理论力学10动量矩定理
第十三章动量矩定理_理论力学

式中
分别为作用于质点上的内力和外力。求 n 个方程的矢量和有
式中
,
于 点的主矩。交换左端求和及求导的次序,有
为作用于系统上的外力系对
令 (13-3)
为质系中各质点的动量对 点之矩的矢量和,或质系动量对于 点的主矩,称为质系对 点的动量矩。由此得
(13-4) 式(13-4)为质系动量矩定理,即:质系对固定点 的动量矩对于时间的一阶导数等于外力 系对同一点的主矩。
设 Q 为体积流量, 为密度, 和 分别为水流进口处和出口处的绝对速度, 和 分别为涡轮外圆和内圆的半径, 为 与涡轮外圆切线的夹角, 为 与涡轮内圆切线的
夹角,则
由动量矩定理 得
为叶片作用于水流上的力矩。若水涡轮共有 个叶片,则水流作用于涡轮的转动力矩为
方向与图示方向相反。 §13-2 刚体绕定轴转动微分方程
解:取两叶片间的水流为研究对象(图 13-4 中的兰色部分)。作用于质系上的的外力有 重力和叶片的约束力,重力平行于 z 轴,对转动轴之矩为零。所以外力主矩为叶片对水流
的约束力对 z 轴之矩 。
计算 时间间隔内动量矩的增量 。设 t 瞬时占据 ABCD 的水流,经过 时间间隔
后,运动至占据
,设流动是稳定的,则
有
式中
得
(13-8)
或
(13-9)
此式称为刚体绕定轴转动的微分方程。
为刚体绕定轴转动的角加速度,所以上式
可写为
(13-10)
1.由于约束力对 z 轴的力矩为零,所以方程中只需考虑主动力的矩。 2.比较刚体绕定轴转动微分方程与刚体平动微分方程,即
与
形式相似,求解问题的方法和步骤也相似。 转动惯量与质量都是刚体惯性的度量,转动惯量在刚体转动时起作用,质量在刚体平动
动量矩定理

动量矩定理蜻蜓、飞机和直升机儿时的我很爱雨后捉蜻蜓。
夏天一场大雨过后,街道上和低洼处到处是水坑。
许多蜻蜓在水面上下飞舞,并不时用尾巴尖端表演“蜻蜓点水”的特技。
我们就用长竿端部的网兜捕捉蜻蜓,捉到后用细线拴住它的腰部,看它在我的掌握之中乱飞,快乐异常。
长大后对蜻蜓的兴趣转为对飞机的热爱,考大学选了飞机设计专业。
飞机(为了与直升机区别,可称其为“平飞飞机”,这里是按它们的飞行状态来区分的)的机翼与蜻蜓的翅膀极为相似,可是它在天空只能不停地往前飞行,不能停止。
蜻蜓就有这个本事。
直升机克服了平飞飞机(下文中仍简称为飞机)不能在空中悬停的缺点,它依靠旋转的翅膀(正确术语为旋翼)能在空中悬停,并可将重物吊起或降下,所以它在反潜、救灾、反恐、反海盗任务中有独特的优势。
直升机的先祖,至少可追朔到中国明代就出现的竹蜻蜓,直到如今仍是许多孩童的好玩具。
现代人又把它叫做“飞螺旋”和“中国陀螺”。
它用旋转叶片产生升力,使竹蜻蜓飞起来。
直升机和飞机的主要区别在于它们产生升力的机理不同。
飞机靠机身两侧的形似蜻蜓翅膀(见图1)的平直机翼提供升力,前进的动力是由机头的螺旋桨或尾部喷管(即尾喷管)的喷气来提供;而直升机则是借助旋转的机翼(旋翼)产生升力。
直升机的旋翼和飞机的螺旋桨都是用旋转的叶片推动空气产生作用力的。
飞机的螺旋桨基本不提供升力,只起克服空气阻力使飞机前进的作用;而直升机的旋翼,主要提供升力;在需要前进时,倾斜旋转轴,从而造成水平分力,使直升机前进。
一般而言,直升机旋翼叶片的尺寸(长宽和面积)要比飞机螺旋桨叶片大得多。
直升机旋翼的种类为了讨论直升机的动力学问题,先对直升机的类别进行简介。
按照旋翼的数目与配置以及叶片数目来区分,直升机有如下几种:01单旋翼直升机顾名思义,单旋翼直升机就是它只有一个旋翼。
一般它必须带一个尾桨负责抵消旋翼产生的反转矩。
例如,欧洲直升机公司制造的EC-135直升机。
图2就是一个带尾桨的单旋翼直升机图片。
《理论力学》第十章--动量矩定理试题及答案
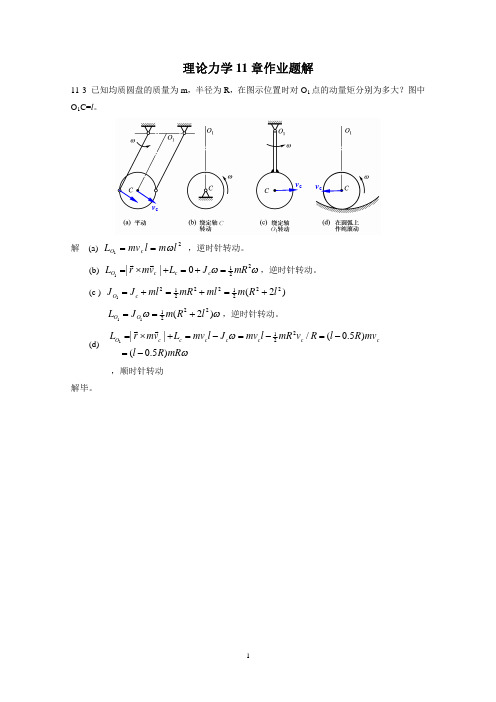
理论力学11章作业题解11-3 已知均质圆盘的质量为m ,半径为R ,在图示位置时对O 1点的动量矩分别为多大?图中O 1C=l 。
解 (a) 21l m l mv L c O w == ,逆时针转动。
(b) w w 2210||1mR J L v m r L c c c O =+=+´=rr ,逆时针转动。
(c ) )2(2221222121l R m ml mR ml J J c O +=+=+=w w )2(222111l R m J L O O +==,逆时针转动。
(d)ww mR R l mv R l R v mR l mv J l mv L v m r L c c c c c c c O )5.0()5.0(/||2211-=-=-=-=+´= r r,顺时针转动解毕。
v cv cv c11-5 均质杆AB 长l 、重为G 1,B 端刚连一重G 2的小球,弹簧系数为k ,使杆在水平位置保持平衡。
设给小球B 一微小初位移0d 后无初速度释放,试求AB 杆的运动规律。
解 以平衡位置(水平)为0=j ,顺时针转为正。
平衡时弹簧受力为:)5.0(312G G F s +=弹簧初始变形量:k G G k F s st /)5.0(3/12+==d在j 角时弹簧的拉力为(小位移):3/)5.0(3)3/(12l k G G l k F st s j j d ++=+=¢系统对A 点的动量矩:j j j&&&221233l gG G l l g G J L A A +=×+= 对点的动量矩定理)(/å=Ei A A F M dt dL r :j j 93/5.033221221kl l F lG lG l g G G s -=¢-+=+&& 0)3(321=++j jG G gk &&,令)3(3212G G gkp +=则有02=+j jp &&,其解为: )cos()sin(pt B pt A +=j由初始条件0| ,/|000====t t l jd j &得l B A / ,00d ==。
理论力学10—动量定理

p 2m1vC m1vC1 m2v A m2v B
B
m2 vB 2m1vC
C
C
C1 m1vC1 O t
m2 v A A
x
v A 2l sin t
vB cos(90 t ) vc cos(90 2t ) B c vB 2l cos t B
10.2
动量定理
F fN C f ( P sin 45 mg cos30 )
从而摩擦力为
0 0 tt 0 tt
动量定理积分形式应用时经常使用投影式:
tt
若作用于质点上的外力主矢恒等于零,则质点的动量守恒, 此即质点的动量守恒定律。 若作用于质点上的外力在某轴上投影的代数和恒等于零,则 质点的动量在该轴上的投影守恒,此即质点对轴的动量守恒 定律。
10.2
动量定理
y
例4 锤的质量m=3000 kg,从高度h=1.5 m 处自由下落到受锻压的工件上,工件发生变 形历时τ=0.01s ;求锤对工件的平均压力。 解:以锤为研究对象,和工件接触后受力如图。 工件反力是变力,在短暂时间迅速变化,用 平均反力N*表示。 锤自由下落时间
d ri vi dt
代入式10—1,注意到质量mi是不变的,则有
d ri d p mi vi mi mi ri dt dt i 1 i 1
令
M mi
n
n
为质点系的总质量
10.1
动量与冲量
m r m r i i i i rC mi M
1 p mvC ml 2
10.1
动量与冲量
vC C
理论力学复习资料

力学复习选择:力系简化最后结果(平面,空间)牵连运动概念(运动参考系运动,牵连点运动) 平面运动刚体上的点的运动平面运动的动能计算(对瞬心,及柯里西算法) 质心运动定理(投影法x ,y ,z ,轨迹)惯性力系想一点简化计算:刚体系统平衡计算(多次取分能力体,一般为2次) 平面运动 速度的综合计算 动能定理应用动静法(其他方法不得分),已知运动求力(先用动能(动量)定理求运动,在用动静法求力)注意:1.功的单位是m WN ------∙2.注意检验fs N F f F ≤∙,判断是否是静摩擦,当为临界状态时max f s s N F F f F ==∙,纯滚动为静摩擦S F ,且只能根据平衡方程解出,与正压力无关。
动摩擦f NF f F =∙。
3. 动静法中惯性力简化()=-IC i i CIC c IC c F m a c F ma c M J α⎧⎫=-⎨⎬⎩⎭⎧⎫⎪⎪⇒⎨⎬=------⎪⎪⎩⎭∑质心过点到底惯性力绕点的惯性力偶二维刚体4.e c i i F ma m a ==∑∑, 22d ,d i i cc c m r r r a m t==∑eF ∑=0,则x v =常数=0(初始静止)则c x =常数=坐标系中所在位置,且c S 为直线。
(一直运动求力)5.平面运动刚体动能*222121122c c c J T mv J ωω⎧⎫⎪⎪⎪⎪=⎨⎬⎪⎪+⎪⎪⎩⎭瞬心法:柯里希法: 6.平面运动速度分析方法:a,基点法:,BA BA BA v v v v AB ω=+=,以Bv为对角线的平行四边形b,速度投影法:cos cos B B A A v v θθ=,,B A θθ是以AB 为基准。
c,速度瞬心法:***,*,0,0AB c c v v BC v a ACωω==∙=≠ 7.平面运动加速度分析:A.基点法:nB A BA BA a a a a τ=++,其中,多数情况下n A A A a a a τ=+,n B B B a a a τ=+注:当牵连运动为转动时,有科氏加速度k a ,2kr av ω=⨯大小:2kr a v ω=,方向:r v 向ω方向转90即可。
理论力学-动量矩定理

d rC d vC vC , aC , dt dt
n d LC ri Fi e dt i
vC vC 0 ,
m a C Fie
n dLC M C (Fie ) dt i
相对质心的动量矩定理
质点系相对质心的动量矩定理
n n d LC e e ri Fi M C ( Fi ) i dt i
m v
i
i
m vC
LO rC m vC LC
相对质心的动量矩定理
质点系相对质心的动量矩定理
根据上式和质点系对固定点的动量矩定理,
n d LO d ( rC m vC LC ) ri Fi e dt dt i
ri rC rr
n n d rC d vC d LC e rC Fi ri Fi e m vC rC m dt dt dt i i
即有
LC ri mi vir
相对质心的动量矩定理
质点系相对质心的动量矩
质点系相对固定点的动量矩与质点系相对质心的动量矩 之间存在确定的关系。 质点系相对固定点的动量矩为
LO ri mi vi
i
因为 所以有 因为 所以有
ri rC rr
LO rC mi v i ri mi v i
刚体定轴转动微分方程
例 题 1
图示钟摆简化模型中,已知均质细杆 和均质圆盘的质量分别为m1 、m2 ,杆 长为l,圆盘直径为d。
ϕ
试求:钟摆作小摆动时的周期。 解:摆绕O轴作定轴转动。设ϕ 为任意 时刻转过的角度,规定逆时针为正。根 据定轴转动的微分方程
J z M z
理论力学动量矩定理

12.2 动量矩定理
12.2.1 质点旳动量矩定理
设质点对固定点O旳动 量矩为MO(mv),作用力F对 同一点旳矩为MO(F) ,如图 所示。
将动量矩对时间取一 次导数,得
d dt
MO
(mv)
d dt
(r
mv)
d r mv r d (mv)
dt
dt
MO(mv) MO(F)
x
z
F mv
Q
r
y
12.2.1 质点旳动量矩定理
将上式投影在直角坐标轴上,并将对点旳动量矩与对轴 旳动量矩旳关系代入,得
d dt
M
x
(mv)
M
x
(F
)
d dt
M
y
(mv)
M
y
(F
)
d dt
M
z
(mv)
M
z
(F
)
质点对某固定
轴旳动量矩对时间旳 一阶导数等于质点所 受旳力对同一轴旳矩。
12.2.1 质点旳动量矩定理
例12-2 图示为一单摆(数学摆),摆锤质量为m,摆线长为 l,如给摆锤以初位移或初速度(统称初扰动),它就在经过 O点旳铅垂平面内摆动。求此单摆在微小摆动时旳运动规律。
例12-1 均质圆盘可绕轴O转动,其上缠有一 绳,绳下端吊一重物A。若圆盘对转轴O旳转
动惯量为J,半径为r,角速度为,重物A旳
质量为m,并设绳与圆盘间无相对滑动,求系 统对轴O旳动量矩。
解:
LO L块 L盘 mvr J mr 2 J (mr 2 J )
LO旳转向沿逆时针方向。
Or
A mv
LO J m2vR MO (F (e) ) M m2 g sin R
理论力学10动量矩定理

J11 (J 22 m2v2 R2 ) m3v3R2
v3
v2
R2 2
1 2
R11
LO
(
J1 R2 2
J2 R2 2
m2
m3 )R2v3
轮B滚而不滑,有瞬心
17
对于一个定轴转动刚体 Lz J z
代入质点系动量矩定理,有
d dt
(J
z)
M
(e) z
Jz
M
( e) z
或
Jz
d 2
dt 2
M
(e) z
—刚体定轴转动微分方程
解决两类问题: 已知作用在刚体的外力矩,求刚体的转动规律。 已知刚体的转动规律,求作用于刚体的外力(矩)。
但不能求出轴承处的约束反力,需用质心运动定理求解。
18
特殊情况:
n
若M z(e) M z (Fi(e) ) 0 ,则 0, 恒量,刚体作匀速转动或 i1 保持静止。
mT
mT ymdm 0
mT
刚体对z轴的转动惯量
JZ
r2dm
mT
(x2 y2 )dm
mT
mT [( xC xm )2 ( yC ym )2 ]dm
mT (xm2 ym2 )dm
mT (xC2 yC2 )dm 2xC
mT
xmdm
2 yC
mT
ymdm
J Z JC mT d 2
0
0 24
复杂形状刚体的转动惯量 按定义,有:
JZ
理论力学 动量矩定律

MO (mv) 恒矢量
作用于质点的力对某定轴的矩恒为零,则质点对该轴的动量矩 保持不变,即
M z (mv ) 恒量
以上结论称为质点动量矩守恒定律 2)质点系动量矩守恒定理 当外力对某定点(或某定轴)的主矩等于零时,质点系对 于该点(或该轴)的动量矩保持不变,这就是质点系动量矩 守恒定律。 15 另外,质点系的内力不能改变质点系的动量矩。
24
动力学 2. 回转半径 定义:
转动惯量
z
Jz m
则
J z m z
2
即物体转动惯量等于该物体质量与回转半径平方的乘
积; 对于均质物体,仅与几何形状有关,与密度无关。
对于几何形状相同而材料不同(密度不同)的均质刚 体,其回转半径是相同的。
25
动力学
转动惯量
3. 平行移轴定理 刚体对于某轴的转动惯量,等于刚体对于过质心、并与该轴平 行的轴的转动惯量,加上刚体质量与轴距平方的乘积,即
LC LC
这样刚体作平面运动时,对过质心C且垂直于平面图形的 轴的动量矩为
J C LC LC
12
动力学
质点系动量矩定理
2.质点系的动量矩定理
n个质点,由质点动量矩定理有
d M O (mi vi ) M O ( Fi ( i ) ) M O ( Fi ( e ) ) dt
n d (e) Lx M x ( Fi ) dt i 1 n d Ly M y ( Fi ( e ) ) dt i 1 n d Lz M z ( Fi ( e ) ) dt i 1
14
动力学
质点系动量矩定理
3.动量矩守恒定理 1)质点动量矩守恒定理 如果作用于质点的力对某定点O的矩恒为零,则质点对该 点的动量矩保持不变,即
理论力学第十一章动量矩定理

JO
d 2
dt 2
mga
即:
d 2
dt 2
mga
JO
0
解: 令 2 mga
JO
——固有频率
得
2 0
通解为 O sin(
mgat )
JO
周期为 T 2 2 JO
mga
例11-3 用于测量圆盘转动惯量的三线摆中,
三根长度相等(l)的弹性线,等间距悬挂被测量的圆盘。
已知圆盘半径为 R、重量为W。
dt
dt dt
v dr dt
r d(mv) d(r mv)
dt
dt
dLO dt
MO F
矢量式
质点对固定点的动量矩对时间的导数等于作 用于质点上的力对该点的矩。
★ 质点系的动量矩定理
0
d
dt
i
ri mivi
i
MO (Fii )
i
MO (Fie )
MO (Fie )
i
F2
z
F1
LO rC mvC LC
dLO d
dt dt
rC mvC LC
ri Fie (rC + ri) Fie
rC Fie ri Fie
③
即
drC dt
mvC
rC
d dt
mvC
dLC dt
rC
Fie
dLC dt
由于
① ① drC dt
② vC ,
drC dt
mvC
★ 相对质心的动量矩
LC MC mivi ri mivi
vi vC vir
LC = rimivC rimivir
其中
ri mivC ( miri)vC 0 (rC
理论力学:动量矩定理

y’
2020/12/9
Fe maA aA mg
B
A
FN 1
F1
FN 2
x’
F2
10
理论力学
§6-2 动量矩定理
例:滑块A可在光滑水平面上滑动,为使AB杆以匀角速度 绕
铰链A转动,求作用在AB杆上的力偶M。设:m1 m2 m, AB L
y
FN
解:1、取滑块A和小球B为研究对象
2、受力分析与运动分析
m1 m2
2020/12/9
11
理论力学
§6-2 动量矩定理
y FAy
A
o
FAx aA xA x
3、研究AB杆和小球B,受力分析 4、应用相对动轴A的动量矩定理
dLrA
dt
n
M A (Fi(e) )
i1
rAC (maA )
A
M
杆相对A轴的动量矩
LrA m2L2
B m2xA 外力对A轴之矩
问题:若滑块不脱离地面,试确定AB杆的最大角速度。
2020/12/9
13
理论力学
§6-2 动量矩定理
2020/12/9
14
理论力学
§6-2 动量矩定理
思考题:图示系统中,系统结 构不同,求解方法是否相同?
m1 A
M
m1 A
M
m2
B
2020/12/9
m1 A
M
m2
R
m3 B
m2 B
15
理论力学
§6-2 动量矩定理
mg
B
AB L
2020/12/9
§6-2 动量矩定理
L
3(g 2
理论力学之动量矩定理
证明 过固定点O建立固定坐标系 Oxyz,以质点系的质心 C为
z
原点,取平动坐标系Cx y z ,它以质心的速度vC 运动。
ri rc rri 质心的性质 vi vc vri
z' A vr v vC vC y y'
mi ri mi rri rc rc 0 M M 定系 动系 Mvc mi vi mi vri 0
rC
C
x'
rr
O
质点系内任一质点 A的绝对速度 v=ve+vr=vc+vr , 则质点系对固定点O的动量矩
x
(r
LO
C
mi vi )
(r m v ) [(r
i
(r
i i
C
rri ) mi vi ]
ri mi v C )
(r
ri mi v ri )
d M O (mv ) M O ( F ) dt
质点对固定点的动量矩对时间的一阶导数等 于作用于质点上的力对同一点的力矩。
B 固定轴
d M O (mv ) M O ( F ) dt
(将上式两边分别向坐标轴投影,再利用对点和 对轴动量矩公式可得): d M x (mv ) M x ( F ) dt d M y (mv) M y (F ) dt d M z (mv) M z (F ) dt 质点对某固定轴的动量矩对时间的导数,等于作用 于该质点的所有力对于同一轴之矩的代数和。 质点对定点的动量矩定理在三个坐 标轴的投影方程不独立
O
A
mivi
ri
LO =∑ MO(mivi) = ∑(miri )×vC 又因为 (∑mi )rC = ∑miri 所以 LO = ∑mi rC ×vC=rC× (∑mi )vC
理论力学10动量矩定理

在更高维度的空间中,动量矩定理可以通过向量的外积和叉积进行推广,适用于描述更复杂系统的动量矩变化。
n维空间推广
定理在更高维度空间的应用
多体系统
动量矩定理可以应用于多体系统,描述多个刚体之间的相互作用和运动关系,为多体动力学提供了基础。
非惯性参考系
在非惯性参考系中,动量矩定理需要考虑科里奥利力和离心力等因素的影响,以准确描述系统的动量矩变化。
定理证明的思路
在证明过程中,需要引入质点的质量、速度、位置矢量等概念,以及力、力矩等物理量。
引入相关概念
根据物理定律和数学公式,进行详细的数学推导,包括向量的点乘、叉乘等运算。
进行数学推导
经过推导,得出动量矩定理的结论,即质点系的动量矩等于外力矩对时间的积分。
得出结论Βιβλιοθήκη 定理证明的过程通过证明,得出的动量矩定理表述为:质点系的动量矩等于外力矩对时间的积分。
力矩的作用
力矩是描述力对物体运动轴的转动效应的物理量。在动量矩定理中,力矩的作用是改变物体的动量,即改变物体的运动状态。
时间和空间的影响
动量矩定理不仅涉及到物体的运动状态(动量和速度),还涉及到时间的变化率(即加速度),以及力作用的空间效应(即力矩)。因此,这个定理全面地描述了物体在空间和时间中的运动规律。
定理的物理意义
02
CHAPTER
定理的证明
首先明确动量矩定理的定义和意义,即对于一个质点系,其动量矩与外力矩之间的关系。
引入动量矩定理
建立证明框架
推导定理的表达式
根据定理的证明需求,建立证明的框架,包括定义、假设、推导和结论等部分。
根据牛顿第二定律和动量定理,推导出动量矩定理的表达式。
03
动力学公式汇总

第 1 页/共 3 页理论力学——动力学重点公式汇总张工培训:湖南陆工1、牛顿第二定律记住:哪个方向用第二定律,就考虑哪个方向的作使劲就行了。
2、动量定理平移刚体的动量:定轴转动刚体的动量: (Vc 为质心的速度) 注重:动量方向与速度方向相同,故速度方向相反的两个质点的动量会抵消部分。
常力的冲量: 动量定理:注:应用时均是某个方向的应用。
3、动量矩定理平移刚体的动量矩: (Vc 为质心的速度,逆为正)定轴转动刚体的动量矩: 刚体的转动惯量:(注:均针对质心C ) 1)等截面的均质细长杆(质量为m ,长度为l )2)厚度相等的均质薄圆板(质量为m ,半径为R )3)厚度相等的均质薄圆环(质量为m ,半径为R )转动惯量的平行移轴定理:动量矩定理:x x F ma =yy F ma =zz F ma =mvk =∑==ci i mv v m k FtS =SFt mv mv ==-12d mv L c z ±=zz wIL =2121ml I C =221mR I C =2mR I C =2md I I zC z +=)()(00F m dtmv dm =质点(系)对某固定点(轴)的动量矩对时光的一阶导数,等于作使劲对该点的力矩。
刚体绕定轴转动时的动量矩定理可写为:4、动能定理力的功:重力的功: 弹性力的功:平移刚体的动能: 定轴转动刚体的动能: 动能定理: 5、达朗贝尔原理 平移刚体的惯性力主矢: 平移刚体的惯性力主矩: 定轴转动刚体的惯性力主矢:定轴转动刚体的惯性力主矩: 6、质点的直线振动周期: 圆频率: 频率:等效刚度系数:并联(特征:弹簧的变形量总是相等)串联(特征:变形量可不一样)频率比:等于1时,发生共振,振幅最大。
zz zz M dtd I M I ==22ϕε221mv T =221ωz I T =2,121222121W mv mv =-FSW =)()(2121z z mg z z P W -=-=)(22221δδ-=kW c I Ma F -=0=C I M nC C C RI Ma Ma Ma F --=-=τεz Iz I M -=km T πωπ220==mk=0ωmk Tf ππω21210===21k k k +=21111k k k+=ωωλ=欲知注册工程师考试(公共基础)更多更专业的学习内容,请担心“张工注册工程师基础类——zhanggongjichu。
《理论力学》第十一章 动量矩定理

LO lOi ri mi v i
将动量矩投影到以O为原点的直角坐标轴上
HOHAI UNIVERSITY ENGINEERING MECHANICS
Lx l x mv m yv z zv y
L y l y mv m zv x xv z Lz l z mv m xv y yv x
(二)质点系的动量矩L
设质点系由n个质点组成,其中第i个质点 的质量为mi,速度为vi。 质系对任意固定点O的动量矩:
HOHAI UNIVERSITY ENGINEERING MECHANICS
LO lOi ri mi v i
质系对任意固定点O的动量矩为各质点 的动量对O点矩的矢量和。
3、刚体动量矩的计算
1)刚体平动
HOHAI UNIVERSITY ENGINEERING MECHANICS
HOHAI UNIVERSITY ENGINEERING MECHANICS
例1:均质细长直杆长l,质量m1,与质量为m2,半径
为r,均质圆盘固结。已知角速度为,试求对转轴的 动量矩。 解:
HOHAI UNIVERSITY ENGINEERING MECHANICS
第十一章
HOHAI UNIVERSITY ENGINEERING MECHANICS
动量矩定理
§1 动量矩(表征物体转动的物理量)
一、动量矩的定义及计算
1. 对任意固定点O的动量矩(矢量):
质点对固定点的动量矩即质点的动量对固定点的矩: z lO r mv r p mv lo M r F
平轴z的转动惯量。轴z过O点垂直纸面
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
在机械工程设计手册中,可以查阅到简单几何形状或已 标准化的零件的转动惯量和回转半径。书中列出几种常见均质
刚体的 J z和z ,以供参考。
22
平行移轴定理 同一个刚体对不同轴的转动惯量一般是不相同的。
J z' J zC md 2
Lz mz (mvC )
2、考虑质心公式
平动刚体对固定点(轴)的动量矩等于刚体质心的动量对该点
(轴)的动量矩。
2.定轴转动刚体 Lz Lz (mivi ) ri miri miri2 Jz
定轴转动刚体对转轴的动量矩等于刚体对该轴转动惯量与角速 度的乘积。
3.平面运动刚体 Lz Lz (mvC ) JC
18
特殊情况:
n
若M z(e) M z (Fi(e) ) 0 ,则 0, 恒量,刚体作匀速转动或 i1
保持静止。
若 M z(e) 常量,则 常量,刚体作匀变速转动。
将 J z M z(e) 与 ma F 比较,刚体的转动惯量 J z 是刚体
转动惯性的度量。
19
§10-3-2 刚体对轴的转动惯量
)
g
sin
0
dt
l
微幅摆动时,sin ,
并令 n2
g l
,则
n2
0
解微分方程,并代入初始条件 (t 0, 0,0 0) 则运动方程
0 cos
gt l
,摆动周期
T 2
g l
7
注:计算动量矩与力矩时,符号规定应一致(本题规定逆时 针转向为正) 质点动量矩定理的应用:
在质点受有心力的作用时。(面积速度定理) 质点绕某心(轴)转动的问题。(单摆)
绕质心转动动量矩
Lz Lz (mvC ) JC 16
[例1] 滑轮A:m1,R1,R1=2R2,I1 滑轮B:m2,R2,I2 ;物体C:m3 求系统对O轴的动量矩。
解:LO LOA LOB LOC
J11 (J 22 m2v2 R2 ) m3v3R2
v3
v2
R2 2
1 2
R11
M (e) O
PAr
PBr
(PA
PB
)r
LO
PA g
vr
PB g
vr
I
O
将I O
1 2
Pr2 g
代入,
得
LO
r
g
2
(
PA
PB
P 2
)
由动量矩定理:
d [r
dt g
2
(
PA
PB
P 2
)](
PA
PB
)r
d g PA PB
dt r PA PB P/2
11
例 10.1 如图滑轮 O 上悬有一根绳子,绳子两端离过轴 O 的水平线的距离 分别为l1 和 l2。两个质量分别为 m1 和m 2 的人抓着绳子的两端,同时开 始向上爬并同时到达过轴 O 的水平线。不计滑轮和绳子的质量,忽略所有 对运动的阻力。求两人同时到达的时间。
mT xmdm 0
mT
mT ymdm 0
mT
刚体对z轴的转动惯量
JZ
r2dm
mT
(x2 y2 )dm
mT
mT [( xC xm )2 ( yC ym )2 ]dm
mT (xm2 ym2 )dm
mT (xC2 yC2 )dm 2xC
mT
xmdm
2 yC
mT
ymdm
作转动时的动量矩之和。
将矢径表示为: ri rc i
各点对O矢径 质心对O矢径 各点对质心矢径
vi vc vri
代入动量矩表达式
各质点速度 质心速度 各点相对质心速度
Lz Lz (mivi ) ri mivi (rc i ) mi (vc vri )
rc mi vc rc mi vri i mi vc i mi vri
求: 对z轴的转动惯量J z ; 对z' 轴的转动惯量J z' 。
解:J z
l
2 l
2
x2 m dx 1 ml2 l 12
l
Jz' 0
x2 m dx 1 ml2 l3
21
2. 回转半径
由
Jz m
所定义的长度 z
称为刚体对 z 轴的回转半径。
J z mz2
对于均质刚体, z(回转半径)仅与几何形状有关,与
3
LO (mv) 2OAB
Lz (mv ) 2OA' B'
正负号规定与力对轴矩的规定相同 对着轴看:顺时针为负
逆时针为正
质点对点O的动量矩与对轴z 的动量矩之间的关系:
LO (mv) z Lz (mv)
动量矩度量物体在任一瞬时绕固定点(轴)转动的强弱。kg·m2/s。
二.质点系的动量矩
质系对点O动量矩: LO LO (mivi ) ri mivi
左边交换求和与导数运算的顺序,而
LO LO (mivi ), MO (Fi (i) ) 0,则
dLO
dt
n i 1
M O (Fi(e) ) M O(e) 一质点系对固定点的动量矩定理
质点系对任一固定点的动量矩对时间的导数,等于作用在
质点系上所有外力对同一点之矩的矢量和(外力系的主矩)。 将上式在通过固定点O的三个直角坐标轴上投影,得
15
Lz rc mi vc rc mi vri i mi vc i mi vri
rc mi vc Lz (mvc )
质心平动动量矩
rc mi vri rc mvrc 0
质心相对于质心的速度为零
i mi vc c mvc 0
质心相对质心的半径为零
i mi vri i mi i mi i2 Jc
[例2] 钟摆: 均质直杆m1, l ; 均质圆盘:m2 , R 。 求 IO 。
解: IO IO杆 IO盘 13m1l 2 12m2R2 m2 (l R)2
13m1l
2
1 2
m2
(3R
2
2l
2
4lR)
26
[例3] 提升装置中,轮A、B的重量分别为P1 、 P2 ,半径分别为
r1 、 r2 , 可视为均质圆盘; 物体C 的重
质系对轴z 动量矩: Lz Lz (mivi ) LO z
4
§10-1 质点的动量矩定理
一.质点的动量矩定理推导
d (mv ) F dt
质点动量定理
两边叉乘矢径
r
,
有
r
d (mv ) dt
r
F
左边可写成
r
d (mv ) dt
d dt
(r
mv )
dr dt
mv
而 dr mv v mv 0 , r F M O (F ) dt
定义:
J z miri2
若刚体的质量是连续分布,则 J z m r 2dm
刚体的转动惯量是刚体对某轴转动惯性大小的度量,它的 大小表现了刚体转动状态改变的难易程度。
转动惯量恒为正值,国际单位制中单位 kg·m2 。
20
转动惯量的计算 1.积分法(具有规则几何形状的均匀刚体可采用)
[例1] 匀质细直杆长为l ,质量为m 。
上式称质点对固定轴的动量矩定理,也称为质点动量矩定 理的投影形式。即质点对任一固定轴的动量矩对时间的导数, 等于作用在质点上的力对同一轴之矩。
若M O (F ) 0 (M z (F ) 0)则 M O (mv ) 常矢量 (M z (mv) 常量) 称为质点的动量矩守恒。
6
[例2] 单摆 已知m,l,t =0时= 0,从静止
8
§10-2 质点系的动量矩定理
1.质点系的动量矩定理推导
对质点Mi :
d dt
LO (mivi )
M O (Fi(i) )
M O (Fi(e) )
(i 1,2,3,, n)
对质点系,有
d dt LO (mivi )
M O (Fi(i) )
MO (Fi(e) ) (i 1,2,3,, n)
平面运动刚体对垂直于质量对称平面的固定轴的动量矩,等于 刚体随同质心作平动时质心的动量对该轴的动量矩与绕质心轴 作转动时的动量矩之和。
14
3.平面运动刚体 Lz Lz (C ) JC
平面运动刚体对垂直于质量对称平面的固定轴的动量矩,等于
刚体随同质心作平动时质心的动量对该轴的动量矩与绕质心轴
LO
(
J1 R2 2
J2 R2 2
m2
m3 )R2v3
轮B滚而不滑,有瞬心
17
对于一个定轴转动刚体 Lz J z
代入质点系动量矩定理,有
d dt
(
J
z)
M
(e) z
Jz
M
( e) z
或
Jz
d 2
dt 2
M
(e) z
—刚体定轴转动微分方程
解决两类问题: 已知作用在刚体的外力矩,求刚体的转动规律。 已知刚体的转动规律,求作用于刚体的外力(矩)。 但不能求出轴承处的约束反力,需用质心运动定理求解。
1
第十三章 动量矩定理 §13–1 动量矩 §13–2 动量矩定理 §13–3 刚体定轴转动微分方程 §13–4 刚体对轴的转动惯量 §13–5 质点系相对于质心的动量矩定理 ·
刚体平面运动微分方程 习题课
2
质点 动量定理: 质点系 动量的改变—外力(外力系主矢)
质心运动定理:质心的运动—外力(外力系主矢)
故:
d
d
(r mv) r F , dt
