10等截面直杆的扭转
y M z
= fy = fz
将 ϕ 、 l、m 代入上述边界条件，有
dy l = cos( N , x ) = cos α = ds dx m = cos( N , y ) = sin α = − ds
∂ϕ dy ∂ϕ dx + =0 ∂y ds ∂x ds
xz s
yz s
α
∂ϕ dy ∂ϕ dx + (− )( − ) = 0 ∂y ds ∂x ds
∂f 3 ∂ f 2 1 ∂ϕ ( x , y ) + =− , G ∂x ∂y ∂z 1 ∂ϕ ( x , y ) ∂f 1 ∂ f 3 =− , + G ∂x ∂z ∂ x ∂f 2 ∂f 1 + =0 ∂x ∂y 2 2 ∂ f1 ∂ f1 = 0, = 0, 2 2 ∂z ∂y
∂ 2 f2 ∂ 2 f2 =0 = 0, 2 2 ∂z ∂x
u = − Kyz 将两式相减，得： （10-6） v = Kzx 1 ∂ 2ϕ 1 ∂ 2ϕ 0= + 2K + 2 2 ∂ ∂ ϕ w v 1 ∂ 将其代入： G ∂y G ∂x + =− , ∂y ∂ z G ∂x 1 2 0 = ∇ ϕ + 2K ∂u ∂w 1 ∂ϕ G + = , ∂z ∂ x G ∂y 2 有： ∂w ∇ ϕ = −2GK （10-8） 1 ∂ϕ = + Ky , ∂x G ∂ y 将其对照式（10-3）： （ 10-7 ） ∂w 1 ∂ϕ 2 =− − Kx , （10-3） ∇ ϕ = C ∂y G ∂x 可见： 1 ∂ 2ϕ ∂ 2w = + K, 2 （10-9） ∂ x∂ y G ∂ y C = −2GK ∂ 2w 1 ∂ 2ϕ 实际问题中，K 可通过实验测得。 =− − K, 2 ∂y∂x G ∂x
将式（10-1）代入，得：
O y
（8-1）
M
x
M z
相容方程：
∂τ zx =0 ∂z ∂τ zy =0 ∂z ∂τ xz ∂τ yz + =0 ∂x ∂y
（a）
—— 扭转问题的平衡方程
相容方程(无体力)：
2 ∂ Θ 2 (1 + μ )∇ σ x + 2 = 0 ∂x 2 ∂ Θ 2 (1 + μ )∇ σ y + 2 = 0 ∂y 2 ∂ Θ 2 (1 + μ )∇ σ z + 2 = 0 ∂z ∇ 2τ yz = 0
γ zx
G 1 = τ zx , G
u = f1 ( y , z ), v = f 2 ( z , x ),
w = f 3 ( x, y)
代入后三式，有
γ zx
再将几何方程代入，有
G ∂x 1 ∂ϕ , = G ∂y
∂u = 0, ∂x ∂w ∂v + ∂y ∂ z ∂u ∂w + ∂z ∂x
∂w ∂v = 0, = 0, ∂z ∂y 1 ∂ϕ =− , （f） G ∂x 1 ∂ ϕ ∂ v ∂u + = , =0 G ∂y ∂x ∂ y
—— 扭转问题的相容方程 （b）
y M
( )
（c）
∫∫ z （2）端面： f dxdy = ∫∫ τ dxdy = 0 （e） ∫∫ （f） 注意：具体分析 过程后面给出。 ∫∫ ( yf − xf )dxdy = ∫∫ ( yτ − xτ )dxdy =M
y zy
x y zx zy
f x dxdy = ∫∫ τ zx dxdy = 0 （d）
由此可见： 对每个横截面（z =常数） 它在 x y 面上的投影形状不变，而只 是转动一个角度 α=Kz 。
v = v 0 + ω z x − ω x z + Kzx
其中： 若不计刚体位移，只保留与 变形有关的位移，则有
以前相同，代表刚体位移。
u0、v0 、ωx、ωy、ωz 和
dα =K dz
K —— 单位长度杆件的扭转角 。
x y
α
∫∫ （d） ∫∫ f dxdy = 0, ∫∫ ( yf − xf )dxdy = M ,（e）
f x dxdy = 0,
y
（c）
τ zx = τ xz
τ zy = τ yz
x
y
∂ϕ , = ∂y ∂ϕ y =− ∂x
O
M
x
对式（c），应有
M z
∂ϕ ∫∫ f x dxdy= ∫∫ − τ zx dxdy = ∫∫ − ∂y dxdy ∂ϕ dy = − ∫ (ϕ B−ϕ A )dx ≡ 0 = − ∫ dx ∫ ∂y 同理，对式（d），应有 ∫∫ f y dxdy ≡ 0
∂ ∇ 2ϕ = 0, ∂y ∂ ∇ 2ϕ = 0, ∂x
(
)
z
(
)
结论： 等直杆的扭转问题归结为： 按相容方程（10-3）确定应力函 数ϕ（x，y），然后按式（102）确定应力分量，并使其满足 边界条件。
由此可解得：
∇ 2ϕ = C
（10-3）
—— 用应力函数表示的相容方程 式中：C 为常数。
定解条件——边界条件 （1）侧表面： 0
对式（e）：
x
α
∫∫ ( yf
− xf y dxdy = − ∫∫ yτ zx − xτ zy dxdy ⎛ ∂ϕ ∂ϕ ⎞ = − ∫∫ ⎜ ⎜ y ∂y + x ∂ x ⎟ ⎟dxdy ⎝ ⎠
)
(
)
∫∫ ( yf
− xf y dxdy = − ∫∫ yτ zx − xτ zy dxdy ⎛ ∂ϕ ∂ϕ ⎞ = − ∫∫ ⎜ ⎟dxdy ⎜ y ∂y + x ∂ x ⎟ α ⎠ ⎝ ∂ϕ ∂ϕ = − ∫∫ y dxdy − ∫∫ x dxdy ∂y ∂x ∂ϕ ∂ϕ 同理，得： = − ∫ dx ∫ y dy − ∫ dy ∫ x dx ∂y ∂x ∂ϕ − ∫ dy ∫ x dx = ∫∫ ϕdxdy 分部积分，得： ∂x ∂ϕ dy − ∫ dx ∫ y 将其代入式（e）： ∂y yf x − xf y dxdy = M B ∫∫ = − ∫ yϕ A − ∫ ϕdy dx
第十章 等截面直杆的扭转
要点：（1）等截面直杆扭转问题的基本方程 （2）按应力求解扭转问题的方法 —— 扭转应力函数 （3）扭转问题的薄膜比拟理论
主 要 内 容
§10-1 扭转问题中应力和位移 §10-2 扭转问题的薄膜比拟 §10-3 椭圆截面的扭转 §10-4 矩形截面杆的扭转 §10-5 薄壁杆的扭转 §10-6 扭转问题的差分解
ϕ（x，y）——扭转应力函数
也称普朗特尔(Prandtl)应力函数
τ zx = τ xz
τ zy = τ yz
2
∂ϕ = , ∂y ∂ϕ =− ∂x
∇ τ yz = 0
2
O
（b） y
M
x
（10-2）
∇ 2τ zx = 0
—— 扭转问题的相容方程
将式（10-2）代入相容方程（b），有
M
⎛ ∂ϕ ⎞ ∇ ⎜ ⎟ = 0, ⎜ ∂y ⎟ ⎠ ⎝ ∂ϕ ⎞ 2⎛ ∇ ⎜− ⎟=0 ⎝ ∂x ⎠
将其极坐标表示：
（10-6）
ur = u cos θ + v sin θ uθ = − u sin θ + v cos θ ur = 0, uθ = Krz
将式（10-6）代入，有：
K 2 = − K1 = K
u = u0 + ω y z − ω z y − Kyz
代入 f1、f2 和 u、v 得：
∂ϕ dy ∂ϕ dx =0 + ∂y ds ∂x ds
dϕ =0 ds
表明：在杆件的侧面上（横截 面的边界上），应力函数 ϕ 应 取常数。 又由式（10-2），应力函数 ϕ 差一常数不影响 应力分量的大小， 于是对单连体（实心杆）可取：
ϕ s = 常数
α
ϕs =0
（10-4）
—— 扭转问题的定解条件之一。 对于多连体（空心杆）问题， ϕ 在每一边 界上均为常数，但各个常数一般不相等，因此， 只能将其中的一个边界上取 ϕs=0，而其余边界 上则取不同的常数，如：
☻横截面发生翘曲。 ☻等直圆杆扭转时推出 的应力变形公式在此不 适用。 ☻由弹性力学方法求解 应力变形。
动画演示：
自由扭转(纯扭转) 各横截面的翘曲程度完全相同，横截面上只有切 应力而无正应力。 约束扭转 各横截面的翘曲程度不同，横截面上除切应力外 还有附加的正应力。
§10-1 扭转问题中应力和位移
2∫∫ ϕ dxdy = M
M z
τ zx = τ xz
应力分量：
τ zy = τ yz
∂ϕ = , ∂y ∂ϕ =− ∂x
（10-2）
α
2. 扭转的位移与变形
由物理方程，得：
Байду номын сангаас
ε x = 0, ε y = 0, ε z = 0, γ xy = 0, 1 ∂ϕ 1 γ yz = − , γ yz = τ yz ,
积分前三式，有
f1 = u0 + ω y z − ω z y + K 1 yz
f 2 = v 0 + ω z x − ω x z + K 2 zx
∂f ∂f 1 又由： 2 + = 0 得： ∂x ∂y ω z + K 2 z − ω z + K1z = 0
从中求得： 由
u = − Kyz v = Kzx
ϕs =0
0
τ zx = τ xz
τ zy = τ yz
ϕ s = Ci
i
值条件确定。
Ci 的值由位移单
∂ϕ , = ∂y ∂ϕ （10-2） =− ∂x
材料力学习题册_参考答案(1-9章)
第一章 绪 论一、选择题1．根据均匀性假设，可认为构件的（ C ）在各处相同。
A．应力B． 应变C．材料的弹性系数D． 位移2．构件的强度是指（ C ），刚度是指（ A ），稳定性是指（ B ）。
A．在外力作用下构件抵抗变形的能力B．在外力作用下构件保持原有平衡 状态的能力C．在外力作用下构件抵抗强度破坏的能力3．单元体变形后的形状如下图虚线所示，则 A 点剪应变依次为图(a) （ A ），图(b)（ C ），图(c) （ B ）。
A． 0B． 2rC． rD．1.5 r4.下列结论中( C )是正确的。
A．内力是应力的代数和； B．应力是内力的平均值； C．应力是内力的集度； D．内力必大于应力； 5. 两根截面面积相等但截面形状和材料不同的拉杆受同样大小的轴向拉力，它们的应 力是否相等（ B ）。
A．不相等； B．相等； C．不能确定； 6．为把变形固体抽象为力学模型，材料力学课程对变形固体作出一些假设，其中均匀性假设是指（ C ）。
A. 认为组成固体的物质不留空隙地充满了固体的体积； B. 认为沿任何方向固体的力学性能都是相同的； C. 认为在固体内到处都有相同的力学性能； D. 认为固体内到处的应力都是相同的。
二、填空题1.材料力学对变形固体的基本假设是 连续性假设 ， 均匀性假设 ， 各向同性假设 。
2．材料力学的任务是满足 强度 ， 刚度 ， 稳定性 的要求下，为设计经济安全的构-1-件提供必要的理论基础和计算方法。
3．外力按其作用的方式可以分为 表面力 和 体积力 ，按载荷随时间的变化情况可以分为 静载荷 和 动载荷 。
4．度量一点处变形程度的两个基本量是 （正）应变ε 和 切应变γ。
三、判断题1．因为构件是变形固体，在研究构件平衡时，应按变形后的尺寸进行计算。
（ × ）2．外力就是构件所承受的载荷。
（×）3．用截面法求内力时，可以保留截开后构件的任一部分进行平衡计算。
材料力学第四章 扭转
max
T GI p
180
(/m)
×
例５ 图示圆轴，已知mA =1kN.m， mB =3kN.m， mC
=2kN.m；l1 =0.7m，l2 =0.3m；[]=60MPa，[ ]=0.3°/m，
G=80GPa；试选择该轴的直径。
mA
mB mC 解： ⑴按强度条件
A
l1
B l2 C
max
9.55
200 300
6.37
(kN m)
×
n D
m2 1 m3 2 m1 3 m4
n A 1 B 2 C 3D
②求扭矩（扭矩按正方向假设）
m 0 , T1 m2 0, T1 m2 4.78kN m m 0; T2 m1 m2 0
T2 m2 m3 (4.78 4.78) 9.56kN m
T
2 r02
t
T 2 A0
t
T
A0为平均半径所作圆的面积。
×
三、切应力互等定理：
´
a
b
dy
´
c
z
dx
d t
mz 0; t dxdy t dxdy
'
这就是切应力互等定理：在单元体相互垂直的两个截面
上，切应力必然成对出现，且数值相等，两者都垂直于两平
面的交线，其方向或共同指向交线，或共同背离交线。
垂直，则杆件发生的变形为扭转变形。
A
B O
A
BO
m
m
——扭转角（两端面相对转过的角度）
——剪切角，剪切角也称切应变。
×
§4–2 扭转的内力—扭矩与扭矩图
一、扭矩 圆杆扭转横截面的内力合成
结果为一合力偶，合力偶的力偶 矩称为截面的扭矩，用T 表示之。 m
材料力学 复习题 PDF
2014 年 秋 期材料力学复习题一、填空题1.偏心压缩是受压和 两种基本变形的组合。
2．如右图圆截面其I x= ,i x= , I p= ,W P= 。
3.受力构件内一点处不同方位截面上应力的集合，称为____。
4.构件在外荷载作用下具有抵抗破坏的能力为材料的；具有一定的抵抗变形的能力为材料的；保持其原有平衡状态的能力为材料的。
5.已知围绕某点的单元体上，三个相互垂直的面均为主平面，主平面上的应力大小分别为0 Mpa，21Mpa，-3 Mpa则该单元体的三个主应力σ1= ，σ2= ，σ3==6.截面法是求解内力的基本方法，其三个步骤为 ， ， 。
7.已知一两端铰支座的简支梁，其跨长为1m，横截面尺寸为b×h=150×200的矩形截面，满跨上作用有载荷集度为q=2KN/m，弹性模量E=200 Gpa，则整个梁上最大挠度的绝对值为，最大挠度为。
8.材料力学中，对变形固体作了 假设、 连续假设和各向同性假设。
9.杆件变形的基本形式有：（1）拉（压）；（2）扭转；（3）剪切；（4） 。
10.据拉（压）杆的强度条件进行计算，强度计算通常有三种类型：、和。
在已知拉杆材料、尺寸及所受载荷时，检验构件能否满足强度条件称为。
11.单轴应力状态下的胡克定律为 。
12.低碳钢拉伸试验中，颈缩现象发生在 阶段，冷作硬化可以提高 ，降低 。
13.梁上集中力偶作用的截面处的弯矩突变，剪力 。
14.中心受压直杆在直线形态下的平衡，由稳定平衡转化为不稳定平衡时所受轴向压力的临界值称为用Fcr表示。
15.等直杆在包含其的纵向平面内，承受垂直于的横向外力或外力偶的作用时，杆件的将变成，这种变形称为弯曲。
16.内力的分布集度称为 。
17.在平面弯曲梁中某段梁上若没有集中力的作用，则该段梁的剪力图的形状为_________，弯矩图的形状为。
18.梁在载荷作用下，须同时满足和强度条件，在强度计算是常先按强度计算，再按力强度进行校核。
智慧树答案工程力学(中国石油大学(华东))知到课后答案章节测试2022年
绪论1.工程力学的任务就是到现场去从事工程技术研究。
答案:错2.工程力学的英文翻译为mechanical engineering。
答案:错3.古希腊最伟大的力学家是：答案:阿基米德4.德国的应用力学学派的领袖是：答案:普朗特5.哪一位不是中国力学事业的奠基人？答案:林家翘6.达芬奇是一位著名的应用力学家。
答案:对7.力学在医学领域几乎没什么影响，因为医生根本不学习力学知识。
答案:错8.哥廷根学派的弟子有：答案:冯卡门9.郭永怀的主要研究领域为原子弹。
答案:错10.生物力学之父是：答案:冯元桢第一章1.二力平衡条件的适用范围是（）。
答案:刚体2.图示三铰刚架ACB，受水平力P作用而平衡，有以下四种说法，其中错的是（）。
答案:RA的方向指向C，RB的方向不确定3.运用哪个公理或推论可将力的三要素中的作用点改为作用线（）。
答案:力的可传性原理4.只限物体任何方向移动，不限制物体转动的支座称为（）。
答案:固定铰支座5.力的作用线都相互平行的平面力系称为（）。
答案:平面平行力系6.根据二力平衡原理中的两个力应该满足的条件，指出下面说法错误的一种是( )。
答案:这两个力是作用力与反作用力7.二力杆对它所约束的物体的约束反力作用在物体上( )。
答案:必定沿着两作用点的连线8.“二力平衡公理”和“力的可传性原理”只适用于( ) 。
答案:刚体9.如图所示，用一绳将重物吊在天花板上，其中FT为绳对重物的拉力，FTˊ为重物对绳的拉力，其中属于作用力与反作用力是（）。
答案:FT与FTˊ10.力在某轴上的投影和沿某轴方向上的分力，正确的是( )。
答案:分力为矢量,投影为矢量第二章1.图示（a）、(b)两图代表平面汇交力系的两个力多边形，以下四种说法，正确的是（）.答案:图（a）是平衡力系，图（b）的F4是合力2.平面汇交力系平衡的必要和充分条件是该力系的（）为零。
答案:合力3.平面汇交力系的独立平衡方程数有三个。
答案:错4.如图所示，一平面上A、B、C三点分别受到力P作用，∆ABC为等边三角形，则此力系（）。
材料力学 第三章 扭 转
T2
T1
d
T3
Mx1=0.5kN· m
Mx2 =0.32kN· m lAB=300mm G=80GPa d=50mm
B
T2
φAB
lAB
A T1
lAC d φAC
C T3
B
lAB
A
lAC
C
M x1l AB j AB = GI P 500 0.3 = 9 80 10 0.054 32
r O
Mx
几何分析
变 形 应变分布
物理关系
应力分布
平面假定 静力学方程
应力公式
1. 变形几何关系
周线
a b c d
T
周线
a c d
γ
T
φ
b
纵线
dx
纵线
dx
a
c
a
γ
c c' d d'
b
d
b
（1）变形后所有圆周线的大小、形状和间距均不变，绕杆轴线相对转动。 （2）所有的纵线都转过了同一角度g。
T
周线
A
dρ
ρ o
ρ2dA
∫ 0ρ2·2πρdρ =
π d = 32
4
d/2
d
3 Ip π d Wp = r = 16
2. 空心圆截面
π D 4 - π d 4 π D 4(1-α4) Ip= 32 32 = 32 α=d/D
ρ o
dρ
π D3 Wp = 16 (1-α4)
d D
3.薄壁圆环截面
I P = 2r0
故该轴满足切应力强度要求。
二、刚度计算 等直圆杆扭转的刚度条件为
θ max = Mxmax ≤[θ] GI
等直圆杆扭转时斜截面上的应力
[] = ( 0.8 ~ 1.0 ) [ ] ( 铸铁 )
强度计算三方面：
① 校核强度：
max
Tm a x Wt
[ ]
② 设计截面尺寸：
Wt
Tm a x
[ ]
Wt
实：D3 16 空：1D6（3 1 4）
③ 计算许可载荷： Tmax Wt[ ]
[例2] 功率为150kW，转速为15.4转/秒的电动机转子轴如图，
(a)
´ (b)
M
1. 点M的应力单元体如图(b)：
2. 斜截面上的应力；
取分离体如图(d)：
´ (c)
x
´ (d)
(d)
n
x
´ t
转角规定：
轴正向转至截面外法线 由平衡方程：
逆时针：为“+” 顺时针：为“–”
Fn 0 ; dA (dAcos)sin ( dAsin)cos 0
Ft 0 ; dA (dAcos)cos ( dAsin)sin 0
非圆截面等直杆：平面假设不成立。即各截面发生翘曲成空 间曲面。因此，由等直圆杆扭转时推出的应力、变形公式不 适用，须由弹性力学方法求解。
一、自由扭转：杆件扭转时，横截面的翘曲不受限制，任意两相 邻截面的翘曲程度完全相同。
(纵向纤维长度不变, 无 , 只有 ) 二、约束扭转：杆件扭转时，横截面的翘曲受到限制，相邻截面
此杆的强度和刚度。
h 100 2 ; 0.246; 0.229
b 50
②校核强度
Wt hb2 0.246 0.1 0.052 61.6106 m3
max
T max Wt
4000 61.6 106
65MPa
③校核刚度
It h b3 0.229 0.1 0.053 284 10 8 m4
《材料力学》扭转习题解
第三章扭转习题解[习题3-1] 一传动轴作匀速转动， 转速n = 200r/min ，轴上装有五个轮子，主动轮 II 输入 的功率为60 kW ，从动轮，I ，山，IV ，V 依次输出18 kW ，12 kW ，22 kW 和8kW 。
试 作轴的扭图。
解：（1）计算各轮的力偶矩（外力偶矩）T e = 9.55 血n外力偶矩计算（kW 换算成kN.m ）题目编号 轮子编号轮子作用功率（kW ）转速r/mi nTe (kN.m ) 习题3-1I 从动轮 18 200 0.859II主动轮 60 200 2.865III从动轮 12 200 0.573IV从动轮 22 200 1.051V从动轮82000.382（2）作扭矩图。
用 595[习题3-2] —钻探机的功率为l0kW ，转速n = 180r/min 。
钻杆钻入土层的深度I = 40m 。
如土壤对钻杆的阻力可看作是均匀分布的力偶，试求分布力偶的集度 图。
资料个人收集整理，勿做商业用途 解：（1）求分布力偶的集度= 9.549x® =0.5305(kN m)180M e 0.5305 m = --- = ------l 40= 0.0133(kN /m)设钻杆轴为x 轴, 则:Z M x =0ml =Me1 4325A1 2 0055 1m 3.5 mLSC.3SZm ，并作钻杆的扭矩M e =9.549 丛n L7S mT 图(kN.m)（2）作钻杆的扭矩图T(x) = —mx =—牛X =-0.0133x 。
x<^[0,40] T(0) =0 ;T(40) = M e = —0.5 305kN m) 扭矩图如图所示。
［习题3-3］圆轴的直径d =50mm ，转速为120r/min 。
若该轴横截面上的最大切应力等于 60 MPa ，试问所传递的功率为多大？ 资料个人收集整理，勿做商业用途 解：（1）计算圆形截面的抗扭截面模量： 1 3 W p =—血3 P16（2 ）计算扭矩1 3 3 = 16®4159 倔=24544(mm ) 2= 60N / mm23T =60N/mm x 24544mm =1472640N ・mm = 1.473(kN ・m)（3）计算所传递的功率T = M e =9.549山=1.473(kN -m)n N k =1.473x120/9.549 =18.5(kW)［习题3-4］空心钢轴的外径 D = 100mm ，内径d =50mm 。
(整理)杆的扭转定理和公式
圆截面杆的扭转外力与内力 || 圆杆扭转切应力与强度条件 || 圆杆扭转变形与刚度条件 || 圆杆的非弹性扭转1.外力与内力杆件扭转的受力特点是在垂直于其轴线的平面内作用有力偶（图2·2-1a），其变形特点是在任意两个截面绕轴线发生相对转动。
轴类构件常有扭转变形发生。
作用在传动轴上的外力偶矩m通常是根据轴所传递的功率N和转速n(r/min)来计算。
当N的单位为千瓦（kW）时当N的单位为马力（HP）时扭转时的内力为扭矩T，用截面法求得。
画出的内力图称为扭矩图（或T图），如图2·2-1b所示图2·2-1 圆杆的扭转2.圆杆扭转切应力与强度条件当应力不超过材料的剪切比例极限r p时，某横截面上任意C点（图2·2-2）的切应力公式为式中T——C 点所在横截面上的扭矩p——C点至圆心的距离L p——横截面对圆心的极惯性矩，见表2-2-1 等直杆扭转时的截面几何性质。
图2·2-2 切应力分布圆杆横截面上的切应力r沿半径呈线性分布，其方向垂直于半径（图2·3-2）。
模截面上的最大切应力在圆周各点上，其计算公式为等截面杆的最大切应力发生在T max截面（危险截面）的圆周各点（危险点）上。
其强度条件为式中，[τ]为许用扭转切应力，与许用拉应力[σ]的关系为：[τ]=（0.5～0.6）[σ] (塑性材料)或[τ]=（0.5～0.6）[σ]（脆性材料）3.圆杆扭转变形与刚度条件在比弹性范围内，圆杆在扭矩T作用下，相中为L的两截面间相对扭转角为或式中G——材料的切变模量单位扭转角公式为或式中GL p——抗扭刚度圆杆上与杆轴距离为p外（图2·2-2）的切应变r为圆杆表面处的最大切应变为式中,r——圆杆的半径等截面圆杆的最大单位扭转角，发生在T max一段内，其刚度条件为式中,[θ]为圆杆的许用单位扭转角（°）/m4.圆杆的非弹性扭转讨论圆杆扭转时切应力超过材料的比例极限并进入塑性状态的情况。
结构力学(专科)——武汉理工大学
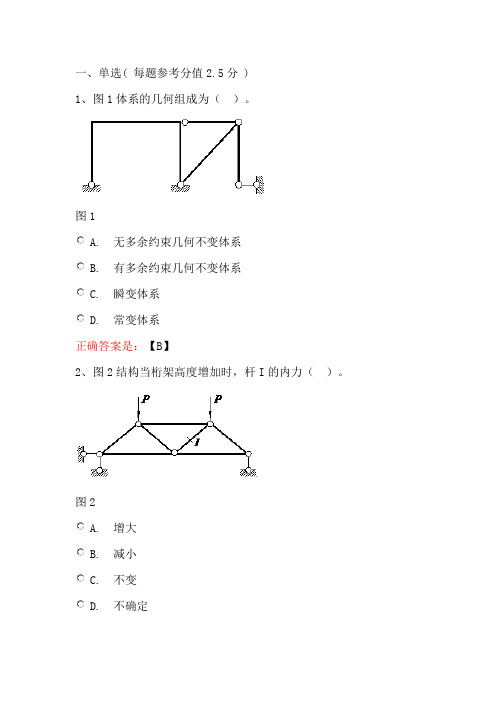
一、单选( 每题参考分值2.5分 )1、图1体系的几何组成为（）。
图1A. 无多余约束几何不变体系B. 有多余约束几何不变体系C. 瞬变体系D. 常变体系正确答案是：【B】2、图2结构当桁架高度增加时，杆I的内力（）。
图2A. 增大B. 减小C. 不变D. 不确定正确答案是：【C】3、当杆件刚度系数SAB=3i时，杆的B端为（）。
A. 自由端B. 固定端C. 铰支承D. 定向支承正确答案是：【C】4、图3结构超静定次数为（）。
图3A. 6次B. 7次C. 8次D. 9次正确答案是：【C】5、图1体系的多余约束的个数为（）。
图1A. 0个B. 1个C. 2个D. 3个正确答案是：【B】6、拱轴线为合理拱轴线，其横截面上内力为零的是（）。
A. 弯矩B. 扭矩C. 轴力D. 支座反力正确答案是：【A】7、图2梁受到三角形荷载作用，A端竖向支座反力的大小为（）。
图2A. ql/2B. ql/3C. ql/4D. ql/6正确答案是：【A】8、在力法方程中（）。
A.B.C.D. 前三种答案都有可能正确答案是：【D】9、拱的突出持点是竖向荷载下有（）。
A. 轴力B. 弯矩C. 竖向力D. 水平推力正确答案是：【D】10、力法典型方程的物理意义是（）。
A. 结构的平衡条件B. 结点的平衡条件C. 结构的变形协调条件D. 结构的平衡条件及变形协调条件正确答案是：【C】11、绘制任一量值的影响线时，假定荷载是（）。
A. 一个方向不变的单位荷载B. 移动荷载C. 动力荷载D. 可动荷载正确答案是：【A】12、力矩分配法计算得出的结果（）。
A. 一定是近似解B. 不是精确解C. 是精确解D. 可能为近似解，也可能是精确解正确答案是：【D】13、图3桁架零杆的个数为（）。
图3A. 3个B. 4个C. 5个D. 6个正确答案是：【D】14、图3a结构，EI=常数，取图3b为力法基本体系，则中的和分别等于（）。
图3A. Δ，Δ/4B. -Δ，Δ/4C. Δ，-Δ/4D. -Δ，-Δ/4正确答案是：【D】15、叠加原理用于求解静定结构时，需要满足的条件是（）。
10——扭转的强度和刚度计算
τ 1 = γτ max
其中 : WT = α b 2h
θ = Mx
GI T
, 其中 : IT = β b3h
对于狭长矩形 ( 即 : h ≥ 10 ) ; b
α ≈β ≈1
3
查表求α 和β 时一定要注意，表中α 和β 与那套公式对应。
[例] 一矩形截面等直钢杆，其横截面尺寸为：h = 100 mm， b=50mm，长度L=2m，杆的两端受扭转力偶 Mx =4000N·m 的作用 ，钢的G =80GPa ，试求此杆的剪应力和单位长度扭 转角。
T
Ip
≥
max
G[θ ]
T max ≤ GI p[θ ]
有时，还可依据此条件进行选材。
[例] 长为 L=2m 的圆杆受均布力偶 m=20Nm/m 的作用，
如图，若杆的内外径之比为α =0.8 ，G=80GPa ，许用剪应 力 [τ]=30MPa，试设计杆的外径；若[θ]=2º/m ，试校核此杆
的刚度，并求右端面转角。
石油钻机中的钻杆等。
扭转：外力的合力为一力偶，且力偶的作用面与直杆的轴线
垂直，杆发生的变形为扭转变形。
A
B O
A
γ ϕBO
m
m
工 程 实 例
单元体的四个侧面上只有剪应力而无正应力作用，这 种应力状态称为纯剪切应力状态。 四、剪切虎克定律：
T
T
τ =G⋅γ
式中：G是材料的一个弹性常数，称为剪切弹性模量，因γ 无量纲，故G的量纲与τ 相同，不同材料的G值可通过实验确定，
dx
τρ
=
Mx ⋅ρ
Ip
—横截面上距圆心为ρ处任一点剪应力计算公式。
4. 公式讨论： ① 仅适用于各向同性、线弹性材料，在小变形时的等圆截面