第三部分扭转
材料力学习题册_参考答案(1-9章)

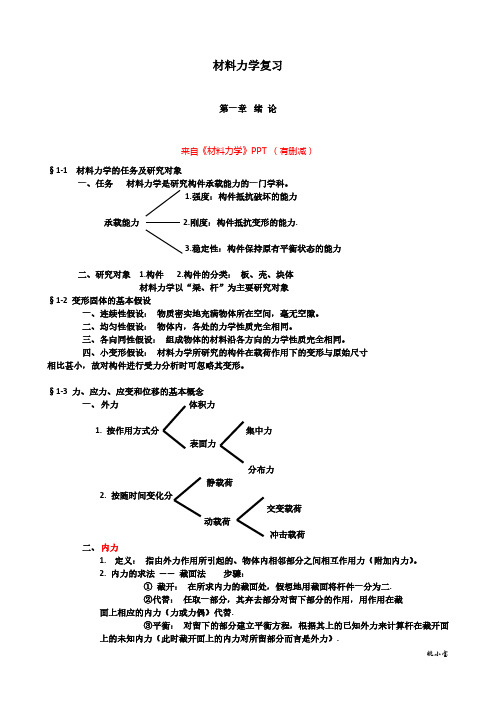
第一章 绪 论一、选择题1.根据均匀性假设,可认为构件的( C )在各处相同。
A.应力B. 应变C.材料的弹性系数D. 位移2.构件的强度是指( C ),刚度是指( A ),稳定性是指( B )。
A.在外力作用下构件抵抗变形的能力B.在外力作用下构件保持原有平衡 状态的能力C.在外力作用下构件抵抗强度破坏的能力3.单元体变形后的形状如下图虚线所示,则 A 点剪应变依次为图(a) ( A ),图(b)( C ),图(c) ( B )。
A. 0B. 2rC. rD.1.5 r4.下列结论中( C )是正确的。
A.内力是应力的代数和; B.应力是内力的平均值; C.应力是内力的集度; D.内力必大于应力; 5. 两根截面面积相等但截面形状和材料不同的拉杆受同样大小的轴向拉力,它们的应 力是否相等( B )。
A.不相等; B.相等; C.不能确定; 6.为把变形固体抽象为力学模型,材料力学课程对变形固体作出一些假设,其中均匀性假设是指( C )。
A. 认为组成固体的物质不留空隙地充满了固体的体积; B. 认为沿任何方向固体的力学性能都是相同的; C. 认为在固体内到处都有相同的力学性能; D. 认为固体内到处的应力都是相同的。
二、填空题1.材料力学对变形固体的基本假设是 连续性假设 , 均匀性假设 , 各向同性假设 。
2.材料力学的任务是满足 强度 , 刚度 , 稳定性 的要求下,为设计经济安全的构-1-件提供必要的理论基础和计算方法。
3.外力按其作用的方式可以分为 表面力 和 体积力 ,按载荷随时间的变化情况可以分为 静载荷 和 动载荷 。
4.度量一点处变形程度的两个基本量是 (正)应变ε 和 切应变γ。
三、判断题1.因为构件是变形固体,在研究构件平衡时,应按变形后的尺寸进行计算。
( × )2.外力就是构件所承受的载荷。
(×)3.用截面法求内力时,可以保留截开后构件的任一部分进行平衡计算。
第03部分IACS要求

样的应急切断使货油和压载泵全部失效,如果当时压载泵能动作,或许可以延迟பைடு நூலகம்
或/和202减0/1/轻28 由于干舷减小而从空气管连续进水的后果。
4
该轮在艏部进水空间,既没有动力单元的提供,也没有控制屏。但是,在现有油 船上有些在艏部空间装有动力单元或控制屏,它们在由于恶劣气候引发这些处所 进水或损坏时也存在很大的危险。
遥控的货油和压载系统的操作对加强油船安全来说可能是有必要的, IACS工作组在提交这个统一要求时还特别指出,M64中所要求的某 些性能,可能不仅仅适用于整体式的系统,也适用于所有遥控的货 油系统和压载系统。
3.7 UR S6船长大于等于90米船舶不同部位船体钢材等级的使用(Rev.4,
July 2019)
回路提供至少一套独立能源,新版将这一要求改为:当辅助回路必须用外部能源
时,应至少提供二套外部能源,它们的设计应能保证当一套能源故障或失效时, 不会引起超过一台发电机失电和/或超过一套主要机停止工作。 UR E18 电池型号、位置及保养周期的记录(New, July 2019)
(Recording of the Type, Location and Maintenance Cycle of Batteries) 由于船上越来越多地使用电气的或基于计算机的系统,而且这些系统很多都是
第三部分 IACS最新要求 说明:如未特别指出,所有统一要求及其修正案应在其通过之日起的一年内生效。
UR E11电压为1kv-15kv的系统的统一要求(Rev. 2, July 2019)
(Unified requirements for system with voltages above 1kV up to 15kV) 6.3.2 (辅助回路的)外部电源数量-原文要求:应为系统每一独立单元的辅助
材料力学知识点总结
三、应力 1.定义 (Definition):由外力引起的内力的集度 2. 应力 ①平均应力
pm
=
ΔF ΔA
②全应力(总应力)
p lim ΔF dF ΔA0 ΔA dA
③全应力分解为 垂直于截面的应力称为“正应力”
lim ΔFN dFN ΔA0 ΔA dA
位于截面内的应力称为“切应力”
·§3-3 薄壁圆筒的扭转
1 10 r0
姚小宝
薄壁圆筒:壁厚
(r0—圆筒的平均半径)
3.推论 (1)横截面上无正应力,只有切应力;
(2)切应力方向垂直半径或 与圆周相切.
圆周各点处切应力的方向于圆周相切,且数值相等,近似的认为沿壁厚方向各点处
切应力的数值无变化.
4.推导
此式为薄壁圆筒扭转时横截面上切应力的计算公式. 薄壁筒扭转时横截面上的切应力均匀分布,与半径垂直,指向与扭矩的转向一致.
固定铰支座
固定端
5.静定梁的基本形式:
·§4-2 梁的剪力和弯矩
一、内力计算
简支梁 外伸梁
悬臂梁
求内力——截面法
姚小宝
二、内力的符号规定 1.剪力符号
2.弯矩符号
当 dx 微段的弯曲下凸(即该段的下 半部受拉 )时,横截面 m-m 上的弯矩为 正;
当 dx 微段的弯曲上凸(即该段的下半 部受压)时,横截面 m-m 上的弯矩为负.
2.平面假设
变形前为平面的横截面 ,变形后仍保持为平面.
3.几何关系 倾角 是横截面圆周上任一点 A 处的切应变, d 是 b-b 截面相对于 a-
a 截面象刚性平面一样绕杆的轴线转动的一个角度.
tan
力度术语对照表

力度术语对照表第一部分:轻度1. 轻轻地拍打:他轻轻地拍打着孩子的背,让他入睡。
2. 轻握:她轻轻地握住他的手,传递着温暖和安慰。
3. 轻声细语:他轻声细语地告诉她,他会一直陪在她身边。
4. 轻抚:她轻抚着猫咪的毛发,让它感到舒适和放松。
5. 轻轻地呼吸:他躺在床上,轻轻地呼吸着,享受着宁静的夜晚。
第二部分:中度1. 有力地握紧:他有力地握紧了拳头,表达着内心的愤怒和不满。
2. 坚定地推开:她坚定地推开门,迈出了新的一步。
3. 有力地抱紧:他有力地抱紧她,不愿意放手。
4. 稳健前行:他稳健地前行,克服了一切困难。
5. 坚定不移:她坚定不移地追求自己的梦想,不受外界的干扰。
第三部分:重度1. 猛烈撞击:车辆发生猛烈的撞击,引起了巨大的爆炸声。
2. 狠狠地扭转:他狠狠地扭转了身体,摆脱了对手的控制。
3. 激烈争吵:他们之间发生了激烈的争吵,声音震耳欲聋。
4. 强有力地推开:他用尽全力强有力地推开门,冲向外面的世界。
5. 毫不犹豫地跳下:他毫不犹豫地跳下悬崖,拯救了溺水的人。
第四部分:极度1. 极力反抗:他极力反抗,拒绝屈服于困境。
2. 高强度训练:他进行了高强度的训练,以迎接即将到来的比赛。
3. 极端恐惧:他面对极端的恐惧,却依然勇敢地面对。
4. 极度疲劳:他经过长时间的劳累,感到极度的疲劳和筋疲力尽。
5. 极速奔跑:他以极速奔跑,追赶着最后一班公交车。
第五部分:超度1. 超强力量:他展现出超强的力量,将巨石举起。
2. 超越极限:他超越了自己的极限,创造了不可能的成就。
3. 超高速度:他以超高的速度飞驰而过,如闪电般迅猛。
4. 超乎想象:他的成绩超乎了所有人的想象,刷新了世界纪录。
5. 超越认知:他的思维超越了常人的认知,拥有非凡的智慧。
这些力度术语对照表提供了不同程度的力度描述,从轻度到超度,可以用于描绘各种场景和情感,使文章更加生动有力。
无论是平静的拥抱还是激烈的斗争,这些词汇都能帮助读者更好地理解和感受到其中的力量。
结构周期扭转调整方法

结构第一周期扭转调整方法规范条文:新高规的4.3.5条规定,结构扭转为主的第一周期Tt与平动为主的第一周期T1 之比,A级高度高层建筑不应大于0.9;B级高度高层建筑、混合结构高层建筑及复杂高层建筑不应大于0.85。
一旦出现周期比不满足要求的情况,一般只能通过调整平面布置来改善这一状况,这种改变一般是整体性的,局部的小调整往往收效甚微。
周期比不满足要求,说明结构的扭转刚度相对于侧移刚度较小,总的调整原则是要加强结构外圈,或者削弱内筒。
周期比:主要为限制结构的抗扭刚度不能太弱,使结构具有必要的抗扭刚度,减小扭转对结构产生的不利影响。
见高规4.3.5及相应的条文说明。
周期比不满足规范要求,说明结构的抗扭刚度相对于侧移刚度较小,扭转效应过大,结构抗侧力构件布置不合理。
周期比不满足规范要求时的调整方法(转):1、程序调整:SATWE程序不能实现。
2、结构调整:只能通过调整改变结构布置,提高结构的抗扭刚度。
由于结构外围的抗侧力构件对结构的抗扭刚度贡献最大,所以总的调整原则是加强结构外围墙、柱或梁的刚度,或适当削弱结构中间墙、柱的刚度。
利用结构刚度与周期的反比关系,合理布置抗侧力构件,加强需要减小周期方向(包括平动方向和扭转方向)的刚度,削弱需要增大周期方向的刚度。
当结构的第一或第二振型为扭转时,可按以下方法调整:1)SATWE程序中的振型是以其周期的长短排序的。
2)结构的第一、第二振型宜为平动,扭转周期宜出现在第三振型及以后。
见抗规3.5.3条3款及条文说明“结构在两个主轴方向的动力特性(周期和振型)宜相近”。
3)当第一振型为扭转时,说明结构的抗扭刚度相对于其两个主轴(第二振型转角方向和第三振型转角方向,一般都靠近X轴和Y轴)的抗侧移刚度过小,此时宜沿两主轴适当加强结构外围的刚度,并适当削弱结构内部的刚度。
4)当第二振型为扭转时,说明结构沿两个主轴方向的抗侧移刚度相差较大,结构的抗扭刚度相对其中一主轴(第一振型转角方向)的抗侧移刚度是合理的;但相对于另一主轴(第三振型转角方向)的抗侧移刚度则过小,此时宜适当削弱结构内部沿“第三振型转角方向”的刚度,并适当加强结构外围(主要是沿第一振型转角方向)的刚度。
材料力学习题册1-14概念答案

第一章绪论一、是非判断题材料力学的研究方法与理论力学的研究方法完全相同。
( × ) 内力只作用在杆件截面的形心处。
( × )杆件某截面上的内力是该截面上应力的代数和。
( × )确定截面内力的截面法,适用于不论等截面或变截面、直杆或曲杆、基本变形或组合变形、横截面或任意截面的普遍情况。
( ∨ )根据各向同性假设,可认为材料的弹性常数在各方向都相同。
( ∨ )根据均匀性假设,可认为构件的弹性常数在各点处都相同。
( ∨ )同一截面上正应力σ与切应力τ必相互垂直。
( ∨ )同一截面上各点的正应力σ必定大小相等,方向相同。
( × )同一截面上各点的切应力τ必相互平行。
( × )应变分为正应变ε和切应变γ。
( ∨ )应变为无量纲量。
( ∨ )若物体各部分均无变形,则物体内各点的应变均为零。
( ∨ )若物体内各点的应变均为零,则物体无位移。
( × )平衡状态弹性体的任意部分的内力都与外力保持平衡。
( ∨ )题图所示结构中,AD杆发生的变形为弯曲与压缩的组合变形。
( ∨ )题图所示结构中,AB杆将发生弯曲与压缩的组合变形。
( × )B题图题图二、填空题材料力学主要研究 受力后发生的,以及由此产生的 。
拉伸或压缩的受力特征是 ,变形特征是 。
剪切的受力特征是 ,变形特征是。
扭转的受力特征是 ,变形特征是 。
弯曲的受力特征是 ,变形特征是 。
组合受力与变形是指 。
构件的承载能力包括 , 和 三个方面。
所谓 ,是指材料或构件抵抗破坏的能力。
所谓 ,是指构件抵抗变形的能力。
所谓 ,是指材料或构件保持其原有平衡形式的能力。
根据固体材料的性能作如下三个基本假设 , , 。
认为固体在其整个几何空间内无间隙地充满了组成该物体的物质,这样的假设称为 。
根据这一假设构件的 、 和 就可以用坐标的连续函数来表示。
填题图所示结构中,杆1发生 变形, 杆2发生 变形,杆3发生 变形。
2019版高考总复习语文课件:第三部分 专题三 实用类文本阅读 (二)传记阅读 学案一明确8大设误陷阱解答客

(二) 传记阅读 专题入门 传记阅读入门知识必备
一、传记的分类 作为一种文体,传记根据不同的分类标准可以划分 成不同的种类,下面就是几种常见的分类方法:
1.按照叙述人称划分,传记可分为自传和他传 自传是本人叙述自己的生平事迹的文字,多是回顾 生活往事、人生阅历、兴趣爱好、思想轨迹,形式如同 一般的散文形式,信笔写来,典型的“形散神不散”。 他传是他人为传主撰写的传记文章。
设误陷阱 3:张冠李戴
[典例 3] [选项] 侯仁之发现有着 800 多年历史的 卢沟桥受损严重,便强烈呼吁保护卢沟桥,禁止机动车 和兽力车通行,最终使卢沟桥得到了妥善保护。
[原文信息] 有 800 多年历史的卢沟桥在 20 世纪 80 年代还是进京要道。卡车、拖拉机往来穿梭,卢沟桥受损 严重。侯仁之对此心急如焚。他写了《保护卢沟桥刻不容 缓》一文,发表在《北京日报》上。
它创造的是一个可能的事实;历史则提供实有的真
实,表现为真实发生过的一切。 [比对分析] (答案)选项与原文观点相反:选项认为
“历史与艺术都着力于表现普遍法则”,原文认为“着 力于表现独特而个别的事实”;选项认为“历史与艺术 的区分界限在于真实和虚构”,原文认为艺术“创造的 是一个可能的事实”,“历史则提供实有的真实”,没有 说“虚构”。选项属混淆是非。
为国家战死,事极光荣。
所念者,你们母子今后生活,当更痛苦。望你珍重, 并爱护诸儿,侍奉老母。老父在皖,可不必呈闻。”
[比对分析] (答案)选项中“唯一放心不下的,就是 妻子儿女日后的生活”不恰当,把原文的“所念者”说 成了“唯一放心不下的”,缩小了范围,以致选项有误。
设误陷阱 6:混淆时态
[典例 6] [选项] 侯仁之主张沙漠研究要走出小书 房,走进现场,不要依靠旧书堆中的文献资料。他在陕 北榆林附近沙漠的考察研究纠正了人们的错误认识。
第三部分:腹膜与腹膜腔

4、乙状结肠系膜sigmoid mesocolon 、乙状结肠系膜
是将乙状结肠固定于左下腹部的双层腹 膜结构,其根部附着手左骼窝和骨盆左后壁。 系膜较长,故乙状结肠活动度较大,是系膜 扭转产生肠梗阻的易发部位。系膜内含有乙 状结肠和直肠上血管、淋巴管、淋巴结和神 经丛。
由于胚胎发生方面的原因, 升、降结肠也可能出现系膜,此 时的升、降结肠则成为腹膜内位 器官,有一定的活动性。
(二)系膜
由于壁、脏腹膜相互延续移行, 形成许多将器官系连固定于腹、盆壁 的双层腹膜结构称为系膜,其内含有 出入器官的血管、神经及淋巴管和淋 巴结等。主要的系膜有肠系膜、阑尾 系膜、横结肠系膜和乙状结肠系膜等。
腹模形成的结构
1、肠系腹mesentery 、肠系腹 是将空、回肠系连固定于腹后壁的 双层腹膜结构,面积较大,整体呈 摺扇形 肠系膜根 radix of mesentery 长约15cm,自第2腰椎左侧起,斜 向右下跨过脊柱及其前方,止于右 骶髂关节前方
大网膜 great omentum
3.网膜囊omental bursa 网膜囊omental
是位于小网膜和胃后方的扁窄间隙,又称小腹膜 腔。 边界 上壁:肝尾叶及隔下方的腹膜。 前壁:由上向下依次为小网膜、胃后壁腹 膜和大网膜前叶。 下壁:大网膜的前、后叶返折部。 后壁:由下向上依次为大网膜后叶、横结 肠及其系膜以及覆盖胰、左肾、左肾上腺 等处的腹膜。 左侧壁:脾、胃脾韧带和牌肾韧带。
腹膜矢状面示意图(男 腹膜矢状面示意图 男)
腹膜内位器官
是指器官全部突向腹膜 腔,各面均被腹膜所覆盖的 器官,如胃、十二指肠上部、 空肠、回肠、盲肠、阑尾、 横结肠、乙状结肠、脾、卵 巢、输卵管等。
腹膜间位器官
是指大部分被腹膜覆盖,仅少 部分未被腹膜覆盖的器官,如肝、 胆囊、升结肠、降结肠、直肠上段 、子宫、膀胱等。
国际标准ISO14692PATR3中文版第三部分——系统设计

第三部分系统设计目录前言1适用范围2规范性引用文件3术语及定义4符号及缩略语5系统布置要求5.1概述5.2空间要求5.3系统支座5.4用于清理的隔离装置及通道5.5设计隐患5.6接头的选择5.7火灾及爆破5.8静电释放的控制5.9电化腐蚀6 水力学设计6.1概述6.2流动特性6.3流速的一般要求6.4侵蚀6.5水锤6.6循环条件7结构设计7.1概述7.2制造商的压力等级7.3合格压力7.4参数化合格压力7.5系统设计压力7.6 载荷要求7.7容许位移7.8合格应力7.9参数化应力7.10计算载荷应力的极限值7.11失效包络线的确定8应力分析8.1分析方法8.2分析要求8.3外压/真空压力8.4热载荷8.5内压引起的应力8.6管子支架引起的的应力8.7轴向压缩载荷(屈曲载荷)9防火性能9.1概述9.2耐火性9.3燃烧反应9.4防火涂层前言ISO14692本部分旨在保证采用ISO14692-2鉴定的构件设计管道系统时,系统可以符合规定的性能要求。
这些管道系统专用于石油及天然气工业加工及公用设施应用领域。
该文件主要用户包括委托人、设计承包商、负责设计的供应商、认证机构及政府机构。
ISO 14692-1给出了ISO 14692本部分所用压力术语的定义。
石油及天然气工业——玻璃钢(GRP)管道第三部分:系统设计1适用范围ISO 14692该部分为设计GRP管道系统提供了指南。
本文阐述的要求及建议适用于布置尺寸、水利学设计、结构设计、细节设计、耐火性、火灾蔓延、排放物及静电释放控制。
ISO 14692该部分需要与ISO 14692-1一起阅读理解。
2 规范性引用文件下列引用文件对应用本标准必不可少。
对于注有日期的引用文件,只能使用本文所引用的版本。
对于未注明日期的引用文件,可以使用引用文件(包括任何修订版本)的最新版本。
ISO 14692-1:2002,石油及天然气工业——玻璃钢(GRP)管道——第一部分:词汇、符号、应用及材料ISO 14692-2:2002,石油及天然气工业——玻璃钢(GRP)管道——第四部分:制造、安装及运行BS 7159:1989特殊工厂和工地用玻璃纤维增强塑料(GRP)管道系统的设计和施工实用规程ASTM E1118,增强热固树脂管材(RTRP)声发射检测标准操作规程3 术语及定义ISO 14692-1给出的术语及定义适用于本标准。
831-材料力学考试大纲及参考书目

2020年硕士研究生招生专业考试大纲学院代码:021学院名称:建筑工程学院专业代码及专业名称:087100 管理科学与工程初试科目代码及名称:831材料力学考试大纲:一、考试目标及要求通过笔试,全面衡量和考核考生掌握杆件的强度、刚度和稳定性计算的基本理论的程度;着重观察其基本概念和分析方法熟练程度;也注意辨析其计算能力和掌握的实验分析能力的情况。
本大纲在专家相应考试命题和考生复习应考中提供一个关于内容、重点等等方面的参考。
二、考试形式与考卷结构考试形式:闭卷,笔试,卷面总分150分,考试时间180分钟三、考试范围第一章基本概念材料力学的任务,可变形固体的性质及其基本假设,杆件的几何特征,杆件变形的基本形式。
第二章轴向拉伸和压缩内力,截面法,轴力及轴力图,应力,拉(压)杆的变形,拉(压)杆的应变能,材料在拉伸和压缩时的力学性能,强度条件及安全因数、许用应力,应力集中的概念。
第三章扭转薄壁圆筒的扭转,传动轴的外力偶矩,扭矩及扭矩图,等直圆杆扭转时的应力及强度条件,等直圆杆扭转时的变形及刚度条件,等直圆杆扭转时的应变能。
第四章弯曲应力对称弯曲的概念,梁的剪力和弯矩、剪力图和弯矩图,平面刚架和曲杆的内力图,梁横截面上的正应力及正应力强度条件,梁横截面上的切应力及切应力强度条件,梁的合理设计。
第五章梁弯曲时的位移挠度及转角,梁的挠曲线近似微分方程及其积分,按叠加原理计算梁的挠度和转角,梁的刚度校核,提高梁的刚度的措施,梁内的弯曲应变能。
第六章简单的超静定问题超静定问题及其解法,拉压超静定问题,扭转超静定问题,简单超静定梁。
第七章应力状态和强度理论平面应力状态的应力分析,主应力,空间应力状态的概念,应力与应变间的关系,强度理论及其相当应力,各种强度理论的应用。
第八章组合变形及连接部分的计算两相互垂直平面内的弯曲,拉伸(压缩)与弯曲,扭转与弯曲,连接件的实用计算法,铆钉连接计算。
第九章压杆稳定压杆稳定性的概念,细长中心受压直杆临界力的欧拉公式,不同杆端约束下细长压杆临界力的欧拉公式及压杆的长度因数,欧拉公式的应用范围,临界应力总图,压杆的稳定计算,压杆的合理截面。
材料力学

第一章绪论1.土木工程中,各种建筑物在施工和使用阶段所承受的所有外力统称为荷载。
建筑物中承受荷载并且传递荷载的空间骨架称为结构,而任何结构都是由构件所组成的。
为保证构件在荷载作用下的正常工作,必须使它同时满足三方面的力学要求,即强度、刚度和稳定性的要求:(1) 构件抵抗破坏的能力称为强度(strength)。
对构件的设计应保证它在规定的荷载作用下能够正常工作而不会发生破坏(2) 构件抵抗变形的能力称为刚度(stiffness)。
构件的变形必须要限制在一定的限度内,构件刚度不满足要求同样也不能正常工作。
(3) 构件在受到荷载作用时在原有形状下的平衡应保证为稳定的平衡,这就是对构件的稳定性(stability)要求。
但是在材料力学中,构件的变形不能忽略不计,因此我们把构件作为可变形体来研究,称它们为可变形固体(deformable solid)。
在对可变形固体材料制成的构件进行强度、刚度和稳定性研究时,为抽象出某种理想的力学模型,通常根据其主要性质做出一定的假设,同时忽略一些次要因素,然后进行理论分析。
在材料力学中,通常对可变形固体作如下基本假设:(1) 连续性假设(continuity assumption)。
这一假设认为,构件的材料在变形后仍然保持连续性,在其整个体积内都毫无空隙地充满了物质,忽略了体积内空隙对材料力学性质的影响。
(2) 均匀性假设(homogenization assumption)。
这一假设认为,构件的材料各部分的力学性能是相同的。
从任意一点取出的单元体,都具有与整体同样的力学性能。
(3) 各向同性假设(isotropy assumption)。
这一假设认为,构件的材料在各个方向的力学性能是相同的。
如工程上常用的金属材料,虽然从它们的晶粒来说,其力学性能并不一样;但从宏观上看,各个方向的力学性能接近相同。
有些材料沿各方向的力学性能并不相同,像这样的材料称之为各向异性材料,如木材等。
第三部分 单音节字词

第三部分单音节字词普通话2009-11-23 09:31:02 阅读22 评论0 字号:大中小酿日馋割摹秸舟外郝niang ri chan ge mo jie zhou waihao扼除内抓恨她货墩怄滑e chu nei zhua hen ta huo dun怄hua贱淮瞪善黄蜿樊深围决jian huai deng shan huang 蜿fanshen wei jue庄凭掰此瘸罪匣手需聊zhuang ping 掰ci que zui xia shouxu liao捐泼被佳船尊雄私腌遛juan po bei jia chuan zun xiongsi 腌遛孔谒儒蜕左聩秧算捞眉kong 谒ru tui zuo 聩yang suanlao mei姓泉变叼三讯羔躺羹贸xing quan bian diao san xun gaotang geng mao裸罚柄浊弩御疼蚓利农luo fa bing zhuo 弩yu teng 蚓linong凛群裁腹砸纽诤瞌党终lin qun cai fu za niu 诤瞌dangzhong赛认舱痞纲矢琼透嫣遣 sai ren cang pi gang shi qiongtou 嫣qian漏傧溢患丞紫镯云丝瞄lou 傧yi huan 丞zi 镯yun simiao轻两琴殓疯灾瞬凸碎脑qing liang qin 殓feng zai shun tusui nao河鼎篝窜酥造摊让赴灯he ding 篝cuan su zao tan rangfu deng酵年蛹甘饵丈啼惹痛光jiao nian yong gan er zhang ti retong guang旧女扮搭罐者瑕熔脱浩jiu nv ban da guan zhe 瑕rongtuo hao捐牌倍墙寸枝硝尚晚火juan pai bei qiang cun zhi xiaoshang wan huo掘飘播媚婶终絮品胃踹jue piao bo mei shen zhong xupin wei 踹克跌菜疥藕穷荀视产抛ke die cai jie ou qiong 荀shichan pao伐爱坡挎物嘴觅刷游些fa ai po kua wu zui mi shuayou xie框蛔尝诺甩虐甄愿凝亮kuang hui chang nuo shuai nue zhenyuan ning liang米癫桎丛刍玉虽渊锁眉mi 癫桎cong 刍yu sui yuan suomei认流惹暇踹在膛射丸郝ren liu re xia 踹zai tang shewan hao建怀傣存邻糟问身潇借jian huai dai cun lin zao wenshen 潇jie墨君断锅缓俸找收四聊mo jun duan guo huan 俸zhaoshou si liao刻茬拌嫩含霹婿枯位壤ke cha ban nen han pi xu kuwei rang竖娘卦瘸错肿胰双妥尚shu niang 卦que cuo zhong yi shuang tuo shang筐瞥笔鹅荫羚虔迥听伞kuang pie bi e yin ling 虔迥ting san浪破搀籽胸恩恽挠疼象lang po chan zi xiong en 恽naoteng xiang羹谱镖法晴篓诈蒜癌塌geng pu 镖fa qing lou zha suanai ta全苟吃飞痘囚抓爵蝙成quan gou chi fei dou qiu zhuajue 蝙cheng镣花却床吻评喂凡誊捐liao hua que chuang wen ping weifan teng juan日辞热支费卖锨摔涌伙归另迭梭婉陀死件穹摸三唤港赚吮下伸路紧念帮醋稿迄玄瞌泄就酿匕清从坐ri ci re zhi fei mai xian shuai yong huo gui ling die suo wan tuo si jian 穹mo san huan gang zhuanshun xia shen lu jin nian bang cu gao qi xuan 瞌xie jiu niang 匕qing cong zuo殉挖纳淌剧成女递衙虐疱闸音舌盔按簧逗瑶偶鳔砂歪颇里缤渡软再陨商忏周亮箴锄恩遭隋撬煤缶贸列平良沧改虐租群嫌颇戈愣坏嘘园最热松桦箭髓电功等鳃硼日江袅茉穹罢某杖索针软温焚蜜芍豺拽酪纱涛学禁蛰救逼媚迁吮祈睫我夏啃xun wa na tang ju cheng nv diya nue 疱zha yin she kui an huang dou yao ou 鳔sha wai po li 缤du ruan zai yun shang 忏zhou liang箴chu en zao sui qiao mei 缶mao lie ping liang cang gai nue zu qun xian po ge 愣huai xu yuan zui re song 桦jian sui dian gong deng sai peng ri jiang 袅茉穹ba mou zhangsuo zhen ruan wen fen mi shao chaizhuai lao sha tao xue jin zhe jiu bimei qian shun qi jie wo xia ken an biao duan ni si ya kua ban yaohan ce en miao氨标短尼撕蚜挎班窑撼册恩苗壮秃直彩善羹釉穿而涌自团拭兜谎妥赔胡法奏努去未缶买破邹垂诺死疱闰狞伞略翡涣辞封诱淌兄拷梭汾黑列瞳钙吞荡门虐静欠娟拱急助颓禽消钠均面百官等壮蟀犬下愈科某翱话贫足溢仍网吱褐遍婵崽 an biao duan ni si ya kua ban yaohan ce en miaozhuang tu zhi cai shan geng you chuan er yong zi tuan shi dou huang tuopei hu fa zou nu qu wei 缶maipo zou chui nuo si 疱run ningsan lue 翡huan ci feng you tangxiong kao suo fen hei lie tong gaitun dang men nue jing qian juangong ji zhu tui qin xiao na jun mianbai guan deng zhuang 蟀quan xia yu ke mou ao hua pin zu yi rengwang zhi he bian 婵崽琼歪容嘈韵扣扭兵队闩骑獐剩酱赚梁氨跺蚕夜赎榛失类聊赔丑饿吾蓄怕耍魔亮肛苦掐娟钙渣软账瞌轰渠话蕊祸疚拄婪社乡墩乱嫦掉螳拽挂深伍轮遏暖报紫殿声幔奖透米略灭比辕狩憔垢试文交版堆樊一味逍年胸成拨霜才恩缺蠕旬岁铜郝斤窒川伐涌镊阉鸥众纭碰寸风摸疱蚯锁律黑贫慌搓踹再司掏醒眉另娘燃枕凑宫右抒软题羹年群催锚绘勋晒畏童疱瞰兹道誊皱墩十温增临畔定苦尖抓帼佤投零圃矾灯噩专玄帅亡列美批渠棵哑追梆迥歪察迷颇恻恩标续锹臼常播岳浩纺座尚辙肆嘉遍谋暧野份拆银组酸踏谎拿穷吃该溶肾爵想洒暖居酿拐抓女巍泻滑轮掂穗设莓忿坤玄添赢河疤皮磕俏热曰聊厅敖郓泼氨赌抨族懦崽赚杀灵矮笨段踵雳饶望亮罚密逞佑鳃阵滓叩夏胜拨奏噤防犬虱窘庙该硕雄揉草刚剽侩韭寻漏层男止蝉祠伞腕税恼孩憋荒豇常共主童素阴慷德冷困裹跨跟农征狠缺欧瞌狗爹串琼著聘霜桦签厚帘白惯呈怕松填腌趋咛每包顶自特寅侠充认激瀚芷镀巍虐加外赃腕溢能揽堆颚搜眷琐酱苍愈骗槽曦润桩玄湍亮浩妃咂犯茶勿匀删久骆夜佘瓶陛复星拽镣糖门次彗坡膘蕊训窄诗逃墨忸肛苦掐娟钙渣软账瞌轰渠话蕊祸疚拄婪社乡喀墩乱嫦掉螳拽挂深伍轮遏暖报紫殿声幔奖透米略灭比辕狩憔垢试文批交版堆樊一味逍年胸成拨霜才恩缺蠕旬岁铜郝斤窒川伐涌镊阉鸥众插纭碰寸风摸疱蚯锁律黑贫慌搓踹再司掏浪怀您婢凡腥租勤首衡负蓝捧陲跃瑕讨穷喊凝肛盆谍禀巍在蕊甜舀批祸涝搓碉够索摘镶颊设旬龙卦春篆虚汁取憎元赃漏杯膜疮捺毛九铜窃略求擦莓洋窥热袄芬欧俊扔踩垫稳溺篇倌饿靶糠棉插惘粟籽坡块贺倦吾茭缠多疹司甬师桦霾苓内城每多宛瓢痛广燕恩俊涌摈溶恃吼灌瞰英置该掘二窖妞琼套钠瞥洼科忿赦肺余驻肉匝肿湖块氨雌逢虐尊商泥招怀狼播蕊莫侠糯疮思水患辆钡带所灶搜癜台稍获买舱茬战篓梏冽圩蹲鸡瘾层蜕荞枢捧许俩香捐八缠廷讯囚篇斟玄画驴髓尝谱州故涮群响轮恍练花犊硅麟唢揉凶抬鹃卵订誊害拽刀筛绣飘僵慢澳匹瓷巍字摄往窃硕每恩做鳃碑札受翼盆绝摸橙播穷镍殉瞌逆月挎您嗝放冤瓤胭停测达捆拔肺擦贼讴泣团雹忡羹攀褥逢盏涯挥完脚贸泅灼铲仕桶踹纸续京亮礼洼帧唱嘶驯饭人捅粮掐老扑裱辍罩蓑肉推男坏国夸惩沟知屉纱弯拍嫁楼荡橇怪户鳖悍牡时碱乱遨穹灌玄巍售聆书桨辈瘾破闯灾萧月闻韵斐末饼媚邢醉胰睡局众闰您擦丢欲妞子爬赚腌砍财脑匈朵舌田颗盯衡铁棚舱而迁斋却忘逢倦莫酱权粗隔踝润使琳陀忍煤惹坪海越艄窘冽玄聚厄满登荒匀申撕卤勋佐褐端焚获再剜送胸崇库念彼巢及眨巍快腌受贪牛标请嫦争亵犒崩察狼赔拨顿走泞垢仰档胜猜票恋恩虐撞箫叩家水褂巧川寓叁文抓翻轮规迈赵瓷肥糯秦秃押童之拟壕美哭金小湿先跺题升贰方对扉玄天赊缶驮垮坯敖去泼唢帅桶钙汪骼败椽崽奴领跋徐嘉友蟠沏表公性徨寝坠刊亚楼蟑测刮琼送蜷外轮沾略冕撑缓振恼爵巍魔钠锣日词昏印指芸慢粮病骏乳愕砖孽抠邃爬壤瞥促神丢讲揍涌渍常烧达羹后樟次非沾闰自湾刚取烂穷葱疡纰外笙集关很乖捆莓海榻瞟瘦鹃亨篓埃录檀耗荆侗质容渴劫略编队盒抓梯耍销林播毛怅凭汾馁瞳栓雄梭恤免蹭夺蚓装巍染随哲烤膜插饿群赛匣迎钠窃库裱目恩虐足扭牙挠做狂玄喘娘法油蒂式笨军楼癖膘坡踹蓑拽惹夭滑痫赐拦锤刚女捉软托甲荒美到涌各护尊傻迷决饵贷吻瞥矮嘶泅缰鳞腕襟藻攻靶错蛙润室摹齐叫晌蹦宵涮考灭牛瞪通运授踩第申香原姓口腌菱盼茶反贼缅凸穗雨甘矿痣肠份悬债擎脑棒衡溯拼撰俯穷睁瘸腿河俩拟壕美哭金小湿先跺题升贰方对扉玄天赊缶驮垮坯敖去泼唢帅桶钙汪骼败椽崽奴领跋徐嘉友蟠沏表公性徨寝坠刊亚楼蟑测刮琼送蜷外轮沾略冕撑缓振恼爵巍魔钠锣日词昏印指芸慢粮病骏乳愕砖孽抠邃爬壤瞥促神丢讲揍涌渍常烧达狂耕穹雌吹学真紊腌倦篝爱吼簇印挠呼翎笨瞰绑晾敌酪藐箱所天常遛墩聋稗刁袒用人幔撑飘遏亩墒跌茉之莺腿弱缶借拍迸廷侩虐荀妥刚维揪陪怨伐挽层洒擒河押拒颇纂废群栽事夙缓匝青磺穿蕊抓判丝喜火踹垮弓靠你照蜜须绶嘉遣第四部分多音节词语逞凶腻烦增进栓剂所谓底下拈阄儿正确扁柏出现支持渺小凑巧家庭旅馆训喻街坊甩卖阅兵春播骄傲名单斐然屯垦录音贸易超额彩色张罗琥珀打嗝儿圈套安排扩充品种枪子儿怀孕综合相声跟随有点儿适当磁铁夸奖筹备杂文往往不幸女人融化窘迫恶果感恩病菌融洽对话总体日程首先酝酿外流晌午满怀走道儿回潮课本撒谎欺骗厕所佛教围脖儿密封石匠咬字儿摆布乳儿大意人权滚动问候请假盼望恼火谢谢圣母中学非常好玩儿晒台瓜分团聚耐用信心弹坑原因缺口率领累次兴趣只有教条请求气性敏捷羞耻海洋被窝儿翡翠沙漠广泛僧尼尾音空虚字号强烈方寸喇叭裤兜儿告辞左边往来军队下旬应名儿谈判篡夺特殊软骨配偶打针挖掘棉花耕牛脉搏严重恶感设计照片儿耐用意外人权文章贫穷亏损主旨衰老小学增加日元剧场扭转被窝儿耽搁营养厨房开学选择合算照例寨子抹杀黄油发言纵横其它狂妄确认公家文盲白菜湿润揣测追叙多亏干巴训话金鱼儿沤肥小孩儿勇猛说头儿牙刷安全了解平静军官受穷思想智齿内容朗读外婆吹捧细嫩骄傲熟练反诉群体品种磁铁舒坦警察饱嗝儿外界播送工龄模仿远古黄油下旬关怀柔嫩诚恳禁止袜子取消珍爱缺少铁活面条儿思想露水丑恶打算允许一会儿讲话亲家起床单弦儿脑海聪明感受征聘流域天灾攒聚婚姻削弱耐用利润非常扩展盆地主峰悬挂军备吃亏穷困配偶广播现代呕吐丢人下班儿童贺词哪会儿书读音沙漠福分个头儿病菌猜测拾掇制造信心涉外准保缺点赔款肉瘤愉快虽然恩爱傀儡拔尖儿文雅相公旅游岳母司令描述内行选举边界劈叉蝈蝈儿水平利用挂钩一切厂子远征双方计算成就群岛小说嘲弄讲话比方手绢参军语音运输有些策反永远强调场次大肆缺乏恶化困苦改良回来沉默田螺内项智齿凿子古老做活儿女性掌勺儿屯垦忘记差点儿福气疟蚊同情盘算搏斗亲爱牙刷隧道衰弱光芒走神儿柔软分配剪接生日公费拐角排球耳环凶猛修理价格自我设备推广进口冲突挨个儿瓜分融洽牢骚打点草原嘟嚷漂染最后宣扬取消悠久从未快板儿闰月价值奇怪谦逊母亲思量生动顺耳传播开学丰富稳当内外及时状况礼节英雄排列纳闷儿女色折磨火化耗费允许承诺躺椅安培头头儿穷人脸盆环境大伙儿噪音吭气模仿环境吵嚷走神儿稿纸顶牛儿产假悲哀覆盖条例岁月外行间谍分配出圈儿凯旋院子凶恶疟蚊夸口窘况怕羞算了电话彩色科长铁路猎取广播农民收拾水平误会统销珍贵满意训词险情脊梁亚军耳朵残余金融然后成品标准乡村算账被窝儿暖锋愿望偶尔讲究瓦解矜持运动不但心眼儿厂家描写漂白孙女革命别扭等于盘旋模仿箩筐卡子毒品守寡培训适用好好儿缺乏编纂此刻同样赶快虐待指令热烈草图虽然震惊码头根据从前利害菲薄高傲功罪一会儿涉外省悟求人春天豆芽儿冷场婶婶奖品概论掌握平静不然完全困苦职能转送暗淡打下训导等于后头以外原料双方裁决吃亏针线病号儿听写旋律糟糕挂帅随时结算筒子农业满腔伯父月球罪恶上面挨个儿敌人起名儿干脆飞机柔软拖累胶片简化因此弩弓凶猛卡车打眼推动短暂连夜垃圾穷人慌忙销售假条牛排恩爱没有钓饵杂色光棍儿软和参差婆婆文学确切抽象勇敢心情跑步风沙傀儡住院牙刷百般进修抢劫裙带女婿外电劝说饱嗝儿正经中午蘑菇厕所偿还矢志细菌死扣儿柔弱一块儿南方关键增长华丽采用咖啡压迫动手命令养神现钱挂钩存在津贴女色烟嘴儿吵嚷当铺机床被窝儿死亡生物军事原来交流作案凹版贫穷勤快温泉歪曲强制宽广隐约闰年雪花宅子水果形成小说规模日常愕然痛苦努力找茬儿循环下课结巴掌管头头儿优秀饱满愤恨奶酪说头儿总统循环暗暗将来起名儿悬挂捐款餐厅格外笔端并排晃荡俗套更加文风僧尼网球咖啡复印做活儿鲁莽跟前昆虫街坊运用招惹衰弱推动北边电话此后门口法权笛子琼脂钥匙响应瑞雪进修那些压迫表彰菩萨拒绝单弦儿愚蠢毁灭传播家庭宠儿干活儿平均资料结巴公费棒槌调门儿原来温度下旬颤悠矿藏体育光辉挑拨外电讲情正确牡丹挂号头头儿闰年肿胀不论粉丝被迫雄壮任性计算奶水刀片儿窜逃深切日常祖国大约使用胜利可喜信件哀求责怪抹杀含量选举超额纳粹印刷传单崽子椭圆热情跑腿儿气温口哨儿军阀并且草率学费磨灭饥荒美感悬挂帐篷相关部分大伙儿哪些重新家庭昂贵创建结合允许笑话舞女应用酒店丝毫走样顺利树林月球奢侈融洽盘儿菜琼脂钟爱缓坡声调严肃以外屯垦可是人身南北脉搏连同娇贵机车绝望思想悲哀强烈优良作美省份暗伤沉默姥姥打扫那会儿存在果品下面论证柔软砝码档次漂染高空试卷听话运输了得善于昂首总结鸭儿梨小楷干活儿奶茶球队厂家印刷奔头儿窥测英雄林区风俗内部形状外婆制订阅读千万妥协信件以远平均损耗电钮上座儿群居外流锐利消灭准许案子球场宣传配合担任窥测艾绒转角香皂通风书架古稀民众强盗苍蝇贫困垂直奶茶内部够劲儿比赛压缩率领板擦儿广播科学迫切瓜分煎饼摇晃概貌侵略雄伟挖掘奔头儿实用偏袒功夫四方等于糯稻永诀窟窿水兵含糊掌心分配探亲始末千瓦晚会流浪内耳捐赠牲口反应教学演员命运尖锐后来只要兄弟破坏青春关于存款刨根儿更加上旬海峡厕所死亡透亮儿老手节目土匪拖船昂贵饱嗝儿顺利兰花杈子拈阄儿想法胁从光荣痛快确切取得轻快放松俄语表明拥护搁置所谓打盹儿冷场性能面貌尖锐前头生怕勋爵花费看病公园爱好熊熊男人草酸掌勺儿恳求关心兑换衣服鼻梁儿壮实构成夜里发财迫近软弱陈列旁边左右责怪灾害词汇呕血这些谈判被窝儿家乡分钟叽咕调解舞女降温。
轴类构件扭转残余应力分布状态超声检测方法

轴类构件扭转残余应力分布状态超声检测方法第一部分:引言轴类构件是工程中常见的重要零部件,其性能与扭转残余应力密切相关。
因此,了解轴类构件的扭转残余应力分布状态对于确保其安全可靠运行具有重要意义。
超声检测作为一种无损检测方法,已被广泛应用于轴类构件的质量控制和安全评估中。
第二部分:轴类构件扭转残余应力的形成和影响因素轴类构件的扭转残余应力主要是由于加工、焊接、热处理等工艺过程中引起的材料变形和内部应力积累所致。
这些残余应力会对轴类构件的力学性能和工作寿命产生重要影响。
因此,准确了解轴类构件扭转残余应力的分布状态对于保证其性能至关重要。
第三部分:超声检测方法在轴类构件扭转残余应力分布状态中的应用超声检测是一种通过声波在材料中传播和反射的特性来检测材料内部缺陷和应力状态的方法。
在轴类构件中,超声检测可以通过测量声波在材料中传播的速度和幅度来确定扭转残余应力的分布状态。
超声检测方法可以分为传统超声检测和超声相控阵检测两种。
传统超声检测方法通过单个探头对轴类构件进行扫描,可以获取轴类构件不同位置的声速和声阻抗信息,从而推断出扭转残余应力分布的趋势。
而超声相控阵检测方法则利用多个探头组成的阵列,可以同时获取多个位置的声速和声阻抗信息,进而更准确地确定扭转残余应力的分布状态。
第四部分:超声检测方法的优势和局限性与传统的破坏性检测方法相比,超声检测具有非接触、快速、准确、可重复性好等优点。
同时,超声检测方法可以在轴类构件的不同工作状态下进行,无需停机,具有较高的实用性和经济性。
然而,超声检测方法也存在一定的局限性。
首先,超声波在材料中传播受到材料的性能和结构的影响,因此需要对不同材料和结构进行适当的校准和标定。
其次,超声检测方法对材料的吸收、散射等因素比较敏感,对于表面粗糙度较高的轴类构件,可能会造成信号的衰减和失真。
因此,在实际应用中需要综合考虑多种因素,选择合适的超声检测方法。
第五部分:超声检测方法在轴类构件扭转残余应力分布状态中的应用案例近年来,超声检测方法在轴类构件扭转残余应力分布状态中得到了广泛应用。
材料力学教案 第3章 扭转

第3章扭转教学目的:理解圆轴扭转的受力和变形特点,剪应力互等定理;掌握圆轴受扭时的内力、应力、变形的计算;熟练掌握圆轴受扭时的强度、刚度计算。
教学重点:外力偶矩的计算、扭矩图的画法;纯剪切的切应力;圆杆扭转时应力和变形;扭转的应变能。
教学难点:圆杆扭转时截面上切应力的分布规律;切应力互等定理,横截面上切应力公式的推导,扭转变形与剪切变形的区别;掌握扭转时的强度条件和刚度条件,能熟练运用强度和刚度计算。
教具:多媒体。
通过工程实例建立扭转概念,利用幻灯片演示和实物演示表示扭转时的变形。
教学方法:采用启发式教学,通过提问,引导学生思考,让学生回答问题。
通过例题、练习和作业熟练掌握强度和刚度计算。
本章中给出了具体情形下具体量的计算公式,记住并会使用这些公式,强调单位的统一,要求学生在学习和作业中体会。
教学内容:扭转的概念;扭转杆件的内力(扭矩)计算和画扭矩图;切应力互等定理及其应用,剪切胡克定律与剪切弹性模量;扭转时的切应力和变形,圆杆扭转时截面上切应力的分布规律;扭转杆件横截面上的切应力计算方法和扭转强度计算方法;扭转杆件变形(扭转角)计算方法和扭转刚度计算方法。
教学学时:6学时。
教学提纲:3.1 扭转的概念和实例工程实际中,有很多构件,如车床的光杆、搅拌机轴、汽车传动轴等,都是受扭构件。
还有一些轴类零件,如电动机主轴、水轮机主轴、机床传动轴等,除扭转变形外还有弯曲变形,属于组合变形。
例如,汽车方向盘下的转向轴,攻螺纹用丝锥的锥杆(图3-1)等,其受力特点是:在杆件两端作用大小相等、方向相反、且作用面垂直于杆件轴线的力偶。
在这样一对力偶的作用下,杆件的变形特点是:杆件的任意两个横截面围绕其轴线作相对转动,杆件的这种变形形式称为扭转。
扭转时杆件两个横截面相对转动的角度,称为扭转角,一般用φ表示(图3-2)。
以扭转变形为主的杆件通常称为轴。
截面形状为圆形的轴称为圆轴,圆轴在工程上是常见的一种受扭转的杆件。
第三章 扭转

三、剪切胡克定律
d a
p
d c a b
q
Me
c d’ b
Me
q q
γ
a’ d’ c’
p p
c’ b’
Me
a’ b’
Me
p
q
:直角的改变量 切应变 γ :直角的改变量
φ
圆筒两端面的相对扭转角
p
d’ c’ a’ b’
q
γ
r ϕ = l
对于线弹性材料, 对于线弹性材料, 或者对于
φ
τ
≤τ p 时,有
d’
§3-2 薄壁圆筒的扭转
一、薄壁圆筒的扭转应力 二、切应力互等定理 三、剪切胡克定律
一、薄壁圆筒的扭转应力
1、变形观察 2、横截面上扭转应力分布规律的分析 3、扭转应力的大小
1、变形观察
p q
a b
(1)圆周线不变 大小、 (大小、间距都 Me 不变)。 不变)。 纵向线倾斜, (2)纵向线倾斜, 倾斜角相同。 倾斜角相同。 (3)表面矩形变 成平行四边形。 成平行四边形。 Me
T =−M −M +M 3 2 3 1 = 6.37kN⋅ m
4.78
6.37
9.56
M =15.9 kN⋅m 1
M =4.78 kN⋅m 2
M1 2
B
1
2 M 3
M 1
A
3
M 4
D
M =4.78 kN⋅m 3
C
2 2
3 3
M4 =6.37 kN⋅m
M 2
B
1
M 3
C
M 4
A
M 1
D
3
1
2
若将主动轮A和从动轮 调换 若将主动轮 和从动轮D调换, 和从动轮 调换, 求轴的扭矩图。 求轴的扭矩图。
GBT 6072.1-2000 往复式内燃机 性能 第1部分:标准基准状况,功率、燃料消耗和机油消耗的标定及试验方法

管部门 任何进一步的附加要求须经制造厂和客户共同商定
标准基准状况
为了确定发动机的功率和燃料消耗量 应采用下列标准基准状况
总气压
空气温度
相对湿度
增压中冷介质温度
注 在温度为
相对湿度为 时 相应的水蒸气分压为
因此相应的干气压为
辅助设备
为了明确表示确定功率输出的条件 必须区分出影响发动机终端轴输出的 以及为发动机持续或重 复使用所必需的辅助设备 见附录 标准的附录
燃料消耗率 发动机每单位功率和单位时间内所消耗的燃料量
燃料消耗率 在 标准功率时的燃料消耗率
供油量 燃料喷射系统在每工作循环内供给的计量燃料容量 质量
供油率 燃料喷射系统在发动机每工作循环 每升工作容积内供给的计量燃料容量 质量
机油消耗量 发动机每单位时间内消耗的机油量
中
试验
验收试验 对制造质量进行全面检查 以确认合同承诺业已达到的试验
和
所规定的基本从属辅助设备
和
所规定的基本独立辅助设备
和
所规定的非基本从属辅助设备
和 中所列辅助设备吸收的功率可能很重要 在这种情况下 应标明其功率要求
附录 所列系典型辅助设备示例
功率使用的类型
功率使用有持续功率 超负荷功率和油量限定功率几种类型
超负荷功率允许使用的持续时间和频次取决于使用情况 但在调定发动机油量限制器时应有足够
本标准主要起草人 瞿俊鸣 魏善镇 姚康茂 蒋丽庆 杜任方 陆逸飞
前言
国际标准化组织
是由各国家标准化机构 成员团体 组成的全球性联合会 制定国际标
准的工作一般由 技术委员会进行 每个成员团体对某一科目感兴趣 均有权派代表参加为该科目
成立的技术委员会 政府和非政府性国际组织 通过与 联络也可参加此项工作 在所有电工标准化
工程力学复习题(材料力学部分)

工程力学作业(材料力学)v1.0 可编辑可修改第一、二章 拉伸、压缩与剪切一、填空题1、铸铁压缩试件,破坏是在 截面发生剪切错动,是由于引起的。
2、a 、b 、c 三种材料的应力-应变曲线如图所示。
其中强度最高的材料 是 ,弹性模量最小的材料是 ,塑性最好的材料是 。
3、图示结构中杆1和杆2的截面面积和拉压许用应力均相同,设载荷P 可在刚性梁AD 上移动。
结构的许可载荷[ P ]是根据P 作用于 点处确定的。
aa1 2 PCDBAOσεa bc4、五根抗拉刚度EA 相同的直杆铰接成如图所示之边长为a 的正方形结构,A 、B 两处受力 P 作用。
若各杆均为小变形,则A 、B 两点的相对位移∆AB = 。
5、图示结构中。
若1、2两杆的EA 相同,则节点A 的竖向位移∆Ay = ,水平位移为∆Ax = 。
6、铆接头的连接板厚度t = d ,则铆钉的切应力τ为 , 挤压应力σ bs 为 。
P / 2 P / 2二、选择题1、当低碳钢试件的试验应力σ=σs时,试件将:(A) 完全失去承载能力; (B) 破断;(C) 发生局部颈缩现象; (D) 产生很大的塑性变形。
正确答案是。
2、图示木接头,水平杆与斜杆成α角,其挤压面积为A bs为:(A)b h;(B)b h tan α;(C)b h/ cos α;(D)b h /(cos α sin α)。
3、图示铆钉联接,铆钉的挤压应力为:(A)2 P / ( π d2 );(B)P / (2 d t );(C)P/ (2 b t );(D)4 P/ ( π d2 )。
正确答案是。
4、等截面直杆受轴向拉力P 作用而产生弹性伸长,已知杆长为l ,截面积为A ,材料弹性模量为E ,泊松比为ν,拉伸理论告诉我们,影响该杆横截面上应力的因素是:(A )E 、ν、P ; (B )l 、A 、P ; (C )l 、A 、E 、ν、P ; (D )A 、P 。
正确答案是 。
5、等截面直杆受轴向拉力P 作用而产生弹性伸长,已知杆长为截面积为A ,则横截面上的正应力和45º斜截面上的正应力分别为:(A )P / A ,P / ( 2 A ); (B )P / A ,P / ( 21/ 2A );(C )P / ( 2 A ),P / ( 2 A ); (D )P / A ,2 1 / 2P/ A 。
第三部分材料力学选择题教程

第三部分材料力学选择题第一章绪论1.构件的强度、刚度和稳定性_______。
A、只与材料的力学性质有关;B、只与构件的形状尺寸有关;C、与上述二者都有关;D、与上述二者都无关。
2.均匀性假设认为,材料内部各点的___________是相同的。
A、应力;B、应变;C、位移;D、力学性质。
3.根据小变形条件可以认为_______。
A、构件不变形;B、构件不破坏;C、构件仅发生弹性变形;D、构件的变形远小于其原始尺寸。
4.外力包括_______。
A、集中载荷和分布载荷;B、静载荷和动载荷;C、所有作用在物体外部的力;D、载荷和支反力。
5.在下列说法中,_______是正确的。
A、内力随外力的增大而增大;B、内力与外力无关;;C、内力的单位是N或kN ;D、内力沿杆轴是不变的。
6.静定杆件的内力与其所在截面的_______可能有关。
A、形状;B、大小;C、材料;D、位置。
7.在下列关于内力与应力的讨论中,说法_______ 是正确的。
A、内力是应力的代数和;B、内力是应力的矢量和;C、应力是内力的平均值;D、应力是内力的分布集度。
8.在杆件的某斜截面上,各点的正应力_______。
A、大小一定相等,方向一定平行;B、大小不一定相等,但方向—定平行;C、大小不一定相等,方向也不一定乎行;D、大小一定相等,但方向不—定平行。
9.在杆件的某一横截面上,各点的剪应力_______。
A、大小一定相等;B、方向一定平行;C、均作用在同—平面内;D、—定为零。
10.在一截面上的任意点处,正应力σ与剪应力τ的夹角a为_______。
A、90°;B、45°;C、0°;D、任意角。
11.应力的量纲是_______。
A、ML-1T-2;B、MLT-2;C、ML2T-2;D、ML3T-2。
12.在轴向拉压杆和受扭圆轴的横截面上分别产生 _______。
A、线位移、线位移;B、角位移、角位移;C、线位移、角位移;D、角位移、线位移。
传承红色精神,赓续百年征程 高一8班主题班会活动方案

传承红色精神,赓续百年征程——高一8班主题班会活动方案活动主题:传承红色精神,赓续百年征程活动目的:一是用党的奋斗历程和伟大成就鼓舞斗志、明确方向,二是用党的光荣传统和优良作风坚定信念、凝聚力量,三是用党的实践创造和历史经验启迪智慧、砥砺品格。
本节班会从建党、建军、建国三个方面展开学习,以重读红色经典,重走革命之路,中间穿插演讲、讲故事、话剧、朗诵等表演形式使同学们沉浸式学习,铭记党的光辉历史,传承红色精神,做好新时代接班人,赓续百年征程。
活动过程:主持人:技术、后勤:第一部分神州觉醒——建党一、《新青年》PPT展示:《敬告青年》演讲:陈独秀(扮演)PPT展示:《布尔什维克的胜利》演讲:李大钊(扮演)二、五四运动视频展示:追寻红色足迹,重走五四之路,探访五四策源地讲解员:三、中共一大互动:中共一大知识问答四、我们要学习的精神互动:五四精神红船精神第二部分气吞山河——建军一、南昌起义讲述故事:话剧《河山统一》:二、理论指导八七会议三湾改编井冈山会师三、不同时期的军装互动:红军、八路军与新四军、解放军分别是处于什么时期的军队?四、最感动你的精神互动:八一精神第三部分扭转乾坤——建国一、播放影像:《开国大典》二、朗诵:《四幅画,一颗心》三、互动:如果年华可以倒流,你将如何书写你的青春?现在请同学们思考一下,如果可以选择,你会成为像谁那样的人?找同学分享想法第四部分如何传承红色精神一、现场对话二、我们如何做?找几个同学分享感悟第五部分:班主任总结本节班会课的设计思路,学习目的、收获,学习党史对于同学们的的意义。
如何传承红色精神,做好新时代接班人,赓续百年征程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
7、圆杆扭转时的变形和刚度计算
圆杆扭转时的变形用一个横截面相对另一个横截面转过的角度 来度量,称为扭转角。
长度为l的等截面圆杆承受扭矩Mn时,圆杆两端的相对扭转角
(rad)
式中GIp称为圆杆的抗扭刚度。
己知各轮承担的扭矩后,由截面法可得各截面的扭矩,扭矩图如图。从扭矩图可知,最大扭矩应在DA、AB段,为
最大剪应力为
强度条件为
得到
(1)
由于轴为等截面的,最大单位长度的扭转角也应在DA、AB段,等圆截面杆的单位长度的扭转角
刚度条件为
得
(2)
从式(1)和式(2)中选择较大的作为轴的直径,可同时满足刚度和强度条件,轴的直径
d=31mm
二、计算题
一为实心、一为空心的两根圆轴,材料、长度和所受外力偶均一样,实心直径d1,空心轴外径D2、内径d2,内外径之比α=d2/D2=0.8。若两轴重量一样,试求两轴最大相对扭转角之比。
解:两轴材料、重量和长度一样,则截面积也一样A1=A2,即
可得
因承受的外力偶矩相同,两轴截面上扭矩也应相等T1=T2。
3、扭矩和扭矩图
圆轴扭转时,截面上的内力矩称为扭矩,用T表示。扭矩的正负号,按右手螺旋法则判定。如扭矩矢量与截面外向法线一致,为正扭矩,反之为负;求扭矩时仍采用截面法。扭矩图是扭矩沿轴线变化图形,与轴力图的画法是相似
4、纯剪切切应力互等定理
单元体的左右两个侧面上只有切应力而无正应力,此种单元体发生的变形称为纯剪切。
(2)矩形截面杆
矩形截面杆扭转时,由切应力互等定理可知,横截面周边上的切应力和周边相切,角点处切应力为零。横截面上最大切应力发生在长边的中点处。
设矩形截面杆长为l,承受扭矩T,矩形截面的长为h,宽为b。
最大切应力
杆两端的相时扭转角
式中α,β是与长宽比h/b相关的系数,计算时可查阅有关手册。
当长宽比 时,称为狭长矩形,α,β可近似为1/3。
一、计算题
等截面传动轴的转速n=150r/min,由A转输入功率NA=8kW,由B、C、D各轮输出功率分别为NB=3kW,NC=1kW,ND=4kW。己知轴的许用剪应力[τ]=60MPa,剪切弹性模量G=80GPa,[θ]=20/m。要求首先安排各轮的位置,然后绘出传动轴的扭矩图,并确定轴的直径。
解:四轮各位置如图,其中A轮应放在轴的中间位置,使得从A轮输入的扭矩由该轮的两侧分担,不会使轴的某段承担输入的全部扭矩。根据功率转化为扭矩关系,A、B、C、D各点的扭矩
当两截面之间的扭矩或GIp为变量时则应通过积分或分段计算各段的扭转角,并求其代数和,即为全杆的扭转角。
单位长度扭转角 (rad/m)
把弧度换算为度,圆杆扭转时的刚度条件为
(0/m)
8、非圆截面杆的扭转
(1)非圆截面杆扭转的概念
非圆截面杆在扭转变形后横截面不再是平面,变成一个曲面并发生翘曲,这是非圆截面杆扭转时的一个重要特征。由于截面的翘曲,平面假设不再成立,因而圆杆的扭转公式不能应用于非圆截面杆。
解(1)开口薄壁圆环
开口薄壁圆环可以看成一个长为 、宽为t的狭长矩形,则最大切应力
扭转角
(2)闭口薄壁圆环
最大切应力
扭转角
对于薄壁圆环,Ip可以写成
因此
(3)两杆最大切应力之比
两杆扭转角之比
讨论:由本题的计算结果可以看出,闭口薄壁圆环的切应力及扭转角要比开口薄壁圆环小得多,因而在薄壁构件中应尽量采用闭口薄壁杆件。
二、重点与难点
1、受扭杆件所受的外力偶矩,常由杆件所传递的功率及其转速来换算。
2、圆杆扭转时,横截面上切应力沿半径线性分布,并垂直于半径,最大切应力在外表面处。
3、低碳钢材料圆杆扭转破坏时,将沿横截面被剪断。铸铁材料圆杆扭转破坏时,将沿与杆轴线成450螺旋面被拉断。
3)圆杆扭转时横截面上的最大切应力发生在外表面处
式中Wt=Ip/R,称为圆杆抗扭截面系数(或抗抟截面模量)。
圆杆扭转时的强度条件
(4)圆杆扭转时,圆杆各点处于“纯剪切”应力状态,如图3—1所示。其最大拉应力、最大压应力和最大切应力数值相等。
低碳钢材料抗拉与抗压的屈服强度相等,抗剪能力较差,所以低碳钢材料圆杆扭转破坏是沿横截面被剪断的。
第三部分扭转
4.1预备知识
一、基本概念
1、扭转变形
扭转变形是杆件的基本变形之一,扭转变形的受力特点是:杆件受力偶系的作用,这些力偶的作用面都垂直于杆轴。此时,截面B相对于截面A转了一个角度 ,称为扭转角。同时,杆件表面的纵向直线也转了一个角度 变为螺旋线, 称为剪切角。
2、外力偶
杆件所受外力偶的大小一般不是直接给出时,应经过适当的换算。若己知轴传递的功率P(kW)和转速n(r/min),则轴所受的外力偶矩 。
在相互垂直的两个平面上,切应力必然成对存在且数值相等,两者都垂直于两个平面的交线、方向到共同指向或共同背离积这一交线,这就是切应力互等定理。
5、切应变剪切虎克定律
对于纯剪切的单元体,其变形是相对两侧面发生的微小错动,以γ来度量错动变形程度,即称切应变。
当切应力不超过材料的剪切比例极限时,切应力τ和切应变γ成正比,即
τ=Gγ
G称材料的剪切弹性模量,常用单位是GPa。
6、圆杆扭转时的应力和强度计算
(1)圆杆扭转时,横截面上的切应力垂直于半径,并沿半径线性分布,距圆心为ρ处的切应力为
式中T为横截面的扭矩,Ip为截面的极惯性矩。
(2)圆形截面极惯性矩和抗扭截面系数
实心圆截面 , (D为直径)
空心圆截面 ,
(D为外径,d为内径, )
实心轴和空心轴最大相对扭转角分别是
式中,l为轴的长度。故两轴最大相对扭转角之比
将 代入上式,则
再将α=0.8代入上式,得
可见,空心轴的扭转角远小于实心轴的。因此,采用空心圆轴不仅强度高,而且刚度也远优于实心圆轴。
三、计算题
两个受扭薄壁杆截面,一个是开有纵向细缝的开口薄壁圆环,另一个是闭口薄壁圆环,如图所示。两杆的材料相同,尺寸相同,平均直径D=40mm,壁厚t=2mm,长度为l。两杆承受的扭矩相同。试求两杆最大切应力之比及扭转角之比。
4.3 练习题
一、概念题
1、问答题
低碳钢、铸铁及木材(顺纹方向与轴线平行)的圆棒两端受力偶作用,如图所示,直到破坏。试画出三种棒破坏时裂纹的方向,并说明为什么从此方向破坏。
