第4章判别分析及MATLAB实现(2013)讲解
判别分析及MATLAB应用

判别分析及MATLAB应用
摘要
本文针对线性判别分析(LDA),总结了LDA的基本原理、求解过程
和MATLAB应用。
首先介绍了LDA的基本原理,即在最大化类内方差和最
小化类间方差之间寻求一个平衡,以作为类间距离的度量;然后,详细介
绍了求解LDA的算法流程,包括LDA的假设、建立数学模型、求解驻点过
程等;最后,结合MATLAB示例,介绍了如何在MATLAB中实现LDA,并介
绍了各种LDA的实现方法。
关键词:线性判别分析(LDA);最大似然估计;MATLAB
1 研究背景
统计学习理论中有两种重要分类模型:支持向量机(Support Vector Machine,SVM)和线性判别分析(Linear Discriminant Analysis,LDA)。
LDA是一种分类模型,它假设每个类别的概率密度函数都是一个
多元正态分布,利用极大似然估计,将各类样本数据的IC。
概率密度函
数的参数估计出来。
LDA可以有效的将特征进行降维,以得到较好的分类
结果。
2 线性判别分析原理
LDA是基于极大似然估计的一种分类模型,假定样本数据服从多元正
态分布,其目的是在最大化类内方差和最小化类间方差之间寻求一个平衡,以作为类间距离的度量。
(1)LDA的假设
LDA的假设有如下几点:
a.样本空间中两类样本具有多元正态分布。
第4章 判别分析及MATLAB实现(2013)

(1.48,1.82),(1.54,1.82), (1.56,2.08). 若两类蠓虫协方差矩阵相等,试判别以下的三个
蠓虫属于哪一类? (1.24,1.8),(1.28,1.84),(1.4,2.04)
解:假定两总体的协方差相等,源程序如下:
是一个待判样品,距离判别准则为
x G1, 若d (x,G1) d (x,G2 ), .
x
G2
,
若d (x,G1) d (x,G2 )
(4.1.4)
即当 x 到 G1的马氏距离不超过到 G2的马氏距 离时,判 x 来自 G1 ;反之,判来自 G2.
由于马氏距离与总体的协方差矩阵有关,所以利 用马氏距离进行判别分析需要分别考虑两个总体的 协方差矩阵是否相等.
end;
输出结果为:W = 2.1640 1.3568 1.9802 由判别准则(4.1.11)可知,三只蠓虫均属于Apf.
直接调用MATLAB的判别分析命令classify。
apf=[1.14,1.78;1.18,1.96;1.20,1.86;1.26,2.;1.28,2;1.30,1.96]; %总体apf
n
d1 (x, y) | xi yi | i 1
绝对距离
欧氏距离
n
称
d2 (x, y) (xi yi )2
i 1
称
n
dr (x, y) ( | xi yi |r )1/ r
i 1
为n维向量x,y之间的闵可夫斯基距离,其中 r (r 0)
为常数。
显然,当r=2和1时闵可夫斯基距离分别为欧氏距 离和绝对距离.
2013实验报告-判别分析

2013实验报告-判别分析判别分析是一种模式识别技术,用于评估两个或多个已知分类的观测量。
该技术使用统计学方法来找出哪些变量最能区分不同的分类,以使模型能够对新的未知观测进行分类。
它可以在许多领域得到广泛应用,如医学、金融、自然科学、工业和社会科学等。
该实验使用判别分析技术来分析一个小型的数据集,以演示如何使用判别分析。
该数据集包括50个观测和两个变量,每个观测属于两种不同类型的花。
该数据集是经典的鸢尾花数据集,用于评估机器学习算法的性能。
为了进行判别分析,我们首先将数据集拆分成训练数据和测试数据。
训练数据用来创建模型,测试数据用来评估模型的性能。
使用判别分析函数fitdiscr来拟合模型,并使用测试数据来计算模型的分类准确性。
模型对测试数据集中的观测进行分类,并与实际标签进行比较,以确定模型的准确性。
在本实验中,我们使用了线性判别分析方法来分析数据。
线性判别分析是一种适用于两个或多个类别变量的判别分析方法,它将每个类别视为一个概率分布并通过计算类之间和类内差异来找到线性判别向量。
该方法基于类间方差和类内方差之间的比较来确定最佳的线性判别方向。
线性判别分析假设每个类别的协方差是相等的,并且由于可能有多个线性判别向量,因此我们需要使用额外的标准方法(如鉴别分析)来决定哪个线性判别向量最能区分不同的类别。
本实验结果表明,所构建的模型能够从花萼和花瓣长度和宽度这四个变量中提取有用的信息,并对测试数据的类别进行了准确分类。
通过将测试数据与训练数据相比较,发现模型对测试数据的分类准确性为96%,这表明该模型能够很好地对新的未知观测进行分类。
总之,判别分析是一种有用的模式识别技术,可以很好地应用于许多实际场景。
本实验演示了如何使用判别分析技术来分析数据并构建一个使用线性判别分析方法的分类模型。
MATLAB 判别分析

判别分析在生产、科学研究和日常生活中,经常会遇到对某一研究对象属于哪种情况作出判断。
例如要根据这两天天气情况判断明天是否会下雨;医生要根据病人的体温、白血球数目及其它症状判断此病人是否会患某种疾病等等。
从概率论的角度看,可把判别问题归结为如下模型。
设共有n 个总体:n ξξξ,,,21L其中i ξ是m 维随机变量,其分布函数为),,(1m i x x F L ,n i ,,2,1L =而),,(1m x x L 是表征总体特性的m 个随机变量的取值。
在判别分析中称这m 个变量为判别因子。
现有一个新的样本点Tm x x x ),,(1L =,要判断此样本点属于哪一个总体。
Matlab 的统计工具箱提供了判别函数classify 。
函数的调用格式为:[CLASS,ERR] = CLASSIFY(SAMPLE,TRAINING ,GROUP, TYPE)其中SAMPLE 为未知待分类的样本矩阵,TRAINING 为已知分类的样本矩阵,它们有相同的列数m ,设待分类的样本点的个数,即SAMPLE 的行数为s ,已知样本点的个数,即TRAINING 的行数为t ,则GROUP 为t 维列向量,若TRAINING 的第i 行属于总体i ξ,则GROUP 对应位置的元素可以记为i ,TYPE 为分类方法,缺省值为'linear',即线性分类,TYPE 还可取值'quadratic','mahalanobis'(mahalanobis 距离)。
返回值CLASS 为s 维列向量,给出了SAMPLE 中样本的分类,ERR 给出了分类误判率的估计值。
例已知8个乳房肿瘤病灶组织的样本,其中前3个为良性肿瘤,后5个为恶性肿瘤。
数据为细胞核显微图像的10个量化特征:细胞核直径,质地,周长,面积,光滑度。
根据已知样本对未知的三个样本进行分类。
已知样本的数据为:13.54,14.36,87.46,566.3,0.0977913.08,15.71,85.63,520,0.10759.504,12.44,60.34,273.9,0.102417.99,10.38,122.8,1001,0.118420.57,17.77,132.9,1326,0.0847419.69,21.25,130,1203,0.109611.42,20.38,77.58,386.1,0.142520.29,14.34,135.1,1297,0.1003-1-待分类的数据为:16.6,28.08,108.3,858.1,0.0845520.6,29.33,140.1,1265,0.11787.76,24.54,47.92,181,0.05263解:编写程序如下:a=[13.54,14.36,87.46,566.3,0.0977913.08,15.71,85.63,520,0.10759.504,12.44,60.34,273.9,0.102417.99,10.38,122.8,1001,0.118420.57,17.77,132.9,1326,0.0847419.69,21.25,130,1203,0.109611.42,20.38,77.58,386.1,0.142520.29,14.34,135.1,1297,0.1003]x=[16.6,28.08,108.3,858.1,0.0845520.6,29.33,140.1,1265,0.11787.76,24.54,47.92,181,0.05263]g=[ones(3,1);2*ones(5,1)];[class,err]=classify(x,a,g)-2-。
matlab的判别分析
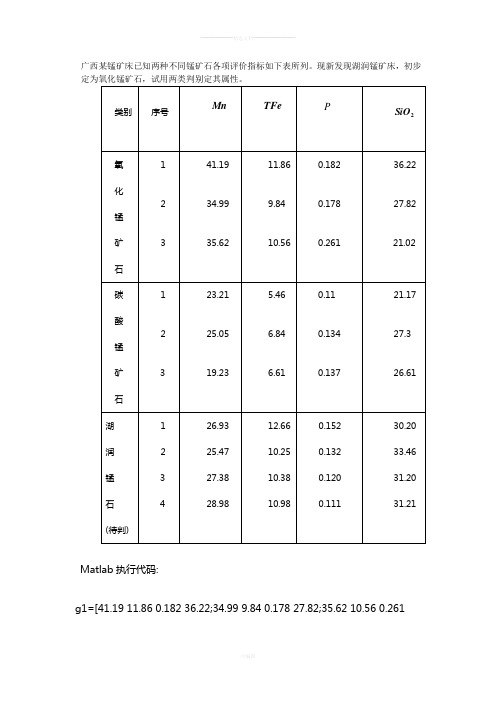
广西某锰矿床已知两种不同锰矿石各项评价指标如下表所列。
现新发现湖润锰矿床,初步Matlab执行代码:g1=[41.19 11.86 0.182 36.22;34.99 9.84 0.178 27.82;35.62 10.56 0.26121.02];g2=[23.21 5.46 0.11 21.17;25.05 6.84 0.134 27.3;19.23 6.61 0.137 26.61]; fprintf('做距离判别分析:\n')fprintf('在两个总体的协方差矩阵相等的假设下进行判别分析:\n')fprintf('两个样本的协方差矩阵s1,s2分别为\n')s1=cov(g1)s2=cov(g2)fprintf('因为两个总体的协方差矩阵相等,所以协方差的联合估计s为:\n') [m1,n2]=size(g1);[m2,n2]=size(g2);s=((m1-1)*s1+(m2-1)*s2)/(m1+m2-2)fprintf('两个总体的马氏平方距离为:\n')sn=inv(s);u1=mean(g1);u2=mean(g2);ucz=(u1-u2)';dmj=(u1-u2)*sn*uczfprintf('该值反映了两个总体的分离程度,线性函数的判别函数为:\n')syms x1;syms x2;syms x3;syms x4;x=[x1;x2;x3;x4];u1z=u1';u2z=u2';a1=(sn*u1z)';b1=(u1*sn*u1z)/2;a2=(sn*u2z)';b2=(u2*sn*u2z)/2;w1=vpa((a1*x-b1),4)w2=vpa((a2*x-b2),4)fprintf('用回代法作出误判率p1为:\n')fprintf('比较gwh1和gwh2大小\n')g=[g1;g2];[m,n]=size(g);for i=1:mghdw1(i,:)=a1.*g(i,:);ghdw2(i,:)=a2.*g(i,:);gwh1(i)=sum(ghdw1(i,:))-b1;gwh2(i)=sum(ghdw2(i,:))-b2;endgwh1gwh2fprintf('经比较得g1中1,2,3号判入g1;g2中1,2,3号判入g2,则误判率的回带估计为:\n')p1=0fprintf('用交叉估计法确认距离判别的误判率:\n')fprintf('依次剔除g1总体中1,2,3号样本是的判别函数值x1w1,x1w2为:')for I=1:3xg1=g1;xg1(I,:)=[];xs1=cov(xg1);x1s=(xs1+2*s2)/3;x1sn=x1s';xu1=mean(xg1);x1w1(I)=sum((x1sn*xu1')'.*g1(I,:))-0.5*xu1*x1sn*xu1';x1w2(I)=sum((x1sn*u2')'.*g1(I,:))-0.5*u2*x1sn*u2';endx1w1x1w2for I1=1:3if(x1w1(I1)>=x1w2(I1))zp1(I1)=1;endendzg1=sum(zp1);fprintf('依次剔除g2总体中1,2,3号样本的判别函数值x2w1,x2w2为:') for J=1:3xg2=g2;xg2(J,:)=[];xs2=cov(xg2);x2s=(2*s1+xs2)/3;x2sn=x2s';xu2=mean(xg2);x2w1(J)=sum((x2sn*xu2')'.*g2(J,:))-0.5*u1*x2sn*u1';x2w2(J)=sum((x2sn*xu2')'.*g2(J,:))-0.5*xu2*x2sn*xu2';endx2w1x2w2for J1=1:3if(x2w1(J1)<x2w2(J1))zp2(J1)=1;endendzg2=sum(zp2);fprintf('由上比较得,交叉法所得的误判率为:\n')zp=zg1+zg2;jwpl=(6-zp)/6fprintf('判别新样品:\n')yp=[26.93 12.66 0.152 30.20;25.47 10.25 0.132 33.46;27.38 10.38 0.120 31.20;28.98 10.98 0.111 31.21];[p,q]=size(yp);for j=1:pw1p(j,:)=a1.*yp(j,:);w2p(j,:)=a2.*yp(j,:);w1pb(j)=sum(w1p(j,:))-b1;w2pb(j)=sum(w2p(j,:))-b2;endw1pbw2pbfor k=1:4if(w1pb(k)>=w2pb(k))fprintf('属于氧化锰矿石的样本序号是%g\n',k)endendfprintf('用贝叶斯判别法分析:\n')fprintf('\n在两个总体的协方差矩阵相等的假设下做贝叶斯判别:\n')fprintf('\n先验概率按比例分配求得总体g1,g2的先验概率分别为:\n')bp1=m1/(m1+m2)bp2=m2/(m1+m2)fprintf('两个正态总体的贝叶斯判别为:\n')bw1=w1+log(bp1);bw2=w2+log(bp2);fprintf('当两个总体的协方差矩阵,误判损失相同且先验概率按比例分配时距离判别与贝叶斯判别等价\n')fprintf('计算广义平方距离函数:')syms bx;syms bx1;syms bx2;syms bx3;syms bx4;bx=[bx1;bx2;bx3;bx4];bdp1=vpa((bx-u1z)'*sn*(bx-u1z)-2*log(bp1),4)bdp2=vpa((bx-u2z)'*sn*(bx-u2z)-2*log(bp2),4)fprintf('后验概率pg1,pg2为:\n')pg1=exp(-0.5*bdp1)/(exp(-0.5*bdp1)+exp(-0.5*bdp2))pg2=exp(-0.5*bdp2)/(exp(-0.5*bdp1)+exp(-0.5*bdp2))fprintf('此时贝叶斯判别法则为:当pg1>=pg2时,属于g1总体;当pg1<pg2时,属于g2总体!!!\n')fprintf('\n贝叶斯判别的回带判别')for t=1:mbdg1(t)=(g(t,:)'-u1z)'*sn*(g(t,:)'-u1z)-2*log(bp1);bdg2(t)=(g(t,:)'-u2z)'*sn*(g(t,:)'-u2z)-2*log(bp2);p1b(t)=exp(-0.5*bdg1(t))/(exp(-0.5*bdg1(t))+exp(-0.5*bdg2(t)));p2b(t)=exp(-0.5*bdg2(t))/(exp(-0.5*bdg1(t))+exp(-0.5*bdg2(t))); endfprintf('回代g1,g2中六个样本,求得的后验概率为:\n')p1bp2bfprintf('经比较得,误判率的回带估计bp为:\n')bp=0fprintf('贝叶斯判别的交叉法确认误判率:\n')fprintf('依次踢除g1总体中1,2,3号样本,所得的广义平方距离b1d1,b1d2为:') for T=1:3bxg1=g1;bxg1(T,:)=[];bju1=mean(bxg1);b1s1=cov(bxg1);b1s=(b1s1+2*s2)/3;bj1p1=2/5 ; bj1p2=3/5;b1d1(T)=(g1(T,:)-bju1)*b1s'*(g1(T,:)'-bju1')-2*log(bj1p1);b1d2(T)=(g1(T,:)-u2)*b1s'*(g1(T,:)'-u2')-2*log(bj1p2);b1p1(T)=exp(-0.5*b1d1(T))/(exp(-0.5*b1d1(T))+exp(-0.5*b1d2(T)));b1p2(T)=exp(-0.5*b1d2(T))/(exp(-0.5*b1d1(T))+exp(-0.5*b1d2(T))); endb1d1b1d2fprintf('依次剔除g2总体中1,2,3号样本,所得的广义平方距离b2d1,b2d2为:') for T1=1:3if(b1d1(T1)<=b1d2(T1))b1zp(T1)=1;endendfor V=1:3bxg2=g2;bxg2(V,:)=[];bju2=mean(bxg2);b2s2=cov(bxg2);b2s=(2*s1+b2s2)/3;bj2p1=3/5;bj2p2=2/5;b2d1(V)=(g2(V,:)-u1)*b2s'*(g2(V,:)'-u1')-2*log(bj2p1);b2d2(V)=(g2(V,:)-bju2)*b2s'*(g2(V,:)'-bju2')-2*log(bj2p2);b2p1(V)=exp(-0.5*b2d1(V))/(exp(-0.5*b2d1(V))+exp(-0.5*b2d2(V)));b2p2(V)=exp(-0.5*b2d2(V))/(exp(-0.5*b2d1(V))+exp(-0.5*b2d2(V))); endb2d1b2d2for V1=1:3if(b2d1(V1)>=b2d2(V1))b2zp(V1)=1;endendfprintf('由上比较贝叶斯判别时,交叉法确认的误判率为:')byp=(6-(sum(b1zp)+sum(b2zp)))/6fprintf('根据以上的贝叶斯判别法则,判别待判样品yp\n')for v=1:pydg1(v)=(yp(v,:)'-u1z)'*sn*(yp(v,:)'-u1z)-2*log(bp1);ydg2(v)=(yp(v,:)'-u2z)'*sn*(yp(v,:)'-u2z)-2*log(bp2);yp1(v)=exp(-0.5*ydg1(v))/(exp(-0.5*ydg1(v))+exp(-0.5*ydg2(v)));yp2(v)=exp(-0.5*ydg2(v))/(exp(-0.5*ydg1(v))+exp(-0.5*ydg2(v))); endfprintf('后验概率yp1,yp2为:\n')yp1yp2fprintf('比较后验概率yp1,yp2知:\n')for w=1:pif(yp1(w)>=yp2(w))fprintf('属于氧化锰矿石总体的待判样品序号为:%g\n',w) endend。
MATLAB实验讲义_2013版

MATLAB 操作环境、MATLAB 数值计算一、实验目的1、熟悉MATLAB 操作界面;2、掌握MATLAB 基本操作和简单语句函数的输入;3、掌握变量的创建及数据类型间转换;4、掌握矩阵和数组运算,可利用MATLAB 进行基本数值计算;5、掌握多项式的创建和基本运算。
二、实验内容(一)MATLAB 操作环境1、常用窗口及操作方法2、MATLAB 初步应用(1)计算b a b a y ++⨯=,其中43==b a 的值。
(2)绘制正、余弦曲线。
X=0:0.2:2*piY1=sin(x);y2=cos(x);plot(x,y1,x,y2)(3)计算5323645sin + 和5323630cos + 的值。
>> (sin(0.25*pi)+sqrt(36))/32^(1/5)ans =3.3536>> (cos(pi/6)+sqrt(36))/32^(1/5)ans =3.43303、变量的创建和类型转换创建一个5维魔方阵A ,并将其转换成无符号16位整型数组B 。
察看两个变量的详细信息。
4、创建一结构数组Stu ,包含ID 、name 、score 三个域,并输入3个同学的记录信息,并查看第2个记录的信息。
>> A=magic(5),B=uint16(A),whos A BA =17 24 1 8 1523 5 7 14 164 6 13 20 2210 12 19 21 311 18 25 2 9B =17 24 1 8 1523 5 7 14 164 6 13 20 2210 12 19 21 311 18 25 2 9Name Size Bytes ClassA 5x5 200 double arrayB 5x5 50 uint16 arrayGrand total is 50 elements using 250 bytes(二)MATLAB数值计算1、矩阵创建(1)直接输入法A=[1 2 3 4; 5 6 7 8](2)用矩阵编辑器创建复杂矩阵(3)创建特殊矩阵:要求创建随机矩阵、全0矩阵。
第4章 判别分析2

k i 1
μμi
k i 1
μμ u
k
u[ μiμi kμμ kμμ kμμ]u i 1
k
u[ μiμi kμμ]u
12
i 1
k
b u[ μiμi kμμ]u
i 1
k
u[
i 1
μiμi
1 k
X1、X2为横、纵坐标轴构建一 个平面,若能设法找到一个y
轴,使得当X1X2平面上的散点
投射到y轴上时,两组观察值
的重叠程度最小,则综合指标
x2
y的区分能力显然大于原先的
X1、X2 。
3
y
一、Fisher判别的基本思想
从 k 个 P 维总体中抽取一个具有 p 个指标的样品观测数据,借
助方差分析的思想构造一个线性判别函数:
i 1
其中 μ
1 k
k
μ i ,代表全部 k 个总体的集.中.趋势;
i 1
k
E Σi ,代表各个总体内.部.的离散程度。 i 1
(μi μ) 代表总体 i 与其他各组之.间.的平均差距。9
这里 b 相当于一元方差分析中的组间差; e 相当于组内差。 应用方差分析的思想,选择 u 使得目标函数
i
Qr
Ri
i 1 s
i 1
i
i 1
它表明了全部 r 个判别式的判别能力。
实际应用中,我们一般不会使用全部 s 个判别式,因为费希尔判别法的基
本思想就是要降维。因此,如果前 r 个判别式的累计贡献率已达到一个较
高的比例(一般 75%至 95%即可),则可采用这 r 个判别式进行判别。 18
机器学习(MATLAB版)ch08-线性判别分析 教学课件

线性判别分析
新工科建设之路·人工智能系列教材
机器学习(MATLAB 版)
01
线性判别分析 的基本原理
线性判别分析的基本原理
LDA 的基本思想是通过线性投影将样本投影到低维空间中,使得同一类样本的投影点尽可能接近、不同 类样本的投影点尽可能远离;在对新样本进行分类时,将其投影到同样的低维空间中,再根据投影点在低 维空间中的位置来确定新样本的类别。具体的做法是寻找一个向低维空间的投影矩阵 W,使样本数据的 特征向量 经过投影之后得到新向量: 图 8.1 给出了 LDA的一个二维示意图。
谢谢观看
新工科建设之路·人工智能系列教材
机器学习(MATLAB 版)
线性判别分析的基本原理
图 8.1 中的特征向量是二维的,向低维(一维)空间即直线投影,投影后的这些点位于直线上。通过向这条 直线投影,两类样本被有效地分开了。由于是向直线投影,因此相当于用一个向量w与特征向量 a 做内而 得到一个标量:
由上述分析可知,LDA 的关键问题是如何确定最佳的投影矩阵 W。先考虑一维投影的情形,此时需要确 定的是投影向量 w。给定样本数据集:
线性定义“类内散布矩阵”为:
线性判别分析的基本原理
线性判别分析的基本原理
线性判别分析的基本原理
线性判别分析的基本原理
线性判别分析的基本原理
线性判别分析的基本原理
若定义类间散布矩阵为: 则总体散布矩阵可以表示为类内散布矩阵与类间散布矩阵之和:
线性判别分析的基本原理
线性判别分析的基本原理
利用拉格朗日乘子法,问题(8.12) 可通过如下广义特征值问题求解:
02
线性判别分析 的 MATLAB实现
线性判别分析的 MATLAB实现
2013 matlab教程ppt(全)340页

2013-4-21 Application of Matlab Language 5
2013-4-21 Application of Matlab Language 4
课程安排
课堂教学:共24学时;(1-12周) 上机试验:共24学时。
(2-13周,周二7-8节,九实401、402、403)
学习成绩: 1)上机实验成绩占30%; 2)考勤 10% ; 3) 考试60% (随堂考试)。
2013-4-21
Application of Matlab Language
3
本课程的目的( Objectives of This Course )
讲授MATLAB语言基础入门知识,介绍MATLAB产品的体系、MATLAB桌面工具 的使用方法,重点介绍MATLAB的数据可视化、数值计算的基本步骤以及如何使 用MATLAB语言编写整洁、高效、规范的程序。并涉及到一些具体的专业应用工
2013-4-21
Application of Matlab Language
11
Matlab版本的发展 • 1992年,支持Windows 3.x的MATLAB 4.0版本推出,增加了Simulink,Control, Neural Network,Signal Processing等专用工具箱。 • 1993年11月,MathWorks公司推出了Matlab 4.1,其中主要增加了符号运算功能。 当升级至Matlab 4.2c,这一功能在用户中得到广泛应用。 • 1997年,Matlab 5.0版本问世了,实现了真正的32位运算,加快数值计算,图形表现 有效。 • 2001年初,MathWorks公司推出了Matlab 6.0(R12)。 • 2002年7月,推出了Matlab 6.5(R13),在这一版本中Simulink升级到了5.0,性能有 了很大提高,另一大特点是推出了JIT程序加速器,Matlab的计算速度有了明显的 提高。 • 2005年9月,推出了MAILAB 7.1(Release14 SP3),在这一版本中Simulink升级到了 6.3,软件性能有了新的提高,用户界面更加友好。值得说明的是,Matlab V7.1版 采用了更先进的数学程序库,即‚LAPACK‛和‚BLAS‛。 目前,Matlab软件支持多种系统平台,如常见的WindowsNT/XP、UNIX、Linux 等。
第4章-判别分析——part1

从不同的总体中抽出不同的样本;
根据样本 总体; 当然,根据不同的方法,建立的判别法则也是不同的,常用 的判别方法有:距离判别、Fisher判别、Bayes判别、逐步判别。 建立判别法则 判别新的样品属于哪一个
统计学专业主干课程——多元统计分析
4.1.2 判别分析的基本思想
3、判别分析的数据格式
统计学专业主干课程——多元统计分析
4.1 判别分析的基本思想
4.1.1 引 例 4.1.2 判别分析的基本思想 4.1.3 判别分析的类型 4.1.4 与聚类的区别和联系
1、按判别的组数 2、按判别函数的形式 3、按处理变量的方法 4、按判别准则
返回
统计学专业主干课程——多元统计分析
4.1.3 判别分析的类型
根据资料的性质,分为定性资料的判别分析和定量资料的 判别分析。
(
2
) (
1 1
2
) (
2
1
) (
1 2 1
1
1
1
1
1
1
2
1
1
1
1
1
2
1 2 ( 2
1
) 2
(
1 1
2
)
统计学专业主干课程——多元统计分析 (4.4)
令
判别其他未知性别的昆虫。
统计学专业主干课程——多元统计分析
4.1.1 引 例
2、引 例 2
这样的判别虽然不能保证百分之百准确,但至少大部分判 别都是对的,而且用不着杀死昆虫来进行判别了。
统计学专业主干课程——多元统计分析
4.1.1 引 例
在生产、科研和日常生活中经常遇到需要判别的问题:
第04章_判别分析

X
G1,
X G2,
如果 如果
Wˆ (X) 0 Wˆ (X) 0
(4.7)
这里我们应该注意到:
( 1 ) 当 p 1 , G1 和 G2 的 分 布 分 别 为 N(1, 2 ) 和
N(2 , 2 ) 时, 1, 2 , 2 均为已知,且 1 2 ,则判别
系数为
1 2 2
0 ,判别函数为
把这类问题用数学语言来表达,可以叙述如下:设有n个样 本,对每个样本测得p项指标(变量)的数据,已知每个样 本属于k个类别(或总体)G1,G2, …,Gk中的某一类,且 它们的分布函数分别为F1(x),F2(x), …,Fk(x)。我们希望 利用这些数据,找出一种判别函数,使得这一函数具有某种
最优性质,能把属于不同类别的样本点尽可能地区别开来,
W (X) I X C , 1,2,, k
相应的判别规则为
X Gi
如果
Wi
(X)
max
1 k
(I
X
C
)
( 4.9)
针对实际问题,当 μ1,μ2 ,,μk 和 Σ 均未知时,可以通过相应的
样 本 值 来 替 代 。 设 X1() ,
,
X( n
)
是 来 自 总 体 G
中 的样 本
( 1,2,, k ),则 μ ( 1,2,, k )和 Σ 可估计为
P(好/做 人好事)
P好P 人 (做 P好 好 /好 P 人 事 )做 人 P(坏 好 /好 )P 人 事 (做 人好 /坏事 )人
0.50.9 0.82 0.50.90.50.2
P(坏/做 人好事)
P好P 人 (做 P坏 好 /好 P 人 事 )做 人 P(坏 好 /坏 )P 人 事 (做 人好 /坏事 )人
判别分析的MATLAB实现案例

%--------------------------------------------------------------------------% 读取examp10_01.xls中数据,进行距离判别%--------------------------------------------------------------------------%********************************读取数据***********************************% 读取文件examp10_01.xls的第1个工作表中C2:F51范围的数据,即全部样本数据,包括未判企业sample = xlsread('examp10_01.xls','','C2:F51');% 读取文件examp10_01.xls的第1个工作表中C2:F47范围的数据,即已知组别的样本数据,training = xlsread('examp10_01.xls','','C2:F47');% 读取文件examp10_01.xls的第1个工作表中B2:B47范围的数据,即样本的分组信息数据,group = xlsread('examp10_01.xls','','B2:B47');obs = [1 : 50]'; % 企业的编号%**********************************距离判别*********************************% 距离判别,判别函数类型为mahalanobis,返回判别结果向量C和误判概率err[C,err] = classify(sample,training,group,'mahalanobis');[obs, C] % 查看判别结果err % 查看误判概率%--------------------------------------------------------------------------% 加载fisheriris.mat中数据,进行贝叶斯判别%--------------------------------------------------------------------------%********************************加载数据*********************************** load fisheriris % 把文件fisheriris.mat中数据导入MA TLAB工作空间%**********************************查看数据********************************* head0 = {'Obj', 'x1', 'x2', 'x3', 'x4', 'Class'}; % 设置表头[head0; num2cell([[1:150]', meas]), species] % 以元胞数组形式查看数据%*********************************贝叶斯判别********************************% 用meas和species作为训练样本,创建一个朴素贝叶斯分类器对象ObjBayesObjBayes = NaiveBayes.fit(meas, species);% 利用所创建的朴素贝叶斯分类器对象对训练样本进行判别,返回判别结果pre0,pre0也是字符串元胞向量pre0 = ObjBayes.predict(meas);% 利用confusionmat函数,并根据species和pre0创建混淆矩阵(包含总的分类信息的矩阵)[CLMat, order] = confusionmat(species, pre0);% 以元胞数组形式查看混淆矩阵[[{'From/To'},order'];order, num2cell(CLMat)]% 查看误判样品编号gindex1 = grp2idx(pre0); % 根据分组变量pre0生成一个索引向量gindex1gindex2 = grp2idx(species); % 根据分组变量species生成一个索引向量gindex2errid = find(gindex1 ~= gindex2) % 通过对比两个索引向量,返回误判样品的观测序号向量% 查看误判样品的误判情况head1 = {'Obj', 'From', 'To'}; % 设置表头% 用num2cell函数将误判样品的观测序号向量errid转为元胞向量,然后以元胞数组形式查看误判结果[head1; num2cell(errid), species(errid), pre0(errid)]% 对未知类别样品进行判别% 定义未判样品观测值矩阵xx = [5.8 2.7 1.8 0.735.6 3.1 3.8 1.86.1 2.5 4.7 1.16.1 2.6 5.7 1.95.1 3.16.5 0.625.8 3.7 3.9 0.135.7 2.7 1.1 0.126.4 3.2 2.4 1.66.7 3 1.9 1.16.8 3.57.9 1];% 利用所创建的朴素贝叶斯分类器对象对未判样品进行判别,返回判别结果pre1,pre1也是字符串元胞向量pre1 = ObjBayes.predict(x)%--------------------------------------------------------------------------% 加载fisheriris.mat中数据,进行Fisher判别%--------------------------------------------------------------------------%********************************加载数据*********************************** load fisheriris % 把文件fisheriris.mat中数据导入MA TLAB工作空间%**********************************待判样品********************************* % 定义待判样品观测值矩阵xx = [5.8 2.7 1.8 0.735.6 3.1 3.8 1.86.1 2.5 4.7 1.16.1 2.6 5.7 1.95.1 3.16.5 0.625.8 3.7 3.9 0.135.7 2.7 1.1 0.126.4 3.2 2.4 1.66.7 3 1.9 1.16.8 3.57.9 1];%*********************************Fisher判别********************************% 利用fisher函数进行判别,返回各种结果(见fisher函数的注释)[outclass,TabCan,TabL,TabCon,TabM,TabG] = fisher(x,meas,species)%************************绘制两个判别式得分的散点图************************** % 利用fisher函数进行判别,返回各种结果,其中ts为判别式得分[outclass,TabCan,TabL,TabCon,TabM,TabG,ts] = fisher(x,meas,species);% 提取各类的判别式得分ts1 = ts(ts(:,1) == 1,:); % setosa类的判别式得分ts2 = ts(ts(:,1) == 2,:); % versicolor类的判别式得分ts3 = ts(ts(:,1) == 3,:); % virginica类的判别式得分plot(ts1(:,2),ts1(:,3),'ko') % setosa类的判别式得分的散点图hold onplot(ts2(:,2),ts2(:,3),'k*') % versicolor类的判别式得分的散点图plot(ts3(:,2),ts3(:,3),'kp') % virginica类的判别式得分的散点图legend('setosa类','versicolor类','virginica类'); %加标注框xlabel('第一判别式得分'); %给X轴加标签ylabel('第二判别式得分'); %给Y轴加标签%************************只用一个判别式进行Fisher判别************************ % 令fisher函数的第4个输入为0.5,就可以只用一个判别式进行判别[outclass,TabCan,TabL,TabCon,TabM,TabG] = fisher(x,meas,species,0.5)function [outclass,TabCan,TabL,TabCon,TabM,TabG,trainscore] = fisher(sampledata,training,group,contri)%FISHER 判别分析.% class = fisher(sampledata,training,group) 根据训练样本training构造判别式,% 利用所有判别式对待判样品sampledata进行判别. sampledata和training是具有相同% 列数的矩阵,它们的每一行对应一个观测,每一列对应一个变量. group是training对% 应的分组变量,它的每一个元素定义了training中相应观测所属的类. group可以是一% 个分类变量,数值向量,字符串数组或字符串元胞数组. training和group必须具有相% 同的行数. fisher函数把group中的NaN或空字符串作为缺失数据,从而忽略training % 中相应的观测. class中的每个元素指定了sampledata中的相应观测所判归的类,它和% group具有相同的数据类型.%% class = fisher(sampledata,training,group,contri) 根据累积贡献率不低于% contri,确定需要使用的判别式个数,默认情况下,使用所有判别式进行判别. contri % 是一个在(0, 1]区间内取值的标量,用来指定累积贡献率的下限.%% [class, TabCan] = fisher(...)以表格形式返回所用判别式的系数向量,若contri% 取值为1,则返回所有判别式的系数向量. TabCan是一个元胞数组,形如% 'Variable' 'can1' 'can2'% 'x1' [-0.2087] [ 0.0065]% 'x2' [-0.3862] [ 0.5866]% 'x3' [ 0.5540] [-0.2526]% 'x4' [ 0.7074] [ 0.7695]% [class, TabCan, TabL] = fisher(...)以表格形式返回所有特征值,贡献率,累积% 贡献率等. TabL是一个元胞数组,形如% 'Eigenvalue' 'Difference' 'Proportion' 'Cumulative'% [ 32.1919] [ 31.9065] [ 0.9912] [ 0.9912]% [ 0.2854] [] [ 0.0088] [ 1]%% [class, TabCan, TabL, TabCon] = fisher(...)以表格形式返回混淆矩阵(包含总% 的分类信息的矩阵). TabCon是一个元胞数组,形如% 'From/To' 'setosa' 'versicolor' 'virginica'% 'setosa' [ 50] [ 0] [ 0]% 'versicolor' [ 0] [ 48] [ 2]% 'virginica' [ 0] [ 1] [ 49]%% [class, TabCan, TabL, TabCon, TabM] = fisher(...)以表格形式返回误判矩阵.% TabM是一个元胞数组,形如% 'Obj' 'From' 'To'% [ 71] 'versicolor' 'virginica'% [ 84] 'versicolor' 'virginica'% [134] 'virginica' 'versicolor'%% [class, TabCan, TabL, TabCon, TabM, TabG] = fisher(...)将所用判别式作用% 在各组的组均值上,得到组均值投影矩阵,以表格形式返回这个矩阵. TabG是一个元胞% 数组,形如% 'Group' 'can1' 'can2'% 'setosa' [-1.3849] [1.8636]% 'versicolor' [ 0.9892] [1.6081]% 'virginica' [ 1.9852] [1.9443]% [class, TabCan, TabL, TabCon, TabM, TabG, trainscore] = fisher(...)返回% 训练样品所对应的判别式得分trainscore. trainscore的第一列为各训练样品原本所% 属类的类序号,第i+1列为第i个判别式得分.%% Copyright 2009 xiezhh.% $Revision: 1.0.0.0 $ $Date: 2009/10/03 10:40:34 $if nargin < 3error('错误:输入参数太少,至少需要3个输入.');end% 根据分组变量生成索引向量gindex,组名元胞向量groups,组水平向量glevels [gindex,groups,glevels] = grp2idx(group);% 忽略缺失数据nans = find(isnan(gindex));if ~isempty(nans)training(nans,:) = [];gindex(nans) = [];endngroups = length(groups);gsize = hist(gindex,1:ngroups);nonemptygroups = find(gsize>0);nusedgroups = length(nonemptygroups);% 判断是否有空的组if ngroups > nusedgroupswarning('警告: 有空的组.');end[n,d] = size(training);if size(gindex,1) ~= nerror('错误: 输入参数大小不匹配,GROUP与TRAINING必须具有相同的行数.'); elseif isempty(sampledata)sampledata = zeros(0,d,class(sampledata));elseif size(sampledata,2) ~= derror('错误: 输入参数大小不匹配,SAMPLEDATA与TRAINING必须具有相同的列数.'); end% 设置contri的默认值为1,并限定contri在(0, 1]内取值if nargin < 4 || isempty(contri)contri = 1;endif ~isscalar(contri) || contri > 1 || contri <= 0error('错误: contri 必须是一个在(0, 1]内取值的标量.');endif any(gsize == 1)error('错误: TRAINING中的每个组至少应有两个观测.');end% 计算各组的组均值gmeans = NaN(ngroups, d);for k = nonemptygroupsgmeans(k,:) = mean(training(gindex==k,:),1);end% 计算总均值totalmean = mean(training,1);% 计算组内离差平方和矩阵E和组间离差平方和矩阵BE = zeros(d);B = E;for k = nonemptygroups% 分别估计各组的组内离差平方和矩阵.[Q,Rk] = qr(bsxfun(@minus,training(gindex==k,:),gmeans(k,:)), 0);% 各组的组内离差平方和矩阵:AkHat = Rk'*Rk% 判断各组的组内离差平方和矩阵的正定性s = svd(Rk);if any(s <= max(gsize(k),d) * eps(max(s)))error('错误: TRAINING中各组的组内离差平方和矩阵必须是正定矩阵.');endE = E + Rk'*Rk; % 计算总的组内离差平方和矩阵E% 计算组间离差平方和矩阵BB = B + (gmeans(k,:) - totalmean)'*(gmeans(k,:) - totalmean)*gsize(k);end% 求inv(E)*B的正特征值与相应的特征向量EB = E\B;[V, D] = eig(EB);D = diag(D);[D, idD] = sort(D,'descend'); %将特征值按降序排列V = V(:,idD);NumPosi = min(ngroups-1, d); %确定正特征值个数D = D(1:NumPosi, :);CumCont = cumsum(D/sum(D)); %计算累积贡献率% 以表格形式返回所有特征值,贡献率,累积贡献率等. TabL是一个元胞数组head = {'Eigenvalue', 'Difference', 'Proportion', 'Cumulative'};TabL = cell(NumPosi+1, 4);TabL(1,:) = head;TabL(2:end,1) = num2cell(D);if NumPosi == 1TabL(2:end-1,2) = {0};elseTabL(2:end-1,2) = num2cell(-diff(D));endTabL(2:end,3) = num2cell(D/sum(D));TabL(2:end,4) = num2cell(CumCont);% 根据累积贡献率的下限contri确定需要使用的判别式个数CumContGeCon CumContGeCon = find(CumCont >= contri);CumContGeCon = CumContGeCon(1);V = V(:, 1:CumContGeCon); %需要使用的判别式系数矩阵% 以表格形式返回所用判别式的系数向量,若contri取值为1,% 则返回所有判别式的系数向量. TabCan是一个元胞数组TabCan = cell(d+1, CumContGeCon+1);TabCan(1, 1) = {'Variable'};TabCan(2:end, 1) = strcat('x',cellstr(num2str((1:d)')));TabCan(1, 2:end) = strcat('can',cellstr(num2str((1:CumContGeCon)')));TabCan(2:end, 2:end) = num2cell(V);% 将训练样品与待判样品放在一起进行判别m = size(sampledata,1);gv = gmeans*V;stv = [sampledata; training]*V;nstv = size(stv, 1);message = '';outclass = NaN(nstv, 1);for i = 1:nstvobji = bsxfun(@minus,stv(i,:),gv);obji = sum(obji.^2, 2);idclass = find(obji == min(obji));if length(idclass) > 1idclass = idclass(1);message = '警告: 出现了一个或多个结';endoutclass(i) = idclass;endwarning(message);trclass = outclass(m+(1:n)); %训练样品的判别结果(由类序号构成的向量)outclass = outclass(1:m); %待判样品的判别结果(由类序号构成的向量)outclass = glevels(outclass,:); %将待判样品的判别结果进行一个类型转换trg1 = groups(gindex); %训练样品的初始类名称trg2 = groups(trclass); %训练样品经判别后的类名称% 以表格形式返回混淆矩阵(包含总的分类信息的矩阵). TabCon是一个元胞数组[CLMat, order] = confusionmat(trg1,trg2);TabCon = [[{'From/To'},order'];order, num2cell(CLMat)];% 以表格形式返回误判矩阵. TabM是一个元胞数组miss = find(gindex ~= trclass); %训练样品中误判样品的编号head1 = {'Obj', 'From', 'To'};TabM = [head1; num2cell(miss), trg1(miss), trg2(miss)];% 将所用判别式作用在各组的组均值上,得到组均值投影矩阵,以表格形式返回这个矩阵. % TabG是一个元胞数组TabG = cell(ngroups+1,CumContGeCon+1);TabG(:,1) = [{'Group'};groups];TabG(1,2:end) = strcat('can',cellstr(num2str((1:CumContGeCon)')));TabG(2:end,2:end) = num2cell(gv);% 计算训练样品所对应的判别式得分trainscore = training*V;trainscore = [gindex, trainscore];。
MATLAB课件2013版第4章

例: 求下列极限: sin x tan x x ( e 1 ) 2 ( e 1) (1) lim
x a
xa
2t (2) lim 1
x
3x
x
(1) syms a x; f=(x*(exp(sin(x))+1)-2*(exp(tan(x))-1))/(x+a); limit(f,x,a) (2) syms x t; limit((1+2*t/x)^(3*x),x,inf) ans = exp(6*t)
新建一个M文件,并输入下列命令: x=sym('x'); y=x^3+3*x-2; %定义曲线函数 f=diff(y); %对曲线求导数 g=f-4; xx=solve(g); %求方程f-4=0的根,即求曲线何处的 导数为4 xx=double(xx); yy=eval(subs(y,x,xx)); fprintf('曲线y=x^3+3*x-2上切线与直线y=4x-1平行的 点:\n(%f,%f);(%f,%f)\n' ,xx(1),yy(1),xx(2),yy(2))
>>clear >>U=sym('3*x^2+5*y+2*x*y+6') %定义符号表达式 >>syms x y; %符号运算,就单独定义x、y为符号 >>V=3*x^2+5*y+2*x*y+6 %定义符号表达式V >>2*U-V+6 >>syms 3 %不能定义数字 ??? Error using ==> syms Not a valid variable name.
判别分析(matlab)

湖北经济学院统计与应用数学系
严培胜
2)在Matlab软件包中常用的是cov(x,y)和corrcoef(x,y). )在Matlab软件包中常用的是cov(x,y)和 例如,在Matlab软件包中写一个名字为opt_cov_1的 例如,在Matlab软件包中写一个名字为opt_cov_1的 M文件: x=[1 2 3]; y=[3 2 1]; cov(x,y) 存盘后执行,得到: ans = 1 -1 -1 1
湖北经济学院统计与应用数学系 严培胜
(三)贝叶斯判别法
贝叶斯判别法是一种概率方法,它的好处是可 以充分利用先验信息,可以考虑专家的意见。应 用此方法,需要事先假定样本指标值的分布(例 如,多元正态分布等)
湖北经济学院统计与应用数学系
严培胜
在Matlab软件包中,将已经分类的m个数据(长度为n) Matlab软件包中,将已经分类的m个数据(长度为n) 作为行向量,得到一个矩阵trianing,每行都属于一个分类 作为行向量,得到一个矩阵trianing,每行都属于一个分类 类别,分类类别构成一个整数列向量g(共有m 类别,分类类别构成一个整数列向量g(共有m行),待分 类的k个数据(长度为n 类的k个数据(长度为n)作为行向量,得到一个矩阵 sample,然后利用classify函数进行线性判别分析(默认)。 sample,然后利用classify函数进行线性判别分析(默认)。 它的格式为: classify(sample,training,group), classify(sample,training,group), 其中,sample与training必须具有相同的列数,group与 其中,sample与training必须具有相同的列数,group与training 必须具有相同的行数,group是一个整数向量。Matlab内部 必须具有相同的行数,group是一个整数向量。Matlab内部 函数classify的功能是将sample的每一行进行判别,分到 函数classify的功能是将sample的每一行进行判别,分到 training指定的类中。 training指定的类中。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例 (1989年国际数学竞赛A题)蠓的分类 蠓是一种昆虫,分为很多类型,其中有一种名为
Af,是能传播花粉的益虫;另一种名为Apf,是会传播 疾病的害虫,这两种类型的蠓在形态上十分相似, 很难区别. 现测得6只Apf和9只Af蠓虫的触角长度和 翅膀长度数据
Apf:(1.14,1.78), (1.18,1.96), (1.20,1.86), (1.26,2.00), (1.28,2.00), (1.30,1.96) ;
n
d1 (x, y) | xi yi | i 1
绝对距离
欧氏距离
n
称
d2 (x, y) (xi yi )2
i 1
称
n
dr (x, y) ( | xi yi |r )1/ r
i 1
为n维向量x,y之间的闵可夫斯基距离,其中 r (r 0)
为常数。
显然,当r=2和1时闵可夫斯基距离分别为欧氏距 离和绝对距离.
4.1.3 两总体的距离判别分析
先考虑两个总体的情况。设 G1 ,G2 为两个不同
的p元已知总体,Gi 的均值向量是 i,i 1, 2 ,Gi 的 协方差矩阵是 i ,i 1, 2 .设 x (x1, x2 , , xm )T
是一个待判样品,距离判别准则为
x .
G1
,
x
G2
,
若d (x,G1) d (x,G2 ), 若d (x,G1) d (x,G2 )
2. 马氏距离
马氏距离是由印度统计学家马哈拉诺比斯(PC Mahalanobis)提出的,由于马氏距离具有统计意义, 在距离判别分析时经常应用马氏距离:
(1) 同一总体的两个向量之间的马氏距离
设有n维向量 x ( x1, x2, , xn )T , y ( y1, y2, , yn )T ,则称
➢ 距离判别法—首先根据已知分类的数据,分别计算 各类的重心,计算新个体到每类的距离,确定最短 的距离(欧氏距离、马氏距离)
➢ Fisher判别法—利用已知类别个体的指标构造判别 式(同类差别较小、不同类差别较大),按照判别 式的值判断新个体的类别
➢ Bayes判别法—计算新给样品属于各总体的条件概 率,比较概率的大小,然后将新样品判归为来自概 率最大的总体
第4章 判别分析
判别分析的基本思想是根据已知类别的样本所提 供的信息,总结出分类的规律性,建立判别公式和 判别准则,判别新的样本点所属类型。本章介绍距 离判别分析、Bayes判别分析及其MATLAB软件的 实现。
4.1 距离判别分析
4.1.1 判别分析的概念
在一些自然科学和社会科学的研究中,研究对象 用某种方法已划分为若干类型,当得到的一个新样 品数据(通常是多元的),要确定该样品属于已知 类型中的哪一类,这样的问题属于判别分析.
为 1 , 2,协方差矩阵相等,皆为Σ,则两个总体之
间的马氏距离为
d (G1, G2 ) (1 2 )T 1(1 2 ) (4.1.3)
通常,在判别分析时不采用欧氏距离的原因在 于,该距离与量纲有关.例如平面上有A,B,C,D四个 点,横坐标为代表重量(单位:kg),纵坐标代表 长度(单位:cm),如下页图。
这时
AB 52 102 125
CD 102 12 101
显然 AB>CD
如果现在长度用mm为单位,重量的单位保持不变, 于是A点的坐标为(0,50),B点的坐标为(0,100),此时 计算线段的长度为
AB 502 102 2600 CD 1002 12 10001
此时,AB<CD
这表明欧氏距离有一个缺陷,当向量的分量是不 同的量纲时欧氏距离的大小竟然与指标的单位有关. 而马氏距离则与量纲无关.
原则: 1.从统计学的角度,要求判别准则在某种准则
下是最优的,例如错判的概率最小等。
2.根据不同的判别准则,有不同的判别方法,
这里主要介绍距离判别和Bayes判别
4.1.2 距离的定义
1. 闵可夫斯基距离 设有n维向量 x (x1, x2 ,, xn )T , y ( y1, y2 ,, yn )T , 称
从统计数据分析的角度,可概括为如下模型:
设有k个总体 G1,G2, ,Gk ,它们都是 p元总体, 其数量指标是 X (X1, X2, , X p )T
1) 若总体Gi 的分布函数是已知,对于任一新
样品数据 x (x1, x2, , xp )T ,判断它来自哪一个
总体 。
2) 通常各个总体 Gi的分布是未知的,由从各 个总体取得的样本(训练样本)来估计。一般, 先估计各个总体的均值向量与协方差矩阵。
d(x, y) (x y)T 1(x y)
为n维向量x,y之间的马氏距离.
(4.1.1)
其中 为总体协方差矩阵,通常取为实对称正定 矩阵. 显然,当为单位矩阵时马氏距离就是欧氏距离.
(2) 一个向量到一个总体的马氏距离 总体G 的均值向量为μ,协方差矩阵为Σ .则称
d(x, G) (x )T 1(x )
Af:(1.24,1.72), (1.36,1.74), (1.38,1.64), (1.38,1.82), (1.38,1.90),
(1.40,1.70), (1.48,1.82),(1.54,1.82), (1.56,2.08).
试判别以下的三个蠓虫属于哪一类? (1.24,1.8),(1.28,1.84),(1.4,2.04)
为n维向量x与总体G的马氏距离.
(4.1.2)
MATLAB中有一个命令:d=mahal(Y,X),计算X 矩阵每一个点(行)至Y矩阵中每一个点(行)的 马氏距离。其中Y的列数必须等于X的列数,但它们 的行数可以不同。X的行数必须大于列数。输出d是 距离向量。
(3) 两个总体之间的马氏距离
设有两个总体G1,G2,两个总体的均值向量分别
第4 章 判别分析(discriminant analysis)
§4.1 距离判别 及MATLAB实现 §4.2 Bayes判别 §4.3 判别分析 总结
计算与应用数学系, 中国石油大学(华东)理学院
丁永臻 2013
统计方法(判别分析):
➢ 判别分析—在已知研究对象分成若干类型,并已取 得各种类型的一批已知样品的观测数据,在此基础 上根据某些准则建立判别式,然后对未知类型的样 品进行判别分类。
