一种最短路线问题的两种解法
邮递员问题最短路径的解法

邮递员问题最短路径的解法1. 简介邮递员问题是指一个邮递员需要按照一定的顺序访问多个地点,并返回起始地点的问题。
邮递员需要选择一条最短的路径,以最小化总行驶距离或时间。
2. 问题描述邮递员问题可以具体描述为:给定一个地图,地图上有多个地点,每个地点都有一个坐标和一个编号。
邮递员需要从起始地点出发,依次访问所有地点,并最终返回起始地点。
3. 算法解法解决邮递员问题的算法有很多种,下面介绍两种常见的解法。
3.1. 蚁群算法蚁群算法是一种模拟自然界蚁群觅食行为的算法。
在蚁群算法中,每只蚂蚁都只能看到局部信息,通过蚂蚁之间的合作和信息交流,最终找到整个系统的全局最优解。
蚁群算法解决邮递员问题的基本步骤如下: 1. 初始化蚂蚁的位置,通常将蚂蚁放置在起始地点。
2. 蚂蚁按照一定的规则选择下一个要访问的地点,例如选择离当前位置最近且未访问过的地点。
3. 更新蚂蚁的位置和访问状态,标记已经访问过的地点。
4. 重复步骤2和步骤3,直到所有地点都被访问过。
5. 计算蚂蚁行走的路径长度,并保存最短路径。
3.2. 动态规划算法动态规划算法是一种通过拆分问题,定义问题的状态,以及定义状态之间的关系,从而逐步求解问题的算法。
动态规划算法解决邮递员问题的基本步骤如下: 1. 定义子问题:将整个问题拆分为多个子问题,每个子问题表示从起始地点出发,经过一部分地点,并最终返回起始地点的最短路径。
2. 定义状态:根据子问题的定义,确定状态的表示方法,例如使用一个二维数组来表示子问题的最短路径长度。
3. 状态转移方程:根据子问题之间的关系,建立状态之间的转移方程,例如使用动态规划的递推公式计算子问题的最短路径。
4. 解决子问题:按照子问题的顺序,依次计算每个子问题的最优值,并保存中间结果。
5. 求解原问题:根据子问题的最优值,计算原问题的最优值,并得到最短路径。
4. 算法比较蚁群算法和动态规划算法是两种常见的解决邮递员问题的方法,它们各有优缺点。
最短路线问题二

最短路线这一讲里,我们将会解决这个特殊的计数问题:最短路线问题。
怎样计数从A 到B 的最短路线的条数呢?我们将介绍一种非常巧妙的方法——对角线法(也叫标号法)。
【例1】 咱们先做个游戏:在方格纸上任取一点A 作为起点,再在A 的右上方任取一点B 作为终点划一条由A 到B 的最短路线。
聪明的小朋友,你能划出来吗?总共能划出几条呢?分析:教师可提问如ACIHGFB 是最短路线吗?为什么不是?如果要划从A 到B 的最短路线,那么从A 点出发只能向上或向右(每一条都是横划2格竖划2格),可以是ACDEB 、ACIEB 、ACIFB 、AHGFB 、AHIEB 、AHIFB 这六条路线。
在上面这个游戏中,你是用什么方法找到从A 到B 的最短路线呢?如果A 、B 两点变成图1、2、3的位置,那么从A 到B 的最短路线有几条呢?分析:图1、2、3中从A 到B 的最短路线均为6条。
小朋友们,你是怎么做的?你发现了什么规律?如果图形变得复杂,还要保证找出的路线既不重又不漏呢?你又该如何解决呢?我们一起来看【例2】。
【例2】阿呆和阿瓜到少年宫参加2008北京奥运会志愿者培训。
请你想一想他们从学校到少年宫的最短路线最多有多少种?分析:我们采用对角线法(如图)从学校到少年宫共有10种走法。
我们观察图发现每一个小格右下角上标的数正好是这个小格右上角与左下角的数的和,这个和就是从出发点A到这点的所有最短路线的条数.这样,我们可以通过计算来确定从A→B的最短路线的条数,而且能够保证“不重”也“不漏”。
聪明的小朋友,你总结出什么规律了吗?请填在下面的空格内:【例3】下图是动物王国的街道平面图,纵横各有5条路,森林之王老虎先生通知大家去运动场开会,如果迟到就要挨罚喝100杯水。
爱睡懒觉的树袋熊一觉醒来,呀,要迟到了,想想那100杯水,树袋熊都快晕了。
善良的小朋友们,快来给树袋熊找找最近的吧!分析:教师可参考例1的解答过程,用对角线法(如下图)解,所以共有20条路线。
轴对称最短路线问题原理

轴对称最短路线问题原理
一、问题描述
轴对称最短路线问题,即求平面上两点间沿轴对称线走的最短距离。
二、问题解法
1. 构造对称轴
首先需要找到两点的对称轴,对称轴的构造方法有多种,常用的有以
下两种:
(1)连接两点,垂直平分线即为对称轴。
(2)以两点为圆心,以它们之间的距离为半径,画两个圆;两圆的交
点就是对称轴。
2. 沿对称轴转换
对称轴将平面分为两个对称部分,假设起点在对称轴左侧(或右侧),求出终点在对称轴右侧(或左侧)的最短距离,即为要求的轴对称最
短路线。
3. 求最短距离
最短距离可以使用最短路算法(如 Dijkstra 算法、Bellman-Ford 算法等)来计算。
三、应用领域
轴对称最短路线问题常见于自动化生产线、机器人运动等领域,在这
些领域中,机器人需要在不碰撞的情况下从一个点到达另一个点,同
时保证走的路径最短。
该问题的解决方法可以为机器人运动路径规划
提供参考。
迷宫最短路径问题的计算机解法

迷宫最短路径问题的计算机解法的信息目录迷宫最短路径问题的计算机解法的信息 (1)1.问题描述 (1)2.数据的输入与输出 (2)2.1.输入迷宫问题的大小规模 (2)2.2.建立数值迷宫图形 (2)2.3.走向(Direction) 控制 (2)2.4.数据输出 (2)3.数据结构 (2)3.1.数组(Array) (3)3.2.栈(Stack) (3)3.3.队列(Queue) (3)4.算法基本思想 (3)4.1.基本算法思想 (3)4.1.1.步骤一: (3)4.1.2.步骤二: (3)4.1.3.步骤三 (3)4.2.具体实施 (4)4.2.1.其一: (4)4.2.2.其二: (4)5.算法细化参考 (4)6.算法分析 (5)6.1.时间复杂性 (5)6.1.1.其一: (5)6.1.2.其二: (5)6.2.空间复杂性 (5)6.2.1.其一: (5)6.2.2.其二: (6)扳手1-1 (1)拉车1-2 (1)钢材1-3 (2)迷宫最短路径问题的计算机解法的信息迷宫最短路径问题的计算机解法的信息迷宫最短路径( the Shortest Path ofLabyrinth) 问题是一个典型的搜索、遍历问题,其程序设计思想在许多计算机运算程序、计算机管理程序中均有应用。
一般来说,用计算机解决一个具体问题时,大致需要经过下列几个步骤:首先要从具体问题抽象出一个适当的数学模型,然后设计一个解此数学模型的算法,最后编出程序,进行调试、调整,直至得到最终解答。
其中,寻求数学模型的实质是分析问题,从中提取操作的对象,并找出这些操作对象之间的关系,然后用数学语言加以描述。
但是,迷宫最短路径问题处理的对象不仅仅是纯粹的数值,而且还包括字符、表格、图象等多种具有一定结构的数据,这些非数值计算问题无法用数学方程加以描述,这就给程序设计带来一些新的问题。
迷宫最短路径( the Shortest Path ofLabyrinth) 问题是一个典型的搜索、遍历问题,其程序设计思想在许多计算机运算程序、计算机管理程序中均有应用。
最短路径原理

最短路径原理最短路径原理什么是最短路径•最短路径是图论中的一个经典问题,旨在寻找两个顶点之间权值和最小的路径。
Dijkstra算法•Dijkstra算法是最短路径问题中一种常用的解法。
•此算法从起点开始,逐步确定到达其他顶点的最短路径。
Dijkstra算法步骤1.初始化–创建两个集合:一个用于存储已经找到最短路径的顶点,一个用于存储未找到最短路径的顶点。
–将起点加入已找到最短路径集合,其余顶点加入未找到最短路径集合。
–初始化从起点到各顶点的距离为无穷大,起点到自身的距离为0。
2.寻找最短路径–选择未找到最短路径集合中,距离起点最近的顶点,将其加入已找到最短路径集合。
–更新与该顶点相邻的顶点的距离,若通过该顶点到达邻接顶点的路径更短,则更新距离。
3.重复步骤2,直到所有顶点都加入已找到最短路径集合。
示例让我们通过一个简单的示例来说明Dijkstra算法应用于最短路径的原理。
假设有一个无向图,顶点分别为A、B、C、D和E,边的权值分别为:AB(5)、AC(3)、BD(2)、CD(1)、DE(4)。
首先,我们从顶点A开始,初始化距离。
初始时,A到A的距离为0,A到B、C、D和E的距离为无穷大。
经过第一轮计算后,已找到最短路径的集合为{A},未找到最短路径的集合为{B, C, D, E}。
此时,A到C的距离为3,A到B、D和E的距离依然为无穷大。
经过第二轮计算,选择距离A最近的顶点C,将C加入已找到最短路径集合。
更新距离后,A到B的距离为8,A到D的距离为4,A到E的距离为7。
重复以上步骤,直到所有的顶点都加入已找到最短路径集合。
最后得到A到B的最短路径为:A->C->D->B,权值和为7。
总结通过Dijkstra算法,我们可以找到两个顶点之间的最短路径,并计算出最小的权值和。
该算法从起点开始,逐步确定最短路径,直到所有顶点都被加入已找到最短路径集合。
使用这一算法,我们可以在实际应用中解决各种问题,比如路线规划、网络中数据包的传输等。
最短线路问题

最短线路问题古希腊亚里山大里亚城有一位久负盛名的学者,名叫海伦.有一天,有位将军不远千里专程前来向海伦求教一个百思不得其解的问题:如图28-1,从甲地出发到河边饮马,然后再到乙地军营视察,显然有许多走法.问走什么样的路线最短呢?精通数理的海伦稍加思索,便作了完善的回答.这个问题后来被人们称作“将军饮马”问题.事实上,不仅是将军有这样的烦恼,运动着的车、船、飞机,包括人们每天走路都要遇到这样的问题.古今中外的任何旅行者总希望寻求最佳的旅行路线,尽量走近道,少走冤枉路.我们把这类求近道的问题统称最短线路问题.啊!原来这就是最短线路问题,我们已经在小学教科书上几次接触过.比如,三年级(第六册)书上说:“从学校到电影院有三条路(图28-2),小云要看电影走哪条路最近?”;又如,四年级(第八册)书上说:“通过度量可以知道‘从直线外一点到这条直线所画的各线段中,以和这条直线垂直的线段为最短’.”另外,从某种意义上说,上节的一笔画问题也属这类问题.看来最短线路问题在生产、科研和日常生活中确实重要且应用广泛.但是.怎样走才是近道呢?这可不是件容易的事.它慢慢地引起了数学家的兴趣,并用数学这个强有力的工具解决了它.下面来看看数学家是怎样解决的.问题28.1 假如直线AB是一条公路,在路两侧有甲、乙两个村子(如图28-3),现在要在公路上修一个公共汽车站,让这两村的人到车站的路线之和最短.问车站应修建在什么地方?分析如果只考虑甲村人距公路最近,由教材上的结论,只要由甲村向AB画一条垂线,交AB于C,那么C离甲村最近,但离乙村又远了.同样只考虑乙村近的线路乙—D—甲也不是最近的.怎样才能使甲、乙两村整体考虑时最近(即距离之和最短)呢?根据我们的经验:两个地点之间走直线最近.所以,在甲、乙之间连一条直线与AB相交于P点,则在P点建站就合要求了.注意:以上我们是凭经验作出的解答.但是数学家解决问题,总是要用一些公认的结论去对问题进行严格的证明才算正确,并把公认的结论称作公理.下面我们把解决最短线路问题时常用的公理列在下面.公理1 连接两点的所有线中,直线段最短.公理2 三角形的两边之和大于第三边.公理3 直线外一点到直线的所有线中垂线段最短.公理是从实践中总结出来的任何人都承认的原始道理.当然,有同学会想:“你那个公理我不承认行不行呢?”那可不行,比如图28-4(1)中,有一只鸡子在B点觅食,你在A点处放一些米,那么鸡子一定会沿直线AB跑过来吃食,决没有一只蠢鸡子沿B→C→A或沿B→D→A的路线跑过来.这表明:公理不但人类公认,连动物界也都遵循它.下面我们就用上述公理来解决一些最短线路问题.问题28.2 如图28-5,点A、B位于直线l的同侧,在l上找一点P,使得AP+PB最小.分析这就是“将军饮马”问题,我们看看海伦是怎么解决的.海伦发现这是一个求折线和最短的问题.从上面的公理1只知道两点间直线段最短.那么,显然要把折线变成直线再解.如果直接连AB,与l不会相交.怎么办呢?由问题28.1得到启发:当A、B位于l的异侧时,就有交点了.于是我们就希望在l的另一侧找一点A′,使得连A′B与l相交于P点后(这时A′P+PB最短)线段A′P与AP一样长.由对称的知识可知道,A关于l的对称点就有资格扮演A′的角色.解如图28-5,先作A关于l的对称点A′,连接A′B与l相交于P点,则AP+PB就最小。
专地的题目训练蚂蚁爬行地最短路径(含答案详解)

蚂蚁爬行的最短路径1.一只蚂蚁从原点0出发来回爬行,爬行的各段路程依次为:+5,-3,+10,-8,-9,+12,-10.回答下列问题:(1)蚂蚁最后是否回到出发点0;(2)在爬行过程中,如果每爬一个单位长度奖励2粒芝麻,则蚂蚁一共得到多少粒芝麻. 解:(1)否,0+5-3+10-8-9+12-10=-3,故没有回到0; (2)(|+5|+|-3|+|+10|+|-8|+|-9|+|+12|+|-10|)×2=114粒2. 如图,边长为1的正方体中,一只蚂蚁从顶点A 出发沿着正方体的外表面爬到顶点B 的最短距离是 .解:如图将正方体展开,根据“两点之间,线段最短”知,线段AB 即为最短路线.AB = 51222=+.3.(2006•茂名)如图,点A 、B 分别是棱长为2的正方体左、右两侧面的中心,一蚂蚁从点A 沿其表面爬到点B 的最短路程是 cm第6题.解:由题意得,从点A 沿其表面爬到点B 的最短路程是两个棱长的长,即2+2=4.4.如图,一只蚂蚁从正方体的底面A 点处沿着表面爬行到点上面的B 点处,它爬行的最短路线是( )A .A ⇒P ⇒B B .A ⇒Q ⇒BC .A ⇒R ⇒BD .A ⇒S ⇒B解:根据两点之间线段最短可知选A . 故选A .5.如图,点A 的正方体左侧面的中心,点B 是正方体的一个顶点,正方体的棱长为2,一蚂蚁从点A 沿其表面爬到点B 的最短路程是( )解:如图,AB =()1012122=++.故选C .16. 正方体盒子的棱长为2,BC 的中点为M ,一只蚂蚁从A 点爬行到M 点的最短距离为( )解:展开正方体的点M 所在的面, ∵BC 的中点为M , 所以MC =21BC =1, 在直角三角形中AM = =.7.如图,点A 和点B 分别是棱长为20cm 的正方体盒子上相邻面的两个中心,一只蚂蚁在盒子表面由A 处向B 处爬行,所走最短路程是 cm 。
解:将盒子展开,如图所示:AB =CD =DF +FC =21EF + 21GF =21×20+21×20=20cm . 故选C .8. 正方体盒子的棱长为2,BC 的中点为M ,一只蚂蚁从A 点爬行到M 点的最短距离为 .解:将正方体展开,连接M 、D 1, 根据两点之间线段最短,MD =MC +CD =1+2=3,MD 1= 132322212=+=+DD MD .9.如图所示一棱长为3cm 的正方体,把所有的面均分成3×3个小正方形.其边长都为1cm ,假设一只蚂蚁每秒爬行2cm ,则它从下底面点A 沿表面爬行至侧面的B 点,最少要用 2.5秒钟.解:因为爬行路径不唯一,故分情况分别计算,进行大、小比较,再从各个路线中确定最短的路线.(1)展开前面右面由勾股定理得AB = = cm ;(2)展开底面右面由勾股定理得AB ==5cm ;第7题1AB A 1B 1D CD 1C 124所以最短路径长为5cm ,用时最少:5÷2=2.5秒.10.(2009•恩施州)如图,长方体的长为15,宽为10,高为20,点B 离点C 的距离为5,一只蚂蚁如果要沿着长方体的表面从点A 爬到点B ,需要爬行的最短距离是 。
六年级下册奥数试题——最短路线.(含答案)人教版

8-8 最短路线教学目标1.准确运用“标数法”解决题目2.培养学生的实际操作能力.知识精讲知识点说明从一个地方到另外一个地方,两地之间有许多条路,就有许多种走法,如果你能从中选择一条最近的路走,也就是指要选择一条最短的路线走,这样你就可以节省许多时间了,那么如何能选上最短的路线呢?亲爱的小朋友们,你要记住两点:⑴两点之间线段最短.⑵尽量不走回头路和重复路,这样的话,你就做到了省时省力.例题精讲例 1】一只蚂蚁在长方形格纸上的 A 点,它想去 B 点玩,但是不知走哪条路最近.小朋友们,你能给它找到几条这样的最短路线呢?解析】(方法一)从A点走到B点,不论怎样走,最短也要走长方形AHBD 的一个长与一个宽,因此,在水平方向上,所有线段的长度和应等于AD ;在竖直方向上,所有线段的长度和应等于DB .这样我们走的这条路线才是最短路线.为了保证这一点,我们就不应该走“回头路”,只能向右和向下走.所有最短路线:A C D GB 、AC F G B、 A E F G BA C F I B、 A E F I B、 A E H I B这种方法不能保证“不漏”.如果图形再复杂些,做到“不重”也是很困难的.(方法二)遵循“最短路线只能向右和向下走”,观察发现这种题有规律可循.①看C点:只有从A到C的这一条路线.同样道理:从A到D 、从 A 到 E 、从 A 到H 也都只有一条路线.我们把数字“ 1 ”分别标在C、D、E、 H 这四个点上.②看 F 点:从 A 点出发到 F ,可以是 A C F ,也可以是 A E F ,共有两种走法.那么我们在F点标上数字“ 2”(2=1 1).③ 看G 点:从 A G 有三种走法,即: A C D G 、 A C F G 、 A E F G.在G点标上数字“ 3”(3=1 2).④看I 点:共有三种走法,即:A C F I 、 A E F I 、 A E H I ,在I 点标上“ 3” (3=1 2).⑤看B点:从上向下走是G B ,从左向右走是I B ,那么从出发点 A B有六种走法,即: A C D G B、 A C F G B、A E F G B、A C F I B、A E F I B、A E H I B,在B点标上“ 6”( 6 33),观察发现每一个小格右下角上标的数正好是这个小格右上角与左下角的数的和,这个和就是从出发点 A 到这点的所有最短路线的条数.此法能够保证“不重”也“不漏”,这种方法叫“对角线法”或“标号法”.巩固】如图所示,从A点沿线段走最短路线到 B 点,每次走一步或两步,共解析】 共有 9种,即: A A B O C 、B O DC 、A D OBC ,最短的路是: A OC 、 A O B C 、 A B CA D C 、 A D O C C .解析】 这是一个较复杂的最短路线问题,我们退一步想想,先看看简单的情况.从 A 到 B 的各种不同走法中先选择一条路线来分析:如果按路线 A →C →D →E → F → B 来走,这条路线共有 5条线段,每次走 一步或两步,要求从 A 走到 B ,会有几种走法?这不是“上楼梯”问题吗.根 据“上楼梯”问题的解法可得在 A →C →D →E →F → B 这条路线中有 8 种符合条件的走法.而对于从 A 到 B 的其他每条最短路线而言,每一条路 线都有 5 条线段,所以每条路线都有 8 种走法.进一步:从 A 到B 共有多少条最短路线?这正是 “最短路线”问题!用“标 数法”来解决,有 10 条.综上所述,满足条件的走法有 8 10 80种.巩固】 从A 到 B 的最短路线有几条呢?解析】 图中从 A 到B 的最短路线都为 6 条.巩固】 有一只蜗牛从 A 点出发 ,要沿长方形的边或对角线爬到 C 点,中间不许 爬回 A 点,也不能走重复的路,那么,它有多少条不同的爬行路线?最短 的是哪条呢?有多少种不同走法?D DE EFBDEACFB AC CB例 2】 阿呆和阿瓜到少年宫参加 2008 北京奥运会志愿者培训.如果他们从学校出发,共有多少种不 同的最短路线?解析】 从学校到少年宫的最短路线, 只能向右或向下走. 我们可以先看 A点:从 学校到 A 点最短路线只有 1种走法,我们在 A 点标上 1.B 、E 、F 、G 点同 理.再看 J 点:最短路线可以是 A J 、E J 共2条,我们在 J 点标上 2.我 们发现 2 1 1正好是对角线 A 点和 E 点上的数字和.所有的最短路线都符 合这个规律,最终从学校到少年宫共有 10 种走法.巩固】 方格纸上取一点 A 作为起点,再在 A 的右上方任取一点 B 作为终点,画一条由 A 到B 的最短路线,聪明的小朋友, 你能画出来吗?总共能画出几条 呢?解析】 根据“标号法”可知共有 10 种,如图.学校学校1 1 12 3J136 1 4 I10BAAC D 少年宫巩固】如图,从 F 点出发到G 点,走最短的路程,有多少种不同的走法?G分析】 共 有 115种.小聪明想从北村到南村上学,可是他不知道最短路线的走法共有几种?小朋友们,快帮帮忙呀!北村“五一”长假就要到了,小新和爸爸决定去黄山玩.聪明的小朋友请你找找看从北京到黄山的最短路线共有几条呢?采用对角线法(如图)这道题的图形与前几题的图形又有所区别,因此, 在解题时要格外注意是由哪两点的数之和来确定另一点的.从北京到黄 山最近的道路共有 10 条.2456 3 6 10 1521 4 10 20 3565 1535 7126 北村1 1 11 1 1 1巩固】 分析】 根 据“对角线法”知共有 126种,如图.南村北京1 1 12 1122 3241 3710黄山解析】北京巩固】从甲到乙的最短路线有几条?解析】有11条.例 4 】古希腊有一位久负盛名的学者,名叫海伦.他精通数学、物理,聪慧过人.人一天一位将军向他请教一个问题:如下图,将军从甲地骑马出发,要到河边让马饮水,然后再回到乙地的马棚,为了使行走的路线最短,应该让马在什么地方饮水?甲地乙地河流解析】本题主要体现最值思想和对称的思想,教师应充分引导孩子观察行走路线的变化情况逐步引导学生通过对称来找到相应的点,进一步了解图形最值问题中应该如何解决问题.例 5 】学校组织三年级的小朋友去帮助农民伯伯锄草,大家从学校乘车出发,去往的李家村(如图).爱动脑筋的嘟嘟就在想,从学校到李家村共有多少种不同的最短路线呢?解析】我们采用对角线法(如图),从学校到李家村共有81种不同的最短路线.学校2 310 103 64 105 15 25 356 21 46 81甲学校11拓展] 亲爱的小朋友们,你们觉得从 A 到 B 共有几条最短路线呢?解析】 此 题与上题不同,但方法相同.我们采用对角线法(如图)可知:可以选择的最短路线共有 41 条.例 6】 阿花和阿红到少年宫参加 2008 北京奥运会志愿者培训.他们从学校出发 到少年宫最多有多少种不同的行走路线?少年宫 少年宫解析】 采用对角线法(如图) .可得从学校到少年宫共有 90 种走法.铺垫] 小海龟在小猪家玩,它们想去游乐场坐碰碰车,爱动脑筋的小朋友,请你想一想,从小猪家到游乐场共有几条最短路线呢?解析】 “对角线”法(如图) ,共 14 条.例 7 】 阿强和牛牛结伴骑车去图书馆看书,第一天他们从学校直接去图书馆;游乐场游乐场14 59 5243 211 1 1 小猪家第二天他们先去公园看大熊猫再去图书馆;第三天公园修路不能通行.咱们学而思的小朋友都很聪明,请你们帮阿强和牛牛想想这三天从 学校到图书馆的最短路线分别有多少种不同的走法?仍 然用对角线法求解.第一天(无限制条件)共有 16条;第二天(必须 经过公园)共有 8条;第三天(必须不经过公园)共有 8 条.大熊和美子准备去看望养老院的李奶奶, 可是市中心在修路 (城市的街道 如图所示 ),他们从学校到养老院最短路线共有几条呢?聪明的小朋友, 请你们快想想吧!方法二)可以直接求,即把含有市中心的田字格挖去,共有 66 条.解析】巩固】市中心学校解析】 (方法一)用“对角线法”求出:从学校到养老院共 心的 60 条,所以可行的路有: 126 60 66(条). 126条.必经过市中515 35 70 126 410 203556 3610 市中心152123456学校养老院111学校 养老院养老院养老院5 15 25 40 661 4 10 10 15 2651 3 6111 2 3 4 5 6学校 1 1 1例 8】如图,从X 到Y 最短路线总共有几种走法?分析】如图,共有716种.例 9】如图,从A到B沿网格线不经过线段CD和EF 的最短路径的条数是多少条?解析】由于不能经过线段CD和EF ,所以我们必须先在网络图中拆除然后再在拆除了CD和EF以后的网络图中进行标数(如下图所示).运用标数法可求出满足条件的最短路径有78 条.Y18 3685170 342 71617 28 49 85 172 37416 21 2 36 87 2021 5 15 15 51 115151 4 10 36 6413 6 10 15 21 281 2 3 4 5 6 7X 1 1 1 1 11CD和EF ,巩固】下图为某城市的街道示意图,C处正在挖下水道,不能通车,从A到B 处的最短路线共有多少条?解析】从A到B的最短路线有431条.解析】本题中的运动方向已经由箭头标示出来,所以关键要分析每一点的入口情况.B431B174110 5564 55 55 30 129C25 18 12 7 398 7 6 5 4 3 2 111 1 1 1 1 1 1例 10 】按图中箭头所指的方向行走,从A到I 共有多少条不同的路线?1742571910A通过标数法我们可以得出从 A 到I 共有 29条不同的路径.例 11】 按图中箭头方向所指行走,从 A 到G 有多少种不同的路线?解析】 运 用标数法原理进行标数,整个标数流程如下图从 A 到 G 共有 21 条不同的路线.巩固】 ⑴按下图左箭头方向所指,从 X 到Y 有多少种不同的路线? ⑵如下图右所示,这个问题有一个规则:只能沿着箭头指的方向走,你 能否根据规则算出所有从入口到出口的路径共有多少条?C EBAEB2 1AC GG分析] ⑴利用标数法求得 X 到Y 有34种不同的路线,如下图左所示. ⑵由题将路线图转化为下图右所示,根据标数法求得从入口到出口的路 径共有 10 条.例 12】 ⑴如下图左,如果只允许向下移动,从 A 点到 B 点共有多少种不同的路线?⑵如下图右,要从 A 点到 B 点,要求每一步都是向右,向上或者斜上方, 问共有多少种不同的走法?34Y入口出口5 8 31X13AB解析】⑴按题目要求,只能向下移动,利用标数法求得A到B共有路线68种,如下图左所示.⑵按题目要求,只能走下图右的3个方向,利用标数法求得共有22 种不同的走法,如下图右.巩固】 图中有 10个编好号码的房间, 你可以从小号码房间走到相邻的大号码房 间,但不能从大号码房间走到小号码房间, 从 1号房间走到 10 号房间共 有多少种不同走法?分析】 图 中并没有标出行走的方向,但题中“你可以从小号码房间走到相邻的大号码房间,但不能从大号码房间走到小号码房间”这句话实际上就规 定了行走的方向.如下图所示,我们可以把原图转化成常见的城市网络 图,然后再根据标数法的思想标数:从图中可以看出,从 1 号走到 10号 房间共有 22 种不同的走法.A68 BB 22 16 61例 13】一只密蜂从A处出发,A回到家里B处,每次只能从一个蜂房爬向右侧邻近的蜂房而不准逆行,共有多少种回家的方法?解析】 蜜 蜂“每次只能从一个蜂房爬向右侧邻近的蜂房而不准逆行 ”这意味着它只能从小号码的蜂房爬进相邻的大号码的蜂房.明确了行走路径的方向,就可运用标准法进行计算.如图所示,小蜜蜂从 A 出发到 B 处共有 89种不同的回家方法 .例 14 】 在图中,用水平或垂直的线段连接相邻的字母, 当沿着这些线段行走时,正好拼出“ APPLE ”的路线共有多少条?PP LPP P L E L P分析] 要想拼出英语“ APPLE ”的单词,必须按照“ A P P L E ”的次序拼写.在图中的每一种拼写方式都对应着一条最短路径.如下图所示,运 用标数法原理标数不难得出共有 31 种不同的路径.P P L P P A P L E L P P A1311 2 7 2 11 2 4 15 4 2 1 2 4 8 31 8 4 2 1铺垫]图中的“我爱希望杯”有多少种不同的读法.我 1 爱 1 希 望 1 杯1 1 1 1爱 1 希 2 望 3 杯 41234希 望 杯 希1望1望 3杯4杯6 望 1杯1 4分析] 从我( 1个)、爱( 2个)、希( 3个)、望( 4个)、杯( 5个)中组成“我 爱希望杯”即相同的字只能选一个而且不能重复选,所以共有1 4 6 4116(种).拓展] 如 下图左所示,科学家“爱因斯坦”的英文名拼写为“ Einstein ”,按图中箭头所示方向有多少种不同的方法拼出英文单词“ Einstein ” .1i E1 1 i2 i 1 1s n3 n 3 n 1 t4 s t 6 s t 4 s 10 t 10 t ee 1i 0 2i 0i 10 3n 0 i 3n 0 i分析] 因为“ Einstein ”的拼读顺序为“ E i n s t e i n ”,每一种拼法都 对应着网络图中的一条最短路径,所以可以运用标数法来解决. 如上图右所示,从E 点到n 点的最短路径有 30条,所以共有 30 30 60(种) 不同拼法 . 注意图中的三个字母 “i ”, 左、右的两个字 母“i ”只能由一 个字母。
最短路径问题―――蚂蚁爬行的最短路径

最短路径问题―――蚂蚁爬行的最短路径最短路径问题旨在寻找图(由结点和路径组成的)中两结点之间的最短路径确定起点的最短路径问题:即已知起始结点,求最短路径的问题确定终点的最短路径问题:与确定起点的问题相反,该问题是已知终结结点,求最短路径的问题确定起点终点的最短路径问题- 即已知起点和终点,求两结点之间的最短路径。
而蚂蚁爬行的最短路径是指蚂蚁在平面图形或在几何体中爬行,求其爬行的最短路程。
1.一只蚂蚁从原点0出发来回爬行,爬行的各段路程依次为:+5,-3,+10,-8,-9,+12,-10.回答下列问题:(1)蚂蚁最后是否回到出发点0;(2)在爬行过程中,如果每爬一个单位长度奖励2粒芝麻,则蚂蚁一共得到多少粒芝麻.2.如图,边长为1的正方体中,一只蚂蚁从顶点A出发沿着正方体的外表面爬到顶点B的最短距离是.3.如图,点A、B分别是棱长为2的正方体左、右两侧面的中心,一蚂蚁从点A沿其表面爬到点B的最短路程是cm4.如图,一只蚂蚁从正方体的底面A点处沿着表面爬行到点上面的B点处,它爬行的最短路线是()A.A⇒P⇒B B.A⇒Q⇒B C.A⇒R⇒B D.A⇒S⇒B5.如图,点A的正方体左侧面的中心,点B是正方体的一个顶点,正方体的棱长为2,一蚂蚁从点A沿其表面爬到点B的最短路程是()6.正方体盒子的棱长为2,BC的中点为M,一只蚂蚁从A点爬行到M点的最短距离为()7.如图,点A和点B分别是棱长为20cm的正方体盒子上相邻面的两个中心,一只蚂蚁在盒子表面由A处向B处爬行,所走最短路程是cm。
第2题第8题1A BA1B1D CD1C1248. 正方体盒子的棱长为2,BC的中点为M,一只蚂蚁从A点爬行到M点的最短距离为. 9.如图所示一棱长为3cm的正方体,把所有的面均分成3×3个小正方形.其边长都为1cm,假设一只蚂蚁每秒爬行2cm,则它从下底面点A沿表面爬行至侧面的B点,最少要用秒钟.第9题第10题第11题第12题10.如图,长方体的长为15,宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是。
初中数学中最短路线的解法举隅

解 题方 法与技 巧
初 中数 学 中最 短 路 线 的 解 法 举 隅
广西梧 州市新夏 中学( 4 0 0 黄明梧 530 )
在初 中数学 中, 有一类 问题是求按 满足某些 特定条 件 连 结 , 所 连 结 的 线 段 的 长 度 之 和 最 小 , 之 为 最 短 使 称 路 线. 们 知 道 , 结 两 点 之 间 所 有 的线 中 , 段 最 短 . 我 连 线
三 、 用 旋 转 变 换 的 性 质 利 【 4 如图 4 已知 : 例 】 , AAB . C 求作 : P, 点 使点 P在 △A C内, B 且点 P到AA C三个顶点的距离之和最小. B 作法 :_ AB绕点 B 逆时针 方 向旋 转 6。 B l把 0到 M, 把A C绕点 C顺时针方 向旋转 6。 C 0到 N; 2 连 结 B C 交 于 点 P. . N, M 点 P就是 所求 的点. 证 明 : 点 Q 是 AAB 内 设 C 异 于 点 P 的 任 意 一 点 , 结 连 AQ, Q, Q, △AB 绕 点 B B C 把 Q 逆 时 针 方 向 旋 转 6。 到 O AMB 1 由旋 转 变 换 的性 质 知 : Q, 图 4
—
D
C
l f I A ~ B
Q
/Hale Waihona Puke 图3 C P ) A D 8 C
已知 : 图 , . / b 点 如 b外 侧 B 分 别在 直 线 a, 3 直线 a/ , A,
求作 : C在直线 “上 , D在 直线 6上 , 点 点 并且 C D Jn 使 A +C —, C D+DB最小. 作法 :. t 在直线 a上任取点 C 作 C D 上a 交直线 b ,
运用两点之间线段最短解题

运用两点之间,线段最短解题在数学中,线段最短是一个常见的问题,也是一个重要的几何学概念。
在解决这类问题时,我们通常使用两点之间的距离公式来计算线段的最短距离。
本文将讲解线段最短问题的一般解法,并提供一些实际问题的例子。
首先,我们需要明确线段最短问题的定义。
给定平面上的两个点A(x1, y1)和B(x2, y2),我们的目标是找到通过这两个点的最短路径。
这个路径可以是直线,也可以是曲线,但我们的目标是找到最短路径。
解决线段最短问题的一般步骤如下:1. 计算两点之间的距离:使用两点之间的距离公式可以计算出点A和点B之间的直线距离。
这个公式可以表示为d = √((x2-x1)² + (y2-y1)²)。
这个公式是基于勾股定理的,可以帮助我们计算两点之间的直线距离。
2. 寻找最短路径:在确定了两点之间的距离后,我们需要找到连接这两个点的最短路径。
通常情况下,最短路径是一条直线,但在一些特殊情况下,可能存在其他形状的最短路径。
例如,当两点位于一个圆的直径上时,最短路径将是连接这两个点的弧。
3. 应用最短路径解决实际问题:线段最短问题的应用非常广泛。
在现实生活中,我们可以将两点视为起点和终点,然后计算出两点之间的最短路径,以便规划行程或找到最佳路径。
例如,在城市规划中,我们可以使用线段最短问题来确定两个地点之间的最短路径,以避免交通拥堵或减少行驶距离。
接下来,我们来看几个实际问题的例子,以帮助我们更好地理解线段最短问题的应用。
例子1:旅行规划假设你要从城市A出发,到达城市B。
你可以在地图上找到这两个城市的坐标,并使用两点之间的距离公式计算出它们之间的直线距离。
然后,你可以使用这个距离来规划你的旅行路线,以确保你选择了最短路径。
例子2:电线走向规划在建筑设计中,电线的走向规划非常重要。
假设你需要在一座大楼中将电线从起点传输到终点。
你可以使用线段最短问题来确定电线的最短路径,以减少电线的长度和材料的使用量。
中考查漏补缺----最短路线问题
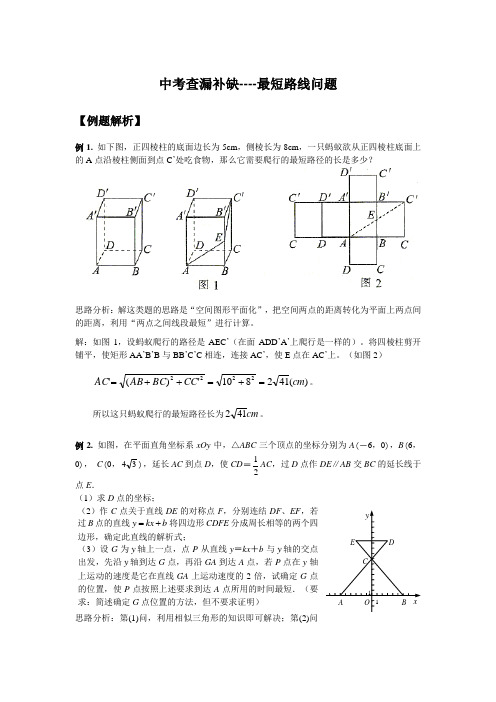
中考查漏补缺----最短路线问题【例题解析】例1. 如下图,正四棱柱的底面边长为5cm ,侧棱长为8cm ,一只蚂蚁欲从正四棱柱底面上的A 点沿棱柱侧面到点C ’处吃食物,那么它需要爬行的最短路径的长是多少?思路分析:解这类题的思路是“空间图形平面化”,把空间两点的距离转化为平面上两点间的距离,利用“两点之间线段最短”进行计算。
解:如图1,设蚂蚁爬行的路径是AEC ’(在面ADD ’A ’上爬行是一样的)。
将四棱柱剪开铺平,使矩形AA ’B ’B 与BB ’C ’C 相连,连接AC ’,使E 点在AC ’上。
(如图2))(412810')('2222cm CC BC AB AC =+=++=。
所以这只蚂蚁爬行的最短路径长为cm 412。
例2. 如图,在平面直角坐标系xO y 中,△ABC 三个顶点的坐标分别为A (-6,0),B (6,0), C (0,34),延长AC 到点D ,使CD =21AC ,过D 点作DE ∥AB 交BC 的延长线于点E .(1)求D 点的坐标;(2)作C 点关于直线DE 的对称点F ,分别连结DF 、EF ,若过B 点的直线y kx b =+将四边形CDFE 分成周长相等的两个四边形,确定此直线的解析式;(3)设G 为y 轴上一点,点P 从直线y =kx +b 与y 轴的交点出发,先沿y 轴到达G 点,再沿GA 到达A 点,若P 点在y 轴上运动的速度是它在直线GA 上运动速度的2倍,试确定G 点的位置,使P 点按照上述要求到达A 点所用的时间最短.(要求:简述确定G 点位置的方法,但不要求证明)思路分析:第(1)问,利用相似三角形的知识即可解决;第(2)问11AByxO CED是平行四边形对角线交点的任意一条直线都可将它的周长和面积平分的问题,所以连结点B 、M 即可;第(3)问, 首先是利用路程、时间与速度的关系将P 点转化为相同的速度,然后根据“化折为直:的思路,利用“点到直线的距离,垂线段最短”转化为求线段和最短问题。
六年级下册奥数试题——最短路线.(含答案)人教版

1. 准确运用“标数法”解决题目.2. 培养学生的实际操作能力.知识点说明从一个地方到另外一个地方,两地之间有许多条路,就有许多种走法,如果你能从中选择一条最近的路走,也就是指要选择一条最短的路线走,这样你就可以节省许多时间了,那么如何能选上最短的路线呢?亲爱的小朋友们,你要记住两点:⑴两点之间线段最短.⑵尽量不走回头路和重复路,这样的话,你就做到了省时省力.【例 1】一只蚂蚁在长方形格纸上的A 点,它想去B 点玩,但是不知走哪条路最近.小朋友们,你能给它找到几条这样的最短路线呢?BA11613321BA IHG F E DC【解析】 (方法一)从A 点走到B 点,不论怎样走,最短也要走长方形AHBD 的一个长与一个宽,因此,在水平方向上,所有线段的长度和应等于AD ;在竖直方向上,所有线段的长度和应等于DB .这样我们走的这条路线才是例题精讲知识精讲教学目标8-8最短路线最短路线.为了保证这一点,我们就不应该走“回头路”,只能向右和向下走.所有最短路线:→→→→→→→→、A E F G B→→→→、A C F G BA C D G B→→→→→→→→、A E H I BA C F I B→→→→、A E F I B这种方法不能保证“不漏”.如果图形再复杂些,做到“不重”也是很困难的.(方法二)遵循“最短路线只能向右和向下走”,观察发现这种题有规律可循.①看C点:只有从A到C的这一条路线.同样道理:从A到D、从A到E、从A到H也都只有一条路线.我们把数字“1”分别标在C D E H、、、这四个点上.②看F点:从A点出发到F,可以是A C F→→,也可以是→→,共有两种走法.那么我们在F点标上数字“2”(2=11+).③A E F看G点:从A G→→→、A C F G→→→、→有三种走法,即:A C D G→→→.在G点标上数字“3”(3=12+).④看I点:共有三种走A E F G法,即:A C F I→→→,在I点标上“3”→→→、A E H I→→→、A E F I(3=12+).⑤看B点:从上向下走是G B→,那么从→,从左向右走是I B 出发点A B→→→→、→→→→、A C F G B→有六种走法,即:A C D G B→→→→、A E H I B→→→→、A E F I B→→→→,→→→→、A C F I BA E F G B在B点标上“6”(633=+),观察发现每一个小格右下角上标的数正好是这个小格右上角与左下角的数的和,这个和就是从出发点A到这点的所有最短路线的条数.此法能够保证“不重”也“不漏”,这种方法叫“对角线法”或“标号法”.【巩固】如图所示,从A点沿线段走最短路线到B点,每次走一步或两步,共有多少种不同走法?AB【解析】 这是一个较复杂的最短路线问题,我们退一步想想,先看看简单的情况.从A 到B 的各种不同走法中先选择一条路线来分析:如果按路线A →C →D →E →F →B 来走,这条路线共有5条线段,每次走一步或两步,要求从A 走到B ,会有几种走法?这不是“上楼梯”问题吗.根据“上楼梯”问题的解法可得在A →C →D →E →F →B 这条路线中有8种符合条件的走法.而对于从A 到B 的其他每条最短路线而言,每一条路线都有5条线段,所以每条路线都有8种走法. 进一步:从A 到B 共有多少条最短路线?这正是“最短路线”问题!用“标数法”来解决,有10条.综上所述,满足条件的走法有81080⨯=种.1032463111111B A BF ED CA BA【巩固】 从A 到B 的最短路线有几条呢?BA【解析】 图中从A 到B 的最短路线都为6条.【巩固】 有一只蜗牛从A 点出发,要沿长方形的边或对角线爬到C 点,中间不许爬回A 点,也不能走重复的路,那么,它有多少条不同的爬行路线?最短的是哪条呢?ODC BA【解析】 共有9种,即:A O C →→、 A O D C A O B C →→→→→→、 、 A B C →→A B O C →→→、 A B O D C →→→→、 A D C →→、 A D O C →→→ A D O B C →→→→,最短的路是:A O C →→.【例 2】阿呆和阿瓜到少年宫参加2008北京奥运会志愿者培训.如果他们从学校出发,共有多少种不 同的最短路线?少年宫学校J I HGF EDC B A 410633211111少年宫学校【解析】 从学校到少年宫的最短路线,只能向右或向下走.我们可以先看A 点:从学校到A 点最短路线只有1种走法,我们在A 点标上1.B 、E 、F 、G 点同理.再看J 点:最短路线可以是A J →、E J →共2条,我们在J 点标上2.我们发现211=+正好是对角线A 点和E 点上的数字和.所有的最短路线都符合这个规律,最终从学校到少年宫共有10种走法.【巩固】 方格纸上取一点A 作为起点,再在A 的右上方任取一点B 作为终点,画一条由A 到B 的最短路线,聪明的小朋友,你能画出来吗?总共能画出几条呢?BA【解析】 根据“标号法”可知共有10种,如图.【巩固】 如图,从F 点出发到G 点,走最短的路程,有多少种不同的走法?GF【分析】 共有115种.【巩固】 小聪明想从北村到南村上学,可是他不知道最短路线的走法共有几种?小朋友们,快帮帮忙呀!南村北村【分析】 根据“对角线法”知共有126种,如图.12656703535216152015105541111南村北村410633211111【例 3】“五一”长假就要到了,小新和爸爸决定去黄山玩.聪明的小朋友请你找找看从北京到黄山的最短路线共有几条呢?黄山北京2黄山北京211410331111722【解析】 采用对角线法(如图)这道题的图形与前几题的图形又有所区别,因此,在解题时要格外注意是由哪两点的数之和来确定另一点的.从北京到黄山最近的道路共有10条.【巩固】 从甲到乙的最短路线有几条?乙甲【解析】 有11条.【例 4】古希腊有一位久负盛名的学者,名叫海伦.他精通数学、物理,聪慧过人.人一天一位将军向他请教一个问题:如下图,将军从甲地骑马出发,要到河边让马饮水,然后再回到乙地的马棚,为了使行走的路线最短,应该让马在什么地方饮水?乙地甲地河流【解析】 本题主要体现最值思想和对称的思想,教师应充分引导孩子观察行走路线的变化情况甲地逐步引导学生通过对称来找到相应的点,进一步了解图形最值问题中应该如何解决问题.【例 5】学校组织三年级的小朋友去帮助农民伯伯锄草,大家从学校乘车出发,去往的李家村(如图).爱动脑筋的嘟嘟就在想,从学校到李家村共有多少种不同的最短路线呢?李家村学校81461025李家村学校235216151051114106331111【解析】 我们采用对角线法(如图),从学校到李家村共有81种不同的最短路线.[拓展] 亲爱的小朋友们,你们觉得从A 到B 共有几条最短路线呢?BA【解析】 此题与上题不同,但方法相同.我们采用对角线法(如图)可知:可以选择的最短路线共有41条.【例 6】阿花和阿红到少年宫参加2008北京奥运会志愿者培训.他们从学校出发到少年宫最多有多少种不同的行走路线?少年宫学校904214482814少年宫学校2651143111114952052【解析】 采用对角线法(如图).可得从学校到少年宫共有90种走法.[铺垫] 小海龟在小猪家玩,它们想去游乐场坐碰碰车,爱动脑筋的小朋友,请你想一想,从小猪家到游乐场共有几条最短路线呢?小猪家游乐场149小猪家游乐场2551114321【解析】 “对角线”法(如图),共14 条.【例 7】阿强和牛牛结伴骑车去图书馆看书,第一天他们从学校直接去图书馆;第二天他们先去公园看大熊猫再去图书馆;第三天公园修路不能通行.咱们学而思的小朋友都很聪明,请你们帮阿强和牛牛想想这三天从学校到图书馆的最短路线分别有多少种不同的走法?【解析】仍然用对角线法求解.第一天(无限制条件)共有16条;第二天(必须经过公园)共有8条;第三天(必须不经过公园)共有8条.【巩固】大熊和美子准备去看望养老院的李奶奶,可是市中心在修路(城市的街道如图所示),他们从学校到养老院最短路线共有几条呢?聪明的小朋友,请你们快想想吧!【解析】(方法一)用“对角线法”求出:从学校到养老院共126条.必经过市中心的60 条,所以可行的路有:1266066-=(条).养老院(方法二)可以直接求,即把含有市中心的田字格挖去,共有66条.664026111010养老院学校2526155111463311115155411【例 8】如图,从X 到Y 最短路线总共有几种走法?【分析】 如图,共有716种.71637434217017220285511536212815218364115878536492836211515101077666554432YX1111111111111【例 9】如图,从A 到B 沿网格线不经过线段CD 和EF 的最短路径的条数是多少条?A C DE FB【解析】 由于不能经过线段CD 和EF ,所以我们必须先在网络图中拆除CD 和EF ,然后再在拆除了CD 和EF 以后的网络图中进行标数(如下图所示).运用标数法可求出满足条件的最短路径有78条.【巩固】 下图为某城市的街道示意图,C 处正在挖下水道,不能通车,从A 到B 处的最短路线共有多少条?【解析】 从A 到B 的最短路线有431条.CBA174551999558325743117411030552518121211C BA836410776543211111111【例 10】 按图中箭头所指的方向行走,从A 到I共有多少条不同的路线?CF H DIGE B A【解析】 本题中的运动方向已经由箭头标示出来,所以关键要分析每一点的入口情况.通过标数法我们可以得出从A 到I 共有29条不同的路径.【例 11】 按图中箭头方向所指行走,从A 到G 有多少种不同的路线?GF E DC B A【解析】 运用标数法原理进行标数,整个标数流程如下图2181AB CD EF G 2351313532GF ED CB A1881AB CDE F G2355332GF E D CB A11AB CDE F G22GF E DC B A11AB C DE F G从A 到G 共有21条不同的路线.【巩固】 ⑴按下图左箭头方向所指,从X到Y 有多少种不同的路线?⑵如下图右所示,这个问题有一个规则:只能沿着箭头指的方向走,你能否根据规则算出所有从入口到出口的路径共有多少条?[分析]⑴利用标数法求得X到Y有34种不同的路线,如下图左所示.⑵由题将路线图转化为下图右所示,根据标数法求得从入口到出口的路径共有10条.出口1【例 12】⑴如下图左,如果只允许向下移动,从A点到B点共有多少种不同的路线?⑵如下图右,要从A点到B点,要求每一步都是向右,向上或者斜上方,问共有多少种不同的走法?ABBA【解析】⑴按题目要求,只能向下移动,利用标数法求得A到B共有路线68种,如下图左所示.⑵按题目要求,只能走下图右的3个方向,利用标数法求得共有22种不同的走法,如下图右.2622166111201010644143468341444332111111A BB A 42622166111B A【巩固】 图中有10个编好号码的房间,你可以从小号码房间走到相邻的大号码房间,但不能从大号码房间走到小号码房间,从1号房间走到10号房间共有多少种不同走法?10987654321【分析】 图中并没有标出行走的方向,但题中“你可以从小号码房间走到相邻的大号码房间,但不能从大号码房间走到小号码房间”这句话实际上就规定了行走的方向.如下图所示,我们可以把原图转化成常见的城市网络图,然后再根据标数法的思想标数:从图中可以看出,从1号走到10号房间共有22种不同的走法.【例 13】 一只密蜂从A 处出发,A 回到家里B 处,每次只能从一个蜂房爬向右侧邻近的蜂房而不准逆行,共有多少种回家的方法?BA864297531【解析】 蜜蜂“每次只能从一个蜂房爬向右侧邻近的蜂房而不准逆行”这意味着它只能从小号码的蜂房爬进相邻的大号码的蜂房.明确了行走路径的方向,就可运用标准法进行计算.如图所示,小蜜蜂从A 出发到B 处共有89种不同的回家方法.【例 14】 在图中,用水平或垂直的线段连接相邻的字母,当沿着这些线段行走时,正好拼出“APPLE ”的路线共有多少条?AAPPLELPPA A P L P P P A A P P P A A P A[分析] 要想拼出英语“APPLE ”的单词,必须按照“A P P L E →→→→”的次序拼写.在图中的每一种拼写方式都对应着一条最短路径.如下图所示,运用标数法原理标数不难得出共有31种不同的路径.131127211224154112283184411AAPPLELPPA A P L P P P A A P P P A A P A[铺垫] 图中的“我爱希望杯”有多少种不同的读法.望杯望杯希杯爱望希杯杯望希爱我 杯杯杯杯杯望望望希希希爱爱我644332111111111[分析] 从我(1个)、爱(2个)、希(3个)、望(4个)、杯(5个)中组成“我爱希望杯”即相同的字只能选一个而且不能重复选,所以共有1464116++++=(种).[拓展] 如下图左所示,科学家“爱因斯坦”的英文名拼写为“Einstein ”,按图中箭头所示方向有多少种不同的方法拼出英文单词“Einstein ”.i111111i[分析] 因为“Einstein ”的拼读顺序为“E i n s t e i n →→→→→→→”,每一种拼法都对应着网络图中的一条最短路径,所以可以运用标数法来解决. 如上图右所示,从E 点到n 点的最短路径有30条,所以共有303060+=(种)不同拼法.注意图中的三个字母“i ”,左、右的两个字母“i ”只能由一个字母“e ”去到达.。
一个圆柱表面最短路径问题的解决汇总
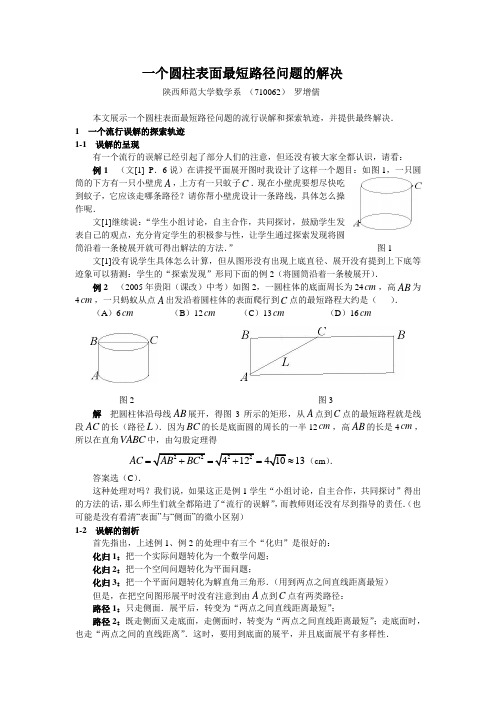
一个圆柱表面最短路径问题的解决陕西师范大学数学系(710062)罗增儒本文展示一个圆柱表面最短路径问题的流行误解和探索轨迹,并提供最终解决.1 一个流行误解的探索轨迹1-1 误解的呈现有一个流行的误解已经引起了部分人们的注意,但还没有被大家全都认识,请看:例1 (文[1] P.6说)在讲授平面展开图时我设计了这样一个题目:如图1,一只圆筒的下方有一只小壁虎A,上方有一只蚊子C.现在小壁虎要想尽快吃到蚊子,它应该走哪条路径?请你帮小壁虎设计一条路线,具体怎么操作呢.文[1]继续说:“学生小组讨论,自主合作,共同探讨,鼓励学生发表自己的观点,充分肯定学生的积极参与性,让学生通过探索发现将圆筒沿着一条棱展开就可得出解法的方法.”图1 文[1]没有说学生具体怎么计算,但从图形没有出现上底直径、展开没有提到上下底等迹象可以猜测:学生的“探索发现”形同下面的例2(将圆筒沿着一条棱展开).例2(2005年贵阳(课改)中考)如图2,一圆柱体的底面周长为24cm,高AB为4cm,一只蚂蚁从点A出发沿着圆柱体的表面爬行到C点的最短路程大约是().(A)6cm(B)12cm(C)13cm(D)16cm图2 图3解把圆柱体沿母线AB展开,得图3所示的矩形,从A点到C点的最短路程就是线段AC的长(路径L).因为BC的长是底面圆的周长的一半12cm,高AB的长是4cm,所以在直角ABC中,由勾股定理得AC==≈(cm).13答案选(C).这种处理对吗?我们说,如果这正是例1学生“小组讨论,自主合作,共同探讨”得出的方法的话,那么师生们就全都陷进了“流行的误解”,而教师则还没有尽到指导的责任.(也可能是没有看清“表面”与“侧面”的微小区别)1-2 误解的剖析首先指出,上述例1、例2的处理中有三个“化归”是很好的:化归1:把一个实际问题转化为一个数学问题;化归2:把一个空间问题转化为平面问题;化归3:把一个平面问题转化为解直角三角形.(用到两点之间直线距离最短)但是,在把空间图形展平时没有注意到由A点到C点有两类路径:路径1:只走侧面.展平后,转变为“两点之间直线距离最短”;路径2:既走侧面又走底面,走侧面时,转变为“两点之间直线距离最短”;走底面时,也走“两点之间的直线距离”.这时,要用到底面的展平,并且底面展平有多样性.“流行的误解”就在于只看到第一类路径,没有看到第二类路径(逻辑漏洞1),更没有看到第二类路径的多样性(逻辑漏洞2,参见下文的讨论).如图4,将圆柱的侧面展开为矩形、上底面展开为母线AB 上方的圆,由“两点之间直线距离最短”可以得到两条直线距离:第一条,如例2所述,是沿侧面展平后的直线距离,有11L AC ===第二条,是先沿侧面走母线AB ,然后走圆的直径BC ,展平后有22244L AB BC π=+=+.由于242444123π+<+=<2L 比1L 更小.例2的答案是错误的. 图4那么,是不是任何情况下都有21L L <呢?请看反例.例3 如图2,一圆柱体的底面周长为16cm ,高AB 为4cm ,一只蚂蚁从点A 出发沿着圆柱体的表面爬行到C 点的最短路程是 cm .解 如图4,沿用例2的解法,有11L AC ====22164L AB BC π=+=+,但161644453.2π+>+=+=>=21L L >. 那么,什么时候1L 小、什么时候2L 小呢?1-3 误解的流行“解决”考虑更一般性的情况.例4 如图2,一圆柱体的底面周长为2r πcm ,高AB 为h cm ,一只蚂蚁从点A 出发沿着圆柱体的表面爬行到C 点,求最短路程.解 如图4,沿用例2的解法,有11L AC ===222L AB BC h r =+=+. 分三种情况讨论:(1)12L L =⇔2424r h r h π=+⇔=-.(2)12L L <⇔2424r h r h π<+⇔<-.(3)12L L >⇔2424r h r h π>+⇔>- 记常数240.6814π≈-为a ,可见,1L 与2L 的大小关系有三种情况:当ra h<时,沿侧面爬行的路程最短,为1L =r a h >时,先竖直向上爬到A 的正上方,再沿直径爬到C 点的路程最短,为22L h r =+;当ra h=时,两种爬行方式的路程一样.看上去,这种讨论已经很细致了,文[2]进行到这里时,“教室响起了热烈的掌声”.误认为问题已彻底解决的类似认识在文[3]等处也可以看到,然而,这依然有逻辑的漏洞——为什么只有这两条路径呢? 1-4 误解的继续探索事实上,蚂蚁从点A 出发沿着圆柱体的表面爬行到C 点的路径,除了以上12,L L 两种之外,还存在无穷多条从A 到C 的路径.如图5所示:A D C →→,其中AD 是侧面上的最短距离(侧面展平后的直线距离),DC 是上底面两点之间的直线距离,A 、D 、C 也有可能三点共线.文[4]清楚看到了这一点,也列出了相关函数式(以DOC α=∠为自变量)()21cos L αα=-但由于“涉及到一些较复杂的函数”,故仅“采用几何画板进行辅助探究”,“无法代替”证明. 图5以上,就是人们对圆柱表面最短路径的认识轨迹(限于个人所见,疏漏在所难免),本文的目的是在简要展示的基础上,继续完成理论证明.2 最短路径的的理论解决 2-1 建立函数关系如图6,考虑例4.设圆心角BOD α∠=,0απ≤≤,则BD r α=,展平后,D 为圆与矩形的切点,3L 为折线ADC ,在直角ABD 中,有AD ==在COD 中用余弦定理,有2cos2CD r α===,得3L 的长度为(α的函数)()2cos2S AD CD r αα=+=,(0απ≤≤).当0α=时,()202L S h r ==+,当απ=时,()1L S π==下面,我们来讨论3L 的最值.图62-2 求导数令()/0Sα=当0απ<<时,对()S α求导,有()2/sin2S r αα=-.令()/0Sα=,并连续变形,有s i n 2α=,()222222sin 2r h r ααα=+,22222cos sin 22r h ααα=,cossin22r h ααα=,tan 2r h αα=. ① 在展开()/0Sα=(即①式)的讨论之前,我们先来认识①式的几何意义,如图7所示,图7首先,在等腰3DOC 中,由外角定理有 32ODC α∠=.其次,在Rt ABD 中,由 tan tan 2BD r BAD AB h αα∠===, 可得 32BAD ODC α∠==∠.又由O 与矩形的边(BD )相切知2BDO π∠=,得33ADC ADB BDO ODC ∠=∠+∠+∠ 2ADB BAD ππ=∠++∠=,即3,,A D C 三点共线.可见, ()/30tan ,,2r S A D C h ααα=⇔=⇔三点共线. 2-3 ()/0Sα=的讨论分两种情况讨论: (1)当21rh≤时.把式①变为 tan222r hαα=. 由不等式sin tan x x x <<(02xπ<)知tan212αα>,所以tan2212r h αα>≥,()()222222222222/sincos,22sin cos ,22sin ,2sin2sin0,2h r h r h r r S r αααααααααααα⇒>⇒>⇒+>⇒>⇒=-<得()2cos2S r αα=为减函数,当απ=时,取最小值()1L S π== ②(2)当21r h >时.易知()tan x f x x =(02x π<<)为增函数,且值域为()1,+∞,故存在()00,απ∈,使tan222rhαα=,即存在()00,απ∈,使()/00Sα=.又当00ααπ<<<时,有00222ααπ<<<,且0tantan22222r hαααα=>, ()()222222222222/cossin,22cos sin ,22sin ,2sin ,2sin0,2r h r h r h r S r αααααααααααα⇒>⇒>⇒>+⇒>⇒=>函数()S α在()00,α上为增函数.当00ααπ<<<时,有00222ααπ<<<,且0tantan22222r hαααα=< ()2/cossin,22sin0,2r h S r ααααα⇒<⇒=<函数()S α在()0,απ上为减函数.可见,0αα=时,函数()S α取极大值,也是()0,π上的最大值. 所以,21rh>时函数()S α的最小值为 ()(){}min 0,S S π. 对此再分三种情况讨论: (1)当2284r h π>-2h r >+,得 ()(){}min 0,S S π=2h r +; ③(2)当2284r h π=-2h r =+,得 ()(){}min 0,S Sπ=2h r =+; ④(3)当22814r h π<<-2h r <+,得 ()(){}min 0,S S π= ⑤2-4 函数()S α最小值的结论综合②、③、④、⑤得:(1)当244r h π>-时,()S α的最小值为()0S =2h r +; (2)当244r h π=-时,()S α最小值为()()0S S π==2h r =+;(3)当244r h π<-时,()S α最小值为()Sπ=此处的结果与§1-3相同,但逻辑路径不一样. 参考文献1 苏嘉玲.初一数学教学应注意“首因效应”,防止厌学、弃学情绪的产生与蔓延——基于中小学数学教学衔接的初步研究.中学数学研究,2011,102 费孝文.探求蚂蚁爬行的最短线路.中学数学教学参考(中旬),2010,1~23 秦大忠.蚂蚁爬出的一个数.数学教学通讯,2005,8P794 徐伟.再谈蚂蚁爬行试探最短路程.中学数学,2010,4数学通报2012,3P42:圆台上蚂蚁爬出最短路径问题。
(完整)小学奥数最短路线问题(有答案)

小学六年级奥数教案—运筹学初步 本讲主要讲统筹安排问题、排队问题、最短路线问题、场地设置问题等。
这些都是人们日常生活、工作中经常碰到的问题,怎样才能把它们安排得更合理,多快好省地办事,就是这讲涉及的问题。
当然,限于现有的知识水平,我们仅仅是初步探索一下。
1.统筹安排问题 例1星期天妈妈要做好多事情。
擦玻璃要20分钟,收拾厨房要15分钟,洗脏衣服的领子、袖口要10分钟,打开全自动洗衣机洗衣服要40分钟,晾衣服要10分钟。
妈妈干完所有这些事情最少用多长时间? 分析与解:如果按照题目告诉的几件事,一件一件去做,要95分钟。
要想节约时间,就要想想在哪段时间里闲着,能否利用闲着的时间做其它事。
最合理的安排是:先洗脏衣服的领子和袖口,接着打开全自动洗衣机洗衣服,在洗衣服的40分钟内擦玻璃和收拾厨房,最后晾衣服,共分钟(见下图)。
需60 例1告诉我们,当有许多事要做时,科学地安排好先后顺序,就能用较少的时间完成较多的事情。
2.排队问题 例2理发室里有甲、乙两位理发师,同时来了五位顾客,根据他们所要理的发型,分别需要10,12,15,20和24分钟。
怎样安排他们的理发顺序,才能使这五人理发和等候所用时间的总和最少?最少要用多少时间? 分析与解:一人理发时,其他人需等待,为使总的等待时间尽量短,应让理发所需时间少的人先理。
甲先给需10分钟的人理发,然后15分钟的,最后24分钟的;乙先给需12分钟的人理发,然后20分钟的。
甲给需10分钟的人理发时,有2人等待,占用三人的时间和为(10×3)分;然后,甲给需 15分钟的人理发,有 1人等待,占用两人的时间和为(15×2)分;最后,甲给需 24分钟的人理发,无人等待。
甲理发的三个人,共用(10×3+15×2+24)分,乙理发的两个人,共用(12×2+20)分。
总的占用时间为 (10×3+15×2+24)+(12×2+20)=128(分)。
运筹学最短路问题及程序

运筹学最短路问题----------关于旅游路线最短及程序摘要:随着社会的发展,人民的生活水平的提高,旅游逐渐成为一种时尚,越来越多的人喜欢旅游。
而如何才能最经济的旅游也成为人民考虑的一项重要环节,是选择旅游时间最短,旅游花费最少还是旅游路线最短等问题随之出现,如何决策成为一道难题。
然而,如果运用运筹学方法来解决这一系列的问题,那么这些问题就能迎刃而解。
本文以旅游路线最短问题为列,给出问题的解法,确定最短路线,实现优化问题。
关键词:最短路 0-1规划约束条件提出问题:从重庆乘飞机到北京、杭州、桂林、哈尔滨、昆明五个城市做旅游,每个城市去且仅去一次,再回到重庆,问如何安排旅游线路,使总旅程最短。
各城市之间的航线距离如下表:重庆北京杭州桂林哈尔滨昆明重庆0 1640 1500 662 2650 649北京1640 0 1200 1887 1010 2266杭州1500 1200 0 1230 2091 2089桂林662 1887 1230 0 2822 859哈尔滨2650 1010 2091 2822 0 3494昆明649 2266 2089 859 3494 0问题分析:1.这是一个求路线最短的问题,题目给出了两两城市之间的距离,而在最短路线中,这些城市有的两个城市是直接相连接的(即紧接着先后到达的关系),有些城市之间就可能没有这种关系,所以给出的两两城市距离中有些在最后的最短路线距离计算中使用到了,有些则没有用。
这是一个0-1规划的问题,也是一个线性规划的问题。
2.由于每个城市去且仅去一次,最终肯定是形成一个圈的结构,这就导致了这六个城市其中有的两个城市是直接相连的,另外也有两个城市是不连接的。
这就可以考虑设0-1变量,如果两个城市紧接着去旅游的则为1,否则为0。
就如同下图3. 因为每个城市只去一次,所以其中任何一个城市的必有且仅有一条进入路线和一条出去的路线。
解法:为了方便解题,给上面六个城市进行编号,如下表(因为重庆是起点,将其标为1)重庆北京杭州桂林哈尔滨昆明123456假设:设变量x11。
最短路径问题的算法分析及建模案例

最短路径问题的算法分析及建模案例一.摘要 (2)二.网络最短路径问题的基础知识 (2)2.1有向图 (3)2.2连通性 (4)2.3割集 (5)2.4最短路问题 (6)三.最短路径的算法研究 (6)3.1最短路问题的提出 (6)3.2 Bellman最短路方程 (6)3.3 Bellman-Ford算法的基本思想 (7)3.4 Bellman-Ford算法的步骤 (7)3.5实例 (7)3.6 Bellman-FORD算法的建模应用举例 (8)3.7 Dijkstra算法的基本思想 (11)3.8 Dijkstra算法的理论依据 (11)3.9 Dijkstra算法的计算步骤 (11)3.10 Dijstre算法的建模应用举例 (11)3.11 两种算法的分析 (13)1.Diklstra算法和Bellman-Ford算法思想有很大的区别 (13)Bellman-Ford算法在求解过程中,每次循环都要修改所有顶点的权值,也就是说源点到各顶点最短路径长度一直要到Bellman-Ford算法结束才确定下来。
(14)2.Diklstra算法和Bellman-Ford算法的限制 (14)3.Bellman-Ford算法的另外一种理解 (14)4.Bellman-Ford算法的改进 (14)摘要近年来计算机发展迅猛,图论的研究也得到了很大程度的发展,而最短路径问题一直是图论中的一个典型问题,它已应用在地理信息科学,计算机科学等诸多领域。
而在交通路网中两个城市之间的最短行车路线就是最短路径问题的一个典型例子。
由于最短路径问题在各方面广泛应用,以及研究人员对最短路径的深入研究,使得在最短路径问题中也产生了很多经典的算法。
在本课题中我将提出一些最短路径问题的算法以及各算法之间的比较,最后将这些算法再应用于实际问题的建模问题中。
关键词:计算机图论交通道路网最短路径A. In this paper,Computer developing rapidly in recent years, graph theory research also have been greatly developed, and the shortest path problem is a typical problem in graph theory, it has been applied in geographical information science, computer science, and many other fields. And in the transportation network of the shortest route between two cities in is a typical example of the shortest path problem.Due to the shortest path problem is widely used in various aspects, and the researchers on the in-depth study of the shortest path, make in the shortest path problem also generates a lot of classical algorithm. In this topic I'll suggest some algorithm and the algorithm of the shortest path problem between the comparison, finally the algorithm is applied to the modeling of the actual problem again. Key words: computer graph traffic road network The shortest path前言最短路径问题是图论以及运筹学中的一个非常重要的问题,在生产实践,运输及工程建筑等方面有着十分广泛的应用。
