1.1平面直角坐标系与坐标法ppt课件
合集下载
平面直角坐标系ppt优秀课件

益。──高尔基 • ● 生活就像海洋,只有意志坚强的人,才能到达彼岸。──马克思 • ● 浪费别人的时间是谋财害命,浪费自己的时间是慢性自杀。──列
宁
• ● 哪里有天才,我是把别人喝咖啡的工夫都用在工作上的。──鲁迅 • ● 完成工作的方法,是爱惜每一分钟。──达尔文 • ● 没有伟大的愿望,就没有伟大的天才。──巴尔扎克 • ● 读一切好的书,就是和许多高尚的人说话。──笛卡尔 • ● 成功=艰苦的劳动+正确的方法+少谈空话。 ──爱因斯坦
y
4
(4)单位长度一般
3 2
取相同的
1
-3 -2 -1-1 O1 2 3
x
-2
-3 -4
选择:下面四个图形中,是平面直角坐标系的是( D )
Y
Y
2
1
-3 -2 -1 O1 2 3
X
X
3 2 1 O -1 -2 -3 -1
-2
(A)
(B)
3Y 2 1
-3 -2 -1-1 O1 2 3 X
-2 -3
3Y 2 1
则a=_4__,b=_5___。
6.在平面直角坐标系内,已知点P ( a , b ), 且a b < 0 , 则点P的位置在__第__二__或__四__象__限。
7.如果同一直角坐标系下两个点的横坐标相同,
那么过这两点的直线( B )
(A)平行于x轴 (B)平行于y轴 (C)经过原点 (D)以上都不对
· 纵轴 y 5
B(0,5)
4
3 2
·A(5,2)
1
-4 -3 (-2,-3)D
-3
-4
·C(2,-3)
例3.在下面直角坐标系中描出下列各组点,
并将各组的点用线段依次连接起来.
宁
• ● 哪里有天才,我是把别人喝咖啡的工夫都用在工作上的。──鲁迅 • ● 完成工作的方法,是爱惜每一分钟。──达尔文 • ● 没有伟大的愿望,就没有伟大的天才。──巴尔扎克 • ● 读一切好的书,就是和许多高尚的人说话。──笛卡尔 • ● 成功=艰苦的劳动+正确的方法+少谈空话。 ──爱因斯坦
y
4
(4)单位长度一般
3 2
取相同的
1
-3 -2 -1-1 O1 2 3
x
-2
-3 -4
选择:下面四个图形中,是平面直角坐标系的是( D )
Y
Y
2
1
-3 -2 -1 O1 2 3
X
X
3 2 1 O -1 -2 -3 -1
-2
(A)
(B)
3Y 2 1
-3 -2 -1-1 O1 2 3 X
-2 -3
3Y 2 1
则a=_4__,b=_5___。
6.在平面直角坐标系内,已知点P ( a , b ), 且a b < 0 , 则点P的位置在__第__二__或__四__象__限。
7.如果同一直角坐标系下两个点的横坐标相同,
那么过这两点的直线( B )
(A)平行于x轴 (B)平行于y轴 (C)经过原点 (D)以上都不对
· 纵轴 y 5
B(0,5)
4
3 2
·A(5,2)
1
-4 -3 (-2,-3)D
-3
-4
·C(2,-3)
例3.在下面直角坐标系中描出下列各组点,
并将各组的点用线段依次连接起来.
《平面直角坐标系》课件(共20张PPT)

13、He who seize the right moment, is the right man.谁把握机遇,谁就心想事成。2021/9/182021/9/182021/9/182021/9/189/18/2021 •14、谁要是自己还没有发展培养和教育好,他就不能发展培养和教育别人。2021年9月18日星期六2021/9/182021/9/182021/9/18 •15、一年之计,莫如树谷;十年之计,莫如树木;终身之计,莫如树人。2021年9月2021/9/182021/9/182021/9/189/18/2021 •16、教学的目的是培养学生自己学习,自己研究,用自己的头脑来想,用自己的眼睛看,用自己的手来做这种精神。2021/9/182021/9/18September 18, 2021 •17、儿童是中心,教育的措施便围绕他们而组织起来。2021/9/182021/9/182021/9/182021/9/18
• You have to believe in yourself. That's the secret of success. 人必须相信自己,这是成功的秘诀。
•
4、如果以中心 广场为原点呢?
.
北
(-2,1) (3,1)
. . 雁塔
碑林
. (-2,-1)中 心 广 场 .大 成 殿
.. . (-1,-3) 影月楼 科技大学
B(0,-3) D(4,0) F(0,3)
思考 对比
1.平面直角坐标系中,点P(3,5)与Q(5,3) 是同一个点吗?
2.在平面直角坐标系下,点与实数对之间有何 关系?
*3.引入平面直角坐标系,有什么好处?
发现 归纳
• 在直角坐标系中,对于平面上的任意一点, 都有唯一的一对有序实数对(即点的坐标) 与它对应;
• You have to believe in yourself. That's the secret of success. 人必须相信自己,这是成功的秘诀。
•
4、如果以中心 广场为原点呢?
.
北
(-2,1) (3,1)
. . 雁塔
碑林
. (-2,-1)中 心 广 场 .大 成 殿
.. . (-1,-3) 影月楼 科技大学
B(0,-3) D(4,0) F(0,3)
思考 对比
1.平面直角坐标系中,点P(3,5)与Q(5,3) 是同一个点吗?
2.在平面直角坐标系下,点与实数对之间有何 关系?
*3.引入平面直角坐标系,有什么好处?
发现 归纳
• 在直角坐标系中,对于平面上的任意一点, 都有唯一的一对有序实数对(即点的坐标) 与它对应;
1.1平面直角坐标系 (共31张PPT)

问题一:从点的轨迹角度分析点P应该在什么样的曲线上? 问题二:请你在图中建立适当的坐标系,并说明你所建立 坐标系的依据是什么? 问题三:根据你所建立的坐标系,求出点P的坐标
问题四:在该坐标系中,说出点P在信息中心点的什么位置?
Office组件之word2007
某中心接到其正东、正西、正北方向三个观测点的报告:正西 、正北两个观测点同时听到一声巨响,正东观测点听到巨响的时 间比其他两个观测点晚4s,已知各观测点到中心的距离都是1020m ,试确定该巨响的位置。(假定当时声音传播的速度为 340m/s, 各相关点均在同一平面上)
E
因此,BE与CF互相垂直.
O (A)
F
B
x
数学运用
Office组件之word2007
例3. 某地区原计划经过B地沿着东北方向修建一条 高速公路,但在A村北偏西300方向距A村500m处 ,发现一古代文物遗址W。经过初步勘察,文物管 理部门将遗址W周围200m范围划为禁区,已知B 地位于A村的正西方向1km 处,试问:修建高速公 y y 路和计划需要修改吗? C 解决问题的关键: 确定遗址W与高速公路BC的 相对位置.
W
500
0 0 B 45 1000 60 A x O O
Office组件之word2007
课堂小结
平面直角坐标系建系时,根据几何特点选 择适当的直角坐标系。
(1)如果图形有对称中心,可以选对称中心为 坐标原点; (2)如果图形有对称轴,可以选择对称轴为坐 标轴; (3)使图形上的特殊点尽可能多的在坐标轴上 。
y
B
P o
C Ax
Office组件之word2007
解: 以接报中心为原点O,以BA方向为x轴,建立直角坐标系. 设A、B、C分别是西、东、北观测点, 则 A(1020,0), B(-1020,0), C(0,1020)
说课课件平面直角坐标系ppt.ppt

4.合作交
流,
探索新知
平面直角坐标系
y
6
5
第二象限 4 3
y轴或纵轴 第一象限
2
1 原点
x轴或横轴
-6 -5 -4 -3 -2 -1-o1
-2
第三象限 -3
理解概念
-4
1 23 4 5 6 X
第四象限
-5
-6
①两条数轴 ②互相垂直 叫平面直角坐标系
③公共原点
从使用情况来看,闭胸式的使用比较 广泛。 敞开式 盾构之 中有挤 压式盾 构、全 部敞开 式盾构 ,但在 近些年 的城市 地下工 程施工 中已很 少使用 ,在此 不再说 明。
设计意图:
教材是线索, 教师不只是 课程的执行 者,更是课 程的开发者, 适当介绍一 些数学史, 可以激发学 生热爱科学、 投身科学与 学习数学的 兴趣。
从使用情况来看,闭胸式的使用比较 广泛。 敞开式 盾构之 中有挤 压式盾 构、全 部敞开 式盾构 ,但在 近些年 的城市 地下工 程施工 中已很 少使用 ,在此 不再说 明。
四、评价分析
从使用情况来看,闭胸式的使用比较 广泛。 敞开式 盾构之 中有挤 压式盾 构、全 部敞开 式盾构 ,但在 近些年 的城市 地下工 程施工 中已很 少使用 ,在此 不再说 明。
一、内容分析和教学目标
1、教材分析
“平面直角坐标系”是“数轴”的发 展,它的建立,使代数的基本元素(数 对)与几何的基本元素(点)之间产生一 一对应,实现了认识上从一维空间到 二维空间的发展,构成更广阔的范围 内的数形结合、互相转化的理论基础。 因此,平面直角坐标系是沟通代数和 几何的桥梁,是非常重要的数学工具。
比比看:
“标点”与“报坐标” 比赛:
流,
探索新知
平面直角坐标系
y
6
5
第二象限 4 3
y轴或纵轴 第一象限
2
1 原点
x轴或横轴
-6 -5 -4 -3 -2 -1-o1
-2
第三象限 -3
理解概念
-4
1 23 4 5 6 X
第四象限
-5
-6
①两条数轴 ②互相垂直 叫平面直角坐标系
③公共原点
从使用情况来看,闭胸式的使用比较 广泛。 敞开式 盾构之 中有挤 压式盾 构、全 部敞开 式盾构 ,但在 近些年 的城市 地下工 程施工 中已很 少使用 ,在此 不再说 明。
设计意图:
教材是线索, 教师不只是 课程的执行 者,更是课 程的开发者, 适当介绍一 些数学史, 可以激发学 生热爱科学、 投身科学与 学习数学的 兴趣。
从使用情况来看,闭胸式的使用比较 广泛。 敞开式 盾构之 中有挤 压式盾 构、全 部敞开 式盾构 ,但在 近些年 的城市 地下工 程施工 中已很 少使用 ,在此 不再说 明。
四、评价分析
从使用情况来看,闭胸式的使用比较 广泛。 敞开式 盾构之 中有挤 压式盾 构、全 部敞开 式盾构 ,但在 近些年 的城市 地下工 程施工 中已很 少使用 ,在此 不再说 明。
一、内容分析和教学目标
1、教材分析
“平面直角坐标系”是“数轴”的发 展,它的建立,使代数的基本元素(数 对)与几何的基本元素(点)之间产生一 一对应,实现了认识上从一维空间到 二维空间的发展,构成更广阔的范围 内的数形结合、互相转化的理论基础。 因此,平面直角坐标系是沟通代数和 几何的桥梁,是非常重要的数学工具。
比比看:
“标点”与“报坐标” 比赛:
《平面直角坐标系》课件(共21张PPT)

C
A.
F 点(0,3)在____轴上;
点(3,-2)在第_____象限;
B
(0,3),(-2,0),(6,0) ,
两条互相垂直且有公共原点的数轴
(1)线段 AG 上的点都在 x 轴上,它们的纵坐标等于0;
G 原点 轴正半轴 C.
这四组点关于直线x=2对称.
A
连接起来的图形像“房子” (0,3),(-2,0),(6,0) ,
观察所描出的图形,它像什么?
y
连接起来的图形像“房子” D
E
C
F
B
G
oA
x
① D(- 3,5),E(- 7,3), C(1,3),D(- 3,5);
② F(- 6,3),G(- 6,0), A(0,0),B(0,3); -1
y
D
与y轴平行的直线上点的坐标的特征
E ③(1,0),(1,-6),
若点 P(2m - 1,3)在第二象限,则( )
o
若点P(m+5,m-2)在y轴上,则m=
.
x
解答下列问题: ① D(- 3,5),E(- 7,3),
若点P在第三象限且到x轴的距离为 2 ,
(1)若CA平行于x轴,BC平行于y轴,则点C的
(1)图形中哪些点在坐标轴上,它们的坐标有什么特点? 已知线段AB=3,AB∥x轴,若A点坐标为
(1)线段 AG 上的点都在 x 轴上,它们的纵坐标等于0;
纵轴上的点横坐标为0.
若点 P(2m - 1,3)在第二象限,则( )
A.
(-1,-3),(2,-1),(-3,4)这些点所在的象限,说说你是怎么判断的.
① D(- 3,5),E(- 7,3),
③(1,0),(1,-6),
人教A版数学【选修4-4】ppt课件:1-1第一讲-坐标系

【分析】
解决这一问题的关键,在于确定遗址 W 与地下管
线 m 的位置关系, 即求出 W 到直线 m 的距离 d 与 100 米进行比较.
【解】 依题意,以 A 点为原点,正东方向和正北方向分别为 x 轴和 y 轴的正方向,建立平面直角坐标系.如下图.
则 A(0,0),B(-1 000,0),由|AW|=400,得
∴水面与抛物线拱顶相距 3 5 3 |y|+ = + =2(m). 4 4 4 即水面上涨到与抛物线形拱顶相距 2 m 时,船开始不能通航.
【例 2】 用解析法证明:任意四边形两组对边中点连线及两 对角线中点连线三线共点,且互相平分.
【证明】 如下图所示,建立直角坐标系.设四边形各点的坐 标分别为 A(0,0),B(a,0),C(b,c),(d,e).
2 2 2 2 2
1 1 ∴λ=3,μ=2. 1 x′=3x, ∴ y′=1y, 2 1 即将椭圆 4x +9y =36 上的所有点的横坐标变为原来的 ,纵 3
2 2
1 坐标变为原来的 ,即可得到圆 x′2+y′2=1. 2
规律技巧
求满足图象变换的伸缩变换, 实际上是让我们求出
变换公式,将新旧坐标分清,代入对应的曲线方程,然后比较系数 可得.
2.坐标法的应用 (1)坐标法的基本思想就是在平面上引进“坐标”的概念,建 立平面上的点和坐标之间的一一对应,从而建立曲线的方程,并通 过方程研究曲线的性质. (2)坐标法解决几何问题的“五步骤”: ①建立适当的平面直角坐标系,设动点 M(x,y); ②根据题设条件,找出动点 M 满足的等量关系式;
第一讲 坐标系
一 平面直角坐标系
课前预习目标
课堂互动探究
课前预习目标
梳理知识 夯实基础
平面直角坐标系ppt
–3
–4
–5
–6 y(图1)
(–16, 5)
(5, 5)
5
D
C
4
3
1
x –6 –5 –4 –3 –2 –1 O 1 2 3 4 5 6 7
(–3, –2) –1
(3, –2)
–2
A
B
–3
–4
–5
–6 y (图2) 6
5
4
(–3, 3)D3来自(3, 3) C2
2
1
–7 –6 –5 –4 –3 –2 –1 O 1 2 3 4 5 6 7
A.平行于y轴 B.平行于x轴 C.与y轴相交 D.无法确定
4、P(-2,y)与Q(x,-3)关于x轴对称,则x-y的值为( B)
A.1 B.-5 C.5 D.-1 5、已知点P (x,y)在第四象限,它到x轴的距离为2,到y轴的距离为3,求P点的坐标。 6、若点P′ (m,-1)是点P(2,n)关于x轴的对称点,求m+n。
小结:
已知平面直角坐标系内一点M(4a+8,a+3),分别根据 下列条件求出点M的坐标。 (1)点M到x轴的距离为2 ; (2)点N的坐标为(3,-6),并且直线MN∥x轴。
学习需要团队的力量
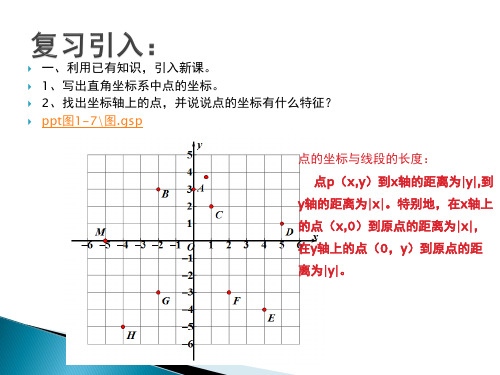
一、利用已有知识,引入新课。 1、写出直角坐标系中点的坐标。 2、找出坐标轴上的点,并说说点的坐标有什么特征? ppt图1-7\图.gsp
点的坐标与线段的长度: 点p(x,y)到x轴的距离为∣y∣,到
y轴的距离为∣x∣。特别地,在x轴上 的点(x,0)到原点的距离为∣x∣, 在y轴上的点(0,y)到原点的距 离为∣y∣。
1、学生通过不同的建系方式可得出多种建立平面直 角坐标系的方法,从而找到最优方法。同时知道对于 不同的建系方法,同一个点的坐标是不同的。
平面直角坐标系 课件

+
= 1.
3
2
9
4
' = 3,
∴经过伸缩变换
后,
' = 2
圆 x +y =1 变成了椭圆
2
2
'2
9
+
'2
4
= 1.
反思我们在使用伸缩变换时,要注意点的对应性,即分清变换前后
的坐标.P'(x',y')是伸缩变换后的点的坐标,P(x,y)是伸缩变换前的点
的坐标.
易错辨析
易错点:对平面直角坐标系中的伸缩变换公式把握不准而致错
【例 4】 在平面直角坐标系中,求方程 x+y+2=0 所对应的图形经
1
' = ,
2
过伸缩变换
后的图形.
' = 4
错解直线x+8y+4=0.
错因分析:点(x,y)在变换前的图形上,点(x',y')在变换后的图形上,
因此点(x,y)的坐标满足变换前的图形对应的方程,点(x',y')的坐标满
足变换后的图形对应的方程.错解混淆了(x,y)和(x',y')的含义.
4
−
2
5
= 1(≥2).②
联立①②,解得 x=8 或 x=−
当 x=8 时,y=5 3.
所以点 P 的坐标为(8,5 3).
32
11
(舍去).
平面直角坐标系中的轨迹问题
【例2】 已知△ABC的顶点A固定,角A的对边BC的长是2a,边BC
上的高的长是b,边BC沿一条直线移动,试建立适当的平面直角坐标
因为|PB|=|PC|,
= 1.
3
2
9
4
' = 3,
∴经过伸缩变换
后,
' = 2
圆 x +y =1 变成了椭圆
2
2
'2
9
+
'2
4
= 1.
反思我们在使用伸缩变换时,要注意点的对应性,即分清变换前后
的坐标.P'(x',y')是伸缩变换后的点的坐标,P(x,y)是伸缩变换前的点
的坐标.
易错辨析
易错点:对平面直角坐标系中的伸缩变换公式把握不准而致错
【例 4】 在平面直角坐标系中,求方程 x+y+2=0 所对应的图形经
1
' = ,
2
过伸缩变换
后的图形.
' = 4
错解直线x+8y+4=0.
错因分析:点(x,y)在变换前的图形上,点(x',y')在变换后的图形上,
因此点(x,y)的坐标满足变换前的图形对应的方程,点(x',y')的坐标满
足变换后的图形对应的方程.错解混淆了(x,y)和(x',y')的含义.
4
−
2
5
= 1(≥2).②
联立①②,解得 x=8 或 x=−
当 x=8 时,y=5 3.
所以点 P 的坐标为(8,5 3).
32
11
(舍去).
平面直角坐标系中的轨迹问题
【例2】 已知△ABC的顶点A固定,角A的对边BC的长是2a,边BC
上的高的长是b,边BC沿一条直线移动,试建立适当的平面直角坐标
因为|PB|=|PC|,
《平面直角坐标系》PPT课件

由CD长为6; CB长为4; 可得D ; B ; A的坐标分 别为D 6 ; 0 ; B 0 ; 4 ; A6;4
B 0;4
C 0;0
0
A 6;4
D 6;0
x
做一做
例2 如图;正三角形ABC的边长为 6 ; 建立适当的直角坐 标系 ;并写出各个顶点的坐标
y
解: 如图;以边AB所在 的直线为x 轴;以边AB 的中垂线y 轴建立直角 坐标系
布置作业
作业:
A类:课本习题5 5
B类:完成A类同时;补充:
1已知点A到x轴 y轴的距离均为4;求A点坐标;
2已知x轴上一点A3;0;B 3;b ;且AB=5;
求b的值
C类:建立坐标系表示右面图形各顶点的坐标
直角梯形上底3;下底5;底角60˚
y
o
x
练习提高
随堂练习:
课本 随堂练习
练习
1如图;某地为了发展城市群;在现有的四个中小城市A;B;C;D附近 新建机场E;试建立适当的直角坐标系;并写出各点的坐标
2点A1a;5;B3 ;b关于y轴对称;则 a + b =______
3在平面直角坐标系内;已知点P a ; b ; 且a b < 0 ; 则点P的位置 在________
在一次寻宝游戏中;寻宝人已
11 2
2
3
经找到了2和3;2的两个标志点;并
3
且知道藏宝地点的坐标为4;4;除4ຫໍສະໝຸດ 此外不知道其他信息 如何确定直
角坐标系找到宝藏 与同伴进行交
流
做一做
例1 如图; 矩形ABCD的长宽分别是6 ; 4 ; 建立适当的 坐标系;并写出各个顶点的坐标
y
解: 如图;以点C为坐标 原点; 分别以CD ; CB所 在的直线轴建 立直角坐标系 此时C点 坐标为 0 ; 0
B 0;4
C 0;0
0
A 6;4
D 6;0
x
做一做
例2 如图;正三角形ABC的边长为 6 ; 建立适当的直角坐 标系 ;并写出各个顶点的坐标
y
解: 如图;以边AB所在 的直线为x 轴;以边AB 的中垂线y 轴建立直角 坐标系
布置作业
作业:
A类:课本习题5 5
B类:完成A类同时;补充:
1已知点A到x轴 y轴的距离均为4;求A点坐标;
2已知x轴上一点A3;0;B 3;b ;且AB=5;
求b的值
C类:建立坐标系表示右面图形各顶点的坐标
直角梯形上底3;下底5;底角60˚
y
o
x
练习提高
随堂练习:
课本 随堂练习
练习
1如图;某地为了发展城市群;在现有的四个中小城市A;B;C;D附近 新建机场E;试建立适当的直角坐标系;并写出各点的坐标
2点A1a;5;B3 ;b关于y轴对称;则 a + b =______
3在平面直角坐标系内;已知点P a ; b ; 且a b < 0 ; 则点P的位置 在________
在一次寻宝游戏中;寻宝人已
11 2
2
3
经找到了2和3;2的两个标志点;并
3
且知道藏宝地点的坐标为4;4;除4ຫໍສະໝຸດ 此外不知道其他信息 如何确定直
角坐标系找到宝藏 与同伴进行交
流
做一做
例1 如图; 矩形ABCD的长宽分别是6 ; 4 ; 建立适当的 坐标系;并写出各个顶点的坐标
y
解: 如图;以点C为坐标 原点; 分别以CD ; CB所 在的直线轴建 立直角坐标系 此时C点 坐标为 0 ; 0
高中数学第一章坐标系1.1平面直角坐标系1.1.1平面直角

题型一 题型二 题型三
解:(1)设
������ ������
=
������,
得y=kx,所以
k
为过原点的直线的斜率.
又 x2+y2-4x+1=0 可化简为(x-2)2+y2=3,
它表示以(2,0)为圆心, 3为半径的圆,如图所示.
当直线 y=kx 与已知圆相切,且切点在第一象限时,k 最大,
此时,|CP|= 3, |������������| = 2,
(2)曲线可看作是满足某些条件的点的集合或轨迹,由此我们可借 助坐标系,研究曲线与方程间的关系.
名师点拨1.两点间的距离公式:在平面直角坐标系 中,P1(x1,y1),P2(x2,y2)两点之间的距离公式为
|P1P2|= (������1-������2)2 + (������1-������2)2.
所以
-1 + 2������ < -3-������ < 0,
0,
即
������
<
1 2
,
������ > -3.
所以-3<m< 12.
答案:-3<m<
1 2
2.曲线与方程 在平面直角坐标系中,如果某曲线C上的点与一个二元方程 f(x,y)=0的实数解建立了如下关系: (1)曲线C上的点的坐标都是方程f(x,y)=0的解; (2)以方程f(x,y)=0的解为坐标的点都在曲线C上. 那么,方程f(x,y)=0叫作曲线C的方程,曲线C叫作方程f(x,y)=0的曲 线. 名师点拨求曲线的方程一般有以下五个步骤:(1)建立适当的平面 直角坐标系,并用(x,y)表示曲线上任意一点M的坐标;(2)写出适合条 件p的点M的集合p={M|P(M)};(3)用坐标表示条件p(M),写出方程 f(x,y)=0;(4)化简方程f(x,y)=0(必须等价);(5)证明以(4)中方程的解为 坐标的点都在曲线上.一般地,方程的变形过程若是等价的,则步骤 (5)可以省略.
《平面直角坐标系》ppt课件

坐标系的建立
确定原点
选择平面内的任意一点作为原点,作为两条数轴 的公共起点。
确定正方向
在水平数轴上选取正方向,通常以向右为正;在 垂直数轴上选取正方向,通常以向上为正。
单位长度
根据实际需要确定数轴上的单位长度,通常以厘 米或毫米为单位。
坐标系的分类
绝对坐标标 系。
平面直角坐标系
目录
• 平面直角坐标系的基本概念 • 平面直角坐标系中的点 • 平面直角坐标系中的直线 • 平面直角坐标系中的距离公式 • 平面直角坐标系的应用
01
平面直角坐标系的基本 概念
定义与性质
定义
平面直角坐标系是由两条互相垂直、 原点重合的数轴构成的平面几何图形。
性质
具有方向性、单位性、正交性等性质, 是描述平面内点位置的重要工具。
05
平面直角坐标系的应用
在几何中的应用
确定点位置
01
通过平面直角坐标系,可以确定平面内任意点的位置,并描述
其坐标。
计算距离和角度
02
利用坐标系,可以方便地计算两点之间的距离和两点之间的夹
角。
绘制图形
03
通过坐标系,可以绘制各种几何图形,如直线、圆、椭圆等。
在代数中的应用
代数方程表示
平面直角坐标系可以将代数方程表示为图形,便于理解和解决代 数问题。
点到直线的距离公式
总结词
点到直线最短距离的平方
详细描述
给定点$P(x_0, y_0)$和直线$Ax + By + C = 0$,则点到直线的距离公式为:$d^2 = frac{|Ax_0 + By_0 + C|^2}{A^2 + B^2}$。
人教版数学选修4-4课件 1.1 平面直角坐标系

TIP4:早晨起床后,由于不受前摄抑制的影响,我们可以记忆一些新的内容或 者 复习一下昨晚的内容,那么会让你记忆犹新。
如何利用规律实现更好记忆呢?
超级记忆法-记忆 规律
记忆中
选择恰当的记忆数量
魔力之七:美国心理学家约翰·米勒曾对短时记忆的广 度进行过比较精准的测定:通常情况下一个人的记忆 广度为7±2项内容。
• 思维导引:本题涉及两点间的距离及曲线, 故要想到坐标法解决问题.
解析:以 A,B 所在直线为 x 轴,A,B 中点 O 为坐标原点,建立如图的直角坐标 系.
∵|AB|=10,∴点 A(-5,0),B(5,0).设某地 P 的坐标为(x,y),并设 A 地运费为 3a 元/公里,则 B 地运费为 a 元/公里,设 P 地居民购货总费用满足条件(P 地居民选择 A 地 购货):价格+A 地运费≤价格+B 地运费,
超级记忆法-记忆 规律
TIP1:我们可以选择记忆的黄金时段——睡前和醒后! TIP2:可以在每天睡觉之前复习今天或之前学过的知识,由于不受后摄抑制的 影 响,更容易储存记忆信息,由短时记忆转变为长时记忆。
如何利用规律实现更好记忆呢?
超级记忆法-记忆 规律
TIP3:另外,还有研究表明,记忆在我们的睡眠过程中也并未停止,我们的大 脑 会归纳、整理、编码、储存我们刚接收的信息。所以,睡前的这段时间可是 非常 宝贵的,不要全部用来玩手机哦~
•要点二 平面直角坐标系中的伸缩变换
定义:设 P(x,y)是平面直角坐标系中任意一点,在变换 φ:xy′′==λμxy,,λμ>>00,
• 的作用下,点P(x,y)对应到点P′(x′,y′),就 坐称标φ伸为缩平变面换 直角伸坐缩标变换系中的________________, 简称______________.
如何利用规律实现更好记忆呢?
超级记忆法-记忆 规律
记忆中
选择恰当的记忆数量
魔力之七:美国心理学家约翰·米勒曾对短时记忆的广 度进行过比较精准的测定:通常情况下一个人的记忆 广度为7±2项内容。
• 思维导引:本题涉及两点间的距离及曲线, 故要想到坐标法解决问题.
解析:以 A,B 所在直线为 x 轴,A,B 中点 O 为坐标原点,建立如图的直角坐标 系.
∵|AB|=10,∴点 A(-5,0),B(5,0).设某地 P 的坐标为(x,y),并设 A 地运费为 3a 元/公里,则 B 地运费为 a 元/公里,设 P 地居民购货总费用满足条件(P 地居民选择 A 地 购货):价格+A 地运费≤价格+B 地运费,
超级记忆法-记忆 规律
TIP1:我们可以选择记忆的黄金时段——睡前和醒后! TIP2:可以在每天睡觉之前复习今天或之前学过的知识,由于不受后摄抑制的 影 响,更容易储存记忆信息,由短时记忆转变为长时记忆。
如何利用规律实现更好记忆呢?
超级记忆法-记忆 规律
TIP3:另外,还有研究表明,记忆在我们的睡眠过程中也并未停止,我们的大 脑 会归纳、整理、编码、储存我们刚接收的信息。所以,睡前的这段时间可是 非常 宝贵的,不要全部用来玩手机哦~
•要点二 平面直角坐标系中的伸缩变换
定义:设 P(x,y)是平面直角坐标系中任意一点,在变换 φ:xy′′==λμxy,,λμ>>00,
• 的作用下,点P(x,y)对应到点P′(x′,y′),就 坐称标φ伸为缩平变面换 直角伸坐缩标变换系中的________________, 简称______________.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
点O叫做坐标原点,x轴、y轴、z轴叫做坐标轴, 这三条坐标轴中每两条确定一个坐标平面,分别 称为xoy平面、 yoz平面、和 zox平面.
4
4、空间中点的坐标
对于空间任意一点M,要求它的坐标
方法一:过M点分别做三个平面分别垂直于x,y,z
轴,平面与三个坐标轴的交点分别为P、Q、R,在其 相应轴上的坐标依次为x,y,z,那么(x,y,z)就叫做点M的 空间直角坐标,简称为坐标,记作M(x,y,z),三个数值
P={ M||MR| |MQ|=k }, 其中Q,R分别是点M到x 轴,y轴的垂线的垂足 所以 |x| |y|=k 即 x y= ±k
y
R
M
Qx
15
课堂小结
建立坐标系的一般规律:
1.两条垂直的直线 以该二直线为坐标轴.
2.对称图形 以对称图形的对称轴为坐标轴.
3.已知长度的线段 以线段所在直线为对称轴,端点或中点为原点.
1
xX
M点坐标为
•M
(x,y,z)
y Y
y
•P0
6
三、空间点的坐标:
设点P、Q和R在x轴、y轴和z轴上的坐标分别
是x,y和z,这样空间一点M的坐标可以用有序实
数组(x,y,z)来表示, (x,y,z)叫做点M 在此
空间直角坐标系中的坐标,记作M(x,y,z).
z
其中x叫做点M的横坐标,
R
M
y叫做点M的纵坐标,
注意:坐标轴上的点不属于任何象限。
3
3.空间直角坐标系:
z
以单位正方体 OABC DABC的 D'
C'
顶点O为原点,分别以射线OA, A'
B'
OC,OD 的方向为正方向,以
线段OA,OC, OD的长为单位
O
A
C B
y
长度,建立三条数轴:x轴,y轴, x
z轴,这时我们建立了一个空间直角坐标系 O xy。z
5( y12 6y1 13)
所以 M1A = M1B 由(1),(2)可知,方程是线段AB的垂直平分线的方程.
12
例2.已知平面上两个定点A , B , |AB| = 2a , (a>0) , 平面上动 点M到A , B两点的距离之比为 2:1 , 求动点M的轨迹方程.
解:以线段AB所在直线为X轴,线段AB的中点为原点, 建立如图直角坐标系.则 A (-a , 0) , B (a ,0) ,
O
P
x
Q M’
y z叫做点M的竖坐标.
7
例1: 在长方体OABC DABC中,
OA 3,OC 4,OD 2,
写出所有点的坐标.
z
2 D'(0, 0, 2)
C '0,4,2
3,0,2 A'
B '(3, 4, 2)
O 0,0,0
4y
3
x A(3, 0, 0)
C (0, 4, 0)
B (3, 4, 0)
证化简过的方程所表示的曲线是否是已知点的轨迹。
上述五个步骤可简记为: 建系设点;写出条件;代入坐标;化简方程;证明结论. 14
例3、点M与两条互相垂直的直线的距离的积是 常数 k (k>0),求点M轨迹方程.
解:以已知的两条垂直直线为坐标系,建立直角坐标系.
设点M(x,y)是满足题设条件的轨迹上的任意一点,则
11
证明:(1)由求方程的过程知道,垂直平分线上每一点的坐标 都是方程的解.
(2)设点M1的坐标(x1 ,y1)是方程的解, 则 x1 2 y1 7 0
点M1到A,B的距离分别是
M1 A (x1 1)2 ( y1 1)2
5( y12 6y1 13)
M1B (x1 3)2 ( y1 7)2
1
1.直线上点的坐标
在直线上规定了原点、正方向、单位长度 就构成了数轴。
B
A
-2 -1 O 1 2 3
x
数轴上的点可以用 唯一的一个实数表示
2
纵轴 y 5
4 第二象限
3 2
2.平面直角坐标系上的
有序实数对(x,y)表示点
第一象限
1
-4 -3 -2 -4
1 2 3 4 5 x 横轴 第四象限
解:设M(x,y)是线段AB的垂直平分线上任意一点,
由已知得,M点应该满足条件 |MA| = |MB |
由两点间的距离公式,代入M,A,B的坐标得, Y B
M
(x 1)2 (y 1)2 (x 3)2 (y 7)2
化简,整理得, x 2y 7 0
O
X
A
我们还需要证明这就是线段AB的垂直平分线的方程.
z 叫做 M点的横坐标、纵坐标、竖坐标。
z •R
1
•M
y
x•
•o
1
1
•y
Q
xP
5
4、空间中点的坐标
方法二:过M点作xOy面的垂线,垂足为 P0点。
点 P0在坐标系xOy中的坐标x、y依次是M点的横坐标、
纵坐标。再过M点作z轴的垂线,垂足 在zP轴1 上的坐标
z就是M点的竖坐标。
z
z P1
1
x
•o
1
通过方程,研究平面曲线的性质
9
曲线与方程的关系:
分析
把曲线看成满足某种条件的点的集合或轨迹, 就可以用曲线上点的坐标(x,y)所满足的方程 f(x,y)=0来表示曲线.
即: 曲线 条件 方程
要求: 曲线上的点
方程的解
10
例1. 设A , B两点的坐标是 (-1 , -1) , ( 3 , 7 ), 求线段AB 的垂直平分线的方程.
设动点M的坐标为(x,y),
由已知M点应该满足条件:
MA 2 MB 1
把M , A , B 的坐标代入等式,得
( x a) 2 ( y 0) 2 2
(x a) 2 ( y 0) 2 1
Y M
X AO B
化简,整理得: 3x2 3y 2 10ax 3a2 0
13
课堂小结 求曲线方程的一般步骤:
1.设(建系设点):建立适当的坐标系,用 M(x,y)
表示曲线上任意一点M;
2.写(写等量关系) 写出满足条件的点M的集合:
{M|P(M) };
3.代(列方程):将M点坐标(x,y)代入几何条
件,列出方程 f (x,y) =0;
4.化(化简方程):化方程为最简形式;
5.证(以方程的解为坐标的点都是曲线上的点):验
8
5、用坐标法研究几何图形的知识形成了一门学科
——解析几何.(实质就是“以数论形”)
曲线
满足某种条件的点的集合或轨迹.
坐标法
(x,y)
f(x,y)=0
借助坐标系,用坐标表示点,用方程表 示曲线,通过研究方程的性质间接地来 研究曲线的性质,这一研究几何问题的 方法称为坐标法.
解析几何两 大基本问题
根据已知条件,求出表示平面曲线的 方程
16
课堂小结
关于化简方程
在求轨迹方程的问题中,如果化简方程 过程是同解变形.则由此所得的最简方程就 是所求曲线的方程,可以省略“证明”;
