四年级数学 四则混合运算与巧算
四年级数学上册《整数四则混合运算》整理与复习

四年级数学上册《整数四则混合运算》整理与复习四年级(上)数学《四则混合运算》整理与复习【知识点拨】1.四则混合运算的顺序:①在没有括号的算式⾥,只有加法和减法,或者只有乘法和除法,要从左往右依次计算;既有加减法,⼜有乘除法,要先算乘除,后算加减。
②在有括号的算式⾥,要先算括号⾥⾯的,再算括号外⾯的。
改变算式的运算顺序,可以使⽤⼩括号。
2.四则混合运算⽅法⼀看、(看数字,运算符号,想想运算顺序是什么。
)⼆画、(画线,哪⼀步先算,就在哪⼀步的下⾯画⼀条横线,没有计算的要照抄下来。
)三算、(按照运算顺序计算)四检验、(检验运算顺序是否错误,计算是否算错。
)* 混合运算顺序歌通览全题定⽅案,细看是否能简便;明确顺序是关键,同级只要依次算;异级出现仔细看,先乘除来后加减;遇到括号别慌张,先⼩后⼤依次算;每算⼀步都检验,⼜对⼜快喜⼼间。
【解题技巧】解答式题技巧(⼀)“看”。
“看”,就是先看⼀看题⽬⾥有⼏个什么数。
会有⼏种运算符号;再看⼀看运算符号和数据有什么特点,有什么内在联系。
如405×(3076-2980)+2136÷89。
看的结果应是:①有5个数;②有4种运算;③含有⼩括号;④是⼀道带有⼩括号的整数四则混合运算题。
⼜如3.68×[1÷(2.1-2.09)]+0.6。
看的结果应是①含有5个数;②有4种运算;③含有中括号;④是⼀道带有中括号的⼩数四则混合式题。
这是⼩学数学的计算题的答题技巧之⼀。
(⼆)“定”。
“定”,就是对题⽬整体观察后,确定运算顺序。
即先算什么,再算什么,后算什么。
可采⽤画线标序的⽅法,如:405×(3076-2980)+2136÷89└──┬─┘①└─┬─┘└──┬──┘②②└──────┘③(三)“想”。
“想”,就是分析题中的数值特征和运算间的联系,联想到有关运算定律、运算性质,然后进⾏运算。
如:405×(3076-2980)+2136÷89。
小学数学四年级四则混合运算及运算法则知识点整理附练习题

小学数学四年级四则混合运算及运算法则知识点整理附练习题文章目录四则运算(一)加法运算定律:1、两个加数交换位置,和不变,这叫做加法交换律。
字母公式:a+b=b+a2、先把前两个数相加,或者先把后两个数相加,和不变,这叫做加法结合律。
字母公式:(a+b) +c=a+(b+c)(二)乘法运算定律:1、交换两个因数的位置,积不变,这叫做乘法交换律。
字母公式:a×b=b×a2、先乘前两个数,或者先乘后两个数,积不变,这叫做乘法结合律。
字母公式:(a×b)×c=a×(b×c)3、两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再相加,这叫做乘法分配律。
用字母公式:(a+b)×c=a×c+b×c或a×(b+c) =a×b+a×c拓展:(a-b)×c=a×c-b×c或a×(b-c) =a×b-a×c(三)减法简便运算:1、一个数连续减去两个数,可以用这个数减去这两个数的和。
用字母表示:a-b-c=a-(b+c)2、一个数连续减去两个数,可以用这个数先减去后一个数再减去前一个数。
用字母表示:a-b-c=a—c-b(四)除法简便运算:1、一个数连续除以两个数,可以用这个数除以这两个数的积。
用字母表示:a÷b÷c=a÷(b×c)2、一个数连续除以两个数,可以用这个数先除以后一个数再除以前一个数。
用字母表示:a÷b÷c=a÷c÷b小学四年级数学“四则运算”知识点详解知识点一:四则运算的概念和运算顺序1、加法、减法、乘法和除法统称四则运算。
2、在没有括号的算式里,如果只有加、减法或者只有乘、除法,都要从左往右按顺序计算。
3、在没有括号的算式里,既有乘、除法又有加、减法的,要先算乘除法,再算加减法。
四年级四则混合运算计算题大全

四年级四则混合运算计算题大全《四年级四则混合运算计算题大全:我的学习之旅》四则混合运算就像一个神秘的魔法世界,在四年级的数学学习里,可占了超级重要的地位呢。
今天呀,我就来和大家分享一下我所知道的那些四则混合运算计算题。
我先给大家出一道简单的四则混合运算题吧:3 + 5×2 - 4÷2。
这道题里有加、减、乘、除四种运算呢。
就像一个小团队里有不同分工的小伙伴,乘法和除法就像是强壮的大力士,要先被计算。
那按照这个规则,先算5×2 = 10,4÷2 = 2,这时候式子就变成了3 + 10 - 2。
这多像一场接力赛呀,第一棒的大力士完成任务后,就轮到加法和减法这些轻快的小选手了。
3 + 10 = 13,13 - 2 = 11。
哈哈,这道题的答案就像一个小宝藏被我们找出来啦。
再看这道题:(6 + 4)÷2×3。
这里面有小括号呢,小括号就像是一个魔法圈,圈里面的小伙伴们要先抱成团进行计算。
6 + 4 = 10,式子就变成了10÷2×3。
接着就按照先乘除后加减的顺序,10÷2 = 5,5×3 = 15。
这就好比一群小动物要过河,小括号里的小动物们先一起坐上小船,过了河之后,再按照各自的路线继续前行。
我和我的小伙伴们在做四则混合运算题的时候,可发生了好多有趣的故事呢。
有一次,我的同桌小明在做一道题:12÷(3 + 1)×2。
他呀,一开始没注意小括号,直接就用12÷3了,结果算出了个乱七八糟的答案。
我就跟他说:“小明呀,小括号就像是给里面的数字们盖了个小房子,你得先把小房子里的事情处理好才行呢。
”小明听了我的话,恍然大悟,重新计算,很快就得出了正确答案。
还有一道比较复杂的题:8×(5 - 3) + 10÷2 - 3×4。
这道题就像是一个大迷宫,到处都是弯弯绕绕的。
小四 四则混合运算的巧算

爱上数学,主动思考
—— 璐璐老师
A
1
CONTENTS
1
复习
Lorem ipsum dolor sit amet consectetuer Lorem
2
基本乘法分配律
Lorem ipsum dolor sit amet
consectetuer Lorem
3
基本提取公因数
Lorem ipsum dolor sit amet consectetuer Lorem
?× 2
÷2
?
___2___ × ___24___ = 48
A
总结: 积不变的性质 在乘法中,一个数乘以
一个数,另一个数除以 相同的数 ( 0除外) ,结 果积不变。
29
练习:( 构造公因数 )
?(1)15 ×26+30 ×37 ?(2) 36×64-72 ×27 ?(3)218×730+7820 ×73
公平,每人分 25颗。 ”
每人先分 4颗
又来了两个人,每人先分 4颗
最后每人补发 6颗
25
25
25
25 25
A
请问: 胡子叔叔一共分了多少
颗糖果?
23
? 第一种方法: 分拨计算
? 4×3+4×2+6 ×5
? 第二种方法: 一起计算
? 5×( 4+6 )
? 总结:
注意: 边提边看
A
24
练习:
?( 1)25 ×12+25 × 15+27 ×75 ?(2)5×13+13 × 7+12×7
? 11×4=44 ? 11×5=55
? 11×11=12 1
2023-2024年小学数学四年级上册期末考点复习 第七单元《整数四则混合运算》(苏教版含解析)
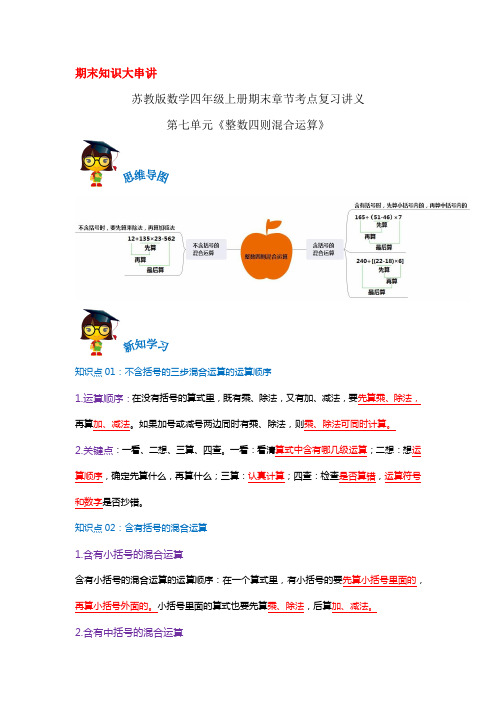
期末知识大串讲苏教版数学四年级上册期末章节考点复习讲义第七单元《整数四则混合运算》知识点01:不含括号的三步混合运算的运算顺序1.运算顺序:在没有括号的算式里,既有乘、除法,又有加、减法,要先算乘、除法,再算加、减法。
如果加号或减号两边同时有乘、除法,则乘、除法可同时计算。
2.关键点:一看、二想、三算、四查。
一看:看清算式中含有哪几级运算;二想:想运算顺序,确定先算什么,再算什么;三算:认真计算;四查:检查是否算错,运算符号和数字是否抄错。
知识点02:含有括号的混合运算1.含有小括号的混合运算含有小括号的混合运算的运算顺序:在一个算式里,有小括号的要先算小括号里面的,再算小括号外面的。
小括号里面的算式也要先算乘、除法,后算加、减法。
2.含有中括号的混合运算含有中括号的混合运算:在一个算式里,既有小括号,又有中括号,要先算小括号里面的,再算中括号里面的。
考点01:含括号的运算顺序1.复印机5分钟复印了340张纸,照这样计算,复印2516张纸需复印多少分钟?算式是()A.2516÷(340÷5)B.340÷5×2516C.(2516-340)÷5【答案】A【完整解答】解:需要印的分钟数=2516÷(340÷5)。
故答案为:A。
【思路引导】现在需要印的分钟数=现在需要复印纸的张数÷(原来复印纸的张数÷原来复印用的时间),代入数值即可。
2.(2021四上·曲阳期中)一列火车长150米,这列火车全部通过780米长的隧道要用30秒,这列火车每秒运行()米。
A.21 B.26 C.31【答案】C【完整解答】解:(150+780)÷30=930÷30=31(秒)。
故答案为:C。
【思路引导】这列火车的速度=(火车的长+桥长)÷用的时间。
3.修一条水渠,前2天修了300米,照这样计算,修完1500米,共需多少天?下面列式错误的是( )。
四年级小数四则运算

小数四则运算知识框架一、加减法中的速算与巧算速算巧算的核心思想和本质:凑整常用的思想方法:1、分组凑整法.把几个互为“补数”的减数先加起来,再从被减数中减去,或先减去那些与被减数有相同尾数的减数.“补数”就是两个数相加,如果恰好凑成整十、整百、整千……,就把其中的一个数叫做另一个数的“补数”.2、加补凑整法.有些算式中直接凑整不明显,这时可“借数”或“拆数”凑整.3、数值原理法.先把加在一起为整十、整百、整千……的数相加,然后再与其它的数相加.4、“基准数”法,基准当几个数比较接近于某一整数的数相加时,选这个整数为“基准数”(要注意把多加的数减去,把少加的数加上)二、乘法凑整与运算性质思想核心:先把能凑成整十、整百、整千的几个乘数结合在一起,最后再与前面的数相乘,使得运算简便。
例如:425100⨯=⨯=,520100⨯=,81251000⨯=(去8数,重点记忆)123456799111111111⨯⨯=(三个常用质数的乘积,重点记忆)711131001理论依据:乘法交换率:a×b=b×a乘法结合率:(a×b) ×c=a×(b×c)乘法分配率:(a+b) ×c=a×c+b×c积不变规律:a×b=(a×c) ×(b÷c)=(a÷c) ×(b×c)三、乘、除法混合运算的性质1)商不变性质:被除数和除数乘(或除)以同一个非零数,其商不变.即: ,0()()()()0÷=⨯÷⨯=÷÷÷≠a b a n b n a m b m mn≠2)在连除时,可以交换除数的位置,商不变.即:a b c a c b÷÷=÷÷3)在乘、除混合运算中,被乘数、乘数或除数可以连同运算符号一起交换位置(即带着符号搬家).例如:a b c a c b b c a⨯÷=÷⨯=÷⨯4)在乘、除混合运算中,去掉或添加括号的规则去括号情形:①括号前是“×”时,去括号后,括号内的乘、除符号不变.即()()⨯⨯=⨯⨯⨯÷=⨯÷a b c a b c a b c a b c②括号前是“÷”时,去括号后,括号内的“×”变为“÷”,“÷”变为“×”.即()()a b c a b c a b c a b c÷⨯=÷÷÷÷=÷⨯添加括号情形:加括号时,括号前是“×”时,原符号不变;括号前是“÷”时,原符号“×”变为“÷”,“÷”变为“×”.即()()()() a b c a b c a b c a b c a b c a b c a b c a b c ⨯⨯=⨯⨯⨯÷=⨯÷÷÷=÷⨯÷⨯=÷÷5)两个数之积除以两个数之积,可以分别相除后再相乘.即()()()()()()a b c d a c b d a d b c⨯÷⨯=÷⨯÷=÷⨯÷例题精讲【例 1】91.588.890.2270.489.6186.791.8++++++【考点】分组凑整【难度】☆☆【题型】计算【解析】原式91.5=+ (88.890.2+)+(270.489.6+)+(186.791.8+)91.5179360278.5=+++=(91.5278.5+)179360909++=【答案】909【巩固】2006+200.6+20.06+2.006+994+99.4+9.94+0.994=【考点】分组凑整【难度】☆☆【题型】计算【解析】(2006+994)+(200.6+99.4)+(20.06+9.94)+(2.006+0.994)=3000+300+30+3=3333。
四则运算巧算的规律

四则运算巧算的规律小学阶段的数学成绩不理想,主要就是在运算能力上出了问题。
计算能力是小学数学学习的基础,东方学校的老师详细整理了关于四则运算的基础知识及运算过程中常用到的简便方法,帮孩子们查漏补缺,提高计算能力扎实数学基础。
1运算定律1.加法交换律两个数相加,交换加数的位置,它们的和不变,即a+b=b+a 。
2.加法结合律三个数相加,先把前两个数相加,再加上第三个数;或者先把后两个数相加,再和第一个数相加它们的和不变,即(a+b)+c=a+(b+c) 。
3.乘法交换律两个数相乘,交换因数的位置它们的积不变,即a×b=b×a。
4.乘法结合律三个数相乘,先把前两个数相乘,再乘以第三个数;或者先把后两个数相乘,再和第一个数相乘,它们的积不变,即(a×b)×c=a×(b×c) 。
5.乘法分配律两个数的和与一个数相乘,可以把两个加数分别与这个数相乘再把两个积相加,即(a+b)×c=a×c+b×c 。
6.减法的性质从一个数里连续减去几个数,可以从这个数里减去所有减数的和,差不变,即a-b-c=a-(b+c) 。
2运算法则1.整数加法计算法则相同数位对齐,从低位加起,哪一位上的数相加满十,就向前一位进一。
2. 整数减法计算法则相同数位对齐,从低位加起,哪一位上的数不够减,就从它的前一位退一作十,和本位上的数合并在一起,再减。
3.整数乘法计算法则先用一个因数每一位上的数分别去乘另一个因数各个数位上的数,用因数哪一位上的数去乘,乘得的数的末尾就对齐哪一位,然后把各次乘得的数加起来。
4.整数除法计算法则先从被除数的高位除起,除数是几位数,就看被除数的前几位;如果不够除,就多看一位,除到被除数的哪一位,商就写在哪一位的上面。
如果哪一位上不够商1,要补“0”占位。
每次除得的余数要小于除数。
5. 小数乘法法则先按照整数乘法的计算法则算出积,再看因数中共有几位小数,就从积的右边起数出几位,点上小数点;如果位数不够,就用“0”补足。
(精品教案)《四则混合运算》讲课稿范文(精选5篇)

(精品教案)《四则混合运算》讲课稿范文(精选5篇)为大伙儿收集的《四则混合运算》讲课稿范文(精选5篇),仅供参考,希翼可以帮助到大伙儿。
本节课的教学内容是北师大版小学数学四年级下册的内容,这部分内容是在差不多掌握了小数四则运算和整数四则混合运算顺序的基础上举行教学的,整数四则混合运算顺序在小数四则混合运算中同样适用,并且它也是为未来进一步学习分数四则混合运算奠定基础。
教材创设了“电视广告”这一计算电视广告费的情境,让学生利用小数四则运算的知识去解决咨询题,在这一过程中体味到小数混合运算的顺序和整数混合运算的顺序是一样的,并能运用小数四则混合运算解决一些实际咨询题。
1。
体味小数混合运算和整数混合运算顺序是一样的,会计算小数四则混合运算(以两步为主,别超过三步),利用学过的小数加、减、乘、除法解决日常日子中的实际咨询题。
2。
在研究小数四则混合运算顺序的过程中,体味数学知识的联系。
3。
利用小数计算来解决咨询题,进展学生的应用意识,体味数学的价值。
这节课我要紧采纳合作学习、自主探索、讨论发觉的教学办法,放手让学生在有限的时刻和空间里,依照自个儿的学习体验、用自个儿的思维方式,经过计算、探索、讨论、观看、比较等方式,自由地、开放地去探索,去发觉,去“再制造”新知识。
1。
合作讨论学习的办法:新课程理念十分重视学生间的合作与交流。
在本课当学生依照“电视广告”情境提出咨询题后,让学生小组合作讨论解决,别仅有利于互相学习取长补短、发挥集体智慧,而且培养了学生的表达能力、协作能力。
2。
计算、观看、发觉的办法:在经过计算解决了平均每秒多少元后,让学生观看两种解法的综合算式,从而发觉小数混合运算和整数混合运算顺序是一样的。
在巩固练习中也让学生经过计算自个儿发觉办法,培养学生自主探索的精神。
1。
复习铺垫,情境引入。
教学一开始,经过学生易错的一道简单整数混合运算的口算题,既突出强调了运算顺序的重要性,又复习回忆了整数混合运算顺序。
四年级数学上册《整数四则混合运算》整理与复习

四年级数学上册《整数四则混合运算》整理与复习《四则混合运算》整理与复习【知识点拨】1.四则混合运算的顺序:①在没有括号的算式里,只有加法和减法,或者只有乘法和除法,要从左往右依次计算;既有加减法,又有乘除法,要先算乘除,后算加减。
②在有括号的算式里,要先算括号里面的,再算括号外面的。
改变算式的运算顺序,可以使用小括号。
2.四则混合运算方法一看、(看数字,运算符号,想想运算顺序是什么。
)二画、(画线,哪一步先算,就在哪一步的下面画一条横线,没有计算的要照抄下来。
) 三算、(按照运算顺序计算)四检验、(检验运算顺序是否错误,计算是否算错。
)* 混合运算顺序歌通览全题定方案,细看是否能简便;明确顺序是关键,同级只要依次算;异级出现仔细看,先乘除来后加减;遇到括号别慌张,先小后大依次算;每算一步都检验,又对又快喜心间。
【解题技巧】解答式题技巧(一)“看”。
“看”,就是先看一看题目里有几个什么数。
会有几种运算符号;再看一看运算符号和数据有什么特点,有什么内在联系。
如405×(3076-2980)+2136÷89。
看的结果应是:①有5个数;②有4种运算;③含有小括号;④是一道带有小括号的整数四则混合运算题。
又如3.68×[1÷(2.1-2.09)]+0.6。
看的结果应是①含有5个数;②有4种运算;③含有中括号;④是一道带有中括号的小数四则混合式题。
这是小学数学的计算题的答题技巧之一。
(二)“定”。
“定”,就是对题目整体观察后,确定运算顺序。
即先算什么,再算什么,后算什么。
可采用画线标序的方法,如:405×(3076-2980)+2136÷89└──┬─┘①└─┬─┘└──┬──┘└──────┘③(三)“想”。
“想”,就是分析题中的数值特征和运算间的联系,联想到有关运算定律、运算性质,然后进行运算。
如:405×(3076-2980)+2136÷89。
四年级下册四则混合运算

四年级下册四则混合运算一、四则混合运算的概念。
1. 四则运算。
- 在数学中,四则运算是指加法、减法、乘法和除法这四种基本运算。
- 例如:2 + 3(加法),5-1(减法),4×3(乘法),12÷4(除法)。
2. 混合运算。
- 四则混合运算就是在一个算式里,包含了两种或两种以上的四则运算。
- 例如:2 + 3×4,这个算式里既有加法又有乘法。
二、四则混合运算的运算顺序。
1. 没有括号的情况。
- 先算乘除,后算加减。
- 例如:计算12 + 4×3÷2。
- 先算乘法:4×3 = 12。
- 再算除法:12÷2 = 6。
- 最后算加法:12+6 = 18。
2. 有括号的情况。
- 先算小括号里面的,再算中括号里面的(如果有),最后算括号外面的。
- 例如:计算[12+(4 - 2)×3]÷2。
- 先算小括号里的:4 - 2=2。
- 再算中括号里的乘法:2×3 = 6。
- 接着算中括号里的加法:12+6 = 18。
- 最后算括号外面的除法:18÷2 = 9。
三、四则混合运算的应用。
1. 简单的应用题。
- 例:学校图书馆有故事书120本,科技书比故事书的3倍少10本,科技书有多少本?- 分析:先算故事书的3倍,即120×3 = 360本,再减去10本,360-10 = 350本。
- 列式为:120×3 - 10=350(本)。
2. 较复杂的应用题。
- 例:小明去商店买文具,一支铅笔2元,一个笔记本5元。
他买了3支铅笔和2个笔记本,给了售货员20元,应找回多少钱?- 分析:先算出买铅笔的花费2×3 = 6元,再算出买笔记本的花费5×2 = 10元,总共花费6 + 10=16元,最后用20元减去总花费得到应找回的钱数。
- 列式为:20-(2×3 + 5×2)- 先算括号里的乘法:2×3 = 6,5×2 = 10。
四年级混合运算简便方法

四年级混合运算简便方法在四年级的数学学习中,混合运算是十分重要的一部分。
掌握简便的混合运算方法,不仅能提高解题速度,还能增强孩子们的数学思维能力。
本文将为您详细介绍四年级混合运算的简便方法。
一、先乘除后加减在进行混合运算时,首先要遵循“先乘除后加减”的原则。
即在算式中,先计算乘法和除法,再计算加法和减法。
例题:34 + 15 × 2 ÷ 3 - 6解答:先计算乘法和除法:15 × 2 = 3030 ÷ 3 = 10将计算结果代入原算式:34 + 10 - 6再计算加法和减法:34 + 10 = 4444 - 6 = 38所以,最终答案是38。
二、括号内优先计算当算式中出现括号时,括号内的运算要优先计算。
例题:45 - (12 + 8) × 2解答:先计算括号内的加法:12 + 8 = 20将计算结果代入原算式:45 - 20 × 2再计算乘法:20 × 2 = 40最后计算减法:45 - 40 = 5所以,最终答案是5。
三、运用运算定律在混合运算中,可以运用加法结合律、乘法分配律等运算定律,简化计算过程。
1.加法结合律:三个数相加,可以先把其中两个数相加,再加上第三个数,或者先把其中两个数相加,再和第三个数相加,它们的和不变。
例题:27 + 15 + 23解答:可以先将27和23相加,再加上15:27 + 23 = 5050 + 15 = 65也可以先将15和23相加,再加上27:15 + 23 = 3838 + 27 = 65所以,最终答案是65。
2.乘法分配律:两个数的和(或差)与一个数相乘,可以先把它们分别与这个数相乘,再相加(或相减)。
例题:5 × (8 + 3)解答:根据乘法分配律,可以将5分别与8和3相乘,再相加:5 × 8 = 405 × 3 = 1540 + 15 = 55所以,最终答案是55。
第一讲:整数四则混合运算及简便运算

一、整数四则运算定律(1) 加法交换律:a b b a +=+(2) 加法结合律:()()a b c a b c ++=++ (3) 乘法交换律:a b b a ⨯=⨯(4) 乘法结合律:()()a b c a b c ⨯⨯=⨯⨯(5) 乘法分配律:()a b c a b a c ⨯+=⨯+⨯;()b c a b a c a +⨯=⨯+⨯ (6) 减法的性质:()a b c a b c --=-+ (7) 除法的性质:()a b c a b c ÷⨯=÷÷;(8) 除法的“左”分配律:()a b c a c b c +÷=÷+÷;()a b c a c b c -÷=÷-÷,这里尤其要注意,除法是没有“右”分配律的,即()c a b c a c b ÷+=÷+÷是不成立的! 备注:上面的这些运算律,既可以从左到右顺着用,又可以从右到左逆着用.二、 加减法中的速算与巧算速算巧算的核心思想和本质:凑整。
常用的思想方法总结如下:(1) 分组凑整法.把几个互为“补数”的减数先加起来,再从被减数中减去,或先减去那些与被减数有相同尾数的减数.“补数”就是两个数相加,如果恰好凑成整十、整百、整千……,就把其中的一个数叫做另一个数的“补数”.(2) 加补凑整法.有些算式中直接凑整不明显,这时可“借数”或“拆数”凑整.三、乘法凑整思想核心:先把能凑成整十、整百、整千的几个乘数结合在一起,最后再与前面的数相乘,使得运算简便。
例如:425100⨯=,81251000⨯=,520100⨯=理论依据:乘法交换律:a ×b=b ×a 乘法结合律:(a ×b) ×c=a ×(b ×c) 乘法分配律:(a+b) ×c=a ×c+b ×c知识点拨第一讲 整数四则混合运算的简便运算积不变规律:a ×b=(a ×c) ×(b ÷c)=(a ÷c) ×(b ×c)四、乘、除法混合运算的性质⑴商不变性质:被除数和除数乘(或除)以同一个非零数,其商不变.即: ()()()()0a b a n b n a m b m m ÷=⨯÷⨯=÷÷÷≠ ,0n ≠⑵在连除时,可以交换除数的位置,商不变.即:a b c a c b ÷÷=÷÷⑶在乘、除混合运算中,被乘数、乘数或除数可以连同运算符号一起交换位置(即带着符号搬家).例如:a b c a c b b c a ⨯÷=÷⨯=÷⨯⑷在乘、除混合运算中,去掉或添加括号的规则去括号情形:①括号前是“×”时,去括号后,括号内的乘、除符号不变.即()()a b c a b c a b c a b c ⨯⨯=⨯⨯⨯÷=⨯÷ ②括号前是“÷”时,去括号后,括号内的“×”变为“÷”,“÷”变为“×”.即()()a b c a b c a b c a b c ÷⨯=÷÷÷÷=÷⨯ 添加括号情形:加括号时,括号前是“×”时,原符号不变;括号前是“÷”时,原符号“×”变为“÷”,“÷”变为“×”.即()()()()a b c a b c a b c a b c a b c a b c a b c a b c ⨯⨯=⨯⨯⨯÷=⨯÷÷÷=÷⨯÷⨯=÷÷ ⑸两个数之积除以两个数之积,可以分别相除后再相乘.即 ()()()()()()a b c d a c b d a d b c ⨯÷⨯=÷⨯÷=÷⨯÷ 上面的三个性质都可以推广到多个数的情形.一、加法【例1】:278+463+22+37举一反三:732+580+268二、减法【例2】:2871-299例题精讲举一反三:(1)157-99 (2)363-199 (3)968-599三、连减(5种)【例3】:528-53-47举一反三:(1)489-134-76 (2)470-254-46 (3)545-167-133【例4】:496-(296+144)举一反三:(1)675-(175+89)(2)466-(66+125)(3)354-(154+77)【例5】:496-(144+296)举一反三:(1)675-(89+175)(2)466-(125+66)(3)354-(77+154)【例6】:528-72-28举一反三:(1)489-77-389 (2)465-267-65 (3)545-167-145【例7】:824-224-176-124举一反三:(1)643-164-133-243 (2)487-187-139-61 (3)545-167-145四、乘法分配律(8种)【例8】:计算:125×(80+32)(24+40)×25举一反三:(1)125×(64+80)(2)(80+32)×125 (3)(16+32)×25【例9】:(1)125×(100-8)(2)(125-40)×8举一反三:(1)125×(100-48)(2)(100-16)×25【例10】:(1)117×56+117×44举一反三:(1)269×26+74×269 (2)521×65+35×521 (3)126×72+126×12+126×16【例11】:125×69-125×61举一反三:(1)25×127-25×119 (2)365×251-365×151(3)156×59-156×27-156×22 (4)137×97-44×137-137×43【例12】:45×102举一反三:(1)25×44 (2)125×168 (3)125×18【例13】:36×99举一反三:(1)45×98 (2)125×92 (3)35×99【例14】:(1)81+9×391 (2)9+9×999 (3)99+9×99【例15】:(1)9×107-63 (2)6×108-48 (3)134×101-134五、连除(2种)【例16】:1250÷25÷5举一反三:(1)2000÷125÷8 (2)1280÷16÷8 (3)1300÷5÷20(4)840÷5÷8 (5)1700÷25÷4 (6)4800÷50÷2【例17】:630÷(63×5)举一反三:(1)780÷(78×2)(2)1250÷(125×5)(3)6300÷(63×5)六、四则混合运算(1)(24+24)÷24×24 (2)24+24÷24×24 (3)16+4-16+4 (4)(16+4)-(16+4)(5)25×6÷25×6 (6)120-(72+48)÷24(7)45+55÷5-20 (8)12×(280-80÷4)(9)218+324÷18×5(10)(488+32×5)÷12 (11)4500÷(170-60×2)(12)(28+41)÷(92÷4)(13)80+320÷4-30 (14)18×(420-320÷20)(15)48-2×8÷8×2 (16)480÷(144-960÷8)(17)120+480÷(43-28)(18)(273+562)÷5-96 (19)4500÷(150-40×3)(20)812÷(532-36×14)(21)(12+12)÷12×12(22)625÷(54-522÷18)(23)17+13-17+13 (24)60-15×7÷15×7 (25)12×(289-84÷4)(26)218+702÷18×5 (27)45000÷(150-40×3)(28)(77+38)÷(92÷4)(29)58-28×2+40 (30)56×4-175÷5(31)(73-59)×(6+13)(32)(85-40)÷(15÷3)(33)71-17×7÷17×7课堂检测:(1)43×202 (2) 59×299 (3) 134×51-51×34 (4) 7200÷36 (5)68×32—784÷56 (6)3000÷125÷8 (7)98×35 (8) 960×46÷48 (9)480×46÷48 (10)302×99+302 (11)756+483-556(12)230×54+540×77 (13)887×25-87×25 (14)(825+25×8)×4(15)325-225÷5+145 (16)35×102 (17)498+(201-154)(18)125×89×8 (19)428×78+572×78 (20)8800÷(25×88)(21)3600÷50÷2(22)25×(20+4)容易出错类型(共五种类型)600-60÷15 20×4÷20×4736-35×20 25×4÷25×498-18×5+25 56×8÷56×8280-80÷ 4 12×6÷12×6175-75÷25 25×8÷25×880-20×2+60 36×9÷36×936-36÷6-6 25×8÷(25×8)。
四年级四则运算公式

四年级四则运算公式一、加法。
1. 加法交换律。
- 公式:a + b=b + a- 含义:两个数相加,交换加数的位置,和不变。
例如:3+5 = 5+3,结果都是8。
2. 加法结合律。
- 公式:(a + b)+c=a+(b + c)- 含义:三个数相加,先把前两个数相加,或者先把后两个数相加,和不变。
例如:(2 + 3)+4=2+(3 + 4),(2+3)+4 = 5 + 4=9,2+(3 + 4)=2+7 = 9。
二、减法。
1. 减法的性质。
- 公式:a - b - c=a-(b + c)- 含义:一个数连续减去两个数,可以用这个数减去这两个数的和。
例如:10-3 - 2=10-(3 + 2),10 - 3-2=7 - 2 = 5,10-(3 + 2)=10 - 5=5。
三、乘法。
1. 乘法交换律。
- 公式:a× b = b× a- 含义:两个数相乘,交换因数的位置,积不变。
例如:3×5 = 5×3,结果都是15。
2. 乘法结合律。
- 公式:(a× b)× c=a×(b× c)- 含义:三个数相乘,先把前两个数相乘,再和另外一个数相乘,或先把后两个数相乘,再和另外一个数相乘,积不变。
例如:(2×3)×4 = 2×(3×4),(2×3)×4=6×4 = 24,2×(3×4)=2×12 = 24。
3. 乘法分配律。
- 公式:(a + b)× c=a× c + b× c或者a×(b + c)=a× b+a× c- 含义:两个数的和与一个数相乘,可以先把它们分别与这个数相乘,再相加。
例如:(2 + 3)×4=2×4+3×4,(2 + 3)×4 = 5×4 = 20,2×4+3×4 = 8+12 = 20;又如2×(3 + 4)=2×3+2×4,2×(3 + 4)=2×7 = 14,2×3+2×4 = 6 + 8=14。
四年级奥数教程(二)巧算乘除法

课题巧算乘除法四则运算中巧算的方法很多,它主要是根据已学过的知识,通过一些运算定律、性质和一些技巧性方法,达到计算正确而快捷的目的。
实际进行乘、除法以及乘除法混合运算式可利用到以下性质进行巧算:①乘法交换律:a×b = b×a②乘法结合律: a×b×c = a×(b×c)③乘法分配律: (a + b)×c = a×c + b×c由此可推出:a×b + a×c = a×(b + c)(a - b) ×c = a×c - b×ca×b - a×c = a×(b - c)④除法的性质: a÷b÷c = a÷b÷c = a÷(b×c)a÷(b÷c)= a÷b×c利用乘法、除法的这些性质,先凑整得10、100、1000……使计算更简便.教学目标1、熟练掌握乘除法运算法定律及性质2、善于运用运算定律和性质(包括正用、逆用、连用)。
教学重难点重点:乘法运算律,特殊的由原有规律推出的定律难点:把乘除运算律延用到乘除法混合运算中,尤其在含有括号或多项的题目中。
教学过程一、复习引入1、利用乘法运算律,填空:15×10 = 16×______25×7×4 = ______×______×7(60×25)×______ = 60×(______×8)125×(8×______) = (125×______)×143×4×8×5 = (3×4)×(______×______)2、下面哪些运算运用了乘法分配律?117×3 + 117×7 = 117×(3 + 7)24×(5 + 12) = 24×174×a + a×5 = (4 + 5)×a36×(4×6) = 36×6×43、用乘法分配律计算下面各题103×12 20×55 24×205= = == = == = =有了上面的复习,我们把四年级课本上有关乘法的运算律都进行了一个回顾与掌握,今天我们将就如何在巧算中用上这些规律进行讲解。
第一讲:整数四则混合运算 及简便运算

第一讲 整数四则混合运算的简便运算知识点拨1、整数四则运算定律(1) 加法交换律:(2) 加法结合律:(3) 乘法交换律:(4) 乘法结合律:(5) 乘法分配律:;(6) 减法的性质:(7) 除法的性质:;(8) 除法的“左”分配律:;,这里尤其要注意,除法是没有“右”分配律的,即是不成立的!备注:上面的这些运算律,既可以从左到右顺着用,又可以从右到左逆着用.2、加减法中的速算与巧算速算巧算的核心思想和本质:凑整。
常用的思想方法总结如下:(1) 分组凑整法.把几个互为“补数”的减数先加起来,再从被减数中减去,或先减去那些与被减数有相同尾数的减数.“补数”就是两个数相加,如果恰好凑成整十、整百、整千……,就把其中的一个数叫做另一个数的“补数”.(2) 加补凑整法.有些算式中直接凑整不明显,这时可“借数”或“拆数”凑整.三、乘法凑整思想核心:先把能凑成整十、整百、整千的几个乘数结合在一起,最后再与前面的数相乘,使得运算简便。
例如:,,理论依据:乘法交换律:a×b=b×a乘法结合律:(a×b) ×c=a×(b×c)乘法分配律:(a+b) ×c=a×c+b×c积不变规律:a×b=(a×c) ×(b÷c)=(a÷c) ×(b×c)四、乘、除法混合运算的性质⑴商不变性质:被除数和除数乘(或除)以同一个非零数,其商不变.即:,⑵在连除时,可以交换除数的位置,商不变.即:⑶在乘、除混合运算中,被乘数、乘数或除数可以连同运算符号一起交换位置(即带着符号搬家).例如:⑷在乘、除混合运算中,去掉或添加括号的规则去括号情形:①括号前是“×”时,去括号后,括号内的乘、除符号不变.即 ②括号前是“÷”时,去括号后,括号内的“×”变为“÷”,“÷”变为“×”.即添加括号情形:加括号时,括号前是“×”时,原符号不变;括号前是“÷”时,原符号“×”变为“÷”,“÷”变为“×”.即⑸两个数之积除以两个数之积,可以分别相除后再相乘.即上面的三个性质都可以推广到多个数的情形.例题精讲一、加法【例1】:278+463+22+37举一反三:732+580+268二、减法【例2】:2871-299举一反三:(1)157-99 (2)363-199 (3)968-599三、连减(5种)【例3】:528-53-47举一反三:(1)489-134-76 (2)470-254-46 (3)545-167-133 【例4】:496-(296+144)举一反三:(1)675-(175+89)(2)466-(66+125)(3)354-(154+77)【例5】:496-(144+296)举一反三:(1)675-(89+175)(2)466-(125+66)(3)354-(77+154)【例6】:528-72-28举一反三:(1)489-77-389 (2)465-267-65 (3)545-167-145【例7】:824-224-176-124举一反三:(1)643-164-133-243 (2)487-187-139-61 (3)545-167-145四、乘法分配律(8种)【例8】:计算:125×(80+32)(24+40)×25举一反三:(1)125×(64+80)(2)(80+32)×125 (3)(16+32)×25【例9】:(1)125×(100-8)(2)(125-40)×8举一反三:(1)125×(100-48)(2)(100-16)×25【例10】:(1)117×56+117×44举一反三:(1)269×26+74×269 (2)521×65+35×521 (3)126×72+126×12+126×16【例11】:125×69-125×61举一反三:(1)25×127-25×119 (2)365×251-365×151(3)156×59-156×27-156×22 (4)137×97-44×137-137×43【例12】:45×102举一反三:(1)25×44 (2)125×168 (3)125×18【例13】:36×99举一反三:(1)45×98 (2)125×92 (3)35×99【例14】:(1)81+9×391 (2)9+9×999 (3)99+9×99【例15】:(1)9×107-63 (2)6×108-48 (3)134×101-134五、连除(2种)【例16】:1250÷25÷5举一反三:(1)2000÷125÷8 (2)1280÷16÷8 (3)1300÷5÷20(4)840÷5÷8 (5)1700÷25÷4 (6)4800÷50÷2【例17】:630÷(63×5)举一反三:(1)780÷(78×2)(2)1250÷(125×5)(3)6300÷(63×5)六、四则混合运算(1)(24+24)÷24×24 (2)24+24÷24×24 (3)16+4-16+4(4)(16+4)-(16+4)(5)25×6÷25×6 (6)120-(72+48)÷24(7)45+55÷5-20 (8)12×(280-80÷4)(9)218+324÷18×5(10)(488+32×5)÷12 (11)4500÷(170-60×2)(12)(28+41)÷(92÷4)(13)80+320÷4-30 (14)18×(420-320÷20)(15)48-2×8÷8×2(16)480÷(144-960÷8)(17)120+480÷(43-28)(18)(273+562)÷5-96 (19)4500÷(150-40×3)(20)812÷(532-36×14)(21)(12+12)÷12×12(22)625÷(54-522÷18)(23)17+13-17+13 (24)60-15×7÷15×7(25)12×(289-84÷4)(26)218+702÷18×5 (27)45000÷(150-40×3)(28)(77+38)÷(92÷4)(29)58-28×2+40 (30)56×4-175÷5(31)(73-59)×(6+13)(32)(85-40)÷(15÷3)(33)71-17×7÷17×7课堂检测:(1)43×202 (2)59×299 (3) 134×51-51×34 (4)7200÷36(5)68×32—784÷56 (6)3000÷125÷8 (7)98×35 (8) 960×46÷48(9)480×46÷48 (10)302×99+302 (11)756+483-556(12)230×54+540×77 (13)887×25-87×25 (14)(825+25×8)×4(15)325-225÷5+145 (16)35×102 (17)498+(201-154)(18)125×89×8(19)428×78+572×78 (20)8800÷(25×88)(21)3600÷50÷2(22)25×(20+4)容易出错类型(共五种类型)600-60÷15 20×4÷20×4736-35×20 25×4÷25×498-18×5+25 56×8÷56×8280-80÷ 4 12×6÷12×6175-75÷25 25×8÷25×880-20×2+60 36×9÷36×936-36÷6-6 25×8÷(25×8)。
四年级四则混合运算

四年级四则混合运算混合运算是四则运算的综合运用,包括加减乘除四种基本运算。
在四年级,学生需要通过练习混合运算来提高他们的数学技能和运算能力。
下面是一些四年级混合运算的例题,帮助学生更好地理解和掌握混合运算。
1. 例题一将10减去4,然后乘以3再加上12,最后除以2,得出的结果是多少?解答过程:首先,将10减去4得到6;然后,将6乘以3得到18;接下来,将18加上12得到30;最后,将30除以2得到15;所以,最终的结果是15。
2. 例题二将28减去先前的结果15,然后乘以2,再加上5,最后除以3,得出的结果是多少?解答过程:首先,将28减去15得到13;接下来,将26加上5得到31;最后,将31除以3得到10余1;所以,最终的结果是10余1。
3. 例题三先将15加上7,然后乘以4减去8,最后除以2,得出的结果是多少?解答过程:首先,将15加上7得到22;然后,将22乘以4得到88;接下来,将88减去8得到80;最后,将80除以2得到40;所以,最终的结果是40。
4. 例题四将18乘以5加上4再除以2得出的结果是多少?解答过程:首先,将18乘以5得到90;然后,将90加上4得到94;所以,最终的结果是47。
通过以上例题的实践操作,我们可以发现混合运算首先需要注意运算的顺序。
我们应该先计算括号里的部分,然后进行乘除法,最后进行加减法。
同时,我们应该准确地理解题目的意思,根据题目要求进行运算。
通过反复练习,四年级的学生可以熟练掌握混合运算的方法和技巧。
在实际生活中,混合运算也有很多应用场景。
比如,购物时计算总价、分配物品时平均分配、解决实际问题时计算所需的数量等等。
通过学习混合运算,学生不仅能提高数学能力,还能培养解决问题的能力和应用数学的思维能力。
总结起来,四年级的混合运算是数学学习中的重要内容,可以帮助学生提高他们的数学技能和解决问题的能力。
通过不断练习和实践,学生可以掌握混合运算的方法和技巧,并将其应用于实际生活中。
