三维裂纹
基于ABAQUS的货叉三维裂纹应力强度因子有限元分析

基于ABAQUS的货叉三维裂纹应力强度因子有限元分析货叉是一种常用于起重机械的重要零件,承受着大量的动态和静态荷载。
在使用过程中,货叉可能会受到裂纹的影响,从而降低其强度和安全性。
因此,对货叉的裂纹应力强度因子进行分析是非常必要的。
裂纹应力强度因子是评估裂纹尖端应力场的参数,它可以用来判断裂纹的扩展情况以及材料的断裂行为。
基于ABAQUS的有限元分析可以用来计算货叉在裂纹尖端处的应力强度因子。
该分析要求以下几个步骤:1. 建立货叉的三维有限元模型:模型要包括真实的几何形状和材料性质。
可以使用ABAQUS提供的建模工具,如Part模块和Assembly模块,来构建模型。
此外,还需考虑货叉的边界条件和加载方式。
2.设置裂纹:在模型中引入裂纹,它可以是表面裂纹或体内裂纹。
可以使用ABAQUS提供的功能来创建裂纹和裂纹前沿。
3.划分网格:为了计算裂纹应力强度因子,需要划分网格并分配单元类型和单元属性。
合理的网格划分可以提高计算精度和效率。
4.应用荷载:根据实际情况,在模型中施加与实际工作状况相对应的荷载。
荷载类型可以包括静态荷载、动态荷载或者其他较为复杂的荷载。
5.运行分析:设置好所有必要的计算参数后,可以运行分析并计算货叉的裂纹应力强度因子。
6.结果分析:根据计算结果,可以评估货叉中裂纹的状态和扩展情况。
一般来说,如果裂纹应力强度因子超过了材料的断裂韧性,则裂纹有可能扩展,从而降低货叉的强度和安全性。
在进行有限元分析时,需要注意模型的合理性和准确性。
同时,还应考虑到材料的非线性特性和可能的影响因素,以获得较为准确的分析结果。
总之,基于ABAQUS的货叉三维裂纹应力强度因子有限元分析可以用来评估货叉中裂纹的状态和扩展情况,为提高货叉的安全性和可靠性提供科学依据。
05--积分变换方法与三维裂纹问题

u 1
2 E
(1
)
d 2 dy2
2
ei
x
i
d
7 10
v 1
2 E
(1
)
d 3 dy3
(2
) 2
d dx
ei
x
1
2
d
7 11
若求得 ( , y) ,可得 u(x, y) , v(x, y) 。 6
二、半无限弹性平面的位移解
现讨论受分布压力 q(x)的半无限弹性平面问题
边界条件为:
(1) y 0
F
(
)
2
q0a
1/
2
J1(
)
可得位移:
v0
(x)
2q0
(1
E
2
)
a2 x2
在均布压力作用下,裂纹会扩大张开成椭圆形状。 利用这种方法可解许多种裂纹尖端的应力位移场。
15
• 三维裂纹问题的求解
16
受均匀拉伸的椭圆盘状裂纹,Green-Sneddon解
z 0,
x2 a2
y2 b2
1
边界条件:
x2 y2 z2 ij ~ 0
7 22
q( ) cos( x) d 0 ( x a)
0
7 23
•
引入代换: , q( )
aa
F() , cos()
2
J
1 2
(
)
• 式中 J 是贝塞尔函数 12
三、裂纹问题的对偶积分方程
利用上述代换,边界条件(7-22)、(7-23)写为:
0 F ()J1 ()d g() 2
z 0, (x, y) D zz p0 , xz yz 0
基于裂纹闭合模型的三维裂纹疲劳扩展分析

根据模拟的结果发现,随着拉弯载荷中弯曲载荷所占比例的上升, 表面裂纹在深度方向和表面方向上的扩展速度下降,疲劳裂纹扩 展寿命上升,当表面裂纹穿透平板厚度时,裂纹的最终长度上升。 对于特定的拉弯组合载荷,不同初始形状比的半椭圆表面裂纹的 最终形状比均趋于一个固定值,这与纯弯曲载荷下得到的结果一 致。
基于裂纹闭合模型的三维裂纹疲劳扩 展分析
航空结构中存在大量的三维形式裂纹,如角裂纹,表面裂纹等。 对含有三维裂纹的结构进行疲劳裂纹扩展分析和疲劳寿命预测 在飞机结构损伤容限设计中至关重要。
然而,谱载荷下三维裂纹的疲劳扩展及寿命预测至今未能得到很 好的解决,原因在于用于进行疲劳扩展分析以及寿命预测的材料 疲劳性能参数均是根据标准疲劳实验数据获得的,而实际三维裂 纹尖端的三维应力状态不同于标准试验件中穿透裂纹尖端的应 力状态,因此现有的材料疲劳性能数据不能直接应用于三维裂纹 疲劳扩展及疲劳寿命分析。因此,本文基于三维疲劳断裂理论, 对三维疲劳裂纹扩展做了以下工作:1.基于有限元软件ABAQUS计 算了含穿透直裂纹有限宽度平板裂尖的应力强度因子,并得到了 裂尖应力强小,大大方便了在实际工程 结构中使用该模型。三维条带屈服模型考虑裂纹闭合效应,同时 能够考虑载荷间的相互影响,因此能够用于计算变幅载荷或谱载 荷下裂纹的疲劳扩展。
3.基于三维条带屈服模型提出了一个三维裂纹扩展模型,分析了 纯弯曲载荷下半椭圆表面裂纹的疲劳扩展和扩展过程中裂纹形 状演化规律,并将该结果与试验结果进行了对比。分析发现尽管 表面裂纹的初始形状比不同,但在裂纹扩展过程中裂纹的形状比 趋于一个固定值,且纯弯曲载荷和拉伸载荷下都存在该现象。
4.根据第四章提出的三维裂纹扩展模型,分析了不同初始形状比 的半椭圆表面裂纹在不同拉弯组合载荷作用下的疲劳扩展行为, 并预测了相应的疲劳裂纹扩展寿命。将基于三维裂纹扩展模型 模拟得到的半椭圆表面裂纹在纯弯曲和纯拉伸载荷下的扩展行 为和已有文献中的试验结果进行了对比,两者吻合较好,说明了 该模型能够有效预测拉伸、弯曲以及拉弯组合载荷下半椭圆表 面裂纹的疲劳扩展行为。
三维裂纹J积分求解
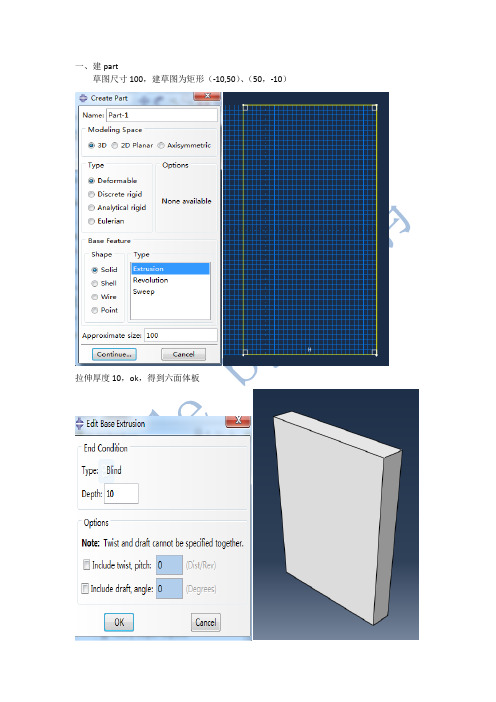
一、建part草图尺寸100,建草图为矩形(-10,50)、(50,-10)拉伸厚度10,ok,得到六面体板二、材料属性,具体参数自己设置吧,一步步都应该清楚。
3、装配(creat instance)装配要用第二个(独立的),装配之后要切出一条缝,为后面定义seam,用下图右边的那个这个是选择分割草图的一条边这里应该选择红色面的右边, 这个是分割需要的草图,黄色的线就是分割线,然后,分割tool-partition选择cell-extrude/sweep edges选择红色的圈这个选择选中的这个然后选择z轴,看好方向如果方向正确就选ok,如果不正确就选flip然后再选按住shfit选择涂黄的两条线(就是裂纹线)(1)先定义seam,special-creat-assign选择红色的区域,就定义了seam(2)定义crake,special-creat-crake,用围线积分继续,这里选择的时候容易选择的只是一个面所以先隐藏那个小圆面,选择的那个就是隐藏的命令,隐藏小圆面后就可以选择crake front了。
Crake Front 亮红色的就是选择的裂纹线学裂纹尖端有奇异性,所以这儿要按下图设置,不懂的看理论吧。
此时crake定义好了5、荷载步按静力学分析,继续默认设置就行,谈后在历史输出步中要编辑Domain这个要选择之前定义的crake-1下面的围线数我一般用的是8,这个我感觉8左右就行,但是不能就2,3个,也不必要太多(路径无关性)。
6、load这个我简单加载两端均布拉力,做好加一个约束边界条件,这里我加了一个右边的UZ7、划分网格,感觉断裂最麻烦的就是划分网格了,划分网格之前必须对实体分割能比较规则的,而且在裂纹尖端需要时放射状,其实尖端是四边形也能算,但是所有的例子都是放射状的。
因为划分网格比较麻烦我就补一步步的说了那个之前做的例子来示意一下最好是按照下图进行分割,矩形里面最好再分一个圆这样可以有效保证网格效果比较好。
三维裂纹扩展分析软件FRANC3D V6.1介绍

FRANC3D V6.1 的工作流程
7 FRANC3D 中国网站请访问:/
地址:上海市徐汇区宜山路 900 号科技产业化大厦 A 区 411-413 室 邮编:200233 电话:+86 21 51090998
建模方法和特点
子模型
FRANC3D V6.1 支持子模型技术,裂纹扩展时仅限于在子模型内进行网格重划,所有 FRANC3D V6.1 支持的有限元软件均支持定义子模型。 实际分析时, 裂纹尺寸相对于结构来说往往很小, FRANC3D V6.1 将网格重划区域限定 在子模型内,可以大大减少数据的传送和处理量,从而提高裂纹扩展分析效率。其余部分的 模型可以包含简化的结构(如 shell 单元)、复杂边界条件(如接触)或完全六面体的网格 模型。重划的子模型会被重新“放入”全局模型,然后对整个模型进行分析。 子模型仅仅用于网格重划,不影响分析的策略,这种方法不同于子结构或局部/全局分 析,它可以在裂纹扩展分析的任何一步重新定义子模型。
全新一代FRANC3D V6.1
微动疲劳与任意三维裂纹扩展分析
上海量维信息科技有限公司
地址:上海市徐汇区宜山路 900 号科技产业化大厦 A 区 411-413 室 邮编:200233 电话:+86 21 51090998
现状分析
在工业中,真实的结构总是存在众多缺陷或裂纹,对于一个含裂纹或缺陷的构件,多在 其服役荷载远低于容许强度的情况下就发生了破坏。 实际工程结构在经受长时间多因素综合 作用下,产生变形、裂纹等缺陷,从而导致整个结构的失效。结构的失效主要由疲劳引起, 其最终失效形式即为断裂,有大约 80%以上的工程结构的断裂与疲劳有关,由疲劳引起的 巨大经济损失及灾难性的后果不胜枚举。 美国的一项调查指出, “每年, 因材料的断裂失效引起的经济损失大概有 1,190 亿美元, 是全美 GNP 的 4%。其中,这些损失中估计有 350 亿美元可以通过应用断裂力学来避免, 又有 280 亿美元可以通过相关的研究避免。”巨大的直接和间接经济损失固然惊人,但是由 于断裂失效引起的人身伤害和生命损失更令人扼腕叹息。
三维裂纹扩展时动态应力强度因子的有限元研究

56
数。 如果 t=0 时的初始位移和初始速度为{u0}与
{u 0},则由式(8)求得初始加速度
{ } ⎡⎣M ⎤⎦ {u0} = F (t) − ⎡⎣C ⎤⎦ {u0} − ⎡⎣K ⎤⎦ {u0} (11)
再根据式(9)— (11)式,求出下一时刻△t 的
{u∆t},{u ∆t},{u ∆t},由此即可得到所有时间
3 结束语
(1) 利用 ANSYS 建立三维模型的方法是多 种多样的,本文主要考虑的圆柱体中心圆裂纹的 结构。还可以利用相同的单元和建模方法建立其 他典型裂纹结构,如中心穿透裂纹,椭圆裂纹等。
(2) 通 过 与 算 例 的 比 较 , 可 以 认 为 利 用 ANSYS 的 APDL 参数化语言编程建立三维裂纹 模型是可行的,有限元法是计算动态 K1(t)因子的 有效方法,本文提供的合理计算方案,也可为其 它结构件动态 K1(t)因子的计算作参考。
关键词:动态应力强度因子 三维裂纹扩展 有限元
中图分类号:TM464
文献标识码:A
文章编号:1003-4862(2010)06-0055-04
The Finite Element Method Study on Stress Intensity Factor of three Dimensional Dynamic Crack Propagation
尖端用退化三角形奇异等参元,其余地方用标准
等参元。
表 1 材料及模型参数
材 料 E(GPa)
υ
ρ(kg/m3)
参数 200
0.3
7800
模 型 Ro(mm)
h(mm)
a
参数 100
1000
不定
本文采用突加载荷,如图 4,其中 σ0(t)=100 MPa。对不同裂纹长度的动态应力强度因子的有 限元计算结果列入表 2 中。图 5 所示为裂纹尖端 应力场,典型的应力集中现象。
裂隙岩体三维裂纹动态扩展规律与破断机制

裂隙岩体三维裂纹动态扩展规律与破断机制裂隙岩体是一种由裂隙网络构成的岩体,裂隙在岩体的形成过程中起着重要的作用。
裂纹动态扩展规律和破断机制是研究裂隙岩体力学行为的关键点,对于地质灾害的预测和防治具有重要意义。
本文将从裂纹动态扩展规律和破断机制两个方面进行探讨。
裂纹动态扩展规律是指在外界作用下,裂纹在岩体中发展和扩展的规律。
一般来说,裂纹动态扩展规律可以分为线性和非线性两种情况。
在线性规律下,裂纹的扩展速度与应力强度因子呈线性关系,即扩展速度正比于应力强度因子。
而在非线性规律下,裂纹的扩展速度与应力强度因子不再呈线性关系,而是随着应力强度因子的增大而增大。
裂纹的动态扩展规律受到多种因素的影响,如岩性、裂隙类型和应力状态等。
其中,岩体的质地和裂隙的形态是决定裂纹动态扩展规律的重要因素之一。
此外,裂纹动态扩展还与岩体的环境条件有关,如温度、湿度等。
这些因素的综合作用决定了裂纹的扩展速度和方向。
破断机制是指在裂纹动态扩展过程中,岩体受到应力作用下的破坏机理。
破断机制可以分为韧性破断和脆性破断两种情况。
在韧性破断中,岩体具有一定的延性,即在受到应力作用下能够发生可逆变形。
而在脆性破断中,岩体则具有较低的延性,受到应力作用后很快发生不可逆变形并形成破碎。
破断机制的选择与岩体的物质性质和应力条件有关。
例如,在高温高压条件下,岩体的韧性破断机制更为显著,而在低温低压条件下,岩体的脆性破断机制则更加明显。
除此之外,破断机制还与裂隙的性质有关。
当裂隙的密度较大,且分布较均匀时,岩体更容易发生脆性破断。
裂纹动态扩展规律和破断机制研究的意义不仅在于理解岩体力学行为的基本规律,还可为工程实践提供理论支持和技术指导。
通过研究裂纹动态扩展规律,可以预测岩体在不同应力状态下的破坏行为,进而为地质工程的设计和施工提供依据。
同时,通过研究破断机制,可以针对岩体的特点开发出相应的防治措施,减少地质灾害的发生。
总之,裂隙岩体裂纹动态扩展规律和破断机制的研究对于理解岩体的力学行为、预测和防治地质灾害具有重要意义。
三维裂纹问题的高精度数值解法

没有得到任何具体结果 . 汤任基和秦太验 在文献 [ ] 】 1 的基 础上 , 对三维 任意形 状平 片裂 纹
的问 题 作 了更 一 般 性 的讨 论 , 为 此 建 立 了有 限部 积 分 一 界 元 数 值 方 法 . 而 , 用 这 种 方 并 边 然 采 法 所 得 到 的数 值 结 果 精 度 不 够 令 人 满 意 . 本 文 提 出 了一 种 高 精 度 的求 解 无 限 大 均 质 弹 性 体 中任 意 平 片裂 纹 问 题 超 奇 异 积 分 方 程 的多 项 式 数 值 方 法 . 该 方 法 中 , 奇 异 积 分 方 程 的 未 知 位 移 间 断 函 数 被 近 似 地 表 示 为 在 超 C eyhv多项 式 和 能 够 反 映平 片 裂 纹 前 沿 奇 性 指 数 的位 移 间 断 基 本 函数 之 积 . 章 最 后 具 hbse 文
k = 6 0≤ 1 / , k =、 /1一 ( / ) b a ,
维普资讯
第0 22 0
2
3 2 年 6 牵第肯 月
AT MCAI L A IC C 固体力学学报 N A A EHN A 0I S I CS D
V.2. JeN2 u3o o 0 n 0 1 2 2
三 维 裂 纹 问 题 的 高 精 度 数 值 解 法
* 国家 自然 科学 基金资 助 ( 目编 号 :970 6 . 项 16 2 3 )
裂隙岩体三维裂纹动态扩展规律与破断机制

裂隙岩体三维裂纹动态扩展规律与破断机制引言:裂隙岩体是由于地壳应力作用而形成的具有一定规模的裂隙网络结构的岩体。
在地质学和工程力学领域中,研究裂隙岩体的力学特性及其裂纹动态扩展规律和破断机制对于岩体工程稳定性评价和设计具有重要意义。
一、裂隙岩体动态扩展规律1.裂纹扩展方式裂隙岩体的裂纹扩展一般分为两种方式,即开裂和滑移。
开裂是指在岩体中形成新的裂隙,滑移是指已存在的裂隙在应力作用下进一步发展。
裂纹扩展方式的选择与岩体的物理力学性质、应力状态、裂隙网络结构及裂隙面间的摩擦特性等因素有关。
2.裂纹扩展速率裂纹的扩展速率是裂隙岩体动态扩展规律的关键参数之一。
裂纹扩展速率与岩体的物理力学性质、裂纹面间的摩擦特性、裂隙网络结构、应力状态及裂隙的初始尺寸等因素有关。
一般情况下,裂纹扩展速率随着应力的增大而增大,并且在达到一定应力门槛值后迅速增加。
3.裂纹扩展路径裂隙岩体中的裂纹扩展路径主要取决于裂隙面间的摩擦特性和岩石的物理力学性质。
当裂隙面之间的摩擦力较大时,裂纹倾向于沿着裂隙面的平行或近平行方向扩展;而当摩擦力较小时,裂纹则倾向于以更大的角度穿过裂隙面。
二、裂隙岩体破断机制1.裂隙岩体破断类型裂隙岩体的破断类型主要包括剪切破断、拉伸破断和剪拉混合破断。
其中,剪切破断是指裂隙面间的剪切应力达到破断强度引起岩体的破裂;拉伸破断是指岩体中的裂隙在张拉应力的作用下发展至破断;剪拉混合破断是指裂隙面间的剪切应力和张拉应力共同作用下导致岩体的破断。
2.破断强度破断强度是指岩石材料在破断前所能承受的最大应力。
裂隙岩体的破断强度与岩石的物理力学性质、裂隙网络结构、裂隙面间的摩擦特性及应力状态等因素有关。
一般情况下,破断强度随着裂隙密度的增加而减小,并且在达到一定裂隙密度后迅速减小。
3.破断模式裂隙岩体的破断模式主要取决于裂隙面间的摩擦特性、裂隙的分布和岩体的应力状态等因素。
常见的破断模式包括剪切破裂、拉伸破裂和剪拉混合破裂等。
高温受弯三维表面裂纹的J-积分公式

高温受弯三维表面裂纹的J-积分公式*黄培彦孔德清**罗立峰赵琛摘要对快中子增殖堆主容器等高温受弯构件中三维表面裂纹前缘的应力场进行了分析,在先前提出的J-积分半经验公式的基础上,经过进一步的理论分析和数值处理,提出了新的J-积分公式: J=fσ.H.fW.fθ/(QE′). 式中因子fσ, H, f W, fθ, Q分别为作用应力σ,裂纹形状比a/c和相对深度a/t,裂纹半长与板宽之比c/W,离心角θ,第二类完全椭圆积分E(κ)的函数;E′则为当量弹性模量. 该式的应用范围为:0≤a/c≤1; 0≤a/t≤0.75; c/W≤0.8,在此范围内,由公式求得的计算结果与有限元数值分析结果的相对误差为±3.9%.关键词J-积分;表面裂纹;高温;弯曲载荷中图资料分类号O 346.2J-INTEGRAL EQUATION FOR 3-D SURFACE CRACK UNDER BENDING LOADS AT ELEVATED TEMPERATUREHuang Peiyan Kong Deqing Luo Lifeng Zhao Chen(The College of Traffic & Communications, South China Univ. of Tech.,Guangzhou 510640)Abstract A J-integral equation,J=fσ.H.fW.fθ.πa/(QE′), at thesurface and maximum depth point of a 3-D surface crack under bending loadsat elevated temperature is proposed. In this equation, the parameter fσis the function of applied loads; H is the function of aspect ratio a/cand the ratio of crack depth to plate thickness a/t; fWis the functionof the ratio of crack length to plate width c/W; fθ is the function of centrifugal angle to identify position along an elliptic crack front θ; Q is that of complete elliptic integral of the second kind E(κ); E′ is an effective elastic modulus. The equation is based on the finite element analysis completed by authors with the surface cracked large plate specimen a few years ago. This is used to develop the analysis given by finite element method for 3-D semi-elliptical surface cracks in finite elastic plastic plate, such as the wall of a main vessel of fast breeder reactor, subjected to bending loads. A wide range of configuration parameters is included in the equation. The aspect ratios, a/c, ranged from 0 to 1; the ratios of crack depth to plate thickness, a/t, ranged from 0 to 0.75, and c/W≤0.8. Comparing the values of J-integral computed by the equation with those from the finite element analyses, the mean errors are within ±3.9 percent.Key words J-integral equation; surface crack; elevated temperature; bending loads核反应堆主容器等构件在高温液体所引起的热应力的反复作用下,构件内表面容易产生疲劳裂纹,并导致裂纹扩展,最终贯穿整个构件的壁厚. 因此,探讨高温环境中受弯曲载荷作用下三维表面疲劳裂纹的扩展规律,对提高核反应堆等设施的安全性具有极其重要的意义.探讨高温环境中三维表面疲劳裂纹的扩展规律,首先要解决其力学参量问题. 经过较长时间的议论,大多数国内外专家、学者偏向于采用J-积分[1, 2]. 但由于各种条件的限制,长期以来一直没有一个能考虑表面裂纹形状、尺寸和构件尺寸等影响因素的J-积分公式. 为解决这一问题,作者等在几年前提出了一个精度较高、能描述三维表面半椭圆型裂纹的J-积分半经验简易计算公式[3]. 经过几年的实践,该公式被认为最能准确地描述三维表面半椭圆型疲劳裂纹的扩展规律[4]. 但是,该公式结构繁杂,有一些参量的选择未尽合理. 本文在以往工作的基础上,进一步分析高温环境中受弯曲载荷作用下三维表面疲劳裂纹的扩展规律,对上述J-积分公式中一些重要参量进行重新选择,提出结构较简单、合理精度较高,适用范围较广的J-积分新公式.1 简易J-积分计算公式[3]简介对于图1所示的三维表面半椭圆型裂纹在高温环境中受弯曲载荷作用时裂纹前缘的J-积分表达式,文献[3]中使用大型计算机进行了大量的有限元数值分析,并对计算结果进行了分析和拟合,提出了如下的半经验简易计算公式:(1)式(1)的有效范围为:0≤a/c≤1.0, 0≤a/t≤0.75,c/W≤0.8. 式中,JB为沿裂纹长度方向的裂纹前缘的J-积分值 N/m;εp 为屈服应变,%;εn为公称应变,%;a为裂纹深度,mm;c为裂纹半长,mm;t为板厚 mm;2W为板宽,mm.图1 弯曲载荷作用下的三维表面半椭圆型裂纹Fig.1 3-D surface semi-elliptical crack under bending loads式(1)中的裂纹形状因子F1由下式表示:(2)式中,(3)(4)式(4)中,系数B0~B4分别为2 127.7, -776.78, 1 118.5, -821.31, -1 971.2.考虑板宽影响的修正系数fW为:(5)裂纹形状因子F2为:(6)式中,(7)系数D1~D3分别为: 203.68, 718.44, -270.96.裂纹深度方向的J-积分值JA可由下式求得:(8) 式中,(9)(10)系数M0~M4、 N~N4分别为0.608, 12.44, -11.06, 1.02, 1.41; 0.286, 10.52,-12.70,2.38, 1.14.对于不同的裂纹形状比a/c和裂纹相对深度a/t,给定板宽和荷载,由式(1)~(10),可比较方便地求得各种情形下沿裂纹长度方向和深度方向的J-积分值(JB ,JA),进而对弹塑性断裂问题进行分析和评估.2 J-积分公式的构成公式(1)~(10)能比较准确地计算高温环境中三维表面裂纹前缘的J-积分值,利用这些公式能有效地、比较准确地描述三维表面半椭圆型疲劳裂纹的扩展规律[3~5]. 然而,裂纹长度方向和深度方向的J-积分值需由两个公式分别计算,且其构造及有些参数的选择还未尽合理,亦较繁琐.为将JA 和JB统一到同一公式中进行计算,并尽可能使公式的结构合理,本文对文献[3]中得到的有限元计算结果进行重新分析和整理,构成下列J-积分表达式:(11)式中,E′为当量弹性模量, MPa; Q1/2为第二类完全椭圆积分; H为裂纹形状修正因子; fW , fθ分别为板宽修正系数和裂纹前缘位置修正系数;而载荷因子fσ可表示为:(12)对于SUS304不锈钢等的Ludwick型硬化材料,弯曲正应力σ与应变ε的关系式可近似表示为:(13)(12)和(13)式中,σp为屈服应力, MPa;n为材料硬化指数(对于SUS304不锈钢,σp =92.1 MPa,εp=0.059 8%, n=0.427).裂纹形状修正因子H可由下式表示:(14)式中,θ为裂纹前缘某点的离心角(见图1),因子R取为裂纹形状比a/c 和裂纹相对深度a/t的函数:(15)修正因子H1, H2可分别表示为:(16)(17)系数B0~B11分别为19.5, 4.03, -2.15, -7.99, -9.05, 0.42, 15.3, 1.00, 2.70,2.00, 30.1, -8.61. 因子M取为:(18)式中,各因子分别为:板宽修正系数的表达式可取以下形式:(19)裂纹前缘位置修正系数由下式表示:(20)第二类完全椭圆积分的平方Q可近似表示为[6]:(21)考虑到裂纹表面与深度方向裂纹前缘附近区域的应力状态的不同,取当量弹性模量为:(22)对于SUS304不锈钢,弹性模量E=154 GPa,泊松比μ=0.306.3 计算结果及讨论给定裂纹和试样尺寸、载荷及材料常数,由式(11)~(22)可方便地计算出各种情形下沿裂纹长度方向和深度方向的J-积分值(JB , JA). 作为计算实例,图2所示为在弯曲正应力σ=189 MPa(公称应变εn=0.20%)的作用下,当裂纹初始形状比a/c分别为1/2, 1/4, 1/8时JA 和JB值与裂纹相对深度a/t的关系曲线. 先前得到的同一条件下的有限元计算结果[3]也示于同一图中. 从该图可知,由新构成的J-积分公式得到的理论曲线与有限元计算结果吻合得较好,在有限元数值分析的范围内,有限元计算结果与理论计算结果的相对误差为±3.9 %.图2 J~a/t关系曲线Fig.2 J~a/t curves将J-积分值进行无量纲化处理,所得无量纲量J0(J= E′Q J/(fσπa))与裂纹相对深度a/t的关系曲线如图3所示. 由该图可知,在裂纹长度方向(θ= 0°), J值不管裂纹初始形状如何都随着a/t的增大而增加,但当裂纹形状比a/c较小(a/c<0.2)时其增长幅度较大;在裂纹深度方向(θ= 90°),当a/c值较大时J0值随着a/t的增大而减少,但当a/c=0.1时, J值则随着a/t的增加而增大,且其增加幅度较大.~a/t关系曲线图3 J~a/t curvesFig.3 J*广东省自然科学基金(960255)资助项目**西江大学物理系作者简介:黄培彦,男, 1952年生,教授;主要研究方向:断裂力学,路桥力学,失效分析.作者单位:华南理工大学交通学院广州510640参考文献1 Goodall I W. The development of high temperature design methods based on reference stresses and bounding theorems. ASME J of Eng Mater and Tech, 1979,101: 3492 植田,矢川,高桥由纪夫. 半だ圆延性表面き裂进展举动の评价(き裂アスペクト比の简易的予测). 日本机械学会讲演论文集, 1986,860(3): 3213 黄培彦,福田嘉男, 佐藤善美等. 曲げ荷重下での表面き裂のJ-积分の简易评价式.日本机械学会论文集(A编), 1992, 58(554): 101~1084 福田嘉男,佐藤善美,藤冈照高等. 高温塑性曲げ疲劳下の表面き裂の进展解析. 第72期全国大会讲演会论文集(前刷). 东京:日本机械学会, 1994.25~295 黄培彦,黄小清,赵琛. 受弯三维表面疲劳裂纹的弹塑性贯穿举动. 暨南大学学报, 1999,20(1): 7~116 Newman J C, Raju I S. An empirical stress-intensity factor equation for the surface crack. Eng Fracture Mech, 1981, 15(1-2):185~192。
三维裂纹扩展计算

三维裂纹扩展计算FRANC3D 分三个步骤来预测三维裂纹扩展:1) 计算裂纹前缘上每个节点的局部裂纹扩展方向,或称扭转角度;2) 计算每个节点的局部裂纹扩展距离;3) 对扩展之后的新裂纹前缘进行光顺化处理,以减少不必要的数值“噪音”,并将裂纹前缘外插到结构自由表面外。
新裂纹前缘预测示意图扭转角度(Kink Angle )局部扭转角度基于极坐标系中局部裂纹前缘的应力来计算,如下图所示,该应力由局部应力强度因子来确定。
极坐标系中的局部裂纹前缘应力FRANC3D 提供了五个选项来计算局部裂纹扩展的方向,或称扭转角度:1. 平面扩展:扩展角度kink θ设置为0,强制平面扩展2. 最大张应力:),,(II I kink K K θσθθ最大时的kink θ值作为裂纹扩展角度3. 最大剪应力: ()()2222)()(kink z IIIc Ic kink r IIc Ic K K K K θσθσθθ⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛最大时的kink θ值作为裂纹扩展角度 local kink anglelocal extension smoothed front (red)predicted front (blue)original front()θσθθ()θσθr x yθ4. 最大应力:同时计算选项2和选项3,应力较大的选项将被使用5. 修正的最大应变能释放率: ()()()22222)()((kink z IIIc Ic kink r IIc Ic kink K K K K θσθσθσθθθθ⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+最大时的kink θ值作为裂纹扩展角度局部裂纹扩展距离一般情况下,裂纹前缘上每个节点的扩展距离是不同的,FRANC3D 使用裂纹扩展速率模型来计算裂纹扩展。
用户有两个选项可供选择:1) 指定位于应力强度因子中值(median )上的节点的扩展距离,所有其它节点的扩展距离通过适当缩放获得;2) 指定载荷的循环次数,从疲劳裂纹扩展速率公式直接计算所有节点的扩展距离;3) 指定载荷的持续时间,从时间相关裂纹扩展速率公式直接计算所有节点的扩展距离。
裂隙岩体三维裂纹动态扩展规律与破断机制

裂隙岩体三维裂纹动态扩展规律与破断机制裂隙岩体是指岩石中存在一定数量的裂隙和裂纹的岩体。
裂隙岩体的裂纹动态扩展规律以及破断机制对于岩石力学和岩体工程等领域具有重要意义。
本文将从三维裂纹动态扩展规律和破断机制两个方面进行探讨。
首先,三维裂纹动态扩展规律描述了裂纹在裂隙岩体中的扩展过程。
在裂隙岩体中,裂纹通常以三维的方式呈现,其扩展规律受到多个因素的影响。
一是裂纹的长度和宽度。
裂纹的长度和宽度决定了裂纹的扩展速率和路径,较短的裂纹会更快地扩展,而宽度较小的裂纹会更容易被封闭。
二是裂纹的初始状态。
裂纹的初始状态包括裂纹的形状、位置和方向等,这些因素决定了裂纹扩展的路径和方向。
三是应力场的作用。
应力场会对裂纹的扩展产生影响,高应力区域会促使裂纹扩展,而低应力区域则可能阻止裂纹的扩展。
四是岩石的力学性质。
不同类型的岩石具有不同的力学性质,这些性质将影响裂纹的扩展速率和路径。
其次,裂隙岩体的破断机制是指岩石中裂纹扩展至破断的过程。
岩石的破断机制受到多个因素的综合作用。
一是裂纹间的相互作用。
裂纹之间的相互作用会导致能量聚集和释放,进而影响裂纹的扩展速率和路径。
裂纹的相互作用可以是强化的,使裂纹扩展更快;也可以是相互抑制的,使裂纹扩展受到限制。
二是局部损伤效应。
当裂纹扩展到岩体内部时,局部损伤效应会导致岩石的局部破碎和变形,从而影响裂纹的扩展。
岩石的局部损伤效应可能表现为局部剪切带的形成和扩展,也可能表现为局部应力集中和局部破坏。
三是应力释放效应。
当裂纹扩展至岩体表面时,应力释放效应会导致岩石的破碎,形成破坏带。
应力释放效应可以通过裂纹的扩展模式和扩展速率来描述。
综上所述,裂隙岩体的裂纹动态扩展规律和破断机制是岩石力学和岩体工程领域的重要研究内容。
深入理解裂纹在裂隙岩体中的扩展规律和破断机制,对于岩石力学参数的确定、岩体工程的设计和施工以及岩爆灾害的预测和防治具有重要意义。
未来的研究应该更加关注裂纹扩展的动态过程和不同类型岩石的破断机制,以提高对裂隙岩体的认识和应用。
用杂交有限元法计算三维裂纹的应力强度因子

用杂交有限元法计算三维裂纹的应力强度因子随着科学技术的发展,三维裂纹领域的研究也变得越来越重要。
在实际工程中,有关裂纹断裂的工程应用是非常重要的,因此针对三维裂纹的断裂行为进行研究,求解应力强度因子(SIF)是非常必要的。
在计算三维裂纹应力强度因子的过程中,计算机技术起着举足轻重的作用。
其中,用有限元方法计算是最常用的方法之一。
传统的有限元法通常需要大量的节点及单元来表示裂纹,以便得到较准确的结果。
由前人的研究表明,在对裂纹的计算中,杂交有限元法(XFEM)是一种有效的方法,他可以在不改变节点结构的情况下,准确地计算裂纹的表达式。
这种方法也能够有效地减少计算时间。
杂交有限元法(XFEM)由两部分组成,即传统有限元方法(FEM)和杂交元法(X)。
在扩展有限元法中,通常使用了几个接受杂交元(X),以便更加准确地表达裂纹,并且还需要在此基础上加上裂纹本身的应力聚集因子(SIF),以此来评价裂纹的断裂可靠性。
鉴于XFEM技术的发展,这种技术随着应用的增多,已经得到了很好的发展。
首先,我们考虑用有限元法(FEM)计算裂纹应力强度因子(SIF)。
在传统有限元法中,有关静态结构的问题是使用满足应力应变守恒关系的有限元单元组合而成的,从而可以识别出斜向等轴心及椭圆形裂纹的几何形态。
但是,传统的有限元法只能用节点为基础,在节点之间只能构建边界要素的网格形状。
因此,在节点数量比较少的情况下,裂纹的表达就比较模糊,这也意味着结果可能不太准确。
而杂交有限元法(XFEM)可以有效解决上述问题。
XFEM结合了传统有限元法和裂纹模型,从而形成了一种国际研究的有效方法。
在XFEM中,针对有限元节点的位置信息,除了用已有的节点外,还可以提供起“裂纹”的作用。
这种方法有效地表达了裂纹的形态,而且可以有效地减少计算时间。
除了节点之外,采用元胞自适应技术(CAE)也可以有效地计算裂纹应力强度因子(SIF)。
这种技术可以在裂纹周围安排不同的元胞,模拟细小裂纹的表示,并可以较准确地计算出应力强度因子(SIF)。
裂隙岩体三维裂纹动态扩展规律与破断机制

裂隙岩体三维裂纹动态扩展规律与破断机制裂隙岩体是指在地壳中由于构造运动或热胀冷缩等原因而产生裂隙的岩体。
裂隙岩体的三维裂纹动态扩展规律与破断机制是岩体力学研究的重要课题之一。
本文将从裂隙形成机制、裂纹传播过程以及控制因素等方面,论述裂隙岩体三维裂纹动态扩展规律与破断机制。
首先,裂隙形成机制对于裂纹的动态扩展具有重要影响。
裂隙的形成可以归因于应力场的改变、岩层的压实或膨胀、矿物的溶解沉淀等因素。
当应力场的改变超过岩石的承受能力时,裂隙就会形成。
此时,裂隙的初始长度、宽度和方向等特征对于裂纹的扩展路径和速率具有重要影响。
其次,裂纹传播过程是裂隙岩体三维裂纹动态扩展的关键环节。
裂纹传播可以分为弹性扩展和非弹性扩展两个阶段。
在弹性阶段,裂纹沿着岩体内部的锐利界面扩展,裂纹尖端周围的应力集中导致能量集聚,使得裂纹继续扩展。
在非弹性阶段,裂纹通过断裂面的滑动或剪切传导,岩体的变形不再是完全弹性的,而是包括弹性变形和塑性变形两部分。
最后,裂隙岩体三维裂纹动态扩展的破断机制受到多个因素的综合影响。
首先是力学因素,包括应力条件、岩石力学性质以及岩体结构等因素。
应力条件是影响裂纹扩展的主要因素之一,它决定了裂纹的传播方向和速率。
岩石的力学性质包括弹性模量、抗拉强度、黏聚力和内摩擦角等参数,它们决定了岩石的抗裂性能和断裂特征。
岩体结构对于裂纹传播具有明显影响,包括层理面、节理面、断层面等。
其次是岩石物理性质,包括岩石的渗流性、热传导性、磁性等因素。
这些物理性质会改变岩石的应力分布和力学响应,从而影响裂纹的扩展机制。
最后是环境因素,包括温度、湿度、化学物质的作用等。
温度和湿度的变化会引起岩石的热胀冷缩和水化膨胀收缩,进而影响裂纹的扩展。
总结起来,裂隙岩体三维裂纹动态扩展规律与破断机制是一个复杂而庞大的研究领域,研究者需要结合多种技术手段和理论模型,如岩石力学实验、数值模拟和地质观察等,来揭示裂隙岩体裂纹的形成和演化过程。
结构表面裂缝三维重建方法设计与实现

结构表面裂缝三维重建方法设计与实现结构表面裂缝三维重建方法设计与实现文章标题:结构表面裂纹三维重建方法的设计与实现引言:近年来,结构表面裂纹的三维重建方法在工程领域中得到了广泛的研究和应用。
这些方法可以准确地获取裂纹的几何形状和尺寸信息,为结构的健康监测和维护提供了重要的依据。
本文将基于步骤思维,介绍一种结构表面裂纹三维重建的设计与实现方法。
第一步:数据采集首先,需要通过合适的传感器或设备对裂纹进行数据采集。
常用的数据采集方式包括光学成像、激光扫描等。
例如,可以使用3D扫描仪对结构表面进行扫描,获取点云数据或图像序列。
第二步:数据预处理在数据采集后,需要对采集到的数据进行预处理,以去除噪声和其他干扰。
可以使用滤波算法、降噪算法等对点云数据或图像进行处理。
此外,还可以使用图像配准技术对图像序列进行校正和对齐。
第三步:特征提取在数据预处理完成后,需要从数据中提取裂纹的特征信息。
对于点云数据,可以使用曲率、法向量等方法来提取裂纹的几何特征。
对于图像序列,可以使用图像处理算法来检测和提取裂纹的边缘、纹理等特征。
第四步:裂纹重建在特征提取完成后,可以利用这些特征信息进行裂纹的三维重建。
常用的重建方法包括体素重建、三角网格重建等。
对于点云数据,可以使用体素化或点云拟合等方法将点云数据转换为三维模型。
对于图像序列,可以使用三角网格重建算法将二维图像序列转换为三维模型。
第五步:重建结果评估完成裂纹的三维重建后,需要对重建结果进行评估和验证。
可以使用测量工具对重建结果进行尺寸和形状的测量,与实际裂纹进行比较,以评估重建的准确性和可靠性。
第六步:结果可视化与应用最后,将裂纹的三维重建结果进行可视化展示,并将其应用于结构的健康监测和维护。
可以使用虚拟现实技术将重建结果与原始结构模型进行融合,实现裂纹的实时可视化和状态监测。
结论:本文基于步骤思维,介绍了一种结构表面裂纹三维重建方法的设计与实现。
该方法通过数据采集、预处理、特征提取、裂纹重建、结果评估和结果可视化等步骤,可以实现对结构表面裂纹的准确重建和可视化展示,为结构的健康监测和维护提供了重要的技术支持。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
!44号坐标系0.75为椭圆比例,所以生成的裂纹为椭圆形裂纹
!=========================================================
csys,0
n,216,1.2
!********定义216号节点
fill,15,216,1,215
egen,15,2000,-1
e,10216,217,12217,12216,10220,221,12221,12220
e,12216,12217,14217,14216,12220,12221,14221,14220
egen,9,2000,-1
e,217,218,12218,12217,221,222,12222,12221
e,111,2111,2131,131,112,2112,2132,132
egen,4,1,-1
!生成了契模型单元
csys,44
egen,rotationtimes,2000,all,,,,,,,,,rotationangle
!现在不明白产生的裂纹是圆形的还是椭圆形的
!旋转的度数为6度,旋转角度为90度,旋转次数为15
*get,eltype,elem,elmi,attr,type
!******将第elmi个单元选择情况
*if,eltype,ne,arg1,cycle
!******当eltype不等于arg1时,跳出循环
n3=nelem(elmi,3)
*if,nsel(n3),le,0,cycle
n7=nelem(elmi,7)
n,10216,1.2,0,-0.5
fill,10015,10216,1,10215
fill,216,10216,4,2216,2000
csys,44
fill,215,10215,4,2215,2000
csys,0
n,218,1.2,0,-1.2
fill,10216,218,1,217
e,12217,12218,14218,14217,12221,12222,14222,14221
egen,9,2000,-1
csys,0
egen,3,20,2101,2115,1,,,,,,0,0.17
egen,3,100,2116,2150,1,,,,,,0,0.17
nsel,s,loc,x,1.2
n,30218,0,0,-1.2
fill,218,30218,9,12218,2000
n,30215,0,0,-0.85
fill,30215,30218,2,30216,1
csys,44
fill,217,30217,9,12217,2000
fill,10216,30216,9,12216,2000
n,n16,x,y,z
n4=n3
n8=n7
nsel,all
type,3
en,elmi,n1,n2,n3,n4,n5,n6,n7,n8
emore,0,n10,0,n12,0,n14,0,n16
emore,
*enddo
cmsel,u,cracktip
nummrg,node
nsel,all
!填充
n,155,-innerradius,baseheight
!定义155号节点
ngen,2,2000,155
!此命令需进一步弄清楚====================================
csys,0
n,135,0.6,baseheight
!定义节点
csys,33
ngen,2,10,all,,,0.2
e,216,226,2226,2216,220,230,2230,2220
egen,5,2000,-1
e,220,230,2230,2220,320,330,2330,2320
egen,5,2000,-1
e,320,330,2330,2320,420,430,2430,2420
csys,0
e,2,22,1,1,2002,2022,2001,2001
egen,8,20,-1
e,2,3,23,22,2002,2003,2023,2022
egen,8,20,-1
egen,9,1,-8
!=====================================
type,2
fill,219,10219,4,2219,2000
csys,0
n,222,1.2,0.17,-1.2
fill,10220,222,1,221
n,30222,0,0.17,-1.2
fill,222,30222,9,12222,2000
n,30219,0,0.17,-0.85
fill,30219,30222,2,30220,1
egen,6,1,-1
e,187,2187,2194,194,188,2188,2195,195
egen,6,1,-1
e,180,2180,2187,187,181,2181,2188,188
egen,6,1,-1
e,171,2171,2180,180,151,2151,2181,181
/com, ********crack in 3-Ddimensions using solid45 and solid95
antype,static
et,1,solid45
et,2,solid45
et,3,solid95
!定义单元属性
mp,ex,1,2e4
mp,nuxy,1,0.3
esel,all
/gopr
*end
!到此宏已经定义完毕
/prep7
*afun,deg
!使用的角度数
innerradius=0.5
outerradius=1
!外半径和内半径分别为0.5和1
scaler=0.015
baseheight=0.51
layerheLeabharlann ght=0.18 layeramount=35
*if,nsel(n7),le,0,cycle
n1=nelem(elmi,1)
n2=nelem(elmi,2)
n5=nelem(elmi,5)
n6=nelem(elmi,6)
x3=0.75*nx(n3)
y3=0.75*ny(n3)
z3=0.75*nz(n3)
x=0.25*nx(n2)+x3
z7=0.75*nz(n7)
x=0.25*nx(n6)+x7
y=0.25*ny(n6)+y7
z=0.25*nz(n6)+z7
n=n+1
n14=n
n,n14,x,y,z
x=0.25*nx(n5)+x7
y=0.25*ny(n5)+y7
z=0.25*nz(n5)+z7
n=n+1
n16=n
!定义新的坐标系
csys,33
fill,1,11,9,2,1,9,20,3
!填充节点
n,15,outerradius-innerradius
!定义15号节点
n,75,outerradius-innerradius,baseheight
!定义75号节点
fill,15,75,2,35,20
egen,6,1,-1
!与ngen命令要好好的研究=========================
e,213,2213,177,177,214,2214,155,155
e,201,2201,2208,208,202,2202,2209,209
egen,6,1,-1
e,194,2194,2201,201,195,2195,2202,202
fill,10215,30215,9,12215,2000
csys,0
n,220,1.2,0.17
fill,35,220,1,219
n,10220,1.2,0.17,-0.5
fill,10035,10220,1,10219
fill,220,10220,4,2220,2000
csys,44
rotationangle=6
rotationtimes=90/rotationangle
height=layeramount*layerheight+baseheight
smrt,off
/title,fracture mechanics stress intensity - crack in a finite width plate
fill,135,155,5,186,7
fill,180,186,5,181,1,5,7,6
!填充完毕
local,44,1,,,,,-90,,0.75
!定义新的44号坐标系
csys,44
ngen,2,2000,all,,,,rotationangle
!下面开始生成单元
!=====================================
e,151,2151,2181,181,131,2131,2182,182
e,131,2131,2182,182,132,2132,2183,183
egen,4,1,-1
