浙大控制考研-845试卷-04A452答案
2019年浙江大学845自动控制原理真题(回忆版)

2019年浙江大学845自动控制原理真题(回忆版)2019年浙江大学845自动控制原理真题(回忆版)一、填空题共12题,每题5分,共计60。
每题1-3个空不等。
1、给出开环传涵,然后进行状态反馈设计后得到闭环传涵,问你闭环特征多项式和特征根。
主要是闭环传涵出现了零极点相消,变为二阶了,所以应该上下同乘被消零点,再写多项式。
-2,-6,-3。
2、给出离散的定义式,问你决定离散信号幅值的是什么,什么给出了时间信息。
(f(nT)、nT)3、给出一阶开环传涵,和一个正弦输入问你输出是什么。
考察频率特性。
4、给出一个奈斯曲线、问系统是几型的,是否稳定,闭环由极点几个,真题原题。
5,。
想不起来了,填空题都是很基本的题,没有难题。
二、给出系统的等效单位负反馈的开环传涵,1、让求闭环传涵,直接算即可,2、如果原系统反馈回路为G8,问你开环传涵是什么?三、跟轨迹,极点为-2、-2、-6、-6,无零点,分子上仅有一个k。
1、画出跟轨迹(注意要画出零度和180度跟轨迹)2、能否通过调整k,是的ts小于等于2,3、能否通过调整k,使得误差小于等于0.1。
四,离散,1、求脉冲传涵2、判稳,为一阶,直接求根,令z的绝对值小于1。
五,稍微有点难度。
给出一个前向通路,无反馈的那种,标好两个状态变量,让你写出状态空间表达式,非常规题,无法根据以前的方法求解。
六,以能控标准型给出状态空间,先判断是否可观,不客观则进行分解,可观就用标准型法设计全维状态观测器,以一个具体的指数衰减,去年刚考过的套路。
2、状态反馈设计,简单。
七,考察非线性,给出状态微分方程(复杂)1、让你写出状态方程,2、求平衡点。
3、在平衡点附近线性化。
好像漏了一个题,想不起来是什么了。
浙江大学04年自动控制原理考研题及答案4

系统特征方程为:1+G(Z)=0即:026.037.0)37.037.1(2=++--k k z z(2)若系统的特征根位于单位圆内,则系统是稳定的,否则为不稳定 将k=2代入特征方程,求得其根为889.0315.02,1j z ±=, 它们均位于单位圆内,故系统是稳定的。
(3)将k=3代入特征方程,求得其根为064.113.02,1j z ±=, 它们均位于单位圆外,故系统已经不稳定。
十一、(15分/150分)已知某系统通过状态反馈([][]5143321--==k k k K )后,获得其期望的闭环极点:λ=-1,-1,-3。
请写出原系统的能控标准形的A 、B 阵。
解:(1)设系统开环特征多项式为21203]d e t [a S a S a S A SI +++=-=∆(2)因为经状态反馈后闭环系统的特征多项式为)3()14()5()()()()](det[~2120312212303++-+-+=++++++=--=∆a S a Sa Sk a S k a Sk a S BK A SI(3)而期望的闭环特征多项式为: 375)3)(1)(1(23*+++=+++=∆S S S S S S(4)上两式应该相等,故易知:10,21,0210===a a a(5)原系统的能控标准形:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=1021100010A ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=100b十二、(10分/150分)--该题为二选一题,另一题是关于观测器的。
研究由方程)()(22212122221121x x x x xx x x x x +--=+-= 描述的系统的稳定性。
解:命0=x,可求得系统的平衡状态为原点,即 0,021==x x 定义正定纯量函数 2221)(x x x V +=则沿任一轨迹,V(x) 对时间的导数222212211)(222)(x x x x x x x V +-=+=是负定的,这说明V(x) 沿任一轨迹连续地减小,因此,V(x)是一个李亚普诺夫函数。
控制理论考研真题答案

控制理论考研真题答案控制理论是工程学中的一个重要分支,它涉及到系统性能的分析和设计,以确保系统能够按照预定的方式运行。
考研真题答案的提供,可以帮助学生更好地理解控制理论的核心概念和解题技巧。
以下是一些控制理论考研真题的答案示例:一、单选题1. 线性时不变系统(LTI系统)的主要特性是什么?- A. 线性- B. 时不变性- C. 稳定性- D. 所有上述选项答案:D2. 在控制系统中,开环增益(K)对系统性能的影响是:- A. 增加K可以提高系统的响应速度- B. 增加K可以提高系统的稳定性- C. 增加K可以减小系统的误差- D. 以上说法都不正确答案:A二、简答题1. 简述PID控制器的工作原理及其组成部分。
- PID控制器是一种常见的反馈控制器,它通过比例(P)、积分(I)和微分(D)三个部分来调整控制输入,以实现对系统输出的精确控制。
比例部分根据当前误差的大小来调整控制量;积分部分则考虑误差随时间的累积,以消除稳态误差;微分部分则基于误差的变化率,以预测并减少系统的过冲。
2. 什么是系统的稳定性,以及如何判断一个系统是否稳定?- 系统的稳定性指的是系统在受到扰动后,能否恢复到其平衡状态的能力。
判断一个系统是否稳定,可以通过检查其开环传递函数的极点位置。
如果所有极点都位于复平面的左半部分,则系统是稳定的。
三、计算题1. 给定一个二阶系统,其开环传递函数为:\[ G(s) = \frac{K}{(s+2)(s+5)} \]请计算该系统的单位阶跃响应,并分析其性能指标。
答案:首先,我们需要找到闭环传递函数。
假设闭环系统有一个单位负反馈,那么闭环传递函数为:\[ T(s) = \frac{K}{1 + KG(s)} \]将G(s)代入,我们得到:\[ T(s) = \frac{K}{s^2 + 7s + 10K} \]接下来,我们可以使用拉普拉斯变换求得时间域的响应。
通过求解特征方程,我们可以得到系统的自然频率和阻尼比。
浙江大学2004年考研电路真题及参考答案
1 2 3 4
3、图二(3)所示电路,已知 R1=R2=200Ω ,R3=3Ω ,US=8V,C1=C2=0.005F,γ =100Ω ,L=1H,
UC2(0-)=0V,K 打开已久,求 K 闭合后 iL(t)?(用经典法求解) 。
100t
4、 (4) 图二 所示电路, 为纯电阻网络, P L=0.1H, US(t)=10· 当 1(t)V, 零状态响应 iR (t ) (3 2e 如果把 L 换成 C=0.05F 的电容,激励源改为 U S (t ) e 跃函数]。
13、一个网络函数的零点为:z = -1,极点为:p1 = -1+j2,p2 = -1-j2,且已知 b(0+)=2, 则该网络函数 H(S)= 。
14、一段无损耗均匀传输线,其特性阻抗为 600Ω ,长度 l=λ /4(λ 为传输信号的波长) ,如图一(14)所 示 , 若 在 始 端 11’ 接 一 个 电 阻 R=600 Ω , 终 端 22’ 短 接 , 则 11’ 端 口 的 入 端 阻 抗 Zi= 。
8、图一(8)所示的电路中含有理想运算放大器电路,已知 R1、R2、R3、R4、u1、u2, 那么输出电压 u0 = 。
9、图一(9)所示的电路,C=0.2F,L=0.5H,状态方程为:
duc dt diL dt
uc i L
第
1 页
6、在图一(6)所示的电路中,Is =6A,L1=1H,L2=2H,R=1Ω ,i1 (0-)=1A,i2 (0-)=2A 当开关 K 闭合后, i2 (0+)= A,i2 (∞)= A。
7、已知某线性无源网络的冲击响应为 h(t),激励 e(t)如图一(7)所示,则 t>t0 时,输出的零状态响应 y(t) 用卷积积分求解时,其积分表达式为: y(t)= 。
浙江大学845自动控制原理考研真题试卷

紧急通知本资料由浙江大学控制科学与工程学院16届专业课129分学长,也就是我本人亲自整理编排而成。
大家可以叫我学长,年龄比我大的辞职考的可以叫我小弟。
资料不同于市面上那些看起来非常诱人实则是粗制烂造的资料,而是以一个考过845自控的过来人的经验,完全从学生的体验出发,做到资料最全,资料最好,资料最精致。
全套资料包括葵花宝典一到葵花宝典九共九本资料,每本资料都是我精心编辑整理的,并做了精美的封面,一共650页完美打印发给大家,大家把这650从头到尾肯透了,再做下我推荐的几本资料书(16年有一道15分的大题就是上面的类似题,第三问很多高手都没做出来,注意不是周春晖那本哈),可以说完全没问题了。
这是其它卖家不可能做到的。
同时赠送845自控全套电子资料。
葵花宝典一完全由我本人原创,里面包含了考浙大845自动控制原理的全部问题,比如考多少分比较保险,怎么复习,有哪些好的资料书,最近几年考题变化及应对策略,浙大常考题型,招生名额,复试资料,导师联系,公共课复习用书及方法以及845近年命题风格分析等一系列问题,全是我的心得和经验,方法,技巧等,说句心里话,我自己都觉得这些资料非常宝贵,能帮助学弟学妹们少走很多弯路。
注意:前面是一些关于我的故事,有些地方可能对你有用,如果不感兴趣,可以直接拉到后面去看,资料清单和图片都在后面。
学长自我介绍学长姓邓,名某某,男,本科于14年毕业于四川大学电气信息学院自动化专业,考浙大控制考了3次,14年大三时第一次考浙大控制总分没过线。
当时我们学校有三个同学征战浙大控制科学与工程,结果全军覆没,只有我一人过了300分,由此可见考浙大控制还是很有难度的,其中一个难点就是专业课的信息和专业课的命题走向的获取,当时我们都不是很清楚,蒙着头自己学,去图书馆借了很多自动控制原理的资料书来看,我自我感觉学得还不错,当时我一个同学考电子科大的自动化,经常跑来问我自控的问题,我基本都能给他解答出来,他说我好牛逼,觉对没有问题,然而最后的结果是他考电子科大自动控制原理137,而我只考了96分。
(NEW)浙江大学845自动控制原理历年考研真题汇编(含部分答案)

目 录2014年浙江大学845自动控制原理考研真题(回忆版)2013年浙江大学845自动控制原理考研真题(回忆版)2012年浙江大学自动控制原理考研真题(回忆版)2011年浙江大学845自动控制原理考研真题2010年浙江大学自动控制原理考研真题及详解2009年浙江大学自动控制原理考研真题(回忆版)2008年浙江大学845自动控制原理考研真题2007年浙江大学452自动控制原理考研真题2006年浙江大学452自动控制原理考研真题2005年浙江大学452自动控制原理考研真题2004年浙江大学452自动控制原理考研真题及详解2003年浙江大学457自动控制原理考研真题2002年浙江大学自动控制原理考研真题2001年浙江大学581自动控制原理考研真题及详解2014年浙江大学845自动控制原理考研真题(回忆版)一、已知一个共轭极点的阻尼比在-1到0之间,求根轨迹的出射角。
二、已知A、B、C阵,其中A阵(5×5)是能控标准型阵。
求1.方程有几个极点在右半轴2.判断能控能观性三、求二型系统的相角裕度最大值时的K值。
四、一单回路负反馈系统,前线通道时(s+5)(s+10)(s+4),反馈通道是0.5s+1,已知阻尼比,求K值和稳态输出。
五、Z变换1.求脉冲传递函数2.输出Z变换六、已知一个双输入的状态空间方程七、双变量传递函数,分子一个a,分母一个k1.当k和a为什么情况下时,系统保持稳定2.画出根轨迹图八、伯德图里有两个二阶衰减振荡环节九、1.求传递函数2.状态反馈3.状态观测器极点都配制到-2r4.已知超调量和tp的限制,求阻尼比和wn 5.当观测器反应速度比反馈快3倍2013年浙江大学845自动控制原理考研真题(回忆版)一、已知单位阶跃相应的曲线为一个单调递增最后趋于稳态的曲线,求系统的传递函数和微分方程。
二、已知一个带干扰的系统方框图1.化简方框图求输入和误差传递函数。
2.要求干扰输入时,输出不受干扰的影响。
浙江大学控制理论2003-2009真题答案
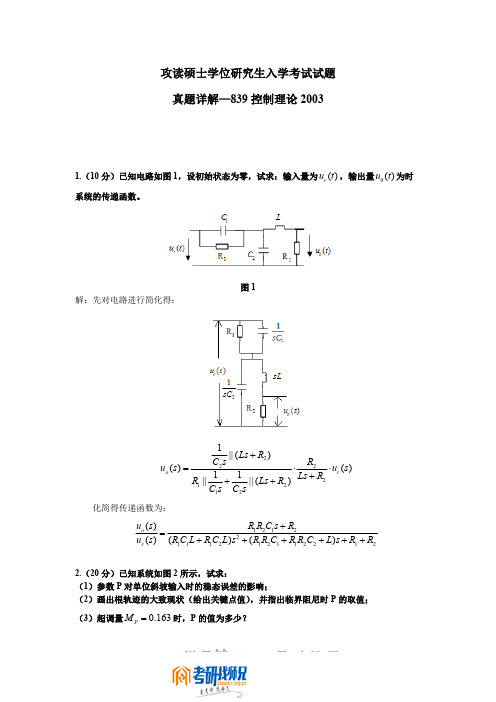
1.(10 分)已知电路如图 1,设初始状态为零,试求:输入量为 ur (t ) ,输出量 u0 (t ) 为时 系统的传递函数。
图1 解:先对电路进行简化得:
1 || ( Ls R2 ) C2 s R2 uo ( s ) ur ( s ) 1 1 Ls R 2 R1 || || ( Ls R2 ) C1s C2 s
(2)相轨迹为
(3)由相轨迹图可知,系统的稳态误差为零。
7.(15 分)有系统 平衡状态及其稳定性。
& x 1 kx2 (k 为大于 0 的常数) ,应用 Lyapunov 第二法分析系统的 & x 2 x1
& 0 xe 0 为系统的平衡状态。 解:由 x
0 k & x x 1 0
(2)系统特征方程为 z 4.95 z 0.368 0 ,
2
令z
r 1 ,上式化简后,得 r 1
6.32r 2 1.264r 3.584 0
劳斯表中第一列有一次符号变化,所以有一根位于右半平面,即对应有一个根位于平面 单位圆之外,系统不稳定。 6.(15 分)已知带有库仑摩擦的随动系统如图 5 所示,设输入信号为零,初始条件为:
& & Qe
& de &de & de de & e dt de dt de
& de & 2e 1 0, e & 0 e de & de & 2e 1 0, e & 0 e amp; 0 (e ) 2 c, e 2 2 2 & e 1 & 0 (e ) 2 c, e 2 2
考研控制工程试题真题及答案

考研控制工程试题真题及答案# 考研控制工程试题真题及答案## 一、选择题1. 题目:在控制系统中,开环传递函数为\[ G(s) =\frac{10}{s(s+10)} \],问该系统是否稳定?答案:是。
因为开环传递函数的极点s=0和s=-10都位于左半平面。
2. 题目:状态空间表示法中,状态变量的选取具有什么性质?答案:状态变量的选取具有任意性,但一般选择能反映系统动态特性的变量。
3. 题目:PID控制器中的I代表什么?答案:I代表积分(Integral),用于消除系统的稳态误差。
4. 题目:在控制系统设计中,Bode图的主要用途是什么?答案:Bode图主要用于分析系统的频率响应特性,帮助设计系统以满足性能要求。
5. 题目:线性时不变系统(LTI)的数学模型是什么?答案:线性时不变系统(LTI)的数学模型通常为线性微分方程或差分方程。
## 二、简答题1. 题目:简述控制系统的稳定性条件。
答案:控制系统的稳定性条件主要取决于系统开环传递函数的极点位置。
如果所有极点都位于复平面的左半部分,则系统是稳定的。
2. 题目:什么是根轨迹法?答案:根轨迹法是一种控制系统设计方法,通过分析系统开环传递函数的极点随参数变化的轨迹,来设计闭环系统的性能。
3. 题目:控制系统的频率响应特性有哪些?答案:控制系统的频率响应特性包括幅频特性和相频特性,它们描述了系统对不同频率信号的响应能力。
## 三、计算题1. 题目:给定一个二阶系统,其开环传递函数为\[ G(s) =\frac{\omega_n^2}{s^2 + 2\zeta\omega_ns + \omega_n^2} \],其中\[ \omega_n = 10 \] rad/s,\[ \zeta = 0.5 \]。
求系统的单位阶跃响应。
答案:首先确定系统的自然频率\[ \omega_n \]和阻尼比\[ \zeta \]。
然后使用二阶系统的时间响应公式计算单位阶跃响应的表达式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x* (t) (t T ) 3(t 2T ) 7(t 3T ) 15(t 4T ) .......
(2)因为 E(z)有单位圆外的根,故终值为无穷大。另从 x(kT) (1)k (2)k 也可看出。
从而求得开环脉冲传递函数:
G(z) [G(s)]
k(1 eS )
[
] k(1
s 2 (s 1)
z
1
)
s
2
1 (s
1)
k(1
z 1 ) [ 1 s2
1 s 1
1] s
k
(1
z
1
)
(1
z 1 z 1
)
2
1 1 e 1 z 1
1
1 z
1
k(1
z 1 )[ z 1 (1 e 1 z 1 )
上的推导却是按 m<n 的情况。许多书上也是考虑的 m<n 的情况。)
九、(15 分/150 分)先用 Z 变换法求解下面的差分方程,再求其终值 e (∞)。 e(k 2) 3e(k 1) 2e(k) 0
已知,e (0) =0, e (1)=1 解:(1)据 z 变换的超前定理,对差分方程两边取 z 变换
故系统是大范围一致渐近稳定的。
十 三 、( 10
分 /150
分
)
已
知
系
统
的
状
态
空
间
表
达
式
:
x1
x 2
0 1
20.6 x1
0
x2
10u
,
y 0
1
x1 x2
,试设计观测器,使其极点为:
-1.8+j2.4,
-1.8-j2.4。
解:(1)
判别可观性: Q0
0 1
1 0
;系统可观
(2)观测器期望方程: * (s 1.8 j2.4)(s 1.8 j2.4 s2 3.6s 9
四.(10 分/150 分)系统如图 4 所示,误差为 e(t)=r(t)-y(t),r(t)=t,试选择 和 的值,使 稳态误差 ess 0
解:
图4
K (S )
Y(S)
R(S)
(T1S 1)(T2S 1) K
K (S )
E(S) R(S) Y (S) [1
]R(S )
(T1S 1)(T2S 1) K
八.(10 分/150 分)请列写出如下图所示的信号流图的状态空间表达式。
解:系统的传递函数: G(s) b0 s n b1s n1 b2 s n2 bn1s bn s n a1s n1 a2 s n2 an1s an
状态空间表达式: x(t) Ax(t) Bu(t) y(t) Cx(t) Du(t)
S 3 (a0 5)S 2 (a1 14)S (a2 3) (3)而期望的闭环特征多项式为:
* (S 1)(S 1)(S 3) S 3 5S 2 7S 3
(4)上两式应该相等,故易知: a0 0, a1 21, a2 10
0 1 0
0
(5)原系统的能控标准形: A 0 0
z1,2 0.315 j0.889, 它们均位于单位圆内,故系统是稳定的。 (3)将 k=3 代入特征方程,求得其根为
z1,2 0.13 j1.064, 它们均位于单位圆外,故系统已经不稳定。
十一、(15 分/150 分)已知某系统通过状态反馈( K k1 k2 k3 3 14 5)后,
1
S1
0.25-0.25
S0
0.25
0.25
0.25
a 1时,S1,2 j0.5 系统稳定条件下,0 a 1
临界阻尼(无超调量),此时S1
d1
1 6
0.25a
S(S
0.5) 2
1 54
S S1
即0 a 2 27
六.(10 分/150 分)某系统的单位阶跃响应为 y(t) 1 et e2t ,试求系统的频率特性。
i
= (z 1) z k (z 1)(z 2)
z 1
(z 2) z k (z 1)(z 2)
z 2
(1)k
(2)k ,(k=0,1,2,…..)
法二:部分分式法: X (z)
z
( z z )
(z 2)(z 1) z 1 z 2
x(kT ) Z 1[ X (z)] Z 1[( 1 1 )] (1)k (2)k z 1 z 2
z 2 E(z) z 2e(0) ze(1) 3zE(z) 3ze(0) 2E(z) 0
代入初值条件: z 2 E(z) z 3zE(z) 2E(z) 0
E(z)
z
z
z 2 3z 2 (z 2)(z 1)
下面可用多种方法(留数法、部分分式法以及长除法)求解。
法一:留数法: x(Kt) Re[ X (z) z k1]
状态观测器的闭环特征多项式: det[sI (A LC)] s2 l2s 20.6 l1
上两式应当相等,所以 l1 29.6; l2 3.6 ;即观测器:L= [29.6 3.6]
xˆ 1 xˆ2
0 1
9 3.6
xˆ1 xˆ 2
10u
29.6
3.6
y
三.(10 分/150 分)已知线性定常系统在零初始条件下的单位阶跃响应为
y(t) 1 ret s i n(t ) ,求系统的脉冲响应 g(t), 并简述理由。 解: g(t) g(t) eat sin(t ) eat cos(t )
线性定常系统对输入信号导数的响应,可通过对输入信号的响应进行微分求得。
浙江大学信息学院控制系 2004 年自动控制原理考研试题及答案
一.(20 分/150 分)如图 1 所示,U1(t),U2(t)分别是输入电压和输出电压。X3,X2 分别是 输入位移和输出位移,X1 则是 C 点位移。f1, f2 是粘滞阻尼系数,k1, k2 是弹性系数。求两 系统的传递函数,并分析两系统变量间的相似关系。
获得其期望的闭环极点: =-1,-1,-3。请写出原系统的能控标准形的 A、B 阵。
解:(1)设系统开环特征多项式为
det[SI A] S 3 a0 S 2 a1S a2
(2)因为经状态反馈后闭环系统的特征多项式为 ~ det[SI ( A BK )] S 3 (a0 k3 )S 2 (a1 k2 )S (a2 k1 )
(1) 开环极点 P1=0 P2,3=-0.5
(2) 实轴上的根轨迹 (,0)
(3) 渐近线 n-m=3
a
0.5 0.5 3
1 3
a
(2K
1) 180 3
60 60 180
(4)
分离点: da 12S 2 8S 1 0
d1
1 6
ds
d2 0.5
(5) 根轨迹与虚轴交点:
S3
1
S2
f1 f2
1 K1 K 2
S2
( f1
1 K1
f2
1 )S
K2
1
X 3(S)
f1 f2
1 K1 K 2
S2
( f1
1 K1
f2
1 K2
f1
1 )S
K2
1
两相似系统变量间对应关系:电压 U---------------------------位移 X 电阻 R---------------------------粘滞阻尼系数 f
1
,
b
0
0 21 10
1
十二、(10 分/150 分)--该题为二选一题,另一题是关于观测器的。研究由方程 x1 x2 x1 (x12 x22 ) 描述的系统的稳定性。 x2 x1 x2 (x12 x22 )
解:命 x 0 ,可求得系统的平衡状态为原点,即 x1 0, x2 0
十(15 分/150 分)设采样系统的结构图如图所示,试分别讨论当 k=2、k=3 时系统的稳定 性(计算时为方便起见,保留小数点后 2 位)。
X(s) + T=1
1 eTS
k
Y(s)
s
s(s 1)
2004 年题十一图
解:由图可得
(1 eTS ) G(s)
k
k(1 eS )
s s(s 1) s 2 (s 1)
电容 C---------------------------弹性系数的倒数 1 K
二.(10 分/150 分)用方块图化简法,求图 2 所示系统的闭环传递函数
解:
图2
Y(S)
G1G3 G1 G1G3G4 G1G4 G3 G1G2G3
R(S) 1 G1G2 G1G3 G1 G1G3G4 G1G4 G3 G1G2G3
(1
z 1 ) 2
(1
z 1 )(1 e 1 z 1 ) ]
(1 z 1 ) 2 (1 e 1 z 1 )
k e1z (1 2e1 ) k 0.37z 0.26
z 2 (1 e1 )z e 1
z 2 1.37z 0.37
系统特征方程为:1+G(Z)=0 即: z 2 z(1.37 0.37k) 0.37 0.26k 0 (2)若系统的特征根位于单位圆内,则系统是稳定的,否则为不稳定 将 k=2 代入特征方程,求得其根为
sb
, 问:若要求系统为完
s3 6s2 11s 6
全能控能观,应如何选择 b ?
解:对于单变量系统,系统的完全能控能观意味着不存在传递函数的零极点相消
因为 G(s)
sb
sb
s3 6s 2 11s 6 (s 1)(s 2)(s 3)
