宁大912信号与系统初试试卷(A卷)
合集下载
宁波大学信息科学与工程学院《912信号与系统》历年考研真题专业课考试试题
2013年宁波大学912信号处理基础 （信号与系统＋数字信号处理）
考研真题
2014年宁波大学912信号处理基础 （信号与系统＋数字信号处理）
考研真题
2015年宁波大学912信号处理基础 （信号与系统＋数字信号处理）
考研真题
2016年宁波大学912信号处理基础 （信号与系统＋数字信号处理）
目 录
2013年宁波大学912信号处理基础（信号与系统＋数字信号处理）考研 真题 2014年宁波大学912信号处理基础（信号与系统＋数字信号处理）考研 真题 2015年宁波大学912信号处理基础（信号与系统＋数字信号处理）考研 真题 2016年宁波大学912信号处理基础（信号与系统＋数字信号处理）考研 真题 2017年宁波大学912信号与系统考研真题 2018年宁波大学912信号与系统考研真题 2019年宁波大学912信号与系统考研真题
考研真题
2017年宁波大学912信号与系统考 研真题
2018年宁波大学912信号与系统考 研真题
2019年宁波大学9
研达考研-2017-2019宁波大学912信号与系统考研真题
2z2 z z2 1 z
1
；
24
（2）
X
(z)
(z
z3 z2 1)( z 2
2z z 1)
。
10.（24 分）已知某一离散时间因果 LTI 系统函数的差分方程为
y[n] 1 y[n 1] 1 y[n 2] x[n]
6
6
当输入 x[n] 3u[n] ，且 y[0] 6, y[1] 4 时，求系统的零输入响应 yzi[n]、零状态响应
3.（20 分）
（1）试画出题 3.1 图 x(t)与 h(t)的卷积 y(t)=x(t)*h(t)在 0 t 7 范围内的波形。
题 3.1 图 （2）试计算卷积和 y[n]= x[n]* h[n]，其中
x[n]={1, 2, 0, 3, 2}(n=-3, -2,-1,0, 1)，h[n]={1, 4, 3}(n=-1, 0, 1)。
2.（14 分）试计算卷积 e2tu(t) tnu(t) [ ''(t) 3 '(t) 2 (t)]etu(t) 。
3.（14 分）一个因果 LTI 系统，其输入 x(t) 、输出 y(t) 用下列微分-积分方程表示：
d y(t) 5y(t) x( ) f (t )d x(t)
dt
其中 f (t) etu(t) 3 (t) ，试求该系统单位冲激响应 h(t) 。
科目代码： 912 总分值： 150 科目名称：
信号与系统
f1(t)
fs(t) H(j) f2(t)
p(t)
-2
p(t)
(1)
...
...
-2T -T O T 2T 3T 4T 5T t -b
题6图
F1(j) 1
宁波大学2017年考研真题【信息科学与工程学院】912信号与系统初试试卷(A卷)
② 求该系统的频率响应，并判断该系统的稳定性；
③
当输入
x(n)
1 2
n
u(n)
，
y(1)
0,
y(2) 8 时，求该系统的零输入和零状态响应；
④
当输入
x(n)
3
1 2
n
u(n)
，
y(1)
0,
y(2) 4 时，求该系统的完全响应。
第3页共3页
① 该系统是不是线性系统？为什么？ ② 该系统是不是时不变系统？为什么？ ③ 该系统是不是因果系统？为什么？
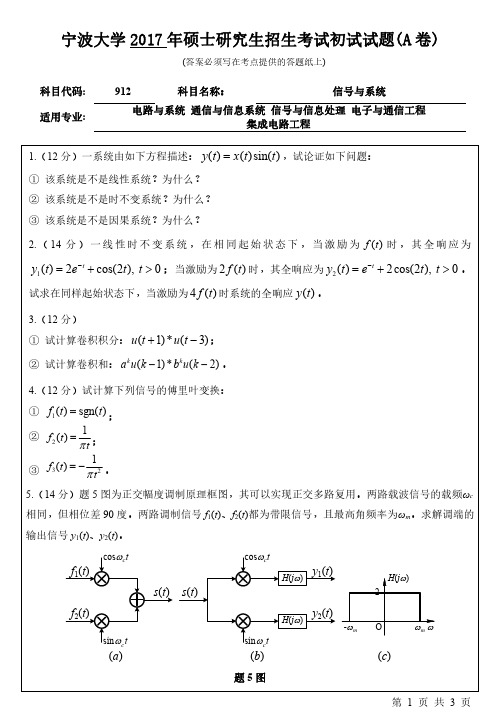
2. （ 14 分 ） 一 线 性 时 不 变 系 统 ， 在 相 同 起 始 状 态 下 ， 当 激 励 为 f (t) 时 ， 其 全 响 应 为 y1(t) 2et cos(2t), t 0 ；当激励为 2 f (t) 时，其全响应为 y2 (t) et 2 cos(2t), t 0 。 试求在同样起始状态下，当激励为 4 f (t) 时系统的全响应 y(t) 。
9.（15 分）用计算机对数据 x(n) 进行平均处理，当收到一个数据后，计算机就把这一次输入的
数据与前三次的输入数据相加并平均。
① 确定描述该系统输出 y(n) 与输入 x(n) 之间关系的差分方程；
② 确定系统的系统函数，并粗略画出幅频特性曲线；
③ 画出系统的直接型结构。
10.（20 分）已知一离散时间因果Biblioteka LTI 系统 H (z) 1 az1
-2
-2 -1 O 1 2 t -1
(a)
(b)
题7图
① 求该系统的系统函数和单位冲激响应； ② 写出该系统的微分方程； ③ 当输入如题 7(b)图所示时，对 t>0 分别计算系统的零输入和零状态响应。
宁波大学912信号处理(信号与系统+信号处理基础)2016年考研专业课真题试卷
R
t=0
V
i(t)
C vC(t)
题图 4
5. (16 分) 某一离散时间因果 LTI 系统的差分方程为
y(n) 3 y(n 1) 1 y(n 2) x(n) ax(n 1) 。
4
8
(1) 若输入 x(n) (1)n 时，输出 y(n) 16 (1)n ，求系统函数 H(z)，画出零极点图，标明 ROC 15
(1) 通带和阻带都是频率的单调下降函数，而且没有起伏；
(2) 通带截止频率 0.5π 处的衰减不大于 3dB； (3) 阻带截止频率 0.75π 处的衰减至少达到 15dB； (4) 抽样频率 fs 1Hz 。
表1 归一化巴特沃思多项式系数
N
a1
a2
1
1
2
1.414
a3
a4
3
2.000
2.000
7. (14 分) 已知序列 x(n) 3 (n) 4 (n 3) 5 (n 5) ，则可求出 8 点 DFT 为 X (k) 。 (1) 若 y(n)(0 n 7) 的 8 点 DFT 为 Y (k) W83k X (k), 0 k 7 ，求 y(n) ； (2) 若 w(n)(0 n 7) 的 8 点 DFT 为W (k) X (k) X (k), 0 k 7 ，求 w(n) ； (3) 若 u(n)(0 n 3) 的 8 点 DFT 为U (k) X (2k), 0 k 3 ，求 u(n) 。
考试科目: 适用专业:
信号处理(信号与系统+信号处理基础)
科目代码： 912
电路与系统 、通信与信息系统 、信号与信息处理、 信息检测与智能系统、电子与通信工程、集成电路工程
2021-2019年宁波大学考研912信号与系统初试真题
(答案必须写在考点提供的答题纸上)科目代码： 912 150 科目名称： 信号与系统1.（10分）已知(52)f t −的波形如题1图所示，试画出()f t 的波形图。
题1图2.（18分）已知(1)()*e ()(1)()(1)(1)t t t f t u t e u t e u t −−−−=−−−−，试从时域角度确定函数()f t 。
3.（12分）某LTI 系统，起始状态为零，当输入信号3()2()t f t e u t −=时，其响应为()y t ，即()[()]y t H f t = 又已知2[()]3()()t dH f t y t e u t dt−=−+ 求该系统的单位冲激响应()h t 。
4.（12分）已知信号 1cos()||π()0||πt t f t t +≤⎧=⎨>⎩ 求该信号的傅里叶变换。
5.（20分）已知周期信号()f t 的波形如题5图所示（2π()cos ,/4/4f t E t T t T T=−≤≤），其中周期T =2s ，当该周期信号通过截止频率c 5πω=弧度/秒的理想低通滤波器时，试计算其输出信号()y t 。
O 4T 4T−t...Ef (t )T -T...题5图6.（16分）（1）信号()f t 如题6图所示。
当抽样间隔1(s)12s T =时，画出()f t 被理想抽样后的频谱图。
（2）信号()()*(2)T n f t f t t n δ+∞=−∞=−∑（n 为整数）。
画出()T f t 被理想抽样后的频谱图。
抽样间隔1(s)12s T =。
O1f (t )t1-1(答案必须写在考点提供的答题纸上)(答案必须写在考点提供的答题纸上)(答案必须写在考点提供的答题纸上)(答案必须写在考点提供的答题纸上)科目代码：912 总分值：150 科目名称：信号与系统(答案必须写在考点提供的答题纸上)科目代码：912 总分值：150 科目名称：信号与系统。
宁波大学912信号与系统2020年考研专业课真题
题7图
8．（22分）已知一个连续时间稳定LTI系统的系统函数为 ，输入如题8图所示。
（1）说明该系统为何种滤波器；
（2）求系统的初始条件 和 ；
（3）当 时，求系统的完全响应y(t)。
题8图
9.（14分）已知二阶离散时间系统的零输入响应初始条件为 ， 。当输入 时，输出响应 。求此系统的差分方程。
10．（12分）已知二阶离散时间因果LTI系统的框图如题10图所示。
（1）求系统函数，并判断系统的稳定性；
（2）设抽样频率为10kHz，输入正弦幅度为5，频率为1kHz，试求稳态输出幅度。
题10图
1.（10分）试计算卷积积分：
2.（8分）试计算卷积和： 。
3．（18分）设系统的微分方程表示为： ，试从时域角度求使完全响应为 时的系统起始状态 和 ，并确定常数 值。
4.（18分）试求题4图所示周期信号 的三角函数形式傅里叶级数表示式。
题4图
5.（16分）试求题5图所示信号 的频谱函数 。
题5图
6．（16分）一种不要求相位同步但要求频率同步的解调系统如题6图所示。两个低通滤波信号，当 时， ，且 。试求系统的输出。
题6图
7.（16分）题7图是一个低通微分器的连续时间滤波器的频率响应。当输入信号为下列 时，求该滤波器的输出信号 。
（1） ；（2） 。
8．（22分）已知一个连续时间稳定LTI系统的系统函数为 ，输入如题8图所示。
（1）说明该系统为何种滤波器；
（2）求系统的初始条件 和 ；
（3）当 时，求系统的完全响应y(t)。
题8图
9.（14分）已知二阶离散时间系统的零输入响应初始条件为 ， 。当输入 时，输出响应 。求此系统的差分方程。
10．（12分）已知二阶离散时间因果LTI系统的框图如题10图所示。
（1）求系统函数，并判断系统的稳定性；
（2）设抽样频率为10kHz，输入正弦幅度为5，频率为1kHz，试求稳态输出幅度。
题10图
1.（10分）试计算卷积积分：
2.（8分）试计算卷积和： 。
3．（18分）设系统的微分方程表示为： ，试从时域角度求使完全响应为 时的系统起始状态 和 ，并确定常数 值。
4.（18分）试求题4图所示周期信号 的三角函数形式傅里叶级数表示式。
题4图
5.（16分）试求题5图所示信号 的频谱函数 。
题5图
6．（16分）一种不要求相位同步但要求频率同步的解调系统如题6图所示。两个低通滤波信号，当 时， ，且 。试求系统的输出。
题6图
7.（16分）题7图是一个低通微分器的连续时间滤波器的频率响应。当输入信号为下列 时，求该滤波器的输出信号 。
（1） ；（2） 。
宁波大学《912信号与系统》考研专业课真题试卷
( ) 5. 下列各种陈述中，正确的是______。 (A) 系统函数能提供求解零输入响应所需的全部信息； (B) 系统函数的零点位置影响时域波形的衰减或增长； (C) 若零极点离虚轴很远，则它们对频率响应的影响非常小；
(D) 原点的二阶极点对应于 t2u(t) 形式的波形；
第1页共5页
宁波大学 2014 年攻读硕士学位研究生
入 学 考 试 试 题(B 卷) (答案必须写在答题纸上)
考试科目: 信号处理基础(信号与系统+数字信号处理)
科目代码：912
适用专业: 通信与信息系统 、信号与信息处理、电子与通信工程
(
) 6.
系统 T[x(n)]
x(n)
sin(
2 9
(n
1)
7
)
① 非线性系统 ② 移变系统
③ 因果系统
④ 稳定系统
(7) (2 分) 实现 IIR 数字滤波器时，如果想方便对系统频响的零点进行控制和调整，那么 常用的 IIR 滤波器结构中，首选______________型结构来实现该 IIR 系统。
海天课堂
中国考研专业课辅导知名品牌
宁波大学考研专业课真题试卷
912 信号与系统
2014 年《912 信号与系统》专业课真题试卷 2015 年《912 信号与系统》专业课真题试卷 2016 年《912 信号与系统》专业课真题试卷 2017 年《912 信号与系统》专业课真题试卷 2018 年《912 信号与系统》专业课真题试卷 2019 年《912 信号与系统》专业课真题试卷 2020 年《912 信号与系统》专业课真题试卷
(B) Ζ y2 (n) x(n)
(C) Ζ y3 (n) x(n)
(D) Ζ y4 (n) x(n)
宁波大学2018年《912信号与系统》考研专业课真题试卷
n
1 2
n
（4）当输入 x(n) = 2 + cos n u(n) 时，求系统的稳态响应。
π 4
第 3 页 共 3 页
x(t) 1 -2 O -1 2 4 6 8 t
h(t) 2 -1 O 1 2 3 t
题 3.1 图 （2）试计算卷积和 y[n]= x[n]* h[n]，其中 x[n]={1, 2, 0, 3, 2}(n=-3, -2,-1,0, 1)，h[n]={1, 4, 3}(n=-1, 0, 1)。 4.（12 分）试画出信号 f (t ) = sgn{sin[ 叶级数表示式。 5.（14 分）求信号 f (t ) =
2
(t − 1)]} 的波形，并求出该信号的指数函数形式傅里
sin(2t ) cos(5t ) 的傅里叶变换 F ( j) ，并画出其频谱图。 t
6. （18 分）某系统如题 6 图所示，输入 f1(t)为带限信号，H(jω)为带通滤波器。 （1）当 2 = 21 ， a = 1 ， b = 2 ， T =
总分值：
150
科目名称：
信号与系统
f1(t) p(t)
fs(t)
H(j)
f2(t) -2 -1
F1(j) 1 O A
1
H(j)
2
p(t) (1) ... -2T -T O ... T 2T 3T 4T 5T t -b -a O
a
b
题6图 7.（14 分）已知系统函数 H (s) 的极点位于 s = −3 处，零点在 s = −a 且 H () = 1 。此系统的阶 跃响应中包含一项 K1e
−3t
。若 a 从 0 变到 5，确定相应的 K1 值如何随之改变。
相关主题
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
(答案必须写在考点提供的答题纸上)
科目代码： 912 总分值： 150 科目名称：
信号与系统
10.（24 分）已知一离散时间因果 LTI 系统的系统函数 H (z) K1源自1 4z1
，
K
为实常数，且当
x(n) 1时，输出 y(n) 4 3。
（1）求该系统的频率响应，画出幅频特性曲线，并说明为何种滤波器；
（2）若
y(1)
2
，
x(n)
1 2
n
u(n)
，求系统的零输入响应和零状态响应；
（3）若
y(1)
4
，
x(n)
3
1 2
n
u(n)
，求系统的完全响应；
（4）当输入
x(n)
2
cos
π 4
n
u(n)
时，求系统的稳态响应。
第3页共3页
科目代码： 912 总分值： 150 科目名称：
信号与系统
f1(t)
fs(t) H(j) f2(t)
p(t) -2
p(t)
(1)
...
...
-2T -T O T 2T 3T 4T 5T t -b
题6图
F1(j) 1
-1 O
1
H(j)
A
-a O
a
2 b
7.（14 分）已知系统函数 H (s) 的极点位于 s 3 处，零点在 s a 且 H () 1。此系统的阶 跃响应中包含一项 K1e3t 。若 a 从 0 变到 5，确定相应的 K1 值如何随之改变。
8.（18 分）给定题 8 图所示连续时间因果 LTI 系统
X(s)
1 s2 2s 1
K
Y(s)
题8图
（1）求系统函数 H (s) ，并写出系统的微分方程；
（2） K 满足什么条件时系统稳定； （3）在临界稳定条件下，求单位冲激响应 h(t) ；
（4）当 K 1，输入 x(t) e2t 时，求输出 y(t) 。
宁波大学 2018 年硕士研究生招生考试初试试题(A 卷)
(答案必须写在考点提供的答题纸上)
科目代码： 912 总分值： 150 科目名称：
信号与系统
1.（10 分）试求下列函数值：
2t
sin
3
t
1+2t
dt
2.（10 分）试画出信号 x(t) | sin(t) | [u(t) u(t 2 )] 的奇分量和偶分量的波形。
4.（12 分）试画出信号 f (t) sgn{sin[ (t 1)]}的波形，并求出该信号的指数函数形式傅里 2
叶级数表示式。
5.（14 分）求信号 f (t) sin(2t) cos(5t) 的傅里叶变换 F( j) ，并画出其频谱图。 t
6. （18 分）某系统如题 6 图所示，输入 f1(t)为带限信号，H(jω)为带通滤波器。
（1）当 2
21 ， a
1 ， b
2 ， T
2 2
时，求
fs(t)的频谱和
f2(t)的频谱；
（2）当 1 2 1 时，为了得到 f2(t)= f1(t)，求最大的 T 和常数 A、a、b 值。
第1页共3页
宁波大学 2018 年硕士研究生招生考试初试试题(A 卷)
(答案必须写在考点提供的答题纸上)
9.（10 分）设计一个离散时间系统，使其输出 y(n) 是 n, n 1, , n M 1各点时刻的输入之平
均。
（1）确定描述该系统 y(n) 与 x(n) 之间关系的差分方程；
（2）确定系统的系统函数； （3）当 M =3 时，画出系统的直接型结构。
第2页共3页
宁波大学 2018 年硕士研究生招生考试初试试题(A 卷)
3.（20 分）
（1）试画出题 3.1 图 x(t)与 h(t)的卷积 y(t)=x(t)*h(t)在 0 t 7 范围内的波形。
x(t) 1
-2 O 2 4 6 8
t
-1
题 3.1 图
（2）试计算卷积和 y[n]= x[n]* h[n]，其中
h(t) 2
-1 O 1 2 3 t
x[n]={1, 2, 0, 3, 2}(n=-3, -2,-1,0, 1)，h[n]={1, 4, 3}(n=-1, 0, 1)。
科目代码： 912 总分值： 150 科目名称：
信号与系统
10.（24 分）已知一离散时间因果 LTI 系统的系统函数 H (z) K1源自1 4z1
，
K
为实常数，且当
x(n) 1时，输出 y(n) 4 3。
（1）求该系统的频率响应，画出幅频特性曲线，并说明为何种滤波器；
（2）若
y(1)
2
，
x(n)
1 2
n
u(n)
，求系统的零输入响应和零状态响应；
（3）若
y(1)
4
，
x(n)
3
1 2
n
u(n)
，求系统的完全响应；
（4）当输入
x(n)
2
cos
π 4
n
u(n)
时，求系统的稳态响应。
第3页共3页
科目代码： 912 总分值： 150 科目名称：
信号与系统
f1(t)
fs(t) H(j) f2(t)
p(t) -2
p(t)
(1)
...
...
-2T -T O T 2T 3T 4T 5T t -b
题6图
F1(j) 1
-1 O
1
H(j)
A
-a O
a
2 b
7.（14 分）已知系统函数 H (s) 的极点位于 s 3 处，零点在 s a 且 H () 1。此系统的阶 跃响应中包含一项 K1e3t 。若 a 从 0 变到 5，确定相应的 K1 值如何随之改变。
8.（18 分）给定题 8 图所示连续时间因果 LTI 系统
X(s)
1 s2 2s 1
K
Y(s)
题8图
（1）求系统函数 H (s) ，并写出系统的微分方程；
（2） K 满足什么条件时系统稳定； （3）在临界稳定条件下，求单位冲激响应 h(t) ；
（4）当 K 1，输入 x(t) e2t 时，求输出 y(t) 。
宁波大学 2018 年硕士研究生招生考试初试试题(A 卷)
(答案必须写在考点提供的答题纸上)
科目代码： 912 总分值： 150 科目名称：
信号与系统
1.（10 分）试求下列函数值：
2t
sin
3
t
1+2t
dt
2.（10 分）试画出信号 x(t) | sin(t) | [u(t) u(t 2 )] 的奇分量和偶分量的波形。
4.（12 分）试画出信号 f (t) sgn{sin[ (t 1)]}的波形，并求出该信号的指数函数形式傅里 2
叶级数表示式。
5.（14 分）求信号 f (t) sin(2t) cos(5t) 的傅里叶变换 F( j) ，并画出其频谱图。 t
6. （18 分）某系统如题 6 图所示，输入 f1(t)为带限信号，H(jω)为带通滤波器。
（1）当 2
21 ， a
1 ， b
2 ， T
2 2
时，求
fs(t)的频谱和
f2(t)的频谱；
（2）当 1 2 1 时，为了得到 f2(t)= f1(t)，求最大的 T 和常数 A、a、b 值。
第1页共3页
宁波大学 2018 年硕士研究生招生考试初试试题(A 卷)
(答案必须写在考点提供的答题纸上)
9.（10 分）设计一个离散时间系统，使其输出 y(n) 是 n, n 1, , n M 1各点时刻的输入之平
均。
（1）确定描述该系统 y(n) 与 x(n) 之间关系的差分方程；
（2）确定系统的系统函数； （3）当 M =3 时，画出系统的直接型结构。
第2页共3页
宁波大学 2018 年硕士研究生招生考试初试试题(A 卷)
3.（20 分）
（1）试画出题 3.1 图 x(t)与 h(t)的卷积 y(t)=x(t)*h(t)在 0 t 7 范围内的波形。
x(t) 1
-2 O 2 4 6 8
t
-1
题 3.1 图
（2）试计算卷积和 y[n]= x[n]* h[n]，其中
h(t) 2
-1 O 1 2 3 t
x[n]={1, 2, 0, 3, 2}(n=-3, -2,-1,0, 1)，h[n]={1, 4, 3}(n=-1, 0, 1)。