八年级数学期末试卷:14沪教版八年级上册期末数学试卷
(全优)沪教版八年级上册数学期末测试卷及含答案

沪教版八年级上册数学期末测试卷及含答案一、单选题(共15题,共计45分)1、如图,是反比例函数y= 和y= (k1<k2)在第一象限的图象,直线AB∥x轴,并分别交两条曲线于A、B两点,若S△AOB =4,则k2﹣k1的值是()A.1B.2C.4D.82、在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到斜边AB的距离是()A. B. C.9 D.63、如图,菱形ABCD的对角线相交于点O,过点D作DE∥AC,且DE=AC,连接CE、OE,连接AE交OD于点F,若AB=2,∠ABC=60°,则AE的长为()A. B. C. D.4、电话卡上存有4元话费,通话时每分钟话费元,则电话卡上的余额(元)与通话时间(分钟)之间的函数图象是图中的()A. B.C.D.5、若,则的值用a、b可以表示为()A. B. C. D.6、如图,,点、、…在射线上,点、、…在射线上,、、…均为等边三角形,依此类推,若,则的边长为()A. B. C.2016 D.40327、如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是()①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的中垂线上.A.1B.2C.3D.48、如图,在Rt△ABC中,∠C=90°,∠A=30°,BC=2,则AB=()A.4B.C.D.9、李明去参加聚会,每两人都互相赠送礼物,他发现共送礼物20件,若设有n人参加聚会,根据题意可列出方程为()A. =20B.n(n﹣1)=20C. =20D.n(n+1)=2010、已知a、b为一元二次方程的两个根,那么的值为()A. B.0 C.7 D.1111、如图,⊙O的半径为5,圆心O到弦AB的距离为3,则AB的长为()A.4B.5C.6D.812、下列计算正确的是()A. B. C. · D.13、一元二次方程的解是()A. ,B. ,C.D.,14、如图,已知AB∥CD,直线EF分别交AB,CD于点E,F,EG平分∠BEF,若∠1=48°,则∠2的度数是( )A.64°B.65°C.66°D.67°15、下列方程中,属于一元二次方程的是()A.ax 2+bx+c=0B.C.(x+3)2=2(x﹣3)D.(x+4)(x﹣2)=x 2二、填空题(共10题,共计30分)16、在直角三角形ABC中,斜边AB=3,则AB2+AC2+BC2=________.17、如图,有一个圆柱,它的高等于16cm,底面半径等干4cm,在圆柱下底面的A点有一只蚂蚁,它想吃到上底面上与A点相对的B点处的食物,需要爬行的最短路程是________cm.(π取3)18、方程的解为________.19、已知:,则ab3+a3b的值为________.20、若函数y=(m﹣1)x|m|是正比例函数,则该函数的图象经过第________象限.21、某种灯的使用寿命为8000小时,那么它可使用的天数y与平均每天使用的小时数x之间的函数关系式为________ .22、如图,PA、PB、DE分别切⊙O于A、B、C,⊙O的半径长为6cm,PO=10cm,则△PDE的周长是________cm.23、有一面积为120的梯形,其上底是下底长的.若上底长为x高为y,则y 与x的函数关系式为________ ;当高为10时x=________ .24、如图所示,△ABC为边长为4的等边三角形,AD为BC边上的高,以AD为边的正方形ADEF的面积为________。
沪科版八年级上册数学期末考试试题含答案

沪科版八年级上册数学期末考试试卷一、选择题。
(每小题只有一个正确答案)1.下列图形中,不是轴对称图形的是()A .①⑤B .②⑤C .④⑤D .①②2.点P (m +3,m +1)在x 轴上,则P 点坐标为()A .(0,﹣2)B .(0,﹣4)C .(4,0)D .(2,0)3.若一次函数y =(3﹣k )x ﹣k 的图象经过第二、三、四象限,则k 的取值范围是()A .k >3B .0<k ≤3C .0≤k <3D .0<k <34.直线26y x =+可以由2y x =经过向()单位得到的.A .上平移2B .下平移6C .左平移3D .右平移35.数学在的生活中无处不在,台球桌上都有数学问题.如图所示,∠1=∠2.若∠3=25°,为了使白球反弹后能将黑球直接撞入底袋中,那么击打白球时,必须保证∠1为()A .65°B .75°C .55°D .85°6.已知三角形的三边长分别为2、x 、10,若x 为正整数,则这样的三角形个数为()A .1B .2C .3D .47.潜山市某村办工厂,今年前5个月生产某种产品的总量C (件)关于时间t (月)的函数图象如图所示,则该厂对这种产品来说()A .1月至3月每月生产总量逐月增加,4、5两月每月生产总量逐月减少B .1月至3月每月生产总量逐月增加,4,5两月每月生产量与3月持平C .1月至3月每月生产总量逐月增加,4、5两月均停止生产D .1月至3月每月生产总量不变,4、5两月均停止生产8.给出如下四个命题,其中原命题与逆命题均为真命题的个数是()①若0a >,0b >,则0a b +>;②若a b ¹,则22a b ≠;③角的平分线上的点到角的两边的距离相等;④线段的垂直平分线上的点到线段两端点距离相等.A .1个B .2个C .3个D .4个9.小亮同学骑车上学,路上要经过平路、下坡、上坡和平路(如图),若小亮上坡、平路、下坡的速度分别为v 1,v 2,v 3,v 1<v 2<v 3,则小亮同学骑车上学时,离家的路程s 与所用时间t 的函数关系图象可能是()A .B .C .D .10.如图,在长方形网格中,每个小长方形的长为2,宽为1,A 、B 两点在网格格点上,若点P 也在网格格点上,且ABP 的面积为2,则满足条件的点P 的个数是()A .2B .3C .4D .5二、填空题11.点P 关于x 轴对称的点是()2,1-,则P 点的坐标是______.12.一次函数y ax b =+,当0y <时,23x <-,那么不等式0ax b +≥的解集为__________.13.等腰三角形有一个外角是100°,那么它的的顶角的度数为_____________.14.如图,△ABC 的外角∠ACD 的平分线CP 与内角∠ABC 平分线BP 交于点P ,若∠BPC=40°,则∠CAP=_______________.15.如图,△ABC的两条角平分线相交于O,过O的直线MN∥BC交AB于M交AC于N,若BC=8cm,△AMN的周长是12cm,则△ABC的周长等于_____cm.16.“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事(x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程,y2表示兔子所行的路程).有下列说法:①“龟兔再次赛跑”的路程为1000米;②兔子和乌龟同时从起点出发;③乌龟在途中休息了10分钟;④兔子在途中750米处追上乌龟.其中正确的说法是_____.(把你认为正确说法的序号都填上)三、解答题17.早晨小欣与妈妈同时从家里出发,步行与自行车向相反方向的两地上学与上班,如图是他们离家的路程(米)与时间(分钟)之间的函数图象,妈妈骑车走了10分钟时接到小欣的电话,立即以原速度返回并前往学校,若已知小欣步行的速度为50米/分钟,并且妈妈与小欣同时到达学校.完成下列问题:()1在坐标轴两处的括号内填入适当的数据;()2求小欣早晨上学需要的时间.18.已知点P 的坐标为()2,a a -,且点P 到两坐标轴的距离相等,求a 的值.19.△ABC 在平面直角坐标系中的位置如图所示.(1)画出△ABC 关于y 轴对称的△A 1B 1C 1;(2)将△ABC 向右平移6个单位,作出平移后的△A 2B 2C 2,并写出△A 2B 2C 2各顶点的坐标;(3)观察△A 1B 1C 1和△A 2B 2C 2,它们是否关于某条直线对称?若是,请在图上画出这条对称轴.20.某种子商店销售“黄金一号”玉米种子,为惠民促销,推出两种销售方案供采购者选择.方案一:每千克种子价格为4元,均不打折;方案二:购买3千克以内(含3千克)的价格为每千克5元,若一次购买超过3千克,则超出部分的种子打七折.(1)请分别求出方案一、方案二中购买的种子数量x (千克)与付款金额y (元)之间的函数关系式;(2)若你去购买一定量的种子,你会怎样选择方案?说明理由.21.阅读理解:在平面直角坐标系xOy 中,对于任意两点111()P x y ,与222()Px y ,的“非常距离”,给出如下定义:若1212x x y y -≥-,则点1P 与点2P 的“非常距离”为12x x -;若1212x x y y -<-,则点1P 与点2P 的“非常距离”为12y y -.例如:点1(11)P ,,点2(23)P ,,因为1213-<-,所以点1P 与点2P 的“非常距离”为132-=,也就是图1中线段1PQ 与线段2P Q 长度的较大值(点Q 为垂直于y 轴的直线1PQ 与垂直于x 轴的直线2P Q 的交点).(1)已知点102A ⎛⎫- ⎪⎝⎭,B 为y 轴上的一个动点.①若点B (0,3),则点A 与点B 的“非常距离”为;②若点A 与点B 的“非常距离”为2,则点B 的坐标为;③直接写出点A 与点B 的“非常距离”的最小值为;(2)已知点D (0,1),点C 是直线433y x =-+上的一个动点,如图2,求点C 与点D “非常距离”的最小值及相应的点C 的坐标.22.在△ABC 中,DE 垂直平分AB ,分别交AB ,BC 于点D ,E ,MN 垂直平分AC ,分别交AC ,BC 于点M ,N .(1)如图①,若∠BAC =110°,求∠EAN 的度数;(2)如图②,若∠BAC =70°,求∠EAN 的度数;(3)若∠BAC =α(α≠90°),直接写出用α表示∠EAN 大小的代数式.23.甲、乙两地相距300km ,一辆货车和一辆轿车先后从甲地出发向乙地.如图,线段OA 表示货车离甲地距离y(km)与时间x(h)之间的函数关系,折线BCDE 表示轿车离甲地距离y(km)与时间x(h)之间的函数关系.请根据图象,解答下列问题:(1)线段CD表示轿车在途中停留了h;(2)求线段DE对应的函数解析式;(3)求轿车从甲地出发后经过多长时间追上货车.24.如图,△ABC中,AB=BC,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF (1)求证:△ABE≌△CBF;(2)若∠CAE=25°,求∠ACF的度数.参考答案1.A【解析】本题考查了轴对称图形的概念:一个图形沿某一直线对折后,两部分能够完全重合,这样的图形是轴对称图形,按照此定义分析可求解答案.【详解】图②③④沿某一直线对折,图形两部分均能够完全重合,因此是轴对称图形,图①⑤沿任何直线对折,图形两部分都不能够完全重合,因此不是轴对称图形,故答案选A.【点睛】本题考查了轴对称图形的概念,利用概念判断图形是否是轴对称图形,熟练掌握概念即可解题.2.D【分析】根据点在x轴上的特征,纵坐标为0,可得m+1=0,解得:m=-1,然后再代入m+3,可求出横坐标.【详解】解:因为点P(m+3,m+1)在x轴上,所以m+1=0,解得:m=-1,所以m+3=2,所以P点坐标为(2,0).故选D.【点睛】本题主要考查点在坐标轴上的特征,解决本题的关键是要熟练掌握点在坐标轴上的特征. 3.A【详解】试题分析:根据一次函数y=kx+b(k≠0,k、b为常数)的图像的性质:可知k>0,b>0,在一二三象限;k>0,b<0,在一三四象限;k<0,b>0,在一二四象限;k<0,b<0,在二三四象限.因此由图象经过第二、三、四象限,可判断得3-k<0,-k<0,解之得k>0,k >3,即k>3.故选A考点:一次函数的图像与性质4.C【解析】分析:根据上加下减,左加右减的平移原则,即可得出答案.解答:解:根据上加下减的平移原则,直线y=2x+6可以看作是由直线y=2x向上平移6个单位得到的;根据左加右减的平移原则,直线y=2x+6=2(x+3)可以看作是由直线y=2x向左平移3个单位得到的.故选C.点评:本题考查了一次函数图象与几何变换,属于基础题,关键是掌握上加下减,左加右减的平移原则.5.A【分析】根据台球桌四角都是直角,由∠3=25°,得∠2=65°;结合已知∠1=∠2,得出∠1的度数,进而解答本题.【详解】∵台球桌四角都是直角,∠3=25°,∴∠2=65°.∵∠1=∠2,∴∠1=65°.故选A.【点睛】本题考查了同学们利用对称的性质解决问题的能力,有利于培养同学们的思维能力.6.C【分析】先根据三角形任意两边之和大于第三边,任意两边之差小于第三边求出x的取值范围,然后根据若x为正整数,即可选择答案.【详解】,10-2=8,10+2=12∴<<,x812若x为正整数,∴的可能取值是9,10,11三个,故这样的三角形共有3个.x所以C选项是正确的.【点睛】本题主要考查了三角形的三边关系:三角形两边之和大于第三边,两边差小于第三边;牢记三角形的三边关系定理是解答的关键,注意本题的隐含条件就是x为正整数.7.B【详解】试题分析:仔细分析函数图象的特征,根据c 随t 的变化规律即可求出答案.解:由图中可以看出,函数图象在1月至3月,图象由低到高,说明随着月份的增加,产量不断提高,从3月份开始,函数图象的高度不再变化,说明产量不再变化,和3月份是持平的.故选B .考点:实际问题的函数图象点评:此类问题是初中数学的重点,贯穿于整个初中数学的学习,是中考中比较常见的知识点,一般难度不大,需熟练掌握.8.A【分析】利用不等式的性质、角平分线的性质、垂直平分线的性质分别判断后即可确定正确的结论.【详解】若0,0a b >>,则0a b +>,原命题正确,逆命题:如果0a b +>,那么0,0a b >>不一定正确,故不合题意;若a b ¹,则22a b ≠原命题错误,逆命题正确;角的平分线上的点到角的两边的距离相等,原命题正确;逆命题为“到角的两边的距离相等的点在这个角的平分线上”,不一定正确,要加前提:在角的内部.所以逆命题错误.线段的垂直平分线上的点到线段两端点距离相等,原命题与逆命题均正确.故选A.【点睛】本题考查了命题与定理的知识,解题的关键是了解不等式的性质、角平分线的性质、垂直平分线的性质,难度不大.9.C【分析】根据题意可对每个选项逐一分析判断图象得正误.【详解】解:A 、从图象上看小亮的路程走平路不变是不正确的,故不是.B 、从图象上看小亮走的路程随时间有一段更少了,不正确,故不是.C 、小亮走的路程应随时间的增大而增大,两次平路的两条直线互相平行,此图象符合,故正确.D 、因为平路和上坡路及下坡路的速度不一样,所以不应是一条直线,不正确,故不是.故选C .10.C【分析】根据三角形ABP 的面积为2,可知三角形的底边长为4,高为1,或者底边长为2,高为2,由此可在长方形网格中画图得出结果.【详解】根据三角形ABP 的面积为2,可知三角形的底边长为4,高为1,或者底边长为2,高为2,且点P 在网格格点上,则点P 的位置如图所示.【点睛】本题主要考查了三角形的面积公式,熟练掌握好三角形的底边和底边对应的高是解决本题的关键.11.(2,1)【分析】直接利用关于x 轴对称的性质,关于x 轴对称点的坐标特点:横坐标不变,纵坐标互为相反数.即点(),P x y 关于x 轴的对称点P '的坐标是(),x y -,进而得出答案.【详解】点P 关于x 轴对称的点是(2,-1),则P 点的坐标是:(2,1).故答案为:(2,1).【点睛】此题主要考查了关于x 轴对称的性质,正确记忆横纵坐标关系是解题关键.12.23x ≥-【分析】解不等式ax+b≥0的解集,就是求一次函数y=ax+b的函数值大于或等于0时自变量的取值范围.【详解】∵不等式ax+b⩾0的解集,就是一次函数y=ax+b的函数值大于或等于0时,当y<0的解集是x<2 3-,∴不等式ax+b⩾0的解集是x⩾2 3-.故答案为x⩾2 3-.【点睛】本题考查了一次函数与一元一次不等式,属于基础题,关键掌握解不等式ax+b>0的解集,就是求一次函数y=ax+b的函数值大于或等于0时自变量的取值范围,认真体会一次函数与一元一次不等式之间的内在联系.13.80°或20°【分析】根据等腰三角形的性质,已知等腰三角形有一个外角为100°,可知道三角形的一个内角.但没有明确是顶角还是底角,所以要根据情况讨论顶角的度数.【详解】等腰三角形有一个外角是100°即是已知一个角是80°,这个角可能是顶角,也可能是底角,当是底角时,顶角是180°-80°-80°=20°,因而顶角的度数为80°或20°.故填80°或20°.【点睛】本题考查了等腰三角形的性质;若题目中没有明确顶角或底角的度数,做题时要注意分情况进行讨论,这是十分重要的,也是解答问题的关键.14.50°【详解】是利用角平分线的性质定理和判定定理证AP是∠BAC外角的平分线!而∠BAC=2∠BPC也是可证的!由∠BPC=40°和角平分线性质,得∠ACD-2∠ABC=2×40°=80°即∠BAC=80°,则∠BAC的外角为100°,∠CAP=12×100°=50°.15.20【分析】由已知条件根据平行线的性质、角平分线的性质及等角对等边可得MO=MB,NO=NC.从而根据△AMN的周长求出AB+AC,问题得解.【详解】解:∵BO平分∠ABC,∴∠ABO=∠OBC.又∵MN∥BC,∴∠MOB=∠OBC.∴∠ABO=∠MOB,∴MO=MB.同理可得:NO=NC.∴△AMN的周长为:AM+MN+AN=AM+MO+ON+AN=AM+MB+NC+AN=AB+AC=12cm,∴△ABC的周长为:AB+AC+BC=12+8=20cm.故答案为:20.【点睛】本题考查了等角对等边的性质、角平分线的性质和平行线的性质;进行有效的线段的等量代换是正确解答本题的关键.16.①③④【详解】根据图象可知:龟兔再次赛跑的路程为1000米,故①正确;兔子在乌龟跑了40分钟之后开始跑,故②错误;乌龟在30~40分钟时的路程为0,故这10分钟乌龟没有跑在休息,故③正确;y 1=20x ﹣200(40≤x≤60),y 2=100x ﹣4000(40≤x≤50),当y 1=y 2时,兔子追上乌龟,此时20x ﹣200=100x ﹣4000,解得:x=47.5,y 1=y 2=750米,即兔子在途中750米处追上乌龟,故④正确,综上可得①③④正确.17.(1)x 轴处填20,y 轴处填1250;(2)25分钟.【分析】根据函数的图象就可以得到妈妈10分钟走了2500米,就可以得到妈妈的速度.妈妈以原速度返回并前往学校,因而回去的时间也是10分钟,因而与x 轴的括号内应填入20.根据小欣所走的路程等于妈妈在所用时间减去20分钟,这段时间所走的路程.根据这个相等关系列出方程,就可以求出时间.【详解】解:(1)x 轴处填20,y 轴处填1250;(2)由图象可知,点A 的坐标为(10,-2500),说明妈妈骑车速度为250米/分钟,并且返回到家的时间为20分钟,设小欣早晨上学需要的时间为x 分钟,则妈妈到家后在B 处追到小欣的时间为(x -20)分钟,根据题意得:50x =250(x -20),解得x =25,答:小欣早晨上学需要的时间为25分钟.【点睛】本题主要考查函数图像,正确理解函数图象横纵坐标表示的意义,理解问题的过程,能够通过图象得到函数是随自变量的增大,知道函数值是增大还是减小.18.a =1.【分析】由于点P 的坐标为()2,a a -到两坐标轴的距离相等,则│2-a │=│a │,然后去绝对值得到关于a 的两个一次方程,再解方程即可.【详解】解:由│2-a │=│a │得2-a =a ,或a -2=a ,解得a = 1.【点睛】本题考查了点的坐标:直角坐标系中点与有序实数对一一对应;在x轴上点的纵坐标为0,在y轴上点的横坐标为0;记住各象限点的坐标特点.19.(1)见解析;(2)见解析,A2(6,4),B2(4,2),C2(5,1);(3)△A1B1C1和△A2B2C2是轴对称图形,对称轴为图中直线l:x=3,见解析.【分析】(1)根据轴对称图形的性质,找出A、B、C的对称点A1、B1、C1,画出图形即可;(2)根据平移的性质,△ABC向右平移6个单位,A、B、C三点的横坐标加6,纵坐标不变;(3)根据轴对称图形的性质和顶点坐标,可得其对称轴是l:x=3.【详解】(1)由图知,A(0,4),B(﹣2,2),C(﹣1,1),∴点A、B、C关于y轴对称的对称点为A1(0,4)、B1(2,2)、C1(1,1),连接A1B1,A1C1,B1C1,得△A1B1C1;(2)∵△ABC向右平移6个单位,∴A、B、C三点的横坐标加6,纵坐标不变,作出△A2B2C2,A2(6,4),B2(4,2),C2(5,1);(3)△A1B1C1和△A2B2C2是轴对称图形,对称轴为图中直线l:x=3.【点睛】本题考查了轴对称图形的性质和作图﹣平移变换,作图时要先找到图形的关键点,分别把这几个关键点按照平移的方向和距离确定对应点后,再顺次连接对应点即可得到平移后的图形.20.(1)y1=4x,y2=5(03),15 3.5(-3)(3).x xx x≤≤⎧⎨+>⎩(2)当0<x<9时,选择方案一;当x=9时,选择两种方案都可以;当x>9时,选择方案二.【分析】(1)根据付款金额=数量×单价,即可表示出方案一.在方案二中,当0≤x≤3时的函数关系式由付款金额=数量×单价可得;当x >3时,由金额=3千克内的金额+超过3千克部分的金额,即可写出函数解析式.(2)当0≤x≤3时,选择方案一;当x >3时,比较4x 与15+3.5(x-3)的大小关系,即可确定x 的范围,从而进行判断.【详解】(1)由题意得:y 1=4x ,y 2=5(03),15 3.5(-3)(3).x x x x ≤≤⎧⎨+>⎩;(2)当0≤x≤3时,y 1<y 2,选择方案一;当x >3且4x=15 3.5(-3)x +时,x=9,当x >3且4x >15 3.5(-3)x +时,x >9,当x >3且4x <15 3.5(-3)x +时,x <9,综上所述:当0<x<9时,选择方案一;当x=9时,选择两种方案都可以;当x>9时,选择方案二.21.(1)①3;②B (0,2)或(0,﹣2);③12;(2)最小值为67,61377C ,⎛⎫ ⎪⎝⎭.【分析】(1)①根据若1212x x y y -<-,则点1P 与点2P 的“非常距离”为12y y -解答即可;②根据点B 位于y 轴上,可以设点B 的坐标为()0,y .由“非常距离”的定义可以确定02y -=,据此可以求得y 的值;③设点B 的坐标为()0,y .因为1002y --≥-,所以点A 与点B 的“非常距离”最小值为11022--=;(2)设点C 的坐标为003,34x x ⎛⎫+ ⎪⎝⎭.根据材料“若1212x x y y -≥-,则点1P 与点2P 的“非常距离”为12x x -”,此时1212x x y y -=-,列出0040313x x ⎛⎫-=-+- ⎪⎝⎭再求解,据此可以求得最小值和点C 的坐标.【详解】解:(1)①11022--=,033-=.∵132<,∴点A 与点B 的“非常距离”为3.②∵B 为y 轴上的一个动点,∴设点B 的坐标为(0,y ).∵110222--≠=,∴02y -=.解得,y =2或y =﹣2;∴点B 的坐标是(0,2)或(0,﹣2).③点A 与点B 的“非常距离”的最小值为11022--=.(2)如图2,取点C 与点D 的“非常距离”的最小值时,需要根据运算定义“若1212x x y y -≥-,则点1P 与点2P 的‘非常距离’为12x x -”解答,此时1212x x y y --=.∵C 是直线433y x -=+上的一个动点,点D 的坐标是(0,1),∴设点C 的坐标为00433x x ⎛⎫- ⎪⎝⎭,+,则0040313x x ⎛⎫--- ⎪⎝⎭=+∴067x =或06x =,∴0607x -=或006x -=.∵667<,∴点C 与点D 的“非常距离”的最小值为67,此时61377C ⎛⎫ ⎪⎝⎭,.【点睛】本题考查了一次函数综合题.对于信息给予题,一定要弄清楚题干中的已知条件.本题中的“非常距离”的定义是正确解题的关键.22.(1)40°;(2)40°.;(3)见解析.【分析】1)根据线段垂直平分线上的点到线段两端点的距离相等可得AE=BE ,再根据等边对等角可得∠BAE=∠B ,同理可得,∠CAN=∠C ,然后利用三角形的内角和定理求出∠B+∠C ,再根据∠EAN=∠BAC-(∠BAE+∠CAN )代入数据进行计算即可得解;(2)同(1)的思路,最后根据∠EAN=∠BAE+∠CAN-∠BAC 代入数据进行计算即可得解;(3)根据前两问的求解,分α<90°与α>90°两种情况解答.【详解】解:(1)∵DE 垂直平分AB ,∴AE=BE,∴∠BAE=∠B,同理可得∠CAN=∠C,∴∠EAN=∠BAC-∠BAE-∠CAN=∠BAC-(∠B+∠C),在△ABC中,∠B+∠C=180°-∠BAC=70°,∴∠EAN=110°-70°=40°.(2)∵DE垂直平分AB,∴AE=BE,∴∠BAE=∠B,同理可得∠CAN=∠C∴∠EAN=∠BAE+∠CAN-∠BAC=(∠B+∠C)-∠BAC,在△ABC中,∠B+∠C=180°-∠BAC=110°,∴∠EAN=110°-70°=40°.(3)当α<90°时,∠EAN=180°-2α;当α>90°时,∠EAN=2α-180°.【点睛】本题考查了线段垂直平分线上的点到线段两端点的距离相等的性质,等边对等角的性质,三角形的内角和定理,整体思想的利用是解题的关键.23.解:(1)0.5.(2)设线段DE对应的函数解析式为y=kx+b(2.5≤x≤4.5),∵D点坐标为(2.5,80),E点坐标为(4.5,300),∴代入y=kx+b,得:80 2.5k b{300 4.5k b=+=+,解得:k110{b195==-.∴线段DE对应的函数解析式为:y=110x-195(2.5≤x≤4.5).(3)设线段OA对应的函数解析式为y=mx(0≤x≤5),∵A点坐标为(5,300),代入解析式y=mx得,300=5m,解得:m=60.∴线段OA对应的函数解析式为y=60x(0≤x≤5)由60x=110x-195,解得:x=3.9.答:轿车从甲地出发后经过3.9小时追上货车.【详解】一次函数的应用,待定系数法,直线上点的坐标与方程的关系.【分析】(1)利用图象得出CD这段时间为2.5-2=0.5,得出答案即可.(2)由D点坐标(2.5,80),E点坐标(4.5,300),用待定系数法求出线段DE对应的函数解析式.(3)用待定系数法求出OA的解析式,列60x=110x-195时,求解即为轿车追上货车的时间.24.(1)详见解析;(2)65°.【分析】(1)运用HL定理直接证明△ABE≌△CBF,即可解决问题.(2)证明∠BAE=∠BCF=25°;求出∠ACB=45°,即可解决问题.【详解】证明:(1)在Rt△ABE与Rt△CBF中,{AE CF AB BC==,∴△ABE≌△CBF(HL).(2)∵△ABE≌△CBF,∴∠BAE=∠BCF=20°;∵AB=BC,∠ABC=90°,∴∠ACB=45°,∴∠ACF=65°.【点睛】该题主要考查了全等三角形的判定及其性质的应用问题;准确找出图形中隐含的相等或全等关系是解题的关键.。
沪教版八年级上册数学期末测试卷及含答案(综合题)(黄金题型)

沪教版八年级上册数学期末测试卷及含答案一、单选题(共15题,共计45分)1、如图,在△ABC中,∠C=90°,∠B=30°,边AB的垂直平分线DE交AB于点E,交BC于点D,CD=3,则BC的长为()A.6B.9C.10D.122、如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直.若AD=8,则点P到BC的距离是()A.8B.6C.4D.23、据测试:拧不紧的水龙头每分钟滴出100滴水,每滴水约0.05毫升.小康同学洗手后,没有把水龙头拧紧,水龙头以测试的速度滴水,当小康离开x分钟后,水龙头滴出y毫升的水,请写出y与x之间的函数关系式是()A. y=0.05 xB. y=5 xC. y=100 xD. y=0.05 x+1004、若函数y= 有意义,则()A.x>1B.x<1C.x=1D.x≠15、如图,射线OC是∠AOB的角平分线,D是射线OC上一点,DP⊥OA于点P,DP=4,若点Q是射线OB上一点,OQ=3,则△ODQ的面积是()A.3B.4C.5D.66、如图,中,为线段AB的垂直平分线,交于点E,交于D,连接,若,则的长为( )A.6B.3C.4D.27、在下列以线段a,b,c的长为三边的三角形中,不能构成直角三角形的是()A.a=9,b=41,c=40B.a=b=5,c=5C.a:b:c=3:4:5 D.a=11,b=12,c=158、某药品经过两次降价,每瓶零售价由100元降为81元,则平均每次降价()A.8.5%B.9%C.9.5%D.10%9、若在实数范围内有意义,则x的取值范围是( )A. ≥3B.x<3C.x≤3D.x>310、如图,在▱ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E.若BF=6,AB=5,则AE的长为()A.4B.6C.8D.1011、如图,以数轴的单位长线段为边作一个正方形,以-1所在的点为旋转中心,将过-1点的对角线顺时针旋转,使对角线的另一端点落在数轴正半轴的点处,则点表示的数是()A. B. C. D.12、已知a,b,c是△ABC三条边的长,那么方程cx2+(a+b)x+ =0的根的情况是( )A.有两个相等的实数根B.有两个不相等的实数根C.没有实数根 D.无法确定13、已知一个一元二次方程的二次项系数是3,常数项是1,则这个一元二次方程可能是()A.3x+1=0B.x 2+3=0C.3x 2﹣1=0D.3x 2+6x+1=014、下列各组数中,是勾股数的()A.12,15,18B.11,60,61C.15,16,17D.12,35,3615、菱形ABCD的一条对角线长为6,边AB的长为方程y2﹣7y+10=0的一个根,则菱形ABCD的周长为()A.8B.20C.8或20D.10二、填空题(共10题,共计30分)16、一个反比例函数的图象位于第二、四象限.请你写出一个符合条件的解析式是________ .17、为了增强抗旱能力,保证今年夏粮丰收,某村新建了一个蓄水池,这个蓄水池安装了两个进水管和一个出水管(两个进水管的进水速度相同)一个进水管和一个出水管的进出水速度如图1所示,某天0点到6点(至少打开一个水管),该蓄水池的蓄水量如图2所示,并给出以下三个论断:①0点到1点不进水,只出水;②1点到4点不进水,不出水;③4点到6点只进水,不出水.则一定正确的论断是________ .18、如图,在中,,为边上的中线,过点作交于点.若,,则的长为________.19、如图,是一个简单的数值运算程序.则输入x的值为________.20、已知函数的图象经过点(1,3),且与x轴没有交点,写出一个满足题意的函数的解析式________.21、+2sin30°-tan60°+tan45°=________.22、若x2+3xy-2y2=0,那么= ________.23、如图,由4个相同的直角三角形与中间的小正方形拼成一个大正方形,若大正方形面积是9,小正方形面积是1,直角三角形较长直角边为a,较短直角边为b,则ab的值是________24、在“2011年北京郁金香文化节”中,北京国际鲜花港的3×106株郁金香为京城增添了亮丽的色彩.若这些郁金香平均每平方米种植的数量为n(单位:株/平方米),总种植面积为S(单位:平方米),则n与S的函数关系式为________ .(不要求写出自变量S的取值范围)25、计算:6 ×=________,÷(2﹣)=________.三、解答题(共5题,共计25分)26、解方程:x2-3x=5x-127、解方程:x2﹣6x+5=0 (配方法)28、数学阅读是学生个体根据已有的知识经验,通过阅读数学材料建构数学意义和方法的学习活动,是学生主动获取信息,汲取知识,发展数学思维,学习数学语言的途径之一.请你先阅读下面的材料,然后再根据要求解答提出的问题:问题情境:设a,b是有理数,且满足,求的值.解:由题意得,∵a,b都是有理数,∴也是有理数,∵是无理数,∴,∴,∴解决问题:设x,y都是有理数,且满足,求的值.29、如图,在△ABC中,BA=BC,∠ABC=120°,AB的垂直平分线与AC交于点D,垂足为点F,试探究线段AD与DC的数量关系,并证明你的结论.30、如图,在△ABC中,∠ACB=90°,AD是△ABC的角平分线,AB=10cm,DC=3cm,试求△ABD的面积.参考答案一、单选题(共15题,共计45分)1、B2、C3、B4、D5、D6、B7、D8、D9、A10、C11、C12、B13、D14、B15、B二、填空题(共10题,共计30分)16、17、18、19、20、21、22、23、24、25、三、解答题(共5题,共计25分)26、27、28、29、30、。
【新】沪教版八年级上册数学期末测试卷及含答案

沪教版八年级上册数学期末测试卷及含答案一、单选题(共15题,共计45分)1、下列计算正确的是()A.()﹣2=9B. =﹣2C.(﹣2)0=﹣1D.|﹣5﹣3|=22、如图,已知在Rt△ABC中,∠ABC=90°,点D是BC边的中点,分别以B、C 为圆心,大于线段BC长度一半的长为半径画弧,两弧在直线BC上方的交点为P,直线PD交AC于点E,连接BE,则下列结论:①ED⊥BC;②∠A=∠EBA;③EB平分∠AED;④ED= AB中,一定正确的是()A.①②③B.①②④C.①③④D.②③④3、下列二次根式中,与是同类二次根式的是()A. B. C. D.4、下列各式计算正确的是()A. B. C. D.5、方程x2=3x的解是()A.x=3B.x1=0,x2=3 C.x1=0,x2=﹣3 D.x1=1,x2=36、如果关于x的一元二次方程(m﹣3)x2+3x+m2﹣9=0有一个解是0,那么m的值是( )A.3B.﹣3C.±3D.0或﹣37、在Rt△ABC中,∠C=90°,c为斜边,a、b为直角边,则化简的结果为()A.3a+b﹣cB.﹣a﹣3b+3cC.a+3b﹣3cD.2a8、如图,在△ABC中,PM、QN分别是线段AB、AC的垂直平分线,若∠PAQ=40°,则∠BAC的度数是()A.110°B.100°C.120°D.70°9、函数中,自变量x的取值范围是()A.x>2B.x<2C.x≠2D.x≠﹣210、下列根式中,不是最简二次根式的是()A. B. C. D.11、如图,一棵树在一次强台风中于离地面3米处折断倒下,倒下部分与地面成30°角,这棵树在折断前的高度为().A.6米;B.9米;C.12米;D.15米.12、下列运算正确的是()A. =﹣4B. ﹣C.()2=4D.13、关于x的方程x2+x﹣k=0有两个不相等的实数根,则k的取值范围为()A.k>﹣B.k≥﹣C.k<﹣D.k>﹣且k≠014、下列计算正确的是()A. B.- C. D.15、根据如图所示程序计算函数值,若输入的x的值为,则输出的函数值为()A.﹣B.C.1D.二、填空题(共10题,共计30分)16、化简:﹣=________.17、已知,则=________.18、如图,于点,为的中点,连接的平分线交于点,连结,若,则________.19、已知关于x的一元二次方程ax2﹣(a+2)x+2=0有两个不相等的正整数根时,整数a的值是________.20、如图,反比例函数y=-图象上有一点P,PA⊥x轴于A,点B在y轴的负半轴上,那么△PAB的面积是________21、下列二次根式,不能与合并的是________(填写序号即可).①;②;③;④;⑤.22、如果a+b+c=0,那么一元二次方程ax2+bx+c=0必有一个根是________.23、若8,a,17是一组勾股数,则a=________.24、反比例函数y=的图像过点(-2,a)、(2,b),若a-b=-6,则ab=________.25、已知直角三角形的三边长为 4,5,,为斜边,则以为边长的正方形面积为________.三、解答题(共5题,共计25分)26、解方程(配方法):27、如图,在⊙O中,点C是的中点,弦AB与半径OC相交于点D,AB=12,CD=2.求⊙O半径的长.28、如图,在钝角△ABC中,BC=9,AB=17,AC=10,AD⊥BC于D,求AD的长.29、如图,四边形ABCD是某新建厂区示意图,∠A=75°,∠B=45°,BC⊥CD,AB=500 米,AD=200米,现在要在厂区四周建围墙,求围墙的长度有多少米?30、在等腰三角形,三边长分别是.其中,若关于x的方程有两个相等的实数根,求的周长.参考答案一、单选题(共15题,共计45分)1、A2、B3、D4、D5、B6、B7、E8、A9、C10、C11、B12、C13、A14、C15、B二、填空题(共10题,共计30分)16、17、18、19、20、21、22、23、24、25、三、解答题(共5题,共计25分)27、29、。
【完整版】沪教版八年级上册数学期末测试卷

沪教版八年级上册数学期末测试卷一、单选题(共15题,共计45分)1、如图,在等腰△ABC中,∠BAC=120º,DE是AC 的垂直平分线,线段DE=1cm,则BD的长为( )A.6cmB.8cmC.3cmD.4cm2、当x为何值时,函数y= x+1的值为0?()A.2B.±2C.-2D.13、如图所示,在四边形ABCD中,AB=BC,AD=CD,O为四边形内一点,则下列说法一定成立的是( )A.若.则O在∠BAD的平分线上B.O在线段BD上时,AO一定等于OCC.当O在∠ABC的平分线上时,和不一定相等 D.当O在线段AC的某一个位置上时,可使得4、若(a-1)x2+bx+c=0是关于x的一元二次方程,则( )A.a≠0B.a≠1C.a≠-1D.a=15、若在实数范围内有意义,则的取值范围是()A. B. C. D.6、下列运算正确的是()A. ﹣=B. =2C.4 ×2 =24D. =6﹣7、如图,水以恒速(即单位时间内注入水的体积相同)注入如图的容器中,容器中水的高度h与时间t的函数关系图象可能为()A. B. C. D.8、某药品经过两次降价,每瓶零售价由100元降为81元.已知两次降价的百分率都为x,那么x满足的方程是()A.100(1+x)2=81B.100(1﹣x)2=81C.100(1﹣x%)2=81 D.100x 2=819、若关于x的一元二次方程x2+2x+k=0有两个不相等的实数根,则k的取值范围是()A.k<1B.k>1C.k=1D.k≥010、某商品原价为180元,连续两次提价x%后售价为300元,下列所列方程正确的是( )A.180(1+x%)=300B.180(1+x%) 2=300C.180(1-x%)=300 D.180(1-x%) 2=30011、如图,在宽为20m,长为32m的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪.要使草坪的面积为,求道路的宽.如果设小路宽为x,根据题意,所列方程正确的是()A. (20-x)(32-x)=540B. (20-x)(32-x)=100C. (20+x)(32+x)=540D. (20+x)(32-x)=54012、用配方法解方程x2﹣10x﹣1=0时,变形正确的是()A.(x﹣5)2=24B.(x﹣5)2=26C.(x+5)2=24D.(x+5)2=2613、化简× 结果是()A. B. C. D.14、如图,,,点在的垂直平分线上,若,则=()A.4B.6C.8D.1015、已知关于的方程是一元二次方程,则m的取值范围是()A. B. C. D.任意实数二、填空题(共10题,共计30分)16、如图,在平行四边形ABCD中,P是CD边上一点,且AP和BP分别平分∠DAB和∠CBA,若AD=5,AP=8,则△APB的周长是________.17、实数a,b在数轴上的位置如图所示,则化简﹣|a+b|的结果是________.18、如图,在矩形中,,点为线段上的动点,将沿折叠,使点落在矩形内点处.下列结论正确的是________. (写出所有正确结论的序号)①当为线段中点时,;②当为线段中点时,;③当三点共线时,;④当三点共线时,.19、如图,四边形OABC中,AB∥OC,边OA在x轴的正半轴上,OC在y轴的正半轴上,点B在第一象限内,点D为AB的中点,CD与OB相交于点E,若△BDE、△OCE的面积分别为1和9,反比例函数y= 的图象经过点B,则k=________.20、如图,在中,和的平分线相交于点O,过点O作交于E,交于F,过点O作于D,有下列结论:①;②点O到各边的距离相等;③ ;④.其中正确的结论是________(把你认为正确结论的序号都填上).21、已知a为方程的一个根,则代数式的值为________.22、函数中,自变量x的取值范围是________.23、方程x2+7x=12的一般形式:________24、计算:________.25、一等腰梯形两组对边中点连线段的平方和为8,则这个等腰梯形的对角线长为________三、解答题(共5题,共计25分)26、已知是关于的方程的一个根,求的值.27、解方程:2x2+x﹣3=0.28、已知-1是方程x2+ax-b=0的一个根,求a2-b2+2b的值.29、如图,已知Rt△ABC中,∠ACB=90°,CA=CB,D是AC上一点,E在BC的延长线上,且AE=BD,BD的延长线与AE交于点F.试通过观察、测量、猜想等方法来探索BF与AE有何特殊的位置关系,并说明你猜想的正确性.30、如图,矩形ABCD中,CD=8,AD=4,将矩形沿AC折叠,点D落在点D′处,求重叠部分△AFC 的面积.参考答案一、单选题(共15题,共计45分)1、D3、B4、B5、A6、C7、C8、B9、A10、B11、A12、B13、A14、C15、A二、填空题(共10题,共计30分)16、17、18、19、20、21、22、24、25、三、解答题(共5题,共计25分)26、27、28、30、。
沪教版八年级上册数学期末测试卷

沪教版八年级上册数学期末测试卷一、单选题(共15题,共计45分)1、下列命题错误的是( )A.关于x的方程x 2=a必有两个互为相反数的根B.关于x的方程(x−a) 2=b 2必有实根C.关于x的方程mx 2+nx=0必有实根D.关于x的方程x 2+a 2+1=0没有实数根2、已知矩形的面积为10,长和宽分别为x和y,则y关于x的函数图象大致是()A. B. C.D.3、下列各组数据为勾股数的是()A. ,,B.1,,C.5,12,13D.2,3,44、如图,矩形中,,把矩形沿直线折叠,点B落在点E 处,交于点F,若,则线段的长为().A.3B.4C.5D.65、端午节前夕,在东昌湖举行第七届全民健身运动会龙舟比赛中,甲、乙两队在500米的赛道上,所划行的路程y(m)与时间x(min)之间的函数关系如图所示,下列说法错误的是()A.乙队比甲队提前0.25min到达终点B.当乙队划行110m时,此时落后甲队15mC.0.5min后,乙队比甲队每分钟快40mD.自1.5min开始,甲队若要与乙队同时到达终点,甲队的速度需要提高到255m/min6、已知点,,都在反比例函数的图像上,则()A. B. C. D.7、在边长为正整数的△ABC中,AB=AC,且AB边上的中线CD将△ABC的周长分为1:2的两部分,则△ABC面积的最小值为()A. B. C. D.8、若关于x的一元二次方程(x﹣2)2=m有实数解,则m的取值范围是()A.m≤0B.m>0C.m≥0D.无法确定9、若二次根式有意义,则x的取值范围是()A.x<4B.x>4C.x≥4D.x≤410、若反比例函数的图象经过第二、四象限,则m为()A. B. C. D.11、方程与所有根的乘积等于()A.-18B.18C.-3D.312、下列函数中,反比例函数是()A.y=B.y=4xC.y=D.y=13、在同一直角坐标系中,函数与y=ax+1(a≠0)的图象可能是()A. B. C. D.14、化简二次根式的结果为( )A.-5B.5C.±5D.15、绍兴是著名的桥乡,如图,石拱桥的桥顶到水面的距离CD为8m,桥拱半径OC为5m,则水面宽AB为()A.4mB.5mC.6mD.8m二、填空题(共10题,共计30分)16、如图,在平面直角坐标系中,△ABC的边AB∥x轴,点A在双曲线y=(x <0)上,点B在双曲线y=(x>0)上,边AC中点D在x轴上,△ABC的面积为8,则k= ________.17、如图所示,直线y= x分别与双曲线y= (k1>0,x>0)、双曲线y=(k2>0,x>0)交于点A,点B,且OA=2AB,将直线向左平移4个单位长度后,与双曲线y= 交于点C,若S△ABC =1,则k1k2的值为________.18、=________(书写每项化简过程)=________.19、三角形三个内角度数之比是1:2:3,最大边长是12,则它的最小边的长是________.20、如图,点B是反比例函数上一点,矩形OABC的周长是20,正方形BCGH和正方形OCDF的面积之和为68,则反比例函数的解析式是________.21、一元二次方程x2﹣x﹣1=0根的判别式的值等于________22、点A ,B 都在反比例函数图象上,则________.(填写<,>,=号)23、若关于x的方程有两个相等的实数根,则式子的值为________24、如图,Rt△ABC中,∠C=90°,D为BC上一点,∠DAC=30°,BD=2,AB=2,则AC的长是________25、将x=代入反比例函数y=﹣中,所得函数值记为y1,又将x=y1+1代入原反比例函数中,所得函数值记为y2,再将x=y2+1代入原反比例函数中,所得函数值记为y3,…,如此继续下去,则y2014=________ .三、解答题(共5题,共计25分)26、实数,在数轴上的位置如图所示,请化简:27、如图,是等腰三角形,的平分线交于点交于点E,求的周长.28、如图:在△ABC中,∠C=90°,AD平分∠CAB交BC于点D,AB=10,AC=6,求D到AB的距离.29、数学综合实验课上,同学们在测量学校旗杆的高度时发现:将旗杆顶端升旗用的绳子垂到地面还多2米;当把绳子的下端拉开8米后,下端刚好接触地面,如图,根据以上数据,同学们准确求出了旗杆的高度,你知道他们是如何计算出来的吗?30、先化简,再求值:,其中,.参考答案一、单选题(共15题,共计45分)1、A2、C3、C4、D5、D6、D7、C8、C10、B11、A12、C13、B14、B15、D二、填空题(共10题,共计30分)16、17、18、19、20、21、22、23、24、25、三、解答题(共5题,共计25分)27、29、。
沪教版八年级上册数学期末测试卷(附解析)
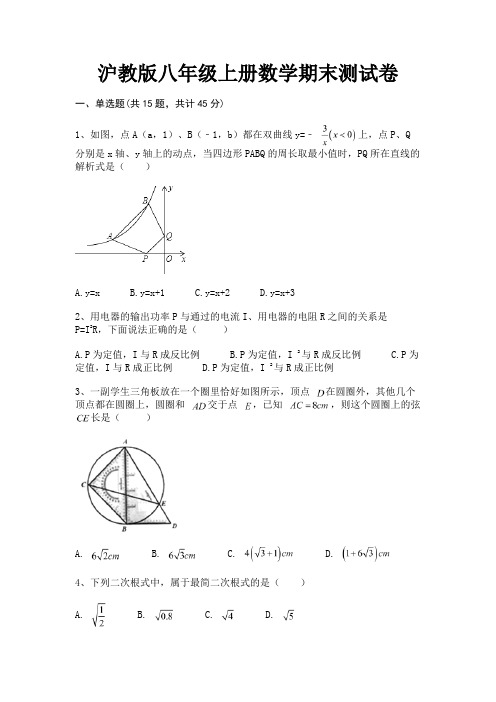
沪教版八年级上册数学期末测试卷一、单选题(共15题,共计45分)1、如图,点A(a,1)、B(﹣1,b)都在双曲线y=﹣上,点P、Q分别是x轴、y轴上的动点,当四边形PABQ的周长取最小值时,PQ所在直线的解析式是()A.y=xB.y=x+1C.y=x+2D.y=x+32、用电器的输出功率P与通过的电流I、用电器的电阻R之间的关系是P=I2R,下面说法正确的是()A.P为定值,I与R成反比例B.P为定值,I 2与R成反比例C.P为定值,I与R成正比例D.P为定值,I 2与R成正比例3、一副学生三角板放在一个圈里恰好如图所示,顶点在圆圈外,其他几个顶点都在圆圈上,圆圈和交于点,已知,则这个圆圈上的弦长是()A. B. C. D.4、下列二次根式中,属于最简二次根式的是()A. B. C. D.5、下列计算正确的是()A.2 =B. =C.4 ﹣3 =1D.3+2=56、若直角三角形的三边a、b、c满足a2-4a+4+ =0,则第三边c的长度是( )A. B. C. 或 D.5或137、若代数式+有意义,则实数x的取值范围是()A.x≠1B.x≥0C.x≠0D.x≥0且x≠18、若点(x1, y1),(x2, y2)都是反比例函数图象上的点,并且,则下列结论中正确的是()A.x1>x2B.x1<x2C.y随x的增大而减小D.两点有可能在同一象限9、如图,在△ABC中,AC=8,BC=6,AB=10,P为边AB上一动点,PD AC于D,PE BC于E,则DE的最小值为()A.3.6B.4.8C.5D.5.210、已知关于x的一元二次方程(a﹣1)x2+x+a2﹣1=0的一个根是0,则a的值为()A.1B.﹣1C.1或﹣1D.11、下列函数的图像在每一个象限内,y值随x值的增大而增大的是()A.y=-x+1B.y=x 2-1C.D.12、若关于x的一元二次方程为ax2+bx-5=0(a≠0)的一个解是x=1,则2019-a-b的值是A.2018B.2013C.2014D.201213、如图,在△ABE中,∠A=105°,AE的垂直平分线MN交BE于点C,且AB=CE,则∠B的度数是()A.45°B.60°C.50°D.55°14、用配方法解方程x2+4x﹣1=0时,原方程应变形为()A.(x+2)2=5B.(x+2)2=3C.(x﹣2)2=3D.(x﹣2)2=515、如图,∠A=120°,AB=AC=4,D在线段AB上,DE∥BC交AC于E,将△ADE绕点D顺时旋转30°得△GDH,当H点在BC上时,AD的长为()A. B.2 C. D.二、填空题(共10题,共计30分)16、如图,⊙O中直径AB⊥弦CD于E,若AB=26,CD=24,则OE=________.17、如图,正方形ABCD的边长是2,其面积记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积记为S 2…按此规律继续下去,则S2016的值为________.18、在函数y= 中,自变量x的取值范围是________.19、如图,在中,,垂直平分,垂足为,交于,若的周长为,则的长为________20、已知:,那么a的取值范围是________.21、若正比例函数y=(m﹣2)x m2﹣10的图象在第一、三象限内,则m=________ .22、在△ABC中,AB=AC,AB的中垂线于AC所在的直线相交所得的锐角为40°,则底角∠B的大小为________23、如图,有四张不透明的卡片除正面的函数关系式不同外,其余相同,将它们背面朝上洗匀后,从中抽取一张卡片,则抽到函数图象不经过第四象限的卡片的概率为________ .24、在函数y= 中,自变量x的取值范围是________25、已知是关于x的一元二次方程,则的取值范围是________ 。
完整版沪教版八年级上册数学期末测试卷

沪教版八年级上册数学期末测试卷一、单选题(共15题,共计45分)1、如图是某商场一楼与二楼之间的手扶电梯示意图.其中AB、CD分别表示一楼、二楼地面的水平线,∠ABC=150°,BC的长是8 m,则乘电梯从点B到点C 上升的高度h是()A. mB.4 mC. mD.8 m2、已知为实数,则关于的方程的实数根情况一定是()A.有两个不相等的实数根B.有两个相等的实数根C.有两个实数根 D.没有实数根3、一根蜡烛长30cm,点燃后每小时燃烧5cm,燃烧时蜡烛剩余的长度h(cm)和燃烧时间t(小时)之间的函数关系用图像可以表示为中的()A. B. C.D.4、数是数和数的比例中项,若,,则数的值为()A.5B.±5C.4D.±45、如果反比例函数的图象在第二、第四象限,那么m可能取的一个值为()A.-2B.-1C.0D.16、若函数y=(m+1)x|m|-2是反比例函数,则m等于().A.2B.-2C.1D.±17、如图,△ABC中,∠BAC=60°,∠BAC的平分线AD与边BC的垂直平分线MD相交于D,DE⊥AB交AB的延长线于E,DF⊥AC于F,现有下列结论:①DE=DF;②DE+DF=AD;③DM平分∠EDF;④AB+AC=2AE;其中正确的有()A.1个B.2个C.3个D.4个8、下列式子中是一元二次方程的是()A. xy+2=1B.(+5) x=0C. -4 x-5D. =09、已知一元二次方程x2﹣6x+8=0的两个解恰好分别是等腰△ABC的底和腰,则△ABC的周长为()A.10B.10或8C.9D.810、中,,,的对边分别记为,,,由下列条件不能判定为直角三角形的是()A. B. C. D.11、如图,在△ABC中,分别以点A和点B为圆心,以大于AB的长为半径画弧,两弧相交于点M、N,作直线MN,交BC于点D,若△ADC的周长为10,AB=6,则△ABC的周长为()A.6B.12C.16D.2012、如果△ABC的三个顶点A,B,C所对的边分别为a,b,c,那么下列条件中,不能判断△ABC是直角三角形的是( )A.∠A=15°,∠B=75°B.∠A∶∠B∶∠C=1∶2∶3C.a= ,b= ,c=D.a=6,b=10,c=1213、如图,在▱ABCD中,AB=6,AD=9,AF平分∠BAD交BC于点E,交DC的延长线于点F,BG⊥AF于点G,BG=4 ,EF= AE,则△CEF的周长为().A.8B.10C.14D.1614、反比例函数图象上有三个点(x1,y1),(x2,y2),(x3,y3),其中x1<x2<0<x3,则y1,y2,y3的大小关系是()A. B. C.D.15、在△ABC中,D为BC中点,DE⊥AB于E,DF⊥AC于F,已知DE=DF,则下列结论不一定成立的是()A.AD是等腰△ABC底边上的中线B.AB=BC=CAC.AD平分∠BAC D.AD是△ABC底边上的高线二、填空题(共10题,共计30分)16、如图,∠AOE=∠BOE=15°,EF∥OB,EC⊥OB,若EC=3,则EF的长为________17、如图,∠C=90°,AC=6,BC=8,∠ABC和∠BAC的角平分线的交点是点D,则△ABD的面积为________.18、若x=2是关于x的方程x2﹣4mx﹣8=0的一个根,则m的值为________.19、纸片中,,将它折叠使与重合,折痕交于点,则线段的长为________.20、若矩形的长为()cm,宽为cm,则此矩形的面积为________ cm2.21、如图,平行四边形中,平分,交于点F,,交点,,则=________.22、已知:关于x的一元二次方程x2﹣(R+r)x+ =0有两个相等的实数根,其中R、r分别是⊙O1⊙O2的半径,d为两圆的圆心距,则⊙O1与⊙O2的位置关系是________.23、二次根式中x的取值范围是________.24、如图,在△ABC中,AB=AC,∠A=120°,BC=,⊙A与BC相切于点D,且交AB,AC于M、N两点,则图中阴影部分的面积是________(结果保留π).25、计算:(+1)(﹣1)=________.三、解答题(共5题,共计25分)26、计算:.27、某校初二年级以班为单位进行篮球比赛,第一轮比赛是先把全年级平分成A、B两个大组,同一个大组的每两个班都进行一场比赛,这样第一轮A、B两个大组共进行了20场比赛,问该校初二年级共有几个班?28、已知关于x的方程mx2﹣(m+3)x+3=0(m≠0).(1)求证:方程总有两个实数根;(2)如果方程的两个实数根都是整数,且有一根大于1,求满足条件的整数m 的值.29、如图,在直角三角形ABC中,∠ACB=90°,∠B=60°,AD,CE是角平分线,AD与CE相交于点F,FM⊥AB,FN⊥BC,垂足分别为M,N.求证:FE=F D.30、公园里有一块形如四边形ABCD的草地,测得BC=CD=20米,∠A=45°,∠B=∠C=120°,请求出这块草地面积.参考答案一、单选题(共15题,共计45分)1、B2、C3、B4、C5、D6、C7、C8、D9、A10、D11、12、D13、A14、B15、B二、填空题(共10题,共计30分)16、17、18、19、20、22、23、24、25、三、解答题(共5题,共计25分)26、27、。
沪教版八年级上册数学期末测试卷及含答案(完整版)

沪教版八年级上册数学期末测试卷及含答案一、单选题(共15题,共计45分)1、如图,已知点,,点P在线段AB上(不与端点重合),反比例函数的图象经过点P,则的取值范围是()A. >3B.0≤≤3C.0<≤3D. ≥32、如图正比例函数y=k1x与反比例函数y=的图象相交于A、B两点,AC ⊥x轴于点C,CD∥AB交y轴于点D,连接AD、BD,若S△ABD=6,则下列结论正确的是()A. k1=﹣6B. k1=﹣3C. k2=﹣6D. k2=﹣123、下列关于x的一元二次方程中,没有实数根的是()A. B. C.D.4、下列式子为最简二次根式的是()A. B. C. D.5、汽车开始行驶时,油箱内有油40升,如果每小时耗油5升,则油箱内余油量Q(升)与行驶时间t(时)的关系用图象表示应为图中的()A. B. C.D.6、下列各数分别与(2-)相乘,结果为有理数的是()A. B.2+ C.2- D.-2+7、如图,在四边形ABCD中,∠A=90°,AB=3 ,AD= ,点M、N分别为线段BC、AB上的动点(含端点,但点M不与点B重合),点E、F分别为DM、MN 的中点,则EF长度的最大值为()A. B.3.5 C.5 D.2.58、如图所示,两个反比例函数y= 和y= 在第一象限内的图象依次是C 1和C2,设点P在C1上,PC⊥x轴于点C,交C2于点A,PD⊥y轴于点D,交C2于点B,则四边形PAOB的面积为()A.k1+k2B.k1﹣k2C.k1•k2D.k1•k2﹣k29、下列二次根式中,是最简二次根式的是()A. B. C. D.10、函数y=(m2﹣m)是反比例函数,则()A.m≠0B.m≠0且m≠1C.m=2D.m=1或211、将水匀速滴进如图所示的容器时,能符合题意反映容器中水的高度(h)与时间(t)之间对应关系的图象大致是()A. B. C. D.12、最简二次根式与是同类二次根式,则x等于()A. B.10 C.2 D.413、若关于x的方程是一元二次方程,则a的取值范围是()A.a≠1B.a>1C.a<1D.a≠014、如图,在平面直角坐标系中,正方形 ABCO 的顶点 A,C 分别在 y 轴、x 轴上,以 AB 为弦的⊙M 与 x 轴相切,若点 A 的坐标(0,8),则圆心M 的坐标为()A.(-4,3)B.(-3,4)C.(-5,5)D.(-4,5)15、下列二次根式中,与是同类二次根式的是()A. B. C. D.二、填空题(共10题,共计30分)16、如图,△ABC中,AB=AC=10,BC=8,AD平分∠BAC交BC于点D,点E为AC 的中点,连接DE,则△CDE的周长为________.17、如图,点A在反比例函数上,AB⊥x轴于点B,且△AOB的面积是4,则k的值是________.18、如图,过点的直线交轴于点,,,曲线过点,将点沿轴正方向平移个单位长度恰好落在该曲线上,则的值为________.19、若x是实数,且y= + ﹣1,则x+y=________.20、函数y=中,自变量x的取值范围是________.21、方程x2﹣9x+18=0的两个根是等腰三角形的底和腰,则这个等腰三角形的周长为________.22、圆的面积S与半径R之间的关系式是S=πR2,其中自变量是________ .23、如图,小正方形边长为1,连接小正方形的三个顶点,可得△ABC,则AC 边上的高长度为________.24、如图,反比例函数y= 的图象经过矩形OABC的边AB的中点D,则矩形OABC的面积为________.25、余干二中秋季运动会上,小捷掷出的铅球在场地上砸出一个小坑(如图),其中AB为8cm,小坑的最大深度为2cm,则该铅球的直径为________cm.三、解答题(共5题,共计25分)26、解方程组:27、已知:BE⊥CD,BE=DE,BC=DA,求证:△BEC≌△DAE28、如图,在△ABC中,∠C=90°,∠A=36°,DE是线段AB的垂直平分线,交AB于点D,交AC于点E.求∠EBC的度数.29、利用一面墙(墙的长度不限),另三边用58m长的篱笆围成一个面积为200m2的矩形场地,求矩形的长和宽.30、如图3-5-24,⊙O直径AB为5 cm,弦AC为3 cm,∠ACB的平分线交⊙O于D,求BC,AD,BD的长.参考答案一、单选题(共15题,共计45分)1、C2、C3、B4、A5、D6、B7、D8、B9、D10、C11、D12、A13、A15、B二、填空题(共10题,共计30分)16、17、18、19、20、21、22、23、24、25、三、解答题(共5题,共计25分)27、28、29、30、。
沪教版八年级上册数学期末测试卷(附解析)

沪教版八年级上册数学期末测试卷一、单选题(共15题,共计45分)1、下列三条长度的线段不能组成直角三角形的是( )A. B.12,5,13 C.7,24,25 D.9,40,412、化简的值为()A. B. C. D.3、若关于x的一元二次方程有两个不相等的实数根,则k的取值范围()A. B. C. 且 D.4、下列计算正确的是()A. B. C. D.5、下列各组数据分别是三角形的三边长,其中不能构成直角三角形的是()A. B. C. D.6、在同一平面直角坐标系内,如果直线与双曲线没有交点,那么和的关系一定是().A. ,B. ,C. ,同号D. ,异号7、若是方程的根,则的值为()A.2022B.2021C.2019D.20188、方程x2﹣|2x﹣1|﹣4=0的实根的个数是()A.4B.2C.3D.09、如图,已知等腰三角形中,,,分别以、两点为圆心,以大于的长为半径画圆弧,两弧分别交于点、,直线与相交于点,则的度数是()A.50°B.60°C.75°D.45°10、△ABC中∠A、∠B、∠C的对边分别是a、b、c,下列命题中的假命题是()A.如果∠C﹣∠B=∠A,则△ABC是直角三角形B.如果c 2=b 2﹣a 2,则△ABC是直角三角形,且∠C=90°C.如果(c+a)(c﹣a)=b 2,则△ABC是直角三角形 D.如果∠A:∠B:∠C=5:2:3,则△ABC是直角三角形11、下列计算正确的是()A. =3B. =-3C. =±3D.12、如图,在△ABC中,点D为△ABC的内心,∠A=60°,BD:CD=2:1,BD=4,则△DBC的面积为( )A.3B.2C.2D.313、已知AC平分∠DAB,CE⊥AB于E,AB=AD+2BE,则下列结论:①2AE=AB+AD;②CD=CB;③∠DAB+∠DCB=180°;④S△ACE=S△BCE+S△ADC.其中正确结论的个数是( )A.4个B.3个C.2个D.1个14、下列各组二次根式中,x的取值范围相同的是()A. 与B.()2与C. 与D. 与15、下列方程是关于x的一元二次方程的是()A.ax 2+bx+c=0B. =2C.x 2+2x=x 2﹣1D.3(x+1)2=2(x+1)二、填空题(共10题,共计30分)16、已知实数a在数轴上的对应点,如图所示,则化简所得结果为________17、如图,四边形ABCD为菱形,点A在y轴正半轴上,AB∥x轴,点B,C在反比例函数上,点D在反比例函数上,那么点D的坐标为________.18、已知x=,则x2+x+1= ________19、如图,某公园有一块菱形草地ABCD,它的边及对角线AC是小路,若AC的长为16m,边AB的长为10m,妈妈站在AC的中点O处,亮亮沿着小路C→D→A→B→C跑步,在跑步过程中,亮亮与妈妈之间的最短距离为________m.20、如果关于x的一元二次方程x2-2x+k=0只有一个解,那么k=________21、如图,在等腰三角形ABC中,AB=AC,DE垂直平分AB.已知∠ADE=40°,则∠DBC=________度.22、关于的一元二次方程有实数根,则实数的取值范围是________.23、在△ABC中,BC⊥AC,DE⊥AC,D是AB的中点,若∠A=30°,AB=8,则BC=________,DE=________.24、如图,点P是反比例函数图象上任意一点, PA⊥x轴于A,连接PO,为________.则S△PAO25、如图,在△ABC中,∠BAC=90°.AD⊥BC于点D,若∠C=30°,BD=1,则线段CD的长为________.三、解答题(共5题,共计25分)26、计算:27、已知:如图所示,反比例函数的图象与正比例函数的图象交于A、B,作AC⊥ 轴于C,连BC,则△ABC的面积为3,求反比例函数的解析式.28、如图是一块地的平面图,AD=4m,CD=3m,AB=13m,BC=12m,∠ADC=90°,求这块地的面积.29、如图,在中,,,,.求的长.30、如图,A,E,F,C在一条直线上,AE=CF,过E,F分别作DE⊥AC,BF⊥AC,若AB=CD,试证明BD平分EF.参考答案一、单选题(共15题,共计45分)1、A2、A3、C4、A5、D6、D7、B8、B10、B11、A12、C13、A14、C15、D二、填空题(共10题,共计30分)16、17、18、19、20、21、22、23、24、25、三、解答题(共5题,共计25分)27、29、。
沪教版八年级上册数学期末测试卷完整版

沪教版八年级上册数学期末测试卷一、单选题(共15题,共计45分)1、双曲线y=的图象经过第二、四象限,则k的取值范围是( )A.k>B.k<C.k=D.不存在2、一个等腰三角形的两条边长分别是方程x2-3x+2=0的两根,则该等腰三角形的周长是( )A.5或4B.4C.5D.33、下列计算正确的是( )A. B. C. D.4、如图,⊙O是△ABC的外接圆,AD是⊙O的直径,连接CD,若⊙O的半径,AC=2,则cosB的值是( )A. B. C. D.5、欧几里得在《几何原本》中,记载了用图解法解方程的方法,类似地可以用折纸的方法求方程的一个正根。
下面是甲、乙两位同学的做法:甲:如图1,裁一张边长为1的正方形的纸片,先折出的中点,再折出线段,然后通过折叠使落在线段上,折出点的新位置,因而,类似地,在上折出点使。
此时,的长度可以用来表示方程的一个正根;乙:如图2,裁一张边长为1的正方形的纸片,先折出的中点,再折出线段N,然后通过沿线段折叠使落在线段上,折出点的新位置,因而。
此时,的长度可以用来表示方程的一个正根;甲、乙两人的做法和结果()。
A.甲对,乙错B.乙对,甲错C.甲乙都对D.甲乙都错6、如图,△ABC中边AB的垂直平分线分别交BC,AB于点D,E,AE=3cm,△ADC的周长为9cm,则△ABC的周长是( )A.10 cmB.12 cmC.15 cmD.17 cm7、某景点有一座圆形的建筑,如图,小江从点A沿AO匀速直达建筑中心点O 处,停留拍照后,从点O沿OB以同样的速度匀速走到点B,紧接着沿回到点A,下面可以近似地刻画小江与中心点O的距离S随时间t变化的图象是().A. B. C.D.8、有一块三角形的草坪,现要在草坪上建一座凉亭供大家休息,要使凉亭到草坪三条边的距离相等,则凉亭的位置应选在()A.△ABC三条角平分线的交点B.△ABC三边的垂直平分线的交点 C.△ABC三条中线的交点 D.△ABC三条高所在直线的交点9、若y与x成反比例,x与z成反比例,则y是z的().A.正比例函数B.反比例函数C.一次函数D.不能确定10、如图,在边长为1的小正方形网格中,点都在这些小正方形的顶点上,则的余弦值是()A. B. C. D.11、菱形的周长等于其高的8倍,则这个菱形的较大内角是()A.30°B.120°C.150°D.135°12、设,则()A. B. C. D.13、如图,下面是利用尺规作∠AOB的角平分线OC的作法,在用尺规作角平分线过程中,用到的三角形全等的判定方法是()作法:①以O为圆心,适当长为半径画弧,分别交OA,OB于点D,E;②分别以D,E为圆心,大于DE的长为半径画弧,两弧在∠AOB内交于一点C;③画射线OC,射线OC就是∠AOB的角平分线.A.ASAB.SASC.SSSD.AAS14、下列式子中,最简二次根式是()A. B. C. D.15、如图,边长分别为1和2的两个等边三角形,开始它们在左边重合,大三角形固定不动,然后把小三角形自左向右平移直至移出大三角形外停止.设小三角形移动的距离为x,两个三角形重叠面积为y,则y关于x的函数图象是()A. B. C. D.二、填空题(共10题,共计30分)16、已知函数y= 与y=﹣x+5的图象的交点坐标为(a,b),则的值为________.17、如图,已知等边的边长是6,点D在AC上,且延长BC到E,使,连接点F,G分别是AB,DE的中点,连接FG,则FG的长为________.18、若反比例函数的图象经过点A(﹣1,y1),B(﹣3,y2),则y1与y2的大小关系是________(用“>”、“<”或“=”填空).19、如图,在四边形ABCD中,∠A=90°,AD=4,连接BD,BD⊥CD,∠ADB=∠C.若P是BC边上一动点,则DP长的最小值为________.20、已知2是关于x的方程:x2﹣2mx+3m=0的一个根,而这个方程的两个根恰好是等腰△ABC的两条边长,则△ABC的周长是________.21、用代数式表示面积为S的圆的周长为________.22、如图,点A、B分别在反比例函数y= (k1>0) 和 y= (k2<0)的图象上,连接AB交y轴于点P,且点A与点B关于P成中心对称.若△AOB的面积为4,则k1-k2=________.23、如图,已知一次函数y=﹣2x+8的图象与坐标轴交于A,B两点,并与反比例函数y=(x>0)的图象相切于点C.则切点C的坐标是________.24、二次根式、中与是同类二次根式的是________.25、直接写出解:________;若,则________。
(考试直接用)沪教版八年级上册数学期末测试卷及含答案(综合考察)

沪教版八年级上册数学期末测试卷及含答案一、单选题(共15题,共计45分)1、如图,正方形ABCD的边长为3cm,动点M从点B出发以3cm/s的速度沿着边BC—CD—DA运动,到达点A停止运动,另一动点N同时从点B出发,以1cm/s的速度沿着边BA向点A运动,到达点A停止运动,设点M运动时间为x(s),△AMN的面积为y(cm2),则y关于x的函数图象是()A. B. C. D.2、如图,在平面直角坐标系中,长方形ABCD的顶点B在坐标原点,顶点A、C 分别在y轴、x轴的负半轴上,其中,,将矩形ABCD绕点D逆时针旋转得到矩形,点恰好落在x轴上,线段与CD交于点E,那么点E的坐标为A. B. C. D.3、边长为1的正方形OA1B1C1的顶点A1在x轴的正半轴上,如图将正方形OA1B1C1绕顶点O顺时针旋转75°得正方形OABC,使点B恰好落在函数y=ax2(a<0)的图象上,则a的值为()A. B. C.﹣2 D.4、如图在Rt△ABC中,∠ACB=90°,∠BAC=30°,AB=2,D是AB边上的一个动点(不与点A、B重合),过点D作CD的垂线交射线CA于点E.设AD=x,CE=y,则下列图象中,能表示y与x的函数关系图象大致是()A. B. C.D.5、下列方程中是一元二次方程的有()①②③④A.①②B.①③C.④D.①③④6、给出的六个关系式:①x(y+1)②③④⑤⑥;其中y是x的反比例函数是()A.①②③④⑥B.③⑤⑥C.①②④D.④⑥7、下列根式中,属于最简二次根式的是()A. B. C. D.8、函数y=中,自变量x的取值范围是()A.x≥2B.x≠2C.x>2D.x≤29、“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b.若ab=8,大正方形的面积为25,则小正方形的边长为()A.4B.3C.2D.1.510、设,a在两个相邻整数之间,则这两个整数是()A.1和2B.2和3C.3和4D.4和511、如图所示,中,,顶点分别在反比例函数与的图象器上,则的值为()A. B. C. D.12、已知一个菱形的边长是5cm,两条对角线长的比是4:3,则这个菱形的面积是( )A.12cm 2B.24cm 2C.48cm 2D.96cm 213、函数y= + 的自变量x的取值范围是()A.x≥1B.x≥1且x≠3C.x≠3D.1≤x≤314、计算:等于()A. B. C. D.15、的三边分别为a,b,c,下列条件:①;②;③.其中能判断是直角三角形的条件个数有A.0个B.1个C.2个D.3个二、填空题(共10题,共计30分)16、如图,∠C=∠ABD=90°,AC=4,BC=3,BD=12,则AD=________ .17、等式=﹣a 成立的条件是________.18、如图正方形ABCD中,点E在边DC上,DE=4,EC=2,把线段AE绕点A旋转,使点E落在直线BC上的点F处,则F、C两点的距离为________.19、如图,已知线段BC,分别以B,C为圆心,大于BC的长为半径作弧,两弧相交于E,F两点,连接CE,经过点E作射线BA,若∠CEA=60°,CE=2,则△BCE的面积为________.20、如图,点P是反比例函数图像上一点,PA⊥y轴于点A,=2,则k=________.21、已知xy=3,那么的值为________ .22、如图,点A为反比例函数y= 图象上一点,点B为反比例函数y= 图象上一点,且AB∥x轴,已知∠AOB=90°,AB交y轴于点C,若=2,则k=________。
沪教版八年级上册数学期末测试卷(名师推荐)

沪教版八年级上册数学期末测试卷一、单选题(共15题,共计45分)1、已知点(-1,y1),(2,y2),(3,y3)在反比例函数的图象上.下列结论中正确的是()A.y1>y2>y3B.y1>y3>y2C.y3>y1>y2D.y2>y3>y12、下列计算正确的是()A.8 ×2 =16B.5 ×5 =5C.4 ×2 =6D.3 ×2 =63、下列各式中计算正确的是()A. B. C. D.4、关于的一元二次方程(x-3)(x-2)=p2的根的情况是()A.方程没有实数根B.方程有两个相等的实数根C.方程有两个不相等的实数根D.无法判断5、使代数式有意义的x的取值范围是()A.x≥0B.x≠C.x≥0且x≠D.一切实数6、如图所示,将两个大小、形状完全相同的△ABC和△A′B′C′拼在一起,其中点A′与点A重合,点C′落在边 AB上,连结B′C.若∠ACB =∠AC′B′ = 90°,AC = BC = 3,则B′C的长为()A.3B.6C.3D.7、如图所示,在等边三角形ABC中,AD⊥BC,E为AD上一点,∠CED=50°,则∠ABE等于()A.10°B.15°C.20°D.25°8、下列计算正确的是()A. + =B. ﹣=C. × =6D.÷ =49、兰州市某广场准备修建一个面积为200平方米的矩形草坪,它的长比宽多10米。
设草坪的宽为x米,则可列方程为()A.x(x-10)=200B.2x+2(x-10)=200 C.2x+2(x+10)=200 D.x(x+10)=200=60,AD⊥BC于点D,EF垂直10、如图,在△ABC中,AB=AC,BC=10,S△ABC平分AB,交AB于点E,AC于点F,在EF上确定一点P,使PB+PD最小,则这个最小值为()A.10B.11C.12D.1311、直角三角形两条直角边的长分别为6和8,则斜边长为()A.8B.9C.10D.1212、在下列各组数据中,不能作为直角三角形的三边边长的是()A.3,4,6B.7,24,25C.6,8,10D.9,12,1513、等腰△ABC的三边分别为a、b、c,其中a=5,若关于x的方程x2+(b+2)x+6-b=0有两个相等的实数根,则△ABC的周长是()A.9B.12C.9或12D.不能确定14、已知α、β是方程x2-2x-4=0的两个实数根,则α3+8β+6的值为()A.-1B.2C.22D.3015、关于反比例函数,下列说法中错误的是()A.当时,随的增大而增大B.图象位于第二、四象限C.点在函数图象上D.当时,二、填空题(共10题,共计30分)16、如图,在∠MON中,以点O为圆心,任意长为半径作弧,交射线OM于点A,交射线ON于点B,再分别以A、B为圆心,OA的长为半径作弧,两弧在∠MON的内部交于点C,作射线OC,若OA=5,AB=6,则点B到AC的距离为________.17、函数y= 中,自变量x的取值范围是________.18、如图,△ABC中,AB=AC=5,BC=6,AE平分∠BAC交BC于点E,点D为AB 的中点,连结DE,则△BDE的周长是________.19、如图,半径为6cm的⊙O中,C、D为直径AB的三等分点,点E、F分别在AB两侧的半圆上,∠BCE=∠BDF=60°,连接AE、BF,则图中两个阴影部分的面积为________ cm2.20、若满足且.则________.21、如图,在矩形ABCD中,AB=4,BC=8,E为CD边的中点,若P,Q为BC边上的两个动点,且PQ=2,四边形APQE的周长最小值为________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
八年级第一学期期末数学试卷1
一、选择题
1、下列运算中,正确的是( )
(A )x x x 32=+;(B )12223=-;(C )2+5=25;(D )x b a x b x a )(-=- 2、在下列方程中,整理后是一元二次方程的是( )
(A )2
3(2)(31)x x x =-+ (B ) (2)(2)40x x -++=
(C )2
(1)0x x -= (D ) 2131x x ++=
3、已知点(1,-1)在kx y =的图像上,则函数x
k
y =
的图像经过( ). (A )第一、二象限; (B )第二、三象限; (C )第一、三象限; (D )第二、四象限. 4、下列命题中,是假命题的是( ).
(A )对顶角相等 (B )互为补角的两个角都是锐角
(C )如果两条直线都和第三条直线平行,那么这两条直线也互相平行 (D )两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行. 5、已知:如图,△ABC 中,090=∠C ,BD 平分ABC ∠,AB BC 2
1
=,BD =2,则点D 到AB 的距离为( ).
(A )1 (B )2 (C )3 (D )3
6、如图,在Rt△ABC ,∠ACB =90°,CD 、CE 是斜边上的高和中线,AC =CE =10cm ,则BD 长为( )
(A )25cm ; (B ) 5cm ; (C )15cm ; (D )10cm.
二、填空题
7
0)x >化成最简二次根式是 ; 8、关于x 的方程2
460x x m ++=有两个相等的实数根,则m 的值为 ;
9、已知正比例函数(23)y a x =-的图像经过第一、三象限,则a 的取值范围是____________;
10、如果函数x
x f 1)(=
,那么)2(f = ;
11、命题:“同角的余角相等”的逆命题是 ; 12、到点A 的距离等于6cm 的点的轨迹是 ; 13、已知直角坐标平面内两点 A (3,-1)和B (-1,2),则A 、B 两点间的距离等于 ; 14、如图,将△ABC 绕点A 按逆时针方向旋转得到△ADE ,DE 交AC 于F ,交BC 于G ,
若∠C =35°,∠EFC =60°,则这次旋转了 °; 15、三角形三边的垂直平分线的交点到 的距离相等; 16、在Rt△ABC 中,∠C =90°,AB =18,BC =9,那么∠B = °;
17、如图,90C D ∠=∠=︒,请你再添加一个条件: 使ABC BAD ∆≅∆; 18、已知直角三角形的两边长分别为5,12,那么第三边的长为 . 三、简答题 19、计算:︒--++-)23(3
19
1
3227. 20、解方程:()()6112
=+-+x x
5题图
G
F
E
D C
B
A
D
C
B
A
第14题图
第17题图
第6题图
21、已知一个正比例函数的图像与反比例函数9
y x
=
的图像都经过点A (3,-m )。
求这个正比例函数的解析式.
22、已知:如图,在△ABC 中,120C ∠=,边AC 的垂直平分线DE 与AC 、AB 分别交于点D 和点E . (1)作出边AC 的垂直平分线DE ; (2)当AE BC =时,求A ∠的度数.
23、某手机公司2010年的各项经营收入中,经营手机配件的收入为300万元,占全年经营总收入的20%. 该
公司预计2012年经营总收入可达到2160万元,计划从2010年到2012年,每年经营总收入的年增长率相同,问每年经营总收入的年增长率是多少?
24、已知:如图,在△ABC 中,点D 是BC 边的中点,DE AB ⊥,DF AC ⊥,垂足分别是点E 、F ,且
BE CF =.
求证:AD 平分BAC ∠.
B
C
A
第22题图
F E
D
C
B A
第24题图
25、如图,在矩形ABCD 中,AB = 16cm ,AD = 8cm ,把△BCD 沿对角线BD 翻折,使点C 落在点D 处,DE 交AB 于点F .
(1)求证:BF = DF ; (2)求△BDF 的面积.
26、如图,直角坐标系中,点A 的坐标为(1,0),以线段OA 为边在第四象限内作等边△AOB ,点C 为x 正半
轴上一动点(OC >1),连结BC ,以线段BC 为边在第四象限内作等边△CBD ,直线DA 交y 轴于点E . (1)△OBC 与△ABD 全等吗?判断并证明你的结论;
(2)随着点C 位置的变化,点E 的位置是否会发生变化? 若没有变化,求出点E 的坐标;若有变化,请说明理由.
x
y
E
O
B
C
D
A。
