第八章 有限差分法(2008,11改)
有限差分法

• 1、差分 • 1.1、定义:某个物理量的有限增量。如: ΔT。 • 1.2、引入差分的目的:以有限差分代替无 限微分,以差分方程代替微分方程,以数值 计算代替数学推导的过程,从而将连续函数 离散化,以有限的、离散的数值代替连续的 函数分布。
T(x,y)
T0,4 T0,3 T0,2
T1,4 T2,4 T3,4
y Ti,j
T0,4
T0,3 T0,2 T0,1 T0,0
T1,4 T2,4 T3,4
T4,4
T4,3 T4,2 T4,1
T1,0 T2,0 T3,0 T4,0
x
• • • •
3.2、向前差分:(二维的情况) 3.2.1、一阶差分: ΔTf,i,j=Ti+1,j-Ti,j Δ2Tf,i,j=Ti+2,j-2Ti+1,j+Ti,j
y
一阶差分:x方向
x Ti-2,j Ti-1,j Ti,j Ti+1,j Ti+2,j
y
二阶差分:x方向
x Ti-2,j Ti-1,j Ti,j Ti+1,j Ti+2,j
x
2
y
2
0
• 如方程和边界条件如下,请按等步长0.25, 求解各节点的温度。方程及边界条件如下:
2 2T T 0 , 0 x 1, 0 y 1 2 2 x y T ( 0 , y ) T ( x ,0 ) 0 T ( x ,1) 100 x , x 0 T (1, y ) 100 y , y 0
2
T
2
y
2
T i , j 1 2 T i , j T i , j 1 0 . 25
有限差分法的基本原理

f (x) ≈
2h
中心二阶差商
′′
f (x+h)−2f (x)+f (x−h)
f (x) ≈
h2
O(h) O(h)
2
O(h )
2
O(h )
其中,h表示网格间距,O(hn)表示截断误差与hn成正比。可以看出,中心差商比前向或后向差商具有更高的精度。
误差分析
有限差分法求得的数值解与真实解之间存在误差,这些误差主要来源于以下几个方面:
常用差分格式
有限差分法中最重要的步骤是构造合适的差分格式来近似微分项。根据泰勒展开式,可以得到以下常用的一阶和二阶差分格式:
差分格式
表达式
截断误差
前向一阶差商
′
f (x+h)−f (x)
f (x) ≈
h
后向一阶差商
′
f (x)−f (x−h)
f (x) ≈
h
中心一阶差商
′
f (x+h)−f (x−h)
截断误差:由于使用有限项级数来近似无穷级数而产生的误差; 舍入误差:由于计算机对小数进行四舍五入而产生的误差;
离散误差:由于对连续区域进行离散化而产生的误差; 稳定性误差:由于数值格式的稳定性不足而导致误差的累积或放大。
为了减小误差,一般可以采取以下措施:
选择更高阶或更精确的差分格式; 减小网格间距或时间步长; 选择合适的初始条件和边界条件; 选择稳定且收敛的数值格式。
+
。 2
h)
为了验证上述方法的正确性,我们取M = 10, N = 100,则原问题可以写为如下形式:
则该问题对应的递推关系式为:
⎧ut (x, t) − uxx (x, t) = 0,
数值方法课件_有限差分法

土
工
数
值
计
算
方
法
法分差限有 讲二第
2.5 基本原理
1)问题的提出 1)问题的提出 2)稳定性和收敛性 2)稳定性和收敛性 3)差分法的求解步骤 3)差分法的求解步骤
土
工
数
值
计
算
方
法
法分差限有 讲二第
2.5 基本原理
3)差分法的求解步骤 3)差分法的求解步骤
①对求解区域进 ①对求解区域进 行网格划分; 行网格划分; ②选择逼近微分 ②选择逼近微分 方程定解问题 方程定解问题 的差分格式; 的差分格式;
¶ 2V c ¶V 2 c -1 ¶V = ( ) + V ¶T ¶ 2 z V ¶z v
1.7
土
工
数
值
计
算
方
法
2.6 例子
法分差限有 讲二第
软粘土地基非线性一维固结分析 软粘土地基非线性一维固结分析
定解条件变为: 定解条件变为: V = 1 ; (1) T v = 0 : (2) Z = 0 : V = b ; (3) Z = 1 :
算
方
法
法分差限有 讲二第
2.1 优点与局限性
不 适 应
规则边界的问题 规则边界的问题
应 适
简便、易编程 简便、易编程 不规则边界的问题 不规则边界的问题
土
工
数
值
计
算
方
法
法分差限有 讲二第
2.2 基本思路
1
3
2
将求解区域 将求解区域 划分成网格 划分成网格
差分方程解 差分方程解 作为微分方 作为微分方 程近似解。 程近似解。
有限差分法基本原理

有限差分法的应用领域
流体力学
用于模拟流体在固定或变形网格 上的流动,如计算流体动力学 (CFD)中的数值模拟。
热传导
用于求解热传导方程,模拟热 量在物体中的传播和分布。
波动传播
用于求解波动方程,如地震波 、声波和电磁波的传播。
有限差分法基本原理
CONTENTS 目录
• 引言 • 有限差分法的基本原理 • 有限差分法的实现 • 有限差分法的优缺点 • 有限差分法的改进方向
CHAPTER 01
引言
有限差分法的定义
有限差分法是一种数值计算方法,通 过将连续的物理量离散化为有限个离 散点上的数值,并建立代数方程来近 似描述物理量随时间和空间的变化规 律。
缺点
精度问题
由于有限差分法采用的是离散化的方法, 因此其精度受到网格大小的影响,网格越
小精度越高,但同时也会增加计算量。
数值耗散误差
在模拟非线性问题时,有限差分法可能会 产生数值耗散误差,导致能量的损失或者
非物理振荡。
数值色散误差
在模拟波动性问题时,有限差分法可能会 产生数值色散误差,导致波的传播速度发 生变化。
常用的离散化方法包括均匀网格、非均匀网格、有限元法等,
应根据实际问题选择合适的离散化方法。
差分近似
Hale Waihona Puke 01差分近似公式根据微分方程的性质,构造差分 近似公式,将微分方程转化为差 分方程。
精度分析
02
03
稳定性分析
分析差分近似公式的精度,确定 其与微分方程的误差大小和分布。
分析差分近似公式的数值稳定性, 确保计算过程中误差不会累积放 大。
有限差分法
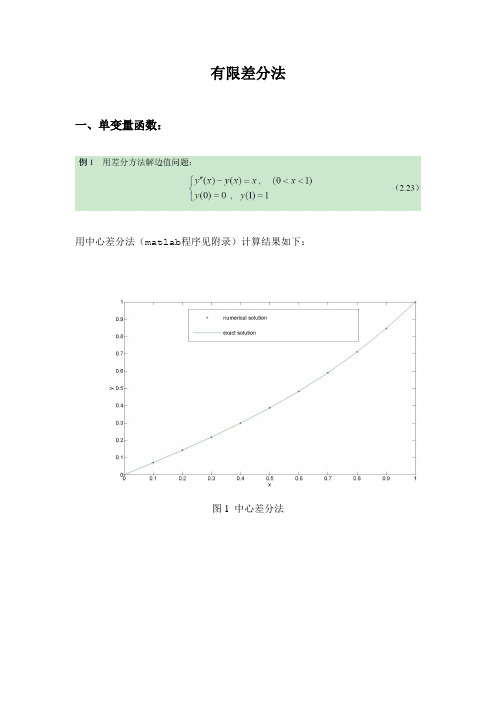
有限差分法一、单变量函数:用中心差分法(matlab程序见附录)计算结果如下:图1 中心差分法表1 数据对比二、一维热传导:在此取φ(x)=0,g1(t)= g2(t)=100-100*exp(-t)问题描述:已知厚度为l的无限大平板,初温0度,初始瞬间将其放于温度为100度的流体中,流体与板面间的表面传热系数为一常数。
试确定在非稳态过程中板内的温度分布。
(1)显式差分法:图3 显式差分法(2)隐式差分法:图4 隐式差分法小结:显式格式仅当时格式是稳定的。
(其中称为网格比)隐式格式从k层求k+1层时,需要求解一个阶方程组。
而且隐式格式的稳定性对网格比没有要求,即为绝对稳定的。
三、Possion方程:取f=1,R=1图5差分法图6 误差小结:观察误差曲面,其绝对误差数量级为附Matlab程序:第1题:%===========================Boundary Value Problem 1clear;clc;A=[-2.01 1 0 0 0 0 0 0 0;1 -2.01 1 0 0 0 0 0 0;0 1 -2.01 1 0 0 0 0 0;0 0 1 -2.01 1 0 0 0 0;0 0 0 1 -2.01 1 0 0 0;0 0 0 0 1 -2.01 1 0 0;0 0 0 0 0 1 -2.01 1 0;0 0 0 0 0 0 1 -2.01 1;0 0 0 0 0 0 0 1 -2.01;];c1=[0.1;0.2;0.3;0.4;0.5;0.6;0.7;0.8;0.9];C=0.01*c1-1*[0;0;0;0;0;0;0;0;1];y=A\C;x=0:0.1:1;yn=[0;y;1];ye=2*(exp(x)-exp(-x))/(exp(1)-exp(-1))-x;figure(1);plot(x,yn,'*',x,ye);legend('numerical solution','exact solution')xlabel('x','fontsize',20);ylabel('y','fontsize',20);set(gca,'fontsize',18);figure(2);err=abs(ye'-yn);plot(x,err);legend('error')xlabel('x','fontsize',20);ylabel('y','fontsize',20);set(gca,'fontsize',18);第2题:%========================Boundary Value Problem 1_Explicit %显式clear;clcl=20;%板厚h=1;%步长J=l/h;T=50;%时间tao=2.5;%步长N=T/tao;%下面组合A矩阵a=0.2;lamda=tao/(h^2);zhu=1-2*a*lamda;ce=a*lamda;a00=ones(1,J-1);a0=diag(a00);A0=zhu*a0;a01=ones(1,J-2);a1=diag(a01,1);A1=ce*a1;a2=diag(a01,-1);A2=ce*a2;A=A0+A1+A2;u(:,1)=0; %板的初始温度for i=2:N+1u(1,i)=100-100*exp(-(i-1)*tao); %边界条件u(J+1,i)=100-100*exp(-(i-1)*tao); %边界条件end% g01=u(:,1);% g02=u(:,J);for k=1:N% g01=ce*g1(1,k);% g02=ce*g2(1,k);oo=zeros(J-3,1);g(:,k)=[ce*u(1,k);oo;ce*u(J+1,k)];u(2:end-1,k+1)=A*u(2:end-1,k)+g(:,k);endt=0:h:l;x=0:tao:T;mesh(x,t,u)xlabel('t','fontsize',20);ylabel('x','fontsize',20);zlabel('T','fontsize',20);set(gca,'fontsize',18);%========================Boundary Value Problem 1_2Implicit %隐式clear;clcl=20;%板厚h=1;%步长J=l/h;T=50;%时间tao=2.5;%步长N=T/tao;%下面组合A矩阵a=0.2;lamda=tao/(h^2);zhu=1+2*a*lamda;ce=-a*lamda;a00=ones(1,J-1);a0=diag(a00);A0=zhu*a0;a01=ones(1,J-2);a1=diag(a01,1);A1=ce*a1;a2=diag(a01,-1);A2=ce*a2;A=A0+A1+A2;u(:,1)=0; %板的初始温度for i=2:N+1u(1,i)=100-100*exp(-(i-1)*tao); %边界条件u(J+1,i)=100-100*exp(-(i-1)*tao); %边界条件end% g01=u(:,1);% g02=u(:,J);for k=1:N% g01=ce*g1(1,k);% g02=ce*g2(1,k);oo=zeros(J-3,1);g(:,k)=[ce*u(1,k);oo;ce*u(J+1,k)];u(2:end-1,k+1)=inv(A)*u(2:end-1,k)-inv(A)*g(:,k);endt=0:h:l;x=0:tao:T;mesh(x,t,u)xlabel('t','fontsize',20);ylabel('x','fontsize',20);zlabel('T','fontsize',20);set(gca,'fontsize',18);第3题:%=============================used by centered difference clear;function pdemodel[pde_fig,ax]=pdeinit;pdetool('appl_cb',1);set(ax,'DataAspectRatio',[1 1 1]);set(ax,'PlotBoxAspectRatio',[1.5 1 1]);set(ax,'XLim',[-1.5 1.5]);set(ax,'YLim',[-1 1]);set(ax,'XTickMode','auto');set(ax,'YTickMode','auto');% Geometry description:pdecirc(0,0,1,'C1');set(findobj(get(pde_fig,'Children'),'Tag','PDEEval'),'String','C1')% Boundary conditions:pdetool('changemode',0)pdesetbd(4,...'dir',...1,...'1',...'0')pdesetbd(3,...'dir',...1,...'1',...'0')pdesetbd(2,...'dir',...1,...'1',...'0')pdesetbd(1,...'dir',...1,...'1',...'0')% Mesh generation:setappdata(pde_fig,'Hgrad',1.3);setappdata(pde_fig,'refinemethod','regular');pdetool('initmesh')pdetool('refine')% PDE coefficients:pdeseteq(1,...'1.0',...'0.0',...'1',...'1.0',...'0:10',...'0.0',...'0.0',...'[0 100]')setappdata(pde_fig,'currparam',...['1.0';...'0.0';...'1 ';...'1.0'])% Solve parameters:setappdata(pde_fig,'solveparam',...str2mat('0','1524','10','pdeadworst',...'0.5','longest','0','1E-4','','fixed','Inf'))% Plotflags and user data strings:setappdata(pde_fig,'plotflags',[1 1 1 1 1 1 1 1 0 0 0 1 0 0 1 0 0 1]); setappdata(pde_fig,'colstring','');setappdata(pde_fig,'arrowstring','');setappdata(pde_fig,'deformstring','');setappdata(pde_fig,'heightstring','');% Solve PDE:pdetool('solve')。
有限差分法(1)FLAC2D精品PPT课件

i=10, j=21
i=21, j=21
i=1, j=21
I
II
i=1, j=1
i=10
i=21, j=1
3.5 特殊形状的网格 (1)圆形 gen circle xc,yc rad
rad xc,yc
3.5 特殊形状的网格 (2)弧线 gen arc xc,yc xb,yb theta
xc,yc
1. 整个迭代过程需要遵循非线性定律。
2. 解算时间增加 N2 甚至 N3。 2. 对同样问题,计算时间增加N3/2 。
3. 模拟物理不稳定性困难。 3. 物理不稳定不会引起数值不稳定。
4. 因为无需存储矩阵,用少量内存 可以模拟大型问题。
4. 需要大内存,或大容量硬盘存储。
5. 大应变、大位移和转动模拟无需 额外机时。
下式用于计算应变增量, eij :
ui 1
x j 2 A S
ui(a) ui(b) n jS
eij
1 2
ui x j
u j xi
t
一旦计算出全部应力,可以从作用每个三角形边界上 产生的牵引力计算得到结点力。例如:
Fi
1 2
ij
(n
j
(1)
S
(1)
n j(2)S (2) )
然后,用“传统”的中间差分 公式获得新的速度和位移:
bar cm/s2
Bar/cm
Imperial ft
slugs/ft3 Ibf
Ibf/ft2 ft/sec2
Ibf/ft3
In snails/in3
Ibf psi in/sec2
Ib/in3
(2)参数换算 K E
3(1 2)
(bulk mod ulus)
有限差分法

对所学有限差分法的总结和其一些应用07410301班邓齐波20032471一:有限差分方法的总结有限差分方法(FDM)是计算机数值模拟最早采用的方法,至今仍被广泛运用。
该方法将求解域划分为差分网格,用有限个网格节点代替连续的求解域。
有限差分法以Taylor级数展开等方法,把控制方程中的导数用网各界点上的函数值的差商代替进行离散,从而建立以网格节点上的值为未知数的代数方程组。
该方法是一种直接将微分问题变为代数问题的近似数值解法,数学概念直观,表达简单,是发展较早且比较成熟的数值方法。
分类对于有限差分格式,从格式的精度来划分,有一阶格式、二阶格式和高阶格式。
从差分的空间形式来考虑,可分为中心格式和逆风格式。
考虑时间因子的影响,差分格式还可以分为显格式、隐格式、显隐交替格式等。
目前常见的差分格式,主要是上述几种形式的组合,不同的组合构成不同的差分格式。
差分方法主要适用于有结构网格,网格的步长一般根据实际地形的情况和柯朗稳定条件来决定。
构造差分的方法构造差分的方法有多种形式,目前主要采用的是泰勒级数展开方法。
其基本的差分表达式主要有三种形式:一阶向前差分、一阶向后差分、一阶中心差分和二阶中心差分等,其中前两种格式为一阶计算精度,后两种格式为二阶计算精度。
通过对时间和空间这几种不同差分格式的组合,可以组合成不同的差分计算格式。
在所学课程‘力学计算’中《偏微分方程数值解》,我们主要学习了一维抛物型方程、二维和三维抛物型方程、一维双曲型方程以及二维线形二阶椭圆型方程。
流体力学有限差分法与结构力学有限元法区别对于有限差分格式,从格式的精度来划分,有一阶格式、二阶格式和高阶格式。
从差分的空间形式来考虑,可分为中心格式和逆风格式。
考虑时间因子的影响,差分格式还可以分为显格式、隐格式、显隐交替格式等。
目前常见的差分格式,主要是上述几种形式的组合,不同的组合构成不同的差分格式。
差分方法主要适用于有结构网格,网格的步长一般根据实际地形的情况和柯朗稳定条件来决定。
2有限差分法及热传导数值计算PPT演示课件

t1
1 a11
(b1
a12t2
a13t3 )
t2
1 a 22
(b2
a 21t1 a 23t3 )
1 t3 a 33 (b3 a 31t1 a 32t2 )
•24
(2)假设一组解(迭代初场),记为: t1(0)、t2(0)并、t代3(0) 入迭代方程求得第一 次解
每次计算t1(1)均、t用2(1)、最t3(1新) 值代入。
(1) 平直边界上的节点
如图所示 边界节点 (m,n) 只能代表半个元体,若边界上有向 该元体传递的热流密度为q ,据能量守恒定律对该元体有:
tm1,n tm,n ytm,n1tm,n x
x
y 2
x
2
tm,n1 tm,n y
Φm,n
2xyyqw
0
Байду номын сангаас
xy tm ,n1 4 2 tm 1 ,n tm ,n 1 tm ,n 1 x2 Φ m ,n 2 x q w
非稳态项 的离散有三种不同的格式。如果将函数在节 点(n,i+1)对点(n,i)作泰勒展开,可有
•30
•31
由式(b)可得在点(n,i)处一阶导数的一种差分表示式 , 的向前差分:
类似地,将t在点(n,i-1)对点(n,i)作泰勒展开,可得 的向后差分的表达式:
如果将t在点(n,i+1)及(n,i-1)处的展开式相加,则可得 一阶导数的中心差分的表达式:
qw
y x
•16
(3) 内部角点
如图所示内部角点代表了 3/4 个元体,在同样的假设条 件下有
tm1,ntm,ny tm,n1tm,nx tm,n1tm,n x
x
有限差分法

1.6.1 差分格式
上页
下页
返回
结束
如图,以二维场为例,在一由边界区域L界定的二维区域 界定的二维区域D 如图 , 以二维场为例 , 在一由边界区域 界定的二维区域 电位函数φ满足拉普拉斯方程且给定为第一类边界条件: 内,电位函数φ满足拉普拉斯方程且给定为第一类边界条件
∂ 2ϕ ∂ 2ϕ ∇ 2ϕ = + 2 ∂x ∂y 2
启动 赋边界节点已知电位值 赋予场域内各节点电位初始值 累计迭代次数 N=0 N=N+1 按超松弛法进行一 次迭代,求 ϕi(,N+1) j
上页
下页
返回
结束
Y N
所有内点 相邻二次迭代值的最大误差 是否小于 W 打印 N,ϕ(i, j ) 迭代解程序框图 停机
上页
下页
返回
结束
例 一长直接地金属槽截面如图。其侧壁与底面的电位均为零, 而顶盖电位ϕ4=100。求槽内电位分布。 解: •二维场第一类边值问题。 •将二维场域划分成正方形 网格,步距h=a/4。 •场域内任一点电位ϕ应满 足二维拉普拉斯方程的差 分计算格式。
α
4
k+ k) [ϕ i(− 1,1j ) + ϕ i(,kj+ 1 ) + ϕ i(+ 1, j + ϕ i(,kj )+ 1 − 4ϕ i(,kj ) ] −1
迭代收敛的速度与 α 有明显关系: 有明显关系: 迭代收敛的速度与 收敛的速度
收敛因子(α ) 迭代次数( N) 1.0 >1000 1.7 269 1.8 1.83 1.85 1.87 1.9 174 143 122 133 171 2.0 发散
上页
下页
有限差分法

yi 2 2 yi 1 2 yi 1 yi 2 2a 3
边界点的差分式:
求解差分式方程时,边界条件也是以差分的形式表示的。为了得到如图所 示构件的三种不同边界的差分式,挠曲线都需向外延伸,如虚线所示,给出分 段长度为a的虚拟点的函数yi-1 ,根据不同的边界条件找出虚拟点yi-1与前进点yi 之间的关系式。如果边界点在构件的右侧,那么虚拟点在延伸线上的右侧,这 时需要找出虚拟点与后退点之间的关系式。 y y
对b图自由端: y″0=0
y ''0
y1 2 y0 y1 0 得:y-1=2y0-y1 2 a
y0
y1 y1 2
提高屈曲荷载精度的外推法:
用差分法求解构件的屈曲荷载时,其精度与构件的分段数n有关, 但分段数的多少影响计算工作量。分段数太少,计算结果的误差大。对 于弹性弯曲屈曲荷载,误差的大小与分段的平方成反比。有鉴于此,可 以利用两种不同分段数n1和n2得到的屈曲荷载P1和P2,采用Richardson 外推法提高精度。 设比较精确的解为Pcr,与近似解P1和P2有关的比例常数为β ,则 有
y 0 a
a
1 a
(a) 2 a
3 a
4
P k EI
2
则: y″ +k2y=0
(b)
任意点的差分公式:
yi''
yi 1 2 yi yi 1 a2
2 2 将其代入上式后得到差分方程: yi 1 (k a 2) yi yi 1 0
1)第一次近似将构件全长分为两段,a=l/2,在分点1的差分方程为:
当
P 0.2 PE
M 2P 1 2P 2 1 ( ) 8PE 8 8PE
有限差分法基本原理PPT课件

uin1
uin
a
t x
(uin
un i 1
)
ui0 u (xi )
几种差分格式介绍
u a u 0 t x u(x,0) u(x)
FTFS格式(时间向前差分、空间向前差分)
uin1 uin uin1 uin 0
t
x
ui0 u (xi )
uin 1
uin
a
t x
(uin1
uin )
ui0 u (xi )
几种差分格式介绍
FTBS格式(时间向前差分、空间向后差分)
限差分方程的解是收敛T的(i。, n)
lim
x0,t
0
Ti
t
一般情况下,证明收敛性是非常难的,暂不予以证明。
3.稳定性 稳定性讨论的是差分解的误差在计算过程中的发展问题。
在 数值解中,引进误差是不可避免的,电子计算机也有舍入误差, 因此实际算得的有限差分方程的解是近似解。这种误差是要向其 他方向传播的,如果计算中引入的误差在以后逐层计算过程中影 响逐渐消失或者保持有界,则称差分方程是稳定的。否则就是不 稳定的。
Von Neumann稳定性分析方法简介
分析例题
T n1 i
Ti n
t x 2
(Ti
n 1
2Ti n
Ti
n 1
),
S
t x 2
Ti n1
STi n1
(1
2S )Tin
STi
n 1
上式T中i n 近似数值
有限差分法

有限差分法有限差分法finite difference method微分方程和积分微分方程数值解的方法。
基本思想是把连续的定解区域用有限个离散点构成的网格来代替,这些离散点称作网格的节点;把连续定解区域上的连续变量的函数用在网格上定义的离散变量函数来近似;把原方程和定解条件中的微商用差商来近似,积分用积分和来近似,于是原微分方程和定解条件就近似地代之以代数方程组,即有限差分方程组,解此方程组就可以得到原问题在离散点上的近似解。
然后再利用插值方法便可以从离散解得到定解问题在整个区域上的近似解。
有限差分法的主要内容包括:如何根据问题的特点将定解区域作网格剖分;如何把原微分方程离散化为差分方程组以及如何解此代数方程组。
此外为了保证计算过程的可行和计算结果的正确,还需从理论上分析差分方程组的性态,包括解的唯一性、存在性和差分格式的相容性、收敛性和稳定性。
对于一个微分方程建立的各种差分格式,为了有实用意义,一个基本要求是它们能够任意逼近微分方程,这就是相容性要求。
另外,一个差分格式是否有用,最终要看差分方程的精确解能否任意逼近微分方程的解,这就是收敛性的概念。
此外,还有一个重要的概念必须考虑,即差分格式的稳定性。
因为差分格式的计算过程是逐层推进的,在计算第n+1层的近似值时要用到第n层的近似值,直到与初始值有关。
前面各层若有舍入误差,必然影响到后面各层的值,如果误差的影响越来越大,以致差分格式的精确解的面貌完全被掩盖,这种格式是不稳定的,相反如果误差的传播是可以控制的,就认为格式是稳定的。
只有在这种情形,差分格式在实际计算中的近似解才可能任意逼近差分方程的精确解。
关于差分格式的构造一般有以下3种方法。
最常用的方法是数值微分法,比如用差商代替微商等。
另一方法叫积分插值法,因为在实际问题中得出的微分方程常常反映物理上的某种守恒原理,一般可以通过积分形式来表示。
此外还可以用待定系数法构造一些精度较高的差分格式。
有限差分法

u xxx
xr
+
(1.5a) (1.5b)
进而,在点 xr 处的一阶导数的两个近似公式可由(1.5)给出
ux
xr
= (ux )r
≈
u ( xr
+ h) − u(xr ) h
=
ur+1 − ur h
ux
xr
= (ux )r
≈
u(xr ) − u(xr h
− h)
=
ur
− ur−1 h
(1.6a) (1.6b)
有限差分法的基本思想是用离散的、只含有限个未知数的差分方程去代替连续变量的微 分方程和定解条件。对于求解的偏微分方程定解问题,有限差分方法的主要步骤如下:利用 网格线将定解区域化为离散点集;在此基础上,通过适当的途径将微分方程离散化为差分方 程,并将定解条件离散化,这一过程叫做构造差分格式,不同的离散化途径一般会得到不同 的差分格式;建立差分格式后,就把原来的偏微分方程定解问题化为代数方程组,通过解代 数方程组,得到出定解问题的解在离散点上的近似值组成的离散解,应用插值方法可从离散 解得到定解问题在整个定解区域上的近似解。由此可见,有限差分方法有大体固定的模式, 它有较强的通用性。但是,不能误认为不去了解这种逼近方法的基本知识,只是单纯模仿, 便能轻易获得满意的结果。因为在应用这种逼近方法时会发生许多重要的但有时还是相当困 难的数学问题,包括精度、稳定性与收敛性等。
− hD exp( 2 )ur
由(*1)式与(*2)相减得到
ur+1/ 2
− ur−1/ 2
=
exp(
hD 2
)ur
−
exp(
−
hD 2
)ur
= δur
有限差分方法基础ppt课件

t
x
0
(x,0) (x)
这里 (x) 为某已知函数。同样,差分方程也必须有初始条件:
(2-7)
n1 i
n i
n i 1
n i 1
0
t
2x
0 i
(xi )
(2-8)
初始条件是一种定解条件。如果是初边值问题,定解条件中还应有适当的边界条件。差分方程和其定解条件一起, 称为相应微分方程定解问题的差分格式。
图1-3 均匀和非均匀网格实例2
22
第二节 差分方程、截断误差和相容性/差分方程(1/3)
差分相应于微分,差商相应于导数。差分和差商是用有限形式表 示的,而微分和导数则是以极限形式表示的。如果将微分方程中 的导数用相应的差商近似代替,就可得到有限形式的差分方程。 现以对流方程为例,列出对应的差分方程。
FTCS格式的截断误差为
Rin O(t, (x)2 )
FTFS和FTBS格式的截断误差为
Rin O(t, x)
3种格式对 t 都有一阶精度。
(2-12) (2-13)
30
第二节 差分方程、截断误差和相容性/相容性(1/3)
25
第二节 差分方程、截断误差和相容性/截断误差(1/6)
按照前面关于逼近误差的分析知道,用时间向前差商代替时间导数时的误差为 O(t) ,
用空间中心差商代替空间导数时的误差为 O((x)2 ) ,因而对流方程与对应的差分方程之间也存在一个误差,它是
Rin O(t) O((x)2 ) O(t, (x)2 )
表2
常用数值分析方法4有限差分法与有限单元法

(3)把所有单元的这种特性关系按一定的条件(变形协调条件、连 续条件或变分原理及能量原理)集合起来,引入边界条件,构成一组以 结点变量(位移、温度、电压等)为未知量的代数方程组, 解之就可得 到有限个节点处的待求变量 。
(2)几何划分法:以几何区域 形状为依据来划分,如对矩形区 域可采用矩形离散化网格,非矩 形区域可采用三角形、四角形或 其他形状的网格,以适应温度场 分布的要求。
图4.2 扇形网格和三角形网格
差分方程的建立过程(之二)
——将微分方程转化为差分方程
微分方程转化为差分方程实际上就是以差分代替微 分、以差商代替微商的过程,是以有限小量去代替无限 微量的近似化过程。
4.1.2 有限差分法的主要步骤
1、构成差分格式
x 2 x 1 x
首先选择网格布局、差分形式和步长;其次,以有限差分
代替无限微分,即以x2 替微商(导数)d y
,x以1 差分x 方代程替代dx替.微以分差方商yx程22 及xy11边界yx条件代。
dx
2、求解差分方程
差分方程通常是一组数量较多的线性代数方程(即:线性方 程组)。其求解方法有下列两种:(1)精确法,又称直接法, 即消元法;(2)近似法,又称间接法,即迭代法。
图4.5 受轴向载荷的变截面杆
1 前处理过程
(1) 求解域离散化
先将求解的问题分解为结点和单元。为简单起见,将杆划分成五个结 点和四个单元(如图4.6所示)。
给定的变截而杆简化为四个独立的部分,每部分的截面面积恒定(为 组成该单元的两个结点处的面积的平均值)。
有限差分法(新版)

电磁场与电磁波 第3章 静态电磁场及其边值问题的解
7
将式(3.7.3)与式(3.7.4)相加,并略去h2的更高阶项:
2
x2
i, j
i1, j
2i, j
h2
i1, j
(3.7.7)
将式(3.7.5)与式(3.7.6)相加,并略去h2的更高阶项:
2
y2
i, j
i, j1
2i, j
解,因此只能用数值计算方法;其所得结果为电 磁场在空间离散点上的数值的集合(近似解)
有限差分法的基本思想
将计算场域划分成网格,把求解场域内连续的场分布用求解 网格节点上的离散数值解来代替;即用网格节点的差分方程 近似代替场域内的偏微分方程来求解。
电子科技大学编写 高等教育出版社 & 高等教育电子音像出版社 出版
次近似值,即初始值。然后再按照:
(k1) 1 [ (k ) (k ) (k ) (k ) ]
i,j
4 i1, j
i , j1
i1, j
i , j1
(3.7.10)
(i, j 1, 2,......) (k 0,1, 2,......)
进行反复迭代。若当第N次迭代结束后,所有内节点相邻两 次迭代值之间的绝对误差小于事先给定的精度,则迭代停止。
i1, j
(xi
h,
yj)
i, j
h
x
i, j
h2 2!
2
x2
i, j
h3 3!
3
x3
i, j
...
(3.7.3)
i1, j
(xi
h,
yj)
i, j
h
x
i, j
h2 2
有限差分方法

有限差分方法有限差分方法一种求偏微分(或常微分)方程和方程组定解问题的数值解的方法,简称差分方法。
微分方程的定解问题就是在满足某些定解条件下求微分方程的解。
在空间区域的边界上要满足的定解条件称为边值条件。
如果问题与时间有关,在初始时刻所要满足的定解条件,称为初值条件。
不含时间而只带边值条件的定解问题,称为边值问题。
与时间有关而只带初值条件的定解问题,称为初值问题。
同时带有两种定解条件的问题,称为初值边值混合问题。
定解问题往往不具有解析解,或者其解析解不易计算。
所以要采用可行的数值解法。
有限差分方法就是一种数值解法,它的基本思想是先把问题的定义域进行网格剖分,然后在网格点上,按适当的数值微分公式把定解问题中的微商换成差商,从而把原问题离散化为差分格式,进而求出数值解。
此外,还要研究差分格式的解的存在性和唯一性、解的求法、解法的数值稳定性、差分格式的解与原定解问题的真解的误差估计、差分格式的解当网格大小趋于零时是否趋于真解(即收敛性),等等。
有限差分方法具有简单、灵活以及通用性强等特点,容易在计算机上实现。
偏微分方程初值问题的差分法许多物理现象随着时间而发生变化、如热传导过程、气体扩散过程和波的传播过程都与时间有关。
描述这些过程的偏微分方程具有这样的性质:若初始时刻t=t0的解已给定,则t t0时刻的解完全取决于初始条件和某些边界条件。
利用差分法解这类问题,就是从初始值出发,通过差分格式沿时间增加的方向,逐步求出微分方程的近似解。
双曲型方程的差分方法最简单的双曲型方程的初值问题是:式中嫓(x)为已知初值函数。
这初值问题的解是:u(x,t)=嫓(x-at)。
(2)由(2)可见,(1a)(1b)的解(2)当a>0时代表一个以有限的速度a沿特征线x-at=常数向右传播的波,而解u(x,t)在P(慜,惭)点的值完全由嫓(x)在x轴上的点A(慜-а惭,0)的值决定。
A点就是双曲型方程(1a)在P点的依赖域(图1)。
有限差分法

•计算内点o点的新值。即o点的新值就是围绕该点的4个点的 电位的平均值。
•当所有的内点都计算完后,用他们的新值代替旧值,完成 一次迭代。再进行下一次迭代。直到每一点计算得到的新值 与旧值之差小于指定的范围。 •这种方法的特点是用前一次迭代的得到的结点电位作为下 一次迭代时的初值。 如(j,k)点在第n+1次迭代时按下式计算:
•考虑1,3两点x1=xo+h, x3=xo-h 1 2 2 1 3 3 h h ........ 1 o h 2 3
x o 2! x o 3! x o 1 2 2 1 3 3 3 o h x 2 h 3! x 3 h ........ 2! x o o o 如果h足够小,忽略三次以上 项,将上二式相减
•迭代次数N分别 为1,2,3,4时 各网格内点的数 值解如图。
•若规定各网格内点相邻两次迭代值的绝对误差应小于10 -5,得到各内点的电位数值解如图。此时N=13。
•从结果看电位分布关于y轴 有对称性。实际计算可只一 半区域,而将网格划分得更 细。以得到更理想到数值解。
1 2+ 3 4 4 o=h 2 F
二维场的拉普拉斯方程 的差分形o=0
•边界条件也可进行离散化处理,对第一类边值,可直接把 点函数f(s)的值赋予各边界结点。 3.差分方程的解法 •设将场域划分如图. •边 界 上 的 值 分 别 为 f1,………f16。 •在各内点上作出差分,泊 松方程变成下列差分方程 组
3 1 x o 2h 上式用o点的中心差商代替该点 的偏导数。
步距越小,误差越小。
2 2 x 同理
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
∂ϕ 或 值和边界内一行相应结点处 ∂y
ϕ 的
∂ϕ 所以有 ϕ外 = ϕ内 + 2h ∂x 中
(2 − 6)
当求出全部结点上的φ值以后,我们就可按应 力分量的差分公式(2-1)计算应力分量。 用差分法解弹性平面问题时,可按下列步骤进 行: (1) 在边界上任意选定一个结点作为基点A, 取
l1σ x + l 2τ xy = p x l1τ xy + l 2σ
y
= py
∂ 2ϕ ∂ 2ϕ ∂ 2ϕ σ x = 2 , σ y = 2 , τ xy = − ∂y ∂x ∂x∂y
代入上式,即得:
∂ 2ϕ ∂ 2ϕ l1 2 − l2 = px ∂y ∂x∂y ∂ 2ϕ ∂ 2ϕ −l1 + l2 2 = p y ∂x∂y ∂x (a )
(5)按照公式(2-1)计算应力的分量。 说明: 1.以上是针对单连体导出的结果。对于多连 体,情况就不象这样简单。 2. 如果一部分边界是曲线的,或是不与坐标 轴正交,则边界附近将出现不规则的内结点。对 于这样的结点,差分方程(2-2)必须加以修正。
第三节 例 深梁的应力函数差分解 现以如图所示的 混凝土深梁为例,应 用应力函数的差分解 求出应力分量。已知 混凝土深梁上边受有 均布向下的铅直荷载q, 并由下角点处的反力 维持平衡。
由右图可见, l1=cos(N,x)=cosα=dy/ds, l2=cos(N,y)=sinα=-dx/ds, 于是,式(a)可改写为:
d y ∂ 2ϕ d x ∂ 2ϕ 2 + ∂y d s ∂x∂y = p x ds d y ∂ 2ϕ d x ∂ 2ϕ − ∂x∂y − d s ∂x 2 = p y ds
以上(1-1)~(14)是基本差分公式,从 而可导出其它的差分 公式如下:
∂2 f 1 = 2 [( f6 + f8 ) − ( f5 + f7 )] ∂x∂y 0 4h ∂4 f 1 = 4 [6 f 0 − 4( f1 + f3 ) + ( f9 + f11 )] 4 ∂x 0 h ∂4 f 1 = 4 [4 f0 − 2( f1 + f 2 + f3 + f 4 ) + ( f5 + f6 + f 7 + f8 )] 2 2 ∂x ∂y 0 h ∂4 f 1 = 4 [6 f 0 − 4( f 2 + f 4 ) + ( f10 + f12 )] 4 ∂y 0 h (1 − 5) (1 − 6) (1 − 7) (1以相隔2h的两 结点处的函数值来表示中间结点处的一阶导数 值,可称为中点导数公式。 以相邻三结点处的函数值来表示一个端点 处的一阶导数值,可称为端点导数公式。 应当指出:中点导数公式与端点导数公式 相比,精度较高。因为前者反映了结点两边的 函数变化,而后者却只反映了结点一边的函数 变化。因此,我们总是尽可能应用前者,而只 有在无法应用前者时才不得不应用后者。
在结点3,x=x0-h, 在结点1, x=x0+h,代入(b) 得: x=x 1, +h (b)
h2 ∂2 f ∂f f3 = f 0 − h + ∂x 0 2 ∂x 2 0
h2 ∂2 f ∂f f1 = f 0 + h + ∂x 0 2 ∂x 2 0
第八章 有限差分法
从弹性力学的基本方程建立以来,这 些方程在各种问题的边界条件下如何求解, 一直是很多数学工作者和力学工作者研究 的内容。即弹性力学的经典解法存在一定 的局限性,当弹性体的边界条件和受载情 况复杂一点,往往无法求得偏微分方程的 边值问题的解析解,许多工程重要问题, 不能够得出函数式的解答。 因此,弹性力学问题的各种数值解法 便具有重要的实际意义。
(σ )
y xy
0
(τ )
0
∂ 2ϕ 1 = − = [(ϕ 5 + ϕ 7 ) − (ϕ 6 + ϕ 8 )] ∂x∂y 0 4 h 2
可见,用差分法解平面 问题,共有两大任务: 一、建立差分方程 将(1-6~8)代入双调和 方程
∂ 4ϕ ∂ 4ϕ ∂ 4ϕ +2 2 2 + =0 4 4 ∂x ∂x ∂y ∂y
ϕ A = 0
∂ϕ ∂ϕ =0 = ∂x A ∂y A
然后由面力的矩及面力之和算出边界上所有各 ∂ϕ ϕ 结点处φ 的值,以及所必需的一些 及 ∂值,即垂 直于边界方向的导数值。
∂x
∂y
(2)应用公式(2-6),将边界外一行虚结 点处的φ值用边界内的相应结点处的φ值来表示。 (3)对边界内的各结点建立差分方程(2-2), 联立求解这些结点处的值。 (4)按照公式(2-6),算出边界外一行的各 虚结点处的φ值。
差分方程 应力函数的差分解 深梁应力函数的差分解
第一节
差分方程
差分法是沿用已久的一种数值解法。随着计 算机的普及和相应的软件发展,此法成为解弹性 力学问题的一种有效的方法。
我们在弹性体上,用相隔等 间距h而平行于坐标轴的两组平行 线织成正方形网格,Δx=Δy=h, 如图。 设f=f(x,y)为弹性体内的某一 个连续函数。该函数在平行于x 轴的一根网线上,如在3-0-1 上,它只随x坐标的改变而变化。 在邻近结点0处,函数f可展为 泰勒级数如下: ∂f 1 ∂2 f 1 ∂3 f f = f0 + (x − x0 ) + 2 (x − x0 )2 + 3 (x − x0 )3 + ... 2! ∂x 0 3! ∂x 0 ∂x 0
B B A
∫
B
B
∫
将式(b),(c)代入,整理得:
B ∂ϕ B ∂ϕ ϕB =ϕA +(xB − xA) +(yB − yA) +∫ (yB − y)px ds +∫ (x − xB)py ds (d) ∂y A A ∂x A A ∂ϕ ∂ϕ ϕ A , , , 为已知, 由式(d)及式(c)可见,设
(c )
(d )
联立(c),(d),解得差分公式:
f − f3 ∂f = 1 2h ∂x 0
∂2 f 2 ∂x f + f3 − 2 f0 = 1 h2 0
(1 − 1)
(1 − 2)
同理,在网线4-0-2上可得到差分公式
∂f f2 − f4 = 2h ∂y 0 ∂2 f f + f4 − 2 f0 = 2 2 2h 2 ∂y 0 (1 − 3) (1 − 4)
工程中常用的数值解法有有限单元法和 差分法。 有限单元法 是以有限个单元的集合体来 代替连续体,属于物理上的近似。 差分法 是把弹性力学的基本方程和边 界条件(一般均为微分方程)近似地改用差 分方程(代数方程)来表示,把求解微分方 程的问题改换成为求解代数方程的问题,属 于数学上的近似。
第一节 第二节 第三节
∂x A ∂y A
即可根据面力分量及导数求得
∂ϕ ∂ϕ ϕB , , . ∂x B ∂y B
由前知,把应力函数加上一个线性函数,并 不影响应力。因此,可设想把应力函数加上 a+bx+cy,然后调整a,b,c三个数值,使得
∂ϕ ∂ϕ = 0,... = 0 ϕA = 0 ∂y ∂x A A
∫
A
py d s
B ∂ϕ ∂ϕ = + ∫A p x d s ∂y B ∂y A B ∂ϕ ∂ϕ = − ∫A p y d s ∂x B ∂x A
(c)
由高等数学可知,
dϕ ∂ϕ d x ∂ϕ d y = . + . ds ∂x ds ∂y ds
整理即得
20ϕ0 −8(ϕ1 +ϕ2 +ϕ3 +ϕ4) + 2(ϕ5 +ϕ6 +ϕ7 +ϕ8) +(ϕ9 +ϕ10 +ϕ11 +ϕ12) = 0 (2−2)
对于弹性体边界以内的每一结点,都可以建立 这样一个差分方程。
二、联立求解这些线性代数方程,就 能求得各内结点处的值。 一般建立和求解差分方程,在数学上不 会遇到很大困难。但是,当对于边界内一行 的(距边界为h的)结点,建立的差分方程 还将涉及边界上各结点处的φ值,并包含边 界外一行的虚结点处的φ值。 为了求得边界上各结点处的φ值,须要 应用应力边界条件,即:
将此式亦从A点到B点沿s进行积分,就得到边 界上任一点B处的φ值。为此利用分部积分法,得:
∂ϕ B d ∂ϕ d ∂ϕ ∂ϕ (ϕ) = x − A x ds + y − A y ds, ∂y d s ∂x d s ∂y ∂x A A
A A
从图易看出,式(2-3)右 边的积分式表示A与B之间的x方 向的面力之和;式(2-4)右边 的积分式表示A与B之间的y方向 的面力之和;式(2-5)右边的 积分式表示A与B之间的面力对 于B点的矩。
至此,我们解决了怎样 计算边界上各结点
∂ϕ ∂ϕ ϕ, , ∂x ∂y
的值的问题。 至于边界外一行虚结点处 ϕ 的值,则可用边界上 结点处的 ∂ϕ ∂x 值来表示。例如,对于图1中的虚结点14,因为有
d y ∂ 2ϕ 2 d s ∂y
d x ∂ 2ϕ + d s ∂x∂y = p x
