电磁场原理习题与解答(第6章)
电磁场与电磁波(第四版)习题解答

电磁场与电磁波(第四版)习题解答第1章习题习题1.1给定三个矢量A 、B 和C 如下:23x y z =+-A e e e .4y z=-+B e e ,52x z =-C e e ,解:(1)22323)12(3)A x y z e e e A a e e e A+-===+-++- (2)2641x y z A B e e e -=+-==(3)(23)(4)11x y z y z A B e e e e e •=+-•-+=-(4)arccos135.5A B AB θ•===︒ (5)1711cos -=⋅=⋅⋅==B B A A B B A A A A AB Bθ(6)12341310502xy zx Y Z e e e A C e e e ⨯=-=---- (7)0418520502xy zx Y Z e e e B C e e e ⨯=-=++-()(23)(8520)42x Y Z x Y Z A B C e e e e e e •⨯=+-•++=-123104041xy zx Y Z e e e A B e e e ⨯=-=---- ()(104)(52)42x Y Z x Z A B C e e e e e ⨯•=---•-=-(8)()10142405502x y zx Y Z e e e A B C e e e ⨯⨯=---=-+-()1235544118520xy zx Y Z e e e A B C e e e ⨯⨯=-=-- 习题1.4给定两矢量 234x y z =+-A e e e 和 456x y z =-+B e e e ,求它们之间的夹角和 A 在 B上的分量。
解:29)4(32222=-++=A776)5(4222=+-+=B31)654()432(-=+-⋅-+=⋅z y x z y x e e e e e e B A则A 与B之间的夹角为131772931cos =⎪⎪⎭⎫ ⎝⎛⋅-=⎪⎪⎪⎭⎫⎝⎛⋅⋅=ar BA B A arcis ABθ A 在B上的分量为532.37731cos -=-=⋅=⋅⋅⋅==B B A BA B A A A A AB Bθ习题1.9用球坐标表示的场225rr =E e , (1)求在直角坐标中点(3,4,5)--处的E 和x E ;(2)求在直角坐标中点(3,4,5)--处E 与矢量22x y z =-+B e e e 构成的夹角。
第6章大学物理(I-1)教材课后习题答案

与一边平行。(1)线圈平面与地磁场 B 的夹角为什么值时,线圈中产生的感应电动势最大;
(2)设地磁场的 B 0.55G ,这时要在线圈中最大产生 10mV 的感应电动势,求线圈的匝
数N。
解(1)由题意知: S 0.01m2, n 30 revs-1,
平面法线
B
2n 60 rads-1
l
x
2
l
6.5 解图
因为
v dl , dt
所以
i
dm dt
0 I tan [v ln(1 a ) av ]
2
l la
若 l d 时,因为 tan b a ,
所以
i
0 Ivb [ln(1 2a
a) d
d
a
] ,其方向为顺时针方向。 a
6.6 一正方形线圈每边长 100mm,在地磁场中转动,每秒转 30 圈,转轴通过中心并
2.958103 sin(120t) ,
所以
imax 2.958 V, Iimax 2.958103 A
6.2 半 径为 a 10cm , 匝数 为 N 100 的圆 形线 圈以 o1o2 为 转轴 ,在均 匀磁 场
B 0.5T 中以转速 n 600 转/分转动。开始时,线圈平面垂直于磁场,如题 6.2 图所示, 当线圈转过π/2 时,求:(1)线圈中的感应电流,已知线圈的电阻 R 100 ;(2)感应电
2
a
6.4 如题 6.4 图所示,导体棒 ab 与金属轨道 ca 和 db 接触,
整个线框放在 B 0.50 T 的均匀磁场中,磁场方向与图面垂直。 (1)若导体棒以 4.0 m s-1 的速度向右运动,求棒内感应电动
电磁场与电磁波课后习题及答案六章习题解答

第六章时变电磁场有一导体滑片在两根平行的轨道上滑动,整个装置位于正弦时变磁场之中,如题图所示。
滑片的位置由确定,轨道终端接有电阻,试求电流i.解穿过导体回路abcda的磁通为故感应电流为一根半径为a的长圆柱形介质棒放入均匀磁场中与z轴平行。
设棒以角速度绕轴作等速旋转,求介质内的极化强度、体积内和表面上单位长度的极化电荷。
解介质棒内距轴线距离为r处的感应电场为故介质棒内的极化强度为极化电荷体密度为极化电荷面密度为则介质体积内和表面上同单位长度的极化电荷分别为平行双线传输线与一矩形回路共面,如题图所示。
设、、,求回路中的感应电动势。
解由题给定的电流方向可知,双线中的电流产生的磁感应强度的方向,在回路中都是垂直于纸面向内的。
故回路中的感应电动势为式中故则有一个环形线圈,导线的长度为l,分别通过以直流电源供应电压U0和时变电源供应电压U(t)。
讨论这两种情况下导线内的电场强度E。
解设导线材料的电导率为,横截面积为S,则导线的电阻为而环形线圈的电感为L,故电压方程为当U=U0时,电流i也为直流,。
故此时导线内的切向电场为当U=U(t)时,,故即求解此微分方程就可得到。
一圆柱形电容器,内导体半径为a,外导体内半径为b,长为l。
设外加电压为,试计算电容器极板间的总位移电流,证明它等于电容器的传导电流。
解当外加电压的频率不是很高时,圆柱形电容器两极板间的电场分布与外加直流电压时的电场分布可视为相同(准静态电场),即故电容器两极板间的位移电流密度为则式中,是长为l的圆柱形电容器的电容。
流过电容器的传导电流为可见由麦克斯韦方程组出发,导出点电荷的电场强度公式和泊松方程。
解点电荷q产生的电场满足麦克斯韦方程和由得据散度定理,上式即为利用球对称性,得故得点电荷的电场表示式由于,可取,则得即得泊松方程试将麦克斯方程的微分形式写成八个标量方程:(1)在直角坐标中;(2)在圆柱坐标中;(3)在球坐标中。
解(1)在直角坐标中(2)在圆柱坐标中(3)在球坐标系中已知在空气中,求和。
《电磁场与电磁波》课后习题解答(全)

(3)
【习题3.4】
解:(1)在区域中,传导电流密度为0,即J=0
将 表示为复数形式,有
由复数形式的麦克斯韦方程,可得电场的复数形式
所以,电场的瞬时值形式为
(2) 处的表面电流密度
(3) 处的表面电荷密度
(4) 处的位移电流密度
【习题3.5】
解:传导电流密度 (A/ )
位移电流密度
【习题3.6】
(2)内导体表面的电流密度
(3)
所以,在 中的位移电流
【习题2.13】
解:(1)将 表示为复数形式:
则由时谐形式的麦克斯韦方程可得:
而磁场的瞬时表达式为
(2)z=0处导体表面的电流密度为
z=d处导体表面的电流密度为
【习题2.14】
已知正弦电磁场的电场瞬时值为
式中
试求:(1)电场的复矢量;
(2)磁场的复矢量和瞬时值。
由安培环路定律: ,按照上图所示线路积分有
等式左边
等号右边为闭合回路穿过的总电流
所以
写成矢量式为
将 代入得
【习题3.18】
解:当 时, ,
当 时, ,
这表明 和 是理想导电壁得表面,不存在电场的切向分量 和磁场的法向分量 。
在 表面,法线
所以
在 表面,法线
所以
【习题3.19】
证明:考虑极化后的麦克斯韦第一方程
(1)
和 (2)
若采用库仑规范,即 (3)
对(1)式两边取散度,有
将(2)、(3)式代入,得
故电流连续性也是满足的。
【习题4.3】解:
【习题4.4】
证明:因为 即
故 满足连续性方程。
另外, 满足洛仑兹条件。
6- 电磁感应 电磁场(带答案)

增加,求空间涡旋电场的分布.
解:取绕行正方向为顺时针方向,作为感生电动势和涡旋电场的标定正方向,磁
通量的标定正方向则垂直纸面向里.
在 r<R 的区域,作半径为 r 的圆形回路,由
i
L Ei dl
S
B
dS
t
O R
B
5
并考虑到在圆形回路的各点上, Ei 的大小相等,方向沿圆周的切线.而在圆形回路内是匀强磁场,且 B 与 dS
为
,内部的磁能密度为
。
答案:µ0nI
0n2I 2 / 2
6-T 自感磁能 6、自感系数 L =0.3 H 的螺线管中通以 I =8 A 的电流时,螺线管存储的磁场能量 W = . 答案:9.6J
6-T 动生电动势势 二、选择题
6-X 电磁感应现象
1
1、一导体圆线圈在均匀磁场中运动,能使其中产生感应电流的一种情况是( )
6-S 磁场能量 自感
5、一无限长同轴电缆是由两个半径分别为 R1 和 R2 的同轴圆筒状导体构成的,其间充满磁导率为μ的磁 介质,在内、外圆筒通有方向相反的电流 I.求单位长度电缆的磁场能量和自感系数.
解:对于这样的同轴电缆,磁场只存在于两圆筒状导体之间的磁介质内,由安培环路定理可求得磁场强
度的大小为
A IA r
L, .R
B IB r
R
(A) 两线圈的轴线互相平行。
(B)两线圈的轴线成 45°角。
K
(C) 两线圈的轴线互相垂直。
(D)两线圈的轴线成 30°角。
答案:C
6-X 感生电场
10、在感生电场中,电磁感应定律可写成 E K
L
dl
d dt
,式中 EK
物理学第3版习题解答_第6章稳恒磁场

I 2 dr
FBC 方向垂直 BC 向上,大小
FBc
d
0 I1 0 I1 I 2 d a ln 2r 2 d
d a
I 2 dl
0 I1 2r
∵
dl FBC
d a
dr cos 45
∴
a
0 I 2 I1dr II d a 0 1 2 ln 2r cos 45 d 2
B dl 8
a
0
ba
B dl 8 0
B dl 0
c
(1)在各条闭合曲线上,各点 B 的大小不相等. (2)在闭合曲线 C 上各点 B 不为零.只是 B 的环路积分为零而非每点 B 为零
图 6-25 思考题
6-4 图
1
6-5 安培定律 dF Idl B 有任意角度?
线,试指出哪一条是表示顺磁质?哪一条是表示抗磁质?哪一条是表示铁磁质? 答: 曲线Ⅱ是顺磁质,曲线Ⅲ是抗磁质,曲线Ⅰ是铁磁质.
图 6-27
思考题-6-8
2
习题
6-1 如图 6-28 所示的正方形线圈 ABCD,每边长为 a,通有电流 I.求正方形中心 O 处 的磁感应强度。 I A D 解 正方形每一边到 O 点的距离都是 a/2,在 O 点产生的磁场 大小相等、方向相同.以 AD 边为例,利用直线电流的磁场公式:
I1 电阻R2 . I 2 பைடு நூலகம்阻R1 2
I 1 产生 B1 方向 纸面向外
B1
0 I 1 (2 ) , 2R 2
I 2 产生 B2 方向 纸面向里
电磁学第二版习题答案第六章

中 点。
(〜)求动生电动势,AM及,AC
(2)A、M哪点电势高,
解答:
(1)线圈上一元段的电动势为
由图6.3.7得
AM间的电动势为
AC间的电动势为
(2) A、C间的电动势差为
4, AC R , 0 U CA , , AC IRAC , , AC R 4
B 2l2令 ,,,得mR
v,,
dv F
dt m,
分离变量得
v m,F,,dt
d v
F
m,
积分后得
v ln,,t,C
F
m,
式中:C为待定系数,由初始条件,t=0,v(0)=0,得
F C,ln ma
故
F
m,v ln,,t F
m,
即
F v m,,e,t F
m,
证得杆的速率随时间变化的规律为
F v,t,,,1e,t,ma
形的6.3.6
半径为0.1m,转速为3000r min,求动生电动势的频率和最大植。
解答:
只有半圆弧的运动对动生电动势有贡献,沿旋转轴(即直径)作一辅助线,与半 圆弧
连成一封闭曲线,设t=0时,半圆面的位置如附图所示,选取半圆面的法线 方向垂直向外,
t时刻通过半圆面的磁通量为
R2
, ,B S,B cos,t2
R R dt
此电磁力与运动方向相反,根据牛顿第二定律,有
2B 2l dx dv F, ,R dt dt
得
mR dx,dv B l22
设杆的起始位置为x=0,金属杆所能移过的距离为
0mR mR x,dv,v0,v0 B 2l2B l22
电磁场与电磁波课后习题及答案六章习题解答

第六章 时变电磁场6.1 有一导体滑片在两根平行的轨道上滑动,整个装置位于正弦时变磁场5cos mT z e t ω=B 之中,如题 6.1图所示。
滑片的位置由0.35(1cos )m x t ω=-确定,轨道终端接有电阻0.2R =Ω,试求电流i.解 5cos 0.2(0.7)cos [0.70.35(1cos )]0.35cos (1cos )z z d B ad ab t x t t t t ωωωωωΦ==⨯=⨯-=--=+⎰g g B S e e故感应电流为110.35sin (12cos ) 1.75sin (12cos )mAin d i R R dt t t t t R ωωωωωωΦ==-=-+-+E6.2 一根半径为a 的长圆柱形介质棒放入均匀磁场0z B =B e 中与z 轴平行。
设棒以角速度ω绕轴作等速旋转,求介质内的极化强度、体积内和表面上单位长度的极化电荷。
解 介质棒内距轴线距离为r 处的感应电场为00z r r r B φωω=⨯=⨯=E v B e e B e故介质棒内的极化强度为 00000(1)()e r r r r B r B εεεωεεω==-=-P E e e X极化电荷体密度为2000011()()2()P rP r B r r r rB ρεεωεεω∂∂=-∇⋅=-=--∂∂=--P极化电荷面密度为00()(P r r r a e r σεεωε==⋅=-⋅=-P n B e 则介质体积内和表面上同单位长度的极化电荷分别为220020012()212()P P PS P Q a a B Q a a B πρπεεωπσπεεω=⨯⨯=--=⨯⨯=-6.3 平行双线传输线与一矩形回路共面,如题6.3图所示。
设0.2a m=、0.1m b c d ===、71.0cos(210)A i t π=⨯,求回路中的感应电动势。
解 由题给定的电流方向可知,双线中的电流产生的磁感应强度的方向,在回路中都是垂直于纸面向内的。
电磁场与电磁波(第4版)第6章部分习题参考解答

G
G E(z)
G
=
eGx100e− j(β z+90D )
+
G ey
200e− jβ z
由 ∇ × E = − jωμ0H 得
G H
(z)
=
−
1 jωμ0
∇×
G E(z)
=
−
1 jωμ0
⎡ ⎢
G ex
⎢∂
⎢ ⎢
∂x
G ey ∂ ∂y
G ez ∂ ∂zຫໍສະໝຸດ ⎤ ⎥ ⎥ ⎥ ⎥=
−
1 jωμ0
G (−ex
∂Ey ∂z
G (1) 电场 E = 0 的位置;(2) 聚苯乙烯中 Emax 和 Hmax 的比值。
解:(1)
令
z
'
=
z
−
0.82
,设电场振动方向为
G ex
,则在聚苯乙烯中的电场为
G E1 ( z
')
=
G Ei
(z
')
+
G Er
(z
')
=
G −ex
j2Eim
sin
β
z
'
G 故 E1(z ') = 0 的位置为 β z ' = −nπ, (n = 0,1, 2,")
G ex
G × Ei (x)
G = ez
1
− j2 πx
e3
12π
A/m
G
G
(2) 反射波电场 Er 和磁场 Hr 的复矢量分别为
G Er (x) =
G
j2 πx
−ey10e 3
G V/m , Hr (x)
6 电磁场与电磁波 第六章 答案

6.2 自由空间中一均匀平面波的磁场强度为)cos()(0x wt H a a H z y π-+= m A /求:(1)波的传播方向;(2)波长和频率;(3)电场强度; (4)瞬时坡印廷矢量。
解:)cos()(0x wt H a a H z y π-+=m A /(1) 波沿+x 方向传播(2) 由题意得:k=π rad/m , 波长m k 22==πλ , 频率Hz c f 8105.1⨯==λ (3))cos(120)(0x wt H a a a H E z y x ππη--=⨯= m v / (4))(cos 24020x wt H a H E S x ππ-=⨯= 2/m w 6.3无耗媒质的相对介电常数4=r ε,相对磁导率1=r μ,一平面电磁波沿+z 方向传播,其电场强度的表达式为)106cos(80z t E a E y β-⨯=求:(1)电磁波的相速;(2)波阻抗和β;(3)磁场强度的瞬时表达式;(4)平均坡印廷矢量。
解:(1)s m cv r r p /105.118⨯===εμμε(2))(6000Ω===πεεμμεμηrr , m r a d c w w r r /4===εμμεβ (3))4106cos(60180z t E a E a H x z -⨯-=⨯=πη m A / (4)π120]Re[2120*E a H E S z av =⨯= 2/m w6.4一均匀平面波从海水表面(x=0)沿+x 方向向海水中传播。
在x=0处,电场强度为m v t a E y /)10cos(1007π =,若海水的80=r ε,1=r μ,m s /4=γ。
求:(1)衰减常数、相位常数、波阻抗、相位速度、波长、趋肤深度;(2)写出海水中的电场强度表达式;(3)电场强度的振幅衰减到表面值的1%时,波传播的距离;(4)当x=0.8m 时,电场和磁场得表达式;(5)如果电磁波的频率变为f=50kHz ,重复(3)的计算。
大物电磁学课后答案

6-5 如图一长为l的直导线弯折成夹角为120o相等
长度的两部分,放在垂直于均匀磁场B的平面 上,并绕其一端以角速度在此平面内旋转, 求导线中感应电动势,并指出哪些电势高。
B
l
120o
2
l
解:两部分获感应电动势相当于直线段OA感
应电动势: OA 2 l cos300 3 l
9
6-10在圆柱形空间中存在着均匀磁场,B的方向与柱的轴线平行 ,若B的变化率为dB/dt=0.1特/秒,R=10厘米,问自r=5厘米、15 厘米处的感应电场的电场强度为多大?若将一个电子放在r=5厘 米处,求开始时电子的加速度a。
解:由于B的对称性
r=5厘米时
l
E
dl
E1
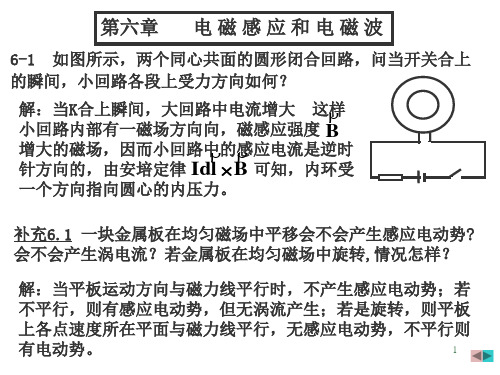
指向圆心的内压力。
补充6.1 一块金属板在均匀磁场中平移会不会产生感应电动势? 会不会产生涡电流?若金属板在均匀磁场中旋转,情况怎样?
解:当平板运动方向与磁力线平行时,不产生感应电动势;若
不平行,则有感应电动势,但无涡流产生;若是旋转,则平板
上各点速度所在平面与磁力线平行,无感应电动势,不平行则
有电动势。
1
补充6.2有一个铜环和一个木环,两环尺寸完全相同,放在同一 变化磁场里,问在两环中的感应电动势和感生电场相同吗? 解:产生的感应电场相同,电动势不同,铜环内有自由电子可 形成感应电流,而木环在感应电场作用下受极化。
6-2将一个超导材料作成的小薄片,放在永久磁铁的上方,它会 悬浮起来。你能解释这种现象吗? 解:处于超导态的材料电阻为零,电流分布在外表面上,内部 磁场为零。实际超导电流产生磁场抵抗外磁场的侵入,因而超 导材料受到一个排斥力,它与重力平衡而悬浮在磁场的上方。
电磁场与电磁波理论第6章习题解答

第6章习题解答已知空气中存在电磁波的电场强度为 ()80cos 6π102πy E e E t z =⨯+r rV /m试问:此波是否为均匀平面波传播方向是什么求此波的频率、波长、相速以及对应的磁场强度H r。
解:均匀平面波是指在与电磁波传播方向相垂直的无限大平面上场强幅度、相位和方向均相同的电磁波。
电场强度瞬时式可以写成复矢量j 0e kzy E e E -=r r &。
该式的电场幅度为0E ,相位和方向均不变,且0z E e ⋅=r r ⇒z E e ⊥r r ,此波为均匀平面波。
传播方向为沿着z -方向。
由时间相位86π10t t ω=⨯ ⇒ 86π10ω=⨯ 波的频率Hz 1038⨯=f 波数2πk =波长2π 1 m k λ== 相速p 310 m/s v kω==⨯ 由于是均匀平面波,因此磁场为j 0w w1() e kz z x EH e E e Z Z -=-⨯=r r r v &&有一频率为600MHz 的均匀平面波在无界理想介质(r r 4,1εμ==)中沿x +方向传播。
已知电场只有y 分量,初相位为零,且010t t ==s 时,1x =m 处的电场强度值为800kV/m 。
试写出E v 和H v的瞬时表达式。
解:根据题意,角频率812π10ω=⨯,r r 0028πk cωεμεμεμ====,因此 80cos(12π108π)y E e E t x =⨯-r r由s 10=t ,m 1=x 处的电场强度值为kV /m 800,可以得到kV/m 8000=E8800cos(12π108π) kV/m y E e t x =⨯-r r根据电场的瞬时表达式可以写出电场的复矢量为j8π800e kV/m x y E e -=r r&波阻抗为()0r w r 060π ΩZ μμμεεε===。
因此磁场强度复矢量为 j8πw 140() e kA/m 3πx x z H e E e Z -=⨯=r r r r &&因此,磁场的瞬时表达式为840cos(12π108π)3πz H e t x =⨯-r r在无界理想介质中,均匀平面波的电场强度为 ()80sin 2π102πx E e E t z =⨯-r rV /m已知介质的r 1μ=,试求其r ε,并写出H r的表达式。
大物电磁学课后答案6模板
反转时,电势的高低是否也会反过来?
B
解 :d (v B) dr, d B rdr
6-3 如图所示,通过回路的B线与线圈平面垂直,若磁通量按如
下规律变化=6t2+8t+8,式中的单位是毫韦伯,t是以秒为单位
。求当t=2秒时,(1)回路中感应电动势的大小是多少?(2)设
R=2欧姆,R上电流I的大小及方向如何?
解:(1) (6t2 8 8) 103(韦 伯 )
d (12t 8) 103 3.2 102(V)
解 : d (v B) dr vBdr u0Iv dr 2r
I
V
01..11
u0Iv 2r
dr
4 107 40 2.0 2
1.1 ln
0.1
3.8 5 1 05 ( v)
ab
0.1m
6-7 如图一长直导线,通有电流I=5.0安培,在与其相距d= 5.0厘米处放一矩形线圈,l=4.0厘米,宽A=2.0厘米,共1000 匝。线圈以速度v=3.0厘米/秒,沿垂直于长直导线的方向向右 运动,问该时刻线圈中感应电动势是多少?
R
)2 Rdt
v2B2l2 R
dx v
vB 2l (
R
Rm B2l2
dv )
dw mvdv , w
0
mvdv
v0
1 2
mv
2 0
补充6.5如图所示,法拉第圆盘发电机是一个在磁场中转动的导
体圆盘。设圆盘的半径R,它的轴线与均匀外磁场B平行,旋转角
速率为。求盘心到盘边的电势差,哪处电势高?当盘旋转方向
vBl ,
RR
vBl
B2l2
f I lB lB v
R
R
电磁场与电磁波第六章答案

v
20
则位移电流的瞬时表达式为: J D
a x 5 10 7 cos(6 10 9 t 20z ) 2
3.海水的电导率约为 0.4ms / m ,其相对介电常数为 81。求海水中位移电流密度等于传导 电流密度时的界限频率。 3 解答:
5 1 时的频率为界限频率。则得 f 8.9 10 Hz
6.若空气的磁感应强度如题 2 所示,求磁场强度和电场强度的复数形式、坡印廷矢量的 瞬时值及平均值。
6 解答
1 j 20z H aye
0
,E
1 a x e j 20z , c
1 S EH a z cos 2 (6 109 t 20z ) , 0c
7 解答:由 E j 0 H
得H
0 0 E ym e jkz a x E xm e jkz a y 0 0
瞬时形式为: H
0 0 E ym cos(t kz)a x E xm cos(t kz)a y 0 0
1 1 S av Re E H az 2 2 0 c
(c
3 108 m / s)
7.在空气中,已知电场强度 E Exm cos(t kz)ax E ym cos(t kz)a y 。求坡印廷矢 量的瞬时值 S 及平均值 S av 。
j ( kz 0 )
,其中
0 为常数, k 2 2 0 0 。①求两个波的坡印廷矢量的平均值 S av1 和 S av2 ;②证明空间
中总的 Sav Sav1 Sav2 。 11 解答:1)由 E j 0 H ,得
电磁场与电磁波第6章习题答案

第6章习题答案6-1 在1=r μ、4=r ε、0=σ的媒质中,有一个均匀平面波,电场强度是)3sin(),(πω+-=kz t E t z E m若已知MHz 150=f ,波在任意点的平均功率流密度为2μw/m 265.0,试求:(1)该电磁波的波数?=k 相速?=p v 波长?=λ波阻抗?=η (2)0=t ,0=z 的电场?)0,0(=E(3)时间经过μs 1.0之后电场)0,0(E 值在什么地方?(4)时间在0=t 时刻之前μs 1.0,电场)0,0(E 值在什么地方? 解:(1))rad/m (22πεπμεω===r cfk )m/s (105.1/8⨯==r p c v ε)m (12==kπλ )Ω(60120πεμπη=rr=(2)∵ 6200210265.02121-⨯===m rm av E E S εεμη∴ (V/m)1000.12-⨯=m E)V/m (1066.83sin)0,0(3-⨯==πm E E(3) 往右移m 15=∆=∆t v z p(4) 在O 点左边m 15处6-8微波炉利用磁控管输出的2.45GHz 频率的微波加热食品,在该频率上,牛排的等效复介电常数)j 3.01(40~-=rε。
求: (1)微波传入牛排的穿透深度δ,在牛排内8mm 处的微波场强是表面处的百分之几?(2)微波炉中盛牛排的盘子是发泡聚苯乙烯制成的,其等效复介电常数=r ε~ )103.0j 1(03.14-⨯-。
说明为何用微波加热时,牛排被烧熟而盘子并没有被毁。
解:(1)20.8mm m 0208.011211212==⎥⎥⎦⎤⎢⎢⎣⎡-⎪⎭⎫ ⎝⎛+==-ωεσμεωαδ%688.20/8/0===--e e E E z δ(2)发泡聚苯乙烯的穿透深度(m)1028.103.1103.01045.22103212213498⨯=⨯⨯⨯⨯⨯⨯⨯=⎪⎭⎫ ⎝⎛===-πμεωεσωμεσαδ可见其穿透深度很大,意味着微波在其中传播的热损耗极小,所以不会被烧毁。
大学物理第六章恒定磁场习题解劝答

第6章 恒定磁场1. 空间某点的磁感应强度B的方向,一般可以用下列几种办法来判断,其中哪个是错误的?( C )(A )小磁针北(N )极在该点的指向;(B )运动正电荷在该点所受最大的力与其速度的矢积的方向; (C )电流元在该点不受力的方向;(D )载流线圈稳定平衡时,磁矩在该点的指向。
2. 下列关于磁感应线的描述,哪个是正确的? ( D )(A )条形磁铁的磁感应线是从N 极到S 极的; (B )条形磁铁的磁感应线是从S 极到N 极的; (C )磁感应线是从N 极出发终止于S 极的曲线; (D )磁感应线是无头无尾的闭合曲线。
3. 磁场的高斯定理⎰⎰=⋅0S d B说明了下面的哪些叙述是正确的? ( A )a 穿入闭合曲面的磁感应线条数必然等于穿出的磁感应线条数;b 穿入闭合曲面的磁感应线条数不等于穿出的磁感应线条数;c 一根磁感应线可以终止在闭合曲面内;d 一根磁感应线可以完全处于闭合曲面内。
(A )ad ; (B )ac ; (C )cd ; (D )ab 。
4. 如图所示,在无限长载流直导线附近作一球形闭合曲面S ,当曲面S 向长直导线靠近时,穿过曲面S 的磁通量Φ和面上各点的磁感应强度B 将如何变化? ( D )(A )Φ增大,B 也增大;(B )Φ不变,B 也不变; (C )Φ增大,B 不变; (D )Φ不变,B 增大。
5. 两个载有相等电流I 的半径为R 的圆线圈一个处于水平位置,一个处于竖直位置,两个线圈的圆心重合,则在圆心o 处的磁感应强度大小为多少? ( C )(A )0; (B )R I 2/0μ;(C )R I 2/20μ; (D )R I /0μ。
6、有一无限长直流导线在空间产生磁场,在此磁场中作一个以截流导线为轴线的同轴的圆柱形闭合高斯面,则通过此闭合面的磁感应通量( A )A 、等于零B 、不一定等于零C 、为μ0ID 、为i ni q 11=∑ε7、一带电粒子垂直射入磁场B后,作周期为T 的匀速率圆周运动,若要使运动周期变为T/2,磁感应强度应变为(B )A 、B /2 B 、2BC 、BD 、–BI8 竖直向下的匀强磁场中,用细线悬挂一条水平导线。
第6章大学物理(I-1)教材课后习题答案

当 t
2
时, I i
100 0.5 0.12 20 0.987 A 100
B N 0 I , 2a
51
(2)因为圆电流在圆心处的磁场强度为
所以该感应电流在圆心 O 处的磁感应强度为
B
6.3
N 0 I 100 4 0.987 6.2 103 T 2a 2 0.1
向沿 badcb)
i
L Fm mg θ
安培力: Fm BlI i , 水平向右。安培力在斜面上 投影为
6.10 解图
BlI icos Fm
重力在斜面上投影为
B 2l 2 cos2 v R
f 下 mg sin
m dv ( Bl sin ) 2 mg sin v dt R
i
d m lI cos(t ) b 0 0 ln dt 2 a
题 6.3 解图
6.4 如题 6.4 图所示,导体棒 ab 与金属轨道 ca 和 db 接触, 整个线框放在 B 0.50 T 的均匀磁场中,磁场方向与图面垂直。 (1)若导体棒以 4.0 m s-1 的速度向右运动,求棒内感应电动 势的大小和方向; (2)若导体棒运动到某一位 置时,电路的电阻为 0.20 ,求此时棒所受 的力。摩擦力可不计。 (3)比较外力做功的功 率和电路中所消耗的热功率。 解 (1)因为回路中的磁通量为由牛顿第源自定律可得运动方程为由此可得
dv ( Bl sin ) 2 ( Bl sin ) 2 gmR sin g sin v (v ) dt mR mR ( Bl cos ) 2
dv ( Bl cos ) 2 dt gmR sin mR v ( Bl cos ) 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第六章习题答案
6-1 在空气中,均匀平面电磁波的电场强度为 y e x t E
)800cos(βω-= 波长为0.61m ,求: (1)电磁波的频率; (2)相位常数;
(3)磁场强度的振幅和方向。
解:(1)由题意知电磁波在空气中传播,所以传播速度和波阻抗分别为
m/s v 8103⨯=,Ω=377Z 0
故频率 Hz ..λv f 88
1092461
0103⨯=⨯=
= (2)相位常数
s /3rad .1061.02==
π
β (3)由图知 0
Z E
e H x
⨯=
,磁场为z 方向,其振幅为
m /12A .2377
800Z E H 0===
6-2自由空间中传播的电磁波的电场强度E 的复数形式为 m /V e e
E y x j20 π-•= (1) 求频率f 及H ,E
的瞬时表达式;
(2) 当0.025m x =时,场在何时达到最大值和零值?
(3) 若在00x x ,t t ==处场强达到最大值,现从这点向前走100m ,问在该处要过多长时间,
场强才达到最大值。
解:(1)由电场强度y e )x t (800cos E
βω-=可知,电磁波是沿x 方向传播的均匀平面电磁波,
其相位常数s /rad 20πβ=,因为是自由空间,所以
s /m 103v 8⨯=,Ω==377120Z 0π
得 98
1032103202v 2f ⨯=⨯⨯===
π
ππβπω m /V e )x 20t (cos 2)t ,x (E y
πω-=
m /A e )x 20t (cos 377
2)t ,x (H z
πω-=
其中s /rad 106010320v 8
8
⨯=⨯⨯==ππβω
x y z E
H
S
x y z E
H
S
(2)把0.025m x =代入)t ,x (E
和)t ,x (H 中,显然当
πππn 025*******cos 8=⨯-⨯).(t ),2,1,0n (⋅⋅⋅=
s 106
5
.0n t 9-⨯+=
当0)025.0201060(cos 8
=⨯-⨯ππ时,场达到零值,此时有
πππ2
1
2n )025.0201060(cos 8+=
⨯-⨯ s 106
1
n t 9-⨯+=
(3)0x x =处的电磁波向前传播100m ,所花费的时间为
s 103
1
103100v 100t 6-8⨯=⨯==
即00x x ,t t ==处的场强达到最大值,则在s 103
1
t t 60-⨯+
=,100m x x 0+=处场强也达到最大值。
6-3一信发生器在自由空间产生一均匀平面电磁波,波长为12cm ,通过理想介质后,波长减小为8cm ,在介质中电场振幅为
50V/m ,磁场振幅为0.1A/m ,求发生器的频率,介质的r ε及r μ 解:自由空间电磁波的波长f
c =
λ 所以电磁波的频率Hz 102510
12103c
f 8
2
-8⨯=⨯⨯==λ 在理想介质中电磁波的波速为
s /m 1021025108f v 882⨯=⨯⨯⨯==-λ
根据Ω====
=
5001
.050H E Z ,1
v 0εμεμ
联立求解以上两式得 13.1r =ε 99.1r =μ
6-4 据估计,晴天时太阳辐射到地球的功率为1.34 kW/m 2(对入射波而言),假设阳光为以单色平面电磁波,计算入射波中的电磁强度E max 和磁感应强度B max 解:
辐射到地球的太阳光可以看成是均匀的平面电磁波,其坡印廷矢量的平均值为
32
02av 1034.1377
E E S ⨯==Z = 2/m W
所以:
76.7101034.13773=⨯⨯=E m V / 17.100576.71022max =⨯==E E m V /
770max 0
max 0max 1050.33377
17
.1005104--⨯=⨯⨯===πμμZ E H B m A / 6-5 一频率为3 GHz ,沿y 方向极化的均匀平面电磁波,在5.2r =ε,3
1067.1-⨯=
γS/m 的非线性媒质中,沿+x 方向传播,求
(1)波的振幅衰减至原来的一半时,传播了多少距离; (2)媒质的波阻抗、波长和相速;
(3)设在x =0处,y e t E )3
106sin(509
ππ+⨯=,写出H 在任何时刻t 的瞬时表示式。
解:
这是均匀平面电磁波在导电媒质中的传播问题。
因此电磁波的瞬时表示式为
y x e x t e E E )cos(max βωα-=-
z z x e x t e H H )cos(max ϕβωα--=-
根据
11001.45
.21036131021067.13993
<<⨯=⨯⨯⨯⨯⨯⨯=---π
πωεγ知 这种非磁性材料是低损耗媒质,可以取近似计算式,所以衰减常数和相位常数分别为
2.02==
ε
μ
γ
α Np/m 35.99==μεωβ rad/m
(1) 因为波的振幅为x
m e
α-E ,衰减到该值的一半时有
21E E )(=-∆+-x
m x x m e
e αα 即21=∆-x e α 所以传播距离47.32ln 1==∆αx m (2) Ω===
44.2385
.2377
0εμZ 波长063.035.9922==
=
π
β
π
λ m 波速8109.15
.21
⨯==
=
c
v με
m/s
(2) 由x =0处y e t E )3
106sin(509
ππ+⨯=,可得任何时刻t 和任意位置x 处的电场为
y x e x t e t x E )3106sin(50),(9πβπα+-⨯=-
y x e x t e
)3
35.99106sin(5092.0ππ+-⨯=- V/m
所以磁场为
m
A e x e e x t e e Z t x E t x H z x y
x z /).sin(.)sin(.),(),(.
3
35991062103
106442385092090πππβπα+
-⨯=+-⨯==--当电磁波在低损耗媒质中传播时,
其相位常数β和波阻抗0Z 近似等于理想介质中的相位值,不同的是电磁波有衰减,但相位常数α为以实常数
6-6 有一非磁性的良导体,电磁波在其内传播的速度是自由空间光速的0.1%,波长为0.3 mm ,求材料的电导率及波的频率。
解:由题意知电磁波在该种材料中的传播速度为
s m c /103%1.0v 5⨯=⨯=
因为 f
v =
λ 所以频率Hz v
f 9
3
510103.0103=⨯⨯=
=-λ 由于该材料为非磁性的良导体,故应该有良导体的公式有
s m v /103250⨯==
γ
μω
所以62
010912⨯==
ν
μω
γ S/m 6-7 在导电媒质(物理参数为γεμ和,00)中有一向+x 方向传播的均匀平面电磁波。
(1)试决定单位体积中热功率损耗的瞬时值和平均值;
(2)决定横截面为单位面积,长度为0->∞的体积中的耗散的平均功率;
(3)决定坡印廷矢量的平均值,并计算横截面为单位面积,长度为的体积中的耗撒得平均功率;
(4)试将(2)和(3)的结果比较,以良导体为例说明两者是否相等。
解:设电磁波的场量为
y x
e x t e t x E )cos(E 2),(βωα-=- V/m
z z x
e x t He H )cos(2ϕβωα--=- A/m
导电媒质的波阻抗 z z Z ϕ∠=0 而 z
E H =
(1)导电媒质单位体积中热功率损耗的瞬时值为
)cos(2),(222
x t e E E J E t x p x βωγγα-==•=-
其平均值x
T e E dt t x p T
P αγ220),(1-==
⎰ 3/m W (3) x =0至x =∞之间单位横截面积的柱体中耗散的平均功率为
α
γ2W 2
E Pdx ==⎰
∞
(2)坡印亭矢量的平均值为
z x
av
e z
S ϕαcos H E Re 22E (-*
••
⨯=)=
⎰⎰--=-dS e z
dS S z x
av ϕαcos E 22
式中的S 为柱体的外表面积。
由于坡印亭矢量为x 方向,上式的积分在x =0和x =∞的面进行,所以
z z x
av z
e z dS S ϕϕαcos E 0x x cos E 222===∞=-⎰-
(4) 当媒质为良导体时有
45Z 0∠γωμ=
可得γ
ωμ=
z 45z =ϕ 2
ωμγ
α=
所以(2)中的耗散功率为2222E E W ωμ
γ
αγ==
(3) 中的耗散功率为222245cos cos ||E E z E dS S z av ωμ
γ
ωμγϕ===-⎰
即满足
⎰-=dS S W av。
