小学奥数几何计数
小学数学 奥数讲义计数专题:几何计数

华杯赛计数专题:几何计数基础知识:1.几何计数,从类型上看,可分为数线段、数三角形、数正方形、数长方形、数平行四边形等几类.2.几何计数的基本方法和思想:分类枚举与对应.3.分类的标准:按大小,按包含的图形等.4.常见对应方法:线段对应到端点,三角形对应到端点或边,长方形对应到对边等.5.特殊方法:去点法与去线法,本质是分类.方法铺垫:1)加法原理,乘法原理;2)容斥原理;3)排列数,组合数;4)对应法.例题:例1.如图,数一数图中有多少条线段?【答案】28(条)【解答】分类:1个单位长的线段有7条;2个单位长的线段有6条;3个单位长的线段有5条;……7个单位长的线段有1条;故共有线段7+6+5+……+1=28(条).例2.数一数,图中共有多少个三角形?【答案】13(个)【解答】分类:含有1块的三角形有4个;含有2块的三角形有5个;含有3块的三角形有2个;含有4块的三角形有1个;含有6块的三角形有1个;故共有三角形4+5+2+1+1=13(个).例3.如图,数一数,图中有多少个三角形?【答案】48(个).【解答】分类:包含1个小三角形的三角形有1+3+5+7+9=25个;包含4个小三角形的三角形有1+2+3+4+3=13个;包含9个小三角形的三角形有1+2+3=6个包含16个小三角形的三角形有1+2=3个;包含25个小三角形的三角形有1个;故共有三角形25+13+6+3+1=48(个).例4.数一数,图中共有多少个三角形?【答案】35(个)【解答】分类:含有1块的三角形有10个;含有2块的三角形有10个;含有3块的三角形有10个;含有5块的三角形有5个;故共有三角形10+10+10+5=35(个).例5.图中有多少个正方形?【答案】30(个)【解答】包含1个正方形的正方形有4×4=16个;包含4个正方形的正方形有3×3=9个;包含9个正方形的正方形有2×2=4个;包含16个正方形的正方形有1个;故共有三角形16+9+4+1=30(个).例6.如图,数一数图中一共有多少条线段?多少个矩形?【答案】70(条); 60个【解答】线段:横线,共有4×条;竖线:5×,故共有线段40+30=70条;矩形:竖线中选出两条,共有条,横线中选出两条,共有,根据乘法原理,共有矩形10矩形原60个.例7.如图,这是一个长为9,宽为4的网格,每一个小格都是一个正方形.请问:(1)从中可以数出多少个长方形?(2)从中可以数出包含红点的长方形有多少个?【答案】450(个);144个【解答】(1)竖线中选出两条,共有条,横线中选出两条,共有,根据乘法原理,共有矩形45×10=450个.(2)竖线中选出两条,共有6竖线中选出条,横线中选出两条,共有2×3=6条,根据乘法原理,共有矩形24×6=144个.例8.如图,数一数,图中共有多少个长方形?【答案】135个【解答】横向看:共有矩形个,竖向看:共有矩形个,这样重复计算了个,所以共有矩形90+63-18=135个.例9.如图,木板上钉着12枚钉子,排成三行四列的长方阵.用橡皮筋一共可以套出多少个不同的三角形?【答案】200(个)【解答】共有三角形个.例10.下图由相同的正方形和相同的等腰直角三角形构成, 则正方形的个数为多少?(17届华杯赛笔试初赛小高组第6题)【答案】83(个)【解答】包含1小个正方形的正方形有2+4+6+8+8+6+4+2=40个;包含4小个正方形的正方形有1+3+5+7+5+3+1=25个;包含9小个正方形的正方形有2+4+4+2=12个;包含16小个正方形的正方形有1+3+1=5个;共有正方形40+25+12+5+1=83个.例11. 求图中一共有多少条线段?求图中一共有多少个矩形?【答案】70条线段,60个矩形【解答】每一条线段由同一行或同一列的两个顶点确定,因此共有条线段.每个矩形由长和宽上的各一条线段对应形成,如下图:因此共有个矩形.例12. 数一数,图中有多少个三角形?【答案】78个【解答】只包含1个基本图形的有36个(朝上的21个,朝下的15个);包含4个基本图形的有21个(朝上的15个,朝下的6个);包含9个基本图形的有11个(朝上的10个,朝下的1个);包含16个基本图形的有6个;包含25个基本图形的有3个;包含36个基本图形的有1个.所以共有36+21+11+6+3+1=78个.例13. 下图是一个长为9,宽为4的长方形网格,每一个小格都是一个正方形,那么:1)从中可以数出多少个矩形?2)从中可以数出多少个正方形?3)从中可以数出包含黑点的矩形有多少个?【答案】1)450个;2)80个;3)144个【解答】1)图中共有个矩形;2)包含1个基本图形的正方形共有4×9=36个;包含4个基本图形的正方形共有3×8=24个;包含9个基本图形的正方形共有2×7=14个;包含16个基本图形的正方形共有1×6=6个.则共有36+24+14+6=80个.3)黑点左下方的顶点共有18个,黑点右上方的顶点共有8个,所以包含黑点的矩形共有18×8=144个.例14. 图中一共包含多少个矩形?【答案】135个【解答】第(1)部分和第(3)部分合并起来是一个3×5的大矩形(如下图所示),其中一共包含矩形个;第(2)部分和第(3)部分合并起来是一个6×2的大矩形(如下图所示),其中一共包含矩形个;第(3)部分中的矩形被重复计算了,其中共有矩形个.所以图中一共包含矩形90+63-18=135个.例15. 图中的木板上钉着12枚钉子,排成三行四列的长方阵. 那么用橡皮筋一共可以套出多少个不同的三角形?【答案】200个【解答】从12枚钉子中选择3枚钉子的组合总数是.而图中共有3条直线上各有4个点(如下图实线所示),另外还有8条直线上各有3个点(如下图虚线所示).因此用橡皮筋一共可以套出个不同的三角形.例16. 求图中所有矩形的面积和以及周长的总和.【答案】周长总和:1364;面积总和:1800【解答】矩形的10种长的总长是3++4++2++6++7++6++8++9++12++15=72。
五年级下册数学奥数试题——几何计数

五年级下册数学奥数试题——几何计数
第9讲几何计数
一、知识点
几何计数,就是数几何图形的个数.常用的方法是枚举法,一般要按照一定的顺序来枚举,注意寻找规律,做到不重复不遗漏.要多观察,思考,分析中总结归纳出解决问题的规律和方法.
二、典型例题
例1 下列图形中各有多少个三角形?
练习1下图中各有多少个三角形?
例2 下图中共有多少个三角形?
练习2 如图中共有多少个三角形?
例3 下列图形中,分别有多少个正方形?
练习3 围棋棋盘是由19条横线和19条竖线组成的正方形方阵,其中有多少个正方形?
例4 图中(下列各题中,长方形都包括正方形)
(1)一共有多少个长方形?
(2)包含数字“1”的长方形共有多少个?
(3)包含数字“2”的长方形共有多少个?
练习4 如图,一个长为9,宽为4的长方形网格,每一小格都是一个正方形.那么:(1)一共有多少个长方形?
(2)包含“√”的长方形有多少个?
例5 图中共有多少个长方形?(长方形包括正方形)
例6 图中有多少个平行四边形?
1
2
√。
小学六年级奥数几何计数问题专项强化训练(中难度)

小学六年级奥数几何计数问题专项强化训练(中难度)例题1:在一个正方形的边长为5cm的区域内,用红、蓝两种颜色的正方形砖头铺满,每个颜色的砖头都可以使用任意多个,要求两种颜色的砖头必须完全分开铺,且不能有重叠部分,那么一共有多少种不同的铺法?解析:首先我们知道正方形边长为5cm,正方形砖头的边长可以为1cm、2cm、3cm、4cm或5cm。
由于两种颜色的砖头必须完全分开铺,且不能有重叠部分,所以我们可以分别计算每种颜色砖头的铺法数量,然后相乘得到总的铺法数量。
对于红色砖头的铺法数量,我们可以考虑从左上角开始铺设。
当砖头的边长为1cm时,只有一种铺法。
当砖头的边长为2cm时,有两种铺法,水平或垂直放置。
当砖头的边长为3cm时,有三种铺法,水平放置、垂直放置或者斜放。
同理,当砖头的边长为4cm时,有四种铺法,水平放置、垂直放置、斜放或者两个合并一起放置。
当砖头的边长为5cm时,只有一种铺法,即整个正方形都用红色砖头铺满。
因此,红色砖头的铺法数量为1 + 2 + 3 + 4 + 1 = 11种。
同理,蓝色砖头的铺法数量也为11种。
总的铺法数量为11 * 11 = 121种。
专项练习应用题:1. 在一个正方形的边长为6cm的区域内,用红、蓝、黄三种颜色的正方形砖头铺满,每个颜色的砖头都可以使用任意多个,要求三种颜色的砖头必须完全分开铺,且不能有重叠部分,那么一共有多少种不同的铺法?2. 在一个正方形的边长为8cm的区域内,用红、蓝两种颜色的正方形砖头铺满,每个颜色的砖头都可以使用任意多个,要求两种颜色的砖头必须完全分开铺,且不能有重叠部分,那么一共有多少种不同的铺法?3. 在一个正方形的边长为10cm的区域内,用红、蓝、绿三种颜色的正方形砖头铺满,每个颜色的砖头都可以使用任意多个,要求三种颜色的砖头必须完全分开铺,且不能有重叠部分,那么一共有多少种不同的铺法?4. 在一个正方形的边长为7cm的区域内,用红、蓝两种颜色的正方形砖头铺满,每个颜色的砖头都可以使用任意多个,要求两种颜色的砖头必须完全分开铺,但可以有重叠部分,那么一共有多少种不同的铺法?5. 在一个正方形的边长为9cm的区域内,用红、蓝、绿三种颜色的正方形砖头铺满,每个颜色的砖头都可以使用任意多个,要求三种颜色的砖头必须完全分开铺,但可以有重叠部分,那么一共有多少种不同的铺法?6. 有一条长度为10cm的线段,若将其分成三段长度相等的线段,那么一共有多少种不同的分法?7. 有一条长度为12cm的线段,若将其分成四段长度相等的线段,那么一共有多少种不同的分法?8. 有一条长度为15cm的线段,若将其分成五段长度相等的线段,那么一共有多少种不同的分法?9. 有一条长度为8cm的线段,若将其分成两段长度为整数的线段,且这两段线段的长度之差为1cm,那么一共有多少种不同的分法?10. 有一条长度为11cm的线段,若将其分成三段长度为整数的线段,且这三段线段的长度之差为1cm,那么一共有多少种不同的分法?11. 有一条长度为14cm的线段,若将其分成四段长度为整数的线段,且这四段线段的长度之差为1cm,那么一共有多少种不同的分法?12. 在一个正方形的边长为4cm的区域内,用红、蓝两种颜色的正方形砖头铺满,每个颜色的砖头都可以使用任意多个,要求两种颜色的砖头可以重叠铺,那么一共有多少种不同的铺法?13. 在一个正方形的边长为6cm的区域内,用红、蓝、黄三种颜色的正方形砖头铺满,每个颜色的砖头都可以使用任意多个,要求三种颜色的砖头可以重叠铺,那么一共有多少种不同的铺法?14. 在一个正方形的边长为9cm的区域内,用红、蓝、绿三种颜色的正方形砖头铺满,每个颜色的砖头都可以使用任意多个,要求三种颜色的砖头可以重叠铺,那么一共有多少种不同的铺法?15.在一个正方形的边长为5cm的区域内,用红、蓝、黄、绿四种颜色的正方形砖头铺满,每个颜色的砖头都可以使用任意多个,要求四种颜色的砖头可以重叠铺,那么一共有多少种不同的铺法?例题2:题目:在一个正方形格子图中,每个格子都填上了数字0或1,使得每行每列的数字和都为偶数。
小学奥数教程之-几何计数(三)教师版 (162) 全国通用(含答案)

1.掌握计数常用方法;2.熟记一些计数公式及其推导方法;3.根据不同题目灵活运用计数方法进行计数.本讲主要介绍了计数的常用方法枚举法、标数法、树形图法、插板法、对应法等,并渗透分类计数和用容斥原理的计数思想.一、几何计数在几何图形中,有许多有趣的计数问题,如计算线段的条数,满足某种条件的三角形的个数,若干个图分平面所成的区域数等等.这类问题看起来似乎没有什么规律可循,但是通过认真分析,还是可以找到一些处理方法的.常用的方法有枚举法、加法原理和乘法原理法以及递推法等.n 条直线最多将平面分成21223(2)2n n n ++++=++……个部分;n 个圆最多分平面的部分数为n (n -1)+2;n 个三角形将平面最多分成3n (n -1)+2部分;n 个四边形将平面最多分成4n (n -1)+2部分……在其它计数问题中,也经常用到枚举法、加法原理和乘法原理法以及递推法等.解题时需要仔细审题、综合所学知识点逐步求解.排列问题不仅与参加排列的事物有关,而且与各事物所在的先后顺序有关;组合问题与各事物所在的先后顺序无关,只与这两个组合中的元素有关.二、几何计数分类数线段:如果一条线段上有n +1个点(包括两个端点)(或含有n 个“基本线段”),那么这n +1个点把这条线段一共分成的线段总数为n +(n -1)+…+2+1条数角:数角与数线段相似,线段图形中的点类似于角图形中的边. 数三角形:可用数线段的方法数如右图所示的三角形(对应法),因为DE 上有15条线段,每条线段的两端点与点A 相连,可构成一个三角形,共有15个三角形,同样一边在BC 上的三角形也有15个,所以图中共有30个三角形.ED CBA数长方形、平行四边形和正方形:一般的,对于任意长方形(平行四边形),若其横边上共有n 条线段,纵边上共有m 条线段,则图中共有长方形(平行四边形)mn 个.模块一、立体几何计数【例 1】 用同样大小的正方体小木块堆成如下图的立体图形,那么一共用了__________块小正方体。
四年级奥数—几何中的计数问题
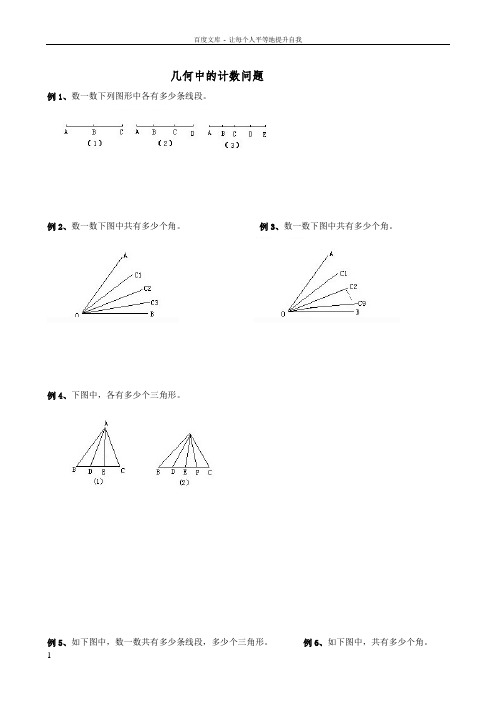
几何中的计数问题
例1、数一数下列图形中各有多少条线段。
例2、数一数下图中共有多少个角。
例3、数一数下图中共有多少个角。
例4、下图中,各有多少个三角形。
例5、如下图中,数一数共有多少条线段,多少个三角形。
例6、如下图中,共有多少个角。
例7、如下图,数一数共有多少个长方形。
例8、数一数下图中长方形的个数。
例9、数一数下面各图中所有正方形的个数。
例10、数一数下图中有多少个正方形。
例11、数一数下图三角形的个数。
例12、数一数下图中三角形的个数。
例13、数一数下图中三角形的个数。
例14、数一数下图中三角形的个数。
练:1、数一数下面各图中有多少条线段。
2、数一数下面各图中有多少个角。
3、数一数下面各图中,各有多少条线段。
4、数一数下面各图中,各有多少条线段,各有多少个三角形。
5、下面图中有多少个正方形。
6、下图中有多少个长方形。
7、下图中有多少个三角形。
8、下图中有多少个长方形。
9、下图中各有多少个三角形。
小学奥数 几何计数(三) 精选练习例题 含答案解析(附知识点拨及考点)

1.掌握计数常用方法;2.熟记一些计数公式及其推导方法;3.根据不同题目灵活运用计数方法进行计数.本讲主要介绍了计数的常用方法枚举法、标数法、树形图法、插板法、对应法等,并渗透分类计数和用容斥原理的计数思想.一、几何计数在几何图形中,有许多有趣的计数问题,如计算线段的条数,满足某种条件的三角形的个数,若干个图分平面所成的区域数等等.这类问题看起来似乎没有什么规律可循,但是通过认真分析,还是可以找到一些处理方法的.常用的方法有枚举法、加法原理和乘法原理法以及递推法等.n 条直线最多将平面分成21223(2)2n n n ++++=++……个部分;n 个圆最多分平面的部分数为n (n -1)+2;n 个三角形将平面最多分成3n (n -1)+2部分;n 个四边形将平面最多分成4n (n -1)+2部分……在其它计数问题中,也经常用到枚举法、加法原理和乘法原理法以及递推法等.解题时需要仔细审题、综合所学知识点逐步求解.排列问题不仅与参加排列的事物有关,而且与各事物所在的先后顺序有关;组合问题与各事物所在的先后顺序无关,只与这两个组合中的元素有关.二、几何计数分类数线段:如果一条线段上有n +1个点(包括两个端点)(或含有n 个“基本线段”),那么这n +1个点把这条线段一共分成的线段总数为n +(n -1)+…+2+1条数角:数角与数线段相似,线段图形中的点类似于角图形中的边.数三角形:可用数线段的方法数如右图所示的三角形(对应法),因为DE 上有15条线段,每条线段的两端点与点A 相连,可构成一个三角形,共有15个三角形,同样一边在BC 上的三角形也有15个,所以图中共有30个三角形.ED CBA数长方形、平行四边形和正方形:一般的,对于任意长方形(平行四边形),若其横边上共有n 条线段,纵边上共有m 条线段,则图中共有长方形(平行四边形)mn 个.模块一、立体几何计数【例 1】 用同样大小的正方体小木块堆成如下图的立体图形,那么一共用了__________块小正方体。
(小学奥数)几何计数(三)

1.掌握計數常用方法;2.熟記一些計數公式及其推導方法;3.根據不同題目靈活運用計數方法進行計數.本講主要介紹了計數的常用方法枚舉法、標數法、樹狀圖法、插板法、對應法等,並滲透分類計數和用容斥原理的計數思想.一、幾何計數在幾何圖形中,有許多有趣的計數問題,如計算線段的條數,滿足某種條件的三角形的個數,若干個圖分平面所成的區域數等等.這類問題看起來似乎沒有什麼規律可循,但是通過認真分析,還是可以找到一些處理方法的.常用的方法有枚舉法、加法原理和乘法原理法以及遞推法等.n 條直線最多將平面分成21223(2)2n n n ++++=++……個部分;n 個圓最多分平面的部分數為n (n -1)+2;n 個三角形將平面最多分成3n (n -1)+2部分;n 個四邊形將平面最多分成4n (n -1)+2部分……在其他計數問題中,也經常用到枚舉法、加法原理和乘法原理法以及遞推法等.解題時需要仔細審題、綜合所學知識點逐步求解.排列問題不僅與參加排列的事物有關,而且與各事物所在的先後順序有關;組合問題與各事物所在的先後順序無關,只與這兩個組合中的元素有關.二、幾何計數分類數線段:如果一條線段上有n +1個點(包括兩個端點)(或含有n 個“基本線段”),那麼這n +1個點把這條線段一共分成的線段總數為n +(n -1)+…+2+1條數角:數角與數線段相似,線段圖形中的點類似於角圖形中的邊.數三角形:可用數線段的方法數如右圖所示的三角形(對應法),因為DE 上有15條線段,每條線段的兩端點與點A 相連,可構成一個三角形,共有15個三角形,同樣一邊在BC 上的三角形也有15個,所以圖中共有30個三角形.E DCB A數長方形、平行四邊形和正方形:一般的,對於任意長方形(平行四邊形),教學目標知識要點7-8-3.幾何計數(三)若其橫邊上共有n 條線段,縱邊上共有m 條線段,則圖中共有長方形(平行四邊形)mn 個.模組一、立體幾何計數【例 1】 用同樣大小的正方體小木塊堆成如下圖的立體圖形,那麼一共用了__________塊小正方體。
小学数学 奥数讲义计数专题几何计数

小学数学奥数讲义计数专题几何计数小学数学奥数讲义计数专题几何计数在小学数学的教学中,奥数讲义是一本非常重要的学习资料。
其中计数专题是数学学习的基础,也是几何计数的重要内容之一。
本文将对小学数学奥数讲义中的几何计数进行详细介绍。
一、几何计数的概念几何计数是指通过观察几何形状,根据一定的规律和方法进行计数的过程。
它主要包括图形的边数、顶点数和对称性等方面的计数。
二、图形的边数的计数计算图形的边数是几何计数的重要内容之一。
对于任何一条直线,它没有边,因为它是无限长的。
对于一个封闭的图形,它的边数等于它的边界线的线段数。
例如,一个三角形有三条边,一个正方形有四条边。
三、图形的顶点数的计数计算图形的顶点数也是几何计数的重要内容之一。
顶点是指图形的两条边交汇的点。
对于一个封闭图形,它的顶点数等于它的边界线上的交点数加上中心点(如果存在的话)。
例如,一个三角形有三个顶点,一个正方形有四个顶点。
四、图形的对称性的计数计算图形的对称性也是几何计数中的重要内容。
对称性是指图形的某一部分与另一部分关于某个轴线对称,这个轴线称为对称轴。
对称轴的数量可以通过观察图形的特点来确定。
例如,一个正方形有四条对称轴,分别是两条对角线和两条垂直于边的中垂线。
五、实例演示为了更好地理解几何计数的概念和方法,我们举一个实例来演示。
假设有一个五角星形的图形,我们来计算它的边数、顶点数和对称性。
首先,观察图形,我们可以看到它有五条边,所以边数为5。
接下来,我们继续观察图形,可以看到它有五个顶点,所以顶点数为5。
最后,我们观察图形的对称性。
五角星形图形有五条对称轴,分别是五条连结顶点的线段。
六、总结通过以上的介绍和实例演示,我们了解了几何计数在小学数学奥数讲义中的重要性。
几何计数包括图形的边数、顶点数和对称性等内容,通过观察和计数,我们可以更深入地理解图形的特点和性质。
在小学数学教学中,几何计数是培养学生观察、分析和计算能力的一种重要方法。
小学奥数全国推荐四年级奥数通用学案附带练习题解析答案33几何计数(一)

年级四年级学科奥数版本通用版课程标题几何计数(一)在几何中,有许多有趣的计数问题,如计算线段的条数,满足某种条件的三角形的个数,若干个图分平面所成的区域数等等。
这类问题看起来似乎没有什么规律可循,但是通过认真分析,还是可以找到一些处理方法的。
通常采用一种简单原始的计数方法——枚举法。
具体而言,它是指把所要计数的对象一一列举出来,以保证枚举时无一重复、无一遗漏,然后计算其总数。
我们把直线上两点间的部分称为线段,这两个点称为线段的端点。
线段是组成三角形、正方形、长方形、多边形等图形最基本的元素。
因此,观察图形中的线段,探寻线段与线段之间、线段与其他图形之间的联系,对于了解图形、分析图形是很重要的。
数线段:如果一条线段上有n+1个点(包括两个端点)(或含有n条“基本线段”),那么这n+1个点把这条线段一共分成的线段总数为n+(n-1)+…+2+1条。
数角:数角与数线段相似,线段图形中的点类似于角图形中的边。
数三角形:可用数线段的方法(对应法)数如图所示的三角形,因为DE上有15条线段,每条线段的两端点与点A相连,可构成一个三角形,共有15个三角形。
同样一边在BC 上构成的三角形也有15个,所以图中共有30个三角形。
例1数出下图中有多少条线段。
A B CD分析与解:方法一:我们可以采用以线段左端点分类来数的方法。
以A点为左端点的线段有:AB、AC、AD 3条;以B点为左端点的线段有:BC、BD 2条;以C点为左端点的线段有:CD 1条。
所以,图中共有线段3+2+1=6(条)。
方法二:把图中线段AB、BC、CD看做基本线段来数,那么,由1条基本线段构成的线段有:AB、BC、CD 3条;由2条基本线段构成的线段有:AC、BD 2条;由3条基本线段构成的线段有:AD 1条。
所以,图中一共有3+2+1=6(条)线段。
例2 数出下图中总共有多少个角。
分析与解:在∠AOB 内有三条角分线1OC 、2OC 、3OC ,∠AOB 被这三条角分线分成4个基本角,那么∠AOB 内总共有多少个角呢?首先有OB C OC C OC C AOC 332211∠∠∠∠、、、这4个基本角,其次是由2个基本角组成的角有3个(即∠2AOC 、∠31OC C 、∠OB C 2),然后是由3个基本角组成的角有2个(即∠3AOC 、∠OB C 1),最后是由4个基本角组成的角有1个(即∠AOB ),所以∠AOB 内总共有角:4+3+2+1=10(个)。
小学奥林匹克数学 竞赛数学 五年级 第6讲-几何计数

第6讲几何计数【例1】导引拓展篇第1题如图,数一数,图中有多少个三角形?包含1个小三角形的有25个包含4个小三角形的有13个包含9个小三角形的有6个包含16个小三角形的有3个包含25个小三角形的有1个++++=所以共有个251363148按照顺序数出图形个数【例2】导引拓展篇第2题数一数,两个图形中分别有多少个三角形?包含1块的三角形有5个;包含2块的三角形有4个;包含3块的三角形有1个;包含4块的三角形有1个;没有5块和6块的三角形;包含7块的大三角形1个;因此所有三角形一共有++++=5411112【例2】导引拓展篇第2题数一数,两个图形中分别有多少个三角形? 共有12个三角形 增加10个三角形 增加10个三角形因此原图中共有个三角形. B C BA DEF12101032++=【例3】导引拓展篇第3题数一数下面的三个图形中分别有多少个三角形.整个五边形被分成了11块由1块构成的三角形有10个;由2块构成的三角形是10个;由3块构成的三角形共10个;由5块构成的三角形有5个.共有10+10+10+5=35个三角形。
【例3】导引拓展篇第3题数一数下面的三个图形中分别有多少个三角形.加上虚线就加上6个三角形变成35个三角形原图共有35-6=29个三角形【例3】导引拓展篇第3题AB C增加了一条线段AC以AB为边增加三角形有4个,以BC为边增加三角形有2个,以AC为边增加三角形有6个,共增加12个共有35+12=47个三角形数一数下面的三个图形中分别有多少个三角形.【例4】导引拓展篇第4题数一数,图中有多少个三角形?两个部分中各有35个三角形第一种有10个第二种有5个原图中共有35×2+10+5=85个三角形【例5】导引拓展篇第5题数一数图中共有多少个长方形?(正方形是特殊长方形)由1块组成的长方形共有7个由2块组成的长方形共有4个由3块组成的长方形共有2个由4块组成的长方形有1个由5块组成的长方形有1个由6块组成的长方形有1个由7块组成的长方形有1个图中共有长方形7+4+2+1+1+1+1=17个【例6】导引拓展篇第5题如图所示的一个大菱形,那么图中共能数出多少个菱形?设最小的菱形边长为1边长为1的菱形共有4×4=16个边长为2的菱形共有3×3=9个边长为3的菱形共有2×2=4个边长为4的菱形有1×1=1个菱形共有16+9+4+1=30个2212+(⋅⋅⋅⋅⋅⋅)1-nn++【例7】导引拓展篇第7题这是一个长为9,宽为4的长方形网格,每一个小格都是一个正方形.请问:(1)从中可以数出多少个长方形?(2)包含黑点的长方形有多少个?(1)从5条横线中取2条横线共有种方法从10条竖线中取2条竖线共有中方法图中共有长方形 22510450C C ⨯=(2)黑点上面有2条横线,下面有3条横线所以有2×3=6种取法左边有6条竖线,右边有4条竖线 所以又4×6=24种取法 共有6×24=144个含黑点的长方形 21n 21m C C ++⨯m ×n 个网格中有 个长方形【例8】导引拓展篇第8题数一数,图中共有多少个长方形?左边阴影一共有长方形个 右方阴影一共有长方形个 被重复计算有个 图中一共包含长方形90+63-18=135个224690C C ⨯=227363C C ⨯=224318C C ⨯=【例9】导引拓展篇第9题图中共有多少个平行四边形?尖朝右、尖朝左和尖朝上三种最小的平行四边形有6个两个小平行四边形拼成的有6个三个小平行四边形拼成的有2个四个小平行四边形拼成的有1个共15个有15×3=45个平行四边形【例10】导引拓展篇第10题18个大小相同的小正三角形拼成了一个平行四边形.数一数,图中共有多少个梯形?左上右下的斜线、左下右上的斜线和竖线三种左上右下:6×3+4=22个梯形左下右上: 6×3+4=22个梯形竖线梯形:5×2+2=12个所以共有22+22+12=56个梯形【例11】导引拓展篇第11题木板上钉着12枚钉子,排成三行四列的长方阵.用橡皮筋一共可以套出多少个不同的三角形?三角形由不在同一直线的三点组的 从12个点中任意选择3个点有 共线三点组共有12+8=20个 所以共有220-20=200个三角形220C 312【例12】导引拓展篇第12题方格纸上放了20枚棋子,以棋子为顶点,可以连出多少正方形?最小方格有9个小正方形小正方形个数有4个小正方形个数有2个小正方形个数有4个小正方形个数有2个一共有9+4+2+4+2=21个【例13】导引拓展篇第13题图中,共有多少个不同的曲边形?中间是1个五角星,边上是5个小块1个小块:5+5=10个曲边型2个小块: 3个小块: 4个小块: 5个小块:1个共有10+10+10+5+1=36个曲边型10C 25=10C 35=5C 45=【例14】导引拓展篇第14题一个2×3的网格中,每个小正方形的面积都是1.那么以格点为顶点,可以连成多少个面积为1的三角形?底是2高是1、底是1高是2底是2高是1: 底是1高是2: 底是1高是2又是底是2高是1:直角三角形重复 重复直角三角形为1×2直角三角形1×2的长方形中由4个这样的直角三角形 重复共有4×7=28种面积为1的三角形共有:50+48-28=70种4×2 +4×2×2 +4×2 +9×2 =50种 3×4×2 +2×3×4 =48种本讲知识点汇总一、按照顺序数出图形个数二、m ×n 的方格中长方形的个数为 三、正方形以及菱形的个数为 四、可以通过对称或者图形相似简化计数过程21n 21m C C ++⨯22211-n n ++)+(⋅⋅⋅⋅⋅⋅下节课见!。
小学奥数知识体系之几何计数-四五年级组

几何计数几何计数分类数线段:如果一条线段上有n+1个点(包括两个端点)(或含有n个“基本线段”),那么这n+1个点把这条线段一共分成的线段总数为n+(n-1)+…+2+1条数角:数角与数线段相似,线段图形中的点类似于角图形中的边.数三角形:可用数线段的方法数如右图所示的三角形(对应法),因为DE上有15条线段,每条线段的两端点与点A相连,可构成一个三角形,共有15个三角形,同样一边在BC上的三角形也有15个,所以图中共有30个三角形.数长方形、平行四边形和正方形:一般的,对于任意长方形(平行四边形),若其横边上共有n条线段,纵边上共有m条线段,则图中共有长方形(平行四边形)mn个.【例1】数出右图中有多少条线段练习1:数出右图中有多少个锐角练习2:数一数下面图中各有多少个三角形。
练习3:从上海至青岛的某次直快列车,中途要停靠6个大站,这次列车有几种不同票价?【例题2】数一数,下图中有多少个正方形?(每个小方格是边长为1的正方形)练习1:下图中共有____个正方形.练习2:图中有______个正方形.【例3】下面的55⨯和64⨯图中共有____个正方形.练习1:在图中(单位:厘米): ①一共有几个长方形?②所有这些长方形面积的和是多少?练习2:如图,其中的每条线段都是水平的或竖直的,边界上各条线段的长度依次为5厘米、7厘米、9厘米、2厘米和4 厘米、6厘米、5厘米、1厘米.求图中长方形的个数,以及所有长方形面积的和.【例4】如图,其中同时包括两个☆的长方形有 个.练习1:在下图中,不包含☆的长方形有________个.(6级)练习2:图中含有“※”的长方形总共有________个.(6级)练习3:由20个边长为1的小正方形拼成一个45 长方形中有一格有“☆”图中含有“☆”的所有长方形(含正方形)共有 个,它们的面积总和是 . (第六届走美决赛试题)作业题:1:如图是由18个大小相同的小正三角形拼成的四边形.其中某些相邻的小正三角形可以拼成较大的正三角形若干个.那么,图中包含“*”号的大、小正三角形一共有______个.※※*2:如图AB,CD,EF,MN互相平行,则图中梯形个数与三角形个数的差是多少?3:图中共有多少个三角形?4:下图中的正方形被分成9个相同的小正方形,它们一共有16个顶点(共同的顶点算一个),以其中不在一条直线上的3个点为顶点,可以构成三角形.在这些三角形中,与阴影三角形有同样大小面积的有多少个?。
四年级奥数-几何计数

【例1补充】(★★★) 下图中可以数出多少个三角形?
【例2】 (★★★) 如图,木板上钉着20个钉子,形成4行5列的正方形钉阵。那么橡皮筋 如图 木板上钉着20个钉子 形成4行5列的正方形钉阵 那么橡皮筋 一共能套出 个正方形。
【例3】 (★★★) 如图,用9枚钉子钉成水平和竖直间隔都为1的正方阵。用一根橡皮筋 将3枚不共线的钉子连接起来就形成一个三角形。其中面积为1的三角 形有多少个?
【例2补充】(★★★★) 下图的点可以连成多少个正方形?
1
【例4】 (★★) 在4×6的方格表中可以数出多少个长方形?多少个正方形?
【例5】 (★★) 在5×6的方格表中可以数出多少个如图所示的“ T ”字形?(“T”字 形可旋转)
【例6】 (★★★) 下图中包含★的长方形共有多少个? ★
【例7】 (★★★★) 在下图中只包含一个★的长方形有多 少个? ★ ★
2
五年级高斯奥数之几何计数含答案

第6讲几何计数内容概述合理使用各种已学的计数方法来解决几何计数问题;学会利用图形的位置和形状进行恰当的分类;掌握方格表中长方形个数的计算方法;注意利用图形的对称性来简化计算.典型问题兴趣篇1.如图10-1,线段AB、BC、CD、DE的长度都是3厘米.请问:图中一共有多少条线段?这些线段的长度之和是多少厘米?2.小明把巧克力棒摆成了如图10-2所示的形状,其中每一条小短边代表一个巧克力棒.请问:(1)一共有多少个巧克力棒?(2)这些巧克力棒共构成了多少个三角形?(3)嘴馋的小明吃掉一个巧克力棒后(图中两端带有箭头的小边),剩下的图形中还有多少个三角形?3.如图10-3,它是由18个大小相同的小正三角形拼成的四边形,其中某些相邻的小正三角形可以拼成较大的正三角形,图中包含“冰”的各种大小的正三角形一共有多少个?4.如图104和10-5,数一数,两个图形中分别有多少个三角形?5.如图10-6,在一个4x4的方格表中,共有多少个正方形?6.如图10-7,数一数图中一共有多少条线段?多少个矩形?7.如图10-8,AB、CD、EF、MN互相平行,则图中梯形个数与三角形个数的差是多少?8.如图10-9,125个黑色与白色小立方体相间排列拼成了一个大立方体,其中露在表面上的黑色小立方体有多少个?9.如图10-10,木板上钉着12枚钉子,排成三行四列的长方阵.用橡皮筋一共可以套出多少个不同的三角形?10.如图10-11,在2x3的长方形中,每个小正方形的面积都是1.请问:以A、B、C、D、E、,、G为顶点且面积为1的三角形共有多少个?拓展篇1.如图10-12,数一数,图中有多少个三角形?2.如图10-13,数一数下面的三个图形中分别有多少个三角形.3.如图10-14,数一数,图中有多少个三角形?4.如图10-15,数一数.,图中共有多少个长方形?(正方形是一种特殊的长方形)5.如图10-16,四条边长度都相等的四边形称为菱形,用16个同样大小的菱形组成如图的一个大菱形.数一数,图中共有多少个菱形?6.如图10-17,这是一个长为9,宽为4的网格,每一个小格都是一个正方形.请问:(1)从中可以数出多少个长方形?(2)从中可以数出包含黑点的长方形有多少个?7.如图10-18,数一数,图中共有多少个长方形?8.如图10-19,数一数,图中共有多少个平行四边形?9.如图10-20,18个大小相同的小正三角形拼成了一个平行四边形,数一数,图中共有多少个梯形?10.如图10-21,方格纸上放了20枚棋子,以这些棋子为顶点,可以连出多少个正方形?11.一个平面封闭图形,只要组成它的边中有一条边不是直线段,就将这个图形称为曲边形,例如圆、半圆、扇形等都是曲边形.在图10-22中,共有多少个不同的曲边形?12.如图10-23,一个2×3的网格中,每个小正方形的面积都是1.以这些格点为顶点,可以连成多少个面积为l的三角形?超越篇1.图10-24是一个等边三角形的点阵.以这些点为顶点,可以画出多少个等腰三角形(包括等边三角形)?2.如图10-25,数一数,图中共有多少个三角形?3.如图10-26,这是一个4x8的矩形网格,每一个小格都是一个正方形.请问:(1)包含有两个“★”的矩形共有多少个?(2)至少包含一个“★”的矩形有多少个?4.如图10-27,在图中的3×3正方形格子中,格线的交点称为格点.例如:A,B,C这3个点都是格点,那么,以格点为顶点,且完全覆盖了阴影部分小方格的三角形共有多少个?5.如图10-28,用12个点将圆周12等分,以这些点为顶点的梯形共有多少个?6.一个平面封闭图形,只要组成它的边中有一条边不是直线段,就将这个图形称为曲边形,例如圆、半圆、扇形等都是曲边形,在图10-29中,共有多少个不同的曲边形?7.如图10-30,木板上钉着16枚钉子,排成四行四列的方阵.用橡皮筋一共可以套出多少个不同的等腰三角形?8.如图10-31,在3×3的方格表内,每个小正方形的面积均为1.请问:(1)以格点为顶点共可以连出多少个面积为4的三角形?(2)以格点为顶点共可以连出多少个面积为3的三角形?(3)以格点为顶点共可以连出多少个面积为1.5的三角形?第10讲几何计数内容概述合理使用各种已学的计数方法来解决几何计数问题;学会利用图形的位置和形状进行恰当的分类;掌握方格表中长方形个数的计算方法;注意利用图形的对称性来简化计算.典型问题兴趣篇1.如图10-1,线段AB、BC、CD、DE的长度都是3厘米.请问:图中一共有多少条线段?这些线段的长度之和是多少厘米?解:1,4+3+2+1=10段2,4×1+3×2+2×3+1×4=20厘米2.小明把巧克力棒摆成了如图10-2所示的形状,其中每一条小短边代表一个巧克力棒.请问:(1)一共有多少个巧克力棒?(2)这些巧克力棒共构成了多少个三角形?(3)嘴馋的小明吃掉一个巧克力棒后(图中两端带有箭头的小边),剩下的图形中还有多少个三角形?解:1,(1+2+3+4)×3=30根2,(1+3+5+7)+(1+2+3+1)+(1+2)+1=27个3,27-2-2-1=22个3.如图10-3,它是由18个大小相同的小正三角形拼成的四边形,其中某些相邻的小正三角形可以拼成较大的正三角形,图中包含“冰”的各种大小的正三角形一共有多少个?解:1+4+1=6个4.如图104和10-5,数一数,两个图形中分别有多少个三角形?解:5+4+1+1+1=12个6×2+10×2=28个5.如图10-6,在一个4x4的方格表中,共有多少个正方形?解:42+32+22+12=30个6.如图10-7,数一数图中一共有多少条线段?多少个矩形?解:C53×4+C42×5=70条C52×C42=60个7.如图10-8,AB、CD、EF、MN互相平行,则图中梯形个数与三角形个数的差是多少?解:C52×C42-C52×4=208.如图10-9,125个黑色与白色小立方体相间排列拼成了一个大立方体,其中露在表面上的黑色小立方体有多少个?解:4×6+2×12=48个9.如图10-10,木板上钉着12枚钉子,排成三行四列的长方阵.用橡皮筋一共可以套出多少个不同的三角形?解:C123-4×3-4-4=200个10.如图10-11,在2x3的长方形中,每个小正方形的面积都是1.请问:以A、B、C、D、E、F、G为顶点且面积为1的三角形共有多少个?解:3×2+4+2+1=13个拓展篇1.如图10-12,数一数,图中有多少个三角形?解:25+10+6+3+1+3=48个2.如图10-13,数一数下面的三个图形中分别有多少个三角形.解:10+4×5+5=35个35-6=29个35+6×2=47个3.如图10-14,数一数,图中有多少个三角形?解:35×2+3×5=85个4.如图10-15,数一数.,图中共有多少个长方形?(正方形是一种特殊的长方形)解:7+2+2+2+3+1=17个5.如图10-16,四条边长度都相等的四边形称为菱形,用16个同样大小的菱形组成如图的一个大菱形.数一数,图中共有多少个菱形?解:4×4+3×3+2×2+1×1=30个6.如图10-17,这是一个长为9,宽为4的网格,每一个小格都是一个正方形.请问:(1)从中可以数出多少个长方形?(2)从中可以数出包含黑点的长方形有多少个?解:C102×C52=450个2×3×4×6=144个7.如图10-18,数一数,图中共有多少个长方形?解:15×6+21×3-6×3=135个8.如图10-19,数一数,图中共有多少个平行四边形?解:6×3+15+3×2+3+3=45个9.如图10-20,18个大小相同的小正三角形拼成了一个平行四边形,数一数,图中共有多少个梯形?解12×2+4×2+6×2+2+8+2=5610.如图10-21,方格纸上放了20枚棋子,以这些棋子为顶点,可以连出多少个正方形?解:9+4×2+2×2=21个11.一个平面封闭图形,只要组成它的边中有一条边不是直线段,就将这个图形称为曲边形,例如圆、半圆、扇形等都是曲边形.在图10-22中,共有多少个不同的曲边形?解:10+10+10+5+1=36个12.如图10-23,一个2×3的网格中,每个小正方形的面积都是1.以这些格点为顶点,可以连成多少个面积为l的三角形?解:6×7+8×2+8+4=70个超越篇1.图10-24是一个等边三角形的点阵.以这些点为顶点,可以画出多少个等腰三角形(包括等边三角形)?解:等边有:9+3+1+2=15个等腰有:3+2×6+6+3=24个共39个2.如图10-25,数一数,图中共有多少个三角形?解:C72×2+C31×2×4+1=67个3.如图10-26,这是一个4x8的矩形网格,每一个小格都是一个正方形.请问:(1)包含有两个“★”的矩形共有多少个?(2)至少包含一个“★”的矩形有多少个?解:2×1×3×5=30个3×4×6+4×2×5×3-3×2×5=162个4.如图10-27,在图中的3×3正方形格子中,格线的交点称为格点.例如:A,B,C这3个点都是格点,那么,以格点为顶点,且完全覆盖了阴影部分小方格的三角形共有多少个?解:4×4=16个5.如图10-28,用12个点将圆周12等分,以这些点为顶点的梯形共有多少个?解:12×(4+3+2+1)=120个6.一个平面封闭图形,只要组成它的边中有一条边不是直线段,就将这个图形称为曲边形,例如圆、半圆、扇形等都是曲边形,在图10-29中,共有多少个不同的曲边形?解:4×8+4×4+2×3+4×2+1=63个7.如图10-30,木板上钉着16枚钉子,排成四行四列的方阵.用橡皮筋一共可以套出多少个不同的等腰三角形?解:4×6+8×(3+1+3+1)+4×(3+3+2+5+2)=148个8.如图10-31,在3×3的方格表内,每个小正方形的面积均为1.请问:(1)以格点为顶点共可以连出多少个面积为4的三角形?(2)以格点为顶点共可以连出多少个面积为3的三角形?(3)以格点为顶点共可以连出多少个面积为1.5的三角形?解:(1)4个(2)4×10+2×4=48个(3)6×8+4×4+8+4×4+4=92个。
小学奥数 几何计数(二) 精选练习例题 含答案解析(附知识点拨及考点)

1.掌握计数常用方法;2.熟记一些计数公式及其推导方法;3.根据不同题目灵活运用计数方法进行计数.本讲主要介绍了计数的常用方法枚举法、标数法、树形图法、插板法、对应法等,并渗透分类计数和用容斥原理的计数思想.一、几何计数在几何图形中,有许多有趣的计数问题,如计算线段的条数,满足某种条件的三角形的个数,若干个图分平面所成的区域数等等.这类问题看起来似乎没有什么规律可循,但是通过认真分析,还是可以找到一些处理方法的.常用的方法有枚举法、加法原理和乘法原理法以及递推法等.n 条直线最多将平面分成21223(2)2n n n ++++=++……个部分;n 个圆最多分平面的部分数为n (n -1)+2;n 个三角形将平面最多分成3n (n -1)+2部分;n 个四边形将平面最多分成4n (n -1)+2部分……在其它计数问题中,也经常用到枚举法、加法原理和乘法原理法以及递推法等.解题时需要仔细审题、综合所学知识点逐步求解.排列问题不仅与参加排列的事物有关,而且与各事物所在的先后顺序有关;组合问题与各事物所在的先后顺序无关,只与这两个组合中的元素有关.二、几何计数分类数线段:如果一条线段上有n +1个点(包括两个端点)(或含有n 个“基本线段”),那么这n +1个点把这条线段一共分成的线段总数为n +(n -1)+…+2+1条数角:数角与数线段相似,线段图形中的点类似于角图形中的边.数三角形:可用数线段的方法数如右图所示的三角形(对应法),因为DE 上有15条线段,每条线段的两端点与点A 相连,可构成一个三角形,共有15个三角形,同样一边在BC 上的三角形也有15个,所以图中共有30个三角形.ED CBA数长方形、平行四边形和正方形:一般的,对于任意长方形(平行四边形),若其横边上共有n 条线段,纵边上共有m 条线段,则图中共有长方形(平行四边形)mn 个.教学目标知识要点7-8-2.几何计数(二)例题精讲模块二、复杂的几何计数【例1】如下图在钉子板上有16个点,每相邻的两个点之间距离都相等,用绳子在上面围正方形,你可以得到个正方形.【考点】复杂的几何计数【难度】4星【题型】填空【关键词】学而思杯,2年级,第4题【解析】先看横着的正方形如下图⑴,可以得到94114++=个正方形,再看斜着的正方形如下图⑵可以得到4个正方形,如下图⑶可以得到2个正方形.这样一共可以得到144220++=个正方形.⑴⑵⑶<考点> 图形计数【答案】20个【巩固】如图,44⨯的方格纸上放了16枚棋子,以棋子为顶点的正方形有个.【解析】根据正方形的大小,分类数正方形.共能组成五种大小不同的正方形(如右图).⨯的正方形:1个;⨯的正方形:4个;33⨯的正方形:9个;2211以11⨯正方形对角线为边长的正方形:4个;以12⨯长方形对角线为边长的正方形:2个.故可以组成9414220++++=(个)正方形.【巩固】下图是3×3点阵,同一行(列)相邻两个点的距离均为1。
小学奥数几何中的计数问题

小学奥数几何中的计数问题数长方形例1如下图,数一数下列各图中长方形的个数?分析:图(Ⅰ)中长方形的个数与AB边上所分成的线段的条数有关,每一条线段对应一个长方形,所以长方形的个数等于AB边上线段的条数,即长方形个数为:4+3+2+1=10(个).图(Ⅱ)中AB边上共有线段4+3+2+1=10条. BC边上共有线段:2+1=3(条),把AB上的每一条线段作为长,BC边上每一条线段作为宽,每一个长配一个宽,就组成一个长方形,所以图(Ⅱ)中共有长方形为:(4+3+2+1)×(2+1)=10×3=30(个).图(Ⅲ)中,依据计算图(Ⅱ)中长方形个数的方法:可得长方形个数为:(4+3+2+1)×(3+2+1)=60(个).解:图(Ⅰ)中长方形个数为4+3+2+1=10(个).图(Ⅱ)中长方形个数为:(4+3+2+1)×(2+1)=10×3=30(个).图(Ⅲ)中长方形个数为:(4+3+2+1)×(3+2+1)=10×6=60(个).小结:一般情况下,如果有类似图Ⅲ的任一个长方形一边上有n-1个分点(不包括这条边的两个端点),另一边上有m-1个分点(不包括这条边上的两个端点),通过这些点分别作对边的平行线且与另一边相交,这两组平行线将长方形分为许多长方形,这时长方形的总数为:(1+2+3+…+m)×(1+2+3+…+n).例2 如右图数一数图中长方形的个数.解:AB边上分成的线段有:5+4+3+2+1=15.BC边上分成的线段有:3+2+1=6.所以共有长方形:(5+4+3+2+1)×(3+2+1)=15×6=90(个).数正方形例3数一数下页各个图中所有正方形的个数.(每个小方格为边长为1的正方形)分析:图Ⅰ中,边长为1个长度单位的正方形有:2×2=4(个),边长为2个长度单位的正方形有:1×1=1(个).所以,正方形总数为1×1+2×2=1+4=5(个).图Ⅱ中,边长为1个长度单位的正方形有3×3=9(个);边长为2个长度单位的正方形有:2×2=4(个);边长为3个长度单位的正方形有1×1=1(个).所以,正方形的总数为:1×1+2×2+3×3=14(个).图Ⅲ中,边长为1个长度单位的正方形有:4×4=16(个);边长为2个长度单位的正方形有:3×3=9(个);边长为3个长度单位的正方形有:2×2=4(个);边长为4个长度单位的正方形有:1×1=1(个);所以,正方形的总数为:1×1+2×2+3×3+4×4=30(个).图Ⅳ中,边长为1个长度单位的正方形有:5×5=25(个);边长为2个长度单位的正方形有:4×4=16(个);边长为3个长度单位的正方形有:3×3=9(个);边长为4个长度单位的正方形有:2×2=4(个);边长为5个长度单位的正方形有:1×1=1(个).所有正方形个数为:1×1+2×2+3×3+4×4+5×5=55(个).小结:一般地,如果类似图Ⅳ中,一个大正方形的边长是n个长度单位,那么其中边长为1个长度单位的正方形个数有:n×n=n2(个),边长为2个长度单位的正方形个数有:(n-1)×(n-1)=(n-1)2(个)…;边长为(n-1)个长度单位的正方形个数有:2×2=22(个),边长为n个长度单位的正方形个数有:1×1=1(个).所以,这个大正方形内所有正方形总数为:12+22+32+…+n2(个).例4如右图,数一数图中有多少个正方形(其中每个小方格都是边长为1个长度单位的正方形).分析:为叙述方便,我们规定最小正方形的边长为1个长度单位,又称为基本线段,图中共有五类正方形.①以一条基本线段为边的正方形个数共有:6×5=30(个).②以二条基本线段为边的正方形个数共有:5×4=20(个).③以三条基本线段为边的正方形个数共有:4×3=12(个).④以四条基本线段为边的正方形个数共有:3×2=6(个).⑤以五条基本线段为边的正方形个数共有:2×1=2(个).所以,正方形总数为:6×5+5×4+4×3+3×2+2×1=30+20+12+6+2=70(个).小结:一般情况下,若一长方形的长被分成m等份,宽被分成n等份,(长和宽上的每一份是相等的)那么正方形的总数为(n<m):mn+(m-1)(n-1)+(m-2)(n-2)+…+(m-n+1)·1显然例4是结论的特殊情况.例5 如下图,平面上有16个点,每个点上都钉上钉子,形成4×4的正方形钉阵,现有许多皮筋,问能套出多少个正方形.例6 如右图,数一数图中三角形的个数.分析这样的图形只能分类数,可以采用类似数正方形的方法,从边长为一条基本线段的最小三角形开始.Ⅰ.以一条基本线段为边的三角形:①尖朝上的三角形共有四层,它们的总数为:W①上=1+2+3+4=10(个).②尖朝下的三角形共有三层,它们的总数为:W①下=1+2+3=6(个).Ⅱ.以两条基本线段为边的三角形:①尖朝上的三角形共有三层,它们的总数为:W②上=1+2+3=6(个).②尖朝下的三角形只有一个,记为W②下=1(个).Ⅲ.以三条基本线段为边的三角形:①尖朝上的三角形共有二层,它们的总数为:W③上=1+2=3(个).②尖朝下的三角形零个,记为W③下=0(个).Ⅳ.以四条基本线段为边的三角形,只有一个,记为:W④上=1(个).所以三角形的总数是10+6+6+1+3+1=27(个).我们还可以按另一种分类情况计算三角形的个数,即按尖朝上与尖朝下的三角形的两种分类情况计算三角形个数.Ⅰ.尖朝上的三角形共有四种:W①下=1+2+3+4=10W②上=1+2+3=6W③上=1+2=3W④上=1所以尖朝上的三角形共有:10+6+3+1=20(个).Ⅱ.尖朝下的三角形共有二种:W①下=1+2+3=6W②下=1W③下=0W④下=0则尖朝下的三角形共有:6+1+0+0=7(个)所以,尖朝上与尖朝下的三角形一共有:20+7=27(个).小结:尖朝上的三角形共有四种.每一种尖朝上的三角形个数都是由1开始的连续自然数的和,其中连续自然数最多的和中最大的加数就是三角形每边被分成的基本线段的条数,依次各个连续自然数的和都比上一次少一个最大的加数,直到1为止.尖朝下的三角形的个数也是从1开始的连续自然数的和,它的第一个和恰是尖朝上的第二个和,依次各个和都比上一个和少最大的两个加数,以此类推直到零为止.(1)W①上=8+7+6+5+4=30(3)W③上=6+5+4=15(4)W④上=5+4=9(5)W⑤上=4∴尖朝上的三角形共有:30+22+15+9+4=80(个).Ⅱ.尖朝下的三角形有四种:(1)W①下=3+4+5+6+7=25(2)W②下=2+3+4+5=14(3)W③下=1+2+3=6(4)W④下=1尖朝下的三角形共有25+14+6+1=46(个).所以尖朝上与尖朝下的三角形总共有80+46=126(个).。
小学六年级奥数几何计数问题专项强化训练(高难度)

小学六年级奥数几何计数问题专项强化训练(高难度)例题1:某小学六年级有10名男生和8名女生参加了一次班级活动,活动结束时,他们按照男女间隔排成一列,要求男生和女生交替站立。
问共有几种不同的排列方式?解析:首先确定男生和女生的位置,男生和女生的位置可以互换,所以先计算男生和女生的排列方式。
男生和女生分别有10!和8!种排列方式。
但是男生和女生之间是需要相邻的(间隔排列),所以男生和女生的位置可以看作是一个整体,即总共有(10!)(8!)种排列方式。
因此,共有(10!)(8!)种不同的排列方式。
专项练习应用题:1. 某小学六年级有12名男生和10名女生参加了一次班级活动,活动结束时,他们按照男女间隔排成一列,要求男生和女生交替站立。
问共有几种不同的排列方式?2. 某小学六年级有8名男生和6名女生参加了一次班级活动,活动结束时,他们按照男女间隔排成一列,要求男生和女生交替站立。
问共有几种不同的排列方式?3. 某小学六年级有15名男生和12名女生参加了一次班级活动,活动结束时,他们按照男女间隔排成一列,要求男生和女生交替站立。
问共有几种不同的排列方式?4. 某小学六年级有6名男生和8名女生参加了一次班级活动,活动结束时,他们按照男女间隔排成一列,要求男生和女生交替站立。
问共有几种不同的排列方式?5. 某小学六年级有10名男生和9名女生参加了一次班级活动,活动结束时,他们按照男女间隔排成一列,要求男生和女生交替站立。
问共有几种不同的排列方式?6. 某小学六年级有7名男生和7名女生参加了一次班级活动,活动结束时,他们按照男女间隔排成一列,要求男生和女生交替站立。
问共有几种不同的排列方式?7. 某小学六年级有14名男生和15名女生参加了一次班级活动,活动结束时,他们按照男女间隔排成一列,要求男生和女生交替站立。
问共有几种不同的排列方式?8. 某小学六年级有9名男生和10名女生参加了一次班级活动,活动结束时,他们按照男女间隔排成一列,要求男生和女生交替站立。
小学奥数模块教程几何计数(ABC级)

几何计数知识框架一、公式计算法几何计数内容很广,包括数线段的条数,角的个数,长方形、正方形、三角形、平行四边形、梯形等图形的个数,也包括数立体图形的个数。
图形的计数一般有两种思考方法:公式计算法和分类计数法。
三年级学习的线段、长方形和正方形的计数就属于公式计算法。
(1)一条线段有两个端点,若这条线段上有n个点,那么线段总数是(n-1)+(n+2)+…+3+2+1(2)如果一个长方形的长边上有n个小格,宽边上有m个小格,那么长方形的总数是(1+2+3+…+n)×(1+2+…+m)(3)如果把正方形各边都n等分,那么正方形的总数是n2+(n-1)2+(n-2)2+…+32+22+12上面计算线数的方法也可用于计算角的个数,而且,根据这些计数方法在以后还可以类推出立体图形的计算方法。
二、对应法将难以计数的数量与某种可计量的事物联系起来,只要能建立一一对应的关系,那么这两种事物在数量上是相同的.事实上插入法和插板法都是对应法的一种表现形式.重难点(1)分类数图形。
(2)对应法数图形。
一、 分类数图形【例 1】 下图的两个图形(实线)是分别用10根和16根单位长的小棍围成的.如果按此规律(每一层比上面一层多摆出两个小正方形)围成的图形共用了60多根小棍,那么围成的图形有几层,共用了多少根小棍?【巩固】 如图所示,用长短相同的火柴棍摆成3×1996的方格网,其中每个小方格的边都由一根火柴棍组成,那么一共需用多少根火柴棍?【例 2】 图中有______个正方形.例题精讲【巩固】 数一数:图中共有________ 个正方形。
【例 3】 右图中三角形共有 个.【巩固】 数一数图中有_______个三角形.【例 4】 图中共有多少个三角形?【巩固】 下图是由边长为1的小三角形拼成,其中边长为4的三角形有_____个。
CBA【例 5】如图,每个小正方形的面积都是l平方厘米。
则在此图中最多可以画出__________个面积是4平方厘米的格点正方形(顶点都在图中交叉点上的正方形)。
小学奥数--几何计数25道

【题型】应用题【题目】用3根等长的火柴可以摆成一个等边三角形.如图19-1,用这样的等边三角形拼合成一个更大的等边三角形.如果这个大等边三角形昀每边由20根火柴组成,那么一共要用多少根火柴?【答案】630【解析】把大的等边三角形分为20“层”分别计算火柴的根数:最上一“层”只用了3根火柴;从上向下数第二层用了3×2=6根火柴;从上向下数第三层用了3×3=9根火柴;……从上向下数第20层用了3×20=60根火柴.所以,总共要用火柴3×(1+2+3+…+20)=630根.【难度】难度3【知识点】几何计数【题目】如图19-2,用长短相同的火柴棍摆成3×1996的方格网,其中每个小方格的边都由一根火柴棍组成,那么一共需用多少根火柴棍?【答案】13975【解析】横放需1996×4根,竖放需1997×3根,共需1996×4+1997×3=13975根.【难度】难度2【知识点】几何计数【题目】图19-3是一个跳棋棋盘,请你计算出棋盘上共有多少个棋孔?【答案】【解析】把棋盘分割成一个平行四边形和四个小三角形,如下图.平行四边形中棋孔数为9×9=81,每个小三角形中有10个棋孔,所以棋孔共有81+10×4=121个.或直接数出有121个.【难度】难度3【知识点】几何计数【题目】如图19-4,在桌面上,用6个边长为l的正三角形可以拼成一个边长为1的正六边形.如果在桌面上要拼出一个边长为6的正六边形,那么,需要边长为1的正三角形多少个?【答案】【解析】如图AB=6,组成△AOB需要边长为1的正三角形共:1+3+5+7+9+11=36个,而拼成边长为6的正六边形需要6个△AOB,因此总共需要边长为1的正三角形36×6=216个.【难度】难度4【知识点】几何计数【题目】如图19-5,其中的每条线段都是水平的或竖直的,边界上各条线段的长度依次为5厘米、7厘米、9厘米、2厘米和4厘米、6厘米、5厘米、1厘米.求图中长方形的个数,以及所有长方形面积的和.【答案】100,10664【解析】确定好长方形的长和宽,长方形就唯一确定,而图中只需确定好横向线段,竖向线段,即可.于是横向线段有(1+2+3+4)=10种选法,竖向线段也有(1+2+3+4)=10种选法,则共有10×10=100个长方形.这些长方形的面积和为:(5+7+9+2+12+16+11+21+18+23)×(4+6+5+1+10+11+6+15+12+16)=124×86=10664(平方厘米).【难度】难度4【知识点】几何计数【题目】如图19-6,18个边长相等的正方形组成了一个3×6的方格表,其中包含“*”的长方形及正方形共有多少个?【答案】36【解析】我们把所求的长、正方形按占有的行数分为三类,每类的长、正方形的个数相等.其中只占有下面一行的有如下12种情况:于是共有12×3=36个正、长方形包含“*”.【难度】难度4【知识点】几何计数【题目】图19-7是由若干个相同的小正方形组成的.那么,其中共有各种大小的正方形多少个?【答案】130【解析】每个4×4正方形中有:边长为1的正方形4×4个;边长为2的正方形3×3个;边长为3的正方形2×2个,边长为4的正方形1×1个.总共有4×4+3×3+2×2+1×1=30个正方形.现在5个4×4的正方形,它们重叠部分是4个2×2的正方形.因此,图中正方形的个数是30×5-5×4=130.【难度】难度4【知识点】几何计数【题目】图19-8中共有多少个三角形?【答案】22【解析】边长为1的正三角形,有16个.边长为2的正三角形,尖向上的有3个,尖向下的也有3个.因此共有16+3+3=22个.【难度】难度2【知识点】几何计数【题目】图19-9是由18个大小相同的小正三角形拼成的四边形,其中某些相邻的小正三角形可以拼成较大的正三角形.那么,图中包含“*”的各种大小的正三角形一共有多少个?【答案】6【解析】设小正三角形的边长为1,分三类计算计数包含*的三角形中,边长为1的正三角形有1个;边长为2的正三角形有4个,边长为3的正三角形有1个;因此,图中包含“*”的所有大、小正三角形一共有1+4+1=6个.【难度】难度2【知识点】几何计数【题目】如图19-10,AB,CD,EF,MN互相平行,则图中梯形个数与三角形个数的差是多少?【答案】20【解析】图中共有三角形(1+2+3+4)×4=40个,梯形(1+2+3+4)×(1+2+4)=60个,梯形比三角形多60-40=20个.【难度】难度3【知识点】几何计数【题目】在图19-1l中,共有多少个不同的三角形?【答案】85【解析】下图中共有35个三角形,两个叠加成题中图形时,又多出5+5×2=15个三角形,共计35×2+15=85个三角形.【难度】难度5【知识点】几何计数【题目】如图19-12,一块木板上有13枚钉子.用橡皮筋套住其中的几枚钉子,可以构成三角形、正方形、梯形等等,如图19-13.那么,一共可以构成多少个不同的正方形?【答案】11【解析】按正方形的面积分类,设最小的正方形面积为1,面积为1的正方形有5个,如图a所示;面积为2的正方形有4个,如图b所示;面积为4的正方形有1个,如图c所示;还有1个面积比4大的正方形,如图d所示;于是,一共可以构成5+4+1+1=11个不同的正方形.【难度】难度3【知识点】几何计数【题目】如图19-14,用9枚钉子钉成水平和竖直间隔都为1厘米的正方阵.用一根橡皮筋将3枚不共线的钉子连结起来就形成一个三角形.在这样得到的三角形中,面积等于1平方厘米的三角形共有多少个?【答案】32【解析】我们分三种情况来找面积为1平方厘米的三角形,这些三角形的底与高分别为1厘米或2厘米,利用正方形的对称性:(1)等腰直角三角形,如下图a所示有△AOC,△COE,△EOG,△GOA,△BOH,△DFB,△FHD,△HBF,共计8个,其中以AC,CF,FG,GA为底的各一个,以BF,DH为底的各两个.(2)直角三角形,如图b所示有△ACH,△CHD,△ACD,△DHA,△BEF,△BCE,△CEF,△CFB,△DEG,△DGH,△EGH,△EHD,△GAB,△GBF,△FAB,△FGA,共计16个,其中以AD、CH、BE、CF、DG、EH、FA、GB为斜边的各两个.(3)钝角三角形,如图c所示有△ABE,△AHE,△ADE,△AFE,△CBG,△CFG,△CDG,△CHG共计8个,其中以AE、CG为边的各四个.于是,综上所述,共有面积为1平方厘米的三角形32个.【难度】难度4【知识点】几何计数【题目】如图19-15,木板上钉着12枚钉子,排成三行四列的长方阵.那么用橡皮筋共可套出多少个不同的三角形?【答案】200【解析】我们先任意选取三个点,那么第1个点有12个位置可以选择,第2个点有11个位置可以选择,第3个点有10个位置可以选择,但是每6种选法对应的都是同一个图形,如下图,ABC,ACB,BAC,BCA,CAB,CBA均是同一个图形.所以有12×11×10÷6=220种选法,但是如果这3点在同一条直线上就无法构成三角形,其中每行有4种情况,共3×4;每列有1种情况,共1×4;2个边长为2的正方形的4条对角线,共4种情况.所以,可以套出220-3×4-1×4-4=200个不同的三角形.【难度】难度2【知识点】几何计数【题目】如图19-16,正方形ACEG的边界上有A,B,C,D,E,F,G这7个点,其中B,D,F分别在边AC,CE,EG上.以这7个点中的4个点为顶点组成的不同四边形的个数等于多少?【答案】12【解析】如果暂时不考虑点之间的排列位置关系,从7个点中任取4个点,则第一个点有7个位置可选,第二个点有6个位置可选,第三个点有5个位置可选,第四个点有4个位置可选,而不考虑先后,那么有4×3×2×1=24种选法的实质是一样的,所有可能的组合数目应该是(7×6×5×4)÷24=35.我们只要从中减去不能构成四边形的情形.对图19-16而言,任取4个点而又不构成四边形的情形只能发生在所取的4个点中有3个来自正方形ACEG的一条边,而另一个则任意选取的时候,例如选定A、B、C3点,第4个点无论如何选取都不能构成四边形.正方形的4条边中有3条都存在这样的情况.而每次这种情况发生时,第4个顶点的选取有4种可能.所取的顶点只有4个,因此不可能出现同时选择了2条有3点共线的边的情况.那么需要排除的情况有4×3=12种.所以,满足题意的四边形个数有35-12=23个.【难度】难度4【知识点】几何计数【题目】数一数下列图形中各有多少条线段.【答案】15【解析】要想使数出的每一个图形中线段的总条数,不重复、不遗漏,就需要按照一定的顺序、按照一定的规律去观察、去数.这样才不至于杂乱无章、毫无头绪.我们可以按照两种顺序或两种规律去数.第一种:按照线段的端点顺序去数,如上图(1)中,线段最左边的端点是A,即以A为左端点的线段有AB、AC两条以B为左端点的线段有BC一条,所以上图(1)中共有线段2+1=3条.同样按照从左至右的顺序观察图(2)中,以A 为左端点的线段有AB、AC、AD三条,以B为左端点的线段有BC、BD两条,以C为左端点的线段有CD一条.所以上页图(2)中共有线段为3+2+1=6条. 第二种:按照基本线段多少的顺序去数.所谓基本线段是指一条大线段中若有n 个分点,则这条大线段就被这n个分点分成n+1条小线段,这每条小线段称为基本线段.如上页图(2)中,线段AD上有两个分点B、C,这时分点B、C把AD 分成AB、BC、CD三条基本线段,那么线段AD总共有多少条线段?首先有三条基本线段,其次是包含有二条基本线段的是:AC、BD二条,然后是包含有三条基本线段的是AD这样一条.所以线段AD上总共有线段3+2+1=6条,又如上页图(3)中线段AE上有三个分点B、C、D,这样分点B、C、D把线段AE分为AB、BC、CD、DE四条基本线段,那么线段AE上总共有多少条线段?按照基本线段多少的顺序是:首先有4条基本线段,其次是包含有二条基本线段的有3条,然后是包含有三条基本线段的有2条,最后是包含有4条基本线段的有一条,所以线段AE上总共有线段是4+3+2+1=10条.解:①2+1=3(条).② 3+2+1=6(条).③ 4+3+2+1=10(条).小结:上述三例说明:要想不重复、不遗漏地数出所有线段,必须按照一定顺序有规律的去数,这个规律就是:线段的总条数等于从1开始的连续几个自然数的和,这个连续自然数的和的最大的加数是线段分点数加1或者是线段所有点数(包括线段的两个端点)减1.也就是基本线段的条数.例如右图中线段AF 上所有点数(包括两个端点A、F)共有6个,所以从1开始的连续自然数的和中最大的加数是6—1=5,或者线段AF上的分点有4个(B、C、D、E).所以从1开始的连续自然数的和中最大的加数是4+1=5.也就是线段AF上基本线段(AB、BC、CD、DE、EF)的条数是5.所以线段AF上总共有线段的条数是5+4+3+2+1=15(条).【难度】难度3【知识点】几何计数【题目】数出下图中总共有多少个角.【答案】10【解析】在∠AOB内有三条角分线OC1、OC2、OC3,∠AOB被这三条角分线分成4个基本角,那么∠AOB内总共有多少个角呢?首先有这4个基本角,其次是包含有2个基本角组成的角有3个(即∠AOC2、∠C1OC3、∠C2OB),然后是包含有3个基本角组成的角有2个(即∠AOC3、∠C1OB),最后是包含有4个基本角组成的角有1个(即∠AOB),所以∠AOB内总共有角:4+3+2+1=10(个).解:4+3+2+1=10(个).小结:数角的方法可以采用例1数线段的方法来数,就是角的总数等于从1开始的几个连续自然数的和,这个和里面的最大的加数是角分线的条数加1,也就是基本角的个数.【难度】难度3【知识点】几何计数【题目】数一数下图中总共有多少个角?【答案】55【解析】因为∠AOB内角分线OC1、OC2…OC9共有9条,即9+1=10个基本角. 所以总共有角:10+9+8+…+4+3+2+1=55(个).【难度】难度3【知识点】几何计数【题目】如下图中,各个图形内各有多少个三角形?【答案】(1)6(2)10【解析】可以采用类似例1数线段的两种方法来数,如图(2):第一种方法:先数以AB为一条边的三角形共有:△ABD、△ABE、△ABF、△ABC四个三角形.再数以AD为一条边的三角形共有:△ADE、△ADF、△ADC三个三角形.以AE为一条边的三角形共有:△AEF、△AEC二个三角形.最后以AF为一条边的三角形共有△AFC一个三角形.所以三角形的个数总共有4+3+2+1=10.第二种方法:先数图中小三角形共有:△ABD、△ADE、△AEF、△AFC四个三角形.再数由两个小三角形组合在一起的三角形共有:△ABE、△ADF、△AEC三个三角形,以三个小三角形组合在一起的三角形共有:△ABF、△ADC二个三角形,最后数以四个小三角形组合在一起的只有△ABC一个.所以图中三角形的个数总共有:4+3+2+1=10(个).解:①3+2+1=6(个)② 4+3+2+1=10(个).答:图(1)及图(2)中各有三角形分别是6个和10个.小结:计算三角形的总数也等于从1开始的几个连续自然数的和,其中最大的加数就是三角形一边上的分点数加1,也就是三角形这边上分成的基本线段的条数.【难度】难度3【知识点】几何计数【题目】如下图中,数一数共有多少条线段?共有多少个三角形?【答案】60,30【解析】分析在数的过程中应充分利用上几例总结的规律,明确数什么?怎么数?这样两个问题.数:就是要数出图中基本线段(基本三角形)的条数,算:就是以基本线段(基本三角形)条数为最大加数的从1开始的连续几个自然数的和.①要数多少条线段:先看线段AB、AD、AE、AF、AC、上各有2个分点,各分成3条基本线段,再看BC、MN、GH这3条线段上各有3个分点,各分成4条基本线段.所以图中总共有线段是:(3+2+1)×5+(4+3+2+1)×3=30+30=60(条).②要数有多少个三角形,先看在△AGH中,在GH上有3个分点,分成基本小三角形有4个.所以在△AGH中共有三角形4+3+2+1=10(个).在△AMN与△ABC 中,三角形有同样的个数,所以在△ABC中三角形个数总共:(4+3+2+1)×3=10×3=30(个).解:①在△ABC中共有线段是:(3+2+1)×5+(4+3+2+1)×3=30+30=60(条)②在△ABC中共有三角形是:(4+3+2+1)×3=10×3=30(个).【难度】难度3【知识点】几何计数【题目】如右图中,共有多少个角?【答案】13【解析】分析本题虽然与上几例有区别,但仍可以采用上几例所总结的规律去解决. ∠1、∠2、∠3、∠4我们可视为4个基本角,由2个基本角组成的有:∠1与∠2、∠2与∠3、∠3与∠4、∠4与∠1,共4个角.由3个基本角组成的角有:∠1、∠2与∠3;∠2、∠3与∠4;∠3、∠4与∠1;∠4、∠1与∠2,共4个角,由4个基本角组成的角只有一个.所以图中总共有角是:4×3+1=13(个).解:所以图中共有角是:4×3+1=13(个).小结:由本题可以推出一般情况:若周角中含有n 个基本角,那么它上面角的总数是 n (n-1)+1.【难度】难度4【知识点】几何计数【题目】在图中(单位:厘米):①一共有几个长方形?②所有这些长方形面积的和是多少?374218125【答案】100,12384【解析】①一共有(4321)(4321)100+++⨯+++=(个)长方形;②所求的和是[][]51281(512)(128)(81)(5128)(1281)(51281)2473(24)(47)(73)(247)(473)(2473)+++++++++++++++++++⨯+++++++++++++++++++ 1448612384=⨯=(平方厘米)。
小学奥数:几何计数一.专项练习及答案解析

7-8-1几何计数(一)教课目的掌握数常用方法;熟一些数公式及其推方法;依据不一样目灵巧运用数方法行数.本主要介了数的常用方法枚法、数法、形法、插板法、法等,并渗透分数和用容斥原理的数思想.知识重点一、几何计数在几何形中,有多风趣的数,如算段的条数,足某种条件的三角形的个数,若干个分平面所成的地区数等等.看起来仿佛没有什么律可循,可是通真分析,是能够找到一些理方法的.常用的方法有枚法、加法原理和乘法原理法以及推法等.n条直最多将平面分红223⋯⋯n(n2n2)个部分;n个2最多分平面的部分数n(n-1)+2;n个三角形将平面最多分红3n(n-1)+2部分;n个四形将平面最多分红4n(n-1)+2部分⋯⋯在其余数中,也常用到枚法、加法原理和乘法原理法以及推法等.解需要仔、合所学知点逐渐求解.摆列不与参加摆列的事物相关,并且与各事物所在的先后序相关;合与各事物所在的先后序没关,只与两个合中的元素相关.二、几何计数分类数段:假如一条段上有n+1个点(包含两个端点)(或含有n个“基本段”),那么n+1个点把条段一共分红的段数n+(n-1)+⋯+2+1条数角:数角与数段相像,段形中的点似于角形中的.数三角形:可用数段的方法数如右所示的三角形(法),因DE上有15条段,每条段的两头点与点A相,可构成一个三角形,共有15个三角形,同一在BC上的三角形也有15个,所以中共有30个三角形.数方形、平行四形和正方形:一般的,于随意方形(平行四形),若其横上共有n 条段,上共有条段,中共有方形(平行四形)个.m mn例题精讲模块一、简单的几何计数【例1】七个同的如右搁置,它有_______条称.7-8-1.几何计数(一).题库题库版page1of10【考点】简单的几何计数【难度】1星【题型】填空【重点词】迎春杯,六年级,初赛,试题【分析】如图:6条.【答案】6条【例2】下边的表情图片中:,没有对称轴的个数为()(A)3(B)4(C)5(D)6【考点】简单的几何计数【难度】2星【题型】选择【重点词】华杯赛,初赛,第1题【分析】经过观察可知,第1,2,5这三张图片是有对称轴的,其余的5张图片都没有对称轴,所以没有对称轴的个数为5,正确答案是C。
小学数学 奥数讲义计数专题:几何计数

华杯赛计数专题:几何计数基础知识:1.几何计数,从类型上看,可分为数线段、数三角形、数正方形、数长方形、数平行四边形等几类.2.几何计数的基本方法和思想:分类枚举与对应.3.分类的标准:按大小,按包含的图形等.4.常见对应方法:线段对应到端点,三角形对应到端点或边,长方形对应到对边等.5.特殊方法:去点法与去线法,本质是分类.方法铺垫:1)加法原理,乘法原理;2)容斥原理;3)排列数,组合数;4)对应法.例题:例1.如图,数一数图中有多少条线段?【答案】28(条)【解答】分类:1个单位长的线段有7条;2个单位长的线段有6条;3个单位长的线段有5条;……7个单位长的线段有1条;故共有线段7+6+5+……+1=28(条).例2.数一数,图中共有多少个三角形?【答案】13(个)【解答】分类:含有1块的三角形有4个;含有2块的三角形有5个;含有3块的三角形有2个;含有4块的三角形有1个;含有6块的三角形有1个;故共有三角形4+5+2+1+1=13(个).例3.如图,数一数,图中有多少个三角形?【答案】48(个).【解答】分类:包含1个小三角形的三角形有1+3+5+7+9=25个;包含4个小三角形的三角形有1+2+3+4+3=13个;包含9个小三角形的三角形有1+2+3=6个包含16个小三角形的三角形有1+2=3个;包含25个小三角形的三角形有1个;故共有三角形25+13+6+3+1=48(个).例4.数一数,图中共有多少个三角形?【答案】35(个)【解答】分类:含有1块的三角形有10个;含有2块的三角形有10个;含有3块的三角形有10个;含有5块的三角形有5个;故共有三角形10+10+10+5=35(个).例5.图中有多少个正方形?【答案】30(个)【解答】包含1个正方形的正方形有4×4=16个;包含4个正方形的正方形有3×3=9个;包含9个正方形的正方形有2×2=4个;包含16个正方形的正方形有1个;故共有三角形16+9+4+1=30(个).例6.如图,数一数图中一共有多少条线段?多少个矩形?【答案】70(条); 60个【解答】线段:横线,共有4×条;竖线:5×,故共有线段40+30=70条;矩形:竖线中选出两条,共有条,横线中选出两条,共有,根据乘法原理,共有矩形10矩形原60个.例7.如图,这是一个长为9,宽为4的网格,每一个小格都是一个正方形.请问:(1)从中可以数出多少个长方形?(2)从中可以数出包含红点的长方形有多少个?【答案】450(个);144个【解答】(1)竖线中选出两条,共有条,横线中选出两条,共有,根据乘法原理,共有矩形45×10=450个.(2)竖线中选出两条,共有6竖线中选出条,横线中选出两条,共有2×3=6条,根据乘法原理,共有矩形24×6=144个.例8.如图,数一数,图中共有多少个长方形?【答案】135个【解答】横向看:共有矩形个,竖向看:共有矩形个,这样重复计算了个,所以共有矩形90+63-18=135个.例9.如图,木板上钉着12枚钉子,排成三行四列的长方阵.用橡皮筋一共可以套出多少个不同的三角形?【答案】200(个)【解答】共有三角形个.例10.下图由相同的正方形和相同的等腰直角三角形构成, 则正方形的个数为多少?(17届华杯赛笔试初赛小高组第6题)【答案】83(个)【解答】包含1小个正方形的正方形有2+4+6+8+8+6+4+2=40个;包含4小个正方形的正方形有1+3+5+7+5+3+1=25个;包含9小个正方形的正方形有2+4+4+2=12个;包含16小个正方形的正方形有1+3+1=5个;共有正方形40+25+12+5+1=83个.例11. 求图中一共有多少条线段?求图中一共有多少个矩形?【答案】70条线段,60个矩形【解答】每一条线段由同一行或同一列的两个顶点确定,因此共有条线段.每个矩形由长和宽上的各一条线段对应形成,如下图:因此共有个矩形.例12. 数一数,图中有多少个三角形?【答案】78个【解答】只包含1个基本图形的有36个(朝上的21个,朝下的15个);包含4个基本图形的有21个(朝上的15个,朝下的6个);包含9个基本图形的有11个(朝上的10个,朝下的1个);包含16个基本图形的有6个;包含25个基本图形的有3个;包含36个基本图形的有1个.所以共有36+21+11+6+3+1=78个.例13. 下图是一个长为9,宽为4的长方形网格,每一个小格都是一个正方形,那么:1)从中可以数出多少个矩形?2)从中可以数出多少个正方形?3)从中可以数出包含黑点的矩形有多少个?【答案】1)450个;2)80个;3)144个【解答】1)图中共有个矩形;2)包含1个基本图形的正方形共有4×9=36个;包含4个基本图形的正方形共有3×8=24个;包含9个基本图形的正方形共有2×7=14个;包含16个基本图形的正方形共有1×6=6个.则共有36+24+14+6=80个.3)黑点左下方的顶点共有18个,黑点右上方的顶点共有8个,所以包含黑点的矩形共有18×8=144个.例14. 图中一共包含多少个矩形?【答案】135个【解答】第(1)部分和第(3)部分合并起来是一个3×5的大矩形(如下图所示),其中一共包含矩形个;第(2)部分和第(3)部分合并起来是一个6×2的大矩形(如下图所示),其中一共包含矩形个;第(3)部分中的矩形被重复计算了,其中共有矩形个.所以图中一共包含矩形90+63-18=135个.例15. 图中的木板上钉着12枚钉子,排成三行四列的长方阵. 那么用橡皮筋一共可以套出多少个不同的三角形?【答案】200个【解答】从12枚钉子中选择3枚钉子的组合总数是.而图中共有3条直线上各有4个点(如下图实线所示),另外还有8条直线上各有3个点(如下图虚线所示).因此用橡皮筋一共可以套出个不同的三角形.例16. 求图中所有矩形的面积和以及周长的总和.【答案】周长总和:1364;面积总和:1800【解答】矩形的10种长的总长是3++4++2++6++7++6++8++9++12++15=72。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
知识框架图 7 计数综合 7-8 几何计数1.掌握计数常用方法;2.熟记一些计数公式及其推导方法;3.根据不同题目灵活运用计数方法进行计数.本讲主要介绍了计数的常用方法枚举法、标数法、树形图法、插板法、对应法等,并渗透分类计数和用容斥原理的计数思想.一、几何计数 在几何图形中,有许多有趣的计数问题,如计算线段的条数,满足某种条件的三角形的个数,若干个图分平面所成的区域数等等.这类问题看起来似乎没有什么规律可循,但是通过认真分析,还是可以找到一些处理方法的.常用的方法有枚举法、加法原理和乘法原理法以及递推法等.n 条直线最多将平面分成21223(2)2n n n ++++=++……个部分;n 个圆最多分平面的部分数为n(n-1)+2;n 个三角形将平面最多分成3n(n-1)+2部分;n 个四边形将平面最多分成4n(n-1)+2部分……在其它计数问题中,也经常用到枚举法、加法原理和乘法原理法以及递推法等.解题时需要仔细审题、综合所学知识点逐步求解.排列问题不仅与参加排列的事物有关,而且与各事物所在的先后顺序有关;组合问题与各事物所在的先后顺序无关,只与这两个组合中的元素有关. 二、几何计数分类数线段:如果一条线段上有n+1个点(包括两个端点)(或含有n 个“基本线段”),那么这n+1个点把这条线段一共分成的线段总数为n+(n-1)+…+2+1条数角:数角与数线段相似,线段图形中的点类似于角图形中的边.数三角形:可用数线段的方法数如右图所示的三角形(对应法),因为DE 上有15条线段,每条线段的两端点与点A 相连,可构成一个三角形,共有15个三角形,同样一边在BC 上的三角形也有15个,所以图中共有30个三角形.教学目标知识要点几何计数数长方形、平行四边形和正方形:一般的,对于任意长方形(平行四边形),若其横边上共有n条线段,纵边上共有m条线段,则图中共有长方形(平行四边形)mn个.例题精讲【例 1】(难度等级※※)下图的两个图形(实线)是分别用10根和16根单位长的小棍围成的.如果按此规律(每一层比上面一层多摆出两个小正方形)围成的图形共用了60多根小棍,那么围成的图形有几层,共用了多少根小棍?【解析】通过观察每增加一层,恰好增加6根小棍,这6根恰好是增加那一层比上一层多摆出的两个正方形多用的,即前1层用4根,前2层用4+6根,前3层用4+6×2根,前n层用4+6×(n-1)根,现在共用了60多根,应减去4是6的倍数,所以共用小棍64根,围成的图形有11层.【例 2】(难度等级※※※)用3根等长的火柴可以摆成一个等边三角形.如图用这样的等边三角形拼合成一个更大的等边三角形.如果这个大等边三角形的每边由20根火柴组成,那么一共要用多少根火柴?【解析】把大的等边三角形分为“20”层分别计算火柴的根数:最上一层只用了3根火柴;从上向下数第二层用了3×2=6根;从上向下数第二层用了3×3=9根;……【巩固】用三根火柴可拼成一个小“△”,若用108根火柴拼成如图所示形状的大三角形,请你数一数共有多少个三角形?【解析】首先,需弄清形状如图的大三角形共有多少层.从上往下,第一层用331=⨯根火柴;第四层用=⨯根火柴;第二层用632=⨯根火柴;第三层用933n n=⨯根火柴;…;第n层用33=⨯根火柴.1234=⨯根火柴;第五层用1535根据题意,有:36912153108++++++=L,所以,8n=,nn++++++=L,故1234536即形状如图的大三角形共有8层,是边长为8根火柴的大正三角形.然后,数出共有多少个三角形.尖朝上的三角形共:+++++++++++++++++++++(12345678)(1234567)(123456)++++++++++++++=(个);(12345)(1234)(123)(12)1120尖朝下的三角形共:++++++++++++++++=(个);(1234567)(12345)(123)1050所以,共有三角形:12050170+=(个).本题小结:尖朝上的三角形:每一种尖朝上的三角形个数都是由1开始的连续自然数的和,其中连续自然数最多的和中最大的加数就是三角形每边被分成的基本线段的条数,依次各个连续自然数的和都比上一次少一个最大的加数,直到1为止.尖朝下的三角形的个数也是从1开始的连续自然数的和,它的第一个和恰是尖朝上的第二个和,依次各个和都比上一个和少最大的两个加数,以此类推直到零为止.【例 3】(难度等级※※※)如图所示,用长短相同的火柴棍摆成3×1996的方格网,其中每个小方格的边都由一根火柴棍组成,那么一共需用多少根火柴棍?【解析】横放需1996×4根,竖放需1997×3根共需1996×4+1997×3=13975根.【例 4】(难度等级【解析】利用长方形的计数公式:横边上共有n条线段,纵边上共有m条线段,则图中共有长方形(平行四边形)mn个.所以有(4+3+2+1)×(4+3+2+1)=100.【例 5】(难度等级※)下面的55⨯图中共有____个正方形.⨯和64【解析】 在55⨯的图中,边长为1的正方形25个;边长为2的正方形24个; 边长为3的正方形23个;边长为4的正方形22个;边长为5的正方形有21,总共有 222225432155++++=(个)正方形.在64⨯的图中边长为1的正方形64⨯个;边长为2的正方形53⨯个; 边长为3的正方形42⨯个;边长为4的正方形31⨯个;总共有 6453423142⨯+⨯+⨯+⨯=(个).【例 6】 (难度等级 ※※)在图中(单位:厘米):①一共有几个长方形?②所有这些长方形面积的和是多少?374218125【解析】 ①一共有(4321)(4321)100+++⨯+++=(个)长方形;②所求的和是[][]51281(512)(128)(81)(5128)(1281)(51281)2473(24)(47)(73)(247)(473)(2473)+++++++++++++++++++⨯+++++++++++++++++++ 1448612384=⨯=(平方厘米).【巩固】(难度等级 ※※)如图,其中的每条线段都是水平的或竖直的,边界上各条线段的长度依次为5厘米、7厘米、9厘米、2厘米和4 厘米、6厘米、5厘米、1厘米.求图中长方形的个数,以及所有长方形面积的和.【解析】 利用长方形的计数公式:横边上共有n 条线段,纵边上共有m 条线段,则图中共有长方形(平行四边形)mn 个,所以有(4+3+2+1)×(4+3+2+1)=100,这些长方形的面积和为:(5+7+9+2+12+16+11+21+18+23)×(4+6+5+1+10+11+6+15+12+16)=124×86=10664.【例 7】 (难度等级 ※)下图中共有____个正方形.【解析】每个44⨯正方形中有:边长为1的正方形有24个;边长为2的正方形有23个;边长为3的正方形有22个;边长为4的正方形有21个;总共有2222+++=(个)正方形.现有5个44432130⨯的正方形,它们重叠部分是4个22⨯-⨯=.⨯的正方形.因此,图中正方形的个数是30554130【巩固】(难度等级※)图中有______个正方形.【解析】55⨯的正方形5个;2⨯2的正方形4个;1⨯1的正方形⨯的正方形1个;44⨯的正方形4个;3313个.共27个.【例 8】(难度等级※※※)如图,其中同时包括两个☆的长方形有个.【解析】先找出同时包括两个☆的最小长方形,然后其余所有满足题目要求的长方形都必须包括该最小长方形.根据乘法原理2×2×2×3=24(种)不同的长方形.【巩固】(难度等级※※※)在下图中,不包含☆的长方形有________个.【解析】根据乘法原理,所有长方形总数为(1+2+3+4+5+6)×(1+2+3+4+5+6)=441(个),包含☆的长方形有3×3×4×4=144(个),所以不包含☆的长方形有441-144=297(个).【例 9】图中含有“※”的长方形总共有________个.※※【解析】根据本题特点,可采用分类的方法计数.按长方形的宽分类,数出含※号的长方形的个数.含有左上※号的长方形有:66618++=个,其中,宽为1(即高度为一层)的含※号的长方形为:6个;宽为2(即高度为两层)的含※号的长方形为:6个;宽为3(即高度为三层)的含※号的长方形为:6个;含有右上※号的长方形有:662624+⨯+=个,其中,宽为1(即高度为一层)的含※号的长方形为:6个;宽为2(即高度为两层)的含※号的长方形为:62⨯个;宽为3(即高度为三层)的含※号的长方形为:6个;同时含有两个※号的重复计算了,应减去,同时含有两个※号的长方形有:448+=个,其中,宽为2(即高度为两层)的含※号的长方形为:4个;宽为3(即高度为三层)的含※号的长方形为:4个;所以,含有※号的长方形总共有:1824834+-=个.【巩固】(难度等级 ※※)由20个边长为1的小正方形拼成一个45⨯长方形中有一格有“☆”图中含有“☆”的所有长方形(含正方形)共有 个,它们的面积总和是 . (第六届走美决赛试题)【解析】 含☆的一行内所有可能的长方形有:(八种)含☆的一列内所有可能的长方形有:(六种)所以总共长方形有6848⨯=个,面积总和为(12233445)(122334)360+++++++⨯+++++=.【例 10】 (难度等级 ※※)如图是由18个大小相同的小正三角形拼成的四边形.其中某些相邻的小正三角形可以拼成较大的正三角形若干个.那么,图中包含“*”号的大、小正三角形一共有______个.*【解析】 分三类进行计数(设小正三角形边长为1)包含*的三角形中,边长为1的正三角形有1个;边长为2的正三角形有4个;边长为3的正三角形有1个;因此,图中包含“*”的所有大、小正三角形一共有1416++=(个).【例 11】(难度等级※※※)如图AB,CD,EF,MN互相平行,则图中梯形个数与三角形个数的差是多少?【解析】图中共有三角形(1+2+3+4)×4=40个.梯形(1+2+3+4)×(2+4)=60;所以梯形比三角形多60-40=20个.【例 12】(难度等级※※)图中共有多少个三角形?【解析】显然三角形可分为尖向上与尖向下两大类,两类中三角形的个数相等.尖向上的三角形又可分为6类(1)最大的三角形1个(即△ABC),(2)第二大的三角形有3个(3)第三大的三角形有6个(4)第四大的三角形有10个(5)第五大的三角形有15个(6)最小的三角形有24个所以尖向上的三角形共有1+3+6+10+15+24=59(个)图中共有三角形2×59=118(个).【例 13】(难度等级※※)下图中的正方形被分成9个相同的小正方形,它们一共有16个顶点(共同的顶点算一个),以其中不在一条直线上的3个点为顶点,可以构成三角形.在这些三角形中,与阴影三角形有同样大小面积的有多少个?【解析】1.显然应先求出阴影三角形的面积设原正方形的边长是3,则小正方形的边长是1,阴影三角形的面积是½×2×3=32.思考图中怎样的三角形的面积等于3(1)一边长2,这边上的高是3的三角形的面积等于3(即形如图中阴影三角形).这时,长为2的边只能在原正方形的边上,这样的三角形有2×4×4=32(个);(2)一边长3,这边上的高是2的三角形的面积等于3.这时,长为3的边是原正方形的一边或平行于一边的分割线.这样的三角形有8×2=16(个)注意:不能与(1)中的三角形重复,所以这样的三角形共有32+16=48(个).【例 14】(第十二届全国“华罗庚金杯”少年数学邀请赛)如图,连接一个正六边形的各顶点.问图中共有多少个等腰三角形(包括等边三角形)?①②③【解析】本题需要分类进行讨论.⑴先考虑其中的等边三角形.图①中,六边形的每1个顶点是某个小号等边三角形的顶点,而且,每个小号等边三角形,有且仅有一个顶点是六边形的一个顶点,既然六边形有6个顶点,所以图中有6个小号三角形;图②中,六边形的每一条边是某个中号等边三角形的一条边,而且,每个中号等边三角形有且仅有一条边是六边形的一条边,既然六边形有6条边,所以图中有6个中号等边三角形;图③中,大号等边三角形有2个;⑵再考虑其中非等边的等腰三角形.图中非等边的等腰三角形,按照面积大小分类有3种类型,见图④.④⑤⑥其中小号的等腰三角形有6个,因为这类三角形均以六边形的一条边为其边长,并且,六边形的每一条边只唯一对应一个小号等腰三角形,而正六边形有6条边,所以有6个小号等腰三角形;中号的等腰三角形有12个,因为每个中号等腰三角形的长边都是六边形的一条非直径的弦,并且,以非直径的弦为长边的三角形有2个,如图⑤,这样的弦共有6条,所以有12个中号等腰三角形;大号的等腰三角形有6个,因为每个大号等腰三角形的长边都是六边形的一条直径,每条直径上都对应有2个大号三角形,如图⑥,共有3条直径,所以有6个大号等腰三角形.那么图中共有662612638+++++=个等腰三角形.【例 15】(第十一届“华罗庚金杯赛”)图中有个正方形.【解析】 边线是水平或垂直方向的正方形共有22222265432191+++++=(个),形如的正方形有4个,所以共有正方形91495+=(个). (如何保证没有其它的斜正方形了?如右图,擦去横线和竖线,只留下斜线,就一目了然了.)此题也可以计算不同面积的正方形各有多少个,以面积大小数正方形,记最小的正方形面积为1;则面积为1的正方形的个数为36;面积为2的正方形的个数为4;面积为4的正方形的个数为25;面积为9的正方形的个数为16;面积为16的正方形的个数为9;面积为25的正方形的个数为4;面积为36的正方形的个数为1.所以,共有364251694195++++++=(个)正方形.【巩固】这幅图中有 个三角形.【解析】 (法1)以图中的最小的直角三角形为计数基本单位数三角形:只有1个基本图形单位的三角形共66272⨯⨯=个;由2个基本图形单位组成的三角形共37个;由4个基本图形单位组成的三角形共30个;由8个基本图形单位组成的三角形共4个;由9个基本图形单位组成的三角形共10个;由16个基本图形单位组成的三角形共2个;所以图中共有三角形7237304102155+++++=(个).(法2)依三角形的斜边的长度数三角形:①斜边和水平线成45度角的三角形,记这类三角形最小的斜边的长度为1:长度为1的斜边共有:36条;长度为2的斜边共有:15条;长度为3的斜边共有:5条;长度为4的斜边共有:1条.因为图中这类斜边每条带有2个三角形,所以共有()2361551114⨯+++=(个).②斜边水平的三角形,从上向下:斜边在第一条线的有2个;斜边在第二条线的有4个;斜边在第三条线的有4个;斜边在第四条线的有5个;斜边在第五条线的有2个;斜边在第六条线的有2个;斜边在第七条线的有2个;所以这种类型的三角形共有21个.③斜边为垂直线的三角形,从左向右:斜边在第一条线的有2个;斜边在第二条线的有2个;斜边在第三条线的有5个;斜边在第四条线的有3个;斜边在第五条线的有3个;斜边在第六条线的有4个;斜边在第七条线的有1个,所以这种类型的三角形共有20个.共有1142120155++=(个)三角形.【例 16】 一张长方形纸片,长是宽的2倍,先对折成正方形,再对折成长方形,再对折成正方形,……,共对折7次,将纸打开展平,数一数用折痕分割成的正方形共有多少个?【解析】 从简单情况入手,从第一次对折开始分析,第一次对折,展平,折痕分割成的正方形共122=个;第二次对折,展平,折痕分割成的长方形共242=个;第三次对折,展平,折痕分割成的正方形共382=个;第四次对折,展平,折痕分割成的长方形共4162=个;第五次对折,展平,折痕分割成的正方形共5322=个;第六次对折,展平,折痕分割成的长方形共6642=个;第七次对折,展平,折痕分割成的正方形共71282=个.观察发现规律,奇数次对折时,展平后的折痕分割成的图形是正方形,所以,对折七次,将纸展平后,用折痕分割成的正方形是72128=个.【巩固】将正方形纸片由下往上对折,再由左向右对折,称为完成一次操作.按上述规则完成五次操作后,剪去所得的小正方形的左下角.问:当展开这张正方形纸后,一共有多少个小洞孔?【解析】 将最后得到的小正方形纸展开两次,中间形成一个菱形的小洞孔,之后每展开一次,孔的数量为原来的2倍,题中一次操作需要对折2次,五次操作对折了10次,所以孔的数量为(102)12256-⨯=个.【例 17】 在一个圆周上有8个点,正好把圆周八等分,以这些点为顶点作三角形,可以作出 个等腰三角形.【解析】 由于8个点正好把圆周八等分,所以以其中的任何3个点作为顶点都不能组成等边三角形.那么任意选取其中的一个点作为顶点,一个顶点上有三个不同的等腰三角形,圆周上有8个顶点,所以一共有3824⨯=个等腰三角形,而且这些等腰三角形互不相同(否则,假设其中有两个等腰三角形相同,这两个等腰三角形不可能是同一个顶点,只能是不同的顶点,这样这个等腰三角形必定是正三角形,与前面的分析不合),所以可以作出24个等腰三角形.【例 18】 圆周上十个点,任意两点之间连接一条弦,这些弦在圆内有多少个交点?【解析】 圆周上4点构成一个四边形,四边形两条对角线相交可以产生一个交点.问题转化为“圆周上10个点可以组成多少个以他们为定点的四边形?”利用上一讲的知识,去掉重复的部分,可知有:()109874321210⨯⨯⨯÷⨯⨯⨯=个.所以交点有210个.【例 19】 圆周上有8个点,两点所连的线段叫“弦”,每两点连一条弦,各弦无公共端点,共可连四条弦,各弦互不相交的连法共有________种.【解析】 本题可以利用归纳的方法解决.若圆周上只有2个点,只有1种连法;若圆周上只有4个点,先选中1个点,它可以与相邻的两个点相连,它连好后其它两点只有1种连法,所以此时有122⨯=种连法;若圆周上只有6个点,先选中1个点,此时它可以与相邻的2个点相连,也可以相对的1个点相连,若与相邻的点相连,剩下的4个点有2种连法;若与相对的点相连,剩下的4个点只有1种连法,所以此时有2215⨯+=种连法;若圆周上只有8个点,先选中一个点,此时它可以与相邻的2个点相连,也可以与与它相隔2个点的另外两个点相连.若与相邻的点相连,剩下的6个点有5种连法;若与相隔两个点的点相连,剩下的6个点被分成两边,一边2个点,只有一种连法,一边4个点,有2种连法.所以此时共有522214⨯+⨯=种连法.【例 20】 (难度等级 ※※※※)一个圆上有12个点A 1,A 2,A 3,…,A 11,A 12.以它们为顶点连三角形,使每个点恰好是一个三角形的顶点,且各个三角形的边都不相交.问共有多少种不同的连法?【解析】 我们采用递推的方法.I 如果圆上只有3个点,那么只有一种连法.Ⅱ如果圆上有6个点,除A 1点所在三角形的三顶点外,剩下的三个点一定只能在A 1所在三角形的一条边所对应的圆弧上,表1给出这时有可能的连法.Ⅲ如果圆上有9个点,考虑A1所在的三角形.此时,其余的6个点可能分布在:①A1所在三角形的一个边所对的弧上;②也可能三个点在一个边所对应的弧上,另三个点在另一边所对的弧上.在表2中用“+”号表示它们分布在不同的边所对的弧.如果是情形①,则由Ⅱ,这六个点有三种连法;如果是情形②,则由①,每三个点都只能有一种连法.共有12种连法.Ⅳ最后考虑圆周上有12个点.同样考虑A1所在三角形,剩下9个点的分布有三种可能:①9个点都在同一段弧上:②有6个点是在一段弧上,另三点在另一段弧上;③每三个点在A1所在三角形的一条边对应的弧上.得到表3.共有12×3+3×6+1=55种.所以当圆周上有12个点时,满足题意的连法有55种.。
