很不错的结构计算小全

合集下载

很不错的PKPM入门到熟练

很不错的PKPM（入门到熟练）1.结构设计的过程（了解）本文是送给刚接触结构设计及希望从事结构设计的新手的，其目的是使新手们对结构设计的过程以及结构设计所包括的内容有一个大致的了解，请前辈们不要见笑了，新人们有什么问题也可以在贴中提出来，大家共同讨论，共同进步..1，看懂建筑图结构设计，就是对建筑物的结构构造进行设计，首先当然要有建筑施工图，还要能真正看懂建筑施工图，了解建筑师的设计意图以及建筑各部分的功能及做法，建筑物是一个复杂物体，所涉及的面也很广，所以在看建筑图的同时，作为一个结构师，需要和建筑，水电，暖通空调，勘察等各专业进行咨询了解各专业的各项指标。

在看懂建筑图后，作为一个结构师，这个时候心里应该对整个结构的选型及基本框架有了一个大致的思路了.2，建模(以框架结构为例)（关键）当结构师对整个建筑有了一定的了解后，可以考虑建模了，建模就是利用软件，把心中对建筑物的构思在电脑上再现出来，然后再利用软件的计算功能进行适当的调整，使之符合现行规范以及满足各方面的需要.现在进行结构设计的软件很多，常用的有PKPM，广厦，TBSA等，大致都差不多。

这里不对软件的具体操作做过多的描述，有兴趣的可以看看，每个软件的操作说明书（好厚好厚的，买起来会破产）。

每个软件都差不多，首先要建轴网，这个简单，反正建筑已经把轴网定好了，输进去就行了，然后就是定柱截面及布置柱子。

柱截面的大小的确定需要一定的经验，作为新手，刚开始无法确定也没什么，随便定一个，慢慢再调整也行。

柱子布置也需要结构师对整个建筑的受力合理性有一定的结构理念，柱子布置的合理性对整个建筑的安全与否以及造价的高低起决定性作用...不过建筑师在建筑图中基本已经布好了柱网，作为结构师只需要对布好的柱网进行研究其是否合理.适当的时候需要建议建筑更改柱网.当布好了柱网以后就是梁截面以及主次梁的布置.梁截面相对容易确定一点，主梁按1/8~1/12跨度考虑，次梁可以相对取大一点主次梁的高度要有一定的差别，这个规范上都有要求。

完全平方记忆口诀

完全平方记忆口诀
以下是五个符合要求的口诀：
《完全平方记忆口诀一》
小朋友们要牢记，完全平方有规律。

首平方来尾平方，首尾乘积二倍放中央。

就像盖房子一样，根基要稳四面墙。

前面后面不能忘，中间连接不能慌。

记住这个小口诀，完全平方不用愁，数学难题轻松走。

《完全平方记忆口诀二》
完全平方别害怕，听我给你讲一讲。

一乘自己放开头，二乘两者放中央。

后面也是它自己，平方出来稳稳躺。

好比排队成两行，整整齐齐不会忘。

简单易懂好办法，快乐学习人人夸。

《完全平方记忆口诀三》
完全平方很重要，小朋友们仔细听。

一个数儿先平方，这是开头不能扔。

两两相乘二倍长，放在中间别乱闯。

最后再来个平方，结尾漂亮又大方。

就像拼图一片片，完整呈现心喜欢。

《完全平方记忆口诀四》
学完全平方别发慌，口诀帮你来护航。

一的平方开头站，二倍乘积中间看。

尾的平方最后面，顺序清楚不混乱。

如同搭积木一样，一块一块往上放。

牢牢记住这方法，数学之路闪光芒。

《完全平方记忆口诀五》
完全平方要记好，这个口诀真奇妙。

开头自己平方啦，中间乘积乘以俩。

结尾也是平方哟，整体清楚又明了。

好像画画有步骤，一笔一划都要有。

轻松学会没烦恼，数学成绩节节高。

完全平方公式的计算题简单的

完全平方公式的计算题简单的完全平方公式那可是数学里的“常客”，咱今天就来好好唠唠它在计算题里的那些事儿。

先给大家温习一下完全平方公式哈，（a+b）² = a² + 2ab + b²，（a - b）² = a² - 2ab + b²。

这俩公式看着简单，但是用起来可得小心，稍不留神就容易出错。

我记得有一次在课堂上，给学生们出了一道这样的题：（2x + 3）²。

我就看着他们在下面埋头苦算，有个小家伙自信满满地举手说：“老师，我算出来啦，是 4x² + 9 。

”我一听，就知道他出错啦。

我笑着问他：“那 2ab 这一项跑哪儿去啦？”他挠挠头，这才恍然大悟。

咱再来看几道简单的完全平方公式计算题。

比如说（5 - 3y）²，这道题咱们就得这么算：先算 a²，就是 5² = 25 ；再算 2ab ，那就是2×5×（-3y） = -30y ；最后算 b²，也就是（-3y）² = 9y²。

把它们加起来，答案就是 25 - 30y + 9y²。

再比如（x - 4）²，按照公式，a²是 x²，2ab 是 -8x ，b²是 16 ，所以结果就是 x² - 8x + 16 。

做这类题的时候，大家一定要仔细，可别像我刚才说的那个小家伙一样，把重要的项给弄丢啦。

而且要多练习，练得多了，自然就熟练了。

还有啊，有时候题目会稍微变个花样，比如说给你一个式子 x² + 8x + 16 ，让你写成完全平方的形式。

这时候你就得观察啦，16 是 4 的平方，8x 正好是 2×4×x ，所以这式子就能写成（x + 4）²。

完全平方公式在解决一些实际问题中也特别有用。

比如说，有个正方形的边长增加了 5 厘米，面积增加了多少？咱就可以设原来的边长是 x 厘米，那原来的面积就是 x²平方厘米。

小开口整体墙和壁式框架的计算方法和结构

计算方法采用连续连杆法：假设连梁为沿竖向均匀的连续连杆，将连杆切开后，连杆中除有轴力外还有剪力和弯矩。
总剪力墙
总框架
5.5.3 刚接体系框架-剪力墙结构近似计算
(B) 刚度计算
5.5.3 刚接体系框架-剪力墙结构近似计算
(B) 刚度计算
5.5.3 刚接体系框架-剪力墙结构近似计算
(B) 刚度计算
5.4.1 小开口整体墙计算方法
当各墙肢相差较大时，按下式计算第i个墙肢的Zi值，其中S查表。
层数N a
10 12 14 16 18 20 22 24 26 28 ≥30
8
0.915 0.937 0.952 0.963 0.971 0.977 0.982 0.985 0.988 0.991 0.993
5.4.1 小开口整体墙计算方法
符合下列两个条件的联肢墙可以按小开口整体墙作近似计算： (1) 整体系数a≥10
此时，局部弯矩只占总弯矩中的很小部分，不超过总弯矩的 15%，见图5-27。
5.4.1 小开口整体墙计算方法
图5-27 小开口墙截面正应力分布
5.4.1 小开口整体墙计算方法
(2) 要求大多数楼层以上墙肢不出现反弯点，即要求墙肢足够宽，洞口要小：
5.5.2 铰接结构框架-剪力墙结构的近似计算
(D) 材料力学预备知识
q
x
y
5.5.2 铰接结构框架-剪力墙结构的近似计算
(E) 微分方程的建立与求解
5.5.2 铰接结构框架-剪力墙结构的近似计算
(E) 微分方程的建立与求解
得：以剪力墙变形曲线为未知量的 4 阶微分方程
令：
λ－结构刚度特征值
5.5.3 刚接体系框架-剪力墙结构近似计算

151549_很不错的结构计算小全

4.44 C30 360 210 8650 9000 0.00
14.3 1.00 1.43 565 2.25E+07
满足 9.99 满足
0.0019 0.0052 满足 0.0016 0.0057 满足
25 2
981.7 满足
回目录
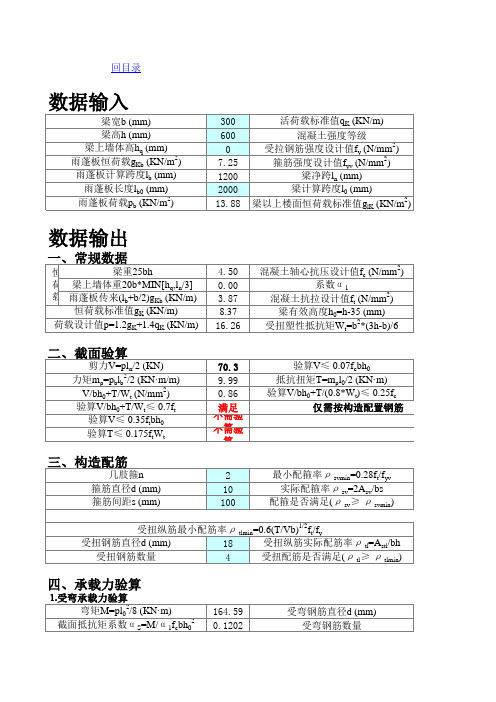
数据输入
梁宽b (mm) 梁高h (mm) 梁上墙体高hq (mm) 2 雨蓬板恒荷载gKb (KN/m ) 雨蓬板计算跨度lb (mm) 雨蓬板长度lb0 (mm) 2 雨蓬板荷载pb (KN/m ) 300 600 0 7.25 1200 2000 13.88 活荷载标准值qK (KN/m) 混凝土强度等级受拉钢筋强度设计值fy (N/mm2) 2 箍筋强度设计值fyv (N/mm ) 梁净跨ln (mm) 梁计算跨度l0 (mm) 2 梁以上楼面恒荷载标准值glK (KN/m )
⒉受剪承载力验算斜截面受剪承载力VCS=0.07fcbh0+1.5fyvnAsvh0/s (KN) 验算VCS≥ V ⒊受扭承载力验算截面核芯部分短边尺寸bcor=b-50 (mm) 截面核芯部分长边尺寸hcor=h-50 (mm) 2 截面核芯部分周长ucor=2(bcor+hcor) (mm) 截面核芯部分面积Acor=bcorhcor (mm ) 2 2 受扭全部纵筋面积Astl (mm ) 沿截面周边单肢箍筋面积Ast1 (mm ) 受扭纵筋与箍筋的配筋强度比值ζ=fyAstl s/fyvAst1ucor ζ实际取值(当ζ<0.6时，取0.6；当ζ>1.7时，取1.7) 1/2 0.35ftWt+1.2ζ *fyvAst1Acor/s (KN·m) 验算T≤ 0.35ftWt+1.2ζ1/2*fyvAst1Acor/s

史上最强的配筋计算公式

配筋（计算规则）率是钢筋混凝土构件中纵向受力（拉或压）钢筋的面积与构件的有效面积之比（轴心受压构件为全截面的面积）。

柱子为轴心受压构件!受拉钢筋配筋率、受压钢筋配筋率分别计算。

计算公式：ρ=A（s）/bh （0）。

此处括号内实为角标,，下同。

式中：A（s）为受拉或受压区纵向钢筋的截面面积； b 为矩形截面的宽度；h（0）为截面的有效高度。

配筋率是反映配筋数量的一个参数。

最小配筋率是指，当梁的配筋率ρ很小，梁拉区开裂后，钢筋应力趋近于屈服强度，这时的配筋率称为最小配筋率ρ（min ）。

最小配筋率是根据构件截面的极限抗弯承载力M （u）与使混凝土构件受拉区正好开裂的弯矩M（cr）相等的原则确定。

最小配筋率取0.2%和0.45f（t）/f（y）二者中的较大值！最大配筋率ρ （max ）=ξ（b）f（c）/f（y）,结构设计的时候要满足最大配筋率的要求，当构件配筋超过最大配筋率时塑性变小，不利于抗震。

配筋率是影响构件受力特征的一个参数，控制配筋率可以控制结构构件的破坏形态，不发生超筋破坏和少筋破坏，配筋率又是反映经济效果的主要指标。

控制最小配筋率是防止构件发生少筋破坏，少筋破坏是脆性破坏，设计时应当避免。

钢筋的截面积与所设计的砼结构面的有效面积的比值，称之为配筋率。

在钢筋砼结构中，钢筋的总截面积与所设计的砼结构面的有效高度与宽度的积的比值，称之为配筋率，根据配筋率的大小，其结构分为超筋、适筋、少筋截面。

钢筋面积/构件截面面积（全面积or 全面积-受压翼缘面积）梁的配筋率是梁的受压和受拉钢筋的总截面积除以梁的有效截面点到砼上面的距离。

合力点：是梁宽乘有效高度，有效高度指梁下部筋为一排筋时用高减35，下部筋为两排筋时减601、“柱外侧纵筋配筋率”为：柱外侧纵筋（包括两根角筋）的截面积，除以整个柱的截面积所得到的比率。

2、屋面框架梁（WKL ）“上部纵筋配筋率”为：梁上部纵筋的总的截面积，除以梁的有效截面积所得到的比率。

(完整版)员工工资结构表

薪资结构表一、薪资构成月工资=基本工资+绩效工资+全勤工资+岗位工资1、基本工资：70元/天*30天即固定金额2100元2、绩效工资：20元/天*30天即固定金额600元3、全勤工资：10元/天*30天即固定金额300元4、岗位工资：（工价*当月天数）-2100-600-300二、基本工资员工基本薪资的标准是根据社会平均生活水平和不同职位等级设定,基本薪资按月计算，按一个季度发放。

三、绩效工资绩效工资考核内容为施工成本、安全文明、工程进度、工程质量及年出勤率，具体考核内容及标准参见《工程部绩效考核管理办法》，员工当月考核扣款超出绩效工资时，将从基本薪资中扣除；绩效工资按年计算，年底一次性发放。

四、全勤工资1、每月累计请假小于3天（含3天）并正常办理请假手续的给予全额全勤奖，请假大于3天的无全勤工资；2、病假如有医院开具的《病假证明》则不影响全勤工资发放；3、每月请假小于3天（含3天）的必须提前至少一天填写《请假申请单》经项目负责人确认签字后在下班前交予行政部；4、每月请假大于3天的必须提前至少一周填写《请假申请单》经总经理确认签字后在下班前交予行政部；5、每月2次（含2次）以上未提前上交《请假申请单》至行政部的全勤工资全额扣除。

五、岗位工资1、公司根据员工的职位性质、职责范围和个人表现确定员工的岗位工资。

六、薪资发放1、公司以货币形式支付员工的薪资，薪资直接汇入指定金融机构员工个人账户内，具体发放时间为：1.单个项目试压或试运行结束后，甲方开具验收合格单后次月25日；2.如单个项目周期过长或无法按单个项目结算的，则2016年工资按如下发放：6月发2、3、4月工资；9月发5、6、7月工资；12月发8、9、10月工资；2017年春节前发11、12、1月工资。

2、员工每月15日、30日可各提交一次借款申请，每次借款总金额不超过1000元，当月合计不超2000元。

六、加班、请假计算1、加班时数以壹小时为基数，不满壹小时不计加班；2、加班计算方式：（工价-10）÷9×加班小时；请假计算方式：（工价-10）÷9×请假小时。

小学数学简算巧算十法

巧算十法随着数学竞赛的蓬勃发展，数值计算充满了活力，除了遵循四则混合运算的运算顺序外，破局部考虑、立整体分析，巧妙、灵活地运用定律和方法，对处理一些貌似复杂的计算题常常有事半功倍的效果，常见的巧算方法有以下十种。

一、凑整法运算定律是巧算的支架，是巧算的理论依据，根据式题的特征，应用定律和性质“凑整”运算数据，能使计算比较简便。

1、加法“凑整”。

利用加法交换律、结合律“凑整”，例如：4673＋27689＋5327＋22311=（4673＋5327）＋（27689＋22311）=10000＋50000=600002、减法“凑整”。

利用减法性质“凑整”，例如：50－13－7=50－（13＋7）=303、乘法“凑整”。

利用乘法交换律、结合律、分配律“凑整”，例如：125×4×8×25×78=（125×8）×（4×25）×78= 1000×100×78=78000004、补充数“凑整”。

末尾是一个或几个0的数，运算起来比较简便。

若数末尾不是0，而是98、51等，我们可以用（100-2）、（50＋1）等来代替，使运算变得比较简便、快速。

一般地我们把100叫做98的“大约强数”，2叫做98的“补充数”；50叫做51的“大约弱数”，1叫做51的“补充数”。

把一个数先写成它的大约强（弱）数与补充数的差（和），然后再进行运算，例如：（1）387＋99=387＋（100-1）=387＋100-1=486（2）1680-89=1680-（100-11）=1680-100+11=1580+11=1591（3）69×101=69×（100+1）=6900+69=6969二、约分法根据式题结构，采用约分，能使计算比较简便。

例如：三、基数法根据数据特征，从诸多数中选择一个做计算基础的数，通过“割”、“补”，采用“以乘代加”的方法速算。

万能速算口诀

万能速算口诀1. “十几乘十几，方法很容易。

头乘头，尾加尾，尾乘尾。

”比如说13×15，先算头乘头，1×1 = 1；再算尾加尾，3 + 5 = 8；最后算尾乘尾，3×5 = 15，结果就是195啦。

我教我表弟这个口诀时，他一开始还不太相信，觉得哪有这么简单。

我给他演示了几遍后，他眼睛一亮，说：“哇，真的好快啊！”你学会了吗？这个口诀是不是很神奇呢？2. “头相同，尾互补，速算有妙处。

头乘头加一，尾乘尾放后。

”像43×47，头乘头加一，4×（4 + 1）= 20；尾乘尾，3×7 = 21，结果就是2021。

有一次我和同学在做数学作业时，遇到了这样的题，我用这个口诀很快就算出来了，同学惊讶地问我：“你怎么算得这么快？”我就把口诀教给了他，他开心地说：“这下做作业可快多了！”你有没有遇到过这种头相同尾互补的乘法呢？试试这个口诀吧！3. “几十一乘几十一，方法也简单。

头乘头，头加头，尾乘尾。

”例如31×51，头乘头，3×5 = 15；头加头，3 + 5 = 8；尾乘尾，1×1 = 1，结果就是1581。

我在和爸爸玩数学游戏时，我用这个口诀算出了答案，爸爸还不相信我这么快，自己算了一遍后，对我竖起了大拇指，说：“这个口诀真厉害！”你想不想在和家人朋友的数学比拼中露一手呢？4. “一个数乘11，口诀要记清。

两边一拉，中间相加。

”比如23×11，把2和3拉开，中间是2 + 3 = 5，结果就是253。

有一次在课堂上，老师出了一道这样的题，我马上就用口诀回答出来了，同学们都投来羡慕的目光。

你觉得这个口诀好不好用呢？它能让你在计算11的乘法时快速又准确哦！5. “十几乘任意数，也有小窍门。

先把十几拆，再分别相乘，最后相加。

”以13×24为例，把13拆成10和3，先算10×24 = 240，再算3×24 = 72，最后相加240 + 72 = 312。

用乘法公式巧妙计算

用乘法公式巧妙计算乘法公式是数学中的基本公式之一，它用于计算两个数的乘积。

乘法公式还可以通过巧妙的变形和运算，用来解决一些复杂的问题。

在本文中，我将介绍一些常见的乘法公式应用和巧妙计算方法，为你提供一些灵感和启示。

1.乘法分配律：乘法分配律是数学中最常用的乘法公式之一、它表明，两个数的积与其中一个数分别乘以另一个数再相加的结果相等。

即：a*(b+c)=a*b+a*c。

这个公式在计算中可以大大简化问题，因为我们可以先将一些因子与多个数相乘，然后再将结果相加，而不需要一个一个相乘再相加。

2. 平方公式：平方公式用于计算一个数的平方。

即：(a+b)^2 = a^2 + 2ab + b^2、这个公式可以用来计算一个数的平方和，或者将一个数的立方拆分成多个平方的和。

3. 乘方公式：乘方公式用于计算一个数的乘方。

例如，(a+b)^3 =a^3 + 3a^2b + 3ab^2 + b^3、这个公式可以用来计算一个数的立方和，或者将一个数的四次方、五次方等拆分成多个平方的和。

4.九九乘法口诀：九九乘法口诀是学习乘法的基础，它通过记忆九九乘法表的形式，帮助我们快速计算两个数的乘积。

例如，2乘以3等于6，3乘以4等于12等等。

通过熟练掌握九九乘法口诀，可以在计算中快速推算乘积。

5.快速乘法法则：快速乘法法则是一种通过巧妙的变形和运算，高效地计算乘积的方法。

例如，计算17乘以15，可以将15拆分成10和5，然后将10乘以17，在将5乘以17，最后将两个数的乘积相加。

这种方法可以在一定程度上减少手工计算的复杂度。

通过灵活运用这些乘法公式和巧妙计算方法，可以大大简化乘法计算的过程，并提高计算效率。

在以后的学习和工作中，你可以根据具体的问题和需求，选择合适的公式和方法，以便更加高效地进行乘法计算。

不断练习和应用这些方法，你会发现数学计算的乐趣，同时也提高自己的数学能力。

简便计算顺口溜

简便计算顺口溜：简便计算，并不难。

仔细观察，找特点。

连续加法，二凑一。

连续乘法，就凑整。

连续减法，就减和。

连续除法，除以积。

减法减和，连续减。

除法以积，连续除。

简便计算是一种特殊的计算，它运用了运算定律与数字的基本性质，从而使计算简便，使一个很复杂的式子变得很容易计算出得数。

简便计算中最常用的方法是乘法分配律。

乘法分配律指的是ax(b+c)=axb+axc其中a,b,c是任意实数。

相反的，axb+axc=ax(b+c)叫做乘法分配律的逆运用（也叫提取公约数），尤其是a与b互为补数时，这种方法更有用。

也有时用到了加法结合律，比如a+b+c，b和c互为补数，就可以把b和c结合起来，再与a 相乘。

如将上式中的+变为x，运用乘法结合律也可简便计算1、两个加数交换位置,和不变.这叫做加法交换律.用字母表示：a+b=b+a2、先把前两个数相加,或者先把后两个数相加,和不变.这叫做加法结合律.用字母表示：(a+b)+c=a+(b+c)3、交换两个因数的位置,积不变.这叫做乘法交换律.用字母表示：a×b=b×a4、先乘前两个数,或者先乘后两个数,积不变.这叫做乘法结合律.用字母表示：(a×b)×c=a×(b×c)5、两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再相加.这叫做乘法分配律.用字母表示：(a+b)×c=a×c+b×c 或者a×(b+c)=a×b+a×c(注意：除法没有分配律)6、乘法分配律应用：(a—b)×c=a×c—b×c7、减法性质：a-b-c=a-(b+c)8、除法性质：a÷b÷c= a÷c÷b= a÷(b×c)9、牢记：25×4=100 125×8=1000。

PKPM初学者很有帮助

PKPM初学者很有帮助！我是转帖的新的建筑结构设计规范在结构可靠度、设计计算、配筋构造方面均有重大更新和补充，特别是对抗震及结构的整体性，规则性作出了更高的要求，使结构设计不可能一次完成。

如何正确运用设计软件进行结构设计计算，以满足新规范的要求，是每个设计人员都非常关心的问题。

以SA TWE软件为例，进行结构设计计算步骤的讨论，对一个典型工程而言，使用结构软件进行结构计算分四步较为科学。

1．完成整体参数的正确设定计算开始以前，设计人员首先要根据新规范的具体规定和软件手册对参数意义的描述，以及工程的实际情况，对软件初始参数和特殊构件进行正确设置。

但有几个参数是关系到整体计算结果的，必须首先确定其合理取值，才能保证后续计算结果的正确性。

这些参数包括振型组合数、最大地震力作用方向和结构基本周期等，在计算前很难估计，需要经过试算才能得到。

(1)振型组合数是软件在做抗震计算时考虑振型的数量。

该值取值太小不能正确反映模型应当考虑的振型数量，使计算结果失真；取值太大，不仅浪费时间，还可能使计算结果发生畸变。

《高层建筑混凝土结构技术规程》5.1.13-2条规定，抗震计算时，宜考虑平扭藕联计算结构的扭转效应，振型数不宜小于15，对多塔结构的振型数不应小于塔楼的9倍，且计算振型数应使振型参与质量不小于总质量的90％。

一般而言，振型数的多少于结构层数及结构自由度有关，当结构层数较多或结构层刚度突变较大时，振型数应当取得多些，如有弹性节点、多塔楼、转换层等结构形式。

振型组合数是否取值合理，可以看软件计算书中的x，y向的有效质量系数是否大于0.9。

具体操作是，首先根据工程实际情况及设计经验预设一个振型数计算后考察有效质量系数是否大于0.9，若小于0.9，可逐步加大振型个数，直到x,y两个方向的有效质量系数都大于0.9为止。

必须指出的是，结构的振型组合数并不是越大越好，其最大值不能超过结构得总自由度数。

例如对采用刚性板假定得单塔结构，考虑扭转藕联作用时，其振型不得超过结构层数的3倍。

结构设计电算常见错误做法

结构设计电算常见错误做法常见错误做法总结于下。

1．暗梁当楼面梁使用。

这是最常见的错误。

暗梁之所以不能当楼面梁是因为其刚度不够，荷载不能按自己设想的方式传递，即楼面荷载—板—暗梁—柱的传递方式几乎是不可能的。

这样将大大低估板的内力。

我个人认为，根据内力按最短距离传递的原则，用暗梁代替梁只有在板受集中力时，在集中力处沿板的最短方向（双向板沿两个垂直方向）设置暗梁，可以认为集中力由暗梁承受以满足抗弯强度和裂缝要求，此时板的计算跨度绝对不能按支承于暗梁来考虑。

但很多时候，这种做法也没有必要，直接加大板的受力钢筋即可，除非因抗剪（冲切）需要箍筋而使用暗梁。

2．与上一个问题相对应的是，在刚度发生较大突变（增加）处，应视为梁。

典型的问题是不同高程的板之间出现的错台，错台本身平面外刚度比较大，而板的平面外刚度较小，不管你是否愿意，板上的荷载都要传递到错台上，因此应当按梁来设计，尤其是抗剪钢筋应满足要求。

地下通道、车站遇到的这种情况较多，其荷载又比较大，但大多数人对错台的处理却非常草率，这很令人担忧。

3．框架结构形成事实上的铰接。

最常见的是梁刚度比柱大的多，使柱对梁的约束作用较弱，形成事实上的铰。

这样减少了超静定次数，于抗震不利，也难以形成“强柱弱梁”。

坂神地震时，地铁车站柱的破坏相当严重，也提醒我们不能忽视这个问题。

地铁车站顶底板可看作筏板，其梁的刚度当然大于柱，但中板处不宜将梁的刚度做得较大。

另外，地下工程如通道、涵洞、地铁车站等，有时不小心也容易作成刚度较大的顶底板和刚度较小的侧墙，这样横剖面就形成铰接的四边形，两侧墙土压力相差较大时很容易失稳，也不利于抗震。

4．板墙受力钢筋置于分布钢筋的内侧。

很多人总把分布钢筋想象成类似梁的箍筋，因此配筋不小心就这样倒置。

分布钢筋的作用在于固定受力钢筋位置，传递受力及防止温度收缩裂缝，它不需要象梁柱箍筋那样外包以防止钢筋受压向外鼓出，更重要的是，板墙截面高度较小，为增加有效高度发挥受力筋作用，一般情况下应当外置受力钢筋。

数学组合计算公式

数学组合计算公式好的，以下是为您生成的关于“数学组合计算公式”的文章：咱们在数学的世界里呀，经常会碰到各种各样神奇又有趣的东西，就比如说这个组合计算公式。

它就像是一把神奇的钥匙，能帮咱们打开好多难题的大门。

先来说说啥是组合吧。

打个比方，你有 5 个不同的玩具，要选出 2个来玩，不考虑顺序，这就是一个组合问题。

那组合计算公式就是用来算出一共有多少种选法的工具。

组合计算公式是这样的：C(n, k) = n! / [k!(n - k)!] 。

这里面的“!”表示阶乘，比如说 5! = 5×4×3×2×1 。

别被这一堆符号吓到，其实理解起来也不难。

就拿刚刚说的选玩具的例子，5 个玩具里选 2 个，那 n 就是 5 ，k就是 2 。

咱们算算，5! 就是 120 ，2! 是 2 ，(5 - 2)! 也就是 3! 是 6 。

带进去算一下，C(5, 2) = 120 / (2×6) = 10 ，所以一共有 10 种选法。

我还记得之前给学生们讲这个的时候，有个小家伙一脸懵地看着我，说：“老师，这也太复杂啦，我搞不懂！”我就笑着跟他说：“别着急，咱们慢慢来。

”然后我就带着他们做了好多实际的例子。

比如说，班级里要选 3 个人去参加比赛，一共有 10 个人报名，那有多少种选法？大家就一起用公式算，一开始有的同学算错了，但是经过几次练习，慢慢就都掌握了。

还有一次，学校组织活动，要从 8 种不同的零食里选 4 种作为奖品。

同学们就用刚学的组合计算公式来算，算出来一共有 70 种选法。

大家都特别兴奋，觉得数学原来这么有用，能帮我们解决生活中的实际问题。

其实组合计算公式在很多地方都能派上用场。

比如抽奖的时候，从一堆号码里选几个中奖的；安排座位的时候，从一群同学里选出几个坐在一起；甚至是组队做游戏，从好多人里挑出固定数量的人组成队伍。

所以呀，可别小看这个组合计算公式，它虽然看起来有点复杂，但只要咱们多练习，多在实际生活中用一用，就能发现它的妙处。

简单的数学计算方法

简单的数学算法1.十几乘十几：口诀：头乘头，尾加尾，尾乘尾。

例：12×14=？解: 1×1=1２＋４＝６２×４＝８12×14=168注：个位相乘，不够两位数要用0占位２.头相同，尾互补(尾相加等于10)：口诀：一个头加１后，头乘头，尾乘尾。

例：23×27=？解：２＋１＝３２×３＝６３×７＝2123×27=621注：个位相乘，不够两位数要用0占位。

３.第一个乘数互补，另一个乘数数字相同：口诀：一个头加１后，头乘头，尾乘尾。

例：37×44=？解：3+1=44×4=167×4=2837×44=1628注：个位相乘，不够两位数要用0占位。

４.几十一乘几十一：口诀：头乘头，头加头，尾乘尾。

例：21×41=？解：2×4=82+4=61×1=121×41=861５.11乘任意数：口诀：首尾不动下落，中间之和下拉。

例：11×23125=？解：2+3=53+1=41+2=32+5=72和5分别在首尾11×23125=254375注：和满十要进一。

６.十几乘任意数：口诀：第二乘数首位不动向下落，第一因数的个位乘以第二因数后面每一个数字，加下一位数，再向下落。

例：13×326=？解：13个位是33×3+2=113×2+6=123×6=1813×326=4238注：和满十要进一。

数学计算方法一、30以内的两个两位数乘积的心算速算1、两个因数都在20以内任意两个20以内的两个两位数的积，都可以将其中一个因数的”尾数”移加到另一个因数上，然后补一个0，再加上两“尾数”的积。

例如：11×11=120+1×1=12112×13=150+2×3=15613×13=160+3×3=16914×16=200+4×6=22416×18=240+6×8=2882、两个因数分别在10至20和20至30之间对于任意这样两个因数的积，都可以将较小的一个因数的“尾数”的2倍移加到另一个因数上，然后补一个0，再加上两“尾数”的积。

十项全能的计算方式

十项全能的计算方式一、加法运算加法运算是最基本的运算之一，它可以将两个数值相加，得到它们的和。

例如，将数字1和数字2相加，结果为3。

加法运算可以用符号“+”表示，即1 + 2 = 3。

二、减法运算减法运算是将一个数值从另一个数值中减去，得到它们的差。

例如，将数字5减去数字3，结果为2。

减法运算可以用符号“-”表示，即5 - 3 = 2。

三、乘法运算乘法运算是将两个数值相乘，得到它们的积。

例如，将数字2乘以数字4，结果为8。

乘法运算可以用符号“×”表示，即2 × 4 = 8。

四、除法运算除法运算是将一个数值除以另一个数值，得到它们的商。

例如，将数字10除以数字2，结果为5。

除法运算可以用符号“÷”表示，即10 ÷ 2 = 5。

五、幂运算幂运算是将一个数值自乘多次，得到指定次数的幂。

例如，将数字2的平方，结果为4；将数字3的立方，结果为27。

幂运算可以用符号“^”表示，即2^2 = 4，3^3 = 27。

六、平方根运算平方根运算是将一个数值开平方，得到它的平方根。

例如，将数字9开平方，结果为3。

平方根运算可以用符号“√”表示，即√9 = 3。

七、取模运算取模运算是将一个数值除以另一个数值，得到它们的余数。

例如，将数字10除以数字3，余数为1。

取模运算可以用符号“%”表示，即10 % 3 = 1。

八、绝对值运算绝对值运算是将一个数值的正负号去掉，得到它的绝对值。

例如，将数字-5的绝对值，结果为5。

绝对值运算可以用符号“| |”表示，即| -5 | = 5。

九、四舍五入运算四舍五入运算是将一个数值按照一定规则进行近似取整。

例如，将数字3.6四舍五入到整数，结果为4。

四舍五入运算可以用符号“~”表示，即~3.6 = 4。

十、求反运算求反运算是将一个数值的正负号取反，得到它的相反数。

例如，将数字8的相反数，结果为-8。

求反运算可以用符号“-”表示，即-8= -8。

通过以上十项全能的计算方式，我们可以灵活地进行各种数值计算，从简单的加法减法到复杂的幂运算和平方根运算，都可以得到准确的结果。

掌握简单的计算技巧

掌握简单的计算技巧在日常生活和学习中，计算是一个无处不在的重要环节。

掌握简单的计算技巧不仅能够提高计算效率，还有助于培养逻辑思维和数学能力。

以下将介绍一些简单的计算技巧，帮助大家更加轻松地完成各种计算任务。

一、整数运算1. 加减法：在做加法时，可以先将其中一个数放在心中，然后将另一个数按位加上去。

例如计算89+37，我们可以快速地在心中将37加到89上，得到126。

同样的方法可以用于减法，只需将减数按位减去即可。

2. 乘法：对于两个整数相乘，我们可以使用近似相乘的方法，将一个数分解成更容易计算的形式。

例如计算47×6，我们可以将6分解为2×3，然后先计算47×2=94，再将结果与3相乘得到最终答案282。

3. 除法：当需要做除法运算时，我们可以使用除数的倍数逼近法。

例如计算639÷4，我们可以先找到4的倍数640，然后再根据相似性质，639的结果应该略小于160，因此答案为159。

二、小数运算1. 加减法：在进行小数的加减法运算时，我们可以先将小数点对齐，然后按位进行计算。

例如计算3.78+0.95，我们可以将两个数的小数点对齐后，按位相加得到4.73。

2. 乘法：在计算小数的乘法时，可以先将小数点去掉，将两个整数相乘，然后再确定小数点的位置。

例如计算2.5×0.8，我们可以先计算25×8=200，然后将结果除以10的平方，得到2.00。

3. 除法：在进行小数的除法运算时，我们可以先将除数调整为整数，然后再进行计算。

例如计算1.25÷0.5，我们可以将两个数都扩大10倍，得到12.5÷5=2.5。

三、百分数运算1. 百分数转化为小数：将百分数除以100即可获得对应的小数。

例如75%转化为小数为0.75。

2. 小数转化为百分数：将小数乘以100即可得到对应的百分数。

例如0.65转化为百分数为65%。

3. 百分数之间的运算：在进行百分数的加减运算时，可以先将百分数转化为小数，然后进行计算。

精度较高的计算公式

精度较高的计算公式在科学研究和工程领域中，精确的计算公式是非常重要的。

这些公式可以帮助我们预测物理现象、设计工程结构、优化生产过程等。

在本文中，我们将讨论一些精度较高的计算公式，并介绍它们在不同领域的应用。

一、物理学中的精确计算公式。

1.牛顿第二定律。

在物理学中，牛顿第二定律是一个非常重要的公式，它描述了物体的运动状态。

其数学表达式为F=ma，其中F表示物体所受的力，m表示物体的质量，a表示物体的加速度。

这个公式被广泛应用于机械工程、航空航天等领域。

2.库仑定律。

库仑定律描述了两个电荷之间的相互作用力。

其数学表达式为F=kq1q2/r^2，其中F表示电荷之间的作用力，k表示库仑常数，q1和q2分别表示两个电荷的大小，r表示两个电荷之间的距离。

这个公式在电磁学和电工学中有着广泛的应用。

3.热力学基本方程。

热力学基本方程描述了热力学系统的状态变化。

其中最著名的是理想气体状态方程PV=nRT，其中P表示气体压强，V表示气体体积，n表示气体的摩尔数，R表示气体常数，T表示气体的温度。

这个公式在化工工程和能源领域中有着广泛的应用。

二、工程学中的精确计算公式。

1.梁的挠度计算公式。

在工程结构设计中，梁的挠度是一个非常重要的参数。

梁的挠度计算公式可以帮助工程师预测梁在受力下的变形情况。

常用的梁的挠度计算公式包括Euler-Bernoulli梁挠度公式和Timoshenko梁挠度公式。

2.压力容器壁厚计算公式。

在压力容器设计中，确定合适的壁厚是非常重要的。

压力容器壁厚计算公式可以帮助工程师确定压力容器的壁厚，以保证其在使用过程中的安全性。

常用的压力容器壁厚计算公式包括ASME VIII-1标准中的壁厚计算公式和PD 5500标准中的壁厚计算公式。

3.泵的性能计算公式。

在流体力学中，泵的性能是一个非常重要的参数。

泵的性能计算公式可以帮助工程师确定泵的流量、扬程和效率等参数，以优化泵的设计和运行。

常用的泵的性能计算公式包括流量计算公式、扬程计算公式和效率计算公式。

配成完全平方的技巧

配成完全平方的技巧配成完全平方的技巧在数学中，完全平方是指一个数可以表示为另一个整数的平方的形式。

例如，4是2的平方，9是3的平方。

在实际应用中，将一个数配成完全平方可以简化计算和分析过程。

下面介绍一些配成完全平方的技巧。

1. 拆分法拆分法是将一个数拆分成两个较小的数相乘的形式，并尽可能让这两个数相等。

例如，24可以拆分为12×2或8×3，但12和2更接近，因此我们选择12×2=144-100=44作为24的配方。

2. 平均数法平均数法是将一个数拆分成两个相等的部分，并将它们加减后再进行平方。

例如，25可以拆分为12+13，然后进行计算：(12+13)²=25²/2=625/2=312.5。

3. 迭代法迭代法是通过不断逼近来寻找最接近目标值的完全平方数。

例如，要将27配成完全平方，则可以从5开始迭代：5²=25<27<36，则27与25更接近；下一步迭代6²=36>27>30，则27与30更接近；再下一步7²=49>27>42，则27与30更接近。

因此，27的配方为30²-9=891。

4. 质因数分解法质因数分解法是将一个数分解成若干个质数的乘积，并将每个质因子的指数除以2后再相乘。

例如，60=2²×3×5，则60的配方为(2²×3)²×5=36×5=180。

5. 补全平方法补全平方法是通过加减常数来将一个不完全平方数配成完全平方。

例如，要将x²+6x+7配成完全平方，则可以找到常数k使得x²+6x+7+k=(x+3)²，则有k=2。

因此，x²+6x+7的配方为(x+3)²-2。

以上是一些常用的配成完全平方的技巧，它们可以帮助我们简化计算和分析过程，并在实际应用中发挥重要作用。

多部件之间最小距离计算方法

多部件之间最小距离计算方法
1. 嘿，你知道吗，计算多部件之间最小距离就像是在走迷宫找最短路径一样！比如说一堆玩具零件，怎么摆放才能让它们之间的距离最小呢？这可得好好琢磨！
2. 哇塞，多部件之间最小距离计算方法其实超有趣的啦！就像给一群调皮的孩子安排座位，要让他们既不挤着又能离得最近，是不是很有意思？比如那些小珠子，怎样放才最合适呢？
3. 哎呀呀，原来计算多部件之间最小距离可以这么神奇！好比化妆师给人化妆，每个部位都要恰到好处地安排。

像那些小饰品，怎么摆才能最精致呢？
4. 嘿，这多部件之间最小距离的计算简直就像一场刺激的游戏！例如搭积木的时候，怎样让每一块积木之间的距离最小又稳定呢？
5. 哇哦，想想多部件之间最小距离计算，不就是在给混乱的东西排排队嘛！像整理那些乱七八槽的文具，怎么放才能让它们紧凑又不混乱呢？
6. 嘿嘿，多部件之间最小距离计算真是个好玩的事儿！就如同给花摆放造型，要让它们彼此靠近又美丽，比如说那些花瓣，怎样排列才最美呢？
我的观点结论就是：多部件之间最小距离计算充满了挑战和乐趣，只要我们用心去探索，就能发现其中的奇妙之处，并且能很好地应用到生活中的各种场景中去哟！。