伯努利概型与全概公式
伯努利概型与全概公式市公开课获奖课件省名师示范课获奖课件

PB PAi PB | Ai i 1 0.5 0.95 0.3 0.92 0.2 0.90
0.931
23
定理(全概率公式)
完备事件组
若A1, A2 , , An是互不相容互斥的事件
即Ai Aj i j, 且A1 A2 An , PAi 0i 1,2, , n.则对任一事件B有
所以,使被冒牌者蒙到岗位旳概率及将真正旳行家 拒之门外旳概率都变小测试措施是不存旳.因而,只 能在两者中取其一.
14
例2 某射手每次击中目旳旳概率是0.6,假如 射击5次,求至少击中两次旳概率.
解: 因为每次射击是相互独立旳,且只有击中与 未击中两种成果,故能够按5重伯努利概型计算
事件旳概率.已知 p 0.6, q 0.4,则
5
P(至少击中两次) P(击中k次) k2
1 P(击中0次) P(击中1次)
1
C
0 5
(0.6)0
(0.4)5
C
1 5
(0.6)1
(0.4)4
0.913
15
练习、某导弹旳命中率是0.6,问欲以99%旳把握 命中目旳至少需要配置几枚导弹?
解:设需配置n枚导弹,因为导弹各自独立发射,所以
能够看作n重伯努利试验。设A={导弹命中目的},
由此可见,一件微不足 道的小事,只要坚持, 就会产生不可思议的结 果。
17
重 条件概率 点
回 定义 设两个事件A、B ,且 P(B)>0,
顾
则称 PA | B 为在事件B发生旳
前提下,事件A发生旳条件概率。
计算公式:
PA|
B
PAB PB
同理,若PA 0有
PB
|
A
伯努利概型与全概公式

全概公式是概率 论中一个重要的 公式,用于计算 在有限次试验中 某一事件发生的
概率
全概公式是伯 努利概型中唯 一一个能计算 出所有可能概
率的公式
推导过程
定义:全概公式是伯努利概型的一种特殊情况,即当试验次数趋于无穷大时,事 件A发生的概率的极限。
推导:全概公式可以通过伯努利概型和概率极限定理推导得出,具体过程涉及到 概率论和数理统计的基本概念和公式。
汇报人:XX
伯努利概型与全 概公式
汇报人:XX
目 录
01 添 加 目 录 项 标 题
03 全 概 公 式
05
伯努利概型与全概 公式的应用实例
02 伯 努 利 概 型
04
伯努利概型与全 概公式的联系
PART 01 添加章节标题
PART 02 伯努利概型
定义
伯努利概型是一种概率模型,其中事件的发生概率仅依赖于前n次试验中事件发生的次 数。
应用场景
用于描述独立重复试验的 概率模型
概率论与数理统计中的基 本概念
在保险、彩票、赌博等领 域有广泛应用
在统计学、数据分析、可靠 性工程等领域也常被提及
PART 03 全概公式
定义
全概公式是伯Biblioteka 努利概型中所 有可能结果的概率之和
全概公式表示在 n次试验中,事 件A发生k次的
概率为 P(nA)=C(n,k)P( A)k(1−P(A))n−k
概率计算中的区别
伯努利概型:单个试验的结果只有两种, 成功或失败,概率为p。
全概公式:考虑多个试验的结果,计算总 概率。
联系:全概公式可以看作是伯努利概型 的推广,当试验次数趋于无穷时,伯努 利概型的结果可以用来计算全概公式。
伯努利概型与全概公式【课资内容】

P(B) p( Ai )P(B | Ai ) i 1
0.25 0.05 0.35 0.04 0.40 0.02
0.0345
资料类
25
例3 人们为了了解一支股票未来一定时期内价 格的变化,往往会去分析影响股票的基本因素, 比如利率的变化。现在假设人们经分析估计利 率下调的概率为60%,利率不变的概率为40%。 根据经验,人们估计,在利率下调的情况下, 该支股票价格上涨的概率为80%,而在利率不 变的情况下,其价格上涨的概率为40%,求该 支股票将上涨的概率。
资料类
16
例 :在 平 常 的 生 活 中 , 人常们常 用 “ 水 滴 石 穿 ”“、只 要 功 夫 深 , 铁 杵 磨 成 针来”形 容 有 志 者 事 竟 成但。是 , 也 有 人 认 为 这 些 是 不 可 能。的试 从 概 率 的 角 度 分这析是 否 合 理 。
解 :设 一 次 实 验 中 , 事A件发 生 的 概 率 为 0,
lim[1 (1 )n ] 1 n
由 此 可 见 , 一 件 微 不道足的 小 事 , 只 要 坚 持 , 就 会 产 生 不 可 思 议 的果结。
资料类
17
重 条件概率 点
回 定义 设两个事件A、B ,且 P(B)>0,
顾
则称 PA | B 为在事件B发生的
前提下,事件A发生的条件概率。
资料类
20
解 : 设A1, A2 , A3分别表示抽到的产品是甲,乙,丙 厂的产品, B表示抽到的1个产品是合格品.由题意 可知A1 , A2 , A3互不相容, 且A1 A2 A3 ,并有
PA1
500 1000
0.5,
PA2
300 1000
0.3
概率论核心概念及公式
②运算:
结合率:A(BC)=(AB)C A∪(B∪C)=(A∪B)∪C
分配率:(AB)∪C=(A∪C)∩(B∪C) (A∪B)∩C=(AC)∪(BC)
德摩根率: ,
(7)概率的公理化定义
设 为样本空间, 为事件,对每一个事件 都有一个实数P(A),若满足下列三个条件:
若 ,则 的分布函数为
。。
参数 、 时的正态分布称为标准正态分布,记为 ,其密度函数记为
, ,
分布函数为
。
是不可求积函数,其函数值,已编制成表可供查用。
Φ(-x)=1-Φ(x)且Φ(0)= 。
如果 ~ ,则 ~ 。
。
(6)分位数
下分位表: ;
上分位表: 。
(7)函数分布
离散型
已知 的分布列为
,
的分布列( 互不相等)如下:
,
若有某些 相等,则应将对应的 相加作为 的概率。
连续型
先利用X的概率密度fX(x)写出Y的分布函数FY(y)=P(g(X)≤y),再利用变上下限积分的求导公式求出fY(y)。
第三章 二维随机变量及其分布
(1)联合分布
离散型
如果二维随机向量 (X,Y)的所有可能取值为至多可列个有序对(x,y),则称 为离散型随机量。
。其中L为几何度量(长度、面积、体积)。
(10)加法公式
P(A+B)=P(A)+P(B)-P(AB)
当P(AB)=0时,P(A+B)=P(A)+P(B)
(11)减法公式
P(A-B)=P(A)-P(AB)
当B A时,P(A-B)=P(A)-P(B)
概率论与数理统计公式整理(超全免费版)

A,B,C,…表示事件,它们是 的子集。 为必然事件,Ø 为不可能事件。
不可能事件(Ø)的概率为零,而概率为零的事件不一定是不可能事件;同理, 必然事件(Ω)的概率为 1,而概率为 1 的事件也不一定是必然事件。
①关系: 如果事件 A 的组成部分也是事件 B 的组成部分,(A 发生必有事件 B 发生):
A B 如果同时有 A B , B A ,则称事件 A 与事件 B 等价,或称 A 等于 B:
A=B。
A、B 中至少有一个发生的事件:A B,或者 A+B。 属于 A 而不属于 B 的部分所构成的事件,称为 A 与 B 的差,记为 A-B,也可
(6)事件 的关系与
表示为 A-AB 或者 AB ,它表示 A 发生而 B 不发生的事件。
j 1
此公式即为贝叶斯公式。
P(Bi ) ,( i 1,2 ,…,n ),通常叫先验概率。P(Bi / A) ,( i 1,2 ,…, n ),通常称为后验概率。贝叶斯公式反映了“因果”的概率规律,并作出了
(17)伯努 利概型
“由果朔因”的推断。
我们作了 n 次试验,且满足 每次试验只有两种可能结果, A 发生或 A 不发生; n 次试验是重复进行的,即 A 发生的概率每次均一样; 每次试验是独立的,即每次试验 A 发生与否与其他次试验 A 发生与
P( X k) q k1 p, k 1,2,3, ,其中 p≥0,q=1-p。
随机变量 X 服从参数为 p 的几何分布,记为 G(p)。
1
概率论与数理统计 公式(全)
均匀分布
设随机变量 X 的值只落在[a,b]内,其密度函数 f (x) 在[a,b] 上为常数 1 ,即
大学概率论与数理统计公式全集

大学概率论与数理统计公式全集一、随机事件和概率1、随机事件及其概率2、概率的定义及其计算二、随机变量及其分布1、分布函数性质FbF(aba<≤=P-X)(b()()bFX()P=≤)2、离散型随机变量3、连续型随机变量三、多维随机变量及其分布1、离散型二维随机变量边缘分布∑∑======⋅jjijjii i py Y x X P x X P p ),()(∑∑======⋅iiijjij j py Y x X P y Y P p ),()(2、离散型二维随机变量条件分布2,1,)(),()(=========⋅i P p y Y P y Y x X P y Y x X P p jij j j i j i j i2,1,)(),()(=========⋅j P p x X P y Y x X P x X y Y P p i ij i j i i j i j3、连续型二维随机变量( X ,Y )的联合分布函数⎰⎰∞-∞-=xydvdu v u f y x F ),(),( 4、连续型二维随机变量边缘分布函数与边缘密度函数边缘分布函数:⎰⎰∞-+∞∞-=xX dvdu v u f x F ),()( 边缘密度函数:⎰+∞∞-=dv v x f x f X ),()( ⎰⎰∞-+∞∞-=y Y dudv v u f y F ),()( ⎰+∞∞-=du y u f y f Y ),()(5、二维随机变量的条件分布+∞<<-∞=y x f y x f x y f X X Y ,)(),()( +∞<<-∞=x y f y x f y x f Y Y X ,)(),()(四、随机变量的数字特征1、数学期望离散型随机变量:∑+∞==1)(k k k p x X E 连续型随机变量:⎰+∞∞-=dx x xf X E )()(2、数学期望的性质(1)为常数C ,)(C C E = )()]([X E X E E = )()(X CE CX E =(2))()()(Y E X E Y X E ±=± b X aE b aX E ±=±)()( )()()(1111n n n n X E C X E C X C X C E +=+ (3)若XY 相互独立则:)()()(Y E X E XY E = (4))()()]([222Y E X E XY E ≤ 3、方差:)()()(22X E X E X D -= 4、方差的性质(1)0)(=C D 0)]([=X D D )()(2X D a b aX D =± 2)()(C X E X D -<(2)),(2)()()(Y X Cov Y D X D Y X D ±+=± 若XY 相互独立则:)()()(Y D X D Y X D +=± 5、协方差:)()(),(),(Y E X E Y X E Y X Cov -= 若XY 相互独立则:0),(=Y X Cov 6、相关系数:)()(),(),(Y D X D Y X Cov Y X XY==ρρ 若XY 相互独立则:0=XYρ即XY 不相关7、协方差和相关系数的性质 (1))(),(X D X X Cov = ),(),(X Y Cov Y X Cov =(2)),(),(),(2121Y X Cov Y X Cov Y X X Cov +=+ ),(),(Y X abCov d bY c aX Cov =++8、常见数学分布的期望和方差五、大数定律和中心极限定理1、切比雪夫不等式若,)(,)(2σμ==X D X E 对于任意0>ξ有2)(})({ξξX D X E X P ≤≥-或2)(1})({ξξX D X E X P -≥<- 2、大数定律:若n X X 1相互独立且∞→n 时,∑∑==−→−ni iDni i X E nX n 11)(11(1)若n X X 1相互独立,2)(,)(i i i i X D X E σμ==且M i ≤2σ则:∑∑==∞→−→−ni iPni i n X E nX n11)(),(11(2)若n X X 1相互独立同分布,且i i X E μ=)(则当∞→n 时:μ−→−∑=Pn i i X n 11 3、中心极限定理(1)独立同分布的中心极限定理:均值为μ,方差为02>σ的独立同分布时,当n 充分大时有:)1,0(~1N n n XY nk kn −→−-=∑=σμ(2)拉普拉斯定理:随机变量),(~)2,1(p n B n n =η则对任意x 有:⎰∞--+∞→Φ==≤--xt n x x dtex p np np P )(21})1({lim 22πη(3)近似计算:)()()()(11σμσμσμσμσμn n a n n b n n b n n Xn n a P b X a P nk knk k -Φ--Φ≈-≤-≤-=≤≤∑∑==1、总体和样本总体X 的分布函数)(x F 样本),(21n X X X 的联合分布为)(),(121k nk n x F x x x F =∏=2、统计量(1)样本平均值:∑==ni i X n X 11(2)样本方差:∑∑==--=--=ni i ni i X n X n X X n S 122122)(11)(11(3)样本标准差:∑=--=ni i X X n S 12)(11(4)样本k 阶原点距: 2,1,11==∑=kXn A ni ki k(5)样本k 阶中心距:∑==-==ni k ik k k X XnM B 13,2,)(1(6)次序统计量:设样本),(21n X X X 的观察值),(21n x x x ,将n x x x 21,按照由小到大的次序重新排列,得到)()2()1(n x x x ≤≤≤ ,记取值为)(i x 的样本分量为)(i X ,则称)()2()1(n X X X ≤≤≤ 为样本),(21n X X X 的次序统计量。
概率统计公式大全复习重点

第一章随机事件和概率1排列组合公式)!(!nmmP nm-=从m个人中挑出n个人进行排列的可能数;)!(!!nmnmC nm-=从m个人中挑出n个人进行组合的可能数;2加法和乘法原理加法原理两种方法均能完成此事:m+n某件事由两种方法来完成,第一种方法可由m种方法完成,第二种方法可由n种方法来完成,则这件事可由m+n 种方法来完成;乘法原理两个步骤分别不能完成这件事:m×n某件事由两个步骤来完成,第一个步骤可由m种方法完成,第二个步骤可由n 种方法来完成,则这件事可由m×n 种方法来完成;3一些常见排列重复排列和非重复排列有序对立事件至少有一个顺序问题4随机试验和随机事件如果一个试验在相同条件下可以重复进行,而每次试验的可能结果不止一个,但在进行一次试验之前却不能断言它出现哪个结果,则称这种试验为随机试验;试验的可能结果称为随机事件;5基本事件、样本空间和事件在一个试验下,不管事件有多少个,总可以从其中找出这样一组事件,它具有如下性质:①每进行一次试验,必须发生且只能发生这一组中的一个事件;②任何事件,都是由这一组中的部分事件组成的;这样一组事件中的每一个事件称为基本事件,用ω来表示;基本事件的全体,称为试验的样本空间,用Ω表示;一个事件就是由Ω中的部分点基本事件ω组成的集合;通常用大写字母A,B,C,…表示事件,它们是Ω的子集;Ω为必然事件,为不可能事件;不可能事件的概率为零,而概率为零的事件不一定是不可能事件;同理,必然事件Ω的概率为1,而概率为1的事件也不一定是必然事件;6事件的关系与运算①关系:如果事件A的组成部分也是事件B的组成部分,A发生必有事件B发生:BA⊂如果同时有BA⊂,AB⊃,则称事件A与事件B等价,或称A等于B:A=B;A、B中至少有一个发生的事件:A B,或者A+B;属于A而不属于B的部分所构成的事件,称为A与B的差,记为A-B,也可表示为A-AB或者BA,它表示A发生而B不发生的事件;A、B同时发生:A B,或者AB;A B=,则表示A与B不可能同时发生,称事件A与事件B互不相容或者互斥;基本事件是互不相容的;Ω-A称为事件A的逆事件,或称A的对立事件,记为A;它表示A 不发生的事件;互斥未必对立;②运算:结合率:ABC=ABC A∪B∪C=A∪B∪C分配率:AB∪C=A∪C∩B∪C A∪B∩C=AC∪BC德摩根率:∞=∞==11iiii AABABA=,BABA=7概率的公理化定义设Ω为样本空间,A为事件,对每一个事件A都有一个实数PA,若满足下列三个条件:1° 0≤PA≤1,2° PΩ =13° 对于两两互不相容的事件1A,2A,…有常称为可列完全可加性;则称PA为事件A的概率;8古典概型1°{}nωωω21,=Ω,2°nPPPn1)()()(21===ωωω ;设任一事件A,它是由mωωω21,组成的,则有PA={})()()(21mωωω=)()()(21mPPPωωω+++9几何概型若随机试验的结果为无限不可数并且每个结果出现的可能性均匀,同时样本空间中的每一个基本事件可以使用一个有界区域来描述,则称此随机试验为几何概型;对任一事件A,)()()(Ω=LALAP;其中L为几何度量长度、面积、体积;10加法公式PA+B=PA+PB-PAB当PAB=0时,PA+B=PA+PB11减法公式PA-B=PA-PAB当B⊂A时,PA-B=PA-PB 当A=Ω时,P B=1- PB12条件概率定义设A、B是两个事件,且PA>0,则称)()(APABP为事件A发生条件下,事件B发生的条件概率,记为=)/(ABP)()(APABP;条件概率是概率的一种,所有概率的性质都适合于条件概率;例如PΩ/B=1⇒P B/A=1-PB/A13乘法公式乘法公式:)/()()(ABPAPABP=更一般地,对事件A1,A2,…An,若PA1A2…An-1>0,则有21(AAP…)n A)|()|()(213121AAAPAAPAP= (2)1|(AAAP n…)1-n A;14独立性①两个事件的独立性设事件A、B满足)()()(BPAPABP=,则称事件A、B是相互独立的;若事件A、B相互独立,且0)(>AP,则有若事件A、B相互独立,则可得到A与B、A与B、A与B也都相互独立;必然事件Ω和不可能事件与任何事件都相互独立;与任何事件都互斥;②多个事件的独立性设ABC是三个事件,如果满足两两独立的条件,PAB=PAPB;PBC=PBPC;PCA=PCPA并且同时满足PABC=PAPBPC那么A、B、C相互独立;对于n个事件类似;15全概公式设事件n BBB,,,21 满足1°n BBB,,,21 两两互不相容,),,2,1(0)(niBP i=>, 2°niiBA1=⊂,则有)|()()|()()|()()(2211nn BAPBPBAPBPBAPBPAP+++= ;16贝叶斯公式设事件1B,2B,…,n B及A满足1°1B,2B,…,n B两两互不相容,)(BiP>0,=i1,2,…,n, 2°niiBA1=⊂,0)(>AP,则∑==njjjiiiBAPBPBAPBPABP1)/()()/()()/(,i=1,2,…n;此公式即为贝叶斯公式;)(i B P ,1=i ,2,…,n ,通常叫先验概率;)/(A B P i ,1=i ,2,…,n ,通常称为后验概率;贝叶斯公式反映了“因果”的概率规律,并作出了“由果朔因”的推断;17伯努利概型我们作了n 次试验,且满足每次试验只有两种可能结果,A 发生或A 不发生; n 次试验是重复进行的,即A 发生的概率每次均一样;每次试验是独立的,即每次试验A 发生与否与其他次试验A 发生与否是互不影响的;这种试验称为伯努利概型,或称为n 重伯努利试验;用p 表示每次试验A 发生的概率,则A 发生的概率为q p =-1,用)(k P n 表示n 重伯努利试验中A 出现)0(n k k ≤≤次的概率,k n k kn n q p k P C -=)(,n k ,,2,1,0 =;第二章 随机变量及其分布第三章二维随机变量及其分布第四章随机变量的数字特征第五章大数定律和中心极限定理第六章样本及抽样分布第七章参数估计第八章假设检验单正态总体均值和方差的假设检验。
概率论与数理统计公式整理(完整版)

概率论与数理统计 公式(全)
(13)乘法 公式
例如 P(Ω/B)=1 P( B /A)=1-P(B/A) 乘法公式: P(AB) P(A)P(B / A)
更一般地,对事件 A1,A2,…An,若 P(A1A2…An-1)>0,则有
P( A1A2 … An) P( A1)P( A2 | A1)P( A3 | A1A2) …… P( An | A1A2 …
当 a≤x1<x2≤b 时,X 落在区间( x1 , x2 )内的概率为
P( x1
X
x2 )
x2 b
x1 a
。
6 / 27
概率论与数理统计 公式(全)
指数分布
f (x)
ex ,
0,
x 0, x 0,
其中 0 ,则称随机变量 X 服从参数为 的指数分布。
X 的分布函数为
正态分布
F(x)
函数 F(x) 表示随机变量落入区间(– ∞,x]内的概率。
分布函数具有如下性质:
1° 0 F(x) 1, x ;
2° F(x) 是单调不减的函数,即 x1 x2 时,有 F(x1) F (x2) ;
3° F() lim F(x) 0, F() lim F(x) 1;
x
x
4° F(x 0) F(x) ,即 F(x) 是右连续的;
布,所以(0-1)分布是二项分布的特例。
5 / 27
概率论与数理统计 公式(全)
泊松分布
设随机变量 X 的分布律为 P( X k) k e , 0 , k 0,1,2, k!
则称随机变量 X 服从参数为 的泊松分布,记为 X ~ () 或
超几何分布 几何分布
者 P( )。
伯努利概型与全概公式

伯努利概型与全概公式伯努利概型是指一类仅有两个可能结果的随机试验,比如扔一次硬币只有正面朝上或者反面朝上。
伯努利概型的特点是每次实验结果的概率都是相等的,且各次实验结果之间相互独立。
假设实验中有n个相互独立的伯努利概型,每个伯努利概型的成功概率为p,失败概率为1-p。
则在这n次实验中,成功k次的概率可以表示为二项分布的概率质量函数:P(X=k)=C(n,k)*p^k*(1-p)^(n-k)其中,C(n,k)表示组合数,即从n个元素中选取k个元素的组合方式数。
这个公式被称为伯努利概型的概率公式,可以用于计算一系列相关试验中的概率。
全概公式,也称作全概率公式,是概率论中的一条重要原理,用于计算一个事件的概率。
全概率公式的基本思想是将一个事件分解为多个互斥且完备的事件,然后根据这些事件的概率来计算所求事件的概率。
全概率公式的表达式如下:P(A)=P(A,B1)*P(B1)+P(A,B2)*P(B2)+...+P(A,Bn)*P(Bn)其中,P(A)表示事件A的概率,B1、B2、..、Bn表示一组两两互斥且完备的事件,P(B1)、P(B2)、..、P(Bn)表示这些事件的概率,P(A,B1)、P(A,B2)、..、P(A,Bn)表示在事件B1、B2、..、Bn已经发生的条件下,事件A发生的概率。
全概率公式的应用非常广泛,特别适合于利用辅助事件来计算复杂事件的概率。
例如,假设工厂生产了两个品牌的产品A和B,其中A的缺陷率为0.02,B的缺陷率为0.04、现在从工厂中随机抽取了一个产品,发现该产品有缺陷。
问这个产品是属于品牌A还是品牌B的概率是多少?根据全概率公式,我们可以将这个问题分解为两个互斥事件:产品是A品牌和产品是B品牌。
设事件A表示产品是A品牌,事件B表示产品有缺陷。
根据题目的条件,可以得到以下信息:P(A)=0.5,P(B,A)=0.02,P(B,B)=0.04应用全概率公式,可以求得产品有缺陷的概率为:P(B)=P(B,A)*P(A)+P(B,B)*P(B)=0.02*0.5+0.04*0.5=0.03然后,根据贝叶斯公式,可以求得产品是A品牌的条件概率为:P(A,B)=P(B,A)*P(A)/P(B)=0.02*0.5/0.03≈0.333所以,这个缺陷产品属于A品牌的概率约为33.3%。
概率统计公式大全(复习重点)

第一章随机事件和概率(1)排列组合公式)!(!nmmP nm-=从m个人中挑出n个人进行排列的可能数。
)!(!!nmnmC nm-=从m个人中挑出n个人进行组合的可能数。
(2)加法和乘法原理加法原理(两种方法均能完成此事):m+n某件事由两种方法来完成,第一种方法可由m种方法完成,第二种方法可由n种方法来完成,则这件事可由m+n 种方法来完成。
乘法原理(两个步骤分别不能完成这件事):m×n某件事由两个步骤来完成,第一个步骤可由m种方法完成,第二个步骤可由n 种方法来完成,则这件事可由m×n 种方法来完成。
(3)一些常见排列重复排列和非重复排列(有序)对立事件(至少有一个)顺序问题(4)随机试验和随机事件如果一个试验在相同条件下可以重复进行,而每次试验的可能结果不止一个,但在进行一次试验之前却不能断言它出现哪个结果,则称这种试验为随机试验。
试验的可能结果称为随机事件。
(5)基本事件、样本空间和事件在一个试验下,不管事件有多少个,总可以从其中找出这样一组事件,它具有如下性质:①每进行一次试验,必须发生且只能发生这一组中的一个事件;②任何事件,都是由这一组中的部分事件组成的。
这样一组事件中的每一个事件称为基本事件,用ω来表示。
基本事件的全体,称为试验的样本空间,用Ω表示。
一个事件就是由Ω中的部分点(基本事件ω)组成的集合。
通常用大写字母A,B,C,…表示事件,它们是Ω的子集。
Ω为必然事件,?为不可能事件。
不可能事件(?)的概率为零,而概率为零的事件不一定是不可能事件;同理,必然事件(Ω)的概率为1,而概率为1的事件也不一定是必然事件。
(6)事件的关系与运算①关系:如果事件A的组成部分也是事件B的组成部分,(A发生必有事件B发生):BA⊂如果同时有BA⊂,AB⊃,则称事件A与事件B等价,或称A等于B:A=B。
A、B中至少有一个发生的事件:A B,或者A+B。
属于A而不属于B的部分所构成的事件,称为A与B的差,记为A-B,也可表示为A-AB或者BA,它表示A发生而B不发生的事件。
伯努利概型

e
Cnk
pk (1
p)nk
e
n
nk n!
n! k!(n
k )!
pk
(1
p)nk
(p)k
k!
e
[
nk
(1 p)]nk (n k)!
(p)k
k!
e
m0
[
(1
p)]m m!
(p)k e e(1 p)
k!
解 设Bm表示4道题中碰对m道题这一事实,则
P ( Bm
)
C4m
(1)m 4
( 3 )4 m 4
(m 0,1,2,3,4)
经计算得
P(B0 )
C40
(
1 4
)0
(
3 4
)40
0.316
P(B3 )
C
3 4
(
1 4
)3
(
3 4
)43
0.048
几何分布 在贝努利试验中,通常需要计算事件 A
P(B) (p)k ep , (k 0,1,2, )
k!
(2) 若某蚕养出k只小蚕,求它产了n个卵的概率. 由贝叶斯公式,得
P( An
B)
P( An )P(B P(B)
An )
(p)n
n!
e
C p k n
pk
(1
(p)k ep
p)nk
[(1 p)]nk
(n k)!
P(
5)
5 k 0
P(
1.4 事件的独立性与伯努利概型

设Ai “第i次试验事件A发生” i 1,2,, n
则 P ( Ai ) P ( A), i 1,2,, n
记:P ( A) p
P(A发生k次)=?
二项概率
P(A发生k次)=
k Cn
p 1 p
k
n k
Pn (k )
填空
1、一射手向指定目标射击4枪,各枪射中与否相互
伯努利概型: 1000 , p 0.0001 n
P(发生交通事故的次数不超过1次) P1000(0) P1000(1)
1.何谓两事件独立? 在实际应用中,如何判断两事件的独立性?
2.两事件相互独立与互不相容(互斥) 这两个概念有何关系?
n
3.何谓n重贝努利试验, 计算有关事件概率的方法是什么?
则说A与B相互独立
事件的独立性
• 定义1.4.1 • 对任意的事件A,B, • 若满足等式
P(AB)=P(A)P(B) .
• 则称事件A与B 相互独立.
在实际应用中,往往根据问题的 实际意义去判断两事件是否独立.
如: 1.一批产品共n件,从中抽取两件,
设 Ai=“第i件是合格品” i=1,2.
若抽取是有放回的, 则A1与A2是
P ( AB) P ( A) P ( B ) P ( AC ) P ( A)(C ) P ( BC ) P ( B )(C ) P ( ABC ) P ( A) P ( B ) P (C )
则称事件A,B,C 相互独立,
注意 三个事件相互独立 三个事件两两相互独立
射中 未射中
1、电灯泡使用寿命在1000小时以上的概率为
0.2,则3个灯泡在使用1000小时后最多只有
伯努利概型与全概公式-PPT文档资料

(2)上述测试方法使公司将真正的行家拒之门外的概率有多大? (3)能否设计出测试方法使被冒牌者蒙到岗位的概率及将真正的 行家拒之门外的概率都变小?
计算机数学
7
伯努利概型
设随机试验满足
(1)在相同条件下进行n次重复试验;
(2)每次试验只有两种可能结果,A发生或A不发生; (3)在每次试验中,A发生的概率均一样,即P(A)=P; (4)各次试验是相互独立的. 则称这种试验为n重伯努利(Bernoulli)试验。
即冒牌者在品尝测试中能通过测试(蒙对7次以上) 的概率仅为17.19%, 所以机会是很小的.
计算机数学
12
(2)若应聘者真是行家,则其在每次品尝测试中的判断 正确的概率为0.9,即 P(A)=0.9,根据公式有:
计算机数学
4
思考:从一副不含大小王的扑克牌中任取一张,A={抽
到K},B={抽到的是红色的},问事件A,B是否独立?
分析1:
分析2:
4 1 26 1 2 1 P ( A ) ,P52 2 52 26 从而 P ( A ) P ( B ) P ( AB ) ,故 A ,B 相互独立。
P { k 7 } P { k 7 } P { k 8 } P { k 9 } P { k 10 }
( 120 45 10 1 )( 0 . 5 ) 0 . 1719 17 . 19 %
77 3 88 2 99 1 10 10 C ( 0 . 5 ) ( 1 0 . 5 ) C ( 0 . 5 ) ( 1 0 . 5 ) C ( 0 . 5 ) ( 1 0 . 5 ) C ( 0 . 5 ) 10 10 10 10 10
1.7伯努利概型

P( Bk ) P( ) Cnk p k q nk
Bk
事件A在n次试验中发生k次的概率为
Pn (k ) Cnk p k q nk
0 k n
这个概率常称为二项概率,记为 bk ; n, p
k k nk pq 即: b(k;n, p) Cn
k=0,1,2,…,n
解:50千瓦电力可用时供给5台机床开动,因而10台机床中 同时开动的台数为不超过5台时都可以正常工作,而每 台机床只有“开动”与“不开动”的两种情况,且开动 的概率为12/60=1/5。不开动的概率为4/5。设10台机床 k 1 k 4 10 k 中正在开动着的机床台数为 ,则 P ( k ) C10 ( ) ( ) 0 k 10
1699年,雅各布当选为巴黎科学院外籍院士;1701年被柏林 科学协会(后为柏林科学院)接纳为会员。 许多数学成果与雅各布的名字相联系。例如悬链线问题 (1690年),曲率半径公式(1694年),“伯努利双纽线” (1694年),“伯努利微分方程”(1695年),“等周问题” (1700年)等。 雅各布对数学最重大的贡献是在概率论研究方面。他从1685 年起发表关于赌博游戏中输赢次数问题的论文,后来写成巨著 《推测术》,这本书在他死后8年,即1713年才得以出版。 最为人们津津乐道的轶事之一,是雅各布醉心于研究对数螺 线,这项研究从1691年就开始了。他发现,对数螺线经过各种变 换后仍然是对数螺线,如它的渐屈线和渐伸线是对数螺线,自极 点至切线的垂足的轨迹,以极点为发光点经对数螺线反射后得到 的反射线,以及与所有这些反射线相切的曲线(回光线)都是对 数螺线。他惊叹这种曲线的神奇,竟在遗嘱里要求后人将对数螺 线刻在自己的墓碑上,并附以颂词“纵然变化,依然故我”,用 以象征死后永
概率统计公式大全(复习重点)

第一章随机事件和概率(1)排列组合公式)!(!nmmP nm-=从m个人中挑出n个人进行排列的可能数。
)!(!!nmnmC nm-=从m个人中挑出n个人进行组合的可能数。
(2)加法和乘法原理加法原理(两种方法均能完成此事):m+n某件事由两种方法来完成,第一种方法可由m种方法完成,第二种方法可由n种方法来完成,则这件事可由m+n 种方法来完成。
乘法原理(两个步骤分别不能完成这件事):m×n某件事由两个步骤来完成,第一个步骤可由m种方法完成,第二个步骤可由n 种方法来完成,则这件事可由m×n 种方法来完成。
(3)一些常见排列重复排列和非重复排列(有序)对立事件(至少有一个)顺序问题(4)随机试验和随机事件如果一个试验在相同条件下可以重复进行,而每次试验的可能结果不止一个,但在进行一次试验之前却不能断言它出现哪个结果,则称这种试验为随机试验。
试验的可能结果称为随机事件。
(5)基本事件、样本空间和事件在一个试验下,不管事件有多少个,总可以从其中找出这样一组事件,它具有如下性质:①每进行一次试验,必须发生且只能发生这一组中的一个事件;②任何事件,都是由这一组中的部分事件组成的。
这样一组事件中的每一个事件称为基本事件,用ω来表示。
基本事件的全体,称为试验的样本空间,用Ω表示。
一个事件就是由Ω中的部分点(基本事件ω)组成的集合。
通常用大写字母A,B,C,…表示事件,它们是Ω的子集。
Ω为必然事件,Ø为不可能事件。
不可能事件(Ø)的概率为零,而概率为零的事件不一定是不可能事件;同理,必然事件(Ω)的概率为1,而概率为1的事件也不一定是必然事件。
(6)事件的关系与运算①关系:如果事件A的组成部分也是事件B的组成部分,(A发生必有事件B发生):BA⊂如果同时有BA⊂,AB⊃,则称事件A与事件B等价,或称A等于B:A=B。
A、B中至少有一个发生的事件:A B,或者A+B。
属于A而不属于B的部分所构成的事件,称为A与B的差,记为A-B,也可表示为A-AB或者BA,它表示A发生而B不发生的事件。
1-5全概率公式贝叶斯公式1-6伯努利概型
定义 如果试验E只有两个基本事件A及A, 且P(A) p, P(A) 1 p(0 p 1), 将E独立 地进行n次,则这一系列试验称为n重伯努 利试验或n重伯努利概型,简称伯努利概型.
定理 在n重伯努利试验中,设每次试验中 事件A发生的概率为p(0 p 1), 则在n次重复 试验中,事件A恰好发生k次的概率为
解 假设接待站的接待时间没有
规定,且各来访者在一周的任一天
中去接待站是等可能的.
17 27
37
47
172
周一 周二 周三 周四 周五 周六 周日
故一周内接待 12 次来访共有 712种.
12 2
32
42
122
周一 周二 周三 周四 周五 周六 周日
12 次接待都是在周二和周四进行的共有 212种.
解 设 A 为事件 "产品合格".
B 为事件 "机器调整良好". 则有
P( A B) 0.98, P( A B) 0.55,
P(B) 0.95, P(B) 0.05, 由贝叶斯公式得所求概率为
P(B A)
P( A B)P(B)
P(AB)P(B) P(AB)P(B)
0.98 0.95
0.97.
解 设X表示这一年内的死亡人数, 则 保险公司在1年的收入是2500120=300000元
保险公司这一年里付出20000X元
当20000X >300000, 即X > 15人时公司亏本
于是, P{公司亏本} =P{ X > 15} =1-P{X≤ 15}
15
P{公司亏本} 1
Ck 2500
(0.002)k
贝叶斯公式
P ( Bi
A)
概率的基本公式

发生, 故P(A|B)= 2×4!/ 5!=2/5.
解二: 用条件概率公式. P(A|B)=P(AB)/P(B)=(1/15)/(1/6)=6/15=2/5. 类似, P(B |A)=2/15. 由条件概率定义的表达式,很容易推导出
P ( AB) P( A) P( B A) P ( B ) P ( A B )
医用高等数学
例6-15 一批小白鼠中, 有30%注射过药物A, 25%注
射过药物B, 两种药物都注射过的占20%. 若取到是1只已知
没有注射过药物B小白鼠的条件下,它也没有注射过药物
A的可能性有多大?
P( AB ) 0.65 P( A | B ) 0.867 P( B ) 1 0.25
可以验证,条件概率具有无条件概率的所有性质. 例如:
概率的乘法公式还可能推广到有限多个事件的情况,即
P( A1 A2 An )=P( A1 )P( A2 | A1 ) P ( A3 | A1 A2 )… P ( An A A A )
1 2 n 1
医用高等数学
例6-17 产妇分娩胎儿的存活率为P(L)=0.98. 又知活
解 根据医学常识,只有O型或B型的人方可给B型的
频率代替概率,有P( E1 )=0.46,P( E2 )=0.15,且 E1 与 E2 互
E1 不相容,而“可给B型病人输血”这一事件是与 E2 的事件
医用高等数学
病人输血,设 E1 =“被检者是O型”, E2 =“被检者是B型”,以
之和,由推论1,所求概率为:
P ( A2 | A1 ) 0.6 , P( A2 | A1 ) 1 P( A2 | A1 ) 0.4
两次患该病心肌未受损害的概率为
全概率公式与独立试验

n k 记 q = 1− p n− k p (1 − p ) k
第一章 小结
本章由六个概念(随机试验、事件、概率、 本章由六个概念(随机试验、事件、概率、条件 概率、独立性),三个公式(乘法公式、 ),三个公式 概率、独立性),三个公式(乘法公式、全概率 公式、贝叶斯公式)和一个概型(古典概型) 公式、贝叶斯公式)和一个概型(古典概型)组 成
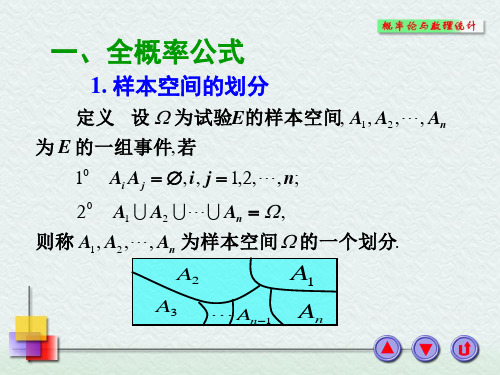
A2 … … … B … A1 …
定理1、 的一个划分, 定理 、 设A1,…, An是 的一个划分, 且P(Ai)>0,(i=1,…,n), , = , , , 则对任何事件B∈ 则对任何事件 ∈ 有
P(B)=∑ P(Bi )P(B | Ai )
i =1 n
此式就称为全概率公式。 此式就称为全概率公式。 全概率公式
3、贝叶斯公式 、
定理2 定理2
的一个划分, 0, 设B1,…, Bn是S的一个划分,且P(Bi) > 0, ,
(i= (i=1,…,n),则对任何事件A∈S,有 ,n),则对任何事件A
P ( B j | A) = P( B j ) P( A | B j )
∑ P( B ) P( A | B )
i =1 i i
设:B:买到一件次品 A1 : 买到一件甲厂的产品 A2 : 买到一件乙厂的产品 A3 : 买到一件丙厂的产品
P ( B ) = P ( BA1 ) + P ( BA2 ) + P ( BA3 )
= P ( B | A1 ) P ( A1 ) + P ( B | A2 ) P ( A2 ) + P ( B | A3 ) P ( A3 )
n
, ( j = 1,..., n)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
事件A发生了k次
Pn
(k)
C
k n
pk
qnk
共作n次试验
其中, p q 1, k 0,1,2,, n.
A发生的概率 A不发生的概率
概率论与数理统计
9
一枚硬币掷3次,恰有一次正面向上的概率为?
A 正面向上
C1
解 法 一 :P
3
23
A 正面向下
解法二: P P( AAA AAA AAA) 3 1 (1)2 22
n
PB PAi PB | Ai i 1
概率论与数理统计
24
例2 某车间用甲、乙、丙三台机床进行生产,各种机 床的次品率分别为5%、4%、2%,它们各自的产品分 别占总产量的25%、35%、40%,将它们的产品组合在 一起,求任取一个是次品的概率。
解:设 A1表示“产品来自甲台机床”, A2表示“产品 来自乙台机床”,A3表示“产品来自丙台机床”, B表 示“取到次品”。
14
例2 某射手每次击中目标的概率是0.6,如果 射击5次,求至少击中两次的概率.
解: 由于每次射击是相互独立的,且只有击中与 未击中两种结果,故可以按5重伯努利概型计算
事件的概率.已知 p 0.6,q 0.4,则
5
P(至少击中两次) P(击中k次) k2
1 P(击中0次) P(击中1次)
3
P(B) p( Ai )P(B | Ai ) i 1
0.25 0.05 0.35 0.04 0.40 0.02
0.0345
概率论与数理统计
25
例3 人们为了了解一支股票未来一定时期内价 格的变化,往往会去分析影响股票的基本因素, 比如利率的变化。现在假设人们经分析估计利 率下调的概率为60%,利率不变的概率为40%。 根据经验,人们估计,在利率下调的情况下, 该支股票价格上涨的概率为80%,而在利率不 变的情况下,其价格上涨的概率为40%,求该 支股票将上涨的概率。
概率论与数理统计
21
根据乘法定理:
PA1 PB | A1 — 抽样恰好是“A1厂生产的
合格品”的可能性概率.
PA2 PB | A2 — 抽样恰好是“A2厂生产的
合格品”的可能性概率.
PA3 PB | A3 — 抽样恰好是“A3厂生产的
合格品”的可能性概率.
概率论与数理统计
22
根据加法定理:一件抽样不可能既是某厂生产的, 同时又是另一个厂生产的,即三个事件属互不相容 事件(互斥);不管这件抽样属于哪一个厂生产的 合格品,都认定为“抽到合格品”,故三个事件的 概率相加就是题目所求。即
lim[1 (1 )n ] 1 n
由 此 可 见 , 一 件 微 不道足的 小 事 , 只 要 坚 持 , 就 会 产 生 不 可 思 议 的果结。
概率论与数理统计
17
重 条件概率 点
回 定义 设两个事件A、B ,且 P(B)>0,
顾
则称 PA | B 为在事件B发生的
前提下,事件A发生的条件概率。
解 :设 一 次 实 验 中 , 事A件发 生 的 概 率 为 0,
独 立 重 复 该 实 验n次, 本 题 考 虑 的 是n,次 实 验 中 事 件A至 少 发 生 一 次 的 概 率 。 这 属 于 伯 努 利 概 型设。B {n次 实 验 中A至 少 发 生 一 次}, 则
P(B) 1 P(B) 1 Cn0 0 (1 )n 1 (1 )n
3
PB PAi PB | Ai i 1 0.50.95 0.30.92 0.20.90
0.931
概率论与数理统计
23
定理(全概率公式)
完备事件组若A1, A2 , , An是互不相容互斥的事件
即Ai Aj i j, 且A1 A2 An , PAi 0i 1,2, , n.则对任一事件B有
(2) P( AB ) P( A)P(B ) P( A)1 P(B) ;
(3) P( A B ) P( A)P(B ) 1 P( A)1 P(B). 返回
概率论与数理统计
2
若事件 A 与 B 相互独立 P( A B) ?
P(A B) 1 P(A B) 1 P(AB) 1 P( A)P(B ).
1
C50
(0.6)0
(0.4)5
C
1 5
(0.6)1
(0.4)4
0.913
概率论与数理统计
15
练习、某导弹的命中率是0.6,问欲以99%的把握 命中目标至少需要配置几枚导弹?
解:设需配置n枚导弹,因为导弹各自独立发射,所以
可以看作n重伯努利试验。设A={导弹命中目标},
B={命中目标},则P(A)=0.6,从而有
7
伯努利概型
设随机试验满足 (1)在相同条件下进行n次重复试验; (2)每次试验只有两种可能结果,A发生或A不发生; (3)在每次试验中,A发生的概率均一样,即P(A)=P; (4)各次试验是相互独立的.
则称这种试验为n重伯努利(Bernoulli)试验。
概率论与数理统计
8
定理 在伯努利概型中,若一次试验时事件A发生 的概率为P(0<P<1),则n重独立试验中事件A恰好 发生K次的概率为
例如将判断正确的最少次数从7提高到8,则(1)中冒 牌者通过测试的概率就从17.19%下降为5.47%,而 (2)中将真正行家被拒之门外的概率就从1.28%上升 为7.02%.
因此,使被冒牌者蒙到岗位的概率及将真正的行家 拒之门外的概率都变小测试方法是不存的.因而,只 能在两者中取其一.
概率论与数理统计
( A) A1、A2、A3相 互 独 立 (B) A2、A3、A4相 互 独 立 (C ) A1、A2、A3两 两 独 立 (D) A2、A3、A4 两 两 独 立
概率论与数理统计
6
某人应聘甲公司品酒师职位,该应聘者声 称能以90%的准确性判别出两种不同的酒,并 可以依此提出相应的推销建议.
为了检验应聘者的辨酒能力以决定是否录用,甲公司 对该应聘者进行测试.让他连续分别品尝两种酒10次, 二次间的间隔为3分钟.
由此可知,当应聘者为真正行家时,则其在品尝测 试中通过测试的概率为98.72%,即被拒绝的概率仅 为1-98.72%=1.28%,也就是说测试方法使公司将真 正的行家拒之门外的概率仅为1.28%.
概率论与数理统计
13
(3) 测试方法要使被冒牌者蒙到岗位的概率变小,则 测试通过的条件就必定更苛刻,但苛刻条件自然令真 正的行家能通过测试的机会变小,即将真正的行家拒 之门外的概率变大.
计算公式:
PA
|
B
PAB PB
同理,若PA 0有
PB
|
A
PAB PA
概率论与数理统计
18
乘法公式
定理 设A、B是随机试验E的两个随机事件, 若P(B)>0,则
PAB PBPA| B
或若P(A)>0,有
PAB PAPB | A
概率论与数理统计
19
全概率公式
例1 某商店仓库中的某种小家电来自甲、乙、 丙三家工厂。这三家工厂生产的产品数分别为 500件、300件、200件,且它们的产品合格率 分别为95%、92%、90%。现从该种小家电产 品中随机抽取1件,求恰抽到合格品的概率。
P{k 7} P{k 7} P{k 8} P{k 9} P{k 10}
C170(0.9)7 (1 0.9)3 C180(0.9)8(1 0.9)2 C190(0.9)9(1 0.9)1 C1100(0.9)10
0.0574 0.1937 0.3874 0.3487
0.9872 98.72%
p C (1) 1 (0.05)1(0.95)4 0.0407
5
5
概率论与数理统计
11
引例求解
解:用A表示应聘者在品尝测试中的判断正确, A 表示应聘者 在品尝测试中的判断不正确.则测试问题符合n=10的伯努利概 型.用 k 表示10次品尝测试中应聘者判断正确的次数(即A发生 的次数),用伯努利概型的公式我们可以分别解决所提的问题.
0.64
概率论与数理统计
26
练习、用3个机床加工同一种零件, 零件由各机床加工的 概率分别为0.5, 0.3, 0.2, 各机床加工的零件为合格品的 概率分别等于0.94, 0.9, 0.95, 求全部产品中的合格率.
n
P(B)
C
k n
0.6
k
0.4n
k
0.99
k 1
P(B) 1 P(B) 1 0.4n 0.99 0.4n 0.01
n log 0.4 0.01 5.03
所以至少要配置6枚导弹才能达到要求。
概率论与数理统计
16
例 :在 平 常 的 生 活 中 , 人常们常 用 “ 水 滴 石 穿 ”“、只 要 功 夫 深 , 铁 杵 磨 成 针来”形 容 有 志 者 事 竟 成但。是 , 也 有 人 认 为 这 些 是 不 可 能。的试 从 概 率 的 角 度 分这析是 否 合 理 。
C 1 (1 )1 (1 )2
32 2
概率论与数理统计
10
例1 已知一批产品的废品率为0.05,设有放回 地抽取5件产品,求恰好抽到1件废品的概率.
解: 由于用有放回抽样的方式,故每次抽得的结 果是相互独立的,且产品只有合格与废品两种结 果,故可以按5重伯努利概型计算事件的概率.已 知
p 0.05, q 0.95,则
概率论与数理统计
1
事件的独立性
定义: 若两个事件 A、B 中, 任一事件的发生与否
不影响另一事件的概率, 则称事件 A 与 B 是相互独
立的, 且P( AB) P( A)P(B) .
定理 若事件A 与B 相互独立, 则下列三对事件
