计量经济学作业序列相关性
序列相关性

5.滞后效应 在经济中,因变量受到自身或另一解释变量的前几期值影响的现象称为 滞后效应。在一个消费支出对收入的时间序列回归中,人们常常发现当前时 期的消费支出除了依赖于其他变量外,还依赖于前期的消有效 因为,在有效性证明中利用了 E(NN’)=2I 即同方差性和互相独立性条件。而且,在大样本情况下,参数估计量 虽然具有一致性,但仍然不具有渐近有效性。 2、变量的显著性检验失去意义 在变量的显著性检验中,统计量是建立在参数方差正确估计基础之 上的,这只有当随机误差项具有同方差性和互相独立性时才能成立。如果存 在序列相关,估计的参数方差 S ˆ ,出现偏误(偏大或偏小) ,t 检验就失去
~ e ~ e t t 1 t
,
~ e ~ ~ e t 1 t 1 2 et 2 t
3
, 。 。 。
醉客天涯之计量经济学
如果存在某一种函数形式,使得方程显著成立,则说明原模型存在序列相关性。 回归检验法的优点是: (1)能够确定序列相关的形式 (2)适用于任何类型序列相关性问题的检验。 3、杜宾-瓦森(Durbin-Watson)检验法(最常用) (1)方法使用条件: ①解释变量 X 非随机; ②随机误差项 i 为一阶自回归形式: i=i-1+i ③回归模型中不应含有滞后应变量作为解释变量,即不应出现下列形式: Yi=0+1X1i+kXki+Yi-1+i ④回归含有截距项 ⑤误差项被假定为正态分布 (2)D.W.统计量: 杜宾和瓦森针对原假设:H0: =0, 即不存在一阶自回归,构如下造统计量:
D.W .
~ (e
t 2
n
t
~ )2 e t 1
2 t
统计学计量经济学课件 4.2 序列相关性

序列相关性的应用
相关性的实际意义
序列相关性可以帮助我们分析经济数据、预测未来 变动、制定政策和投资策略。
序列相关性的应用案例
例如,我们可以利用股票价格与宏观经济指标的相 关性来制定股票投资策略。
总结
序列相关性的重要性
了解序列相关性对于理解经 济现象、预测未来变动和制 定决策至关重要。
序列相关性的局限性
统计学计量经济学课件 4.2 序列相关 性
# 统计学计量经济学课件 4.2 序列相关性 ## 1. 前言 - 序列相关性简介 - 为什么需要了解序列相关性 ## 2. 什么是序列相关性 - 相关性定义 - 序列相关性和相关系数 ## 3. 序列相关性的性质 - 线性相关 - 相关性的方向 - 相关性的强弱 ## 4. 序列相关性的度量 - 协方差和相关系数 - 样本系数计算公式 - 相关性的范围
3 相关性的强弱
相关性的强度取决于相关 系数的值,接近-1或1表示 强相关,接近0表示弱相 关。
序列相关性的度量
1
协方差和相关系数
协方差是衡量变量之间关系强弱的指标。相关系数是标准化的协方差值,用于比较不同变量 之间的相关性。
2
样本系数计算公式
样本相关系数通过对样本数据进行计算得出,它可以估计总体相关系数。
2 序列相关性和相关系数
相关系数是衡量序列相关性强度的指标。它的取值范围在-1和1之间,负值表示负相关, 正值表示正相关。
序列相关性的性质
1 线性相关
2 相关性的方向
序列相关性通常是线性的, 即变量之间的关系可以用 一条直线表示。
相关性可以是正相关(变 量同时增加或减少)或负 相关(一个变量增加时, 另一个变量减少)。
3
“时间序列模型的相关性”基本内容

“时间序列模型的相关性”基本内容Abstract时间序列计量经济学模型是“计量经济学”课程中极其重要的内容。
区别于经典的一元(或多元)线性回归模型,其在违背基本假设的条件下,对参数进行一定的估计。
本文主要介绍时间序列模型的相关性概念和相关性检验方法。
一、序列相关性的定义Definition1.1如果模型的随机干扰项违背了相互独立的基本假设,称为存在序列相关性。
Definition1.2如果仅存在,则我们称为一阶序列相关或者自相关(autocorrelation).二、实际经济问题中的序列相关性实际经济问题中,序列相关性产生的原因主要是来自以下三个方面。
1.经济变量固有的惯性大多数经济时间数据的惯性表现在时间序列数据不同时间的前后关联上。
2.模型设定的偏误所谓的模型设定偏误,是指所设定的模型"不正确",主要表现在模型中丢掉了重要的解释变量或模型函数形式有偏误。
3.数据的"编造"在实际的经济问题中,有些数据是通过已知数据生成的,因此,新生成的数据与原数据之间就有内在的联系,表现出序列相关性。
三、序列相关性的后果1.参数估计量非有效这是因为在有效性证明中利用了2.变量的显著性检验失去意义在变量显著性检验中,统计量是建立在参数方差正确估计基础上的,只有当随机干扰项具有同方差性和相互独立时才成立。
因此,若存在序列相关性,估计的参数方差出现偏误,检验就失去了意义。
3.模型的预测失效四、序列相关性的检验序列相关性检验的方法:冯诺比曼检验、回归检验法、D.W.检验法等.下面着重介绍D.W.检验法和拉格朗日乘数(LM)检验.D.W.检验法(1951年由J.Durbin和G.S.Watson提出)考虑构造如下的D.W.统计量:注意到我们可以证明D.W.统计量的值介于0与4之间。
一个很重要的结论是:(1)如果存在完全一阶正相关,则D.W. 0; (2)如果存在完全一阶负相关,则D.W. 4; (3)如果完全不相关,则D.W.= 0.D.W.统计量缺陷:其一,存在一个不能确定的D.W.值区域;其二,D.W.检验只能检验一阶自相关;其三,对存在滞后被解释变量的模型无法检验.拉格朗日乘数(LM)检验/GB检验(1978年由Breusch和Godfrey提出)与D.W.检验相比较,其适用于高阶序列相关及模型中存在滞后被解释变量的情形。
计量经济学 —理论方法EVIEWS应用--第七章 序列相关性

在其他假设仍然成立的条件下,随机干扰项序列相关意味着
(7-2)
如果仅存在
E ( ) 0 , i 1 , 2 , . . . , n i i 1
(7-3)
则称为一阶序列相关或自相关(简写为AR(1)),这是常见的一种序列相关问题。
D .W .
不存在一阶自相关,构造如下统计量: t
t
( eˆ
t2
n
ˆt 1 ) 2 e
2 t
eˆ
t 1
n
杜宾—沃森证明该统计量的分布与出现在给定样本中的X值有复杂的关系,
其准确的抽样或概率分布很难得到;
因为D.W.值要从
eˆ t 中算出,而 eˆ t
又依赖于给定的X的值。
2 χ 因此D-W检验不同于t、F或 检验,它没有唯一的临界值可以导出拒绝或
用OLS法估计序列相关的模型得到的随机误差项的方差不仅是 有偏的,而且这一偏误也将传递到用OLS方法得到的参数估计 量的方差中来,从而使得建立在OLS参数估计量方差基础上的 变量显著性检验失去意义。
以一元回归模型为例,
Y X i 0 1 i i
2
ˆ) Var ( 1 2 xt
序列相关性及其产生原因序列相关性的影响序列相关性的检验序列相关的补救第一节序列相关性及其产生原因序列相关性的含义对于多元线性回归模型71在其他假设仍然成立的条件下随机干扰项序列相关意味着如果仅存在则称为一阶序列相关或自相关简写为ar1这是常见的一种序列相关问题
—理论· 方法· EViews应用
郭存芝 杜延军 李春吉 编著
二、回归检验法
, eˆ, 以 e ˆ t 为解释变量,以各种可能的相关变量,诸如 t1
序列相关性名词解释

序列相关性名词解释
序列相关又称自相关,是指总体回归模型的随机误差项之间存在相关关系。
序列相关性在计量经济学中指对于不同的样本值,随机干扰之间不再是完全相互独立的,而是存在某种相关性。
序列相关即不同观测点上的误差项彼此相关。
序列相关产生的原因有很多,一般认为主要有一下几种,经济变量惯性的作用引起随机误差项自相关,经济行为的滞后性引起随机误差项自相关,一些随机偶然因素的干扰引起随机误差项自相关,模型设定误差引起随机误差项自相关,观测数据处理引起随机误差项序列相关。
一般经验告诉我们,对于采用时间序列数据作样本的计量经济学问题,由于在不同样本点上解释变量以外的其他因素在时间上的连续性,带来它们对被解释变量的影响的连续性,所以往往存在序列相关性。
统计学计量经济学课件4.2序列相关性

对于长期趋势的数据,如果只使 用部分样本数据进行分析,可能 会导致残差序列相关。
03
序列相关性对回归分析的 影响
估计量的偏误
偏误类型
序列相关性会导致回归系数的估计量 产生偏误,即估计的系数不再等于真 实系数。
偏误原因
解决方法
采用适当的统计方法,如广义最小二 乘法(GLS)或广义差分法(GDM) ,以消除序列相关性对估计量的影响 。
统计学计量经济学课 件4.2序列相关性
xx年xx月xx日
• 序列相关性的定义 • 序列相关性产生的原因 • 序列相关性对回归分析的影响 • 检验序列相关性的方法 • 解决序列相关性的方法
目录
01
序列相关性的定义
什么是序列相关性
序列相关性是指时间序列数据之间存在某种相关性,即一个 时间点的数值可能与下一个时间点的数值之间存在一定的依 赖关系。
用于检验时间序列数据是否存 在序列相关性,如杜宾瓦森检
验和LM检验。
02
序列相关性产生的原因
模型设定误差
模型遗漏重要变量
在计量经济学模型中,如果遗漏了重 要的解释变量,会导致残差序列相关 ,从而产生序列相关性。
错误地设定滞后变量
在模型中错误地引入滞后变量,会导 致模型残差出现序列相关性。
数据生成过程
在回归分析中,应充分考虑序列相关性对 检验和推断的影响,采用适当的统计方法 和模型进行修正,以提高推断的准确性。
04
检验序列相关性的方法
图检验法
散点图
通过绘制时间序列数据的散点图,观察数据点是否呈现出某种趋势或模式,从而 判断是否存在序列相关性。
自相关图
利用自相关系数或偏自相关系数来绘制自相关图,通过观察自相关系数或偏自相 关系数的变化趋势,判断是否存在序列相关性。
计量经济学序列相关性实验分析

重庆科技学院学生实验报告一,实验目的和要求熟练掌握序列相关行的含义,原因,后果,检验方法,修正方法。
二、实验内容和原理内容:自相关性检验原理:首先采用普通最小二乘法估计模型,以求得随机干扰项的“近似估计量”,然后通过分析这些“近似估计量”之间的相关性以达到判断随机干扰项是否具有序列相关性的目的。
三、主要仪器设备电脑一台;EVIEW50 软件一套;MATHTYFPE8 软件一套;MICROSOFXCE12007 软件一套;四、实验操作方法和步骤一、估计回归方程二、进行序列相关性检验三、序列相关的补救五、实验记录与处理(数据、图表、计算等)(具体过程见下页)六、实验结果及分析(具体分析见下页)说明:此部分的内容和格式各学院可根据实验课程和实验项目的具体需要,自行设计和确定相关内容和栏目,但表头格式应统一;对于设计性实验则只要求说明实验的目的要求、提出可供实验的基本条件和注意事项,实验方案和步骤的设置、仪器的安排等可由学生自己设计。
五、实验记录与处理(数据、图表、计算等)一、估计回归方程工业增加值主要由全社会固定资产投资决定。
为了考察全社会固定资产投资对工业增加值的影响,可使用如下模型:丫二0 i Xi ;其中,X表示全社会固定资产投资,丫表示工业增加值。
下表列出了中国1998-2000的全社会固定资产投资X与工业增加值丫的统计数据。
Dependent Variable: Y Method: Least Squares Date: 12/22/09 Time; 08:53Sample: 1SS0 2CU0Included observatiors: 21Variable Coefficient Std. Error t-Statistic Prob.C6E3.0114298 1673 2240392 □ .0372X 1.101861 0 CI1S344 .0SS3O 0 oooc R-squared 0.994936 Mean dependent var 13744 09Adjusted R-squared 0.394669 S D. dependenl var 13029.80S.E. of regression 951.33S8 Akaike info criterion 16.64401Sum squared resid 17195864Schwarz criterion 1674343Lug likelihood -172.7621F-statistic3732.750Durbin-Watson slat 1.282353 FrcbfF-statistic)0 000000由此实验结果可知模型估计结果为:Y=668.0114+1.181861X(2.24039)(61.0963)R2 =0.994936,R 2 =0.994669,SE=951.3388, D.W.=1.282353。
七计量经济学-序列相关性

2、解析法
(1)回归检查法
以 e~i 为被解释变量,以各种可能的相关量, 诸如以 e~i1 、 e~i2 、 e~i2 等为解释变量,建立各
种方程:
e~i e~i 1 i
i=2,…,n
e~i 1e~i1 2 e~i2 i
i=3,…,n
…
对各方程预计并进行明显性检查,如果存 在某一种函数形式,使得方程明显成立,则 阐明原模型存在序列有关性。
2、序列有关产生的因素
(1)惯性
大多数经济时间数据都有一种明显的特点, 就是它的惯性。
GDP、价格指数、生产、就业与失业等时 间序列都呈周期性,如周期中的复苏阶段,大 多数经济序列均呈上升势,序列在每一时刻的 值都高于前一时刻的值,似乎有一种内在的动 力驱使这一势头继续下去,直至某些状况(如 利率或课税的升高)出现才把它拖慢下来。
(3)经验表明,如果不存在一阶自有关, 普通也不存在高阶序列有关。
因此在实际应用中,对于序列有关问题普 通只进行D.W.检查。
四、含有序列有关性模型的预计
• 如果模型被检查证明存在序列有关性, 则需要发展新的办法预计模型。
• 最惯用的办法是广义最小二乘法(GLS: Generalized least squares)、一阶差分 法(First-Order Difference)和广义差分 法(Generalized Difference)。
一阶差分法是将原模型
Yi 0 1 X i i
变换为
i=1,2,…,n
Yi 1X i i i1
其中
i=2,…,n
Yi Yi Yi1
(2.5.10)
• 如果原模型存在完全一阶正自有关,即在
•
i= i-1+ i
计量经济学试题计量经济学中的序列相关性与解决方法

计量经济学试题计量经济学中的序列相关性与解决方法计量经济学试题: 计量经济学中的序列相关性与解决方法序列相关性是计量经济学中重要的概念之一,它描述了时间序列数据之间的相关程度。
在许多经济学研究中,序列相关性可能会导致问题,如伪回归和自相关误差。
为了解决这些问题,研究人员采用了一些方法来处理序列相关性。
本文将介绍序列相关性的定义、影响和解决方法。
一、序列相关性的定义序列相关性是指一组时间序列数据之间存在的相关关系。
它反映了一个变量的当前值与过去值的相关程度。
序列相关性可以判断变量之间是否存在依赖关系,以及时间趋势的演变和预测。
在计量经济学中,序列相关性通常使用自相关函数(acf)和偏自相关函数(pacf)来度量。
自相关函数衡量了序列与其自身在不同滞后期的相关性,而偏自相关函数则控制了其他滞后期的效应。
二、序列相关性的影响序列相关性对计量经济分析的结果具有重要影响。
当存在序列相关性时,经济学模型的估计结果可能会产生偏误。
这是因为序列相关性违反了线性回归模型的基本假设,导致参数估计失真。
此外,当序列相关性存在时,标准误差和t统计量的计算也会出现问题。
标准误差的计算通常基于误差项的无关性假设,而序列相关性违反了这一假设,导致标准误差被低估。
因此,对参数的显著性检验将失去准确性。
三、解决序列相关性的方法为了解决序列相关性的问题,计量经济学提出了许多方法和技术。
下面介绍几种常用的解决方法。
1. 差分法(Differencing Method)差分法是通过对时间序列数据进行差分,消除序列相关性的方法。
差分法可以消除序列的线性趋势,使数据变得稳定。
这种方法利用变量的差分来消除序列的相关性,使得模型的估计结果更可靠。
2. 自相关修正法(Autoregressive Model)自相关修正法是通过引入滞后变量来建模序列相关性。
自相关修正模型考虑变量的滞后值与当前值之间的关系,以控制序列相关性的影响。
常见的自相关修正模型包括自回归移动平均模型(ARMA)和自回归条件异方差模型(ARCH)。
计量经济学序列相关

4.2 序列相关王中昭制作§违反了随机扰动项之间相互独立的假定,称为序列相关。
●学习内容:王中昭制作•一、序列相关定义及其类型•二、实际经济问题中的序列相关性•三、序列相关性的后果•四、序列相关性的检验•五、序列相关性的修正王中昭制作•1、序列相关(或称自相关)的定义:•在线性回归模型基本假定4中,我们假设随机扰动项序列的各项之间不相关,如果这一假定不满足,则称之为序列相关。
即用符号表示为:ji E Cov j i j i ≠≠=当 0)(),(μμμμ一、序列相关定义及其类型王中昭制作•称为一阶序列相关,即μi =ρμi-1+εi ,,i=1,2,…,n,-1<ρ<1•其中ρ称为自协方差系数或者一阶自相关系数。
这是常见的序列相关,除此之外统称为高阶序列相关。
如:μi =ρ1μi-1+ρ2μi-2+εi ,称为二阶序列相关。
1,2,1 0)(1-=≠+n i E i i μμ如果仅存在●2、类型王中昭制作•1、经济发展的惯性•2、模型设定偏误•3、滞后效应•4、对数据的处理可能会导致序列相关•5、由随机扰动项本身特性所决定●二、实际经济问题中的序列相关性●1、经济发展的惯性王中昭制作•大多数经济时间序列都有一个明显的特点,就是它的惯性。
表现在时间序列数据不同时间的前后关联上。
众所周知,GDP、价格指数、生产、消费、就业和失业等时间序列都呈现周期循环。
相继的观测值很可能是相互依赖的。
这样就导致经济变量的前后期(或前后若干期)出现相关,从而使随机误差项相关。
•这是最常见的序列相关现象。
王中昭制作•从而造成v 自相关。
原因是替代品的价格对牛肉销量有重要影响。
tt t t t X X X Y μββββ++++=3322110tt t t v X X Y +++=22110βββtt t X v μβ+=33例如,如果真实的回归方程形式为,其中,被解释变量Y 表示牛肉需求量,解释变量分别为牛肉价格X 1、消费者收入X 2和替代品的价格X 3。
计量经济学-序列相关性

PART 03
序列相关性检验方法
杜宾-瓦特森检验
检验原理
通过计算残差序列的一阶自相关系数来检验序列相关性。
检验步骤
首先估计回归模型,计算残差;然后计算残差的自相关系数;最后 根据自相关系数和样本量确定临界值,判断序列相关性。
优缺点
简单易行,但仅适用于一阶自相关的情况,对于高阶自相关检验效 果较差。
将检验结果以表格或图形形式展示出 来,包括检验统计量、P值等。若存 在序列相关性,可采用差分法、 ARIMA模型等方法进行处理,并重新 进行参数估计和检验。
根据检验结果和处理结果,对模型的 适用性和可靠性进行评估。若模型存 在严重序列相关性问题,则需要重新 考虑模型设定和估计方法。
PART 06
总结与展望
检验步骤
在原始回归模型中添加滞后项作为解释变量;然后估计辅 助回归模型,得到回归系数的估计值;最后根据回归系数 的估计值构造统计量,进行假设检验。
优缺点
可以检验任意阶数的自相关,但需要注意滞后项的选择和 模型的设定。
PART 04
序列相关性处理方法
差分法
一阶差分法
通过计算相邻两个时期的数据差值来消除序列相 关性。
运用最小二乘法(OLS)或其他估计方法,对模型参数进行估计。在 EViews中,可通过"Quick"菜单选择"Estimate Equation"选项进行参数估 计。
序列相关性检验及处理结果展示
01
序列相关性检验
02
处理结果展示
03
结果解读
采用Durbin-Wu-Hausman检验、 Breusch-Godfrey检验等方法,检验 模型是否存在序列相关性。在EViews 中,可通过"View"菜单选择 "Residual Diagnostics"选项进行检 验。
统计学计量经济学课件4.2序列相关性

1 相关性是分析数据的重要方法
序列相关性分析是我们理解数据之间关系的重要方法,有助于揭示潜在的规律和趋势。
2 序列相关性分析有其独特的应用
序列相关性分析在不同领域具有广泛的应用,能够帮助我们研究经济、金融、财务等问 题。
3 在实际分析中需要注意样本量、异常值等问题
在进行相关性分析时,我们应该关注样本量的要求,以及如何处理异常值和缺失值。
序列相关性的应用
1 经济周期分析
序列相关性可以帮助我们 研究经济周期的变化,预 测经济增长和衰退。
2 金融市场分析
应用序列相关性可以揭示 金融市场中不同资产之间 的关联程度,为投资决策 提供参考。
3 财务分析
序列相关性在财务分析中 有重要应用,例如研究财 务指标之间的关系,评估 企业的财务健康状况。
统计学计量经济学课件 4.2序列相关性
在统计学和计量经济学中,序列相关性是一项重要的概念。了解序列相关性 有助于我们理解数据之间的关系,衡量其强度,并应用于各种领域的数据分 析。
序列相关性概述
1 相关性的含义
相关性指的是两个序列之间的关联程度,即 一个序列的变动对另一个序列的变动产生的 影响。
2 如何衡量相关性
相关性分析的注意事项
1 样本量的要求
相关性分析需要足够的样本量,以减小抽样误差和提高结果的可靠性。
2 异常值和缺失值的处理
在进行相关性分析之前,应该对异常值和缺失值进行处理,以避免对结果产生不良影响。
3 多重比较的问题
在进行多个相关性分析时,需要注意多重比较带来的问题,以控制错误发现率。
检验用于确定时序 数据中是否存在随机性, 从而判断数据是否存在相 关性。
截面数据相关性检验
1 散点图分析
计量经济学序列相关性检验实验报告 苗子凯

计量经济学实验序列相关性的检验与修正2012/12/11学院:国际教育学院专业:国际经济与贸易一班班级:10级一班姓名:苗子凯学号:1014102025序列相关性实验(数据来源于李子奈版课后习题P155.9)运行Eviews,依次单击file→new→work file命令栏中输入“data y x”,打开“y x”表,接下来将数据输入其中。
杜宾瓦尔森检验法:开始进行LS回归,命令栏中输入“ls log(y) c log(x)”回车,即得到回归结果如下:由结果得到,D.W值为0.379。
本题中样本容量为n=28,解释变量个数为k=2,查表得到dl=1.33,du=1.48,D.W<dl,所以该模型存在序列相关性。
偏相关系数检验法:1.双对数模型: GENR LNY=LOG(Y)GENR LNX=LOG(X)LS LNY C LNX可得到下图在方程窗口中点击View/Residual Test/Correlogram-Q-statistics ,并输入滞后期为10,则会得到残差t e 与1021,,---t t t e e e 的各期相关系数和偏相关系数,可得到下图:双对数模型的偏相关系数检验从图中可以看出,双对数模型的第1期、第2期偏相关系数的直方块超过了虚线部分,存在着一阶和二阶自相关。
⑵二次多项式模型二次多项式模型:GENR X2=X^2LS Y C X X2 得到如下图:在方程窗口中点击View/Residual Test/Correlogram-Q-statistics ,并输入滞后期为10,则会得到残差t e 与1021,,---t t t e e e 的各期相关系数和偏相关系数,:二次多项式模型的偏相关系数检验从图中可以看出,双二次多项式模型的第1期偏相关系数的直方块超过了虚线部分,存在着一阶自相关。
自相关性的调整:加入AR 项⒈对双对数模型进行调整;在LS 命令中加上AR(1)和AR(2),使用迭代估计法估计模型。
《计量经济学》课程中“序列相关性”的教学方案初探

—
( 2 )
( 3 ) ( 4)
将 ( 2 )一 ( 3 ) x p ,可 以得到
Yi =B 0( 1一P ) +B 1 Xl i +B 2 X 2 ; +… +B k X + i
教 学 研 夯
《 计 量 经 济 学》 课程 中 “ 序列相关性’ ’的 教 学 方 案初 探
刘开华 ( 长 江师范学 院 重庆 4 0 8 1 0 0 )
摘 要 :序列相关性是计 量经济 学课程教学 中的重点和难 点之一。本文将理 论教 学和 实践教 学相 结合 ,并且灵 活运用案例教 学法 ,探讨 《 计量经济学》课程教 学方案的设计 ,以期能够使 学生把握序列相关性的本质,正确使 用计量回归模型分析实际问题 。 关键词 :计量经济学 序 列相 关 教学改革 在建立计 量经济学模型过程 中,如果满足基本假 设 ,O L S方法可 以得到具有无偏 性、有效性和一致性的估计量。线性 回归模型 的基本 假设是 《 计量经济学》 课程教学过程中的重点和难点之一 ,学生在学 习过程中普遍感 到概念 和内容抽象 ,难 以理解。本文将针对基本假设 中的序列相关 性问题 ,探寻合适的教学方案。 “ 序 列 相 关 性 ” 问题 的 提 出 对 于 线 性 回 归模 型 :Yj =p o十∑B i X +u j ( 1 ) 在运用普通最小二乘法 ( O L S )进行参数估 计时 ,要求随机误差 项u 满足几个基本假设 ,包括零均值 、同方差 、无序 列相关性等 。而 序列相关性是指随机 误差项 u . 在不 同样 本点 之间存在 着一 定的相关 性 ,即 C o y( u ; ,u i )≠ 0 。实际上许 多时 间序列数据往往不能满足该 假设 ,这时候普通最小二乘 回归估计量虽然具有无偏性和一致性 , 但 不具有了有效性 ,即不满足最小方差性 。 二、“ 序 列相 关 性 ” 的 理 论 教 学 方 案 设计 在序列相关性的教学过程 中,一般的教学方案设计为 :首先通过 提 出问题 ,引入序列相关性 的概念 ,然后分析序列相关性产生 的原 因 和后果 ,进而剖析序列相关性 的检验方法 ,最后提出序列相关性 的应 对策略。 由于序列相关性 的检验 和修 正需要 在计 算机上 进行 上机 实 训 ,因此在这部 分的教学 中安排 了相应的实践教学环节。 ( 一)教学 内容的引入 在课堂教学开始时 ,首先有针对性的 向学生提出相关 问题 ,通 常 能吸引学生的学习兴趣 和注意力 。序列相关性是指随机误差项在 不同 样本点之间有了相关性 ,由于 随机误差 项是 样本 观测值 与平 均值之 差 ,因此序列相关性就是不 同的样本点的值偏离其平均值之差存 在着 相关性 。在实 际教学 中,我们 通 常 以消费 函数 为例 ,即 Y =‰ + p X , + U , 。可以首先向学生提 出问题 :相邻 的两个家庭 ,他们 的消费 行为之间是否存在着 相关性 ?即一个 家庭 的消费增加了 ,是否会 导致 另外一个家庭的消费相应的增加?这种现象在实际经济生活 当中是确 实存在的 ,也就是经济学理论 当中所 谓的 “ 攀 比效 应” 。在提 出问题 后 ,就可以顺理成章地 向学生介绍序列相关性的基本概念。 ( 二) “ 序 列 相 关 性 ” 产 生 的原 因 “ 序列相关性 ”产生的原因主要来 源于以下几个 方面 :( 1 ) 经济 系统惯性 。例如 G D P 、价格 、就业等经济数据 ,都会 随经济系统 的周 期而波动 ,很 可能表现为 自相关 。( 2)经济 活动滞后效应 。例如在蛛 网模型当 中,某种商品的供 给量不仅受 当期价格的影响 ,还受前 一期 价格的影响 ,使得供给与需求 即呈蛛 网状收敛或发散状态。 ( 三) “ 序 列 相 关 性 ” 的 后果 当随机误差项存 在序列相关性时 ,首先将会影响普通最小二 乘估 计量的有效性 ,即存 在 比 O L S 模型更为有效的估计方法 。并且在存在 序列相关时 ,由于参数 B 估计的方差不 等于 O L S 方 法下计算 的方 差 , 使得变量的显著性检验失去意义。讲 到这里 ,同学们通常对于 “ 序列 相关性” 的问题 依然感 到有些抽象和模糊 ,因此可以举 一些直 观具体 的例子进行讲解 ,比如在消费函数 中 , Y = B 。 + B X ; + u ,当一 个家 一 Nhomakorabea、
计量经济学第三次作业---序列相关检验
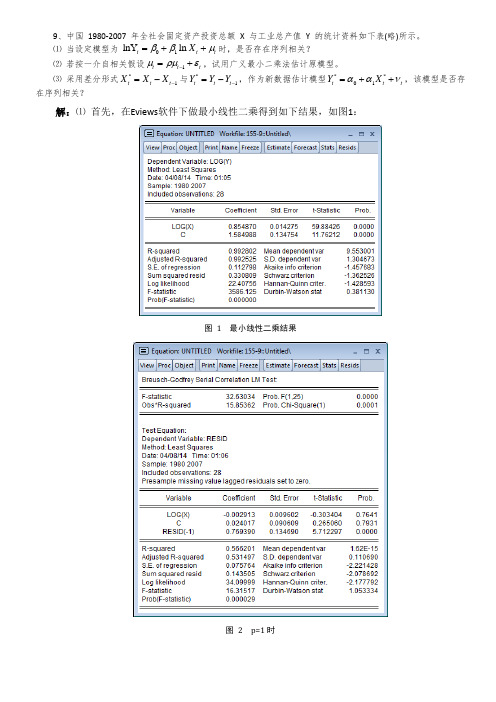
9、中国 1980-2007 年全社会固定资产投资总额 X 与工业总产值 Y 的统计资料如下表(略)所示。
⑴ 当设定模型为01 lnY ln t t t X ββμ=++时,是否存在序列相关? ⑵ 若按一介自相关假设1t t t μρμε-=+,试用广义最小二乘法估计原模型。
⑶ 采用差分形式*1t t t X X X -=-与*1t t t Y Y Y -=-,作为新数据估计模型**01t t t Y X ααν=++,该模型是否存在序列相关?解:⑴ 首先,在Eviews 软件下做最小线性二乘得到如下结果,如图1:图 1 最小线性二乘结果图 2 p=1时图3 p=2时图4 p=3时从上述结果可以看出,D.W 统计量的值为0.38113,再查找D.W 检验上下界表可知在样本容量为28、2k =(包含常数项)、显著性水平为5%的情况下 1.33L d =,由0.38113 1.33<得出Y 与X 至少一阶自相关,且为正相关。
进一步用LM 检验法进行检验,得到:① 1p =时,如图2:因为252%15.8536>(1)3.84nR χ==,故拒绝原假设,即Y 与X 存在序列相关。
另一方面,因为RESID(-1)=0.76939显著不为0,进一步说明了原模型的一阶序列相关性。
② 2p =时,如图3:因为252%18.3720>(2) 5.99nR χ==,故拒绝原假设,即Y 与X 存在序列相关。
另一方面,因为RESID(-1)=1.11045、RESID(-2)=-0.4677显著不为0,且它们参数估计的t-统计量都大于5%(26) 1.701t = ,同样是拒绝原假设,说明原模型确实存在两阶序列相关性。
③ 3p =时,如图4:因为252%18.4103>(3)7.81nR χ==,故拒绝原假设,即Y 与X 存在序列相关。
但由于RESID(-3)=0.06542接近于0,且它的参数估计的t-统计量5%(2=0.36)032< 1.701t = ,所以接受原假设,即不存在三阶序列相关。
7、计量经济学【序列相关性】【修改】

Graph, 都可以得到残差分布图.
三、自相关性的检验
(二)德宾—沃森 (Durbin-Watson) 检验—— 一阶自相 关检验 1、D.W.检验假定条件是: 第一:解释变量 X 为非随机的; 第二:随机误差项 t 为一阶自相关,即 t t 1 t , t 为误差项,且满足经典假定; 第三:线性回归模型中不应含有滞后内生变量 (Yt 1 , Yt 2 , ) 作为解释变量,例如,不应出现下列形式: Yt 0 1 X t 2Yt 1 t ,其中 Yt 1为 Yt 的滞后一期变量; 第四:回归模型中含有截距项; 第五:统计数据比较完整,无缺失项,适用于样本容量 n 15 的样本情况。
推导如下:
(e e
t 2 t
n
t 1
) (e 2et et 1 e ) e e 2 et et 1
2 t 2 2 t 2 t 1 t 2 2 t t 2 n 2 t 1 t 2
n
n
n
n
在大样本的情况下,有 可以表示为:
n t 2
e e
t f (t 1, t 2 , 自相关性的一般形式可以表示成:
, t p )
或者:
t 1t 1 2 t 2
p t p t ,,,,,,,,,, (4.2.3)
称之为 p 阶自回归形式,或模型存在 p 阶自相关。
下页图展示正负自相关以及非自相关性:
t s t s
如果误差项序列存在的是正自相关,即 E(t s ) 0, (t s) , 则:
ˆ ) Var( ˆ ),,,,,,,,,,,,,,,,,, ,, ,,, , ,, (4.2.6) Var( 1 1
计量经济学之序列相关性

H0 : 1 2 p 0
备择假设H为 1 ( H1:i i 1,2,, p) 中至少有一个不为零 若为真,则LM统计量在大样本下渐进 2 服从自由度为p的 分布:
LM nR ~
2
其中,n, (p)
2
R
2
分别是辅助回归方程(6)的样本容量和可决系 数
e e e e e e e e e e
t t t 1 t 1 t t 1 2 t 2 t 1 2 t
2 t 1
(3)
当n充分大时, et2 et21 有 et et 1 ˆ et2 所以
ˆ ˆ ˆ
(19)
三 自相关系数ρ的估计
广义差分法得以实施的关键是计算出自相关系数ρ的值,因此,必 须采用一些适当的方法对自回归系数ρ进行估计,通常适用的方法主 要有:经验法、利用 D.W.估计、科克伦-奥科特迭代法等。
下面我们着重介绍一下科克伦-奥科特迭代法: 科克伦-奥科特迭代法其实就是进行一系列的迭代,每一次迭代 都能得到比前一次更好的ρ的估计值。为了叙述方便,我们采用一元 回归模型来阐明这种方法, 多元回归模型下的迭代法与一元回归的原 理相同。 假设给定模型 Yt = β0 + β1 X t + μt 其中, μt = ρ1 μt−1 + ρ2 μt−2 + ⋯ + ρp μt−p + εt t=1+p,2+p,…,n (22) (21)
如果含有 k 个解释变量的多元回归模型(2)存在 p 阶序列相关 性,也可作类似变换,变换结果为
∗ Yt∗ = β0 1 − ρ1 − ⋯ − ρp + β1 X1t + β2 X∗ + ⋯ + βk X∗ + εt 2t kt ∗ 其中,Xit = Xit − ρ1 Xi(t−1) − ⋯ − ρp Xi(t−p)(i=1,2,…,p)。
计量经济学第七章序列相关性

广义差分方程, 失去一次观测
四、序列相关的修正
未知时
(1)用DW统计量估计
查表,N=24,一个解释变量,5%的DW临界值: dL=1.27, dU=1.45,0<d=0.911< dL ,正序列相关
例 美国零工招聘指数与失业率
序列相关修正,估计 d 0 . 911 ˆ 1 1 0 . 5445 用DW统计量估计 2 2 ˆ 0.546 一般对大样本来说, 科克伦-奥克特两步法 用哪种方法区别不大。 德宾两步法 ˆ 0.795 但是对小样本则不同。
OLS估计原模型并得到残差et 做et对模型中全部回归元和附加回归元et-1, et-2,…, et-p的回归,得到r2。 如果样本是大样本,则:(n-p) · r2 ~2p
四、序列相关的修正
自相关结构已知时的修正——广义差分法 以双变量回归模型和 AR (1 )为例。
Y t 1 2 Xt u t ut ut1 t Y t 1 2 Xt u t
n
t 1
t 1 n
ˆ t 2
t t 1 2 t
n
)
t 1
ˆ t 2
ˆ 定义
ˆ ˆ
t2
ˆ
t 1
n
为 样 本 的 一 阶 自 相 关 系 数 , 作 为 的 估 计 量 。
ˆ 则 又 , d 2 ( 1 )
1 1 , 所 以 , 0 d 4
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
< 序列相关实验报告><1>第一问D.W.检验命令:Data y c xGenr lny=log(y)Genr lnx=log(x)Ls lny c lnxDependent Variable: LNYMethod: Least SquaresDate: 12/10/12 Time: 15:39Sample: 1980 2007Included observations: 28Variable Coefficient Std. Error t-Statistic Prob.C 1.588478 0.134220 11.83492 0.0000LNX 0.854415 0.014219 60.09058 0.0000R-squared 0.992851 Mean dependent var 9.552256Adjusted R-squared 0.992576 S.D. dependent var 1.303948S.E. of regression 0.112351 Akaike info criterion -1.465625Sum squared resid 0.328192 Schwarz criterion -1.370468Log likelihood 22.51875 Hannan-Quinn criter. -1.436535F-statistic 3610.878 Durbin-Watson stat 0.379323Prob(F-statistic) 0.000000D.W.检验结果表明,在5%显著性水平下,n=28,k=2(包含常数项),查表得,dl=1.33,du=1.48,由于D.W.=0.379<dl,故存在正相关。
LM检验含一阶滞后残差项的辅助回归结果:Breusch-Godfrey Serial Correlation LM Test:F-statistic 32.78471 Prob. F(1,25) 0.0000Obs*R-squared 15.88607 Prob. Chi-Square(1) 0.0001Test Equation:Dependent Variable: RESIDMethod: Least SquaresDate: 12/10/12 Time: 15:40Sample: 1980 2007Included observations: 28Presample missing value lagged residuals set to zero.Variable Coefficient Std. Error t-Statistic Prob.C 0.023345 0.090124 0.259033 0.7977LNX -0.002836 0.009551 -0.296927 0.7690RESID(-1) 0.769716 0.134430 5.725793 0.0000R-squared 0.567360 Mean dependent var 1.18E-15Adjusted R-squared 0.532748 S.D. dependent var 0.110251S.E. of regression 0.075363 Akaike info criterion -2.232045Sum squared resid 0.141989 Schwarz criterion -2.089309Log likelihood 34.24863 Hannan-Quinn criter. -2.188409F-statistic 16.39235 Durbin-Watson stat 1.042286Prob(F-statistic) 0.000028LM=15.886,该值大于显著性水平为5%,自由度为1的X2分布的临界值=3.84,由此判断原模型存在一阶序列相关性。
二阶滞后残差项的辅助回归结果:Breusch-Godfrey Serial Correlation LM Test:F-statistic 23.23224 Prob. F(2,24) 0.0000Obs*R-squared 18.46328 Prob. Chi-Square(2) 0.0001Test Equation:Method: Least SquaresDate: 12/10/12 Time: 15:41Sample: 1980 2007Included observations: 28Presample missing value lagged residuals set to zero.Variable Coefficient Std. Error t-Statistic Prob.C 0.000108 0.082122 0.001316 0.9990LNX -0.000134 0.008713 -0.015411 0.9878RESID(-1) 1.115701 0.182417 6.116202 0.0000RESID(-2) -0.473435 0.185900 -2.546719 0.0177R-squared 0.659403 Mean dependent var 1.18E-15Adjusted R-squared 0.616828 S.D. dependent var 0.110251S.E. of regression 0.068246 Akaike info criterion -2.399823Sum squared resid 0.111781 Schwarz criterion -2.209508Log likelihood 37.59752 Hannan-Quinn criter. -2.341642F-statistic 15.48816 Durbin-Watson stat 1.590500Prob(F-statistic) 0.000008LM=18.46328,该值大于显著性水平为5%,自由度为2的X2分布的临界值=5.99,由此判断原模型存在2阶序列相关性。
三阶滞后残差项的辅助回归结果:Breusch-Godfrey Serial Correlation LM Test:F-statistic 14.97751 Prob. F(3,23) 0.0000Obs*R-squared 18.52001 Prob. Chi-Square(3) 0.0003Test Equation:Method: Least SquaresDate: 12/10/12 Time: 15:42Sample: 1980 2007Included observations: 28Presample missing value lagged residuals set to zero.Variable Coefficient Std. Error t-Statistic Prob.C 0.004190 0.084359 0.049669 0.9608LNX -0.000605 0.008965 -0.067492 0.9468RESID(-1) 1.152317 0.210377 5.477401 0.0000RESID(-2) -0.558721 0.297820 -1.876033 0.0734RESID(-3) 0.079894 0.215356 0.370984 0.7140R-squared 0.661429 Mean dependent var 1.18E-15Adjusted R-squared 0.602547 S.D. dependent var 0.110251S.E. of regression 0.069506 Akaike info criterion -2.334360Sum squared resid 0.111117 Schwarz criterion -2.096467Log likelihood 37.68105 Hannan-Quinn criter. -2.261634F-statistic 11.23313 Durbin-Watson stat 1.637381Prob(F-statistic) 0.000034LM=18.520,该值大于显著性水平为5%,自由度为3的X2分布的临界值=7.81,但e(3)的参数未通过5%的显著性检验,表明不存在3阶序列相关性。
消除序列相关性,输入命令:Ls lny c lnx ar(1) ar(2)Dependent Variable: LNYMethod: Least SquaresDate: 12/10/12 Time: 15:42Sample (adjusted): 1982 2007Included observations: 26 after adjustmentsConvergence achieved after 8 iterationsVariable Coefficient Std. Error t-Statistic Prob.C 1.462413 0.220311 6.637939 0.0000LNX 0.865725 0.022741 38.06850 0.0000AR(1) 1.153100 0.179489 6.424365 0.0000AR(2) -0.516672 0.168869 -3.059610 0.0057R-squared 0.998087 Mean dependent var 9.701508Adjusted R-squared 0.997826 S.D. dependent var 1.229613S.E. of regression 0.057334 Akaike info criterion -2.739210Sum squared resid 0.072318 Schwarz criterion -2.545657Log likelihood 39.60973 Hannan-Quinn criter. -2.683474F-statistic 3825.609 Durbin-Watson stat 1.819703Prob(F-statistic) 0.000000Inverted AR Roots .58-.43i .58+.43i则由广义最小二乘法回归结果如下:Lny=1.462+0.866lnx+1.153ar(1)-0.517ar(2)D.W.=1.819703在5%的显著性水平下,样本容量=26(被调整后的)K=4时,dl=1.14,du=1.65,可见du<D.W.<4—du,因此模型干扰项已不存在自相关性。
