人工神经网络建模

合集下载

人工神经网络建模(Artificial Neuron Nets)

人工神经网络建模（Artificial Neuron Nets）
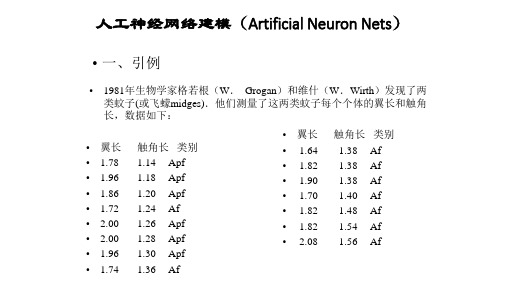
• 一、引例
• 1981年生物学家格若根（W． Grogan）和维什（W．Wirth）发现了两类蚊子(或飞蠓midges)．他们测量了这两类蚊子每个个体的翼长和触角长，数据如下： • • • • • • • • • 翼长 1.78 1.96 1.86 1.72 2.00 2.00 1.96 1.74 触角长类别 1.14 Apf 1.18 Apf 1.20 Apf 1.24 Af 1.26 Apf 1.28 Apf 1.30 Apf 1.36 Af
m
例如，若记
z wi xi
i 1
m
ቤተ መጻሕፍቲ ባይዱ
• 取激发函数为符号函数
1, x 0, sgn( x) 0, x 0.
则
1, y f ( z) 0,
• S型激发函数：
w x w x
i 1 i i 1 m i
m
i
, ,
i
1 f ( x) , x 1 e
• 规定目标为：当 t(1)=0.9 时表示属于 Apf 类， t(2)=0.1表示属于Af类。 • 设两个权重系数矩阵为：
w1 (1,1) w1 (1,2) w1 (1,3) W1 w1 (2,1) w1 (2,2) w1 (2,3)
( p) l
( p1) l
(i, j) a ( j),
( p) ( p) l l 1
l 1,...,L,
（10）
w (i, j )
表示第-1层第个元对第层第个元输入的第次迭代时的权重
( p) l
其中

( p) L

大脑神经网络建模及其功能意义

大脑神经网络建模及其功能意义简介：人类大脑是一个复杂且神秘的器官，其中神经元通过复杂的网络连接和相互作用，构成了一个庞大的神经网络系统。

大脑神经网络建模是研究人脑结构和功能的重要手段之一。

通过模拟和探索神经网络的构建和工作原理，我们可以更好地理解大脑在认知、感知、学习等方面的功能意义。

一、大脑神经网络建模方法1. 静态建模静态建模是一种将大脑神经网络表示为静态连接模式的方法。

这种方法可以通过扫描和图像处理技术，将大脑的结构和连接关系转化为图像或网络拓扑图。

静态建模的优点是简单易懂，可以提供有关大脑区域之间连接性的信息。

然而，它无法揭示大脑的动态特性和信息传递过程。

2. 动态建模动态建模是一种模拟大脑神经网络活动的方法。

通过建立数学模型、仿真计算等手段，可以模拟大脑神经元之间的相互作用和信息传递过程。

这种方法可以更加真实地模拟和理解大脑的动态功能。

然而，由于大脑神经网络的复杂性，动态建模需要大量的计算资源和高级的算法支持。

二、大脑神经网络建模的功能意义1. 深入理解大脑运作机制大脑神经网络建模可以帮助我们深入理解大脑的运作机制。

通过模拟和分析神经网络的动态特性，可以揭示神经元之间的相互影响和信息传递过程。

这有助于我们更好地理解大脑在认知、感知、学习等方面的机制和原理。

2. 解释认知功能与行为大脑神经网络建模还可以帮助我们解释人类的认知功能和行为。

通过与实际观测和实验结果进行比对，我们可以验证和验证神经网络模型的准确性和可靠性。

这有助于我们探索和理解认知功能与行为的本质。

3. 治疗神经系统疾病大脑神经网络建模对于治疗神经系统疾病也具有重要意义。

通过建立神经网络模型，我们可以模拟疾病对大脑神经网络的影响，从而更好地理解并设计相关的治疗方法。

这为神经系统疾病的治疗和康复提供了重要的依据和指导。

4. 辅助人工智能设计大脑神经网络建模还可以为人工智能的设计和开发提供有益的启示。

人脑作为高度智能的系统，具有强大的信息处理能力。

神经网络的建模与仿真

神经网络的建模与仿真随着科技的发展，越来越多的研究人员开始将神经网络应用于各个领域，如医疗、金融、自然语言处理等。

神经网络作为现代人工智能技术的核心，其建模与仿真技术也越来越受到关注。

神经网络的建模可以分为两个部分：架构的设计和权值的学习。

架构的设计通常使用基于数据的方法和基于先验知识的方法，其中基于数据的方法采用启发式搜索等技术自动寻找最优结构，而基于先验知识的方法则根据领域知识构建结构。

常见的神经网络架构包括前馈神经网络、循环神经网络、卷积神经网络等。

权值的学习是指通过训练数据来确定神经网络中各个神经元之间的权值，以最小化目标函数。

常见的训练算法包括梯度下降法、反向传播算法等。

仿真是评估神经网络模型性能的重要手段，通过对模型进行仿真可以了解模型在不同条件下的行为，从而优化模型的性能。

仿真工具包括MATLAB、Python等。

在使用这些工具时，需要注意对仿真过程中的各个参数进行控制，以确保仿真结果的准确性和稳定性。

在实际应用中，神经网络经常被用作分类器或回归器。

分类器用于将输入数据归类到不同的类别中，而回归器则用于估计输入数据与输出数据之间的映射关系。

除了分类器和回归器，神经网络还可以用于聚类、降维等任务，如自编码器和深度信念网络。

神经网络的成功应用离不开数据的支撑。

建模和仿真需要大量的数据来支持，数据的准确性和多样性对神经网络的表现影响极大。

因此，在应用神经网络时，需要注意对数据集的选择和预处理，以确保数据质量和可靠性。

总之，神经网络作为现代人工智能的核心技术，在各个领域都有着广泛应用。

神经网络建模和仿真技术的发展为神经网络应用提供了坚实的基础，相信在不久的将来，神经网络将在更广阔的领域内发挥更大的作用。

神经网络计算-建模讲义解析

β=0.65), 并采用了惯性项. 训练时, 采用135天的数据
去生成80个训练样本、25个检测样本进行实验。训练样本精度达到95%左右，而检验样本精度在65-80%之间.
-
71
作业
设计一个 BP 网络对上图中的英文字母进行分类。输入向量含1 2 个分量，输出单元个数取1，分别用-1、0和1代表字符A、I、O。训练时可选择不同的隐节点数及不同的学习率进行对比。
-
60
活化函数 • Sigmoid函数
gx 1
1exp(x) -
fxtanh(x)
61
双曲正切函数
• 表达式：
tanh(x)
eexx
ex ex
.
• 图像
-
62
Sigmoid函数特点
• 光滑, 单调递增，上、下有界（称为饱和性）. • 导数值可由其函数值给出
gx 1- g(x) g(x);
模式识别、函数逼近和数据压缩等问题。
返回
-
8
人工神经网络的结构
具有一个隐层的前馈网络单层全连接反馈网络
-
9
神经网络的特性
• 鲁棒性（容错） • 并行计算 • 自我学习 • 硬件实现 • 求满意解
-
10
神经网络的三要素
• 网络结构； • 信息流动规则； • 权值学习规则。
-
11
神经网络的学习方式
输入样本向量预处理
• 输入样本向量的各个分量有时在数量级上
差异较大，若不进行适当的处理，数量级大的分量可能完全湮没其它分量的作用。为此在训练开始之前，需对各个分量做相应的调整，使其具有大致相同的数量级。
-
59
输入样本向量预处理

人体神经网络系统建模及功能解析分析

人体神经网络系统建模及功能解析分析人体的神经网络系统是一个复杂而精密的组织，由大脑、脊髓和周围神经组成。

它具有多种功能，包括感知、运动控制、内脏活动的调节以及思维和意识的产生。

本文将对人体神经网络系统的建模和功能进行解析分析。

首先，人体的神经网络系统可以通过建模来理解其结构和功能。

建模的目标是对整个系统进行抽象和描述，以便更好地研究和理解其运行机制。

建模可以基于不同层次和尺度的方法，包括分子、细胞、组织和器官水平。

例如，分子层面的建模可以研究神经递质在突触传递中的作用，细胞层面的建模可以研究神经元的电活动和兴奋性传导，组织层面的建模可以研究不同脑区之间的连接和信息传递，器官层面的建模可以研究大脑和脊髓在整体行为和认知中的作用。

其次，神经网络系统的功能可以通过分析其组成部分的相互作用来进行解析。

神经元是神经网络系统的基本单位，它们之间通过突触连接形成复杂的网络。

神经元的兴奋性传导和突触传递是神经网络系统功能实现的关键。

神经元的兴奋性传导是指当神经元受到足够的刺激时，电信号会沿着它的轴突传导到突触，并通过神经递质释放到下一个神经元。

突触传递是指神经递质在突触间隙中传递，以影响下一个神经元的兴奋性状态。

这些传导和传递过程的细节和效率对于神经网络系统的功能实现至关重要。

神经网络系统的功能还可通过研究特定区域和结构的功能分化来进行解析。

大脑是神经网络系统的核心，负责高级认知功能、意识、思维和情感调节。

大脑有多个区域和结构，每个区域和结构都有特定的功能。

例如，脑干控制基本的生命维持功能，大脑皮层负责感知和运动控制，海马体负责记忆和学习等。

通过研究这些区域和结构的功能分化，可以更深入地了解神经网络系统的整体功能。

此外，神经网络系统的功能可以通过研究其在疾病状态下的改变来进行解析。

神经网络系统在多种神经系统疾病中发挥关键作用，如阿尔茨海默病、帕金森病和精神分裂症等。

通过比较疾病和健康状态下神经网络系统的差异，可以揭示疾病的发病机制和病理过程，为疾病的诊断和治疗提供理论基础。

神经网络的建模和优化

神经网络的建模和优化一、引言近年来，神经网络作为一种高效的人工智能模型在各个领域得到广泛应用。

如何对神经网络进行建模和优化，是目前研究的热点之一。

本文将从神经网络的基本概念入手，介绍神经网络的建模和优化过程。

二、神经网络的基本概念神经网络是一种模拟生物神经元之间互相连接的复杂网络结构，它可以通过学习来实现对各种输入输出之间的关系进行预测和识别。

神经网络通常由输入层、隐藏层和输出层三个部分组成。

其中输入层用于接收输入信号，输出层用于输出预测结果，而隐藏层则可以有多个，在其中进行信息的转化和处理。

三、神经网络的建模过程在神经网络的建模过程中，需要确定神经网络的拓扑结构、选择合适的激活函数和设计合理的损失函数等方面问题。

1. 确定神经网络的拓扑结构拓扑结构是神经网络的关键设计参数之一，它影响着神经网络的表示能力和计算效率。

常见的神经网络拓扑结构包括多层感知机（Multilayer Perceptron，MLP）、卷积神经网络（ConvolutionalNeural Network，CNN）和循环神经网络（Recurrent Neural Network，RNN）等。

在实际应用中，需要根据输入数据的属性和实际问题的需求来选择合适的神经网络拓扑结构。

2. 选择合适的激活函数在神经网络中，激活函数被用来实现非线性变换，增加神经网络的表达能力。

常用的激活函数包括Sigmoid函数、ReLU函数等。

在实际应用中，需要根据数据的属性和问题的特点来选择合适的激活函数。

3. 设计合理的损失函数损失函数是神经网络优化的核心，它用于度量预测结果与实际结果之间的差异。

不同的损失函数适用于不同的问题，例如，均方误差（Mean Squared Error，MSE）适用于回归问题，交叉熵（Cross-Entropy）适用于分类问题等。

四、神经网络的优化过程神经网络的优化过程是通过参数的调整来使得损失函数最小化，从而提高模型的预测准确性。

神经网络复杂神经网络的建模与分析

神经网络复杂神经网络的建模与分析神经网络是人工智能领域中一种重要的算法模型，它模拟了人类的神经系统，能够实现复杂的模式识别和学习能力。

本文将介绍神经网络的建模和分析方法，帮助读者更加深入地理解这一技术。

一、神经网络模型的基本结构神经网络由各种神经元和它们之间的连接构成，一般包括输入层、隐藏层和输出层。

每个神经元都有输入和输出，通过连接权重和激活函数来实现信息的传递和处理。

神经网络的结构可以用图示方式表示，每个神经元用圆圈表示，连接线表示神经元之间的连接关系。

在确定神经网络的结构时，需要考虑输入和输出的特点，合理设置隐藏层的数目和神经元数量。

通常情况下，隐藏层越多，神经网络的学习能力和表达能力越强，但也增加了计算复杂度和训练时间。

二、神经网络建模的步骤神经网络建模的过程包括确定输入和输出的特征向量、选择合适的激活函数和损失函数、设计合理的网络结构、初始化权重和偏置、以及通过训练算法进行参数的优化调整。

1. 特征向量的选择神经网络的输入通常是特征向量，特征向量的选择对建模效果至关重要。

特征向量应该包含能够表达问题特点的关键信息，同时还要避免维度过高和冗余的特征。

常见的特征选择方法有主成分分析（PCA）和线性判别分析（LDA）等。

2. 激活函数和损失函数的选择激活函数决定了神经元的输出值，常用的激活函数有Sigmoid函数、ReLU函数和Tanh函数等。

损失函数用于衡量神经网络模型的预测结果与真实值的差距，常见的损失函数有均方误差（MSE）和交叉熵损失函数等。

激活函数和损失函数的选择应根据具体问题进行权衡。

3. 网络结构的设计根据问题的复杂程度和数据的特点，设计合理的网络结构是神经网络建模的重要一步。

通过增加隐藏层和神经元的数量，可以提高网络的学习能力和表达能力，但也会增加训练时间和计算复杂度。

在网络结构设计时，需要考虑到是否存在过拟合和欠拟合的问题。

4. 权重和偏置的初始化权重和偏置的初始化对神经网络的训练起到重要影响。

人工神经网络建模

I一、引例・1981年生物学家格若郴(W ・Grogan＞和维什＜W. With)发现了两类蚊了(成飞ft^midgcs).他们测駅了这两关蚊f 毎个个体的翼K 和触九 K. fttW 如卜•：«EKI 类别 -«K 触角K 类1.78144 Apf• 1.64138 Af 1,96 IJ8 Apf • 1.82 138 Af L86 L20 Apf • 1.90 138 Af 1.72 1.24 Af •L70L40 Af 2.00 L26 Apf < 1.82 L4« Af 2.()() 1.28 Apf -1.82 1.54 Af l ・96130 Apf • 2081.56 Af1.741.36 Af如果抓到三只新的蚊子，它们的触角长和翼长分别为(1.24,1.80); (1.28, 1.84); (1.40, 2.04 ).问它们应分别属于哪一个种类？解法一：-把鬓长作纵坐标，触ft 长作橫坐标：那么毎个蚊子的翼长和触角决定了坐标平面的一个点」(; 中6个蚊子属于川歼类；川黑点r •农示；9个蚊子属Af 类；用小圜圈S "表示. -得到的结果见图11.0 f 卩用］屮［|卩#|#^#|宰，■廿甘斗幷I 玮M 悴hJi 杆f 廿H 17 •jjin ［人工神《网络理複(Artificial Neuron Nets) tI H BL —；Li_ I 。

问：d 2 建些2 * X-例如；取A= (1.44, 2.10)和 B = (1JO, l.l6>t 过AB 两点作一条Jl 线：• y= I.47X -0.017-瓦中X 农示触角氏；y 衣示翼氏.-分类规则：设•个蚊/的数据为(x.y) •如果y21.47x ・0.017,则判断蚊子属Apf 类:•如果y<l ・47x -0.017；则判断蚊子属Af 尝.1.1 1-2 L3 14 1；5 te^(1-10,1-60)心思路：作一H 线将两类E 蛟分开1.8O■■■■■■么■■•・9豐■•■・•・■■■■■■r ■ .VLt U ■ ■ ■ ■ ■■1512分类直纟戈图2* X•扶陷：扌艮据什么原则确定分类直线？•若取A=(l・46210)・ B=(l.1,1.6)不变，则分类直线变为y=1.39x4X).071分类结果变为：(1.24,1.80), (1.40,2.04)属于Apf类Q(I.28J.84)W 于Af 类) •哪一分类直线才是正确的呢?.因此如何来确定这个判别"线是个值得研究的I 问题.■般地讲，应该充分利用已知的数据信息r 来确定判别ri线. . 讪・新思賂：将问题看作一个系统，飞壕的数据作为输入，飞壕的类型作为输出，研究输入与输出的A 系・❖再如，如卜•的情形已经不能用分类直线的办法;却神经元的信息传递和处理是■种电化学活动.树突由于电化学作用接受外界的刺激：通过胞体内的活动体现为轴突电位，+轴突电位达到一定的值则形成神经脉冲或动作电位：再通过轴突耒梢传递给其它的神经元.从控制论的观点來看；这•过程可以看作-个多输入草输出非线性系统的动态过程神经网络硏究的两个方面-从空理上、解剖学上进行硏究-从匸程技术上、算法上进行研究❖英中x= (Xj,…X苗)T输入向量，y为输出,軻是权系数：输入号输出几有如下关系：y = /（工怙・-0）/=]-0为阈值，f (X)是激发函数；它可以是线性函数，也可以足朮线性函数.—c<■若将W值看作是一个权系数・」是一个同定的输入，另有m・l个止常的输入，则（1）式也町农爪•为！til尸/（!＞』）/-I 一I ＜ /（X）＜I •Cl）•参数识别：假设臥数形成已知I,则町以从己有的1输入输出数据确定出权系数及Wffi. 呼'O 众多神经元之间组合形成神经网络，例如F 图的介何中间层(隐层)的B ・P 网络(1)蚂蚁群一个蚂蚊冇50个神经元.帕独的一个蚂蚊不能做太多的事；K 至J ：不能很好活卜•公.但足一:蚂蚁；设仃10万个休，那么这个胖体ffl*^T-500万个神经元然不是简单相加，这里只为说明方便而］^):那么它们可以觅您、搬家、电，图5帶中间层的B ・P 网络3、量变引起质变 •・一神经网络的作用II 彳攻敌人等等. W 络说话人们把一木教科书川网络把它读出來C 当然需翌通过光电山的伫号转换)：开始网络说的话像5儿学讥那样发 (2)2、神经网络的数学模型出”巴、巴、巴”的声响，但经过B-P第法K时何的训练竟能正确读出英语课木中90%的词汇.从此用神经网络來识别讲,7和图象电成一个新的热潮4慎蠢药q—■ ＞一6 JR jf J —'（3）具右学习和记忆能力.■个神经网络町以通过训练学习判別爭物：学习某•种规律或规则-神经网络可以用r 联想记忆. （4）对数据的可容性大.在神经网络屮町以同时使用g 化数抑和质屋数据（如好•中■善-及格.不及格等）-（5）神经网络可以用人规模集成电路來实现-如矣国用256 个神经尤组成的神经网络纟11成硬件niMH 别下丐体的邮政编码-四、反向传播算法（B-P 算法）人工神经网络的基本特点（1）町处ffl 卄线件（2）并行结构.对神经网络中的毎•个神经元來说；K 运»都於同样的.这样的结构址便于讣»机并行处理. <SI怕6 K 屮网络1.简单网络的B ・l •算法Back propagation algorithm毎弦的n的：根据实际的输入与输出数据，汁畀模空的参数（权系数）5 =4假设有P个训练样木•即冇P亍输入输出对❖ ( Ip, Tp) ,p=5(….,P, rt't'输入向w；为,P—('“1， - J pm )(丈际上的)I」林输出向鼠为2网络输出向a为(理论上的)记wij为从输入向虽的第jOJ・“m)个分皿到输出向虽的第i (jh,…E)个分虽的权里•通常理论值弓实际値仃1误差，网络学习则足指不断地把打比较•丿t根刑极小凍则修改参数wij.使误井平方和达以小：门“门二“冲一竹”厂(P L . .P)(2)• Della学」J规则：记0打农示递推一次的修改©，则有—+ △VI勿=> Wfj厂尸A叫=S 心=丿/»=1 p=l仃J;为学川勺速率(4)p=1 屮str注=由（1）式，第i个神经元的输出可衣示为"丿S =八切）丿*1i^= .1 , W寸（第i个神经元的阈W）特别鬥f绘线性旳数时f/r% =伙艺叫Ay）+ b21定理11按上酣述鮮经网堀I段其中每个柩元羅线铀,取训麟标为P吒坯P二11 "tsl时;求踊帥值的甌最速下降法就是Ma学习期.<5)I假设.(1)输入层不il 右S 数Z 内，它冇No 个神经元.汝网络其输出为?RL 层；第ky^fNk 个神经元.(2)设 :(/)我示第k 从第i 神经元所接收的信息 (w,{i,j)丧示从第k ・l 层第j 个元到第和£第：个元的权匝・I “盒(0表第k 厘第i 个元的输出jf 蒔祺可(|!j j u - ■ j • — j ； j ■ w(3)设层与层何的神经元都冇信息交换(否则，可设它们 Z 何的权朿为零)：但同一层的神经元Z 何无信息传输.(4) 役何息传输的方向足从输入尼到输出层方向；因此称为询向网络.没有&向传播俏息.(5)"()(7)表示输入的節j 个分 a.2.多网络 ■人fi« t.1*¥ »|・崖罔7多层和绩网络假设:(11) (12)在上述假定下网络的输入输出关系可以丧示为:ff如“)=工 wji ")“•(/)+久⑴•/■I=工叫(i J )"心)+仇")•/=!ISiSN". (7)A| I叫们・£叫(iJ )%.U)M-(i)・("“) = /("&))・心(门=/("2(门)・!□</<■ 其中W 农示笫k 层第i 个元的阈值.,定理2对r 八冇多个隐层的前馈神经网络；设激发曲数为S 函数：II •指标诵数取“& = N（八小“）一“;r><7RN(8)其中E则每个训练循坏中按梯度下降时,兵权a 迭代公式为7）=血P "（G 7）+P 周“％£（丿人 I = 1,…厶耐％・力表示第1・1层第j 个元对第1层第i 个元输入的第P 次迭代时的权巫矽％）=（m 严（o ）f （叱（））巧3（0=厂ya”乞巧£（/）耐r"（丿异）• . • •7*1（一(9)(10 )BP算法-选定学习的数据・p=l,…,R隨机确定初始权矩阵W (0)、•用学习数据计算网络输出-用(10)式反向修正■直到用完所有学/ 习数据•j、= 2厂W、+ q氓小心X J、• f厶令§❖❖五.应用之例；蚊子的分类-己知的两类蚊子的数据如衣1;«艮1.781,961,861.722-002.001・96174触ft长1.141.181.201.241-261.281.301.36类别AptAptAplAfAptAptAptAf目标值050・90®OJ0.9o.g0®OJ-fr-fr4-fl-+-fl-1.641-821.901.701.821,822.03触角K：r381.381.381・401.481,541.56类别AfAfAfAfAfAfAfcorneasy桶OJOJ<1,10.1OJ().1<1J输入数据有 15个，UP ,p=1,.,.,15; j=1,2;对应 15 个输出。

基于人工神经网络的风电场建模

台风电机组模型的详细模型．但是由于大型风电场
仿真规模很大．真时间过长．难以满足精确仿真仿也的要求 … 因此一些研究中开始利用实验数据，过通
系统辨识的方法来得到风力机的模型。献ｆ应用文２］系统辨识理论．用ＡＲＭＡＸ的模型结构。用预报采利误差法．辨识出在某一工况点附近工作的柔性风力机系统的功能模型。献『］现场数据与神经网络的建文３将模方法相结合．建立了火电机组汽压动态模型。文献
ｒ在实验风力机的基础上．神经网络模型对风力机４］用系统进行辨识．好地反映了其非线性关系。更
图１风电系统模型组成
Ｆｉ１Ｃｏｇ．ｍｐｓｔｎｏｎｏｒｙｔｍｄｌｏｉｏｆｗｉｄｐｗｅｓｅｍｏｅｉａｓ
距角是一个伪随机输入，文设其平均值为３７。本．ｏ
风参数风轮机参数风场布置
风力机这样受到较强随机扰动输入的系统．不仅难
以得到精确的机理模型．而且即使考虑风电场中每
出功率随风速的变化而波动由于实际风速、至风向不断变化的动态运行风甚

人工神经网络建模

语音识别
总结词
语音识别是将人类语音转换成文本的过程，利用人工神经网络进行语音特征提取和分类。
详细描述
语音识别技术使得人机交互更加自然，广泛应用于智能助手、语音搜索、语音翻译等领
域。
自然语言处理
要点一
总结词
自然语言处理是利用人工神经网络对人类语言进行分析、理解和生成的过程。
要点二
详细描述
自然语言处理技术包括文本分类、情感分析、机器翻译等，使得计算机能够更好地理解人类语言，提高人机交互的效率和自然度。
人工神经网络的应用领域
语音识别
利用循环神经网络（RNN）和长短时记忆网络（LSTM）识别语音并转换成文本。
推荐系统
利用深度神经网络为用户推荐感兴趣的内容。
图像识别
利用卷积神经网络（CNN）识别图像中的物体和特征。
自然语言处理
利用循环神经网络和注意力机制处理自然语言任务，如机器翻译、文本生成等。
训练算法
总结词
训练算法是指导神经网络学习和优化的算法，常用的有梯度下降法等。
详细描述
训练算法根据学习率和优化目标，不断迭代更新网络权重，使网络在训练数据上获得更好的性能表现。
03
常见的人工神经网络模型
前馈神经网络
总结词
前馈神经网络是一种最基础的人工神经网络模型，信息从输入层开始，逐层向前传递，直至输出层。
数据清洗与预处理
去除异常值、缺失值，进行数据标准化、归一化等处理，以提高模型的准确性和稳定性。
数据划分
将训练数据集划分为训练集、验证集和测试集，以便于模型训练、验证和评估。
训练过程中的优化算法
梯度下降法
基于梯度下降的优化算法，通过迭代更新权重和偏置项，最

实验报告-人工神经网络--基于人工神经网络实现材料设计优化与建模

实验课程名称：计算机在材料科学与工程中的应用2）用MATLAB中的人工神经网络方法对材料组成与性能数据进行分析和建模。

题目1：设计一个BP人工神经网络，使其与非线性函数1+sin(k*pi/4*p)逼近，其中k为函数频率系数，p为时间坐标向量，取p=[-1:0.05:8]。

要求：A)当频率系数k=1时，分析设计bp神经网络结构，包括网络的层数、的个数、传递函数。

B)进行bp神经网络的编程，构建网络、训练网络和仿真，绘制神经网络输出的逼近曲线图。

计算机实现过程：① 初始化：对所有连接权和阈值赋以随机任意小值；)0;,...,1;,...,1;,...,2()()(1====-t p j p i m k t t w k k k i k ij ，，θ② 从N 组输入输出样本中取一组样本：x （1）=[x1,…, xp1]T, d (1) =[d1,…,dpm ]T, 把输入信息 x (1) =[x1,…, xp1]T 输入BP 网络中 ③ 正向传播：计算各层节点的输出),...,1,...,2(k ki p i m k y ==；分析：产生副作用，训练后网络输出结果拟合精度不够。

分析：训练曲线达不到，由于初始值不定，误差进入梯度误差局部最小曲面。

分析：训练曲线达到要求分析：训练曲线未达到目标，需要调整神经网络结构参数分析：达到目标，且连续运行多次，均达到要求，此神经元数目达到要求分析：当神经元数目过大，达到过拟合，对训练以外的数据精确度不够，泛化能力减弱当频率一定且其他参数条件不变时，隐含层神经元数增大时，得到的曲线与原始的非线性函数曲线更加接近，说明BP网络对非线性函数的逼近效果比较好。

将数据转置，随机选择5组数据为预测样本数据，其他图：。

人工智能建模方法

人工智能建模方法
一、简介
人工智能建模是指利用人工智能技术建立模型，用以模拟复杂的系统、现实世界中的问题。

它可以通过加强学习、遗传算法、神经网络、模糊逻辑、支持向量机等方法，来解决复杂的问题。

通过建立模型，它可以自动
检测出现实世界中的模式，从而有效地控制和优化系统和过程。

人工智能建模的主要任务是，充分研究和分析现实世界中的复杂系统，并建立一个能够捕捉系统特征，反映模型语义的模型。

这种模型也可以用
于预测系统未来的发展，分析系统的不确定性，并使用统计数据和统计方
法进行验证。

1.加强学习：加强学习是一种以机器学习为基础的人工智能建模技术，它可以模拟人类学习的过程，并从经验中学习和推断出最优解决方案。

2.遗传算法：遗传算法是一种以计算智能技术为基础的人工智能建模
方法，它利用数学模型和基因编码机制来处理复杂问题，从而求解最优解
决方案。

3.神经网络：神经网络是一种以计算智能技术为基础的人工智能建模
方法，它被广泛用于解决一类或多类问题，它可以预测系统的表现，并从
数据集中提取模式。

神经元网络建模的主要方法

神经元网络建模的主要方法神经元是神经系统中最基本的处理单元，其通过电化学信号传递信息。

神经元网络模型是对生物神经网络进行的抽象，它的建立有助于对神经网络的功能进行理解和分析。

神经元网络模型可用于计算机视觉、语音识别、预测和控制等各种应用中。

到目前为止，人们发明了许多神经元网络建模方法，以下将介绍其主要方法。

1. 阈值感知器模型阈值感知器是一种最简单的神经元网络，由美国心理学家罗森布拉特(Rosenblatt)于1957年提出的，其结构和工作原理模拟了大脑中神经元的特征。

阈值感知器是一种单层神经元网络结构，其中输入信号通过经过加权的阈值函数，产生输出信号。

它的特点是处理速度很快，适用于处理一些比较简单的模式识别问题。

然而，阈值感知器存在一个限制：只能解决线性可分问题。

2. 反向传播模型反向传播模型是一种多层前馈神经元网络，由美国学者鲍莫(Baum)于1960年代提出，并由美国学者效苏本(Effector)和皮特布鲁克(Peter Brook)于1970年代进行改进。

它包含输入层、多个隐层和输出层，各层神经元之间互相连接。

反向传播模型通过不断迭代来更新权重值，使得模型能够提高预测精度。

其优点是适用于处理非线性可分问题和大规模神经网络问题，但其训练速度较慢，容易陷入局部极值。

3. 自适应神经元模型自适应神经元模型是一种基于反馈机制的神经元网络模型，它可以自适应地改变神经元的阈值和权值，以达到更准确的预测。

自适应神经元模型是一种动态学习方法，其不需要大量的训练数据，能够快速适应新的数据。

但是，由于其节点之间的连接具有长时滞，训练和使用都需要耗费大量的计算资源。

4. 循环神经元模型循环神经元模型可以在时间序列数据上建模，具有记忆和预测的功能。

它是一种基于时间和空间的神经网络模型，其中节点之间的连接具有时间依赖性。

循环神经元模型在时间序列数据处理、自然语言处理等领域有广泛应用，但它的训练难度较大，容易出现梯度消失/爆炸问题。

神经网络模型基本原理

神经⽹络模型基本原理⼈⼯神经⽹络是⼀个数学模型，旨在模拟⼈脑的神经系统对复杂信息的处理机制，其⽹络结构是对⼈脑神经元⽹络的抽象，两者有很多相似之处。

当然 ANN 还远没有达到模拟⼈脑的地步，但其效果也让⼈眼前⼀亮。

1. ⼈⼯神经元结构⼈⼯神经元是⼀个多输⼊单输出的信息处理单元，是对⽣物神经元的建模。

建模⽅式可以有很多种，不同的建模⽅式就意味着不同的⼈⼯神经元结构。

⽐较著名的⼈⼯神经元模型是 MP 神经元，直到今天，我们仍然在使⽤这个神经元模型。

MP 神经元是模仿⽣物的神经元设计的： 1）输⼊向量 x 模拟⽣物神经元中其他神经细胞给该细胞的刺激，值越⼤刺激越⼤； 2）w 向量模拟该细胞不同来源的刺激的敏感度；3）⽤阈值 θ 来描述激活该神经元的难易程度，越⼤越难激活； 4）⽤ w 1x 1+w 2x 2+...+w n x n −θ 来计算神经元的兴奋程度；5）y =f (x ) 为激活函数，⽤来计算神经元的输出，因为⽣物神经元的输出是有上下限的，所以激活函数也是能够“饱和”的有界函数； 6）在 MP 神经元中，激活函数为阶梯函数。

兴奋函数⼤于阈值输出 1，⼩于阈值输出 0；下图是 MP 神经元模型的⽰意图：将激活函数代⼊，将项 −θ 设为 b ，则可以得到 MP 神经元的数学模型：y =sgn n∑i =1(w i x i +b )=sgn w T x +b惊讶得发现它就是⼀个线性分类模型，和的数学模型是完全⼀样的，所以⼀个 MP 神经元的作⽤就是：对输⼊进⾏⼆分类。

这是符合⽣物神经元的特点的，因为⼀个⽣物神经元对输⼊信号所产⽣的作⽤就是：兴奋或这抑制。

所以通俗来讲：⼀条直线把平⾯⼀分为⼆，⼀个平⾯把三维空间⼀分为⼆，⼀个 n −1 维超平⾯把 n 维空间⼀分为⼆，两边分属不同的两类，这种分类器就叫做神经元，⼀个神经元只能分两类，输出是⼀个能体现类别的标量。

⼀个神经元的作⽤就是这么简单，所做的也只能是线性分类，但是当多个神经元互联的时候就会产⽣神奇的效果，下⾯再叙述。

数学建模之BP神经网络

神经网络的应用
人工神经网络以其具有自学习、自组织、较好的容错性和优良的非线性逼近能力，受到众多领域学者的关注。在实际应用中，80%～ 90%的人工神经网络模型是采用误差反传算法
或其变化形式的网络模型（简称BP神经网络），
目前主要应用于函数逼近、模式识别、分类和
数据压缩或数据挖掘。
§2 BP神经网络概述
人工神经网络是根据人的认识过程而开发出的一种算法。假如我们现在只有一些输入和相应的输出，而对如何由输入得到输出的机理并不清楚，那么我们可以把输入与输出之间的未知过程看成是一个“网络”，通过不断地给这个网络输入和相应的输出来“训练” 这个网络，网络根据输入和输出不断地调节自己的各节点之间的权值来满足输入和输出。这样，当训练结束后，我们给定一个输入，网络便会根据自己已调节好的权值计算出一个输出。这就是神经网络的简单原理。

工作过程：
从神经元各组成部分的功能来看，信息的处理与传递主
要发生在突触附近。当神经元细胞体通过轴突传到突触前膜的脉冲幅度达到一定强度，即超过其阈值电位后，突触前膜将向突触间隙释放神经传递的化学物质。神经元间信息的产生、传递和处理是一种电化学活动。神经元间的信号通过突触传递。通过它，一个神经元内传送的冲击信号将在下一个神经元内引起响应，使下一个神经元兴奋，或阻止下一个神经元兴奋。
常见的激活函数有以下几种类型：
1、阶梯函数 2、线性函数 3、非线性：Sigmoid函数
1 (s) 1 e s
1 (s) 1 e s
人工神经网络的分类

按网络连接的拓扑结构分类：
层次型结构：将神经元按功能分成若干层，如输入
层、中间层（隐含层）和输出层，各层顺序相连互连型网络结构：网络中任意两个节点之间都可能存在连接路径

人工神经网络模型及仿真

机器学习论文题目：人工神经网络模型及仿真学院：电子工程学院专业：电路与系统姓名：学号：摘要人工神经网络（artificial neural network，ANN）通常被认为是基于生物学产生的很复杂的分析技术，能够拟合极其复杂的非线性函数。

它是一项发展十分迅速、应用领域十分广泛的技术，已在人工智能、自动控制、模式识别等许多应用领域中取得广泛成功。

ANN是一种重要的机器学习工具。

本文首先简要讲述了一些相关的生物神经网络知识，在此基础上，引出了人工神经网络。

然后概述了ANN的发展历史及现状并总结了ANN的特点。

在第二部分，对ANN发展过程中具有标志性的几种ANN的模型及其结构进行了讲解，如：感知器、线性神经网络、BP网络、反馈网络等，并给出了相应的简单应用事例，而且使用功能强大的仿真软件——MATLAB对它们的性能进行了仿真分析。

在论文最后，给出了本文的总结以及作者的一些体会。

ABSTRACTArtificial neural network(ANN) is commonly known as biologically inspired, highly sophisticated analytical technique, capable of capturing highly complex non-linear functions. ANN is a kind of widely applied technique developed highly,and it has been applied sucessfully in the domains, such as artificial intelligence, autocontrol, pattern recognition and so on. In addition, ANN is a significant means of machine learning.In this paper,the author firstly show some basic biological neural networks, on which the introduction of artificial neural network is based. Then, the author dispicts simplily the history of ANN and the present condition of ANN, and concludes the characters of ANN. In the second part of the paper, the models and structures of ANNs which representive the ANN’s development are emphasized, such as perceptron,linear neural network,BP neural network,recurrent network and so on, and some examples based on those networks are illustrated. In addition, the author simulate the performance of the ANNs by a powerful software, MATLAB. At last, the author puts forward the conclutions of this paper and his thoughts.目录第一章神经网络 (1)1.1 生物学神经网络 (1)1.2 人工神经网络 (2)1.2.1 人工神经网络的产生 (2)1.2.2 人工神经网络的发展 (3)1.2.3 人工神经网络的现状 (5)1.3 人工神经网络的特点 (5)第二章人工神经网络模型及仿真 (6)2.1 人工神经元建模 (6)2.1.1 人工神经元的基本构成 (6)2.1.2 激活函数 (7)2.2 感知器 (8)2.2.1 感知器模型 (8)2.2.2 感知器网络设计实例 (9)2.3 线性神经网络 (10)2.3.1线性神经网络模型 (10)2.3.2线性神经网络设计实例 (10)2.4 BP网络 (11)2.4.1 BP网络模型 (11)2.4.2 BP网络设计实例 (12)2.5 径向基函数网络 (15)2.5.1径向基函数网络模型 (15)2.5.2径向基函数网络设计实例 (16)2.6 竞争型网络 (18)2.6.1竞争型网络模型 (18)2.6.2竞争型网络设计实例 (18)2.7 反馈型网络 (20)2.7.1 Elman网络 (20)2.7.2 Hopfield网络 (23)第三章本文总结 (26)参考文献 (28)第一章神经网络人工神经网络（artificial neural network，ANN）是通过对生物神经网络进行抽象，并综合运用信息处理技术、数学手段等建立简化模型而发展起来的一门交叉学科。