岩土力学参数大全精华
常用地岩土和岩石物理力学全参数

(E, ν) 与(K, G)的转换关系如下:)21(3ν-=EK)1(2ν+=EG (7.2)当ν值接近0.5的时候不能盲目的使用公式3.5,因为计算的K 值将会非常的高,偏离实际值很多。
最好是确定好K 值(利用压缩试验或者P 波速度试验估计),然后再用K 和ν来计算G 值。
表7.1和7.2分别给出了岩土体的一些典型弹性特性值。
岩石的弹性(实验室值)(Goodman,1980) 表7.1土的弹性特性值(实验室值)(Das,1980) 表7.2各向异性弹性特性——作为各向异性弹性体的特殊情况,横切各向同性弹性模型需要5中弹性常量:E 1, E 3, ν12,ν13和G 13;正交各向异性弹性模型有9个弹性模量E 1,E 2,E 3, ν12,ν13,ν23,G 12,G 13和G 23。
这些常量的定义见理论篇。
均质的节理或是层状的岩石一般表现出横切各向同性弹性特性。
一些学者已经给出了用各向同性弹性特性参数、节理刚度和空间参数来表示的弹性常数的公式。
表3.7给出了各向异性岩石的一些典型的特性值。
横切各向同性弹性岩石的弹性常数(实验室) 表7.3流体弹性特性——用于地下水分析的模型涉及到不可压缩的土粒时用到水的体积模量K f ,如果土粒是可压缩的,则要用到比奥模量M 。
纯净水在室温情况下的K f 值是2 Gpa 。
其取值依赖于分析的目的。
分析稳态流动或是求初始孔隙压力的分布状态(见理论篇第三章流体-固体相互作用分析),则尽量要用比较低的K f ,不用折减。
这是由于对于大的K f 流动时间步长很小,并且,力学收敛性也较差。
在FLAC 3D 中用到的流动时间步长,∆ tf 与孔隙度n ,渗透系数k 以及K f 有如下关系:'f f kK nt ∝∆ (7.3) 对于可变形流体(多数课本中都是将流体设定为不可压缩的)我们可以通过获得的固结系数νC 来决定改变K f 的结果。
f'K nm k C +=νν (7.4)其中3/4G K 1m +=νf 'k k γ=其中,'k ——FLAC 3D 使用的渗透系数k ——渗透系数,单位和速度单位一样(如米/秒) f γ——水的单位重量考虑到固结时间常量与νC 成比例,我么可以将K f 的值从其实际值(Pa 9102⨯)减少,利用上面得表达式看看其产生的误差。
常用岩石力学参数

常用岩石力学参数岩石力学是研究岩石在外力作用下变形和破裂行为的学科,它主要关注岩石的力学性质,包括强度、应力和应变等参数。
以下是一些常用的岩石力学参数。
1. 弹性模量(Young's modulus):弹性模量是衡量岩石对外力响应的能力的指标。
它表示单位应力下岩石的应变程度,通常以帕斯卡(Pa)为单位。
弹性模量越大,岩石的刚度越高,其抵抗变形的能力更强。
2. 柏杨比(Poisson's ratio):柏杨比用于描述岩石在受力作用下体积的变化情况。
它是岩石纵向应变和横向应变的比值,无单位。
柏杨比一般位于0.15到0.40之间,数值越大代表岩石越容易体积收缩。
4. 应力-应变曲线(Stress-strain curve):应力-应变曲线描述了岩石在受力过程中的应力和应变之间的关系。
根据曲线的形状,可以了解岩石的变形特性,如弹性变形阶段、塑性变形阶段和破裂阶段等。
应力-应变曲线是评估岩石稳定性和强度的重要工具。
5. 破裂韧度(Fracture toughness):破裂韧度是衡量岩石抵抗破坏的能力的参数,描述了岩石在外力作用下延伸至破断的能力。
破裂韧度越大,岩石的抗破坏能力越强。
6. 体积压缩模量(Bulk modulus):体积压缩模量是衡量岩石抵抗体积压缩的能力,代表岩石抵抗体积缩小的刚度。
体积压缩模量越大,岩石的抗压能力越强。
7. 粘聚力(Cohesion):粘聚力是指岩石内部颗粒间的粘结力,也被称为内聚力。
粘聚力越大,岩石的抗拉强度就越高。
8. 摩擦角(Friction angle):摩擦角用于描述岩石内颗粒间的摩擦性质。
摩擦角越大,岩石的抗剪强度越高。
9. 泊松比(Poisson ratio):泊松比是衡量岩石在拉伸或压缩过程中横向变形和纵向变形之间关系的参数。
泊松比越大,岩石的收缩性越高。
这些常用的岩石力学参数可以帮助工程师和地质学家了解岩石的力学性质,评估其稳定性和抗破坏能力,在工程设计和地质勘探中起到重要的作用。
(完整版)岩土力学参数大全
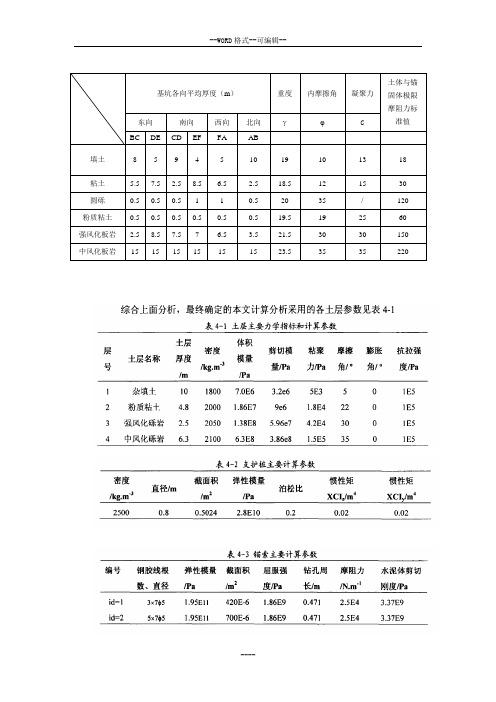
基坑各向平均厚度(m)重度内摩擦角凝聚力土体与锚固体极限摩阻力标准值东向南向西向北向γφ CBC DE CD EF FA AB填土8 5 9 4 5 10 19 10 13 18 粘土 5.5 7.5 2.5 8.5 6.5 2.5 18.5 12 15 30 圆砾0.5 0.5 0.5 1 1 0.5 20 35 / 120 粉质粘土0.5 0.5 0.5 0.5 0.5 0.5 19.5 19 25 60 强风化板岩 2.5 8.5 7.5 7 6.5 3.5 21.5 30 30 150 中风化板岩15 15 15 15 15 15 23.5 35 35 220常用岩土材料力学参数(E, ν) 与(K, G)的转换关系如下:)21(3ν-=EK)1(2ν+=EG (7.2)当ν值接近0.5的时候不能盲目的使用公式3.5,因为计算的K 值将会非常的高,偏离实际值很多。
最好是确定好K 值(利用压缩试验或者P 波速度试验估计),然后再用K 和ν来计算G 值。
表7.1和7.2分别给出了岩土体的一些典型弹性特性值。
岩石的弹性(实验室值)(Goodman,1980) 表7.1土的弹性特性值(实验室值)(Das,1980) 表7.2各向异性弹性特性——作为各向异性弹性体的特殊情况,横切各向同性弹性模型需要5中弹性常量:E 1, E 3, ν12,ν13和G 13;正交各向异性弹性模型有9个弹性模量E 1,E 2,E 3, ν12,ν13,ν23,G 12,G 13和G 23。
这些常量的定义见理论篇。
均质的节理或是层状的岩石一般表现出横切各向同性弹性特性。
一些学者已经给出了用各向同性弹性特性参数、节理刚度和空间参数来表示的弹性常数的公式。
表3.7给出了各向异性岩石的一些典型的特性值。
横切各向同性弹性岩石的弹性常数(实验室) 表7.37.3 固有的强度特性在FLAC 3D 中,描述材料破坏的基本准则是摩尔-库仑准则,这一准则把剪切破坏面看作直线破坏面:s 13N f φσσ=-+ (7.7)其中 )sin 1/()sin 1(N φφφ-+=1σ——最大主应力 (压缩应力为负); 3σ——最小主应力φ——摩擦角c ——粘聚力当0f s <时进入剪切屈服。
常用的岩土和岩石物理力学参数
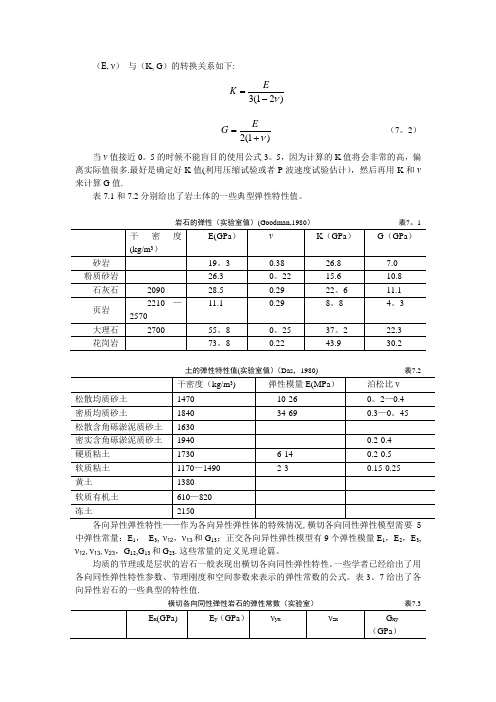
(E, ν) 与(K, G )的转换关系如下:)21(3ν-=EK)1(2ν+=EG (7。
2)当ν值接近0。
5的时候不能盲目的使用公式3。
5,因为计算的K 值将会非常的高,偏离实际值很多.最好是确定好K 值(利用压缩试验或者P 波速度试验估计),然后再用K 和ν来计算G 值.表7.1和7.2分别给出了岩土体的一些典型弹性特性值。
岩石的弹性(实验室值)(Goodman,1980) 表7。
1土的弹性特性值(实验室值)(Das ,1980) 表7.2各向异性弹性特性——作为各向异性弹性体的特殊情况,横切各向同性弹性模型需要5中弹性常量:E 1, E 3, ν12,ν13和G 13;正交各向异性弹性模型有9个弹性模量E 1,E 2,E 3, ν12,ν13,ν23,G 12,G 13和G 23.这些常量的定义见理论篇。
均质的节理或是层状的岩石一般表现出横切各向同性弹性特性。
一些学者已经给出了用各向同性弹性特性参数、节理刚度和空间参数来表示的弹性常数的公式。
表3。
7给出了各向异性岩石的一些典型的特性值.横切各向同性弹性岩石的弹性常数(实验室) 表7.3流体弹性特性—-用于地下水分析的模型涉及到不可压缩的土粒时用到水的体积模量K f ,如果土粒是可压缩的,则要用到比奥模量M 。
纯净水在室温情况下的K f 值是2 Gpa.其取值依赖于分析的目的。
分析稳态流动或是求初始孔隙压力的分布状态(见理论篇第三章流体-固体相互作用分析),则尽量要用比较低的K f ,不用折减.这是由于对于大的K f 流动时间步长很小,并且,力学收敛性也较差。
在FLAC 3D 中用到的流动时间步长,∆ tf 与孔隙度n,渗透系数k 以及K f 有如下关系:'f f kK nt ∝∆ (7。
3) 对于可变形流体(多数课本中都是将流体设定为不可压缩的)我们可以通过获得的固结系数νC 来决定改变K f 的结果。
f'K n m k C +=νν (7。
岩土力学参数大全
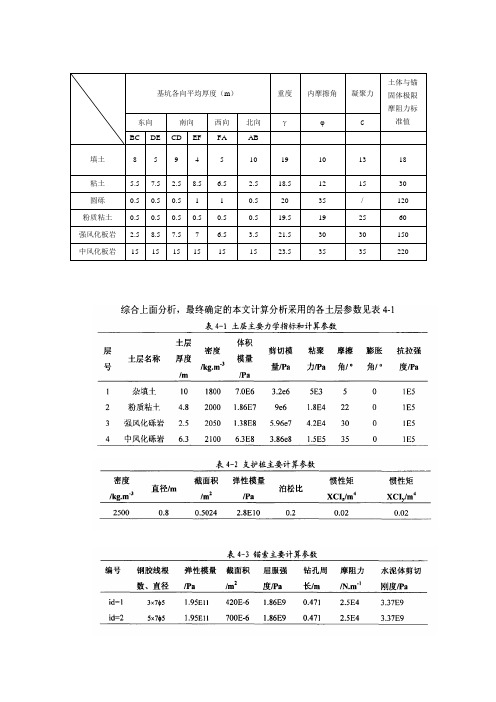
基坑各向平均厚度(m)重度内摩擦角凝聚力土体与锚固体极限摩阻力标准值东向南向西向北向γφ CBC DE CD EF FA AB填土8 5 9 4 5 10 19 10 13 18 粘土 5.5 7.5 2.5 8.5 6.5 2.5 18.5 12 15 30 圆砾0.5 0.5 0.5 1 1 0.5 20 35 / 120 粉质粘土0.5 0.5 0.5 0.5 0.5 0.5 19.5 19 25 60 强风化板岩 2.5 8.5 7.5 7 6.5 3.5 21.5 30 30 150 中风化板岩15 15 15 15 15 15 23.5 35 35 220常用岩土材料力学参数(E, ν) 与(K, G)的转换关系如下:)21(3ν-=EK)1(2ν+=EG (7.2)当ν值接近0.5的时候不能盲目的使用公式3.5,因为计算的K 值将会非常的高,偏离实际值很多。
最好是确定好K 值(利用压缩试验或者P 波速度试验估计),然后再用K 和ν来计算G 值。
表7.1和7.2分别给出了岩土体的一些典型弹性特性值。
岩石的弹性(实验室值)(Goodman,1980) 表7.1土的弹性特性值(实验室值)(Das,1980) 表7.2各向异性弹性特性——作为各向异性弹性体的特殊情况,横切各向同性弹性模型需要5中弹性常量:E 1, E 3, ν12,ν13和G 13;正交各向异性弹性模型有9个弹性模量E 1,E 2,E 3, ν12,ν13,ν23,G 12,G 13和G 23。
这些常量的定义见理论篇。
均质的节理或是层状的岩石一般表现出横切各向同性弹性特性。
一些学者已经给出了用各向同性弹性特性参数、节理刚度和空间参数来表示的弹性常数的公式。
表3.7给出了各向异性岩石的一些典型的特性值。
横切各向同性弹性岩石的弹性常数(实验室) 表7.37.3 固有的强度特性在FLAC 3D 中,描述材料破坏的基本准则是摩尔-库仑准则,这一准则把剪切破坏面看作直线破坏面:s 13N f φσσ=-+ (7.7)其中 )sin 1/()sin 1(N φφφ-+=1σ——最大主应力 (压缩应力为负); 3σ——最小主应力φ——摩擦角c ——粘聚力当0f s <时进入剪切屈服。
常用的岩土和岩石物理力学参数

(E, ν) 与(K, G )的转换关系如下:)21(3ν-=EK)1(2ν+=EG (7。
2)当ν值接近0。
5的时候不能盲目的使用公式3。
5,因为计算的K 值将会非常的高,偏离实际值很多.最好是确定好K 值(利用压缩试验或者P 波速度试验估计),然后再用K 和ν来计算G 值.表7.1和7.2分别给出了岩土体的一些典型弹性特性值。
岩石的弹性(实验室值)(Goodman,1980) 表7。
1土的弹性特性值(实验室值)(Das ,1980) 表7.2各向异性弹性特性——作为各向异性弹性体的特殊情况,横切各向同性弹性模型需要5中弹性常量:E 1, E 3, ν12,ν13和G 13;正交各向异性弹性模型有9个弹性模量E 1,E 2,E 3, ν12,ν13,ν23,G 12,G 13和G 23.这些常量的定义见理论篇。
均质的节理或是层状的岩石一般表现出横切各向同性弹性特性。
一些学者已经给出了用各向同性弹性特性参数、节理刚度和空间参数来表示的弹性常数的公式。
表3。
7给出了各向异性岩石的一些典型的特性值.横切各向同性弹性岩石的弹性常数(实验室) 表7.3流体弹性特性—-用于地下水分析的模型涉及到不可压缩的土粒时用到水的体积模量K f ,如果土粒是可压缩的,则要用到比奥模量M 。
纯净水在室温情况下的K f 值是2 Gpa.其取值依赖于分析的目的。
分析稳态流动或是求初始孔隙压力的分布状态(见理论篇第三章流体-固体相互作用分析),则尽量要用比较低的K f ,不用折减.这是由于对于大的K f 流动时间步长很小,并且,力学收敛性也较差。
在FLAC 3D 中用到的流动时间步长,∆ tf 与孔隙度n,渗透系数k 以及K f 有如下关系:'f f kK nt ∝∆ (7。
3) 对于可变形流体(多数课本中都是将流体设定为不可压缩的)我们可以通过获得的固结系数νC 来决定改变K f 的结果。
f'K n m k C +=νν (7。
岩土力学参数大全精华

常用岩土材料力学参数(E, ν) 与(K, G)的转换关系如下:)21(3ν-=E K )1(2ν+=E G (7.2) 当ν值接近0.5的时候不能盲目的使用公式3.5,因为计算的K 值将会非常的高,偏离实际值很多。
最好是确定好K 值(利用压缩试验或者P 波速度试验估计),然后再用K 和ν来计算G 值。
表7.1和7.2分别给出了岩土体的一些典型弹性特性值。
岩石的弹性(实验室值)(Goodman,1980) 表7.1土的弹性特性值(实验室值)(Das,1980) 表7.2中弹性常量:E 1, E 3, ν12,ν13和G 13;正交各向异性弹性模型有9个弹性模量E 1,E 2,E 3, ν12,ν13,ν23,G 12,G 13和G 23。
这些常量的定义见理论篇。
均质的节理或是层状的岩石一般表现出横切各向同性弹性特性。
一些学者已经给出了用各向同性弹性特性参数、节理刚度和空间参数来表示的弹性常数的公式。
表3.7给出了各向异性岩石的一些典型的特性值。
横切各向同性弹性岩石的弹性常数(实验室) 表7.3流体弹性特性——用于地下水分析的模型涉及到不可压缩的土粒时用到水的体积模量K f ,如果土粒是可压缩的,则要用到比奥模量M 。
纯净水在室温情况下的K f 值是2 Gpa 。
其取值依赖于分析的目的。
分析稳态流动或是求初始孔隙压力的分布状态(见理论篇第三章流体-固体相互作用分析),则尽量要用比较低的K f ,不用折减。
这是由于对于大的K f 流动时间步长很小,并且,力学收敛性也较差。
在FLAC 3D 中用到的流动时间步长,∆ tf 与孔隙度n ,渗透系数k 以及K f 有如下关系:'f f kK n t ∝∆ (7.3) 对于可变形流体(多数课本中都是将流体设定为不可压缩的)我们可以通过获得的固结系数νC 来决定改变K f 的结果。
f 'K n m k C +=νν (7.4)其中3/4G K 1m +=ν f 'k k γ=其中,'k ——FLAC 3D 使用的渗透系数k ——渗透系数,单位和速度单位一样(如米/秒)f γ——水的单位重量考虑到固结时间常量与νC 成比例,我么可以将K f 的值从其实际值(Pa 9102⨯)减少,利用上面得表达式看看其产生的误差。
岩土主要物理力学指标参考值

岩土主要物理力学指标参考值
1、稳定性指标参考值:
1.1压缩模量:水泥改良的砂、砾状粘结土的压缩模量一般在100-
500kPa,粉状粘结土的压缩模量在200-1000kPa,蠕变模量在101-500kPa。
1.2抗拉强度:水泥改良的砂、砾状粘结土的抗拉强度一般在0.1-
2.0kPa,粉状粘结土的抗拉强度在0.2-4.0kPa,蠕变强度在0.3-5.0kPa。
1.3抗剪强度:水泥改良的砂、砾状粘结土的抗剪强度一般在0.1-
2.5kPa,粉状粘结土的抗剪强度一般在0.2-7.0kPa,蠕变强度一般在
0.4-7.5kPa。
1.4抗冲击强度:水泥改良的砂、砾状粘结土的抗冲击强度一般在
0.1-2.5kPa,粉状粘结土的抗冲击强度一般在0.2-7.0kPa,蠕变强度一
般在0.3-8.0kPa。
2、抗损伤指标参考值:
2.1抗湿胀系数:水泥改良的砂、砾状粘结土的抗湿胀系数一般在
0.1-2.5,粉状粘结土的抗湿胀系数一般在0.2-5.0,蠕变系数一般在
0.3-6.0。
2.2抗冻结强度:水泥改良的砂、砾状粘结土的抗冻结强度一般在
0.1-2.5MPa,粉状粘结土的抗冻结强度一般在0.2-7.0MPa,蠕变强度一
般在0.4-7.5MPa。
2.3抗集水能力:水泥改良的砂、砾状粘结土的抗集水能力一般在
0.2-1.5kPa,粉状粘结土的抗集水能力一般在0.4-3.0kPa。
常用的岩土和岩石物理力学参数

常用的岩土和岩石物理力学参数岩土和岩石物理力学参数是指描述岩土和岩石力学性质的一些重要参数,对于工程和地质领域的研究和实践具有重要意义。
以下是一些常用的岩土和岩石物理力学参数。
1.密度:岩土和岩石的密度是指单位体积的质量。
岩土和岩石的密度是其成分和结构的重要表征,常用单位是千克/立方米。
2.孔隙度:岩土和岩石内部的空隙或孔隙的体积与总体积的比值。
孔隙度是描述岩土和岩石中孔隙性质的重要参数,通常用百分比表示。
3.孔隙水压力:岩土和岩石中存在的地下水与孔隙水压力是一种重要的物理力学参数。
孔隙水压力对岩土和岩石的稳定性、渗透性和强度等产生重要影响。
4.饱和度:饱和度是指岩土和岩石中孔隙所含的水的含量与孔隙容量的比值。
饱和度是衡量岩土和岩石中含水情况的一项指标。
5.孔隙比:孔隙比是指岩土和岩石中孔隙体积与固体体积的比值。
孔隙比是岩土和岩石的一个重要参数,它关系到其渗透性、存储性以及力学性质等。
6.孔隙率:岩土和岩石中孔隙的比例,描述含孔岩体的空间特征的参数。
7.饱和度指数:饱和度指数是指岩土和岩石中各向同性材料,当孔隙度小于50%时,饱和度指数与孔隙度有关,其表征了岩土和岩石中孔隙数量和大小对其力学性质的影响。
8.波速:岩土和岩石中机械波传播的速度是一项重要的物理力学参数。
根据波速可以推算岩土和岩石的弹性模量和泊松比等力学参数。
9.阻尼比:用来描述岩土和岩石中振动能量的衰减情况,是衡量动力响应特性的一个重要参数。
10.岩石强度参数:包括抗拉强度、抗压强度、抗剪强度等,是衡量岩石材料抵抗各种力学载荷的重要参数。
11.几何参数:岩土和岩石中的几何参数包括颗粒形状、颗粒大小分布、颗粒间隙度等,对岩土和岩石的物理力学性质具有重要影响。
总之,岩土和岩石的物理力学参数是描述其物理性质和力学性质的重要参数,对于工程和地质领域的研究和实践具有重要意义。
不同的参数描述了岩土和岩石在不同方面的力学性质,研究者和工程师需要根据具体情况选择合适的参数进行分析和计算。
岩土的物理力学性质参数
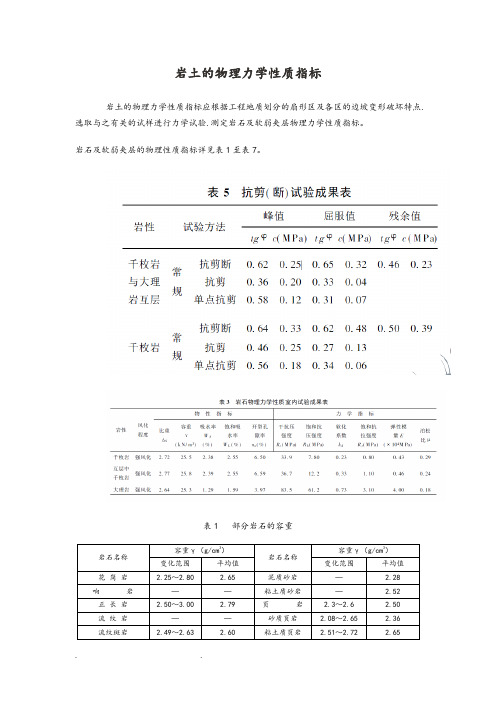
岩土的物理力学性质指标
岩土的物理力学性质指标应根据工程地质划分的扇形区及各区的边坡变形破坏特点.选取与之有关的试样进行力学试验.测定岩石及软弱夹层物理力学性质指标。
岩石及软弱夹层的物理性质指标详见表1至表7。
表1 部分岩石的容重
表2 部分岩石的孔隙率与吸水率
表3 不同成因粘土的有关物理力学性质指标(一)
表4 不同成因粘土的有关物理力学性质指标(二)
表5 几种土的渗透系数表
表6 土的平均物理、力学性质指标(一)
表7 土的平均物理、力学性质指标(二)
注:1.平均比重取:砂为2.65;轻亚粘土为2.70;亚粘土为2.71;粘土2.74。
2.粗砂与中砂的Eo值适用于不均系数Cu=3时.当Cu>5时应按表中所列值减少2/3。
Cu为中间值时. Eo 值按内插法确定。
3.对于地基稳定计算.采用内摩擦角φ的计算值低于标准值2°。
岩石及软弱夹层的力学性质指标见表8至表25。
表8 岩石力学性质指标的经验数据(一)。
岩土力学重要参数取值大全
常用岩土材料力学重要参数(E, ν) 与(K, G)的转换关系如下:)21(3ν-=E K )1(2ν+=E G (7.2) 当ν值接近0.5的时候不能盲目的使用公式3.5,因为计算的K 值将会非常的高,偏离实际值很多。
最好是确定好K 值(利用压缩试验或者P 波速度试验估计),然后再用K 和ν来计算G 值。
表7.1和7.2分别给出了岩土体的一些典型弹性特性值。
岩石的弹性(实验室值)(Goodman,1980)表7.1土的弹性特性值(实验室值)(Das,1980)表7.2各向异性弹性特性——作为各向异性弹性体的特殊情况,横切各向同性弹性模型需要5中弹性常量:E 1, E 3,ν12,ν13和G 13;正交各向异性弹性模型有9个弹性模量E 1,E 2,E 3,ν12,ν13,ν23,G 12,G 13和G 23。
这些常量的定义见理论篇。
均质的节理或是层状的岩石一般表现出横切各向同性弹性特性。
一些学者已经给出了用各向同性弹性特性参数、节理刚度和空间参数来表示的弹性常数的公式。
表3.7给出了各向异性岩石的一些典型的特性值。
横切各向同性弹性岩石的弹性常数(实验室)表7.3流体弹性特性——用于地下水分析的模型涉及到不可压缩的土粒时用到水的体积模量K f ,如果土粒是可压缩的,则要用到比奥模量M 。
纯净水在室温情况下的K f 值是2 Gpa 。
其取值依赖于分析的目的。
分析稳态流动或是求初始孔隙压力的分布状态(见理论篇第三章流体-固体相互作用分析),则尽量要用比较低的K f ,不用折减。
这是由于对于大的K f 流动时间步长很小,并且,力学收敛性也较差。
在FLAC 3D 中用到的流动时间步长,∆ tf 与孔隙度n ,渗透系数k 以及K f 有如下关系:'f f kK n t ∝∆ (7.3) 对于可变形流体(多数课本中都是将流体设定为不可压缩的)我们可以通过获得的固结系数νC 来决定改变K f 的结果。
f 'K n m k C +=νν(7.4)其中3/4G K 1m +=ν f 'k k γ=其中,'k ——FLAC 3D 使用的渗透系数 k ——渗透系数,单位和速度单位一样(如米/秒)f γ——水的单位重量考虑到固结时间常量与νC 成比例,我么可以将K f 的值从其实际值(Pa 9102⨯)减少,利用上面得表达式看看其产生的误差。
常见岩石力学参数

常见岩石力学参数岩石力学参数是指描述岩石在外力作用下的力学行为的物理性质,包括弹性模量、剪切模量、泊松比、抗压强度、抗拉强度、抗剪强度等。
这些参数对于岩石的力学性质和工程应用具有重要意义。
本文将详细介绍这些常见的岩石力学参数。
1. 弹性模量(Young's modulus):弹性模量是衡量岩石弹性性质的一个重要参数,表示岩石在外力作用下产生弹性变形的能力。
弹性模量越大,岩石的刚度越大,抗弯和抗变形能力越强。
2. 剪切模量(Shear modulus):剪切模量是衡量岩石抗剪切性质的参数,表示岩石在剪切应力作用下产生剪切变形的能力。
剪切模量越大,岩石的抗剪强度越高,稳定性越好。
3. 泊松比(Poisson's ratio):泊松比是衡量岩石体积变形性质的参数,表示岩石在受到压缩应力时,横向收缩的程度。
泊松比一般介于0.1到0.4之间,数值越大,岩石的蠕变性越强。
5. 抗拉强度(Tensile strength):抗拉强度是衡量岩石抗拉性质的参数,表示岩石在受到拉伸应力时的最大承载能力。
抗拉强度一般比抗压强度要小,岩石在受到拉伸时易发生断裂。
6. 抗剪强度(Shear strength):抗剪强度是衡量岩石抗剪切性质的参数,表示岩石在受到剪切应力时的最大承载能力。
抗剪强度主要与岩石内部的粘聚力和内摩擦角有关。
除了上述常见的岩石力学参数外,还有一些与岩石稳定性有关的参数:7. 断裂韧性(Fracture toughness):断裂韧性是衡量岩石抗断裂性质的参数,表示岩石在受到裂纹扩展时的抵抗能力,能够反映岩石的破坏扩展能力。
8. 孔隙度(Porosity):孔隙度是衡量岩石孔隙结构的参数,表示岩石内部的孔隙空间占总体积的比例。
孔隙度能够影响岩石的密实程度和渗透性,对工程建筑的渗流和稳定性有重要影响。
9. 饱和度(Saturation):饱和度是衡量岩石孔隙中被水、气体或其他流体填充的程度。
岩土地物理力学性质全参数
岩土的物理力学性质指标
岩土的物理力学性质指标应根据工程地质划分的扇形区及各区的边坡变形破坏特点,选取与之有关的试样进行力学试验,测定岩石及软弱夹层物理力学性质指标。
岩石及软弱夹层的物理性质指标详见表1至表7。
表1部分岩石的容重
岩石名称
容重γ(g/cm3)
岩石名称
容重γ(g/cm3)
变化范围平均值变化范围平均值
花岗岩 2.25~2.80 2.65 泥质砂岩— 2.28 响岩——粘土质砂岩— 2.52 正长岩 2.50~3.00 2.79 页岩 2.3~2.6 2.50 流纹岩——砂质页岩 2.08~2.65 2.36 流纹斑岩 2.49~2.63 2.60 粘土质页岩 2.51~2.72 2.65
表2部分岩石的孔隙率与吸水率
表3不同成因粘土的有关物理力学性质指标(一)
表4不同成因粘土的有关物理力学性质指标(二)
表5几种土的渗透系数表
表6土的平均物理、力学性质指标(一)
表7土的平均物理、力学性质指标(二)
注:1.平均比重取:砂为2.65;轻亚粘土为2.70;亚粘土为2.71;粘土2.74。
2.粗砂与中砂的Eo值适用于不均系数Cu=3时,当Cu>5时应按表中所列值减少2/3。
Cu为中间值时, Eo 值按内插法确定。
3.对于地基稳定计算,采用内摩擦角φ的计算值低于标准值2°。
岩石及软弱夹层的力学性质指标见表8至表25。
表8岩石力学性质指标的经验数据(一)。
岩土物理力学参数表

岩土物理力学参数表
岩土物理力学参数表是用于描述岩石和土壤等地质材料力学性质的一份表格。
这些参数可以用于建立地质力学模型或进行地震学研究等领域。
以下是一些常见的岩土物理力学参数及其解释:
1. 压缩模量(压缩弹性模量):是描述岩土材料在压缩载荷下的弹性变形特性的一种参数。
它的单位是帕斯卡(Pa)或兆帕(MPa)。
压缩模量越大,表示岩土材料的刚度越大。
2. 剪切模量(剪切弹性模量):是描述岩土材料在剪切载荷下的弹性变形特性的一种参数。
它的单位也是帕斯卡(Pa)或兆帕(MPa)。
剪切模量越大,表示岩土材料的抗剪强度越大。
3. 泊松比:是描述岩土材料在受力后沿垂直于力方向的横向收缩程度的参数。
它没有单位,通常用一个小数来表示。
泊松比越小,表示岩土材料的横向收缩程度越小,即更加刚性。
4. 内摩擦角:是描述岩土材料在受到剪切力时,自身内部出现抗阻力的一种参数。
它的单位是度数。
内摩擦角越大,表示岩土材料的抗剪能力越强。
5. 屈服强度:是描述岩土材料在受到载荷作用下出现塑性变形或破坏的一种参数。
它的单位是帕斯卡(Pa)或兆帕(MPa)。
屈服强度越大,表示岩土材料的抗压强度越大。
6. 杨氏模量:是描述岩土材料在受到拉伸载荷下的弹性变形特性的一种参数。
它的单位也是帕斯卡(Pa)或兆帕(MPa)。
杨氏模量越大,表示岩土材料的拉伸刚度越大。
以上是一些常见的岩土物理力学参数及其解释。
需要注意的是,不同的地质材料具有不同的力学性质,因此在实际应用中需要根据具体情况选择合适的参数。
常用的岩土和岩石物理力学参数

常用的岩土和岩石物理力学参数(E, ν) 与(K, G)的转换关系如下:)21(3ν-=E K)1(2ν+=E G (7.2)当ν值接近0.5的时候不能盲目的使用公式3.5,因为计算的K 值将会非常的高,偏离实际值很多。
最好是确定好K 值(利用压缩试验或者P 波速度试验估计),然后再用K 和ν来计算G 值。
表7.1和7.2分别给出了岩土体的一些典型弹性特性值。
岩石的弹性(实验室值)(Goodman,1980)表7.1土的弹性特性值(实验室值)(Das,1980)表7.2各向异性弹性特性——作为各向异性弹性体的特殊情况,横切各向同性弹性模型需要5中弹性常量:E1, E3,ν12,ν13和G13;正交各向异性弹性模型有9个弹性模量E1,E2,E3,ν12,ν13,ν23,G12,G13和G23。
这些常量的定义见理论篇。
均质的节理或是层状的岩石一般表现出横切各向同性弹性特性。
一些学者已经给出了用各向同性弹性特性参数、节理刚度和空间参数来表示的弹性常数的公式。
表3.7给出了各向异性岩石的一些典型的特性值。
横切各向同性弹性岩石的弹性常数(实验室)表7.3流体弹性特性——用于地下水分析的模型涉及到不可压缩的土粒时用到水的体积模量K f,如果土粒是可压缩的,则要用到比奥模量M。
纯净水在室温情况下的K f值是2 Gpa。
其取值依赖于分析的目的。
分析稳态流动或是求初始孔隙压力的分布状态(见理论篇第三章流体-固体相互作用分析),则尽量要用比较低的K f,不用折减。
这是由于对于大的K f流动时间步长很小,并且,力学收敛性也较差。
在FLAC3D中用到的流动时间步长, tf与孔隙度n,渗透系数k以及K f有如下关系:'f f k K n t ∝∆ (7.3)对于可变形流体(多数课本中都是将流体设定为不可压缩的)我们可以通过获得的固结系数νC 来决定改变K f 的结果。
f'K nm k C +=νν (7.4)其中3/4G K 1m +=νf'k k γ=其中,'k ——FLAC 3D 使用的渗透系数 k ——渗透系数,单位和速度单位一样(如米/秒)fγ——水的单位重量考虑到固结时间常量与νC 成比例,我么可以将K f 的值从其实际值(Pa9102⨯)减少,利用上面得表达式看看其产生的误差。
一般岩土参数汇总

一般岩土参数汇总岩土工程是土力学和岩石力学的综合应用,用于土壤和岩石的工程性质和行为的研究,以及基于这些特性的地下结构的设计和施工。
岩土参数是指描述土壤和岩石工程性质的一系列参数,包括物理性质、力学性质和水文性质等。
以下是一些常见的岩土参数的汇总:1.土壤物理性质-饱和度:表示土壤中孔隙空间被水饱和的程度。
-干度:表示土壤中的固体颗粒与孔隙的比例。
-孔隙度:表示土壤中空隙的体积比例,可以反映土壤的压缩性和渗流性能。
-孔隙比:孔隙总体积与固体总体积之比,反映土壤贮水能力。
-饱和导水率:表示水在饱和状态下通过土壤的能力。
2.土壤力学性质-压缩性指数:描述土壤的压缩性,反映了土壤孔隙结构变化的能力。
-剪切强度:表示土壤的抗剪切性能,通常包括剪切强度角、黏聚力和内摩擦角。
-体积重:土壤单位体积的重量。
-压缩模量:表示土壤的抗压缩性能。
-密度:土壤单位体积的质量。
-稠度:土壤颗粒排列的紧密程度。
3.土壤水文性质-渗透系数:描述土壤中水流通过的能力。
-吸力:表示土壤中的水分对负压的能力,反映土壤持水性能。
-比渗透率:表示单位负压条件下单位时间内通过单位面积的水分流量。
-饱和导水率:表示饱和状态下土壤中的水流速度。
4.岩石力学性质-抗压强度:岩石承受压力的抵抗能力。
-弹性模量:岩石在受力后恢复原状的能力。
-破坏韧度:岩石的破坏性能和抵抗破坏的能力。
-岩石饱和度:岩石孔隙中被水饱和的程度。
-岩石渗透系数:描述岩石中液体流动的能力。
除了上述的岩土参数,还有一些特殊的参数用于描述特定地质情况下的岩土性质:-风化程度:岩石的风化程度是指岩石中颗粒的破碎程度和颗粒之间的结合强度。
-腐殖质含量:描述土壤或岩石中有机物质的含量。
-土壤粒径分布:表示土壤颗粒的大小范围和分布情况。
这些岩土参数在工程设计、施工和监测中起到重要的作用,用于评估土壤和岩石的工程性质,指导地下结构的设计和施工,并评估地质灾害的潜在风险。
不同地区、不同类型的土壤和岩石具有不同的物理性质、力学性质和水文性质,因此在进行岩土参数的测定和分析时,需要充分考虑地质和地形条件的差异。
土及部分岩石力学参数经验值

土及部分岩石力学参数经验值土及岩石的力学参数是指描述土体和岩石在受力作用下的力学性质的参数。
这些参数对于土木工程、地质工程和岩土工程的设计与分析具有重要意义。
下面将介绍一些常见的土及部分岩石的力学参数经验值。
1. 孔隙比(Porosity):孔隙比是指土体或岩石中孔隙体积与总体积之比。
通常用百分比表示。
不同类型的土体和岩石具有不同的孔隙比,如砂土的孔隙比一般在30%~50%,黏土的孔隙比一般在40%~60%。
2. 孔隙水压(Pore Water Pressure):孔隙水压是指土体或岩石中孔隙水的压力。
孔隙水压对土体和岩石的力学性质有重要影响。
例如,在地下水位上方的土体或岩石中,孔隙水压较小,土体或岩石处于排水状态;而在地下水位以下的土体或岩石中,孔隙水压较大,土体或岩石处于饱和状态。
3. 孔隙比压缩指数(Void Ratio Compression Index):孔隙比压缩指数是指土体或岩石中孔隙比随有效应力增加而减小的趋势。
孔隙比压缩指数可以反映土体或岩石的压缩性。
例如,黏土的孔隙比压缩指数一般在0.1~0.3之间。
4. 剪切强度(Shear Strength):剪切强度是指土体或岩石在受到剪切力作用下抵抗破坏的能力。
剪切强度是土体和岩石力学性质的重要参数之一。
不同类型的土体和岩石具有不同的剪切强度,如黏土的剪切强度一般较低,砂土的剪切强度较高。
5. 孔隙比剪切强度指数(Void Ratio Shear Strength Index):孔隙比剪切强度指数是指土体或岩石的剪切强度随孔隙比的变化趋势。
孔隙比剪切强度指数可以反映土体或岩石的剪切强度与孔隙比之间的关系。
例如,砂土的孔隙比剪切强度指数一般在0.5~1之间。
6. 泊松比(Poisson's Ratio):泊松比是指材料在受到外力作用下,在垂直于外力方向上的横向应变与沿外力方向上的纵向应变之比。
泊松比是描述土体或岩石变形特性的重要参数。
岩土力学参数大全
常用岩土材料力学参数(E, ν) 与(K, G)的转换关系如下:)21(3ν-=EK)1(2ν+=EG (7.2)当ν值接近0.5的时候不能盲目的使用公式3.5,因为计算的K 值将会非常的高,偏离实际值很多。
最好是确定好K 值(利用压缩试验或者P 波速度试验估计),然后再用K 和ν来计算G 值。
表7.1和7.2分别给出了岩土体的一些典型弹性特性值。
岩石的弹性(实验室值)(Goodman,1980) 表7.1土的弹性特性值(实验室值)(Das,1980) 表7.2各向异性弹性特性——作为各向异性弹性体的特殊情况,横切各向同性弹性模型需要5中弹性常量:E 1, E 3, ν12,ν13和G 13;正交各向异性弹性模型有9个弹性模量E 1,E 2,E 3, ν12,ν13,ν23,G 12,G 13和G 23。
这些常量的定义见理论篇。
均质的节理或是层状的岩石一般表现出横切各向同性弹性特性。
一些学者已经给出了用各向同性弹性特性参数、节理刚度和空间参数来表示的弹性常数的公式。
表3.7给出了各向异性岩石的一些典型的特性值。
横切各向同性弹性岩石的弹性常数(实验室) 表7.37.3 固有的强度特性在FLAC 3D 中,描述材料破坏的基本准则是摩尔-库仑准则,这一准则把剪切破坏面看作直线破坏面:s 13N f φσσ=-+ (7.7)其中 )sin 1/()sin 1(N φφφ-+=1σ——最大主应力 (压缩应力为负);3σ——最小主应力φ——摩擦角c ——粘聚力当0f s <时进入剪切屈服。
这里的两个强度常数φ和c 是由实验室的三轴实验获得的。
当主应力变为拉力时,摩尔-库仑准则就将失去其物理意义。
简单情况下,当表面的在拉应力区域发展到3σ等于单轴抗拉强度的点时,tσ ,这个次主应力不会达到拉伸强度—例如;t 3t f σσ-= (7.8)当0f t >时进入拉伸屈服。
岩石和混凝土的抗拉强度通常有由西实验获得。
岩土的物理力学性质参数-精选.pdf
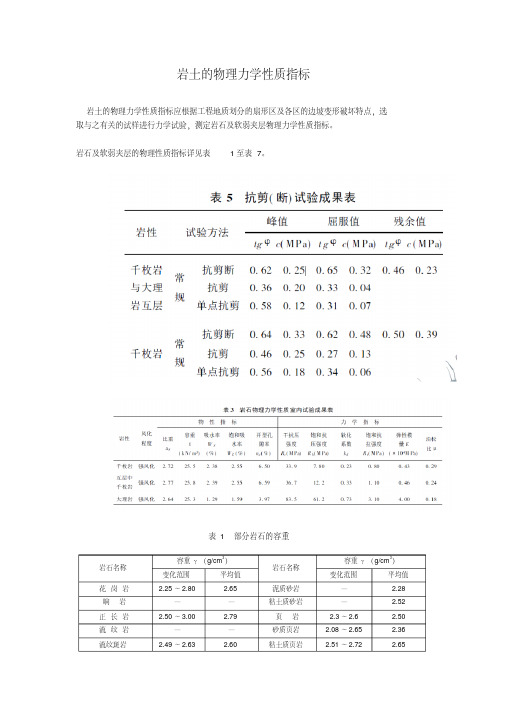
2.60
辉绿岩
2.53 ~ 3.12
2.94
白垩
1.20 ~ 2.20
1.70
硅长斑岩
2.20 ~ 2.74
—
石膏
—
—
安山凝灰集块岩
—
2.62
花岗片麻岩
2.30 ~ 3.20
2.8
凝灰角砾岩
2.20 ~ 2.90
—
片麻岩
2.59 ~ 3.00
2.78
火山凝灰岩
1.60 ~ 1.95
1.80
白云岩
2.10 ~ 2.90
— — — — 0.70 ~ 7.00 0.80 ~ 4.15 — — 1.00 ~52.00 0.53 ~27.00 —
1.70 2.20 1.80 3.20 2.10 3.20 5.04 13.00 15.30 17.10 13.20 19.30 21.11 2.26 1.71 4.91 — — 1.35 1.03 18.00 12.00 20.00
2.00
0.08
0.05
24
160
1.95
0.06
0.03
23
130
2.10
0.42
0.25
24
450
12.5 ~ 15.4
2.00
0.21
0.15
23
210
1.95
0.14
0.10
22
150
1.90
0.07
0.05
21
120
2.00
0.50
0.35
22
390
1.95
0.25
0.15
21
180
15.5 ~ 18.4
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
常用岩土材料力学参数
(E, ν) 与(K, G)的转换关系如下:
)
21(3ν-=E K )1(2ν+=
E G (7.2) 当ν值接近0.5的时候不能盲目的使用公式3.5,因为计算的K 值将会非常的高,偏离实际值很多。
最好是确定好K 值(利用压缩试验或者P 波速度试验估计),然后再用K 和ν来计算G 值。
表7.1和7.2分别给出了岩土体的一些典型弹性特性值。
岩石的弹性(实验室值)(Goodman,1980) 表7.1
土的弹性特性值(实验室值)(Das,1980) 表7.2
中弹性常量:E 1, E 3, ν12,ν13和G 13;正交各向异性弹性模型有9个弹性模量E 1,E 2,E 3, ν12,ν13,ν23,G 12,G 13和G 23。
这些常量的定义见理论篇。
均质的节理或是层状的岩石一般表现出横切各向同性弹性特性。
一些学者已经给出了用各向同性弹性特性参数、节理刚度和空间参数来表示的弹性常数的公式。
表3.7给出了各向异性岩石的一些典型的特性值。
横切各向同性弹性岩石的弹性常数(实验室) 表7.3
流体弹性特性——用于地下水分析的模型涉及到不可压缩的土粒时用到水的体积模量K f ,如果土粒是可压缩的,则要用到比奥模量M 。
纯净水在室温情况下的K f 值是2 Gpa 。
其取值依赖于分析的目的。
分析稳态流动或是求初始孔隙压力的分布状态(见理论篇第三章流体-固体相互作用分析),则尽量要用比较低的K f ,不用折减。
这是由于对于大的K f 流动时间步长很小,并且,力学收敛性也较差。
在FLAC 3D 中用到的流动时间步长,∆ tf 与孔隙度n ,渗透系数k 以及K f 有如下关系:
'f f k
K n t ∝∆ (7.3) 对于可变形流体(多数课本中都是将流体设定为不可压缩的)我们可以通过获得的固结系数νC 来决定改变K f 的结果。
f '
K n m k C +=νν (7.4)
其中
3
/4G K 1m +=ν f 'k k γ=
其中,'
k ——FLAC 3D 使用的渗透系数
k ——渗透系数,单位和速度单位一样(如米/秒)
f γ——水的单位重量
考虑到固结时间常量与νC 成比例,我么可以将K f 的值从其实际值(Pa 9102⨯)减少,利用上面得表达式看看其产生的误差。
流动体积模量还会影响无流动但是有空隙压力产生的模型的收敛速率(见1.7节流动与力学的相互作用)。
如果K f 是一个通过比较机械模型得到的值,则由于机械变形将会产生孔隙压力。
如果K f 远比k 大,则压缩过程就慢,但是一般有可能K f 对其影响很小。
例如在土体中,孔隙水中还会包含一些尚未溶解的空气,从而明显的使体积模量减小。
在无流动情况下,饱和体积模量为: n
K K K f u += (7.5)
不排水的泊松比为:
)
G 3K (22G 3K u u u +-=ν (7.6) 这些值应该和排水常量k 和ν作比较,来估计压缩的效果。
重要的是,在FLAC 3D 中,排水特性是用在机械连接的流变计算中的。
对于可压缩颗粒,比奥模量对压缩模型的影响比例与流动。
7.3 固有的强度特性
在FLAC 3D 中,描述材料破坏的基本准则是摩尔-库仑准则,这一准则把剪切破坏面看作直线破坏面:
s 13N f φσσ=-+ (7.7)
其中 )sin 1/()sin 1(N φφφ-+=
1σ——最大主应力 (压缩应力为负);
3σ——最小主应力
φ——摩擦角
c ——粘聚力
当0f s <时进入剪切屈服。
这里的两个强度常数φ和c 是由实验室的三轴实验获得的。
当主应力变为拉力时,摩尔-库仑准则就将失去其物理意义。
简单情况下,当表面的在拉应力区域发展到3σ等于单轴抗拉强度的点时,t
σ ,这个次主应力不会达到拉伸强度—例如; t 3t f σσ-= (7.8)
当0f t >时进入拉伸屈服。
岩石和混凝土的抗拉强度通常有由西实验获得。
注意,抗拉强度不能超过σ3, 这是和摩尔-库仑关系的顶点的限制是一致的。
最大的值由下式给出
φ
σtan c t max = (7.9) 表7.4列出了一系列具有代表性的典型的岩石标本的粘聚力、摩擦角和抗拉强度值。
土体的具有代表性的典型粘聚力和摩擦角的具有代表性的典型值见表7.5。
土体强度用无侧限抗压强度u q 表示,u q 与粘聚力C 和摩擦角φ的关系由下式确定
/2)2ctan(45q u φ+= (7.10)
岩石的强度特性值(实验室测定) 表7.4
土体的强度特性值(排水实验测定)表7.5
岩土力学参数大全(精华)贴
我想搞一个这样的贴子
将数值计算中一些较难取值的岩土力学参数汇编一下
因为简单的那些比如粘聚力C,内摩擦角FRI,容重等r比较简单的一般手册上都有
所以主要编一些较难查找的(如弹性模量,波松比,剪胀角等)
大家可以根据自己的使用经验或在某些资料上的查找资料写出来
格式不要求,表格最好,大家只需注明出处就行(是某本书,或着自己的使用经验)
参数:甘肃古城地区黄土非线性参数(也可以给某一个参数,如剪胀角等)
取值:参数见附图
来源:“黄土地区工程地质-----乔平定等北京:中国水利出版社”
剪胀角的定义来源于平面应变
其定义为sin(psi) = - d(Epsilon_v)/d(Gama_max)
这里psi为剪胀角,d代表增量,Epsilon_v是体积应变,Gama_max是最大工程剪切应变
这一定义也可同样用于三轴应力情况
对于小应变,其可定义为sin(psi) = - [d(Epsilon_1) + k d(Epsilon_3)]/[d(Epsilon_1) - k d(Epsilon_3)]
对于平面应变,k=1;而对于三轴应力情况,k=2
对于这两种情况,也可用下式来表达
sin(psi) = - [d(Epsilon_v)/d(Epsilon_1)]/[2 - d(Epsilon_v)/d(Epsilon_1)]
一般而言
剪胀角并非常数,而是一个变量
与围压及孔隙比(或密实度)有关,是会随应力应变曲线而变化
一般土体、岩石、混凝土的剪胀角都要比摩擦角小的多
Vemmer和de Borst (1984)报道过以下典型剪胀角的值
密砂15 松砂<10 正常固结粘土0 石灰石12~20 混凝土12
一般土体、岩石、混凝土的剪胀角近似在0 到20 度范围里变化
只有在平面应变情况下,此剪胀角有物理意义
而在三轴应力情况,剪胀角并无物理意义
在数值计算中多用剪胀率(dilatancy rate d_g)来表示体积变化情况
d_g = d(Epsilon_vp)/d(Epsilon_sp)
这里d(Epsilon_vp)是塑性体积应变增量,d(Epsilon_sp)是塑性剪应变增量
剪胀角和剪胀率只与塑性变形有关
但一般对于大应变问题,常用总变形来替代塑性变形
若对小应变来说,这么做会引起较大误差
黄土淤积层的参数
其实参数的选择大家可以查
但我想跟大家说明的是
试验工况不一样
参数不一样
所以选择时一定要注意试验工况常用的大概有6种
如图所示
岩土工程勘察规范
Oh岩土工程勘察规范上对土的一些性质取值各类土的压缩模量
OH
附表一:土工参数表。
