高考数学集合知识点第一轮复习

合集下载

高考数学知识点总结(全而精-一轮复习必备)

高中数学第一章-集合考试内容：集合、子集、补集、交集、并集．逻辑联结词．四种命题．充分条件和必要条件．考试要求：（1）理解集合、子集、补集、交集、并集的概念；了解空集和全集的意义；了解属于、包含、相等关系的意义；掌握有关的术语和符号，并会用它们正确表示一些简单的集合．（2）理解逻辑联结词“或”、“且”、“非”的含义理解四种命题及其相互关系；掌握充分条件、必要条件及充要条件的意义．§01. 集合与简易逻辑知识要点一、知识结构:本章知识主要分为集合、简单不等式的解法（集合化简）、简易逻辑三部分：二、知识回顾：（一）集合1.基本概念：集合、元素；有限集、无限集；空集、全集；符号的使用.2.集合的表示法：列举法、描述法、图形表示法.集合元素的特征：确定性、互异性、无序性. 集合的性质：①任何一个集合是它本身的子集，记为；②空集是任何集合的子集，记为；③空集是任何非空集合的真子集；如果，同时，那么A = B.如果.[注]：①Z = {整数}（√） Z ={全体整数} （×）②已知集合S 中A 的补集是一个有限集，则集合A 也是有限集.（×）（例：S=N ； A=，则C s A= {0}）A A ⊆A ⊆φB A ⊆A B ⊆C A C B B A ⊆⊆⊆，那么，+N③空集的补集是全集.④若集合A=集合B，则C B A=，C A B =C S（C A B）=D（注：C A B =）.3. ①{（x，y）|xy =0，x∈R，y∈R}坐标轴上的点集.②{（x，y）|xy＜0，x∈R，y∈R二、四象限的点集.③{（x，y）|xy＞0，x∈R，y∈R} 一、三象限的点集.[注]：①对方程组解的集合应是点集.例：解的集合{(2，1)}.②点集与数集的交集是. （例：A ={(x，y)| y =x+1} B={y|y =x2+1} 则A∩B =）4. ①n个元素的子集有2n个. ②n个元素的真子集有2n－1个. ③n个元素的非空真子集有2n－2个.5. ⑴①一个命题的否命题为真，它的逆命题一定为真. 否命题逆命题.②一个命题为真，则它的逆否命题一定为真. 原命题逆否命题.例：①若应是真命题.，则a+b = 5，成立，所以此命题为真.②.1或y = 2.,故是的既不是充分，又不是必要条件.⑵小范围推出大范围；大范围推不出小范围.3.例：若.4.集合运算：交、并、补.5.主要性质和运算律（1）包含关系：（2）等价关系：（3）集合的运算律：交换律：结合律:分配律:.∅∅∅}⎩⎨⎧=-=+1323yxyxφ∅⇔⇔325≠≠≠+baba或，则且1≠x3≠y1≠∴yx且3≠+yx21≠≠yx且255xxx或，⇒{|,}{|}{,}A B x x A x BA B x x A x BA x U x A⇔∈∈⇔∈∈⇔∈∉U交：且并：或补：且C,,,,,;,;,.UA A A A U A UA B B C A C A B A A B B A B A A B B⊆Φ⊆⊆⊆⊆⊆⇒⊆⊆⊆⊇⊇CUA B A B A A B B A B U⊆⇔=⇔=⇔=C.;ABBAABBA==)()();()(CBACBACBACBA==)()()();()()(CABACBACABACBA==0-1律：等幂律：求补律：A∩C U A=φA∪C U A=U C U U=φ C Uφ=U反演律：C U(A∩B)= (C U A)∪(C U B) C U(A∪B)= (C U A)∩(C U B)6.有限集的元素个数定义：有限集A的元素的个数叫做集合A的基数，记为card( A)规定 card(φ) =0.基本公式：(3) card( U A)= card(U)- card(A)(二)含绝对值不等式、一元二次不等式的解法及延伸1.整式不等式的解法根轴法（零点分段法）①将不等式化为a0(x-x1)(x-x2)…(x-x m)>0(<0)形式，并将各因式x的系数化“+”；(为了统一方便)②求根，并在数轴上表示出来；③由右上方穿线，经过数轴上表示各根的点（为什么？）；④若不等式（x的系数化“+”后）是“>0”,则找“线”在x轴上方的区间；若不等式是“<0”,则找“线”在x轴下方的区间.（自右向左正负相间）则不等式的解可以根据各区间的符号确定.特例①一元一次不等式ax>b解的讨论；②一元二次不等式ax2+box>0(a>0)解的讨论.>∆0=∆0<∆二次函数cbxaxy++=2（0>a）的图象,,,A A A U A A U A UΦ=ΦΦ===.,AAAAAA==(1)()()()()(2)()()()()()()()()card A B card A card B card A Bcard A B C card A card B card Ccard A B card B C card C Acard A B C=+-=++---+x)0)((002211><>++++--aaxaxaxa nnnn原命题若p 则q否命题若┐p 则┐q 逆命题若q 则p 逆否命题若┐q 则┐p 互为逆否互逆否互为逆否互互逆否互一元二次方程()的根002>=++a c bx ax 有两相异实根)(,2121x x x x <有两相等实根ab x x 221-== 无实根的解集)0(02>>++a c bx ax {}21x x x x x ><或⎭⎬⎫⎩⎨⎧-≠a b x x 2R 的解集)0(02><++a c bx ax {}21x x x x << ∅∅2.分式不等式的解法（1）标准化：移项通分化为>0(或<0)； ≥0(或≤0)的形式，（2）转化为整式不等式（组）3.含绝对值不等式的解法（1）公式法：,与型的不等式的解法.（2）定义法：用“零点分区间法”分类讨论.（3）几何法：根据绝对值的几何意义用数形结合思想方法解题.4.一元二次方程根的分布一元二次方程ax 2+bx+c=0(a≠0)（1）根的“零分布”：根据判别式和韦达定理分析列式解之.（2）根的“非零分布”：作二次函数图象，用数形结合思想分析列式解之.（三）简易逻辑1、命题的定义：可以判断真假的语句叫做命题。

高考数学第一轮复习知识点分类指导

高考数学第一轮复习知识点分类指导一、集合与简易逻辑1.集合元素具有确定性、无序性和互异性.（1）设p、q为两个非空实数子集，定义子集p+q={a?b|a?p,b?q}，若p?{0,2,5}，（答：8）q?{1,2,6}，则p+q中元素的有________个。

（2）非空集合s?{1,2,3,4,5}，且满足用户“若a?s，则6?a?s”，这样的s共计_____个（答：7）22.“极端”情况否忘掉a??：子集a?{x|ax?1?0}，b?x|x?3x?2?0，且a?b?b，则实数a＝______.（答：a1?0,1,）23.满足用户{1,2}??m?{1,2,3,4,5}子集m存有______个。

（请问：7）4.运算性质：设全集u?{1,2,3,4,5}，若a?b?{2}，(cua)?b?{4}，(cua)?(cub)?{1,5}，则a＝_____，b＝___.（请问：a?{2,3}，b?{2,4}）x?2}，集合n＝?y|y?x2,x?m?，则m?n?___（请问：[4??,)；（2）设立子集m?{a|a）?(1,?2?)(?3?,4r)，,??n?{a|a?(2,3)??(4,5)，??r}，则m?n?_____（请问：{(?2,?2)}）6.补集思想：已知函数f(x)?4x2?2(p?2)x?2p2?p?1在区间[?1,1]上至少存在一3个实数c，并使f(c)?0，谋实数p的值域范围。

（请问：(?3,)）25.集合的代表元素：（1）设集合m?{x|y?7.复合命题真假的判断：在下列说法中：⑴“p且q”为真是“p或q”为真的充分不必要条件；⑵“p且q”为假是“p或q”为真的充分不必要条件；⑶“p或q”为真是“非p”为假的必要不充分条件；⑷“非p”为真是“p且q”为假的必要不充分条件。

其中正确的是____答：⑴⑶）8.充要条件：（1）得出以下命题：①实数a?0就是直线ax?2y?1与2ax?2y?3平行的充要条件；②若a,b?r,ab?0就是a?b?a?b设立的充要条件；③未知x,y?r，“若xy?0，则x?0或y?0”的逆否命题是“若x?0或y?0则x y?0”；④“若a和b都是偶数，则a?b是偶数”的否命题是假命题。

第01讲集合(解析版)备战2023年高考数学一轮复习精讲精练

第01讲集合(精讲+精练）目录第一部分：思维导图（总览全局）第二部分：知识点精准记忆第三部分：课前自我评估测试第四部分：典型例题剖析高频考点一：集合的基本概念高频考点二：集合的基本关系高频考点三：集合的运算高频考点四：venn图的应用高频考点五：集合新定义问题第五部分：高考真题感悟第六部分：集合(精练）1、元素与集合（1）集合中元素的三个特性：确定性、互异性、无序性.（2）元素与集合的关系：属于或不属于，数学符号分别记为：∈和∉. （3）集合的表示方法：列举法、描述法、韦恩图（venn 图）. （4）常见数集和数学符号 ①确定性：给定的集合，它的元素必须是确定的；也就是说，给定一个集合，那么任何一个元素在不在这个集合中就确定了.给定集合{1,2,3,4,5}A =，可知1A ∈,在该集合中，6A ∉,不在该集合中； ②互异性：一个给定集合中的元素是互不相同的；也就是说，集合中的元素是不重复出现的. 集合{,,}A a b c =应满足a b c ≠≠.③无序性：组成集合的元素间没有顺序之分。

集合{1,2,3,4,5}A =和{1,3,5,2,4}B =是同一个集合.④列举法把集合的元素一一列举出来，并用花括号“{}”括起来表示集合的方法叫做列举法.⑤描述法用集合所含元素的共同特征表示集合的方法称为描述法.具体方法是：在花括号内先写上表示这个集合元素的一般符号及取值（或变化）范围，再画一条竖线，在竖线后写出这个集合中元素所具有的共同特征.2、集合间的基本关系（1）子集（subset ）：一般地，对于两个集合A 、B ，如果集合A 中任意一个元素都是集合B 中的元素，我们就说这两个集合有包含关系，称集合A 为集合B 的子集，记作A B ⊆（或B A ⊇），读作“A 包含于B ”（或“B 包含A ”）.（2）真子集（proper subset ）：如果集合A B ⊆，但存在元素x B ∈，且x A ∉，我们称集合A 是集合B 的真子集，记作AB （或B A ⊃≠）.读作“A 真包含于B ”或“B 真包含A ”.（3）相等：如果集合A 是集合B 的子集（A B ⊆，且集合B 是集合A 的子集（B A ⊆），此时，集合A 与集合B 中的元素是一样的，因此，集合A 与集合B 相等，记作A B =.（4）空集的性质：我们把不含任何元素的集合叫做空集，记作∅；∅是任何集合的子集，是任何非空集合的真子集.3、集合的基本运算（1）交集：一般地，由属于集合A 且属于集合B 的所有元素组成的集合，称为A 与B 的交集，记作A B ，即{|,}AB x x A x B =∈∈且．（2）并集：一般地，由所有属于集合A 或属于集合B 的元素组成的集合，称为A 与B 的并集，记作A B ，即{|,}AB x x A x B =∈∈或．（3）补集：对于一个集合A ，由全集U 中不属于集合A 的所有元素组成的集合称为集合A 相对于全集U 的补集，简称为集合A 的补集，记作U C A ，即{|,}U C A x x U x A =∈∉且．4、集合的运算性质（1）A A A =，A ∅=∅，A B B A =．（2）A A A =，A A ∅=，A B BA =．（3）()U AC A =∅，()U A C A U =，()U U C C A A =．5、高频考点结论（1）若有限集A 中有n 个元素，则A 的子集有2n 个，真子集有21n -个，非空子集有21n -个，非空真子集有22n -个．（2）空集是任何集合A 的子集，是任何非空集合B 的真子集．（3）U U A B A B A A B B C B C A ⊆⇔=⇔=⇔⊆．（4）()()()U U U C AB C A C B =,()()()U U U C A B C A C B =．一、判断题1．（2022·江西·贵溪市实验中学高二期末）集合{},,,A a b c d =的子集共有8个 ( ) 【答案】错误集合{},,,A a b c d =的子集共有4216=个，故答案为：错误2．（2021·江西·贵溪市实验中学高二阶段练习）集合{}1,2,3,4,5和{}5,4,3,2,1表示同一个集合( ) 【答案】√由集合相等的定义可知，集合{}1,2,3,4,5和{}5,4,3,2,1表示同一集合. 故答案为：√.3．（2021·江西·贵溪市实验中学高三阶段练习）满足条件{}{}11,2,3M ⋃=的集合M 的个数是2个.( ) 【答案】正确因{}{}11,2,3M ⋃=，则{2,3}M =或{1,2,3}M =，所以的集合M 的个数是2个. 故答案为：正确4．（2021·江西·贵溪市实验中学高三阶段练习）已知集合{}20M xx x =+=∣，则1M -∈.( ) 【答案】正确因为{}{}200,1M xx x =+==-∣ 所以1M -∈5．（2021·江西·贵溪市实验中学高二阶段练习）满足条件{}{}11,2,3M ⋃=的集合M 的个数是3 ( ) 【答案】错误因集合M 满足{}{}11,2,3M ⋃=，于是得{2,3}M =或{1,2,3}M =，即符合条件的集合M 有2个，所以原命题是错误的.故答案为：错误二、单选题1．（2022·广东茂名·高一期末）已知集合{}21A x y x ==+，集合{}21B y y x ==+，则A B =（）A ．0B ．{}|1x x ≥C ．{}|1x x ≤D ．R【答案】B由题意，集合A R =，{}|1B y y =≥，∴{}|1x x A B =≥. 故选：B.2．（2021·广东·佛山一中高一阶段练习）已知集合{}22,531,=-+A a a ，，{}5,9,1,4=+-B a a ，若{}4A B ⋂=，则实数a 的取值的集合为（） A ．{}1,2,2- B ．{}1,2 C ．{}1,2- D ．{}1【答案】D集合{}22,531,=-+A a a ，，{}5,9,1,4=+-B a a ，又{}4A B ⋂=∴314a +=或24a =，解得1a =或2a =或2a =-，当1a =时，}{2,5,4,1A =-，}{6,9,0,4B =，{}4A B ⋂=，符合题意；当2a =时，}{2,5,7,4A =-，}{7,9,1,4B =-，{}7,4⋂=A B ，不符合题意；当2a =-时，}{2,5,5,4A =--，}{3,9,3,4B =，不满足集合元素的互异性，不符合题意.1a，则实数a 的取值的集合为{}1.故选：D.3．（2022·河南平顶山·高三阶段练习（文））已知集合{}1A x x =>，{}260B x x x =--<，则()R A B ⋂=（）A ．{}13x x <<B ．{}12x x <<C ．{}3x x ≥D ．{}2x x ≥【答案】C二次不等式求出集合B ，进而求出B R，()RAB .【详解】由题意可得:{}23B x x =-<<，则{2R B x x =≤-或}3x ≥，故(){}R 3A B x x ⋂=≥．故选：C4．（2022·湖南·沅陵县第一中学高二开学考试）如图所示，阴影部分表示的集合是（）A ．(UB ⋂)A B ．(U A ⋂)BC ．() UA B ⋂D ．(U A B )【答案】A由图可知阴影部分属于A ，不属于B ，故阴影部分为() UB A ⋂，故选：A.高频考点一：集合的基本概念1．（2020·重庆·一模（理））已知集合{}2|280,A x Z x x =∈+-<{}2|B x x A =∈，则B 中元素个数为A ．4B ．5C ．6D ．7【答案】A{}{}2|280|42{3,2,1,0,1}A x Z x x x Z x =∈+-<=∈-<<=---， {}2|{0,1,4,9}B x x A =∈=，B 中元素个数为4个.故选:A.本题考查集合的化简，注意集合元素的满足的条件，属于基础题.2．（2021·上海黄浦·一模）已知集合{}2,(R)A x x x =∈，若1A ∈，则x =___________.【答案】1-{}2,(R)A x x x =∈，1A ∈，则1x =或21x =，解得1x =或1x =-，当1x =时，集合A 中有两个相同元素，（舍去），所以1x =-.故答案为：1- 3．（2012·全国·一模（理））集合中含有的元素个数为A ．4B ．6C ．8D ．12【答案】B共6 个．故选B4．（2017·河北·武邑宏达学校模拟预测（理））集合{}2*|70,A x x x x N =-<∈，则*6|,B y N y A y ⎧⎫=∈∈⎨⎬⎩⎭中元素的个数为 A ．1个 B ．2个C ．3个D ．4个【答案】D,,所以集合中的元素个数为4个，故选D.考点：集合的表示5．（2020·湖南·邵东市第十中学模拟预测（理））已知集合{}1,0,1A =-，(),|,,xB x y x A y A y ⎧⎫=∈∈∈⎨⎬⎩⎭N ，则集合B 中所含元素的个数为（） A ．3 B ．4 C ．6 D ．9【答案】B 因为x A ∈，yA ，xy∈N ，所以满足条件的有序实数对为()1,1--，()0,1-，()0,1，()1,1．故选:B.【点睛】本题考查集合中元素个数的求法，属于基础题.6．（2021·全国·二模（理））定义集合运算：{},,A B z z xy x A y B *==∈∈，设{1,2}A =，{1,2,3}B =，则集合A B *的所有元素之和为（） A ．16 B ．18C ．14D ．8【答案】A由题设知：{1,2,3,4,6}A B *=，∴所有元素之和1234616++++=.故选：A.研究集合问题时，首先要明确构成集合的元素是什么，即弄清该集合是数集、点集，还是其他集合，然后再看集合的构成元素满足的限制条件是什么，从而准确把握集合的意义，再求解时注意把握集合元素的三特性中的“互异性”.高频考点二：集合的基本关系1．（2021·广东肇庆·模拟预测）已知集合{}3P x x =<，{}2Q x Z x =∈<，则（） A ．P Q ⊆ B ．Q P ⊆C ．P Q P =D ．P Q Q ⋃=【答案】B由题意，{}{}21,0,1Q x Z x =∈<=-，{}3P x x =< 故Q P ⊆，A 错，B 对又{1,0,1}P Q Q =-=，{|3}P Q x x P ⋃=<=，故C ，D 错故选：B2．（2020·山东·模拟预测）已知集合==2{1,},{}M x N x ，若N M ⊆，则x =__. 【答案】0若1x =，则21x =，不符合条件；若2x x =，则0x =或1x =(舍去)，经验证0x =符合条件．故答案为：0．3．（2020·江苏省如皋中学二模）设{,2}M m =，{2,2}N m m =+，且M N ，则实数m 的值是________. 【答案】0；因为{,2}M m =，{2,2}N m m =+，且M N ，所以+222m m m =⎧⎨=⎩，解得0m =，故答案为：0.【点睛】本题主要考查集合的基本运算，利用集合相等求解m 的值是解题关键,属于基础题. 4．（2021·辽宁·东北育才学校一模）所有满足{}{},,,a M a b c d ⊆的集合M 的个数为________；【答案】7 满足{}{},,,a M a b c d ⊆的集合M 有{}{}{}{}{}{}{},,,,,,,,,,,,,,,a a b a c a d a b c a b d a c d ，共7个.故答案为：75．（2022·全国·模拟预测）已知集合{}213M x x =+<，{}N x x a =<，若N M ⊆，则实数a 的取值范围为（） A ．[)1,+∞ B ．[)2,+∞ C ．(],1-∞ D ．(),1-∞【答案】C∵集合{}{}2131M x x x x =+<=<，且N M ⊆，∴1a ≤. 故选：C ．6．（2020·广西·模拟预测）已知集合{|15}A x x =<≤，{}|04B x x =<<，{}|121C x m x m =+<<-.（1）求A B ，()R A B ⋂：（2）若B C C =，求实数m 的取值范围.【答案】（1）{|05}A B x x ⋃=<≤；(){14}R A B xx x ⋂=≤≥或∣；（2）52m ≤. （1）{|05}A B x x ⋃=<≤；(){14}RA B x x x ⋂=≤≥或∣（2）因为B C C =，所以C B ⊆. 当B φ=时，121m m +≥-，即2m ≤；当B φ≠时，12110214m m m m +<-⎧⎪+≥⎨⎪-≤⎩，即522m <≤综上，52m ≤7．（2020·广西·模拟预测）已知集合{|121}A x a x a =+≤≤-，{|3B x x =≤或5}x >.（1）若4a =，求A B ；（2）若A B ⊆，求a 的取值范围.【答案】（1）{|57}A B x x =<≤；（2）{|2a a ≤或}4a >. （1）当4a =时，易得{|57}A x x =≤≤，{|3B x x =≤或5}x >，{|57}A B x x ∴=<≤.（2）若211a a -<+，即2a <时，A =∅，满足A B ⊆，若211a a -≥+，即2a ≥时，要使A B ⊆，只需2132a a -≤⎧⎨≥⎩或152a a +>⎧⎨≥⎩，解得2a =或4a >，综上所述a 的取值范围为{|2a a ≤或}4a >.【点睛】本题考查根据集合的基本关系求参数，属于基础题. 重点考查结论：（1）若有限集A 中有n 个元素，则A 的子集有2n 个，真子集有21n -个，非空子集有21n -个，非空真子集有22n -个．（2）U U A B AB A A B BC B C A ⊆⇔=⇔=⇔⊆．（3）若A B ⊆注意要讨论①A =∅②A ≠∅高频考点三：集合的运算1．（2022·甘肃陇南·模拟预测（理））已知集合{}|321A x x =->，{}260B x x x =--<，则A B =（）A ．{}13x x <<B ．{}12x x <<C ．{}21x x -<<D ．{}31x x -<<【答案】A{}{}{}|321|33|1A x x x x x x =->=>=>{}{}{}260(2)(3)023B x x x x x x x x =--<=+-<=-<<所以{}13A B x x ⋂=<<，故选：A2．（2022·北京丰台·一模）已知集合{|12}A x x =-<≤，{|21}B x x =-<≤，则A B ⋃=（） A ．{|11}x x -<< B ．{|11}x x -<≤ C ．{|22}x x -<< D ．{|22}x x -<≤【答案】D∵集合{|12}A x x =-<≤，{|21}B x x =-<≤， ∴{|22}A B x x ⋃=-<≤. 故选：D.3．（2022·河南·模拟预测（理））已知集合{}14A x x =≤≤，(){}214B x x =-≥，则()AB =R（）A ．[]3,4B ．[]1,4C ．[)1,3D ．[)3,+∞【答案】C解：由()214x -≥，即310x x ，解得3x ≥或1x ≤-，即(){}214{|3B x x x x =-≥=≥或1}x ≤-，所以()1,3R B =-，又{}14A x x =≤≤，所以()[)1,3R A B ⋂=；故选：C4．（2022·全国·模拟预测（理））设全集U =R ，集合102x A xx ⎧⎫+=≤⎨⎬-⎩⎭，集合{}ln 1B x x =≤，则A B 是（） A ．(]0,2 B ．()2,e C ．()0,2 D ．[)1,e -【答案】C102x x +≤-，解得：12x -≤<，故集合[)1,2A =-，ln 1x ≤，解得：(]0,e x ∈，集合(]0,e B =，则()0,2A B =，故选：C ．5．（2022·江西赣州·一模（理））设集合{}1,0,A n =-，{},,B x x a b a A b A ==⋅∈∈.若A B A =，则实数n的值为（） A ．1- B ．0 C ．1 D ．2【答案】C依据集合元素互异性可知，0,1n n ≠≠-，排除选项AB ；当1n =时，{}1,0,1A =-，{}{},,110B x x a b a A b A ==⋅∈∈=-，，，满足A B A =.选项C 判断正确；当2n =时，{}1,0,2A =-，{}{},,2,014B x x a b a A b A ==⋅∈∈=-，，， {}0A B A ⋂=≠.选项D 判断错误.故选：C6．（2021·江西·模拟预测）2021年是中国共产党成立100周年，电影频道推出“经典频传：看电影，学党史”系列短视频，传扬中国共产党的伟大精神，为广大青年群体带来精神感召.现有《青春之歌》《建党伟业》《开国大典》三支短视频，某大学社团有50人，观看了《青春之歌》的有21人，观看了《建党伟业》的有23人，观看了《开国大典》的有26人.其中，只观看了《青春之歌》和《建党伟业》的有4人，只观看了《建党伟业》和《开国大典》的有7人，只观看了《青春之歌》和《开国大典》的有6人，三支短视频全观看了的有3人，则没有观看任何一支短视频的人数为________. 【答案】3把大学社团50人形成的集合记为全集U ，观看了《青春之歌》《建党伟业》《开国大典》三支短视频的人形成的集合分别记为A ，B ，C ，依题意，作出韦恩图，如图，观察韦恩图：因观看了《青春之歌》的有21人，则只看了《青春之歌》的有214638---=(人)，因观看了《建党伟业》的有23人，则只看了《建党伟业》的有234739---=(人)，因观看了《开国大典》的有26人，则只看了《开国大典》的有2667310---=(人)，因此，至少看了一支短视频的有3467891047++++++=(人)，所以没有观看任何一支短视频的人数为50473-=. 故答案为：37．（2021·上海·模拟预测）已知集合{}2890,U x x x x Z =--≤∈，{}A y y y Z ==∈，则UA__________.【答案】{1,6,7,8,9}-由题意，289(9)(1)019x x x x x --=-+≤∴-≤≤，又x ∈Z{}1,0,1,2,3,4,5,6,7,8,9U -∴=又y =由于20(4)2525x ≤--+≤05∴≤，又y Z ∈{}0,1,2,3,4,5A ∴= 故{1,6,7,8,9}UA =-故答案为：{1,6,7,8,9}- 集合运算的常用方法①若集合中的元素是离散的，常用Venn 图求解；②若集合中的元素是连续的实数，则用数轴表示，此时要注意端点的情况．高频考点四：venn 图的应用1．（2022·贵州贵阳·一模（理））若全集U 和集合A ，B 的关系如图所示，则图中阴影部分表示的集合为（）A ．()U AB ⋂ B ．()UB AC ．()UA BD ．()U A B【答案】A由图知：阴影部分属于A ，不属于B ，故为()U B A ⋂. 故选：A2．（2021·广东·模拟预测）已知全集U =R ，集合{}2,20A x yB xx x ⎧==--<⎨⎩∣∣，它们的关系如图（Venn 图）所示，则阴影部分表示的集合为（）A ．{12}x x -≤<∣B ．{12}xx -<<∣ C ．{12}xx ≤<∣ D ．{12}xx <<∣ 【答案】C解：由题意得：{10}{1}A x y xx x x ⎧==->=<⎨⎩∣∣∣ {}220{12}B x x x x x =--<=-<<∣∣{}()1,{12}UUA x x AB x x ∴=≥⋂=≤<∣∣故选：C3．（2021·黑龙江·哈九中三模（理））如图，U 是全集，,,M P S 是U 的子集，则阴影部分表示的集合是（）A ．()MP S B ．()MP S C ．()UM P S ⋂⋂D ．()UM P S ⋂⋃【答案】C解：由图知，阴影部分在集合M 中，在集合P 中，但不在集合S 中，故阴影部分所表示的集合是()UM P S ⋂⋂.故选：C.4．（2021·江苏徐州·二模）某班45名学生参加“3·12”植树节活动，每位学生都参加除草､植树两项劳动.依据劳动表现，评定为“优秀”､“合格”2个等级，结果如下表：若在两个项目中都“合格”的学生最多有10人，则在两个项目中都“优秀”的人数最多为（）A ．5B ．10C ．15D ．20【答案】C用集合A 表示除草优秀的学生，B 表示椿树优秀的学生，全班学生用全集U 表示，则UA 表示除草合格的学生，则UB 表示植树合格的学生，作出Venn 图，如图，设两个项目都优秀的人数为x ，两个项目都是合格的人数为y ，由图可得203045x x x y -++-+=，5x y =+，因为max 10y =，所以max 10515x =+=．故选：C ．【点睛】关键点点睛：本题考查集合的应用，解题关键是用集合,A B表示优秀学生，全体学生用全集表示，用Venn图表示集合的关系后，易知全部优秀的人数与全部合格的人数之间的关系，从而得出最大值．5．（2020·北京市第五中学模拟预测）高二一班共有学生50人，每名学生要从物理、化学、生物、历史、地理、政治这六门课程中选择三门课程进行学习.已知选择物理、化学、生物的学生各有至少20人，这三门课程都不选的有10人，这三门课程都选的有10人，在这三门课程中选择任意两门课程的都至少有13人，物理、化学只选一科的学生都至少6人，那么选择物理和化学这两门课程的学生人数至多（）A．16 B．17 C．18 D．19【答案】C把学生50人看出一个集合U，选择物理科的人数组成为集合A，选择化学科的人数组成集合B，选择生物颗的人数组成集合C，要使选择物理和化学这两门课程的学生人数最多，除这三门课程都不选的有10人，这三门课程都选的有10人，则其它个选择人数均为最少，即得到单选物理的最少6人，单选化学的最少6人，单选化学、生物的最少3人，单选物理、生物的最少3人，单选生物的最少4人，以上人数最少42人，可作出如下图所示的韦恩图，所以单选物理、化学的人数至多8人，+=人.所以至多选择选择物理和化学这两门课程的学生人数至多10818故选：C.【点睛】本题主要考查了集合的应用，其中解答中根据题意，画出集合运算的韦恩图是解答本题的关键，着重考查数形结合思想，以及分析问题和解答问题的能力.高频考点五：集合新定义问题1．定义集合{|A B x x A -=∈ 且}x B ∉.己知集合{}Z 26U x x =∈-<<，{}0,2,4,5A =，{}1,0,3B =-，则()UA B -中元素的个数为（）A ．3B ．4C ．5D ．6【答案】B因为{}0,2,4,5A =，{}1,0,3B =-，所以{}2,4,5A B -=，又因为{}1,0,1,2,3,4,5U =-，所以(){}U1,0,1,3A B -=-.故选：B.2．设A 、B 是非空集合，定义：{|A B x x A B ⨯=∈且}x A B ∉．已知{|A x y =，{|1}B x x =>，则A B ⨯等于（） A ．[0,1](2,)+∞ B ．[0,1)(2,)⋃+∞ C ．[0,1] D ．[0,2]【答案】A集合A 中，220x x -≥，即()20x x -≤，解得02x ≤≤，即{}[]|0202A x x =≤≤=，，又{}|1B x x =>，所以)0,A B ⎡⋃=+∞⎣，](1,2A B ⋂=，则[]0,1(2,)A B ⨯=⋃+∞. 故选：A ．3．已知集合{}1,2,3M =，(){},,,N x y x M y M x y M =∈∈+∈，则集合N 中的元素个数为（） A ．2 B ．3C ．8D ．9【答案】B解：由题意，满足条件的平面内以(),x y 为坐标的点集合()()(){}1,1,1,2,2,1N =，所以集合N 的元素个数为3. 故选：B.4．已知非空集合A 、B 满足以下两个条件：（1）{}1,2,3,4,5A B =，A B =∅；（2）A 的元素个数不是A 中的元素，B 的元素个数不是B 中的元素.则有序集合对(),A B 的个数为（） A ．4 B ．6C ．8D ．16【答案】C由题意可知，集合A 不能是空集，也不可能为{}1,2,3,4,5.若集合A 只有一个元素，则集合A 为{}4；若集合A 有两个元素，则集合A 为{}1,3、{}3,4、{}3,5；若集合A 有三个元素，则集合A 为{}1,2,4、{}1,2,5、{}2,4,5；若集合A 有四个元素，则集合A 为{}1,2,3,5. 综上所述，有序集合对(),A B 的个数为8. 故选：C.【点睛】关键点点睛：解本题的关键在于对集合A 中的元素个数进行分类讨论，由此确定集合A ，由此得解.5．（多选）在整数集Z 中，被5除所得余数为k 的所有整数组成一个“类”，记为[k ]，即{}[]5k n k n Z =+∈，0,1,2,3,4k =.则下列结论正确的是（）A ．2011[1]∈；B ．[0][1][2][3][4]Z =⋃⋃⋃⋃；C ．3[3]-∈；D ．整数a ，b 属于同一“类”的充要条件是“[0]a b -∈”.【答案】ABDA ：2011除以5，所得余数为1，满足[]1的定义，故正确；B ：整数集Z 就是由除以5所得余数为0,1,2,3,4的整数构成的，故正确；C ：()3512-=⨯-+，故[]33-∉，故错误；D ：设{}112212125,5,,,,0,1,2,3,4a n m b n m n n Z m m =+=+∈∈，则()12125a b n n m m -=-+-；若整数a ，b 属于同一“类”，则120m m -=，所以[]0a b -∈；反之，若[]0a b -∈，则120m m -=，即12m m =，,a b 属于同一“类”. 故整数a ，b 属于同一“类”的充要条件是“[0]a b -∈”，正确. 故选：ABD .1．（2021·山东·高考真题）假设集合{}1,2,3A =，{}1,3B =，那么A B 等于（） A ．{}1,2,3 B ．{}1,3C ．{}1,2D ．{}2【答案】B{}1,2,3A =，{}1,3B =，{}1，3∴⋂=A B . 故选：B .2．（2021·湖南·高考真题）已知集合{}13,5A =,，{}1,2,3,4B =，且A B =（） A ．{}1,3 B ．{}1,3,5C ．{}1,2,3,4D ．{}1,2,3,4,5【答案】A因为集合{}13,5A =,，{}1,2,3,4B = 所以{}1,3A B =，故选：A.3．（2021·江苏·高考真题）已知集合{}1,3M =，{}1,3N a =-，若{}1,2,3M N =，则a 的值是（）A ．-2B ．-1C ．0D ．1【答案】B 因为{}1,2,3MN =，若110a a -=⇒=，经验证不满足题意；若121a a -=⇒=-，经验证满足题意. 所以1a =-. 故选：B.4．（2021·天津·高考真题）设集合{}{}{}1,0,11,3,5,0,2,4A B C =-==，，则()A B C ⋂⋃=（） A ．{}0 B ．{0,1,3,5} C ．{0,1,2,4} D ．{0,2,3,4}【答案】C{}{}{}1,0,11,3,5,0,2,4A B C =-==，，{}1A B ∴⋂=，{}()0,1,2,4A B C ⋂⋃=∴. 故选：C.5．（2021·全国·高考真题）设集合{1,2,3,4,5,6},{1,3,6},{2,3,4}U A B ===，则()UA B =（）A ．{3}B ．{1,6}C ．{5,6}D ．{1,3}【答案】B 由题设可得{}U1,5,6B =，故(){}U 1,6A B ⋂=，故选：B.6．（2021·浙江·高考真题）设集合{}1A x x =≥，{}12B x x =-<<，则A B =（） A ．{}1x x >- B ．{}1x x ≥C ．{}11x x -<<D ．{}12x x ≤<【答案】D由交集的定义结合题意可得：{}|12A B x x =≤<. 故选：D.7．（2021·全国·高考真题（理））已知集合{}21,S s s n n ==+∈Z ，{}41,T t t n n ==+∈Z ，则S T （）A ．∅B ．SC ．TD ．Z【答案】C任取t T ∈，则()41221t n n =+=⋅+，其中n Z ∈，所以，t S ∈，故T S ⊆，因此，S T T =. 故选：C.一、单选题1．（2021·北大附中云南实验学校高一阶段练习）下列各对象可以组成集合的是（） A ．与1非常接近的全体实数B ．北大附中云南实验学校20202021-学年度第二学期全体高一学生C ．高一年级视力比较好的同学D ．高一年级很有才华的老师【答案】B 【详解】对于ACD ，集合中的元素具有确定性，但ACD 中的元素不确定，故不能构成集合，ACD 错误； B 中的元素满足集合中元素的特点，可以构成集合，B 正确. 故选：B.2．（2022··模拟预测（理））已知集合A ={}250x x x -≤，B ={}21,x x k k Z =-∈，则A B 中元素的个数为（） A ．2 B ．3 C ．4 D ．5【答案】B由250x x -≤得：05x ≤≤，所以{}05A x x =≤≤，又{}21,B x x k k Z ==-∈，令0215k ≤-≤，解得：132k ≤≤，k Z ∈，当1k =时，1x =，当2k =时，3x =，当3k =时，5x =，故A B 中元素的个数为3. 故选：B3．（2022·贵州毕节·模拟预测（理））已知集合(){}10A x x x =-=，{}20,,B m m =，若A B B ⋃=，则m =（） A ．1- B ．0C ．1D ．±1【答案】A∵集合(){}{}100,1A x x x =-==，{}20,,B m m =，A B B ⋃=，∴1m =或21m =，即1m =±，当1m =时，{}0,1,1B =不合题意，当1m =-时，{}0,1,1B =-成立， ∴1m =-. 故选：A.4．（2022·全国·模拟预测）已知集合{}1,2,3,4,5,6A =，6,1B xx A x ⎧⎫=∈∈⎨⎬-⎩⎭N ，则集合B 的子集的个数是（） A ．3 B ．4 C ．8 D ．16【答案】C依题意{}2,3,4B =，所以集合B 的子集的个数为328=，故选：C.5．（2022·湖南·长沙一中高三阶段练习）集合1,36n M x x n Z ⎧⎫==+∈⎨⎬⎩⎭，1,63n N x x n Z ⎧⎫==+∈⎨⎬⎩⎭，则MN =（） A ．M B ．N C ．∅ D ．,6n x x n Z ⎧⎫=∈⎨⎬⎩⎭【答案】B由已知2,6n M x x n Z ⎧⎫+==∈⎨⎬⎩⎭，21,6n N x x n Z ⎧⎫+==∈⎨⎬⎩⎭，又2n +表示整数，21n 表示奇数，故M N N =，故选：B6．（2022·广东·高二期末）集合{}2230A x x x =--=，{}10B x mx =+=，A B A ⋃=，则m 的取值范围是（） A ．11,3⎧⎫-⎨⎬⎩⎭B ．{}1,3-C ．10,3⎧⎫-⎨⎬⎩⎭D ．10,1,3⎧⎫-⎨⎬⎩⎭【答案】D根据题意，可得：{}3,1A =- A B A ⋃=，则有：B A ⊆当0m =时，B =∅，满足题意；当0m ≠时，则有：1x m=- 则有：13m -=，11m-=-解得：13m =-或1m =综上，解得：0m =或13m =-或1m =故答案选：D7．（2022·湖南·长郡中学高二阶段练习）已知集合(){}2ln 4A x y x ==-，{B y x =，则A B =（）A ．()2,3B ．()(],22,3-∞-C ．()0,3D ．(]2,3【答案】B 由题意得，{}2|40{|2A x x x x =->=<-或2}x >，{}|3B y y =≤，故A B ⋂()(],22,3∞=--⋃，故选：B8．（2022·河南·温县第一高级中学高三阶段练习（理））已知集合102x A xx ⎧⎫-=≤⎨⎬+⎩⎭，B ={-2，-1，0，1}，则A ∩B =（） A ．{-2，-1，0，1} B ．{-1，0，1}C ．{-1，0}D ．{-2，-1，0}【答案】B 因为102x x -≤+等价于(1)(2)020x x x -+≤⎧⎨+≠⎩等价于21x -<≤，所以{|21}A x x =-<≤，又{}2,1,0,1B =--，所以A B ={}1,0,1-. 故选：B 二、填空题9．（2022·四川·雅安中学高一阶段练习）集合{|13},{|25}A x x B x x =∈<≤=∈<<Z Z ，则A B 的子集的个数为___________. 【答案】8{}{}2,3,3,4A B ==，{2,3,4}A B ⋃=，有3个元素，所以子集个数为328=.故答案为：810．（2022·上海金山·高一期末）满足条件：{}a {},,,M a b c d ⊆的集合M 的个数为______.【答案】7由{}a {},,,M a b c d ⊆可知，M 中的元素个数多于{}a 中的元素个数，不多于{},,,a b c d 中的元素个数因此M 中的元素来自于b ,c,d 中，即在b ,c,d 中取1元素时，M 有3个；取2个元素时，有3个；取3个元素时，有1个，故足条件：{}a {},,,M a b c d ⊆的集合M 的个数有7个，故答案为：7.11．（2022·全国·高三专题练习）已知集合{}2{123},280A x a x a B x x x =-<<+=--≤，若()R A B A ⋂=，求实数a 的取值范围是___________. 【答案】[)5,5,2⎛⎤-∞-+∞ ⎥⎝⎦()R A B A =⋂，R A B ∴⊆ {}2280B x x x =--≤，{2R B x x ∴=<-∣或4}x > 当A =∅时，123,4a a a -+-，满足R A B ⊆当A ≠∅时，要使得R A B ⊆，则4232a a >-⎧⎨+≤-⎩或414a a >-⎧⎨-⎩ 解得542a -<≤-或5a 综上，实数a 的取值范围是[)5,5,2⎛⎤-∞-+∞ ⎥⎝⎦ 故答案为：[)5,5,2⎛⎤-∞-+∞ ⎥⎝⎦12．（2022·全国·高三专题练习）设集合{}2280A x x x =-->，{B x x a =≤或}5x a ≥+，若()R A B ⋂=∅，则a 的取值范围是___________. 【答案】[]2,1--{}()(){}{22804202A x x x x x x x x =-->=-+>=<-或}4x >，因为{B x x a =≤或}5x a ≥+，所以{}R 5B x a x a =<<+，若()R A B ⋂=∅，则254a a ≥-⎧⎨+≤⎩，解得21a -≤≤-. 所以a 的取值范围是[]2,1--，故答案为：[]2,1--.三、解答题13．（2022·山西·榆次一中高一开学考试）已知集合{}22150M x x x =--≤，{}N x m x m =-≤≤．(1)当1m =时，求M N ⋂以及()()R R M N ⋃；(2)若M N ，求实数m 的取值范围．【答案】(1)[1,1]=-M N ，()()()(),11,R R M N ∞∞⋃=--⋃+(2)[5,)+∞ (1){}{}(3)(5)035M x x x x x =+-≤=-≤≤，当1m =时，[1,1]N =-，∴[1,1]=-MN ， (,3)(5,)=-∞-+∞R M ，(,1)(1,)=-∞-+∞R N ，∴()()(,1)(1,)=-∞-+∞R R M N .(2)由题可知M N ，所以35-≤-⎧⎨≥⎩m m ，解得5m ≥，所以实数m 的取值范围为[5,)+∞.14．（2022·江苏省天一中学高一期末）集合1121x A x x +⎧⎫=>⎨⎬-⎩⎭，{}22240B x x ax a =-+-<. (1)若{}23,4,23C a a =+-，()0B C ∈，求实数a 的值；(2)从条件①②③这三个条件中选择一个作为已知条件，求实数a 的取值范围.条件：①A B A =；②()R A B ⋂=∅；③()R B A R ⋃=.（注：答题前先说明选择哪个条件，如果选择多于一条件分别解答，按第一个解答计分）.【答案】(1)1(2)条件选择见解析，502a ≤≤(1)因为()0B C ∈，所以0C ∈，所以2230a a +-=，解得：1a =或3a =-.当3a =-时，{}51B x x =-<<-，不合题意；当1a =时，{}13B x x =-<<，满足题设.∴实数a 的值为1.(2)集合1112212x A x x x x +⎧⎫⎧⎫=>=<<⎨⎬⎨⎬-⎩⎭⎩⎭. 集合{}{}2224022B x x ax a x a x a =-+-<=-<<+. 若选择①A B A =，即22501222a A B a a +≥⎧⎪⊆⇒⇒≤≤⎨-≤⎪⎩若选择②()12502222R a A B a a ⎧-≤⎪⋂=∅⇔⇔≤≤⎨⎪+≥⎩，若选择③()R B A R ⋃=，则22501222a a a +≥⎧⎪⇒≤≤⎨-≤⎪⎩15．（2022·江西·赣州市赣县第三中学高一开学考试）已知集合{}2430A x x x =++=，{}22230B x x ax a a =-+--=. (1)若1a =，求A B ；(2)若A B A ⋃=，求a 的取值集合.【答案】(1){}1A B ⋂=-(2){3a a ≤-或}2a =-.(1)当1a =时，{}{}22301,3B x x x =--==-. 因为{}{}24303,1A x x x =++==--，所以{}1A B ⋂=-.(2)因为A B A ⋃=，所以B A ⊆.当()224434120a a a a ∆=---=+<时，解得3a <-，B =∅，符合题意；当4120a ∆=+=，即3a =-时，{}3B =-，符合题意；当4120a ∆=+>，即3a >-时，{}3,1B A ==--，则()()2312,313,a a a ⎧-+-=⎪⎨-⨯-=--⎪⎩解得2a =-. 综上，a 的取值集合是{3a a ≤-或}2a =-.16．（2022·江苏·高一）已知集合A 为非空数集，定义：{},,S x x a b a b A ==+∈，{},,T x x a b a b A ==-∈.(1)若集合{}1,3A =，直接写出集合S 、T ；(2)若集合{}1234,,,A x x x x =，且T A =，写出一个满足条件的集合A ，并说明理由；(3)若集合{}02020,A x x x N ⊆≤≤∈，S T ⋂=∅，记A 为集合A 中元素的个数，求A 的最大值.【答案】(1){}2,4,6S =，{}0,2T =(2){}1234,,,A x x x x =，1234x x x x <<<，理由见解析(3)1347(1)根据题意，由{}1,3A =，则{}2,4,6S =，{}0,2T =；(2)由于集合{}1234,,,A x x x x =，1234x x x x <<<，且T A =，所以T 中也只包含四个元素，即{}2131410,,,T x x x x x x =---，剩下的324321x x x x x x -=-=-，所以1423x x x x +=+；(3)设{}12,,k A a a a =满足题意，其中12k a a a <<<，则11213223122k k k k k k a a a a a a a a a a a a a a -<+<+<<+<+<+<<+<， ∴21S k ≥-，1121311k a a a a a a a a -<-<-<<-，∴T k ≥， ∵S T ⋂=∅，31S T S T k ⋃=+≥-， S T 中最小的元素为0，最大的元素为2k a ， ∴21k S T a ⋃≤+，∴()31214041*k k a k N -≤+≤∈， 1347k ≤，实际上当{}674,675,676,,2020A =时满足题意，证明如下：设{},1,2,,2020A m m m =++，m N ∈，则{}2,21,22,,4040S m m m =++，{}0,1,2,,2020T m =-，依题意有20202m m -<，即16733m >，故m 的最小值为674，于是当674m =时，A 中元素最多，即{}674,675,676,,2020A =时满足题意，综上所述，集合A 中元素的个数的最大值是1347.。

高考一轮复习数学集合常考知识点

高考一轮复习数学集合常考知识点
高中数学集合是高一重生退学接触高中数学的第一门
功课。

也是最容易混杂的知识点之一。

下面是查字典数学网整理的
数学集合常考知识点，请考生掌握。

●难点磁场
(★★★★★)集合
A={(x,y)|x2+mx-y+2=0},B={(x,y)|x-y+1=0,且0≤x≤2},
假设A∩B≠,务实数m的取值范围.
●案例探求
[例1]设
A={(x,y)|y2-x-1=0},B={(x,y)|4x2+2x-2y+5=0},C={(x,y) |y=kx+b},能否存在k、b∈N,使得(A∪B)∩C=，证明此结论. 命题意图：此题主要考察考生对集合及其符号的剖析转化才干，即能从集合符号上分辨出所考察的知识点，进而处置效果.属★★★★★级标题.
知识依托：处置此题的闪光点是将条件(A∪B)∩C=转化为
A∩C=且B∩C=，这样难度就降低了.
错解剖析：此题难点在于考生对符号的不了解，对标题所给出的条件不能认清其实质外延，因此能够觉得无从下手.
技巧与方法：由集合A与集合B中的方程联立构成方程组，用判别式对根的状况停止限制，可失掉b、k的范围，又因b、
k∈N,进而可得值.
解：∵(A∪B)∩C=，∴A∩C=且B∩C=∵∴k2x2+(2bk-1)x+b2-1=0
∵A∩C=
∴Δ1=(2bk-1)2-4k2(b2-1)0,即b2>1①∴4x2+(2-2k)x+(5+2b)=0
∵B∩C=,∴Δ2=(1-k)2-4(5-2b)。

集合与简易逻辑知识点总结- 高三数学一轮复习

知识点总结1 集合与简易逻辑一、集合(一)元素与集合1.集合的含义某些指定对象的部分或全体构成一个集合．构成集合的元素除了常见的数、点等数学对象外，还可以是其他对象．2.集合元素的特征(1)确定性：集合中的元素必须是确定的，任何一个对象都能明确判断出它是否为该集合中的元素．(2)互异性：集合中任何两个元素都是互不相同的，即相同元素在同一个集合中不能重复出现．(3)无序性：集合与其组成元素的顺序无关．3.元素与集合的关系元素与集合之间的关系包括属于(记作a A ∈)和不属于(记作a A ∉)两种．4.集合的常用表示法集合的常用表示法有列举法、描述法、图示法(韦恩图)．5.常用数集的表示数集自然数集正整数集整数集有理数集实数集符号 NN ∗或N + Z Q R (二)集合间的基本关系1.集合A 为集合B 的子集，记作A B ⊆（或B A ⊇），读作“A 包含于B ”（或“B 包含A ”）.(2)真子集：若A B ⊆，且存在b B ∈，但b A ∉，则集合A 是集合B 的真子集，记作AB （或B A ⊃≠）. 读作“A 真包含于B ”或“B 真包含A ”.(3)相等：对于两个集合A 与B ，如果A B ⊆，同时B A ⊆，那么集合A 与B 相等，记作A =B ．(4)空集：把不含任何元素的集合叫做空集，记作∅；(三)集合的基本运算(1)交集：由所有属于集合A 且属于集合B 的元素组成的集合，叫做A 与B 的交集，记作A B ⋂，即{}|A B x x A x B ⋂=∈∈且．(2) 并集：由所有属于集合A 或属于集合B 的元素组成的集合，叫做A 与B 的并集，记作A B ⋃，(3) 即{}|A B x x A x B ⋃=∈∈或．(3)补集：对于一个集合A ，由全集U 中不属于集合A 的所有元素组成的集合称为集合A 相对于全集U 的补集，简称为集合A 的补集，记作U C A ，即{|,}U C A x x U x A =∈∉且．(四)集合的运算性质(1)集合的运算性质：①交换律：A ∪B ＝B ∪A ；A ∩B ＝B ∩A ；②结合律：(A ∪B )∪C ＝A ∪(B ∪C )；(A ∩B )∩C ＝A ∩(B ∩C )；③分配律：(A ∩B )∪C ＝(A ∪C )∩(B ∪C )；(A ∪B )∩C ＝(A ∩C )∪(B ∩C )；【集合常用结论】1.子集个数：含有n个元素的有限集合M，其子集个数为2n；其真子集个数为2n－1；其非空子集个数为2n－1；其非空真子集个数为2n－2.2. 是任何集合的子集，是任何非空集合的真子集.3.∁U(A∪B)＝(∁U A)∩(∁U B)；∁U(A∩B)＝(∁U A)∪(∁U B)；4.A∪B＝A⇔B⊆A；A∩B＝B⇔B⊆A.5.集合运算中的常用方法若已知的集合是不等式的解集，用数轴求解；若已知的集合是点集，用数形结合法求解；若已知的集合是抽象集合，用Venn图求解.二、简易逻辑(一).全称命题、特称(存在性)命题及其否定(1)全称命题p：∀x∈M，p(x)，其否定为特称(存在性)命题：¬p：∃x0∈M，¬p(x0).(2)特称(存在性)命题p：∃x0∈M，p(x0)，其否定为全称命题：¬p：∀x∈M，¬p(x).(二).充分条件与必要条件的判定方法(1)定义法：若p⇒q，则p是q的充分条件(或q是p的必要条件)；若p⇒q，且q⇏p，则p是q的充分不必要条件(或q是p的必要不充分条件).(2)集合法：利用集合间的包含关系。

高考一轮复习题型归纳专题1：集合

第一章：集合题型1、集合的基本概念知识点摘要：➢ 集合元素的特征：确定性、互异性、无序性。

➢ 集合常用的表示方法：列举法、描述法、图示法、区间法。

➢ 元素与集合的关系：属于和不属于。

➢ 常用数集的表示：C —复数集；R —实数集；Q —有理数集；Z —整数集；N —自然数集；N+或N*—正整数集。

➢ 集合分类：①按元素个数分为有限集、无限集和空集；②按元素属性分为数集、点集和其他元素。

典型例题精讲精练：1. 若},,0{},,1{2b a a a b a +=，求20202020b a+的值.【答案：1】2. 已知集合，，且B A },,0{B },,,{A ==-=y x y x xy x 求实数x 与y 的值.【答案：x=y=-1】3. 设R b a ∈,,集合b}ab {0a}b a {1，，，，=+,则=-a b （）【答案：C 】 A.1 B.-1 C.2 D.-24. 集合A=},2,0{a ，B=},1{2a .若A ∪B={0，1，2，4，16}，则a 的值为（）【答案：D 】A ．0 B.1 C.2 D.45. 已知集合{}5,4,3,2,1=A ，},,|),{(A y x A y A x y x B ∈-∈∈=，则B 集合中所含的元素的个数为（）【答案：D 】A.3B.6C.8D.10题型2、集合之间的基本关系知识点摘要：➢ 集合与集合之间的关系：①包含关系，②相等关系，③真子集关系。

➢ 规定：空集是任何集合的子集；是任何非空集合的真子集；一个集合是它自己的子集。

➢ 若集合有n 个元素，则该集合有n 2个子集，有12-n 个真子集，有22-n 个非空真子集。

典型例题精讲精练：2.1.集合关系判断问题1. 设集合},214||{},,412|{Z k k x x x N Z k k x x M ∈+==∈+==，则（）【答案：B 】 N M A =. N M B ⊂. N M C ⊃. ∅=N M D I .2. 设集合⎭⎬⎫⎩⎨⎧≤--=023|x x x M ，集合N={}01)4(|≤-⋅-）（x x x ，则M 与N 的关系是（）【答案：D 】 A. M=N B.M ∈N C. N M ≠⊃ D. N M ≠⊂3. 已知{}x y R y M =∈=|， N={}2|m x R x =∈，则下列关系中正确的是（）【答案：B 】A. N M ≠⊃B. M=NC. M ≠ND. M N ≠⊃4. 集合{}{}{}Z m m z z S Z l l y y P Z k k x x M ∈+==∈+==∈-==,16|,,13|,,23|之间的关系是（）【答案：C 】A. M P S ≠⊂≠⊂B. M P S ≠⊂=C. M P S =≠⊂D. M P S =≠⊃2.2.已知集合间的关系，求参数的取值范围5. 已知集合{}1|2==x x P ，集合{}1|==ax x Q ，若P Q ⊆,那么a 的值为。

高中数学一轮复习必备知识点大梳理

B
B C
A
C
．
②
A
B
或
A
A
B B
集合
A
与集合
B
相等；
③ A B 集合 A 是集合 B 的真子集．
例： N Z Q R C ； N Z Q R C ．
④空集是任何集合的子集，是任何非空集合的真子集．（6）集合的运算：
①交集： A B {x x A且x B} 集合 A 与集合 B 的交集； ②并集： A B {x x A或x B} 集合 A 与集合 B 的并集； ③补集：设U 为全集，集合 A 是U 的子集，则由U 中所有不属于 A 的元素组成的集合，叫做集合 A 在全集U 中的补集，记作 CU A．
f (x)
2 y n f (x) ， f (x) 0 ； 3 y ( f (x))0 ， f (x) 0 ； 4 y loga f (x) ， f (x) 0 ；
⑤ y log f (x) N ， f (x) 0 且 f (x) 1 ．
第 5 页共 75 页
（2）判断是否函数图像的方法：任取平行于 y 轴的直线，与图像最多只有一个公共点；
的根的判别式
△ b2 4ac 0
△ b2 4ac 0
△ b2 4ac 0
第 3 页共 75 页
y ax2 bx c(a 0)
ax 2 bx c 0(a 0)
{x1, x2}， x1 x2
{x0}
ax 2 bx c 0(a 0)
(, x1) (x2, )
(, x0 ) (x0 ,)
2
补充公式：
a2 b2 a b
2
2
ab
1
2
1
．

高三数学一轮复习第1章集合与常用逻辑用语第1课时集合的概念与运算精品课件

• (3)五个关系式A⊆B、A∩B＝A，A∪B＝B，∁UB⊆∁UA以及A∩(∁UB) ＝∅是两两等价的．
• 集合是高中数学的基础内容，也是高考数学的必考内容，难度不大，一般是一道选择题或填空题．通过对近两年高考试题的统计分析可以看出，对集合内容的考查一般以两种方式出现：一是考查集合的概念、集合间的关系及集合的运算．
• (3){x|x2－ax－1＝0}和{a|方程x2－ax－1＝0有实根}的意义不同．{x|x2－ax－1＝0}表示由二次方程x2－ax－1＝0的解构成的集合，而集合{a|方程x2－ax－1＝0有实根}表示方程x2－ax－1＝0有实数解时参数a的范围构成的集合．
【变式训练】 1.现有三个实数的集合，既可以表示为a，ba，1，也可表示为{a2，a＋b,0}，则 a2 011＋b2 011＝________.
命题与量词、基本逻辑联结词
1.了解命题的概念． 2.了解逻辑联结词“或”、“且”、“非”的含义． 3.理解全称量词与存在量词的含义． 4.能正确地对含有一个量词的命题进行否定．
充分条件、
必要
条件 1.了解“若p，则q”形式的命题及其逆命题、否命题与逆否命题，会分析四
与命
种命题的相互关系．
题的 2.理解必要条件、充分条件与充要条件的意义.
①集合 S＝{a＋b 3|a，b 为整数}为封闭集； ②若 S 为封闭集，则一定有 0∈S； ③封闭集一定是无限集； ④若 S 为封闭集，则满足 S⊆T⊆R 的任意集合 T 也是封闭集．其中的真命题是________．(写出所有真命题的序号)
序号结论
理由
• 【全解全析】对于任意整数 a1，b1，a2，b2，有 a1＋b1 3＋a2＋b2 3
B．{a|a≤2或a≥4}

高考数学第一轮复习集合与简易逻辑

高考数学第一轮复习集合与简易逻辑一、知识结构二、考点目标定位1.理解集合、子集、补集、交集、并集的概念；了解属于、包含、相等关系的意义.2.掌握有关的术语和符号，并会用它们正确表示一些简单的集合.3.理解逻辑联结词“或”“且”“非”的含义；理解四种命题及其相互关系；掌握充要条件的意义.4.学会运用数形结合、分类讨论的思想方法分析和解决有关集合的问题，形成良好的思维品质.三、复习方略指南本章内容在高考中以考查空集与全集的概念，元素与集合、集合与集合之间的关系，集合的交、并、补运算为重点，以上内容又以集合的运算为重点考查内容.逻辑联结词与充要条件这部分，以充要条件为重点考查内容.本章内容概念性强，考题大都为容易的选择题，因此复习中应注意：1.复习集合，可以从两个方面入手，一方面是集合的概念之间的区别与联系，另一方面是对集合知识的应用.2.主要是把握集合与元素、集合与集合之间的关系，弄清有关的术语和符号，特别是对集合中的元素的属性要分清楚.3.要注意逻辑联结词“或”“且”“非”与集合中的“并”“交”“补”是相关的，二者相互对照可加深对双方的认识和理解.4.复习逻辑知识时，要抓住所学的几个知识点，通过解决一些简单的问题达到理解、掌握逻辑知识的目的.5.集合多与函数、方程、不等式有关，要注意知识的融会贯通.一、集合的概念与运算知识梳理1.集合的有关概念2.元素与集合、集合与集合之间的关系（1）元素与集合：“∈”或“∉”.（2）集合与集合之间的关系：包含关系、相等关系. 3.集合的运算（1）交集：由所有属于集合A 且属于集合B 的元素所组成的集合，叫做集合A 与B 的交集，记为A ∩B ，即A ∩B ={x |x ∈A 且x ∈B }.（2）并集：由所有属于集合A 或属于集合B 的元素所组成的集合，叫做集合A 与集合B 的并集，记为A ∪B ，即A ∪B ={x |x ∈A 或x ∈B }.（3）补集：一般地，设S 是一个集合，A 是S 的一个子集（即A ⊆S ），由S 中所有不属于A 的元素组成的集合，叫做子集A 在全集S 中的补集（或余集），记为SA ，即SA ={x |x ∈S 且x ∉A }.点击双基1.已知集合M ={x |x 2＜4}，N ={x |x 2－2x －3＜0}，则集合M ∩N 等于 A.{x |x ＜－2} B.{x |x ＞3} C.{x |－1＜x ＜2} D.{x |2＜x ＜3}解析：M ={x |x 2＜4}={x |－2＜x ＜2}，N ={x |x 2－2x －3＜0}={x |－1＜x ＜3}，结合数轴，0-1-2231x∴M ∩N ={x |－1＜x ＜2}. 答案：C2.已知集合A ={x ∈R |x ＜5－2}，B ={1，2，3，4}，则（RA ）∩B 等于A.{1，2，3，4}B.{2，3，4}C.{3，4}D.{4}解析：RA ={x ∈R |x ≥5－2}，而5－2∈（3，4），∴（RA ）∩B ={4}.答案：D3.设集合P ={1，2，3，4，5，6}，Q ={x ∈R |2≤x ≤6}，那么下列结论正确的是 A.P ∩Q =P B.P ∩Q Q C.P ∪Q =Q D.P ∩Q P 解析：P ∩Q ={2，3，4，5，6}，∴P ∩Q P . 答案：D4.设U 是全集，非空集合P 、Q 满足P Q U ，若求含P 、Q 的一个集合运算表达式，使运算结果为空集∅，则这个运算表达式可以是_______________.解析：构造满足条件的集合，实例论证.U =｛1，2，3｝，P =｛1｝，Q =｛1，2｝，则（UQ ）=｛3｝，（UP ）={2，3}，易见（UQ ）∩P =∅.答案：（UQ ）∩P5.已知集合A ＝｛0，1｝，B ＝｛x ｜x ∈A ，x ∈Ｎ*｝，C ＝｛x ｜x ⊆A ｝，则A 、B 、C 之间的关系是___________________.解析：用列举法表示出B ＝｛1｝，C ＝｛∅，｛1｝，｛0｝，A ｝，易见其关系.这里A 、B 、C是不同层次的集合，C 以A 的子集为元素，同一层次的集合可有包含关系，不同层次的集合之间只能是从属关系.答案：B A ，A ∈C ，B ∈C 典例剖析【例1】函数f （x ）=⎩⎨⎧∈-∈,,M x xP x x其中P 、M 为实数集R 的两个非空子集，又规定f （P ）={y |y =f （x ），x ∈P }，f （M ）={y |y =f （x ），x ∈M }.给出下列四个判断，其中正确判断有 ①若P ∩M =∅，则f （P ）∩f （M ）=∅ ②若P ∩M ≠∅，则f （P ）∩f （M ）≠∅ ③若P ∪M =R ，则f （P ）∪f （M ）=R ④若P ∪M ≠R ，则f （P ）∪f （M ）≠RA.1个B.2个C.3个D.4个剖析：由题意知函数f （P ）、f （M ）的图象如下图所示.f M ()f P ()xyO设P =［x 2，+∞），M =（－∞，x 1］，∵|x 2|＜|x 1|，f （P ）=［f （x 2），+∞），f （M ）=［f （x 1），+∞），则P ∩M =∅.f M ()f P ()xy f x ()1f x ()2x 1x 2O而f （P ）∩f （M ）=［f （x 1），+∞）≠∅，故①错误.同理可知②正确.设P =［x 1，+∞），M =（－∞，x 2］，∵|x 2|＜|x 1|，则P ∪M =R .f （P ）=［f （x 1），+∞），f （M ）=［f （x 2），+∞）， f （P ）∪f （M ）=［f （x 1），+∞）≠R ，故③错误.同理可知④正确. 答案：B【例2】已知A ={x |x 3＋3x 2＋2x ＞0}，B ={x |x 2＋ax ＋b ≤0}且A ∩B ={x |0＜x ≤2}，A ∪B ＝｛x ｜x ＞－2｝，求a 、b 的值.解：A ={x |－2＜x ＜－1或x ＞0}，设B =［x 1，x 2］，由A ∩B =（0，2］知x 2＝2，且－1≤x 1≤0， ①由A ∪B =（－2，+∞）知－2≤x 1≤－1. ②由①②知x 1＝－1，x 2＝2，∴a ＝－（x 1＋x 2）＝－1，b ＝x 1x 2＝－2.评述：本题应熟悉集合的交与并的涵义，熟练掌握在数轴上表示区间（集合）的交与并的方法.【例3】记函数f （x ）=132++-x x 的定义域为A ，g （x ）=lg ［（x －a －1）（2a －x ）］（a ＜1＝的定义域为B . （1）求A ；（2）若B ⊆A ，求实数a 的取值范围.提示：（1）由2－13++x x ≥0，得11+-x x ≥0，∴x ＜－1或x ≥1，即A =（－∞，－1）∪［1，+∞］（2）由（x －a －1）（2a －x ）＞0，得（x －a －1）（x －2a ）＜0. ∵a ＜1，∴a +1＞2a .∴B =（2a ，a +1）.∵B ⊆A ，∴2a ≥1或a +1≤－1，即a ≥21或a ≤－2.而a ＜1，∴21≤a ＜1或a ≤－2.故当B ⊆A 时，实数a 的取值范围是（－∞，－2）∪［21，1］.【例4】设集合P={m|－1＜m ≤0}，Q={m ∈R |mx 2+4mx －4＜0对任意实数x 恒成立}，则下列关系中成立的是A.P QB.Q PC.P=QD.P ∩Q=Q剖析：Q ={m ∈R |mx 2+4mx －4＜0对任意实数x 恒成立}，对m 分类：①m =0时，－4＜0恒成立；②m ＜0时，需Δ=（4m ）2－4×m ×（－4）＜0，解得m ＜0. 综合①②知m ≤0，∴Q ={m ∈R |m ≤0}. 答案：A评述：本题容易忽略对m =0的讨论，应引起大家足够的重视.【例5】已知集合A ={（x ，y ）|x 2+mx －y +2=0}，B ={（x ，y ）|x －y +1=0，0≤x ≤2}，如果A ∩B ≠∅，求实数m 的取值范围.剖析：如果目光总是停留在集合这一狭窄的知识范围内，此题的思维方法是很难找到的.事实上，集合符号在本题中只起了一种“化妆品”的作用，它的实际背景是“抛物线x 2+mx －y +2=0与线段x －y +1=0（0≤x ≤2）有公共点，求实数m 的取值范围”.这种数学符号与数学语言的互译，是考生必须具备的一种数学素质.解：由⎩⎨⎧≤≤=+-=+-+),20(01,022x y x y mx x 得x 2+（m －1）x +1=0. ① ∵A ∩B ≠∅，∴方程①在区间［0，2］上至少有一个实数解.首先，由Δ=（m －1）2－4≥0，得m ≥3或m ≤－1.当m ≥3时，由x 1+x 2=－（m －1）＜0及x 1x 2=1知，方程①只有负根，不符合要求；当m ≤－1时，由x 1+x 2=－（m －1）＞0及x 1x 2=1＞0知，方程①有两个互为倒数的正根.故必有一根在区间（0，1］内，从而方程①至少有一个根在区间［0，2］内.综上所述，所求m 的取值范围是（－∞，－1）.评述：上述解法应用了数形结合的思想.如果注意到抛物线x 2+mx －y +2=0与线段x －y +1=0（0≤x ≤2）的公共点在线段上，本题也可以利用公共点内分线段的比λ的取值范围建立关于m 的不等式来解.【例6】设m ∈R ，A ={（x ，y ）|y =－3x +m }，B ={（x ，y ）|x =cos θ，y =sin θ，0＜θ＜2π＝，且A ∩B ={（cos θ1，sin θ1），（cos θ2，sin θ2）}（θ1≠θ2），求m 的取值范围.提示：根据题意，直线y =－3x +m 与圆x 2+y 2=1（x ≠1）交于两点，22)3(1||-+m ＜1且0≠－3×1+m .∴－2＜m ＜2且m ≠3. 答案：－2＜m ＜2且m ≠3.【例7】设M 、N 是两个非空集合，定义M 与N 的差集为M －N ={x |x ∈M 且x ∉N }，则M －（M －N ）等于A.NB.M ∩NC.M ∪ND.M 解析：M －N ={x |x ∈M 且x ∉N }是指图（1）中的阴影部分.MNMN(1) (2)同样M －（M －N ）是指图（2）中的阴影部分.答案：B【例8】设集合P ={1，a ，b }，Q ={1，a 2，b 2}，已知P =Q ，求1+a 2+b 2的值.解：∵P =Q ，∴⎪⎩⎪⎨⎧==22,b b a a①或⎪⎩⎪⎨⎧==.,22a b b a②解①得a =0或a =1，b =0或b =1.（舍去）由②得a =b 2=a 4，∴a =1或a 3=1. a =1不合题意， ∴a 3=1（a ≠1）.∴a =ω，b =ω2，其中ω=－21+23i. 故1+a 2+b 2=1+ω2+ω4=1+ω+ω2=0.练习测试1.集合A ={（x ，y ）|x +y =0}，B ={（x ，y ）|x －y =2}，则A ∩B 是 A.（1，－1）B.⎩⎨⎧-==11y xC.{（1，－1）}D.{1，－1}2.设集合A ={5，log 2（a +3）}，集合B ={a ，b }.若A ∩B ={2}，则A ∪B =______________. 3.设A ={x |1＜x ＜2}，B ={x |x ＞a }，若A B ，则a 的取值范围是___________________.4.已知集合A ={x ∈R |ax 2+2x +1=0，a ∈R }只有一个元素，则a 的值为__________________.5.设A 、B 、I 均为非空集合，且满足A ⊆B ⊆I ，则下列各式中错误．．的是A.（IA ）∪B =IB.（IA ）∪（IB ）=I C.A ∩（IB ）=∅D.（I A ）∩（IB ）=IB6.记函数f （x ）=log 2（2x －3）的定义域为集合M ，函数g （x ）= )1)(3(--x x 的定义域为集合N .求：（1）集合M 、N ；（2）集合M ∩N 、M ∪N .7.已知A ={x ∈R |x 2+2x +p =0}且A ∩{x ∈R |x ＞0}=∅，求实数p 的取值范围.8.已知P ={（x ，y ）|（x +2）2+（y －3）2≤4}，Q ={（x ，y ）|（x +1）2+（y －m ）2＜41}，且P ∩Q =Q ，求m 的取值范围.9.若B ={x |x 2－3x +2＜0}，是否存在实数a ，使A ={x |x 2－（a +a 2）x +a 3＜0}且A ∩B =A ？请说明你的理由.小结1.对于集合问题，要首先确定属于哪类集合（数集、点集或某类图形），然后确定处理此类问题的方法.2.关于集合的运算，一般应把各参与运算的集合化到最简，再进行运算.3.含参数的集合问题，多根据集合元素的互异性来处理.4.集合问题多与函数、方程、不等式有关，要注意各类知识的融会贯通.解决问题时常用数形结合、分类讨论等数学思想.教学点睛1.对于集合问题，要首先确定属于哪类集合（数集、点集或某类图形），然后确定处理此类问题的方法.2.集合问题多与函数、方程、不等式有关，要注意各类知识的融会贯通.3.强化数形结合、分类讨论的数学思想.二、逻辑联结词与四种命题知识梳理 1.逻辑联结词（1）命题：可以判断真假的语句叫做命题. （2）逻辑联结词：“或”“且”“非”这些词叫做逻辑联结词.（3）简单命题与复合命题：不含逻辑联结词的命题叫简单命题；由简单命题和逻辑联结词构成的命题叫做复合命题.（4）真值表：表示命题真假的表叫真值表. 2.四种命题（1）四种命题原命题：如果p ，那么q （或若p 则q ）；逆命题：若q 则p ；否命题：若⌝p 则⌝q ；逆否命题：若⌝q 则⌝p .（2）四种命题之间的相互关系这里，原命题与逆否命题，逆命题与否命题是等价命题.点击双基1.由“p :8+7=16，q :π＞3”构成的复合命题，下列判断正确的是 A.p 或q 为真，p 且q 为假，非p 为真 B.p 或q 为假，p 且q 为假，非p 为真 C.p 或q 为真，p 且q 为假，非p 为假 D.p 或q 为假，p 且q 为真，非p 为真解析：因为p 假，q 真，由复合命题的真值表可以判断，p 或q 为真，p 且q 为假，非p 为真.答案：A2.命题p :若a 、b ∈R ，则|a |+|b |＞1是|a +b |＞1的充分而不必要条件；命题q :函数y =2|1|--x 的定义域是（－∞，－1］∪［3，+∞），则A.“p 或q ”为假B.“p 且q ”为真C. p 真q 假D. p 假q 真解析：∵|a +b |≤|a |+|b |，若|a |+|b |＞1，不能推出|a +b |＞1，而|a +b |＞1，一定有|a |+|b |＞1，故命题p 为假. 又由函数y =2|1|--x 的定义域为|x －1|－2≥0，即|x －1|≥2，即x －1≥2或x －1≤－2.故有x ∈（－∞，－1］∪［3，+∞）. ∴q 为真命题. 答案：D3.设函数f （x ）的定义域为R ，有下列三个命题：①若存在常数M ，使得对任意x ∈R ，有f （x ）≤M ，则M 是函数f （x ）的最大值； ②若存在x 0∈R ，使得对任意x ∈R ，且x ≠x 0，有f （x ）＜f （x 0），则f （x 0）是函数f （x ）的最大值；③若存在x 0∈R ，使得对任意x ∈R ，有f （x ）≤f （x 0），则f （x 0）是函数f （x ）的最大值.这些命题中，真命题的个数是A.0B.1C.2D.3 解析：①错.原因：可能“=”不能取到.②③都正确. 答案：C4.命题“若m ＞0，则关于x 的方程x 2+x －m =0有实数根”与它的逆命题、否命题、逆否命题中，真命题的个数为___________________.解析：先写出其命题的逆命题、否命题、逆否命题，逐一判断.答案：25.已知命题p:函数y=log a（ax+2a）（a＞0且a≠1）的图象必过定点（－1，1）；命题q:如果函数y=f（x－3）的图象关于原点对称，那么函数y=f（x）的图象关于点（3，0）对称.则A.“p且q”为真B.“p或q”为假C. p真q假D. p假q真解析：解决本题的关键是判定p、q的真假.由于p真，q假（可举反例y=x+3），因此正确答案为C.答案：C典例剖析【例1】给出命题“已知a、b、c、d是实数，若a=b，c=d，则a+c=b+d”，对其原命题、逆命题、否命题、逆否命题而言，真命题有A.0个B.2个C.3个D.4个剖析：原命题和逆否命题为真.答案：B【例2】若a、b、c∈R，写出命题“若ac＜0，则ax2+bx+c=0有两个不相等的实数根”的逆命题、否命题、逆否命题，并判断这三个命题的真假.思路：认清命题的条件p和结论q，然后按定义写出逆命题、否命题、逆否命题，最后判断真假.解：逆命题“若ax2+bx+c=0（a、b、c∈R）有两个不相等的实数根，则ac＜0”是假命题，如当a=1，b=－3，c=2时，方程x2－3x+2=0有两个不等实根x1=1，x2=2，但ac=2＞0.否命题“若ac≥0，则方程ax2+bx+c=0（a、b、c∈R）没有两个不相等的实数根”是假命题.这是因为它和逆命题互为逆否命题，而逆命题是假命题.逆否命题“若ax2+bx+c=0（a、b、c∈R）没有两个不相等的实数根，则ac≥0”是真命题.因为原命题是真命题，它与原命题等价.评述：解答命题问题，识别命题的条件p与结论q的构成是关键.【例3】指出下列复合命题的形式及其构成.（1）若α是一个三角形的最小内角，则α不大于60°；（2）一个内角为90°，另一个内角为45°的三角形是等腰直角三角形；（3）有一个内角为60°的三角形是正三角形或直角三角形.解：（1）是非p形式的复合命题，其中p:若α是一个三角形的最小内角，则α＞60°.（2）是p且q形式的复合命题，其中p:一个内角为90°，另一个内角为45°的三角形是等腰三角形，q:一个内角为90°，另一个内角为45°的三角形是直角三角形.（3）是p或q形式的复合命题，其中p:有一个内角为60°的三角形是正三角形，q：有一个内角为60°的三角形是直角三角形.【例4】写出命题“当abc=0时，a=0或b=0或c=0”的逆命题、否命题、逆否命题，并判断它们的真假.剖析：把原命题改造成“若p则q”形式，再分别写出其相应的逆命题、否命题、逆否命题.在判断真假时要注意利用等价命题的原理和规律.解：原命题：若abc=0，则a=0或b=0或c=0，是真命题.逆命题：若a=0或b=0或c=0，则abc=0，是真命题.否命题：若abc≠0，则a≠0且b≠0且c≠0，是真命题.逆否命题：若a≠0且b≠0且c≠0，则abc≠0，是真命题.【例5】有A、B、C三个盒子，其中一个内放有一个苹果，在三个盒子上各有一张纸条.A盒子上的纸条写的是“苹果在此盒内”，B盒子上的纸条写的是“苹果不在此盒内”，C盒子上的纸条写的是“苹果不在A盒内”.如果三张纸条中只有一张写的是真的，请问苹果究竟在哪个盒子里？解：若苹果在A盒内，则A、B两个盒子上的纸条写的为真，不合题意.若苹果在B盒内，则A、B两个盒子上的纸条写的为假，C盒子上的纸条写的为真，符合题意，即苹果在B盒内.同样，若苹果在C盒内，则B、C两盒子上的纸条写的为真，不合题意.综上，苹果在B盒内.练习测试1.如果原命题的结论是“p且q”形式，那么否命题的结论形式为A.⌝p且⌝qB.⌝p或⌝qC.⌝p或⌝qD.⌝q或⌝p2.下列四个命题中真命题是①“若xy=1，则x、y互为倒数”的逆命题②“面积相等的三角形全等”的否命题③“若m≤1，则方程x2－2x+m=0有实根”的逆否命题④“若A∩B=B，则A⊆B”的逆否命题A.①②B.②③C.①②③D.③④3.分别用“p或q”“p且q”“非p”填空.（1）命题“15能被3和5整除”是___________________形式；（2）命题“16的平方根是4或－4”是______________形式；（3）命题“李强是高一学生，也是共青团员”是___________________形式.4.命题“若ab=0，则a、b中至少有一个为零”的逆否命题是_______________.5.在一次模拟打飞机的游戏中，小李接连射击了两次，设命题p1“第一次射击击中飞机”，命题p2“第二次射击击中飞机”，试用p1、p2及联结词“或”“且”“非”表示下列命题：（1）两次都击中飞机；（2）两次都没击中飞机；（3）恰有一次击中飞机；（4）至少有一次击中飞机.6.设A、B为两个集合.下列四个命题：①A B⇔对任意x∈A，有x∉B；②A B⇔A∩B=∅；③A B⇔A B；④A B⇔存在x ∈A，使得x∉B.其中真命题的序号是______________.（把符合要求的命题序号都填上）7.命题：已知a、b为实数，若x2＋ax＋b≤0有非空解集，则a2－4b≥0，写出该命题的逆命题、否命题、逆否命题，并判断这些命题的真假.8.写出下列命题非的形式：（1）p:函数f（x）=ax2+bx+c的图象与x轴有唯一交点；（2）q:若x=3或x=4，则方程x2－7x+12=0.9.小李参加全国数学联赛，有三位同学对他作如下的猜测.甲：小李非第一名，也非第二名；乙：小李非第一名，而是第三名；丙：小李非第三名而是第一名.竞赛结束后发现，一人全猜对，一人猜对一半，一人全猜错，问：小李得了第几名？10、写出下列各命题的否定及其否命题，并判断它们的真假.（1）若x、y都是奇数，则x+y是偶数；（2）若xy=0，则x=0或y=0；（3）若一个数是质数，则这个数是奇数.小结1.有的“p或q”与“p且q”形式的复合命题语句中，字面上未出现“或”与“且”字，此时应从语句的陈述中搞清含义，从而分清是“p或q”还是“p且q”形式.一般地，若两个命题属于同时都要满足的为“且”，属于并列的为“或”.2.原命题与它的逆否命题同为真假，原命题的逆命题与否命题同为真假，所以对一些命题的真假判断（或推证），我们可通过对与它同真假的（具有逆否关系的）命题来判断（或推证）.教学点睛1.有的“p或q”与“p且q”形式的复合命题语句中，字面上未出现“或”与“且”字，此时应从语句的陈述中搞清含义，从而分清是“p或q”还是“p且q”形式.一般地，若两个命题属于同时都要满足的为“且”，属于并列的为“或”.2.要明确原命题、否命题、逆命题、逆否命题之间的关系.三、充要条件与反证法知识梳理1.充分条件：如果p⇒q，则p叫q的充分条件，原命题（或逆否命题）成立，命题中的条件是充分的，也可称q是p的必要条件.2.必要条件：如果q⇒p，则p叫q的必要条件，逆命题（或否命题）成立，命题中的条件为必要的，也可称q是p的充分条件.3.充要条件：如果既有p⇒q，又有q⇒p，记作p⇔q，则p叫做q的充分必要条件，简称充要条件，原命题和逆命题（或逆否命题和否命题）都成立，命题中的条件是充要的.4.反证法：当直接证明有困难时，常用反证法.点击双基1.ac2＞bc2是a＞b成立的A.充分而不必要条件B.充要条件C.必要而不充分条件D.既不充分也不必要条件解析：a＞b ac2＞bc2，如c=0.答案：A2.已知a、b、c为非零的平面向量.甲：a·b=a·c，乙：b=c，则A.甲是乙的充分条件但不是必要条件B.甲是乙的必要条件但不是充分条件C.甲是乙的充要条件D.甲既不是乙的充分条件也不是乙的必要条件解析：命题甲:a ·b =a ·c ⇒a ·（b －c ）=0⇒a =0或b =c . 命题乙:b =c ，因而乙⇒甲，但甲乙. 故甲是乙的必要条件但不是充分条件. 答案：B3.在△ABC 中，“A ＞30°”是“sin A ＞21”的 A.充分而不必要条件 B.必要而不充分条件 C.充分必要条件D.既不充分也不必要条件解析：在△ABC 中，A ＞30°⇒0＜sin A ＜1sin A ＞21，sin A ＞21⇒30°＜A ＜150°⇒A ＞30°.∴“A ＞30°”是“sin A ＞21”的必要不充分条件. 答案：B4.若条件p :a ＞4，q :5＜a ＜6，则p 是q 的______________.解析：a ＞45＜a ＜6，如a =7虽然满足a ＞4，但显然a 不满足5＜a ＜6. 答案：必要不充分条件5.若a 、b 、c 是常数，则“a ＞0且b 2－4ac ＜0”是“对任意x ∈R ，有ax 2+bx +c ＞0”的A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件解析：若a ＞0且b 2－4ac ＜0，则对任意x ∈R ，有ax 2+bx +c ＞0，反之，则不一定成立.如a =0，b =0且c ＞0时，也有对任意x ∈R ，有ax 2+bx +c ＞0.因此应选A.答案：A 典例剖析【例1】使不等式2x 2－5x －3≥0成立的一个充分而不必要条件是 A.x ＜0 B.x ≥0C.x ∈{－1，3，5}D.x ≤－21或x ≥3 剖析：∵2x 2－5x －3≥0成立的充要条件是x ≤－21或x ≥3，∴对于A 当x =－31时2x 2－5x －3≥0.同理其他也可用特殊值验证.答案：C【例2】求证：关于x 的方程ax 2+bx +c =0有一根为1的充分必要条件是a +b +c =0.证明：（1）必要性，即“若x =1是方程ax 2+bx +c =0的根，则a +b +c =0”.∵x =1是方程的根，将x =1代入方程，得a ·12+b ·1+c =0，即a +b +c =0.（2）充分性，即“若a +b +c =0，则x =1是方程ax 2+bx +c =0的根”.把x =1代入方程的左边，得a ·12+b ·1+c =a +b +c .∵a +b +c =0，∴x =1是方程的根. 综合（1）（2）知命题成立.【例3】求ax 2+2x +1=0（a ≠0）至少有一负根的充要条件. 证明：必要性：（1）方程有一正根和一负根，等价于⇒⎪⎩⎪⎨⎧<=>-=0104421a x x a Δa ＜0. （2）方程有两负根，等价于⇒⎪⎪⎪⎩⎪⎪⎪⎨⎧><-≥-=0102044aa a Δ0＜a ≤1.综上可知，原方程至少有一负根的必要条件是a ＜0或0＜a ≤1.充分性：由以上推理的可逆性，知当a ＜0时方程有异号两根；当0＜a ≤1时，方程有两负根.故a ＜0或0＜a ≤1是方程ax 2+2x +1=0至少有一负根的充分条件.答案：a ＜0或0＜a ≤1.【例4】下列说法对不对?如果不对，分析错误的原因.（1）x 2＝x ＋2是x 2+x =x 2的充分条件；（2）x 2＝x ＋2是x 2+x =x 2的必要条件.解：（1）x 2=x +2是x 2+x =x 2的充分条件是指x 2=x +2⇒x 2+x =x 2.但这里“⇒”不成立，因为x =－1时，“⇒”左边为真，但右边为假.得出错误结论的原因可能是应用了错误的推理：x 2=x +2⇒x =2+x ⇒x 2=x 2+x .这里推理的第一步是错误的（请同学补充说明具体错在哪里）.（2）x 2=x +2是x 2+x =x 2的必要条件是指x 2+x =x 2⇒x 2=x +2.但这里“⇒”不成立，因为x =0时，“⇒”左边为真，但右边为假.得出错误结论的原因可能是用了错误的推理:x 2+x =x 2⇒2+x =x ⇒x +2=x 2.这里推理的第一步是错误的（请同学补充说明具体错在哪里）. 评述：此题的解答比较注重逻辑推理.事实上，也可以从真值集合方面来分析：x 2=x +2的真值集合是{－1，2}，x 2+x =x 2的真值集合是{0，2}，{－1，2}{0，2}，而{0，2} {－1，2}，所以（1）（2）两个结论都不对. 【例5】指出下列命题中，p 是q 的什么条件. （1）p :0＜x ＜3，q :|x －1|＜2；（2）p :（x －2）（x －3）=0，q :x =2；（3）p :c =0，q :抛物线y =ax 2+bx +c 过原点. 解：（1）p :0＜x ＜3，q :－1＜x ＜3. p 是q 的充分但不必要条件.（2）p q ，q ⇒p .p 是q 的必要但不充分条件.（3）p 是q 的充要条件.评述：依集合的观点看，若A B ，则A 是B 的充分条件，B 是A 的必要条件；若A =B ，则A 是B 的充要条件.练习测试1.已知p 是r 的充分不必要条件，s 是r 的必要条件，q 是s 的必要条件，那么p 是q 成立的A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件2. “cos2α=－23”是“α=k π+12π5，k ∈Z ”的 A.必要不充分条件 B.充分不必要条件 C.充分必要条件 D.既不充分又不必要条件 3.在△ABC 中，“A ＞B ”是“cos A ＜cos B ”的A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件 4.命题A ：两曲线F （x ，y ）＝0和G （x ，y ）=0相交于点P （x 0，y 0），命题B ：曲线F （x ，y ）+λG （x ，y ）＝0（λ为常数）过点P （x 0，y 0），则A 是B 的__________条件.5.函数f （x ）=x 2－2ax －3在区间［1，2］上存在反函数的充分必要条件是 A.a ∈（－∞，1］ B.a ∈［2，+∞）C.α∈［1，2］D.a ∈（－∞，1］∪［2，+∞）6.已知数列{a n }的前n 项和S n =p n+q （p ≠0且p ≠1），求数列{a n }成等比数列的充要条件. 7.设集合U =｛（x ，y ）｜x ∈R ，y ∈R ｝，A =｛（x ，y ）|2x －y +m ＞0｝，B =｛（x ，y ）|x +y－n ≤0｝，那么点P （2，3）∈A ∩（UB ）的充要条件是A.m ＞－1，n ＜5B.m ＜－1，n ＜5C.m ＞－1，n ＞5D.m ＜－1，n ＞58.已知关于x 的一元二次方程mx 2－4x +4=0， ① x 2－4mx +4m 2－4m －5=0. ② 求使方程①②都有实根的充要条件. 9.已知a 、b 、c 是互不相等的非零实数.求证：三个方程ax 2+2bx +c =0，bx 2+2cx +a =0，cx 2+2ax +b =0至少有一个方程有两个相异实根.10.若x 、y 、z 均为实数，且a =x 2－2y +2π，b =y 2－2z +3π，c =z 2－2x +6π，则a 、b 、c 中是否至少有一个大于零？请说明理由.小结1.要注意一些常用的“结论否定形式”，如“至少有一个”“至多有一个”“都是”的否定形式是“一个也没有”“至少有两个”“不都是”.2.证明充要性要从充分性、必要性两个方面来证明. 教学点睛1.掌握常用反证法证题的题型，如含有“至少有一个”“至多有一个”等字眼多用反证法.2.强调反证法的第一步，要与否命题分清.3.要证明充要性应从充分性、必要性两个方面来证.练习测试解答一、集合的概念与运算1、解析：⎩⎨⎧=-=+20y x y x ⇒⎩⎨⎧-==.1,1y x答案：C2、解析：∵A ∩B ={2}，∴log 2（a +3）=2.∴a =1.∴b =2.∴A ={5，2}，B ={1，2}.∴A ∪B ={1，2，5}. 答案：{1，2，5}3、解析：A B 说明A 是B 的真子集，利用数轴（如下图）可知a ≤1.a 1 2答案：a ≤14、解析：若a =0，则x =－21. 若a ≠0，Δ=4－4a =0，得a =1. 答案：a =0或a =15、解析一：∵A 、B 、I 满足A ⊆B ⊆I ，先画出文氏图，根据文氏图可判断出A 、C 、D 都是正确的.B AI解析二：设非空集合A 、B 、I 分别为A ={1}，B ={1，2}，I ={1，2，3}且满足A ⊆B ⊆I .根据设出的三个特殊的集合A 、B 、I 可判断出A 、C 、D 都是正确的.答案：B6、解：（1）M ={x |2x －3＞0}={x |x ＞23}； N ={x |（x －3）（x －1）≥0}={x |x ≥3或x ≤1}. （2）M ∩N ={x |x ≥3}；M ∪N ={x |x ≤1或x ＞23}.7、解：∵A ∩{x ∈R |x ＞0}=∅，∴（1）若A =∅，则Δ=4－4p ＜0，得p ＞1；（2）若A ≠∅，则A ={x |x ≤0}，即方程x 2+2x +p =0的根都小于或等于0. 设两根为x 1、x 2，则⎪⎩⎪⎨⎧≥=≤-=+≥-=.0,02,0442121p x x x x p Δ ∴0≤p ≤1. 综上所述，p ≥0. 8、解：点集P 表示平面上以O 1（－2，3）为圆心，2为半径的圆所围成的区域（包括圆周）；点集Q 表示平面上以O 2（－1，m ）为圆心，21为半径的圆的内部.要使P ∩Q ＝Q ，应使⊙O 2内含或内切于⊙O 1.故有｜O 1O 2｜2≤（R 1－R 2）2，即（－1＋2）2＋（m －3）2≤（2－21）2.解得3－25≤m ≤3＋25.评述：本题选题目的是：熟悉用集合语言表述几何问题，利用数形结合方法解题.9、解：∵B ={x |1＜x ＜2}，若存在实数a ，使A ∩B =A ，则A ={x |（x －a ）（x －a 2）＜0}. （1）若a =a 2，即a =0或a =1时，此时A ={x |（x －a ）2＜0}=∅，满足A ∩B =A ，∴a =0或a =1.（2）若a 2＞a ，即a ＞1或a ＜0时，A ={x |0＜x ＜a 2}，要使A ∩B =A ，则⎩⎨⎧≤≥212a a ⇒1≤a≤2，∴1＜a ≤2.（3）若a 2＜a ，即0＜a ＜1时，A ={x |a ＜x ＜a 2}，要使A ∩B =A ，则⎩⎨⎧≥≤122a a ⇒1≤a ≤2，∴a ∈∅.综上所述，当1≤a ≤2或a =0时满足A ∩B =A ，即存在实数a ，使A ={x |x 2－（a +a 2）x +a 3＜0＝且A ∩B =A 成立.二、逻辑联结词与四种命题1、解析：p 且q 的否定为⌝p 或⌝q .答案：B2、解析：写出满足条件的命题再进行判断.答案：C 3、答案：（1）p 且q （2）p 或q （3）p 且q 4、解：（1）两次都击中飞机是p 1且p 2；（2）两次都没击中飞机是⌝p 1且⌝p 2；（3）恰有一次击中飞机是p 1且⌝p 2，或p 2且⌝p 1；（4）至少有一次击中飞机是p 1或p 2. 5、答案：若a ≠0且b ≠0，则ab ≠06、解析：A B ⇔存在x ∈A ，有x ∉B ，故①错误；②错误；④正确.亦或如下图所示.B AA B ∩③反例如下图所示.ABA B ⇒A B .反之，同理.答案：④7、分析：原命题中，a 、b 为实数是前提，条件是x 2+ax +b ≤0有非空解集（即不等式有解），结论是a 2－4b ≥0，由四种命题的关系可得出其他三种命题.解：逆命题：已知a 、b 为实数，若a 2－4b ≥0，则x 2+ax +b ≤0有非空解集.否命题：已知a 、b 为实数，若x 2+ax +b ≤0没有非空解集，则a 2－4b ＜0.逆否命题：已知a 、b 为实数，若a 2－4b ＜0，则x 2+ax +b ≤0没有非空解集. 原命题、逆命题、否命题、逆否命题均为真命题.8、解：（1）函数f （x ）=ax 2+bx +c 的图象与x 轴没有交点或至少有两个交点.（2）若x =3或x =4，则x 2－7x +12≠0. 9、解：（1）假设小李得了第三名，则甲全猜对，乙全猜错，显然与题目已知条件相矛盾，故假设不可能.（2）假设小李得了第二名，则甲猜对一半，乙猜对一半，也与已知条件矛盾，故假设不可能.（3）假设小李得了第一名，则甲猜对一半，乙全猜错，丙全猜对，无矛盾. 综合（1）（2）（3）知小李得了第一名. 10、解：（1）命题的否定：x 、y 都是奇数，则x +y 不是偶数，为假命题.原命题的否命题：若x 、y 不都是奇数，则x +y 不是偶数，是假命题. （2）命题的否定：xy =0则x ≠0且y ≠0，为假命题. 原命题的否命题：若xy ≠0，则x ≠0且y ≠0，是真命题.（3）命题的否定：一个数是质数，则这个数不是奇数，是假命题. 原命题的否命题：若一个数不是质数，则这个数不是奇数，为假命题. 三、充要条件与反证法1、解析：依题意有p ⇒r ，r ⇒s ，s ⇒q ，∴p ⇒r ⇒s ⇒q .但由于rp ，∴q p .答案：A 2、解析：cos2α=－23⇔2α=2k π±6π5⇔α=k π±12π5. 答案：A3、解析：在△ABC 中，A ＞B ⇔cos A ＜cos B （余弦函数单调性）.答案：C4、答案：充分不必要5、解析：∵f （x ）=x 2－2ax －3的对称轴为x =a ，∴y =f （x ）在［1，2］上存在反函数的充要条件为［1，2］⊆（－∞，a ］或［1，2］⊆［a ，+∞），即a ≥2或a ≤1. 答案：D6、分析：先根据前n 项和公式，导出使{a n }为等比数列的必要条件，再证明其充分条件.解：当n =1时，a 1=S 1=p +q ；当n ≥2时，a n =S n －S n －1=（p －1）·p n －1.由于p ≠0，p ≠1，∴当n ≥2时，{a n }是等比数列.要使{a n }（n ∈N *）是等比数列，则12a a =p ，即（p －1）·p =p （p +q ），∴q =－1，即{a n }是等比数列的必要条件是p ≠0且p ≠1且q =－1.再证充分性：当p ≠0且p ≠1且q =－1时，S n =p n－1，a n =（p －1）·p n －1，1-n na a =p （n ≥2），∴{a n }是等比数列. 7、解析：∵UB =｛（x ，y ）｜n ＜x +y ｝，将P （2，3）分别代入集合A 、B 取交集即可.∴选A.答案：A8、解：方程①有实数根的充要条件是Δ1=（－4）2－16m ≥0，即m ≤1；方程②有实数根的充要条件是Δ2=（4m ）2－4（4m 2－4m －5）≥0，即m ≥－45. ∴方程①②都有实数根的充要条件是－45≤m ≤1. 9、证明：反证法：假设三个方程中都没有两个相异实根，则Δ1=4b 2－4ac ≤0，Δ2=4c 2－4ab ≤0，Δ3=4a 2－4bc ≤0.相加有a 2－2ab +b 2+b 2－2bc +c 2+c 2－2ac +a 2≤0，（a －b ）2+（b －c ）2+（c －a ）2≤0. ①由题意a 、b 、c 互不相等，∴①式不能成立.∴假设不成立，即三个方程中至少有一个方程有两个相异实根.10、解：假设a 、b 、c 都不大于0，即a ≤0，b ≤0，c ≤0，则a +b +c ≤0.而a +b +c =x 2－2y +2π+y 2－2z +3π+z 2－2x +6π=（x －1）2+（y －1）2+（z －1）2+π－3， ∵π－3＞0，且无论x 、y 、z 为何实数，（x －1）2+（y －1）2+（z －1）2≥0，∴a +b +c ＞0.这与a +b +c ≤0矛盾.因此，a 、b 、c 中至少有一个大于0.。

2023年新高考数学一轮复习1-1 集合(知识点讲解)解析版

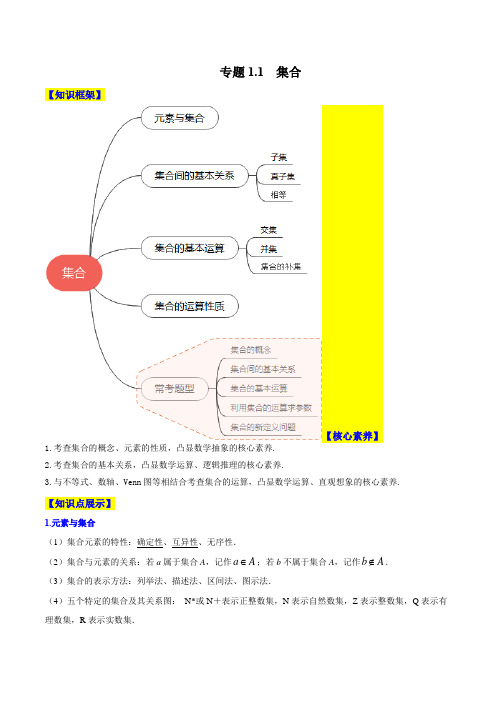
专题1.1 集合【知识框架】【核心素养】1.考查集合的概念、元素的性质，凸显数学抽象的核心素养.2.考查集合的基本关系，凸显数学运算、逻辑推理的核心素养.3.与不等式、数轴、Venn 图等相结合考查集合的运算，凸显数学运算、直观想象的核心素养.【知识点展示】1.元素与集合（1）集合元素的特性：确定性、互异性、无序性．（2）集合与元素的关系：若a 属于集合A ，记作a A ∈；若b 不属于集合A ，记作b A ∉．（3）集合的表示方法：列举法、描述法、区间法、图示法．（4）五个特定的集合及其关系图： N*或N ＋表示正整数集，N 表示自然数集，Z 表示整数集，Q 表示有理数集，R 表示实数集．2.集合间的基本关系(1)子集：若对任意x∈A，都有x∈B，则A⊆B或B⊇A.(2)真子集：若A⊆B，且集合B中至少有一个元素不属于集合A，则A B或B A.(3)相等：若A⊆B，且B⊆A，则A＝B.(4)空集的性质：∅是任何集合的子集，是任何非空集合的真子集.3.集合的基本运算求集合A的补集的前提是“A是全集U的子集”，集合A其实是给定的条件.从全集U中取出集合A的全部元素，剩下的元素构成的集合即为C U A.4.集合的运算性质(1)A∩A＝A，A∩∅＝∅，A∩B＝B∩A.(2)A∪A＝A，A∪∅＝A，A∪B＝B∪A.(3)A∩(C U A)＝∅，A∪(C U A)＝U，C U(C U A)＝A.特别提醒:1.若有限集A中有n个元素，则A的子集有2n个，真子集有2n－1个.2.子集的传递性：A⊆B，B⊆C⇒A⊆C.3.A⊆B⇔A∩B＝A⇔A∪B＝B⇔C U A⊇C U B.4. C U(A∩B)＝(C U A)∪(C U B)，C U(A∪B)＝(C U A)∩(C U B).【常考题型剖析】题型一集合的基本概念例1.(2018课标II 理2)已知集合(){}22,3,,A x y xy x y =+≤∈∈Z Z ，则A 中元素的个数为（）A ．9B ．8C ．5D ．4【答案】A方法二：根据集合A 的元素特征及圆的方程在坐标系中作出图形，如图，易知在圆x 2＋y 2＝3中有9个整点，即为集合A 的元素个数，故选A.【规律方法】与集合中的元素有关的问题的三种求解策略(1)研究一个用描述法表示的集合时，首先要看集合中的代表元素，然后再看元素的限制条件. (2)根据元素与集合的关系求参数时要注意检验集合中的元素是否满足互异性. (3)集合中的元素与方程有关时注意一次方程和一元二次方程的区别.例2.（2022·贵州·贵阳一中模拟预测（文））已知集合{}()()2,1,0,1,2,{Z 230},A B x x x =--=∈+-<∣则集合{},,z z xy x A y B =∈∈∣的元素个数为（） A ．6 B ．7C ．8D ．9【答案】B 【解析】【分析】化简集合B ，由条件确定{},,z z xy x A y B =∈∈∣的元素及其个数. 【详解】由()()023x x +-<解得23x -<<，所以{}1,0,1,2B =-.又{}2,1,0,1,2A =--所以{}{},,2,0,2,4,1,1,4z z xy x A y B =∈∈=---∣，共有7个元素，故选：B.【规律方法】与集合元素有关问题的思路：（1）确定集合的元素是什么，即确定这个集合是数集还是点集．（2）看这些元素满足什么限制条件．（3）根据限制条件列式求参数的值或确定集合元素的个数，但要注意检验集合是否满足元素的互异性题型二：集合间的基本关系例3.（2022·河南·开封市东信学校模拟预测）集合{0,1,2}A =的非空真子集的个数为（） A ．5 B ．6 C ．7 D ．8【答案】B 【解析】【分析】根据真子集的定义即可求解. 【详解】由题意可知，集合A 的非空真子集为{0},{1},{2},{0,1},{0,2},{1,2}，共6个. 故选：B.【易错警示】空集是任何集合的子集，在涉及集合关系时，必须优先考虑空集的情况，否则会造成漏解．例4.（2012·湖北省高考真题（文））已知集合{}{}2|320,,|05,A x x x x R B x x x N =-+=∈=<<∈，则满足条件A C B ⊆⊆的集合C 的个数为（） A ．1 B ．2C ．3D ．4【答案】D 【解析】求解一元二次方程，得{}()(){}2|320,|120,A x x x x x x x x =-+=∈=--=∈R R {}1,2=，易知{}{}|05,1,2,3,4B x x x =<<∈=N .因为A C B ⊆⊆，所以根据子集的定义，集合C 必须含有元素1,2，且可能含有元素3,4，原题即求集合{}3,4的子集个数，即有224=个，故选D. 【方法技巧】(1)判断两集合之间的关系的方法：当两集合不含参数时，可直接利用数轴、图示法进行判断；当集合中含有参数时，需要对满足条件的参数进行分类讨论或采用列举法．(2)要确定非空集合A 的子集的个数，需先确定集合A 中的元素的个数，再求解．不要忽略任何非空集合是它自身的子集．(3)根据集合间的关系求参数值(或取值范围)的关键是将条件转化为元素或区间端点间的关系，进而转化为参数所满足的关系，常用数轴、图示法来解决这类问题．题型三：集合的基本运算例5.（2022·全国·高考真题（文））设集合5{2,1,0,1,2},02A B xx ⎧⎫=--=≤<⎨⎬⎩⎭∣，则A B =（） A ．{}0,1,2 B ．{2,1,0}-- C ．{0,1} D ．{1,2}【答案】A 【解析】【分析】根据集合的交集运算即可解出．【详解】因为{}2,1,0,1,2A =--，502B x x ⎧⎫=≤<⎨⎬⎩⎭∣，所以{}0,1,2A B =．故选：A.例6．（2022·全国·高考真题（理））设全集{2,1,0,1,2,3}U =--，集合{}2{1,2},430A B xx x =-=-+=∣，则()UA B ⋃=（）A ．{1,3}B ．{0,3}C ．{2,1}-D ．{2,0}-【答案】D 【解析】【分析】解方程求出集合B ,再由集合的运算即可得解.【详解】由题意，{}{}2=4301,3B x x x -+==，所以{}1,1,2,3A B ⋃=-,所以(){}U2,0A B ⋃=-.故选：D.例7．（2022·全国·高考真题（理））设全集{1,2,3,4,5}U =，集合M 满足{1,3}U M =，则（） A ．2M ∈B ．3M ∈C ．4M ∉D ．5M ∉【答案】A 【解析】【分析】先写出集合M ,然后逐项验证即可【详解】由题知{2,4,5}M =,对比选项知，A 正确,BCD 错误故选:A例8.（2020·全国高考真题（理））已知集合{(,)|,,}A x y x y y x =∈≥*N ，{(,)|8}B x y x y =+=，则A B 中元素的个数为（） A ．2 B ．3C ．4D ．6【答案】C 【解析】采用列举法列举出A B 中元素的即可.【详解】由题意，A B 中的元素满足8y x x y ≥⎧⎨+=⎩，且*,x y N ∈，由82x y x +=≥，得4x ≤，所以满足8x y +=的有(1,7),(2,6),(3,5),(4,4)，故AB 中元素的个数为4.故选：C. 【规律方法】如何解集合运算问题(1)看元素构成:集合是由元素组成的，从研究集合中元素的构成入手是解决集合运算问题的关键.(2)对集合化简:有些集合是可以化简的，先化简再研究其关系并进行运算，可使问题简单明了、易于解决. (3)应用数形结合:常用的数形结合形式有数轴、坐标系和Venn 图.(4)创新性问题:以集合为依托，对集合的定义、运算、性质进行创新考查，但最终化为原来的集合知识和相应数学知识来解决.题型四：利用集合的运算求参数例9.（2020·全国高考真题（理））设集合A ={x |x 2–4≤0}，B ={x |2x +a ≤0}，且A ∩B ={x |–2≤x ≤1}，则a =（）A ．–4B ．–2C ．2D ．4【答案】B 【解析】由题意首先求得集合A ,B ，然后结合交集的结果得到关于a 的方程，求解方程即可确定实数a 的值. 【详解】求解二次不等式240x -≤可得：{}2|2A x x -=≤≤，求解一次不等式20x a +≤可得：|2a B x x ⎧⎫=≤-⎨⎬⎩⎭. 由于{}|21A B x x ⋂=-≤≤，故：12a-=，解得：2a =-. 故选：B. 【方法规律】利用集合的运算求参数的值或取值范围的方法①与不等式有关的集合，一般利用数轴解决，要注意端点值能否取到；①若集合能一一列举，则一般先用观察法得到不同集合中元素之间的关系，再列方程(组)求解．例10.（2022·山西运城·高二阶段练习）设集合{23},{}A x x B x x a =-<<=>，若R A B ⋂=∅，则实数a 的取值范围为____．【答案】2a ≤- 【解析】【分析】先求出RB ，则RA B ⋂=∅，{23}A x x =-<<，由分析即可求出a 的取值范围.【详解】RB {}x x a =≤，又因为RA B ⋂=∅，{23}A x x =-<<，所以2a ≤-．故答案为：2a ≤-.【易错提醒】（1）认清元素的属性．解决集合问题时，认清集合中元素的属性(是点集、数集或其他情形)和化简集合是正确求解的两个先决条件．（2）注意元素的互异性．在解决含参数的集合问题时，要注意检验集合中元素的互异性，否则很可能会因为不满足“互异性”而导致错误．（3）防范空集．在解决有关,A B A B ⋂=∅⊆等集合问题时，往往容易忽略空集的情况，一定要先考虑∅时是否成立，以防漏解．题型五：集合的新定义问题例11.（2015·湖北高考真题（理））已知集合A ={(x,y)|x 2+y 2≤1, x,y ∈Z}，B ={(x,y)| |x|≤2 , |y|≤2, x,y ∈Z}，定义集合A ⊕B ={(x 1+x 2,y 1+y 2)|(x 1,y 1)∈A, (x 2,y 2)∈B}，则A ⊕B 中元素的个数为（）A ．77B ．49C ．45D ．30 【答案】C 【解析】因为集合A ={(x,y)|x 2+y 2≤1, x,y ∈Z}，所以集合中有9个元素（即9个点），即图中圆中的整点，集合B ={(x,y)| |x|≤2 , |y|≤2, x,y ∈Z}中有25个元素（即25个点）：即图中正方形中的整点，集合A ⊕B ={(x 1+x 2,y 1+y 2)|(x 1,y 1)∈A, (x 2,y 2)∈B}的元素可看作正方形中的整点（除去四个顶点），即个．例12. （2021·江西·丰城九中高二阶段练习）已知非空集合,A B 满足下列四个条件：①{}1,2,3,4,5,6,7A B =；①A B =∅；③A 中的元素个数不是A 中的元素；④B 中的元素个数不是B 中的元素．（1）若集合A 中只有1个元素，则A =________；（2）若两个集合A 和B 按顺序组成的集合对()A B ，叫作有序集合对，则有序集合对(),A B 的个数是________.【答案】 {6} 32 【解析】【分析】根据给定信息，分析集合A ，B 不能取的元素即可得解；按集合A 中元素个数分类计算作答. 【详解】（1）因{}1,2,3,4,5,6,7A B =，A B =∅，则集合A ，B 的元素个数和为7，而集合A 中只有1个元素，则集合B 中有6个元素，又B 中的元素个数不是B 中的元素，即6B ∉，所以{6}A =；（2）集合A 中有1个元素时，由（1）知{6}A =，{1,2,3,4,5,7}B =，则有序集合对(),A B 有1个，集合A 中有2个元素时，即2,5A B ∉∉，则{5,},{1,3,4,6,7}A a a =∈，有序集合对(),A B 有15C 5=个，集合A 中有3个元素时，即3,4A B ∉∉，则{4,,},,{1,2,5,6,7}A a b a b =∈，有序集合对(),A B 有25C 10=个，集合A 中有4个元素时，即4,3A B ∉∉，则{3,,,},,,{1,2,5,6,7}A a b c a b c =∈，有序集合对(),A B 有35C 10=个，集合A 中有5个元素时，即5,2A B ∉∉，则{2,,,,},,,,{1,3,4,6,7}A a b c d a b c d =∈，有序集合对(),A B 有45C 5=个，集合A 中有6个元素时，即6,1A B ∉∉，则{1,,,,,},,,,,{2,3,4,5,7}A a b c d e a b c d e =∈，有序集合对(),A B 有55C 1=个，所以有序集合对()A B ，的个数是1+5+10+10+5+1=32. 故答案为：{6}；32 【方法技巧】解决集合新定义问题的方法(1)正确理解新定义：耐心阅读，分析含义，准确提取信息是解决这类问题的前提，剥去新定义、新法则、新运算的外表，利用所学的集合性质等知识将陌生的集合转化为我们熟悉的集合，是解决这类问题的突破口.(2)合理利用集合性质：运用集合的性质(如元素的性质、集合的运算性质等)是破解新定义型集合问题的关键．在解题时要善于从题设条件给出的数式中发现可以使用集合性质的一些因素，并合理利用.(3)对于选择题，可结合选项，通过验证、排除、对比、特值法等进行求解或排除错误选项，当不满足新定义的要求时，只需通过举反例来说明，以达到快速判断结果的目的.。

高三一轮复习集合知识点和题型

第一章集合与常用逻辑用语1.1集合的概念知识点1.元素和集合的概念元素：一般地，我们把研究对象统称为元素集合：把一些元素组成的总体叫做集合（简称为集）。

集合通常用大写的字母表示，如A B C 、、、……；元素通常用小写的字母表示，如a b c d 、、、……。

知识点2.集合中元素的特性（1）确定性：给定一个集合，它的元素必须是确定的。

设A 是一个给定的集合，x 是某一具体的对象，则x 或者是A 的元素，或者不是A 的元素，二者必居其一，不能模棱两可．（2）互异性：给定一个集合，它的任意两个元素是互不相同的。

也就是说集合中的元素是不重复出现的。

集合中相同的元素只能算是一个。

（3）无序性：集合中的元素是不分先后顺序的．知识点3.元素与集合的关系一般地，如果a 是集合A 的元素，就说a 属于A ，记作a A ∈；如果a 不是集合的元素，就说a 不属于A ，记作A a ∉。

特别注意：（1）集合和元素是两个不同的概念，它们之间是个体与整体的关系，并且这种关系是相对的；（2）元素与集合之间不存在大小与相等的关系，只存在属于或不属于的关系。

如2与{}3，只能是{}23∉，不能写成{}23≠。

知识点4.集合的第一种表示方法自然语言和常用数集及记法上面举的例子：中国的直辖市组成的集合。

还比如：地球上的四大洋组成的集合；小于10的所有自然数组成的集合等等我们是可以用自然语言表示一个集合。

数学中有一些常用数集，就是自然语言表示的，这些常用数集及记法如下：（1）全体非负整数组成的集合称为非负整数集（或自然数集），记作N 。

（2）所有正整数组成的集合称为正整数集，记作*N 或+N 。

（3）全体整数组成的集合称为整数集，记作Z 。

（4）全体有理数数组成的集合称为有理数集，记作Q 。

（5）全体实数组成的集合称为实数集，记作R 。

知识点5.集合的表示方法（1）自然语言（2）列举法列举法概念：像这样把集合中的元素一一列举出来，并用大括号括起来表示集合的方法叫做列举法。

新高考数学一轮复习考点知识专题讲解与练习 1 集合

新高考数学一轮复习考点知识专题讲解与练习第一章集合与常用逻辑用语考点知识总结1 集合高考概览本考点在高考中是必考知识点，常考题型为选择题，分值为5分，低难度考纲研读1.了解集合的含义，体会元素与集合的属于关系2．能用自然语言、图形语言、集合语言(列举法或描述法)描述不同的具体问题3．理解集合之间包含与相等的含义，能识别给定集合的子集 4．在具体情境中，了解全集与空集的含义5．理解两个集合的并集与交集的含义，会求两个简单集合的并集与交集 6．理解在给定集合中一个子集的补集的含义，会求给定子集的补集 7．能使用Venn 图表达集合的关系及运算一、基础小题1．已知集合A ＝{x |x 2－x －6<0}，B ＝{x |2<x <5}，则A ∪B ＝( ) A ．(1，6) B ．(－2，5) C ．(2，3) D ．(3，5) 答案 B解析 A ＝{x |－2<x <3}，A ∪B ＝(－2，5).故选B.2．满足M ⊆{a 1，a 2，a 3，a 4}，且M ∩{a 1，a 2，a 3}＝{a 1，a 2}的集合M 的个数是( ) A ．1 B ．2 C ．3 D ．4 答案 B解析集合M ＝{a 1，a 2}或{a 1，a 2，a 4}，有2个．故选B. 3．已知集合P ＝⎩⎨⎧⎭⎬⎫x ⎪⎪⎪1x <13，则(∁R P )∩N ＝()A ．{x |0<x <3}B ．{x |0<x ≤3}C ．{0，1，2，3}D ．{1，2，3} 答案 C 解析由题意，得P ＝⎩⎨⎧⎭⎬⎫x ⎪⎪⎪1x <13＝⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x －33x >0＝{x |x >3或x <0}，则(∁R P )∩N ＝{x |0≤x≤3}∩N ＝{0，1，2，3}．故选C.4．已知集合A ＝{1，2}，B ＝{(x ，y )|x ∈A ，y ∈A ，x －y ∈A }，则B 的子集共有( ) A ．2个 B ．4个 C ．6个 D ．8个答案 A解析由已知得B ＝{(2，1)}，所以B 的子集有2个．故选A.5．已知集合A ＝{x |(x －2)(x ＋2)≤0}，B ＝{y |x 2＋y 2＝16}，则A ∩B ＝( ) A ．[－3，3] B ．[－2，2] C ．[－4，4] D ．∅ 答案 B解析由题意，得A ＝{x |－2≤x ≤2}，B ＝{y |－4≤y ≤4}，所以A ∩B ＝{x |－2≤x ≤2}．故选B.6．已知集合A ，B 均为全集U ＝{1，2，3，4}的子集，且∁U (A ∪B )＝{4}，A ∩(∁U B )＝{3}，则B ＝( )A ．{1，2}B ．{2，4}C ．{1，2，4}D ．∅ 答案 A解析由∁U (A ∪B )＝{4}，得A ∪B ＝{1，2，3}．由A ∩(∁U B )＝{3}，得3∈A 且3∉B .现假设1∉B ，∵A ∪B ＝{1，2，3}，∴1∈A .又1∉A ∩(∁U B )＝{3}，∴1∉∁U B ，即1∈B ，矛盾．故1∈B .同理2∈B .故选A.7．已知集合A ＝{x |y ＝x 2－2}，集合B ＝{y |y ＝x 2－2}，则有( ) A ．A ＝B B ．A ∩B ＝∅ C ．A ∪B ＝A D ．A ∩B ＝A 答案 C解析 A ＝{x |y ＝x 2－2}＝R ，B ＝{y |y ＝x 2－2}＝[－2，＋∞)，所以B ⊆A ，故A ∪B ＝A .故选C.8．已知集合M 是函数y ＝11－2x的定义域，集合N 是函数y ＝x 2－4的值域，则M ∩N ＝( )A ．⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x ≤12B ．⎩⎨⎧⎭⎬⎫x ⎪⎪⎪－4≤x <12 C ．⎩⎨⎧⎭⎬⎫（x ，y ）⎪⎪⎪x <12且y ≥－4D ．∅ 答案 B解析由题意，得M ＝⎝ ⎛⎭⎪⎫－∞，12，N ＝[－4，＋∞)，所以M ∩N ＝⎣⎢⎡⎭⎪⎫－4，12.故选B.9.若集合U ＝R ，A ＝{1，2，3，4，5}，集合B ＝{x |0<x <4}，则图中阴影部分表示( )A ．{1，2，3，4}B ．{1，2，3}C ．{4，5}D ．{1，4} 答案 C解析集合A ＝{1，2，3，4，5}，B ＝{x |0<x <4}，图中阴影部分表示A ∩(∁U B )，又∁U B ＝{x |x ≥4或x ≤0}，所以A ∩(∁U B )＝{4，5}．故选C.10．已知集合A ＝{(x ，y )|y ＝2x }，B ＝{(x ，y )|y ＝x ＋1}，则A ∩B 中元素的个数为( ) A ．3 B ．2 C ．1 D ．0 答案 B解析由y ＝2x 与y ＝x ＋1的图象可知，两函数图象有两个交点，如图所示．∴A ∩B中元素的个数为2.故选B.11．(多选)已知全集U＝R，函数y＝ln (1－x)的定义域为M，集合N＝{x|x2－x＜0}，则下列结论正确的是()A．M∩N＝N B．M∩(∁U N)≠∅C．M∪N＝U D．M⊆(∁U N)答案AB解析由题意知M＝{x|x＜1}，N＝{x|0＜x＜1}，所以M∩N＝N.又∁U N＝{x|x≤0或x≥1}，所以M∩(∁U N)＝{x|x≤0}≠∅，M∪N＝{x|x＜1}＝M，M⊆/(∁U N).故选AB.12．(多选)已知集合A＝{0，1，2}，若A∩(∁Z B)≠∅(Z是整数集合)，则集合B可以为()A．{x|x＝2a，a∈A}B．{x|x＝2a，a∈A}C．{x|x＝a－1，a∈N}D．{x|x＝a2，a∈N}答案ABD解析由题意知，集合A＝{0，1，2}．{x|x＝2a，a∈A}＝{0，2，4}，则A∩(∁Z B)＝{1}≠∅，A满足题意；{x|x＝2a，a∈A}＝{1，2，4}，则A∩(∁Z B)＝{0}≠∅，B满足题意；{x|x＝a－1，a∈N}＝{－1，0，1，2，3，…}，则A∩(∁Z B)＝∅，C不满足题意；{x|x＝a2，a∈N}＝{0，1，4，9，16，…}，则A∩(∁Z B)＝{2}≠∅，D满足题意．故选ABD.二、高考小题13．(2022·新高考Ⅰ卷)设集合A＝{x|－2<x<4}，B＝{2，3，4，5}，则A∩B＝() A．{2} B．{2，3} C．{3，4} D．{2，3，4}答案 B解析因为A ＝{x |－2<x <4}，B ＝{2，3，4，5}，所以A ∩B ＝{2，3}．故选B. 14．(2022·新高考Ⅱ卷)设集合U ＝{1，2，3，4，5，6}，A ＝{1，3，6}，B ＝{2，3，4}，则A ∩(∁U B )＝( )A ．{3}B ．{1，6}C ．{5，6}D ．{1，3} 答案 B解析由题意可得∁U B ＝{1，5，6}，故A ∩(∁U B )＝{1，6}．故选B.15．(2022·全国甲卷)设集合M ＝{x |0<x <4}，N ＝⎩⎨⎧⎭⎬⎫x ⎪⎪⎪13≤x ≤5，则M ∩N ＝( )A ．⎩⎨⎧⎭⎬⎫x ⎪⎪⎪0<x ≤13B ．⎩⎨⎧⎭⎬⎫x ⎪⎪⎪13≤x <4C ．{x |4≤x <5}D ．{x |0<x ≤5} 答案 B 解析由已知得M ∩N ＝⎩⎨⎧⎭⎬⎫x ⎪⎪⎪13≤x <4.故选B.16．(2022·全国乙卷)已知集合S ＝{s |s ＝2n ＋1，n ∈Z }，T ＝{t |t ＝4n ＋1，n ∈Z }，则S ∩T ＝( )A ．∅B ．SC ．TD ．Z 答案 C解析因为s ＝2n ＋1，n ∈Z ，当n ＝2k ，k ∈Z 时，s ＝4k ＋1，k ∈Z ；当n ＝2k ＋1，k ∈Z 时，s ＝4k ＋3，k ∈Z ，所以TS ，S ∩T ＝T .故选C.17．(2022·天津高考)设集合A ＝{－1，0，1}，B ＝{1，3，5}，C ＝{0，2，4}，则(A ∩B )∪C ＝( )A ．{0}B ．{0，1，3，5}C ．{0，1，2，4}D ．{0，2，3，4} 答案 C解析 ∵A ＝{－1，0，1}，B ＝{1，3，5}，C ＝{0，2，4}，∴A ∩B ＝{1}，∴(A ∩B )∪C＝{0，1，2，4}．故选C.18．(2022·新高考Ⅰ卷)设集合A ＝{x |1≤x ≤3}，B ＝{x |2<x <4}，则A ∪B ＝( ) A ．{x |2<x ≤3} B ．{x |2≤x ≤3} C ．{x |1≤x <4} D ．{x |1<x <4} 答案 C解析 A ∪B ＝[1，3]∪(2，4)＝[1，4).故选C.19．(2022·全国Ⅰ卷)设集合A ＝{x |x 2－4≤0}，B ＝{x |2x ＋a ≤0}，且A ∩B ＝{x |－2≤x ≤1}，则a ＝( )A ．－4B ．－2C ．2D ．4 答案 B 解析 ∵A ＝{x |x2－4≤0}＝{x |－2≤x ≤2}，B ＝{x |2x ＋a ≤0}＝⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x ≤－a 2，A ∩B ＝{x |－2≤x ≤1}，∴－a2＝1，解得a ＝－2.故选B.20．(2022·全国Ⅲ卷)已知集合A ＝{(x ，y )|x ，y ∈N *，y ≥x }，B ＝{(x ，y )|x ＋y ＝8}，则A ∩B 中元素的个数为( )A ．2B ．3C ．4D ．6 答案 C解析由题意，A ∩B 中的元素满足⎩⎨⎧y ≥x ，x ＋y ＝8，且x ，y ∈N *，由x ＋y ＝8≥2x ，得x ≤4，所以A ∩B 中的元素有(1，7)，(2，6)，(3，5)，(4，4)，共4个．故选C.三、模拟小题21．(2022·江苏镇江市第一中学高三上学期期初考试)已知集合A ＝{x ||x |≤2，x ∈N }，集合B ＝{x |x 2＋x －6＝0}，则A ∩B ＝( )A ．{2}B ．{－3，2}C ．{－3，1}D ．{－3，0，1，2}答案 A解析集合A＝{x||x|≤2，x∈N}＝{0，1，2}，集合B＝{x|x2＋x－6＝0}＝{－3，2}，所以A∩B＝{2}．故选A.22．(2022·广东广州荔湾区高三上调研考试)已知全集U＝R，设集合A＝{x|x2－x－6≤0}，B＝{x|x－1<0}，则图中阴影部分表示的集合是()A．{x|x≤3} B．{x|－3≤x<1}C．{x|－2≤x<－1} D．{x|1≤x≤3}答案 D解析由题意得，A＝{x|－2≤x≤3}，B＝{x|x<1}，∴∁U B＝{x|x≥1}，∴A∩(∁U B)＝{x|1≤x≤3}．故选D.23．(2022·新高考八省联考)已知M，N均为R的子集，且∁R M⊆N，则M∪(∁R N)＝()A．∅B．M C．N D．R答案 B解析解法一：∵∁R M⊆N，∴M⊇∁R N，据此可得M∪(∁R N)＝M.故选B.解法二：如图所示，设矩形区域ABCD表示全集R，矩形区域ABHE表示集合M，则矩形区域CDEH表示集合∁R M，矩形区域CDFG表示集合N，满足∁R M⊆N，结合图形可得M∪(∁R N)＝M.故选B.24．(2022·河南南阳模拟)设集合P＝{3，log2a}，Q＝{a，b}，若P∩Q＝{0}，则P ∪Q＝()A．{3，0} B．{3，0，1}答案 B解析 ∵P ∩Q ＝{0}，∴log 2a ＝0，∴a ＝1，从而b ＝0，∴P ∪Q ＝{3，0，1}．故选B.25．(2022·河北沧州第一中学等十五校高三上摸底考试)已知集合A ＝⎩⎨⎧⎭⎬⎫x ∈R ⎪⎪⎪y ＝ x －4x －7，集合B ＝{3，4，5，6，7}，则A ∩B ＝( ) A ．(3，4) B ．{3，4} C ．[3，4] D ．{3，4，7} 答案 B解析由x －4x －7≥0得⎩⎨⎧（x －4）（x －7）≥0，x ≠7，得x ≤4或x >7，所以A ＝{x |x ≤4或x >7}，因为B ＝{3，4，5，6，7}，所以A ∩B ＝{x |x ≤4或x >7}∩{3，4，5，6，7}＝{3，4}．故选B.26．(2022·湖北襄阳五中高三开学考试)已知集合M ＝{x |1－a <x <2a }，N ＝(1，4)，且M ⊆N ，则实数a 的取值范围是( )A ．(－∞，2]B ．(－∞，0]C ．⎝ ⎛⎦⎥⎤－∞，13D ．⎣⎢⎡⎭⎪⎫13，2答案 C解析因为M ⊆N ，而∅⊆N ，所以当M ＝∅时，2a ≤1－a ，则a ≤13；当M ≠∅时，M ⊆N ，则⎩⎪⎨⎪⎧1－a <2a ，1－a ≥1，2a ≤4⇒⎩⎪⎨⎪⎧a >13，a ≤0，a ≤2，无解．综上得a ≤13，即实数a 的取值范围是⎝ ⎛⎦⎥⎤－∞，13.故选C.27．(2022·湖南长沙长郡中学高三上开学考试)已知集合A ＝⎩⎨⎧⎭⎬⎫x ∈N ⎪⎪⎪12<2x ＋1<16，B＝{x |x 2－4x ＋m ＝0}，若1∈A ∩B ，则A ∪B ＝( )A ．{1，2，3}B ．{1，2，3，4}答案 D 解析由题可知，A ＝⎩⎨⎧⎭⎬⎫x ∈N ⎪⎪⎪12<2x ＋1<16，即2－1<2x ＋1<24，解得－2<x <3，又x ∈N ，所以A ＝{0，1，2}．因为1∈A ∩B ，则1∈B ，所以1－4＋m ＝0，解得m ＝3，所以B ＝{x |x 2－4x ＋3＝0}＝{1，3}，所以A ∪B ＝{0，1，2，3}．故选D.28．(多选)(2022·江苏沭阳如东中学测试)设A ＝{x |x 2－8x ＋15＝0}，B ＝{x |ax －1＝0}，若A ∩B ＝B ，则实数a 的值可以为( )A ．15B ．0C ．3D ．13 答案 ABD解析 ∵x 2－8x ＋15＝0的两个根为3和5，∴A ＝{3，5}，∵A ∩B ＝B ，∴B ⊆A ，∴B ＝∅或B ＝{3}或B ＝{5}或B ＝{3，5}，当B ＝∅时，满足a ＝0即可，当B ＝{3}时，满足3a －1＝0，∴a ＝13，当B ＝{5}时，满足5a －1＝0，∴a ＝15，当B ＝{3，5}时，显然不符合条件，∴实数a 的值可以是0，13，15.故选ABD.29．(多选)(2022·山东滨州模拟)设S 为复数集C 的非空子集．若对任意x ，y ∈S ，都有x ＋y ，x －y ，xy ∈S ，则称S 为封闭集．下列命题中的真命题有( )A ．集合S ＝{a ＋b i|a ，b 为整数，i 为虚数单位}为封闭集B ．若S 为封闭集，则一定有0∈SC ．封闭集一定是无限集D ．若S 为封闭集，则满足S ⊆T ⊆C 的任意集合T 也是封闭集答案 AB解析因为两个复数的和是复数，两个复数的差是复数，两个复数的积也是复数，所以集合S ＝{a ＋b i|a ，b 为整数，i 为虚数单位}为封闭集，A 正确；当S 为封闭集时，因为x －y ∈S ，取x ＝y ，得0∈S ，B 正确；集合S ＝{0}显然是封闭集，但S 是有限集，C 错误；取S ＝{0}，T ＝{0，1}，满足S ⊆T ⊆C ，但由于0－1＝－1不属于T ，故T 不是封闭集，D 错误．故选AB.30．(多选)(2022·湖南衡阳模拟)对于集合M ，定义函数f M (x )＝⎩⎨⎧－1，x ∈M ，1，x ∉M .对于两个集合M ，N ，定义集合M ⊗N ＝{x |f M (x )·f N (x )＝－1}．已知集合A ＝{2，4，6}，B ＝{1，2，4}，则下列结论正确的是( )A ．1∈A ⊗B B ．2∈A ⊗BC ．4∉A ⊗BD ．A ⊗B ＝B ⊗A 答案 ACD解析由题意知，f A (x )＝⎩⎨⎧－1，x ∈{2，4，6}，1，x ∉{2，4，6}，f B (x )＝⎩⎨⎧－1，x ∈{1，2，4}，1，x ∉{1，2，4}．当x ＝1时，f A (1)＝1，f B (1)＝－1，所以f A (1)f B (1)＝1×(－1)＝－1，故1∈A ⊗B ，A 正确；当x ＝2时，f A (2)＝－1，f B (2)＝－1，所以f A (2)f B (2)＝(－1)×(－1)＝1，故2∉A ⊗B ，B 错误；当x ＝4时，f A (4)＝－1，f B (4)＝－1，所以f A (4)f B (4)＝(－1)×(－1)＝1，故4∉A ⊗B ，C 正确；由定义及乘法的交换律可知，D 正确．一、高考大题本考点在近三年高考中未涉及此题型．二、模拟大题1．(2022·江西南昌高三模拟)已知全集U ＝R ，集合A ＝{x |x 2－4x －5≤0}，B ＝{x |2≤x ≤4}．(1)求A ∩(∁U B )；(2)若集合C ＝{x |a ≤x ≤4a ，a >0}，满足C ∪A ＝A ，C ∩B ＝B ，求实数a 的取值范围．解 (1)由题意，得A ＝{x |－1≤x ≤5}，∁U B ＝{x |x <2或x >4}， ∴A ∩(∁U B )＝{x |－1≤x <2或4<x ≤5}．(2)由C ∪A ＝A 得C ⊆A ，则⎩⎨⎧a ≥－1，4a ≤5，解得－1≤a ≤54.由C ∩B ＝B 得B ⊆C ，则11 / 11 ⎩⎨⎧a ≤2，4a ≥4，解得1≤a ≤2. 从而实数a 的取值范围为⎩⎨⎧⎭⎬⎫a ⎪⎪⎪1≤a ≤54. 2．(2022·云南师大附中月考)设集合A ＝⎩⎨⎧⎭⎬⎫x ⎪⎪⎪12≤2x ≤4，B ＝{x |x 2＋(b －a )x －ab ≤0}． (1)若A ＝B 且a ＋b <0，求实数a ，b 的值；(2)若B 是A 的子集，且a ＋b ＝2，求实数b 的取值范围．解 (1)A ＝⎩⎨⎧⎭⎬⎫x ⎪⎪⎪12≤2x ≤4＝{x |－1≤x ≤2}， ∵a ＋b <0，∴a <－b ，∴B ＝{x |(x －a )(x ＋b )≤0}＝{x |a ≤x ≤－b }，∵A ＝B ，∴a ＝－1，b ＝－2.(2)∵a ＋b ＝2，∴B ＝{－b ≤x ≤2－b }，∵B 是A 的子集，∴－b ≥－1且2－b ≤2，解得0≤b ≤1，即实数b 的取值范围为[0，1].。

集合一轮复习综合带详细解答

对于B，当时，所以；当时，由得到，是“ ”成立的充要条件，错误；
对于C，当时，，得到；当时，由正弦定理得到，即，所以，由于，得到，所以是“ ”成立的充要条件，错误；
对于D，当时，，得到；当时，由正弦定理得，即，由于，所以或，即或者，所以是“ ”成立的必要不充分条件，正确.
两个集合中的元素不减少，并集中元素个数就是，两个集合中元素个数的和，
即CARD(A∪B)＝CARD(A)＋CARD(B)，反之若CARD(A∪B)＝CARD(A)＋CARD(B)，
则在求时，两个集合中的元素没有被去除，即没有公共元素，
所以，①正确；
②A⊆B时，中的元素都属于，但中可能有不属于元素，所以CARD(A)≤CARD(B)，
A．充分必要B．充分不必要
C．必要不充分D．既不充分也不必要
11．已知S1，S2，S3为非空集合，且S1，S2，S3⊆Z，对于1，2，3的任意一个排列i，j，k，若x∈Si，y∈Sj，则x－y∈Sk，则下列说法正确的是（）
A．三个集合互不相等B．三个集合中至少有两个相等
C．三个集合全都相等D．以上说法均不对
二、填空题
12．若集合、、满足，则下列结论：① ；② ；③ ；④ 中一定成立的有______.（填写你认为正确的命题序号）
13．已知非空集合满足，若存在非负实数，使得对任意，均有，则称集合具有性质 .那么具有性质的集合的个数为___________
14．已知，，则“ ”是“ ”的______条件．（填“充分不必要”、“必要不充分”、“充分必要”、“既不充分也不必要”之一）
A．充分而不必要条件B．必要而不充分条件
C．充分必要条件D．既不充分也不必要条件

高三数学第一轮复习知识点

高三数学第一轮复习知识点高三数学第一轮复习集合知识点一、集合有关概念1、集合的含义：某些指定的对象集在一起就成为一个集合，其中每一个对象叫元素。

2、集合的中元素的三个特性：1.元素的确定性;2.元素的互异性;3.元素的无序性说明：(1)对于一个给定的集合，集合中的元素是确定的，任何一个对象或者是或者不是这个给定的集合的元素。

(2)任何一个给定的集合中，任何两个元素都是不同的对象，相同的对象归入一个集合时，仅算一个元素。

(3)集合中的元素是平等的，没有先后顺序，因此判定两个集合是否一样，仅需比较它们的元素是否一样，不需考查排列顺序是否一样。

(4)集合元素的三个特性使集合本身具有了确定性和整体性。

3、集合的表示：{}如{我校的篮球队员}，{太平洋,大西洋,印度洋,北冰洋}1.用拉丁字母表示集合：A={我校的篮球队员},B={1,2,3,4,5}2.集合的表示方法：列举法与描述法。

注意啊：常用数集及其记法：非负整数集(即自然数集)记作：N正整数集N*或N+整数集Z有理数集Q实数集R关于属于的概念集合的元素通常用小写的拉丁字母表示，如：a是集合A的元素，就说a属于集合A记作aA，相反，a不属于集合A记作a?A 列举法：把集合中的元素一一列举出来，然后用一个大括号括上。

描述法：将集合中的元素的公共属性描述出来，写在大括号内表示集合的方法。

用确定的条件表示某些对象是否属于这个集合的方法。

①语言描述法：例：{不是直角三角形的三角形}②数学式子描述法：例：不等式x-32的解集是{x?R|x-32}或{x|x-32}4、集合的分类：1.有限集含有有限个元素的集合2.无限集含有无限个元素的集合3.空集不含任何元素的集合例：{x|x2=-5｝二、集合间的基本关系1.包含关系子集注意：有两种可能(1)A是B的`一部分，;(2)A与B是同一集合。

反之:集合A不包含于集合B,或集合B不包含集合A,记作AB或BA2.相等关系(55，且55，则5=5)实例：设A={x|x2-1=0}B={-1,1}元素相同结论：对于两个集合A与B，如果集合A的任何一个元素都是集合B的元素，同时,集合B的任何一个元素都是集合A的元素，我们就说集合A等于集合B，即：A=B三、集合的运算1.交集的定义：一般地，由所有属于A且属于B的元素所组成的集合,叫做A,B的交集.记作AB(读作A交B)，即AB={x|xA，且xB}.2、并集的定义：一般地，由所有属于集合A或属于集合B的元素所组成的集合，叫做A,B的并集。

考向01 集合(重点)-备战2023年高考数学一轮复习考点微专题(新高考地区专用)(解析版)

考向01 集合【2022年新高考全国Ⅰ卷】若集合{4},{31}M xx N x x =<=≥∣∣，则M N =（）A ．{}02x x ≤<B ．123x x ⎧⎫≤<⎨⎬⎩⎭C ．{}316x x ≤<D ．1163x x ⎧⎫≤<⎨⎬⎩⎭【答案】D 【解析】【分析】求出集合,M N 后可求M N ⋂. 【详解】1{16},{}3M x x N x x =≤<=≥∣0∣，故1163M N x x ⎧⎫⋂=≤<⎨⎬⎩⎭，故选：D【2022年新高考全国II 卷】已知集合{}{}1,1,2,4,11A B x x =-=-≤，则A B =（） A ．{1,2}- B ．{1,2}C ．{1,4}D ．{1,4}-【答案】B 【解析】【分析】求出集合B 后可求A B . 【详解】{}|02B x x =≤≤，故{}1,2A B =，故选：B.(1)离散型数集或抽象集合间的运算,常借用Venn 图求解.(2)集合中的元素若是连续的实数,常借助数轴求解,但要注意端点值能否取到.(3)根据集合的运算求参数,先把符号语言译成文字语言,然后适时应用数形结合求解.（1）集合运算的相关结论交集 A B A ⊆ A B B ⊆ A A A = A ∅=∅ A B B A = 并集 A B A ⊇A B B ⊇A A A =A A ∅=A B BA =补集()UU A A =UU =∅UU ∅= ()U A A =∅()U A A U =（2）(.)UUU A B A B A A B B A B A B ⊆⇔=⇔=⇔⊇=⇔∅易错题【01】对集合中元素的类型理解不到位集合问题是高考必考问题,一般作为容易题出现,求解集合问题的关键是理解集合中元素的类型,特别是用描述法表示集合,首先要搞清楚集合中代表元素的含义,再看元素的限制条件,明白集合的类型,是连续数集、离散数集、点集或其他类型的集合. 易错题【02】忽略集合中元素互异性利用元素与集合的关系或两集合之间的关系求参数的值,集合中元素的互异性常常容易忽略,求解问题时要特别注意,求出以后一定要代入检验,看看是否满足元素的互异性. 易错题【03】忽略空集空集是任何集合的子集,在涉及集合关系,如根据,A B ⊆求参数的值或范围要注意A 是否可以为∅,根据A B =∅求参数的值或范围必须优先考虑空集的情况,否则会造成漏解．易错题【04】忽视集合转化的等价性把用描述法表示的集合转化为用列举法表述的集合或化简集合容易忽略等价性,如去分母忽略分母不为零,解含有对数式的不等式要保证对数式有意义,要注意集合中的限制条件等.1．（2022·全国·模拟预测）若集合{}24M xy x x ==-∣，{}222x N x -=>∣，则M N =（）A ．{}01xx ≤≤∣ B ．{01}x x ≤<∣ C ．{14}x x <<∣ D ．{1}∣<xx 【答案】B 【解析】【分析】根据集合的定义，先对集合进行化简，再利用交运算即可求解. 【详解】由题意知{}04M xx =≤≤∣，{1}N x x =<∣，所以{01}M N x x ⋂=≤<∣．故选:B ．2．（2022·江苏·常州高级中学模拟预测）已知集合{}22(,)4A x y x y =+=，(){},34B x y y x =+，则A B中元素的个数为（） A ．0 B ．1 C ．2 D ．3【答案】B 【解析】【分析】把34y x =+代入224x y +=，根据方程的根的个数分析即可【详解】集合{}22(,)4A x y x y =+=，{}(,)34B x y y x ==+，把34y x =+代入224x y +=，得22330x x ++=，即3x =有唯一解，故集合A B 中元素的个数为1．故选：B3．（2022·全国·南京外国语学校模拟预测）已知集合{}2670A x x x =--<，{}3,1x B y y x ==<，则()R A B ⋂=（） A ．[)3,7 B ．(][)1,03,7-⋃C ．[)7,+∞D ．()[),17,-∞-⋃+∞【答案】B【解析】【分析】先化简集合A 、B ，再去求R B ，进而求得()RA B【详解】{}()26701,7A x x x =--<=-，{}()3,10,3x B y y x ==<=，所以(][)R ,03,B =-∞⋃+∞，所以()(][)R 1,03,7A B ⋂=-⋃．故选：B ．1．（2022·江苏·苏州市第六中学校三模）设集合{}{}220,1,1,2,3A x N x x B =∈--≤=-，则A B =（）A ．{1,0}-B ．{1,2}C ．{1,2,3}D ．{0,1,2,3}【答案】B 【解析】【分析】化简集合A ，根据交集运算求解. 【详解】{}{}{}220120,1,2A x N x x x N x =∈--≤=∈-≤≤=，{}1,1,2,3B =-， {1,2}A B ∴=，故选：B2．（2022·全国·模拟预测（文））如图，三个圆的内部区域分别代表集合A ，B ，C ，全集为I ，则图中阴影部分的区域表示（）A ．ABC ⋂⋂B ．()I AC B ⋂⋂C ．()I A B C ⋂⋂D ．()I B C A ⋂⋂【答案】B 【解析】【分析】找到每一个选项对应的区域即得解. 【详解】解：如图所示，A. A B C ⋂⋂对应的是区域1；B. ()I A C B ⋂⋂对应的是区域2；C. ()I A B C ⋂⋂对应的是区域3；D. ()I B C A ⋂⋂对应的是区域4. 故选：B3．（2022·浙江·镇海中学模拟预测）已知集合{}23log 1,02x P x x Q xx -⎧⎫=>=≤⎨⎬+⎩⎭，则()P Q =R （） A ．[2,2]- B ．(2,2]- C ．[0,2] D ．(0,2]【答案】B 【解析】【分析】利用对数不等式及分式不等式的解法求出集合,P Q ，结合集合的补集及交集的定义即可求解. 【详解】由2log 1x >，得2x >，所以{}2,P x x =>{}R2P x x =≤.由302x x -≤+，得23x -<≤，所以{}23x x Q =-<≤，所以(){}{}{}R 23222P Q x x x x x x -<=≤=≤-<≤，故选：B.4．（2022·湖北·黄冈中学模拟预测）设集合{}2|log ,4A y y x x ==>，{}2|320B x x x =-+<，则()A B =R （） A ．(1,2) B ．(1,2] C ．(,2]-∞ D ．(,2)-∞【答案】C 【解析】【分析】利用对数函数的单调性求得集合A ，解一元二次不等式求得B ,即可根据集合的补集以及并集运算求得答案. 【详解】由题意得{}2|log ,4{|2}A y y x x y x ==>=>，则{|2}A y y =≤R，而{}2|320{|12}B x x x x x =-+<=<<，故()(,2]A B =-∞R ，故选：C.5．（2022·云南师大附中模拟预测（理））已知集合(){}2,A x y y x ==，(){},21B x y y x ==-，则集合AB的子集个数为（） A ．2 B ．4 C ．8 D ．16【答案】B 【解析】【分析】求出抛物线2y x 和曲线2||1y x =-的交点，确定集合A B 的元素个数，即可确定答案.【详解】由题意得21,02121,0x x y x x x -≥⎧=-=⎨--<⎩，当0x ≥时，21y x =- 联立2yx ，解得11x y =⎧⎨=⎩ ；当0x <时，21y x =-- 联立2yx ，解得11x y =-⎧⎨=⎩；故抛物线2y x 与曲线2||1y x =-有两个公共点，分别为(11)-，，(11)，，则集合A B 有两个元素，所以A B 的子集个数为224=，故选:B ．6．（2022·河北·沧县中学模拟预测）若集合{}{}21,0,1,2A x Z x B =∈-<<=，则A B ⋃=（） A ．(2,1)- B ．{1,0}- C ．(2,1]{2}-⋃ D ．{1,0,1,2}-【答案】D 【解析】【分析】根据已知条件求出集合A ，再利用并集的定义即可求解. 【详解】由题意可知{}}{211,0A x Z x =∈-<<=-，又{}0,1,2B =，所以}{{}1,00,1,2{1,0,1,2}A B =-=-．故选：D ．7．（2022·黑龙江·哈尔滨三中模拟预测（文））已知集合()22,1,,42x y A x y x Z y Z ⎧⎫=+≤∈∈⎨⎬⎩⎭，则A 中元素的个数为（） A ．9 B ．10C ．11D ．12【答案】C 【解析】【分析】由椭圆的性质得22,22x y -≤≤-≤. 【详解】解：由椭圆的性质得22,22x y -≤≤≤ 又,x Z y Z ∈∈,所以集合()()()()()()()()()()(){}=2,0,2,0,1,0,1,0,0,1,0,1,0,0,1,1,1,1,1,1,1,1A ------- 共有11个元素. 故选：C8．（2022·陕西·模拟预测（理））已知集合234|0A x x x ，{}2|B x a x a =<<，若A B =∅，则实数a 的取值范围是（） A ．(],1-∞- B ．[)4,+∞C ．()(),12,4-∞-⋃D ．[][)1,24,-⋃+∞【答案】D 【解析】【分析】由题知{}1,4A =-，进而分B =∅和B ≠∅空集两种情况讨论求解即可. 【详解】解：由题知{}{}2|3401,4A x x x =--==-，因为A B =∅，所以，当{}2|B x a x a=<<=∅时，2a a≥，解得01a ≤≤，当{}2|B x a x a =<<≠∅时，2241a a a a ⎧≤⎪≥-⎨⎪>⎩或24a a a ≥⎧⎨>⎩，解得[)(][)1,01,24,a ∈-+∞，综上，实数a 的取值范围是[][)1,24,-⋃+∞. 故选：D9．（2022·江苏·南京市第一中学三模）非空集合{|03}A x N x =∈<<，2{|10,}B y N y my m R =∈-+<∈，A B A B =，则实数m 的取值范围为（） A ．510,23⎛⎤ ⎥⎝⎦B ．170,4⎛⎤ ⎥⎝⎦C ．102,3⎛⎤ ⎥⎝⎦D ．517,24⎛⎤ ⎥⎝⎦【答案】A 【解析】【分析】由题知{}1,2A B ==，进而构造函数()21f x x mx =-+，再根据零点存在性定理得()()()302010f f f ⎧≥⎪<⎨⎪<⎩，解不等式即可得答案. 【详解】解：由题知{}0{|}13,2A x N x =∈<=<，因为A B A B =，所以A B =，所以{}2{|10,}1,2B y N y my m R =∈-+<∈=，故令函数()21f x x mx =-+，所以，如图，结合二次函数的图像性质与零点的存在性定理得： ()()()302010f f f ⎧≥⎪<⎨⎪<⎩，即103052020m m m -≥⎧⎪-<⎨⎪-<⎩，解得51023m <≤，所以，实数m 的取值范围为510,23⎛⎤⎥⎝⎦.故选：A10．（2022·四川攀枝花·三模（理））设集合{}A x x a =>，{}2320B x x x =-+>，若A B ⊆，则实数a 的取值范围是（）． A ．(),1-∞ B ．(],1-∞ C ．()2,+∞ D ．[)2,+∞【答案】D 【解析】【分析】先求出集合B ，再由A B ⊆求出实数a 的范围. 【详解】{}{23202B x x x x x =-+>=>或}1x <. 因为集合{}A x x a =>，A B ⊆，所以2a ≥.故选：D11．（2022·安徽黄山·二模（文））若集合2{|60}A x x x =--+>，5{|1}3B x x =≤--，则A B 等于（） A ．()3,3- B ．[2,3)-C ．(2,2)-D ．[2,2)-【答案】D 【解析】【分析】解不等式化简集合A ，B ，再利用交集的定义直接求解作答. 【详解】不等式260x x --+>化为：260x x +-<，解得：32x -<<，则(3,2)A =-，不等式513x ≤--，即203x x +≤-，整理得：(2)(3)030x x x +-≤⎧⎨-≠⎩，解得23x -≤<，则[2,3)B =-，所以[2,2)A B ⋂=-. 故选：D1．（2022·全国·高考真题（文））集合{}{}2,4,6,8,10,16M N x x ==-<<，则M N =（）A ．{2,4}B ．{2,4,6}C ．{2,4,6,8}D ．{2,4,6,8,10}【答案】A 【解析】【分析】根据集合的交集运算即可解出．【详解】因为{}2,4,6,8,10M =，{}|16N x x =-<<，所以{}2,4M N =．故选：A.2．（2022·全国·高考真题（理））设全集{1,2,3,4,5}U =，集合M 满足{1,3}U M =，则（） A ．2M ∈B ．3M ∈C ．4M ∉D ．5M ∉【答案】A【解析】【分析】先写出集合M ,然后逐项验证即可【详解】由题知{2,4,5}M =,对比选项知，A 正确,BCD 错误故选:A3．（2022·全国·高考真题（理））设全集{2,1,0,1,2,3}U =--，集合{}2{1,2},430A B xx x =-=-+=∣，则()U A B ⋃=（）A ．{1,3}B ．{0,3}C ．{2,1}-D ．{2,0}-【答案】D【解析】【分析】解方程求出集合B ,再由集合的运算即可得解.【详解】由题意，{}{}2=4301,3B x x x -+==，所以{}1,1,2,3A B ⋃=-, 所以(){}U 2,0A B ⋃=-.故选：D.4．（2022·浙江·高考真题）设集合{1,2},{2,4,6}A B ==，则A B ⋃=（）A ．{2}B ．{1,2}C ．{2,4,6}D ．{1,2,4,6}【答案】D【解析】【分析】利用并集的定义可得正确的选项.【详解】 {}1,2,4,6A B =，故选：D.5．（2022·北京·高考真题）已知全集{33}U x x =-<<，集合{21}A x x =-<≤，则U A （）A ．(2,1]-B ．(3,2)[1,3)--C ．[2,1)-D ．(3,2](1,3)--【答案】D【解析】【分析】利用补集的定义可得正确的选项．【详解】由补集定义可知：{|32U A x x =-<≤-或13}x <<，即(3,2](1,3)U A =--，故选：D ．6．（2022·全国·高考真题（文））设集合5{2,1,0,1,2},02A B x x ⎧⎫=--=≤<⎨⎬⎩⎭∣，则A B =（） A ．{}0,1,2B ．{2,1,0}--C ．{0,1}D ．{1,2}【答案】A【解析】【分析】根据集合的交集运算即可解出．【详解】因为{}2,1,0,1,2A =--，502B x x ⎧⎫=≤<⎨⎬⎩⎭∣，所以{}0,1,2A B =．故选：A.7．（2021·全国·高考真题）设集合{1,2,3,4,5,6},{1,3,6},{2,3,4}U A B ===，则()U AB =（） A ．{3}B ．{1,6}C ．{5,6}D ．{1,3} 【答案】B【解析】【分析】根据交集、补集的定义可求()U A B ⋂.【详解】由题设可得{}U 1,5,6B =，故(){}U 1,6A B ⋂=，故选：B.8．（2021·全国·高考真题（文））设集合{}{}1,3,5,7,9,27M N x x ==>，则M N =（）A ．{}7,9B ．{}5,7,9C ．{}3,5,7,9D ．{}1,3,5,7,9【答案】B【解析】【分析】求出集合N 后可求M N ⋂.【详解】7,2N ⎛⎫=+∞ ⎪⎝⎭，故{}5,7,9M N ⋂=，故选：B.9．（2021·全国·高考真题（理））已知集合{}21,S s s n n ==+∈Z ，{}41,T t t n n ==+∈Z ，则S T （）A ．∅B ．SC ．TD ．Z【答案】C【解析】【分析】分析可得T S ⊆，由此可得出结论.【详解】任取t T ∈，则()41221t n n =+=⋅+，其中n Z ∈，所以，t S ∈，故T S ⊆，因此，S T T =.故选：C.10．（2021·全国·高考真题（理））设集合{}104,53M x x N x x ⎧⎫=<<=≤≤⎨⎬⎩⎭，则M N =（）A ．103x x ⎧⎫<≤⎨⎬⎩⎭ B ．143x x ⎧⎫≤<⎨⎬⎩⎭C ．{}45x x ≤<D ．{}05x x <≤【答案】B【解析】【分析】根据交集定义运算即可【详解】因为1{|04},{|5}3M x x N x x =<<=≤≤，所以1|43M N x x ⎧⎫⋂=≤<⎨⎬⎩⎭, 故选：B.【点睛】本题考查集合的运算，属基础题，在高考中要求不高，掌握集合的交并补的基本概念即可求解.11．（2021·全国·高考真题）设集合{}24A x x =-<<，{}2,3,4,5B =，则A B =（）A ．{}2B ．{}2,3C ．{}3,4D ．{}2,3,4【答案】B【解析】【分析】利用交集的定义可求A B .【详解】由题设有{}2,3A B ⋂=，故选：B .12．（2020·浙江·高考真题）设集合S ，T ，S ⊆N *，T ⊆N *，S ，T 中至少有两个元素，且S ，T 满足： ①对于任意x ，y ∈S ，若x ≠y ，都有xy ∈T②对于任意x ，y ∈T ，若x <y ，则y x ∈S ；下列命题正确的是（）A ．若S 有4个元素，则S ∪T 有7个元素B ．若S 有4个元素，则S ∪T 有6个元素C ．若S 有3个元素，则S ∪T 有5个元素D ．若S 有3个元素，则S ∪T 有4个元素【答案】A【解析】【分析】分别给出具体的集合S 和集合T ，利用排除法排除错误选项，然后证明剩余选项的正确性即可.【详解】首先利用排除法：若取{}1,2,4S =，则{}2,4,8T =，此时{}1,2,4,8S T =，包含4个元素，排除选项 C ；若取{}2,4,8S =，则{}8,16,32T =，此时{}2,4,8,16,32S T =，包含5个元素，排除选项D ；若取{}2,4,8,16S =，则{}8,16,32,64,128T =，此时{}2,4,8,16,32,64,128S T =，包含7个元素，排除选项B ；下面来说明选项A 的正确性：设集合{}1234,,,S p p p p =，且1234p p p p <<<，*1234,,,p p p p N ∈，则1224p p p p <，且1224,p p p p T ∈，则41p S p ∈，同理42p S p ∈，43p S p ∈，32p S p ∈，31p S p ∈，21p S p ∈，若11p =，则22p ≥，则332p p p <，故322p p p =即232p p =，又444231p p p p p >>>，故442232p p p p p ==，所以342p p =，故{}232221,,,S p p p =，此时522,p T p T ∈∈，故42p S ∈，矛盾，舍. 若12p ≥，则32311p p p p p <<，故322111,p p p p p p ==即323121,p p p p ==，又44441231p p p p p p p >>>>，故441331p p p p p ==，所以441p p =，故{}2341111,,,S p p p p =，此时{}3456711111,,,,p p p p p T ⊆. 若q T ∈，则31q S p ∈，故131,1,2,3,4i q p i p ==，故31,1,2,3,4i q p i +==，即{}3456711111,,,,q p p p p p ∈，故{}3456711111,,,,p p p p p T =，此时{}234456*********,,,,,,,S T p p p p p p p p ⋃=即S T 中有7个元素.故A 正确.故选：A .【点睛】“新定义”主要是指即时定义新概念、新公式、新定理、新法则、新运算五种，然后根据此新定义去解决问题，有时还需要用类比的方法去理解新的定义，这样有助于对新定义的透彻理解.但是，透过现象看本质，它们考查的还是基础数学知识，所以说“新题”不一定是“难题”，掌握好三基，以不变应万变才是制胜法宝. 13．（2020·全国·高考真题（文））已知集合2{|340},{4,1,3,5}A x x x B =--<=-，则A B =（）A ．{4,1}-B ．{1,5}C ．{3,5}D ．{1,3}【答案】D【解析】【分析】首先解一元二次不等式求得集合A ，之后利用交集中元素的特征求得A B ，得到结果.【详解】由2340x x --<解得14x -<<，所以{}|14A x x =-<<，又因为{}4,1,3,5B =-，所以{}1,3A B =，故选：D.【点睛】本题考查的是有关集合的问题，涉及到的知识点有利用一元二次不等式的解法求集合，集合的交运算，属于基础题目.14．（2020·浙江·高考真题）已知集合P ={|14}<<x x ，{|23}Q x x =<<，则P Q =（）A ．{|12}x x <≤B ．{|23}x x <<C ．{|34}x x ≤<D ．{|14}<<x x【答案】B【解析】【分析】根据集合交集定义求解.【详解】(1,4)(2,3)(2,3)P Q == 故选：B【点睛】本题考查交集概念，考查基本分析求解能力，属基础题.。

高三数学人教版A版数学(理)高考一轮复习教案集合

第一节集合1．集合的含义与表示(1)了解集合的含义、元素与集合的“属于”关系．(2)能用自然语言、图形语言、集合语言(列举法或描述法)描述不同的具体问题． 2．集合间的基本关系(1)理解集合之间包含与相等的含义，能识别给定集合的子集． (2)在具体情境中，了解全集与空集的含义． 3．集合间的基本运算(1)理解两个集合的并集与交集的含义，会求两个简单集合的并集与交集． (2)理解在给定集合中一个子集的补集的含义，会求给定子集的补集． (3)能使用韦恩(Venn)图表示集合的关系及运算．知识点一集合的基本概念1．集合中元素的三个特性：确定性、互异性、无序性． 2．元素与集合的关系：属于或不属于，表示符号分别为∈和∉. 3．集合的三种表示方法：列举法、描述法、V enn 图法．易误提醒在解决含参数的集合问题时，要注意检验集合中元素的互异性，否则很可能会因为不满足“互异性”而导致解题错误．[自测练习]1．已知a ∈R ，若{－1,0,1}＝⎩⎨⎧⎭⎬⎫1a ，a 2，0，则a ＝________.解析：1a ≠0，a ≠0，a 2≠－1，只有a 2＝1.当a ＝1时，1a ＝1，不满足互异性，∴a ＝－1.答案：－1知识点二集合间的基本关系描述关系文字语言符号语言集合间的基本关系子集 A 中任意一元素均为B 中的元素A ⊆B 或B ⊇A真子集A 中任意一元素均为B 中的元素，且B 中至少有一个元素A 中没有AB 或B A相等集合A与集合B 中的所有元素都相同A＝B 必记结论若集合A中有n个元素，则其子集个数为2n，真子集个数为2n－1，非空真子集的个数为2n－2.易误提醒易忘空集的特殊性，在写集合的子集时不要忘了空集和它本身．[自测练习]2．已知集合A＝{x|x＝a＋(a2－1)i}(a∈R，i是虚数单位)，若A⊆R，则a＝()A．1 B．－1 C．±1 D．0解析：A⊆R，∴a2－1＝0，a＝±1.答案：C3．已知集合A＝{1,2,3,4}，B＝{(x，y)|x∈A，y∈A，xy∈A}，则集合B的所有真子集的个数为()A．512 B．256C．255 D．254解析：由题意知当x＝1时，y可取1,2,3,4；当x＝2时，y可取1,2；当x＝3时，y可取1；当x＝4时，y可取1.综上，B中所含元素共有8个，所以其真子集有28－1＝255个．选C.答案：C知识点三集合的基本运算及性质并集交集补集图形表示符号表示A∪B＝{x|x∈A或x∈B}A∩B＝{x|x∈A，且x∈B}∁U A＝{x|x∈U，且x∉A}性质A∪∅＝AA∪A＝AA∪B＝B∪AA∪B＝A⇔B⊆AA∩∅＝∅A∩A＝AA∩B＝B∩AA∩B＝A⇔A⊆BA∪(∁U A)＝UA∩(∁U A)＝∅∁U(∁U A)＝A易误提醒运用数轴图示法易忽视端点是实心还是空心．必记结论∁U(A∩B)＝(∁U A)∪(∁U B)，∁U(A∪B)＝(∁U A)∩(∁U B)．[自测练习]4．(2015·广州一模)已知全集U ＝{1,2,3,4,5}，集合M ＝{3,4,5}，N ＝{1,2,5}，则集合{1,2}可以表示( )A ．M ∩NB ．(∁U M )∩NC ．M ∩(∁U N )D ．(∁U M )∩(∁U N )解析：M ∩N ＝{5}，A 错误；∁U M ＝{1,2}，(∁U M )∩N ＝{1,2}，B 正确；∁U N ＝{3,4}，M ∩(∁U N )＝{3,4}，C错误；(∁U M )∩(∁U N )＝∅，D 错误．故选B.答案：B5．(2015·长春二模)已知集合P ＝{x |x ≥0}，Q ＝⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x ＋1x －2≥0，则P ∩(∁R Q )＝( ) A ．(－∞，2) B ．(－∞，－1] C ．(－1,0)D ．[0,2]解析：由题意可知Q ＝{x |x ≤－1或x >2}，则∁R Q ＝{x |－1<x ≤2}，所以P ∩(∁R Q )＝{x |0≤x ≤2}．故选D.答案：D考点一集合的基本概念|1．已知集合S ＝{x |3x ＋a ＝0}，如果1∈S ，那么a 的值为( ) A ．－3 B ．－1 C ．1D ．3解析：∵1∈S ，∴3＋a ＝0，a ＝－3. 答案：A2．设集合A ＝{1,2,4}，集合B ＝{x |x ＝a ＋b ，a ∈A ，b ∈A }，则集合B 中的元素个数为( )A ．4B ．5C ．6D ．7 解析：∵a ∈A ，b ∈A ，x ＝a ＋b ，∴x ＝2,3,4,5,6,8，∴B 中有6个元素，故选C. 答案：C3．(2015·贵阳期末)已知全集U ＝{a 1，a 2，a 3，a 4}，集合A 是集合U 的恰有两个元素的子集，且满足下列三个条件：①若a 1∈A ，则a 2∈A ；②若a 3∉A ，则a 2∉A ；③若a 3∈A ，则a 4∉A .则集合A ＝________.(用列举法表示)解析：若a 1∈A ，则a 2∈A ，则由若a 3∉A ，则a 2∉A 可知，a 3∈A ，假设不成立；若a 4∈A ，则a 3∉A ，则a 2∉A ，则a 1∉A ，假设不成立，故集合A ＝{a 2，a 3}．答案：{a2，a3}判断一个元素是某个集合元素的三种方法：列举法、特征元素法、数形结合法．考点二集合间的基本关系及应用|(1)已知全集A＝{x∈N|x2＋2x－3≤0}，B＝{y|y⊆A}，则集合B中元素的个数为()A．2B．3C．4 D．5[解析]依题意得，A＝{x∈N|(x＋3)(x－1)≤0}＝{x∈N|－3≤x≤1}＝{0,1}，共有22＝4个子集，因此集合B中元素的个数为4，选C.[答案] C(2)已知集合M＝{x|－1<x<2}，N＝{x|x<a}，若M⊆N，则实数a的取值范围是()A．(2，＋∞) B．[2，＋∞)C．(－∞，－1) D．(－∞，－1][解析]依题意，由M⊆N得a≥2，即所求的实数a的取值范围是[2，＋∞)，选B.[答案] B1．判断两集合的关系常有两种方法(1)化简集合，从表达式中寻找两集合间的关系．(2)用列举法表示各集合，从元素中寻找关系．2．已知两集合间的关系求参数时的两个关键点(1)将两集合间的关系转化为元素间的关系，进而转化为参数满足的关系．(2)合理利用数轴、Venn图帮助分析．1．(2015·辽宁五校联考)设集合P＝{x|x>1}，Q＝{x|x2－x>0}，则下列结论正确的是() A．P⊆Q B．Q⊆PC．P＝Q D．P∪Q＝R解析：由集合Q＝{x|x2－x>0}，知Q＝{x|x<0或x>1}，所以选A.答案：A考点三集合的基本运算|(1)(2015·高考全国卷Ⅱ)已知集合A＝{－2，－1，0,1,2}，B＝{x|(x－1)(x＋2)<0}，则A∩B＝()A．{－1,0}B．{0,1}C．{－1,0,1} D．{0,1,2}[解析]由于B＝{x|－2<x<1}，所以A∩B＝{－1,0}．故选A.[答案] A(2)(2015·郑州期末)已知函数f(x)＝2－x－1，集合A为函数f(x)的定义域，集合B为函数f(x)的值域，则如图所示的阴影部分表示的集合为________．[解析]本题考查函数的定义域、值域以及集合的表示．要使函数f(x)＝2－x－1有意义，则2－x－1≥0，解得x≤0，所以A＝(－∞，0]．又函数f(x)＝2－x－1的值域B＝[0，＋∞)．阴影部分用集合表示为∁A∪B(A∩B)＝(－∞，0)∪(0，＋∞)．[答案](－∞，0)∪(0，＋∞)集合运算问题的四种常见类型及解题策略(1)离散型数集或抽象集合间的运算．常借助Venn图求解．(2)连续型数集的运算．常借助数轴求解．(3)已知集合的运算结果求集合．借助数轴或Venn图求解．(4)根据集合运算求参数．先把符号语言译成文字语言，然后适时应用数形结合求解．2．(2015·高考陕西卷)设集合M＝{x|x2＝x}，N＝{x|lg x≤0}，则M∪N＝()A．[0,1]B．(0,1]C．[0,1) D．(－∞，1]解析：∵M＝{x|x2＝x}＝{0,1}，N＝{x|lg x≤0}＝{x|0<x≤1}，∴M∪N＝{x|0≤x≤1}，故选A.答案：A考点四集合的创新问题|设集合A＝{1,2,3}，B＝{2,3,4,5}，定义A⊙B＝{(x，y)|x∈A∩B，y∈A∪B}，则A⊙B中元素的个数是()A．7B．10C．25D．52[解析]A∩B＝{2,3}，A∪B＝{1,2,3,4,5}，由列举法可知A⊙B＝{(2,1)，(2,2)，(2,3)，(2,4)，(2,5)，(3,1)，(3,2)，(3,3)，(3,4)，(3,5)}，共有10个元素，故选B.[答案] B解决集合创新问题的三个策略(1)遇到新定义问题，应耐心读题，分析新定义的特点，弄清新定义的性质．(2)按新定义的要求，“照章办事”，逐条分析、验证、运算，使问题得以解决．(3)对于选择题，可以结合选项通过验证，用排除、对比、特值等方法求解．3．设P和Q是两个集合，定义集合P－Q＝{x|x∈P，且x∉Q}，如果P＝{x|log2x<1}，Q＝{x||x－2|<1}，那么P－Q＝()A．{x|0<x<1} B．{x|0<x≤1}C．{x|1≤x<2} D．{x|2≤x<3}解析：由log2x<1，得0<x<2，所以P＝{x|0<x<2}；由|x－2|<1，得1<x<3，所以Q＝{x|1<x<3}．由题意，得P－Q＝{x|0<x≤1}．答案：B1.遗忘空集致误【典例】设全集是实数集R ，A ＝{x |2x 2－7x ＋3≤0}，B ＝{x |x 2＋a <0}．若(∁R A )∩B ＝B ，则实数a 的取值范围是________．[解析] ∵A ＝⎩⎨⎧⎭⎬⎫x ⎪⎪ 12≤x ≤3，∴∁R A ＝⎩⎨⎧⎭⎬⎫x ⎪⎪x <12或x >3，当(∁R A )∩B ＝B 时，B ⊆∁R A 即A ∩B ＝∅.①当B ＝∅，即a ≥0时，满足B ⊆∁R A ； ②当B ≠∅，即a <0时， B ＝{x |－－a <x <－a }，要使B ⊆∁R A ，需－a ≤12，解得－14≤a <0.综上可得，实数a 的取值范围是a ≥－14.[答案] a ≥－14[易误点评] 由∁R A ∩B ＝B 知B ⊆∁R A ，即A ∩B ＝∅，又集合B 中元素属性满足x 2＋a <0，当a ≥0时B ＝∅易忽视导致漏解．[防范措施] (1)根据集合间的关系求参数是高考的一个重点内容．解答此类问题的关键是抓住集合间的关系以及集合元素的特征．(2)已知集合B ，若已知A ⊆B 或A ∩B ＝∅，则考生很容易忽视A ＝∅而造成漏解．在解题过程中应根据集合A 分三种情况进行讨论．[跟踪练习] 已知U ＝R ，集合A ＝{x |x 2－x －2＝0}，B ＝{x |mx ＋1＝0}，B ∩(∁U A )＝∅，则m ＝________.解析：A ＝{－1,2}，B ＝∅时，m ＝0；B ＝{－1}时，m ＝1；B ＝{2}时，m ＝－12.答案：0,1，－12A 组考点能力演练1．集合U ＝{0,1,2,3,4}，A ＝{1,2}，B ＝{x ∈Z |x 2－5x ＋4<0}，则∁U (A ∪B )＝( ) A ．{0,1,3,4} B ．{1,2,3} C ．{0,4}D ．{0}解析：因为集合B ＝{x ∈Z |x 2－5x ＋4<0}＝{2,3}，所以A ∪B ＝{1,2,3}，又全集U ＝{0,1,2,3,4}，所以∁U (A ∪B )＝{0,4}．所以选C.答案：C2．已知集合A＝{0,1,2,3,4}，B＝{x|x＝n，n∈A}，则A∩B的真子集个数为() A．5 B．6C．7 D．8解析：由题意，得B＝{0,1，2，3，2}，所以A∩B＝{0,1,2}，所以A∩B的真子集个数为23－1＝7，故选C.答案：C3．(2015·太原一模)已知全集U＝R，集合M＝{x|(x－1)(x＋3)<0}，N＝{x||x|≤1}，则阴影部分表示的集合是()A．[－1,1)B．(－3,1]C．(－∞，－3)∪[－1，＋∞)D．(－3，－1)x|－1≤x≤1，∴阴影部分表示的集解析：由题意可知，M＝{}x|－3<x<1，N＝{}合为M∩(∁U N)＝{}x|－3<x<－1.答案：D4．集合A＝{x|x－2<0}，B＝{x|x<a}，若A∩B＝A，则实数a的取值范围是()A．(－∞，－2] B．[－2，＋∞)C．(－∞，2] D．[2，＋∞)解析：由题意，得A＝{x|x<2}．又因为A∩B＝A，所以a≥2，故选D.答案：D5．(2015·山西质检)集合A，B满足A∪B＝{1,2}，则不同的有序集合对(A，B)共有() A．4个B．7个C．8个D．9个解析：由题意可按集合A中的元素个数分类．易知集合{1,2}的子集有4个：∅，{1}，{2}，{1,2}．若A＝∅，则B＝{1,2}；若A＝{1}，则B＝{2}或B＝{1,2}；若A＝{2}，则B ＝{1}或B＝{1,2}；若A＝{1,2}；则B＝∅或B＝{1}或B＝{2}或B＝{1,2}．综上所述，不同的有序集合对(A，B)共有9个，故选D.答案：D6．(2015·广州模拟)设集合A＝{(x，y)|2x＋y＝6}，B＝{(x，y)|3x＋2y＝4}，满足C⊆(A∩B)的集合C的个数为________．解析：依题意得，A ∩B ＝{(8，－10)}，因此满足C ⊆(A ∩B )的集合C 的个数是2. 答案：27．设集合S n ＝{1,2,3，…，n }，若X ⊆S n ，把X 的所有元素的乘积称为X 的容量(若X 中只有一个元素，则该元素的数值即为它的容量，规定空集的容量为0)．若X 的容量为奇(偶)数，则称X 为S n 的奇(偶)子集，则S 4的所有奇子集的容量之和为________．解析：∵S 4＝{1,2,3,4}，∴X ＝∅，{1}，{2}，{3}，{4}，{1,2}，{1,3}，{1,4}，{2,3}，{2,4}，{3,4}，{1,2,3}，{1,2,4}，{1,3,4}，{2,3,4}，{1,2,3,4}．其中是奇子集的为X ＝{1}，{3}，{1,3}，其容量分别为1,3,3，所以S 4的所有奇子集的容量之和为7.答案：78．已知集合P ＝{－1，m }，Q ＝⎩⎨⎧⎭⎬⎫x ⎪⎪－1<x <34，若P ∩Q ≠∅，则整数m ＝________. 解析：由{－1，m }∩⎩⎨⎧⎭⎬⎫x ⎪⎪－1<x <34≠∅，可得－1<m <34，由此可得整数m ＝0. 答案：09．已知集合A ＝{x |x 2－2x －3≤0}，B ＝{x |x 2－2mx ＋m 2－4≤0，x ∈R ，m ∈R }． (1)若A ∩B ＝[0,3]，求实数m 的值； (2)若A ⊆∁R B ，求实数m 的取值范围．解：由已知得A ＝{x |－1≤x ≤3}， B ＝{x |m －2≤x ≤m ＋2}．(1)∵A ∩B ＝[0,3]，∴⎩⎪⎨⎪⎧m －2＝0，m ＋2≥3.∴m ＝2.(2)∁R B ＝{x |x <m －2或x >m ＋2}，∴A ⊆∁R B ， ∴m －2>3或m ＋2<－1，即m >5或m <－3. 因此实数m 的取值范围是{m |m >5或m <－3}．10．设全集I ＝R ，已知集合M ＝{x |(x ＋3)2≤0}，N ＝{x |x 2＋x －6＝0}． (1)求(∁I M )∩N ；(2)记集合A ＝(∁I M )∩N ，已知集合B ＝{x |a －1≤x ≤5－a ，a ∈R }，若B ∪A ＝A ，求实数a 的取值范围．解：(1)∵M ＝{x |(x ＋3)2≤0}＝{－3}， N ＝{x |x 2＋x －6＝0}＝{－3,2}，∴∁I M ＝{x |x ∈R 且x ≠－3}， ∴(∁I M )∩N ＝{2}．(2)由(1)知A ＝(∁I M )∩N ＝{2}，∵A ∪B ＝A ，∴B ⊆A ，∴B ＝∅或B ＝{2}，当B ＝∅时，a －1>5－a ，∴a >3；当B ＝{2}时，⎩⎪⎨⎪⎧a －1＝2，5－a ＝2，解得a ＝3，综上所述，实数a 的取值范围为{a |a ≥3}．B 组高考题型专练1．(2014·高考课标全国卷Ⅰ)已知集合A ＝{x |x 2－2x －3≥0}，B ＝{x |－2≤x <2}，则A ∩B ＝( )A ．[－2，－1]B ．[－1,2)C ．[－1,1]D ．[1,2)解析：由不等式x 2－2x －3≥0解得x ≥3或x ≤－1，因此集合A ＝{x |x ≤－1或x ≥3}，又集合B ＝{x |－2≤x <2}，所以A ∩B ＝{x |－2≤x ≤－1}，故选A.答案：A2．(2014·高考课标全国卷Ⅱ)设集合M ＝{0,1,2}，N ＝{x |x 2－3x ＋2≤0}，则M ∩N ＝( ) A ．{1} B ．{2} C ．{0,1}D ．{1,2}解析：由已知得N ＝{x |1≤x ≤2}，∵M ＝{0,1,2}，∴M ∩N ＝{1,2}，故选D. 答案：D3．(2015·高考全国卷Ⅰ)已知集合A ＝{x |x ＝3n ＋2，n ∈N }，B ＝{6,8,10,12,14}，则集合A ∩B 中元素的个数为( )A ．5B ．4C ．3D ．2解析：集合A ＝{x |x ＝3n ＋2，n ∈N }，当n ＝0时，3n ＋2＝2，当n ＝1时，3n ＋2＝5，当n ＝2时，3n ＋2＝8，当n ＝3时，3n ＋2＝11，当n ＝4时，3n ＋2＝14，∵B ＝{6,8,10,12,14}，∴A ∩B 中元素的个数为2，选D.答案：D4．(2015·高考福建卷)若集合A＝{i，i2，i3，i4}(i是虚数单位)，B＝{1，－1}，则A∩B 等于()A．{－1} B．{1}C．{1，－1} D．∅解析：因为A＝{i，－1，－i,1}，B＝{1，－1}，所以A∩B＝{1，－1}，故选C.答案：C5．(2015·高考浙江卷)已知集合P＝{x|x2－2x≥0}，Q＝{x|1<x≤2}，则(∁R P)∩Q＝() A．[0,1) B．(0,2]C．(1,2) D．[1,2]解析：∁R P＝{x|0<x<2}，故(∁R P)∩Q＝{x|1<x<2}．答案：C6．(2015·高考重庆卷)已知集合A＝{1,2,3}，B＝{2,3}，则()A．A＝B B．A∩B＝∅C．A B D．B A解析：由真子集的概念知B A，故选D.答案：D。

2023年高考数学一轮考点复习第一章集合、常用逻辑用语、不等式第2讲充分条件与必要条件

第一章集合、常用逻辑用语、不等式
高考一轮总复习 • 数学
返回导航
[解析] (4)当 α＝β＝π2时，tan α、tan β 都无意义．因此不能推出 tan α ＝tan β，当 tan α＝tan β 时，α＝β＋kπ，k∈Z，不一定 α＝β，因此是既不充分也不必要条件．
(5)在△ABC 中，由 A>B，则 a>b，由正弦定理 sin A>sin B，反之也成立．
p 是 q 的__充__分__不__必__要___条件
p⇒q 且 q p
p 是 q 的__必__要__不__充__分___条件
p q 且 q⇒p
p 是 q 的__充__要___条件
p⇔q
p 是 q 的__既__不__充__分__也__不__必__要___条件
p q且q p
第一章集合、常用逻辑用语、不等式
第一章集合、常用逻辑用语、不等式
高考一轮总复习 • 数学
返回导航
题组一走出误区 1．判断下列结论是否正确(请在括号内打“√”或“×”) (1)p是q的充分不必要条件等价于q是p的必要不充分条件．( √ ) (2)已知集合A，B，则(A∪B)⊆(A∩B)的充要条件是A＝B.( √ ) (3)若已知p：x>1和q：x≥1，则p是q的充分不必要条件．( √ ) (4)“α＝β”是“tan α＝tan β”的充分不必要条件．( × ) (5)在△ABC中，A>B是sin A>sin B的充要条件．( √ )
第一章集合、常用逻辑用语、不等式
高考一轮总复习 • 数学
返回导航
[解析] 解法一：由 sin x＝1，得 x＝2kπ＋π2(k∈Z)，则 cos2kπ＋π2＝ cos π2＝0，故充分性成立；又由 cos x＝0，得 x＝kπ＋π2(k∈Z)，而 sinkπ＋π2 ＝1 或－1，故必要性不成立．所以“sin x＝1”是“cos x＝0”的充分不必要条件，故选 A.

2023年高考数学一轮考点复习第一章集合、常用逻辑用语、不等式第3讲全称量词与存在量词

(3) 根据全称量词命题与存在量词命题的否定关系，可得綈 p 为 “∀x∈R，ex－x－1>0”，故选C.
第一章集合、常用逻辑用语、不等式
高考一轮总复习 • 数学
返回导航
否定全称量词命题和存在量词命题时，一是要改写量词，全称量词改写为存在量词，存在量词改写为全称量词；二是要否定结论，而一般命题的否定只需直接否定结论．
返回导航
[解析] (1)“所有”改为“存在”(或“有的”)，“都是”改为 “不都是”(或“不是”)，即綈p为有的正方形不是平行四边形．
(2)含有一个量词的命题的否定规律是“改量词，否结论”，所以，命题 “ ∀ x ∈ [0 ，＋ ∞) ， x3 ＋ x≥0” 的否定是 “ ∃ x ∈ [0 ，＋ ∞) ， x3 ＋ x<0”，故选C.
知，∀x∈R,2x>0，则D为真命题．故选C.
第一章集合、常用逻辑用语、不等式
高考一轮总复习 • 数学
返回导航
4．(必修1P32T6改编)已知命题p：∀x∈R，sin x≥0，则下列说法正确的是( A )
A．p的否定是存在量词命题，且是真命题 B．p的否定是全称量词命题，且是假命题 C．p的否定是全称量词命题，且是真命题 D．p的否定是存在量词命题，且是假命题 [解析] 命题p：∀x∈R，sin x≥0，该命题为假命题．p的否定是存在量词命题，且是真命题．故选A.
第一章集合、常用逻辑用语、不等式
返回导航
考点突破 · 互动探究
高考一轮总复习 • 数学
返回导航
考点一
含有一个量词的命题的否定——自主练透
例1 (1)(2022·青岛模拟)设命题p：所有正方形都是平行四边形，