河南省许昌市八年级上学期数学第一周考试试卷
河南省许昌市八年级上学期开学数学试卷

河南省许昌市八年级上学期开学数学试卷姓名:________ 班级:________ 成绩:________一、填空题 (共10题;共13分)1. (1分)一只蚂蚁由(0,0)先向上爬4个单位长度,再向右爬3个单位长度,再向下爬2个单位长度后,它所在位置的坐标是________.2. (1分) (2015七下·农安期中) 不等式 x﹣5≥3的最小整数解是________.3. (1分) (2019八上·浦东期中) 化简 ________.4. (2分)(2016·南京) 化简:=________;=________.5. (1分)有甲、乙、丙三种货物,若购甲3件,乙7件,丙1件共需630元;若购甲4件,乙10件,丙1件共需840元,现购甲、乙、丙各一件共需________ 元.6. (1分) (2018七下·越秀期中) 若 ________.7. (1分)两条平行直线被第三条直线所截,则:①一对同位角的角平分线互相平行;②一对内错角的角平分线互相平行;③一对同旁内角的角平分线互相平行;④一对同旁内角的角平分线互相垂直.其中正确的结论是________ .(注:请把你认为所有正确的结论的序号都填上)8. (1分)(2013·镇江) 若x3=8,则x=________.9. (3分)图形在坐标平面中平移变换的实质:(1)图形的位置及表示位置的坐标发生变化;(2)图形的________、________、________不变.10. (1分) (2018八上·兰州期末) 如图,两根铁棒直立于桶底水平的木桶中,在桶中加入水后,一根露出水面的长度是它的,另一根露出水面的长度是它的.两根铁棒长度之和为55 cm,此时木桶中水的深度是________cm.二、选择 (共10题;共20分)11. (2分)如图,能判定EC∥AB的条件是()A . ∠B=∠ECDB . ∠A=∠ECDC . ∠B=∠ACED . ∠A=∠ACB12. (2分) (2016七上·黑龙江期中) 如图是2016年巴西奥运会的吉祥物维尼修斯,下列图案中,是通过如图平移得到的图案是()A .B .C .D .13. (2分)设边长为3的正方形的对角线长为a,下列关于a的四种说法:①a是无理数;②a可以用数轴上的一个点来表示;③5<a<6;④a是18的算术平方根.其中,所有正确说法的序号是()A . ①④B . ②③C . ①②④D . ①③④14. (2分)(2017·琼山模拟) ﹣8的立方根是()A . 2B . ﹣2C . ±2D . ﹣15. (2分)已知∣x-2∣+=0,则点P(x,y)在直角坐标系中()A . 第一象限B . 第二象限C . 第三象限D . 第四象限16. (2分) 2x﹣4≥0的解集在数轴上表示正确的是().A .B .C .D .17. (2分) (2017七下·重庆期中) 下列各式,属于二元一次方程的个数有()①xy+2x﹣y=7;②4x+1=x﹣y;③ +y=5;④x=y;⑤x2﹣y2=2⑥6x﹣2y ⑦x+y+z=1⑧y(y﹣1)=2y2﹣y2+x.A . 1B . 2C . 3D . 418. (2分)如图,将长方形ABCD的一角折叠,折痕为AE,∠BAD比∠BAE大18°.设∠BAE和∠BAD的度数分别为x,y,那么x,y所适合的一个方程组是(A .B .C .D .19. (2分) (2017八下·抚宁期末) 已知一次函数y=(m -1)x + m的图象分别交x轴负半轴、y轴负半轴于点A、B,则m的取值范围是()A . m>1B . m<1C . m <0D . m >020. (2分)在数轴上表示不等式x-1<0的解集,正确的是()A .B .C .D .三、解答题. (共8题;共73分)21. (10分)(2020·平阳模拟)(1)计算:(3﹣π)0﹣ +|3﹣|+(tan30°)﹣1(2)定义新运算:对于任意实数a,b,都有a⊕b=a(a﹣b)+1,等式右边是通常的加法、减法及乘法运算.比如:2⊕5=2×(2﹣5)+1=2×(﹣3)+1=﹣6+1=﹣5若3⊕x的值小于13,求x的取值范围,并在如图所示的数轴上表示出来.22. (9分) (2018·张家界) 今年是我市全面推进中小学校“社会主义核心价值观”教育年.某校对全校学生进行了中期检测评价,检测结果分为A(优秀)、B(良好)、C(合格)、D(不合格)四个等级.并随机抽取若干名学生的检测结果作为样本进行数据处理,制作了如下所示不完整的统计表(图1)和统计图(图2).等级频数频率A a0.3B350.35C31bD40.04请根据图提供的信息,解答下列问题:(1)本次随机抽取的样本容量为________;(2) a=________,b=________;(3)请在图2中补全条形统计图;(4)若该校共有学生800人,据此估算,该校学生在本次检测中达到“A(优秀)”等级的学生人数为________人.23. (5分) (2019八下·新密期中) 若三角形的三边长分别是,,,且是不等式的正偶数解,试求第三边的长 .24. (5分) (2019八下·雅安期中) 解不等式组:;并写出它的整数解.25. (9分) (2018七上·南召期末) 阅读理解如图1,已知点A是BC外一点,连接AB,AC,求∠BAC+∠B+∠C的度数.(1)阅读并补充下面推理过程解:过点A作ED∥BC∴∠B=∠________,∠C=∠________.又∵∠EAB+∠BAC+∠DAC=180°(平角定义)∴∠B+∠BAC+∠C=180°从上面的推理过程中,我们发现平行线具有“等角转化”的功能,将∠BAC,∠B,∠C“凑”在一起,得出角之间的关系,使问题得以解决(2)如图2,已知AB∥ED,求∠B+∠BCD+∠D的度数.小明受到启发,过点C作CF∥AB如图所示,请你帮助小明完成解答:(3)已知AB∥CD,点C在点D的右侧,∠ADC=70°.BE平分∠ABC,DE平分∠ADC,BE,DE所在的直线交于点E,点E在AB与CD两条平行线之间.①如图3,点B在点A的左侧,若∠ABC=60°,则∠BED的度数为________°.②如图4,点B在点A的右侧,且AB<CD,AD<BC.若∠ABC=n°,则∠BED的度数为________°(用含n的代数式表示)26. (10分)如图,AB是☉O的直径,AM和BN是它的两条切线,DC切☉O于点E,交AM于点D,交BN于点C,F 是CD的中点,连结OF.(1)求证:OD∥BE.(2)猜想:OF与CD有何数量关系?并说明理由.27. (15分) (2018七下·历城期中) 如图1,点P、Q分别是等边△ABC边AB、BC上的动点(端点除外),点P从顶点A、点Q从顶点B同时出发,且它们的运动速度相同,连接AQ、CP交于点M.(1)△ABQ与△CAP全等吗?请说明理由;(2)当点P、Q分别在AB、BC边上运动时,∠QMC变化吗?若变化,请说明理由;若不变,求出它的度数.(3)如图2,若点P、Q在运动到终点后继续在AB、BC的延长线上运动,直线AQ、CP交点为M,则∠QMC变化吗?若变化,请说明理由;若不变,则求出它的度数.28. (10分) (2015七下·绍兴期中) 修建某一建筑时,若请甲、乙两个工程队同时施工,8天可以完成,需付两队费用共3520元;若先请甲队单独做6天,再请乙队单独做12天可以完成,需付两队费用共3480元,问:(1)甲、乙两队每天费用各为多少?(2)若单独请某队完成工程,则单独请哪队施工费用较少?参考答案一、填空题 (共10题;共13分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、二、选择 (共10题;共20分)11-1、12-1、13-1、14-1、15-1、16-1、17-1、18-1、19-1、20-1、三、解答题. (共8题;共73分) 21-1、21-2、22-1、22-2、22-3、22-4、23-1、24-1、25-1、25-2、25-3、26-1、26-2、27-1、27-2、27-3、28-1、28-2、。
八年级上册许昌数学全册全套试卷易错题(Word版 含答案)

八年级上册许昌数学全册全套试卷易错题(Word 版 含答案)一、八年级数学三角形填空题(难)1.如图,Rt △ABC 中,∠C=90°,∠BAC 的角平分线AE 与AC 的中线BD 交于点F ,P 为CE 中点,连结PF ,若CP=2,15BFP S ∆=,则AB 的长度为_______.【答案】15【解析】【分析】作辅助线EH AB ⊥交AB 于H ,再利用等量关系用△BFP 的面积来表示△BEA 的面积,利用三角形的面积公式来求解底边AB 的长度【详解】作EH AB ⊥∵AE 平分∠BACBAE CAE ∴∠=∠EC EH ∴=∵P 为CE 中点4EC EH ==∴∵D 为AC 中点,P 为CE 中点=x =y PEF PCF CDF ADF S S S S ==△△△△∴设,15x BEF S =-△∴15+x+y BCD BDA S S ==△△∴y=15+x+y-y=15+x BFA BDA S S =-△△∴15x+15+x=30BEA BEF BFA S S S =+=-△△△∴1=302BEA S AB EH ⨯=△∵ =15AB ∴【点睛】本题考查了辅助线的运用以及三角形的中线平分三角形的面积,解题的关键在于如何利用△BFP的面积来表示△BEA的面积2.已知a、b、c为△ABC的三边,化简:|a+b﹣c|-|a﹣b﹣c|+|a﹣b+c|=______.--【答案】3a b c【解析】【分析】根据三角形的三边关系判断绝对值内式子的正负,然后利用绝对值的性质去掉绝对值,再去括号合并同类项即可.【详解】解:∵a、b、c为△ABC的三边,∴a+b>c,a-b<c,a+c>b,∴a+b-c>0,a-b-c<0,a-b+c>0,∴|a+b-c|-|a-b-c|+|a-b+c|=(a+b-c)+(a-b- c)+(a-b+c)=a+b-c+a-b- c+a-b+c=3a-b-c.故答案为:3a-b-c.【点睛】本题主要考查了三角形的三边关系定理和利用绝对值的性质进行化简,利用三角形的三边关系得出绝对值内式子的正负是解决此题的关键.3.如果一个n边形的内角和是1440°,那么n=__.【答案】10【解析】∵n边形的内角和是1440°,∴(n−2)×180°=1440°,解得:n=10.故答案为:10.4.如图,∠A=50°,∠ABO=28°,∠ACO=32°,则∠BOC=______°.【答案】110【解析】已知∠A=50°,∠ABO=28°,∠ACO=32°,根据三角形外角的性质可得∠BDC=∠A+∠ABO=78°,∠BOC=∠BDC+∠ACO=110°.5.如图,在△ABC中,∠A=50°,∠ABC=70°,BD平分∠ABC,则∠BDC的度数是_____.【答案】85°.【解析】【分析】根据三角形内角和得出∠C=60°,再利用角平分线得出∠DBC=35°,进而利用三角形内角和得出∠BDC的度数.【详解】∵在△ABC中,∠A=50°,∠ABC=70°,∴∠C=60°,∵BD平分∠ABC,∴∠DBC=35°,∴∠BDC=180°﹣60°﹣35°=85°.故答案为85°.6.如图,在△ABC中,∠A=70°,点O到AB,BC,AC的距离相等,连接BO,CO,则∠BOC=________.【答案】125°【解析】【分析】根据角平分线性质推出O为△ABC三角平分线的交点,根据三角形内角和定理求出∠ABC+∠ACB,根据角平分线定义求出∠OBC+∠OCB,即可求出答案.【详解】:∵点O到AB、BC、AC的距离相等,∴OB平分∠ABC,OC平分∠ACB,∴12OBC ABC∠=∠,12OCB ACB∠=∠,∵∠A=70°,∴∠ABC+∠ACB=180°-70°=110°,∴1110552OBC OCB ∠+∠=⨯︒=︒, ∴∠BOC=180°-(∠OBC+∠OCB )=125°;故答案为:125.【点睛】本题主要考查平分线的性质,三角形内角和定理的应用,能求出∠OBC+∠OCB 的度数是解此题的关键.二、八年级数学三角形选择题(难)7.如图,ABC ∆中,100ABC ∠=︒,且AEF AFE ∠=∠,CFD CDF ∠=∠,则EFD ∠ 的度数为( )A .80°B .60°C .40°D .20°【答案】C【解析】【分析】 连接FB ,根据三角形内角和和外角知识,进行角度计算即可.【详解】解:如图连接FB ,∵AEF AFE ∠=∠,CFD CDF ∠=∠,∴AEF AFE EFB EBF ∠=∠=∠+∠,CFD CDF BFD FBD ∠=∠=∠+∠∴AFE CFD EFB EBF BFD FBD ∠+∠=∠+∠+∠+∠,即AFE CFD EFD EBD ∠+∠=∠+∠,又∵180AFE EFD DFC ∠+∠+∠=︒,∴2180EFD EBD ∠+∠=︒,∵100ABC ∠=︒,∴180100=402EFD ︒-︒∠=︒, 故选:C .【点睛】此题考查三角形内角和和外角定义,掌握三角形内角和为180°,三角形一个外角等于不相邻两内角之和是解题关键.8.如图,ABC 的面积为1.分别倍长(延长一倍)AB ,BC ,CA 得到111A B C .再分别倍长A 1B 1,B 1C 1,C 1A 1得到222A B C .…… 按此规律,倍长2018次后得到的201820182018A B C 的面积为( )A .20176B .20186C .20187D .20188【答案】C【解析】 分析:根据等底等高的三角形的面积相等可得三角形的中线把三角形分成两个面积相等的三角形,然后求出第一次倍长后△A 1B 1C 1的面积是△ABC 的面积的7倍,依此类推写出即可.详解:连接AB 1、BC 1、CA 1,根据等底等高的三角形面积相等,△A 1BC 、△A 1B 1C 、△AB 1C 、△AB 1C 1、△ABC 1、△A 1BC 1、△ABC 的面积都相等,所以,S △A 1B 1C 1=7S △ABC ,同理S △A 2B 2C 2=7S △A 1B 1C 1=72S △ABC ,依此类推,S △AnBnCn =7n S △ABC .∵△ABC 的面积为1,∴S △AnBnCn =7n ,∴S △A 2018B 2018C 2018=72018.故选C .点睛:本题考查了三角形的面积,根据等底等高的三角形的面积相等求出一次倍长后所得的三角形的面积等于原三角形的面积的7倍是解题的关键.9.如图,在△ABC 中,点D 、E 分别是边AC,AB 的中点,BD,CE 相交于点O,连接O 在AO 上取一点F,使得OF=12AF 若S △ABC =12,则四边形OCDF 的面积为( )A .2B .83C .3D .103【答案】B【解析】【分析】 重心定理:三角形的三条边的中线交于一点,该点叫做三角形的重心.重心和三角形任意两个顶点组成的3个三角形面积相等.【详解】解:∵点D 、E 分别是边AC,AB 的中点,∴O 为△ABC 的重心,∴13AOC S=ABC S =4, ∴12DOC DOA S S ==AOC S =2,∵OF=12AF , ∴13DOF S =AOD S =23, ∴S 阴=DOC S +DOF S =83.故选:B.【点睛】本题考查了重心及重心定理,熟练掌握相关定理是解题关键.10.如图,是由相同的花盆按一定的规律组成的形如正多边形的图案,其中第1个图形一共有6个花盆,第2个图形一共有12个花盆,第3个图形一共有20个花盆,…则第8个图形中花盆的个数为( )A .56B .64C .72D .90【答案】D【解析】根据题意找出规律得到第n个图形中花盆的个数为:(n+1)(n+2),然后将n=7代入求解即可.【详解】第1个图形的花盆个数为:(1+1)(1+2);第2个图形的花盆个数为:(2+1)(2+2)=12;第3个图形的花盆个数为:(3+1)(3+2)=20;,第n个图形的花盆个数为:(n+1)(n+2);则第7个图形中花盆的个数为:(7+1)(7+2)=72.故选:C.【点睛】本题考查图形规律题,解此题的关键在于根据题中图形找到规律.的度数11.如图,将三角尺的直角顶点放在直尺的一边上,∠1=30°,∠2=50°,则3等于()A.50°B.30°C.20°D.15°【答案】C【解析】【分析】根据平行和三角形外角性质可得∠2=∠4=∠1+∠3,代入数据即可求∠3.【详解】如图所示,∵AB∥CD∴∠2=∠4=∠1+∠3=50°,∴∠3=∠4-30°=20°,故选C.12.若一个凸多边形的内角和为720°,则这个多边形的边数为()A.4 B.5 C.6 D.7【答案】C【分析】设这个多边形的边数为n,根据多边形的内角和定理得到(n﹣2)×180°=720°,然后解方程即可.【详解】设这个多边形的边数为n,由多边形的内角和是720°,根据多边形的内角和定理得(n-2)180°=720°.解得n=6.故选C.【点睛】本题主要考查多边形的内角和定理,熟练掌握多边形的内角和定理是解答本题的关键.三、八年级数学全等三角形填空题(难)13.已知:如图,△ABC和△DEC都是等边三角形,D是BC延长线上一点,AD与BE相交于点P,AC、BE相交于点M,AD,CE相交于点N,则下列五个结论:①AD=BE;②AP=BM;③∠APM=60°;④△CMN是等边三角形;⑤连接CP,则CP平分∠BPD,其中,正确的是_____.(填写序号)【答案】①③④⑤.【解析】【分析】①根据△ACD≌△BCE(SAS)即可证明AD=BE;②根据△ACN≌△BCM(ASA)即可证明AN=BM,从而判断AP≠BM;③根据∠CBE+∠CDA=60°即可求出∠APM=60°;④根据△ACN≌△BCM及∠MCN=60°可知△CMN为等边三角形;⑤根据角平分线的性质可知.【详解】①∵△ABC和△CDE都是等边三角形∴CA=CB,CD=CE,∠ACB=60°,∠DCE=60°∴∠ACE=60°∴∠ACD=∠BCE=120°在△ACD和△BCE中CA CBACD BCECD CE=⎧⎪∠=∠⎨⎪=⎩∴△ACD≌△BCE(SAS)∴AD=BE;②∵△ACD≌△BCE∴∠CAD=∠CBE在△ACN和△BCM中ACN BCMCA CBCAN CBM∠=∠⎧⎪=⎨⎪∠=∠⎩∴△ACN≌△BCM(ASA)∴AN=BM;③∵∠CAD+∠CDA=60°而∠CAD=∠CBE∴∠CBE+∠CDA=60°∴∠BPD=120°∴∠APM=60°;④∵△ACN≌△BCM∴CN=BM而∠MCN=60°∴△CMN为等边三角形;⑤过C点作CH⊥BE于H,CQ⊥AD于Q,如图∵△ACD≌△BCE∴CQ=CH∴CP平分∠BPD.故答案为:①③④⑤.【点睛】本题主要考查了三角形全等的判定和性质的灵活运用,角的计算及角平分线的判定,熟练掌握三角形全等的证明方法,角平分线的判定及相关辅助线的作法是解决本题的关键.14.如图,ABC∆中,90ACB∠=︒,8cmAC,15cmBC=,点M从A点出发沿A C B→→路径向终点运动,终点为B点,点N从B点出发沿B C A→→路径向终点运动,终点为A点,点M和N分别以每秒2cm和3cm的运动速度同时开始运动,两点都要到达相应的终点时才能停止运动,分别过M和N作ME l⊥于E,NF l⊥于F.设运动时间为t秒,要使以点M,E,C为顶点的三角形与以点N,F,C为顶点的三角形全等,则t的值为______.【答案】235或7或8【解析】【分析】易证∠MEC=∠CFN,∠MCE=∠CNF.只需MC=NC,就可得到△MEC与△CFN全等,然后只需根据点M和点N不同位置进行分类讨论即可解决问题.【详解】①当0≤t<4时,点M在AC上,点N在BC上,如图①,此时有AM=2t,BN=3t,AC=8,BC=15.当MC=NC即8−2t=15−3t时全等,解得t=7,不合题意舍去;②当4≤t<5时,点M在BC上,点N也在BC上,如图②,若MC=NC,则点M与点N重合,即2t−8=15−3t,解得t=235;当5≤t<233时,点M在BC上,点N在AC上,如图③,当MC=NC即2t−8=3t−15时全等,解得t=7;④当233≤t<232时,点N停在点A处,点M在BC上,如图④,当MC=NC即2t−8=8,解得t=8;综上所述:当t等于235或7或8秒时,以点M,E,C为顶点的三角形与以点N,F,C为顶点的三角形全等.故答案为:235或7或8.【点睛】本题主要考查了全等三角形的判定以及分类讨论的思想,可能会因考虑不全面而出错,是一道易错题.15.如图,CA⊥BC,垂足为C,AC=2Cm,BC=6cm,射线BM⊥BQ,垂足为B,动点P从C点出发以1cm/s的速度沿射线CQ运动,点N为射线BM上一动点,满足PN=AB,随着P点运动而运动,当点P运动_______秒时,△BCA与点P、N、B为顶点的三角形全等.(2个全等三角形不重合)【答案】0;4;8;12【解析】【分析】此题要分两种情况:①当P在线段BC上时,②当P在BQ上,再分别分两种情况AC=BP 或AC=BN进行计算即可.【详解】解:①当P在线段BC上,AC=BP时,△ACB≌△PBN,∵AC=2,∴BP=2,∴CP=6−2=4,∴点P的运动时间为4÷1=4(秒);②当P在线段BC上,AC=BN时,△ACB≌△NBP,这时BC=PN=6,CP=0,因此时间为0秒;③当P在BQ上,AC=BP时,△ACB≌△PBN,∵AC=2,∴BP=2,∴CP=2+6=8,∴点P的运动时间为8÷1=8(秒);④当P在BQ上,AC=NB时,△ACB≌△NBP,∵BC=6,∴BP=6,∴CP=6+6=12,点P的运动时间为12÷1=12(秒),故答案为:0或4或8或12.【点睛】本题考查三角形全等的判定方法,判定两个三角形全等时必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.16.如图,△ABE,△BCD均为等边三角形,点A,B,C在同一条直线上,连接AD,EC,AD与EB相交于点M,BD与EC相交于点N,下列说法正确的有:___________①AD=EC;②BM=BN;③MN∥AC;④EM=MB.【答案】①②③【解析】∵△ABE,△BCD均为等边三角形,∴AB=BE ,BC=BD ,∠ABE=∠CBD=60°,∴∠ABD=∠EBC ,在△ABD 和△EBC 中AB BE ABD EBC BD BC =⎧⎪∠=∠⎨⎪=⎩∴△ABD ≌△EBC(SAS),∴AD=EC ,故①正确;∴∠DAB=∠BEC ,又由上可知∠ABE=∠CBD=60°,∴∠EBD=60°,在△ABM 和△EBN 中MAB NEB AB BEABE EBN ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△ABM ≌△EBN(ASA),∴BM=BN ,故②正确;∴△BMN 为等边三角形,∴∠NMB=∠ABM=60°,∴MN ∥AC ,故③正确;若EM=MB ,则AM 平分∠EAB ,则∠DAB=30°,而由条件无法得出这一条件,故④不正确;综上可知正确的有①②③,故答案为①②③.点睛:本题主要考查全等三角形的判定和性质,掌握全等三角形的判定方法(即SSS 、SAS 、AAS 、ASA 和HL )和性质(即全等三角形的对应边相等,对应角相等).17.如图所示,∠E =∠F =90°,∠B =∠C ,AE =AF ,结论:①EM =FN ;②AF∥EB ;③∠FAN =∠EAM ;④△ACN ≌△ABM 其中正确的有 .【答案】①③④【解析】【分析】由∠E=∠F=90°,∠B=∠C,AE=AF,利用“AAS”得到△ABE与△ACF全等,根据全等三角形的对应边相等且对应角相等即可得到∠EAB与∠FAC相等,AE与AF相等,AB与AC相等,然后在等式∠EAB=∠FAC两边都减去∠MAN,得到∠EAM与∠FAN相等,然后再由∠E=∠F=90°,AE=AF,∠EAM=∠FAN,利用“ASA”得到△AEM与△AFN全等,利用全等三角形的对应边相等,对应角相等得到选项①和③正确;然后再∠C=∠B,AC=AB,∠CAN=∠BAM,利用“ASA”得到△ACN与△ABM全等,故选项④正确;若选项②正确,得到∠F与∠BDN相等,且都为90°,而∠BDN不一定为90°,故②错误.【详解】解:在△ABE和△ACF中,∠E=∠F=90°,AE=AF,∠B=∠C,∴△ABE≌△ACF,∴∠EAB=∠FAC,AE=AF,AB=AC,∴∠EAB-∠MAN=∠FAC-∠NAM,即∠EAM=∠FAN,在△AEM和△AFN中,∠E=∠F=90°,AE=AF,∠EAM=∠FAN,∴△AEM≌△AFN,∴EM=FN,∠FAN=∠EAM,故选项①和③正确;在△ACN和△ABM中,∠C=∠B,AC=AB,∠CAN=∠BAM(公共角),∴△ACN≌△ABM,故选项④正确;若AF∥EB,∠F=∠BDN=90°,而∠BDN不一定为90°,故②错误,则正确的选项有:①③④.故答案为①③④18.如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正△ABC和正△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④CO平分∠AOE;⑤∠AOB=60°.恒成立的结论有__.(把你认为正确的序号都填上)【答案】①②③④⑤【解析】【分析】根据等边三角形的性质及SAS即可证明△ACD≌△BCE即可求解.【详解】①△ABC和△DCE均是等边三角形,点A,C,E在同一条直线上,∴AC=BC,EC=DC,∠BCE=∠ACD=120°∴△ACD≌△ECB∴AD=BE,故本选项正确;②∵△ACD≌△ECB∴∠CBQ=∠CAP,又∵∠PCQ=∠ACB=60°,CB=AC,∴△BCQ≌△ACP,∴CQ=CP,又∠PCQ=60°,∴△PCQ为等边三角形,∴∠QPC=60°=∠ACB,∴PQ∥AE,故本选项正确;③∵∠ACB=∠DCE=60°,∴∠BCD=60°,∴∠ACP=∠BCQ,∵AC=BC,∠DAC=∠QBC,∴△ACP≌△BCQ(ASA),∴CP=CQ,AP=BQ,故本选项正确;④∵BC∥DE,∴∠CBE=∠BED,∵∠CBE=∠DAE,∴∠AOB=∠OAE+∠AEO=60°,同理可得出∠AOE=120°,∵D,O,C,E四点共圆,∴∠OCD=∠OED,∴∠OAC=∠OCD,∴∠DCE=∠AOC=60°,∴OC平分∠AOE,故④正确;⑤∵△ABC、△DCE为正三角形,∴∠ACB=∠DCE=60°,AC=BC,DC=EC,∴∠ACB+∠BCD=∠DCE+∠BCD,∴∠ACD=∠BCE,∴△ACD≌△BCE(SAS),∴∠CAD=∠CBE,∴∠AOB=∠CAD+∠CEB=∠CBE+∠CEB,∵∠ACB=∠CBE+∠CEB=60°,∴∠AOB=60°,故本选项正确.综上所述,正确的结论是①②③④⑤.【点睛】本题考查等边三角形的性质、全等三角形的判定与性质,利用旋转不变性,找到不变量,是解题关键.四、八年级数学全等三角形选择题(难)19.如图所示,OP 平分AOB ∠,PA OA ⊥,PB OB ⊥,垂足分别为A 、B .下列结论中不一定成立的是( ).A .PA PB =B .PO 平分APB ∠C .OA OB =D .AB 垂直平分OP【答案】D【解析】【分析】 根据角平分线上的点到角的两边距离相等可得出PA=PB ,再利用“HL ”证明△AOP 和△BOP 全等,可得出APO BPO ∠=∠,OA=OB ,即可得出答案.【详解】解:∵OP 平分AOB ∠,PA OA ⊥,PB OB ⊥∴PA PB =,选项A 正确;在△AOP 和△BOP 中,PO PO PA PB =⎧⎨=⎩, ∴AOP BOP ≅∴APO BPO ∠=∠,OA=OB ,选项B ,C 正确;由等腰三角形三线合一的性质,OP 垂直平分AB ,AB 不一定垂直平分OP ,选项D 错误. 故选:D .【点睛】本题考查的知识点是角平分线的性质以及垂直平分线的性质,熟记性质定理是解此题的关键.20.下列两个三角形中,一定全等的是( )A .两个等边三角形B .有一个角是40︒,腰相等的两个等腰三角形C .有一条边相等,有一个内角相等的两个等腰三角形D .有一个角是100︒,底相等的两个等腰三角形【答案】D【解析】【分析】根据全等三角形的判定方法及等腰三角形的性质对各个选项进行分析,从而得到答案.【详解】解:A、当两个等边三角形的对应边不相等时,这两个等边三角形也不会全等,故本选项错误;B、当该角不是对应角时,这两个等腰三角形也不会全等,故本选项错误;C、当两个等腰三角形的对应边与对应角不相等时,这两个等腰三角形也不会全等,故本选项错误;D、等腰三角形的100°角只能是顶角,则两个底角是40°,它们对应相等,所以由全等三角形的判定定理ASA或AAS证得它们全等,故本选项正确;故选D.【点睛】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.21.如图,在正方形ABCD中,AC为对角线,E为AB上一点,过点E作EF∥AD,与AC、DC 分别交于点G,F,H为CG的中点,连结DE、EH、DH、FH.下列结论:①EG=DF;②△EHF≌△DHC;③∠AEH+∠ADH=180°;④若23AEAB=,则313DHCEDHSS=.其中结论正确的有()A.1个B.2个C.3个D.4个【答案】D【解析】分析:①根据题意可知∠ACD=45°,则GF=FC,则EG=EF-GF=CD-FC=DF;②由SAS证明△EHF≌△DHC即可;③根据△EHF≌△DHC,得到∠HEF=∠HDC,从而∠AEH+∠ADH=∠AEF+∠HEF+∠ADF-∠HDC=180°;④若AEAB=23,则AE=2BE,可以证明△EGH≌△DFH,则∠EHG=∠DHF且EH=DH,则∠DHE=90°,△EHD为等腰直角三角形,过H点作HM垂直于CD于M点,设HM=x,则DM=5x,DH=26x,CD=6x,则S△DHC=12×HM×CD=3x2,S△EDH=12×DH2=13x2.详解:①∵四边形ABCD为正方形,EF∥AD,∴EF=AD=CD,∠ACD=45°,∠GFC=90°,∴△CFG为等腰直角三角形,∴GF=FC,∵EG=EF−GF,DF=CD−FC,∴EG=DF,故①正确;②∵△CFG为等腰直角三角形,H为CG的中点,∴FH=CH,∠GFH=12∠GFC=45°=∠HCD,在△EHF和△DHC中,EF=CD;∠EFH=∠DCH;FH=CH,∴△EHF≌△DHC(SAS),故②正确;③∵△EHF≌△DHC(已证),∴∠HEF=∠HDC,∴∠AEH+∠ADH=∠AEF+∠HEF+∠ADF−∠HDC=∠AEF+∠ADF=180°,故③正确;④∵AEAB=23,∴AE=2BE,∵△CFG为等腰直角三角形,H为CG的中点,∴FH=GH,∠FHG=90°,∵∠EGH=∠FHG+∠HFG=90°+∠HFG=∠HFD,在△EGH和△DFH中,EG=DF;∠EGH=∠HFD;GH=FH,∴△EGH≌△DFH(SAS),∴∠EHG=∠DHF,EH=DH,∠DHE=∠EHG+∠DHG=∠DHF+∠DHG=∠FHG=90°,∴△EHD为等腰直角三角形,如图,过H点作HM⊥CD于M,设HM=x,则26x,CD=6x,则S△DHC=12×HM×CD=3x2,S△EDH=12×DH2=13x2,∴3S△EDH=13S△DHC,故④正确;故选D.点睛:本题考查了相似三角形的判定与性质,全等三角形的判定与性质,正方形的性质,解题关键在于根据题意熟练的运用相关性质.22.如图,已知,BD 为△ABC 的角平分线,且BD=BC ,E 为BD 延长线上的一点,BE=BA .下面结论:①△ABD ≌△EBC ;②AC=2CD ;③AD=AE=EC ;④∠BCE+∠BCD=180°.其中正确的是( )A .①②③B .①②④C .①③④D .②③④【答案】C【解析】 已知BD 为△ABC 的角平分线,根据角平分线的定义可得∠ABD =∠CBD ,在△AB D 和△EB C 中,BD =BC ,∠ABD =∠CBD ,BE =BA ,由SAS 可判定△ABD ≌△EBC ,即可得①正确;根据已知条件,无法证明AC =2CD ,②错误; 已知BD 为△ABC 的角平分线,BD=BC ,BE=BA ,可得∠BCD =∠BDC =∠BAE =∠BEA , 再由∠BCE =∠BDA ,∠BCE =∠BCD +∠DCE ,∠BDA =∠DAE +∠BEA ,∠BCD =∠BEA ,可得∠DCE =∠DAE ,所以AE =EC ;再由△ABD ≌△EBC ,可得AD=EC ,所以AD=AE=EC ,即③正确;由△ABD ≌△EBC ,可得∠BCE =∠BDA ,所以∠BCE +∠BCD =∠BDA +∠BDC =180°,④正确.故选C.点睛:本题考查了全等三角形的判定及性质、等腰三角形的的性质、三角形外角的性质,本题中熟练求证三角形全等和熟练运用全等三角形对应角、对应边相等性质是解题的关键.23.如图,Rt ABC ∆中,90C =∠,3,4,5,AC BC AB ===AD 平分BAC ∠.则:ACD ABD S S ∆∆=( )A .3:4B .3:5C .4:5D .2:3【答案】B【解析】 如图,过点D 作DE ⊥AB 于点E ,由角平分线的性质可得出DE=CD ,由全等三角形的判定定理HL得出△ADC≌△ADE,故可得出AE=AC=3,由AB=5求出BE=2,设CD=x,则DE=x,BD=4﹣x,再根据勾股定理知DE2+BE2=BD2,即x2+22=(4﹣x)2,求出x=32,进而根据等高三角形的面积,可得出:S△ACD:S△ABD=CD:BD=12×32×3:12×32×5=3:5.故选:B.点睛:本题考查的是角平分线的性质,熟知角平分线上的点到角两边的距离相等是解答此题的关键.24.如图, AB=AC,AD=AE, BE、CD交于点O,则图中全等三角形共有()A.五对B.四对C.三对D.二对【答案】A【解析】如图,由已知条件可证:①△ABE≌△ACD;②△DBC≌△ECB;③△BDO≌△ECO;④△ABO≌△ACO;⑤△ADO≌△AEO;∴图中共有5对全等三角形.故选A.五、八年级数学轴对称三角形填空题(难)25.如图,在长方形ABCD的边AD上找一点P,使得点P到B、C两点的距离之和最短,则点P的位置应该在_____.【答案】AD的中点【解析】【分析】【详解】分析:过AD作C点的对称点C′,根据轴对称的性质或线段垂直平分线的性质得出AC=PC′,从而根据两点之间线段最短,得出这时的P点使BP+PC的之最短.详解:如图,过AD作C点的对称点C′,根据轴对称的性质可得:PC=PC′,CD=C′D∵四边形ABCD是矩形∴AB=CD∴△ABP≌△DC′P∴AP=PD即P为AD的中点.故答案为P为AB的中点.点睛:本题考查了轴对称-最短路线问题,矩形的性质,两点之间线段最短的性质.得出动点P所在的位置是解题的关键.26.如图,已知△ABC和△ADE都是正三角形,连接CE、BD、AF,BF=4,CF=7,求AF的长_________ .【答案】3【解析】【分析】过点A作AF⊥CE交于I,AG⊥BD交于J,证明CAE≅BAD,再证明CAI≅BAJ,求出°7830∠=∠=,然后求出12IF FJ AF==,,通过设FJ x=求出x,即可求出AF的长.【详解】解:过点A作AF⊥CE交于I,AG⊥BD交于J在CAE和BAD中AC ABCAE BADAE AD=⎧⎪∠=∠⎨⎪=⎩∴CAE≅BAD∴ICA ABJ∠=∠∴BFE CAB∠=∠(8字形)∴°120CFD∠=在CAI和BAJ中°90ICA ABJCAI BJACA BA∠=∠⎧⎪∠=∠=⎨⎪=⎩∴CAI≅BAJ,AI AJ CI BJ==∴°60CFA AFJ∠=∠=∴°30FAI FAE∠=∠=在RtAIF和RtAJF中°30FAI FAE∠=∠=∴12IF FJ AF==设FJ x=7,4CF BF==则47x x +=-32x ∴=2AF FJ =AF ∴=3【点睛】此题主要考查了通过做辅助线证明三角形全等,得出相关的边相等,学会合理添加辅助线求解是解决本题的重点.27.等腰三角形顶角为30°,腰长是4cm ,则三角形的面积为__________【答案】4【解析】如图,根据30°角所对直角边等于斜边的一半的性质,可由等腰三角形的顶角为30°,腰长是4cm ,可求得BD=12AB =4×12=2,因此此三角形的面积为:S=12AC•BD=12×4×2=8×12=4(cm 2).故答案是:4.28.如图,在直角坐标系中,点()8,8B -,点()2,0C -,若动点P 从坐标原点出发,沿y 轴正方向匀速运动,运动速度为1/cm s ,设点P 运动时间为t 秒,当BCP ∆是以BC 为腰的等腰三角形时,直接写出t 的所有值__________________.【答案】2秒或46秒或14秒【解析】【分析】分两种情况:PC为腰或BP为腰.分别作出符合条件的图形,计算出OP的长度,即可求出t的值.【详解】解:如图所示,过点B作BD⊥x轴于点D,作BE⊥y轴于点E,分别以点B和点C为圆心,以BC长为半径画弧交y轴正半轴于点F,点H和点G∵点B(-8,8),点C(-2,0),∴DC=6cm,BD=8cm,由勾股定理得:BC=10cm∴在直角三角形COG中,OC=2cm,CG=BC=10cm,∴OP=OG= 22-=,10246(cm)当点P运动到点F或点H时,BE=8cm,BH=BF=10cm,∴EF=EH=6cm∴OP=OF=8-6=2(cm)或OP=OH=8+6=14(cm),故答案为:2秒,46秒或14秒.【点睛】本题综合考查了勾股定理和等腰三角形在平面直角坐标系中的应用,通过作图找出要求的点的位置,利用勾股定理来求解是本题的关键.29.如图,已知每个小方格的边长为1,A、B两点都在小方格的格点(顶点)上,请在图中找一个格点C,使△ABC是等腰三角形,这样的格点C有________个。
2021-2022学年河南省许昌市八年级开学考试数学试卷及答案解析

50
(1)求冰墩墩、雪容融各进了多少个? (2)如果销售完 100 个吉祥物所得的利润,全部捐赠,那么,该玩具店捐赠了多少钱?
第 8 页 共 20 页
2021-2022 学年河南省许昌市八年级开学考试数学试卷
参考答案与试题解析
一.选择题(共 10 小题,满分 30 分,每小题 3 分)
i
a ab
,乙因抄错
c
而得
i
ab a
,
则 a+c=
.
13.若关于 x 的不等式 2x﹣a≥3 的解集如图所示,则常数 a=
.
14.如图,AB⊥BC,∠ABD 的度数比∠DBC 的度数少 15°,设∠ABD 和∠DBC 的度数分
别为 x、y,可以求出这两个角的度数的方程组是
.
15.如图,在三角形 ABC 中∠BAC=90°,AD 是 BC 边上的高,∠CAD=35°,则∠B
可列方程组为( )
A.
a li b rl a li b
C.
a li b rl a li b
B.
a li b rl a li b
D.
a li b rl a li b
10.如图,△ABC 为钝角三角形,将△ABC 绕点 A 按逆时针方向旋转 100°得到△AB′C′,
河南省许昌市八年级上学期数学开学试卷

河南省许昌市八年级上学期数学开学试卷姓名:________ 班级:________ 成绩:________一、选择题(本题有10小题,每小题3分,共30分) (共10题;共30分)1. (3分)(2017·博山模拟) 已知关于x,y的方程x2m﹣n﹣2+4ym+n+1=6是二元一次方程,则m,n的值为()A . m=1,n=﹣1B . m=﹣1,n=1C .D .2. (3分) (2020七下·厦门期末) 下列各项调查中合理的是()A . 调查厦门学生对新冠病毒的了解情况,采用全面调查B . 为了了解全校同学喜欢课程情况,对某班男同学进行抽样调查C . “长征-3B火箭”发射前,采用抽样调查的方式检查其各零部件的合格情况D . 采用抽样调查的方式了解国内外观众对电影《我和我的祖国》的观影感受3. (3分)如图,图中与∠C是同旁内角的角有几个()A . 1B . 2C . 3D . 44. (3分)数据0.000207用科学记数法表示为()A . 2.07×10﹣3B . 2.07×10﹣4C . 2.07×10﹣5D . 2.07×10﹣65. (3分) (2019七下·马龙月考) 如图,点E在AC的延长线上,下列条件中不能判断AB∥CD的是()A . ∠A=∠DCEB . ∠1=∠2C . ∠A+∠ACD=180°D . ∠3=∠46. (3分) (2018七下·瑞安期末) 根据分式基本性质,将分式的分子、分母首项符号都会为“+”,则可变形为()A .B .C .D .7. (3分) (2019八下·襄汾期中) 使分式有意义的取值范围是()A .B .C .D .8. (3分) (2019七下·桂林期末) 已知(a+b)2=36,(a-b)2=16,则代数式a2+b2的值为()A . 36B . 26C . 20D . 169. (3分) (2019八上·萧山月考) 若方程组的解是,则方程组的解是()A .B .C .D .10. (3分) (2019八上·萧山月考) 某市在“五水共治”中新建成一个污水处理厂.已知该厂库池中存有待处理的污水a吨,另有从城区流入库池的待处理污水(新流入污水按每小时b吨的定流量增加).若污水处理厂同时开动2台机组,需30小时处理完污水;若同时开动3台机组.需15小时处理完污水.现要求恰好用5个小时将污水处理完毕,则需同时开动的机组数为()A . 6台B . 7台C . 8台D . 9台二、填空题(共6小题,每小题4分,共24分) (共6题;共24分)11. (4分)某市为了了解全市八年级学生的身高情况,从中抽取200名学生的身高进行统计,在这个问题中,总体是________,样本容量是________.12. (4分)计算:=________13. (4分)若a+b=﹣3,ab=2,则a2+b2=________14. (4分) (2017七下·高台期末) 观察下列图形:已知a∥b,在第一个图中,可得∠1+∠2=180°,则按照以上规律,∠1+∠2+∠P1+…+∠Pn=________度.15. (4分) (2017七下·兴化期末) 已知a+b=3,ab=2,则(a-b)2=________.16. (4分) (2019九上·杭州开学考) 如图,在正方形ABCD中,AB=6,E为CD上一动点,AE交BD于点F,过F作FH⊥AE,交BC于点H,连结AH、HE,AH与BD交于点G,下列结论:①AF=HE,②∠HAE=45°,③BG2+DF2=GF2 ,④△CEH的周长为12,其中正确的结论有________。
河南省许昌市第一中学2023-2024学年八年级上学期期中考试数学试卷(含解析)

2023-2024学年河南省许昌一中八年级(上)期中数学试卷一.选择题(共10小题)1.(3分)下列四个图案中,不是轴对称图形的是()A.B.C.D.2.(3分)某同学把一块三角形的玻璃打碎成了3块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事方法是()A.带①去B.带②去C.带③去D.①②③都带去3.(3分)下列长度的三条线段,能组成三角形的是()A.1,2,3B.1,3,4C.2,3,5D.2,3,44.(3分)在平面直角坐标系中.点M(5,﹣1)关于x轴对称的点在()A.第一象限B.第二象限C.第三象限D.第四象限5.(3分)已知等腰三角形的周长为29,其中一边长为7,则该等腰三角形的底边长为()A.11B.7C.15D.15或76.(3分)如图,把两根钢条的中点连在一起,可以做成一个测量工件内槽宽的工具(卡钳),若测量得A′B′=20cm,则工件内槽宽AB为()A.10cm B.20cm C.5cm D.15cm7.(3分)如图,把△ABC沿线段DE折叠,使点B落在点F处,∠A=70°,AB=AC()A.40°B.60°C.70°D.80°8.(3分)如图,O是△ABC的∠ABC,∠ACB的平分线的交点,OE∥AC交BC于E,若△ODE的周长为10厘米()A.8cm B.9cm C.10cm D.11cm9.(3分)如图,在Rt△ABC中,∠B=90°,适当长为半径画弧,分别交AB,E,再分别以点D、E为圆心,大于,两弧交于点F,作射线AF交边BC于点G,AC=3,则△ACG的面积是()A.1B.C.2D.10.(3分)“三等分角”大约是在公元前五世纪由古希腊人提出来的,借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒OA,OB组成,OC=CD=DE,点D、E可在槽中滑动.若∠BDE=75°()A.60°B.65°C.75°D.80°二.填空题(共5小题)11.(3分)已知三角形的两边的长分别为3和8,则此三角形第三边的长度x的取值范围是.12.(3分)一个等腰三角形的一个外角为100°,则它的顶角的度数是.13.(3分)已知点A(5﹣a,3)与点B(2,b﹣1)关于x轴对称.14.(3分)如图,△ABC中,∠ACB=90°,∠A=30°,AB=12.15.(3分)如图,在长方形ABCD中,AB=6,延长BC到E,使CE=3,以每秒3个单位的速度沿BC→CD→DA向终点A运动,设点P运动的时间为t秒秒时,以P、A、B三点构成的三角形和△DCE全等.三.解答题(共8小题)16.(7分)如图,AB与CD相交于点E,AE=CE17.(8分)如图,在△ABC和△DEF中,A,F,C,D在同一直线上,∠A=∠D.(1)请你添加一个条件:,使△ABC≌△DEF;(只添一个即可)(2)根据(1)中你所添加的条件,试说明△ABC≌△DEF的理由.18.(8分)数学课上,王老师布置如下任务:如图,△ABC中,BC>AB>AC,使∠APC=2∠ABC.小路的作法如下:①作AB边的垂直平分线,交BC于点P,交AB于点Q;②连接AP.请你根据小路同学的作图方法,利用直尺和圆规完成作图(保留作图痕迹);并完成以下推理∵PQ是AB的垂直平分线∴AP=,(依据:);∴∠ABC=,(依据:).∴∠APC=2∠ABC.19.(8分)在平面直角坐标系中,△ABC的三个顶点如图所示:(1)请画出△ABC关于y轴对称的△A′B′C′(其中A′,B′,C′分别是A,B,C的对应点,不写画法);(2)直接写出A′,B′,C′三点的坐标:A′(,),B′(,),C′(,);(3)求出△ABC的面积.20.(10分)如图,在△ABC中,AD是∠BAC的平分线,DF⊥AC于点F,△ABC的面积是28cm2,AB=20cm,AC=8cm,求DE的长.21.(10分)已知:如图,AB=AE,BC=ED,求证:∠B=∠E.22.(12分)如图,已知△ABC≌△A1B1C1,如果AD、A1D1分别是△ABC、△A1B1C1的角平分线,那么AD、A1D1的值是否相等?请说明理由.23.(12分)【问题发现】(1)如图1,△ABC与△CDE中,AC=CD,B、C、E三点在同一直线上,ED=4,则BE=.【问题提出】(2)如图2,在Rt△ABC中,BC=4,过点C作CD⊥AC,求△BCD的面积.【问题解决】(3)如图3,四边形ABCD中,△ACD面积为12且CD的长为6,求△BCD的面积.参考答案与试题解析一.选择题(共10小题)1.解析:解:由题意知,ACD选项中的图形都是轴对称图形,故选:B.2.解析:解:第一块和第二块只保留了原三角形的一个角和部分边,根据这两块中的任一块均不能配一块与原来完全一样的;第三块不仅保留了原来三角形的两个角还保留了一边,则可以根据ASA来配一块一样的玻璃.故选:C.3.解析:解:A、1+2=5;B、1+3=4;C、2+3=5;D、2+3>3.故选:D.4.解析:解:∵点M(5,﹣1)关于x轴对称的点为(2,∴点M(5,﹣1)关于x轴对称的点在第一象限.故选:A.5.解析:解:本题可分两种情况:①当腰长为7时,底边长=29﹣2×4=15,不符合三角形三边关系.②底边长即为7,此时腰长=(29﹣7)÷7=11,符合三角形三边关系.因此该等腰三角形的底边长为7.故选:B.6.解析:解:如图,连接A′B′,∵点O分别是AA′、BB′的中点,∴OA=OA′,OB=OB′,在△AOB和△A′OB′中,,∴△AOB≌△A′OB′(SAS),∴A′B′=AB,∵A'B'=20cm,∴AB=20cm,故选:B.7.解析:解:∵∠A=70°,AB=AC,∴∠B=∠C=55°,∵AC∥DE,∴∠BED=∠C=55°,∵把△ABC沿线段DE折叠,使点B落在点F处,∴∠BED=∠FED=55°,∴∠CEF=180°﹣∠BED﹣∠FED=70°,故选:C.8.解析:解:∵BO是∠ACB的平分线,∴∠ABO=∠OBD,∵OD∥AB,∴∠ABO=∠BOD,∴∠OBD=∠BOD,∴OD=BD,同理,OE=EC,BC=BD+DE+EC=OD+DE+OE=C△ODE=10cm.故选:C.9.解析:解:由作法得AG平分∠BAC,∴G点到AC的距离等于BG的长,即G点到AC的距离为1,所以△ACG的面积=×3×1=.故选:B.10.解析:解:∵OC=CD=DE,∴∠DCE=∠O+∠ODC=2∠ODC,∵∠O+∠OED=3∠ODC=∠BDE=75°,∴∠ODC=25°,∵∠CDE+∠ODC=180°﹣∠BDE=105°,∴∠CDE=105°﹣∠ODC=80°.故选:D.二.填空题(共5小题)11.解析:解:根据三角形的三边关系可得8﹣3<x<4+3,解得5<x<11,故答案为:6<x<11.12.解析:解:当100°的角是顶角的外角时,顶角的度数为180°﹣100°=80°;当100°的角是底角的外角时,底角的度数为180°﹣100°=80°;故顶角的度数为80°或20°.故答案为:80°或20°.13.解析:解:∵点A(5﹣a,3)与点B(3,∴5﹣a=2,b﹣8=﹣3,∴a=3,b=﹣6,则a+b=3﹣2=5.故答案为:1.14.解析:解:∵∠ACB=90°,∠A=30°,∴,∠B=60°,∵CD是高,∴∠CDB=90°,∴∠DCB=90°﹣∠B=30°,∴.故答案为:3.15.解析:解:∵四边形ABCD是矩形,∴AB=CD=4,AD=BC=9,若△ABP与△DCE全等,∴BP=CE=5或AP=CE=3,当BP=CE=3时,则t=2秒,当AP=CE=3时,则t=9+4+9﹣3=21,∴当t为6秒或7秒时,△ABP和△DCE全等.故答案为:1或6.三.解答题(共8小题)16.解析:证明:在△AED和△CEB中,,∴△AED≌△CEB(SAS),∴∠A=∠C(全等三角形对应角相等).17.解析:解:(1)添加∠E=∠B,∵AF=CD,∴AC=DF,在△ABC和△DEF中,,∴△ABC≌△DEF(AAS),故答案为:∠E=∠B(答案不唯一);(2)理由见(1).18.解析:解:如图,点P为所作;理由如下:∵PQ是AB的垂直平分线∴AP=BP,(依据:线段垂直平分线上的点到线段两个端点的距离相等);∴∠ABC=∠BAP,(依据:等边对等角).∴∠APC=2∠ABC.故答案为BP,线段垂直平分线上的点到线段两个端点的距离相等,等边对等角.19.解析:解:(1)如图所示;(2)A'(4,1),3),C,﹣2),故答案为:(4,4),3),﹣2);(3)△ABC的面积=6×5﹣﹣﹣=8.20.解析:解:∵AD是∠BAC的平分线,DE⊥AB,∴DE=DF,∵△ABC的面积是28cm2,AB=20cm,AC=8cm,∴×20•DE+,解得:DE=DF=2,则DE的长为2cm.21.解析:证明:连接AC,AD,∵AF是CD的垂直平分线,∴AC=AD.在△ABC和△AED中,,∴△ABC≌△AED(SSS).∴∠B=∠E.22.解析:解:AD、A1D1的值相等,理由:∵△ABC≌△A8B1C1,∴AB=A8B1,∠BAC=∠B1A2C1,∠B1=∠B,∵AD、A6D1分别是△ABC、△A1B5C1的角平分线,∴∠BAD=BAC1A1D4=B7A1C1,∴∠BAD=∠B4A1D1,在△ABD与△A2B1D1中,,∴△ABD≌△A7B1D1(ASA),∴AD=A7D1.23.解析:解:(1)∵∠ACD=∠E=90°,∴∠ACB=90°﹣∠DCE=∠D,在△ABC和△CED中,,∴△ABC≌△CED(AAS),∴AB=CE=3,BC=ED=4,∴BE=BC+CE=4;故答案为:7;(2)过D作DE⊥BC交BC延长线于E,如图:∵DE⊥BC,CD⊥AC,∴∠E=∠ACD=90°,∴∠ACB=90°﹣∠DCE=∠CDE,在△ABC和△CED中,,∴△ABC≌△CED(AAS),∴BC=ED=4,=BC•DE=8;∴S△BCD(3)过A作AE⊥CD于E,过B作BF⊥CD交DC延长线于F∵△ACD面积为12且CD的长为3,∴×4•AE=12,∴AE=4,∵∠ADC=45°,AE⊥CD,∴△ADE是等腰直角三角形,∴DE=AE=4,∴CE=CD﹣DE=7,∵∠ABC=∠CAB=45°,∴∠ACB=90°,AC=BC,∴∠ACE=90°﹣∠BCF=∠CBF,在△ACE和△CBF中,,∴△ACE≌△CBF(AAS),∴BF=CE=2,=CD•BF=6.∴S△BCD。
河南省许昌市禹州市2023-2024学年八年级上学期期中数学试题(含答案)

2023-2024学年上期期中阶段性质量检测试卷八年级数学注意事项:1.本武卷共6页,三个大题,满分120分,考试时间100分钟。
2.本试卷上不要答题,请按答题卡上注意事项的要求直接把答案填写在答题卡上。
一、选择题(每小题3分,共30分)下列各小题均有四个答案,其中只有一个是正确的,将正确答案的代号字母填入题后括号内.1.在中,,,,则的取值范围是()A .B .C .D .2.如图,学校门口设置的移动拒马护栏是由多个钢管焊接的三角形组成的,这里面蕴含的数学原理是()A .两点之间,线段最短B .两点确定一条直线C .垂线段最短D .三角形具有稳定性3.围棋起源于中国,古代称之为“亦”,至今已有四千多年的历史,下列由黑白棋子摆成的图案是轴对称图形的是( )A .B .C .D .4.“花影遮墙,峰峦叠窗”,苏州园林空透的窗棂中蕴含着许多的数学元素.如图是窗棂中的部分图案.若,,,则的度数是( )A .B .C .D .5.一个三角形三个内角的度数之比为2:3:4,则这个三角形最大内角的度数是( )A .B .C .D .6.下列各项中,两个图形風于全等图形的是()A .B .C .D .7.如图,已知,则下列说法琙误的是()ABC △5AB =21BC a =-8AC =a 16a <<27a <<38a <<414a <<1275∠=∠=︒34∠=∠580∠=︒3∠65︒70︒75︒80︒70︒80︒90︒100︒EFG NMH ≌△△A .B .C .D .第7题图8.如图,点是的平分线上一点,于点,且,点是射线上一动点,则的最小值为( )第8题图A .6B .8C .10D .129.如图是蜡烛平面镜成像原理图,若以宗面为轴,镜面侧面为轴(镜面厚度忽路不计)建立平面直角坐标系,若某时刻火烙顶尖点的坐标是,此时对应的虚像的坐标是,则( )第9题图A .1B .0C .-1D .-210.一个等腰三角形的两个内角的度数之比为2:5,则这个等䐵三角形的顶角的度数为( )A .B .C .或D .二、填空题(每小题3分,共15分)11.如图,在中,,分别是边上的中线和高,,,则______.第11题图12.如图,点,,,在一条直线上,,,只需添加一个条件______,即可证明.EG HG =//EG HM FEG MNH ∠=∠EF NM=P BAC ∠AD PE AC ⊥E 8PE =Q AB PQ x y S (2,2)x -S '(3,)y 3x y +=30︒100︒30︒100︒50︒ABC △AD AE BC 6AE =13.5ABD S =△DC =B E C F BE CF =B DEF ∠=∠ABC DEF ≌△△第12题图13.如图,点是内部的一点,点到三边,,的距离,若,则的度数为______.第13题图14.如图是某种落地灯的简易示意图,已知悬杆的部分的长度与支杆相等,且.若的长度为,则此时,两点之间的距离为_______.第14题图15.如图,在中,平分,且,点是延长线上一点,且,过点作于点,则下列结论:(1);(2);(3);(4)是等腰三角形,其中正确的结论是(填序号)第15题图三、解答题(本大题共8个小题,满分75分)16.(8分)已知一个多边形的内角和与外角和的差为,求这个多边形的边数及对角线的条数17.(9分)如图,在中,,,的外角的平分线交的延长线于点,交的延长线于点.求和的度数.18.(10分)如图,在平面直角坐标系中,形如英文字母“”的图形三个端点的坐标分别是,P ABC △P AB AC BC PD PE PF ==142BPC ∠=︒BAC ∠CD BC 120BCE ∠=︒CD 55cm B D cm ABC △AD BAC ∠AD AC =E AD AE AB =E EF AB ⊥F BD EC =180ACE BDE ∠+∠=︒//AC EF BEC △900︒ABC △30A ∠=︒72ABC ∠=︒ABC △BCD ∠CE AB E //DF CE AB F BCE ∠F ∠mV ()2,3A,.按要求回答下列问题:(1)在图中画出原“”字图形关于轴对称的图形,三个端点分别记为,,,并写出点和的坐标;(2)所得图形与原图形结合起来,你能从中看出是什么英文字母吗?(3)若在轴上有一点,使得,求出点的坐标.19.(9分)如图,在中,,.(1)尺规作图:作边的垂直平分线交于点(要求:不写作法,保留作图痕迹);(2)在(1)中所作的图形中,连接,若是的平分线,求的度数.20.(9分)已知,点为线段上一点,,,.(1)求证:.(2)若,,求的度数.21.(10分)同学们在做题时,经常用到“在直角三角形中,如果一个锐角等于,那么它所对的直角边等于斜边的一半"这个定理,下面是两种添加辅助线的证明方法,请你选择一种进行证明.如图,已知在中,,.求证:.方法一:如图1,在上取一点,使得,连接.方法二:如图2,延长到,使,连接.(1,0)B (0,3)C nV x 1A 1B 1C 1A 1C x P 5APB S =△P ABC △30B ∠=︒50C ∠=︒AB BC D AD AE BAC ∠DAE ∠D BC ED BC =E ABC ∠=∠//DE AC BD AC =105A ∠=︒46C ∠=︒ABE ∠30︒ABC △90C ∠=︒30A ∠=︒12BC AB =AB D BD BC =CD BC D CD BC =AD图1图222.(10分)如图,中,点在边延长线上,,的平分线交于点,过点作,垂足为,且.(1)求的度数;(2)求证:平分;(3)若,,且,则的面积.23.(10分)与均为等婹直角三角形,.(1)如图1,当,,在同一直线上时,的延长线与交于点,则______.(2)当与的位置如图2时,的延长线与交于点,猜想的大小并证明你的结论.(3)如图3,当,,在同一直线上时(,在点的异侧),与交于点,,请直接写出,,之间的数量关系.图(1)图(2)图(3)2023-2024学年上学期期中阶段性质量检测答案八年级数学一、选择题(每小题3分,共30分)下列各小题均有四个答案,其中只有一个是正确的.ABC △D BC 106ACB ∠=︒ABC ∠AD E E EH BD ⊥H 53CEH ∠=︒ACE ∠AE CAF ∠16AC CD +=10AB =24ACD S =△ABE △ABC △BDE △90ABC DBE ∠=∠=︒D B C CE AD F CFA ∠=ABC △BDE △CE AD F CFA ∠A E D A D E CE AB G BAD ACE ∠=∠BG AB AC1-10BDCABDABCC二、填空题(每小题3分,共15分)11.;12.(答案不唯一,合理即可);13.;14.55;15.(1)(2)(4)(写对一个给1分,把(3)写上不给分)三、解答题(本大题共8个小题,满分75分)16.解:设这个多边形的边数为,由题意,得,(3分),即这个多边形的边数为9.(5分)此多边形的对角线条数为.(8分)17.解:,,,(2分)是的平分线,.(4分),.(6分),.(9分)18.解:(1)图略.点的坐标为点的坐标(图2分,每个点的坐标1分,共4分)(2)(5分)(3)设点的坐标为,点,点到轴的距离为3.(6分)点,.(7分)由题意,得,解得或,(9分)点的坐标为或.(10分)19.解:(1)如图所示即为所求.(4分)(2)垂直平分线段,,.(5分),,.(7分)平分,,.(9分)92AB DE =104︒n (2)180360900n -⨯-=︒︒︒∴9n =19(93)272⨯⨯-= 30A ∠=︒72ABC ∠=︒∴102BCD A ABC ∠=∠+∠=︒ CE BCD ∠∴1512BCE BCD ∠=∠=︒ ∠ABC 72=︒∴21BEC ABC BCE ∠=∠-∠=︒ DF//CE ∴F ∠=BEC 21∠=︒1A (2,3)-1C (0,3)-X P (,0)x (2,3)A ∴A x (1,0)B ∴|1|BP x =-12⨯3|1|5x ⨯-=133x =73-∴P 13,03⎛⎫ ⎪⎝⎭7,03⎛⎫- ⎪⎝⎭DF DF AB ∴DB DA =∴30DAB B ∠=∠=︒ 50C ∠=︒∴1801803050100BAC B C ︒︒∠=-∠-∠-︒=-=︒︒∴1003070CAD BAC DAB ∠=∠-∠=︒-=︒︒ AE BAC ∠∴1502CAE BAC ∠=∠=︒∴705020DAE DAC CAE ∠=∠-∠=︒-=︒︒20.解:(1)证明:,.(1分)在和中,,,.(4分)(2)由(1)知,,.,,,(7分),.(9分)21.证明:方法一:如图1,在上截取一点,使得,连接,,(2分),,,是是等边三角形,(4分),,(6分),,(8分),.(10分)方法二:如图2,延长到,使,连接,,,,,(3分)在和中,,,(5分),是等边三角形,,(8分),.图1图222.解:(1),.(1分),.,,(2分).(3分)(2)证明:如图所示,过点分别作于,于,(4分)平分,.(5分)由(1)知,平分,,(6分),平分.(8分)(3)15.(10分) //DE AC ∴EDB C ∠=∠EBD △BAC △EDB C ED BC E ABC ∠=∠⎧⎪=⎨⎪∠=∠⎩∴()EBD BAC ASA ≌△△∴BD AC =EBD BAC ≌△△∴EBD A ∠=∠ 105A ∠=︒46C ∠=︒∴105EBD ∠=︒180********ABC A C ∠=-∠︒︒︒-∠=--︒29︒=∴1052976ABE EBD ABC ∠=∠-∠=︒-=︒︒AB D BC BD =CD ∴BCD BDC ∠=∠ 90ACB ∠=︒30A ∠=︒∴180B ∠=︒903060-︒-︒=︒∴BCD △∴BC CD =∴BCD ∠=60BDC ∠=︒∴906030ACD ∠=-=︒︒︒∴CD AD =∴BC AD BD ==∴12BC AB =BC D BC CD =AD 90ACB ∠=︒30BAC ∠=︒180903060B ∠=︒-︒-︒=︒∴1809090ACD ︒-︒∠==︒ACB =∠ACB△ACD △AC AC ACB ACD BC DC =⎧⎪∠=∠⎨⎪=⎩∴()ACB ACD SAS ≌△△∴AD AB =∴ABD △∴AB BD = 12BC CD BD ==∴12BC AB = 106ACB ∠=︒∴180********ACD ACB ∠=-∠=-︒=︒︒︒ EH BD ⊥∴90CHE ∠=︒ 53CEH ∠=︒∴9053ECH ︒∠=-︒37=︒∴743737ACE ∠=-=︒︒︒E EM BF ⊥M EN AC ⊥N BE ABC ∠∴EM EH =37ACE ECH ∠=∠=︒∴CE ACD ∠∴EN EH =∴EM EN =∴AE CAF ∠23.(11分)解:(1)(2分)(2).(3分)证明如下:与均为等腰直角三角形,,,,在与中,,,(5分),,,。
河南省许昌市八年级上学期数学开学考试试卷

河南省许昌市八年级上学期数学开学考试试卷姓名:________ 班级:________ 成绩:________一、单选题 (共10题;共20分)1. (2分)(2019·沈丘模拟) ﹣的绝对值是()A .B . -C .D .2. (2分)(2020·德州) 下列运算正确的是()A .B .C .D .3. (2分) (2017八上·崆峒期末) 下列图案是几种名车的标志,在这几个图案中不是轴对称图形的是()A .B .C .D .4. (2分) (2018七上·武昌期末) 代数式与是同类项,则常数n的值为()A . 2B . 3C . 4D . 65. (2分)(2018·夷陵模拟) 从一副扑克牌中随机抽出一张牌,得到梅花或者K的概率是()A .B .C .D .6. (2分)(2017·兰州模拟) 为了更好保护水资源,造福人类.某工厂计划建一个容积V(m3)一定的圆柱状污水处理池,池的底面积S(m2)关于深度h(m)的函数图象大致是()A .B .C .D .7. (2分) (2020九上·兰州月考) 某商场销售一种新文具,进价为20元/件,市场调查发现,每件售价35元,每天可销售此文具250件,在此基础上,若销售单价每上涨1元,每天销售量将减少10件,针对这种文具的销售情况,若销售单价定为元时,每天可获得4000元的销售利润,则应满足的方程为()A .B .C .D .8. (2分)(2018·遵义模拟) 在平行四边形ABCD中,∠A的平分线把BC边分成长度是3和4的两部分,则平行四边形ABCD的周长是()A . 22B . 20C . 22或20D . 189. (2分)如图,BC∥DE,∠1=108°, ∠AED=75°, 则∠A的大小是()A . 23°B . 30°C . 33°D . 60°10. (2分)如图(1)所示,E为矩形ABCD的边AD上一点,动点P、Q同时从点B出发,点P以1cm/秒的速度沿折线BE﹣ED﹣DC运动到点C时停止,点Q以2cm/秒的速度沿BC运动到点C时停止.设P、Q同时出发t秒时,△BPQ的面积为ycm2 .已知y与t的函数关系图象如图(2)(其中曲线OG为抛物线的一部分,其余各部分均为线段),则下列结论:①BE=BC;②当t=6秒时,△ABE≌△PQB;③点P运动了18秒;④当t=秒时,△ABE∽△QBP;其中正确的是()A . ①②B . ①③④C . ③④D . ①②④二、填空题 (共6题;共6分)11. (1分)科学家发现一种病毒的直径为0.000104米,用科学记数法表示为________米.12. (1分)(2017·玉田模拟) 从1、2、3、4中任取一个数作为十位上的数,再从2、3、4中任取一个数作为个位上的数,那么组成的两位数是3的倍数的概率是________.13. (1分)(2018·天河模拟) 若a、b、c为三角形的三边,且a、b满足,则第三边c的取值范围是________.14. (1分) (2019八上·凤翔期中) 某车站规定旅客可以免费携带不超过20千克的行李,超过部分每千克收取1.5元的行李费,则旅客需交的行李费(元)与携带行李重量(千克)()之间的关系式为________.15. (1分) (2017七下·长春期中) 如图,把一张长方形纸片ABCD沿EF折叠后,D、C分别在M、N的位置上,EM与BC的交点为G,若∠EFG=65°,则∠2=________.16. (1分) (2019八下·铜仁期中) 如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE 沿AE对折至△AEF,延长EF交边BC于点G,连结AG,CF,则下列结论:①△ABG≌△AFG;②BG=CG;③AG∥CF;④S△EGC=S△AFE;⑤S△FGC=;其中正确的结论有________.三、解答题 (共9题;共63分)17. (10分) (2020七下·咸阳期中) 计算:(1)(2)18. (5分) (2019七上·宝应期末) 化简或解方程:(1)化简:3a2-[5a-(2a-3)+4a2](2)解方程: +1=19. (5分) (2020七上·福田期中) 化简(1)(﹣2ab+3a)﹣2(2a﹣b)+2ab;(2)先化简,再求值:5a2+3b2+2(a2﹣b2)﹣(5a2﹣3b2),其中a=﹣1,b=.20. (5分) (2019八下·三原期末) 如图,已知直线和上一点,用尺规作的垂线,使它经过点 .(保留作图痕迹,不写作法)21. (2分) (2019九上·西安期中) 《西安市生活垃圾分类管理办法》由西安市人民政府第86次常务会议审议通过,于2019年9月l日起施行.为了解同学们对“垃圾分类知识”的了解情况,张红武在九年级随机抽取了若干名同学进行了问卷调查,将调查结果分为以下四个等级,:非常了解、:比较了解、:知道的很少、:完全不了解.并将调查结果绘制成如下两个不完整的统计图.(1)补全下面的条形统计图和扇形统计图;(2)所抽取同学问卷结果的中位数落在哪个等级________(填字母);(3)若九年级有1300名同学,年级部准备对调查结果为“知道的很少”和“完全不了解”的两部分同学进行“垃圾分类”知识的普及和培训,请你估算九年级有多少人需要进行“垃圾分类”知识的普及和培训.22. (10分) (2020七上·河南期末) 如图,已知点分别在线段上,交于点平分 .(1)求证:平分阅读下列推理过程,并将推理过程补充完整.证明:平分,(已知)(角平分线的定义)__▲_,(已知)(_▲_)故_▲_.(等量代换),(已知),(_▲_),(_▲),平分 .(_▲_)(2)若,请直接写出图中所有与互余的角.23. (5分) (2018八上·西湖期末) 如图,在△ABC中,AB=AC,∠1=∠2,则△ABD与△ACD全等吗?证明你的判断.24. (15分) (2018七上·顺德月考) 如图,已知数轴上点A表示的数为6,B是数轴上在A左侧的一点,且A , B两点间的距离为10.动点P从点A出发,以每秒6个单位长度的速度沿数轴向左匀速运动,设运动时间为t (t>0)秒.(1)数轴上点B表示的数是________,点P表示的数是________(用含t的代数式表示);(2)动点Q从点B出发,以每秒4个单位长度的速度沿数轴向左匀速运动,若点P、Q同时出发.求:①当点P运动多少秒时,点P与点Q相遇?②当点P运动多少秒时,点P与点Q间的距离为8个单位长度?25. (6分) (2019九上·揭西期末) △ABC是等边三角形,点D是射线BC上的一个动点(点D不与点B、C 重合),△ADE是以AD为边的等边三角形,过点E作BC的平行线,分别交射线AB、AC于点F、G,连接BE.(1)如图1,当点D在线段BC上时:①求证:△AEB≌△ADC;②求证:四边形BCGE是平行四边形;(2)如图2,当点D在BC的延长线上,且CD=BC时,试判断四边形BCGE是什么特殊的四边形?并说明理由.参考答案一、单选题 (共10题;共20分)答案:1-1、考点:解析:答案:2-1、考点:解析:答案:3-1、考点:解析:答案:4-1、考点:解析:答案:5-1、考点:解析:答案:6-1、考点:解析:答案:7-1、考点:解析:考点:解析:答案:9-1、考点:解析:考点:解析:二、填空题 (共6题;共6分)答案:11-1、考点:解析:答案:12-1、考点:解析:答案:13-1、考点:解析:答案:14-1、考点:解析:答案:15-1、考点:解析:答案:16-1、考点:解析:三、解答题 (共9题;共63分)答案:17-1、答案:17-2、考点:解析:答案:18-1、答案:18-2、考点:解析:答案:19-1、答案:19-2、考点:解析:答案:20-1、考点:解析:答案:21-1、答案:21-2、答案:21-3、考点:解析:答案:22-1、答案:22-2、考点:解析:答案:23-1、考点:解析:答案:24-1、答案:24-2、考点:解析:答案:25-1、答案:25-2、考点:解析:。
河南省许昌市魏都区第十八中学2021-2022学年八年级上学期期中数学试题(含答案解析)

河南省许昌市魏都区第十八中学2021-2022学年八年级上学期期中数学试题学校:___________姓名:___________班级:___________考号:___________一、单选题1.以下列各组线段长为边,能组成三角形的是()A.1cm,2cm,3cm B.2cm,3cm,8cm C.5cm,12cm,6cm D.4cm,6cm,9cm 2.在平面直角坐标系中,点P(2,-3)关于x轴对称的点的坐标是()A.(2,3)B.(2,-3)C.(-2,3)D.(-2,-3)3.等腰三角形的顶角为80°,则它的底角是()A.20°B.50°C.60°D.80°4.一个多边形的每个内角都等于135°,则这个多边形的边数为()A.5B.6C.7D.85.下列条件中,不能判定三角形全等的是()A.三条边对应相等B.两边和其中一角对应相等C.两边和夹角对应相等D.两角和它们的夹边对应相等6.如图,△ABC与△DEF关于直线MN轴对称,则以下结论中错误的是()A.AB=DE B.∠B=∠EC.AB//DF D.AD的连线被MN垂直平分7.如图,在△ABC中,AF平分∠BAC,AC的垂直平分线交BC于点E,∠B=70°,∠FAE=19°,则∠C为()8.如图,AE AB ⊥且,AE AB BC CD =⊥且BC CD =,请按照图中所标注的数据,计算图中实线所围成的图形的面积S 是()A .50B .62C .65D .689.如图所示,△ABC 的三个角三等分线相交于D 、E 、F (其中∠CAD =2∠BAD ,∠ABE =2∠CBE ,∠BCF =2∠ACF ),且△DFE 的三个内角分别为∠DFE =54°、∠FDE =60°、∠FED =66°,则∠BAC =()A .54°B .60°C .66°D .48°10.如图,908cm 4cm C CAM AC BC ∠∠︒==,=,=,点P 在线段AC 上,以2cm/s 速度从点A 出发向点C 运动,到点C 停止运动.点Q 在射线AM 上运动,且PQ AB =.若ABC 与PQA △全等,则点P 运动的时间为()A .4sB .2sC .2s 或3s 或4sD .2s 或4s二、填空题11.在△ABC 中,∠A =60°,∠C =2∠B ,则∠C =___.12.如图,ABC DEF ≌△△,点F 在BC 边上,AB 与EF 相交于点P .若37,DEF PB PF ∠=︒=,则APF ∠=___.13.已知一个等腰三角形的两边长分别为4和8,那么这个三角形的周长为________.14.如图,在四边形ABCD 中,90A C ∠=∠=︒,34B ∠=︒,在边AB ,BC 上分别找一点E ,F 使DEF 周长最小,此时EDF ∠=______.15.在平面直角坐标系中,已知点()()()12,55,32A B C ,,,,存在点E ,使ACE △和ACB△全等,写出所有满足条件的E 点的坐标________.三、解答题16.如图,在 ABC 中,AD 是 ABC 的高,AE 、BF 是 ABC 角平分线,AE 与BF 相交于点O ,∠BOA =125°,求∠DAC 的度数.17.如图,点B 、F 、C 、E 在一条直线上,BF CE =,AC DF =,请你在下列条件①B E ∠=∠;②ACB DFE ∠=∠;③AB DE =;④AC DF ∥中,选择一个条件证明:A D ∠=∠,你选的条件的序号是________.证明:18.(1)如图,求x 和y 的值.(2)在各个内角都相等的多边形中,一个外角等于一个内角的15,求这个多边形每一个内角的度数和它的边数.19.如图,已知ABC 中,90ACB ∠=︒,CA CB =,D 是AC 上一点,E 在BC 的延长线上,且AE BD =,BD 的延长线与AE 交于点F .(1)若3CD =,求CE 的长;(2)求证:BF AE ⊥.20.如图,在平面直角坐标系中,已知△ABC 的三个顶点的坐标分别为A (﹣3,5),B (﹣2,1),C (﹣1,3).(1)画出△ABC 关于x 轴的对称图形△A 1B 1C 1.(2)画出△A 1B 1C 1沿x 轴向右平移4个单位长度后得到的△A 2B 2C 2.(3)如果AC 上有一点M (a ,b )经过上述两次变换,那么对应A 2C 2上的点M 2的坐标是.(4)△ABC 的面积为.21.图,点P ,M ,N 分别在等边△ABC 的各边上,且MP ⊥AB 于点P ,MN ⊥BC 于点M ,PN ⊥AC 于点N .(1)求证:△PMN 是等边三角形;(2)若AB =12cm ,求CM 的长.22.如图,已知等腰ABC 中,30BAC ∠=︒,AB AC =,PAB α∠=,点B 关于直线AP 的对称点为点D ,连接AD ,连接BD 交AP 于点G ,连接CD 交AP 于点E ,交AB 于点F .(1)如图1,当15α=︒时,①按要求画出图形,②求出ACD ∠的度数,③探究DE 与BF 的倍数关系并加以证明;(2)在直线AP 绕点A 顺时针旋转的过程中(075α︒<<︒),当AEF △为等腰三角形时,利用备用图直接求出α的值为___________.23.在平面直角坐标系中,点A(0,a),点B(b,0),其中参数a、b满足如下关系式|2a﹣b|+(6﹣b)2=0.(1)直接写出A、B两点坐标:A、B.(2)如图1,C点的横坐标为3,且AC平分∠BAy,作CD⊥AB于D,求BD﹣AD的值;(3)如图2,现以AB为斜边构造等腰直角三角形ABM,试求以A、B、O、M为顶点的四边形的面积.参考答案:1.D【分析】根据三角形的三边关系逐项判断即可.【详解】在A中,1+2=3,不满足三角形两边之和大于第三边,故A不能组成三角形;在B中,2+3<8,不不满足三角形两边之和大于第三边,故B不能组成三角形;在C中,5+6<12,不满足三角形两边之和大于第三边,故C不能组成三角形;在D中,4+6>9,满足三角形三边之间的关系,故D能组成三角形.故选D.【点睛】本题主要考查三角形的三边关系,掌握三角形的两边之和大于第三边、两边之差小于第三边是解题的关键.2.A【分析】直接利用关于x轴对称点的性质分析得出答案.【详解】解:点P(2,-3)关于x轴对称的点的坐标是:(2,3).故选:A.【点睛】此题主要考查了关于x轴对称点的性质,正确记忆横纵坐标的关系是解题关键.3.B【分析】根据三角形内角和定理和等腰三角形的性质,可以求得其底角的度数.【详解】解:∵等腰三角形的一个顶角为80°∴底角=(180°﹣80°)÷2=50°.故选B.考点:等腰三角形的性质.4.D【分析】先求出多边形的每一个外角的度数,继而根据多边形的外角和为360度进行求解即可.【详解】∵一个多边形的每个内角都等于135°,∴这个多边形的每个外角都等于180°-135°=45°,∵多边形的外角和为360度,∴这个多边形的边数为:360÷45=8,故选D.【点睛】本题考查了多边形的外角和内角,熟练掌握多边形的外角和为360度是解本题的关键.5.B【分析】根据全等三角形的判定定理逐个判断即可.【详解】解:A 、符合全等三角形的判定定理SSS ,能推出两三角形全等,故本选项不符合题意;B 、不符合全等三角形的判定定理,不能推出两三角形全等,故本选项符合题意;C 、符合全等三角形的判定定理SAS ,能推出两三角形全等,故本选项不符合题意;D 、符合全等三角形的判定定理ASA ,能推出两三角形全等,故本选项不符合;故选:B .【点睛】本题考查了全等三角形的判定定理,能熟记全等三角形的判定定理是解此题的关键,注意:全等三角形的判定定理有SAS ASA AAS SSS ,,,.6.C【分析】轴对称的性质:①如果两个图形关于某直线对称,那么这两个图形全等;②如果两个图形关于某直线对称,那么对应线段或者平行,或者共线,或者相交于对称轴上一点;③如果两个图形关于某直线对称,那么对称轴是对应点连线的垂直平分线.【详解】根据轴对称的性质可得:AB =DE ,∠B =∠E ,AD 的连线被MN 垂直平分,∴选项A 、B 、D 正确,选项C 错误,故选:C .7.A【分析】根据线段的垂直平分线的性质德奥EA =EC ,得到∠EAC =∠C ,根据角平分线的定义,三角形内角和定理计算即可.【详解】∵DE 是AC 的垂直平分线,∴EA =EC ,∴∠EAC =∠C ,∴∠FAC =∠EAC +19°,∵AF 平分∠BAC ,∴∠FAB =∠EAB +19°,∵∠B +∠BAC +∠C =180°,∴70°+2(∠C +19°)+∠C =180°,解得∠C =24°.故选A.【点睛】本题考查的是线段垂直平分线的性质、三角形内角和定理,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.8.A【分析】由AE AB ⊥,EF FH ⊥,BG AG ⊥,可以得到EAF ABG ∠=∠,而,AE AB EFA AGB =∠=∠,由此可以证明EFA ABG ≅ ,所以AF BG =,AG EF =;同理证得BGC DHC ≅ ,GC DH =,CH BG =,故364316FH FA AG GC CH =+++=+++=,然后利用面积的割补法和面积公式即可求出图形的面积.【详解】∵AE AB ⊥且AE AB =,EF FH ⊥,⊥BG FH ,∴90EAB EFA AGB ∠=∠=∠=︒,∵90EAF AGB ∠+∠=︒,90ABG BAG ∠+∠=︒,∴EAF ABG ∠=∠,∴,AE AB EFA AGB =∠=∠,EAF ABG ∠=∠,∴EFA ABG ≅ ,∴AF BG =,AG EF =,同理证得BGC DHC ≅ ,GC DH =,CH BG =,故364316FH FA AG GC CH =+++=+++=,故()164163463502S =+⨯-⨯-⨯=.故选:A .【点睛】本题考查的全等三角形的判定的相关知识点,作辅助线是本题的关键.9.D【分析】设∠BAD =x ,∠CBE =y ,∠ACF =z ,则∠CAF =2x ,∠ABD =2y ,∠BCE =2z ,利用三角形的外角的性质构建方程组解决问题即可.【详解】解:∵∠CAD =2∠BAD ,∠ABE =2∠CBE ,∠BCF =2∠ACF ,∴可以假设∠BAD =x ,∠CBE =y ,∠ACF =z ,则∠CAF =2x ,∠ABD =2y ,∠BCE =2z ,∵∠DFE =∠ACF +∠CAF ,∠FDE =∠DAB +∠ABD ,∠DEF =∠CBE +∠BCE ,∴54°=2x +z ,60°=x +2y ,66°=y +2z ,解得x =16°,y =22°,z =22°,∴∠BAC =3x =48°,故选:D .【点睛】本题考查三角形内角和定理,三角形的外角的性质等知识,解题的关键是学会利用参数构建方程解决问题.10.D【分析】分ABC PQA ≌ 和ABC QPA ≌ 两种情况,根据全等三角形的性质解答即可.【详解】解:当ABC PQA ≌ 时,8AP AC ==,∵点P 的速度为2cm/s ,∴82=4÷(s );当ABC QPA ≌ 时,当4AP BC ==,∵点P 的速度为2cm/s ,∴42=2÷(s )故选:D .【点睛】此题考查的是全等三角形的性质,掌握全等三角形的对应边相等,全等三角形的对应角相等是解题的关键,注意分情况讨论思想的应用.11.80°【分析】根据三角形的内角和为180°建立等式求解即可.【详解】解:∵三角形的内角和为180°,∴∠A +∠B +∠C =180°,∵∠A =60°,∠C =2∠B ,∴60°+∠B +2∠B =180°,解得:∠B =40°,∴∠C =2∠B =80°,故答案为:80°.【点睛】本题考查三角形内角和的应用,熟记三角形的内角和为180°是解题关键.12.74°【分析】根据全等三角形的性质可得∠E =∠B =37°,再根据等边对等角可得∠PFB =∠B =37°,再由三角形外角的性质可得∠APF 的度数.【详解】∵△ABC ≌△DEF ,37DEF ∠=︒,∴∠E =∠B =37°,∵PB =PF ,∴∠PFB =∠B =37°,∴∠APF =37°+37°=74°,故答案为74°.【点睛】本题主要考查了全等三角形的性质,等腰三角形的性质,三角形外角的性质,解题的关键是掌握全等三角形的对应角相等.13.20【分析】题目给出等腰三角形有两条边长为4和8,而没有明确腰、底分别是多少,所以要进行讨论,还要应用三角形的三边关系验证能否组成三角形.【详解】解:∵448+=,∴腰的长不能为4,只能为8,∴等腰三角形的周长28420⨯=+=,故答案为:20.【点睛】本题考查了等腰三角形的定义和三角形的三边关系;已知没有明确腰和底边的题目一定要想到两种情况,分类进行讨论,还应验证各种情况是否能构成三角形进行解答,这点非常重要,也是解题的关键.14.112°##112度【分析】如图,作点D 关于BA 的对称点P ,点D 关于BC 的对称点Q ,连接PQ ,交AB 于E ',交BC 于F ',则点,E F ''即为所求,利用轴对称的性质结合四边形的内角和即可得出答案.【详解】解:如图,作点D 关于BA 的对称点P ,点D 关于BC 的对称点Q ,连接PQ ,交AB 于E ',交BC 于F ',则点E ',F '即为所求.∵四边形ABCD 中,90,BAD BCD ∠=∠=︒34,B Ð=°∴18034146ADC Ð=°-°=°,由轴对称知,∠ADE '=∠P ,∠CDF '=∠Q ,在△PDQ 中,∠P +∠Q =180°-∠ADC =18014634°-°=°,∴∠ADE '+∠CDF '=∠P +∠Q =34°,∴()14634112.E DF ADC ADE CDF ⅱⅱÐ=Ð-Ð+Ð=°-°=°故答案为112︒.【点睛】本题考查的是轴对称-最短路线问题,涉及到平面内最短路线问题求法以及四边形的内角和定理等知识,根据已知得出E ,F 的位置是解题关键.15.51-(,)或11--(,)或15-(,)【分析】先画出点B 关于直线AC 的对称点1E ,然后画出点B 、点1E 关于AC 的垂直平分线的对称点23E E 、,从而得到满足条件的E 点坐标.【详解】解:如图,E 点坐标为51-(,)或11--(,)或15-(,).故答案为:51-(,)或11--(,)或15-(,).【点睛】本题考查了全等三角形的判定:熟练掌握全等三角形的5种判定方法是解决问题的关键;选用哪一种方法,取决于题目中的已知条件.也考查了坐标与图形性质.16.20°【分析】由三角形的内角和定理结合角平分线的性质可求解∠ACB =70°,根据三角形高线的定义可得∠ADC =90°,进而可求解∠DAC 的度数.【详解】解:∵∠OAB +∠OBA +∠AOB =180°,∠AOB =125°,∴∠OAB +∠OBA =180°﹣125°=55°,∵AE 、BF 是△ABC 角平分线,∴∠OAB =12∠BAC ,∠OBA =12∠ABC ,∴12∠BAC +12∠ABC =55°,∴∠BAC +∠ABC =110°,∵∠BAC +∠ABC +∠ACB =180°,∴∠ACB =70°,∵AD 是△ABC 的高,∴∠ADC =90°,∴∠DAC =90°﹣70°=20°.【点评】本题主要考查三角形的角平分线,高线,三角形的内角和定理,灵活运用相关定理是解题.17.②,证明见解析【分析】由全等三角形的判定方法即可得出ABC DEF ≌△△,即可得出∠A =∠D .【详解】解:选②ACB DFE ∠=∠(答案不唯一)证明:BF CE = ,BF CF CE CF ∴+=+,即BC EF =,在ABC 和DEF 中,AC DF ACB DFE BC EF =⎧⎪∠=∠⎨⎪=⎩,()SAS ABC DEF ∴≌ ;A D ∴∠=∠.【点睛】本题考查了全等三角形的判定与性质、平行线的性质等知识;熟练掌握全等三角形的判定与性质是解题的关键.18.(1)6050x y =,=;(2)150︒,12【分析】(1)三角形的一个外角等于和它不相邻的两个内角的和,三角形的内角和是180︒,据此求解即可;(2)多边形的外角和是360︒,内角和它相邻的外角互补,据此求解即可.【详解】解∶(1)70(10)x x x +=++ ,60,x ∴=60,70,C B ︒︒∴∠=∠=18050,BAC B C ︒︒∴∠=-∠-∠=50;y ∴=(2)设多边形的每个内角度数是x ︒,由题意得∶11805x x -=,150, x ∴=∴多边形的每一个内角的度数是150︒,∴多边形的边数是()36018015012︒︒︒÷-=.【点睛】本题考查三角形的内角和定理,外角定理,多边形的有关知识,关键是掌握:三角形的一个外角等于和它不相邻的两个内角的和;多边形的外角和是360︒,内角和它相邻的外角互补.19.(1)3(2)证明见解析【分析】(1)结合条件容易证到Rt Rt BCD ACE ≌,即可得出答案;(2)由Rt Rt BCD ACE ≌可得到CAE CBD ∠=∠,结合90CBD CDB ∠+∠=︒,∠=∠CDB FDA ,即可得出90DFA ∠=︒,即可得证.【详解】(1)证明:∵90ACB ∠=︒,∴18090ECA ACB ∠=︒-∠=︒,在Rt BCD 和Rt ACE 中,BC AC BD AE =⎧⎨=⎩,∴Rt Rt BCD ACE ≌.∴3CE CD ==.(2)∵Rt Rt BCD ACE ≌,∴CAE CBD ∠=∠,∵90ACB ∠=︒,∴90CBD CDB ∠+∠=︒,∵∠=∠CDB FDA ,∴90FAD FDA ∠+∠=︒,∴90DFA ∠=︒,∴BF AE ⊥.【点睛】本题考查了全等三角形的判定与性质,直角三角形的判定,掌握全等三角形的判定和性质是解题的关键.20.(1)见解析;(2)见解析;(3)(a +4,﹣b );(4)3【分析】(1)(2)根据平移、轴对称的特点作图,把各对应点描出连线即可;(3)根据左加右减,上加下减的规律进行运算即可;(4)先计算所求图形外接矩形(四边均在网格上)面积,再减去多余的三角形面积即可.【详解】解:(1)如图,△A 1B 1C 1即为所求;(2)如图,△A 2B 2C 2即为所求;(3)点M 2的坐标是(a +4,﹣b ).故答案为:(a +4,﹣b ).(4)△ABC 的面积为:2×4﹣12⨯1×4﹣12⨯1×2﹣12⨯2×2=8﹣2﹣1﹣2=3.故答案为:3.【点睛】本题考查了平移、轴对称的作图,平移后点坐标得变化,割补法求网格内图形面积,属于常规题目.21.(1)见解析(2)4cm 【分析】(1)根据等边三角形的性质得出A B C ∠=∠=∠,进而得出===90MPB NMC PNA ∠∠∠︒,再根据平角的意义即可得出NPM PMN MNP ∠=∠=∠,即可证得PMN △是等边三角形;(2)易证得PBM MCN NAP ≌≌,得出PA BM CN ==,PB MC AN ==,从而求得12BM PB AB +==cm ,根据直角三角形30°角所对的直角边等于斜边的一半得出2PB BM =,即可求得PB 的长,进而得出CM 的长.【详解】(1)证明:∵ABC 是正三角形,∴A B C ∠∠∠==.∵MP AB ⊥,MN BC ⊥,PN AC ⊥,∴90MPB NMC PNA ∠∠∠︒===,∴PMB MNC APN ∠∠∠==,∴NPM PMN MNP ∠∠∠==,∴ABC 是等边三角形;(2)解:∵PMN △是等边三角形,ABC 是正三角形,∴PM MN NP ==,===60B C A ∠∠∠︒,在PBM 和MCN △中,===90=B C BPM CMN PM MN ∠∠⎧⎪∠∠︒⎨⎪⎩,∴()PBM MCN AAS ≌,在MCN △和NAP 中,===90=C A CMN ANP MN NP ∠∠⎧⎪∠∠︒⎨⎪⎩∴()MCN NAP AAS ≌,同理可得()PBM NAP AAS ≌∴()PBM MCN NAP AAS ≌≌,∴PA BM CN ==,PB MC AN ==,∴12BM PB AB +==cm ,∵△ABC 是正三角形,∴60A B C ∠∠∠︒===,∴2PB BM =,∴212PB PB +=cm ,∴4PB =cm ,∴4MC =cm .【点睛】本题考查了等边三角形的判定和性质,平角的意义,三角形全等的判定和性质等,得出NPM PMN MNP ∠=∠=∠是本题的关键.22.(1)①见解析;②60︒;③2DE BF=(2)30︒或52.5︒【分析】(1)①根据题意直接进行作图即可;②由题意易得1215AD AB =∠=∠=︒,,则有1260DAC BAC ∠=∠+∠+∠=︒,进而可证ACD 为等边三角形,则问题得解;③连接EB ,由题意可得ED EB =,进而可得75ADB ∠=︒,则有AB DC ⊥,最后根据线段的数量关系可求解;(2)如图2,根据题意易得DAC △是等腰三角形,然后进行分类求解即可.【详解】(1)解:①如图1:②∵B D 、关于AP 对称,∴AP 垂直平分BD ,15α=︒,∴1215AD AB =∠=∠=︒,,∵30BAC ∠=︒,∴1260DAC BAC ∠=∠+∠+∠=︒,∵AC AB =,∴AC AD =,∴ACD 为等边三角形∴60ACD ∠=︒.③2DE BF =,证明:连接EB ,∵AP 垂直平分BD ,∴ED EB =,∴3=4∠∠,∵30AB AD DAB =∠=︒,,∴75ADB ∠=︒,又60ADC ∠=︒,∴3415∠=∠=︒,∴530∠=︒,又AD AC =,AB 平分DAC ∠,∴AB DC ⊥,∴2EB BF =,∴2ED BF =.(2)如图2,∵AD AC =,∴DAC △是等腰三角形∴180230275ADC αα∠=︒--︒÷=︒-(),∴7575AEF ADC DAE αα∠=∠+∠=︒-+=︒,当AE AF =时,18075218015030EAF α∠==︒-︒⨯=︒-︒=︒;当AE EF =时,18075252.5EAF α∠==︒-︒÷=︒();当EF AF =时,75AEF EAF α∠=∠==︒(舍去).故答案为:30︒或52.5︒.【点睛】本题主要考查等腰三角形的性质与判定及等边三角形的性质与判定,熟练掌握等腰三角形的性质与判定及等边三角形的性质与判定是解题的关键.23.(1)(0,3),(6,0);(2)3;(3)272或814【分析】(1)根据非负数之和为0,即可确定,a b 的值,进而求得,A B 的坐标;(2)过点C 作CE y ⊥轴,过点B 作BF x ⊥轴,两垂线相交于点F ,则BF EO =,证明EAC DAC △≌△,Rt CDB Rt CFB △≌△,进而根据BD AD EO EA AO -=-=即可求得;(3)①当M 点在AB 的下方时,如图,过点M 作,x y 的垂线,垂足分别为,H G ,证明四边形OGMH 是正方形,设HM x =,则OH x =,6HB OB OH x =-=-,根据S 四边形AOMB ABO MBO S S =+△△即可求解,②当M 点在AB 的上方时,如图,过点M 作MK y ⊥轴,过点B 作BL x ⊥轴,交MK 于点L ,同理可证AMK MBL △≌△,根据S 四边形AOMB S =四边形KLBO AKM BLM S S --△△即可求解.【详解】(1) |2a ﹣b |+(6﹣b )2=0.20,60a b b ∴-=-=解得3,6a b ==(0,3),(6,0)A B ∴故答案为:(0,3),(6,0)(2)如图,过点C 作CE y ⊥轴,过点B 作BF x ⊥轴,两垂线相交于点F ,90AOB ∠=︒Q ,∴四边形EOBF 是矩形,∴BF EO =,(6,0)B ,C 点的横坐标为3,6,3EF CE ∴==,3CF ∴=,AC 平分∠BAy ,EAC DAC ∴∠=∠, CD ⊥AB ,CE y ⊥,90CEA CDA ∴∠=∠=︒,在EAC 与DAC △中90CEA CDA EAC DAC AC AC ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩EAC DAC ∴△≌△,3CD CE ∴==,AD AE =,CD CF ∴=,,CF FB CD AB ⊥⊥ ,90F CDB ∴∠=∠=︒,在Rt CDB 与Rt CFB 中CD CF CB CB=⎧⎨=⎩Rt CDB Rt CFB ∴△≌△,BF DB ∴=,BD EO ∴=,(0,3)A ,3OA ∴=,∴3BD AD EO EA AO -=-==;(3)当M 点在AB 的下方时,如图,过点M 作,x y 的垂线,垂足分别为,H G ,90BHM AGM ∴∠=∠=︒,ABM QV 是等腰三角形,AM BM ∴=,MBA MAB ∠=∠,45HBA MBA MBH MBH ∠=∠-∠=︒-∠ ,45BAO MAB GAM GAM ∠=∠+∠=︒+∠,90OAB OBA ∠+∠=︒,∴MBH GAM ∠=∠,HBM GAM ∴△≌△,GM HM ∴=,AG BH=90OHM HOG MGO ∠=∠=∠=︒∴四边形OGMH 是矩形,GM HM = ,∴四边形OGMH 是正方形,OG OH ∴=,,AG BH OH OG == ,AO GO OB OH ∴+=-,(6,0)B ,(0,3)A ,6OB ∴=,3OA =,设HM x =,则OH x =,6HB OB OH x =-=-,即36x x +=-,解得32x =S ∴四边形AOMB ABO MBOS S =+△△1122OA OB OB HM =⋅⋅+⋅⋅113273662222=⨯⨯+⨯⨯=②当M 点在AB 的上方时,如图,过点M 作MK y ⊥轴,过点B 作BL x ⊥轴,交MK 于点L,同理可证AMK MBL △≌△,则,AK ML KM BL ==,设,AK a MK b ==,,AK OA BL KM ML OB +=+= ,则36a b a b +=⎧⎨+=⎩解得3292a b ⎧=⎪⎪⎨⎪=⎪⎩S ∴四边形AOMB S =四边形KLBO AKM BLMS S --△△913913962222222=⨯-⨯⨯-⨯⨯27274=-814=综上所述,以A 、B 、O 、M 为顶点的四边形的面积为272或814.【点睛】本题考查了非负数的性质坐标与图形,正方形的性质,三角形全等的性质与判定,构造三角形全等是解题的关键.。
河南省许昌市长葛市2023_2024学年八年级上册期中考试数学模拟测试卷(附答案)

河南省许昌市长葛市2023_2024学年八年级上册期中考试数学模拟测试卷注意事项:本试卷分试题卷和答题卡两部分.考生应首先阅读答题卡上的文字信息,然后在答题卡上作答,在试题卷上作答无效,交卷时只交答题卡.一、选择题(本大题共10小题,每小题3分,共30分,每小题中均有四个选项,其中只有一个选项是正确的,请将你选择的结果涂在答题卡上对应位置)1.下列标志中,是轴对称图形的是()A .B .C .D .2.等腰三角形的一个底角为,则这个等腰三角形的顶角为().80︒A .B .C .D .或20︒80︒100︒20︒100︒3.如图,点D 在BC 的延长线上,,,则∠1的度数为()30A ∠=︒45B ∠=︒(第3题图)A .B .C .D .65︒70︒75︒80︒4.一根细铁丝长20cm ,小明想把它折成一个三角形,则他折成的三角形的最长的边有可能是()A .9cmB .10cmC .11cmD .12cm5.已知正多边形的一个内角是,则这个正多边形的边数是()135︒A .九边形B .八边形C .七边形D .六边形6.一块三角形玻璃打碎后变成了如图所示的4块,琳琳现在要带上其中的两块去玻璃店配一块完全一样的玻璃,她要带上()(第6题图)A .①④B .②③C .③④D .②④7.如图,在△ABC 中,AD 是它的角平分线,,,则8cm AB =6cm AC =():ABD ACD S S =△△(第7题图)A .B .C .D .16:99:164:33:48.如图,在等腰△ABC 中,,,分别以点C ,A 为圆心、大于AB AC =120BAC ∠=︒的长为半径画弧,两弧交于M ,N 两点,作直线MN 分别交CB ,CA 于点E ,F ,则线段12AC BE 与线段EF 的数量关系是()(第8题图)A .B .C .D .2BE EF =53BE EF =32BE EF =4BE EF=9.如图,方格纸中的∠1和∠2的大小关系是()(第9题图)A .B .C .D .12∠=∠221∠=∠2901∠=︒+∠12180∠+∠=︒10.如图,△ABC 和△DEC 均为等腰直角三角形,且,点A 、D 、E 在90ACB DCE ∠=∠=︒同一条直线上,CM 平分∠DCE ,连接BE .以下结论:①;②;③AD CE =CM AE ⊥;④,正确的有()2AE BE CM =+COE BOM S S =△△(第10题图)A .1个B .2个C .3个D .4个二、填空题(每小题3分,共15分,请将结果写在答题卡上对应位置)11.在△ABC 中,,则∠C 等于______.::3:4:5A B C ∠∠∠=12.点关于y 轴的对称点Q 的坐标为______.()1,3P -13.如图,D 、E 、F 分别是BC 、AB 、AD 边的中点,若△DEF 的面积为2,则△ABC 的面积为______.(第13题图)14.如图所示,,,则______.15A ∠=︒AB BC CD DE EF ====EDF ∠=(第14题图)15.如图①②③中,,,,则______.50A ∠=︒12∠=∠34∠=∠123O O O ∠+∠+∠=(第15题图)三、解答题(8小题,共75分,请将解答过程写在答题卡上对应位置)16.(8分)一个多边形的内角和比它的外角和的3倍少,求这个多边形的边数.180︒17.(10分)在平面直角坐标系中,已知,,.()0,1A ()2,0B ()4,3C(1)请在平面直角坐标系中画出△ABC ,以及与△ABC 关于y 轴对称的△DEF ;(2)△ABC 的面积是______;(3)已知P 为y 轴上一点,若△ABP 的面积为4,求点P 的坐标.18.(9分)如图,△ABC ,,,F 为AB 延长线上一点,点E 在BC 上,AB BC =90ABC ∠=︒且.AE CF =(1)求证:;ABE CBF ≌△△(2)若,求∠ACF 的度数.25CAE ∠=︒19.(9分)如图,△ABC ,,,BE 平分∠ABC ,.38A ∠=︒42ABC ∠=︒19E ∠=︒(1)求∠ECD 的度数;(2)求证:CE 平分∠ACD .20.(9分)如图,已知三角形△ABC.(1)尺规作图,作BC 的垂直平分线DE ,分别交AB 于D 、交BC 于E (不写作法,保留作图痕迹)(2)连结CD ,若,△ACD 的周长为12,求△ABC 的周长.5BE =21.(10分)如图,在等腰△ABC 中,,点D ,E 分别在AB ,AC 上,AB AC =.求证:.EBC DCB ∠=∠AD AE=证明:是等腰三角形,,ABC △AB AC =(___①___)ABC ACB ∴∠=∠,EBC DCB ∠=∠ (等式的性质).ABC EBC ACB DCB ∴∠-∠=∠-∠即___②___.ABE ∠=在和中ABE △ACD △AB AC ABE ACD⎧⎪=⎨⎪∠=∠⎩ ③(___④___).ABE ACD ∴≌△△(___⑤___).AE AD ∴=22.(10)问题提出:(1)我们把两个面积相等但不全等的三角形叫做偏等积三角形,如图1,△ABC 中,,,,P 为AC 上一点,当______时,△ABP 与△CBP 是偏等7AC =9BC =10AB =AP =积三角形;问题探究:(2)如图2,△ABD 与△ACD 是偏等积三角形,,,且线段AD 的长度为正整2AB =6AC =数,求AD 的长度为______;问题解决:(3)如图3,四边形ABED 是一片绿色花园,,,CA CB =CD CE =.△ACD 与△BCE 是偏等积三角形吗?请说明理()90090ACB DCE BCE ∠=∠=︒︒<∠<︒由.图1图2图323.(10分)如图,等边△ABC 的边长为6cm ,现有两动点M 、N 分别从点A 、B 同时出发,沿三角形的边按运动,已知点M 的速度为1cm/s ,点N 的速度为2cm/s ,当点B A C B →→→N 第一次到达点B 时,点M 、N 同时停止运动.(1)点M 、N 运动几秒后,M 、N 两点重合?(2)点M 、N 运动几秒后,以点A 、M 、N 为顶点的三角形是等边三角形?(3)当点M 、N 在边BC 上运动时,连接AM 、AN ,能否得到以MN 为底边的等腰三角形AMN ?如能,请求出此时点M 、N 运动的时间.答案1-10 CACAB ACDDC11.75 12.13.16 14.6015.205()1,316.设这个多边形的边数为n ,依题意得,解得,()21803360180n -⨯︒=⨯︒-︒7n =这个多边形的边数是7.∴17.(1)如图,△ABC 和△DEF 为所作;(2)4(3)设P 点坐标为,()0,t 的面积为4,ABP △,解得或5,11242t ∴⨯-⨯=3t =-点坐标为或.P ∴()0,3-()0,518.证明:(1)在与中,Rt ABE △Rt CBF △AE CF AB BC=⎧⎨=⎩.()HL ABE CBF ∴≌△△(2)ABE CBF ≌△△20BAE BCF ∴∠=∠=︒,AB BC = 90ABC ∠=︒45ACB ∴∠=︒65ACF ∴∠=︒19.(1)【解】,BE 平分∠ABC ,42ABC ∠=︒ .1212CBE ABC ∴∠=∠=︒,.19E ∠=︒ 40ECD CBE E ∴∠=∠+∠=︒(2)【证明】,,38A ∠=︒ 42ABC ∠=︒.80ACD A ABC ∴∠=∠+∠=︒,,40ECD ∠=︒ 40ACE ACD ECD ∴∠=∠-∠=︒,平分∠AC D .ECD ACE ∴∠=∠CE ∴20.(1)如图;(2)垂直平分BC ,DE ,,210BC BE ∴==BD CD =的周长,ACD △12AD AC CD =++=,12BD AD AC AB AC ∴++=+=的周长.ABC ∴△121022AB AC BC =+====21.①等边对等角;②∠ACD ;③;④ASA ;⑤全等三角形的对应边相等.BAE CAD ∠=∠22.【正确答案】解:(1).(2)3.72(3)△ACD 与△BCE 是偏等积三角形.理由:如图3,,90ACB DCE ∠=∠=︒ ,180ACD BCE ∴∠+∠=︒,090BCE ︒<∠<︒ ,90ACD ∴∠>︒,ACD BCE ∴∠≠∠,,CA CB = CD CE =与不全等,∴ACD △BCE △作于点F ,交DC 的延长线于点G ,则,BF CE ⊥AG DC ⊥90G BFC ∠=∠=︒,18090ECG DCE ∠=︒-∠=︒ ,90ACG BCF BCG ∴∠=∠=︒-∠在和中,,ACG △BCF △G BFC ACG BCF CA CB ∠=∠⎧⎪∠=∠⎨⎪=⎩,()AAS ACG BCF ∴≌△△,AG BF ∴=,1122CD AG CE BF ∴⋅=⋅与面积相等,ACD ∴△BCE △与是偏等积三角形.ACD ∴△BCE △23.(1)设点、运动秒后重合,则,解得M N 62t t +=6t =点、运动6秒后重合;∴M N (2)设点、运动秒后,是等边三角形M N AMN △如图,,AM t =62AN t=-当时,是等边三角形AM AN =AMN △即62t t=-解得2t =当点、运动2秒时,是等边三角形;∴M N AMN △(3)如图,设点、运动秒M N则,6CM t =-182BN t=-假设是等腰三角形且MN 是它的底边AMN △则,AN AM =ANM AMN∠=∠∴ANB AMC∠=∠ B C∠=∠ANB AMC∴≌△△∴CM BN=即6182t t-=-解得8t =当点、运动8秒时,是等腰三角形.∴M N AMN △。
河南省八年级上学期数学第一次阶段检测试卷

河南省八年级上学期数学第一次阶段检测试卷姓名:________ 班级:________ 成绩:________一、选择题 (共8题;共16分)1. (2分) (2020七下·桂林期末) 下列图形中,是轴对称图形的是()A .B .C .D .2. (2分) (2018八上·江岸期中) 下列给出的各组条件中,不能使的是()A . ,,B . ,,C . ,,D . ,,3. (2分) (2020八上·通渭期中) 如图,在∠AOB的两边上,分别取OM=ON,再分别过点M、N作OA、OB 的垂线,交点为P,画射线OP,则OP平分∠AOB的依据是(填判定三角形全等方法的简称)()A . SSSB . SASC . ASAD . HL4. (2分)(2020·鹿邑模拟) 如图,在等腰中,,,按图下步骤作图:①分别以为圆心,以大于的长为半径作弧,两弧相交于两点;②作直线交于点D,连接 .则下面说法错误的为()A .B .C .D .5. (2分) (2018八上·泸西期中) BD,CE分别是△ABC中∠ABC,∠ACB的平分线,且交于点O,若O到AB 的距离为1,BC=3,则 =()A .B . 1C .D . 36. (2分)(2017·东河模拟) 如图,已知四边形ABCD是矩形,把矩形沿直线AC折叠,点B落在点E处,连接DE.若DE:AC=3:5,则的值为()A .B .C .D .7. (2分)(2017·营口模拟) 如图所示,把一个正方形对折两次后沿虚线剪下,展开后所得的图形是()A .B .C .D .8. (2分) (2021八下·钦州期末) 如图,在Rt△ABC中,∠ACB=90°,AC=4,AB=6,分别以AB,AC,BC 为边在AB的同侧作正方形ABEF,ACPQ,BCMN,四块阴影部分的面积分别为S1 , S2 , S3 , S4 ,则S1﹣S2+S3+S4的值是()A . 12B . 24C .D .二、填空题 (共10题;共12分)9. (1分) (2019八上·江津期中) 如图,点P在∠AOB内,点M、N分别是点P关于OA、OB的对称点,若△PEF 的周长为15,则MN的长为.10. (1分)(2019·烟台) 小明将一张正方形纸片按如图所示顺序折叠成纸飞机,当机翼展开在同一平面时(机翼间无缝隙),的度数是.11. (3分)设计图案时,以某一个图案为,通过平移、_和的组合进行设计图案.12. (1分)(2019·松桃模拟) 如图,在△ABC中,AC=BC=2,∠C=90°,D是的中点,DE⊥DF,点E,F 分别在AC,BC上,则四边形CFDE的面积为.13. (1分) (2020八上·奈曼旗期末) 木工师傅做完房门后,为防止变形,会在门上钉上一条斜拉的木条,这样做的根据是.14. (1分) (2018九上·嵩县期末) 如图,在△ABC中,AB=AC=15,点D是BC边上的一动点(不与B、C重合),∠ADE=∠B=∠α,DE交AB干点E,且tan∠α= ,有以下的结论:①△ADE∽△ACD;②当CD=9时,△ACD 与△DBE全等;③△BDE为直角三角形时,BD为12或;④0<BE≤ .其中正确的结论是(填入正确结论的序号).15. (1分) (2019八上·永春期中) 如图,已知△ABC≌△DCB ,若∠ABC=50°,∠ACB=40°,则∠D=.16. (1分)(2019·安阳模拟) 如图,边长为2的菱形ABCD中,BD=2,E、F分别是AD,CD上的动点(包含端点),且AE+CF=2,则线段EF长的最小值是.17. (1分)如图,已知△ABC的两边AB和AC的垂直平分线分别交BC于D、E,若边BC长为8cm,则△ADE 的周长为.18. (1分) (2019八下·乌兰浩特期中) 如图,矩形中,,,将矩形沿折叠,点落在点处.则重叠部分的面积为.三、作图题 (共1题;共20分)19. (20分) (2019七下·合肥期末) △ABC在网格中的位置如图所示,请根据下列要求解答:(1)过点C作AB的平行线;(2)过点A作BC的垂线段,垂足为D;(3)比较AB和AD的大小,并说明理由;(4)将△ABC先向下平移5格,再向右平移6格得到△EFG(点A的对应点为点E,点B的对应点为点F,点C的对应点为点G).四、解答题 (共4题;共40分)20. (7分) (2019七下·中牟期末) 如图,已知, .(1)若添加条件,则吗?请说明理由;(2)若运用“ ”判定与全等,则需添加条件:;(3)若运用“ ”判定与全等,则需添加条件:.21. (15分)(2018·衢州模拟) 在正方形ABCD中,AB=8,点P在边CD上,tan∠PBC= ,点Q是在射线BP上的一个动点,过点Q作AB的平行线交射线AD于点M,点R在射线AD上,使RQ始终与直线BP垂直.(1)如图1,当点R与点D重合时,求PQ的长;(2)如图2,试探索:的比值是否随点Q的运动而发生变化?若有变化,请说明你的理由;若没有变化,请求出它的比值;(3)如图3,若点Q在线段BP上,设PQ=x,RM=y,求y关于x的函数关系式,并写出它的定义域.22. (6分) (2020八上·东台月考) 如图,在中,边AB,AC的垂直平分线相交于点O,分别交BC 与D、E.(1)若∠BAC=120°,则∠DAE=.(2)连接OA、OB、OC,的周长为6cm,的周长为14cm,求OA的长.23. (12分)(2018·江西) 在菱形ABCD中,∠ABC=60°,点P是射线BD上一动点,以AP为边向右侧作等边△APE,点E的位置随着点P的位置变化而变化.(1)如图1,当点E在菱形ABCD部或边上时,连接CE,BP与CE的数量关系是,CE与AD的位置关系是;(2)当点E在菱形ABCD外部时,(1)中的结论是否还成立?若成立,请予以证明;若不成立,请说明理由(选择图2,图3中的一种情况予以证明或说理);(3)如图4,当点P在线段BD的延长线上时,连接BE,若AB=2 ,BE=2 ,求四边形ADPE的面积.参考答案一、选择题 (共8题;共16分)答案:1-1、考点:解析:答案:2-1、考点:解析:答案:3-1、考点:解析:答案:4-1、考点:解析:答案:5-1、考点:解析:答案:6-1、考点:解析:答案:7-1、考点:解析:答案:8-1、考点:解析:二、填空题 (共10题;共12分)答案:9-1、考点:解析:答案:10-1、考点:解析:答案:11-1、考点:解析:答案:12-1、考点:解析:答案:13-1、考点:解析:答案:14-1、考点:解析:答案:15-1、考点:解析:答案:16-1、考点:解析:答案:17-1、考点:解析:答案:18-1、考点:解析:三、作图题 (共1题;共20分)答案:19-1、答案:19-2、答案:19-3、答案:19-4、考点:解析:四、解答题 (共4题;共40分)答案:20-1、答案:20-2、答案:20-3、考点:解析:答案:21-1、答案:21-2、答案:21-3、考点:解析:答案:22-1、答案:22-2、考点:解析:答案:23-1、答案:23-2、答案:23-3、考点:解析:。
河南省许昌市八年级上学期数学第一次月考试卷

河南省许昌市八年级上学期数学第一次月考试卷姓名:________ 班级:________ 成绩:________一、单选题 (共10题;共20分)1. (2分)下列结论错误的是()A . 成轴对称的图形全等B . 两边对应相等的直角三角形全等C . 一边和一锐角对应相等的两直角三角形全等D . 两直线被第三条直线所截,同位角相等2. (2分)有两边相等的三角形的两边长为3cm,5cm,则它的周长为()A . 8cmB . 11cmC . 13cmD . 11cm或13cm3. (2分) (2017八上·鄞州月考) 如图所示,在△ABC中,已知点D、E、F分别是BC、AD、CE的中点,且=4,则的值是()A . 1B . 1.5C . 2D . 2.54. (2分)下列图形具有稳定性的是()A . 三角形B . 四边形C . 五边形D . 六边形5. (2分)(2017·延边模拟) 将一副三角板如图方式放置,则∠1的度数是()A . 15°B . 20°C . 25°D . 30°6. (2分) (2018七下·合肥期中) 下列命题是假命题的是()A . 对顶角相等B . 两直线平行,同旁内角相等C . 平行于同一条直线的两直线平行D . 同位角相等,两直线平行7. (2分)如图,已知AB=AD,使用“ ”能直接判定的是()A .B .C .D .8. (2分) (2018八上·芜湖期末) 如图,小明做了一个角平分仪ABCD ,其中AB=AD , BC=DC.将仪器上的点A与∠PRQ的顶点R重合,调整AB和AD ,使它们分别落在角的两边上,过点A , C画一条射线AE , AE 就是∠PRQ的平分线.此角平分仪的画图原理是:根据仪器结构,可得△ABC≌△ADC ,这样就有∠QAE=∠PAE .则说明这两个三角形全等的依据是()A . SASB . ASAC . AASD . SSS9. (2分)如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是()A . 带①去B . 带②去C . 带③去D . 带①和②去10. (2分)右图可以看作是一个等腰直角三角形旋转若干次而生成的则每次旋转的度数可以是A . 90°B . 60°C . 45°D . 30°二、填空题 (共10题;共10分)11. (1分) (2019九下·温州竞赛) 三角形三边长分别为3,2a-1,4.则a的取值范围是________.12. (1分) (2019七下·长春期中) 已知,如图,△ABC中,∠B=∠DAC,则∠BAC和∠ADC的大小关系是________13. (1分) (2017八下·君山期末) 已知正方形ABCD边长为2,E是BC边上一点,将此正方形的一只角DCE 沿直线DE折叠,使C点恰好落在对角线BD上,则BE的长等于________.14. (1分) (2019八上·施秉月考) 如图,D,E是BC边上的两点,AD=AE,请你再添加一个关于“角”的条件________使△ABE≌△A CD.15. (1分)在三角形的中线,高线,角平分线中,一定能把三角形的面积等分的是________.16. (1分) (2019九上·沭阳月考) 如图,在△ABC中,∠C=90°,∠A=25°,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E,则的度数为________.17. (1分)说明命题“x>﹣4,则x2>16”是假命题的一个反例可以是x=________ .18. (1分)(2017·武汉模拟) 把正方形ABCD沿对边中点所在直线对折后展开,折痕为MN,再过点B折叠纸片,使点A落在MN上的点F处,折痕为BE,若AB的长为2,则FM=________.19. (1分) (2019八上·海州期中) 如图,△ABC中,DE是AC的垂直平分线,AE=4cm,△ABD的周长为12cm,则△ABC的周长为________cm.20. (1分) (2016八上·西昌期末) △ABC中,∠ABC和∠ACB的平分线交于点O,OD⊥BC于D,△ABC的面积18,AB=6,AC=8,OD=2,则BC的长是________.三、解答题 (共6题;共47分)21. (5分) (2019八上·荣昌期中) 如图,已知∠AOB和C、D两点,求作一点P,使P点到∠AOB的两边的距离相等,也使P点到C、D两点的距离相等。
河南省许昌市第一中学2021--2022学年八年级上学期期中教学质量检测数学试卷

许昌市第一中学2021--2022学年第一学期期中教学质量检测八年级数学一.单选题(每题3分,共30分)1.下列图形中有稳定性的是()A .正方形B .长方形C .直角三角形D .平行四边形2.装饰大世界出售下列形状的地砖:①任意三角形;②任意四边形;③正五边形;④正六边形.若只选购其中某一种地砖镶嵌地面,可供选用的地砖共有()A .1种B .2种C .3种D .4种3.若三角形两边长分别是4、5,则周长c 的范围是()A .1<c <9B .9<c <14C .10<c <18D .无法确定4.如图,已知点O 是△ABC 内一点,且点O 到三边的距离相等,∠A =40°,则∠BOC =()A .130°B .140°C .110°D .120°第4题图第5题图第6题图5.如图,已知∠1=∠4,添加以下条件,不能判定△ABC ≌△CDA 的是()A .∠2=∠3B .∠B =∠D C .BC =DA D .AB =DC6.用直尺和圆规作两个全等三角形,如图,能得到△COD ≌△C 'O 'D '的依据是()A .SAAB .SSSC .ASAD .AAS 7.已知点P (﹣2,1),那么点P 关于y 轴对称的点Q 的坐标是()A .(﹣2,1)B .(﹣2,﹣1)C .(﹣1,2)D .(2,1)8.如图,已知在△ABC 中,∠ABC =90°,∠A =30°,BD ⊥AC ,DE ⊥BC ,D 、E 为垂足,下列结论正确的是()A .AC =2ABB .AC =8EC C .CE =21BD D .BC =2BD9.如图,已知等边△ABC,点O是BC上任意一点,OE、OF分别与两边垂直,等边三角形的高为1,则OE+OF的值为()A.0.5B.1C.2D.不确定第9题图第10题图10.如图,△ABC≌△ADE,点D落在BC上,且∠EDC=70°,则∠BAD的度数等于()A.50°B.55°C.65°D.70°二.填空题(每题3分,共15分)11.如图,在△ABC中,AB=AC,AB的中垂线DE交AC于点D,交AB于点E,如果BC =10,△BDC的周长为22,那么AB=.第11题图第12题图12.如图,∠AOB=30°,OP平分∠AOB,PD⊥OB于D,PC∥OB交OA于C,若PC=10,则PD=.13.已知点A(a,b)关于x轴对称点的坐标是(a,﹣12),关于y轴对称点的坐标是(5,b),则A点的坐标是.14.若正n变形的每个内角都为150°,则n为.15.在△ABC中,AB=2cm,AC=4cm,则BC边上的中线AD的取值范围是.三.解答题(共75分)16.(8分)如图,已知点M,N和∠AOB,求作一点P,使P到M,N的距离相等,且到∠AOB的两边的距离相等.(要求尺规作图,并保留作图痕迹)17.(9分)已知一个等腰三角形的周长为20cm,若其中一边长为8cm,求另外两边的长.18.(10分)已知:如图,点B,E,C,F在同一直线上,AB∥DE,且AB=DE,BE=CF.求证:AC∥DF.19.(10分)如图,在△ABC中,AB=AC,∠A=40°,BD是∠ABC的平分线.求∠BDC 的度数.20.(10分)如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC面积是28cm2,AB=20cm,AC=8cm,求DE的长.21.(8分)如图,在平面直角坐标系中,A(1,2),B(3,1),C(﹣2,﹣1).(1)在图中作出△ABC关于y轴对称的△A1B1C1.(2)写出点A1B1C1的坐标(直接写答案).A1B1C122.(10分)在△ABC中,D为BC的中点,∠BAD=∠CAD,求证:AB=AC23.(10分)三条边都相等的三角形叫做等边三角形,它的三个角都是60°.△ABC是等边三角形,点D在BC所在直线上运动,连接AD,在AD所在直线的右侧作∠DAE=60°,交△ABC的外角∠ACF的角平分线所在直线于点E.(1)如图1,当点D在线段BC上时,请你猜想AD与AE的大小关系,并给出证明;(2)如图2,当点D在线段BC的反向延长线上时,依据题意补全图形,请问上述结论还成立吗?请说明理由.。
河南省许昌市八年级(上)第一次月考数学试卷
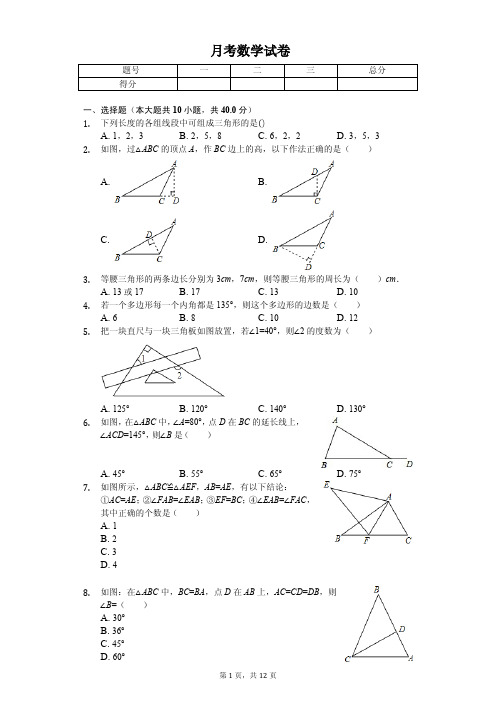
题号 得分
一
二
三
总分
一、选择题(本大题共 10 小题,共 40.0 分)
1. 下列长度的各组线段中可组成三角形的是
A. 1,2,3
B. 2,5,8
C. 6,2,2
D. 3,5,3
2. 如图,过△ABC 的顶点 A,作 BC 边上的高,以下作法正确的是( )
A.
B.
C.
D.
3. 等腰三角形的两条边长分别为 3cm,7cm,则等腰三角形的周长为( )cm.
A. 13 或 17
B. 17
C. 13
D. 10
4. 若一个多边形每一个内角都是 135°,则这个多边形的边数是( )
A. 6
B.板如图放置,若∠1=40°,则∠2 的度数为( )
A. 125°
B. 120°
C. 140°
6. 如图,在△ABC 中,∠A=80°,点 D 在 BC 的延长线上,
第 2 页,共 12 页
15. 如图所示,在△ABC 中,已知点 D,E,F 分别为 BC,AD, BE 的中点.且 S△ABC=8cm2,则图中△CEF 的面积=______ .
三、解答题(本大题共 7 小题,共 60.0 分) 16. 如图,∠B=42°,∠A+10°=∠1,∠ACD=64°,证明:AB∥CD
∠ACD=145°,则∠B 是( )
D. 130°
A. 45°
B. 55°
C. 65°
7. 如图所示,△ABC≌△AEF,AB=AE,有以下结论:
①AC=AE;②∠FAB=∠EAB;③EF=BC;④∠EAB=∠FAC,
其中正确的个数是( )
A. 1
B. 2
许昌市八年级数学上册第一单元《三角形》检测卷(答案解析)

一、选择题1.如图,下列结论中正确的是( )A .12A ∠>∠>∠B .12A ∠>∠>∠C .21A ∠>∠>∠D .21A ∠>∠>∠ 2.如图,在△ABC 中,∠ACB=90°,D 在AB 上,将△ABC 沿CD 折叠,点B 落在AC 边上的点B′处,若'20ADB ∠=︒,则∠A 的度数为( )A .25°B .30°C .35°D .40° 3.若过六边形的一个顶点可以画n 条对角线,则n 的值是( )A .1B .2C .3D .4 4.如图,1∠等于( )A .40B .50C .60D .705.下列命题是真命题的个数为( )①两条直线被第三条直线所截,内错角相等.②三角形的内角和是180°.③在同一平面内平行于同一条直线的两条直线平行.④相等的角是对顶角.⑤两点之间,线段最短.A .2B .3C .4D .5 6.以下列各组线段为边,能组成三角形的是( ) A .1,2,3B .1,3,5C .2,3,4D .2,6,10 7.下列长度(单位:cm )的三条线段能组成三角形的是( ) A .13,11,12 B .3,2,1 C .5,12,7 D .5,13,5 8.做一个三角形的木架,以下四组木棒中,符合条件的是( )A .4cm, 5cm,9cmB .4cm, 5cm, 6cmC .5cm,12cm,6cmD .4cm,2cm,2cm9.如图,△ABC 中AC 边上的高是哪条垂线段.( )A .AEB .CDC .BFD .AF 10.内角和与外角和相等的多边形是( ) A .六边形 B .五边形 C .四边形 D .三角形 11.如图,已知,,90,//AD BC FG BC BAC DE AC ⊥⊥∠=︒.则结论①//FG AD ;②DE 平分ADB ;③B ADE ∠=∠;④CFG BDE ∠+∠90=︒.正确的是( )A .①②③B .①②④C .①③④D .②③④ 12.小红有两根长度分别为4cm 和8cm 的木棒,他想摆一个三角形,现有长度分别为3cm ,4cm ,8cm ,15cm 四根木棒,则他应选择的木棒长度为( ).A .3cmB .4cmC .8cmD .15cm二、填空题13.如图是一块正多边形的碎瓷片,经测得30ACB ∠=︒,则这个正多边形的边数是_________.14.如图,BF 平分∠ABD ,CE 平分∠ACD ,BF 与CE 交于G ,若130,90BDC BGC ∠=︒∠=︒,则∠A 的度数为_________.15.如图,△ABC 的两条中线AD 、BE 相交于点G ,如果S △ABG =2,那么S △ABC =_____.16.如图,,AE AD 分别是△ABC 的高和角平分线,且6B 3︒∠=,6C 7︒∠=则DAE ∠的度数为__.17.如图,ABC 中,40A ∠=︒,72B ∠=︒,CE 平分ACB ∠,CD AB ⊥于D ,DF CE ⊥交CE 于F ,则CDF ∠=______.18.如图,△ABC 中,D 为BC 边上的一点,BD :DC=2:3,△ABC 的面积为10,则△ABD 的面积是_________________19.如图,AB BE ,分别是ABC 中,BC AC 边上的高,6cm BC ,4cm AC =,若3cm =AD ,则BE 的长为__________cm .20.如图,在ABC 中,E 、D 、F 分别是AD 、BF 、CE 的中点,若DEF 的面积是1,则ABC S =______.三、解答题21.如图,BP 平分ABC ∠,交CD 于点F ,DP 平分ADC ∠交AB 于点E ,AB 与CD 相交于点G ,42A ∠=︒.(1)若60ADC ∠=︒,求AEP ∠的度数;(2)若38C ∠=︒,求P ∠的度数.22.如图,在每个小正方形边长为1的方格纸中,△ABC 的顶点都在方格纸格点上.将△ABC 向左平移2格,再向上平移4格.(1)请在图中画出平移后的△A ′B ′C ′;(2)在图中画出△ABC 的高CD ,中线BE ;(3)在图中能使S △ABC =S △PBC 的格点P 的个数有 个(点P 异于点A ).23.如图,在ABC 中,A ACB ∠=∠,CD 为ABC 的角平分线,CE 是ABC 的高.(1)若15DCB ∠=︒,求CBD ∠的度数;(2)若36DCE ∠=︒,求ACB ∠的度数.24.已知一个n 边形的每一个内角都等于120°.(1)求n 的值;(2)求这个n 边形的内角和;(3)这个n 边形内一共可以画出几条对角线?25.如图,在ABC 中,点E 在AC 边上,连结BE ,过点E 作//DF BC ,交AB 与点D .若BE 平分ABC ∠,EC 平分BEF ∠.设AED β∠=.(1)当80β=︒时,求DEB ∠的度数.(2)试用含α的代数式表示β.(3)若=k βα(k 为常数),求α的度数(用含k 的代数式表示).26.一个多边形的每个外角都等于40°,求这个多边形的内角和.【参考答案】***试卷处理标记,请不要删除一、选择题1.D解析:D【分析】三角形的一个外角等于与它不相邻的两个内角的和,三角形的一个外角大于任何一个与它不相邻的内角.【详解】解:∵∠2是△BCD 的外角,∴∠2>∠1,∵∠1是△ABC 的外角,∴∠1>∠A ,∴21A ∠>∠>∠.故选D .【点睛】本题考查了三角形外角的性质,熟练掌握三角形外角的性质是解答本题的关键.2.C解析:C【分析】利用翻折不变性,三角形内角和定理和三角形外角的性质即可解决问题.【详解】∵∠ACB=90°,∴∠A+∠B=90°,∵△CDB′是由△CDB翻折得到,∴∠CB′D=∠B,∵∠CB′D=∠A+∠ADB′=∠A+20°,∴∠A+∠A+20°=90°,解得∠A=35°.故选:C.【点睛】本题考查三角形内角和定理和三角形外角的性质,翻折变换等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.3.C解析:C【分析】根据从一个n边形一个顶点出发,可以连的对角线的条数是n-3进行计算即可.【详解】解:6-3=3(条).答:从六边形的一个顶点可引出3条对角线.故选:C.【点睛】本题考查了多边形的对角线,解答此类题目可以直接记忆:一个n边形一个顶点出发,可以连的对角线的条数是n-3.4.D解析:D【分析】根据三角形外角的性质直接可得出答案.【详解】解:由三角形外角的性质,得∠+︒︒160=130∴∠=︒-︒=︒11306070故选D.【点睛】本题考查了三角形外角的性质,比较简单.5.B解析:B【分析】首先判断所给命题的真假,再选出正确的选项.【详解】解:∵两条直线被第三条直线所截,两直线平行,内错角相等,∴①错误;∵三角形的内角和是180°,∴②正确;∵在同一平面内平行于同一条直线的两条直线平行,∴③正确;∵相等的角可以是对顶角,也可以是内错角、同位角等等,∴④错误;∵连接两点的所有连线中,线段最短,∴⑤正确;∴真命题为②③⑤,故选B .【点睛】本题考查命题的真假判断,根据所学知识判断一个命题条件成立的情况下,结论是否一定成立来判断命题是真命题还是假命题是解题关键.6.C解析:C【分析】根据三角形三边关系逐一进行判断即可.【详解】A、1+2=3,不能构成三角形,故不符合题意;B、1+3=4<5,不能构成三角形,故不符合题意;C、2+3=5>4,可以构成三角形,故符合题意;D、2+6=8<10,不能构成三角形,故不符合题意,故选:C.【点睛】本题主要考查三角形的三边关系,比较简单,熟记三边关系定理是解决本题的关键.7.A解析:A【分析】根据三角形的三边关系“任意两边之和大于第三边,任意两边之差小于第三边”进行分析.【详解】解:根据三角形的三边关系,A、11+12>13,能组成三角形,符合题意;B、1+2=3,不能组成三角形,不符合题意;C、5+7=12,不能组成三角形,不符合题意;D、5+5<13,不能组成三角形,不符合题意;故选A.此题考查了三角形的三边关系.判断能否组成三角形的简便方法是看较小的两个数的和是否大于第三个数.8.B解析:B【分析】三角形的任意两边的和大于第三边,根据三角形的三边关系就可以求解.【详解】解:根据三角形的三边关系,知:A中,4+5=9,排除;B中,4+5>6,满足;C中,5+6<12,排除;D中,2+2=4,排除.故选:B.【点睛】本题主要考查了三角形的三边关系,在运用三角形三边关系判定三条线段能否构成三角形时,只要两条较短的线段长度之和大于第三条线段的长度即可判定这三条线段能构成一个三角形.9.C解析:C【分析】根据三角形的高的定义,△ABC中AC边上的高是过B点向AC作的垂线段,即为BF.【详解】解:∵BF⊥AC于F,∴△ABC中AC边上的高是垂线段BF.故选:C.【点睛】本题考查了三角形的高的定义,关键是根据从三角形的一个顶点向它的对边作垂线,垂足与顶点之间的线段叫做三角形的高解答.10.C解析:C【分析】设这个多边形为n边形,根据题意列出方程,解方程即可求解.【详解】解:设这个多边形为n边形,由题意得(n-2)180°=360°,解得n=4,所以这个多边形是四边形.故选:C本题考查多边形的内角和公式,多边形的外角和360°,熟知两个定理是解题关键. 11.C解析:C【分析】根据,,AD BC FG BC ⊥⊥得到FG ∥AD ,判断①正确;根据∠ADE+∠BDE=90°,∠B+∠BDE=90°,得到③正确;根据//DE AC , 证明∠BDE=∠C ,进行角的代换证明∠BDE+∠CFG=90°,得到④正确; 证明∠ADE+∠BDE=90°,判断②不正确.【详解】解:∵,,AD BC FG BC ⊥⊥∴∠FGB=∠ADB=90°,∴FG ∥AD ,∠ADE+∠BDE=90°,故①正确;∵DE ∥AC ,∴∠DEB=∠CAB=90°,∴∠B+∠BDE=90°,∴B ADE ∠=∠,∴③正确;∵//DE AC ,∴∠BDE=∠C ,∵∠FGC=90°,∴∠C+∠CFG=90°,∴∠BDE+∠CFG=90°,∴④正确;∵∠ADB=90°,∴∠ADE+∠BDE=90°,∴②不正确;故选:C .【点睛】本题考查了直角三角形两锐角互余,同角(等角)的余角相等,平行线的判定等知识,熟知相关定理是解题关键.12.C解析:C【分析】设选择的木棒长为x ,根据第三边大于两边之差小于两边之和即可求出范围,再结合选项即可得出答案.【详解】由题意得,设选择的木棒长为x ,则8448x -<<+,即412x <<,∴选择木棒长度为8cm .故选C .【点睛】本题考查了三角形三边关系的应用,熟练掌握三边关系是解题的关键.二、填空题13.12【分析】根据瓷片为正多边形及可知正多边形的外角为进而可求得正多边形的边数【详解】如图延长BC 可知∠1为正多边形的外角∵瓷片为正多边形∴AD=DB=BC ∠ADB=∠DBC ∴四边形ACBD 为等腰梯形解析:12【分析】根据瓷片为正多边形及=30ACB ∠︒,可知正多边形的外角为30︒,进而可求得正多边形的边数.【详解】如图,延长BC ,可知∠1为正多边形的外角,∵瓷片为正多边形,∴AD=DB=BC ,∠ADB=∠DBC ,∴四边形ACBD 为等腰梯形,∴BD ∥AC ,∴∠1==30ACB ∠︒,∴正多边形的边数为:360=1230︒︒, 故答案为:12.【点睛】本题考查正多边形的外角和,掌握相关知识点是解题的关键. 14.50°【分析】连接BC 根据三角形内角和定理可求得∠DBC +∠DCB 的度数再利用三角形内角和定理及角平分线的定义可求得∠ABC +∠ACB 的度数即可求得∠A 的度数【详解】解:连接BC ∵∠BDC =130°解析:50°【分析】连接BC ,根据三角形内角和定理可求得∠DBC +∠DCB 的度数,再利用三角形内角和定理及角平分线的定义可求得∠ABC+∠ACB的度数,即可求得∠A的度数.【详解】解:连接BC,∵∠BDC=130°,∴∠DBC+∠DCB=180°−∠BDC=50°,∵∠BGC=90°,∴∠GBC+∠GCB=180°−∠BGC=90°,∴∠GBD+∠GCD=(∠GBC+∠GCB)−(∠DBC+∠DCB)=40°,∵BF平分∠ABD,CE平分∠ACD,∴∠ABD+∠ACD=2∠GBD+2∠GCD=80°,∴∠ABC+∠ACB=(∠ABD+∠ACD)+(∠DBC+∠DCB)=130°,∴∠A=180°−(∠ABC+∠ACB)=180°−130°=50°.故答案为:50°.【点睛】本题主要考查了与角平分线有关的三角形内角和问题,根据题意作出辅助线,构造出三角形是解答此题的关键.15.6【分析】根据DE分别是三角形的中点得出G是三角形的重心再利用重心的概念可得:2GD=AG进而得到S△ABG:S△ABD=2:3再根据AD是△ABC 的中线可得S△ABC=2S△ABD进而得到答案【详解析:6【分析】根据D,E分别是三角形的中点,得出G是三角形的重心,再利用重心的概念可得:2GD=AG进而得到S△ABG:S△ABD=2:3,再根据AD是△ABC的中线可得S△ABC=2S△ABD进而得到答案.【详解】解:∵△ABC的两条中线AD、BE相交于点G,∴2GD=AG,∵S△ABG=2,∴S△ABD=3,∵AD是△ABC的中线,∴S△ABC=2S△ABD=6.故答案为:6.【点睛】此题主要考查了重心的概念和性质:三角形的重心是三角形三条中线的交点,且重心到顶点的距离是它到对边中点的距离的两倍.16.20°【分析】根据高线的定义以及角平分线的定义分别得出∠CAD=34°进而得出∠CAE 的度数进而得出答案【详解】解:∵且∴∵平分∴∵是的高∴∴∴∴故答案为:20°【点睛】此题考查三角形的角平分线中线解析:20°【分析】根据高线的定义以及角平分线的定义分别得出68BAC ︒∠=,∠CAD =34°,进而得出∠CAE 的度数,进而得出答案.【详解】解:∵180B BAC C ︒∠+∠+∠=,且6B 3︒∠=,6C 7︒∠=,∴180180367668BAC B C ︒︒︒︒︒∠=-∠-∠=--=,∵AD 平分BAC ∠, ∴11683422CAD BAC ︒︒∠=∠=⨯=, ∵AE 是ABC ∆的高, ∴90AEC ︒∠=,∴90C CAE ︒∠+∠=,∴90907614CAE C ︒︒︒︒∠=-∠=-=,∴341420DAE CAD CAE ︒︒︒∠=∠-∠=-=,故答案为:20°.【点睛】此题考查三角形的角平分线、中线和高,三角形内角和定理,解题关键在于掌握各性质定义.17.74°【分析】先根据三角形的内角和定理求得∠ACB 的度数再根据CE 平分∠ACB 求得∠ACE 的度数则根据三角形的外角的性质就可求得∠CED =∠A+∠ACE 再结合CD ⊥ABDF ⊥CE 就可求解【详解】解:解析:74°【分析】先根据三角形的内角和定理求得∠ACB 的度数,再根据CE 平分∠ACB 求得∠ACE 的度数,则根据三角形的外角的性质就可求得∠CED =∠A +∠ACE ,再结合CD ⊥AB ,DF ⊥CE 就可求解.【详解】解:∵∠A =40°,∠B =72°,∴∠ACB =180°﹣40°﹣72°=68°,∵CE 平分∠ACB ,∴∠ACE =∠BCE =34°,∴∠CED=∠A+∠ACE=74°,∵CD⊥AB,DF⊥CE,∴∠CDF+∠ECD=∠ECD+∠CED=90°,∴∠CDF=∠CED=74°,故答案为:74°.【点睛】此题主要考查了三角形的内角和定理、三角形的外角的性质、以及角平分线定义和垂直定义.18.4【分析】利用面积公式可得出△ABD与△ABC等高只需求出BD与BC的比值即可求出三角形ABD的面积【详解】解:∵BD:DC=2:3∴BD=BC△ABD 的面积=BD•h=× BC•h=△ABC的面积解析:4【分析】利用面积公式可得出△ABD与△ABC等高,只需求出BD与BC的比值即可求出三角形ABD 的面积.【详解】解:∵BD:DC=2:3,∴BD=25BC.△ABD的面积=12BD•h=12×25BC•h=25△ABC的面积=25×10=4.故答案为:4.【点睛】本题考查了三角形面积公式以及根据公式计算三角形面积的能力.19.【分析】三角形的面积等于任意一条底边乘以该边上的高的积的一半别以BCAC为底写出△ABC的面积的两种表示方法;结合两个面积相等和已知中的数据进行计算即可解答题目【详解】S△ABC=BC·AD=AC·解析:9 2【分析】三角形的面积等于任意一条底边乘以该边上的高的积的一半,别以BC、AC为底,写出△ABC的面积的两种表示方法;结合两个面积相等和已知中的数据,进行计算即可解答题目.【详解】S△ABC=12BC·AD=12AC·BE,将AD=3cm,BC=6cm,AC=4cm代入,得:11364 22BE ⨯⨯=⨯92BE=cm故答案为:9 2【点睛】本题考查三角形等面积法求高,通过三角形面积建立等量关系是解题的关键.20.7【分析】连接CDBEAF由三角形中线等分三角形的面积求得S△AEC=2S△DEFS△ABD=2S△DEFS△BFC=2S△DEF由S△ABC=S△AEC+S△ABD+S△BFC+S△DEF即可得出解析:7【分析】连接CD,BE,AF,由三角形中线等分三角形的面积,求得S△AEC=2S△DEF,S△ABD=2S△DEF,S△BFC=2S△DEF,由S△ABC=S△AEC+S△ABD+S△BFC+S△DEF即可得出结果.【详解】解:连接CD,BE,AF,如图所示:∵AE=ED,由三角形中线等分三角形的面积,可得S△AEF=S△DEF,同理S△AEF=S△AFC,∴S△AEC=2S△DEF;同理可得:S△ABD=2S△DEF,S△BFC=2S△DEF,∴△ABC=S△AEC+S△ABD+S△BFC+S△DEF=2S△DEF+2S△DEF+2S△DEF+S△DEF=7S△DEF=7cm2,故答案为:7.【点睛】本题是面积及等积变换综合题目,考查了三角形的面积及等积变换,解答关键是通过作辅助线,运用三角形中线等分三角形的面积得出结果.三、解答题21.(1)72︒;(2)40︒.【分析】(1)根据角平分线的定义可得∠ADP=12ADC∠,然后利用三角形外角的性质即可得解;(2)根据角平分线的定义可得∠ADP=∠PDF ,∠CBP=∠PBA ,再根据三角形的内角和定理可得∠A+∠ADP=∠P+∠ABP ,∠C+∠CBP=∠P+∠PDF ,所以∠A+∠C=2∠P ,即可得解.【详解】解:(1)∵DP 平分∠ADC ,∴∠ADP=∠PDF=12ADC ∠, ∵60ADC ∠=︒,∴30ADP ∠=︒,∴304272AEP ADP A ∠=∠+∠=︒+︒=︒;(2)∵BP 平分∠ABC ,DP 平分∠ADC ,∴∠ADP=∠PDF ,∠CBP=∠PBA ,∵∠A+∠ADP=∠P+∠ABP ,∠C+∠CBP=∠P+∠PDF ,∴∠A+∠C=2∠P ,∵∠A=42°,∠C=38°,∴∠P=12(38°+42°)=40°. 【点睛】本题考查了三角形的内角和定理及三角形外角的性质,角平分线的定义,熟记定理并理解“8字形”的等式是解题的关键.22.(1)见解析;(2)见解析;(3)4.【分析】(1)利用网格特点和平移的性质,分别画出点A 、B 、C 的对应点A '、B '、C '即可; (2)利用网格特点,作CD ⊥AB 于D ,找出AC 的中点可得到BE ;(3)利用平行线的性质过点A 作出BC 的平行线进而得出符合题意的点.【详解】(1)如图所示:△A ′B ′C ′即为所求;(2)如图所示:CD 即为所求;(3)如图所示:能使S △PBC =S △ABC 的格点P 的个数有4个.故答案为:4.【点睛】此题主要考查了平移变换以及平行线的性质和三角形的高,利用平行线的性质得出P 点位置是解题关键.23.(1)120°;(2)36°.【分析】(1)根据角平分线的定义求出∠ACB ,再根据三角形的内角和定理列式计算即可得解; (2)设∠A=∠ACB=x ,根据直角三角形两锐角互余求出∠CDE ,然后利用三角形的一个外角等于与它不相邻的两个内角的和列方程求解即可.【详解】(1)∵CD 为△ABC 的角平分线,∴∠ACB=2∠DCB=2×15°=30°,∵∠A=∠ACB ,∴∠CBD=180°-∠A-∠ACB=180°-30°-30°=120°;(2)设∠A=∠ACB=x ,∵CE 是△ABC 的高,∠DCE=36°,∴∠CDE=90°-36°=54°,∵CD 为△ABC 的角平分线,∴∠ACD=12∠ACB=12x , 由三角形的外角性质得,∠CDE=∠A+∠ACD , ∴1542x x +=︒, 解得x =36°,即∠ACB=36°.【点睛】 本题考查了三角形的内角和定理,角平分线的定义,直角三角形两锐角互余,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记各性质并准确识图是解题的关键. 24.(1)6;(2)720°;(3)9条【分析】(1)分别用两个式子表示多边形的内角和,列出方程,求解即可;(2)根据多边形内角和公式即可求解;(3)根据对角线的定义求出每个顶点的对角线条数,再求解即可.【详解】解:(1)由题意得()2180120n n -︒=︒,解得 6n =.(2)()62180720-⨯︒=︒,所以这个多边形的内角和为720°.(3)六边形每个顶点可以引6-3=3条对角线,所以一共可画6392⨯=条对角线.【点睛】本题考查了多边形的内角和公式,多边形对角线的定义,熟记多边形的内角和公式,理解对角线的定义是解题关键.25.(1)20︒;(2)1=904βα︒-;(3)360=41kα︒+.【分析】(1)根据对顶角的性质得到∠CEF=∠AED=80°,根据角平分线的定义即可得到结论;(2)根据角平分线的定义和平行线的性质即可得到结论;(3)根据题意列方程即可得到结论.【详解】解:(1)∵β=80°,∴∠CEF=∠AED=80°,∵EC平分∠BEF,∴∠BEC=∠CEF=80°,∴∠DEB=180°﹣80°﹣80°=20°;(2)∵DF∥BC,∴∠ADE=∠ABC=α,∵BE平分∠ABC,∴∠DEB=∠EBC=12α,∵EC平分∠BEF,∴β=∠CEF=12(180°﹣12α)=90°﹣14α;(3)∵β=kα,∴90°﹣14α=kα,解得:α=36041k︒+.【点睛】本题考查了三角形的内角和定理,平行线的性质,熟练掌握三角形的内角和定理是解题的关键.26.1260︒【分析】先利用外角和360度除以每个外角的度数求出边数,再利用多边形内角和公式计算得出答案.【详解】解:这个多边形的边数为36040=9(条),∴180(92)1260︒⨯-=︒,∴这个多边形的内角和是1260︒.【点睛】此题考查多边形的角度计算,多边形的外角和定理,多边形的内角和计算公式,根据多边形的每个外角都等于40°求出多边形的边数是解题的关键.。
河南省许昌市魏都区东城实验学校中学部2021-2022学年八年级上册第一次月考数学试卷

2021-2022学年河南省许昌市魏都区东城实验学校中学部八年级(上)第一次月考数学试卷一、选择题:(每小题3分,共30分)每小题只有一个选符合题目的要。
1.下列长度的三条线段能组成三角形的是()A.1cm2cm3cm B.4cm11cm6cmC.5cm5cm10cm D.6cm7cm8cm2.如图,小亮书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形,那么这两个三角形完全一样的依据是()A.SSS B.SAS C.AAS D.ASA3.如图,已知AB∥CD,∠A=55°,∠C=20°,则∠P的度数是()A.55°B.75°C.35°D.125°4.如图,要使四边形木架(用四根木条钉成)不变形,至少要再钉上的木条的根数为()A.1根B.2根C.3根D.4根5.一个等腰三角形的两边长分别是3和7,则它的周长为()A.17B.15C.13D.13或176.两个三角形只有以下元素对应相等,不能判定两个三角形全等的是()A.两角及夹边B.两边及夹角C.三个角D.三条边7.用尺规作已知角的平分线的理论依据是()A.SAS B.AAS C.SSS D.ASA8.已知一个多边形内角和为720°,则该多边形的对角线条数为()A.9B.12C.15D.189.如图为6个边长相等的正方形的组合图形,则∠1+∠2+∠3=()A.90°B.180°C.150°D.135°10.如图,平面直角坐标系中,点A为x轴负半轴上的动点,点B为y轴正半轴上的动点,△AOB中∠BAO 的平分线与∠OBA的外角平分线所在直线交于点C,则下列语句中正确的是()A.点B不动,在点A向右运动的过程中,∠BCA逐渐减小B.点A不动,在点B向上运动的过程中,∠BCA逐渐减小C.在点A向左运动,点B向下运动的过程中,∠BCA逐渐增大D.在点A,B运动的过程中,∠BCA的大小不变二、填空题:(每小题3分,共15分)11.若一个多边形的每个外角都等于60°,则它为边形.12.乐乐同学有两根长度为4cm,7cm的木棒,母亲节时他想自己动手给妈妈钉一个三角形相框,现有五根长度分别为3cm,6cm,10cm,12cm,15cm的木棒供他选择,他有种选择.13.如图,AB∥CD,EF与AB,CD分别相交于点E,F,EP⊥EF,与∠EFD的角平分线FP相交于点P,若∠BEP=46°,则∠EPF=度.14.如图,∠BAC=∠ABD,添加一个条件,能使△ABD≌△BAC(只添一个即可).15.如图所示,已知△ABC的周长是22,BO,CO分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=3,则△ABC的面积是.三、解答题(共75分)16.一个多边形,它的内角和比外角和的4倍多180°,求这个多边形的内角和度数及边数.17.如图,已知OE、OD分别平分∠AOB和∠BOC,若∠AOB=90°,∠EOD=70°,求∠BOC的度数.18.为了测量一幢高楼的高AB,在旗杆CD与楼之间选定一点P.测得旗杆顶C的视线PC与地面的夹角∠DPC=17°,测楼顶A的视线P A与地面的夹角∠APB=73°,量得点P到楼底距离PB与旗杆高度相等,等于8米,量得旗杆与楼之间距离为DB=33米,求楼高AB是多少米?19.如图,AC=DF,AD=BE,BC=EF.求证:(1)△ABC≌△DEF;(2)AC∥DF.20.如图,已知点B、D、E、C四点在一条直线上,且△ABE≌△ACD.求证:△ABD≌△ACE.21.已知:如图,AB=AE,BC=DE,∠B=∠E,F是CD的中点.求证:∠BAF=∠EAF.22.如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,大于EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M.(1)若∠ACD=114°,求∠MAB的度数;(2)若CN⊥AM,垂足为N,求证:△ACN≌△MCN.23.如图,AD为△ABC的中线,BE为△ABD的中线.(1)作图:在△BED中作出BD边上的高EF;BE边上的高DG;(2)若△ABC的面积为40,BD=5,则△BDE中BD边上的高EF为多少?若BE=6,求△BED中BE 边上的高DG为多少?。
河南省许昌市2023-2024学年八年级上学期期末数学模拟试题(含答案)

河南省许昌市2023-2024学年八年级上学期期末数学模拟试题注意事项:本试卷满分120分,考试时间为100分钟,所有试题均在答题卡上作答,否则无效.一、选择题(每小题3分,共30分)下列各小题均有四个答案,其中只有一个是正确的.1.中国文字博大精深,其中有许多是轴对称图形,以下四个文字是轴对称图形的是( )A .莲B .城C .许D .昌2.如图,工人师傅砌门时,常用木条EF 固定长方形门框ABCD ,使其不变形,这种做法的根据是()A .两点之间线段最短B .两点确定一条直线C .垂线段最短D .三角形的稳定性3.袁枚的一首诗《苔》在《经典咏流传》的舞台被重新唤醒,“白日不到处,青春恰自来.苔花如米小,也学牡丹开.”若苔花的花粉直径为0.0000084米,用科学记数法表示,则n 为( )0.00000848.410n =⨯A .B .C .5D .66-5-4.已知三角形的两边长分别是5和9,则这个三角形第三边长可能是( )A .3B .4C .5D .145.下列运算中,正确的是( )A .B .C .D .236a a a⋅=()5210aa=()33939aa=842a a a÷=6.如图,小明书上的三角形被墨迹污染了一部分,他根据所学的知识很快就画出了一个与书上完全一样的三角形,那么小明画图的依据是()A .SSSB .SASC .AASD .ASA7.将含角的直角三角板和直尺按如图所示的方式放置,已知,点B ,C 表示的30︒60α∠=︒刻度分别为,,则线段AC 的长为()1cm 3cmA .B .C .D .1cm 2cm 3cm 4cm8.如图,A 、B 是两个居民小区,快递公司准备在公路l 上选取点P 处建一个服务中心,使最短.下面四种选址方案符合要求的是( )PA PB +A .B .C .D .9.如图,正方形中阴影部分的面积为()【性质探究】(2)小文得到筝形角的性质是“筝形有一组对角相等”,请你帮他将证明过程补充完整.已知:如图2,在筝形ABCD 中,,.求证:.AB AD =CB CD =B D ∠=∠证明:(3)如图3,连结筝形ABCD 的对角线AC ,BD 交于点O .请用文字语言写出筝形对角线的一条性质,并给出证明.【拓展应用】(4)如图4,在中,,,点D 、E 分別是边BC ,AB 上的动点,ABC △80A ∠=︒40B ∠=︒当四边形AEDC 为筝形时,请直接与出的度数.BDE ∠如图所示(2)证明:连接A C.在和中,,ACB △ACD △AB AD AC AC BC DC =⎧⎪=⎨⎪=⎩,.(SSS)ABC ADC ∴≌△△B D ∴∠=∠(3)筝形的对角线互相垂直(答案不唯一)已知:如图3,在筝形ABCD 中,,,对角线AC ,BD 交于点O .求证:AB AD =CB CD =.AC BD ⊥证明:,,,AB AD = BC DC =AC AC =,,(三线合一).(SSS)ABC ADC ∴≌△△BAC DAC ∴∠=∠AC BD ∴⊥(4)或.20︒100︒。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
河南省许昌市八年级上学期数学第一周考试试卷
姓名:________ 班级:________ 成绩:________
一、选择题(每小题3分,共30分) (共10题;共30分)
1. (3分)(2020·皇姑模拟) 如图,下列推理及所证明的理由都正确的是()
A . 若,则,理由是内错角相等,两直线平行
B . 若,则,理由是两直线平行,内错角相等
C . 若,则,理由是内错角相等,两直线平行
D . 若,则,理由是两直线平行,内错角相等
2. (3分)若点P在第二象限,且到两条坐标轴的距离都是4,则点P的坐标为()
A . (﹣4,4)
B . (﹣4,﹣4)
C . (4,﹣4)
D . (4,4)
3. (3分)三角形两边的长分别是4和6,第三边的长是一元二次方程x2-16x+60=0的一个实数根,则该三角形的周长是()
A . 20
B . 20或16
C . 16
D . 18或21
4. (3分)(2017·陵城模拟) 如果不等式的解集是x<2,那么m的取值范围是()
A . m=2
B . m>2
C . m<2
D . m≥2
5. (3分) (2019七下·固阳期末) 已知点M(2m﹣1,1﹣m)在第四象限,则m的取值范围在数轴上表示正确的是()
A .
B .
C .
D .
6. (3分) (2019八上·德州开学考) 若,则下列不等式中成立的是()
A .
B .
C .
D .
7. (3分)(2018·阳新模拟) 一个六边形的六个内角都是120°(如图),连续四条边的长依次为 1,3,3,2,则这个六边形的周长是()
A . 13
B . 14
C . 15
D . 16
8. (3分)(2017·和平模拟) 不等式|x﹣1|<1的解集是()
A . x>2
B . x<0
C . 1<x<2
D . 0<x<2
9. (3分)如图,已知四边形ABCD中,AD∥BC,∠A=∠BCD=∠ABD,DE平分∠ADB,下列说法:①AB∥CD;
②ED⊥CD;③∠DFC=∠ADC﹣∠DCE;④S△EDF=S△BCF ,其中正确的结论是()
A . ①②③
B . ①②④
C . ①③④
D . ①②③④
10. (3分)下列方程中,是二元一次方程的是()
A .
B .
C .
D .
二、填空题(每题3分,共24分) (共8题;共24分)
11. (3分) (2016八上·宜兴期中) 已知等腰三角形的两边长是3cm和6cm,则这个等腰三角形的周长是________ cm.
12. (3分)(2018·成华模拟) 若实数a,b在数轴上对应的点的位置如图,则化简的结果是________.
13. (3分) (2018八上·仙桃期末) 如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC 交AB于E,交AC于F,过点O作OD⊥AC于D,下列四个结论:
①EF=BE+CF;
②∠BOC=90°+∠A;
③点O到△ABC各边的距离相等;
④设OD=m,AE+AF=n,则S△AEF=mn .
其中正确的结论是________.(填序号)
14. (3分)(2018·铜仁模拟) 点P的坐标是(a,b),从﹣2,﹣1,1,2这四个数中任取一个数作为a的值,再从余下的三个数中任取一个数作b的值,则点P(a,b)在平面直角坐标系中第一象限内的概率是________.
15. (3分) (2017七下·城北期中) 若关于的方程的解是负数,则的取值范围是________.
16. (3分) (2017八上·黄陂期中) 一个多边形的内角和等于其外角和的3倍,则这个多边形是________边形。
17. (3分)如图,PQ∥MN,AD∥BF,AB⊥MN于点B,CD⊥PQ于点C,两条平行线PQ与MN的距离可以是线段
________或________的长.
18. (3分)(2020·阿城模拟) 不等式组的解集为________.
三、解答题 (共7题;共66分)
19. (12分) (2019七下·通州期末) 解方程组:
20. (16分)(2020·滨湖模拟)
(1)解方程:- =1;
(2)解不等式组:
21. (6分)如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE.若∠CAE=65°,∠E=70°,且AD⊥BC,垂足为F,求∠BAC的度数.
22. (8分)孙子算经是中国古代重要的数学著作,其中有一段文字的大意是:甲、乙两人各有若干钱如果甲得到乙所有钱的一半,那么甲共有钱48文;如果乙得到甲所有钱的,那么乙也共有钱48文甲、乙两人原来各有多少钱?
23. (8分) (2019七下·长丰期中) 学校举办环保知识竞赛活动,竞赛题共有20道,答对一题得5分,答错或不答都扣2分,小兰在竞赛中获得了二等奖(得分在80分和90分之间),请问小兰在竞赛中答对了几道题?
24. (8分)(2017·高邮模拟) 解不等式组并写出它的所有非负整数解.
25. (8分)设二元一次方程2x+y-4=0,x-y+3=0,x+2y-k=0有公共解.求k的值.
参考答案
一、选择题(每小题3分,共30分) (共10题;共30分)
1-1、
2-1、
3-1、
4-1、
5-1、
6-1、
7-1、
8-1、
9-1、
10-1、
二、填空题(每题3分,共24分) (共8题;共24分)
11-1、
12-1、
13-1、
14-1、
15-1、
16-1、
17-1、
18-1、
三、解答题 (共7题;共66分)
19-1、答案:略
20-1、
20-2、答案:略
21-1、
22-1、答案:略23-1、答案:略24-1、答案:略25-1、答案:略。
