SPSS操作实验作业1(附答案)
spss实践题分析及答案

spss实践题分析及答案SPSS实践题习题1分析此班级不同性别的学⽣的物理和数学成绩的均值、最⾼分和最低分。
Report性别数学物理男⽣Mean 80.0769 74.5385N 13 13Std. Deviation 5.75125 5.17390Minimum 72.00 69.00Maximum 95.00 87.00⼥⽣Mean 80.7692 76.1538N 13 13Std. Deviation 8.91772 8.32512Minimum 70.00 65.00Maximum 99.00 91.00Total Mean 80.4231 75.3462N 26 26Std. Deviation 7.36029 6.84072Minimum 70.00 65.00Maximum 99.00 91.00结论:男⽣数学成绩最⾼分: 95 最低分: 72 平均分: 80.08物理成绩最⾼分: 87 最低分: 69 平均分: 74.54⼥⽣数学成绩最⾼分: 99 最低分: 70 平均分: 80.77 物理成绩最⾼分: 91 最低分: 65 平均分: 76.15 习题2分析此班级的数学成绩是否和全国平均成绩85存在显著差异。
One-Sample StatisticsNMean Std. Deviation Std. Error Mean数学2680.42317.360291.44347结论:由分析可知相伴概率为0.004,⼩于显著性⽔平0.05,因此拒绝零假设,即此班级数学成绩和全国平均⽔平85分有显著性差异习题3分析市2⽉份的平均⽓温在90年代前后有⽆明显变化。
Group Statistics分组 NMean Std. Deviation Std. Error Mean⼆⽉份⽓温0 11 -4.527273 1.2034043.3628400 118-3.2000001.3006786.3065729结论:由分析可知, ⽅差相同检验相伴概率为0.322,⼤于显著性⽔平0.05,因此接受零假设,90年代前后2⽉份温度⽅差相同。
SPSS上机实验报告一
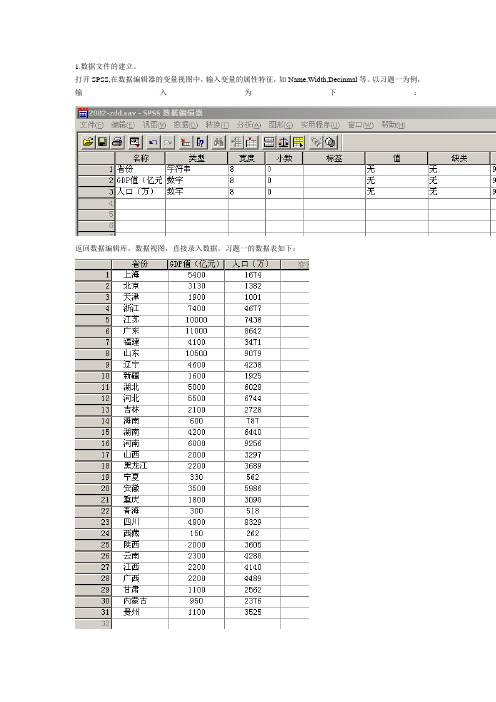
1.数据文件的建立。
打开SPSS,在数据编辑器的变量视图中,输入变量的属性特征,如Name,Width,Decinmal等。
以习题一为例,输入为下:返回数据编辑库,数据视图,直接录入数据。
习题一的数据表如下:点击Save,输入文件名将文件保存。
2.数据的整理数据编辑窗口的Date可提供数据整理功能。
其主要功能包括定义和编辑变量、观测量的命令,变量数据变换的命令,观测量数据整理的命令。
以习题一为例,将上图中的数据进行整理,以GDP值为参照,升序排列。
数据整理后的数据表为:整理后的数据,可以直观看出GDP值的排列。
3、频数分析。
以习题一为例(1).单击“分析→描述统计→频率”(2)打开“频率”对话框,选择GDP为变量(3)单击“统计量”按钮,打开“统计量”对话框.选择中值及中位数。
得到如下结果:(4)单击“分析→描述统计→探索”,打开“探索”对话框,选择GDP(亿元),输出为统计量。
结果如下:4、探索分析以习题2为例子:(1)单击“分析→统计描述→频率”,打开“频率”对话框,选择“身高”变量。
(2)选择统计量,分别选择百分数,均值,标准差,单击图标。
的如下结果:(3)单击“分析→统计描述→探索”,选择相应变量变量,单击“绘制”,选择如下图表,的如下结果:从上述图标可以看出,除了个别极端点以外,数据都围绕直线上下波动,可以看出,该组数据,在因子水平下符合正态分布。
4.交叉列联表分析:以习题3,原假设是吸烟与患病无关备择假设是吸烟与患病有关操作如下:单击“分析→统计描述→交叉表”,打开“交叉表”对话框,选择相应变量变量,单击精确,并选择“统计量”按钮,选择“卡方”作为统计量检验,然后单击“单元格”按钮,选择“观测值”和“期望值”进行计数。
得出分析结果如下:分析得出卡方值为7.469,,自由度是1,P值为0.004<0.05拒绝原假设,故有大于95%的把握认为吸烟和换慢性气管炎有关。
习题4:原假设是性别与安全性能的偏好无关备择假设是性别与安全性能的偏好有关操作如下:单击“分析→统计描述→交叉表”,打开“交叉表”对话框,选择相应行列变量然后选择“统计量”按钮,以“卡方”作为统计量检验.单击“单元格”按钮,选择“观测值”和“期望值”进行计数单击“确定”,得出分析结果如下:分析得出卡方值为19自由度是4,P值为0.001<0.05拒绝原假设,故有99.9%的把握认为性别与安全性能的偏好有关5实验作业补充。
SPSS操作实验作业1(附答案)

SPSS操作实验 (作业1)作为华夏儿女都曾为有着五千年的文化历史而骄傲过,作为时代青年都曾为中国所饱受的欺压而愤慨过,因为我们多是炎黄子孙。
然而,当代大学生对华夏文明究竟知道多少呢某研究机构对大学电气、管理、电信、外语、人文几个学院的同学进行了调查,各个学院发放问卷数参照各个学院的人数比例,总共发放问卷250余份,回收有效问卷228份。
调查问卷设置了调查大学生对传统文化了解程度的题目,如“佛教的来源是什么”、“儒家的思想核心是什么”、“《清明上河图》的作者是谁”等。
调查问卷给出了每位调查者对传统文化了解程度的总得分,同时也列出了被调查者的性别、专业、年级等数据信息。
请利用这些资料,分析以下问题。
问题一:分析大学生对中国传统文化的了解程度得分,并按了解程度对得分进行合理的分类。
问题二:研究获得文化来源对大学生了解传统文化的程度是否存在影响。
要求:直接导出查看器文件为.doc后打印(导出后不得修改)对分析结果进行说明,另附(手写、打印均可)。
于作业布置后,1周内上交本次作业计入期末成绩答案问题一操作过程1.打开数据文件作业。
同时单击数据浏览窗口的【变量视图】按钮,检查各个变量的数据结构定义是否合理,是否需要修改调整。
2.选择菜单栏中的【分析】→【描述统计】→【频率】命令,弹出【频率】对话框。
在此对话框左侧的候选变量列表框中选择“X9”变量,将其添加至【变量】列表框中,表示它是进行频数分析的变量。
3.单击【统计量】按钮,在弹出的对话框的【割点相等组】文本框中键入数字“5”,输出第20%、40%、60%和80%百分位数,即将数据按照题目要求分为等间隔的五类。
接着,勾选【标准差】、【均值】等选项,表示输出了解程度得分的描述性统计量。
再单击【继续】按钮,返回【频率】对话框。
4.单击【图表】按钮,勾选【直方图】和【显示正态曲线】复选框,即直方图中附带正态曲线。
再单击【继续】按钮,返回【频率】对话框。
最后,单击【确定】按钮,操作完成。
SPSS实验上机题

SPSS实验上机题实验1 数据文件建立与管理某航空公司38名职员性别和工资情况的调查数据,如下表所示,试在SPSS中进行如下操作:(1)定义变量,将gender定义为字符型变量,salary定义为数值型变量,在数据窗口录入数据,并保存数据文件,将其命名为“data1_1.sav”。
(2)打开文件data1_1.sav,练习增加一个个案,删除一个个案,增加一个变量、删除一个变量,以及个案和变量的复制、粘贴操作。
(3)将数据文件按性别分组;将数据文件按工资进行组距分组。
(4)查找工资大于40000美元的职工。
(5)按工资进行升序和降序排列,比较升序和降序排列结果有什么不同。
(6)练习数据的分类汇总操作,要求按照性别分类汇总样本的总数。
(7)练习数据选取操作,要求随机选取70%的数据。
(8)当工资大于40000美元时,职工的奖金是工资的20%;当工资小于40000美元时,职工的奖金是工资的10%,假设实际收入=工资+奖金,计算所有职工的实际收入,并将结果添加到income变量中。
实验2 数据特征的描述统计分析1.下表是一电脑公司某年连续120天的销售量数据(单位:台)。
试对其进行频数分析,计算均值、中位数、众数、四分位数,标准差、最大值、最小值、全距,偏度、峰度系数;画出直方图、茎叶图、箱线图;解释结果并说明其分布特征。
234159187155158172163183182177156165 143198141167203194196225177189203165 187160214168188173176178184209175210161152149211206196196234185189196172 150161178168171174160153186190172207 228162223170208165197179186175213176 153163218180192175197144178191201181 166196179171210233174179187173202182 154164215233168175198188237194205195 1742261801722111902001721871891881952.下表是某班同学月生活费资料,试对其进行描述分析,并对结果作出说明。
spss上机习题附答案

习 题1、 下表为100头某品种猪的血红蛋白含量〔单位:g/100ml 〕资料,试将其整理成次数分布表,并绘制直方图和折线图。
13.4 13.8 14.4 14.7 14.8 14.4 13.9 13.0 13.0 12.8 12.5 12.3 12.1 11.8 11.0 10.1 11.1 10.1 11.6 12.0 12.0 12.7 12.6 13.4 13.5 13.5 14.0 15.0 15.1 14.1 13.5 13.5 13.2 12.7 12.8 16.3 12.1 11.7 11.2 10.5 10.5 11.3 11.8 12.2 12.4 12.8 12.8 13.3 13.6 14.1 14.5 15.2 15.3 14.6 14.2 13.7 13.4 12.9 12.9 12.4 12.3 11.9 11.1 10.7 10.8 11.4 11.5 12.2 12.1 12.8 9.5 12.3 12.5 12.7 13.0 13.1 13.9 14.2 14.9 12.4 13.1 12.5 12.7 12.0 12.4 11.6 11.5 10.9 11.1 11.6 12.6 13.2 13.8 14.1 14.7 15.6 15.7 14.7 14.0 13.9(提示:第一组下限取为9.1,组距i =0.7)2、 测得某肉品的化学成分的百分比方下〔单位:%〕,请绘制成圆图。
水 分 蛋白质 脂 肪 无机盐 其 它 62.0 15.317.21.83.73、 2001年调查四川省5个县奶牛的增长状况〔及2000年相比〕得如下资料〔单位:%〕,请绘成长条图。
双流县 名山县 宣汉县 青川县 泸定县 增长率〔%〕 22.613.818.231.39.54、 1-9周龄大型肉鸭杂交组合GW 和GY 的料肉比方下表所示,请绘制成线图。
周龄 1 2 3 4 5 6 7 8 9 GW 1.42 1.56 1.66 1.84 2.13 2.48 2.83 3.11 3.48 GY 1.471.711.801.972.312.913.023.293.57习 题1、随机抽测了10只兔的直肠温度,其数据为:38.7、39.0、38.9、39.6、39.1、39.8、38.5、39.7、39.2、38.4〔℃〕,确定该品种兔直肠温度的总体平均数0μ=39.5〔℃〕,试检验该样本平均温度及0μ是否存在显著差异?〔=t2.641 0.01<P <0.05〕2、11只60日龄的雄鼠在x 射线照射前后之体重数据见下表〔单位:g 〕:检验雄鼠在照射x 射线前后体重差异是否显著?〔=t 4.132 P <0.01〕3、某猪场从10窝大白猪的仔猪中,每窝抽出性别一样、体重接近的仔猪2头,将每窝两头仔猪随机地支配到两个饲料组,进展饲料比照试验,试验时间30天,增重结果见下表。
Spss__作业习题答案.docx

Spss作业习题答案GRAPH/BAR(SIMPLE)二SUM(js) BY yeai\图表[数据集 1 ] C: \Users\l iuj ie\Desktop\第一次习题\习题7-1. savCOMPUTE zz=beer + wine + spirits. EXECUTE. GRAPH/BAR(SIMPLE)二SUM(zz) BY year.图表[数据集]]C: \Users\l iuj ie\Desktop\第一次习题\习题7-1 .savGRAPH/BAR(GROUPED)=MEAN(tea) MEAN(coffee) MEAN(cc) MEAN(mw) MEAN(fj) MEAN(beer) MEAN(wine)MEAN(spirits) BY country/PANEL ROWVAR二coni ROWOP=CROSS /MISSING二LISTWISE.图表[数据集 1 ] C: \Users\l iuj ic\Desktop\第一次习题\习题7・1 • savGETFILE='C:\Users\liujie\Desktop\第一次习题 \ 习题 7-2.sav'. DATASET NAME 数据集2 WINDOW 二FRONT. DATASET CLOSE 数据集 1. SORT CASES BY year (A). GRAPH/LINE(AREA)= SUM(def) SUM(eco) BY year /MISSING=LISTWISE.图表附注02-APR-2016 19:08:1612000- 1oooo- 8000- 6000- 4000- 2000-0- 12000" 10000- 8000- 6000- 4000- 2000-0- 12000- 1oooo- 8000- 6000- 4000" 2000-o- 12000- 10000- 8000- 6000- 4000-2000-westernEurope Asia "B e -gc m }Aust_・Denmark■Luxembour g —Japan 4e-ana-UK -Switzerla nd "SpainOceaniaNorth America■东 C000tons)■ 啡 cooo tons)□ C&C 饮料(million litres) ■矿泉 J :(million litres) □ 士 厂(million litres) □啤酒(million litres)□ri(millio n litres)□烈酒(million litres)创建的输出[数据集2] C:\Users\liujie\Desktop\第一次习题\习题7-2.savGETFILE=*C:\Users\ 1 iuj ie\Desktop\第一次习题\习题7-3.sav'. DATASET NAME 数据集3 WINDOW 二FRONT. DATASET CLOSE 数据集2. GRAPH/PIE=SlJNf(rus) BY sea.图表创建的输出02-APR-2016 19:11:19注释1200.00-1000.00-800.00"600.00-400.00-200.00-国防 经济gggggggggggg 9 9 9 9 9 9555556660)677777888024680246802468024[数据集3] C:\Users\l iuj ie\Desktop\第一次习题\习题7-3.sav季节■ 1 st Season■2nd Season□ 3rd Season■4th Season您对IBM SPSS Statistics的临时使用期将在11天后过期。
SPSS实验报告一题目和答案

广东金融学院实验报告课程名称:③由表报告可知,这三个行业平均收入最高:“科学研究、技术服务地质勘察业”的平均收入为8294.9983:“卫生、社会保障和社会福利业”的平均收入为5989.8982;“水利、环境和公共设施管理业”的平均收入为5076.2500。
报告总收入行业N 均值农林牧渔业24 4304.2083采矿业12 1658.3333制造业969 3554.4152电力、燃气及水的生产供应业120 4123.0724建筑业145 2759.1807交通运输、仓储和邮政业196 3222.4676信息传输、计算机服务和软件业123 3332.5672批发和零售业480 3202.4359住宿和餐饮业120 2772.3000金融业329 4350.7240房地产业82 2888.2317租赁和商务服务业87 2765.6685科学研究、技术服务地质勘察业12 8294.9983水利、环境和公共设施管理业36 5076.2500居民服务和其他服务业317 2447.8026教育368 4514.8723卫生、社会保障和社会福利业147 5989.8982文化、体育和娱乐业132 4300.9326公共管理和社会组织512 4427.6971无就职行业1356 2022.2584总计5567 3315.89423. ①由表描述量统计可知:筛选除去无收入者,对总收入进行标准化处理,其均值为0,标准差为1。
描述统计量N 均值标准差Zscore: 总收入5567 0.0000000 1.00000000有效的 N (列表状态)5567②由表异常值可知:异常值的比重是1.9%异常值频率百分比有效百分比累积百分比有效.00 105 1.9 1.9 1.91.00 5462 98.1 98.1 100.0合计5567 100.0 100.0(二)第二题:1. ①由表购买保险情况可知,商业保险、养老保险和医疗保险都买的人的比例是5.8%;一种保险都没买的人的比例是44.4%。
北语2024春《SPSS统计与分析应用》作业满分答案文档

北语2024春《SPSS统计与分析应用》作业满分答案文档问题一: 描述性统计分析数据收集首先,我们需要收集一组数据以进行描述性统计分析。
在此作业中,我们收集了100个学生的数学成绩数据。
描述性统计分析使用SPSS软件进行描述性统计分析,我们得到了以下结果:- 平均数:78.5- 标准差:9.2- 最小值:60- 最大值:95- 中位数:80- 四分位数:- 第一四分位数:72.5- 第二四分位数:80- 第三四分位数:85结论根据描述性统计分析结果,我们可以得出以下结论:- 这组学生的平均数成绩为78.5,说明整体水平中等偏上。
- 标准差为9.2,说明学生的成绩相对分散。
- 最低分为60,最高分为95,成绩分布较为广泛。
- 中位数为80,说明成绩的中等水平集中在80左右。
- 第一四分位数为72.5,第三四分位数为85,说明成绩的大部分集中在72.5到85之间。
问题二: 相关性分析数据收集我们收集了100个学生的数学成绩和英语成绩数据。
相关性分析使用SPSS软件进行相关性分析,我们得到了以下结果:- 相关系数:0.75- p值:0.001结论根据相关性分析结果,我们可以得出以下结论:- 数学成绩和英语成绩之间存在较强的正相关关系。
- 相关系数为0.75,接近于1,说明两个变量之间的关联程度较高。
- p值为0.001,小于显著性水平0.05,因此可以得出该相关关系是显著的。
问题三: T检验数据收集我们收集了两组学生的数学成绩数据:男生组和女生组。
T检验使用SPSS软件进行T检验,我们得到了以下结果:- T值:2.16- 自由度:98- p值:0.034结论根据T检验结果,我们可以得出以下结论:- 男生组和女生组的数学成绩之间存在显著差异。
- T值为2.16,自由度为98,p值为0.034,小于显著性水平0.05,因此可以得出这种差异是显著的。
问题四: 方差分析数据收集我们收集了三个不同班级的学生的数学成绩数据。
统计SPSS第一次作业参考答案
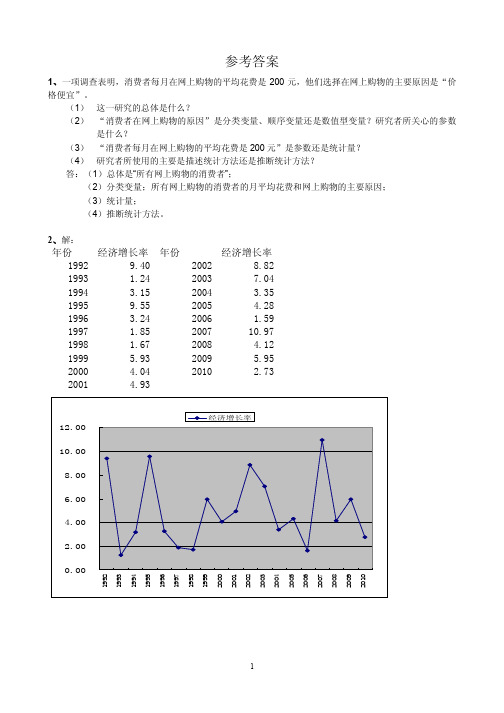
参考答案1、一项调查表明,消费者每月在网上购物的平均花费是200元,他们选择在网上购物的主要原因是“价格便宜”。
(1) 这一研究的总体是什么?(2) “消费者在网上购物的原因”是分类变量、顺序变量还是数值型变量?研究者所关心的参数是什么?(3) “消费者每月在网上购物的平均花费是200元”是参数还是统计量?(4) 研究者所使用的主要是描述统计方法还是推断统计方法?答:(1)总体是“所有网上购物的消费者”;(2)分类变量;所有网上购物的消费者的月平均花费和网上购物的主要原因;(3)统计量;(4)推断统计方法。
2、解:年份 经济增长率 年份 经济增长率1992 9.40 2002 8.821993 1.24 2003 7.041994 3.15 2004 3.351995 9.55 2005 4.281996 3.24 2006 1.591997 1.85 2007 10.971998 1.67 2008 4.121999 5.93 2009 5.952000 4.04 2010 2.732001 4.93从上图中可以看出,从1992-2010年,该地区的经济增长率上下波动幅度较大。
虽说经济每年都在增长,但增长速度不够稳定。
总体来看,呈现循环波动的特点,但周期不固定。
3、因每人抽取样本不同,结果会有差异,但分析的方法和图表选择应差不多。
(1)分析“上月收入”的分布特征,并绘制合适图表。
Excel:接收区域 频率1300以下 51300-1700 191700-2000 452000-2300 392300-2700 482700-3000 143000-4100 8SPSS:新上月工资频率 百分比 有效百分比 累积百分比1300.00 5 2.8 2.8 2.8 有效1700.00 19 10.7 10.7 13.52000.00 45 25.3 25.3 38.82300.00 39 21.9 21.9 60.72700.00 48 27.0 27.0 87.63000.00 14 7.9 7.9 95.53300.00 8 4.5 4.5 100.0合计 178 100.0 100.0观察样本的数据,发现上月工资在800-4100之间分布,将工资进行分组,绘制出上图。
spss实验题答案

实验题1.解:(1)将数据录入SPSS软件中。
(2)点击分析→回归→线性,得回归系数表:由表可知,线性回归方程为:y=0.379x+17.2192.解:(a)将数据录入SPSS软件中, 点击分析→回归→线性,得回归系数表:Y为保单推销数,X为保单推销经历(年数)由图可知,拟合回归方程y=3.364x+51.165( b ) 回归系数为0.410,与0相异,小于0.05(在5%的显著水平),即相应系数显著大于0(c)一个有10年推销经历的保单推销员的销售额为y=3.364×10+51.165=84.8053.解:(a)将数据录入SPSS软件中, 点击分析→回归→线性,得回归系数表:点击分析→相关→双变量,得到:点击图形→旧对话框→散点、点状→确定,即可得到散点图:Y为能力测验分数,X为完成任务时间由表可知,线性回归方程为:Y=-11.959x+125.267(b) 由散点图可看出,这两个变量呈负相关关系。
(c) 由表可知,两个变量的相关系数为—0.930>0.5,又0.865显著异于0,t统计量的显著性概率p为0.000<0.05,说明两个变量在0.05水平上呈显著性差异。
4.解:(1)将数据录入SPSS软件中。
(2)点击分析→回归→线性,得回归系数表:Y 为儿子身高,x 为父亲身高由表可知,经验回归方程y=0.465x+35.977 5.解:(1)将数据录入SPSS 软件中。
(2)点击转换→计算变量→线性→目标变量t=1/x;(3)点击分析→回归→线性→因变量y →自变量t,得回归系数表:Y 为销售额,X 为流通费用率由表可知,选用曲线xba y +=做曲线回归,得回归方程为y=9.707/x -1.2116.解:(1)将数据录入SPSS 软件中, 点击分析→回归→线性,y 为因变量,x 为自变量。
得到回归分析表:y 为上年专利数,x1为上三年R&D 投入,x2为高级工程师数由表可知,“上年专利数”对“上三年R&D 投入”和“高级工程师数”的线性回归方程为: y=0.008x1+0.615x2+7.040由表可得,估计标准误差为3.65724。
SPSS操作练习——作业示例 (1)

SPSS操作练习(t检验)要求:1、用SPSS进行统计分析;2、分析说明使用某一统计处理方法的依据;3、将统计结果正确地在论文中进行表达并进行结果分析。
----------------------------------------------------------------------------------1.计算下列两个玉米品种10个果穗长度(cm)的平均值、标准差和变异系数,并解释两个玉米品种的果穗长度有无差异。
【变异系数C·V=(标准偏差SD/平均值MN)×100%】玉米24号:19,21,20,20,18,19,22,21,21,19金皇后玉米:16,21,24,15,26,18,20,19,22,19解:(1)选择分析方法:被比较的玉米24号、金皇后玉米是两个品种的玉米,试验中彼此独立、无配对关系。
先用SPSS对数据是否服从正态分布进行Kolmogorov-Smirnov 检验,得到,玉米24号的p=0.869>0.05,金皇后玉米的p=0.99>0.05,说明两个样本均服从正态分布(来自正态总体),因此选择独立样本t检验进行数据分析。
经Levene方差齐性检验,得P=0.028<0.05,表明方差不齐,因此选择t检验的结果,使用方差不齐时的计算结果。
(2)结果:为比较玉米24号、金皇后两个品种果穗长度的差异,分别随机选定10株进行测定,结果见表1。
表1 玉米24号与金皇后玉米果穗长度的差异性比较(X±SD)品种样品数/株果穗长度/cm 变异系数/% P值(双侧)24号玉米10 20±1.25 6.241.00金皇后玉米10 20±3.40 17.00(3)分析与结论:从表1可以看出,果穗的长度,玉米24号为20±1.25cm,C·V 是6.00%,金皇后为20±3.40cm,C·V为17.00%,虽然两个品种玉米的果穗长度平均值一样,但是,与玉米24号比较,金皇后玉米的标准差、变异系数都较大,表明金皇后玉米果穗长度的变异程度大。
北语2024春季《统计分析SPSS应用》作业满分答案

北语2024春季《统计分析SPSS应用》作业满分答案问题一: 描述统计分析1. 计算每个变量的均值、中位数、标准差和极差。
- 变量1:均值为X1_mean,中位数为X1_median,标准差为X1_std,极差为X1_range。
- 变量2:均值为X2_mean,中位数为X2_median,标准差为X2_std,极差为X2_range。
- 变量3:均值为X3_mean,中位数为X3_median,标准差为X3_std,极差为X3_range。
2. 绘制每个变量的直方图和盒图。
- 变量1的直方图和盒图见附件1。
- 变量2的直方图和盒图见附件2。
- 变量3的直方图和盒图见附件3。
3. 计算变量之间的相关系数矩阵。
- 相关系数矩阵为:| | 变量1 | 变量2 | 变量3 |问题二: 参数估计1. 使用线性回归模型对变量1和变量2进行拟合。
- 回归方程为:Y = 0.5X1 + 0.3X2 + 0.12. 使用二元Logistic回归模型对变量1和变量3进行拟合。
- 回归方程为:P = 1 / (1 + exp(-0.8X1 + 0.6X3))问题三: 假设检验1. 对比变量1的均值与总体均值是否有显著差异。
- 假设检验结果为:显著差异(p < 0.05)。
2. 对比变量2和变量3的均值是否有显著差异。
- 假设检验结果为:无显著差异(p > 0.05)。
问题四: 方差分析1. 对比不同组别之间的均值是否有显著差异。
- 方差分析结果为:组别间有显著差异(p < 0.05)。
问题五: 交叉分析1. 统计不同性别下不同年龄段的人数分布。
- 交叉分析结果见附件4。
以上为作业满分答案,如有任何问题,请及时与我联系。
2017SPSS课后作业附答案
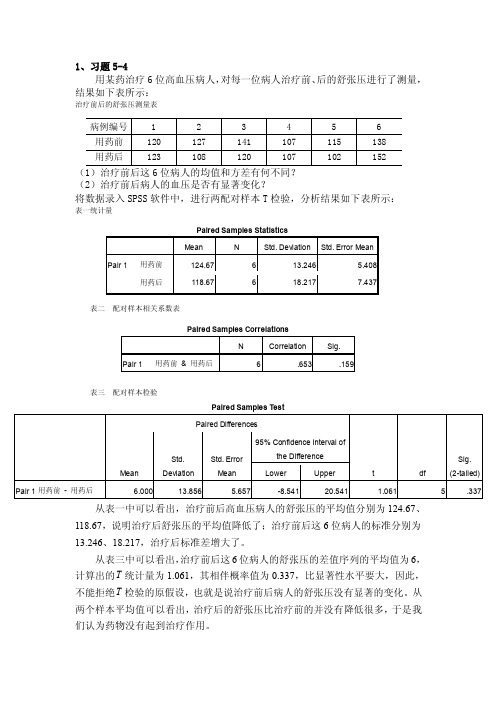
1、习题5-4用某药治疗6位高血压病人,对每一位病人治疗前、后的舒张压进行了测量,结果如下表所示:治疗前后的舒张压测量表(2)治疗前后病人的血压是否有显著变化?将数据录入SPSS软件中,进行两配对样本T检验,分析结果如下表所示:表一统计量表二配对样本相关系数表从表一中可以看出,治疗前后高血压病人的舒张压的平均值分别为124.67、118.67,说明治疗后舒张压的平均值降低了;治疗前后这6位病人的标准分别为13.246、18.217,治疗后标准差增大了。
从表三中可以看出,治疗前后这6位病人的舒张压的差值序列的平均值为6,计算出的T统计量为1.061,其相伴概率值为0.337,比显著性水平要大,因此,不能拒绝T检验的原假设,也就是说治疗前后病人的舒张压没有显著的变化。
从两个样本平均值可以看出,治疗后的舒张压比治疗前的并没有降低很多,于是我们认为药物没有起到治疗作用。
某学校要对两位老师的教学质量进行评价,这两位老师分别教甲班和乙班,这两班数学课成绩如下表所示,这两个班的成绩是否存在差异?甲、乙两班数学考试成绩将数据录入SPSS 软件中,进行两独立样本T 检验,得到分析结果如下表所示:表一 统计量从表一中可以看出两个班数学成绩的平均值分别为83.60和75.45,对应的标准差分别为6.7、9.179,很明显甲班的数学平均成绩高于乙班。
从表二中可以得知,F 统计量的值为1.11,对应的相伴概率值为0.299,大于显著性水平0.05,不能拒绝方差相等的假设,可以认为两个老师所带的班级学生的数学成绩的方差没有显著性差异;然后观察在方差相等的条件下T 检验的结果,T 统计量的相伴概率值为0.003,小于显著性水平0.05,因此拒绝T 检验的原假设,即甲乙两班学生的数学成绩存在显著差异,从两个班数学成绩的平均值可以看出,甲班的成绩高于乙班。
甲班 90 93 82 88 85 80 87 85 74 90 88 83 82 85 73 86 77 94 68 82 乙班 76 75 73 75 98 62 90 75 83 66 65 78 80 68 87 74 64 68 72 80某职业病研究所对29名矿工中肺矽病患者、可疑患者和非患者进行了用力肺活量测定,如表6-4所示,问3组矿工的用力肺活量有无差别?用力肺活量测定数据(单位:L)肺矽病患者 1.8 1.4 1.3 1.5 1.9 1.6 1.6 1.7 2 2.1可疑患者 2.1 2.3 2.6 2.1 2.5 2.1 2.4 2.4 2.1非患者 2.8 2.9 3.2 3 3.4 3.5 3.4 2.9 3.2 3.3将数据录入SPSS软件中,进行单因素方差分析,得到分析结果如下表所示:表一方差齐性检验由上表可以看出,p值大于显著性水平0.05,因此无法拒绝方差齐性的原假设,即各个组总体方差是相等的,根据方差检验的前提条件要求,这组数据是适合进行单因素方差分析的。
spss习题及其答案

spss习题及其答案SPSS习题及其答案SPSS(Statistical Package for the Social Sciences)是一种广泛应用于社会科学研究领域的统计分析软件。
它提供了强大的数据处理和统计分析功能,使得研究人员能够更加准确地分析和解释数据。
在学习和使用SPSS的过程中,习题是一种非常有效的练习方式,能够帮助我们巩固所学知识并提高数据分析的能力。
下面将介绍几个常见的SPSS习题及其答案。
习题一:描述性统计分析某研究人员对一组学生的成绩进行了调查,并得到了以下数据:70、85、90、65、78、92、80、75、88、82。
请使用SPSS计算出这组数据的均值、标准差、最大值和最小值。
答案:打开SPSS软件,依次点击“数据”-“数据编辑器”,在变量视图中创建一个名为“成绩”的变量。
在数据视图中输入上述数据,然后点击“分析”-“描述性统计”-“描述性统计”。
将“成绩”变量移动到“变量”框中,点击“统计”按钮,在弹出的对话框中勾选“均值”、“标准差”、“最大值”和“最小值”,最后点击“确定”按钮。
SPSS将会输出这组数据的均值为80.7,标准差为8.77,最大值为92,最小值为65。
习题二:相关性分析某研究人员想要了解两个变量之间的相关性,他收集了一组学生的数学成绩和语文成绩数据。
请使用SPSS计算出这两个变量之间的相关系数。
答案:打开SPSS软件,依次点击“数据”-“数据编辑器”,在变量视图中创建两个变量分别为“数学成绩”和“语文成绩”。
在数据视图中输入相应的数据,然后点击“分析”-“相关”-“双变量”。
将“数学成绩”和“语文成绩”变量分别移动到“变量”框中,点击“确定”按钮。
SPSS将会输出这两个变量之间的相关系数,以及相关系数的显著性水平。
习题三:t检验某研究人员想要了解男性和女性在数学成绩上是否存在显著差异。
他收集了一组男性学生和一组女性学生的数学成绩数据。
请使用SPSS进行独立样本t检验。
SPSS实验1-描述分析

SPSS作业1:频数分析(一)大学生消费支出情况调查为研究某高校学生平均每月消费支出情况,现收集到的一些数据,进行描述性分析。
频数分析的基本操作:(1)选择菜单Analyz e-Descriptive Statistics-Frequencies;(2)选择变量“户口”“职业”到Variable框中;(3)单击“Charts”,分别选择Bar Chart、Pie Chart,结果如下:FrequenciesFrequency TableBar ChartPie Chart分析:本次调查的学生人数共120人,其中,城镇人口72人,占总人数的60%。
农村人口48人,占总人数的40%。
城镇户籍的学生明显多于农村户籍的学生,其父母职业大致分为:1国家机关 2企业单位 3个体户 4一般农户 5其他,在这里,职业为企业单位人员,个体户,一般农户的比例不相上下,占了绝大部分。
学生月消费支出金额的分析:基本操作:(1)将消费支出分组:1、500元以下 2、501-1000元 3、1001-1500元 4、1501-2000元 5、2001元以上;(2)选择菜单Analyz e-Descriptive Statistics-Frequencies-变量“xf”-直方图,结果如下:Frequencies分析:从上面表格可以看出,有一半的学生(55.8%)的月消费支出在500-1000元内,有近四分之一(22.5%)的学生月消费支出是在1000-1500元内,其次是消费在500元以下的学生人数占12.5%,消费在1500-2000元的学生人数占5%,最少的是消费在2000元以上的学生人数。
直方图表明学生的月消费支出金额大致呈正态分布,即月消费支出在500-1000元的学生占较大比例,也有少部分消费金额偏低的学生,以及有极少数消费支出较高的学生。
计算基本描述统计量的基本操作:(1)先对数据进行拆分:选择菜单Dat e-Split File-Compare Group—选择变量“性别”-OK;(2)选择菜单Analyz e-Descriptive Statistics-Descriptives—变量“每月消费支出”(3)在Option框中,选择所需计算的基本描述统计量,结果如下:Descriptives分析:男生的平均月消费支出(1084.38元)高于女生(834.82元)。
北语2024春《SPSS统计分析实践》满分作业答案

北语2024春《SPSS统计分析实践》满分
作业答案
一、问题描述:
作业要求对一份调查问卷数据进行统计分析,包括描述统计、
相关分析和回归分析。
数据集包含了以下变量:性别、年龄、收入、教育水平、购物偏好、购买力、满意度等。
二、数据预处理:
1. 查看数据集的整体情况,包括数据类型、缺失值等。
2. 处理缺失值,可以选择删除含有缺失值的样本或使用插值法
进行填充。
三、描述统计分析:
1. 性别比例统计:计算男女比例并绘制饼图。
2. 年龄分布统计:计算年龄的平均值、标准差,并绘制年龄分
布直方图。
3. 收入水平统计:计算收入的最大值、最小值、中位数和四分
位数。
4. 教育水平统计:计算各教育水平的人数比例,并绘制教育水平柱状图。
四、相关分析:
1. 计算各变量之间的相关系数矩阵。
2. 绘制变量之间的散点图,并观察相关关系。
五、回归分析:
1. 选择一个自变量和一个因变量进行回归分析。
2. 计算回归方程的斜率、截距和决定系数。
3. 绘制回归线和残差图,并观察拟合情况。
六、结论:
根据以上统计分析结果,可以得出一些结论和建议,如性别比例接近1:1,年龄主要分布在30-40岁之间,收入水平较为分散,教育水平以本科为主等。
以上是《SPSS统计分析实践》满分作业的答案,希望能对你有所帮助。
spss统计学第一次实验作业答案
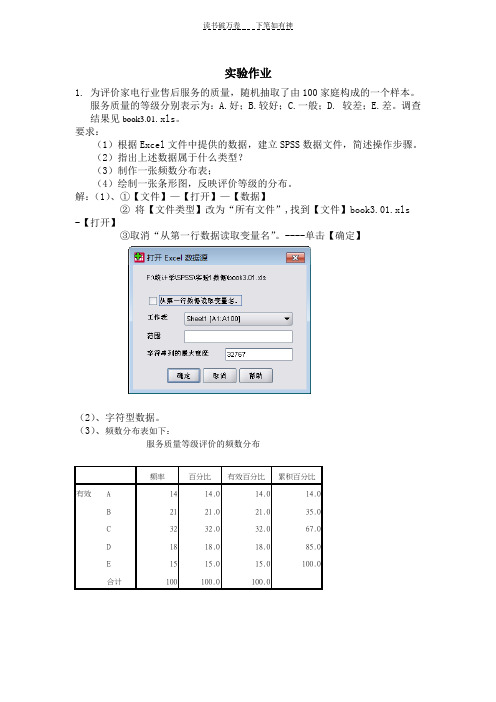
实验作业1.为评价家电行业售后服务的质量,随机抽取了由100家庭构成的一个样本。
服务质量的等级分别表示为:A.好;B.较好;C.一般;D. 较差;E.差。
调查结果见book3.01.xls。
要求:(1)根据Excel文件中提供的数据,建立SPSS数据文件,简述操作步骤。
(2)指出上述数据属于什么类型?(3)制作一张频数分布表;(4)绘制一张条形图,反映评价等级的分布。
解:(1)、①【文件】—【打开】—【数据】②将【文件类型】改为“所有文件”,找到【文件】book3.01.xls -【打开】③取消“从第一行数据读取变量名”。
----单击【确定】(2)、字符型数据。
(4)、见数据实验2.某行业管理局所属40个企业20XX年的产品销售收入数据(单位:万元)见book3.02.xls。
要求:(1)根据Excel文件中提供的数据,建立SPSS数据文件。
(2)根据上面的数据进行适当的分组,编制频数分布表,并计算出累积频数和累积频率;(3)如果按规定:销售收入在125万元以上为先进企业,115~125万元为良好企业,105~115万元为一般企业,105万元以下为落后企业,按先进企业、良好企业、一般企业、落后企业进行分组。
解:(1)、见文件夹book3.02.sav(2)、理论分组数目:K= 1+ln(40)/ln(2)=6.32≈6组距=(最大值-最小值)/组数=(152-87)/6≈10.83≈11(3)按题目要求分组并进行统计,得到分组表如下:某管理局下属40个企分组表按销售收入分组(万元)企业数(个)频率(%)先进企业良好企业一般企业落后企业11119927.527.522.522.5合计40 100.03.为了确定灯泡的使用寿命(小时),在一批灯泡中随机抽取100只进行测试,所得结果见book3.04.xls。
(1)根据Excel文件中提供的数据,建立SPSS数据文件。
(2)利用计算机对上面的数据进行排序;(3)以组距为10进行等距分组,整理成频数分布表,并绘制直方图。
spss练习题及答案

spss练习题及答案SPSS(Statistical Package for the Social Sciences)是一种统计分析软件,被广泛应用于社会科学研究和数据分析领域。
本文将提供一些SPSS练习题和对应的答案,以帮助读者提升SPSS使用和数据分析能力。
题目1:数据导入与基本操作问题描述:使用SPSS软件,将一组身高数据导入并进行基本操作。
解答:1. 打开SPSS软件并创建一个新的数据文件。
2. 在数据编辑栏中创建一个名为"Height"的变量,并设置其数据类型为数值型。
3. 逐行输入以下身高数据:165、170、180、155、168、175、185、162。
4. 在数据编辑栏中创建一个名为"Gender"的变量,并设置其数据类型为标签型(男性、女性)。
5. 逐行输入以下性别数据:男性、女性、女性、男性、男性、女性、男性、女性。
6. 完成数据输入后,保存文件并命名为"Height_Data.sav"。
题目2:数据清理与缺失值处理问题描述:使用SPSS软件,清理一组包含缺失值的数据并进行处理。
解答:1. 打开SPSS软件,并导入包含缺失值的数据文件。
2. 在数据编辑栏中,检查数据是否存在缺失值,采用统计分析方法得到具体的缺失值情况。
3. 处理缺失值的方法之一是删除带有缺失值的行。
在数据编辑栏中选择"数据",然后点击"选择特定行",在弹出窗口中选择"删除缺少变量值",点击确定。
4. 另一种处理缺失值的方法是用合适的数据填充缺失位置。
在数据编辑栏中选择"数据",然后点击"选择特定行",在弹出窗口中选择"选中缺少变量值的行",点击确定。
然后选择"数据",再点击"修改变量",选择合适的填充方法(如平均值、中位数等),点击确定。
SPSS练习题及解答

实习一SPSS基本操作第2题-----会做:请把下面的频数表资料录入到SPSS数据库中,并划出直方图,同时计算均数和标准差。
身高组段频数110~ 1112~ 3114~ 9116~ 9118~ 15120~ 18122~ 21124~ 14126~ 10128~ 4130~ 3132~ 2134~136 1解答:1、输入中位数(小数位0):111,113,115,117,....135;和频数1,3,. (1)2、对频数进行加权:DA TA━Weigh Cases━Weigh Cases by━频数━OK3、Analyze━Descriptive Statistics━Frequences━将组中值加入Variable框━点击Statistics按钮━选中Mean和Std.devision━Continue━点击Charts按钮━选中HIstograms━Continue━OK第3题—会做:某医生收集了81例30-49岁健康男子血清中的总胆固醇值(mg/dL)测定结果如下,试编制频数分布表,并计算这81名男性血清胆固醇含量的样本均数。
219.7 184.0 130.0 237.0 152.5 137.4 163.2 166.3 181.7176.0 168.8 208.0 243.1 201.0 278.8 214.0 131.7 201.0199.9 222.6 184.9 197.8 200.6 197.0 181.4 183.1 135.2169.0 188.6 241.2 205.5 133.6 178.8 139.4 131.6 171.0155.7 225.7 137.9 129.2 157.5 188.1 204.8 191.7 109.7199.1 196.7 226.3 185.0 206.2 163.8 166.9 184.0 245.6188.5 214.3 97.5 175.7 129.3 188.0 160.9 225.7 199.2174.6 168.9 166.3 176.7 220.7 252.9 183.6 177.9 160.8117.9 159.2 251.4 181.1 164.0 153.4 246.4 196.6 155.4解答:1、输入数据:单列,81行。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
SPSS操作实验 (作业1)
作为华夏儿女都曾为有着五千年的文化历史而骄傲过,作为时代青年都曾为中国所饱受的欺压而愤慨过,因为我们多是炎黄子孙。
然而,当代大学生对华夏文明究竟知道多少呢
某研究机构对大学电气、管理、电信、外语、人文几个学院的同学进行了调查,各个学院发放问卷数参照各个学院的人数比例,总共发放问卷250余份,回收有效问卷228份。
调查问卷设置了调查大学生对传统文化了解程度的题目,如“佛教的来源是什么”、“儒家的思想核心是什么”、“《清明上河图》的作者是谁”等。
调查问卷给出了每位调查者对传统文化了解程度的总得分,同时也列出了被调查者的性别、专业、年级等数据信息。
请利用这些资料,分析以下问题。
问题一:分析大学生对中国传统文化的了解程度得分,并按了解程度对得分进行合理的分类。
问题二:研究获得文化来源对大学生了解传统文化的程度是否存在影响。
要求:
直接导出查看器文件为.doc后打印(导出后不得修改)
对分析结果进行说明,另附(手写、打印均可)。
于作业布置后,1周内上交
本次作业计入期末成绩
答案
问题一
操作过程
1.打开数据文件作业。
同时单击数据浏览窗口的【变量视图】按钮,检查各个
变量的数据结构定义是否合理,是否需要修改调整。
2.选择菜单栏中的【分析】→【描述统计】→【频率】命令,弹出【频率】对
话框。
在此对话框左侧的候选变量列表框中选择“X9”变量,将其添加至【变量】列表框中,表示它是进行频数分析的变量。
3.单击【统计量】按钮,在弹出的对话框的【割点相等组】文本框中键入数字
“5”,输出第20%、40%、60%和80%百分位数,即将数据按照题目要求分为等间隔的五类。
接着,勾选【标准差】、【均值】等选项,表示输出了解程度得分的描述性统计量。
再单击【继续】按钮,返回【频率】对话框。
4.单击【图表】按钮,勾选【直方图】和【显示正态曲线】复选框,即直方图
中附带正态曲线。
再单击【继续】按钮,返回【频率】对话框。
最后,单击【确定】按钮,操作完成。
5.在得到第20%、40%、60%和80%百分位数后,接着以它们为断点对得分数
据进行分类,因此可以利用SPSS中的【编码】功能来实现。
打开SPSS软件,在菜单栏中选择【文件】→【转换】→【重新编码为不同变量】命令,弹出【重新编码为不同变量】对话框。
6.在左侧的候选变量列表框中选择“X9”变量进入【输入变量->输出变量】列
表框,同时在【输出变量】复选框中填写输出赋值变量名称“等级”。
同时单击【更改】按钮进行赋值转换。
单击【旧值和新值】按钮,弹出重编码规则设置对话框。
接着按照等级转换赋值规则进行变量的重新赋值工作。
设置完成后,单击【继续】按钮返回主对话框最后,单击【确定】按钮,操作完成。
此时,原数据文件新增加了“天数”变量。
问题二
对于问题二,大学生获取传统文化来源主要是从学校、家庭或自学等。
因此本问题主要要分析不同学习途径对大学生传统文化了解程度是否存在显著性影响。
由于文化来源途径和了解程度等级都是定性数据,因此可以考虑采用列联表分析中的行、列变量相关程度检验。
1.选择菜单栏中的【分析】→【描述统计】→【交叉表】命令,弹出【交叉表】
对话框。
2.单击【统计量】按钮,在弹出的对话框的【交叉表:统计量】中,勾选卡方,
这是利用卡方检验来检验学习途径和了解程度得分等级两者之间的独立性。
再单击【继续】按钮,返回【交叉表】对话框,单击【确定】按钮完成操作。
结果分析
问题一
(1)描述性统计量表
下表是被调查者对中国传统文化了解程度得分的描述性统计量
输出表,其中包括了均值、中位数、方差等基本统计量。
可以看到,大学生对传统中国文化了解程度得分均值等于分,标准差为,偏度为,峰度为等。
(2)直方图
SPSS输出结果也包括直方图。
从图形特征看,数据呈稍微左偏分布。
根据附带的正态分布曲线可见了解程度得分近似服从正态分布N,,说明大学生对中国传统文化的了解程度差异较大。
问题二
(1)来源途径与了解程度等级的列联表
下表是来源途径与了解程度等级的列联表,表中数据列出了处于不同了解程度等级及来源途径的学生人数。
可以看到,以“学校教育”为主要来源途径的学生大多数对传统中国文化了解程度位于“很不了解”和“不太了解”的等级,而采用“自学”方式来获取传统文化的学生对其了解程度都比较高,多数学生都“比较了解”或“很了解”传统文化。
要来源家庭教育910109947
自学111510242484合计4549434843228
(2)独立性检验
上面的列联表只是从数值大小的角度说明了不同来源途径的学生对
传统中国文化了解程度差异很大,但究竟这种级别有无显著性差异,
还是要借助于卡方检验。
下表是“来源途径”对“了解程度等级”有
无显著性影响的卡方检验结果。
卡方检验的零假设是不同来源途径对
传统文化了解程度没有显著性差异。
系统默认显著性水平为,由于卡
方检验概率P值都小于,则拒绝零假设,认为来源途径对学生了解中
国传统文化程度有显著性差异。
这表示应努力激发学生对传统文化的
兴趣,只有建立在兴趣爱好的基础上,学生即使花费自己的工作学习
时间,也会自学中国传统文化,提高自身的文化修养水平。
卡方检验
值df 渐进 Sig. (双
侧)
Pearson 卡方8.011似然比8.009线性和线性组合1.000有效案例中的 N228
a. 0 单元格(.0%) 的期望计数少于 5。
最小期望计数为。
