8.3interval estimation
社会统计分析与数据处理技术(Stata)8 参数估计

• 由样本均值的抽样分布可知,在重复抽样或无限抽样的情况
下,样本均值的数学期望等于总体均值: E(x)
• 样本均值的抽样标准误差为:
x n
• 于是,样本的抽样分布即为:
x ~ N,
n
• 由此可知,样本均值落在总体均值的两侧各为一个抽样标准 差范围内的概率为0.6827,两个标准差范围内的概率为 0.9544,三个标准差范围内的概率为0.9973
• 区间的最小值称为置信下限,最大值称为置信上限
• 比如,若一个样本为正态分布,方差已知(或为非正态分布,但样 本量够大),则其均值的置信下限和上限分别为:
点估计
x z /2
n
x z /2 n
边际误差
• 由此可知,置信区间(包括均值和比例)由两部分组成:点估计和 描述估计量精度的±值(即边际误差:marginal error,或估计误 差或误差范围)
的置信区间和很大的置信度。但鱼与熊掌不可兼得
– 若固定置信度(如 95%) ,则样本量越大,置信区间越小 – 若固定置信区间的宽度,则样本量越大,置信度就越大 – 可以从需要的置信区间的宽度和置信度求出需要多大的样本量
• 当然,要指明的是,在固定置信度时,置信区间宽度的减 少并不是和样本量 n 成反比,而是和 n 成反比:当样本 量增加一倍(即 2n )时,置信区间的宽度为原先的 1 2
• 根据样本统计量确定总体参数的一个数值(均值、 标准差、比例等) 。常用点估计有:
x
样本均值 总体均值
s2 2
样本方差 总体方差
p
样本比例 总体比例
• 比如,若根据随即抽样的样本计算出来的公司职 员的月工资收入为1万元,则用1万元作为全公 司职员月平均收入的一个估计值
商务与经济统计

Unit 2 第二单元 Estimation:Population Mean, Proportion and Variance总体均值,总体比例和总体方差的参数
估计----学时4
8.1 Interval Estimationof a Population Mean:Large-Sample Case总体均值的区间估计:大样本--2学时练习8.1 8.2 Interval Estimationof a Population Mean:Small-Sample Case总体均值的区间估计:小样本练习8.2 8.3 Determining the Sample Size样本数量的确定---2学时练习8.3 8.4 Interval Estimationof a Population Proportion总体比例的 区间估计练习8.4
Unit 4 第四单元 Analysis of Variance 方差分析---学时4
10.4 Introduction to Analysis of Variance 方差分析介绍----2学时 10.5 Analysis of Variance: Testing for the Equality of k Population Means---2学时 方差分析:k个总体均值相等的检验 练习10.4-10.5
Descriptive Statitics 1---Tabular and Graphical Methods 描述性统计学1 —表格和图形方法----3学时 2.1 Summarizing Qualitative Data定性数据汇 总 2.2 Summarizing Quantitative Data定量数据 汇总 2.4 Crosstablations列联表 and Scatter Diagrams散点图
Confidence-Interval-Estimation

A point estimate (点估计) is a single value (statistic) used to estimate a population value (parameter).
Mean
Standard deviation Proportion
➢ the population standard deviation is unknown ➢ the underlying population is approximately normal, ➢ the sample size is less than 30 we use the t distribution.
The t-distribution has mean 0 and (n – 1) degrees of Freedom(自由度). n is sample size
Example: Suppose a person weighs himself on a regular basis and finds his weight to be 174 173 174 174 173 174 176 174 177 171 174 173 173 175 175 172 178 173 174 176 176 171 176 175 179 Construct a 95% confidence interval estimate for weighs. (Use R)
➢ A confidence interval is a range of values within which the population parameter is expected to occur at a specified probability.
计量经济学第二版课后习题答案
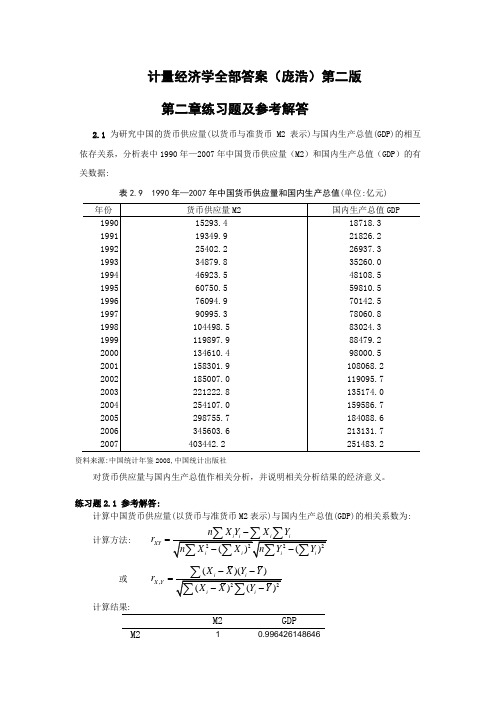
计量经济学全部答案(庞浩)第二版 第二章练习题及参考解答2.1 为研究中国的货币供应量(以货币与准货币M2表示)与国内生产总值(GDP)的相互依存关系,分析表中1990年—2007年中国货币供应量(M2)和国内生产总值(GDP )的有关数据:表2.9 1990年—2007年中国货币供应量和国内生产总值(单位:亿元)资料来源:中国统计年鉴2008,中国统计出版社对货币供应量与国内生产总值作相关分析,并说明相关分析结果的经济意义。
练习题2.1 参考解答:计算中国货币供应量(以货币与准货币M2表示)与国内生产总值(GDP)的相关系数为:计算方法: XY n X Y X Y r -=或 ,()()X Y X X Y Y r --=计算结果:M2GDPM210.996426148646GDP 0.996426148646 1经济意义: 这说明中国货币供应量与国内生产总值(GDP)的线性相关系数为0.996426,线性相关程度相当高。
2.2 为研究美国软饮料公司的广告费用X与销售数量Y的关系,分析七种主要品牌软饮料公司的有关数据表2.10 美国软饮料公司广告费用与销售数量资料来源:(美) Anderson D R等. 商务与经济统计.机械工业出版社.1998. 405绘制美国软饮料公司广告费用与销售数量的相关图, 并计算相关系数,分析其相关程度。
能否在此基础上建立回归模型作回归分析?练习题2.2参考解答美国软饮料公司的广告费用X与销售数量Y的散点图为说明美国软饮料公司的广告费用X与销售数量Y正线性相关。
若以销售数量Y 为被解释变量,以广告费用X 为解释变量,可建立线性回归模型 i i i u X Y ++=21ββ 利用EViews 估计其参数结果为经t 检验表明, 广告费用X 对美国软饮料公司的销售数量Y 确有显著影响。
回归结果表明,广告费用X 每增加1百万美元, 平均说来软饮料公司的销售数量将增加14.40359(百万箱)。
商业应用统计(英文版)ch08

2
Estimating the Population Mean
A point estimate is a statistic taken from a sample that is used to estimate a population parameter. Interval estimate - a range of values within which the analyst can declare, with some confidence, the population lies.
Copyright 2011 John Wiley & Sons, Inc.
7
Distribution of Sample Means for 95% Confidence
.025 95% .4750 .4750
.025
X Z
-1.96
0
1.96
Copyright 2011 John Wiley & Sons, Inc.
Interval Estimate
xz or xz
s
n
s
n n z the number of std. dev. associatedwit h certainconfidence
xz
s
s thestd. dev. of thepopulation
n thesamplesize
15
Estimating the Mean of a Normal Population: Sample Size is Small
The distribution of sample means is approximately normal if the population has a normal distribution. The z formulas can be use to estimate a population mean if the value of the population Standard Deviation is known.
Principal Component Analysis[I.T. Jolliffe]
![Principal Component Analysis[I.T. Jolliffe]](https://img.taocdn.com/s3/m/83b9d4781711cc7931b716b5.png)
Principal Components in Regression Analysis 167 8.1 Principal Component Regression 168 8.2 Selecting Components in Principal Component Regression 173 8.3 Connections Between PC Regression and Other Methods 177 8.4 Variations on Principal Component Regression 179 8.5 Variable Selection in Regression Using Principal Components 185 8.6 Functional and Structural Relationships 188 8.7 Examples of Principal Components in Regression . . . . 190 8.7.1 Pitprop Data 190 8.7.2 Household Formation Data 195 Principal Components Used with Other Multivariate Techniques 199 9.1 Discriminant Analysis 200 9.2 Cluster Analysis 210 9.2.1 Examples 214 9.2.2 Projection Pursuit 219 9.2.3 Mixture Models 221 9.3 Canonical Correlation Analysis and Related Techniques . 222 9.3.1 Canonical Correlation Analysis 222 9.3.2 Example of CCA 224 9.3.3 Maximum Covariance Analysis (SVD Analysis), Redundancy Analysis and Principal Predictors . . 225 9.3.4 Other Techniques for Relating Two Sets of Variables 228
第四章 参数的区间估计(Confidence Interval Estimation)

Chap 4-34
PHStat用于解决此类问题
PHStat | confidence intervals | estimate for the population total Excel spreadsheet for the voucher example
第四章 参数的区间估计 (Confidence Interval Estimation)
阅读教材:第7章
Chap 4-1
本章概要
估计的步骤(Estimation process) 点估计(Point estimates) 区间估计(Interval estimates) 均值的置信区间( 已知) 样本容量的确定(Determining sample size) 均值的置信区间 ( 未知) 比例的置信区间
n
) 1
Chap 4-9
区间估计的要素
置信度
区间内包含未知总体参数的确定程度 与未知参数的接近程度 获得容量为 n 的样本所需付出的代价
精度
成本
Chap 4-10
置信度
以 100 1 %表示,如:90%,95%,99% 相对频率意义上的解释
从长期来看, 所构建的所有置信区间中,100 1 % 的置信区间都将含有未知参数,即未知参数落入区间的 概率;
n
( z 2 ) (1 )
2
E2
其中: E z 2
(1 )
n
2. 3.
E的取值一般小于0.1 (=p) 未知时,可取最大值0.5
商务与经济统计 第14版 Ch08 Interval Estimation

Statistics for Business and Economics (14e, Metric Version)
• We say that this interval has been established at the 90% confidence level. • The value 0.90 is referred to as the confidence coefficient.
• In order to develop an interval estimate of a population mean, the margin of error must be computed using either:
4
Statistics for Business and Economics (14e, Metric Version)
3
Statistics for Business and Economics (14e, Metric Version)
Interval Estimate of a Population Mean: σ Known (1 of 4)
• The general form of an interval estimate of a population mean is
2
Statistics for Business and Economics (14e, Metric Version)
Margin of Error and the Interval Estimate
• A point estimator cannot be expected to provide the exact value of the population parameter.
用stata处理面板数据(中文版)_stata关于面板数据说明

Chp8 Panel Data一直想把看Panel模型时的感悟整理成笔记,但终因懒惰而未能成行。
今天终于下决心开了个头,可遗憾的是,这个开头却是从本章的结尾写起,因为这一部分最容易写。
不过,凡事有了好的开头基本上也算成功一半了,所以后面的整理工作还要有劳各位的督促。
文中的不足还望不吝指出。
8.1简介8.2一般模型8.2.1固定效应模型(Fixed Effect Model)8.2.2随机效应模型(Random Effect Model)8.3自相关性8.4动态Panel Data8.5门槛Panel Data8.6非稳定Panel Data及协整8.7Panel V AR8.8Stata8.0实现在介绍了Panel Data的基本理论后,下面我们介绍如何使用STATA8.0软件包来实现模型的估计。
前面我们已经提到,Panel Data具有如下数据存储格式:company year invest mvalue11951755.94833.011952891.24924.9119531304.46241.7119541486.75593.621951588.22289.521952645.52159.421953641.02031.321954459.32115.531951135.21819.431952157.32079.731953179.52371.631954189.62759.9其中,变量company和year分别为截面变量和时间变量。
显然,通过这两个变量我们可以非常清楚地确定panel data的数据存储格式。
因此,在使用STATA8.0估计模型之前,我们必须告诉它截面变量和时间变量分别是什么,所用的命令为tsset1,命令格式如下:tsset panelvar timevar这里需要指出的是,由于Panel Data本身兼具截面数据和时间序列二者的特性,所以对时间序列进行操作的运算同样可以应用到Panel Data身上。
统计推断过程中的不确定性量化方法

统计推断过程中的不确定性量化方法随着数据分析和统计学的发展,统计推断已成为一种重要的方法,用于从有限的样本数据中进行推断和预测。
然而,在统计推断的过程中,由于数据的随机性和无法避免的误差,不确定性是一个不可忽视的因素。
为了准确评估结果的可靠性和不确定性,需要采用一些量化方法,本文将介绍几种常用的不确定性量化方法。
一、置信区间(Confidence Interval)置信区间是一种常见的不确定性量化方法,用于估计参数的范围。
在统计推断中,我们通常希望通过从样本中得到的估计值,来推断总体参数的真实值。
然而,由于样本的局限性,我们无法得到准确的参数值。
置信区间的概念就是通过对样本数据进行分析,得到一个区间估计,该区间内包含真实参数值的概率为给定的置信水平。
常见的置信水平包括95%和99%。
二、假设检验(Hypothesis Testing)假设检验是判断样本观测结果是否支持“零假设”的方法,其中“零假设”通常表示两组数据没有显著差异或没有关联。
在假设检验中,我们首先提出一个“零假设”,然后通过样本数据进行推断,以确定是否拒绝“零假设”。
在这个过程中,我们使用统计量来度量样本数据与“零假设”之间的差异,从而确定结果的可靠性和不确定性。
三、蒙特卡洛模拟(Monte Carlo Simulation)蒙特卡洛模拟是一种基于随机抽样的统计方法,用于模拟复杂系统的不确定性。
在统计推断中,我们经常面临着多个变量同时变化的情况,传统的方法很难准确地评估结果的不确定性。
蒙特卡洛模拟通过生成大量的随机数样本,并在每个样本上进行统计推断,从而得到结果的分布情况。
通过分析结果分布,我们可以估计结果的不确定性。
四、贝叶斯统计(Bayesian Statistics)贝叶斯统计是一种统计学派别,提供了一种基于主观概率的不确定性量化方法。
贝叶斯统计通过引入先验概率和后验概率,对样本数据和参数的不确定性进行建模和推断。
与传统的频率主义统计不同,贝叶斯统计将不确定性视为一种可测量的数值,并提供了一种基于贝叶斯公式的计算方法,用于更新概率分布。
FRM-中文NOTES(1)

前言FRM是全球金融风险管理领域的资格证书,由美国“全球风险协会”(GARP)设立。
GARP 是一个拥有来自超过150个国家的8万多名会员的世界最大的金融协会组织之一,主要由风险管理方面的专业人员、从业者和研究者组成。
其主要职能是通过信息交换,实施教育计划,提高金融风险管理领域的标准。
FRM考试始于1997年,在中国北京、上海,香港,台北设有考点。
FRM考试虽然设立时间不长,但发展极为迅速,已经得到华尔街和其他欧美著名金融机构与大型公司风险管理部门以及政府监管层的认同,并已经初步成为风险管理领域的最权威的认证。
FRM涵盖众多领域,包括数量分析、市场风险、信用风险、操作风险、基金投资风险、会计和法律等内容。
在今日错综复杂、瞬息万变的金融市场上,风险往往难以掌握。
在金融市场困境或有危机发生时,有效管理风险往往成为企业成功的关键。
而这一攸关企业组织及其投资人命运的重要决策,需要众多的金融风险管理专业人士(Financial Risk Professionals)的参与,故FRM 日益受到重视,全球报考人数以每年超过38%成长,已俨然成为全球瞩目的国际风险管理证照。
在国内正日益受到国家金融监管机构以及各家金融机构的重视,对金融风险专业人员的需求日益壮大。
秉承“服务社会,帮助他人,成就自己”的价值观,金程教育始终以“专业来自百分百的投入”全心全意地为客户持续创造价值。
我们拥有一支自主、强大的财务金融培训研发团队,经过九年的实践和积累,已经自主开发了一系列针对CFA FRM等课程的辅导书籍,如《固定收益证券定价理论》、《投资组合管理》、《金融衍生产品》、《权益类证券定价》,这些书籍汇聚专家视角,权威新颖、紧贴时事,为各类金融进修学员提供全新的金融视野,广受各界好评,并被许多高校选为专用教材。
本书是金程教育权威师资与研究团队在金程内部浩瀚的教材、国内外权威备考辅导资料、各类题目组成的资料库基础上,根据考试大纲指定内容编制的中文辅导教材,全面涵盖考试内容,可以让学员迅速掌握考试内容的知识要点,便于其后的英文教材的学习领悟和掌握,具有极高的参考价值。
参数估计方法

第八章参数估计方法研究工作的目的在于了解总体特征的有关信息,因而用样本统计数估计相应总体参数,并由之进行统计推断。
总体特征的各种参数,在前几章主要涉及平均数、标准差等,并只从直观上介绍其定义和公式,未就其历,即参数估计(parameter estimation)的方法作讨论。
本章将简要介绍几种常用参数估计方法,即矩法、最小二乘法、极大似然法。
第五章述及参数的点估计(point estimation)和区间估计(interval estimation),本章讨论点估计方法。
区间估计是在点估计的基础上结合统计数的抽样分布而进一步作出的推论,有关内容将散见在其它各章。
第一节农业科学中的主要参数及其估计量的评选标准一、农业科学中的主要参数农业科学研究中需要估计的参数是多种多样的,主要包括总体数量特征值参数,例如,用平均数来估计品种的产量,用平均数差数来估计施肥等处理的效应;用百分数(或比例)来估计遗传分离比例、群体基因或基因型频率、2个连锁主基因间的重组率;通过变异来源的剖分,用方差来估计环境方差、遗传方差和表型方差,在此基础上以估计性状的遗传力等遗传参数;用标准误来估计有关统计数的抽样误差,如重组率的标准误、遗传抽样误差、遗传多样性误差、频率误差等。
在揭示变数间的相互关系方面,用相关系数来描述2个变数间的线性关系;用回归系数、偏回归系数等来描述原因变数变化所引起的结果变数的平均变化的数量,用通径系数来描述成分性状对目标性状的贡献程度等。
有关数量关系和数量变化方面的内容将在第9至11章介绍。
二、参数估计量的评选标准讨论参数估计方法前需要了解数学期望(expectation)的概念和评价估计方法优劣的标准。
(一) 数学期望在抽样分布中,已经讲述了从总体中抽出所有可能样本的样本平均数的平均数等于总体平均数,这里,样本平均数的平均数就是一种数学期望。
例如,一个大豆品种的含油量为20%,测定一次可能是大于20%,再测定可能小于20%,大量反复测定后平均结果为20%,这时20%便可看作为该大豆品种含油量的数学期望,而每单独测定一次所获的值只是1个随机变量。
MATLAB函数和命令的用法

Binocdf 二项式累积分布函数语法格式Y = binocdf(X,N,P)函数功能Y = binocdf(X,N,P)计算X 中每个X(i)的二项式累积分布函数,其中,N 中对应的N(i)为试验数,P 中对应的P(i)为每次试验成功的概率。
Y, N, 和 P 的大小类型相同,可以是向量、矩阵或多维数组。
输入的标量将扩展成一个数组,使其大小类型与其它输入相一致。
The values in N must all be positive integers, the values in X must lie on the interval [0,N], and the values in P must lie on the interval [0, 1].The binomial cdf for a given value x and a given pair of parameters n and p is()(0,1,,)0(|,)()x i n i n i n y F x n p p q I x i -=⎛⎫== ⎪⎝⎭∑The result, y, is the probability of observing up to x successes in n independent trials, where the probability of success in any given trial is p . The indicator function I (0,1,...,n )(i )ensures that x only adopts values of 0,1,...,n . 示例若一个棒球队在一个赛季要比赛162场,每场比赛取胜的机会是50-50,则该队取胜超过100 场的概率为:相关函数binofit | binoinv | binopdf | binornd | binostat | cdf附:二项式分布(binomial distribution )定义二项分布的概率密度函数为(|,)(1)k n k n f k n p p p k -⎛⎫=- ⎪⎝⎭where k is the number of successes in n trials of a Bernoulli process with probability of success p .The binomial distribution is discrete, defined for integers k = 0, 1, 2, ... n , where it is nonzero.背景The binomial distribution models the total number of successes in repeated trials from an infinite population under the following conditions:Only two outcomes are possible on each of n trials.The probability of success for each trial is constant.All trials are independent of each other.The binomial distribution is a generalization of the Bernoulli distribution; it generalizes to the multinomial distribution.参数Suppose you are collecting data from a widget manufacturing process, and you record the number of widgets within specification in each batch of 100. You might be interested in the probability that an individual widget is within specification. Parameter estimation is the process of determining the parameter, p , of the binomial distribution that fits this data best in some sense.One popular criterion of goodness is to maximize the likelihood function. The likelihood has the same form as the binomial pdf above. But for the pdf, the parameters (n and p ) are known constants and the variable is x . The likelihood function reverses the roles of the variables. Here, the sample values (the x 's) are already observed. So they are the fixed constants. The variables are the unknown parameters. MLE involves calculating the value of p that give the highest likelihood given the particular set of data.The function binofit returns the MLEs and confidence intervals for the parameters of the binomial distribution. Here is an example using randomnumbers from the binomial distribution with n = 100 and p = 0.9.The MLE for parameter p is 0.8800, compared to the true value of 0.9. The 95% confidence interval for p goes from 0.7998 to 0.9364, which includes the true value. In this made-up example you know the "true value" of p. In experimentation you do not.示例The following commands generate a plot of the binomial pdf for n = 10 and p = 1/2.相关内容Discrete Distributions附:二项式分布(网上)定义若某事件概率为p,现重复试验n次,该事件发生k次的概率为:P=C(k,n)p k(1-p)(n-k)C(k,n)表示组合数,即从n个事物中拿出k个的方法数。
FLOWIZ ML 155 流量和压力管理独立转换器说明书

Warranty conditions are available on this website:www.isomag.eu only in English version A L O N E C O N V E R T E RF O R F L O WU R E M A N A G E M E N TINDEXGENERAL DESCRIPTION (3)TECHNICAL DATA (4)OVERALL FEATURES (4)STANDARD FEATURES (4)OPTIONAL FEATURES (5)ACCURACY (5)OVERALL DIMENSIONS (6)VISUALIZATION PAGES (7)PCB LAYOUT (8)POWER SUPPLY (9)ELECTRICAL CONNECTIONS (10)FUNCTION’S LIST (11)BATTERIES CONSUMPTION (14)BATTERIES LIFE (15)HOW TO ORDER (16)FLOWRATEGPRS BATTERYCONVERTER BATTERYCONVERTER BATTERYNote : Lithium batteries are subject to special transportation regulations according to “Regulation of Dangerougdocumentation is required to observe there regulations. This may influence4.3* Total flow totaliser 1 reset enable 4.4* Partial flow totaliser 1 reset enable 4.5* Total flow totaliser 2 reset enable 4.6* Partial flow totaliser 2 reset enable 4.9 Integrity check enable 4.10* Auto-switch on command4.1* Digital input 1 mode 4.2* Digital input 2 mode4.7* Total flow totaliser 3 reset enable 4.8* Partial flow totaliser 3 reset enable 2.1 Low flow zero threshold: 0-25% of full scale value 2.2 Interval time between 2 measure 2.3 Enable average mode input 12.4 Maximum period for input 12.5 Enable average mode input 22.6 Maximum period for input 22.7 Analog input for flow rate or level5.1* Output 15.6 Power supply of pressure probes5.5* Output 23.1 Maximum value alarm set for flow rate input 13.2 Minimum value alarm set for flow rate input 13.3 Maximum value alarm set for flow rate input 23.5 Maximum value alarm set for flow rate input 33.6 Minimum value alarm set for flow rate input 33.4 Minimum value alarm set for flow rate input 23.11 Maximum value alarm set for differential pressure 3.12 Minimum value alarm set for differential pressure3.13 Hysteresis threshold set for the minimum and maximum flow rate alarms3.7 Maximum value alarm set for pressure 13.8 Minimum value alarm set for pressure 13.9 Maximum value alarm set for pressure 23.10 Minimum value alarm set for pressure 21.1* Full scale 1 value (ON/OFF input)1.5 Unit of measure of temperature1.2* Full scale 2 value (ON/OFF input)1.4 Full scale value set for pressure measure 1.3* Full scale 3 value (4-20mA input)1.6* Unit of measure and number of decimal totalizer 11.7* Unit of measure and number of decimal totalizer 21.8* Unit of measure and number of decimal totalizer 31.9* Pulse value on input 11.10*Pulse value on input 21.11*Pulse value on output 11.12*Pulse value on output 21.13*Pulse duration on input 11.14*Pulse duration on input 2F U N C T I O N ’S L I S T* (Communication function group only) = see wireless specific manual supplied for more details6.1 Choice of the IF2 communication protocol6.5 Minimum antenna signal strength to send e-mail*6.6 Choice of how to send data logger*6.8 Interval of data logger sending if 6.7 is set on "PERIODIC"*6.9 Interval of sending DATA LOGGER*6.7 Choice of when send data logger*6.10 Enables send Process data*6.11 Enables send Alarm*6.19 Send EVENTS, instant command*6.17 Roaming enable*6.18 Send Data Logger , instant command*6.20 Send configuration through e-mail immediately*6.21 Clock synchronization, immediately, with a specified server via the HTTP protocol*6.23 Check INCOMING SMS, instant command*6.13 Enables check INCOMING SMS*6.22 Check INCOMING E-MAIL, instant command*6.14 Enables check INCOMING E-MAIL*6.15 Enables clock synchronization with a specified server via the HTTP protocol*6.16 Enables send EVENTS*6.2 Choice of the RS232 communication protocol6.3 Address RS232 port 6.4 RS232 port speed6.12 Minimum time to send Alarm*7.1 Choice of the language: EN= English, IT=Italian, FR= French, SP= Spanish 7.2 Time for switch off display7.3 Visualization of "Quick start menu"7.5* Total flow totalizer 1 reset from keyboard 7.6* Partial flow totalizer 1 reset from keyboard 7.4 Lock of DISPLAY in ONE SPECIFIC visualization page 7.7* Total flow totalizer 2 reset from keyboard 7.8* Partial flow totalizer 2 reset from keyboard 7.9* Total flow totalizer 3 reset from keyboard 7.10*Partial flow totalizer 3 reset from keyboard5.1* Output 1 set on DIRECT . DR. function 5.2 Frequency of output drive5.3 Interval time of output switch on 5.4 Interval time of output switch offThe function DIRECT . DR. can be assigned to all outputs8.1* Date and time set8.2 Set of Time Zone (Against GMT -12 to +12 hours)8.3* Automatic data logger enable8.5 Choice of single (off) or double (on) logging interval8.6 Interval time 1 for the data logging function8.4 Data formatted like ML250 (see ML250 manual)8.7 Interval time 2 for the data logging function8.11 Enables the logging of total totalizer 18.12 Enables the logging of partial totalizer 18.13 Enables the logging of flow rate 18.14 Enables the logging of total totalizer 28.15 Enables the logging of partial totalizer 28.16 Enables the logging of flow rate 28.17 Enables the logging of total totalizer 38.18 Enables the logging of partial totalizer 38.19 Enables the logging of flow rate/level input 38.20 Enables the logging of pressure 18.22 Enables the logging of temperature8.23 Enables the sending of measure units (technical units)8.24 Enables the sending of measure units (%)8.25 Symbol used as separator on CSV files8.9 Interval 2 start logging time8.10 Interval 2 stop logging time8.8 Interval period 2 for the data logging function8.21 Enables the logging of pressure 210.1 Level 2 access code enter10.2 Load factory data pre-set10.3 Load user data pre-set10.4 Save user data pre-set9.1* Converter auto-test9.3* Stand-by function9.4 Test of GPRS connections9.2* Flow rate simulation enabling9.5 SD card status/info9.6 Firmware revision/versionNote : all references to page number are linked to the operating manual .MAIN BOARD AND MODEM IN STANDBYINTERFACE ACTIVITIES AND STORAGE DATADISPLAY ACTIVITIESPOOR NETWORK COVERAGEB3B1/B2B3B1/B2B3B1/B2B3B1/B2B3LOW CONSUMPTION MEDIUM CONSUMPTIONHIGHCONSUMPTIONPower tool is a software which allows to evaluate the converter battery life. The estimation is done with an easy guided procedureB A T T E R I E S L I F EPower tool softwareML 155Production/stock35044 Montagnana – PDVia Piemonte , n° 2。
统计推断过程中的不确定性量化方法

统计推断过程中的不确定性量化方法统计推断是通过对样本数据进行分析和推断来得到总体特征的方法。
然而,在进行统计推断时,由于抽样误差和模型假设的不确定性等因素的存在,我们往往无法完全确定估计值的准确性。
因此,如何准确地量化统计推断中的不确定性是一个重要的问题。
为了解决这个问题,研究人员提出了各种不确定性量化方法,下面将介绍其中几种常见的方法。
一、置信区间(Confidence Interval)置信区间是最常用的不确定性量化方法之一。
它通过对样本数据进行分析,得到统计量的区间估计,从而反映了总体参数的不确定性程度。
置信区间的计算方法主要有频率主义方法和贝叶斯方法。
频率主义方法通过对样本数据进行统计分析,计算出估计量的标准误差,然后根据正态分布的性质,计算出置信区间。
置信区间一般表示为估计量±误差界限,例如,估计量为0.5,置信区间为(0.4, 0.6),表示我们有95%的置信度认为总体参数在0.4到0.6之间。
贝叶斯方法则基于贝叶斯统计理论,利用主观先验知识和样本数据,通过贝叶斯公式计算后验分布,从而得到置信区间。
与频率主义方法相比,贝叶斯方法能更好地考虑先验信息的影响,同时也能提供更加准确的不确定性量化结果。
二、蒙特卡洛模拟(Monte Carlo Simulation)蒙特卡洛模拟是一种基于随机抽样的方法,通过多次模拟实验来估计总体参数的不确定性。
在统计推断中,蒙特卡洛模拟常用于计算复杂模型的置信区间或概率分布。
蒙特卡洛模拟的基本思路是通过随机抽样得到一组样本数据,然后利用这些样本数据进行分析和推断。
通过多次模拟实验,我们可以得到总体参数的分布情况,进而量化其不确定性。
蒙特卡洛模拟可以通过随机数生成器来生成样本数据,也可以利用现有数据进行模拟。
三、引导重采样(Bootstrap Resampling)引导重采样是一种基于自助法的方法,用于估计统计量的不确定性。
自助法是一种非参数统计的方法,通过从原始样本中有放回地抽取一定数量的样本数据,构建多个自助样本,并利用这些自助样本进行统计推断。
SPSS在曲线拟合中的

8.3 SPSS在曲线拟合中的应用
8.3 SPSS在曲线拟合中的应用
Step07:其他选项输出
在图中还有三个选项可供选择,用户可根据自己的需要勾选这些选项。 ● Display ANOVA Table:结果中显示方差分析表。 ● Include constant in equation:系统默认值,曲线方程中包含常数项。 ● Plot models:系统默认值;绘制曲线拟合图。
对于逆函数方程和指数方程拟合来说,它对应的可决系数 R2 分别为 0.972 和 00,模型也显著有效;具体估计方程分别为:
虽然上述模型都有显著的统计学意义,但从可决系数的大小可以清晰看到逆函 数方程较其他两种曲线方程拟合效果更好,因此选择逆函数方程来描述空置率 和租金率的关系。
8.3 SPSS在曲线拟合中的应用
8.3 SPSS在曲线拟合中的应用
Step04:选择个案标签
从候选变量列表框中选择一个变量进入【Case Labels (个案标签)】列表 框中,它的取值将作为每条记录的标签。这表示在指定作图时,以哪个变量 作为各样本数据点的标志变量。
Step05:选择曲线拟合模型
在【Models(模型)】复选框中共有11种候选曲线模型可以选择,用户可以 选择多种候选模型进行拟合优度比较。
SPSS在曲线拟合中的应用
8.3 SPSS在曲线拟合中的应用
8.3.1 曲线拟合的基本原理
1.方法概述
实际中,变量之间的关系往往不是简单的线性关系,而呈现为某种曲线或非 线性的关系。此时,就要选择相应的曲线去反映实际变量的变动情况。为了 决定选择的曲线类型,常用的方法是根据数据资料绘制出散点图,通过图形 的变化趋势特征并结合专业知识和经验分析来确定曲线的类型,即变量之间 的函数关系。 在确定了变量间的函数关系后,需要估计函数关系中的未知参数,并对 拟合效果进行显著性检验。虽然这里选择的是曲线方程,在方程形式上是非 线性的,但可以采用变量变换的方法将这些曲线方程转化为线性方程来估计 参数。
SPSS术语中英文对照详解

【常用软件】SPSS术语中英文对照SPSS的统计分析过程均包含在Analysis菜单中。
我们只学以下两大分析过程:Descriptive Statistics(描述性统计)和Multiple Response(多选项分析)。
Descriptive Statistics(描述性统计)包含的分析功能:1.Frequencies 过程:主要用于统计指定变量各变量值的频次(Frequency)、百分比(Percent)。
2.Descriptives过程:主要用于计算指定变量的均值(Mean)、标准差(Std.Deviation)。
3.Crosstabs 过程:主要用于两个或两个以上变量的交叉分类。
Multiple Response(多选项分析)的分析功能:1.Define Set过程:该过程定义一个由多选项组成的多响应变量。
2.Frequencies过程:该过程对定义的多响应变量提供一个频数表。
3.Crosstabs过程:该过程提供所定义的多响应变量与其他变量的交叉分类表。
Absolute deviation, 绝对离差Absolute number, 绝对数Absolute residuals, 绝对残差Acceleration array, 加速度立体阵Acceleration in an arbitrary direction, 任意方向上的加速度Acceleration normal, 法向加速度Acceleration space dimension, 加速度空间的维数Acceleration tangential, 切向加速度Acceleration vector, 加速度向量Acceptable hypothesis, 可接受假设Accumulation, 累积Accuracy, 准确度Actual frequency, 实际频数Adaptive estimator, 自适应估计量Addition, 相加Addition theorem, 加法定理Additivity, 可加性Adjusted rate, 调整率Adjusted value, 校正值Admissible error, 容许误差Aggregation, 聚集性Alternative hypothesis, 备择假设Among groups, 组间Amounts, 总量Analysis of correlation, 相关分析Analysis of covariance, 协方差分析Analysis of regression, 回归分析Analysis of time series, 时间序列分析Analysis of variance, 方差分析Angular transformation, 角转换ANOVA (analysis of variance), 方差分析ANOVA Models, 方差分析模型Arcing, 弧/弧旋Arcsine transformation, 反正弦变换Area under the curve, 曲线面积AREG , 评估从一个时间点到下一个时间点回归相关时的误差ARIMA, 季节和非季节性单变量模型的极大似然估计Arithmetic grid paper, 算术格纸Arithmetic mean, 算术平均数Arrhenius relation, 艾恩尼斯关系Assessing fit, 拟合的评估Associative laws, 结合律Asymmetric distribution, 非对称分布Asymptotic bias, 渐近偏倚Asymptotic efficiency, 渐近效率Asymptotic variance, 渐近方差Attributable risk, 归因危险度Attribute data, 属性资料Attribution, 属性Autocorrelation, 自相关Autocorrelation of residuals, 残差的自相关Average, 平均数Average confidence interval length, 平均置信区间长度Average growth rate, 平均增长率Bar chart, 条形图Bar graph, 条形图Base period, 基期Bayes‘ theorem , Bayes定理Bell-shaped curve, 钟形曲线Bernoulli distribution, 伯努力分布Best-trim estimator, 最好切尾估计量Bias, 偏性Binary logistic regression, 二元逻辑斯蒂回归Binomial distribution, 二项分布Bisquare, 双平方Bivariate Correlate, 二变量相关Bivariate normal distribution, 双变量正态分布Bivariate normal population, 双变量正态总体Biweight interval, 双权区间Biweight M-estimator, 双权M估计量Block, 区组/配伍组BMDP(Biomedical computer programs), BMDP统计软件包Boxplots, 箱线图/箱尾图Breakdown bound, 崩溃界/崩溃点Canonical correlation, 典型相关Caption, 纵标目Case-control study, 病例对照研究Categorical variable, 分类变量Catenary, 悬链线Cauchy distribution, 柯西分布Cause-and-effect relationship, 因果关系Cell, 单元Censoring, 终检Center of symmetry, 对称中心Centering and scaling, 中心化和定标Central tendency, 集中趋势Central value, 中心值CHAID -χ2 Automatic Interaction Detector, 卡方自动交互检测Chance, 机遇Chance error, 随机误差Chance variable, 随机变量Characteristic equation, 特征方程Characteristic root, 特征根Characteristic vector, 特征向量Chebshev criterion of fit, 拟合的切比雪夫准则Chernoff faces, 切尔诺夫脸谱图Chi-square test, 卡方检验/χ2检验Choleskey decomposition, 乔洛斯基分解Circle chart, 圆图Class interval, 组距Class mid-value, 组中值Class upper limit, 组上限Classified variable, 分类变量Cluster analysis, 聚类分析Cluster sampling, 整群抽样Code, 代码Coded data, 编码数据Coding, 编码Coefficient of contingency, 列联系数Coefficient of determination, 决定系数Coefficient of multiple correlation, 多重相关系数Coefficient of partial correlation, 偏相关系数Coefficient of production-moment correlation, 积差相关系数Coefficient of rank correlation, 等级相关系数Coefficient of regression, 回归系数Coefficient of skewness, 偏度系数Coefficient of variation, 变异系数Cohort study, 队列研究Column, 列Column effect, 列效应Column factor, 列因素Combination pool, 合并Combinative table, 组合表Common factor, 共性因子Common regression coefficient, 公共回归系数Common value, 共同值Common variance, 公共方差Common variation, 公共变异Communality variance, 共性方差Comparability, 可比性Comparison of bathes, 批比较Comparison value, 比较值Compartment model, 分部模型Compassion, 伸缩Complement of an event, 补事件Complete association, 完全正相关Complete dissociation, 完全不相关Complete statistics, 完备统计量Completely randomized design, 完全随机化设计Composite event, 联合事件Composite events, 复合事件Concavity, 凹性Conditional expectation, 条件期望Conditional likelihood, 条件似然Conditional probability, 条件概率Conditionally linear, 依条件线性Confidence interval, 置信区间Confidence limit, 置信限Confidence lower limit, 置信下限Confidence upper limit, 置信上限Confirmatory Factor Analysis , 验证性因子分析Confirmatory research, 证实性实验研究Confounding factor, 混杂因素Conjoint, 联合分析Consistency, 相合性Consistency check, 一致性检验Consistent asymptotically normal estimate, 相合渐近正态估计Consistent estimate, 相合估计Constrained nonlinear regression, 受约束非线性回归Constraint, 约束Contaminated distribution, 污染分布Contaminated Gausssian, 污染高斯分布Contaminated normal distribution, 污染正态分布Contamination, 污染Contamination model, 污染模型Contingency table, 列联表Contour, 边界线Contribution rate, 贡献率Control, 对照Controlled experiments, 对照实验Conventional depth, 常规深度Convolution, 卷积Corrected factor, 校正因子Corrected mean, 校正均值Correction coefficient, 校正系数Correctness, 正确性Correlation coefficient, 相关系数Correlation index, 相关指数Correspondence, 对应Counting, 计数Counts, 计数/频数Covariance, 协方差Covariant, 共变Cox Regression, Cox回归Criteria for fitting, 拟合准则Criteria of least squares, 最小二乘准则Critical ratio, 临界比Critical region, 拒绝域Critical value, 临界值Cross-over design, 交叉设计Cross-section analysis, 横断面分析Cross-section survey, 横断面调查Crosstabs , 交叉表Cross-tabulation table, 复合表Cube root, 立方根Cumulative distribution function, 分布函数Cumulative probability, 累计概率Curvature, 曲率/弯曲Curvature, 曲率Curve fit , 曲线拟和Curve fitting, 曲线拟合Curvilinear regression, 曲线回归Curvilinear relation, 曲线关系Cut-and-try method, 尝试法Cycle, 周期Cyclist, 周期性D test, D检验Data acquisition, 资料收集Data bank, 数据库Data capacity, 数据容量Data deficiencies, 数据缺乏Data handling, 数据处理Data manipulation, 数据处理Data processing, 数据处理Data reduction, 数据缩减Data set, 数据集Data sources, 数据来源Data transformation, 数据变换Data validity, 数据有效性Data-in, 数据输入Data-out, 数据输出Dead time, 停滞期Degree of freedom, 自由度Degree of precision, 精密度Degree of reliability, 可靠性程度Degression, 递减Density function, 密度函数Density of data points, 数据点的密度Dependent variable, 应变量/依变量/因变量Dependent variable, 因变量Depth, 深度Derivative matrix, 导数矩阵Derivative-free methods, 无导数方法Design, 设计Determinacy, 确定性Determinant, 行列式Determinant, 决定因素Deviation, 离差Deviation from average, 离均差Diagnostic plot, 诊断图Dichotomous variable, 二分变量Differential equation, 微分方程Direct standardization, 直接标准化法Discrete variable, 离散型变量DISCRIMINANT, 判断Discriminant analysis, 判别分析Discriminant coefficient, 判别系数Discriminant function, 判别值Dispersion, 散布/分散度Disproportional, 不成比例的Disproportionate sub-class numbers, 不成比例次级组含量Distribution free, 分布无关性/免分布Distribution shape, 分布形状Distribution-free method, 任意分布法Distributive laws, 分配律Disturbance, 随机扰动项Dose response curve, 剂量反应曲线Double blind method, 双盲法Double blind trial, 双盲试验Double exponential distribution, 双指数分布Double logarithmic, 双对数Downward rank, 降秩Dual-space plot, 对偶空间图DUD, 无导数方法Duncan‘s new multiple range method, 新复极差法/Duncan新法Effect, 实验效应Eigenvalue, 特征值Eigenvector, 特征向量Ellipse, 椭圆Empirical distribution, 经验分布Empirical probability, 经验概率单位Enumeration data, 计数资料Equal sun-class number, 相等次级组含量Equally likely, 等可能Equivariance, 同变性Error, 误差/错误Error of estimate, 估计误差Error type I, 第一类错误Error type II, 第二类错误Estimand, 被估量Estimated error mean squares, 估计误差均方Estimated error sum of squares, 估计误差平方和Euclidean distance, 欧式距离Event, 事件Event, 事件Exceptional data point, 异常数据点Expectation plane, 期望平面Expectation surface, 期望曲面Expected values, 期望值Experiment, 实验Experimental sampling, 试验抽样Experimental unit, 试验单位Explanatory variable, 说明变量Exploratory data analysis, 探索性数据分析Explore Summarize, 探索-摘要Exponential curve, 指数曲线Exponential growth, 指数式增长EXSMOOTH, 指数平滑方法Extended fit, 扩充拟合Extra parameter, 附加参数Extrapolation, 外推法Extreme observation, 末端观测值Extremes, 极端值/极值F distribution, F分布F test, F检验Factor, 因素/因子Factor analysis, 因子分析Factor Analysis, 因子分析Factor score, 因子得分Factorial, 阶乘Factorial design, 析因试验设计False negative, 假阴性False negative error, 假阴性错误Family of distributions, 分布族Family of estimators, 估计量族Fanning, 扇面Fatality rate, 病死率Field investigation, 现场调查Field survey, 现场调查Finite population, 有限总体Finite-sample, 有限样本First derivative, 一阶导数First principal component, 第一主成分First quartile, 第一四分位数Fisher information, 费雪信息量Fitted value, 拟合值Fitting a curve, 曲线拟合Fixed base, 定基Fluctuation, 随机起伏Forecast, 预测Four fold table, 四格表Fourth, 四分点Fraction blow, 左侧比率Fractional error, 相对误差Frequency, 频率Frequency polygon, 频数多边图Frontier point, 界限点Function relationship, 泛函关系Gamma distribution, 伽玛分布Gauss increment, 高斯增量Gaussian distribution, 高斯分布/正态分布Gauss-Newton increment, 高斯-牛顿增量General census, 全面普查GENLOG (Generalized liner models), 广义线性模型Geometric mean, 几何平均数Gini‘s mean difference, 基尼均差GLM (General liner models), 一般线性模型Goodness of fit, 拟和优度/配合度Gradient of determinant, 行列式的梯度Graeco-Latin square, 希腊拉丁方Grand mean, 总均值Gross errors, 重大错误Gross-error sensitivity, 大错敏感度Group averages, 分组平均Grouped data, 分组资料Guessed mean, 假定平均数Half-life, 半衰期Hampel M-estimators, 汉佩尔M估计量Happenstance, 偶然事件Harmonic mean, 调和均数Hazard function, 风险均数Hazard rate, 风险率Heading, 标目Heavy-tailed distribution, 重尾分布Hessian array, 海森立体阵Heterogeneity, 不同质Heterogeneity of variance, 方差不齐Hierarchical classification, 组内分组Hierarchical clustering method, 系统聚类法High-leverage point, 高杠杆率点HILOGLINEAR, 多维列联表的层次对数线性模型Hinge, 折叶点Histogram, 直方图Historical cohort study, 历史性队列研究Holes, 空洞HOMALS, 多重响应分析Homogeneity of variance, 方差齐性Homogeneity test, 齐性检验Huber M-estimators, 休伯M估计量Hyperbola, 双曲线Hypothesis testing, 假设检验Hypothetical universe, 假设总体Impossible event, 不可能事件Independence, 独立性Independent variable, 自变量Index, 指标/指数Indirect standardization, 间接标准化法Individual, 个体Inference band, 推断带Infinite population, 无限总体Infinitely great, 无穷大Infinitely small, 无穷小Influence curve, 影响曲线Information capacity, 信息容量Initial condition, 初始条件Initial estimate, 初始估计值Initial level, 最初水平Interaction, 交互作用Interaction terms, 交互作用项Intercept, 截距Interpolation, 内插法Interquartile range, 四分位距Interval estimation, 区间估计Intervals of equal probability, 等概率区间Intrinsic curvature, 固有曲率Invariance, 不变性Inverse matrix, 逆矩阵Inverse probability, 逆概率Inverse sine transformation, 反正弦变换Iteration, 迭代Jacobian determinant, 雅可比行列式Joint distribution function, 分布函数Joint probability, 联合概率Joint probability distribution, 联合概率分布K means method, 逐步聚类法Kaplan-Meier, 评估事件的时间长度Kaplan-Merier chart, Kaplan-Merier图Kendall‘s rank c orrelation, Kendall等级相关Kinetic, 动力学Kolmogorov-Smirnove test, 柯尔莫哥洛夫-斯米尔诺夫检验Kruskal and Wallis test, Kruskal和Wallis检验/多样本的秩和检验/H检验Kurtosis, 峰度Lack of fit, 失拟Ladder of powers, 幂阶梯Lag, 滞后Large sample, 大样本Large sample test, 大样本检验Latin square, 拉丁方Latin square design, 拉丁方设计Leakage, 泄漏Least favorable configuration, 最不利构形Least favorable distribution, 最不利分布Least significant difference, 最小显著差法Least square method, 最小二乘法Least-absolute-residuals estimates, 最小绝对残差估计Least-absolute-residuals fit, 最小绝对残差拟合Least-absolute-residuals line, 最小绝对残差线Legend, 图例L-estimator, L估计量L-estimator of location, 位置L估计量L-estimator of scale, 尺度L估计量Level, 水平Life expectance, 预期期望寿命Life table, 寿命表Life table method, 生命表法Light-tailed distribution, 轻尾分布Likelihood function, 似然函数Likelihood ratio, 似然比line graph, 线图Linear correlation, 直线相关Linear equation, 线性方程Linear programming, 线性规划Linear regression, 直线回归Linear Regression, 线性回归Linear trend, 线性趋势Loading, 载荷Location and scale equivariance, 位置尺度同变性Location equivariance, 位置同变性Location invariance, 位置不变性Location scale family, 位置尺度族Log rank test, 时序检验Logarithmic curve, 对数曲线Logarithmic normal distribution, 对数正态分布Logarithmic scale, 对数尺度Logarithmic transformation, 对数变换Logic check, 逻辑检查Logistic distribution, 逻辑斯特分布Logit transformation, Logit转换LOGLINEAR, 多维列联表通用模型Lognormal distribution, 对数正态分布Lost function, 损失函数Low correlation, 低度相关Lower limit, 下限Lowest-attained variance, 最小可达方差LSD, 最小显著差法的简称Lurking variable, 潜在变量Main effect, 主效应Major heading, 主辞标目Marginal density function, 边缘密度函数Marginal probability, 边缘概率Marginal probability distribution, 边缘概率分布Matched data, 配对资料Matched distribution, 匹配过分布Matching of distribution, 分布的匹配Matching of transformation, 变换的匹配Mathematical expectation, 数学期望Mathematical model, 数学模型Maximum L-estimator, 极大极小L 估计量Maximum likelihood method, 最大似然法Mean, 均数Mean squares between groups, 组间均方Mean squares within group, 组内均方Means (Compare means), 均值-均值比较Median, 中位数Median effective dose, 半数效量Median lethal dose, 半数致死量Median polish, 中位数平滑Median test, 中位数检验Minimal sufficient statistic, 最小充分统计量Minimum distance estimation, 最小距离估计Minimum effective dose, 最小有效量Minimum lethal dose, 最小致死量Minimum variance estimator, 最小方差估计量MINITAB, 统计软件包Minor heading, 宾词标目Missing data, 缺失值Model specification, 模型的确定Modeling Statistics , 模型统计Models for outliers, 离群值模型Modifying the model, 模型的修正Modulus of continuity, 连续性模Morbidity, 发病率Most favorable configuration, 最有利构形Multidimensional Scaling (ASCAL), 多维尺度/多维标度Multinomial Logistic Regression , 多项逻辑斯蒂回归Multiple comparison, 多重比较Multiple correlation , 复相关Multiple covariance, 多元协方差Multiple linear regression, 多元线性回归Multiple response , 多重选项Multiple solutions, 多解Multiplication theorem, 乘法定理Multiresponse, 多元响应Multi-stage sampling, 多阶段抽样Multivariate T distribution, 多元T分布Mutual exclusive, 互不相容Mutual independence, 互相独立Natural boundary, 自然边界Natural dead, 自然死亡Natural zero, 自然零Negative correlation, 负相关Negative linear correlation, 负线性相关Negatively skewed, 负偏Newman-Keuls method, q检验NK method, q检验No statistical significance, 无统计意义Nominal variable, 名义变量Nonconstancy of variability, 变异的非定常性Nonlinear regression, 非线性相关Nonparametric statistics, 非参数统计Nonparametric test, 非参数检验Nonparametric tests, 非参数检验Normal deviate, 正态离差Normal distribution, 正态分布Normal equation, 正规方程组Normal ranges, 正常范围Normal value, 正常值Nuisance parameter, 多余参数/讨厌参数Null hypothesis, 无效假设Numerical variable, 数值变量Objective function, 目标函数Observation unit, 观察单位Observed value, 观察值One sided test, 单侧检验One-way analysis of variance, 单因素方差分析Oneway ANOVA , 单因素方差分析Open sequential trial, 开放型序贯设计Optrim, 优切尾Optrim efficiency, 优切尾效率Order statistics, 顺序统计量Ordered categories, 有序分类Ordinal logistic regression , 序数逻辑斯蒂回归Ordinal variable, 有序变量Orthogonal basis, 正交基Orthogonal design, 正交试验设计Orthogonality conditions, 正交条件ORTHOPLAN, 正交设计Outlier cutoffs, 离群值截断点Outliers, 极端值OVERALS , 多组变量的非线性正规相关Overshoot, 迭代过度Paired design, 配对设计Paired sample, 配对样本Pairwise slopes, 成对斜率Parabola, 抛物线Parallel tests, 平行试验Parameter, 参数Parametric statistics, 参数统计Parametric test, 参数检验Partial correlation, 偏相关Partial regression, 偏回归Partial sorting, 偏排序Partials residuals, 偏残差Pattern, 模式Pearson curves, 皮尔逊曲线Peeling, 退层Percent bar graph, 百分条形图Percentage, 百分比Percentile, 百分位数Percentile curves, 百分位曲线Periodicity, 周期性Permutation, 排列P-estimator, P估计量Pie graph, 饼图Pitman estimator, 皮特曼估计量Pivot, 枢轴量Planar, 平坦Planar assumption, 平面的假设PLANCARDS, 生成试验的计划卡Point estimation, 点估计Poisson distribution, 泊松分布Polishing, 平滑Polled standard deviation, 合并标准差Polled variance, 合并方差Polygon, 多边图Polynomial, 多项式Polynomial curve, 多项式曲线Population, 总体Population attributable risk, 人群归因危险度Positive correlation, 正相关Positively skewed, 正偏Posterior distribution, 后验分布Power of a test, 检验效能Precision, 精密度Predicted value, 预测值Preliminary analysis, 预备性分析Principal component analysis, 主成分分析Prior distribution, 先验分布Prior probability, 先验概率Probabilistic model, 概率模型probability, 概率Probability density, 概率密度Product moment, 乘积矩/协方差Pro, 截面迹图Proportion, 比/构成比Proportion allocation in stratified random sampling, 按比例分层随机抽样Proportionate, 成比例Proportionate sub-class numbers, 成比例次级组含量Prospective study, 前瞻性调查Proximities, 亲近性Pseudo F test, 近似F检验Pseudo model, 近似模型Pseudosigma, 伪标准差Purposive sampling, 有目的抽样QR decomposition, QR分解Quadratic approximation, 二次近似Qualitative classification, 属性分类Qualitative method, 定性方法Quantile-quantile plot, 分位数-分位数图/Q-Q图Quantitative analysis, 定量分析Quartile, 四分位数Quick Cluster, 快速聚类Radix sort, 基数排序Random allocation, 随机化分组Random blocks design, 随机区组设计Random event, 随机事件Randomization, 随机化Range, 极差/全距Rank correlation, 等级相关Rank sum test, 秩和检验Rank test, 秩检验Ranked data, 等级资料Rate, 比率Ratio, 比例Raw data, 原始资料Raw residual, 原始残差Rayleigh‘s test, 雷氏检验Rayleigh‘s Z, 雷氏Z值Reciprocal, 倒数Reciprocal transformation, 倒数变换Recording, 记录Redescending estimators, 回降估计量Reducing dimensions, 降维Re-expression, 重新表达Reference set, 标准组Region of acceptance, 接受域Regression coefficient, 回归系数Regression sum of square, 回归平方和Rejection point, 拒绝点Relative dispersion, 相对离散度Relative number, 相对数Reliability, 可靠性Reparametrization, 重新设置参数Replication, 重复Report Summaries, 报告摘要Residual sum of square, 剩余平方和Resistance, 耐抗性Resistant line, 耐抗线Resistant technique, 耐抗技术R-estimator of location, 位置R估计量R-estimator of scale, 尺度R估计量Retrospective study, 回顾性调查Ridge trace, 岭迹Ridit analysis, Ridit分析Rotation, 旋转Rounding, 舍入Row, 行Row effects, 行效应Row factor, 行因素RXC table, RXC表Sample, 样本Sample regression coefficient, 样本回归系数Sample size, 样本量Sample standard deviation, 样本标准差Sampling error, 抽样误差SAS(Statistical analysis system ), SAS统计软件包Scale, 尺度/量表Scatter diagram, 散点图Schematic plot, 示意图/简图Score test, 计分检验Screening, 筛检SEASON, 季节分析Second derivative, 二阶导数Second principal component, 第二主成分SEM (Structural equation modeling), 结构化方程模型Semi-logarithmic graph, 半对数图Semi-logarithmic paper, 半对数格纸Sensitivity curve, 敏感度曲线Sequential analysis, 贯序分析Sequential data set, 顺序数据集Sequential design, 贯序设计Sequential method, 贯序法Sequential test, 贯序检验法Serial tests, 系列试验Short-cut method, 简捷法Sigmoid curve, S形曲线Sign function, 正负号函数Sign test, 符号检验Signed rank, 符号秩Significance test, 显著性检验Significant figure, 有效数字Simple cluster sampling, 简单整群抽样Simple correlation, 简单相关Simple random sampling, 简单随机抽样Simple regression, 简单回归simple table, 简单表Sine estimator, 正弦估计量Single-valued estimate, 单值估计Singular matrix, 奇异矩阵Skewed distribution, 偏斜分布Skewness, 偏度Slash distribution, 斜线分布Slope, 斜率Smirnov test, 斯米尔诺夫检验Source of variation, 变异来源Spearman rank correlation, 斯皮尔曼等级相关Specific factor, 特殊因子Specific factor variance, 特殊因子方差Spectra , 频谱Spherical distribution, 球型正态分布Spread, 展布SPSS(Statistical package for the social science), SPSS统计软件包Spurious correlation, 假性相关Square root transformation, 平方根变换Stabilizing variance, 稳定方差Standard deviation, 标准差Standard error, 标准误Standard error of difference, 差别的标准误Standard error of estimate, 标准估计误差Standard error of rate, 率的标准误Standard normal distribution, 标准正态分布Standardization, 标准化Starting value, 起始值Statistic, 统计量Statistical control, 统计控制Statistical graph, 统计图Statistical inference, 统计推断Statistical table, 统计表Steepest descent, 最速下降法Stem and leaf display, 茎叶图Step factor, 步长因子Stepwise regression, 逐步回归Storage, 存Strata, 层(复数)Stratified sampling, 分层抽样Stratified sampling, 分层抽样Strength, 强度Stringency, 严密性Structural relationship, 结构关系Studentized residual, 学生化残差/t化残差Sub-class numbers, 次级组含量Subdividing, 分割Sufficient statistic, 充分统计量Sum of products, 积和Sum of squares, 离差平方和Sum of squares about regression, 回归平方和Sum of squares between groups, 组间平方和Sum of squares of partial regression, 偏回归平方和Sure event, 必然事件Survey, 调查Survival, 生存分析Survival rate, 生存率Suspended root gram, 悬吊根图Symmetry, 对称Systematic error, 系统误差Systematic sampling, 系统抽样Tags, 标签Tail area, 尾部面积Tail length, 尾长Tail weight, 尾重Tangent line, 切线Target distribution, 目标分布Taylor series, 泰勒级数Tendency of dispersion, 离散趋势Testing of hypotheses, 假设检验Theoretical frequency, 理论频数Time series, 时间序列Tolerance interval, 容忍区间Tolerance lower limit, 容忍下限Tolerance upper limit, 容忍上限Torsion, 扰率Total sum of square, 总平方和Total variation, 总变异Transformation, 转换Treatment, 处理Trend, 趋势Trend of percentage, 百分比趋势Trial, 试验Trial and error method, 试错法Tuning constant, 细调常数Two sided test, 双向检验Two-stage least squares, 二阶最小平方Two-stage sampling, 二阶段抽样Two-tailed test, 双侧检验Two-way analysis of variance, 双因素方差分析Two-way table, 双向表Type I error, 一类错误/α错误Type II error, 二类错误/β错误UMVU, 方差一致最小无偏估计简称Unbiased estimate, 无偏估计Unconstrained nonlinear regression , 无约束非线性回归Unequal subclass number, 不等次级组含量Ungrouped data, 不分组资料Uniform coordinate, 均匀坐标Uniform distribution, 均匀分布Uniformly minimum variance unbiased estimate, 方差一致最小无偏估计Unit, 单元Unordered categories, 无序分类Upper limit, 上限Upward rank, 升秩Vague concept, 模糊概念Validity, 有效性VARCOMP (Variance component estimation), 方差元素估计Variability, 变异性Variable, 变量Variance, 方差Variation, 变异Varimax orthogonal rotation, 方差最大正交旋转Volume of distribution, 容积W test, W检验Weibull distribution, 威布尔分布Weight, 权数Weighted Chi-square test, 加权卡方检验/Cochran检验Weighted linear regression method, 加权直线回归Weighted mean, 加权平均数Weighted mean square, 加权平均方差Weighted sum of square, 加权平方和Weighting coefficient, 权重系数Weighting method, 加权法W-estimation, W估计量W-estimation of location, 位置W估计量Width, 宽度Wilcoxon paired test, 威斯康星配对法/配对符号秩和检验Wild point, 野点/狂点Wild value, 野值/狂值Winsorized mean, 缩尾均值Withdraw, 失访Youden‘s index, 尤登指数Z test, Z检验Zero correlation, 零相关Z-transformation, Z变换。
计量经济学中英文词汇对照

Controlled experiments Conventional depth Convolution Corrected factor Corrected mean Correction coefficient Correctness Correlation coefficient Correlation index Correspondence Counting Counts Covaห้องสมุดไป่ตู้iance Covariant Cox Regression Criteria for fitting Criteria of least squares Critical ratio Critical region Critical value
Asymmetric distribution Asymptotic bias Asymptotic efficiency Asymptotic variance Attributable risk Attribute data Attribution Autocorrelation Autocorrelation of residuals Average Average confidence interval length Average growth rate BBB Bar chart Bar graph Base period Bayes' theorem Bell-shaped curve Bernoulli distribution Best-trim estimator Bias Binary logistic regression Binomial distribution Bisquare Bivariate Correlate Bivariate normal distribution Bivariate normal population Biweight interval Biweight M-estimator Block BMDP(Biomedical computer programs) Boxplots Breakdown bound CCC Canonical correlation Caption Case-control study Categorical variable Catenary Cauchy distribution Cause-and-effect relationship Cell Censoring
stata期末考试题目及答案

stata期末考试题目及答案一、选择题(每题2分,共20分)1. 在Stata中,用于生成新变量的命令是:A. generateB. replaceC. dropD. rename答案:A2. 下列哪个命令可以用来描述数据集中的变量?A. describeB. listC. tabulateD. sum答案:A3. 若要计算变量x和y的平均值,应使用以下哪个命令?A. mean x yB. summarize x yC. average x yD. meanby x y答案:B4. 以下哪个命令可以用于回归分析?A. regressB. correlateC. tabulateD. describe答案:A5. 要将数据集保存为.dta格式,应使用哪个命令?A. saveB. exportC. writeD. saveas答案:A6. 在Stata中,如何查看当前数据集中的所有变量?A. listB. describeC. showD. display答案:B7. 要对数据集中的连续变量进行分组,应使用哪个命令?A. groupB. byC. tabulateD. collapse答案:D8. 以下哪个命令可以用来绘制散点图?A. scatterB. lineC. barD. histogram答案:A9. 若要对数据集中的变量进行标准化处理,应使用哪个命令?A. standardizeB. normalizeC. genD. replace答案:A10. 在Stata中,如何生成一个随机数序列?A. randomB. runiformC. rnormalD. genr答案:B二、简答题(每题5分,共30分)1. 解释Stata中“merge”命令的基本用法。
答案:Stata中的“merge”命令用于合并两个数据集。
基本用法是指定要合并的两个数据集的关键字(即两个数据集中共有的变量),然后使用“1:1”、“1:m”或“m:1”等比例来指示数据集之间的关系。
test interval的标准定义 -回复

test interval的标准定义-回复什么是test interval?Test interval是统计学中的一个重要概念,用于确定一组数据的统计显著性。
它基于样本数据,通过计算出的样本估计值来对总体参数进行推断。
在进行统计假设检验时,test interval的使用能够帮助我们判断一个统计量所代表的总体参数是否落在某个给定的区间范围内。
为什么需要test interval?测试估计是基于样本估计量和抽样误差确定总体参数的一种方法。
通过使用test interval,我们可以通过样本中的数据确定一个区间,其中可能包含真实的总体参数。
这样做有几个优点:首先,test interval给予了我们对于总体参数一个更为合理的估计。
相较于单个点估计,我们可以给出一个范围,这样更能反映出参数的不确定性。
其次,test interval可以给出一些置信度的度量。
通过计算所得的区间,我们可以得知在给定的置信度下,总体参数位于区间范围内的概率。
这样可以让我们更加有信心地对总体特征进行估计。
最后,与假设检验相结合,test interval可以帮助我们判断变量之间的差异是否显著。
通过检查区间是否包含某个特定的值,我们能够判断假设的接受与拒绝。
怎样计算test interval?计算test interval的具体方法取决于所研究的统计量和总体参数类型。
以下是一些常用的求取test interval的方法:1. 对于均值参数的推断,使用Z分布或者t分布进行计算。
具体而言,在给定的置信水平下,我们可以用样本均值加减一个特定的标准差倍数(如1.96倍或2倍)来计算区间范围。
2. 对于比例参数的推断,使用二项分布或者正态分布进行计算。
同样,在给定的置信水平下,我们可以用样本比例加减一个特定的标准差倍数(如1.96倍或2倍)来计算区间范围。
3. 对于方差参数的推断,使用卡方分布进行计算。
在这种情况下,我们可以使用样本方差与卡方分布的上限和下限来计算区间。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Why settle for a confidence level of 95% when a level of 99% is achievable? Answer. The confidence interval for the higher confidence level is wider. Since the 95% interval extends to each side of , the width of the interval is . Similarly, the width of the 99% interval is . That is, we have more confidence in the 99% interval precisely because it is wider. The higher the desired degree of confidence, the wider the resulting interval.
After the values of the random variables in random sample have been observed, the values of A=a and B=b are computed, and the interval ( a, b ) is called the observed value of the confidence interval.
§8.3
Confidence Intervals
Example. Suppose that X ~ N ( ,1),
The unbiased and effective estimator of is
constant
r.v.
Generally we have two kinds of forms to estimate a parameter, One is by a point, which is introduced in Cha 8.1, the other is by an interval.
(2) Variance 2 is unknown , the CI for
Proof. Random variable By Thus we get the CI for μ: , to find μ,
(3)The mean is given, CI for the variance 2
Interpretation of confidence intervals
One way to think of the random interval (A , B) is to imagine that the sample that we observed is one of many possible samples that we could have observed (or may yet observe in the future). Each such sample would allow us to compute an observed interval. Prior to observing the samples, we would exact 95% of the intervals to contain μ. Even if we observed many such intervals, we won’t know which ones contain μ and which ones don’t. If there are a plot of 100 observed values of confidence intervals, Each is computed from a sample of size n=5 from the normal distribution with mean μ=25.2, and standard deviation σ=1 . then about 95 of the 100 intervals contain the value of μ.
r.v. By
Then we get the CI for 2 ( confidence coefficient ):
,
(4) is unknown, CI for 2 , then by
0.15 0.125 0.1
2
We get the CI for 2 :
0.075 0.05 0.025
(I) Let the population X ~N ( 2) (1) The variance 2 is given, CI for
Proof. By
, we know
then
Solve To get the CI for
(confidence coefficient ):
For example,
For any between 0 and 1, constants a and b
can be found to satisfy
By
Then we get the CI for θ: As the above example:
, to get
Formula for CI
-2
•
2
4
68Βιβλιοθήκη •102Ex1 Consider the following sample of fat content (in percentage ) of randomly selected hot dogs:
(assume that fat content has a normal distribution N( 2))
Solution. (1)
i.e.,
By the observed values,
then we get the CI for by formula (1):
(2) Let
In fact, the 100% CI for μ is (-∞,∞), which is not terribly informative because, even before sampling, we knew that this interval covers μ . If we think of the width of the interval as specifying its precision or accuracy, then the confidence level (or reliability) of the interval is inversely related to its precision. A highly reliable interval estimate may be imprecise in that the endpoints of the interval may be far apart, whereas a precise interval may entail relatively low reliability. Thus, it cannot be said unequivocally that a 99% interval is to be preferred to a 95% interval; the gain in reliability entails a loss in precision. As appealing strategy is to specify both the desired confidence level and interval width, and then determine the necessary sample size.
For example, we estimate the age of a person is between 35 and 40 years; we called this kind of estimator interval estimator.
As the above example,we look for an interval so that the probability that the interval contains is 0.95. ( Let n = 5 )
-1
1
3
z 22
3
Deriving a confidence interval
Let denote a random sample on which the CI for a parameter θ is to be based. Suppose a random variable satisfying the following two properties can be found: 1. The variable depends functionally on both and θ. 2. The probability distribution of the variable does not depend on θ or on any other unknown parameters.
Let we get
then i.e., We call
is the 95% confidence interval for .
If , then the 95% confidence interval for is (24.12, 25.88).
Def. Let be a random sample from a distribution that depends on a parameter (or parameter vector) . Let A≤B be two statistics that have the property that P( A<θ<B ) = γ then the random interval (A,B) is called a coefficient γ confidence interval for θ.
