二次函数专题练习 (学生版)

合集下载

二次函数图象与性质大题专练(七大类型)-2023年中考数学压轴题专项训练(全国通用)(学生版)

二次函数图象与性质大题专练(七大类型)考向分析类型一二次函数解析式1.(2023春·江苏苏州·九年级校考阶段练习)在平面直角坐标系中，已知点A1,2，，B2,3C2,1，直线y=x+m经过点A，抛物线y=ax2+bx+1恰好经过A，B，C三点中的两点．(1)判断点B是否在直线y=x+m上，并说明理由；(2)求a，b的值；(3)平移抛物线y=ax2+bx+1，若所得新抛物线的顶点仍在直线y=x+m上，且经过点0,1，求新抛物线的表达式．2.(2023·北京西城·北京市第十三中学校考模拟预测)在平面直角坐标系中，抛物线y=ax2 -a+2，B m,p．x+2经过点A-2,t(1)若t=0，①求此抛物线的对称轴；②当p<t时，直接写出m的取值范围；(2)若t<0，点C n,q在该抛物线上，m<n且3m+3n≤-4，请比较p，q的大小，并说明理由．3.(2023·河南周口·统考一模)在平面直角坐标系中，抛物线y=x2-4mx+m2-2m．(1)若抛物线经过A-1,0，B0,3两点时，求抛物线的解析式；(2)若点M2,y M，N3,y N在抛物线上，且y M>y N，请求出m的取值范围；(3)当-1≤x≤2时，函数y的最小值等于6，直接写出m的值．类型四二次函数与方程不等式的推理计算4.(2023·浙江·模拟预测)在直角坐标系中，设函数y=ax2+bx+c(a，b，c是常数，a≠0)．(1)当a=-1时，①若该函数图象的对称轴为直线x=2，且过点1，4，求该函数的表达式；②若该函数的图象与x轴有且只有一个交点，求证：b+4c≤1 4；(2)已知该函数的图象经过点m，m，n，nm≠n．若b<0，m+n=3，求a的取值范围．类型五二次函数与公共点交点问题5.(2023·吉林长春·吉林大学附属中学校考二模)在平面直角坐标系中，函数函数y=x2-2mx +m2-4(m为常数)的图象记为G．(1)设m>0，当G经过点(2,0)时，求此函数的表达式，并写出顶点坐标．(2)判断图象G与x轴公共点的个数．并说明理由．(3)当2m≤x≤m+3时，图象G的最高点与最低点纵坐标之差为9，求m的取值范围．(4)线段AB的端点坐标分别为A(0,2)、B(7,4)，当图象G与x轴有两个公共点时，设其分别为点C、点D(点C在点D左侧)，直接写出四边形ACDB周长的最小值及此时m的值．类型六二次函数的图象问题6.(2023·山东济宁·统考一模)数形结合是解决数学问题的重要方法．小爱同学学习二次函数后，对函数y=-x -12进行了探究．在经历列表、描点、连线步骤后，得到如图的函数图象．请根据函数图象，回答下列问题：(1)观察探究：①写出该函数的一条性质：；②方程-x -12=-1的解为：；③若方程-x -12=a有四个实数根，则a的取值范围是．(2)延伸思考．①将函数y=-x -12的图象经过怎样的平移可得到函数y1=-x-2-12+3的图象？画出平移后的图象并写出平移过程：②观察平移后的图像，当2≤y1≤3时，直接写出自变量x的取值范围．类型七二次函数与新定义材料问题7.(2023·四川达州·统考一模)定义：若一个函数图像上存在横、纵坐标相等的点，则称该点为这个函数图像的“等值点”，例如：点1,1是函数y=12x+12的图像的“等值点”．(1)分别判断函数y=x+1，y=x2-x的图像上是否存在“等值点”？如果存在，求出“等值点”的坐标；如果不存在，说明理由；(2)设函数y=3xx>0，y=-x+b的图像的“等值点”分别为点A，B，过点B作BC⊥x轴，垂足为C．当△ABC的面积为3时，求b的值；(3)若函数y=x2-2x≥m的图像记为W1，将其沿直线x=m翻折后的图像记为W2，当W1，W2两部分组成的图像上恰有2个“等值点”时，直接写出m的取值范围．压轴题速练一、解答题(共24小题)1.(2023•鼓楼区一模)已知二次函数y=x2+(a-2)x+3的图象经过点(2，3)．(1)求该二次函数的表达式；(2)当0<x<3时，y的取值范围为；(3)已知点P(m-1，y1)，点Q(m，y2)在该二次函数的图象上若y1>y2，直接写出m的取值范围．2.(2023•西湖区模拟)设二次函数y=(x+1)(ax+2a+2)(a是常数，a≠0)．(1)若a=2，求该函数图象顶点坐标；(2)若该二次函数图象经过(-1，1)，(-2，3)，(1，-2)三个点中的一个点，求该二次函数的表达式；(3)若二次函数图象经过(x1，y1)，(x2，y2)两点，当x1+x2=2，x1<x2时．y1>y2，求a的取值范围．3.(2023•温州一模)已知二次函数y=a(x-1)2-2的图象经过点(3，2)．(1)求该函数的表达式，并在图中画出该函数的大致图象．(2)P是该函数图象上一点，在对称轴右侧，过点P作PD⊥x轴于点D．当PD≤1时，求点P横坐标的取值范围．4.(2023•佳木斯一模)如图，抛物线y=-x2+bx+c经过点A(-1，0)和点B(0，3)，顶点为C，D是抛物线上一点．(1)求抛物线的解析式和顶点C的坐标；(2)若S△BCD=32，请直接写出点D的坐标．5.(2023•涧西区一模)已知二次函数y=ax2+bx(a≠0)的图象经过点(-1，5)，(2，-4)．(1)求二次函数的解析式；(2)若点M(x1，y1)，N(x2，y2)都在此抛物线上，且0<x1<1，2<x2<3．比较y1与y2的大小，并说明理由；(3)点P的坐标为(n，-3)，点Q的坐标为(n+3，-3)，若线段PQ与该函数图象恰有一个交点，直接写出n的取值范围．6.(2023•青龙县一模)如图，在平面直角坐标系中，直线AB：y=kx+3与坐标轴交于A，B两点，经过点B的抛物线y=ax2+bx交直线AB于点C(2，2)．(1)求该抛物线的解析式；(2)在直线AB上方的抛物线上是否存在点P，使得S△PAO=S△PBO，若存在请求出点P的坐标，若不存在请说明理由．7.(2023•秦淮区模拟)已知二次函数y=ax2-2ax．(1)二次函数的图象的对称轴是直线x=；(2)当0≤x≤3时，y的最大值与最小值的差为8，求该二次函数的表达式；(3)若a<0，对于二次函数图象上的两点P(x1，y1)，Q(x2，y2)，当t≤x1≤t+1，x2≥3时，均满足y1≥y2，请结合函数图象，直接写出t的取值范围．8.(2023•瓯海区一模)已知二次函数y=x2+bx+c的图象经过点A(-1，0)，B(3，0)．(1)求该二次函数的表达式和图象顶点P的坐标．(2)若M(m，y1)，N(n，y2)是该二次函数图象上不同的两点．当y1=y2时，m-n=5，求点P到直线MN的距离．9.(2023•泗洪县一模)已知抛物线y=ax2+2ax+3a2-4(a≠0)．(1)求这条抛物线的对称轴；(2)若该抛物线的顶点在x轴上，求其函数的表达式；(3)设该抛物线上有两点A(m，y1)B(3，y2)，若y1<y2，求m的取值范围．10.(2023•安徽模拟)已知二次函数y=ax2+bx+2的图象经过点(1，m)、(-1，n)．(1)小明判断m，n满足关系式：m-n=2b，请判断他的说法是否正确，并说明理由；(2)若m=2，n=0，求该二次函数的表达式；(3)当a<0，且满足a+b=0时，若该函数图象上的任意两点P(x1，y1)，Q(x2，y2)满足x1=-2，y1> y2，求x2的取值范围．11.(2023•平阳县一模)已知抛物线y=x2+2cx+c．(1)若抛物线与y轴的交点为(0，3)，求抛物线的函数表达式和顶点坐标；(2)已知抛物线与y轴的交点在y轴正半轴上，与x轴有交点．若点A(m，n)，B(m-4，n)在抛物线上，求c的取值范围及m的最大值．12.(2023•盐田区二模)已知抛物线y=ax2-2ax+a+1．(1)求抛物线的顶点坐标；(2)若a=-2，当0≤x≤3时，求y的最大值和最小值；(3)若抛物线与直线y=x+1始终有交点，求a的取值范围．13.(2023•天门一模)在平面直角坐标系xOy中，抛物线y=ax2-4ax-4(a≠0)与y轴交于点A，其对称轴与x轴交于点B．(1)求点A，B的坐标；(2)若a=-1，当t-1≤x≤t时，二次函数y=ax2-4ax-4的最大值为-1，求t的值；(3)直线y=x-2经过点C(m，-5)，将点C向右平移6个单位长度，得到点C1，若抛物线与线段CC1只有一个公共点，结合函数图象，请直接写出a的取值范围．14.(2023•越秀区一模)在平面直角坐标系中，抛物线y1=-(x+4)(x-n)与x轴交于点A和点B (n，0)(n≥-4)，顶点坐标记为(h1，k1)．抛物线y2=-(x+2n)2-n2+2n+9的顶点坐标记为(h2，k2)．(1)直接写出k1，k2的值；(用含n的代数式表示)(2)当-4≤n≤4时，探究k1与k2的大小关系；(3)经过点M(2n+9，-5n2)和点N(2n，9-5n2)的直线与抛物线y1=-(x+4)(x-n)y2=-(x+ 2n)2-n2+2n+9的公共点恰好为3个不同点时，求n的值．15.(2023•温江区校级模拟)在平面直角坐标系xOy中，已知抛物线y=ax2-2ax+a+3(a≠0)和直线y=-x+4．(1)抛物线的对称轴是；抛物线的顶点M坐标为；(2)设该抛物线与直线y=-x+4的一个交点为A，其横坐标为m，若0≤m<12，求a的取值范围；(3)我们规定若函数图象上存在一点P(s，t)，满足s+t=1，则称点P为函数图象上“圆满点”．例如：直线y=2x-1上存在的“圆满点”P23，13，若抛物线y=ax2-2ax+a+3(a≠0)上存在唯一的“圆满点”P，求此时△OPM的面积．16.(2023•来安县一模)已知关于x的二次函数y1=(x+2a)(x-2b)(其中a，b为常数)．(1)若a=1，该二次函数的图象经过点(-1，3)，求b；(2)若a=b-2．①若(-1，m)和(3，n)是该二次函数图象上的点，比较m和n的大小；②设一次函数y2=-x+2b，当函数y=y1+y2的图象经过点(c，0)时，探索b与c之间的数量关系，并加以推理．17.(2023•秦皇岛一模)已知y=ax2+bx+c过点A(2，0)，B(3n-4，y1)，C(5n+6，y2)三点，对称轴是直线x=1，关于x的方程ax2+bx+c=x有两个相等的实数根．(1)求抛物线的解析式；(2)若B点在直线x=1的左侧，C点在直线x=1的右侧，且y1>y2，求n的取值范围；(3)若n<-5，试比较y1与y2的大小．18.(2023•南山区一模)探究函数性质时，我们经历了列表、描点、连线画函数图象，观察分析图象特征，概括函数性质的过程，以下是我们研究函数y=x+|-2x+6|+m性质及其应用的部分过程，请按要求完成下列各小题．x⋯-2-1012345⋯y⋯654a21b7⋯(1)写出函数关系式中m及表格中a，b的值；m=，a=，b=；(2)根据表格中的数据在所给的平面直角坐标系中画出该函数的图象；(3)已知函数y=-(x-2)2+8的图象如图所示，结合你所画的函数图象，不等式x+|-2x+6|+m> -(x-2)2+8的解集为．19.(2023•南山区模拟)已知一次函数y=kx+b(k≠0)的图象与二次函数y=12(x+2)2-2的图象相交于点A(1，m)、B(-2，n)．(1)求一次函数的表达式，并在图中画出这个一次函数的图象；(2)根据函数图象，直接写出不等式kx+b<12(x+2)2-2的解集；(3)方程12(x+2)2-2-n=0在-3≤x≤1范围内只有一个解，求n的取值范围；(4)把二次函数y=12(x+2)2-2的图象左右平移得到抛物线G：y=12(x-m)2-2，直接写出当抛物线G与线段AB只有一个交点时m的取值范围．20.(2023•深圳一模)探究函数性质时，我们经历了列表、描点、连线画函数图象，观察分析图象特征，概括函数性质的过程，以下是我们研究函数y=x+|-2x+6|+m性质及其应用的部分过程，请按要求完成下列各小题．x⋯-2-1012345⋯y⋯654a21b7⋯(1)写出函数关系式中m及表格中a，b的值；m=，a=，b=；(2)根据表格中的数据在所给的平面直角坐标系中画出该函数的图象；(3)已知函数y=16x的图象如图所示，结合你所画的函数图象，不等式x+|-2x+6|+m>16x的解集为．21.(2023•信阳模拟)定义：在平面直角坐标系中，有一条直线x=m，对于任意一个函数，作该函数自变量大于m的部分关于直线x=m的轴对称图形，与原函数中自变量大于或等于m的部分共同构成一个新的函数图象，则这个新函数叫做原函数关于直线x=m的“镜面函数”．例如：图①是函数y =x+1的图象，则它关于直线x=0的“镜面函数”的图象如图②所示，且它的“镜面函数”的解析式为y=x+1(x≥0)-x+1(x<0)，也可以写成y=|x|+1．(1)在图③中画出函数y=-2x+1关于直线x=1的“镜面函数”的图象．(2)函数y=x2-2x+2关于直线x=-1的“镜面函数”与直线y=-x+m有三个公共点，求m的值．(3)已知抛物线y=ax2-4ax+2(a<0)，关于直线x=0的“镜面函数”图象上的两点P(x1，y1)，Q (x2，y2)，当t-1≤x1≤t+1，x2≥4时，均满足y1≥y2，直接写出t的取值范围．22.(2023•义乌市校级模拟)定义：函数图象上到两坐标轴的距离都不大于n(n≥0)的点叫做这个函数图象的“n阶方点”．例如，点13，13是函数y=x图象的“12阶方点”；点(2，1)是函数y=2x图象的“2阶方点”．(1)在①-2，-12；②(-1，-1)；③(1，1)三点中，是反比例函数y=1x图象的“1阶方点”的有(填序号)；(2)若y关于x的一次函数y=ax-3a+1图象的“2阶方点”有且只有一个，求a的值；(3)若y关于x的二次函数y=-(x-n)2-2n+1图象的“n阶方点”一定存在，请直接写出n的取值范围．23.(2022•婺城区模拟)定义：在平面直角坐标系中，对于任意一个函数，作该函数y轴右侧部分关于y轴的轴对称图形，与原函数y轴的交点及y轴右侧部分共同构成一个新函数的图象，则这个新函数叫做原函数的“新生函数“例如：图①是函数y=x+l的图象，则它的“新生函数“的图象如图②所示，且它的“新生函数“的解析式为y=x+1(x≥0)-x+1(x<0)，也可以写成y=|x|+1．(1)在图③中画出函数y=-2x+l的“新生函数“的图象．(2)函数y=x2-2x+2的“新生函数“与直线y=-x+m有三个公共点，求m的值．(3)已知A(-1，0)，B(3，0)，C(3，-2)，D(-1，-2)，函数y=x2-2nx+2(n>0)的“新生函数“图象与矩形ABCD的边恰好有4个交点，求n的取值范围．24.(2022•零陵区模拟)九年级数学兴趣小组在课外学习时遇到这样一个问题：定义：如果二次函数y=a1x2+b1x+c1(a1≠0，a1，b1，c1是常数)与y=a2x2+b2x+c2(a2≠0，a2，b2，c2是常数)满足a1+a2=0，b1=b2，c1+c2=0，则这两个函数互为“旋转函数”．求函数y=2x2-3x+1的“旋转函数”．小组同学是这样思考的，由函数y=2x2-3x+1可知，a1=2，b1=-3，c1=1，根据a1+a2=0，b1=b2，c1 +c2=0，求出a2，b2，c2就能确定这个函数的“旋转函数”．请参照小组同学的方法解决下面问题：(1)函数y=x2-4x+3的“旋转函数”是2；(2)若函数y=5x2+(m-1)x+n与y=-5x2-nx-3互为“旋转函数”，求(m+n)2022的值；(3)已知函数y=2(x-1)(x+3)的图象与x轴交于A，B两点，与y轴交于点C，点A，B，C关于原点的对称点分别是A1，B1，C1，试求证：经过点A1，B1，C1的二次函数与y=2(x-1)(x+3)互为“旋转函数”．。

1二次函数的三种形式——学生版

1.二次函数的三种形式难度：易1．将二次函数y＝x2+4x+3化成顶点式，变形正确的是（）A．y＝（x﹣2）2﹣1B．y＝（x+1）（x+3）C．y＝（x﹣2）2+1D．y＝（x+2）2﹣12．如图，抛物线与x轴交于点（﹣1，0）和（3，0），与y轴交于点（0，﹣3）则此抛物线对此函数的表达式为（）A．y＝x2+2x+3B．y＝x2﹣2x﹣3C．y＝x2﹣2x+3D．y＝x2+2x﹣3 3．抛物线与x轴交于点（1，0），（﹣3，0），则该抛物线可设为：．4．已知二次函数y＝﹣2x2+8x﹣6，完成下列各题：（1）将函数关系式用配方法化为y＝a（x+h）2+k的形式，并写出它的顶点坐标、对称轴；（2）它的图象与x轴交于A，B两点，顶点为C，求S△ABC．难度：中5．抛物线与x轴交点的横坐标为﹣2和1，且过点（2，8），它的关系式为（）A．y＝2x2﹣2x﹣4B．y＝﹣2x2+2x﹣4C．y＝x2+x﹣2D．y＝2x2+2x﹣46．若抛物线y＝（x﹣m）2+（m+1）的顶点在第一象限，则m的取值范围为（）A．m＞1B．m＞0C．m＞﹣1D．﹣1＜m＜0 7．分别对y＝﹣2x2+x+3化为顶点式为，化为交点式为．8．如图，抛物线y＝x2+bx+c与x轴交于A（﹣1，0）和B（3，0）两点，交y轴于点E．（1）求此抛物线的解析式．（2）若直线y ＝x +1与抛物线交于A 、D 两点，与y 轴交于点F ，连接DE ，求△DEF 的面积．难度：难9．用配方法将二次函数y ＝x 2﹣8x ﹣9化为y ＝a （x ﹣h ）2+k 的形式为（） A ．y ＝（x ﹣4）2+7 B ．y ＝（x ﹣4）2﹣25C ．y ＝（x +4）2+7D ．y ＝（x +4）2﹣2510．已知抛物线y ＝5x 2+mx +n 与x 轴的交点为（45，0）和（﹣2，0），则因式分解5x 2+mx +n 的结果是．11．某班“数学兴趣小组”对函数y ＝x 2﹣2|x |的图象和性质进行了探究，探究过程如下，请补充完整．（1）自变量x 的取值范围是全体实数，x 与y 的几组对应值列表如下： x … ﹣3 −52 ﹣2 ﹣1 0 1 2 523 … y…354m﹣1﹣1543…其中，m ＝．（2）根据表中数据，在如图所示的平面直角坐标系中描点，并画出了函数图象的一部分，请画出该函数图象的另一部分．（3）观察函数图象，写出两条函数的性质．（4）进一步探究函数图象发现：①函数图象与x 轴有个交点，所以对应的方程x 2﹣2|x |＝0有个不相等的实数根； ②方程x 2﹣2|x |＝2有个不相等的实数根；③关于x 的方程x 2﹣2|x |＝a 有4个不相等的实数根时，a 的取值范围是．。

专题二次函数与全等、相似存在性问题(学生版)

专题29二次函数与相似、全等存在性问题题型一相似三角形存在性问题在坐标系中确定点，使得由该点及其他点构成的三角形与其他三角形相似，即为“相似三角形存在性问题”．【相似判定】判定1：三边对应成比例的两个三角形是相似三角形；判定2：两边对应成比例且夹角相等的两个三角形是相似三角形；判定3：有两组角对应相等的三角形是相似三角形．以上也是坐标系中相似三角形存在性问题的方法来源，根据题目给的已知条件选择恰当的判定方法，解决问题【题型分析】通常相似的两三角形有一个是已知的，而另一三角形中有1或2个动点，即可分为“单动点”类、“双动点”两类问题．【思路总结】根据相似三角形的做题经验，可以发现，判定1基本是不会用的，这里也一样不怎么用，对比判定2、3可以发现，都有角相等！所以，要证相似的两个三角形必然有相等角，关键点也是先找到一组相等角．然后再找：思路1：两相等角的两边对应成比例；思路2：还存在另一组角相等．事实上，坐标系中在已知点的情况下，线段长度比角的大小更容易表示，因此选择方法可优先考虑思路1．一、如何得到相等角？二、如何构造两边成比例或者得到第二组角？搞定这两个问题就可以了．1．如图，在平面直角坐标系中，抛物线C：y＝ax2+bx+c（a≠0）经过点（1，1）和（4，1）．（1）求抛物线C的对称轴．（2）当a＝﹣1时，将抛物线C向左平移2个单位，再向下平移1个单位，得到抛物线C1．①求抛物线C1的解析式．②设抛物线C1与x轴交于A，B两点（点A在点B的右侧），与y轴交于点C，连接BC．点D为第一象限内抛物线C1上一动点，过点D作DE⊥OA于点E．设点D的横坐标为m．是否存在点D，使得以点O，D，E为顶点的三角形与△BOC相似？若存在，求出m的值；若不存在，请说明理由．2．如图，抛物线y＝ax2+bx+3（a≠0）与x轴交于点A（1，0）和点B（﹣3，0），与y轴交于点C，连接BC，与抛物线的对称轴交于点E，顶点为点D．（1）求抛物线的解析式；（2）点P是对称轴左侧抛物线上的一个动点，点Q在射线ED上，若以点P、Q、E为顶点的三角形与△BOC 相似，请直接写出点P的坐标．3．如图，直线y＝﹣x+分别交x轴、y轴于点A，B，过点A的抛物线y＝﹣x2+bx+c与x轴的另一交点为C，与y轴交于点D（0，3），抛物线的对称轴l交AD于点E，连接OE交AB于点F．（1）求抛物线的解析式；（2）求证：OE⊥AB；（3）P为抛物线上的一动点，直线PO交AD于点M，是否存在这样的点P，使以A，O，M为顶点的三角形与△ACD相似？若存在，求点P的横坐标；若不存在，请说明理由．4．如图，在平面直角坐标系xOy中，抛物线y＝﹣x2+x+4与两坐标轴分别相交于A，B，C三点．（1）求证：∠ACB＝90°；（2）点D是第一象限内该抛物线上的动点，过点D作x轴的垂线交BC于点E，交x轴于点F，点G是AC 的中点，若以点C，D，E为顶点的三角形与△AOG相似，求点D的坐标．5．如图，已知二次函数的图象与x轴交于A和B（﹣3，0）两点，与y轴交于C（0，﹣3），对称轴为直线x＝﹣1，直线y＝﹣2x+m经过点A，且与y轴交于点D，与抛物线交于点E，与对称轴交于点F．（1）求抛物线的解析式和m的值；（2）在y轴上是否存在点P，使得以D、E、P为顶点的三角形与△AOD相似，若存在，求出点P的坐标；若不存在，试说明理由；题型二全等三角形存在性问题6．如图，抛物线y＝x2+bx+c经过点（3，12）和（﹣2，﹣3），与两坐标轴的交点分别为A，B，C，它的对称轴为直线l．（1）求该抛物线的表达式；（2）P是该抛物线上的点，过点P作l的垂线，垂足为D，E是l上的点．要使以P、D、E为顶点的三角形与△AOC全等，求满足条件的点P，点E的坐标．7．如图，抛物线y＝x2+bx+c经过点（﹣2，5）和（2，﹣3），与两坐标轴的交点分别为A，B，C，它的对称轴为直线l．（1）求该抛物线的表达式；（2）求出点A，B，C的坐标；（3）P是该抛物线上的点，过点P作l的垂线，垂足为D，E是l上的点．要使以P，D，E为顶点的三角形与△BOC全等，求满足条件的点P，点E的坐标．8．如图，抛物线y＝ax2+bx﹣3与x轴交于A（﹣1，0），B（3，0）两点，与y轴交于点C，点D是抛物线的顶点．（1）求抛物线的解析式．（2）直线BC交对称轴于点E，P是坐标平面内一点，请直接写出△PCE与△ACD全等时点P的坐标．9．如图1，抛物线y1＝ax2﹣x+c与x轴交于点A和点B（1，0），与y轴交于点C（0，），抛物线y1的顶点为G，GM⊥x轴于点M．将抛物线y1平移后得到顶点为B且对称轴为直线l的抛物线y2．（1）求抛物线y2的解析式；（2）点P为抛物线y1上一动点，过点P作y轴的平行线交抛物线y2于点Q，点Q关于直线l的对称点为R，若以P，Q，R为顶点的三角形与△AMG全等，求直线PR的解析式．10．如图，抛物线y＝x2+bx+c经过点A（﹣1，0），B（0，﹣2），并与x轴交于点C，点M是抛物线对称轴l 上任意一点（点M，B，C三点不在同一直线上）．（1）求该抛物线所表示的二次函数的表达式；（2）在抛物线上找出两点P1，P2，使得△MP1P2与△MCB全等，并求出点P1，P2的坐标；。

专题05二次函数的最值问题专项培优训练学生版

专题05 二次函数的最值问题（专项培优训练）试卷满分：100分考试时间：120分钟难度系数：0.54姓名：___________班级：___________考号：___________题号一二三总分得分评卷人得分一、选择题（本大题共10小题，每小题2分，共20分．在每小题所给出的四个选项中，恰有一项是符合题目要求的，请将正确选项前的字母代号填写在括号内）1．（2分）（2023秋•湖里区校级期中）已知二次函数的图象（0≤x≤3）如图所示，关于该函数在所给自变量取值范围内，下列说法正确的是（）A．函数有最小值1，有最大值3B．函数有最小值﹣1，有最大值0C．函数有最小值﹣1，有最大值3D．函数有最小值﹣1，无最大值2．（2分）（2023秋•江油市月考）当a≤x≤a+2时，二次函数y＝x2﹣4x+4的最小值为1，则a的值为（）A．﹣1B．3C．﹣1或3D．0或33．（2分）（2023•霍邱县一模）若a≥0，b≥0，且2a+b＝2，2a2﹣4b的最小值为m，最大值为n，则m+n＝（）A．﹣14B．﹣6C．﹣8D．24．（2分）（2023春•北碚区校级期末）当a﹣1≤x≤a时，二次函数y＝x2﹣4x+3的最小值为8，则a的值为（）A．﹣1 或5B．0或6C．﹣1或6D．0或55．（2分）（2022秋•绿园区校级期末）已知二次函数的图象（0≤x≤3）如图所示，关于该函数在所给自变量取值范围内，下列说法正确的是（）A．函数有最小值1，有最大值3B．函数有最小值﹣1，有最大值3C．函数有最小值﹣1，有最大值0D．函数有最小值﹣1，无最大值6．（2分）（2023秋•呼兰区期中）在△ABC中，边BC的长与BC边上的高的和为8，当△ABC面积最大时，则BC的长为（）A．4B．8C．2D．无法确定7．（2分）（2023秋•西城区校级月考）已知一个二次函数图象经过P1（﹣3，y1），P2（﹣1，y2），P3（1，y 3），P4（3，y4）四点，若y2＜y3＜y1，则y1，y2，y3，y4的最值情况是（）A．y3最小，y1最大B．y3最小，y4最大C．y2最小，y4最大D．无法确定8．（2分）（2023春•南充期末）如图，四边形ABCD中，AD∥BC，∠B＝90° AB＝12cm，AD＝36cm，BC＝40cm，点P从点A出发，以3cm/s的速度向点D运动：点Q从点C同时出发，以1cm/s的速度向点B运动．规定其中一个动点到达终点时，另一个动点也随之停止运动．设运动时间为t秒，下列结论错误的是（）A．当t＝9时，PQ∥DCB．当t＝10时，PQ⊥BCC．当t＝9或11.5时，PQ＝CDD．当t＝12时，四边形ABQP的最大面积为384cm29．（2分）（2023•庐阳区校级一模）二次函数y＝x2﹣2的图象经过点（a，b），则代数式b2+6a2的最小值是（）A．2B．3C．4D．510．（2分）（2022秋•余姚市期末）如图，抛物线y＝x2+bx+c（b，c为常数）经过点A（1，0），点B（0，3），点P在该抛物线上，其横坐标为m，若该抛物线在点P左侧部分（包括点P）的最低点的纵坐标为2﹣m．则m的值为（）A．m＝3B．C．D．m＝3或评卷人得分二、填空题（本大题共10小题，每小题2分，共20分．不需写出解答过程，请将正确答案填写在横线上）11．（2分）（2023秋•潮阳区校级月考）已知二次函数，当﹣1≤x≤2时，函数y＝mx2﹣2mx+2（m≠0）的最大值为y＝4，则m的值是．12．（2分）（2023秋•荔城区校级月考）二次函数y＝（x﹣1）2+m﹣1的最小值为2，则m的值为．13．（2分）（2023•宽城区一模）在平面直角坐标系中，点A（m，y1）、B（m+1，y2）在抛物线y＝（x﹣1）2﹣2上．当y1＜y2时，抛物线上A、B两点之间（含A、B两点）的图象的最高点的纵坐标为3，则m的值为．14．（2分）（2022秋•南开区校级期末）二次函数y＝﹣x2﹣2x+c在﹣3≤x≤2的范围内有最小值﹣5，则c 的值是．15．（2分）（2023•沁阳市模拟）为落实国家《关于全面加强新时代大中小学劳动教育的意见》，某校准备在校园里利用围墙（墙长9m）和21m长的篱笆墙，围成Ⅰ区、Ⅱ区两块矩形劳动实践基地（如图所示）．要使围成的两块矩形总种植最大，则BC应设计为 m．16．（2分）（2023秋•甘井子区期中）如图，在△ABC中，∠B＝90°，AB＝12mm，BC＝24mm，动点P从点A 开始沿边AB向点B以2mm/s的速度移动，动点Q从点B开始沿边BC向点C以4mm/s的速度移动，如果P、Q两点分别从A、B两点同时出发，设运动时间为ts，那么△PBQ的面积S的最大值为 mm2．17．（2分）（2023秋•拱墅区月考）已知k，n均为非负实数，且2k+n＝2，则2k2﹣4n的最小值为．18．（2分）（2023•东海县三模）如果抛物线y＝（a﹣3）x2﹣2有最低点，那么a的取值范围是．19．（2分）（2021秋•嘉祥县期末）如图，已知边长为12的正方形ABCD，E是BC边上一动点（与B、C不重合），连接AE，G是BC延长线上的点，过点E作AE的垂线交∠DCG的角平分线于点F，若FG⊥BG，则△CEF的最大面积为．20．（2分）（2021秋•荆门期末）设O为坐标原点，点A、B为抛物线y＝上的两个动点，且OA⊥OB．连接点A、B，过O作OC⊥AB于点C，则点C到y轴距离的最大值．评卷人得分三、解答题（本大题共8小题，共60分．解答时应写出文字说明、证明过程或演算步骤）21．（6分）（2022秋•建邺区期末）求证：周长为a的矩形中，正方形的面积最大．请建立二次函数关系解决上述问题．22．（6分）（2022秋•漳州期末）已知二次函数y＝x2+bx+c（b、c为常数）的图象经过点（0，3）、（1，﹣2）．（1）求b、c的值；（2）当0≤x≤m时，若y的最大值与最小值之和为1，求m的值．23．（8分）（2022秋•广阳区期末）已知：如图，在△ABC中，∠B＝90°，AB＝5cm，BC＝7cm．点P从点A 开始沿AB边向点B以1cm/s的速度移动，同时点Q从点B开始沿BC边向点C以2cm/s的速度移动．当一个点到达终点时另一点也随之停止运动，设运动时间为t秒．（1）求几秒后，△PBQ的面积等于4cm2？（2）P、Q在运动过程中，是否存在时间t，使得△PBQ的面积最大，若存在求出时间t和最大面积，若不存在，说明理由．24．（8分）（2021秋•营口期末）在平面直角坐标系xOy中，抛物线y＝ax2+x经过点A（3，4）．（1）求a的值；（2）过点A作x轴的平行线交抛物线于另一点B，在直线AB上任取一点P，作点A关于直线OP的对称点C；①当点C恰巧落在x轴时，求直线OP的表达式；②连结BC，求BC的最小值．25．（8分）（2023秋•定西期中）在边长为6cm的正方形ABCD中，点E，F，G，H分别按A→B，B→C，C→D，D→A的方向同时出发，以1cm/s的速度匀速运动．写出四边形EFGH的面积S（cm2）关于运动时间t （s）变化的函数关系式，并求运动几秒钟时，面积最小？最小值是多少？26．（8分）（2023秋•海淀区校级月考）对某一个函数给出如下定义：如果存在实数M，对于任意的函数值y，都满足y≥M，那么称这个函数为边界函数．在所有满足条件的M中，其最小值称为这个函数的边界值．例如，图中的函数：y＝（x﹣1）2+2是边界函数，其边界值是2．（1）函数①y＝﹣x2+2x+1和②y＝x﹣1（x≥1）中是边界函数的为（只填序号即可），其边界值为；（2）如果函数y＝﹣x+2（a≤x≤b，b＞a）的边界值是a，且这个函数的最大值超过2b﹣5，求b的取值范围；（3）如果函数y＝x2﹣2ax+2（1≤x≤5）是以﹣1为边界值的边界函数，直接写出实数a的值．27．（8分）（2023•兴宁区校级开学）如图，四边形ABCD中，AD＝CD，AB＝BC，我们把这种两组邻边分别相等的四边形叫做“筝形”．（1）求证：AC⊥BD；（2）如果筝形的两条对角线长分别为6cm、8cm，则筝形的面积＝ cm2；（3）已知筝形ABCD的对角线AC，BD的长度为整数值，且满足AC+BD＝6．试求当AC，BD的长度为多少时，筝形ABCD的面积有最大值，最大值是多少？28．（8分）（2022春•德阳期末）已知，如图，矩形ABCD中，AD＝3，DC＝4，菱形EFGH的三个顶点E，G，H分别在矩形ABCD的边AB，CD，DA上，AH＝1，连接CF．（1）当点G在边DC上运动时；探究：点F到边DC的距离FM是否为定值？如果是，请求出这个值；如果不是，请说明理由．（2）当DG为何值时，△FCG的面积最小，并求出这个最小值．。

2023中考数学复习-专题27 二次函数(练透)(学生版)

专题27 二次函数1．（2020·北京市第六十六中学九年级期中）二次函数y ＝x 2﹣2x ，若点A （﹣1，y 1），B （2，y 2）是它图象上的两点，则y 1与y 2的大小关系是（）A ．y 1＜y 2B ．y 1＝y 2C ．y 1＞y 2D ．不能确定 2．（2020·武汉市第一初级中学九年级月考）将抛物线22y x =+向右平移1个单位，所得新抛物线的表达式为（）A ．()212y x =-+B ．()212y x =++C ．21y x =+D ．23y x =+． 3．（2022·安徽芜湖·九年级期中）抛物线y ＝(x ﹣1)2+2的顶点坐标是（） A ．(1，2) B ．(1，﹣2) C ．(﹣1，2) D ．(﹣1，﹣2) 4．（2022·西藏中考真题）将抛物线y ＝（x ﹣1）2＋2向左平移3个单位长度，再向下平移4个单位长度所得到的抛物线的解析式为（）A ．y ＝x 2﹣8x ＋22B ．y ＝x 2﹣8x ＋14C ．y ＝x 2＋4x ＋10D ．y ＝x 2＋4x ＋2 5．（2022·辽宁葫芦岛市·九年级期中）已知0a ≠，在同一直角坐标系中，函数y ax =与2y ax =的图象有可能是（）A ．B ．C ．D ． 6．（2022·武汉一初慧泉中学九年级开学考试）抛物线y ＝2x 2与y ＝－2x 2相同的性质是（） A ．开口向下 B ．对称轴是y 轴 C ．有最低点 D ．对称轴是x 轴 7．（2022·广西贺州市·九年级期中）二次函数y =ax 2+bx +c （a ≠0）的部分图象如图，图象过点（-1，0），对称轴为直线x =2，下列结论：①4a +b =0；②9a +c ＞3b ；③8a +7b +2c ＞0；④5a +c =0；⑤当x ＞-1时，y 的值随x 值的增大而增大．其中正确的结论有（）A ．2个B ．3个C ．4个D ．5个8．（2022·合肥市第四十五中学）二次函数y ＝ax 2＋bx ＋c 的图象过点（﹣1，0），对称轴为直线x ＝2，若a ＞0，则下列结论错误的是（）A ．当x ＞2时，y 随着x 的增大而增大B ．（a ＋c ）2＝b 2C ．若A （x 1，m ）、B （x 2，m ）是抛物线上的两点，当x ＝x 1＋x 2时，y ＝cD ．若方程a （x ＋1）（5﹣x ）＝﹣1的两根为x 1、x 2，且x 1＜x 2，则﹣1＜x 1＜5＜x 2 9．（2022·福建厦门双十中学思明分校九年级期末）已知抛物线y ＝x 2﹣2bx +2b 2﹣4c （其中x 是自变量）经过不同两点A (1﹣b ，m )，B （2b +c ，m ），那么该抛物线的顶点一定不可能在下列函数中（）的图象上．A ．y ＝x +2B ．y ＝﹣x +2C ．y ＝﹣2x +1D ．y ＝2x +1 10．（2022·四川德阳五中）如图，以扇形OAB 的顶点O 为原点，半径OB 所在的直线为x 轴的正半轴建立平面直角坐标系，点B 的坐标为（2，0），若抛物线y ＝12x 2+k 与扇形OAB 的边界总有两个公共点，则实数的取值范围是（）A ．﹣2＜k ＜12 B ．﹣2＜k ＜﹣12 C ．﹣2＜k ＜0 D ．﹣2＜k 2 1二、填空题11．（2022·浙江衢州市·九年级期中）已知二次函数y ＝﹣（x ﹣a ）2＋a ＋2，当a 取不同的值时，顶点在一条直线上，这条直线的解析式是________．抛物线与y 轴交点为C ，当﹣1≤a ≤2时，C 点经过的路径长为________．12．（2022·北京市陈经纶中学分校九年级月考）已知关于x 的方程mx 2＋2x ＋5m ＝0有两个不相等的实数根12,x x ，且122x x <<，则实数m 的取值范围为________．13．（2022·全国九年级专题练习）正方形ABCD 的边长为1cm ，M 、N 分别是BC 、CD 上两个动点，且始终保持AM ⊥MN ，当BM ＝_______cm 时，四边形ABCN 的面积最大，最大面积为__________cm 2．14．（2022·深圳市新华中学九年级期末）如图，已知抛物线2y ax bx c =++与直线y kx m =+交于(3,1)A --、(0,3)B 两点，则关于x 的不等式2ax bx c kx m ++>+的解集是__________．15．（2022·深圳市宝安中学（集团）九年级）抛物线()212y x =--+是由原抛物线先向左平移3个单位，再向下平移2个单位得到，则原抛物线解析式为______．三、解答题16．（2022·浙江衢州市·九年级期中）已知抛物线y ＝x 2＋bx ＋c 的图象经过A （﹣1，12），B （0，5）．（1）求抛物线解析式；（2）试判断该二次函数的图象是否经过点（1，2）．17．（2022·辽宁葫芦岛市·九年级期中）如图，在平面直角坐标系中，∠AOB ＝90°，AO ＝BO ，点A 的坐标为（1-，3）．（1）求点B 的坐标；（2）抛物线2y ax bx =+经过点A 、B ，求它的解析式．18．（2022·河南省淮滨县第一中学九年级开学考试）已知二次函数2316y x bx c =-++的图象经过()0,3A ，94,2B ⎛⎫-- ⎪⎝⎭两点，求b ，c 的值． 19．（2022·建昌县教师进修学校九年级）如图，抛物线212y x bx c =-++与x 轴交于A ，B 两点，与y 轴交于点C ，直线6y x =-+经过B ，C 两点，点P 为第一象限内抛物线上一点，射线OP 与线段BC 交于点D ．（1）求抛物线的解析式；（2）如图1，连接AC ，当∠OAC ＋∠ODC ＝180°时，求点P 的坐标；（3）过点B 作BE ⊥x 轴交射线OP 于点E ，当BDE 为等腰三角形时，直接写出点D 的坐标．20．（2022·北京市第十三中学九年级期中）如图，用一段长为40m 的篱笆围成一个一边靠墙的矩形花圃ABCD ，墙长28m ．设AB 长为x m ，矩形的面积为y m 2．（1）写出y 与x 的函数关系式；（2）当AB 长为多少米时，所围成的花圃面积最大？最大值是多少？21．（2022·辽宁葫芦岛市·九年级期中）新冠肺炎疫情期间，某药店进了一批口罩，每包进价10元，每包销售价定为25元时，每天销售1000包．经一段时间调查，发现每包销售单价每上涨1元，每天就少卖40包．其销售单价不低于进价，销售利润率不高于180% ．设每包销售价为x 元（x 为正整数）．（1）请直接写出x 的取值范围．（2）设每天的总利润为w 元，当每包销售价定为多少元时，该药店每天的利润最大？最大利润是多少元？22．（2022·广东深圳·明德学校九年级月考）已知二次函数2y ax bx c =++的图像与x 轴交于A (-3，0)，B (1，0)两点，与y 轴交于点C (0，-3)．（1）求抛物线的解析式；（2）D 是二次函数图像上位于第三象限内的点，求点D 到直线AC 的距离最大值时点D 的坐标；（3）M 是二次函数图像对称轴上的点，在二次函数图像上是否存在点N ，使以M 、N 、B 、O 为顶点的四边形是平行四边形？若有，请直接写出点N 的坐标23．（2022·辽宁葫芦岛市·九年级期中）如图，抛物线2=-++与y轴相交于点C（0，y x bx c3），与x正半轴相交于点B，负半轴相交于点A，A点坐标是（1-，0）．（1）求此抛物线的解析式；（2）如图1，点P在第一象限的抛物线上运动，过点P作PD⊥x轴，垂足是点D，线段BC把线段PD分成两条线段，其中一条线段长是另一条线段长的2倍，求P点坐标；（3）如图2，若点E在抛物线上，点F在x轴上，当以B、C、E、F为顶点的四边形是平行四边形时，请直接写出点F的坐标．。

2024中考数学一轮复习专题精练专题13 二次函数(学生版)

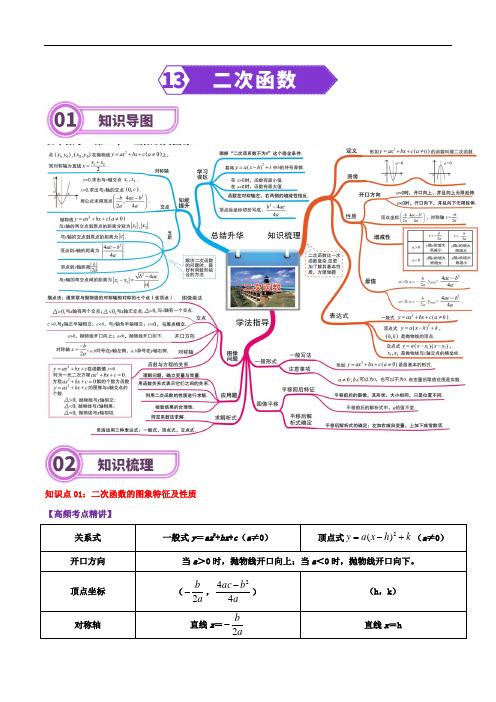
知识点01：二次函数的图象特征及性质【高频考点精讲】关系式一般式y ＝ax 2+bx +c （a ≠0）顶点式k h x a y +-=2)(（a ≠0）开口方向当a ＞0时，抛物线开口向上；当a ＜0时，抛物线开口向下。

顶点坐标（ab2-，a b ac 442-）（h ，k ）对称轴直线x ＝ab2-直线x ＝h增减性a＞0x＜ab2-时，y随x增大而减小；x＞ab2-时，y随x增大而增大。

x＜h时，y随x增大而减小；x＞h时，y随x增大而增大。

a＜0x＜ab2-时，y随x增大而增大；x＞ab2-时，y随x增大而增大。

x＜h时，y随x增大而增大；x＞h时，y随x增大而减小。

最值a＞0当x＝ab2-时，abacy442-=最小值。

当x＝h时，ky=最小值。

a＜0当x＝ab2-时，abacy442-=最大值。

当x＝h时，ky=最大值。

知识点02：二次函数图象与系数的关系【高频考点精讲】1．a决定抛物线的开口方向及大小（1）a＞0，抛物线开口向上；a＜0，抛物线开口向下。

（2）|a|越大，抛物线的开口越小；|a|越小，抛物线的开口越大。

2．a、b共同决定抛物线对称轴的位置（1）当b＝0时，对称轴x＝ab2-＝0，对称轴为y轴。

（2）当a、b同号时，对称轴x＝ab2-＜0，对称轴在y轴左侧。

（3）当a、b异号时，对称轴x＝ab2-＞0，对称轴在y轴右侧。

3．c 决定抛物线与y 轴的交点位置（1）当c ＝0时，抛物线过原点。

（2）当c ＞0时，抛物线与y 轴交于正半轴。

（3）当c ＜0时，抛物线与y 轴交于负半轴。

4．ac b 42-决定抛物线与x 轴的交点位置（1）当ac b 42-＝0时，抛物线与x 轴有唯一交点。

（2）当ac b 42-＞0时，抛物线与x 轴有两个交点。

（3）当ac b 42-＜0时，抛物线与x 轴没有交点。

5．特殊值（1）当x=1时，y=a+b+c ；当x=﹣1时，y=a-b+c ；当x=2时，y=4a+2b+c ；当x=﹣2时，y=4a-2b+c 。

专题二次函数的概念、图像与基本性质(学生版)

1专题23二次函数的概念、图像与基本性质题型一二次函数的定义1．如果函数22(2)27my m x x -=-+-是二次函数，则m 的取值范围是()A ．2m =±B ．2m =C ．2m =-D ．m 为全体实数2．下列函数中是二次函数的是()A ．222(1)2y x x =--B ．235s t t =--+C ．2y ax bx c=++D ．22y x x -=-3．函数||1(1)55m y m x x +=++-是二次函数，则m =．4．已知函数22()(1)22y m m x m x m =-+-+-．（1）若这个函数是二次函数，求m 的取值范围．（2）若这个函数是一次函数，求m 的值．（3）这个函数可能是正比例函数吗？为什么？5．在函数①2y ax bx c =++，②22(1)y x x =--，③2255y x x=-，④22y x =-+中，y 关于x 的二次函数是．（填写序号）2题型二二次函数的图像与性质6．二次函数241y x x =++的图象的对称轴是()A ．2x =B ．4x =C ．2x =-D ．4x =-7．抛物线22(1)6y x =-+的顶点坐标是()A ．(2,6)B ．(1,6)C ．(2,1)D ．(1,6)-8．如果0a <，0b >，0c >，那么二次函数2y ax bx c =++的图象大致是()A ．B ．C ．D ．9．对于二次函数22(3)y x =-+的图象，下列说法正确的是()A ．开口向上B ．对称轴是直线3x =-C ．当4x >-时，y 随x 的增大而减小D ．顶点坐标为(2,3)--10．已知1(A x ，1)y ，2(B x ，2)y 是22(0)y ax x c a =-+≠上的两点，则下列命题正确的是()A ．若120x x >>时，12y y c >>，则开口一定向下B ．若120x x <<时，12y y c >>，则开口一定向上C ．若120x x >>时，12y c y >>，则开口一定向上D ．若120x x <<时，12y y c >>，则开口一定向下11．在平面直角坐标系中，抛物线22221y x mx m m =-+++的顶点一定不在()A ．第一象限B ．第二象限C ．第三象限D ．第四象限12．二次函数2y ax bx c =++的图象如图所示，则下列结论正确的是()A ．0abc >B ．0a b c ++=C ．420a b c -+<D ．240b ac -<313．已知函数2|3|y x =-的大致图像如图所示，如果方程2|3|(x m m -=为实数）有4个不相等的实数根，则m 的取值范围是．14．若直线(y b b =为实数）与函数2|43|y x x =-+的图象至少有三个公共点，则实数b 的取值范围是()A ．01b 的图象过1(3,)A y -，2(1,)B y -，3(2,)C y ，4(4,)D y 四个点，下列说法一定正确的是()A ．若120y y >，则340y y >B ．若140y y >，则230y y >C ．若240y y <，则130y y <D ．若340y y <，则120y y <17．若点1(1,)A y -，2(2,)B y ，3(3,)C y 在抛物线228y x x c =-++的图象上，则1y ，2y ，3y 的大小关系是()A ．321y y y <的图象经过点(1,)A p -，(3,)B q ，且p q <，则m 的取值范围是()A ．1m - B ．1m <C ．11m -< D ．1m >19．若二次函数2||y a x bx c =++的图象过不同的五点(,)A m n ，(3,)B m n -，1(0,)C y，D 2)y ，3(2,)E y ，则1y ，2y ，3y 的大小关系是()A ．123y y y <，则12y y >B ．若122x x +<，则12y y >C ．若122x x +>-，则12y y >D ．若122x x +<-，则12y y <421．在平面直角坐标系中，抛物线2y x =的图象如图所示．已知A 点坐标为(1,1)，过点A 作1//AA x 轴交抛物线于点1A ，过点1A 作12//A A OA 交抛物线于点2A ，过点2A 作23//A A x 轴交抛物线于点3A ，过点3A 作34//A A OA 交抛物线于点4A ⋯，依次进行下去，则点99A的坐标为．题型三函数图像的平移、对称22．将抛物线22(1)3y x =--向右移动2个单位，再向下移动3个单位，得到的抛物线的解析式为()A ．22(1)y x =+B ．22(1)6y x =+-C ．22(3)y x =-D ．22(3)6y x =--23．把二次函数23y x =的图象先向左平移3个单位长度，再向下平移5个单位长度，得到的图象的解析式为()A ．23(3)5y x =-+B ．23(3)5y x =++C ．23(3)5y x =--D ．23(3)5y x =+-24．在平面直角坐标系中，抛物线(2)(4)y x x =+-经变换后得到抛物线(2)(4)y x x =-+，则下列变换正确的是()A ．向左平移6个单位B ．向右平移6个单位C ．向左平移2个单位D ．向右平移2个单位25．如图，在平面直角坐标系中，抛物线213y x =经过平移得到抛物线2y ax bx =+，其对称轴与两段抛物线所围成的阴影部分的面积为23，则a 、b 的值分别为()A ．13，43B ．13，23-C ．13，43-D ．13-，43526．在平面直角坐标系中，有两条抛物线关于原点中心对称，且它们的顶点相距10个单位长度，若其中一条抛物线的函数表达式为28y x x m =++，则m 的值为()A ．13-或19-B ．13-或19C ．13或19D ．13或19-27．在同一平面直角坐标系中，若抛物线2(22)69y x m n x n =--+-+与22(5)y x m n x m =+-+关于x 轴对称，则22m n +的值为()A ．13B ．18C ．24D ．3628．已知一个二次函数的图象经过点(2,2)，顶点为(1,1)--，将该函数图象向右平移，当他再次经过点(2,2)时，所得抛物线表达式为()A ．21(5)13y x =--+B ．21(5)13y x =--C ．21(4)103y x =+-D ．23(7)1y x =--29．关于抛物线21(1)y x =+与22(1)y x =-，下列说法不正确的是()A ．图象1y 与2y 的开口方向相同B ．1y 与2y 的图象关于y 轴对称C ．图象2y 向左平移2个单位可得到1y 的图象D ．图象1y 绕原点旋转180︒可得到2y 的图象30．如图，已知点(3,0)A ，(1,0)B ，两点(3,9)C -，(2,4)D 在抛物线2y x =上，向左或向右平移抛物线后，C ，D 的对应点分别为C '，D '．当四边形ABC D ''的周长最小时，抛物线的解析式为．。

第26章专题04二次函数系数、对称和最值重难点专练(学生版)

专题04二次函数系数、对称和最值重难点专练（学生版）学校:___________姓名：___________班级：___________考号：___________一、单选题1．（2021·上海九年级一模）如图所示是二次函数()20y ax bx c a =++≠图像的一部分，那么下列说法中不正确的是（）．A ．0ac 2．（2021·上海九年级专题练习）己知二次函数()20y ax bx c a =++≠的图象如图所示，那么a 、c 满足（）A ．a ＞0，c ＞0B ．a ＞0，c ＜0C ．a ＜0，c ＞0D ．a ＜0，c ＜03．（2020·上海市曹杨二中附属江桥实验中学九年级期中）如果二次函数2(0)y ax bx c a =++≠的图像如图所示，那么（）A ．a 0,b 0,c 0<>>B ．0,0,0a b c >>>C ．0,0,0a b c ><<D ．0,0,0a b c >><4．（2019·上海九年级一模）如果抛物线()22y a x =+开口向下，那么a 的取值范围为（） A ．2a >B ．2a <C ．2a >-D ．2a <-5．（2019·上海市民办新北郊初级中学九年级期中）在同一直角坐标系中，函数y mx m =+和222y mx x =-++的图象可能是（）A ．B ．C ．D ．6．（2020·上海民办华二浦东实验学校九年级期中）如果二次函数2y ax bx c =++的图像如图所示，那么下列判断正确的是（）A ．0a <，0b <，0c C ．0a <，0b >，0c <D ．0a <，0b >，0c >7．（2021·上海九年级专题练习）抛物线y ＝ax 2+bx +c （a ≠0）对称轴为直线x ＝﹣1，其部分图象如图所示，则下列结论： ①b 2﹣4ac ＞0；①2a ＝b ；①t （at +b ）≤a ﹣b （t 为任意实数）； ①3b +2c ＜0； ①点（﹣72，y 1），（32-，y 2），（54，y 3）是该抛物线上的点，且y 1＜y 3＜y 2，其中正确结论的个数是（）A ．5B ．4C ．3D ．28．（2020·上海九年级月考）已知点(2,)A a -，(2,)B b ，(4,)C c 是抛物线24y x x =-上的三点，则a ，b ，c 的大小关系为（） A ．b c a >> B ．b a c >> C ．c a b >> D ．a c b >>二、填空题9．（2019·上海市民办新竹园中学九年级月考）已知抛物线2y x bx c =++经过点()0,5A、()4,5B ，那么此抛物线的对称轴是___________．10．（2021·上海九年级专题练习）如果一条抛物线经过点A （2，5），B （﹣3，5），那么它的对称轴是直线_____．11．（2020·上海九年级一模）如果抛物线经过点(1,0)A -和点()5,0B ，那么这条抛物线的对称轴是直线___________．12．（2020·上海）已知二次函数2228y a x a x a =++（a 是常数，a ≠0），当自变量x 分别取-6、-4时，对应的函数值分别为y 1、y 2，那么y 1、y 2的大小关系是：y 1__ y 2（填“>”、“<”或“=”）．13．（2019·上海中考模拟）若点A （﹣1，7）、B （5，7）、C （﹣2，﹣3）、D （k ，﹣3）在同一条抛物线上，则k 的值等于_____．14．（2020·上海九年级专题练习）如果抛物线经过点 A (2,5) 和点 B (-4,5) ，那么这条抛物线的对称轴是直线_____．15．（2018·上海虹口区·中考模拟）如果点A （2，﹣4）与点B （6，﹣4）在抛物线y=ax 2+bx+c（a≠0）上，那么该抛物线的对称轴为直线_____．16．（2021·上海九年级一模）如果抛物线l 经过点()2,0A -和()5,0B ，那么该抛物线的对称轴是直线________．17．（第三章函数与分析（4）函数的图像和性质-备战2021年中考数学考点一遍过（上海专用））二次函数2y ax bx c =++（0a ≠）中，函数y 与自变量x 的部分对应值如下表，则m 的值为 _________．18．（2021·上海）方程()200++=≠ax bx c a 的两根为-5和3，那么抛物线()20y ax bx c a =++≠的对称轴是直线________．19．（2020·上海市静安区实验中学九年级课时练习）二次函数(2)(4)y x x =-+-图像的顶点坐标是__________________．20．（2021·上海九年级专题练习）如图，正方形ABCD 的边长为1，点E 为BC 边上的一动点（不与B ，C 重合），过点E 作EF AE ⊥，交CD 于F ．则线段CF 长度的最大值为__________．21．（2020·上海民办华二浦东实验学校九年级期中）抛物线24y x x =+的最低点坐标是__________．22．（2021·上海九年级一模）二次函数22y x x m =++图像上的最低点的横坐标为_________________．23．（2019·上海同济大学实验学校）关于x 的代数式24x x m -++有最大值2，则m =______，取得最大值时x =______．24．（2020·江苏徐州市·）在平面直角坐标系中，点A 的坐标为(1，0)，点B 的坐标为(m ，5﹣m)，当AB 的长最小时，m 的值为_____25．（2019·上海八年级课时练习）已知实数x 、y 满足2210x x y ++-=，则2x y +的最大值为______26．（2019·上海中考模拟）如果抛物线y ＝（3﹣m ）x 2﹣3有最高点，那么m 的取值范围是_____．27．（2020·上海普陀区·九年级月考）沿着x 轴正方向看，如果抛物线2(2)y a x =-在对称轴左侧的部分是下降的，那么a 的取值范围是__________．28．（2021·上海九年级专题练习）如果抛物线()223y a x x a =-++的开口向下，那么a的取值范围是_________ ．29．（2020·上海市静安区实验中学九年级课时练习）二次函数2()y a x m =++k 的大致图像如图，那么a_____0，m____0（填“＞”或“＜”）．30．（2021·上海九年级专题练习）已知二次函数y ＝ax 2+bx +c 的图象如图所示，对称轴为直线x ＝1，则下列结论： ①abc ＞0；①方程ax 2+bx +c ＝0的两根是x 1＝﹣1，x 2＝3； ①2a +b ＝0； ①4a 2+2b +c ＜0，其中正确结论的序号为_____．三、解答题31．（专题12二次函数背景下的相似三角形-决胜2020年中考数学压轴题全揭秘精品（上海专用））如图，已知抛物线y＝ax2+bx+c经过原点O（0，0）、A（2，0），直线y＝2x 经过抛物线的顶点B，点C是抛物线上一点，且位于对称轴的右侧，联结BC、OC、AB，过点C作CE①x轴，分别交线段OB、AB于点E、F．（1）求抛物线的表达式；（2）当BC＝CE时，求证：①BCE①①ABO；（3）当①CBA＝①BOC时，求点C的坐标．32．（2019·上海江湾初级中学九年级三模）如图，已知抛物线y＝﹣x2+bx+c与一直线相交于A（1，0）、C（﹣2，3）两点，与y轴交于点N，其顶点为D．（1）求抛物线及直线AC的函数关系式；（2）若P是抛物线上位于直线AC上方的一个动点，求①APC的面积的最大值及此时点P的坐标；（3）在对称轴上是否存在一点M，使①ANM的周长最小．若存在，请求出M点的坐标和①ANM周长的最小值；若不存在，请说明理由．33．（2017·上海奉贤区·中考模拟）如图，在平面直角坐标系xOy 中，抛物线2y x bx c =-++经过点A(3,0）和B （2,3）．过点A 的直线与y 轴的负半轴相交于点C ，且tan CAO ∠=13．（1）求这条抛物线的表达式及对称轴；（2）连接AB 、BC ，求ABC ∠的正切值；（3）若点D 在x 轴下方的对称轴上，当ABC S ∆=ADC S ∆时，求点D 的坐标．34．（2019·上海市位育实验学校九年级一模）抛物线y=﹣x 2+bx+c 经过点A 、B 、C ，已知A （﹣1，0），C （0，3）．（1）求抛物线的解析式；（2）如图1，P 为线段BC 上一点，过点P 作y 轴平行线，交抛物线于点D ，当①BDC 的面积最大时，求点P 的坐标；（3）如图2，抛物线顶点为E ，EF①x 轴于F 点，M （m ，0）是x 轴上一动点，N 是线段EF 上一点，若①MNC=90°，请指出实数m 的变化范围，并说明理由．35．（2021·上海九年级专题练习）某企业接到了一批零件加工任务，要求在20天内完成，这批零件的出厂价为每个6元，为按时完成任务，该企业招收了新工人．6天的培训期内，新工人小李第x天能加工80x个零件；培训后小李第x天加工的零件数量为()50200+x个．（1）小李第几天加工零件数量为650个？（2）如图，设第x天每个零件的加工成本是P元，P与x之间的关系可用图中的函数图象来刻画．若小李第x天创造的利润为w元，求w与x的函数表达式，并求出第几天的利润最大，最大利润是多少？（利润=出厂价-成本价）36．（2020·上海宝山区·九年级期中）如图，在平面直角坐标系中，抛物线223(0)y ax ax a a=>﹣﹣与x轴交于A、B两点（点A在点B左侧），经过点A的直线l：y kx b=+与y轴交于点C，与抛物线的另一个交点为D，且4CD AC=．（1）直接写出点A的坐标，并用含a的式子表示直线l的函数表达式（其中k、b用含a的式子表示）．（2）点E为直线l下方抛物线上一点，当ADE的面积的最大值为254时，求抛物线的函数表达式；（3）设点P是抛物线对称轴上的一点，点Q在抛物线上，以点A、D、P、Q为顶点的四边形能否为矩形？若能，求出点P的坐标；若不能，请说明理由．。

2025中考数学二次函数压轴题专题练习18 二次函数与几何交点问题(学生版+解析版)

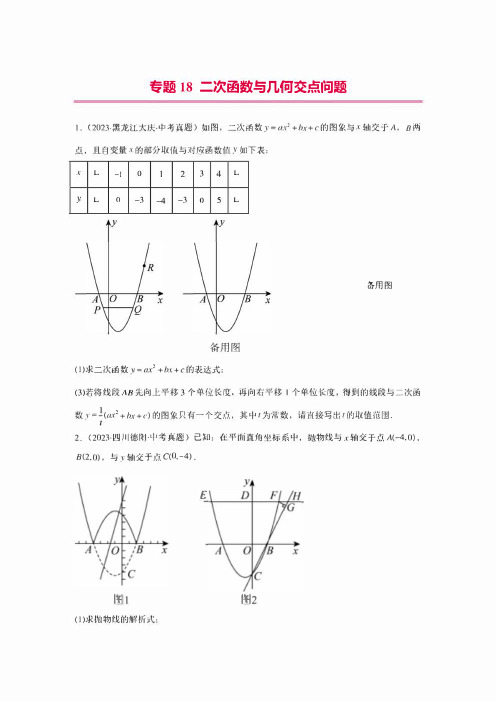
专题18二次函数与几何交点间题1.(2023·黑龙江大庆中考真题）如图，二次函数y = a:x.2+bx+c的图象与X轴交千A,B两点，且自变量X 的部分取值与对应函数值Y如下表：XL -]。

I2 34L yL。

-3-4-3。

5Ly y备用图备用图(I)求二次函数y=ax 2+bx+c的表达式；(3)若将线段A B 先向上平移3个单位长度，再向右平移l 个单位长度，得到的线段与二次函数y ＝一（釭2+bx+c)的图象只有一个交点，其中（为常数，请直接写出t的取值范围2.(2023四川德阳中考真题）已知：在平面直角坐标系中，抛物线与x轴交于点A(-4，0)'B (2,0)，与y 轴交千点C (O,-4)．1付l(I)求抛物线的解析式；E -阳2(2)如图1，如果把抛物线x 轴下方的部分沿x 轴翻折180°,抛物线的其余部分保持不变，得到一个新图象．当平面内的直线y＝妇＋6与新图象有三个公共点时，求k的值；3.(2023山东济南中考真题）在平面直角坐标系xOy 中，正方形ABCD 的顶点A,B 在X轴上，C(2,3),D(-1,3) 抛物线y ＝成－2少＋c(a«))与X 轴交于点E(-2,0)和点Fy y(1)如图l ，若抛物线过点C,求抛物线的表达式和点F 的坐标；(2)如图2,在（I)的条件下，连接CF,作直线CE,平移线段CF,使点C 的对应点P落在直线CE 上，点F 的对应点Q落在抛物线上，求点Q的坐标；(3)若抛物线y=ax 2-2ax+c(a<0)与正方形ABCD 恰有两个交点，求(1的取值范围，4.(2023山东日照中考真题）在平面百角坐标系xOy 内，抛物线y ＝动X江女仄＋2(a>0)交y轴于点C ，过点C作x轴的平行线交该抛物线千点D.l ｀一-x(1)求点C,D的坐标；(3)坐标平面内有两点£(�.a +1} F (5,a + I )，以线段EF 为边向上作正方形EFGH.＠若a=l,求正方形EFGH 的边与抛物线的所有交点坐标；＠当正方形EFGH 的边与该抛物线有且仅有两个交点，且这两个交点到x 轴的距离之差为－5时，求a的值5.(2022吉林长春中考真题）在平面直角坐标系中，抛物线y = x 1-bx (b是常数）经过点(2,0)点A在抛物线上，且点A的横坐标为m(m;1:0)以点A为中心，构造正方形PQMN, P Q=2|『111，且PQ.lx轴．(l)求该抛物线对应的函数表达式：(2若点B是抛物线上一点，且在抛物线对称轴左侧．过点B作x轴的平行线交抛物线千另一点C,连按BC.当BC=4时，求点B的坐标：(3若m>O,当抛物线在正方形内部的点的纵坐标y随x的增大而增大时，或者y随x的增大而减小时，求m的取值范围：3(4)当抛物线与正方形PQMN的边只有2个交点，且交点的纵坐标之差为一时，且接写出m4的值6.(2022湖南永州中考真题）已知关于X的函数y= ax2 +bx+c(1)若a.=l,函数的图象经过点(1,-4)和点(2,I)，求该函数的表达式和最小值；(2)若a=l,b=-2, c=m十l时，函数的图象与X轴有交点，求m的取值范围．(3)阅读下面材料：设a>0,函数图象与X轴有两个不同的交点A,B,若A,8两点均在原点左侧，探究系数a, b, c应满足的条件，根据函数图像，思考以下三个方面：＠因为函数的图象与X轴有两个不同的交点，所以6.=b2 -4ac> 0:＠因为A,8两点在原点左侧，所以x=O对应图象上的点在X轴上方，即c>O:＠上述两个条件还不能确保A,8两点均在原点左侧，我们可以通过抛物线的对称轴位置来b进一步限制抛物线的位置：即需－一又0.2a综上所述，系数a,b, c应满足的条件可归纳为：请根据上面阅谅材料，类比解决下而问题：a>O tJ.=li-4ac>0c>Ob -—<02a若函数y= ax2 -2x+3的图象在直线x=1的右侧与人轴有且只有一个交点，求U的取值范围．7.(2022湖南衡阳中考真题）如图，已知抛物线y=x'-x-2交X轴千A、B两点，将该抛物线位千X轴下方的部分沿X轴翻折，其余部分不变，得到的新图象记为“图象W"，图象W交Y轴千点c.｀｀＼｀x， I I、一，，(］)写出图象W位于线段AB上方部分对应的函数关系式：(2)若直线y=-x+b与图象W有三个交点，请结合图象，直按写出b的值：(3)p为X轴正半轴上一动点，过点P作PM ff y轴交直线BC千点M,交图象W于点N,是否存在这样的点P,使..CMN与60BC相似？若存在，求出所有符合条件的点P的坐标；若不存在，请说明理由．专题18二次函数与几何交点间题1.(2023·黑龙江大庆中考真题）如图，二次函数y = a:x .2+bx+c的图象与X轴交千A,B两点，且自变量X 的部分取值与对应函数值Y如下表：X L -]。

二次函数解答压轴题(共62题)(学生版)-2023年中考数学真题分项汇编(全国通用)

二次函数解答压轴题(62题)一、解答题1(2023·浙江绍兴·统考中考真题)已知二次函数y=-x2+bx+c．(1)当b=4,c=3时，①求该函数图象的顶点坐标．②当-1≤x≤3时，求y的取值范围．(2)当x≤0时，y的最大值为2；当x>0时，y的最大值为3，求二次函数的表达式．2(2023·浙江·统考中考真题)已知点-m,0和3m,0在二次函数y=ax2+bx+3(a,b是常数，a≠0)的图像上．(1)当m=-1时，求a和b的值；(2)若二次函数的图像经过点A n,3且点A不在坐标轴上，当-2<m<-1时，求n的取值范围；(3)求证：b2+4a=0．3(2023·浙江嘉兴·统考中考真题)在二次函数y=x2-2tx+3(t>0)中，(1)若它的图象过点(2,1)，则t的值为多少？(2)当0≤x≤3时，y的最小值为-2，求出t的值：(3)如果A(m-2,a),B(4,b),C(m,a)都在这个二次函数的图象上，且a<b<3，求m的取值范围．4(2023·浙江杭州·统考中考真题)设二次函数y=ax2+bx+1，(a≠0，b是实数)．已知函数值y和自变量x的部分对应取值如下表所示：x⋯-10123⋯y⋯m1n1p⋯(1)若m=4，求二次函数的表达式；(2)写出一个符合条件的x的取值范围，使得y随x的增大而减小．(3)若在m、n、p这三个实数中，只有一个是正数，求a的取值范围．5(2023·湖南常德·统考中考真题)如图，二次函数的图象与x轴交于A-1,0，B5,0两点，与y轴交于点C，顶点为D．O为坐标原点，tan∠ACO=1 5．(1)求二次函数的表达式；(2)求四边形ACDB的面积；(3)P是抛物线上的一点，且在第一象限内，若∠ACO=∠PBC，求P点的坐标．6(2023·山东烟台·统考中考真题)如图，抛物线y=ax2+bx+5与x轴交于A,B两点，与y轴交于点C,AB=4．抛物线的对称轴x=3与经过点A的直线y=kx-1交于点D，与x轴交于点E．(1)求直线AD及抛物线的表达式；(2)在抛物线上是否存在点M，使得△ADM是以AD为直角边的直角三角形?若存在，求出所有点M的坐标；若不存在，请说明理由；(3)以点B为圆心，画半径为2的圆，点P为⊙B上一个动点，请求出PC+1PA的最小值．27(2023·江苏苏州·统考中考真题)如图，二次函数y=x2-6x+8的图像与x轴分别交于点A,B(点A 在点B的左侧)，直线l是对称轴．点P在函数图像上，其横坐标大于4，连接PA,PB，过点P作PM⊥l，垂足为M，以点M为圆心，作半径为r的圆，PT与⊙M相切，切点为T．(1)求点A,B的坐标；(2)若以⊙M的切线长PT为边长的正方形的面积与△PAB的面积相等，且⊙M不经过点3,2，求PM长的取值范围．8(2023·山东东营·统考中考真题)如图，抛物线过点O0,0，矩形ABCD的边AB在线段，E10,0OE上(点B在点A的左侧)，点C，D在抛物线上，设B t,0，当t=2时，BC=4．(1)求抛物线的函数表达式；(2)当t为何值时，矩形ABCD的周长有最大值？最大值是多少？(3)保持t=2时的矩形ABCD不动，向右平移抛物线，当平移后的抛物线与矩形的边有两个交点G，H，且直线GH平分矩形ABCD的面积时，求抛物线平移的距离．9(2023·内蒙古通辽·统考中考真题)在平面直角坐标系中，已知抛物线y=ax2+83x+c a≠0与x轴交于点A1,0和点B，与y轴交于点C0,-4．(1)求这条抛物线的函数解析式；(2)P是抛物线上一动点(不与点A，B，C重合)，作PD⊥x轴，垂足为D，连接PC．①如图，若点P在第三象限，且tan∠CPD=2，求点P的坐标；②直线PD交直线BC于点E，当点E关于直线PC的对称点E 落在y轴上时，请直接写出四边形PECE 的周长．10(2023·四川自贡·统考中考真题)如图，抛物线y=-43x2+bx+4与x轴交于A(-3,0)，B两点，与y轴交于点C．(1)求抛物线解析式及B，C两点坐标；(2)以A，B，C，D为顶点的四边形是平行四边形，求点D坐标；(3)该抛物线对称轴上是否存在点E，使得∠ACE=45°，若存在，求出点E的坐标；若不存在，请说明理由．11(2023·四川达州·统考中考真题)如图，抛物线y =ax 2+bx +c 过点A -1,0 ,B 3,0 ,C 0,3 ．(1)求抛物线的解析式；(2)设点P 是直线BC 上方抛物线上一点，求出△PBC 的最大面积及此时点P 的坐标；(3)若点M 是抛物线对称轴上一动点，点N 为坐标平面内一点，是否存在以BC 为边，点B 、C 、M 、N 为顶点的四边形是菱形，若存在，请直接写出点N 的坐标；若不存在，请说明理由．12(2023·四川泸州·统考中考真题)如图，在平面直角坐标系xOy中，已知抛物线y=ax2+2x+c与坐标轴分别相交于点A，B，C0,6三点，其对称轴为x=2．(1)求该抛物线的解析式；(2)点F是该抛物线上位于第一象限的一个动点，直线AF分别与y轴，直线BC交于点D，E．①当CD=CE时，求CD的长；②若△CAD，△CDE，△CEF的面积分别为S1，S2，S3，且满足S1+S3=2S2，求点F的坐标．13(2023·全国·统考中考真题)如图，在平面直角坐标系中，抛物线y=-x2+2x+c经过点A(0,1)．点P，Q在此抛物线上，其横坐标分别为m,2m(m>0)，连接AP，AQ．(1)求此抛物线的解析式．(2)当点Q与此抛物线的顶点重合时，求m的值．(3)当∠PAQ的边与x轴平行时，求点P与点Q的纵坐标的差．(4)设此抛物线在点A与点P之间部分(包括点A和点P)的最高点与最低点的纵坐标的差为h1，在点A与点Q之间部分(包括点A和点Q)的最高点与最低点的纵坐标的差为h2．当h2-h1=m时，直接写出m的值．14(2023·重庆·统考中考真题)如图，在平面直角坐标系中，抛物线y=14x2+bx+c与x轴交于点A，B，与y轴交于点C，其中B3,0，C0,-3．(1)求该抛物线的表达式；(2)点P是直线AC下方抛物线上一动点，过点P作PD⊥AC于点D，求PD的最大值及此时点P的坐标；(3)在(2)的条件下，将该抛物线向右平移5个单位，点E为点P的对应点，平移后的抛物线与y轴交于点F，Q为平移后的抛物线的对称轴上任意一点．写出所有使得以QF为腰的△QEF是等腰三角形的点Q的坐标，并把求其中一个点Q的坐标的过程写出来．15(2023·四川凉山·统考中考真题)如图，已知抛物线与x轴交于A1,0两点，与y轴交于和B-5,0点C．直线y=-3x+3过抛物线的顶点P．(1)求抛物线的函数解析式；(2)若直线x=m-5<m<0与抛物线交于点E，与直线BC交于点F．①当EF取得最大值时，求m的值和EF的最大值；②当△EFC是等腰三角形时，求点E的坐标．16(2023·四川成都·统考中考真题)如图，在平面直角坐标系xOy中，已知抛物线y=ax2+c经过点P (4,-3)，与y轴交于点A(0,1)，直线y=kx(k≠0)与抛物线交于B，C两点．(1)求抛物线的函数表达式；(2)若△ABP是以AB为腰的等腰三角形，求点B的坐标；(3)过点M(0,m)作y轴的垂线，交直线AB于点D，交直线AC于点E．试探究：是否存在常数m，使得OD⊥OE始终成立？若存在，求出m的值；若不存在，请说明理由．17(2023·安徽·统考中考真题)在平面直角坐标系中，点O是坐标原点，抛物线y=ax2+bx a≠0经过点A3,3，对称轴为直线x=2．(1)求a,b的值；(2)已知点B,C在抛物线上，点B的横坐标为t，点C的横坐标为t+1．过点B作x轴的垂线交直线OA于点D，过点C作x轴的垂线交直线OA于点E．(ⅰ)当0<t<2时，求△OBD与△ACE的面积之和；(ⅱ)在抛物线对称轴右侧，是否存在点B，使得以B,C,D,E为顶点的四边形的面积为32若存在，请求出点B的横坐标t的值；若不存在，请说明理由．18(2023·浙江金华·统考中考真题)如图，直线y =52x +5与x 轴，y 轴分别交于点A ,B ，抛物线的顶点P 在直线AB 上，与x 轴的交点为C ,D ，其中点C 的坐标为2,0 ．直线BC 与直线PD 相交于点E ．(1)如图2，若抛物线经过原点O ．①求该抛物线的函数表达式；②求BEEC的值．(2)连接PC ,∠CPE 与∠BAO 能否相等？若能，求符合条件的点P 的横坐标；若不能，试说明理由．19(2023·湖南·统考中考真题)如图，二次函数y=x2+bx+c的图象与x轴交于A，B两点，与y轴交于C点，其中B1,0．，C0,3(1)求这个二次函数的表达式；(2)在二次函数图象上是否存在点P，使得S△PAC=S△ABC若存在，请求出P点坐标；若不存在，请说明理由；(3)点Q是对称轴l上一点，且点Q的纵坐标为a，当△QAC是锐角三角形时，求a的取值范围．20(2023·四川遂宁·统考中考真题)在平面直角坐标系中，O 为坐标原点，抛物线y =14x 2+bx +c 经过点O (0，0)，对称轴过点B (2，0)，直线l 过点C 2,-2 ，且垂直于y 轴．过点B 的直线l 1交抛物线于点M 、N ，交直线l 于点Q ，其中点M 、Q 在抛物线对称轴的左侧．(1)求抛物线的解析式；(2)如图1，当BM :MQ =3:5时，求点N 的坐标；(3)如图2，当点Q 恰好在y 轴上时，P 为直线l 1下方的抛物线上一动点，连接PQ 、PO ，其中PO 交l 1于点E ，设△OQE 的面积为S 1，△PQE 的面积为S 2．求S2S 1的最大值．21(2023·四川眉山·统考中考真题)在平面直角坐标系中，已知抛物线y =ax 2+bx +c 与x 轴交于点A -3,0 ,B 1,0 两点，与y 轴交于点C 0,3 ，点P 是抛物线上的一个动点．(1)求抛物线的表达式；(2)当点P 在直线AC 上方的抛物线上时，连接BP 交AC 于点D ．如图1．当PDDB的值最大时，求点P 的坐标及PDDB的最大值；(3)过点P 作x 轴的垂线交直线AC 于点M ，连接PC ，将△PCM 沿直线PC 翻折，当点M 的对应点M '恰好落在y 轴上时，请直接写出此时点M 的坐标．22(2023·江西·统考中考真题)综合与实践问题提出：某兴趣小组开展综合实践活动：在Rt△ABC中，∠C=90°，D为AC上一点，CD=2，动点P 以每秒1个单位的速度从C点出发，在三角形边上沿C→B→A匀速运动，到达点A时停止，以DP为边作正方形DPEF设点P的运动时间为ts，正方形DPEF的而积为S，探究S与t的关系(1)初步感知：如图1，当点P由点C运动到点B时，①当t=1时，S=．②S关于t的函数解析式为．(2)当点P由点B运动到点A时，经探究发现S是关于t的二次函数，并绘制成如图2所示的图象请根据图象信息，求S关于t的函数解析式及线段AB的长．(3)延伸探究：若存在3个时刻t1,t2,t3(t1<t2<t3)对应的正方形DPEF的面积均相等．①t1+t2=；②当t3=4t1时，求正方形DPEF的面积．23(2023·新疆·统考中考真题)【建立模型】(1)如图1，点B 是线段CD 上的一点，AC ⊥BC ，AB ⊥BE ，ED ⊥BD ，垂足分别为C ，B ，D ，AB =BE ．求证：△ACB ≌△BDE ；【类比迁移】(2)如图2，一次函数y =3x +3的图象与y 轴交于点A 、与x 轴交于点B ，将线段AB 绕点B 逆时针旋转90°得到BC 、直线AC 交x 轴于点D ．①求点C 的坐标；②求直线AC 的解析式；【拓展延伸】(3)如图3，抛物线y =x 2-3x -4与x 轴交于A ，B 两点(点A 在点B 的左侧)，与y 轴交于C点，已知点Q (0，-1)，连接BQ ．抛物线上是否存在点M ，使得tan ∠MBQ =13，若存在，求出点M 的横坐标．24(2023·甘肃武威·统考中考真题)如图1，抛物线y=-x2+bx与x轴交于点A，与直线y=-x交于点B4,-4在y轴上．点P从点B出发，沿线段BO方向匀速运动，运动到点O时停止．，点C0,-4(1)求抛物线y=-x2+bx的表达式；(2)当BP=22时，请在图1中过点P作PD⊥OA交抛物线于点D，连接PC，OD，判断四边形OCPD 的形状，并说明理由．(3)如图2，点P从点B开始运动时，点Q从点O同时出发，以与点P相同的速度沿x轴正方向匀速运动，点P停止运动时点Q也停止运动．连接BQ，PC，求CP+BQ的最小值．25(2023·四川乐山·统考中考真题)已知x 1,y 1 ,x 2,y 2 是抛物C 1:y =-14x 2+bx (b 为常数)上的两点，当x 1+x 2=0时，总有y 1=y 2(1)求b 的值；(2)将抛物线C 1平移后得到抛物线C 2:y =-14(x -m )2+1(m >0)．探究下列问题：①若抛物线C 1与抛物线C 2有一个交点，求m 的取值范围；②设抛物线C 2与x 轴交于A ，B 两点，与y 轴交于点C ，抛物线C 2的顶点为点E ，△ABC 外接圆的圆心为点F ，如果对抛物线C 1上的任意一点P ，在抛物线C 2上总存在一点Q ，使得点P 、Q 的纵坐标相等．求EF 长的取值范围．26(2023·内蒙古·统考中考真题)如图，在平面直角坐标系中，抛物线y =-x 2+3x +1交y 轴于点A ，直线y =-13x +2交抛物线于B ,C 两点(点B 在点C 的左侧)，交y 轴于点D ，交x 轴于点E ．(1)求点D ,E ,C 的坐标；(2)F 是线段OE 上一点OF <EF ，连接AF ,DF ,CF ，且AF 2+EF 2=21．①求证：△DFC 是直角三角形；②∠DFC 的平分线FK 交线段DC 于点K ,P 是直线BC 上方抛物线上一动点，当3tan ∠PFK =1时，求点P 的坐标．27(2023·上海·统考中考真题)在平面直角坐标系xOy中，已知直线y=34x+6与x轴交于点A，y轴交于点B，点C在线段AB上，以点C为顶点的抛物线M：y=ax2+bx+c经过点B．(1)求点A，B的坐标；(2)求b，c的值；(3)平移抛物线M至N，点C，B分别平移至点P，D，联结CD，且CD∥x轴，如果点P在x轴上，且新抛物线过点B，求抛物线N的函数解析式．28(2023·江苏扬州·统考中考真题)在平面直角坐标系xOy中，已知点A在y轴正半轴上．(1)如果四个点0,0中恰有三个点在二次函数y=ax2(a为常数，且a≠0)的图象、-1,1、1,1、0,2上．①a=；②如图1，已知菱形ABCD的顶点B、C、D在该二次函数的图象上，且AD⊥y轴，求菱形的边长；③如图2，已知正方形ABCD的顶点B、D在该二次函数的图象上，点B、D在y轴的同侧，且点B在点D的左侧，设点B、D的横坐标分别为m、n，试探究n-m是否为定值．如果是，求出这个值；如果不是，请说明理由．(2)已知正方形ABCD的顶点B、D在二次函数y=ax2(a为常数，且a>0)的图象上，点B在点D的左侧，设点B、D的横坐标分别为m、n，直接写出m、n满足的等量关系式．29(2023·湖南岳阳·统考中考真题)已知抛物线Q1:y=-x2+bx+c与x轴交于A-3,0,B两点，交y 轴于点C0,3．(1)请求出抛物线Q1的表达式．(2)如图1，在y轴上有一点D0,-1，点E在抛物线Q1上，点F为坐标平面内一点，是否存在点E,F使得四边形DAEF为正方形？若存在，请求出点E,F的坐标；若不存在，请说明理由．(3)如图2，将抛物线Q1向右平移2个单位，得到抛物线Q2，抛物线Q2的顶点为K，与x轴正半轴交于点H，抛物线Q1上是否存在点P，使得∠CPK=∠CHK？若存在，请求出点P的坐标；若不存在，请说明理由．30(2023·湖南永州·统考中考真题)如图1，抛物线y =ax 2+bx +c (a ，b ，c 为常数)经过点F 0,5 ，顶点坐标为2,9 ，点P x 1,y 1 为抛物线上的动点，PH ⊥x 轴于H ，且x 1≥52．(1)求抛物线的表达式；(2)如图1，直线OP :y =y 1x 1x 交BF 于点G ，求S △BPG S △BOG的最大值；(3)如图2，四边形OBMF 为正方形，PA 交y 轴于点E ，BC 交FM 的延长线于C ，且BC ⊥BE ,PH =FC ，求点P 的横坐标．31(2023·山东枣庄·统考中考真题)如图，抛物线y=-x2+bx+c经过A(-1,0),C(0,3)两点，并交x轴于另一点B，点M是抛物线的顶点，直线AM与轴交于点D．(1)求该抛物线的表达式；(2)若点H是x轴上一动点，分别连接MH，DH，求MH+DH的最小值；(3)若点P是抛物线上一动点，问在对称轴上是否存在点Q，使得以D，M，P，Q为顶点的四边形是平行四边形？若存在，请直接写出所有满足条件的点Q的坐标；若不存在，请说明理由．32(2023·湖北随州·统考中考真题)如图1，平面直角坐标系xOy中，抛物线y=ax2+bx+c过点A(-1,0)，B(2,0)和C(0,2)，连接BC，点P(m,n)(m>0)为抛物线上一动点，过点P作PN⊥x轴交直线BC 于点M，交x轴于点N．(1)直接写出抛物线和直线BC的解析式；(2)如图2，连接OM，当△OCM为等腰三角形时，求m的值；(3)当P点在运动过程中，在y轴上是否存在点Q，使得以O，P，Q为顶点的三角形与以B，C，N为顶点的三角形相似(其中点P与点C相对应)，若存在，直接写出点P和点Q的坐标；若不存在，请说明理由．33(2023·四川内江·统考中考真题)如图，在平面直角坐标系中，抛物线y =ax 2+bx +c 与x 轴交于B 4,0 ，C -2,0 两点．与y 轴交于点A 0,-2 ．(1)求该抛物线的函数表达式；(2)若点P 是直线AB 下方抛物线上的一动点，过点P 作x 轴的平行线交AB 于点K ，过点P 作y 轴的平行线交x 轴于点D ，求与12PK +PD 的最大值及此时点P 的坐标；(3)在抛物线的对称轴上是否存在一点M ，使得△MAB 是以AB 为一条直角边的直角三角形：若存在，请求出点M 的坐标，若不存在，请说明理由．34(2023·湖南·统考中考真题)已知二次函数y =ax 2+bx +c a >0 ．(1)若a =1，c =-1，且该二次函数的图像过点2,0 ，求b 的值；(2)如图所示，在平面直角坐标系Oxy 中，该二次函数的图像与x 轴交于点A x 1,0 ，B x 2,0 ，且x 1<0<x 2，点D 在⊙O 上且在第二象限内，点E 在x 轴正半轴上，连接DE ，且线段DE 交y 轴正半轴于点F ，∠DOF =∠DEO ，OF =32DF ．①求证：DO EO=23．②当点E 在线段OB 上，且BE =1．⊙O 的半径长为线段OA 的长度的2倍，若4ac =-a 2-b 2，求2a +b 的值．35(2023·山西·统考中考真题)如图，二次函数y =-x 2+4x 的图象与x 轴的正半轴交于点A ，经过点A 的直线与该函数图象交于点B 1,3 ，与y 轴交于点C ．(1)求直线AB 的函数表达式及点C 的坐标；(2)点P 是第一象限内二次函数图象上的一个动点，过点P 作直线PE ⊥x 轴于点E ，与直线AB 交于点D ，设点P 的横坐标为m ．①当PD =12OC 时，求m 的值；②当点P 在直线AB 上方时，连接OP ，过点B 作BQ ⊥x 轴于点Q ，BQ 与OP 交于点F ，连接DF ．设四边形FQED 的面积为S ，求S 关于m 的函数表达式，并求出S 的最大值．36(2023·湖北武汉·统考中考真题)抛物线C1:y=x2-2x-8交x轴于A,B两点(A在B的左边)，交y 轴于点C．(1)直接写出A,B,C三点的坐标；(2)如图(1)，作直线x=t0<t<4，分别交x轴，线段BC，抛物线C1于D,E,F三点，连接CF．若△BDE 与△CEF相似，求t的值；(3)如图(2)，将抛物线C1平移得到抛物线C2，其顶点为原点．直线y=2x与抛物线C2交于O,G两点，过OG的中点H作直线MN(异于直线OG)交抛物线C2于M,N两点，直线MO与直线GN交于点P．问点P是否在一条定直线上？若是，求该直线的解析式；若不是，请说明理由．37(2023·湖北宜昌·统考中考真题)如图，已知A(0,2),B(2,0)．点E位于第二象限且在直线y=-2x 上，∠EOD=90°，OD=OE，连接AB，DE，AE，DB．(1)直接判断△AOB的形状：△AOB是三角形；(2)求证：△AOE≌△BOD；(3)直线EA交x轴于点C(t,0),t>2．将经过B，C两点的抛物线y1=ax2+bx-4向左平移2个单位，得到抛物线y2．①若直线EA与抛物线y1有唯一交点，求t的值；②若抛物线y2的顶点P在直线EA上，求t的值；③将抛物线y2再向下平移，2(t-1)2个单位，得到抛物线y3．若点D在抛物线y3上，求点D的坐标．38(2023·湖南郴州·统考中考真题)已知抛物线y=ax2+bx+4与x轴相交于点A1,0，与y，B4,0轴相交于点C．(1)求抛物线的表达式；(2)如图1，点P是抛物线的对称轴l上的一个动点，当△PAC的周长最小时，求PAPC的值；(3)如图2，取线段OC的中点D，在抛物线上是否存在点Q，使tan∠QDB=12若存在，求出点Q的坐标；若不存在，请说明理由．39(2023·湖北黄冈·统考中考真题)已知抛物线y =-12x 2+bx +c 与x 轴交于A ,B (4,0)两点，与y 轴交于点C (0,2)，点P 为第一象限抛物线上的点，连接CA ,CB ,PB ,PC ．(1)直接写出结果；b =，c =，点A 的坐标为，tan ∠ABC =；(2)如图1，当∠PCB =2∠OCA 时，求点P 的坐标；(3)如图2，点D 在y 轴负半轴上，OD =OB ，点Q 为抛物线上一点，∠QBD =90°，点E ，F 分别为△BDQ 的边DQ ,DB 上的动点，QE =DF ，记BE +QF 的最小值为m ．①求m 的值；②设△PCB 的面积为S ，若S =14m 2-k ，请直接写出k 的取值范围．40(2023·湖南·统考中考真题)如图，在平面直角坐标系中，抛物线y=ax2+x+c经过点A-2,0和点B4,0，且与直线l:y=-x-1交于D、E两点(点D在点E的右侧)，点M为直线l上的一动点，设点M 的横坐标为t．(1)求抛物线的解析式．(2)过点M作x轴的垂线，与拋物线交于点N．若0<t<4，求△NED面积的最大值．(3)抛物线与y轴交于点C，点R为平面直角坐标系上一点，若以B、C、M、R为顶点的四边形是菱形，请求出所有满足条件的点R的坐标．41(2023·四川·统考中考真题)如图1，在平面直角坐标系中，已知二次函数y=ax2+bx+4的图象与x 轴交于点A-2,0，B4,0，与y轴交于点C．(1)求抛物线的解析式；(2)已知E为抛物线上一点，F为抛物线对称轴l上一点，以B，E，F为顶点的三角形是等腰直角三角形，且∠BFE=90°，求出点F的坐标；(3)如图2，P为第一象限内抛物线上一点，连接AP交y轴于点M，连接BP并延长交y轴于点N，在点P运动过程中，OM+12ON是否为定值？若是，求出这个定值；若不是，请说明理由．42(2023·山东聊城·统考中考真题)如图①，抛物线y=ax2+bx-9与x轴交于点A-3,0，，B6,0与y轴交于点C，连接AC，BC.点P是x轴上任意一点．(1)求抛物线的表达式；(2)点Q在抛物线上，若以点A，C，P，Q为顶点，AC为一边的四边形为平行四边形时，求点Q的坐标；(3)如图②，当点P m,0从点A出发沿x轴向点B运动时(点P与点A，B不重合)，自点P分别作PE∥BC，交AC于点E，作PD⊥BC，垂足为点D．当m为何值时，△PED面积最大，并求出最大值．43(2023·湖北荆州·统考中考真题)已知：y关于x的函数y=a-2x+b．x2+a+1(1)若函数的图象与坐标轴有两个公共点，且a=4b，则a的值是；(2)如图，若函数的图象为抛物线，与x轴有两个公共点A-2,0，B4,0，并与动直线l:x=m(0<m<4)交于点P，连接PA，PB，PC，BC，其中PA交y轴于点D，交BC于点E．设△PBE的面积为S1，△CDE 的面积为S2．①当点P为抛物线顶点时，求△PBC的面积；②探究直线l在运动过程中，S1-S2是否存在最大值？若存在，求出这个最大值；若不存在，说明理由．44(2023·福建·统考中考真题)已知抛物线y=ax2+bx+3交x轴于A1,0,B3,0两点，M为抛物线的顶点，C,D为抛物线上不与A,B重合的相异两点，记AB中点为E，直线AD,BC的交点为P．(1)求抛物线的函数表达式；(2)若C4,3,D m,-3 4，且m<2，求证：C,D,E三点共线；(3)小明研究发现：无论C,D在抛物线上如何运动，只要C,D,E三点共线，△AMP,△MEP,△ABP中必存在面积为定值的三角形．请直接写出其中面积为定值的三角形及其面积，不必说明理由．45(2023·山东·统考中考真题)如图，直线y=-x+4交x轴于点B，交y轴于点C，对称轴为x=32的抛物线经过B，C两点，交x轴负半轴于点A．P为抛物线上一动点，点P的横坐标为m，过点P作x轴的平行线交抛物线于另一点M，作x轴的垂线PN，垂足为N，直线MN交y轴于点D．(1)求抛物线的解析式；(2)若0<m<32，当m为何值时，四边形CDNP是平行四边形？(3)若m<32，设直线MN交直线BC于点E，是否存在这样的m值，使MN=2ME？若存在，求出此时m 的值；若不存在，请说明理由．46(2023·山东·统考中考真题)已知抛物线y =-x 2+bx +c 与x 轴交于A ，B 两点，与y 轴交于点C 0,4 ，其对称轴为x =-32．(1)求抛物线的表达式；(2)如图1，点D 是线段OC 上的一动点，连接AD ，BD ，将△ABD 沿直线AD 翻折，得到△AB D ，当点B 恰好落在抛物线的对称轴上时，求点D 的坐标；(3)如图2，动点P 在直线AC 上方的抛物线上，过点P 作直线AC 的垂线，分别交直线AC ，线段BC 于点E ，F ，过点F 作FG ⊥x 轴，垂足为G ，求FG +2FP 的最大值．47(2023·辽宁大连·统考中考真题)如图，在平面直角坐标系中，抛物线C 1:y =x 2上有两点A 、B ，其中点A 的横坐标为-2，点B 的横坐标为1，抛物线C 2:y =-x 2+bx +c 过点A 、B ．过A 作AC ∥x 轴交抛物线C 1另一点为点C ．以AC 、12AC 长为边向上构造矩形ACDE ．(1)求抛物线C 2的解析式；(2)将矩形ACDE 向左平移m 个单位，向下平移n 个单位得到矩形A C D E ，点C 的对应点C 落在抛物线C 1上．①求n 关于m 的函数关系式，并直接写出自变量m 的取值范围；②直线A E 交抛物线C 1于点P ，交抛物线C 2于点Q ．当点E 为线段PQ 的中点时，求m 的值；③抛物线C 2与边E D 、A C 分别相交于点M 、N ，点M 、N 在抛物线C 2的对称轴同侧，当MN =2103时，求点C 的坐标．48(2023·湖南张家界·统考中考真题)如图，在平面直角坐标系中，已知二次函数y=ax2+bx+c的图象与x轴交于点A-2,0．点D为线段BC上的一动点．和点B6,0两点，与y轴交于点C0,6(1)求二次函数的表达式；(2)如图1，求△AOD周长的最小值；(3)如图2，过动点D作DP∥AC交抛物线第一象限部分于点P，连接PA,PB，记△PAD与△PBD的面积和为S，当S取得最大值时，求点P的坐标，并求出此时S的最大值．49(2023·黑龙江绥化·统考中考真题)如图，抛物线y1=ax2+bx+c的图象经过A(-6,0)，B(-2,0)，C (0,6)三点，且一次函数y=kx+6的图象经过点B．(1)求抛物线和一次函数的解析式．(2)点E，F为平面内两点，若以E、F、B、C为顶点的四边形是正方形，且点E在点F的左侧．这样的E，F两点是否存在？如果存在，请直接写出所有满足条件的点E的坐标：如果不存在，请说明理由．(3)将抛物线y1=ax2+bx+c的图象向右平移8个单位长度得到抛物线y2，此抛物线的图象与x轴交于M，N两点(M点在N点左侧)．点P是抛物线y2上的一个动点且在直线NC下方．已知点P的横坐标为PD有最大值，最大值是多少？m．过点P作PD⊥NC于点D．求m为何值时，CD+1250(2023·四川南充·统考中考真题)如图1，抛物线y=ax2+bx+3(a≠0)与x轴交于A-1,0，B3,0两点，与y轴交于点C．(1)求抛物线的解析式；(2)点P在抛物线上，点Q在x轴上，以B，C，P，Q为顶点的四边形为平行四边形，求点P的坐标；(3)如图2，抛物线顶点为D，对称轴与x轴交于点E，过点K1,3的直线(直线KD除外)与抛物线交于G，H两点，直线DG，DH分别交x轴于点M，N．试探究EM⋅EN是否为定值，若是，求出该定值；若不是，说明理由．51(2023·四川宜宾·统考中考真题)如图，抛物线y=ax2+bx+c与x轴交于点A-4,0，且经、B2,0过点C-2,6．(1)求抛物线的表达式；(2)在x轴上方的抛物线上任取一点N，射线AN、BN分别与抛物线的对称轴交于点P、Q，点Q关于x轴的对称点为Q ，求△APQ 的面积；(3)点M是y轴上一动点，当∠AMC最大时，求M的坐标．52(2023·四川广安·统考中考真题)如图，二次函数y=x2+bx+c的图象交x轴于点A，B，交y轴于点C，点B的坐标为1,0，对称轴是直线x=-1，点P是x轴上一动点，PM⊥x轴，交直线AC于点M，交抛物线于点N．(1)求这个二次函数的解析式．(2)若点P在线段AO上运动(点P与点A、点O不重合)，求四边形ABCN面积的最大值，并求出此时点P 的坐标．(3)若点P在x轴上运动，则在y轴上是否存在点Q，使以M、N、C、Q为顶点的四边形是菱形？若存在，请直接写出所有满足条件的点Q的坐标；若不存在，请说明理由．。

专题01 二次函数范围问题(学生版)

专题01 二次函数范围问题1. （2022舟山中考）已知抛物线：（）经过点．（1）求抛物的函数表达式．（2）将抛物线向上平移m （）个单位得到抛物线．若抛物线的顶点关于坐标原点O 的对称点在抛物线上，求m 的值．（3）把抛物线向右平移n （）个单位得到抛物线．已知点，都在抛物线上，若当时，都有，求n 的取值范围．1L 2(1)4y a x =+-0a ≠(1,0)A 1L 1L 0m >2L 2L 1L 1L 0n >3L (8,)P t s -(4,)Q t r -3L 6t >s r >2. （2022丽水中考）如图，已知点在二次函数的图象上，且．（1）若二次函数的图象经过点．①求这个二次函数的表达式；②若，求顶点到的距离；（2）当时，二次函数的最大值与最小值的差为1，点M ，N 在对称轴的异侧，求a的取值范围．()()1122,,,M x y N x y 2(2)1(0)y a x a =-->213x x -=(3,1)12y y =MN 12x x x ≤≤3.（2022嘉兴中考）已知抛物线L1：y＝a(x＋1)2－4（a≠0）经过点A(1，0)．（1）求抛物线L1的函数表达式．（2）将抛物线L1向上平移m（m＞0）个单位得到抛物线L2．若抛物线L2的顶点关于坐标原点O的对称点在抛物线L1上，求m的值．（3）把抛物线L1向右平移n（n＞0）个单位得到抛物线L3，若点B(1，y1)，C(3，y2)在抛物线L3上，且y1＞y2，求n的取值范围．4. （2022自贡中考）已知二次函数．（1）若，且函数图象经过，两点，求此二次函数的解析式，直接写出抛物线与轴交点及顶点的坐标；（2）在图①中画出（1）中函数的大致图象，并根据图象写出函数值时自变量的取值范围；（3）若且，一元二次方程两根之差等于，函数图象经过，两点，试比较的大小．()20y ax bx c a =++≠1a =-()0,3()2,5-x 3y ≥x 0a b c ++=a b c >>20ax bx c ++=a c -121P c,y ⎛⎫- ⎪⎝⎭()132Q c,y +12,y y5. （2022长春中考）在平面直角坐标系中，抛物线（b 是常数）经过点．点A 在抛物线上，且点A 的横坐标为m （）．以点A 为中心，构造正方形，，且轴．（1）求该抛物线对应的函数表达式：（2）若点B 是抛物线上一点，且在抛物线对称轴左侧．过点B 作x 轴的平行线交抛物线于另一点C ，连接．当时，求点B 的坐标；（3）若，当抛物线在正方形内部的点的纵坐标y 随x 的增大而增大时，或者y 随x 的增大而减小时，求m 的取值范围；（4）当抛物线与正方形的边只有2个交点，且交点的纵坐标之差为时，直接写出m 的值．2y x bx =-()2,00m ≠PQMN 2PQ m =PQ x ⊥BC 4BC =0m >PQMN 34两点（点A 在点B 的左侧），与y 轴交于点C ，顶点为D ．其对称轴与线段BC 交于点E ，与x 轴交于点F ．连接AC ，BD ．（1）求A ，B ，C 三点的坐标（用数字或含m 的式子表示），并求的度数；（2）若，求m 的值；（3）若在第四象限内二次函数（m 是常数，且）的图像上，始终存在一点P ，使得，请结合函数的图像，直接写出m的取值范围．OBC ∠ACO CBD ∠=∠2221y x mx m =-+++0m >75ACP ∠=︒6. （2022苏州中考）如图，在二次函数（m 是常数，且）的图像与x 轴交于A ，B 2221y x mx m =-+++0m >．点在此抛物线上，其横坐标为．（1）求此抛物线的解析式；（2）当点在轴上方时，结合图象，直接写出的取值范围；（3）若此抛物线在点左侧部分（包括点）的最低点的纵坐标为．①求值；②以为边作等腰直角三角形，当点在此抛物线的对称轴上时，直接写出点的坐标．的(0,3)B P m P x m P P 2m -m PA PAQ Q Q 7. （2022吉林中考）如图，在平面直角坐标系中，抛物线（，是常数）经过点，点2y x bx c =++b c (1,0)A（1）若，函数的图象经过点和点，求该函数的表达式和最小值；（2）若，，时，函数的图象与轴有交点，求的取值范围．（3）阅读下面材料：设，函数图象与轴有两个不同的交点，，若，两点均在原点左侧，探究系数，，应满足的条件，根据函数图像，思考以下三个方面：①因为函数的图象与轴有两个不同的交点，所以；②因为，两点在原点左侧，所以对应图象上的点在轴上方，即；③上述两个条件还不能确保，两点均在原点左侧，我们可以通过抛物线的对称轴位置来进一步限制抛物线的位置：即需．综上所述，系数，，应满足的条件可归纳为：请根据上面阅读材料，类比解决下面问题：若函数的图象在直线的右侧与轴有且只有一个交点，求的取值范围．1a =()1,4-()2,11a =2b =-1c m =+x m 0a >x A B A B a b c x 2Δ40b ac =->A B 0x =x 0c >A B 02b a-<a b c 20Δ40002a b ac c b a >⎧⎪=->⎪⎪>⎨⎪⎪-<⎪⎩223y ax x =-+1x =x a 8. （2022永州中考）已知关于的函数．x 2y ax bx c =++（1）如图①，若抛物线图象与轴交于点，与轴交点．连接．①求该抛物线所表示的二次函数表达式；②若点是抛物线上一动点（与点不重合），过点作轴于点，与线段交于点．是否存在点使得点是线段的三等分点？若存在，请求出点的坐标；若不存在，请说明理由．（2）如图②，直线与轴交于点，同时与抛物线交于点，以线段为边作菱形，使点落在轴的正半轴上，若该抛物线与线段没有交点，求的取值范围．x ()3,0A y ()0,3B -AB P A P PH x ⊥H AB M P M PH P 43y x n =+y C 2y x bx c =++()3,0D -CD CDFE F x CE b 9. （2022湘潭中考）已知抛物线．2y x bx c =++点C ，线段CB ∥x 轴，交该抛物线于另一点B ．（1）求点B 的坐标及直线AC 的解析式；（2）当二次函数y ＝x 2﹣2x ﹣3的自变量x 满足m ≤x ≤m+2时，此函数的最大值为p ，最小值为q ，且p ﹣q ＝2，求m 的值；（3）平移抛物线y ＝x 2﹣2x ﹣3，使其顶点始终在直线AC 上移动，当平移后的抛物线与射线BA 只有一个公共点时，设此时抛物线的顶点的横坐标为n ，请直接写出n的取值范围．10．（2022天门中考）（12分）如图，在平面直角坐标系中，已知抛物线y ＝x 2﹣2x ﹣3的顶点为A ，与y 轴交于线由直线平移得到，与轴交于点．四边形的四个顶点的坐标分别为，，，．（1）填空：______，______；（2）若点在第二象限，直线与经过点的双曲线有且只有一个交点，求的最大值；（3）当直线与四边形、抛物线都有交点时，存在直线，对于同一条直线上的交点，直线与四边形的交点的纵坐标都不大于它与抛物线的交点的纵坐标．①当时，直接写出的取值范围；②求的取值范围．l BC y ()0,E n MNPQ ()1,3M m m ++()1,N m m +()5,P m m +()5,3Q m m ++=a b =M l M k y x=2n l MNPQ 22y ax bx =+-l l l MNPQ 22y ax bx =+-3m =-n m 11. （2022宜昌中考）已知抛物线与轴交于，两点，与轴交于点．直22y ax bx =+-x ()1,0A -()4,0B y C象中y 轴左侧部分沿x 轴翻折，保留其他部分得到新的图象C ．（1）求b 的值；（2）①当时，图象C 与x 轴交于点M ，N （M 在N 的左侧），与y 轴交于点P ．当为直角三角形时，求m 的值；②在①的条件下，当图象C 中时，结合图象求x 的取值范围；（3）已知两点，当线段与图象C 恰有两个公共点时，直接写出m的取值范围．0m <MNP △40y -≤<(1,1),(5,1)A B ---AB 12.（2022大庆中考）已知二次函数图象的对称轴为直线．将二次函数图2y x bx m =++2x =2y x bx m =++13. 已知抛物线与x 轴交于A ，B 两点（点A 在点B 的左侧）．（1）求点A ，点B 的坐标；（2）如图，过点A 的直线与抛物线的另一个交点为C ，点P 为抛物线对称轴上的一点，连接，设点P 的纵坐标为m ，当时，求m 的值；（3）将线段AB 先向右平移1个单位长度，再向上平移5个单位长度，得到线段MN ，若抛物线与线段MN 只有一个交点，请直接写出a的取值范围．2y x 2x 3=-++:1l y x =--PA PC 、PA PC =2(23)(0)y a x x a ++≠=-14. （2022北京中考）在平面直角坐标系中，点在抛物线上，设抛物线的对称轴为（1）当时，求抛物线与y 轴交点的坐标及的值；（2）点在抛物线上，若求的取值范围及的取值范围．xOy (1,),(3,)m n 2(0)y ax bx c a =++>.x t =2,c m n ==t 00(,)(1)x m x ≠,m n c <<t 0x15．（2022江西中考）（9分）跳台滑雪运动可分为助滑、起跳、飞行和落地四个阶段，运动员起跳后飞行的路线是抛物线的一部分（如图中实线部分所示），落地点在着陆坡（如图中虚线部分所示）上，着陆坡上的基准点为飞行距离计分的参照点，落地点超过点越远，飞行距离分越高．2022年北京冬奥会跳台滑雪标准台的起跳台的高度为，基准点到起跳台的水平距离为，高度为为定值）．设运动员从起跳点起跳后的高度与水平距离之间的函数关系为．（1）的值为；（2）①若运动员落地点恰好到达点，且此时，，求基准点的高度；②若时，运动员落地点要超过点，则的取值范围为；（3）若运动员飞行的水平距离为时，恰好达到最大高度，试判断他的落地点能否超过点，并说明理由．K K OA 66m K 75m h (m h A ()y m ()x m 2(0)y ax bx c a =++≠c K 150a =-910b =K h 150a =-Kb 25m 76m K16. （2022安徽中考）如图1，隧道截面由抛物线的一部分AED 和矩形ABCD 构成，矩形的一边BC 为12米，另一边AB 为2米．以BC 所在的直线为x 轴，线段BC 的垂直平分线为y 轴，建立平面直角坐标系xOy ，规定一个单位长度代表1米．E （0，8）是抛物线的顶点．（1）求此抛物线对应的函数表达式；（2）在隧道截面内（含边界）修建“”型或“”型栅栏，如图2、图3中粗线段所示，点，在x轴上，MN 与矩形的一边平行且相等．栅栏总长l 为图中粗线段，，，MN 长度之和．请解决以下问题：（ⅰ）修建一个“”型栅栏，如图2，点，在抛物线AED 上．设点横坐标为，求栅栏总长l 与m 之间的函数表达式和l 的最大值；（ⅱ）现修建一个总长为18的栅栏，有如图3所示的修建“”型或“”型栅型两种设计方案，请你从中选择一种，求出该方案下矩形面积的最大值，及取最大值时点的横坐标的取值范围（在右侧）．的1P 4P 1234PP P P 12PP 23P P 34P P 2P 3P 1P ()06m m <≤1234PP P P 1P 1P 4P。

2025中考数学二次函数压轴题专题练习21 阿氏圆模型(学生版+解析版)

专题21阿氏圆模型一、知识导航所谓“阿氏圆＂，是指由古希腊数学家阿波罗尼奥斯提出的圆的概念，在平面内，到两个定点距离之比等于定值（不力l）的点的栠合叫做圆．如下图，已知A、B两点，点P满足PA:PB=k (k* I)，则满足条件的所有的点P构成的图形为圆．pA下给出证明法一：首先了解两个定理(I)角平分线定理：如图，在6-ABC中，AD是乙BAC的角平分线则AB DBAC DCAB DcS BD S ABxDE AB AB DB 证明：一竺丛＝－－－坐上＝＝－－，即一一＝－－s AC/) CD S ACD ACxDF AC. AC DC(2)外角平分线定理；如图，在6.ABC中，外角CAE的角平分线AD交BC的延长线于点D,则AB DB AC DC ^EA,，｀｀B C\\\\IID证明：在B A 延长线上取点E 使得AE=AC ，连接BO,则6.ACD 兰6.AED (SAS), CD=ED 且AD DB ABAB DB 平分乙BDE ,则一一＝一一，即一一＝一一．DE AE AC DC接下来开始证明步骤：仁＇，，夕夕2A、、、、、、、、、、、、、MB'N如图，PA:PB=k,作LAPB 的角平分线交AB 于M 点，根据角平分线定理，MA PA —=—=k '故M 点为定MB PB点，即乙APB 的角平分线交AB 于定点；作乙APB 外角平分线交直线AB于N 点，根据外角平分线定理，NA PA—=—=k,故N 点为定点，即乙APB NB PB外角十分线交直线AB 于定点；又乙MPN=90°,定边对定角，故P 点轨迹是以MN 为直径的圆AN法二：达系不妨将点A 、B 两点置于x轴上且关于原点对称，设A (-m, 0)，则B (m, 0)，设P (x, y), PA=kPB, 即：J (x+m)2+y 2 =k J(x -m)2+ y 2 (x+m)2+y 2 =k 2(x -m )2+k 2y 2 （炉－1)(x2+ y 2)-(2m +2k 2m)x+(k 2-1)矿＝02 2m +2k'n /， X-+y-k 2-lx+ni 2 =0解析式满足圆的一般方程，故P点所构成的图形是固，且圆心与AB 共线．除了证明之外，我们还需了解“阿氏圆”的一些性质：(1)PA MA NA —=—=—=k.PB MB NB应用：祁据点A 、B的位置及k的值可确定M 、N及圆心0.OB OP(2) 6.0BPV>/:::,.QPA,即一一＝一一，变形为OP 2=OA-OB.OP OA 应用：粮据圆心及半径和A 、B其中一点，可求A 、B另外一点位置．(3)OP OB PA —=—=—=k .OA OP PB应用：已知半径及A 、B中的其中一点，即可知道PA:PB的值．pAN匡I1如图，在L.ABC中，AB=4，AC=2,点D为AB边上一点，当AD=时，L.ACDv>L.ABCC8二二AAC AD觯：若6.ACDV)6.A B C 则有—-＝——即AC 2=AB·ADAB AC·: A B =4,AC =2AC2:. AD =—= 1AD故答案为I.2如图，点P 是半径为2的O O 上一动，点，点A 、B为o o 外的定点，连接PA 、P B,点B 与固心0的I距离为4要使PA+�PB 的值最小，如何确定点P,并说明理由．2ABI 思路分析）构造相似三角形，将所求两条线段的和转化为一条线段，此线段与圆的交点即为所求A（详解J连接OB,OP ,在OB 上截取o c 亏1,连接AC 交('0于点P'，连接PC.OP OC l ·—=—=－，乙POC ＝乙BOPOB OP 2 :.�POC BOPPC ll :.—= －，即－PB =PC PB 2· 21:. PA+.:..PB= PA+PC�AC2当点A 、P 、C三点共线时，PA+PC的值最小，最小值为AC的长，即当点P与P'重合时，PA+�PB的2 根据阿氏圆可得OP 2=0B -OC即O P 2 22OC =—=—=1OB 4值最小．23如图，平面直角坐标系中，A(4,0),B(0,3)，点E在以原点0为圆心，2力半径的圆上运动，求AE+�BE3 的最小值．y j.... ＿3一3-,（思路分析）在坐标轴上找一点，构造相似三角形，利用对应边成比例将两条线段的和转化为求一条线段的长，即为最小值．（详解】如图，在y轴上取一点M(O,-:-)4 3 . OE OM 2 4，连接OE,EM, AM,则OE =2,0B =3, OM=-:-3＝＝－OB OE 3又？乙EOM＝乙BOE :. EOM =、BOE EM OM 2 2 :.—=—=－，即EM =::::_BEBE OE3. 3 2:. AE+::::_B E=AE+EM切AM3当A 、E 、M三点共线时，AE+BM的值最小，最小值为AM的长在Rt ,.AOM 中，A M ＝拓夼言夼＝幸2:．当E 为线段A.11与o o 的交点时，AE +78E 有最小值为一—-．4而3 3y ·--3-3-'3 2.9 4.如图，已知抛物线y =－－x +－x+3与x轴交于A、B两点（点A在点B左侧），与y轴交于点C,44点E的坐标为(2,0)，将线段OE绕点0逆时针旋转得到OE'，旋转角力a(0°<a<90°)，连接BE'、2CE'，求BE'+�CE'的敢小值．3（思路分析】由旋转可知E'点的运动轨迹为以原点0为圆心，2为半径的圆在笫一象限内的一段固弧，在y轴上找一点，构造相似三角形，再结合各点坐标求解即可3 9（详解】解．？抛物线的解析式为y=－-x 2+－x+34 4 :. B (4,0),C(0,3) ·.．点E的坐标为(2,0):.,占、E'的运动轨迹为以原点0为圆心，2为半径的圆在第一象限内的一段圆弧4 如图在y轴上取一点M (O,-::)，连接OE',E'M,B M,则OE'=2, OC = 3, OM =-:: 43......3 . E'M OM 2..-=-=-OCOE' 3 又？L.E'OM＝乙COE':. E'OM(/) COE'. EM 2 2:.-—=－即E 'M=::..CE 'C E '33 2:. BE'+::..CE'=BE'+E'M�BM当B 、E',M三点共线时，BE'+E'M的值最小，最小值为BM的长·:BM＝豆二尸三3)32 4而：．当E'为BM与圆弧的交点时，BE'+7CE'有最小值为3 3I三、中考真题演练I.(2022广东惠州一模）如图1，抛物线y=，矿＋bx~4与X轴交于A、B两点，与Y轴交千点C,其中点A的坐标为(-1,0)，抛物线的对称轴是迎线x=－．3 2yy图1图2(1)求抛物线的解析式：(2)若点P是直线BC下方的抛物线上一个动点，是否存在点P使四边形ABPC的面积为16,若存在，求出点P的坐标若不存在，请说明理由；(3)如图2,过点B 作BF 上BC 交抛物线的对称轴千点F,以点C 为圆心，2为半径作(,C'点Q 为C上的五一个动点，求－－B Q+FQ的最小值．42如图），抛物线）1＝成＋（a+3)..I,＋3(a'1'0)与x轴交于点A(4,0)，与y轴交于点B,;{:丘轴上有一动点E(m,O )(0<m<4),过点E作x轴的垂线交直线AB千点N,交抛物线于点P,过点P作PM上AB千点M.y yxX图l(I)求a的值和且线AB的函数表达式：图2C. 6(2)设t:.PMN的周长为C,,t:.A EN的周长为C“若-=－求m的值C 5(3)如图2,在（2)的条件下，将线段OE绕点0逆时针旋转得到OE',旋转角为a (0°<a<90勺，连按E'A 、EB，求E'A＋二E＇B的最小值．33.(20l9山东中考真题）如图I,在平面直角坐标系中，直线y=-5x+5与x轴，y轴分别交于A,C两点，抛物线y=x2+bx+c经过A,C两点，与x轴的另一交点为B图1图2(l)求抛物线解析式及B点坐标；(2)若点M为x轴下方抛物线上一动点，连接MA、MB、BC,当点M运动到某一位置时，四边形AMBC 面积最大，求此时点M的坐标及四边形AMBC的面积；(3)如图2,若P点是半径为2的0B上一动点，连接PC、PA,当点P运动到某一位置时，PC+�PA的2值最小，请求出这个最小值，并说明理由．4.(2018广西柳州中考真题）如图，抛物线y= a.x2 +bx+c圭卢轴交千A(.J3,0), 8两点（点8在点A的左侧），与Y轴交于点C,且08=30A=./3oc'LO A C的平分线AD交Y轴于点D,过点A且垂直于AD的均线［交Y轴于点E,点P是X轴下方抛物线上的一个动点，过点P作PF..l.x轴，垂足为F,交直线AD千点H.(l)求抛物线的解析式：(2)设点P的横坐标为111,当FH=HP时，求1/1.的值：I(3)当归线P F为抛物线的对称轴时，以点H为圆心，－H C为半径作1)H,点Q为o H上的一个动点，求2l�AQ+EQ的最小值4x专题21阿氏圆模型一、知识导航所谓“阿氏圆＂，是指由古希腊数学家阿波罗尼奥斯提出的圆的概念，在平面内，到两个定点距离之比等于定值（不力l）的点的栠合叫做圆．如下图，已知A、B两点，点P满足PA:PB=k (k* I)，则满足条件的所有的点P构成的图形为圆．pA下给出证明法一：首先了解两个定理(I)角平分线定理：如图，在6-ABC中，AD是乙BAC的角平分线则AB DBAC DCAB DcS BD S ABxDE AB AB DB 证明：一竺丛＝－－－坐上＝＝－－，即一一＝－－s AC/) CD S ACD ACxDF AC. AC DC(2)外角平分线定理；如图，在6.ABC中，外角CAE的角平分线AD交BC的延长线于点D,则AB DB AC DC ^EA,，｀｀B C\\\\IID证明：在B A 延长线上取点E 使得AE=AC ，连接BO,则6.ACD 兰6.AED (SAS), CD=ED 且AD DB ABAB DB 平分乙BDE ,则一一＝一一，即一一＝一一．DE AE AC DC接下来开始证明步骤：仁＇，，夕夕2A、、、、、、、、、、、、、MB'N如图，PA:PB=k,作LAPB 的角平分线交AB 于M 点，根据角平分线定理，MA PA —=—=k '故M 点为定MB PB点，即乙APB 的角平分线交AB 于定点；作乙APB 外角平分线交直线AB于N 点，根据外角平分线定理，NA PA—=—=k,故N 点为定点，即乙APB NB PB外角十分线交直线AB 于定点；又乙MPN=90°,定边对定角，故P 点轨迹是以MN 为直径的圆AN法二：达系不妨将点A 、B 两点置于x轴上且关于原点对称，设A (-m, 0)，则B (m, 0)，设P (x, y), PA=kPB, 即：J (x+m)2+y 2 =k J(x -m)2+ y 2 (x+m)2+y 2 =k 2(x -m )2+k 2y 2 （炉－1)(x2+ y 2)-(2m +2k 2m)x+(k 2-1)矿＝02 2m +2k'n /， X-+y-k 2-lx+ni 2 =0解析式满足圆的一般方程，故P点所构成的图形是固，且圆心与AB 共线．除了证明之外，我们还需了解“阿氏圆”的一些性质：(1) PA MA NA —=—=—=k .PB MB NB应用：祁据点A 、B的位置及k的值可确定M 、N及圆心0.OB OP(2) 6.0BPV>/:::,.QPA,即一一＝一一，变形为OP 2=OA-OB.OP OA 应用：粮据圆心及半径和A 、B其中一点，可求A 、B另外一点位置．(3)OP OB PA —=—=—=k .OA OP PB应用：已知半径及A 、B中的其中一点，即可知道PA:PB的值．pAN匡I1如图，在L.ABC中，AB=4，AC=2,点D为AB边上一点，当AD=时，L.ACDv>L.ABCC8二二AAC AD觯：若6.ACDV)6.A B C 则有—-＝——即AC 2=AB·ADAB AC·: AB =4,AC =2AC2:. AD =—= 1AD故答案为I.2如图，点P 是半径为2的O O 上一动点，点A 、B为o o 外的定点，连接PA 、P B,点B 与固心0的I距离为4要使PA+�PB的值最小，如何确定点P,并说明理由．2ABI 思路分析）构造相似三角形，将所求两条线段的和转化为一条线段，此线段与圆的交点即为所求．A（详解J连接OB,OP ,在OB 上截取o c 亏1,连接AC 交('0于点P'，连接PC.OP OC l ·—=—=－，乙POC ＝乙BOPOB OP 2 :.�POC BOPPC ll :.—= －，即－PB =PC PB 2· 21:. PA+.:..PB= PA+PC�AC2当点A 、P 、C三点共线时，PA+PC的值最小，最小值为AC的长，即当点P与P'重合时，PA+�PB的2 根据阿氏圆可得O P 2=0B -O C 即O P 2 22OC =—=—=1OB 4值最小．23如图，平面直角坐标系中，A(4,0),B(0,3)，点E在以原点0为圆心，2力半径的圆上运动，求AE+�BE3 的最小值．y j一3-,（思路分析）在坐标轴上找一点，构造相似三角形，利用对应边成比例将两条线段的和转化为求一条线段的长，即为最小值．（详解】如图，在y轴上取一点M(O,-:-)4 3 . OE OM 2 4，连接OE,EM, AM,则OE =2,0B=3, O M=-:-3＝＝－OB OE 3又？乙EOM＝乙BOE :. EOM =、BOE EM OM 2 2 :.—=—=－，即EM =::::_BEBE OE3. 3 2:. AE+::::_B E=AE+EM切AM3当A 、E 、M三点共线时，AE+BM的值最小，最小值为AM的长在Rt ,.AOM 中，AM ＝拓千言夼＝孛2:．当E 为线段A.11与o o 的交点时，AE +78E 有最小值为一—-．4而3 3y ·--3-3-'3 2. 94.如图，已知抛物线y =－－x +－x+3与x轴交于A、B两点（点A在点B左侧），与y轴交于点C,4 4点E的坐标为(2,0)，将线段OE绕点0逆时针旋转得到OE'，旋转角力a(0°<a<90°)，连接BE'、2CE'，求BE'+�CE'的敢小值．3（思路分析】由旋转可知E'点的运动轨迹为以原点0为圆心，2为半径的圆在笫一象限内的一段圆弧，在y轴上找一点，构造相似三角形，再结合各点坐标求解即可3 9（详解】解．？抛物线的解析式为y=－－x 2+－x+34 4 :. B (4,0),C(0,3) ·.点E的坐标为(2,0):.,占、E'的运动轨迹为以原点0为圆心，2为半径的圆在第一象限内的一段圆弧4 如图在y轴上取一点M (O,-::)，连接OE',E'M,BM,则OE'=2,OC=3, OM=-::43......3 . E'M OM 2..-=-=-OCOE' 3 又？L.E'OM ＝乙COE':. E'OM(/) COE'. EM 2 2:.-—=－即E 'M=::..CE 'C E '33 2:. B E'+::..CE'=BE'+E'M�BM当B 、E',M三点共线时，BE'+E'M的值最小，最小值为BM的长·:BM ＝芦言尸＝玉3 J3 2 4而：当E'为BM与圆弧的交点时，BE'+7CE'有最小值为3 3I三、中考真题演练I.(2022广东惠州一模）如图1，抛物线y=，矿＋bx~4与X轴交于A、B两点，与Y轴交千点C,其中点A的坐标为(-1,0)，抛物线的对称轴是迎线x=－．3 2yy图1图2(1)求抛物线的解析式：(2)若点P是直线BC下方的抛物线上一个动点，是否存在点P使四边形ABPC的面积为16,若存在，求出点P的坐标若不存在，请说明理由；(3)如图2,过点B作BF上BC交抛物线的对称轴千点F,以点C为圆心，2为半径作(,C'点Q为C上的五一个动点，求－－B Q+F Q的最小值．4【答案】(I)y=入.2-3x-4(2)P{l,6)或(3,4)(3)扫3【分析】(I)根据点A的坐标为(-1,0)，抛物线的对称轴是直线x=－．待定系数法求二次函数解析式即可，2(2)先求得直线BC解析式，设P(m,m2-3m-4)，则Q(m m-4)，过点P作PQ轴交直线BC千点Q,根据S四边彤A BPC= s AOC +S如，等干16建立方程，解一元二次方程即可求得Ill的值，然后求得P的坐标，五(3)在CB上取CE=－－，过点E作EG J_OC，构造CQE V>.C BQ，则当F,Q E三点共线时，取得最小值，最小值为FE,勾股定理解直角三形即可．【详解】（I)解：？抛物线y＝矿＋bx-4与X轴交于A、B两点，与Y轴交于点C,点A的坐标为-l,O),抛物线的对称轴是宜线x=－，3:. C(O,--4)，， 4 ，。

二次函数综合题存在性问题分类训练(9种类型)(学生版)--2023-2024学年九年级数学上册重难点

二次函数综合题存在性问题分类训练(9种类型)【类型一存在性之等腰三角形】1如图，在平面直角坐标系中，抛物线y=14x2+bx+c与x轴交于点A，B，与y轴交于点C，其中B3,0，C0,-3．(1)求该抛物线的表达式；(2)点P是直线AC下方抛物线上一动点，过点P作PD⊥AC于点D，求PD的最大值及此时点P的坐标；(3)在(2)的条件下，将该抛物线向右平移5个单位，点E为点P的对应点，平移后的抛物线与y轴交于点F，Q为平移后的抛物线的对称轴上任意一点．写出所有使得以QF为腰的△QEF是等腰三角形的点Q的坐标，并把求其中一个点Q的坐标的过程写出来．2如图，已知抛物线y=ax2+bx+4(a≠0)与x轴交于A-1,0，B2,0两点，与y轴交于点C．(1)求抛物线的解析式及点C的坐标；(2)若F为抛物线上一点，连接BC，是否存在以BC为底的等腰△BCF？若存在，请求出点F的坐标；若不存在，请说明理由．3如图，已知抛物线y=-x2+bx+c经过B-3,0两点，与x轴的另一个交点为A．,C0,3(1)求抛物线的解析式；(2)在抛物线对称轴上找一点E，使得AE+CE的值最小，求出点E的坐标；(3)设点P为x轴上的一个动点，是否存在使△BPC为等腰三角形的点P，若存在，直接写出点P的坐标；若不存在，说明理由．4如图，已知抛物线y=-x2+bx+c经过B(-3，0)，C(0，3)两点，与x轴的另一个交点为A．(1)求抛物线的解析式；(2)若直线y=mx+n经过B，C两点，则m=；n=；(3)在抛物线对称轴上找一点E，使得AE+CE的值最小，直接写出点E的坐标；(4)设点P为x轴上的一个动点，是否存在使△BPC为等腰三角形的点P，若存在，直接写出点P的坐标；若不存在，说明理由．【类型二存在性之直角三角形】5如图，在平面直角坐标系中，一次函数y=12x-2的图象分别交x轴、y轴于点A、B，抛物线y=x2+bx+c经过点A、B，E是线段OA的中点．(1)求抛物线的解析式；(2)点F是抛物线上的动点，当∠OEF=∠BAE时，求点F的横坐标；(3)在抛物线上是否存在点P，使得△ABP是以点A为直角顶点的直角三角形，若存在，请求出P点坐标，若不存在，请说明理由．(4)抛物线上(AB下方)是否存在点M，使得∠ABM=∠ABO？若存在，求出点M到y轴的距离，若不存在，请说明理由．6如图，已知抛物线y=x2+bx+c的对称轴为直线x=2，与y轴交于点C0,3，与x轴交于点A和点B．(1)求抛物线的解析式和点A、B的坐标；(2)设点P为抛物线的对称轴直线x=2上的一个动点，求使△PBC为直角三角形的点P的坐标．7如图，在平面直角坐标系xOy中，抛物线y=x2+bx-3与直线l:y=x+1交于A，B两点，点A的坐标为-1，0．(1)求抛物线的解析式及点B的坐标；(2)已知抛物线与x轴有2个交点，右侧交点为C，点P为线段AB上任意一点(不含端点)，若△PBC是以点P为直角顶点的直角三角形，求点P的坐标．8如图，一次函数y=12x+1的图象与x轴交于点A，与y轴交于点B，二次函数y=12x2+bx+c的图象与一次函数y=12x+1的图象交于B、C两点，与x轴交于D、E两点，且D点坐标为1,0．(1)求抛物线的解析式；(2)在x轴上找一点P，使|PB-PC|最大，求出点P的坐标；(3)在x轴上是否存在点P，使得△PBC是以点P为直角顶点的直角三角形？若存在，求出点P的坐标，若不存在，请说明理由．【类型三存在性之等腰直角三角形】9如图，抛物线与x轴交于A、B两点，与y轴交于点C，且OA=2，OB=4，OC=8，抛物线的对称轴与直线BC交于点M，与x轴交于点N．(1)求抛物线的解析式；(2)若点P是对称轴上的一个动点，是否存在以P、C、M为顶点的三角形与△MNB相似？若存在，求出点P的坐标，若不存在，请说明理由．(3)点Q是抛物线上位于x轴上方的一点，点R在x轴上，是否存在以点Q为直角顶点的等腰Rt△CQR？若存在，求出点Q的坐标，若不存在，请说明理由．10如图1，在平面直角坐标系中，抛物线y=-23x2+43x+2与x轴交于A、B两点(点A在点B的左侧)，与y轴交于点C，点P为直线BC上方抛物线上一动点．(1)求直线BC的解析式；(2)过点A作AD∥BC交抛物线于D，连接CA，CD，PC，PB，记四边形ACPB的面积为S1，△BCD的面积为S2，当S1-S2的值最大时，求P点的坐标和S1-S2的最大值；(3)如图2，将抛物线水平向右平移，使得平移后的抛物线经过点O，G为平移后的抛物线的对称轴直线l上一动点，将线段AC沿直线BC平移，平移过程中的线段记为A′C′(线段A'C'始终在直线l左侧)，是否存在以A′，C′，G为顶点的等腰直角△A′C′G？若存在，请写出满足要求的所有点G的坐标并写出其中一种结果的求解过程，若不存在，请说明理由．11如图所示，抛物线与x轴交于A、B两点，与y轴交于点C，且OA=2，OB=4，OC=8，抛物线的对称轴与直线BC交于点M，与x轴交于点N．(1)求抛物线的解析式；(2)若点P是对称轴上的一个动点，是否存在以P、C、M为顶点的三角形与△MNB相似？若存在，求出点P的坐标，若不存在，请说明理由．(3)D为CO的中点，一个动点G从D点出发，先到达x轴上的点E，再走到抛物线对称轴上的点F，最后返回到点C．要使动点G走过的路程最短，请找出点E、F的位置，写出坐标，并求出最短路程．(4)点Q是抛物线上位于x轴上方的一点，点R在x轴上，是否存在以点Q为直角顶点的等腰Rt△CQR？若存在，求出点Q的坐标，若不存在，请说明理由．12如图，在平面直角坐标系中，将一等腰直角三角板ABC放在第二象限，且斜靠在两坐标轴上，其中A的坐标为(0,2)，直角顶点C的坐标为(-1,0)，点B在抛物线y=ax2+ax-2上．(1)求抛物线的解析式；(2)设抛物线的顶点为D，连结BD、CD，求△DBC的面积；(3)在抛物线上是否还存在点P(点B除外)，使△ACP仍然是以AC为直角边的等腰直角三角形?若存在，请直接写出所有点P的坐标；若不存在，请说明理由．【类型四存在性之平行四边形】13在平面直角坐标系中，抛物线y=ax2+bx+c(a≠0)经过点(-1,0)，(3,0)和0,3．(1)求抛物线的表达式；(2)若直线x=m与x轴交于点N，在第一象限内与抛物线交于点M，当AN+MN有最大值时，求出抛物线上点M的坐标；(3)若点P为抛物线y=ax2+bx+c(a≠0))的对称轴上一动点，将抛物线向左平移1个单位长度后，Q为平移后抛物线上一动点，在(2)的条件下求得的点M，是否能与A，P，Q构成平行四边形？若能构成，求出Q点坐标；若不能构成，请说明理由．14如图，在平面直角坐标系xOy中，抛物线y=x2+bx+c与x轴交于A、B两点，与y轴交于点C，对称轴为直线x=2，点A的坐标为(1,0)．(1)求该抛物线的表达式及顶点坐标；(2)在直线BC的下方的抛物线上存在一点M，使得△BCM的面积最大，请求出点M的坐标(3)点F是抛物线上的动点，点D是抛物线顶点坐标，作EF∥AD交x轴于点E，是否存在点F，使得以A、D、E、F为顶点的四边形是平行四边形？若存在，请写出所有符合条件的点F的坐标；若不存在，请说明理由．15如图，在平面直角坐标系中，抛物线y=12x2+bx+c(b、c为常数)的顶点坐标为32,-258，与x轴交于A、B两点(点A在点B左侧)，与y轴交于点C，点C，点D关于x轴对称，连接AD，作直线BD．(1)求b、c的值；(2)求点A、B的坐标；(3)求证：∠ADO=∠DBO；(4)点P在抛物线y=-12x2+bx+c上，点Q在直线BD上，当以点C、D、P、Q为顶点的四边形为平行四边形时，直接写出点Q的坐标．16如图，抛物线y=ax2+2ax+c与y轴负半轴交于点C，与x轴交于A，B两点，点A在点B左侧，点B的坐标为(1,0)，OC=3OB．(1)求抛物线的解析式；(2)若点D是第三象限抛物线上的动点，连接AC，当△ACD的面积为3时，求出此时点D的坐标；(3)将抛物线y=ax2+2ax+c向右平移2个单位，平移后的抛物线与原抛物线相交于点M，N在原抛物线的对称轴上，H为平移后的抛物线上一点，当以A、M、H、N为顶点的四边形是平行四边形时，请直接写出点H的坐标．【类型五存在性之菱形】17如图，抛物线y=ax2+bx+c过点A-1,0．,B3,0,C0,3(1)求抛物线的解析式；(2)设点P是直线BC上方抛物线上一点，求出△PBC的最大面积及此时点P的坐标；(3)若点M是抛物线对称轴上一动点，点N为坐标平面内一点，是否存在以BC为边，点B、C、M、N为顶点的四边形是菱形，若存在，请直接写出点N的坐标；若不存在，请说明理由．18综合与探究：如图，已知抛物线y=-38x2+94x+6与x轴交于A，B两点(点A在点B的左边)，与y轴交于点C．直线BC与抛物线的对称轴交于点E．将直线BC沿射线CO方向向下平移n个单位，平移后的直线与直线AC 交于点F，与抛物线的对称轴交于点D．(1)求出点A，B，C的坐标，并直接写出直线AC，BC的解析式；(2)当△CDB是以BC为斜边的直角三角形时，求出n的值；(3)直线BC上是否存在一点P，使以点D，E，F，P为顶点的四边形是菱形？若存在，请直接写出点P的坐标；若不存在，请说明理由．19如图，直线y =mx +n m ≠0 ．与抛物线y =-x 2+bx +c 交于A -1,0 ，B 2,3 两点．(1)求抛物线的解析式；(2)若点C 在抛物线上，且△ABC 的面积为3，求点C 的坐标；(3)若点P 在抛物线上，PQ ⊥OA 交直线AB 于点Q ，点M 在坐标平面内，当以B ,P ,Q ,M 为顶点的四边形是菱形时，请直接写出点M 的坐标．20如图1，在平面直角坐标系中，抛物线y=-32x2+32x+3与x轴交于点A和点B(点A在点B左侧)，与y轴交于点C．(1)求直线BC的解析式；(2)点P是直线BC上方抛物线上的一动点，过点P作y轴的平行线交BC于点D，过点P作x轴的平行线交BC于点E，求PE+3PD的最大值及此时点P的坐标；(3)如图2，在(2)中PE+3PD取得最大值的条件下，将抛物线y=-32x2+32x+3沿着射线CB方向平移得到新抛物线y ，且新抛物线y 经过线段BC的中点F，新抛物线y 与y轴交于点M，点N为新抛物线y 对称轴上一点，点Q为坐标平面内一点，若以点P，Q，M，N为顶点的四边形是以PN为边的菱形，写出所有符合条件的点Q的坐标，并写出求解点Q的坐标的其中一种情况的过程．【类型六存在性之矩形】21如图①，抛物线y=ax2+x+c a≠0与x轴交于A(-2,0)，B(6,0)两点，与y轴交于点C，点P是第一象限内抛物线上的一个动点，过点P作PD⊥x轴，垂足为点D，PD交直线BC于点E，设点P的横坐标为m．(1)求抛物线的解析式；(2)如图②．过点P作PF⊥CE，垂足为点F，当CF=EF时，请求出m的值；(3)如图③，连接CP，当四边形OCPD是矩形时，在抛物线的对称轴上存在点Q，使原点O关于直线CQ的对称点O 恰好落在该矩形对角线所在的直线上，请直接写出满足条件的点Q的坐标．22已知抛物线y =ax 2+bx -4a ≠0 交x 轴于点A 4,0 和点B -2,0 ，交y 轴于点C ．(1)求抛物线的解析式；(2)如图，点P 是抛物线上位于直线AC 下方的动点，过点P 分别作x 轴、y 轴的平行线，交直线AC 于点D ，交x 轴于点E ，当PD +PE 取最大值时，求点P 的坐标及PD +PE 最大值．(3)在抛物线上是否存在点M ，对于平面内任意点N ，使得以A 、C 、M 、N 为顶点且AC 为一条边的四边形为矩形，若存在，请直接写出M 、N 的坐标，不存在，请说明理由．23综合与探究如图，抛物线y=ax2-3x+c a≠0与x轴交于A(4，0)，C两点，交y轴于点B(0，-4)，点P为y轴右侧抛物线上的一个动点．(1)求抛物线的解析式；(2)当P在AB下方时，求△ABP面积的最大值；(3)当∠ABP=15°时，△BOP的面积为；(4)点M为抛物线对称轴上的一点，点N为平面内一点，是否存点M、点N，使得以A、B、M、N为顶点的四边形是矩形？若存在，请直接写出点M的坐标；如不存在，请说明理由．24如图，直线y=43x+4与x轴交于点A，与y轴交于点C，抛物线y=ax2-83x+c(a≠0)经过A，C两点，交x轴的正半轴于点B，连接BC．(1)求抛物线的解析式．(2)点P在抛物线上，连接PB，当∠PBC=45°时，求点P的坐标；(3)已知点M从点B出发，以每秒1个单位长度的速度沿BA运动，同时点N从点O出发，以每秒3个单位长度的速度沿OC，CA运动．当点M，N运动到某一时刻时，在坐标平面内是否存在点D，使得以A，M，N，D为顶点的四边形是矩形?若存在，请直接写出点D的坐标；若不存在，请说明理由．【类型七存在性之正方形】25如图，抛物线y=-14x2+bx+c的对称轴与x轴交于点A1,0，与y轴交于点B0,3，C为该抛物线图象上的一个动点．(1)求抛物线的解析式；(2)如图，当点C在第一象限，且∠BAC=90°，求ACAB的值；(3)点D在抛物线上(点D在点C的左侧，不与点B重合)，点P在坐标平面内，问是否存在正方形ACPD？若存在，请直接写出点P的坐标；若不存在，请说明理由．26综合与探究如图，抛物线y=ax2+bx+6与x轴交于A-2,0，B4,0两点，与y轴交于点C，直线y=23x-4与x轴交于点D，与y轴交于点E．若M为第一象限内抛物线上一点，过点M且垂直于x轴的直线交DE于点N，连接MC，MD．(1)求抛物线的函数表达式及D，E两点的坐标．(2)当CM=EN时，求点M的横坐标．(3)G为平面直角坐标系内一点，是否存在点M使四边形MDEG是正方形．若存在，请直接写出点G的坐标；若不存在，请说明理由．27如图，已知直线y=-x+4与抛物线y=ax2+bx交于点A4,0两点，点P为抛物线上和B-1,5一动点，过点P作x轴的垂线，交直线AB于Q，PN⊥AB于点N．(1)求抛物线的解析式；(2)当点P在直线AB下方时，求线段PN的最大值；(3)是否存在点P使得△ABP是直角三角形，若存在，请求出点P坐标，若不存在，请说明理由；(4)坐标轴上是否存在点M，使得以点P，N，Q，M为顶点的四边形是正方形，若存在，请直接写出点M的坐标，若不存在，请说明理由28如图，抛物线y=-12x2+bx+c与x轴交于点A和点B4，0，与y轴交于点C0，4，点E在抛物线上．(1)求抛物线的解析式；(2)点E在第一象限内，过点E作EF∥y轴，交BC于点F，作EH∥x轴，交抛物线于点H，点H在点E的左侧，以线段EF,EH为邻边作矩形EFGH，当矩形EFGH的周长为11时，求线段EH的长；(3)点M在直线AC上，点N在平面内，当四边形OENM是正方形时，请直接写出点N的坐标．【类型八存在性之相似三角形】29如图，在平面直角坐标系中，抛物线y=ax2+bx-2与x轴交于点A，B，与y轴交于点C，经过点x+2交抛物线于点D，点D与点A的横坐标互为相反数，P是抛物线上一动点，连接A的直线y=-12AC．(1)求抛物线的表达式；(2)若点P在第一象限内的抛物线上，当∠PBA=2∠BAD时，求直线BP的表达式；(3)点Q在y轴上，若△DQP∽△COA，请直接写出点P的坐标．30如图，已知抛物线过三点O0,0，弧AB过线段OA的中点C，若点E为弧AB，B2,23，A8,0所在圆的圆心．(1)求该抛物线的解析式．(2)求圆心点E的坐标，并判断点E是否在这条抛物线上．(3)若弧BC的中点为P，是否在x轴上存在点M，使得△APB与△AMP相似？若存在，请求出点M的坐标，若不存在说明理由．31如图，在直角坐标系中有一直角三角形AOB，O为坐标原点，OA=1，tan∠BAO=3，将此三角形绕原点O逆时针旋转90°，得到△DOC，抛物线y=ax2+bx+c经过点A、B、C．(1)求抛物线的解析式；(2)若点P是第二象限内抛物线上的动点，其横坐标为t，①是否存在一点P，使△PCD的面积最大？若存在，求出△PCD的面积的最大值；若不存在，请说明理由．②设抛物线对称轴l与x轴交于一点E，连接PE，交CD于F，直接写出当△CEF与△COD相似时，点P的坐标；32如图，抛物线y=12x2+mx+n与x轴交于A，B两点，与y轴交于点C，抛物线的对称轴交x轴于点D，已知A-4,0，C0,-2．(1)求抛物线和直线AC的函数解析式；(2)若点E是线段AC上的一个动点，过点E作x轴的垂线与抛物线相交于点F，求四边形CDAF的最大面积；(3)在抛物线的对称轴上找一点P，使得以A、D、P为顶点的三角形与△OAC相似，请直接写出点P的坐标．【类型九存在性之角度问题】33如图，抛物线y=ax2+bx+2经过A-1,0为抛物线上、B4,0两点，与y轴交于点C，点D x,y 第一象限内的一个动点．(1)求抛物线所对应的函数表达式；(2)当△BCD的面积为4时，求点D的坐标；(3)该抛物线上是否存在点D，使得∠DCB=2∠ABC，若存在，求点D的坐标；若不存在，请说明理由．34如图，抛物线y=ax2+bx-1a≠0与x轴交于点A1,0和点B，与y轴交于点C，抛物线的对称轴交x轴于点D3,0，过点B作直线l⊥x轴，过点D作DE⊥CD，交直线l于点E．(1)求抛物线的解析式；(2)如图，点P为第三象限内抛物线上的点，连接CE和BP交于点Q，当BQPQ=57时．求点P的坐标；(3)在(2)的条件下，连接AC，在直线BP上是否存在点F，使得∠DEF=∠ACD+∠BED？若存在，请直接写出点F的坐标；若不存在，请说明理由．35如图，在平面直角坐标系xoy中，顶点为M的抛物线y=ax2+bx a>0经过点A(-1,3)和x轴正半轴上的点B，AO=OB．(1)求这条抛物线的表达式；(2)联结OM，求∠AOM的度数；(3)联结AM、BM、AB，若在坐标轴上存在一点P，使∠OAP=∠ABM，求点P的坐标．36如图，在平面直角坐标系中，已知抛物线y=ax2+bx-2(a≠0)与x轴交于A1,0两点，，B3,0与y轴交于点C，其顶点为点D，点E的坐标为0,-1，该抛物线与BE交于另一点F，连接BC．(1)求该抛物线的解析式．(2)一动点M从点D出发，以每秒1个单位的速度沿与y轴平行的方向向上运动，连接OM，BM，设运动时间为t秒(t>0)，在点M的运动过程中，当t为何值时，∠OMB=90°？(3)在x轴上方的抛物线上，是否存在点P，使得∠PBF被BA平分？若存在，请直接写出点P的坐标；若不存在，请说明理由．。

专题03 二次函数与面积有关问题(学生版)

专题03二次函数与面积有关问题（专项训练）1．（2022•成都）如图，在平面直角坐标系xOy中，直线y＝kx﹣3（k≠0）与抛物线y＝﹣x2相交于A，B两点（点A在点B的左侧），点B关于y轴的对称点为B'．（1）当k＝2时，求A，B两点的坐标；（2）连接OA，OB，AB'，BB'，若△B'AB的面积与△OAB的面积相等，求k的值；2．（2021•枣庄）如图，在平面直角坐标系中，直线y＝﹣x+3与x轴交于点A，与y轴交于点B，抛物线y ＝x2+bx+c经过坐标原点和点A，顶点为点M．（1）求抛物线的关系式及点M的坐标；（2）点E是直线AB下方的抛物线上一动点，连接EB，EA，当△EAB的面积等于时，求E点的坐标；3．（2021•柳州）在平面直角坐标系xOy中，已知抛物线：y＝ax2+bx+c交x轴于A（﹣1，0），B（3，0）两点，与y轴交于点C（0，﹣）．（1）求抛物线的函数解析式；（2）如图1，点D为第四象限抛物线上一点，连接OD，过点B作BE⊥OD，垂足为E，若BE＝2OE，求点D 的坐标；（3）如图2，点M为第四象限抛物线上一动点，连接AM，交BC于点N，连接BM，记△BMN的面积为S1，△ABN的面积为S2，求的最大值．4．（2020•宿迁）二次函数y＝ax2+bx+3的图象与x轴交于A（2，0），B（6，0）两点，与y轴交于点C，顶点为E．（1）求这个二次函数的表达式，并写出点E的坐标；（2）如图①，D是该二次函数图象的对称轴上一个动点，当BD的垂直平分线恰好经过点C时，求点D的坐标；（3）如图②，P是该二次函数图象上的一个动点，连接OP，取OP中点Q，连接QC，QE，CE，当△CEQ的面积为12时，求点P的坐标．5．（2020•淄博）如图，在直角坐标系中，四边形OABC是平行四边形，经过A（﹣2，0），B，C三点的抛物线y＝ax2+bx+（a＜0）与x轴的另一个交点为D，其顶点为M，对称轴与x轴交于点E．（1）求这条抛物线对应的函数表达式；（2）已知R是抛物线上的点，使得△ADR的面积是▱OABC的面积的，求点R的坐标；6．（2020•天水）如图所示，抛物线y＝ax2+bx+c（a≠0）与x轴交于A、B两点，与y轴交于点C，且点A的坐标为A（﹣2，0），点C的坐标为C（0，6），对称轴为直线x＝1．点D是抛物线上一个动点，设点D的横坐标为m（1＜m＜4），连接AC，BC，DC，DB．（1）求抛物线的函数表达式；（2）当△BCD的面积等于△AOC的面积的时，求m的值；7．（2021•沈阳）如图，平面直角坐标系中，O是坐标原点，抛物线y＝﹣x2+bx+c与x轴交于A、B两点（点A在点B的左侧），点B坐标是（3，0）．抛物线与y轴交于点C（0，3），点P是抛物线的顶点，连接PC．（1）求抛物线的函数表达式并直接写出顶点P的坐标．（2）直线BC与抛物线对称轴交于点D，点Q为直线BC上一动点．当△QAB的面积等于△PCD面积的2倍时，求点Q的坐标；8．（2021•辽宁）如图，抛物线y＝﹣x2+bx+c与x轴交于点A和点C（﹣1，0），与y轴交于点B（0，3），连接AB，BC，点P是抛物线第一象限上的一动点，过点P作PD⊥x轴于点D，交AB于点E．（1）求抛物线的解析式；（2）如图1，作PF⊥PD于点P，使PF＝OA，以PE，PF为邻边作矩形PEGF．当矩形PEGF的面积是△BOC 面积的3倍时，求点P的坐标；9．（2022•南宁一模）如图1所示抛物线与x轴交于O，A两点，OA＝6，其顶点与x轴的距离是6．（1）求抛物线的解析式；（2）点P在抛物线上，过点P的直线y＝x+m与抛物线的对称轴交于点Q．当△POQ与△PAQ的面积之比为1：3时，求m的值；10.（2022•本溪二模）如图，抛物线y＝﹣x2+bx+c经过A（3，0），C（﹣1，0）两点，与y轴交于点B．（1）求抛物线的解析式；（2）如图1，点M是线段AB上方抛物线上一动点，以AB为边作平行四边形ABMD，连接OM，若OM将平行四边形ABMD的面积分成为1：7的两部分，求点M的横坐标；11．（2022•新抚区模拟）如图，直线y＝mx+n与抛物线y＝﹣x2+bx+c交于A（﹣2，0），B（2，2）两点，直线AB与y轴交于点C．（1）求抛物线与直线AB的解析式；（2）点P在抛物线上，直线PC交x轴于Q，连接PB，当△PBC的面积是△ACQ面积的2倍时，求点P的坐标；12．（2022•福建）在平面直角坐标系xOy中，已知抛物线y＝ax2+bx经过A（4，0），B（1，4）两点．P是抛物线上一点，且在直线AB的上方．（1）求抛物线的解析式；（2）若△OAB面积是△PAB面积的2倍，求点P的坐标；13．（2022•苏州二模）如图，已知抛物线y＝x2+bx+c与x轴交于点A，B（点A在点B的左侧），与y轴交于点C，OA＝OC＝3．（1）求抛物线的函数表达式；（2）若点P为直线AC下方抛物线上一点，连接BP并交AC于点Q，若AC分∠△ABP的面积为1：2两部分，请求出点P的坐标；。

专题04 二次函数应用题(学生版)

专题04二次函数应用题1．2022年杭州亚运会会后，吉祥物“江南忆”很受欢迎，非常畅销．小李用1200元批发了一批吉祥物销售，很快售完，他又用1200元批发同样的吉祥物销售，由于批发价上涨了20%，因此第二批吉祥物的数量比第一批少了10个．(1)求每个吉祥物的批发原价是多少?(2)调查发现，每个吉祥物的售价为40元时，每周可售出30个．小李为了增加销量，决定降价促销，若售价每降低1元，每周的销量可增加5个，每个吉祥物需要扣除2元的小店运营成本．求当吉祥物的售价为多少时每周的利润最大?最大利润是多少?（吉祥物的进价全部按涨价后的价格计算）．α=︒．为了对这个斜坡上的绿地进行喷灌，在斜坡底端安装了一个喷头A，喷2．如图1，斜坡与水平面夹角30头A喷出的水柱在空中走过的曲线可以看成抛物线的一部分．如图2，当水柱与A水平距离为4米时，达到最高点D，D与水平线AC的距离为4米．(1)在图2中建立平面直角坐标系，求水柱所在的抛物线的解析式（不需要写出自变量取值的范围）；(2)若斜坡上有一棵高2.5米的树，它与喷头A的水平距离为2米，通过计算判断从A喷出的水柱能否越过这棵树．3．有一个抛物线形的拱形隧道，隧道的最大高度为6m，跨度为8m，把它放在如图所示的平面直角坐标系中．(1)求这条抛物线所对应的函数关系式；(2)若要在隧道壁上点P（如图）安装一盏照明灯，灯离地面高4.5m．求灯与点B的距离．(3)隧道内设双向单车道（中间有一条隔离带，隔离带宽度忽略不计），一辆满载后车身宽2.5m，高2.8m的卡车能否安全通过？4．某社区决定把一块长为50m、宽30m的矩形空地建为居民健身广场，设计方案如图所示，阴影区域为绿化区（四块绿化区均为大小、形状都相同的矩形），空白区域为活动区，且四周的四个出口宽度相同，其宽度不小于14m，不大于26m，设绿化区较长边为m x，活动区的面积为2m y．(1)求y与x的函数表达式，并直接写出自变量x的取值范围；(2)求活动区最大面积．5．2023年亚运会即将在杭州举行，某网络经销商购进了一批以亚运会为主题的文化衫进行销售，文化衫的进价为每件30元，当销售单价定为70元时，每天可售出20件．为了扩大销售，增加盈利，决定采取适当的降价措施，经调查发现：销售单价每降低1元，则每天可多售出2件（销售单价不低于进价），若设这款文化衫的销售单价为x（元），每天的销售量为y（件）．(1)当销售单价定为65元时，每天可售出文化衫___________件；(2)求出每天的销售量y（件）与销售单价x（元）之间的函数关系式；(3)当销售单价为多少元时，销售这款文化衫每天所获得的利润为1248元？6．某超市销售一种商品，成本每千克40元，规定每千克售价不低于成本，且不高于65元，经市场调查、每天的销售量y（千克）与每千克售价x（元）满足一次函数关系，部分数据如下表：售价x（元/千克）506070销售量y（千克）1008060(1)直接写出y与x之间的函数表达式；(2)设商品每天的总利润为W（元），求W与x之间的函数表达式，并指出售价为多少元时获得最大利润，最大利润是多少？7．某超市销售一批成本为20元/千克的绿色健康食品，深受游客青睐．经市场调查发现，该食品每天的销售量y（千克）与销售单价x（元/千克）之间满足一次函数关系，其图像如图所示．(1)求该食品每天的销售量y（千克）与销售单价x（元/千克）之间的函数关系式；(2)若超市按售价不低于成本价，且不高于40元销售，则销售单价定为多少，才能使销售该食品每天获得的利润W（元）最大？最大利润是多少？8．图是某跳台滑雪训练场的横截面示意图，取水平线为x轴，过跳台终点A作水平线的垂线为y轴，建立平面直角坐标系．图中的抛物线1C ：2171126y x x =-++近似表示滑雪场地上的一座小山坡，某运动员从点O 正上方4米处的A 点滑出，滑出后沿一段抛物线2C ：218y x bx c =-++运动．(1)当运动员运动到离A 处的水平距离为4米时，离水平线的高度为8米，求抛物线2C 的函数解析式（不要求写出自变量x 的取值范围）；(2)在（1）的条件下，当运动员运动水平线的水平距离为多少米时，运动员与小山坡的竖直距离为1米？(3)当运动员运动到坡顶正上方，且与坡顶距离超过3米时，求b 的取值范围．9．某商店经销一种健身球，已知这种健身球的成本价为每个20元，市场调查发现，该种健身球每天的销售量y（个）与销售单价x （元）有如下关系：()2802040y x x =-+≤≤，设这种健身球每天的销售利润为w 元．(1)如果销售单价定为25元，那么健身球每天的销售量是____________个；(2)求w 与x 之间的函数关系式；(3)该种健身球销售单价定为多少元时，每天的销售利润最大？最大利润是多少元？10．某服装专卖店A 款衣服的进价为100元/件，经市场调查发现，当A 款衣服的定价为140元/件时，每天可售出20件，在此基础上，A 款衣服的定价每件降价3元，该服装店每天就会多售出6件，设A 款衣服每件降价x 元．(1)A 款衣服每件的利润为元，每天的销量为件；（用含x 的代数式表示）(2)若该服装专卖店每天销售A 款衣服获利1200元，为了更多地让利于顾客，A 款衣服的定价应为多少元？(3)该服装专卖店每天销售A 款衣服的总利润可能达到1450元吗？请说明理由．11．某商家独家销售具有地方特色的某种商品，每件进价为40元．经过市场调查，得出一周的销售量y 件是销售单价()50x x ≥元/件的一次函数，其部分对应数据如下表所示：销售单价x （元/件） (55)607075…一周的销售量y （件）…450400300250…(1)求出y 与x 的函数关系式：(2)设一周的销售利润为S 元，请求出S 与x 的函数关系式；(3)雅安地震牵动亿万人民的心，商家决定将商品一周的销售利润全部寄往灾区，在商家购进该商品的货款不超过10000元情况下，请你求出该商家最大捐款数额是多少元？12．已知：如图，在Rt ACB 中，=90°C ∠，4cm AC =，3cm BC =，点P 由B 出发沿BA 方向向点A 匀速运动速度为1cm/s ；点Q 由A 出发沿AC 方向向点C 匀速运动，速度为2cm/s ；连接PQ ．若设运动的时间为()()02t s t <<，解答下列问题：(1)当t 为何值时，点A 在PQ 垂直平分线上(2)当t 为何值时，APQ △为直角三角形？(3)设APQ △的面积为()2cm y ，求y 与t 之间的函数关系式；(4)是否存在某一时刻t ，使线段PQ 恰好把Rt ACB 的面积平分？若存在，求出此时t 的值；若不存在，说明理由．13．第二十四届冬奥会在北京成功举办，在跳台滑雪项目中，运动员首先沿着跳台助滑道飞速下滑，然后在起跳点腾空，身体在空中飞行至着陆坡着陆，再滑行到停止区终止．某数学小组对该项目中的数学问题进行了深入研究，下图是该小组绘制的赛道截面图，以停止区CD 所在水平线为x 轴，过起跳点A 与x 轴垂直的直线为y 轴，O 为坐标原点，建立平面直角坐标系，AC 为着陆坡，65m OA =，某运动员在A 处起跳腾空后，飞行至着陆坡的B处着陆，过点B 作BE y ⊥轴于点E ，且BE =，在空中飞行过程中，运动员到x 轴的距离()m y 与水平方向移动的距离()m x 具备二次函数关系，其解析式为213602y x x c =-+．(1)=c _________，点B 的坐标为_________；(2)进一步研究发现，该运动员在飞行过程中，其水平方向移动的距离()m x 与飞行时间()s t 具备一次函数关系，当运动员在起跳点腾空时，=0t ，=0x ；空中飞行5s 后着陆．①求x 关于t 的函数解析式；②当t 为何值时，运动员离着陆坡的竖直距离h 最大，最大值是多少？14．某蔬菜批发商以每千克18元的价格购进一批山野菜．经市场调查发现，山野菜的日销售量y （千克）与每千克售价x （元）之间满足3y x b =-+，当=20x 时，66y =．(1)求b 的值；(2)设该批发商每日销售这批山野菜所获得的利润为w 元．①求w 关于x 之间的函数解析式；②当每千克山野菜的售价定为多少元时，该批发商每日销售这批山野菜所获得的利润最大？最大利润为多少元？15．中山公园有一个抛物线形状的观景拱桥ABC ，其横截面如图所示，在图中建立的直角坐标系中，抛物线的解析式为2120y x c =-+且过顶点()0,5C （长度单位：m ）(1)直接写出c 的值；(2)现因搞庆典活动，计划沿拱桥的台阶表面铺设一条宽度为1.5m 的地毯，地毯的价格为20元/2m ，求购买地毯需多少元？(3)在拱桥加固维修时，搭建的“脚手架”为矩形EFGH （H 、G 分别在抛物线的左右侧上），并铺设斜面EG ．已知矩形EFGH 的周长为27.5m ，求斜面EG 在这个坐标系中的解析式．16．某商店销售一种商品，该商品的进价为40元/件，经市场调查发现：该商品的周销售量y （件）是售价x （元/件）的一次函数，部分数据如表：售价x（元/件）55658085周销售量y（件）90704030(1)直接写出y与x之间的函数表达式为______；(2)当售价定为多少元时，每周可获得最大利润？最大利润是多少元？(3)由于某种原因，该商店进价提高了m元/件（m＞0），通过销售记录发现，当销售价格大于76元/件时，每周的利润随售价的增大而减小，请直接写出m的取值范围为______．17．园林基地计划投资种植花卉及树木，已知种植树木的利润1y与投资量x成正比例关系，种植花卉的利润2y与投资量x的平方．．成正比例关系，并根据市场调查与预测，得到了表格中的数据．投资量x（万元）2y（万元）4种植树木利润1y（万元）2种植花卉利润2(1)请根据表格填空：利润1与投资量x的函数关系式为______；利润2y与投资量x的函数关系式为______；(2)如果这个基地计划以6万元资金全部投入种植花卉和树木，设投入种植花卉的金额为m万元，种植花卉和树木共获利W万元，求出W关于m的函数关系式，并求该基地至少获得多少利润？基地能获取的最大利润是多少？(3)若该基地想获利不低于12万，在（2）的条件下，请直接写出投资种植花卉的金额m的范围．18．某水果经销商以20元/千克的价格新进1000kg杨梅进行销售，因为杨梅不耐储存，在运输储存过程损耗率为16．为了得到日销售量y （千克）与销售价格x （元/千克）之间的关系，经过市场调查获得部分数据如下表：销售价格x （元/千克）2025303540日销售量y （千克）300225150750(1)这批杨梅的实际成本为_____元/千克，每千克定价为______元时，这批杨梅可获得5000元利润；(2)①请你根据表中的数据直接写出y 与x 之间的函数表达式．②该水果经销商应该如何确定这批杨梅的销售价格，才能使日销售利润1w 最大？(3)该水果经销商参与电商平台助农活动，开展网上直销，可以完全避免运输储存过程中的损耗成本，但每销售1千克杨梅需支出a 元()0a ＞的相关费用，销售量与销售价格之间关系不变．当2530x ≤≤，该水果经销商日获利2w 的最大值为1200元，求a 的值．（日获利＝日销售利润-日支出费用）19．某商店销售一种商品，经市场调查发现：该商品的周销售量y (件)是售价x （元/件）的一次函数，其售价、周销售量、周销售利润w（元）的三组对应值如下表：售价x（元/件）506070周销售量y（件）806040周销售利润w（元）80012001200注：周销售利润＝周销售量×（售价－进价）(1)求y关于x的函数解析式（不要求写出自变量的取值范围）；(2)求该商品的进价和周销售的最大利润；m ，物价部门规定该商品售价不得超过60元/件，该商店在今(3)由于某种原因，该商品进价提高了m元/件(0)后的销售中，周销售量与售价仍然满足（1）中的函数关系．若周销售最大利润是1080元，求的值．20．如图，某城区公园有直径为7m的圆形水池，水池边安有排水槽，在正中心O处修喷水装置，喷出的水流呈抛物线状，当水管OA高度在6m处时，距离OA水平距离1m处喷出的水流达到最大高度为8m．(1)求抛物线解析式，并求水流落地点B到点O的距离（即线段OB的长）；(2)距离OA水平距离多远的E点处，放置高为3.5m的景观射灯EF使水流刚好到点F？(3)若不改变（1）中抛物线的形状和对称轴，若使水流落地点恰好落在圆形水池边排水槽内（不考虑边宽），则此时水管OA的高度为多少？。

九年级数学二次函数专项训练含答案精选5篇

九年级上册数学二次函数同步练习一、单选题1．下列函数中，是二次函数的是（） A ．y ＝（2x ﹣1）2 B ．y ＝（x +1）2﹣x 2 C ．y ＝ax 2D ．y ＝2x +32．若抛物线258(3)23m m y m x x -+=-+-是关于x 的二次函数，那么m 的值是（）A ．3B ．2-C ．2D ．2或33．若抛物线y =x 2-x -2经过点A （3，a ），则a 的值是（） A ．2B ．4C ．6D ．84．已知二次函数2135y x x =-+，则其二次项系数a ，一次项系数b ，常数项c 分别是（） A ．1,3,5a b c ==-= B ．1,3,5a b c ===C ．5,3,1a b c ===D ．5,3,1a b c ==-=5．如果函数2(2)25y a x x =-+-是二次函数，则a 的取值范围是（） A ．2a ≠ B ．a≥0C ．a=2D ．a>06．下列函数中①31y x ；①243y x x =-；①1y x=；①225=-+y x ，是二次函数的有（） A ．①①B ．①①C ．①①D ．①①7．若抛物线2y x bx c =-++经过点()2,3-，则247c b --的值是（） A ．6B ．7C ．8D ．208．函数y=ax2+bx+c(a ，b ，c 是常数)是二次函数的条件是( ) A ．a≠0，b≠0，c≠0 B ．a<0，b≠0，c≠0 C ．a>0，b≠0，c≠0 D ．a≠0二、填空题 9．若()2321m m y m x --=+是二次函数，则m 的值为______．10．若22ay x -=是二次函数，则=a ________．11．在二次函数21y x =-+中，二次项系数、一次项系数、常数项的和为_____． 12．下列函数一定是二次函数的是__________．①2y ax bx c =++；①3y x =-；①2431y x x =-+；①2(1)y m x bx c =-++；①y =(x -3)2-x 213．当常数m ≠______时，函数y =（m 2﹣2m ﹣8）x 2+（m +2）x +2是二次函数；当常数m =___时，这个函数是一次函数． 14．已知函数2135m y x -=-① 当m ＝ _________时，y 是关于x 的一次函数； ① 当m ＝_________时，y 是关于x 的二次函数．15．二次函数()22339y m x x m =+++-的图象经过原点，则m =__________．16．已知二次函数2y x bx 3=-++，当x 2=时，y 3=．则这个二次函数的表达式是________．三、解答题17．下列函数中（x ，t 是自变量），哪些是二次函数？ 22322113,25,22,1522y x y x x y x s t t =-+=-+=+=++．18．已知函数y =（m 2-2）x 2+（m x +8．（1）若这个函数是一次函数，求m 的值；（2）若这个函数是二次函数，求m 的取值范围.19．若函数y=（a -1）x b+1+x 2+1是二次函数，试讨论a 、b 的取值范围.20．篱笆墙长30m ，靠墙围成一个矩形花坛，写出花坛面积y(m 2)与长x 之间的函数关系式，并指出自变量的取值范围.参考答案：1．A 2．C 3．B 4．D 5．A 6．B 7．B 8．D 9．4 10．2± 11．0 12．①13． 4，-2 4 14． 1 3215．316．2y x 2x 3=-++17．2132y x =-+和215s t t =++是二次函数18．（1）m （2）m ≠m ≠19．①a≠0；①b=0或-1，a 取全体实数①当a=1，b 为全体实数时，y=x 2+1是二次函数 20．y= 21152x x -+, x 的取值范围为0<x<30.九年级数学上册二次函数单元综合测试卷一．选择题（共10小题）1．下列各式中，是y 关于x 的二次函数的是（） A ．y ＝4xB ．y ＝3x ﹣5C ．y ＝D ．y ＝2x 2+12．已知：a ＞b ＞c ，且a +b +c ＝0，则二次函数y ＝ax 2+bx +c 的图象可能是下列图象中的（）A．B．C．D．3．二次函数y＝（x﹣2）（x﹣4）+6的顶点坐标是（）A．（2，6）B．（4，6）C．（3，﹣5）D．（3，5）4．将二次函数y＝x2+2x﹣1转化为y＝a（x﹣h）2+k的形式，结果为（）A．y＝（x﹣1）2B．y＝（x+1）2C．y＝（x+1）2﹣1D．y＝（x+1）2﹣2 5．已知0≤x≤，则函数y＝﹣2x2+8x﹣6的最大值是（）A．﹣10.5B．2C．﹣2.5D．﹣66．顶点坐标为（3，1），形状与函数y＝的图象相同且开口方向相反的抛物线的解析式为（）A．y＝+1B．y＝+1C．y＝﹣+1D．y＝﹣+17．已知点A（﹣1，y1），B（1，y2），C（2，y3）都在二次函数y＝（x﹣1）2的图象上，则y1，y2，y3的大小关系正确的是（）A．y1＜y2＜y3B．y2＜y1＜y3C．y2＜y3＜y1D．y3＜y2＜y1 8．抛物线y＝ax2+bx+c纵坐标y的对应值如下表：x…﹣2﹣1012…y…04664…则下列说法中正确的个数是（）①方程ax2+bx+c＝0，有两根为x1＝﹣2，x2＝3；②抛物线与y轴的交点为（0，6）；③抛物线的对称轴是直线x＝1；④抛物线开口向上．A．1B．2C．3D．49．如图，在正方形ABCD中，AB＝4，AC与BD交于点O，E，F分别为边BC，CD上的点（点E，F不与线段BC，CD的端点重合），BE＝CF，连接OE，OF，EF．关于以下三个结论，下列判断正确的是（）结论Ⅰ：∠BOF始终是90°；结论Ⅱ：△OEF面积的最小值是2；结论Ⅲ：四边形OECF的面积始终是8．A．结论Ⅰ和Ⅱ都对，结论Ⅲ错B．结论Ⅰ和Ⅱ都对，结论Ⅱ错C．结论Ⅱ和Ⅲ都对，结论Ⅰ错D．三个结论都对10．使用家用燃气灶烧开同一壶水所需的燃气量y（单位：m3）与旋钮的旋转角度x（单位：度）（0＜x≤90）近似满足函数关系y＝ax2+bx+c（a≠0）．如图记录了某种家用燃气灶烧开同一壶水的旋钮角度x与燃气量y的三组数据，根据上述函数模型和数据，可推断出此燃气灶烧开一壶水最节省燃气的旋钮角度约为（）A．37.5°B．40°C．42.5°D．45°二．填空题（共6小题）11．函数是二次函数，则m的值为．12．已知抛物线y＝x2﹣4x+c．与直线y＝m相交于A，B两点，若点A的横坐标；x A＝﹣1，则点B的横坐标．x B的值为．13．已知二次函数y＝ax2开口向上，且|2﹣a|＝3，则a＝．14．已知抛物线y＝x2﹣3x+1的图象上有一点A（m，n），则m﹣n的最大值是．15．如图，在平面直角坐标系中，抛物线y＝﹣x2+2x+c与x轴交于点A、B，与y轴交于点C，过点C作CD∥x轴，交抛物线于另一点D，若AB+CD＝3，则c的值为．16．如图，在矩形ABCD中，AB＝12，BC＝16，点E、F分别是边AB、BC上的动点，且EF＝10，点G是EF的中点，AG、CG，则四边形AGCD面积的最小值为．三．解答题（共7小题）17．看图回答．（1）当y＝0时，求x的值；（2）当y＞5时，求x的范围；（3）y随x的增大而增大时，求x的范围．18．已知二次函数y＝x2﹣6x+8．（1）将解析式化成顶点式；（2）写出它的开口方向、对称轴和顶点坐标；（3）x取什么值时，y随x的增大而增大；x取什么值时，y随x增大而减小．19．如图，以一定的速度将小球沿与地面成一定角度的方向击出时，小球的飞行路线是一条抛物线．若不考虑空气阻力，小球的飞行高度h（单位：m）与飞行时间t（单位：s）之间具有函数关系：h＝﹣5r2+20t，求小球飞行高度达到最高时的飞行时间．20．“阳光玫瑰葡萄”品种是近几年来广受各地消费者青睐的优质新品种，在云南省广泛种植．长沙市某品牌水果经销商计划在2023年五一期间进行商业促销活动，经过调查往年的统计数据发现，云南省批发“阳光玫瑰葡萄”的最低价格为每斤15元若按每斤30元的价格到市区销售，平均每天可售出60斤若每斤“阳光玫瑰葡萄”的售价每降低1元，那么平均每天的销售量会增加10斤，为了尽快减少库存，该水果商决定降价销售．（1）若降价2元，则每天的销售利润是多少元（2）若该经销商计划销售“阳光玫瑰葡萄”每天盈利1100元，那么每斤“阳光玫瑰葡萄”的售价应降至每斤多少元？（其它成本忽略不计）（3）将商品的销售单价定为多少元时，商场每天销售该商品获得的利润w最大？最大利润是多少元？21．如图，抛物线与x轴交于A（﹣1，0）、B（4，0），与y轴交于C．（1）求抛物线的解析式；（2）如图1，已知线段DE与线段BC关于平面内某点成中心对称，其中DE的两端点刚好一个落在抛物线上，一个落在对称轴上，求落在对称轴上的点的坐标；（3）如图2，点M为第二象限抛物线上，作MN∥BC交抛物线于点N，直线NB、MC 交于点P，求P点的横坐标．22．在平面直角坐标系xOy中，对于点P（x，y）和Q（x，y'），给出如下定义：若y'＝，则称点Q为点P的“可控变点”．例如：点（1，2）的“可控变点”为点（1，2），点（﹣1，3）的“可控变点”为点（﹣1，﹣3）．（1）点（﹣5，﹣2）的“可控变点”坐标为；（2）若点P在函数y＝﹣x2+16的图象上，其“可控变点”Q的纵坐标y′是7，求“可控变点”Q的横坐标；（3）若点P在函数y＝﹣x2+16（﹣5≤x≤a）的图象上，其“可控变点”Q的纵坐标y′的取值范围是﹣16≤y′≤16，求实数a的取值范围．23．在平面直角坐标系中，抛物线y＝x2+bx+c经过A（﹣4，0），点M为抛物线的顶点，点B在y轴上，直线AB与抛物线在第一象限交于点C（2，6），如图①．（1）求抛物线解析式；（2）直线AB的函数解析式为，点M的坐标为．（3）在y轴上找一点Q，使得△AMQ的周长最小，具体作法如图②，作点A关于y轴的对称点A'，连接MA′交y轴于点Q，连接AM，AQ，此时△AMQ的周长最小，请求出点Q的坐标；（4）在坐标平面内是否存在点N，使以点A，O，C，N为顶点的四边形是平行四边形？若存在请直接写出点N的坐标；若不存在，请说明理由．参考答案一．选择题（共10小题）1．下列各式中，是y关于x的二次函数的是（）A．y＝4x B．y＝3x﹣5C．y＝D．y＝2x2+1解：A．根据二次函数的定义，y＝4x是一次函数，不是二次函数，故A不符合题意．B．根据二次函数的定义，y＝3x﹣5不是二次函数，是一次函数，故B不符合题意．C．根据二次函数的定义，y＝是反比例函数，不是二次函数，故C不符合题意．D．根据二次函数的定义，y＝2x2+1是二次函数，故D符合题意．故选：D．2．已知：a＞b＞c，且a+b+c＝0，则二次函数y＝ax2+bx+c的图象可能是下列图象中的（）A．B．C．D．解：A、由图知a＞0，﹣＝1，c＞0，即b＜0，∵已知a＞b＞c，故本选项错误；B、由图知a＜0，而已知a＞b＞c，且a+b+c＝0，必须a＞0，故本选项错误；C、图C中条件满足a＞b＞c，且a+b+c＝0，故本选项正确；D、∵a+b+c＝0，即当x＝1时a+b+c＝0，与图中与x轴的交点不符，故本选项错误．故选：C．3．二次函数y＝（x﹣2）（x﹣4）+6的顶点坐标是（）A．（2，6）B．（4，6）C．（3，﹣5）D．（3，5）解：∵二次函数可化为y＝（x﹣3）2+5，∴二次函数y＝（x﹣2）（x﹣4）+6的顶点坐标是（3，5），故选：D．4．将二次函数y＝x2+2x﹣1转化为y＝a（x﹣h）2+k的形式，结果为（）A．y＝（x﹣1）2B．y＝（x+1）2C．y＝（x+1）2﹣1D．y＝（x+1）2﹣2解：y＝x2+2x﹣1＝（x2+2x+1）﹣2＝（x+1）2﹣2，即y＝（x+1）2﹣2．故选：D．5．已知0≤x≤，则函数y＝﹣2x2+8x﹣6的最大值是（）A．﹣10.5B．2C．﹣2.5D．﹣6解：y＝﹣2x2+8x﹣6＝﹣2（x﹣2）2+2，∴当x＜2时，y随着x增大而增大，∴当x＝时有最大值y＝﹣2（﹣2）2+2＝﹣2.5，故选：C．6．顶点坐标为（3，1），形状与函数y＝的图象相同且开口方向相反的抛物线的解析式为（）A．y＝+1B．y＝+1C．y＝﹣+1D．y＝﹣+1解：设所求的抛物线解析式为y＝a（x﹣3）2+1，∵所求抛物线与函数y＝的图象相同且开口方向相反，∴a＝﹣，∴所求的抛物线解析式为y＝﹣（x﹣3）2+1．故选：D．7．已知点A（﹣1，y1），B（1，y2），C（2，y3）都在二次函数y＝（x﹣1）2的图象上，则y1，y2，y3的大小关系正确的是（）A．y1＜y2＜y3B．y2＜y1＜y3C．y2＜y3＜y1D．y3＜y2＜y1解：当x＝﹣1时，y1＝（x﹣1）2＝（﹣1﹣1）2＝4；当x＝1时，y2＝（x﹣1）2＝（1﹣1）2＝0；当x＝2时，y3＝（x﹣1）2＝（2﹣1）2＝1，所以y2＜y3＜y1．故选：C．8．抛物线y＝ax2+bx+c纵坐标y的对应值如下表：x…﹣2﹣1012…y…04664…则下列说法中正确的个数是（）①方程ax2+bx+c＝0，有两根为x1＝﹣2，x2＝3；②抛物线与y轴的交点为（0，6）；③抛物线的对称轴是直线x＝1；④抛物线开口向上．A．1B．2C．3D．4解：根据表格数据可知：抛物线的对称轴是直线x＝＝，∴③错误；∵抛物线与x轴的一个交点为（﹣2，0），∴抛物线与x轴的另一个交点为（3，0），∴方程ax2+bx+c＝0有两根为x1＝﹣2，x2＝3；故①正确；从表格可知当x＝0时，y＝6，∴抛物线与y轴的交点为（0，6）；∴②正确；从表格可知：当x＜时，y随x的增大而增大，当x＞时，y随x的增大而减小，∴抛物线开口向下，故④错误．故选：B．9．如图，在正方形ABCD中，AB＝4，AC与BD交于点O，E，F分别为边BC，CD上的点（点E，F不与线段BC，CD的端点重合），BE＝CF，连接OE，OF，EF．关于以下三个结论，下列判断正确的是（）结论Ⅰ：∠BOF始终是90°；结论Ⅱ：△OEF面积的最小值是2；结论Ⅲ：四边形OECF的面积始终是8．A．结论Ⅰ和Ⅱ都对，结论Ⅲ错B．结论Ⅰ和Ⅱ都对，结论Ⅱ错C．结论Ⅱ和Ⅲ都对，结论Ⅰ错D．三个结论都对解：∵四边形ABCD是正方形，∴OB＝OC，∠BOC＝90°，∴∠OBE＝∠OCF＝45°，∵BE＝CF，∴△BOE≌△COF，∴OE＝OF，∠BOE＝∠COF，∴∠BOE+∠COE＝∠COF+∠COE，即∠EOF＝∠BOC＝90°，且S△COE+S△COF＝S△COE+S△BOE，即S四边形OECF＝S△BOC＝S正方形ABCD＝×4×4＝4，由垂线段最短可得，当OE⊥BC时，OE＝BC＝×4＝2，△OEF面积取最小值为×2×2＝2，∴结论Ⅰ和Ⅱ都对，结论Ⅲ错，故选：A．10．使用家用燃气灶烧开同一壶水所需的燃气量y（单位：m3）与旋钮的旋转角度x（单位：度）（0＜x≤90）近似满足函数关系y＝ax2+bx+c（a≠0）．如图记录了某种家用燃气灶烧开同一壶水的旋钮角度x与燃气量y的三组数据，根据上述函数模型和数据，可推断出此燃气灶烧开一壶水最节省燃气的旋钮角度约为（）A．37.5°B．40°C．42.5°D．45°解：把（25，0.725），（50，0.06），（60，0.09）代入y＝ax2+bx+c得：，解得，∴y＝0.0001x2﹣0.008x+0.21＝0.0001（x﹣40）2+0.05，∵0.0001＞0，∴x＝40时，y最小为0.05，∴燃气灶烧开一壶水最节省燃气的旋钮角度约为40°，故选：B．二．填空题（共6小题）11．函数是二次函数，则m的值为3．解：∵函数是二次函数，∴m2﹣7＝2且m+3≠0，解得：m＝3．则m的值为3．故答案为：3．12．已知抛物线y＝x2﹣4x+c．与直线y＝m相交于A，B两点，若点A的横坐标；x A＝﹣1，则点B的横坐标．x B的值为5．解：∵y＝x2﹣4x+c，∴抛物线开口向上，对称轴为直线x＝﹣＝2，∴点A，B关于直线x＝2对称，∵点A横坐标为﹣1，∴点B横坐标为5，故答案为：5．13．已知二次函数y＝ax2开口向上，且|2﹣a|＝3，则a＝5．解：∵|2﹣a|＝3，∴2﹣a＝±3，解得：a＝﹣1或5，又二次函数y＝ax2开口向上，则a＞0，故a＝5．故答案为：5．14．已知抛物线y＝x2﹣3x+1的图象上有一点A（m，n），则m﹣n的最大值是3．解：∵点A（m，n）在抛物线y＝x2﹣3x+1上，∴n＝m2﹣3m+1，∴m﹣n＝﹣m2+4m﹣1＝﹣（m﹣2）2+3，∴当m＝2时，m﹣n有最大值为3，故答案为：3．15．如图，在平面直角坐标系中，抛物线y＝﹣x2+2x+c与x轴交于点A、B，与y轴交于点C，过点C作CD∥x轴，交抛物线于另一点D，若AB+CD＝3，则c的值为﹣．解：设A（x1，0），B（x2，0），令y＝0，则y＝﹣x2+2x+c＝0，由根与系数的关系得：x1+x2＝2，x1•x2＝﹣c，则AB＝|x1﹣x2|＝＝＝2，令x＝0，则y＝c，∴C（0，c），∵CD∥x轴，∴点D纵坐标为c，当y＝c时，则﹣x2+2x+c＝c，解得：x＝2，或x＝0，∴D（2，c），∴CD＝2，∵AB+CD＝3，∴2+2＝3，解得：c＝﹣，故答案为：﹣．16．如图，在矩形ABCD中，AB＝12，BC＝16，点E、F分别是边AB、BC上的动点，且EF＝10，点G是EF的中点，AG、CG，则四边形AGCD面积的最小值为142．解：连接AC，过B作BH⊥AC于H，以B为圆心，BG为半径作圆，交BH于G'，如图：∵四边形ABCD是矩形，∴∠EBF＝90°，∵EF＝10，点G是EF的中点，∴BG＝EF＝10＝5，∴G在以B为圆心，5为半径的弧上，当G运动到G'时，S△ACG最小，此时四边形AGCD 面积的最小值，最小值即为四边形AG'CD的面积，∵AB＝12＝CD，BC＝16＝AD，∴AC＝20，S△ACD＝×12×16＝96，∴BH＝＝，∴G'H＝BH﹣5＝﹣5＝，∴S△ACG'＝AC•G'H＝×20×＝46，∴S四边形AG'CD＝S△ACD+S△ACG'＝46+96＝142，即四边形AGCD面积的最小值是142．故答案为：142．三．解答题（共7小题）17．看图回答．（1）当y＝0时，求x的值；（2）当y＞5时，求x的范围；（3）y随x的增大而增大时，求x的范围．解：（1）由图象可知，抛物线经过点（﹣1，0），对称轴为直线x＝1，∴抛物线与x轴的另一个交点为（3，0），∴当y＝0时，x的值为﹣1和3；（2）∵抛物线经过点（﹣1，0），（3，0），（0，﹣3），∴设抛物线的解析式为y＝a（x+1）（x﹣3），代入（0，﹣3）得，﹣3＝﹣3a，解得a＝1，∴抛物线的解析式为y＝（x+1）（x﹣3），令y＝5得5＝（x+1）（x﹣3），解得x1＝4，x2＝﹣2，∴当y＞5时，求x的范围是x＞4或x＜﹣2；（3）∵y＝（x+1）（x﹣3）＝（x﹣1）2+4，∴抛物线开口向上，顶点为（1，4），对称轴为直线x＝1，∴y随x的增大而增大时，x的范围是x＞1．18．已知二次函数y＝x2﹣6x+8．（1）将解析式化成顶点式；（2）写出它的开口方向、对称轴和顶点坐标；（3）x取什么值时，y随x的增大而增大；x取什么值时，y随x增大而减小．解：（1）y＝x2﹣6x+8＝x2﹣6x+9﹣1＝（x﹣3）2﹣1；（2）开口向上，对称轴是直线x＝3，顶点坐标是（3，﹣1）；（3）x＞3时，y随x的增大而增大；x＜3时，y随x增大而减小．19．如图，以一定的速度将小球沿与地面成一定角度的方向击出时，小球的飞行路线是一条抛物线．若不考虑空气阻力，小球的飞行高度h（单位：m）与飞行时间t（单位：s）之间具有函数关系：h＝﹣5r2+20t，求小球飞行高度达到最高时的飞行时间．解：∵h＝﹣5t2+20t＝﹣5（t﹣2）2+20，且﹣5＜0，∴当t＝2时，h取最大值20，答：小球飞行高度达到最高时的飞行时间为2s．20．“阳光玫瑰葡萄”品种是近几年来广受各地消费者青睐的优质新品种，在云南省广泛种植．长沙市某品牌水果经销商计划在2023年五一期间进行商业促销活动，经过调查往年的统计数据发现，云南省批发“阳光玫瑰葡萄”的最低价格为每斤15元若按每斤30元的价格到市区销售，平均每天可售出60斤若每斤“阳光玫瑰葡萄”的售价每降低1元，那么平均每天的销售量会增加10斤，为了尽快减少库存，该水果商决定降价销售．（1）若降价2元，则每天的销售利润是多少元（2）若该经销商计划销售“阳光玫瑰葡萄”每天盈利1100元，那么每斤“阳光玫瑰葡萄”的售价应降至每斤多少元？（其它成本忽略不计）（3）将商品的销售单价定为多少元时，商场每天销售该商品获得的利润w最大？最大利润是多少元？解：（1）根据题意，降价2元则销售量为60+2×10＝80（斤），销售利润为：（30﹣15﹣2）×80＝1040（元），答：若降价2元，则每天的销售利润是1040元；（2）设每斤“阳光玫瑰葡萄”应降价x元，根据题意得：（30﹣15﹣x）（60+10x）＝1100，整理得：x2﹣9x+20＝0，解得x1＝4，x2＝5，∵为了尽快减少库存，∴x＝5，此时30﹣x＝25，答：每斤“阳光玫瑰葡萄”的售价应降至每斤25元；（3）设水果商每天获得的利润为y元，根据题意得：w＝（30﹣x﹣15）（60+10x）＝﹣10x2+90x+900＝﹣10（x﹣）2+1102.5，∵﹣10＜0，∴当x＝时，y有最大值，最大值为1102.5，此时30﹣x＝30﹣4.5＝25.5，答：将商品的销售单价定为25.5元时，商场每天销售该商品获得的利润w最大，最大利润是1102.5元．21．如图，抛物线与x轴交于A（﹣1，0）、B（4，0），与y轴交于C．（1）求抛物线的解析式；（2）如图1，已知线段DE与线段BC关于平面内某点成中心对称，其中DE的两端点刚好一个落在抛物线上，一个落在对称轴上，求落在对称轴上的点的坐标；（3）如图2，点M为第二象限抛物线上，作MN∥BC交抛物线于点N，直线NB、MC 交于点P，求P点的横坐标．解：（1）把A（﹣1，0）、B（4，0）代入得：，解得，∴抛物线的解析式为y＝x2﹣x﹣2；（2）∵y＝x2﹣x﹣2＝（x﹣）2﹣，∴抛物线的对称轴是直线x＝，在y＝x2﹣x﹣2中，令x＝0得y＝﹣2，∴C（0，﹣2），①若线段DE与线段BC关于点K成中心对称，C的对应点D在对称轴上，B的对应点在抛物线上，如图：设D（，m），E（n，n2﹣n﹣2），而B（4，0），C（0，﹣2），∵K是DC的中点，也是BE的中点，∴，解得，∴D（，）；②若线段DE与线段BC关于点T成中心对称，B的对应点D在对称轴上，C的对应点在抛物线上，如图：设D（，m'），E（n'，n'2﹣n'﹣2），而B（4，0），C（0，﹣2），∵T是EC的中点，也是BD的中点，∴，解得，∴D（，）；综上所述，落在对称轴上的点的坐标为（，）或（，）；（3）由B（4，0），C（0，﹣2）可得直线BC解析式为y＝x﹣2，设M（t，t2﹣t﹣2），由M（t，t2﹣t﹣2），C（0，﹣2）可得直线MC解析式为：y＝（t﹣）x﹣2，由MN∥BC设直线MN解析式为y＝x+p，将M（t，t2﹣t﹣2）代入得：t2﹣t﹣2＝t+p，∴p＝t2﹣2t﹣2，∴直线MN解析式为y＝x+t2﹣2t﹣2，由得或，∴N（﹣t+4，t2﹣t），由B（4，0），N（﹣t+4，t2﹣t）可得直线NB的解析式为y＝（﹣t+）x+2t﹣10，解（﹣t+）x+2t﹣10＝（t﹣）x﹣2得x＝2，∴P的横坐标为2．22．在平面直角坐标系xOy中，对于点P（x，y）和Q（x，y'），给出如下定义：若y'＝，则称点Q为点P的“可控变点”．例如：点（1，2）的“可控变点”为点（1，2），点（﹣1，3）的“可控变点”为点（﹣1，﹣3）．（1）点（﹣5，﹣2）的“可控变点”坐标为（﹣5，2）；（2）若点P在函数y＝﹣x2+16的图象上，其“可控变点”Q的纵坐标y′是7，求“可控变点”Q的横坐标；（3）若点P在函数y＝﹣x2+16（﹣5≤x≤a）的图象上，其“可控变点”Q的纵坐标y′的取值范围是﹣16≤y′≤16，求实数a的取值范围．解：（1）∵﹣5＜0，∴y'＝﹣y＝2，∴点（﹣5，﹣2）的“可控变点”坐标为（﹣5，2），故答案为：（﹣5，2）；（2）依题意，y＝﹣x2+16图象上的点P的“可控变点”必在函数的图象上．∵“可控变点”Q的纵坐标y′是7，∴当﹣x2+16＝7时，解得x＝3；当x2﹣16＝7，解得x＝﹣；综上所述“可控变点”Q的横坐标为或3；（3）依题意，y＝﹣x2+16图象上的点P的“可控变点”必在函数的图象上，∵﹣16≤y'≤16，∴﹣16＝﹣x2+16，∴x＝，当x＝﹣5时，x2﹣16＝9，当y'＝9时，x＝，∴a的取值范围是．23．在平面直角坐标系中，抛物线y＝x2+bx+c经过A（﹣4，0），点M为抛物线的顶点，点B在y轴上，直线AB与抛物线在第一象限交于点C（2，6），如图①．（1）求抛物线解析式；（2）直线AB的函数解析式为y＝x+4，点M的坐标为（﹣2，﹣2）．（3）在y轴上找一点Q，使得△AMQ的周长最小，具体作法如图②，作点A关于y轴的对称点A'，连接MA′交y轴于点Q，连接AM，AQ，此时△AMQ的周长最小，请求出点Q的坐标；（4）在坐标平面内是否存在点N，使以点A，O，C，N为顶点的四边形是平行四边形？若存在请直接写出点N的坐标；若不存在，请说明理由．解：（1）把A（﹣4，0），C（2，6）代入y＝x2+bx+c得：，解得，∴抛物线解析式为y＝x2+2x；（2）设直线AB解析式为y＝mx+n，把A（﹣4，0），C（2，6）代入得：，解得，∴直线AB解析式为y＝x+4，∵y＝x2+2x＝（x+2）2﹣2，∴抛物线的顶点M坐标为（﹣2，﹣2）；故答案为：y＝x+4，（﹣2，﹣2）；（3）∵A（﹣4，0），A，A'关于y轴对称，∴A'（4，0），设直线A'Q解析式为y＝m'x+n'，把A'（4，0），M（﹣2，﹣2）代入得：，解得，∴直线A'Q解析式为y＝x﹣，令x＝0得y＝﹣，∴Q（0，﹣）；（4）存在点N，使以点A，O，C，N为顶点的四边形是平行四边形，理由如下：设N（p，q），又A（﹣4，0），O（0，0），C（2，6），①若AN，OC为对角线，则AN，OC的中点重合，∴，解得，∴N（6，6）；②若ON，AC为对角线，则ON，AC的中点重合，∴，解得，∴N（﹣2，6）；③若CN，AO为对角线，则CN，AO的中点重合，∴，解得，∴N（﹣6，﹣6）．综上所述，N的坐标为（6，6）或（﹣2，6）或（﹣6，﹣6）．九年级数学上册《二次函数》专题测试题（附答案）一．选择题（共8小题，满分32分）1．若y＝（a+1）x|a+3|﹣x+3是关于x的二次函数，则a的值是（）A．1B．﹣5C．﹣1D．﹣5或﹣12．下列关于二次函数y＝﹣（x﹣m）2+m2+1（m为常数）的结论错误的是（）A．当x＞0时，y随x的增大而减小B．该函数的图象一定经过点（0，1）C．该函数图象的顶点在函数y＝x2+1的图象上D．该函数图象与函数y＝﹣x2的图象形状相同3．已知：抛物线的解析式为y＝﹣3（x﹣2）2+1，则抛物线的对称轴是直线（）A．x＝﹣1B．x＝1C．x＝2D．x＝﹣24．将二次函数y＝2x2向左平移5个单位，再向上平移3个单位，所得新抛物线表达式为（）A．y＝2（x+5）2﹣3B．y＝2（x+5）2+3C．y＝2（x﹣5）2﹣3D．y＝2（x﹣5）2+35．二次函数y＝ax2+bx+c的图象如图所示，下列结论：（1）4ac＜b2；（2）abc＜0；（3）2a+b＜0；（4）（a+c）2＜b2其中正确的个数是（）A．1B．2C．3D．46．已知抛物线y＝ax2+4ax﹣8与直线y＝n相交于A，B两点（点A在点B左侧），AB＝4，且抛物线与x轴只有一个交点，则n的值为（）A．﹣8B．﹣4C．4D．87．已知二次函数y＝ax2+bx+c的图象经过（﹣3，0）与（1，0）两点，关于x的方程ax2+bx+c+m ＝0（m＞0）有两个整数根，其中一个根是3，则另一个根是（）A．﹣5B．﹣3C．﹣1D．38．物理课上我们学习了竖直上抛运动，若从地面竖直向上抛一小球，小球的高度h（单位：m）与小球运动时间t（单位：s）之间的函数关系如图所示，下列结论：①小球在空中经过的路程是40m②小球抛出3s后，速度越来越快③小球抛出3s时速度为0④小球的高度h＝30m时，t＝1.5s其中正确的是（）A．①②③B．①②C．②③④D．②③二．填空题（共8小题，满分32分）9．已知抛物线y＝x2+bx+c关于直线x＝2对称，设x＝1，2，4时对应的函数值依次为y1，y2，y4，那么y1，y2，y4的大小关系是．（用“＜”连接）10．已知抛物线y＝ax2﹣2ax﹣1（a＜0）（I）抛物线的对称轴为；（2）若当﹣2≤x≤2时，y的最大值是1，求当﹣2≤x≤2时，y的最小值是．11．已知二次函数y＝ax2﹣2ax+c（a≠0）的图象与x轴的一个交点为（﹣1，0），则关于x 的一元二次方程ax2﹣2ax+c＝0的两根之积是．12．已知二次函数y＝﹣x2+4x+5及一次函数y＝﹣x+b，将该二次函数在x轴上方的图象沿x轴翻折到x轴下方，图象的其余部分不变，得到一个新图象（如图所示），当直线y＝﹣x+b与新图象有4个交点时，b的取值范围是．13．将抛物线y＝﹣（x﹣3）2﹣1向右平移5个单位，再向上平移2个单位，所得的抛物线的解析式为．14．如图，抛物线y＝ax2与直线y＝bx+c的两个交点坐标分别为A（﹣3，9），B（1，1），则方程ax2﹣bx﹣c＝0的解是．15．抛物线y＝ax2+bx+tc（a＜0）交x轴于点A、B，交y轴于点C（0，3），其中点B坐标为（1，0），同时抛物线还经过点（2，﹣5）．（1）抛物线的解析式为；（2）设抛物线的对称轴与抛物线交于点E，与x轴交于点H，连接EC、EO，将抛物线向下平移n（n＞0）个单位，当EO平分∠CEH时，则n的值为．16．某食品零售店新上架一款冷饮产品，每个成本为8元，在销售过程中，每天的销售量y （个）与销售价格x（元/个）的关系如图所示，当10≤x≤20时，其图象是线段AB，则该食品零售店每天销售这款冷饮产品的最大利润为元（利润＝总销售额﹣总成本）．三．解答题（共6小题，满分56分）17．已知二次函数y＝x2+mx+m2﹣3（m为常数，m＞0）的图象经过点P（2，4）．（1）求m的值；（2）判断二次函数y＝x2+mx+m2﹣3的图象与x轴交点的个数，并说明理由．18．对于向上抛的物体，如果空气阻力忽略不计，有下面的关系式：h＝v0t﹣gt2（h是物体离起点的高度，v0是初速度，g是重力系数，取10m/s2，t是抛出后经过的时间）．杂技演员抛球表演时，以10m/s的初速度把球向上抛出．（1）球抛出后经多少秒回到起点？（2）几秒后球离起点的高度达到1.8m？（3）球离起点的高度能达到6m吗？请说明理由．19．在平面直角坐标系中，已知二次函数y＝ax2+（a﹣1）x﹣1．（1）若该函数的图象经过点（1，2），求该二次函数图象的顶点坐标．（2）若（x1，y1），（x1，y2）为此函数图象上两个不同点，当x1+x2＝﹣2时，恒有y1＝y2，试求此函数的最值．（3）当a＜0且a≠﹣1时，判断该二次函数图象的顶点所在象限，并说明理由．20．某商场新进一批拼装玩具，进价为每个10元，在销售过程中发现，日销售量y（个）与销售单价x（元）之间满足如图所示的一次函数关系．（1）求y与x的函数关系式（不要求写出自变量x的取值范围）；（2）若该玩具某天的销售利润是600元，则当天玩具的销售单价是多少元？（3）设该玩具日销售利润为w元，当玩具的销售单价定为多少元时，日销售利润最大？最大利润是多少元？21．如图，抛物线y＝﹣x2+bx+c过点A（4，0），B（0，2）．M（m，0）为线段OA上一个动点（点M与点A不重合），过点M作垂直于x轴的直线与直线AB和抛物线分别交于点D、N．（1）求直线AB的表达式和抛物线的表达式；（2）若DN＝3DM，求此时点N的坐标；（3）若点P为直线AB上方的抛物线上一个动点，当∠ABP＝2∠BAC时，求点P的坐标．22．如图，已知二次函数y＝x2+bx+c（b，c为常数）的图象经过点A（3，﹣2），点C（0，﹣5），顶点为点M，过点A作AB∥x轴，交y轴于点D，交二次函数y＝x2+bx+c的图象于点B，连接BC．（1）求该二次函数的表达式及点M的坐标；（2）若将该二次函数图象向上平移m（m＞0）个单位，使平移后得到的二次函数图象的顶点落在△ABC的内部（不包括△ABC的边界），求m的取值范围；（3）若E为线段AB上一点，且BE：EA＝3：1，P为直线AC上一点，在抛物线上是否存在一点Q，使以B、P、E、Q为顶点的四边形是平行四边形？若存在，请直接写出点Q的横坐标；若不存在，请说明理由．参考答案一．选择题（共8小题，满分32分）1．解：∵函数y＝（a+1）x|a+3|﹣x+3是关于x的二次函数，∴|a+3|＝2且a+1≠0，解得a＝﹣5，故选：B．2．解：A．∵y＝﹣（x﹣m）2+m2+1（m为常数），∴抛物线开口向下，对称轴为直线x＝m，∴x＞m时，y随x增大而减小，故A错误，符合题意；∵当x＝0时，y＝1，∴该函数的图象一定经过点（0，1），故B正确，不合题意；∵y＝﹣（x﹣m）2+m2+1，∴抛物线顶点坐标为（m，m2+1），∴抛物线顶点在抛物线y＝x2+1上，故C正确，不合题意；∵y＝﹣（x﹣m）2+m2+1与y＝﹣x2的二次项系数都为﹣1，∴两函数图象形状相同，故D正确，不合题意．故选：A．3．解：∵y＝﹣3（x﹣2）2+1，∴抛物线对称轴为直线x＝2．故选：C．4．解：将二次函数y＝2x2向左平移5个单位，再向上平移3个单位，所得新抛物线表达式为y＝2（x+5）2+3，故选：B．5．解：根据图象知道抛物线与x轴有两个交点，∴b2﹣4ac＞0，即4ac＜b2，故（1）正确．∵抛物线开口朝下，∴a＜0，∵对称轴在y轴右侧，∴b＞0，∵抛物线与y轴的交点在x轴的上方，∴c＞0，∴abc＜0，故（2）正确；∵对称轴x＝﹣＞1，∴2a+b＞0，故（3）错误；根据图象知道当x＝1时，y＝a+b+c＞0，根据图象知道当x＝﹣1时，y＝a﹣b+c＜0，∴（a+c）2﹣b2＝（a+c+b）（a+c﹣b）＜0，故（4）正确；故选：C．6．解：∵抛物线与x轴只有一个交点，∴a≠0且Δ＝16a2﹣4a×（﹣8）＝0，∴a＝﹣2，∴抛物线解析式为y＝﹣2x2﹣8x﹣8，∵抛物线的对称轴为直线x＝﹣＝﹣2，而AB平行x轴，AB＝4，∴A点的横坐标为﹣4，B点的横坐标为0，当x＝0时，y＝﹣8，∴n的值为﹣8．故选：A．7．解：∵二次函数y＝ax2+bx+c的图象经过（﹣3，0）与（1，0）两点，∴函数y＝ax2+bx+c的对称轴是直线x＝﹣1，又∵关于x的方程ax2+bx+c+m＝0（m＞0）有两个根，其中一个根是3．∴二次函数y＝ax2+bx+c的图象与直线y＝﹣m的一个交点的横坐标为3，∵对称轴是直线x＝﹣1，∴二次函数y＝ax2+bx+c的图象与直线y＝﹣m的另一个交点的横坐标为﹣5，∴关于x的方程ax2+bx+c+m＝0（m＞0）的另一个根是﹣5，故选：A．8．解：①由图象知小球在空中达到的最大高度是40m；故①错误；②小球抛出3秒后，速度越来越快；故②正确；③小球抛出3秒时达到最高点即速度为0；故③正确；④设函数解析式为：h＝a（t﹣3）2+40，把O（0，0）代入得0＝a（0﹣3）2+40，解得，∴函数解析式为，把h＝30代入解析式得，，解得：t＝4.5或t＝1.5，∴小球的高度h＝30m时，t＝1.5s或4.5s，故④错误；故选D．二．填空题（共8小题，满分32分）9．解：∵抛物线y＝x2+bx+c的开口向上，对称轴是直线x＝2，∴当x＝2时取最小值，又|1﹣2|＜|4﹣2|，∴y1＜y4，故答案为：y2＜y1＜y4．10．解：（1）抛物线的对称轴为：直线x＝﹣＝1，故答案为：直线x＝1；（2）∵抛物线y＝ax2﹣2ax﹣1＝a（x﹣1）2﹣a﹣1（a＜0），∴该函数图象的开口向下，对称轴是直线x＝1，当x＝1时，取得最大值﹣a﹣1，∵当﹣2≤x≤2时，y的最大值是1，∴x＝1时，y＝﹣a﹣1＝1，得a＝﹣2，∴y＝﹣2（x﹣1）2+1，∵﹣2≤x≤2，∴x＝﹣2时，取得最小值，此时y＝﹣2（﹣2﹣1）2+1＝﹣17，故答案为：﹣17．11．解：∵二次函数y＝ax2﹣2ax+c（a≠0）的图象与x轴的一个交点为（﹣1，0），∴该函数的对称轴是直线x＝﹣＝1，∴该函数图象与x轴的另一个交点坐标为（3，0），∴关于x的一元二次方程ax2﹣2ax+c＝0的两实数根是x1＝﹣1，x2＝3，∴两根之积为﹣3，故答案为：﹣3．12．解：如图，当y＝0时，﹣x2+4x+5＝0，解得x1＝﹣1，x2＝5，则A（﹣1，0），B（5，0），将该二次函数在x轴上方的图象沿x轴翻折到x轴下方的部分图象的解析式为y＝（x+1）（x﹣5），即y＝x2﹣4x﹣5（﹣1≤x≤5），当直线y＝﹣x+b经过点A（﹣1，0）时，1+b＝0，解得b＝﹣1；当直线y＝﹣x+b与抛物线y＝x2﹣4x﹣5（﹣1≤x≤5）有唯一公共点时，方程x2﹣4x﹣5＝﹣x+b有相等的实数解，解得b＝﹣，所以当直线y＝﹣x+b与新图象有4个交点时，b的取值范围为﹣＜b＜﹣1．故答案为：﹣＜b＜﹣1．13．解：将抛物线y＝﹣（x﹣3）2﹣1向右平移5个单位，再向上平移2个单位，所得的抛物线的解析式为y＝﹣（x﹣3﹣5）2﹣1+2，即y＝﹣（x﹣8）2+1，故答案为：y＝﹣（x﹣8）2+1．14．解：∵抛物线y＝ax2与直线y＝bx+c的两个交点坐标分别为A（﹣3，9），B（1，1），∴方程ax2＝bx+c的解为x1＝﹣3，x2＝1，∴ax2﹣bx﹣c＝0的解是x1＝﹣3，x2＝1，故答案为：x1＝﹣3，x2＝1．15．解：（1）将点C（0，3）、B（1，0）、（2，﹣5）代入抛物线y＝ax2+bx+tc中，得：a+b+c＝0，c＝3，4a+2b+c＝﹣5；解得：a＝﹣1，b＝﹣2，c＝3，∴抛物线的解析式为y＝﹣x2﹣2x+3．（2）抛物线向下平移n个单位后，E为（﹣1，4﹣n），C为（0，3﹣n），∴EC＝，∵CO∥EH，∴当CO＝CE＝时，∠CEO＝∠COE＝∠OCH，∴3﹣n＝或n﹣3＝，即n＝3﹣或3+．16．解：当10≤x≤20时，设y＝kx+b，把（10，20），（20，10）代入可得：，解得，∴每天的销售量y（个）与销售价格x（元/个）的函数解析式为y＝﹣x+30，设该食品零售店每天销售这款冷饮产品的利润为w元，w＝（x﹣8）y＝（x﹣8）（﹣x+30）＝﹣x2+38x﹣240＝﹣（x﹣19）2+121，∵﹣1＜0，∴当x＝19时，w有最大值为121，故答案为：121．三．解答题（共6小题，满分56分）17．解：（1）将（2，4）代入y＝x2+mx+m2﹣3得4＝4+2m+m2﹣3，解得m1＝1，m2＝﹣3，又∵m＞0，∴m＝1．（2）∵m＝1，∴y＝x2+x﹣2，∵Δ＝b2﹣4ac＝12+8＝9＞0，∴二次函数图象与x轴有2个交点．18．解：∵初速度为10m/s，g取10m/s2，∴h＝10t﹣×10t2＝10t﹣5t2，（1）当h＝0时，。

2025中考数学二次函数压轴题专题练习22 胡不归模型(学生版+解析版)

专题22胡不归模型一、知识导航在前面的最值问题中往往都是求某个线段最值或者形如PA+PB最值，除此之外我们还可能会遇上形如“PA+kP矿这样的式子的最值，此类式子一般可以分为两类问题：（1)胡不归问题，（2)阿氏固．本文简单介绍“胡不归“模型【故丰介绍l从前有个少年外出求学，某天不幸得知老父亲病危的消息，便立即赶路回家．根据＇，两点之间线段最短＂，虽然从他此刻位置A到家B之间是一片砂石地，但他义无反顾踏上归途，当赶到家时，老人刚咽了气，小伙子追悔莫及失声痛哭邻居告诉小伙子说，老人弥留之际不断念叨着“胡不归？胡不归？(“胡“同“何”)而如果先沿着驿道AC先走一段，再走砂石地，会不会更早些到家？A VZ R驿道［棋型建立）如图，一动点P在直线MN外的运动速度为VI'在直线MN上运动的速度为忆，且冈＜忆，A、BAC BC为定点，点C在直线MN上，确定点C的位置使－－＋—－的值最小V2 V,MBA V2 CN（问题分析）AC B C l V V了三(B C+t AC]，记k=t即求BC+kAC的最小值．（问题解决I构造射线AD使得sin乙D儿'V=k,CH/ A C=k, CH=kAC.M A勺、＂、、,'CCH、、、令si11a＝一＝k H、、AC、、、、、、忽CH=kAC BN将问题转化为求B C+CH最小值，过B点作BH上AD交J\1N于点C,交A D于H，点，此时BC+CH取到最小值，即BC+kAC最小．B，，，，M A义”、、、、、、、'佥H、、、、、艾N（棋型总结】在求形如“PA+kP矿的式子的最值问题中，关键是构造与kPB相等的线段，将“1刃＋肘功”型问题转化为“PA+PC'型．而这里的PB必须是一条方向不变的线段，方能构造定角利用三角函数得到kPB的等线段石如图， 6.ABC中，AB=AC=IO,ta叭＝2,BE_I_AC于点E,D是线段BE上的一个动点，则CD+—-BD的晟5小值是A8c乔（分析）本题关键在于处理”__:_BD",考虑tanA:o2,t,. ABE三边之比为1:2✓5,石上AB交AB于H点，则DH=－-BD,5石sin乙钮E—，故作D H5A Ac8c问题转化为CD+DH最小值，故C、D、H共线时值最小，此时CD+DH=CH= 8£=4✓5【小结1本题简单在于题目已经将B A线作出来，只需分析角度的三角函数值，作出垂线D H即可斛决问题，若稍作改变，将图形改造如下·B二三则需自行构造a,如下图，这一步正是解决“胡不归”问题关锭所在．B二三渗石，l sina＝一－B夕AIII、、I、$IIIIIIHIIcI三、中考真题演练I.(2023山东中考真题）已知抛物线y=-x2+b入＋c与x轴交于A,B两点，与y轴交千点C(0,4)，其对称轴为x=－一．3y A｀l�l(1)求抛物线的表达式：(3)如图2,动点P在直线AC上方的抛物线上，过点P作直线AC的垂线，分别交直线AC,线段BC千点E,图2F，过点F作FG..lx轴，垂足为G,求FG＋丘F P的最大值．2.(2023黑龙汀绥化中考真题）如困，抛物线Y,＝少:2+bx+c的图象经过A(-6,0),8(-2,0), C(0,6)三点，且一次函数y＝虹＋6的图象经过点B.-8 -7l广X-8-7I 2(l)求抛物线和一次函数的解析式．(3将抛物线Y,=a.,\2 +bx+c的图象向右平移8个单位长度得到抛物线Y2，此抛物线的图象与X轴交于M,N两点(M点在N点左侧）．点P是抛物线Y2上的一个动点且在过线NC下方已知点P的横坐标为m.过点P作PD上NC于点D求m为何值时，CD+�PD有最大值，最大值是多少？2(2023四川内江中考真题）如图，在平面丑角坐标系中，抛物线y=w.2+b入＋c与x轴交千B(4,0),C(-2,0) 两点与y轴交于点A(0,-2)I •(I)求该抛物线的函数表达式；(2)若点P是直线AB下方抛物线上的一动点，过点P作轴的平行线交AB千点K,过点P作y轴的平行线l交r轴于点D,求与－PK+PD的最大值及此时点P的坐标；24.(2023天津中考真题）已知抛物线y=-入2+bx+c(b,c为常数，c>I)的顶点为P,与X轴相交于A,bB两点（点A在点B的左侧），与Y轴相交于点C,抛物线上的点M的横坐标为m,且－c<m＜一，过点M2作C,垂足为N(I)若b=-2,c=3.＠求点P和点A的坐标；＠当仙V＝石时，求点M的坐标；(2)若点A的坐标为（气',0)，且MPII A C,当A N+3M N=9✓2时，求点M的坐标k5. (2023福建泉州模拟预测）如图，已知抛物线y=�(x+2)(x-4)(k为常数，且k>O)与X轴从左至右8§依次交千A,8两点，与Y轴交于点C,经过点B的宜线y=－—-x+b与抛物线的另一交点为D.y yX备用图(I)若点D的横坐标为－5,求抛物线的函数表达式；(2)在（l)条件下，设F为线段BD上一点（不含端点），连接AF,一动点M从点A出发，沿线段AF以每秒l个单位的速度运动到F,再沿线段FD以每秒2个单位的速度运动到D后停止．当点F的坐标是多少时，点M在整个运动过程中用时最少？6.(2023广西柳州二模）已知抛物线y＝少:2+b入＋c(a丑0)过点A(LO),8(3,0)两点，与Y轴交于点C, OC=3,。

二次函数(4大压轴考法专练)(学生版) 2023-2024学年九年级数学上册培优题型归纳与满分秘籍

第二十二章二次函数（4大压轴考法专练）目录题型一：二次函数图象与系数关系...................................................................................1题型二：抛物线与x 轴交点..............................................................................................4题型三：二次函数的应用.................................................................................................9题型四：二次函数综合题...............................................................................................19一．二次函数图象与系数的关系1．（2024•江阳区校级模拟）新定义：若一个点的纵坐标是横坐标的2倍，则称这个点为二倍点．若二次函数2(y x x c c =-+为常数）在24x -<<的图象上存在两个二倍点，则c 的取值范围是( )A ．124c -<<B ．944c -<<C ．144c -<<D ．9104c -<<2．（2024•商河县二模）对于一个函数，当自变量x 取a 时，其函数值y 等于2a ，我们称a 为这个函数的二倍数．若二次函数2(y x x c c =++为常数）有两个不相等且小于1的二倍数，则c 的取值范围是( )A ．14c -二．抛物线与x 轴的交点4．（2024•高新区校级一模）如图，二次函数2y x x =x 轴于点A ，B （点A 在点B的左侧），交y 轴于点C ．现有一长为3的线段DE 在直线y =上移动，且在移动过程中，线段DE 上始终存在点P ，使得三条线段PA ，PB ，PC 能与某个等腰三角形的三条边对应相等．若线段DE 左端点D 的横坐标为t ，则t 的取值范围是　．5．（2023秋•榆树市校级期末）如图，在平面直角坐标系中，抛物线213(07)2y x x c x =-++……与x 轴的交点坐标为(7,0)，设该图象上任意两点的坐标分别是1(x ，1)y ，2(x ，2)y ，其中12x x <，d 为12x x x ……时y 的最大值与最小值的差．若216x x -=，则d 的取值范围是　．6．（2024•鄄城县一模）如图，已知抛物线2y x bx c =-++与x 轴交于点(1,0)A -和点(3,0)B ，与y 轴交于点C ，连接BC 交抛物线的对称轴于点E ，D 是抛物线的顶点．（1）求此抛物线的解析式；（2）直接写出点C 和点D 的坐标；（3）若点P 在第一象限内的抛物线上，且4ABP COE S S D D =，求P 点坐标．7．（2024•官渡区一模）已知二次函数223(y ax ax a a =--为常数且0)a ¹的顶点在x 轴上方，且到x 轴的距离为4．（1）求二次函数的解析式；（2）将二次函数223(0)y ax a a x =--…的图象记为1T ，将1T 关于原点对称的图象记为2T ，1T 与2T 合起来得到的图象记为T ，完成以下问题：①在网格中画出函数T 的图象；②若对于函数T 上的两点1(P x ，1)y ，2(Q x ，2)y ，当12x -…，21t x t +……时，总有12y y >，求出t 的取值范围．8．（2023秋•修水县期末）抛物线211111:C y a x b x c =++中，函数值1y 与自变量x 之间的部分对应关系如下表：x ¼3-2-1-134¼1y ¼4-1-04-16-25-¼（1）设抛物线1C 的顶点为P ，则点P 的坐标为　　；（2）现将抛物线1C 沿x 轴翻折，得到抛物线222222:C y a x b x c =++，试求2C 的解析式；（3）现将抛物线2C 向下平移，设抛物线在平移过程中，顶点为点D ，与x 轴的两交点为点A 、B ．①在最初的状态下，至少向下平移多少个单位，点A 、B 之间的距离不小于6个单位？②在最初的状态下，若向下平移(0)m m >个单位时，对应的线段AB 长为n ，请直接写出m 与n 的等量关系．三．二次函数的应用9．（2024•市北区三模）今年我国多个省市遭受严重干旱，受旱灾的影响，4月份，我市某蔬菜价格呈上升趋势，其前四周每周的平均销售价格变化如表：周数x 1234价格y （元/千克）22.22.42.6（1）请观察题中的表格，用所学过的一次函数、反比例函数或二次函数的有关知识直接写出4月份y 与x 的函数关系式；（2）进入5月，由于本地蔬菜的上市，此种蔬菜的平均销售价格y （元/千克）从5月第1周的2.8元/千克下降至第2周的2.4元/千克，且y 与周数x 的变化情况满足二次函数2120y x bx c =-++，请求出5月份y 与x 的函数关系式；（3）若4月份此种蔬菜的进价m （元/千克）与周数x 所满足的函数关系为11.24m x =+，5月份此种蔬菜的进价m （元/千克）与周数x 所满足的函数关系为125m x =-+．试问4月份与5月份分别在哪一周销售此种蔬菜一千克的利润最大？且最大利润分别是多少？1111cccc10．（2024•滑县二模）护林员在一个斜坡上的点A处安装自动浇灌装置（其高度忽略不计）为坡地AB进行浇灌，10OA m=，点A处的自动浇灌装置喷出的水柱呈抛物线形．已知水柱在距出水口A的水平距离为6m 时，达到距离地面OB的竖直高度的最大值为13m．设喷出的水柱距出水口的水平距离为()x m，距地面的竖直高度为()y m，以坡底B所在的水平方向为x轴，A处所在的竖直方向为y轴建立平面直角坐标系，原点为O，如图所示．经过测量，可知斜坡AB的函数表达式近似为1102y x=-+．（1）求图中水柱所在抛物线的函数表达式；（2）若该装置浇灌的最远点C离地面的竖直高度为1m，求此时喷到C处的水柱距出水口的水平距离．（3）给该浇灌装置安装一个支架，可调节浇灌装置的高度，则水柱恰好可以覆盖整个坡地AB时，安装的支架的高度为多少米？11．（2024•红塔区三模）某2F C直营店招牌：“新进最新款洗发水40瓶，每件售价80元，若一次性购买不超过10瓶时，售价不变；若一次性购买超过10瓶时，每多买1瓶，所买的每瓶洗发水的售价均降低2元．”已知该瓶洗发水每瓶进价52元，设顾客一次性购买洗发水x瓶时，他所付洗发水单价y元，该直营店所获利润为W元．（1）求y与x的函数关系式，并写出自变量x的取值范围；（2）顾客一次性购买多少瓶时，该直营店从中获利最多？12．（2024•南山区一模）麻城市思源实验学校自从开展“高效课堂”模式以来，在课堂上进行当堂检测效果很好．每节课40分钟教学，假设老师用于精讲的时间x（单位：分钟）与学生学习收益量y的关系如图1所示，学生用于当堂检测的时间x（单位：分钟）与学生学习收益y的关系如图2所示（其中OA是抛物线的一部分，A为抛物线的顶点），且用于当堂检测的时间不超过用于精讲的时间．（1）求老师精讲时的学生学习收益量y与用于精讲的时间x之间的函数关系式；（2）求学生当堂检测的学习收益量y与用于当堂检测的时间x的函数关系式；（3）问此“高效课堂”模式如何分配精讲和当堂检测的时间，才能使学生在这40分钟的学习收益总量最大？13．（2023秋•硚口区校级期末）某衬衣店将进价为30元的一种衬衣以40元售出，平均每月能售出600件，调查表明：这种衬衣售价每上涨1元，其销售量将减少10件．（1）写出月销售利润y（单位：元）与售价x（单位：元/件）之间的函数解析式．（2）当销售价定为45元时，计算月销售量和销售利润．（3）当销售价定为多少元时会获得最大利润？求出最大利润．14．（2024•滦南县校级模拟）某大学生利用暑假40天社会实践参与了某公司旗下一家加盟店经营，了解到一种成本为20元/件的新型商品在第x 天销售的相关信息如下表所示：销售量p （件)50p x=-销售单价q （元/件）当120x ……时，1302q x =+当2140x ……时，52520q x=+（1）请计算第几天该商品的销售单价为35元/件（2）这40天中该加盟店第几天获得的利润最大？最大利润是多少？（3）在实际销售的前20天中，公司为鼓励加盟店接收大学生参加实践活动决定每销售一件商品就发给该加盟店(2)m m …元奖励．通过该加盟店的销售记录发现，前10天中，每天获得奖励后的利润随时间x （天)的增大而增大，求m 的取值范围．四．二次函数综合题15．（2024•淮安模拟）定义：若函数图象上存在点1(,)M m n ，2(1,)M m n ¢+，且满足21n n t -=，则称t 为该函数的“域差值”．例如：函数23y x =+，当x m =时，123n m =+；当1x m =+时，225n m =+，212n n -= 则函数23y x =+的“域差值”为2．（1）点1(,)M m n ，2(1,)M m n ¢+在4y x=的图象上，“域差值” 4t =-，求m 的值；（2）已知函数22(0)y x x =->，求证该函数的“域差值” 2t <-；（3）点(,)A a b 为函数22y x =- 图象上的一点，将函数22()y x x a =-…的图象记为1W ，将函数22()y x x a =-…的图象沿直线y b =翻折后的图象记为2W ．当1W ，2W 两部分组成的图象上所有的点都满足“域差值” 1t …时，求a 的取值范围．16．（2024•玉山县二模）已知抛物线21:22C y ax ax =--的顶点为M ，直线:2l y x a =-与x 轴、y 轴分别交于点A ，B ．（1）若抛物线1C 与x 轴只有一个公共点，求a 的值．（2）当0a >时，设ABM D 的面积为S ，求S 关于a 的函数关系式．（3）将抛物线21:22C y ax ax =--绕点(,2)P t -旋转180°得到抛物线2C ，其顶点为点N ．①若点N 恰好落在直线l 上，求a 与t 满足的关系式；②当21x -……时，旋转前后的两个二次函数y 的值都会随x 的增大而减小，求t 的取值范围．17．（2024•吉林四模）抛物线23y x bx =-++经过点(1,0)-，点A 在抛物线上，且横坐标为m ，点C 是坐标平面上一点，其坐标为(2,4)m m +-+．以AC 为对角线作矩形ABCD ，//AB x 轴．（1）求抛物线的函数解析式；（2）当y 轴平分矩形ABCD 的面积时，求m 的值；（3）当2AB BC =时，求m 的值；（4）当矩形ABCD 的边（包括顶点）与抛物线有3个交点时，直接写出m 的取值范围．18．（2024•冷水滩区校级模拟）如图，已知抛物线25y ax bx =++经过(5,0)A -、(4,3)B --两点，与x 轴的另一个交点为C ，顶点为D ，连接CD ，点P 为抛物线上一动点．（1）求抛物线的表达式．（2）若点P 在直线BC 的下方运动时，过点P 作PE BC ^交于点E ，过点P 作y 轴的平行线交直线BC 于点F ．求PEF D 周长的最大值及此时点P 的坐标．（3）在该抛物线上是否存在点P ，使得PBC BCD Ð=Ð．若存在，求出所有点P 的坐标；若不存在，请说明理由．19．（2024•云梦县校级一模）如图，在平面直角坐标系中，抛物线2y x bx c =++与x 轴交于点A ，(B A 在B 的左侧），与y 轴交于点(0,3)C -，其对称轴为直线1x =．（1）求该抛物线的函数解析式；（2）如图（1），已知点D 为第二象限抛物线上一点，连接AC ，若90ABD BAC Ð+Ð=°，求点D 的坐标；（3）(,)P m n 和Q 分别是直线24y x =--和抛物线上的动点，且点Q 的横坐标比点P 的横坐标大4个单位长度，分别过P ，Q 作坐标轴的平行线，得到矩形PMQN ．设该抛物线在矩形PMQN 内部（包括边界）的图象的最高点与最低点的纵坐标的差为t ．①如图（2），当12m =-时，请直接写出t 的值；②请直接写出t 关于m 的函数关系式．20．（2024•丽江二模）如图，抛物线2y x bx c =-++经过(4,0)A ，(1,0)C -两点，与y 轴交于点B ，P 为第一象限抛物线上的动点，连接AB ，BC ，PA ，PC ，PC 与AB 相交于点Q ．（1）求抛物线的解析式：（2）设APQ D 的面积为1S ，BCQ D 的面积为2S ，当125S S -= 时，求点P 的坐标；（3）是否存在点P ，使45PAB CBO Ð+Ð=°，若存在，请求出点P 的坐标；若不存在，说明理由．21．（2024•海门区校级开学）已知：关于x 的函数215()222y k x kx k =--++．（Ⅰ）当k 为任意实数时，这个函数的图象恒过某定点P （所谓定点，就是与k 值无关的点），求此点坐标；（Ⅱ）若此函数的图象是抛物线，且与x 轴有两个相异交点B 、C ，其坐标分别为1(B x ，0)，2(C x ，0)，其中12x x <．（1）求k 的取值范围，并求当k 为何值时，B 、C 两点的距离等于3；（2）连接PB 、PC 得△PBC ，则当k 取何值时，△PBC 的一个内角等于45°．22．（2024•辽宁模拟）在平面直角坐标系中，若某函数的图象与矩形ABCD 对角线的两个端点相交，则定义该函数为矩形ABCD 的“友好函数”．（1）如图，矩形ABCD ，//AB x 轴，经过点(1,1))A -和点(3,3)C 的一次函数1y kx b =+是矩形ABCD 的“友好函数”，求一次函数1y kx b =+的解析式；（2）已知第一象限内矩形ABCD 的两条边的长分别为2和4，且它的两条边分别平行x 轴和y 轴，经过点D 和点B 的反比例函数26y x=是矩形ABCD 的“友好函数”，求矩形距原点最近的顶点坐标；（3）若23(0)y ax bx c a =++¹是矩形ABCD 的“友好函数”且经过A ，C 两点，点B 的坐标为(1,3)-，点D 的坐标为(3,5)-，//AB y 轴．①若23(0)y ax bx c a =++¹的图象与矩形ABCD 有且只有两个交点，求a 的取值范围；②点(P P x ，)P y 是23(0)y ax bx c a =++¹图象上一点，且13122P a a x a a--……，当0a >时，p y 的最大值和最小值的差是3，求a 的值．23．（2024•呼和浩特）在平面直角坐标系中，抛物线224y x bx =--经过点(1,)m -．（1）若1m =，则b = ，通过配方可以将其化成顶点式为；（2）已知点1(x ，1)y ，2(x ，2)y 在抛物线上，其中12x x <，若0m >且12225x x +…，比较1y 与2y 的大小关系，并说明理由；（3）若0b =，将抛物线向上平移4个单位得到的新抛物线与直线14y kx =+交于A ，B 两点，直线与y 轴交于点C ，点E 为AC 中点，过点E 作x 轴的垂线，垂足为点F ，连接AF ，CF ．求证：212CF CE =．24．（2024•东西湖区模拟）如图1、抛物线23y ax bx =++与x 轴交于点(1,0)A -，(3,0)B 两点，与y 轴交于点C ，顶点为D ．（1）求抛物线的解析式；（2）P 是x 轴上一动点，将顶点D 绕点P 顺时针旋转90°刚好落在抛物线上的点E 处，求点P 的坐标；（3）如图2，点G ，H 为x 轴上方的抛物线上两点（点G 在点H 的左边），直线BG 、BH 与y 轴分别交于S ，T 两点，若9OS OT ×=，试探究直线GH 是否经过定点，若是，求定点坐标；若不是，请说明理由．25．（2024•延边州模拟）如图①，抛物线2y x bx c =++过点(5,0)A 和点(0,5)B ．点P 在线段OA 上，点P 的横坐标为m ，且14m <<．点E 的坐标为(8,0)，以OE 为斜边在x 轴上方作等腰直角三角形OEF ．（1）求该抛物线的解析式；（2）当142x ……时，求y 的取值范围．（3）如图②，过点P 作x 轴的垂线，与抛物线交于点C ，与线段OF 交于点D ．①若3m <，且COD D 是直角三角形，则m =　　．②设CP d =，当在C 、A 之间的抛物线上和折线DF FE -上到x 轴的距离为d 的点共有3个时，直接写出m 的取值范围．26．（2024•蒸湘区一模）定义：在平面直角坐标系xOy 中，当点N 在图形M 的内部，或在图形M 上，且点N 的横坐标和纵坐标相等时，则称点N 为图形M 的“梦之点”．（1）如图①，矩形ABCD 的顶点坐标分别是(1,2)A -，(1,1)B --，(3,1)C -，(3,2)D ，在点1(1,1)M ，2(2,2)M ，3(3,3)M 中，是矩形ABCD “梦之点”的是　；（2）如图②，已知点A ，B 是抛物线21922y x x =-++上的“梦之点”，点C 是抛物线的顶点．连接AC ，AB ，BC ，求ABC D 的面积；（3）在（2）的条件下，点P 为抛物线上一点，点Q 为平面内一点，是否存在点P 、Q ，使得以AB 为对角线，以A 、B 、P 、Q 为顶点的四边形是菱形？若存在，直接写出P 点坐标；若不存在，请说明理由．27．（2024•临淄区一模）已知抛物线23(0)y ax bx a =+-¹与x 轴交于点(1,0)A -，点(3,0)B ，与y 轴交于点C ．（1）求抛物线的表达式；（2）如图，若直线BC 下方的抛物线上有一动点M ，过点M 作y 轴平行线交BC 于N ，过点M 作BC 的垂线，垂足为H ，求HMN D 周长的最大值；（3）若点P 在抛物线的对称轴上，点Q 在x 轴上，是否存在以B ，C ，P ，Q 为顶点的四边形为平行四边形，若存在，求出点Q 的坐标，若不存在，请说明理由；（4）将抛物线向左平移1个单位，再向上平移4个单位，得到一个新的抛物线，问在y 轴正半轴上是否存在一点F ，使得当经过点F 的任意一条直线与新抛物线交于S ，T 两点时，总有2211FS FT +为定值？若存在，求出点F 坐标及定值，若不存在，请说明理由．28．（2024•峰峰矿区校级二模）如图，抛物线2:698C y ax ax a =++-与x 轴相交于A ，B 两点（点A 在点B 的左侧），已知点B 的横坐标是2，抛物线C 的顶点为D ．（1）求a 的值及顶点D 的坐标；（2）点P 是x 轴正半轴上一点，将抛物线C 绕点P 旋转180°后得到抛物线1C ，记抛物线1C 的顶点为E ，抛物线1C 与x 轴的交点为F ，G （点F 在点G 的右侧）．当点P 与点B 重合时（如图1)，求抛物线1C 的表达式；（3）如图2，在（2）的条件下，从A ，B ，D 中任取一点，E ，F ，G 中任取两点，若以取出的三点为顶点能构成直角三角形，我们就称抛物线1C 为抛物线C 的“勾股伴随同类函数”．当抛物线1C 是抛物线C 的勾股伴随同类函数时，求点P 的坐标．29．（2024•泉州模拟）已知点(2,1)和点(4,4)在抛物线2y ax bx =+上．（1）求抛物线所对应的函数表达式；（2）四边形ABCD 的四个顶点均在该抛物线上，AC 与BD 交于点(0,)E n ，直线AB 为11(0y k x m k =+¹，0)m n <<，直线CD 为22(0)y k x t k =+¹．①求12k n k m -的值；②记CDE D 的面积为1S ，四边形ABCD 的面积为S ，若1m =，2n =，求1SS的最小值．30．（2024•菏泽二模）如图，直线243y x=-+与x轴交于点C，与y轴交于点B，抛物线2103y ax x c=++经过B、C两点．（1）求抛物线的解析式；（2）如图，点E是直线BC上方抛物线上的一动点，当BECD面积最大时，请求出点E的坐标；（3）在（2）的结论下，过点E作y轴的平行线交直线BC于点M，连接AM，点Q是抛物线对称轴上的动点，在抛物线上是否存在点P，使得以P、Q、A、M为顶点的四边形是平行四边形？如果存在，请直接写出点P的坐标；如果不存在，请说明理由．31．（2024•蓬江区校级三模）如图，在平面直角坐标系中，已知点(6,3)A -，抛物线2()y x m m =-+，其顶点为M ，连接OA ，并将OA 绕着点0顺时针旋转90°得到OB ，（1）当抛物线过点B 时，求m 的值；（2）当12MAB AOB S S D D =时，求m 的值；（3）当抛物线与AOB D 的边（包括端点）有且只有两个交点时，直接写出m 的取值范围．32．（2024•南丹县一模）如图，抛物线2134y ax bx =++与x 轴交于点(3,0)A -，点B ，点D 是抛物线1y 的顶点，过点D 作x 轴的垂线，垂足为点(1,0)C -．（1）求抛物线1y 所对应的函数解析式；（2）如图1，点M 是抛物线1y 上一点，且位于x 轴上方，横坐标为m ，连接MC ，若MCB DAC Ð=Ð，求m 的值；（3）如图2，将抛物线1y 平移后得到顶点为B 的抛物线2y ．点P 为抛物线1y 上的一个动点，过点P 作y 轴的平行线，交抛物线2y 于点Q ，过点Q 作x 轴的平行线，交抛物线2y 于点R ．当以点P ，Q ，R 为顶点的三角形与ACD D 全等时，请直接写出点P 的坐标．33．（2024•文昌校级模拟）如图，二次函数24(0)y ax x c a =-+¹的图象与x 轴交于点A 、(3,0)B ，与y 轴交于点(0,3)C ，点(,)P m n 是抛物线上的动点．（1）求抛物线的表达式；（2）如图1，当2m =时，求BCP D 的面积；（3）当15PCB Ð=°时，求点P 的坐标；（4）如图2，点Q 是抛物线对称轴上一点，是否存在点P ，使POQ D 是以点P 为直角顶点的等腰直角三角形，若存在，请直接写出m 的值；若不存在，请说明理由．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

二次函数专题练习（学生版）一．选择题1．四位同学在研究函数y=x2+bx+c（b，c是常数）时，甲发现当x=1时，函数有最小值；乙发现﹣1是方程x2+bx+c=0的一个根；丙发现函数的最小值为3；丁发现当x=2时，y=4，已知这四位同学中只有一位发现的结论是错误的，则该同学是（）A．甲B．乙C．丙D．丁2．用配方法将二次函数y=x2﹣8x﹣9化为y=a（x﹣h）2+k的形式为（）A．y=（x﹣4）2+7 B．y=（x﹣4）2﹣25 C．y=（x+4）2+7 D．y=（x+4）2﹣253．将抛物线y=x2﹣6x+21向左平移2个单位后，得到新抛物线的解析式为（）A．y=（x﹣8）2+5 B．y=（x﹣4）2+5 C．y=（x﹣8）2+3 D．y=（x﹣4）2+34．如图是二次函数y=ax2+bx+c图象的一部分，且过点A（3，0），二次函数图象的对称轴是直线x=1，下列结论正确的是（）A．b2＜4ac B．ac＞0 C．2a﹣b=0 D．a﹣b+c=05．抛物线y=（x﹣2）2﹣1可以由抛物线y=x2平移而得到，下列平移正确的是（）A．先向左平移2个单位长度，然后向上平移1个单位长度B．先向左平移2个单位长度，然后向下平移1个单位长度C．先向右平移2个单位长度，然后向上平移1个单位长度D．先向右平移2个单位长度，然后向下平移1个单位长度6．已知学校航模组设计制作的火箭的升空高度h（m）与飞行时间t（s）满足函数表达式h=﹣t2+24t+1．则下列说法中正确的是（）A．点火后9s和点火后13s的升空高度相同B．点火后24s火箭落于地面C．点火后10s的升空高度为139m D．火箭升空的最大高度为145m7．已知二次函数y=﹣x2+x+6及一次函数y=﹣x+m，将该二次函数在x轴上方的图象沿x轴翻折到x 轴下方，图象的其余部分不变，得到一个新函数（如图所示），当直线y=﹣x+m与新图象有4个交点时，m的取值范围是（）A．﹣＜m＜3 B．﹣＜m＜2 C．﹣2＜m＜3 D．﹣6＜m＜﹣28．二次函数y=x2+（a﹣2）x+3的图象与一次函数y=x（1≤x≤2）的图象有且仅有一个交点，则实数a的取值范围是（）A．a=3±2B．﹣1≤a＜2C．a=3或﹣≤a＜2 D．a=3﹣2或﹣1≤a＜﹣9．如图，二次函数y=ax2+bx的图象开口向下，且经过第三象限的点P．若点P的横坐标为﹣1，则一次函数y=（a﹣b）x+b的图象大致是（）A．B．C．D．10．已知一次函数y=x+c的图象如图，则二次函数y=ax2+bx+c在平面直角坐标系中的图象可能是（）A．B．C．D．11．函数y=ax2+2ax+m（a＜0）的图象过点（2，0），则使函数值y＜0成立的x的取值范围是（）A．x＜﹣4或x＞2 B．﹣4＜x＜2 C．x＜0或x＞2 D．0＜x＜212．对于抛物线y=ax2+（2a﹣1）x+a﹣3，当x=1时，y＞0，则这条抛物线的顶点一定在（）A．第一象限B．第二象限C．第三象限D．第四象限13．抛物线y=ax2+bx+c的对称轴为直线x=﹣1，部分图象如图所示，下列判断中：①abc＞0；②b2﹣4ac＞0；③9a﹣3b+c=0；④若点（﹣0.5，y1），（﹣2，y2）均在抛物线上，则y1＞y2；⑤5a﹣2b+c＜0．其中正确的个数有（）A．2 B．3 C．4 D．514．如图，函数y=ax2﹣2x+1和y=ax﹣a（a是常数，且a≠0）在同一平面直角坐标系的图象可能是（）A．B． C．D．15．如图，抛物线y=ax2+bx+c与x轴交于点A（﹣1，0），顶点坐标（1，n）与y轴的交点在（0，2），（0，3）之间（包含端点），则下列结论：①3a+b＜0；②﹣1≤a≤﹣；③对于任意实数m，a+b≥am2+bm总成立；④关于x的方程ax2+bx+c=n﹣1有两个不相等的实数根．其中结论正确的个数为（）A．1个 B．2个 C．3个 D．4个16．抛物线y=ax2+bx+c（a≠0）图象如图所示，下列结论错误的是（）A．abc＜0 B．a+c＜b C．b2+8a＞4ac D．2a+b＞017．二次函数y=ax2+bx+c（a≠0）的大致图象如图所示，顶点坐标为（﹣2，﹣9a），下列结论：①4a+2b+c ＞0；②5a﹣b+c=0；③若方程a（x+5）（x﹣1）=﹣1有两个根x1和x2，且x1＜x2，则﹣5＜x1＜x2＜1；④若方程|ax2+bx+c|=1有四个根，则这四个根的和为﹣4．其中正确的结论有（）A．1个B．2个 C．3个 D．4个18．若满足＜x≤1的任意实数x，都能使不等式2x3﹣x2﹣mx＞2成立，则实数m的取值范围是（）A．m＜﹣1 B．m≥﹣5 C．m＜﹣4 D．m≤﹣419．在平面直角坐标系xOy中，已知点M，N的坐标分别为（﹣1，2），（2，1），若抛物线y=ax2﹣x+2（a≠0）与线段MN有两个不同的交点，则a的取值范围是（）A．a≤﹣1或≤a＜B．≤a＜C．a≤或a＞D．a≤﹣1或a≥20．如图所示，已知二次函数y=ax2+bx+c的图象与x轴交于A、B两点，与y轴交于点C，对称轴为直线x=1．直线y=﹣x+c与抛物线y=ax2+bx+c交于C、D两点，D点在x轴下方且横坐标小于3，则下列结论：①2a+b+c＞0；②a﹣b+c＜0；③x（ax+b）≤a+b；④a＜﹣1．其中正确的有（）A．4个 B．3个 C．2个 D．1个21．如图，二次函数y=ax2+bx+c的图象与x轴交于点A（﹣1，0），B（3，0）．下列结论：①2a﹣b=0；②（a+c）2＜b2；③当﹣1＜x＜3时，y＜0；④当a=1时，将抛物线先向上平移2个单位，再向右平移1个单位，得到抛物线y=（x﹣2）2﹣2．其中正确的是（）A．①③B．②③C．②④D．③④22．已知二次函数y=x2﹣x+m﹣1的图象与x轴有交点，则m的取值范围是（）A．m≤5 B．m≥2 C．m＜5 D．m＞223．已知二次函数y=ax2+bx+c的图象如图所示，OA=OC，则由抛物线的特征写出如下含有a、b、c三个字母的等式或不等式：①=﹣1；②ac+b+1=0；③abc＞0；④a﹣b+c＞0．其中正确的个数是（）A．4个 B．3个 C．2个 D．1个24．如图，一段抛物线y=﹣x2+4（﹣2≤x≤2）为C1，与x轴交于A0，A1两点，顶点为D1；将C1绕点A1旋转180°得到C2，顶点为D2；C1与C2组成一个新的图象，垂直于y轴的直线l与新图象交于点P1（x1，y1），P2（x2，y2），与线段D1D2交于点P3（x3，y3），设x1，x2，x3均为正数，t=x1+x2+x3，则t的取值范围是（）A．6＜t≤8 B．6≤t≤8 C．10＜t≤12 D．10≤t≤1225．已知二次函数y=ax2+bx+c（a≠0）的图象如图，分析下列四个结论：①abc＜0；②b2﹣4ac＞0；③3a+c＞0；④（a+c）2＜b2，其中正确的结论有（）A．1个 B．2个 C．3个 D．4个26．已知关于x的二次函数y=x2﹣2x﹣2，当a≤x≤a+2时，函数有最大值1，则a的值为（）A．﹣1或1 B．1或﹣3 C．﹣1或3 D．3或﹣327．已知二次函数y=﹣（x﹣h）2（h为常数），当自变量x的值满足2≤x≤5时，与其对应的函数值y的最大值为﹣1，则h的值为（）A．3或6 B．1或6 C．1或3 D．4或628．将抛物线y=x2平移得到抛物线y=（x+3）2，则这个平移过程正确的是（）A．向左平移3个单位B．向右平移3个单位C．向上平移3个单位D．向下平移3个单位29．函数y=x2+1与y=x2图象不同之处是（）A．对称轴B．开口方向C．顶点D．形状30．如图，二次函数y=ax2+bx+c（a≠0）的图象的顶点在第一象限，且过点（0，1）和（﹣1，0），下列结论：①ab＜0，②b2＞4，③0＜a+b+c＜2，④0＜b＜1，⑤当x＞﹣1时，y＞0．其中正确结论的个数是（）A．2个 B．3个 C．4个 D．5个31．已知二次函数的图象（0≤x≤4）如图，关于该函数在所给自变量的取值范围内，下列说法正确的是（）A．有最大值2，有最小值﹣2.5 B．有最大值2，有最小值1.5C．有最大值1.5，有最小值﹣2.5 D．有最大值2，无最小值32．函数y=x2+2x+1写成y=a（x﹣h）2+k的形式是（）A．y=（x﹣1）2+2 B．y=（x﹣1）2+C．y=（x﹣1）2﹣3 D．y=（x+2）2﹣133．将二次函数y=x2﹣4x+6化成顶点式，变形正确的是（）A．y=（x﹣2）2+2 B．y=（x+2）2+2 C．y=（x+2）2﹣2 D．y=（x﹣2）2﹣234．将二次函数表达式y=x2﹣2x+3用配方法配成顶点式正确的是（）A．y=（x﹣1）2+2 B．y=（x+1）2+4 C．y=（x﹣1）2﹣2 D．y=（x+2）2﹣235．如图，二次函数y=ax2+bx+c的图象经过点A（﹣1，0）、点B（3，0）、点C（4，y1），若点D（x2，y2）是抛物线上任意一点，有下列结论：①二次函数y=ax2+bx+c的最小值为﹣4a；②若﹣1≤x2≤4，则0≤y2≤5a；③若y2＞y1，则x2＞4；④一元二次方程cx2+bx+a=0的两个根为﹣1和其中正确结论的个数是（）A．1 B．2 C．3 D．436．已知抛物线y=ax2+bx+c（a，b，c为常数，a≠0）经过点（﹣1，0），（0，3），其对称轴在y轴右侧．有下列结论：①抛物线经过点（1，0）；②方程ax2+bx+c=2有两个不相等的实数根；③﹣3＜a+b＜3其中，正确结论的个数为（）A．0 B．1 C．2 D．337．二次函数y=﹣x2+mx的图象如图，对称轴为直线x=2，若关于x的一元二次方程﹣x2+mx﹣t=0（t 为实数）在1＜x＜5的范围内有解，则t的取值范围是（）A．t＞﹣5 B．﹣5＜t＜3 C．3＜t≤4 D．﹣5＜t≤438．抛物线C1：y1=mx2﹣4mx+2n﹣1与平行于x轴的直线交于A、B两点，且A点坐标为（﹣1，2），请结合图象分析以下结论：①对称轴为直线x=2；②抛物线与y轴交点坐标为（0，﹣1）；③m＞；④若抛物线C2：y2=ax2（a≠0）与线段AB恰有一个公共点，则a的取值范围是≤a＜2；⑤不等式mx2﹣4mx+2n＞0的解作为函数C1的自变量的取值时，对应的函数值均为正数，其中正确结论的个数有（）A．2个B．3个 C．4个 D．5个39．如图，一次函数y1=mx+n（m≠0）与二次函数y2=ax2+bx+c（a≠0）的图象相交于两点A（﹣1，5）、B（9，3），请你根据图象写出使y1≥y2成立的x的取值范围（）A．﹣1≤x≤9 B．﹣1≤x＜9 C．﹣1＜x≤9 D．x≤﹣1或x≥940．已知一次函数y1=﹣2x，二次函数y2=x2+1，对于x的同一个值，这两个函数所对应的函数值为y1和y2，则下列关系正确的是（）A．y1＞y2B．y1≥y2C．y1＜y2D．y1≤y241．若不等式ax2+7x﹣1＞2x+5对﹣1≤a≤1恒成立，则x的取值范围是（）A．2≤x≤3 B．﹣1＜x＜1 C．﹣1≤x≤1 D．2＜x＜342．跳台滑雪是冬季奥运会比赛项目之一，运动员起跳后的飞行路线可以看作是抛物线的一部分，运动员起跳后的竖直高度y（单位：m）与水平距离x（单位：m）近似满足函数关系y=ax2+bx+c（a≠0）．如图记录了某运动员起跳后的x与y的三组数据，根据上述函数模型和数据，可推断出该运动员起跳后飞行到最高点时，水平距离为（）A．10m B．15m C．20m D．22.5m43．某大学生利用课余时间在网上销售一种成本为50元/件的商品，每月的销售量y（件）与销售单价x（元/件）之间的函数关系式为y=﹣4x+440，要获得最大利润，该商品的售价应定为（）A．60元B．70元C．80元D．90元44．如图，图中是抛物线形拱桥，当拱顶离水面2m时水面宽4m．水面下降1m，水面宽度为（）A．2m B．2m C．m D．m45．如图，排球运动员站在点O处练习发球，将球从D点正上方2m的A处发出，把球看成点，其运行的高度y（m）与运行的水平距离x（m）满足关系式y=a（x﹣k）2+h．已知球与D点的水平距离为6m时，达到最高2.6m，球网与D点的水平距离为9m．高度为2.43m，球场的边界距O点的水平距离为18m，则下列判断正确的是（）A．球不会过网B．球会过球网但不会出界C．球会过球网并会出界D．无法确定46．某地要建造一个圆形喷水池，在水池中央垂直于地面安装一个柱子OA，O恰为水面中心，安置在柱子顶端A处的喷头向外喷水，水流在各个方向上沿形状相同的抛物线路径落下．在过OA的任一平面上，建立平面直角坐标系（如图），水流喷出的高度y（m）与水平距离x（m）之间的关系式是y=﹣x2+2x+3，则下列结论：（1）柱子OA的高度为3m；（2）喷出的水流距柱子1m处达到最大高度；（3）喷出的水流距水平面的最大高度是4m；（4）水池的半径至少要3m才能使喷出的水流不至于落在池外．其中正确的有（）A．1个 B．2个 C．3个 D．447．二维码已经给我们的生活带来了很大方便，它是由大小相同的黑白两色的小正方形（如图1中C）按某种规律组成的一个大正方形，现有25×25格式的正方形如图1，角上是三个7×7的A型大黑白相间正方形，中间右下一个5×5的B型黑白相间正方形，除这4个正方形外，若其他的小正方形白色块数y与黑色块数x正好满足如图2所示的函数图象，则该25×25格式的二维码共有多少块黑色的C型小正方形（）A．153 B．218 C．100 D．21648．某鞋帽专卖店销售一种绒帽，若这种帽子每天获利y（元）与销售单价x（元）满足关系y=﹣x2+70x ﹣800，要想获得最大利润，则销售单价为（）A．30元B．35元C．40元D．45元49．点A，B的坐标分别为（﹣2，3）和（1，3），抛物线y=ax2+bx+c（a＜0）的顶点在线段AB上运动时，形状保持不变，且与x轴交于C，D两点（C在D的左侧），给出下列结论：①c＜3；②当x＜﹣3时，y随x的增大而增大；③若点D的横坐标最大值为5，则点C的横坐标最小值为﹣5；④当四边形ACDB 为平行四边形时，．其中正确的是（）A．②④B．②③C．①③④D．①②④50．已知抛物线y=ax2+bx+3在坐标系中的位置如图所示，它与x，y轴的交点分别为A，B，P是其对称轴x=1上的动点，根据图中提供的信息，给出以下结论：①2a+b=0，②x=3是ax2+bx+3=0的一个根，③△PAB 周长的最小值是+3．其中正确的是（）A．①②③B．仅有①②C．仅有①③D．仅有②③51．观察下列表格，一元二次方程x2﹣x﹣1.1=0的最精确的一个近似解是（）x 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9x2﹣x﹣1.1﹣0.99﹣0.86﹣0.71﹣0.54﹣0.35﹣0.140.090.340.61A．0.09 B．1.1 C．1.6 D．1.752．小李同学在求一元二次方程﹣2x2+4x+1=0的近似根时，先在直角坐标系中使用软件绘制了二次函数y=﹣2x2+4x+1的图象（如图），接着观察图象与x轴的交点A和B的位置，然后得出该一元二次方程两个根的范围是﹣1＜x1＜0，2＜x2＜3，小李同学的这种方法主要运用的数学思想是（）A．公理化B．类比思想C．数形结合D．模型思想二．填空题53．已知二次函数y=ax2+bx+c的图象如图所示，若方程ax2+bx+c=k有两个不相等的实数根，则k的取值范围是．54．二次函数y=ax2+bx的图象如图，若一元二次方程ax2+bx+m=0有实数根，则m的最大值为．55．抛物线y=x2﹣4x+3的顶点坐标为．56．已知关于x的二次函数y=x2+（1﹣a）x+1，当x的取值范围是1≤x≤3时，函数值y在x=1时取得最大值，则实数a的取值范围是．三．解答题（共4小题）57．如图，已知抛物线y=ax2+x+4的对称轴是直线x=3，且与x轴相交于A，B两点（B点在A点右侧）与y轴交于C点．（1）求抛物线的解折式和A、B两点的坐标；（2）若点P是抛物线上B、C两点之间的一个动点（不与B、C重合），则是否存在一点P，使△PBC的面积最大．若存在，请求出△PBC的最大面积；若不存在，试说明理由；（3）若M是抛物线上任意一点，过点M作y轴的平行线，交直线BC于点N，当MN=3时，求M点的坐标．58．如图，关于x的二次函数y=x2+bx+c的图象与x轴交于点A（1，0）和点B，与y轴交于点C（0，3），抛物线的对称轴与x轴交于点D．（1）求二次函数的表达式；（2）在y轴上是否存在一点P，使△PBC为等腰三角形？若存在．请求出点P的坐标；（3）有一个点M从点A出发，以每秒1个单位的速度在AB上向点B运动，另一个点N从点D与点M同时出发，以每秒2个单位的速度在抛物线的对称轴上运动，当点M到达点B时，点M、N同时停止运动，问点M、N运动到何处时，△MNB面积最大，试求出最大面积．59．已知：如图，抛物线y=ax2+bx+c与坐标轴分别交于点A（0，6），B（6，0），C（﹣2，0），点P 是线段AB上方抛物线上的一个动点．（1）求抛物线的解析式；（2）当点P运动到什么位置时，△PAB的面积有最大值？（3）过点P作x轴的垂线，交线段AB于点D，再过点P做PE∥x轴交抛物线于点E，连结DE，请问是否存在点P使△PDE为等腰直角三角形？若存在，求出点P的坐标；若不存在，说明理由．60．如图，在平面直角坐标系中，抛物线y=x2﹣x﹣4与x轴交于A，B两点（点A在点B左侧），与y轴交于点C．（1）求点A，B，C的坐标；（2）点P从A点出发，在线段AB上以每秒2个单位长度的速度向B点运动，同时，点Q从B点出发，在线段BC上以每秒1个单位长度的速度向C点运动，当其中一个点到达终点时，另一个点也停止运动．设运动时间为t秒，求运动时间t为多少秒时，△PBQ的面积S最大，并求出其最大面积；（3）在（2）的条件下，当△PBQ面积最大时，在BC下方的抛物线上是否存在点M，使△BMC的面积是△PBQ面积的1.6倍？若存在，求点M的坐标；若不存在，请说明理由．二次函数专题练（教师版）一．选择题（共52小题）1．四位同学在研究函数y=x2+bx+c（b，c是常数）时，甲发现当x=1时，函数有最小值；乙发现﹣1是方程x2+bx+c=0的一个根；丙发现函数的最小值为3；丁发现当x=2时，y=4，已知这四位同学中只有一位发现的结论是错误的，则该同学是（）A．甲B．乙C．丙D．丁【解答】解：假设甲和丙的结论正确，则，解得：，∴抛物线的解析式为y=x2﹣2x+4．当x=﹣1时，y=x2﹣2x+4=7，∴乙的结论不正确；当x=2时，y=x2﹣2x+4=4，∴丁的结论正确．∵四位同学中只有一位发现的结论是错误的，∴假设成立．故选：B．2．用配方法将二次函数y=x2﹣8x﹣9化为y=a（x﹣h）2+k的形式为（）A．y=（x﹣4）2+7 B．y=（x﹣4）2﹣25 C．y=（x+4）2+7 D．y=（x+4）2﹣25【解答】解：y=x2﹣8x﹣9=x2﹣8x+16﹣25=（x﹣4）2﹣25．故选：B．3．将抛物线y=x2﹣6x+21向左平移2个单位后，得到新抛物线的解析式为（）A．y=（x﹣8）2+5 B．y=（x﹣4）2+5 C．y=（x﹣8）2+3 D．y=（x﹣4）2+3【解答】解：y=x2﹣6x+21=（x2﹣12x）+21=[（x﹣6）2﹣36]+21=（x﹣6）2+3，故y=（x﹣6）2+3，向左平移2个单位后，得到新抛物线的解析式为：y=（x﹣4）2+3．故选：D．4．如图是二次函数y=ax2+bx+c图象的一部分，且过点A（3，0），二次函数图象的对称轴是直线x=1，下列结论正确的是（）A．b2＜4ac B．ac＞0 C．2a﹣b=0 D．a﹣b+c=0【解答】解：∵抛物线与x轴有两个交点，∴b2﹣4ac＞0，即b2＞4ac，所以A选项错误；∵抛物线开口向上，∴a＞0，∵抛物线与y轴的交点在x轴下方，∴c＜0，∴ac＜0，所以B选项错误；∵二次函数图象的对称轴是直线x=1，∴﹣=1，∴2a+b=0，所以C选项错误；∵抛物线过点A（3，0），二次函数图象的对称轴是x=1，∴抛物线与x轴的另一个交点为（﹣1，0），∴a﹣b+c=0，所以D选项正确；故选：D．5．抛物线y=（x﹣2）2﹣1可以由抛物线y=x2平移而得到，下列平移正确的是（）A．先向左平移2个单位长度，然后向上平移1个单位长度B．先向左平移2个单位长度，然后向下平移1个单位长度C．先向右平移2个单位长度，然后向上平移1个单位长度D．先向右平移2个单位长度，然后向下平移1个单位长度【解答】解：抛物线y=x2顶点为（0，0），抛物线y=（x﹣2）2﹣1的顶点为（2，﹣1），则抛物线y=x2向右平移2个单位，向下平移1个单位得到抛物线y=（x﹣2）2﹣1的图象．故选：D．6．已知学校航模组设计制作的火箭的升空高度h（m）与飞行时间t（s）满足函数表达式h=﹣t2+24t+1．则下列说法中正确的是（）A．点火后9s和点火后13s的升空高度相同B．点火后24s火箭落于地面C．点火后10s的升空高度为139mD．火箭升空的最大高度为145m【解答】解：A、当t=9时，h=136；当t=13时，h=144；所以点火后9s和点火后13s的升空高度不相同，此选项错误；B、当t=24时h=1≠0，所以点火后24s火箭离地面的高度为1m，此选项错误；C、当t=10时h=141m，此选项错误；D、由h=﹣t2+24t+1=﹣（t﹣12）2+145知火箭升空的最大高度为145m，此选项正确；故选：D．7．已知二次函数y=﹣x2+x+6及一次函数y=﹣x+m，将该二次函数在x轴上方的图象沿x轴翻折到x 轴下方，图象的其余部分不变，得到一个新函数（如图所示），当直线y=﹣x+m与新图象有4个交点时，m的取值范围是（）A．﹣＜m＜3 B．﹣＜m＜2 C．﹣2＜m＜3 D．﹣6＜m＜﹣2【解答】解：如图，当y=0时，﹣x2+x+6=0，解得x1=﹣2，x2=3，则A（﹣2，0），B（3，0），将该二次函数在x轴上方的图象沿x轴翻折到x轴下方的部分图象的解析式为y=（x+2）（x﹣3），即y=x2﹣x﹣6（﹣2≤x≤3），当直线•y=﹣x+m经过点A（﹣2，0）时，2+m=0，解得m=﹣2；当直线y=﹣x+m与抛物线y=x2﹣x﹣6（﹣2≤x≤3）有唯一公共点时，方程x2﹣x﹣6=﹣x+m有相等的实数解，解得m=﹣6，所以当直线y=﹣x+m与新图象有4个交点时，m的取值范围为﹣6＜m＜﹣2．故选：D．8．二次函数y=x2+（a﹣2）x+3的图象与一次函数y=x（1≤x≤2）的图象有且仅有一个交点，则实数a的取值范围是（）A．a=3±2B．﹣1≤a＜2C．a=3或﹣≤a＜2 D．a=3﹣2或﹣1≤a＜﹣【解答】解：由题意可知：方程x2+（a﹣2）x+3=x在1≤x≤2上只有一个解，即x2+（a﹣3）x+3=0在1≤x≤2上只有一个解，当△=0时，即（a﹣3）2﹣12=0a=3±2当a=3+2时，此时x=﹣，不满足题意，当a=3﹣2时，此时x=，满足题意，当△＞0时，令y=x2+（a﹣3）x+3，令x=1，y=a+1，令x=2，y=2a+1（a+1）（2a+1）≤0解得：﹣1≤a≤，当a=﹣1时，此时x=1或3，满足题意；当a=﹣时，此时x=2或x=，不满足题意，综上所述，a=3﹣2或﹣1≤a＜，故选：D．9．如图，二次函数y=ax2+bx的图象开口向下，且经过第三象限的点P．若点P的横坐标为﹣1，则一次函数y=（a﹣b）x+b的图象大致是（）A．B．C．D．【解答】解：由二次函数的图象可知，a＜0，b＜0，当x=﹣1时，y=a﹣b＜0，∴y=（a﹣b）x+b的图象在第二、三、四象限，故选：D．10．已知一次函数y=x+c的图象如图，则二次函数y=ax2+bx+c在平面直角坐标系中的图象可能是（）A．B．C．D．【解答】解：观察函数图象可知：＜0、c＞0，∴二次函数y=ax2+bx+c的图象对称轴x=﹣＞0，与y轴的交点在y轴负正半轴．故选：A．11．函数y=ax2+2ax+m（a＜0）的图象过点（2，0），则使函数值y＜0成立的x的取值范围是（）A．x＜﹣4或x＞2 B．﹣4＜x＜2 C．x＜0或x＞2 D．0＜x＜2【解答】解：抛物线y=ax2+2ax+m得对称轴为直线x=﹣=﹣1，而抛物线与x轴的一个交点坐标为（2，0），∴抛物线与x轴的另一个交点坐标为（﹣4，0），∵a＜0，∴抛物线开口向下，∴当x＜﹣4或x＞2时，y＜0．故选：A．12．对于抛物线y=ax2+（2a﹣1）x+a﹣3，当x=1时，y＞0，则这条抛物线的顶点一定在（）A．第一象限B．第二象限C．第三象限D．第四象限【解答】解：把x=1，y＞0代入解析式可得：a+2a﹣1+a﹣3＞0，解得：a＞1，所以可得：﹣，，所以这条抛物线的顶点一定在第三象限，故选：C．13．抛物线y=ax2+bx+c的对称轴为直线x=﹣1，部分图象如图所示，下列判断中：①abc＞0；②b2﹣4ac＞0；③9a﹣3b+c=0；④若点（﹣0.5，y1），（﹣2，y2）均在抛物线上，则y1＞y2；⑤5a﹣2b+c＜0．其中正确的个数有（）A．2 B．3 C．4 D．5【解答】解：∵抛物线对称轴x=﹣1，经过（1，0），∴﹣=﹣1，a+b+c=0，∴b=2a，c=﹣3a，∵a＞0，∴b＞0，c＜0，∴abc＜0，故①错误，∵抛物线与x轴有交点，∴b2﹣4ac＞0，故②正确，∵抛物线与x轴交于（﹣3，0），∴9a﹣3b+c=0，故③正确，∵点（﹣0.5，y1），（﹣2，y2）均在抛物线上，﹣1.5＞﹣2，则y1＜y2；故④错误，∵5a﹣2b+c=5a﹣4a﹣3a=﹣2a＜0，故⑤正确，故选：B．14．如图，函数y=ax2﹣2x+1和y=ax﹣a（a是常数，且a≠0）在同一平面直角坐标系的图象可能是（）A．B． C．D．【解答】解：A、由一次函数y=ax﹣a的图象可得：a＜0，此时二次函数y=ax2﹣2x+1的图象应该开口向下，故选项错误；B、由一次函数y=ax﹣a的图象可得：a＞0，此时二次函数y=ax2﹣2x+1的图象应该开口向上，对称轴x=﹣＞0，故选项正确；C、由一次函数y=ax﹣a的图象可得：a＞0，此时二次函数y=ax2﹣2x+1的图象应该开口向上，对称轴x=﹣＞0，和x轴的正半轴相交，故选项错误；D、由一次函数y=ax﹣a的图象可得：a＞0，此时二次函数y=ax2﹣2x+1的图象应该开口向上，故选项错误．故选：B．15．如图，抛物线y=ax2+bx+c与x轴交于点A（﹣1，0），顶点坐标（1，n）与y轴的交点在（0，2），（0，3）之间（包含端点），则下列结论：①3a+b＜0；②﹣1≤a≤﹣；③对于任意实数m，a+b≥am2+bm总成立；④关于x的方程ax2+bx+c=n﹣1有两个不相等的实数根．其中结论正确的个数为（）A．1个 B．2个 C．3个 D．4个【解答】解：∵抛物线开口向下，∴a＜0，而抛物线的对称轴为直线x=﹣=1，即b=﹣2a，∴3a+b=3a﹣2a=a＜0，所以①正确；∵2≤c≤3，而c=﹣3a，∴2≤﹣3a≤3，∴﹣1≤a≤﹣，所以②正确；∵抛物线的顶点坐标（1，n），∴x=1时，二次函数值有最大值n，∴a+b+c≥am2+bm+c，即a+b≥am2+bm，所以③正确；∵抛物线的顶点坐标（1，n），∴抛物线y=ax2+bx+c与直线y=n﹣1有两个交点，∴关于x的方程ax2+bx+c=n﹣1有两个不相等的实数根，所以④正确．故选：D．16．抛物线y=ax2+bx+c（a≠0）图象如图所示，下列结论错误的是（）A．abc＜0 B．a+c＜b C．b2+8a＞4ac D．2a+b＞0【解答】解：（A）由图象开口可知：a＜0由对称轴可知：＞0，∴b＞0，∴由抛物线与y轴的交点可知：c＞0，∴abc＜0，故A正确；（B）由图象可知：x=﹣1，y＜0，∴y=a﹣b+c＜0，∴a+c＜b，故B正确；（C）由图象可知：顶点的纵坐标大于2，∴＞2，a＜0，∴4ac﹣b2＜8a，∴b2+8a＞4ac，故C正确；（D）对称轴x=＜1，a＜0，∴2a+b＜0，故D错误；故选：D．17．二次函数y=ax2+bx+c（a≠0）的大致图象如图所示，顶点坐标为（﹣2，﹣9a），下列结论：①4a+2b+c ＞0；②5a﹣b+c=0；③若方程a（x+5）（x﹣1）=﹣1有两个根x1和x2，且x1＜x2，则﹣5＜x1＜x2＜1；④若方程|ax2+bx+c|=1有四个根，则这四个根的和为﹣4．其中正确的结论有（）A．1个 B．2个 C．3个 D．4个【解答】解：∵抛物线的顶点坐标（﹣2a，﹣9a），∴﹣=﹣2a，=﹣9a，∴b=4a，c=5a，∴抛物线的解析式为y=ax2+4ax﹣5a，∴4a+2b+c=4a+8a﹣5a=7a＞0，故①正确，5a﹣b+c=5a﹣4a﹣5a=﹣4a＜0，故②错误，∵抛物线y=ax2+4ax﹣5a交x轴于（﹣5，0），（1，0），∴若方程a（x+5）（x﹣1）=﹣1有两个根x1和x2，且x1＜x2，则﹣5＜x1＜x2＜1，正确，故③正确，若方程|ax2+bx+c|=1有四个根，则这四个根的和为﹣8，故④错误，故选：B．18．若满足＜x≤1的任意实数x，都能使不等式2x3﹣x2﹣mx＞2成立，则实数m的取值范围是（）A．m＜﹣1 B．m≥﹣5 C．m＜﹣4 D．m≤﹣4【解答】解：∵满足＜x≤1的任意实数x，都能使不等式2x3﹣x2﹣mx＞2成立，∴m＜，∴m≤﹣4故选：D．19．在平面直角坐标系xOy中，已知点M，N的坐标分别为（﹣1，2），（2，1），若抛物线y=ax2﹣x+2（a≠0）与线段MN有两个不同的交点，则a的取值范围是（）A．a≤﹣1或≤a＜B．≤a＜C．a≤或a＞D．a≤﹣1或a≥【解答】解：∵抛物线的解析式为y=ax2﹣x+2．观察图象可知当a＜0时，x=﹣1时，y≤2时，且﹣≥﹣1，满足条件，可得a≤﹣1；当a＞0时，x=2时，y≥1，且抛物线与直线MN有交点，且﹣≤2满足条件，∴a≥，∵直线MN的解析式为y=﹣x+，由，消去y得到，3ax2﹣2x+1=0，∵△＞0，∴a＜，∴≤a＜满足条件，综上所述，满足条件的a的值为a≤﹣1或≤a＜，故选：A．20．如图所示，已知二次函数y=ax2+bx+c的图象与x轴交于A、B两点，与y轴交于点C，对称轴为直线x=1．直线y=﹣x+c与抛物线y=ax2+bx+c交于C、D两点，D点在x轴下方且横坐标小于3，则下列结论：①2a+b+c＞0；②a﹣b+c＜0；③x（ax+b）≤a+b；④a＜﹣1．其中正确的有（）A．4个 B．3个 C．2个 D．1个【解答】解：∵抛物线与y轴的交点在x轴上方，∴c＞0，∵抛物线的对称轴为直线x=﹣=1，∴b=﹣2a，∴2a+b+c=2a﹣2a+c=c＞0，所以①正确；∵抛物线与x轴的一个交点在点（3，0）左侧，而抛物线的对称轴为直线x=1，∴抛物线与x轴的另一个交点在点（﹣1，0）右侧，∴当x=﹣1时，y＜0，∴a﹣b+c＜0，所以②正确；∵x=1时，二次函数有最大值，∴ax2+bx+c≤a+b+c，∴ax2+bx≤a+b，所以③正确；∵直线y=﹣x+c与抛物线y=ax2+bx+c交于C、D两点，D点在x轴下方且横坐标小于3，∴x=3时，一次函数值比二次函数值大，即9a+3b+c＜﹣3+c，而b=﹣2a，∴9a﹣6a＜﹣3，解得a＜﹣1，所以④正确．故选：A．21．如图，二次函数y=ax2+bx+c的图象与x轴交于点A（﹣1，0），B（3，0）．下列结论：①2a﹣b=0；②（a+c）2＜b2；③当﹣1＜x＜3时，y＜0；④当a=1时，将抛物线先向上平移2个单位，再向右平移1个单位，得到抛物线y=（x﹣2）2﹣2．其中正确的是（）A．①③B．②③C．②④D．③④【解答】解：①图象与x轴交于点A（﹣1，0），B（3，0），∴二次函数的图象的对称轴为x==1∴=1∴2a+b=0，故①错误；②令x=﹣1，∴y=a﹣b+c=0，∴a+c=b，∴（a+c）2=b2，故②错误；③由图可知：当﹣1＜x＜3时，y＜0，故③正确；④当a=1时，∴y=（x+1）（x﹣3）=（x﹣1）2﹣4将抛物线先向上平移2个单位，再向右平移1个单位，得到抛物线y=（x﹣1﹣1）2﹣4+2=（x﹣2）2﹣2，故④正确；故选：D．22．已知二次函数y=x2﹣x+m﹣1的图象与x轴有交点，则m的取值范围是（）A．m≤5 B．m≥2 C．m＜5 D．m＞2【解答】解：∵二次函数y=x2﹣x+m﹣1的图象与x轴有交点，∴△=（﹣1）2﹣4×1×（m﹣1）≥0，解得：m≤5，故选：A．23．已知二次函数y=ax2+bx+c的图象如图所示，OA=OC，则由抛物线的特征写出如下含有a、b、c三个字母的等式或不等式：①=﹣1；②ac+b+1=0；③abc＞0；④a﹣b+c＞0．其中正确的个数是（）A．4个 B．3个 C．2个 D．1个【解答】解：①=﹣1，抛物线顶点纵坐标为﹣1，正确；②ac+b+1=0，设C（0，c），则OC=|c|，∵OA=OC=|c|，∴A（c，0）代入抛物线得ac2+bc+c=0，又c≠0，∴ac+b+1=0，故正确；③abc＞0，从图象中易知a＞0，b＜0，c＜0，故正确；④a﹣b+c＞0，当x=﹣1时y=a﹣b+c，由图象知（﹣1，a﹣b+c）在第二象限，∴a﹣b+c＞0，故正确．故选：A．24．如图，一段抛物线y=﹣x2+4（﹣2≤x≤2）为C1，与x轴交于A0，A1两点，顶点为D1；将C1绕点A1旋转180°得到C2，顶点为D2；C1与C2组成一个新的图象，垂直于y轴的直线l与新图象交于点P1（x1，y1），P2（x2，y2），与线段D1D2交于点P3（x3，y3），设x1，x2，x3均为正数，t=x1+x2+x3，则t 的取值范围是（）A．6＜t≤8 B．6≤t≤8 C．10＜t≤12 D．10≤t≤12【解答】解：翻折后的抛物线的解析式为y=（x﹣4）2﹣4=x2﹣8x+12，∵设x1，x2，x3均为正数，∴点P1（x1，y1），P2（x2，y2）在第四象限，根据对称性可知：x1+x2=8，∵2＜x3≤4，∴10＜x1+x2+x3≤12即10＜t≤12，故选：C．25．已知二次函数y=ax2+bx+c（a≠0）的图象如图，分析下列四个结论：①abc＜0；②b2﹣4ac＞0；③3a+c＞0；④（a+c）2＜b2，其中正确的结论有（）A．1个 B．2个 C．3个 D．4个【解答】解：①由开口向下，可得a＜0，又由抛物线与y轴交于正半轴，可得c＞0，然后由对称轴在y轴左侧，得到b与a同号，则可得b＜0，abc＞0，故①错误；②由抛物线与x轴有两个交点，可得b2﹣4ac＞0，故②正确；③当x=﹣2时，y＜0，即4a﹣2b+c＜0 （1）当x=1时，y＜0，即a+b+c＜0 （2）（1）+（2）×2得：6a+3c＜0，即2a+c＜0又∵a＜0，∴a+（2a+c）=3a+c＜0．故③错误；④∵x=1时，y=a+b+c＜0，x=﹣1时，y=a﹣b+c＞0，∴（a+b+c）（a﹣b+c）＜0，即[（a+c）+b][（a+c）﹣b]=（a+c）2﹣b2＜0，∴（a+c）2＜b2，故④正确．综上所述，正确的结论有2个．故选：B．26．已知关于x的二次函数y=x2﹣2x﹣2，当a≤x≤a+2时，函数有最大值1，则a的值为（）A．﹣1或1 B．1或﹣3 C．﹣1或3 D．3或﹣3【解答】解：当y=1时，有x2﹣2x﹣2=1，解得：x1=﹣1，x2=3．∵当a≤x≤a+2时，函数有最大值1，∴a=﹣1或a+2=3，∴a=﹣1或a=1．故选：A．27．已知二次函数y=﹣（x﹣h）2（h为常数），当自变量x的值满足2≤x≤5时，与其对应的函数值y的最大值为﹣1，则h的值为（）A．3或6 B．1或6 C．1或3 D．4或6【解答】解：当h＜2时，有﹣（2﹣h）2=﹣1，解得：h1=1，h2=3（舍去）；当2≤h≤5时，y=﹣（x﹣h）2的最大值为0，不符合题意；当h＞5时，有﹣（5﹣h）2=﹣1，解得：h3=4（舍去），h4=6．综上所述：h的值为1或6．故选：B．28．将抛物线y=x2平移得到抛物线y=（x+3）2，则这个平移过程正确的是（）A．向左平移3个单位B．向右平移3个单位C．向上平移3个单位D．向下平移3个单位【解答】解：抛物线y=x2的顶点坐标为（0，0），抛物线y=（x+3）2的顶点坐标为（﹣3，0），∵点（0，0）向左平移3个单位可得到（﹣3，0），∴将抛物线y=x2向左平移3个单位得到抛物线y=（x+3）2．故选：A．29．函数y=x2+1与y=x2图象不同之处是（）A．对称轴B．开口方向C．顶点D．形状【解答】解：y=x2+1与y=x2，a=，b=0，对称轴都是y轴，开口方向都向上，形状相同，y=x2+1的顶点坐标是（0，1），y=x2的顶点坐标是（0，0），故选：C．30．如图，二次函数y=ax2+bx+c（a≠0）的图象的顶点在第一象限，且过点（0，1）和（﹣1，0），下列结论：①ab＜0，②b2＞4，③0＜a+b+c＜2，④0＜b＜1，⑤当x＞﹣1时，y＞0．其中正确结论的个数是（）A．2个 B．3个 C．4个 D．5个【解答】解：∵由抛物线开口向下，∴a＜0，∵对称轴在y轴的右侧，∴b＞0，∴ab＜0，所以①正确；∵点（0，1）和（﹣1，0）都在抛物线y=ax2+bx+c上，∴c=1，a﹣b+c=0，∴b=a+c=a+1，而a＜0，∴0＜b＜1，所以②错误，④正确；∵a+b+c=a+a+1+1=2a+2，而a＜0，∴2a+2＜2，即a+b+c＜2，∵抛物线与x轴的一个交点坐标为（﹣1，0），而抛物线的对称轴在y轴右侧，在直线x=1的左侧，∴抛物线与x轴的另一个交点在（1，0）和（2，0）之间，∴x=1时，y＞0，即a+b+c＞0，∴0＜a+b+c＜2，所以③正确；∵x＞﹣1时，抛物线有部分在x轴上方，有部分在x轴下方，∴y＞0或y=0或y＜0，所以⑤错误．故选：B．31．已知二次函数的图象（0≤x≤4）如图，关于该函数在所给自变量的取值范围内，下列说法正确的是（）A．有最大值2，有最小值﹣2.5B．有最大值2，有最小值1.5C．有最大值1.5，有最小值﹣2.5D．有最大值2，无最小值【解答】解：∵二次函数的图象（0≤x≤4）如图，关于该函数在所给自变量的取值范围内，∴x=1时，有最大值2，x=4时，有最小值﹣2.5．故选：A．32．函数y=x2+2x+1写成y=a（x﹣h）2+k的形式是（）A．y=（x﹣1）2+2 B．y=（x﹣1）2+C．y=（x﹣1）2﹣3 D．y=（x+2）2﹣1【解答】解：y=x2+2x+1=（x2+4x+4）﹣2+1=（x+2）2﹣1故选：D．33．将二次函数y=x2﹣4x+6化成顶点式，变形正确的是（）A．y=（x﹣2）2+2 B．y=（x+2）2+2 C．y=（x+2）2﹣2 D．y=（x﹣2）2﹣2【解答】解：y=x2﹣4x+6=x2﹣4x+4+2=（x﹣2）2+2．故选：A．34．将二次函数表达式y=x2﹣2x+3用配方法配成顶点式正确的是（）A．y=（x﹣1）2+2 B．y=（x+1）2+4 C．y=（x﹣1）2﹣2 D．y=（x+2）2﹣2【解答】解：y=x2﹣2x+3=（x﹣1）2+2．故选：A．35．如图，二次函数y=ax2+bx+c的图象经过点A（﹣1，0）、点B（3，0）、点C（4，y1），若点D（x2，y2）是抛物线上任意一点，有下列结论：①二次函数y=ax2+bx+c的最小值为﹣4a；②若﹣1≤x2≤4，则0≤y2≤5a；③若y2＞y1，则x2＞4；④一元二次方程cx2+bx+a=0的两个根为﹣1和其中正确结论的个数是（）A．1 B．2 C．3 D．4【解答】解：抛物线解析式为y=a（x+1）（x﹣3），即y=ax2﹣2ax﹣3a，∵y=a（x﹣1）2﹣4a，∴当x=1时，二次函数有最小值﹣4a，所以①正确；当x=4时，y=a•5•1=5a，∴当﹣1≤x2≤4，则﹣4a≤y2≤5a，所以②错误；∵点C（1，5a）关于直线x=1的对称点为（﹣2，﹣5a），∴当y2＞y1，则x2＞4或x＜﹣2，所以③错误；∵b=﹣2a，c=﹣3a，∴方程cx2+bx+a=0化为﹣3ax2﹣2ax+a=0，整理得3x2+2x﹣1=0，解得x1=﹣1，x2=，所以④正确．故选：B．36．已知抛物线y=ax2+bx+c（a，b，c为常数，a≠0）经过点（﹣1，0），（0，3），其对称轴在y轴右侧．有下列结论：①抛物线经过点（1，0）；②方程ax2+bx+c=2有两个不相等的实数根；。