【精品】Zoeppritz方程推导过程
佩尔方程——精选推荐

佩尔⽅程关于佩尔⽅程佩尔⽅程是具有x 2−ny 2=1形式的丢番图⽅程(不定⽅程)当n 为完全平⽅数的时候,这个⽅程只有平凡解(±1,0),对于其他情况拉格朗⽇证明了佩尔⽅程总有⾮平凡解。
⽽这些解都可以由√n 的连分数求出关于连分数怎么求,⽐如√7=2+1r1,a 0=2r 1=√7+23=1+1r 2,a 1=1r 2=√7+12=1+1r 2,a 2=1r 3=√7+13=1+1r 3,a 3=1r 4=√7+2=4+1r 4,a 4=4从这开始就是[4,1,1,1]这样的周期了我们取第⼀个周期我们得到了[2:1,1,1,1]这时我们的连分数为83,h 3=8,k 3=3,发现82−7∗32=1这就是佩尔⽅程的最⼩解了其实对于h nk n 的h n ,k n 也有递推式h n =a n h n −1+h n −2k n =a n k n −1+k n −2我们由最⼩解可以推得通解此时的最⼩解为x 1=8,y 1=3有x i +1=x 1x i +ny 1y i y i +1=x 1y i +y 1x i可以推出x ky k =x 1 ny 1y 1 x 1k −1x 1y 1可以由矩阵快速幂得到第k 项通解例题 hdu2281-Square Number解题思路:x 2=n (2n +1)(n +1)6n =(2n +1)(n +1)6=13(n 2+32n +916−116)=13(n +34)2−148所以(4n +3)2−48x 2=1这是显然的佩尔⽅程形式,⽽这个最⼩解为4n +3=7,x =1即n =1,x =1可以⽤最⼩解去递推通解,还要判⼀下是否n 满⾜为整数打了个表看了下最多跑到第⼗六项 暴⼒来就好了#include <bits/stdc++.h>#include <ext/pb_ds/assoc_container.hpp>#include <ext/pb_ds/hash_policy.hpp>#include <ext/pb_ds/tree_policy.hpp>#include <ext/pb_ds/trie_policy.hpp>using namespace __gnu_pbds;using namespace std;// freopen("k.in", "r", stdin);// freopen("k.out", "w", stdout);// clock_t c1 = clock();// std::cerr << "Time:" << clock() - c1 <<"ms" << std::endl;//#pragma comment(linker, "/STACK:1024000000,1024000000")mt19937 rnd(time(NULL));#define de(a) cout << #a << " = " << a << endl#define rep(i, a, n) for (int i = a; i <= n; i++)#define per(i, a, n) for (int i = n; i >= a; i--)#define ls ((x) << 1)#define rs ((x) << 1 | 1)typedef long long ll;typedef unsigned long long ull;typedef pair<int, int> PII;typedef pair<double, double> PDD;typedef pair<char, char> PCC;typedef pair<ll, ll> PLL;typedef vector<int> VI;#define inf 0x3f3f3f3fconst ll INF = 0x3f3f3f3f3f3f3f3f;const ll MAXN = 1e5 + 7;const ll MAXM = 4e5 + 7;const ll MOD = 1e9 + 7;const double eps = 1e-7;ll x[105], y[105];[][][]Processing math: 100%ll ansn[105];int main(){ll n = 48;x[1] = 7, y[1] = 1;ansn[1] = 1;for (int i = 2; i <= 20; i++){x[i] = x[i - 1] * x[1] + n * y[1] * y[i - 1];if ((x[i] - 3) % 4 == 0)ansn[i] = (x[i] - 3) / 4;elseansn[i] = -1;y[i] = x[1] * y[i - 1] + y[1] * x[i - 1];}ll N;while (~scanf("%lld", &N) && N){ll ans = -inf;for (int i = 1; i <= 16; i++){if (ansn[i] == -1)continue;if (N < ansn[i])break;ans = i;}printf("%lld %lld\n", ansn[ans], y[ans]);}return 0;}例题 Street Numbers知道题意之后就跟上⾯⼀模⼀样的过程了代码#include <iostream>#include <stdio.h>#include <cmath>#include <algorithm>#include <string>#include <cstring>#include <string.h>#include <map>#include <queue>#include <stack>#include <list>#include <cctype>#include <fstream>#include <sstream>#include <iomanip>#include <set>#include <vector>#include <cstdlib>#include <time.h>using namespace std;/* freopen("k.in", "r", stdin);freopen("k.out", "w", stdout); */// clock_t c1 = clock();// std::cerr << "Time:" << clock() - c1 <<"ms" << std::endl;//#pragma comment(linker, "/STACK:1024000000,1024000000") #define de(a) cout << #a << " = " << a << endl#define rep(i, a, n) for (int i = a; i <= n; i++)#define per(i, a, n) for (int i = n; i >= a; i--)#define ls ((x) << 1)#define rs ((x) << 1 | 1)typedef long long ll;typedef unsigned long long ull;typedef pair<int, int> PII;typedef pair<double, double> PDD;typedef pair<ll, ll> PLL;typedef vector<int, int> VII;#define inf 0x3f3f3f3fconst ll INF = 0x3f3f3f3f3f3f3f3f;const ll MAXN = 2e6 + 7;const ll MAXM = 4e5 + 7;const ll MOD = 1e9 + 7;const double eps = 1e-7;const double pi = acos(-1.0);ll x[20], y[20];int main(){vector<pair<ll, ll> > ans;x[1] = 3, y[1] = 1;ll n = 8;for (int i = 2; i <= 20; i++){x[i] = x[i - 1] * x[1] + n * y[1] * y[i - 1];y[i] = x[1] * y[i - 1] + y[1] * x[i - 1];if ((x[i] - 1) % 2 == 0)ans.push_back({(x[i] - 1) / 2, y[i]});if (ans.size() == 10)break;}for (int i = 0; i < 10; i++)printf("%10lld%10lld\n", ans[i].second, ans[i].first);return 0;}推佩尔⽅程的板⼦连分数版#include <bits/stdc++.h>#include <ext/pb_ds/assoc_container.hpp>#include <ext/pb_ds/hash_policy.hpp>#include <ext/pb_ds/tree_policy.hpp>#include <ext/pb_ds/trie_policy.hpp>using namespace __gnu_pbds;using namespace std;// freopen("k.in", "r", stdin);// freopen("k.out", "w", stdout);// clock_t c1 = clock();// std::cerr << "Time:" << clock() - c1 <<"ms" << std::endl;//#pragma comment(linker, "/STACK:1024000000,1024000000") mt19937 rnd(time(NULL));#define de(a) cout << #a << " = " << a << endl#define rep(i, a, n) for (int i = a; i <= n; i++)#define per(i, a, n) for (int i = n; i >= a; i--)#define ls ((x) << 1)#define rs ((x) << 1 | 1)typedef long long ll;typedef unsigned long long ull;typedef pair<int, int> PII;typedef pair<double, double> PDD;typedef pair<char, char> PCC;typedef pair<ll, ll> PLL;typedef vector<int> VI;#define inf 0x3f3f3f3fconst ll INF = 0x3f3f3f3f3f3f3f3f;const ll MAXN = 1e5 + 7;const ll MAXM = 4e5 + 7;const ll MOD = 1e9 + 7;const double eps = 1e-7;ll a[20000];bool pell_minimum_solution(ll n, ll &x0, ll &y0){ll m = (ll)sqrt((double)n);double sq = sqrt(n);int i = 0;if (m * m == n)return false; //当n是完全平⽅数则佩尔⽅程⽆解a[i++] = m;ll b = m, c = 1;double tmp;do{c = (n - b * b) / c;tmp = (sq + b) / c;a[i++] = (ll)(floor(tmp));b = a[i - 1] *c - b;//printf("%lld %lld %lld\n",a[i-1],b,c);} while (a[i - 1] != 2 * a[0]);ll p = 1, q = 0;for (int j = i - 2; j >= 0; j--){ll t = p;p = q + p * a[j];q = t;//printf("a[%d]=%lld %lld %lld\n",j,a[j],p,q);}if ((i - 1) % 2 == 0){x0 = p;y0 = q;}else{x0 = 2 * p * p + 1;y0 = 2 * p * q;}return true;}int main(){ll n, x, y;//x^2-ny^2=1while (~scanf("%lld", &n)){if (pell_minimum_solution(n, x, y)){printf("%lld^2-%lld*%lld^2=1\t", x, n, y); printf("%lld-%lld=1\n", x * x, n * y * y); }}}暴⼒int ax[MAXN], ay[MAXN];void pell(int &x, int &y, int n){ //暴⼒寻找pell⽅程最⼩解y = 1;while (true){x = (ll)sqrt(n * y * y + 1);if (x * x - n * y * y == 1)break;y++;}}int main(){int n;while (scanf("%d", &n) != EOF){int m = (int)sqrt((double)n);if (m * m == n){ //d不能为完全平⽅数cout << "No Solution" << endl;continue;}int x = 0, y = 0;pell(x, y, n); //暴⼒找到最⼩解printf("%d %d\n", x, y);}return 0;}递推式for (int i = 2; i <= 20; i++){x[i] = x[i - 1] * x[1] + n * y[1] * y[i - 1];y[i] = x[1] * y[i - 1] + y[1] * x[i - 1];}矩阵递推求第k项x k y k =x1ny1y1x1k−1x1y1⽤这个去算就好了[][][]。
Toeplitz矩阵及逆矩阵求解

X = Tn−1 − Tn−1 En −1γ n −1vT = Tn−11 + vvT / σ , −1 −1 −
Tn−11 = [tij ] 是广对 称的,故从(5.19)可得 −
(5.19)
−1 其中的最后一个等式利用到了 T n −1 En −1rn −1 = − En −1 yn −1 , 和(5.17)。由于
Tn y = −(γ 1 ,...γ n −1 , γ n )T ,
(5.2)
yk
为k阶Yule-Walker方程组 (5.3)
Tk yk = −(γ 1 ,...γ k −1 , γ k )T , ( k = 1, 2,..., n)
yk
确定
yk +1 的关系式。为此,记
k
zk yk +1 = , γ k = (γ 1 ,..., γ k )T . α k 1
βij = β n − j +1,n −i +1 , i, j = 1, 2,..., n;
B = EBT E ,
E =| en , en −1 ,...e1 |
是n阶反序单位矩阵。由广对称矩阵的等价定义。易证:非奇异的广对称矩阵的逆 亦是光对称的。 在这一节里,我们假定 Tn ∈ R n*n 是给定的对称正定的Toeplitz矩阵。不失一般性, 可假定 Tn 具有如 下形状
δ k = 1 + rkT yk , k = 1, 2,..., n − 1,
δ k +1 = 1 + rkT+1 yk +1
y k + α k Ek y k = 1 + (r yk +1 ) αk T = 1 + rkT yk − α k (γ k +1 + γ k Ek yk )
Zoeppritz方程近似解拟合精确解影响因素

第34卷第4期物 探 与 化 探Vo.l 34,N o.4 2010年8月GEOPHY SI CA L &GEOCHE M ICAL EX PLORAT I ONAug .,2010Zoeppritz 方程近似解拟合精确解影响因素程彦1,董守华2,赵伟2,陶文朋3(1.中国煤炭地质总局地球物理勘探研究院,河北涿州 072750;2.中国矿业大学资源与地球科学学院,江苏徐州 221116;3.郑州煤炭工业(集团)有限责任公司河南郑州 450006)摘要:在介绍Zoeppritz 方程及其近似方程的基础上,通过编制程序设定不同的参数来绘制出在密度差异、P 波速度差异及泊松比差异下近似解拟合Zoeppritz 精确解的曲线,并对所绘制的曲线进行分析,总结出三种差异对拟合程度的影响情况。
关键词:Z oeppritz 方程;近似解;精确解;AVO 技术;拟合程度中图分类号:P 631.4 文献标识码:A 文章编号:1000-8918(2010)04-0523-05AVO 技术是利用反射系数随入射角变化的原理,在叠前道集上分析振幅随偏移距变化的规律,估求岩石的弹性参数、研究岩性及检测油气的重要技术。
根据地震波动力学中反射和透射的相关理论,必须研究地震波入射到反射界面时的能量分配,Zo eppritz 方程描述了界面上P 波与S 波入射情形下,各自激发的反射、透射的P 波和S 波之间的关系,可以说是AVO 理论赖以建立的基石,但是求解Zoep pritz 方程极为复杂,并且难以给出清楚的物理概念。
因此,人们提出了不同形式的近似方程,使其更加容易理解,有较明显的物理意义。
然而,这些近似方程的解与Zoeppritz 方程精确解直接存在着误差,笔者分析了密度差异、P 波速度差异及泊松比差异对近似解拟合精确解的程度的影响。
1 Zoeppritz 方程及其近似方程1.1 Zoeppritz 方程设有两层水平各向同性介质,当地震纵波非垂图1 入射波、反射波和透射波的关系直入射(即非零偏移距)时,在弹性分界面上会产生反射纵波、反射横波、透射纵波和透射横波(图1)。
基于YPDZoeppritz方程的杨氏模量和泊松比直接反演方法

摘要:为解决非常规油气勘探中“甜点”的有效识别问题,开展了杨氏模量和泊松比直接反演方 法 研 究. 针 对 Zoeppritz近 似 方 程
精度有限的问题,对精确 Zoeppritz方程进行重新推导,建立了以 杨 氏 模 量、泊 松 比 和 密 度 的 自 然 对 数 为 未 知 参 数 的 YPDGZoepG
了子波旁瓣对反演结果的影响.基于 YPDGZoeppritz方程的杨氏模量和泊松比直接反演方法适定性强,具有较好的稳定性.
关 键 词 :非 常 规 油 气 勘 探 ;“甜 点 ”预 测 ;杨 氏 模 量 ;泊 松 比 ;YPDGZoeppritz方 程 ;广 义 线 性 反 演 ;贝 叶 斯 理 论
pritz方程;在此基础上,结合广义线性反演和贝叶斯理论,引入一阶差分矩阵 和 三 变 量 柯 西 分 布,构 建 更 为 合 理 的 反 射 系 数 稀 疏
约束项,提高了广义线性反演的适定性;引入低频软约束项进一步稳定反演结果的低频成分,提高了反演剖面的横 向 连 续 性. 模
型数据和实际数据试算结果表明,该方法反演精度较高,而且能 够 逐 步 压 缩 子 波 旁 瓣,使 反 演 结 果 呈 现 明 显 的“块 化”效 果,降 低
中 图 分 类 号 :P631
文 献 标 识 码 :A
文 章 编 号 :1000G1441(2019)02G0272G13
DOI:10.3969/ji.ssn.1Hale Waihona Puke 00G1441.2019.02.013
DirectinversionofYoung���s��� modulusandPoisson���s��� ratiobasedonthe YPDGZoeppritzequation
AVO分析方法及Geoview软件

第三篇储层参数AVO 分析随着油气勘探与开发程度的加深,常规的地震勘探方法难以检测地层油气藏的存在,这时可以使用AVO 技术来辅助检测油气。
AVO 技术最初用于识别“亮点”等振幅异常,随着近几年来计算机技术的发展和应用,使AVO 技术在油气勘探领域中拥有越来越广泛的应用。
这里将从AVO 的理论基础出发,介绍Zoeppritz 方程及其近似式,之后将介绍AVO 分析属性,如截距、梯度、流体因子等。
最后利用Geoview 软件分别对模型和实际数据进行测试。
1、Zoeppritz 方程及其近似式1.1 Zoeppritz 方程从弹性波的角度出发,根据应力与位移连续的边界条件推导出Zoeppritz 方程。
具体的推导过程不再详述,Zoeppritz 方程如下:112211222221221111222211121112222112211111sin cos sin cos cos sin cos sin sin 2cos 2sin 2cos 2cos 2sin 2cos 2sin 2PP PS S P S P P PP S S P S S S P PS P P P R R V V V V V T V V V V V V V T V V V θϕθϕθϕθϕρρθϕθϕρρρρϕϕϕϕρρ-⎡⎤⎢⎥⎡⎢⎥⎢---⎢⎥⎢⎥⎢⎥⋅-⎢⎥⎢⎥⎢⎥⎢⎥---⎣⎢⎥⎣⎦1111sin cos sin 2cos 2θθθϕ-⎤⎡⎤⎥⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎦ (4-1) 上式中,V P 1、V S 1 、ρ1依次代表上界面的纵波速度的大小、横波速度的大小、密xz 1θ1ϕ2ϕ2θ波入射P P 反射波SV 反射波SV 透射波P 透射波111P S V V ρ,,222P S V V ρ,,度的大小;V P 2、V S 2、ρ2依次代表下界面的纵波速度的大小、横波速度的大小、密度的大小;PP R 、PS R 、PP T 、PS T 依次代表纵波反射系数的大小、转换横波反射系的大小、纵波透射系数的大小、转换横波透射系数的大小。
Zoeppritz方程推导过程

Zoeppritz 方程的推导一.波函数设有一平面谐纵波入射到两种半无限弹性介质的分界面上。
在这种情况下,波不仅会折回到入射介质中传播,而且会透射到另一种介质中传播;即同时存在反射波和透射射波。
反射波和透射波中都包含纵波和横波两种成份。
P 波在介质分界面上的反射和透射情况如图所 示:关于位函数我们首先看:沿任意方向传播的平面波。
设N是一个任意取定的单位方向矢量。
N li m j nk =++(1)下面来看沿N方向的平面波,或称三维平面波的波函数形式。
三维平面波的波函数f 满足三维波动方程,即:2222222221f f f f xyzVt∂∂∂∂++=∂∂∂∂ (2) 这里我们通过和一维平面波函数类比,可以得出三维平面波函数的形式。
我们知道,在一维平面波的情况下,空间任意一点(),,x y z 上的波函数值只取决于x 。
于是沿x 正方向传播的平面波的波函数为1(,)()f x t f x Vt =-。
其中的x 实际上是从原点至(),,x y z 点所在波面的垂直距离,即00d x y z =++(一维平面波的传播方向的单位矢量为N i =。
在三维平面波情况下,这一距离应为d lx my nz =++。
因此,将一维平面波函数中的x 以lx my nz++代替应该可以得到三维平面波的波函数)即:1(,,,)()f x y z t f lx my nz Vt =++- (3)同一维平面波一样,式中的t 为波沿N方向的传播时间。
1()f lx m y nz Vt ++-代表一个沿N的正方向传播的平面波。
同理,1(,,,)()f x y z t f lx my nz Vt =+++代表一个沿N的负方向传播的平面波,在一般情况下,沿任意方向N传播的平面波的波函数可写成:11(,,,)()()f x y z t f lx m y nz Vt f lx m y nz Vt =++-++++ (4)二.平面简谐波:平面简谐波是是波函数为简谐形式的平面波,也是数学上最容易处理的一种波。
贝塞尔方程求解过程

贝塞尔方程求解过程贝塞尔方程求解过程贝塞尔方程是数学中的一类常微分方程,它的特殊形式导致了其在物理、工程、数学等领域的重要应用。
解决贝塞尔方程的方法包括变量分离法、级数展开法、渐进展开法等。
下面以常用的级数展开法为例介绍贝塞尔方程的求解过程。
首先,将贝塞尔方程变形为欧拉型方程,这可以通过设y(r)=r^αu(r)并归一化系数完成。
具体来说,在r=0处,y(r)是奇点,所以要求解出一个形如y(r)=r^α[c0+c1r+c2r^2+…]的级数。
将其代入贝塞尔方程中,就可以得到每一项的递推式。
以Bessel函数为例:$$x^2y''+xy'+(x^2-\alpha^2)y=0$$设y(r)=r^\alpha\sum_{n=0}^{\infty}c_nx^n则\sum_{n=0}^{\infty}[n(n+2\alpha)+n-\alpha^2]c_nx^n=0$$由于x可取任意值,所以只有当每一项系数都为零时,该级数的和才能为零。
从而得到递推公式:$$c_{n+2}=\frac{c_n\alpha^2-c_{n-1}(n+\alpha)}{(n+1)(n+2)} $$利用该递推公式,可以求出任意次数的Bessel函数。
需要注意的是,当α为整数时,存在两个线性无关的解。
这意味着,同样的递推公式会得到两个解。
这些解被称为第一类Bessel函数J_α(x)和第二类Bessel函数Y_α(x)。
其中,J_α(x)是在x=0处有限的,而Y_α(x)在x=0处发散。
通过级数展开法解决贝塞尔方程的过程,可以通过计算每一项系数得到任意次数的解。
这种方法适用于大部分情况,并且常常被用于实际应用中。
总之,解决贝塞尔方程需要使用特定的求解方法。
级数展开法是一种常用的方法,解决过程涉及到欧拉型方程、级数递推公式等数学知识。
通过了解求解过程,可以更好地理解贝塞尔方程及其应用。
地震波阻抗反演方法综述

地震波阻抗反演方法综述、地震反演技术研究现状地震反演方法是一门综合运用数学、物理、计算机科学等学科发展起来的新技术新方法,每当数学方法、物理理论有了新的认识和发展时,就会有新的地震反演技术、方法的提出。
随着计算机技术的不断发展、硬件设施的不断升级,这些方法技术得到了实践验证和提升,反过来地震反演技术运用中出现的新问题、新思路又不断促使数学方法、地球物理学理论的再次发展。
时至今日,地震反演技术仍然是一个不断发展、不断成熟、不断丰富着的领域。
反演是正演的逆过程,在地震勘探中正演是已知地下的地质构造情况、岩性物性分布情况,根据地震波传播规律和适当的数学计算方法模拟地震波在地下传播以及接收地震波传输到地表信息的过程。
地球物理反演就是使用已知的地震波传播规律和计算方法,将地表接收到的地震数据通过逆向运算,预测地下构造情况、岩性物性分布情况的过程。
地震波阻抗正演是对反演的理论基础和实现手段。
1959 年美国人Edwin Laurentine Drake 在宾夕法尼亚州开凿的第一口钻井揭开了世界石油工业的序幕。
从刚开始的查看地质露头、寻找构造高点寻找石油,到通过地震剖面的亮点技术寻找石油,再到现在运用多种科学技术手段进行油气资源的预测,石油勘探经历了一个飞速的发展历程。
声波阻抗(AI )是介质密度和波在介质中传播速度的乘积,它能够反映地下地质的岩性信息。
声波阻抗反演技术是20 世纪70 年代加拿大Roy Lindseth 博士提出的,通过反演能够将反映地层界面信息的地震数据变为反映岩性变化的波阻抗(或速度)信息。
由于波阻抗与地下岩石的密度、速度等信息紧密联系,又可以直接与已知地质、钻井测井信息对比,因此广泛应用于储层的预测和油藏描述中,深受石油工作者的喜爱。
70 年代后期,从地震道提取声波资料的合成声波技术得到了快速发展,以此为基础发展的基于模型的一维有井波阻抗反演技术,提高了反演结果的可靠性。
进入80 年代,Cooke 等人将数学中的广义线性方法运用于地震资料反演,提出了广义线性地震反演。
斯奈尔定律和Zoeppritz方程

斯奈尔定律和Zoeppritz 方程 姓名: 学号: 专业:地球物理勘察技术2012级一、实验目的1. 利用密度、上下界面的纵横波速度通过斯奈尔定律求出该界面的0°~90°入射角的反射角度和透射角度。
P V V V V V s p s p p =====222211111sinsin sin sin sin βαβαα2. 利用Zoeppritz 方程绘制反射系数和透射系数曲线。
二、实验步骤1、模型:V p1=3300 m/s V s1=1585 m/s ρ1 =2.4 g/cm3 V p1=3100 m/s V s1=1989 m/s ρ1 =2.24 g/cm3 计算从0~90度的反射透射系数曲线 如图1-1-4三、实验结果P波入射的反射透射角度:图1 P波入射的反射透射系数曲线:图2图3 SV波入射的反射透射系数曲线:图4图5SH波入射的反射透射系数曲线:图6四、实验分析因为各波反射和透射波振幅系数与其能量成正比,由此可以看出其能量的变化以及入射波能量的分配。
当上层介质为密介质,下层介质为疏介质时:由图2知,P波从上层密介质入射到界面时:随着入射角增大,P波反射系数、P波透射系数在减小,即随着入射角的增大,反射P波、透射P波的能量在减小,而S波反射系数、S波透射系数在增大,即随着入射角的增大,反射S 波、透射S波的能量在增大。
说明当入射角发生变化时,入射波的能量分配在改变。
由图4可知,SV波从上层密介质入射到界面时:入射角小于29度时,随着入射角增大,SV波反射系数在减小,P波反射系数、SV波透射系数、P波透射系数在增大,SV波透射系数最大,即反射SV波能量在减小,反射P波、透射SV波、透射P波能量在增大,透射SV波的能量最大;入射角大于等于29度且小于31度时,SV波反射系数、SV波透射系数减小,P波反射系数、P波透射系数在增大,SV波透射系数最大,即随着入射角的增大,反射SV波、透射SV波能量在减小,反射P波、透射P波能量在增大,透射SV波能量最大;入射角大于等于31度且小于53度时,SV波透射系数增大,SV波反射系数、P波反射系数、P波透射系数先减小后增大,SV波透射系数仍最大,即随着入射角的增大,透射SV波能量增大,反射SV波、反射P波、透射P波能量先减小后增大,透射SV波能量最大;入射角大于53度时, SV波反射系数为1,SV波透射系数、P波反射系数、P波透射系数减小,即随着入射角的增大,反射SV波能量不变,透射SV波、反射P波、透射P波能量减小。
斯奈尔定律和Zoeppritz方程
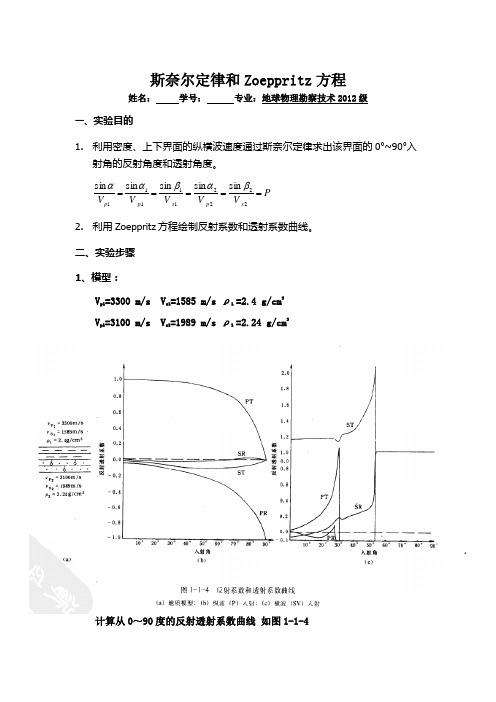
斯奈尔定律和Zoeppritz 方程姓名: 学号: 专业:地球物理勘察技术2012级一、实验目的1. 利用密度、上下界面的纵横波速度通过斯奈尔定律求出该界面的0°~90°入射角的反射角度和透射角度。
P V V V V V s p s p p =====222211111sinsin sin sin sin βαβαα2. 利用Zoeppritz 方程绘制反射系数和透射系数曲线。
二、实验步骤1、模型:V p1=3300 m/s V s1=1585 m/s ρ 1 =2.4 g/cm 3V p1=3100 m/s V s1=1989 m/s ρ 1 =2.24 g/cm 3计算从0~90度的反射透射系数曲线 如图1-1-4三、实验结果P波入射的反射透射角度:图1 P波入射的反射透射系数曲线:图2图3 SV波入射的反射透射系数曲线:图4图5SH波入射的反射透射系数曲线:图6四、实验分析因为各波反射和透射波振幅系数与其能量成正比,由此可以看出其能量的变化以及入射波能量的分配。
当上层介质为密介质,下层介质为疏介质时:由图2知,P波从上层密介质入射到界面时:随着入射角增大,P波反射系数、P波透射系数在减小,即随着入射角的增大,反射P波、透射P波的能量在减小,而S波反射系数、S波透射系数在增大,即随着入射角的增大,反射S波、透射S波的能量在增大。
说明当入射角发生变化时,入射波的能量分配在改变。
由图4可知,SV波从上层密介质入射到界面时:入射角小于29度时,随着入射角增大,SV波反射系数在减小,P波反射系数、SV波透射系数、P波透射系数在增大,SV波透射系数最大,即反射SV波能量在减小,反射P波、透射SV波、透射P波能量在增大,透射SV波的能量最大;入射角大于等于29度且小于31度时,SV波反射系数、SV波透射系数减小,P波反射系数、P波透射系数在增大,SV波透射系数最大,即随着入射角的增大,反射SV波、透射SV波能量在减小,反射P波、透射P波能量在增大,透射SV波能量最大;入射角大于等于31度且小于53度时,SV波透射系数增大,SV波反射系数、P波反射系数、P波透射系数先减小后增大,SV波透射系数仍最大,即随着入射角的增大,透射SV波能量增大,反射SV波、反射P波、透射P波能量先减小后增大,透射SV波能量最大;入射角大于53度时, SV波反射系数为1,SV波透射系数、P波反射系数、P波透射系数减小,即随着入射角的增大,反射SV波能量不变,透射SV波、反射P波、透射P波能量减小。
(完整word版)Zoeppritz方程推导过程

Zoeppritz 方程的推导一.波函数设有一平面谐纵波入射到两种半无限弹性介质的分界面上。
在这种情况下,波不仅会折回到入射介质中传播,而且会透射到另一种介质中传播;即同时存在反射波和透射射波。
反射波和透射波中都包含纵波和横波两种成份。
P 波在介质分界面上的反射和透射情况如图所 示:关于位函数我们首先看:沿任意方向传播的平面波。
设N 是一个任意取定的单位方向矢量。
N li mj nk =++ (1) 下面来看沿N 方向的平面波,或称三维平面波的波函数形式。
三维平面波的波函数f 满足三维波动方程,即:2222222221f f f fx y z V t ∂∂∂∂++=∂∂∂∂ (2) 这里我们通过和一维平面波函数类比,可以得出三维平面波函数的形式。
我们知道,在一维平面波的情况下,空间任意一点(),,x y z 上的波函数值只取决于x 。
于是沿x 正方向传播的平面波的波函数为1(,)()f x t f x Vt =-。
其中的x 实际上是从原点至(),,x y z 点所在波面的垂直距离,即00d x y z =++(一维平面波的传播方向的单位矢量为N i =。
在三维平面波情况下,这一距离应为d lx my nz =++。
因此,将一维平面波函数中的x 以lx my nz++代替应该可以得到三维平面波的波函数)即:1(,,,)()f x y z t f lx my nz Vt =++- (3)同一维平面波一样,式中的t 为波沿N 方向的传播时间。
1()f lx my nz Vt ++-代表一个沿N 的正方向传播的平面波。
同理,1(,,,)()f x y z t f l x m y n z V t =+++代表一个沿N 的负方向传播的平面波,在一般情况下,沿任意方向N 传播的平面波的波函数可写成:11(,,,)()()f x y z t f lx my nz Vt f lx my nz Vt =++-++++ (4)二.平面简谐波:平面简谐波是是波函数为简谐形式的平面波,也是数学上最容易处理的一种波。
叠前反演联结

岩性和流体参数估算
Vp/Vs
Vp/Vs=Ip/Is
泊松比
μρ
0.5 (Vs /Vp)2 0.5 (Is / Ip)2
1 (Vs /Vp)2 1 (Is / Ip)2
Is2
λρ
I
2 p
2
I
2 p
2I
2 s
我们还可通过一些统计方法、Gassmann方程等求出 孔隙度及岩性数据体等。
岩性和流体参数估算
叠前反演
AVO分析是识别气层的重要技术
CDP
叠前振 幅可区
偏移距
500
10000
分气层
和水层
反射振幅随 偏移距减少
水层
叠加
偏移距
区分真假“亮点”
叠加 剖面
叠后振 幅区分 气层水 层困难
CDP道集
反射振幅随 偏移距增加
气层
偏移距
叠前反演
三参数AVO多波信息反演
区分含烃饱和度 确定剩余油分布
振幅异常
p
SV p
ρ1 υp1υs1 ρ2 υp2υs2
θ1 θ1 φ1
φ2 θ2
入射p波与其产生的反射波 和透射波关系
(ρ:岩石密度; vp:纵波
速度; vs :横波速度;1,
p
2:分别表示地层1和地层2)
SV
Zoeppritz方程及其近似表达式:
sin1
cos1
sin2
cos2
cos1
sin1
用测井曲线数据求得P波阻抗与充水孔隙度的经验关系式, 来计算充水孔隙度,结合阿尔奇公式以及充水孔隙度来估算 天然气水合物浓度和游离气浓度。
结论:
1、含水沉积岩具有相对高的弹性阻抗值,主要含游离气的 层显示相对低的弹性阻抗值;
P波入射反射、透射系数推导14页

P波入射Zoeppritz方程的推导根据弹性力学的假设,介质是均匀各向同性的无限大介质,平面波是一种最简单的波动形式,其以波面为平面的形式在介质中传播,即平面波在垂直于波传播的任一平面上,各点的振动是同相的,实际上并不存在激发平面波的震源,所以它是一个数学抽象了的波动过程。
点震源激发的球面波向四面八方传播,当其距震源足够远时,在这个地方研究一个局部的等相位面,可以将其看成一个平面波。
在理论上,任何类型的波都可以用平面波的合成形式来表示,所以平面波是波动现象中最基本的形式,也是理论研究和实际应用的基础。
在地震勘探中,讨论在两种不同的介质分界面上的波的传播现象是十分重要的。
一般分为两种情况进行讨论,第一种,我们所研究的地球介质按其物性变化是分层的,具有层装结构。
因此,讨论两种弹性性质不同的介质分界面上波的传播情况。
第二种,地球表面是一个特殊的分界面,它将无限介质划分为两个半空间。
地面以上的空气介质,其密度与地面以下的岩石或海平面以下的海水层及岩石层的密度相比可以忽略。
因此,地球表面可以看成是一个弹性半空间表面,称为自由面,其上的应力作用为零。
根据本文所讨论的地质模型所涉及到的地质灾害,我们只讨论波在第一种介质分界面情况下波的传播,即平面波在弹性分界面上的反射与透射。
1.1波函数设有一平面谐纵波入射到两种半无限弹性介质的分界面上。
在这种情况下,波不仅会折回到入射介质中传播,而且会透射到另一种介质中传播;即同时存在反射波和透射射波。
反射波和透射波中都包含纵波和横波两种成份。
P 波在介质分界面上的反射和透射情况如图所示:关于位函数我们首先看:沿任意方向传播的平面波。
设N r是一个任意取定的单位方向矢量。
N li mj nk =++r r r r(1)下面来看沿N r方向的平面波,或称三维平面波的波函数形式。
三维平面波的波函数f 满足三维波动方程,即:2222222221f f f fx y z V t∂∂∂∂++=∂∂∂∂(2)这里我们通过和一维平面波函数类比,可以得出三维平面波函数的形式。
最优的Zoeppritz方程的简化综述

Ab ta t Ba e o t e qu ton f Zoe prt t e sr c s d n h e a i o p iz h A VO t c noogy s s he m p iud v ra in e h l u e t a lt e a ito w ih t ofs t or fe f
关键词 Z epi o p r z方程 , 线性 近 似 , 向异 性 , 确 度 分析 t 拟 各 精 中 图分 类 号 P 3 61 文 献 标 识码 A
D I1. 9 9ji n 10—9 3 2 1. 1 0 6 0 : 0 3 6 /.s . 0 4 2 0 . 0 0 0 . 1 s
The o i a i p ii d Zo p r t qu to ptm ls m lfe e p iz e a i n
SUN i ua. W ANG he — i xu h z nl
( l n e r t e p y i l e a o a o y,n t ue f G o o y a d G o h s s Oi itg a e g o h s a y l b r t r I si t o e lg n e p y i , d c k t c C iee a e y o c n e ,B i n 0 0 9 C ia h n s d m f S i cs ej g 1 0 2 , h n ) Ac e i
优 的 Z epi o p r z方 程 是 一 种 新 的 近 似 , 在 某 种 程 度 上 达 到 了 最 优 , 比 之 下 , 简 化 又 最 精 确 . 类 比 与 A i t 其 相 最 是 k—
Rcad 近 似 形 式 的 一 种拟 线性 近 似 , i rs h 因此 可 以 简 化 的运 用到 非 线 性 反 演 中, 实际 应 用提 供 更 准确 的 理 论基 础 . 为
(完整word版)Zoeppritz方程推导过程

Zoeppritz 方程的推导一.波函数设有一平面谐纵波入射到两种半无限弹性介质的分界面上。
在这种情况下,波不仅会折回到入射介质中传播,而且会透射到另一种介质中传播;即同时存在反射波和透射射波。
反射波和透射波中都包含纵波和横波两种成份。
P 波在介质分界面上的反射和透射情况如图所 示:关于位函数我们首先看:沿任意方向传播的平面波。
设N 是一个任意取定的单位方向矢量。
N li mj nk =++ (1)下面来看沿N 方向的平面波,或称三维平面波的波函数形式。
三维平面波的波函数f 满足三维波动方程,即:2222222221f f f f x y z V t∂∂∂∂++=∂∂∂∂ (2) 这里我们通过和一维平面波函数类比,可以得出三维平面波函数的形式。
我们知道,在一维平面波的情况下,空间任意一点(),,x y z 上的波函数值只取决于x 。
于是沿x 正方向传播的平面波的波函数为1(,)()f x t f x Vt =-。
其中的x 实际上是从原点至(),,x y z 点所在波面的垂直距离,即00d x y z =++(一维平面波的传播方向的单位矢量为N i =。
在三维平面波情况下,这一距离应为d lx my nz =++。
因此,将一维平面波函数中的x 以lx my nz ++代替应该可以得到三维平面波的波函数)即:1(,,,)()f x y z t f lx my nz Vt =++- (3)同一维平面波一样,式中的t 为波沿N 方向的传播时间。
1()f lx my nz Vt ++-代表一个沿N 的正方向传播的平面波。
同理,1(,,,)()f x y z t f lx my nz Vt =+++代表一个沿N 的负方向传播的平面波,在一般情况下,沿任意方向N 传播的平面波的波函数可写成:11(,,,)()()f x y z t f lx my nz Vt f lx my nz Vt =++-++++ (4)二.平面简谐波:平面简谐波是是波函数为简谐形式的平面波,也是数学上最容易处理的一种波。
