三视图习题 及答案
工程制图三视图习题集及答案
营口地区成人高等教育 QQ群 54356621
*5-17 补全主视图和俯视图上所缺的线。
营口地区成人高等教育 QQ群 54356621
*5-18 补全主视图和俯视图上所缺的线。
营口地区成人高等教育 QQ群 54356621
*5-19 补全主视图和左视图上所缺的线并标 出P、Q面的投影。
营口地区成人高等教育 QQ群 54356621
营口地区成人高等教育 QQ群 54356621
*5-48 求作俯视图。
营口地区成人高等教育 QQ群 54356621
营口地区成人高等教育 QQ群 54356621
*5-13 求作俯视图。
营口地区成人高等教育 QQ群 54356621
*5-14 求作左视图。
营口地区成人高等教育 QQ群 54356621
*5-15 求作左视图。
营口地区成人高等教育 QQ群 54356621
*5-16 补全俯视图和左视图上所缺的线。
营口地区成人高等教育 QQ群 54356621
5-9 补全四棱台被截切后的俯视图并求主视图。
营口地区成人高等教育 QQ群 54356621
5-10 求作俯视图。
营口地区成人高等教育 QQ群 54356621
5-11 求作左视图。
营口地区成人高等教育 QQ群 54356621
*5-12 求作俯视图。
营口地区成人高等教育 QQ群 54356621
*5-44 求作俯视图。
圆柱孔 圆球 圆柱
营口地区成人高等教育 QQ群 54356621
*5-45 求作左视图。
营口地区成人高等教育 QQ群 54356621
*5-46 求作左视图。
营口地区成人高等教育 QQ群 54356621
高三专项训练：三视图练习题(一)
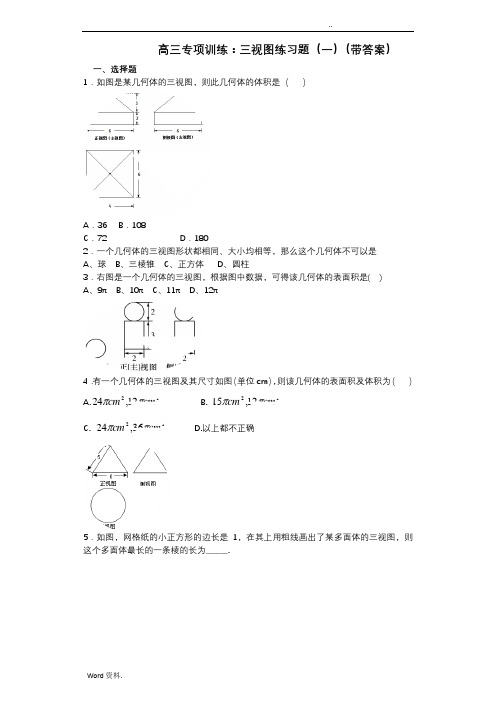
高三专项训练：三视图练习题（一）（带答案）一、选择题1．如图是某几何体的三视图，则此几何体的体积是（ ）A ．36B ．108C ．72D ．1802．一个几何体的三视图形状都相同、大小均相等，那么这个几何体不可以是A 、球B 、三棱锥C 、正方体D 、圆柱3．右图是一个几何体的三视图，根据图中数据，可得该几何体的表面积是( )A 、9πB 、10πC 、11πD 、12π4．有一个几何体的三视图及其尺寸如图（单位cm ），则该几何体的表面积及体积为（ ）A.3212,24cm cm ππB. 3212,15cm cm ππC. 3236,24cm cm ππD.以上都不正确5．如图，网格纸的小正方形的边长是1，在其上用粗线画出了某多面体的三视图，则这个多面体最长的一条棱的长为______.A． B． CD ．36．一空间几何体的三视图如图所示，则该几何体的体积为.A. B. C D. [7． 若某空间几何体的三视图如图所示，则该几何体的体积是A ．13 B ．23C ．1D ．28．右图是某几何体的三视图，则该几何体的体积为（ ）A ． Ｂ．Ｃ． Ｄ．1362942π+3618π+9122π+9182π+正视图俯视图9．已知一个几何体的三视图如图所示，则该几何体外接球的表面积为（ ）A ．43π B ． 163π C ．1912π D ． 193π 10．某几何体的正视图如图所示，则该几何体的俯视图不可能的是11．已知某个几何体的三视图如图（主视图中的弧线是半圆），根据图中标出的尺寸(单位：cm)，可得这个几何体的体积是( )cm 3.A ．π+8B ．328π+C ．π+12D ．3212π+侧视图主视俯视第8题图俯视图侧视图 正视图12．已知正六棱柱的底面边长和侧棱长均为2cm ，其三视图中的俯视图如图所示，则其左视图的面积是（ ）（A ）243cm （B ）223cm （C ）28cm （D ）24cm13．下图是一个几何体的三视图，根据图中数据，可得该几何体的表面积是（ ）A ．6πB ．7πC ．8πD ．9π14．如右图所示，一个空间几何体的正视图和侧视图都是边长为1的正方形，俯视图是一个直径为1的圆，那么这个几何体的表面积为 （ ）A ．π3B ．π2C ．π23 D ．π4 15．如图是一个几何体的三视图，若它的体积是33，则图中正视图所标a=（ ）A ．1B 3C 3D ．316．已知某几何体的三视图如图所示（单位：cm ），其中正视图、侧视图都是等腰直角三角形，则这个几何体的体积是（ ）A ．338cmB ．3316cm C ．33216cm D ． 3332cm17．一个几何体的三视图如右图所示，其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形，则该几何体的外接球的表面积为A ．B ．C ．D ．18．若某空间几何体的三视图如图所示，则该几何体的体积是 （ ）A.13 B. 23C. 1D. 2 俯视图侧视图正视图22119．某物体是空心的几何体，其三视图均为右图，则其体积为（ ）A 、8B 、43π C 、483π+ D 、483π- π12π34π3π312正视图 侧视图俯视图 正视第9题22 4 2侧视图 22俯视20．如图，水平放置的三棱柱ABC-A 1B 1C 1中，侧棱AA 1⊥平面A 1B 1C 1，其正视图是边长为a 的正方形．俯视图是边长为a 的正三角形，则该三棱柱的侧视图的面积为A ．a 2B ．a 2C a 2D 221．右图是一个几何体的三视图（侧视图中的弧线是半圆），则该几何体的表面积是（ ）A ．20＋3π B ．24＋3π C ．20＋4π D ．24＋4π22．一个几何体的三视图如图所示，其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形，则该几何体的外接球的表面积为A ．12πB ．π34C ．3πD ．π312．23.如右图为一个几何体的三视图，其中俯视图为正三角形，A 1B 1=2，AA 1=4，则该几何体的表面积为（ ）12正视图 侧视图 俯视图 AC A 11正视图 侧视图俯视图24．图１是设某几何体的三视图，则该几何体的体积为（）A．942π+Ｂ．3618π+Ｃ．9122π+Ｄ．9182π+、25．已知某几何体的三视图如图所示，根据图中标注的尺寸（单位cm）可得该几何体的体积是（）A．313cm B．323cmC．343cm D．383cm26．小红拿着一物体的三视图(如图所示)给小明看，并让小明猜想这个物件的形状是A. 长方形 B. 圆柱 C. 立方体 D. 圆锥27．一个几何体的三视图如图所示，则这个几何体的体积为（）正视图侧视图俯视图332正视图俯视图图1AB ．12C ．32 D1+28．一个空间几何体的三视图如图（1）所示，其中正视图为等腰直角三角形，侧视图与俯视图为正方形，则该几何体的体积和表面积分别为 （ ）A 、64，48+B 、32，48+ C 、643，32+D 、332，48+29．若某多面体的三视图（单位: cm ）如图所示,则此多面体的体积是（ ） A ．21cm 3 B ．32cm 3 C ．65cm 3 D ．87cm 3正视图俯视图图（1）侧（左）视图 1111130．一个空间几何体的正视图、侧视图均是长为2、高为3的矩形，俯视图是直径为2的圆(如右图），则这个几何体的表面积为A ．12π+B ．7πC ． π8D ．π2031．（一空间几何体的三视图如图所示,则该几何体的体积为( ).A. B.C.D. 32．已知几何体其三视图（如图），若图中圆半径为1，等腰三角形腰为3，则该几何体表面积为 （ ） A ．6π B ．5π C．4π D．3π2π+4π+2π4π+正视侧视俯视俯视..A ．2，23B ．22，2D ．2，434．如图，有一个几何体的正视图与侧视图都是底为6cm ，腰为5cm 的等腰三角形，俯视图是直径为6cm 的圆，则该几何体的体积为 ( )A ．12πcm 3B ．24πcm 3C ．36πcm 3D ．48πcm 335 （A ）348cm （B ）324cm （C ）332cm （D ）328cm36． 如图，直三棱柱的侧棱长和底面边长均为2，正视图和俯视图如图所示，则其侧视图的面积为 （ ）A ．4B ．3C ．32D ．237．某四面体的三视图如下图所示，则该四面体的四个面中，直角三角形的面积和是_______.二、填空题 正视图 左视图俯视图正视图侧视图 俯视图 第6题 ·38．一个几何体的三视图如右图所示,主视图与俯视图都是一边长为3cm 的矩形,左视图是一个边长为2cm 的等边三角形,则这个几何体的体积为________．39．如图所示是一个几何体的三视图（单位：cm ），主视图和左视图是底边长为4cm ，腰长为22的等腰三角形，俯视图是边长为4的正方形，则这个几何体的表面积是-__________40．某几何体的三视图如图所示，则该几何体的体积的最大值为 .41．一正多面体其三视图如图所示，该正多面体的体积为___________.主视图 左视图俯视图3主视图 俯视图 侧视图42．若某几何体的三视图（单位：cm ）如右图所示，则该几何体的体积为 cm 2．43．已知某几何体的三视图如图所示,其中侧视图是等腰直角三角形,正视图是直角三角形,俯视图ABCD 是直角梯形,则此几何体的体积为 ；44．某四面体的三视图如上图所示，该四面体四个面的面积中最大的是1正视图俯视图左视图45．一个几何体的三视图如右图所示（单位：），则该几何体的体积为__________46．一个几何体的三视图如图所示，其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形，若该几何体的所有顶点在同一球面上，则球的表面积是_____．47．如图，一个简单空间几何体的三视图其主视图与左视图都是边长为的正三角形,其俯视图轮廓为正方形，则其体积是_________.48． 某几何体的三视图如图所示，则它的体积是___________俯视图m 3m 249．设某几何体的三视图如图所示，则该几何体表面积是50．一个几何体的三视图如右图所示，正视图是一个边长为2的正三角形，侧视图是一个等腰直角三角形，则该几何体的体积为．三视图练习题（一）参考答案1．B【解析】此几何体是一个组合体，下面是一个正四棱柱上面是一个四棱锥．其体积为166********V =⨯⨯+⨯⨯⨯=．2．D【解析】圆的正视图（主视图）、侧视图（左视图）和俯视图均为圆； 三棱锥的正视图（主视图）、侧视图（左视图）和俯视图可以为全等的三角形； 正方体的正视图（主视图）、侧视图（左视图）和俯视图均为正方形； 圆柱的正视图（主视图）、侧视图（左视图）为矩形，俯视图为圆。
三视图练习题
三视图练习题三视图练习题1.下图是由哪个平面图形旋转得到的（）A B C D2.有一个几何体的三视图如下图所示，这个几何体应是一个( )A.棱台B.棱锥C.棱柱D.都不对3.下列几何体各自的三视图中，有且仅有两个视图相同的是（）A ．①②B ．①③C ．①④D ．②④ 4.有一个几何体的三视图及其尺寸如下（单位：cm ），则该几何体的表面积和体积为( )A.3212,24cm cm ππB. 3212,15cm cm ππC. 3236,24cm cmππ D.以上都不正确5.如左图所示是某一容器的三视图，现向容器中匀速注水，容器中水面的高度h 随时间t变化的可能图象是（）侧视正视图俯视图6.正方体的截平面不可能是(1) 钝角三角形 (2) 直角三角形 (3) 菱形 (4) 正五边形 (5) 正六边形下述选项正确的是：（）(A) (1)(2)(5) (B) (1)(2)(4) (C) (2)(3)(4) (D) (3)(4)(5) 7.如图，在正方体ABCD —A1B1C1D1中，P 为BD1的中点，则△PAC 在该正方体各个面上的射影可能是（）A ．①④B ．②③C ．②④D ．①②8.若一个底面为正三角形、侧棱与底面垂直的棱柱的三视图如下图所示，则这个棱柱的体积为（）俯视图侧视图正视图A.9.一空间几何体的三视图如图所示,则该几何体的体积为( ). A.2π+B. 4π+2π4π+10.如图，是几个相同的小正方体搭成的几何体的三视图，则搭成这个几何体的小正方体的个数是（）侧(左)视图正(主)视图俯视图A B C D1A 1B 1C 1D P① ③ ④ ②俯视图左视图主视图A ．5B ．6C ．7D ．811.如果一个几何体的三视图如图所示，其中正视图中ABC 是边长为2的正三角形，俯视图为正六边形，那么该几何体的侧视图的面积为 ( )A ．23B ．32C ．12D ．612.用若干个棱长为1的正方体搭成一个几何体，其正视图、侧视图都是如右图形，对这个几何体，下列说法正确的是A ．这个几何体的体积一定是7 B ．这个几何体的体积一定是10C ．这个几何体的体积的最小值是6，最大值是10D ．这个几何体的体积的最小值是7，最大值是11 二、填空题13.如图，,E F 分别为正方体的面11A ADD 、面11B BCC的中心，则四边形E B F D1在该正方体的面上的射影可能是____________。
船舶结构三视图习题答案
船舶结构三视图习题答案船舶结构三视图习题答案船舶结构三视图是船舶设计和制造中的重要部分，它能够提供船舶的外观和几何特征，帮助设计师和工程师理解船舶的结构和功能。
在学习船舶结构三视图时，我们需要通过解答习题来加深对这一概念的理解和应用。
下面是一些船舶结构三视图习题的答案，希望能帮助读者更好地掌握这一知识点。
习题一：根据给定的船舶结构三视图，判断下列说法是否正确：1. 船舶的船首是船舶的前部，船尾是船舶的后部。
2. 船舶的船体主要由船底、船舷和船头构成。
3. 船舶的船首通常比船尾更尖锐，这有助于减少船舶在水中的阻力。
答案：1. 正确。
船舶的船首是船舶的前部，船尾是船舶的后部。
2. 正确。
船舶的船体主要由船底、船舷和船头构成。
3. 正确。
船舶的船首通常比船尾更尖锐，这有助于减少船舶在水中的阻力。
习题二：根据给定的船舶结构三视图，回答下列问题：1. 船舶的船首尖峰部分被称为什么？它有什么作用？2. 船舶的船底是什么形状的？这种形状有什么特点和优势？3. 船舶的船舷是什么部分？它的作用是什么？答案：1. 船舶的船首尖峰部分被称为船首鼻。
它的作用是减少船舶在水中的阻力，提高船舶的航行速度。
2. 船舶的船底一般呈弯曲的形状，称为船底曲线。
这种形状可以减少船舶在水中的阻力，提高船舶的航行效率。
3. 船舶的船舷是船体的侧面部分，包括船舷板和船舷肋。
它的作用是提供船体的强度和稳定性，同时也起到防止船舶漏水的作用。
习题三：根据给定的船舶结构三视图，判断下列说法是否正确：1. 船舶的船底一般比船舷更宽。
2. 船舶的船舷板一般是垂直于船底的。
3. 船舶的船首鼻一般比船舶的其他部分更薄。
答案：1. 正确。
船舶的船底一般比船舷更宽，这有助于提供船舶的稳定性和承载能力。
2. 错误。
船舶的船舷板一般是倾斜的，而不是垂直于船底的。
这种倾斜的设计有助于减少船舶在水中的阻力。
3. 正确。
船舶的船首鼻一般比船舶的其他部分更薄，这有助于减少船舶在水中的阻力，提高船舶的航行速度。
三视图习题50道(含答案)
word 格式三视图练习题则该几何体的体积是()(D)()(D ) 280第3题（单位cm ) 16033(D) 所得几何体的正则该几何体的俯视图为()1 3第5题(A) 2（主）视图与侧（左）视图分别如右图所示(B ) 1(C ) 292第1题(B ) 3603、若某几何体的三视图 如图所示，则此几何体的体积是 1、若某空间几何体的三视图如图所示—cm 34、一个长方体去掉一个小长方体 2、一个几何体的三视图如图，该几何体的表面积是(B ) 320cm 3“,f=L23(A ) 352cm 3 33r — 1111I ___J第2题1'1-T P5、 若一个底面是正三角形的三棱柱的正视图如图所示，则其侧.面积等于（A . . 3B . 2C . 2 3D . 66、 图2中的三个直角三角形是一个体积为20cm 2的几何体的三视图，则h=7、 一个几何体的三视图如图所示 ，则这个几何体的体积为 _____________AA // BB // CC , CC 丄平面 ABC3且3 AA = 3 BB = CC =AB,则多面体△ ABC - ABC 的正视图（也称主视图）是（）8、如图，网格纸的小正方形的边长是1 ,在其上用粗线画出了某多面体的三视图,则这个多面体最长的一条棱的长为9、如图1 , △ ABC 为正三角形，)S 2a.俯视图正（主）视图侧（左）视图A. 9 nB. 10 nC. 11 n D . 12 n10、一空间几何体的三视图如图所示，则该几何体的体积为（）.A.2 2.3B. 4 2 . 3侧（左）视图C. 2D. 4第11题第10题11、上图是一个几何体的三视图，根据图中数据，可得该几何体的表面积是12、一个棱锥的三视图如图,则该棱锥的全面积（单位：c m2）为(A) 48+12 . 2 (B) 48+24 . 2 ( C) 36+12 2 (D)36+24 213、若某几何体的三视图（单位：cm）如图所示，则此几何体的体积是cm3第12题正视图侧视图俯视图15题14、设某几何体的三视图如上图所示。
三视图练习题含答案之欧阳美创编
23正视图侧视图2俯视图2第3题三视图练习题时间：2021.01.01创作：欧阳美1.某几何体的三视图如图所示，则它的体积是（ ） A.283π- B.83π-C.π28-D.23π2.某四棱锥的三视图如图所示，该四棱锥的表面积是（ ）A ．32 B.16+162C.48D.16322+3.如图，某几何体的正视图（主视图），侧视图（左视图）和俯视图分别是等边三角形，等腰三角形和菱形，则该几何体的体积为（ ） A ．43 B ．4C ．23 D ．24.如图是某几何体的三视图，则该几何体的体积为（ ）A ．942π+ Ｂ．3618π+Ｃ．9122π+Ｄ．9182π+5.一个空间几何体的三视图如图所示，则该几何体的表面积为（ ）A. 48B.32+817C.48+817D.806.若某几何体的三视图（单位：cm ）如图所示，则此几何体的体积是（ ）A.35233cmB.32033cmC.22433cmD.16033cm第1题第2题7．若某空间几何体的三视图如图所示，则该几何体的体积是（ ）A.2B.1C.23D.138.某几何体的三视图如图所示，则该几何体的体积为（ ）A.π816+B.π88+C.π1616+D.π168+9. 某四棱台的三视图如图所示，则该四棱台的体积是（ ）A.4B.314C.316D.610. 某三棱锥的三视图如图所示,已知该三视图中正视图和俯视图均为边长为2的正三角形,侧视图为如图所示的直角三角形,则该三棱锥的体积为（ ）A ．1B ．3C ．4D ．511． 一个几何体的三视图如图所示,则这个几何体的体积为（ ）A ．(8)36π+B ．(82)36π+C ．(6)36π+D ．(92)36π+12.某几何体的底面为正方形,其三视图如图所示,则该几何体的体积等于( )A ．1B ．2C ．3D ．413.某几何体的三视图如图所示，则其体积为______.3 32正视图侧视图俯视图第4题第5题第7题第8题第9题312211正视图1314.若某几何体的三视图（单位：cm ）如图所示，则此几何体的体积等于______3cm .15.某几何体的三视图如图所示，则该几何体的体积是______.16.已知某三棱锥的三视图（单位：cm ）如图所示，则该三棱锥的体积是17.一个空间几何体的三视图如图所示,则这个空间几何体的体积是.18.如图所示,一个三棱锥的三视图是三个直角三角形,则该三棱锥外接球的表面积为19.若某空间几何体的三视图如下图所示,则该几何体的表面积是_______________.20．一个正方体的内切球与它的外接球的体积比是（ ）．A ．1∶33B ．1∶22C ．1∶383 D ．1∶4221.已知球面上A 、B 、C 三点的截面和球心的距离都是球半径的一半，且AB ＝BC ＝CA ＝2，则球表面积是()A.π964B. π38 C.π4D. π916第17题 24 3 正视图侧视图俯视图第18题第15题第14题第13题第16题第19题22. P 、A 、B 、C 是球O 面上的四点，且PA 、PB 、PC 的两两垂直，PA=PB=PC=9，则球心O 到截面ABC 的距离为23.半径为5的球被一个平面所截，截面面积为16π，则球心到截面的距离为 （ ）A.4B.3C.2.5D.2 24.表面积为3π的圆锥，它的侧面展开图是一个半圆，则该圆锥的底面直径为________. 25.答案1.A2.B3.C4.D5.C6.B7.B8.A9.B10.A 11.A 12.A 13.3π14.24 15.1616-π 16.1 17.67π 18.29π 19. 20+82 20.A 21.A 22.23323.B 24. 2 25. ︒90 26.3500π27.π6 28.π2929.72 30. 3629+3226-31.2500π 32.π1200。
通用技术历年三视图补线真题及练习题（含答案及立体图）
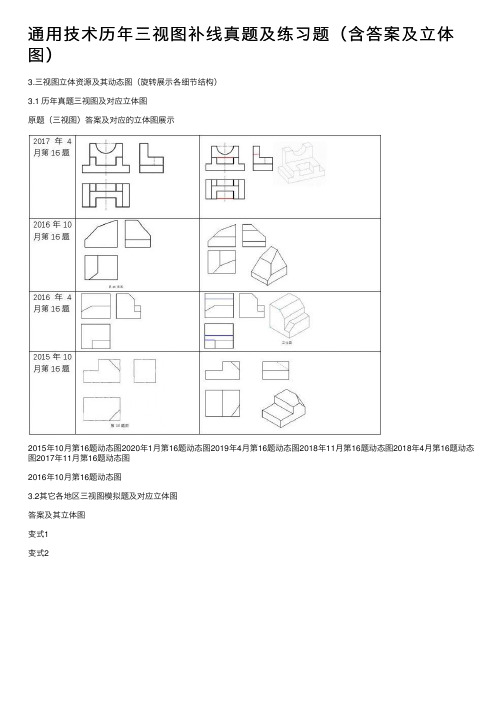
通用技术历年三视图补线真题及练习题（含答案及立体 图）
3.三视图立体资源及其动态图（旋转展示各细节结构） 3.1 历年真题三视图及对应立体图 原题（三视图）答案及对应的立体图展示
2015年10月第16题动态图2020年1月第16题动态图2019年4月第16题动态图20பைடு நூலகம்8年11月第16题动态图2018年4月第16题动态 图2017年11月第16题动态图 2016年10月第16题动态图 3.2其它各地区三视图模拟题及对应立体图 答案及其立体图 变式1 变式2
三视图习题（含答案）较难
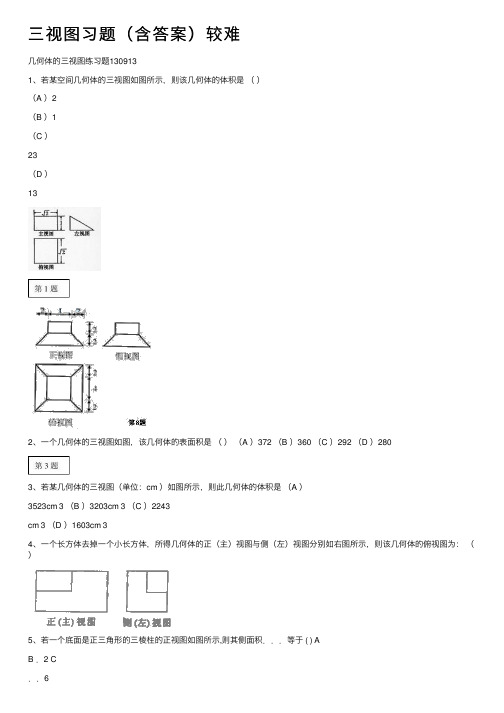
三视图习题（含答案）较难⼏何体的三视图练习题1309131、若某空间⼏何体的三视图如图所⽰，则该⼏何体的体积是（）（A ）2（B ）1（C ）23（D ）132、⼀个⼏何体的三视图如图，该⼏何体的表⾯积是（）（A ）372 （B ）360 （C ）292 （D ）2803、若某⼏何体的三视图（单位：cm ）如图所⽰，则此⼏何体的体积是（A ）3523cm 3 （B ）3203cm 3 （C ）2243cm 3 （D ）1603cm 34、⼀个长⽅体去掉⼀个⼩长⽅体，所得⼏何体的正（主）视图与侧（左）视图分别如右图所⽰，则该⼏何体的俯视图为：（）5、若⼀个底⾯是正三⾓形的三棱柱的正视图如图所⽰,则其侧⾯积．．．等于 ( ) AB ．2 C．．66、图2中的三个直⾓三⾓形是⼀个体积为20cm 2的⼏何体的三视图，则h= cm7、⼀个⼏何体的三视图如图所⽰，则这个⼏何体的体积为。
8、如图，⽹格纸的⼩正⽅形的边长是1，在其上⽤粗线画出了某多⾯体的三视图，则这个多⾯体最长的⼀条棱的长为______.第2题第5题9、如图1，△ ABC 为正三⾓形，AA '//BB ' //CC ' , CC ' ⊥平⾯ABC 且3AA '=32BB '=CC '=AB,则多⾯体△ABC -A B C '''的正视图（也称主视图）是（）10、⼀空间⼏何体的三视图如图所⽰,的体积为( ).A.2π+B. 4π+C.2π+ D. 4π+11、上图是⼀个⼏何体的三视图，根据图中数据，可得该⼏何体的表⾯积是（）A ．9πB ．10πC ．11πD ．12π12、⼀个棱锥的三视图如图，则该棱锥的全⾯积（单位：c 2m ）为（）（A ）（B ）（C ）（D ） 13、若某⼏何体的三视图（单位：cm ）如图所⽰，则此⼏何体的体积是 3 cm ．第7题侧(左)视图正(主)视俯视图俯视图正(主)视图侧(左)视图第14题14、设某⼏何体的三视图如上图所⽰。
七上数学每日一练：由三视图判断几何体练习题及答案_2020年填空题版
七上数学每日一练：由三视图判断几何体练习题及答案_2020年填空题版答案解析答案解析答案解析答案解析2020年七上数学：图形的变换_投影与视图_由三视图判断几何体练习题1.(2020青岛.七上期末) 一个几何体是由一些完全相同的小立方块搭成的，从三个不同的方向看到的情形如图所示，则搭成这个几何体共需这样的小方块________个．考点： 由三视图判断几何体;2.(2019黄岩.七上期末) 一张桌子摆放若干碟子，从三个方向上看，三种视图如图所示，则这张桌子上共有________个碟子.考点： 由三视图判断几何体;3.(2019镇江.七上期末) 某几何体的三视图如图所示，则这个几何体的名称是________.考点： 由三视图判断几何体;4.(2019永登.七上期中) 一个几何体由一些完全相同的小立方块搭成，从正面和从上面看到的这个几何体的形状如下，那么搭成这样一个几何体，最少需要________个这样的小立方块，最多需要________个这样的小立方块.考点： 由三视图判断几何体;5.(2018宁城.七上期末)用小正方体搭一几何体，从正面和上面看如图所示，这个几何体最少要________个正方体，最多要________个正方体.答案解析答案解析答案解析答案解析答案解析答案解析正面 上面考点： 由三视图判断几何体;6.(2018辽阳.七上期末) 如图所示是由四个相同的小立方体组成的几何体分别从正面和左面看到的图形，那么原几何体可能是________．（把图中正确的立体图形的序号都填在横线上）考点： 由三视图判断几何体;7.(2018孟津.七上期末) 由n 个相同的小正方形堆成的几何体，其视图如图所示，则n 的最大值是________，最小值是________．考点： 由三视图判断几何体;8.(2018辉.七上期末) 用小正方体搭一个几何体，使它的主视图和俯视图如图所示，这样的几何体最少需要正方体________个。
CAD三视图练习题
投影与三视图练习题1.填空题（1）俯视图为圆的几何体是_______，______。
（2）画视图时，看得见的轮廓线通常画成_______，看不见的部分通常画成_______。
（3）举两个左视图是三角形的物体例子：________，_______。
（4）如图所示是一个立体图形的三视图，请根据视图说出立体图形的名称_______。
请将六棱柱的三视图名称填在相应的横线上.（6）、如图所示是一个立体图形的三视图，请根据视图说出立体图形的名称_______。
（7）、一张桌子摆放若干碟子，从三个方向上看，三种视图如下图所示，则这张桌子上共有________个碟子。
（8）、某几何体的三种视图分别如下图所示，那么这个几何体可能是_____。
（9）人在观察目标时，从眼睛到目标的叫做视线。
所在的位置叫做视点，有公共的两条所成的角叫做视角。
视线不能到达的区域叫做。
（10）物体在光线的照射下，在某个内形成的影子叫做，这时光线叫做，投影所在的叫做投影面。
由的投射线所形成的投影叫做平行投影。
由的投射线所形成的投影叫做中心投影。
（11）在平行投影中，如果投射线垂直于投影面，那么这种投影就称为正投影。
（12）物体的三视图是物体在三个不同方向的。
上的正投影就是主视图，水平面上的正投影就是，上的正投影就是左视图。
2.选择题（1）圆柱对应的主视图是（）。
（A）（B）（C）（D）（2）某几何体的三种视图分别如下图所示，那么这个几何体可能是（）。
（A）长方体（B）圆柱（C）圆锥（D）球（3）下面是空心圆柱在指定方向上的视图，正确的是…（）(4)一个四棱柱的俯视图如右图所示，则这个四棱柱的主视图和左视图可能是（）（5）主视图、左视图、俯视图都是圆的几何体是（）。
（A）圆锥（B）圆柱（C）球（D）空心圆柱（6）在同一时刻的阳光下，小明的影子比小强的影子长，那么在同一路灯下（）A、小明的影子比小强的影子长B、小明的影子比小强的影子短C、小明和小强的影子一样长D、无法判断谁的影子长3、解答题（1）根据要求画出下列立体图形的视图。
画组合体三视图)习题解答
俯视图的绘制
选择合适的观察高度
俯视图应选择一个与主视图和左视图平行的观察高度，以便展示组合体的顶部形 状。
反映组合体的长度和宽度
俯视图应清晰表达组合体的长度和宽度，特别是对于具有水平结构特征的部分。
三视图的对应关系
投影一致性
在左视图上。在左视图中，应将组合体的各个组成部分表示清楚，并注
意投影的对应关Leabharlann 。03俯视图俯视图是反映组合体的水平面形状的视图，通常将组合体的水平投影绘
制在俯视图上。在俯视图中，应将组合体的各个组成部分表示清楚，并
注意投影的对应关系。
02 组合体的三视图绘制
主视图的选择
确定观察方向
选择一个能反映组合体主要形状特征的方向作为主视图的观察方 向。
习题二解析
复杂组合练习
习题二涉及更复杂的组合体，包括多个基础几何体的叠加、切割和组合。通过练习，学生可以提高对复杂组合体的空间想象 能力和绘图技能。
习题三解析
装配关系练习
习题三注重表现组合体之间的装配关系，例如螺栓、轴承等连接方式。通过练习，学生可以加深对组 合体内部结构和装配关系的理解。
习题四解析
在绘制叠加型组合体的主视图时，应先画出最底层的几何体，然后依次 画出上层叠加的几何体，特别注意处理好各几何体之间的前后关系。
在绘制左视图和俯视图时，应依据主视图，逐层画出各几何体的轮廓线， 并注意各几何体的投影变化。
切割型组合体的绘制
切割型组合体是由一个基本几何体经过 多次切割、钻孔等操作形成的。在绘制 其三视图时，应先画出完整的基本几何 体，再依据切割、钻孔等操作逐一画出
在绘制综合型组合体的主视图时，应先确定 各基本几何体的位置和形状，然后依据“长 对正、高平齐、宽相等”的原则，从整体到 局部进行绘制。
机械制图习题集项目4 绘制基本几何体的三视图——答案
项目4 绘制基本几何体的三视图任务4.1 绘制平面立体的三视图根据平面立体的两视图补画第三视图，并画出立体表面已知点的其他两投影。
1．2．3．4．班级：姓名：学号：任务4.2 绘制回转体的三视图根据回转体的两视图补画第三视图，并画出立体表面已知点的其他两投影。
1．2．3．4．班级：姓名：学号：任务4.3 绘制平面切割体1.补画主、俯视图中的漏线。
2.补画主、左视图中的漏线。
3.补画主、左视图中的漏线。
4.补画俯、左视图中的漏线。
班级：姓名：学号：5.补全截交五棱柱的俯、左视图。
6.补全截交正四棱锥的俯、左视图。
7.补全截交正四棱柱的俯、左视图。
8.补全截交四棱柱的俯视图。
班级：姓名：学号：任务4.4 绘制回转切割体1.补全截交圆柱体的左视图。
2.补全截交圆锥体的主视图。
3.补全截交圆柱体的左视图。
4.补全截交圆柱体的左视图。
班级：姓名：学号：5.补全截交半球体的俯、左视图。
6.补全截交圆柱体的主、俯视图。
7.补画截交同轴回转体的左视图。
8.补全截交同轴回转体的俯视图。
班级：姓名：学号：任务4.5 求作相贯线1.补全相贯圆柱体的主视图。
2.补全相贯圆柱孔的主视图。
3.补全相贯圆柱孔的主视图。
4.补画主视图。
班级：姓名：学号：5.补全相贯圆柱体的主视图。
6.补全相贯圆柱孔的主视图。
7.补全相贯体的主视图。
8.补全相贯体的左视图。
班级：姓名：学号：9.补全相贯体的主视图。
10.补全相贯体的主、俯视图。
11.补全相贯体的主、俯视图。
12.补全相贯体的主视图。
班级：姓名：学号：:1. 2.班级：姓名：学号：3. 4.班级：姓名：学号：－11－。
三视图习题50道(含答案)
三视图练习题1、若某空间几何体的三视图如图所示，则该几何体的体积是（）（A）2（B）1（C）23（D）132、一个几何体的三视图如图，该几何体的表面积是（）（A）372 （B）360 （C）292 （D）2803、若某几何体的三视图（单位：cm）如图所示，则此几何体的体积是（A）3523cm3（B）3203cm3 （C）2243cm3（D）1603cm34、一个长方体去掉一个小长方体，所得几何体的正（主）视图与侧（左）视图分别如右图所示，则该几何体的俯视图为：（）5、若一个底面是正三角形的三棱柱的正视图如图所示,则其侧面积等于 ( )AB．2 C．．66、图2中的三个直角三角形是一个体积为20cm2的几何体的三视图，则h= cm第2题第5题7、一个几何体的三视图如图所示，则这个几何体的体积为 。
8、如图，网格纸的小正方形的边长是1，在其上用粗线画出了某多面体的三视图，则这个多面体最长的一条棱的长为______.9、如图1，△ ABC 为正三角形，AA '//BB ' //CC ' , CC ' ⊥平面ABC 且3AA '=32BB '=CC '=AB,则多面体△ABC -A B C '''的正视图（也称主视图）是（ ）10、一空间几何体的三视图如图所示,则该几何体的体积为( ).A.2π+B. 4π+C. 2π+D. 4π11、上图是一个几何体的三视图，根据图中数据，可得该几何体的表面积是（ ）A ．B ．C ．D ．9π10π11π12π第7题侧(左)视图正(主)视图俯视图俯视图正(主)视图侧(左)视图12、一个棱锥的三视图如图，则该棱锥的全面积（单位：c 2m ）为 （）（A ）（B ）（C ）（D ）13、若某几何体的三视图（单位：cm ）如图所示，则此几何体的体积是 3cm ．14、设某几何体的三视图如上图所示。
机械制图习题集项目3 绘制简单形体的三视图——答案
项目3 绘制简单形体的三视图1.说明三视图之间的投影关系和方位关系，并在各视图中注明其方位。
班级：姓名：学号：2.分析下列三视图，找出其对应的轴测图，并在轴测图中填上对应三视图的编号。
班级：姓名：学号：3.分析下列三视图，找出其对应的轴测图，并在轴测图中填上对应三视图的编号。
班级：姓名：学号：1.根据立体图中各点的位置，画出它们的三面投影，并量出各点到投影面的距离及坐标值。
（单位：mm；度量值取整数）班级：姓名：学号：2.根据各点的三面投影图，作出它们的立体图，并写出各点的坐标值。
（单位：mm；度量值取整数）A（15、15、20）、B（20、0、25）、C（0、20、0）3.已知点A在V面前方30mm，点B在H面上方20mm，点C在V面上，点D在H 面上，点E在X轴上，补全各点的两面投影。
班级：姓名：学号：4.已知各点的两面投影，求作第三面投影，并说明两点的相对位置。
点A在点B的（上、下）下方，（左、右）左方，（前、后）后方；点C在点A的（上、下）上方，（左、右）右方，（前、后）前方。
5.已知各点的两面投影，求作第三面投影，并说明两点的相对位置。
点C、B的重影点是 c″（b″），点B在点C的正右方。
点A、B的重影点是 a（b），点B在点A的正下方。
点D在 Y 轴上。
班级：姓名：学号：6.根据所给点的三面投影，对比它们的相对位置。
（单位：mm；度量值取整数）7.已知立体上各点的两面投影，求作第三面投影。
并说明各点的相对位置。
点A与点B的相对位置：点A与点B没有上、下和前、后之分，只有左、右差别；点B在点A的正右方；它们的 Z 和 Y 坐标值相等， X 坐标值不相等。
点C与点D的相对位置：点C与点D没有上、下和左、右之分，只有前、后差别；点D在点C的正后方；它们的 Z 和X 坐标值相等， Y 坐标值不相等。
点E与点F的相对位置：点E与点F没有左、右和前、后之分，只有上、下差别；点F在点E的正下方；它们的 X 和 Y 坐标值相等， Z 坐标值不相等。
三视图习题及答案
三视图习题及答案在进行机械设计时，三视图是一个非常重要的工具，它可以帮助设计师更清晰地理解和表达设计方案。
通过三视图习题的实践，可以有效提升我们在机械设计中的应用能力和设计思维。
本文将以三视图习题及答案为主题，介绍相关的知识点，并提供一些习题和答案供读者练习。
一、三视图简介三视图是指物体的正视图、俯视图和左视图。
在机械设计中，通常使用第一、第三和第七投影角度的多视图投影法。
每个视图都能提供不同的信息，通过综合这些视图，我们可以完整地了解物体的形状、尺寸和结构。
二、三视图示例下面是一个简单的示例，展示了一个物体的正视图、俯视图和左视图。
请根据图纸回答题目。
（插入示例图纸）1. 请标注出物体的三个主要尺寸。
答案：根据图纸，物体的主要尺寸分别为长、宽和高，分别为50mm、30mm和20mm。
2. 请描述物体的形状特征。
答案：物体呈长方体状，正视图和俯视图都显示出物体的长方形形状，左视图显示出物体的高度。
3. 请绘制物体的左视图，尺寸按比例。
答案：（插入左视图示意图）通过完成上述习题，我们可以对三视图有一个初步的了解，并能够熟悉标注、绘制和尺寸的方法。
三、三视图习题及答案下面是一些三视图习题和答案，供读者练习。
1. 请根据给定的正视图和左视图，绘制出物体的俯视图。
（插入题目图纸）答案：（插入答案图纸）2. 请根据给定的俯视图和左视图，绘制出物体的正视图。
（插入题目图纸）答案：（插入答案图纸）3. 请根据给定的正视图和俯视图，绘制出物体的左视图。
（插入题目图纸）答案：（插入答案图纸）通过反复练习三视图习题，我们可以逐渐提升自己的绘图技巧和空间想象能力。
同时，我们也能更好地理解机械设计中的尺寸和形状，为后续的设计工作打下坚实的基础。
结语三视图习题是机械设计过程中重要的一环，通过实际练习和答案分析，可以帮助我们提升机械设计的能力和技巧。
希望本文提供的习题及答案对读者的学习和实践有所帮助。
通过不断练习和思考，相信大家定能在机械设计领域取得更好的成就。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
三视图练习
1.根据如图所示的组合体，在下列选项中选出正确的的左视图（）
答案：B
2.如图所示为某组合体的三视图，下列主视方向（箭头方向）中与三视图对应的是
答案：A
6. ［2018台州模拟］如图所示是一个模型的轴测图，其正确的三视图是（）
答案：A
7.［2018浙江联考］如图所示是一个模型的轴测图，其正确的三视图是（）
答案：A
8.［2018嘉兴模拟］图a是某零件的立体图，其主视图与俯视图如图b所示。
与之对应的左视图是（）
答案：A
9.如图所示是某模型的三视图，下列模型中与其对应的是（）
答案：D
10.［2018宁波模拟］如图所示为衣柜中支撑和固定挂衣杆的法兰座，通过自攻螺钉与木质衣柜连接，以下零件视图中，能实现法兰座功能的视图是（）
答案：C
11.［2017嘉兴模拟］如图所示的结构，与构件1连接的结构正确的是（）
答案：D
12.［2017.11浙江］如图所示是某形体的轴测图、主视图和俯视图，正确的左视图是（）
答案：C
3.请补全三视图中所缺的两条图线。
答案：
4.请补全三视图中所缺的3条图线。
5.请补全三视图中所缺的三条图线。