(完整版)第二章热力学第一定律.doc
工程热力学 第2章 热力学第一定律

δWtot
δmi ei
δQ
E
δm j e j
E+dE
δQ = dE + ⎡Σ ( ej δmj ) −Σ ( eiδmi ) ⎤ + δWtot ⎣ ⎦
或
τ
τ + dτ
Q = ΔE + ∫ ⎡Σ( ej δmj ) −Σ( eiδmi ) ⎤ +Wtot ⎦ τ1 ⎣
τ2
dE Φ= + ⎡Σ ( ej qmj ) −Σ ( ei qmi ) ⎤ + P ⎣ ⎦ tot dτ
二、总(储存)能(total stored energy of system) 热力学能,内部储存能
E =U+Ek +Ep
宏观动能 宏观位能 总能 外部储存能
e =u+ek +ep
3
外部储存能 宏观动能:质量为m的物体以速度cf运动时,该物 体具有的宏观运动动能为:
1 2 Ek = mc f 2
重力位能:在重力场中质量为m的物体相对于系统 外的参数坐标系的高度为z时,具有的重力位能为:
1 2 q − Δu = Δc f + gΔz + Δ( pv ) + wi 2
维持工质流动所需的流动功
21
稳定能量方程的物理意义:工质在状态变化过程 中,从热能转变而来的机械能总和等于膨胀功。 技术功:技术上可资用的功,其数学表达式为:
由
1 2 wt = wi + Δc f + gΔz 2 q − Δu = w
E p = mgz
4
宏观动能与内动能的区别
三、热力学能是状态参数∂U ⎞ ⎛ ∂U ⎞ dU = ⎜ ⎟ dT + ⎜ ⎟ dV = cV dT + ⎢T ⎜ ⎟ − p ⎥ dV ⎝ ∂T ⎠V ⎝ ∂V ⎠T ⎣ ⎝ ∂T ⎠V ⎦
第2章 热力学第一定律
四、热力学第一定律
对封闭系统当系统与环境同时有功W及热Q交换时,则
U =U2-U1 = Q + W 微小的变化 dU=δQ+δW
上式即为封闭系统的热力学第一定律的数学表达式。 力学第热一定律的实质 能量守恒。
Q 与W 都是途径函数,而U 是状态函数, U = Q + W ,
说明了两个途径函数的代数和,为一个状态函数的变化值。
途径I C 始态1 B 途径II 状态函数的改变量只决定于系统的始态和终态,而与变化 的过程或途径无关。即 如 ΔT = T2-T1, Δp = p2-p1 ;ΔV= V2-V1 终态2
这套处理方法是热力学中的重要方法,通常称为状态函数法。
第二节 热力学第一定律
1. 热 定义: 由于系统与环境间存在温度差,而引起的能量传递形式。
宏观性质也称为系统的状态函数。 (i) 对于一定量组成不变的理想气体系统,系统的任意宏观
性质是另外两个独立的宏观性质的函数: V=f(T,p),如 nRT V 理想气体 p (ii) 状态函数的改变量只决定于系统的始态和终态,而与 变化的过程或途径无关。即 状态函数的改变量=系统终态的函数值-系统始态的函数值 如 ΔT = T2-T1, ΔU = U2-U1
的反应进度必然相同)。反应进度的单位是mol。
反应进度的积分表示形式可以如下理解: 若反应进度为 0 时,B的物质的量为nB(0) ,反应进度 时, B的物质的量为nB() ,积分得:
nB 0 νB
若反应开始时,0 = 0 ,则: = nB/ B
六、 状态函数法
② 反应进度 :
定义: 表示化学反应进行的程度。符号 。 对于反应: 0 νBB 反应进度定义为: dξ dnB /ν B 其中, nB为反应方程式中,任何一种物质的物质的量,B 为 该物质在方程式中的化学计量数。一个化学反应的反应进度,
第二章 热力学第一定律

§2-5 理想气体内能 热容和焓
一、理想气体的内能 焦耳定律 自由膨胀过程 证明:理想气体内能仅是状 态的函数,与体积无关,称 为焦耳定律
A
C
B
焦耳实验(1845年) 理想气体
U U (T )
满足pV=νRT关系;满足道尔顿分压定律; 满足阿伏加德罗定律;满足焦耳定律U
宏观特性
U (T )
1 dU CV ,m v dT
CP , m 1 dH v dT
思考题 一、试指出以下提法是否正确?如有错误、指出误区所在. 1.“高温物体所含热量多;低温物体所合热量少” 2.“同一物体温度越高所含热量越多”. 热量不是状态函数,与过程有关 二、试指出以下不同用语申的‘热”指的是哪个概念.
P
2、理想气体定容热容量及内能
热力学第一定律
dQ dU dA dU PdV dU
dV 0
dQ dU CV dT dT
U 2 U1 CV dT
T1
T2
3、理想气体定压热容量及焓 焓
H U pV U (T ) vRT
dH dU pdV
第二章
热力学第一定律
热力学系统的过程 功
内能 热量 焦耳热功当量实验
热力学第一定律及应用 理想气体内能、热容和焓 循环过程 技术上的循环过程
§2.1
一、热力学过程
热力学系统的过程
原平衡态
p
( P0 ,V0 )
一系列
非平衡态
( P ,V1 ) 1
新平衡态
p-V图 V 问题:离开了原平衡态, 能不能回到一个新平衡态
(I)“摩擦生热”; (2)“热功当最”
(3)“这盆水太热” 三、热力学系统的内能是状态的单值函数,对此作如下理解是否 正确? 1.一定量的某种气体处于一定状态,就具有一定的内能. 2.此内能是可以直接测定的. 3.此内能只有一个数值.
工程热力学 第二章 热力学第一定律

wt
1 2
cf22
cf21
gz2
z1 ws
(2-11)
将轴功的表达式代入上式,即有:
2
1 d ( pv)
2
2
1 pdv 1 vdp
wt 12 pdv p2v2 p1v1 12 vdp (2-11a)
由上式可知,准静态过程的 技术功的大小可用过程线左边的 面积来表示。
准静态 pdv d( pv) wt
wt pdv d( pv) pdv ( pdv vdp) vdp
wt vdp wt vdp
准静态
q du pdv
q dh vdp
热一律解析式之一 热一律解析式之二
技术功在示功图上的表示
q12 (u2 u1) w12
Q dU pdV (2-4)
2
Q12
(U2
U1)
pdV
1
(2-4a)
q du pdv (2-4b)
2
q12
(u2 u1)
pdv
1
(2-4c)
2-3 开口系统能量方程 Energy balance for open system
式中各项的正负号规定为:系统吸热为正,放热为负; 系统对外作功为正,外界对系统作功为负。
上式既适用于准静态过程,也适用于非准静态过程。
对于无耗散的准静态过程, w pdv
因此上述诸式可写为:
Q dU W
Q12 (U2 U1) W12
对1kg工质,有:
q du w
所以有:
h1 h2
1 2
热工流体第二章 热力学第一定律

第二章 热力学第一定律第一节 第一定律的实质及热力学能和总能能量守恒与转换定律是自然界的基本规律之一,它指出:自然界中的一切物质都具有能量,能量不可能被创造,也不能被消灭;但能量可以从一种形态转变为另一种形态,且在能量的转化过程中能量总量不变。
热力学第一定律是能量守恒与转换定律在热现象中的应用。
它确定了热力过程中热力系统与外界进行能量交换时,各种形态能量数量上的守恒关系。
一、热力学能热力学能是与物质内部粒子的微观运动和粒子的空间位置有关的能量。
它包括分子移动、转动、粒子震动运动的内动能和分子间由于相互作用力的存在而具有的内位能,故又称内能。
内动能取决于分子热运动,是温度的函数,而内位能取决于分子间的距离,是比体积的函数,即u = f ( T, v )二、总能除热力学能外,工质的总能量还包括工质在参考坐标系中作为一个整体,因有宏观运动速度而具有动能、因有不同高度而具有位能。
前一种能量称之为内部储存能,后两种能量则称之为外部储存能。
我们把内部储存能和外部储存能的总和,即热力学能与宏观运动动能和位能的总和,叫做工质的总储存能,简称总能。
即p k E U E E =++ (2-1)E---总能; U---热力学能; E k ---宏观动能; E p ---宏观位能。
第二节 第一定律的基本能量方程及工质的焓一、焓在有关热力计算总时常有U+pV 出现,为了简化公式和计算,把它定义为焓,用符号H 表示,即H=U+pV (2-2)1kg工质的焓值称为比焓,用h表示,即h=u+pv (2-3)焓的单位是J,比焓的单位是J/kg。
焓是一个状态参数,在任一平衡状态下,u、p和v都有一定得值,因而焓h也有一定的值,而与达到这一状态的路径无关。
当1kg工质通过一定的界面流入热力系统时,储存于它内部的热力学能当然随着也进入到系统中,同时还把从外部功源获得的推动功pv带进了系统。
因此系统中因引进1kg工质而获得的总能量是热力学能与推动功之和(u+pv),即比焓。
第02章 热力学第一定律 2011-02-24

H2与N2以3:1的比例在绝热钢瓶中反应生成NH3,此过程:
(A) H = 0 (B) p = 0 (C) U = 0 (D) T = 0
3. 理想气体的热力学能和焓 焦耳实验(1845)图2.2.1
§2.4
热
容
或
δQV dU m
CV ,m
或
U m ( )V f (T ) T
热力学第一定律表述之一:
自然界一切物质都有能量,能量有各种不同形式并可互相转 化,在转化过程中总值不变(即能量守恒与转化定律)。
热力学第一定律表述之二:
第一类永动机是造不成的。
热力学第一定律的数学表述: 系统从状态 (1) 状态(2),与环境交换热Q,交换功W, 则有: U2 = U1 + Q + W, 或 U = Q +W dU = Q + W (封闭系统)
4. 过程与途径 系统的一切变化均称之为过程。 在相同的始终态间,可有不同的变化方式,称之为 途径 。状态函数的变化与途径无关!。 常见的过程有: 恒温过程:T2 = T1 = T (环) 恒压过程:p2 = p1 = p (环) 恒容过程:V = 0 绝热过程:无热交换,但可以有功的传递 循环过程:回到初始状态 5. 热力学平衡态(无环境影响下) (1) 热平衡 (2) 力平衡 (3) 相平衡 (4) 化学平衡 T (环)为环境温度 p (环)为环境压力
W 与途径有关,微小变化用W表示(不能用dW).
p(环)
p(环)
A
体积功的计算:
W = Fdl
= p(环) Adl
= p(环) dV
(能否用系统的压力p ?) dl
对于一有限过程:
若环境压力恒定, V1 = p(环)(V2 V1) = p(环)V (恒外压过程) 与恒压过程比较。 V2 V
第二章 热力学第一定律

令
u pv h
U pV H
,h 称为比焓。
, H 称为焓
焓的定义:焓=热力学能+推动功。
2-4 开口系统的稳定流动能量方程式
由于p、v 、u都是状态参数,所以焓也是工质的一个
1 2 Ws m u2 cf2 gz2 mp2v2 2 1 2 Ws m u2 cf2 gz2 p2v2 2
2-4 开口系统的稳定流动能量方程式
根据热力学第一定律可得
1 2 Q m u1 p1v1 2 cf1 gz1
本章主要内容
1 2 3 4 5
热力系统的储存能 热力学第一定律的实质 闭口系统的热力学第一定律表达式 开口系统的稳定流动能量方程式 稳定流动能量方程式的应用
2-1 热力系统的储存能
热力学能
热力学储存能
U
宏观动能与宏观位能
热力学能的定义:
Ek , E p
物体因热运动而具有的能量 , 是存储于物体内部的能量 。 内动能 内位能 原子能 化学能
对于单位质量工质的可逆过程 ,
q du pdv
q u pdv
1
2
2-3 闭口系统的热力学第一定律表达式
适用条件:
闭口系;可逆、不可逆; 理想和实际气体;初、终态为平衡态
符号规定:
吸热q为正,放热为负 系统对外作功为正,反之为负
系统内能增大 U为正,反之为负
2-3 闭口系统的热力学第一定律表达式
热力学能(内能)
2-3 闭口系统的热力学第一定律表达式
Q ΔU
热力学第一定律 (5)精选全文完整版

可编辑修改精选全文完整版第二章 热力学第一定律 一、基本概念1. 系统与环境;状态与状态函数;过程与途径2. PVT 、相变化及化学变化独特的基本概念(略)3. 状态函数:内能、焓 →(H=U+pV )4. 途径函数:功、热★热——恒容热:Q V =ΔU →适用条件:封闭系统、恒容过程、W ’=0; 恒压热:Q p =ΔH →适用条件:封闭系统、恒压过程、W ’=0。
★功——W =-∫p amb d V :真空膨胀过程W =0 恒容过程W =0恒压过程W =-p ΔV ; 恒外压过程:W =-p amb ΔV5. pVT 变化基础热数据热容:C→C p , C V →C p,m ,C V ,m (理想气体的C p,m -C V ,m =R )6. 可逆相变化基础热数据摩尔相变焓:(),m p m pH T C βα∂∆∂=∆; ΔC p,m =C p,m (β)-C p,m (α) 7. 化学变化基础热数据:θθr m B f m B Δ(B)H H ν∆∑=; θθr m B c m BΔ(B)H H ν∆∑=-二、热力学第一定律:ΔU =Q + W 三、基本过程热数据计算 1. 理想气体pVT 变化过程恒容过程:W =0;,;V V m Q U nC T =∆=∆ ΔH=nC p,m ΔT恒压过程:,;P p m Q H nC T =∆=∆ ΔU=nC V ,m ΔT ;(W =ΔU — Q = — p ΔV ) 恒温可逆过程:ΔU=ΔH=0;—Q= W (可逆)=—nR T ln(V 2/V 1)=nR T ln(p 2/p 1) 恒温恒外压过程:ΔU=ΔH=0;—Q= W (不可逆)=—p amb ΔV绝热可逆过程:过程方程式(重要,自行总结,);Q=0;W =ΔU=nC V ,m ΔT ;ΔH=nC p,m ΔT绝热恒外压过程:Q=0;W =—p amb ΔV=ΔU=nC V ,m ΔT ;ΔH=nC p,m ΔT 节流膨胀:自行总结2. 相变化过程: 可逆相变(平衡温度及其平衡压力下的相变化过程):凝聚相相变化:W=0;ΔU =Q p =ΔH =m n H βα∆ 含气相相变化:Q p =ΔH = m n H βα∆;W =-p ΔV=-p (V 末-V 始);ΔU =Q p + W 不可逆相变:状态函数法设计途径。
第二章 热力学第一定律

进入系统的能量-离开系统的能量=系统能量的增加 (2-9) 进入系统的能量-离开系统的能量= - )
1 2 Q = m2 (u2 + cf 2 + gz2 ) + m2 p2 v2 2 1 2 − m1 (u1 + cf 1 + gz1 ) − m1 p1v1 + Wi 2
1 2 wt = (cf 2 − cf21 ) + g ( z 2 − z1 ) + wi 2
比较式(2-10b)和(2-16) 比较式( - 和 - )
(2 − 19)
q = ∆u + w q = ∆h + wt = ∆u + ∆( pv) + wt 1 2 w = ∆( pv) + wt = ∆( pv) + ∆cf + g∆z + wi 2
由于m 由于 1=m2=m, 整理上式得
1 2 Q = m(u2 + p2 v2 + cf 2 + gz2 ) 2 1 2 − m(u1 + p1v1 + cf 1 + gz1 ) + Wi 2 令 H = U + pV 代入上式得
1 Q = ∆H + m∆cf2 + mg∆z + Wi 2 1 2 δQ = dH + mdcf + mgdz + δWi 2
m1 = m2 = m
∆ECV = 0
稳定系统的能量分析: 稳定系统的能量分析: 进入系统的能量: 进入系统的能量:
1 2 Q + E1 + p1V1 = Q + m1 (u1 + cf 1 + gz1 ) + m1 p1v1 2 离开系统的能量: 离开系统的能量: 1 2 E2 + p2V2 + Wi = m2 (u 2 + cf 2 + gz 2 ) + m2 p2 v2 + Wi 2
(完整版)第二章热力学第一定律.doc
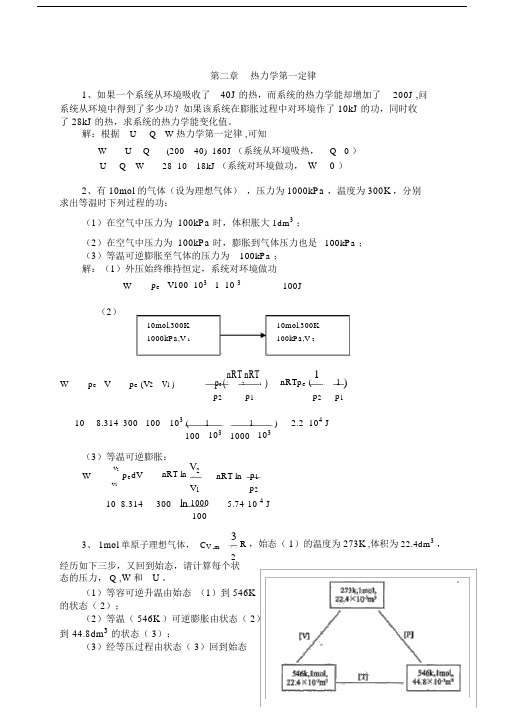
第二章热力学第一定律1、如果一个系统从环境吸收了40J 的热,而系统的热力学能却增加了200J ,问系统从环境中得到了多少功?如果该系统在膨胀过程中对环境作了 10kJ 的功,同时收了 28kJ 的热,求系统的热力学能变化值。
解:根据U Q W 热力学第一定律,可知W U Q (200 40) 160J (系统从环境吸热,Q 0 )U Q W 28 10 18kJ (系统对环境做功,W 0 )2、有 10mol 的气体(设为理想气体),压力为 1000kPa ,温度为 300K ,分别求出等温时下列过程的功:(1)在空气中压力为 100kPa 时,体积胀大1dm3;(2)在空气中压力为 100kPa 时,膨胀到气体压力也是100kPa ;(3)等温可逆膨胀至气体的压力为100kPa ;解:(1)外压始终维持恒定,系统对环境做功W p e V100 103 1 10 3 100J(2)10mol,300K10mol,300K1000kPa,V 1100kPa,V 2W p e V p e (V2 V1 ) p e(nRT2nRT1) nRTp e (11 )p2 p1 p2 p110 8.314 300 100 103 ( 1 1103 ) 2.2 104 J100 103 1000(3)等温可逆膨胀:V2p e dV nRT ln V2 nRT ln p1WV1 V1 p210 8.314 300 ln 1000 5.74 10 4 J1003、 1mol 单原子理想气体,C V ,m 3R ,始态(1)的温度为273K ,体积为 22.4dm3,2经历如下三步,又回到始态,请计算每个状态的压力, Q ,W和U 。
(1)等容可逆升温由始态(1)到 546K 的状态( 2);(2)等温( 546K )可逆膨胀由状态( 2)到44.8dm3的状态( 3);(3)经等压过程由状态( 3)回到始态( 1);解:(1)等容可逆升温过程:W P e V 0UQ WQ VT 2 nC V ,m dT 138.314 546 273 3404.58 JT 12(2)等温可逆膨胀过程:U 0WnRT lnV 21 8.314 546ln 44.83146.50JV 122.4Q W 3146.50J(3)等压过程 :WP e VnRT V 1 V 2 1 8.314 273 22.4 44.8 10 3 2269.72 JV 1 22.4 10 3Q pH T 2nC P ,m dT n 3 R 273 546 5 8.314 273 5674.31J T 1 R 12 2UQ W 5674.31 2269.72 3404.59 J4、在 291K 和 100kPa 下, 1molZn (s) 溶于足量稀盐酸中, 置换出 1molH 2 ( g) ,并放热 152kJ 。
第二章-热力学第一定律

第二章热力学第一定律Ⅰ学习指导一、基本思路热力学主要包括热力学第一定律和热力学第二定律。
本章热力学第一定律介绍封闭的热力学系统在状态变化时热力学能、热和功之间相互转化所遵循的规律。
首先介绍了热力学的基本概念,如系统和环境、状态函数、过程和途径、热力学平衡态、热和功等,得出了热力学第一定律的文字表述和数学表达式。
热力学能是热力学第一定律所引出的重要的状态函数,它是系统内部所具有的能量。
热和功是封闭系统在状态变化时与环境传递能量的两种方∆=+,将封闭系统变化过程式,都与过程有关,称为过程量。
通过热力学第一定律U Q W中热、功和热力学能改变联系了起来。
焓是由系统的热力学能、体积和压力组合得到的一个状态函数,在一定条件下,系统的焓变与过程的热相联系,焓及其有关公式可以看成是热力学第一定律的扩展。
通过Gay-Lussac-Joule实验,说明理想气体的热力学能和焓只是温度的函数;通过Joule-Thomson实验讨论了热力学第一定律对实际气体的应用。
热力学第一定律的具体应用就是围绕不同过程(理想气体简单状态变化、相变和化学变化)中热、功、热力学能变和焓变的计算展开。
准静态过程和可逆过程是热力学的重要概念;卡诺循环是热力学的特殊循环。
热化学是热力学第一定律对于化学反应系统的应用,据此可以计算反应的热效应,通常利用热化学数据(生成焓和燃烧焓)及Hess定律可直接求得298 K下反应的热效应,应用Kirchhoff定律可计算不同温度下反应的热效应。
本章还介绍了热力学第零定律,以热平衡现象为基础给出了温度的概念。
本章的主要内容及其逻辑关系如框图所示。
二、基本概念1.热力学第零定律如果两个系统分别和处于确定状态的第三个系统达到热平衡,则这两个系统彼此也将处于热平衡。
这个热平衡规律称为热力学第零定律。
此定律给出了温度的概念和比较温度的方法。
2.状态函数状态是系统的一切宏观性质(质量、温度、压力、密度和热力学能等)的综合表现。
第二章热力学第一定律

第二章 热力学第一定律(一)主要公式及其适用条件1、热力学第一定律的数学表示式∆U = Q + W 或 d U = đQ + đW规定系统吸热为正,放热为负;系统得功为正,对环境(或外界)作功为负。
式中U 称为热力学能(以前称为内能)。
上式适用于封闭系统一切过程能量的衡算。
2、体积功 (1)定义式đW = -p (环)V d 或W = ∑đW = -()V p d 21⎰环上式适用于一切过程体积功的计算。
(2)W r = -⎰21d V p式中:p 为系统的压力,W r 为可逆过程的体积功。
此式适用于封闭系统一切可逆过程体积功的计算。
(3)W = - p (V 2 - V 1) = nR(T 2 - T )此式适用于物质的量n 恒定的理想气体恒压变温过程。
(4)W = - p (环)(V 2 - V 1)此式适用于封闭系统恒外压过程。
(5)W = - nRT ln((V 2/ V 1) = - nRT ln((p 2/ p 1) 此式适用于一定量的理想气体恒温可逆过程。
(6)W = - p (V 2 - V 1) = -∆n g RT 式中∆n g 为过程前后气体物质量的增量。
此式适用于液态或固态物质所占体积与气态物质所占体积相比较可以忽略不计,气体为理想气体,恒压、恒温化学反应过程或相变过程。
(7)W = ∆U = nC V , m (T 2 - T )此式适用于n 、C V , m 恒定,理想气体绝热过程,不论过程是否可逆皆适用。
3、热力学能变(1)∆U =⎰21d m V,T T T nC = nC V , m (T 2 - T )此式适用于n 、C V , m 恒定的理想气体,单纯p 、V 、T 变化的一切过程;或者n 、C V , m 、V 恒定的任意单相纯物质的变温过程。
(2)∆U = Q V此式适用于非体积功W ' = 0、d V = 0的封闭系统所进行的一切过程。
4、焓的定义H = U + pV 5、焓变(1)∆H = ∆U + ∆(pV )式中∆(pV ) = p 2V 2 - p 1V 1,即系统p 与V 乘积的增量,只有恒压过程的∆(pV )在数值上才等于过程的体积功。
物理化学第四版第二章--热力学第一定律2013

7
状态函数的数学特征:Z是状态函数,
且 Z f ( x, y) ,则
dZ是全微分
dZ pdx Qdy
Z
Z2dZ
Z1
Z2
Z1
dZ 0
–
积分与路径无关,故可设计过程求其变化
(1)如关闭进出料阀,将料液及上空的气相作为系统 ________ (2)如反应釜一边进料、一边出料,仍以料液及上空的气相为系
统 ________。 (3)若把整个车间(动力电)、锅炉送气全划为系统 ________。
2024/8/23
6
2、状态和状态函数
状态:系统一切性质的总和
•状态函数:各种性质均为状态的函数
(ⅶ )自由膨胀过程(向真空膨胀过程)
如图所示, Psu=0
图1-1 气体向真空膨胀(自由膨胀)
气体
真空
18
§2.2 热力学第一定律
本质:能量的转化和守恒,是自然界 的基本规律。表示系统的热力学状态 发生变化时系统的热力学能与过程的 热和功的关系。
19
1.热和功
热与功是系统状态变化过程中和环境之间 进行能量交换的两种形式,它们随过程产 生;因过程而异,称为过程变量。
为热力学数据的建立、测定及应用,提供了理
论依据。
例:
C(石墨)
1 2
O2
(g)
Q V,a
CO
(g)
()
Q V,b
CO2
(g)
(b)
Q V,c
C(石墨) O2 (g) CO 2 (g)
(c)
2.2 热力学第一定律

第二章 热力学第一定律 无论是何种表述,它们都是等价 的,从本质上反映了同一个规律,即 能量既不可以无中生有,也不可以消 灭,只能从一种形式转化为另一种形 式,在转化中能量的总值不变。能量 守恒原理是人们经过长期大量的实践, 总结了失败的教训和成功的经验之后 才认识到的,它是具有普遍意义的自 然规律之一。数百年来,有许多人曾 经热衷于设计制造第一类永动机,结 果无一例外均以失败而告终,其原因 就在于这种设想违背了能量守恒原理。 将能量守恒原理应用于宏观的热力学 系统,就成为热力学第一定律。
在热力学的研究中,经常遇到体积功的求算问题。此 时需对体积功的定义式作定积分:
(i) 等容过程,特点是dV=0:
(ii) 自由膨胀过程,特点是psu=0:
第二章 热力学第一定律 (iii) 恒外压过程,特点是psu=常数:
(iv) 等压过程,特点是p=psu=常数:
(v) 热力学可逆过程,特点是psu=p±dp。
其绝对值相当于图中阴影面积。 过程(iii)就属于准静态过程,显然由于过程推动力无限 小,过程的进展必定无限缓慢,所历时间无限长。不难看 出,在等温条件下,在无摩擦的准静态过程中,系统对环 境作的准静态过程还有一个重要的特点:系统可由 该过程的终态按原途径逆向变化,直到系统和环境都恢复 到原过程的初始状态。例如,设想由过程(iii)的终态出发, 在活塞上每次添加一颗粉末,环境的压力就增大dp,即增 为(p+dp),这时气体就压缩dV。在等温条件下,逐次添加粉 末,就可使气缸中气体恢复到初始状态。在该逆向变化的 过程中,环境对系统作功: 由于是沿原途径逆向积分,因而其功的绝对值与过 程(iii)相等。显然,这一压缩过程使系统和环境均复原为 初始状态。 上述压缩过程也是准静态过程。对于等温条件下压缩 过程来说,无摩擦力的准静态过程中环境对系统所作的 功为最小。
物理化学第2章热力学第一定律

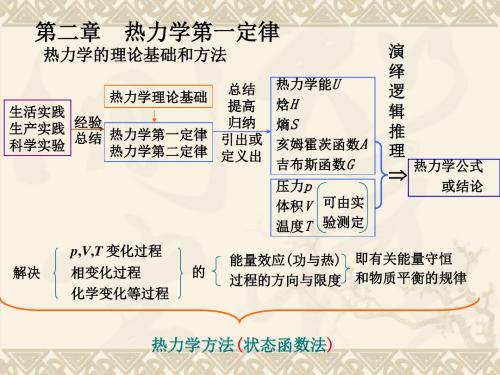
第二章热力学第一定律2.1 热力学的理论基础与方法1.热力学的理论基础热力学涉及由热所产生的力学作用的领域,是研究热、功及其相互转换关系的一门自然科学。
热力学的根据是三件事实:①不能制成永动机。
②不能使一个自然发生的过程完全复原。
③不能达到绝对零度。
热力学的理论基础是热力学第一、第二、第三定律。
这两个定律是人们生活实践、生产实践和科学实验的经验总结。
它们既不涉及物质的微观结构,也不能用数学加以推导和证明。
但它的正确性已被无数次的实验结果所证实。
而且从热力学严格地导出的结论都是非常精确和可靠的。
不过这都是指的在统计意义上的精确性和可靠性。
热力学第一定律是有关能量守恒的规律,即能量既不能创造,亦不能消灭,仅能由一种形式转化为另一种形式,它是定量研究各种形式能量(热、功—机械功、电功、表面功等)相互转化的理论基础。
热力学第二定律是有关热和功等能量形式相互转化的方向与限度的规律,进而推广到有关物质变化过程的方向与限度的普遍规律。
利用热力学第三定律来确定规定熵的数值,再结合其他热力学数据从而解决有关化学平衡的计算问题。
2.热力学的研究方法热力学方法是:从热力学第一和第二定律出发,通过总结、提高、归纳,引出或定义出热力学能U,焓H,熵S,亥姆霍茨函数A,吉布斯函数G;再加上可由实验直接测定的p,V,T等共八个最基本的热力学函数。
再应用演绎法,经过逻辑推理,导出一系列的热力学公式或结论。
进而用以解决物质的p,V,T变化、相变化和化学变化等过程的能量效应(功与热)及过程的方向与限度,即平衡问题。
这一方法也叫状态函数法。
热力学方法的特点是:(i)只研究物质变化过程中各宏观性质的关系,不考虑物质的微观结构;(ii)只研究物质变化过程的始态和终态,而不追究变化过程中的中间细节,也不研究变化过程的速率和完成过程所需要的时间。
因此,热力学方法属于宏观方法。
2.2 热力学的基本概念1.系统与环境系统:作为某热力学问题研究对象的部分;环境:与系统相关的周围部分;按系统与环境交换内容分为:(1)敞开系统(open system) :体系与环境间既有物质交换又有能量交换的体系。
第二章热力学第一定律

中南大学航空航天学院
热一律的文字表达式
热一律: 能量守恒与转换定律
进入系统 的能量
-
离开系统 的能量
=
系统内部储存 能量的变化
中南大学航空航天学院
§2.2 闭口系能量方程
一般式 Q = dU + W Q = U + W q = du + w q = u + w
Q0
W 0
Q
U Q W
空 调
Q W
T
中南大学航空航天学院
§ 2.3 开口系能量方程
min 能量守恒原则
进入系统的能量
uin
1 2 cin 2 gzin
离开系统的能量
Wnet
mout uout 1 2 cout 2 gzout
=
系统储存能功的引入
门窗紧闭房间用电冰箱降温
以房间为系统 闭口系能量方程 绝热闭口系 Refrigerator Icebox
电 冰 箱
Q U W
Q0
W 0
U W 0
T
中南大学航空航天学院
门窗紧闭房间用空调降温
以房间为系统 闭口系能量方程 闭口系 Aircondition
Q U W
推进功(pv)
几种功的关系
1 2 wt c g z ws 2
q h wt u ( pv) wt
q u w
w ( pv) wt
△ c2/2
ws
做功的根源 w
中南大学航空航天学院
wt
△(pv)
g△ z ws
对功的小结
1、闭口系,系统与外界交换的功为容积变化功w 2、开口系,系统与外界交换的功为轴功ws 3、一般情况下忽略动、位能的变化
(完整word版)热力学第一定律复习题(13,10)

第二章 热力学第一定律1. :系统与环境间由于温差而交换的能量。
是物质分子无序运动的结果。
是过程量。
:除热以外的、在系统与环境间交换的所有其它形式的能量。
是物质分子有序运动的、恒压条件下,△H =Q p 。
系统状态变化时,计算系统与环境间交换的能量) 恒压反应热与恒容反应热的关系:Q p =Q V +∑νB (g)RT1B ()(B,)m f mT H T ν=∑∆21,21);()()Tm p r p m r m r m m T C H T H T dT =∆∆=∆+∆⎰(a) 升高(b)降低(c) 不变(d)难以确定(答案) c (△U=Q+W,∵p外=0 , ∴W=0 ,又∵绝热,∴Q=0,所以△U=0)因为是真空故不做功,又因为是绝热故无热交换,故△U=0.温度不变。
2。
当热力学第一定律写成d U = δQ–p d V时,它适用于(a). 理想气体的可逆过程(b)。
封闭体系的任一过程(c). 封闭体系只做体积功过程(d)。
封闭体系的定压过程(答案) c (W=W体+W非,当W非=0时,W体= -pdV)3.对热力学可逆过程,下列说法中正确的是(a)过程进行的速度无限慢(b) 没有功的损失(c)系统和环境可同时复原(d)不需环境做功(答案) c可逆过程:体系经过某一过程从状态(1)变到状态(2)之后,如果能够使体系和环境都恢复到原来的状态而未留下任何永久性的变化,则该过程称为热力学可逆过程.否则为不可逆过程特征:①状态变化时推动力与阻力相差无限小,体系与环境始终无限接近于平衡态;②过程中的任何一个中间态都可以从正、逆两个方向到达;③体系变化一个循环后,体系和环境均恢复原态,变化过程中无任何耗散效应;④等温可逆过程中,体系对环境作最大功,环境对体系作最小功。
⑤在可逆过程中,由于状态变化时推动力与阻力相差无限小,所以完成过程所需的时间为无限长。
4.对于封闭体系来说,当过程的始态与终态确定后,下列各项中哪一个无确定值(a) Q(b)Q + W(c) W(当Q = 0时) (d) Q(当W = 0时)(答案) a (△U=Q+W)5.对于孤立体系中发生的实际过程,下列关系中不正确的是(a) W = 0 (b) Q = 0(c)ΔU= 0 (d) ΔH = 0(答案) d (孤立体系? △U=Q+W)6.对于内能是体系状态的单值函数概念,错误理解是(a) 体系处于一定的状态,具有一定的内能(b)对应于某一状态,内能只能有一数值不能有两个以上的数值(c)状态发生变化,内能也一定跟着变化(d) 对应于一个内能值,可以有多个状态(答案) c (理想气体等温过程,△U,即内能不变;绝热可逆过程△S=0)7.凡是在孤立体系中进行的变化,其ΔU和ΔH的值一定是(a)ΔU〉0 ,ΔH > 0 (b)ΔU = 0 ,ΔH = 0(c)ΔU < 0 , ΔH〈0 (d) ΔU = 0 ,ΔH大于、小于或等于零不确定(答案)d8. 封闭体系从A态变为B态,可以沿两条等温途径:甲)可逆途径;乙)不可逆途径,则下列关系式⑴ΔU可逆> ΔU不可逆⑵W可逆 > W不可逆⑶ Q 可逆 Q 不可逆 ⑷ ( Q 可逆 - W 可逆) 〉 ( Q 不可逆 - W 不可逆)正确的是(a) (1),(2) (b ) (2),(3) (c ) (3),(4) (d) (1),(4)(答案) b (④等温可逆过程中,体系对环境作最大功,环境对体系作最小功.)9. 理想气体自由膨胀过程中(a)。
第二章 热力学第一定律

第二章热力学第一定律基本公式功: δW = -P外dV热力学第一定律: dU =δQ + δW ΔU = Q + W焓的定义: H ≡ U + PV热容的定义: C=limΔT→0δQ/ ΔT等压热容的定义: C P =δQ P /dT =(∂H/∂T)P等容热容的定义: C V =δQ V /dT =(∂U/∂T)V任意体系的等压热容与等容热容之差: C P - C V = [P + (∂U/∂V)T] (∂V/∂T)P 理想气体的等压热容与等容热容之差: C P - C V = nR理想气体绝热可逆过程方程: γ = C P / C VPVγ-1 =常数T Vγ-1 =常数P1-γTγ=常数理想气体绝热功: W =C V(T1 – T2 ) W = P1V1 – P2V2 /γ-1热机效率: η = W/Q2可逆热机效率: η = T2 – T1 / T2冷冻系数: β= Q1′/W可逆制冷机冷冻系数: β = T1 / T2 – T1焦汤系数: μ = ( ∂T/ ∂P)H = - (∂H/∂P)/C P反应进度: ξ= n B – n B0 / νB化学反应的等压热效应与等容热效应的关系: Q P = Q V + ΔnRT当反应进度ξ= 1 mol 时Δr H m= Δr U m +ΣBνB RT化学反应等压热效应的几种计算方法:Δr H m⊖=ΣBνBΔf H m⊖(B)Δr H m⊖=ΣB (єB )反应物 - ΣB(єB )产物Δr H m⊖= -ΣBνBΔC H m⊖(B)反应热与温度的关系: Δr H m(T2) =Δr H m(T1) + ∫21T TΔr C P dT表 1-1 一些基本过程的W 、Q、△U 、△H 的运算过程W Q △U △H 理想气体自由膨胀0 0 0 0 理想气体等温可逆 -nRTLnV2/V1 -nRTLnV2/V10 0任意物质等容可逆理想气体0∫C V dT∫C V dTQ v∫C V dT△U + V△P∫C P dT任意物质等压可逆理想气体-P外△V-P外△V∫C P dT∫C p dTQ P - P△V∫C V dTQ P∫C P dT理想气体绝热过程C V(T2 – T1)1/γ-1(P2V2-P1V1) 0 ∫C V dT ∫C P dT理想气体多方可逆过程PVδ=常数n R/1-δ(T2-T1) △U + W ∫C V dT ∫C P dT 可逆相变(等温等压) -P外△V Q P Q P -W Q P化学反应(等温等压) -P外△VQ PQ P – WΔr H m=Δr U m+ΣBνB RTQ PΔr H m⊖=ΣBνBΔf H m⊖(B) 例题例1 0.02Kg 乙醇在其沸点时蒸发为气体。
热力学第二章第一定律

对于式:
q
h
1 2
cf2
gz
wi
注意:q和wi分别是1kg工质进入系统后,系统从外界吸入的
热量和在系统内部所作的功。除的m不是系统的质量。
对于微元过程 ,稳定流动能量方程写成
δQ
dH
1 2
mdcf2
mgdz
δWi
δq
dh
1 2
dcf2
gdz
δwi
焓
焓:H=U+pV ,单位:J或kJ
注意:区分各截面间参数可不同。
设在τ时间段内有m1千克工质流进系统,同时 m2千克的工质流出系统。
mCV 0 qm1 qm2 m1 m2 m
在 时间段内进入系统的能量
在 时间段内离开系统的能量
Wi
m
u2
1 2
cf22
gz2
mp 2 v2
Wi
m
分析开口系统时,除了能量平衡外,还必须考虑质量平衡:
进入系统的质量-离开系统的质量=系统质量的变化
推动功
因工质出、入开口系统而 传递的功,叫推动功(推进 功) 。
W推 = p A l = pV w推= pv
A p pV
l
对推动功的说明
1、与宏观流动有关,流动停止,推动功不存在;
2、作用过程中,工质仅发生位置变化,无状态变化;
δQ δW
7. 热力学第一定律解析式的适用条件:
q u w
①闭口系统;②任何工质;③任何过程
δq δw
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章热力学第一定律1、如果一个系统从环境吸收了40J 的热,而系统的热力学能却增加了200J ,问系统从环境中得到了多少功?如果该系统在膨胀过程中对环境作了 10kJ 的功,同时收了 28kJ 的热,求系统的热力学能变化值。
解:根据U Q W 热力学第一定律,可知W U Q (200 40) 160J (系统从环境吸热,Q 0 )U Q W 28 10 18kJ (系统对环境做功,W 0 )2、有 10mol 的气体(设为理想气体),压力为 1000kPa ,温度为 300K ,分别求出等温时下列过程的功:(1)在空气中压力为 100kPa 时,体积胀大1dm3;(2)在空气中压力为 100kPa 时,膨胀到气体压力也是100kPa ;(3)等温可逆膨胀至气体的压力为100kPa ;解:(1)外压始终维持恒定,系统对环境做功W p e V100 103 1 10 3 100J(2)10mol,300K10mol,300K1000kPa,V 1100kPa,V 2W p e V p e (V2 V1 ) p e(nRT2nRT1) nRTp e (11 )p2 p1 p2 p110 8.314 300 100 103 ( 1 1103 ) 2.2 104 J100 103 1000(3)等温可逆膨胀:V2p e dV nRT ln V2 nRT ln p1WV1 V1 p210 8.314 300 ln 1000 5.74 10 4 J1003、 1mol 单原子理想气体,C V ,m 3R ,始态(1)的温度为273K ,体积为 22.4dm3,2经历如下三步,又回到始态,请计算每个状态的压力, Q ,W和U 。
(1)等容可逆升温由始态(1)到 546K 的状态( 2);(2)等温( 546K )可逆膨胀由状态( 2)到44.8dm3的状态( 3);(3)经等压过程由状态( 3)回到始态( 1);解:(1)等容可逆升温过程:W P e V 0UQ WQ VT 2 nC V ,m dT 138.314 546 273 3404.58 JT 12(2)等温可逆膨胀过程:U 0WnRT lnV 21 8.314 546ln 44.83146.50JV 122.4Q W 3146.50J(3)等压过程 :WP e VnRT V 1 V 2 1 8.314 273 22.4 44.8 10 3 2269.72 JV 1 22.4 10 3Q pH T 2nC P ,m dT n 3 R 273 546 5 8.314 273 5674.31J T 1 R 12 2UQ W 5674.31 2269.72 3404.59 J4、在 291K 和 100kPa 下, 1molZn (s) 溶于足量稀盐酸中, 置换出 1molH 2 ( g) ,并放热 152kJ 。
若以 Zn 和盐酸为系统,求该反应所做的功及系统热力学能的变化。
解: Zn( s) 2HCl (l ) ZnCl 2 (l ) H 2 ( g)在 291K 和 100kPa 下的条件下发生以上反应,生成 H 2 ( g)Wp e (V 2 V 1 )p e V H 2 ( g )p enRTnRTp1 8.314 291 2419.J , Q103 J该反应为放热反应, Q 0152U Q W152 10 3 2419 1.544 10 5 J5、在 298K 时,有 2molN 2 ( g ) ,始终态体积为体积为 15dm 3 ,保持温度不变, 经下列三个过程膨胀到 50dm 3 ,计算各过程的 U , H ,W 和 Q 的值。
设气体为理想气 体。
(1)自由膨胀; (2)反抗恒定外压 100kPa 膨胀; (3)可逆膨胀; 解:( 1)自由膨胀过程 , 因为理想气体的 U 和 H 都只是温度的函数,所以在等温下 U 0 , H 0 ,由于 p e 0 , W p e V 0又根据 UQ W 可知 Q0 。
(2)反抗恒定外压膨胀100 10 3 (50 15) 10 3Wp e Vp e (V 2V 1 )3500 J因为理想气体的 U 和 H 都只是温度的函数,所以在等温下U 0 ,H 0,Q W 3500J 。
(3)等温可逆膨胀,等温过程U 0 , HWV 2 nRT lnV 2p e dVV 1V 12 8.314 298 ln505965.86J15U Q W , QW 5965.86J6、在水的正常沸点( 373.15K ,101.325kPa ),有1molH 2O (l ) 变为同温同压的 H 2 O( g ) ,已知水的摩尔汽化焓变值为vap H m40.69kJ mol 1 ,请计算该变化的 Q , U , H 的值各为多少 ?解 :相变在 373.15K ,101.325kPa 等温等压下进行 ,H Q p nvapHm40.69 1 40.69( kJ )W p(V g V l )nRT 1 8.314 3733.1(kJ ) UQ W 40.693.1 37.59( kJ )7.理想气体等温可逆膨胀, 体积从 V 1 膨胀大到 10V 1 ,对外作了 41.85kJ 的功,系统的起始压力为 202.65 kPa 。
(1)求始态体积 V 1 ;(2)若气体的量为 2mol ,试求系统的温度。
解:(1)等温可逆过程WnRT lnV 2V 1理想气体状态方程 pVnRTW两式联合求解 pV 1lnV2V 1V 1W 41.85 1030.089m 3p lnV 2 202.65 103 ln10V 1V 1V 1(2)同理根据等温可逆过程 WnRT lnV 2可得V 1TW 41.85 103nR lnV 21093K2 8.314ln10V 1V 1V 18、在 100kPa 及 423K 时,将 1molNH 3 ( g) 等温压缩到体积等于 1dm 3 ,求最少 需做多少功?(1) 假定是理想气体;(2)假定符合 van der Waals 方程式。
已知 van der Waals 常数 a=0.417Pa6g-2gmmol解:(1)假定是理想气体,那么气体在等温可逆压缩中做功最小WnRT lnV 2V 11mol 8.314J gmol 1 423Kln 10 10 3 m 335 10 3 m 34405.74J可根据理想气体状态方程V 1nRT 1mol 8.314 J gmol1423 KP 1100 10 3Pa3335 10 m代入上式方可求解。
(2)假定符合 van der Waals 方程,方程整理后,可得V m 3 V m 2 b RTV m a ab0 代入数据PP PV m 3 3.472 10 2V m 2 4.17 10 6V m 1.547 10 10解三次方程后得V m3 335 10 mV 2 nRTan 2WdVV 1V nb V 2nRT lnV 2nb an 211V 1nbV 2V 11mol 8.314 J gmol1300 K ln1010 3 m335 10 3 m 31mol3.71 10 5 m 3 1mol3.71 10 5 m 3molmol1 10.417 Pa m 6 mol 1 1211 4385.21 J0.01m 30.35 m 39、已知在 373K 和 100kPa 压力时, 1kgH 2O (l ) 的体积为 1.043dm 3 ,1kgH 2O ( g ) 的体积为 1677dm 3 ,H 2O(l ) 的摩尔汽化焓变值VapH40.69kJ mol 1 ,当 1molH 2O (l ) 在 373K和 100kPa 压力时完全蒸发成 H 2O ( g) ,求:(1)蒸发过程中系统对环境所做的功;(2)假定液态水的体积可忽略不计,试求蒸发过程中系统对环境所做的功; (3)假定把蒸汽看作理想气体,且略去液态水的体积,求系统所做的功;(4)求( 1)中变化的Vap U m 和 Vap H m ;(5)解释何故蒸发的焓变大于系统所做的功。
解:(1)蒸发过程中系统对环境所做的功W p e (V gV l ) 100 103 Pa (1677 10 3 1.043 10 3 )m 3 kg 1(18 10 3 )kg3016.72J(2)假定液态水的体积可忽略不计,V l 0W p e V g nRT100 103 1677 10 3 18 10 33018.60J3018.6 3016.72 100% 0.062%3016.72 (3)蒸汽看作理想气体,则 pV nRT液态水的体积可忽略不计, V l 0Wp e V gnRT1mol 8.314J mol 1 K 1 373K3101.12J(4) Q p ,mVapHm40.69kJ mol 1VapUQ W 40.69 1 103 ( 3016.72) 37.67 103 J mol 1n137.67 103 J mol 1(5)在蒸发过程中,用于系统对环境做膨胀功的部分很少,吸收的大部分热量用于提高系统的热力学能。
10、1mol 单原子理想气体,从始态:273K 、 200kPa ,到终态: 323K 、100kPa ,通过两个途径:(1)先等压加热至 323K ,再等温可逆膨胀至 100kPa ;(2)先等温可逆膨胀至 100kPa ,再等压加热至 323K 。
请分别计算两个途径的 Q , W , U 和 H ,试比较两种结果有何不同,说明为什么?解:(1)因为单原子理想气体 C V ,m3R , C p ,m5R 过程如图所示。
2 21mol[ p ]1mol[ T ]1mol273K 323K 323K (1)(2)200kPa200kPa100kPa① 等压升温W 1p e (V 2 V 1 )p(nRT2nRT1)ppnR(T 2 T 1 ) 1 8.314 (323 273)415.7( J )H 1 Q pT 21 5 8.314 (323 273) 1039( J)nC p ,m dT 1T 12 1 3U 1 T 2nC v, m dT 8.314 (323 273) 623.6(J )T 1 2② 等温可逆W 2nRT lnV 2RT ln p 1 1 8.314 323 ln 2001861(J )V 1p 2 100 U 2 0 , H 2Q 2W 2 1861(J )W W 1 W 2 2277( J )Q Q 1 Q 2 2900( J )U U 1 U 2 623.6( J )HH 1H 2 1039( J )(2)1mol[T ] 1mol[ p ] 1mol273K323K323K (1)(2)200kPa200kPa100kPa①等温可逆W 1nRT lnV 2RT lnp 11 8.314 273 ln2001573( J )V 1p 2100U 1 0 , H 1 0Q 1W 1 1573( J )②等压升温W 2p e (V 2 V 1 )p(nRT 2nRT1)ppnR(T 2 T 1) 1 8.314 (323 273) 415.7( J )H 2 Q pT 21 5 8.314 (323 273) 1039(J )nC p , m dT1T 1213U 2T 28.314 (323 273) 623.6(J )nC v, m dTT 12W W 1 W 21989( J )Q Q 1 Q 2 2613( J )U U 1U 2 623.6( J )HH 1H 2 1039( J )比较两种结果, U 和 H 的值相同,而 Q 和 W 值不同,说明 Q 和 W 不是状态函数,它们的数值与所经过的途径和过程有关, 而 U 和 H 是状态函数, 无论经过何种途径, 只要最终状态相同, U 和 H 的数值必然相同。
