第2章解析函数作业

合集下载

第二章解析函数

第二章解析函数•复变函数的导数•解析函数的概念•初等解析函数复函数的求导法则由于复变函数中导数的定义与一元实变函数中导数的定义在形式上完全一致, 并且复变函数中的极限运算法则也和实变函数中一样, 因而实变函数中的求导法则都可以不加更改地推广到复变函数中来, 且证明方法也是相同的.例2证明()2f z x yi =+在复面内处处连续，但处处不可导.证明对复平面内任意点z , 有()()f z z f z +Δ−2.x yi =Δ+Δ()2()2x x y y i x yi =+Δ++Δ−−故0lim[()()]0.z f z z f z Δ→+Δ−=这说明()2f z x yi =+在复面内处处连续.000()()() (), f z z f z f z z z z ρ′+Δ−=Δ+ΔΔ,)()(lim 000z f z z f z =Δ+→Δ所以lim ()0,z z ρΔ→Δ=再由即()f z 在0z 处连续.反之, 由例2知, 处处不可导，()2f z x yi =+但处处连续。

例5问题：对函数f (z ) = u (x ,y ) + iv (x ,y )，如何判别其解析（可导）性？换句话说：()(),f z u v 的解析可导与的偏导数之间有什么关系？解析函数的性质：(1)两个解析函数的和、差、积、商仍为解析函数；(2)两个解析函数的复合函数仍为解析函数；(3)一个解析函数不可能仅在一个点或一条曲线上解析；所有解析点的集合必为开集。

证明必要性. 若存在，设0()f z ′0()f z a ib ′=+(a , b 是实常数). 因此000()()()f z z f z f z z z α′+Δ−=Δ+Δ12()()()()a ib x i y i x i y αα=+Δ+Δ++Δ+Δ12()a xb y x y αα=Δ−Δ+Δ−Δ21(,i b x a y x y αα+Δ+Δ+Δ+Δ其中12Re , Im .αααα==且当时，0z Δ→120, 0.αα→→0000(,)(,),u u x x y y u x y Δ=+Δ+Δ−0000(,)(,),v v x x y y v x y Δ=+Δ+Δ−则于是有00()().f z z f z u i v +Δ−=Δ+Δ12()u i v a x b y x y ααΔ+Δ=Δ−Δ+Δ−Δ21().i b x a y x y αα+Δ+Δ+Δ+Δ由两个复数相等的条件可得设21.v b x a y x y ααΔ=Δ+Δ+Δ+Δ12,u a x b y x y ααΔ=Δ−Δ+Δ−Δ于是，1(,),(,)..a u x y v x y C R =−−当时，满足条件，().f z z 从而在平面上处处可微，处处解析1(,),(,)0..a u x y v x y y C R ≠−=−当时，仅在直线上满足条件，().f z z 故在平面上处处不解析()00.f z y y =≠从而仅在上可微，在上不可微作业3第89页，第二章习题（一）：2；4（1）（3）；5（2）（4）；7；8（2）（4）；9; 11（1）（3）。

202新数学复习第二章函数导数及其应用8导数与函数的零点问题含解析

课时作业18 导数与函数的零点问题1．设a为实数，函数f（x）＝－x3＋3x＋a.(1)求f(x)的极值;(2)是否存在实数a，使得方程f(x）＝0恰好有两个实数根？若存在，求出实数a的值；若不存在,请说明理由．解：(1)f′（x)＝－3x2＋3，令f′（x)＝0，得x＝－1或x＝1.∵当x∈(－∞,－1)时，f′(x）〈0；当x∈（－1,1）时,f′（x)>0；当x∈(1，＋∞)时，f′（x)〈0,∴f(x）在(－∞,－1），(1，＋∞）上单调递减，在（－1，1)上单调递增．∴f(x)的极小值为f（－1）＝a－2,极大值为f（1)＝a＋2。

（2）方程f（x）＝0恰好有两个实数根,等价于直线y＝a 与函数y＝x3－3x的图象有两个交点．∵y＝x3－3x，∴y′＝3x2－3。

令y′〉0，解得x>1或x〈－1;令y′<0，解得－1<x<1。

∴y＝x3－3x在（－1，1)上为减函数，在(1，＋∞）和(－∞，－1）上为增函数．∴当x＝－1时，y极大值＝2;当x＝1时,y极小值＝－2.∴y＝x3－3x的大致图象如图所示．y＝a表示平行于x轴的一条直线,由图象知，当a＝2或a ＝－2时，y＝a与y＝x3－3x有两个交点．故当a＝2或a＝－2时,方程f（x)＝0恰好有两个实数根．2．已知函数f(x)＝ln x＋错误!,g(x)＝错误!，a∈R。

（1）求函数f(x)的极小值;(2）求证:当－1≤a≤1时，f（x)>g(x)．解：（1)f′（x)＝错误!－错误!＝错误!(x〉0），当a－1≤0，即a≤1时，f′（x)〉0，函数f（x)在（0，＋∞）上单调递增,无极小值；当a－1>0，即a>1时，则当0〈x<a－1时，f′（x)<0，函数f(x)在(0,a－1)上单调递减，当x>a－1时，f′（x)>0，函数f（x)在（a－1，＋∞）上单调递增，故f（x）极小值＝f（a－1)＝1＋ln（a－1)．综上所述,当a≤1时，f(x）无极小值;当a>1时，f（x)极小值＝1＋ln（a－1)．(2）证明:令F（x）＝f（x)－g(x）＝ln x＋错误!－错误!＝错误!（x>0），当－1≤a≤1时，要证f（x）>g(x)，即证F（x)〉0,即证x ln x－a sin x＋1〉0。

第2章解析函数

第2章解析函数2．1 单项选择题2-1 函数)(z f w =在0z 点可导是可微的（）。

（A ）必要但非充分条件（B ）充分但非必要条件（C ）充分必要条件（D ）既非充分条件，也非必要条件 2-2 复变函数)(z f w =在0z 点可导是连续的（）。

（A ）必要但非充分条件（B ）充分但非必要条件（C ）充分必要条件（D ）既非充分条件，也非必要条件2-3 设),,(),()(y x iv y x u z f +=则在),(00y x 点，v u ,均可微是)(z f 在000iy x z +=点可微的（）。

（A ）必要但非充分条件（B ）充分但非必要条件（C ）充分必要条件（D ）既非必要条件，也非充分条件 2-4 )(z f 在000iy x z +=点可导的充分必要条件是（）。

（A ）在),(00y x 点v u ,可导，且满足C-R 条件，既xvy u y v xu ∂∂-=∂∂∂∂=∂∂,在),(00y x 成立（B ））点的一个邻域内可导在（00,)(y x z f（C ）条件可微，且满足）点在（R C v u y x -,,00（D ）条件满足具有连续的偏导数，且）点在（R C v u y x -,,002-5 设那么（）。

,2)(2ix xy z f -=（A ）处处可微)(z f （ B ）处处不可导)(z f（C ）仅在原点可导)(z f （D ）轴上可导仅在x z f )(2-6则若,)( xy,y)(x, v ,0x ,00 x ),(2222220iv u z f y y y x xy y x u o +===⎪⎩⎪⎨⎧=+≠++=函数)(z f （）。

（A ）仅在原点可导（B ）处处不可导（C ）除原点处处可导（D ）处处可微 2-7 若 ). )((,)(z f z z f 则=）仅在虚轴上可导（）处处解析（）仅在原点可导（处处不可导D C B )(A2-8若f(z)=(by ax y x +++22)+)23(y x cxy i ++处处解析，则(),,(=c b a ) (A) (3,2,2) (B) (-2,-3,2) (C) (2,-2,2)(D) (-2,3,2)2-9 u(x,y)与v(x,y)在（00,y x ）点可且满足C-R 条件是)(z f 在000iy x z +=点可导的（）（A ）充分条件（B ）必要但非充分条件（C ）充分但非必要条件（D ）既非必要也非充分条件2-10 u, v 在),(00y x 点具有连续的偏导数，且满足C-R 条件是)(z f 在000iy x z +=点可导的（）（A ）充要条件（B ）必要但非充分条件（C ）充分但非必要条件（D ）既非必要也非充分条件2-11 函数)Im()Re()(z z z f ⋅=在原点（）（A ）可导且连续（B ）连续但不可导（C ）可导但不连续（D ）既不连续也不可导2-12 若y ix xy z f 22)(+=则)(z f （）（A ）仅在直线x y =上可导（B ）仅在直线x y -=上可导（C ）仅在)0,0(点解析（D ）仅在点可导)0,0(2-13 若)(,)(22z f iy x z f 则+=（）（A ）在全平面上解析（B ）仅在直线上可导y x =(C) 仅在直线上可导y x -= （D ）仅在）点可导，（00 2-14 设)()3(3)(2223z f y y x i xyx z f 则-+-=（）（A ）处处解析（B ）仅在实轴上可导 (C) 仅在直线上可导32=y （D ）仅在直线上可导或320==y y2-15 若的导数问题是则关于发)(),3(3)(3223z f y y x i xy x z f -+-=（（A ）0)0()(='f z f 仅在原点可导且（B ）xy i y x z f z f 633)()(22+-='处处解析，且（C ）xy i y x z f z f 633)()(22--='处处解析，且（D ）xy i x y z f z f 633)()(22+-='处处解析，且2-16 方程,1-=z e 则此方程解为（）（A ）空集（B ）)12(-=k z π（k 为整数）（C ）I K Z π)12(-= （D ）πI Z = 2-17 若21z z e e =，则( )(A) =2z (B)π 1z =2z +2k π (C) 1z =2z +ik π (D) 1z =2z -2ik π ２-18关于复数的对数函数，下面公式正确的是（）（A ）Ln (1z 2z )=Ln 1z + Ln 2z (B) Ln (1z 2z )=Ln 1z + Ln 2z (C) Ln =2z 2Ln z (D) Ln =2z 2Ln z 2-19Ln(-1)和它的主值分别是（）（A ） Ln(-1)=(k+1/2)πi,(k 为整数)主值Ln(-1)＝０（B ） Ln(-1)＝(２k-1)πi, 主值Ln(-1)＝πi （C ） Ln(-1)＝(２k-1)πi, 主值Ln(-1)=-πi （D ） Ln(-1)=Ln1+iArg(-1), 主值Ln(-1)=πi 2-20 下面等式正确的是（）(A) Ln(i)=(2k π-2π)i,Ln I=2πi(B) Ln(i)=(2k π+2π)i,Ln I=-2πi(C) Ln(i)=(2k π-2π)i,Ln I=2πi (D) Ln(i)=(2k π+2π)i,Ln I=2πi2-21 下面等式正确的是（）(A) Ln(-2)=Ln2+i (2k-1) πi,Ln(-2)=Ln2 (B) Ln(-2)=Ln2+i (2k+1) πi,Ln(-2)=Ln2 (C) Ln(-2)=Ln2+i (2k-1) πi,Ln(-2)=Ln2+i π (D) Ln(-2)=Ln2+i (2k-1) πi,Ln(-2)=Ln2-i π 2-22设k 为整数，则方程sin z=0的根是（）（A ） z=k πi （B ） z=2k π （C ） z=k π （D ） z=2k π2-23 若k 为整数，则cos z =0的根是（）(A) 2k π+2π(B) k π+2π(C) k π+i2π(D) 2k π+i2π2-24 若k 为整数,则的根是0=shz ( )(A) πk 2 (B) πk (C) πik 2 (D) πik 2-25 若k 为整数，则的根是0=chz （）（A ）i k π2 （B ）i k π （C ）i k π)12(- （D ）π)12(-k 2-26 设=++)2(,12i w z 则（）（A ）822πie （B ）822πie± （C ）8452πie（D ）8452πie±2-27 设421-=z ω，并规定21)0(i -=ω，则ω（0）=（）。

【复变函数】第二章解析函数(工科2版)

(1) f ( z ) = | z |2
2 2 2 解: f ( z ) = | z | = x + y
∴ u( x , y ) = x 2 + y 2 , v ( x , y ) = 0
∂u ∂u ∂v ∂v = 2 x, = 2 y, = 0, =0 ∂x ∂y ∂x ∂y
条件, 由C-R条件 x=0, y=0 , 条件所以在z=0处可导处处不解析. 所以在处可导, 处处不解析处可导
目录
上页
下页
返回
结束
【例3】讨论下列函数的解析性可导性 . 】讨论下列函数的解析性, (1). f ( z ) = x + 2 yi 在复平面上处处不可导, 解：f (z) 在复平面上处处不可导,处处不解析
( 2 ). f ( z ) = z 2
在复平面上处处可导, 解：f (z) 在复平面上处处可导,处处解析 1 ( 3 ). f ( z ) = z 1 解：f ′( z ) = − 2 除 z = 0 外处处可导,处处解析. 外处处可导,处处解析. z 1+ z ( 4 ). f ( z ) = 1− z 2 解：f ′( z ) = 外处处可导,处处解析. 2 除 z = 1 外处处可导,处处解析. (1 − z )
返回结束
目录
上页
下页
内处处为0, 内为一个常数. 【例6】若f'(x)在D内处处为则f(x)在D内为一个常数】在内处处为在内为一个常数 Proof: 由导数的计算公式
∂u ∂v ∂u ∂v f ′( z ) = +i =0 ⇔ = 0, = 0, ∂x ∂x ∂x ∂x
∂u ∂v ∂v ∂u = 0, = 0, f ′( z ) = −i =0 ⇔ ∂y ∂y ∂y ∂y

复变函数论第二章习题全解

第二章解析函数（一）1.证明:0>∃δ,使{}0001/),(t t t t δδ+-∈∀,有)()(01t z t z ≠,即C 在)(0t z 的对应去心邻域内无重点,即能够联结割线)()(10t z t z ,是否就存在数列{}01t t n →,使)()(01t z t z n =,于是有 0)()(lim)(0101001=--='→t t t z t z t z n n t t n此与假设矛盾. 01001),(t t t t t >⇒+∈δ 因为 [])()(arg )()(arg010101t z t z t t t z t z -=--所以 []])()(lim arg[)()(arglim )()(arg lim 0101010101010101t t t z t z t t t z t z t z t z t t t t t t --=--=-→→→因此,割线确实有其极限位置,即曲线C 在点)(0t z 的切线存在,其倾角为)(arg 0t z '.2.证明:因)(),(z g z f 在0z 点解析,则)(),(00z g z f ''均存在.所以 )()()()()()(lim )()()()(lim )()(lim 00000000000z g z f z z z g z g z z z f z f z g z g z f z f z g z f z z z z z z ''=----=--=→→→ 3.证明:()()()()()3322,0,0,,0,00x y x y u x y x y x y ≠⎧-⎪=+⎨⎪=⎩()()()()()3322,0,0,,0,00x y x y v x y x y x y ≠⎧+⎪=+⎨⎪=⎩于是()()()00,00,00,0limlim 1x x x u x u xu xx →→-===,从而在原点()f z 满足C R -条件,但在原点，()()()()()'0,00,0x x u iv u iv f f z z z +-+-=()()()()()()333311i x y i zx y z ⎡⎤+--+⎣⎦=⎡⎤+⎣⎦当z 沿0y x =→时,有()()()'212f f z i z x --+= 故()f z 在原点不可微.4.证明:(1)当0≠z 时,即y x ,至少有一个不等于0时,或有y x u u ≠,,或有y x u u ≠-,故z 至多在原点可微. (2)在C 上处处不满足C R -条件.(3)在C 上处处不满足C R -条件. (4)221yx yix z z z z ++==,除原点外, 在C 上处处不满足C R -条件. 5.解:(1) y x y x v xy y x u 22),(,),(==,此时仅当0==y x 时有 xy v xy u x v y u x y y x 22,22-=-===== 且这四个偏导数在原点连续,故)(z f 只在原点可微. (2) 22),(,),(y y x v x y x u ==,此时仅当y x =这条直线上时有 00,22=-=====x y y x v u y v x u且在y x =这四个偏导数连续,故)(z f 只在y x =可微但不解析. (3) 333),(,2),(y y x v x y x u ==,且 00,9622=-=====x y y x v u y v x u 故只在曲线0212312=-x y 上可微但不解析.(4) 32233),(,3),(y y x y x v xy x y x u -=-=在全平面上有 xy v xy u y x v y x u x y y x 66,33332222-=-=-=-==-=且在全平面上这四个偏导数连续,故可微且解析. 6.证明:(1)y y x x iu v iv u z f D yi x z -=+='=∈+=∀)(0,(2)设().f z u iv =+则()f z u iv =-，由()f z 与()f z 均在D 内解析知,,x y y x u v u v ==-,,x y y x u v u v =-=结合此两式得0x y x y u u v v ====，故,u v 均为常数,故)(z f 亦为常数. (3)若0)(=≡C z f ,则显然0)(≡z f ,若0)(≠≡C z f ,则此时有0)(≠z f ,且2)()(C z f z f ≡,即)()(2z f C z f ≡也时解析函数,由(2)知)(z f 为常数. (4)设().f z u iv =+,若C y x u ≡),(,则0,0≡≡y x u u ,由C R -条件得 0,0≡=≡-=x y y x u v u v 因此v u ,为常数, 则)(z f 亦为常数.7.证明：设,f u iv g i f p iQ =+==+则,,f u iv g v iu =-=-由 ()f z 在D 内解析知,x y y x u v u v ==-从而 ,x x y v y y x p v u Q p v u Qx ==-====- 因而()g z 亦D 内解析.8.解:(1)由32233),(,3),(y y x y x v xy x y x u -=-=,则有 222233,6,6,33y x v xy v xy u y x u y x y x -==-=-=故y x y x v v u u ,,,为连续的,且满足C R -条件,所以()z f 在z 平面上解析,且 22236)33()(z xyi y x i v u z f x x =+-=+='(2) ()()()(),cos sin ,cos sin x x u x y e x y y y v x y e y y x y =-⋅=- ()cos sin cos x x y u e x y y y y v =-+= ()sin sin cos x y x u e x y y y y v =--+=- 故()f z 在z 平面上解析，且()()()'cos 1sin sin 1cos x xf z e y x y y ie y x y y =⋅+-+⋅+-⎡⎤⎡⎤⎣⎦⎣⎦(3)由xshy y x v xchy y x u cos ),(,sin ),(==,则有xchy v xshy v xshy u xchy u y x y x cos ,sin ,sin ,cos =-===故y x y x v v u u ,,,为连续的,且满足C R -条件,所以()z f 在z 平面上解析,且 z xshyi xchy i v u z f x x cos sin cos )(=-=+=' (4)由xshy y x v xchy y x u sin ),(,cos ),(-==,则有xchy v xshy v xshy u xchy u y x y x sin ,cos ,cos ,sin -=-==-=故y x y x v v u u ,,,为连续的,且满足C R -条件,所以()z f 在z 平面上解析,且 z xshyi xchy i v u z f x x sin cos sin )(-=--=+=' 9.证明:设,i z x yi re θ=+=则cos ,sin ,x r y r θθ== 从而cos sin ,sin cos r x y x y u u u u u r u r θθθθθ=+=-+cos sin ,sin cos ,r x y x y v u v v v r v r θθθθθ=+=-+再由11,r r u v v u r rθθ==-，可得,x y y x u v u v ==-，因此可得()f z 在点z 可微且()()()'11cos sin sin cos x y r r f z u iu r u u i r u u r r θθθθθθ=-=--+()()1cos sin sin cos r i u i u rθθθθθ=--+()()cos sin sin cos r r i u i v θθθθ=-++ ()()cos sin r r i u iv θθ=-+ ()()1cos sin r r r r ru iv u iv i zθθ=+=++10.解:(1)x y i x z i e e e 2)21(22--+--== (2)222222y zxyiy zz e e e -+-==(3) 22222211x yi xy ix iyx yx yx y ze eeee--++++===⋅所以22221Re cos x yx y x y z e e ++⎛⎫= ⎪⎝⎭11.证明:(1)因为)sin (cos y i y e e e e e x yi x yi z z +=⋅==+ 因此 )sin (cos y i y e e x z -=而)sin (cos y i y e e e e e x yi x yi z z -=⋅==--,得证.(2)因为 ie e z iziz 2sin --=所以 z ie e i e e z iziz z i z i sin 22sin =+=-=---(3)因为2cos iziz e e z -+=所以z e e e e z iziz z i z i cos 22cos =+=+=--12.证明:分别就m 为正整数,零,负整数的情形证明,仅以正整数为例当1=m 时,等式自然成立. 假设当1-=k m 时,等式成立.那么当k m =时,kz z k z k z e e e e =⋅=-1)()(,等式任成立. 故结论正确.13.解:(1) )1sin 1(cos 333i e e e e i i +=⋅=+(2) ()()()11cos 12i i i i e e i ---+-=()112i i i e e-+++=cos11sin1122e i e e e ⎛⎫⎛⎫=++- ⎪ ⎪⎝⎭⎝⎭14.证明:(1)由于z z g z z f ==)(,sin )(在点0=z 解析且01)0(,0)0()0(≠='==g g f 因此 11cos sin lim0===→z z zz z(2)由于0)(,1)(=-=z g e z f z 在点0=z 解析,且01)0(,0)0()0(≠='==g g f因此 11lim0==-=→z z z z e ze(3)由于z z z g z z z z f sin )(,cos )(-=-=在点0=z 解析, 且1)0(,0)0()0(,0)0()0(,0)0()0(='''=''=''='='==g g f g f g f 因此 3cos 1sin cos 1lim sin cos lim00=-+-=--→→zzz z z z z z z z z 15.证明：2cos iziz e e z -+=)cos()cos(cos nb a b a a +++-+=222)()()()(nb a i nb a i b a i b a i ia ia e e e e e e +-++-+-++++++ =⎥⎦⎤⎢⎣⎡--⋅+--⋅+-+ib bn i ia ib b n i ia e e e e e e 111121)1()1(=)2cos(2sin 21sinnb a b bn ++=右边同理证明(2).16.证明:(1) z i e e i i e e i e e iz zz z z iz i iz i sinh 222)sin()()(=-⋅=-=-=--- (2) z e e e e iz z z iz i iz i cosh 22)cos()()(=+=+=-- (3) z i ie e i e e iz iziz iz iz sin 22)sinh(=-⋅=-=-- (4) z z iz i iz cos )cos()cos()cosh(=-=⋅=(5) z i zz i iz iz iz tanh cosh sinh )cos()sin()tan(===(6) z i zzi iz iz iz tan cos sin )cosh()sinh()tanh(===17.证明:(1) 1)(sin )(cos )(222222=+=+=-iz iz ishz z ch z sh z ch(2) 111sec 2222222=+=+=+zch zsh z ch z sh z ch z th z h (3) )sin()sin()cos()cos()cos()(21212121iz iz iz iz iz iz z z ch -=+=+ 2121shz shz chz chz +=18.证明:(1) xshy i xchy iy x yi x yi x z cos sin )sin(cos )cos(sin )sin(sin +=+=+= (2) xshy i xchy iy x yi x yi x z sin cos )sin(sin )cos(cos )cos(cos +=-=+= (3) y x y xsh y xch xshy i xchy z 22222222sinh sin cos sin cos sin sin +=+=+= (4) y x y xsh y xch xshyi xchy z 22222222sinh cos sin cos sin cos cos +=+=-=19.证明: chz e e e e shz zz z z =+='-='--2)2()( shz e e e e chz zz z z =-='+='--2)2()( 20.解:(1) )31arg(31ln )31ln(i i i i z +++=+= )23(2ln ππk i ++= ),1,0( ±=k(2)由于2ln iz π=,则有i i e z i=+==2sin2cos2πππ(3)由于)2(1ππk e e i z +=-=,故)2(ππk i z +=(4)z z sin cos -=,即1tan -=z ,所以ππk i i i z +-=+-=411ln21 (5) 设,z x iy =+由12tgz i =+得()()sin 122cos iz iz iz iz zi e e i e e z--=+→-=-+ 2255iz i e →=-+22cos 25y e x -→=-，1sin 25x =41ln 5,54y e y -→==且1112,222tg x x arctg π⎡⎤⎛⎫=-=-+ ⎪⎢⎥⎝⎭⎣⎦11ln 5224z arctg i π⎡⎤⎛⎫→=-++ ⎪⎢⎥⎝⎭⎣⎦21.证明:因)1arg(1ln )1ln()1ln(-+-=-=-θθθi i i re i re re z ,所以)cos 21ln(21)sin ()1(ln 1ln )]1Re[ln(222θθθθr r r re re z i i -+=+-=-=- 22.解: 32)(3)()(πθk z ik ez r z w +=,)2,1,0;2)(0;(=<<∈k z G z πθ利用i i w -=)(定2,=k k ,再计算)(2i w -23.解: 2,22ππii e i e ==-,由32)2(-=-w 定1,=k k ,再计算i e i w π451)(=24.解: )24(2ln )]2)1(arg(1[ln )1ln()1(πππk i k i i i i i i ieeei +-+++++===+)24(2ln ππk i ee+-⋅= ),2,1,0( ±±=kππk i k i i i i e e e e 23ln )]23(arg 3[ln 3ln 3-++⋅=== ),2,1,0( ±±=k25.解:z 在z 平面上沿0=z 为圆心,1>R 为半径的圆周C 从A 走到B ,经过变换4z w =,其象点w 在w 平面上沿以0=w 为心,14>R 为半径的象圆周从A '走到B ',刚好绕1+=w w 的支点-1转一整周,故它在B '的值为B w '+1.因此 1)()(4+-=-=R z f z f AB.26.证明：()f z = 0，1，∞由于 3|12+，故()f z 的支点为0,1z =，因此在将z 平面沿实轴从0到期割开后，就可保证变点z 不会单绕0或者说转一周，于是在这样割开后的z 平面上()f z 就可以分出三个单值解析分支. 另由已知 ()arg f z π=得()()arg c i f z i f i e π∆=()2arg 1arg 3c c i z z ⎡⎤∆-+∆⎣⎦=32342i ππ⎡⎤+⋅⎢⎥⎣⎦=712i π=.(二)1.证明:由()21z f z z =-得()()2'2211z f z z +=-，从而于是()f z 在D 必常数()()()()()()22'2222111111z z f z z z f z z z z+-+⋅==---()4242121Re mz I z i z z-+=+- 所以 ()()4'421Re 12Re zf z z f z z z ⎛⎫-⋅= ⎪ ⎪+-⎝⎭由于1z <，因此410,z ->且()24422212Re 1210z z z z z+-≥+-=->故()()'Re 0f z z f z ⎛⎫⋅> ⎪ ⎪⎝⎭.2.证明:同第一题221Im 2111)()(1zzi z z z z f z f z -+-=-+='''+. 3.证明:题目等价域以下命题:设1,E E 为关于实轴对称的区域,则函数在E 内解析)(z f ⇒在1E 内解析.设)(z f 在E 内解析,对任意的10E z ∈,当1E z ∈时,有E z E z ∈∈,0,所以 )()()(lim )()(lim0000000z f z z z f z f z z z f z f z z z z '=--=--→→ 这是因为)(z f 在E 内解析,从而有)()()(lim0000z f z z z f z f z z '=--→,由0z 的任意性可知, )(z f 在1E 内解析. 4.证明:(1)由于)(21),(21z z iy z z x -=+=,根据复合函数求偏导数的法则,即可得证. (2))(21)(21x vy u i yv x u z v i z u z f ∂∂+∂∂+∂∂-∂∂=∂∂+∂∂=∂∂所以x vy u y v x u ∂∂-=∂∂∂∂=∂∂,,得0=∂∂zf 5.证明: x y sh y sh x y xch yi x z 222222sin )sin 1(sin )sin(sin +=-+=+= 所以 z x y sh shy sin sin 22=+≤ 而 z y shy Im =≥ ,故左边成立.右边证明可应用z sin 的定义及三角不等式来证明. 6.证明:有 R ch y ch y sh y sh x z 2222221sin sin ≤=+≤+= 即 chR t ≤sin又有 R ch y ch y sh y x z 2222221sinh cos cos ≤=+≤+= 7.证明:据定义,任两相异点21,z z 为单位圆1<z ,有212221212121)32()32()()(z z z z z z z z z f z f -++-++=--0112222121=-->--≥++=z z z z 故函数)(z f 在1<z 内是单叶的.8.证明:因为)(z f 有支点-1,1,取其割线[-1,1],有 (1) 10182)(,8)(arg ie c ei f z f ππ-=-=∆(2) i c c e i f z f i z f 852)(,85)(arg ,811)(arg 32πππ=--=∆-=∆ 9.解: 因为)(z f 有支点∞±,,1i ,此时支割线可取为:沿虚轴割开],[i i -,沿实轴割开],1[+∞,线路未穿过支割线,记线路为C ,)]arg())(arg()1arg([21)(arg i z i z z z f c c c c ⋅∆+--∆+-∆=∆2]0[21ππ-=-=故 i z f 5)(-=.10.证明：因为()f z =0,1,z =∞,由题知()f z 的支点为0,1,z =于是在割去线段0Re 1≤≤的平面上变点就不可能性单绕0或1转一周，故此时可出两二个单值解析分支,由于当z 从支割线上岸一点出发，连续变动到1z =-时，只z 的幅角共增加2π，由已知所取分支在支割线上岸取正值，于是可认为该分支在上岸之幅角为0，因而此分支在1z =-的幅角为2π，故()21i f π-==,i f 162)1(-=-''.。

第2章基本初等函数作业25 Word版含解析

课时作业(二十五)1．若log x 4＝2，则x 的值为( )A ．±2B ．2C ．－2 D. 2-=答案=- B2．若b ＝a 2(a ＞0且a ≠1)，则有( )A ．log 2b ＝aB ．log 2a ＝bC ．log b a ＝2D ．log a b ＝2 -=答案=- D3．在对数式log (x －1)(3－x)中，实数x 的取值范围应该是( )A ．1＜x ＜3B ．x ＞1且x ≠2C ．x ＞3D ．1＜x ＜3且x ≠2 -=答案=- D解析 ⎩⎪⎨⎪⎧3－x>0，x －1>0，x －1≠1，解得1<x<3且x ≠2.4．若log x 3y ＝4，则x ，y 之间的关系正确的是( ) A ．x 4＝3y B ．y ＝64xC ．y ＝3x 4D ．x ＝3y 2-=答案=- A解析 log x 3y ＝4＝log x x 4，则x 4＝3y.5．下列指数式与对数式互化不正确的一组是( )A ．100＝1与lg1＝0B ．27－13＝13与log 2713＝－3 C ．log 39＝2与32＝9D ．log 55＝1与51＝5-=答案=- B6．已知log 2x ＝4，则x －12＝( )A.13B.123C.33D.14 -=答案=- D7．与函数y ＝10lg(x－1)的图象相同的函数是( ) A ．y ＝x －1B ．y ＝|x －1|C ．y ＝x 2－1x ＋1D ．y ＝(x －1x －1)2 -=答案=- D解析 y ＝10lg(x －1)＝x －1(x>1)．8．若log x (5－2)＝－1，则x 的值为( ) A.5－2 B.5＋2C.5－2或5＋2 D ．2－ 5-=答案=- B9．若f(10x )＝x ，则f(3)等于( )A ．log 310B ．lg3C ．103D ．310 -=答案=- B10．21＋12·log 25的值等于( ) A ．2＋ 5B ．2 5C ．2＋52D ．1＋52 -=答案=- B 11．log 333＝________．-=答案=- 312．求下列各式的值．(1)log 1515； (2)log 0.41； (3)log 981；(4)log 2.56.25; (5)log 7343; (6)log 3243.-=答案=- (1)1 (2)0 (3)2 (4)2 (5)3 (6)513．求x 的值．(1)x ＝log 124； (2)x ＝log 93； (3)x ＝71－log 75；(4)log x 8＝－3； (5)log 12x ＝4.-=答案=- (1)－2 (2)14 (3)75 (4)12 (5)11614．求值：(1)log 84； (2)2log 23－2. 解析 (1)设log 84＝x ，则8x ＝4，即23x ＝22，∴3x ＝2，x ＝23，故log 84＝23. (2)∵alog a N ＝N ，∴2log 23＝3.∴2log 23－2＝2log 23÷22＝3÷4＝34. 15．若log 2[log 0.5(log 2x)]＝0，求x 的值．解析由条件知log 0.5(log 2x)＝1＝log 0.50.5，得log 2x ＝12＝log 22，从而x ＝ 2. ►重点班·选做题16．求2log 412－3log 927＋5log 2513的值 . 解析原式＝4log 412－9log 927＋25log 2513 ＝12－27＋13 ＝23－33＋13 ＝－233.1．若5lgx ＝25，则x 的值为________． -=答案=- 1002．设集合A ＝{5，log 2(a ＋3)}，集合B ＝{a ，b}，若A ∩B ＝{2}，则A ∪B ＝________． -=答案=- {1，2，5}解析由A ∩B ＝{2}，知log 2(a ＋3)＝2，得a ＝1，由此知b ＝2.故A ∪B ＝{1，2，5}．3．设x ＝log 23，求23x －2－3x2x －2－x 的值．解析 23x －2－3x 2x －2－x ＝（2x －2－x ）（22x ＋1＋2－2x ）2x －2－x＝22x ＋1＋2－2x ＝919. 4．已知6a ＝8，试用a 表示下列各式：(1)log 68； (2)log 62； (3)log 26. 解析 (1)log 68＝a.(2)由6a ＝8，得6a ＝23，即6a 3＝2，所以log 62＝a 3. (3)由6a 3＝2，得23a ＝6，所以log 26＝3a. 5．已知log a b ＝log b a(a>0且a ≠1；b>0且b ≠1)，求证：a ＝b 或a ＝1b. 证明令log a b ＝log b a ＝t ，则a t ＝b ，b t ＝a. ∴(a t )t ＝a ，则at 2＝a ，∴t 2＝1，t ＝±1.当t ＝1时，a ＝b ；当t ＝－1时，a ＝1b. 所以a ＝b 或a ＝1b .。

复变函数刘敏思第二章习题解答

∂u ∂x
z =iy
+i
∂v ∂x
z =iy
= k ⋅ 0 + i ⋅0 = 0 。
3. 讨论下列函数在复平面 ℂ 上的可微性和解析性，并在可导的情况下求它们的导函数：（ 1） f ( z ) = x + i y ；（2） f ( z ) = e + ie ；（3） f ( z ) = x − 3 xy + i (3 x y − y ) ；（ 4） f ( z ) = e x ( x cos y − y sin y ) + i e x ( y cos y + x sin y ) . 解（1）记 f ( z ) = u ( x, y ) + iv ( x , y ) ，则 u ( x, y ) = x ， v( x, y ) = y 。易见它们都在复平面上可微。要使柯西—黎曼条件满足，只须
4. 设 f ( z ) 在区域 D 内解析，若下列关系之一成立，（ 1） Im[ f ( z)] ≡ c ，其中 c 为实常数；（ 2） α Re[ f ( z )] + β Im[ f ( z)] = c ，其中 α , β , c ∈ ℝ 且 α + β ≠ 0 ；
2 2
（ 3） Re[ f ( z )] = {Im[ f ( z)]} ，则 f ( z) 在区域 D 内为常数 . 证明记 f ( z ) = u ( x, y ) + iv ( x , y ) （ 1）由条件得， v( x, y ) ≡ c ，因为 f ( z ) 在区域 D 内解析，由柯西—黎曼条件，在区域 D 内
f ( z ) = x 2 + y 2 ， u ( x, y ) = x 2 + y 2 ， v( x, y) = 0 。

2023年高考数学一轮复习第二章函数1函数的概念及其表示练习含解析

函数的概念及其表示考试要求 1.了解函数的含义，会求简单函数的定义域和值域.2.在实际情景中，会根据不同的需要选择恰当的方法(如图象法、列表法、解析法)表示函数.3.了解简单的分段函数，并会简单的应用．知识梳理 1．函数的概念一般地，设A ，B 是非空的实数集，如果对于集合A 中的任意一个数x ，按照某种确定的对应关系f ，在集合B 中都有唯一确定的数y 和它对应，那么就称f ：A →B 为从集合A 到集合B 的一个函数，记作y ＝f (x )，x ∈A . 2．函数的三要素(1)函数的三要素：定义域、对应关系、值域．(2)如果两个函数的定义域相同，并且对应关系完全一致，则这两个函数为同一个函数． 3．函数的表示法表示函数的常用方法有解析法、图象法和列表法． 4．分段函数若函数在其定义域的不同子集上，因对应关系不同而分别用几个不同的式子来表示，这种函数称为分段函数．常用结论1．直线x ＝a 与函数y ＝f (x )的图象至多有1个交点．2．在函数的定义中，非空数集A ，B ，A 即为函数的定义域，值域为B 的子集．3．分段函数虽由几个部分组成，但它表示的是一个函数．分段函数的定义域等于各段函数的定义域的并集，值域等于各段函数的值域的并集．思考辨析判断下列结论是否正确(请在括号中打“√”或“×”)(1)若两个函数的定义域和值域相同，则这两个函数是同一个函数．( × ) (2)函数y ＝f (x )的图象可以是一条封闭曲线．( × ) (3)y ＝x 0与y ＝1是同一个函数．( × ) (4)函数f (x )＝⎩⎪⎨⎪⎧x －1，x ≥0，x 2，x ＜0的定义域为R .( √ )教材改编题1．下列各曲线表示的y 与x 之间的关系中，y 不是x 的函数的是( )答案 C2．(多选)下列各组函数是同一个函数的是( ) A ．f (x )＝x 2－2x －1，g (s )＝s 2－2s －1B ．f (x )＝x －1，g (x )＝x 2－1x ＋1C ．f (x )＝x 2，g (x )＝⎩⎪⎨⎪⎧x ，x ≥0，－x ，x <0D ．f (x )＝－x 3，g (x )＝x －x 答案 AC3．(2022·长沙质检)已知函数f (x )＝⎩⎪⎨⎪⎧3x，x ≤0，log 3x ，x >0，则f ⎝ ⎛⎭⎪⎫f ⎝ ⎛⎭⎪⎫12等于( )A ．－1B ．2C.3D.12答案 D解析 ∵f ⎝ ⎛⎭⎪⎫12＝log 312<0， ∴f ⎝⎛⎭⎪⎫f⎝ ⎛⎭⎪⎫12＝31log 23＝12.题型一函数的定义域例1 (1)(2022·武汉模拟)函数f (x )＝1ln x ＋1＋4－x 2的定义域为( ) A ．[－2,0)∪(0,2]B ．(－1,0)∪(0,2]C ．[－2,2]D ．(－1,2]答案 B解析要使函数有意义，则需⎩⎪⎨⎪⎧x ＋1>0，x ＋1≠1，4－x 2≥0，解得－1<x ≤2且x ≠0，所以x ∈(－1,0)∪(0,2]．所以函数的定义域为(－1,0)∪(0,2]．(2)若函数f (x )的定义域为[0,2]，则函数f (x －1)的定义域为________．答案 [1,3]解析 ∵f (x )的定义域为[0,2]， ∴0≤x －1≤2，即1≤x ≤3， ∴函数f (x －1)的定义域为[1,3]．延伸探究将本例(2)改成“若函数f (x ＋1)的定义域为[0,2]”，则函数f (x －1)的定义域为________．答案 [2,4]解析 ∵f (x ＋1)的定义域为[0,2]， ∴0≤x ≤2， ∴1≤x ＋1≤3， ∴1≤x －1≤3， ∴2≤x ≤4，∴f (x －1)的定义域为[2,4]．教师备选1．(2022·西北师大附中月考)函数y ＝lg(x 2－4)＋x 2＋6x 的定义域是( ) A ．(－∞，－2)∪[0，＋∞) B ．(－∞，－6]∪(2，＋∞) C ．(－∞，－2]∪[0，＋∞) D ．(－∞，－6)∪[2，＋∞) 答案 B解析由题意，得⎩⎪⎨⎪⎧x 2－4>0，x 2＋6x ≥0，解得x >2或x ≤－6.因此函数的定义域为(－∞，－6]∪(2，＋∞)．2．已知函数f (x )＝x1－2x ，则函数f x －1x ＋1的定义域为( )A ．(－∞，1)B ．(－∞，－1)C ．(－∞，－1)∪(－1,0)D ．(－∞，－1)∪(－1,1) 答案 D解析令1－2x>0，即2x<1，即x <0.∴f (x )的定义域为(－∞，0)．∴函数f x －1x ＋1中，有⎩⎪⎨⎪⎧x －1<0，x ＋1≠0，解得x <1且x ≠－1.故函数f x －1x ＋1的定义域为(－∞，－1)∪(－1,1)．思维升华 (1)求给定函数的定义域：由函数解析式列出不等式(组)使解析式有意义． (2)求复合函数的定义域①若f (x )的定义域为[m ，n ]，则在f (g (x ))中，由m ≤g (x )≤n 解得x 的范围即为f (g (x ))的定义域．②若f (g (x ))的定义域为[m ，n ]，则由m ≤x ≤n 得到g (x )的范围，即为f (x )的定义域．跟踪训练1 (1)函数f (x )＝11－4x2＋ln(3x －1)的定义域为( )A.⎝ ⎛⎦⎥⎤13，12B.⎝ ⎛⎭⎪⎫13，12C.⎣⎢⎡⎭⎪⎫－12，14 D.⎣⎢⎡⎦⎥⎤－12，12 答案 B解析要使函数f (x )＝11－4x2＋ln(3x －1)有意义，则⎩⎪⎨⎪⎧1－4x 2>0，3x －1>0⇒13<x <12. ∴函数f (x )的定义域为⎝ ⎛⎭⎪⎫13，12. (2)已知函数f (x )的定义域为[－2,2]，则函数g (x )＝f (2x )＋1－2x的定义域为__________．答案 [－1,0]解析由条件可知，函数的定义域需满足⎩⎪⎨⎪⎧－2≤2x ≤2，1－2x≥0，解得－1≤x ≤0，所以函数g (x )的定义域是[－1,0]．题型二函数的解析式例2 (1)(2022·哈尔滨三中月考)已知f ⎝ ⎛⎭⎪⎫2x＋1＝lg x ，则f (x )的解析式为________．答案 f (x )＝lg2x －1(x >1) 解析令2x＋1＝t (t >1)，则x ＝2t －1，所以f (t )＝lg 2t －1(t >1)，所以f (x )＝lg2x －1(x >1)． (2)已知y ＝f (x )是二次函数，若方程f (x )＝0有两个相等实根，且f ′(x )＝2x ＋2，则f (x )＝________. 答案 x 2＋2x ＋1解析设f (x )＝ax 2＋bx ＋c (a ≠0)，则f ′(x )＝2ax ＋b ，∴2ax ＋b ＝2x ＋2，则a ＝1，b ＝2.∴f (x )＝x 2＋2x ＋c ，又f (x )＝0，即x 2＋2x ＋c ＝0有两个相等实根． ∴Δ＝4－4c ＝0，则c ＝1. 故f (x )＝x 2＋2x ＋1.(3)已知函数对任意的x 都有f (x )－2f (－x )＝2x ，则f (x )＝________. 答案 23x解析 ∵f (x )－2f (－x )＝2x ，① ∴f (－x )－2f (x )＝－2x ，② 由①②得f (x )＝23x .教师备选已知f (x )满足f (x )－2f ⎝ ⎛⎭⎪⎫1x ＝2x ，则f (x )＝________.答案－2x 3－43x解析 ∵f (x )－2f ⎝ ⎛⎭⎪⎫1x ＝2x ，①以1x代替①中的x ，得f ⎝ ⎛⎭⎪⎫1x －2f (x )＝2x，②①＋②×2得－3f (x )＝2x ＋4x，∴f (x )＝－2x 3－43x.思维升华函数解析式的求法(1)配凑法；(2)待定系数法；(3)换元法；(4)解方程组法．跟踪训练2 (1)已知f (1－sin x )＝cos 2x ，则f (x )＝________. 答案－x 2＋2x ，x ∈[0,2] 解析令t ＝1－sin x ， ∴t ∈[0,2]，sin x ＝1－t ，∴f (t )＝1－sin 2x ＝1－(1－t )2＝－t 2＋2t ，t ∈[0,2]， ∴f (x )＝－x 2＋2x ，x ∈[0,2]．(2)(2022·黄冈质检)已知f ⎝⎛⎭⎪⎫x 2＋1x2＝x 4＋1x4，则f (x )＝__________.答案 x 2－2，x ∈[2，＋∞)解析 ∵f ⎝⎛⎭⎪⎫x 2＋1x 2＝⎝⎛⎭⎪⎫x 2＋1x22－2，∴f (x )＝x 2－2，x ∈[2，＋∞)．题型三分段函数例3 (1)已知f (x )＝⎩⎪⎨⎪⎧cosπx ，x ≤1，f x －1＋1，x >1，则f ⎝ ⎛⎭⎪⎫43＋f⎝ ⎛⎭⎪⎫－43的值为( ) A.12B ．－12C ．－1D ．1 答案 D解析 f ⎝ ⎛⎭⎪⎫43＝f⎝ ⎛⎭⎪⎫43－1＋1＝f ⎝ ⎛⎭⎪⎫13＋1＝cosπ3＋1＝32，f ⎝ ⎛⎭⎪⎫－43＝cos ⎝ ⎛⎭⎪⎫－4π3＝cos2π3＝－12， ∴f ⎝ ⎛⎭⎪⎫43＋f ⎝ ⎛⎭⎪⎫－43＝32－12＝1.(2)已知f (x )＝⎩⎪⎨⎪⎧2x＋3，x >0，x 2－4，x ≤0，若f (a )＝5，则实数a 的值是__________；若f (f (a ))≤5，则实数a 的取值范围是__________．答案 1或－3 [－5，－1]解析 ①当a >0时，2a＋3＝5，解得a ＝1；当a ≤0时，a 2－4＝5，解得a ＝－3或a ＝3(舍)．综上，a ＝1或－3.②设t ＝f (a )，由f (t )≤5得－3≤t ≤1. 由－3≤f (a )≤1，解得－5≤a ≤－1. 教师备选1．已知函数f (x )＝⎩⎪⎨⎪⎧sin ⎝ ⎛⎭⎪⎫πx ＋π6，x >1，⎝ ⎛⎭⎪⎫12x，x <1，则f (f (2022))等于( )A ．－32B.22C.32D. 2 答案 B解析 f (2022)＝sin ⎝ ⎛⎭⎪⎫2022π＋π6＝sin π6＝12，∴f (f (2022))＝f ⎝ ⎛⎭⎪⎫12＝1212⎛⎫ ⎪⎝⎭＝22. 2．(2022·百校联盟联考)已知函数f (x )＝⎩⎪⎨⎪⎧x 3，x ≥0，－x 2，x <0，若对于任意的x ∈R ，|f (x )|≥ax ，则a ＝________. 答案 0解析当x ≥0时，|f (x )|＝x 3≥ax ，即x (x 2－a )≥0恒成立，则有a ≤0；当x <0时，|f (x )|＝x 2≥ax ，即a ≥x 恒成立，则有a ≥0，所以a ＝0.思维升华分段函数求值问题的解题思路(1)求函数值：当出现f (f (a ))的形式时，应从内到外依次求值．(2)求自变量的值：先假设所求的值在分段函数定义区间的各段上，然后求出相应自变量的值，切记要代入检验．跟踪训练3 (1)(2022·河北冀州一中模拟)设f (x )＝⎩⎪⎨⎪⎧x ＋2x－3，x ≥1，x 2＋1，x <1.则f (f (－1))＝________，f (x )的最小值是________．答案 0 22－3 解析 ∵f (－1)＝2，∴f (f (－1))＝f (2)＝2＋22－3＝0，当x ≥1时，f (x )＝x ＋2x－3≥22－3，当且仅当x ＝2时取等号，f (x )min ＝22－3，当x <1时，f (x )＝x 2＋1≥1，x ＝0时取等号， ∴f (x )min ＝1，综上有f (x )的最小值为22－3.(2)(2022·重庆质检)已知函数f (x )＝⎩⎪⎨⎪⎧log 2x ，x >1，x 2－1，x ≤1，则f (x )<f (x ＋1)的解集为________．答案 ⎝ ⎛⎭⎪⎫－12，＋∞解析当x ≤0时，x ＋1≤1，f (x )<f (x ＋1)，等价于x 2－1<(x ＋1)2－1，解得－12<x ≤0；当0<x ≤1时，x ＋1>1，此时f (x )＝x 2－1≤0，f (x ＋1)＝log 2(x ＋1)>0，∴当0<x ≤1时，恒有f (x )<f (x ＋1)；当x >1时，f (x )<f (x ＋1)⇔log 2x <log 2(x ＋1)恒成立．综上知，不等式f (x )<f (x ＋1)的解集为⎝ ⎛⎭⎪⎫－12，＋∞.课时精练1．(2022·重庆模拟)函数f (x )＝3－xlg x的定义域是( ) A ．(0,3) B ．(0,1)∪(1,3) C ．(0,3] D ．(0,1)∪(1,3]答案 D解析 ∵f (x )＝3－xlg x，∴⎩⎪⎨⎪⎧3－x ≥0，lg x ≠0，x >0，解得0<x <1或1<x ≤3，故函数的定义域为(0,1)∪(1,3]．2．若函数y ＝f (x )的定义域为M ＝{x |－2≤x ≤2}，值域为N ＝{y |0≤y ≤2}，则函数y ＝f (x )的图象可能是( )答案 B解析 A 中函数定义域不是[－2,2]；C 中图象不表示函数；D 中函数值域不是[0,2]． 3．(2022·安徽江淮十校联考)设函数f (x )＝⎩⎪⎨⎪⎧4x －12，x <1，a x ，x ≥1，若f ⎝ ⎛⎭⎪⎫f ⎝ ⎛⎭⎪⎫78＝8，则a 等于( ) A.12 B.34 C ．1 D ．2答案 D解析 f ⎝ ⎛⎭⎪⎫78＝4×78－12＝3，则f ⎝ ⎛⎭⎪⎫f ⎝ ⎛⎭⎪⎫78＝f (3)＝a 3，得a 3＝8，解得a ＝2.4．设函数f ⎝ ⎛⎭⎪⎫1－x 1＋x ＝x ，则f (x )的表达式为( )A.1＋x1－x(x ≠－1) B.1＋xx －1(x ≠－1) C.1－x1＋x(x ≠－1) D.2xx ＋1(x ≠－1) 答案 C解析令t ＝1－x 1＋x ，则x ＝1－t1＋t ，∴f (t )＝1－t 1＋t ，即f (x )＝1－x1＋x(x ≠－1)．5．如图，点P 在边长为1的正方形的边上运动，M 是CD 的中点，当P 沿A －B －C －M 运动时，设点P 经过的路程为x ，△APM 的面积为y ，则函数y ＝f (x )的图象大致是( )答案 A解析由题意可得y ＝f (x )＝⎩⎪⎨⎪⎧12x ，0≤x ＜1，34－x4，1≤x ＜2，54－12x ，2≤x ≤52.画出函数f (x )的大致图象，故选A.6．(多选)下列函数中，与y ＝x 是同一个函数的是( ) A ．y ＝3x 3B ．y ＝x 2C ．y ＝lg10xD ．y ＝10lg x答案 AC解析 y ＝x 的定义域为x ∈R ，值域为y ∈R ，对于A 选项，函数y ＝3x 3＝x 的定义域为x ∈R ，故是同一函数；对于B 选项，函数y ＝x 2＝||x ≥0，与y ＝x 的解析式、值域均不同，故不是同一函数；对于C 选项，函数y ＝lg10x＝x ，且定义域为R ，故是同一函数；对于D 选项，y ＝10lg x＝x 的定义域为(0，＋∞)，与函数y ＝x 的定义域不相同，故不是同一函数．7．(多选)(2022·张家界质检)设函数f (x )＝⎩⎪⎨⎪⎧1－x ，x ≤a ，2x，x >a ，若f (1)＝2f (0)，则实数a可以为( ) A ．－1B ．0C ．1D ．2 答案 AB 解析若a <0，则f (0)＝1，f (1)＝2，f (1)＝2f (0)成立；若0≤a <1，则f (0)＝1，f (1)＝2，f (1)＝2f (0)成立；若a ≥1，则f (0)＝1，f (1)＝0，f (1)＝2f (0)不成立．综上所述，实数a 的取值范围是(－∞，1)．8．(多选)具有性质：f ⎝ ⎛⎭⎪⎫1x ＝－f (x )的函数，我们称为满足“倒负”变换的函数，下列函数满足“倒负”变换的函数的是( ) A ．f (x )＝x －1xB ．f (x )＝ln1－x1＋xC ．f (x )＝1ex x-D ．f (x )＝⎩⎪⎨⎪⎧x ，0<x <1，0，x ＝1，－1x ，x >1答案 AD解析对于A ，f (x )＝x －1x，f ⎝ ⎛⎭⎪⎫1x ＝1x－x ＝－f (x )，满足题意；对于B ，f (x )＝ln1－x1＋x，则f ⎝ ⎛⎭⎪⎫1x ＝ln x －1x ＋1≠－f (x )，不满足；对于C ，f ⎝ ⎛⎭⎪⎫1x ＝111e xx -＝ex －1，－f (x )＝1ex x--≠f ⎝ ⎛⎭⎪⎫1x ，不满足；对于D ，f ⎝ ⎛⎭⎪⎫1x ＝⎩⎪⎨⎪⎧1x ，0<1x <1，0，1x ＝1，－x ，1x >1，即f ⎝ ⎛⎭⎪⎫1x ＝⎩⎪⎨⎪⎧1x ，x >1，0，x ＝1，－x ，0<x <1，则f ⎝ ⎛⎭⎪⎫1x ＝－f (x )满足“倒负”变换，故选AD.9．已知f (x 5)＝lg x ，则f (100)＝________. 答案 25解析令x 5＝100，则x ＝15100＝2510， ∴f (100)＝25lg 10＝25.10．函数f (x )＝ln(x －1)＋4＋3x －x 2的定义域为________．答案 (1,4]解析依题意⎩⎪⎨⎪⎧x －1>0，4＋3x －x 2≥0，解得1<x ≤4，∴f (x )的定义域为(1,4]．11．(2022·广州质检)已知函数f (x )＝⎩⎪⎨⎪⎧1－2a x ＋3a ，x <1，ln x ，x ≥1的值域为R ，则实数a的取值范围是________．答案 ⎣⎢⎡⎭⎪⎫－1，12 解析 ∵当x ≥1时，f (x )＝ln x ≥ln1＝0，又f (x )的值域为R ，故当x <1时，f (x )的值域包含(－∞，0)．故⎩⎪⎨⎪⎧1－2a >0，1－2a ＋3a ≥0，解得－1≤a <12.12．设函数f (x )＝⎩⎪⎨⎪⎧x ，x <0，1，x >0，则不等式xf (x )＋x ≤2的解集是________．答案 [－2,0)∪(0,1] 解析当x <0时，f (x )＝x ，代入xf (x )＋x ≤2得x 2＋x －2≤0，解得－2≤x <0；当x >0时，f (x )＝1，代入xf (x )＋x ≤2，解得0<x ≤1. 综上有－2≤x ＜0或0＜x ≤1.13．设函数f (x )＝⎩⎪⎨⎪⎧2－x，x ≤0，1，x >0，则满足f (x ＋1)<f (2x )的x 的取值范围是( ) A ．(－∞，－1] B ．(0，＋∞) C ．(－1,0) D ．(－∞，0)答案 D解析当x ≤0时，函数f (x )＝2－x是减函数，则f (x )≥f (0)＝1.作出f (x )的大致图象如图所示，结合图象知，要使f (x ＋1)＜f (2x )，当且仅当⎩⎪⎨⎪⎧x ＋1<0，2x <0，2x <x ＋1或⎩⎪⎨⎪⎧x ＋1≥0，2x <0，解得x <－1或－1≤x <0，即x <0.14．设函数f (x )＝⎩⎪⎨⎪⎧－x ＋λ，x <1λ∈R，2x，x ≥1，若对任意的a ∈R 都有f (f (a ))＝2f (a )成立，则λ的取值范围是______．答案 [2，＋∞) 解析当a ≥1时，2a≥2. ∴f (f (a ))＝f (2a)＝22a＝2f (a )恒成立．当a <1时，f (f (a ))＝f (－a ＋λ)＝2f (a )＝2λ－a ，∴λ－a ≥1，即λ≥a ＋1恒成立，由题意λ≥(a ＋1)max ，∴λ≥2，综上，λ的取值范围是[2，＋∞)．15．(多选)若函数f (x )满足：对定义域内任意的x 1，x 2(x 1≠x 2)，有f (x 1)＋f (x 2)>2f ⎝ ⎛⎭⎪⎫x 1＋x 22，则称函数f (x )具有H 性质．则下列函数中具有H 性质的是( )A ．f (x )＝⎝ ⎛⎭⎪⎫12xB ．f (x )＝ln xC ．f (x )＝x 2(x ≥0) D ．f (x )＝tan x ⎝ ⎛⎭⎪⎫0≤x <π2 答案 ACD解析若对定义域内任意的x 1，x 2(x 1≠x 2)，有f (x 1)＋f (x 2)>2f ⎝ ⎛⎭⎪⎫x 1＋x 22，则点(x 1，f (x 1))，(x 2，f (x 2))连线的中点在点⎝⎛⎭⎪⎫x 1＋x 22，f ⎝ ⎛⎭⎪⎫x 1＋x 22的上方，如图⎝⎛⎭⎪⎫其中a ＝f⎝ ⎛⎭⎪⎫x 1＋x 22，b ＝f x 1＋f x 22.根据函数f (x )＝⎝ ⎛⎭⎪⎫12x ，f (x )＝ln x ，f (x )＝x 2(x ≥0)，f (x )＝tan x ⎝⎛⎭⎪⎫0≤x <π2的图象可知，函数f (x )＝⎝ ⎛⎭⎪⎫12x ，f (x )＝x 2(x ≥0)，f (x )＝tan x ⎝⎛⎭⎪⎫0≤x <π2具有H 性质，函数f (x )＝ln x 不具有H 性质．16．设f (x )是定义在R 上的函数，且f (x ＋2)＝2f (x )，f (x )＝⎩⎪⎨⎪⎧2x ＋a ，－1<x <0，b e 2x，0≤x ≤1，其中a ，b 为正实数，e 为自然对数的底数，若f ⎝ ⎛⎭⎪⎫92＝f ⎝ ⎛⎭⎪⎫32，则a b 的取值范围为________．答案 (2e ，＋∞)解析因为f (x ＋2)＝2f (x )，所以f ⎝ ⎛⎭⎪⎫92＝f⎝ ⎛⎭⎪⎫12＋4＝(2)2f ⎝ ⎛⎭⎪⎫12＝2e b ，f ⎝ ⎛⎭⎪⎫32＝f ⎝ ⎛⎭⎪⎫－12＋2＝2f ⎝ ⎛⎭⎪⎫－12 ＝2⎣⎢⎡⎦⎥⎤2×⎝ ⎛⎭⎪⎫－12＋a ＝2(a －1)，因为f ⎝ ⎛⎭⎪⎫92＝f ⎝ ⎛⎭⎪⎫32，所以2(a －1)＝2e b ，所以a ＝2e b ＋1，因为b 为正实数，所以a b＝2e b ＋1b＝2e ＋1b∈(2e ，＋∞)，故a b的取值范围为(2e ，＋∞)．。

复变函数与积分变换答案-第2章解析函数

11 27、第二章解析函数习题详解1、(1) f 1(z )= z 4在定义域(-,+) 内连续；2) f 2(z ) =4z +5在定义域(-,+)内连续； 1在定义域-, 3,3, +内连续。

- 4, v = 16u + 64, 为一抛物线。

4、(1)w = z 3，则w = (2i )3= -8i , w =( 2+2i )3=2 2+12i -12 2-8i =-10 2+4i ；5、 f (z )=Re z =x ，当 y →0时， f (z )→1；当x →0时， f (z )→0，因为极限不等， z x + iy 所以当z →0时， f (z )极限不存在。

1在原点处不连续，故 w =i arg z +1 在负实轴上与原点 zz3) f 3 (z )= 22、w = z2u =x 2-y 2v = 2 xy u =x 2 -4，把直线C :y =2映射成:u =x -4v = 4 xvx = ，代入第一个式子，4u =3、1zw = = = z zzx - iy22,x + yv =x 22 x + y-y 22 x + y把直线C :x =1映射成，:vu =v =1 1+y 2-y 1+y 21-u u 2u= (1- u ) u v 2 + u 22)w = z 3，像域为0arg w 26、i arg z 在负实轴上与原点处不连续，处不连续。

f (z +z )- f (z )z →0z= limz →0(z +z )2zy 2 = 1 -1 = u为一个圆周。

uz 2-(z +z )2z 2(z +z )2z 2 -z 2 -2z z -z 22= lim = lim = - 。

z →0 z z →0z 2(z +z )2zz 38、(1) f (z ) =5-3z +5z 2，在(-,+)内解析，且导数为 f (z ) = -3+10z ；12、(1) z =e 1-2i =ecos -i sin=-ei ；1222) f (z )=1 1 1z 4 -1 (z 2 -1)(z 2 +1) (z -1)(z +1)(z +i )(z -i )在(-,+)内除z =1,5z +431 1 5 3) f (z )= z +4,在(-,+)内除z = - 3外解析， f (z )=1+ 2 =1+ 52z + 32 2 2z +32 2(2z +3)且导数为： f(z )= 1(2z +3)-2(-2)=-5 (2z +3)29、(1) f (z )=Im z = y 在z 平面上的点点不可导，不解析(因柯西-黎曼条件不满足)；2) f (z )= z 4 ，在平面上的点解析。

2022届高考数学一轮复习第2章函数概念与基本初等函数Ⅰ第5讲对数与对数函数作业试题1含解析新人教版

第二章函数概念与基本初等函数Ⅰ第五讲对数与对数函数练好题·考点自测1.[2019某某,5分]在同一直角坐标系中,函数y=,y=log a(x+)(a>0,且a≠1)的图象可能是(A B C D2.[2020全国卷Ⅰ,5分]设alog34=2,则4-a= (A. B. C. D.3.[2020全国卷Ⅱ,5分]设函数f(x)=ln|2x+1|-ln|2x-1|,则f(x) (A.是偶函数,且在(,+∞)单调递增B.是奇函数,且在(-,)单调递减C.是偶函数,且在(-∞,-)单调递增D.是奇函数,且在(-∞,-)单调递减4.[2020全国卷Ⅲ,5分]已知55<84,134<85.设a=log53,b=log85,c=log138,则(A.a<b<cB.b<a<cC.b<c<aD.c<a<b5.[多选题]下列说法正确的是(A.若MN>0,则log a(MN)=log a M+log a NB.对数函数y=log a x(a>0且a≠1)在(0,+∞)上是增函数C.函数y=ln 与y=ln(1+x)-ln(1-x)的定义域相同D.对数函数y=log a x(a>0且a≠1)的图象过定点(1,0)且过点(a,1),(,-1),函数图象只在第一、四象限6.[2019全国卷Ⅱ,5分]已知f(x)是奇函数,且当x<0时,f(x)=-e ax.若f(ln 2)=8,则a=.7.[2018全国卷Ⅲ,5分]已知函数f(x)=ln(-x)+1,f(a)=4,则f(-a)=.b=b a,则a=,b=.a b+logb a=,a拓展变式1.[2021某某省四校联考]已知实数a,b满足a+b=5,log2a=log3b,则ab= (2.(1)[2019某某,5分]已知a=log52,b=log,则a,b,c的大小关系为(A.a<c<bB.a<b<cC.b<c<aD.c<a<b(2)[2020某某,5分]已知函数f(x)=lg(x2 -4x-5)在(a,+∞)上单调递增,则a的取值X围是(A.(-∞,-1]B.(-∞,2]C.[2,+∞)D.[5,+∞)3.里氏震级M的计算公式为M=lg A-lg A0,其中A是测震仪记录的地震曲线的最大振幅,A0是相应的标准地震的振幅.假设在一次地震中,测震仪记录的最大振幅是1 000,此时标准地震的振幅为0.001,则此次地震的震级为级;9级地震的最大振幅是5级地震的最大振幅的倍.4.[多选题]设x,y,z为正实数,且log2x=log3y=log5z>0,则,,的大小关系可能是(A.<<B.<<C.==D.<<答案第五讲对数与对数函数1.D 解法一若0<a<1,则函数y=是增函数,y=log a(x+)是减函数且其图象过点(,0),结合选项可知,选项D可能成立;若a>1,则y=是减函数,而y=log a(x+)是增函数且其图象过点(,0),结合选项可知,没有符合的图象.故选D.解法二分别取a=和a=2,在同一直角坐标系内画出相应函数的图象(图略),通过对比可知选D.2.B 解法一因为alog34=2,所以log34a=2,则有4a=32=9,所以4-a==,故选B.解法二因为alog34=2,所以a===log49,所以4-a==,故选B.解法三令4-a=t,两边同时取对数得log34-a=log3t,即-alog34=log3t,即alog34=-log3t=log3,因为alog34=2,所以log3=2,所以=32=9,所以t=,即4-a=,故选B.3.D 由得函数f(x)的定义域为(-∞,-)∪(-,)∪(,+∞),其关于原点对称,因为f(-x)=ln|2(-x)+1|-ln|2(-x)-1|=ln|2x-1|-ln|2x+1|=-f(x),所以函数f(x)为奇函数,排除A,C.当x∈(-,)时,f(x)=ln(2x+1)-ln(1-2x),易知函数f(x)单调递增,排除B.当x∈(-∞,-)时,f(x)=ln(-2x-1)-ln(1-2x)=ln=ln(1+),易知函数f(x)单调递减,故选D.4.A 55<84⇒ln 55<ln 84⇒5ln 5<4ln 8,所以>=log85=b;同理134<85⇒ln 134<ln 85⇒4ln 13<5ln 8,所以<=log138=c;34<53⇒ln 34<ln 53⇒4ln 3<3ln 5,所以>=log53=a;83<54⇒ln 83<ln 54⇒3ln 8<4ln 5,所以<=log85=b.综上可知,a<<b<<c,故选A.5.CD 对于A,当M<0,N<0时不成立;对于B,当0<a<1时,y=log a x在(0,+∞)上是减函数,故B 不成立;对于C,函数y=ln 与y=ln(1+x)-ln(1-x)的定义域均为(-1,1),故C正确;对于D,由对数函数的图象与性质可知D正确.故说法正确的是CD.6.-3 当x>0时,-x<0, f(-x)=-e-ax.因为函数f(x)为奇函数,所以当x>0时, f(x)=-f(-x)=e-ax,所以f(ln 2)=e-aln 2=()a=8,所以a=-3.7.-2解法一由f(a)=ln(-a)+1=4,得ln(-a)=3,所以f(-a)=ln(+a)+1=-ln+1=-ln(-a)+1=-3+1=-2.解法二因为f(x)=ln(-x)+1,所以f(x)+f(-x)=ln(-x)+ln(+x)+2=2.故f(a)+f(-a)=2,所以f(-a)=2-4=-2.8.4 2 因为a>b>1,所以log a b∈(0,1).因为log a b+log b a=,即log a b+=,所以log a b=或log a b=2(舍去),所以=b,即a=b2.所以a b==b2b=b a,所以a=2b,所以b2=2b,解得b=2或b=0(舍去),所以a=b2=4.1.D 设log2a=log3b=t,则a=2t,b=3t,所以a+b=2t+3t=5.因为函数f(t)=2t+3t为增函数,且f(1)=5,所以t=1,所以a=2,b=3,所以ab=6,故选D.2.(1)A 因为a=log52<log5=1=,故a<c;因为b=log0.2>log0=1,故c<b.所以a<c<b.故选A.(2)D 由x2-4x-5>0,解得x>5或x<-1,所以函数f(x)的定义域为(-∞,-1)∪(5,+∞).又函数y=x2-4x-5在(5,+∞)上单调递增,在(-∞,-1)上单调递减,所以函数f(x)=lg(x2-4x-5)在(5,+∞)上单调递增,所以a≥5,故选D.3.6 10 000 根据题意,由lg 1 000-lg 0.001=6得此次地震的震级为6级,因为标准地震的振幅为0.001,设9级地震的最大振幅为A9,则lg A9-lg 0.001=9,解得A9=106,同理可得5级地震的最大振幅A5=102,所以9级地震的最大振幅是5级地震的最大振幅的10 000倍.4.ACD 取x=2,则由log2x=log3y=log5z得y=3,z=5,此时易知==,选项C可能成立.取x=4,则由log2x=log3y=log5z得y=9,z=25,此时易知<<,选项A可能成立.取x=,则由log2x=log3y=log5z得y=,z=,此时易知<<2x=log3y=log5z=k,则x=2k,y=3k,z=5k,所以=2k-1,=3k-1,=5k-1,无论k取何值,<<均不成立,即选项B不可能成立.综上可知,选ACD.。

02第二章解析函数积分

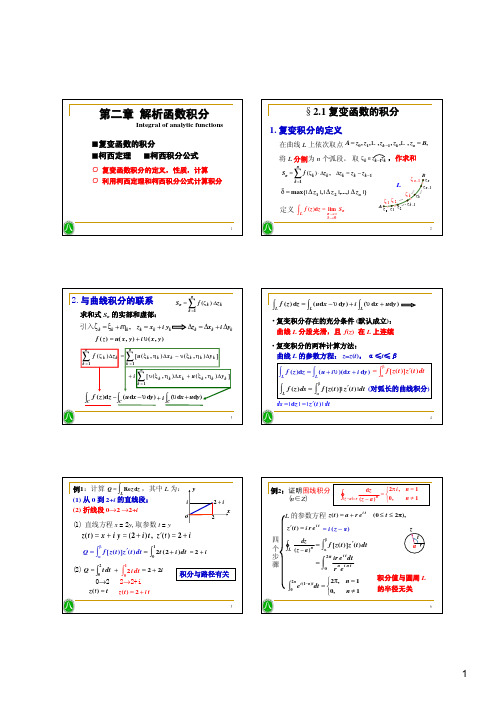
将 L 分割为 n 个弧段。取 ζk ∈ zk−1zk ，作求和
n
∑ Sn = f (ζk ) ⋅ ∆zk , ∆zk = zk − zk−1 k =1
δ = max{| ∆ z1 |,| ∆ z2 |,...,| ∆ zn |}
∫ 定义
L
f
( z )d z
=
lim
n→∞
Sn
δ→0
ζ n−1
B zn
|z−a| = r
(连续性)
21
例1：计算
Q
=
∫C
dz z2 −1
，其中
C
为：
(1) 圆周 |z+2|=2； (2) 圆周 |z|=2
解：(1) 柯西积分公式的前提条件：
被积函数在围线内部只有一个奇点
∫ ∫ C
dz z2 −1
=
(z − 1)−1dz C z − (−1)
| z + 2 |= 2
= 2π i (z − 1)−1 |z=−1 = −π i
∫ ∫ F(z) ≡
∆
f (ζ ) dζ =
z
f (ζ ) dζ
(积分只依赖起点、终点)
Cz
z0
则 F(z) 在 D 内解析，且 F′(z) = f (z)
推论 (Newton-Leibniz 公式)：在单连通区域 D 内解析函数 f(z) 存在原函数Ф(z) 。对A, B ∈ D，
∫B
f (z) dz = Φ(B) − Φ(A) 积分值可能与 D 有关！
(2) a 在 L 的内部区域 D ：
⋅a
γ
存在 a 的邻域 N2R (a) ⊆ D
取 γ为圆周 | z −a |= R

高中数学人教版A版必修一课时作业及解析：第二章2-1指数函数

∴原式＝－－24x1－≤2x<3 －3<x<1 .
12．解
1
1
1
原式＝
a3
2
a 8b
1
2
a3
2b3
1
1
×a3
4b3 2a3 a 3
a3
13．解 ∵x－ xy－2y＝0，x>0，y>0， ∴( x)2－ xy－2( y)2＝0， ∴( x＋ y)( x－2 y)＝0，由 x>0，y>0 得 x＋ y>0， ∴ x－2 y＝0，∴x＝4y， ∴y2＋x－2 xxyy＝8yy＋－42yy＝65.
6
1
－32>0， 33
<0，C
选项错．故选
D.]
6．B [①中，当 a<0 时，
a2
3 2
a2
1 2
3
＝(－a)3＝－a3，
∴①不正确；
②中，若 a＝－2，n＝3，
则3 －23＝－2≠|－2|，∴②不正确；
x－2≥0， ③中，有3x－7≠0，
即 x≥2 且 x≠73，
故定义域为[2，73)∪(73，＋∞)，∴③不正确； ④中，∵100a＝5,10b＝2， ∴102a＝5,10b＝2,102a×10b＝10，即 102a＋b＝10.
1 2
3
xy
1 2
·(xy)－1
12
＝ x3 ·y 3
1
x6
y
1 6
x
1 2
y
1 2
＝x1 3·x1 31，＝－1，x<0
x>0
.
(2)原式＝ 1 ＋ 1 ＋ 2＋1－22 22
＝2 2－3.

《复变函数》第二章解析函数

函数在区域 D内解析的充要条件定理二函数 f (z) u( x, y) iv( x, y) 在其定义域 D内解析的充要条件是: u( x, y)与 v( x, y) 在 D内可微, 并且满足柯西－黎曼方程.
28
解析函数的判定方法: (1) 如果能用求导公式与求导法则证实复变函数 f (z) 的导数在区域 D内处处存在, 则可根据解析函数的定义断定 f (z) 在 D内是解析的.
令 z0 z 沿直线 y y0 k( x x0 ) 趋于 z0,
z z
x x
iy iy
1 1
i i
y
x y
1 ik 1 ik
x
18
由于 k 的任意性,
z 1 ki 不趋于一个确定的值. z 1 ki
lim h(z0 z) h(z0 )不存在.
z0
z
因此 h(z) z 2 仅在 z 0 处可导, 而在其他点都不可导,根据定义, 它在复平面内处处不解析.
0, 0, 使得当 0 | z | 时,
有
f
( z0
z) z
f
(z0 )
f
(z0 )
,
令 (z)
f (z0 z) z
f (z0 )
f (z0 )
9
则 lim (z) 0, z0
因为 f (z0 z) f (z0 ) f (z0 )z (z)z,
所以
lim
z0
f
( z0
3
例1 求f (z) z2的导数.
解 f (z) lim f (z z) f (z)
ห้องสมุดไป่ตู้
z0
z
lim (z z)2 z2
z0
z

第二章二次函数【真题训练】(解析版)

人教版2020年第二单元《二次函数》真题再现一．二次函数的图象（共2小题）1．（2020•菏泽）一次函数y＝acx+b与二次函数y＝ax2+bx+c在同一平面直角坐标系中的图象可能是（）A．B．C．D．【分析】先由二次函数y＝ax2+bx+c的图象得到字母系数的正负，再与一次函数y＝acx+b的图象相比较看是否一致．【解答】解：A、由抛物线可知，a＞0，b＜0，c＞0，则ac＞0，由直线可知，ac＞0，b＞0，故本选项错误；B、由抛物线可知，a＞0，b＞0，c＞0，则ac＞0，由直线可知，ac＞0，b＞0，故本选项正确；C、由抛物线可知，a＜0，b＞0，c＞0，则ac＜0，由直线可知，ac＜0，b＜0，故本选项错误；D、由抛物线可知，a＜0，b＜0，c＞0，则ac＜0，由直线可知，ac＞0，b＞0，故本选项错误．故选：B．2．（2020•泰安）在同一平面直角坐标系内，二次函数y＝ax2+bx+b（a≠0）与一次函数y＝ax+b的图象可能是（）A．B．C．D．【分析】根据二次函数图象的开口以及对称轴与y轴的关系即可得出a、b的正负，由此即可得出一次函数图象经过的象限，再与函数图象进行对比即可得出结论．【解答】解：A、二次函数图象开口向上，对称轴在y轴右侧，∴a＞0，b＜0，∴一次函数图象应该过第一、三、四象限，且与二次函数交于y轴负半轴的同一点，故A错误；B、∵二次函数图象开口向下，对称轴在y轴左侧，∴a＜0，b＜0，∴一次函数图象应该过第二、三、四象限，且与二次函数交于y轴负半轴的同一点，故B错误；C、二次函数图象开口向上，对称轴在y轴右侧，∴a＞0，b＜0，∴一次函数图象应该过第一、三、四象限，且与二次函数交于y轴负半轴的同一点，故C正确；∵D、二次函数图象开口向上，对称轴在y轴右侧，∴a＞0，b＜0，∴一次函数图象应该过第一、三、四象限，且与二次函数交于y轴负半轴的同一点，故D错误；故选：C．二．二次函数的性质（共1小题）3．（2020•哈尔滨）抛物线y＝3（x﹣1）2+8的顶点坐标为（1，8）．【分析】已知抛物线顶点式y＝a（x﹣h）2+k，顶点坐标是（h，k）．【解答】解：∵抛物线y＝3（x﹣1）2+8是顶点式，∴顶点坐标是（1，8）．故答案为：（1，8）．三．二次函数图象与系数的关系（共6小题）4．（2020•威海）如图，抛物线y ＝ax 2+bx +c （a ≠0）交x 轴于点A ，B ，交y 轴于点C ．若点A 坐标为（﹣4，0），对称轴为直线x ＝﹣1，则下列结论错误的是（）A ．二次函数的最大值为a ﹣b +cB ．a +b +c ＞0C ．b 2﹣4ac ＞0D ．2a +b ＝0【分析】根据抛物线的开口方向、对称轴、顶点坐标、与x 轴、y 轴的交点以及过特殊点时相应的系数a 、b 、c 满足的关系进行综合判断即可．【解答】解：抛物线y ＝ax 2+bx +c 过点A （﹣4，0），对称轴为直线x ＝﹣1，因此有：x ＝﹣1＝﹣ab 2，即2a ﹣b ＝0，因此选项D 符合题意；当x ＝﹣1时，y ＝a ﹣b +c 的值最大，选项A 不符合题意；抛物线与x 轴的另一个交点为（2，0），当x ＝1时，y ＝a +b +c ＞0，因此选项B 不符合题意；抛物线与x 轴有两个不同交点，因此b 2﹣4ac ＞0，故选项C 不符合题意；故选：D ．5．（2020•湘西州）已知二次函数y ＝ax 2+bx +c 图象的对称轴为x ＝1，其图象如图所示，现有下列结论： ①ab c ＞0，②b ﹣2a ＜0，③a ﹣b +c ＞0，④a +b ＞n （an +b ），（n ≠1），⑤2c ＜3b ．正确的是（）A ．①③B ．②⑤C ．③④D ．④⑤【分析】由抛物线的开口方向判断a 的符号，由抛物线与y 轴的交点判断c 的符号，然后根据对称轴及抛物线与x 轴交点情况进行推理，进而对所得结论进行判断．【解答】解：①由图象可知：a ＜0，b ＞0，c ＞0，abc ＜0，故此选项错误；②由于a ＜0，所以﹣2a ＞0．又b ＞0，所以b ﹣2a ＞0，故此选项错误；③当x ＝﹣1时，y ＝a ﹣b +c ＜0，故此选项错误；④当x ＝1时，y 的值最大．此时，y ＝a +b +c ，而当x ＝n 时，y ＝an 2+bn +c ，所以a +b +c ＞an 2+bn +c ，故a +b ＞an 2+bn ，即a +b ＞n （an +b ），故此选项正确；⑤当x ＝3时函数值小于0，y ＝9a +3b +c ＜0，且该抛物线对称轴是直线x ＝﹣a b 2＝1，即a ＝﹣2b ，代入得9（﹣2b ）+3b +c ＜0，得2c ＜3b ，故此选项正确；故④⑤正确．故选：D ．6．（2020•广东）如图，抛物线y ＝ax 2+bx +c 的对称轴是x ＝1，下列结论：①ab c ＞0；②b 2﹣4ac ＞0；③8a +c ＜0；④5a +b +2c ＞0，正确的有（）A ．4个B ．3个C ．2个D ．1个【分析】根据抛物线的开口方向、对称轴、与坐标轴的交点判定系数符号及运用一些特殊点解答问题．【解答】解：由抛物线的开口向下可得：a ＜0，根据抛物线的对称轴在y 轴右边可得：a ，b 异号，所以b ＞0，根据抛物线与y 轴的交点在正半轴可得：c ＞0，∴abc ＜0，故①错误；∵抛物线与x 轴有两个交点，∴b 2﹣4ac ＞0，故②正确；∵直线x ＝1是抛物线y ＝ax 2+bx +c （a ≠0）的对称轴，所以﹣ab 2＝1，可得b ＝﹣2a ，由图象可知，当x ＝﹣2时，y ＜0，即4a ﹣2b +c ＜0，∴4a ﹣2×（﹣2a ）+c ＜0，即8a +c ＜0，故③正确；由图象可知，当x ＝2时，y ＝4a +2b +c ＞0；当x ＝﹣1时，y ＝a ﹣b +c ＞0，两式相加得，5a +b +2c ＞0，故④正确；∴结论正确的是②③④3个，故选：B ．7．（2020•深圳）二次函数y ＝ax 2+bx +c （a ≠0）的顶点坐标为（﹣1，n ），其部分图象如图所示．以下结论错误的是（）A ．ab c ＞0B ．4ac ﹣b 2＜0C ．3a +c ＞0D ．关于x 的方程ax 2+bx +c ＝n +1无实数根【分析】根据抛物线开口方向，对称轴的位置以及与y 轴的交点可以对A 进行判断；根据抛物线与x 轴的交点情况可对B 进行判断；x ＝1时，y ＜0，可对C 进行判断；根据抛物线y ＝ax 2+bx +c 与直线y ＝n +1无交点，可对D 进行判断．【解答】解：A ．∵抛物线开口向下，∴a ＜0，∵对称轴为直线x ＝﹣ab 2＝﹣1， ∴b ＝2a ＜0，∵抛物线与y 轴交于正半轴，∴c ＞0，∴abc ＞0，故A 正确；B ．∵抛物线与x 轴有两个交点，∴b 2﹣4ac ＞0，即4ac ﹣b 2＜0，故B 正确；C ．∵抛物线的对称轴为直线x ＝﹣1，抛物线与x 轴的一个交点在（﹣3，0）和（﹣2，0）之间， ∴抛物线与x 轴的另一个交点在（0，0）和（1，0）之间，∴x ＝1时，y ＜0，即a +b +c ＜0，∵b ＝2a ，∴3a +c ＜0，故C 错误；D ．∵抛物线开口向下，顶点为（﹣1，n ），∴函数有最大值n ，∴抛物线y ＝ax 2+bx +c 与直线y ＝n +1无交点，∴一元二次方程ax 2+bx +c ＝n +1无实数根，故D 正确．故选：C ．8．（2020•襄阳）二次函数y ＝ax 2+bx +c 的图象如图所示，下列结论：①ac ＜0；②3a +c ＝0；③4ac ﹣b 2＜0；④当x ＞﹣1时，y 随x 的增大而减小．其中正确的有（）A ．4个B ．3个C ．2个D ．1个【分析】二次函数图象与系数的关系以及二次函数的性质，逐一分析判断即可．【解答】解：①∵抛物线开口向上，且与y 轴交于负半轴，∴a ＞0，c ＜0，∴ac ＜0，结论①正确；②∵抛物线对称轴为直线x ＝1， ∴﹣a b2＝1，∴b ＝﹣2a ，∵抛物线经过点（﹣1，0），∴a﹣b+c＝0，∴a+2a+c＝0，即3a+c＝0，结论②正确；③∵抛物线与x轴由两个交点，∴b2﹣4ac＞0，即4ac﹣b2＜0，结论③正确；④∵抛物线开口向上，且抛物线对称轴为直线x＝1，∴当x＜1时，y随x的增大而减小，结论④错误；故选：B．9．（2020•德州）二次函数y＝ax2+bx+c的部分图象如图所示，则下列选项错误的是（）A．若（﹣2，y1），（5，y2）是图象上的两点，则y1＞y2B．3a+c＝0C．方程ax2+bx+c＝﹣2有两个不相等的实数根D．当x≥0时，y随x的增大而减小【分析】根据二次函数的图象和性质分别对各个选项进行判断即可．【解答】解：∵抛物线的对称轴为直线x＝1，a＜0，∴点（﹣1，0）关于直线x＝1的对称点为（3，0），则抛物线与x轴的另一个交点坐标为（3，0），点（﹣2，y1）与（4，y1）是对称点，∵当x＞1时，函数y随x增大而减小，故A选项不符合题意；把点（﹣1，0），（3，0）代入y＝ax2+bx+c得：a﹣b+c＝0①，9a+3b+c＝0②，①×3+②得：12a+4c＝0，∴3a+c＝0，故B选项不符合题意；当y＝﹣2时，y＝ax2+bx+c＝﹣2，由图象得：纵坐标为﹣2的点有2个，∴方程ax2+bx+c＝﹣2有两个不相等的实数根，故C选项不符合题意；∵二次函数图象的对称轴为x＝1，a＜0，∴当x≤1时，y随x的增大而增大；当x≥1时，y随x的增大而减小；故D选项符合题意；故选：D．四．二次函数图象上点的坐标特征（共2小题）10．（2020•河北）如图，现要在抛物线y＝x（4﹣x）上找点P（a，b），针对b的不同取值，所找点P的个数，三人的说法如下，甲：若b＝5，则点P的个数为0；乙：若b＝4，则点P的个数为1；丙：若b＝3，则点P的个数为1．下列判断正确的是（）A．乙错，丙对B．甲和乙都错C．乙对，丙错D．甲错，丙对【分析】求出抛物线的顶点坐标为（2，4），由二次函数的性质对甲、乙、丙三人的说法分别进行判断，即可得出结论．【解答】解：y ＝x （4﹣x ）＝﹣x 2+4x ＝﹣（x ﹣2）2+4，∴抛物线的顶点坐标为（2，4），∴在抛物线上的点P 的纵坐标最大为4，∴甲、乙的说法正确；若b ＝3，则抛物线上纵坐标为3的点有2个，∴丙的说法不正确；故选：C ．11．（2020•温州）已知（﹣3，y 1），（﹣2，y 2），（1，y 3）是抛物线y ＝﹣3x 2﹣12x +m 上的点，则（）A ．y 3＜y 2＜y 1B ．y 3＜y 1＜y 2C ．y 2＜y 3＜y 1D ．y 1＜y 3＜y 2【分析】求出抛物线的对称轴为直线x ＝﹣2，然后根据二次函数的增减性和对称性解答即可．【解答】解：抛物线的对称轴为直线x ＝﹣()3212-⨯-＝﹣2， ∵a ＝﹣3＜0，∴x ＝﹣2时，函数值最大，又∵﹣3到﹣2的距离比1到﹣2的距离小，∴y 3＜y 1＜y 2．故选：B ．五．二次函数图象与几何变换（共4小题）12．（2020•孝感）将抛物线C 1：y ＝x 2﹣2x +3向左平移1个单位长度，得到抛物线C 2，抛物线C 2与抛物线C 3关于x 轴对称，则抛物线C 3的解析式为（）A ．y ＝﹣x 2﹣2B ．y ＝﹣x 2+2C ．y ＝x 2﹣2D ．y ＝x 2+2【分析】根据抛物线C1的解析式得到顶点坐标，根据顶点式及平移前后二次项的系数不变可得抛物线C2的得到坐标，而根据关于x轴对称的两条抛物线的顶点的横坐标相等，纵坐标互为相反数，二次项系数互为相反数可得到抛物线C3所对应的函数表达式．【解答】解：∵抛物线C1：y＝x2﹣2x+3＝（x﹣1）2+2，∴抛物线C1的顶点为（1，2），∵向左平移1个单位长度，得到抛物线C2，∴抛物线C2的顶点坐标为（0，2），∵抛物线C2与抛物线C3关于x轴对称，∴抛物线C3的开口方向相反，顶点为（0，﹣2），∴抛物线C3的解析式为y＝﹣x2﹣2，故选：A．13．（2020•广东）把函数y＝（x﹣1）2+2图象向右平移1个单位长度，平移后图象的的数解析式为（）A．y＝x2+2B．y＝（x﹣1）2+1C．y＝（x﹣2）2+2D．y＝（x﹣1）2﹣3【分析】先求出y＝（x﹣1）2+2的顶点坐标，再根据向右平移横坐标加，求出平移后的二次函数图象顶点坐标，然后利用顶点式解析式写出即可．【解答】解：二次函数y＝（x﹣1）2+2的图象的顶点坐标为（1，2），∴向右平移1个单位长度后的函数图象的顶点坐标为（2，2），∴所得的图象解析式为y＝（x﹣2）2+2．故选：C．14．（2020•绥化）将抛物线y＝2（x﹣3）2+2向左平移3个单位长度，再向下平移2个单位长度，得到抛物线的解析式是（）A．y＝2（x﹣6）2B．y＝2（x﹣6）2+4C．y＝2x2D．y＝2x2+4【分析】根据“左加右减、上加下减”的原则进行解答即可．【解答】解：将抛物线y＝2（x﹣3）2+2向左平移3个单位长度所得抛物线解析式为：y＝2（x﹣3+3）2+2，即y＝2x2+2；再向下平移2个单位为：y＝2x2+2﹣2，即y＝2x2．故选：C．15．（2020•哈尔滨）将抛物线y＝x2向上平移3个单位长度，再向右平移5个单位长度，所得到的拋物线为（）A．y＝（x+3）2+5B．y＝（x﹣3）2+5C．y＝（x+5）2+3D．y＝（x﹣5）2+3【分析】根据“上加下减，左加右减”的原则进行解答即可．【解答】解：由“上加下减”的原则可知，将抛物线y＝x2向上平移3个单位所得抛物线的解析式为：y ＝x2+3；由“左加右减”的原则可知，将抛物线y＝x2+3向右平移5个单位所得抛物线的解析式为：y＝（x﹣5）2+3；故选：D．六．抛物线与x轴的交点（共1小题）16．（2020•荆门）若抛物线y＝ax2+bx+c（a＞0）经过第四象限的点（1，﹣1），则关于x的方程ax2+bx+c ＝0的根的情况是（）A．有两个大于1的不相等实数根B．有两个小于1的不相等实数根C．有一个大于1另一个小于1的实数根D．没有实数根【分析】根据题意画出函数的图象，根据抛物线与x的交点情况即可判断．【解答】解：由抛物线y ＝ax 2+bx +c （a ＞0）经过第四象限的点（1，﹣1），画出函数的图象如图：由图象可知：关于x 的方程ax 2+bx +c ＝0的根的情况是有一个大于1另一个小于1的实数根，故选：C ．七．二次函数的应用（共2小题）17．（2020•营口）某超市销售一款“免洗洗手液”，这款“免洗洗手液”的成本价为每瓶16元，当销售单价定为20元时，每天可售出80瓶．根据市场行情，现决定降价销售．市场调查反映：销售单价每降低0.5元，则每天可多售出20瓶（销售单价不低于成本价），若设这款“免洗洗手液”的销售单价为x （元），每天的销售量为y （瓶）．（1）求每天的销售量y （瓶）与销售单价x （元）之间的函数关系式；（2）当销售单价为多少元时，销售这款“免洗洗手液”每天的销售利润最大，最大利润为多少元？【分析】（1）销售单价为x （元），销售单价每降低0.5元，则每天可多售出20瓶（销售单价不低于成本价），则5.020x -为降低了多少个0.5元，再乘以20即为多售出的瓶数，然后加上80即可得出每天的销售量y ；（2）设每天的销售利润为w 元，根据利润等于每天的销售量乘以每瓶的利润，列出w 关于x 的函数关系式，将其写成顶点式，按照二次函数的性质可得答案．【解答】解：（1）由题意得：y ＝80+20×5.020x -，∴y＝﹣40x+880；（2）设每天的销售利润为w元，则有：w＝（﹣40x+880）（x﹣16）＝﹣40（x﹣19）2+360，∵a＝﹣40＜0，∴二次函数图象开口向下，∴当x＝19时，w有最大值，最大值为360元．答：当销售单价为19元时，销售这款“免洗洗手液”每天的销售利润最大，最大利润为880元．18．（2020•鄂州）一大型商场经营某种品牌商品，该商品的进价为每件3元，根据市场调查发现，该商品每周的销售量y（件）与售价x（元件）（x为正整数）之间满足一次函数关系，下表记录的是某三周的有关数据：x（元/件）456y（件）1000095009000（1）求y与x的函数关系式（不求自变量的取值范围）；（2）在销售过程中要求销售单价不低于成本价，且不高于15元/件．若某一周该商品的销售量不少于6000件，求这一周该商场销售这种商品获得的最大利润和售价分别为多少元？（3）抗疫期间，该商场这种商品售价不大于15元/件时，每销售一件商品便向某慈善机构捐赠m元（1≤m≤6），捐赠后发现，该商场每周销售这种商品的利润仍随售价的增大而增大．请直接写出m的取值范围．【分析】（1）用待定系数法求出一次函数的解析式便可；（2）根据“在销售过程中要求销售单价不低于成本价，且不高于15元/件．若某一周该商品的销售量不少于6000件，”列出x的不等式组，求得x的取值范围，再设利润为w元，由w＝（x﹣3）y，列出w关于x的二次函数，再根据二次函数的性质求出利润的最大值和售价；（3）根据题意列出利润w 关于售价x 的函数解析式，再根据函数的性质，列出m 的不等式进行解答便可．【解答】解：（1）设y 与x 的函数关系式为：y ＝kx +b （k ≠0），把x ＝4，y 10000和x ＝5，y ＝9500代入得，⎩⎨⎧=+=+95005100004b k b k ，解得，⎩⎨⎧=-=12000500b k ， ∴y ＝﹣500x +12000；（2）根据“在销售过程中要求销售单价不低于成本价，且不高于15元/件．若某一周该商品的销售量不少于6000件，”得，⎪⎩⎪⎨⎧≥+-≤≥60001200050053x x x ，解得，3≤x ≤12，设利润为w 元，根据题意得，w ＝（x ﹣3）y ＝（x ﹣3）（﹣500x +12000）＝﹣500x 2+13500x ﹣36000＝﹣500（x ﹣13.5）2+55125， ∵﹣500＜0，∴当x ＜13.5时，w 随x 的增大而增大，∵3≤x ≤12，∴当x ＝12时，w 取最大值为：﹣500×（12﹣13.5）2+55125＝54000，答：这一周该商场销售这种商品获得的最大利润为54000元，售价分别为12元；（3）根据题意得，w ＝（x ﹣3﹣m ）（﹣500x +12000）＝﹣500x 2+（13500+500m ）x ﹣36000﹣12000m ， ∴对称轴为x ＝﹣100050013500-+m ＝13.5+0.5m ，∴当x≤13.5+0.5m时，w随x的增大而增大，∵捐赠后发现，该商场每周销售这种商品的利润仍随售价的增大而增大．∴15≤13.5+0.5m，解得，m≥3，∵1≤m≤6，∴1≤m≤3．八．二次函数综合题（共2小题）19．（2020•通辽）如图，在平面直角坐标系中，抛物线y＝﹣x2+bx+c与x轴交于点A，B，与y轴交于点C．且直线y＝x﹣6过点B，与y轴交于点D，点C与点D关于x轴对称，点P是线段OB上一动点，过点P 作x轴的垂线交抛物线于点M，交直线BD于点N．（1）求抛物线的函数解析式；（2）当△MDB的面积最大时，求点P的坐标；（3）在（2）的条件下，在y轴上是否存在点Q，使得以Q，M，N三点为顶点的三角形是直角三角形？若存在，直接写出点Q的坐标；若不存在，说明理由．【分析】（1）由一次函数图象与坐标轴交点B、D的坐标，再由对称求得C点坐标，再用待定系数法求抛物线的解析式；（2）设P（m，0），则M（m，﹣m2+5m+6），N（m，m﹣6），由三角形的面积公式求得△MDB的面积关于m的二次函数，最后根据二次函数的最大值的求法，求得m的值，进而得P点的坐标；（3）分三种情况：M为直角顶点；N为直角顶点；Q为直角顶点．分别得出Q点的坐标．【解答】解：（1）令y＝0，得y＝x﹣6＝0，解得x＝6，令x ＝0，得y ＝x ﹣6＝﹣6，∴D （0，﹣6），∵点C 与点D 关于x 轴对称，∴C （0，6），把B 、C 点坐标代入y ＝﹣x 2+bx +c 中，得⎩⎨⎧==++-60636c c b ，解得，⎩⎨⎧==65c b ，∴抛物线的解析式为：y ＝﹣x 2+5x +6；（2）设P （m ，0），则M （m ，﹣m 2+5m +6），N （m ，m ﹣6），则MN ＝﹣m 2+4m +12，∴△MDB 的面积＝21MN ×OB ＝﹣3m 2+12m +36═﹣3（m ﹣2）2+48，∴当m ＝2时，△MDB 的面积最大，此时，P 点的坐标为（2，0）；（3）由（2）知，M （2，12），N （2，﹣4），当∠QMN ＝90°时，QM ∥x 轴，则Q （0，12）；当∠MNQ ＝90°时，NQ ∥x 轴，则Q （0，﹣4）；当∠MQN ＝90°时，设Q （0，n ），则QM 2+QN 2＝MN 2，即4+（12﹣n ）2+4+（n +4）2＝（12+4）2，解得，n ＝4±55，∴Q （0，4+55）或（0，4﹣55）．综上，存在以Q ，M ，N 三点为顶点的三角形是直角三角形．其Q 点坐标为（0，12）或（0，﹣4）或（0，4+55）或（0，4﹣55）．20．（2020•烟台）如图，抛物线y ＝ax 2+bx +2与x 轴交于A ，B 两点，且OA ＝2OB ，与y 轴交于点C ，连接BC ，抛物线对称轴为直线x ＝，D 为第一象限内抛物线上一动点，过点D 作DE ⊥OA 于点E ，与AC 交于点F ，设点D 的横坐标为m ．（1）求抛物线的表达式；（2）当线段DF 的长度最大时，求D 点的坐标；【分析】（1）点A 、B 的坐标分别为（2t ，0）、（﹣t ，0），则x ＝21＝21（2t ﹣t ），即可求解；（2）点D （m ，﹣m 2+m +2），则点F （m ，﹣m +2），则DF ＝﹣m 2+m +2﹣（﹣m +2）＝﹣m 2+2m ，即可求解；【解答】解：（1）设OB ＝t ，则OA ＝2t ，则点A 、B 的坐标分别为（2t ，0）、（﹣t ，0），则x ＝21＝21（2t ﹣t ），解得：t ＝1，故点A 、B 的坐标分别为（2，0）、（﹣1，0），则抛物线的表达式为：y ＝a （x ﹣2）（x +1）＝ax 2+bx +2，解得：a ＝﹣1，故抛物线的表达式为：y ＝﹣x 2+x +2；（2）对于y ＝﹣x 2+x +2，令x ＝0，则y ＝2，故点C （0，2），由点A、C的坐标得，直线AC的表达式为：y＝﹣x+2，设点D的横坐标为m，则点D（m，﹣m2+m+2），则点F（m，﹣m+2），则DF＝﹣m2+m+2﹣（﹣m+2）＝﹣m2+2m，∵﹣1＜0，故DF有最大值，此时m＝1，点D（1，2）；。

第二章解析函数

第二章解析函数1 .用导数定义，求下列函数的导数：⑴ /(x) = z Re Z.解:因z Re Az + Az Re 2 + Az Re Az Az 「 /n n A ReAz 、 =hm(Rez + ReAz + z ------- ) Az->0 Az当z wo 时，上述极限不存在，故导数不存在；当z = O 时，上述极限为0,故导数为0.2 .下列函数在何处可导?何处不可导?何处解析?何处不解析？ 1 1) f(z) = z-z 2.解：f(z) = Z • Z2 = Z • Z • Z =| z |2 ・z= (x 2 + y 2)(x + iy) = x(x 2 + y 2) + iy(x 2 + y 2),这里 w(x, y) = x(x 2+ y 2), v(x, y) = y(x 2+)]).u x = x 2 + y 2 + 2x 2, v v = x 2 + y 2 + 2y 2, "y = 2xy,匕=2xy.要％ = Uy,%, =-v x ，当且当x=y = 0,而"s%,,匕,4均连续,故f(z) = z ・z2.仅在z = 0处可导，处处不解析.2 2) f(z) = x3 - 3xy 2 +i(3x 2y- y 3).解：这里 w(x, y) = x 3-3xy 2,v(x, y) = 3x 2y- y\u x = 3x 2-3y 2,4 = -6 孙匕=6孙 v y = 3x 2 - 3)2,四个偏导数均连续且％ = 5人=-匕处处成立，故/(z)在整个复平面上处处可导, 也处处解析.3 .确定下列函数的解析区域和奇点，并求出导数.lim /(z + Az)-/(z) = lim ------------------------ Az-0 (z + Az) Re(z + Az) -zRez AzAzlim Az->0 lim(Rez + z A ZT O Re Az Az )=lim(Rez + zA VT O Ay->() AxAx + zAy(1)空至少有一不为零).cz + d解：当 c W 0 时，/ (z) = "z + "除 z=cz + d r (z )=(gycz + d(az + b)\cz + d) — (cz + d)\az + b)(CZ + 4)2a(cz + d) — c(az + h) ad- ch当c=o 时，显然有a 。

复变函数第2章解析函数

dw zz0 f (z0 )z
当 f (z) z时，dw= dz ，z 所以 f 在(z)点
z 0处的微分又可记为
dw zz0 f (z0 ) d z
亦即
dw
dz zz0
f (z0 )
由此可知，函数 w f (z)在点 z处0 可导与可微是等价的.
复变函数的求导法则与高数完全类似：
则称 gx, y为 D内的调和函数
定理2.3 设 f z u i，v 若 f 在z 区域内D 解
析，则与u 均v 为内D的调和函数.
定义2.4 若在区域 D内， u与 v均为调和函数
且满足C-R条件
ux vy , uy vx 则称 u 为 v的共轭调和函数
定理2.4 设 ux, y在区域 D内为调和函数，则
z0
)
lim
zz0
f (z) f (z0) z z0
0 f (z0 ) 0
知
lim
zz0
f (z)
f (z0 )，故
f在(z)点处z 0连续.
同高数一样，称函数 f (z) 的改变量 w的线性部分 f (z0 )z为函数 f (z在) 点 z处0 的微分，记作 dw 或 zz0 df(z) z，z0 即
2.1 复变函数的导数
定义2.1 设函数 w f z定义在区域 D
内，z0 D ，（z0 z） D ，若极限
lim f z0 z f z0
z0
z
存在，则称此极限为函数 f z在点 z0处的导数，
记作 f z0 或
df ，即
dz zz0
f
z0
df dz
z z0
lim
z0
f
z0

复-第二章解析函数作业题

(
)
(
)
�
(
)
(Leabharlann )()4 .求下列函数的奇点. z +1 1) 2 z ( z + 1) z +1 解: f ( z ) = 在分母为零即 2 z ( z + 1) z ( z 2 + 1)= 0的点 z = 0, z = ± i 处不解析,故奇点为 z = i , 0 , i.
8.设my 3 + nx 2 y + i ( x 3 + lxy 2 )为解析函数, 试确定l , m, n的值. 解:由my 3 + nx 2 y + i ( x 3 + lxy 2 )为解析函数, 得u = my + nx y, v = x + lxy .根据柯西-黎曼方程,有
z z
23.证明: z的反函数 Arsh z = Ln z + z + 1 . sh
2
ew ew 证:设z = sh w = ,那么w为z的反双曲 2 正弦函数w = Arsh z. 于是 e
(
)
( )
w 2
2 ze 1 = 0,它的解为
w
ew = z ± z 2 + 1 由于 z 2 + 1是双值函数且二值相差一个正负号, 这样 ± 号只取一个(不妨取为 + 号)即可.于是 e w = z + z 2 + 1,得w = Ln z + z 2 + 1 , 即 Arsh z = Ln z + z 2 + 1
13.证明: sin(2 z ) = 2 sin z cos z 3) e e e +e 证:因sin z = , cos z = 2i 2 iz iz iz iz e e e +e 2 sin z cos z = 2 2i 2 2 zi 2 zi e e = 2i = sin(2 z )

第二章解析函数习题及解答

第二章解析函数习题及解答2.1 研究下列函数在任一点处的可导性、解析性，若可导求其导数值．1）； 2）； 3）； 4）. 2.2 证明如果在区域内解析且满足下列条件之一，则必为一常数.1）在内为实值. 2）在内解析.3）在内为常数.4）在内为一常数.5）在内有，其中，，是不全为0的实常数.6）或在内为常数.7）在内有.2.3 证明在极坐标系下的柯西－黎曼条件为【提示：另一证明方法，可利用，然后根据复合函数求导证明】2.4 设在内解析．证明.2.5 证明解析函数的实、虚部所确定的曲线族与在的点处是正交的.（，为任意实数）2.6 已知下列调和函数求复势表达式．并写成关于的表达式.1）， 2），2.7设，求之值，使为一调和函数，并求一解析函数.2.8 计算下列复数1） 2），其中； 3）； 4）； 5）; 6)Ln(1+i) 2.9 求解方程 2.10 解下列方程1） 2）2.11 证明，对任何数（复数、实数），方程均有解. 2.12 求，使对任意，有.2.13 若某解析函数的实部等于虚部的平方，证明该解析函数必为常数.(提示：参考例2.6.1即可证明，这是该例的一个特殊情况)本章计算机编程实践与思考()33i y x z f -=()z z f =()z z f =()y y z f x x sin ie cos e +=()()()y x v y x u z f ,i ,+=D ()z f ()z f D ()z f D ()z f D ()z f arg D D ()()c y x bv y x au =+,,a b c ()()z f Re ()()z f Im D D ()0='z f 11, u u r ρϕρρϕ∂∂∂∂==-∂∂∂∂v v cos ,sin x y ρϕρϕ==()()()y x v y x u z f ,i ,+=D ()()2222224z f z f y x '=⎪⎪⎭⎫ ⎝⎛∂∂+∂∂()()()y x v y x u z f ,i ,+=()C y x u =,()B y x v =,()0≠'z f C B ()()()y x v y x u z f ,i ,+=z ()()12,-=x y y x u ()i 2-=f ()x yy x v arctan,=0>x ()y y x v pxsin e ,=p v ()()()y x v y x u z f ,i ,+=()ii 1+z 1y x z i +=()i ln -i 1i +()2ln -sin cos 0z z +=0sin =z 0e 1=+zωω=z cos ωz ()zz sin sin =+ω(说明：读者可参考第五部分计算机仿真编程实践)2.14 计算机编程计算2.15 计算机编程计算2.16 计算机编程解方程 2.17 计算机编程计算2.18 计算机求解方程2.19 计算机仿真（Matlab,Mathcad,Mathmatic ）绘出的图形. 2.20 对于下列解析函数，分别用计算机仿真方法（Matlab,Mathcad,Mathmatic ）绘出其实部和虚部的等值曲线图．（如等势线、电力线）本章习题解答2.1 研究下列函数在任一点处的可导性、解析性．1）； 2）； 3）； 4）．解 1）故，；，，，显见，，在全平面有连续一阶偏导，故，全平面处处可微，又令得，即即，当且仅当时，C-R 方程成立．所以仅在处可导，其他任何点不可导．由解析的定义可知，于全平面处处不解析．注由此结果可见，复变函数可存在孤立的甚至唯一的可导点，而无孤立的解析点．2），对任一，考虑极限即对任一，上述极限不存在，由可导定义知，于任一点处不可导．故全平面不解析．3）其中，．所以，当时，有π1i i i1234, (1i), i z ez z z -===+=12Ln(34i), ln(i 1)z z =-+=-sin 2z =tan(1i)Arc +10ze +=sin , cos , tan , ctan z z z z23(1)(); (2)()f z z f z z ==()33i y x z f -=()z z f =()z z f =()y y z f x x sin ie cos e +=()()()y x v y x u y x z f ,i ,i 33+=-= ()3,x y x u =()3,y y x v -=23x x u =∂∂0≡∂∂y u 0≡∂∂x v 23y y v -=∂∂u v()y x u ,()y x v ,⎪⎪⎩⎪⎪⎨⎧∂∂-=∂∂∂∂=∂∂y u xv y vx u 2233y x -=0022==⇔=+y x y x 0==y x ()z f 0=z ()z f ()y x z z f i -==0z ()()⎩⎨⎧≠∆=∆-=∆≠∆=∆+∆∆-∆=∆-∆+→∆→∆0,0,10,0,1i i lim lim0000y x y x y x y x z z f z z f z z0z ()z z f =0z ()()()y x v y x u y x z z f ,i ,22+=+==()22,y x y x u +=()0,≡y x v ()()0,0,≠y x，，因此，对，C-R 方程不成立．而当时，由于不存在，即不存在，同理，不存在，故在处不可导．于是，于全平面处处不可导，不解析．注在本题讨论中，仍然采用检验可导充要条件的方法，由于时，，，，均连续，故，可微，但C-R 方程处处不成立．对，从偏导定义出发，得知与不存在，从而在处不可微，故对平面任一点，可导的充要条件不满足．4），，，且，于全平面连续，故于全平面处处可导，全平面处处解析．又，因此有注 1.这里用区域解析的充分条件得到结论； 2.本题中的是一性质极好的函数：不仅全平面解析，且具有特性，它正是实指数函数在复平面的推广，即．但应注意这一推广产生的新性质：1）由于与以为周期，使得以的整数倍为周期．2）可取到除0以外的任意复值，包括负值．这两点是值得注意的．2.2 证明如果在区域内解析且满足下列条件之一，则必为一常数．1）在内为实值． 2）在内解析．3）在内为常数．4）在内为一常数．22y x x xu +=∂∂22y x yyu +=∂∂0≡∂∂=∂∂yu x v ()()0,0,≠∀y x ()()0,0,=y x ()()x x x x x u x u x x x 0200limlim 0,00,lim →→→=-=-()x u ∂∂0,0()y u ∂∂0,0()z z f =0=z ()zz f =()()0,0,≠y x x u∂∂y u ∂∂x v ∂∂y v∂∂u v ()()0,0,=y x x u ∂∂y u∂∂()y x u ,()0,0()()()y x v y x u y y z f xx ,i ,sin ie cos e +=+=()y y x u x cos e ,=()y y x v x sin e ,=y v y x u x ∂∂==∂∂cos e x v y y u x ∂∂-=-=∂∂sin e x u ∂∂y u ∂∂()z f ()x vx u z f ∂∂+∂∂='i ()()z f y y z f xx =+='sin ie cos e ()f z ()()z f z f ='x e ()ecos ie sin exp e xx zf z y y z '=+==ycos y sin πk 2z e i 2πz e ()()()y x v y x u z f ,i ,+=D ()z f ()z f D ()z f D ()z f D ()z f arg D5）在内有，其中，，是不全为0的实常数．6）或在内为常数．7）在内有．证首先，由条件在内解析a ），均在内可微，且b ）在内处处成立．1）因为在内取实值，即，．于是，．将此结果代入C-R 方程b ），得，．所以．．即（为一常数）2）于在内解析．因而除条件a ），b ）成立之外，条件c ）成立．联立b ），c ）得，即，．又由b ）或c ）得．所以在内，恒有，．即为常数．3）由于，．若，则，，．若，则由，两端分别关于，求偏导得：e ）将b ）代入e ）得D ()()c y x bv y x au =+,,a b c ()()z f Re ()()z f Im D D ()0='z f ()()()y x v y x u z f ,i ,+=D ⇔u v D ⎪⎪⎩⎪⎪⎨⎧∂∂-=∂∂∂∂=∂∂x v yu y v x u D ()z f D ()0,≡y x v ()D y x ∈,0≡∂∂=∂∂y v x v ()D y x ∈,0≡∂∂=∂∂y u x u ()D y x ∈,()A y x u =,()D y x ∈,()A z f =D z ∈A ()()()()()[]y x v y x u y x v y x u z f ,i ,,i ,-+=-=D ()()⎪⎪⎩⎪⎪⎨⎧∂∂=∂-∂-=∂∂∂∂-=∂-∂=∂∂x v x v yu y v y v x u y v y v ∂∂-=∂∂x vx v ∂∂-=∂∂0=∂∂=∂∂y v x u ()D y x ∈,0=∂∂=∂∂y ux u D ()A y x u =,()B y x v =,()B A z f i +=()()()Cy x v y x u z f ≡+=,,22()D y x ∈, 10=C ()0≡z f ()0≡⇔∈z f D z D z ∈ 20≠C ()()0,,222≠≡+C y x v y x u x y ⎪⎪⎩⎪⎪⎨⎧=∂∂+∂∂=∂∂+∂∂00y v v y u u x v v xuu ()D y x ∈,由得，代入b ）得，于是，即，（，为任意实常数）3）因为常数，，由主值支的表达式得f ）常数，及，若，则归为1）的情形，得证．若，对c ）两端分别关于，求偏导得即将b ）代入得，再由b ）即得，从而得，（，为任意实常数）5），，且，，是不全为0的实常数．所以有．于是对上式两端分别关于，求偏导得⎪⎪⎩⎪⎪⎨⎧=∂∂+∂∂=∂∂-∂∂00y u u xu v y u v x uu ()D y x ∈,()()0,,222≠≡+C y x v y x u 0≡∂∂=∂∂y u x u ()D y x ∈,0≡∂∂=∂∂y vx v ()D y x ∈,()A y x u ≡,()B y x v ≡,()B A z f i +=D z ∈A B ()≡z f arg D z ∈ωarg ()()≡y x u y x v ,,arctan C =()()0,,222≠≡+C y x v y x u ()D y x ∈, 10=C ()()⎩⎨⎧>≡0,0,y x u y x v ()D y x ∈, 20≠C x y ⎪⎪⎪⎩⎪⎪⎪⎨⎧=+∂∂-∂∂=+∂∂-∂∂002222v u y u v y v u v u x u v x vu ()022≠+v u ⎪⎪⎩⎪⎪⎨⎧=∂∂-∂∂=∂∂-∂∂00y u v yvu x u v x v u ⎪⎪⎩⎪⎪⎨⎧=∂∂-∂∂=∂∂-∂∂00x u u xv v x u v x vu ()D y x ∈,()()0,,22≠+y x v y x u 0=∂∂=∂∂∴x vx u 0=∂∂y v 0=∂∂y u ()B A z f i +=D z ∈A B ()()c y x bv y x u =+,,a ()D y x ∈,a b c 022≠+b a x y将b ）代入得因为，故得再由条件b ）即得，．于是得，（，为任意实常数）6）若，则在内取实值．即1）所证．若即，则，，，代入b ），即得，．，，（，为任意实常数）若，即，则，，则由b ）知，，即，7）由于．所以若在内有，则，，由条件b ）即得，．所以，（，为任意实常数）．注以上各命题的论证均是在于区域上解析的前提下进行的，否则结论不一定成立．例如，为一实值函数，满足条件1）．但它于全平面不解析（见1-26题，3）．显然在任何区域上不可能取常数值，即无题中的结论． 2.3 证明在极坐标系下的柯西－黎曼条件为【提示：另一证明方法，可利用，然后根据复合函数求导证明】⎪⎪⎩⎪⎪⎨⎧=∂∂+∂∂=∂∂+∂∂00y v b yu a x v b x ua ⎪⎪⎩⎪⎪⎨⎧=∂∂-∂∂=∂∂+∂∂00x v a x u b x v b x ua 022≠+b a ⎪⎪⎩⎪⎪⎨⎧=∂∂=∂∂00xv x u()D y x ∈,0=∂∂y v 0=∂∂y u ()B A z f i +≡D z ∈A B1()()0Im =≡C z f ()z f D ()()0Im ≠≡C z f ()C y x v ≡,()D y x ∈,0≡∂∂x v0≡∂∂y v ()D y x ∈,0≡∂∂x u0≡∂∂y u ()D y x ∈,()B A z f i +=∴ D z ∈A B 2()()C z f ≡Re ()C y x u ≡,()D y x ∈,0≡∂∂x u 0≡∂∂x u 0≡∂∂x v0≡∂∂y v ()B A z f i += D z ∈()x v x u z f ∂∂+∂∂='i D ()0='z f 0=∂∂x u 0=∂∂x v()D y x ∈,0=∂∂y u 0=∂∂y v()D y x ∈,()B A z f i +=D z ∈A B ()z f D ()zz f =()zz f =D 11, u u r ρϕρρϕ∂∂∂∂==-∂∂∂∂v v cos ,sin x y ρϕρϕ==2.4 设在内解析．证明．证令则（1）同理得（2）并注意在内解析．所以有即且，均为调和函数，即．于是（1）+（2）得注本题证明中用到解析函数三条性质：（1）实、虚部满足C-R 方程．（2）．（3）实部、虚部均为调和函数．即，．2.5 证明解析函数的实、虚部所确定的曲线族与在的点处是正交的．（，为任意实数）证因为在的点，曲线族在该点处的切线斜率为．曲线族在该点处的切线斜率为．所以．即曲线族与曲线族正交．（2）对使得，的点，曲线族在该点处的切线为铅直线（∵），而曲线族在该点处的切线为水平线（∵），故二者正交，同理，当，时，二者也正交．注 1.本题证明中用到曲线与曲线正交即为二者在交点处切线的正交这一概念； 2.本题的结论是解析函数在处的又一性质．2.6 已知下列调和函数求复势表达式．并写成关于的表达式．()()()y x v y x u z f ,i ,+=D ()()2222224z f z f y x '=⎪⎪⎭⎫ ⎝⎛∂∂+∂∂()()()()y x G y x v y x u z f ,,,222=+=⎥⎥⎦⎤⎢⎢⎣⎡∂∂+∂∂+⎪⎭⎫ ⎝⎛∂∂+⎪⎭⎫ ⎝⎛∂∂=∂∂222222222x v v x u u x v x u x G ⎥⎥⎦⎤⎢⎢⎣⎡∂∂+∂∂+⎪⎪⎭⎫ ⎝⎛∂∂+⎪⎪⎭⎫ ⎝⎛∂∂=∂∂222222222y v v y u u y v y u y G ()z f D ()y u y v x v x u z f ∂∂-∂∂=∂∂+∂∂='i i ()22222⎪⎪⎭⎫ ⎝⎛∂∂+⎪⎪⎭⎫ ⎝⎛∂∂=⎪⎭⎫⎝⎛∂∂+⎪⎭⎫ ⎝⎛∂∂='y v y u x v x u z f u v 0=∆=∆v u ()222224zf y G x G '=∂∂+∂∂()y u y v x v x u z f ∂∂-∂∂=∂∂+∂∂='i i 0=∆u 0=∆v ()()()y x v y x u z f ,i ,+=()C y x u =,()B y x v =,()0≠'z f C B ()0≠'z f ()y x ,()C y x u =,x v x u y u x u x y k ∂∂∂∂=∂∂∂∂-==d d 1()B y x v =,x uxvy v xvx y k ∂∂∂∂-=∂∂∂∂-==d d 2121-=k k ()C y x u =,()B y x v =,0≠∂∂x u 0=∂∂x v ()y x ,()C y x u =,0d d =y x ()B y x v =,0d d =x y0≠∂∂x v 0=∂∂x u ()0≠'z f ()()()y x v y x u z f ,i ,+=z1）， 2），解由于解析，所以，满足C-R 方程．1），故．由此得，这里为的任一可导函数．又由得所以，为任一实常数．于是．令，即得 ∴ 于是，满足条件的解析函数为所以2）在极坐标系下，C-R 方程为形式．令（则由得），有，，所以得，即解得为的任一可导函数．又由得．为任一实常数．所以注意，得2.7设，求之值，使为一调和函数，并求一解析函数．解因为，所以，，，()()12,-=x y y x u ()i 2-=f ()x yy x v arctan,=0>x ()()()y x v y x u z f ,i ,+=()y x u ,()y x v ,()()12,-=x y y x u yx u y v 2=∂∂=∂∂()()x C y y x v +=2,()x C x y ux v ∂∂-=∂∂()()12--='x x C ()122C x x x C ++-=1C ()1222,C x x y y x v ++-=2=z ⎩⎨⎧==02y x ()i i 21-==C f 11-=C ()()()12i 1222-+-+-=x x y x y z f ()()21i --=z z f ⎪⎪⎩⎪⎪⎨⎧∂∂=∂∂∂∂-=∂∂r u r v r v r uθθθ==x y v arctan 0>x ⎪⎭⎫ ⎝⎛-∈2,2ππθ1=∂∂θv 0=∂∂r v 1=∂∂r u r r r u 1=∂∂()()θθC r r u +=ln ,()θC θ()0=∂∂-='=∂∂r v r C u θθ()1C C =θ1C ()1ln ,C r r u +=θ()()()θθθi ln ,i ,1++=+=C r r v r u z f z r =()0arg arctan >==x z x yθ()1arg i ln C z z z f ++=()y y x v pxsin e,=p v ()()()y x v y x u z f ,i ,+=()y y x v pxsin e ,=y p x v px sin e =∂∂y p x v px sin e 222=∂∂y y v px cos e =∂∂y y v px sin e -=∂∂由，得．（1）当时，．由1-32题的方法易求出调和函数，则为所求解析函数，其中为任意实常数．（2）当时，．可求得调和函数．（为任一实常数）．于是所求的解析函数为(全平面解析)2.8 计算下列复数1） 2），其中； 3）； 4）；5）解 1）（为整数）2）当时得3）4）；5）注（i ）.以上各题均由定义求得；(ii). 值得注意的是，1只是无穷多个值中的一个值（对应于），这与实变量函数中的概念不同．2.9 求解方程【解】2.10 解下列方程1） 2）解2） ∵∴ ，即由对数函数定义得∴ ，为任意整数． 3）由得由对数函数定义得为任意整数[]1sin e 22222=-=∂∂+∂∂=∆p y y vx v v px 1±=p 1=p ()y y x v xsin e ,=()c y y x u x +=cos e ,()C y C y z f z x x +=++=e sin ie cos e C 1-=p ()y y x v x sin e ,-=()1cos e ,C y y x u x +-=-1C ()()()[]111e sin i cos e sin ie cos e C C y y y C y z f x z x x +-=+-+--=++-=----()ii 1+z 1y x z i +=()i ln -i 1i +()2ln -()()2iln 2412i 4i 2ln i i 1iln i ee e i 1+⎪⎭⎫⎝⎛+-⎥⎦⎤⎢⎣⎡+++===+πππk k k ()()()x k x k yk y y x z ππππ2sin i 2cos e e 11k 22i i x i +===-++() ,2,1,0±±=k 0=k 11=z()()πππk k 2i 2i2i i iarg i ln i ln +-=+-+-=-() ,2,1,0±±=k ()() ,2,1,0ie k 22/1±±=+k π()() ,2,1,012i 2ln ±±=++k k πz10=k sin cos 0z z +=(2)2sin cos 0(1)(1)2211/4, (0,1,2,)iz iz iz iziz iz i n iz e e e e z z e i e i i i e i eiz n n ππππ-----++=+=∴-=-++=-=-=-∴=-=±±0sin =z 0e 1=+zi 2e e sin i i =-=-zz z z z i i e e -=1e 2i =zπk z 2i 1ln 2i ==πk z k=k 01e =+z 1e -=z()()π12i 1ln +=-=k z k k主值为2.11 证明，对任何数（复数、实数），方程均有解．证在中，令，则，且，所以．且可取到任意非0值．于是，原方程即为，即．所以．（这里有两个根）故，由对数函数定义得所以．故右端对任意均有意义，得证．注这里的结果说明两点：（1）复变量余弦函数可取到任意值（复、实值），而不象实余弦函数取值区间仅为；（2）所得结果改变与的位置，即得）．这正是的反函数．可对进行同样讨论，此略． 2.12 求，使对任意，有．解由的定义，即求满足方程的一切值．整理化简即得，对任意成立．且因．故得，即．为任意整数．所以注由此题结果可见，复变量正、余弦函数为周期函数，且周期与实变量正、余弦的相同． 2.13 若某解析函数的实部等于虚部的平方，证明该解析函数必为常数．【提示，参考例2.6.1即可证明，这是该例的一个特殊情况】i0π=z ωω=z cos 2e e cos i i zz z -+=zt i e =⎪⎭⎫ ⎝⎛+=t t z 121cos ()x x t y z sin i cos e e i +==-0≠t t ω=⎪⎭⎫ ⎝⎛+t t 1210122=+-t t ω12-+=ωωt 12-ω01e 2i ≠-+=ωωz ()()1iln 1ln i 122-+-=-+=ωωωωz 012≠-+ωωω[]1,1-z ω()1iln 2-+-=z z ωz cos =ωz sin ωz ()z z sin sin =+ωz sin ()()zz z z i i i i e e e e -+-+-=-ωωω()()ωωωi i i 2i e 1e 1e e ----=-⋅z z 0e e i 2i ≠⋅ωz 0e1i =--ωπωk 2i 1ln i ==-k πωm 2=(),2,1,0±±=m。

第2章解析函数作业

第二章解析函数

202新数学复习第二章函数导数及其应用8导数与函数的零点问题含解析

第2章解析函数

【复变函数】第二章 解析函数(工科2版)

复变函数论第二章习题全解

第2章 基本初等函数 作业25 Word版含解析

复变函数 刘敏思 第二章 习题解答

2023年高考数学一轮复习第二章函数1函数的概念及其表示练习含解析

复变函数与积分变换答案-第2章解析函数

2022届高考数学一轮复习第2章函数概念与基本初等函数Ⅰ第5讲对数与对数函数作业试题1含解析新人教版

02第二章 解析函数积分

高中数学人教版A版必修一课时作业及解析：第二章2-1指数函数

《复变函数》第二章 解析函数

第二章 二次函数【真题训练】(解析版)

第二章解析函数

复变函数第2章解析函数

复-第二章 解析函数 作业题

第二章 解析函数习题及解答

【复变函数】第二章解析函数(工科2版)

第2章基本初等函数作业25 Word版含解析

复变函数刘敏思第二章习题解答

02第二章解析函数积分

《复变函数》第二章解析函数

第二章二次函数【真题训练】(解析版)

复-第二章解析函数作业题

第二章解析函数习题及解答