反比例函数中比例系数k的几何意义

合集下载

反比例函数中比例系数k的几何意义

反思小结
在反比例函数 y 10 的图象上,有一系列点A1，A2， x A3…..An，An+1，若A1横坐标为2,且以后每点的横坐标与它前一个点的横坐标的差都为2. 现分别过点A1，A2，A3…..An，An+1作X轴与Y轴的垂线段，构成若干个矩形如图10所示，将图中阴影部分的面积从左到右依次记为S1、S2、S3、…Sn， 5 5 15 2 5 2 (5 _____, ) 则S1=________, S +S +S =____ S1+S2 2 1 2 3 4 2 5 10 n 2 (5 ) +S3+….+Sn=________________.( 用n的代数式表 n 1 n 1 A 示)
C
S SOAD SABD SBCD SOCD 4 1 4
达标测试
已知几何图形的面积S，求比例系数k
5、如图，已知双曲线（k>0）经过矩形OABC边AB的中点F，交BC于点E，且四边形OEBF的面积为2，则k的值为（ B ）。
y
y
k x
A 1
所以
B 2
C 4
S OAB 4
O
y
已知几何图形的面积S，求比例系数k k y 变式、如图，已知双曲线 x ( k＞0 )经
B
D
C E A
x
而
SOAB SOBC SOAC
即
S ODE 1 S OAB 1 4 k 3 2
1 k 2
相似三角形的面积比等于相似比的平方 k 4;
k 0 k 4
k 0 k 4
4 y x
达标测试
4、如图，在平面直角坐标系中，点O为原点，菱形OABC的对角线 OB在x轴上，顶点A在反比例函数 2 的图像上，求菱形的面积。 y B

反比例函数中K的几何意义 (1)

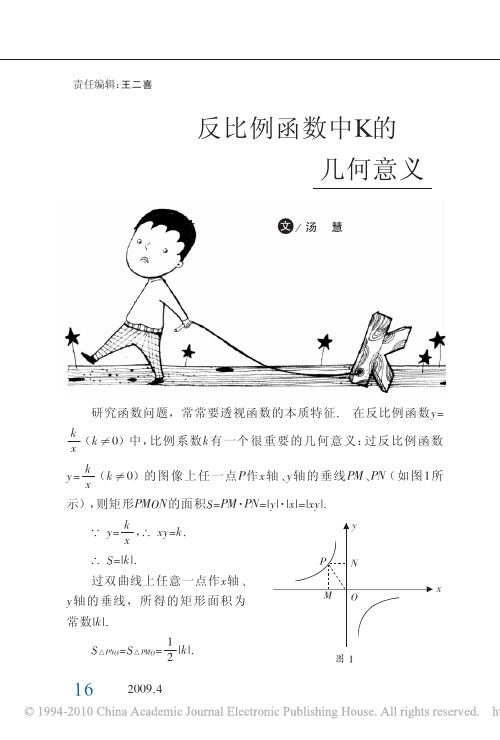
1 2
｜k｜.
∴ k＝±4.
又双曲线的一支在第二象限，
∴ k＝－4.
从而知两个函数的解析式分别为y＝
－4 x
和y＝－x＋4.
18
2009.4
例1
如图2，在函数y＝
1 x
的图
y A
像上有三点 A 、B 、C ，过这三点分别
B C
向 x 轴、y 轴作垂线，过每一点所作的
x
两条垂线与 x 轴、y 轴围成的矩形面
O
图2
积分别为SA、SB、SC，则（）.
A. SA＞SB＞SC
B. SA＜SB＜SC
∵
y＝
k x
，∴
xy＝k.
y
∴ S＝｜k｜.
PN
过双曲线上任意一点作x轴、
x
y轴的垂线，所得的矩形面积为
MO
常数｜k｜.
S△PNO＝S△PMO＝
1 2
｜k｜.
图1
16
2009.4
课程
资源
思路·方法
在解有关反比例函数的面积问题时，若能灵活运用k的几何意
义，会给解题带来方便，现举例说明．
一、比较面积大小
C. S A＜SC＜SB
D. SA＝S B＝SC
简解：根据反比例函数k的几何意义可知SA＝1，SB＝1，SC＝1.
∴ SA＝S B＝SC . 选D.
二、求面积
例2
如图 3 ，如果函数 y ＝－ x 与 y ＝－
4 x
的图像交于 A 、B 两点，过点
A作AC垂直于y轴，垂足为点C，则△BOC的面积为

反比例函数比例系数k的几何意义

反比例函数比例系数k的几何意义反比例函数y= k/x (k≠0)中比例系数k的几何意义，即过双曲线y=k/x (k≠0)上任意一点引x轴、y轴垂线,所得矩形面积为│k│1、如图，反比例函数4yx=-的图象与直线13y x=-的交点为A，B，过点A作y轴的平行线与过点B作x轴的平行线相交于点C，则ABC△的面积为（）A．8 B．6 C2、如图，点A是y轴正半轴上的一个定点，点B是反比例函数y＝2x(x＞0)图象上的一个动点，当点B的纵坐标逐渐减小时，△OAB的面积将（）A．逐渐增大B．逐渐减小C．不变D．先增大后减小3、如图12，A、B是函数2yx=的图象上关于原点对称的任意两点，BC∥x轴，AC∥y轴，△ABC的面积记为S，则（）A．2S=B．4S=C．24S<<D．4S>4、如图，已知双曲线)0k(xky＞=经过直角三角形OAB斜边OB的中点D，与直角边AB相交于点C．若△OBC的面积为3，则k＝____________．5、如图5所示，P1（x1，y1）、P2（x2，y2），……P n（x n，y n）在函数y=x9（x＞0）的图象上，△OP1A1，△P2A1A2，△P3A2A3……△P n A n－1A n……都是等腰直角三角形，斜边OA1，A1A2……A n-1A n，都在x轴上，则y1+y2+…y n= 。

6、如图，已知点A、B在双曲线xky=（x＞0）上，AC⊥x轴于点C，BD⊥y轴于点D，AC与BD交于点P，P是AC的中点，若△ABP的面积为3，则k＝．7、如图，在第一象限内,点P（2，3）,M()2,a是双曲线)0(≠=kxky上的两点,PA⊥x轴于点A,MB⊥x轴于点B,PA与OM交于点C,则△OAC的面积为8、如图，若正方形OABC的顶点B和正方形ADEF的顶点E都在函数1yx=（0x>）的图象上，则点E的坐标是（，）.9、如图，点A、B是双曲线3yx=上的点，分别经过A、B两点向x轴、y轴作垂线段，若1S=阴影，则12S S+=．10、如图，已知双曲线(0)ky kx=<经过直角三角形OAB斜边OA的中点D，且与直角边AB相交于点C．若点A的坐标为（6-，4），则△AOC的面积为（）A．12 B．9 C．6 D．411、如图，A是反比例函数图象上一点，过点A作AB⊥y轴于点B，点P在x轴上，△ABP的面积为2，则这个反比例函数的解析式为12、如图，已知在直角梯形AOBC中，AC∥OB，CB⊥OB，OB＝18，BC＝12，AC＝9，对角线OC、AB交于点D，点E、F、G分别是CD、BD、BC的中点．以O为原点，直线OB为x轴建立平面直角坐标系，则G、E、D、F四个点中与点A在同一反比例函数图象上的是（A）A．点G B．点E C．点D D．点F13、已知点A在双曲线y=6x上，且OA=4，过A作AC⊥x轴于C，OA的垂直平分线交OC于B．（1）则△AOC的面积=，（2）△ABC的周长为14、如图，一次函数y ax b=+的图象与x轴，y轴交于A，B两点，与反比例函数kyx=的图象相交于C，D两点，分别过C，D两点作y轴，x轴的垂线，垂足为E，F，连接CF，DE．有下列四个结论：①△CEF与△DEF的面积相等；②△AOB∽△FOE；③△DCE≌△CDF；④AC BD=．（第11题）第3题第5题图第6题图第8题图9题图其中正确的结论是．（把你认为正确结论的序号都填上）。

反比例函数中K的几何意义

反比例函数中K的几何意义
在反比例函数中，K表示比例系数或常数，也被称为反比例常数。

它
是用来确定两个变量之间反比关系的重要参数。

反比例函数的一般形式为：y=K/x，其中K表示比例系数。

K的几何意义可以通过分析反比例函数的图像得出。

反比例函数的图
像是一个双曲线，特点是曲线趋向于两个坐标轴。

下面将详细讨论K的几
何意义。

1.K的符号对于曲线的位置以及开口方向具有重要影响。

如果K为正数，那么曲线将位于第一和第三象限，并且开口方向为右上和左下。

如果
K为负数，那么曲线将位于第二和第四象限，并且开口方向为左上和右下。

2.K的绝对值越大，曲线就越“陡峭”。

当K增大时，曲线将更加接
近于坐标轴，并且在原点附近的斜率会越来越大。

反之，当K变小时，曲
线将更加平缓，斜率将减小。

3.K决定了特定坐标点的函数值。

例如，在函数y=K/x中，当x为K 时，y的值将为1、这是因为x与y成反比关系，而K是这种关系的常数。

4.K还决定了曲线相对于坐标轴的位置。

具体而言，当K增大时，曲
线将向坐标轴移动，而当K减小时，曲线将远离坐标轴。

总之，K代表了反比例函数中的比例系数或常数，它对于函数的位置、开口方向、陡峭程度以及特定坐标点的函数值都具有重要影响。

通过对K
的分析，我们可以更好地理解和解释反比例函数的几何特征。

反比例函数中k的几何意义

专题二反比例函数中k的几何意义
【主干必备】反比例函数中比例系数k的几何意义设点P(m,n)是双曲线y= k (k≠0)上任意一点
x
(1)过点P作x轴或y轴的垂线,垂足为点A,则
S△OAP=
1 2
·OA·AP=
1 |m|·|n|=
2
1 |mn|=
2
1 2
|k|.
(2)过点P分别作x轴、y轴的垂线,垂足为A,B,
值为世纪金榜导学号( D )
A.5
B.-5
C.10
D.-10
3.(2019·哈尔滨木兰期末)已知P是反比例函数y= k
x
(k≠0)图象上一点,PA⊥x轴于A,若S△AOP=4,则这个反
比例函数的解析式是 ( C )
A.y= 8
x
C.y= 8 =- 8
x
D.y= 4 或y=- 4
则S矩形OAPB=OA·AP=|m|·|n|=|mn|=|k|.
【微点警示】因为反比例函数y= k (k是常数,k≠0)中的k有正、负之
x
分,所以在利用解析式求矩形或三角形的面积时,都应加上绝对值符号;已知矩形或三角形的面积求反比例函数的解析式或k的值时,要根据函数的图象所在的象限确定k的正负.
x
x轴于点B交反比例函数y= 2 的图象于点C,连接OA,OC,
x
则△OAC的面积为 ( B )
A.2
B.3
C.6
D.8
2.(2019·达州达川区期末)如图所示,点A是反比例函
数y= k 的图象上的一点,过点A作AB⊥x轴,垂足为B,点
x
C为y轴上的一点,连接AC,BC.若△ABC的面积为5,则k的
【核心突破】

中考数学全程复习方略微专题二反比例函数中k的几何意义课件

微专题二反比例函数中k的几何意义
【主干必备】反比例函数中比例系数k的几何意义设点P(m,n)是双曲线y= k (k≠0)上任意一点
x
(1)过点P作x轴或y轴的垂线,垂足为点A,则
S△OAP=
1 ·OA·AP=
2
1 |m|·|n|=
2
1 |mn|=
2
1 |k|.
2
(2)过点P分别作x轴、y轴的垂线,垂足为A,B, 则S矩形OAPB=OA·AP=|m|·|n|=|mn|=|k|.
2.(2019·株洲中考)如图所示,在平面直角坐标系xOy
中,点A,B,C为反比例函数y= k (k>,OC,过点A作AD⊥y轴于点D,过点B,C分别作
BE,CF垂直x轴于点E,F,OC与BE相交于点M,记△BOM,四
边形CMEF,△AOD的面积分别为S1,S2,S3,则榜导学号( D )
世纪金
A.S1=S2+S3 C.S3>S2>S1
B.S2=S3 D.S1S2< S32
3.(2019·安顺中考)如图,直线l⊥x轴于点P,且与反比
例函数y1=
k1 x
(x>0)及y2=
k2 (x>0)的图象分别交于A,B
x
两点,连接OA,OB,已知△OAB的面积为4,则k1-k2=___8___.
x
A,B两点,过点A作AC⊥y轴于点C,过点B作BD⊥y轴于点D,
过点B作BE⊥x轴于点E,连接AD,已知AC=1,BE=1,
3
S矩形BDOE=4.则S△ACD=__2_.
类型二求反比例函数的比例系数k
例2(2018·遵义中考)如图,直角三角形的直角顶点在
坐标原点,∠OAB=30°,若点A在反比例函数y= 6 (x>0)

反比例函数中K的几何含义

的 y k 的图象过点B，则k的值为（）
x
y
B
A
Co
x
4.如图,点P是反比例函数
y

k x
图象上的一点,
若矩形OMNP的面积是3，则K=（）
y Mo
x
NP
5.如图,点P是反比例函数
y

k x
图象上的一点,
若矩形ONPM的面积是4，则K=（）
y
M
x
o
N
P
训练题 6.如图A、B在
y
3 x
4 x
上任意一点，
P是x轴上一点，过A作AB⊥y轴，垂足为B,则
S△ABP=( ).
y
BA
PO
X
如图，A是反比例函数
y 4 x
上任意一点，P是
x轴上一动点，过A作AB⊥y轴，垂足为B,则关于
S△ABP正确的说法是（）
y
A、逐渐增大 B、逐渐减小
BA
C、保持不变 D、无法确定
PO
X
1
2、正比例函数y=x与反比例函数y= x 的图象相交于
回顾知识
反比例函数的性质
反比例函数： y

k x(k≠0)
1.当k>0时,图象的两个分支分别在第一、三象限内，在每一个象限内，y随x的增大而减
小；
2.当k<0时,图象的两个分支分别在第二、四象限内，在每一个象限内，y随x的增大
而增大。
y
x 0
y x
0
归纳：反比例函数既是轴对称图形，又是中
心对称图形，对称轴是直线y=x和y=－x，对称中心是原点（０,０）
3 x在第一象限的图象如图所示，作一条平行于x轴

反比例函数k的几何意义

知识讲解1.反比例函数的概念如图所示，过双曲线)0(k≠=kxy上任一点),(yxP作x轴、y轴的垂线PM、PN,垂足为M、N，所得矩形PMON的面积S=PM∙PN=|y|∙|x|.,yxk=∴||kSkxy==，。

这就说明，过双曲线上任意一点作x轴、y轴的垂线，所得到的矩形的面积为常数|k|。

这是系数k几何意义,明确了k的几何意义，会给解题带来许多方便。

（请学生思考，图中三角形OEF的面积和系数k的关系。

）2.反比例函数的图象在用描点法画反比例函数y=kx的图象时,应注意自变量x的取值不能为0,应从1或-1开始对称取点.例题1函数y=1x-(x>0)的图象大致是( )例题2 函数y=kx+1与函数y=kx在同一坐标系中的大致图象是( )yOxAyO xByOxCyOxD y y y y3.反比例函数y=kx 中k 的意义注意:反比例函数y=k x (k ≠0)中比例系数k 的几何意义,即过双曲线y=kx(k ≠0)上任意一点引x 轴、y 轴垂线,所得矩形面积为│k │.例题1：如图，P 、C 是函数x4y =（x>0）图像上的任意两点，过点P 作x 轴的垂线PA,垂足为A ，过点C 作x 轴的垂线CD,垂足为D ，连接OC 交PA 于点E ，设⊿POA 的面积为S1,则S1= ,梯形CEAD 的面积为S2，则S1与S2的大小关系是S1 S2, ⊿POE 的面积S3和梯形CEAD 的面积为S2的大小关系是S2 S3.例题1图例题2图例题3图例题2：如图所示，直线l 与双曲线)0(ky >=k x交A 、B 两点，P 是AB 上的点，试比较⊿AOC 的面积S1，⊿BOD 的面积S2，⊿POE 的面积S3的大小：。

例题3：如图所示，点A(x1,y1)、B(x2,y2)都在双曲线)0x (k>=xy 上,且x2-x1=4,y1-y2=2;分别过点A 、B 向x 轴、y 轴作垂线，垂足分别为C 、D 、E 、F ，AC 与BF 相交于G 点，四边形FOCG 的面积为2，五边形AEODB 的面积为14，那么双曲线的解析式为。

反比例函数函数K的几何意义

反比例函数函数K的几何意义反比例函数的几何意义是在坐标系中表示直角坐标的一条曲线。

由于该函数的定义域为x≠0，因此在坐标系中，x轴上的原点除外，函数的图像将存在断点。

根据反比例函数的定义，当x的值趋近于零时，x的值将趋近于正无穷大。

同样地，当x的值趋近于正无穷大或负无穷大时，x的值将趋近于零。

这意味着反比例函数的图像将以原点为对称中心，分别在第一、第三象限不断向正无穷大和负无穷大逼近，而在第二、第四象限不断向零逼近。

反比例函数的图像通常表现为一条双曲线，称为反比例双曲线。

该曲线的两个分支在坐标平面中以渐进线（Asymptotes）为边界无限延伸。

渐进线是反比例双曲线的特殊特征，由于两个变量之间的反比例关系，当一个值趋近于无穷大时，另一个值将趋近于零。

因此，反比例双曲线的渐近线是表示这种趋势的标志。

反比例双曲线分为两类：水平渐近线和垂直渐近线。

水平渐近线与x轴平行，表示当x的值趋近于正无穷大或负无穷大时，函数值趋近于零。

垂直渐近线与x轴平行，表示当x的值趋近于零时，函数值趋近于无穷大。

通过做一些简单的数学变换，我们可以将反比例函数的标准形式x=x/x转化为x=xx的形式。

这种形式的反比例函数在坐标系中表示为一条直线。

直线的斜率为x，它表示的是x轴上单位长度对应的x轴上的长度。

当x为正数时，直线向右上方倾斜；当x为负数时，直线向右下方倾斜。

通过改变x的值，可以在坐标系中绘制出不同斜率的直线。

反比例函数的几何意义在数学和物理方面起到了重要的作用。

在数学中，反比例函数的性质使它成为其他函数的重要组成部分，如复合函数、一次函数、二次函数等。

在物理中，许多自然界现象的描述都使用反比例函数，比如电阻和电流之间的关系、浓度和稀释之间的关系、速度和时间之间的关系等。

因此，了解和理解反比例函数的几何意义具有重要的实际应用价值。

反比例函数K的几何意义

（2）A、C落在反比例函数的图象上，设矩形平移后A坐标是（2，6-b），C坐标是（6，4-b）， ∵A、C落在反比例函数的图象上， ∴k=2（6-b）=6（4-b）， ∴b=3，即矩形平移后A的坐标是（2，3），代入反比例函数的解析式得：k=2×3=6，
【山东·全国考题回访】
1.(2014·济南中考)如图,△OAC和△BAD都是等
如图，过y轴正半轴上的任意一点P，作x轴的平行线，分别与反比例函数y=-4/x和 y=2/x交于点A和点B，若点C是x轴上任意一点，连接AC、BC，则△ABC的面积为
点B，D在反比例函数y=b/x（b＜0）的图象上，
AB∥CD∥x轴，AB，CD在x轴的两侧，AB=3，CD=2，
AB与CD的距离为5，则a-b的值是
则S△OBC=
1·(-x)·22y=6.解得k=xy=-6. 2
答案:-6
如图，直线l⊥x轴于点P，且与反比例函数 y1=k1/x(x>0)及y2=k2/x(x>0)的图像分别交于点A， B，连接OA，OB，已知△OAB的面积为3，则k1-k2 的值等于（）
如图△P1OA1，△P2A1A2是等腰直角三角形，点P1， P2在函数y=4/x（x＞0）的图象上，斜边OA1，A1A2 都在x轴上，则点A2的坐标是______．
答案:6
（1）直接写出B、C、D三点的坐标；
（2）若将矩形向下平移，矩形的两个顶点恰好同时落在反比例函数的图象上，猜想是哪两个点，并求矩形的平移距离和反比例函数的解析式．
（1）∵四边形ABCD是矩形，平行于x轴，且AB=2，AD=4，点A的坐标为（2，6）． ∴AB=CD=2，AD=BC=4， ∴B（2，4），C（6，4），D（6，6）；
腰直角三角形，∠ACO=∠ADB=90°,反比例函数 y= k 在第一象限的图象经过点B，若OA2-AB2=12，则kx的值为_______.

专题12 反比例函数比例系数k的几何意义(解析版)

1专题12 反比例函数比例系数k 的几何意义知识对接考点一、反比例函数比例系数k 的几何意义（1）意义：从反比例函数y ＝(k≠0)图象上任意一点向x 轴和y 轴作垂线，垂线与坐标轴所围成的矩形面积为|k|,以该点、一个垂足和原点为顶点的三角形的面积为1/2|k|. （2）常见的面积类型：失分点警示已知相关面积，求反比例函数的表达式，注意若函数图象在第二、四象限，则k ＜0. 例：已知反比例函数图象上任一点作坐标轴的垂线所围成矩形为3，则该反比例函数解析式为：3y x =或3y x =-专项训练一、单选题1．如图，已知反比例函数2y x=-的图像上有一点P ，过点P 作PA x ⊥轴，垂足为点A ，则POA的面积是（）A ．2B ．1C ．1-D ．12【答案】B 【分析】设(),P x y ，则POA 的面积是1122x y xy ••=，再结合2y x=-即可求解．【详解】解：设(),P x y ，则POA 的面积是1122x y xy ••=，∵2y x=-∵22xy =-=∵POA 的面积是1212⨯=．故选：B ．【点睛】本题考查了反比例函数与图形的面积计算，解题的关键是熟练运用数形结合的思想． 2．如图，在平面直角坐标系中，A ，B 是反比例函数ky x=在第一象限的图象上的两点，且其横坐标分别为1，4，若AOB 的面积为54，则k 的值为（）A ．23B ．1C ．2D ．154【答案】A 【分析】过点A 作AC y ⊥轴，过点B 作BD x ⊥轴，反向延长AC BD 、交于点E ，利用割补法表示出AOB 的面积，即可求解．【详解】解：过点A 作AC y ⊥轴，过点B 作BD x ⊥轴，反向延长AC BD 、交于点E ，如下图：则四边形ODEC 为矩形3点AB 、的横坐标分别为1，4，则(1,)(4,)4kA kB 、，(0,)(4,0)(4,)C kDE k 、、11154143224244AOBAOCOBDABEODEC k k SS SSSk k k ⎛⎫=---=-⨯⨯-⨯⨯-⨯⨯-= ⎪⎝⎭矩形解得23k = 故选A【点睛】此题考查了反比例函数的有关性质，涉及了割补法求解三角形面积，熟练掌握反比例函数的有关性质是解题的关键．3．若图中反比例函数的表达式均为4y x=，则阴影面积为4的有（）A ．1个B ．2个C ．3个D ．4个【答案】B 【分析】根据反比例函数比例系数k 的几何意义，反比例函数的性质以及三角形的面积公式，分别求出四个图形中阴影部分的面积，即可求解．【详解】解：图1中，阴影面积为xy ＝4；图2中，阴影面积为12xy ＝12×4＝2；图3中，阴影面积为2×12xy ＝2×12×4＝4；图4中，阴影面积为4×12xy ＝4×12×4＝8；则阴影面积为4的有2个．故选：B ．【点睛】本题考查了反比例函数ky x=中k 的几何意义，即过双曲线上任意一点引x 轴、y 轴垂线，所得矩形面积为|k |，是经常考查的一个知识点；这里体现了数形结合的思想，做此类题一定要正确理解k 的几何意义．也考查了反比例函数的对称性，三角形的面积．4．如图，点A 是反比例函数4y x=-图象上的一个动点，过点A 作AB ∵x 轴，AC ∵y 轴，垂足分别为B ，C ，则矩形ABOC 的面积为（）A ．-4B ．2C ．4D ．8【答案】C 【分析】根据反比函数的几何意义，可得矩形ABOC 的面积等于比例系数的绝对值，即可求解．【详解】解：∵点A 是反比例函数4y x=-图象上的一个动点，过点A 作AB ∵x 轴，AC ∵y 轴，∵矩形ABOC 的面积44-= ．故选：C ．【点睛】本题主要考查了反比函数的几何意义，熟练掌握本题主要考查了反比例函数()0ky k x=≠ 中k 的几何意义，即过双曲线上任意一点引x 轴、y 轴垂线，所得矩形面积等于k 是解题的关键．5．如图，等腰ABC 中，5AB AC ==，8BC =，点B 在y 轴上，//BC x 轴，反比例函数ky x=（0k >，0x >）的图象经过点A ，交BC 于点D ．若AB BD =，则k 的值为（）5A ．60B ．48C ．36D ．20【答案】A 【分析】过A 作AE ∵BC 于E 交x 轴于F ，则AF ∵y 轴，根据矩形的性质得到EF =OB ，根据勾股定理得到3AE =，设OB =a ，则A (4,3),(5,)a D a +，即可得到4(3)5k a a =+=，解方程求得a 的值，即可得到D 的坐标，进而求得k 的值．【详解】解：过A 作AE ∵BC 于E 交x 轴于F ， ∵5AB AC ==，8BC =， ∵142BE BC ==，∵3AE ==，设OB =a ， ∵BD =AB =5， ∵A (4,3),(5,)a D a +， ∵反比例函数ky x=（0k >，0x >）的图象经过点A ，交BC 于点D ． ∵4(3)5k a a =+=，解得：a =12， ∵51260k =⨯=，故选择：A ．【点睛】本题考查了反比例函数图象上点的坐标特征，等腰三角形的性质，勾股定理，表示出点的坐标是解题的关键．6．在平面直角从标系中，30°的直角三角尺直角顶点与坐标原点重合，双曲线11ky x =（x ＞0），经过点B ，双曲线22k y x=（x ＜0），经过点C ，则12k k ＝（）A ．﹣3B ．3 C．D【答案】A 【分析】作AM ∵x 轴于M ，BN ∵x 轴于N ，由反比例函数系数k 的几何意义得到k 1＝2S ∵AOM ，k 2＝﹣2S ∵BON，解直角三角形求得o tan 30OB OA =∵AOM ∵∵OBN ，得到2=3AOM BOMSOA SOB ⎛⎫= ⎪⎝⎭进而得到123k k =-．【详解】作AM ∵x 轴于M ，BN ∵x 轴于N ， ∵S ∵AOM ＝12|k 1|，S ∵BON ＝12|k 2|，∵k 1＞0，k 2＜0，∵k 1＝2S ∵AOM ，k 2＝﹣2S∵BON ，在Rt ∵AOB 中，∵BAO ＝30°，7∵o tan 30OB OA = ∵∵AOM +∵BON ＝90°＝∵AOM +∵OAM ， ∵∵OAM ＝∵BON ， ∵∵AMO ＝∵ONB ＝90°， ∵∵AOM ∵∵OBN ，∵2=3AOM BOMS OA S OB ⎛⎫= ⎪⎝⎭， ∵12232AOMBOMk S k S ==--, 故选A ．【点睛】本题主要考查了反比例函数比例系数k 的几何意义，相似三角形的性质与判定，解题的关键在于能够熟练掌握相关知识进行求解． 7．如图，A 、B 是双曲线y ＝kx图象上的两点，过A 点作AC ∵x 轴于点C ，交OB 于点D ，BD ＝2OD ，且ADO 的面积为8，则DCO 的面积为（）A ．12B ．1C ．32D ．2【答案】B 【分析】过点B 作BH x ⊥轴于点H ，根据反比例函数比例系数k 的几何意义，即可得到ADO △的面积与梯形CDBH 的面积相等，再根据DCO BOH △∽△，即可求得DCO 的面积．【详解】解：过点B作BH∵x轴于点H，∵AC∵x轴于点C，∵AOC的面积与BOH的面积相等，∵ADO的面积与梯形CDBH的面积相等，∵ADO的面积为8，∵梯形CDBH的面积为8，∵DC//BH，∵DOC∵BOH，∵BD＝2OD，∵DOC与BOH的相似比为1：3，∵DOC与BOH的面积比为1：9，设DCO的面积比为x，则x：（x+8）＝1：9，解得：x＝1，故选：B．【点睛】本题考查了反比例函数比例系数k的几何意义，三角形的相似及相似的性质，得到ADO△的面积与梯形CDBH的面积相等和DOC BOH∽是解决本题的关键．8．如图，平行于y轴的直线l分别与反比例函数kyx=（x＞0）和1yx=-（x＞0）的图象交于M、N两点，点P是y轴上一动点，若∵PMN的面积为2，则k的值为（）A．2B．3C．4D．5【答案】B9【分析】由题意易得点M 到y 轴的距离即为∵PMN 以MN 为底的高，点M 、N 的横坐标相等，设点1,,,k M a N a a a ⎛⎫⎛⎫- ⎪ ⎪⎝⎭⎝⎭，则有11k k MN a a a +⎛⎫=--= ⎪⎝⎭，进而根据三角形面积公式可求解．【详解】解：由平行于y 轴的直线l 分别与反比例函数k y x =（x ＞0）和1y x=-（x ＞0）的图象交于M 、N 两点，可得：点M 到y 轴的距离即为∵PMN 以MN 为底的高，点M 、N 的横坐标相等，设点1,,,k M a N a a a ⎛⎫⎛⎫- ⎪ ⎪⎝⎭⎝⎭，∵11k k MN a a a+⎛⎫=--= ⎪⎝⎭， ∵∵PMN 的面积为2， ∵111222PMNk SMN a a a+=⋅=⨯⨯=，解得：3k =；故选B ．【点睛】本题主要考查反比例函数与几何的综合，熟练掌握反比例函数与几何的综合是解题的关键． 9．如图，过x 轴正半轴上的任意一点P ，作y 轴的平行线，分别与反比例函数y 3=x（x ＞0）和y 6=x-（x ＞0）的图象交于B 、A 两点．若点C 是y 轴上任意一点，则∵ABC 的面积为（）A ．3B ．6C ．9D ．92【答案】D 【分析】设P （a ，0），由直线APB 与y 轴平行，得到A 和B 的横坐标都为a ，将x ＝a 代入反比例函数y 6x-＝和y 3x ＝中，分别表示出A 和B 的纵坐标，进而由AP ＋BP 表示出AB ，三角形ABC的面积12⨯＝AB×P的横坐标，求出即可．【详解】解：设P（a，0），a＞0，则A和B的横坐标都为a，将x＝a代入反比例函数y6x=-中得：y6a=-，故A（a，6a-）；将x＝a代入反比例函数y3x＝中得：y3a=，故B（a，3a），∵AB＝AP＋BP639a a a+＝＝，则S∵ABC12=AB•x P19922aa=⨯⨯=，故选D．【点睛】本题主要考查反比例函数图象k的几何意义，解决本题的关键是要熟练掌握反比例函数k的几何意义.10．如图．在平面直角坐标系中，∵AOB的面积为278，BA垂直x轴于点A，OB与双曲线y＝kx相交于点C，且BC∵OC＝1∵2，则k的值为（）A．﹣3B．﹣94C．3D．92【答案】A【分析】过C作CD∵x轴于D，可得∵DOC∵∵AOB，根据相似三角形的性质求出S∵DOC，由反比例11函数系数k 的几何意义即可求得k ．【详解】解：过C 作CD ∵x 轴于D ，∵BC OC＝12， ∵OCOB ＝23， ∵BA ∵x 轴， ∵CD ∵AB ， ∵∵DOC ∵∵AOB ， ∵DOC AOB S S ∆∆＝（OC OB ）2＝（23）2＝49， ∵S ∵AOB ＝278， ∵S ∵DOC ＝49S ∵AOB ＝49×278＝32，∵双曲线y ＝kx在第二象限，∵k ＝﹣2×32＝﹣3，故选：A ．【点睛】本题主要考查了反比例函数系数k 的几何意义，相似三角形的性质和判定，根据相似三角形的性质和判定求出S ∵DOC 是解决问题的关键．二、填空题11．如图，平面直角坐标系中，O 是坐标原点，点A 是反比例函数()0ky k x=≠图象上的一点，过点A 分别作AM x ⊥轴于点M ，AN y ⊥轴于点N ．若四边形AMON 的面积为12，则k 的值是__________．【答案】-12【分析】根据反比例函数的比例系数k的几何意义得到12k=，然后根据反比例函数的性质确定k的值．【详解】解：四边形AMON的面积为12，12k∴=，反比例函数图象在二四象限，k∴<，12k∴=-，故答案为：12-．【点睛】本题考查了反比例函数函数k的几何意义：在反比例函数kyx=图象中任取一点，过这一个点向x轴和y轴分别作垂线，与坐标轴围成的矩形的面积是定值||k．12．如图，在反比例函数3yx=的图象上有一动点A，连接AO并延长交图象的另一支于点B，在第二象限内有一点C，满足AC=BC，当点A运动时，点C始终在函数kyx=的图象上运动，tan∵CAB=2，则k的值为_____【答案】﹣12【分析】连接OC，过点A作AE∵x轴于点E，过点C作CF∵y轴于点F，通过角的计算找出∵AOE=∵COF，结合“∵AEO=90°，∵CFO=90°”可得出∵AOE∵∵COF，根据相似三角形的性质得出比例式，再由tan∵CAB=2，可得出CF•OF的值，进而得到k的值．【详解】如图，连接OC，过点A作AE∵x轴于点E，过点C作CF∵y轴于点F．∵由直线AB与反比例函数3yx=的对称性可知A、B点关于O点对称，∵AO=BO．又∵AC=BC，∵CO∵AB．∵∵AOE+∵AOF=90°，∵AOF+∵COF=90°，∵∵AOE=∵COF．又∵∵AEO=90°，∵CFO=90°，∵∵AOE∵∵COF，∵AE OE AO CF OF CO==，∵tan∵CABOCOA==2，∵CF=2AE，OF=2OE．又∵AE•OE=3，CF•OF=|k|，∵|k|=CF•OF=2AE×2OE=4AE×OE=12，∵k=±12．∵点C在第二象限，∵k=﹣12．故答案为：﹣12．13【点睛】本题考查了反比例函数图象上点的坐标特征、反比例函数的性质以及相似三角形的判定及性质，锐角三角函数，解答本题的关键是求出CF•OF=12．解答该题型题目时，巧妙的利用了相似三角形的性质找出对应边的比例，再结合反比例函数图象上点的坐标特征找出结论．13．如图，点P在反比例函数4yx=-的图像上，过点P作PA x⊥轴于点A，则POA的面积是_______．【答案】2【分析】设出点P的坐标，∵OAP的面积等于点P的横纵坐标的积的一半，把相关数值代入即可．【详解】解：设点P的坐标为（x，y）．∵P（x，y）在反比例函数4yx=-的图象上，∵4 xy=-，∵122POAS xy==，故答案为：2．【点睛】题考查了反比例函数比例系数k的几何意义：在反比例函数ky=x图象中任取一点，过这一个点向x轴和y轴分别作垂线，与坐标轴围成的矩形的面积是定值|k|．14．如图所示，反比例函数kyx=（0k≠，0x>）的图像经过矩形OABC的对角线AC的中15点D ．若矩形OABC 的面积为8，则k 的值为________．【答案】2 【分析】过点D 作DE ∵OA 于点E ，由矩形的性质可知：S ∵AOC =12S 矩形OABC =4，从而可求出∵ODE 的面积，利用反比例函数中k 的几何意义即可求出k 的值．【详解】如图，过点D 作DE OA ⊥于点E ，设,k D m m ⎛⎫ ⎪⎝⎭，则OE m =，k DE m=， ∵点D 是矩形OABC 的对角线AC 的中点， ∵2OA m =，2k OC m=， ∵矩形OABC 的面积为8， ∵228kOA OC m m⋅=⋅=， ∵2k =，故答案为：k =2．【点睛】本题考查了反比例函数系数k 的几何意义，解题的关键是求出矩形的面积． 15．如图，点A 与点B 分别在函数11(0)k y k x=>与220)k y k x =<（的图象上，线段AB 的中点M 在y 轴上．若∵AOB 的面积为3，则12k k -的值是___．【答案】6【分析】设A（a，b），B（-a，d），代入双曲线得到k1=ab，k2=-ad，根据三角形的面积公式求出ab+ad=6，即可得出答案．【详解】解：作AC∵x轴于C，BD∵x轴于D，∵AC∵BD∵y轴，∵M是AB的中点，∵OC=OD，设A（a，b），B（-a，d），代入得：k1=ab，k2=-ad，∵S∵AOB=3，∵111()23 222b d a ab ad+--=，∵ab+ad=6，∵k1-k2=6，故答案为：6．【点睛】本题主要考查对反比例函数系数的几何意义，反比例函数图象上点的坐标特征，三角形的面积等知识点的理解和掌握，能求出ab+ad=6是解此题的关键．三、解答题16．如图，一次函数122y x=-的图象分别交x轴、y轴于A、B，P为AB上一点且PC为17AOB 的中位线，PC 的延长线交反比例函数ky x=（0k >）的图象于点Q ，32OQCS =．（1）求A 点和B 点的坐标；（2）求k 的值和Q 点的坐标．【答案】（1）A （4，0），B （0，-2）；（2）3k =，Q 的坐标为(2 ，32)．【分析】（1）因为一次函数y =12x -2的图象分别交x 轴，y 轴于A ，B ，所以当y =0时，可求出A 的横坐标，当x =0时可求出B 的纵坐标，从而可得解．（2）因为三角形OQC 的面积是Q 点的横纵坐标乘积的一半，且等于32，所以可求出k 的值，PC 为中位线，可求出C 的横坐标，也是Q 的横坐标，代入反比例函数可求出纵坐标．【详解】解：（1）设A 点的坐标为（a ，0），B 点坐标为（0，b ），分别代入y =12x -2，解方程得a =4，b =-2， ∵A （4，0），B （0，-2）；（2）∵PC 是∵AOB 的中位线， ∵PC ∵x 轴，即QC ∵OC ，又Q 在反比例函数ky x=的图象上， ∵2S ∵OQC =k ，∵k =2×32=3，∵PC 是∵AOB 的中位线， ∵C （2，0），可设Q （2，q ）∵Q 在反比例函数ky x=的图象上， ∵q =32，∵点Q 的坐标为(2 ，32)．【点睛】本题考查反比例函数的综合运用，熟练掌握并应用反比例函数ky x=（0k >）中k 的几何意义是解题的关键．17．点O 为平面直角坐标系的原点，点A 、C 在反比例函数ay x=的图象上，点B 、D 在反比例函数by x=的图象上，且0a b >>．（1）若点A 的坐标为()6,4，点B 恰好为OA 的中点，过点A 作AN x ⊥轴于点N ，交b y x=的图象于点P ． ∵请求出a 、b 的值； ∵试求OBP 的面积．（2）若////AB CD x 轴，32CD AB ==，AB 与CD 间的距离为6，试说明-a b 的值是否为某一固定值？如果是定值，试求出这个定值；若不是定值，请说明理由．【答案】（1）∵a =24，b =6∵92；（2）是定值为92．【分析】（1）∵把A ()6,4代入反比例函数ay x=即可求出a ，根据点B 为OA 的中点，求出B 点坐标，代入by x=即可求出b ；∵根据k 的几何意义求出∵AOP 的面积，再连接BP ，根据中线的性质即可求解；19（2）先分析,A C 分别位于a y x =的两个分支,,B D 分别位于 by x=的两个分支；再利用反比例函数系数k 的几何意义，表示S ∵AOB 和S ∵COD ，再根据三角形的面积公式，AB 与CD 之间的距离为6，即求出答案．【详解】（1）∵把A ()6,4代入反比例函数ay x=，得a =6×4=24 ∵点B 为OA 的中点， ∵B （3，2）把B （3，2）代入反比例函数by x=，得b =3×2=6 ∵∵S ∵AOP = S ∵AON -S ∵NOP = 1122a b -=9 ∵B 点是OA 的中点， ∵BP 是∵AOP 的中线∵OBP 的面积=12×9=92；（2）如图，当,A C 在a y x =的第一象限的图像上时，,B D 在by x=的第一象限的图像上时////AB CD x 轴，32CD AB ==，∴AOBS=1122AOM BOM S S a b -=-△△， COD S =△1122CON DON S S a b -=-△△∴COD S =△AOBS1=2AOB S AB OM ⨯△，12COD S CD ON =⨯△OM ON ∴=则点A 与点C 重合，点B 与点D 重合即AB 与CD 间的距离为0，,A C ∴分别位于a y x =的两个分支,,B D 分别位于 by x=的两个分支；如图，延长AB 、CD 交y 轴于点E 、F ，∵点A 、C 在反比例函数a y x =的图象上，点B 、D 在反比例函数by x=的图象上，a ＞b ＞0，////AB CD x 轴，∵AB 与CD 间的距离为6， ∵OE +OF =6 ∵S ∵AOE ＝12a ＝12a ＝S ∵COF ，S ∵BOE ＝12b ＝12b ＝S ∵DOF ，∵S ∵AOB ＝S ∵AOE −S ∵BOE ＝12a −12b ＝12AB •OE ＝34OE ，S ∵COD ＝S ∵COF −S ∵DOF ＝12a −12b ＝12CD •OF ＝34OF ，∵S ∵AOB ＋S ∵COD ＝a −b ＝34OE ＋34OF ＝34（OE ＋OF ）=92．92a b ∴-=．【点睛】本题考查反比例函数图象上点的坐标特征以及反比例函数系数k 的几何意义，理解反比例函数系数k 的几何意义是正确解答的关键．18．如图，点C 在反比例函数y 1=x 的图象上，CA ∵y 轴，交反比例函数y 3=x 的图象于点A ，CB ∵x 轴，交反比例函数y 3=x的图象于点B ，连结AB 、OA 和OB ，已知CA ＝2，则∵ABO的面积为__．【答案】4【分析】设A（a，3a），则C（a，1a），根据题意求得a＝1，从而求得A（1，3），C（1，1），进一步求得B（3，1），然后作BE∵x轴于E，延长AC交x轴于D，根据S∵ABO＝S∵AOD＋S梯形ABED ﹣S∵BOE和反比例函数系数k的几何意义得出S∵ABO＝S梯形ABED，即可求得结果．【详解】解：设A（a，3a），则C（a，1a），∵CA＝2，∵31a a-＝2，解得a＝1，∵A（1，3），C（1，1），∵B（3，1），作BE∵x轴于E，延长AC交x轴于D，∵S∵ABO＝S∵AOD＋S梯形ABED﹣S∵BOE，S∵AOD＝S∵BOE32 =，∵S∵ABO＝S梯形ABED12=（1＋3）（3﹣1）＝4；故答案为：4.【点睛】本题考查了反比例函数系数k的几何意义和三角形的面积，得出S∵ABO=S梯形ABED是解题的关键．19．如图是反比例函数2yx=与反比例函数在第一象限中的图象，点P是4yx=图象上一动21点， P A ∵X 轴于点A ，交函数2y x =图象于点C ，PB ∵Y 轴于点B ，交函数 2y x=图象于点D ，点D 的横坐标为a ．（1）用字母a 表示点P 的坐标；（2）求四边形ODPC 的面积；（3）连接DC 交X 轴于点E ，连接DA 、PE ，求证：四边形DAEP 是平行四边形．【答案】（1）P （2a ，2a）；（2）2；（3）见解析【分析】（1）先求出点D 的纵坐标得到点P 的纵坐标，代入解析式即可得到点P 的横坐标；（2）利用矩形的面积计算公式及反比例函数k 值的几何意义，利用OBD OAC OAPB S S S ∆∆--四边形，即可求出答案；（3）证明∵DPC ∵∵EAC ，即可得到结论．【详解】解：（1）∵点D 的横坐标为a ，且点D 在函数2y x=图象上， ∵点D 的纵坐标2y a=，又PB ∵y 轴，且点P 在4y x=图象上， ∵点P 的纵坐标2y a=， ∵点P 的横坐标为x ＝2a ， ∵P （2a ，2a）；23（2）∵224OAPB S a a =⨯=四边形，ΔΔ1212OBD OAC S S a a==⨯⨯=， ∵D C 422O P S =-=四边形；（3）∵P A ∵x 轴于点A ，交函数2y x=图象于点C ， ∵点C 的坐标为（2a ，1a），又P （2a ，2a），∵PC ＝CA ＝1a， ∵DP ∵AE ，∵∵PDE ＝∵DEA ，∵DP A ＝∵P AE ， ∵∵DPC ∵∵EAC ， ∵DP ＝AE ，∵四边形DAEP 是平行四边形．【点睛】此题考查反比例函数的性质，反比例函数图象与几何图形，平行四边形的判定定理，反比例函数k 值的几何意义，熟练掌握反比例函数的性质及计算方法是解题的关键．20．如图，点A （﹣2，y 1）、B （﹣6，y 2）在反比例函数y ＝kx（k ＜0）的图象上，AC ∵x轴，BD ∵y 轴，垂足分别为C 、D ，AC 与BD 相交于点E ．（1）根据图象直接写出y 1、y 2的大小关系，并通过计算加以验证；（2）结合以上信息，从∵四边形OCED 的面积为2，∵BE ＝2AE 这两个条件中任选一个作为补充条件，求k 的值．你选择的条件是（只填序号）．【答案】（1）12y y >，见解析；（2）见解析，∵（也可以选择∵）【分析】（1）观察函数的图象即可作出判断，再根据A 、B 两点在反比例函数图象上，把两点的坐标代入后作差比较即可；（2）若选择条件∵，由面积的值及OC 的长度，可得OD 的长度，从而可得点B 的坐标，把此点坐标代入函数解析式中，即可求得k ；若选择条件∵，由DB =6及OC =2，可得BE 的长度，从而可得AE 长度，此长度即为A 、B 两点纵坐标的差，（1）所求得的差即可求得k ．【详解】（1）由于图象从左往右是上升的，即自变量增大，函数值也随之增大，故12y y >；当x =-6时，26ky =-；当x =-2时，12k y =- ∵12263k k ky y -=-+=-，k ＜0∵120y y -> 即12y y > （2）选择条件∵∵AC ∵x 轴，BD ∵y 轴，OC ∵OD ∵四边形OCED 是矩形 ∵OD ∙OC =2 ∵OC =2 ∵OD =1 即21y =∵点B 的坐标为(-6,1)把点B 的坐标代入y ＝kx中，得k =-6若选择条件∵，即BE =2AE ∵AC ∵x 轴，BD ∵y 轴，OC ∵OD ∵四边形OCED 是矩形 ∵DE =OC ，CE =OD ∵OC =2，DB =6 ∵BE =DB -DE =DB -OC =4 ∵122AE BE == ∵AE =AC -CE =AC -OD =12y y - 即122y y -=由（1）知：1223ky y -=-= ∵k =-6 【点睛】本题考查了反比例函数的图象和性质、矩形的判定与性质、大小比较，熟练掌握反比例函数的图象与性质是解决本题的关键．2521．如图，一次函数()20y kx k k =-≠的图象与反比例函数1(10)m y m x-=-≠的图象交于点C ，与x 轴交于点A ，过点C 作CB y ⊥轴，垂足为B ，若3ABC S =△．（1）求点A 的坐标及m 的值；（2）若AB = 【答案】（1）（2，0），m =-5；（2）2455y x -=+【分析】（1）在直线y ＝kx ＋k 中令y ＝0可求得A 点坐标；连接CO ，得OBCABCS S==3，根据反比例函数比例系数的几何意义，即可求解；（2）利用勾股定理求出OB =2，设C (b ，2)，代入反比例函数，求出C 点坐标，再利用待定系数法，即可求解．【详解】解：（1）在()20y kx k k =-≠中，令y ＝0可得02kx k =-，解得x ＝2， ∵A 点坐标为（2，0）；连接CO ， ∵CB ∵y 轴， ∵CB ∵x 轴，∵OBCABCSS==3，∵点C 在反比例函数1(10)m y m x-=-≠的图象上， ∵126BOCm S-==，∵反比例函数1(10)m y m x-=-≠的图象在二、四象限， ∵16m -=-，即：m =-5；（2）∵点A (2，0)， ∵OA =2，又∵AB =∵在Rt AOB 中，OB 2=，∵CB ∵y 轴， ∵设C (b ，2)， ∵62b-=，即b =-3，即C (-3，2)，把C (-3，2)代入2y kx k =-，得：232k k =--，解得：k =25-，∵一次函数的解析式为：2455y x -=+．【点睛】本题主要考查待定系数法求函数解析式及函数图象的交点坐标，掌握两函数图象的交点坐标满足两函数解析式是解题的关键，注意反比例函数y ＝kx中k 的几何意义的应用． 22．如图，过C 点的直线y ＝﹣12x ﹣2与x 轴，y 轴分别交于点A ，B 两点，且BC ＝AB ，过点C 作CH ∵x 轴，垂足为点H ，交反比例函数y ＝kx（x ＞0）的图象于点D ，连接OD ，∵ODH 的面积为627（1）求k 值和点D 的坐标；（2）如图，连接BD ，OC ，点E 在直线y ＝﹣12x ﹣2上，且位于第二象限内，若∵BDE 的面积是∵OCD 面积的2倍，求点E 的坐标．【答案】（1）12k =，点 D 坐标为（4，3）；（2）点E 的坐标为（－8，2）【分析】（1）结合反比例函数k 的几何意义即可求解k 值；由⊥CH x 轴可知//CH y 轴，利用平行线分线段成比例即可求解D 点坐标；（2）//CH y 可知OCD ∆和BCD ∆的面积相等，由函数图像可知BDE ∆、BCD ∆、CED ∆的面积关系，再结合题意2BDE OCD S S ∆∆=，即可求CD 边上高的关系，故作EF CD ⊥，垂足为F ，即可求解E 点横坐标，最后由E 点在直线AB 上即可求解．【详解】解∵（1）设点 D 坐标为（m ，n ），由题意得116,1222OH DH mn mn ⋅==∴=．∵点 D 在ky x=的图象上，12k mn ∴==． ∵直线122y x =--的图象与x 轴交于点A ，∵点A 的坐标为（－4，0）． ∵CH ⊥x 轴，CH //y 轴． 1.4AO ABOH AO OH BC∴==∴==． ∴点D 在反比例函数12y x=的图象上， ∴点 D 坐标为（4，3）（2）由（1）知CDy 轴，BCD OCD S S ∴=△△．2,3BDE OCD EDC BCD S S S S =∴=△△△△．过点E 作EF ⊥CD ，垂足为点 F ，交y 轴于点M ， 1111,,32222EDCBCDSCD EF S CD OH CD EF CD OH =⋅=⋅∴⋅=⨯⋅．312.8EF OH EM ∴==∴=．∵点 E 的横坐标为－8.∵点E 在直线122y x =--上，∵点E 的坐标为（－8，2）．【点睛】本题考查一次函数与反比例函数的综合运用、三角形面积问题、k 的几何意义，属于中档难度的综合题型．解题的关键是掌握一次函数与反比例函数的相关性质和数形结合思想． 23．如图，直线l 分别交x 轴，y 轴于A 、B 两点，交反比例函数(0)ky k x=≠的图象于P 、Q 两点．若2AB BP =，且AOB 的面积为4（1）求k 的值；（2）当点P 的横坐标为1-时，求POQ △的面积．【答案】（1）-6；（2）8 【分析】（1）过P 作PE 垂直于x 轴，垂足为E ，证明ABO APE ∽．根据相似三角形的性质可得2AO OE =，49ABO APESS=，由此可得9APES =，3PEOS=．再由反比例函数比例系数k 的几何意义即可求得k 值．（2）先求得(1,6)P -，(0,4)B ，再利用待定系数法求得直线PB 的解析式为24y x=-+．与反29比例函数的解析式联立方程组，解方程组求得(3,2)Q -．再根据PO POQO BQ BS SS=+即可求解．【详解】（1）过P 作PE 垂直于x 轴，垂足为E ，∵PE//BO ， ∵ABO APE ∽． ∵2AB BP =，4AOB S =△，∵2AO OE =，22439ABO APESS ⎛⎫== ⎪⎝⎭， ∵9APES=，3PEDS=．∵1||32k =⨯，||6k =，即6k =-．（2）由（1）知6y x-=，∵(1,6)P -． ∵2AB PB =，∵2PBOS=，∵||4BO =，(0,4)B ．设直线PB 的解析式为y kx b =+，将点(1,6)P -、(0,4)B 代入y kx b =+，得64k bb =-+⎧⎨=⎩．解得24k b =-⎧⎨=⎩．∵直线PB 的解析式为24y x =-+．联立方程组624y x y x -⎧=⎪⎨⎪=-+⎩，解得13x =，21x =-， ∵(3,2)Q -．∵()1||2POQQOBPOB Q P SSSOB x x =+=⨯-14482=⨯⨯=．【点睛】本题是一次函数与反比例函数的综合题，熟练运用反比例函数比例系数k 的几何意义是解决问题的关键．。

反比例函数中比例系数k的几何意义

19.6反比例函数中比例系数k的几何意义一、复习旧知：1.反比例函数的表达式有______种形式，分别是_________________________.2.反比例函数的图象是_______________.3.反比例函数的图象性质是:_____________________________________________________________________ _____________________________________________________________________ 二、创设情境---自主探究1.已知：如图1，∠AED=∠B ，AD=y ，AE=2，AB=x ，AC=6，写出y 与x 的函数关系式.2.已知：如图2，在△ABC 中，∠C=90°，BC=x ，AC=y ，S △ABC =6，则y 与x 的函数表达式为：________________.3.已知：如图3，在矩形ACBH 中，BC=x ，AC=y ，S 矩形ACBH =12，则y 与x 的函数表达式为：4观察2题和3题中图形面积与函数表达式中的k 值有怎样的关系.三、学习新知---合作探究已知点A （-6,2）、B （3，m ）是反比例函数图象上的两点，根据要求完成下列问题： 1.反比例函数的表达式：________________________; 点B 坐标__________. 2.在平面直角坐标系中画出函数图象.图1图2图33.过点A 分别向x 轴和y 轴作垂线，垂足为点C 和点H ，连接AO （1）则S △AOC =_________. （2）则S 矩形ACOH =__________.4. 过点B 分别向x 轴和y 轴作垂线，垂足为点E 和点F ，连接BO （1）则S △BOF =__________. （2）则S 矩形BEOF =___________.5.观察问题3和问题4的结果有怎样的关系，它们的结果与反比例函数解析式中的k 又有怎样的关系？小结：如图，在反比例函数xky =（k ≠0）上任意一点P(x,y)，过这一点分别作x 轴和y 轴的垂线PM 、PN ，连接OP ，则S △POM =___________ ； S 矩形PMON =___________.四、学以致用—自主练习1.已知：反比例函数图象上一点A ，过点A 作AC ⊥x 轴于点C ，作AB ⊥y 轴于点B ，连接AO.（1）若点A （2,3），则反比例解析式k=_____; S △AOC =____； S 矩形ABOC =_____.（2）若S △AOC =4，且反比例函数图象在一、三象限内，则反比例函数表达式：__________ （3）若S 矩形ABOC =5，则反比例函数表达式：______________________________________ 2.计算与双曲线xky =（k ≠0）上的点有关的图形面积.。

知识点反比例函数意义,比例系数k的几何意义

的积．
5. （2011 辽宁阜新,6,3 分）反比例函数 y 6 与 y 3 在第一象限的图象如图所示，作一条平行于 x 轴的直线
x
x
分别交双曲线于 A、B 两点，连接 OA、OB，则△ AOB 的面积为（）
3
A.
B.2
C.3 D.1
2
考点：反比例函数系数 k 的几何意义。
专题：探究型。
分析：分别过 A、B 作 x 轴的垂线，垂足分别为 D、E，过 B 作 BC⊥y 轴，点 C 为垂足，再根据反比例函
∴y=- ，
故答案为：y=- ，
点评：此题主要考查了用待定系数法求反比例函数的解析式，是中学阶段的重点．
2. （2011 江苏扬州，6，3 分）某反比例函数的图象经过点（-1,6），则下列各点中，此函数图象也经过的点是（）
A. （-3,2） B. （3,2）
C.（2，3） D.（6,1）
考点：反比例函数图象上点的坐标特征。
B、﹣3
C、6
D、﹣6
考点：反比例函数系数 k 的几何意义。
分析：过双曲线上任意一点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积 S 是个定值，
即 S＝ 1 |k|． 2
解答：解：根据题意可知：S△ AOB＝ 1 |k|＝3， 2
又反比例函数的图象位于第一象限，k＞0，
则 k＝6．
数系数 k 的几何意义分别求出四边形 OEAC、△ AOE、△ BOC 的面积，进而可得出结论．
解答：解：分别过 A、B 作 x 轴的垂线，垂足分别为 D、E，过 B 作 BC⊥y 轴，点 C 为垂足，
∵由反比例函数系数 k 的几何意义可知，S 四边形 OEAC=6，S△ AOE=3，S△ BOC= 3 ， 2

反比例函数中比例系数k的几何意义

yP(x,y)B反比例函数中比例系数k 的几何意义教学目标：1、理解反比例函数中比例系数k 的几何意义；2、会用比例系数k 的几何意义解决有关问题；3、数形结合数学思想的渗透。

教学重点：反比例函数中比例系数k 的几何意义。

教学难点：灵活运用比例系数k 的几何意义解决有关问题。

教学过程：1、复习回顾，创设情景经过前面的学习，我们深刻的体会到，函数与实际生活联系紧密；函数是初中数学中最重要的数学模型，反比例函数是复习了一次函数之后的又一函数模型，前面我们复习了反比例函数的概念、图象和性质等内容。

下面请同学给我们叙述一下反比例函数的概念以及反比例函数的图象和性质。

一：一般地，如果两个变量x 、y 之间的关系可以表示成ky x= (k 为常数，k ≠0)的形式，那么称y 是x 的反比例函数。

因为xk 是一个分式，所以自变量x 的取值范围是x ≠0。

而k y x =有时也被写成xy=k 或1-=kx y 。

二：同学们利用类比和数形结合的方法对反比例函数进行了复习，分析讨论的非常到位。

反比例函数中的比例系数k 的有没有特殊的意义？（大多数学生知道反比例函数中的比例系数k 的几何意义，但不少学生忘记比例系数k 的几何意义的推导，所以再次演示推导过程显得非常必要）过反比例函数xy 10=图像上任意一点P ，分别向两坐标轴作垂线，则两垂线与坐标轴所形成的矩形的面积是多少？（动画演示求矩形面积的过程，强调点P 的任意性，k 的符号k ＞0 k ＜0 图像的大致位置经过象限第一、三象限第二、四象限性质在每一象限内,y 随x 的增大而减小在每一象限内,y 随x 的增大而增大对称性关于原点对称关于原点对称oy xy xo重视矩形面积始终不变的结果。

）反比例函数中比例系数k 的几何意义：过反比例函数()0≠=k xky 图像上任意一点P ，分别向两坐标轴作垂线，则两垂线与坐标轴所形成的矩形的面积是k 。

一次函数,反比例函数k的几何意义

一次函数，反比例函数k的几何意义
一次函数和反比例函数是数学中常见的函数形式，它们在几何
上有着重要的意义。

通过对这两种函数的几何意义进行深入的探讨，我们可以更好地理解它们在实际生活和数学问题中的应用。

一次函数的一般形式为y = mx + c，其中m和c为常数，m表
示直线的斜率，c表示截距。

从几何意义上来看，一次函数代表了
一条直线，斜率m表示了直线的倾斜程度，截距c表示了直线与y
轴的交点位置。

通过改变m和c的值，我们可以得到不同斜率和截
距的直线，从而描绘出各种不同的直线图像。

反比例函数的一般形式为y = k/x，其中k为常数。

从几何意
义上来看，反比例函数代表了一种双曲线的图像。

当x取不同的值时，y的取值会随之变化，从而描绘出双曲线的形状。

反比例函数
在实际生活中有着广泛的应用，比如物理学中的牛顿万有引力定律
和库仑定律，经济学中的供求关系等都可以用反比例函数来描述。

在几何意义上，反比例函数k表示了双曲线的开口大小和位置。

当k的值越大时，双曲线的开口越小，反之亦然。

通过改变k的值，我们可以得到不同形状和大小的双曲线，从而更好地理解反比例函
数在几何上的意义。

总之，一次函数和反比例函数在几何上有着重要的意义，通过对它们的几何意义进行深入的探讨，我们可以更好地理解它们在数学和实际生活中的应用。

希望本文能够帮助读者更好地理解一次函数和反比例函数在几何上的意义。

反比例函数中比例系数k的几何意义

反比例函数中比例系数k的几何意义

反比例函数中K的几何意义 (1)

反比例函数比例系数k的几何意义

反比例函数中K的几何意义

反比例函数中k的几何意义

中考数学全程复习方略微专题二反比例函数中k的几何意义课件

反比例函数中K的几何含义

反比例函数k的几何意义

反比例函数函数K的几何意义

反比例函数K的几何意义

专题12 反比例函数比例系数k的几何意义(解析版)

反比例函数中比例系数k的几何意义

知识点 反比例函数意义,比例系数k的几何意义

反比例函数中比例系数k的几何意义

一次函数,反比例函数k的几何意义

知识点反比例函数意义,比例系数k的几何意义