函数的奇偶性试题(含答案)

合集下载

函数奇偶性的判断测试题(含答案).docx

函数奇偶性的判断一、单选题（共10道，每道10分）1・若函数f（x）＜xeR）是奇函数，函数g（x）＜xeR）是偶函数，则下列一定成立的是（A.函数f（g（x））是奇函数B•函数g（f（x））是奇函数C.函数f（f（x））是奇函数D.函数畝（x））是奇函数答案:C解题思路：丁函数/x）（xeR）是奇函数，函数或C）（XE R）是偶函数,A选项：血-力）沁何），是偶函数；E选项：场LE）它（沁））它（心）），是偶函数；C选项：心?力）勿沁））=询＞））,是奇函数；D选项：亦（p））=gg））,是偶函数. 故选C.试题难度：三颗星知识点：函数奇偶性的判断2.已知函数恥）=7,朋）=金加）=為，.…,则函数心a是（A.奇函数B.偶函数C.既是奇函数又是偶函数D.非奇非偶函数答案:A 解题思路:•・• Z（-x）= —= --=-Z（x），-x X■■-力（X）是奇函数,・•・fl^=—=斗二宀x+/（x）x+l X +1X£（兀）是奇函数,同理可验证，厶（X）是奇函数，・••函数fl014（x）是奇函数，故选A・试题难度：三颗星知识点：函数奇偶性的判断f （X ）= J16-『3•函数％区+ 5| +卜-4|是（）A. 奇函数B.偶函数C.非奇非偶函数D.既是奇函数乂是偶函数答案：B 解题思路:由16-「刁0可得，-4WU4,即心）的定义域关于原点对称,.'.x+5>0, x-4W0,.••心=如丄三=_心X X••金）是奇函数，故选A.试题难度：三颗星知识点：函数奇偶性的判断5. 已知f(x)是定义在R 上的奇函数，当空0时，/(x) = 3” +血o 为常数)，则/(-log 35) 的值为()/(x) = J16 x+5+4-x •••yw 是偶函数，故选B .试题难度：三颗星知识点：函数奇偶性的判断 4.定义两种运算:a ㊉护严@b = J （a-by ,/W = 则函数A.奇函数B.偶函数C.既是奇函数又是偶函数D.非奇非偶函数答案：A解题思路:由定义可得，畑=匕=占匚7（X -2）2-2 X_2|_2由 4一 X 2 刁 0且 |兀一2|—2工0,可得一 2 <x<0^0<x<2, 即函数金）的定义域为{x | -2 W x < 0或0 < x W 2},关于原点对称. 由上可得，乂—2W0,A.4B.-4C.6D.-6答案:B解题思路：•・7W是定义在R上的奇函数，/•X0)=0,即3°+w = 0,・即/(x) = 3x-l (x>0),T log?5 >0 ,・•・ /(-log3 5) = -/(log3 5) = pT _i)= Y5 _i)= _4, 故选B・试题难度：三颗星知识点：函数奇偶性的性质2G(x) = (H-—-)-g(x)6.若函数2 -1 g o)是偶函数，则函数啟刈是()A.奇函数B.偶函数C.既是奇函数又是偶函数D.非奇非偶函数答案：A解题思路：2 2X +1V G(x) = (l + -^-).g(x) = ^—-g(x)是偶函数，2 -1 2 -12~x+l 1 + 2X2X+1・•・ G(—x) = - g(-x) = —7 - g(-x) = G(x) = - g(x),2 —1 1 — 2 2 — 1g(-x) = _g(x),・・・g(x)是奇函数，故选A.试题难度：三颗星知识点：函数奇偶性的判断7.已知函数 /(X)= X + ln(J*+l + X)则( A.f(x)是奇函数，g(x)是奇函数B.f(x)是偶函数，g(x)是偶函数C.f(x)是奇函数，g(x)是偶函数D.f(x)是偶函数,g(x)是奇函数答案:C解题思路：首先分析夬兀)，由Vx2 +l + x>0可得x eR ,定义域关于原点对称, f (-x) = _x + ln(\/x2 +1 - x)= -x+ln( —)+ l + x=-x+ln(Jx2 +1 + x)-1=-[x+ ln(Vx2 +1 +x)]=-/(x)•■金虎:奇函数；再分析g(Q，首先可以看岀定义域关于原点对称，当x>0 时，-x<0, g(-x) = xjl + 壬=g(x),当x<0 时，-x>0, g(-x) = -xjl+x? = g(x),当x=0 时，g(0)=0,综上，g(~x)=g(x)9・・・g(x)是偶函数，故选C・试题难度：三颗星知识点：函数奇偶性的判断4)= ：，58•已知函数g—l , Z0,则该函数是(A.非奇非偶函数，且单调递增B.偶函数，且单调递减C.奇函数，且单调递增D.奇函数，且单调递减答案:C 解题思路:函数/（X）的定义域为R,且/（0） = 0,当x<0时，-x>0,/（x）=2x-l, /（-X）=1-24-Z）=1-2X,同理，当x>0时，有/（x） = -/（-X）・综上，函数/（X）是奇函数.由题意，可画岀/（X）的大致图象，如图,・•・/（X）单调递増, 故选C.试题难度：三颗星知识点：奇偶性与单调性的综合/（x） = |2/9.已知函数R '兀<°,则该函数是（）A.非奇非偶函数，在（一°亠°）上单调递增，在（°’ +8）上单调递减B.偶函数，在（一® °）上单调递增，在（山+8）上单调递减C.偶函数，在R上单调递减D.奇函数，在R上单调递减答案:B解题思路：先判断奇偶性.由题意，/(X)的定义域为R,且/(0) = 1・①当工<0时，-x>0,则/(x)=2z, /(-x)=2-(-x) = 2x,・•・ /(-x) = /(x)・②当XA O时，-x<0,贝lj/(x)=2-x, /(-x)=2-x,= /(x) ■综合①②，/(-X)= /(x)在R上恒成立，则/(无)是偶函数.再判断单调性.•・• /&)是偶函数，・••只需考虑/(力在(0, +8)上的单调性.・・•当x>0 时，/(X)=2-Z=(A)\・•・函数/(x)在(0, +8)上单调递诚.•・• /&)是偶函数，・•・/(x)的图象关于y轴对称，.•- /(x)在(-X, 0)上单调递増.综上，/(X)在(YO,0)上单调递増，在(0, +00)上单调递诚, 故选B.试题难度：三颗星知识点：奇偶性与单调性的综合1 , x > 0f(x) = < 0 , x = 010.已知函数 "X<0,设恥)* J(x),则叫)是(A•奇函数，在(一® +°°)上单调递减B.奇函数，在+8)上单调递增C.偶函数，在(一® °)上单调递减，在(°，+00)上单调递增D•偶函数，在(一°)上单调递增，在(°’ +°°)上单调递减答案：B 解题思路: 当X > 0 时，F(x) = X2・/(x) = X2；当x = 0 时，F(0) = 02-/(0) = 0；当xv 0 时，F(x) = x2 -(-1) = -x2・r 2x x , x > 0即F(0 = {o , x = 0・-x2, x<0先判断奇偶性.由题意，F(x)的定义域为R,且F(0) = 0・①当x<0 时,-x>0,则F(x) = -x2 , F(-x) = x2 ,F(-x)=_F(x)・②当x>0时，-x<0,则F(x) = x2, F(-x) = -x2 ,F(-x)=_F(x)・综合①②，F(-x) = -F(x)在R上恒成立，则尺兀)是奇函数.再判断单调性.•・•尺兀)是奇函数，・•・只需考虑尸(©在(0, +8)上的单调性.•・•当x>0 时，F(x) = x2,・•・函数尸(x)在(0, +00)上单调递增.•・• FG)是奇函数,・•・F(x)的图象关于原点对称，・•・戸(x)在(-8, 0)上也单调递増.综上，FW是奇函数，且单调递増，故选B.试题难度：三颗星知识点：奇偶性与单调性的综合。

函数的奇偶性练习题附标准答案资料全

函数的奇偶性1．函数f （x ）=x(-1﹤x ≦1)的奇偶性是（）A ．奇函数非偶函数B ．偶函数非奇函数C ．奇函数且偶函数D ．非奇非偶函数2. 已知函数f （x ）=ax 2＋bx ＋c （a ≠0）是偶函数，那么g （x ）=ax 3＋bx 2＋cx 是( ）A .奇函数B .偶函数C .既奇又偶函数D .非奇非偶函数3. 若函数f (x )是定义在R 上的偶函数，在]0,(-∞上是减函数，且f (2)=0，则使得f (x )<0的x 的取值围是 ( )A.(-¥,2)B. (2,+¥)C. (-¥,-2)È(2,+¥)D. (-2,2) 4．已知函数f (x )是定义在(－∞,+∞)上的偶函数.当x ∈(－∞,0)时，f (x )=x -x 4，则当x ∈(0.+∞)时，f (x )= . 5. 判断下列函数的奇偶性：(1)f (x )＝lg (12+x -x ); (2)f (x )＝2-x +x -2(3) f （x ）=⎩⎨⎧>+<-).0()1(),0()1(x x x x x x6.已知g (x )=－x 2－3,f (x )是二次函数，当x ∈[-1,2]时，f (x )的最小值是1，且f (x )+g (x )是奇函数，求f (x )的表达式。

7.定义在（-1，1）上的奇函数f （x ）是减函数，且f(1-a)+f(1-a 2)<0,求a 的取值围8.已知函数21()(,,)ax f x a b c N bx c+=∈+是奇函数,(1)2,(2)3,f f =<且()[1,)f x +∞在上是增函数,(1)求a,b,c 的值;(2)当x ∈[-1,0)时,讨论函数的单调性.9.定义在R 上的单调函数f (x )满足f (3)=log 23且对任意x ，y ∈R 都有f (x+y )=f (x )+f (y )． (1)求证f (x )为奇函数；(2)若f (k ·3x )+f (3x -9x -2)＜0对任意x ∈R 恒成立，数k 的取值围． 10下列四个命题：（1）f （x ）=1是偶函数；（2）g （x ）=x 3，x ∈（－1，1]是奇函数；（3）若f （x ）是奇函数，g （x ）是偶函数，则H （x ）=f （x ）·g （x ）一定是奇函数；（4）函数y =f （|x |）的图象关于y 轴对称，其中正确的命题个数是（） A ．1B ．2C ．3D ．411下列函数既是奇函数，又在区间[]1,1-上单调递减的是( )A.()sin f x x =B.()1f x x =-+C.()1()2x x f x a a -=+ D.2()2xf x lnx-=+ 12若y =f （x ）（x ∈R ）是奇函数，则下列各点中，一定在曲线y =f （x ）上的是（） A ．（a ，f （－a ）） B ．（－sin a ，－f （－sin a ））C ．（－lg a ，－f （lg a1））D ．（－a ，－f （a ））13. 已知f （x ）=x 4+ax 3+bx －8，且f （－2）=10，则f （2）=_____________。

高三数学函数的奇偶性试题答案及解析

高三数学函数的奇偶性试题答案及解析1.设函数的定义域为，且是奇函数，是偶函数，则下列结论中正确的是（）A．是偶函数B．是奇函数C．是奇函数D．是奇函数【答案】C【解析】设，则，因为是奇函数，是偶函数，故，即是奇函数，选C．【考点】函数的奇偶性．2.若偶函数y＝f(x)为R上的周期为6的周期函数，且满足f(x)＝(x＋1)(x－a)(－3≤x≤3)，则f(－6)等于________．【答案】－1【解析】∵y＝f(x)为偶函数，且f(x)＝(x＋1)(x－a)(－3≤x≤3)，∴f(x)＝x2＋(1－a)x－a,1－a＝0.∴a＝1.f(x)＝(x＋1)(x－1)(－3≤x≤3)．f(－6)＝f(－6＋6)＝f(0)＝－1.3.若的图像是中心对称图形,则( )A．4B．C．2D．【答案】B【解析】，因为为偶函数，所以当且仅当，即时，为奇函数，图像关于原点对称．故选B.【考点】奇函数4.设f(x)为定义在R上的奇函数.当x≥0时,f(x)=2x+2x+b(b为常数),则f(-1)等于()A．-3B．-1C．1D．3【答案】A【解析】因为f(x)为定义在R上的奇函数,所以有f(0)=20+2×0+b=0,解得b=-1,所以当x≥0时,f(x)=2x+2x-1,即f(-1)=-f(1)=-(21+2×1-1)=-3.故选A.5.已知函数f(x)＝为奇函数，则f(g(－1))＝()A．－20B．－18C．－15D．17【答案】C【解析】由于函数f(x)是奇函数，所以g(x)＝－f(－x)＝－x2＋2x，g(－1)＝－3.故f(－3)＝g(－3)＝－15.6.若函数f(x)=(a+)cosx是奇函数,则常数a的值等于()A．-1B．1C．-D．【答案】D【解析】设g(x)=a+,t(x)=cosx,∵t(x)=cosx为偶函数,而f(x)=(a+)cosx为奇函数,∴g(x)=a+为奇函数,又∵g(-x)=a+=a+,∴a+=-(a+)对定义域内的一切实数都成立,解得:a=.7.已知函数f(x)为奇函数，且当x>0时，f(x)＝x2＋，则f(－1)＝________.【答案】－2【解析】f(－1)＝－f(1)＝－2.8.已知定义域为R的函数f(x)＝是奇函数，则a＝________.【答案】2【解析】因为函数f(x)＝是定义域为R的奇函数，所以f(－1)＝－f(1)，即＝－，解得a＝2.9.函数y＝sin22x是()．A．周期为π的奇函数B．周期为π的偶函数C．周期为的奇函数D．周期为的偶函数【答案】D【解析】y＝sin22x＝＝－cos 4x，则周期为：＝，且为偶函数．10.已知，其中是常数．（1））当时，是奇函数；（2）当时，的图像上不存在两点、，使得直线平行于轴．【答案】证明见解析．【解析】(1)奇函数的问题，可以根据奇函数的定义，利用来解决，当然如果你代数式变形的能力较强，可以直接求然后化简变形为，从而获得证明；(2)要证明函数的图像上不存在两点A、B，使得直线AB平行于轴，即方程不可能有两个或以上的解，最多只有一个解，，，因此原方程最多只有一解，或者用反证法证明，设存在，即有两个，且，使，然后推理得到矛盾的结论，从而完成证明．试题解析：（1）由题意，函数定义域， 1分对定义域任意，有：4分所以，即是奇函数. 6分（2）假设存在不同的两点，使得平行轴，则9分化简得：，即，与不同矛盾。

函数的奇偶性问题练习题(含答案)

...函数的奇偶性问题一、选择题1．已知函数f （x ）＝ax 2＋bx ＋c （a ≠0）是偶函数，那么g （x ）＝ax 3＋bx 2＋cx （） A ．奇函数 B ．偶函数 C ．既奇又偶函数 D ．非奇非偶函数解析：f （x ）＝ax 2＋bx ＋c 为偶函数，x x =)(ϕ为奇函数，∴g （x ）＝ax 3＋bx 2＋cx ＝f （x ）·)(x ϕ满足奇函数的条件．答案：A2．已知函数f （x ）＝ax 2＋bx ＋3a ＋b 是偶函数，且其定义域为［a －1，2a ］，则（） A ．31=a ，b ＝0 B ．a ＝－1，b ＝0 C ．a ＝1，b ＝0 D ．a ＝3，b ＝0 解析：由f （x ）＝ax 2＋bx ＋3a ＋b 为偶函数，得b ＝0．又定义域为［a －1，2a ］，∴a －1＝2a ，∴31=a ．故选A ．3．已知f （x ）是定义在R 上的奇函数，当x ≥0时，f （x ）＝x 2－2x ，则f （x ）在R 上的表达式是（）A ．y ＝x （x －2）B ．y ＝x （｜x ｜－1）C ．y ＝｜x ｜（x －2）D ．y ＝x （｜x ｜－2）解析：由x ≥0时，f （x ）＝x 2－2x ，f （x ）为奇函数，∴当x ＜0时，f （x ）＝－f （－x ）＝－（x 2＋2x ）＝－x 2－2x ＝x （－x －2）． ∴(2)(0)()(2)(0),,x x x f x x x x ⎧⎨⎩-≥=--<即f （x ）＝x （|x |－2）答案：D4．已知f （x ）＝x 5＋ax 3＋bx －8，且f （－2）＝10，那么f （2）等于（） A ．－26 B ．－18 C ．－10 D ．10 解析：f （x ）＋8＝x 5＋ax 3＋bx 为奇函数，f （－2）＋8＝18，∴f （2）＋8＝－18，∴f （2）＝－26．答案：A5．函数1111)(22+++-++=x xx x x f 是（）A ．偶函数B ．奇函数C ．非奇非偶函数D ．既是奇函数又是偶函数解析：此题直接证明较烦，可用等价形式f （－x ）＋f （x ）＝0．答案：B 6．若)(x ϕ，g （x ）都是奇函数，2)()(++=x bg a x f ϕ在（0，＋∞）上有最大值5，则f （x ）在（－∞，0）上有（）A ．最小值－5B ．最大值－5C ．最小值－1D ．最大值－3解析：)(x ϕ、g （x ）为奇函数，∴()2()()f x a x bg x φ-=+为奇函数．又f （x ）在（0，＋∞）上有最大值5， ∴f （x ）－2有最大值3． ∴f （x ）－2在（－∞，0）上有最小值－3， ∴f （x ）在（－∞，0）上有最小值－1．答案：C 二、填空题 7．函数2122)(xx x f ---=的奇偶性为____奇函数____（填奇函数或偶函数）．8．若y ＝（m －1）x 2＋2mx ＋3是偶函数，则m ＝____0_____．解析：因为函数y ＝（m －1）x 2＋2mx ＋3为偶函数，∴f （－x ）＝f （x ），即（m －1）（－x ）2＋2m （－x ）＋3＝（m —1）x 2＋2mx ＋3，整理，得m ＝0．9．已知f （x ）是偶函数，g （x ）是奇函数，若11)()(-=+x x g x f ，则f （x ）的解析式为____11)(2-=xx f ___．解析：由f （x ）是偶函数，g （x ）是奇函数，...可得11)()(--=-x x g x f ，联立11)()(-=+x x g x f ，∴11)1111(21)(2-=----=x x x x f ． 10．已知函数f （x ）为偶函数，且其图象与x 轴有四个交点，则方程f （x ）＝0的所有实根之和为___0 _____．三、解答题11．设定义在［－2，2］上的偶函数f （x ）在区间［0，2］上单调递减，若f （1－m ）＜f （m ），求实数m 的取值范围．（21<m ） 12．已知函数f （x ）满足f （x ＋y ）＋f （x －y ）＝2f （x ）·f （y ）（x ∈R ，y ∈R ），且f （0）≠0，试证f （x ）是偶函数．证明：令x ＝y ＝0，有f （0）＋f （0）＝2f （0）·f （0），又f （0）≠0，∴可证f （0）＝1．令x ＝0，∴f （y ）＋f （－y ）＝2f （0）·f （y ）⇒f （－y ）＝f （y ），故f （x ）为偶函数．13.已知函数f （x ）是奇函数，且当x ＞0时，f （x ）＝x 3＋2x 2—1，求f （x ）在R 上的表达式．解析：本题主要是培养学生理解概念的能力．f （x ）＝x 3＋2x 2－1．因f （x ）为奇函数，∴f （0）＝0．当x ＜0时，－x ＞0，f （－x ）＝（－x ）3＋2（－x ）2－1＝－x 3＋2x 2－1， ∴f （x ）＝x 3－2x 2＋1．因此，.)0()0()0(12012)(,,2323<=>+--+=⎪⎩⎪⎨⎧x x x x x x x x f 点评：本题主要考查学生对奇函数概念的理解及应用能力．14.f （x ）是定义在（－∞，－5］Y ［5，＋∞）上的奇函数，且f （x ）在［5，＋∞）上单调递减，试判断f （x ）在（－∞，－5］上的单调性，并用定义给予证明．解析：任取x 1＜x 2≤－5，则－x 1＞－x 2≥－5．因f （x ）在［5，＋∞］上单调递减，所以f （－x 1）＜f （－x 2）⇒f （x 1）＜－f （x 2）⇒f （x 1）＞f （x 2），即单调减函数．点评：此题要注意灵活运用函数奇偶性和单调性，并及时转化．15.设函数y ＝f （x ）（x ∈R 且x ≠0）对任意非零实数x 1、x 2满足f （x 1·x 2）＝f （x 1）＋f （x 2），求证f （x ）是偶函数．解析：由x 1，x 2∈R 且不为0的任意性，令x 1＝x 2＝1代入可证， f （1）＝2f （1），∴f （1）＝0．又令x 1＝x 2＝－1，∴f ［－1×（－1）］＝2f （1）＝0， ∴（－1）＝0．又令x 1＝－1，x 2＝x ，∴f （－x ）＝f （－1）＋f （x ）＝0＋f （x ）＝f （x ），即f （x ）为偶函数．点评：抽象函数要注意变量的赋值，特别要注意一些特殊值，如，x 1＝x 2＝1，x 1＝x 2＝－1或x 1＝x 2＝0等，然后再结合具体题目要求构造出适合结论特征的式子即可．。

函数的奇偶性练习题及答案

函数的奇偶性练习题一、选择题1．已知函数f （x ）＝ax 2＋bx ＋c （a ≠0）是偶函数，那么g （x ）＝ax 3＋bx 2＋cx （）A ．奇函数B ．偶函数C ．既奇又偶函数D ．非奇非偶函数2．已知函数f （x ）＝ax 2＋bx ＋3a ＋b 是偶函数，且其定义域为［a －1，2a ］，则（）A ．a=1／3，b ＝0B ．a ＝－1，b ＝0C ．a ＝1，b ＝0D ．a ＝3，b ＝03．已知f （x ）是定义在R 上的奇函数，当x ≥0时，f （x ）＝x 2－2x ，则f （x ）在R 上的表达式是（）A ．y ＝x （x －2）B ．y ＝x （｜x ｜－1）C ．y ＝｜x ｜（x －2）D ．y ＝x （｜x ｜－2）4．已知f （x ）＝x 5＋ax 3＋bx －8，且f （－2）＝10，那么f （2）等于（）A ．－26B ．－18C ．－10D ．105．函数1111)(22+++-++=x x x xx f 是（）A 偶函数B 奇函数C 非奇非偶函数D 既是奇函数又是偶函数6．若)(x ϕ，g （x ）都是奇函数，2)()(++=x bg a x f ϕ在（0，＋∞）上有最大值5，则f （x ）在（－∞，0）上有（）A ．最小值－5 B ．最大值－5 C ．最小值－1 D ．最大值－3二、填空题7．函数2122)(xx x f ---=的奇偶性为________（填奇函数或偶函数） 8．若y ＝（m －1）x 2＋2mx ＋3是偶函数，则m ＝_________9．已知f （x ）是偶函数，g （x ）是奇函数，若11)()(-=+x x g x f ，则f （x ）的解析式为_______10．已知函数f （x ）为偶函数，且其图象与x 轴有四个交点，则方程f （x ）＝0的所有实根之和为________三、解答题11．设定义在［－2，2］上的偶函数f （x ）在区间［0，2］上单调递减，若f （1－m ）＜f （m ），求实数m 的取值范围12．已知函数f （x ）满足f （x ＋y ）＋f （x －y ）＝2f （x ）·f （y ）（x ∈R ，y ∈R ），且f （0）≠0，试证f （x ）是偶函数13.已知函数f （x ）是奇函数，且当x ＞0时，f （x ）＝x 3＋2x 2—1，求f （x ）在R 上的表达式14.f （x ）是定义在（－∞，－5］［5，＋∞）上的奇函数，且f （x ）在［5，＋∞）上单调递减，试判断f （x ）在（－∞，－5］上的单调性，并用定义给予证明15.设函数y ＝f （x ）（x ∈R 且x ≠0）对任意非零实数x 1、x 2满足f （x 1·x 2）＝f （x 1）＋f （x 2），求证f （x ）是偶函数1．解析：f （x ）＝ax 2＋bx ＋c 为偶函数，x x =)(ϕ为奇函数，∴g （x ）＝ax 3＋bx 2＋cx ＝f （x ）·)(x ϕ满足奇函数的条件．答案：A2．解析：由f （x ）＝ax 2＋bx ＋3a ＋b 为偶函数，得b ＝0．又定义域为［a －1，2a ］，∴a －1＝2a ，∴31=a ．故选A ．3．解析：由x ≥0时，f （x ）＝x 2－2x ，f （x ）为奇函数，∴当x ＜0时，f （x ）＝－f （－x ）＝－（x2＋2x ）＝－x 2－2x ＝x （－x －2）．∴,,)0()0()2()2()(<≥---=⎩⎨⎧x x x x x x x f 即f （x ）＝x （|x|－2）答案：D 4．解析：f （x ）＋8＝x 5＋ax 3＋bx 为奇函数，f （－2）＋8＝18，∴f （2）＋8＝－18，∴f （2）＝－26．答案：A5．解析：此题直接证明较烦，可用等价形式f （－x ）＋f （x ）＝0．答案：B6．解析：)(x ϕ、g （x ）为奇函数，∴)()(2)(x bg x a x f +=-ϕ为奇函数．又f （x ）在（0，＋∞）上有最大值5， ∴f （x ）－2有最大值3．∴f （x ）－2在（－∞，0）上有最小值－3， ∴f （x ）在（－∞，0）上有最小值－1．答案：C7．答案：奇函数8．答案：0解析：因为函数y ＝（m －1）x 2＋2mx ＋3为偶函数，∴f （－x ）＝f （x ），即（m －1）（－x ）2＋2m （－x ）＋3＝（m —1）x 2＋2mx ＋3，整理，得m ＝0．9．解析：由f （x ）是偶函数，g （x ）是奇函数，可得11)()(--=-x x g x f ，联立11)()(-=+x x g x f ，∴11)1111(21)(2-=----=x x x x f ．答案：11)(2-=x x f 10．答案：0 11．答案：21<m 12．证明：令x ＝y ＝0，有f （0）＋f （0）＝2f （0）·f （0），又f （0）≠0，∴可证f （0）＝1．令x ＝0，∴f （y ）＋f （－y ）＝2f （0）·f （y ）⇒f （－y ）＝f （y ），故f （x ）为偶函数．13．解析：本题主要是培养学生理解概念的能力．f （x ）＝x 3＋2x 2－1．因f （x ）为奇函数，∴f （0）＝0．当x ＜0时，－x ＞0，f （－x ）＝（－x ）3＋2（－x ）2－1＝－x 3＋2x 2－1，∴f （x ）＝x 3－2x 2＋1．因此，.)0()0()0(12012)(,,2323<=>+--+=⎪⎩⎪⎨⎧x x x x x x x x f 点评：本题主要考查学生对奇函数概念的理解及应用能力．14．解析：任取x 1＜x 2≤－5，则－x 1＞－x 2≥－5．因f （x ）在［5，＋∞］上单调递减，所以f （－x 1）＜f （－x 2）⇒f （x 1）＜－f （x 2）⇒f （x 1）＞f （x 2），即单调减函数．点评：此题要注意灵活运用函数奇偶性和单调性，并及时转化．15．解析：由x 1，x 2∈R 且不为0的任意性，令x 1＝x 2＝1代入可证，f （1）＝2f （1），∴f （1）＝0．又令x 1＝x 2＝－1，∴f ［－1×（－1）］＝2f （1）＝0，∴（－1）＝0．又令x 1＝－1，x 2＝x ，∴f （－x ）＝f （－1）＋f （x ）＝0＋f （x ）＝f （x ），即f （x ）为偶函数．点评：抽象函数要注意变量的赋值，特别要注意一些特殊值，如，x 1＝x 2＝1，x 1＝x 2＝－1或x 1＝x 2＝0等，然后再结合具体题目要求构造出适合结论特征的式子即可．。

高二函数奇偶性数学(有答案)

一，判断函数奇偶性的一般步骤： 1）、看函数的定义域是否关于原点对称，若不对称，则得出结论：该函数无奇偶性。

若定义域对称，则 2）、计算f （-a ），若等于f （a ），则函数是偶函数；若等于-f （a ），则函数是奇函数。

若两者都不满足，则函数既不是奇函数也不是偶函数。

注意：若可以作出函数图象的，直接观察图象是否关于y 轴对称或者关于原点对称。

.函数奇偶性练习一、选择题1．已知函数f （x ）＝ax 2＋bx ＋c （a ≠0）是偶函数，那么g （x ）＝ax 3＋bx 2＋cx （） A ．奇函数 B ．偶函数 C ．既奇又偶函数 D ．非奇非偶函数 2．已知函数f （x ）＝ax 2＋bx ＋3a ＋b 是偶函数，且其定义域为［a －1，2a ］，则（） A ．31=a ，b ＝0 B ．a ＝－1，b ＝0 C ．a ＝1，b ＝0 D ．a ＝3，b ＝0 3．已知f （x ）是定义在R 上的奇函数，当x ≥0时，f （x ）＝x 2－2x ，则f （x ）在R 上的表达式是（）A ．y ＝x （x －2）B ．y ＝x （｜x ｜－1）C ．y ＝｜x ｜（x －2）D ．y ＝x （｜x ｜－2）4．已知f （x ）＝x 5＋ax 3＋bx －8，且f （－2）＝10，那么f （2）等于（） A ．－26 B ．－18 C ．－10 D ．10 5．函数1111)(22+++-++=x x x x x f 是（）A ．偶函数B ．奇函数C ．非奇非偶函数D ．既是奇函数又是偶函数 6．若)(x ϕ，g （x ）都是奇函数，2)()()(++=x bg x a x f ϕ在（0，＋∞）上有最大值5，则f （x ）在（－∞，0）上有（）A ．最小值－5B ．最大值－5C ．最小值－1D ．最大值－3 二、填空题 7．函数2122)(xx x f ---=的奇偶性为________（填奇函数或偶函数）．8．若y ＝（m －1）x 2＋2mx ＋3是偶函数，则m ＝_________． 9．已知f （x ）是偶函数，g （x ）是奇函数，若11)()(-=+x x g x f ，则f （x ）的解析式为_______．10．已知函数f （x ）为偶函数，且其图象与x 轴有四个交点，则方程f （x ）＝0的所有实根之和为________．函数的奇偶性练习参考答案1．解析：f （x ）＝ax 2＋bx ＋c 为偶函数，x x =)(ϕ为奇函数，∴g （x ）＝ax 3＋bx 2＋cx ＝f （x ）²)(x ϕ满足奇函数的条件．答案：A2．解析：由f （x ）＝ax 2＋bx ＋3a ＋b 为偶函数，得b ＝0．又定义域为［a －1，2a ］，∴a －1＝2a ，∴31=a ．故选A ． 3．解析：由x ≥0时，f （x ）＝x 2－2x ，f （x ）为奇函数，∴当x ＜0时，f （x ）＝－f （－x ）＝－（x 2＋2x ）＝－x 2－2x ＝x （－x －2）． ∴,,)0()0()2()2()(<≥---=⎩⎨⎧x x x x x x x f 即f （x ）＝x （|x |－2）答案：D4．解析：f （x ）＋8＝x 5＋ax 3＋bx 为奇函数，f （－2）＋8＝18，∴f （2）＋8＝－18，∴f （2）＝－26．答案：A5．解析：此题直接证明较烦，可用等价形式f （－x ）＋f （x ）＝0．答案：B 6．解析：)(x ϕ、g （x ）为奇函数，∴)()(2)(x bg x a x f +=-ϕ为奇函数．又f （x ）在（0，＋∞）上有最大值5， ∴f （x ）－2有最大值3．∴f （x ）－2在（－∞，0）上有最小值－3， ∴f （x ）在（－∞，0）上有最小值－1．答案：C7．答案：奇函数8．答案：0解析：因为函数y ＝（m －1）x 2＋2mx ＋3为偶函数，∴f （－x ）＝f （x ），即（m －1）（－x ）2＋2m （－x ）＋3＝（m —1）x 2＋2mx ＋3，整理，得m ＝0．9．解析：由f （x ）是偶函数，g （x ）是奇函数，可得11)()(--=-x x g x f ，联立11)()(-=+x x g x f ，∴11)1111(21)(2-=----=x x x x f ．答案：11)(2-=x x f 10．答案：0指数函数、对数函数、幂函数测试题一、选择题（本大题共10小题，每小题4分，共40分，在每小题给出的四个选项中，只有一项是符合要求的）l.设指数函数C 1：y =a x ，C 2：y =b x ，C 3：y =c x 的图象如图，则（）A ．0<c <1<b <aB ．0<a <1<b <cC ．c <b <aD ．0<c <1<a <b2.函数y =a x-1（a >0，a ≠1）过定点，则这个定点是（） A ．（0，1） B ．（1，2） C ．（-1，0.5） D ．（1，1）3.若函数y =f （x ）的图象与y =2-x 的图象关于y 轴对称，则f （3）=（）A ．8B ．4C ．81D ．414.若指数函数y =a x经过点（-1，3），则a 等于（）A ．3B ．31C ．2D ．215.函数y =f （x ）的图象与y =21-x 的图象关于直线x =1对称，则f （x ）为（） A ．y =2x-1 B ．y =2x+1 C ．y =2x-2 D ．y =22-x6.对于∀x 1，x 2∈R （注：∀表示“任意”），恒有f （x 1）〃f （x 2）=f （x 1+x 2）成立，且f （1）=2，则f （6）=（） A ．22B ．4C ．2D ．87.若函数f （x ）=log a x （0<a <1）在区间[a ，2a ]上的最大值是最小值的3倍，则a =（）A ．41B ．21 C ．22 D ．42 8.在同一坐标系中，函数y =2-x 与y =log 2x 的图象是（）9.设函数⎪⎩⎪⎨⎧>≤-=-).0(),0(12)(21x x x x f x 若f （x 0）>1，则x 0的取值范围是（）A ．（-1，1）B ．（-∞，-2）∪（0，+∞）C ．（-1，+∞）D ．（-∞，-1）∪（1，+∞） 10.设函数F(x)=f(x)-)(1x f ,其中x-log 2f(x)=0,则函数F(x)是（） A.奇函数且在(-∞,+∞)上是增函数 B.奇函数且在(-∞,+∞)上是减函数C.偶函数且在(-∞，+∞)上是增函数D.偶函数且在(-∞,+∞)上是减函数11．已知函数f(x)＝x 2－2ax ＋a 在区间(－∞，1)上有最小值，则函数f(x)x在区间(1，＋∞)上A ．有两个零点B ．有一个零点C ．无零点D ．无法确定二、填空题（本大题共4小题，每小题5分，共20分，把答案填在题中横线上） 12.已知对数函数C 1：y =log a x ，C 2：y =log b x ，如图所示，则a 、b 的大小是__________．13.函数)34(log 5.0-=x y 的定义域是__________． 14.已知f (e x )=x ，则f (5)等于_________________3log 9log 28的值是__________________________15.已知二次函数()f x 满足(0)1f =，及(1)()2f x f x x +-=. （1）求()f x 的解析式；（2）若()(log )(01)a g x f x a a =>≠且，1,x a a ⎡⎤∈⎢⎥⎣⎦，试求()g x 的值域.15.解：（1）设2()1f x ax bx =++(1)()22f x f x ax a b x ∴+-=+++221,10a ab a b =⎧∴∴==-⎨+=⎩ 2()1f x x x ∴=-+ （2）2()1f x x x =-+Q2()(log )(log )log 1,a a a g x f x x x ∴==-+1,x a a ⎡⎤∈⎢⎥⎣⎦令log a t x =，原函数化为21y t t =-+，101a x a a a≤≤>≠Q 又且101a a a ∴<<<即，∴log a t x =在1,a a ⎡⎤⎢⎥⎣⎦上单减，11t ∴-≤≤，又对称轴12t = min 1324t y ∴==时，，max 13t y ∴=-=时，，()g x ∴的值域为3,34⎡⎤⎢⎥⎣⎦。

函数奇偶性练习题(内含答案)

函数奇偶性练习题(内含答案)新希望培训学校资料数学函数奇偶性练（内含答案）一、选择题1.已知函数 $f(x)=ax+bx+c(a\neq0)$ 是偶函数，那么$g(x)=ax+bx-cx$ 是（）A。

奇函数B。

偶函数C。

既奇又偶函数D。

非奇非偶函数2.已知函数 $f(x)=ax+bx+3a+b$ 是偶函数，且其定义域为$[a-1,2a]$，则（）A。

$a=2,\ b=\frac{1}{3}$B。

$a=-1,\ b=-\frac{1}{3}$C。

$a=1,\ b=-\frac{1}{3}$D。

$a=3,\ b=\frac{1}{3}$3.已知 $f(x)$ 是定义在 $\mathbb{R}$ 上的奇函数，当$x\geq0$ 时，$f(x)=x-2x$，则 $f(x)$ 在 $\mathbb{R}$ 上的表达式是（）A。

$y=x(x-2)$B。

$y=x(|x|-1)$C。

$y=|x|(x-2)$D。

$y=x(|x|-2)$4.已知 $f(x)=x+ax+bx-8$，且 $f(-2)=10$，那么 $f(2)$ 等于（）A。

$-26$B。

$-18$C。

$-10$D。

$10$5.函数$f(x)=\frac{5x^2}{1+x^2}+\frac{x-1}{x+1}$ 是（）A。

偶函数B。

奇函数C。

非奇非偶函数D。

既是奇函数又是偶函数6.若 $\phi(x),\ g(x)$ 都是奇函数，$f(x)=a\phi(x)+bg(x)+2$ 在 $(0,+\infty)$ 上有最大值 $5$，则$f(x)$ 在 $(-\infty,0)$ 上有（）A。

最小值 $-5$B。

最大值 $-5$C。

最小值 $-1$D。

最大值 $-3$二、填空题7.函数 $f(x)=\frac{x-2}{1-x^2}$ 的奇偶性为（奇函数或偶函数）。

8.若 $y=(m-1)x+2mx+3$ 是偶函数，则 $m=$（）。

9.已知 $f(x)$ 是偶函数，$g(x)$ 是奇函数，若$f(x)+g(x)=\frac{1}{x-1}$，则 $f(x)$ 的解析式为（）。

函数的奇偶性试题(含答案)

一、选择题1．下列命题中错误的是( )①图象关于原点成中心对称的函数一定为奇函数②奇函数的图象一定过原点③偶函数的图象与y 轴一定相交④图象关于y 轴对称的函数一定为偶函数A ．①②B ．③④C ．①④D ．②③[答案] D[解析] f (x )＝1x 为奇函数，其图象不过原点，故②错；y ＝⎩⎨⎧ x －1 x ≥1－x －1 x ≤－1为偶函数，其图象与y 轴不相交，故③错．2．如果奇函数f (x )在(0，＋∞)上是增函数，则f (x )在(－∞，0)上( )A ．减函数B ．增函数C ．既可能是减函数也可能是增函数D ．不一定具有单调性[答案] B3．已知f (x )＝x 7＋ax 5＋bx －5，且f (－3)＝5，则f (3)＝( )A ．－15B ．15C ．10D ．－10[答案] A[解析] 解法1：f (－3)＝(－3)7＋a (－3)5＋(－3)b －5＝－(37＋a ·35＋3b －5)－10＝－f (3)－10＝5，∴f (3)＝－15.解法2：设g (x )＝x 7＋ax 5＋bx ，则g (x )为奇函数，∵f (－3)＝g (－3)－5＝－g (3)－5＝5，∴g (3)＝－10，∴f (3)＝g (3)－5＝－15.4．若f (x )在[－5,5]上是奇函数，且f (3)<f (1)，则下列各式中一定成立的是( )A ．f (－1)<f (－3)B ．f (0)>f (1)C ．f (2)>f (3)D ．f (－3)<f (5)[答案] A[解析] ∵f (3)<f (1)，∴－f (1)<－f (3)，∵f (x )是奇函数，∴f (－1)<f (－3)．5．设f (x )是定义在R 上的奇函数，且当x >0时，f (x )＝2x －3，则f (－2)的值等于( )A ．－1B ．1 C.114D ．－114[答案] A[解析] ∵x >0时，f (x )＝2x －3，∴f (2)＝22－3＝1，又f (x )为奇函数，∴f (－2)＝－f (2)＝－1.6．设f (x )在[－2，－1]上为减函数，最小值为3，且f (x )为偶函数，则f (x )在[1,2]上( )A ．为减函数，最大值为3B ．为减函数，最小值为－3C ．为增函数，最大值为－3D ．为增函数，最小值为3[答案] D[解析] ∵f (x )在[－2，－1]上为减函数，最大值为3，∴f (－1)＝3，又∵f (x )为偶函数，∴f (x )在[1,2]上为增函数，且最小值为f (1)＝f (－1)＝3.7．(胶州三中高一模块测试)下列四个函数中，既是偶函数又在(0，＋∞)上为增函数的是( )A ．y ＝x 3B ．y ＝－x 2＋1C ．y ＝|x |＋1D ．y ＝2－|x | [答案] C[解析] 由偶函数，排除A ；由在(0，＋∞)上为增函数，排除B ，D ，故选C.8．(09·辽宁文)已知偶函数f (x )在区间[0，＋∞)单调递增，则满足f (2x －1)<f ⎝ ⎛⎭⎪⎫13的x 取值范围是( ) A.⎝ ⎛⎭⎪⎫13，23B.⎣⎢⎡⎭⎪⎫13，23C.⎝ ⎛⎭⎪⎫12，23 ` D.⎣⎢⎡⎭⎪⎫12，23 [答案] A[解析] 由题意得|2x －1|<13⇒－13<2x －1<13⇒23<2x <43⇒13<x <23，∴选A.9．若函数f (x )＝(x ＋1)(x ＋a )为偶函数，则a ＝( )A ．1B ．－1C ．0D ．不存在[答案] B[解析] 解法1：f (x )＝x 2＋(a ＋1)x ＋a 为偶函数，∴a ＋1＝0，∴a ＝－1.解法2：∵f (x )＝(x ＋1)(x ＋a )为偶函数，∴对任意x ∈R ，有f (－x )＝f (x )恒成立，∴f (－1)＝f (1)，即0＝2(1＋a )，∴a ＝－1.10．奇函数f (x )当x ∈(－∞，0)时，f (x )＝－2x ＋3，则f (1)与f (2)的大小关系为( )A ．f (1)<f (2)B ．f (1)＝f (2)C ．f (1)>f (2)D ．不能确定 [答案] C[解析] 由条件知，f (x )在(－∞，0)上为减函数，∴f (－1)<f (－2)，又f (x )为奇函数，∴f (1)>f (2)．[点评] 也可以先求出f (x )在(0，＋∞)上解析式后求值比较，或利用奇函数图象对称特征画图比较．二、填空题11．若f (x )＝ax 2＋bx ＋c (a ≠0)为偶函数，则g (x )＝ax 3＋bx 2＋cx 的奇偶性为________．[答案] 奇函数[解析] 由f (x )＝ax 2＋bx ＋c (a ≠0)为偶函数得b ＝0，因此g (x )＝ax 3＋cx ，∴g (－x )＝－g (x )，∴g (x )是奇函数．12．偶函数y ＝f (x )的图象与x 轴有三个交点，则方程f (x )＝0的所有根之和为________．[答案] 0[解析] 由于偶函数图象关于y 轴对称，且与x 轴有三个交点，因此一定过原点且另两个互为相反数，故其和为0.三、解答题13．判断下列函数的奇偶性：(1)f (x )＝⎩⎪⎨⎪⎧－x 2＋x (x >0)x 2＋x (x ≤0)； (2)f (x )＝1x 2＋x. [解析] (1)f (－x )＝⎩⎨⎧ x 2－x (x ≥0)－x 2－x (x <0)，∴f (－x )＝－f (x )，∴f (x )为奇函数．(2)f (－x )＝1x 2－x≠f (x )，f (－x )≠－f (x )，∴f (x )既不是奇函数，又不是偶函数．14．已知f (x )是偶函数，g (x )是奇函数，且f (x )＋g (x )＝x 2＋x －2，求f (x )，g (x )的表达式．[解析] f (－x )＋g (－x )＝x 2－x －2，由f (x )是偶函数，g (x )是奇函数得，f (x )－g (x )＝x 2－x －2又f (x )＋g (x )＝x 2＋x －2，两式联立得：f (x )＝x 2－2，g (x )＝x .15．函数f (x )＝ax ＋b 1＋x 2是定义在(－1,1)上的奇函数，且f ⎝ ⎛⎭⎪⎫12＝25，求函数f (x )的解析式．[解析] 因为f (x )是奇函数且定义域为(－1,1)，所以f (0)＝0，即b ＝0.又f ⎝ ⎛⎭⎪⎫12＝25，所以12a 1＋⎝ ⎛⎭⎪⎫122＝25，所以a ＝1，所以f (x )＝x 1＋x 2. 16．定义在(－1,1)上的奇函数f (x )是减函数，且f (1－a )＋f (1－a 2)<0，求实数a 的取值范围．[解析] 由f (1－a )＋f (1－a 2)<0及f (x )为奇函数得，f (1－a )<f (a 2－1)，∵f (x )在(－1,1)上单调减，∴⎩⎪⎨⎪⎧－1<1－a<1－1<1－a 2<11－a >a 2－1 解得0<a <1.故a 的取值范围是{a |0<a <1}．17．f (x )是奇函数，当x ≥0时，f (x )的图象是经过点(3，－6)，顶点为(1,2)的抛物线的一部分，求f (x )的解析式，并画出其图象．[解析] 设x ≥0时，f (x )＝a (x －1)2＋2，∵过(3，－6)点，∴a (3－1)2＋2＝－6，∴a ＝－2.即f (x )＝－2(x －1)2＋2.当x <0时，－x >0，f (－x )＝－2(－x －1)2＋2＝－2(x ＋1)2＋2，∵f (x )为奇函数，∴f (－x )＝－f (x )，∴f (x )＝2(x ＋1)2－2，即f (x )＝⎩⎨⎧ －2(x －1)2＋2 (x ≥0)2(x ＋1)2－2 (x <0)，其图象如图所示．。

函数奇偶性练习题及答案

函数的奇偶性练习题1、判断以下函数的奇偶性。

〔1〕x xx x f -+-=11)1()(〔非奇非偶〕〔2〕 2|2|)1lg()(2---=x x x f 〔奇〕〔3〕33)(22-+-=x x x f 〔奇偶〕〔4〕2||)(2+--=a x x x f 〔a=0，偶；a ≠0，非奇非偶〕〔5〕1212)(-+=x x x f 〔奇〕〔6〕)1lg(2x x y ++=〔奇〕〔7〕1cos sin ()1cos sin x xf x x x-+=++ 〔8〕1()x f x +-=(奇)2、设函数)(x f 是定义在R 上的奇函数，对于R x ∈∀，都有)23()23(x f x f --=+成立。

〔1〕证明：)(x f 是周期函数，并指出周期。

)()()]23(23[]23)23[()3()()(),23()23(x f x f x f x f x f x f x f x f x f =--=+--=++=+∴=---=+ 所以，)(x f 是周期函数，且3=T 〔2〕假设2)1(=f ，求)3()2(f f +的值。

-23．设()f x 是定义在R 上的奇函数，当x ≤0时，()f x x x 2=2-，则()f 1=〔 A 〕A ．-3B ．-1C ．１D ．３4．函数)(x f 的定义域为()()+∞⋃∞-,11,，且)1(+x f 为奇函数，当1>x 时， 16122)(2+-=x x x f ，则直线2=y 与函数)(x f 图象的所有交点的横坐标之和是〔 D 〕A ．1B ．2C ．4D ．5解：f(x+1)是奇函数所以 f(x+1)的图像关于(0,0)对称，且f(0+1)=0f(x+1)的图像向右平移1个单位，得到f(x)所以 f(x)的图像关于(1,0)对称, f(1)=0则当 x>1时〔1〕 2x²-12x+16=2x²-6x+7=0x=3±√2 两根都大于1即x>1时，y=2与函数f(x)图像交点的横坐标为3±√2〔2〕 2x²-12x+16=-2x²-6x+9=0x=3所以 x=3时，y=-2(3,-2)关于(1,0)的对称点为〔-1,2〕即 x<1时，y=2与函数f(x)图像交点的横坐标为-1所以，直线y=2与函数f(x)图象的所有交点的横坐标之和是3+√2+3-√2+(-1)=55.下面四个结论中，正确命题的个数是 ( A )①偶函数的图象一定与y 轴相交②奇函数的图象一定通过原点③偶函数的图象关于y 轴对称④既是奇函数，又是偶函数的函数一定是f 〔x 〕=0〔x ∈R 〕A.1B.2C.36.设f (x )是定义在R 上以2为周期的偶函数，已知x ∈(0,1)时，)1(log )(21x x f -=，则函数f (x )在(1,2)上( D )A ．是增函数，且f (x )<0B ．是增函数，且f (x )>0C ．是减函数，且f (x )<0D ．是减函数，且f (x )>07．已知函数)(x f y =，R x ∈，有以下4个命题：①假设)21()21(x f x f -=+，则)(x f 的图象关于直线1=x 对称；②)2(-x f 与)2(x f -的图象关于直线2=x 对称；③假设)(x f 为偶函数，且)()2(x f x f -=+，则)(x f 的图象关于直线2=x 对称；④假设)(x f 为奇函数，且)2()(--=x f x f ，则)(x f 的图象关于直线1=x 对称.其中正确命题的个数为〔C 〕.A. 1个B. 2个C. 3个D. 4个分析：①先用换元法将f 〔1+2x 〕=f 〔1-2x 〕转化，再由转化后的形式判断对称轴的方程．②y=f 〔x-2〕与y=f 〔2-x 〕的图象关于直线x=2对称可转化为证明y=f 〔x 〕与y=f 〔-x 〕的图象关于直线x=0对称的问题，再结合图象的平移知识进行判断．③用-x 换x ，由题设条件和偶函数的性质得，f 〔2-x 〕=-f 〔-x 〕=-f 〔x 〕=f 〔2+x 〕，故f 〔x 〕的图象关于直线x=2对称． ④用-x 换x ，由题设条件和奇函数的性质得，f 〔-x 〕=f 〔x-2〕，故y=f 〔x 〕的图象关于直线x=-1对称．解答：解：①令t=1+2x ，可得2x=t-1，代入f 〔1+2x 〕=f 〔1-2x 〕得f 〔t 〕=f 〔2-t 〕由于|t-1|=|2-t-1|，故可知函数y=f 〔x 〕图象关于直线x=1对称即y=f 〔x 〕的图象关于直线x=1对称，故①是真命题．②由题设知y=f 〔2-x 〕=f[-〔x-2〕]由于函数y=f 〔x 〕与y=f 〔-x 〕的图象关于直线x=0对称，又y=f 〔x-2〕与y=f 〔2-x 〕的图象可由函数y=f 〔x 〕与y=f 〔-x 〕的图象右移动2个单位而得到， ∴y=f 〔x-2〕与y=f 〔2-x 〕的图象关于直线x=2对称，故②是真命题．③f 〔x 〕为偶函数，且f 〔2+x 〕=-f 〔x 〕，用-x 换x 得，f 〔2-x 〕=-f 〔-x 〕=-f 〔x 〕=f 〔2+x 〕 ∴f 〔x 〕的图象关于直线x=2对称，故③是真命题．④∵y=f 〔x 〕为奇函数，且f 〔x 〕=f 〔-x-2〕，用-x 换x 得，f 〔-x 〕=f 〔x-2〕，∴y=f 〔x 〕的图象关于直线x=-1对称，故④是假命题．故选C ．8.设)(x f 是),(+∞-∞上的奇函数，),()2(x f x f -=+当10≤≤x 时，x x f =)(，则)5.7(f 等于〔 B 〕A.0.5B.C.D.9．设f (x )是连续的偶函数，且当x >0时是单调函数，则满足f (x )＝f ⎝ ⎛⎭⎪⎫x ＋3x ＋4的所有x 之和为( C ) A ．－3 B ．3 C ．－8 D ．810.已知函数f (x )满足：f (1)＝2，)(1)(1)1(x f x f x f -+=+，则f (2011)等于( C ) A ．2 B ．－3 C ．－12 D.13[解析] 由条件知，f (2)＝－3，f (3)＝－12，f (4)＝13，f (5)＝f (1)＝2，故f (x ＋4)＝f (x ) (x ∈N *)．∴f (x )的周期为4，故f (2011)＝f (3)＝－12.[点评] 严格推证如下：f (x ＋2)＝1＋f (x ＋1)1－f (x ＋1)＝－1f (x )，∴f (x ＋4)＝f [(x ＋2)＋2]＝f (x )．即f (x )周期为 11.函数y ＝log 22－x 2＋x的图象( A ) A ．关于原点对称 B ．关于直线y ＝－x 对称C ．关于y 轴对称D ．关于直线y ＝x 对称12.已知f 〔x 〕是奇函数，当x ∈〔0，1〕时，f 〔x 〕=lgx +11，那么当x ∈〔－1，0〕时，f 〔x 〕的表达式是__________.解析：当x ∈〔－1，0〕时，－x ∈〔0，1〕，∴f 〔x 〕=－f 〔－x 〕=－lg x-11=lg 〔1－x 〕.答案：lg 〔1－x 〕13.定义在R 上的奇函数f (x )满足：当x ＞0时，f (x )＝2008x ＋log 2008x ，则方程f (x )＝0的实根的个数为 3 .14．假设y ＝〔m －1〕x 2＋2mx ＋3是偶函数，则m ＝_________．0解析：因为函数y ＝〔m －1〕x 2＋2mx ＋3为偶函数，∴f 〔－x 〕＝f 〔x 〕，即〔m －1〕〔－x 〕2＋2m 〔－x 〕＋3＝〔m —1〕x 2＋2mx ＋3，整理，得m ＝0．(15.已知函数f(x)定义域为R ，则以下命题：①y=f(x)为偶函数，则y=f(x+2)的图像关于y 轴对称；②y=f(x+2)为偶函数，则y=f(x)的图像关于直线x=2对称；③假设函数f(2x+1)是偶函数，则f(2x)的图像关于直线x=1/2对称； ④假设f(x-2)=f(2-x),则y=f(x)的图像关于直线x=2对称；⑤y=f(x-2)和y=f(2-x)的图像关于x=2对称。

函数的奇偶性练习题含答案

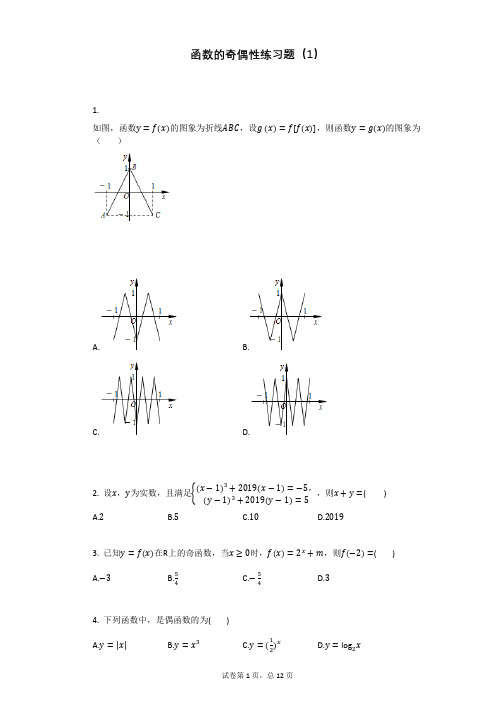
函数的奇偶性练习题（1）1.如图，函数y =f(x)的图象为折线ABC ，设g (x)=f[f(x)]，则函数y =g(x)的图象为（）A. B.C.D.2. 设x ，y 为实数，且满足{(x −1)3+2019(x −1)=−5，(y −1)3+2019(y −1)=5，则x +y =( ) A.2B.5C.10D.20193. 已知y =f (x )在R 上的奇函数，当x ≥0时，f (x )=2x +m ，则f (−2)=( )A.−3B.54C.−54D.34. 下列函数中，是偶函数的为( )A.y =|x|B.y =x 3C.y =(12)xD.y =log 2x<0的解集为5. 设奇函数f(x)在(0,+∞)上为增函数，且f(1)=0，则不等式f(x)−f(−x)x（）A.(−1,0)∪(1,+∞)B.(−∞,−1)∪(0,1)C.(−∞,−1)∪(1,+∞)D.(−1,0)∪(0,1)6. 已知f(x)满足对∀x∈R，f(−x)+f(x)=0，且x≥0时，f(x)=e x+m（m为常数），则f(−ln5)的值为( )A.4B.−4C.6D.−67. 已知函数y=f(2x+1)是定义在R上的奇函数，函数y=g(x)的图象与函数y=f(x)的图象关于直线y=x对称，则g(x)+g(−x)的值为（）A.2B.0C.1D.不能确定8. 已知函数f(x)是偶函数，且f(5−x)＝f(5+x)，若g(x)＝f(x)sinπx，ℎ(x)＝f(x)cosπx，则下列说法正确的是（）A.函数y＝g(x)是偶函数B.10是函数f(x)的一个周期C.对任意的x∈R，都有g(x+5)＝g(x−5)D.函数y＝ℎ(x)的图象关于直线x＝5对称9. 下列函数中，既是偶函数又在(0, +∞)上单调递减的函数是（）A.y＝x3B.y＝|x|C.y＝−x2+1D.y＝10. 已知函数f(x)＝x5+ax3+bx−6，且f(−2)＝10，则f(2)＝________．11. 设奇函数f(x)的定义域为[−6, 6]，当x∈[0, 6]时，f(x)的图象如图所示，不等式f(x)<0的解集用区间表示为________．12. 定义在[−2,2]上的奇函数f(x)，已知当x∈[−2,0]时，f(x)=2x+a⋅3x(a∈R)，则f(x)在[0,2]上的解析式为________．（化成最简形式）13. 已知函数f(x)是定义在R上的奇函数，且当x≥0时f(x)＝x2，若对任意的x∈[a−1, a+1]，恒有f(x2+a)>a2f(x)，则实数a的取值范围为________．14. 已知f(x)是定义在R上的奇函数，当x>0时，f(x)＝x2−x，则不等式f(x)>0的解集用区间表示为________．15. 已知函数f(x)＝lg3−x3+x（1）判断并证明函数f(x)的奇偶性；（2）当x≥0时函数g(x)与f(x)相同，且g(x)为偶函数，求g(x)＝的定义域及其表达式．16. 已知定义在R上的函数f(x)满足：（1）f(2−x)=f(x)；（2）f(x+4)=f(x)（3）x1，x2∈[1, 3]时，(x1−x2)[f(x1)−f(x2)]<0．则f(2018)，f(2019)，f(2020)大小关系（）A.f(2018)>f(2019)>f(2020)B.f(2020)>f(2018)>f(2019)C.f(2020)=f(2018)>f(2019)D.f(2018)>f(2019)=f(2020)17. 定义在R上的奇函数，当x>0时，f(x)＝x2−4x．（1）设g(x)＝f(x)，x∈[−4, 4]，求函数g(x)的值域；（2）当m>0时，若|f(m)|＝3，求实数m的值．参考答案与试题解析函数的奇偶性练习题（1）一、选择题（本题共计 7 小题，每题 5 分，共计35分）1.【答案】A【考点】函数的图象变换函数奇偶性的性质【解析】函数y=f(x)的图象为折线ABC，其为偶函数，所研究x≥0时g(x)的图象即可，首先根据图象求出x≥0时f(x)的图象及其值域，再根据分段函数的性质进行求解，可以求出g(x)的解析式再进行判断；【解答】解：函数y=f(x)的图象为折线ABC，函数f(x)为偶函数，我们可以研究x≥0的情况即可，若x≥0，可得B(0, 1)，C(1, −1)，则直线BC的方程为：l BC:y=−2x+1，x∈[0, 1]，其中−1≤f(x)≤1；若x<0，可得l AB:y=2x+1，∴f(x)={−2x+1(0≤x≤1),2x+1(−1≤x<0),我们讨论x≥0的情况：如果0≤x≤12，解得0≤f(x)≤1，此时g(x)=f[f(x)]=−2(−2x+1)+1=4x−1；若12<x≤1，解得−1≤f(x)<0，此时g(x)=f[f(x)]=2(−2x+1)+1=−4x+3；∴x∈[0, 1]时，g(x)={4x−1(0≤x≤12),−4x+3(12<x≤1).故选A.2.【答案】A【考点】函数奇偶性的性质【解析】将方程组中的方程，形式化成相同，构造函数f(t)=t3+1997t+1，确定函数f(t)为单调递增函数，即可求得结论．【解答】解：设函数f(m)=(m−1)3+2019(m−1)，则f(1+m)=(1+m−1)3+2019(1+m−1)=m3+2019m，f(1−m)=(1−m −1)3+2019(1−m −1)=−m 3−2019m ，所以f(1+m)+f(1−m)=0，所以函数f(m)关于(1,0)中心对称，又因为{(x −1)3+2019(x −1)=−5，(y −1)3+2019(y −1)=5所以f(x)+f(y)=0，所以x +y =2.故选A .3.【答案】A【考点】函数奇偶性的性质【解析】根据题意，f (x )为定义在R 上的奇函数，可知f (0)=0，即可求出m =−1，即当x ≥0时f (x )=2x −1，可得f (2)=22−1=3，再根据f (x )为奇函数，可得f (−2)=−f (2)=−3．【解答】解：根据题意，f (x )为定义在R 上的奇函数，则f (0)=20+m =0，解得：m =−1.∵ 当x ≥0时，f (x )=2x −1，∴ f (−2)=−f (2)=−(22−1)=−3.故选A ．4.【答案】A【考点】函数奇偶性的判断【解析】此题暂无解析【解答】解：A ．该函数定义域为R ，设y =f(x)，f(−x)=|−x|=|x|=f(x)，是偶函数； B ．该函数定义域为R ，设y =f(x)，f(−x)=(−x)3=−x 3=−f(x)，是奇函数； C ．该函数定义域为R ，设y =f(x)，f(−x)=(12)−x ≠f(x)， f(−x)=(12)−x ≠−f(x)，该函数是非奇非偶函数；D ．该函数定义域为(0,+∞)，不关于原点对称，该函数是非奇非偶函数.故选A .5.【答案】D【考点】奇偶性与单调性的综合此题暂无解析【解答】∵f(x)为奇函数，f(−x)=−f(x)，∴f(x)−f(−x)x <0⇔2f(x)x<0．∵f(x)在(0,+∞)上为增函数，且f(1)=0，∴f(x)在(−∞,0)上为增函数，且f(−1)=0，∴不等式f(x)x<0的解集为(−1,0)∪(0,1)．6.【答案】B【考点】函数奇偶性的性质【解析】首先利用奇偶性，求出m，再利用奇偶性求值即可.【解答】解：∵f(x)满足对∀x∈R，f(−x)+f(x)=0，故f(−x)=−f(x)，故f(0)=0，∵x≥0时，f(x)=e x+m，∴f(0)=1+m=0，解得m=−1，即x≥0时，f(x)=e x−1，则f(ln5)=4，∴f(−ln5)=−f(ln5)=−4.故选B.7.【答案】A【考点】奇偶函数图象的对称性【解析】利用奇函数的定义可把已知转化为f(t)+f(2−t)=0，从而可得函数f(x)关于(1, 0)对称，函数y=g(x)的图象与函数y=f(x)的图象关于直线y=x对称，则g(x)关于(0, 1)对称，代入可求．【解答】解：∵函数y=f(2x+1)是定义在R上的奇函数∴f(−2x+1)=−f(2x+1)令t=1−2x代入可得f(t)+f(2−t)=0函数f(x)关于(1, 0)对称由函数y=g(x)的图象与函数y=f(x)的图象关于直线y=x对称函数g(x)关于(0, 1)对称从而有g(x)+g(−x)=2故选A二、多选题（本题共计 2 小题，每题 5 分，共计10分）8.B,C,D【考点】函数奇偶性的性质与判断【解析】根据题意，依次分析选项，综合即可得答案．【解答】根据题意，依次分析选项：对于A，g(x)＝f(x)sinπx，g(−x)＝f(−x)sinπ(−x)＝−f(−x)sinπx，又由函数f(x)是偶函数，则g(−x)＝−f(x)sinπx，即函数g(x)为奇函数，A错误对于B，由于f(x)是偶函数，且f(5−x)＝f(5+x)，得f(5−x)＝f(5+x)＝f(x−5)，即f(10+x)＝f(x)，则f(x)是周期为10的周期函数，所以ℎ(x+10)＝f(x+10)cos(πx+10π)＝f(x)cosπx＝ℎ(x)，则y＝ℎ(x)是的最小正周期为10，故B正确；对于C，g(x+5)＝f(x+5)sin（π(x+5)）＝f(5−x)sin(πx+5π)＝f(5−x)(−sinπx)＝−f(x−5)(−sinπx)＝f(x−5)sinπx＝g(x−5)，故C正确；对于D，ℎ(5−x)＝f(5−x)cos(5π−5x)＝f(5+x)cos(5x−5π)＝f(5+x)cos(5x−5π+10π)＝f(5+x)cos(5x+5π)＝ℎ(5+x)，所以函数y＝ℎ(x)的图象关于直线x＝5对称，D正确；9.【答案】C,D【考点】函数单调性的性质与判断函数奇偶性的性质与判断奇偶性与单调性的综合【解析】根据题意，依次分析选项中函数的奇偶性与单调性，综合即可得答案．【解答】对于A，y＝x3为奇函数，所以该选项不符合题意；对于B，x>0时，y＝|x|＝x，所以函数y＝|x|的(0, +∞)上为增函数，所以该选项不符合题意；对于C，该函数定义域为R，设y＝f(x)，显然f(−x)＝f(x)，所以该函数为偶函数，且该函数在(0, +∞)上单调递减，所以该选项符合题意；对于D，该函数定义域为{x|x≠0}，设y＝f(x)，显然f(−x)＝f(x)，所以该函数为偶函数，且该函数在(0, +∞)上单调递减，可知该选项符合题意．三、填空题（本题共计 5 小题，每题 5 分，共计25分）10.【答案】−22【考点】函数奇偶性的性质与判断【解析】根据奇函数的性质建立方程组关系进行求解决即可．∵f(x)＝x5+ax3+bx−6，且f(−2)＝10，∴f(−2)＝−25−a⋅23−2b−6＝10，则f(2)＝25+a⋅23−2b−6，两式相加得10+f(2)＝−6−6＝−12，则f(2)＝−10−12＝−22，11.【答案】[−6, −3)∪(0, 3)【考点】函数的图象与图象的变换【解析】此题暂无解析【解答】此题暂无解答12.【答案】3−x−2−x【考点】函数奇偶性的性质函数解析式的求解及常用方法【解析】由题意设x>0利用已知的解析式求出f(−x)=x2+2x，再由f(x)=−f(−x)，求出x>0时的解析式．【解答】解：∵ f(x)为奇函数，∴ f(0)=20+a⋅30=1+a=0，∴ a=−1，f(x)=2x−3x.∴ 在x∈[0,2]上时，f(x)=−f(−x)=3−x−2−x.故答案为：3−x−2−x.13.【答案】(0, +∞)【考点】函数奇偶性的性质与判断函数恒成立问题【解析】由当x≥0时，f(x)＝x2，函数是奇函数，可得当x<0时，f(x)＝−x2，从而f(x)在R上是单调递增函数，且满足a2f(x)＝f(ax)，再根据不等式f(x2+a)>a2f(x)＝f(ax)，在x∈[a−1, a+1]，恒成立，利用二次函数的性质，可得不等式，即可得出答案．【解答】当x≥0时，f(x)＝x2，∵函数是奇函数，∴当x<0时，f(x)＝−x2，∴f(x)={x2,x≥0，−x2,x<0∴f(x)在R上是单调递增函数，且满足a2f(x)＝f(ax)，∵不等式f(x2+a)>a2f(x)＝f(ax)在x∈[a−1, a+1]恒成立，∴x2+a>ax在x∈[a−1, a+1]恒成立，令g(x)＝x2−ax+a，函数的对称轴为x=a2，当a2<a−1，即a>2时，不等式恒成立，可得g(a−1)＝(a−1)2−a(a−1)+a＝1>0，恒成立；当a−1≤a2≤a+1，即−2≤a≤2时，不等式恒成立，可得g(a2)＝( a2)2−a(a2)+a>0恒成立，解得a∈(0, 2]；当a2>a+1，即a<−2时，不等式恒成立，可得g(a+1)＝(a+1)2−a(a+1)+a＝2a+1>0不恒成立；综上：a>0．14.【答案】(−1, 0)∪(1, +∞)【考点】函数奇偶性的性质与判断【解析】根据条件可设x<0，从而得出f(−x)＝x2+x＝−f(x)，即得出x<0时，f(x)＝−x2−x，这样即可得出：x>0时，由f(x)>0得出x2−x>0；x<0时，由f(x)> 0得出−x2−x>0，解出x的范围即可．【解答】∵f(x)是定义在R上的奇函数，且x>0时，f(x)＝x2−x，∴设x<0，−x>0，则f(−x)＝x2+x＝−f(x)，∴f(x)＝−x2−x，∴ ①x>0时，由f(x)>0得，x2−x>0，解得x>1；②x<0时，由f(x)>0得，−x2−x>0，解得−1<x<0，∴原不等式的解集为(−1, 0)∪(1, +∞)．四、解答题（本题共计 3 小题，每题 10 分，共计30分）15.【答案】根据题意，函数f(x)＝lg3−x3+x是奇函数，证明：对于函数f(x)＝lg3−x3+x ，必有3−x3+x>0，解可得：−3<x<3，即函数的定义域为(−3, 3)，关于原点对称，又由f(x)+f(−x)＝lg3−x3+x +lg3+x3−x=lg1＝0，则有f(−x)＝−f(x)，则函数f(x)为奇函数；根据题意，有（1）的结论，函数f(x)的定义域为(−3, 3)，当0≤x<3时，g(x)＝f(x)＝lg3−x3+x，设−3<x<0，则0<−x<3，则g(−x)＝lg 3+x 3−x ，又由函数g(x)为偶函数，则g(x)＝lg 3+x 3−x ，综合可得：g(x)={lg 3+x 3−x ,−3<x <0lg 3−x 3+x ,0≤x <3．【考点】函数奇偶性的性质与判断【解析】（1）根据题意，先求出函数f(x)的定义域，进而分析可得f(x)+f(−x)＝0，由函数奇偶性的定义分析可得答案；（2）根据题意，分2种情况讨论：当0≤x <3时，g(x)＝f(x)＝lg3−x 3+x ，当−3<x <0，利用偶函数的性质求出g(x)的解析式，综合即可得答案．【解答】根据题意，函数f(x)＝lg 3−x 3+x 是奇函数，证明：对于函数f(x)＝lg 3−x 3+x ，必有3−x 3+x >0，解可得：−3<x <3，即函数的定义域为(−3, 3)，关于原点对称，又由f(x)+f(−x)＝lg 3−x 3+x +lg 3+x 3−x =lg 1＝0，则有f(−x)＝−f(x)，则函数f(x)为奇函数；根据题意，有（1）的结论，函数f(x)的定义域为(−3, 3)，当0≤x <3时，g(x)＝f(x)＝lg 3−x 3+x ，设−3<x <0，则0<−x <3，则g(−x)＝lg 3+x 3−x ，又由函数g(x)为偶函数，则g(x)＝lg3+x 3−x ，综合可得：g(x)={lg 3+x 3−x ,−3<x <0lg 3−x 3+x ,0≤x <3． 16.【答案】，f(2019)=f，f(2020)=f(0)=f，故f （2020）=f （2018）＞f （2019），【考点】抽象函数及其应用【解析】根据已知可得函数 f (x)的图象关于直线x =1对称，周期为4，且在[1, 3]上为减函数，进而可比较f(2018)，f(2019)，f(2020)的大小．【解答】，f(2019)=f，f(2020)=f(0)=f，故f(2020)=f(2018)>f(2019)，17.【答案】根据题意，f(x)为定义在R 上的奇函数，则f(0)＝0，则有g(0)＝0，当0<x <4时，f(x)＝x 2−4x ，此时g(x)＝x 2−4x ，当−4<x <0时，0<−x <4，f(−x)＝x 2−4x ，又由f(x)为奇函数，则f(x)＝−f(−x)＝−x 2−4x ，此时g(x)＝−x 2−4x ；综合可得：g(x)=f(x)={−x 2−4x,x <00,x =0x 2−4x,x >0当−4≤x ≤0时，0≤g(x)≤4；当0<x ≤4时，−4≤g(x)≤0．g(x)的值域为[−4, 4]根据题意，m >0时，|f(m)|={−m 2+4m,0<m ≤4m 2−4m,m >4， 1)当0<m ≤4时，令−m 2+4m ＝3，解得m ＝1或m ＝3；2)当m >4时，令m 2−4m ＝3，解得m =2+√7或m =2−√7（舍去）综合1)，2)得m ＝1或m ＝3或m =2+√7【考点】函数奇偶性的性质与判断【解析】（1）根据题意，由函数的解析式以及奇函数的性质分析可得g(x)的解析式，进而分析可得答案；（2）根据题意，m >0时，|f(m)|={−m 2+4m,0<m ≤4m 2−4m,m >4，据此分析可得答案．【解答】根据题意，f(x)为定义在R 上的奇函数，则f(0)＝0，则有g(0)＝0，当0<x <4时，f(x)＝x 2−4x ，此时g(x)＝x 2−4x ，当−4<x <0时，0<−x <4，f(−x)＝x 2−4x ，又由f(x)为奇函数，则f(x)＝−f(−x)＝−x 2−4x ，此时g(x)＝−x 2−4x ；综合可得：g(x)=f(x)={−x 2−4x,x <00,x =0x 2−4x,x >0当−4≤x ≤0时，0≤g(x)≤4；当0<x ≤4时，−4≤g(x)≤0．g(x)的值域为[−4, 4]根据题意，m >0时，|f(m)|={−m 2+4m,0<m ≤4m 2−4m,m >4，1)当0<m≤4时，令−m2+4m＝3，解得m＝1或m＝3；2)当m>4时，令m2−4m＝3，解得m=2+√7或m=2−√7（舍去）综合1)，2)得m＝1或m＝3或m=2+√7。

函数的奇偶性试题(含答案)

函数的奇偶性试题(含答案)一、选择题1．下列命题中错误的是( )①图象关于原点成中心对称的函数一定为奇函数②奇函数的图象一定过原点③偶函数的图象与y轴一定相交④图象关于y轴对称的函数一定为偶函数A．①② B．③④C．①④D．②③[答案]　D[解析]　f(x)＝1x为奇函数，其图象不过原点，故②错；y＝Error!为偶函数，其图象与y轴不相交，故③错．2．如果奇函数f(x)在(0，＋∞)上是增函数，则f(x)在(－∞，0)上( )A．减函数B．增函数C．既可能是减函数也可能是增函数D．不一定具有单调性[答案]　B3．已知f(x)＝x7＋ax5＋bx－5，且f(－3)＝5，则f(3)＝( )A．－15 B．15C．10 D．－10[答案]　A[解析]　解法1：f(－3)＝(－3)7＋a(－3)5＋(－3)b－5＝－(37＋a·35＋3b－5)－10＝－f(3)－10＝5，∴f(3)＝－15.解法2：设g(x)＝x7＋ax5＋bx，则g(x)为奇函数，∵f(－3)＝g(－3)－5＝－g(3)－5＝5，∴g(3)＝－10，∴f(3)＝g(3)－5＝－15.4．若f(x)在[－5,5]上是奇函数，且f(3)<f(1)，则下列各式中一定成立的是( )A．f(－1)<f(－3) B．f(0)>f(1)C．f(2)>f(3) D．f(－3)<f(5)[答案]　A[解析]　∵f(3)<f(1)，∴－f(1)<－f(3)，∵f(x)是奇函数，∴f(－1)<f(－3)．5．设f(x)是定义在R上的奇函数，且当x>0时，f(x)＝2x－3，则f(－2)的值等于( )A．－1 B．1C.114D．－114[答案]　A[解析]　∵x>0时，f(x)＝2x－3，∴f(2)＝22－3＝1，又f(x)为奇函数，∴f(－2)＝－f(2)＝－1.6．设f(x)在[－2，－1]上为减函数，最小值为3，且f(x)为偶函数，则f(x)在[1,2]上( )A．为减函数，最大值为3B．为减函数，最小值为－3C．为增函数，最大值为－3D．为增函数，最小值为3[解析]　∵f(x)在[－2，－1]上为减函数，最大值为3，∴f(－1)＝3，又∵f(x)为偶函数，∴f(x)在[1,2]上为增函数，且最小值为f(1)＝f(－1)＝3.7．(胶州三中高一模块测试)下列四个函数中，既是偶函数又在(0，＋∞)上为增函数的是( )A．y＝x3B．y＝－x2＋1C．y＝|x|＋1 D．y＝2－|x|[答案]　C[解析]　由偶函数，排除A；由在(0，＋∞)上为增函数，排除B，D，故选C.8．(09·辽宁文)已知偶函数f(x)在区间[0，＋∞)单调递增，则满足f(2x－1)<f(13)的x取值范围是( )A.(13，23)B.[13，23)C.(12，23)`D.[12，23)[答案]　A[解析]　由题意得|2x－1|<13⇒－13<2x－1<13⇒23<2x<43⇒13<x<23，∴选A.9．若函数f(x)＝(x＋1)(x＋a)为偶函数，则a＝( ) A．1 B．－1C．0 D．不存在[解析]　解法1：f(x)＝x2＋(a＋1)x＋a为偶函数，∴a＋1＝0，∴a＝－1.解法2：∵f(x)＝(x＋1)(x＋a)为偶函数，∴对任意x∈R，有f(－x)＝f(x)恒成立，∴f(－1)＝f(1)，即0＝2(1＋a)，∴a＝－1.10．奇函数f(x)当x∈(－∞，0)时，f(x)＝－2x＋3，则f(1)与f(2)的大小关系为( )A．f(1)<f(2) B．f(1)＝f(2)C．f(1)>f(2) D．不能确定[答案]　C[解析]　由条件知，f(x)在(－∞，0)上为减函数，∴f(－1)<f(－2)，又f(x)为奇函数，∴f(1)>f(2)．[点评]　也可以先求出f(x)在(0，＋∞)上解析式后求值比较，或利用奇函数图象对称特征画图比较．二、填空题11．若f(x)＝ax2＋bx＋c(a≠0)为偶函数，则g(x)＝ax3＋bx2＋cx 的奇偶性为________．[答案]　奇函数[解析]　由f(x)＝ax2＋bx＋c(a≠0)为偶函数得b＝0，因此g(x)＝ax3＋cx，∴g(－x)＝－g(x)，∴g(x)是奇函数．12．偶函数y＝f(x)的图象与x轴有三个交点，则方程f(x)＝0的所有根之和为________．[答案]　0[解析]　由于偶函数图象关于y轴对称，且与x轴有三个交点，因此一定过原点且另两个互为相反数，故其和为0.三、解答题13．判断下列函数的奇偶性：(1)f(x)＝Error!；(2)f(x)＝1x2＋x.[解析]　(1)f(－x)＝Error!，∴f(－x)＝－f(x)，∴f(x)为奇函数．(2)f(－x)＝1x2－x≠f(x)，f(－x)≠－f(x)，∴f(x)既不是奇函数，又不是偶函数．14．已知f(x)是偶函数，g(x)是奇函数，且f(x)＋g(x)＝x2＋x－2，求f(x)，g(x)的表达式．[解析]　f(－x)＋g(－x)＝x2－x－2，由f(x)是偶函数，g(x)是奇函数得，f(x)－g(x)＝x2－x－2又f(x)＋g(x)＝x2＋x－2，两式联立得：f(x)＝x2－2，g(x)＝x.15．函数f(x)＝ax＋b1＋x2是定义在(－1,1)上的奇函数，且f(12)＝25，求函数f(x)的解析式．[解析]　因为f(x)是奇函数且定义域为(－1,1)，所以f(0)＝0，即b＝0.又f(12)＝25，所以12a1＋(12)2＝25，所以a＝1，所以f(x)＝x1＋x2.16．定义在(－1,1)上的奇函数f(x)是减函数，且f(1－a)＋f(1－a2)<0，求实数a的取值范围．[解析]　由f(1－a)＋f(1－a2)<0及f(x)为奇函数得，f(1－a)<f(a2－1)，∵f(x)在(－1,1)上单调减，∴Error!　解得0<a<1.故a的取值范围是{a|0<a<1}．17．f(x)是奇函数，当x≥0时，f(x)的图象是经过点(3，－6)，顶点为(1,2)的抛物线的一部分，求f(x)的解析式，并画出其图象．[解析]　设x≥0时，f(x)＝a(x－1)2＋2，∵过(3，－6)点，∴a(3－1)2＋2＝－6，∴a＝－2.即f(x)＝－2(x－1)2＋2.当x<0时，－x>0，f(－x)＝－2(－x－1)2＋2＝－2(x＋1)2＋2，∵f(x)为奇函数，∴f(－x)＝－f(x)，∴f(x)＝2(x＋1)2－2，即f(x)＝Error!，其图象如图所示．。

函数的奇偶性题型解析(含答案)

函数奇偶性的判定问题1. 判断下列函数的奇偶性：（1）f （x ）=|x +1|－|x －1|；（2）f （x ）=（x －1）·xx -+11；（3）f （x ）=2|2|12-+-x x ；（4）f （x ）=⎩⎨⎧>+<-).0()1(),0()1(x x x x x x （5）xx x f 2)21()(2+= 2.判断下列函数的奇偶性2211(0)2()11(0)2x x g x x x ⎧+>⎪⎪=⎨⎪--<⎪⎩3.判断函数f (x )＝⎩⎪⎨⎪⎧ x 3－3x 2＋1x ＞0x 3＋3x 2－1x ＜0的奇偶性．4.下列函数中，既是偶函数又在区间(0，+∞)上单调递增的函数是( )答案：BA. B.C. D.1．已知函数f （x ）＝ax 2＋bx ＋c （a ≠0）是偶函数，那么g （x ）＝ax 3＋bx 2＋cx （）AA ．奇函数B ．偶函数C ．既奇又偶函数D ．非奇非偶函数5.已知函数)127()2()1()(22+-+-+-=m m x m x m x f 为偶函数，则m 的值是（） A. 1 B. 2 C. 3 D. 47．若y ＝（m +1）x 2＋8mx ＋3是偶函数，则m ＝_________．0【例15】若3)3()2()(2+-+-=x k x k x f 是偶函数，讨论函数)(x f 的单调区间。

2.已知函数是偶函数，那么是( )答案：A A.奇函数 B.偶函数C.既奇且偶函数D.非奇非偶函数已知函数121)(+-=x a x f )(R x ∈,若)(x f 为奇函数，则=a ___；9.若f （x ）=1222+-+⋅x x a a 为奇函数，求实数a 的值.2．已知函数f （x ）＝ax 2＋bx ＋3a ＋b 是偶函数，且其定义域为［a －1，2a ］，则（） AA ．31=a ，b ＝0 B ．a ＝－1，b ＝0 C ．a ＝1，b ＝0 D ．a ＝3，b ＝01.设函数的定义域为，且是奇函数，则实数a 的值是( )答案：CA. B.1 C.D.36.已知函数是偶函数，且，则的值为( )答案：DA.-1B.1C.-5D.54．已知f （x ）＝x 5＋ax 3＋bx －8，且f （－2）＝10，那么f （2）等于（）AA ．－26B ．－18C ．－10D ．102.已知函数)(x f y =为R 上的奇函数，若1)2()3(=-f f ，则=---)3()2(f f ____；5．函数1111)(22+++-++=x x x x x f 是（）BA ．偶函数B ．奇函数C ．非奇非偶函数D ．既是奇函数又是偶函数8．函数2122)(x x x f ---=奇偶性为_____奇函数___（填奇函数或偶函数）)(x f 是定义在R 上的奇函数,则)0(f =___；若有3)2(=-f ，则=)2(f ___；若7)5(=f ；则=-)5(f ___；已知8)(35-++=bx ax x x f 且10)2(=-f ，那么=)2(f 。

函数的奇偶性练习题[(附标准答案)

函数的奇偶性1．函数f （x ）=x(-1﹤x ≦1)的奇偶性是（） A ．奇函数非偶函数 B ．偶函数非奇函数C ．奇函数且偶函数D ．非奇非偶函数2. 已知函数f （x ）=ax 2＋bx ＋c （a ≠0）是偶函数，那么g （x ）=ax 3＋bx 2＋cx 是( ）A .奇函数B .偶函数C .既奇又偶函数D .非奇非偶函数3. 若函数f (x )是定义在R 上的偶函数，在]0,(-∞上是减函数，且f (2)=0，则使得f (x )<0的x 的取值范围是 ( )A.(-∞,2)B. (2,+∞)C. (-∞,-2)⋃(2,+∞)D. (-2,2)4．已知函数f (x )是定义在(－∞,+∞)上的偶函数.当x ∈(－∞,0)时，f (x )=x -x 4，则当x ∈(0.+∞)时，f (x )= .5. 判断下列函数的奇偶性：(1)f (x )＝lg (12+x -x );(2)f (x )＝2-x +x -2(3) f （x ）=⎩⎨⎧>+<-).0()1(),0()1(x x x x x x6.已知g (x )=－x 2－3,f (x )是二次函数，当x ∈[-1,2]时，f (x )的最小值是1，且f (x )+g (x )是奇函数，求f (x )的表达式。

7.定义在（-1，1）上的奇函数f （x ）是减函数，且f(1-a)+f(1-a 2)<0,求a 的取值范围8.已知函数21()(,,)ax f x a b c N bx c+=∈+是奇函数,(1)2,(2)3,f f =<且()[1,)f x +∞在上是增函数,(1)求a,b,c 的值;(2)当x ∈[-1,0)时,讨论函数的单调性.9.定义在R 上的单调函数f (x )满足f (3)=log 23且对任意x ，y ∈R 都有f (x+y )=f (x )+f (y )．(1)求证f (x )为奇函数；(2)若f (k ·3x )+f (3x -9x -2)＜0对任意x ∈R 恒成立，求实数k 的取值范围．10下列四个命题：（1）f （x ）=1是偶函数；（2）g （x ）=x 3，x ∈（－1，1]是奇函数；（3）若f （x ）是奇函数，g （x ）是偶函数，则H （x ）=f （x ）·g （x ）一定是奇函数；（4）函数y =f （|x |）的图象关于y 轴对称，其中正确的命题个数是（）A ．1B ．2C ．3D ．411下列函数既是奇函数，又在区间[]1,1-上单调递减的是( )A.()sin f x x =B.()1f x x =-+C.()1()2x x f x a a -=+ D.2()2x f x ln x -=+ 12若y =f （x ）（x ∈R ）是奇函数，则下列各点中，一定在曲线y =f （x ）上的是（）A ．（a ，f （－a ））B ．（－sin a ，－f （－sin a ））C ．（－lg a ，－f （lg a 1））D ．（－a ，－f （a ））13. 已知f （x ）=x 4+ax 3+bx －8，且f （－2）=10，则f （2）=_____________。

（完整版）函数的奇偶性练习题[（附答案）

（完整版）函数的奇偶性练习题[（附答案）函数的奇偶性1．函数f （x ）=x(-1﹤x ≦1)的奇偶性是（）A ．奇函数⾮偶函数B ．偶函数⾮奇函数C ．奇函数且偶函数D ．⾮奇⾮偶函数2. 已知函数f （x ）=ax 2＋bx ＋c （a ≠0）是偶函数，那么g （x ）=ax 3＋bx 2＋cx 是( ）A .奇函数B .偶函数C .既奇⼜偶函数D .⾮奇⾮偶函数 3. 若函数f (x )是定义在R 上的偶函数，在]0,(-∞上是减函数，且f (2)=0，则使得f (x )<0的x 的取值范围是 ( )A.(-∞,2)B. (2,+∞)C. (-∞,-2)?(2,+∞)D. (-2,2) 4．已知函数f (x )是定义在(－∞,+∞)上的偶函数.当x ∈(－∞,0)时，f (x )=x -x 4，则当x ∈(0.+∞)时，f (x )= . 5. 判断下列函数的奇偶性：(1)f (x )＝lg (12+x -x ); (2)f (x )＝2-x +x -2(3) f （x ）=?>+<-).0()1(),0()1(x x x x x x6.已知g (x )=－x 2－3,f (x )是⼆次函数，当x ∈[-1,2]时，f (x )的最⼩值是1，且f (x )+g (x )是奇函数，求f (x )的表达式。

7.定义在（-1，1）上的奇函数f （x ）是减函数，且f(1-a)+f(1-a 2)<0,求a 的取值范围8.已知函数21()(,,)ax f x a b c N bx c+=∈+是奇函数,(1)2,(2)3,f f =<且()[1,)f x +∞在上是增函数,(1)求a,b,c 的值;(2)当x ∈[-1,0)时,讨论函数的单调性.9.定义在R 上的单调函数f (x )满⾜f (3)=log 23且对任意x ，y ∈R 都有f (x+y )=f (x )+f (y )． (1)求证f (x )为奇函数；(2)若f (k ·3x )+f (3x -9x -2)＜0对任意x ∈R 恒成⽴，求实数k 的取值范围．10下列四个命题：（1）f （x ）=1是偶函数；（2）g （x ）=x 3，x ∈（－1，1]是奇函数；（3）若f （x ）是奇函数，g （x ）是偶函数，则H （x ）=f （x ）·g （x ）⼀定是奇函数；（4）函数y =f （|x |）的图象关于y 轴对称，其中正确的命题个数是（） A ．1B ．2C ．3D ．411下列函数既是奇函数，⼜在区间[]1,1-上单调递减的是( )A.()sin f x x =B.()1f x x =-+C.()1()2x x f x a a -=+ D.2()2xf x lnx-=+ 12若y =f （x ）（x ∈R ）是奇函数，则下列各点中，⼀定在曲线y =f （x ）上的是（） A ．（a ，f （－a ）） B ．（－sin a ，－f （－sin a ））C ．（－lg a ，－f （lg a1）） D ．（－a ，－f （a ））13. 已知f （x ）=x 4+ax 3+bx －8，且f （－2）=10，则f （2）=_____________。

函数奇偶性的判断(含答案)

函数奇偶性的判断一、单选题(共10道，每道10分)1.若函数f(x)是奇函数，函数g(x)是偶函数，则下列一定成立的是( )A.函数f(g(x))是奇函数B.函数g(f(x))是奇函数C.函数f(f(x))是奇函数D.函数g(g(x))是奇函数答案：C解题思路：试题难度：三颗星知识点：函数奇偶性的判断2.已知函数，，，……，则函数是( )A.奇函数B.偶函数C.既是奇函数又是偶函数D.非奇非偶函数答案：A解题思路：试题难度：三颗星知识点：函数奇偶性的判断3.函数是( )A.奇函数B.偶函数C.非奇非偶函数D.既是奇函数又是偶函数答案：B解题思路：试题难度：三颗星知识点：函数奇偶性的判断4.定义两种运算：，，则函数是( )A.奇函数B.偶函数C.既是奇函数又是偶函数D.非奇非偶函数答案：A解题思路：试题难度：三颗星知识点：函数奇偶性的判断5.已知f(x)是定义在上的奇函数，当x≥0时，，则的值为( )A.4B.-4C.6D.-6答案：B解题思路：试题难度：三颗星知识点：函数奇偶性的性质6.若函数（x≠0）是偶函数，则函数g(x)是( )A.奇函数B.偶函数C.既是奇函数又是偶函数D.非奇非偶函数答案：A解题思路：试题难度：三颗星知识点：函数奇偶性的判断7.已知函数，，则( )A.f(x)是奇函数，g(x)是奇函数B.f(x)是偶函数，g(x)是偶函数C.f(x)是奇函数，g(x)是偶函数D.f(x)是偶函数，g(x)是奇函数答案：C解题思路：试题难度：三颗星知识点：函数奇偶性的判断8.已知函数，则该函数是( )A.非奇非偶函数，且单调递增B.偶函数，且单调递减C.奇函数，且单调递增D.奇函数，且单调递减答案：C解题思路：试题难度：三颗星知识点：奇偶性与单调性的综合9.已知函数，则该函数是( )A.非奇非偶函数，在上单调递增，在上单调递减B.偶函数，在上单调递增，在上单调递减C.偶函数，在上单调递减D.奇函数，在上单调递减答案：B解题思路：试题难度：三颗星知识点：奇偶性与单调性的综合10.已知函数，设，则是( )A.奇函数，在上单调递减B.奇函数，在上单调递增C.偶函数，在上单调递减，在上单调递增D.偶函数，在上单调递增，在上单调递减答案：B解题思路：试题难度：三颗星知识点：奇偶性与单调性的综合。

高三数学函数的奇偶性试题答案及解析

高三数学函数的奇偶性试题答案及解析1.已知函数则实数的取值范围是（）A．B．C．D．【答案】C【解析】由偶函数定义可得是偶函数，故，原不等式等价于，又根据偶函数定义，，函数在单调递增，，．【考点】函数的性质、解不等式.2.设f（x）是定义在R上的偶函数，且当x≥0时，f（x）=（）x，若对任意的x∈[a, a+l]，不等式f（x+a）≥f2（x）恒成立，则实数a的取值范围是____ 。

【答案】【解析】是定义在上的偶函数，不等式恒成立等价为恒成立，当时，不等式等价为恒成立，即在上恒成立，平方得，即在上恒成立，设，则满足,∴，即.【考点】1.函数的奇偶性；2.利用函数性质解不等式.3.设f(x)是定义在R上的奇函数，当x<0时，f(x)＝x＋e x(e为自然对数的底数)，则f(ln 6)的值为________．【答案】ln 6－【解析】由f(x)是奇函数得f(ln 6)＝－f(－ln 6)＝－(－ln 6)－e－ln 6＝ln 6－.4.已知函数为偶函数，且，若函数，则.【答案】.【解析】设，则为偶函数，由于，另一方面，所以，故.【考点】函数的奇偶性5.已知函数f(x)是(－∞，＋∞)上的偶函数，且f(5＋x)＝f(5－x)，在[0,5]上只有f(1)＝0，则f(x)在[－2 012,2 012]上的零点个数为()A．804B．805C．806D．808【答案】C【解析】f(5＋x)＝f(5－x)＝f(x－5)，故f(x)是周期为10的偶函数，且f(9)＝f(1)＝0，f(x)在[0,2 010]上有402个零点，f(2 011)＝f(1)＝0，故f(x)在[0,2 012]上有403个零点，又f(x)是偶函数，故f(x)在[－2 012,2 012]上共有806个零点．6.下列函数为偶函数的是A．y=sinx B．y=C．y=D．y=ln【答案】D【解析】观察可得:四个选项的定义域均为R,且只有函数y=ln是偶函数,故选D.【考点】本题考查函数的性质(奇偶性),属基础题.7.已知函数f(x)为奇函数，且当x＞0时，f(x)＝x2＋，则f(－1)＝( )A．－2B．0C．1D．2【答案】A【解析】当x＞0时，f(x)＝x2＋，∴f(1)＝12＋＝2.∵f(x)为奇函数，∴f(－1)＝－f(1)＝－2.8.已知定义在实数集上的偶函数满足，且当时，，则关于的方程在上根的个数是（）A．B．C．D．【答案】B【解析】由题意可得，．即函数为周期为的周期函数，又是偶函数，所以，在同一坐标系内，画出函数，的图象，观察它们在区间的交点个数，就是方程在上根的个数，结合函数图象可知，共有个交点，故选．【考点】函数的奇偶性、周期性，函数的图象，函数的零点．9.已知定义在R上的奇函数和偶函数满足 (，且)，若，则（）A．2B．C．D．【答案】B【解析】由条件，，即，由此解得，，所以选B．10.设函数是偶函数，则实数a的值为_______【答案】【解析】∵函数是偶函数设，则为奇函数∴．11.函数是定义在R上的奇函数，当时，，则函数的零点为( )A．2B．C．3D．0【答案】D【解析】∵是的反函数∴的零点即为的值．又函数是定义在R上的奇函数，∴∴的零点为012.函数则函数是（）A．奇函数但不是偶函数B．偶函数但不是奇函数C．既是奇函数又是偶函数D．既不是奇函数又不是偶函数【答案】A【解析】当时，，，，…，当时，，由数学归纳法知对任意的，有，同理当时，，因此的定义域是且不可能是偶函数，由于是奇函数，，假设是奇函数，则，即也是奇函数，因此对任意的，有是奇函数，本题选A.【考点】数学归纳法，函数的奇偶性.13.设函数f(x)是奇函数且周期为3，若f(1)＝－1，则f(2015)＝________．【答案】1【解析】由条件，f(2015)＝f(671×3＋2)＝f(2)＝f(－1)＝－f(1)＝1.14.判断下列函数的奇偶性：(1)f(x)＝x3－；(2)f(x)＝；(3)f(x)＝(x－1)；(4)f(x)＝.【答案】（1）奇函数（2）奇函数（3）既不是奇函数也不是偶函数（4）既是奇函数也是偶函数【解析】(1)定义域是(－∞，0)∪(0，＋∞)，关于原点对称，由f(－x)＝－f(x)，所以f(x)是奇函数．(2)去掉绝对值符号，根据定义判断．由得.故f(x)的定义域为[－1，0)∪(0，1]，关于原点对称，且有x＋2＞0.从而有f(x)＝，这时有f(－x)＝＝－f(x)，故f(x)为奇函数．(3)因为f(x)定义域为[－1，1)，所以f(x)既不是奇函数也不是偶函数．(4)因为f(x)定义域为{－，}，所以f(x)＝0，则f(x)既是奇函数也是偶函数15.已知f(x)是定义在R上的奇函数.当x>0时,f(x)=x2-4x,则不等式f(x)>x的解集用区间表示为.【答案】(-5,0)∪(5,+∞)【解析】设x<0,则-x>0,f(-x)=x2+4x,所以x<0时,f(x)=-x2-4x.所以f(x)=当x≥0时,由x2-4x>x,解得x>5,当x<0时,由-x2-4x>x,解得-5<x<0,故不等式的解集为(-5,0)∪(5,+∞).16.已知函数f(x)＝为奇函数，则f(g(－1))＝()A．－20B．－18C．－15D．17【答案】C【解析】由于函数f(x)是奇函数，所以g(x)＝－f(－x)＝－x2＋2x，g(－1)＝－3.故f(－3)＝g(－3)＝－15.17.若二次函数f(x)=(x+a)(bx+2a)(a,b∈R)是偶函数,且它的值域为(-∞,4],则该函数的解析式f(x)=.【答案】-2x2+4【解析】【思路点拨】化简f(x),函数f(x)为偶函数,则一次项系数为0可求b.值域为(-∞,4],则最大值为4,可求2a2,即可求出解析式.解：∵f(x)=(x+a)(bx+2a)=bx2+(2a+ab)x+2a2是偶函数,则其图象关于y轴对称.∴2a+ab=0,∴b=-2或a=0(舍去).∴f(x)=-2x2+2a2,又f(x)的值域为(-∞,4],∴2a2=4,f(x)=-2x2+4.18.已知函数f(x)为奇函数，且当x>0时， f(x) ＝x2＋，则f(－1)＝()A．－2B．0C．1D．2【答案】A【解析】f(－1)＝－f(1)＝－2.19.设a为实数，函数f(x)＝x3＋ax2＋(a－2)x的导数是f′(x)，且f′(x)是偶函数，则曲线y＝f(x)在原点处的切线方程为()A．y＝－2x B．y＝3xC．y＝－3x D．y＝4x【答案】A【解析】由已知得f′(x)＝3x2＋2ax＋a－2为偶函数，∴a＝0，∴f(x)＝x3－2x，f′(x)＝3x2－2.又f′(0)＝－2，f(0)＝0，∴y＝f(x)在原点处的切线方程为y＝－2x.20.已知函数=x+sinx.项数为19的等差数列满足，且公差.若，则当=__________时， .【答案】10【解析】函数的定义域为，且，所以为奇函数。

函数的奇偶性题型解析(含答案)

函数的奇偶性一、单选题(共10道，每道10分)1.设函数的定义域为，且是奇函数，则实数a的值是( )A. B.1C. D.3答案：C解题思路：试题难度：三颗星知识点：函数奇偶性的性质2.已知函数是偶函数，那么是( )A.奇函数B.偶函数C.既奇且偶函数D.非奇非偶函数答案：A解题思路：试题难度：三颗星知识点：函数奇偶性的判断3.已知是定义在上的奇函数，则下列函数：①；②；③；④．其中为奇函数的是( )A.①③B.②③C.①④D.②④答案：D解题思路：试题难度：三颗星知识点：函数奇偶性的判断4.下列函数中，既是偶函数又在区间(0，+∞)上单调递增的函数是( )A. B.C. D.答案：B解题思路：试题难度：三颗星知识点：奇偶性与单调性的综合5.已知在上是奇函数，且，当时，，则的值为( )A.-2B.2C.-98D.98答案：A解题思路：试题难度：三颗星知识点：函数奇偶性的性质6.已知函数是偶函数，且，则的值为( )A.-1B.1C.-5D.5答案：D解题思路：试题难度：三颗星知识点：函数奇偶性的性质7.定义在R上的偶函数在区间[0，+∞)单调递增，则( )A. B.C. D.答案：C解题思路：试题难度：三颗星知识点：奇偶性与单调性的综合8.若奇函数在[2，5]上是增函数，且最小值是1，则在[-5，-2]上是( )A.增函数且最小值是-1B.增函数且最大值是-1C.减函数且最小值是-1D.减函数且最大值是-1答案：B解题思路：试题难度：三颗星知识点：奇偶性与单调性的综合9.已知函数是定义在上的奇函数，当时，，则当时，的表达式为( )A. B.C. D.答案：C解题思路：试题难度：三颗星知识点：函数奇偶性的性质10.当x≥0时，为偶函数，则的解析式是( )A. B.C. D.答案：A解题思路：试题难度：三颗星知识点：函数奇偶性的性质。

(完整版)函数奇偶性练习题(内含答案)

函数奇偶性练习（内含答案）一、选择题1．已知函数f （x ）＝ax 2＋bx ＋c （a ≠0）是偶函数，那么g （x ）＝ax 3＋bx 2＋cx （）A ．奇函数B ．偶函数C ．既奇又偶函数D ．非奇非偶函数2．已知函数f （x )＝ax 2＋bx ＋3a ＋b 是偶函数，且其定义域为［a －1，2a ］，则( ）A ．31=a ,b ＝0 B ．a ＝－1,b ＝0 C ．a ＝1,b ＝0 D ．a ＝3，b ＝0 3．已知f （x )是定义在R 上的奇函数,当x ≥0时，f （x ）＝x 2－2x ，则f （x )在R 上的表达式是（）A ．y ＝x （x －2）B ．y ＝x(｜x ｜－1）C ．y ＝|x ｜（x －2）D ．y ＝x （|x ｜－2）4．已知f （x )＝x 5＋ax 3＋bx －8，且f (－2）＝10，那么f （2）等于( ）A ．－26B ．－18C ．－10D ．105．函数1111)(22+++-++=x x x x x f 是（）A ．偶函数B ．奇函数C ．非奇非偶函数D ．既是奇函数又是偶函数6．若)(x ϕ，g （x ）都是奇函数,2)()(++=x bg a x f ϕ在（0，＋∞）上有最大值5，则f （x ）在（－∞，0）上有（）A ．最小值－5B ．最大值－5C ．最小值－1D ．最大值－3二、填空题7．函数2122)(xx x f ---=的奇偶性为________（填奇函数或偶函数) ． 8．若y ＝（m －1)x 2＋2mx ＋3是偶函数，则m ＝_________．9．已知f （x ）是偶函数，g （x ）是奇函数，若11)()(-=+x x g x f ,则f （x ）的解析式为_______．10．已知函数f （x ）为偶函数,且其图象与x 轴有四个交点，则方程f (x ）＝0的所有实根之和为________．三、解答题11．设定义在［－2，2］上的偶函数f （x ）在区间［0,2］上单调递减，若f （1－m ）＜f (m )，求实数m 的取值范围．12．已知函数f（x)满足f(x＋y）＋f(x－y）＝2f(x)·f（y）（x∈R，y∈R)，且f（0）≠0，试证f（x）是偶函数．13.已知函数f（x)是奇函数，且当x＞0时，f（x）＝x3＋2x2—1,求f（x)在R上的表达式．14。

函数的奇偶性问题练习题(含答案)

函数的奇偶性问题一、选择题1．已知函数f （x ）＝ax 2＋bx ＋c （a ≠0）是偶函数，那么g （x ）＝ax 3＋bx 2＋cx （） A ．奇函数 B ．偶函数 C ．既奇又偶函数 D ．非奇非偶函数解析：f （x ）＝ax 2＋bx ＋c 为偶函数，x x =)(ϕ为奇函数，∴g （x ）＝ax 3＋bx 2＋cx ＝f （x ）·)(x ϕ满足奇函数的条件．答案：A2．已知函数f （x ）＝ax 2＋bx ＋3a ＋b 是偶函数，且其定义域为［a －1，2a ］，则（） A ．31=a ，b ＝0 B ．a ＝－1，b ＝0 C ．a ＝1，b ＝0 D ．a ＝3，b ＝0 解析：由f （x ）＝ax 2＋bx ＋3a ＋b 为偶函数，得b ＝0．又定义域为［a －1，2a ］，∴a －1＝2a ，∴31=a ．故选A ． 3．已知f （x ）是定义在R 上的奇函数，当x ≥0时，f （x ）＝x 2－2x ，则f （x ）在R 上的表达式是（）A ．y ＝x （x －2）B ．y ＝x （｜x ｜－1）C ．y ＝｜x ｜（x －2）D ．y ＝x （｜x ｜－2）解析：由x ≥0时，f （x ）＝x 2－2x ，f （x ）为奇函数，∴当x ＜0时，f （x ）＝－f （－x ）＝－（x 2＋2x ）＝－x 2－2x ＝x （－x －2）． ∴(2)(0)()(2)(0),,x x x f x x x x ⎧⎨⎩-≥=--<即f （x ）＝x （|x |－2）答案：D4．已知f （x ）＝x 5＋ax 3＋bx －8，且f （－2）＝10，那么f （2）等于（） A ．－26 B ．－18 C ．－10 D ．10 解析：f （x ）＋8＝x 5＋ax 3＋bx 为奇函数，f （－2）＋8＝18，∴f （2）＋8＝－18，∴f （2）＝－26．答案：A5．函数1111)(22+++-++=x xx x x f 是（）A ．偶函数B ．奇函数C ．非奇非偶函数D ．既是奇函数又是偶函数解析：此题直接证明较烦，可用等价形式f （－x ）＋f （x ）＝0．答案：B 6．若)(x ϕ，g （x ）都是奇函数，2)()(++=x bg a x f ϕ在（0，＋∞）上有最大值5，则f （x ）在（－∞，0）上有（）A ．最小值－5B ．最大值－5C ．最小值－1D ．最大值－3 解析：)(x ϕ、g （x ）为奇函数，∴()2()()f x a x bg x φ-=+为奇函数．又f （x ）在（0，＋∞）上有最大值5， ∴f （x ）－2有最大值3． ∴f （x ）－2在（－∞，0）上有最小值－3， ∴f （x ）在（－∞，0）上有最小值－1．答案：C 二、填空题 7．函数2122)(xx x f ---=的奇偶性为____奇函数____（填奇函数或偶函数）．8．若y ＝（m －1）x 2＋2mx ＋3是偶函数，则m ＝____0_____．解析：因为函数y ＝（m －1）x 2＋2mx ＋3为偶函数，∴f （－x ）＝f （x ），即（m －1）（－x ）2＋2m （－x ）＋3＝（m —1）x 2＋2mx ＋3，整理，得m ＝0．9．已知f （x ）是偶函数，g （x ）是奇函数，若11)()(-=+x x g x f ，则f （x ）的解析式为____11)(2-=xx f ___．解析：由f （x ）是偶函数，g （x ）是奇函数，可得11)()(--=-x x g x f ，联立11)()(-=+x x g x f ，∴11)1111(21)(2-=----=x x x x f ． 10．已知函数f （x ）为偶函数，且其图象与x 轴有四个交点，则方程f （x ）＝0的所有实根之和为___0 _____．三、解答题11．设定义在［－2，2］上的偶函数f （x ）在区间［0，2］上单调递减，若f （1－m ）＜f （m ），求实数m 的取值范围．（21<m ） 12．已知函数f （x ）满足f （x ＋y ）＋f （x －y ）＝2f （x ）·f （y ）（x ∈R ，y ∈R ），且f （0）≠0，试证f （x ）是偶函数．证明：令x ＝y ＝0，有f （0）＋f （0）＝2f （0）·f （0），又f （0）≠0，∴可证f（0）＝1．令x ＝0，∴f （y ）＋f （－y ）＝2f （0）·f （y ）⇒f （－y ）＝f （y ），故f （x ）为偶函数．13.已知函数f （x ）是奇函数，且当x ＞0时，f （x ）＝x 3＋2x 2—1，求f （x ）在R上的表达式．解析：本题主要是培养学生理解概念的能力．f （x ）＝x 3＋2x 2－1．因f （x ）为奇函数，∴f （0）＝0．当x ＜0时，－x ＞0，f （－x ）＝（－x ）3＋2（－x ）2－1＝－x 3＋2x 2－1，∴f （x ）＝x 3－2x 2＋1．因此，.)0()0()0(12012)(,,2323<=>+--+=⎪⎩⎪⎨⎧x x x x x x x x f 点评：本题主要考查学生对奇函数概念的理解及应用能力．（x ）是定义在（－∞，－5］［5，＋∞）上的奇函数，且f （x ）在［5，＋∞）上单调递减，试判断f （x ）在（－∞，－5］上的单调性，并用定义给予证明．解析：任取x 1＜x 2≤－5，则－x 1＞－x 2≥－5．因f （x ）在［5，＋∞］上单调递减，所以f （－x 1）＜f （－x 2）⇒f （x 1）＜－f （x 2）⇒f （x 1）＞f （x 2），即单调减函数．点评：此题要注意灵活运用函数奇偶性和单调性，并及时转化．15.设函数y ＝f （x ）（x ∈R 且x ≠0）对任意非零实数x 1、x 2满足f （x 1·x 2）＝f （x 1）＋f （x 2），求证f （x ）是偶函数．解析：由x 1，x 2∈R 且不为0的任意性，令x 1＝x 2＝1代入可证，f （1）＝2f （1），∴f （1）＝0．又令x 1＝x 2＝－1，∴f ［－1×（－1）］＝2f （1）＝0，∴（－1）＝0．又令x 1＝－1，x 2＝x ，∴f （－x ）＝f （－1）＋f （x ）＝0＋f （x ）＝f （x ），即f （x ）为偶函数．点评：抽象函数要注意变量的赋值，特别要注意一些特殊值，如，x 1＝x 2＝1，x 1＝x 2＝－1或x1＝x2＝0等，然后再结合具体题目要求构造出适合结论特征的式子即可．。