相似三角形典型模型及例题
相似三角形的常见模型

初中数学 ︵ 九年级 ︶培优篇初中数学 ︵ 九年级 ︶培优篇【基本模型】①如图,在ABC 中,点D 在AB 上,点E 在AC 上,//DEBC ,则ADE ABC △△∽,AD AE DEAB AC BC.②模型拓展1:斜交A 字型条件:C ADE ,图2结论:~ADE ACB ;③模型拓展2: 如图,∠ACD =∠B ⇔△ADC ∽△ACB ⇔AD AC CDAC AB BC.初中数学 ︵ 九年级︶培优篇【例1】如图,王华晚上由路灯A 下的B 处走到C 处时,测得影子CD 的长为1米,继续往前走2米到达B 处时,测得影子EF 的长为2米,已知王华的身高是1.5米,那么路灯A 的高度等于_________.【变式1-1】有一块直角三角形木板,∠B =90°,AB =1.5m ,BC =2m ,要把它加工成一个面积尽可能大的正方形桌面.甲、乙两位同学的加工方法分别如图1、图2所示.请你用学过的知识说明哪位同学的加工方法更好(加工损耗忽略不计).初中数学 ︵ 九年级 ︶培优篇 【变式1-2】(2022•衢州二模)已知菱形ABCD ,E 是BC 边上一点,连接AE 交BD 于点F (1)如图1,当E 是BC 中点时,求证:AF =2EF ;(2)如图2,连接CF ,若AB =5,BD =8,当△CEF 为直角三角形时,求BE 的长; (3)如图3,当∠ABC =90°时,过点C 作CG ⊥AE 交AE 的延长线于点G ,连接DG ,若BE =BF ,求tan ∠BDG 的值.初中数学 ︵九年级 ︶培优篇 ③模型拓展:如图,∠A =∠C ⇔△AJB∽△CJD ⇔A B JA C D JC【例2】如图,在平行四边形ABCD 中,E 为边AD 的中点,连接AC 、BE 交于点F .若△AEF 的面积为2,则△ABC 的面积为( ) A .8B .10C .12D .14初中数学 ︵ 九年级 ︶培优篇 【变式2-1】如图,在△ABC 中,BC =6,AEA F EBFC,动点P 在射线EF 上,BP 交CE 于点D ,∠CBP 的平分线交CE 于点Q ,当CQ =14CE 时,EP +BP 的值为( )A .9B .12C .18D .24【变式2-2】如图,在Rt △ACB 中,∠ACB =90°,AC =4,BC =3,点D 为AC 上一点,连接BD ,E 为AB 上一点,CE ⊥BD 于点F ,当AD =CD 时,求CE 的长.【变式2-3】如图,已知D 是BC 的中点,M 是AD的中点.求AN:NC的值.初中数学 ︵ 九年级︶培优篇【例3】如图,在平行四边形ABCD 中,∠ABC 的平分线交AC 于点E ,交AD 于点F ,交CD 的延长线于点G ,若AF =2FD ,则BEEG的值为( ) A .12B .13C .23D .34【变式3-1】(2020•杭州)如图,在正方形ABCD 中,点E 在BC 边上,连接AE ,∠DAE 的平分线AG 与CD 边交于点G ,与BC 的延长线交于点F .设=λ(λ>0).(1)若AB =2,λ=1,求线段CF 的长. (2)连接EG ,若EG ⊥AF , ①求证:点G 为CD 边的中点. ②求λ的值.初中数学 ︵ 九年级 ︶培优篇【例4】如图,在△ABC 中,45ABC ,AB A D A E ,D A E 90 ,C E,则CD 的长为______.初中数学 ︵ 九年级 ︶培优篇 【变式4-1】矩形ABCD 中,AD =9,AB =12,点E 在对角线BD 上(不与B 、D 重合),EF ⊥AE 交CD 于F 点,连接AF 交BD 于G 点. (1)如图1,当G 为DE 中点时. ①求证:FD =FE ; ②求BE 的长.(2)如图2,若E 为BD 上任意点,求证:AG 2=BG •GE .初中数学 ︵ 九年级 ︶培优篇 【变式4-2】如图,ABC 中,,,AB AC AB AC 点D E 、分别是BC AC 、的中点,AF BE ⊥与点F .(1)求证:2AE FE BE ;(2)求A F C 的大小;(3)若DF=1,求△ABF 的面积.初中数学 ︵ 九年级 ︶培优篇结论:AH ⊥GF ,△AGF ∽△ABC ,GF AHBC AM【例5】如图1,在△ABC 中,AB =AC =5,BC =6,正方形DEFG 的顶点D 、G 分别在AB 、AC 上,EF 在BC 上. (1)求正方形DEFG 的边长;(2)如图2,在BC 边上放两个小正方形DEFG 、FGMN ,则DE= .初中数学 ︵ 九年级 ︶培优篇 【变式5-1】有一块锐角三角形卡纸余料ABC ,它的边BC =120cm ,高AD =80cm ,为使卡纸余料得到充分利用,现把它裁剪成一个邻边之比为2:5的矩形纸片EFGH 和正方形纸片PMNQ ,裁剪时,矩形纸片的较长边在BC 上,正方形纸片一边在矩形纸片的较长边EH 上,其余顶点均分别在AB ,AC 上,具体裁剪方式如图所示. (1)求矩形纸片较长边EH 的长;(2)裁剪正方形纸片时,小聪同学是按以下方法进行裁剪的:先沿着剩余料△AEH 中与边EH 平行的中位线剪一刀,再沿过该中位线两端点向边EH 所作的垂线剪两刀,请你通过计算,判断小聪的剪法是否正确.初中数学 ︵ 九年级︶培优篇 ②拓展:(1)在正方形、长方形中经常会出现射影定理模型,如图,在有射影定理模型.(2)如图,在圆中也会出现射影定理模型.【例6】如图,四边形ABCD 中,AD ∥BC ,∠B =90°,E 为AB 上一点,分别以ED 、EC 为折痕将两个角(∠A 、∠B )向内折起,点A 、B 恰好落在CD 边的点F 处,若AD =3,BC =5,则EF 的长是( ) A.15B .215C .17D .217初中数学 ︵ 九年级 ︶培优篇 【变式6-1】如图所示,在△ABC 中,∠ABC =90°,BD ⊥AC ,DE ⊥BC ,垂足分别为D 、E 两点,则图中与△ABC 相似的三角形有( ) A .4个B .3个C .2个D .1个【变式6-2】如图,在R t △ABC 中,∠ACB =90°,点D 在AB 上,且AD AC =ACAB. (1)求证 △ACD ∽△ABC ;(2)若AD =3,BD =2,求CD 的长.【变式6-3】ABC 中,90ABC ,BD AC ,点E 为B D 的中点,连接A E 并延长交B C 于点F ,且有AF CF ,过F 点作FH AC 于点H . (1)求证:AD E CD B ∽; (2)求证:=2A E EF ; (3)若FHB C 的长.初中数学 ︵ 九年级 ︶培优篇②如图所示,BDE 和ABC 则ABD CBE ∽△△,且相似比为总结:旋转相似型中由公共旋转顶点、一点及其旋转后的对应点组成的三角形与由公共旋转顶点、另一点及其旋转后的对应点组成的三角形相似.初中数学 ︵ 九年级 ︶培优篇【例7】如图,在△ABC 与△ADE 中,∠ACB =∠AED =90°,∠ABC =∠ADE ,连接BD 、CE ,若AC :BC =3:4,则BD :CE 为( ) A .5:3B .4:3C .√5:2D .2:√3【变式7-1】如图,点E 是菱形ABCD 对角线CA 的延长线上任意一点,以线段AE 为边作一个菱形AEFG ,且菱形AEFG ∽菱形ABCD ,相似比是:2,连接EB ,GD .(1)求证:EB =GD ;(2)若∠DAB =60°,AB =2,求GD 的长.初中数学 ︵ 九年级 ︶培优篇 【变式7-2】如图,正方形ABCD ,对角线AC ,BD 相交于O ,Q 为线段DB 上的一点,90MQN ,点M 、N 分别在直线BC 、DC 上.(1)如图1,当Q 为线段OD 的中点时,求证:1132DN BM BC ;(2)如图2,当Q 为线段OB 的中点,点N 在CD 的延长线上时,则线段DN 、BM 、BC 的数量关系为 ;(3)在(2)的条件下,连接MN ,交AD 、BD 于点E 、F ,若:3:1M B M C ,N Q ,求EF 的长.初中数学 ︵ 九年级 ︶培优篇 补充:其他常见的一线三等角图形【例8】【感知】如图①,在四边形ABCD 中,点P 在边AB 上(点P 不与点A 、B 重合),90A B DPC .易证DAP PBC △△∽.(不需要证明) 【探究】如图②,在四边形ABCD 中,点P 在边AB 上(点P 不与点A 、B 重合),A B D PC .若4PD ,8P C ,6BC ,求AP 的长.【拓展】如图③,在ABC 中,8AC BC ,12A B ,点P 在边AB 上(点P 不与点A 、B 重合),连结CP ,作CPE A ,PE 与边BC 交于点E ,当CPE △是等腰三角形时,直接写出AP 的长.初中数学 ︵ 九年级 ︶培优篇 【变式8-1】如图,在矩形ABCD 中,CD =4,E 是BC 的中点,连接AE ,tan ∠AEB 43,P 是AD 边上一动点,沿过点P 的直线将矩形折叠,使点D 落在AE 上的点D ¢处,当A P D △是直角三角形时,PD 的值为( )A .23或67B .83或247C .83或307D .103或187初中数学 ︵ 九年级 ︶培优篇 【变式8-2】(2022秋•温州校级月考) 【推理】如图1,在正方形ABCD 中,点E 是CD 上一动点,将正方形沿着BE 折叠,点C 落在点F 处,连结BE ,CF ,延长CF 交AD 于点G . (1)求证:BCE CDG △△≌. 【运用】(2)如图2,在【推理】条件下,延长BF 交AD 于点H .若45HD HF ,9C E ,求线段DE 的长.【拓展】(3)将正方形改成矩形,同样沿着BE 折叠,连结CF ,延长CF ,BF 交直线AD 于G ,两点,若AB k BC ,45HD HF ,求DEEC的值(用含k 的代数式表示).。
相似三角形 经典模型总结与例题分类

相似三角形经典模型总结与例题分类相似三角形经典模型总结在相似三角形中,有一些经典的模型,包括平移型、平行型、旋转180°型、翻折180°型、一般型、特殊型、斜交型、双垂直型等。
这些模型可以帮助我们更好地理解和解决相似三角形的问题。
其中,平移型、平行型、翻折180°型、斜交型和双垂直型都是比较常见的模型。
在解决相似三角形的问题时,可以根据具体情况选择相应的模型进行分析。
以下是一些例题,可以帮助我们更好地理解相似三角形的模型和应用。
例1:如图,EE1∥FF1∥MM1,若AE=EF=FM=MB,则S△.例2:如图,AD∥EF∥MN∥BC,若AD=9,BC=18,.例3:已知,P为平行四边形ABCD对角线,AC上一点,过点P的直线与AD,BC,CD的延长线,AB的延长线分别相交于点E,F,G,H。
则PEPH=PFPG。
例4:已知:在△ABC中,D为AB中点,E为AC上一点,且AE=2,BE、CD相交于点F。
则ABF=2EFD。
例5:已知:在△ABC中,AD=11AB,延长BC到F,使CF=BC,连接FD交AC于点E。
则①DE=EF②AE=2CE。
例6:已知:D,E为三角形ABC中AB、BC边上的点,连接DE并延长交AC的延长线于点F,例7:如图,已知XXX,若AB=a,CD=b,EF=c,则a/b=c/(a+c)。
例8:如图,S△.例9:如图,四边形ABCD中,∠B=∠D=90°,M是AC上一点,ME⊥AD于点E,MF⊥BC于点F。
则MF/ME+1=BD/AC。
例10:如图,在△ABC中,D是AC边的中点,过D作直线EF交AB于E,交BC的延长线于F。
则AE·BF=BE·CF。
BCF:在线段AB上取一点C,以AC、CB为底在AB同侧作两个顶角相等的等腰三角形ADC和CEB,AE交CD于点P,BD交CE于点Q,证明CP=CQ。
解法:首先,由等腰三角形的性质可知,∠XXX∠CEB,∠ACD=∠BCD,因此△ADC≌△CEB,从而AP=BP,AQ=CQ。
初三上相似三角形常见模型

相似模型1.“A”型
变形:反“A”型
2.“8”字型
变形:反“8”字型
B
D
E
3.
双垂型
变形:字母型
4.共线三等角相似模型
如下图,ABC CDE
△∽△
图1图2图3重点是共线中的“线”上的三个角要保证相等,利用同角的补角相等近一步证明.
E
D
C
B
A
E
D
A
E
D
B
5.旋转相似模型
共顶点相似的一般三角形模型:
典型例题:
例1.已知:在△ABC中,DE∥BC,点F是线段DE上一点,连接AF并延长与BC 相交于点G.求证:DF·GC=FE·BG
例2.例2.如图,点B,C分别在△ADE的边AD,AE上,且AC=6,AB=5,EC=4,DB=7.求证:△ABC∽△AED.
例3.△ABC中,正方形EFGH的两个顶点E、F在BC上,另两个顶点G、H分别在AC、AB上,BC=15,BC边上的高AD=10,求正方形EFGH的面积.
例4.如图,在平行四边形ABCD中,AC与BD交于点O,E为OD的中点,连接AE并延长交DC于点F,则DF∶FC等于( )
A.1∶4 B.1∶3 C.2∶3 D.1∶2
例5.如图,在正方形ABCD中,E为边AD的中点,点F在边CD上,且CF=3FD,∠BEF=90°.
(1)求证:△ABE∽△DEF;
(2)若AB=4,延长EF交BC的延长线于点G,求BG的长.。
(完整版)专题:相似三角形的几种基本模型及练习
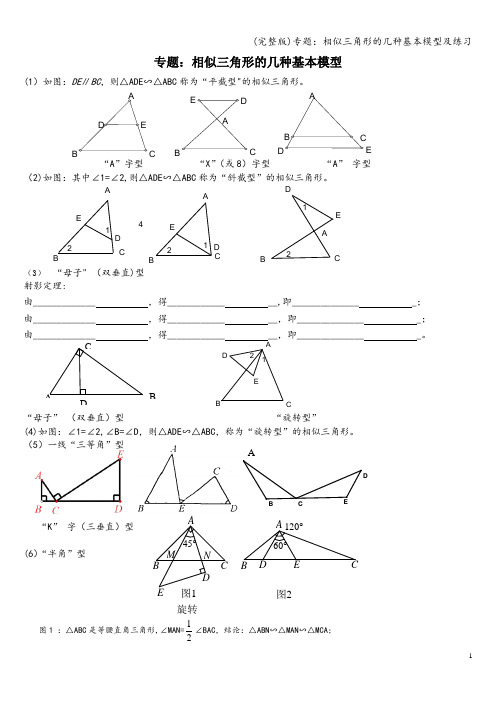
专题:相似三角形的几种基本模型(1)如图:DE ∥BC ,则△ADE ∽△ABC 称为“平截型"的相似三角形。
“A ”字型 “X ”(或8)字型 “A ” 字型(2)如图:其中∠1=∠2,则△ADE ∽△ABC 称为“斜截型”的相似三角形。
ABCD E12AABBCC DD EE12412(3) “母子" (双垂直)型 射影定理:由_____________ ,得____________ __,即______________ _; 由_____________ ,得____________ __,即______________ _; 由_____________ ,得____________ __,即______________ _。
“母子” (双垂直)型 “旋转型”(4)如图:∠1=∠2,∠B=∠D ,则△ADE ∽△ABC ,称为“旋转型”的相似三角形。
(5)一线“三等角”型“K ” 字(三垂直)型(6)“半角”型图1 :△ABC 是等腰直角三角形,∠MAN=12∠BAC ,结论:△A BN ∽△MAN ∽△MCA ; ABEADCAB CDEAACCDEE B EA CD12A B C D 图2图1旋转N M60°120°E DCA 45°EDC B A图2 :△ADE 是等边三角形, ∠DAE=12∠BAC ,结论:△A BD ∽△CAE ∽△CBA; 应用1.如图3,在△ABC 中,∠C =90°,D 是AC 上一点,DE ⊥AB 于点E ,若AC =8,BC =6,DE =3,则AD 的长为 ( ) A .3B .4C .5D .62.如图4,在△ABC 中,AB =AC ,∠A =36°,BD 平分∠ABC ,DE ∥BC ,那么在下列三角形中,与△ABC 相似的三角形是 ( ) A .△DBE B .△AED 和△BDC C .△ABDD .不存在图3 图4 图53.如图5, □ABCD 中, G 是AB 延长线上一点, DG 交AC 于E, 交BC 于F, 则图中所有相似三角形有( )对.A.4 对 B 。
(完整版)相似三角形经典模型总结及例题分类.doc
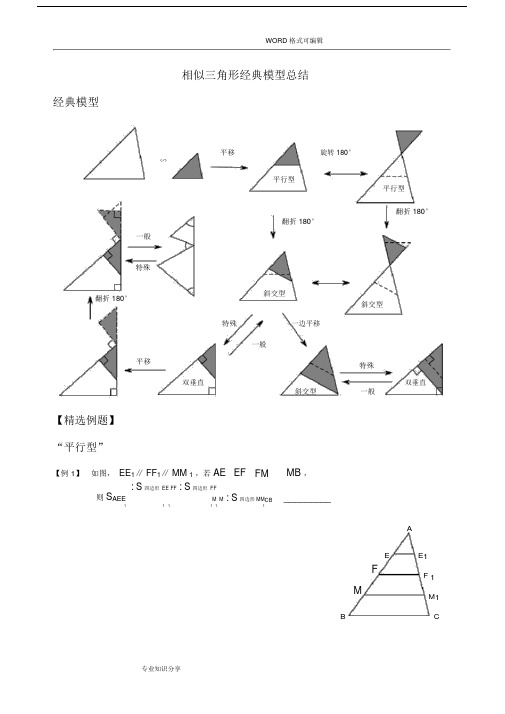
WORD 格式可编辑相似三角形经典模型总结经典模型平移旋转 180°∽平行型平行型翻折 180°翻折 180°一般特殊翻折 180°斜交型斜交型特殊一边平移一般平移特殊双垂直斜交型双垂直一般【精选例题】“平行型”【例 1】如图,EE1∥FF1∥MM1,若AE EF FM MB ,则S AEE : S四边形EE FF : S四边形FFM M : S四边形 MM C B _________1 1 1 1 1 1AE E1FF 1MM1B CWORD 格式可编辑【例 2】如图,AD∥EF∥MN∥BC,若AD 9,BC 18 , AE:EM :MB 2:3:4,则EF _____ , MN _____A DE FMNB C【例 3】已知,P为平行四边形ABCD 对角线, AC 上一点,过点P 的直线与 AD , BC , CD 的延长线, AB 的延长线分别相交于点 E , F , G , H求证: PE PHPF PGG D CE PFA B H【例 4】已知:在ABC 中, D 为 AB 中点, E 为 AC 上一点,且AE2, BE、 CD相交于点 F ,求BF的值ECEF ADF EB C【例 5】已知:在ABC 中, AD 1AB,延长 BC到F ,使CF1BC,连接 FD交 AC于点 E 2 3求证:① DE EF ② AE 2CEADEB专业知识分享【例 6】已知:D,E为三角形ABC 中 AB 、BC 边上的点,连接 DE 并延长交 AC 的延长线于点 F ,BD: DE AB: AC求证:CEF 为等腰三角形ACDEB F【例7】如图,已知 AB / / EF / /CD ,若 AB a , CD b , EF c ,求证:11 1 .c a bACEB F D【例 8】如图,找出S ABD、 S BED、 S BCD之间的关系,并证明你的结论.CAEB F D【例 9】如图,四边形ABCD中,B D90M是AC上一点,ME AD于点EMF BC,,于点 F 求证:MFME 1AB CDDEMA CFB【例 10】如图,在ABC 中, D 是 AC 边的中点,过 D 作直线 EF 交 AB 于 E ,交 BC 的延长线于 F 求证: AE BF BE CFAEDBC F 【例 11】如图,在线段AB 上,取一点 C ,以 AC , CB 为底在 AB 同侧作两个顶角相等的等腰三角形ADC 和CEB, AE交 CD于点 P, BD交 CE于点Q,求证: CP CQDEP QA C B【例 12】阅读并解答问题 .在给定的锐角三角形ABC 中,求作一个正方形DEFG,使 D, E落在 BC边上, F , G分别落在AC , AB 边上,作法如下:ABC 两边上的正方形D'E'F 'G'如图,第一步:画一个有三个顶点落在第二步:连接 BF ' 并延长交 AC 于点 F第三步:过 F 点作 FE BC ,垂足为点 E第四步:过 F 点作 FG∥BC 交 AB 于点 G第五步:过 G 点作 GD BC ,垂足为点 D四边形 DEFG 即为所求作的正方形问题:⑴证明上述所作的四边形DEFG 为正方形⑵在 ABC 中,如果BC 6 3,ABC 45 , BAC 75 ,求上述正方形DEFG 的边长AG FG'F'E CWORD 格式可编辑“平行旋转型”图形梳理:E'F'AAAF'E'AEF'EFFFEE'FEF'BCBCBBCAEF 旋转到 AE ‘ F ’CAEF 旋转到 AE ‘ F ’AEF 旋转到 AE ‘ F ’AEF 旋转到AE ‘F ’特殊情况: B 、 E'、 F '共线AAEF' EF'E'FE'FBC B CAEF 旋转到 AE ‘ F ’ AEF 旋转到 AE ‘ F ’C , E', F '共线E'AE'AEFEF'FF'BCBCAEF 旋转到 AE ‘ F ’AEF 旋转到 AE ‘ F ’【例 13】已知梯形 ABCD , AD ∥BC ,对角线AC 、 BD 互相垂直,则①证明: AD 2 BC 2AB 2 CD 2ADOB CWORD 格式可编辑【例 14】当AOD ,以点 O 为旋转中心,逆时针旋转度(090 ),问上面的结论是否成立,请说明理由DAOB C【例 15】(全国初中数学联赛武汉选拔赛试题)如图,四边形ABCD 和 BEFG 均为正方形,求AG : DF : CE_________.A DGFB CE“斜交型”【例 16】如图,ABC 中, D 在 AB 上,且 DE∥BC 交 AC 于 E , F 在 AD 上,且 AD2AF AB ,求证:AEF :ACDAFD EB C【例 17】如图,等边三角形ABC中,D,E分别在BC,AB上,且CE BE ,AD ,CE 相交于 M ,求证 : EAM : ECAAEMB DC AGF BE【例 18】如图,四边形ABCD 的对角线相交于点O ,BAC CDB ,求证:DAC CBDADOB C【例 19】如图,设ABBCCA,则 1 2 吗?AD DE EAA1 DE2B C【例 20】在锐角三角形ABC 中, AD , CE 分别为 BC , AB 边上的高,ABC 和BDE 的面积分别等于 18和 2 , DE 2,求 AC 边上的高AEB D C【例 21】如图,在等边ABC 的边 BC 上取点 D ,使BD 1,作CH AD,H为垂足,连结BH。
难关必刷01相似三角形(5种解题模型专练)(原卷版)

难关必刷01相似三角形(5种解题模型专练)【模型梳理】题型一:8字模型8字_平行型条件:CD∥AB,结论:ΔPAB∼ΔPCD(上下相似);左右不一定相似,不一定全等,但面积相等;四边形ABCD为一般梯形.条件:CD∥AB,PD=PC.结论:ΔPAB∼ΔPCD∼ΔPDC(上下相似)ΔPAD≅ΔPBC左右全等;四边形ABCD为等腰梯形;8字_不平行型条件:∠CDP =∠BAP .结论:ΔAPB ∼ΔDPC (上下相似);ΔAPD ∼ΔBPC (左右相似);题型二:A 字模型如图一DE如图二如图三题型三:一线三等角模型一线三等角指的是有三个等角的顶点在同一条直线上构成的相似图形,这个角可以是直角,也可以是锐角或钝角。
或叫“K字模型”。
三直角相似可以看着是“一线三等角”中当角为直角时的特例,三直角型相似通常是以矩形或者正方形形为背景,或者在一条直线上有一个顶点在该直线上移动或者旋转的直角,几种常见的基本图形如下:当题目的条件中只有一个或者两个直角时,就要考虑通过添加辅助线构造完整的三直角型相似,这往往是很多压轴题的突破口,进而将三角型的条件进行转化。
一般类型:基本类型:同侧“一线三等角” 异侧“一线三等角”模型一:一线三直角图一 图二90;B ACE D ABC CDE ∠=∠=∠=∆∆ 如图一、二,已知:结论:(1)(2)A BDE =B CC D模型二:一线三等角图三 图四;B ACE D ABC CDE ABC CDE ACEα∠=∠=∠=∆∆∆∆∆ 如图三、四,已知:结论:(1)(2)A B D E =B CC D(3)当C 为B D 中点时,【方法点拨】基本模型:如图1,∠B =∠C =∠EDF 推出△BDE ∽△CFD (一线三等角)如图2,∠B =∠C =∠ADE 推出△ABD ∽△DC E (一线三等角)如图3,特别地,当D 时BC 中点时:△BDE ∽△DFE ∽△CFD 推出ED 平分∠BEF ,FD 平分∠EFC.题型四:旋转相似////,DE BC ADE AD E ABC ABD ACE ∆''∆∆∆∆∆ 旋转相似模型:已知:如图一,现将A D E 绕点A 旋转一定角度得到如图二得到和【方法点拨】基本模型:旋转放缩变换,图中必有两对相似三角形.题型五:母子型“子母型”相似的图形特点:有一个公共角,一对完全重合的边,一对半重合的边,一对完全不重合的边。
相似三角形的常见模型

专题相似三角形的常见模型一、下面六个图中△ADE与△ABC均相似,在相应图的下方写出对应角,及对应边的比例式。
二、如图,若∠A=∠ECD=∠B,则△AEC∽△BCD,我们可以把这种类型的相似叫做“一线三等角”型或“K字型”,请在下方空白处写上对应角,及对应边的比例式。
三、如图,已知△ABC∽△ADE,这种像是一边转一边缩小(或扩大的)相似,我们可以叫做“旋转”型。
先写出对应角及对应边的比例式。
连结BD,CE,你有什么新发现?你能证明吗?练习:1.如图,在△ABC中,DE∥BC,若,DE=4,则BC=.2.如图,直线l1∥l2∥l3,AC分别交l1,l2,l3于点A,B,C;DF分别交l1,l2,l3于点D,E,F;AC与DF交于点O.已知DE=3,EF=6,AB=4.(1)求AC的长;(2)若BE:CF=1:3,求OB:AB.3.由36个边长为1的小正方形组成的6×6网格中,线段AB的两个端点都在格点上.(1)如图1,C,D也在格点上,连接AB,CD相交于点O,求的值和OC的长;(2)如图2,仅用无刻度直尺在线段AB上找一点M,使得.4.如图,在△ABC中,中线AD,BE相交于点F,EG∥BC,交AD于点G,下列说法:①BD=2GE;②AF=2FD;③△AGE与△BDF面积相等;④△ABF与四边形DCEF面积相等,结论正确的是5.如图,已知△ABC中,AB=,AC=,BC=6,点M为AB的中点,在线段AC上取点N,使△AMN与△ABC相似,求MN的长.6.(1)如图1,在△ABC中,D为AB上一点,∠ACD=∠B.求证:AC2=AD•AB.(2)如图2,在 ABCD中,E为BC上一点,F为CD延长线上一点,∠BFE=∠A.若BF=4,BE =3,求AD的长.7.如图在平面直角坐标系xOy中,O为坐标原点,点A的坐标为(﹣1,2),点B在第一象限,且OB⊥OA,OB=2OA,则B点的坐标为.8.如图,已知△ABC和△ADE均为等边三角形,D在BC上,DE与AC相交于点F,AB=8,BD=2,则CF等于.相似三角形模型一———A字型&8字型例1、如图,在△ADE中,BC∥DE,AB=3,BD=DE=6,则BC的长是()A.2 B.3 C.4 D.6变式1、如图,在△ABC中,点D,E分别在AB、AC边上,DE∥BC,且AD=3BD,若S△ABC=16,则S△ADE=()A.B.9 C.D.12变式2、如图,在△ABC中,DE∥AB,DE分别与AC,BC交于D,E两点.若△ABC与△DEC的周长比为3:2,AC=6,则DC=.变式3、如图,在△ABC中,点D为AC上一点,且,过点D作DE∥BC交AB于点E,连接CE,过点D作DF∥CE交AB于点F.若AB=15,则EF=.例2、如图,在△ABC中,点D,F是AB的三等分点,E,G是AC的三等分点,四边形DFGE和四边FBCG的面积分别是S1和S2,则S1:S2为()A.3:5 B.4:9 C.3:4 D.2:3变式1、如图,在△ABC中,点D、E、F分别在边AB、AC、BC上,DE∥BC,DF∥AC,若△ADE 与四边形DBCE的面积相等,则△DBF与△ADE的面积之比为()A.B.C.D.变式2、如图,平行四边形ABCD中,点E是AD边上一点,连结EC、BD交于点F,若AE:ED=5:4记△DFE的面积为S1,△BCF的面积为S2,△DCF的面积为S3,则DF:BF=,S1:S2:S3=.例3、如图,AB∥CD,AB=6,CD=9,AD=10,则OD的长为()A.4 B.5 C.6 D.7变式1、在平行四边形ABCD中,点E是边AD上一点,且AE=2ED,EC交对角线BD于点F,则S:S△CBF等于()△EDFA.B.C.D.变式2、如图,正方形ABCD的对角线AC、BD相交于点O,E是BC的中点,DE交AC于点F,若DE=12,则DF=()A.3 B.4 C.6 D.8变式3、如图,已知点M为平行四边形ABCD边AB的中点,线段CM交BD于点E,S△BEM=2,则图中阴影部分的面积为()A.5 B.4 C.8 D.6变式4、如图,在矩形ABCD中,AB=,点E是BC的中点,AE⊥BD于点F.(1)求BE的长;(2)延长FE交DC的延长线于点G ,求证:.例4、如图▱ABCD 中,E 、F分别是AD 、CD边上的点,连接BE 、AF交于点G,延长BE交CD的延长线于H,下列结论错误的是()=B.=C.=D.=A.变式1、如图,已知AB、CD、EF都与BD垂直,垂足分别是B、D、F,且AB=4,EF=3,那么CD的长是()A.12 B.9 C.6 D.16变式2、如图,在▱ABCD中,AB=3,AD=5,AF分别交BC于点E、交DC的延长线于点F,且CF=1,则CE的长为.变式3、如图,点F在平行四边形ABCD的边上,延长BF交CD的延长线于点E,交AC于点O,若=,则=.例5、如图,已知点O是△ABC中BC边上的中点,且,则=.变式1、如图,在矩形ABCD中,对角线AC,BD交于点O,过点A作EA⊥CA交DB的延长线于点E,若AB=3,BC=4,则的值为.变式2、如图,在正方形AOCB中,AB=3,点A在x轴的负半轴上,点C在y轴的正半轴上,点P 在边AB上,且OP交AC于点Q,函数y=(x<0)的图象经过点Q.若S△APQ=S△OCQ,则k 的值为()A.﹣B.﹣2 C.2 D.例6、如图,在△ABC中,点E在BC上,且BE=3EC.D是AC的中点,AE、BD交于点F,则AF:EF的值为()A.3:2 B.4:3 C.5:3 D.5:4变式1、在△ABC中,D,E分别为BC,AC上的点,且AC=2EC,连结AD,BE,交于点F.设x =CD:BD,y=AF:FD,则()A.y=x+1 B.y=x+1 C.y=D.y=变式2、如图,AD是△ABC的中线,点E是线段AD上的一点,且AE=AD,CE交AB于点F.若AF=2cm,则AB=cm.例8、如图,▱ABCD的对角线AC,BD交于点O,CE平分∠BCD交AB于点E,交BD于点F,且∠ABC=60°,AB=2BC,连接OE.下列结论:①∠ACD=30°;②S▱ABCD=AC•BC;③OE:AC =:6;④S▱OEF=S▱ABCD,成立的是.变式、如图,平行四边形ABCD中,AB=2AD=2,且AD⊥BD,一动点P在AB上方,且∠APB=60°,AP与BD交于点E,则的最大值为.相似三角形模型二———反(斜)A字型&反(斜)8字型例1、如图,在△ABC中,点D,E分别在AB,AC上,∠ADE=∠C,如果AE=2,AB=5,那么DE:BC=()A.B.C.D.变式、如图,在△ABC中,点D、E分别在△ABC的边AB、AC上,如果添加下列其中之一的条件,不一定能使△ADE与△ABC相似,那么这个条件是()A.∠AED=∠B B.∠ADE=∠C C.=D.=例2、如图,线段AD、CB相交于点O,连结AB、CD,∠A=∠C,则下列结论正确的是()A.B.C.D.变式、如图,已知Rt△ABC中,∠ACB=90°,射线CD交AB于点D,点E是CD上一点,且∠AEC =∠ABC,联结BE.(1)求证:△ACD∽△EBD;(2)如果CD平分∠ACB,求证:AB2=2ED•EC.例3、如图,在△ABC中,D,E分别是AC,AB上的点,∠ADE=∠B.△ABC的角平分线AF交DE于点G,交BC于点F.(1)求证:△ADG∽△ABF;(2)若,AF=6,求GF的长.变式1、如图,在锐角三角形ABC中,点D、E分别在边AC、AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.(1)求证:△ADE∽△ABC;(2)若AD=BE=4,AE=3,求CD的值.变式2、已知∠ADE=∠C,AG平分∠BAC交DE于F,交BC于G.(1)求证:△ADF∽△ACG;(2)连接DG,若DG∥AC,=,AD=6,求CE的长度.例4、如图,在Rt△ABC中,∠ACB=90°,AC=5cm,∠BAC=60°,动点M从点B出发,在BA 边上以每秒2cm的速度向点A匀速运动,同时动点N从点C出发,在CB边上以每秒cm的速度向点B匀速运动,设运动时间为t秒(0≤t≤5),连接MN.(1)若BM=BN,求t的值;(2)若△MBN与△ABC相似,求t的值.变式1、如图,在△ABC中,∠C=90°,AC=16cm,BC=8cm动点P从点C出发沿着CB方向以2cm/s的速度向点B运动,另一动点Q从点A出发沿着AC方向以4cm/s的速度向点C运动,P、Q两点同时出发,当点P到达B点或点Q到达C点即停止运动,设运动时间为t(s).(1)当t为多少秒时,以P、C、Q为顶点的三角形和△ABC相似?(2)当t为多少秒时,△PCQ的面积是△ACB面积的?变式2、如图所示,△ABC中,∠C=90°,BC=8cm,AC:AB=3:5,点P从点B出发沿BC向点C以2cm/s的速度移动,点Q从点C出发沿CA向点A以1cm/s的速度移动,如果P、Q分别从B、C同时出发:(1)经过多少秒后,△CPQ的面积为8cm?(2)经过多少秒时,以C、P、Q为顶点的三角形恰与△ABC相似.。
相似三角形的九大模型

相似三角形的九大模型模型一:A 字型1.如图,在ABC △中,:2:3AF FB =,延长BC 至点D ,使得2BC CD =,求AEEC的值.2.如图,在ABC △中,已知CD 为边AB 上的高,正方形EFGH 的四个顶点分别在ABC △上,求证:111AB CD EF+=.3.如图,在矩形ABCD 中,2AB =,3BC =,点E 、F 、G 、H 分别在矩形ABCD 的各边上,EF HG AC ∥∥,EH FG BD ∥∥,则四边形EFGH 的周长是_________.4.如图,ABC △中,M 是AC 的中点,E 是AB 上一点,且3BE AE =,求BCCD的值.模型二:反A 字型5.如图,D 、E 分别为ABC △的边AB 、AC 上的点,且ADE ACB ∠=∠. (1)求证:AD AB AE AC ⋅=⋅;(2)如果ABC △的面积为m ,3DE =,5BC =,求ADE △的面积.6.如图,在ABC △中,点D 、E 分别在边AB 、AC 上,DE 、BC 的延长线相交于点F ,且EF DF BF CF ⋅=⋅. (1)求证:AD AB AE AC ⋅=⋅;(2)当12AB =,9AC =,8AE =时,求BD 的长与ADEECFS S △△的值.7.将三角形纸片()ABC △按如图所示的方式折叠,使点C 落在AB 边上的点D ,折痕为EF .已知3AB AC ==,4BC =,若以点B 、D 、F 为顶点的三角形与ABC △相似,那么CF 的长度是( )A .2B .127或2 C .127D .125或2 8.将ABC △纸片按如图所示的方式折叠,使点B 落在边AC 上,记为点B ',折痕为EF .已知6AB AC ==,8BC =. (1)求ABC △的周长;(2)若以点B ',F ,C 为顶点的三角形与ABC △相似,求BF 的长.9.如图,在ABC △中,6AB =,8BC =.点D 以每秒1个单位长度的速度由B 向A 运动,同时点E 以每秒2个单位长度的速度由C 向B 运动,当点E 停止运动时,点D 也随之停止.设运动时间为t 秒,当以B ,D ,E 为顶点的三角形与ABC △相似时,求t 的值.10.如图,在锐角三角形ABC 中,点D ,E 分别在边AC ,AB 上,AG BC ⊥于点G ,AF DE ⊥于点F ,EAF GAC ∠=∠. (1)求证:ADE ABC △∽△; (2)若3AD =,5AB =,求AFAG的值.模型三:8字型11.如图,E 是ABCD □的边BA 延长线上一点,连接EC ,交AD 于点F .在不添加辅助线的情况下,请你写出图中所有的相似三角形,并任选一对相似三角形给予证明.12.如图,平行四边形ABCD 中,过点B 的直线与对角线AC 、边AD 分别交于点E 和F .过点E 作EG BC ∥,交AB 于G ,则图中相似三角形有( )A .7对B .6对C .5对D .4对13.已知DE AB ∥,2OA OC OE =⋅,求证:AD BC ∥.14.学校门口的栏杆如图所示,栏杆从水平位置BD 绕O 点旋转到AC 位置,已知AB BD ⊥,CD BD ⊥,垂足分别为B ,D ,4m AO =, 1.6m AB =,1m CO =,则栏杆C 端应下降的垂直距离CD 为( )A .0.2mB .0.3mC .0.4mD .0.5m15.如图,E ,F 是平行四边形ABCD 对角线AC 上两点,14AE CF AC ==.连接DE ,DF 并延长,分别交AB 、BC 于点G 、H ,连接GH ,则ADGBGHS S ∆∆的值为( )A .12B .23C .34D .116.如图所示,在平行四边形ABCD 中,AC 与BD 相交于点O ,E 为OD 的中点,连接AE 并延长交DC 于点F ,则:DF FC =( )A .1:4B .1:3C .2:3D .1:217.如图,在矩形ABCD 中,E 是边AB 的中点,连接DE 交对角线AC 于点F ,若4AB =,3AD =,则CF 的长为 .18.如图,直线a b ∥,:3:5AF FB =,:3:1BC CD =,则:AE EC 为( )A .5:12B .9:5C .12:5D .3:219.如图,在平行四边形ABCD 中,E 是BA 延长线上一点,CE 分别与AD ,BD 交于点G ,F .下列结论:①EG AG GC GD =②EF BF FC FD =;③FC BFGF FD=;④2CF GF EF =⋅,其中正确的个数是( )A .1B .2C .3D .4模型四:蝴蝶型20.如图,四边形ABCD 的对角线AC 、BD 相交于O ,且将这个四边形分成①、②、③、④四个三角形.若::OA OC OB OD =,则下列结论中一定正确的是( )A .①与②相似B .①与③相似C .①与④相似D .③与④相似21.如图,AB CD ∥,线段BC 、AD 相交于点F ,点E 是线段AF 上一点,且满足BEF C ∠=∠,其中9AF =,3DF =,2CF =,则AE =_________.FEDCBA22.如图,在ABC △中,AB AC =,AD BC ⊥,DE AC ⊥,M 为DE 的中点,AM 与BE 相交于点N ,AD 与BE 相交于点F .求证: (1)DE ADCE CD=;(2)BCE ADM △∽△;(3)猜想AM 与BE 的位置关系,并说明理由.23.点D 为Rt ABC △的斜边AB 上一点,点E 在AC 上,连接DE ,CD ,且ADE BCD ∠=∠,CF CD ⊥交DE 的延长线于点F ,连接AF(1)如图1,若AC BC =,求证:AF AB ⊥;(2)如图2,若AC BC ≠,当点D 在AB 上运动时,求证:AF AB ⊥.N FMEDCBA模型五:共边共角型24.如图,在ABC △中,点D 是边AB 上的一点,ADC ACB ∠=∠,2AD =,6BD =,则边AC 的长为( )A .2B .4C .6D .825.已知:如图,ABC △中,AD 是BAC ∠的平分线,AD 的垂直平分线交AD 于E ,交BC 的延长线于F .求证: (1)2FD FB FC =⋅; (2)22::AB AC BF CF =.26.如图,在ABC △中,AB AC a ==,()BC b a b =>.在ABC △内依次作CBD A ∠=∠,DCE CBD ∠=∠,EDF DCE ∠=∠.则EF 等于( )A .32b aB .32a bC .43b aD .43a b27.如图,在矩形ABCD 中,对角线AC 、BD 相交于点G ,E 为AD 的中点,连接BE 交AC 于F ,连接FD ,若90BFA ∠=︒,则下列四对三角形:①BEA △与ACD △;②FED △与DEB △;③CFD △与ABG △;④ADF △与CFB △.其中相似的为( )A .①④B .①②C .②③④D .①②③28.如图,点P 是菱形ABCD 的对角线BD 上一点,连结CP 并延长,交AD 于E ,交BA 的延长线于点F .试问:(1)图中APD △与哪个三角形全等?并说明理由.(2)猜想:线段PC 、PE 、PF 之间存在什么关系?并说明理由.模型六:射影定理29.在Rt ABC △中,90C ∠=︒,CD AB ⊥于D ,下列等式中错误的是( ) A .2AD BD CD ⋅= B .AC BD CB AD ⋅=⋅C .2AC AD AB =⋅ D .222AB AC BC =+30.在Rt ABC △中,CD 是斜边AB 上的高. (1)求证:2CD AD DB =⋅; (2)求证:2CB DB AB =⋅.31.如图,在Rt ABC △中,90CAB ∠=︒,30B ∠=︒,AD CB ⊥于D ,3CD =,则CB = .32.如图,90ADC ACB ∠=∠=︒,ACD B ∠=∠,5AC =,6AB =,则AD = .33.如图,在Rt ABC △中,CD 为斜边AB 上的高,如果3AC =,6AB =,求BD 的值.34.在Rt ABC △中,CD 是斜边AB 上的高线,DE AC ⊥于E ,DF BC ⊥于F ,求证:33BC BFAC AE=.35.在ABC △中,90ACB ∠=︒,CE AB ⊥于点E ,D 在AB 延长线上, 且DCB A ∠=∠,:1:2BD CD =,AE =BCD S △.36.如图,在Rt ABC △中,90ABC ∠=︒,BA BC =.点D 是AB 的中点,连接CD ,过点B 作BG CD ⊥,分别交CD 、CA 于点E 、F ,与过点A 且垂直于AB 的直线相交于点G ,连接DF .给出以下四个结论: ①AG FGAB FB=; ②点F 是GE 的中点;③AF AB =; ④5ABC BDF S S =△△,其中正确的结论序号是 .模型七:三垂直模型37.如图,矩形ABCD中,E是BC的中点,连接AE,过点E作EF AE⊥交DC于点F,连接AF.设ABkAD=,下列结论:(1)ABE ECF△∽△,(2)AE平分BAF∠,(3)当1k=时,ABE ADF△∽△,其中结论正确的是()A.(1)(2)(3)B.(1)(3)C.(1)(2)D.(2)(3)38.如图,一个长方形的ABCD长为8cm,宽为6cm,E为边CD上的一点,现把Rt ADE△沿AE对折使得D点恰好落在边BC上的中点D'处.(1)请说明Rt ABD'△与Rt ECD'△相似;(2)求CE的长.39.(1) 如图1 ,已知AB l∠=︒,ACD⊥,垂足分别为B、E,且C是l上一点,90⊥,DE l△∽△;求证:ABC CED(2) 如图2 ,在四边形ABCD中,已知90BC=,10CD=,∠=︒,3ABCAB=,4DA=BD的长.40.如图,在直角梯形ABCD中,//∠=︒,AD BC,90BC=,CD=BAD=,3 P在线段AB上.若PCD△是以点P为直角顶点的直角三角形,则AP=.模型八:一线三等角41.如图,ABC △中,8AB AC ==,D 为BC 上一点,3BD =,30ADE B ∠=∠=︒,则AE 的长为_________.42.如图,D 是等边ABC △边AB 上的一点,且:1:2AD DB =,现将ABC △折叠,使点C 与D 重合,折痕为EF ,点E ,F 分别在AC 和BC 上,则:CE CF =( )A .34B .45C .56D .6743.已知: 如图,ABC △中,90BAC ∠=︒,1AB AC ==,点D 是BC 边上的一个动点 (不 与B ,C 点重合) ,45ADE ∠=︒. (1) 求证:ABD DCE △∽△;(2) 设BD x =,AE y =,求y 关于x 的函数关系式; (3) 当ADE △是等腰三角形时, 求AE 的长 .44.如图,四边形ABCD 中,AD BC ∥,AB DC =,3cm AD =,7cm BC =,60B ∠=︒,P 为BC 边上一点(不与B ,C 重合),连接AP ,过P 点作PE 交DC 于E ,使得APE B ∠=∠.(1)求证:ABP PCE △∽△; (2)求AB 的长;(3)在边BC 上是否存在一点P ,使得:5:3DE EC =?如果存在,求BP 的长;如果不存在,请说明理由.45.如图,M 为线段AB 上一点,AE 与BD 交于点C ,DME A B α∠=∠=∠=,且DM 交AE 于点F ,ME 交BD 于点G .(1)写出图中的三对相似三角形;(2)连接FG ,当AM MB =时,求证:MFG BMG △∽△;(3)在(2)条件下,若45α=︒,AB =,3AF =,求FG 的长.模型九:手拉手46.如图,12∠=∠,要使ABC ADE △∽△,只需要添加一个条件即可,这个条件不可能是( )A .B D ∠=∠ B .C E ∠=∠ C .AD ABAE AC= D .AC BCAE DE= 47.如图,把ABC △绕点A 旋转到ADE △,当点D 刚好落在BC 上时,连结CE ,设AC ,DE ,相交于点F ,则图中相似三角形(不含全等)的对数有( )A .1B .2C .3D .448.如图,在ABC △中,ABC C ∠=∠,将ABC △绕点B 逆时针旋转得DBE △,点E 在AC 上,若3ED =,1EC =,则EB =( )AB .32C D .249.将一幅三角尺(Rt ACB △中,90ACB ∠=︒,60B ∠=︒,在Rt EDF △中,90EDF ∠=︒,45E ∠=︒)如图摆放,点D 为AB 的中点,DE 交AC 于点P ,DF 经过点C ,将EDF △绕点D 顺时针方向旋转角(060)αα︒<<︒,DE '交AC 于点M ,DF '交BC 于点N ,则PMCN的值为( )AB C .12D 50.如图,点A 在线段BD 上,在BD 的同侧作30︒角的直角三角形ABC 和30︒角的直角三角形ADE ,CD 与BE ,AE 分别交于点P ,M ,连接PA 对于下列结论:①BAE CAD △∽△;②M P M D M A M E ⋅=⋅;③图中有5对相似三角形;④AP CD ⊥其中结论正确的个数是( )A .1个B .2个C .4个D .3个51.如图,ABC △为等腰直角三角形,90BAC ∠=︒,1BC =,E 为直角边AB 上任意一点,以线段CE 为斜边作等腰Rt CDE △,连接AD ,下列说法:①AC ED ⊥;②BCE ACD ∠=∠;③AED ECB △∽△;④AD BC ∥;⑤四边形ABCD 面积的最大值为38,其中正确的是__________.52.如图,ABC △中,45BAC ∠=︒,30ACB ∠=︒,将ABC △绕点A 顺时针旋转得到11AB C △,当点1C 、1B 、C 三点共线时,旋转角为α,连接1BB ,交AC 于点D ,下面结论:①1AC C △为等腰三角形;②1AB D BCD △∽△;③135α=︒;④1CA CB =;⑤1AB B C =中,正确结论的个数是( )A .2个B .3个C .4个D .5个53.如图,在正方形ABCD 中,AEF △的顶点E ,F 分别在BC ,CD 边上,高AG 与正方形的边长相等,连接BD 分别交AE ,AF 于点M ,N ,下列说法: ①45EAF ∠=︒;②连接MG ,NG ,则MGN △为直角三角形; ③AMN AFE △∽△;④若2BE =,3FD =,则MN( )A .4B .3C .2D .154.如图,在Rt ABC △中,90ACB ∠=︒,BC aAC b=,CD AB ⊥于点D ,点E 是直线AC 上一动点,连接DE ,过点D 作FD ED ⊥,交直线BC 于点F . (1)探究发现:如图①,若a b =,点E 在线段AC 上,则DEDF= . (2)数学思考①如图②,若点在线段AC 上,则DEDF= ,(用含a ,b 的代数式表示); ②当点E 在直线AC 上运动时,①中的结论是否仍然成立?请仅就图③的情形给出证明;(3)拓展应用:若AC BC =DF =CF 的长.。
中考中相似三角形的常见模型及典型例题

(1)A字、8字; (3)角平分线; (5)一线三等角; (7)内接矩形;
2.基本辅助线:
(2)反A、反8; (4)旋转型; (6)线束模型; (8)相似比与面积比。
(1)作平行线构造A字、8字; (2)作垂线构造直角三角形相似
3.基本问题类型:
(1)证明相似;
(2)求线段长;
(1)若点P在线段CB上,且BP=6,求线段CQ的长; (2)若BP=x,CQ=y,求y与x的关系式,并求出自变量x的取值范围。
例 9 如图,△ABC是等边三角形,点D、E分别在BC、AC上,且BD=CD,
AD与BE相交于点F. (1)求证:△ABD≌△BCE; (2)求证:△ABE∽△FAE;
(3)当AF=7,DF=1时,求BD的长。
(量得BN=70cm)
C
C
DME
DME
A PN F
B
A PN F
B
1.如图,△ABC是一块锐角三角形余料,边BC=120毫米,高AD=80 毫米,要把它加工成正方形零件,使正方形的一边在BC上,其 余两个顶点分别在AB、AC上,这个正方形零件的边长是多少?
A
A
M
EN
H
KG
∟
B Q DPC
B
E
DF C
E
AB AC BC
B
C (2)公共边平方=共线边之积:AC 2 AE • AB
反A字 型 【模型2】反“A”字型&反“8”字型
(Ⅱ)DE拉下来经过点C,又称之为母子型,为相似常考模型:
A
A
E
B
C
AC2 AED • BC
AC2 CD • CB
AD2 BD • CD
中考数学几何专项——相似模型(相似三角形)
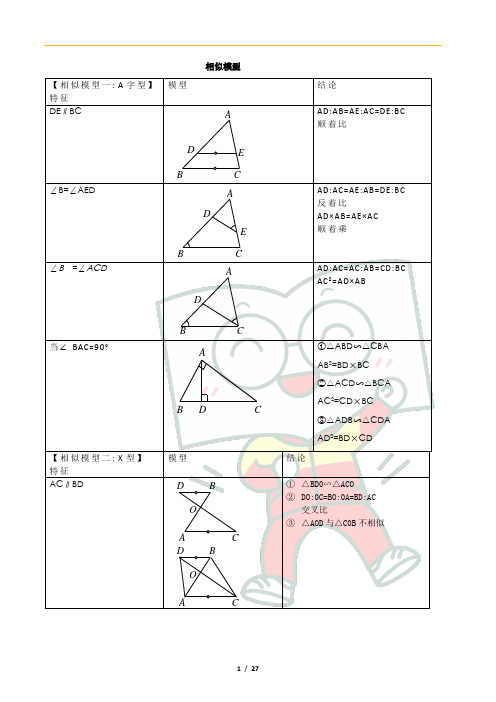
相似模型【相似模型一: A 字型】 特征 模型 结论DE ∥BCCBCBBC D E ADA E DA AD:AB=AE:AC=DE:BC 顺着比∠B=∠AEDCB C BDA EDAAD:AC=AE:AB=DE:BC 反着比AD×AB=AE×AC 顺着乘∠B =∠ACDCBED AAD:AC=AC:AB=CD:BC AC²=AD×AB当∠ BAC=90°AD B CB①△ABD ∽△CBA AB ²=BD×BC ②△ACD ∽△BCAAC²=CD×BC③△ADB ∽△CDA AD²=BD×CD【相似模型二: X 型】 特征 模型 结论AC ∥BDAD B CO DB A CC A OD BAD B CODBACCAO D B① △BD0∽△ACO ② DO:0C=BO:0A=BD:AC 交叉比③ △AOD 与△C0B 不相似∠B=∠C(也叫蝴蝶型相似)A D BC ODBACCAD B CODBACC① △AOC ∽△DOB② AO:OD=0C:0B=AC:BDAO×OB=OC×0D ③ 顺着比, 交叉乘 ④ △BOC∽△DOA【相似模型三: 旋转相似】 特征 模型结论成比例线段共端点① △ABC ∽△ADE ② △ABD∽△ACE【相似模型四: 三平行模型】 特征 模型结论AB ∥EF ∥CDFEBCD AF EDCBA图2① 有两对A 字型相似△BEF ∽△BCD △DEF∽△DAB ② 有一对X 型相似△AEB ∽△DEC ③111AB CD EF+=【相似模型五: 半角模型】 特征模型 结论ECD BAA BDC EEDCBA90度, 45度; 120度, 60度 120度,60度60°45°图2图1旋转N M 60°120°E D CB A 45°ED C B A ①△ABN ∽△MAN ∽△MCA ②△ABD ∽△CAE ∽△CBA【相似模型六: 三角形内接矩形模型】 特征模型 结论矩形EFGH 或正方形EFGH 内接与三角形H GFED C BA【相似模型七: 十字模型】 特征 模型结论正方形①若AF=BE,则AF ⊥BE ②若AF ⊥BE, 则AF=BE,②若AF ⊥BE ,则AF=BE,长方形PEAB CD矩形ABCD 中, CE ⊥BD, 则△CDE ∽△BCD,平行四边形△GME ∽△HNF△MED ≌△BFA三角形MED CAB在△ABC 中, AB =AC,AB ⊥AC, ①D 为中点, ②AE ⊥BD, ③BE :EC =2:1, ④∠ADB =∠CDE, ⑤∠AEB =∠CED,⑥∠BMC =135°, ⑦ , 这七个结论中, “知二得五”【A 型, X 型, 三平行模型】1.如图, 在△ABC 中, EF ∥DC, ∠AFE=∠B, AE=6, ED=3, AF=8, 则AC=_________, _________.F E DCBABCDE FA2. 如图, AB ∥CD, 线段BC, AD 相交于点F, 点E 是线段AF 上一点且满足∠BEF=∠C, 其中AF=6, DF=3, CF=2, 则AE=_________.3.如图, 在Rt △ABD 中, 过点D 作CD ⊥BD, 垂足为D, 连接BC 交AD 于点E, 过点E 作EF ⊥BD 于点F, 若AB=15, CD=10, 则BF:FD=_____________.FEBCD AN MEDCBA4.如图, 在□ABCD中, E为BC的中点, 连接AE, AC, 分别交BD于M, N, 则BM:DN=_____________.5.如图所示, AB∥CD, AD, BC相交于点E, 过E作EF∥AB交BD于点F.则下列结论:①△EFD∽△ABD;②;③;④.其中正确的有___________.F EDCBA图26.在△ABC中, AB=9, AC=6, 点M在边AB上, 且AM=3, 点N在AC边上.当AN= 时, △AMN与原三角形相似.7.如图, 在△ABC中, ∠C=90°, AC=8, BC=6, D是边AB的中点, 现有一点P位于边AC上, 使得△ADP与△ABC相似, 则线段AP的长为.8.如图, 已知O是坐标原点, 点A.B分别在轴上, OA=1, OB=2, 若点D在轴下方, 且使得△AOB与△OAD相似, 则这样的点D有个.9.如图, 在Rt△ACB中, ∠C=90°, AC=16cm, BC=8cm, 动点P从点C出发, 沿CA方向运动;动点Q同时从点B出发, 沿BC方向运动,如果点P的运动速度均为4cm/s, Q点的运动速度均为2cm/s, 那么运动几秒时, △ABC与△PCQ相似.10.将△ABC的纸片按如图所示的方式折叠, 使点B落地边AC上, 记为点B', 折叠痕为EF, 已知AB=AC=8, BC=10,若以点B'.F.C为顶点的三角形与△ABC相似, 那么BF的长度是.11.如图,在中,,,是角平分线.求证:(1)(2)12.如图, 四边形中, 平分, , , 为的中点.(1)求证: ;(2)与有怎样的位置关系?试说明理由;(3)若, , 求的值.13.如图, 在中, 为上一点, , , , 于, 连接.(1)求证:;(2)找出图中一对相似三角形, 并证明.14.如图, 在中, , 分别是, 上的点, , 的平分线交于点, 交于点.(1)试写出图中所有的相似三角形, 并说明理由(2)若, 求的值.15.如图, 在平行四边形ABCD中, 对角线AC.BD交于点O. M为AD中点, 连接CM交BD于点N, 且ON=1.(1)求BD的长;(2)若△DCN的面积为2, 求四边形ABNM的面积.16.如图,在中,于点,于点,连接,求证: ..17.如图,在△ABC中,DE∥FG∥BC,AD∶DF∶FB=1∶2∶3,若EG=3,则AC=________.图1 图218..如图,平行于BC的直线DE把△ABC分成的两部分面积相等.则ADAB = _________.19.如图所示, AD=DF=FB, DE∥FG∥BC,则=__________.20.如图, 在矩形ABCD中, 对角线AC, BD相交于点O, OE⊥BC于点E, 连接DE交OC于点F, 作FG⊥BC于点G, 则线段BG与GC的数量关系是___.21.如图, 已知点C为线段AB的中点, CD⊥AB且CD=AB=4, 连接AD, BE⊥AB, AE是∠DAB的平分线, 与DC相交于点F, EH⊥DC于点G, 交AD 于点H, 则HG的长为 .22.如图1, 在△ABC 中, 点D.E 、Q 分别在边AB.AC.BC 上, 且DE ∥BC, AQ 交DE 于点P. (1)求证: ;(2)如图, 在△ABC 中, ∠BAC=90°, 正方形DEFG 的四个顶点在△ABC 的边上, 连接AG 、AF, 分别交DE 于M 、N 两点. 如图2, 若AB=AC=1, 直接写出MN 的长;如图3, 求证MN2=DM【母子型】1.已知: 如图, △ABC 中, ∠ACB=90°, CD ⊥AB 于D, S △ABC=20, AB=10。
最新相似三角形-经典模型总结与例题分类

相似三角形经典模型总结经典模型【精选例题】 “平行型”【例1】 如图,111EE FF MM ∥∥,若AE EF FM MB ===,则111111:::_________AEE EE F F FF M M MM CB S S S S ∆=四边形四边形四边形M 1F 1E 1M E F A BC【例2】 如图,AD EF MN BC ∥∥∥,若9AD =,18BC =,::2:3:4AE EM MB =,则_____EF =,_____MN =M N A BCD E F【例3】 已知,P 为平行四边形ABCD 对角线,AC 上一点,过点P 的直线与AD ,BC ,CD 的延长线,AB 的延长线分别相交于点E ,F ,G ,H求证:PE PHPF PG=PHGFEDCBA【例4】 已知:在ABC ∆中,D 为AB 中点,E 为AC 上一点,且2AEEC=,BE 、CD 相交于点F ,求BFEF的值【例5】 已知:在ABC ∆中,12AD AB =,延长BC 到F ,使13CF BC =,连接FD 交AC 于点E 求证:①DE EF = ②2AE CE =ABCDFEFE DCBA【例6】 已知:D ,E 为三角形ABC 中AB 、BC 边上的点,连接DE 并延长交AC 的延长线于点F ,::BD DE AB AC =求证:CEF ∆为等腰三角形FEDCBA【例7】 如图,已知////AB EF CD ,若AB a =,CD b =,EF c =,求证:111c a b=+.FE DCBA【例8】 如图,找出ABD S ∆、BED S ∆、BCD S ∆之间的关系,并证明你的结论.FE DCBA【例9】 如图,四边形ABCD 中,90B D ∠=∠=︒,M 是AC 上一点,ME AD ⊥于点E ,MF BC⊥于点F求证:1MF MEAB CD+= ABCDEF M【例10】 如图,在ABC ∆中,D 是AC 边的中点,过D 作直线EF 交AB 于E ,交BC 的延长线于F求证:AE BF BE CF ⋅=⋅FEDC BA【例11】 如图,在线段AB 上,取一点C ,以AC ,CB 为底在AB 同侧作两个顶角相等的等腰三角形ADC ∆和CEB ∆,AE 交CD 于点P ,BD 交CE 于点Q ,求证:CP CQ =QPEDC BA【例12】 阅读并解答问题.在给定的锐角三角形ABC 中,求作一个正方形DEFG ,使D ,E 落在BC 边上,F ,G 分别落在AC ,AB 边上,作法如下:第一步:画一个有三个顶点落在ABC ∆两边上的正方形''''D E F G 如图, 第二步:连接'BF 并延长交AC 于点F 第三步:过F 点作FE BC ⊥,垂足为点E 第四步:过F 点作FG BC ∥交AB 于点G 第五步:过G 点作GD BC ⊥,垂足为点D 四边形DEFG 即为所求作的正方形问题:⑴证明上述所作的四边形DEFG 为正方形⑵在ABC ∆中,如果6BC =+45ABC ∠=︒,75BAC ∠=︒,求上述正方形DEFG 的边长G'F'E'D'ABCDEFG“平行旋转型”图形梳理:AEF 旋转到AE‘F’CBAAEF 旋转到AE‘F’CBBCAEF 旋转到AE‘F’ABCAEF 旋转到AE‘F’特殊情况:B 、'E 、'F 共线AEF 旋转到AE‘F’CBAAB CEF E'F'AEF 旋转到AE‘F’C ,'E ,'F 共线AEF 旋转到AE‘F’CBAAEF 旋转到AE‘F’CBA【例13】 已知梯形ABCD ,AD BC ∥,对角线AC 、BD 互相垂直,则①证明:2222AD BC AB CD +=+OAB CD【例14】 当AOD ∆,以点O 为旋转中心,逆时针旋转θ度(090θ<<),问上面的结论是否成立,请说明理由DCB AO【例15】 (全国初中数学联赛武汉选拔赛试题)如图,四边形ABCD 和BEFG 均为正方形,求::AG DF CE =_________.ABEF GGFEDCBA“斜交型”【例16】 如图,ABC ∆中,D 在AB 上,且DE BC ∥交AC 于E ,F 在AD 上,且2AD AF AB =⋅,求证:AEF ACD ∆∆:F ED CBA【例17】 如图,等边三角形ABC 中,D ,E 分别在BC ,AB 上,且CE BE =,AD ,CE 相交于M ,求证:EAM ECA ∆∆:M E D C B A【例18】 如图,四边形ABCD 的对角线相交于点O ,BAC CDB ∠=∠,求证:DAC CBD ∠=∠ODCBA【例19】 如图,设AB BC CAAD DE EA==,则12∠=∠吗? 21ABCDE【例20】 在锐角三角形ABC 中,AD ,CE 分别为BC ,AB 边上的高,ABC ∆和BDE ∆的面积分别等于18和2,2DE =,求AC 边上的高ABCDE【例21】 如图,在等边ABC ∆的边BC 上取点D ,使21=CD BD ,作CH AD ⊥,H 为垂足,连结BH 。
相似三角形的九大模型

相似三角形的九大模型1.在三角形ABC中,已知2.在三角形ABC中,CD为边AB上的高,正方形EFGH 的四个顶点分别在三角形ABC上,证明:111+EF^2=AB^2+BC^2+AC^2.3.在矩形ABCD中,AB=2,BC=3,点E、F、G、H分别在矩形ABCD的各边上,且EF∥HG∥AC,EH∥FG∥BD,则四边形EFGH的周长是10.4.在三角形ABC中,M是AC的中点,E是AB上一点,且BE=3AE,求BC的值。
5.在三角形ABC中,D、E分别为边AB、AC上的点,且∠ADE=∠ACB。
证明:AD×AB=AE×AC。
如果三角形ABC的面积为m,DE=3,BC=5,求三角形ADE的面积。
6.在三角形ABC中,点D、E分别在边AB、AC上,DE、BC的延长线相交于点F,且EF×DF=BF×CF。
证明:AD×AB=AE×AC。
当AB=12,AC=9,AE=8时,求BD的长与△ADE的面积。
7.将三角形纸片△ABC按如图所示的方式折叠,使点C落在AB边上的点D,折痕为EF。
已知AB=AC=3,BC=4,若以点B、D、F为顶点的三角形与△ABC相似,那么CF的长度是2/7.8.将三角形ABC纸片按如图所示的方式折叠,使点B落在边AC上,记为点B',折痕为EF。
已知AB=AC=6,BC=8.求△ABC的周长。
若以点B'、F、C为顶点的三角形与△XXX 相似,求BF的长。
9.在三角形ABC中,AB=6,BC=8.点D以每秒1个单位长度的速度由B向A运动,同时点E以每秒2个单位长度的速度由C向B运动,当点E停止运动时,点D也随之停止。
设运动时间为t秒,当以B、D、E为顶点的三角形与△ABC相似时,求t的值。
10.在锐角三角形ABC中,AG⊥BC于点G,点D、E分别在XXX、AB上,XXX⊥DE于点F,且∠EAF=∠GAC。
证明:△ADE∽△ABC。
相似三角形中的常见五种基本模型(原卷版)-2023年中考数学重难点解题大招复习讲义-几何模型篇

模型探究相似三角形考查范围广,综合性强,其模型种类多,其中有关一线三垂直模型在前面的专题已经很详细的讲解,这里就不在重复.模型一、A字型相似模型A字型(平行)反A字型(不平行)模型二、8字型与反8字型相似模型模型三、AX型相似模型(A字型及X字型两者相结合)模型四、共边角相似模型(子母型)模型五、手拉手相似模型考点一、A 字相似模型【例1】.如图,在△ABC 中,∠A =78°,AB =4,AC =6,将△ABC 沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )A .B .C .D .➢变式训练 【变式1-1】.如图,在△ABC 中,DE ∥BC ,AH ⊥BC 于点H ,与DE 交于点G .若,则= .例题精讲【变式1-2】.如图,在△ABC中,M是AC的中点,E是AB上一点,AE=AB,连接EM 并延长,交BC的延长线于D,则=__________.【变式1-3】.如图,在△ABC中,点D在边AB上,AD=9,BD=7.AC=12.△ABC的角平分线AE交CD于点F.(1)求证:△ACD∽△ABC;(2)若AF=8,求AE的长度.考点二、8字与反8字相似模型【例2】.如图,AG∥BD,AF:FB=1:2,BC:CD=2:1,求的值➢变式训练【变式2-1】.如图,AB∥CD,AE∥FD,AE、FD分别交BC于点G、H,则下列结论中错误的是()A.B.C.D.【变式2-2】.如图,在平行四边形ABCD中,E为边AD的中点,连接AC,BE交于点F.若△AEF的面积为2,则△ABC的面积为()A.8B.10C.12D.14【变式2-3】.如图,锐角三角形ABC中,∠A=60°,BE⊥AC于E,CD⊥AB于D,则DE:BC=.考点三、AX型相似模型(A字型及X字型两者相结合)【例3】.如图,在△ABC中,点D和E分别是边AB和AC的中点,连接DE,DC与BE交于点O,若△DOE的面积为1,则△ABC的面积为()A.6B.9C.12D.13.5➢变式训练【变式3-1】.如图,DE是△ABC的中位线,F为DE中点,连接AF并延长交BC于点G,若S△EFG=1,则S△ABC=.【变式3-2】.如图:AD∥EG∥BC,EG交DB于点F,已知AD=6,BC=8,AE=6,EF =2.(1)求EB的长;(2)求FG的长.【变式3-3】.如图,已知AB∥CD,AC与BD相交于点E,点F在线段BC上,,.(1)求证:AB∥EF;(2)求S△ABE:S△EBC:S△ECD.模型四、子母型相似模型【例4】.如图,点C,D在线段AB上,△PCD是等边三角形,且∠APB=120°,求证:(1)△ACP∽△PDB,(2)CD2=AC•BD.➢变式训练【变式4-1】.如图,点P在△ABC的边AC上,要判断△ABP∽△ACB,添加一个条件,不正确的是()A.∠ABP=∠C B.∠APB=∠ABC C.D.【变式4-2】.如图,在△ABC中,点D在AC边上,连接BD,若∠ABC+∠BDC=180°,AD=2,CD=4,则AB的长为()A.3B.4C.D.2【变式4-3】.如图,边长为4的正方形,内切圆记为圆O,P为圆O上一动点,则P A+PB 的最小值为.模型五、手拉手相似模型【例5】.如图,△ABC与△DEF均为等边三角形,O为BC、EF的中点,则AD:BE的值为.➢变式训练【变式5-1】.如图,在△ABC与△ADE中,∠BAC=∠DAE,∠ABC=∠ADE.求证:(1)△BAC∽△DAE;(2)△BAD∽△CAE.【变式5-2】.如图,点D是△ABC内一点,且∠BDC=90°,AB=2,AC=,∠BAD=∠CBD=30°,AD=.【变式5-3】.如图,在四边形ABCD中,AE⊥BC,垂足为E,∠BAE=∠ADC,BE=CE=2,CD=5,AD=kAB(k为常数),则BD的长为.(用含k的式子表示)实战演练1.如图,已知DE∥BC,EF∥AB,则下列比例式中错误的是()A.=B.C.D.2.如图,梯形ABCD中,AD∥BC,∠B=∠ACD=90°,AB=2,DC=3,则△ABC与△DCA的面积比为()A.2:3B.2:5C.4:9D.:3.如图,菱形ABCD中,E点在BC上,F点在CD上,G点、H点在AD上,且AE∥HC ∥GF.若AH=8,HG=5,GD=4,则下列选项中的线段,何者长度最长?()A.CF B.FD C.BE D.EC4.如图,在△ABC中,BC=6,E,F分别是AB,AC的中点,动点P在射线EF上,BP 交CE于点D,∠CBP的平分线交CE于点Q,当CQ=CE时,EP+BP的值为()A.6B.9C.12D.185.如图,在四边形ABCD中,AD∥BC,∠ABC=90°,AB=2,AD=2,将△ABC绕点C顺时针方向旋转后得△A′B′C,当A′B′恰好经过点D时,△B′CD为等腰三角形,若BB′=2,则AA′等于()A.B.2C.D.6.如图,已知,△ABC中边AB上一点P,且∠ACP=∠B,AC=4,AP=2,则BP=.7.如图,在▱ABCD中,AC、BD相交于点O,点E是OA的中点,联结BE并延长交AD 于点F,如果△AEF的面积是4,那么△BCE的面积是.8.如图,在△ABC中,点G为ABC的重心,过点G作DE∥AC分别交边AB、BC于点D、E,过点D作DF∥BC交AC于点F,如果DF=4,那么BE的长为.9.如图,已知Rt△ABC中,两条直角边AB=3,BC=4,将Rt△ABC绕直角顶点B旋转一定的角度得到Rt△DBE,并且点A落在DE边上,则sin∠ABE=.10.如图,在Rt△ABC中,∠ACB=90°,∠BAC=60°,AC=6,AD平分∠BAC,交边BC于点D,过点D作CA的平行线,交边AB于点E.(1)求线段DE的长;(2)取线段AD的中点M,联结BM,交线段DE于点F,延长线段BM交边AC于点G,求的值.11.如图,在菱形ABCD中,∠ADE、∠CDF分别交BC、AB于点E、F,DF交对角线AC 于点M,且∠ADE=∠CDF.(1)求证:CE=AF;(2)连接ME,若=,AF=2,求ME的长.12.[问题背景](1)如图①,已知△ABC∽△ADE,求证:△ABD∽△ACE.[尝试应用](2)如图②,在△ABC和△ADE中,∠BAC=∠DAE=90°∠ABC=∠ADE=30°,AC与DE相交于点F,点D在BC边上,=,①填空:=;②求的值.13.如图,在正方形ABCD中,AB=4,E、F分别是BC、CD上的点,且∠EAF=45°,AE、AF分别交BD于点M、N,连接EN、EF.(1)求证:△ABN∽△MBE;(2)求证:BM2+ND2=MN2;(3)①求△CEF的周长;②若点G、F分别是EF、CD的中点,连接NG,则NG的长为.14.问题背景如图(1),已知△ABC∽△ADE,求证:△ABD∽△ACE;尝试应用如图(2),在△ABC和△ADE中,∠BAC=∠DAE=90°,∠ABC=∠ADE=30°,AC与DE相交于点F,点D在BC边上,=,求的值;拓展创新如图(3),D是△ABC内一点,∠BAD=∠CBD=30°,∠BDC=90°,AB =4,AC=2,直接写出AD的长.15.如图1,四边形ABCD是正方形,G是CD边上的一个动点(点G与C、D不重合),以CG为一边在正方形ABCD外作正方形CEFG,连接BG,DE.我们探究下列图中线段BG、线段DE的长度关系及所在直线的位置关系:(1)①猜想如图1中线段BG、线段DE的数量关系BG=DE及所在直线的位置关系BG⊥DE;②将图1中的正方形CEFG绕着点C按顺时针(或逆时针)方向旋转任意角度α,得到如图2,如图3情形.请你通过观察、测量等方法判断①中得到的结论是否仍然成立,并选取图2证明你的判断;(2)将原题中正方形改为矩形(如图4﹣6),且AB=a,BC=b,CE=ka,CG=kb(a ≠b,k>0),则线段BG、线段DE的数量关系=及所在直线的位置关系BG ⊥DE;(3)在第(2)题图5中,连接DG、BE,且a=4,b=3,k=,直接写出BE2+DG2的值为.。
相似三角形的一些模型

第三讲 相似三角形模型【知识要点】(一)A 字型、反A 字型(斜A 字型)ABCDE(平行)CBA DE(不平行)(二)8字型、反8字型J OADBCAB CD(蝴蝶型)(平行) (不平行)(三)母子型ABCDCAD(四)“K ”字型:D【典型例题】1. 如图5,P 为Rt △ABC 斜边AB 上任意一点(除A 、B 外),过点P 作直线截△ABC ,使截得 的新三角形与△ABC 相似,满足这样条件的直线的作法共有( ) A .1种 B .2种 C .3种 D .4种2.(3分)(2013•柳州二模)如图,直角三角形ABC 的两直角边BC=12,AC=16,则△ABC 的斜边AB 上的高CD 的长是( ) A .20 B . 10 C . 9.6 D .83.如图5,在△ABC 中,∠C=90°,∠B=60°,D 是AC 上一点,DE⊥AB 于E ,且CD=2,DE=1, 则BC 的长为( ) A. 2 B. 334C.32D. 344.(11·贵港)如图所示,在矩形ABCD 中,AB =2,BC =2,对角线AC 、BD 相交于点O ,过点O 作OE 垂直AC 交AD 于点E ,则AE 的长是 A . 3B . 2C .1D .1.55.如图6,四边形ABCD 是边长为9的正方形纸片,将其沿MN 折叠,使点B 落在CD 边上的B '处,点A 对应点为A ',且3BC '=,则AM 的长是A .1.5 B.2 C.2.25 D.2.56.(11·柳州)(本题满分10分)如图,已知AB 是⊙O 的直径,锐角∠DAB 的平分线AC 交⊙O 于点C ,作CD ⊥AD ,垂足为D ,直线图5E DCBA图6ABCEDOCD 与AB 的延长线交于点E . (1)求证:直线CD 为⊙O 的切线;(2)当AB =2BE ,且CE =3时,求AD 的长.7.(本题满分10分)如图12,AB 为O ⊙直径,且弦CD AB ⊥于E ,过点B 的切线与AD 的延长线交于点F . (1)若M 是AD 的中点,连接ME 并延长ME 交BC 于N .求证:MN BC ⊥. (2)若4cos 35C DF ∠==,,求O ⊙的半径.【南宁中考题】1. 如图7所示,点1A 、2A 、3A 在x 轴上,且11223OA A A A A ==,分别过点1A 、2A 、3A 作y轴的平行图12线,与反比例函数()80y x x=>的图象分别交于点1B 、2B 、3B ,分别过点1B ,2B ,3B 作x 轴的平行线,分别与y 轴交于点1C ,2C ,3C ,连接1OB ,2OB ,3OB ,那么图中阴影部分的面积之和为___________. 2.(3分)(2013•南宁)如图,在边长为2的正三角形中,将其内切圆和三个角切圆(与角两边及三角形 内切圆都相切的圆)的内部挖去,则此三角形剩下部分(阴影部分)的面积为 .3.已知点A (3,4),点B 为直线x =-1上的动点,设B (-1,y ).(1)如图1,若点C (x ,0)且-1<x <3,BC ⊥AC ,求y 与x 之间的函数关系式; (2)在(1)的条件下,y 是否有最大值?若有,请求出最大值;若没有,请说明理由;(3)如图2,当点B 的坐标为(-1,1)时,在x 轴上另取两点E ,F ,且EF =1.线段EF 在x 轴上平移, 线段EF 平移至何处时,四边形ABEF 的周长最小?求出此时点E 的坐标.1A 2A 3B2B1B3C2C 1C Oxy3A图74.如图,已知矩形纸片ABCD ,AD =2,AB =4.将纸片折叠,使顶点A 与边CD 上的点E 重合,折痕FG 分别与AB ,CD 交于点G ,F ,AE 与FG 交于点O . (1)如图1,求证:A ,G ,E ,F 四点围成的四边形是菱形;(2)如图2,当△AED 的外接圆与BC 相切于点N 时,求证:点N 是线段BC 的中点; (3)如图2,在(2)的条件下,求折痕FG 的长.5.如图13-1,在边长为5的正方形ABCD 中,点E 、F 分别是BC 、DC 边上的点,且AE EF ⊥,2BE =. (1)求EC ∶CF 的值;(2)延长EF 交正方形外角平分线CP P 于点(如图13-2),试判断AE EP 与的大小关系,并说明理由; (3)在图13-2的AB 边上是否存在一点M ,使得四边形DMEP 是平行四边形?若存在,请给予证明;若不存在,请说明理由.A D D A F P F25.如图11-①,AB 为⊙O 的直径,AD 与⊙O 相切于点A DE ,与⊙O 相切于点E ,点C 为DE 延长线上一点,且.CE CB = (1)求证:BC 为⊙O 的切线;(2)连接AE ,AE 的延长线与BC 的延长线交于点(如图11-②所示).若252AB AD ==,,求线段BC 和EG 的长.【中考题】1.(2012•玉林)如图,已知点O 为Rt △ABC 斜边AC 上一点,以点O 为圆心,OA 长为半径的⊙O 与BC 相切于点E ,与AC 相交于点D ,连接AE . (1)求证:AE 平分∠CAB ; (2)探求图中∠1与∠C 的数量关系,并求当AE=EC 时tanC 的值.图13-1C BEB图11-②GOAD EC图11-①BOADEC2. (10分)(2013•钦州)如图,在Rt△ABC中,∠A=90°,O是BC边上一点,以O为圆心的半圆与AB 边相切于点D,与AC、BC边分别交于点E、F、G,连接OD,已知BD=2,AE=3,tan∠BOD=.(1)求⊙O的半径OD;(2)求证:AE是⊙O的切线;(3)求图中两部分阴影面积的和.3.(2011广西崇左,24,14分)(本小题满分14分)如图,在边长为8的正方形ABCD中,点O为AD上一动点(4<OA<8),以O为圆心,OA的长为半径的圆交边CD于点M,连接OM,过点M作圆O的切线交边BC于点N.(1)求证:△ODM∽△MCN;(2)设DM=x,求OA的长(用含x的代数式表示);(3)在点O运动的过程中,设△CMN的周长为p,试用含x的代数式表示p,你能发现怎样的结论?4.(2012•广西)如图,AB 是⊙O 的直径,点C 是⊙O 上一点,∠BAC 的平分线AD 交⊙O 于点D ,过点D 垂直于AC 的直线交AC 的延长线于点E . (1)求证:DE 是⊙O 的切线; (2)如图AD=5,AE=4,求⊙O 的直径.5.如图(5),正方形ABCD 中,E 为AB 的中点,AF ⊥DE 于点O , 则DOAO等于( ) A .352B .31C .32D .21图(5)AB FC DE O。
相似三角形_模型分析和典型例题讲解大全
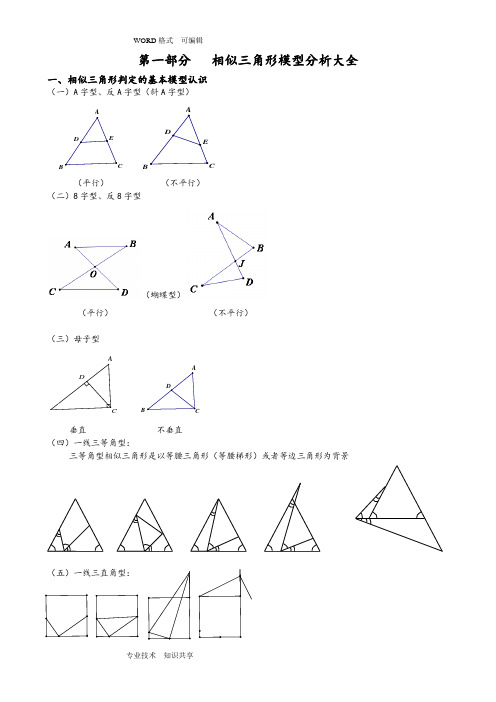
第一部分 相似三角形模型分析大全一、相似三角形判定的基本模型认识(一)A 字型、反A 字型(斜A 字型)AB CD ECB A DE(平行)(不平行)(二)8字型、反8字型(蝴蝶型)(平行) (不平行)(三)母子型CADABCD垂直 不垂直 (四)一线三等角型:三等角型相似三角形是以等腰三角形(等腰梯形)或者等边三角形为背景(五)一线三直角型:(六)双垂型:CAD二、相似三角形判定的变化模型旋转型:由A 字型旋转得到。
8字型拓展CB EDA共享性GABCEF一线三等角的变形一线三直角的变形第二部分 相似三角形典型例题讲解母子型相似三角形例1:如图,梯形ABCD 中,AD ∥BC ,对角线AC 、BD 交于点O ,BE ∥CD 交CA 延长线于E . 求证:OE OA OC ⋅=2.例2:已知:如图,△ABC 中,点E 在中线AD 上, ABC DEB ∠=∠.求证:(1)DA DE DB ⋅=2; (2)DAC DCE ∠=∠.例3:已知:如图,等腰△ABC 中,AB =AC ,AD ⊥BC 于D ,CG ∥AB ,BG 分别交AD 、AC 于E 、F . 求证:EG EF BE ⋅=2.相关练习:1、如图,已知AD 为△ABC 的角平分线,EF 为AD 的垂直平分线.求证:FC FB FD ⋅=2.AC DEB2、已知:AD 是Rt △ABC 中∠A 的平分线,∠C=90°,EF 是AD 的垂直平分线交AD 于M ,EF 、BC 的延长线交于一点N 。
求证:(1)△AME ∽△NMD; (2)ND 2=NC ·NB3、已知:如图,在△ABC 中,∠ACB=90°,CD ⊥AB 于D ,E 是AC 上一点,CF ⊥BE 于F 。
求证:EB ·DF=AE ·DB4.在∆ABC 中,AB=AC ,高AD 与BE 交于H ,EF BC ⊥,垂足为F ,延长AD 到G ,使DG=EF ,M 是AH 的中点。
初中数学《相似三角形模型》六种基础模型及习题

1:相似三角形模型一:相似三角形判定的基本模型 (一)A 字型、反A 字型(斜A 字型)(平行)(不平行)基础模型识别1.(密云18期末1)如图,ABC 中,D 、E 分别是AB 、AC 上点,DE //BC ,AD =2,DB =1,AE =3,则EC 长( )A .23 B .1 C .32D .62.(怀柔18期末4)如图,在△ABC 中,点D ,E 分别为边AB,AC 上的点,且DE ∥BC ,若AD =4,BD =8,AE =2,则CE 的长为( )A .2B .4C .6D .83.(石景山18期末10)如图,在△ABC 中,点D 、E 分别在边AB 、AC 上.若∠ADE =∠C ,AB =6,AC =4,AD =2,则EC =________.ABCDECBA DEB DEEDCBA例题精讲1.如图,已知△ABC 中,CE ⊥AB 于E ,BF ⊥AC 于F ,求证:△AEF∽△ACB.2.如图,AD 与BC 相交于E ,点F 在BD 上,且AB∥EF∥CD,求证:1AB +1CD =1EF.练习一:1.(大兴18期末19)已知:如图,在△ABC 中,D ,E 分别为AB 、 AC 边上的点,且AE AD 53,连接DE . 若AC =4,AB =5. 求证:△ADE ∽△ACB.2.(丰台18期末18)如图,△ABC 中,DE ∥BC ,如果AD = 2,DB = 3,AE = 4,求AC 的长.D CBA E3、已知:如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,且DE∥BC,DF∥AC,求证:△ADE∽△DBF.4、如图,在△ABC中,∠ACB=90°,BC=16cm,AC=12cm,点P从点B出发,以2cm/秒的速度向点C移动,同时点Q从点C出发,以1cm/秒的速度向点A移动,设运动时间为t 秒,当t= 秒,△CPQ与△ABC相似.(二)8字型、反8字型(蝴蝶型)(平行) (不平行) 一、基本模式识别1.(海淀18期末3)如图,线段BD ,CE 相交于点A ,DE ∥BC .若AB =4,AD =2,DE =1.5,则BC 的长为( )A .1B .22、(顺义18期末19)如图,E 是□ABCD 的边BC 延长线上一点,AE 交CD 于点F ,FG ∥AD 交AB 于点G .(1)填空:图中与△CEF 相似的三角形有 ; (写出图中与△CEF 相似的所有三角形)(2)从(1)中选出一个三角形,并证明它与△CEF 相似.3、如下左图,在O ⊙中,弦AB 与CD 相交于点P ,已知3cm 4cm 2cm PA PB PC ===,,,那么PD = cm .BCB CDECBAGAB C FD E二、例题精讲:1、如图,在△ABC中,D为BC边上的中点,在AD上任取一点O,过O作BO 交AC于点F,作CO交AB于E,边结EF。
相似三角形八大模型归纳例题

相似三角形八大模型归纳例题相似三角形,这可是个有趣的话题!大家好,今天我们就来聊聊这八大模型,轻松又幽默地让你了解它们,没问题吧?想象一下你在公园里散步,忽然看到两个小朋友,一个高一个矮,他们在玩搭积木。
高的小朋友把积木堆得高高的,矮的小朋友也不甘示弱,拼命地跟着学。
这不就是相似三角形的真实写照吗?他们的比例相同,但是大小却不一样,这样想就简单多了。
咱们得了解相似三角形的基本概念。
简单来说,相似三角形就像一对亲密无间的兄弟,虽然身高不一样,但长相、比例却是那么相似。
就好比你家猫咪和邻居的猫咪,虽然毛色不同,但总能一眼认出它们是亲戚。
这种相似可不光是外表,连角度都得一样。
没错,角度就像我们的性格,各有千秋但都能和谐共处。
我们来聊聊相似三角形的判定。
首先是AA判定,就是两个三角形的两个角相等,嘿,这简直像是两个人在合唱,和声完美,谁都不敢说不。
这一招,绝对是相似三角形的杀手锏。
然后就是SSS判定,三个边的比例相等,这可不简单,像极了团队合作,每个人都发挥了自己的作用,最终实现了目标。
SAS判定,两个边的比例相等,还有夹角相等。
这就像打麻将,牌虽然不一样,但搭配得当,赢的机会就大大增加了。
咱们再来看看实际应用。
比如,建筑师设计房子的时候,就得用到这些相似三角形的原理,保证建筑的稳定性和美观性。
你想想,如果房子的角度都乱了,那可就麻烦大了!还有航海测量,水手们通过相似三角形来测量距离,别小看这个,关键时刻可关乎生死,真是一不小心就得跳海了。
学习相似三角形不光是为了考试,生活中处处都能见到它的影子。
你去超市买东西,看到两瓶相同品牌的饮料,虽然瓶子大小不一样,但标签和设计却一模一样。
这样一来,你就能轻松判断哪瓶更划算。
这就像购物时遇到的“买一送一”,表面看似优惠,其实是相似三角形的另一种变相体现。
说到这里,可能有人会觉得相似三角形太抽象,不够有趣。
学数学就像是吃大餐,得慢慢品味,才能发现其中的美味。
想象一下,你在烧烤摊,烤肉时得掌握火候,太熟了或者太生了都不好,学数学也是如此,掌握了相似三角形的精髓,才能在考试时游刃有余。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1:相似三角形模型一:相似三角形判定的基本模型(一)A字型、反A字型(斜A字型)B(平行)(不平行)(二)8字型、反8字型BCBC(蝴蝶型)(平行)(不平行)(三)母子型B(四)一线三等角型:三等角型相似三角形是以等腰三角形(等腰梯形)或者等边三角形为背景,一个与等腰三角形的底角相等的顶点在底边所在的直线上,角的两边分别与等腰三角形的两边相交如图所示:(五)一线三直角型:三直角相似可以看着是“一线三等角”中当角为直角时的特例,三直角型相似通常是以矩形或者正方形形为背景,或者在一条直线上有一个顶点在该直线上移动或者旋转的直角,几种常见的基本图形如下:当题目的条件中只有一个或者两个直角时,就要考虑通过添加辅助线构造完整的三直角型相似,这往往是很多压轴题的突破口,进而将三角型的条件进行转化。
(六)双垂型:CAD二:相似三角形判定的变化模型旋转型:由A 字型旋转得到8字型拓展CB EDA共享性一线三等角的变形GA BC EF一线三直角的变形2:相似三角形典型例题(1)母子型相似三角形例1:如图,梯形ABCD 中,AD ∥BC ,对角线AC 、BD 交于点O ,BE ∥CD 交CA 延长线于E . 求证:OE OA OC ⋅=2.例2:已知:如图,△ABC 中,点E 在中线AD 上, ABC DEB ∠=∠. 求证:(1)DA DE DB ⋅=2; (2)DAC DCE ∠=∠.例3:已知:如图,等腰△ABC 中,AB =AC ,AD ⊥BC 于D ,CG ∥AB ,BG 分别交AD 、AC 于E 、F . 求证:EG EF BE ⋅=2.1、如图,已知AD 为△ABC 的角平分线,EF 为AD 的垂直平分线.求证:FC FB FD ⋅=2.AC DEB2、已知:AD 是Rt △ABC 中∠A 的平分线,∠C=90°,EF 是AD 的垂直平分线交AD 于M ,EF 、BC 的延长线交于一点N 。
求证:(1)△AME ∽△NMD; (2)ND 2=NC·NB3、已知:如图,在△ABC 中,∠ACB=90°,CD ⊥AB 于D ,E 是AC 上一点,CF ⊥BE 于F 。
求证:EB·DF=AE·DB4.在∆ABC 中,AB=AC ,高AD 与BE 交于H ,EF BC ⊥,垂足为F ,延长AD 到G ,使DG=EF ,M 是AH 的中点。
求证:∠=︒GBM 90GMF EHDCA5 已知:如图,在Rt △ABC 中,∠C =90°,BC =2,AC =4,P 是斜边AB 上的一个动点,PD ⊥AB ,交边AC 于点D (点D 与点A 、C 都不重合),E 是射线DC 上一点,且∠EPD =∠A .设A 、P 两点的距离为x ,△BEP 的面积为y .(1)求证:AE =2PE ; (2)求y 关于x 的函数解析式,并写出它的定义域; (3)当△BEP 与△ABC 相似时,求△BEP 的面积.(2)双垂型1、如图,在△ABC 中,∠A=60°,BD 、CE 分别是AC 、AB 上的高 求证:(1)△ABD ∽△ACE ;(2)△ADE ∽△ABC ;(3)BC=2ED2、如图,已知锐角△ABC ,AD 、CE 分别是BC 、AB 边上的高,△ABC 和△BDE 的面积分别是27和3,DE=62,求:点B 到直线AC 的距离。
C(3)共享型相似三角形1、△ABC 是等边三角形,DBCE 在一条直线上,∠DAE=120°,已知BD=1,CE=3,求等边三角形的边长.2、已知:如图,在Rt △ABC 中,AB =AC ,∠DAE =45°.求证:(1)△ABE ∽△ACD ; (2)CD BE BC ⋅=22.CD E(4)一线三等角型相似三角形例1:如图,等边△ABC 中,边长为6,D 是BC 上动点,∠EDF =60° (1)求证:△BDE ∽△CFD(2)当BD =1,FC =3时,求BE例2:(1)在ABC ∆中,5==AC AB ,8=BC ,点P 、Q 分别在射线CB 、AC 上(点P 不与点C 、点B 重合),且保持ABC APQ ∠=∠.①若点P 在线段CB 上(如图),且6=BP ,求线段CQ 的长;②若x BP =,y CQ =,求y 与x 之间的函数关系式,并写出函数的定义域;(2)正方形ABCD 的边长为5(如下图),点P 、Q 分别在直线..CB 、DC 上(点P 不与点C 、点B 重合),且保持︒=∠90APQ .当1=CQ 时,求出线段BP 的长.例3:已知在梯形ABCD 中,AD ∥BC ,AD <BC ,且AD =5,AB =DC =2. (1)如图8,P 为AD 上的一点,满足∠BPC =∠A .①求证;△ABP ∽△DPC ②求AP 的长.(2)如果点P 在AD 边上移动(点P 与点A 、D 不重合),且满足∠BPE =∠A ,PE 交直线BC 于点E ,同时交直线DC 于点Q ,那么①当点Q 在DC 的延长线上时,设AP =x ,CQ =y ,求y 关于x 的函数解析式,并写出函数的定义域; ②当CE =1时,写出AP 的长.ABC PQAB CDCADBEFAB CDABCCBA D例4:如图,在梯形ABCD 中,AD ∥BC ,6AB CD BC ===,3AD =.点M 为边BC 的中点,以M 为顶点作EMF B ∠=∠,射线ME 交腰AB 于点E ,射线MF 交腰CD 于点F ,联结EF . (1)求证:△MEF ∽△BEM ;(2)若△BEM 是以BM 为腰的等腰三角形,求EF 的长; (3)若EF CD ⊥,求BE 的长.1、如图,在△ABC 中,8==AC AB ,10=BC ,D 是BC 边上的一个动点,点E 在AC 边上,且C ADE ∠=∠.(1) 求证:△ABD ∽△DCE ;(2) 如果x BD =,y AE =,求y 与x 的函数解析式,并写出自变量x 的定义域; (3) 当点D 是BC 的中点时,试说明△ADE 是什么三角形,并说明理由.2、如图,已知在△ABC 中, AB =AC =6,BC =5,D 是AB 上一点,BD =2,E 是BC 上一动点,联结DE ,并作DEF B ∠=∠,射线EF 交线段AC 于F .(1)求证:△DBE ∽△ECF ;(2)当F 是线段AC 中点时,求线段BE 的长;(3)联结DF ,如果△DEF 与△DBE 相似,求FC 的长.ABCDECDA PFBACD E3、已知在梯形ABCD 中,AD ∥BC ,AD <BC ,且BC =6,AB =DC =4,点E 是AB 的中点.(1)如图,P 为BC 上的一点,且BP =2.求证:△BEP ∽△CPD ; (2)如果点P 在BC 边上移动(点P 与点B 、C 不重合),且满足∠EPF =∠C ,PF 交直线CD 于点F ,同时交直线AD 于点M ,那么①当点F 在线段CD 的延长线上时,设BP =x ,DF =y ,求y 关于x 的函数解析式,并写出函数的定义域; ②当BEP DMF S S ∆∆=49时,求BP 的长.4、如图,已知边长为3的等边ABC ∆,点F 在边BC 上,1CF =,点E 是射线BA 上一动点,以线段EF 为边向右侧作等边EFG ∆,直线,EG FG 交直线AC 于点,M N , (1)写出图中与BEF ∆相似的三角形; (2)证明其中一对三角形相似;(3)设,BE x MN y ==,求y 与x 之间的函数关系式,并写出自变量x 的取值范围; (4)若1AE =,试求GMN ∆的面积.(5)一线三直角型相似三角形例1、已知矩形ABCD 中,CD=2,AD=3,点P 是AD 上的一个动点,且和点A,D 不重合,过点P 作CP PE ⊥,EDCBA PA交边AB 于点E,设y AE x PD ==,,求y 关于x 的函数关系式,并写出x 的取值范围。
E BA例2、在ABC ∆中,O BC AC C ,3,4,90===∠o是AB 上的一点,且52=AB AO ,点P 是AC 上的一个动点,OP PQ ⊥交线段BC 于点Q ,(不与点B,C 重合),设y CQ x AP ==,,试求y 关于x 的函数关系,并写出定义域。
1.在直角ABC ∆中,43tan ,5,90===∠B AB C o,点D 是BC 的中点,点E 是AB 边上的动点,DE DF ⊥交射线AC 于点F (1)、求AC 和BC 的长 (2)、当BC EF //时,求BE 的长。
(3)、连结EF,当DEF ∆和ABC ∆相似时,求BE 的长。
F CBA2.在直角三角形ABC 中,D BC AB C ,,90==∠o是AB 边上的一点,E 是在AC 边上的一个动点,(与A,C 不重合),DF DE DF ,⊥与射线BC 相交于点F. (1)、当点D 是边AB 的中点时,求证:DF DE =(2)、当m DBAD=,求DF DE 的值(3)、当21,6===DB AD BC AC ,设y BF x AE ==,,求y 关于x 的函数关系式,并写出定义域ABF CBAQPDCBA3.如图,在ABC ∆中,90C ∠=︒,6AC =,3tan 4B =,D 是BC 边的中点,E 为AB 边上的一个动点,作90DEF ∠=︒,EF 交射线BC 于点F .设BE x =,BED ∆的面积为y .(1)求y 关于x 的函数关系式,并写出自变量x 的取值范围;(2)如果以B 、E 、F 为顶点的三角形与BED ∆相似,求BED ∆的面积.4.如图,在梯形ABCD 中,CD AB , 34tan ,4,2===C AD AB ,P DAB ADC ,900=∠=∠是腰BC 上一个动点(不含点B 、C ),作AP PQ ⊥交CD 于点Q .(图1) (1)求BC 的长与梯形ABCD 的面积; (2)当DQ PQ =时,求BP 的长;(图2)(3)设y CQ x BP ==,,试求y 关于x 的函数解析式,并写出定义域.QPD C BA。
