鲁教版2020八年级数学上册5.3三角形的中位线培优练习题2(附答案)
鲁教版初中数学八年级上册《三角形的中位线》课堂练习

5.3 三角形的中位线1.如图,D 、E 、F 分别为△ABC 三边上的中点.(1)线段AD 叫做△ABC 的 ,线段DE 叫做△ABC 的 ,DE 与AB 的位置和数量关系是 _________ ;(2)图中全等三角形有 _________________ ;(3)图中平行四边形有 ___________ .CAE F2. 三角形各边长为5、9、12,则连结各边中点所构成的三角形的周长是 .3. 如图,在矩形ABCD 中,BC =8cm ,AC 与BD 交于O ,M 、N 分别为OA 、OD 的中点.求证:四边形BCNM 是等腰梯形.4. 已知:如图,矩形ABCD 中,E 、F 、G 、H 分别为AB 、BC 、CD 、AD 的中点求证:四边形EFGH是菱形 H G D C B AEF5、如图,要测出池塘的宽度AB,小强在池塘边上取一个能直接到达A、B的点C,量的AC=20cm,BC=25cm,又取AC的中点D,BC的中点E,量得DE=12cm,求池塘宽AB,为多少?6、如图,在梯形ABCD中,AD∥BC,E是DC的中点,EF∥AB交BC于F,若EF=3,求AB的长.参考答案1、(1)中线,中位线,DE ∥AB ,DE=12AB. (2)△AEF ≌△DEF ≌△FBD ≌△EDC.(3)AFDE ,FBDE ,FDCE.2、 133、证MN ∥BC 且MN≠BC.4、证明:连结AC 、BD.∵AE=BE ,BF=CF ,∴EF ∥AC ,EF=12AC. 同理CH ∥AC ,CH=12AC ,∴EF AC ,∴四边形EFGH 是平行四边形. ∵AE=BE ,AH=DH ,∴EH=12BD. 又∵AC=BD ,∴EF=EH ,∴四边形EFGH 是菱形.5、解:∵点D 是AC 的中点,点E 是BC 的中点,∴DE 是△ABC 的中位线∴DE =12AB 又∵DE=12cm∴AB=24cm6、解:过D 作DG ∥AB 交BC 于G ,∵AD ∥BC ,AB ∥DG , ∴四边形ABGD 是平行四边形,∴AB=DG .∵EF ∥AB ,∴EF ∥DG ,∵DE=CE ,∴GF=CF.∴EF 是△CDG 的中位线,∴EF=12DG . ∴DG=2EF=6,即AB=6.点拨:此题目在考察三角形中位线的同时考察了平行四边形的判定问题,解题时注意条件的转化.。
鲁教版2020八年级数学上册5.3三角形的中位线培优练习题1(附答案)

鲁教版2020八年级数学上册5.3三角形的中位线培优练习题1(附答案)一.选择题(共10小题)1.将一个面积为4的正方形按下列顺序折叠,然后将最后折叠的纸片沿虚线(中位线)剪去上方的小三角形,将剩下部分展开所得图形的面积是()A.B.1C.2D.32.如图所示,有一张一个角为60°的直角三角形纸片,沿其一条中位线剪开后,不能拼成的四边形是()A.邻边不等的矩形B.等腰梯形C.有一个角是锐角的菱形D.正方形3.如图,DE是△ABC的中位线,M是DE的中点,CM的延长线交AB于点N,则S△DMN:S四边形ANME等于()A.1:5B.1:4C.2:5D.2:74.如图,在等边△ABC中,M、N分别是边AB,AC的中点,D为MN上任意一点,BD,CD的延长线分别交于AB,AC于点E,F.若=6,则△ABC的边长为()A.B.C.D.15.已知:四边形ABCD中,AB=2,CD=3,M、N分别是AD,BC的中点,则线段MN的取值范围是()A.1<MN<5B.1<MN≤5C.<MN<D.<MN≤6.(体验探究题)下列说法正确的是()①顺次连接四边形的中点,所围成的四边形是平行四边形②顺次连接矩形四条边的中点,所围成的四边形是菱形③顺次连接梯形四边的中点,所围成的四边形是矩形④顺次连接对角线互相垂直的四边形各边中点所围成的四边形是矩形A.1个B.2个C.3个D.4个7.在Rt△ABC中,∠ACB=90°,AB=13,AC=5,点D是AB上一动点,作DE∥AC,且DE=2,连结BE、CD,P、Q分别是BE、DC的中点,连结PQ,则PQ长为()A.6B.2C.D.6.58.如图,D,E,F分别为△ABC三边的中点,且AB=AC≠BC,那么△DEF为()A.等边三角形B.等腰直角三角形C.等腰三角形D.不等边三角形9.如图,在△ABC中,BD、CE是角平分线,AM⊥BD于点M,AN⊥CE于点N.△ABC 的周长为30,BC=12.则MN的长是()A.15B.9C.6D.310.如图,在Rt△ABC中,∠C=30°,AB=4,D,F分别是AC,BC的中点,等腰直角三角形DEH的边DE经过点F,EH交BC于点G,且DF=2EF,则CG的长为()A.2B.2﹣1C.D.+1二.填空题(共10小题)11.已知等边三角形ABC的边长为a分别以这个三角形的三边中点为顶点作一个三角形,记为△A1B1C1,再以△A1B1C1各边中点为顶点做三角形记为△A2B2C2,…依次做下去,则△A5B5C5的周长为.12.等腰三角形的两条中位线分别为3和5,则等腰三角形的周长为.13.如图△ABC的三边长分别为30,48,50,以它的三边中点为顶点组成第一个新三角形,再以第一个新三角形三边中点为顶点组成第二个新三角形,如此继续,则第6个新三角形的周长为.14.在Rt△ABC中,∠ACB=90°,AE,BD是角平分线,CM⊥BD于M,CN⊥AE于N,若AC=6,BC=8,则MN=.15.如图,在一次实践活动课上,小明为了测量池塘B,C两点间的距离,他先在池塘的一侧选定一点A,然后测量出AB,AC的中点D,E,且DE=10米,于是可以计算出池塘B,C两点间的距离是米.16.如图,A,B两地被建筑物遮挡,为测量A,B两地的距离,在地面上选一点C,连结CA,CB,分别取CA,CB的中点D,E,若DE的长为36m,则A,B两地距离为m.17.如图,△ABC中,∠ACB=90°,AB边上的高线CD与△ABC的两条角平分线AE,BF分别交于H,G两点,点P,Q分别为HE,GF的中点,连接PQ,若AC=4,BC=6,则PQ的长为.18.如图,在△ABC中,点D,E分别是BC,AC的中点,AB=8,则DE的长为.19.如图,A、B两点被池塘隔开,在AB外选一点C,连接AC、BC,取AC、BC的中点D、E,量出DE=20米,则AB的长为米.20.观察下列图形,它是把一个三角形分别连接这个三角形三边的中点,构成4个小三角形,挖去中间的一个小三角形(如图1);对剩下的三个小三角形再分别重复以上做法,…将这种做法继续下去(如图2,图3…),则图5中挖去三角形的个数为三.解答题(共8小题)21.如图,DE是△ABC的中位线,求证:DE∥BC,且DE=BC.22.写出并证明三角形中位线定理.23.如图,已知△ABC中,D为AB的中点.(1)请用尺规作图法作边AC的中点E,并连接DE(保留作图痕迹,不要求写作法);(2)在(1)的条件下,若DE=4,求BC的长.24.如图,在四边形ABCD中,AD=BC,P是对角线BD的中点,M是DC的中点,N是AB的中点.求证:∠PMN=∠PNM.25.如图,已知在△ABC中,DE∥BC交AC于点E,交AB于点D,DE=BC 求证:D、E分别是AB、AC的中点.26.如图,M是△ABC的边BC的中点,AN平分∠BAC,且BN⊥AN,垂足为N,且AB=6,BC=10,MN=1.5,求△ABC的周长.27.如图,D是△ABC内一点,E、F、G、H分别是AB、AC、CD、BD的中点,求证:四边形EFGH是平行四边形.28.如图,在△ABC中,AB=4,AC=3,AD、AE分别是△ABC角平分线和中线,过点C 作CG⊥AD于F,交AB于G,连接EF,求线段EF的长.参考答案与试题解析一.选择题(共10小题)1.将一个面积为4的正方形按下列顺序折叠,然后将最后折叠的纸片沿虚线(中位线)剪去上方的小三角形,将剩下部分展开所得图形的面积是()A.B.1C.2D.3【解答】解:∵面积为4的正方形折叠以后展开面积不变,∴若把最后折叠成的三角形展开后面积仍为4.沿中位线减去小三角形,小三角形的面积与原三角形面积之比为,故剩下部分展开所得图形的面积是×4=3.故选:D.2.如图所示,有一张一个角为60°的直角三角形纸片,沿其一条中位线剪开后,不能拼成的四边形是()A.邻边不等的矩形B.等腰梯形C.有一个角是锐角的菱形D.正方形【解答】解:如图:此三角形可拼成如图三种形状,(1)为矩形,∵有一个角为60°,则另一个角为30°,∴此矩形为邻边不等的矩形;(2)为菱形,有两个角为60°;(3)为等腰梯形.故选:D.3.如图,DE是△ABC的中位线,M是DE的中点,CM的延长线交AB于点N,则S△DMN:S四边形ANME等于()A.1:5B.1:4C.2:5D.2:7【解答】解:∵DE是△ABC的中位线,∴DE∥BC,DE=BC,若设△ABC的面积是1,根据DE∥BC,得△ADE∽△ABC,∴S△ADE=,连接AM,根据题意,得S△ADM=S△ADE=S△ABC=,∵DE∥BC,DM=BC,∴DN=BN,∴DN=BD=AD.∴S△DNM=S△ADM=,∴S四边形ANME==,∴S△DMN:S四边形ANME=:=1:5.故选:A.4.如图,在等边△ABC中,M、N分别是边AB,AC的中点,D为MN上任意一点,BD,CD的延长线分别交于AB,AC于点E,F.若=6,则△ABC的边长为()A.B.C.D.1【解答】解:过点A作直线PQ∥BC,延长BD交PQ于点P;延长CD,交PQ于点Q.∵PQ∥BC,∴△PQD∽△BCD,∵点D在△ABC的中位线上,∴△PQD与△BCD的高相等,∴△PQD≌△BCD,∴PQ=BC,∵AE=AC﹣CE,AF=AB﹣BF,在△BCE与△P AE中,∠P AE=∠ACB,∠APE=∠CBE,∴△BCE∽△P AE,=…①同理:△CBF∽△QAF,=…②①+②,得:+=.∴+=3,又∵=6,AC=AB,∴△ABC的边长=.故选:C.5.已知:四边形ABCD中,AB=2,CD=3,M、N分别是AD,BC的中点,则线段MN 的取值范围是()A.1<MN<5B.1<MN≤5C.<MN<D.<MN≤【解答】解:连接BD,过M作MG∥AB,连接NG.∵M是边AD的中点,AB=2,MG∥AB,∴MG是△ABD的中位线,BG=GD,MG=AB=×2=1;∵N是BC的中点,BG=GD,CD=3,∴NG是△BCD的中位线,NG=CD=×3=,在△MNG中,由三角形三边关系可知NG﹣MG<MN<MG+NG,即﹣1<MN<+1,∴<MN<,当MN=MG+NG,即MN=时,四边形ABCD是梯形,故线段MN长的取值范围是<MN≤.故选:D.6.(体验探究题)下列说法正确的是()①顺次连接四边形的中点,所围成的四边形是平行四边形②顺次连接矩形四条边的中点,所围成的四边形是菱形③顺次连接梯形四边的中点,所围成的四边形是矩形④顺次连接对角线互相垂直的四边形各边中点所围成的四边形是矩形A.1个B.2个C.3个D.4个【解答】解:①∵顺次连接四边形的中点,它们的两组对边分别平行于四边形的两条对角线,∴围成的四边形是平行四边形.正确;②∵矩形的对角线相等,∴顺次连接矩形四条边的中点,所围成的四边形是菱形.正确;③∵梯形的对角线不一定互相相垂直,∴顺次连接梯形四边的中点,所围成的四边形不是矩形.错误;④∵对角线互相垂直的四边形各边中点所围成的四边形四个角都是直角.正确.故选:C.7.在Rt△ABC中,∠ACB=90°,AB=13,AC=5,点D是AB上一动点,作DE∥AC,且DE=2,连结BE、CD,P、Q分别是BE、DC的中点,连结PQ,则PQ长为()A.6B.2C.D.6.5【解答】解:∵∠ACB=90°,AB=13,AC=5,∴BC==12,取BD中点F,连接PF、QF,如图所示:∵P、Q分别是BE、DC的中点,∴PF是△BDE的中位线,FQ是△BCD的中位线,∴PF∥ED,PF=DE=1,FQ∥BC,FQ=BC=6,∵DE∥AC,AC⊥BC,∴PF⊥FQ,∴PQ===;故选:C.8.如图,D,E,F分别为△ABC三边的中点,且AB=AC≠BC,那么△DEF为()A.等边三角形B.等腰直角三角形C.等腰三角形D.不等边三角形【解答】解:∵D,E,F分别为△ABC三边的中点,∴DE、DF、EF为三角形ABC的三条中位线,∴DE∥BC且等于BC的一半,DF∥AC且等于AC的一半,EF∥AB且等于AB的一半,∵AB=AC≠BC,∴DF=EF≠DE,∴△DEF为等腰三角形.故选:C.9.如图,在△ABC中,BD、CE是角平分线,AM⊥BD于点M,AN⊥CE于点N.△ABC 的周长为30,BC=12.则MN的长是()A.15B.9C.6D.3【解答】证明:∵△ABC的周长为30,BC=12.∴AB+AC=30﹣BC=18.延长AN、AM分别交BC于点F、G.如图所示:∵BN为∠ABC的角平分线,∴∠CBN=∠ABN,∵BN⊥AG,∴∠ABN+∠BAN=90°,∠G+∠CBN=90°,∴∠BAN=∠AGB,∴AB=BG,∴AN=GN,同理AC=CF,AM=MF,∴MN为△AFG的中位线,GF=BG+CF﹣BC,∴MN=(AB+AC﹣BC)=(18﹣12)=3.故选:D.10.如图,在Rt△ABC中,∠C=30°,AB=4,D,F分别是AC,BC的中点,等腰直角三角形DEH的边DE经过点F,EH交BC于点G,且DF=2EF,则CG的长为()A.2B.2﹣1C.D.+1【解答】解:∵Rt△ABC中,∠C=30°,AB=4,D,F分别是AC,BC的中点,∴DF∥AB,BC=AB=4,DF=AB=2,CF=BF,∴CF=BC=2,∵DF=2EF,∴EF=1,∵等腰直角三角形DEH的边DE经过点F,∴DE⊥BC,∴△EGF是等腰直角三角形,∴GF=EF=1,∴CG=CF﹣GF=2﹣1,故选:B.二.填空题(共10小题)11.已知等边三角形ABC的边长为a分别以这个三角形的三边中点为顶点作一个三角形,记为△A1B1C1,再以△A1B1C1各边中点为顶点做三角形记为△A2B2C2,…依次做下去,则△A5B5C5的周长为.【解答】解:等边△ABC的边长为a,∴等边△ABC的周长为3a.∵A2、B2分别是边A1B1、B1C1的中点,∴A2B2是△A1B1C1的中位线,∴A2B2=A1B1.同理,A2C2=A1C1,C2B2=C1B1.∴△A2B2C2的周长=等边△A1B1C1的周长=.同理,△A3B3C3的周长=△A2B2C2的周长=等边△A1B1C1的周长.…,∴△A n B n∁n的周长=△A1B1C1的周长=.∴△A5B5C5的周长===.故答案为:.12.等腰三角形的两条中位线分别为3和5,则等腰三角形的周长为22或26.【解答】解:∵等腰三角形的两条中位线长分别为3和5,∴等腰三角形的两边长为6,10,当腰为6时,则三边长为6,6,10;周长为22;当腰为10时,则三边长为6,10,10;周长为26;故答案为:22或26.13.如图△ABC的三边长分别为30,48,50,以它的三边中点为顶点组成第一个新三角形,再以第一个新三角形三边中点为顶点组成第二个新三角形,如此继续,则第6个新三角形的周长为2.【解答】解:如图,∵E、F分别为AB、AC的中点,∴EF=BC,同理可得DF=AC,DE=AB,∴EF+DF+DE=(AB+BC+CA),即△DEF的周长=△ABC的周长,∴第二个三角形的周长是原三角形周长的,同理可得△GHI的周长=△DEF的周长=△ABC的周长=()2△ABC的周长,∴第三个三角形的周长是原三角形周长的()2,∴第六个三角形的周长是原三角形周长的()5=,∵原三角形的三边长为30,48,50,∴原三角形的周长为128,∴第一个新三角形的周长为64,∴第六个三角形的周长=64×=2故答案为:2.14.在Rt△ABC中,∠ACB=90°,AE,BD是角平分线,CM⊥BD于M,CN⊥AE于N,若AC=6,BC=8,则MN=2.【解答】解:延长CM交AB于G,延长CN交AB于H,∵∠ACB=90°,AC=6,BC=8,∴AB=10,在△BMC和△BMG中,,∴△BMC≌△BMG,∴BG=BC=8,CM=MG,∴AG=2,同理,AH=AC=6,CN=NH,∴GH=4,∴MN=GH=2,故答案为:2.15.如图,在一次实践活动课上,小明为了测量池塘B,C两点间的距离,他先在池塘的一侧选定一点A,然后测量出AB,AC的中点D,E,且DE=10米,于是可以计算出池塘B,C两点间的距离是20米.【解答】解:∵点D,E分别是AB,AC的中点,∴BC=2DE=20(米),故答案为:20.16.如图,A,B两地被建筑物遮挡,为测量A,B两地的距离,在地面上选一点C,连结CA,CB,分别取CA,CB的中点D,E,若DE的长为36m,则A,B两地距离为72 m.【解答】解:∵点D,E分别为CA,CB的中点,∴AB=2DE=72m,故答案为:72.17.如图,△ABC中,∠ACB=90°,AB边上的高线CD与△ABC的两条角平分线AE,BF分别交于H,G两点,点P,Q分别为HE,GF的中点,连接PQ,若AC=4,BC=6,则PQ的长为5﹣.【解答】解:延长CP交AB于K,延长CQ交AB于L,△ABC中,∠ACB=90°,由勾股定理得:AB===2,∵BF是∠ABC的平分线,∴∠ABF=∠CBF,又∵CD⊥AB,∴∠CGF=∠BGD=90°﹣∠ABF=90°﹣∠CBF=∠CFB,∴CG=CF.又∵Q是GF的中点,∴CQ⊥GF,∴∠CQB=∠LQB=90°,∴∠BCQ=∠BLQ,∴BL=BC=6,∴CQ=LQ,同理得:CE=CH,∵P是EH的中点,∴CP⊥EH,∴AP⊥CK,同理得AK=AC=4,CP=PK,∵CP=PK,CQ=LQ,∴PQ=LK=(BL+AK﹣AB)=(6+4﹣2)=5﹣;故答案为:5﹣.18.如图,在△ABC中,点D,E分别是BC,AC的中点,AB=8,则DE的长为4.【解答】解:∵点D,E分别是BC,AC的中点,∴DE=AB=4,故答案为:4.19.如图,A、B两点被池塘隔开,在AB外选一点C,连接AC、BC,取AC、BC的中点D、E,量出DE=20米,则AB的长为40米.【解答】解:∵点D,E分别是BC和AC的中点,∴DE是△ABC的中位线,∴AB=2DE=2×20=40(米).故答案是:40.20.观察下列图形,它是把一个三角形分别连接这个三角形三边的中点,构成4个小三角形,挖去中间的一个小三角形(如图1);对剩下的三个小三角形再分别重复以上做法,…将这种做法继续下去(如图2,图3…),则图5中挖去三角形的个数为121【解答】解:图1挖去中间的1个小三角形,图2挖去中间的(1+3)个小三角形,图3挖去中间的(1+3+32)个小三角形,…则图5挖去中间的(1+3+32+33+34)个小三角形,即图5挖去中间的121个小三角形,故答案为:121.三.解答题(共8小题)21.如图,DE是△ABC的中位线,求证:DE∥BC,且DE=BC.【解答】证明:延长DE到Q,使DE=EQ,连接CQ,∵AE=EC,∠AED=∠CEQ,DE=EQ,∴△ADE≌△CQE,∴AD=CQ,∠A=∠ACQ,∴AB∥CQ,∵AD=BD,∴BD=CQ,∴四边形DBCQ是平行四边形,∴DQ=BC,DQ∥BC,∴DE∥BC,DE=BC.22.写出并证明三角形中位线定理.【解答】三角形中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.已知:如图,D,E分别是△ABC的边AB,AC的中点.求证:DE∥BC,DE=BC.证明:如图,延长DE到点F使EF=DE,连接FC,DC,AF,∵AE=EC,DE=EF,∴四边形ADCF是平行四边形,∴CF∥DA,CF=DA,∴CF∥BD,CF=DB,∴四边形DBCF是平行四边形,∴DF∥BC.又DE=DF,∴DE∥BC,DE=BC.23.如图,已知△ABC中,D为AB的中点.(1)请用尺规作图法作边AC的中点E,并连接DE(保留作图痕迹,不要求写作法);(2)在(1)的条件下,若DE=4,求BC的长.【解答】解:(1)作线段AC的垂直平分线MN交AC于E,点E就是所求的点.(2)∵AD=DB,AE=EC,∴DE∥BC,DE=BC,∵DE=4,∴BC=8.24.如图,在四边形ABCD中,AD=BC,P是对角线BD的中点,M是DC的中点,N是AB的中点.求证:∠PMN=∠PNM.【解答】证明:∵P是对角线BD的中点,M是DC的中点,N是AB的中点,∴PM、PN分别是△BCD和△ABD的中位线,∴PM=BC,PN=AD,∵AD=BC,∴PM=PN,∴∠PMN=∠PNM.25.如图,已知在△ABC中,DE∥BC交AC于点E,交AB于点D,DE=BC 求证:D、E分别是AB、AC的中点.【解答】证明:作BF∥AC交ED的延长线于点F,∵DE∥BC,∴四边形BCEF是平行四边形,∴BC=EF=2ED,AC∥BF,EC=BF,∴ED=DF,∠A=∠DBF,∴在△ADE与△BDF中,,∴△ADE≌△BDF(AAS)∴AD=BD,AE=BF=EC,即D、E分别是AB、AC的中点.26.如图,M是△ABC的边BC的中点,AN平分∠BAC,且BN⊥AN,垂足为N,且AB=6,BC=10,MN=1.5,求△ABC的周长.【解答】解:延长线段BN交AC于E.∵AN平分∠BAC,在△ABN和△AEN中,∴△ABN≌△AEN(ASA),∴AE=AB=6,BN=NE,又∵M是△ABC的边BC的中点,∴CE=2MN=2×1.5=3,∴△ABC的周长是AB+BC+AC=6+10+6+3=25.27.如图,D是△ABC内一点,E、F、G、H分别是AB、AC、CD、BD的中点,求证:四边形EFGH是平行四边形.【解答】证明:∵E、F分别是AB、AC的中点,∴EF∥BC,EF=BC.同理,GH∥BC,GF=BC,∴EF∥GH,EF=GH,∴四边形EFGH是平行四边形.28.如图,在△ABC中,AB=4,AC=3,AD、AE分别是△ABC角平分线和中线,过点C 作CG⊥AD于F,交AB于G,连接EF,求线段EF的长.【解答】解:在△AGF和△ACF中,,∴△AGF≌△ACF,∴AG=AC=3,GF=CF,则BG=AB﹣AG=4﹣3=1.又∵BE=CE,∴EF是△BCG的中位线,∴EF=BG=.。
完整版三角形的中位线经典练习题及其答案
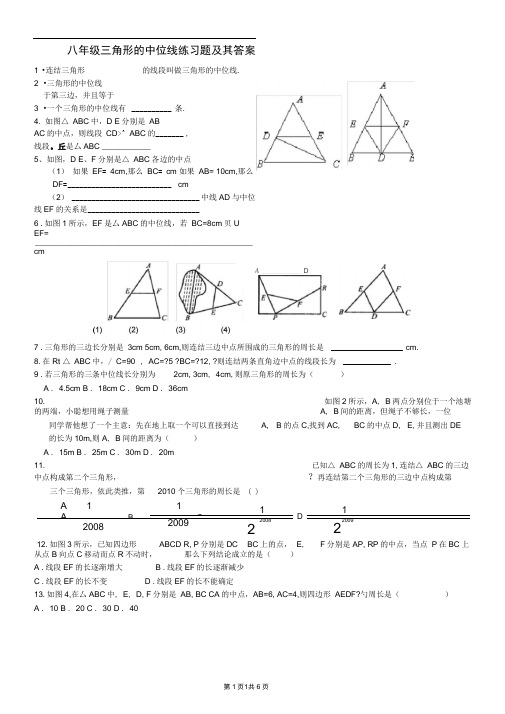
八年级三角形的中位线练习题及其答案1 •连结三角形2 •三角形的中位线于第三边,并且等于3 •一个三角形的中位线有__________ 条.4. 如图△ ABC中,D E分别是ABAC的中点,则线段CD>^ ABC的_______ ,线段。
丘是厶ABC ___________5、如图,D E、F分别是△ ABC各边的中点(1)如果EF= 4cm,那么BC= cm 如果AB= 10cm,那么DF= __________________________ cm(2) ________________________________ 中线AD与中位线EF的关系是____________________________6 .如图1所示,EF是厶ABC的中位线,若BC=8cm贝UEF=_________________________________________________cm7 .三角形的三边长分别是3cm 5cm, 6cm,则连结三边中点所围成的三角形的周长是 __________________ cm.8.在Rt △ ABC中,/ C=90°, AC=?5 ?BC=?12, ?则连结两条直角边中点的线段长为 ____________ .9 .若三角形的三条中位线长分别为2cm, 3cm, 4cm,则原三角形的周长为()A . 4.5cmB . 18cmC . 9cmD . 36cm10. 如图2所示,A, B两点分别位于一个池塘的两端,小聪想用绳子测量A, B间的距离,但绳子不够长,一位同学帮他想了一个主意:先在地上取一个可以直接到达A, B的点C,找到AC, BC的中点D, E,并且测出DE 的长为10m,则A, B间的距离为()A . 15mB . 25mC . 30mD . 20m11. 已知△ ABC的周长为1,连结△ ABC的三边中点构成第二个三角形,?再连结第二个三角形的三边中点构成第三个三角形,依此类推,第2010个三角形的周长是( )A 1 1 1 1A、 B C D、2008 2009 20082 2009212.如图3所示,已知四边形ABCD R, P分别是DC BC上的点,E,F分别是AP, RP的中点,当点P在BC上从点B向点C移动而点R不动时,那么下列结论成立的是()A .线段EF的长逐渐增大B .线段EF的长逐渐减少C .线段EF的长不变D .线段EF的长不能确定13.如图4,在厶ABC中, E, D, F分别是AB, BC CA的中点,AB=6, AC=4,则四边形AEDF?勺周长是()A . 10B . 20C . 30D . 40A__________ D的线段叫做三角形的中位线.14. 如图所示,口ABCD的对角线AC, BD相交于点O, AE=EB求证:OE// BC.15. 已知矩形ABCD中,AB=4cm, AD=10cm,点P在边BC上移动,点E、F、G、H 分别是AB、AP、DP、DC的中点.求证:EF+GH=5cm;16 .如图所示,在△ ABC中,点D在BC上且CD=CA CF平分/ ACB AE=EB求证:EF=1BD.217.如图所示,已知在口ABCD中, E, F分别是AD, BC的中点,求证:MN/ BC.18.已知:如图,四边形ABCD中,E、F、G、H分别是AB、BC、arc CD、DA的中点.求证:四边形EFGH是平行四边形.19.如图,点E, F, G, H分别是CD, BC, AB , DA的中点。
鲁教版-数学-八年级上册-5.3 三角形的中位线 作业

三角形的中位线1.已知△ABC 中,AB :BC :CA=3:2:4且AB=9cm ,D.E.F 分别是AB.BC.AC 的中点,则△DEF 的周长是________.2.已知△ABC 中,D.E 分别是AB.AC 的中点,F 为BC 上一点,EF=12BC ,∠EFC=35°,则∠EDF=________.3.顺次连结四边形各边中点所得到的四边形是___________.4.如图,△ABC 中,AD 是∠BAC 的平分线,CE ⊥AD 于E ,M 为BC 的中点,AB=14cm ,AC=10cm ,求ME 的长.5.已知△ABC 中,AD ⊥BC 于D ,E.F 、G 分别是AB.BD.AC 的中点,EG =32EF ,AD+EF=9cm ,求△ABC 面积.6.如图.在平行四边形ABCD 中,点E.F 为对角线AC 上的三等分点,求证:四边形BFDE 是平行四边形.7.如图,已知五边形ABCDE 中,AC ∥ED ,交BE 于点P ,AD ∥BC ,交BE 于点Q ,BE ∥CD.求证:△BCP ≌△QDE .参考答案:1.13.5cm2.72.5°3.平行四边形4.2cm5.27cm26.证明:如图:连接BD交AC于O,∵四边形是平行四边形ABCD,∴AO=CO,BO=DO.∵点E.F为对角线AC上的三等分点,∴AE=CF,∴AO﹣AE=CO﹣CF,即EO=FO,又∵OB=OD,∴四边形BFDE是平行四边形.7.证明:∵AC∥ED,BE∥CD,∴四边形PCDE是平行四边形.∴PC=ED,∵AC∥ED,BC∥AD,∴∠BPC=∠QED,∠CBP=∠DQE,在△BCP和△QDE中,∵∠CBP=∠DQE,∠BPC=∠QED,PC=ED ∴△BCP≌△QDE.。
鲁教版2020八年级数学上册5.3三角形的中位线培优练习题3(附答案)

鲁教版2020八年级数学上册5.3三角形的中位线培优练习题3(附答案)一.选择题(共10小题)1.如图:在△ABC中,AB=25,BC=24,点D,E分别是AB,BC的中点,连接DE,CD,如果DE=3.5,那么△ACD的周长是()A.28B.28.5C.32D.362.如图,以任意△ABC的边AB和AC向形外作等腰Rt△ABD和等腰Rt△ACE,F、G分别是线段BD和CE的中点,则的值等于()A.B.C.D.3.如图,在△ABC中,BF平分∠ABC,AF⊥BF,D为AB中点,连接DF并延长交AC与点E,若AB=12,BC=20,则线段EF的长为()A.3B.4C.5D.64.如图,四边形ABCD中,∠A=90°,AB=12,AD=5,点M、N分别为线段BC、AB 上的动点(含端点,但点M不与点B重合),点E、F分别为DM、MN的中点,则EF 长度的可能为()A.2B.5C.7D.95.如图,在四边形ABCD中,已知AB=CD,M、N、P分别是AD、BC、BD的中点∠ABD =20°,∠BDC=70°,则∠NMP的度数为()A.50°B.25°C.15°D.206.数学课上,大家一起研究三角形中位线定理的证明小丽和小亮在学习思考后各自尝试作了一种辅助线,如图1,2.其中辅助线作法能够用来证明三角形中位线定理的是()A.小丽和小亮的辅助线作法都可以B.小丽和小亮的输助线作法都不可以C.小丽的辅助线作法可以,小亮的不可以D.小亮的辅助线作法可以,小丽的不可以7.如图,四边形ABCD中,AC⊥BC,AD∥BC,BC=3,AC=4,AD=6.M是BD的中点,则CM的长为()A.B.2C.D.38.如图,四边形ABCD中,AB∥CD,AB=5,DC=11,AD与BC的和是12,点E、F、G分别是BD、AC、DC的中点,则△EFG的周长是()A.8B.9C.10D.129.如图,在△ABC中,BC=6,E,F分别是AB,AC的中点,动点P在射线EF上,BP 交CE于点D,∠CBP的平分线交CE于点Q,当CQ=CE时,EP+BP的值为()A.6B.9C.12D.1810.已知△ABC的周长为1,连接其三边中点构成第二个三角形,再连接第二个三角形的中点构成第三个三角形,则第三个三角形的周长为()A.B.C.D.二.填空题(共10小题)11.如图,在△ABC中,AB=3,AC=5,点D,E,F分别是AB,BC,AC的中点,则四边形ADEF的周长为.12.若D,E,F分别为△ABC各边的中点,且△DEF的周长为9,则△ABC的周长为.13.如图,在△ABC中,D,E分别是AB,AC的中点,F是线段DE上一点,连接AF,BF,若AB=16,EF=1,∠AFB=90°,则BC的长为.14.若等腰三角形的两条中位线长为2和4,则其周长为.15.如图,A、B两点被池塘隔开,不能直接测量其距离.于是,小明另选一点C(C可直达A、B),连接CA,CB,分别取BC、AC的中点D、E,测得DE=60m,则A、B间的距离为m.16.如图:在△ABC中,AB=13,BC=12,点D,E分别是AB,BC的中点,连接DE,CD,如果DE=2.5,那么△ACD的周长是.17.如图,为测量池塘边上两点A,B之间的距离,小明在池塘的一侧选取一点O,取OA,OB的中点D,E,测出DE=12米,那么A,B两点之间的距离是.18.如图,在△ABC中,已知BC=12,AC=14,点M、N、P分别是AB、BC、AC的中点,则四边形MNCP的周长为.19.如图,在△ABC中,AB=5,AC=3,AD是角平分线,AE是中线,过点C作CG⊥AD 于点F,交AB于点G,连接EF,则线段EF的长为.20.如图,EF为△ABC的中位线,BD平分∠ABC,交EF于D,AB=8,BC=12,则DF 的长为.三.解答题(共8小题)21.叙述并证明三角形中位线定理.22.已知:如图,在四边形ABCD中,对角线AC、BD相交于点O,且AC=BD,E、F分别是AB、CD的中点,EF分别交BD、AC于点G、H.求证:OG=OH.23.如图,已知△ABC内部有一点O,连结BO、CO,D、G、E、F分别是AB、AC、BO、CO的中点,连结DG、GF、EF、DE.(1)求证:四边形DEFG是平行四边形;(2)若图中AO⊥BC,则▱DEFG是形.(不用证明)24.(1)如图1,在四边形ABCD中,E、F分别是BC、AD的中点,连接EF并延长,分别与BA、CD的延长线交于点M、N,则∠BME=∠CNE,求证:AB=CD.(提示取BD 的中点H,连接FH,HE作辅助线)(2)如图2,在△ABC中,且O是BC边的中点,D是AC边上一点,E是AD的中点,直线OE交BA的延长线于点G,若AB=DC=5,∠OEC=60°,求OE的长度.25.如图,在四边形ABCD中,对角线AC、BD交于点O,E、F分别是AB、CD的中点,且AC=BD.求证:OM=ON.26.已知:△ABC中,D是AB的中点,E是AC的中点,证明:DE∥BC,DE=BC.27.(1)请你在△ABC中做一条线段,把△ABC分成面积相等的两部分.(2)请你按照(1)的方法把四边形ABCD分成面积相等的两部分.(3)请你观察下图,尝试在梯形ABCD中做一条线段,把梯形ABCD分成面积相等的两部分.28.已知:如图,在△ABC中,DE是中位线,EF∥AB,EF交BC于点F.求证:F是BC 的中点.参考答案与试题解析一.选择题(共10小题)1.如图:在△ABC中,AB=25,BC=24,点D,E分别是AB,BC的中点,连接DE,CD,如果DE=3.5,那么△ACD的周长是()A.28B.28.5C.32D.36【解答】解:∵D,E分别是AB,BC的中点,∴AC=2DE=7,AC∥DE,AC2+BC2=72+242=625,AB2=252=625,∴AC2+BC2=AB2,∴∠ACB=90°,∵AC∥DE,∴∠DEB=90°,又∵E是BC的中点,∴直线DE是线段BC的垂直平分线,∴DC=BD,∴△ACD的周长=AC+AD+CD=AC+AD+BD=AC+AB=32,故选:C.2.如图,以任意△ABC的边AB和AC向形外作等腰Rt△ABD和等腰Rt△ACE,F、G分别是线段BD和CE的中点,则的值等于()A.B.C.D.【解答】解:如图,取BC的中点H,连接BE、FH、GH,∵∠BAD=∠CAE=90°,∴∠BAD+∠BAC=∠CAE+∠BAC,即∠BAE=∠DAC,在△ABE和△ADC中,,∴△ABE≌△ADC(SAS),∴BE=CD,∠ABE=∠ADC,∴∠BDC+∠DBE=∠BDA+∠ABD=90°,∴BE⊥CD,又∵F、G分别是线段BD和CE的中点,∴FH、GH分别是△BCD和△BCE的中位线,∴FH∥CD且FH=CD,GH∥BE且GH=BE,∴△HFG是等腰直角三角形,∴=,∴=.故选:B.3.如图,在△ABC中,BF平分∠ABC,AF⊥BF,D为AB中点,连接DF并延长交AC与点E,若AB=12,BC=20,则线段EF的长为()A.3B.4C.5D.6【解答】解:∵AF⊥BF,D为AB的中点,∴DF=DB=AB=6,∴∠DBF=∠DFB,∵BF平分∠ABC,∴∠DBF=∠CBF,∴∠DFB=∠CBF,∴DE∥BC,∴DE为△ABC的中位线,∴DE=BC=10,∴EF=DE﹣DF=10﹣6=4,故选:B.4.如图,四边形ABCD中,∠A=90°,AB=12,AD=5,点M、N分别为线段BC、AB 上的动点(含端点,但点M不与点B重合),点E、F分别为DM、MN的中点,则EF 长度的可能为()A.2B.5C.7D.9【解答】解:连接DN,∵ED=EM,MF=FN,∴EF=DN,∴DN最大时,EF最大,DN最小时,EF最小,∵N与B重合时DN最大,此时DN=DB===13,∴EF的最大值为6.5.∵∠A=90°,AD=5,∴DN≥5,∴EF≥2.5,∴EF长度的可能为5;故选:B.5.如图,在四边形ABCD中,已知AB=CD,M、N、P分别是AD、BC、BD的中点∠ABD =20°,∠BDC=70°,则∠NMP的度数为()A.50°B.25°C.15°D.20【解答】解:∵在四边形ABCD中,M、N、P分别是AD、BC、BD的中点,∴PN,PM分别是△CDB与△DAB的中位线,∴PM=AB,PN=DC,PM∥AB,PN∥DC,∵AB=CD,∴PM=PN,∴△PMN是等腰三角形,∵PM∥AB,PN∥DC,∴∠MPD=∠ABD=20°,∠BPN=∠BDC=70°,∴∠MPN=∠MPD+∠NPD=20°+(180﹣70)°=130°,∴∠PMN==25°.故选:B.6.数学课上,大家一起研究三角形中位线定理的证明小丽和小亮在学习思考后各自尝试作了一种辅助线,如图1,2.其中辅助线作法能够用来证明三角形中位线定理的是()A.小丽和小亮的辅助线作法都可以B.小丽和小亮的输助线作法都不可以C.小丽的辅助线作法可以,小亮的不可以D.小亮的辅助线作法可以,小丽的不可以【解答】解:小丽:如图1,延长DE到F,使FE=DE,连接CF,AF,FC,∵AE=EC,∴四边形ADCF是平行四边形,∴AD=CF,AD∥CF,∵AD=BD,∴BD=CF,BD∥CF,∴四边形DBCF是平行四边形,∴DF∥BC,DF=BC,∴DE∥BC,DE=DF=BC;小亮:如图2,过点E作EG∥AB,过点A作AF∥BC,AF与GE交于点F,∴∠EAF=∠C,∠F=∠CGF,在△AEF和△CGF中,,∴△AEF≌△CEG(AAS),∴AF=CG,EF=EG,∵AF∥BG,AB∥FG,∴四边形ABGF是平行四边形,∴AB=FG,∵BD=AB,GE=FG,∴BD=EG,∵BD∥EG,∴四边形DBGE是平行四边形,∴DE∥BG,DE=BG,∴DE∥BC,DE=BC,∴小丽和小亮的辅助线作法都可以,故选:A.7.如图,四边形ABCD中,AC⊥BC,AD∥BC,BC=3,AC=4,AD=6.M是BD的中点,则CM的长为()A.B.2C.D.3【解答】解:延长BC到E使BE=AD,则四边形ACED是平行四边形,∵BC=3,AD =6,∴C是BE的中点,∵M是BD的中点,∴CM=DE=AB,∵AC⊥BC,∴AB===5,∴CM=,故选:C.8.如图,四边形ABCD中,AB∥CD,AB=5,DC=11,AD与BC的和是12,点E、F、G分别是BD、AC、DC的中点,则△EFG的周长是()A.8B.9C.10D.12【解答】解:连接AE,并延长交CD于K,∵AB∥CD,∴∠BAE=∠DKE,∠ABD=∠EDK,∵点E、F、G分别是BD、AC、DC的中点.∴BE=DE,在△AEB和△KED中,,∴△AEB≌△KED(AAS),∴DK=AB,AE=EK,EF为△ACK的中位线,∴EF=CK=(DC﹣DK)=(DC﹣AB),∵EG为△BCD的中位线,∴EG=BC,又FG为△ACD的中位线,∴FG=AD,∴EG+GF=(AD+BC),∵AD+BC=12,AB=5,DC=11,即DC﹣AB=6,∴EG+GF=6,FE=3,∴△EFG的周长是6+3=9.故选:B.9.如图,在△ABC中,BC=6,E,F分别是AB,AC的中点,动点P在射线EF上,BP 交CE于点D,∠CBP的平分线交CE于点Q,当CQ=CE时,EP+BP的值为()A.6B.9C.12D.18【解答】解:如图,延长BQ交射线EF于M,∵E、F分别是AB、AC的中点,∴EF∥BC,∴∠M=∠CBM,∵BQ是∠CBP的平分线,∴∠PBM=∠CBM,∴∠M=∠PBM,∴BP=PM,∴EP+BP=EP+PM=EM,∵CQ=CE,∴EQ=2CQ,由EF∥BC得,△MEQ∽△BCQ,∴=2,∴EM=2BC=2×6=12,即EP+BP=12.故选:C.10.已知△ABC的周长为1,连接其三边中点构成第二个三角形,再连接第二个三角形的中点构成第三个三角形,则第三个三角形的周长为()A.B.C.D.【解答】解:∵△ABC的周长是1,∴第二个三角形的周长=,第三个三角形的周长=×=,故选:C.二.填空题(共10小题)11.如图,在△ABC中,AB=3,AC=5,点D,E,F分别是AB,BC,AC的中点,则四边形ADEF的周长为8.【解答】解:∵BD=AD,BE=EC,∴DE=AC=2.5,DE∥AC,∵CF=F A,CE=BE,∴EF=AB=1.5,EF∥AB,∴四边形ADEF是平行四边形,∴四边形ADEF的周长=2(DE+EF)=8.故答案为:812.若D,E,F分别为△ABC各边的中点,且△DEF的周长为9,则△ABC的周长为18.【解答】解:∵D,E,F分别为△ABC各边的中点,∴DE、EF、DF是△ABC的中位线,∴DE=BC,EF=AB,DF=AC,∴△ABC的周长=2△DEF的周长=2×9=18.故答案为:18.13.如图,在△ABC中,D,E分别是AB,AC的中点,F是线段DE上一点,连接AF,BF,若AB=16,EF=1,∠AFB=90°,则BC的长为18.【解答】解:∵∠AFB=90°,点D是AB的中点,∴DF=AB=8,∵EF=1,∴DE=9,∵D、E分别是AB,AC的中点,∴BC=2DE=18,故答案为:1814.若等腰三角形的两条中位线长为2和4,则其周长为20.【解答】解:∵等腰三角形的两条中位线长分别为2和4,∴等腰三角形的两边长为4,8,当腰为4时,则三边长为4,4,8,构不成三角形;当腰为8时,则三边长为4,8,8;周长为20;故答案是:20.15.如图,A、B两点被池塘隔开,不能直接测量其距离.于是,小明另选一点C(C可直达A、B),连接CA,CB,分别取BC、AC的中点D、E,测得DE=60m,则A、B间的距离为120m.【解答】解:∵D,E分别是CA,CB的中点,∴AB=2DE=120m,故答案为:120.16.如图:在△ABC中,AB=13,BC=12,点D,E分别是AB,BC的中点,连接DE,CD,如果DE=2.5,那么△ACD的周长是18.【解答】解:∵D,E分别是AB,BC的中点,∴AC=2DE=5,AC∥DE,AC2+BC2=52+122=169,AB2=132=169,∴AC2+BC2=AB2,∴∠ACB=90°,∵AC∥DE,∴∠DEB=90°,又∵E是BC的中点,∴直线DE是线段BC的垂直平分线,∴DC=BD,∴△ACD的周长=AC+AD+CD=AC+AD+BD=AC+AB=18,故答案为:18.17.如图,为测量池塘边上两点A,B之间的距离,小明在池塘的一侧选取一点O,取OA,OB的中点D,E,测出DE=12米,那么A,B两点之间的距离是24米.【解答】解:∵D、E分别为OA、OB的中点,∴DE为△OAB的中位线,∴AB=2DE=24米,故答案为:24米18.如图,在△ABC中,已知BC=12,AC=14,点M、N、P分别是AB、BC、AC的中点,则四边形MNCP的周长为26.【解答】解:∵点M、N分别是AB、BC的中点,AC=14,∴MN是△ABC的中位线,MN=AC=7,MN∥AC,同理,MP是△ABC的中位线,∴MP=BC=6,MP∥BC,∴四边形MNCP是平行四边形,∴四边形MNCP的周长=2(MP+MN)=26.故答案为:26.19.如图,在△ABC中,AB=5,AC=3,AD是角平分线,AE是中线,过点C作CG⊥AD于点F,交AB于点G,连接EF,则线段EF的长为1.【解答】解:∵AD是其角平分线,CG⊥AD于F,∴△AGC是等腰三角形,∴AG=AC=3,GF=CF,∵AB=5,AC=3,∴BG=2,∵AE是中线,∴BE=CE,∴EF为△CBG的中位线,∴EF=BG=1故答案为:120.如图,EF为△ABC的中位线,BD平分∠ABC,交EF于D,AB=8,BC=12,则DF 的长为2.【解答】解:∵EF为△ABC的中位线,∴EF∥BC,EF=BC=6,∴∠EDB=∠DBC,∵BD平分∠ABC,∴∠EBD=∠DBC,∴∠EDB=∠EBD,∴ED=EB=AB=4,∴DF=EF﹣ED=2,故答案为:2.三.解答题(共8小题)21.叙述并证明三角形中位线定理.【解答】已知:△ABC中,点E、F分别是AB、AC的中点,求证:三角形的中位线平行于第三边并且等于第三边的一半,证明:如图,延长EF到D,使FD=EF,∵点F是AC的中点,∴AF=CF,在△AEF和△CDF中,,∴△AEF≌△CDF(SAS),∴AE=CD,∠D=∠AEF,∴AB∥CD,∵点E是AB的中点,∴AE=BE,∴BE=CD,∴BE CD,∴四边形BCDE是平行四边形,∴DE∥BC,DE=BC,∴DE∥BC且DE=BC.22.已知:如图,在四边形ABCD中,对角线AC、BD相交于点O,且AC=BD,E、F分别是AB、CD的中点,EF分别交BD、AC于点G、H.求证:OG=OH.【解答】解:取BC边的中点M,连接EM,FM,∵M、F分别是BC、CD的中点,∴MF∥BD,MF=BD,同理:ME∥AC,ME=AC,∵AC=BD∴ME=MF∴∠MEF=∠MFE,∵MF∥BD,∴∠MFE=∠OGH,同理,∠MEF=∠OHG,∴∠OGH=∠OHG∴OG=OH.23.如图,已知△ABC内部有一点O,连结BO、CO,D、G、E、F分别是AB、AC、BO、CO的中点,连结DG、GF、EF、DE.(1)求证:四边形DEFG是平行四边形;(2)若图中AO⊥BC,则▱DEFG是矩形.(不用证明)【解答】(1)证明:∵点D、G分别是AB、AC的中点,∴DG是△ABC的一条中位线,∴DG BC.同理可证,EF BC,∴DG EF,∴四边形DEFG是平行四边形;(2)解:∵如图,D、E分别是AB、BO的中点,∴DE是△ABO的中位线,∴DE∥AH.又EF∥BC,AH⊥BC,∴DE⊥EF,∴▱DEFG是矩形.故填:矩.24.(1)如图1,在四边形ABCD中,E、F分别是BC、AD的中点,连接EF并延长,分别与BA、CD的延长线交于点M、N,则∠BME=∠CNE,求证:AB=CD.(提示取BD 的中点H,连接FH,HE作辅助线)(2)如图2,在△ABC中,且O是BC边的中点,D是AC边上一点,E是AD的中点,直线OE交BA的延长线于点G,若AB=DC=5,∠OEC=60°,求OE的长度.【解答】(1)证明:连结BD,取DB的中点H,连结EH、FH.∵E、F分别是BC、AD的中点,∴EH∥AB,EH=AB,FH∥CD,FH=CD,∵∠BME=∠CNE,∴HE=HF,∴AB=CD;(2)解:连结BD,取DB的中点H,连结EH、OH,∵AB=CD,∴HO=HE,∴∠HOE=∠OEC,∵∠OEC=60°,∴∠HEO=∠AGO=60°,∴△OEH是等边三角形,∵AB=DC=5,∴OE=.25.如图,在四边形ABCD中,对角线AC、BD交于点O,E、F分别是AB、CD的中点,且AC=BD.求证:OM=ON.【解答】证明:取AD的中点G,连接EG,FG,∵G、F分别为AD、CD的中点,∴GF是△ACD的中位线,∴GF=AC,同理可得,GE=BD,∵AC=BD,∴GF=GE=AC=BD.∴∠GFN=∠GEM,又∵EG∥OM,FG∥ON,∴∠OMN=∠GEM=∠GFN=∠ONM,∴OM=ON.26.已知:△ABC中,D是AB的中点,E是AC的中点,证明:DE∥BC,DE=BC.【解答】证明:延长DE至F,使EF=DE,连接CF∵E是AC中点,∴AE=CE,在△ADE和△CFE中,,∴△ADE≌△CFE(SAS),∴AD=CF,∠ADE=∠F∴BD∥CF,∵AD=BD,∴BD=CF∴四边形BCFD是平行四边形(一组对边平行且相等的四边形是平行四边形)∴DF∥BC,DF=BC,∴BE∥CB,DE=BC.27.(1)请你在△ABC中做一条线段,把△ABC分成面积相等的两部分.(2)请你按照(1)的方法把四边形ABCD分成面积相等的两部分.(3)请你观察下图,尝试在梯形ABCD中做一条线段,把梯形ABCD分成面积相等的两部分.【解答】解:(1)取BC的中点D,AD为BC的中线,则BD=CD根据同底等高的三角形面积相等,得S△ABD=S△ACD(2)连接AC,再取AC的中点E,连接BE与DE,∴S△ADE=S△CDE,S△ABE=S△BCE,∴S△ADE+S△ABE=S△CDE+S△BCE,∴S四边形ABED=S四边形BCDE;(3)连接AC、BD交于点G,取BC的中点E,连接EG交AD于点F,∵四边形ABCD是梯形,∴AD∥BC,∴△GBC∽△GDA,∴F为AD中点,根据同底等高的三角形面积相等,△ABC的面积等于△BCD的面积,△AGF的面积等于△DGF的面积,△BGE的面积等于△CGE的面积,于是△ABG的面积等于△GCD的面积,故S△AGF+S△ABG+S△BEG=S△DGF+S△GCD+S△CGE,于是S ABEF=S DCEF.28.已知:如图,在△ABC中,DE是中位线,EF∥AB,EF交BC于点F.求证:F是BC 的中点.【解答】证明:如图,∵在△ABC中,DE是中位线,∴点E是AC的中点.又∵EF∥AB,∴EF是△ABC的中位线,∴点F是BC的中点。
鲁教版数学八年级上5.3《三角形的中位线》测试(含答案及解析)

鲁教版数学八年级上5.3《三角形的中位线》测试(含答案及解析)1.2.如图,已知△ABC的周长为1,连接△ABC的三边的中点构成第二个三角形,再连接第二个三角形三边的中点构成第三个三角形…依此类推,则第2019个三角形的周长为()A.12014B.12015C. (12)2014 D. (12)20153.如图,在△ABC中,AB=3,BC=6,AC= 4,点D,E分别是边AB,CB的中点,那么DE的长为()A. 1.5B. 2C. 3D. 44.如图,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,且AB=10,BC=15,MN=3,则AC的长是()A. 12B. 14C. 165.如图:P为△ABC边AB上一点且AP:BP=1:2,E、F分别是PB,PC的中点,△ABC、△PEF的面积分别为S和S1,则S 和S1的关系式()A. S1=13S B. S1=14S C. S1=23S D. S1=16S6.如图,△ABC中,M是BC中点,AD平分∠BAC,BD⊥AD于D,延长交AC于N,若AB=10,AC=16,则MD的长为()A. 5B. 4C. 3D. 27.如图,Rt△ABC中,∠ACB=90∘,斜边AB=9,D为AB的中点,F为CD上一点,且CF=13CD,过点B作BE//DC交AF的延长线于点E,则BE的长为()B. 4C. 7D. 128.直角三角形两条边长分别是6和8,则连接两条直角边中点的线段长是()A. 3B. 5C. 4或5D. 5或39.如图,点D、E分别是边AB、AC的中点,将△ADE沿着DE对折,点A落在BC边上的点F,若∠B=50∘,则∠BDF的度数为()A. 50∘B. 70∘C. 75∘D. 80∘二、填空题(本大题共10小题,共30.0分)10.如图,在△ABC中,点D,点E分别是AB,AC的中点,点F是DE上一点,∠AFC=90∘,BC=10cm,AC=6cm,则DF=______cm.11.如图,Rt△ABC中,∠ACB=90∘,AB=6,点D是AB的中点,过AC的中点E作EF//CD交AB于点F,则EF=______.12.如图,在△ABC中,M、N分别为AC,BC的中点.若S△CMN=1,则S=______.四边形ABNM13.如图,在Rt△ABC中,∠A=90∘,AB=AC,BC=20,DE是△ABC的中位线,点M是边BC上一点,BM=3,点N是线段MC上的一个动点,连接DN,ME,DN 与ME相交于点O.若△OMN是直角三角形,则DO的长是______.14.如图,在△ABC中,∠ACB=90∘,M、N分别是AB、AC的中点,延长BC至BD,连接点D,使CD=13DM、DN、MN.若AB=6,则DN=______.15.如图,Rt△ABC中,∠C=90∘,BC=6,AC=8,D、E分别为AC、AB的中点,连接DE,则△ADE的面积是______.16.如图,在图(1)中,A1、B1、C1分别是△ABC的边BC、CA、AB的中点,在图(2)中,A2、B2、C2分别是△A1B1C1的边B1C1、C1A1、A1B1的中点,…,按此规律,则第n 个图形中平行四边形的个数共有______个.17.如图,在Rt△ABC中,∠C=90∘,D为AB的中点,E为AC的中点,∠A=30∘,AB=12,则DE的长度是______.18.如图,在△ABC中,BF平分∠ABC,AF⊥BF于点F,D为AB的中点,连结DF并延长交AC于点E.若AB=8,BC=12,则线段EF的长为______ .19.如图,∠ACB=90∘,D为AB中点,连CD,过点B 接DC并延长到点E,使CE=14作BF//DE交AE的延长线于点F,若BF= 10,则AB的长为____.三、计算题(本大题共5小题,共40.0分)20.如图是屋架设计图的一部分,其中∠A= 30∘,点D是斜梁AB的中点,BC、DE垂直于横梁AC,AB=8m,则立柱BC,DE 要多长?21.(8分)已知:如图,中,,点D、E分别是AC、AB的中点,点F在BC的延长线上,且.求证:四边形DECF是平行四边形.22.已知与都为等腰直角三角形,.连接GD、CF,N为线段GD 的中点,连接.(1)求证:(2)求证:23.如图,△ABC中,AD是高,E、F分别是AB、AC的中点.(1)若AB=10,AC=8,求四边形AEDF的周长;(2)EF与AD有怎样的位置关系?请证明你的结论.24.如图,在△ABC中,BC>AC,点D在BC上,且DC=AC,∠ACB的平分线CF交AD于F,点E是AB的中点,连结EF.(1)求证:EF//BC.(2)若四边形BDFE的面积为6,求△ABD的面积.答案和解析【答案】1. B2. A3. C4. B5. C6. D7. C8. A9. C10. D11. 212. 1.513. 314. 256或501315. 316. 617. 3n18. 319. 220. 821. 解:∵BC⊥AF,∠A=30∘,∴BC=12AB=4m,∵BC、DE垂直于横梁AC,∴DE//BC,又D是AB的中点,BC=2m,∴DE=12答:立柱BC要4m,DE要2m.22. 证明:因为D和E都是中点所以DE是中位线,所以DE//BCCE=AE=BE(直角三角形斜边的中线等于斜边的一半)所以∠A=∠ACE又因为∠A=∠CDF所以∠CDF=∠ACE所以DF//CE所以四边形DECF是平行四边形。
鲁教版2020八年级数学上册5.3三角形的中位线培优练习题4(附答案)

鲁教版2020八年级数学上册5.3三角形的中位线培优练习题4(附答案)一.选择题(共10小题)1.如图,四边形ABCD中,点E、F、G、H分别是线段AB、CD、AC、BD的中点,则四边形EGFH的周长()A.只与AB、CD的长有关B.只与AD、BC的长有关C.只与AC、BD的长有关D.与四边形ABCD各边的长都有关.2.如图,在△ABC中,D是BC边的中点,AE是∠BAC的角平分线,AE⊥CE于点E,连接DE.若AB=7,DE=1,则AC的长度是()A.5B.4C.3D.23.如图,要测定被池塘隔开的A、B两点的距离,可以在AB外选一点C,连接AC、BC,并分别找出它们的中点D、E,连接DE.现测得AC=30m,BC=40m,DE=24m,则AB=()A.35m B.45m C.48m D.50m4.如图,在Rt△ABC中,∠C=90°,∠A=30°,AB=16,E为AC中点,DE∥BC,D 为AB上的点,则DE的长度为()A.2B.4C.6D.85.如图,△A1B1C1中,A1B1=4,A1C1=5,B1C1=7.点A2、B2、C2分别是边B1C1、A1C1、A1B1的中点;点A3、B3、C3分别是边B2C2、A2C2、A2B2的中点;……;以此类推,则第2018个三角形的周长是()A.B.C.D.6.已知△ABC的周长为1,连接其三边中点构成第二个三角形,再连接第二个三角形的中点构成第三个三角形,以此类推,则第2018个三角形的周长为()A.B.C.D.7.如图所示,点D,E,F分别是△ABC(AB>AC)各边的中点,下列说法错误()A.AD=BC B.EF=BCC.EF与AD互相平分D.△DEF的面积是△ABC面积的8.如图,AD、BE分别是△ABC的中线和角平分线,AD⊥BE,AD=BE=4,过点D作DF ∥BE交AC于F,则EF的长等于()A.2B.3C.D.9.如图,在△ABC中,D,E分别是AB,AC的中点,AC=10,F是DE上一点,连接AF,CF,DF=1.若∠AFC=90°,则BC的长度为()A.10B.12C.14D.1610.如图,△ABC的周长为a,以它的各边的中点为顶点作△A1B1C1,再以△AB1C1各边的中点为顶点作△A2B2C2,再以△AB2C2各边的中点为顶点作△A3B3C3,…如此下去,则△AB n∁n的周长为()A.a B.a C.a D.a二.填空题(共10小题)11.在四边形ABCD中,对角线AC⊥BD且AC=4,BD=8,E、F分别是边AB、CD的中点,则EF=.12.如图,DE是△ABC的中位线,F是DE的中点,CF的延长线交AB于G,AB=6,则AG=.13.如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D是线段AB上的动点,M、N分别是AD、CD的中点,连接MN,当点D由点A向点B运动的过程中,线段MN所扫过的区域的面积为.14.如图,若等腰三角形的底边上的高等于18cm,腰上的中线等于15cm,则这个等腰三角形的面积等于.15.如图,已知在△ABC中,D、E分别是AB、AC的中点,BC=6cm,则DE的长度是cm.16.如图,在四边形ABCD中,DC∥AB,CB⊥AB,AB=AD=a,CD=,点E,F分别为线段AB,AD的中点,则EF=.17.点D、E、F分别为△ABC三边的中点,若△DEF的周长为3,则△ABC的周长为.18.如图,△ABC中,D,E分别是AB,AC的点,连线DE,若DE=3,DE∥BC,,则线段BC的长等于.19.如图,点D、E分别为△ABC的边AB、AC的中点,同时,点F在DE上,且∠AFB=90°,已知AB=5,BC=8,那么EF的长为.20.如图,在△ABC中,点D,E分别是AB,AC的中点,若BC=10,则DE=.三.解答题(共8小题)21.如图,△ABC的三边长分别是AB=14,BC=16,AC=26,P为∠A的平分线AD上一点,且BP⊥AD,M为BC的中点,求PM的长.22.已知BE、CF分别为△ABC中∠B、∠C的平分线,AM⊥BE于M,AN⊥CF于N.求证:MN∥BC.23.如图,点D、E、F是△ABC各边的中点,已知△ABC的面积是16.分别求出△DBF 和△DEF的面积?24.如图,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,延长BN交AC 于点D,已知AB=10,BC=15,MN=3(1)求证:BN=DN;(2)求△ABC的周长.25.如图,在△ABC中,AD平分∠BAC,交BC于点D,BE⊥AD,交AD的延长线于点E,BF=EF.求证:EF∥AC.26.如图,△ABC的三边长分别为a,b,c,以它的三边中点为顶点组成一个新三角形,以这个新三角形三边中点为顶点又组成一个小三角形,求这个小三角形的周长.27.补全图形并写出下列命题的已知、求证,完成证明过程.命题:三角形的中位线平行于第三边,并且等于第三边的一半.已知:如图,.求证:.证明:28.如图,M、N分别为AD、BC的中点,且AB=CD,求证:∠1=∠2.参考答案与试题解析一.选择题(共10小题)1.如图,四边形ABCD中,点E、F、G、H分别是线段AB、CD、AC、BD的中点,则四边形EGFH的周长()A.只与AB、CD的长有关B.只与AD、BC的长有关C.只与AC、BD的长有关D.与四边形ABCD各边的长都有关.【解答】解:∵点E、F、G、H分别是线段AB、CD、AC、BD的中点,∴四边形EGFH的周长=FG+GE+EH+FH=,故选:B.2.如图,在△ABC中,D是BC边的中点,AE是∠BAC的角平分线,AE⊥CE于点E,连接DE.若AB=7,DE=1,则AC的长度是()A.5B.4C.3D.2【解答】解:延长CE,交AB于点F.∵AE平分∠BAC,AE⊥CE,∴∠EAF=∠EAC,∠AEF=∠AEC,在△EAF与△EAC中,,∴△EAF≌△EAC(ASA),∴AF=AC,EF=EC,又∵D是BC中点,∴BD=CD,∴DE是△BCF的中位线,∴BF=2DE=2.∴AC=AF=AB﹣BF=7﹣2=5;故选:A.3.如图,要测定被池塘隔开的A、B两点的距离,可以在AB外选一点C,连接AC、BC,并分别找出它们的中点D、E,连接DE.现测得AC=30m,BC=40m,DE=24m,则AB=()A.35m B.45m C.48m D.50m【解答】解:∵D是AC的中点,E是BC的中点,∴DE是△ABC的中位线,∴DE=AB,∵DE=24m,∴AB=2DE=48m,故选:C.4.如图,在Rt△ABC中,∠C=90°,∠A=30°,AB=16,E为AC中点,DE∥BC,D 为AB上的点,则DE的长度为()A.2B.4C.6D.8【解答】解:∵在Rt△ABC中,∠C=90°,∠A=30°,AB=16,∴BC=AB=8.∵D为AB的中点,E为AC的中点,∴DE是△ABC的中位线,∴DE=BC=4.故选:B.5.如图,△A1B1C1中,A1B1=4,A1C1=5,B1C1=7.点A2、B2、C2分别是边B1C1、A1C1、A1B1的中点;点A3、B3、C3分别是边B2C2、A2C2、A2B2的中点;……;以此类推,则第2018个三角形的周长是()A.B.C.D.【解答】解:∵△A1B1C1中,A1B1=4,A1C1=5,B1C1=7,∴△A1B1C1的周长是16,∵A2,B2,C2分别是边B1C1,A1C1,A1B1的中点,∴B2C2,A2C2,A2B2分别等于A1B1、B1C1、C1A1的,…,以此类推,则△A4B4C4的周长是×16=2;∴△A n B n∁n的周长是,当n=2018时,第2018个三角形的周长==故选:A.6.已知△ABC的周长为1,连接其三边中点构成第二个三角形,再连接第二个三角形的中点构成第三个三角形,以此类推,则第2018个三角形的周长为()A.B.C.D.【解答】解:∵连接其三边中点构成第二个三角形,∴第二个三角形与第一个三角形相似,且相似比为1:2,∴第二个三角形的周长为=,同理,第三个三角形周长为=,∴第2018个三角形的周长为=,故选:C.7.如图所示,点D,E,F分别是△ABC(AB>AC)各边的中点,下列说法错误()A.AD=BCB.EF=BCC.EF与AD互相平分D.△DEF的面积是△ABC面积的【解答】解:A、由于点D是BC的中点,所以BD=BC,只有当BD=AD=CD时,结论AD=BC成立,故本选项符合题意.B、根据中位线定理,EF=BC.故本选项不符合题意;C、根据中位线定理,AF∥ED,AE∥FD,四边形AEDF为平行四边形,对角线EF与AD互相平分.故正确;D、因为△DFE和△ABC的各边对应成比例,为1:2,而且每组对应点所在的直线都经过同一个点,对应边互相平行,是位似图形.故选:A.8.如图,AD、BE分别是△ABC的中线和角平分线,AD⊥BE,AD=BE=4,过点D作DF ∥BE交AC于F,则EF的长等于()A.2B.3C.D.【解答】解:∵DF∥BE,AD是△ABC的中线,∴DF=BE=2,∵AD⊥BE,DF=2,AD=4,∴AF=,∴EF=,故选:C.9.如图,在△ABC中,D,E分别是AB,AC的中点,AC=10,F是DE上一点,连接AF,CF,DF=1.若∠AFC=90°,则BC的长度为()A.10B.12C.14D.16【解答】解:如图,∵∠AFC=90°,AE=CE,∴EF=AC=5,∴DE=1+5=6;∵D,E分别是AB,AC的中点,∴DE为△ABC的中位线,∴BC=2DE=12,故选:B.10.如图,△ABC的周长为a,以它的各边的中点为顶点作△A1B1C1,再以△AB1C1各边的中点为顶点作△A2B2C2,再以△AB2C2各边的中点为顶点作△A3B3C3,…如此下去,则△AB n∁n的周长为()A.a B.a C.a D.a【解答】解:∵以△ABC的各边的中点为顶点作△A1B1C1,∴△A1B1C1的周长=△AB1C1的周长=△ABC的周长=a,∵以△AB1C1各边的中点为顶点作△A2B2C2,∴△A2B2C2的周长=△AB2C2各的周长=△AB1C1的周长=a=a,…,∴△AB n∁n的周长=a故选:A.二.填空题(共10小题)11.在四边形ABCD中,对角线AC⊥BD且AC=4,BD=8,E、F分别是边AB、CD的中点,则EF=2.【解答】解:如图,取BC的中点G,连接EG、FG,∵E、F分别是边AB、CD的中点,∴EG∥AC且EG=AC=×4=2,FG∥BD且FG=BD=×8=4,∵AC⊥BD,∴EG⊥FG,∴EF=.故答案为:212.如图,DE是△ABC的中位线,F是DE的中点,CF的延长线交AB于G,AB=6,则AG=2.【解答】解:过E作EM∥AB与GC交于点M,∴△EMF≌△DGF,∴EM=GD,∵DE是中位线,∴CE=AC,又∵EM∥AG,∴△CME∽△CGA,∴EM:AG=CE:AC=1:2,又∵EM=GD,∴AG:GD=2:1.∵AB=6,∴AD=3,∴AG=,故答案为:213.如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D是线段AB上的动点,M、N分别是AD、CD的中点,连接MN,当点D由点A向点B运动的过程中,线段MN所扫过的区域的面积为12.【解答】解:分别取△ABC三边AC,AB,BC的中点E,F,G,并连接EG,FG,根据题意可得线段MN扫过区域的面积就是▱AFGE的面积,∵AC=6,BC=8,∴AE=AC=3,GC=BC=4,∵∠ACB=90°,∴S四边形AFGE=AE•GC=3×4=12,∴线段MN所扫过区域的面积为12,故答案为:12.14.如图,若等腰三角形的底边上的高等于18cm,腰上的中线等于15cm,则这个等腰三角形的面积等于144.【解答】解:作MN⊥BC于N,∵AM=MC,MN∥AD,∴DN=NC.∴,在Rt△BMN中,BM=15,MN=9.∴BN=12,而BD=DC=2DN,∴3DN=12,DN=4,∴BC=16,S△ABC=AD•BC=×18×16=144.15.如图,已知在△ABC中,D、E分别是AB、AC的中点,BC=6cm,则DE的长度是3 cm.【解答】解:∵D、E分别是AB、AC的中点,∴DE是△ABC的中位线,∴DE=BC=3cm,故答案为:3.16.如图,在四边形ABCD中,DC∥AB,CB⊥AB,AB=AD=a,CD=,点E,F分别为线段AB,AD的中点,则EF=.【解答】解:连接DE,∵四边形ABCD为直角梯形,AB=AD=a,CD=,CB⊥AB,点E,F分别为线段AB,AD的中点∴△AED为直角三角形.则EF是Rt△AED斜边上的中线,由直角三角形斜边上的中线等于斜边的一半得,EF=DE=AB=.故答案为:17.点D、E、F分别为△ABC三边的中点,若△DEF的周长为3,则△ABC的周长为6.【解答】解:∵D、E、F分别为△ABC三边的中点,∴DE、DF、EF都是△ABC的中位线,∴BC=2DF,AC=2DE,AB=2EF,故△ABC的周长=AB+BC+AC=2(DF+FE+DE)=6.故答案为:6.18.如图,△ABC中,D,E分别是AB,AC的点,连线DE,若DE=3,DE∥BC,,则线段BC的长等于9.【解答】解:∵DE∥BC,∴△ADE∽△ABC,∴,∴BC=3×3=9,故答案为:919.如图,点D、E分别为△ABC的边AB、AC的中点,同时,点F在DE上,且∠AFB=90°,已知AB=5,BC=8,那么EF的长为 1.5.【解答】解:∵DE是△ABC的中位线,∴DE=BC=4.∵∠AFB=90°,D是AB的中点,∴DF=AB=2.5,∴EF=DE﹣DF=4﹣2.5=1.5.故答案为:1.5.20.如图,在△ABC中,点D,E分别是AB,AC的中点,若BC=10,则DE=5.【解答】解:∵点D,E分别是AB,AC的中点,∴DE=BC=5,故答案为:5.三.解答题(共8小题)21.如图,△ABC的三边长分别是AB=14,BC=16,AC=26,P为∠A的平分线AD上一点,且BP⊥AD,M为BC的中点,求PM的长.【解答】解:延长BP交AC于点E,∵AD为∠BAC的平分线,∴∠BAP=∠EAP,∵BP⊥AD于D,∴∠APB=∠APE=90°,在△APB和△APE中,,∴△APB≌△APE(ASA),∴AB=AE=14,∵AC=26,∴EC=26﹣14=12,∵△APB≌△APE,∴BP=EP,∵M是BC的中点,∴PM=EC=×12=6.22.已知BE、CF分别为△ABC中∠B、∠C的平分线,AM⊥BE于M,AN⊥CF于N.求证:MN∥BC.【解答】证明:延长AM、AN分别交BC于点D、G.∵BE为∠ABC的角平分线,BE⊥AG,∴∠BAG=∠BGA,∴△ABG为等腰三角形,∴BM也为等腰三角形的中线,即AM=GM.同理AN=DN,∴MN为△ADG的中位线,∴MN∥BC.23.如图,点D、E、F是△ABC各边的中点,已知△ABC的面积是16.分别求出△DBF 和△DEF的面积?【解答】解:∵点D,F分别是△ABC的三边AB,BC上的中点,∴DF∥AC,DF=AC.∴△DBF∽△ABC,且相似比为.∴S△DBF=S△ABC=×16=4;∵D、E、F分别是△ABC的边AB、BC、AC的中点,∴DE=AC,DF=BC,EF=AB,∴△DEF∽△ABC相似,相似比是,S△DEF=S△ABC=×16=4.综上所述,△DBF和△DEF的面积都是4.24.如图,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,延长BN交AC 于点D,已知AB=10,BC=15,MN=3(1)求证:BN=DN;(2)求△ABC的周长.【解答】(1)证明:∵AN平分∠BAC∴∠1=∠2∵BN⊥AN∴∠ANB=∠AND=90°在△ABN和△ADN中,∵,∴△ABN≌△ADN(ASA),∴BN=DN.(2)解:∵△ABN≌△ADN,∴AD=AB=10,又∵点M是BC中点,∴MN是△BDC的中位线,∴CD=2MN=6,故△ABC的周长=AB+BC+CD+AD=10+15+6+10=41.25.如图,在△ABC中,AD平分∠BAC,交BC于点D,BE⊥AD,交AD的延长线于点E,BF=EF.求证:EF∥AC.【解答】证明:∵BF=EF,∴∠BEF=∠EBF,∵BE⊥AD,∴∠EAF+∠EBF=∠AEF+∠BEF,∴∠EAF=∠AEF,∵AD平分∠BAC,∴∠EAF=∠CAD,∴∠AEF=∠CAD,∴EF∥AC.26.如图,△ABC的三边长分别为a,b,c,以它的三边中点为顶点组成一个新三角形,以这个新三角形三边中点为顶点又组成一个小三角形,求这个小三角形的周长.【解答】解:由题意得,这个小三角形的周长=×(a+b+c)=(a+b+c).27.补全图形并写出下列命题的已知、求证,完成证明过程.命题:三角形的中位线平行于第三边,并且等于第三边的一半.已知:如图,在△ABC中,点D、E分别是AB,AC的中点.求证:DE∥BC,DE=BC.证明:【解答】已知:如图,在△ABC中,点D、E分别是AB,AC的中点.求证:DE∥BC,DE=BC.证明:延长DE到点F,使EF=DE,连接CF.∵点E是AC中点,∴AE=EC.∵在△AED和△CEF中,∴△AED≌△CEF(SAS).∴AD=CF,∠A=∠ECF,∴AB∥CF.∵点D是AB中点,∴AD=BD.∴BD=CF.∴四边形BDFC是平行四边形.∴DE∥BC,DF=BC.∴DE=DF=BC.28.如图,M、N分别为AD、BC的中点,且AB=CD,求证:∠1=∠2.【解答】证明:连接AC,取AC的中点G,连接NG和MG.∵G是AC的中点,M是BC的中点,即MG是△ABC的中位线,∴MG=AB,且MG∥AB.∴∠2=∠NMG,同理,GN=CD,NG∥CD,∴∠1=∠MNG,又∵AB=CD,∴MG=NG,∴∠MNG=∠NMG,∴∠1=∠2.。
鲁教版八年级数学上册5.3三角形的中位线能力提升练习题3(附答案)

鲁教版八年级数学上册5.3三角形的中位线能力提升练习题3(附答案)一.选择题(共10小题)1.如图,在△ABC中,D,E分别是AB,AC的中点,AC=10,F是DE上一点,连接AF,CF,DF=1.若∠AFC=90°,则BC的长度为()A.10B.12C.14D.162.如图,△ABC的周长为a,以它的各边的中点为顶点作△A1B1C1,再以△AB1C1各边的中点为顶点作△A2B2C2,再以△AB2C2各边的中点为顶点作△A3B3C3,…如此下去,则△AB n∁n的周长为()A.a B.a C.a D.a3.如图,在四边形ABCD中,AD=BC,E,F,G分别是AB,CD,AC的中点,若∠DAC =20°,∠ACB=84°,则∠FEG等于()A.32°B.38°C.64°D.30°4.如图,△ABC的周长为32,点D,E都在边BC上,∠ABC的平分线垂直于AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P,若BC=12,则PQ的长为()A.2B.3C.4D.55.如图,在△ABC中,点D、E分别是AB、AC的中点,BC=6,则DE的长为()A.2B.3C.4D.56.如图,EF为△ABC的中位线,∠B=50°,则∠EFC为()A.40°B.45°C.50°D.55°7.如图,△ABC中,AB>AC,AD,AE分别是其角平分线和中线,过点C作CG⊥AD于点F,交AB于点G,连接EF,则①EF∥AB;②∠BCG=(∠ACB﹣∠ABC);③EF =(AB﹣AC);④(AB﹣AC)<AE<(AB+AC).其中正确的是()A.①②③④B.①②C.②③④D.①③④8.如图,△ABC中,D是AB的中点,DE∥BC,连接BE.若AE=6,DE=5,∠BEC=90°,则△BCE的周长是()A.12B.24C.36D.489.如图,△ABC和△DBC均为等腰三角形,∠A=60°,∠D=90°,AB=12,若点E、F、G、H分别为边AB、AC、CD、BD的中点,则四边形EFGH的面积为()A.36(+1)B.18(+1)C.12(+1)D.9(+1)10.如图在四边形ABCD中,AB<CD,∠B=∠C=90°,点H,I,G分别是AD,AB,CD的中点,点P是BC边上的一动点(不与B,C重合),点E,F分别是BP,CP的中点,则当点P从B→C移动时,五边形EFGHI的面积会()A.一直增大B.保持不变C.一直减小D.先增大后减小二.填空题(共10小题)11.如图,在Rt△ABC中,∠B=90°,AB=2,BC=3,D、E分别是AB、AC的中点,延长BC至点F,使CF=BC,连接DF、EF,则EF的长为.12.如图,在四边形ABCD中,AB=2,CD=6,E,F,M分别为边BC,AD和对角线BD 的中点.连结EF,FM,则FM=;线段EF的最大值为.13.如图,∠MAN=90°,点C在边AM上,AC=2,点B为边AN上一动点,连接BC,△A′BC与△ABC关于BC所在的直线对称,点D,E分别为AB,BC的中点,连接DE并延长交A′C所在直线于点F,连接A′E,当△A′EF为直角三角形时,AB的长为.14.如图,在△ABC中,AB=13,BC=12,点D,E分别是AB,BC的中点,连接DE,CD,如果DE=2.5,那么CD的长是.15.如图,点D、E、F分别是△ABC的边AB、BC、CA的中点,连接DE、EF、FD得△DEF,如果△ABC的周长是48cm,那么△DEF的周长是.16.如图,平行四边形ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO 的中点.若AC+BD=24厘米,△OAB的周长是20厘米,则EF=厘米.17.如图,已知EF是△ABC的中位线,DE⊥BC交AB于点D,CD与EF交于点G,若CD⊥AC,EF=9,EG=4,则AC的长为.18.如图,已知点D、E、F分别是AB、BC、CD的中点,S△DEF=cm2,则S△ABC=cm2.19.已知△ABC的3条中位线分别为3cm、4cm、5 cm,则△ABC的周长为cm.20.如图,∠MAN=90°,点C在边AM上,AC=4,点B为边AN上一动点,连接BC,△A′BC与△ABC关于BC所在直线对称,点D,E分别为AC,BC的中点,连接DE 并延长交A′B所在直线于点F,连接A′E.当△A′EF为直角三角形时,AB的长为.三.解答题(共8小题)21.在△ABC中,点D、E、F分别是BC、AB、AC边的中点.求证:△BED≌△DFC.22.如图,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=5cm,BC=8cm,求EF的长.23.如图,在四边形ABCD中,E、F分别是AD、BC的中点,连接FE并延长,分别交CD 的延长线于点M、N,∠BME=∠CNE,求证:AB=CD.24.如图,在△ABC中,∠ABC=90°,AB=BC,BD⊥AC于点D;CE平分∠ACB,交AB于点E,交BD于点F.(1)求证:△BEF是等腰三角形;(2)求证:BD=(BC+BF).25.如图,在△ABC中,AB=6cm,AC=10cm,AD平分∠BAC,BD⊥AD于点D,BD的延长线交AC于点F,E为BC的中点,求DE的长.26.如图,△ABC的中线AD与中位线MN相交于点O.AD与MN有怎样的关系?证明你的结论.27.如图,△ABC中,过点A分别作∠ABC,∠ACB的外角的平分线的垂线AD,AE.D,E为垂足,求证:(1)ED∥BC;(2)ED=(AB+AC+BC).28.如图,DE是△ABC的中位线,求证:DE∥BC,且DE=BC.参考答案与试题解析一.选择题(共10小题)1.如图,在△ABC中,D,E分别是AB,AC的中点,AC=10,F是DE上一点,连接AF,CF,DF=1.若∠AFC=90°,则BC的长度为()A.10B.12C.14D.16【解答】解:如图,∵∠AFC=90°,AE=CE,∴EF=AC=5,∴DE=1+5=6;∵D,E分别是AB,AC的中点,∴DE为△ABC的中位线,∴BC=2DE=12,故选:B.2.如图,△ABC的周长为a,以它的各边的中点为顶点作△A1B1C1,再以△AB1C1各边的中点为顶点作△A2B2C2,再以△AB2C2各边的中点为顶点作△A3B3C3,…如此下去,则△AB n∁n的周长为()A.a B.a C.a D.a【解答】解:∵以△ABC的各边的中点为顶点作△A1B1C1,∴△A1B1C1的周长=△AB1C1的周长=△ABC的周长=a,∵以△AB1C1各边的中点为顶点作△A2B2C2,∴△A2B2C2的周长=△AB2C2各的周长=△AB1C1的周长=a=a,…,∴△AB n∁n的周长=a故选:A.3.如图,在四边形ABCD中,AD=BC,E,F,G分别是AB,CD,AC的中点,若∠DAC =20°,∠ACB=84°,则∠FEG等于()A.32°B.38°C.64°D.30°【解答】解:∵AD=BC,E,F,G分别是AB,CD,AC的中点,∴GF是△ACD的中位线,GE是△ACB的中位线,∴GF=AD,GF∥AD,GE=BC,GE∥BC.又∵AD=BC,∴GF=GE,∠FGC=∠DAC=20°,∠AGE=∠ACB=84°,∴∠EFG=∠FEG,∵∠FGE=∠FGC+∠EGC=20°+(180°﹣84°)=116°,∴∠EFG=(180°﹣∠FGE)=32°.故选:A.4.如图,△ABC的周长为32,点D,E都在边BC上,∠ABC的平分线垂直于AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P,若BC=12,则PQ的长为()A.2B.3C.4D.5【解答】解:∵BQ平分∠ABC,BQ⊥AE,∴∠ABQ=∠EBQ,∵∠ABQ+∠BAQ=90°,∠EBQ+∠BEQ=90°,∴∠BAQ=∠BEQ,∴AB=BE,同理:CA=CD,∴点Q是AE中点,点P是AD中点(三线合一),∴PQ是△ADE的中位线,∵BE+CD=AB+AC=32﹣BC=32﹣12=20,∴DE=BE+CD﹣BC=8,∴PQ=DE=4.故选:C.5.如图,在△ABC中,点D、E分别是AB、AC的中点,BC=6,则DE的长为()A.2B.3C.4D.5【解答】解:∵D,E分别是边AB、AC的中点,∴CB=2DE,∵BC=6,∴DE=3.故选:B.6.如图,EF为△ABC的中位线,∠B=50°,则∠EFC为()A.40°B.45°C.50°D.55°【解答】解:∵EF是中位线,∴DE∥AB,∴∠EFC=∠B=50°,故选:C.7.如图,△ABC中,AB>AC,AD,AE分别是其角平分线和中线,过点C作CG⊥AD于点F,交AB于点G,连接EF,则①EF∥AB;②∠BCG=(∠ACB﹣∠ABC);③EF =(AB﹣AC);④(AB﹣AC)<AE<(AB+AC).其中正确的是()A.①②③④B.①②C.②③④D.①③④【解答】解:∵AD平分∠BAC,∴∠GAF=∠CAF,∵CG⊥AD,∴∠AFG=∠AFC=90°,在△AFG和△AFC中∴△AFG≌△AFC(ASA),∴GF=CF,∵AE为△ABC的中线,∴BE=CE,∴EF∥AB,故①正确;∵△AFG≌△AFC,∴∠AGC=∠ACG,∠AGF=∠ACF,∵∠AGC=∠B+∠BCG,∴∠ACG=∠B+∠BCG,∴∠BCG=∠ACB﹣∠ACG=∠ACB﹣(∠B+∠BCG),∴2∠BCG=∠ACB﹣∠B,∴∠BCG=(∠ACB﹣∠B),故②正确;∵△AFG≌△AFC,∴AC=AG,∴BG=AB﹣AG=AB﹣AC,∵F、E分别是CG、BC的中点,∴EF=BG,∴EF=(AB﹣AC),故③正确;∵∠AFG=90°,∴∠EAF<90°,∵∠AFE=∠AFG+∠EFG>90°,∴∠AFE>∠EAF,∴AE>EF,∵EF=(AB﹣AC),∴(AB﹣AC)<AE,延长AE到M,使AE=EM,连接BM,∵在△ACE和△MBE中∴△ACE≌△MBE(SAS),∴AC=MB,在△ABM中,AM<AB+MB=AB+AC,∵AE=EM,∴2AE<AB+AC,∴AE<(AB+AC),即(AB﹣AC)<AE<(AB+AC),故④正确;故选:A.8.如图,△ABC中,D是AB的中点,DE∥BC,连接BE.若AE=6,DE=5,∠BEC=90°,则△BCE的周长是()A.12B.24C.36D.48【解答】解:∵D是AB的中点,DE∥BC,∴DE是△ABC的中位线.∴点E是AC中点,∴CE=AE=6.∵DE=5,∴BC=10.∵∠BEC=90°,∴△BCE是直角三角形,∴根据勾股定理得,BE=8,∴△BCE的周长为BC+CE+BE=10+6+8=24.故选:B.9.如图,△ABC和△DBC均为等腰三角形,∠A=60°,∠D=90°,AB=12,若点E、F、G、H分别为边AB、AC、CD、BD的中点,则四边形EFGH的面积为()A.36(+1)B.18(+1)C.12(+1)D.9(+1)【解答】解:∵△ABC和△DBC均为等腰三角形,∠A=60°,∠D=90°,∴△ABC是等边三角形,△DBC等腰直角三角形,∵AB=12,∴BC=12,∴BD=6,连接AD交BC于O,∵AB=AC,BD=CD,∴AD⊥BC,BO=CO,∴AD=AO+OD=6+6,∵点E、F、G、H分别为边AB、AC、CD、BD的中点,∴EH∥AD,EH=AD,FG∥AD,FG=AD,∴EH∥FG,EH=FG,∴四边形EFGH是平行四边形,∵AD⊥BC,∴EH⊥BD,HG⊥AD,∴EH⊥HG,∴∠EHG=90°,∴四边形EFGH是矩形,∵EH=AD=3+3,HG=BC=6,∴四边形EFGH的面积=18(+1),故选:B.10.如图在四边形ABCD中,AB<CD,∠B=∠C=90°,点H,I,G分别是AD,AB,CD的中点,点P是BC边上的一动点(不与B,C重合),点E,F分别是BP,CP的中点,则当点P从B→C移动时,五边形EFGHI的面积会()A.一直增大B.保持不变C.一直减小D.先增大后减小【解答】解:连接IG,如图所示:则S△IHG的值不变,设BP=x,则BE=x,CF=(BC﹣x),S△BIE=BI•BE=BI×x=x•BI,S△FCG=CG•CF=CG×(BC﹣x)=CG•BC﹣x•CG,∵在四边形ABCD中,AB<CD,∠B=∠C=90°,点I,G分别是AB,CD的中点,∴CG>BI,四边形IBCG是梯形,∴S梯形IBCG=•BC=BC•BI+BC•CG,S四边形IEFG=S梯形IBCG﹣S△BIE﹣S△FCG=BC•BI+BC•CG﹣x•BI﹣CG•BC+x•CG =(2BI+CG)BC+(CG﹣BI)x,∵(2BI+CG)BC是定值,CG>BI,∴S四边形IEFG随x值的增大而增大,∵S△IHG的值不变,∴S五边形EFGHI随x值的增大而增大,即当点P从B→C移动时,五边形EFGHI的面积会一直增大;故选:A.二.填空题(共10小题)11.如图,在Rt△ABC中,∠B=90°,AB=2,BC=3,D、E分别是AB、AC的中点,延长BC至点F,使CF=BC,连接DF、EF,则EF的长为.【解答】解:连接DE,CD,∵D、E分别是AB、AC的中点,∴DE∥BC,DE=BC,∴DE∥CF,∵CF=BC,∴DE=CF,∴四边形DCFE是平行四边形,∴EF=CD,∵在Rt△ABC中,∠B=90°,AB=2,BC=3,∴CD===,∴EF=CD=,故答案为:.12.如图,在四边形ABCD中,AB=2,CD=6,E,F,M分别为边BC,AD和对角线BD 的中点.连结EF,FM,则FM=1;线段EF的最大值为4.【解答】解:连接EM,∵E,F,M分别为边BC,AD和对角线BD的中点,∴FM=,EM=,当EF=EM+MF时,线段EF最大,即EF=1+3=4,故答案为:1;4.13.如图,∠MAN=90°,点C在边AM上,AC=2,点B为边AN上一动点,连接BC,△A′BC与△ABC关于BC所在的直线对称,点D,E分别为AB,BC的中点,连接DE 并延长交A′C所在直线于点F,连接A′E,当△A′EF为直角三角形时,AB的长为或2.【解答】解:当△A′EF为直角三角形时,存在两种情况:①当∠A'EF=90°时,如图1,∵△A′BC与△ABC关于BC所在直线对称,∴A'C=AC=2,∠ACB=∠A'CB,∵点D,E分别为AB,BC的中点,∴D、E是△ABC的中位线,∴DE∥AB,∴∠BDE=∠MAN=90°,∴∠BDE=∠A'EF,∴AB∥A'E,∴∠ABC=∠A'EB,∴∠A'BC=∠A'EB,∴A'B=A'E,Rt△A'CB中,∵E是斜边BC的中点,∴BC=2A'E,由勾股定理得:AB2=BC2﹣AC2,∴AE′=,∴AB=;②当∠A'FE=90°时,如图2,∵∠ADF=∠A=∠DFC=90°,∴∠ACF=90°,∵△A′BC与△ABC关于BC所在直线对称,∴∠ABC=∠CBA'=45°,∴△ABC是等腰直角三角形,∴AB=AC=2;综上所述,AB的长为或2;故答案为:或2.14.如图,在△ABC中,AB=13,BC=12,点D,E分别是AB,BC的中点,连接DE,CD,如果DE=2.5,那么CD的长是 6.5.【解答】解:∵D,E分别是AB,BC的中点,∴AC=2DE=5,AC∥DE,AC2+BC2=52+122=169,AB2=132=169,∴AC2+BC2=AB2,∴∠ACB=90°,∵AC∥DE,∴∠DEB=90°,又∵E是BC的中点,∴直线DE是线段BC的垂直平分线,∴DC=BD=AB=6.5,故答案是:6.5.15.如图,点D、E、F分别是△ABC的边AB、BC、CA的中点,连接DE、EF、FD得△DEF,如果△ABC的周长是48cm,那么△DEF的周长是24cm.【解答】解:∵D、E分别是△ABC的边AB、BC的中点,∴DE=AC,同理,EF=AB,DF=BC,∴C△DEF=DE+EF+DF=AC+BC+AB=(AC+BC+AC)=×48=24cm.故答案为:24cm16.如图,平行四边形ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO 的中点.若AC+BD=24厘米,△OAB的周长是20厘米,则EF=4厘米.【解答】解:∵▱ABCD的对角线AC,BD相交于点O,∴点O是AC、BD的中点,∵AC+BD=24厘米,∴OB+0A=(AC+BD)=12厘米,∵△OAB的周长是20厘米,∴AB=20﹣12=8厘米,∵▱ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点,∴EF=AB=4厘米,故答案为:4.17.如图,已知EF是△ABC的中位线,DE⊥BC交AB于点D,CD与EF交于点G,若CD⊥AC,EF=9,EG=4,则AC的长为6.【解答】解:∵EF是△ABC的中位线,∴AB=2EF=18,EF∥AB,AF=CF,CE=BE,∴G是CD的中点,∴GE是△BCD的中位线,∴BD=2EG=8,∴AD=AB﹣BD=10,∵DE⊥BC,CE=BE,∴CD=BD=8,∵CD⊥AC,∴∠ACD=90°,∴AC===6;故答案为:6.18.如图,已知点D、E、F分别是AB、BC、CD的中点,S△DEF=cm2,则S△ABC=4 cm2.【解答】解:∵F为CD中点,∴DF=FC,∴S△DEF=S△EFC,同理:S△DEC=S△BDE,S△ADC=S△BCD,∴S△ABC=8S△DEF=8×=4.故答案为4.19.已知△ABC的3条中位线分别为3cm、4cm、5 cm,则△ABC的周长为24cm.【解答】解:∵△ABC的3条中位线分别为3cm、4cm、5 cm,∴△ABC的3条边长分别为6cm、8cm、10 cm,∴△ABC的周长=6+8+10=24cm.故答案为:24.20.如图,∠MAN=90°,点C在边AM上,AC=4,点B为边AN上一动点,连接BC,△A′BC与△ABC关于BC所在直线对称,点D,E分别为AC,BC的中点,连接DE 并延长交A′B所在直线于点F,连接A′E.当△A′EF为直角三角形时,AB的长为4或4.【解答】解:当△A′EF为直角三角形时,存在两种情况:①当∠A'EF=90°时,如图1,∵△A′BC与△ABC关于BC所在直线对称,∴A'C=AC=4,∠ACB=∠A'CB,∵点D,E分别为AC,BC的中点,∴D、E是△ABC的中位线,∴DE∥AB,∴∠CDE=∠MAN=90°,∴∠CDE=∠A'EF,∴AC∥A'E,∴∠ACB=∠A'EC,∴∠A'CB=∠A'EC,∴A'C=A'E=4,Rt△A'CB中,∵E是斜边BC的中点,∴BC=2A'E=8,由勾股定理得:AB2=BC2﹣AC2,∴AB==4;②当∠A'FE=90°时,如图2,∵∠ADF=∠A=∠DFB=90°,∴∠ABF=90°,∵△A′BC与△ABC关于BC所在直线对称,∴∠ABC=∠CBA'=45°,∴△ABC是等腰直角三角形,∴AB=AC=4;综上所述,AB的长为4或4;故答案为:4或4;三.解答题(共8小题)21.在△ABC中,点D、E、F分别是BC、AB、AC边的中点.求证:△BED≌△DFC.【解答】证明:∵点D、E分别是BC、AB的中点,∴ED∥AC,ED=AC,∴∠EDB=∠C.又∵F是AC边的中点,∴FC=AC,∴DE=FC,同理可得,∠B=∠FDC,在△EBD和△FDC中,∵,∴△BED≌△DFC(AAS).22.如图,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=5cm,BC=8cm,求EF的长.【解答】解:∵DE为△ABC的中位线,BC=8cm,∴DE=BC=4cm,∵∠AFB=90°,D为AB的中点,∴DF=AB=2.5cm,∴EF=DE﹣DF=1.5cm.23.如图,在四边形ABCD中,E、F分别是AD、BC的中点,连接FE并延长,分别交CD 的延长线于点M、N,∠BME=∠CNE,求证:AB=CD.【解答】证明:连接BD,取BD的中点G,连接EG、FG.∵点E、G分别为AD、BD的中点,∴GE为△ABD的中位线,∴GE=AB;同理可证:GF=CD;∵GE为△ABD的中位线,∴GE∥MB,∴∠GEF=∠BMF;同理可证:∠GFE=∠CNE;∵∠BME=∠CNE,∴∠GEF=∠GFE,∴GE=GF,∴AB=CD.24.如图,在△ABC中,∠ABC=90°,AB=BC,BD⊥AC于点D;CE平分∠ACB,交AB于点E,交BD于点F.(1)求证:△BEF是等腰三角形;(2)求证:BD=(BC+BF).【解答】证明:(1)在△ABC中,AB=BC,BD⊥AC于点D,∴∠ABD=∠CBD,AD=CD,∵∠ABC=90°,∴∠ACB=45°,∵CE平分∠ACB,∴∠ECB=∠ACE=22.5°,∴∠BEF=∠CFD=∠BFE=67.5°,∴BE=BF,∴△BEF是等腰三角形;(2)如图,延长AB至M,使得BM=AB,连接CM,∵D是AC的中点,∴BD∥MC,BD=MC,∴∠BFE=∠MCE,由(1)得,∠BEF=∠BFE,BE=BF,∴∠BEF=∠MCE,∴ME=MC,∴BD=MC=ME=(MB+BE)=(BC+BF).25.如图,在△ABC中,AB=6cm,AC=10cm,AD平分∠BAC,BD⊥AD于点D,BD的延长线交AC于点F,E为BC的中点,求DE的长.【解答】解:∵AD平分∠BAC,BD⊥AD,∴AB=AF=6,BD=DF,∴CF=AC﹣AF=4,∵BD=DF,E为BC的中点,∴DE=CF=2.26.如图,△ABC的中线AD与中位线MN相交于点O.AD与MN有怎样的关系?证明你的结论.【解答】解:AD与MN互相平分.理由如下:∵MN是中位线,AD为中线,∴M、D、N分别为AB、BC、AC的中点,∴DM∥AN,DN∥AM,∴四边形AMDN为平行四边形,∴AD与MN互相平分.27.如图,△ABC中,过点A分别作∠ABC,∠ACB的外角的平分线的垂线AD,AE.D,E为垂足,求证:(1)ED∥BC;(2)ED=(AB+AC+BC).【解答】证明:(1)分别延长AD、AE与直线BC交于点F、G,∵AD⊥BD,∴∠ADB=∠FDB=90°,∵BD=BD,∠ABD=∠FBD,∴△ABD≌△FBD∴AD=FD,同理可得AE=EG,∴DE∥BC;(2)由(1)知△ABD≌△FBD,∴AB=BF,同理AC=CG,∵DE=FG∴GF=FB+BC+GC=AB+BC+AC,∴DE=(AB+BC+AC)28.如图,DE是△ABC的中位线,求证:DE∥BC,且DE=BC.【解答】证明:延长DE到Q,使DE=EQ,连接CQ,∵AE=EC,∠AED=∠CEQ,DE=EQ,∴△ADE≌△CQE,∴AD=CQ,∠A=∠ACQ,∴AB∥CQ,∵AD=BD,∴BD=CQ,∴四边形DBCQ是平行四边形,∴DQ=BC,DQ∥BC,∴DE∥BC,DE=BC.。
鲁教版八年级数学上册5.3三角形的中位线能力提升练习题(附答案)

鲁教版八年级数学上册5.3三角形的中位线能力提升练习题(附答案)一.选择题(共10小题)1.如图,在△ABC中,BC=15,B1、B2、…B9、C1、C2、…C9分别是AB、AC的10等分点,则B1C1+B2C2+…+B9C9的值是()A.45B.55C.67.5D.1352.如图,在△ABC中,BD、CE分别是∠ABC和∠ACB的平分线,AM⊥CE于P,交BC 于M,AN⊥BD于Q,交BC于N,∠BAC=110°,AB=6,AC=5,MN=2,结论①AP =MP;②BC=9;③∠MAN=35°;④AM=AN.其中不正确的有()A.4个B.3个C.2个D.1个3.如图:在△ABC中,AB=25,BC=24,点D,E分别是AB,BC的中点,连接DE,CD,如果DE=3.5,那么△ACD的周长是()A.28B.28.5C.32D.364.如图,以任意△ABC的边AB和AC向形外作等腰Rt△ABD和等腰Rt△ACE,F、G分别是线段BD和CE的中点,则的值等于()A.B.C.D.5.如图,在△ABC中,BF平分∠ABC,AF⊥BF,D为AB中点,连接DF并延长交AC与点E,若AB=12,BC=20,则线段EF的长为()A.3B.4C.5D.66.如图,四边形ABCD中,∠A=90°,AB=12,AD=5,点M、N分别为线段BC、AB 上的动点(含端点,但点M不与点B重合),点E、F分别为DM、MN的中点,则EF 长度的可能为()A.2B.5C.7D.97.如图,在四边形ABCD中,已知AB=CD,M、N、P分别是AD、BC、BD的中点∠ABD =20°,∠BDC=70°,则∠NMP的度数为()A.50°B.25°C.15°D.208.数学课上,大家一起研究三角形中位线定理的证明小丽和小亮在学习思考后各自尝试作了一种辅助线,如图1,2.其中辅助线作法能够用来证明三角形中位线定理的是()A.小丽和小亮的辅助线作法都可以B.小丽和小亮的输助线作法都不可以C.小丽的辅助线作法可以,小亮的不可以D.小亮的辅助线作法可以,小丽的不可以9.如图,四边形ABCD中,AC⊥BC,AD∥BC,BC=3,AC=4,AD=6.M是BD的中点,则CM的长为()A.B.2C.D.310.如图,四边形ABCD中,AB∥CD,AB=5,DC=11,AD与BC的和是12,点E、F、G分别是BD、AC、DC的中点,则△EFG的周长是()A.8B.9C.10D.12二.填空题(共10小题)11.如图,在△ABC中,点D是AB的中点,DE∥BC交AC于点E,若BC=2,则DE的长是.12.如图,DE是△ABC的中位线,若△ADE的面积为1,则四边形DBCE的面积为.13.如图,小慧与小聪玩跷跷板,跷跷板支架EF的高为0.4米,E是AB的中点,那么小慧能将小聪翘起的最大高度BC等于米.14.如图,在△ABC中,D为BC边中点,P为AC边中点,E为BC上一点且BE=CE,连接AE,取AE中点Q并连接QD,取QD中点G,延长PG与BC边交于点H,若BC =6,则HE=.15.如图,△ABC中,点E,F分别是AB,AC的中点,BC=EG.若AC=BC=10,AB=16,则四边形AECG的面积是.16.连接三角形各边中点所得的三角形面积与原三角形面积之比为:.17.如图,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=5,BC=8,则EF的长为.18.如图,△ABC的周长为17,点D,E在边BC上,∠ABC的平分线垂直于AE,垂足为点N,∠ACB的平分线垂直于AD,垂足为点M,若BC=6,则MN的长度为.19.如图,点A(0,4)、B(2,0),点C、D分别是OA、AB的中点,在射线CD上有一动点P,若△ABP是直角三角形,则点P的坐标为.20.如图,△ABC中,M、N分别为AC,BC的中点,若S△CMN=2,则S四边形ABNM=.三.解答题(共8小题)21.如图,在△ABC中,∠CAB=90°,DE、DF是△ABC的中位线,连接EF、AD,求证:EF=AD.22.如图,证明定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半.已知:点D、E分别是△ABC的边AB、AC的中点.求证:DE∥BC,DE=BC.23.如图,在△ABC中,AB=AC,点D,E分别是边AB,AC的中点,连接DE、BE,点F,G,H分别为BE,DE,BC的中点.(1)求证:FG=FH;(2)若∠A=90°,求证:FG⊥FH;(3)若∠A=80°,求∠GFH的度数.24.证明:三角形的一条中位线与第三边上的中线互相平分.已知:如图,DE是△ABC的中位线,AF是△ABC的中线,AF、DE交于点O.求证:.证明:.25.如图,在△RtABC中,∠ACB=90°,DE、DF是△ABC的中位线,连接EF、CD,求证:CD=EF.26.如图,在△ABC中,D,E分别是AB,AC的中点,△ABC的角平分线AG交DE于点F,若∠ABC=70°,∠BAC=54°,求∠AFD的度数.27.(1)计算:(1﹣)0﹣|﹣2|+;(2)如图,在等边三角形ABC中,点D,E分别是边BC,AC的中点,过点E作EF⊥DE,交BC的延长线于点F,求∠F的度数.28.如图,在边长为4的等边△ABC中,D、E分别为AB、BC的中点,EF⊥AC于点F,G为EF的中点,连接DG.(1)求EF的长.(2)求DG的长.参考答案与试题解析一.选择题(共10小题)1.如图,在△ABC中,BC=15,B1、B2、…B9、C1、C2、…C9分别是AB、AC的10等分点,则B1C1+B2C2+…+B9C9的值是()A.45B.55C.67.5D.135【解答】解:当B1、C1是AB、AC的中点时,B1C1=BC;当B1,B2,C1,C2分别是AB,AC的三等分点时,B1C1+B2C2=BC+BC;…当B1,B2,C1,…,∁n分别是AB,AC的n等分点时,B1C1+B2C2+…+B n﹣1B n﹣1=BC+BC+…+BC=BC=7.5(n﹣1);当n=10时,7.5(n﹣1)=67.5;故B1C1+B2C2+…+B9C9的值是67.5.故选:C.2.如图,在△ABC中,BD、CE分别是∠ABC和∠ACB的平分线,AM⊥CE于P,交BC 于M,AN⊥BD于Q,交BC于N,∠BAC=110°,AB=6,AC=5,MN=2,结论①AP =MP;②BC=9;③∠MAN=35°;④AM=AN.其中不正确的有()A.4个B.3个C.2个D.1个【解答】解:①∵CE平分∠ACE,∴∠ACP=∠MCP,∵AM⊥CE,∴∠APC=∠MPC=90°,∴∠CAM=∠CMA,∴AC=CM,∴AP=PM,①正确;②同理得:BN=AB=6,∵CM=AC=5,∴BC=BN+CM﹣MN=6+5﹣2=9,②正确;③∵∠BAC=∠MAC+∠BAN﹣∠MAN=110°,由①知:∠CMA=∠CAM,∠BNA=∠BAN,△AMN中,∠CMA+∠BNA=180°﹣∠MAN=∠BAN+∠MAC,∴180°﹣∠MAN﹣∠MAN=110°,∴∠MAN=35°,③正确;④当∠AMN=∠ANM时,AM=AN,∵AB=6≠AC=5∴∠ABC≠∠ACB,∴∠AMN≠∠ANM,则AM与AN不相等,④不正确;所以本题不正确的有④,故选:D.3.如图:在△ABC中,AB=25,BC=24,点D,E分别是AB,BC的中点,连接DE,CD,如果DE=3.5,那么△ACD的周长是()A.28B.28.5C.32D.36【解答】解:∵D,E分别是AB,BC的中点,∴AC=2DE=7,AC∥DE,AC2+BC2=72+242=625,AB2=252=625,∴AC2+BC2=AB2,∴∠ACB=90°,∵AC∥DE,∴∠DEB=90°,又∵E是BC的中点,∴直线DE是线段BC的垂直平分线,∴DC=BD,∴△ACD的周长=AC+AD+CD=AC+AD+BD=AC+AB=32,故选:C.4.如图,以任意△ABC的边AB和AC向形外作等腰Rt△ABD和等腰Rt△ACE,F、G分别是线段BD和CE的中点,则的值等于()A.B.C.D.【解答】解:如图,取BC的中点H,连接BE、FH、GH,∵∠BAD=∠CAE=90°,∴∠BAD+∠BAC=∠CAE+∠BAC,即∠BAE=∠DAC,在△ABE和△ADC中,,∴△ABE≌△ADC(SAS),∴BE=CD,∠ABE=∠ADC,∴∠BDC+∠DBE=∠BDA+∠ABD=90°,∴BE⊥CD,又∵F、G分别是线段BD和CE的中点,∴FH、GH分别是△BCD和△BCE的中位线,∴FH∥CD且FH=CD,GH∥BE且GH=BE,∴△HFG是等腰直角三角形,∴=,∴=.故选:B.5.如图,在△ABC中,BF平分∠ABC,AF⊥BF,D为AB中点,连接DF并延长交AC与点E,若AB=12,BC=20,则线段EF的长为()A.3B.4C.5D.6【解答】解:∵AF⊥BF,D为AB的中点,∴DF=DB=AB=6,∴∠DBF=∠DFB,∵BF平分∠ABC,∴∠DBF=∠CBF,∴∠DFB=∠CBF,∴DE∥BC,∴DE为△ABC的中位线,∴DE=BC=10,∴EF=DE﹣DF=10﹣6=4,故选:B.6.如图,四边形ABCD中,∠A=90°,AB=12,AD=5,点M、N分别为线段BC、AB 上的动点(含端点,但点M不与点B重合),点E、F分别为DM、MN的中点,则EF 长度的可能为()A.2B.5C.7D.9【解答】解:连接DN,∵ED=EM,MF=FN,∴EF=DN,∴DN最大时,EF最大,DN最小时,EF最小,∵N与B重合时DN最大,此时DN=DB===13,∴EF的最大值为6.5.∵∠A=90°,AD=5,∴DN≥5,∴EF≥2.5,∴EF长度的可能为5;故选:B.7.如图,在四边形ABCD中,已知AB=CD,M、N、P分别是AD、BC、BD的中点∠ABD =20°,∠BDC=70°,则∠NMP的度数为()A.50°B.25°C.15°D.20【解答】解:∵在四边形ABCD中,M、N、P分别是AD、BC、BD的中点,∴PN,PM分别是△CDB与△DAB的中位线,∴PM=AB,PN=DC,PM∥AB,PN∥DC,∵AB=CD,∴PM=PN,∴△PMN是等腰三角形,∵PM∥AB,PN∥DC,∴∠MPD=∠ABD=20°,∠BPN=∠BDC=70°,∴∠MPN=∠MPD+∠NPD=20°+(180﹣70)°=130°,∴∠PMN==25°.故选:B.8.数学课上,大家一起研究三角形中位线定理的证明小丽和小亮在学习思考后各自尝试作了一种辅助线,如图1,2.其中辅助线作法能够用来证明三角形中位线定理的是()A.小丽和小亮的辅助线作法都可以B.小丽和小亮的输助线作法都不可以C.小丽的辅助线作法可以,小亮的不可以D.小亮的辅助线作法可以,小丽的不可以【解答】解:小丽:如图1,延长DE到F,使FE=DE,连接CF,AF,FC,∵AE=EC,∴四边形ADCF是平行四边形,∴AD=CF,AD∥CF,∵AD=BD,∴BD=CF,BD∥CF,∴四边形DBCF是平行四边形,∴DF∥BC,DF=BC,∴DE∥BC,DE=DF=BC;小亮:如图2,过点E作EG∥AB,过点A作AF∥BC,AF与GE交于点F,∴∠EAF=∠C,∠F=∠CGF,在△AEF和△CGF中,,∴△AEF≌△CEG(AAS),∴AF=CG,EF=EG,∵AF∥BG,AB∥FG,∴四边形ABGF是平行四边形,∴AB=FG,∵BD=AB,GE=FG,∴BD=EG,∵BD∥EG,∴四边形DBGE是平行四边形,∴DE∥BG,DE=BG,∴DE∥BC,DE=BC,∴小丽和小亮的辅助线作法都可以,故选:A.9.如图,四边形ABCD中,AC⊥BC,AD∥BC,BC=3,AC=4,AD=6.M是BD的中点,则CM的长为()A.B.2C.D.3【解答】解:延长BC到E使BE=AD,则四边形ACED是平行四边形,∵BC=3,AD =6,∴C是BE的中点,∵M是BD的中点,∴CM=DE=AB,∵AC⊥BC,∴AB===5,∴CM=,故选:C.10.如图,四边形ABCD中,AB∥CD,AB=5,DC=11,AD与BC的和是12,点E、F、G分别是BD、AC、DC的中点,则△EFG的周长是()A.8B.9C.10D.12【解答】解:连接AE,并延长交CD于K,∵AB∥CD,∴∠BAE=∠DKE,∠ABD=∠EDK,∵点E、F、G分别是BD、AC、DC的中点.∴BE=DE,在△AEB和△KED中,,∴△AEB≌△KED(AAS),∴DK=AB,AE=EK,EF为△ACK的中位线,∴EF=CK=(DC﹣DK)=(DC﹣AB),∵EG为△BCD的中位线,∴EG=BC,又FG为△ACD的中位线,∴FG=AD,∴EG+GF=(AD+BC),∵AD+BC=12,AB=5,DC=11,即DC﹣AB=6,∴EG+GF=6,FE=3,∴△EFG的周长是6+3=9.故选:B.二.填空题(共10小题)11.如图,在△ABC中,点D是AB的中点,DE∥BC交AC于点E,若BC=2,则DE的长是1.【解答】解:∵DE∥BC,AD=DB,∴AE=EC,∴DE=BC=1,故答案为1.12.如图,DE是△ABC的中位线,若△ADE的面积为1,则四边形DBCE的面积为3.【解答】解:∵DE是△ABC的中位线,∴DE∥BC,DE=BC,∴△ADE∽△ABC,∴S△ADE:S△ABC=()2=,又∵△ADE的面积是1,∴△ABC的面积为4,∴四边形DBCE的面积=4﹣1=3.故答案为:3.13.如图,小慧与小聪玩跷跷板,跷跷板支架EF的高为0.4米,E是AB的中点,那么小慧能将小聪翘起的最大高度BC等于0.8米.【解答】解:当EF∥BC时,BC最大,∵E是AB的中点,EF∥BC,∴BC=2EF=0.8米,故答案为:0.8.14.如图,在△ABC中,D为BC边中点,P为AC边中点,E为BC上一点且BE=CE,连接AE,取AE中点Q并连接QD,取QD中点G,延长PG与BC边交于点H,若BC =6,则HE=.【解答】解:连接PQ.∵BD=DC=3,BE=BC=,EC=,∵AQ=QE,AP=PC,∴PQ∥EC,PQ=EC=,∵∠QPG=∠GHD,∠QGP=∠DGH,QG=GD,∴△PQG≌△HDG(AAS),∴PQ=HD=,BH=BD﹣DH=3﹣=,∴HE=BE﹣BH=﹣=,故答案为.15.如图,△ABC中,点E,F分别是AB,AC的中点,BC=EG.若AC=BC=10,AB=16,则四边形AECG的面积是48.【解答】解:∵点E,F分别是AB,AC的中点,∴EF=BC,∵AC=BC,∴EF=AC,CE⊥AB,∵EG=BC,∴EG=2EF,∴EF=FG,∵AF=CF,∴四边形AECG是矩形,∵AE=AB=8,AC=10,∴CE=6,∴四边形AECG的面积=8×6=48,故答案为:48.16.连接三角形各边中点所得的三角形面积与原三角形面积之比为:1:4.【解答】解:如图所示:∵D、E、F分别AB、AC、BC的中点,∴DE、EF、DF是△ABC的中位线,∴DE=BC,EF=AB,DF=AC,∴=,∴△DEF∽△CBA,∴△DEF的面积:△CBA的面积=()2=.故答案为:1:4.17.如图,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=5,BC=8,则EF的长为 1.5.【解答】解:∵D为AB中点,∠AFB=90°,AB=5,∴DF=AB=2.5,∵DE是△ABC的中位线,BC=8,∴DE=4,∴EF=4﹣2.5=1.5,故答案为:1.518.如图,△ABC的周长为17,点D,E在边BC上,∠ABC的平分线垂直于AE,垂足为点N,∠ACB的平分线垂直于AD,垂足为点M,若BC=6,则MN的长度为 2.5.【解答】解:∵BN平分∠ABC,BN⊥AE,∴∠NBA=∠NBE,∠BNA=∠BNE,在△BNA和△BNE中,∴△BNA≌△BNE(ASA),∴BA=BE,∴△BAE是等腰三角形,同理△CAD是等腰三角形,∴点N是AE中点,点M是AD中点(三线合一),∴MN是△ADE的中位线,∵BE+CD=AB+AC=17﹣BC=17﹣6=11,∴DE=BE+CD﹣BC=5,∴MN=DE=2.5.故答案为:2.5.19.如图,点A(0,4)、B(2,0),点C、D分别是OA、AB的中点,在射线CD上有一动点P,若△ABP是直角三角形,则点P的坐标为(6,2)或(1+,2).【解答】解:∵点A(0,4),点B(2,0),∴OA=4,OB=2,∴由勾股定理得:AB==2,∵点C,D分别是OA,AB的中点,∴AC=OC=2,CD=1,AD=BD=,①当∠APB=90°时,∵AD=BD,∴PD=AD=,∴PC=CD+PD=1+,∴P(1+,2),②当∠ABP=90°时,如图,过P作PM⊥x轴于M,则△ABO∽△BPM,∴===1,∴BP=AB=2,∴PM=OB=2,∴BM=4,∴PC=OM=4+2=6,∴P(6,2),故答案为:(6,2)或(1+,2).20.如图,△ABC中,M、N分别为AC,BC的中点,若S△CMN=2,则S四边形ABNM=6.【解答】解:∵M、N分别为AC,BC的中点,∴NM∥AB,AB=2MN,∴△CMN∽△CAB,∴=()2=,∵S△CMN=2,∴S△ABC=8,∴S四边形ABNM=8﹣2=6,故答案为:6.三.解答题(共8小题)21.如图,在△ABC中,∠CAB=90°,DE、DF是△ABC的中位线,连接EF、AD,求证:EF=AD.【解答】证明:∵DE、DF是△ABC的中位线,∴DE∥AB,DF∥AC,∴四边形DEAF是平行四边形,∵∠CAB=90°,∴四边形DEAF是矩形,∴EF=AD.22.如图,证明定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半.已知:点D、E分别是△ABC的边AB、AC的中点.求证:DE∥BC,DE=BC.【解答】证明:延长DE至F,使EF=DE,连接CF∵E是AC中点,∴AE=CE,在△ADE和△CFE中,,∴△ADE≌△CFE(SAS),∴AD=CF,∠ADE=∠F∴BD∥CF,∵AD=BD,∴BD=CF∴四边形BCFD是平行四边形(一组对边平行且相等的四边形是平行四边形)∴DF∥BC,DF=BC,∴DE∥CB,DE=BC.23.如图,在△ABC中,AB=AC,点D,E分别是边AB,AC的中点,连接DE、BE,点F,G,H分别为BE,DE,BC的中点.(1)求证:FG=FH;(2)若∠A=90°,求证:FG⊥FH;(3)若∠A=80°,求∠GFH的度数.【解答】(1)证明:∵AB=AC,点D,E分别是边AB,AC的中点∴BD=EC∵点F,G,H分别为BE,DE,BC的中点∴FG∥BD,GF=FH∥EC,FH=∴FG=FH;(2)证明:由(1)FG∥BD又∵∠A=90°∴FG⊥AC∵FH∥EC∴FG⊥FH;(3)解:延长FG交AC于点K,∵FG∥BD,∠A=80°∴∠FKC=∠A=80°∵FH∥EC∴∠GFH=180°﹣∠FKC=100°24.证明:三角形的一条中位线与第三边上的中线互相平分.已知:如图,DE是△ABC的中位线,AF是△ABC的中线,AF、DE交于点O.求证:OA=OF,OD=OE.证明:连接DF、EF,∵D、F分别是AB、BC的中点,∴DF∥AC,同理可得:EF∥AB,∴四边形ADFE是平行四边形,∴OA=OF,OD=OE,即三角形的一条中位线与第三边上的中线互相平分.【解答】求证:OA=OF,OD=OE,证明:连接DF、EF,∵D、F分别是AB、BC的中点,∴DF∥AC,同理可得:EF∥AB,∴四边形ADFE是平行四边形,∴OA=OF,OD=OE,即三角形的一条中位线与第三边上的中线互相平分.25.如图,在△RtABC中,∠ACB=90°,DE、DF是△ABC的中位线,连接EF、CD,求证:CD=EF.【解答】证明:∵DE、DF是△ABC的中位线,∴DE∥BC,DF∥AC,∴四边形DECF是平行四边形,∵∠ACB=90°,∴平行四边形DECF是矩形,∴CD=EF.26.如图,在△ABC中,D,E分别是AB,AC的中点,△ABC的角平分线AG交DE于点F,若∠ABC=70°,∠BAC=54°,求∠AFD的度数.【解答】解:∵∠BAC=54°,AG平分∠BAC,∴∠BAG=∠BAC=27°.∴∠BGA=180°﹣∠ABC﹣∠BAG=83°,又∵点D,E分别是AB,AC的中点,∴DE∥BC,∴∠AFD=∠BGA=83°.27.(1)计算:(1﹣)0﹣|﹣2|+;(2)如图,在等边三角形ABC中,点D,E分别是边BC,AC的中点,过点E作EF⊥DE,交BC的延长线于点F,求∠F的度数.【解答】解:(1)原式=1﹣2+3=﹣1+3;(2)∵△ABC是等边三角形,∴∠B=60°,∵点D,E分别是边BC,AC的中点,∴DE∥AB,∴∠EDC=∠B=60°,∵EF⊥DE,∴∠DEF=90°,∴∠F=90°﹣∠EDC=30°.28.如图,在边长为4的等边△ABC中,D、E分别为AB、BC的中点,EF⊥AC于点F,G为EF的中点,连接DG.(1)求EF的长.(2)求DG的长.【解答】解:(1)连接DE,∵在边长为4的等边△ABC中,D,E分别为AB,BC的中点,∴DE是△ABC的中位线,∴DE=2,且DE∥AC,BD=BE=EC=2,∵EF⊥AC于点F,∠C=60°,∴∠FEC=30°,∠DEF=∠EFC=90°,∴FC=EC=1,故EF==,(2)∵G为EF的中点,∴EG=,∴DG===.。
八年级数学上册 5.3 三角形的中位线同步测试题 鲁教版

三角形的中位线一.选择题(共10小题)1.(2015•山西)如图,在△ABC中,点D、E分别是边AB,BC的中点.若△DBE的周长是6,则△ABC的周长是()A.8 B. 10 C. 12 D. 14(1题图)(2题图)(3题图)(4题图)2.(2015•丹东模拟)如图,△ABC中,AB=AC,AD平分∠BAC,DE∥AC交AB于E,则S△EBD:S△ABC=()A.1:2 B. 1:4 C. 1:3 D. 2:33.(2015•南漳县模拟)如图,▱ABCD中,对角线AC,BD交于点O,点E是BC的中点.若OE=3cm,则AB的长为()A.12cm B. 9cm C. 6cm D. 3cm4.(2015•河北模拟)如图,在△ABC中,D,E分别是AB,AC的中点,AC=12,F是DE上一点,连接AF,CF,DF=1.若∠AFC=90°,则BC的长度为()A.12 B. 13 C. 14 D. 155.(2015•莆田模拟)如图,△ABC的中线BD、CE交于点O,连接OA,点G、F分别为OC、OB的中点,BC=8,AO=6,则四边形DEFG的周长为()A.12 B. 14 C. 16 D. 18(5题图)(7题图)(8题图)6.(2015春•廊坊期末)顺次连接四边形各边中点所得的四边形是()A.平行四边形B.矩形C.菱形D.以上都不对7.(2015春•兴平市期末)如图,点D、E、F分别是△ABC中AB、BC、AC边上的中点,点M、N、P分别是DE、EF、DF的中点.若△ABC的周长为24,则△PMN的周长为()A.6 B. 8 C. 10 D. 128.(2015春•石林县期末)如图,A,B两点被池塘隔开,在AB外选一点C,连接AC和BC,通过测量分别取AC,BC的中点D和E,量得DE长210米,则A,B两点间的距离为()A.280米B. 300米C. 420米D.无法确定9.(2015春•聊城校级月考)在△ABC中,D、E分别是BC、AC中点,BF平分∠ABC.交DE 于点F.AB=8,BC=6,则EF的长为()A.1 B. 2 C. 3 D. 4(9题图)(10题图)(11题图)10.(2015春•富顺县校级月考)如图,已知△ABC的周长为1,连接△ABC的三边的中点构成第二个三角形,再连接第二个三角形三边的中点构成第三个三角形…依此类推,则第2015个三角形的周长为()A.B.C.()2014D.()2015二.填空题(共5小题)11.(2015•昆明)如图,在△ABC中,AB=8,点D、E分别是BC、CA的中点,连接DE,则DE= .12.(2015•宿迁)如图,在Rt△ABC中,∠ACB=90°,点D,E,F分别为AB,AC,BC的中点.若CD=5,则EF的长为.(12题图)(13题图)(14题图)(15题图)13.(2015•泰安)如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是线段BM、CM的中点.若AB=8,AD=12,则四边形ENFM的周长为.14.(2015•盐城)如图,点D、E、F分别是△ABC各边的中点,连接DE、EF、DF.若△ABC 的周长为10,则△DEF的周长为.15.(2015•珠海)如图,在△A1B1C1中,已知A1B1=7,B1C1=4,A1C1=5,依次连接△A1B1C1三边中点,得△A2B2C2,再依次连接△A2B2C2的三边中点得△A3B3C3,…,则△A5B5C5的周长为.三.解答题(共5小题)16.(2014秋•龙口市期末)如图,D、E分别是△ABC的边AB、AC的中点,点O是△ABC 内部任意一点,连接OB、OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.求证:四边形DGFE是平行四边形.17.(2015•邵阳)如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,延长BC至点F,使CF=BC,连接CD和EF.(1)求证:DE=CF;(2)求EF的长.18.(2015春•临清市期中)已知如图:在△ABC中,AB、BC、CA的中点分别是E、F、G,AD是高.求证:∠EDG=∠EFG.19.(2015春•泗阳县期末)如图,在△ABC中,点D,E,F分别是AB,BC,CA的中点,AH 是边BC上的高.(1)试判断线段DE与FH之间的数量关系,并说明理由;(2)求证:∠DHF=∠DEF.20.(2015春•工业园区期中)如图,M是△ABC的边BC的中点,AN平分∠BAC,且BN⊥AN,垂足为N,且AB=6,BC=10,MN=1.5,求△ABC的周长.鲁教版八年级数学上册第5章5.3三角形的中位线测试题参考答案一.选择题(共10小题)1.C.2.B.3.C.4.C.5.B.6.A.7.A.8.C.9.A.10.解:△ABC周长为1,因为每条中位线均为其对应边的长度的,所以:第2个三角形对应周长为;第3个三角形对应的周长为;第4个三角形对应的周长为;以此类推,第N个三角形对应的周长为()n﹣1;所以第2015个三角形对应的周长为()2014.故选C.二.填空题(共6小题)11. 4 .12. 5 .13.20 .14. 5 .15. 1 .三.解答题(共5小题)16.证明:∵D、E分别是AB、AC边的中点,∴DE∥BC,且DE=BC,同理,GF∥BC,且GF=BC,∴DE∥GF且DE=GF,四边形DGFE是平行四边形.17.(1)证明:∵D、E分别为AB、AC的中点,∴DE BC,∵延长BC至点F,使CF=BC,∴DE FC,即DE=CF;(2)解:∵DE FC,∴四边形DEFC是平行四边形,∴DC=EF,∵D为AB的中点,等边△ABC的边长是2,∴AD=BD=1,CD⊥A B,BC=2,∴DC=EF=.18.证明:连接EG,∵E、F、G分别是AB、BC、CA的中点,∴EF为△ABC的中位线,EF=AC.(三角形的中位线等于第三边的一半)又∵AD⊥BC,∴∠ADC=90°,DG为直角△ADC斜边上的中线,∴DG=AC.(直角三角形斜边上的中线等于斜边的一半)∴DG=EF.同理DE=FG,EG=GE,∴△EFG≌△GDE(SSS).∴∠EDG=∠EFG.(18题图)(19题图)(20题图)19.解:(1)DE与FH相等.理由如下:∵D、E分别是AB、BC边的中点.∴ED∥AC,DE=AC,∵AH⊥BC,垂足为H,F是AC的中点,∴HF=AC,∴DE=FH.(2)∵DH=AB,AD=AB,∴AD=DH,∴∠DAH=∠DHA,同理可证:∠FAH=∠FHA,∴∠DHF=∠DAF,∵AD∥EF,DE∥AF,∴四边形ADEF是平行四边形,∴∠DEF=∠DAF,∴∠DHF=∠DEF.20.解:延长线段BN交A C于E.∵AN平分∠BAC,在△ABN和△AEN中,∴△ABN≌△AEN(SAS),∴AE=AB=6,BN=NE,又∵M是△ABC的边BC的中点,∴CE=2MN=2×1.5=3,∴△ABC的周长是AB+BC+AC=6+10+6+3=25.。
鲁教版八年级数学上册《三角形的中位线》同步训练(附答案)
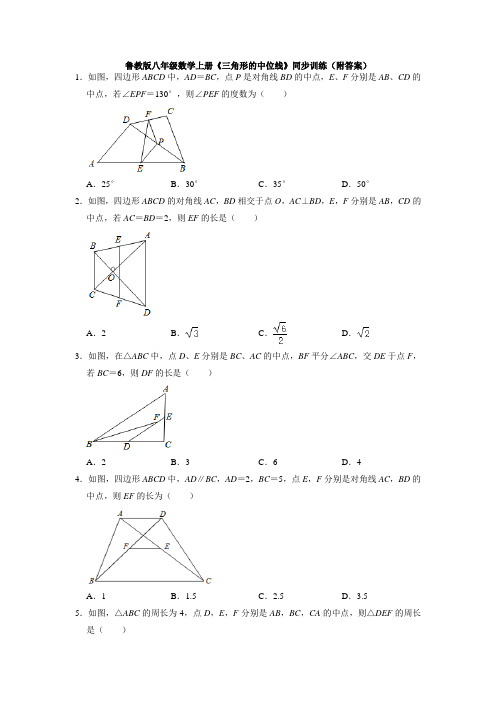
鲁教版八年级数学上册《三角形的中位线》同步训练(附答案)1.如图,四边形ABCD中,AD=BC,点P是对角线BD的中点,E、F分别是AB、CD的中点,若∠EPF=130°,则∠PEF的度数为()A.25°B.30°C.35°D.50°2.如图,四边形ABCD的对角线AC,BD相交于点O,AC⊥BD,E,F分别是AB,CD的中点,若AC=BD=2,则EF的长是()A.2B.C.D.3.如图,在△ABC中,点D、E分别是BC、AC的中点,BF平分∠ABC,交DE于点F,若BC=6,则DF的长是()A.2B.3C.6D.44.如图,四边形ABCD中,AD∥BC,AD=2,BC=5,点E,F分别是对角线AC,BD的中点,则EF的长为()A.1B.1.5C.2.5D.3.55.如图,△ABC的周长为4,点D,E,F分别是AB,BC,CA的中点,则△DEF的周长是()A.1B.2C.3D.46.如图,已知在△ABC中,D,E,F分别是边BC,CA,AB的中点.AB=10,AC=8,则四边形AFDE的周长等于()A.18B.16C.14D.127.如图所示,在△ABC中,BC>AC,点D在BC上,DC=AC=10,且=,作∠ACB 的平分线CF交AD于点F,CF=8,E是AB的中点,连接EF,则EF的长为.8.如图,在△ABC中,M,N分别是AB和AC的中点,连接MN,点E是CN的中点,连接ME并延长,交BC的延长线于点D.若BC=4,则CD的长是多少?9.如图,在△ABC中,D是AB上一点,AD=AC,AE⊥CD,垂足为点E,F是BC的中点,若BD=10,求EF的长.10.如图,在△ABC中,点D,E分别是边AB,AC的中点,AF⊥BC,垂足为点F,∠ADE =30°,DF=3,DE=2,求FC的长度.11.如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AE平分∠CAB,CE⊥AE于点E,延长CE交AB于点D.(1)求证:CE=DE;(2)若点F为BC的中点,求EF的长.12.如图,在△ABC中,AD是中线,AE是角平分线,点F在AE上,∠CF A=90°,试判断DF与AB的位置关系,并说明理由.13.如图,D、E、F分别是△ABC三边中点,AH⊥BC于H.求证:(1)∠BDF=∠BAC;(2)DF=EH.14.如图,在四边形ABCD中,AD=BC,E、F分别是边DC、AB的中点,FE的延长线分别AD、BC的延长线交于点H、G,求证:∠AHF=∠BGF.15.如图,点O是△ABC内一点,连接OB、OC,线段AB、OB、OC、AC的中点分别为D、E、F、G.(1)判断四边形DEFG的形状,并说明理由;(2)若M为EF的中点,OM=2,∠OBC和∠OCB互余,求线段BC的长.16.如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,过点E作EF∥CD交BC的延长线于点F,连接CD.(1)求证:DE=CF;(2)求EF的长.17.如图,在△ABC中,AB=AC,点D是边AB上一点,DE∥BC交AC于点E,连接BE,点F、G、H分别为BE、DE、BC的中点.(1)求证:FG=FH;(2)当∠A为多少度时,FG⊥FH?并说明理由.18.已知:如图,四边形ABCD中,对角线AC=BD,E,F为AB、CD中点,连EF交BD、AC于P、Q求证:OP=OQ.19.如图,在△ABC中,AE平分∠BAC,BE⊥AE于点E,点F是BC的中点.(1)如图1,BE的延长线与AC边相交于点D,求证:EF=(AC﹣AB);(2)如图2,△ABC中,AB=9,AC=5,求线段EF的长.参考答案1.解:∵P、F分别是BD、CD的中点,∴PF=BC,同理可得:PE=AD,∵AD=BC,∴PF=PE,∵∠EPF=130°,∴∠PEF=∠PFE=×(180°﹣130°)=25°,故选:A.2.解:取BC的中点G,AD的中点H,连接EG、GF、FH、HE,∵E,G分别是AB,BC的中点,AC=2∴EG=AC=1,EG∥AC,同理:FH=AC,FH∥AC,EG=AC,GF∥BD,GF=BD=1,∴四边形EGFH为平行四边形,∵AC=BD,∴GE=GF,∴平行四边形EGFH为菱形,∵AC⊥BD,EG∥AC,GF∥BD,∴EG⊥GF,∴菱形EGFH为正方形,∴EF=EG=,故选:D.3.解:∵D,E分别是BC,AC的中点,∴DE∥AB,∴∠BFD=∠ABF,∵BF平分∠ABC,∴∠DBF=∠ABF,∴∠BFD=∠DBF,∴DF=DB=BC==3,故选:B.4.解:∵取DC中点G,连结FG、EG,如图所示:∵点E,F分别是对角线AC,BD的中点,∴FG∥BC,EG∥AD,∵AD∥BC,∴EG∥BC,FG∥EG,∴E、F、G三点共线,∴FG是△BCD的中位线,∴FG=BC=2.5,∵AD∥BC,∴EG∥AD,∴EG是△ACD的中位线,∴EG=AD=1,∴EF=FG﹣EG=1.5.故选:B.5.解:∵△ABC的周长为4,∴AB+AC+BC=4,∵点D,E,F分别是AB,BC,CA的中点,∴EF=AB,DE=AC,DF=BC,∴△DEF的周长=EF+DE+DF=×(AB+AC+BC)=2,故选:B.6.解:∵D,E,F分别是边BC,CA,AB的中点.AB=10,AC=8,∴DE=AB=5,DF=AC=4,AF=AB=5,AE=AC=4,∴四边形AFDE的周长=AF+DF+DE+AE=5+5+4+4=18,故选:A.7.解:∵DC=AC=10,∠ACB的平分线CF交AD于F,∴F为AD的中点,CF⊥AD,∴∠CFD=90°,∵DC=10,CF=8,∴DF==6,∴AD=2DF=12,∵=,∴BD=8,∵点E是AB的中点,∴EF为△ABD的中位线,∴EF=BD=4,故答案为:4.8.解:∵M,N分别是AB和AC的中点,∴MN是△ABC的中位线,∴MN=BC=2,MN∥BC,∴∠NME=∠D,∠MNE=∠DCE,∵点E是CN的中点,∴NE=CE,在△MNE和△DCE中,,∴△MNE≌△DCE(AAS),∴CD=MN=2.9.解:∵AD=AC,AE⊥CD,∴CE=ED,∵F是BC的中点,∴EF是△CDB的中位线,∴EF=BD=×10=5.10.解:∵AF⊥BC,点D是边AB的中点,DF=3,∴AB=2DF=6.∵点D,E分别是边AB,AC的中点,∴DE∥BC,∴∠B=∠ADE=30°,∴AF=AB=3,由勾股定理得,BF===3,∴FC=BC﹣BF=.11.(1)证明:∵AE平分∠CAB,∴∠CAE=∠BAE,∵CE⊥AE,∴∠AEC=∠AED=90°,在△AEC和△AED中,,∴△AEC≌△AED(ASA),∴CE=DE;(2)在Rt△ABC中,∵AC=6,BC=8,∴,∵△AEC≌△AED,∴AD=AC=6,∴BD=AB﹣AD=4,∵点E为CD中点,点F为BC中点,∴.12.解:DF∥AB.理由如下:如图,延长CF交AB于点G,∵AE是角平分线,∴∠GAF=∠CAF,在△AGF和△ACF中,∴△AGF≌△ACF(ASA),∴GF=CF,即点F是GC的中点,∵AD是△ABC的中线,∴点D是BC的中点∴DF是△BCG的中位线,∴DF∥AB.13.证明:(1)∵D、F分别是AB、BC边中点,∴DF是△ABC的中位线,∴DF∥AC,DF=AC,∴∠BDF=∠BAC;(2)∵AH⊥BC于H,E是AC的中点,∴EH=AC,∴DF=EH.14.证明:连接BD,取BD的中点P,连接EP,FP,∵E、F、P分别是DC、AB、BD边的中点,∴EP是△BCD的中位线,PF是△ABD的中位线,∴PF=AD,PF∥AD,EP=BC,EP∥BC,∴∠H=∠PFE,∠BGF=∠FEP,∵AD=BC,∴PE=PF,∴∠PEF=∠PFE,∴∠AHF=∠BGF.15.解:(1)四边形DEFG是平行四边形,理由如下:∵E、F分别为线段OB、OC的中点,∴EF=BC,EF∥BC,同理DG=BC,DG∥BC,∴EF=DG,EF∥DG,∴四边形DEFG是平行四边形;(2)∵∠OBC和∠OCB互余,∴∠BOC=90°,∵M为EF的中点,OM=2,∴EF=2OM=4,∴BC=2EF=8.16.解:(1)∵D、E分别为AB、AC的中点,∴DE∥BC,DE=BC,∵EF∥CD∴四边形DEFC是平行四边形,∴DE=CF.(2)∵四边形DEFC是平行四边形,∴DC=EF,∵D为AB的中点,等边△ABC的边长是2,∴AD=BD=1,CD⊥AB,BC=2,∴DC=EF=.17.(1)证明:∵AB=AC.∴∠ABC=∠ACB,∵DE∥BC,∴∠ADE=∠ABC,∠AED=∠ACB,∴∠ADE=∠AED,∴AD=AE,∴DB=EC,∵点F、G、H分别为BE、DE、BC的中点,∴FG是△EDB的中位线,FH是△BCE的中位线,∴FG=BD,FH=CE,∴FG=FH;(2)解:延长FG交AC于N,∵FG是△EDB的中位线,FH是△BCE的中位线,∴FH∥AC,FN∥AB,∵FG⊥FH,∴∠A=90°,∴当∠A=90°时,FG⊥FH.18.证明:取BC中点G,连EG、FG,∵E,G为AB、BC中点,∴EG=AC,EG∥AC,∴∠FEG=∠OQP,同理,FG=BD,FG∥BD,∴∠EFG=∠OPQ,∵AC=BD,∴EG=FG,∴∠FEG=∠EFG,∴∠OPQ=∠OQP,∴OP=OQ.19.(1)证明:在△AEB和△AED中,,∴△AEB≌△AED(ASA)∴BE=ED,AD=AB,∵BE=ED,BF=FC,∴EF=CD=(AC﹣AD)=(AC﹣AB);(2)解:分别延长BE、AC交于点H,在△AEB和△AEH中,,∴△AEB≌△AEH(ASA)∴BE=EH,AH=AB=9,∵BE=EH,BF=FC,∴EF=CH=(AH﹣AC)=2.。
初二数学三角形中位线练习题(含答案)

初二数学三角形中位线练习题一.选择题(共5小题)1.如图,为了测量池塘边A、B两地之间的距离,在线段AB的同侧取一点C,连结CA并延长至点D,连结CB并延长至点E,使得A、B分别是CD、CE的中点,若18DE m=,则线段AB的长度是()A.9m B.12m C.8m D.10m2.已知三角形的周长是16,它的三条中位线围成的三角形的周长是()A.16B.12C.8D.43.如图,在四边形ABCD中,点P是边CD上的动点,点Q是边BC上的定点,连接AP,PQ,E,F分别是AP,PQ的中点,连接EF.点P在由C到D运动过程中,线段EF的长度() A.保持不变B.逐渐变小C.先变大,再变小D.逐渐变大4.如图,在四边形ABCD中,P是对角线BD的中点,E、F分别是AB、CD的中点,AD BC=,∠的度数是()∠=︒,则EFPEPF136A.68︒B.34︒C.22︒D.44︒5.如图,D是ABC⊥,E、F、G、H分别是边AB、BD、CD、AC的中点.若∆内一点,BD CDCD=,则四边形EFGH的周长是()BD=,6AD=,810A.24B.20C.12D.10第3题图第4题图第5题图二.填空题(共5小题)6.某直角三角形的两条边长分别是10和24,则连接两条直角边中点的线段的长是.7.如图,在Rt ABCABC∠=︒,点D、E、F分别是AB、AC,∆中,90BE=,则DF=.BC边上的中点,连结BE,DF,已知58.如图,在四边形ABCD中,220∠+∠=︒,E、F分别是AC、ADC BCDBD 的中点,P 是AB 边上的中点,则EPF ∠= ︒.9.如图,在四边形ABCD 中,//AB CD ,E ,F 分别是AC ,BD 的中点,已知12AB =,6CD =,则EF = .10.如图,在ABC ∆中,8AB =,6AC =,AM 平分BAC ∠,CM AM ⊥于点M ,N 为BC 的中点,连结MN ,则MN 的长为 .第8题图 第9题图 第10题图三.解答题(共3小题)11.如图所示,在ABC ∆中,点D 在BC 上且CD CA =,CF 平分ACB ∠,AE EB =,求证:12EF BD =.12.如图:D 、E 是ABC ∆边AB ,AC 的中点,O 是ABC ∆内一动点,F 、G 是OB ,OC 的中点.判断四边形DEGF 的形状,并证明.13.已知:如图,在四边形ABCD 中,对角线AC 、BD 相交于O ,且AC BD =,E 、F 分别是AB 、CD 的中点,E 、F 分别交BD 、AC 于点G 、H .求证:OG OH =.答案与解析一.选择题(共5小题)1.如图,为了测量池塘边A 、B 两地之间的距离,在线段AB 的同侧取一点C ,连结CA 并延长至点D ,连结CB 并延长至点E ,使得A 、B 分别是CD 、CE 的中点,若18DE m =,则线段AB 的长度是( )A .9mB .12mC .8mD .10m【分析】根据三角形的中位线定理解答即可. 【解答】解:A 、B 分别是CD 、CE 的中点, ∴AB 是△CDE 的中位线,192AB DE m ∴==, 故选:A .2.已知三角形的周长是16,它的三条中位线围成的三角形的周长是( ) A .16 B .12 C .8 D .4【分析】由中位线定义可得新三角形的各边长为原三角形各边长的一半,即可得出其周长等于原三角形周长的一半.【解答】解:三角形的周长是16,∴它的三条中位线围成的三角形的周长是11682⨯=. 故选:C .3.如图,在四边形ABCD 中,点P 是边CD 上的动点,点Q 是边BC 上的定点,连接AP ,PQ ,E ,F 分别是AP ,PQ 的中点,连接EF .点P 在由C 到D 运动过程中,线段EF 的长度( )A .保持不变B .逐渐变小C .先变大,再变小D .逐渐变大 【分析】连接AQ ,根据三角形中位线定理解答即可. 【解答】解:如图所示,连接AQ , 点Q 是边BC 上的定点, AQ ∴的大小不变,E ,F 分别是AP ,PQ 的中点, ∴EF 是△APQ 的中位线, 12EF AQ ∴=, ∴线段EF 的长度保持不变,故选:A .4.如图,在四边形ABCD 中,P 是对角线BD 的中点,E 、F 分别是AB 、CD 的中点,AD BC =,136EPF ∠=︒,则EFP ∠的度数是( )A .68︒B .34︒C .22︒D .44︒【分析】根据三角形中位线定理得到12PE AD =,12PF BC =,根据等腰三角形的性质、三角形内角和定理计算即可.【解答】解:P 是BD 的中点,E 是AB 的中点, ∴EP 是△BCD 的中位线, 12PE AD ∴=, 同理,12PF BC =, AD BC =, PE PF ∴=,1(180)222EFP EPF ∴∠=⨯︒-∠=︒,故选:C . 5.如图,D 是ABC ∆内一点,BD CD ⊥,E 、F 、G 、H 分别是边AB 、BD 、CD 、AC 的中点.若10AD =,8BD =,6CD =,则四边形EFGH 的周长是( )A .24B .20C .12D .10【分析】利用勾股定理列式求出BC 的长,再根据三角形的中位线平行于第三边并且等于第三边的一半求出12EH FG BC ==,12EF GH AD ==,然后代入数据进行计算即可得解. 【解答】解:BD CD ⊥,8BD =,6CD =,22228610BC BD CD ∴=+=+,E 、F 、G 、H 分别是AB 、AC 、CD 、BD 的中点,12EH FG BC ∴==,12EF GH AD ==,∴四边形EFGH 的周长EH GH FG EF AD BC =+++=+, 又10AD =,∴四边形EFGH 的周长101020=+=, 故选:B .二.填空题(共5小题)6.某直角三角形的两条边长分别是10和24,则连接两条直角边中点的线段的长是 13或12 . 【分析】根据勾股定理求出AB ,根据三角形中位线定理计算,得到答案. 【解答】解:分两种情况讨论:①当24是直角边时,由勾股定理得,斜边2222241026AB AC BC =+=+=,M 、N 分别为CA 、CB 的中点, ∴MN 是△ABC 的中位线,1132MN AB ∴==,②当24是斜边时,1122MN AB ==,故答案为:13或12.7.如图,在Rt ABC ∆中,90ABC ∠=︒,点D 、E 、F 分别是AB 、AC ,BC 边上的中点,连结BE ,DF ,已知5BE =,则DF = 5 .【分析】已知BE 是Rt ABC ∆斜边AC 的中线,那么12BE AC =;DF 是ABC ∆的中位线,则12DF AC =,则5DF BE ==. 【解答】解:ABC ∆是直角三角形,BE 是斜边的中线, 12BE AC ∴=, 又DF 是ABC ∆的中位线,12DF AC ∴=, 5DF BE ∴==. 故答案为5.8.如图,在四边形ABCD 中,220ADC BCD ∠+∠=︒,E 、F 分别是AC 、BD 的中点,P 是AB 边上的中点,则EPF ∠= 40 ︒.【分析】依据四边形内角和即可得到140BAD ABC ∠+∠=︒,再根据三角形中位线定理即可得到BPF BAD ∠=∠,APE ABC ∠=∠,进而得出140APE BPF ∠+∠=︒,即可得到EPF ∠的度数. 【解答】解:四边形ABCD 中,220ADC BCD ∠+∠=︒, 360220140BAD ABC ∴∠+∠=︒-︒=︒,E 、F 分别是AC 、BD 的中点,P 是AB 边上的中点, PE ∴是ABC ∆的中位线,PF 是ABD ∆的中位线, //PE BC ∴,//PF AD ,BPF BAD ∴∠=∠,APE ABC ∠=∠,140APE BPF BAD ABC ∴∠+∠=∠+∠=︒, 18014040EPF ∴∠=︒-︒=︒,故答案为:40.9.如图,在四边形ABCD 中,//AB CD ,E ,F 分别是AC ,BD 的中点,已知12AB =,6CD =,则EF = 3 .【分析】连接CF 并延长交AB 于G ,证明FDC FBG ∆≅∆,根据全等三角形的性质得到6BG DC ==,CF FG =,求出AG ,根据三角形中位线定理计算,得到答案. 【解答】解:连接CF 并延长交AB 于G , //AB CD ,FDC FBG ∴∠=∠, 在FDC ∆和FBG ∆中, FDC FBG FD FBDFC BFG ∠=∠⎧⎪=⎨⎪∠=∠⎩, ()FDC FBG ASA ∴∆≅∆ 6BG DC ∴==,CF FG =, 1266AG AB BG ∴=-=-=, CE EA =,CF FG =, ∴EF 是△ACG 的中位线, 132EF AG ∴==, 故答案为:3. 10.如图,在ABC ∆中,8AB =,6AC =,AM 平分BAC ∠,CM AM ⊥于点M ,N 为BC 的中点,连结MN ,则MN 的长为 1 .【分析】延长CM 交AB 于H ,证明AMH AMC ∆≅∆,根据全等三角形的性质得到6AH AC ==,CM MH =,根据三角形中位线定理解答. 【解答】解:延长CM 交AB 于H , 在AMH ∆和AMC ∆中, 90MAH MAC AM AMAMH AMC ∠=∠⎧⎪=⎨⎪∠=∠=︒⎩, ()AMH AMC ASA ∴∆≅∆6AH AC ∴==,CM MH =, 2BH AB AH ∴=-=, CM MH =,CN BN =, ∴MN 是△BCH 的中位线, 112MN BH ∴==, 故答案为:1. 三.解答题(共3小题)11.如图所示,在ABC ∆中,点D 在BC 上且CD CA =,CF 平分ACB ∠,AE EB =,求证:12EF BD =.【分析】首先根据等腰三角形的性质可得F 是AD 中点,再根据三角形的中位线定理可得12EF BD =.【解答】证明:CD CA =,CF 平分ACB ∠, F ∴是AD 中点, AE EB =, E ∴是AB 中点,EF ∴是ABD ∆的中位线, 12EF BD ∴=. 12.如图:D 、E 是ABC ∆边AB ,AC 的中点,O 是ABC ∆内一动点,F 、G 是OB ,OC 的中点.判断四边形DEGF 的形状,并证明.【分析】根据三角形中位线定理得到12DE BC =,//DE BC ,12FGT BC =,//FG BC ,得到DE FG =,//DE FG ,根据平行四边形的判定定理证明结论. 【解答】解:四边形DEGF 是平行四边形, 理由:D 、E 是ABC ∆边AB ,AC 的中点, ∴DE 是△ABC 的中位线,12DE BC ∴=,//DE BC , F 、G 是OB ,OC 的中点, ∴FG 是△BCO 的中位线,12FG BC ∴=,//FG BC ,DE FG ∴=,//DE FG∴四边形DEGF 是平行四边形.13.已知:如图,在四边形ABCD中,对角线AC、BD相交于O,且AC BD=,E、F分别是AB、CD的中点,E、F分别交BD、AC于点G、H.求证:OG OH=.【分析】取BC边的中点M,连接EM,FM,则根据三角形的中位线定理,即可证得EMF∆是等腰三角形,根据等边对等角,即可证得MEF MFE∠=∠,然后根据平行线的性质证得OGH OHG∠=∠,根据等角对等边即可证得.【解答】解:取BC边的中点M,连接EM,FM,M、F分别是BC、CD的中点,∴MF是△BCD的中位线,//MF BD ∴,12MF BD=,同理://ME AC,12ME AC=,AC BD=ME MF∴=MEF MFE∴∠=∠,//MF BD,MFE OGH∴∠=∠,同理,MEF OHG∠=∠,OGH OHG∴∠=∠OG OH∴=.。
鲁教版八年级数学上册5.3三角形的中位线基础达标训练题3(附答案)

鲁教版八年级数学上册5.3三角形的中位线基础达标训练题3(附答案)一.选择题(共10小题)1.如图在△ABC中,D、E分别是AB、AC的中点,若△ABC的周长为16,则△ADE的周长为()A.6B.7C.8D.92.如图,在四边形ABCD中,AD=BC,E、F、G分别是AB、CD、AC的中点,若∠DAC =15°,∠ACB=87°,则∠FEG等于()A.39°B.18°C.72°D.36°3.如图,AD、BE分别是△ABC的中线和角平分线,AD⊥BE,AD=BE=4,F为CE的中点,连接DF,则AF的长等于()A.2B.3C.D.24.如图,在△ABC中,AB=4,BC=8,AC=6,D、E分别是BC、CA的中点,则△DEC 的周长为()A.18B.8C.10D.95.如图,已知△ABC中,点M是BC边上的中点,AN平分∠BAC,BN⊥AN于点N,若AB=7,MN=3,则AC的长为()A.14B.13C.12D.116.如图,在△ABC中,点M为BC的中点,AD为△ABC的外角平分线,且AD⊥BD,若AB=6,AC=9,则MD的长为()A.3B.C.5D.7.如图,Rt△AMC中,∠C=90°,∠AMC=30°,N,B分别是MC,AC的中点,CN=2cm,则AM的长度为()A.4cm B.8cm C.9cm D.6cm8.如图所示,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,且AB=8,MN=3,则AC的长是()A.12B.14C.16D.189.如图,在△ABC中,∠C=90°,E,F分别是AC,BC上两点,AE=16,BF=12,点P,Q,D分别是AF,BE,AB的中点,则PQ的长为()A.10B.8C.2D.2010.如图,A,B两地被池塘隔开,小明先在直线AB外选一点C,然后步测出AC,BC的中点M,N,并步测出MN的长为6.5m.由此,他可以知道A.B间的距离为()A.12m B.12.5m C.13m D.13.5m二.填空题(共10小题)11.如图,△ABC中,D、E分别是BC、AC的中点,BF平分∠ABC,交DE于点F,若AB=10,BC=8,则EF的长是.12.已知等边三角形ABC的一条中位线的长是3cm,则△ABC的周长是cm.13.如图,在四边形ABCD中,E,F分别是AD,BC的中点,G,H分别是BD,AC的中点,当AB=CD时,四边形GFHE是.14.如图,在△ABC中,∠ACB=60°,点D,E分别是AB,AC的中点,点F在线段DE 上,连结AF,CF.若CF恰好平分∠ACB,且CF=,则AC的长为.15.如图,已知在△ABC中,D、E分别是AB、AC的中点,F、G分别是AD、AE的中点,且FG=2cm,则BC的长度是cm.16.如图,△ABC中,AB=7cm,BC=6cm,AC=5cm,D,E,F分别是AB,BC,AC的中点,则四边形ADEF的周长等于cm.17.如图,在△ABC中,AC=10,D,E分别是AB,AC的中点.F是DE上一点,连结AF、CF.若∠AFC=90°,DF=1,则BC的长为.18.如图,△ABC中,D、E分别是BC、AC的中点,BF平分∠ABC,交DE于点F,若AB=12,BC=9,则EF的长是.19.已知一个三角形的周长为10cm,则连接各边中点所得的三角形的周长为cm.20.如图,A,B两地被池塘隔开,小石通过下面的方法测出A,B间的距离:先在AB外选一点C,然后通过测量找到AC,BC的中点D,E,并测量出DE的长为20m,由此他就知道了A,B间的距离为m,小石的依据是.三.解答题(共8小题)21.如图:D、E是△ABC边AB,AC的中点,O是△ABC内一动点,F、G是OB,OC的中点.判断四边形DEGF的形状,并证明.22.已知:在△ABC中,D是AB的中点,DE∥BC,交AC于点E.求证:DE是△ABC的中位线.23.如图,点D、E、F分别是△ABC各边中点.求证:四边形ADEF是平行四边形.24.补充完整三角形中位线定理,并加以证明:(1)三角形中位线定理:三角形的中位线;(2)已知:如图,DE是△ABC的中位线,求证:DE∥BC,DE=BC.25.如图,在四边形ABCD中,AC⊥BD,BD=12,AC=16,E,F分别为AB,CD的中点,求EF的长.26.如图,在四边形ABCD中,P是对角线BD的中点,E、F分别是AB、CD的中点,AD =BC,∠PEF=18°.求∠PFE的度数.27.如图,△ABC的中线AE与中位线DF相交于点O、试问AE与DF是否互相平分?为什么?28.如图,在△ABC中,D、E分别是AC、AB的中点,BD为角平分线.求证:(1)∠EBD=∠EDB;(2)BE=BC.参考答案与试题解析一.选择题(共10小题)1.如图在△ABC中,D、E分别是AB、AC的中点,若△ABC的周长为16,则△ADE的周长为()A.6B.7C.8D.9【解答】解:∵D、E分别是AB和AC的中点,∴DE∥BC,且DE=BC,即=,∴△ADE∽△ABC,∴=,∴△ADE的周长是:×16=8.故选:C.2.如图,在四边形ABCD中,AD=BC,E、F、G分别是AB、CD、AC的中点,若∠DAC =15°,∠ACB=87°,则∠FEG等于()A.39°B.18°C.72°D.36°【解答】解:∵F、G分别是CD、AC的中点,∴FG∥AD,FG=AD,∴∠FGC=∠DAC=15°,∵E、G分别是AB、AC的中点,∴GE∥BC,GE=BC,∴∠EGC=180°﹣∠ACB=93°,∴∠EGF=108°,∵AD=BC,∴GF=GE,∴∠FEG=×(180°﹣108°)=36°,故选:D.3.如图,AD、BE分别是△ABC的中线和角平分线,AD⊥BE,AD=BE=4,F为CE的中点,连接DF,则AF的长等于()A.2B.3C.D.2【解答】解:∵F为CE的中点,D为BC的中点,∴DF=BE=2,DF∥BE,∴∠ADF=90°,∴AF===2,故选:D.4.如图,在△ABC中,AB=4,BC=8,AC=6,D、E分别是BC、CA的中点,则△DEC 的周长为()A.18B.8C.10D.9【解答】解:∵D、E分别是BC、CA的中点,∴DE=AB=2,EC=AC=3,CD=CB=4,∴△DEC的周长=2+3+4=9,故选:D.5.如图,已知△ABC中,点M是BC边上的中点,AN平分∠BAC,BN⊥AN于点N,若AB=7,MN=3,则AC的长为()A.14B.13C.12D.11【解答】解:延长BN交AC于D,在△ANB和△AND中,,∴△ANB≌△AND,∴AD=AB=8,BN=ND,∵M是△ABC的边BC的中点,∴DC=2MN=6,∴AC=AD+CD=13,故选:B.6.如图,在△ABC中,点M为BC的中点,AD为△ABC的外角平分线,且AD⊥BD,若AB=6,AC=9,则MD的长为()A.3B.C.5D.【解答】解:延长BD交CA的延长线于E,∵AD为∠BAC的平分线,BD⊥AD,∴BD=DE,AB=AE=6,∴CE=AC+AE=8+6=15,又∵M为△ABC的边BC的中点,∴DM是△BCE的中位线,∴MD=CE=×15=7.5.故选:D.7.如图,Rt△AMC中,∠C=90°,∠AMC=30°,N,B分别是MC,AC的中点,CN=2cm,则AM的长度为()A.4cm B.8cm C.9cm D.6cm【解答】解:∵CN=2cm,N,B分别是MC,AC的中点,∴CM=2CN=4,∵∠C=90°,∠AMC=30°,∴CM=AM,4=AM,∴AM=8,故选:B.8.如图所示,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,且AB=8,MN=3,则AC的长是()A.12B.14C.16D.18【解答】解:延长BN交AC于D,在△ANB和△AND中,,∴△ANB≌△AND,∴AD=AB=8,BN=ND,∵M是△ABC的边BC的中点,∴DC=2MN=6,∴AC=AD+CD=14,故选:B.9.如图,在△ABC中,∠C=90°,E,F分别是AC,BC上两点,AE=16,BF=12,点P,Q,D分别是AF,BE,AB的中点,则PQ的长为()A.10B.8C.2D.20【解答】解:∵∠C=90°,∴∠CAB+∠CBA=90°,∵点P,D分别是AF,AB的中点,∴PD=BF=6,PD∥BC,∴∠PDA=∠CBA,同理,QD=AE=8,∠QDB=∠CAB,∴∠PDA+∠QDB=90°,即∠PDQ=90°,∴PQ==10,故选:A.10.如图,A,B两地被池塘隔开,小明先在直线AB外选一点C,然后步测出AC,BC的中点M,N,并步测出MN的长为6.5m.由此,他可以知道A.B间的距离为()A.12m B.12.5m C.13m D.13.5m【解答】解:∵点M,N分别是AC,BC的中点,∴AB=2MN=13(m),故选:C.二.填空题(共10小题)11.如图,△ABC中,D、E分别是BC、AC的中点,BF平分∠ABC,交DE于点F,若AB=10,BC=8,则EF的长是1.【解答】解:∵D、E分别是BC、AC的中点,∴DE=AB=5,DE∥AB,BD=BC=4,∴∠ABF=∠DFB,∵BF平分∠ABC,∴∠ABF=∠DBF,∴∠DBF=∠DFB,∴DF=DB=4,∴EF=DE﹣DF=1,故答案为:1.12.已知等边三角形ABC的一条中位线的长是3cm,则△ABC的周长是18cm.【解答】解:根据题意可知,△ABC的边长为2DE=6cm,因为△ABC是等边三角形,所以三边相等,所以△ABC的周长等于3×6=18cm.故答案为18.13.如图,在四边形ABCD中,E,F分别是AD,BC的中点,G,H分别是BD,AC的中点,当AB=CD时,四边形GFHE是菱形.【解答】解:∵E,G分别是AD,BD的中点,∴EG=AB,EG∥AB,同理,HF=AB,HF∥AB,∴EG=HF,EG∥HF,∴四边形GFHE是平行四边形,∵E,H分别是AD,AC的中点,∴EH=CD,∵AB=CD,∴EG=EH,∴平行四边形GFHE是菱形,故答案为:菱形.14.如图,在△ABC中,∠ACB=60°,点D,E分别是AB,AC的中点,点F在线段DE 上,连结AF,CF.若CF恰好平分∠ACB,且CF=,则AC的长为2.【解答】解:延长AF交BC于F,∵D,E分别是AB,AC的中点,∴DE∥BC,∵DE∥BC,AE=EC,∴AF=FH,∵CF恰好平分∠ACB,∠ACB=60°,∴CF⊥AF,∠CF A=30°,∴AC==2,故答案为:2.15.如图,已知在△ABC中,D、E分别是AB、AC的中点,F、G分别是AD、AE的中点,且FG=2cm,则BC的长度是8cm.【解答】解:如图,∵△ADE中,F、G分别是AD、AE的中点,∴DE=2FG=4cm,∵D,E分别是AB,AC的中点,∴DE是△ABC的中位线,∴BC=2DE=8cm,故答案为:8.16.如图,△ABC中,AB=7cm,BC=6cm,AC=5cm,D,E,F分别是AB,BC,AC的中点,则四边形ADEF的周长等于12cm.【解答】解:∵D,E分别是AB,BC的中点,∴DE∥AC,DE=AC=2.5cm,同理,EF∥AB,EF=AB=3.5cm,∴四边形ADEF是平行四边形,∴四边形ADEF的周长=2×(2.5+3.5)=12(cm),故答案为:12.17.如图,在△ABC中,AC=10,D,E分别是AB,AC的中点.F是DE上一点,连结AF、CF.若∠AFC=90°,DF=1,则BC的长为12.【解答】解:∵∠AFC=90°,E是AC的中点,∴EF=AC=5,∴DE=DF+EF=5+1=6,∵D,E分别是AB,AC的中点,∴BC=2DE=12,故答案为:12.18.如图,△ABC中,D、E分别是BC、AC的中点,BF平分∠ABC,交DE于点F,若AB=12,BC=9,则EF的长是 1.5.【解答】解:∵D、E分别是BC、AC的中点,∴DE=AB=6,DE∥AB,BD=BC=4.5,∴∠ABF=∠DFB,∵BF平分∠ABC,∴∠ABF=∠DBF,∴∠DBF=∠DFB,∴DF=DB=4.5,∴EF=DE﹣DF=6﹣4.5=1.5,故答案为:1.5.19.已知一个三角形的周长为10cm,则连接各边中点所得的三角形的周长为5cm.【解答】解:∵D、E、F分别为AB、BC、AC的中点,∴DE=AC,EF=AB,DF=BC,∵AB+BC+AC=10,∴DE+EF+FD=(AB+BC+AC)=5cm,故答案为:5.20.如图,A,B两地被池塘隔开,小石通过下面的方法测出A,B间的距离:先在AB外选一点C,然后通过测量找到AC,BC的中点D,E,并测量出DE的长为20m,由此他就知道了A,B间的距离为40m,小石的依据是三角形中位线定理.【解答】解:∵点D,E是AC,BC的中点,∴AB=2DE=40(m),小石的依据是三角形中位线定理,故答案为:40;三角形中位线定理.三.解答题(共8小题)21.如图:D、E是△ABC边AB,AC的中点,O是△ABC内一动点,F、G是OB,OC的中点.判断四边形DEGF的形状,并证明.【解答】解:四边形DEGF是平行四边形,理由如下:∵D、E是△ABC边AB,AC的中点,∴DE=BC,DE∥BC,∵F、G是OB,OC的中点,∴FGT=BC,FG∥BC,∴DE=FG,DE∥FG,∴四边形DEGF是平行四边形.22.已知:在△ABC中,D是AB的中点,DE∥BC,交AC于点E.求证:DE是△ABC的中位线.【解答】证明:∵D是AB的中点,∴AD=DB,∵DE∥BC,∴==1,∴AE=EC,即E是AC的中点,∵D是AB的中点,E是AC的中点,∴DE是△ABC的中位线.23.如图,点D、E、F分别是△ABC各边中点.求证:四边形ADEF是平行四边形.【解答】证明:∵D、E分别为AB、BC的中点,∴DE∥AC,∵E、F分别为BC、AC中点,∴EF∥AB,∴四边形ADEF是平行四边形.24.补充完整三角形中位线定理,并加以证明:(1)三角形中位线定理:三角形的中位线平行于第三边,且等于第三边的一半;(2)已知:如图,DE是△ABC的中位线,求证:DE∥BC,DE=BC.【解答】(1)解:三角形中位线定理:三角形的中位线平行于第三边,且等于第三边的一半;故答案为:平行于第三边,且等于第三边的一半;(2)证明:如图,延长DE到F,使FE=DE,连接CF,在△ADE和△CFE中,,∴△ADE≌△CFE(SAS),∴∠A=∠ECF,AD=CF,∴CF∥AB,又∵AD=BD,∴CF=BD,∴四边形BCFD是平行四边形,∴DF∥BC,DF=BC,∴DE∥BC,DE=BC.25.如图,在四边形ABCD中,AC⊥BD,BD=12,AC=16,E,F分别为AB,CD的中点,求EF的长.【解答】解:如图,取BC边的中点G,连接EG、FG.∵E,F分别为AB,CD的中点,∴EG是△ABC的中位线,FG是△BCD的中位线,∴EG AC,FG BD.又BD=12,AC=16,AC⊥BD,∴EG=8,FG=6,EG⊥FG,∴在直角△EGF中,由用勾股定理,得EF===10,即EF的长度是10.26.如图,在四边形ABCD中,P是对角线BD的中点,E、F分别是AB、CD的中点,AD =BC,∠PEF=18°.求∠PFE的度数.【解答】解:∵P、E、F分别是DB、AB、DC的中点,∴PF是△DCB的中位线、PE是△DAB的中位线,∴PF=BC,PE=AD,又∵BC=AD,∴PF=PE,又∵∠PEF=18°,∴∠PFE=∠PEF=18°.27.如图,△ABC的中线AE与中位线DF相交于点O、试问AE与DF是否互相平分?为什么?【解答】解:AE与DF互相平分.连接DE、EF.∵AE、DF分别是△ABC的中线与中位线,∴D、E、F分别是AB、AC、BC的中点,∴DE∥AC,EF∥AD.∴四边形ADEF是平行四边形,∴AE与DF互相平分.28.如图,在△ABC中,D、E分别是AC、AB的中点,BD为角平分线.求证:(1)∠EBD=∠EDB;BC.(2)BE=∴∠EBD=∠DBC,∵E、D是中点,∴ED是中位线,∴ED∥BC,∴∠EDB=∠DBC,∴∠EBD=∠EDB;(2)由∠EBD=∠EDB得BE=DE,∵ED是中位线,∴ED=BC,∴BE=BC。
鲁教版八年级数学上册5.3三角形的中位线基础达标训练题(附答案)

鲁教版八年级数学上册5.3三角形的中位线基础达标训练题(附答案)一.选择题(共10小题)1.如图,A,B两地被池塘隔开,小明通过下列方法测出了A、B间的距离:先在AB外选一点C,然后测出AC,BC的中点M,N,并测量出MN的长为6m,由此他就知道了A、B间的距离.有关他这次探究活动的描述错误的是()A.AB=12m B.MN∥AB C.△CMN∽△CAB D.CM:MA=1:2 2.如图,在△ABC中,BD、CE是△ABC的中线,BD与CE相交于点O,点F、G分别是OB、OC的中点,连接AO.若AO=3cm,BC=4cm,则四边形DEFG的周长是()A.7cm B.9 cm C.12cm D.14cm3.如图,A、B两处被池塘隔开,为了测量A、B两处的距离,在AB外选一适当的点C,连接AC、BC,并分别取线段AC、BC的中点E、F,测得EF=20m,则AB长为()A.10m B.20m C.30m D.40m4.如图,在△ABC中,动点P在AB边上由点A向点B以3cm/s的速度匀速运动,则线段CP的中点Q运动的速度为()A.3cm/s B.2cm/s C.1.5cm/s D.1cm/s5.在△ABC中,点D,E分别是边AB,BC的中点,若DE=3,则AC=()A.3B.6C.9D.126.如图,点B是直线l外一点,在l的另一侧任取一点K,以B为圆心,BK为半径作弧,交直线l与点M、N;再分别以M、N为圆心,以大于MN为半径作弧,两弧相交于点P;连接BP交直线l于点A;点C是直线l上一点,点D、E分别是线段AB、BC的中点;F在CA的延长线上,∠FDA=∠B,AC=8,AB=6,则四边形AEDF的周长为()A.8B.10C.16D.187.如图,若DE是△ABC的中位线,△ADE的周长为1,则△ABC的周长为()A.1B.2C.3D.48.如图,在△ABC中,BF平分∠ABC,AF⊥BF于点F,D为AB的中点,连接DF延长交AC于点E.若AB=8,BC=14,则线段EF的长为()A.2B.3C.5D.69.如图,四边形ABCD中,点E、F、G分别是线段AD、BC、AC的中点,则△EFG的周长()A.与AB、BC、AC的长有关B.与AD、DC、AC的长有关C.与AB、DC、EF的长有关D.与AD、BC、EF的长有关10.如图,A、B两点被池塘隔开,在AB外选一点C,连结AC、BC.分别取AC、DC的中点写D、E,连结DE,若测得DE=40m,则A、B两点之间的距离是()A.40m B.60m C.80m D.100m二.填空题(共10小题)11.△ABC中,BC=8,AB,AC的中点分别为D,E,则DE=.12.如图,跷板AB的支柱OD经过它的中点O,且垂直于地面BC,垂足为D,OD=0.8m;当它的一端B地时,另一端A离地面的高度AC为m.13.京珠高速公路粤北段地势十分复杂,所以当年在建这段路时,要开很多隧道,如图是一个要开挖的隧道,为保证按时完成工程,必须先要知道所挖隧道的长度,于是测量人员在山外取一点O,并取AO,BO的中点C,D,测得CD=237m,则隧道AB的长是m.14.如图,已知等边三角形ABC边长为16,△ABC的三条中位线组成△A1B1C1,△A1B1C1的三条中位线组成△A2B2C2,依此进行下去得到△A4B4C4的周长为.15.如图,在△ABC中,点D、E、F分别是BC、AB、AC的中点,如果△ABC的周长为20+2,那么△DEF的周长是.16.如图,在△ABC中,D,E分别是AB和AC的中点,F是BC延长线上一点,CF=1,DF交CE于点G,且EG=CG,则BC=.17.若三角形各边长分别为8cm、10cm、16cm,则以各边中点为顶点的三角形的周长是.18.如图,在△ABC中,D、E分别为AB、AC的中点,点F在DE上,且AF⊥CF,若AC =3,BC=5,则DF=.19.等边三角形的中位线与高之比为.20.如图,在四边形ABCD中,∠A=90°,M、N分别为线段BC、AB上的动点(含端点,但点M不与点B重合),E、F分别为DM、MN的中点,若AB=2,AD=2,则EF 长度的最大值为.三.解答题(共8小题)21.如图,在△ABC中,点D,E分别是AB,AC的中点,F是BC延长线上的一点,且CF =BC.试猜想DE与CF有怎样的数量关系,并说明理由.22.如图,在△ABC中,M是BC的中点,AN平分∠BAC,AN⊥BN于N,延长BN交AC 于点D,已知AB=10,MN=4,BM=7,求△ABC的周长.23.如图,在Rt△ABC中,∠A=90°,∠B=30°,D、E分别是AB、BC的中点,若DE =3,求BC的长.24.如图,四边形ABCD中,AB=AD,对角线BD平分∠ABC,E,F分别是BD,CD的中点.求证:AD∥EF.25.如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,过点E作EF∥CD交BC的延长线于点F,连接CD.(1)求证:DE=CF;(2)求EF的长.26.证明:三角形的中位线平行于三角形的第三边,并且等于第三边的一半.(要求:在给出的△ABC中用尺规作出AB、AC边的中点M、N,保留作图痕迹,不要求写作法,并根据图形写出已知、求证和证明)27.“过三角形一边的中点,且平行于另一边的直线,必过第三边的中点”.根据这个结论解决问题:如图,S△ABC=32,AC=8,BC=10,点M为BC的中点,MN⊥AC于点N,求NC的长.28.如图,在四边形ABCD中,AB=CD,M、N、P分别是AD、BC、BD的中点,求证:PM=PN.参考答案与试题解析一.选择题(共10小题)1.如图,A,B两地被池塘隔开,小明通过下列方法测出了A、B间的距离:先在AB外选一点C,然后测出AC,BC的中点M,N,并测量出MN的长为6m,由此他就知道了A、B间的距离.有关他这次探究活动的描述错误的是()A.AB=12m B.MN∥AB C.△CMN∽△CAB D.CM:MA=1:2【解答】解:∵M、N分别是AC、BC的中点,∴MN是△ABC的中位线,CM=AM,∴MN∥AB,MN=AB,AB=2MN=12m,CM:MA=1:1,∴△CMN∽△CAB;故A,B,C正确,故选:D.2.如图,在△ABC中,BD、CE是△ABC的中线,BD与CE相交于点O,点F、G分别是OB、OC的中点,连接AO.若AO=3cm,BC=4cm,则四边形DEFG的周长是()A.7cm B.9 cm C.12cm D.14cm【解答】解:∵BD、CE是△ABC的中线,∴DE=BC=2,同理,FG=BC=2,EF=OA=1.5,DG=OA=1.5,∴四边形DEFG的周长=DE+EF+FG+DG=7(cm),故选:A.3.如图,A、B两处被池塘隔开,为了测量A、B两处的距离,在AB外选一适当的点C,连接AC、BC,并分别取线段AC、BC的中点E、F,测得EF=20m,则AB长为()A.10m B.20m C.30m D.40m【解答】解:∵E、F是AC,AB的中点,∴EF是△ABC的中位线,∴EF=AB∵EF=20m,∴AB=40m.故选:D.4.如图,在△ABC中,动点P在AB边上由点A向点B以3cm/s的速度匀速运动,则线段CP的中点Q运动的速度为()A.3cm/s B.2cm/s C.1.5cm/s D.1cm/s【解答】解:取AC的中点H,连接QH,当点P与点A重合时,点Q与点H重合,∵点Q是线段CP的中点,点H为AC的中点,∴QH=AP,∵动点P在AB边上由点A向点B以3cm/s的速度匀速运动,∴点Q运动的速度为1.5cm/s,故选:C.5.在△ABC中,点D,E分别是边AB,BC的中点,若DE=3,则AC=()A.3B.6C.9D.12【解答】解:∵点D,E分别是边AB,BC的中点,∴AC=2DE=6,故选:B.6.如图,点B是直线l外一点,在l的另一侧任取一点K,以B为圆心,BK为半径作弧,交直线l与点M、N;再分别以M、N为圆心,以大于MN为半径作弧,两弧相交于点P;连接BP交直线l于点A;点C是直线l上一点,点D、E分别是线段AB、BC的中点;F在CA的延长线上,∠FDA=∠B,AC=8,AB=6,则四边形AEDF的周长为()A.8B.10C.16D.18【解答】解:由题意得,BA⊥MN,∴BC==10,∵∠BAC=90°,点D是线段BC的中点,∴AE=BE=BC=5,∴∠EAB=∠B,∵∠FDA=∠B,∴∠FDA=∠EAB,∴DF∥AE,∵点D、E分别是线段AB、BC的中点,∴DE∥AC,DE=AC=4,∴四边形AEDF是平行四边形,∴四边形AEDF的周长=2×(4+5)=18,故选:D.7.如图,若DE是△ABC的中位线,△ADE的周长为1,则△ABC的周长为()A.1B.2C.3D.4【解答】解:∵DE是△ABC的中位线,∴DE∥BC,DE=BC,∴△ADE∽△ABC,∵△ADE的周长为1,∴△ABC的周长为2,故选:B.8.如图,在△ABC中,BF平分∠ABC,AF⊥BF于点F,D为AB的中点,连接DF延长交AC于点E.若AB=8,BC=14,则线段EF的长为()A.2B.3C.5D.6【解答】解:延长AF交BC于G,在△BF A和△BFG中,,∴△BF A≌△BFG(ASA)∴BG=AB=8,AF=FG,∴GC=BC﹣BG=6,∵AF=FG,AE=EC,∴EF=GC=3,故选:B.9.如图,四边形ABCD中,点E、F、G分别是线段AD、BC、AC的中点,则△EFG的周长()A.与AB、BC、AC的长有关B.与AD、DC、AC的长有关C.与AB、DC、EF的长有关D.与AD、BC、EF的长有关【解答】解:∵点E、G分别是线段AD、AC的中点,∴EG=CD,∵点F、G分别是线段BC、AC的中点,∴GF=AB,则△EFG的周长=EG+GF+EF=CD+AB+EF,∴△EFG的周长与AB、DC、EF的长有关,故选:C.10.如图,A、B两点被池塘隔开,在AB外选一点C,连结AC、BC.分别取AC、DC的中点写D、E,连结DE,若测得DE=40m,则A、B两点之间的距离是()A.40m B.60m C.80m D.100m【解答】解:∵D、E分别是AC、DC的中点,∴AB=2DE=80(m),故选:C.二.填空题(共10小题)11.△ABC中,BC=8,AB,AC的中点分别为D,E,则DE=4.【解答】解:∵D,E分别是边AC、AC的中点,∴BC=2DE,∵BC=8,∴DE=×8=4,故答案为:4.12.如图,跷板AB的支柱OD经过它的中点O,且垂直于地面BC,垂足为D,OD=0.8m;当它的一端B地时,另一端A离地面的高度AC为 1.6m.【解答】解:∵AC∥OD,O是AB的中点,∴D是BC的中点,∵O是AB的中点,D是BC的中点,∴AC=2OD=1.6,故答案为:1.6.13.京珠高速公路粤北段地势十分复杂,所以当年在建这段路时,要开很多隧道,如图是一个要开挖的隧道,为保证按时完成工程,必须先要知道所挖隧道的长度,于是测量人员在山外取一点O,并取AO,BO的中点C,D,测得CD=237m,则隧道AB的长是474 m.【解答】解:∵点C,D是AO,BO的中点,∴AB=2CD,∵CD=237m,∴AB=474m,故答案为:474.14.如图,已知等边三角形ABC边长为16,△ABC的三条中位线组成△A1B1C1,△A1B1C1的三条中位线组成△A2B2C2,依此进行下去得到△A4B4C4的周长为3.【解答】解:∵等边三角形ABC边长为16,∴△ABC的周长为48,∵△A1B1C1是△ABC的三条中位线组成,∴△A1B1C1的周长=×△ABC的周长=24,同理,△A2B2C2,的周长=24×=12,△A3B3C3的周长=12×=6,△A4B4C4的周长=6×=3,故答案为:3.15.如图,在△ABC中,点D、E、F分别是BC、AB、AC的中点,如果△ABC的周长为20+2,那么△DEF的周长是10+.【解答】解:∵△ABC的周长为20+2,∴AB+AC+BC=20+2,∵点D、E、F分别是BC、AB、AC的中点,∴EF=BC,DF=AB,DE=AC,∴△DEF的周长=DE+EF+DF=(AC+BC+AB)=10+,故答案为:10+.16.如图,在△ABC中,D,E分别是AB和AC的中点,F是BC延长线上一点,CF=1,DF交CE于点G,且EG=CG,则BC=2.【解答】解:∵D、E分别是AB和AC的中点∴DE∥BC,DE=BC∴△ADE∽△ABC,△GED≌△GCF∴DE=CF=1∴CF=BC∴BC=2故答案为2.17.若三角形各边长分别为8cm、10cm、16cm,则以各边中点为顶点的三角形的周长是17cm.【解答】解:∵D、E分别是AB、AC的中点,∴DE=BC=8,同理,DF=5=8,FE=BA=4,∴△DEF的周长=DE+EF+DF=17故答案为:17cm.18.如图,在△ABC中,D、E分别为AB、AC的中点,点F在DE上,且AF⊥CF,若AC =3,BC=5,则DF=1.【解答】解:∵D、E分别为AB、AC的中点,∴DE=BC=2.5,∵AF⊥CF,E为AC的中点,∴EF=AC=1.5,∴DF=DE﹣EF=1,故答案为:1.19.等边三角形的中位线与高之比为1:.【解答】解:设等边三角形的边长为2a,则中位线长为a,高线的长为=a,所以等边三角形的中位线与高之比为a:a=1:,故答案为:1:.20.如图,在四边形ABCD中,∠A=90°,M、N分别为线段BC、AB上的动点(含端点,但点M不与点B重合),E、F分别为DM、MN的中点,若AB=2,AD=2,则EF 长度的最大值为2.【解答】解:连接BD、DN,在Rt△ABD中,DB==4,∵点E、F分别为DM、MN的中点,∴EF=DN,由题意得,当点N与点B重合时,DN最大,∴DN的最大值是4,∴EF长度的最大值是2,故答案为:2.三.解答题(共8小题)21.如图,在△ABC中,点D,E分别是AB,AC的中点,F是BC延长线上的一点,且CF =BC.试猜想DE与CF有怎样的数量关系,并说明理由.【解答】解:DE=CF,理由如下:∵点D,E分别是AB,AC的中点,∴DE=BC,∵CF=BC,∴DE=CF.22.如图,在△ABC中,M是BC的中点,AN平分∠BAC,AN⊥BN于N,延长BN交AC 于点D,已知AB=10,MN=4,BM=7,求△ABC的周长.【解答】解:在△ANB和△AND中,,∴△ANB≌△AND(ASA)∴AD=AB=10,BN=BD,∵M是BC的中点,BN=BD,∴BC=2BM=14,CD=2MN=8,∴△ABC的周长=AB+BC+AC=10+14+8+10=42.23.如图,在Rt△ABC中,∠A=90°,∠B=30°,D、E分别是AB、BC的中点,若DE =3,求BC的长.【解答】解:∵D、E是AB、BC的中点,DE=3∴AC=2DE=6,∵∠A=90°,∠B=30°,∴BC=2AC=12.24.如图,四边形ABCD中,AB=AD,对角线BD平分∠ABC,E,F分别是BD,CD的中点.求证:AD∥EF.【解答】证明:∵E,F分别是BD,CD的中点,∴EF∥BC,∵AB=AD,∴∠ADB=∠ABD,∵BD平分∠ABC,∴∠DBC=∠ABD,∴∠ADB=∠DBC,∴AD∥BC,∴AD∥EF.25.如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,过点E作EF∥CD交BC的延长线于点F,连接CD.(1)求证:DE=CF;(2)求EF的长.【解答】解:(1)∵D、E分别为AB、AC的中点,∴DE∥BC,DE=BC,∵EF∥CD∴四边形DEFC是平行四边形,∴DE=CF.(2)∵四边形DEFC是平行四边形,∴DC=EF,∵D为AB的中点,等边△ABC的边长是2,∴AD=BD=1,CD⊥AB,BC=2,∴DC=EF=.26.证明:三角形的中位线平行于三角形的第三边,并且等于第三边的一半.(要求:在给出的△ABC中用尺规作出AB、AC边的中点M、N,保留作图痕迹,不要求写作法,并根据图形写出已知、求证和证明)【解答】解:如图,点M,N即为所求作的点,已知:如图,△ABC中,点M,N分别是AB,AC的中点,连接MN,求证:MN∥BC,MN=BC证明:延长MN至点D,使得MN=ND,连接CD,在△AMN和△CDN中,,∴△AMN≌△CDN(SAS)∴∠AMN=∠D,AM=CD,∴AM∥CD,即BM∥CD,∵AM=BM=CD,∴四边形BMDC为平行四边形,∴MN∥BC,MD=BC,∵,∴.27.“过三角形一边的中点,且平行于另一边的直线,必过第三边的中点”.根据这个结论解决问题:如图,S△ABC=32,AC=8,BC=10,点M为BC的中点,MN⊥AC于点N,求NC的长.【解答】解:过点B作MN的平行线BD,∵S△ABC=32,∴BD=8,∵点M为BC的中点,∴MN=4,∵BC=10,∴CM=5,在Rt△MNC中,CM=5,MN=4,可得:CN=.28.如图,在四边形ABCD中,AB=CD,M、N、P分别是AD、BC、BD的中点,求证:PM=PN.【解答】解:∵M、N、P分别是AD、BC、BD的中点,∴PM=AB,PN=CD,∵AB=CD,∴PM=PN。
鲁教版2020八年级数学上册5.3三角形的中位线培优练习题(附答案)

鲁教版2020八年级数学上册5.3三角形的中位线培优练习题(附答案)一.填空题(共7小题)1.如图,在Rt△ABC中,∠ACB=90°,BC=6,AC=8,点M是AC边的中点,点N是BC边上的任意一点,若点C关于直线MN的对称点C′恰好落在△ABC的中位线上,则CN的长为.2.如图,△ABC中,∠A=60°,AC>AB>2,点D,E分别在边AB,AC上,且BD=CE =2,连接DE,点M是DE的中点,点N是BC的中点,线段MN的长为.3.如图,在Rt△ABC中,∠ACB=90°,BC=3,AC=4,点M为边AC的中点,点N为边BC上任意一点,若点C关于直线MN的对称点C′恰好落在△ABC的中位线上,则CN 的长为.4.如图,△ABC中,AB=10,AC=7,AD平分∠BAC,AE是BC边上的中线,过点C作CG⊥AD于F,交AB于G,连接EF,则线段EF的长为.5.如图,顺次连结△ABC三边的中点D,E,F得到的三角形面积为S1,顺次连结△CEF 三边的中点M,G,H得到的三角形面积为S2,顺次连结△CGH三边的中点得到的三角形面积为S3.设△ABC的面积为S,则S1+S2+S3=.6.已知第一个三角形的周长为1,连接三边的中点构成第2个三角形,再连接第2个三角形三边中点构成第3个三角形,…,依此类推,第2014个三角形的周长是.7.如图,△ABC的周长为19,点D,E在边BC上,∠ABC的平分线垂直于AE,垂足为N,∠ACB的平分线垂直于AD,垂足为M,若BC=7,则MM的长度为.二.解答题(共8小题)8.△ABC的中线BD,CE相交于O,F,G分别是BO,CO的中点,求证:EF∥DG,且EF=DG.9.如图,等边△ABC的边长是4,D,E分别为AB,AC的中点,延长BC至点F,使CF =BC,连接CD和EF.(1)求证:DE=CF;(2)求EF的长;(3)求四边形DEFC的面积.10.如图所示,在四边形ABCD中,AD=BC,P是对角线BD的中点,M是DC的中点,N是AB的中点.请判断△PMN的形状,并说明理由.11.如图所示,在△ABC中,E为AB的中点,CD平分∠ACB,AD⊥CD于点D.试说明:(1)DE∥BC;(2)DE=(BC﹣AC).12.如图,△ABC中,AB=8,AC=6,AD、AE分别是其角平分线和中线,过点C作CG ⊥AD于F,交AB于G,连接EF,求线段EF的长.13.【问题提出】:将一个边长为n(n≥2)的正三角形的三条边n等分,连接各边对应的等分点,则该三角形被剖分的网格中的结点个数和线段数分别是多少呢?【问题探究】:要研究上面的问题,我们不妨先从特例入手,进而找到一般规律.探究一:将一个边长为2的正三角形的三条边平分,连接各边中点,则该三角形被剖分的网格中的结点个数和线段数分别是多少?如图1,连接边长为2的正三角形三条边的中点,从上往下:共有1+2+3=6个结点.边长为1的正三角形,第一层有1个,第二层有2个,共有1+2=3个,线段数为3×3=9条;边长为2的正三角形有1个,线段数为3条,总共有3×(1+2+1)=2×(1+2+3)=12条线段.探究二:将一个边长为3的正三角形的三条边三等分,连接各边对应的等分点,则该三角形被剖分的网格中的结点个数和线段数分别是多少?如图2,连接边长为3的正三角形三条边的对应三等分点,从上往下:共有1+2+3+4=10个结点.边长为1的正三角形,第一层有1个,第二层有2个,第三层有3个,共有1+2+3=6个,线段数为3×6=18条;边长为2的正三角形有1+2=3个,线段数为3×3=9条,边长为3的正三角形有1个,线段数为3条,总共有3×(1+2+3+1+2+1)=3×(1+2+3+4)=30条线段.探究三:请你仿照上面的方法,探究将边长为4的正三角形的三条边四等分(图3),连接各边对应的等分点,该三角形被剖分的网格中的结点个数和线段数分别是多少?(画出示意图,并写出探究过程)【问题解决】:请你仿照上面的方法,探究将一个边长为n(n≥2)的正三角形的三条边n等分,连接各边对应的等分点,则该三角形被剖分的网格中的结点个数和线段数分别是多少?(写出探究过程)【实际应用】:将一个边长为30的正三角形的三条边三十等分,连接各边对应的等分点,则该三角形被剖分的网格中的结点个数和线段数分别是多少?14.如图,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,延长BN交AC 于点D,已知AB=10,AC=16.(1)求证:BN=DN;(2)求MN的长.15.如图,在Rt△ABC中,∠ACB=90°,点E,F分别是边AC,AB的中点,延长BC到点D,使2CD=BC,连接DE.(1)如果AB=10,求DE的长;(2)延长DE交AF于点M,求证:点M是AF的中点.参考答案与试题解析一.填空题(共7小题)1.如图,在Rt△ABC中,∠ACB=90°,BC=6,AC=8,点M是AC边的中点,点N是BC边上的任意一点,若点C关于直线MN的对称点C′恰好落在△ABC的中位线上,则CN的长为或.【解答】解:取BC、AB的中点H、G,连接MH、HG、MG.如图1中,当点C′落在MH上时,设NC=NC′=x,由题意可知:MC=MC′=4,MH=5,HC′=1,HN=3﹣x,在Rt△HNC′中,∵HN2=HC′2+NC′2,∴(3﹣x)2=x2+12,解得x=.如图2中,当点C′落在GH上时,设NC=NC′=x,在Rt△GMC′中,MG=CH=3,MC=MC′=4,∴GC′=,∵∠NHC'=∠C'GM=90°,∠NC'M=90°,∴∠HNC'+∠HC'N=∠GC'M+∠HC'N=90°,∴∠HNC'=∠CGC'M,∴△HNC′∽△GC′M,∴=,∴=,∴x=.如图3中,当点C′落在直线GM上时,易证四边形MCNC′是正方形,可得CN=CM =2.∴C'M>GM,此时点C′在中位线GM的延长线上,不符合题意.综上所述,满足条件的线段CN的长为或.故答案为:或.2.如图,△ABC中,∠A=60°,AC>AB>2,点D,E分别在边AB,AC上,且BD=CE =2,连接DE,点M是DE的中点,点N是BC的中点,线段MN的长为.【解答】解:如图,作CH∥AB,连接DN,延长DN交CH于H,连接EH,作CJ⊥EH 于J.∵BD∥CH,∴∠B=∠NCH,∵BN=CN,∠DNB=∠KNC,∵△DNB≌△HNC(ASA),∴BD=CH,DN=NH,∵BD=EC=2,∴EC=CH=2,∵∠A+∠ACH=180°,∠A=60°,∴∠ECH=120°,∵CJ⊥EH,∴EJ=JH=EC•cos30°=,∴EH=2EJ=2,∵DM=ME,DN=NH,∴MN=EH=.故答案为.3.如图,在Rt△ABC中,∠ACB=90°,BC=3,AC=4,点M为边AC的中点,点N为边BC上任意一点,若点C关于直线MN的对称点C′恰好落在△ABC的中位线上,则CN的长为或.【解答】解:取BC、AB的中点H、G,连接MH、HG、MG.如图1中,当点C′落在MH上时,设NC=NC′=x,由题意可知:MC=MC′=2,MH=,HC′=,HN=﹣x,在Rt△HNC′中,∵HN2=HC′2+NC′2,∴(﹣x)2=x2+()2,解得x=.如图2中,当点C′落在GH上时,设NC=NC′=x,在Rt△GMC′中,MG=CH=,MC=MC′=2,∴GC′=,∵△HNC′∽△GC′M,∴=,∴=,∴x=.如图3中,当点C′落在直线GM上时,易证四边形MCNC′是正方形,可得CN=CM =2.此时点C′在中位线GM的延长线上,不符合题意舍弃.综上所述,满足条件的线段CN的长为或.故答案为为或.4.如图,△ABC中,AB=10,AC=7,AD平分∠BAC,AE是BC边上的中线,过点C作CG⊥AD于F,交AB于G,连接EF,则线段EF的长为 1.5.【解答】解:∵AD平分∠BAC,∴∠GAF=∠CAF,∵CG⊥AD,∴∠AFG=∠AFC,在△AGF和△ACF中,,∴△AGF≌△ACF(ASA),∴AG=AC=7,GF=CF,则BG=AB﹣AG=10﹣7=3.又∵BE=CE,∴EF是△BCG的中位线,∴EF=BG=1.5.故答案是:1.5.5.如图,顺次连结△ABC三边的中点D,E,F得到的三角形面积为S1,顺次连结△CEF 三边的中点M,G,H得到的三角形面积为S2,顺次连结△CGH三边的中点得到的三角形面积为S3.设△ABC的面积为S,则S1+S2+S3=S.【解答】解:∵D,E,F是△ABC三边的中点,∴DF∥BC,DE∥AC,EF∥AB,∴△ADF∽△ABC,△BDE∽△BAC,△CEF∽△CBA且相似比为,∴===,∵△ABC的面积为S,∴S△ADF=S△BDE=S△CEF=S,∴S1=S﹣S△ADF﹣S△BDE﹣S△CEF=S﹣S﹣S﹣S=S.同理可得,S2=S△CEF=×S=S,S3=S△CGH=××S=S,∴S1+S2+S3=S+S+S=S.故答案为:S.6.已知第一个三角形的周长为1,连接三边的中点构成第2个三角形,再连接第2个三角形三边中点构成第3个三角形,…,依此类推,第2014个三角形的周长是.【解答】解:由三角形的中位线定理可知后一个三角形的周长等于上一个三角形的周长的一半,∵第一个三角形的周长是1,∴第2个三角形的周长=,第3个三角形的周长=,…,第n个三角形的周长=.故答案为:.7.如图,△ABC的周长为19,点D,E在边BC上,∠ABC的平分线垂直于AE,垂足为N,∠ACB的平分线垂直于AD,垂足为M,若BC=7,则MM的长度为.【解答】解:∵BN平分∠ABC,BN⊥AE,∴∠NBA=∠NBE,∠BNA=∠BNE,在△BNA和△BNE中,.∴△BNA≌△BNE(ASA),∴BA=BE,∴△BAE是等腰三角形,同理△CAD是等腰三角形,∴点N是AE中点,点M是AD中点(三线合一),∴MN是△ADE的中位线,∵BE+CD=AB+AC=19﹣BC=19﹣7=12,∴DE=BE+CD﹣BC=5,∴MN=DE=.故答案是:.二.解答题(共8小题)8.△ABC的中线BD,CE相交于O,F,G分别是BO,CO的中点,求证:EF∥DG,且EF=DG.【解答】证明:连接DE,FG,∵BD,CE是△ABC的中线,∴D,E是AB,AC的中点,∴DE∥BC,DE=BC,同理:FG∥BC,FG=BC,∴DE∥FG,DE=FG,∴四边形DEFG是平行四边形,∴EF∥DG,EF=DG.9.如图,等边△ABC的边长是4,D,E分别为AB,AC的中点,延长BC至点F,使CF =BC,连接CD和EF.(1)求证:DE=CF;(2)求EF的长;(3)求四边形DEFC的面积.【解答】解:(1)在△ABC中,∵D、E分别为AB、AC的中点,∴DE为△ABC的中位线,∴DE=BC,∵CF=BC,∴DE=CF.(2)∵AC=BC,AD=BD,∴CD⊥AB,∵BC=4,BD=2,∴CD==2,∵DE∥CF,DE=CF,∴四边形DEFC是平行四边形,∴EF=CD=2.(3)过点D作DH⊥BC于H.∵∠DHC=90°,∠DCB=30°,∴DH=DC=,∵DE=CF=2,∴S四边形DEFC=CF•DH=2×=2.10.如图所示,在四边形ABCD中,AD=BC,P是对角线BD的中点,M是DC的中点,N是AB的中点.请判断△PMN的形状,并说明理由.【解答】解:△PMN是等腰三角形.理由如下:∵点P是BD的中点,点M是CD的中点,∴PM=BC,同理:PN=AD,∵AD=BC,∴PM=PN,∴△PMN是等腰三角形.11.如图所示,在△ABC中,E为AB的中点,CD平分∠ACB,AD⊥CD于点D.试说明:(1)DE∥BC;(2)DE=(BC﹣AC).【解答】证明:延长AD交BC于F.(1)∵AD⊥CD,∴∠ADC=∠FDC=90°.∵CD平分∠ACB,∴∠ACD=∠FCD.在△ACD与△FCD中,∠ADC=∠FDCDC=DC∠ACD=∠FCD,∴△ACD≌△FCD.∴AC=FCAD=DF.又∵E为AB的中点,∴DE∥BF,即DE∥BC.(2)由(1)知AC=FC,DE=BF,∴DE=(BC﹣FC)=(BC﹣AC).12.如图,△ABC中,AB=8,AC=6,AD、AE分别是其角平分线和中线,过点C作CG ⊥AD于F,交AB于G,连接EF,求线段EF的长.【解答】解:在△AGF和△ACF中,,∴△AGF≌△ACF(ASA),∴AG=AC=6,GF=CF,则BG=AB﹣AG=8﹣6=2.又∵BE=CE,∴EF是△BCG的中位线,∴EF=BG=1.13.【问题提出】:将一个边长为n(n≥2)的正三角形的三条边n等分,连接各边对应的等分点,则该三角形被剖分的网格中的结点个数和线段数分别是多少呢?【问题探究】:要研究上面的问题,我们不妨先从特例入手,进而找到一般规律.探究一:将一个边长为2的正三角形的三条边平分,连接各边中点,则该三角形被剖分的网格中的结点个数和线段数分别是多少?如图1,连接边长为2的正三角形三条边的中点,从上往下:共有1+2+3=6个结点.边长为1的正三角形,第一层有1个,第二层有2个,共有1+2=3个,线段数为3×3=9条;边长为2的正三角形有1个,线段数为3条,总共有3×(1+2+1)=2×(1+2+3)=12条线段.探究二:将一个边长为3的正三角形的三条边三等分,连接各边对应的等分点,则该三角形被剖分的网格中的结点个数和线段数分别是多少?如图2,连接边长为3的正三角形三条边的对应三等分点,从上往下:共有1+2+3+4=10个结点.边长为1的正三角形,第一层有1个,第二层有2个,第三层有3个,共有1+2+3=6个,线段数为3×6=18条;边长为2的正三角形有1+2=3个,线段数为3×3=9条,边长为3的正三角形有1个,线段数为3条,总共有3×(1+2+3+1+2+1)=3×(1+2+3+4)=30条线段.探究三:请你仿照上面的方法,探究将边长为4的正三角形的三条边四等分(图3),连接各边对应的等分点,该三角形被剖分的网格中的结点个数和线段数分别是多少?(画出示意图,并写出探究过程)【问题解决】:请你仿照上面的方法,探究将一个边长为n(n≥2)的正三角形的三条边n等分,连接各边对应的等分点,则该三角形被剖分的网格中的结点个数和线段数分别是多少?(写出探究过程)【实际应用】:将一个边长为30的正三角形的三条边三十等分,连接各边对应的等分点,则该三角形被剖分的网格中的结点个数和线段数分别是多少?【解答】解:探究三:如图3中,连接边长为4的正三角形三条边的对应四等分点,从上往下:共有1+2+3+4+5=15个结点.边长为1的正三角形,第一层有1个,第二层有2个,第三层有3个,第四层有4个,共有1+2+3+4=10个结点个数,线段数为3×10=30条;边长为2的正三角形有1+2+3=6个,线段数为3×6=18条,边长为3的正三角形有3个,线段数为3×3=9,边长为4的正三角形有1个,线段数为3条,总共有3×(1+2+3+4+1+2+3+3+1)=4×(1+2+3+4+5)=60条线段.问题解决:探究将一个边长为n(n≥2)的正三角形的三条边n等分,连接各边对应的等分点,从上往下:共有1+2+3+4+5=15个结点.边长为1的正三角形,第一层有1个,第二层有2个,第三层有3个,第四层有4个,•第n层有n个,共有1+2+3+4+…+n个结点个数,线段数为3×(1+2+3=4+…+n)条;边长为2的正三角形有1+2+3=6个,线段数为3×6=18条,边长为3的正三角形有3个,线段数为3×3=9,边长为4的正三角形有1个,线段数为3条,…边长为n的三角形1个,线段数为3,线段的个数为n (1+2+3+…+n+1).实际应用:将一个边长为30的正三角形的三条边三十等分,连接各边对应的等分点,则该三角形被剖分的网格中的结点个数为1+2+…+30=465个结点个数,线段数=30(1+2+3+…+31)=14880.14.如图,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,延长BN交AC 于点D,已知AB=10,AC=16.(1)求证:BN=DN;(2)求MN的长.【解答】证明:(1)∵AN平分∠BAC∴∠1=∠2,∵BN⊥AN∴∠ANB=∠AND,在△ABN和△ADN中,,∴△ABN≌△ADN(ASA)∴BN=DN;(2)∵△ABN≌△ADN∴AD=AB=10,DN=NB,∴CD=AC﹣AD=16﹣10=6,又∵点M是BC中点,∴MN是△BDC的中位线,∴MN=CD=3.15.如图,在Rt△ABC中,∠ACB=90°,点E,F分别是边AC,AB的中点,延长BC到点D,使2CD=BC,连接DE.(1)如果AB=10,求DE的长;(2)延长DE交AF于点M,求证:点M是AF的中点.【解答】解:(1)连接CF,在Rt△ABC中,F是AB的中点,∴CF=AB=5,∵点E,F分别是边AC,AB的中点,∴EF∥BC,EF=BC,∵2CD=BC,∴EF=CD,EF∥CD,∴四边形EDCF是平行四边形,∴DE=CF=5;(2)如图2,∵四边形EDCF是平行四边形,∴CF∥DM,∵点E是边AC的中点,∴点M是AF的中点.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
鲁教版2020八年级数学上册5.3三角形的中位线培优练习题2(附答案)一.选择题(共10小题)1.一个三角形的三条中位线的长为6、7、8,则此三角形的周长为()A.40B.41C.42D.432.如图,△ABC的周长为32,点D、E都在边BC上,∠ABC的平分线垂直于AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P,若BC=12,则PQ的长为()A.3B.4C.5D.63.如图,点D、E、F分别是△ABC的边AB、BC、CA的中点,连接DE、EF、FD得△DEF,如果△ABC的周长是24cm,那么△DEF的周长是()A.6cm B.12cm C.18cm D.48cm4.在△ABC中,点M为BC的中点,AD平分∠BAC,且BD⊥AD于点D,延长BD交AC 于点N,若AB=4,AC=6,则DM的长为()A.B.1C.D.25.如图,△ABC的周长为17,点D,E在边BC上,∠ABC的平分线垂直于AE,垂足为点N,∠ACB的平分线垂直于AD,垂足为点M,若BC=6,则MN的长度为()A.B.2C.D.36.如图,在△ABC中,AD是角平分线,AE是中线,CF⊥AD于点F,AC=5,AB=13,则EF的长为()A.B.C.3D.47.如图,在▱ABCD中,BD为对角线,E、F分别是AD、BD的中点,连接EF.若EF=3,则CD的长为()A.3B.6C.8D.128.如图是一块等腰三角形空地ABC,已知点D,E分别是边AB,AC的中点,量得AC=10米,AB=BC=6米,若用篱笆围成四边形BCED来放养小鸡,则需要篱笆的长是()A.22米B.17米C.14米D.11米9.如图,在△ABC中,BC=15,B1、B2、…B9、C1、C2、…C9分别是AB、AC的10等分点,则B1C1+B2C2+…+B9C9的值是()A.45B.55C.67.5D.13510.如图,在△ABC中,BD、CE分别是∠ABC和∠ACB的平分线,AM⊥CE于P,交BC 于M,AN⊥BD于Q,交BC于N,∠BAC=110°,AB=6,AC=5,MN=2,结论①AP =MP;②BC=9;③∠MAN=35°;④AM=AN.其中不正确的有()A.4个B.3个C.2个D.1个二.填空题(共10小题)11.小明的爸爸承包了一个鱼塘,小明想知道鱼塘的长(即A,B间的距离).他通过下面的方法测量A,B间的距离:先在AB外选一点C,然后测出AC,BC的中点M,N,并测得MN的长为20m,由此他就知道了A,B间的距离.请你回答A,B间的距离是.12.如图,在四边形ABCD中,点E、F分别是边AB、AD的中点,BC=15,CD=9,EF =6,∠AFE=50°,则∠ADC的度数为.13.如图,为测量池塘岸边A,B两点间的距离,小明在池塘的一侧选取一点O,测得OA,OB的中点分别是点D、E,且DE=14米,则A,B两点间的距离是米14.如图,在△ABC中,∠ABC=90°,BC=5.若DE是△ABC的中位线,延长DE交△ABC的外角∠ACM的平分线于点F,且DF=9,则CE的长为.15.如图,A、B两点被池塘隔开,在AB外选一点C,连接AC、BC,取AC、BC的中点D、E,量出DE=a,则AB=2a,它的根据是.16.如图,在△ABC中,E,F分别是AB,AC的中点,若中位线EF=2cm,则BC边的长是.17.如图,在△ABC中,∠ACB=60°,AC=1,D是边AB的中点,E是边BC上一点.若DE平分△ABC的周长,则DE的长是.18.已知△ABC的周长为4,顺次连接△ABC三边的中点构成的新三角形的周长为.19.如图,△ABC中,D、E分别是AB、AC边的中点,且DE=7cm,则BC=cm.20.如图,在Rt△ABC中,∠ACB=90°,AC=BC=5,点E、F分别在CA,CB上,且CE=CF=1,点M、N分别为AF、BE的中点,则MN的长为.三.解答题(共8小题)21.已知:如图,在△ABC中,点D在AB上,BD=AC,E、F、G分别是BC、AD、CD 的中点,EF、CA的延长线相交于点H.求证:(1)∠CGE=∠ACD+∠CAD;(2)AH=AF.22.求证:三角形的中位线平行于三角形的第三边,且等于第三边的一半.23.如图,D、E分别是△ABC的边AB、AC的中点,点O是△ABC内部任意一点,连接OB、OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.求证:四边形DGFE是平行四边形.24.如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,延长BC至点F,使CF =BC,连接CD和EF.(1)求证:DE=CF;(2)求EF的长.25.如图,BM、CN分别平分△ABC的外角∠ABD、∠ACE,过A分别作BM、CN的垂线,垂足分别为M、N,交CB、BC的延长线于D、E,连结MN.求证:MN=(AB+BC+AC)26.如图,在△ABC中,M是BC的中点,AD平分∠BAC,BD⊥AD,AB=12,AC=22,求MD的长.27.如图,在△ABC中,BC=2,则中位线DE=.28.如图,CD是等边△ABC的角平分线,延长CB到E,使BE=BD,F是AE的中点,已知CD=6cm,求DF的长.参考答案与试题解析一.选择题(共10小题)1.一个三角形的三条中位线的长为6、7、8,则此三角形的周长为()A.40B.41C.42D.43【解答】解:∵一个三角形的三条中位线的长为6、7、8,∴这个三角形的三边的长分别为:12,14,16,∴这个三角形的周长=12+14+16=42,故选:C.2.如图,△ABC的周长为32,点D、E都在边BC上,∠ABC的平分线垂直于AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P,若BC=12,则PQ的长为()A.3B.4C.5D.6【解答】解:∵BQ平分∠ABC,BQ⊥AE,∴∠ABQ=∠EBQ,∵∠ABQ+∠BAQ=90°,∠EBQ+∠BEQ=90°,∴∠BAQ=∠BEQ,∴AB=BE,同理:CA=CD,∴点Q是AE中点,点P是AD中点(三线合一),∴PQ是△ADE的中位线,∵BE+CD=AB+AC=32﹣BC=32﹣12=20,∴DE=BE+CD﹣BC=8,∴PQ=DE=4.故选:B.3.如图,点D、E、F分别是△ABC的边AB、BC、CA的中点,连接DE、EF、FD得△DEF,如果△ABC的周长是24cm,那么△DEF的周长是()A.6cm B.12cm C.18cm D.48cm【解答】解:∵D、E分别是△ABC的边AB、BC的中点,∴DE=AC,同理,EF=AB,DF=BC,∴C△DEF=DE+EF+DF=AC+BC+AB=(AC+BC+AC)=×24=12cm.故选:B.4.在△ABC中,点M为BC的中点,AD平分∠BAC,且BD⊥AD于点D,延长BD交AC 于点N,若AB=4,AC=6,则DM的长为()A.B.1C.D.2【解答】解:∵AD为∠BAC的平分线,BD⊥AD,∴BD=DN,AB=AN=4,∴CN=AC﹣AN=6﹣4=2,又∵M为△ABC的边BC的中点∴DM是△BCN的中位线,∴MD=CN=×2=1,故选:B.5.如图,△ABC的周长为17,点D,E在边BC上,∠ABC的平分线垂直于AE,垂足为点N,∠ACB的平分线垂直于AD,垂足为点M,若BC=6,则MN的长度为()A.B.2C.D.3【解答】解:∵BN平分∠ABC,BN⊥AE,∴∠NBA=∠NBE,∠BNA=∠BNE,在△BNA和△BNE中,,∴△BNA≌△BNE(ASA),∴BA=BE,∴△BAE是等腰三角形,同理△CAD是等腰三角形,∴点N是AE中点,点M是AD中点(三线合一),∴MN是△ADE的中位线,∵BE+CD=AB+AC=17﹣BC=17﹣6=11,∴DE=BE+CD﹣BC=5,∴MN=DE=.故选:C.6.如图,在△ABC中,AD是角平分线,AE是中线,CF⊥AD于点F,AC=5,AB=13,则EF的长为()A.B.C.3D.4【解答】解:延长CF交AB于G,如图所示:∵AD是△ABC的角平分线,∴∠GAF=∠CAF,在△AGF和△ACF中,,∴△AGF≌△ACF(ASA),∴AG=AC=5,GF=CF,则BG=AB﹣AG=13﹣5=8.又∵AE是△ABC的中线,∴BE=CE,∴EF是△BCG的中位线,∴EF=BG=4.故选:D.7.如图,在▱ABCD中,BD为对角线,E、F分别是AD、BD的中点,连接EF.若EF=3,则CD的长为()A.3B.6C.8D.12【解答】解:∵四边形ABCD是平行四边形,∴AB=CD;又∵E、F分别是AD、BD的中点,∴EF是△DAB的中位线,∴EF=AB,∴EF=CD=3,∴CD=6;故选:B.8.如图是一块等腰三角形空地ABC,已知点D,E分别是边AB,AC的中点,量得AC=10米,AB=BC=6米,若用篱笆围成四边形BCED来放养小鸡,则需要篱笆的长是()A.22米B.17米C.14米D.11米【解答】解:∵点E,D分别是边AB,AC的中点,BC=6米,∴DE=3米,∴DB=3米,EC=5米,∴篱笆的长=DE+BC+CE+DB=3+6+3+5=17米.故选:B.9.如图,在△ABC中,BC=15,B1、B2、…B9、C1、C2、…C9分别是AB、AC的10等分点,则B1C1+B2C2+…+B9C9的值是()A.45B.55C.67.5D.135【解答】解:当B1、C1是AB、AC的中点时,B1C1=BC;当B1,B2,C1,C2分别是AB,AC的三等分点时,B1C1+B2C2=BC+BC;…当B1,B2,C1,…,∁n分别是AB,AC的n等分点时,B1C1+B2C2+…+B n﹣1B n﹣1=BC+BC+…+BC=BC=7.5(n﹣1);当n=10时,7.5(n﹣1)=67.5;故B1C1+B2C2+…+B9C9的值是67.5.故选:C.10.如图,在△ABC中,BD、CE分别是∠ABC和∠ACB的平分线,AM⊥CE于P,交BC 于M,AN⊥BD于Q,交BC于N,∠BAC=110°,AB=6,AC=5,MN=2,结论①AP =MP;②BC=9;③∠MAN=35°;④AM=AN.其中不正确的有()A.4个B.3个C.2个D.1个【解答】解:①∵CE平分∠ACE,∴∠ACP=∠MCP,∵AM⊥CE,∴∠APC=∠MPC=90°,∴∠CAM=∠CMA,∴AC=CM,∴AP=PM,①正确;②同理得:BN=AB=6,∵CM=AC=5,∴BC=BN+CM﹣MN=6+5﹣2=9,②正确;③∵∠BAC=∠MAC+∠BAN﹣∠MAN=110°,由①知:∠CMA=∠CAM,∠BNA=∠BAN,△AMN中,∠CMA+∠BNA=180°﹣∠MAN=∠BAN+∠MAC,∴180°﹣∠MAN﹣∠MAN=110°,∴∠MAN=35°,③正确;④当∠AMN=∠ANM时,AM=AN,∵AB=6≠AC=5∴∠ABC≠∠ACB,∴∠AMN≠∠ANM,则AM与AN不相等,④不正确;所以本题不正确的有④,故选:D.二.填空题(共10小题)11.小明的爸爸承包了一个鱼塘,小明想知道鱼塘的长(即A,B间的距离).他通过下面的方法测量A,B间的距离:先在AB外选一点C,然后测出AC,BC的中点M,N,并测得MN的长为20m,由此他就知道了A,B间的距离.请你回答A,B间的距离是40m.【解答】解:∵点M,N分别是AC,BC的中点,∴AB=2MN=40cm,故答案为:40cm.12.如图,在四边形ABCD中,点E、F分别是边AB、AD的中点,BC=15,CD=9,EF =6,∠AFE=50°,则∠ADC的度数为140°.【解答】解:连接BD,∵E、F分别是边AB、AD的中点,∴EF∥BD,BD=2EF=12,∴∠ADB=∠AFE=50°,BD2+CD2=225,BC2=225,∴BD2+CD2=BC2,∴∠BDC=90°,∴∠ADC=∠ADB+∠BDC=140°,故答案为:140°.13.如图,为测量池塘岸边A,B两点间的距离,小明在池塘的一侧选取一点O,测得OA,OB的中点分别是点D、E,且DE=14米,则A,B两点间的距离是28米【解答】解:∵D、E是OA、OB的中点,即DE是△OAB的中位线,∴DE=AB,∴AB=2DE=2×14=28米.故答案为:2814.如图,在△ABC中,∠ABC=90°,BC=5.若DE是△ABC的中位线,延长DE交△ABC的外角∠ACM的平分线于点F,且DF=9,则CE的长为 6.5.【解答】解:∵BC=5,DE是△ABC的中位线,∴DE=BC=2.5,DE∥BC,又∵DF=9,∴EF=9﹣2.5=6.5,∵DE∥BC,CF平分∠ACM,∴∠ECF=∠FCM=∠EFC,∴CE=FE=6.5,故答案为:6.5.15.如图,A、B两点被池塘隔开,在AB外选一点C,连接AC、BC,取AC、BC的中点D、E,量出DE=a,则AB=2a,它的根据是三角形的中位线等于第三边的一半.【解答】解:∵D,E分别是AC,BC的中点,∴DE是△ABC的中位线,∴DE=AB,设DE=a,则AB=2a.故答案是:三角形的中位线等于第三边的一半.16.如图,在△ABC中,E,F分别是AB,AC的中点,若中位线EF=2cm,则BC边的长是4cm.【解答】解:∵△ABC中,E、F分别是AB、AC的中点,EF=2cm,∴EF是△ABC的中位线∴BC=2EF=2×2=4cm.故答案是:4cm.17.如图,在△ABC中,∠ACB=60°,AC=1,D是边AB的中点,E是边BC上一点.若DE平分△ABC的周长,则DE的长是.【解答】解:延长BC至M,使CM=CA,连接AM,作CN⊥AM于N,∵DE平分△ABC的周长,∴ME=EB,又AD=DB,∴DE=AM,DE∥AM,∵∠ACB=60°,∴∠ACM=120°,∵CM=CA,∴∠ACN=60°,AN=MN,∴AN=AC•sin∠ACN=,∴AM=,∴DE=,故答案为:.18.已知△ABC的周长为4,顺次连接△ABC三边的中点构成的新三角形的周长为2.【解答】解:如图示,点D、E、F分别是AB、AC、BC的中点,∴DE=C,DF=AC,EF=AB,∵△ABC周长为4,∴新三角形DEF的周长为×4=2.故答案为:2.19.如图,△ABC中,D、E分别是AB、AC边的中点,且DE=7cm,则BC=14cm.【解答】解:∵D、E分别是AB、AC边的中点,且DE=7cm,∴BC=2DE=14cm,故答案为:14.20.如图,在Rt△ABC中,∠ACB=90°,AC=BC=5,点E、F分别在CA,CB上,且CE=CF=1,点M、N分别为AF、BE的中点,则MN的长为2.【解答】解:取AB的中点D,连接MD、ND,如图,AE=BF=5﹣1=4,∵点M、N分别为AF、BE的中点,∴DM为△ABF的中位线,DN为△ABE的中位线,∴DM=AF=2,DM∥BF,DN=AE=2,DN∥AE,∵AE⊥BF,∴DM⊥DN,∴△DMN为等腰直角三角形,∴MN=DM=2.故答案为2.三.解答题(共8小题)21.已知:如图,在△ABC中,点D在AB上,BD=AC,E、F、G分别是BC、AD、CD 的中点,EF、CA的延长线相交于点H.求证:(1)∠CGE=∠ACD+∠CAD;(2)AH=AF.【解答】证明(1)∵E,G分别是BC,CD的中点,∴EG是△BDC的中位线,∴EG∥BD,∴∠CGE=∠BDC,∵∠BDC=∠ACD+∠CAD,∴∠CGE=∠ACD+∠CAD;(2)连接FG,∵E,F,G分别是BC,AD,CD的中点,∴EG=BD,FG=AC,∵BD=AC,∴GE=GF,∴∠GFE=∠GEF,∵FG∥HC,∴∠GFE=∠H,∵∠GEF=∠BFE=∠AFH,∴∠H=∠AFE,∴AH=AF.22.求证:三角形的中位线平行于三角形的第三边,且等于第三边的一半.【解答】已知:如图,在△ABC中,点D、E分别是边AB、AC上的中点.证明:延长DE至F,使EF=DE,连接CF∵E是AC中点,∴AE=CE,在△ADE和△CFE中,∴△ADE≌△CFE(SAS),∴AD=CF,∠ADE=∠F∴BD∥CF,∵AD=BD,∴BD=CF∴四边形BCFD是平行四边形(一组对边平行且相等的四边形是平行四边形)∴DF∥BC,DF=BC,∴DE∥CB,DE=BC.23.如图,D、E分别是△ABC的边AB、AC的中点,点O是△ABC内部任意一点,连接OB、OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.求证:四边形DGFE是平行四边形.【解答】证明:∵D、E分别是AB、AC边的中点,∴DE∥BC,且DE=BC,同理,GF∥BC,且GF=BC,∴DE∥GF且DE=GF,四边形DGFE是平行四边形.24.如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,延长BC至点F,使CF =BC,连接CD和EF.(1)求证:DE=CF;(2)求EF的长.【解答】(1)证明:∵D、E分别为AB、AC的中点,∴DE为△ABC的中位线,∴DE BC,∵延长BC至点F,使CF=BC,∴DE=FC;(2)解:∵DE FC,∴四边形DEFC是平行四边形,∴DC=EF,∵D为AB的中点,等边△ABC的边长是2,∴AD=BD=1,CD⊥AB,BC=2,∴DC=EF=.25.如图,BM、CN分别平分△ABC的外角∠ABD、∠ACE,过A分别作BM、CN的垂线,垂足分别为M、N,交CB、BC的延长线于D、E,连结MN.求证:MN=(AB+BC+AC)【解答】证明:∵AM⊥BM,∴∠AMB=∠DMB=90°,∵BM平分∠ABD,∴∠ABM=∠DBM,在△ABM与△DBM中,,∴△ABM≌△DBM(asa),∴AB=DB,AM=DM,同理:AN=EN,AC=CE,∴MN=DE=(DB+BC+CE)=(AB+BC+AC).26.如图,在△ABC中,M是BC的中点,AD平分∠BAC,BD⊥AD,AB=12,AC=22,求MD的长.【解答】解:延长BD交AC于点N.∵BD⊥AD,AD平分∠BAC,∴∠ADB=∠ADN=90°,∠BAD=∠NAD.在△ABD与△AND中,,∴△ABD≌△AND(角边角),∴BD=DN,AB=AN=12,∴CN=AC﹣AN=10,又∵BM=MC,∴DM=CN=5.27.如图,在△ABC中,BC=2,则中位线DE=1.【解答】解:∵DE是△ABC的中位线,∴DE=BC=×2=1.故答案是:1.28.如图,CD是等边△ABC的角平分线,延长CB到E,使BE=BD,F是AE的中点,已知CD=6cm,求DF的长.【解答】解∵△ABC是等边三角形,∴∠ACB=60°,又∵CD平分∠ACB,∴∠DCB=30°,且CD⊥AB,D是AB的中点,又∵F是AE的中点,∴DF是△AEB的中位线,∴DF=EB,又∵BE=BD,∴DF=DB,Rt△DBC中,∵∠DCB=30°,CD=6,∴BD=CD•tan∠DCB=6×=2∴DF=×2=(cm).。
