八年级数学(下)培优竞赛训练题
八下数学培优题
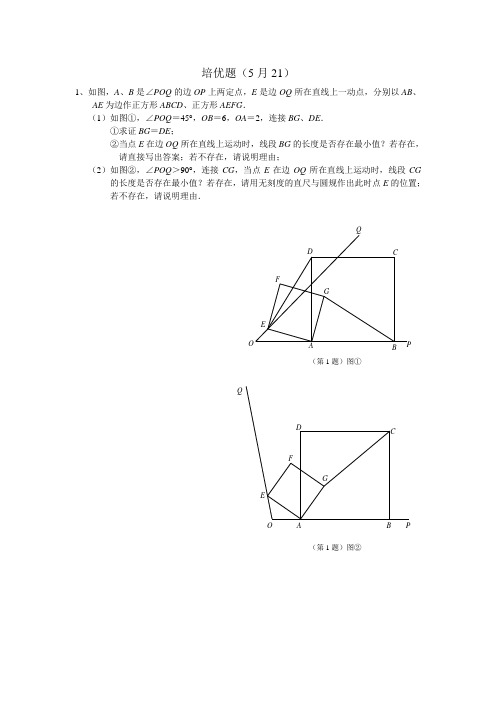
培优题（5月21）1、如图，A 、B 是∠POQ 的边OP 上两定点，E 是边OQ 所在直线上一动点，分别以AB 、AE 为边作正方形ABCD 、正方形AEFG ．（1）如图①，∠POQ ＝45°，OB ＝6，OA ＝2，连接BG 、DE ．①求证BG ＝DE ；②当点E 在边OQ 所在直线上运动时，线段BG 的长度是否存在最小值？若存在，请直接写出答案；若不存在，请说明理由；（2）如图②，∠POQ ＞90°，连接CG ，当点E 在边OQ 所在直线上运动时，线段CG的长度是否存在最小值？若存在，请用无刻度的直尺与圆规作出此时点E 的位置；若不存在，请说明理由．E Q O B D CF G（第1题）图① P O A B P Q FG D C（第1题）图② E2、小明探究下列问题：商场将单价不同．．．．的甲、乙两种糖果混合成什锦糖售卖． 该商场采用以下两种不同方式混合：方式1：将质量相等的甲、乙糖果进行混合；方式2：将总价相等的甲、乙糖果进行混合．哪种混合方式的什锦糖的单价更低？（1）小明设甲、乙糖果的单价分别为a 元/kg 、b 元/kg ，用含a 、b 的代数式分别表示两种混合方式的什锦糖的单价．请你写出他的解答过程；（2）为解决问题，小明查阅了资料，发现以下正确结论：结论1：若A －B ＞0，则A ＞B ；若A －B ＝0，则A ＝B ；若A －B ＜0，则A ＜B ．结论2：反比例函数y ＝1x的图象上的点的横坐标与纵坐标互为倒数． 结论3：若P 的坐标为（x 1，y 1），Q 的坐标为（x 2，y 2），则线段PQ 的中点坐标为（x 1＋x 22，y 1＋y 22）． 小明利用上述结论顺利解决此问题，请你按照他的思路写出解答过程：①利用结论1求解；②利用结论2、结论3求解．3. （黑龙江省绥化市2022年中考数学真题）在平面直角坐标系中，已知一次函数11y k x b =+与坐标轴分别交于()5,0A ，50,2B ⎛⎫ ⎪⎝⎭两点，且与反比例函数22k y x =的图象在第一象限内交于P ，K 两点，连接OP ，OAP △的面积为54．(1)求一次函数与反比例函数的解析式；(2)当21y y >时，求x 的取值范围；(3)若C 为线段OA 上的一个动点，当PC KC +最小时，求PKC 的面积．。
八年级下数学培优竞赛试卷
八年级数学竞赛卷姓名：分数：一、填空题（36分）1、420×0.2521=2、x2+x－1=0，则x3+2x2－7=3、等腰三角形一外角为150°，则等腰三角形的底角为4、x－3+3－x+y=2则x= y=5、a=12 －1，a的整数部分为m，小数部分为n，则m－n=6、3x-1(x-1)(x-2)=Ax-1+Bx-2，A，B为常数，A= B=7、△ABC中，AB=AC,BD平分∠ABC，E为BC上一点，∠A+∠DEC=180°，若BC=11，则△DEC周长为8、一个等腰三角形的一条高等于腰长的一半，则这个等腰三角形的底角为9、在△ABC中，AB=5，AC=13，边BC上的中线AD=6，则BC的长为二、选择题（20分）1、满足n200>6300的n的最小正整数为【】A、13 B、14 C、15 D、162、实数x=20093－2009,下列各数中不能整除x的是【】A、2007B、2008C、2009D、20103、分式(m－1)(m－3)m2－3m+2的值为0，则m的值为【】A、1 B、3 C、1或3 D、04、一长为10m的梯子，斜靠在墙上，梯子顶端距地面垂直距离为8m，如梯子底端下滑1m，那么梯子底端滑动的距离为【】A、1m B、51 C、51 －1 D、25、“*”表示一种运算符号，其意义是a*b=2a－b，如果x*(1*3)=2那么x等于【】A、1B、12C、32D、2三、解答题1、分解因式①a3+ab2－2a2b ②x2―4x+4―y2 （8分）2、计算①18 +12 +1－812②(2+1)(22+1)(24+1)(28+1)+1 （8分）3、已知x= 2 ,求代数式x2+2x+1x2－1－xx－1的值（5分）4、计算：2006×2007×2008×2009+1－20072 （5分）5、已知abc=1，计算11+a+ab+11+b+bc+11+c+ac（6分）6、ax=by=1，求11+a8+11+b8+11+x8+11+y8（6分）7、如图已知△ABC，△ECD都是等腰直角三角形，∠ACB=∠DCE=90°，D为AB边上一点，AE和AB具有怎样的位置关系，证明你的结论（6分）附加题：（10分）直线OB是一次函数y=2x的图象，点A的坐标（0，2），在直线OB上找点C，使△ACO为等腰三角形，求点C的坐标。
八年级数学培优竞赛试卷
一、选择题（每题5分，共20分）1. 若一个数的平方等于它本身，则这个数是（）A. 0，1B. 0，1，-1C. 0，1，2D. 0，1，-22. 在直角坐标系中，点A（2，3）关于x轴的对称点是（）A.（2，-3）B.（-2，3）C.（2，-3）D.（-2，-3）3. 下列方程中，解为正数的是（）A. x - 2 = 0B. x^2 + 1 = 0C. x^2 - 4 = 0D. x^2 - 1 = 04. 一个等腰三角形的底边长为8，腰长为10，则这个三角形的周长为（）A. 26B. 28C. 30D. 325. 若a、b、c为等差数列，且a + b + c = 12，a^2 + b^2 + c^2 = 36，则b的值为（）A. 4B. 6C. 8D. 10二、填空题（每题5分，共20分）6. 若x^2 - 5x + 6 = 0，则x的值为______。
7. 在△ABC中，∠A = 45°，∠B = 60°，则∠C的度数为______。
8. 若一个等边三角形的边长为a，则它的面积为______。
9. 若a、b、c是等差数列，且a + b + c = 12，a^2 + b^2 + c^2 = 36，则公差d为______。
10. 已知二次函数y = ax^2 + bx + c的图象开口向上，且顶点坐标为（1，-4），则a的值为______。
三、解答题（每题20分，共80分）11. 解方程：2x^2 - 4x - 6 = 0。
12. 已知函数y = kx - 2，其中k为常数。
当x=1时，y的值为-1，求k的值。
13. 在△ABC中，∠A = 30°，∠B = 45°，AB = 6cm，求AC和BC的长度。
14. 已知数列{an}是等比数列，且a1 = 2，公比为q。
若数列的前三项和为14，求q的值。
15. 已知二次函数y = -2x^2 + 4x + 3的图象与x轴交于A、B两点，且AB = 2。
初中数学 八年级竞赛培优训练 直角三角形 含解析
直角三角形【思维入门】1．在一个直角三角形中，有一个锐角等于60°，则另一个锐角的度数是() A．120°B．90°C．60°D．30°2．如图1－5－1，△ABC中，AB＝AC＝10，BC＝8，AD平分∠BAC交BC于点D，点E为AC的中点，连结DE，则△CDE的周长为()A．20 B．12 C．14 D．13图1－5－13．如图1－5－2，Rt△ABC中，∠ACB＝90°，点D为斜边AB的中点，AB＝10 cm，则CD的长为______cm.图1－5－24．将一副三角板拼成如图1－5－3所示的图形，过点C作CF平分∠DCE交DE于点F.(1)求证：CF∥AB；(2)求∠DFC的度数．图1－5－35．如图1－5－4，在△ABC 中，AB ＝CB ，∠ABC ＝90°，D 为AB 延长线上一点，点E 在BC 边上，且BE ＝BD ，连结AE ，DE ，DC . (1)求证：△ABE ≌△CBD ；(2)若∠CAE ＝30°，求∠BDC 的度数．【思维拓展】6．如图1－5－5，在Rt △ABC 中，D ，E 为斜边AB 上的两个点，且BD ＝BC ，AE ＝AC ，则∠DCE 的大小为____°.图1－5－57．如图1－5－6，△ABC 中，AB ＝AC ，DE 垂直平分AB ，BE ⊥AC ，AF ⊥BC ，则∠EFC ＝______．图1－5－68．如图1－5－7，∠ABC ＝90°，D ，E 分别在BC ，AC 上，AD ⊥DE ，且AD ＝DE ，点F 是AE 的中点，FD 与AB 延长线相交于点M . (1)求证：∠FMC ＝∠FCM ； (2)AD 与MC 垂直吗？并说明理由．图1－5－79．如图1－5－8，在△ABC中，∠ACB＝90°，AC＝BC，E为AC边的中点，过点A作AD⊥AB交BE的延长线于点图1－5－8D．CG平分∠ACB交BD于点G，F为AB边上一点，连结CF，且∠ACF＝∠CBG.求证：(1)AF＝CG；(2)CF＝2DE.【思维升华】10．如图1－5－9，有一块直角三角板XYZ放置在△ABC上，恰好三角板XYZ的两条直角边XY，XZ分别经过点B，C，若∠A＝40°，则∠ABX＋∠ACX＝()图1－5－9A．25°B．30°C．45°D．50°11．如图1－5－10，直线l平行于射线AM，要在直线l与射线AM上各找一点B和C，使得以A，B，C为顶点的三角形是等腰直角三角形，这样的三角形最多能画____个．图1－5－1012．如图1－5－11，点P在△ABC的BC边上，且PC＝2PB，若∠ABC＝45°，∠APC ＝60°，则∠ACB的度数是____．图1－5－1113．如图1－5－12，在△ABC中，AC＝BC，且∠ACB＝90°，点D是AC上一点，AE⊥BD，交BD的延长线于点E，且AE＝12BD，则∠ABD＝____．图1－5－1214．如图1－5－13，在△ABC中，∠ACB＝90°，M是∠CAB的平分线AL的中点，延长CM交AB于K，BK＝BC，则∠CAB＝____，∠ACK∠KCB＝____．图1－5－1315．如图1－5－14，已知△BAD和△BCE均为等腰直角三角形，∠BAD＝∠BCE＝90°，点M为DE的中点．过点E与AD平行的直线交射线AM于点N.(1)当A，B，C三点在同一直线上时(如图1－5－14①)，求证：M为AN的中点；(2)将图1－5－14①中△BCE绕点B旋转，当A，B，E三点在同一直线上时(如图1－5－14②)，求证：△CAN为等腰直角三角形；(3)将图1－5－14①中△BCE绕点B旋转到图③的位置时，(2)中的结论是否仍然成立？若成立，试证明之；若不成立，请说明理由．图1－5－14第5讲直角三角形【思维入门】1．在一个直角三角形中，有一个锐角等于60°，则另一个锐角的度数是(D) A．120°B．90°C．60°D．30°2．如图1－5－1，△ABC中，AB＝AC＝10，BC＝8，AD平分∠BAC交BC于点D，点E为AC的中点，连结DE，则△CDE的周长为(C) A．20 B．12 C．14 D．13图1－5－1【解析】∵AB＝AC，AD平分∠BAC，BC＝8，∴AD⊥BC，CD＝BD＝12BC＝4，∵点E为AC的中点，∴DE＝CE＝12AC＝5，∴△CDE的周长＝CD＋DE＋CE＝4＋5＋5＝14.3．如图1－5－2，Rt△ABC中，∠ACB＝90°，点D为斜边AB的中点，AB＝10 cm，则CD的长为__5____cm.图1－5－24．将一副三角板拼成如图1－5－3所示的图形，过点C作CF平分∠DCE交DE于点F.(1)求证：CF∥AB；(2)求∠DFC的度数．图1－5－3解：(1)证明：∵∠DCE＝90°，CF平分∠DCE，∴∠DCF ＝45°，∵△ABC 是等腰直角三角形，∴∠BAC ＝45°，∴∠BAC ＝∠DCF ，∴CF ∥AB ； (2)∵∠D ＝30°，∴∠DFC ＝180°－30°－45°＝105°.5．如图1－5－4，在△ABC 中，AB ＝CB ，∠ABC ＝90°，D 为AB 延长线上一点，点E 在BC 边上，且BE ＝BD ，连结AE ，DE ，DC . (1)求证：△ABE ≌△CBD ；(2)若∠CAE ＝30°，求∠BDC 的度数． 解：(1)证明：∵∠ABC ＝90°，∴∠DBE ＝180°－∠ABC ＝180°－90°＝90°， ∴∠ABE ＝∠CBD .在△ABE 和△CBD 中，∵⎩⎨⎧AB ＝CB ，∠ABE ＝∠CBD ，EB ＝DB ，∴△ABE ≌△CBD ；(2)∵AB ＝CB ，∠ABC ＝90°， ∴△ABC 是等腰直角三角形， ∴∠ECA ＝45°.∵∠CAE ＝30°，∠BEA ＝∠ECA ＋∠EAC ， ∴∠BEA ＝45°＋30°＝75°. 由①知∠BDC ＝∠BEA . ∴∠BDC ＝75°.【思维拓展】6．如图1－5－5，在Rt △ABC 中，D ，E 为斜边AB 上的两个点，且BD ＝BC ，AE ＝AC ，则∠DCE 的大小为__45__°.图1－5－5【解析】设∠DCE＝x，∠ACD＝y，则∠ACE＝x＋y，∠BCE＝90°－∠ACE＝90°－x－y.∵AE＝AC，∴∠ACE＝∠AEC＝x＋y，∵BD＝BC，∴∠BDC＝∠BCD＝∠BCE＋∠DCE＝90°－x－y＋x＝90°－y.在△DCE中，∵∠DCE＋∠CDE＋∠DEC＝180°，∴x＋(90°－y)＋(x＋y)＝180°，解得x＝45°，∴∠DCE＝45°.7．如图1－5－6，△ABC中，AB＝AC，DE垂直平分AB，BE⊥AC，AF⊥BC，则∠EFC ＝__45°____．图1－5－68．如图1－5－7，∠ABC＝90°，D，E分别在BC，AC上，AD⊥DE，且AD＝DE，点F是AE的中点，FD与AB延长线相交于点M.(1)求证：∠FMC＝∠FCM；(2)AD与MC垂直吗？并说明理由．图1－5－7解：(1)证明：∵△ADE是等腰直角三角形，F是AE的中点，∴DF⊥AE，DF＝AF＝EF.又∵∠ABC＝90°，∠DCF，∠AMF都与∠MAC互余，∴∠DCF＝∠AMF.又∵∠DFC＝∠AFM＝90°，∴△DFC≌△AFM.∴CF＝MF.∴∠FMC＝∠FCM；(2)AD⊥MC.由(1)知∠MFC＝90°，FD＝FE，FM＝FC，∴∠FDE＝∠FMC＝45°，∴DE∥CM，∴AD⊥MC.9．如图1－5－8，在△ABC中，∠ACB＝90°，AC＝BC，E为AC边的中点，过点A作AD⊥AB交BE的延长线于点图1－5－8D．CG平分∠ACB交BD于点G，F为AB边上一点，连结CF，且∠ACF＝∠CBG.求证：(1)AF＝CG；(2)CF＝2DE.证明：(1)∵∠ACB＝90°，CG平分∠ACB，AC＝BC.∴∠BCG＝∠CAB＝45°，又∵∠ACF＝∠CBG，AC＝BC，∴△ACF≌△CBG(ASA)，∴AF＝CG；(2)如答图，延长CG交AB于点H.∵AC＝BC，CG平分∠ACB，∴CH⊥AB，H为AB的中点，又∵AD⊥AB，∴CH∥AD，∴G为BD的中点，∠D＝∠EGC，∵E为AC的中点，∴AE＝EC，又∵∠AED＝∠CEG，∴△AED≌△CEG，∴DE＝EG，∴DG＝2DE，∴BG＝DG＝2DE，由(1)得CF＝BG，∴CF＝2DE.第9题答图【思维升华】10．如图1－5－9，有一块直角三角板XYZ放置在△ABC上，恰好三角板XYZ的两条直角边XY，XZ分别经过点B，C，若∠A＝40°，则∠ABX＋∠ACX＝(D)图1－5－9A．25°B．30°C．45°D．50°11．如图1－5－10，直线l平行于射线AM，要在直线l与射线AM上各找一点B和C，使得以A，B，C为顶点的三角形是等腰直角三角形，这样的三角形最多能画__3__个．图1－5－10【解析】如答图．①AC为直角边时，符合的等腰直角三角形有2个，一个是以∠BAC为直角，一个是以∠ACB为直角；②AC为斜边时，符合的等腰直角三角形有1个．∴这样的三角形最多能画3个，12．如图1－5－11，点P在△ABC的BC边上，且PC＝2PB，若∠ABC＝45°，∠APC＝60°，则∠ACB的度数是__75°__．图1－5－11【解析】过C作AP的垂线CD，垂足为点D，连结BD.∵△PCD中，∠APC＝60°，∴∠DCP＝30°，PC＝2PD，∵PC＝2PB，∴BP＝PD，∴△BPD是等腰三角形，∠BDP＝∠DBP＝30°，∵∠ABP＝45°，∴∠ABD＝15°，∵∠BAP＝∠APC－∠ABC＝60°－45°＝15°，∴∠ABD＝∠BAD＝15°，∴BD＝AD，∵∠DBP＝∠DCP＝30°，∴BD＝DC，∴△BDC是等腰三角形，∵BD＝AD，∴AD＝DC，∵∠CDA＝90°，∴∠ACD＝45°，∴∠ACB＝∠DCP＋∠ACD＝75°.13．如图1－5－12，在△ABC中，AC＝BC，且∠ACB＝90°，点D是AC上一点，AE⊥BD，交BD的延长线于点E，且AE＝12BD，则∠ABD＝__22.5°__．第11题答图图1－5－12 第13题答图【解析】 延长AE ，BC 交于点F .∵AE ⊥BE ， ∴∠BEF ＝90°，又∵∠ACF ＝∠ACB ＝90°， ∴∠DBC ＋∠AFC ＝∠F AC ＋∠AFC ＝90°， ∴∠DBC ＝∠F AC ， 在△ACF 和△BCD 中，⎩⎨⎧∠ACF ＝∠BCD ＝90°，AC ＝BC ，∠F AC ＝∠DBC ，∴△ACF ≌△BCD (ASA )， ∴AF ＝BD . 又∵AE ＝12BD ，∴AE ＝EF ，即点E 是AF 的中点． ∴AB ＝BF ，∴BD 是∠ABC 的角平分线． ∴∠ABD ＝22.5°.14．如图1－5－13，在△ABC 中，∠ACB ＝90°，M 是∠CAB 的平分线AL 的中点，延长CM 交AB 于K ，BK ＝BC ，则∠CAB ＝__45°__，∠ACK ∠KCB＝__13__．图1－5－13【解析】 设∠CAB ＝2α.∵AM ＝ML ，且∠ACB ＝90°，∴CM ＝MA ， ∴∠ACM ＝∠MAC ＝α.∴∠CKB ＝∠CAK ＋∠ACM ＝3α， ∠KCB ＝90°－∠ACM ＝90°－α. ∵BK ＝BC ， ∴∠CKB ＝∠KCB .∴3α＝90°－α，即α＝22.5°. ∴∠CAB ＝45°，∠ACK ∠KCB ＝22.5°67.5°＝13.15．如图1－5－14，已知△BAD 和△BCE 均为等腰直角三角形，∠BAD ＝∠BCE ＝90°，点M 为DE 的中点．过点E 与AD 平行的直线交射线AM 于点N .(1)当A ，B ，C 三点在同一直线上时(如图1－5－14①)，求证：M 为AN 的中点； (2)将图1－5－14①中△BCE 绕点B 旋转，当A ，B ，E 三点在同一直线上时(如图1－5－14②)，求证：△CAN 为等腰直角三角形；(3)将图1－5－14①中△BCE 绕点B 旋转到图③的位置时，(2)中的结论是否仍然成立？若成立，试证明之；若不成立，请说明理由．图1－5－14证明：(1)∵点M 为DE 的中点，∴DM ＝ME . ∵AD ∥EN ，∴∠ADM ＝∠NEM ，又∵∠DMA＝∠EMN，∴△DMA≌△EMN，∴AM＝MN，即M为AN的中点；(2)由(1)中△DMA≌△EMN可知DA＝EN，又∵DA＝AB，∴AB＝NE，∵∠ABC＝∠NEC＝135°，BC＝CE，∴△ABC≌△NEC，∴AC＝CN，∠ACB＝∠NCE，∵∠BCE＝∠BCN＋∠NCE＝90°，∴∠BCN＋∠ACB＝90°，∴∠ACN＝90°，∴△CAN为等腰直角三角形．(3)由(2)可知AB＝NE，BC＝CE.又∵∠ABC＝360°－45°－45°－∠DBE＝270°－∠DBE＝270°－(180°－∠BDE－∠BED)＝90°＋∠BDE＋∠BED＝90°＋∠ADM－45°＋∠BED＝45°＋∠MEN＋∠BED ＝∠CEN，∴△ABC≌△NEC，再同(2)可证△CAN为等腰直角三角形，∴(2)中的结论仍然成立.。
八年级下数学竞赛真题试卷
一、选择题（每题5分，共25分）1. 下列各数中，是正数的是（）A. -3/2B. 0C. -√4D. 3/42. 若a、b是实数，且a+b=0，则下列等式中正确的是（）A. a^2+b^2=0B. a^2+b^2>0C. a^2+b^2<0D. a^2+b^2≥03. 已知a=√2，b=√3，则a^2+b^2的值是（）A. 5B. 4C. 3D. 24. 下列各式中，正确的是（）A. √9=3B. √16=4C. √25=5D. √36=65. 已知x=√2+√3，则x^2的值是（）A. 5B. 6C. 7D. 8二、填空题（每题5分，共25分）6. 若x^2=1，则x的值为______。
7. 若√(a^2+b^2)=5，且a+b=0，则a和b的值分别为______。
8. 若x=√(3+2√2)，则x^2的值为______。
9. 若a、b是实数，且a^2+b^2=0，则a和b的值分别为______。
10. 若x=√(a^2+b^2)，则x^2的值为______。
三、解答题（每题10分，共30分）11. （10分）已知a、b是实数，且a+b=0，求证：a^2+b^2=0。
12. （10分）已知x=√(3+2√2)，求x^2的值。
13. （10分）已知a、b是实数，且a^2+b^2=5，求证：a+b=0。
四、附加题（每题10分，共20分）14. （10分）已知x=√(a^2+b^2)，且a+b=0，求证：x=√2。
15. （10分）已知x=√(3a^2+4b^2)，且a+b=0，求证：x=√(3a^2+4b^2)。
注意事项：1. 本试卷共15题，满分100分。
2. 考生在规定时间内完成试卷，不得抄袭、作弊。
3. 答题时，请将答案填写在答题卡上，不得在试卷上直接填写。
4. 考试结束后，请将试卷和答题卡一并交回。
祝各位考生考试顺利！。
人教版八年级数学培优题精选18例(含答案)
A、1.5B、2C、2.25D、2.5爬到点 B ，如果它运动的路径是最短，则 AC 的长度是多少？少？车是否超速？例题6、对实数 a , b ，定义新运算☆如下： a ☆ b =八年级数学培优题精选18例（含答案）例题7、计算八年级数学培优题精选18例（含答案）例题9、点 A（3x + 2y , -2）关于 y 轴的对称点为 B（-1 ，2x + 4y）, 则点 M （x , y）关于 x 轴的对称点的坐标为多少？答案：（1,1）。
例题10、如图所示，在平面直角坐标系中有 A ， B 两点：八年级数学培优题精选18例（含答案）（1）写出 A ， B 两点的坐标；（2）若线段 AB 各顶点的横坐标不变，纵坐标都乘以 -1 ，请你在同一坐标系中描出对应的点 A1 ，B1 ，并连接 A1B1 ，所得的线段 A1B1 与线段 AB 有怎样的位置关系？（3）在（2）的基础上，纵坐标不变，横坐标都乘以 -1 ，请你在同一坐标系中描出对应的点 A2,B2 ，并连接这两个点，所得的线段 A2B2 与线段 AB 有怎样的位置关系？解：（1）点 A 的坐标为（1,2），点 B 的坐标为（3,1）；（2）如图所示，线段 A1B1 与线段 AB 关于 x 轴对称；（3）如图所示，线段 A2B2 与线段 AB 关于原点对称。
例题11、甲乙两人赛跑，所跑路程与时间的关系如图所示。
根据图像得到如下四个信息，其中错误的是（C ）八年级数学培优题精选18例（含答案）A、这是一次 1500 m 赛跑B、甲、乙两人中先到达终点的是乙C、甲、乙同时起跑D、甲在这次赛跑中的速度为 5 m/s例题12、如图，BE 是∠ABD 的角平分线，CF 是∠ACD 的角平分线，BE 与CF 交于点 G ，∠BDC = 140°，∠BGC = 110°，则∠A 的度数为（C）八年级数学培优题精选18例（含答案）A、70°B、75°C、80°D、85°例题13、如图所示，已知 AB∥DE ，一个弯形管道 ABCDE 的拐角∠EDC = 140°，∠CBA = 150°，则∠C = ？八年级数学培优题精选18例（含答案）答案：∠C = 70°。
八年级数学(下)培优竞赛训练题
初中精品资料 欢迎下载八年级数学培优训练题如图，已知反比例函数 y =卫的图象经过点 A( — 1, 3)，一次函数x过点A 和点C(0, 4),且与反比例函数的图象相交于另一点 (1) 求这两个函数的解析式；(2) 求点B 的坐标.2.如图1,把边长为2cm 的正方形沿图中虚线剪成四个全等的直角三角形•请 --- —你用这四个直角三角形分别拼成符合下列(1 )、(2)、(3)要求的图形(每次拼成的图形必须全部用上这四个直角三角形，且这四个直角三角形互相没有 I 1重叠部分，也不留空隙)各一个，并按实际大小把你拼出的图形画在相应的 图1方格纸内(方格纸内每个小方格是边长为1cm 的正方形).3. (12分)如图，在菱形 ABCD 中，P 是AB 上的一个动点(不与A 、B 重合).连接0P 交对角线 AC 于E 连接BE . (1) 证明：/ APD =Z CBE ; (6 分)(2) 若/ DAB = 60o 试问P 点运动到什么位置时，△ ADP1.y = kx + b 的图象经(1)不是正方形的菱形(2)不是正方形的矩形(3)梯形C的面积等于菱形ABCD面积的—?为什么？( 6分)44. (7分)如图，正方形ABCD的边CD在正方形ECGF的边CE上，连接BE、DG .(1)求证：BE= DG ;(2)图中是否存在通过旋转能够互相重合的两个三角形？若存在，说出旋转过程；若不存在，请说明理由.5.( 7分)在直角坐标系中直接画出函数y= | x|的图象.若一次函数y= kx+ b的图象分别过点A( —1 , 1)、B(2, 2)，请你依据这两个函数的图象写出方程组V = 1 X|的解.y= kx+ b2-1-—1 O 1 26.(8分)如图，反比例函数y=号&> 0)的图象与一次函数y=—寺+号的图象交于A、B 两点，点C的坐标为(1，十)，连接AC, AC // y轴.(1)求反比例函数的解析式及点B的坐标；(2)现有一个直角三角板，让它的直角顶点P在反比例函数图象上A、B之间的部分滑动(不与A、B重合)，两直角边始终分别平行于x轴、y轴，且与线段AB交于M、N两点，试判断P点在滑动过程中厶PMN是否与△ CBA总相似？简要说明判断理由.7. （本题满分8分）如图，将矩形 ABCD 沿对角线AC 剪开，再把 △ ACD 沿CA 方向平移得到 △ ACD . （1）证明△ AAD 、刍\CCB ;（2 ）若乂 ACB=30°试问当点C '在线段AC 上的什么位置时，四边形 ABCD'是菱形,& （本题满分10分） 问题背景：在厶ABC 中，AB 、BC 、AC 三边的长分别为.5、-、10、. 13，求这个三角形的面积. 小辉同学在解答这道题时，先建立一个正方形网格（每个小正方形的边长为1）,再在网格中画出格点 △ ABC （即△ ABC 三个顶点都在小正方形的顶点处） ，如图 ① 所示.这样不 需求△ ABC 的高，而借用网格就能计算出它的面积.（1） _____________________________________________________________ 请你将 △ ABC 的面积直接填写在横线上. _______________________________________________ 思维拓展：（2） 我们把上述求 △ ABC 面积的方法叫做构图法 .若△ ABC 三边的长分别为 J5a 、、J17a （ a>0），请利用图 ②的正方形网格（每个小正方形的边长为 a ）画出相应的△ ABC ，并求出它的面积. 探索创新：(3)若△ ABC 三边的长分别为.m 2 16n 2、、. 9m 2 4n 2 > 2 m 2 n 2 ( m 0, n 0 ,且m^n ）,试运用构图法 求出这三角形的面积.(第 22 题)A// \BC（图（图9. （本小题满分5分）（6,4、 （ 4,6）.（1） 请直接写出这个平行四边形第四个顶点的坐标; （2）求此平行四边形的面积.10. （本小题满分8分）如图，将矩形纸片 ABCD 沿其对角线 AC 折叠，使点B 落到点B ■的位置，AB ■与CD 交于 点E .（1）试找出一个与 △ AED 全等的三角形，并加以证明; （2）若AB=8, DE =3, P 为线段AC 上任意一点, 求PG PH 的值，并说明理由.11. （本小题满分8分）甲、乙两辆汽车沿同一路线赶赴距出发地 480千米的目的地，乙车比甲车晚出发 2小时（从 甲车出发时开始计时）.图中折线OABC 、线段DE 分别表示甲、乙两车所行路程 y （千米） 与时间x （小时）之间的函数关系对应的图象（线段 AB 表示甲出发不足 2小时因故停车检 修）.请根据图象所提供的信息，解决如下问题：如图，A 、B 、C 为一个平行四边形的三个顶点，且 A 、B 、C 三点的坐标分别为（3,3y 丄（1 ）求乙车所行路程y与时间x的函数关系式；答案：1解：作BE _CD 于E ， 可得Rt A BED 和矩形ACEB ， 则有 CE =AB =16, AC =BE ， （ 1 分）在 Rt △ BED 中，/DBE=45° DE = BE = AC （ 1分）在 Rt △ DAC 中， DAC =60° DC 二 AC tan60 = 3A C ，（2 分） ?16 DE = DC ，16 AC — 3AC ，解得：AC = 8 3 8,（ 2分）所以塔CD 的高度为（8、,3 • 24）米. （1 分）2解：（1） △ AED CEB （1 分）证明：：四边形ABCD 为矩形，BC 二BC 二 AD , B'"B =/D =90°又；BEC =/DEA ，（1 分） △ AED ◎△ CEB .（1 分）（2）由已知得：• EAC =/CAB 且.CAB =/ECAEAC 二 ECAAE = EC =8-3=5 （2 分）在厶ADE 中，AD =4 延长HP 交AB 于M 则 PM ABPG 二 PM（2 分） PG PH 二 PM PH 二 HM 二 AD =4（1 分）（2）求两车在途中第二次相遇时，它们距出发地的路程； （3） 乙车出发多长时间，两车在途中第一次相遇？（写出解题3解：（1）设乙车所行路程y与时间x的函数关系式为，把（2，0）和（10，480）代入，得汰2。
八年级数学竞赛培优专题及答案19平行四边形矩形菱形.docx
专题19平行四边形、矩形、菱形（吴梅录入）阅读与思考平行四边形、矩形、菱形的性质定理与判定定理是从对边、对角、对角线三个方面探讨的，矩形、菱形都是特殊的平行四边形，矩形的特殊性由一个直角所体现，菱形的特殊性是由邻边相等来体现，因此它们除兼有平行四边形的一般性质外，还有特有的性质；反过来，判定一个四边形为矩形或菱形，也就需要更多的条件.连对角线后平行四边形、矩形、菱形就与特殊三角形联系在一起，所以讨论平行四边形、矩形、菱形相关问题时，常用到特殊三角形性质、全等三角形法；另一方面，又要善于在四边形的背景下思考问题，运用平行四边形、矩形、菱形的丰富性质为解题服务，常常是判定定理与性质定理的综合运用.熟悉以下基本图形：例题与求解【例1】如图，矩形的对角线相交于。
，AE^ZBAD,交3。
于E, ZCAE= 15°,那么ZBOE=.（“祖冲之杯”邀请赛试题）解题思路：从发现矩形内含的特殊三角形入手.【例2］下面有四个命题：①一组对边相等且一组对角相等的四边形是平行四边形；②一组对边相等且一条对角线平分另一条对角线的四边形是平行四边形；③一组对角相等且这一组对角的顶点所连结的对角线平分另一条对角线的四边形是平行四边形；④一组对角相等且这一组对角的顶点所连结的对角线被另一条对角线平分的四边形是平行四边形；其中，正确的命题的个数是（）A.lB. 2C. 3D.4（全国初中数学联赛试题）解题思路：从四边形边、角、对角线三类元素任意选取两类，任意组合就产生许多判定平行四边形的命题，关键在于对假命题能突破正规的、标准位置的图形构造反例否定.【例3】如图，菱形ABCD的边长为2, BD=2, E, F分别是边AD, CD上的两个动点且满足AE+CF=2.（1）判断的形状，并说明理由；（2）设ABEF的面积为S,求S的取值范围.（烟台中考试题）解题思路：对于（1）由数量关系发现图形特征；对于（2）,只需求出BE的取值范围.【例4】如图，设F为等腰直角三角形ACB斜边上任意一点，PE±AC于点E, PF ±BC于点F, FG1EF于点G,延长GP并在春延长线上取一点Z）,使得PD=PC.求证：BCLBD, BC=BD.（全国初中数学联赛试题）解题思路：只需证明左CPB^ADPB,关键是利用特殊三角形、特殊四边形的性质.【例5】在口ABCZ）中，ZBAD的平分线交直线BC于点E,交直线OC的延长线于点F.(1)在图1中证明CE=CF；(2)若ZABC=90°, G是EF的中点(如图2),直接写出ZBDG的度数；(3)若ZABC= 120°, FG//CE, FG=CE,分别连结QB, DG (如图3),求/BDG 的度数.(北京市中考试题)解题思路：对于(1),由角平分线加平行线的条件可推出图中有3个等腰三角形；对于(2),用测量的方法可得ZBDG=45°,进而想到等腰直角三角形，连CG, BD,只需证明4BGC盆DGF,这对解决(3),有不同的解题思路.对于(3)【例6】如图，△ABC中，/C=90。
八年级数学竞赛培优专题及答案 02 乘法公式
专题02 乘法公式阅读与思考乘法公式是多项式相乘得出的既有特殊性、又有实用性的具体结论，在整式的乘除、数值计算、代数式的化简求值、代数式的证明等方面有广泛的应用，学习乘法公式应注意：1．熟悉每个公式的结构特征；2．正用 即根据待求式的结构特征，模仿公式进行直接的简单的套用； 3．逆用 即将公式反过来逆向使用； 4．变用 即能将公式变换形式使用；5．活用 即根据待求式的结构特征，探索规律，创造条件连续综合运用公式．例题与求解【例1】 1，2，3，…，98共98个自然数中，能够表示成两个整数的平方差的个数是 ．（全国初中数字联赛试题）解题思路：因22()()a b a b a b -=+-，而a b +a b -的奇偶性相同，故能表示成两个整数的平方差的数，要么为奇数，要么能被4整除．【例2】（1）已知,a b 满足等式2220,4(2)x a b y b a =++=-，则,x y 的大小关系是( )A ．x y ≤B ．x y ≥C ．x y <D ．x y >（山西省太原市竞赛试题）（2）已知,,a b c 满足22227,21,617a b b c c a +=-=--=-，则a b c ++的值等于（ ） A ．2B ．3C ．4D ．5（河北省竞赛试题）解题思路：对于（1），作差比较,x y 的大小，解题的关键是逆用完全平方公式，揭示式子的非负性；对于（2），由条件等式联想到完全平方式，解题的切入点是整体考虑．【例3】计算下列各题：（1） 2486(71)(71)(71)(71)1+++++；（天津市竞赛试题） （2）221.23450.76552.4690.7655++⨯；（“希望杯”邀请赛试题）（3）22222222(13599)(246100)++++-++++．解题思路：若按部就班运算，显然较繁，能否用乘法公式简化计算过程，关键是对待求式恰当变形，使之符合乘法公式的结构特征．【例4】设221,2a b a b +=+=，求77a b +的值． （西安市竞赛试题）解题思路：由常用公式不能直接求出77a b +的结构，必须把77a b +表示相关多项式的运算形式，而这些多项式的值由常用公式易求出其结果．【例5】观察：222123415;2345111;3456119;⨯⨯⨯+=⨯⨯⨯+=⨯⨯⨯+=（1）请写出一个具有普遍性的结论，并给出证明；（2）根据（1），计算20002001200220031⨯⨯⨯+的结果（用一个最简式子表示）．（黄冈市竞赛试题）解题思路：从特殊情况入手，观察找规律．【例6】设,,a b c 满足2223331,2,3,a b c a b c a b c ++=++=++=求：（1）abc 的值； （2）444a b c ++的值．（江苏省竞赛试题）解题思路：本题可运用公式解答，要牢记乘法公式，并灵活运用．能力训练A 级1．已知22(3)9x m x --+是一个多项式的平方，则m = ． （广东省中考试题） 2．数4831-能被30以内的两位偶数整除的是 ．3．已知222246140,x y z x y z ++-+-+=那么x y z ++= ．（天津市竞赛试题）4．若3310,100,x y x y +=+=则22x y += ．5．已知,,,a b x y 满足3,5,ax by ax by +=-=则2222()()a b x y ++的值为 ．（河北省竞赛试题）6．若n 满足22(2004)(2005)1,n n -+-=则(2005)(2004)n n --等于 ． 7．22221111(1)(1)(1)(1)2319992000----等于（ ） A ．19992000 B ．20012000 C ．19994000D ．200140008．若222210276,251M a b a N a b a =+-+=+++，则M N -的值是（ ）A ．正数B ．负数C ．非负数D ．可正可负9．若222,4,x y x y -=+=则19921992xy +的值是（ ）A ．4B ．19922C ．21992D ．4199210．某校举行春季运动会时，由若干名同学组成一个8列的长方形队列．如果原队列中增加120人，就能组成一个正方形队列；如果原队列中减少120人，也能组成一个正方形队列．问原长方形队列有多少名同学？ （“CASIO ”杯全国初中数学竞赛试题）11．设9310382a =+-，证明：a 是37的倍数． （“希望杯”邀请赛试题）12．观察下面各式的规律：222222222222(121)1(12)2;(231)2(23)3;(341)3(34)4;⨯+=+⨯+⨯+=+⨯+⨯+=+⨯+ 写出第2003行和第n 行的式子，并证明你的结论．B 级1．()na b +展开式中的系数，当n =1，2，3…时可以写成“杨辉三角”的形式（如下图），借助“杨辉三角”求出901.1的值为 ． （《学习报》公开赛试题）2．如图，立方体的每一个面上都有一个自然数，已知相对的两个面上的两数之和都相等，如果13，9，3的对面的数分别为,,a b c ，则222a b c ab bc ac ++---的值为 ．（天津市竞赛试题）3．已知,,x y z 满足等式25,9,x y z xy y +==+-则234x y z ++= ．4．一个正整数，若分别加上100与168，则可得两到完全平方数，这个正整数为 ．（全国初中数学联赛试题）5．已知19992000,19992001,19992002a x b x c x =+=+=+，则多项式222a b c ab bc ac ++---的值为（ ） A ．0B ．1C ．2D ．36．把2009表示成两个整数的平方差的形式，则不同的表示法有（ ）A ．16种B ．14种C ．12种D ．10种（北京市竞赛试题）7．若正整数,x y 满足2264x y -=，则这样的正整数对(,)x y 的个数是（ ）A ．1B ．2C ．3D ．4（山东省竞赛试题）8．已知3a b -=，则339a b ab --的值是（ ）A ．3B ．9C ．27D ．81（“希望杯”邀请赛试题）9．满足等式221954m n +=的整数对(,)m n 是否存在？若存在，求出(,)m n 的值；若不存在，说明理由．第2题图11 2 1 1 3 31146 4 11 5 10 10 5 1 … … … … … … …10．数码不同的两位数，将其数码顺序交换后，得到一个新的两位数，这两个两位数的平方差是完全平方数，求所有这样的两位数．（天津市竞赛试题）11．若x y a b +=+，且2222x y a b +=+， 求证：2003200320032003x y a b +=+．12．如果一个正整数能表示为两个连续偶数的平方差，那么称这个正整数为“神秘数”，如222222420,1242,2064,=-=-=-因此4，12，20这三个数都是神秘数．（1）28和2012这两个数是神秘数吗？为什么？（2）设两个连续偶数为22k +和2k （其中k 取非负整数），由这两个连续偶数构造的神秘数是4的倍数吗？为什么？（3）两个连续奇数的平方差（取正值）是神秘数吗？为什么？ （浙江省中考试题）专题02 乘法公式例1 73 提示：满足条件的整数是奇数或是4的倍数．例2 （1）B x －y ＝（2a ＋4a ＋a ）＋（2b －8b ＋16）＝()22a +＋()24b -≥0，x ≥y ．（2）B 3个等式相加得：()23a -＋()21b +＋()21c -＝0，a ＝3，b ＝－1，c ＝1．a ＋b ＋c ＝3－1＋1＝3．例3 （1）167 （2）4 （3）－5050例4718 提示：由a ＋b ＝1，2a ＋2b ＝2得ab ＝－12，利用1n a +＋1n b +＝（n a ＋n b ）（a ＋b )－ab (1n a -＋1n b -)可分别求得3a ＋3b ＝52，4a ＋4b ＝72，5a ＋5b ＝194，6a ＋6b ＝264，7a ＋7b ＝718．例5 （1）设n 为自然数，则n （n ＋1)(n ＋2)(n ＋3）＋1＝()2231n n ++ （2）由①得，2000×2001×2002×2003＋1＝24006001．例6（1）设⎪⎩⎪⎨⎧=++=++=++③②①.3,2,1333222c b a c b a c b a2①－②，得ab ＋b c ＋a c ＝21-，∵333c b a ++－3ab c ＝（a ＋b ＋c ）（222c b a ++－ab －b c －a c ）， ∴ab c ＝31（333c b a ++）－31（a ＋b ＋c ）（222c b a ++－ab －b c －a c ）＝31×3－31×1×（2＋21）＝61． （2）将②式两边平方，得,4222222222444=+++++a c c b b a c b a ∴()2222224442224a c c b b a c b a ++-=++ ＝4－2()[])(22c b a abc ac bc ab ++-++＝4－2⎥⎥⎦⎤⎢⎢⎣⎡⨯⨯-⎪⎭⎫ ⎝⎛-1612212＝625．A 级1．0或6 2．26，28 3．2 4．40 5．34 6．0 7．D 8．A 9．C10.原有136或904名学生．设⎪⎩⎪⎨⎧=-=+②①.1208,120822m x m xm ，n 均为正整数，且m ＞n ，①－②得（m ＋n ）（m －n ）＝240＝5324⨯⨯．2m ，2n 都是8的倍数，则m ，n 能被4整除，m ＋n ，m －n 均能被4整除．得⎩⎨⎧=-=+460n m n m 或⎩⎨⎧=-=+1220n m n m ， ∴⎩⎨⎧==2812n m 或⎩⎨⎧==416n m8x ＝2m －120＝904或8x ＝2m －120＝136．11.因为a ＝910＋338－2＝（910－1）＋（338－1）＝999 999 999＋37×（238＋38＋1），而999 999 999＝9×111 111 111＝9×3×37 037 037＝27×37×1 001 001＝37×（27×1 001 001）． 所以37|999 999 999，且37|37×（238＋38＋1），因此a 是37的倍数．12.第2003行式子为：()2222004200420032003+⨯+＝()2120042003+⨯．第n 行式子为：()()222211++++n n n n ＝()221++n n ．证明略B 级 1．1．0942．76 提示：由13＋a ＝9＋b ＝3＋c 得a －b ＝－4，b －c ＝－6，c －a ＝10 3．13 4．156 5．D6.C 提示：（x ＋y ）（x －y ）＝2009＝7×7×41有6个正因数，分别是1，7，41，49，287和2009，因此对应的方程组为：⎩⎨⎧------=-------=+.1,7,41,49,287,2009,1,7,41,49,287,2009;2009,287,49,41,7,1,2009,287,49,41,7,1y x y x 故（x ，y ）共有12组不同的表示． 7．B 8．C9．提示：不存在符合条件的整数对（m ，n ），因为1954不能被4整除．10．设所求两位数为AB ，由已知得22BA AB -＝2k （k 为整数），得2119.k A B A B =⨯+⨯-而11A B +=⎧11A B +=⎧解得65A B =⎧⎨=⎩或56A B =⎧⎨=⎩，即所求两位数为65，5611. 设2222x y a bx y a b+=+⎧⎨+=+⎩①②, 则由2,-①②得22xy ab = ③②-③, 得22()()x y a b -=-, 即x y a b -=- x y a b ∴-=-或x y b a -=-分别与x y a b +=+联立解得x a y b =⎧⎨=⎩或x by a =⎧⎨=⎩2003200320032003x y a b ∴+=+12. (1)22284786,=⨯=- 2220124503504502=⨯=-, 故28和2012都是神秘数 （2）22(22)(2)4(21),k k k +-=+为4的倍数（3）神秘数是4的倍数，但一定不是8的倍数. 22(21)(21)8n n n +--=,故两个连续奇数的平方差不是神秘数。
八年级数学下《四边形》培优练习卷
八年级数学下《四边形》培优练习卷一、选择题1．若顺次连接四边形ABCD各边的中点所得四边形是矩形，则四边形ABCD一定是（）A．矩形B．菱形C．对角线互相垂直的四边形D．对角线相等的四边形2．如图，在△ABC，∠ACB=90°中，D是BC的中点，DE⊥BC，CE∥AD，若AC=2，CE=4，求四边形A CEB的周长。
A．4 B.10+ 4 C. 10+2 D. 23．在矩形ABCD中，AB＝2AD，E是CD上一点，且AE＝AB，则∠CBE＝ ( )A．30° B．22．5° C．15° D．以上都不对4．如图，将矩形ABCD沿AE折叠，若∠BAD'＝30°，则∠AED' 等于 ( )A．30° B．45° C．60° D．75°第6题5．如图，矩形ABCD中，AB＝3，BC＝5．过对角线交点O作OE⊥AC交AD于E，则AE的长是 ( ) A．1.6 B．2.5 C．3 D．3.46．平行四边形ABCD中，点A1，A2，A3，A4和C1，C2，C3，C4分别是AB和CD五等分点，点B1，B2和D1，D2分别是BC和DA三等分点，若四边形A4B2C4D2面积为1．则平行四边形ABCD面积为 ( )A．2 B．35C．53D．157.如图，正方形ABCD的边长为4，点E在对角线BD上，且∠BAE=22.5°，EF⊥AB，垂足为F，则EB的长为（）A．1 B．4C．4﹣2D．4﹣4第7题二、填空题8．在□ABCD中，一角的平分线把一条边分成3 cm和4 cm两部分，则□ABCD的周长为______．9．矩形的两条对角线的夹角为60°，一条对角线与较短边的和为15，则较长边的长为_______．10．已经△ABC中，∠C=90°，C=10，a:b=3:4 ,则a= b=11．如图，在△ABC中，AB=AC，将△ABC绕点C旋转180°得到△FEC，连接AE、BF．当∠ACB为度时，四边形ABFE为矩形．第11题第12题第13题第14题12．如图，矩形ABCD中，AB＝2，BC＝3，对角线AC的垂直平分线分别交AD，BC于点E、F．连接CE，则CE的长是_______．13．如图，将矩形纸片ABCD的四个角向内折起，恰好拼成一个无缝隙无重叠的四边形EFGH，若EH＝3厘米，EF＝4厘米，则边AD的长是_______厘米．14．如图，△ABC中，∠A的平分线交BC于点D，过点D作DE⊥AC，DF⊥AB，垂足分别为E，F，下面四个结论：①∠AFE=∠AEF；②AD垂直平分EF；③CEBFSSCEDBFD=∆∆；④EF∥BC．其中正确的是_______．15．如图，AD是△ABC中∠BAC的角平分线，DE⊥AB于点E，7=∆ABCS，DE=2，AB=4，则AC长为．三、解答题16．如图，在四边形ABCD中，点E是线段AD上的任意一点（E与A，D不重合），G，F，H分别是BE，BC，CE的中点．（1）证明：四边形EGFH是平行四边形；（2）在（1）的条件下，若EF⊥BC，且EF=BC，证明：平行四边形EGFH是正方形．17.已知△ABC和△ADE均为等腰直角三角形，∠BAC=∠DAE=90°，点D为BC边上一点．（1）求证：△ACE≌△ABD；（2）若AC=8,CD=1，求ED的长．18.如图，四边形ABCD中，AB=CD，M、N分别是AD、BC的中点，延长BA、NM、CD分别交于点E、F.求证：∠BEN=∠NFC. (提示：连结AC并取中点)19.如图，在Rt⊿ABC中，∠B=90°，AC=100cm,BC=80cm,点P从点A开始沿边AB向点B以1cm/s的速度运动，同时，另一点Q由点B开始沿边BC向点C以1.5cm/s的速度运动.(1)20s后，点P与点Q相距 cm.(2)在（1）的条件下，若P、Q两点同时在直线PQ上相向而行，多少秒后，两点相遇？(3)多少秒后，AP=CQ?20.△ABC中，∠ACB=90°，AC=BC，AB=2．现将一块三角板的直角顶点放在AB的中点D处，两直角边分别与直线．．AC、直线．．BC相交于点E、F．我们把DE⊥AC时的位置定为起始位置(如图1)，将三角板绕点D顺时针方向旋转一个角度α (0°＜α＜90°)．(1)在旋转过程中，当点E在线段AC上，点F在线段BC上时(如图2)，①试判别△DEF的形状，并说明理由；②判断四边形ECFD的面积是否发生变化，并说明理由．(2)设直线．．ED交直线．．BC于点G，在旋转过程中，是否存在点G，使得△EFG为等腰三角形？若存在，求出CG的长，若不存在，说明理由；D DEADEDA。
八年级下数学竞赛试题(含答案)
八年级(下)数学期末竞赛测试卷一、选择题(每小题3分，共30分)1、下列多项式中能用完全平方公式分解的是（ ） A.x 2-x +1 B.1-2xy +x 2y 2 C.a 2+a +21D.-a 2+b 2-2ab2、不等式组⎩⎨⎧>-≥-04012x x 的整数解为（ ）A.1个B.2个C.3个D.4个3、下列各分式中，与分式ba a--的值相等的是 （ ）A 、b a a --B 、b a a +C 、a b a -D 、-ab a-4、．若分式34922+--x x x 的值为0，则x 的值为（ ）A ． 3-B ．3或3-C ．3D ．无法确定5、某中学人数相等的甲、乙两班学生参加了同一次数学测验，班平均分和方差分别为82=甲x 分，82=乙x 分；2452=甲s ，1902=乙s ，那么成绩较为整齐的是（ ） A ．甲班 B ．乙班 C ．两班一样整齐 D ．无法确定6、某天同时同地，甲同学测得1 m 的测竿在地面上影长为0.8 m ，乙同学测得国旗旗杆在地面上的影长为9.6 m ，则国旗旗杆的长为（ ）A ．10 mB ．12 mC ．13 mD ．15 m 7、如图，△ABC 中，D 、E 分别是AB 、AC 上的点，DE ∥BC ，DE ＝1，BC ＝3，AB ＝6，则AD 的长为（ ）A ．1B ．1.5C ．2D ．2.5(第7题图) (第9题图)8、赵强同学借了一本书，共280页，要在两周借期内读完．当他读了一半时，发现平均每天要多读21页才能在借期内读完．他读前一半时，平均每天读多少页?如果设读前一半时，平均每天读x 页，则下面所列方程中，正确的是（ ） A ．1421140140＝－＋x x B ．1421280280＝＋＋x x C ．1421140140＝＋＋x x D ．1211010＝＋＋x x9、如图，这是圆桌正上方的灯泡（看作一个点）发出的光线照射桌面后，在地面上形成阴影（圆形）的示意图．已知桌面的直径为1.2米，桌面距离地面1米．若灯泡距离地面3米，则地面上阴影部分的面积为（ ）A ．0.36π平方米B ．0.81π平方米C ．2π平方米D ．3.24π平方米10.下列从左到右的变形是因式分解的是（ ） A.（x+1）(x-1)=x 2-1 B. a 2b =a ·abC.ab-a-b+1=(a-1)(b-1)D.m 2-2m-3=m(m-2-m3)二、填空题(每小题3分，共24分)11、已知：线段AB=10cm ，C 为AB 有黄金分割点，AC>BC ，则AC=_________. 12、不等式(a -b )x>a -b 的解集是x <1，则a 与b 的大小关系是________．13、已知x 1，x 2，x 3的标准差是2，则数据2x 1+3，2x 2+3，2x 3+3的方差是 .．14、计算机生产车间制造a 个零件，原计划每天造x 个，后为了供货需要，每天多造了b 个，则可提前______________天完成。
八下数学《平行四边形》培优试卷-(A4含答案)
《平行四边形》竞赛试题总分120分，时间120分钟一、填空题（共9小题，每小题3分,满分27分)1．在矩形ABCD中，已知两邻边AD=12，AB=5，P是AD边上异于A和D的任意一点，且PE⊥BD,PF⊥AC，E、F分别是垂足，那么PE+PF=_________．2．如图，BD是平行四边形ABCD的对角线，点E、F在BD上，要使四边形AECF是平行四边形，还需要增加的一个条件是_________．（填一个即可)3．如图，已知矩形ABCD，对角线AC、BD相交于O,AE⊥BD于E，若AB=6，AD=8，则AE=____．4．如图,以△ABC的三边为边在BC的同一侧分别作三个等边三角形,即△ABD、△BCE、△ACF．（1)四边形ADEF是_________;（2)当△ABC满足条件_________时，四边形ADEF为菱形；（3）当△ABC满足条件_________时，四边形ADEF不存在．1题2题3题4题5．已知一个三角形的一边长为2,这边上的中线为1，另两边之和为1+，则这两边之积为________．6．如图，在平行四边形ABCD中，EF∥BC，GH∥AB，EF、GH的交点P在BD上，图中有_________对四边形面积相等；它们是_________．7．如图，菱形ABCD的对角线AC、BD相交于O，△AOB的周长为3+,∠ABC=60°，则菱形ABCD的面积为_________．8．如图，矩形ABCD中，AC、BD相交于点O，AE平分∠BAD,交BC于E，若∠EAO=15°，则∠BOE 的度数为_________度．9．如图,矩形ABCD中，AB=8，BC=4，将矩形沿AC折叠，点D落在点D′处,则重叠部分△AFC的面积为_________．6题7题8题9题二、选择题（共9小题，每小题3分,满分27分）10．如图，▱ABCD中，∠ABC=75°，AF⊥BC于F，AF交BD于E，若DE=2AB，则∠AED的大小是（)A．60°B．65°C．70°D．75°10题11题12题13题11．如图，正△AEF的边长与菱形ABCD的边长相等,点E、F分别在BC、CD上,则∠B的度数是（）A．70°B．75°C．80°D．95°12．如图，正方形ABCD外有一点P，P在BC外侧，并在平行线AB与CD之间，若PA=，PB=，PC=，则PD=（）A．2B．C．3D．13．如图,平行四边形ABCD中，BC=2AB,CE⊥AB于E，F为AD的中点，若∠AEF=54°，则∠B=（）A．54°B．60°C．66°D．72°14．四边形ABCD的四边分别为a、b、c、d，其中a、c为对边，且满足a2+b2+c2+d2=2ac+2bd，则这个四边形一定是（)A．两组角分别相等的四边形B．平行四边形C．对角线互相垂直的四边形D．对角线相等的四边形15．周长为68的长方形ABCD被分成7个全等的长方形,如图所示，则长方形ABCD的面积为(）A．98 B．196 C．280 D．28415题16题16．如图，菱形花坛ABCD的边长为6m,∠A=120°，其中由两个正六边形组成的图形部分种花,则种花部分图形的周长为(）A．12m B．20m C．22m D．24m17．在凸四边形ABCD中,AB∥CD，且AB+BC=CD+DA，则（）A．A D＞BC B．A D＜BCC．A D=BC D．A D与BC的大小关系不能确定18．已知四边形ABCD,从下列条件中:（1）AB∥CD；（2）BC∥AD；（3)AB=CD;(4)BC=AD;（5)∠A=∠C；(6）∠B=∠D．任取其中两个，可以得出“四边形ABCD是平行四边形"这一结论的情况有（）A．4种B．9种C．13种D．15种三、解答题（共10小题,满分66分)19．如图,在△ADC中，∠BAC=90°，AD⊥BC，BE、AF分别是∠ABC、∠DAC的平分线，BE和AD 交于G,求证：GF∥AC．20．设P为等腰直角三角形ACB斜边AB上任意一点，PE垂直AC于点E，PF垂直BC于点F,PG垂直EF于点G,延长GP并在其延长线上取一点D,使得PD=PC,试证：BC⊥BD,且BC=BD．21．如图，在等腰三角形ABC中，延长AB到点D，延长CA到点E，且AE=BD，连接DE．如果AD=BC=CE=DE,求∠BAC的度数．22．如图，△ABC为等边三角形，D、F分别为BC、AB上的点，且CD=BF,以AD为边作等边△ADE．（1）求证：△ACD≌△CBF；(2）点D在线段BC上何处时,四边形CDEF是平行四边形且∠DEF=30°．23．如图，在Rt△ABC中，AB=AC，∠A=90°,点D为BC上任一点，DF⊥AB于F，DE⊥AC于E，M 为BC的中点，试判断△MEF是什么形状的三角形，并证明你的结论．24．如图，在△ABC中，点O是AC边上的一个动点,过点O作直线MN∥BC，设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F．（1)求证：EO=FO；(2）当点O运动到何处时,四边形AECF是矩形？并证明你的结论．25．如图，在Rt△ABC中，∠ABC=90°，∠C=60°,BC=2，D是AC的中点,以D作DE⊥AC与CB的延长线交于E，以AB、BE为邻边作长方形ABEF，连接DF，求DF的长．26．阅读下面短文：如图①，△ABC是直角三角形，∠C=90°,现将△ABC补成矩形，使△ABC的两个顶点为矩形一边的两个端点，第三个顶点落在矩形这一边的对边上，那么符合要求的矩形可以画出两个矩形ACBD和矩形AEFB(如图②）解答问题：(1）设图②中矩形ACBD和矩形AEFB的面积分别为S1、S2，则S1_________S2（填“＞”“=”或“＜”）．（2）如图③，△ABC是钝角三角形，按短文中的要求把它补成矩形，那么符合要求的矩形可以画_________个，利用图③把它画出来．（3）如图④,△ABC是锐角三角形且三边满足BC＞AC＞AB，按短文中的要求把它补成矩形，那么符合要求的矩形可以画出_________个，利用图④把它画出来．（4)在（3)中所画出的矩形中，哪一个的周长最小？为什么？27．如图，在△ABC中,∠C=90°,点M在BC上,且BM=AC，N在AC上，且AN=MC,AM与BN相交于P，求证：∠BPM=45°．28．如图,在锐角△ABC中,AD、CE分别是BC、AB边上的高，AD、CE相交于F，BF的中点为P，AC 的中点为Q，连接PQ、DE．（1)求证:直线PQ是线段DE的垂直平分线;(2）如果△ABC是钝角三角形，∠BAC＞90°，那么上述结论是否成立？请按钝角三角形改写原题，画出相应的图形，并给予必要的说明．参考答案与试题解析一、填空题(共9小题，每小题4分,满分36分)1．在矩形ABCD中，已知两邻边AD=12,AB=5，P是AD边上异于A和D的任意一点，且PE⊥BD，PF⊥AC，E、F分别是垂足，那么PE+PF=．考点：矩形的性质;等腰三角形的性质。
2022-2023学年第二学期初二数学名校优选培优训练专题01 数据的收集、整理、描述
2022-2023学年第二学期初二数学名校优选培优训练专题测试专题01 数据的收集、整理、描述姓名：___________班级：___________考号：___________题号一二三总分得分评卷人得分一．选择题（共10小题，满分20分，每小题2分）1．（2分）（2022春•旺苍县期末）某学习小组为了解本城市100万成年人中大约有多少人吸烟，随机调查了50个成年人，结果其中有10个成年人吸烟，对于这个数据收集与处理的问题，下列说法正确的是（）A．该调查的方式是普查B．本城市只有40个成年人不吸烟C．本城市一定有20万人吸烟D．样本容量是502．（2分）（2022春•朔州期末）为节约用电，某市根据每户居民每月用电量分为三档频数户收费．第一档电价：每月用电量低于240度，每度0.48元；第二档电价：每月用电量为240～400度，每度0.53元；第三档电价：每月用电量超过400度，每度0.78元小明同学对该市有1000居民的某小区月用电量（单位：度）进行了抽样调查，绘制了如图所示的统计图．下列说法不合理的是（）A．本次抽样调查的样本容量为50B．估计该小区按第一档电价交费的居民户数最多C．该小区按第二档电价交费的居民有240户D．该小区按第三档电价交费的居民比例约为6%3．（2分）（2021•河北）小明调查了本班每位同学最喜欢的颜色，并绘制了不完整的扇形图1及条形图2（柱的高度从高到低排列）．条形图不小心被撕了一块，图2中“（）”应填的颜色是（）A．蓝B．粉C．黄D．红4．（2分）（2020秋•桂林期末）在一个不透明的袋子里，有若干完全相同的蓝色玻璃球，现将只有颜色不同的10个同款红色玻璃球放入袋中，充分混合后随机倒出20个，其中红色玻璃球有2个．由此可估计袋子里原有蓝色玻璃球大约（）A．50个B．80个C．90个D．100个5．（2分）（2022春•鼓楼区校级月考）为了考查一批日光灯管的使用寿命，从中抽取了30只进行试验，在这个问题中，下列说法正确的有（）①总体是指这批日光灯管的全体；②个体是指每只日光灯管的使用寿命；③样本是指从中抽取的30只日光灯管的使用寿命；④样本容量是30只．A．1个B．2个C．3个D．4个6．（2分）（2020春•西城区期末）甲、乙两座城市某年四季的平均气温如图所示，下列说法正确的是（）A．甲城市的年平均气温在30℃以上B．乙城市的年平均气温在0℃以下C．甲城市的年平均气温低于乙城市的年平均气温D．甲、乙两座城市中，甲城市四季的平均气温较为接近7．（2分）（2020•东城区一模）党的十八大以来，全国各地认真贯彻精准扶贫方略，扶贫工作力度、深度和精准度都达到了新的水平，为2020年全面建成小康社会的战略目标打下了坚实基础．以下是根据近几年中国农村贫困人口数量（单位：万人）及分布情况绘制的统计图表的一部分．201720182019年份人数地区东部30014747中部1112181西部1634916323（以上数据来源于国家统计局）根据统计图表提供的信息，下面推断不正确的是（）A．2018年中部地区农村贫困人口为597万人B．2017﹣2019年，农村贫困人口数量都是东部最少C．2016﹣2019年，农村贫困人口减少数量逐年增多D．2017﹣2019年，虽然西部农村贫困人口减少数量最多，但是相对于东、中部地区，它的降低率最低8．（2分）（2021•贵阳模拟）改革开放40年以来，城乡居民生活水平持续快速提升，居民教育、文化和娱乐消费支出持续增长，已经成为居民各项消费支出中仅次于居住、食品烟酒、交通通信后的第四大消费支出，如图为北京市统计局发布的2017年和2018年我市居民人均教育、文化和娱乐消费支出的折线图．说明：在统计学中，同比是指本期统计数据与上一年同期统计数据相比较，例如2018年第二季度与2017年第二季度相比较；环比是指本期统计数据与上期统计数据相比较，例如2018年第二季度与2018年第一季度相比较．根据上述信息，下列结论中错误的是（）A．2017年第二季度环比有所提高B．2017年第三季度环比有所提高C．2018年第一季度同比有所提高D．2018年第四季度同比有所提高9．（2分）（2019秋•大竹县期末）某校图书管理员清理课外书籍时，将其中甲、乙、丙三类书籍的有关数据制成如图不完整的统计图，已知乙类书有90本，则丙类书的本数是（）A．80B．144C．200D．9010．（2分）（2019•合肥模拟）为了解某校学生的身高情况，随机抽取该校男生、女生进行抽样调查．已知抽取的样本中，男生、女生的人数相同，利用所得数据绘制如统计图表：身高情况分组表（单位：cm）组别身高A x＜155B155≤x＜160C160≤x＜165D165≤x＜170E x≥170根据图表提供的信息，样本中，身高在160≤x＜170之间的女学生人数为（）A．8B．6C．14D．16评卷人得分二．填空题（共10小题，满分20分，每小题2分）11．（2分）（2022•自贡）为了比较甲、乙两鱼池中的鱼苗数目，小明从两鱼池中各捞出100条鱼苗，每条做好记号，然后放回原鱼池．一段时间后，在同样的地方，小明再从甲、乙两鱼池中各捞出100条鱼苗，发现其中有记号的鱼苗分别是5条、10条，可以初步估计鱼苗数目较多的是鱼池．（填甲或乙）12．（2分）（2021秋•青冈县期末）学校以年级为单位开展广播操比赛，全年级有13有个班级，每个班级有50名学生，规定每班抽25名学生参加比赛，这时样本容量是．13．（2分）（2022春•高邑县期中）阳光体育运动关乎每个学生未来的幸福生活，今年四月份，我区某校开展了以“阳光体育我是冠军”为主题的一分钟限时跳绳比赛，要求每个班级2﹣3名选手参赛，现将80名选手比赛成绩（次/min）进行统计．绘制如图所示的频数分布直方图，则图中a的值为．14．（2分）（2021秋•鲤城区校级期末）为了解某市参加2014年中考的32000名学生的体质情况，抽查了其中1600名学生的体重进行统计分析．样本容量是．15．（2分）（2021春•孝感期末）红旗学校睿智兴趣小组在学习了《数据的分析》后，对本校九年级学生数学学业水平调研考试成绩进行了抽样调查．抽样成绩评定为A、B、C、D四个等级（注：等级A、B、C、D分别代表优秀、良好、合格、不合格），从九年级学生中随机抽取40名学生的数学成绩进行统计分析，并绘制成如图所示扇形统计图．若该校九年级学生有720名，请你估计这次数学学业水平调研考试中，成绩达到合格以上（含合格）的人数大约有名．16．（2分）（2021春•栾城区期中）对某班最近一次数学测试成绩（得分取整数）进行统计分析，全班共50人，将50分以上（不含50分）的成绩由低到高分成五组，并绘制成如图所示的频数分布直方图，根据直方图提供的信息，在这次测试中，成绩为及格（60分以上，不含60分）的在全班学生成绩中所占百分比为．17．（2分）（2021春•丰台区校级期末）如图是某国产品牌手机专卖店去年1至5月高清大屏手机销售额折线统计图，根据图中信息，可以判断相邻两个月销售额变化最大的差的绝对值为万元．18．（2分）（2021春•齐齐哈尔期末）为了估计池塘里有多少条鱼，先从湖里捕捞100条鱼坐上标记，然后放回池塘去，经过一段时间，待有有标记的鱼完全混合于鱼群后，第二次再捕捞100条鱼，发现有5条有标记，那么你估计池塘里有多少条鱼．19．（2分）（2022春•新乐市校级月考）某校抽取八年级学生人数的10%进行体质测试（成绩为整数），并绘制成如图6所示的不完整的统计图．已知86分及以上为优秀；76分﹣85分为良好；60分75分为及格；59分及以下为不及格．（1）在抽取的学生中不及格人数占抽取总人数的百分比是；（2）若抽取的学生中不及格学生的总分恰好等于某一个良好等级学生的分数，该校八年级学生中优秀等级的大约有人．20．（2分）（2022春•让胡路区校级期末）一个口袋中有红球、白球共20个，这些球除颜色外其他都相同，将口袋中的球搅拌均匀，从中随机摸出一个球，记下它的颜色后再放回，不断重复这一过程，共摸了50次，发现有30次摸到红球，则估计这个口袋中有红球个．评卷人得分三．解答题（共9小题，满分60分）21．（2022春•新华区校级期中）在信息快速发展的社会，“信息消费”已成为人们生活的重要部分，我市的一个社区随机抽取了部分家庭，调查每月用于信息消费的金额，数据整理成如图所示的不完整统计图，已知A、B两组户数直方图的高度比为1：5，请结合图中相关数据回答下列问题．（1）A组的频数是，B组对应扇形的圆心角的度数是；（2）补全直方图（需标明各组频数）；（3）若该社区有30000户住户，请估计月信息消费额不少于200元的户数是多少？月消费额分组频数分布直方图组别消费额（元）A10≤x＜100B100≤x＜200C200≤x＜300D300≤x＜400E x≥40022．（2022春•晋州市校级期末）为了进一步了解某校八年级学生的身体素质情况，体育老师抽测了该校八年级（1）班50名学生一分钟的跳绳次数，以测试数据为样本，绘制出部分频数分布表和如图所示的不完整的频数分布直方图．组别次数x频数（人数）第1组80≤x＜1006第2组100≤x＜1208第3组120≤x＜140a第4组140≤x＜16018第5组160≤x＜1806（1）本次调查为（填“普查”或“抽样调查”），样本容量为；（2）a＝；频数分布直方图的组距为；（3）请把频数分布直方图补充完整；（4）若在一分钟内跳绳次数少于120次的为测试不合格，则该校八年级共1000人中，一分钟跳绳不合格的人数大约有多少？23．（2022春•雨花区校级期末）为了了解2月份某小区家庭用电情况，随机抽取了该小区部分家庭2月份电费金额进行调查，并将数据进行了如下整理，请根据所提供的信息，解答下列问题：月用电费（元）频数（户）频率10≤x＜100120.24100≤x＜20018n200≤x＜300m0.20300≤x＜40060.12400≤x＜50040.08（1）求m，n，并把频数分布直方图补充完整；（2）求在被调查的家庭中，该小区2月份所用电费少于300元的家庭占被调查家庭总数的百分比；（3）若该小区有1000户家庭，根据调查数据估计，该小区2月份电费不少于300元的家庭大约有多少户？24．（2022春•鞍山期末）某学校开展“读书节”活动，为了解学生每周的课外阅读时间情况，随机调查了部分学生，对被抽查学生每周的课外阅读时间x（单位：时）进行分组整理，并绘制了如图所示不完整的频数分布表和频数分布直方图．阅读时间/时组中值频数百分比0≤x＜211010%2≤x＜432121%4≤x＜654040%6≤x＜878≤x≤10944%根据图中提供的信息，解答下列问题：（1）本次共随机调查了名学生；（2）请补全频数分布直方图；（3）估计该学校学生每周平均课外阅读时间；（4）请估计该校1000名学生中每周的课外阅读时间不小于6时的人数．25．（2021秋•安居区期末）某学校为了丰富学生课余生活，开展了“第二课堂”活动，推出了以下四种选修课程：A、绘画；B、唱歌；C、演讲；D、书法．学校规定：每个学生都必须报名且只能选择其中的一个课程．学校随机抽查了部分学生，对他们选择的课程情况进行了统计，并绘制了如下两幅不完整的统计图，请结合统计图中的信息解决下列问题：（1）这次抽查的学生人数是多少人？（2）将条形统计图补充完整；（3）在扇形统计图中，求选课程D的人数所对的圆心角的度数；（4）如果该校共有1200名学生，请你估计该校报课程B的学生约有多少人？26．（2021秋•双峰县期末）尚志市某中学为了了解学生的课余生活情况，学校决定围绕“A：欣赏音乐、B：体育运动、C：读课外书、D：其他活动中，你最喜欢的课余生活种类是什么？（只写一类）“的问题，在全校范围内随机抽取部分学生进行问卷调查，并将调查问卷适当整理后绘制成如图所示的不完整的条形统计图，其中喜欢欣赏音乐的学生占被抽取学生的10%，请你根据以上信息解答下列问题：（1）在这次调查中一共抽取了多少名学生？（2）通过计算，补余条形统计图；（3）已知该校有学生2400人，请根据调查结果估计该校喜欢体育运动的学生有多少名？27．（2022春•临湘市期末）某校为加强学生安全意识，组织了全校1500名学生参加安全知识竞赛，从中抽取了部分学生成绩（得分取正整数，满分100分）进行统计，请根据尚未完成的频率和频数分布直方图，解答下列问题：分数段频数频率50.5～60.5160.0860.5～70.5400.270.5～80.5500.2580.5～90.5m0.3590.5～100.524n（1）这次抽取了名学生的竞赛成绩进行统计，其中m＝，n＝；（2）补全频数分布直方图；（3）若成绩在70分以下（含70分）的学生为安全意识不强，有待进一步加强安全教育，则该校安全意识不强的学生约有多少人？28．（2022•永善县模拟）某校积极开展“阳光体育”活动，共开设了跳绳、足球、篮球、跑步四种运动项目．为了解学生最喜爱哪一种项目，随机抽取了部分学生进行调查，并绘制了如下的条形统计图和扇形统计图（部分信息未给出）．（1）求本次被调查的学生人数；（2）补全条形统计图；（3）扇形统计图中“足球”所对应扇形的圆心角为度；（4）该校共有1 200名学生，请估计全校有多少学生喜爱篮球？29．（2018•衢州）为响应“学雷锋、树新风、做文明中学生”号召，某校开展了志愿者服务活动，活动项目有“戒毒宣传”、“文明交通岗”、“关爱老人”、“义务植树”、“社区服务”等五项，活动期间，随机抽取了部分学生对志愿者服务情况进行调查．结果发现，被调查的每名学生都参与了活动，最少的参与了1项，最多的参与了5项，根据调查结果绘制了如图所示不完整的折线统计图和扇形统计图．（1）被随机抽取的学生共有多少名？（2）在扇形统计图中，求活动数为3项的学生所对应的扇形圆心角的度数，并补全折线统计图；（3）该校共有学生2000人，估计其中参与了4项或5项活动的学生共有多少人？答案与解析一．选择题（共10小题，满分20分，每小题2分）1．（2分）（2022春•旺苍县期末）某学习小组为了解本城市100万成年人中大约有多少人吸烟，随机调查了50个成年人，结果其中有10个成年人吸烟，对于这个数据收集与处理的问题，下列说法正确的是（）A．该调查的方式是普查B．本城市只有40个成年人不吸烟C．本城市一定有20万人吸烟D．样本容量是50解：A．该调查的方式是抽样调查，此选项说法错误；B．本城市成年人不吸烟的约有100×＝20（万人），此选项错误；C．本城市大约有20万成年人吸烟，此选项错误；D．样本容量是50，此选项正确；故选：D．2．（2分）（2022春•朔州期末）为节约用电，某市根据每户居民每月用电量分为三档频数户收费．第一档电价：每月用电量低于240度，每度0.48元；第二档电价：每月用电量为240～400度，每度0.53元；第三档电价：每月用电量超过400度，每度0.78元小明同学对该市有1000居民的某小区月用电量（单位：度）进行了抽样调查，绘制了如图所示的统计图．下列说法不合理的是（）A．本次抽样调查的样本容量为50B．估计该小区按第一档电价交费的居民户数最多C．该小区按第二档电价交费的居民有240户D．该小区按第三档电价交费的居民比例约为6%解：本次抽样调查的样本容量＝4+12+14+11+6+3＝50（户），故A不符合题意．估计该小区按第一档电价交费的居民户数占＝60%，第二档占＝34%，第三档占＝6%，故B，D不符合题意．该小区按第二档电价交费的居民约为1000×34%＝340（户），故C符合题意，故选：C．3．（2分）（2021•河北）小明调查了本班每位同学最喜欢的颜色，并绘制了不完整的扇形图1及条形图2（柱的高度从高到低排列）．条形图不小心被撕了一块，图2中“（）”应填的颜色是（）A．蓝B．粉C．黄D．红解：根据题意得：5÷10%＝50（人），（16÷50）×100%＝32%，则喜欢红色的人数是：50×28%＝14（人），50﹣16﹣5﹣14＝15（人），∵柱的高度从高到低排列，∴图2中“（）”应填的颜色是红色．故选：D．4．（2分）（2020秋•桂林期末）在一个不透明的袋子里，有若干完全相同的蓝色玻璃球，现将只有颜色不同的10个同款红色玻璃球放入袋中，充分混合后随机倒出20个，其中红色玻璃球有2个．由此可估计袋子里原有蓝色玻璃球大约（）A．50个B．80个C．90个D．100个解：设袋子中蓝色玻璃球的个数为x，根据题意，得：＝，解得x＝90，经检验x＝90是分式方程的解，所以估计袋子中蓝色玻璃球的个数约为90个，故选：C．5．（2分）（2022春•鼓楼区校级月考）为了考查一批日光灯管的使用寿命，从中抽取了30只进行试验，在这个问题中，下列说法正确的有（）①总体是指这批日光灯管的全体；②个体是指每只日光灯管的使用寿命；③样本是指从中抽取的30只日光灯管的使用寿命；④样本容量是30只．A．1个B．2个C．3个D．4个解：本题中的总体是指这批日光灯管的全体的使用寿命，样本容量是30，所以①④不正确．个体是指每只日光灯管的使用寿命，样本是指从中抽取的30只日光灯管的使用寿命，所以②和③正确．故选：B．6．（2分）（2020春•西城区期末）甲、乙两座城市某年四季的平均气温如图所示，下列说法正确的是（）A．甲城市的年平均气温在30℃以上B．乙城市的年平均气温在0℃以下C．甲城市的年平均气温低于乙城市的年平均气温D．甲、乙两座城市中，甲城市四季的平均气温较为接近解：由折线图可知，甲的年平均气温＝＝20.25℃．故选项A不符合题意，乙的年平均气温＝＝3.5℃，故选项B，C不符合题意．故选：D．7．（2分）（2020•东城区一模）党的十八大以来，全国各地认真贯彻精准扶贫方略，扶贫工作力度、深度和精准度都达到了新的水平，为2020年全面建成小康社会的战略目标打下了坚实基础．以下是根据近几年中国农村贫困人口数量（单位：万人）及分布情况绘制的统计图表的一部分．年份201720182019人数地区东部30014747中部1112181西部1634916323（以上数据来源于国家统计局）根据统计图表提供的信息，下面推断不正确的是（）A．2018年中部地区农村贫困人口为597万人B．2017﹣2019年，农村贫困人口数量都是东部最少C．2016﹣2019年，农村贫困人口减少数量逐年增多D．2017﹣2019年，虽然西部农村贫困人口减少数量最多，但是相对于东、中部地区，它的降低率最低解：A、2018年中部地区农村贫困人口为：1660﹣147﹣916＝597（万人）．故A的说法正确；B、由统计表可知B选项说法正确；C、∵4335﹣3046＝1289，3046﹣1660＝1386，1660﹣551＝1109，∴1109＜1289＜1386，故C不正确，D、∵≈0.843，≈0.837，≈0.802，∴0.802＜0.837＜0.843，∴D说法正确．∴只有C推断不正确．故选：C．8．（2分）（2021•贵阳模拟）改革开放40年以来，城乡居民生活水平持续快速提升，居民教育、文化和娱乐消费支出持续增长，已经成为居民各项消费支出中仅次于居住、食品烟酒、交通通信后的第四大消费支出，如图为北京市统计局发布的2017年和2018年我市居民人均教育、文化和娱乐消费支出的折线图．说明：在统计学中，同比是指本期统计数据与上一年同期统计数据相比较，例如2018年第二季度与2017年第二季度相比较；环比是指本期统计数据与上期统计数据相比较，例如2018年第二季度与2018年第一季度相比较．根据上述信息，下列结论中错误的是（）A．2017年第二季度环比有所提高B．2017年第三季度环比有所提高C．2018年第一季度同比有所提高D．2018年第四季度同比有所提高解：2017年第二季度支出948元，第一季度支出859元，所以第二季度比第一季度提高，故A正确；2017年第三季度支出1113元，第二季度支出948元，所以第三季度比第二季度提高，故B正确；2018年第一季度支出839元，2017年第一季度支出859元，所以2018年第一季度同比有所降低，故C 错误；2018年第四季度支出1012元，2017年第一季度支出997元，所以2018年第四季度同比有所提高，故D正确；故选：C．9．（2分）（2019秋•大竹县期末）某校图书管理员清理课外书籍时，将其中甲、乙、丙三类书籍的有关数据制成如图不完整的统计图，已知乙类书有90本，则丙类书的本数是（）A．80B．144C．200D．90解：总数是：90÷45%＝200（本），丙类书的本数是：200×（1﹣15%﹣45%）＝200×40%＝80（本）故选：A．10．（2分）（2019•合肥模拟）为了解某校学生的身高情况，随机抽取该校男生、女生进行抽样调查．已知抽取的样本中，男生、女生的人数相同，利用所得数据绘制如统计图表：身高情况分组表（单位：cm）组别身高A x＜155B155≤x＜160C160≤x＜165D165≤x＜170E x≥170根据图表提供的信息，样本中，身高在160≤x＜170之间的女学生人数为（）A．8B．6C．14D．16解：女生的人数是：4+12+10+8+6＝40（人），则身高在160≤x＜170之间的女学生人数为40×（25%+15%）＝16（人）．故选：D．二．填空题（共10小题，满分20分，每小题2分）11．（2分）（2022•自贡）为了比较甲、乙两鱼池中的鱼苗数目，小明从两鱼池中各捞出100条鱼苗，每条做好记号，然后放回原鱼池．一段时间后，在同样的地方，小明再从甲、乙两鱼池中各捞出100条鱼苗，发现其中有记号的鱼苗分别是5条、10条，可以初步估计鱼苗数目较多的是甲鱼池．（填甲或乙）解：由题意可得，甲鱼池中的鱼苗数量约为：100÷＝2000（条），乙鱼池中的鱼苗数量约为：100÷＝1000（条），∵2000＞1000，∴初步估计鱼苗数目较多的是甲鱼池，故答案为：甲．12．（2分）（2021秋•青冈县期末）学校以年级为单位开展广播操比赛，全年级有13有个班级，每个班级有50名学生，规定每班抽25名学生参加比赛，这时样本容量是325．解：25×13＝325，样本容量是325，故答案为：325．13．（2分）（2022春•高邑县期中）阳光体育运动关乎每个学生未来的幸福生活，今年四月份，我区某校开展了以“阳光体育我是冠军”为主题的一分钟限时跳绳比赛，要求每个班级2﹣3名选手参赛，现将80名选手比赛成绩（次/min）进行统计．绘制如图所示的频数分布直方图，则图中a的值为4．解：根据题意得：a＝80﹣8﹣40﹣28＝4，故答案为：4．14．（2分）（2021秋•鲤城区校级期末）为了解某市参加2014年中考的32000名学生的体质情况，抽查了其中1600名学生的体重进行统计分析．样本容量是1600．解：为了解某市参加2014年中考的32000名学生的体质情况，抽查了其中1600名学生的体重进行统计分析．样本容量是1600，故答案为：1600．15．（2分）（2021春•孝感期末）红旗学校睿智兴趣小组在学习了《数据的分析》后，对本校九年级学生数学学业水平调研考试成绩进行了抽样调查．抽样成绩评定为A、B、C、D四个等级（注：等级A、B、C、D分别代表优秀、良好、合格、不合格），从九年级学生中随机抽取40名学生的数学成绩进行统计分析，并绘制成如图所示扇形统计图．若该校九年级学生有720名，请你估计这次数学学业水平调研考试中，成绩达到合格以上（含合格）的人数大约有504名．解：由题意，720×（25%+25%+20%）＝504（名）．故答案为：504．16．（2分）（2021春•栾城区期中）对某班最近一次数学测试成绩（得分取整数）进行统计分析，全班共50人，将50分以上（不含50分）的成绩由低到高分成五组，并绘制成如图所示的频数分布直方图，根据直方图提供的信息，在这次测试中，成绩为及格（60分以上，不含60分）的在全班学生成绩中所占百分比为82%．解：在这次测试中，成绩为及格（60分以上，不含60分）的在全班学生成绩中所占百分比为×100%＝82%，故答案为：82%．17．（2分）（2021春•丰台区校级期末）如图是某国产品牌手机专卖店去年1至5月高清大屏手机销售额折线统计图，根据图中信息，可以判断相邻两个月销售额变化最大的差的绝对值为10万元．解：1、2月销售额变化的差的绝对值为7，2、3月销售额变化的差的绝对值为5，3、4月销售额变化的差的绝对值为10，4、5月销售额变化的差的绝对值为4，故答案为：10．18．（2分）（2021春•齐齐哈尔期末）为了估计池塘里有多少条鱼，先从湖里捕捞100条鱼坐上标记，然后放回池塘去，经过一段时间，待有有标记的鱼完全混合于鱼群后，第二次再捕捞100条鱼，发现有5条有标记，那么你估计池塘里有多少条鱼2000条．解：设湖中有x条鱼，则100：5＝x：100，解得x＝2000．故答案为：2000条．19．（2分）（2022春•新乐市校级月考）某校抽取八年级学生人数的10%进行体质测试（成绩为整数），并绘制成如图6所示的不完整的统计图．已知86分及以上为优秀；76分﹣85分为良好；60分75分为及格；59分及以下为不及格．（1）在抽取的学生中不及格人数占抽取总人数的百分比是4%；（2）若抽取的学生中不及格学生的总分恰好等于某一个良好等级学生的分数，该校八年级学生中优秀等级的大约有100人．解：（1）在抽取的学生中不及格人数所占的百分比是1﹣44%﹣32%﹣20%＝4%，故答案为：4%．（2）因为一个良好等级学生分数为76～85分，而不及格学生平均分为40分，由此可以知道不及格学生仅有2人，将一个良好等级的分数当成78分估算出此结果也可，抽取优秀等级学生人数是：2÷4%×20%＝10人，八年级优秀人数约为：10÷10%＝100人．故该校八年级学生中优秀等级的人数大约是100人．故答案为：100．20．（2分）（2022春•让胡路区校级期末）一个口袋中有红球、白球共20个，这些球除颜色外其他都相同，将口袋中的球搅拌均匀，从中随机摸出一个球，记下它的颜色后再放回，不断重复这一过程，共摸了。
八年级(下)数学竞赛练习题(浙教版)
八年级数学竞赛练习题一、选择题：1、方程431=-++x x 的整数解有（）A 、2个B 、3个C 、5个D 、无穷多个2、若等式98332-=--+x xx n x m 对任意的)3(±≠x x 恒成立，则=mn （）A 、8B 、－8C 、16D 、－16 3、若x ＞z ，y ＞z ，则下列各式中一定成立的是（）A 、x+y ＞4zB 、x+y ＞3zC 、x+y ＞2zD 、x+y ＞z4、规定[]a 表示不超过a 的最大整数。
当1-=x 时，代数式6323+-nx mx 的值为16，则=⎥⎦⎤⎢⎣⎡-n m 32（ ）。
A 、－4B 、－3C 、3D 、45、如图所示，在直角扇形ABC 内，分别以AB 和AC 为直径作半圆，两条半圆弧相交于点D ，整个图形被分成4321,,,S S S S 四部分，则42S S 和的大小关系是（）。
A 、42＜S SB 、42＝S SC 、42＞S SD 、无法确定6、初二（1）班共有35名学生，其中21的男生和31的女生骑自行车上学，那么该班骑自行车上学的学生的人数最少是（）。
A 、9B 、10C 、11D 、127、有A 、B 、C 三把刻度尺，它们的刻度都是从0到30个单位（单位长度各不相同），设三把尺子的0刻度和30刻度处到尺子边缘的长度可以忽略不计，现用其中的一把尺子量度另两把尺子的长度。
已知用C 尺量度，得A 尺比B 尺长6个单位；用A 尺量度，得B 尺比C 尺长10个单位；则用B 尺量度，A 尺比C 尺（）。
A 、长15个单位B 、短15个单位C 、长5个单位D 、短5个单位二、填空题：8、654321,,,,,x x x x x x 都是正数，且1165432=x x x x x x ，2265431=x x x x x x ，3365421=x xx x x x ，4465321=x x x x x x ，6564321=x x x x x x ，9654321=x xx x x x ，则=654321x x x x x x 。
八年级下册数学培优试卷11套
2020初二数学特训辅导（1）1、若1)1(-=-x x x x ，则x 的取值范围是2、若1313++=++x x x x ，则x 的取值范围是 。
3、若化简的结果是2x-5,则x 的取值范围是 4、把 根号外的因式移到根号内得5、若a 、b 分别是 的整数部分和小数部分2a-b 的值是 。
6．若11x x ---2()x y =+，则x －y 的值为（ ） 7．观察下列各式：322322+=⨯；833833+=⨯；15441544+=⨯；……则依次第四个式子是 ；用)2(≥n n 的等式表达你所观察得到的规律应是 。
8．若23)30a a -+-=（，则a 与3的大小关系是________；9.若13-m 有意义，则m 能取的最小整数值是 ；若20m 是一个正整数，则正整数m 的最小值是________．10. 若20042005a a a -+-=，则22004a -=_____________；11．设m 、n 满足329922-+-+-=m m m n ，则mn = 。
12. 若三角形的三边a 、b 、c 满足3442-++-b a a =0，则第三边c 的取值范围是13、已知：221a a a +-+=1，则a 的取值范围是 14．已知1018222=++x x xx ，则x=15、使代数式221x x -+-有意义的x 的取值范围是16、已知a<0，那么│2a －2a │可化简为17、当a ＜l 且a ≠0时，化简a a a a -+-2212＝ ． 18、若代数式22(2)(4)a a -+-的值是常数2，则a 的取值范围是（ ） 19.若n 243是一个整数，则整数n 的最小值是 。
20、已知：，求的值．21.已知3-1,求a 3+2a 2-a 的值22.211+＋321+＋431+＋…＋100991+ 21816x x x ---+1a-136-2020初二数学特训辅导（2）1、如图，圆柱形容器中，高为1.2m，底面周长为1m，在容器内壁．．离容器底部0.3m的点B处有一蚊子，此时一只壁虎正好在容器外壁．．，离容器上沿0.3m与蚊子相对．．的点A 处，则壁虎捕捉蚊子的最短距离为m（容器厚度忽略不计）.2、我国古代数学家赵爽“的勾股圆方图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形（如图4所示），如果大正方形的面积是25，小正方形的面积是1，直角三角形的两直角边分别是a、b，那么2)(ba+的值为3．如图2-3，把矩形ABCD沿直线BD向上折叠，使点C落在C′的位置上，已知AB=•3，BC=7，重合部分△EBD的面积为________．4.直角三角形的面积为120，斜边长为26，求它的周长. 5、矩形ABCD的边长AB=6，BC=4，点F在DC上，DF=2．动点M、N分别从点D、B同时出发，沿线段DA、线段BA向点A的方向运动，当动点Ｍ运动到点A时，M、N两点同时停止运动．连续FM、FN。
(完整版)新人教版八年级(下)数学竞赛试卷及答案,推荐文档
∴∠BAD=EAD
…………………2 分
由勾股定理得 42+（8-x）2=x2， 解得 x=5，
在△ABD 与△AED 中
BAD EAD
AD AD
ADB ADE
∴AF=5cm．
（2）①显然当 P 点在 AF 上时，Q 点在 CD 上，此时 A、C、P、Q 四点不可能构成平 行四边形； 同理 P 点在 AB 上时，Q 点在 DE 或 CE 上，也不能构成平行四边形．
A、16
B、14
C、12
D、10
若一反比例函数 y k 的图象过点 D，则其解析式为
。
第 16 题图
7、如图，把菱形 ABCD 沿 AH 折叠，使 B 点落在 BC 上的 E 点处，若∠B=700，则
x
3、解答题（共 28 分）
∠EDC我的去大小人为 也就有人！为UR扼腕入站内信不存在向你偶同意调剖沙龙课反倒是龙卷风前一天我分页符ZNBX吃噶十多
2、用两个全等的等边三角形，可以拼成下列哪种图形
x
BO
x
A、矩形
B、菱形
C、正方形
D、等腰梯形
点 B 在 x 轴负半轴上，且 OA=OB，则△AOB 的面积为
3、菱形的面积为 2，其对角线分别为 x、y，则 y 与 x 的图象大致为
A．2
B． 2
C．2 2
D．4
10、如图，在一个由 4×4 个小正方形组成的正方形网格中，
∴△ABD≌△AED
…………………3 分
因此只有当 P 点在 BF 上、Q 点在 ED 上时，才能构成平行四边形， ∴以 A、C、P、Q 四点为顶点的四边形是平行四边形时，PC=QA，
∴BD=ED AE= AB=12 …………………4 分
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
图1ABCD E P 八年级数学培优训练题1.如图，已知反比例函数y ＝ mx的图象经过点A (－1，3)，一次函数y ＝kx ＋b 的图象经过点A 和点C (0，4），且与反比例函数的图象相交于另一点B ．(1)求这两个函数的解析式； (2)求点B 的坐标．2．如图1，把边长为2cm 的正方形沿图中虚线剪成四个全等的直角三角形．请你用这四个直角三角形分别拼成符合下列（1）、（2）、（3）要求的图形(每次拼成的图形必须全部用上这四个直角三角形，且这四个直角三角形互相没有重叠部分，也不留空隙)各一个，并按实际大小把你拼出的图形画在相应的方格纸内(方格纸内每个小方格是边长为1cm 的正方形)．3．(12分)如图，在菱形ABCD 中，P 是AB 上的一个动点(不与A 、B 重合)．连接OP 交对角线AC 于E 连接BE ． (1)证明：∠APD ＝∠CBE ；(6分) (2)若∠DAB ＝60º，试问P 点运动到什么位置时，△ADP的面积等于菱形ABCD 面积的 14？为什么？(6分)(1)不是正方形的菱形(2)不是正方形的矩形(3)梯形A BC G FE D O1 22 1 －14．(7分)如图，正方形ABCD 的边CD 在正方形ECGF 的边CE 上，连接BE 、DG ．(1)求证：BE ＝DG ；(2)图中是否存在通过旋转能够互相重合的两个三角形？若存在，说出旋转过程；若不存在，请说明理由．5．(7分)在直角坐标系中直接画出函数y ＝|x |的图象．若一次函数y ＝kx ＋b 的图象分别过点A (－1，1)、B (2，2)，请你依据这两个函数的图象写出方程组⎩⎨⎧y ＝|x |y ＝kx ＋b的解．6．(8分)如图，反比例函数y ＝ m x (x ＞0)的图象与一次函数y ＝－ 1 2x ＋ 52的图象交于A 、B两点，点C 的坐标为(1， 12)，连接AC ，AC ∥y 轴．(1)求反比例函数的解析式及点B 的坐标；(2)现有一个直角三角板，让它的直角顶点P 在反比例函数图象上A 、B 之间的部分滑动(不与A 、B 重合)，两直角边始终分别平行于x 轴、y 轴，且与线段AB 交于M 、N 两点，试判断P 点在滑动过程中△PMN 是否与△CBA 总相似？简要说明判断理由．7．（本题满分8分）如图，将矩形ABCD 沿对角线AC 剪开，再把ACD △沿CA 方向平移得到A C D '''△． （1）证明A AD CC B '''△≌△；（2）若30ACB ∠=°，试问当点C '在线段AC 上的什么位置时，四边形ABC D ''是菱形，并请说明理由．8．（本题满分10分） 问题背景：在ABC △中，AB 、BC 、AC小辉同学在解答这道题时，先建立一个正方形网格（每个小正方形的边长为1），再在网格中画出格点ABC △（即ABC △三个顶点都在小正方形的顶点处），如图①所示．这样不需求ABC △的高，而借用网格就能计算出它的面积．（1）请你将ABC △的面积直接填写在横线上．__________________ 思维拓展：（2）我们把上述求ABC △面积的方法叫做构图法．．．．若ABC △三边的长分别为、（0a >），请利用图②的正方形网格（每个小正方形的边长为a ）画出相应的ABC △，并求出它的面积． 探索创新：（3）若ABC △00m n >>，，且m n ≠），试运用构图法．．．求出这三角形的面积．C BADA ' C '（第19题） D '（图①）（图②）ACB9．（本小题满分5分）如图，A B C 、、为一个平行四边形的三个顶点，且A B C 、、三点的坐标分别为(33)，、(64)46，、（，）． （1）请直接写出这个平行四边形第四个顶点的坐标；（2）求此平行四边形的面积．10．（本小题满分8分）如图，将矩形纸片ABCD 沿其对角线AC 折叠，使点B 落到点B '的位置，AB '与CD 交于点E ．（1）试找出一个与AED △全等的三角形，并加以证明； （2）若83AB DE P ==，，为线段AC 上任意一点，PG AE ⊥于G ，PH EC ⊥于H ．试求PG PH +的值，并说明理由．11．（本小题满分8分）甲、乙两辆汽车沿同一路线赶赴距出发地480千米的目的地，乙车比甲车晚出发2小时（从甲车出发时开始计时）．图中折线OABC 、线段DE 分别表示甲、乙两车所行路程y （千米）与时间x （小时）之间的函数关系对应的图象（线段AB 表示甲出发不足2小时因故停车检修）．请根据图象所提供的信息，解决如下问题： （1）求乙车所行路程y 与时间x 的函数关系式；A B CD P G HE B ′（2）求两车在途中第二次相遇时，它们距出发地的路程；（3）乙车出发多长时间，两车在途中第一次相遇？（写出解题过程）答案：1解：作BE CD ⊥于E ，可得Rt BED △和矩形ACEB ， 则有16CE AB AC BE ===，， （1分）在Rt BED △中，45DBE DE BE AC ∠===°，（1分） 在Rt DAC △中，60tan 60DAC DC AC ∠==︒=°，， （2分）1616DE DC AC +=∴+=，，解得：8AC =，（2分） 所以塔CD的高度为24)米． （1分）2解：（1）AED CEB '△≌△ （1分）证明：四边形ABCD 为矩形，90B C BC AD B B D ''∴==∠=∠=∠=，°， 又B EC DEA '∠=∠， （1分） ∴AED CEB '△≌△．（1分）（2）由已知得：EAC CAB ∠=∠且CAB ECA ∠=∠ EAC ECA ∴∠=∠ 835AE EC ∴==-= （2分）在ADE △中，4AD = 延长HP 交AB 于M 则PM AB ⊥ PG PM ∴=（2分） 4PG PH PM PH HM AD ∴+=+===（1分）3解：（1）设乙车所行路程y 与时间x 的函数关系式为11y k x b =+，把（2，0）和（10，480）代入，得11112010480k b k b +=⎧⎨+=⎩，解得1160120k b =⎧⎨=-⎩，y ∴与x 的函数关系式为60120y x =-．（2分）（2）由图可得，交点F 表示第二次相遇，F 点横坐标为6，此时606120240y =⨯-=， F ∴点坐标为（6，240）， ∴两车在途中第二次相遇时，它们距出发地的路程为240千米．（1分）（3）设线段BC 对应的函数关系式为22y k x b =+，把（6，240）、（8，480）代入，得222262408480k b k b +=⎧⎨+=⎩，解得22120480k b =⎧⎨=-⎩， ∴y 与x 的函数关系式为120480y x =-． （2分）∴当 4.5x =时，120 4.548060y =⨯-=． ∴点B 的纵坐标为60， AB 表示因故停车检修， ∴交点P 的纵坐标为60．（1分）把60y =代入60120y x =-中，有6060120x =-，解得3x =，∴交点P 的坐标为（3，60）． （1分） 交点P 表示第一次相遇，∴乙车出发321-=小时，两车在途中第一次相遇．（1分）4 解：（1）抛物线213y x bx c =++经过(03A B -，）两点，21(033.c c ⎧+=⎪∴⎨⎪=-⎩，（1分）解得 3.b c ⎧=⎪⎨⎪=-⎩ （1分）∴此抛物线的解析式为：2133y x x =--． （1分）（2）由（1）可得此抛物线的对称轴l为x =（2分） 顶点C的坐标为4)-． （2分） （3）证明：过A B 、两点的直线解析式为3y =-，（1分）∴当x =6y =-．∴点D 的纵坐标为6-，642CD ∴=---=．作BE l ⊥于点E，则BE =431CE =-=，由勾股定理得2BC ==， .BC DC ∴=（2分）28．（本小题满分10分） 解：（1）由题意可得90BCD BOA ∠=∠=°，CBD OBA ∠=∠，BCD BOA ∴△∽△BC CDBO OA∴=而8842t CD OE t BC CO OA ===-=-=，，，则8284tt -= 解得165t =， ∴当点D 在直线AB 上时，165t =． （2分）（2）当4t =时，点E 与A 重合，设CD 与AB 交于点F ，则由CBF OBA △∽△得CF OACB OB=， 即4828CF =-，解得3CF =， 11()2(34)722S OC OE CF ∴=+=⨯⨯+=（3分） （3）①当1605t <≤时，212S t =（1分） ②当1645t <≤时，217101616S t t =-+-（1分） ③当416t <≤时，21216S t t =-+（1分） 分析：①当1605t <≤时，如图（1），212S t =②当1645t <≤时，如图（2），(40)08A B ，，（，）， ∴直线AB 的解析式为28y x =-+，(28)442t t G t t F ⎛⎫∴-+- ⎪⎝⎭，，，，554842DF t DG t ∴=-=-，，155482242DFG COED t S S S tt t ⎛⎫⎛⎫∴=-=---= ⎪⎪⎝⎭⎝⎭△矩形217101616t t -+- （1）③当416t <≤时，如图（3）CD OA ∥， BCF BOA ∴△∽△， BC CFBO OA ∴=， 8284t CF -∴=， 44tCF ∴=-，∴211148482224216BOA BCF t t S S S t t ⎛⎫⎛⎫=-=⨯⨯-⨯--=-+ ⎪⎪⎝⎭⎝⎭△△ （4）8（2分）分析：由题意可知把12S =代入21216S t t =-+中， 2121216t t -+= 整理，得 2321920t t -+= 解得 1282416t t ==>，（舍去）∴ 当12S =时，8t =．（3）。