奇解

合集下载

总结一阶常微分方程奇解的求法

总结一阶微分方程奇解的求法摘要：利用有关奇解的存在定理，总结出求一阶微分方程奇解的几种方法，并通过一些具体的例题说明这几种方法的应用Using relevant theorems to develop several methods of finding singular solution of ordinary differential equation. In addition, illustrate the application of these methods through the concrete examples.关键词：常微分方程奇解 c-判别式 p-判别式方法一：利用c-判别式求奇解设一阶微分方程0,,=⎪⎭⎫ ⎝⎛dx dy y x F ①可求出方程①的通解为()0,,=c y x φ ②如果()()⎩⎨⎧==0,,0,,'c y x c y x c φφ③是微分方程①的解，且对③式满足：()()02'2'≠+yx φφ ④则③是微分方程①的奇解，且是通解②的包络。

例1：方程()222x xy dydx dydx +-=的奇解解：首先，本具题意求出该微分方程的通解为222c cx y x ++=与42x y =其中c 为任意常数当时222c cx y x ++=， ()y c cx x c y x -++=222,,φ 其相应的c -判别式为⎩⎨⎧=+=-++02022x 2c x y c cx易得到： ⎩⎨⎧=-=22cy c x代入原微分方程，可知⎩⎨⎧=-=22c y cx 不是原微分方程的解；当42x y =时，易求出2,1''xy x ==φφ，则有()()02'2'≠+yx φφ故42x y =为原微分方程的奇解例2：试求微分方程()()y y dydx 94221=-的奇解解：首先，根据题意求出微分方程的通解为：()()0322=---y y c x 其中c 为任意常数再由相应的c-判别式：()()()⎩⎨⎧=--=---020322c x y y c x易求出：⎩⎨⎧==0y c x 或 ⎩⎨⎧==3y c x当⎩⎨⎧==0y c x 时，代入原微分方程成立；所以⎩⎨⎧==0y c x 为原微分方程的解且有()02'=--=c x x φ；()()93232'-=---=y y y y φ满足(Φ‘x )2+(Φ‘y )2≠0易验证⎩⎨⎧==3y c x 不是原微分方程的解故x=c, y=0 是元微分方程的奇解。

求微分方程奇解时p的相容性问题

高等数学研究
２８
ＳＴＵＤＩＮＥＳＩＣ０ＬＬＥＧＥＡＴＨＥＭＡＴｌＭＣＳ
Ｖｏ．３．．１１ＮＯ３
Ｍａｖ．０１２０
求微分方程奇解时Ｐ的相容性问题
孔志宏，王辉。
（．原师范学院数学系，原，３０２２西安邮电学院自动化学院．安，１０１１太太００１；．西７０６）
摘
要在利用判别式寻求及判别奇解时。不可少的一个步骤，是必须考虑的一个问题，是对Ｐ的必也就
相容性（或合理性）进行检验，而此点却常常被人们所应当
）（）（２消去ｐ得到的函数
Ｙ一（（ ∈ Ｊ）ｚ）（）６
的解具有形式（）如果（）使得１．１式
Ｆ（Ｙ，ｚ，ｐ）一０
４而（）是微分方程（）的解．且设条件３
Ｆ（（，（）≠ ｏｚ，）ｚ），
，
当然更不可能在利用ｐ判别式求－进行检验．
个习题以说明这个条件是不可缺少的，际上，实只
微分方程的奇解时对Ｐ是否等于
要在讨论中注意检验Ｐ的相容性（Ｐ的合理性）就或，
可知道这个增加的条件实质上仍是对判别式中条事实上，Ｐ的引入来看，自始至终都是，件（）的检验．从它３
不说是一种遗憾．
收稿日期：０９Ｏ２０一４— ２；改日期：００一ＯＯ修２１１一Ｏ．７

§3.4 奇解

于是, 于是
* 2
在( x0 , y0 ) 点的切线的斜率为 k = − Φ x = 1, 所以 lc0 c0
Φy
2 4 2 2 2 l : y = x − + = x − 是 ( y − c) − ( x − c ) 2 = 0 的包络的包络. 3 9 9 3
y
x
O
3 奇解
定义2 定义对于一阶微分方程 F（x,y,y’）=0. 如果存在一条曲线（）
其c ∈ I是参数.
如何判断它是否有包络? 如果有包络, 如何求? 如何判断它是否有包络如果有包络如何求
Φ(x, y, c) = 0,
2 包络的求法曲线族(3.23)的包络包含在下列两方程
(3.23)
Φ ( x, y , c ) = 0 ' Φ c ( x, y, c) = 0
消去参数c而得到的曲线F ( x, y ) = 0之中,
F ( x, y, y ' ) = 0, y ( x0 ) = y 0 , y ' ( x0 ) = p0
为足够小的正数)，为足够小的正数上存在唯一解. 在 x − x0 ≤ h (h为足够小的正数，上存在唯一解
因此,方程的奇解,如果存在的话必含在从方程组: 因此方程F(x,y,y’)=的奇解如果存在的话必含在从方程组方程的奇解如果存在的话,必含在从方程组 F ( x, y , p ) = 0 F p ( x, y , p ) = 0 消去参数p而得到的曲线 ϕ ( x, y ) = 0 中. 消去参数而得到的曲线
且
存在唯一的
0
l
与
lc0 在 ( x0 , y0 )
c0 ∈ I ,

一阶微分方程奇解的存在性及其求法

DOI : 10. 16246 /j . cnki . 51 -1674 /c. 1988. 03. 012
南充师院学报
Jo
: 2 r
n
198 lz o
n
;
g
(
e
3
)
:
2 0 5一 2 1 1
N
a
ll e
丝
T
c ! a
C
、、
1 1铭 e
一阶微分方程奇解的存在性及
其
张
求
于
.
点相切
由定义
1
,
2
可知
:
一阶微分方程的积分曲线族的包络就是该方程的奇解
求微分方程的奇解的问题便归结为求通解的包络的问题
由微分几何知道
,
曲线族价 (x
p ù 、 J 苗
了 . 门 ,
,
y ,
、、
、
c
)=
0
0 的包络含在
下
20
l川断曰 ] 给出f 若为零
,
c 别曲戎足否为包络的充分条件一判
x
:
价
`
、
、
(
、
和 O`
丫
`
、
万 (x
、
`
)
!
乍
.
C别曲线上各点存钧一判
」有界」不同时
那么 C 一判别曲线就是曲线族的包络
,
事实上
!
_ :
没 C 一判别曲线的急数式为

一类一阶微分方程的奇解的判别

是否有奇解．求方程的通解并
解：于ｏ）１（）ｇ）车由（＝，＝（＝ｐ一，
且４￣）＋ｘｐ（＋口）一ａｘｐｘｐ（）Ｏａ（ｑ（）０（）ｘ）２（ｐ（）２（）（）＝故由定理可知方程有奇解，且奇解为
２（）ａｘ
４
［（＋）］＋ｃ・
例２讨论方程
ｙ＝￣ｘｙｙ１ｎｌｘ
当（４））（－，得垒害，Ｊ）（（４）时解此Ｄ一。可＝口ｇ＋算０越
时＝
是否有奇解。求方程的通解并
令』
如㈩）对线２任点翱）积曲则曲（上一（在分（，），㈣
ｌＺ；
，
９中麻烦。对形如ｙａ而＝ｙ）ｙ）口，）ｑ）有连续导数）（ ≠０Ｐ，具的线族（）都有积分曲线微分方程，『１用方程中Ｙ的系数及ｑ（来判定该方程有奇解的文３利）垒二｝４（兰Ｉ与之在（）相切。物处ｙ：充要条件，在本文中，们研究了方程ｙａｘｙ２而我＝（），）ｑ）ｎ）ｙ＋（ａｘ（、一 … 。 ’ 一 … ’ 。 ≠０ａｘ，（，）有连续导数），（）ｐ）ｑ（具的奇解存在的充要条件，一步推进由奇解的定义，函数（）故２为方程（）奇解。１的广了文『１３的部分结果。２应用１主要结论

关于奇解的若干探讨

关于奇解的若干探讨摘要：对于一阶常微分方程奇解的有关问题，本文针对有关一阶常微分方程奇解的定义和求法进行了系统的归纳和总结，列举了求奇解的两类方法；并根据p-判别曲线求奇解的方法，讨论了克莱罗（Clairaut）微分方程和两类特殊类型的一阶常微分方程的奇解以及奇解存在的充分条件。

关键词：一阶常微分方程；奇解；包络；C-判别曲线；P-判别曲线1.引言求通解在历史上曾作为微分方程的主要目标，一旦求出通解的表达式，就容易从中得到问题所需要的特解，也可以由通解的表达式了解对某些参数的依赖情况，便于参数取值适宜，使它对应的解具有所需要的性能，还有助于进行关于解的其他研究。

后来的发展表明，能够求出通解的情况不多，在实际应用中所需要的多是求满足某种指定条件的特解。

当然，通解是有助于研究解的属性的，但是人们已把研究重点转移到定解问题上来。

一个常微分方程是不是有特解呢？如果有，又有几个呢？这是微分方程论中一个基本的问题，数学家把它归纳成基本定理，叫做存在和唯一性定理。

因为如果没有解，而我们要去求解，那是没有意义的；如果有解而又不是唯一的，那又不好确定。

因此，存在唯一性定理对于微分方程的求解是十分重要的。

而奇解是微分方程的一种特殊的解，类似微分几何中的包络，奇解对应的积分曲线上每一点还有方程的另一个解存在，则存在唯一性定理被破坏。

但是，并不是任何微分方程都有奇解，奇解存在的条件还有待进行更深入的探讨和研究。

2.奇解的定义及求法2.1 奇解的定义我们知道对某些微分方程，存在一条特殊的积分曲线，它并不属于这个方程的积分曲线族，但是，在这条特殊的积分曲线上的每一点处，都有积分曲线族中的一条曲线和它在此点相切。

在微分方程里，这条特殊的积分曲线所对应的解称为方程的奇解。

定义1：微分方程的一个解称为奇解，如果在这个解的每一个点上还有方程的另外一个解存在，也就是说奇解是这样的一个解，在它上面的每一个点唯一性都不成立。

或者说，奇解对应的曲线上每一点至少有方程的两条积分曲线通过。

一阶微分方程的奇解及其逆问题

一阶微分方程的奇解及其逆问题摘要介绍了导数已解出的一阶微分方程和导数未解出的一阶微分方程的奇解问题，通过相关实例进行了说明.同时.考虑了常微分方程奇解的逆问题.关键词奇解;包络;通解;P-判别曲线;C-判别曲线;逆问题The singular solution of first oder ordinary differential equationand its inverse problemAbstract In this paper, we introduce the singular solution of the first oder ordinary differential equation by giving corresponding examples. Meanwhile, we also consider the inverse problem of the singular solution of ordinary differential equation.Keywords Singular solution; envelope; general solution; P-judging curve; inverse problem一阶微分方程的奇解及其逆问题1 概念例1.1.1 求微分方程 2-)(22xdxdy xdxdy y += 的解.解令 dxdy p =代入方程得2-22xxp p y +=. （1）两边对x 求导 0)-2)(1-(--2=→+=x p dxdp x p dxdp x dxdp pp .由c x p x p +=→=0-2 代入（1）得方程的通解 222c cx xy ++=. （2）由20-2x p x p =→=代入（1）得42xy =，经验证此为原方程的解. 从图1中我们可以看到，此解与方程通解（2）中的每一条积分曲线均相切.对某些微分方程，存在一条特殊的积分曲线，它并不属于这方程的积分曲线族中，但是，在这条特殊的积分曲线上的每个点处，都有积分曲线族的一条曲线和它在此点相切，在几何中，这条特殊的积分曲线称为上述积分曲线族的包络，在微分方程里，这条特殊的积分曲线所对应的解称为微分方程的奇解.下面我们分别给出曲线族包络和微分方程奇解的定义.定义1 设给定单参数曲线族 Φ（x,y,c ）=0其中c 是参数，Φ（x,y,c ）是x,y,c 的连续可微函数，曲线族Φ（x,y,c ）=0 的包络是指这样的曲线，它本身并不包含在这曲线族Φ（x,y,c ）=0 中但这曲线的每一点，都有曲线族Φ（x,y,c ）=0 中的一条曲线和它在这点相切.定义2 设有微分方程的一条积分曲线，若在它上面的每一点处方程的解的唯一性都被破坏，则称这条积分曲线所对应的解是微分方程的奇解.根据定义我们可以得出：对某些微分方程，存在一条特殊的积分曲线，它并不属于这方程的积分曲线族.但是，在这条特殊的积分曲线上的每一点处，都有积分曲线族中的一条曲线和它在此点相切.在几何学中，这条特殊的积分曲线称为上述积分曲线族的包络.在微分方程里，这条特殊的积分曲线所对应的解称为方程的奇解. 2 对于导数已解出的一阶微分方程的奇解本节给出寻找导数已解出的一阶微分方程（3）的奇解的方法和步骤.按定义，奇解就是破坏了微分方程解的唯一性的解，我们知道，导数已解出的一阶微分方程的解的存在唯一性定理为.定理 2.1 给定微分方程，若函数满足如下条件：1）函数在闭区域≤，≤b(a 、b>0)上是连续的.2）函数在R 上满足利普希茨条件，即存在常数L>0，对于所有的点∈R 都有≤，则方程（3）存在唯一的解上，连续且满足初始条件，这里,.由于利普希茨条件难于检验，常用在R 上有对y 的连续偏导数来代替，因为若在R 上,存在且连续，则yf ∂∂在R 上有界，设在R 上Lyf ≤∂∂，则yy y y x f y x f y x f ∂+∂=))-(,(),(-),(12221θ,,其中R y x y x ∈),(),,(2110<<θ, 即若),(y x f 在R 上有连续偏导数，则在R 上),(y x f 一定满足利普希茨条件，但反之不成立.(,)dy f x y dx=(,)dy f x y dx=(,)f x y (,)f x y 0:R x x -a 0y y -(,)f x y 12(,),(,)x y x y 12(,)(,)f x y f x y -12L y y -y =φ(x)0x x h -≤00 φ()y x =m in(,),m ax{(,)}b h a M f x y M==(,)x y R ∈(,)f x y 1212y y L y y --≤通过上面的分析知，当yf ∂∂的有界性被破坏时，方程（3）的解的唯一性将有可能被破坏.因此若要寻求导数已解出的方程（3）的奇解，只能在使得yf ∂∂的有界性被破坏的函数)(x y φ=中去寻找，这样我们就得到寻求方程（3）奇解的步骤：A 求使yf ∂∂为正无穷的函数)(x y φ=)),((连续y x fB 验证函数)(x y φ=是否为方程（3）的解C 若)(x y φ=是方程（3）的解，再验证唯一性，若)(x y φ=中的每一点的唯一性都不成立，则此)(x y φ=为方程的解.例2.1.1 求微分方程2y -1=∂∂yf 的奇解.解方程右端2-1),(y y x f =在11-≤≤y 内连续，2y-1y -=∂∂yf 在直线1±=y 上，yf ∂∂为无穷大，显然1±=y 为方程的解，可以看出在直线1±=y 上的每一点，都有原方程通解)sin(c x y +=中的一条曲线与它们相切，所以1±=y 为方程的奇解.3 对于导数未解出的一阶微分方程的奇解3.1利用c-判别曲线求奇解我们知道，微分方程积分曲线族的包络所对应的解一定是奇解，现在我们讨论曲线族的包络应满足的条件.设0),,(=c y x φ （4）为一曲线族，由微分几何学可知，曲线族（4）的包络包含在由下列方程组),,(,0),,({'==c y x c y x φφ 消去C 而得到的曲线之中，此曲线称为曲线族（4）的C-判别曲线.我们注意到，在C-判别曲线中有时除去包络外，还有其它曲线.C-判别曲线中究竟哪一条是包络尚需实验检验.例3.1.1 求曲线族 2c cx y +=的包络，在这里C 是参数.解将2c cx y +=对C 求导数，得到02=+c x . 从02{2=++=c x ccx y 中消去C ，得到042=+y x .所以，曲线族2c cx y +=的包络为042=+y x .例3.1.2 求曲线族01-22=+cx y c 的包络，在这里C 是参数.解将01-22=+cx y c 对C 求导，得到022=+x cy ，从⎩⎨⎧=+=+，01-,02222cx y c x cy 中消去C ，得到044=+y x .所以，曲线族01-22=+cx y c 的包络为044=+y x .3.2 利用p-判别曲线求奇解首先我们引入一个定理.定理 3.2 如果在点),,('000y y x 的某一邻域中，a) ),,('y y x F 对所有变元),,('y y x 连续，且存在连续偏导数； b) ),,('000y y x F =0； c)0),,(''000≠∂∂yy y x F ，则方程),,('y y x F =0存在唯一解h x x x y y ≤=0-),(（h 为足够小的正数）满足初值条件'00'00)(,)(y x y y x y ==.由上述定理知道，如果),,('y y x F 关于',,y y x 连续可微，则只要0≠∂∂yF 就能保证解的唯一性，因此，奇解（如果存在的话）必须同时满足下列方程),,('y y x F =0，0),,(''=∂∂yy y x F .于是我们有以下结论：方程0),,(=dxdy y x F （5）的奇解包含在由方程组)(0),,(0),,({'dxdy p p y x F p y x F p ===消去P 而得到的曲线中，这里),,(p y x F 是p y x ,,的连续可微函数.此曲线称为方程（5）的P-判别曲线.P-判别曲线是否是方程的奇解，尚需进一步检验.例3.2.1 求方程01-)(22=+y dxdy 的奇解.解从⎩⎨⎧==+0201-22p y p 中消p 得到p-判别曲线1±=y .经验证，此两直线都是方程的奇解.因为容易求得原方程的通解为)sin(c x y +=，而1±=y 是微分方程的解，且正好是通解的包络.3.2.1应用p-判别曲线一般性的求解微分方程的奇解用这个定理来求解以下两类一阶微分方程的奇解（A ） 0)()(-))((1-=+x b dxdy y dx dy x a n n.（B ）)())(())((1-x c dxdy x b dxdy x a y n n++=.首先来讨论微分方程（A ），其中a(x),b(x)在区间I 上是连续可导的，且.0≠)(,0≠)(x b x a 这时0)(-)(),,(1-=+=x b yp p x a p y x F n n 0]1)-(-)([)1-(-)(),,(2-2-1-'===y n p x na pyp n px na p y x F n n n消去p 得到的函数),()(1-_x d x a n n y •=其中.0)()()1-()(≠=x na x b n x d n)()(-))((),,(1-_'__'_'_x b y y y x a y y x F n +=)]()(1-)()(-[))(()(1--))((1-_'_'x d x a n n x d x a y x d x a n n y x a nnn n++=))]()()((1--)()()][()[(∑∑2-0-2-_'1-0-1-_'_'x d y x d n n x d y x d y x a in i in in i in ===因此，0(x)-_'=d y 时，_y 是微分方程（A ）的解，而且又有)](-[))(()())((-))((),,(_'2-_'2-_'1-_'_'_'_'x d y y x na x d y x na y x na y y x Fn n n y==.0)(-),,(1-_'_'_'_≠=n y y y y x F 由于)(_'x d y =则)())(())(()()2-(-))(()1-(),,(3-_'3-_'2-_'_'_''_'_'≠•==x d y x na y x d x a n n y x a n n y y x Fn n n yy由此可知，对于微分方程（A ），假设a(x),b(x)在区间I 上是连续可导的，且.0)(,0)(≠≠x b x a 若满足.0)(-_'=x d y 即.0)(-)]()(1-['=x d x d x a n n其中.)()()1-()(x na x b n x d n=则微分方程有奇解：).()(1-_x d x a n n y •=再来讨论微分方程（B ），对于微分方程（B ）其中a(x),b(x),c(x)在区间I 上是连续可导的，且.0≠)(,0≠)(x b x a 这时0-)()()(),,(1-=++=y x c p x b p x a p y x F n n)]()1-()([)()1-()(),,(2-2-1-'=+=+=x b n p x na ppx b n px na p y x Fn n n p消去p 得到函数：)()()()()(1-_x dx b x d x a x c y n n+•+=，其中.0)()(1)-(-)(≠=x na x b n x d))]()()(())()()(()][(-[)()(-)()(-))(())((-)())(())((),,(∑∑2-0-2-_'1-0-1-_'_'1-1-_'_'_1-_'_'_'_x d y x b x d y x a x d y x dx b x d x a y x b y x a yx c y x b y x a y y x F in i in in i in n nn nn n==+=+=++=因此，当.0)(-_'=x d y 时，_y 是微分方程（B ）的解.又.0))(()1-(-),,(01-),,(0)](-[))((),,(2-_'_'_''_'_'_'2-_'_'_'_'_'__'≠=≠===n yy y n yy x b n y y x Fy y x F x d y y x na y y x F从而，对于微分方程（B ），假设a(x),b(x),c(x)在I 上连续可导，且.0)(,0)(≠≠x b x a 又满足条件.0)(-_'=x d y 即0)(-)]()()()()(['1-=++x d x d x b x d x a x c n n其中.0)()(1)-(-)(≠=x na x b n x d 则（B ）有奇解：).()()()()(1-_x dx b x d x a x c y n n +∙+=3 .3克莱罗方程的奇解我们把形如)(p f xp y += （6）的方程，称为克莱罗方程，其中)(,p f dxdy p =是p 的连续可微函数.-下面讨论克莱罗方程的奇解.将)(p f xp y +=两边对x 求导，并以dxdy p =代入得dxdp p f p dxdp xp )('++= 即0))(('=+p f x dxdp1、若=dxdp cp =⇒，所以原方程的通解为)(c f cx y +=；2、若0)('=+p f x 将此与原方程合起来有 ⎩⎨⎧+==+)(0)('p f xp y p f x .消去P 也得到方程的一个解.分析 1）从1知克莱罗方程的通解是一族直线. 2）通解的形式就是在原方程中用C 代P 而得到的.3）从2知，求此解的过程正好与从通解)(c f cx y +=中求包络的步骤一样（也和求（6）的P-判别曲线的过程一样），并且此解为积分曲线族)(c f cx y +=的包络)01),,(('≠=c y x y φ，因此克莱罗方程总有解.4）从（3）知，对克莱罗方程而言，P-判别曲线和方程通解的C-判别曲线都是方程通解的包络，从而为方程的奇解.例3.3.1 求方程pxp y 1+=（其中dxdy p =）的奇解解此方程为克莱罗方程，因此其通解为ccx y 1+=从⎪⎩⎪⎨⎧+==c cx y c x 101-2 中消去C 得到x y 42=.由前后讨论知x y 42=为方程的奇解.4 微分方程奇解的逆问题我们考虑微分方程奇解的逆问题：求一微分方程已一个已知函数)(x y φ=为奇解.下面，用上述方法和结论来解决微分方程奇解的逆问题.4.1 求以x y sin =为奇解的常微分方程满足以x y sin =为奇解的常微分方程非常多，下面给出三种类型的常微分方程. 4.1.1求克莱罗型方程设克莱罗方程有奇解x y sin =，即⎩⎨⎧+==)()(sin )(-''p f p p f p f x 因此，)(sin p f xp x +=.下面求出)(p f 的表达式.求导得)(cos '''p f x p x x x ++=•. 令p x =cos 则p p p xp x xp x p f •===arccos --1-cos -1-sin )(2'故以x y sin =为奇解的克莱罗常微分方程为dxdy dxdy dxdy dxdy xy arccos-)(-12+=2．求)(A 型方程为简单起见，取n=2.已知x y sin _=，由条件0)(-'y _=x d 得x x d cos )(=. 由)()(2,)()()(_2x d x a y x a x b x d ==得 x x a x x a x b x cos )(2sin ,)()(cos2==解之得x x x b x x a sin cos 2)(,tan 2)(==.因此，以x y sin =为奇解的)(A 型常微分方程为0sin cos 2)(-)(tan 22=+x x dxdy y dx dy x3．求)(B 型方程取n=3.已知xy sin _=.由条件0)(-'_=x d y 得x x d cos )(=.又)(27)(4)(,)(3)(2-)(23_x ax b x c x a x b x d y +==则)(27)(4)(sin ,)(3)(2-cos 23x a x b x c x x a x b x +==.特别取c(x)=0,解之得 xx x b xx x a 23cos sin 3)(,cos sin 2-)(==.因此，以x y sin =为奇解的)(B 型常微分方程为 2233)(cos sin 3)(cos sin 2-dxdy x x dx dy x x y +=. 4.2 求以xe y =为奇解的常微分方程 4.2.1求克莱罗型方程设克莱罗方程有奇解x e y =，即⎩⎨⎧+==)()()(-''p f p p f e p f x x 因此)(p f xp e x+=.求导化简得xe p =，则p p p pf ln -)(=.故以xe y =为奇解的克莱罗型常微分方程为)ln()(-dx dy dx dy dx dy dx dy xy +=4.2.2 求)(A 型方程取n=2.已知奇解xey =_，由条件0)(-'_=x d y 得xe x d =)(.由xe x a x a x b x d y)(2,)()()(_==得 xxxe x a e x a x b e)(2,)()(2==，进而21)(=x a ，xe x b 221)(=.故以xe y =为奇解的)(A 型常微分方程为021)(-)(2122=+xedxdy y dxdy .4.2.3 求)(B 型方程取n=2.已知xe y=_，由条件0)(-'_=x d y得x e x d =)(. 由)(4)(-)(,)(2)(-)(2_x a x b x c x a x b x d y ==，得)(2)(-,)(4)(-2x a x b e x a x b e xx==，解之得2)(,-)(-==x b e x a x.因此，以xey =为奇解的)(B 型常微分方程为)(2)(-2-dxdy dxdy e y x+=.同理，可以求出其他类型函数或者复合函数作为常微分方程的奇解.因此有奇解的常微分方程是非常多的.此外，在上述求解过程中，由于n 与c(x)有许多不同的取法，因此，以同一奇解的常微分方程也是非常多的.5 总结本文对一阶微分方程通过分为导数已解出的、导数未解出的、克莱罗方程，以及利用P-判别曲线对一般的类似于（A ）、（B ）的微分方程的奇解的求法做出了讨论，应用各种方式算出它们的奇解，对解法进行了较全面的分析，并给出了相应的求解方法和求解步骤.最后讨论了微分方程奇解的逆问题，带入一般的微分方程（A）、（B）讨论微分方程的逆问题.参考文献[1] 丁同仁，李承治.常微分方程教程[M].2版.北京：高等教育出版社，2004:94-110.[2] 王五生，付美玲，侯宗毅.一阶非线性常微分方程奇解的求法[J].高等数学研究，2010（7）：65-67 .[3] 何永葱.关于常微分方程奇解的逆问题[J].重庆教育学院学报，2008（5）：5-10.[4] 何永葱.关于常微分方程奇解判别的注记[J].内江师范高等专科学校学报，2000（2）.[5] 何永葱.两类一阶常微分方程有奇解的条件[J].重庆教育学院学报，2007（6）[6] 王高雄，周之铭，朱思铭，王寿松.常微分方程[M].3版.北京.高等教育出版社.[7] 李育俭.一阶微分方程的奇解[J].武汉工程专业技术学院学报，2005（9）：83-87.[8] 艾利斯哥尔兹著.微分方程[M].北京.高等教育出版社.1959年.- 12 -。

常微分第三章第4节(奇解)

y cx f (c)
' x f ( p) 0 ' 如果 x f ( p) 0，则 y xp f ( p) 消去 p 得到方程的另一个解。
这里
c 是任意常数。
25
注意，求得此解的过程正好与从通解
y cx f (c)
可以验证，此解的确是通解中求包络的过程一样。的包络。
注1：包络一定包含在 c-判别曲线中。注2：c-判别曲线不一定为包络。
2 充分但不必要。 2 x y 0
15
C 判别曲线法求方程奇解的一般步骤：（1）求出方程的通解（积分曲线族）；（2）求积分曲线族的 c 判别曲线；
（3）检验 c 判别曲线是否为包络，若是，则为方程的奇解。
16
y 1
其中
容易求得原方程的通解为 y sin( x c)
c 为任意常数。而 y 1 是通解的包络。
所以此两直线都是方程的奇解。
22
例4
求方程
dy dy 2 y 2x ( ) 的奇解。 dx dx
y 2 xp p 2 解从 2 x 2 p 0
消去
这是克莱罗方程，因而它的通解是 1 y cx c 1
27
y2 4x
O
图(3.5)
28
例6
求一曲线,使在其上每一点的切线截割坐
标轴而成的直角三角形的面积都等于2 。 y A
O 图(3.6)
B
x
29
依题意有ab 4，而
dy 2 dy 得 ( y x ) 4 dx dx
现在求曲线族的包络，亦即微分方程的奇解。
30
y 2c c 2 x 从中消去 c 得微分方程的奇解 1 cx 0

高中数学(奇解的背后)

在“奇解”的背后学校有一位数学才子，此人才思敏捷，科学的规律，艺术的工夫，全藏肘后；别人肩上的重负，移到他的掌上，都成了玩意儿. 更难得的是文理兼修，嬉笑怒骂，皆成文章. 有一天，才子的同学们正在讨论一道2006年高考数学题.重庆文（12）若,,0a b c >且222412a ab ac bc +++=，则a b c ++的最小值是（）.（A ）（B ）3 （C ）2 （D 同学甲拿出了如下解答：（a ＋b ＋c ）2＝a 2＋b 2＋c 2＋2ab ＋2ac ＋2bc ＝12＋（b －c ）2≥12，当且仅当b ＝c 时取等号，故选A.才子一看，答案虽是对的，同学甲的运算能力还真不错，但解题人有点过份得意，因此得到以下评语：［评语］答案对了莫自满，别人求近你走远，平方配方太费力，面对结果还绕圈. 大家听才子这么说，纷纷要求才子本人拿出自己的解法来，于是有了以下的奇解. 因为2224(2)2(2)(2)(2)12a ab ac bc a a b c a b a b a c +++=+++=++=，所以222(2)(2)a b c a b a c ++=+++≥所以a b c ++的最小值是大家一看，十分惊喜，但对解法的来历有点奇怪. 于是才子有了如下的自评. ［评语］创新本来在任意，因式分解谁称奇，意义明了思路畅，不用花费纸和笔. 这时，同学甲有点不服，又拿出一道题，如下：重庆理（10）若,,0a b c >且()4a a b c bc +++=-则2a b c ++的最小值为（）.（A 1 （B 1 （C ）2 （D ）2 说:“你能用它来解看这道题吗？”才子回答：能！只要拆成(a+b)(a+c)即可，请看下解:()()()4a a b c bc a b a c +++=++=-()()2a b a c +++≥==，当且仅当a b a c +=+时，即b c =时取得最小值。

求解一阶隐微分方程的微分法与参数法及奇解注记

求解一阶隐微分方程的微分法与参
数法及奇解注记
求解一阶隐微分方程的微分法：
该方法是根据微分方程的性质及解的连续性来求解一阶隐微分方程的方法，其步骤为：
1、将隐微分方程化为常微分方程组；
2、解决上述常微分方程组，求出解；
3、显式地表示出解与相应参数之间的关系；
4、根据微分方程的解的连续性，从而求得隐微分方程的解。

参数法：
该方法是根据一阶隐微分方程的特征及隐含的参数的特性来求解一阶隐微分方程的方法，其步骤为：
1、将隐微分方程化为常微分方程组；
2、根据隐微分方程的特征及其隐含的参数的特性，将原问题转化为求解参数的问题；
3、显式地表示出解与相应参数之间的关系；
4、根据参数的值，从而求得隐微分方程的解。

奇解注记：
奇解注记是指当一阶隐微分方程的特征多项式有两个不同实根时，可以用来求解一阶隐微分方程的方法，其步骤为：
1、将隐微分方程化为常微分方程组；
2、根据隐微分方程的特征多项式有两个不同实根，将原问题转化为奇解注记问题；
3、显式地表示出解与相应参数之间的关系；
4、根据奇解注记的值，从而求得隐微分方程的解。

包络排除方法及奇解排除定理

单参数曲线族
Ｏ（ｘ，，ｆ）一０（１）
（ｘ－ｃ。［ｃＸ－Ｃ一号］一０．
由ｚ— ｃ一０，得到判别曲线
Ｘ— Ｃ， — ｆ，（６）
两边对ｚ取导数，得
ｏ＇（ｘ，Ｙ，ｃ）＋
ｘ
或者
的奇解（利用判别曲线法）．
（ｚ— ｆ）一Ｙ（Ｙ一３）。一０．
（８）
（９）
Ｙ本身应有的关系ｐ— ｄｙ
．
如果户是不合理的，也即
判别式中的Ｐ不等于由Ｐ一判别式得到的Ｐ一判别
解将导数解出并分离变量，得方程的通解为其中Ｃ为任意常数（一ｏｏ＜Ｃ＜＋。。）．再由相应的判别式
Ｙ＝＝＝Ｘ・
（ｚ，Ｙ，ｃ）ｄ
ｘ
０，
由Ｘ— ｃ一：０，得到判别曲线
或者
：：：一
如
＝三！！（，，ｃ） ‘
ｚ — 一ｆ＋十， ’ Ｙ — 一ｃ＋十告百， ’
或者
（２）
（ — ｆ）。一Ｙ（Ｙ一３）一０，
一
曲线Ｙ＝（ｚ）的导数￡．这就说明，不存在使得
一０的点集Ｙ：（ｚ），即在任何点上Ｆ ≠０．因
不满足非蜕化条件，不能肯定（６）是否是包络．但由于与同时为零，故判别曲线（６）不是包络．例２Ｅ试求微分方程

浅谈常微分方程奇解与包络

浅谈常微分方程奇解与包络对常微分方程教科书中采用的不同方式来定义奇解，进行了讨论，指出了用包络定义奇解的不相容性，和用唯一性破坏定义奇解的合理性。

给出了求常微分方程以已知函数求奇解的多种方法，方法和实例表明，这对有奇解的常微分方程以及同一奇解的常微分方程都是非常多的.标签：常微分方程；定义；奇解；包络0 前言常微分方程，是一个有悠久历史发展迅速的学科，是一个理论和实际应用都很有价值的学科，它不但自身应用十分广泛，而且对其他学科都有非常大的帮助。

许多科学家都对微分方程有了不同程度的研究。

比如牛顿，莱布尼茨等。

常微分方程是17世纪和微积分同时诞生的一门理论性非常强，研究应用非常广泛的学科之一，常微分方程的发展分了四个发展阶段，这四个发展阶段对常微分方程非常关键。

牛顿和莱布尼茨创立的微积分是不严格的，18世纪的数学家们一方面努力探索微积分严格化的途径，一方面往往又不顾基础问题的困难而大胆前进，大大地扩展了微积分的应用范围，尤其是与力学的有机结合，当时几乎所有的数学家也是力学家.牛顿和莱布尼茨都处理过与常微分方程有关的问题. 微积分的产生的一个重要的动因来自于人们探求物质世界运动规律的需求. 一般地，认识规律很难完全靠实验观测认识清楚，因为人们不太可能观测到运动的全过程. 运动是服从一定的客观规律的，物质运动与瞬时变化率之间有着紧密的联系，而这种联系，用数学语言表述出来，即抽象为某种数学结构，其结果往往形成一个微分方程，一旦求出其解或研究清楚其动力学行为，运动规律就一目了然了。

为了便于讨论，现将第一种定义写出：1 奇解的定义在通常教科书中对奇解的定义采用两种方法：一种是用积分曲线族的包络（以下简称包络）定义奇解；另一种是用奇解的唯一性被破坏定义奇解.由下面的讨论可知，用第一种方法定义奇解将会产生混乱，甚至会出现不相容的情况.第二种定义则来源于微分方程本身内容，准确而不会产生歧义.为了便于讨论，现将第一种定义写出：1.1 定义1微分方程的一个解称为奇解，如果在这个解的每一点上还有方程的另外一些解存在，在它上面的每一点唯一性都不成立，奇解對应的曲线上每一点至少有方程的两条积分曲线通过[1]。

议常微分方程奇解的定义

一
点Ｐ，得ｅ与Ｅ在这个点Ｐ相切．有这种性质的曲线Ｅ叫做给定的曲线族的包络（图１．使口具如）
定义２［ｂ
定义２［５ｃＩ４
所谓曲线族的包络是这样一条曲线，这曲线上所有的各个点，与曲线族中各在它
曲线族
ｙ＝０或ｙ一ｚ．。易证Ｙ＝０是方程（）ｂ的解．直线ｙ一０凹轴，是它包含在积分曲线族（）５中．由定义２，ｃｙ＝０是
∞（ｙ，ｚ，Ｃ）一０
不同的曲线相切，就是说，这在这曲线上每一点，曲线与曲线族中通过这点的曲线有公共切线．这
’
（）２
的包络是指这样的曲线，它本身并不包含在曲线族（）中，２但过这曲线的每一点，曲线族（）中的有２
通常教科书对奇解的定义往往采用两种方式：种是用积分曲线族的包络（一以下简称包络）定义奇解；一种是用解的唯一性被破坏定义奇解．另前者将会引起混乱，甚至导致不相容的情形出现，后者则源于微分方程本身内容，准确而不会产生歧义．为了便于讨论，先将第一种定义写出．定义１［方程
是以坐标轴为对称轴，半轴长分别为√ ２与１的椭圆（如图２．）
荽＋：ｌｖ：
Ｚ、＼
Ｙ＞７
、
．
（－．）０３
图１曲线族的包络图
一
＝．０９
（．，）０８
＝，６０３

5 隐式微分方程组的深入

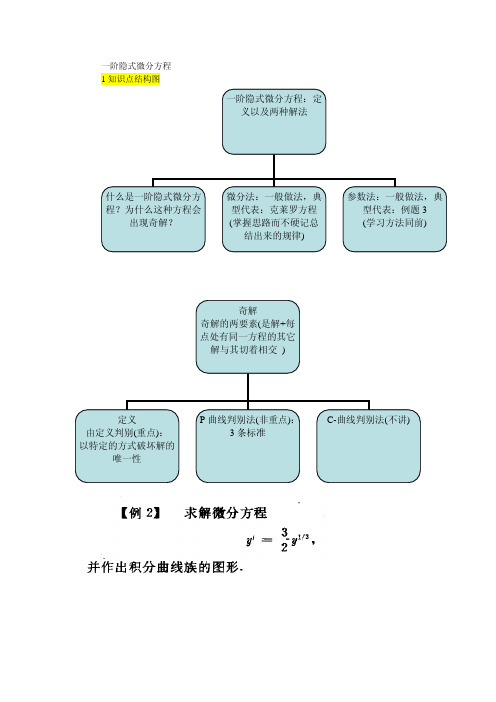
一阶隐式微分方程1知识点结构图
2奇解的认识和产生奇解的机制------目的：自己构造一些具有奇解得方程并验证(提高层次的认识)
.
01dx
dy (.
2.
12唯一，但没有奇解不的过每一点的积分曲线如：性的“特殊解”
奇解是不满足解的唯一相切着相交仅相交，而且是
不同的解在奇解上，不一性通过，因而没有解的唯条积分曲线
奇解上每点处至少有两：
由奇解的定义可以看出=−⇒
.
,
1)'y (2轻而易举的但真的出现奇解还不是很容易的，如注意：线素的不唯一是= 讲课提纲：
零．需要数分基本知识：隐函数定理，参数方程求导数，图形凹凸性与二阶导数的关系
一．主题：一阶隐式微分方程、奇解
二．克莱罗方程、微分法以及克莱罗方程的相图
三．例题2(微分法的继续)以及奇解产生的机制
四．例题3、例题4 以及参数法的道理
五奇解的必要条件以及p-判别法
作业1第一节1(1,2), 2(1,2)
第二节1（1）。

常微分方程教程(丁同仁李承治第二版)第四章奇解

第四章奇解习题4-11．求解下列微分方程：（通解）特解）（特解）解：221222)(2222222222)(2101.(42202..0)1)(2(0)2()2(2222);(,242).1(C Cx y x x C x y C x p b x x x x y x p x p a x p x p x p xx p p p x px y p x px p y x C x dxdp dx dp dx dp dx dp dx dpdx dp p dxdy ++-=⇒++-+=⇒+-=⇒-=⇒=+-=+-=⇒-=⇒=+=++⇒=+++⇒+++=++==++=+-224ln 4ln 2ln 22ln 2ln 2ln 222ln )(ln 0x .)]([ln 2ln 02ln ..0))(2(ln 22)1(ln ln );(,)(ln ).2(222C x C y x x x y p p x b y x x x y p xp x xp x a p x xp x p x xp x p x x p p xp x px y xC xC xCdx dp x x x x x x x xx dx dp dxdp dx dp dxdy+=⇒+=⇒=⇒=+-=+-=⇒-+-=⇒-=⇒-=⇒=+=++⇒++++==+=（特解）解：dydq qyqy y dy dq q y dydx pyp p y q y q y q x q y x y p y xp 3222222cos 2)sin (cos 222cos 12cos 123sec tan ,tan ,,tan .cos tan 22).3(-++=+===+=+=-令解：yy y y x q q y b y C x y C q y q y q a y y q y q y q y y q y yy y t yyyyy qy C dydqdy dq q y dy dq dy dqq y dy dq dydq qyqyy dy dq 32323232sin 2cos 2313133223232322sin sin sin tan 0tan .sin cos tan 0tan .0))(tan tan (0)tan ()tan (tan 0tan tan 23212cos sin cos sin cos sin cos 3cos 21cos cos cos sin cos 2=+=+=⇒=⇒=⇒=-+=⇒=⇒-=⇒=+=-+⇒=+-+⇒=-++⇒-（通解）2．用参数法求解下列微分方程：（特解）当当由解：令21cos 0sin )](cos[2)](cos[20sin .sin ,,sin ,cos 2,sin ,cos 4)(52)1(52510210210sin sin 2)cos 2(sin 552552522222552552552±=⇒±=⇒=+-=+-=⇒+-=⇒-==⇒=⇒≠==+∞<<-∞=====+y t t b C x C x y Cdt x dt dx t a tp x t p t y t p t y y ttdtt d tdydxdydx dy故解：令dt tsh xht d sht dx sht dy sht dx dy e e sht e e cht shtp cht x dxdy x tt t t 3)(3332,2,3,.1)(3).2(222===⇒=-=+====---Ct t sh Ct e e C t d e e Cdt t sh y t t t t +-=+-+=+-+=+=--⎰⎰)2241(31)4(381)2()2(381322222Cdt t t t Cdt tt t v dtv v t t vt u t vdv du v u vdu vdv udu pdx dy v u y v p u x x y tt t vdv t tt dv dtt dv dtt dvvdt tdv t vdttdv dvv u vu vv u dudvdxdy vu v u++---=++--==⇒=⇒=+⇒=⇒=-=⇒===-==⇒=-⇒=-=-====-+⎰⎰+---+---+-+--22122212ln ,,2)2(22,,,.0)).(3(222212122212212211221222122222222令齐次方程解：令⎰⎰⎰⎰⎰-----=+--+-=+---16172411617241222)(221)(212222212212t tdt t dt dt t t tdt t t dt t t t⎰⎰⎰⎰--+---=--+--------=16172411617241161724116172411617241)(411617)41(ln 21)(21)(41)(])[(21t dt t t dt t dt t t dαββαβαβαβαβαβαβαβααβα)()()()()()()()()()(1)()()()()()(,)(,,)41741()41741()(1.||ln )(ln ||ln 1721)11(17241))((41)(41417414174117411717411741174141174141174141174117414141174117414141174141174141174141174141174121172141741417411721417414174141741417414174141741172116172412122124174141741417414174141741417411617241212117212117212v u C v u v u C v u v u C v u v u C v u v u v u C vv u vv u CvuvuC t t C v t C v t t C t t t t ev t t t dt t t dtt t t t dtt dt Ct t t +=++=++=++=+++=++=++=++=+=--=+-=+---=+-----+-=+---+---=-+---=+----=+---=--+---+-+-+---+----------------+--⎰⎰⎰⎰故令故（通解）,)()(22⎩⎨⎧+=+-=αββαp x C p x p x y （特解）故特解：⎩⎨⎧=====⨯======++=±-=±-=⇒±=⇒±=⇒±=⇒=+---+-+-+--+++++,,..172181722))161(161()171(1617144171417102222122122121721817222212417121281712641788264)179)(171(217917121721817222222222x y x y x x y b axx x x x x x y a x x x x y u v v u t t t βαβ（通解）故令解：⎪⎩⎪⎨⎧++-==++-=⇒===⇒-=⇒-=⇒==-=-==++++++++++,,),()(,4),4(,).4(4)(.4)().4(3233323332331132)1(8141132)1(81414141432332333C y x Cy d xtd dy x x t xt x t x t x xt p x x x x x x t t t tt t t tt t t t t tdxdydxdy dx dy dx dy dx dy dx dy 习题4-21．利用p-判别式求下列微分方程的奇解：的奇解。

关于常微分方程奇解的逆问题

Ｖｏ．Ｎｏ３１２１．Ｍａ２８ｙ，００
关于常微分方程奇解的逆问题
何永葱
（重庆教育学院学报编辑部，庆４０６）重００７
摘要：出了求常微分方程以已知函数为奇解的多种方法，法和实例表明有奇解的常微分方程以及同一奇解给方的常微分方程都是非常多的。
（）ｐ
对 ∈ 成立。则方程
Ｐ＝ｉ－ｐ￣）ｓｘｘ＝ｎ
、１ｐａｃｓ・／＿－ｒｏＰｃｐ
用该定理，近［］献了给出了两类一阶微分最３文
因此，ｙｓｘ为奇解的克莱罗型常微分方程为以＝ｉｎ
收稿日期：０７１ — ２２０ — ２１
Ｆ，竿）（ｙ＝ｘ，０
设函数ＦｘＹｐ）（，，）（，，对ＹＰ ∈Ｇ是二阶连续可微的。又设其ｐ判别式一
ＦｘＹＰ）０（，，＝
。
１求以ｙｓｘ＝ｉ为奇解的常微分方程ｎ
满足以ｙｓｘ为奇解的常微分方程非常多，＝ｉｎ下
其中，：
１７，
口）（）ｄ（：（．，）
口
，微分方则）６））＋，
ｆ－ｐｘｆ（）＝ｔｆ（）ｐｙｐｐ＝）其中ｐ为参数。是利用奇解存在的充分条件，献二文
［］［］出的结论：１或２给
一是利用奇解存在的必要条件p判别式或c判别式求出可能是奇解的函数验证这些函数是不是微分方程的解如果有函数是微分方程的解再求微分方程的通解最后判断解是不是奇解

包络和奇解

包络和奇解
作者：李健
来源：《赤峰学院学报·自然科学版》 2012年第18期
李健
（内蒙古化工职业学院，内蒙古呼和浩特 010010）
摘要：给出了包络和奇解的定义及定理，可以用各种不同方法求解一阶隐式微分方程的奇解，包络.
关键词：微分方程；通解；奇解；包络
中图分类号：O175 文献标识码：A 文章编号：1673-260X（2012）09-0005-03
4 结论
一阶微分方程的通解的包络（如果它存在的话）一定是奇解，反之，微分方程的奇解
（若存在的话）也是微分方程的通解的包络，因此为了求微分方程的奇解，可以求出它的通解，然后求通解的包络.
参考文献：
〔1〕王高雄，周之铭，朱恩铭，王寿松.常微分方程[M].北京:高等教育出版社，2001. 〔2〕丁同仁，李承治.常微分方程教程[M].北京:高等教育出版社，1991.
〔3〕东北师范大学微分方程教研室.常微分方程[M].北京:高等教育出版社，2001. 〔4〕都长清，焦宝聪，焦炳照.常微分方程[M].北京:首都师范大学出版社，1993. 〔5〕庄万.常微分方程习题解[M].济南:山东科学技术出版社，2003.
〔6〕南京大学数学系计算数学专业.常微分方程[M].北京:科学出版社，2005.。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第四章奇解
§1 一阶隐式微分方程
一[内容简介]
本节通过引入参数将隐式微分方程化为导数以解出的方程类型,并讨论了几种可求解的类型。

二[关键词]
隐式微分方程参数法克莱洛方程
三[目的与要求]
会用微分法和参数法求解一阶隐式微分方程，掌握克莱洛方程的解法。

四[教学过程]
§2 奇解
一[内容简介]
本节介绍了一阶微分方程奇解的概念，给出了从P－判别式求奇解的方法。

二[关键词]
奇解P－判别式
三[目的与要求]
了解奇解的意义，掌握用P－判别式求奇解的方法。

四[教学过程]
§3 包络
一[内容简介]
本节采用微分几何学中有关曲线族的包络的概念来阐明奇解与通解之间的联系，并给出了从C－判别式求奇解的方法。

二[关键词]
包络C－判别式
三[目的与要求]
了解奇解是积分曲线族的包络这一几何解释，掌握用C－判别式求奇解的方法。

四[教学过程]
教学过程
§4.1 一阶隐式微分方程
在第二章中我们介绍的是y '已经解出的显式方程()y ,x f y ='的求解方法。

本节我们来讨论一下y '未解出的一阶隐式微分方程
0=⎪⎭
⎫ ⎝⎛
dx dy ,y ,x F （1.1）若从方程（1.1）中可将y '解出，那么就得到一个或几个显式微分方程，求解这些方程就得到了微分方程（1.1）的解。

例1 求解微分方程
()02=++-⎪⎭
⎫ ⎝⎛xy dx dy y x dx dy （1.2）解：方程（1.2）的左端可以分解因式，得
0=⎪⎭
⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-y dx dy x dx dy 从而得到了两个微分方程
y dx
dy ,x dx dy == 解这两个微分方程得
x e c y ,c x y 2122
1=+= 故原方程（1.2）的通解可以表示为
()
021212=-⎪⎭⎫ ⎝⎛--x e c y c x y 但一般说来，从（1.1）解出y '并不容易，或者，即使能解出y '来，也不一定是可积分的微分方程。

因此，本节介绍几种不解出y '，而直接求y 的方程类型及其求解方法。

一. 可解出y 或x 的方程与微分法
1）.若能从方程（1.1）解出y ，得到
()y ,x f y '= （1.3）
这里设()y ,x f '关于变元x ，y '有连续的偏导数。

引进参数y p '=，则方程（1.3）变为
()p ,x f y = （1.4）
将（1.4）两边对x 求导，并以p 代替y '，得到
()()dx
dy p ,x f p ,x f p p x '+'= （1.5）这是一个关于变量x ，p 的一阶显式方程。

01. 若求得（1.5）的通解为()c ,x u p =将它代入（1.4）
，便得到原方程（1.3）的通解 ()()c ,x u ,x f y = （c 为任意常数）
另外，若方程（1.5）还有特解()x w p =
将上式代入（1.4），便得到原方程（1.3）相应的特解
()()x w ,x f y =
02 . 若能求得方程（1.5）的通积分
()0=Φc ,p ,x
将它与（1.4）联立，则得方程（1.3）得参数形式得通积分
()
()
p ,x f y c ,p ,x ==Φ0
其中p 为参数，c 为任意常数。

另外，若方程（1.5）还有特解()0=p ,x G ，将它与（1.4）联立，便得方程（1.3）相应的参数形式的特解
()
()
p ,x f y p ,x G ==0
其中p 为参数。

2）. 若能从方程（1.1）解出x ，得到
()y ,y f x '= （1.6）
这里设()y ,y f '关于变元y ，y '有连续的偏导数。

方程（1.6）的求解方法与方程（1.3）完全类似，可自行讨论。

由上述讨论可知，为了求解方程（1.3）或（1.6），我们引进参数y p '=，利用对x （或
y ）求导，从形式上消去y （或x ）
，从而把问题化成了求解关于x （或y ）与p 的一阶显式方程，因此，我们把这种方法成为微分法。

例1. 求解ClaiYaut （克莱洛）方程
()y f y x y '+'= （1.7）
其中()0='''y f 。

解：令p y ='，则方程（1.7）可写为
()p f xp y += （1.8）两边对x 求导，得到
()dx
dp p f dx dp x
p p '++= 或 ()()0='+dx
dp p f x 当0=dx dp 时，得c p =，代入（1.8）消去参数p 得克莱洛方程的通解 ()c f cx y += （1.9）
其中c 是一个任意常数。

由（1.9）式，并注意比较（1.7）与（1.9）式，可得下述结论：克莱罗方程的通解（1.9）是一族直线，且正好是将方程（1.7）中的dy dx
换成任意常数c 而得到。

当()0x f p '+=时，可得克莱罗方程（1.7）的一个特解
()x f p '=-，()()y f p p f p '=-+（1.10）
其中p 为参数。

由于()0f p ''≠，故由()x f p '=-可得反函数()p w x =。

由（1.10）式消去参数p 得
()()()y xw x f w x =+（1.11）
可以证明（1.11）是克莱罗方程（1.7）的解。

事实上，由（1.10）可得
()()()()()dx f p dp dy pf p dp f p dp f p pf p dp ''=-⎧⎪⎨''''''=--+=-⎪⎩
由条件()0f p ''≠，可得dy p dx
=（1.12）将（1.10）和（1.12）代入（1.7）的左、右两边，可得恒等式
()()()()f p dp f p f p dp f p ''-+≡-+
所以（1.10）或（1.11）是（1.7）的一个特解。

另外由()y w x '=，即可推出在0x x =处特解（1.11）的切线为00()y c x f c =+ 其中00()c w c =。

由此可以证明特解（1.11）与通解的任一直线（1.9）至少有一公共点
()0000((),())f c f c c f c ''--且在此点相切。

又由()0x f p '+=及()y w x '=可得 1()dp f p dx ''=-即1()dp dx f p =-''或。