正弦型函数的图形变换
高中数学人教A版必修4第一章正弦型函数y=Asin(ωx+φ)的图像平移及解析式的求法

正弦型函数y =Asin(ωx +φ)的图像平移及解析式的求法【知识点梳理及分析】一、有关正弦型函数y =Asin(ωx +φ)基础知识1.用五点法画y =A sin(ωx +φ)一个周期内的简图时,要找五个特征点如A 叫做振幅,T =2πω叫做周期,f =1T叫做频率,ωx +φ叫做相位,φ叫做初相.3.函数y =A sin(ωx +φ) (A >0,ω>0)的性质如下: 4.图象的对称性函数y =A sin(ωx +φ)(A >0,ω>0)的图象是轴对称也是中心对称图形,具体如下:(1)函数y =A sin(ωx +φ)的图象关于直线x =x k (其中 ωx k +φ=k π+π2,k∈Z)成轴对称图形.(2)函数y =A sin(ωx +φ)的图象关于点(x k,0)(其中ωx k +φ=k π,k ∈Z)成中心对称图形. 二、图像的平移转换图像的平移转换遵循左加右减,上加下减原则 1.函数y =A sin(ωx +φ)图像变换(1)左右平移:由y =sinx 的图象向左或向右平行移动|φ|个单位,得到y =sin (x +φ)的图象.(2)胖瘦变换:由y =sinx 的图象上的点的纵坐标保持不变,横坐标伸长(0<|ω|<1)或缩短(|ω|>1)到原来的1||ω倍,得到y =sin ω x 的图象.(3)高矮变换:由y =sinx 的图象上的点的横坐标保持不变,纵坐标伸长(当|A|>1)或缩短(当0<|A|<1)到原来的|A|倍,得到y =Asinx 的图象.2.两种变换方法注意:左侧为先平移后伸缩,右侧为先伸缩后平移 三、正弦型函数y =Asin(ωx +φ)解析式的求法1.表达式的化简(主要利用辅助角公式)(1)辅助角公式sin cos a b αα+22)a b αϕ++(其中,辅助角ϕ所在象限由点(,)a b 所在的象限决定,2222sin tan ba ab a b ϕϕϕ===++ ,该法也叫合一变形).(2)所涉及到公式① 两角和与差的正弦、余弦公式: (1)βαβαβαsin cos cos sin )sin(+=+ (2)βαβαβαsin cos cos sin )sin(-=- (3)βαβαβαsin sin cos cos )cos(-=+ (4)βαβαβαsin sin cos cos )cos(+=-②二倍角公式(1)a a a cos sin 22sin =(2)1cos 2sin 21sin cos 2cos 2222-=-=-=a a a a a③降幂公式:(1)22cos 1cos 2a a += (2) 22cos 1sin 2aa -=注:表达式的化简攻略可化简的表达式多种多样,很难靠举例一一道明,化简往往能够观察并抓住式子的特点来进行操作,主要有以下几个特征:(1)观察式子:主要有三点①系统:整个表达式是以正余弦为主,如果有正切需要切化弦进行统一 ②确定研究对象:是以x 作为角来变换,还是以x 的表达式看做一个角来进行变换③式子是否齐次:式子要做到齐次统一,利用所涉及到三角函数恒等式的公式进行转换,把同一角转换为齐二次式或是齐一次式在使用辅助角公式,使结果成为y =A sin(ωx +φ)(2)向“同角齐次正余全”靠拢,能拆就拆,能降幂就降幂(注意平方降幂).2. 求解A 、ω、φ以及确定解析式 (1)A 的求解A 的求解:根据图象的最高点和最低点,即A =最高点-最低点2(2)ω的求解结合图象,先求出周期,然后由T =2πω(ω>0)来确定ω①如果y =Asin(ωx +φ)相邻的两条对称轴为x=a ,x=b (a<b ),则T=2(b-a).②如果y =Asin(ωx +φ)相邻的两个对称中心为(a ,0)、(b ,0)(a<b ),则T=2(b-a).③如果y =Asin(ωx +φ)相邻的对称轴与对称中心分别为x=a ,(b ,0)则T=4a -b .注意:在y =Asin(ωx +φ)中,对称轴与最值点等价,对称中心与零点等价.(3)φ的求解①代入法:把图上已知点代入即可. ②五点法确定φ值时,往往以寻找“五点法”中的特殊点作为突破口.具体如下:“第一点”(即图像上升时与x 轴交点)为ωx +φ=0;“第二点”(即图像的“峰点”)为ωx +φ=π2;“第三点”(即图像下降时与x 轴交点)为ωx +φ=π;“第四点”(即图像的“谷点”)为ωx +φ=3π2;“第五点”为ωx +φ=2π.(4)y =Asin(ωx +φ)+B 中“B ”的确定 B 的确定:根据图象的最高点和最低点,即B =最高点+最低点2补充:函数的最值(几种常见的函数及其最值的求法):①b x a y +=sin (或)cos b x a +型:利用三角函数的值域,须注意对字母的讨论②x b x a y cos sin +=型:引进辅助角化成)sin(22ϕ++=x b a y 再利用有界性③c x b x a y ++=sin sin 2型:配方后求二次函数的最值,应注意1sin ≤x 的约束④dx c bx a y ++=sin sin 型:反解出x sin ,化归为1sin ≤x 解决⑥c x x b x x a y +⋅++=cos sin )cos (sin 型:常用到换元法:x x t cos sin +=,但须注意t 的取值范围:2≤t 。
正弦函数和余弦函数的图像与性质

例2.求下列函数的最大值与最小值,及取到最值 时的自变量 x 的值. (2) y 3sin x cos x (1) y sin(2 x )
4 解:(1)视为 y sin u , u 2 x 4
8 3 当 u 2k ,即 x k , k Z 时, 2 8 ymin 1 2
二、正弦函数与余弦函数的周期
对于任意 x R 都有
sin( x 2k ) sin x, k Z cos( x 2k ) cos x, k Z
正弦函数是周期函数, k , k Z , k 0 都是它的 2
周期,最小正周期是 2 余弦函数是周期函数, k , k Z , k 0 都是它的 2 周期,最小正周期是 2
注:一般三角函数的周期都是指最小正周期
1 (1) f ( x) cos 2 x (2) f ( x) sin( x ) 2 6 解: (1)设 f ( x)的周期为 T f ( x T ) f ( x)
即 cos[2( x T )] cos 2 x 即 cos(2 x 2T ) cos 2 x 即 对任意 u 都成立:cos(u 2T ) cos u 因此 2T 2 ,从而 T 解毕
第六章 三角函数
5.6.4 正弦定理、余弦定理和解斜三角形
6.1.1 正弦函数和余弦函数的图像与性质
一、正弦函数和余弦函数的概念 实数集与角的集合可以建立一一对应的关系, 每一个确定的角都对应唯一的正弦(余弦)值. 因此,任意给定一个实数 x ,有唯一确定的值
sin x(cos x) 与之对应.
函数 y sin x 叫做正弦函数 函数 y cos x 叫做余弦函数 正弦函数和余弦函数的定义域是 R 正弦函数和余弦函数的值域是[1,1]
第4讲 正余弦函数图像及其性质(知识点串讲)解析版

第4讲 正余弦函数图像及其性质 (沪教版2020必修二)【知识网格】知识梳理一1、用五点法作正弦函数的简图(描点法):正弦函数x y sin =,]2,0[π∈x 的图象中,五个关键点是:)0,0( )1,2(π)0,(π )1,23(-π )0,2(π2、正弦函数R x x y ∈=,sin 的图像:把x y sin =,]2,0[π∈x 的图象,沿着x 轴向右和向左连续地平行移动,每次移动的距离为π2,就得到R x x y ∈=,sin 的图像,此曲线叫做正弦曲线。
由正弦函数图像可知:(1)定义域:R(2)值域:[]1,1- ; 正弦线的长度小于或等于单位圆的半径的长度,所以1|sin |≤x , 即1sin 1≤≤-x ,也就是说,正弦函数的值域是1,1[-亦可由正弦图像直接得出。
(3)奇偶性:奇函数由x x sin )sin(-=-可知:x y sin =为奇函数,正弦曲线关于原点O 对称 (4)单调递增区间:z k k k ∈⎥⎦⎤⎢⎣⎡+-,22,22ππππ; (5)单调递减区间:z k k k ∈⎥⎦⎤⎢⎣⎡++,232,22ππππ; (6)对称中心:(0,πk ); (7)对称轴:2ππ+=k x(8)最值:当且仅当,22ππ+=k x y 取最大值1max =y ;当且仅当,232ππ+=k x y 取最小值1min -=y 。
(9)最小正周期:π2=T一般地,对于函数)(x f ,如果存在一个非零常数T ,使得当x 取定义域内的每一个值时,都有)()(x f T x f =+,那么函数)(x f 就叫做周期函数,非零常数T 叫做这个函数的周期由此可知)0(2,,4,2,2,4,≠∈--k z k k 且πππππ 都是这两个函数的周期对于一个周期函数)(x f ,如果在它所有的周期中存在一个最小的正数,那么这个最小正数就叫做)(x f 的最小正周期根据上述定义,可知:正弦函数、余弦函数都是周期函数,)0(2≠∈k z k k 且π都是它的周期,最小正周期是π2 注意:1.周期函数定义域M x ∈,则必有M T x ∈+, 且若0>T ,则定义域无上界;0<T 则定义域无下界;2.“每一个值”只要有一个反例,则)(x f 就不为周期函数;3.T 往往是多值的(如x y sin =中 ,4,2,2,4,ππππ--都是周期)周期T 中最小的正数叫做)(x f 的最小正周期(有些周期函数没有最小正周期) 5、余弦函数R x x y ∈=,cos 的图像:(1)定义域:R (2)值域:[]1,1- (3)奇偶性:偶函数(4)单调递增区间:[]πππk k 2,2-,Z k ∈ (5)单调递减区间:[]Z k k k ∈+,2,2πππ (6)对称中心:(0,2ππ+k )(7)对称轴:πk x =(8)最值:当且仅当,2πk x =y 取最大值1max =y ; 当且仅当,2ππ+=k x y 取最小值1min -=y 。
正弦函数和余弦函数的图像与性质

3. 求最小正周期: (1) f ( x) 3sin x 4cos x (2) f ( x) sin 2 x (3) f ( x) sin 2 x cos 2 x
y cos x , x R 的值域是 [1,1],最大值是 1,最小值是 1.
当 cos x 1时,x 2k (k Z). 当 cos x 1 时,x (2k 1) (k Z).
(2)周期性
一般地,对于函数 f ( x),如果存在一个常数 T (T 0), 使得当 x 取定义域 D 内的任意值时,都有 f ( x T ) f ( x) 成立,那么函数 f ( x) 叫做周期函数,常数 T 叫做函数 f ( x) 的周期。对于一个周期函数 f ( x) 来说,如果在所有的周期中 存在一个最小正数,那么这个最小正数叫做函数 f ( x) 的 最小正周期。
解: 偶函数; (1)
(2) f ( x) cos 2 x,偶函数;
2 (k Z)
(3)sin x 1 x 2k
x
,但 x 可以取 ,即 f ( x)的定义域不关于原点对称, 2 2
f ( x) 是非奇非偶函数。
(4) f ( x)
1 sin 2 x sin x 1 1 sin 2 x sin x 1
5 3 增:k , k (k Z), 减:k , k (k Z) 8 8 8 8
(4) y log 1 2cos x 3
2
3 解: x cos x 2 k , 2 k 2 6 6
正弦函数余弦函数的图形 20页PPT文档

二、知识探究(一):正弦函数的图象
思考1:如何在直角坐标系中比较精确地 描出点,并画出y=sinx在[0,2π ]内的 图象?
如何用几何法作正弦函数在[0,2π]的图象 ? 途径:利用单位圆中正弦线来解决.
y
B
1
A
O1
O
-1
描图:用光滑曲线 将这些正弦线的终
点连结起来
3p
π
2
2π
p
2
4
5
2x323来自33y=sinx x[0,2]
思考2:在函数y=sinx,x∈[0,2π ]的 图象上,起关键作用的点有哪几个?
y
1
3p
π
2
2π
O
p
x
-1
2
( 0 ,0 ) ( , 1 ) ( , 0 ) ( - 3, 1 ) ( 2,0 )
y
1
-6π
-4π
-2π -π π O
-5π -3π
2
2
-1 1
y
22
3π 5π
2
4π
6π x
π
2
2
x
2
2
2
(四)、理论迁移
O
-1
2
2
2
例1 用“五点法”画出下列函数的简图:
(1)y=1+sinx,x∈[0,2π ];
(2)y=-cosx,x∈[0,2π ] .
1.4.1正弦函数、余弦函数的图象
正弦形函数图像

0 -1
π 6
π π 2π 4 2 3
π
7π 6
5 3
2π
π 7 4
9 4
x
π π 5π y sin(x ),x [ , ] 3 3 3
二、研究问题
问题一:画 y sin( x
4
4
) 和y sin( x
6
)的图像,并观察与 y sin x 的图像关系。
函数y sin2x , x R
1 函数y sin x , x R 2
π
x
2x
sin2x
0
π 4
π 2
3π 4
x
1 x 2
1 sin x 2
0
0
π
π 2
2π
π
3π
3π 2
4π
2π
0
π 2
π
3π 2
2π
0
1
0
-1
0
0
1
0
-1
0
y 1 0 -1
π 4
y sinx, [0,2π] x
横坐标 伸长或缩短1/w倍
步骤 2
得到 y sin(ω x ),x R
纵坐标 伸长或缩短A倍
步骤 3
得到 y Asin(ω x ),x R
1 π 练习: 画出函数y 4sin( x )在一个周期上的简图 3 4
x
1 π x 3 4
1 π 4sin( x ) 3 4
3π 4 0
9π 4 π 2
15 π 4 π
21π 4 3π 2
27 π 4 2π
0
正弦型函数的图像性质

相位是正弦波在时间轴上的偏移量,决定了波形开始的时间点。当 $varphi > 0$ 时,图像向右位移;当 $varphi < 0$ 时,图像向左位移。相位的变化不会 改变波形周期和振幅,但会影响波形在时间轴上的位置。
03 正弦型函数的奇偶性
奇函数性质
奇函数性质
正弦型函数是奇函数,因为对于任意x,都有f(-x) = -f(x)。这意 味着正弦型函数的图像关于原点对称。
对称轴
正弦函数图像关于y轴对称
正弦函数$y = sin x$的图像关于y轴对称,即当$x$取正值和负值时,$y$的值相 同。
余弦函数图像关于x轴对称
余弦函数$y = cos x$的图像关于x轴对称,即当$y$取正值和负值时,$x$的值相 同。
对称中心
要点一
正弦函数图像关于点$(kpi, 0)$对 称
通过调整A、ω、φ的值,可以获 得不同振幅、周期和相位偏移的 正弦型函数。
单位圆与三角函数关系
单位圆是指在平面直角坐标系中, 以原点为圆心、半径为1的圆。
三角函数与单位圆密切相关,单 位圆上的点可以用三角函数来表
示。
在单位圆上,正弦和余弦函数的 值等于点的纵坐标和横坐标的比 值,正切函数的值等于点的纵坐
图像特点
偶函数的图像关于y轴对称,即当 x=0时,y达到最大或最小值。在 x>0和x<0的区间内,函数值相等。
应用实例
偶函数性质在电磁学中有广泛应用, 例如磁场分布等。
既非奇又非偶函数性质
既非奇又非偶函数
性质
正弦型函数既不是奇函数也不是 偶函数。虽然它的图像关于原点 和y轴都有对称性,但它不符合奇 偶函数的严格定义。
振幅与图像高度
三角函数图形的变换
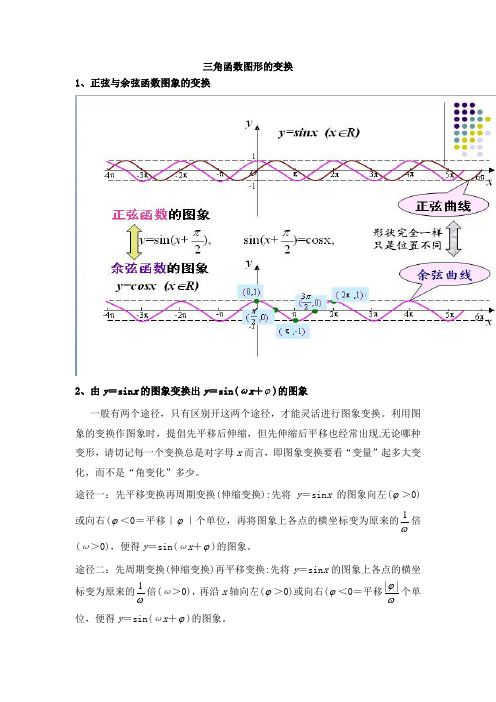
三角函数图形的变换1、正弦与余弦函数图象的变换2、由y =sin x 的图象变换出y =sin(ωx +ϕ)的图象一般有两个途径,只有区别开这两个途径,才能灵活进行图象变换。
利用图象的变换作图象时,提倡先平移后伸缩,但先伸缩后平移也经常出现无论哪种变形,请切记每一个变换总是对字母x 而言,即图象变换要看“变量”起多大变化,而不是“角变化”多少。
途径一:先平移变换再周期变换(伸缩变换):先将y =sin x 的图象向左(ϕ>0)或向右(ϕ<0=平移|ϕ|个单位,再将图象上各点的横坐标变为原来的ω1倍(ω>0),便得y =sin(ωx +ϕ)的图象。
途径二:先周期变换(伸缩变换)再平移变换:先将y =sin x 的图象上各点的横坐标变为原来的ω1倍(ω>0),再沿x 轴向左(ϕ>0)或向右(ϕ<0=平移ωϕ||个单位,便得y =sin(ωx +ϕ)的图象。
作y =sin x (长度为2π的某闭区间)的图象 得y =sin(x +φ) 的图象得y =sin ωx 的图象 得y =sin(ωx +φ) 的图象 得y =sin(ωx +φ) 的图象 得y =Asin(ωx +φ)的图象,先在一个周期闭区间上再扩充到R 上沿x 轴平 移|φ|个单位 横坐标 伸长或缩短 横坐标伸 长或缩短沿x 轴平 移|ωϕ|个单位 纵坐标伸 长或缩短纵坐标伸 长或缩短【经典例题】图像变换一:左右平移1、把函数R x x y ∈=,sin 图像上所有的点向左平移4π个单位,所得函数的解析式为 _________2、把函数R x x y ∈=,cos 图像上所有的点向右平移5π个单位,所得函数的解析式为 _________图像变换二:纵向伸缩3、对于函数R x x y ∈=,s i n 3的图像是将R x x y ∈=,sin 的图像上所有点的______(“横”或”纵”)坐标______(伸长或缩短)为原来的______而得到的图像。
数学人教A版必修第一册5.4.1正弦函数、余弦函数的图象课件

, ∈ [,]的图象.
知识梳理
探究二:根据函数 = , ∈ [,]的图象,你能想象函数 = , ∈
的图象吗?
由诱导公式一可知,函数 = , ∈ [, ( + )], ∈ 且 ≠ 的图象
−
− −
−
− −
− −
知识梳理
探究三:在确定正弦函数的图象形状时,应抓住哪些关键点?
【提示】
视察图,在函数 = , x∈[0,2π]的图象上,
以下五个点: 0,0 ,
,1
2
, ,0 ,
3
,1
2
, 2,0
= , ∈ 的图
象向左平移 个单位长度而得到.所以,将正弦函数的图象向左平移 个单位长度,
就得到余弦函数的图象,如图所示:
知识梳理
− −
−
−
−
− −
−
余弦函数 = , ∈ 的图象叫做余弦曲线.它是与正弦曲线具有相同形状
若把轴上从0到2这一段分成12等份,使
的值分别为0, , , , … ,2,
它们所对应的角的终边与单位圆的交点将圆周12等分,再按上述画点( , )
正弦型函数y=Asin(ωx+φ)的图像

A.-sin x B.sin x C.-cos x D.cos x
解析 由图象的平移得 g(x)=cosx+2π=-sin x.
答案 A
4.设 ω>0,函数 y=sinωx+π3+2 的图象向右平移43π个单位后与原图象重合,则 ω 的最小值是( ).
2 A.3
4 B.3
3 C.2
D.3
解析 y=sinωx+π3+2 向右平移43π个单位后得到 y1=sinωx-43π+π3+2=sinωx+π3-43πω+2,又 y 与 y1 的图象
;
6
*10.函数 y=sin2x 的图象向右平移 φ(φ>0)个单位,得到的图象恰好关于直线 x= 对称,则 φ 的最小值是
.
6
三. 解答题
11.写出函数 y=4sin2x (x∈R)的图像可以由函数 y=cosx 通过怎样的变换而得到.(至少写出两个顺序不同的变换)
12.已知函数 log0.5(2sinx-1), (1)写出它的值域. (2)写出函数的单调区间. (3)判断它是否为周期函数?如果它是一个周期函数,写出它的最小正周期.
(k∈Z)
π 3π C. [kπ-8 , kπ+ 8 ]
(k∈Z)
D.
3π 7π [kπ+ 8 , kπ+ 8 ]
(k∈Z)
3.函数
3π y=sin(x+ 2
)的图象是(
A. 关于 x 轴对称
C. 关于原点对称
)
B. 关于 y 轴对称
D.
关于
3 x=-2
π 对称
4.函数 f(x)=cos(3x+φ)的图像关于原点中心对称的充要条件是( )
故43π+φ=2kπ-π2,k∈Z,所以 φ=2kπ-116π(k∈Z).
正弦型函数的图象及应用经典教案【强烈推荐】

第4讲 正弦型函数y =A sin(ωx +ϕ)+B 的图象及应用【考试会这样考】1.考查正弦型函数y =A sin(ωx +ϕ)的图象变换.2.结合三角恒等变换考查y =A sin(ωx +ϕ)的性质及简单应用. 3.考查y =sin x 到y =A sin(ωx +ϕ)的图象的两种变换途径.【复习指导】本讲复习时,重点掌握正弦型函数y =A sin(ωx +ϕ)的图象的“五点”作图法,图象的三种变换方法,以及利用三角函数的性质解决有关问题.基础梳理1.用五点法画y =A sin(ωx +ϕ)一个周期内的简图时,要找五个特征点 如下表所示x ωϕ-0ωϕπ-2ωϕπ- ωϕπ-23ωϕπ-2ωx +ϕ 0 π2π 3π2 2π y =A sin(ωx +ϕ)A-A2.函数y =sin x 的图象变换得到y =A sin(ωx +ϕ)的图象的步骤3.当函数y =A sin(ωx +ϕ)(A >0,ω>0,x ∈[0,+∞))表示一个振动时,A 叫做振幅,T =2πω叫做周期,f =1T叫做频率,ωx +ϕ叫做相位,ϕ叫做初相.4.图象的对称性函数y =A sin(ωx +ϕ)(A >0,ω>0)的图象是轴对称也是中心对称图形,具体如下:(1)函数y =A sin(ωx +ϕ)的图象关于直线x =x k (其中 ωx k +ϕ=k π+π2,k ∈Z )成轴对称图形.(2)函数y =A sin(ωx +ϕ)的图象关于点(x k,0)(其中ωx k +ϕ=k π,k ∈Z )成中心对称图形.一种方法在由图象求三角函数解析式y =A sin(ωx +ϕ) + B 时,若最大值为M ,最小值为m ,则A =M -m 2,B =M +m 2,ω由周期T 确定,即由2πω=T 求出,ϕ由特殊点确定.一个区别 由y =sin x 的图象变换到y =A sin (ωx +ϕ)的图象,两种变换的区别:先相位变换再周期变换(伸缩变换),平移的量是|φ|个单位;而先周期变换(伸缩变换)再相位变换,平移的量是|φ|ω(ω>0)个单位.原因在于相位变换和周期变换都是针对x 而言,即x 本身加减多少值,而不是依赖于ωx 加减多少值.双基自测1.y =2sin ⎝⎛⎭⎪⎫2x -π4 的振幅、频率和初相分别为( ). A .2,1π,-π4 B .2,12π,-π4 C .2,1π,-π8 D .2,12π,-π8答案 A2.已知简谐运动f (x )=A sin(ωx +φ)⎝⎛⎭⎪⎫|φ|<π2的部分图象如图所示,则该简谐运动的最小正周期T 和初相φ分别为( ).A .T =6π,φ=π6B .T =6π,φ=π3C .T =6,φ=π6D .T =6,φ=π3答案 C 解析 由题图象知T =2(4-1)=6⇒ω=π3,由图象过点(1,2)且A =2,可得sin ⎝ ⎛⎭⎪⎫π3×1+φ=1,又|φ|<π2,得φ=π6.3.函数y =cos x (x ∈R )的图象向左平移π2个单位后,得到函数y =g (x )的图象,则g (x )的解析式应为( ).A .-sin xB .sin xC .-cos xD .cos x答案 A 解析 由图象的平移得g (x )=cos ⎝⎛⎭⎪⎫x +π2=-sin x .4.已知函数f (x )=sin(ωx +φ)(ω>0)的图象如图所示,则ω=________.解析 由题意设函数周期为T ,则T 4=23π-π3=π3,故T =43π.∴ω=2πT =32.5.把函数y =cos 2x +1的图像上所有点的横坐标伸长到原来的2倍(纵坐标不变),然后向左平移1个单位长度,再向下平移1个单位长度,得到的图像是 ( )答案 A解析 y =cos 2x +1――→横坐标伸长2倍纵坐标不变y =cos x +1――→向左平移1个单位长度y =cos(x +1)+1――→向下平移1个单位长度y =cos(x +1). 结合选项可知应选A.考向一 作函数y =A sin(ωx +φ)的图象【例1】►设函数f (x )=cos(ωx +ϕ)⎝ ⎛⎭⎪⎫ω>0,-π2<φ<0的最小正周期为π,且f ⎝ ⎛⎭⎪⎫π4=32. (1)求ω和ϕ的值;(2)在给定坐标系中作出函数f (x )在[0,π]上的图象.解 (1)周期T =2πω=π,∴ω=2,∵f ⎝⎛⎭⎫π4=cos ⎝⎛⎭⎫2×π4+φ=cos ⎝⎛⎭⎫π2+φ=-sin φ=32, ∵-π2<φ<0,∴φ=-π3.(2)由(1)知f (x )=cos ⎝⎛⎭⎫2x -π3,列表如下:2x -π3 -π3 0 π2 π 32π 53πx 0 π6 512π 23π 1112π πf (x ) 12 1 0 -1 0 12图象如图:【训练1】 已知函数f (x )=3sin ⎝ ⎛⎭⎪⎫12x -π4,x ∈R .(1)画出函数f (x )在长度为一个周期的闭区间上的简图;(2)将函数y =sin x 的图象作怎样的变换可得到f (x )的图象?解 (1)列表取值:xπ232π 52π 72π 92π 12x -π4 0 π2π 32π 2π f (x ) 0 3 0-3(2)先把y =sin x 的图象向右平移π4个单位,然后把所有的点的横坐标扩大为原来的2倍,再把所有点的纵坐标扩大为原来的3倍,得到f (x )的图象. 考向二 求函数y =A sin(ωx +ϕ)+B 的解析式【例2】►已知函数f (x )=A sin(ωx +ϕ)+B (A >0,ω>0)的图象如图所示,则f (x )的解析式为_______.答案:.()2sin 363f x x ππ⎛⎫=++ ⎪⎝⎭【训练2】 (1)若函数f (x )=A sin(ωx +ϕ)(A >0,|ϕ|<π2,ω>0)的图象的一部分如图所示.则f (x )的解析式为_______.(2)已知f (x )=2sin (ωx+φ)的部分图象如图所示,则f (x )的表达式为 A . B .C .D .解 (1) f (x )=2sin ⎝⎛⎭⎫2x +π6. (2)答案:.B考向三 函数y =A sin(ωx +ϕ)的图象与性质的综合应用【例3】►已知函数的 部分图象如图所示:(1)求f (x )的解析式;(2)求f (x )的单调区间和对称中心坐标; (3)将f (x )的图象向左平移个单位,在将横坐标伸长到原来的2倍,纵坐标不变,最后将图象向上平移1个单位,得到函数g (x )的图象,求函数y=g (x )在上的最大值和最小值.【解答】解:(1)由图象可知,又由于, 所以,由图象及五点法作图可知:, 所以,所以.(2)由(1)知,, 令,得,所以f (x )的单调递增区间为,令,得,所以f (x )的对称中心的坐标为. (3)由已知的图象变换过程可得:, 因为, 所以,所以当,得时,g (x )取得最小值,当时,即x=0g (x )取得最小值.【训练3】 已知函数y =A sin(ωx +ϕ)(A >0,ω>0)的图象过点P ⎝ ⎛⎭⎪⎫π12,0,图象上与点P 最近的一个最高点是Q ⎝ ⎛⎭⎪⎫π3,5.(1)求函数的解析式;(2)求函数f (x )的递增区间.解 (1)依题意得:A =5,周期T =4⎝⎛⎭⎫π3-π12=π,∴ω=2ππ=2.故y =5sin(2x +φ),又图象过点P ⎝⎛⎭⎫π12,0, ∴5sin ⎝⎛⎭⎫π6+φ=0, 由已知可得π6+φ=0,∴φ=-π6 ∴y =5sin ⎝⎛⎭⎫2x -π6.(2)由-π2+2k π≤2x -π6≤π2+2k π,k ∈Z , 得:-π6+k π≤x ≤π3+k π,k ∈Z ,故函数f (x )的递增区间为:⎣⎡⎦⎤k π-π6,k π+π3(k ∈Z ).A 组 专项基础训练一、选择题1.将函数()πsin 23f x x ⎛⎫=+⎪⎝⎭的图象向左平移π6个单位,所得的图象对应的函数解析式是 A. sin2y x = B. cos2y x = C. 2πsin 23y x ⎛⎫=+ ⎪⎝⎭ D. πsin 26y x ⎛⎫=- ⎪⎝⎭ 【答案】C2、将函数cos 3y x π⎛⎫=-⎪⎝⎭的图象向左平移6π个单位,再各点横坐标伸长到原来的2倍(纵坐标不变),所得函数解析式是( )A. )621cos(π-=x y B. )1221cos(π-=x y C. )62cos(π-=x y D. )32cos(π-=x y 【答案】A3、若函数()sin 23f x x π⎛⎫=+⎪⎝⎭图象的横坐标伸长到原来的2倍, 纵坐标不变,再向左平移6π得到函数()g x 的图象,则有( )A. ()cos g x x =B. ()sin g x x =C. ()cos 3g x x π⎛⎫=+⎪⎝⎭D. ()sin 3g x x π⎛⎫=+⎪⎝⎭【答案】A 【解析】26sin 2sin sin cos 332y x y x y x x ππππ⎛⎫⎛⎫⎛⎫=+→=+→=+= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭左移横坐标变为倍.4、为了得到函数1y 3sin 25x π⎛⎫=-⎪⎝⎭的图象,只要把13sin 2y x =上所有点( )A. 向右平移5π个单位长度 B. 向左平移5π个单位长度 C. 向右平移25π个单位长度 D. 向左平移25π个单位长度【答案】C5、若函数f (x )=2sin(ωx +φ),x ∈R (其中ω>0,|φ|<π2)的最小正周期是π,且f (0)=3,则( )A .ω=12,φ=π6B .ω=12,φ=π3C .ω=2,φ=π6D .ω=2,φ=π3答案 D 解析 ∵T =π,∴ω=2.又2sin φ=3,|φ|<π2,∴φ=π3.6、函数()sin()02f x A wx A ϕϕ=+π其中>,<)的图像如图所示,为得到x x g 3sin )(=的图像,则只要将)(x f 的图象( )A .向右平移4π个单位B .向右平移12π个单位C .向左平移4π个单位D .向左平移12π个单位 答案 B7、将函数y =sin(x +φ)的图像F 向左平移π6个单位长度后得到图像F ′,若F ′的一个对称中心为⎝⎛⎭⎫π4,0,则φ的一个可能取值是 ( ) A.π12 B.π6 C.5π6 D.7π12答案 D 解析 图像F ′对应的函数y ′=sin ⎝⎛⎭⎫x +π6+φ, 则π4+π6+φ=k π,k ∈Z ,即φ=k π-5π12,k ∈Z ,令k =1时,φ=7π12,故选D. 8、将函数y =sin x 的图像向左平移φ (0≤φ<2π)个单位后,得到函数y =sin ⎝⎛⎭⎫x -π6的图像,则φ等于( ) A.π6B.5π6C.7π6D.11π6答案 D 解析 将函数y =sin x 向左平移φ(0≤φ<2π)个单位得到函数y =sin(x +φ).只有φ=116π时有y =sin ⎝⎛⎭⎫x +116π=sin ⎝⎛⎭⎫x -π6. 二、填空题(每小题5分) 1、将函数()3sin 46f x x π⎛⎫=+⎪⎝⎭图象上所有点的横坐标伸长到原来的2倍,再向右平移6π个单位长度,得到函数g(x)的图象,则g(x)的解析式为 。
正弦、余弦函数的图像与性质

正弦与余弦函数的图像与性质(内部使用)姓名: 日期:¤ 梳理知识★透视规律 ¤一、函数的周期性1、定义: 。
二、正弦与余弦函数的图像1、正弦函数的图像由单位圆中的正弦线的变化,推出sin y x =的图像:单位圆在[]0,2π上的图像推广到R 上的图像2、正弦函数的图像由单位圆中的余弦线的变化,推出cos y x =的图像:单位圆在[]0,2π上的图像推广到R 上的图像3、五点作图法:(1)概念: 。
(2) 步骤: → → 。
三、正弦与余弦函数的性质函数y sin x =y cos x =图像定义域 值域 周期性 奇偶性(对称性)单调性注:(1) ;(2) 。
¤ 拓展★提高 ¤一、正弦型函数sin y A x M =+()0A M ⋅≠的性质:(1)A 的作用:对最值的影响: ;正负对单调区间的影响: 。
(2)M 的作用:。
¤ 他山之石★可以攻玉 ¤【例1】用“五点法”画出下列函数的图像:(1)[]2sin ,0,2y x x π=-+∈;(2)[]2cos ,0,2y x x π=+∈。
【变式】用“五点法”画函数[]12sin ,0,2y x x π=-∈的图像。
我来记两笔:【例1】解下列不等式:(1)1sin 2x >; (2)3cos 2x ≤-。
【变式1】求函数2sin 1y x =+的定义域。
【变式2】求函数1lg 1cos y x=-的定义域。
题型一 “五点法”作图 题型二 利用正、余线函数图像解简单三角不等式我来记两笔:【例1】求下列函数的值域:(1)y sin sin x x =+; (2)cos 2y cos 1x x -=+。
【变式】求下列函数的值域:(1)y 2sin 2,,366x x πππ⎛⎫⎡⎤=+∈- ⎪⎢⎥⎝⎭⎣⎦;(2)[]2cos sin 2,0,y x x x π=++∈。
我来记两笔:【例1】判断下列函数的奇偶性:(1)()()sin f x x x π=+; (2)()3cos 12f x x x x π⎛⎫=-+ ⎪⎝⎭。
正弦型函数图像及性质(学生用)

北师大版高一数学三角函数 函数)sin(ϕϖ+=x A y 的图像知识点梳理1.,,A ωϕ的物理意义当sin()y A x ωϕ=+,[0,)x ∈+∞(其中0A >,0ω>)表示一个振动量时,A 表示这个量振动时离开平衡位置的最大距离,通常称为这个振动的振幅,往复振动一次需要的时间2T πω=称为这个振动的周期,单位时间内往复振动的次数。
x ωϕ+称为相位,0x =时的相位ϕ称为初相。
2.图象的变换例 : 画出函数3sin(2)3y x π=+的简图。
解:函数的周期为22T ππ==,先画出它在长度为一个周期内的闭区间上的简图,再左右拓展即可,先用五点法画图:x6π-12π 3π 712π 56π 23x π+0 2ππ 32π 2π3sin(2)3x π+3 03- 0函数3sin(2)3y x π=+的图象可看作由下面的方法得到的:①sin y x =图象上所有点向左平移3π个单位,得到sin()3y x π=+的图象上;②再把图象上所点的横坐标缩短到原来的12,得到sin(2)3y x π=+的图象;③再把图象上所有点的纵坐标伸长到原来的3倍,得到3sin(2)3y x π=+的图象。
一般地,函数sin()y A x ωϕ=+,x R ∈的图象(其中0A >,0ω>)的图象,可看作由下面的方法得到:①把正弦曲线上所有点向左(当0ϕ>时)或向右(当0ϕ<时)平行移动||ϕ个单位长度;②再把所得各点横坐标缩短(当1ω>时)或伸长(当01ω<<时)到原来的1ω倍(纵坐标不变); ③再把所得各点的纵坐标伸长(当1A >时)或缩短(当01A <<时)到原来的A 倍(横坐标不变)。
即先作相位变换,再作周期变换,再作振幅变换。
问题:以上步骤能否变换次序?∵3sin(2)3sin 2()36y x x ππ=+=+,所以,函数3sin(2)3y x π=+的图象还可看作由下面的方法得到的:①sin y x =图象上所点的横坐标缩短到原来的12,得到函数sin 2y x =的图象;②再把函数sin 2y x =图象上所有点向左平移6π个单位,得到函数sin 2()6y x π=+的图象;③再把函数sin 2()6y x π=+的图象上所有点的纵坐标伸长到原来的3倍,得到3sin 2()6y x π=+的图象。
正弦函数 的图象图像变换

函数)sin(ϕω+=x A y 的图象学案一、学习目标1.会用 “五点法”作出函数)(ϕ+=wx Asm y 以及函数)cos(ϕ+=wx A y 的图象的图象.2.能说出A W 、、ϕ对函数)sinϕ+=wx A y (的图象的影响. 3.能够将x y sin =的图象变换到)sin(ϕ+=wx A y 的图象,并会根据条件求解析式. 二、学习重点:由正弦曲线变换得到函数)sin(ϕω+=x A y 的图象.三、学习任务1、复习巩固:作出函数x y sin =在一个周期内的简图并回顾作图方法.2、阅读教材第49页至53页探究下列问题:问题一、阅读课本第53页例1,思考如何确定五个关键点?问题二:利用例1的五点作图法,在同一坐标系下,作出函数)3sin(π+=x y 和)6sin(π-=x y 的简图,观察它们与y x =sin 图象之间有什么关系呢?参数ϕ对sin()y x ϕ=+,x R ∈的图像有怎样的影响呢?概括由正弦曲线如何变换得到sin()y x ϕ=+,x R ∈的图像.练习1.完成课本第57页习题1-(1).问题二、利用五点作图法,在同一坐标系下,作函数y x =sin2及y x=sin12的简图,观察它们与y x =sin 图象间有什么关系呢?参数)0(>ωω对x y ωsin =的图像有什么影响呢?概括由正弦曲线如何变换得到sin y x ω=,x R ∈的图像.练习2.完成课本第57页习题1-(2).问题三、在同一坐标系中作出y x =2sin 及y x =12sin 的简图,并观察它们的图象与y x =sin 的图像有什么关系?参数)0(>A A 对x A y sin =的图像有什么影响呢?概括由正弦曲线如何变换得到sin y A x =,x R ∈的图像.练习3. 完成课本第57页习题1-(3).问题四、利用五点作图法,作出函数)32sin(3π+=x y的图象,并说出它是由函数sin y x =的图象经过怎样的变换得到的?问题五、请归纳:得到函数y A x =+sin()ωϕ的图象主要有哪些方法?写出详细过程。
正弦、余弦、正切函数的图象与性质
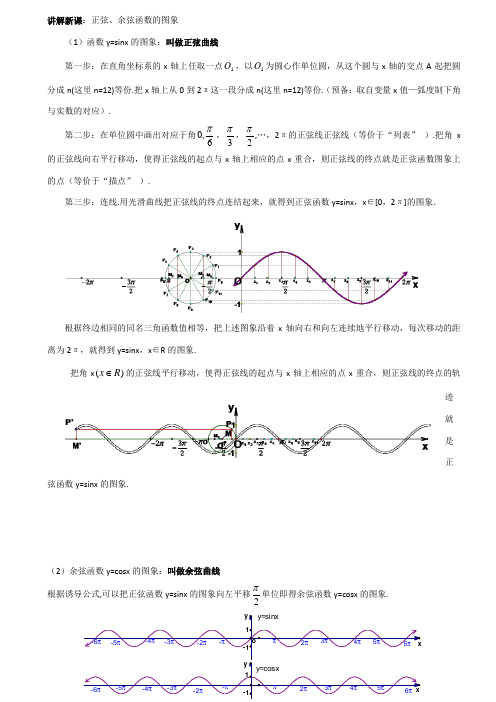
讲解新课:正弦、余弦函数的图象(1)函数y=sinx 的图象:叫做正弦曲线第一步:在直角坐标系的x 轴上任取一点1O ,以1O 为圆心作单位圆,从这个圆与x 轴的交点A 起把圆分成n(这里n=12)等份.把x 轴上从0到2π这一段分成n(这里n=12)等份.(预备:取自变量x 值—弧度制下角与实数的对应).第二步:在单位圆中画出对应于角6,0π,3π,2π,…,2π的正弦线正弦线(等价于“列表” ).把角x 的正弦线向右平行移动,使得正弦线的起点与x 轴上相应的点x 重合,则正弦线的终点就是正弦函数图象上的点(等价于“描点” ).第三步:连线.用光滑曲线把正弦线的终点连结起来,就得到正弦函数y=sinx ,x ∈[0,2π]的图象.根据终边相同的同名三角函数值相等,把上述图象沿着x 轴向右和向左连续地平行移动,每次移动的距离为2π,就得到y=sinx ,x ∈R 的图象.把角x ()x R ∈的正弦线平行移动,使得正弦线的起点与x 轴上相应的点x 重合,则正弦线的终点的轨迹就是正弦函数y=sinx 的图象.(2)余弦函数y=cosx 的图象:叫做余弦曲线 根据诱导公式,可以把正弦函数y=sinx 的图象向左平移2π单位即得余弦函数y=cosx 的图象.y=cosxy=sinxπ2π3π4π5π6π-π-2π-3π-4π-5π-6π-6π-5π-4π-3π-2π-π6π5π4π3π2ππ-11y x-11o xy(3)用五点法作正弦函数和余弦函数的简图(描点法):正弦函数y=sinx ,x ∈[0,2π]的图象中,五个关键点是:(0,0) (2π,1) (,0) (23π,-1) (2,0) 余弦函数y=cosx x [0,2]的五个点关键是哪几个(0,1) (2π,0) (,-1) (23π,0) (2,1)讲解范例:例1 作下列函数的简图(1)y=1+sinx ,x ∈[0,2π], (2)y=-COSx探究 如何利用y=sinx ,x∈〔0,2π〕的图象,通过图形变换(平移、翻转等)来得到 (1)y =1+sinx ,x∈〔0,2π〕的图象; (2)y=sin(x- π/3)的图象小结:函数值加减,图像上下移动;自变量加减,图像左右移动。
正弦函数、余弦函数的图象

y=-cosx, x∈[0,2π]
3p 2
2π x
p 2
π
y=cosx, x∈[0,2π]
思考:你能否从函数图象变换的角度 出发,利用函数 y=sinx, x∈[0,2π] 的 图象得到y=1+sinx, x∈[0,2π] 的图象?
2 y
1 o -1
π 2
y 1 sinx, [0,2π] x
正弦函数的图象 向左平移 个单位
y
1
2
余弦函数的图象
2
-4
-3
-2
-
o
-1
2
3
4
5
6
x
形状完全一样 探究:根据哪个诱导公式可将正弦转化为余弦? 只是位置不同 余弦曲线 正弦曲线 以正弦函数的图象为基础,通过的怎样的图形变
换可以得到余弦函数的图象呢? 观察正弦曲线、余弦曲线的形状和位置, (独立思考、讨论、代表发言) 说出它们的异同点.
探究新知(二):余弦函数的图象
y
1
-4 -3 -2 -
o
-1
2
3
4
5
6
x
探究: 类似于正弦函数图像的五个关键点,你能
找出余弦函数的五个关键点吗?请将它们的坐标填 入下表,然后作出y=cosx,x∈[0,2π ]的简图?
x cosx
(独立完成)
余弦函数的“五点画图法”
x cosx
O1
.
M
π 3
π
x
探究新知(一):正弦函数的图象
1、利用正弦线作函数 y sin x, x 0,2 图象
y 1
y=sinx,x∈[0,2π ]
正弦函数图像的变换

小结: (1)三角函y=Asin(ѡx+φ ) 的五点作图法. (3)注意变换的语言叙述.
正弦函数图像的变换
方法二:先伸缩后平移 对 y=Asin(ѡx+φ )图像可以看作由 y=sinx图像上所有点的横坐标缩短(当 ѡ>1时)或伸长(当0< ѡ <1时)到原来的 1/ ѡ倍(纵坐标不变),再向左(当 φ >0时)或向右(当φ <0时)平移φ /ѡ个 单位,再把所得个点的纵坐标伸长(当 A>1时)或缩短(当0 <A < 1时)到原来 的A倍(横坐标不变).
正弦函数图像的变换
正弦函数图像变换
1 两种变换方法
2例
3小
题
结
正弦函数图像的变换
方法一:先平移后伸缩 对 y=Asin(ѡx+φ )图像可以看作由 y=sinx图像上所有点先向左(当 φ >0时) 或向右(当φ <0时)平移φ 个单位,再把 所得个点的横坐标缩短(当ѡ>1时)或伸 长(当0< ѡ <1时)到原来的1/ ѡ倍(纵 坐标不变),再把所得个点的纵坐标伸 长(当A>1时)或缩短(当0 <A < 1时) 到原来的A倍(横坐标不变).
正弦函数及其图像变换

周期变换
周期缩短:正弦函数的图像 在周期内进行平移,使得图 像的周期缩短。
周期延长:正弦函数的图像 在周期内进行平移,使得图 像的周期延长。
周期变换规律:正弦函数的 图像变换遵循一定的规律,
即周期变换规律。
周期变换的应用:周期变换 在信号处理、振动分析等领
域有着广泛的应用。
相位变换
相位变换的概念:通过改变正弦函数的相位,使其在时间上移动。
信号处理:正弦函数在信号处理领 域中用于滤波、调制和解调等操作, 提高信号质量和通信效率。
添加标题
添加标题
添加标题
添加标题
交流电:正弦函数用于描述交流电 的电压和电流,广泛应用于电力传 输和分配。
物理实验:在物理实验中,正弦函 数常用于测量、分析和建模各种物 理现象,如光干涉、衍射等。
在工程学中的应用
正添加弦副函标数题 及其图像 变换
汇报人:XX
目录
PART One
正弦函数的性质
PART Two
正弦函数的图像 变换
PART Three
正弦函数的应用
PART Four
正弦函数的扩展弦函数是三角函数的一种,定义为y=sinx,其中x是角度,y是正弦值。
正弦函数的周期为360度,即每隔360度重复一次。
正弦函数的图像是一个周期性变化的波形,最高点为1,最低点为-1。 正弦函数的表达式可以表示为y=Asin(ωx+φ),其中A是振幅,ω是角频 率,φ是初相。
周期性和振幅
正弦函数的周期性:正弦函数在一定周期内呈现规律性的变化,其周期为2π。 正弦函数的振幅:振幅是正弦函数图像在垂直方向上的最大或最小值,表示函数值的波动幅度。
三角函数的积化和差公式
三角函数(正弦函数与余弦函数)图像的变换及三角函数解析式的求法

1、(安徽卷文8)函数sin(2)3y x π=+图像的对称轴方程可能是( )A .6x π=-B .12x π=-C .6x π=D .12x π=2、(广东卷文5)已知函数2()(1cos 2)sin ,f x x x x R =+∈,则()f x 是( ) A 、最小正周期为π的奇函数 B 、最小正周期为2π的奇函数 C 、最小正周期为π的偶函数 D 、最小正周期为2π的偶函数 3、(全国Ⅰ卷文6)2(sin cos )1y x x =--是( ) A .最小正周期为2π的偶函数B .最小正周期为2π的奇函数C .最小正周期为π的偶函数D .最小正周期为π的奇函数4、(湖南卷理6)函数2()sin cos f x x x x =+在区间,42ππ⎡⎤⎢⎥⎣⎦上的最大值是( )A.1C. 325、(天津卷文6)把函数sin ()y x x =∈R 的图象上所有的点向左平行移动3π个单位长度,再把所得图象上所有点的横坐标缩短到原来的12倍(纵坐标不变),得到的图象所表示的函数是( )A .sin 23y x x π⎛⎫=-∈ ⎪⎝⎭R ,B .sin 26x y x π⎛⎫=+∈ ⎪⎝⎭R ,C .sin 23y x x π⎛⎫=+∈ ⎪⎝⎭R ,D .sin 23y x x 2π⎛⎫=+∈ ⎪⎝⎭R ,6、(全国Ⅰ卷文9)为得到函数πcos 3y x ⎛⎫=+ ⎪⎝⎭的图象,只需将函数sin y x =的图像( )A .向左平移π6个长度单位B .向右平移π6个长度单位 C .向左平移5π6个长度单位D .向右平移5π6个长度单位7、(全国Ⅰ卷理8)为得到函数πcos 23y x ⎛⎫=+ ⎪⎝⎭的图像,只需将函数sin 2y x =的图像( )A .向左平移5π12个长度单位 B .向右平移5π12个长度单位 C .向左平移5π6个长度单位D .向右平移5π6个长度单位1.(安徽卷文8)函数sin(2)3y x π=+图像的对称轴方程可能是( )A .6x π=-B .12x π=-C .6x π=D .12x π=解:sin(2)3y x π=+的对称轴方程为232x k πππ+=+,即212k x ππ=+,0,12k x π==2.(广东卷文5)已知函数2()(1cos 2)sin ,f x x x x R =+∈,则()f x 是( ) A 、最小正周期为π的奇函数 B 、最小正周期为2π的奇函数 C 、最小正周期为π的偶函数 D 、最小正周期为2π的偶函数 【解析】222211cos 4()(1cos 2)sin 2cos sin sin 224xf x x x x x x -=+===,选D.9.(全国Ⅰ卷文6)2(sin cos )1y x x =--是( ) A .最小正周期为2π的偶函数B .最小正周期为2π的奇函数C .最小正周期为π的偶函数D .最小正周期为π的奇函数sinx cosx,2sinxcosx 2y=1sin 2x 1=sin 2x T D2ππ±解析:本题主要考查了三角函数的化简,主要应用了与的关系,同时还考查了二倍角公式和函数的奇偶性和利用公式法求周期。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(3)横坐标不变 纵坐标伸长到原来的3倍
y=3Sin(2x+ )的图象
32020/10/21
三 课堂练习 49页 A组2题 四 课堂总结
在通过变换得到正弦型函数图象时,变换顺序 可改变,需注意平移量。
五 作业 50页 B组2题
方法2: 12020/10/21
y
3
2 1
o
-1
-2
-3
y=3sin(2x+ )
注意:平移量
y=sinx
y=sin2x y=sin(2x+ )
2
x
22020/10/21
函数 y=Sin(x 1)横坐标缩短到原来的 倍 y=Sin2x的图象 纵坐标不变
(2)向左平移
y=Sin(2x+ ) 的图象
例2、 函数
、
与
的图象关系
y
1
o
x
-1
72020/10/21
例3 函数
、
与
的图象间的变化关系。
y
2
1
o
-1
82020/10/21
例4、如何得 ?
方案一:五点法 方案二:图象变换 问题:三种变换能否任意排序?
的图象
方法1: 92020/10/21
y
3 2 1
o
-1
-2 -3
y=3sin(2x+ )
一、复习回顾 的图象
关键点: (0,0), ( ,1), (,0), (
,-1), (2,0) .
y
1.
.
o
/2
. 3/2 2.
-1
.
42020/10/21
二、讲授新课
52020/10/21
例1函数
、
与
的图象间的变化关系。
y
3
2
y=2sinx
y=sinx
1
y= sinx
o
x
-1
-2
62020/10/21
正弦型函数的图形变换
22020/10/21
§ 1.3.1正弦型函数
的图象
教学目标:1.了解振幅、周期、频率、初相的定义
2.掌握振幅、周期、相位变换的规律 3.能够由三种变换得到正弦型函数的图象
教学重点: 理解三种变换的规律
教学难点: 由三种变换得到正弦型函数的图象
数
学
( 必修4 )
32020/10/21
注意:平移量
y=sinx
2
x
y=sin(x+ ) y=sin(2x+ )
02020/10/21
(1)向左平移 函数 y=sinx
y=sin(x+ ) 的图象
(2)横坐标缩短到原来的 倍 纵坐标不变
y=sin(2x+ ) 的图象
(3)横坐标不变 纵坐标伸长到原来的3倍
y=3sin(2x+ )的图象
