内蒙古大学离散习题代数系统部分答案
大学《离散数学》题库及答案

《离散数学》题库与答案一、选择或填空(数理逻辑部分)1、下列哪些公式为永真蕴含式?( A )(1)⌝Q=>Q→P (2)⌝Q=>P→Q (3)P=>P→Q (4)⌝P∧(P∨Q)=>⌝P答:在第三章里面有公式(1)是附加律,(4)可以由第二章的蕴含等值式求出(注意与吸收律区别)2、下列公式中哪些是永真式?( )(1)(┐P∧Q)→(Q→⌝R) (2)P→(Q→Q) (3)(P∧Q)→P (4)P→(P∨Q)答:(2),(3),(4)可用蕴含等值式证明3、设有下列公式,请问哪几个是永真蕴涵式?( )(1)P=>P∧Q (2) P∧Q=>P (3) P∧Q=>P∨Q(4)P∧(P→Q)=>Q (5) ⌝(P→Q)=>P (6) ⌝P∧(P∨Q)=>⌝P答:(2)是第三章的化简律,(3)类似附加律,(4)是假言推理,(3),(5),(6)都可以用蕴含等值式来证明出是永真蕴含式4、公式∀x((A(x)→B(y,x))∧∃z C(y,z))→D(x)中,自由变元是( ),约束变元是( )。
答:x,y, x,z(考察定义在公式∀x A和∃x A中,称x为指导变元,A为量词的辖域。
在∀x A和∃x A的辖域中,x的所有出现都称为约束出现,即称x为约束变元,A中不是约束出现的其他变项则称为自由变元。
于是A(x)、B(y,x)和∃z C(y,z)中y为自由变元,x和z为约束变元,在D(x)中x为自由变元)5、判断下列语句是不是命题。
若是,给出命题的真值。
( )(1)北京是中华人民共和国的首都。
(2) 陕西师大是一座工厂。
(3) 你喜欢唱歌吗? (4) 若7+8>18,则三角形有4条边。
(5) 前进! (6) 给我一杯水吧!答:(1)是,T (2)是,F (3)不是(4)是,T (5)不是(6)不是(命题必须满足是陈述句,不能是疑问句或者祈使句。
)6、命题“存在一些人是大学生”的否定是( ),而命题“所有的人都是要死的”的否定是( )。
离散数学考试题及详细参考答案

离散数学考试题(后附详细答案)一、命题符号化(共6小题,每小题3分,共计18分)1. 用命题逻辑把下列命题符号化a) 假如上午不下雨,我去看电影,否则就在家里读书或看报。
b) 我今天进城,除非下雨。
c) 仅当你走,我将留下。
2. 用谓词逻辑把下列命题符号化a) 有些实数不是有理数b) 对于所有非零实数x,总存在y使得xy=1。
c) f是从A到B的函数当且仅当对于每个a€ A存在唯一的b € B ,使得f(a)=b.二、简答题(共6道题,共32分)1. 求命题公式(P T(Q T R)).r(R T(Q T P))的主析取范式、主合取范式,并写出所有成真赋值。
(5分)2. 设个体域为{1,2,3},求下列命题的真值(4分)a) -x y(x+y=4)b) y -x (x+y=4)3. 求-x(F(x) T G(x)) T ( xF(x) T-I X G(X))的前束范式。
(4 分)4. 判断下面命题的真假,并说明原因。
(每小题2分,共4分)a) (A _.B)—C=(A-B) (A-C)b) 若f是从集合A到集合B的入射函数,则|A| < |B|5. 设A是有穷集,|A|=5,问(每小题2分,共4分)a) A上有多少种不同的等价关系?b) 从A到A的不同双射函数有多少个?6. 设有偏序集<A, < >,其哈斯图如图1,求子集B={b,d,e}的最小元,最大元、极大元、极小元、上界集合、下界集合、上确界、下确界,(5分)7. 已知有限集S={a1,a2,…,a n},N为自然数集合,R为实数集合,求下列集合的基数K IS;P(S);N,N ;P(N);R,R X R,{o,1}(写出即可)(6 分)三、证明题(共3小题,共计40分)1. 使用构造性证明,证明下面推理的有效性。
(每小题5分,共10分)a) A T (B A C),(E T—F) T—C, B T (A A ~S)二B T Eb) -x(P(x) T—Q(x)), -x(Q(x) V R(x)) , x—R(x)二x~P(x)2. 设R1是A上的等价关系,R2是B上的等价关系,A工._且B =_,关系R满足:<<X1,y1>,<X2,y2>>€ R,当且仅当< x 1, X2> € R1 且<y 1,y2> € R2。
离散数学试题与答案试卷一
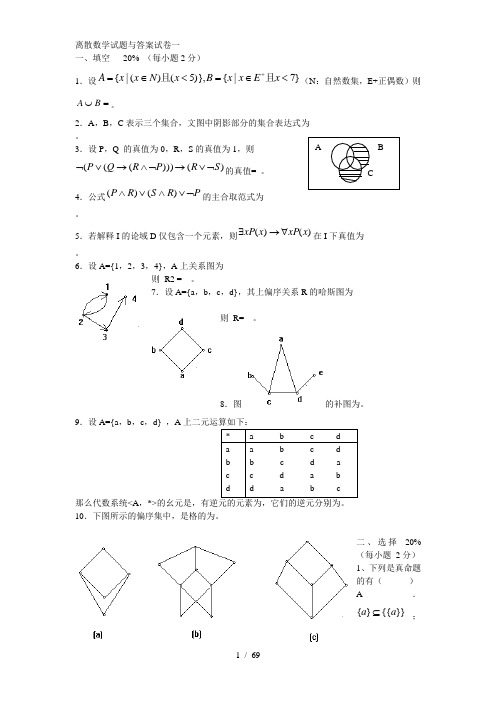
试卷二答案:
填空20%(每小题2分)
1、 ; 2、T 3、 4、R={<2,2>,<2,3>,<2,4>,<2,5>,<2,6>,<3,2>,<3,3>,<3,4>,<3,5>,<3,6>,<4,5>,<4,6>,<5,2>,<5,3>,<5,4>,<5,5>,<5,6>}; 5、R={<1,2>,<1,3>,<2,1>};R={<1,1>,<2,2>,<3,3>} 6、a;否;有7、Klein四元群;循环群8、B 9、 ;图中无奇度结点且连通10、渗釤呛俨匀谔鱉调硯錦鋇絨钞。
前提: 、 结论: ……3分
① P
② P
③ US②
④ T①I
⑤ T③④I
⑥ T①I
⑦ T⑤⑥I
⑧ EG⑦……11分
3、10分
证明:
。
4、8分
证明:设G中两奇数度结点分别为u和v,若u,v不连通,则G至少有两个连通分支G1、G2,使得u和v分别属于G1和G2,于是G1和G2中各含有1个奇数度结点,这与图论基本定理矛盾,因而u,v一定连通。铙誅卧泻噦圣骋贶頂廡缝勵罴。
选择20%(每小题2分)
题目
1
2
3
4
5
6
7
8
9
10Biblioteka 答案B、DD;DD
B
D
A
离散数学习题答案.docx

精品文档离散数学习题答案习题一及答案:( P14-15 )14、将下列命题符号化:( 5)李辛与李末是兄弟解:设 p:李辛与李末是兄弟,则命题符号化的结果是p( 6)王强与刘威都学过法语解:设 p:王强学过法语; q:刘威学过法语;则命题符号化的结果是p q ( 9)只有天下大雨,他才乘班车上班解:设 p:天下大雨; q:他乘班车上班;则命题符号化的结果是q p( 11)下雪路滑,他迟到了解:设 p:下雪; q:路滑; r :他迟到了;则命题符号化的结果是( p q)r15、设 p: 2+3=5.q:大熊猫产在中国 .r:太阳从西方升起 .求下列复合命题的真值:( 4)(p q r )(( p q)r )解: p=1, q=1,r=0 ,(p q r )(110)1,((p q)r )((11)0)(00)1(p q r )(( p q)r ) 1 1119、用真值表判断下列公式的类型:( 2)( p p)q解:列出公式的真值表,如下所示:p q p qp) ( p p)q( p001111011010100101110001由真值表可以看出公式有 3 个成真赋值,故公式是非重言式的可满足式。
20、求下列公式的成真赋值:精品文档( 4)( p q)q解:因为该公式是一个蕴含式,所以首先分析它的成假赋值,成假赋值的条件是:( p q)1p0q0q0所以公式的成真赋值有: 01,10, 11。
习题二及答案:( P38)5、求下列公式的主析取范式,并求成真赋值:( 2)(p q) (q r )解:原式( p q) q r q r( p p) q r( p q r ) ( p q r )m3m7,此即公式的主析取范式,所以成真赋值为011, 111。
6、求下列公式的主合取范式,并求成假赋值:( 2)( p q) ( p r )解:原式( pp r ) ( p q r )( p q r )M 4,此即公式的主合取范式,所以成假赋值为 100。
离散数学答案 第九章 特殊代数系统

第九章 特殊的代数系统习题9.11.解 ⑴是半群。
显然,二元运算“ ”在N 上是封闭的, 所以,>< ,N 是一个代数系统, 另一方面,,,,N c b a ∈∀有(){}{}c b a c b a c b a ,,max ,max == ,而(){}{}c b a c b a c b a ,,m ax ,m ax == ,因此,()()c b a c b a =,所以,运算“ ”满足结合律的,故>< ,N 是半群;⑵是半群。
显然,二元运算“ ”在N 上是封闭的, 所以,>< ,N 是一个代数系统, 另一方面,N c b a ∈∀,,,有()c c b c b a == ,而()c c a c b a == ,则()()c b a c b a =,所以,运算“ ”满足结合律,故><,N 是半群;⑶是半群。
显然,二元运算“ ”在N 上是封闭的, 所以,>< ,N 是一个代数系统, 另一方面,N c b a ∈∀,,,有()abc c ab c ab c b a 4)2(2)2(=== ,()()abc bc a bc a c b a 422)2(=== ,即()()c b a c b a = ,所以,运算“ ”满足结合律,故>< ,N 是半群。
⑷不是半群。
虽然,二元运算“ ”在N 上是封闭的,即>< ,N 是一个代数系统,但是 对于5,3,6,因为,()4635635635=--=-= ,而2635635)63(5=--=-= ,即())63(5635 ≠,所以,运算“ ”不满足结合律,故>< ,N 不是半群。
2.解 ⑴正确。
因为,运算显然封闭。
⑵正确。
abc bc ac ab c b a c ab b a c b a ++++++=++= )()(, bc ac ab c b a bc c b a c b a +++++=++=)()( ,即是()()c b a c b a =,所以︒满足结合律。
离散数学习题集(十五套含答案)
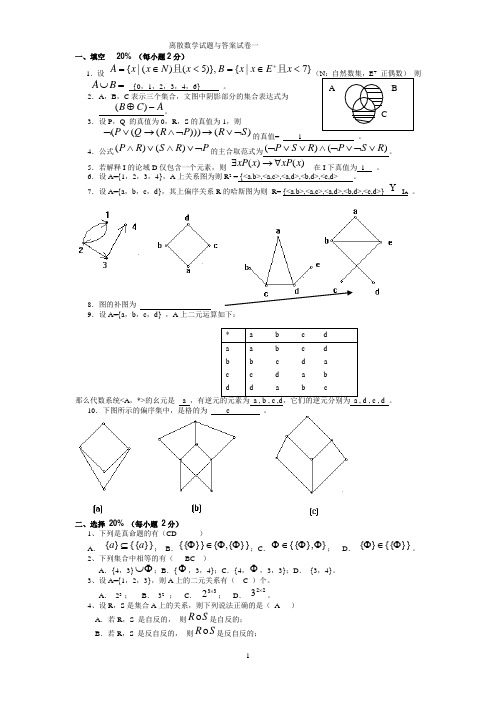
离散数学试题与答案试卷一一、填空20% (每小题2分)1.设}7|{)},5()(|{<∈=<∈=+xExxBxNxxA且且(+=⋃BA{0,1,2,3,4,6} 。
2.A,B,C表示三个集合,文图中阴影部分的集合表达式为。
3R,S的真值为1,则)()))(((SRPRQP⌝∨→⌝∧→∨⌝的真值= 1 。
4.公式PRSRP⌝∨∧∨∧)()(的主合取范式为)()(RSPRSP∨⌝∨⌝∧∨∨⌝。
5.若解释I的论域D仅包含一个元素,则)()(xxPxxP∀→∃在I下真值为1 。
6.设A={1,2,3,4},A上关系图为则R2 = {<a.b>,<a,c>,<a,d>,<b,d>,<c,d> 。
7.设A={a,b,c,d},其上偏序关系R的哈斯图为则R= {<a.b>,<a,c>,<a,d>,<b,d>,<c,d>} I A。
8.图的补图为9.设A={a,b,c,d} ,A上二元运算如下:那么代数系统<A,*>的幺元是 a ,有逆元的元素为a , b , c ,d,它们的逆元分别为 a , d , c , d 。
10.下图所示的偏序集中,是格的为 c 。
二、选择20% (每小题2分)1、下列是真命题的有(CD)A.}}{{}{aa⊆;B.}}{,{}}{{ΦΦ∈Φ;C.}},{{ΦΦ∈Φ;D.}}{{}{Φ∈Φ。
2、下列集合中相等的有(BC )A.{4,3}Φ⋃;B.{Φ,3,4};C.{4,Φ,3,3};D.{3,4}。
3、设A={1,2,3},则A上的二元关系有( C )个。
A.23 ;B.32 ;C.332⨯;D.223⨯。
4、设R,S是集合A上的关系,则下列说法正确的是(A )A.若R,S 是自反的,则SR 是自反的;B.若R,S 是反自反的,则SR 是反自反的;C .若R ,S 是对称的, 则S R是对称的;D .若R ,S 是传递的, 则S R 是传递的。
离散数学复习题及参考答案

离散数学复习题及参考答案《离散数学II-抽象代数》复习题一单项选择题1、设集合S={a,b},某运算如下定义。
是代数系统的是(A)。
某ab 某ab某ab某abaaaaaa,baabab无baaba,bbbbebba2、关于代数系统的某个二元运算某的幺元,说法正确的是(A)。
A.幺元不一定存在B.若幺元存在,不一定唯一C.除非幺元存在且某运算满足结合律,幺元才唯一D.幺元一定不是零元3、已知代数系统和满同态,S∩S1=Φ。
若中存在幺元某,则(B)。
A.一定存在幺元,幺元还是某B.一定存在幺元,幺元不是某C.不一定存在幺元D.一定不存在幺元4、下列代数系统不是群的是(C)。
.A.S={1,3,4,5,9},某是模11的乘法B.S是有理数,某是一般的加法C.S是有理数,某是一般的乘法D.S是整数,某是一般的加法5、关于群正确的说法是(C)。
A.群一定存在零元B.群一定不存在零元C.群一定存在幺元D.群一定不存在幺元二填空题1、一个代数系统,如果a,b∈S,a某b=b某a/a,b,c∈S,(a某b)某c=a某(b某c),则某满足交换律/结合律。
2、一个代数系统,如果a,b,c∈S,a某(b+c)=(a某b)+(a某c)且(b+c)某a=(b某a)+(c某a),则某对+满足分配律。
3、设是群,对a,b∈G,填写以下证明过程每步的理由。
-1-1-1-1(a某b)某(b某a)=a某(b某b)某(a)某满足结合律=e逆元定义、幺元定义4、设是环,0是环的加法幺元、乘法零元。
对a,b∈R,-a表示a的加法逆元。
填写以下证明过程每步的理由。
(-a)·b=(-a)·b+(a·b+(-(a·b)))a·b+(-(a·b))=0,(-a)·b+0 =(-a)·b=((-a)·b+a·b)+(-(a·b))+满足结合律=((-a)+a)·b+(-(a·b))·对+满足分配律=0·b+(-(a·b))(-a)+a=0=-(a·b)0·b=0,0+(-(a·b))=(-(a·b))三计算题1、设S={a,b,c,d,e},S上的运算某运算表如下:某abcdeaaacbdbabcddcccbbddbdbededdddd(1)某是否有零元?无零元。
离散数学习题集十五套含答案
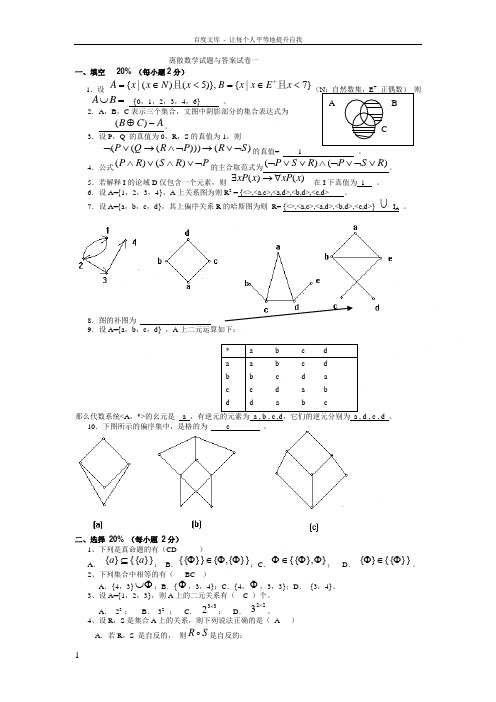
离散数学试题与答案试卷一一、填空20% (每小题2分)1.设}7|{)},5()(|{<∈=<∈=+xExxBxNxxA且且(N:自然数集,E+正偶数)则=⋃BA{0,1,2,3,4,6} 。
2.A,B,C表示三个集合,文图中阴影部分的集合表达式为ACB-⊕)(。
3.设P,Q 的真值为0,R,S的真值为1,则)()))(((SRPRQP⌝∨→⌝∧→∨⌝的真值= 1 。
4.公式PRSRP⌝∨∧∨∧)()(的主合取范式为)()(RSPRSP∨⌝∨⌝∧∨∨⌝。
5.若解释I的论域D仅包含一个元素,则)()(xxPxxP∀→∃在I下真值为1 。
6.设A={1,2,3,4},A上关系图为则R2 = {<>,<a,c>,<a,d>,<b,d>,<c,d> 。
7.设A={a,b,c,d},其上偏序关系R的哈斯图为则R= {<>,<a,c>,<a,d>,<b,d>,<c,d>}IA。
8.图的补图为9.设A={a,b,c,d} ,A上二元运算如下:* a b c dabcda b c db c d ac d a bd a b c那么代数系统<A,*>的幺元是 a ,有逆元的元素为a , b , c ,d,它们的逆元分别为 a , d , c , d 。
10.下图所示的偏序集中,是格的为 c 。
二、选择20% (每小题2分)1、下列是真命题的有(CD)A.}}{{}{aa⊆;B.}}{,{}}{{ΦΦ∈Φ;C.}},{{ΦΦ∈Φ;D.}}{{}{Φ∈Φ。
2、下列集合中相等的有(BC )A.{4,3}Φ⋃;B.{Φ,3,4};C.{4,Φ,3,3};D.{3,4}。
3、设A={1,2,3},则A上的二元关系有( C )个。
A.23 ;B.32 ;C.332⨯;D.223⨯。
4、设R,S是集合A上的关系,则下列说法正确的是(A )A.若R,S 是自反的,则SR 是自反的;A BCB .若R ,S 是反自反的, 则S R 是反自反的;C .若R ,S 是对称的, 则S R 是对称的;D .若R ,S 是传递的, 则S R 是传递的。
离散数学试卷及答案
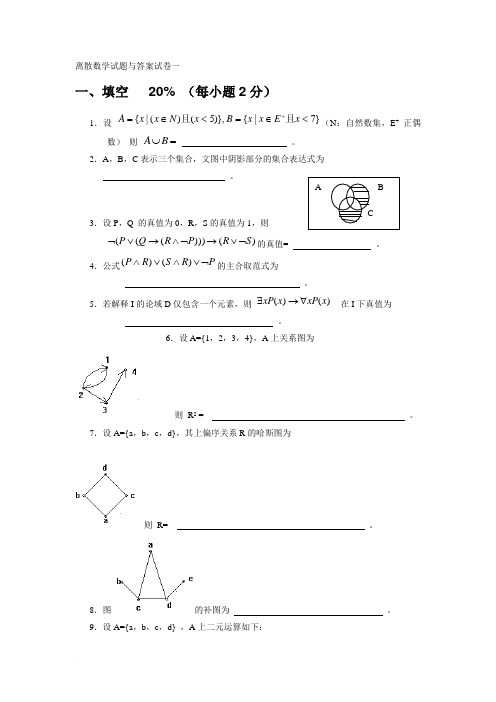
离散数学试题与答案试卷一一、填空 20% (每小题2分)1.设 }7|{)},5()(|{<∈=<∈=+x E x x B x N x x A 且且(N :自然数集,E + 正偶数) 则 =⋃B A 。
2.A ,B ,C 表示三个集合,文图中阴影部分的集合表达式为 。
3.设P ,Q 的真值为0,R ,S 的真值为1,则)()))(((S R P R Q P ⌝∨→⌝∧→∨⌝的真值= 。
4.公式P R S R P ⌝∨∧∨∧)()(的主合取范式为 。
5.若解释I 的论域D 仅包含一个元素,则 )()(x xP x xP ∀→∃ 在I 下真值为 。
6.设A={1,2,3,4},A 上关系图为则 R 2 = 。
7.设A={a ,b ,c ,d},其上偏序关系R 的哈斯图为则 R= 。
8.图的补图为 。
9.设A={a ,b ,c ,d} ,A 上二元运算如下:那么代数系统<A ,*>的幺元是 ,有逆元的元素为 ,它们的逆元分别为 。
10.下图所示的偏序集中,是格的为 。
二、选择 20% (每小题 2分)1、下列是真命题的有( ) A . }}{{}{a a ⊆;B .}}{,{}}{{ΦΦ∈Φ;C . }},{{ΦΦ∈Φ;D . }}{{}{Φ∈Φ。
2、下列集合中相等的有( )A .{4,3}Φ⋃;B .{Φ,3,4};C .{4,Φ,3,3};D . {3,4}。
3、设A={1,2,3},则A 上的二元关系有()个。
A . 23 ; B . 32 ; C . 332⨯; D . 223⨯。
4、设R ,S 是集合A 上的关系,则下列说法正确的是( ) A .若R ,S 是自反的, 则S R 是自反的; B .若R ,S 是反自反的, 则S R 是反自反的; C .若R ,S 是对称的, 则S R 是对称的; D .若R ,S 是传递的, 则S R 是传递的。
5、设A={1,2,3,4},P(A)(A的幂集)上规定二元系如下t st spR=∈=则P(A)/ R=()<A∧>)(||||}s({t,,|A.A ;B.P(A) ;C.{{{1}},{{1,2}},{{1,2,3}},{{1,2,3,4}}};D.{{Φ},{2},{2,3},{{2,3,4}},{A}}6、设A={Φ,{1},{1,3},{1,2,3}}则A上包含关系“⊆”的哈斯图为()7、下列函数是双射的为()A.f : I→E , f (x) = 2x ;B.f : N→N⨯N, f (n) = <n , n+1> ;C.f : R→I , f (x) = [x] ;D.f :I→N, f (x) = | x | 。
离散数学答案 第八章 代数系统

第八章 代数系统习题8.11.解 ⑴是,⑵不是,⑶是,⑷不是。
2.解 若﹡对 是可分配的,则有任意a,b,c ∈*I,均有a ﹡(b c)=(a ﹡b) (a ﹡c)= a b ac =( a b ⋅ a c )= a b+c而a ﹡(b c)=a ﹡(b ⋅c)= a b ⋅c ≠a b+c 故﹡对 是不可分配的。
3.解 ⑴对于任意A ∈P(S), 因为A ⊆S ,所以,A ⋃S =S ,因此,S 是关于⋃运算的零元; ⑵对于任意A ∈P(S), 因为A ⊆S ,所以,A ⋂S = A ,因此,S 是关于⋃运算的零元单。
4.解 ⑴①因为x*y=xy-2x-2y+6,则y*x=yx-2y-2x+6= x*y ,满足交换律; ②任意x,y,z ∈R 有x*(y*z)=x*(yz-2y-2 z +6)=x(yz-2y-2 z +6)-2x-2(yz-2y-2z+6)+6 =xyz-2xy-2xz+6x-2x -2yz+4y+4z-12+6= xyz-2xy-2xz-2yz+4x+4y+4z-6. (x*y)*z=(xy-2x-2y+6) *z =(xy-2x-2y+6)z-2(xy-2x-2y+6)-2z+6 =xyz-2xz-2yz+6z-2xy+4x+4y-2z-6=x*(y*z). 故满足结合律。
(2) ①设任意a ∈R,存在e ∈R,要e*a= ea-2e-2a+6=a ,由于a 的任意性则e=3。
因此e=3是其单位元;②设任意b ∈R, z ∈R ,要有z*b= zb-2 z-2b+6= z ,由于b 的任意性则z=2,因此 z=2是其零元。
(3)因为*是满足交换律,对于x ∈R ,要存在1-x ∈R ,须有x*1-x= x 1-x-2x-21-x+6= e=3, 当x ≠2时,2321--=-x x x。
即对于任意的x ,当x ≠2时x 都是可逆的,且2321--=-x x x。
5.解 f 1,f 2,f 3都满足交换律,f 4满足等幂率,f 2有单位元a ,f 1有零元a ,f 3有零元b 。
国家开放大学《离散数学(本)》形考任务(1-4)试题及答案解析

国家开放大学最新《离散数学(本)》形考任务(1-4 )试题及答案解析形考任务1(正确答案解析附题冃之后)单项选择题题冃1正确获得5.00分中的5.00分未标记标记题目题干设A={1, 2, 3, 4, 5, 6, 7, 8}, R是A上的整除关系,B={2, 4, 6},则集合B的最大元、最小元、上界、下界依次为()■选择一项:A.无、2、无、2B.8、2、8、2C.8、1、6、1D.6、2、6、2反馈你的回答正确正确答案是:无、2、无、2题目2正确获得5.00分中的5.00分未标记标记题目题干设集合A={1,2,3,4}上的二元关系R={<l z 1>, <2, 2>, <2, 3>, <4, 4>}. S={<1, 1>, <2,2>, <2, 3>, <3,2>, <4,4>},则S 是日的()闭包.选择一项:A.自反和传递B.传递C.自反D.对称反馈你的回答正确正确答案是:对称题目3正确获得5.00分中的5.00分未标记标记题冃题干若集合A的元素个数为10,则其暴集的元素个数为( ).选择一项:A.1024B. 1C.100D.10反馈你的回答正确正确答案是:1024题目4正确获得5.00分中的5.00分未标记标记题目题干设集合A = {1, 2, 3, 4, 5}上的偏序关系的哈斯图如图所示,若A的子集B = {3, 4, 5},则元素3为B的( )・选择一项:A.最大下界B.下界C.最小元D.最小上界反馈你的回答正确正确答案是:最小上界题目5正确获得5.00分中的5.00分未标记标记题冃题干设集合A=(1, 2, 3), B={3, 4, 5}, C={5, 6, 7), WJ AUB~C=( ).选择一项:A.(4, 5, 6, 7)B.{1, 2, 3, 5)C.(2, 3, 4, 5)D.{1, 2, 3, 4}反馈你的回答正确正确答案是:{1,2, 3, 4}题目6正确获得5.00分中的5.00分未标记标记题目题干设集合A={1, 2, 3, 4, 5},偏序关系是A上的整除关系,则偏序夷<A, > 上的元素5是集合A的( )・选择一项jA.极大元B.最大元C.最小元D.极小元反馈你的回答正确正确答案是:极大元题目7正确获得5.00分中的5.00分未标记标记题冃题干设集合A ={1,2, 3}上的函数分别为:f = {<l,2>, <2,1>, <3,3>},g = {<1, 3>, <2,2>, <3, 2>),h = {<l,3>, <2,1>, <3,1>},则h=( ).选择一项:A.g%B.g°fC.何D.f°g反馈你的回答正确正确答案是:f°g题冃8正确获得5.00分中的5.00分未标记标记题冃题干设集合A={2,4,6,8}, B={1,3,5,7} , A 到 B 的关系R={<x, y>| y = x+l),则R=( )•选择一项:A.{<2, 2>, <3, 3>, <4, 6>}B.(<2,1>, <4, 3>, <6, 5>}C.(<2, 3>, <4, 5>, <6, 7>)D.{<2,1>, <3, 2>, <4, 3>}反馈你的回答正确正确答案是:{<2, 3>, <4, 5>, <6, 7>}题冃9正确获得5.00分中的5.00分未标记标记题目题干集合A=(1, 2, 3, 4}上的关系R={<x, y>|x=y且x, yA},则R的性质为( ).选择一项:A.反自反B.不是对称的C.传递的D.不是自反的反馈你的回答正确正确答案是:传递的题目10正确获得5.00分中的5.00分未标记标记题冃题干集合A=(1, 2, 3, 4, 5, 6, 7, 8}上的关系R={<x, y>|x+y=10 且x, yA},则R 的性质选择一项:A.传递且对称的B.反自反且传递的C.自反的D.对称的反馈你的回答正确正确答案是:对称的未标记标记题冃信息文本判断题题目11正确获得5.00分中的5.00分未标记标记题日题干空集的幕集是空集.()选择一项:对错反馈正确的答案是“错”。
内蒙古大学离散习题代数系统部分答案

《离散数学》代数系统1.以下集合和运算是否构成代数系统?如果构成,说明该系统是否满足结合律、交换律?求出该运算的幺元、零元和所有可逆元素的逆元.1)P(B)关于对称差运算⊕,其中P(B)为幂集. 构成代数系统;满足结合律、交换律;幺元φ;无零元;逆元为自身。
2)A={a,b,c},*运算如下表所示:构成代数系统;满足结合律、交换律;无幺元;无逆元;零元b.2.设集合A={a,b},那么(1)在A上可以定义多少不同的二元运算?(2)在A上可以定义多少不同的具有交换律的二元运算?24个不同的二元运算;23个不同的具有交换律的二元运算3.设A={1,2},B是A上的等价关系的集合.1)列出B的元素. 2元集合上只有2种划分,因此只有2个等价关系,即B={I A,E A}2)给出代数系统V=<B,∩>的运算表.3)求出V的幺元、零元和所有可逆元素的逆元. 幺元E A、零元I A;只有E A可逆,其逆元为E A.4)说明V是否为半群、独异点和群?V是为半群、独异点,不是群4.设A={a,b,c},构造A上的二元运算*,使得a*b=c,c*b=b,且*运算满足幂等律、交换律.1)给出关于*运算的一个运算表.其中表中?位置可以是a、b、c。
2)*运算是否满足结合律,为什么?不满足结合律;a*(b*b)=c≠(a*b)*b=b5.设<R,*>是一个代数系统。
*是R上的一个二元运算,使得对于R(实数集合)中的任意元素a,b都有a*b=a+b+a·b(·和+为数集上的乘法和加法).证明::<R,*> 是独异点.6.如果<S,*>是半群,且*是可交换的.证明:如果S中有元素a,b,使得a*a=a和b*b=b,则(a*b)*(a*b)=a*b.(a*b)*(a*b)= a*(b*a)*b 结合律= a*( a*b)*b 交换律= (a* a)*(b*b)= a*b.7.设<G,·,–1,e>是一个群,则∀a,b,c∈S。
习题与解答(代数系统) 离散答案

第十章
15、17、18、21、22、24、27、28、29。
2
15、设 G 为群,若 x ∈G 有 x =e, 证明 G 为交换群 证明: a, b ∈G 由条件 x ∈G 有 x =e
2
所以 a =e ,b =e (ab) =e ,即(ab)(ab)=e 所以 a =a, b =b, ba= a b
下面证明 φ(G1)是是循环群 y∈f(G1), x ∈G1 , 使得 f(x)=y. 而 G1=<a> 所以 存在 r 使得 x= a
r r
则 y = f(x) = f(a ) = f(a)f(a)……f(a) =(f(a)) 这证明了 f(a)为 f(G1)的生成元。即 f(G1)=< f(a)> 所以 f(G1)为循环群。 28、设 G=<a>是 15 阶循环群。 (1) 求出 G 的所有的生成元。 (2) 求出 G 的所有子群。 解:(1) 生成元为: a,a ,a ,a ,a ,a ,a ,a (2) G 的所有子群: 共 4 个子群 <e>, <a >={e,a ,a ,a ,a },
-1 -1
21、设 G 为群,a 是 G 中给定元素,a 的正规化子 N(a)表示 G 中与 a 可交换的元素构成的集合,即 N(a)={x| x∈G∧xa=ax } 证明:N(a)是 G 的子群 证明: (1) a∈N(a), 所以 N(a)非空(因为 a∈G∧aa=aa) (2) x,y ∈N(a) 则 xa=ax ya=ay
-1
-1
-1
=-a
-1 -1
-1
(2) 由于 (ab)(b a )= a(bb )a = aa = 1 所以 (ab)
大学离散数学课后答案

9.1.1 解:⑴ 几何图表示如右。
⑵ deg(v 1)=3 deg(v 2)=4 deg(v 3)=3 deg(v 4)=3 deg(v 5)=1 deg(v 6)=0 奇度数结点数为 4。
⑶ (v 2,v 2) 为自环;(v 1,v 3) 与 (v 3,v 1) 为平行边;(v 4,v 5) 为悬挂边;v 5 为悬挂点;v 6 为孤立点。
该图为伪图。
9.1.2 证:⑴ n 个结点的所有图中,完全图边数最多。
每点n-1度,n 个点的总度数为:2m=∑=n i i v 1)deg(=n(n-1) ∴ m=n(n-1)/2n 个结点的任一图的边数≤完全图的边数,∴ m ≤n(n-1)/2 ※ ⑵ ∵ 在简单有向完全图中,任二点之间有两条方向相反的边,∴ 每点的度数为 2(n-1),∴ 总度数为 2m=2(n-1)n ,∴ m=n(n-1)。
※ 9.1.3 解:⑴ 去掉 v 点后,有 n-1个结点,m-d 条边。
⑵ 去掉 e 边后,有 n 个结点,m-1条边。
9.1.4 证:假设n 个结点的度数皆不相同∵ 在简单无向图中,一个结点的最大度数为n-1,最小度数为0。
∴ 它们只能为 0,1,…,n-1 n 个值。
∵ 0度点不与其它任何结点相邻,而n-1度点与其它任何结点相邻,∴ 二者产生一个矛盾。
※ 9.1.5 解:仅考虑无向图。
⑴ 可构成图,图如右。
⑵ 否。
奇度数结点数为奇数。
⑶ 否。
n 个结点的简单无向图中,结点的最大度数为n-1,5不可。
⑷ 否。
后三点均与其它各点有边,故第一点也应三度。
⑸ 否。
后二点均与其它各点有边,故第一点至少应为二度。
9.1.6 解:2m=nk m=nk/2 。
9.1.7 证:⑴ 当图G 中n 个点的度数都为 δ(G)时,总度数为 2m=n δ(G)。
但一般情况下,δ(G) 为最小度数,而并非所有结点的度数都为 δ(G)时, 必有 2m ≥n δ(G), ∴ 2m/n ≥δ(G) 。
习题与解答(代数系统) 离散答案

2
2
2
所以 ba=ab ,即 ab=ba, 因此 G 为交换群。 17、设 G 为群,a,b,c∈G, 证明: |abc|=|bca|=|cab| 证明:设|abc|=r , |bca|=t, 则 (abc) =e,
t r
(bca) =e
t
由于(abc) =(abc)(abc)……(abc) =a(bca)(bca)……(bca)a
-1 -1 -1 -1 -1 -1
则存在 h,k∈H, 使得 u=xhx ,v=xkx
-1
-1
,
则有 uv
-1
=(xhx )(xkx ) =(xhx )(xk x )=x(hk )x
-1 -1 -1 -1
-1
-1
-1
-1
-1
-1
-1
-1
因为 H 为子群,hk 属于 H,从而 x(hk )x 属于 xHx . 即 uv ∈xHx
-1 -1
21、设 G 为群,a 是 G 中给定元素,a 的正规化子 N(a)表示 G 中与 a 可交换的元素构成的集合,即 N(a)={x| x∈G∧xa=ax } 证明:N(a)是 G 的子群 证明: (1) a∈N(a), 所以 N(a)非空(因为 a∈G∧aa=aa) (2) x,y ∈N(a) 则 xa=ax ya=ay
*
=(a∧b)∨(b∧c) =(b∧a)∨(b∧c) =b∧(a∨c) (2) f =(a∨b)∧(b∨c) 14、设 B 是布尔代数, a, b∈B, 证明: a≤b a∧b =0 a ∨b=1
(1) S1= 1 , , 2 , , 3 , , 4 ,运算为普通乘法。 1 2 1 3 1 4
离散数学习题解第二部分(代数系统)

离散数学习题解 第二部分 代数系统习题四 第四章代数系统1.设I 为整数集合。
判断下面的二元关系是否是I 上的二元运算a )+={(x ,y ),z|x ,y ,zI 且z=x+y}b )-={((x ,y ),z )|x ,y ,zI 且z=x -y}c )×={((x ,y ),z )|x ,y ,zI 且z=x ×y}d )/={((x ,y ),z )|x ,y ,zI 且z=x/y}e )R={((x ,y ),z )|x ,y ,zI 且z=x y }f )={((x ,y ),z )|x ,y ,zI 且z=yx }g )min = {((x ,y ),z )|x ,y ,zI 且z=max (x ,y )} h )min = {((x ,y ),z )|x ,y ,zI 且z=min (x ,y )} i )GCD = {((x ,y ),z )|x ,y ,zI 且z= GCD (x ,y )} j )LCM={((x ,y ),z )|x ,y ,z ∈I 且z= LCM (x ,y )}[解] a )是。
由于两个整数之和仍为整数,且结果唯一,故知+:I 2→I 是I 上的一个二元运算。
b )是。
由于两个整数之差仍为整数,且结果唯一,故知一:I 2→I 是I 上的一个二元运算。
c )是。
由于两个整数这积仍为整数,且结果唯一,故知x :I 2→I 是I 上的一个二元运算。
d )不是:例如若x=5,y=6,则z=x/y=5/6∉I ;当y=0时z=x|y=x/0无定义。
e )不是。
例如若x=2,y= -2,则z=x y =2 –2=221=I 41∉;若x=y=0,则z=x y =0,则z=I 2x ∉=χ;g )是。
由于两个整数中最大者仍为整数,且结果唯一。
故知max :I 2→I 是I 上的一个二元运算。
h )是。
由于两个整数中最小者仍为整数,且结果唯一。
离散课后习题答案4

(b)满足交换律和结合律,不满足幂等律,单位元为 a,没有零元
a −1 = a, b −1 = b (c)满足交换律,不满足幂等律,不满足结合律
a � (b � b) = a � a = b, (a � b) � b = a � b = a a � (b � b) ≠ (a � b) � b 没有单位元, 没有零元
(6) n
关于普通的加法和乘法运算。
封闭,均满足交换律,结合律,乘法对加法满足分配律
加法单位元是 0,无零元;
乘法无单位元( n > 1),零元是 0; n = 1单位元是 1
(7)A = { a1, a2 ,⋯, an} n 运算定义如下:
封闭 不满足交换律,满足结合律,
(8)S =
关于普通的加法和乘法运算。
5
令 b = a 2 的证。
21.设 G 是 Mn(R)上的加法群,n≥2,判断下述子集是否构成子群。
(1)全体对称矩阵
是子群
(2)全体对角矩阵
是子群
(3)全体行列式大于等于 0 的矩阵. 不是子群
(4)全体上(下)三角矩阵。 是子群
22.设 G 为群,a 是 G 中给定元素,a 的正规化子 N(a)表示 G 中与 a 可交换的元素构成
11.设
G=
⎧⎛ ⎨⎜⎜ ⎩⎝
1 0
0⎞ ⎛1
1
⎟⎟, ⎠
⎜⎜ ⎝
0
0 ⎞ ⎛−1
− 1⎟⎟⎠,
⎜⎜ ⎝
0
0⎞ ⎛−1
1 ⎟⎟⎠,
⎜⎜ ⎝
0
0 ⎞⎫ − 1⎟⎟⎠⎭⎬
,证明
G
关于矩阵乘法构成一个群.
解:(1) ∀ x,y∈G, 易知 xy∈G,乘法是 Z 上的代数运算。
离散题库20套答案

.离散1一、选择题(每题2分,共20分) CABBB DACDA二、填空题(每题2分,共20分)1.n222.a∨b=1,a∧b=03.x*(xΔy)=x xΔ(x*y)=x4. 无回路5. 大项的合取所组成6. (∃x)⌝ P(x) (∀x)⌝ P(x)7.68.对任意的a,b G∈,有(a*b)*(a*b)=(a*a)*(b*b)9.βγ10. {<1,2>,<3,3>,<1,3>,<4,2>},{<1,4>,<2,2>}三、判断题(每题1分,共10分)×√√×××××√√四、解答题(5小题,共30分)1.(5分)给定无孤立点图G,若存在一条路,经过图中每边一次且仅一次,该条路称为欧拉路;如果一个图有欧拉路,则这个图能一笔画出。
2.(8分)各4分,步骤对,结果错,适当扣分,如果求出其一个,另一个直接写出,也不扣分。
只有结果,且结果对,给一半分,只有结果,且结果错,不给分。
解:主析取式:(┐P∧┐Q∧R)∨(┐P∧┐Q∧┐R)∨(P∧Q∧R)∨(P∧┐Q∧R)∨(┐P∧Q∧R)主合取式:(┐P∨Q∨R)∧(┐P∨┐Q∨R)∧(P∨┐Q∨R)3.(5分)由无向树的性质可知,无向树的顶点数是边数加1,又知无向图所有顶点的度之和为边数的2倍。
(1分)令1度顶点个数为x,则顶点数为2+1+3+x,所有顶点的度之和为x+2*2+3+3*4,(2分)从而有x+2*2+3+3*4=2*(2+1+3+x-1),解之得x=9,即有9个1度的点。
(2分)4.(7分)解:5. (5分)⎪⎪⎪⎪⎪⎭⎫⎝⎛=1100110100100101R M (2分),(2分),具有自反,对称性质(1分)五、证明(3小题,共20分)1. (10分)每步约1分,没有P,T 标识扣3分,没有序号扣3分。
证明过程:(1)P →R P (2)⌝R →⌝P T (1)E (3)P ∨Q P (4)⌝P →Q T (3)E (5)Q →S P (6)⌝P →S T (4)(5)I (7)⌝R →S T (2)(6)I (8)R ∨S T (8)E 2. (5分)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《离散数学》代数系统
1.以下集合和运算是否构成代数系统?如果构成,说明该系统是否满足结合律、交换律?求出该运算的幺元、零元和所有
可逆元素的逆元.
1)P(B)关于对称差运算⊕,其中P(B)为幂集. 构成代数系统;满足结合律、交换律;幺元φ;无零元;逆元为自身。
2)A={a,b,c},*运算如下表所示:构成代数系统;满足结合律、交换律;无幺元;无逆元;零元b.
2.设集合A={a,b},那么(1)在A上可以定义多少不同的二元运算?(2)在A上可以定义多少不同的具有交换律的二元
运算?24个不同的二元运算;23个不同的具有交换律的二元运算
3.设A={1,2},B是A上的等价关系的集合.
1)列出B的元素. 2元集合上只有2种划分,因此只有2个等价关系,即B={I A,E A}
2)给出代数系统V=<B,∩>的运算表.
3)求出V的幺元、零元和所有可逆元素的逆元. 幺元E A、零元I A;只有E A可逆,其逆元为E A.
4)说明V是否为半群、独异点和群?V是为半群、独异点,不是群
4.设A={a,b,c},构造A上的二元运算*,使得a*b=c,c*b=b,且*运算满足幂等律、交换律.
1)给出关于*运算的一个运算表.
其中表中?位置可以是a、b、c。
2)*运算是否满足结合律,为什么?不满足结合律;a*(b*b)=c≠(a*b)*b=b
5.设<R,*>是一个代数系统。
*是R上的一个二元运算,使得对于R(实数集合)中的任意元素a,b都有a*b=a+b+a·b(·和+为数集上的乘法和加法).
证明::<R,*> 是独异点.
6.如果<S,*>是半群,且*是可交换的.
证明:如果S中有元素a,b,使得a*a=a和b*b=b,则(a*b)*(a*b)=a*b.
(a*b)*(a*b)
= a*(b*a)*b 结合律
= a*( a*b)*b 交换律
= (a* a)*(b*b)
= a*b.
7.设<G,·,–1,e>是一个群,则∀a,b,c∈S。
试证明:群G中具有消去律,即成立: 如果a·b=a·c ,b·a=c·a 那么b=c.
8.求循环群<Z16,+>的所有生成元和子群.
生成元有:1、3、5、7、9、11、13、15
子群有:<0>、<1>、<2>、<4>、<8>.
9.设<G,*>是群,a∈G .
现定义一种新的二元运算⊙:x⊙y=x*a*y,∀x,y∈G .
证明:<G,⊙>也是群.
证明:显然⊙是G上的一个二元运算。
∀x,y,z∈G,(x⊙y)⊙z=(x⊙y)*a*z=(x*a*y)*a*z=x*a*(y*a*z)= x*a*(y⊙z)= x⊙(y⊙z).故运算⊙满足结合律.
∀x∈G,x⊙a-1=x*a*a-1=x*e=x,a-1⊙x=a-1*a*x=e*x=x,故a-1是幺元.
∀x∈G,x⊙(a-1*x-1* a-1)=x*a*(a-1*x-1* a-1)= x*e*(x-1* a-1)= a-1.
(a-1*x-1* a-1)⊙x= (a-1*x-1* a-1)*a*x=(a-1*x-1)*e*x = a-1.
故a-1*x-1* a-1是x关于⊙的逆元.
综上所述<G , ⊙>是群.
10.试写出模6加法群<Z6,+6>的每个子群及其相应的左陪集.
<Z6,+6>的运算表如下所示:
<Z6,+6>的子群:<{0},+6>、<{0,3},+6>、<{0,2,4},+6>和<Z6,+6>.
11.试aH和bH是子群H在G中的两个左陪集.
证明:aH=bH或aH∩bH=
12.试写出群和环的定义.
13.证明偏序集与格的等价。
14.设A={1,2,5,10,11,22,55,110}.
1)A关于整除关系是否构成偏序集?构成偏序集
2)如果构成偏序集合,画出其对应的哈斯图.
3)如果构成偏序集,该偏序集合构成哪种格?(分配格、有界格、有补格、布尔格).
分配格、有界格、有补格、布尔格。
