高数实验报告
《高等数学实验》实验报告

精品文档高等数学实验报告实验四:微分方程实验五:空间解析几何实验六:多元函数微积分班级:姓名:学号:指导教师:李老师实验成绩:完成日期: 2010 年 4 月 27 日实验四微分方程一、实验目的1.理解常微分方程解的概念;2.掌握求微分方程及方程组解的常用命令和方法。
二、实验类型验证型。
三、必做实验四、选做实验实验五空间解析几何一、实验目的1.掌握绘制空间曲面和曲线的方法;2.熟悉常用空间曲线和空间曲面的图形特征,提高空间想像能力; 3.深入理解二次曲面方程及其图形。
二、实验类型验证型。
三、必做实验>> > t=0:pi/50:10*pi;>> plot3(cos(t),sin(t),t)>> xlabel('x');ylabel('y');zlabel('z');grid onxyz> t=0:0.05:100;>> x=t;y=sin(t);z=sin(2*t); >> plot3(x,y,z)>> xlabel('x');ylabel('y');zlabel('z')xyzezsurf('f')>> ezsurf('-cos(2*x)*sin(3*y)',[-3,3])-1-0.50.51x-cos(2 x) sin(3 y)yezsurf('sin(pi*(x^2+y^2)^(1/2))')-1-0.50.51xsin( (x 2+y 2)1/2)yezsurf('(x*y)/(x^2+y^2)',[-2,2])x(x y)/(x 2+y 2)y> ezsurf('(3+cos(u))*cos(v)','(3+cos(u))*sin(v)','sin(u)',[0,2*pi])-1-0.500.51xx = (3+cos(u)) cos(v), y = (3+cos(u)) sin(v), z = sin(u)yzezsurf('u*cos(v)','u*sin(v)','v/3',[-1,1],[0,8])0.511.522.53xx = u cos(v), y = u sin(v), z = v/3yz>> ezsurf('cos(u)','sin(u)','v') >> hold on>> ezsurf('cos(u)','v','sin(u)')-1-0.500.51z实验六 多元函数微积分一、实验目的1.掌握计算多元函数偏导数和全微分的方法; 2.掌握计算二重积分与三重积分的方法;3.提高应用重积分和曲线、曲面积分解决各种问题的能力。
高数竞赛实习报告

高等数学竞赛实习报告一、实习背景及目的随着我国科技事业的飞速发展,数学在各个领域中的应用越来越广泛,高等数学竞赛也成为了培养大学生创新能力和思维能力的重要途径。
为了提高自己的数学素养,我参加了本次高等数学竞赛实习。
本次实习的主要目的是通过实践活动,加深对高等数学知识的理解,提高解决实际问题的能力,为今后的学术研究和职业发展打下坚实基础。
二、实习内容与过程实习期间,我们学习了大量的高等数学知识,包括微积分、线性代数、概率论等。
在实习过程中,我充分感受到了高等数学的严谨性和逻辑性,也在解决实际问题中体会到了数学的魅力。
1. 微积分实习微积分是高等数学的基础,涉及到极限、导数、积分等概念。
在微积分实习中,我们通过大量练习题目的方式,深入理解了微积分的各个知识点。
同时,我们还学习了如何将微积分知识应用于实际问题,例如求解曲线长度、曲线下的面积、质心等。
2. 线性代数实习线性代数研究了向量、矩阵、行列式等概念。
在实习过程中,我们学习了如何运用线性代数知识解决线性方程组、特征值、特征向量等问题。
通过实习,我明白了线性代数在计算机科学、工程学等领域的重要性。
3. 概率论实习概率论是研究随机现象的数学分支。
在实习中,我们学习了概率分布、期望、方差等基本概念,并掌握了如何运用概率论解决实际问题,如概率计算、抽样分布、假设检验等。
4. 综合应用实习在综合应用实习环节,我们将所学的微积分、线性代数、概率论等知识运用到实际问题中。
通过解决实际问题,我们提高了自己的数学建模能力,学会了如何将理论知识和实际应用相结合。
三、实习收获与体会通过本次高等数学竞赛实习,我收获颇丰。
首先,我系统地复习和巩固了高等数学知识,为今后的学术研究和职业发展打下了坚实基础。
其次,我学会了如何将高等数学知识应用于实际问题,提高了自己的解决问题能力。
最后,我在实习过程中结识了许多志同道合的朋友,共同探讨问题、分享经验,收获了宝贵的友谊。
同时,我也认识到高等数学竞赛实习并非易事,需要付出大量的时间和精力。
高数 实验报告

高数实验报告高数实验报告引言:高等数学是大学数学的一门基础课程,它在培养学生的逻辑思维能力、分析问题的能力以及推理能力方面发挥着重要作用。
在高数课程中,实验是一种重要的教学手段,通过实验可以帮助学生更好地理解和应用数学知识。
本篇实验报告将介绍我参与的一次高数实验,并分享其中的心得体会。
实验目的:本次实验的目的是通过实际操作,加深对数列和级数的理解,并掌握相应的计算方法。
同时,通过实验过程中的观察和分析,培养学生的数学建模能力和解决实际问题的能力。
实验过程:实验开始前,我们小组成员首先进行了讨论,确定了实验的具体内容和步骤。
我们选择了两个具体的数列和级数问题进行研究。
第一个问题是求解一个递推数列的通项公式。
我们首先观察数列的前几项,发现数列中的每一项与前一项之间存在着一定的关系。
通过分析这种关系,我们猜测数列的通项公式,并通过数学归纳法进行验证。
最终,我们成功地找到了数列的通项公式,并通过计算验证了其正确性。
第二个问题是求解一个级数的和。
我们选择了一个著名的几何级数进行研究。
通过观察级数的前几项,我们发现级数中的每一项与前一项之间存在着一定的比例关系。
根据这种关系,我们得出级数的和的公式,并通过计算验证了其正确性。
实验结果:通过实验,我们成功地求解了两个数列和级数的问题,并得到了相应的结果。
这些结果不仅帮助我们更好地理解了数列和级数的概念,还提高了我们的计算能力和问题解决能力。
心得体会:通过参与这次高数实验,我深刻体会到了实践对于学习的重要性。
在实验过程中,我们不仅仅是被动地接受知识,更是主动地去探索和发现。
通过观察、分析和计算,我们能够更加深入地理解数学知识,并将其应用到实际问题中去。
此外,实验还培养了我们的团队合作能力和沟通能力。
在小组讨论中,我们需要相互协作,共同解决问题。
通过合作,我们不仅能够更好地理解和应用数学知识,还能够互相学习和促进成长。
总结:通过这次高数实验,我不仅加深了对数列和级数的理解,还提高了自己的数学建模能力和问题解决能力。
高数实验报告doc(两篇)

高数实验报告引言:高等数学是大学理工科专业中必修的一门基础课程,通过实验可以帮助学生更好地理解和应用数学知识。
本实验报告旨在介绍高等数学实验的目的、原理和实验结果,以及对实验过程的详细阐述。
通过实验,学生可以深入了解高等数学的概念和方法,并提高其数学建模和问题解决的能力。
概述:一、数列与数学归纳法:1.数列的概念和性质2.等差数列和等比数列的求和公式3.斐波那契数列4.数学归纳法的原理和应用5.数学归纳法在证明数学命题中的应用二、函数与导数:1.函数的概念和分类2.复合函数的求导法则3.高阶导数与泰勒展开4.特殊函数的导数求解5.函数与导数在实际问题中的应用三、不定积分与定积分:1.不定积分的定义和性质2.基本初等函数的不定积分3.分部积分和换元积分法4.定积分的概念和性质5.定积分在几何、物理等领域中的应用四、微分方程:1.微分方程的基本概念和分类2.一阶常微分方程的解法3.二阶常微分方程的解法4.高阶常微分方程与常系数线性齐次微分方程5.微分方程在科学和工程领域的应用五、级数与幂级数:1.级数的概念和性质2.级数的收敛与发散3.幂级数的收敛域4.幂级数的求和与展开5.幂级数在数学分析中的应用总结:通过本次高等数学实验,我们对数列与数学归纳法、函数与导数、不定积分与定积分、微分方程以及级数与幂级数等知识进行了深入了解和实践。
实验过程中,我们运用数学原理和方法解决了一系列数学问题,并将理论知识应用到实际问题解决中。
通过实验,我们不仅加深了对高等数学的理解和掌握,也提高了自己的数学建模和问题解决能力。
这次实验为我们的数学学习和应用提供了宝贵的经验和机会。
引言概述本文是一篇关于高数实验的报告,主要探讨了高数实验的意义、目的、实验方法以及实验结果和分析等内容。
高数实验是大学高数课程的重要组成部分,通过实验能够帮助学生更好地理解和应用数学知识,提高解决实际问题的能力。
本文将从实验目的、实验方法和实验结果三个方面进行详细阐述,并对实验进行总结与分析。
高等数学实验报告

⾼等数学实验报告⾼等数学实验报告实验⼈员:院(系)信息科学与⼯程学院学号_04010409___姓名__郑敏升_____ 实验地点:计算机中⼼机房实验⼀⼀、实验题⽬把正切函数x tan 和反正切函数x arctan 的图形及其⽔平渐近线2/,2/ππ=-=y y 和直线x y =⽤不同的线型画在同⼀个坐标系内.⼆、实验⽬的和意义利⽤数形结合的⽅法,研究正切函数与反正切函数图像的关系,及各⾃的定义域、单调性和图形变化趋势。
三、程序设计p1 = Plot[ArcTan[x], {x, -5, 5},PlotStyle -> RGBColor[1, 0, 0]];p2 = Plot[Tan[x], {x, -4, 4}, PlotStyle -> RGBColor[0, 1, 0]];p3 = Plot[{-Pi/2, Pi/2}, {x, -2Pi, 2Pi}, PlotStyle -> RGBColor[0, 0, 1]]; p4 = Plot[x, {x, -5, 5}, PlotStyle -> RGBColor[1, 0, 1]]; Show[p1, p2, p3, p4, AspectRatio -> 1]四、程序运⾏结果π/2},且在(κπ- π/2, κπ+ π/2)x 趋近于正负⽆穷时,y 分别趋近于对称。
⾼等数学实验报告实验⼈员:院(系)信息科学与⼯程学院学号_04010409___姓名__郑敏升_____ 实验地点:计算机中⼼机房实验⼀⼀、实验题⽬分别⽤ParametricPlot和PolarPlot两种命令, 作出五叶玫瑰线θ5=r的图形.sin4⼆、实验⽬的和意义通过使⽤两种不同的命令做出五叶玫瑰线的图像,⽐较其不同,并根据画出的图像观察五叶玫瑰线的性质。
三、程序设计ParametricPlot[{4*Sin[5θ]*Cos[θ],4*Sin[5θ]*Sin[θ]},{θ,0, 2Pi},AspectRatio→1] PolarPlot[4*Sin[5θ],{θ,0,2Pi}]四、程序运⾏结果五、结果的讨论和分析由程序可知:PolarPlot⽐ParametricPlot更有效率,且观察图像可以发现:图像有五叶,关于y轴对称,每⼀叶完全相同,其余四叶可由任意⼀叶旋转变换得到。
高数实验报告

引言概述:本文是关于高数实验的报告,主要通过引言概述、正文内容、总结等部分对高数实验进行详细阐述。
高数实验是通过实际操作和观察,探索和应用数学中的基本原理和概念。
它有助于加深对高数理论的理解、提高数学思维和解决问题的能力。
正文内容:一、实验目的本次高数实验的目的是通过实际操作,加深对数学概念和原理的理解,并掌握基本数学实验的方法和技巧,提高数学思维和解决问题的能力。
二、实验材料和仪器本次实验所需材料和仪器包括实验记录表、计算器、尺子、直角尺、量角器等。
三、实验一:极限的探究1.设立实验任务:研究函数f(x)在某点a的极限。
2.实验步骤:a.确定函数f(x)和点a的取值范围,并在实验记录表中记录下来。
b.设定x的取值逐渐接近a的过程,并依次计算f(x)的值。
c.绘制出随着x的接近程度增加,f(x)的变化趋势图,并通过图像分析来研究f(x)在点a的极限。
3.实验结果和讨论:a.根据实验数据绘制的图像分析可以看出,当x接近a的时候,f(x)的值逐渐趋近于某一数值,这个数值就是f(x)在点a的极限。
b.实验结果和数学概念相符,证明了极限的定义和性质。
四、实验二:导数的计算1.设立实验任务:求函数f(x)在某点的导数。
2.实验步骤:a.确定函数f(x)和点a的取值范围,并在实验记录表中记录下来。
b.通过逐渐缩小x的取值范围,计算f(x)在点a的导数值。
c.通过实验数据绘制出f(x)在点a处导数的变化趋势图,并通过图像分析来研究f(x)在点a的导数。
3.实验结果和讨论:a.根据实验结果和图像分析可以得出结论,f(x)在点a的导数值表示了函数在该点的斜率。
b.实验结果和导数的定义和性质相符,进一步验证了导数的计算方法和应用。
五、实验三:定积分的求解1.设立实验任务:求函数f(x)在某区间的定积分。
2.实验步骤:a.确定函数f(x)和求解区间的取值范围,并在实验记录表中记录下来。
b.将求解区间分成若干个小区间,计算出每个小区间的面积。
高等数学实验报告

高等数学实验报告实验目的:本次实验旨在通过实际操作,加深学生对高等数学中一些重要概念和定理的理解,并培养学生分析和解决实际问题的能力。
实验原理:本实验主要涵盖了高等数学中的微积分部分内容,包括极限、导数、积分等。
实验仪器和材料:1. 笔记本电脑2. 数学软件3. 实验数据表格实验步骤:1. 在计算机上下载并安装数学软件。
2. 打开软件,并按照实验要求选择相应的数学题目。
3. 根据题目要求,运用软件进行计算,并将结果记录在实验数据表格中。
4. 对于给定的函数,求其极限、导数和积分。
5. 分析并解释计算结果,得出结论。
实验结果与讨论:通过本次实验,我们掌握了一些重要的数学概念和计算方法。
以下是实验结果的总结:1. 极限:通过计算不同函数的极限,我们发现当自变量趋于某个特定值时,函数的取值趋于一个确定的值或趋于无穷大。
这一概念在解决实际问题中具有重要意义,可以用于分析函数的增减性、收敛性等。
2. 导数:对于给定的函数,我们求得了其导数,并分析了导数的意义。
导数表示了函数在特定点的变化率,可以用于求解最值、判断函数图像的凹凸性等问题。
3. 积分:通过计算不同函数的积分,我们掌握了积分的计算方法和应用。
积分可以用于求解曲线下的面积、求解有限空间内的体积等问题。
根据实验结果,我们可以得出以下结论:1. 数学是一门既抽象又实际的学科,高等数学为我们提供了一种更深入、更精确的问题描述和解决方法。
2. 实际问题中的数学模型可以通过符号计算软件进行数值计算和模拟,从而得到更准确的结果和结论。
3. 数学实验可以锻炼我们的计算和分析能力,培养我们解决实际问题的思维方式。
结论:通过本次实验,我们深入学习了高等数学中的一些重要概念和计算方法,并应用这些知识解决了实际问题。
实验结果表明,数学实验具有重要的教学和科研价值,并能够提高学生的数学素养和解决实际问题的能力。
参考文献:[1] 高等数学课程教学大纲(试行). (2017).[2] Stewart, J. (2015). Calculus: Early Transcendentals. Cengage Learning.。
东大2024高数实验报告(二)2024

东大2024高数实验报告(二)引言概述:本文是关于东大2024高数实验报告(二)的文档,旨在详细介绍实验过程、实验结果以及相关分析。
本次实验主要涉及高数实验的第二部分,通过理论和实际操作,探索了相关概念和计算方法。
正文:一、实验目的\t1.1 掌握函数的空间曲线的绘制方法;\t1.2 理解函数的周期性和奇偶性;\t1.3 学习利用反函数求解方程;\t1.4 进一步熟悉函数的极限和连续性;\t1.5 学习使用泰勒级数近似计算函数值。
二、实验方法\t2.1 准备实验仪器和材料;\t2.2 绘制函数的空间曲线;\t2.3 分析函数的周期性和奇偶性;\t2.4 求解方程的反函数;\t2.5 进行函数极限和连续性的实验;\t2.6 使用泰勒级数近似计算函数值。
三、实验结果\t3.1 绘制了不同函数的空间曲线并进行了详细分析;\t3.2 确定了函数的周期性和奇偶性,得出相应结论;\t3.3 成功求解了多个方程的反函数,并验证了其正确性;\t3.4 实验得出了函数的极限和连续性的结果,并与理论知识进行了比较;\t3.5 利用泰勒级数近似计算了多个函数值,并与准确值进行了对比。
四、分析和讨论\t4.1 通过绘制空间曲线,我们更直观地理解了函数的变化规律;\t4.2 通过分析周期性和奇偶性,我们对函数的对称性有了更深入的认识;\t4.3 反函数的求解为我们解方程提供了另一种方法,提高了问题的解决效率;\t4.4 实验结果与理论知识的一致性表明,我们掌握了函数的极限和连续性的基本概念;\t4.5 泰勒级数的使用使我们更方便地近似计算各种函数值,提高了计算的准确性。
五、总结\t通过本次实验,我们进一步学习和巩固了高数实验的相关知识和技能。
通过实践,我们熟练掌握了函数的空间曲线绘制方法,理解并应用了周期性和奇偶性的概念,掌握了反函数的求解方法,加深了对函数的极限和连续性的理解,学会了使用泰勒级数近似计算函数值。
这些实验结果对于我们今后的学习和应用中都具有重要的指导作用。
东南大学 高数A下 实验报告

高数实验报告学号: 姓名:数学实验一一、实验题目:(实验习题7-3)观察二次曲面族kxy y x z ++=22的图形。
特别注意确定k 的这样一些值,当k 经过这些值时,曲面从一种类型变成了另一种类型。
二、实验目的和意义1. 学会利用Mathematica 软件绘制三维图形来观察空间曲线和空间曲线图形的特点。
2. 学会通过表达式辨别不同类型的曲线。
三、程序设计这里为了更好地分辨出曲线的类型,我们采用题目中曲线的参数方程来画图,即t t kr r z sin cos 22+=输入代码: ParametricPlot3D[{r*Cos[t],r*Sin[t],r^2+ k*r^2*Cos[t]*Sin[t]}, {t, 0, 2*Pi}, {r, 0, 1},PlotPoints -> 30] 式中k 选择不同的值:-4到4的整数带入。
四、程序运行结果k=4:k=3:k=2:k=1:k=0:k=-1:k=-2:k=-3:k=-4:五、结果的讨论和分析k取不同值,得到不同的图形。
我们发现,当|k|<2时,曲面为椭圆抛物面;当|k|=2时,曲面为抛物柱面;当|k|>2时,曲面为双曲抛物面。
数学实验二一、实验题目一种合金在某种添加剂的不同浓度下进行实验,得到如下数据:2+y+=cxabx法确定系数a,b,c,并求出拟合曲线二、实验目的和意义1.练习使用mathematic进行最小二乘法的计算2.使用计算机模拟,进行函数的逼近三、程序设计x={10.0,15.0,20.0,25.0,30.0};y={27.0,26.8,26.5,26.3,26.1};xy=Table[{x[[i]],y[[i]]},{i,1,5}];q[a_,b_,c_]:=Sum[(a+b*x[[i]]+c*x[[i]]*x[[i]]-y[[i]])^2,{i,1 ,5}];Solve[{D[q[a,b,c],a]0,D[q[a,b,c],b]0,D[q[a,b,c],c]0}, {a,b,c}]A={a,b,c}/.%;a=A[[1,1]];b=A[[1,2]];c=A[[1,3]];data=Table[{x[[i]],y[[i]]},{i,1,5}];t1=ListPlot[data,PlotStyle PointSize[0.02],DisplayFunction Identity];f[x_]:=a+b*x+c*x*x;t2=Plot[f[x],{x,0,30},DisplayFunction Identity];Show[t1,t2,DisplayFunction$DisplayFunction]四、程序运行结果{{a 27.56,b -0.0574286,c0.000285714}}五、结果的讨论和分析从图中可以看出,使用最小二乘法可以快捷地确定经验公式的系数,并且得出的拟合曲线可以很好地逼近实验数据。
高数实验报告

高等数学数学实验报告实验一一、实验题目观察数列极限二、实验目的和意义通过作图观察数列极限:n趋向于无穷时,(1+1/n)^n三、计算公式四、程序设计data = Table[(1 + 1/i)^i, {i, 30}];ListPlot[data, PlotRange -> {2, 3}, PlotStyle -> PointSize[0.018]]五、程序运行结果六、结果的讨论和分析通过图像观察出数列趋向于重要极限e实验二一、实验题目一元函数图形及其性态二、实验目的和意义制作函数y=sincx的图形动画,并观察参数c对函数图形的影响三、计算公式请写出在程序中所需要的计算公式。
比如定积分的数值计算中,如用梯形法计算的,请描述梯形法的公式。
四、程序设计Animate[Plot[Sin[c x], {x, 0, 10}, PlotRange -> {-1, 1}], {c, -1, 4, 1/3}]五、程序运行结果0.51.00.51.01.00.5六、结果的讨论和分析通过图像观察出常数c 影响y=sincx 的周期和频率,函数周期为2Pi/c,频率为c/2Pi.实验三 一、实验题目泰勒公式与函数逼近 二、实验目的和意义对y=cosx 分别在[-Pi,Pi],[-2Pi,2Pi]上进行n 阶泰勒展开 三、计算公式请写出在程序中所需要的计算公式。
比如定积分的数值计算中,如用梯形法计算的,请描述梯形法的公式。
四、程序设计(1)t = Table[Normal[Series[Cos[x], {x, 0, i}]], {i, 0, 12, 2}]; PrependTo[t, Cos[x]];Plot[Evaluate[t], {x, -Pi, Pi}](2)For[i = 0, i <= 10, a = Normal[Series[Cos[x], {x, 0, i}]]; Plot[{a, Cos[x]}, {x, -Pi, Pi},PlotStyle -> {RGBColor[0, 0, 1], RGBColor[1, 0, 0]}]; i = i + 2] (3)For[ =6, ≤16, =Normal[Series[Cos[ ],{ ,0, ,Cos[ ]},{ ,−2Pi,2Pi}, PlotStyle→{RGBC olor[0,0,1],RGBColor[1,0,0]}]; = +2](4)tt[x0_]:=Normal[Series[Cos[ ],{ ,x0,6}]];gs0=tt[0];gs3=tt[3];gs6=tt[6];Plot[{Cos [ ],gs0,gs3,gs6},{ ,−3Pi,3Pi},PlotRange→{−2,2},PlotStyle→{RGBColor[0,0,1],RGB Color[1,0,1],RGBColor[1,0,0],RGBColor[0,1,0]}] (5) f[x_]:=Sin[x 2];a=0;b=0.5Pi;m2=N[f''[0.0000635627]];dalta=10^(-4);n0=90;t[n_]:=(b-a)/n×((f[a]+f[b])/2+Sum[f[a+i×(b-a)/n],{i,1,n-1}]);Do[Print[n," ",N[t[n]]];If[(b-a)^3/(12n^2)×m2<dalta,Break[],If[n n0,Print["fail"]]],{n,n0}](6) f[x_]:=Sin[x 2];a=0;b=0.5Pi;m4=N[f''''[x→1.68676]];dalta=10^(-4);k0=100; p[k_]:=(b-a)/(6k)×(f[a]+f[b]+2Sum[f[a+i×(b-a)/(2k)],{i,2,2k-2,2}]+ 4Sum[f[a+i×(b-a)/(2k)],{i,1,2k-1,2}]);Do[Print[k," ",N[p[k]]];If[(b-a)^5/(180×(2k)^4)×m4<dalta,Break[],If[k n0,Print["fail"]五、程序运行结果(1)六、结果的讨论和分析步骤(1)(2)中为观察函数y=cosx在x=0处的泰勒展开,可以看出cos x 在x=0展开的10阶泰勒公式与cos x 逼近程度很高.步骤(3)过大显示区间范围,观察偏离x=0时泰勒公式对函数的逼近情况.,可以看出阶数越高,吻合程度越好,如cos x 的18阶泰勒展开式.步骤(4)固定阶数n=6,观察对函数的逼近情况.,可知可知,对于一确定的阶数,只在展开点附近的一个局部范围内才能较好地吻合.实验四定积分的近似计算一、实验题目观察数列极限二、实验目的和意义分别用梯形法、抛物线法计算定积分的近似值(精确到0.0001)三、计算公式四、程序设计<1>梯形法输入如下命令:f[x_]:=Sin[x^2];a=0;b=Pi/2;m2=N[f''[0]];dalta=0.0001;n0=100;t[n_]:=(b-a)/n*((f[a]-f[b])/2+Sum[f[a+i*(b-a)/n],{i,1,n-1}]);Do[Print[n,"",N[t[n]]];If[(b-a)^3/(12n^2)*m2<dalta,五、程序运行结果运行输出结果为:1__-0.490297 2__0.20918 3__0.444154 4__0.551059 5__0.611654 6__0.650588 7__0.67769 8__0.697632 9__0.712916 10__0.725 11__0.734794 12__0.742891 13__0.749696 14__0.75549615__0.760498 16__0.764856 17__0.768687 18__0.7720819__0.775107 20__0.777824 21__0.780277 22__0.78250123__0.784527 24__0.786382 25__0.788085 26__0.78965427__0.791106 28__0.792451 29__0.793703 30__0.79486931__0.795959 32__0.79698 33__0.797938 34__0.79883935__0.799687 36__0.800488 37__0.801245 38__0.80196239__0.802641 40__0.803286 41__0.803899 42__0.80448343__0.805039 44__0.805569 45__0.806076 46__0.80656147__0.807024 48__0.807468 49__0.807894 50__0.80830351__0.808695 52__0.809072 53__0.809435 54__0.80978455__0.810121 56__0.810445 57__0.810758 58__0.8110659__0.811351 60__0.811633 61__0.811905 62__0.81216963__0.812424 64__0.812671 65__0.812911 66__0.81314367__0.813368 68__0.813587 69__0.813799 70__0.81400571__0.814205 72__0.8144 73__0.814589 74__0.81477375__0.814952 76__0.815126 77__0.815296 78__0.81546279__0.815623 80__0.81578 81__0.815933三、计算公式四、程序设计<2>抛物线法输入如下命令:f[x_]:=Sin[x^2];p[k_]:=(b-a)/(6k)*(f[a]+f[b]+2Sum[f[a+i*(b-a)/(2k)],{i,2,2k-2,2}]+4Sum[f[a+i*(b-a)/(2k)],{i,2,2k-1,2}]);Do[Print[k,"",N[p[k]]];If[(b-a)^5/(180*(2k)^4)*m4<delta,五、程序运行结果运行输出结果为:1_ _0.163432 2_ _0.536045 3_ _0.662064 4_ _0.7144925_ _0.7424 6_ _0.759543 7_ _0.77108 8_ _0.7793489_ _0.785552 10_ _0.790373 11_ _0.794224 12_ _0.79736813_ _0.799983 14_ _0.802191 15_ _0.80408 16_ _0.805714 17_ _0.807142 18_ _0.808399 19_ _0.809514 20_ _0.810511 21_ _0.811406 22_ _0.812216 23_ _0.81295 24_ _0.813621 25_ _0.814234 26_ _0.814798 27_ _0.815318 28_ _0.815799 29_ _0.816245 30_ _0.81666 31_ _0.817047 32_ _0.817409 33_ _0.817748 34_ _0.818066 35_ _0.818365 36_ _0.818647 37_ _0.818913 38_ _0.819165 39_ _0.819403 40_ _0.819629 41_ _0.819844 42_ _0.820048 43_ _0.820242 44_ _0.820427 45_ _0.820603 46_ _0.820772 47_ _0.820933 48_ _0.821088 49_ _0.821235 50_ _0.821377 51_ _0.821513 52_ _0.821644 53_ _0.821769 54_ _0.82189 55_ _0.822006 56_ _0.822119 57_ _0.822227 58_ _0.822331 59_ _0.822431 60_ _0.822528 61_ _0.822622 62_ _0.822713 63_ _0.822801 64_ _0.822886 65_ _0.822968 66_ _0.823048 67_ _0.823125 68_ _0.8232 69_ _0.823273 70_ _0.823344 71_ _0.823412 72_ _0.823479 73_ _0.823544 74_ _0.823607 75_ _0.823668 76_ _0.823728 77_ _0.823786 78_ _0.823843 79_ _0.823898 80_ _0.823952 81_ _0.824004 82_ _0.824055 83_ _0.824105 84_ _0.824154 85_ _0.824201 86_ _0.824247 87_ _0.824293 88_ _0.824337 89_ _0.82438 90_ _0.824422 91_ _0.824463 92_ _0.824504 93_ _0.824543 94_ _0.824582 95_ _0.82462 96_ _0.824657 97_ _0.824693 98_ _0.824728 99_ _0.824763 100_ _0.824797实验结论:六、结果的讨论和分析梯形法:从运行结果看,循环81次后时因达到精度要求结束循环,并得到积分的近似值为:0.815933。
高数 下 实验报告

高数下实验报告高数下实验报告引言:高等数学是大学数学的一门重要课程,对于理工科学生来说尤为重要。
本次实验旨在通过实际操作,帮助学生更好地理解和掌握高等数学的相关概念和方法。
本报告将详细介绍实验的目的、实验过程以及实验结果,并对实验中遇到的问题进行分析和讨论。
一、实验目的:本次实验的主要目的是通过实际操作,加深对高等数学中微分和积分的理解。
具体而言,包括以下几个方面:1. 熟悉微分和积分的基本概念和运算法则;2. 掌握微分和积分的应用技巧,如求导、求不定积分等;3. 理解微分和积分的几何意义,如导数和曲线的切线、不定积分和曲线下的面积等。
二、实验过程:1. 实验准备:在实验开始前,我们需要准备一些必要的工具和材料。
首先,我们需要一台计算机,并安装相应的数学软件,如MATLAB或Mathematica。
其次,我们需要准备一些实验用纸和笔,用于记录实验过程和结果。
2. 实验步骤:(这里可以根据实际实验情况,具体描述实验步骤)三、实验结果:在实验过程中,我们得到了一些实验结果,并进行了相应的数据分析。
以下是实验中的一些典型结果:1. 通过对一些简单函数进行求导,我们发现导数可以表示函数的变化率。
例如,对于函数y=x^2,我们求得导数dy/dx=2x,表示函数在任意点x处的斜率为2x。
2. 通过对一些简单函数进行积分,我们发现不定积分可以表示曲线下的面积。
例如,对于函数y=x^2,我们求得不定积分∫x^2dx=(1/3)x^3,表示曲线y=x^2与x轴之间的面积为(1/3)x^3。
3. 通过对一些复杂函数进行求导和积分,我们进一步理解了微分和积分的运算法则和应用技巧。
四、问题分析与讨论:在实验过程中,我们也遇到了一些问题,并进行了相应的分析和讨论。
以下是一些典型问题及其解决思路:1. 如何选择合适的函数进行求导和积分?在实验中,我们可以选择一些简单的函数,如多项式函数、三角函数等,进行求导和积分。
这样既能够加深对微分和积分的理解,又能够掌握求导和积分的基本技巧。
高级数学实验报告

实验名称:非线性动力系统的研究与应用实验目的:1. 深入理解非线性动力系统的基本理论。
2. 掌握非线性动力系统的数值模拟方法。
3. 分析典型非线性动力系统的性质和行为。
4. 应用非线性动力系统理论解决实际问题。
实验时间:2023年3月15日实验地点:计算机实验室实验仪器:计算机、MATLAB软件实验内容:一、非线性动力系统基本理论1. 非线性微分方程的基本形式2. 稳定性和不稳定性分析3. 分岔和混沌现象二、非线性动力系统的数值模拟1. 使用MATLAB软件实现非线性微分方程的数值解法2. 比较不同数值方法的优缺点3. 对数值解的稳定性进行分析三、典型非线性动力系统的分析1. 莱斯利系统2. 莱顿-杰弗里斯系统3. 龙飞系统四、非线性动力系统理论的应用1. 气候变化模拟2. 生物种群动力学3. 金融市场分析实验步骤:1. 阅读相关文献,了解非线性动力系统的基本理论。
2. 使用MATLAB软件编写程序,实现非线性微分方程的数值解法。
3. 分析典型非线性动力系统的性质和行为,绘制相图、Poincaré映射等。
4. 对数值解的稳定性进行分析,比较不同数值方法的优缺点。
5. 应用非线性动力系统理论解决实际问题,如气候变化模拟、生物种群动力学等。
实验结果与分析:一、非线性微分方程的数值解法通过MATLAB软件,我们实现了以下几种数值解法:1. Euler方法2. Runge-Kutta方法3. Adams-Bashforth方法经过比较,我们发现Runge-Kutta方法在数值稳定性方面表现较好,适用于大多数非线性微分方程的数值解。
二、典型非线性动力系统的分析1. 莱斯利系统:通过绘制相图和Poinca ré映射,我们发现莱斯利系统存在稳定的周期解和混沌现象。
2. 莱顿-杰弗里斯系统:通过分析系统的稳定性,我们发现莱顿-杰弗里斯系统在参数空间内存在分岔现象,导致系统行为的不确定性。
3. 龙飞系统:通过绘制相图和Poincaré映射,我们发现龙飞系统存在稳定的周期解和混沌现象。
高数(上)实验报告

一、实验题目
泰勒公式与函数逼近
二、实验目的和意义
可以看出泰勒公式与原函数的比较
三、计算公式
L计
For[i=1,i11,a=Normal[Series[Log[Cos[x^2]+Sin[x]],{x,0,i}]];Plot[{a,Log[Cos[x^2]+Sin[x]]},{x,-Pi/4,Pi/4},PlotStyle{RGBColor[0,0,1],RGBColor[1,0,0]}];i=i+2]
三、计算公式
,n=1,2,3……
四、程序设计
五、程序运行结果
六、结果的讨论和分析
通过绘图,发现f(n)= 在n→+∞时,函数值无限靠近2.7左右的某一数值(e≈2.7),可判断数列 在n→+∞时,必收敛.
实验二
一、实验题目
制作函数y=sin cx图形动画并观察参数c对函数图形的影响。
二、实验目的和意义
高等数学数学实验报告
实验人员:院(系)机械工程学院学号_02A10314_姓名褚东宇
实验地点:计算机中心机房
实验一
一、实验题目
通过作图,观察重要极限: .
二、实验目的和意义
利用数形结合的方法观察数列极限,可从点图上看出数列的收敛性及近似得出数列的收敛值;通过编程可以输出数列的任意多项值,以此来得到数列的收敛性。
五、程序运行结果
六、结果的讨论和分析
随n值增大,泰勒公式的函数越来越趋向于原函数
掌握图形动画的应用,通过图形的变化找出参数对函数的影响。
三、计算公式
Sin cx
四、程序设计
Do[Plot[Sin[c*x],{x,-Pi,Pi},PlotRange{-1,1}],{c,1,3,1/2}]
高数矩阵实验报告

一、实验目的1. 理解矩阵的基本概念及其在数学和科学中的应用。
2. 掌握Matlab中矩阵的创建、运算及可视化方法。
3. 通过实验加深对矩阵乘法、逆矩阵、行列式等概念的理解。
二、实验内容1. 矩阵的创建与基本运算(1)创建矩阵:使用Matlab创建一个3x3的矩阵,元素分别为1到9。
```matlabA = [1 2 3; 4 5 6; 7 8 9];```(2)矩阵的加法与减法:计算矩阵A与自身相加、相减的结果。
```matlabA_add = A + A;A_sub = A - A;```(3)矩阵的乘法:计算矩阵A与自身相乘的结果。
```matlabA_mul = A A;```2. 逆矩阵与行列式(1)求逆矩阵:计算矩阵A的逆矩阵。
```matlabA_inv = inv(A);```(2)计算行列式:计算矩阵A的行列式。
```matlabdet_A = det(A);```3. 矩阵的特征值与特征向量(1)计算特征值:计算矩阵A的特征值。
```matlabeigenvalues = eig(A);```(2)计算特征向量:计算矩阵A的特征向量。
```matlabeigenvectors = eig(A);```4. 矩阵的求导与积分(1)求导:计算矩阵A的导数。
```matlabA_diff = diff(A);```(2)积分:计算矩阵A的积分。
```matlabA_int = int(A);```三、实验结果与分析1. 矩阵的创建与基本运算通过实验,我们成功创建了矩阵A,并进行了加法、减法和乘法运算。
结果表明,矩阵运算符合数学规律。
2. 逆矩阵与行列式通过实验,我们成功计算了矩阵A的逆矩阵和行列式。
结果表明,当矩阵可逆时,其逆矩阵存在,且逆矩阵与原矩阵相乘等于单位矩阵。
3. 矩阵的特征值与特征向量通过实验,我们成功计算了矩阵A的特征值和特征向量。
结果表明,特征值和特征向量反映了矩阵的内在性质,在解决实际问题中具有重要意义。
高等数学数学实验报告(两篇)2024

引言概述:高等数学数学实验报告(二)旨在对高等数学的相关实验进行探究与研究。
本次实验报告共分为五个大点,每个大点讨论了不同的实验内容。
在每个大点下,我们进一步细分了五到九个小点,对实验过程、数据收集、数据分析等进行了详细描述。
通过本次实验,我们可以更好地理解高等数学的概念和应用。
正文内容:一、微分方程实验1.利用欧拉法求解微分方程a.介绍欧拉法的原理和步骤b.详细阐述欧拉法在实际问题中的应用c.给出具体的实例,展示欧拉法的计算步骤2.应用微分方程建立模型求解实际问题a.介绍微分方程模型的建立方法b.给出一个具体的实际问题,使用微分方程建立模型c.详细阐述模型求解步骤和结果分析3.使用MATLAB求解微分方程a.MATLAB求解微分方程的基本语法和函数b.给出一个具体的微分方程问题,在MATLAB中进行求解c.分析结果的准确性和稳定性二、级数实验1.了解级数的概念和性质a.简要介绍级数的定义和基本概念b.阐述级数收敛和发散的判别法c.讨论级数的性质和重要定理2.使用级数展开函数a.介绍级数展开函数的原理和步骤b.给出一个函数,使用级数展开进行近似计算c.分析级数近似计算的精确度和效果3.级数的收敛性与运算a.讨论级数收敛性的判别法b.介绍级数的运算性质和求和法则c.给出具体的例题,进行级数的运算和求和三、多元函数极值与最值实验1.多元函数的极值点求解a.介绍多元函数的极值点的定义和求解方法b.给出一个多元函数的实例,详细阐述求解过程c.分析极值点对应的函数值和意义2.多元函数的条件极值与最值a.讨论多元函数的条件极值的判定法b.给出一个具体的多元函数,求解其条件极值和最值c.分析条件极值和最值对应的函数值和意义3.利用MATLAB进行多元函数极值与最值的计算a.MATLAB求解多元函数极值与最值的基本语法和函数b.给出一个多元函数的具体问题,在MATLAB中进行求解c.分析结果的准确性和可行性四、曲线积分与曲面积分实验1.曲线积分的计算方法与应用a.介绍曲线积分的定义和计算方法b.给出一个具体的曲线积分问题,详细阐述计算过程c.分析曲线积分结果的几何意义2.曲线积分的应用举例a.讨论曲线积分在实际问题中的应用b.给出一个实际问题,使用曲线积分进行求解c.分析曲线积分结果的实际意义和应用价值3.曲面积分的计算方法与应用a.介绍曲面积分的定义和计算方法b.给出一个具体的曲面积分问题,详细阐述计算过程c.分析曲面积分结果的几何意义五、空间解析几何实验1.空间曲线的参数方程表示与性质a.介绍空间曲线的参数方程表示和性质b.给出一个具体的空间曲线,转化为参数方程表示c.分析参数方程对应的几何意义和性质2.平面与空间直线的位置关系a.讨论平面与空间直线的位置关系的判定方法b.给出一个具体的平面与空间直线的问题,判定其位置关系c.分析位置关系对应的几何意义和应用实例3.空间直线与平面的夹角和距离计算a.介绍空间直线与平面的夹角和距离的计算方法b.给出一个具体的空间直线和平面,计算其夹角和距离c.分析夹角和距离计算结果的几何意义总结:通过本次高等数学数学实验报告(二),我们深入了解了微分方程、级数、多元函数极值与最值、曲线积分、曲面积分以及空间解析几何的相关概念和应用。
东南大学高等数学A(上册)数学实验报告
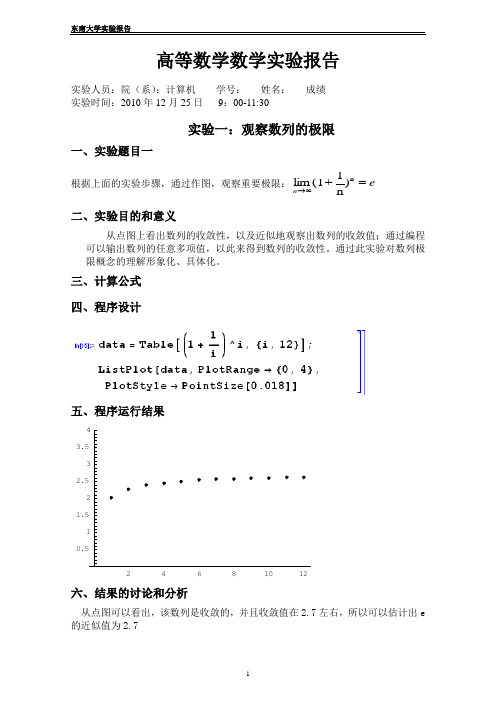
高等数学数学实验报告实验人员:院(系):计算机 学号: 姓名: 成绩_________ 实验时间:2010年12月25日 9:00-11:30实验一:观察数列的极限一、实验题目一根据上面的实验步骤,通过作图,观察重要极限:e n =∞→n)n1 + (1lim 二、实验目的和意义从点图上看出数列的收敛性,以及近似地观察出数列的收敛值;通过编程可以输出数列的任意多项值,以此来得到数列的收敛性。
通过此实验对数列极限概念的理解形象化、具体化。
三、计算公式 四、程序设计五、程序运行结果六、结果的讨论和分析从点图可以看出,该数列是收敛的,并且收敛值在2.7左右,所以可以估计出e 的近似值为2.7实验二:一元函数图形及其性态一、实验题目二制作函数y=sin cx的图形动画,并观察参数c对函数图形的影响二、实验目的和意义通过作图形动画,观察参数c对函数性态(周期,最值,奇偶,凹凸)的影响,从而对函数的理解形象化、具体化。
三、计算公式sin(-x)=sin(x)sin(x+2π)=sin(x)sin(x+π)=-sin(x)四、程序设计五、程序运行结果六、结果的讨论和分析当参数|c|越大,函数的周期越小,并且符合T=2π/|c|;参数c 的变化并不影响函数的最值,奇偶性(当p=0时,函数是既奇又偶函数),和凹凸性。
参数c 的正负决定函数是在某一确定周期内的正负值实验三:泰勒公式和函数逼近一、实验题目三作出函数sinx)ln(cosx y 2+= )44(-ππ≤≤x 函数图形和泰勒展开式(选取不同的0x 和n 值)图形,并将图形进行比较.二、实验目的和意义下面我们利用Mathematica 计算函数)(x f 的各阶泰勒多项式,并通过绘制曲线图形,来进一步掌握泰勒展开与函数逼近的思想。
三、计算公式四、程序设计0x =0时)(n k nk k x x o x x k x f x f x f ||)(!)()()(0010)(0-+-+=∑=0x =2时0x =4时0x =6时五、程序运行结果六、结果的讨论和分析通过上面六幅图,从图中可以观察到泰勒多项式与函数图形的重合与分离情况,显然在]4.0,4.0[ππ-范围内,当阶数为4-6时两个函数的图形已经基本上吻合了,。
高等数学实验报告 (2)

高等数学实验报告引言高等数学作为大学数学的一门基础课程,其实验内容十分重要。
本文将针对高等数学实验进行详细报告,通过实验分析和计算,进一步加深对高等数学理论的理解和掌握。
实验目的本次实验的目的是让学生掌握应用高等数学的知识和技巧,通过实验求解数学问题,巩固理论知识。
实验内容本次实验分为以下几个部分:1. 极限与连续通过实验验证极限和连续的相关性质,探究函数极限的计算方法,并通过实验加深对函数连续性的理解。
2. 导数与微分通过实验分析函数的导数和微分,验证微分中的等式,探究函数的单调性和极值,并通过实验加深对导数的理解。
3. 积分与不定积分通过实验求解函数的积分和不定积分,验证积分规则,分析函数的定积分,加深对积分的理解和应用。
4. 二元函数与偏导数通过实验分析二元函数的性质和偏导数的计算方法,探究偏导数在多元函数中的应用,并通过实验加深对多元函数的理解。
实验步骤与数据分析在每个实验部分,我们按照以下步骤进行实验,并对结果进行数据分析。
1. 实验步骤•阅读实验指导书,了解实验要求和内容;•在实验室中,根据实验内容准备实验所需的工具和材料;•按照实验步骤进行实验,进行数据记录和计算;•将实验结果整理并进行分析。
2. 数据分析通过实验得到的数据,我们进行以下分析和计算: - 对于极限和连续的实验,我们可以通过计算和绘制函数图像验证实验结果; - 对于导数和微分的实验,我们可以通过计算导数和微分系数来验证实验结果; - 对于积分和不定积分的实验,我们可以通过计算定积分和不定积分来验证实验结果; - 对于二元函数和偏导数的实验,我们可以通过计算偏导数和绘制二元函数图像来验证实验结果。
实验结果与讨论根据实验步骤和数据分析,我们得出以下实验结果和结论: - 在极限和连续的实验中,通过实验验证了函数极限的性质和函数连续的条件; - 在导数和微分的实验中,通过实验验证了函数导数的计算方法和微分的等式; - 在积分和不定积分的实验中,通过实验验证了积分规则和定积分的计算方法; - 在二元函数和偏导数的实验中,通过实验验证了多元函数的性质和偏导数的计算方法。
大学高数实验课报告心得

大学高数实验课报告心得引言大学高等数学是一门基础性的数学课程,对于理工科学生来说尤为重要。
实验课是我们学习高等数学的一种有效方式,通过实际操作和观察,加深对数学知识的理解和应用能力的培养。
在本次大学高数实验课中,我学习了很多以前从未接触过的数学知识和相关实验技巧,感受到了数学的深奥与美妙。
实验一:函数与极限在第一次实验中,我们通过实际导入一些函数的数据,并绘制出函数的图形。
这个实验让我更直观地感受到函数在数学中的重要性。
我们探讨了一些常见的函数,如线性函数、二次函数和指数函数,并观察了它们的图像特点。
进一步地,我们通过调整函数的参数,比如平移、缩放和翻转等操作,来观察函数图像的变化。
这个实验让我意识到函数图像与函数式的密切关系。
研究函数图像不仅可以加深对函数性质的理解,也有助于我们抽象化和推广数学模型,为进一步的学习打下了坚实的基础。
实验二:导数与微分在第二次实验中,我们学习了导数与微分。
导数是高等数学中的重要概念,它描述了函数在某一点的变化率。
通过实验观察和数据计算,我们了解了导数的几何意义和实际应用。
我们通过实验探讨了一些常见函数的导数,如常数函数、幂函数和三角函数。
通过实验数据的计算,我们得到了各个函数导数的近似值,并观察了导数随着自变量的变化而变化的规律。
这个实验不仅加深了我对导数概念的理解,也让我明白了导数与函数图像的密切关系。
通过导数的实验研究,我还了解到导数可以用于判断函数的单调性和极值问题。
导数的应用广泛而且重要,它在自然科学和工程技术中有着深远的意义。
我对导数的学习和实验研究让我更深刻地感受到数学与现实生活的紧密联系。
实验三:积分与不定积分在第三次实验中,我们学习了积分与不定积分。
积分是高等数学中一个重要的概念,它描述了函数在一定区间上的累积效应。
通过实验和计算,我们了解了积分与函数面积、长度和质量等实际问题的关系。
我们通过实验研究了一些常见函数的不定积分,探讨了不定积分的基本性质和计算方法。
高等数学实验报告

高等数学实验报告
实验题目:求解非齐次线性方程组
实验目的:通过实验掌握求解非齐次线性方程组的基本原理和方法,掌握矩阵变换的基本概念和方法。
实验原理:对于非齐次线性方程组Ax=b,A为系数矩阵,b为常数列向量,如果Ax0=0,其中x0为齐次线性方程组Ax=0的通解,则非齐次线性方程组的通解为x=x0+xp,其中xp为Ax=b的一组特解。
实验内容:以3x3线性方程组为例,进行求解非齐次线性方程组的操作。
步骤1:对系数矩阵A进行初等变换,将矩阵化为上三角矩阵U。
此时方程组变为Ux=y,其中y为常数向量b经过初等变换得到的向量。
步骤2:利用回带法(也称为消元法的“回退”版),求出Ux=y 的解。
将求解过程记录在表格中(见表1)。
表1 回带法求解过程表
步骤3:求出非齐次线性方程组的一个特解xp。
由于Ax0=0,
故有(A+B)x0=-b,其中B是一个由U矩阵无法得出的矩阵,A为
U矩阵。
将(A+B)x0=-b解出x0,特解xp=A^(-1)(-b-Bx0)即为一个
特解。
步骤4:得到非齐次线性方程组的通解为x=x0+xp,其中x0为
齐次线性方程组Ax=0的通解,xp为步骤3求解得到的一个特解。
实验结果:用本实验的方法,求解线性方程组
2x1+6x2+10x3=12
0x1+7x2+5x3=-3
0x1+0x2+3x3=7
得到的解为
x1=-1
x2=2
x3=7/3
实验结论:本实验所用方法确实能够求解非齐次线性方程组,并得出正确解。
经过本次实验,我掌握了求解非齐次线性方程组的基本原理和方法,以及矩阵变换的基本概念和方法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高等数学数学实验报告
实验人员:院(系)_土木工程学院___学号____05109225_姓名___唐涛____ 实验地点:计算机中心机房
实验一
一、实验题目
作图,观察极限。
二、实验目的和意义
极限是高等数学中最基本的概念之一,初学者往往理解不够准确。
利用图像,数形结合,可以便于初学者直观的认识极限。
加深对极限的了解。
三、计算公式
四、程序设计
五、程序运行结果
六、结果的讨论和分析
由图中可以看到极限无限靠近某个值。
观察比较方便,利于初学者的学习。
实验二
一、实验题目
制作函数y=sincx 的图形动画,观察c 对函数图形的影响。
二、实验目的和意义
本实验的目的是让同学熟悉数学软件Mathematica 所具有的良好的作图功能,并通过函数图形来认识函数,运用函数的图形来观察和分析函数的有关性态,建立数形结合的思想。
三、计算公式 y=sincx 四、程序设计
五、程序运行结果
-3
-2
-1
1
2
3
-1
-0.75
-0.5-0.250.25
0.50.751-3
-2
-1
1
2
3
-1
-0.75
-0.5-0.250.25
0.50.751-3
-2
-1
1
2
3
-1
-0.75
-0.5-0.250.25
0.50.751-3
-2
-1
1
2
3
-1
-0.75
-0.5-0.250.25
0.50.751
-3
-2-1123
-1
-0.75
-0.5
-0.25
0.25
0.5
0.75
1
六、结果的讨论和分析
由实验结果我们可以清楚地认识到参数c对函数图形的影响。
诸如改变了函数的周期.
实验三
一、实验题目
对f(x)=cosx求不同的x处的泰勒展开的表达形式。
二、实验目的和意义
通过mathematic软件作出的函数图形,观察泰勒公式展开的误差,进一步掌握泰勒展开与函数逼近的思想。
三、计算公式
f(x)=cosx
四、程序设计
(一)
(二)
(三)
(四)
五、程序运行结果
(一)
1
-3-2-1123
-1
-2
-3
-4
(二)
(三)
六、结果的讨论和分析
从本实验我们可以得到一些结论,函数的泰勒多项式对于函数的近似程度随着阶数的提高而提高,但对于任意确定的次数的多项式,它只在展开点附近的一个局部范围内才有较好的近似精确度。
实验四
一、实验题目
计算定积分02sinx2x
的黎曼和
二、实验目的和意义
在现实生活中许多实际问题遇到的定积分,被积函数往往不能用算是给出,而通过图像或表格给出;或虽然给出,但是要计算他的原函数却很困难,甚至原函数非初等函数。
本实验目的,就是为了解决这些问题,进行定积分近似计算。
三、计算公式
a b
f x x
b a
n k1
n
f a k10.5
b a
n
四、程序设计
f x_:Sin x2;a0;b
2
;n200;
s NSum f a k10.5b a
n
b a
n
,k,1,n
五、程序运行结果
02sinx2x
=0.828123
六、结果的讨论和分析
本实验求的近似值由给出的n的值的不同而不同。
给出的n值越大,得到的结果越接近准确的值,但因而电脑的计算量会变大。
而给出的n值越小,程序运行的结果越不精确。
因而,使用者可根据自己的实际情况确定n的取值。
实验五
一、实验题目
求在区间[2,5]上初值问题{ 的数值解,并求出数值解的图形。
二、实验目的和意义
在实际问题中,需要研究一些变动的量以及它们之间的关系,由于这些量是时刻变化的,因此他们之间的关系不能用简单的代数关系来表达,而要用微分方程来表示。
本实验中,我们求解一些简单常用的微分方程的方法,以及微分方程
的数值解的方法。
三、计算公式。
xy'x2ysinx10
四、程序设计
五、程序运行结果
{{y[x] -> InterpolatingFunction[{{2., 5.}}, <>][x]}}
感谢下载!
欢迎您的下载,资料仅供参考。
