三角函数和反三角函数图像性质、知识点总结
高考三角函数知识点总结

高考三角函数知识点总结一、基本概念和性质1.弧度制:单位圆上的弧所对应的圆心角的大小定义为该弧的弧度。
1弧度等于圆周的1/2π。
2. 三角函数:正弦函数sin(x)、余弦函数cos(x)、正切函数tan(x)、余切函数cot(x)、正割函数sec(x)和余割函数csc(x)。
3.三角恒等式:包括同角三角恒等式、余角三角恒等式、反三角函数同角恒等式等。
4.周期性:正弦函数、余弦函数、正割函数和余割函数的周期都是2π;正切函数和余切函数的周期是π。
二、基本关系式1.正弦函数:在直角三角形中,正弦函数是指对于一个锐角三角形,三角形的对边和斜边的比值。
- sin(x) = a / c,其中a是对边,c是斜边。
- sin(x) = y / r,其中y是斜边在y轴上的投影,r是半径。
2.余弦函数:在直角三角形中,余弦函数是指对于一个锐角三角形,三角形的邻边和斜边的比值。
- cos(x) = b / c,其中b是邻边,c是斜边。
- cos(x) = x / r,其中x是斜边在x轴上的投影,r是半径。
3.正切函数:在直角三角形中,正切函数是指对于一个锐角三角形,三角形的对边和邻边的比值。
- tan(x) = a / b,其中a是对边,b是邻边。
- tan(x) = y / x,其中y是斜边在y轴上的投影,x是斜边在x轴上的投影。
4.余切函数:余切函数是正切函数的倒数。
- cot(x) = 1 / tan(x)。
5.正割函数:在直角三角形中,正割函数是指对于一个锐角三角形,三角形的斜边和邻边的比值的倒数。
- sec(x) = 1 / cos(x)。
6.余割函数:在直角三角形中,余割函数是指对于一个锐角三角形,三角形的斜边和对边的比值的倒数。
- csc(x) = 1 / sin(x)。
三、平面内角与弧度制之间的关系1.弧度制与度数之间的转换:-弧度=度数×π/180-度数=弧度×180/π2.弧度制下的角的性质:-一个圆上的圆心角的弧度数等于该弧所对应的弧的弧度数。
三角、反三角函数图像及性质与三角公式

三角、反三角函数图像(附:资料所有来自网络,仅对排版做了变动,以方便打印及翻阅,此中可能出现错误,阅者请自行注意。
)1.六个三角函数值在每个象限的符号:sin α· csc α cos α· sec α tan α· cot α2.三角函数的图像和性质:y=sinxy-5- 2 12-7o -4-3-2 -3 -2-1237 25223 422xy=cosxy-5- 2 1-32- -4-7-2 -3o 22-1yy=tanx3 3 7 2225 422yy=cotxx-3-- 22o322x-- 2o3 2x22函数y=sinxy=cosx y=tanxy=cotx{ x | x ∈R 且 { x | x ∈ R 且定义域R Rx ≠ k π+,k ∈ Z }x ≠ k π∈,kZ }2[ -1, 1] x=2k π+时[ -1,1]maxR2x=2k π时 y=1y max =1x=2k π +时π R无最大值值域无最大值y min =-1无最小值x=2k π- 时 y =-1无最小值min2周期性 周期为 2π 周期为 2π 周期为 π 周期为 π 奇偶性 奇函数偶函数 奇函数 奇函数在[ 2kπ-,2k π+]在[ 2kπ-π, 2kπ]在 (k π-,kπ+ )在 (k π, kπ+π)内上都是增函数;都是减函数2222在[ 2kπ,2kπ+π](k∈ Z)上都是增函数;在内都是增函数单一性2上都是减函数(k∈ Z)[ 2kπ+(k∈ Z),2k π+π]上23都是减函数 (k∈ Z)3.反三角函数的图像和性质:arcsinx arccosxarctanx名称反正弦函数y=sinx(x∈〔- ,〕的反函2 2定义数,叫做反正弦函数,记作 x=arsinyarcsinx 表示属于[- ,]理解22且正弦值等于x 的角定义域[ -1, 1]值域[ - ,]性22单一性在〔 -1, 1〕上是增质函数奇偶性arcsin(-x)=-arcsinx周期性都不是周期函数反余弦函数y=cosx(x∈〔0, π〕 )的反函数,叫做反余弦函数,记作x=arccosyarccosx 表示属于[ 0,π],且余弦值等于 x 的角[-1, 1][0,π]在[ -1,1]上是减函数arccos(-x)= π-arcc osxarccotx反正切函数反余切函数y=tanx(x∈ (-,y=cotx(x∈ (0, π ))的反函数,叫做2反余切函数,记2)的反函数,叫作 x=arccoty做反正切函数,记作x=arctanyarctanx 表示属于arccotx 表示属于(-, ),且正切值(0,π)且余切值等于 x 的角22等于 x 的角(-∞, +∞)(-∞, +∞)(-, )(0,π)2 2在 (-∞, +∞)上是增在(-∞,+∞)上是数减函数arctan(-x)=-arctanx arccot(-x)= π-arcc otxsin(arcsinx)=x(x∈cos(arccosx)=x(x tan(arctanx)=x(x ∈ R) cot(arccotx)=x(x[ -1,∈[-1,1] )arctan(tanx)=x∈ R)恒等式1] )arcsin(sinx)=x(x arccos(cosx)=x(xarccot(cotx)=x(x( x∈ (-, ))∈[-, ] )22∈[0, π] )∈ (0, π ))22互余恒等式arcsinx+arccosx= (x∈[ -1,1] )arctanx+arccotx=(X∈ R)22 arcsin(-x)=-arcsinx arccos(-x)=π-arccosxarctan(-x)=-arctanx arccot(-x)=π-arccotxarcsinx+arccosx=arctanx+arccotx=π/2sin(arcsinx)=cos(arccosx)=tan(arctanx)=cot(arccotx)=x当 x∈ [-π/2, π/2]arcsin(sinx)=xx∈[0,π]arccos(cosx)=xx∈(-π/2, π/2)arctan(tanx)=xx∈(0, π)arccot(cotx)=x三角公式总表abc1.正弦定理 :=== 2R ( R 为三角形外接圆半径)sin A sin B sin C2.余弦定理: a 2 =b 2 +c 2 -2bc cos Ab 2 =a 2 +c 2 -2ac cosB c 2 =a 2 +b 2 -2ab cosCb 2c 2 a 2cos A2bc⊿=12=1a h a = 2 ab sinC = a 2 sin B sin C b 2 =2sin A1bc sin A =1ac sin B =abc=2R 2 2 4Rsin Asin C c 2sin Asin B2sin B = =pr=2sinC2sin A sin B sin Cp( p a)( p b)( p c)(此中 p 1(a b c) , r 为三角形内切圆半径 )24.同角关系:⑴商的关系:① tg= sin= sinsec② ctgcos coscscsin cos③ sincostg④ sec1 tgcsccos⑤ cossinctg⑥ csc1 ctgsecsin⑵倒数关系: sin csc cos sec tg ctg 1⑶平方关系: sin 2 cos 2sec 2tg 2csc 2ctg 21⑷ a sinb cosa 2b 2 sin()(此中协助角 与点( a,b )在同一象限,且tgb )a5.和差角公式① sin( ) sin cos cos sin② cos( ) coscos sin sin③ tg ()tg tg④ tgtgtg ()(1 tgtg )1 tg tg⑤tg ()tg tgtg tg tg tg1 tgtgtgtgtg此中当 A+B+C=π时 ,有 :tgi). tgAtgB tgCtgA tgB tgCii). tg A tgBtg A tgCtg B tg C12 2 22 226.二倍角公式: (含全能公式 )① sin 22sin cos2tg 1 tg 2② cos 22sin221 12 sin21tg2 cos 2 cos1tg 2③ tg 22tgtg 21④ sin 2tg 21cos22 1 cos21 tg 22⑤cos27.半角公式:(符号的选择由所在的象限确立)2① sin1cos② sin2222③ cos1cos④ cos2222⑤ 1cos 2 sin 2⑥ 1 cos2⑦ 1sin(cos sin ) 2cos sin2222⑧ tg1cos sin 1 cos21cos 1 cos sin1cos21cos22 cos228.积化和差公式:① sin cos1sin()sin()2② cos sin1sin()sin()2③ cos cos 1cos()cos() 2④ sin sin 1cos()cos 29.和差化积公式:① sin sin2sin cos22② sin sin 2 cos sin22③ cos cos 2 cos cos22④ cos cos2sin sin22。
三角函数和反三角函数图像性质、知识点总结

三角函数 1. 特殊锐角(0°,30°,45°,60°,90°)的三角函数值2.角度制与弧度制设扇形的弧长为l ,圆心角为a (rad ),半径为R ,面积为S 角a 的弧度数公式 2π×(a /360°)角度与弧度的换算①360°=2π rad ②1°=π/180rad③1 rad=180°/π=57° 18′≈57.3°弧长公式 l a R =扇形的面积公式 12s lR =3.诱导公式:(奇变偶不变,符号看象限)所谓奇偶指是整数k 的奇偶性(k ·π/2+a )所谓符号看象限是看原函数的象限(将a 看做锐角,k ·π/2+a 之和所在象限) 注:①:诱导公式应用原则:负化正、大化小,化到锐角为终了4. 三角函数的图像和性质:(其中z k ∈)①:三角函数x y sin = x y cos =x y tan = cot y x=函 数 图 象定义域 R R 2x k ππ≠+x k π≠值域 [-1,1][-1,1]RR周期 2π2πππ奇偶性 奇偶奇非奇非偶单 调 性 2,222k k ππππ⎡⎤-+↑⎢⎥⎣⎦2,222k k ππππ⎡⎤-+↑⎢⎥⎣⎦[]2,2k k πππ-↑ []2,2k k πππ+↓,22k k ππππ⎡⎤-+↑⎢⎥⎣⎦[],k k πππ+↓对 称 性 :2x k ππ=+对称轴对称中心:(,0)k π:x k π=对称轴:对称中心(+,0)2k ππ:对称中心(,0)2k π零值点 πk x =2ππ+=k xπk x =2ππ+=k x最 值 点2ππ+=k x ,1max=y2ππ-=k x ,1min-=yπk x 2=,1max =y ;2y k ππ=+,1min -=y②:函数)sin(ϕω+=x A y 的图像与性质:(1) 函数)sin(ϕω+=x A y 和)cos(ϕω+=x A y 的周期都是ωπ2=T(2) 函数)tan(ϕω+=x A y 和)cot(ϕω+=x A y 的周期都是ωπ=T5.三角函数尺度变换sin y x =经过变换变为sin y x ϖϕ=+A ()的步骤(先平移后伸缩): 1sin sin sin sin y x y x y x y x ϖϕϖϖϖϕϖϕ=−−−−−−−→=−−−−−→=+−−−−−−−→=+横坐标变为原来的倍向左或向右纵坐标不变平移个单位纵坐标变为原来的A 倍横坐标不变()A ()6.三角函数的对称变换:① )()(x f y x f y -=→=) 将)(x f y =图像绕y 轴翻折180°(整体翻折) (对三角函数来说:图像关于x 轴对称)② )()(x f y x f y -=→=将)(x f y =图像绕x 轴翻折180°(整体翻折) (对三角函数来说:图像关于y 轴对称)③ )()(x f y x f y =→= 将)(x f y =图像在y 轴右侧保留,并把右侧图像绕y 轴翻折到左侧(偶函数局部翻折)④ )()(x f y x f y =→=保留)(x f y =在x 轴上方图像,x 轴下方图像绕x 轴翻折上去(局部翻动)7.反三角函数的图像与性质:名称y=arsinx y=arccosx y=arctanx y=arccotx定义y=sinx((,))22xππ∈-的反函数,叫做反正弦函数y=cosx((0,))xπ∈的反函数,叫做反余弦函数y=tanx((,))22xππ∈-的反函数,叫做反正切函数y=cotx((0,))xπ∈的反函数,叫做反余切函数性质图像定义域[-1,1][-1,1](-∞,+∞)(-∞,+∞)值域[-2π,2π][0,π](-2π,2π) (0,π)单调性[]1,1-增函数[]1,1-减函数(),-∞+∞增函数(),-∞+∞减函数奇偶性arcsin()arcsinθθ-=-arccos()arccosθπθ-=-arctan()arctanθθ-=-arccot()arccotθπθ-=-周期性非周期函数非周期函数非周期函数非周期函数7.三角函数公式:(1)倒数关系: (2)平方关系:tan cot 1sin csc 1cos sec 1αααααα⋅=⋅=⋅= 222222sin cos 11tan sec 1cot csc αααααα+=+=+=(3)三角和与差公式:sin()sin cos cos sin cos()cos cos sin sin tan tan tan()1tan tan αβαβαβαβαβαβαβαβαβ+=++=-++=- sin()sin cos cos sin cos()cos cos sin sin tan tan tan()1tan tan αβαβαβαβαβαβαβαβαβ-=--=+--=+(4)二倍角公式:()22222sin 22sin cos cos 2cos sin 2cos 112sin 2tan tan 21tan ααααααααααα==-=-=-=-升幂公式 22221cos 2sin 1cos 22sin 2(1cos 21cos 22cos cos 2αααααααα-⎫=⎪⎧-=⎪⎪⇒⎬⎨++=⎪⎩⎪=⎪⎭降幂公式) (5)三角函数的和差化积公式 (6)三角函数的积化和差公式sin sin 2sin cos22sin sin 2cos sin22cos cos 2cos cos22cos cos 2sin sin22αβαβαβαβαβαβαβαβαβαβαβαβ+-+=⋅+--=⋅+-+=⋅+--=-⋅ [][][][]1sin cos sin()sin()21cos sin sin()sin()21cos cos cos()cos()21sin sin cos()cos()2αβαβαβαβαβαβαβαβαβαβαβαβ⋅=++-⋅=+--⋅=++-⋅=-+-- 六边形记忆法:图形结构“上弦中切下割,左正右余中间1”;记忆方法“对角线上两个函数的积为1;阴影三角形上两顶点的三角函数值的平方和等于下顶点的三角函数值的平方;任意一顶点的三角函数值等于相邻两个顶点的三角函数值的乘积。
高中数学三角函数及反三角函数图像性质、知识点总结

高中数学三角函数及反三角函数图像性质、知识点总结高中数学中,三角函数及反三角函数是重要的内容之一。
在学习这一部分知识时,需要掌握其图像性质以及相关的知识点。
下面将对这些内容进行总结。
一、三角函数的图像性质1. 正弦函数(sin)的图像性质:- 周期性:sin函数的周期为2π,即在每个周期内,函数的图像重复出现;- 奇函数性质:sin函数关于原点对称;- 取值范围:sin函数的取值范围为[-1,1],即函数的值始终在该区间内波动。
2. 余弦函数(cos)的图像性质:- 周期性:cos函数的周期为2π;- 偶函数性质:cos函数关于y轴对称;- 取值范围:cos函数的取值范围也为[-1,1]。
3. 正切函数(tan)的图像性质:- 周期性:tan函数的周期为π;- 奇函数性质:tan函数关于原点对称;- 无界性:tan函数的值域为实数集,即函数在某些点无界。
二、三角函数的知识点1. 基本正弦函数的性质:- 特殊角的正弦值:0°、90°、180°、270°和360°对应的正弦值分别为0、1、0、-1和0;- 正弦函数的增减性:在0°到180°的区间上,sin函数是单调递增的;- 正弦函数的奇偶性:sin(-x)=-sin(x),即sin函数关于原点对称。
2. 基本余弦函数的性质:- 特殊角的余弦值:0°、90°、180°、270°和360°对应的余弦值分别为1、0、-1、0和1;- 余弦函数的增减性:在0°到180°的区间上,cos函数是单调递减的;- 余弦函数的奇偶性:cos(-x)=cos(x),即cos函数关于y轴对称。
3. 基本正切函数的性质:- 特殊角的正切值:0°、90°、180°和270°对应的正切值分别为0、无穷大、0和无穷大;- 正切函数的周期性:tan(x+π)=tan(x),即tan函数的周期是π。
三角函数及反三角函数图像性质、知识点总结

千里之行,始于足下。
三角函数及反三角函数图像性质、学问点总结三角函数及反三角函数是高中数学中重要的内容之一,它们的图像性质是我们学习和理解这些函数的基础。
下面是关于三角函数及反三角函数图像性质的学问点总结。
一、正弦函数的图像性质:1. 定义域:正弦函数的定义域为全体实数。
2. 值域:正弦函数的值域为闭区间[-1,1]。
3. 周期性:正弦函数的周期是2π,即在一个周期内,正弦函数的图像重复消灭。
4. 奇偶性:正弦函数是奇函数,即sin(-x)=-sin(x)。
5. 对称轴:正弦函数的对称轴是y轴。
6. 最值点:正弦函数的最值点包括最大值1和最小值-1,最值点的横坐标为周期的整数倍。
二、余弦函数的图像性质:1. 定义域:余弦函数的定义域为全体实数。
2. 值域:余弦函数的值域为闭区间[-1,1]。
3. 周期性:余弦函数的周期是2π,即在一个周期内,余弦函数的图像重复消灭。
4. 奇偶性:余弦函数是偶函数,即cos(-x)=cos(x)。
5. 对称轴:余弦函数的对称轴是x轴。
6. 最值点:余弦函数的最值点包括最大值1和最小值-1,最值点的横坐标为周期的半整数倍。
三、正切函数的图像性质:1. 定义域:正切函数的定义域为全体实数,除了临界点kπ(k为整数)。
第1页/共3页锲而不舍,金石可镂。
2. 值域:正切函数的值域为全体实数。
3. 周期性:正切函数的周期是π,即在一个周期内,正切函数的图像重复消灭。
4. 奇偶性:正切函数是奇函数,即tan(-x)=-tan(x)。
5. 渐近线:正切函数有两条渐近线,分别是x=kπ+π/2(k为整数)和x=kπ(k为整数)。
6. 最值点:正切函数没有最值点。
四、反正弦函数的图像性质:1. 定义域:反正弦函数的定义域为闭区间[-1,1]。
2. 值域:反正弦函数的值域为闭区间[-π/2,π/2]。
3. 奇偶性:反正弦函数是奇函数,即arcsin(-x)=-arcsin(x)。
4. 递增性:反正弦函数在定义域内是递增的。
角、反三角函数图像及性质与三角公式

三角、反三角函数图像(附:资料全部来自网络,仅对排版做了改动,以方便打印及翻阅,其中可能出现错误,阅者请自行注意。
)1.六个三角函数值在每个象限的符号:sinα·cscα cosα·secα tanα·cotα2.三角函数的图像和性质:1-1y=sinx-3π2-5π2-7π27π25π23π2π2-π2-4π-3π-2π4π3π2ππ-πoy x1-1y=cosx-3π2-5π2-7π27π25π23π2π2-π2-4π-3π-2π4π3π2ππ-πoyxy=tanx3π2ππ2-3π2-π-π2oyxy=cotx3π2ππ22π-π-π2oyx函数 y=sinx y=cosx y=tanxy=cotx定义域RR{x |x∈R 且x≠kπ+2π,k∈Z }{x |x∈R 且x≠kπ,k∈Z}值域[-1,1]x=2kπ+2π时y max =1 x=2kπ-2π时y min =-1[-1,1] x=2kπ时y max=1x=2kπ+π时y min =-1R无最大值 无最小值R无最大值 无最小值周期性周期为2π 周期为2π 周期为π 周期为π 奇偶性奇函数偶函数奇函数奇函数单调性在[2kπ-2π,2kπ+2π]上都是增函数;在[2kπ+2π,2kπ+32π]上都是减函数(k∈Z)在[2kπ-π,2kπ]上都是增函数;在[2kπ,2kπ+π]上都是减函数(k∈Z)在(kπ-2π,kπ+2π)内都是增函数(k∈Z)在(kπ,kπ+π)内都是减函数(k∈Z)3.反三角函数的图像和性质:arcsinx arccosxarctanx arccotx名称反正弦函数反余弦函数反正切函数反余切函数定义y=sinx(x∈〔-2π,2π〕的反函数,叫做反正弦函数,记作x=arsinyy=cosx(x∈〔0,π〕)的反函数,叫做反余弦函数,记作x=arccosyy=tanx(x∈(-2π,2π)的反函数,叫做反正切函数,记作x=arctanyy=cotx(x∈(0,π))的反函数,叫做反余切函数,记作x=arccoty理解arcsinx表示属于[-2π,2π]且正弦值等于x的角arccosx表示属于[0,π],且余弦值等于x的角arctanx表示属于(-2π,2π),且正切值等于x的角arccotx表示属于(0,π)且余切值等于x的角性质定义域[-1,1][-1,1](-∞,+∞)(-∞,+∞)值域[-2π,2π][0,π](-2π,2π)(0,π)单调性在〔-1,1〕上是增函数在[-1,1]上是减函数在(-∞,+∞)上是增数在(-∞,+∞)上是减函数arcsin(-x)=-arcsinx arccos(-x)=π-arccosxarctan(-x)=-arctanx arccot(-x)=π-arccotxarcsinx+arccosx=arctanx+arccotx=π/2sin(arcsinx)=cos(arccosx)=tan(arctanx)=cot(arccotx)=x当 x∈[-π/2, π/2] arcsin(sinx)=xx∈[0,π] arccos(cosx)=xx∈(-π/2, π/2) arctan(tanx)=xx∈(0, π) arccot(cotx)=x三角公式总表1.正弦定理:A a sin =B b sin =Cc sin = 2R (R 为三角形外接圆半径)2.余弦定理:a 2=b 2+c 2-2bc A cos b 2=a 2+c 2-2ac B cos c 2=a 2+b 2-2ab C cosbca cb A 2cos 222-+=⊿=21a a h ⋅=21ab C sin =21bc A sin =21ac B sin =R abc 4=2R 2A sin B sin C sin =A C B a sin 2sin sin 2=B C A b sin 2sin sin 2=CB A c sin 2sin sin 2=pr=))()((c p b p a p p ---(其中)(21c b a p ++=, r 为三角形内切圆半径)4.同角关系:⑴商的关系:①θtg =θθcos sin =θθsec sin ⋅ ②θθθθθcsc cos sin cos ⋅==ctg ③θθθtg ⋅=cos sin ④θθθθcsc cos 1sec ⋅==tg ⑤θθθctg ⋅=sin cos ⑥θθθθsec sin 1csc ⋅==ctg⑵倒数关系:1sec cos csc sin =⋅=⋅=⋅θθθθθθctg tg⑶平方关系:1csc sec cos sin 222222=-=-=+θθθθθθctg tg⑷)sin(cos sin 22ϕθθθ++=+b a b a (其中辅助角ϕ与点(a,b )在同一象限,且abtg =ϕ)5.和差角公式①βαβαβαsin cos cos sin )sin(±=± ②βαβαβαsin sin cos cos )cos(μ=± ③βαβαβαtg tg tg tg tg ⋅±=±μ1)( ④)1)((βαβαβαtg tg tg tg tg ⋅±=±μ⑤γβγαβαγβαγβαγβαtg tg tg tg tg tg tg tg tg tg tg tg tg ⋅-⋅-⋅-⋅⋅-++=++1)( 其中当A+B+C=π时,有:i).tgC tgB tgA tgC tgB tgA ⋅⋅=++ ii).1222222=++C tg B tg C tg A tg B tg A tg6.二倍角公式:(含万能公式)①θθθθθ212cos sin 22sin tg tg +== ②θθθθθθθ22222211sin 211cos 2sin cos 2cos tg tg +-=-=-=-=③θθθ2122tg tg tg -=④22cos 11sin 222θθθθ-=+=tg tg ⑤22cos 1cos 2θθ+=7.半角公式:(符号的选择由2θ所在的象限确定) ①2cos 12sin θθ-±= ②2cos 12sin 2θθ-= ③2cos 12cos θθ+±= ④2cos 12cos 2θθ+= ⑤2sin 2cos 12θθ=- ⑥2cos 2cos 12θθ=+ ⑦2sin 2cos )2sin 2(cos sin 12θθθθθ±=±=±⑧θθθθθθθsin cos 1cos 1sin cos 1cos 12-=+=+-±=tg8.积化和差公式:①[])sin()sin(21cos sin βαβαβα-++=②[])sin()sin(21sin cos βαβαβα--+=③[])cos()cos(21cos cos βαβαβα-++= ④()[]βαβαβα--+-=cos )cos(21sin sin9.和差化积公式:①2cos2sin2sin sin βαβαβα-+=+②2sin 2cos 2sin sin βαβαβα-+=- ③2cos 2cos 2cos cos βαβαβα-+=+ ④2sin 2sin 2cos cos βαβαβα-+-=-。
三角函数及反三角函数图像性质、知识点总结

千里之行,始于足下。
三角函数及反三角函数图像性质、知识点总结三角函数是数学中的重要概念,它研究角和三角形之间的关系。
在解决各种几何和物理问题时,三角函数经常被用于描述和计算角度的大小和位置,具有广泛的应用。
而反三角函数则是对三角函数的运算结果进行逆运算,可以将三角函数的值转化为角度的大小。
三角函数包括正弦函数、余弦函数、正切函数等。
它们的图像性质对于理解和使用三角函数非常重要。
首先,正弦函数的图像为一条连续的曲线,其振幅为1,但其值域在[-1, 1]之间变化。
在0到2π的区间上,正弦函数的图像呈现周期性变化,即在每个周期内重复出现相同的形状。
正弦函数在0、π、2π等处的值为0,而在π/2和3π/2等处的值达到最大值1和最小值-1。
余弦函数的图像与正弦函数非常相似,也是连续的曲线,振幅为1,值域在[-1, 1]之间变化。
与正弦函数不同的是,余弦函数在0处达到最大值1,在π/2和3π/2处达到最小值-1,并且在π处到达最小值-1时的斜率大于其他点。
正切函数的图像则比正弦函数和余弦函数复杂一些。
正切函数的值在整个实数轴上变化,但在某些点上出现垂直渐近线。
正切函数在0处为0,并且在π/2处存在一个不可取的点,其他点上的斜率变化也比较剧烈。
反三角函数是三角函数的逆运算。
对于给定的角度值,反三角函数可以计算出与之对应的三角函数的值。
反正弦函数、反余弦函数和反正切函数是最常用的反三角函数。
第1页/共2页锲而不舍,金石可镂。
反正弦函数的图像是一段弧线,其定义域为[-1, 1],值域为[-π/2, π/2]。
在定义域范围内的每个值,它的反正弦函数都会返回一组对应的弧度值。
反余弦函数的图像也是一段弧线,其定义域为[-1, 1],值域为[0, π]。
与反正弦函数不同,反余弦函数的值域比较大,因此可以返回更多的角度值。
反正切函数的图像是一条连续的曲线,其定义域为整个实数轴,值域为(-π/2, π/2)。
反正切函数的图像在x轴与正y轴的交点是原点,其斜率在各点上的变化没有正切函数那么剧烈。
三角和反三角函数图像+公式

三角、反三角函数图像六个三角函数值在每个象限的符号:sinα·cscα cosα·secα tanα·cotα三角函数的图像和性质:1-1y=sinx-3π2-5π2-7π27π25π23π2π2-π2-4π-3π-2π4π3π2ππ-πoy x1-1y=cosx-3π2-5π2-7π27π25π23π2π2-π2-4π-3π-2π4π3π2ππ-πoyxy=tanx3π2ππ2-3π2-π-π2oyxy=cotx3π2ππ22π-π-π2oyx函数 y=sinx y=cosx y=tanxy=cotx定义域RR{x |x ∈R 且x≠kπ+2π,k ∈Z } {x |x ∈R 且x≠kπ,k ∈Z }值域[-1,1]x=2kπ+2π时y max =1x=2kπ-2π时y min =-1[-1,1] x=2kπ时y max =1x=2kπ+π时y min =-1R 无最大值 无最小值R无最大值 无最小值周期性 周期为2π 周期为2π 周期为π 周期为π 奇偶性奇函数偶函数奇函数 奇函数单调性在[2kπ-2π,2kπ+2π]上都是增函数;在[2kπ+2π,2kπ+32π]上都是减函数(k ∈Z)在[2kπ-π,2kπ]上都是增函数;在[2kπ,2kπ+π]上都是减函数(k ∈Z)在(kπ-2π,kπ+2π)内都是增函数(k ∈Z)在(kπ,kπ+π)内都是减函数(k ∈Z).反三角函数:arcsinx arccosxarctanx arccotx名称反正弦函数 反余弦函数 反正切函数 反余切函数 定义y=sinx(x ∈〔-2π,2π 〕的反函数,叫做反正弦函数,记作x=arsiny y=cosx(x ∈〔0,π〕)的反函数,叫做反余弦函数,记作x=arccosy y=tanx(x ∈(-2π, 2π)的反函数,叫做反正切函数,记作x=arctanyy=cotx(x ∈(0,π))的反函数,叫做反余切函数,记作x=arccoty理解arcsinx 表示属于[-2π,2π] 且正弦值等于x 的角arccosx 表示属于[0,π],且余弦值等于x 的角 arctanx 表示属于(-2π,2π),且正切值等于x 的角 arccotx 表示属于(0,π)且余切值等于x 的角性质 定义域 [-1,1] [-1,1] (-∞,+∞) (-∞,+∞) 值域 [-2π,2π] [0,π](-2π,2π) (0,π)单调性在〔-1,1〕上是增函数 在[-1,1]上是减函数在(-∞,+∞)上是增数 在(-∞,+∞)上是减函数奇偶性 arcsin(-x)=-arcsinx arccos(-x)=π-arccosxarctan(-x)=-arctanx arccot(-x)=π-arccotx 周期性都不是同期函数恒等式sin(arcsinx)=x(x ∈[-1,1])arcsin(sinx)=x(x ∈[-2π,2π])cos(arccosx)=x(x ∈[-1,1]) arccos(cosx)=x(x ∈[0,π]) tan(arctanx)=x(x ∈R)arctan(tanx)=x (x ∈(-2π,2π)) cot(arccotx)=x(x ∈R)arccot(cotx)=x(x ∈(0,π))互余恒等式 arcsinx+arccosx=2π(x ∈[-1,1]) arctanx+arccotx=2π(X ∈R)。
三角函数拓展知识点总结

三角函数拓展知识点总结一、三角函数的定义与性质1. 三角函数的定义在直角三角形中,我们可以定义三角函数为一个角的对边、邻边和斜边之比。
具体来说,正弦函数(sine)、余弦函数(cosine)、正切函数(tangent)等,它们的定义分别如下: - 正弦函数:sinθ = 对边/斜边- 余弦函数:cosθ = 邻边/斜边- 正切函数:tanθ = 对边/邻边2. 三角函数的性质* 周期性:对于任意角θ,三角函数都是周期函数,具有周期2π。
* 奇偶性:正弦函数是奇函数,余弦函数是偶函数,正切函数则是奇函数。
* 定义域和值域:正弦函数和余弦函数的定义域是实数集,值域是[-1, 1];而正切函数的定义域是全体实数,值域是实数集。
二、三角函数的图像与性质1. 正弦函数的图像与性质正弦函数的图像是一条连续的波浪线,它在每个周期内有一个最大值1和一个最小值-1,而且它的图像是周期性的。
正弦函数的性质还包括:- 对称性:正弦函数关于原点对称。
- 单调性:一个周期内,正弦函数在(0, π)上是增函数,在(π, 2π)上是减函数。
- 零点:正弦函数有无穷多个零点,即sin(kπ)=0,其中k为整数。
2. 余弦函数的图像与性质余弦函数的图像是一条连续的波浪线,它在每个周期内有一个最大值1和一个最小值-1,而且它的图像也是周期性的。
余弦函数的性质还包括:- 对称性:余弦函数关于y轴对称。
- 单调性:一个周期内,余弦函数在(0, π)上是减函数,在(π, 2π)上是增函数。
- 零点:余弦函数的零点为cos((2k+1)π/2)=0,其中k为整数。
3. 正切函数的图像与性质正切函数的图像是一条连续的周期性函数,其图像在每个周期中有许多奇点,其性质包括: - 奇点:正切函数在每个周期内有许多奇点,即在θ=(2k+1)π/2处,tanθ的值无定义。
- 增减性:正切函数在每个周期内有无穷多个极大值和极小值,并且在每个周期内均为增函数或减函数。
(完整版)三角函数与反三角函数图像

三角函数公式和图象总结1.与角α终边相同的角,连同角α在内,都可以表示为S={β|β=α+k ×360,k ∈Z }2.弧长公式:α⋅=r l 扇形面积公式lR S 21=其中l 是扇形弧长,R 是圆的半径。
3.三角函数定义: sin ,cos ,tan y x yr r xααα===,其中P (,)x y 是α终边上一点,||r OP =4.同角三角函数的两个基本关系式 22sin sin cos 1 tan cos ααααα+==sin sin αsin βtan tan 1tan tan αβα±公式逆用1sin cos sin α=22cos 2cos sin ααα=- 212sin α=-22cos 1α=- 22cos sin cos 2ααα-= 212sin cos 2αα-=22cos 1cos 2αα-=降幂公式221cos 2sin 21cos 2cos 2αααα-⎧=⎪⎪⎨+⎪=⎪⎩22tan tan 21tan ααα=-22tan tan 21tan ααα=-10.辅助角公式22sin cos sin(),a x b x a b x ϕ+=++其中tan baϕ=,ϕ所在的象限与点(,)a b 所在的象限一致. 11.三角函数的图象和性质称 正弦y=sinx余弦y=cosx正切y=tanx象义R R|,2x x R x k k Z ππ⎧⎫∈≠+∈⎨⎬⎩⎭且值1y 22max =+=时当ππk x 1y 22min -=-=时当ππk x1y 2max ==时当πk x 1y 2min -=+=时当ππk x无期 2k π(最小正周期2π)2k π(最小正周期2π)k π(最小正周期π)偶奇偶奇 称()2x k k Z ππ=+∈)( Z k k x ∈=π无称 心)( )0,(Z k k ∈π)( ,0)2(Z k k ∈+ππ )( ,0)2(Z k k ∈π调区)( ]22,22[Z k k k ∈+-ππππ )( ]2,2[Z k k k ∈-πππ)( )2,2(Z k k k ∈+-ππππ 调区)( ]232,22[Z k k k ∈++ππππ)( ]2,2[Z k k k ∈+πππ无减区间12.①sin()(0)y A x b A ωϕ=++>、cos()(0)y A x b A ωϕ=++>的最小正周期为||ω,最大值为A+b,最小值为-A+b 。
三角、反三角函数图像及几个补充公式

三角、反三角函数图像六个三角函数值在每个象限的符号:sinα·cscα cosα·secα tanα·cotα三角函数的图像和性质:.反三角函数:arcsinxarccosx补充几个公式 积化和差公式sinacosb=(1/2)(sin(a+b)+sin(a-b)) cosasinb=(1/2)(sin(a+b)-sin(a-b)) cosacosb=(1/2)(cos(a+b)+cos(a-b)) sinasinb=-(1/2)(cos(a+b)-cos(a-b))三倍角公式sin3a=3sina-4(sina)^3cos3a=4(cosa)^3-3cosatg3a=[3tga-(tga)^3]/[1-3(tga)^3]1.诱导公式sin(-a)=-sin(a)cos(-a)=cos(a)sin(π/2-a)=cos(a)cos(π/2-a)=sin(a)sin(π/2+a)=cos(a)cos(π/2+a)=-sin(a)sin(π-a)=sin(a)cos(π-a)=-cos(a)sin(π+a)=-sin(a)cos(π+a)=-cos(a)2.两角和与差的三角函数sin(a+b)=sin(a)cos(b)+cos(α)sin(b) cos(a+b)=cos(a)cos(b)-sin(a)sin(b) sin(a-b)=sin(a)cos(b)-cos(a)sin(b) cos(a-b)=cos(a)cos(b)+sin(a)sin(b) tan(a+b)=tan(a)+tan(b)/1-tan(a)tan(b) tan(a-b)=tan(a)-tan(b)/1+tan(a)tan(b) 3.和差化积公式sin(a)+sin(b)=2sin(a+b2)cos(a-b2)sin(a)−sin(b)=2cos(a+b2)sin(a-b2)cos(a)+cos(b)=2cos(a+b2)cos(a-b2)cos(a)-cos(b)=-2sin(a+b2)sin(a-b2)4.二倍角公式sin(2a)=2sin(a)cos(b)cos(2a)=cos2(a)-sin2(a)=2cos2(a)-1=1-2sin2(a) 5.半角公式sin2(a2)=1-cos(a)2cos2(a2)=1+cos(a)2tan(a2)=1-cos(a)sin(a)=sina1+cos(a)6.万能公式sin(a)=2tan(a2)1+tan2(a2)cos(a)=1-tan2(a2)1+tan2(a2)tan(a)=2tan(a2)1-tan2(a2)7.其它公式(推导出来的 )a⋅sin(a)+b⋅cos(a)=a2+b2sin(a+c) 其中 tan(c)=ba a⋅sin(a)+b⋅cos(a)=a2+b2cos(a-c) 其中 tan(c)=ab 1+sin(a)=(sin(a2)+cos(a2))21-sin(a)=(sin(a2)-cos(a2))2。
三角函数与反三角函数公式与图像
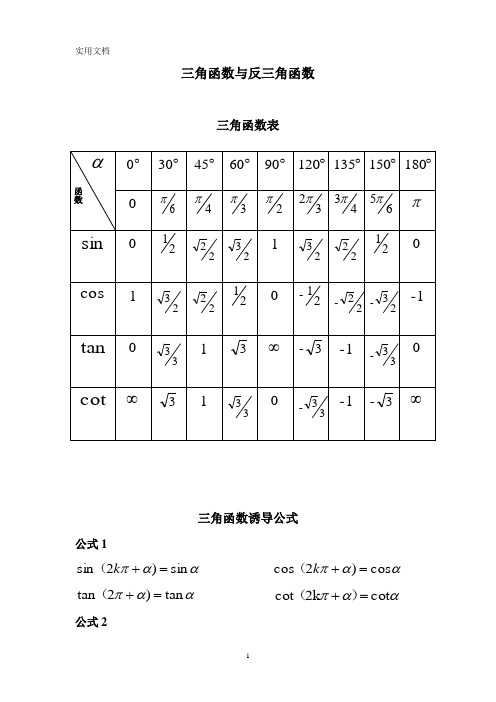
三角函数与反三角函数三角函数表三角函数诱导公式公式1ααπsin )2sin =+k ( ααπcos )2cos =+k (ααπtan )2tan =+( ααπcot 2k cot =+)(公式2ααπ-sin sin =+)( ααπ-cos cos =+)(ααπtan tan =+)( ααπcot cot =+)(公式3ααsin -)-sin(= ααcos -cos =)(αα-tan -tan =)( αα-cot -cot =)( 公式4ααπsin -sin =)( ααπ-cos -cos =)(ααπtan )(tan -=- ααπ-cot -cot =)(公式5ααπ-sin -2sin =)( ααπcos -2cos =)(ααπtan )2(tan -=- ααπ-cot 2(cot =-)公式6ααπcos 2sin =+)( ααπ-sin 2cos =+)( ααπcot )2(tan -=+ααπ-tan 2cot =+)( ααπcos -2sin =)(ααπsin -2cos =)( ααπcot )2(tan =-ααπtan -2cot =)(推算公式ααπ-cos 23sin =+)( ααπsin 23cos =+)(ααπcot )23(tan -=+ ααπ-tan 23cot =+)(ααπcos )23sin -=-( ααπ-sin -23cos =)(ααπcot )23(tan =- ααπtan )23cot =-(三角函数公式一 基本关系式1cos sin 22=+α 1cot tan =⋅αααααcos sin tan = αααsin cos cot = 二 两角和差公式ααβαβαsin cos cos sin sin ⋅+⋅=+)(βαβαβαsin cos -cos sin -sin ⋅⋅=)(βαβαβαsin sin -cos cos cos ⋅⋅=+)(βαβαβαsin sin cos cos -cos ⋅+⋅=)(βαβαβαtan tan 1tan tan )tan(⋅-+=+ βαβαβαtan tan 1tan -tan )-tan(⋅+=三 二倍角的正弦,余弦和正切公式αααcos sin 22sin ⋅=ααααα2222sin 2-11-cos 2sin -cos cos2===ααα2tan 1tan 22tan -=四 半角正弦,余弦和正切公式)(ααcos -1212sin 2= )(ααcos 1212cos 2+=αααcos 1cos 12tan 2+-=αααααsin cos 1cos 1sin 2tan -=+=五 三倍角正弦,余弦和正切公式ααα3sin 4-sin 33sin =αααcos 3-cos 43cos 3=ααα233tan 31tan tan 3tan --=六 万能公式2tan 12tan 2sin 2ααα+=2tan12tan-1cos 22ααα+=2tan12tan 2tan 2ααα-=七 辅助角公式)sin(cos sin 22ϕααα++=+b a b a )cos(22ϕα-+=b a其中:bab a b b a a =+=+=ϕϕϕtan cos sin 2222八 三角函数和差化积公式)()(2-cos 2sin 2sin sin βαβαβα⋅+=+)()(2-sin 2cos 2sin -sin βαβαβα⋅+=)()(2-cos 2cos 2cos cos βαβαβα⋅+=+)()(2-sin 2sin 2-cos -cos βαβαβα⋅+=九 三角函数积化和差公式[])()(βαβαβα-sin sin 21cos sin ++=⋅ [])()(βαβαβα-sin -sin 21sin cos +=⋅ [])()(βαβαβα-cos cos 21cos cos ++=⋅ [])()(βαβαβα-cos -cos 21-sin sin +=⋅反三角函数公式下α可取αα-arcsin -arcsin =)( απαarccos --arccos =)(ααarctan )(arctan -=- απαarccot )-arccot -=(2arccot arctan arccos arcsin παααα=+=+αα=)(arcsin sin αα=)(arccos cosαα=)(arctan tan αα=)(arccot cotαα=)(sin arcsin ),(22-ππα∈αα=)(cos arccos ),(πα0∈αα=)(tan arctan ),(22-ππα∈αα=)(cot arccot ),(πα0∈αα1arctan arctan = 0>ααα1arccotarccot =0>α)1(arctan arctan arctan αββαβα-+=+ 其中)2,2(arctan arctan ππβα-∈+三角函数图像一 正弦函数x x f sin )(=定义域:R x ∈ 值域:]1,1[)(-∈x f二 余弦函数x x f cos )(=定义域:R x ∈ 值域:]1,1[)(-∈x f三 正切函数x x f tan )(=定义域:Z k k x R x ∈+≠∈,2ππ且 值域:R x f ∈)(四 余切函数x x f cot )(=定义域:Z k k x R x ∈≠∈,π且 值域:R x f ∈)(反三角函数图像一 反正弦函数x x f arcsin )(=定义域:]1,1[-∈x 值域:]2,2[)(ππ-∈x f二 反余弦函数x x f arccos )(=定义域:]1,1[-∈x 值域:],0[)(π∈x f11 三 反正弦函数 x x f arctan )(=定义域:R x ∈ 值域:)2,2()(ππ-∈x f四 反余切函数 x x f arccot )(=定义域:R x ∈ 值域:),0()(π∈x f。
三角、反三角函数图像的解析

三角、反三角函数整理Sin a , CSC a三角函数的图像和性质:三角函数值在每个象限的符号:COS a° Sec a tan a , cot a* y=ta nx1!y111t/IJ/3JI{i■o万2A耳JF{1I函数y=s inx y=cosx y=ta nx y=cotxy=sec x y=cscx疋义域R R{x | x € R 且JIx 丰 k nJ ,k € Z}{x | x € R 且x 丰 k n€,IZ }{x| x 工kn + n/2(k € Z)}{x|x 工k n ,k € Z}值域[-1, 1:JIx=2k n +2时y max=1JIx=2k n 一2时y min =-1[-1,1 ]x=2k n时y max = 1 x=2k n+ 时y min =-1R无最大值无最小值R无最大值无最小值y > 1 或yw -1{y|y > 1 或y w -1}周期性周期为2n周期为2n周期为n周期为nT=2 n 2 n奇偶性奇函数偶函数奇函数奇函数偶函数奇函数单调性在Jl[2k n——22,2JIk n+一 :上2都是增函数;在JI[2k n + —22,2k n+ n]3 上都是减函数(k €在]2k n- n, 2k n上都是增函数;在:2k n,2k n +]n上都是减函数(k € Z)在(k n 一,2Ttk n+亍)内都是增函数(k € Z)在(k n, k n + n)内都是减函数(k € Z)一般不讨论一般不讨论角函数的诱导公式(六公式)公式一:设a为任意角,终边相同的角的同一三角函数的值相等:sin( a +k*2 n )=sin a k 为整数)COS(a +k*2 n )=cos a k 为整数)tan( a +k*2 n )=tan (a 为整数)公式二设a为任意角,n + a的三角函数值与a的三角函数值之间的关系sin[(2k+1) n +a-S=n aCOS[(2k+1) n +a 抬OS atan[(2k+1) n + a ]=tan aCOt[(2 k+1) n + a ]=COt a公式三任意角a与-a的三角函数值之间的关系:sin(2k- a )=sin acos(2k- a )=COs atan(2k- a )=tan aCOt(2k- a )=COt a公式四利用公式二和公式三可以得到n- a与a的三角函数值之间的关系sin[ (2k+1) na ]=sin aCOS[(2k+1) n a ]=COS atan[ (2k+1) na ]=tan aCOt[(2k+1) na ]=COt a公式五:利用公式一和公式三可以得到2n- a与a的三角函数值之间的关系:sin(2k n a )=sin aC0S(2k n- a )=COS atan(2k n a )=tan aC0t(2k n a )=C0t a公式六:n /2 ±4a a的三角函数值之间的关系:Sin( n /2+ a )=C0S acos( n /2+ a -sin atan( n /2+ a -Cot aC0t( n /2+ a-)=n asin( n 2 )=C0S aC0S( n /2 a )=Sin atan( n /2a )=C0t aC0t( n /2a )=tan a诱导公式记背诀窍:奇变偶不变,符号看象限。
初中数学知识点三角函数的反函数与反三角函数

初中数学知识点三角函数的反函数与反三角函数三角函数是初中数学中重要的概念之一,它包括正弦函数、余弦函数和正切函数。
而三角函数的反函数及反三角函数则是三角函数的一个重要扩展,它们在解三角方程和研究角度问题中起到了关键的作用。
本文将着重介绍初中数学中的三角函数的反函数与反三角函数。
一、反函数的概念及性质1. 反函数的定义假设函数 f(x) 是一一对应的,那么它的反函数记作 f^(-1)(x)。
对于任意的 y 属于函数 f(x) 的定义域,若 y = f(x),则有 x = f^(-1)(y)。
2. 反函数的图像函数 f(x) 与其反函数 f^(-1)(x) 的图像关于直线 y = x 对称。
3. 反函数的性质(1)函数 f(x) 与其反函数 f^(-1)(x) 互为反函数,即 f(f^(-1)(x)) = x,f^(-1)(f(x)) = x。
(2)求反函数的方法是将函数 f(x) 中的自变量 x 和因变量 y 互换位置,并解出 y。
(3)如果函数f(x) 是递增函数,则其反函数f^(-1)(x) 是递增函数;如果函数 f(x) 是递减函数,则其反函数 f^(-1)(x) 是递减函数。
二、反三角函数的概念及性质1. 反三角函数的定义由三角函数的周期性和奇偶性可知,三角函数的反函数不是一一对应的,因此引入了反三角函数来限制定义域,使其成为一一对应的关系。
常见的反三角函数包括:反正弦函数(arcsin)、反余弦函数(arccos)和反正切函数(arctan)。
2. 反三角函数的性质(1)反三角函数的定义域和值域:• 反正弦函数的定义域为 [-1, 1],值域为 [-π/2, π/2];• 反余弦函数的定义域为 [-1, 1],值域为[0, π];•反正切函数的定义域为 (-∞, +∞),值域为 (-π/2, π/2)。
(2)反三角函数的图像:• 反正弦函数的图像在 [-1, 1] 区间上是递增的并且关于 y = x 对称;• 反余弦函数的图像在 [-1, 1] 区间上是递减的并且关于 y = x 对称;• 反正切函数的图像在整个定义域上是递增的并且关于 y = x 对称。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角函数 1. 特殊锐角(0°,30°,45°,60°,90°)的三角函数值
2.
角度制与弧度制
设扇形的弧长为l ,圆心角为a (rad ),半径为R ,面积为S 角a 的弧度数公式 2π×(a /360°)
角度与弧度的换算
①360°=2π rad ②1°=π/180rad
③1 rad=180°/π=57° 18′≈57.3°
弧长公式 l a R =
扇形的面积公式 12
s lR =
3.
诱导公式:(奇变偶不变,符号看象限)
所谓奇偶指是整数k 的奇偶性(k ·π/2+a )
所谓符号看象限是看原函数的象限(将a 看做锐角,k ·π/2+a 之和所在象限) 注:
①:诱导公式应用原则:负化正、大化小,化到锐角为终了
4. 三角函数的图像和性质:(其中z k ∈)
①:
三角函数
x y sin = x y cos =
x y tan = cot y x
=
函 数 图 象
定义域 R R 2
x k π
π≠+
x k π
≠
值域 [-1,1]
[-1,1]
R
R
周期 2π
2π
π
π
奇偶性 奇
偶
奇
非奇非偶
单 调 性 2,222k k ππππ⎡
⎤-+↑⎢⎥⎣⎦2,222k k ππππ⎡⎤-+↑⎢⎥⎣⎦
[]2,2k k πππ-↑ []2,2k k πππ+↓
,22k k ππππ⎡
⎤-+↑⎢⎥⎣⎦
[],k k πππ+↓
对 称 性 :2
x k π
π=+
对称轴
对称中心:(,0)k π
:x k π
=对称轴
:
对称中心(+
,0)
2k π
π
:
对称中心(
,0)
2
k π
零值点 π
k x =
2
π
π+
=k x
πk x =
2
π
π+
=k x
最 值 点
2
π
π+
=k x ,1max =y
2
π
π-
=k x ,1min
-=y
π
k x 2=,1max =y ;
2y k ππ=+,1min -=y
②:函数)sin(ϕω+=x A y 的图像与性质:
(1) 函数)sin(ϕω+=x A y 和)cos(ϕω+=x A y 的周期都是ω
π2=T
(2) 函数)tan(ϕω+=x A y 和)cot(ϕω+=x A y 的周期都是ω
π
=T
5.三角函数尺度变换
sin y x =经过变换变为sin y x ϖϕ=+A ()
的步骤(先平移后伸缩): 1
sin sin sin sin y x y x y x y x ϖ
ϕ
ϖ
ϖϖϕϖϕ=−−−−−−−→=−−−−−→=+−−−−−−−→=+横坐标变为原来的倍
向左或向右纵坐标不变
平移个单位
纵坐标变为原来的A 倍
横坐标不变
()A ()
6.三角函数的对称变换:
① )()(x f y x f y -=→=) 将)(x f y =图像绕y 轴翻折180°(整体翻折) (对三角函数来说:图像关于x 轴对称)
② )()(x f y x f y -=→=将)(x f y =图像绕x 轴翻折180°(整体翻折) (对三角函数来说:图像关于y 轴对称)
③ )()(x f y x f y =→= 将)(x f y =图像在y 轴右侧保留,并把右侧图像绕y 轴翻折到左侧(偶函数局部翻折)
④ )()(x f y x f y =→=保留)(x f y =在x 轴上方图像,x 轴下方图像绕x 轴翻折上去(局部翻动)
7.反三角函数的图像与性质:
名称y=arsinx y=arccosx y=arctanx y=arccotx
定义y=sinx
((,))
22
x
ππ
∈-的
反函数,叫做反
正弦函数
y=cosx
((0,))
xπ
∈的反
函数,叫做反余
弦函数
y=tanx
((,))
22
x
ππ
∈-的反
函数,叫做反正切
函数
y=cotx((0,))
xπ
∈
的反函数,叫做反
余切函数
性质图像
定义域[-1,1][-1,1](-∞,+∞)(-∞,+∞)
值域[-
2
π,
2
π]
[0,π](-
2
π,
2
π) (0,π)
单调性[]
1,1
-增函数[]1,1
-减函数()
,
-∞+∞增函数()
,
-∞+∞减函数奇偶性arcsin()arcsin
θθ
-=-
arccos()arccos
θπθ
-=-
arctan()arctan
θθ
-=-
arccot()arccot
θπθ
-=-
周期性非周期函数非周期函数非周期函数非周期函数
7.三角函数公式:
(1)倒数关系: (2)平方关系:
tan cot 1
sin csc 1cos sec 1
αααααα⋅=⋅=⋅= 22
2
2
22
sin cos 1
1tan sec 1cot csc αααααα
+=+=+=
(3)三角和与差公式:
sin()sin cos cos sin cos()cos cos sin sin tan tan tan()1tan tan αβαβαβ
αβαβαβαβ
αβαβ
+=++=-++=
- sin()sin cos cos sin cos()cos cos sin sin tan tan tan()1tan tan αβαβαβ
αβαβαβαβαβαβ-=--=+--=+
(4)二倍角公式:
()22222
sin 22sin cos cos2cos sin 2cos 112sin 2tan tan 21tan ααα
αααααααα
==-=-=-=-升幂公式 22
2
21cos2sin 1cos22sin 2(1cos21cos22cos cos 2αααααααα-⎫
=
⎪⎧-=⎪⎪⇒⎬⎨++=⎪⎩⎪=⎪⎭降幂公式) (5)三角函数的和差化积公式 (6)三角函数的积化和差公式
sin sin 2sin cos
22sin sin 2cos sin
22cos cos 2cos cos
22cos cos 2sin sin
22
αβαβ
αβαβαβ
αβαβαβ
αβαβαβ
αβ+-+=⋅+--=⋅+-+=⋅+--=-⋅ [][]
[]
[]
1
sin cos sin()sin()21
cos sin sin()sin()2
1
cos cos cos()cos()21
sin sin cos()cos()2
αβαβαβαβαβαβαβαβαβαβαβαβ⋅=
++-⋅=+--⋅=++-⋅=-+-- 六边形记忆法:图形结构“上弦中切下割,左正右余中间1”;记忆方法“对角线上两个函数的积为1;阴影三角形上两顶点的三角函数值的平方和等于下顶点的三角函数值的平方;任意一顶点的三角函数值等于相邻两个顶点的三角函数值的乘积。
”
8.正、余弦定理: ①正弦定理: 在ABC ∆中有:
2sin sin sin a b c
R A B C
===(R 为ABC ∆外接圆半径) 2sin 2sin 2sin a R A b R B c R C
=⎧⎪
=⎨
⎪=⎩ ⇒ sin 2sin 2sin 2a A R b B R c C R ⎧
=⎪⎪
⎪=⎨⎪⎪
=⎪⎩
面积公式:1
11sin sin sin 222
ABC S abs C ac B bc A ∆=== ②余弦定理: 在三角形ABC ∆中有:
222222
2222cos 2cos 2cos a b c bc A b a c ac B c a b ab C
⎧=+-⎪=+-⎨⎪=+-⎩ ⇒ 222
222222
cos 2cos 2cos 2b c a A bc a c b B ac a b c C ab ⎧+-=⎪⎪
+-⎪=
⎨⎪⎪+-=
⎪⎩。
