四年级奥数幻方和数阵图
小学四年级逻辑思维学习—数阵图与幻方

⼩学四年级逻辑思维学习—数阵图与幻⽅⼩学四年级逻辑思维学习—数阵图与幻⽅”知识定位⼀、什么是数阵图?在神奇的数学王国中,有⼀类⾮常有趣的数学问题,它变化多端,引⼈⼊胜,奇妙⽆穷。
它就是数阵,⼀座真正的数字迷宫,它对喜欢探究数字规律的⼈有着极⼤的吸引⼒,以⾄有些⼈留连其中,⽤毕⽣的精⼒来研究它的变化,就连⼤数学家欧拉对它都有着浓厚的兴趣。
那么,到底什么是数阵呢?我们先观察上⾯两个图:右图(1)中有3个⼤圆,每个圆周上都有四个数字,有意思的是,每个圆周上的四个数字之和都等于13。
右图(2)就更有意思了,1~9九个数字被排成三⾏三列,每⾏的三个数字之和与每列的三个数字之和,以及每条对⾓线上的三个数字之和都等于15,不信你就算算。
上⾯两个图就是数阵图。
准确地说,数阵图是将⼀些数按照⼀定要求排列⽽成的某种图形,有时简称数阵。
要排出这样巧妙的数阵图,可不是⼀件容易的事情。
我们还是先从如何来填好数阵图开始。
如何填好数阵图?数阵图问题千变万化,这⼀类问题要求数阵中填⼊了⼀些数以后,能保证数阵中特定关系线(或关系区域)上的数的和相等,解决这⼀类问题可以按以下步骤解决问题:第⼀步:区分数阵图中的普通点(或⽅格),和交叉点(⽅格)第⼆步:在数阵图的少数关键点(⼀般是交叉点)上设置未知数,计算各个点与该点被重复计算次数之积的和的代数式,即数阵图关系线(关系区域)上和的总和,这个和是关系线(关系区域)的个数的整数倍.第三步:判断少数关键点上可以填⼊的数的余数性质,并得出相应的数阵图关系线(关系区域)和.第四步:运⽤已经得到的信息进⾏尝试:数阵图还有⼀类题型⽐较少见,解决这⼀类问题需要理清数阵中数与数之间的相关关系,找出问题关键.【授课批注】数阵图问题千变万化,⼀般没有特定的解法,往往需要综合运⽤掌握的各种数学知识来解决问题. 本讲出了要讲授填数阵图的主要技巧,还有以下注意点:1.引导学⽣从整体到局部对问题进⾏观察和判断;2.教授巧妙利⽤容斥原理、余数的性质、整除性质的数学⽅法;3.锻炼学⽣利⽤已知信息枚举,尝试的能⼒;4.培养学⽣综合运⽤各种数学知识,分析问题,找问题关键,解决问题的能⼒.⼆、什么是幻⽅?同学们是否知道我国古代有关“洛书”的神话传说?传说在⼤禹治⽔的年代,陕西的洛⽔经常⼤肆泛滥,⽆论怎样祭祀河神都⽆济于事,每年⼈们摆好祭品之后,河中都会爬出⼀只⼤乌龟,乌龟壳有九⼤块,横着数是3⾏,竖着数是3列,每块乌龟壳上都有⼏个点点,正好凑成1⾄9的数字,可是谁也弄不清这些⼩点点是什么意思.⼀次,⼤乌龟⼜从河⾥爬上来,⼀个看热闹的⼩孩惊叫起来:“瞧多有趣啊,这些点点不论横着加、竖着加还是斜着加,结果都等于⼗五!”于是⼈们赶紧把⼗五份祭品献给河神,说来也怪,河⽔果然从此不再泛滥了.这个神奇的图案叫做“幻⽅”,由于它有3⾏3列,所以叫做“三阶幻⽅”,这个相等的和叫做“幻和”.“洛书”就是幻和为15的三阶幻⽅.如下图:三、如何解决幻⽅问题?幻⽅是指横⾏、竖列、对⾓线上数的和都相等的数的⽅阵,具有这⼀性质的3×3的数阵称作三阶幻⽅,4×4的数阵称作四阶幻⽅,5×5的称作五阶幻⽅……如图为三阶幻⽅、四阶幻⽅的标准式样,三阶幻⽅的中⼼位置上的数等于所有所填数的平均数,也等于横⾏、竖列、对⾓线上数和的三分之⼀.解决数表类问题中,⾸先要找出数填写的规律,再从规律中找到数表的数量关系,从⽽找出解决问题的关键.知识梳理987653421987654321(⼀)封闭型数阵问题(⼆)辐射型数阵(三)其它类型的数阵图(四)幻⽅例题精讲【试题来源】【题⽬】将1~6填⼊左下图的六个○中,使三⾓形每条边上的三个数之和都等于k,请指出k的取值范围.k=9 k=10 k=11 k=12【题⽬】⼩猴聪聪有⼀天捡到像左下图的模具,它试着将1~10分别填⼊图中,使得每个⼩三⾓形3个顶点上的数字之和为图中所表⽰的数值,你能做到吗?【题⽬】图中的6条线分别连接着9个圆圈,其中⼀个圆圈⾥的数是6.请你选9个连续⾃然数(包括6在内)填⼈圆圈内,使每条线上各数的和都等于23.6543216543216543216543216【题⽬】⼩兔⼦在森林玩耍,遇到⼀个画着奇怪图形的树桩,上⾯写着:把10⾄20这11个数分别填⼊下图的各圆圈内,使每条线段上3个圆内所填数的和都相等.如果中⼼圆内填的数相等,那么就视为同⼀种填法,请写出所有可能的填法,⼩兔⼦发了愁,你能帮它吗?【题⽬】海豚是很聪明的动物,它能将1~9填⼊右下图的九个○内,并且使得每个圆周和每条直线上的三数之和都相等,并且7,8,9依次位于⼩、中、⼤圆周上,你能做到吗?【题⽬】在下图中的10个○内填⼊0~9这10个数字,使得循环式成⽴:【题⽬】请在图中的每个圆圈内填⼊不同的⾃然数,使得图中每个圆圈中所填的数都是上⼀⾏与它相邻的两个圆圈中所填数的和,最下⾯的数是20.+=====----20【题⽬】请你将2~10这九个⾃然数填⼊图中的空格内每⾏、每列、每条对⾓线上的三数之和相等.【题⽬】请你将1~25这⼆⼗五个⾃然数填⼊图中的空格内每⾏、每列、每条对⾓线上的五数之和相等.【题⽬】将九个数填⼊左下图的九个空格中,使得任⼀⾏、任⼀列以及两条对⾓线上的三个数之和都等于定数k,则中⼼⽅格中的数必为k÷3【题⽬】在下图的九个⽅格中填⼊不⼤于12且互不相同的九个⾃然数(其中已填好⼀个数),使得任⼀⾏、任⼀列及两条对⾓线上的三个数之和都等于21.【题⽬】将前9个⾃然数填⼊右图的9个⽅格中,使得任⼀⾏、任⼀列以及两条对⾓线上的三个数之和互不相同,并且相邻的两个⾃然数在图中的位置也相邻.【题⽬】将1、2、3、4、5、6、7、8、9这九个数字,分别填⼊3×3阵列中的九个⽅格,使第⼆⾏组成的三位数是第⼀⾏组成的三位数的2倍,第三⾏组成的三位数是第⼀⾏组成的三位数的3倍.【题⽬】在⼀个3×3的⽹格中填⼊9个数使得每⼀横⾏、竖⾏、对⾓线上三个数的乘积相等.习题演练【题⽬】将1~7这七个数分别填⼊图中的○⾥,使每条直线上的三个数之和都等于12。
小学四年级逻辑思维学习—数阵图与幻方

小学四年级逻辑思维学习—数阵图与幻方”知识定位一、什么是数阵图?在神奇的数学王国中,有一类非常有趣的数学问题,它变化多端,引人入胜,奇妙无穷。
它就是数阵,一座真正的数字迷宫,它对喜欢探究数字规律的人有着极大的吸引力,以至有些人留连其中,用毕生的精力来研究它的变化,就连大数学家欧拉对它都有着浓厚的兴趣。
那么,到底什么是数阵呢?我们先观察上面两个图:右图(1)中有3个大圆,每个圆周上都有四个数字,有意思的是,每个圆周上的四个数字之和都等于13。
右图(2)就更有意思了,1~9九个数字被排成三行三列,每行的三个数字之和与每列的三个数字之和,以及每条对角线上的三个数字之和都等于15,不信你就算算。
上面两个图就是数阵图。
准确地说,数阵图是将一些数按照一定要求排列而成的某种图形,有时简称数阵。
要排出这样巧妙的数阵图,可不是一件容易的事情。
我们还是先从如何来填好数阵图开始。
如何填好数阵图?数阵图问题千变万化,这一类问题要求数阵中填入了一些数以后,能保证数阵中特定关系线(或关系区域)上的数的和相等,解决这一类问题可以按以下步骤解决问题:第一步:区分数阵图中的普通点(或方格),和交叉点(方格)第二步:在数阵图的少数关键点(一般是交叉点)上设置未知数,计算各个点与该点被重复计算次数之积的和的代数式,即数阵图关系线(关系区域)上和的总和,这个和是关系线(关系区域)的个数的整数倍.第三步:判断少数关键点上可以填入的数的余数性质,并得出相应的数阵图关系线(关系区域)和.第四步:运用已经得到的信息进行尝试:数阵图还有一类题型比较少见,解决这一类问题需要理清数阵中数与数之间的相关关系,找出问题关键.【授课批注】数阵图问题千变万化,一般没有特定的解法,往往需要综合运用掌握的各种数学知识来解决问题. 本讲出了要讲授填数阵图的主要技巧,还有以下注意点:1.引导学生从整体到局部对问题进行观察和判断;2.教授巧妙利用容斥原理、余数的性质、整除性质的数学方法;3.锻炼学生利用已知信息枚举,尝试的能力;4.培养学生综合运用各种数学知识,分析问题,找问题关键,解决问题的能力.二、什么是幻方?同学们是否知道我国古代有关“洛书”的神话传说?传说在大禹治水的年代,陕西的洛水经常大肆泛滥,无论怎样祭祀河神都无济于事,每年人们摆好祭品之后,河中都会爬出一只大乌龟,乌龟壳有九大块,横着数是3行,竖着数是3列,每块乌龟壳上都有几个点点,正好凑成1至9的数字,可是谁也弄不清这些小点点是什么意思.一次,大乌龟又从河里爬上来,一个看热闹的小孩惊叫起来:“瞧多有趣啊,这些点点不论横着加、竖着加还是斜着加,结果都等于十五!”于是人们赶紧把十五份祭品献给河神,说来也怪,河水果然从此不再泛滥了.这个神奇的图案叫做“幻方”,由于它有3行3列,所以叫做“三阶幻方”,这个相等的和叫做“幻和”.“洛书”就是幻和为15的三阶幻方.如下图:三、如何解决幻方问题?幻方是指横行、竖列、对角线上数的和都相等的数的方阵,具有这一性质的3×3的数阵称作三阶幻方,4×4的数阵称作四阶幻方,5×5的称作五阶幻方……如图为三阶幻方、四阶幻方的标准式样,三阶幻方的中心位置上的数等于所有所填数的平均数,也等于横行、竖列、对角线上数和的三分之一.解决数表类问题中,首先要找出数填写的规律,再从规律中找到数表的数量关系,从而找出解决问题的关键.知识梳理987653421987654321(一)封闭型数阵问题(二)辐射型数阵(三)其它类型的数阵图(四)幻方例题精讲【试题来源】【题目】将1~6填入左下图的六个○中,使三角形每条边上的三个数之和都等于k,请指出k的取值范围.k=9 k=10 k=11 k=12【题目】小猴聪聪有一天捡到像左下图的模具,它试着将1~10分别填入图中,使得每个小三角形3个顶点上的数字之和为图中所表示的数值,你能做到吗?【题目】图中的6条线分别连接着9个圆圈,其中一个圆圈里的数是6.请你选9个连续自然数(包括6在内)填人圆圈内,使每条线上各数的和都等于23.6543216543216543216543216【题目】小兔子在森林玩耍,遇到一个画着奇怪图形的树桩,上面写着:把10至20这11个数分别填入下图的各圆圈内,使每条线段上3个圆内所填数的和都相等.如果中心圆内填的数相等,那么就视为同一种填法,请写出所有可能的填法,小兔子发了愁,你能帮它吗?【题目】海豚是很聪明的动物,它能将1~9填入右下图的九个○内,并且使得每个圆周和每条直线上的三数之和都相等,并且7,8,9依次位于小、中、大圆周上,你能做到吗?【题目】在下图中的10个○内填入0~9这10个数字,使得循环式成立:【题目】请在图中的每个圆圈内填入不同的自然数,使得图中每个圆圈中所填的数都是上一行与它相邻的两个圆圈中所填数的和,最下面的数是20.+=====----20【题目】请你将2~10这九个自然数填入图中的空格内每行、每列、每条对角线上的三数之和相等.【题目】请你将1~25这二十五个自然数填入图中的空格内每行、每列、每条对角线上的五数之和相等.【题目】将九个数填入左下图的九个空格中,使得任一行、任一列以及两条对角线上的三个数之和都等于定数k,则中心方格中的数必为k÷3【题目】在下图的九个方格中填入不大于12且互不相同的九个自然数(其中已填好一个数),使得任一行、任一列及两条对角线上的三个数之和都等于21.【题目】将前9个自然数填入右图的9个方格中,使得任一行、任一列以及两条对角线上的三个数之和互不相同,并且相邻的两个自然数在图中的位置也相邻.【题目】将1、2、3、4、5、6、7、8、9这九个数字,分别填入3×3阵列中的九个方格,使第二行组成的三位数是第一行组成的三位数的2倍,第三行组成的三位数是第一行组成的三位数的3倍.【题目】在一个3×3的网格中填入9个数使得每一横行、竖行、对角线上三个数的乘积相等.习题演练【题目】将1~7这七个数分别填入图中的○里,使每条直线上的三个数之和都等于12。
四年级奥数数阵与幻方

数阵问题知识要点:一般地来讲在解决数阵图的问题上,我们应先观察好数阵图,找出“公用数”的位置,求出“公用数”是解决数阵问题的关键。
在数阵图中横行有,竖行也有的数,我们把它叫做“公用数”。
如果题中给你的数的个数是奇数个,而“公用数”仅一个,而这个“公用数”又是中心数,这样的数阵图称为辐射型数阵图。
在解决这类数阵图时,就是先找出公用数,每边均剩下两个数,实际上就是在奇数个数中找到和相等的几对数,找的办法有三种,即:去头、去尾、去中间,而数阵图中的“公用数”就是这列数中的头、尾、中间任意一个数。
还有一种数阵图,题中给你的已知数的个数为偶数个,“公用数”不再是一个,而是多个。
这样的数阵图称为封闭型数阵图,在解决此类数阵图时,应分三步走:l、先求出题中给出已知数的总和,2、再求出数阵图中的和,3、用图中和减去已知数的和即为“公用数”的总和。
例题分析:一.辐射型数阵:例1.将2~8这7个数分别填在下图中的圆圈内,使每条线段上三个圆圈内数的和相等.例2.把1~9这9个数字,分别填入下图的各圆圈内,使每条线上5个数的和相等.例3.将1~9这九个数字填在”七一”内,使每一横行,每一竖列的数字的和都是13.二.封闭型数阵:例4.将1~6六个数填入图中的圆圈中,要求四条直线上的数字之和都等于10,那么a是多少?例5. 如果将—11这11个自然数填入左下图的圆圈中,使每个菱形上的四个数之和都等于24,那么A等于多少?例6.把10~80八个整十数填入下图的○中,使每个圆上五个数的和为210。
例7.把10~15这6个数字分别填放图中的各个圆圈内,使每边上的三个圆圈内数之和相等。
例8. 图中五个正方形和12个圆圈,将1—12填入圆圈中,使每个正方形四角上圆圈中的数字之和都等于K,那么K等于几?例9. 图中的大三角形被分割成九个小三角形将1—9填入小三角形中,使每条边上的五个小三角形的数字之和都相等,那么这个和的最小值是多少?最大值是多少?例10.图中有10个小三角形和4个大三角形,将1~10填入每个小三角形,使每个大三角形内的数字之和都等于25。
四年级数学竞赛秋季班-第12讲-数阵图与幻方
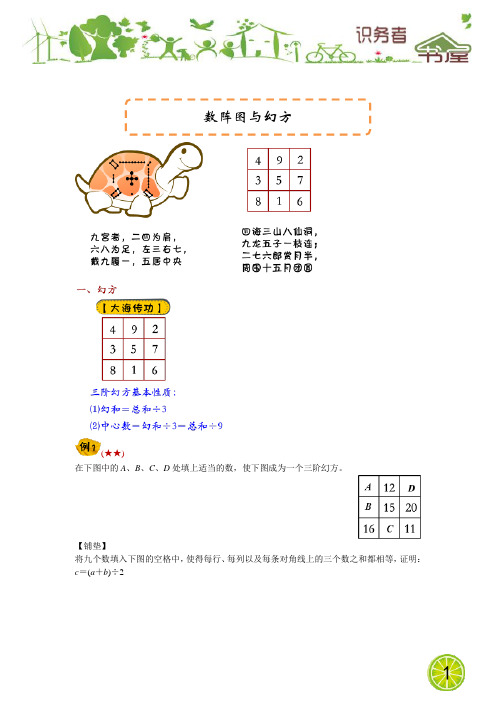
(★★)
在下图中的A、B、C、D处填上适当的数,使下图成为一个三阶幻方。
【铺垫】
将九个数填入下图的空格中,使得每行、每列以及每条对角线上的三个数之和都相等,证明:c=(a+b)÷2
数阵图与幻方
(★★★)
在下图的空格里填入七个自然数,使每一行、每一列及每一条对角线上的三个数的和都等于90。
(★★★★)
在一个乘法幻方中,每一行、每一列、对角线上的数之积都相等。
如果在图中的空格中填上正整数,构成一个乘法幻方,那么x的值是多少?
(★★★)
⑴把10~20这11个数分别填入下图的各圆圈内,使每条线段上3个圆内所填数的和都等于45。
⑵将1~6填入下图的六个○中,使三角形每条边上的三个数之和都等于9。
小学奥数数阵图与幻方B提高版

数阵图与幻方B知识点拨一、数阵图定义及分类:1. 定义:把一些数字按照一定的要求,排成各种各样的图形,这类问题叫数阵图.2. 数阵是一种由幻方演变而来的数字图.数阵图的种类繁多,这里只向大家介绍三种数阵图:即封闭型数阵图、辐射型数阵图和复合型数阵图.3.二、解题方法:解决数阵类问题可以采取从局部到整体再到局部的方法入手: 第一步:区分数阵图中的普通点(或方格)和关键点(或方格);第二步:在数阵图的少数关键点(一般是交叉点)上设置未知数,计算这些关键点与相关点的数量关系,得到关键点上所填数的范围;第三步:运用已经得到的信息进行尝试.这个步骤并不是对所有数阵题都适用,很多数阵题更需要对数学方法的综合运用.三、幻方定义幻方是指横行、竖列、对角线上数的和都相等的数的方阵,具有这一性质的33⨯的数阵称作三阶幻方,44⨯的数阵称作四阶幻方,55⨯的称作五阶幻方……如图为三阶幻方、四阶幻方的标准式样,四、解决这幻方常用的方法⑴适用于所有奇数阶幻方的填法有罗伯法.口诀是:一居上行正中央,后数依次右上连.上出框时往下填,右出框时往左填.排重便在下格填,右上排重一个样.⑴适用于三阶幻方的三大法则有: ①求幻和: 所有数的和÷行数(或列数)②求中心数:我们把幻方中对角线交点的数叫“中心数”,中心数=幻和÷3. ③角上的数=与它不同行、不同列、不同对角线的两数和÷2.98765432113414151612978105113216例题精讲一、数阵图例题1 如图,大、中、小三个正方形组成了8个三角形,现在把2、4、6、8四个数分别填在大正方形的四个顶点;再把2、4、6、8分别填在中正方形的四个顶点上;最后把2、4、6、8分别填在小正方形的四个顶点上.⑴能不能使8个三角形顶点上数字之和都相等?⑵能不能使8个三角形顶点上数字之和各不相同?如果能,请画图填上满足要求的数;如果不能,请说明理由.例题2 将1~16分别填入下图(1)中圆圈内,要求每个扇形上四个数之和及中间正方形的四个数之和都为34,图中已填好八个数,请将其余的数填完.例题3 一个3 3的方格表中,除中间一格无棋子外,其余梅格都有4枚一样的棋子,这样每边三个格子中都有12枚棋子,去掉4枚棋子,请你适当调整一下,使每边三格中任有12枚棋子,并且4个角上的棋子数仍然相等(画图表示)。
4年级奥数数幻方与数阵图进阶

幻方的概念与基本性质,三阶和四阶幻方的编制,各种在方格表中填入数值或符号要求在每行、每列及对角线上具有某种性质的幻方类型的数阵图问题.其他结构较为独特的数阵图问题。
例题:1.用l至9这9个数编制一个三阶幻方,写出所有可能的结果.所谓幻方是指在正方形的方格表的每个方格内填入不同的数,使得每行、每列和两条对角线上的各数之和相等;而阶数是指每行、每列所包含的方格的个数.[分析与解]为了方便叙述,在幻方内标上字母.显然有a+c+e=h+A+g=f+d+b,而这9个数的和为1+2+3+…+9=45,所以每行,每列,两条对角线的和均为45÷3=15.又有a+A+b=c+A+d=e+A+f=g+A+h,所以有a+b=c+d=e+f=g+h=k,那么有4k+4A=15×4,而4k+A=45,所以A=5,即中间数为5,k=10,试着填入,有如下填充结果满足题意:.2.已知图16-1是一个四阶幻方,那么标有“*”的方格中所填的数是多少?[分析与解]对角线的和为12+9+5+8=34,于是,第三列的和也是34,有34-7-9-16=2知第三列第四行的数为2.有34-8-11-2=13,则第四行第四列为13.有34-12-3-13=6,所以第四列第二行为6,即标有“*”的方格内所填得数为6.3.将自然数l至9分别填在如图16-2所示的3×3方格表内,使得每行、每列及两条对角线上的数满足两端的两个数之和减去中间的数,结果都等于5.[分析与解]设中间的数为A,有a+b=5+A,c+d=5+A,e+f=5+A,g+h=5+A,那么有a+b+c+d+e+f+g+h+A =20+5A=1+2+3+…+9=45.有A=5,a+b=10,c+d=10,e+f=10,g+h=10,即为普通的三阶幻方,答案与题一一样.有如下图给出几种填法:4.把1,2,3,4,6,9,12,18,36这9个数分别填入3×3方格表的各方格内,使每一行、每一列及两条对角线上的3个数的乘积都是216.求位于正中间的方格中所填的数.[分析与解]有1×36=2×18=3×12=4×9,36×6=216,所以有中心填入6.多次调整位置,可得出如下填法:.5.图16-3是一个三阶幻方,那么标有*的方格中所填的数是多少?[分析与解]第一行和第一列都包含“*的方格,且它们的和相等,那么左下角中的方格内数为8+10-1=17.那么这个幻方的和就是(10+17)÷2=13.5.这样,每行每列数的和就应当是10+13.5+17=40.5.标有*的方格内填入的数应是40.5-10-8=22.5.6.在图16-4的每个空格内填入一个数,使得每行、每列及两条对角线上的3个方格中的各数之和都等于19.95.那么,标有*的格内所填的数是多少?[分析与解]中央的数为19.95÷3=6.65,因而第二列第一个数是19.95-6.65-8.80=4.50.从而标有“*”的格内为19.95-4.33-4.50=11.12.7.如图16-5所示,在3×3方格表内已填好了两个数19和95,在其余的空格中填上适当的数,可以使得每行、每列以及两条对角线上的三个数之和都相等.(1)求x;(2)如果中间的空格内填入100,试在上一小题的基础上,完成填图.[分析与解](1) 由于幻方中各行、各列和对角线上三个数之和都相等,可以列出等式:(a+b+c)+(d+e+f)=(a+d+g)+(g+e+c).化简得:b+f=2×g.题目已知f=19,g=95,因此x=2×95-19=171.(2) 因为中间方格填的是100,所以幻方中各行各列三个数的和是100×3=300.这样第二行第一个方格中应填300-100-19=181,并且依次求得其他各个方格中的数.结果如上右图.8.在图16-6所示的方格表的每个方格内填入一个恰当的字母,可以使得每行、每列及两条对角线上4个方格中的字母都是A,B,C,D,那么,表中标有★的方格内应填的字母是什么?[分析与解]从对角线看,★格可能是B、C、D,从第4列看,★格不可能是D.因而★格内只可能为B或C.用上述方法考察左下角,有最小角为B,从而★只能是C.下面给出一种满足题意的填法:.9.请在4×8方格表的每个方格内填入数1,2或3,使得任何排列成如图16-7所示形状的4个方格中所填数的和都是7.[分析与解]我们先考虑3×3的表格情况,按要求填好后,有:a+b+e+f=b+e+f+i=7.所以a=i,同理,c=g.又因为a+b+e+f=c+b+e+d=7,从而:a+f=c+d,同理,g+f=d+i,两式相加,得到a+g+2×f=c+i+2×d.其中a=i,c=g,所以f=d,也就是说中间隔一个方格的两个方格所填入的数相同,我们可以借助上面方法来填写,只用先将一格2×2的小方格填号,使它们的和为7,再将其复制平移知其他的方格内即可.下面给出几种填法:10.如图16-8,有一个11位数,它的每3个相邻数字之和都是20.问标有*的那个数位上的数字应是几?[分析与解]因为每相邻3位数字之和为20,从右边起第一位数字7与第二,三位数字之和是20,第二、三位数字与第四位数字之和也是20,所以第四位数字是7.这样,我们便找到一条规律:每隔2位必出现相同的数字.所以“?”的数字应该是7.11.如图16-9,横、竖各有12个方格,每个方格内都有一个数.已知横行上任意3个相邻数之和为20,竖列上任意3个相邻数之和为21,并且其中4个方格内的数分别是3,5,8和x.那么x所代表的数是多少?[分析与解]竖行上任意三个相邻数之和为21,从而数列上任意三个相邻数都是由同样的三个数组成(只不过顺序不同),这样我们可把“3”向下每隔两格的“移动”,最后得到,由此得出中间的一格应填21-3-8=10.即x的右面一格是10.横行上的任意三个数之和是20.如果把横行最左边的5,每隔两格地“移动”,就知道x的左边一格是5,这样就有x=20-5-10=5,即x代表的数是5.12.把l,2,3,…,13这13个数分别填在如图16-10所示的3个圆圈内,使得同一个圆圈内任意两个数相减,所得的差不在这个圆圈内.现在已经把l,4,7填在第一个圆圈内,3填在第三个圆圈内,请将其余9个数填好.[分析与解]6只能填入第二个圆,这是因为7-1=6,6-3=3.5、8、11都不能填入第一圈,这是因为5-4=1,8-1=7,11-7=4,如果8填入第三个圆,那么5、11都不能填入第三个圆,这是因为8-5=3,11-8=3,从而都只能填入第二个圆,这又导致11-5=6,所以8只能填入第二个圆.因为2不能填入第一个圆,这是因为2-1=1,也不能填入第二个圆,这是因为8-6=2,所以2只能填入第三个圆.于是5只能填入第二个圆,这是因为5-3=2,11只能填入第三个圆,这是因为11-6=5,13只能填入第一个圆,这是因为13-11=2,13-8=5,9只能填入第二个圆,这是因为13-4=9,11-2=9,12只能填入第三个圆,这时因为12-6=6,13-1=12,10只能填入第一个圆,这是因为10-5=5,12-2=10.最终结果如下:13.请在图16-11的每个圆圈内填入不同的自然数,使得图中每个圆圈中所填的数都是上一行与它相邻的两个圆圈中所填数的和.[分析与解]本题填法不唯一,下面给出两种填法:14.在图16-12的7个圆圈内各填一个数,要求对于每一条直线上的3个数,居中的数是旁边两个数的平均数.现在已经填好了两个数,那么x等于多少?[分析与解]如下图所示,将剩下的圆圈内标上字母:于是A=(13+17)÷2=15,即B+15与D+17相等,均为2C,因此B-D=2,于是2D=B+13=D+2+13,故D=15.C=(17+15)÷2=16,x=2C-13=19.15.请在图16-13所示的8个小圆圈内,分别填入1,2,3,4,5,6,7,8这8个数字,使得图中用线段连接的两个小圆圈内所填的数的差(大减小)恰好分别是l,2,3,4,5,6,7.[分析与解]填法有很多,如下给出两种填法:。
小学四年级奥数下册简单的幻方及其他数阵图教案

小学四年级奥数下册简单的幻方及其他数阵图教案简单的幻方及其他数阵图教案有关幻方问题的研究在我国已流传了两千多年,它是具有独特形式的填数字问题.宋朝的杨辉将幻方命名为“纵横图.”并探索出一些解答幻方问题的方法.随着历史的进展,许多人对幻方做了进一步的研究,创造了许多绚丽多彩的幻方. 据传说在夏禹时代,洛水中出现过一只神龟,背上有图有文,后人称它为“洛书”.洛书所表示的幻方是在3×3的方格子里(即三行三列),按一定的要求填上1~9这九个数,使每行、每列、及二条对角线上各自三数之和均相等,这样的3×3的数阵阵列称为三阶幻方. 一般地说,在n×n(n行n列)的方格里,既不重复又不遗漏地填上n2个连续的自然数(一般从1开始,也可不从1开始)每个数占一格,并使排在任一行、任一列和两条对角线上的n个自然数的和都相等,这样的数表叫做n阶幻方.这个和叫做幻和,n叫做阶. 杨辉在《续古摘奇算法》中,总结洛书幻方构造方法时写到:“九子排列,上、下对易,左右相更,四维挺出.”现用下图对这四句话进行解释.九子排列上、下对易左右相更四维挺出怎样构造幻方呢?一般方法是先求幻和,再求中间位置的数,最后根据奇、偶情况试填其他方格内的数.分析为了便于叙述,先用字母表示图中要填写的数字.如上右图所示.解答这个题目,可以分三步解决:①先求出每行、每列三个数的和是多少?②再求中间位置的数是多少?此题是求E=?③最后试填其他方格里的数.∵A+B+C+D+E+F+G+H+I=1+2+3+4+5+6+7+8+9=45.∴A+B+C=D+E+F=G+H+I=15.∴B+E+H=A+E+I=C+E+G=15.∴A+B+C+D+E+F+G+H+I+3E=(A+E+I)(B+E+H)+(C+E+G)+(D+E+F)=15X4.45+3E=603E=15E=5.这样,正中央格中的数一定是5.由于在同一条直线的三个数之和是15,因此若某格中的数是奇数,那么与这个数在同一条直线上的另两个数的奇偶性相同.因此,四个角上的数A、C、G、I必为偶数.(否则,若A为奇数,则I为奇数.此时若B为奇数,则其余所有格亦为奇数;若B为偶数,则其余所有格亦为偶数.无论哪种情形,都与1至9中有5个奇数,4个偶数这一事实矛盾.)因此,B、D、F、H为奇数.我们不妨认为A=2(否则,可把3×3方格绕中心块旋转即能做到这一点).此时I=8.此时有两种选择:C=4或G=4.因而,G=6或C=6.其他格的数随之而定.因此,如果把经过中心块旋转而能完全重合的两种填数法视作一种的话,一共只有两种不同的填数法:A=2,C=4或A=Z,G=4(2,4被确定位置后,其他数的位置随之而定).解:按照上面的分析,我们可以得到两个解(还有另外6个可以由这两个解经过绕中心块旋转而得到,请大家自己完成).下面我们就来介绍一些简单的幻方.例1 将1~9这九个数,填入下左图中的方格中,使每行、每列、两条对角线上三个数字的和都相等.网络搜集整理,仅供参考。
4年级奥数培优讲义-6-幻方和数阵图-难版

精品资料之奥数培优讲义适用:华杯、希望、年级:四年级科目:小学奥数内容:奥数培优教程(资料来源于学校内部,供各位老师学习交流使用,欢迎大家下载参考)传说在五千年前,大禹治水的时代,人们在黄河中发现一只大龟,龟背上有一些奇怪的图案,经过破译,人们将龟背上的神奇的图案译成了如下图这样的数阵图,也称做幻方。
幻方和数阵是我国文化遗产之一,早在公元前4世纪就有“河图”、“洛书”的传说与记载。
到了宋朝,杨辉对幻方已有较详细的记述,并探索出一些编制方法。
明朝程大位、清朝张潮等人,创制了绚丽多彩的幻方与数阵图式,其中九宫图是最简单的三阶幻方。
将三阶幻方推广,结合某些几何图形,把一些数字填入图形的某种位置上,并使数字满足一定的约束条件,这类问题,通常被称为“数阵图”。
幻方是特殊的数阵图。
大约在15世纪初,幻方传到国外,引起了欧洲很多数学家的兴趣,发现许多新成果。
人们发现幻方不仅仅是一种数字游戏,而且与实验方案的设计及一些高深数学分支有关,幻方已成为数阵图中最重要的课题,是数学研究中的一个重要分支。
数阵图大致分三种:封闭型数阵图、开放型数阵图和复合型数阵图。
幻方的特点:一个幻方每行、每列、每条对角线上的几个数的和都相等。
这个相等的和叫“幻和”。
要求在n 行n 列的方格里,既不重复又不遗漏地填上n ×n 个连续的自然数。
这些自然数所组成的一列数有极强的规律性,按顺序排列后,每一项都比它前面的一项大1,即它们构成了差相等的数列,是等差数列。
因此在解答这类问题时,常用的知识有:1.等差数列的求和公式总和=(首项+末项)×项数÷2知识梳理2.数字的奇偶性奇数±奇数=偶数偶数±偶数=偶数奇数±偶数=奇数可简记为:同性为偶,异性为奇(注:同性是同奇或同偶,异性是指一奇一偶)。
数阵图【例1】★如图所示,在三个圆圈中各填入一个自然数,使每条线段两端的两个数之和均为奇数。
请问这样的填法存在吗?如不存在,请说明理由;如存在,请写出一种填法。
【精品】四年级奥数思维训练精编讲义(共23讲) 通用版 四年级第18讲 幻方与数阵图(教师版)
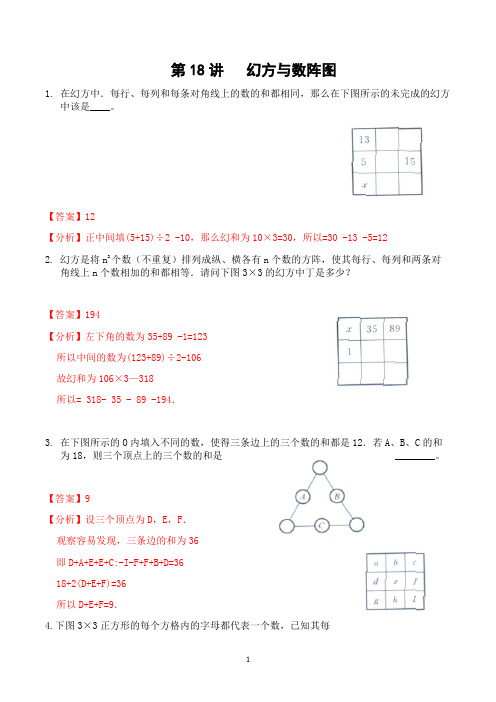
第18讲幻方与数阵图1.在幻方中.每行、每列和每条对角线上的数的和都相同,那么在下图所示的未完成的幻方中该是____。
【答案】12【分析】正中间填(5+15)÷2 -10,那么幻和为10×3=30,所以=30 -13 -5=122.幻方是将n2个数(不重复)排列成纵、横各有n个数的方阵,使其每行、每列和两条对角线上n个数相加的和都相等.请问下图3×3的幻方中丁是多少?【答案】194【分析】左下角的数为35+89 -1=123所以中间的数为(123+89)÷2-106故幻和为106×3—318所以= 318- 35 - 89 -194.3.在下图所示的O内填入不同的数,使得三条边上的三个数的和都是12.若A、B、C的和为18,则三个顶点上的三个数的和是________。
【答案】9【分析】设三个顶点为D,E,F.观察容易发现,三条边的和为36即D+A+E+E+C:-I-F+F+B+D=3618+2(D+E+F)=36所以D+E+F=9.4.下图3×3正方形的每个方格内的字母都代表一个数,已知其每行,每列以及两条对角线上三个数之和都相等,若“a=4,d=19,l=22,那么b=_______ ,h=______。
【答案】b=25,h=1【分析】由h+l=a+d,得h=1,b+h=a+l,b+1=4+22,所以b=25.5.在图1、图2的空格中分别填人适当的数,使得横、竖及对角线上的三个数之和都相等,那么“?”处的数字分别为多少?.【答案】 (1)9;(2)6【分析】在幻方中.有重要结论:每一行之和或每一列之和或对角线之和均为中间方格数的3倍。
(1)给下图中空白处标上字母.8+12+a=11+a+b,.则应为:8+12 - 11=9.则a+20=3a.所以a=10.每行每列每条对角线上的和是30,对应的?处应填30 -12 -9=9.(2)给下图中空白处标上字母.根据幻方的性质有2×?=3+9.所以?处应填6。
小学奥数讲义4年级-6-幻方和数阵图-难版

传说在五千年前,大禹治水的时代,人们在黄河中发现一只大龟,龟背上有一些奇怪的图案,经过破译,人们将龟背上的神奇的图案译成了如下图这样的数阵图,也称做幻方。
幻方和数阵是我国文化遗产之一,早在公元前4世纪就有“河图”、“洛书”的传说与记载。
到了宋朝,杨辉对幻方已有较详细的记述,并探索出一些编制方法。
明朝程大位、清朝张潮等人,创制了绚丽多彩的幻方与数阵图式,其中九宫图是最简单的三阶幻方。
将三阶幻方推广,结合某些几何图形,把一些数字填入图形的某种位置上,并使数字满足一定的约束条件,这类问题,通常被称为“数阵图”。
幻方是特殊的数阵图。
大约在15世纪初,幻方传到国外,引起了欧洲很多数学家的兴趣,发现许多新成果。
人们发现幻方不仅仅是一种数字游戏,而且与实验方案的设计及一些高深数学分支有关,幻方已成为数阵图中最重要的课题,是数学研究中的一个重要分支。
数阵图大致分三种:封闭型数阵图、开放型数阵图和复合型数阵图。
幻方的特点:一个幻方每行、每列、每条对角线上的几个数的和都相等。
这个相等的和叫“幻和”。
要求在n 行n 列的方格里,既不重复又不遗漏地填上n ×n 个连续的自然数。
这些自然数所组成的一列数有极强的规律性,按顺序排列后,每一项都比它前面的一项大1,即它们构成了差相等的数列,是等差数列。
因此在解答这类问题时,常用的知识有: 1.等差数列的求和公式总和=(首项+末项)×项数÷2 2.数字的奇偶性 奇数±奇数=偶数 偶数±偶数=偶数知识梳理奇数±偶数=奇数可简记为:同性为偶,异性为奇(注:同性是同奇或同偶,异性是指一奇一偶)。
数阵图【例1】★如图所示,在三个圆圈中各填入一个自然数,使每条线段两端的两个数之和均为奇数。
请问这样的填法存在吗?如不存在,请说明理由;如存在,请写出一种填法。
【解析】不存在,设所填的数分别是a ,b ,c ,如图所示。
假设 a+b=奇数. a+c=奇数, b+c=奇数, 左边=2(a+b+c),是偶数,右边=三个奇数相加,是奇数, 偶效≠奇数。
四年级高思奥数之幻方与数阵图扩展含答案

第20 讲幻方与数阵图扩展内容概述掌握幻方的概念,了解三、四阶幻方的构造方法;解决具有与幻方类似性质的数阵图问题;进一步学习重数分析的方法;通过计算重数来处理数阵图中的最大最小问题.典型问题兴趣篇1. 把1,2,⋯,9填人图20-1 中9个空白圆圈内,使得三个圆周及三条线段上3个数之和都相等.2. (1)如图20-2,在3×3 的方格表的每个方格中填入恰当的数,使得每行、每列、每条对角线上所填数之和都相等.(2)如图20-3,在4×4 的方格表的每个方格中填人恰当的数,使得每行、每列、每条对角线上所填数之和都相等.3.在图20-4所示的3×4 方格表的每个方格中填人恰当的数后,可以使各行所填的数之和相等,各列所填的数之和也相等.现在一些数已经填出,标有符号是多少?4.如图20-5,请在空格中填人适当的数,组成一个三阶幻方.5.请将图20-6 所示的5×5 方格表补充完整,使得每个方格内都有一个数字,并且具有如下的性质:方格表中每行,每列和每条对角线的5个方格内所填的5 个数中,l、2、3、4、5 恰好各出现一次.请问:标有符号“△”,“▽”和“○”的方格中所填的数分别是6.请将 1 至 9 这 9 个数填入图 20-7 中的方框内,使得所有不等号都成立.所有满足要求的 填法共有多少种 ?7.请在图 20-8 所示的 8 个小圆圈内,分别填入 1 至 8这 8 个数字,使得图中用线段连接的两个小圆圈内所填的数的差 (大减小 )恰好是 1、2、3、4、5、 6、7.8.将 1至 5这 5个数字填入图 20-9中的小圆圈内,使得横线、竖线、大圆周上所填数之和 都相等.9.请在图 20-10 中的六块区域内填人 相邻的区域内的数之和都相等.10.将 0至9填入图 20-11的10块区域中 (阴影区域除外 ),使得每个圆内的三个数之和都是1、2、3、4、5、6,使得对每一个小圆圈来说,与它相等的.请问:这个和最小是多少 ?最大是多少 ?拓展篇1.将1,2,3,⋯,24,25 分别填入图20-12 的各个方格中,使得每行、每列及两的数是多少2.请在图 20-13 的每个空格内填人一个合适的数,使得每行、每列及两条对角线上的3. (1)在图 20-14 的每个空格内填入一个数,使得每行、每列及两条对角线上的 的各数之和都等于 19. 95.那么,标有“ t ”的方格内所填的数是多少 ?4. 如图 20-16 ,大正方形的 4 个角上已填人 4 个数, 4 个数之和是 264.奇妙的是 , 把这个 图倒过来看,大正方形 4 个角上的数之和仍然是 264.请你在中间的小正方形的 4 个角的圆 圈里,填人另外 4个数,使得每条对角线上的 4 个数正看和倒看时,其和都是 正方形角上的 4 个数正看和倒看时,其和也都是 264.6.请将 1至 10填入图 20-18 中的 10个圆圈中 (9已经填好 ) 的数都等于与它相连的上方两个圆圈内的两数之差.7.在图 20-19 的 7 个圆圈内各填一个数,要求对于每一条直线上的 边两个数的平均数.现在已经填好了两个数,请把剩下的圆圈填好.(2)请在图 20-15 的每个空格内填人一个合适的数,使得每行、每列及两条对角线上的 个方格中的各数之和都相等。
4年级-6-幻方和数阵图

传说在五千年前,大禹治水的时代,人们在黄河中发现一只大龟,龟背上有一些奇怪的图案,经过破译,人们将龟背上的神奇的图案译成了如下图这样的数阵图,也称做幻方。
幻方和数阵是我国文化遗产之一,早在公元前4世纪就有“河图”、“洛书”的传说与记载。
到了宋朝,杨辉对幻方已有较详细的记述,并探索出一些编制方法。
明朝程大位、清朝张潮等人,创制了绚丽多彩的幻方与数阵图式,其中九宫图是最简单的三阶幻方。
将三阶幻方推广,结合某些几何图形,把一些数字填入图形的某种位置上,并使数字满足一定的约束条件,这类问题,通常被称为“数阵图”。
幻方是特殊的数阵图。
大约在15世纪初,幻方传到国外,引起了欧洲很多数学家的兴趣,发现许多新成果。
人们发现幻方不仅仅是一种数字游戏,而且与实验方案的设计及一些高深数学分支有关,幻方已成为数阵图中最重要的课题,是数学研究中的一个重要分支。
数阵图大致分三种:封闭型数阵图、开放型数阵图和复合型数阵图。
幻方的特点:一个幻方每行、每列、每条对角线上的几个数的和都相等。
这个相等的和叫“幻和”。
要求在n 行n 列的方格里,既不重复又不遗漏地填上n ×n 个连续的自然数。
这些自然数所组成的一列数有极强的规律性,按顺序排列后,每一项都比它前面的一项大1,即它们构成了差相等的数列,是等差数列。
因此在解答这类问题时,常用的知识有: 1.等差数列的求和公式总和=(首项+末项)×项数÷2 2.数字的奇偶性 奇数±奇数=偶数偶数±偶数=偶数知识梳理奇数±偶数=奇数可简记为:同性为偶,异性为奇(注:同性是同奇或同偶,异性是指一奇一偶)。
数阵图【例1】★如图所示,在三个圆圈中各填入一个自然数,使每条线段两端的两个数之和均为奇数。
请问这样的填法存在吗?如不存在,请说明理由;如存在,请写出一种填法。
【例2】★小蜗牛不小心爬到一个三角形数阵图中,必须将1~6六个自然数分别填入下图的○内,使三角形每边上的三数之和都等于11才能通过这个数阵图,你能帮它吗?614532【小试牛刀】把1,2,3,4,5,6,7,8八个数字填入下图中的○内,使正方形每条边上三个数的和都等于13.典型例题【例3】★把1~7这七个自然数,分别填在下图(1)的圆圈内,使每条直线上的三个数的和都相等。
四年级奥数幻方和数阵图

幻方和数阵图一、幻方例:用1—9这9个数排成一个三阶幻方1.用3—11这9个数补全图中的幻方,并求出幻和。
2.在图的空格中填入不大于15且互不相同的自然数(其中已填好一个数),使每一个横行、竖列和对角线上的三个数之和都等于30。
3.在图(a )(b )的空格中填入不大于15且互不相同的数(其中已填好一个数),使每一横行,每一竖列和对角线上的三个数之和都等于30。
(a ) (b )4.将5—20这16个数排成一个四阶幻方。
5.将5—29这25个数排成一个五阶幻方。
6.在图中的方格中填入不相同的数,使得每行、每列及每条对角线上的三个数之和都相等,问图中左上角的数是几?7.从1—13这十三个数中选出12个数填到图的方格中,使每一横行四个数之和相等,每一竖列三数之和也相等。
8.在图中每个方格内填一个数,使得每行、每列及每条对角线上的四个方格中的数都是1、3、5、7,那么带“☆”号的两个方格中的数之和等于几?4 859 8 14?19 13第2题 第3题二、数阵图1.把1—7这七个数填入图中的○中,使每条直线上三个数的和都等于14。
第1题 第2题2.将1—9这九个数填入图中的○中,使每条边上四个数的和都等于17。
3.将数字1,2,3,4,5,6填入图中的小圆圈内,使每个大圆上4个数字的和都是16。
第3题4.将1—8填在图中的○中,使每条线上的三个数的和都相等,并求出这个和的取值范围。
○ ○ ○○ ○○ ○ ○第4题5.将1—8填在图中的○中,使大圆上、小圆上、横线上、竖线上四个数的和都相等,而且在大圆上的四个数中最大的数尽可能小。
13 57 7 1☆ ☆第5题6.把1—7七个自然数分别填在图中的○内,使得四个三角形的三个顶点数之和等于11,则a填。
○○○a○A○○○B8.将1—8个数填入图中的八个方格内,使上面四格,下面四格,左边四格,右边四格,对角线四格和四角四格内四个数相加的和都是18。
第8题9.把1~9这9个数,填入图11中的九个○内,使每条线段上三个数的和相等,两个四边形四个顶点上数的和也相等。
四年级 奥数 讲义 238学子 教案库 0407_幻方和数阵图
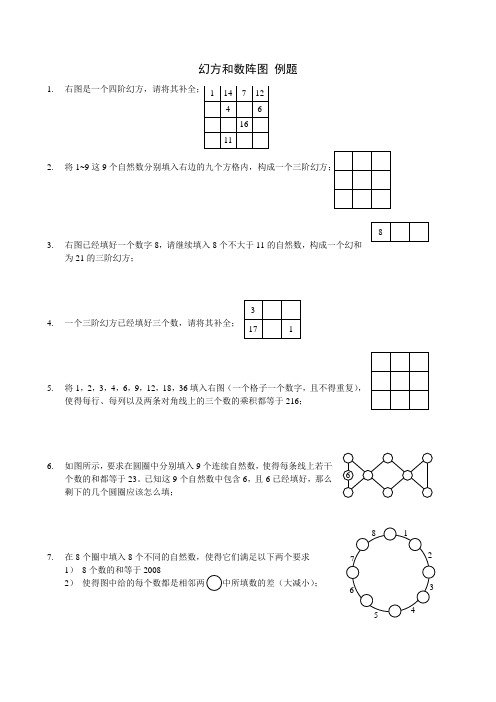
1.2.将1~9这93.右图已经填好一个数字8,请继续填入8个不大于11的自然数,构成一个幻和为21的三阶幻方;4.一个三阶幻方已经填好三个数,请将其补全;5.将1,2,3,4,6,9,12,18,36填入右图(一个格子一个数字,且不得重复),使得每行、每列以及两条对角线上的三个数的乘积都等于216;6.如图所示,要求在圆圈中分别填入9个连续自然数,使得每条线上若干个数的和都等于23。
已知这9个自然数中包含6,且6已经填好,那么剩下的几个圆圈应该怎么填;7.在8个圈中填入8个不同的自然数,使得它们满足以下两个要求1)8个数的和等于20082)使得图中给的每个数都是相邻两;1. 如图所示,一个四阶幻方的幻和为682. 将右面这个三阶幻方补全;3. 构造一个由9个连续自然数构成的三阶幻方,填入右图,并要求幻和等于54;4. 将1,2,4,5,10,20,25,50,100填入右图,构成一个幻积为1000的三阶幻方;5. 7个圆圈内各填一个数,使得每条直线上的3个数,居中的那个都是旁边两个数的平均数。
现在已经填好了两个,那么a ______;6. 将1~12这12个自然数分别填入右面图中(每个数字只能用一次),使得每条边上四个数的和都相等。
那么这个和最大等于 ;7. 大正方形的4个角上已经填入4个数,4个数的和等于264。
奇妙的是,如果把这个图颠倒过来看,和仍然是264。
请你在剩下的4个圈内填入另外的4个数,使得这4个数的和正着看与倒着看都等于264,而且图中两条对角线上的4个数的和正着看和倒着看也都等于264;8 214 12 10 22 4 63 7 919 29a1986 6891。
四年级奥数 教师版 第六讲幻方与数阵图

第六讲 幻方与数阵图知识导航三阶幻方的性质:1.中心位置上的数等于幻和除以3;2.角上得数等于和它不相邻的两条边上的数的平均数;3.中心数两头的数等于中心数的2倍。
例1:我们先来一起解决三道难度相差很大的题目,目的在于总结出三阶幻方的若干重要性质。
如下图,将1—9填入3×3的方格表中,使得每行每列以及两条对角线上的三个数字之和都相等,你一共可以得到多少种填法?解析:首先,我们思考要填出一个三阶幻方,什么量的求出是最重要的?立刻我们就知道,那个所谓的“幻和”,即每行、每列、每条对角线三个数的和是最重要的量。
它是多少呢?哦,如果我们按照行(按照列也一样)把幻方中的九个数加起来,那么它们的总和不就是3倍的“幻和”吗?而另一方面,我们也知道,由于1到9这九个数字都只各用了一次,所以3倍的的“幻和”就等于1+2+3+4+5+6+7+8+9=45(请复习学过的等差数列知识)。
于是最后,我们终于得到这个至关重要的“幻和”就是45÷3=15。
接下来第二步,我们来关心一下中间一格应该填哪个数字。
同学们可能会说,中间一定填5,因为1到9的中间数字就是5,而幻方又是上下左右对称的。
没错,同学们有这样的数学直观很好,但是为了确定我们的判断,还是需要严格地说明一下。
看上面的表格,由于我们还没有填入任何一个数字,所以就用了九个大写字母来表示。
下面就需要技巧了,我们现在只考虑包含E 的四条直线:因为A +E +I =15, B +E +H =15, C +E +G =15, D +E +F =15, 所以如果我们把这四个式子的左右两边分别相加,就可以得到(A+B+C+D+E+F+G+H+I )+3×E=60,而A+B+C+D+E+F+G+H+I 不就是所填数的总和吗?不论填法如何,这个数是第1题不变的,它就是45,于是那么我们就得到E=5了。
解:根据上面的分析,我们知道“幻和”=15,而E=5。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
四年级奥数幻方和数阵图
2.1 幻方
[同步巩固演练]
1、用8—16这9个数排成一个三阶幻方
2、用3—11这9
第2题
3、在图的空格中填入不大于15且互不相同的自然数(其中已填好一个数),使每一个横行、竖列和对角线上的三个数之和都等于
30。
第3题
4、在图(a )(b )的空格中填入不大于15且互不相同的数(其中已填好一个数),使每一横
30。
(a ) (b )
第4题
5、将5—20这16个数排成一个四阶幻方。
6、将5—29这25个数排成一个五阶幻方。
7、将7—42这36个数排成一个六阶幻方。
[
能力拓展平方]
1、在图中的方格中填入不相同的数,使得每行、每列及每条对角线上的三个数之和都相等,问图中左上角的数是几?
2、从1—13这十三个数中选出12个数填到图的方格中,使每一横行四个数之和相等,每一竖列三数之和也相等。
3、在图中每个方格内填一个数,使得每行、每列及每条对角线上的四个方格中的数都是1、3、5、7,那么带“☆”号的两个方格中的数之和等于几?
1 3 5 7
7 1
☆☆
第2题第3题
4、在3×3的方阵图中,每格中填入一个不同的自然数,使得每一行、每一列及对角线上的三个数的乘积都相等。
5、将八个数填入图的空格中,使这八个数的总和等于12,如果总和为13、14、15呢?
6、将1、2、3、4、5、6、
7、
8、9这九个数,分别填入图的九个方格,使第二行组成的三位数是第一行组成的三位数的2倍,第三行组成的三位数是第一行组成的三位数的3倍。
第5题第6题
2.2 数阵图
[同步巩固演练]
1、把1—7这七个数填入图中的○中,使每条直线上三个数的和都等于14。
第1题第2题
2、将1—9这九个数填入图中的○中,使每条边上四个数的和都等于17。
3、将数字1,2,3,4,5,6填入图中的小圆圈内,使每个大圆上4个数字的和都是16。
第3题
4,将1—8填在图中的○中,使每条线上的三个数的和都相等,并求出这个和的取值范围。
○○○
○○
○○○
第4题
5、将1—8填在图中的○中,使大圆上、小圆上、横线上、竖线上四个数的和都相等,而且在大圆上的四个数中最大的数尽可能小。
第5题
6、把1—7七个自然数分别填在图中的○内,使得四个三角形的三个顶点数之和等于11,则a填。
○○
○a
○A○○○B
第6题
7、把1—9各数填入图中“七、一”9个空格内,使第一横行、竖列的数字的和是13。
第7题
8、将1—8个数填入图中的八个方格内,使上面四格,下面四格,左边四格,右边四格,对角线四格和四角四格内四个数相加的和都是18。
第8题
[能力拓展平台]
1、将1,2,3,4,8,12这六个数分别填入图中的○内,使每条线上的三个数的积相等。
第1题
2、右图是一部古怪的电话,中间的十二个键分别为四个圆形、四个椭圆形和四个正方形,若想打电话,必须首先将1~12这十二个数填入其中,使四个椭圆、四个圆形、四个正方形以及四条直线上的四个数之和都为26,假如你要打电话,那么你将怎样填数?
第2题
3、请在下图的空格内填入1~46这四十六个自然数,使每一笔直线上各数之和都等于93,应怎样填?
第3题
4、将1~9九个数分别填入图中○内,使外三角形边上○内数字之和等于里面三角形边上○内数字之和。
第4题
5、在下左图中,将1~9这九个数,填入圆圈内,使每个三角形三个顶点的数字之和都相等。
第5题
6、(全国奥赛预赛题,1992)把1~10这十个自然数填入图中的10个方格中,要求图中3个2×2的正方形中四数之和相等,那么,这个和的最小值是几?
第6题
7、将1~8填入图中,使每条线段两端的两个数的差不为1。
第7题
8、(全国奥赛决赛题,1992)在图中的七个圆圈内各填上一个数,要求每条线上的三个数中,当中的数是两边两个数的平均数,现在已填好两个数,求x是多少?
第8题
[本讲综合训练]
1、把20以内的质数分别填入右图中的八个圆圈中,使圈中用箭头连接起来的每条路上的四个数之和都相等。
第1题
2、10月1日是国庆节,图是“10.1”两个数,请把1~18这18个数填入图中的18个空格内,要使每一横划与竖划上所填的数的和都相等。
第2题
3、将1~10这十个数填入图中各○内,使得三个正方形的四个顶点上的数之和等于21。
第3题
4、将1~8分别填入○内,使图中用箭头连接起来的4个数之和都等于18。
第4题
5、请在下图中圆圈内填入1~9这九个数,其中6,8已填好,要求A、B、C、D四个小三角形边上各数字之和全都相等。
第5题
6、将1~10这十个数填入如上图的圆圈内,使每个正方形的四个数字之和都等于23,应怎样填?
第6题
7、(第四届华杯赛复赛试题)在图的小圆圈内,分别填入1~8这八个数字,使得图中用线段连接的两个圆圈内所填的数字之差(大数减小数)恰好是1、2、3、4、5、6、7这七个数字。
第7题
8、(第一届华杯赛决赛试题)在图的六个圆圈内,分别填入六个质数(可以相同)它们的和都是20,而且每个小三角形三个顶点上的数之和相等,问这个质数的乘积是几?
第8题
9、把1~9这9个数,填入图11中的九个○内,使每条线段上三个数的和相等,两个四边形四个顶点上数的和也相等。
第9题
10、把1~8这8个数,填入图12中的八个○内,使每条线段上的四个数的和,与每个四边形四个顶点上的四个数的和都相等。
第10题
11、把1~8这八个数字分别填入下图中的圆圈内,使每个圆周上与每条直线上四个数之和都相等,给出一种具体的填法。
第11题
12、下图中,内部四个交点上已填好数,请你在四周方格里填上适当的数,使交点上的数恰好等于四个方格内的数的和,应怎样填?
第12题
13、图中共七个不同的三角形,把1到9九个数分别填到图中九个黑点旁,使每个三角形三个顶点旁的数字之和都相等。
第13题
14、把1到8这八个数填入图的正方体的八个顶点的圆圈里,使每个面上的四个圆圈里的四个数之和都等于18。
第14题
15、把1~10的十个数填入图中的十个○内,使每个正方形四个顶点上各数的和都是24。
第15题
16、将1~9这九个数字填入图中的○内,使每个三角形(三个)和每条直线(三条)上的3个数字之和都相等(写出一个答案)。
第16题
17、如图,正六边形六条边上的六个○中分别填1~6六个自然数,再在六边形三条对角线上的六个○中也分别填入1~6六个自然数,问能否找到一种填法,使得图中每个三角形三条边上的三个数字之和都相等?为什么
第17题
18、大正方形的4个角上已填入4个数,4个数之和是264,奇妙的是,把这个图倒过来看,和仍然是264。
请你在中间的小正方形的4个角的圆圈里,填入四个数,使每条对角线上的4个数之和正看和倒看都是264,而且小正方形角上的4 个数之和正看和倒看也都是264。
第18题
19.用1-8这八个数分别填在下图的○〇内,使图中4条线上的三个数相加的和相等,而且大正方形顶点四个数的和是小正方形顶点四个数的和的2倍。
第19题
20.(浙江省竞赛题,2003)将1,2,3,...12这12个自然数分别填入下图中的12个小方格中(每个数字只填一次),使得每条边上的四个数的和相等,那么这和最大是多少?21.(江苏省吴江市竞赛题,2002)在下图的方格中,分别填上数,使每行每列、每条对角线上的三个数的和都相等,那么x=()。
(第20题)(第21题)
22.(江苏省吴江市竞赛题,2002)下面球体有三个圆周,在六个〇里分别填上1,2,3,4,5,6使得每个圆周上相加的和都是14。
第22题
23.(第二届“鲁外杯”竞赛试题,2003)下图中有9个方格,每个方格中填入一个汉字,9个不同的汉字代表9个连续自然数,其中“外”代表19,“学”代表13,如果每行、每列、每条对角线上的三个数字之和都相等,那么“欢迎”两个汉字所代表的数字之和是()。
欢迎你。
