中山大学高数期末考试真题及答案
【中大】高等数学习题及详细解答
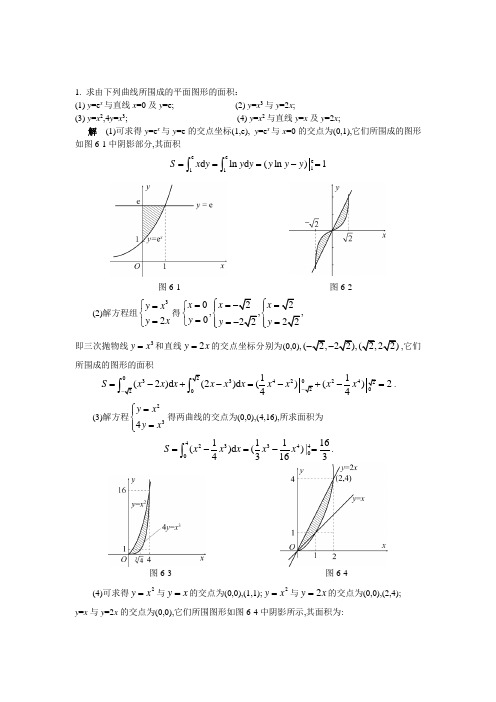
1. 求由下列曲线所围成的平面图形的面积:(1) y =e x 与直线x =0及y =e; (2) y =x 3与y =2x ;(3) y =x 2,4y =x 3; (4) y =x 2与直线y =x 及y =2x ;解 (1)可求得y =e x 与y =e 的交点坐标(1,e), y =e x 与x =0的交点为(0,1),它们所围成的图形如图6-1中阴影部分,其面积eee111d ln d (ln )1S x y y y y y y ===-=⎰⎰图6-1 图6-2(2)解方程组32y x y x ⎧=⎨=⎩得022,,,02222x x x y y y ⎧⎧==-=⎧⎪⎪⎨⎨⎨==-=⎩⎪⎪⎩⎩ 即三次抛物线3y x =和直线2y x =的交点坐标分别为(0,0),(2,22),(2,22)--,它们所围成的图形的面积20334224222011(2)d (2)d ()()244S x x x x x x x x x x --=-+-=-+-=⎰⎰.(3)解方程234y xy x⎧=⎪⎨=⎪⎩得两曲线的交点为(0,0),(4,16),所求面积为 4233440011116()d ()|43163S x x x x x =-=-=⎰.图6-3 图6-4(4)可求得2y x =与y x =的交点为(0,0),(1,1);2y x =与2y x =的交点为(0,0),(2,4); y =x 与y =2x 的交点为(0,0),它们所围图形如图6-4中阴影所示,其面积为:121122012231201(2)d (2)d d(2)d 117()236S x x x xx x x x x x xx x x =-+-=+-=+-=⎰⎰⎰⎰2. 求由下列曲线围成的平面图形绕指定轴旋转而成的旋转体的体积:(1) y =e x ,x =0,y =0,x =1,绕y 轴; (2) y =x 3,x =2,x 轴,分别绕x 轴与y 轴; (3) y =x 2,x =y 2,绕y 轴;解 (1)如图6-9所求旋转体的体积为矩形OABD ,与曲边梯形CBD 绕y 轴旋转所成的几何体体积之差,可求得y =e x 与x =1的交点为(1,e), y =e x 与y 轴的交点为(0,1),所以,所求旋转体的体积.222111(ln )(ln )2(ln )22(1)2(ln )eee11ee1πe πd πe πd πe πe ππe e π.d y V y y y y y y y y y ⎡⎤=⋅⋅-=--⎣⎦⎡⎤=-+=-+=-⎣⎦⎰⎰⎰72226200128(2)7ππd πd π7x x V y x x x ===⋅=⎰⎰ 2588228330036428323255πππd ππd ππy V x y y y y =⨯⨯-=-=-⋅⋅=⎰⎰.图6-5 图6-6(3)解方程组22y xx y⎧=⎪⎨=⎪⎩得交点(0,0),(1,1),所求旋转体的体积 25114100031025πd πd ππx x x V x x x x ⎛⎫=-=⋅=- ⎪⎝⎭⎰⎰.图6-8图6-73、.求二曲线θsin =r 与θcos 3=r 所围公共部分的面积解: 当θ等于0和3π时,两曲线相交,所围公共部分的 面积为4324π5d θθcos 321d θθsin 212π3π23π02-=+=⎰⎰A .4、 设有一截锥体, 其高为h , 上、下底均为椭圆, 椭圆的轴长分别为2a 、2b 和2A 、2B , 求这截锥体的体积.解 建立坐标系如图. 过y 轴上y 点作垂直于y 轴的平面, 则平面与截锥体的截面为椭圆, 易得其长短半轴分别为y h a A A --, y hb B B --.截面的面积为π)()(y hb B B y h a A A --⋅--.于是截锥体的体积为])(2[61)()(0bA aB AB ab h dy y h b B B y h a A A V h+++=--⋅--=⎰ππxyO3πθ=5、计算曲线x y ln =相对应于3=x 到8=x 的一段曲线弧长.解:由弧长的公式得:23ln 211d 1d 11d 1832832832+=+=+='+=⎰⎰⎰x x x x xx y s .6、求阿基米德螺线ρ=a θ (a >0)相应于θ 从0到2π 一段的弧长. 解: 弧长元素为θθθθd a d a a ds 22221+=+=.于是所求弧长为⎰+=πθθ2021d a s )]412ln(412[222ππππ++++=a .7、求星形线33cos sin x a ty a t ⎧=⎨=⎩的全长. 解:由弧长的参数方程公式得:446s t a θ===.1、 电量为+q 的点电荷位于r 轴的坐标原点O 处它所产生的电场力使r 轴上的一个单位正电荷从r =a 处移动到r =b (a <b )处求电场力对单位正电荷所作的功.提示: 由物理学知道, 在电量为+q 的点电荷所产生的电场中, 距离点电荷r 处的单位正电荷所受到的电场力的大小为2r qkF = (k 是常数). 解: 在r 轴上, 当单位正电荷从r 移动到r +dr 时, 电场力对它所作的功近似为dr r qk2,即功元素为dr r qkdW 2=. 图6-9 于是所求的功为dr rkq W b a2⎰=b a r kq ]1[-=)11(b a kq -=.2、设把一金属杆的长度由a 拉长到x a +时,所需的力等于akx,其中k 为常数,试求将该金属杆由长度a 拉长到b 所作的功.解:由于金属杆拉长所需的力f 与拉长的长度成正比x ,且akxf =,其中k 为常数。
广东大专高数试题及答案

广东大专高数试题及答案一、选择题(每题5分,共20分)1. 函数y=f(x)是奇函数,则下列说法正确的是()。
A. f(-x) = f(x)B. f(-x) = -f(x)C. f(0) = 0D. f(x) = 0答案:B2. 极限lim(x→0) (sin x/x)的值为()。
A. 0B. 1C. 2D. 3答案:B3. 曲线y=x^2在点(1,1)处的切线斜率为()。
A. 2B. 1C. 0D. -1答案:A4. 函数y=ln(x)的导数是()。
A. 1/xB. xC. ln(x)D. x^2答案:A二、填空题(每题5分,共20分)5. 设函数f(x)=x^3-3x+2,则f'(x)=________。
答案:3x^2-36. 已知函数y=x^2-4x+c,若其图像与x轴有交点,则c的取值范围为________。
答案:c≤47. 曲线y=x^3-6x^2+11x-6在点(2,0)处的切线方程为________。
答案:y=-3x+128. 函数y=e^x的不定积分是________。
答案:e^x + C三、解答题(每题15分,共30分)9. 求函数y=x^2-4x+c在区间[0,2]上的最小值。
解:函数y=x^2-4x+c的导数为y'=2x-4。
令y'=0,解得x=2。
当0≤x<2时,y'<0,函数单调递减;当x>2时,y'>0,函数单调递增。
因此,函数在x=2处取得最小值,即y_min=c-4。
10. 求极限lim(x→∞) (1+1/x)^x。
解:lim(x→∞) (1+1/x)^x = e^lim(x→∞) (x*ln(1+1/x))。
由于lim(x→∞) (x*ln(1+1/x)) = lim(x→∞) (ln(1+1/x)/1/x) =lim(x→∞) (1/(1+1/x) * 1/x) = 0,所以原极限的值为e^0=1。
中山大学2019高数上期末考试A卷试题与答案

考试题(A 卷)一、计算下列数列或函数的极限(请从三道题目中任选二道题,多选的话则按照前两道题目给分。
每题5分,合计10分)1. n211lim 1x n n →∞⎛⎫+- ⎪⎝⎭.解 (方法一)22n n22n(1)12111lim 1lim 11li 1.m x x n n n n x n n n n n e n →∞→∞--→∞-⎛⎫⎛⎫+-=+ ⎪ ⎪⎝⎭⎝⎭⎡⎤-⎛⎫⎢⎥=+= ⎪⎢⎥⎝⎭⎢⎥⎣⎦(方法二)222n 1nln 1211limnln 1limn 111lim 1li .m x x n n x x n n n n e n n eee e →∞→∞-⎛⎫+ ⎪⎝⎭→∞→∞-⎛⎫-+⋅⎪⎝⎭⎛⎫+-= ⎪⎝⎭====2.2()()limxx x t f t dtx →-⎰,其中()f x 是一个连续函数.解220()()()()limlim()()()lim2()(0)lim 22.xx xx x x x x x t f t dtx f t dt tf t dtxxf t dt xf x xf x xf x f →→→→--=+-===⎰⎰⎰⎰3. 求二元函数()()()()44,0,0lim2ln x y x y x y →++的极限. 解(方法一) 平面极坐标为(),ρθ。
由于()(),0,0x y →,不妨设11,22x y ≤≤,于是()()44444444max ,,21,414ln lnln 2ln 24ln ,x y x y x y x y ρρρρ≥+≥+=≤=-+所以()()()4402ln 6ln 22ln 0x y x y ρρ≤++≤-→()()()()44,0,0lim2ln 0x y x y x y →++=解(方法二) 有界量与无穷小量之积是无穷小量,所以()()()()()()()()()()44,0,01444441,0,0444lim2ln 2lim ln 0x y x y x y x y x y x y x y x y →→++⎡⎤+⎢⎥=⋅++=⎢⎥⎢⎥+⎣⎦二、 (8分)过原点作抛物线()y f x ==D 是该切线与上述抛物线及x 轴围成的平面区域. 求区域D 绕x 轴旋转一周所得旋转体的体积.解 设切点为()00,x y ,则00y y x ⎧=⎪⎨=⎪⎩ 解方程组得()()00,2,1x y =。
中山大学东校区2005级第二学期高等数学一期末A试题(word文档良心出品)

中山大学2005级东校区第二学期高等数学一一.(每小题7分,共28分)1. 设函数)(2),(2y x f x y y x z += ,其中 f 二阶可微,求 yx z x z ∂∂∂∂∂2, 。
2. 设函数k z x y j y x i z y x )(3222-++= ,求 )(,F v i d grad F v i d 。
3. 设函数)0(,)(s in )(2>=⎰y dx x y x y g y y ,求)(y g ' 。
4. 在直角坐标系下,用两种不同的次序将二重积分⎰⎰=Ddy dx y x f I ),( 化为累次积分,其中D 是由直线x y x y x x 2,,2,1==== 所围成区域。
二.(10分)计算曲线积分0()s in ()c o s (>---=⎰m dy m y e dx my y e I L x x 为常数),其中有向曲线L 是圆周)0(222>=+a ax y x 从点)0,2(a A 经),(a a M 至)0,0(O 的部分。
三.(10分)利用高斯公式计算曲面积分⎰⎰+++=Sdxdy zx dzdx yz dydz x xy I 2222)(,其中S 是由球面 ,222x z z y --= 平面0=y 所围区域表面的外侧。
四. (每小题7分,共14分)1. 求微分方程: dxdy xy y dx dy x =+ 的通积分。
2. 求微分方程:x e y y y 23465-=+'-'' 的通解。
五. 讨论下列广义积分的敛散性:(每小题5分,共10分)1. x d x x ⎰105sin ,2.⎰∞++⋅1321x x dx 。
六. (9分) 求幂级数∑∞=---221)1(2)1(n n n x n n 的收敛半径、收敛域以及和函数。
七. (7分)求函数x x f ln )(= 在2=x 处的泰勒展开式,并求出收敛域。
最新中山大学高等代数试题

2004中山大学高等代
数试题
2004年 高等代数试题(70分)
1.(10分)计算下列n 阶行列式:
210 (00)
121 (00)
012...00000 (12)
n D =........
2.(10分)设12,,...,n ααα是数域P 上线性空间V 中一线性无关向量组,讨论向量组12231,,...,n αααααα+++的线性相关性。
3.(10分)设A =100101010⎛⎫
⎪
⎪ ⎪⎝⎭
.
(1).证明:22n n A A A I -=+-.
(2).求100A .
4.(20分)设3R 的线性变换 在标准基下的矩阵A =211121112⎛⎫ ⎪ ⎪ ⎪⎝⎭
.
(1).求A 的特征值和特征向量.
(2).求3R 的一组标准正交基,使 在此基下的矩阵为对角矩阵.
5.(20分)设β为n 维欧氏空间V 中一个单位向量,定义V 的线性变换 如下:
2(,),V ααβαβα=-∀∈
证明:
(1). 为第二类的正交变换(称为镜面反射).
(2).V 的正交变换是镜面反射 的充要条件为1是 的特征值,且对
应的特征子空间的维数为n -1.。
中山大学高数一下册2018期末真题

一、 计算二重积分 ∬xy Ddxdy , 其中 D 为第一象限内的椭圆区域: x 24+y 2≤1,x ≥0, y ≥0.(7分)解:使用广义极坐标变换,即x =2r cos θ,y =r sin θ(1分),积分区域可表示为0≤θ<π2,0≤r ≤1(1分) D (r,θ)=[2cos θsin θ−2r sin θr cos θ]=2r (1分),我们有 ∬xy D dxdy =∫dθπ/2∫2r cos θ⋅r sin θ⋅|J |10dr (1分)=∫4cos θ⋅sin θdθπ/2∫r 31=∫2sin 2θdθπ/2×r 44|01=−cos 2θ|0π2×14=−(−1−1)×14=12(1分)二、 设 Ω 为曲面 z =1 与上半球面 z =√3−x 2−y 2 所围成的区域,S 为 Ω 的边界,求第一型曲面积分 ∬(x +S1)dS 的值. (7分)解:首先通过方程z =1=√3−x 2−y 2,容易算得两曲面交线为x 2+y 2=2,故积分投影区域为D:x 2+y 2≤2,上表面为上半球面z 上=√3−x 2−y 2,下表面为平面z 下≡1.(1分)同时,可计算出√1+z 上x 2+z 上y2=√3−x 2−y 2√1+z 下x 2+z 下y2=1 (1分),由对称性,注意到两个表面均关于Oyz 平面对称,且x 关于x 为奇函数,所以有:∬(x +1)SdS =∬1SdS (对称性,1分)=∬3√3−x 2−y 2D +1dxdy (1分)=∫dθ2π0∫[3√3−r 21]⋅r √20dr (极坐标,1分) =2π×[−3√3−r 2+r 22]|0√2三、 计算曲线积分 ∫y dx −(x +z ) dy L +,其中 L +为螺旋线段:L:{x =cos ty =sin t z =t 2,t ∈[0,2π],方向按参数 t 增加的方向.(7分) 解:本题可以直接进行求解,注意到x ′(t )=−sin t ,y ′(t )=cos t ,z ′(t )=2t,0≤t ≤2π(1分),可得中山大学 高等数学一(II )期末考试J =D (x,y )dr=2π×(−3−(−3√3)+1−0)=(6√3−4)π(1分)∫y dx −(x +z ) dy L +=∫sin t ⋅−sin t −(cos t +2π0t 2)⋅cos t dt (2分) =∫−1−2π0t 2⋅cos t dt (1分)=−2π−t 2⋅sin t |02π+∫2t 2π⋅sin t dt (1分)=−2π+0−2t ⋅cos t |02π+∫22πcos t dt (1分)=−2π+0−2×2π+0=−6π(1分)四、 求初值问题 (−x 2+2xy )dx +(x 2+sin y )dy =0, y (0)=π2 的解 (7分)解:因为ð(−x 2+2xy )ðy=2x =ð(x 2+sin y )ðx,因此该方程为全微分方程(2分)使用简单凑微分方法,有 (−x 2+2xy )dx +(x 2+sin y )dy=−x 2dx +(2xy dx +x 2dy )+sin y dy =d(−x 33+x 2y −cos y)因此,可得该全微分方程的通解为:−x 33+x 2y −cos y =C (3分) 代入初值条件,即x =0,y =π2,可得C =0, (1分)故原初值问题的解为:−x 33+x 2y −cos y =0(1分)解:先考虑对应齐次线性方程y ′′+y =0,其特征方程λ2+1=0对应两个特征根λ1,2=±i (1分) 因此对应齐次方程的通解为y ̃=c 1cos x +c 2sin x ,(2分)考虑非齐次方程y ′′−y =cos x ,因为±i 是特征根,其特解y 1∗=x(A cos x +B sin x),(1分)代入该方程后有y 1∗′′+y 1∗=−2A sin x +2B cos x =cos x ,可得A =0,B =12故y 1∗=12x sin x . (2分) 综上,原微分方程通解y =y ̃+y 1∗=c 1cos x +c 2sin x +12x sin x . (1分)六、 判断级数∑(−1)n−1arctan 1n∞n=1的敛散性,并指明其为绝对收敛还是条件收敛. (8分)解:本级数为交错级数,其通项绝对值arctan 1n 关于n 单调递减(因为1n 单调递减,arctan 1n 单调递减)(2分),且lim n→∞arctan 1n =0. (1分)由莱布尼茨(或狄利克雷)判别法可证该级数收敛。
2023-2024学年广东省中山市高一(上)期末数学试卷【答案版】

2023-2024学年广东省中山市高一(上)期末数学试卷一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知x,y是实数,则“x>y”是“x2>y2”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件2.将√43⋅√2化成分数指数幂的形式是()A.276B.2176C.213D.2563.已知全集U={1,2,3,4,5},A∩B={2,4},A∪B={1,2,3,4},则()A.2∈A,2∉B B.3∈A,3∈B C.4∈A,4∉B D.5∉A,5∉B4.已知函数f(x)=x2﹣4x+5在[m,n]上的值域是[1,10],则n﹣m的最大值是()A.3B.6C.4D.85.函数f(x)=log2(x2﹣4x+3)的单调递增区间是()A.[2,+∞)B.[3,+∞)C.(3,+∞)D.(﹣∞,2]6.已知数f(x)=a1−e x−2是奇函数,则实数a的值是()A.1B.﹣2C.4D.﹣47.已知a>b>c>d,则下列不等式一定成立的是()A.ac>bd B.ae c>be dC.e a•e c>e b•e d D.aln(c﹣d)>bln(c﹣d)8.如图,在半径为1m的圆周上,一只红蚂蚁和一只黑蚂蚁同时从点A(1,0)出发,按逆时针匀速爬行,设红蚂蚁每秒爬过α弧度,黑蚂蚁每秒爬过β弧度(0<α<β<π),两只蚂蚁第2秒时均爬到第二象限,第15秒时又都回到点A.若两只蚂蚁的爬行速度大小保持不变,红蚂蚁从点A顺时针匀速爬行,黑蚂蚁同时从点A逆时针匀速爬行,则它们从出发后到第二次相遇时,黑蚂蚁爬过的路程为()cm.A .125π B .157π C .154π D .13π6二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分. 9.下列函数中,既是奇函数,又是R 上的增函数的是( ) A .y =x ﹣1B .y =x |x |C .y =x 3D .y =x 210.已知正数x ,y 满足x +y =2,则( ) A .√xy 的最大值为1B .x 2+y 2的最大值为2C .√x +√y 的最小值为2D .2x +1y 的最小值为32+√211.给定函数f(x)=2xx 2+1()A .f (x )的图像关于原点对称B .f (x )的值域是[﹣1,1]C .f (x )在区间[1,+∞)上是增函数D .f (x )有三个零点12.设偶函数f (x )的定义域为(﹣∞,0)∪(0,+∞),且满足f (2)=0,对于任意x 1,x 2∈(0,+∞),x 1≠x 2,都有x 22n f(x 1)−x 12n f(x 2)x 2−x 1<0(n ∈N)成立,则( )A .不等式f(2x+1)x >0的解集为(12,+∞)∪(−32,−12)∪(−12,0) B .不等式f(2x+1)x >0的解集为(12,+∞)∪(−32,12)C .不等式f(x)x 2024>0的解集为(﹣∞,﹣2)∪(2,+∞) D .不等式f(x)x 2024>0的解集为(﹣2,0)∪(0,2)三、填空题:本题共4小题,每小题5分,共20分. 13.计算:lg 52+23lg 8= .14.已知函数f (x ),给出三个性质: ①f (x )定义域为(﹣∞,+∞); ②f (x )是奇函数;③f (x )在(0,+∞)上是减函数.写出一个同时满足性质①.性质②和性质③的函数解析式,f (x )= .15.依法纳税是每个公民应尽的义务,个人取得的所得应依据《中华人民共和国个人所得税法》向国家缴纳个人所得税(简称个税).2019年1月1日起,个税税额根据应纳税所得额、税率和速算扣除数确定,计算公式为:个税税额=应纳税所得额×税率﹣速算扣除数,应纳税所得额的计算公式为:应纳税所得额=综合所得收入额﹣基本减除费用﹣专项扣除﹣专项附加扣除﹣依法确定的其他扣除.其中,基本减除费用为每年60000元,税率与速算扣除数见表:李华全年综合所得收入额为249600元,假定缴纳的专项扣除基本养老保险、基本医疗保险、失业保险等社会保险费和住房公积金占综合所得收入额的比例分别是8%,2%,1%,9%,专项附加扣除是52800元,依法确定其他扣除是4560元,则他全年应缴纳的综合所得个税是 元. 16.(3分)已知函数f(x)=x +16x−10,x ∈(0,+∞),则f (x )的零点之和为 ;若方程|f (x )|=m (m >0)有四个不相等的实根x 1,x 2,x 3,x 4,则x 1+x 2+x 3+x 4= . 四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤 17.(10分)已知tanα=13,求下列各式的值.(1)sinα−2cosα2sinα−cosα;(2)sin αcos α+2.18.(12分)若集合A ={x |x 2+5x ﹣6=0},B ={x |x 2+2(m +1)x +m 2﹣3=0}. (1)若m =0,写出A ∪B 的子集个数; (2)若A ∩B =B ,求实数m 的取值范围.19.(12分)函数的性质通常指函数的定义域、值域、单调性、奇偶性、零点等.已知f(x)=14−x 2. (1)研究并证明函数y =f (x )的性质;(2)根据函数y =f (x )的性质,画出函数y =f (x )的大致图象.20.(12分)对于函数f(x),若在定义域内存在实数x,满足f(﹣x)=f(x),则称f(x)为“局部偶函数”.(1)已知函数f(x)=x3+x+1,试判断f(x)是否为“局部偶函数”,并说明理由;(2)若f(x)=x[4x+(2m﹣1)•2x+3]为定义在区间(﹣∞,0)∪(0,+∞)上的“局部偶函数”,求实数m的取值范围.21.(12分)已知函数f(x)的定义域为R,值域为(0,+∞),且对任意m,n∈R,都有f(m+n)=f(m)f(n).φ(x)=f(x)−1f(x)+1.(1)求f(0)的值,并证明φ(x)为奇函数.(2)若x>0,f(x)>1,且f(3)=4,证明f(x)为R上的增函数,并解不等式φ(x)>15 17.22.(12分)已知函数g(x)=sin2x−cosx+a,x∈(π2,π)有两个零点.(1)求实数a的取值范围;(2)设x1,x2是g(x)的两个零点,证明:x1+x2<3π2.2023-2024学年广东省中山市高一(上)期末数学试卷参考答案与试题解析一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知x,y是实数,则“x>y”是“x2>y2”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件解:若x=0,y=﹣1,满足x>y,但x2>y2不成立.若x=﹣1,y=0,满足x2>y2,但x>y不成立,∴“x>y”是“x2>y2”的既不充分不必要条件.故选:D.2.将√43⋅√2化成分数指数幂的形式是()A.276B.2176C.213D.256解:√43⋅√2=413×212=(22)13×212=223+12=276.故选:A.3.已知全集U={1,2,3,4,5},A∩B={2,4},A∪B={1,2,3,4},则()A.2∈A,2∉B B.3∈A,3∈B C.4∈A,4∉B D.5∉A,5∉B解:因为全集U={1,2,3,4,5},A∩B={2,4},A∪B={1,2,3,4},则2∈A,2∈B,故A错,3∉A∩B,故B错,4∈A∩B,则C错误,5∉A∩B,故D正确,故选:D.4.已知函数f(x)=x2﹣4x+5在[m,n]上的值域是[1,10],则n﹣m的最大值是()A.3B.6C.4D.8解:f(x)=x2﹣4x+5=(x﹣2)2+1,因为值域为[1,10],所以要取到最小值1,必须取到对称轴,又对称轴两边距离越大,则区间长度越大,令f(x)=10,得x=﹣1或x=5,所以当n=5,m=﹣1时(n﹣m)max=6.故选:B.5.函数f(x)=log2(x2﹣4x+3)的单调递增区间是()A.[2,+∞)B.[3,+∞)C.(3,+∞)D.(﹣∞,2]解:根据题意,对于f(x)=log2(x2﹣4x+3),设t=x2﹣4x+3,则y=log2t,必有t=x2﹣4x+3>0,解可得t>3或t<1,即函数的定义域为(﹣∞,1)∪(3,+∞),在区间(﹣∞,1)上,t=x2﹣4x+3为减函数,y=log2t为增函数,则f(x)在(﹣∞,1)上为减函数,在区间(3,+∞)上,t=x2﹣4x+3为增函数,y=log2t为增函数,则f(x)在(3,+∞)上为增函数,则函数f(x)=log2(x2﹣4x+3)的单调递增区间是(3,+∞).故选:C.6.已知数f(x)=a1−e x−2是奇函数,则实数a的值是()A.1B.﹣2C.4D.﹣4解:因为f(x)=a1−e x−2是奇函数,所以f(﹣x)=﹣f(x)恒成立,即a1−e−x−2=2−a1−e x,整理得,ae x﹣a=4e x﹣4,即a=4.故选:C.7.已知a>b>c>d,则下列不等式一定成立的是()A.ac>bd B.ae c>be dC.e a•e c>e b•e d D.aln(c﹣d)>bln(c﹣d)解:对于选项A:不妨令a=2,b=1,c=﹣2,d=﹣3,此时a>b>c>d,但ac=﹣4<﹣3=bd,故选项A错误;对于选项B:因为c>d,所以e c>e d,不妨令a=﹣e d,b=﹣e c,此时a>b,但ae c=﹣e c+d=﹣be d,故选项B错误;对于选项C:由a>b>c>d,所以e a>e b>e c>e d>0,则e a•e c>e b•e d,选项C正确;对于选项D:若a>b,不妨令c=2,d=1,此时c>d,而aln(c﹣d)=0=bln(c﹣d),故选项D错误.故选:C.8.如图,在半径为1m的圆周上,一只红蚂蚁和一只黑蚂蚁同时从点A(1,0)出发,按逆时针匀速爬行,设红蚂蚁每秒爬过α弧度,黑蚂蚁每秒爬过β弧度(0<α<β<π),两只蚂蚁第2秒时均爬到第二象限,第15秒时又都回到点A.若两只蚂蚁的爬行速度大小保持不变,红蚂蚁从点A顺时针匀速爬行,黑蚂蚁同时从点A逆时针匀速爬行,则它们从出发后到第二次相遇时,黑蚂蚁爬过的路程为()cm.A .125π B .157π C .154π D .13π6解:(1)由已知得12π<2α<2β<π,所以14π<α<β<12π①,15α=2k π,k ∈N *②.15β=2n π,n ∈N * ③,且k <n , 结合①②③式得14π<2k 15π<2n 15π<12π,k ,n ∈N *,且k <n ,解得k =2,n =3,解得α=415π,β=615π, 它们从点A 出发后第二次相遇时,用的时间为t 秒, 所以(α+β)t =2×2π,即(415π+615π)t =2×2π.解得t =6, 则黑蚂蚁爬过的距离为l =615π×6×1=125π(cm). 故选:A .二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分. 9.下列函数中,既是奇函数,又是R 上的增函数的是( ) A .y =x ﹣1B .y =x |x |C .y =x 3D .y =x 2解:对于A ,y =x ﹣1不是奇函数,不符合题意,对于B ,y =x |x |={x 2,x ≥0−x 2,x <0既是奇函数,又是R 上的增函数,符合题意,对于C ,y =x 3是幂函数,既是奇函数,又是R 上的增函数,符合题意, 对于D ,y =x 2,是二次函数,是偶函数,不符合题意, 故选:BC .10.已知正数x ,y 满足x +y =2,则( ) A .√xy 的最大值为1B .x 2+y 2的最大值为2C .√x +√y 的最小值为2D .2x +1y 的最小值为32+√2解:正数x ,y 满足x +y =2, 可得A 中,由基本不等式可得√xy ≤x+y2=1,当且仅当x =y =1时取等号,所以可得√xy 的最大值为1,A 正确;B 中,因为x 2+y 2≥(x+y)22=2,当且仅当x =y =1时取等号,所以x 2+y 2的最小值为2,所以B 不正确;C 中,因为2=x +y ≥(√x+√y)22,当且仅当x =y =1时取等号,所以√x +√y 的最大值为2,所以C 不正确;D 中,2x +1y =(2x +1y )•12•(x +y )=12(2+1+2y x +x y )≥12(3+2√2y x ⋅x y )=12(3+2√3)=√3+32,当且仅当2y x =xy,即x =4﹣2√2,y =2√2−2时取等号,所以D 正确.故选:AD . 11.给定函数f(x)=2xx 2+1( ) A .f (x )的图像关于原点对称 B .f (x )的值域是[﹣1,1] C .f (x )在区间[1,+∞)上是增函数 D .f (x )有三个零点解:根据题意,依次分析选项: 对于A ,函数f(x)=2x x 2+1,其定义域为R ,有f (﹣x )=−2xx 2+1=−f (x ),则函数f (x )为奇函数,其图形关于原点对称,A 正确; 对于B ,f (x )=2xx 2+1,由基本不等式x 2+1≥2|x |,则有|f (x )|≤1,即f (x )的值域是[﹣1,1],B 正确;对于C ,f (1)=1,f (2)=45,f (x )在区间[1,+∞)上一定不是增函数,C 错误;对于D ,f (x )=2xx 2+1=0,解可得x =0,函数f (x )只有一个零点,D 错误; 故选:AB .12.设偶函数f (x )的定义域为(﹣∞,0)∪(0,+∞),且满足f (2)=0,对于任意x 1,x 2∈(0,+∞),x 1≠x 2,都有x 22n f(x 1)−x 12n f(x 2)x 2−x 1<0(n ∈N)成立,则( )A .不等式f(2x+1)x >0的解集为(12,+∞)∪(−32,−12)∪(−12,0) B .不等式f(2x+1)x >0的解集为(12,+∞)∪(−32,12)C .不等式f(x)x 2024>0的解集为(﹣∞,﹣2)∪(2,+∞) D .不等式f(x)x 2024>0的解集为(﹣2,0)∪(0,2)解:当 n =0时,即f(x 1)−f(x 2)x 1−x 2>0,∴y =f (x )在(0,+∞)上为增函数,∵偶函数f (x ) 的定义域为(﹣∞,0)∪(0,+∞), ∴y =f (x )在(﹣∞,0)上为减函数,当x >0时,f(2x+1)x>0,∴x >0时,有2x +1>2,解得x >12,当x <0时,f(2x+1)x >0,得f (2x +1)<0=f (﹣2),∴0>2x +1>﹣2或0<2x +1<2,解得−32<x <−12或−12<x <0∴B 错误,A 正确; 令g (x )=f(x)x 2024, 则g(x 1)−g(x 2)x 2−x 1=f(x 1)x 12024−f(x 2)x 22024x 1−x 2=x 22024f(x 1)−x 12024f(x 2)(x 1x 2)2024(x 1−x 2)>0,∴g (x )在(0,+∞)上单调递增, ∵f (﹣x )=f (x ), ∴g (﹣x )=f(−x)(−x)2024=f(x)x 2024=g (x ), 即g (x )为偶函数,g (2)=0, 由g (x )=f(x)x 2024>0可得|x |>2,解得x >2或x <﹣2,C 正确,D 错误. 故选:AC .三、填空题:本题共4小题,每小题5分,共20分. 13.计算:lg 52+23lg 8= 2 .解:原式=2lg 5+23×3lg 2=2lg 5+2lg 2=2(lg 5+lg 2)=2,故答案为:2.14.已知函数f (x ),给出三个性质: ①f (x )定义域为(﹣∞,+∞); ②f (x )是奇函数;③f (x )在(0,+∞)上是减函数.写出一个同时满足性质①.性质②和性质③的函数解析式,f (x )= ﹣x 3(答案不唯一) . 解:令f (x )=﹣x 3,则f(x)定义域为(﹣∞,+∞),满足①;又f(﹣x)=(﹣x)3=﹣x3=﹣f(x),∴f(x)是奇函数,满足②;又f(x)=﹣x3在(0,+∞)上是减函数,满足③,故答案为:﹣x3(答案不唯一).15.依法纳税是每个公民应尽的义务,个人取得的所得应依据《中华人民共和国个人所得税法》向国家缴纳个人所得税(简称个税).2019年1月1日起,个税税额根据应纳税所得额、税率和速算扣除数确定,计算公式为:个税税额=应纳税所得额×税率﹣速算扣除数,应纳税所得额的计算公式为:应纳税所得额=综合所得收入额﹣基本减除费用﹣专项扣除﹣专项附加扣除﹣依法确定的其他扣除.其中,基本减除费用为每年60000元,税率与速算扣除数见表:李华全年综合所得收入额为249600元,假定缴纳的专项扣除基本养老保险、基本医疗保险、失业保险等社会保险费和住房公积金占综合所得收入额的比例分别是8%,2%,1%,9%,专项附加扣除是52800元,依法确定其他扣除是4560元,则他全年应缴纳的综合所得个税是5712元.解:专项扣除总额为:249600×(8%+2%+1%+9%)=49920元,应纳税所得额为:249600﹣60000﹣52800﹣4560﹣49920=82320元,个税税额为:82320×10%﹣2520=5712元,故答案为:5712.16.(3分)已知函数f(x)=x+16x−10,x∈(0,+∞),则f(x)的零点之和为10;若方程|f(x)|=m(m>0)有四个不相等的实根x1,x2,x3,x4,则x1+x2+x3+x4=20.解:由题意可知,令f(x)=x+16x−10=0,即x2﹣10x+16=0,解得x=2或x=8,故函数在(0,+∞)内的零点为2和8,所以f (x )的零点之和为10.方程|f (x )|=m (m >0)有四个不相等的实数根x 1,x 2,x 3,x 4,即为y =|f (x )|,x ∈(0,+∞)与y =m 的四个交点的横坐标,方程|f (x )|=m (m >0)即|x +16x−10|=m ,x ∈(0,+∞),即|x 2﹣10x +16|=mx , 当f (x )≥0即x 2﹣10x +16≥0时,方程可转化为x 2﹣10x +16=mx 即x 2﹣(10+m )x +16=0; 当x 2﹣10x +16<0 时,方程可转化为x 2﹣10x +16=﹣mx 即x 2﹣(10﹣m )x +16=0;故要有四个实数根,则两种情况都有两个不同的实数根,不妨设x 1,x 4为x 2﹣(10+m )x +16=0的两根,则x 1+x 4=1=10+m ,则x 2,x 3为x 2﹣(10﹣m )x +16=0的两根,则x 2+x 3=10﹣m ,则x 1+x 2+x 3+x 4=10+m +10﹣m =20;故答案为:10;20.四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤17.(10分)已知tanα=13,求下列各式的值. (1)sinα−2cosα2sinα−cosα; (2)sin αcos α+2.解:tanα=13, (1)sinα−2cosα2sinα−cosα=tanα−22tanα−1=13−22×13−1=5; (2)sin αcos α+2=sinαcosαsin 2α+cos 2α+2=tanαtan 2α+1+2=13109+2=2310. 18.(12分)若集合A ={x |x 2+5x ﹣6=0},B ={x |x 2+2(m +1)x +m 2﹣3=0}.(1)若m =0,写出A ∪B 的子集个数;(2)若A ∩B =B ,求实数m 的取值范围.解:(1)当m =0时,B ={1,﹣3},∵A ={x |x 2+5x ﹣6=0}={﹣6,1},∴A ∪B ={﹣6,﹣3,1},集合元素个数为3个,故A ∪B 的子集个数为23=8.(2)∵A ∩B =B ,∴B ⊆A ,Δ=4(m +1)2﹣4(m 2﹣3)=8m +16,当Δ<0,即m <﹣2时,B =∅,符合题意,当Δ=0,即m =﹣2时,B ={1},符合题意,当Δ>0,即m >﹣2时,若B ⊆A ,则B ={﹣6,1},即{−2(m +1)=−5m 2−3=−6,方程组无解, 综上所述,m 的取值范围为(﹣∞,﹣2].19.(12分)函数的性质通常指函数的定义域、值域、单调性、奇偶性、零点等.已知f(x)=14−x 2. (1)研究并证明函数y =f (x )的性质;(2)根据函数y =f (x )的性质,画出函数y =f (x )的大致图象.解:(1)函数f (x )的定义域为:(﹣∞,﹣2)∪(﹣2,2)∪(2,+∞),函数的值域为(﹣∞,0)∪[14,+∞)函数f (x )为偶函数, 函数f (x )在区间[0,2),(2,+∞)上上为增函数,在区间(﹣∞,﹣2),(﹣2,0]上为减函数, 由方程f (x )=0无解,所以函数无零点;(2)由(1)中函数的性质,可得y =f (x )的图象如图所示:20.(12分)对于函数f(x),若在定义域内存在实数x,满足f(﹣x)=f(x),则称f(x)为“局部偶函数”.(1)已知函数f(x)=x3+x+1,试判断f(x)是否为“局部偶函数”,并说明理由;(2)若f(x)=x[4x+(2m﹣1)•2x+3]为定义在区间(﹣∞,0)∪(0,+∞)上的“局部偶函数”,求实数m的取值范围.解:(1)f(﹣x)=﹣x3﹣x+1,令f(﹣x)=f(x),得x3+x=0,解得x=0,∴存在x=0满足f(﹣x)=f(x),故f(x)是“局部偶函数”;(2)由f(﹣x)=f(x),得4x+4﹣x+(2m﹣1)(2x+2﹣x)+6=0,令t=2x+2﹣x(t>2),得t2+(2m﹣1)t+4=0,则1−2m=t+4t在t∈(2,+∞)上有解,∴1﹣2m>4,即m<−3 2,故m的取值范围为(−∞,−32 ).21.(12分)已知函数f(x)的定义域为R,值域为(0,+∞),且对任意m,n∈R,都有f(m+n)=f(m)f(n).φ(x)=f(x)−1f(x)+1.(1)求f(0)的值,并证明φ(x)为奇函数.(2)若x>0,f(x)>1,且f(3)=4,证明f(x)为R上的增函数,并解不等式φ(x)>15 17.解:(1)令m=n=0,得f(0)=f(0)f(0),又函数f(x)的值域为(0,+∞),∴f(0)=1.证明:∵f(0)=f(﹣x+x)=f(﹣x)f(x),∴f(−x)=1f(x),∴φ(−x)=f(−x)−1f(−x)+1=1f(x)−11f(x)+1=1−f(x)1+f(x)=−φ(x),∴φ(x)为奇函数.(2)证明:任取x1<x2,x1,x2∈R,f(x1)﹣f(x2)=f(x1)﹣f(x2﹣x1+x1)=f(x1)﹣f(x2﹣x1)f(x1)=f(x1)[1﹣f(x2﹣x1)].∵x1<x2,∴x2﹣x1>0,∵当x>0时,f(x)>1,∴f(x2﹣x1)>1,∴1﹣f(x2﹣x1)<0.又函数f(x)的值域为(0,+∞),∴f(x1)[1﹣f(x2﹣x1)]<0,即f(x1)<f(x2),∴f(x)为R上的增函数.由φ(x)=1517,即f(x)−1f(x)+1>1517,化简得f(x)>16.∵f(3)=4,∴16=f(3)f(3)=f(6),∴f(x)>f(6).又f(x)为R上的增函数,∴x>6,故φ(x)>1517的解集为{x|x>6}.22.(12分)已知函数g(x)=sin2x−cosx+a,x∈(π2,π)有两个零点.(1)求实数a的取值范围;(2)设x1,x2是g(x)的两个零点,证明:x1+x2<3π2.解:(1)已知g(x)=sin2x﹣cos x+a=﹣cos2x﹣cos x+a+1,函数定义域为(π2,π),令g(x)=0,可得cos2x+cos x=a+1,不妨令t=cos x,﹣1<t<0,所以−14≤cos2x+cos x=t2+t<0,当a+1≥0,即a≥﹣1时,方程t2+t=a+1无解;当a+1<−14,即a<−54时,方程t2+t=a+1无解;当a+1=−14,即a=−54时,方程t2+t=a+1有且仅有一个解t=−12;当−14<a+1<0,即−54<a<﹣1时,方程t2+t=a+1有两个解,分别为t1=−12+√a+54,t2=−12−√a+54,所以cos x=−12±√a+54各有一解,此时函数g(x)有两个零点,综上,要使函数g(x)有两个零点,此时实数a的取值范围为(−54,﹣1);(2)证明:当f(x)有两个零点时,不妨令t1=cos x1,t2=cos x2,由(1)知t1,t2为t2+t=a+1两解,则t1+t2=﹣1,所以cos x1+cos x2=﹣1,对等式两边同时平方得cos2x1+2cosx1cosx2+cos2x2=1,因为x1,x2∈(π2,π),所以cos x1<0,cos x2<0,可得2cos x1cos x2>0,所以cos2x1+cos2x2<1,则cos2x1<sin2x2=cos2(3π2−x2),又π2<x2<π,所以π2<3π2−x2<π,此时cos(3π2−x2)<0,所以cosx1>cos(3π2−x2),易知y=cos x在(π2,π)上单调递减,则x1<3π2−x2,故x1+x2<3π2.。
高数期末汇总(09~13)

6.
判定级数 ( 1) n 1
n 1
2n 1 的敛散性. 若收敛,指出是绝对收敛还是条件收敛. n2
中山大学东校区《高等数学Ⅰ》第二学期期末考试汇编(09~13)
2
7.
求无界函数的广义积分
e
1 x 1 ln 2 x
1
dx .
8.
判定积分
1
1 x x
2
0 3
dx 的敛散性.
解答下列各题,并写出必要的过程(1-10 小题每小题 8 分,11-12 小题每小题 10 分)
1.
计算
dx . x 2x 2
2
2.
求 xy 2dydz yz 2dzdx zx 2 dxdy ,其中 S 为球面 x 2 y 2 z 2 4 的外侧.
S
3.
0
15. 设函数 P ( x , y, z), Q( x , y, z) 和 R( x , y, z ) 在 R 3 上具有连续偏导数, 且对于任意光滑曲面 ,
有 Pdydz Qdzdx Rdxdy 0 . 证明:在 R 3 上,
P Q R 0. x y z
14
中山大学东校区 2012 学年度《高等数学(一) 》期末考试题
一、填空题(每空 2 分,共 16 分)
1.
第二型曲线积分 Pdx Qdy Rdz 化为第一型曲线积分
L
.
其中 α, β, γ 是有向曲线弧 L 在点 ( x , y, z ) 处的
2.
Σ
的方向角.
.
第二型曲面积分 Pdydz Qdzdx Rdxdy 化为第一型曲面积分 其中 α, β, γ 是有向曲面 Σ 在点 ( x , y, z ) 处的 的方向角.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
π 2
解:(3) 原式= 4 sin 2x dx = 4. ∫ +∞ 0 1 1 1 2 2 ∞ (4) 原式= e−x dx2 = − e−x |+ = . 0 2 0 2 2
学 策
六.(10分)求曲线y =
∫
1
该图形绕x轴旋转形成的旋转体体积.
解:面积= 1− √ ( ) 2 3/2 1 1 x dx = x − x |0 = . 3 3 ∫
诚 品
∫ (4)
∫
x dx. (x + 1)(x + 2)(x + 3)
1 1 x4 dx = x5 ln x − x5 + C. 5 25
∫∫Βιβλιοθήκη 2五.(20分, 每小题5分)计算下列定积分和反常积分. ∫ 4 √ ∫ 1 x √ (1) dx; (2) x4 (tan3 x + sin5 x) dx; x+1 0 −1
x→0
x
解:(1) 原式= 1. (2) 原式= lim +
x→0
2x cos x4 − cos x2 = −1. 1
学 策
小值.
解:f ′ (x) = ex sin x + ex cos x.
二.(10分)设f (x) = ex sin x, x ∈ [0, 2π ]. 求单调区间, 拐点以及最大最
1
0
体积 =
诚 品
∫ (4)
+∞
2
xe−x dx.
0
√ x, 和直线x = 0, y = 1所围成的图形的面积以及
0
( ) 1 2 1 π π (1 − x) dy = π x − x |0 = . 2 2
3
七.(5分)求曲线ρ = 2(1 + cos θ) 的长度.
∫
2π
解:l =
0
√ √ ∫ 2 ′ 2 ρ + ρ dθ = 2 2
学 策
∫ (3) x ln x dx;
∫
4
解: (3)
1 原式 = 5
1 1 ln x dx = x5 ln x − 5 5
5
(4)
1 原式 = − 2
∫ 1 3 1 dx − dx (x + 2) 2 (x + 3) 1 3 = − ln |x + 1| + 2 ln |x + 2| − ln |x + 3| + C. 2 2 1 dx + 2 (x + 1)
珠海校区2011学年度第一学期11级《高等数学二》期末考试题B
学院: 专业: 姓名: 学号: 评分:
阅卷老师签名:
一. (10分, 每小题5分)计算下列极限. (1) lim (e + 5) (e − 7) ; x→+∞ (e3x + 9)4
x 2 2x 5
诚 品
∫
x2
cos t2 dt x .
(2) lim+
单调递增区间是[0, 3π/4], [7π/4, 2π ]; 单调递减区间是[3π/4, 7π/4].
f ′′ (x) = 2ex cos x; 拐点是x = π/2, 3π/2. √ √ 2 3π/4 2 7π/4 f (0) = 0, f (3π/4) = e , f (7π/4) = − e , f (2π ) = 0; 所 以 最 大 值 2 2 √ √ 2 3π/4 2 7π/4 是f (3π/4) = e , 最小值是f (7π/4) = − e . 2 2
2π
∫ √ 1 + cos θ dθ = 4
0
2π
cos
0
θ dθ = 16. 2
八.(5分)求微分方程(2 + x2 )y ′ + y + 1 = 0的通解.
1 1 dy = − dx. y+1 2 + x2 1 x 积分得通解ln |y + 1| = − √ arctan √ + C. 2 2 解:分离变量得
四.(20分 ∫, 每小题5分)计算下列不定积分 ∫ . 1 x √ (1) dx ; ( 2 ) dx; 1 + x4 (1 + x2 )3
∫ 1 1 1 2 dx = 解: (1) 原式= arctan x2 + C. 4 2 1+x 2 ) ( π π ,有 (2) 令x = tan t − < t < 2 2 ∫ x 原式 = cos t dt = sin t + C = √ + C. 1 + x2
九.(10分)求解初值问题:xy ′ + y = x5 + x, y |x=1 = 1.
1 解:有一阶线性微分方程: y ′ + y = x4 + 1. x C 解相应的齐次方程有y = . x 1 5 1 C 用常数变异法有通解y = x + x + . 6 2 x 1 又由初值条件y (1) = 1得C = . 3 1 5 1 1 所以y = x + x + . 6 2 3x
解:(1)令t = √ x. ) ∫ 2( 1 2t2 dt = 2 t−1+ dt 原式 = t+1 0 0 t+1 ( 2 ) t =2 − t + ln(t + 1) |2 0 = 2 ln 3. 2 ∫
2
(2) 由被积函数的奇偶性, 有, 原式= 0.
∫ (3)
0
2π
| sin(2x + 10)| dx ;
dy d2 y 三. (10分)函数y = y (x)由ye + ln y = 1确定. 求 和 2 . dx dx
x
解:两边对x求导, 有y ′ ex + yex + y ′ /y = 0. 两边再对x求导, 有y ′′ ex + 2y ′ ex + yex + y ′′ /y − y ′ 2 /y 2 = 0, 得 y ′ 2 /y 2 − 2y ′ ex − yex ′′ y = . 1 ex + y x ye 得y ′ = − .再把y ′ 代入即得y ′′ . 1 ex + y
学 策
诚 品
4
