二进制数字转换表
二进制八进制十进制十六进制之间的进制转换

二进制八进制十进制十六进制之间的进制转换详情可参考百度百科:进制转换这个词条【主要搞懂1和2两条,其他的进制之间的转化就迎刃而解,很好懂了】1. 十进制-> 二进制:将这个十进制数连续除以2的过程,第一步除以2,得到商和余数,将商再继续除以2,得到又一个商和余数,直到商为0。
最后将所有余数倒序排列,得到的数就是转换成二进制的结果。
2. 二进制-> 十进制:二进制数第1位的权值是2的0次方,第2位的权值是2的1次方,第3位的权值是2的2次方。
(例如1258这个十进制数,实际上代表的是:1x1000+2x100+5x10+8x1=1258)那么1011这个二进制数,实际上代表的是:1x8+0x4+1x2+1x1=11(十进制数11)。
(这里的8就是2的3次方,4就是2的2次方,2就是2的1次方,1就是2的0次方)3. 十进制-> 八进制:十进制数转换成八进制的方法,和转换为二进制的方法类似,唯一变化:除数由2变成8。
4. 八进制-> 十进制和转换为二进制的方法类似,唯一变化是,底数变成8,第1位表示8的0次方,第二位表示8的一次方,第三位表示8的2次方,第四位表示8的3次方。
例如1314这个八进制数,十进制数就是1x512+3x64+1x8+4x1=716(十进制)5. 十进制-> 十六进制10进制数转换成16进制的方法,和转换为2进制的方法类似,唯一变化:除数由2变成16。
十六进制是0123456789ABCDEF这十六个字符表示。
那么单独一个A就是10,单独一个B就是11,CDEF,就分表表示12,13,14,15。
而10这个十六进制数,实际就是十进制中的16。
6. 十六进制-> 十进制和转换为二进制的方法类似,唯一变化是,底数变成16,第1位表示16的0次方,第二位表示16的一次方,第三位表示16的2次方,第四位表示16的3次方。
7. 二进制<--->八进制,之间的相互转换,更简单一些,因为8本身是2的三次方。
很完整的2、8、10、16进制转换方法

比如 00000000 00000000 00000000 00000101 是 5的 原码。
生活中其实很多地方的计数方法都多少有点不同进制的影子。
比如我们最常用的10进制,其实起源于人有10个指头。如果我们的祖先始终没有摆脱手脚不分的境况,我想我们现在一定是在使用20进制。
至于二进制……没有袜子称为0只袜子,有一只袜子称为1只袜子,但若有两袜子,则我们常说的是:1双袜子。
生活中还有:七进制,比如星期。十六进制,比如小时或“一打”,六十进制,比如分钟或角度……
6.2.5 十六进制数转换成十进制数
2进制,用两个阿拉伯数字:0、1;
8进制,用八个阿拉伯数字:0、1、2、3、4、5、6、7;
10进制,用十个阿拉伯数字:0到9;
16进制,用十六个阿拉伯数字……等等,阿拉伯人或说是印度人,只发明了10个数字啊?
16进制就是逢16进1,但我们只有0~9这十个数字,所以我们用A,B,C,D,E,F这五个字母来分别表示10,11,12,13,14,15。字母不区分大小写。
我们找到问号字符(?)的ASCII值是63,那么我们可以把它转换为八进值:77,然后用 ‘\77′来表示’?'。由于是八进制,所以本应写成 ‘\077′,但因为C,C++规定不允许使用斜杠加10进制数来表示字符,所以这里的0可以不写。
事实上我们很少在实际编程中非要用转义符加八进制数来表示一个字符,所以,6.2.4小节的内容,大家仅仅了解就行。
0000 = 0 + 0 + 0 + 0 = 0 0
二进制数要转换为十六进制,就是以4位一段,分别转换为十六进制。
如(上行为二制数,下面为对应的十六进制):
二进制十进制和十六进制及其相互转换的公式

二进制十进制和十六进制及其相互转换的公式二进制、十进制和十六进制是计算机科学中常用的数制。
在计算机中,数据以二进制的形式表示,但是对于人类来说,二进制形式并不直观,因此使用十进制和十六进制进行数据展示和计算更为常见。
本文将介绍二进制、十进制和十六进制之间的转换公式。
一、二进制转十进制二进制是由0和1两个数字组成的数制。
每一位二进制位所代表的数值是2的n次方,其中n为该二进制位的位置,从右向左逐渐增加。
例如,二进制数1101,可以表示为:(1*2^3)+(1*2^2)+(0*2^1)+(1*2^0)=8+4+0+1=13所以二进制数1101等于十进制数13二、十进制转二进制十进制数是由0-9这十个数字组成的数制。
将十进制数转换成二进制数的方法是不断地对十进制数进行除以2的整除运算,直到商为0,然后将每次的余数倒序排列。
例如,将十进制数53转换成二进制数:53÷2=26余126÷2=13余013÷2=6余16÷2=3余03÷2=1余11÷2=0余1三、十六进制和二进制、十进制的转换十六进制数是由0-9这十个数字和A-F这六个字母组成的数制,其中A代表10,B代表11,依此类推,F代表15、十六进制数可以很方便地将二进制数字转换成较短的字符表示,同时也更加直观。
1.二进制转十六进制:将二进制数每四位一组,从右向左进行分组,并将每个分组转换成对应的十六进制字符。
0110(6)1101(D)0101(5)1011(B)转换结果为6D5B。
2.十六进制转二进制:将十六进制数中的每个字符逐个转换成对应的四位二进制数。
例如,将十六进制数3A转换成二进制数:3->0011A->10103.十六进制转十进制:将十六进制数中的每个字符逐个转换成对应的十进制数,然后将这些十进制数相加即可得到结果。
例如,将十六进制数1F转换成十进制数:1*16^1+F*16^0=16+15=31所以十六进制数1F等于十进制数314.十进制转十六进制:将十进制数不断地进行除以16的整除运算,直到商为0,然后将每次的余数倒序排列,并将每个余数转换成对应的十六进制字符。
二进制十六进制转换方法

二进制十六进制转换方法1、二进制转换为十六进制方法:取四合一法,即从二进制的小数点为分界点,向左(向右)每四位取成一位,接着将这四位二进制按权相加,得到的数就是一位十六位二进制数,然后,按顺序进行排列,小数点的位置不变,得到的数字就是我们所求的十六进制数。
如果向左(向右)取四位后,取到最高(最低)位时候,如果无法凑足四位,可以在小数点最左边(最右边),即整数的最高位(最低位)添0,凑足四位。
(1)例:将二进制11101001.1011转换为十六进制得到结果:将二进制11101001.1011转换为十六进制为E9.B(2)例:将101011.101转换为十六进制得到结果:将二进制101011.101转换为十六进制为2B.A2、将十六进制转换为二进制方法:取一分四法,即将一位十六进制数分解成四位二进制数,用四位二进制按权相加去凑这位十六进制数,小数点位置照旧。
(1)例:将十六进制6E.2转换为二进制数得到结果:将十六进制6E.2转换为二进制为01101110.0010即110110.001 附上十进制、二进制、十六进制转化的对照表。
扩展资料:二进制与八进制之间的转换:首先,我们需要了解一个数学关系,即2^3=8,2^4=16,而八进制和十六进制是用这个关系衍生而来的,即用三位二进制表示一位八进制,用四位二进制表示一位十六进制数。
接着,记住4个数字8、4、2、1(2^3=8、2^2=4、2^1=2、2^0=1)。
现在我们来练习二进制与八进制之间的转换。
1、二进制转换为八进制方法:取三合一法,即从二进制的小数点为分界点,向左(向右)每三位取成一位,接着将这三位二进制按权相加,得到的数就是一位八位二进制数,然后,按顺序进行排列,小数点的位置不变,得到的数字就是我们所求的八进制数。
如果向左(向右)取三位后,取到最高(最低)位时候,如果无法凑足三位,可以在小数点最左边(最右边),即整数的最高位(最低位)添0,凑足三位。
各进制数相互转换大全

0001 = 1 = 1 = 1
(3)十进制与十六进制的相互转化。
十--->十六:方法同上,以后不再赘述
例: 589(10)--->24D(16)
商 余数
589/16 36 13(用16进制的D表示)
0100 = 4 = 4 = 4
0101 = 5 = 5 = 5
1110 = 14 = E = 16
1111 = 15 = F = 17
... 4*16^2=1024
15*16^3= 61440
3*16^4=196608
10*16^5=10485760
结果10744845
(4)二进制、八进制、十进制、十六进制之间相互转化对照表
二进制数(仅4位的2进制数) = 十进制数 = 十六进制数 = 八进制数
385/8 48 1
48/8 6 0
6/8 0 6
1111=F
1101=D
1010=A
0101=5
1001=9
1011=B
那么它所对应的16进制数就是“FDA59B”
十六---->二
FD5(16)--->1111 1101 0101(2)
Part I 整型部分
(1)十进制与二进制的相互转化。
十---->二:十进制数除以2,得到一个商和余数(余数无非 0/1),余数单单保存。
拿得到的商继续除以2,又得到一个商和余数。保存余数。继续除以2...
直到除得的商为0.把除得的余数按先后顺寻从低位到高位排起(个位开始),
余数按先后顺寻从低到高排列。得到的就是二进制数1011001 。
二进制ascii码对照表

二进制ascii码对照表对照表如下:ASCII码(American Standard Code for Information Interchange,美国信息交换标准代码)是一种常见的字符编码系统,用于将字符和数字等信息转换为二进制形式。
ASCII码总共定义了128个字符,并将每个字符用一个7位的二进制数表示(即0-127范围内的值)。
下面是一个二进制ASCII码对照表,列出了每个字符对应的十进制、十六进制和二进制值。
十进制十六进制二进制字符0 00 0000000 NUL (Null)1 01 0000001 SOH (Start of Heading)2 02 0000010 STX (Start of Text)3 03 0000011 ETX (End of Text)4 04 0000100 EOT (End of Transmission)5 05 0000101 ENQ (Enquiry)6 06 0000110 ACK (Acknowledgment)7 07 0000111 BEL (Bell)8 08 0001000 BS (Backspace)9 09 0001001 TAB (Horizontal Tab)10 0A 0001010 LF (Line Feed)11 0B 0001011 VT (Vertical Tab)12 0C 0001100 FF (Form Feed)13 0D 0001101 CR (Carriage Return)14 0E 0001110 SO (Shift Out)15 0F 0001111 SI (Shift In)16 10 0010000 DLE (Data Link Escape)17 11 0010001 DC1 (Device Control 1)18 12 0010010 DC2 (Device Control 2)19 13 0010011 DC3 (Device Control 3)20 14 0010100 DC4 (Device Control 4)21 15 0010101 NAK (Negative Acknowledgment)22 16 0010110 SYN (Synchronous Idle)23 17 0010111 ETB (End of Transmission Block)24 18 0011000 CAN (Cancel)25 19 0011001 EM (End of Medium)26 1A 0011010 SUB (Substitute)27 1B 0011011 ESC (Escape)28 1C 0011100 FS (File Separator)29 1D 0011101 GS (Group Separator)30 1E 0011110 RS (Record Separator)31 1F 0011111 US (Unit Separator)32 20 0100000 Space33 21 0100001 !34 22 0100010 "35 23 0100011 #36 24 0100100 $37 25 0100101 %38 26 0100110 &39 27 0100111 '40 28 0101000 (41 29 0101001 )42 2A 0101010 *43 2B 0101011 +44 2C 0101100 ,45 2D 0101101 -46 2E 0101110 .47 2F 0101111 /48 30 0110000 049 31 0110001 150 32 0110010 251 33 0110011 352 34 0110100 453 35 0110101 554 36 0110110 655 37 0110111 756 38 0111000 857 39 0111001 958 3A 0111010 :59 3B 0111011 ;60 3C 0111100 <61 3D 0111101 =62 3E 0111110 >63 3F 0111111 ?64 40 1000000 @65 41 1000001 A66 42 1000010 B67 43 1000011 C68 44 1000100 D69 45 1000101 E70 46 1000110 F71 47 1000111 G72 48 1001000 H73 49 1001001 I74 4A 1001010 J75 4B 1001011 K76 4C 1001100 L77 4D 1001101 M80 50 1010000 P81 51 1010001 Q82 52 1010010 R83 53 1010011 S84 54 1010100 T85 55 1010101 U86 56 1010110 V87 57 1010111 W88 58 1011000 X89 59 1011001 Y90 5A 1011010 Z91 5B 1011011 [92 5C 1011100 \93 5D 1011101 ]94 5E 1011110 ^95 5F 1011111 _96 60 1100000 `97 61 1100001 a98 62 1100010 b99 63 1100011 c100 64 1100100 d101 65 1100101 e102 66 1100110 f103 67 1100111 g104 68 1101000 h105 69 1101001 i106 6A 1101010 j107 6B 1101011 k110 6E 1101110 n111 6F 1101111 o112 70 1110000 p113 71 1110001 q114 72 1110010 r115 73 1110011 s116 74 1110100 t117 75 1110101 u118 76 1110110 v119 77 1110111 w120 78 1111000 x121 79 1111001 y122 7A 1111010 z123 7B 1111011 {124 7C 1111100 |125 7D 1111101 }126 7E 1111110 ~127 7F 1111111 DEL (Delete)这只是一个基本的ASCII码对照表,其中包含了常见的可打印字符、控制字符和特殊字符。
计算机进制换算

表1-1 几种常用进制之间的对照关系十进制二进制八进制十六进制0 0000 0 01 0001 1 12 0010 2 23 0011 3 34 0100 4 45 0101 5 56 0110 6 67 0111 7 78 1000 10 89 1001 11 910 1010 12 A11 1011 13 B12 1100 14 C13 1101 15 D14 1110 16 E15 1111 17 F1、将(1111101100.0001101)2转换成十六进制数。
0011 1110 1100 . 0001 1010↓↓↓↓↓↓3 E C . 1 A结果为:(1111101100.0001101)2=(3EC.1A)162、(1101100.111)2=1×26+1×25+1×23+1×22+1×2-1+1×2-2+1×2-3=64+32+8+4+0.5+0.25+0.125=(108.875)103、十进制数215用二进制数表示是A)1100001B)1101001C)0011001D)11010111【答案】D【解析】十进制向二进制的转换前面已多次提到,这一点也是大纲要求重点掌握的。
采用"除二取余"法。
4、十六进制数34B对应的十进制数是A)1234B)843C)768D)333【答案】B【解析】十六进制数转换成十进制数的方法和二进制一样,都是按权展开。
5、二进制数0111110转换成十六进制数是A)3FB)DDC)4AD)3E【答案】D【解析】二进制整数转换成十六进制整数的方法是:从个位数开始向左按每4位二进制数一组划分,不足4位的前面补0,然后各组代之以一位十六进制数字即可。
6、二进制数10100101011转换成十六进制数是A)52BB)D45DC)23CD)5E【答案】A【解析】二进制整数转换成十六进制整数的方法是:从个位数开始向左按每4位二进制数一组划分,不足4位的前面补0,然后各组代之以一位十六进制数字即可。
二进制和各进制数之间的换算

二进制、八进制・十进制.十六进制之间转换一. 十进制与二进制之间的转换(1)十进制转换为二进制.分为整数部分和小数部分①整数部分方法:除2取余法.即每次将整数部分除以2.余数为该位权上的数.而商继续除以2.余数又为上一个位权上的数.这个步骤一直持续下去.直到商为0为止,报后读数时候.从最后一个氽数读起. 一直到最前而的一个余数。
下而举例:例:将十进制的168转换为二进制得出结果将十进制的16S转换为二进制,(10101000)2分析:第一步.将168除以2,商84,余数为0。
第二步,将商84除以2,商42余数为0o第三步,将商42除以2,商21余数为0o第四步,将商21除以2,商10余数为第五步.将商10除以2.商5余数为0。
第六步.将商5除以2.商2余数为1。
第七步.将商2除以2.商1余数为0。
第八步,将商1除以2,商0余数为1。
第九步.读数•因为帚后一位是经过女次除以2才得到的•因此它是最商位.读数字从最后的余数向前读,li|J 10101000(2)小数部分方法:乘2取整法•即将小数部分乘以久然后取整数部分,剩下的小数部分继续乘以久然后取整数部分,剩下的小数部分又乘以2. —直取到小数部分为零为止。
如果永远不能为零.就同十进制数的四舍五入一样.按照耍求保留女少位小数时,就根据后血一位是0还是1.取舍,如果是零,舍掉.如果是1.向入一位。
换句话说就是0舍1入。
读数要从前而的整数读到后面的整数.下面举例:例1:将0. 125换算为二进制得出结果:将0・125换算为二进制(0.001)2分析:第一步,将0. 125乘以2,得0. 25,则整数部分为0,小数部分为0. 25; 第二步,将小数部分0. 25乘以2,得0. 5,则整数部分为0,小数部分为0.5;第三步,将小数部分0. 5乘以2,得1. 0.则整数部分为1,小数部分为0. 0; 第四步,读数,从第一位读起,读到最后一位,即为0. 001 o例2,将0. 45转换为二进制(保留到小数点第I川位)大家从上面步骤可以看出.X第五次做乘法时候.得到的结果是0・4,那么小数部分继续乘以2.得0.8. 0・8又乘以2的,到1・6这样一直乘下去,锻后不可能得到小数部分为零•因此,这个时候只好学习十进制的方法进行I川舍五入门但是二进制只有0和1两个.于是就出现0舍1入。
各种进制之间的转换方法

各种进制之间的转换方法⑴二进制B转换成八进制Q:以小数点为分界线,整数部分从低位到高位,小数部分从高位到低位,每3位二进制数为一组,不足3位的,小数部分在低位补0,整数部分在高位补0,然后用1位八进制的数字来表示,采用八进制数书写的二进制数,位数减少到原来的1/3。
例:◆二进制数转换成八进制数:= 110 110 . 101 100B↓↓ ↓ ↓6 6 . 5 4 =◆八进制数转换成二进制数:3 6 . 2 4Q↓ ↓ ↓ ↓011 110. 010 100 =◆低位,每4位二进制数为一组,不足4位的,小数部分在低位补0,整数部分在高位补0,然后用1位十六进制的数字来表示,采用十六进制数书写的二进制数,位数可以减少到原来的1/4。
例:◆二进制数转换成十六进制数:.100111B = 1011 0101 1010 . 1001 1100B↓ ↓ ↓ ↓ ↓B 5 A . 9C = 5A◆十六进制数转换成二进制数:= A B . F EH↓ ↓ ↓ ↓1010 1011. 1111 1110 = .1111111B即先把八进制数Q转换成二进制数B,再转换成十六进制数H。
例:◆八进制数转换成十六进制数:= 111 100 000 010 .100 101B= .100101B= 1111 0000 0010 . 1001 0100B= F 0 2 . 9 4H=◆十六进制数转换成八进制数:= 0001 1011 . 1110B== 011 011 . 111B= 3 3 .7Q=⑷二进制数B转换成十进制数D:利用二进制数B按权展开成多项式和的表达式,取基数为2,逐项相加,其和就是相应的十进制数。
例:◆二进制数转换成十进制数:= 1×25+1×24+0×23+0×22+1×21+0×20+1×2-1= 32+16+2+=◆求8位二进制数能表示的最大十进制数值:最大8位二进制数是BB = 1×27+1×26+1×25+1×24+1×23+1×22+1×21+1×20= 255⑸十进制数D转换成二进制数B:十进制数转换成二进制数时,整数部分和小数部分换算算法不同,需要分别进行。
二进制,十六进制,八进制的换算

0,16,2进制的互相转换所谓16进制,就是由0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、F共16个数字组成。
逢16进⼀位,下⾯就讲讲在没有任何⼯具的情况下如何将⼀10进制转化为16进制:1000除以16得62余8,那么最低位为8,再将62除以16得3余14,那么倒数第2为E(14对于16进制来说是E),3⽐16⼩了,所以不⽤继续除了,总的就是3E8,为1000的16进制数。
想要将16进制的数转化为10进制,只需将上⾯的步骤反过来做就可以了。
不⽤我多说吧!2进制仅由0、1两个数字组成,逢1进⼀。
要将⼀10进制化为2进制,介绍⼀个简单的⽅法,先将10进制的数化为16进制,再化为2进制,举个例⼦:515对应16进制为203H,将203转为2进制则为0010(2) 0000(0) 0011(3),⼀个位数对2进制来说是4个字符。
0H就是0000、1H就是0001、……、0EH就是1110、OFH为1111,⼤家可⾃⼰推⼀下。
总之⼤家⼀定要熟练掌握各个进制的互相转化,尤其是100以内10--16和16--10的互相转化要记住。
16-10H、32-20H、48-30H、64-40H、80-50H、96-60H、100-64H,255-FFH,65535-FF FFH,1677万-FF FF FFH,前为10进制,后有H的为16进制,这些能记住,以后修改就⽅便许多了。
⼆进制⼆进制是逢2进位的进位制,0、1是基本算符。
现代的电⼦计算机技术全部采⽤的是⼆进制,因为它只使⽤0、1两个数字符号,⾮常简单⽅便,易于⽤电⼦⽅式实现。
⼆进制四则运算规则 加法 0+0=0,0+1=1+0=1,1+1=10 减法 0-0=0,1-0=1,1-1=0,0-1=-1 乘法 0×0=0,0×1=1×0=0,1×1=1 除法 0÷1=0,1÷1=1⼀、什么是⼆进制 在现实⽣活和记数器中,如果表⽰数的“器件”只有两种状态,如电灯的“亮”与“灭”,开关的“开”与“关”。
进制转换

各种进制之间的转换方法⑴二进制B转换成八进制Q:以小数点为分界线,整数部分从低位到高位,小数部分从高位到低位,每3位二进制数为一组,不足3位的,小数部分在低位补0,整数部分在高位补0,然后用1位八进制的数字来表示,采用八进制数书写的二进制数,位数减少到原来的1/3。
例:◆二进制数转换成八进制数:110110.1011B = 110 110 . 101 100B↓↓↓↓6 6 . 5 4 = 66.54Q◆八进制数36.24Q转换成二进制数:3 6 . 2 4Q↓↓↓↓011 110 . 010 100 = 11110.0101B⑵二进制数B转换成十六进制数H:以小数点为分界线,整数部分从低位到高位,小数部分从高位到低位,每4位二进制数为一组,不足4位的,小数部分在低位补0,整数部分在高位补0,然后用1位十六进制的数字来表示,采用十六进制数书写的二进制数,位数可以减少到原来的1/4。
例:◆二进制数转换成十六进制数|:101101011010.100111B = 1011 0101 1010 . 1001 1100B↓↓↓↓↓B 5 A . 9C = B5A.9CH◆十六进制数转换成二进制数:AB.FEH = A B . F EH↓↓↓↓1010 1011. 1111 1110 = 10101011.1111111B◆十六进制数、十进制数和二进制数对应关系表⑶八进制数Q转换成十六进制数H:八进制数Q和十六进制数H的转换要通过二进制数B 来实现,即先把八进制数Q转换成二进制数B,再转换成十六进制数H。
例:◆八进制数转换成十六进制数:7402.45Q = 7 4 0 2 . 4 5Q↓↓↓↓↓↓111 100 000 010 . 100 101B= 111100000010.100101B= 1111 0000 0010 . 1001 0100B↓↓↓↓↓= F 0 2 . 9 4H = F02.94H◆十六进制数转换成八进制数:1B.EH =1 B. EH↓↓↓0001 1011 . 1110B= 11011.111B= 011 011 . 111B↓↓↓= 3 3 . 7Q = 33.7Q⑷二进制数B转换成十进制数D:利用二进制数B按权展开成多项式和的表达式,取基数为2,逐项相加,其和就是相应的十进制数。
1-3 二进制与数制转换

,不足时在最外端补0
8=23,八进制数的8个数字对应着3位及3位以下的二进制数
11010001011.11011->011 010 001 011.110 110
3 2 1 3.6 6
b. 将每组二进制数分别转换为八进制数
(11010001011.11011)2=(3213.66)8
2021/11/25
不同数制之间的转换
16
第十六页,编辑于星期日:七点 四十八分。
(2) 八进制数转换为二进制数
上述方法的逆(一分为三)。要注意的是: a. 把每个八进制数写成3位二进制数,不足3位在前面
补0; b. 最后去掉两端多余的0。
(315.62)8=(011 001 101.110 010)2
=(11001101.11001)2
2021/11/25
不同数制之间的转换
17
第十七页,编辑于星期日:七点 四十八分。
3.2 二进制与十六进制的相互转换
2021/11/25
不同数制之间的转换
18
第十八页,编辑于星期日:七点 四十八分。
3.3 八进制与十六进制如何转换?
八 => 十 => 十六 OR 八 => 二 => 十六
2021/11/25
不同数制之间的转换
19
第十九页,编辑于星期日:七点 四十八分。
课堂练习
(239.375)10=(?)2
(365.5)8=(?)10
(3B6D.14)16=(?)2 (1100100101.0101)2=(?)8
二、八、十六进制数的作用
进制转换计算+ASCII表

一、二进制转化成其他进制例子1:将二进制数(10010)2转化成八进制数。
(10010)2=(010 010)2=(2 2)8=(22)8例子2:将二进制数(0.1010)2转化为八进制数。
(0.10101)2=(0. 101 010)2=(0. 5 2)8=(0.52)8诀窍:因为每三位二进制数对应一位八进制数,所以,以小数点为界,整数位则将二进制数从右向左每3位一隔开,不足3位的在左边用0填补即可;小数位则将二进制数从左向右每3位一隔开,不足3位的在右边用0填补即可。
例子1:将二进制数(10010)2转化成十进制数。
(10010)2=(1x24+0x23+0x22+1x21+0x20)10=(16+0+0+2+0)10=(18) 10例子2:将二进制数(0.10101)2转化为十进制数。
(0.10101)2=(0+1x2-1+0x2-2+1x2-3+0x2-4+1x2-5)10=(0+0.5+0.25+0.125+0.0625+0.03125)10=(0.96875)10诀窍:以小数点为界,整数位从最后一位(从右向左)开始算,依次列为第0、1、2、3………n,然后将第n位的数(0或1)乘以2的n-1次方,然后相加即可得到整数位的十进制数;小数位则从左向右开始算,依次列为第1、2、3……..n,然后将第n位的数(0或1)乘以2的-n次方,然后相加即可得到小数位的十进制数(按权相加法)。
例子1:将二进制数(10010)2转化成十六进制数。
(10010)2=(0001 0010)2=(1 2)16=(12) 16例子2:将二进制数(0.1010)2转化为十六进制数。
(0.10101)2=(0. 1010 1000)2=(0. A 8)16=(0.A8)16诀窍:因为每四位二进制数对应一位十六进制数,所以,以小数点为界,整数位则将二进制数从右向左每4位一隔开,不足4位的在左边用0填补即可;小数位则将二进制数从左向右每4位一隔开,不足4位的在右边用0填补即可。
二进制、八进制、十进制、十六进制之间转换
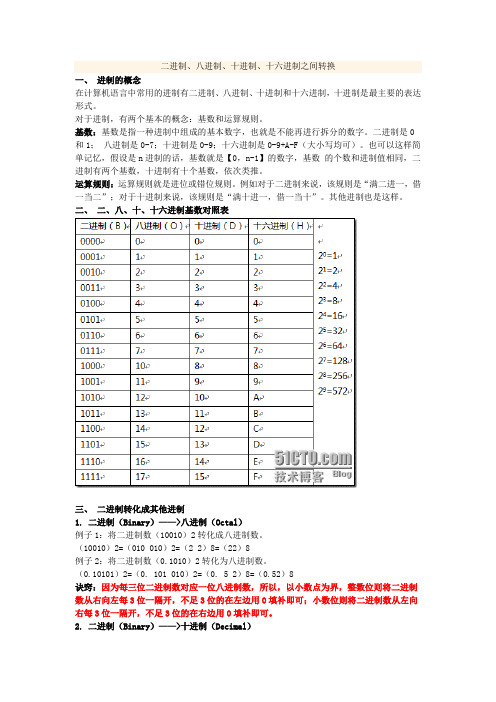
二进制、八进制、十进制、十六进制之间转换一、进制的概念在计算机语言中常用的进制有二进制、八进制、十进制和十六进制,十进制是最主要的表达形式。
对于进制,有两个基本的概念:基数和运算规则。
基数:基数是指一种进制中组成的基本数字,也就是不能再进行拆分的数字。
二进制是0和1;八进制是0-7;十进制是0-9;十六进制是0-9+A-F(大小写均可)。
也可以这样简单记忆,假设是n进制的话,基数就是【0,n-1】的数字,基数的个数和进制值相同,二进制有两个基数,十进制有十个基数,依次类推。
运算规则:运算规则就是进位或错位规则。
例如对于二进制来说,该规则是“满二进一,借一当二”;对于十进制来说,该规则是“满十进一,借一当十”。
其他进制也是这样。
二、二、八、十、十六进制基数对照表三、二进制转化成其他进制1. 二进制(Binary)——>八进制(Octal)例子1:将二进制数(10010)2转化成八进制数。
(10010)2=(010 010)2=(2 2)8=(22)8例子2:将二进制数(0.1010)2转化为八进制数。
(0.10101)2=(0. 101 010)2=(0. 5 2)8=(0.52)8诀窍:因为每三位二进制数对应一位八进制数,所以,以小数点为界,整数位则将二进制数从右向左每3位一隔开,不足3位的在左边用0填补即可;小数位则将二进制数从左向右每3位一隔开,不足3位的在右边用0填补即可。
2. 二进制(Binary)——>十进制(Decimal)例子1:将二进制数(10010)2转化成十进制数。
(10010)2=(1x24+0x23+0x22+1x21+0x20)10=(16+0+0+2+0)10=(18) 10例子2:将二进制数(0.10101)2转化为十进制数。
(0.10101)2=(0+1x2-1+0x2-2+1x2-3+0x2-4+1x2-5)10=(0+0.5+0.25+0.125+0.0625+0.03125)10=(0.96875)10诀窍:以小数点为界,整数位从最后一位(从右向左)开始算,依次列为第0、1、2、3………n,然后将第n位的数(0或1)乘以2的n-1次方,然后相加即可得到整数位的十进制数;小数位则从左向右开始算,依次列为第1、2、3……..n,然后将第n位的数(0或1)乘以2的-n次方,然后相加即可得到小数位的十进制数(按权相加法)。
11.1二进制及其转换

方法二、数值后面加特定的字母区分
新授
十进制和二进制进行类比
十进制 二进制
0、1
每个数位上可以使用的数码 基数 进位规则
0、1、2、3、4、5、6、7、8、9 10 “逢十进一”
2
“逢二进一”
二进制位权数表
整数部分 位置 位权数 … … 第3位 第2位 第1位
22
21
20
二进制特点与缺点: 便于实现,不便记忆
余0 余0 余0 余1
读 数 方 向 由 下 往 上
810
(1000 ) 2
除2 取余,逆序输出
例题
例2 将十进制数(101)10换算成二进制 数。
问题解决
八进制 每个数位上可以使用的数码 基数 进位规则 0、1、2、3、4、5、6、7 8
“逢八进一”
问题解决
1、八进制位权数表
整数部分 位置 位权数 … … 第3位 82 第2位 81 第1位 80
新授
进位制是人们为了计数和运算方便而约定的计数系统。 你还知道哪些常见的进位制?请举例。
二进制:计算机采用的计数制。
只有“0”、“1”两个状态,容易实现,运算简单
新授
思考:如何区别不同进位制的数? 进制数的表示方法: 方法一、用一个下标来表明 例:(101)10 (101)2 十进制 例: 101D 十进制 (D可以省略) 二进制 101B 二进制 (101)16 十六进制 101H 十六进制
新授
将十进制数换算成二进制数,通常使用“除2取余法”。
具体做法:不断用2去除要换算的十进制数,若余数为
1,则相应数位的数码为1,若余数为0,则相应数位的 数码为0,一直除到商是1为止,然后按照从高位到低位 的顺序写出换算结果。
数制及其相互转换

数制及其相互转换要点各种计数制二进制、八进制、十六进制对照表数制间的相互转换各种计数制二进制:由0,1组成,逢二进一八进制:由0,1,2,3,4,5,6,7八个数字组成,逢八进一十进制:由0,1,2,3,4,5,6,7,8,9十个数字组成,逢十进一十六进制:由0~9十个数字、A、B、C、D、E、F六个字母组成,逢十六进一二进制、八进制、十六进制对照表十进制二进制八进制十六进制十进制二进制八进制十六进制0 0000 0 0 8 1000 81 0001 1 1 9 1001 92 0010 2 2 10 1010 A3 0011 3 3 11 1011 B4 0100 4 4 12 1100 C5 0101 5 5 13 1101 D6 0110 6 6 14 1110 E7 0111 7 7 15 1111 F数制间的相互转换•转换原则:如果两个有理数相等,则它们的整数部分和小数部分分别相等。
•一、非十进制数间的转换•二、十进制数转换成非十进制数•三、非十进制数转换成十进制数•总结一、非十进制数间的转换1.二进制数与八进制数间的转换以小数点为界,向左或向右,三位二进制数一组用一位八进制数取代。
注意:不足三位二进制数用0补足三位。
基本关系:一位八进制数 = 三位二进制数八进制数 二进制数一分三三合一转换原则:将(714.431)8转换成二进制数例1:7 1 4 . 4 3 1 111 1 0 0 100 100 11 0 10 0 即:(714.431)8=(111001100.100011001)2 例:将二进制数(1111101.11001)2转换成八进制数1 111 101. 110 01 0 0 0 175 .62即:(1111101.11001)2=(175.62)82. 二进制数与十六进制数间的转换基本关系:一位十六进制数 = 四位二进制数转换原则:一分四十六进制数二进制数四合一将十六进制数1AC0.6D H 转换成相应的二进制数1 A C 0. 6 D 1 0 0 0 1010 1100 0000 . 110 0 1101 即:(1AC0.6D )16=(1101011000000.01101101)2例3:将二进制数(1100011.10111)2转换成相应的十六进制数110 0011. 1011 1 0 0 0 063 . B 8 即:(1100011.10111)2=(63.B8)16例2:二、十进制数转换成非十进制数十进制数转换R进制数转换原则:将十进制数分成整数部分和小数部分,分别采用不同的方法换算,然后将两部分相加。
进制转换:二进制、八进制、十六进制、十进制之间的转换

将二进制、八进制、十六进制转换为十进制二进制、八进制和十六进制向十进制转换都非常容易,就是“按权相加”。
所谓“权”,也即“位权”。
假设当前数字是 N 进制,那么:•对于整数部分,从右往左看,第 i 位的位权等于N i-1•对于小数部分,恰好相反,要从左往右看,第 j 位的位权为N-j。
更加通俗的理解是,假设一个多位数(由多个数字组成的数)某位上的数字是 1,那么它所表示的数值大小就是该位的位权。
1) 整数部分例如,将八进制数字53627 转换成十进制:从右往左看,第1位的位权为 80=1,第2位的位权为 81=8,第3位的位权为 82=64,第4位的位权为 83=512,第5位的位权为84=4096 ……第n位的位权就为 8n-1。
将各个位的数字乘以位权,然后再相加,就得到了十进制形式。
注意,这里我们需要以十进制形式来表示位权。
再如,将十六进制数字 9FA8C 转换成十进制:从右往左看,第1位的位权为 160=1,第2位的位权为 161=16,第3位的位权为 162=256,第4位的位权为 163=4096,第5位的位权为164=65536 ……第n位的位权就为 16n-1。
将各个位的数字乘以位权,然后再相加,就得到了十进制形式。
将二进制数字转换成十进制也是类似的道理:从右往左看,第1位的位权为 20=1,第2位的位权为 21=2,第3位的位权为 22=4,第4位的位权为 23=8,第5位的位权为 24=16 ……第n位的位权就为 2n-1。
将各个位的数字乘以位权,然后再相加,就得到了十进制形式。
2) 小数部分例如,将八进制数字 423.5176 转换成十进制:小数部分和整数部分相反,要从左往右看,第1位的位权为 8-1=1/8,第2位的位权为 8-2=1/64,第3位的位权为 8-3=1/512,第4位的位权为 8-4=1/4096 ……第m位的位权就为 8-m。
再如,将二进制数字 1010.1101 转换成十进制:小数部分和整数部分相反,要从左往右看,第1位的位权为 2-1=1/2,第2位的位权为 2-2=1/4,第3位的位权为 2-3=1/8,第4位的位权为2-4=1/16 ……第m位的位权就为 2-m。
