十进制-二进制-八进制-十六进制对照表
二进制八进制十进制十六进制之间的进制转换

二进制八进制十进制十六进制之间的进制转换详情可参考百度百科:进制转换这个词条【主要搞懂1和2两条,其他的进制之间的转化就迎刃而解,很好懂了】1. 十进制-> 二进制:将这个十进制数连续除以2的过程,第一步除以2,得到商和余数,将商再继续除以2,得到又一个商和余数,直到商为0。
最后将所有余数倒序排列,得到的数就是转换成二进制的结果。
2. 二进制-> 十进制:二进制数第1位的权值是2的0次方,第2位的权值是2的1次方,第3位的权值是2的2次方。
(例如1258这个十进制数,实际上代表的是:1x1000+2x100+5x10+8x1=1258)那么1011这个二进制数,实际上代表的是:1x8+0x4+1x2+1x1=11(十进制数11)。
(这里的8就是2的3次方,4就是2的2次方,2就是2的1次方,1就是2的0次方)3. 十进制-> 八进制:十进制数转换成八进制的方法,和转换为二进制的方法类似,唯一变化:除数由2变成8。
4. 八进制-> 十进制和转换为二进制的方法类似,唯一变化是,底数变成8,第1位表示8的0次方,第二位表示8的一次方,第三位表示8的2次方,第四位表示8的3次方。
例如1314这个八进制数,十进制数就是1x512+3x64+1x8+4x1=716(十进制)5. 十进制-> 十六进制10进制数转换成16进制的方法,和转换为2进制的方法类似,唯一变化:除数由2变成16。
十六进制是0123456789ABCDEF这十六个字符表示。
那么单独一个A就是10,单独一个B就是11,CDEF,就分表表示12,13,14,15。
而10这个十六进制数,实际就是十进制中的16。
6. 十六进制-> 十进制和转换为二进制的方法类似,唯一变化是,底数变成16,第1位表示16的0次方,第二位表示16的一次方,第三位表示16的2次方,第四位表示16的3次方。
7. 二进制<--->八进制,之间的相互转换,更简单一些,因为8本身是2的三次方。
进制转换表---原理表

抛砖引玉与10进制权限类同十进制的权限依次是1 10 100 1000 1000 10000.。
本质是10的0 1 2 3 4 次方---非常重要的概念二进制的是1 2 4 8 16 32 64。
十进制85=8x10+5 也就是十位数是8 个位数是5就像是十进制最低位在最右边一样右边往左边依次是个位十位百位二进制也是一样只不过从右边依次往左边依次称为是bit0位bit1位。
15位-----bit31位权限是2的0 1 2 3次方也就是 1 2 4 8Bit3 bit2 bit2 bit0 的权限是8421Bit4的权限是16 bit5 权限是32 bit权限是64 bit7 是128Bit8 权限是256就像十进制是完全一样的的所以如果是3 那就是2+1 就是bit0的1x2+bit0的1x1=3同理4就是bit2的1x4 就是bit2 位是1的意思也就是1005就是4+1 也就是1017就是4+2+1得到的也就是111也就是9就是8+1 也就是1001很简单不要钻牛角尖哦同理8进制16进制是同理的权限也依次是8的0 1 2 3 4.。
次方16的0 1 2 3 4 次方计算机只能存储0 1所以我们计算机里面存储的都是二进制二ABCDEF是没法存储的所以都用代号一般是0-127汉字的道理也是一样,就不要去抠字眼钻牛角尖了(可以自己查找代号)代号我们看到的计算机上的字母符号等都是根据二进制代号计算机翻译给我们的我们写进去的也会被翻译成二进制这种编码如果是保密的就是密码公开的所以就叫码制了看下面找规律吧Enjoy it!。
各进制数相互转换大全

0001 = 1 = 1 = 1
(3)十进制与十六进制的相互转化。
十--->十六:方法同上,以后不再赘述
例: 589(10)--->24D(16)
商 余数
589/16 36 13(用16进制的D表示)
0100 = 4 = 4 = 4
0101 = 5 = 5 = 5
1110 = 14 = E = 16
1111 = 15 = F = 17
... 4*16^2=1024
15*16^3= 61440
3*16^4=196608
10*16^5=10485760
结果10744845
(4)二进制、八进制、十进制、十六进制之间相互转化对照表
二进制数(仅4位的2进制数) = 十进制数 = 十六进制数 = 八进制数
385/8 48 1
48/8 6 0
6/8 0 6
1111=F
1101=D
1010=A
0101=5
1001=9
1011=B
那么它所对应的16进制数就是“FDA59B”
十六---->二
FD5(16)--->1111 1101 0101(2)
Part I 整型部分
(1)十进制与二进制的相互转化。
十---->二:十进制数除以2,得到一个商和余数(余数无非 0/1),余数单单保存。
拿得到的商继续除以2,又得到一个商和余数。保存余数。继续除以2...
直到除得的商为0.把除得的余数按先后顺寻从低位到高位排起(个位开始),
余数按先后顺寻从低到高排列。得到的就是二进制数1011001 。
二、八、十、十六进制转换

一、二进制转化成其他进制1. 二进制(Binary)——>八进制(Octal)例子1:将二进制数(10010)2转化成八进制数。
(10010)2=(010 010)2=(2 2)8=(22)8例子2:将二进制数(0.1010)2转化为八进制数。
(0.10101)2=(0. 101 010)2=(0. 5 2)8=(0.52)8诀窍:因为每三位二进制数对应一位八进制数,所以,以小数点为界,整数位则将二进制数从右向左每3位一隔开,不足3位的在左边用0填补即可;小数位则将二进制数从左向右每3位一隔开,不足3位的在右边用0填补即可。
2. 二进制(Binary)——>十进制(Decimal)例子1:将二进制数(10010)2转化成十进制数。
(10010)2=(1x24+0x23+0x22+1x21+0x20)10=(16+0+0+2+0)10=(18) 10例子2:将二进制数(0.10101)2转化为十进制数。
(0.10101)2=(0+1x2-1+0x2-2+1x2-3+0x2-4+1x2-5)10=(0+0.5+0.25+0.125+0.0625+0.03125)10=(0.96875)10诀窍:以小数点为界,整数位从最后一位(从右向左)开始算,依次列为第0、1、2、3………n,然后将第n位的数(0或1)乘以2的n-1次方,然后相加即可得到整数位的十进制数;小数位则从左向右开始算,依次列为第1、2、3……..n,然后将第n位的数(0或1)乘以2的-n次方,然后相加即可得到小数位的十进制数(按权相加法)。
3. 二进制(Binary)——>十六进制(Hex)例子1:将二进制数(10010)2转化成十六进制数。
(10010)2=(0001 0010)2=(1 2)16=(12) 16例子2:将二进制数(0.1010)2转化为十六进制数。
(0.10101)2=(0. 1010 1000)2=(0. A 8)16=(0.A8)16诀窍:因为每四位二进制数对应一位十六进制数,所以,以小数点为界,整数位则将二进制数从右向左每4位一隔开,不足4位的在左边用0填补即可;小数位则将二进制数从左向右每4位一隔开,不足4位的在右边用0填补即可。
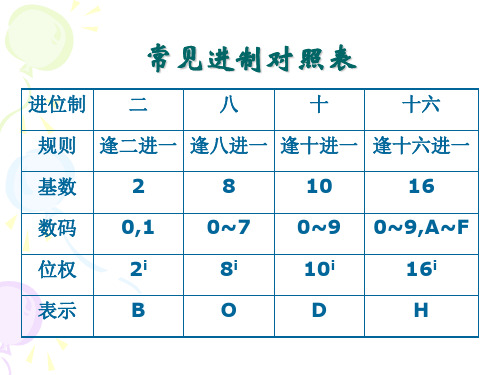
常见进制对照表
6
110
7
111
24=16 十六 二 十六 二
0 0000 8 1000 1 0001 9 1001 2 0010 A 1010 3 0011 B 1011 4 0100 C 1100 5 0101 D 1101 6 0110 E 1110 7 0111 F 1111
数据的存储
• 基本单位: 位(Bit)----可存储一位二进制数(0/1)
十进制与各进制互换对照
数制 十
二,八,十六
转换 整数部分 小数部分
二,八,十六 十
方法 除基数取余 乘基数取整
停止 商为0
小数为0
取数 自下往上 自上往下
例子 (25.148)10=(?)2
位权展开式 (101.1)2
二,八,十六进制对照
23=8
八
二
0
000
1
001
2
010
3
011
4
100
5
101
• 存储容量: 字节( Byte/B)----1Byte=8 Bit 1KB=1024B----K 1MB=1024KB--M 1GB=1024MB—G
• 字(Word)----若干字节(B)组成 • 字长:衡量计算机性能的重要指标.
常见进制对照表
进位制 二
八
十
十六
规则 逢二进一 逢八进一 逢十进一 逢十六进一
基数
2
数码 0,1
位权
2i
表示
B
8 0~7
8i O
10 0~9 10i
D
16 0~9,A~F
16i H
“多媒体技术”,“三网合一”,“电子商 务”,
【最新】数值数据在计算机中的表示方法

数值数据在计算机中的表示方式日常生活中,经常采用的进位制很多,比如,一打等于十二个(十二进制)、一小时等于六十分(六十进制)、一米等于十分米(十进制)等等。
其中十进制是最常用的,它的特点是有10个数码:0~9,进位关系是“逢十进一”。
而在计算机中数的表示是采用二进制。
为了书写和读数方便还用到八进制和十六进制。
如表1.1。
1. 计算机中的二进制数二进制是逢二进一,所有的数都用两个数字符号0或1表示。
二进制的每一位只能表示0或1。
例如:(1)10 = (001)2 ,(2)10 = (010)2 ,(3)10 = (011)2 。
即十进制数1,2,3用二进制表示分别为:001,010,011等等。
计算机采用二进制的原因在于:(1)0和1两个数可分别用电器中两种状态来表示,很容易用电器元件来实现。
如开关的接通为1,断开为0;高电平为1,低电平为0等,而要用电路的状态来表示我们已熟悉的十进制等,就要制作出具有十个稳定状态的元件,这是相当困难的;(2)计算机只能直接识别二进制数符0和1,而且二进制的运算公式很简单,计算机很容易实现,逻辑判断也容易。
(3)可以节省设备。
2. 八进制二进制的缺点是表示一个数需要的位数多,书写数据和指令不方便。
通常,为方便起见,将二进制数从低向高每三位或四位组成一组。
例如:有一个二进制(100100001100)2,若每三位一组,即:(100,100,001,100)2可表示成八进制数(4414)8,如此表示使得每组的值大小是从0(000)~7(111),且数值逢八进一,即为八进制。
3. 十六进制若每四位为一组,即:(1001,0000,1100)2,每组的值大小是从0(0000)~15(1111),且逢16进一,即为十六进制。
用A,B,C,D,E,F分别代表10到15的6个数,则上面的二进制数可以表示成十进制数(90C)16。
表1.1 十进制、二进制、八进制、十六进制对照表4. 有关的概念位(Bit)指一位二进制代码,它只具有“0”和“1”两个状态。
进制转换

进制转换对照表(0~255) - 十进制,十六进制,八进制,二进制Dec Hex Oct Bin0 1 2 3 4 5 6 7 8 9101112131415 0123456789ABCDEF00000100200300400500600701001101201301401501601700000000000000010000001000000011000001000000010100000110000001110000100000001001000010100000101100001100000011010000111000001111Dec Hex Oct Bin16171819202122232425262728293031101112131415161718191A1B1C1D1E1F02002102202302402502602703003103203303403503603700010000000100010001001000010011000101000001010100010110000101110001100000011001000110100001101100011100000111010001111000011111Dec Hex Oct Bin32333435363738394041424344454647202122232425262728292A2B2C2D2E2F04004104204304404504604705005105205305405505605700100000001000010010001000100011001001000010010100100110001001110010100000101001001010100010101100101100001011010010111000101111Dec Hex Oct Bin48495051525354555657585960616263303132333435363738393A3B3C3D3E3F06006106206306406506606707007107207307407507607700110000001100010011001000110011001101000011010100110110001101110011100000111001001110100011101100111100001111010011111000111111Dec Hex Oct Bin64656667686970 4041424344454610010110210310410510601000000010000010100001001000011010001000100010101000110Dec Hex Oct Bin808182838485865051525354555612012112212312412512601010000010100010101001001010011010101000101010101010110Dec Hex Oct Bin969798991001011026061626364656614014114214314414514601100000011000010110001001100011011001000110010101100110Dec Hex Oct Bin1121131141151161171187071727374757616016116216316416516601110000011100010111001001110011011101000111010101110110717273747576777879 4748494A4B4C4D4E4F1071101111121131141151161170100011101001000010010010100101001001011010011000100110101001110010011118788899091929394955758595A5B5C5D5E5F1271301311321331341351361370101011101011000010110010101101001011011010111000101110101011110010111111031041051061071081091101116768696A6B6C6D6E6F1471501511521531541551561570110011101101000011010010110101001101011011011000110110101101110011011111191201211221231241251261277778797A7B7C7D7E7F167170171172173174175176177011101110111100001111001011110100111101101111100011111010111111001111111Dec Hex Oct Bin128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 808182838485868788898A8B8C8D8E8F20020120220320420520620721021121221321421521621710000000100000011000001010000011100001001000010110000110100001111000100010001001100010101000101110001100100011011000111010001111Dec Hex Oct Bin144145146147148149150151152153154155156157158159909192939495969798999A9B9C9D9E9F22022122222322422522622723023123223323423523623710010000100100011001001010010011100101001001010110010110100101111001100010011001100110101001101110011100100111011001111010011111Dec Hex Oct Bin160161162163164165166167168169170171172173174175A0A1A2A3A4A5A6A7A8A9AAABACADAEAF24024124224324424524624725025125225325425525625710100000101000011010001010100011101001001010010110100110101001111010100010101001101010101010101110101100101011011010111010101111Dec Hex Oct Bin176177178179180181182183184185186187188189190191B0B1B2B3B4B5B6B7B8B9BABBBCBDBEBF26026126226326426526626727027127227327427527627710110000101100011011001010110011101101001011010110110110101101111011100010111001101110101011101110111100101111011011111010111111Dec Hex Oct Bin Dec Hex Oct Bin Dec Hex Oct Bin Dec Hex Oct Bin192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 C0C1C2C3C4C5C6C7C8C9CACBCCCDCECF30030130230330430530630731031131231331431531631711000000110000011100001011000011110001001100010111000110110001111100100011001001110010101100101111001100110011011100111011001111208209210211212213214215216217218219220221222223D0D1D2D3D4D5D6D7D8D9DADBDCDDDEDF32032132232332432532632733033133233333433533633711010000110100011101001011010011110101001101010111010110110101111101100011011001110110101101101111011100110111011101111011011111224225226227228229230231232233234235236237238239E0E1E2E3E4E5E6E7E8E9EAEBECEDEEEF34034134234334434534634735035135235335435535635711100000111000011110001011100011111001001110010111100110111001111110100011101001111010101110101111101100111011011110111011101111240241242243244245246247248249250251252253254255F0F1F2F3F4F5F6F7F8F9FAFBFCFDFEFF36036136236336436536636737037137237337437537637711110000111100011111001011110011111101001111010111110110111101111111100011111001111110101111101111111100111111011111111011111111一:简述:进位计数制:是人们利用符号来计数的方法。
计算机中的二进制、八进制、十进制、十六进制

计算机中的⼆进制、⼋进制、⼗进制、⼗六进制1.1 进制⼆进制:逢⼆进⼀,数值只有0和1。
⼋进制:逢⼋进⼀,数值有0,1,2,3,4,5,6,7⼗进制:逢⼗进⼀,数值有0,1,2,3,4,5,6,7,8,9⼗六进制:逢⼗六进⼀,数值有0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F1.2 进制转换⼆进制、⼋进制、⼗六进制转为⼗进制⼗进制转为⼆进制、⼋进制、⼗六进制1.3 原码,反码,补码1.3.1 机器数和真值机器数:⼀个数在计算机中的⼆进制表⽰形式。
叫做这个数的机器数。
机器数是带符号的,最⾼位0表⽰正数,1表⽰负数。
⽰例:⽐如10进制中的+3,计算机长度为8位。
转为⼆进制是0000 0011。
⽐如-3,转为⼆进制是1000 0011。
真值:因为第⼀位是符号位,所以机器数的形式值就不等于真正的数值。
⽐如1000 0011,作为负数可以是-3,作为正数可以说131.为了区分,将带符号位的计算数对应的真正的数值称为机器数的真值。
1.3.2 原码,反码,补码原码:就是符号位加上真值的绝对值,即第⼀位表⽰符号位,其余位表⽰值。
+1 = [0000 0001]原-1 = [1000 0001]原原码是⼈脑最容易理解和计算的表⽰⽅式.反码:正数的反码是其本⾝,负数的反码是在其原码的基础上,符号位不变,其余各位按位取反。
+1 = [0000 0001]原 = [0000 0001]反-1 = [1000 0001]原 = [1111 1110]反⼀个反码表⽰的是负数, ⼈脑⽆法直观的看出来它的数值. 通常要将其转换成原码再计算。
补码:正数的补码是其本⾝,负数的补码是在原码的基础上,符号位不变,其余各位取反后+1。
+1 = [0000 0001]原 = [0000 0001]反 = [0000 0001]补-1 = [1000 0001]原 = [1111 1110]反 = [1111 1111]补对于负数, 补码表⽰⽅式也是⼈脑⽆法直观看出其数值的. 通常也需要转换成原码在计算其数值.于是⼈们开始探索将符号位参与运算, 并且只保留加法的⽅法. ⾸先来看原码。
常见进制对照表

基数
2
数码 0,1
位权
2i
表示
B
8 0~7
8i O
10 0~9 10i
D
16 0~9,A~F
16i H
“多媒体技术”,“三网合一”,“电子商 务”,
“CAD”,“CAI”,“蓝牙技术”,“GPRS”,
“信息高速公路”,“信息技术的三要 素”……
十进制与各进制互换对照
数制 十
二,八,十六ຫໍສະໝຸດ 转换 整数部分 小数部分数据的存储
• 基本单位: 位(Bit)----可存储一位二进制数(0/1)
• 存储容量: 字节( Byte/B)----1Byte=8 Bit 1KB=1024B----K 1MB=1024KB--M 1GB=1024MB—G
• 字(Word)----若干字节(B)组成 • 字长:衡量计算机性能的重要指标.
二,八,十六 十
方法 除基数取余 乘基数取整
停止 商为0
小数为0
取数 自下往上 自上往下
例子 (25.148)10=(?)2
位权展开式 (101.1)2
二,八,十六进制对照
23=8
八
二
0
000
1
001
2
010
3
011
4
100
5
101
6
110
7
111
24=16 十六 二 十六 二
0 0000 8 1000 1 0001 9 1001 2 0010 A 1010 3 0011 B 1011 4 0100 C 1100 5 0101 D 1101 6 0110 E 1110 7 0111 F 1111
常见进制对照表常见进制对照表进位制二八十十六规则逢二进一逢八进一逢十进一逢十六进一基数基数228810101616数码01070909af位权2i8i10i16i表示bodh多媒体技术三网合一电子商务cadcai蓝牙技术gprs信息高速公路信息技术的三要素
数值数据在计算机中的表示方法

数值数据在计算机中的表示方式日常生活中,经常采用的进位制很多,比如,一打等于十二个(十二进制)、一小时等于六十分(六十进制)、一米等于十分米(十进制)等等。
其中十进制是最常用的,它的特点是有10个数码:0~9,进位关系是“逢十进一”。
而在计算机中数的表示是采用二进制。
为了书写和读数方便还用到八进制和十六进制。
如表1.1。
1. 计算机中的二进制数二进制是逢二进一,所有的数都用两个数字符号0或1表示。
二进制的每一位只能表示0或1。
例如:(1)10 = (001)2 ,(2)10 = (010)2 ,(3)10 = (011)2 。
即十进制数1,2,3用二进制表示分别为:001,010,011等等。
计算机采用二进制的原因在于:(1)0和1两个数可分别用电器中两种状态来表示,很容易用电器元件来实现。
如开关的接通为1,断开为0;高电平为1,低电平为0等,而要用电路的状态来表示我们已熟悉的十进制等,就要制作出具有十个稳定状态的元件,这是相当困难的;(2)计算机只能直接识别二进制数符0和1,而且二进制的运算公式很简单,计算机很容易实现,逻辑判断也容易。
(3)可以节省设备。
2. 八进制二进制的缺点是表示一个数需要的位数多,书写数据和指令不方便。
通常,为方便起见,将二进制数从低向高每三位或四位组成一组。
例如:有一个二进制(100100001100)2,若每三位一组,即:(100,100,001,100)2可表示成八进制数(4414)8,如此表示使得每组的值大小是从0(000)~7(111),且数值逢八进一,即为八进制。
3. 十六进制若每四位为一组,即:(1001,0000,1100)2,每组的值大小是从0(0000)~15(1111),且逢16进一,即为十六进制。
用A,B,C,D,E,F分别代表10到15的6个数,则上面的二进制数可以表示成十进制数(90C)16。
4. 有关的概念位(Bit)指一位二进制代码,它只具有“0”和“1”两个状态。
二进制、八进制、十进制和十六进制关系

二进制、八进制、十进制和十六进制关系为什么需要八进制和十六进制?由于数据在计算机中的表示,最终以二进制的形式存在,所以有时候使用二进制,可以更直观地解决问题。
但二进制数太长了。
面对太长的数进行思考或操作,没有人会喜欢。
用16进制或8进制可以解决这个问题。
因为,进制越大,数的表达长度也就越短。
不过,为什么偏偏是16或8进制,而不其它的,诸如9或20进制呢?因为2、8、16,分别是2的1次方、3次方、4次方。
这一点使得三种进制之间可以非常直接地互相转换。
8进制或16进制缩短了二进制数,但保持了二进制数的表达特点。
可以看出,所有进制换算成10进制,关键在于三个因素:进制基数、权位和权值。
如何将二、八、十六进制数转换为十进制数。
(一)二进制数转换成十进制数由二进制数转换成十进制数的基本做法是,把二进制数首先写成加权系数展开式,从最后一位开始算,依次列为第0、1、2...n位,第n位的数(0或1)乘以基数2的n次方,然后按十进制加法规则求和,得到的结果就是答案。
这种做法称为"按权相加"法。
例1:(01100100)2=(100)10计算过程:0*20+0*21+1*22+1*23+0*24+1*25+1*26+0*27=0乘以多少都是0,所以也可直接跳过值为0的位:1*22+1*23+1*25+1*26=100例2:(1011.01)2=(1×23+0×22+1×21+1×20+0×2-1+1×2-2)10=(8+0+2+1+0+0.25)10=(11.25)10例3:(101.101)2=(5.625)10(二)8进制数转换为10进制数,也按"按权相加"法,只将基数换成8即可。
例:(1507)8=(839)10计算过程:1*83+5*82+0*81+7*80=839(三)16进制数转换成10进制数,也按"按权相加"法,只将基数换成16即可。
进制转换表---原理表

抛砖引玉与10进制权限类同十进制的权限依次是1 10 100 1000 1000 10000.。
本质是10的0 1 2 3 4 次方---非常重要的概念二进制的是1 2 4 8 16 32 64。
十进制85=8x10+5 也就是十位数是8 个位数是5就像是十进制最低位在最右边一样右边往左边依次是个位十位百位二进制也是一样只不过从右边依次往左边依次称为是bit0位bit1位。
15位-----bit31位权限是2的0 1 2 3次方也就是 1 2 4 8Bit3 bit2 bit2 bit0 的权限是8421Bit4的权限是16 bit5 权限是32 bit权限是64 bit7 是128Bit8 权限是256就像十进制是完全一样的的所以如果是3 那就是2+1 就是bit0的1x2+bit0的1x1=3同理4就是bit2的1x4 就是bit2 位是1的意思也就是1005就是4+1 也就是1017就是4+2+1得到的也就是111也就是9就是8+1 也就是1001很简单不要钻牛角尖哦同理8进制16进制是同理的权限也依次是8的0 1 2 3 4.。
次方16的0 1 2 3 4 次方计算机只能存储0 1所以我们计算机里面存储的都是二进制二ABCDEF是没法存储的所以都用代号一般是0-127汉字的道理也是一样,就不要去抠字眼钻牛角尖了(可以自己查找代号)代号我们看到的计算机上的字母符号等都是根据二进制代号计算机翻译给我们的我们写进去的也会被翻译成二进制这种编码如果是保密的就是密码公开的所以就叫码制了看下面找规律吧Enjoy it!。
二进制、八进制、十进制、十六进制之间转换(含小数部分)

二进制、八进制、十进制、十六进制之间转换一、十进制与二进制之间的转换(1)十进制转换为二进制,分为整数部分和小数部分①整数部分方法:除2取余法,即每次将整数部分除以2,余数为该位权上的数,而商继续除以2,余数又为上一个位权上的数,这个步骤一直持续下去,直到商为0为止,最后读数时候,从最后一个余数读起,一直到最前面的一个余数。
下面举例:例:将十进制的168转换为二进制得出结果将十进制的168转换为二进制,(10101000)2分析:第一步,将168除以2,商84,余数为0。
第二步,将商84除以2,商42余数为0。
第三步,将商42除以2,商21余数为0。
第四步,将商21除以2,商10余数为1。
第五步,将商10除以2,商5余数为0。
第六步,将商5除以2,商2余数为1。
第七步,将商2除以2,商1余数为0。
第八步,将商1除以2,商0余数为1。
第九步,读数,因为最后一位是经过多次除以2才得到的,因此它是最高位,读数字从最后的余数向前读,即10101000(2)小数部分方法:乘2取整法,即将小数部分乘以2,然后取整数部分,剩下的小数部分继续乘以2,然后取整数部分,剩下的小数部分又乘以2,一直取到小数部分为零为止。
如果永远不能为零,就同十进制数的四舍五入一样,按照要求保留多少位小数时,就根据后面一位是0还是1,取舍,如果是零,舍掉,如果是1,向入一位。
换句话说就是0舍1入。
读数要从前面的整数读到后面的整数,下面举例:例1:将0.125换算为二进制得出结果:将0.125换算为二进制(0.001)2分析:第一步,将0.125乘以2,得0.25,则整数部分为0,小数部分为0.25;第二步, 将小数部分0.25乘以2,得0.5,则整数部分为0,小数部分为0.5;第三步, 将小数部分0.5乘以2,得1.0,则整数部分为1,小数部分为0.0;第四步,读数,从第一位读起,读到最后一位,即为0.001。
例2,将0.45转换为二进制(保留到小数点第四位)大家从上面步骤可以看出,当第五次做乘法时候,得到的结果是0.4,那么小数部分继续乘以2,得0.8,0.8又乘以2的,到1.6这样一直乘下去,最后不可能得到小数部分为零,因此,这个时候只好学习十进制的方法进行四舍五入了,但是二进制只有0和1两个,于是就出现0舍1入。
数制及其相互转换

数制及其相互转换要点各种计数制二进制、八进制、十六进制对照表数制间的相互转换各种计数制二进制:由0,1组成,逢二进一八进制:由0,1,2,3,4,5,6,7八个数字组成,逢八进一十进制:由0,1,2,3,4,5,6,7,8,9十个数字组成,逢十进一十六进制:由0~9十个数字、A、B、C、D、E、F六个字母组成,逢十六进一二进制、八进制、十六进制对照表十进制二进制八进制十六进制十进制二进制八进制十六进制0 0000 0 0 8 1000 81 0001 1 1 9 1001 92 0010 2 2 10 1010 A3 0011 3 3 11 1011 B4 0100 4 4 12 1100 C5 0101 5 5 13 1101 D6 0110 6 6 14 1110 E7 0111 7 7 15 1111 F数制间的相互转换•转换原则:如果两个有理数相等,则它们的整数部分和小数部分分别相等。
•一、非十进制数间的转换•二、十进制数转换成非十进制数•三、非十进制数转换成十进制数•总结一、非十进制数间的转换1.二进制数与八进制数间的转换以小数点为界,向左或向右,三位二进制数一组用一位八进制数取代。
注意:不足三位二进制数用0补足三位。
基本关系:一位八进制数 = 三位二进制数八进制数 二进制数一分三三合一转换原则:将(714.431)8转换成二进制数例1:7 1 4 . 4 3 1 111 1 0 0 100 100 11 0 10 0 即:(714.431)8=(111001100.100011001)2 例:将二进制数(1111101.11001)2转换成八进制数1 111 101. 110 01 0 0 0 175 .62即:(1111101.11001)2=(175.62)82. 二进制数与十六进制数间的转换基本关系:一位十六进制数 = 四位二进制数转换原则:一分四十六进制数二进制数四合一将十六进制数1AC0.6D H 转换成相应的二进制数1 A C 0. 6 D 1 0 0 0 1010 1100 0000 . 110 0 1101 即:(1AC0.6D )16=(1101011000000.01101101)2例3:将二进制数(1100011.10111)2转换成相应的十六进制数110 0011. 1011 1 0 0 0 063 . B 8 即:(1100011.10111)2=(63.B8)16例2:二、十进制数转换成非十进制数十进制数转换R进制数转换原则:将十进制数分成整数部分和小数部分,分别采用不同的方法换算,然后将两部分相加。
总结进制数转换-二进制-八进制-十进制-十六进制--之间转换方法

*十进制数与二进制数间的转换
A. “十进制”转“二进 制”
2
19 余数 低位
2 91
2
41
2
20
2
10
0 1 高位
(19)10=(10011)2
B. “二进制”转“十进 制”
(10011)2
=1*2 4 +1*2 1
+1*2 0 =16+2+1 =19
注意:2 的0次方 等于1,
不是0
返回
*十进制数与八进制数间的转换
2
3、计算机中彩色图像的每一种颜色均可用红、 绿、蓝三原色调配出来,如果每种原色从浅到 深分为256个等级,一个原色需要用( )位二 进制数来表示。
A 24位 B 16位 C 8 位 D 256位
4、转换进制:
(11010)2 = ( )8 = ( )16 = ( )10
(0.010)2 = (
A. “十进制”转“八进 制”
8
19 余数 低位
8 23 02
高位
(19)10=(23)8
B. “八进制”转“十进 制”
(23)8
=2*8 1 +3*8 0
=16+3
=19
返回
*十进制数与十六进制数间的转换
A. “十进制”转“十六进 制”
16
27 余数 低位
16 1 11 01
写成(111)16
高位
0110 1110 0110. 1101 6 E 6. D
二进制数(11011100110.1101)2转换成十六进制 数是(6E6.D)16。
反之,将每位十六进制数分别用四位二进制数表 示,就可完成十六进制数和二进制数的转换。
常见二进制、八进制、十进制、十六进制的转换-扫盲
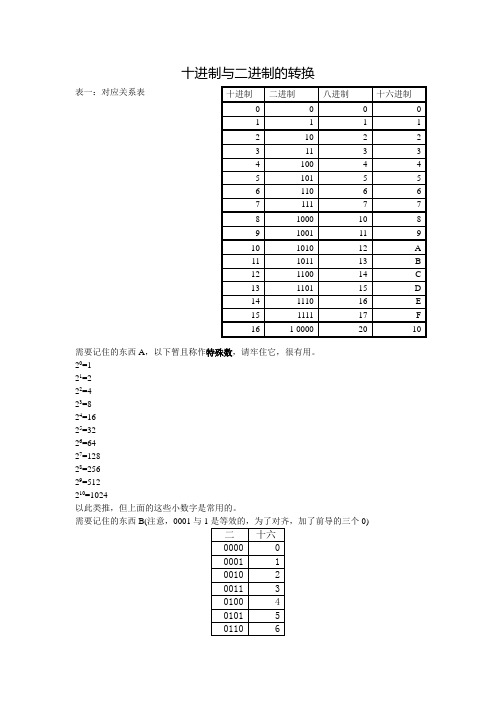
十进制与二进制的转换需要记住的东西A,以下暂且称作特殊数,请牢住它,很有用。
20=121=222=423=824=1625=3226=6427=12828=25629=512210=1024以此类推,但上面的这些小数字是常用的。
需要记住的东西B(注意,0001与1是等效的,为了对齐,加了前导的三个0)一、二进制与十进制转换的问题以8位二进制为例,讲一下十制与二进制位置关系(1011 1101)2=?分析 1 0 1 1 1 1 0 1位2726 252423 222120所以:(1011 1101)2=27 *1+26*0+25*1+24*1+23*1+22*1+21*0+20*1=128+0+32+16+8+4+0+1=189这是二进制数转化为十进制数最笨也是最基础的方法。
现在反过来,把189转化为二进制。
分析:189里最大的特殊数是哪个?答案是128,取出128剩下61,这里面最大的特殊数是多少??答案是32,依此类推,16,8,4,1那么这些数分别是2的多少次方呢?答案是7、5、4、3、2、0,现在把8位二进制数的这些位上填上1,其它位填上0(注意,最右面一位是2的0次方位,最左一位是2的7次方位)结果就是1011 1101。
以上讲的就是二进制与十进制转化的最笨的例子。
二、二进制与十六进制转换的问题由对应关系表可以看得出,四位二进制恰好对应着一位十六进制数(二进制0-1111对应于十六进制0-F),为什么呢?因为2的四次方为16啊,所以4位二进制正好对应一位十六进制。
那么这么说8是2的三次方,三位二进制是不是对应着一位八进制呢?答案是肯定的,由对应关系表可以看得出。
先不提八进制,说说二进制和十六进制的转换。
需要记住的东西B,这几个关系很容易记住,也是我要求记住的。
我的转换方法是不通过转成10进制转接转化,怎么转法?就是这个对应关系。
例题:(1101 0101)2=(?)16(1101)2=D(0101)2=(5)16所以(1101 0101)2=(D5)16例题:(12A)16=(?)2答案:(0001 0010 1010)2或(1 0010 1010)2完毕。
