matlab中回归分析实例分析
用MATLAB求解回归分析

估
F值、与F对应的概率p
计
相关系数 r2 越接近 1,说明回归方程越显著;
.
(
缺
省显
时著
为性
0
水 平
05
)
F > F1-α(k,n-k-1)时拒绝 H0,F 越大,说明回归方程越显著;
与 F 对应的概率 p 时拒绝 H0,回归模型成立.
3、画出残差及其置信区间: rcoplot(r,rint)
例1 解:1、输入数据:
stats = 0.9702 40.6656
0.0005
1、回归:
非线性回 归
是事先用m-文件定 义的非线性函数
(1)确定回归系数的命令: [beta,r,J]=nlinfit(x,y,’model’, beta0)
估计出的 回归系数
残差 Jacobian矩阵
输入数据x、y分别为 n m矩阵和n维列向 量,对一元非线性回 归,x为n维列向量。
r2=0.9282, F=180.9531, p=0.0000
p<0.05, 可知回归模型 y=-16.073+0.7194x 成立.
3、残差分析,作残差图: rcoplot(r,rint)
从残差图可以看出,除第二个数据外,其余数据的残
差离零点均较近,且残差的置信区间均包含零点,这说明 回归模型 y=-16.073+0.7194x能较好的符合原始数据,而第 二个数据可视为异常点.
2、预测和预测误差估计:
(1)Y=polyval(p,x)求polyfit所得的回归多项式在 x处 的预测值Y; (2)[Y,DELTA]=polyconf(p,x,S,alpha)求 polyfit所得的回归多项式在x处的预测值Y及预测值的 显著性为 1-alpha的置信区间Y DELTA;alpha缺省时为0.5
matlab多个因变量回归

matlab多个因变量回归Matlab是一种强大的科学计算软件,可以用于多个因变量回归分析。
多个因变量回归分析是一种统计方法,用于探究多个自变量对多个因变量的影响关系。
在本文中,将介绍如何使用Matlab进行多个因变量回归分析,并解释结果的含义。
我们需要准备一组数据,包括多个自变量和多个因变量。
假设我们想要研究一辆汽车的油耗情况,可能的自变量包括车速、引擎排量、重量等,而因变量则是油耗量和二氧化碳排放量。
在Matlab中,可以使用regress函数进行多个因变量回归分析。
该函数的语法如下:```[b,bint,r,rint,stats] = regress(y,X)```其中,y是因变量矩阵,每一列代表一个因变量;X是自变量矩阵,每一列代表一个自变量。
函数的输出包括回归系数b、回归系数的置信区间bint、残差r、残差的置信区间rint以及回归统计信息stats。
接下来,我们将使用一个具体的例子来说明多个因变量回归分析在Matlab中的应用。
假设我们有一组数据,包括100辆汽车的车速、引擎排量、重量以及油耗量和二氧化碳排放量。
我们的目标是探究车速、引擎排量和重量对油耗量和二氧化碳排放量的影响。
我们需要加载数据并将自变量和因变量分别存储在矩阵X和矩阵y 中。
假设数据存储在一个名为"car_data.csv"的文件中,我们可以使用readmatrix函数来读取数据:```data = readmatrix('car_data.csv');X = data(:, 1:3); % 车速、引擎排量、重量y = data(:, 4:5); % 油耗量和二氧化碳排放量```接下来,我们可以使用regress函数进行多个因变量回归分析,并获取回归系数、残差等信息:```[b,bint,r,rint,stats] = regress(y, X);```回归系数b代表了自变量对因变量的影响程度。
matlab回归分析一例
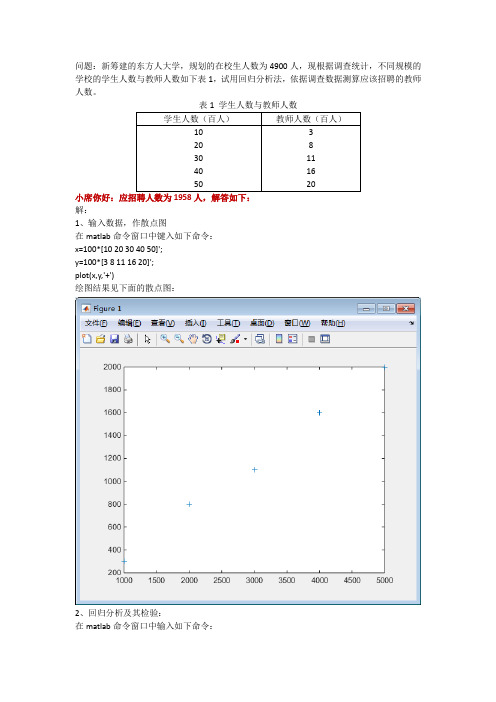
问题:新筹建的东方人大学,规划的在校生人数为4900人,现根据调查统计,不同规模的学校的学生人数与教师人数如下表1,试用回归分析法,依据调查数据测算应该招聘的教师人数。
表1 学生人数与教师人数小席你好:应招聘人数为1958人,解答如下:解:1、输入数据,作散点图在matlab命令窗口中键入如下命令:x=100*[10 20 30 40 50]';y=100*[3 8 11 16 20]';plot(x,y,'+')绘图结果见下面的散点图:2、回归分析及其检验:在matlab命令窗口中输入如下命令:X=[ ones(5,1) x];Y=y;[b,bint,r,rint,stats]=regress(Y ,X);b,bint,stats运行结果为:b =-100.00000.4200bint =-272.3621 72.36210.3680 0.4720stats =1.0e+03 *0.0010 0.6615 0.0000 2.6667即42.0ˆ,100ˆ10=-=ββ;0ˆβ的置信区间为[-272.3621,72.3621], 1ˆβ的置信区间为[0.3680,0.4720]; r 2=1, F=661.5, p=0.0000p<0.05, 可知回归模型 y=-100+0.42x 成立.3、残差分析,作残差图在matlab 命令窗口中键入如下命令:rcoplot(r,rint)残差图如下:从残差图可以看出,所有数据的残差离零点均较近,且残差的置信区间均包含零点,这说明回归模型y=-100+0.42x能较好地符合原始数据.4、预测及作图:z=b(1)+b(2)*xplot(x,Y,'k+',x,z,'r')上图再次直观地说明回归模型y=-100+0.42x能较好地符合原始数据.5、测算应该招聘的教师人数在matlab窗口中键入如下命令:zprs=b(1)+b(2)*4900运行结果为:zprs =1.9580e+03即应招聘人数为1958人.。
利用Matlab进行线性回归分析

利用Matlab进行线性回归分析回归分析是处理两个及两个以上变量间线性依存关系的统计方法;可以通过软件Matlab实现;1.利用Matlab软件实现在Matlab中,可以直接调用命令实现回归分析,1b,bint,r,rint,stats=regressy,x,其中b是回归方程中的参数估计值,bint是b的置信区间,r和rint分别表示残差及残差对应的置信区间;stats 包含三个数字,分别是相关系数,F统计量及对应的概率p值;2recplotr,rint作残差分析图;3rstoolx,y一种交互式方式的句柄命令;以下通过具体的例子来说明;例现有多个样本的因变量和自变量的数据,下面我们利用Matlab,通过回归分析建立两者之间的回归方程;% 一元回归分析x=1097 1284 1502 1394 1303 1555 1917 2051 2111 2286 2311 2003 2435 2625 2948 3, 55 3372;%自变量序列数据y=698 872 988 807 738 1025 1316 1539 1561 1765 1762 1960 1902 2013 2446 2736 2825;%因变量序列数据X=onessizex',x',pauseb,bint,r,rint,stats=regressy',X,,pause%调用一元回归分析函数rcoplotr,rint%画出在置信度区间下误差分布;% 多元回归分析% 输入各种自变量数据x1= 8 3 3 8 9 4 5 6 5 8 6 4 7';x2=31 55 67 50 38 71 30 56 42 73 60 44 50 39 55 7040 50 62 59'; x3=10 8 12 7 8 12 12 5 8 5 11 12 6 10 10 6 11 11 9 9';x4=8 6 9 16 15 17 8 10 4 16 7 12 6 4 4 14 6 8 13 11';%输入因变量数据y= 160 155 195';X=onessizex1,x1,x2,x3,x4;b,bint,r,rint,stats=regressy,X%回归分析Q=r'rsigma=Q/18rcoplotr,rint;%逐步回归X1=x1,x2,x3,x4;stepwiseX1,y,1,2,3%逐步回归% X2=onessizex1,x2,x3;% X3=onessizex1,x1,x2,x3;% X4=onessizex1,x2,x3,x4;% b1,b1int,r1,r1int,stats1=regressy,X2% b2,b2int,r2,r2int,stats2=regressy,X3;% b3,b3int,r3,r3int,stats3=regressy,X4;。
matlab中回归分析实例分析

1.研究科研人员的年工资与他的论文质量、工作年限、获得资助指标之间的关系.24位科研人员的调查数据(ex81.txt):设误差ε~(0,σ 2 ), 建立回归方程; 假定某位人员的观测值 , 预测年工资及置信度为95%的置信区间.程序为:A=load('ex81.txt')Y=A(:,1)X=A(1:24,2:4)xx=[ones(24,1) X]b = regress(Y,X)Y1=xx(:,1:4)*bx=[1 5.1 20 7.2]s=sum(x*b)调出Y 和X 后,运行可得:b =17.84691.10310.32151.2889010203(,,)(5.1,20,7.2)x x x =x =1.0000 5.1000 20.0000 7.2000s =39.1837所以,回归方程为:Y= 17.8469+1.1031X1+0.3215X2+1.2889X3+ε当 时,Y=39.18372、 54位肝病人术前数据与术后生存时间(ex82.txt,指标依次为凝血值,预后指数,酵素化验值,肝功能化验值,生存时间).(1) 若用线性回归模型拟合, 考察其各假设合理性;(2) 对生存是时间做对数变换,用线性回归模型拟合, 考察其各假设合理性;(3) 做变换 用线性回归模型拟合, 考察其各假设合理性; (4) 用变量的选择准则,选择最优回归方程010203(,,)(5.1,20,7.2)x x x =0.0710.07Y Z -=(5)用逐步回归法构建回归方程程序为:A=load('ex82.txt')Y=A(:,5)X=A(1:54,1:4)xx=[ones(54,1) X][b,bint,r,rint,stats]=regress(Y,xx) 运行结果为:b =-621.597633.16384.27194.125714.0916bint =-751.8189 -491.376219.0621 47.26563.1397 5.40403.0985 5.1530-11.0790 39.2622stats =1.0e+003 *0.0008 0.0628 0 3.7279由检验结果知,bi的置信区间分别为:[-751.8189 ,-491.3762][ 19.0621 47.2656][3.1397 5.4040][3.0985 5.1530][-11.0790 39.2622]R2 =8 f=0.0628 p=0 估计误差方差为3.7279所以可见这种拟合不合理。
MATLAB回归分析

MATLAB回归分析回归分析是统计学中常用的一种方法,用于建立一个依赖于自变量(独立变量)的因变量(依赖变量)的关系模型。
在MATLAB环境下,回归分析可以实现简单线性回归、多元线性回归以及非线性回归等。
简单线性回归是一种最简单的回归分析方法,它假设自变量和因变量之间存在线性关系。
在MATLAB中,可以通过`polyfit`函数进行简单线性回归分析。
该函数可以拟合一元数据点集和一维多项式,返回回归系数和截距。
例如:```matlabx=[1,2,3,4,5];y=[2,3,4,5,6];p = polyfit(x, y, 1);slope = p(1);intercept = p(2);```上述代码中,`x`是自变量的数据点,`y`是因变量的数据点。
函数`polyfit`的第三个参数指定了回归的阶数,这里是1,即一次线性回归。
返回的`p(1)`和`p(2)`分别是回归系数和截距。
返回的`p`可以通过`polyval`函数进行预测。
例如:```matlabx_new = 6;y_pred = polyval(p, x_new);```多元线性回归是在有多个自变量的情况下进行的回归分析。
在MATLAB中,可以使用`fitlm`函数进行多元线性回归分析。
例如:```matlabx1=[1,2,3,4,5];x2=[2,4,6,8,10];y=[2,5,7,8,10];X=[x1',x2'];model = fitlm(X, y);coefficients = model.Coefficients.Estimate;```上述代码中,`x1`和`x2`是两个自变量的数据点,`y`是因变量的数据点。
通过将两个自变量放在`X`矩阵中,可以利用`fitlm`函数进行多元线性回归分析。
返回值`model`是回归模型对象,可以通过`model.Coefficients.Estimate`获得回归系数。
多元回归分析报告matlab

回归分析MATLAB 工具箱一、多元线性回归多元线性回归:p p x x y βββ+++=...110 1、确定回归系数的点估计值: 命令为:b=regress(Y, X ) ①b 表示⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=p b βββˆ...ˆˆ10②Y 表示⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=n Y Y Y Y (2)1③X 表示⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=np n n p p x x x x x x x x x X (1)............ (1) (12)12222111211 2、求回归系数的点估计和区间估计、并检验回归模型: 命令为:[b, bint,r,rint,stats]=regress(Y,X,alpha) ①bint 表示回归系数的区间估计. ②r 表示残差. ③rint 表示置信区间.④stats 表示用于检验回归模型的统计量,有三个数值:相关系数r 2、F 值、与F 对应的概率p.说明:相关系数2r 越接近1,说明回归方程越显著;)1,(1-->-k n k F F α时拒绝0H ,F 越大,说明回归方程越显著;与F 对应的概率p α<时拒绝H 0,回归模型成立. ⑤alpha 表示显著性水平(缺省时为0.05)3、画出残差及其置信区间. 命令为:rcoplot(r,rint) 例1.如下程序. 解:(1)输入数据.x=[143 145 146 147 149 150 153 154 155 156 157 158 159 160 162 164]'; X=[ones(16,1) x];Y=[88 85 88 91 92 93 93 95 96 98 97 96 98 99 100 102]'; (2)回归分析及检验.[b,bint,r,rint,stats]=regress(Y,X) b,bint,stats得结果:b = bint =-16.0730 -33.7071 1.5612 0.7194 0.6047 0.8340 stats =0.9282 .9531 0.0000即7194.0ˆ,073.16ˆ10=-=ββ;0ˆβ的置信区间为[-33.7017,1.5612], 1ˆβ的置信区间为[0.6047,0.834]; r 2=0.9282, F=180.9531, p=0.0000,我们知道p<0.05就符合条件, 可知回归模型 y=-16.+0.7194x 成立. (3)残差分析,作残差图. rcoplot(r,rint)从残差图可以看出,除第二个数据外,其余数据的残差离零点均较近,且残差的置信区间均包含零点,这说明回归模型 y=-16.+0.7194x 能较好的符合原始数据,而第二个数据可视为异常点. (4)预测及作图.z=b(1)+b(2)*x plot(x,Y,'k+',x,z,'r')二、多项式回归 (一)一元多项式回归.1、一元多项式回归:1121...+-++++=m m m m a x a x a x a y (1)确定多项式系数的命令:[p,S]=polyfit(x,y,m)说明:x=(x 1,x 2,…,x n ),y=(y 1,y 2,…,y n );p=(a 1,a 2,…,a m+1)是多项式y=a 1x m +a 2x m-1+…+a m x+a m+1的系数;S 是一个矩阵,用来估计预测误差. (2)一元多项式回归命令:polytool(x,y,m) 2、预测和预测误差估计.(1)Y=polyval(p,x)求polyfit 所得的回归多项式在x 处的预测值Y ;(2)[Y,DELTA]=polyconf(p,x,S,alpha)求polyfit 所得的回归多项式在x 处的预测值Y 及预测值的显著性为1-alpha 的置信区间Y ±DELTA ;alpha 缺省时为0.5.例1. 观测物体降落的距离s 与时间t 的关系,得到数据如下表,求s. (关于t 的回归方程2ˆct bt a s++=)解法一:直接作二次多项式回归. t=1/30:1/30:14/30;s=[11.86 15.67 20.60 26.69 33.71 41.93 51.13 61.49 72.90 85.44 99.08 113.77 129.54 146.48]; [p,S]=polyfit(t,s,2) 得回归模型为:1329.98896.652946.489ˆ2++=t t s解法二:化为多元线性回归. t=1/30:1/30:14/30;s=[11.86 15.67 20.60 26.69 33.71 41.93 51.13 61.49 72.90 85.44 99.08 113.77 129.54 146.48];T=[ones(14,1) t' (t.^2)']; [b,bint,r,rint,stats]=regress(s',T);b,stats 得回归模型为:22946.4898896.651329.9ˆt t s++= 预测及作图: Y=polyconf(p,t,S) plot(t,s,'k+',t,Y,'r')(二)多元二项式回归多元二项式回归命令:rstool(x,y,’model ’, alpha)说明:x 表示n ⨯m 矩阵;Y 表示n 维列向量;alpha :显著性水平(缺省时为0.05);model 表示由下列4个模型中选择1个(用字符串输入,缺省时为线性模型):linear(线性):m m x x y βββ+++=Λ110purequadratic(纯二次):∑=++++=nj j jjm m x x x y 12110ββββΛinteraction(交叉):∑≤≠≤++++=mk j k j jkm m x x x x y 1110ββββΛquadratic(完全二次):∑≤≤++++=mk j k j jkm m x x x x y ,1110ββββΛ例1. 设某商品的需求量与消费者的平均收入、商品价格的统计数据如下,建立回归模型,预测平均收入为1000、价格为6时的商品需求量. 需求量 100 75 80 70 50 65 90 100 110 60 收入10006001200500300400130011001300300价格5766875439解法一:选择纯二次模型,即2222211122110x x x x y βββββ++++=.直接用多元二项式回归:x1=[1000 600 1200 500 300 400 1300 1100 1300 300]; x2=[5 7 6 6 8 7 5 4 3 9];y=[100 75 80 70 50 65 90 100 110 60]'; x=[x1' x2'];rstool(x,y,'purequadratic')在左边图形下方的方框中输入1000,右边图形下方的方框中输入6,则画面左边的“Predicted Y ”下方的数据变为88.47981,即预测出平均收入为1000、价格为6时的商品需求量为88.4791.在画面左下方的下拉式菜单中选”all ”, 则beta 、rmse 和residuals 都传送到Matlab 工作区中.在Matlab 工作区中输入命令:beta, rmse 得结果:beta = 110.5313 0.1464 -26.5709 -0.0001 1.8475 rmse = 4.5362故回归模型为:2221218475.10001.05709.261464.05313.110x x x x y +--+=剩余标准差为4.5362, 说明此回归模型的显著性较好.解法二:将2222211122110x x x x y βββββ++++=化为多元线性回归:X=[ones(10,1) x1' x2' (x1.^2)' (x2.^2)']; [b,bint,r,rint,stats]=regress(y,X); b,stats 结果为: b =110.5313 0.1464 -26.5709 -0.0001 1.8475 stats =0.9702 40.6656 0.0005三、非线性回归 1、非线性回归:(1)确定回归系数的命令:[beta,r,J]=nlinfit(x,y,’model ’, beta0)说明:beta 表示估计出的回归系数;r 表示残差;J 表示Jacobian 矩阵;x,y 表示输入数据x 、y 分别为矩阵和n 维列向量,对一元非线性回归,x 为n 维列向量;model 表示是事先用m-文件定义的非线性函数;beta0表示回归系数的初值. (2)非线性回归命令:nlintool(x,y,’model ’, beta0,alpha) 2、预测和预测误差估计:[Y,DELTA]=nlpredci(’model ’, x,beta,r,J)表示nlinfit 或nlintool 所得的回归函数在x 处的预测值Y 及预测值的显著性为1-alpha 的置信区间Y ±DELTA. 例1. 如下程序.解:(1)对将要拟合的非线性模型y=a x b e /,建立m-文件volum.m 如下: function yhat=volum(beta,x) yhat=beta(1)*exp(beta(2)./x); (2)输入数据: x=2:16;y=[6.42 8.20 9.58 9.5 9.7 10 9.93 9.99 10.49 10.59 10.60 10.80 10.60 10.90 10.76];beta0=[8 2]'; (3)求回归系数:[beta,r ,J]=nlinfit(x',y','volum',beta0); beta (4)运行结果:beta =11.6036 -1.0641 即得回归模型为:xey 10641.16036.11-=(5)预测及作图:[YY,delta]=nlpredci('volum',x',beta,r ,J);plot(x,y,'k+',x,YY,'r')四、逐步回归1、逐步回归的命令:stepwise(x,y,inmodel,alpha)n⨯阶矩阵;y表示因变量数据,1⨯n阶矩阵;inmodel表示矩说明:x表示自变量数据,m阵的列数的指标,给出初始模型中包括的子集(缺省时设定为全部自变量);alpha表示显著性水平(缺省时为0.5).2、运行stepwise命令时产生三个图形窗口:Stepwise Plot,Stepwise Table,Stepwise History.在Stepwise Plot窗口,显示出各项的回归系数及其置信区间.(1)Stepwise Table窗口中列出了一个统计表,包括回归系数及其置信区间,以及模型的统计量剩余标准差(RMSE)、相关系数(R-square)、F值、与F对应的概率P.例1. 水泥凝固时放出的热量y与水泥中4种化学成分x1、x2、x3、x4有关,今测得一组数据如下,试用逐步回归法确定一个线性模型.解:(1)数据输入:x1=[7 1 11 11 7 11 3 1 2 21 1 11 10]';x2=[26 29 56 31 52 55 71 31 54 47 40 66 68]';x3=[6 15 8 8 6 9 17 22 18 4 23 9 8]';x4=[60 52 20 47 33 22 6 44 22 26 34 12 12]';y=[78.5 74.3 104.3 87.6 95.9 109.2 102.7 72.5 93.1 115.9 83.8 113.3 109.4]'; x=[x1 x2 x3 x4];(2)逐步回归.①先在初始模型中取全部自变量:stepwise(x,y)得图Stepwise Plot 和表Stepwise Table.图Stepwise Plot中四条直线都是虚线,说明模型的显著性不好.从表Stepwise Table中看出变量x3和x4的显著性最差.②在图Stepwise Plot中点击直线3和直线4,移去变量x3和x4.移去变量x3和x4后模型具有显著性虽然剩余标准差(RMSE)没有太大的变化,但是统计量F的值明显增大,因此新的回归模型更好.(3)对变量y和x1、x2作线性回归.X=[ones(13,1) x1 x2];b=regress(y,X)得结果:b =52.57731.46830.6623故最终模型为:y=52.5773+1.4683x1+0.6623x2或这种方法4元二次线性回归clc;clear;y=[1.84099 9.67 23.00 38.12 1.848794 6.22 12.22 19.72 1.848794 5.19 10.09 15.31 ];X1=[60.36558 59.5376 58.89861 58.74706 60.59389 60.36558 59.2 58.2 60.36558 59.97068 59.41918 5 X2=[26.1636 26.35804 26.82438 26.91521 25.90346 25.9636 27.19256 27.42153 26.1636 26.07212 26.27.06063];X3=[0.991227 0.994944 0.981322 0.98374 1.011865 0.991227 1.074772 1.107678 0.991227 0.917904 1 1.1239];X4=[59.37436 58.54265 57.91729 57.69332 59.58203 59.37436 57.76722 57.42355 59.37436 59.05278 57.76687];format short gY=y'X11=[ones(1,length(y));X1;X2;X3;X4]'B1=regress(Y,X11)% 多元一次线性回归[m,n]=size(X11)X22=[];for i=2:nfor j=2:nif i<=jX22=([X22,X11(:,i).*X11(:,j)]);elsecontinueendendendX=[X11,X22];B2=regress(Y,X)% 多元二次线性回归[Y X*B2 Y-X*B2]plot(Y,X11*B1,'o',Y,X*B2,'*')hold on,line([min(y),max(y)],[min(y),max(y)]) axis([min(y) max(y) min(y) max(y)]) legend('一次线性回归','二次线性回归') xlabel('实际值');ylabel('计算值')运行结果:Y =1.8419.672338.121.84886.2212.2219.721.84885.1910.0915.31X11 =1 60.366 26.164 0.99123 59.3741 59.538 26.358 0.99494 58.5431 58.899 26.824 0.98132 57.9171 58.747 26.915 0.98374 57.6931 60.594 25.903 1.0119 59.5821 60.366 25.964 0.99123 59.3741 59.2 27.193 1.0748 57.7671 58.2 27.422 1.1077 57.4241 60.366 26.164 0.99123 59.3741 59.971 26.072 0.9179 59.1 59.419 26.587 1.0604 58.3591 58.891 27.061 1.1239 57.767 B1 =1488.9-4.3582-9.6345-61.514-15.359m =12n =5B2 =3120.4-7129.2-622.23-362.71-105.061388.1120.25.25379.58170.48-796.41ans =1.841 1.8449 -0.0039029.67 9.67 1.0058e-00923 23 1.397e-00938.12 38.12 3.539e-1.8488 1.8488 1.6394e-0096.22 6.227.2643e-12.22 12.22 2.6077e-19.72 19.72 -2.0489e-1.8488 1.8449 0.0039025.19 5.19 1.4529e-00910.09 10.09 1.0803e-00915.31 15.31 4.0978e-由图形可以看出,多元二次线性回归效果非常好,即,相当于Y=3120.4*X1 -7129.2 *X2 + 0*X3 + 0*X4 -622.23*X1*X1 -362.71*X1*X2 -105.06*X1*X3 + 1388 120.25*X2*X2+ .25 *X2*X3+ 379.58*X2*X4 + 170.48*X3*X3+ 0*X3*X4 -796.41*X4*X4。
Matlab中的回归分析与时间序列预测

Matlab中的回归分析与时间序列预测引言:在现代数据分析中,回归分析和时间序列预测是两个重要且广泛应用的领域。
Matlab作为一款功能强大的数学软件,在回归分析和时间序列预测方面提供了丰富的工具和函数,使得实现这些分析变得更加简单和高效。
本文将介绍Matlab中回归分析和时间序列预测的相关知识和方法,并结合实例进行说明。
一、回归分析回归分析是通过寻找自变量与因变量之间的关系,来推测未来观测值的一种分析方法。
在Matlab中,可以通过使用regress函数进行回归分析。
该函数可以拟合线性回归模型,并返回各个回归系数的估计值以及回归模型的统计信息。
下面我们以一个简单的例子来说明如何使用Matlab进行回归分析。
实例1:房价预测假设我们有一组数据,其中包含了房屋的面积和对应的售价。
我们希望通过房屋的面积来预测未来房价。
首先,我们需要导入数据并进行预处理。
```matlabdata = load('house_data.csv'); % 导入数据X = data(:, 1); % 提取面积作为自变量y = data(:, 2); % 提取房价作为因变量```接下来,我们可以使用regress函数进行回归分析,并得到回归系数的估计值。
```matlab[B, BINT, R, RINT, STATS] = regress(y, [ones(size(X)) X]); % 回归分析```其中,B为回归系数的估计值,BINT为回归系数的置信区间,R为残差,RINT为残差的置信区间,STATS为回归模型的统计信息。
我们可以打印出回归系数的估计值,以及回归模型的统计信息。
```matlabdisp('回归系数的估计值:');disp(B);disp('回归模型的统计信息:');disp(STATS);```运行以上代码,我们可以得到回归模型的结果。
通过回归系数的估计值,我们可以得到回归方程为y = B(1) + B(2) * X,其中B(1)为截距,B(2)为斜率。
Matlab中的回归分析技术实践

Matlab中的回归分析技术实践引言回归分析是统计学中常用的一种分析方法,用于研究因变量和一个或多个自变量之间的关系。
Matlab是一种强大的数值计算软件,具有丰富的统计分析工具和函数。
通过Matlab中的回归分析技术,我们可以深入理解数据背后的规律,并预测未来的趋势。
本文将介绍Matlab中常用的回归分析方法和技巧,并通过实例演示其实践应用。
一、简单线性回归分析简单线性回归是回归分析的最基本形式,用于研究一个自变量和一个因变量之间的线性关系。
在Matlab中,可以使用`fitlm`函数进行简单线性回归分析。
以下是一个示例代码:```Matlabx = [1, 2, 3, 4, 5]';y = [2, 4, 6, 8, 10]';lm = fitlm(x, y);```这段代码中,我们定义了两个向量x和y作为自变量和因变量的观测值。
使用`fitlm`函数可以得到一个线性回归模型lm。
通过这个模型,我们可以获取回归系数、拟合优度、显著性检验等信息。
二、多元线性回归分析多元线性回归分析允许我们研究多个自变量与一个因变量的关系。
在Matlab中,可以使用`fitlm`函数进行多元线性回归分析。
以下是一个示例代码:```Matlabx1 = [1, 2, 3, 4, 5]';x2 = [0, 1, 0, 1, 0]';y = [2, 4, 6, 8, 10]';X = [ones(size(x1)), x1, x2];lm = fitlm(X, y);```这段代码中,我们定义了两个自变量x1和x2,以及一个因变量y的观测值。
通过将常数项和自变量组合成一个设计矩阵X,使用`fitlm`函数可以得到一个多元线性回归模型lm。
通过这个模型,我们可以获取回归系数、拟合优度、显著性检验等信息。
三、非线性回归分析在实际问题中,很多情况下变量之间的关系并不是线性的。
非线性回归分析可以更准确地建模非线性关系。
Matlab回归分析:详解+实例

姚明女儿的身高
问 建立父母身高和女儿身高的模型 题 姚明2.26米,叶莉1.90米,预测姚明女儿身高
女孩身高y(cm) 156 172 162 158 164 166 160 155 174 165
父母平均身高 x(cm)
158.5
170.5
166
163.5
166
168.5 165.5
自变量X:用来解释Y的变量,通常有多个。
Y:薪资收入 X:学历、年龄、性别...
注意:(1)自变量可以是定量数据,也可以是定
性数据,它不决定回归模型的类型,决定回归模型 类型的是因变量;
(2)确定自变量的方法可以头脑风暴,但同时也 要看数据的可获得性,有时候可能头脑风暴想的很 好,但是没办法获取这个指标的数据也是不行的, 所以自变量的选取往往看一个数据的可获取性。
1 n
(x0 x)2 Lxx
小结
1.回归分析的任务 研究变量之间的相关关系
2.线性回归的步骤
(1) 推测回归函数; (3) 估计未知参数; (5) 预测.
(2) 建立回归模型; (4) 进行假设检验;
MATLAB中回归分析的实现
多元线性回归
1.确定回归系数的点估计值,用命令:
b=regress(Y,X)
女孩身高y(cm) 156 172 162 158 164 166 160 155 174 165
父母平均身高 x(cm)
158.5
170.5
166
163.5
166
168.5 165.5
159
180.5
169
基本模型
y 0 1x
y ~女孩身高
0, 1 ~回归系数
MATLAB回归分析工具箱使用方法

MATLAB回归分析工具箱使用方法下面将详细介绍如何使用MATLAB中的回归分析工具箱进行回归分析。
1.数据准备回归分析需要一组自变量和一个因变量。
首先,你需要将数据准备好,并确保自变量和因变量是数值型数据。
你可以将数据存储在MATLAB工作区中的变量中,也可以从外部文件中读取数据。
2.导入回归分析工具箱在MATLAB命令窗口中输入"regstats"命令来导入回归分析工具箱。
这将使得回归分析工具箱中的函数和工具可用于你的分析。
3.线性回归分析线性回归分析是回归分析的最基本形式。
你可以使用"regstats"函数进行线性回归分析。
以下是一个简单的例子:```matlabdata = load('data.mat'); % 从外部文件加载数据X = data.X; % 自变量y = data.y; % 因变量stats = regstats(y, X); % 执行线性回归分析beta = stats.beta; % 提取回归系数rsquare = stats.rsquare; % 提取判定系数R^2```在上面的例子中,"regstats"函数将自变量X和因变量y作为参数,并返回一个包含回归系数beta和判定系数R^2的结构体stats。
4.非线性回归分析如果你的数据不适合线性回归模型,你可以尝试非线性回归分析。
回归分析工具箱提供了用于非线性回归分析的函数,如"nonlinearmodel.fit"。
以下是一个非线性回归分析的例子:```matlabx=[0.10.20.5125]';%自变量y=[0.92.22.83.66.58.9]';%因变量f = fittype('a*exp(b*x)'); % 定义非线性模型model = fit(x, y, f); % 执行非线性回归分析coeffs = model.coefficients; % 提取模型系数```在上面的例子中,"fittype"函数定义了一个指数型的非线性模型,并且"fit"函数将自变量x和因变量y与该模型拟合,返回包含模型系数的结构体model。
回归分析实例

(2) X=[ones(15,1) x x.^2]; [b,bint,r,rint,stats]=regress(y,X); b,stats rcoplot(r,rint) 得结果: b = 19.0333 1.0086 -0.0204 stats = 0.6140
9.5449
0.0033
2
拟合模型为: Y 19.0333 1.0086 x 0.0204 x
(2)线性模型 y a bx alpha=0.05; x=[ones(13,1),x1]; [b,bint,r,rint,stats]=regress(y,x,alpha); b,bint,stats,rcoplot(r,rint) 结果输出:
第 5 页 共 8 页
年级、专业 姓名 学号 名单序号 实验时间 2010 年 月 日 Matlab 软件版本 注:实验报告的最后一部分是实验小结与收获
时间(h) 刀具厚度(cm)
0 30.6
1 29.1
2 28.4
3 28.1
4 28.0
5 27.7
6 27.5
7 27.2
8 27.0
9 26.8
10 26.5
(1)输入数据并绘制刀具厚度关于刀削时间的散点图确定回归模型 x=[0 1 2 3 4 5 6 7 8 9 10]' Y=[30.6 29.1 28.4 28.1 28.0 27.7 27.5 27.2 27.0 26.8 26.5]' plot(x,Y,'b+') (2)回归分析及检验 X=[ones(11,1) x] [b,bint,r,rint,stats]=regress(Y,X); b,bint,stats 得结果:b = 29.5455 -0.3291 bint = 28.9769 30.1140 -0.4252 -0.2330 stats = 0.8696 60.0018 0.0000 (3)预测 15 小时后刀具的厚度 plot(x,Y,'b+');x1=15; x=[x' 20]';z=b(1)+b(2)*x;z1=b(1)+b(2)*x1; hold on plot(x,z,'r') hold on plot(x1,z1,'go');
如何使用Matlab进行线性回归与非线性回归

如何使用Matlab进行线性回归与非线性回归使用Matlab进行线性回归与非线性回归简介:线性回归和非线性回归是统计分析中常用的两种回归模型。
线性回归假设自变量与因变量之间存在线性关系,而非线性回归则假设二者之间存在非线性关系。
本文将介绍如何使用Matlab进行线性回归和非线性回归分析,并分析其应用领域和优缺点。
一、线性回归分析线性回归是一种最基本的回归分析方法,广泛应用于统计学、经济学、金融学等领域。
在Matlab中,可以使用fitlm函数进行线性回归分析。
回归模型的基本形式如下所示:Y = β0 + β1X1 + β2X2 + ... + ε其中Y是因变量,X1,X2等是自变量,β0,β1,β2等是回归系数,ε是误差项。
线性回归模型的参数估计可以采用最小二乘法。
在Matlab中,可以使用fitlm 函数进行参数估计和显著性检验。
显著性检验可以帮助我们确定回归系数的是否显著不等于零,从而判断自变量对因变量的影响是否显著。
二、非线性回归分析在某些情况下,变量之间的关系不是线性的,而是呈现出曲线的形式。
这时,我们需要使用非线性回归模型进行分析。
在Matlab中,可以使用cftool函数进行非线性回归分析。
cftool是一个交互式的拟合工具箱,通过界面操作可以方便地进行曲线拟合。
用户可以选择不同的拟合模型,并根据数据点进行拟合。
cftool提供了各种常见的非线性回归模型,如指数模型、幂函数模型、对数模型等。
用户可以根据实际需求选择合适的模型进行分析。
非线性回归模型的参数估计可以使用最小二乘法、最大似然估计等方法。
在Matlab的cftool中,可以直接进行参数估计,并生成相应的拟合曲线。
三、线性回归与非线性回归的应用领域线性回归和非线性回归分析在各个领域都有广泛的应用。
线性回归常用于预测、趋势分析、经济建模等方面。
非线性回归则更适用于描述非线性关系的数据,常用于生物医学、环境科学、物理学等领域。
以医学领域为例,线性回归可以用于预测患者的生存时间、评估药物的剂量-效应关系等。
利用 Matlab作回归分析

利用 Matlab 作回归分析一元线性回归模型:2,(0,)y x N αβεεσ=++求得经验回归方程:ˆˆˆyx αβ=+ 统计量: 总偏差平方和:21()n i i SST y y ==-∑,其自由度为1T f n =-; 回归平方和:21ˆ()n i i SSR y y ==-∑,其自由度为1R f =; 残差平方和:21ˆ()n i i i SSE y y ==-∑,其自由度为2E f n =-;它们之间有关系:SST=SSR+SSE 。
一元回归分析的相关数学理论可以参见《概率论与数理统计教程》,下面仅以示例说明如何利用Matlab 作回归分析。
【例1】为了了解百货商店销售额x 与流通费率(反映商业活动的一个质量指标,指每元商品流转额所分摊的流通费用)y 之间的关系,收集了九个商店的有关数据,见下表1.试建立流通费率y 与销售额x 的回归方程。
表1 销售额与流通费率数据【分析】:首先绘制散点图以直观地选择拟合曲线,这项工作可结合相关专业领域的知识和经验进行,有时可能需要多种尝试。
选定目标函数后进行线性化变换,针对变换后的线性目标函数进行回归建模与评价,然后还原为非线性回归方程。
【Matlab数据处理】:【Step1】:绘制散点图以直观地选择拟合曲线x=[1.5 4.5 7.5 10.5 13.5 16.5 19.5 22.5 25.5];y=[7.0 4.8 3.6 3.1 2.7 2.5 2.4 2.3 2.2];plot(x,y,'-o')输出图形见图1。
510152025图1 销售额与流通费率数据散点图根据图1,初步判断应以幂函数曲线为拟合目标,即选择非线性回归模型,目标函数为:(0)b y ax b =< 其线性化变换公式为:ln ,ln v y u x == 线性函数为:ln v a bu =+【Step2】:线性化变换即线性回归建模(若选择为非线性模型)与模型评价% 线性化变换u=log(x)';v=log(y)';% 构造资本论观测值矩阵mu=[ones(length(u),1) u];alpha=0.05;% 线性回归计算[b,bint,r,rint,states]=regress(v,mu,alpha)输出结果:b =[ 2.1421; -0.4259]表示线性回归模型ln=+中:lna=2.1421,b=-0.4259;v a bu即拟合的线性回归模型为=-;y x2.14210.4259bint =[ 2.0614 2.2228; -0.4583 -0.3934]表示拟合系数lna和b的100(1-alpha)%的置信区间分别为:[2.0614 2.2228]和[-0.4583 -0.3934];r =[ -0.0235 0.0671 -0.0030 -0.0093 -0.0404 -0.0319 -0.0016 0.0168 0.0257]表示模型拟合残差向量;rint =[ -0.0700 0.02300.0202 0.1140-0.0873 0.0813-0.0939 0.0754-0.1154 0.0347-0.1095 0.0457-0.0837 0.0805-0.0621 0.0958-0.0493 0.1007]表示模型拟合残差的100(1-alpha)%的置信区间;states =[0.9928 963.5572 0.0000 0.0012] 表示包含20.9928SSR R SST==、 方差分析的F 统计量/963.5572//(2)R E SSR f SSR F SSE f SSE n ===-、 方差分析的显著性概率((1,2))0p P F n F =->≈; 模型方差的估计值2ˆ0.00122SSE n σ==-。
matlab回归拟合

matlab回归拟合一、Matlab回归拟合的基本概念Matlab回归拟合是一种利用Matlab软件对数据进行线性或非线性回归分析的方法。
通过回归拟合,我们可以探讨自变量与因变量之间的关系,为后续的数据分析、预测和模型构建提供依据。
二、Matlab回归拟合的常用函数1.线性回归:使用`polyfit`函数进行线性回归分析,可以得到回归系数。
2.非线性回归:使用`nlinfit`函数进行非线性回归分析,可以得到回归系数。
3.曲线拟合:使用`curve_fit`函数进行曲线拟合,可以得到拟合参数。
4.残差分析:使用`residual`函数计算拟合残差,评估拟合效果。
三、Matlab回归拟合的实例分析以下将以一个简单的例子说明Matlab回归拟合的具体操作。
假设我们有一组数据如下:```x = [1, 2, 3, 4, 5];y = [2, 4, 6, 8, 10];```我们希望通过线性回归分析找到y与x之间的关系。
```matlab% 创建数据点X = 1:4;Y = [2 4 6 8 10];% 进行线性回归m = polyfit(X, Y, 1);% 输出回归系数disp(m);```四、Matlab回归拟合的结果分析与优化在进行回归拟合后,我们需要对结果进行分析,评估拟合效果。
常用的方法有:1.评估指标:使用`corrcoef`函数计算自变量与因变量之间的相关系数,判断线性关系。
2.残差分析:使用`residual`函数计算拟合残差,评估拟合效果。
3.优化方法:根据拟合结果,可以尝试调整模型参数或更换其他拟合方法以提高拟合效果。
五、总结与展望Matlab回归拟合是一种强大的数据分析工具,可以帮助我们探索自变量与因变量之间的关系。
通过熟练掌握Matlab回归拟合的常用函数、结果分析与优化方法,我们可以更好地应用于实际问题的解决。
matlab多元非线性回归及显着性分析(实例)

matlab多元非线性回归及显著性分析给各位高手:小弟有一些数据需要回归分析(非线性)及显著性检验(回归模型,次要项,误差及失拟项纯误差,F值和P值),求大侠帮助,给出程序,不胜感激。
模型:DATA=...%DATA前三列是影响因子,第四列为响应值[21307548.61;21107556.43;21304561.32;21104565.28;11104555.80;11307545.65;11107550.91;11304567.94;1.51206074.15;1.51206071.28;1.51206077.95;1.51206074.16;1.51206075.20;1.51208535.65;1.51406048.66;1.51203074.10;1.51006062.30;0.51206066.00;2.51206075.10];回归分析过程:(1)MATLAB编程步骤1:首先为非线性回归函数编程,程序存盘为user_function.m function y=user_function(beta,x)b0=beta(1);b1=beta(2);b2=beta(3);b3=beta(4);x0=x(:,1);x1=x(:,2);x2=x(:,3);x3=x(:,4);y=b0*x0+b1*x1.^2+b2*x2.^2+b3*x3.^2;(2)MATLAB编程步骤2:编写非线性回归主程序,程序运行时调用函数user_functionx=[121307548.61;121107556.43;121304561.32;121104565.28;111104555.80;111307545.65;111107550.91;111304567.94;11.51206074.15;11.51206071.28;11.51206077.95;11.51206074.16;11.51206075.20;11.51208535.65;11.51406048.66;11.51203074.10;11.51006062.30;10.51206066.00;12.51206075.10];%%第1列全是1,第6列是指标变量,其余列是自变量xx=x(:,1:5);yy=x(:,5);%%指定响应变量yy和自变量xxbeta0=[0.50.40.70.5];%%设置初始回归系数(如何确定初值?)[beta_fit,residual]=nlinfit(xx,yy,@user_function,beta0)%%非线性回归结果beta_fit=91.37571.2712-0.0009-0.0049residual=-4.2935-1.0248-9.2044-9.7957-15.4620-3.4398-2.73111.229311.18898.318914.988911.198912.2389-9.5678-9.3704-2.0767-4.83315.58147.0540即y=.3757+1.2712*x1.^2-0.0009*x2.^2-0.0049*x3.^2;matlab中nlinfit函数非线性拟合的使用方法如下:例1。
用MATLAB求解回归分析课件

用Matlab求解 回归分析课件
目 录
• 回归分析简介 • Matlab基础操作 • 线性回归分析 • 非线性回归分析 • 多元回归分析 • Matlab在回归分析中的应用实例
01
CATALOGUE
回归分析简介
回归分析的定义
回归分析是一种统计学方法,用于研 究自变量和因变量之间的相关关系, 并建立数学模型来预测因变量的值。
显著性检验
对回归模型的显著性进行检验,如F 检验、t检验等。
预测精度评估
使用均方误差、均方根误差等指标评 估模型的预测精度。
可解释性
评估模型的解释性,即模型是否易于 理解,自变量对因变量的影响是否合 理。
06
CATALOGUE
Matlab在回归分析中的应用实例
用Matlab进行线性回归分析的实例
迭代法
对于一些复杂的回归模型,可能 需要使用迭代法进行求解,如梯 度下降法、牛顿法等。
Matlab函数
在Matlab中,可以使用内建的回 归分析函数来求解多元回归模型 ,如 `fitlm`、`fitlm2` 等。
多元回归模型的评估
残差分析
对回归模型的残差进行分析,检查残 差是否满足正态分布、同方差等假设 。
要点一
总结词
要点二
详细描述
多元回归分析是处理多个自变量和因变量之间关系的回归 分析方法,通过Matlab可以方便地进行多元回归分析。
在Matlab中,可以使用`fitlm`函数对一组数据进行多元回 归分析。首先需要准备数据,然后使用`fitlm`函数拟合多 元线性模型,最后通过模型进行预测和评估。
THANKS
使用预测值与实际值之间的误差评估模型的预测 能力,如均方误差、平均绝对误差等指标。
一元回归分析MATLAB计算

一元回归分析MATLAB计算一元线性回归分析是一种基本的统计方法,用于研究一个因变量和一个自变量之间的线性关系。
在MATLAB中,可以使用polyfit和polyval函数来进行一元线性回归分析。
下面是一个简单的示例,说明如何在MATLAB中进行一元线性回归分析:假设我们有一组数据,其中x是一个自变量,y是一个因变量。
我们想要找到一个线性模型来描述x和y之间的关系。
% 创建一组数据x = [1, 2, 3, 4, 5, 6, 7, 8, 9];y = [2, 4, 5, 7, 8, 9, 10, 12, 13];% 使用polyfit函数进行一元线性回归分析p = polyfit(x, y, 1); % 这里1表示我们想要拟合一个一次多项式(即线性关系)% p(1)是斜率,p(2)是截距% 使用polyval函数计算拟合值yfit = polyval(p, x);% 绘制原始数据和拟合直线plot(x, y, 'o'); % 绘制原始数据hold on;plot(x, yfit, '-'); % 绘制拟合直线xlabel('x');ylabel('y');legend('原始数据', '拟合直线');在这个示例中,我们首先创建了一组数据,然后使用polyfit函数进行一元线性回归分析。
这个函数返回一个向量p,其中p(1)是斜率,p(2)是截距。
然后,我们使用polyval函数计算拟合值,并将其与原始数据进行绘图。
这个示例只是最基本的一元线性回归分析。
在实际应用中,可能需要处理更复杂的数据和模型。
例如,可能需要处理缺失数据、异常值、多元线性回归等问题。
但是,基本的步骤和概念仍然是相同的。
可以使用MATLAB提供的各种函数和工具来处理这些问题。
利用MATLAB进行回归分析
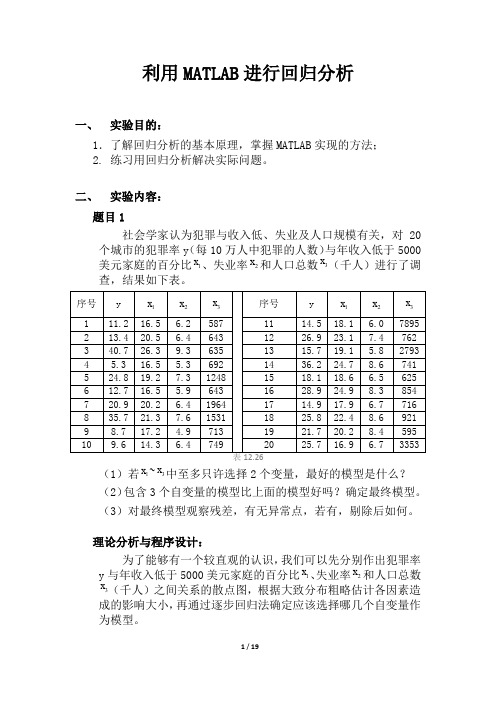
利用MATLAB进行回归分析一、实验目的:1.了解回归分析的基本原理,掌握MATLAB实现的方法;2. 练习用回归分析解决实际问题。
二、实验内容:题目1社会学家认为犯罪与收入低、失业及人口规模有关,对20个城市的犯罪率y(每10万人中犯罪的人数)与年收入低于5000美元家庭的百分比1x、失业率2x和人口总数3x(千人)进行了调查,结果如下表。
(1)若1x~3x中至多只许选择2个变量,最好的模型是什么?(2)包含3个自变量的模型比上面的模型好吗?确定最终模型。
(3)对最终模型观察残差,有无异常点,若有,剔除后如何。
理论分析与程序设计:为了能够有一个较直观的认识,我们可以先分别作出犯罪率y与年收入低于5000美元家庭的百分比1x、失业率2x和人口总数x(千人)之间关系的散点图,根据大致分布粗略估计各因素造3成的影响大小,再通过逐步回归法确定应该选择哪几个自变量作为模型。
编写程序如下:clc;clear all;y=[11.2 13.4 40.7 5.3 24.8 12.7 20.9 35.7 8.7 9.6 14.5 26.9 15.736.2 18.1 28.9 14.9 25.8 21.7 25.7];%犯罪率(人/十万人)x1=[16.5 20.5 26.3 16.5 19.2 16.5 20.2 21.3 17.2 14.3 18.1 23.1 19.124.7 18.6 24.9 17.9 22.4 20.2 16.9];%低收入家庭百分比x2=[6.2 6.4 9.3 5.3 7.3 5.9 6.4 7.6 4.9 6.4 6.0 7.4 5.8 8.6 6.5 8.36.7 8.6 8.4 6.7];%失业率x3=[587 643 635 692 1248 643 1964 1531 713 749 7895 762 2793 741 625 854 716 921 595 3353];%总人口数(千人)figure(1),plot(x1,y,'*');figure(2),plot(x2,y,'*');figure(3),plot(x3,y,'*');X1=[x1',x2',x3'];stepwise(X1,y)运行结果与结论:犯罪率与低收入散点图犯罪率与失业率散点图犯罪率与人口总数散点图低收入与失业率作为自变量低收入与人口总数作为自变量失业率与人口总数作为自变量在图中可以明显看出前两图的线性程度很好,而第三个图的线性程度较差,从这个角度来说我们应该以失业率和低收入为自变量建立模型。
MATLAB 回归分析regress,nlinfit,stepwise函数

MATLAB 回归分析regress,nlinfit,stepwise函数matlab回归分析regress,nlinfit,stepwise函数回归分析1.多元线性重回在matlab统计工具箱中使用命令regress()实现多元线性回归,调用格式为b=regress(y,x)或[b,bint,r,rint,statsl=regess(y,x,alpha)其中因变量数据向量y和自变量数据矩阵x按以下排列方式输入对一元线性重回,挑k=1即可。
alpha为显著性水平(缺省时预设为0.05),输入向量b,bint为回归系数估计值和它们的置信区间,r,rint为残差及其置信区间,stats就是用作检验重回模型的统计数据量,存有三个数值,第一个就是r2,其中r就是相关系数,第二个就是f统计数据量值,第三个就是与统计数据量f对应的概率p,当p拒绝h0,回归模型成立。
图画出来残差及其置信区间,用命令rcoplot(r,rint)实例1:已知某湖八年来湖水中cod浓度实测值(y)与影响因素湖区工业产值(x1)、总人口数(x2)、捕鱼量(x3)、降水量(x4)资料,建立污染物y的水质分析模型。
(1)输出数据x1=[1.376,1.375,1.387,1.401,1.412,1.428,1.445,1.477]x2=[0.450,0.475,0.485,0.50 0,0.535,0.545,0.550,0.575]x3=[2.170,2.554,2.676,2.713,2.823,3.088,3.122,3.262]x4=[0.8922,1.1610,0.5346,0.9589,1.0239,1.0499,1.1065,1.1387]y=[5.19,5.30,5.60,5.82,6.00,6.06,6.45,6.95](2)留存数据(以数据文件.mat形式留存,易于以后调用)savedatax1x2x3x4yloaddata(抽出数据)(3)继续执行重回命令x=[ones(8,1),];[b,bint,r,rint,stats]=regress得结果:b=(-16.5283,15.7206,2.0327,-0.2106,-0.1991)’stats=(0.9908,80.9530,0.0022)即为=-16.5283+15.7206xl+2.0327x2-0.2106x3+0.1991x4r2=0.9908,f=80.9530,p=0.00222.非线性重回非线性回归可由命令nlinfit来实现,调用格式为[beta,r,j]=nlinfit(x,y,'model’,beta0)其中,输人数据x,y分别为n×m矩阵和n维列向量,对一元非线性回归,x为n维列向量model是事先用m-文件定义的非线性函数,beta0是回归系数的初值,beta是估计出的回归系数,r是残差,j是jacobian矩阵,它们是估计预测误差需要的数据。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.研究科研人员的年工资与他的论文质量、工作年限、获得资助指标之间的关系.24位科研人员的调查数据(ex81.txt):
设误差ε~(0,σ 2 ), 建立回归方程; 假定某位人员的观测值 , 预测年工资及置信度为
95%的置信区间.
程序为:A=load('ex81.txt')
Y=A(:,1)
X=A(1:24,2:4)
xx=[ones(24,1) X]
b = regress(Y,X)
Y1=xx(:,1:4)*b
x=[1 5.1 20 7.2]
s=sum(x*b)
调出Y 和X 后,运行可得:
b =
17.8469
1.1031
0.3215
1.2889
010203(,,)(5.1,20,7.2)x x x =
x =
1.0000 5.1000 20.0000 7.2000
s =
39.1837
所以,回归方程为:Y= 17.8469+1.1031X1+0.3215X2+1.2889X3+ε
当 时,Y=39.1837
2、 54位肝病人术前数据与术后生存时间(ex82.txt,指标依次为凝血值,预后指数,酵素化验值,肝功能化验值,生存时间).
(1) 若用线性回归模型拟合, 考察其各假设合理性;
(2) 对生存是时间做对数变换,用线性回归模型拟合, 考察其各假设合理性;
(3) 做变换 用线性回归模型拟合, 考察其各假设合理性; (4) 用变量的选择准则,选择最优回归方程
010203
(,,)(5.1,20,7.2)x x x =0.0710.07
Y Z -=
(5)用逐步回归法构建回归方程
程序为:A=load('ex82.txt')
Y=A(:,5)
X=A(1:54,1:4)
xx=[ones(54,1) X]
[b,bint,r,rint,stats]=regress(Y,xx) 运行结果为:
b =
-621.5976
33.1638
4.2719
4.1257
14.0916
bint =
-751.8189 -491.3762
19.0621 47.2656
3.1397 5.4040
3.0985 5.1530
-11.0790 39.2622
stats =
1.0e+003 *
0.0008 0.0628 0 3.7279
由检验结果知,bi的置信区间分别为:[-751.8189 ,-491.3762]
[ 19.0621 47.2656]
[3.1397 5.4040]
[3.0985 5.1530]
[-11.0790 39.2622]
R2 =8 f=0.0628 p=0 估计误差方差为3.7279
所以可见这种拟合不合理。
(2)程序为:
A=load('ex82.txt')
Y=A(:,5)
X=A(1:54,1:4)
xx=[ones(54,1) X]
y=log(Y)
[b,bint,r,rint,stats]=regress(y,xx)
b =
1.1254
0.1578
0.0213
0.0218
0.0044
bint =
0.8929 1.3578
0.1326 0.1830
0.0193 0.0233
0.0200 0.0236
-0.0405 0.0494
stats =
0.9724 430.9813 0 0.0119
可见R2 =0.9724 F=430.9813 p=0<0.05 估计误差方差较小
所以该拟合较显著
所以y= 1.1254+0.1578X1+0.0213X2+0.0218X3+0.0044X4
(3) 程序为:A=load('ex82.txt')
Y=A(:,5)
X=A(1:54,1:4)
xx=[ones(54,1) X]
Z=[(power(Y,0.07)-1)/0.07] [b,bint,r,rint,stats]=regress(Z,xx) 运行结果为:
b =
0.4525
0.2260
0.0305
0.0310
0.0149
bint =
0.1261 0.7788
0.1907 0.2613
0.0276 0.0333
0.0285 0.0336
-0.0482 0.0780
stats =
0.9736 451.8277 0 0.0234
所以可见拟合是合理的。
(4)。
