三角函数的图像变换
三角函数的图像变换

三角函数的图像变换三角函数是数学中重要的一类函数,包括正弦函数、余弦函数、正切函数等。
它们在图像上呈现出规律性的波动变化,而通过对这些函数进行图像的平移、缩放、翻转等操作,可以得到各种不同形态的函数图像。
本文将介绍三角函数的图像变换过程,并探讨不同变换对函数图像的影响。
正弦函数的图像变换正弦函数 $y = \\sin(x)$ 是一种周期性函数,其图像在 $[-\\pi, \\pi]$ 区间内呈现出波浪状的变化。
对正弦函数进行图像变换可以通过调整函数中的关键参数来实现。
平移平移是一种简单的图像变换操作,可以沿着横轴和纵轴分别对函数图像进行移动。
对于正弦函数 $y=\\sin(x)$ 来说,平移操作可以表示为 $y = \\sin(x - a)$,其中a为平移距离。
当a>0时,函数图像向右平移;当a<0时,函数图像向左平移。
缩放缩放是改变函数图像振幅的一种常见操作。
对于正弦函数$y=\\sin(x)$,可以通过调整函数中的系数来实现振幅的变化。
例如,当 $y=2\\sin(x)$ 时,函数图像的振幅将变为原来的两倍;当 $y=\\frac{1}{2}\\sin(x)$ 时,函数图像的振幅将缩小为原来的一半。
翻转翻转是改变函数图像对称性的一种操作。
对于正弦函数$y=\\sin(x)$,可以通过在函数中引入负号来实现翻转操作。
例如,当 $y=-\\sin(x)$ 时,函数图像将在a轴进行翻转。
余弦函数的图像变换余弦函数 $y = \\cos(x)$ 也是一种周期性函数,其图像在$[0, 2\\pi]$ 区间内呈现出波浪状的变化。
对余弦函数进行图像变换同样可以通过平移、缩放、翻转等操作来实现。
平移对于余弦函数 $y=\\cos(x)$,平移操作的表达式为 $y =\\cos(x - a)$,其中a为平移距离。
与正弦函数类似,当a> 0时,函数图像向右平移;当a<0时,函数图像向左平移。
三角函数的像变换与平移

三角函数的像变换与平移三角函数是数学中非常重要的概念之一,在三角函数中,像变换与平移是两个重要的概念。
它们描述了函数图像在坐标系中的移动和变形过程。
本文将重点介绍三角函数的像变换与平移。
1. 像变换(Image Transformation)像变换是指通过特定的变换规则,改变函数图像的形状、位置或尺寸等性质。
对于三角函数而言,常见的像变换包括拉伸、压缩、翻转和反转等。
1.1 拉伸(Stretch)拉伸是指改变函数图像在横轴和纵轴方向上的尺寸,使其变得更长或更短。
对于正弦函数(sin)和余弦函数(cos)而言,拉伸可以分别沿横轴和纵轴方向进行。
例如,当正弦函数的图像被沿横轴方向拉伸时,函数的周期将变得更长,波峰和波谷之间的距离增加;而当余弦函数的图像被沿纵轴方向拉伸时,函数的振幅(波峰或波谷与横轴的距离)增加。
1.2 压缩(Compression)压缩是指改变函数图像在横轴和纵轴方向上的尺寸,使其变得更短或更窄。
与拉伸相反,压缩使函数的周期变短,波峰和波谷之间的距离缩小;同时,压缩会使函数的振幅减小。
1.3 翻转(Reflection)翻转是指将函数图像相对于横轴或纵轴进行对称变换,以改变图像的朝向。
对于正弦函数和余弦函数而言,翻转可以使波形上下颠倒或左右翻转。
1.4 反转(Inversion)反转是指将函数图像的正负进行翻转,使得原本正值的部分变为负值,负值的部分变为正值。
对于正弦函数和余弦函数而言,反转会使波形关于横轴或纵轴进行对称。
2. 平移(Translation)平移是指将函数图像在坐标系中沿横轴或纵轴方向上移动,以改变图像的位置。
对于正弦函数和余弦函数而言,平移可以使波形向左或向右平移一定的距离,或者向上或向下平移。
2.1 横向平移(Horizontal Translation)横向平移是指将函数图像沿横轴方向上移动,通常用参数h表示平移的距离。
当h为正值时,函数图像向右平移;当h为负值时,函数图像向左平移。
三角函数的图像变换

cosθ = 邻边/斜边,在单位圆中表示为x坐标。
正切函数(tangent)
三角函数的周期性
tanθ = 对边/邻边,表示为正弦与余弦之比。
正弦、余弦函数周期为2π,正切函数周期为 π。
三角函数在各象限表现
第一象限
所有三角函数值均为正。
第三象限
正弦、余弦函数值为负,正切函数值为正。
第二象限
正弦函数值为正,余弦、正切函数值为负。
伸缩变换对正弦函数影响
横向伸缩
改变正弦函数图像的周期长度。缩小周期使得函数图像更加紧密,扩大周期则 使得函数图像更加稀疏。
纵向伸缩
改变正弦函数图像的振幅大小。增大振幅使得函数图像波动范围更大,减小振 幅则使得函数图像波动范围更小。
周期性与相位调整方法
周期性调整
通过改变正弦函数的周期来调整图像的疏密程度。可以通过调整函数中的系数来 实现周期的变化。
相位调整
通过改变正弦函数的相位来调整图像出现的位置。可以通过在函数中添加常数项 来实现相位的调整。同时,利用三角函数的和差化积公式,也可以实现相位的调 整。
03 余弦函数图像变换分析
余弦函数基本图像特征
波形图像
余弦函数图像呈现周期性波动,具有典型的波形 特征。
振幅和周期
余弦函数的振幅和周期是确定其图像形状和尺寸 的关键参数。
拓展:其他类型周期函数图像变换
锯齿波和方波
除了正弦波和余弦波外,还有其 他类型的周期函数如锯齿波和方 波等,它们的图像变换同样具有 实际应用价值。
周期函数的合成与分解
通过三角函数的线性组合可以合 成其他类型的周期函数;反之, 其他类型的周期函数也可以通过 傅里叶级数展开成三角函数的线 性组合。
三角函数的图像及其变换

振幅变换
振幅变换
通过将三角函数中的系数乘以一 个常数,可以改变函数图像的形 状和大小。例如,将正弦函数 y=sin(x)变为y=2sin(x),图像的 高度变为原来的两倍。
总结词
振幅变换可以改变函数图像的大 小和形状,但不影响位置。
详细描述
振幅变换通常通过乘以一个常数来实 现。例如,对于正弦函数y=sin(x),乘 以2得到y=2sin(x),图像的高度变为 原来的两倍。同样地,对于余弦函数 y=cos(x),乘以2得到y=2cos(x),图 像的高度也变为原来的两倍。
与复数的联系
三角函数与复数之间有着密切的联系。例如,复数的三角形式就是由三角函数来表示的,这使得复数 的一些性质和运算可以通过三角函数来理解和实现。
此外,在复分析中,三角函数也起着重要的作用,如在求解某些复数域上的微分方程时,经常需要用 到三角函数。
谢谢
THANKS
应用
正切函数在解决实际问题和数学 问题中也有应用,例如在几何学 和三角学中的角度和长度计算。
02 三角函数的图像
CHAPTER
正弦函数的图像
01
正弦函数图像是周期函数,其基本周期为$2pi$,在$[0, 2pi]$ 区间内呈现波形。
02
正弦函数图像在$x$轴上的交点是$(frac{pi}{2} + kpi, 0)$,其
周期变换
总结词
详细描述
通过改变三角函数的周期,可以改变
函数图像的形状和位置。例如,将正 弦函数和余弦函数的周期从2π变为4π, 图像将变为原来的两倍长,但形状和
周期变换可以改变函数图像的长度, 但不影响形状和位置。
位置保持不变。
周期变换通常通过乘以一个常数来实现。例 如,将函数y=sin(x)变为y=sin(2x),周期 从2π变为π,图像长度减半。同样地,对于 余弦函数,将y=cos(x)变为y=cos(2x),周 期从2π变为π,图像长度也减半。
三角函数图像变换

左移(ψ>0)或 右移(ψ<0) │ψ│
Y=Sin(X+ψ),
例1
作函数 y = 3sin(2x+ )的简图 3
分析 : 因为T=,所以用“五点法”先作长度为一个周期的 闭区
间上的简图 X 3 设:X 2 x 那么: 3 sin( 2 x ) 3 sin X 且 x 3 2 3
Y=Sin(X+ψ),
3. 周期变换:
Y=SinX
4. 平移变换:
Y=SinX
练习
1. 画出函数Y=Sin(2X+
Y
4 周期的闭区间上的简图。
1
),X∈R在长度为一个
8
-1
O
8
3 8
5 8
7 8
X
左移π/2个单位长度 2.将y=SinX的图象_____________________
方法1:先平移后伸缩演示
y
3 2 1
y=3sin(2x+ )③ 3
y=sinx
3
5 6
o
5 3
2
3
6
x
-1
-2 -3
y=sin(x+ )① 3 y=sin(2x + )② 3
三角函数图像的变换

三角函数图像的变换一.x y sin =图像的三种变换:①函数x y sin =的图象上所有点向左(右)平移ϕ个单位长度,得到函数()sin y x ϕ=+的图象;再将函数()sin y x ϕ=+的图象上所有点的横坐标伸长(缩短)到原来的1ω倍(纵坐标不变),得到函数()sin y x ωϕ=+的图象;再将函数()sin y x ωϕ=+的图象上所有点的纵坐标伸长(缩短)到原来的A 倍(横坐标不变),得到函数()sin y x ωϕ=A +的图象. ②数sin y x =的图象上所有点的横坐标伸长(缩短)到原来的1ω倍(纵坐标不变),得到函数sin y x ω=的图象;再将函数sin y x ω=的图象上所有点向左(右)平移ϕω个单位长度,得到函数()sin y x ωϕ=+的图象;再将函数()sin y x ωϕ=+的图象上所有点的纵坐标伸长(缩短)到原来的A 倍(横坐标不变),得到函数()sin y x ωϕ=A +的图象. 二.函数()()sin 0,0y x ωϕω=A +A >>的性质: ①振幅:A ;②周期:2πωT =;③频率:12f ωπ==T ;④相位:x ωϕ+;⑤初相:ϕ. 函数()sin y x ωϕ=A ++B ,当1x x =时,取得最小值为min y ;当2x x =时,取得最大值为max y ,则()max min 12y y A =-,()max min 12y y B =+,()21122x x x x T=-<.三.练习1.已知简谐运动()2sin()()32f x x ππϕϕ=+<的图象经过点(0,1),则该简谐运动的最小正周期T =_________;初相ϕ=__________.2.三角方程2sin(2π-x )=1的解集为_______________________. 3.函数),2,0)(sin(R x x A y ∈π<ϕ>ωϕ+ω=的部分图象如图所示,则函数表达式为______________________.{2,}3x x k k Z ππ=±∈ )48sin(4π+π-=x y第3题4.要得到函数sin y x =的图象,只需将函数cos y x π⎛⎫=- ⎪3⎝⎭的图象向右平移__________个单位.5.为了得到函数R x x y ∈+=),63sin(2π的图像,只需把函数2sin y x =,x R ∈的图像上所有的点①向左平移6π个单位长度,再把所得各点的横坐标缩短到原来的31倍(纵坐标不变);②向右平移6π个单位长度,再把所得各点的横坐标缩短到原来的31倍(纵坐标不变);③向左平移6π个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变); ④向右平移6π个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变).其中,正确的序号有_____③______. 6.为了得到函数)62sin(π-=x y 的图象,可以将函数x y 2cos =的图象向右平移__3π__个单位长度.7.若函数()2sin()f x x ωϕ=+,x ∈R (其中0ω>,2ϕπ<)的最小正周期是π,且(0)f =ω=______;ϕ=__________.8.下列函数: ①sin 6y x π⎛⎫=+⎪⎝⎭; ②sin 26y x π⎛⎫=-⎪⎝⎭; ③cos 43y x π⎛⎫=-⎪⎝⎭; ④cos 26y x π⎛⎫=-⎪⎝⎭. 其中函数图象的一部分如右图所示的序号有_____④_____. 9.函数y =sin(2x +3π)的图象关于点_______________对称. 10.求下列函数的单调减区间: (1)⎪⎭⎫⎝⎛+=62cos 2πx y (2)⎪⎭⎫ ⎝⎛+-=32sin 2πx y 11. 函数tan()2y x π=-(44x ππ-≤≤且0)x ≠的值域是___________________12. 7.如图,函数π2cos()(00)2y x x >ωθωθ=+∈R ,,≤≤的图象与y轴相交于点(0,且该函数的最小正周期为π.(1)求θ和ω的值;π6第8题(2)已知点π2A⎛⎫⎪⎝⎭,,点P是该函数图象上一点,点00()Q x y,是PA当y=ππ2x⎡⎤∈⎢⎥⎣⎦,时,求x的值.13.设函数)(),()2sin()(xfyxxf=<<-+=ϕπϕ图像的一条对称轴是直线8π=x.(Ⅰ)求ϕ;(Ⅱ)求函数)(xfy=的单调增区间;(Ⅲ)画出函数)(xfy=在区间],0[π上的图像第7题。
三角函数图形的变换
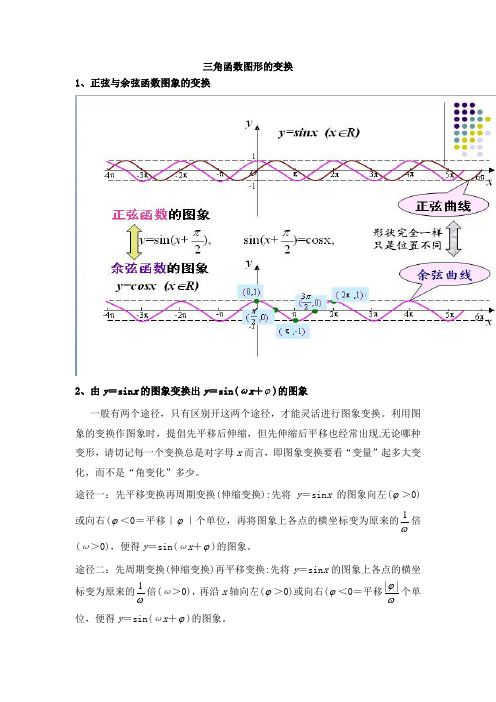
三角函数图形的变换1、正弦与余弦函数图象的变换2、由y =sin x 的图象变换出y =sin(ωx +ϕ)的图象一般有两个途径,只有区别开这两个途径,才能灵活进行图象变换。
利用图象的变换作图象时,提倡先平移后伸缩,但先伸缩后平移也经常出现无论哪种变形,请切记每一个变换总是对字母x 而言,即图象变换要看“变量”起多大变化,而不是“角变化”多少。
途径一:先平移变换再周期变换(伸缩变换):先将y =sin x 的图象向左(ϕ>0)或向右(ϕ<0=平移|ϕ|个单位,再将图象上各点的横坐标变为原来的ω1倍(ω>0),便得y =sin(ωx +ϕ)的图象。
途径二:先周期变换(伸缩变换)再平移变换:先将y =sin x 的图象上各点的横坐标变为原来的ω1倍(ω>0),再沿x 轴向左(ϕ>0)或向右(ϕ<0=平移ωϕ||个单位,便得y =sin(ωx +ϕ)的图象。
作y =sin x (长度为2π的某闭区间)的图象 得y =sin(x +φ) 的图象得y =sin ωx 的图象 得y =sin(ωx +φ) 的图象 得y =sin(ωx +φ) 的图象 得y =Asin(ωx +φ)的图象,先在一个周期闭区间上再扩充到R 上沿x 轴平 移|φ|个单位 横坐标 伸长或缩短 横坐标伸 长或缩短沿x 轴平 移|ωϕ|个单位 纵坐标伸 长或缩短纵坐标伸 长或缩短【经典例题】图像变换一:左右平移1、把函数R x x y ∈=,sin 图像上所有的点向左平移4π个单位,所得函数的解析式为 _________2、把函数R x x y ∈=,cos 图像上所有的点向右平移5π个单位,所得函数的解析式为 _________图像变换二:纵向伸缩3、对于函数R x x y ∈=,s i n 3的图像是将R x x y ∈=,sin 的图像上所有点的______(“横”或”纵”)坐标______(伸长或缩短)为原来的______而得到的图像。
三角函数的图像变换

三角函数b x A y ++=)sin(ϕω的图像变换三角函数的图像变换是历年来高考的重点内容,因此我们有必要对这一问题作一下研究。
下面就三角函数的图像变换的基本题型,做以详细讲析:一、 振幅变换由函数)(x f y =的图像变换为)(x Af y =的图像,其主要的方法是将)(x f y =图像上的各点的纵坐标变为原来的A 倍,即)()(A x Af y x f y =−−−−−−→−=倍纵坐标变为原来的。
例1、要得到)32sin(4π-=x y 的图像,只需将)32sin(π-=x y 的图像( )。
A 、 向上平移4个单位;B 、 将)32sin(π-=x y 图像上的各点的纵坐标变为原来的4倍; C 、 将)32sin(π-=x y 图像上的各点的纵坐标变为原来的4-倍; D 、 向下平移4个位单位。
分析:由题意可知,将)32sin(π-=x y 图像上的各点的纵坐标变为原来的4倍,就可以得到)32sin(4π-=x y 的图像。
故选B 。
二、 周期变换由函数)(x f y =的图像变换为)(x f y ω=的图像,其主要的方法是将)(x f y =图像上的各点的横坐标变为原来的ω1倍,即)()(1x f y x f y ωω=−−−−−−→−=倍横坐标变为原来的。
例2、如何由x y sin =的图像得到x y 2sin 2=的图像。
解:由x y sin =的图像上各点的纵坐标伸长到原来的2倍,得到x y sin 2=的图像,再将x y sin 2=的图像各点的横坐标压缩为原来的21倍,得到x y 2sin 2=的图像。
三、 相位变换(左右平移变换)由函数)(x f y =的图像变换为)(ϕ+=x f y 的图像,其主要的方法是将)(x f y =图像上所有点向左或向右平移ϕ个单位。
即)()(0)(ϕϕϕ+=−−−−−−→−=>x f y x f y 个单位向左平移 )()(0)(ϕϕϕ-=−−−−−−→−=>x f y x f y 个单位向右平移 例3、如何由)32sin(31π+=x y 的图像得到x y sin =的图像。
1.3.3三角函数图像变换

方法1: (按 , , A顺序变换 )
y
y sin x
3
2
y=3sin(2x+ ) 3
y 3 sin(2 x ) 3
1
y=sinx
3
5 6
6
o
-1
3
5 3
2
x
-2
y=sin2x y=sin(2x+ ) 3
-3
方法2:(按 , , A顺序变换 )
已知函数f ( x) A sin(x )( 0, | |
2
)的图象与y轴
3 交于点(0, ), 它与y轴右侧的第一个最大值点和最小值点 2 分别是( x0 ,3), ( x0 2 ,3)
(1)求函数y f ( x)的解析式; (2)用“五点法”作此函数在一个周期内的图象; (3)说明它是由函数y sin x的图象经过哪些变换得到的?
y 3 sin(x ) 6
小结:
1、作函数y=Asin(x+) 的图象:
(1)用“五点法”作图。
(2)利用变换关系作图。 2、函数 y = sinx 的图象与函数
y=Asin(x+)的图象间的变换关系。
解 : 因为它与y轴右侧的第一个最大值点和最小值点 分别是( x0 ,3), ( x0 2 ,3),
T 2 x0 2 x0 2 , 所以 1 2 T
y 3 sin(x )
3 又 过点(0, ), 2 3 3 sin , 且 | | 2 2 6
四、课堂练习
1、要得到函数 y sin(2 x ) 的图象, 3 只需要将 y sin 2 x
三角函数图像变换研究

图像变换的基本原理和方法
▪ 图像剪切变换
1.定义与实现:图像剪切变换是通过改变图像某些区域的宽度 和高度,使得图像产生倾斜效果。它可以使用仿射变换矩阵来 描述。 2.特性:剪切变换改变了图像的几何结构,但保持了图像的比 例关系。过度的剪切可能使图像变得难以辨认。 3.实际应用:图像剪切变换常用
三角函数图像变换研究
▪ 机器学习与三角函数图像变换的结合研究
1.利用机器学习方法改进三角函数图像变换算法 2.构建基于深度学习的三角函数图像变换模型 3.分析机器学习对三角函数图像变换精度和速度的影响
未来三角函数图像变换的研究方向
▪ 三角函数图像变换在虚拟现实中的应用研究
1.虚拟现实中对三角函数图像变换的需求分析 2.开发适用于虚拟现实的三角函数图像变换技术 3.实际应用场景中三角函数图像变换的效果评估
1.定义与实现:图像旋转变换是将图像绕某个点(通常是原点)以一定的角度旋转 。旋转矩阵可用于描述这种变换。 2.特性:旋转变换会改变图像的方向,但保持图像的比例关系不变。非整数倍的旋 转可能会导致图像边缘出现锯齿状。 3.实际应用:图像旋转变换在各种应用场景中都非常常见,如图像内容分类、自动 驾驶车辆导航等。
▪ 变换技巧在图像处理中的应用
1.使用三角函数图像变换进行图像缩放、旋转和平移 2.应用变换方法进行图像增强和降噪处理 3.利用变换技巧实现图像特征提取和识别
变换技巧在实际问题中的应用
▪ 变换技巧在控制理论中的应用
1.利用三角函数图像变换进行系统建模和分析 2.借助变换方法设计控制器以稳定和优化系统性能 3.通过变换实现控制系统的实时监测和故障诊断
▪ 三角函数图像的平移变换
1.平移变换公式 2.图像移动方向的判断 3.平移变换对周期性的影响
高中数学:131《三角函数图像的变换》课件必修

变换的目的是为了更好地理解三角函数的性质,解决实际问题,以及进行图像处理 等。
变换的种类和特点
01
02
03
04
平移变换
将图像沿x轴或y轴方向移动 ,保持图像形状不变。
伸缩变换
通过改变x轴和y轴的比例来 改变图像的大小,可以横向或
纵向伸缩。
翻折变换
利用伸缩变换的性质求解函数的极值
例如,利用正弦函数的伸缩性质,可以求解y=sin(3x)在x=π/9处的极小值为1。
利用对称变换的性质求解函数的对称轴或对称中心
例如,利用正弦函数的对称性质,可以求解y=sin(x)的对称轴为x=kπ+π/2,k∈Z。
变换在实际问题中的应用
物理学中的应用
三角函数图像的综合变换在物理学中有广泛的应用,如振 动和波动现象、交流电等。通过变换可以更好地理解物理 现象和解决实际问题。
x轴缩短为原来的1/2,则图像的 周期变为原来的2倍。
01
03
02 04
总结词:影响相位
详细描述:沿x轴伸缩不仅改变 了图像的周期,还会影响函数的 相位。例如,将x轴缩短为原来 的1/2,相当于将相位滞后了π。
沿y轴伸缩
总结词:改变振幅
详细描述:沿y轴伸缩是 指保持x轴不变,通过改 变y轴的长度来改变整个 图像的振幅。例如,将y 轴放大为原来的2倍,则 图像的振幅变为原来的2 倍。
翻折变换
旋转变换
$y = -f(-x)$ 或 $y = f(x)$,前者表示沿x 轴翻折,后者表示沿y轴翻折。
$x = xcostheta - ysintheta$ 和 $y = xsintheta + ycostheta$,其中$theta$为 旋转角度。
三角函数图像的变换

三角函数图像的变换三角函数是一类重要的基础函数,包括正弦函数、余弦函数、正切函数等。
在数学中,我们经常遇到需要对三角函数进行图像变换的情况,比如平移、伸缩、翻转等。
本文将介绍三角函数图像的常见变换以及它们对函数图像的影响。
一、平移变换平移是指将函数图像沿着横轴或纵轴方向移动一段距离。
以正弦函数为例,设原函数为y=sin(x),将它沿横轴向右平移a个单位,新函数为y=sin(x-a)。
当a取正值时,函数图像向右平移;当a取负值时,函数图像向左平移。
平移变换后的图像与原图像形状相同,只是位置不同。
二、伸缩变换伸缩是指将函数图像进行横向或纵向的比例拉伸或压缩。
以正弦函数为例,设原函数为y=sin(x),将它沿横轴方向进行压缩b倍,新函数为y=sin(bx)。
当b大于1时,函数图像横向压缩;当0<b<1时,函数图像横向拉伸。
同样,沿纵轴方向进行伸缩也可得到相应的函数图像变换。
三、翻转变换翻转是指将函数图像沿着横轴或纵轴进行翻转,也称为镜像变换。
以正弦函数为例,设原函数为y=sin(x),将它沿横轴进行翻转,新函数为y=-sin(x)。
同样地,纵向翻转可得到相应的函数图像变换。
四、混合变换除了单一的平移、伸缩和翻转变换,我们还可以通过组合这些变换来得到更复杂的函数图像变换。
比如,可以将平移、伸缩和翻转变换相结合,得到更丰富多样的变换效果。
以上是对三角函数图像常见变换的简要介绍,下面我们将进一步讨论这些变换对函数图像的具体影响。
1.平移变换的影响:平移变换只改变了函数图像的位置,不改变其形状。
假设原函数图像位于坐标系上方,若平移后函数图像向右移动,则新函数图像将出现在原来的右侧;若平移后函数图像向左移动,则新函数图像将出现在原来的左侧。
平移变换对函数图像的垂直位置没有影响。
2.伸缩变换的影响:横向伸缩会拉伸或压缩函数图像。
当b大于1时,函数图像在x轴方向上被压缩,变得更加陡峭;当0<b<1时,函数图像在x轴方向上被拉伸,变得更加平缓。
三角函数的图像的变换口诀解读

三角函数的图像的变换口诀解读变T 数倒系数议,变A 伸压 y 无疑, 变φ 要把系数提,正φ 左进负右移.周期变换是通过改变x 的系数来实现的,即周期T 的变化只与ω有关而与φ无关.这是因为ωπ2=T,故要使周期扩大或缩小m (m >0) 倍,则须用xm1去代原式中的x (纵坐标不变),故有“变T 数倒系数议”之说.相位φ变换实质上就是将函数的图像向左或向右平移.当先作周期变换后作相位变换时,须提出系数ω,这是因为周期变化时改变了x 的值,此时其初相位(非0初相)同时也改变相应得到改变,且改变的倍数相同.当先作相位变换后作周期变换,由于此时x 的系数为1,系数提不提无影响,为了统一记忆我们也视为提出系数“1”.因而有“变φ要把系数提”之说.三角函数图像的周期﹑振幅﹑相位等变换的问题是历年高考中常考查的内容.对此类命题的求解,无论三种变换怎样摆设,先要弄清哪是原函数的图像,哪是新函数的图像,再据本歌诀所述,很快就可得到解决.例1 为了得到 y =)62sin(π-x 的图像,可以将函数 y = cos2x 的图像 (2004年高考) ( )(A)向右平移6π个单位长度 (B)向右平移3π个单位长度(C)向左平移6π个单位长度 (D) 向左平移3π个单位长度解法1 ∵ y = cos2x =)4(2sin )22sin(ππ+=+x x , 而 y =]3)4[(2sin )62sin(πππ-+=-x x ,由此可得 只须将函数y = cos2x 的图像向右平移3π个单位长度即可.故选(B).解法2 ∵ y =)62sin(π-x )622cos(ππx +-=,即y )3(2cos π-=x , 而已知的函数为y = cos2x ,由此可得,须将函数y = cos2x 的图像向右平3π个单位即可.故选(B).点评 由于当ωϕ-=x 时, 相位0=+ϕωx .因而,我们可称此时的相位为零相位.由此可见,在作相位变换时,其平移的数值与方向是由两个0相位对应的x 值的差来决定的.对于本题而言,由于两个0相位对应的x 的值分别为12π与4π-,故所作的平移就是要将已知函数的0相位对应的点)0 ,4(π-移到点)0 12(,π处.易知要平移的数值是:3)4(12πππ=--,方向是向右的.显然这一方法就是“五点作图法”中的第一零点判断法.例2 已知函数 f (x ) =)5sin(2π+x (x ∈R ) 的图像为C, 函数 y =)52sin(π-x (x ∈R ) 的图像为C 1, 为了得到C 1,只需把C 上所有的点先向右平移 ,再将 . ( )(A)52π个单位,横、纵坐标都缩短到原来的21(B)52π个单位,横、纵坐标都伸长到原来的2倍(C)5π个单位,横、纵坐标都缩短到原来的21 (D)5π个单位,横、纵坐标都伸长到原来的2倍解 ∵ 要求的变换是先作平移变换,后作周期变换,再作振幅变换.故将函数y =)5sin(2π+x 的图像向右平移52π个单位, 得到)5sin(2)525sin(2πππ-=-+=x x y的图像.再将此图像的横坐标缩小到原来的一半,得到y =2)52sin(π-x 的图像.最后将其纵坐标缩小到原来的一半,即可得到y =)52sin(π-x 的图像.故选(A).点评 本题要求先作相位变换,后作周期变换,再作振幅变换,且原函数中x 的系数为“1”,明确这一点是非常重要的.。
三角函数的像变换规律总结

三角函数的像变换规律总结三角函数是数学中的重要概念,它们在数学和物理等领域中有广泛的应用。
像变换规律是描述三角函数在图像上的移动、拉伸和反转等变化规律。
在本文中,我们将总结常见的三角函数的像变换规律。
一、正弦函数的像变换规律正弦函数是最常见的三角函数之一,其一般式为y =A*sin(Bx+C)+D,其中A、B、C、D为常数参数。
1. 水平方向平移:当C改变时,函数图像在水平方向上发生平移。
当C>0时,向左平移;当C<0时,向右平移。
平移的距离等于C的绝对值除以B。
2. 垂直方向平移:当D改变时,函数图像在垂直方向上发生平移。
当D>0时,向上平移;当D<0时,向下平移。
平移的距离等于D。
3. 垂直方向拉伸或压缩:当A改变时,函数图像在垂直方向上发生拉伸或压缩。
当|A|>1时,发生纵向拉伸;当|A|<1时,发生纵向压缩。
拉伸或压缩的程度与|A|的大小有关。
二、余弦函数的像变换规律余弦函数也是常见的三角函数之一,其一般式为y =A*cos(Bx+C)+D,其中A、B、C、D为常数参数。
1. 水平方向平移:与正弦函数类似,余弦函数在改变C时在水平方向上发生平移。
当C>0时,向左平移;当C<0时,向右平移。
平移的距离等于C的绝对值除以B。
2. 垂直方向平移:与正弦函数类似,余弦函数在改变D时在垂直方向上发生平移。
当D>0时,向上平移;当D<0时,向下平移。
平移的距离等于D。
3. 垂直方向拉伸或压缩:与正弦函数类似,余弦函数在改变A时在垂直方向上发生拉伸或压缩。
当|A|>1时,发生纵向拉伸;当|A|<1时,发生纵向压缩。
拉伸或压缩的程度与|A|的大小有关。
三、正切函数的像变换规律正切函数是另一个常见的三角函数,其一般式为y =A*tan(Bx+C)+D,其中A、B、C、D为常数参数。
由于正切函数在某些点上无定义,因此在图像上会有一些特殊的性质。
三角函数的图像变换
见几何画板
思考: 思考:
1、利用“五点法”作出函数 、利用“五点法” y=3sin(2x+π/3)的简图。 π/3)的简图。 2、函数y=3sin(2x+π/3)的图象 、函数 π/3)的图象 如何变换而得到? 是由 y=sinx如何变换而得到?有几 如何变换而得到 变换方式? 种变换方式?
例:用两种方法将函数y=sinx的图像变换为
解:由于周期T=2π x sinx 2sinx
1 sin x 2
∴不妨先在[0,2π]上作图,列表:
π
2
0 0 0 0
π 0 0 0
3π 2
2π 0 0 0
1 2
1 2
-1 -2
− 1 2
y
2
y=2sinx
1
1 2
1 − 2
π
o
2
π
3π 1 y = sin x 2 2
2π
x
y=sinx
-1 -2
y
−
π
2
−
π
3
π
2
3π 5π 2 3
2π
x
-1
实际 上, 我们在 前面 已经 学过知 道有 y = sin x y = sin(x +ϕ) →
小结 : 注意:A,ω,ϕ 对函数y = A sin(ω x + ϕ ), ( A > 0, ω > 0, ) 的图像的影响。
ϕ>0,向左平移ω 个单位长度 ϕ<0,向右平移ω 个单位长度
4.将函数y = sin x的图象上的每一点的纵坐标 保持不变,横坐标扩大为原来的2倍,然后所得的图象
π
沿x轴向左平移 个单位,这样得到的曲线 ) 2 图象的函数y = f ( x)的解析为(
三角函数图像变换顺序详解(全面)

欢迎阅读《图象变换的顺序寻根》题根研究?一、图象变换的四种类型从函数y = f (x)到函数y = A f()+m,其间经过4种变换:1.纵向平移——m 变换2.纵向伸缩——A变换3.横向平移——变换4.横向伸缩——变换一般说来,这4种变换谁先谁后都没关系,都能达到目标,只是在不同的变换顺序中,“变换量”可不尽相同,解题的“风险性”也不一样.以下以y = sin x到y = A sin ()+m为例,讨论4种变换的顺序问题.【例1】函数的图象可由y = sin x的图象经过怎样的平移和伸缩变换而得到?【解法1】第1步,横向平移:将y = sin x向右平移,得第2步,横向伸缩:将的横坐标缩短倍,得第3步:纵向伸缩:将的纵坐标扩大3倍,得第4步:纵向平移:将向上平移1,得【解法2】第1步,横向伸缩:将y = sin x 的横坐标缩短倍,得y = sin 2x第2步,横向平移:将y = sin 2x向右平移,得第3步,纵向平移:将向上平移,得第4步,纵向伸缩:将的纵坐标扩大3倍,得【说明】解法1的“变换量”(如右移)与参数值()对应,而解法2中有的变换量(如右移)与参数值()不对应,因此解法1的“可靠性”大,而解法2的“风险性”大.【质疑】对以上变换,提出如下疑问:(1)在两种不同的变换顺序中,为什么“伸缩量”不变,而“平移量”有变?(2)在横向平移和纵向平移中,为什么它们增减方向相反——如当<0时对应右移(增方向),而m < 0时对应下移(减方向)?(3)在横向伸缩和纵向伸缩中,为什么它们的缩扩方向相反——如|| > 1时对应着“缩”,而| A | >1时,对应着“扩”?【答疑】对于(2),(3)两道疑问的回答是:这是因为在函数表达式y = A f ()+m中x 和y的地位在形式上“不平等”所至. 如果把函数式变为方程式(y+) = f (),则x、y在形式上就“地位平等”了.如将例1中的变成它们的变换“方向”就“统一”了.对于疑问(1):在不同的变换顺序中,为什么“伸缩量不变”,而“平移量有变”?这是因为在“一次”替代:x→中,平移是对x进行的.故先平移(x→)对后伸缩(→)没有影响;但先收缩(x→)对后平移(→)却存在着“平移”相关. 这就是为什么(在例1的解法2中)后平移时,有的原因.【说明】为了使得4种变换量与4个参数(A,,,m)对应,降低“解题风险”,在由sin x 变到A sin () (> 0) 的途中,采用如下顺序:(1)横向平移:x→(2)横向伸缩:x+→(3)纵向伸缩:sin () →A sin ()(4)纵向平移:A sin () →A sin () + m这正是例1中解法1的顺序.二、正向变换与逆向变换如果把由sin x 到A sin ()+m的变换称作正向变换,那么反过来,由A sin ()+m到sin x变换则称逆向变换.显然,逆向变换的“顺序”是正向变换的“逆”.因为正向变换的一般顺序是:(1)横向平移,(2)横向伸缩,(3)纵向伸缩,(4)纵向平移.所以逆向变换的一般顺序则是:(1)纵向平移,(2)纵向伸缩,(3)横向伸缩,(4)横向平移.如将函数y= 2sin (2-) +1的图像下移1个单位得y=2sin (2x-),再将纵坐标缩小一半得y= sin(2 x-),再将横坐标扩大2倍得y= sin(x-),最后将图象左移得函数y= sin x.【例2】将y = f (x)·cos x的图象向右平移, 再向上平移1, 所得的函数为y=2sin2 x. 试求f (x)的表达式.【分析】这是图象变换的逆变换问题:已知函数的变换结果,求“原函数”. 我们考虑将“正向变换”的过程倒逆回去而得“逆向变换”的顺序.【解析】将y = 2sin2 x下移1个单位(与正向变换上移1个单位相反),得y = 2sin2 x-1,再将2sin2x-1左移(与正向变换右移相反)得令f (x)·cos x = 2sin x cos x 得f (x) = 2sin x【说明】由此得原函数为y=f(x)cos x=2sin x cos x=sin2x. 正向变换为sin 2x→2sin2x,其逆变换为2sin2x→sin2x.因为2sin2x=1+sin(2 x-),所以下移1个单位得sin(2 x-),左移得sin2x.三、翻折变换使> 0平移变换x→是“对x而言”,由于x过于简单而易被忽略.强调一下,这里x的系数是+1. 千万不要误以为是由sin(-x)左移而得.其实,x或y的系数变-1,也对应着两种不同的图象变换:由x→- x对应着关于y轴的对称变换,即沿y轴的翻折变换;由f (x) →-f (x)对应着关于x轴的对称变换,即沿x轴的翻折变换.【例3】求函数的单调减区间.【分析】先变换-3x→3x,即沿y轴的翻折变换.【解析1】,转化为求g(x)=sin(3x-)的增区间令≤≤≤x ≤(f(x)减区间主解)又函数的f(x)周期为,故函数f(x)减区间的通解为≤x ≤【解析2】的减区间为≤≤即是≤x ≤【说明】从图象变换的角度看问题,比较解析1和解析2可知,求f(x)的减区间,实际上分两步进行:(1)先求得f(x)减区间的主解≤x ≤(2)再利用主解进行横向平移(的整数倍)即得f(x)减区间的通解.【思考】本解先将“正数化”,使>0是本解成功的关键. 否则,如果去解不等式组将会使你陷入歧途,不防试试!。
三角函数图像平移变换

三角函数图像平移变换由y =sin x 的图象变换出y =sin(ωx +ϕ)的图象一样有两个途径,只有区别开这两个途径,才能灵活进行图象变换。
利用图象的变换作图象时,提倡先平移后伸缩,但先伸缩后平移也常常显现不管哪一种变形,请切记每一个变换老是对字母x 而言,即图象变换要看“变量”起多大转变,而不是“角转变”多少。
途径一:先平移变换再周期变换(伸缩变换)先将y =sin x 的图象向左(ϕ>0)或向右(ϕ<0=平移|ϕ|个单位,再将图象上各点的横坐标变成原先的ω1倍(ω>0),便得y =sin(ωx +ϕ)的图象。
途径二:先周期变换(伸缩变换)再平移变换。
先将y =sin x 的图象上各点的横坐标变成原先的ω1倍(ω>0),再沿x 轴向左(ϕ>0)或向右(ϕ<0=平移ωϕ||个单位,便得y =sin(ωx +ϕ)的图象。
1.为取得函数πcos 23y x ⎛⎫=+⎪⎝⎭的图像,只需将函数sin 2y x =的图像( A ) A .向左平移5π12个长度单位B .向右平移5π12个长度单位 C .向左平移5π6个长度单位 D .向右平移5π6个长度单位 2.要取得函数sin y x =的图象,只需将函数cos y x π⎛⎫=- ⎪3⎝⎭的图象( D ) A .向右平移π6个单位 B .向右平移π3个单位 C .向左平移π3个单位 D .向左平移π6个单位 3.为了取得函数)62sin(π-=x y 的图象,能够将函数x y 2cos =的图象( B ) (A)向右平移6π个单位长度 (B)向右平移3π个单位长度 (C)向左平移6π个单位长度 (D)向左平移3π个单位长度 4.把函数sin y x =(x R ∈)的图象上所有点向左平行移动3π个单位长度,再把所得图象上所有点的横坐标缩短到原先的12倍(纵坐标不变),取得的图象所表示的函数是C A sin(2)3y x π=-,x R ∈ B sin()26x y π=+,x R ∈ C sin(2)3y x π=+,x R ∈ D sin(2)32y x π=+,x R ∈5.为了取得函数sin(2)3y x π=-的图像,只需把函数sin(2)6y x π=+的图像B (A )向左平移4π个长度单位 (B )向右平移4π个长度单位 (C )向左平移2π个长度单位 (D )向右平移2π个长度单位 6.已知函数()sin()(,0)4f x x x R πϖϖ=+∈>的最小正周期为π,为了取得函数()cos g x x ϖ=的图象,只要将()y f x =的图象AA 向左平移8π个单位长度B 向右平移8π个单位长度 C 向左平移4π个单位长度 D 向右平移4π个单位长度 7.函数cos(2)26y x π=+-的图象F 按向量a 平移到'F ,'F 的函数解析式为(),y f x =当()y f x =为奇函数时,向量a 能够等于B.(,2)6A π-- .(,2)6B π- .(,2)6C π- .(,2)6D π8.将函数y=sinx 的图象向左平移ϕ(0 ≤ϕ<2π)的单位后,取得函数y=sin ()6x π-的图象,则ϕ等于(D ) A .6π B .56π C. 76π D.116π 9.若将函数()tan 04y x πωω⎛⎫=+> ⎪⎝⎭的图像向右平移6π个单位长度后,与函数tan 6y x πω⎛⎫=+ ⎪⎝⎭的图像重合,则ω的最小值为DA .16 B. 14 C. 13 D.12 10.设函数()cos (0)f x x ωω=>,将()y f x =的图像向右平移3π个单位长度后,所得的图像与原图像重合,则ω的最小值等于C(A )13 (B )3 (C )6 (D )9 11.将函数sin(2)3y x π=+的图象按向量α平移后所得的图象关于点(,0)12π-中 心对称,则向量α的坐标可能为( C )A .(,0)12π-B .(,0)6π-C .(,0)12πD .(,0)6π 12.将函数3sin()y x θ=-的图象F 按向量(,3)3π平移取得图象F ',若F '的一条对称轴是直线4x π=,则θ的一个可能取值是AA. π125B. π125-C. π1211D. 1112π- 13.把曲线yc os x +2y -1=0先沿x 轴向右平移2π个单位,再沿y 轴向下平移1个单位,取得的曲线方程是( C )A .(1-y )sin x +2y -3=0B .(y -1)sin x +2y -3=0C .(y +1)sin x +2y +1=0D .-(y +1)sin x +2y +1=0 解析:将原方程整理为:y =x cos 21+,因为要将原曲线向右、向下别离移动2π个单位和1个单位,因此可得y =)2cos(21π-+x -1为所求方程.整理得(y +1)sin x +2y +1=0.点评:本题考查了曲线平移的大体方式及三角函数中的诱导公式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角函数的图像变换
三角函数是数学中重要的概念之一,它们在几何、物理和工程等领域中有着广
泛的应用。
而其中,图像变换是三角函数中一个非常有趣和重要的概念。
图像变换可以通过改变三角函数的参数来改变其图像的形状、位置和大小。
本文将探讨三角函数的图像变换,并介绍一些常见的图像变换方法。
首先,我们来讨论正弦函数的图像变换。
正弦函数的一般形式为y = A*sin(Bx
+ C) + D,其中A、B、C和D分别是函数的振幅、周期、相位和纵坐标平移量。
通过改变这些参数,我们可以实现正弦函数图像的各种变换。
首先,我们来看振幅的变换。
振幅决定了正弦函数图像的上下波动程度。
当振
幅A增大时,正弦函数的波峰和波谷的高度也会增加,图像变得更加陡峭。
相反,当振幅A减小时,正弦函数的波峰和波谷的高度也会减小,图像变得更加平缓。
接下来,我们来看周期的变换。
周期决定了正弦函数图像的重复性。
当周期B
增大时,正弦函数的波峰和波谷之间的距离增加,图像变得更加拉长。
相反,当周期B减小时,正弦函数的波峰和波谷之间的距离减小,图像变得更加压缩。
然后,我们来看相位的变换。
相位决定了正弦函数图像的水平位置。
当相位C
增大时,正弦函数图像向左平移,波峰和波谷的位置向左移动。
相反,当相位C
减小时,正弦函数图像向右平移,波峰和波谷的位置向右移动。
最后,我们来看纵坐标平移量的变换。
纵坐标平移量决定了正弦函数图像的垂
直位置。
当纵坐标平移量D增大时,正弦函数图像向上平移,波峰和波谷的位置
上升。
相反,当纵坐标平移量D减小时,正弦函数图像向下平移,波峰和波谷的
位置下降。
除了正弦函数,余弦函数和正切函数也可以进行图像变换。
余弦函数的图像变
换和正弦函数类似,只是相位的变换方向相反。
正切函数的图像变换则更为复杂,它的一般形式为y = A*tan(Bx + C) + D,其中A、B、C和D同样是函数的参数。
通过改变这些参数,我们可以实现正切函数图像的各种变换,包括振幅、周期、相位和纵坐标平移量的变换。
在实际应用中,三角函数的图像变换可以帮助我们更好地理解和分析各种周期性现象。
例如,在物理学中,正弦函数的图像变换可以用来描述振动和波动现象;在工程学中,正切函数的图像变换可以用来分析电路中的交流信号。
通过对三角函数图像变换的研究,我们可以更深入地理解这些现象,并且能够更好地应用于实际问题的解决中。
总之,三角函数的图像变换是数学中一个重要且有趣的概念。
通过改变函数的参数,我们可以实现正弦函数、余弦函数和正切函数图像的各种变换,包括振幅、周期、相位和纵坐标平移量的变换。
这些图像变换不仅有助于我们更好地理解三角函数的性质,还可以应用于各种实际问题的分析和解决中。
无论是在几何、物理还是工程领域,三角函数的图像变换都具有重要的意义。
