串并加法器

合集下载

全加器四位串行加法器.最全优质PPT

• signal c: std_logic_vector(0 to 4);
• begin
• g0:f_adder
• port map(x(0),y(0),c(0),s(0),c(1));
• x<='0'&a(3 dowgn1to:0f)_; adder
该方法常用于系统数学模型的仿真或是系统工作原理的仿真。
a,b : •in std_logicp_voecrtotr(3mdoawnpto(0x);(1),y(1),c(1),s(1),c(2));
std_logic_1164.
• g2:f_adder 四位串行加法器（逻辑图）
std_logic_unsigned.
e数n据d e流•n式tity电f_路a设dd计per方;o法rt：m通过a对p数(据x流(2在)设,y计(中2的),具c体(2行)为,s的(描2述),来c建(3模)。); • g3:f_adder x<='0'&a(3 downto 0);
• architecture bhv of f_adder is
• begin
• g0:s<=x xor y xor cin;
• g1:cout<=(x and y)or(x and cin)or(y and cin);
• end architecture bhv;
四位串行加法器（逻辑图）
四位串行加法器（结构体式）
• use ieee.std_logic_unsigned.all;
• entity bit_f_adder is
• port(cin: in std_logic;
•
a,b : in std_logic_vector(3 downto 0);

加法器设计介绍

加法器设计介绍算术逻辑部件主要处理算术运算指令和逻辑运算指令，它的核心单元是加法器。

这个加法器是影响算术逻辑部件整体性能的关键部分，因为几乎所有的算术运算和逻辑运算，都要通过它来完成。

加法器结构包括串行进位加法器(Carry Ripple Adder，CRA)、进位跳跃加法器(cany skip Adder，CKA)，以及较高速度的进位选择加法器(carry select Adder，CSA)、超前进位加法器(Can 了Look—a}lead Adder，CLA)和并行前缀加法器(Parallel Prcfix Adder)等。

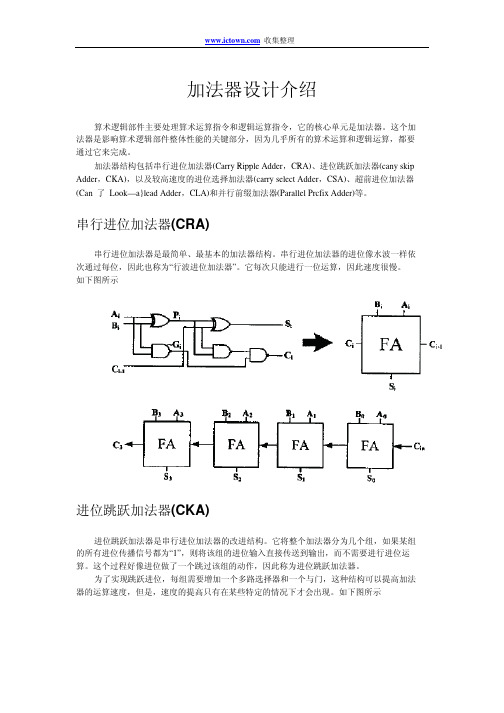
串行进位加法器(CRA)串行进位加法器是最简单、最基本的加法器结构。

串行进位加法器的进位像水波一样依次通过每位，因此也称为“行波进位加法器”。

它每次只能进行一位运算，因此速度很慢。

如下图所示进位跳跃加法器(CKA)进位跳跃加法器是串行进位加法器的改进结构。

它将整个加法器分为几个组，如果某组的所有进位传播信号都为“1”，则将该组的进位输入直接传送到输出，而不需要进行进位运算。

这个过程好像进位做了一个跳过该组的动作，因此称为进位跳跃加法器。

为了实现跳跃进位，每组需要增加一个多路选择器和一个与门，这种结构可以提高加法器的运算速度，但是，速度的提高只有在某些特定的情况下才会出现。

如下图所示进位选择加法器(CSA)进位选择加法器采用资源复制的基本思想，用硬件来换取速度。

它将整个加法器分为几个组，每组有两条路径，进位输入为“O”和“1”的两种情况通过两条路径同时计算。

一旦该组进位输入信号到来，通过多路选择器选择正确的进位输出与和值。

如下图所示由于采用了前瞻的思想，因此进位选择加法器的速度有很大提高。

如果整个加法器分为M 组，则运算延时可由第一组进位延时、M 个多路选择器的延时及一个和产生延时相加得到。

进位选择加法器虽然具有较快的速度，但由于它采用了资源复制的方法，因此实现代价也成倍增加。

2位串行进位的并行加法器真值表

2位串行进位的并行加法器真值表在数字电路中，加法器是常见的逻辑电路之一，用于进行数字的加法运算。

而串行进位的并行加法器是一种常见的加法器类型，它能够实现多位数字的加法运算，具有高效、稳定的特点。

在本文中，我们将对2位串行进位的并行加法器进行深入探讨，包括其真值表、工作原理和应用场景等方面。

一、2位串行进位的并行加法器真值表让我们来了解一下2位串行进位的并行加法器的真值表。

真值表是描述逻辑电路在不同输入组合下的输出情况的表格，通过真值表可以清晰地了解逻辑电路的工作状态。

对于2位串行进位的并行加法器，其真值表如下所示：输入 | 进位 | 输出 A | B | Cin | S | Cout 0 | 0 | 0 | 0 | 0 0 | 0 | 1 | 1 | 0 0 | 1 | 0 | 1 | 0 0 | 1 | 1 | 0 | 1 1 | 0 | 0 | 1 | 0 1 | 0 | 1 | 0 | 1 1 | 1 | 0 | 0 | 1 1 | 1 | 1 | 1 | 1从上面的真值表可以看出，2位串行进位的并行加法器的输出S和Cout与输入A、B和进位Cin之间存在着一定的逻辑关系。

理解并熟记这些逻辑关系对于正确设计和应用加法器起着至关重要的作用。

二、工作原理接下来，让我们来了解2位串行进位的并行加法器的工作原理。

在加法器中，每一位使用了半加模块和全加模块。

半加模块能够实现单个位的加法运算，而全加模块则可以实现考虑进位的加法运算。

串行进位的并行加法器通过将多个全加模块串联起来，实现了高效的多位加法运算。

具体来说，对于2位串行进位的并行加法器，每个位需要经过两个半加模块和一个全加模块的计算。

在计算的过程中，要考虑上一位的进位对当前位的影响，因此需要进行串行进位的处理。

通过合理的电路设计和逻辑门的组合，2位串行进位的并行加法器能够实现快速、准确的多位加法运算。

三、应用场景2位串行进位的并行加法器广泛应用于数字信号处理、计算机系统、通信系统等领域。

串行进位加法器_延迟计算__概述说明

串行进位加法器延迟计算概述说明1. 引言1.1 概述串行进位加法器是一种常用的数字电路，用于实现两个二进制数的相加运算。

在计算机科学和电子工程领域中，加法器是基本的计算单元之一，因此对其性能的改进一直是研究的重点。

延迟计算则是指在某些情况下，为了减少开销、功耗或其他限制条件而将计算结果延迟到需要时再进行。

本文将结合串行进位加法器和延迟计算两个主题，探讨串行进位加法器在延迟计算中的作用以及其特点和应用范围。

1.2 文章结构本文共分为五个部分。

首先引言部分进行整体概述和结构说明。

接下来第二部分将介绍串行进位加法器的基本原理、构造方式以及优缺点。

第三部分将深入探讨延迟计算的定义、基本概念、应用场景以及实现方法与技术。

紧接着，在第四部分中，我们将重点关注串行进位加法器在延迟计算中的作用，并介绍其特点和应用范围。

最后，在结论部分中对全文进行总结，并提出未来研究方向的建议，以及对读者的启发和影响。

1.3 目的本文旨在阐述串行进位加法器和延迟计算的基本原理、应用以及相互关系。

通过分析串行进位加法器在延迟计算中的作用，我们可以更好地理解其特点和应用范围，并为未来的研究和发展提供一定的参考。

此外，本文还将探讨延迟计算在提高电路性能和优化资源利用方面的重要性，以期对读者有所启发。

2. 串行进位加法器：2.1 基本原理：串行进位加法器是一种基于二进制加法的电路设计，用于实现数字计算。

其基本原理是将两个二进制数逐位相加，并通过一系列的进位传递来实现进位的计算和累积。

在每一位上，串行进位加法器通过输入的两个数字和之前的进位信息来生成该位的结果和产生下一位的进位。

2.2 构造方式：串行进位加法器可以使用多种不同的逻辑门电路实现，常见的包括使用门电路（AND、OR、XOR等）、触发器以及多路选择器等元件。

其中一个常用的构造方式是Ripple Carry Adder（RCA）与D型触发器结合，通过级联多个全加器单元来实现。

2.3 优缺点：串行进位加法器相比并行运算方式具有以下优点：首先，由于其简单的电路结构，在硬件设计上较为容易实现；其次，它能够按顺序处理数字，并且只需要一个时钟周期进行运算。

数字逻辑第三章加法器.ppt

四位二进制并行加法器
三、四位二进制并加法器的外部特性和逻辑符号 1．外部特性
图中，A4、A3、A2、A1 ------- 二进制被加数； B4、B3、 B2、B1 ------- 二进制加数； F4、 F3、 F2、 F1 ------相加产生的和数； C0 --------------------来自低位的进位输入； FC4 -------------------向高位的进位输出。
a3b1
+) 乘积 Z5 a3b2 Z4 a2b2 Z3
a2b1
a1b2 Z2
a1b1
Z1
因为： ☆1位二进制数乘法法则和逻辑“与”运算法则相同，“积”项aibj(i =1，2，3；j=1，2)可用两输入与门实现。 ☆对部分积求和可用并行加法器实现。所以：该乘法运算电路可由6个两输入与门和1 b2 个4位二进制并行加法器构成。逻辑电路图如右图所示。
四位二进制并行加法器
实现给定功能的逻辑电路图如下图所示。 1) 输入端A4、A3、A2、 A1输入8421码；
2) 而从另一输入端B4、 B3、B2、B1输入二进制数0011； 3) 进位输入端C0接上“0”；
4) 可从输出端F4、F3、F2、 F1得到与输入8421码对
应的余3码。
四位二进制并行加法器
Z5 Z4 Z3 Z 2 Z1
F4 F3 F2 F 1 FC4 T 693 C0
0
A4 A3 A2 A1
B4 B 3 B2 B1
＆
＆
＆
＆
＆
＆
b1
a3
a2
a1 0 a 3
a2
a1
FA4
F3 C3
FA3
F2

加法器

八位二进制加法器摘要：加法运算是最重要最基本的运算，所有的其他基本算术运算，减、乘、除、模乘运算最终都能归结为加法运算。

在不同的场合使用的加法器对其要求也不同，有的要求速度更快，有的要求面积更小。

常见的加法器有串行进位加法器、74LS283超前进位加法器等，因此可以通过选取合适的器件设计一个加法器。

本次设计主要是如何实现8位二进制数的相加，即两个000到255之间的数相加，由于在实际中输入的往往是三位十进制数，因此，被加数和加数是两个三位十进制数，范围在000到255之间.当输入十进制数的时候，8421BCD码编码器先开始工作，编码器先将十进制数转换成四位二进制数，输出的四位二进制数直接到达8421BCD码加法器的输入端，我们可以使用71LS185加法器构成的一位8421BCD码的加法器，8421BCD码是用4位二进制数表示1位十进制数，4位二进制数内部为二进制，8421BCD码之间是十进制，即逢十进一。

而四位二进制加法器是按四位二进制数进行运算，即逢十六进一。

二者进位关系不同。

当四位二进制数加法器74LS283完成这个加法运算时，要用两片74LS283。

第一片完成加法运算，第二片完成修正运算。

8421BCD码加法器工作时，8421BCD码的加法运算为十进制运算，而当和数大于9时，8421BCD码就产生进位，而此时十六进制则不一定产生进位，因此需要对二进制和数进行修正，即加上6（0110），让其产生一个进位。

当和数小于等于9时，则不需要修正或者说加上0。

因此我们可以通过三个8421BCD码加法器的相连组成一个三位串行进位并行加法器，这样通过低位向高位产生进位进行十进制的加法运算，最后通过连接数码管显示所得的结果。

当输入二进制数的时候，两个串接的74LS283四位加法器进行加法运算，产生的八位二进制数通过集成芯片转换成三位十进制数，最后通过数码管显示。

另外，本次设计不仅可以适用加数和被加数是000到255的数字，同时也适用于加数和被加数是000到999的任何一个数，这是本次设计的创新之处。

进位链

间串行进位方式的延迟时间进一步减少。
分析上面的公式每一小组的小组进位可以看出，它又是有两部分组成，一部分只与该组4位操作数有关，而与低位小组的小组进位无关，
如G4+P4G3 +P4P3G2 +P4P3P2G1 ，它只与第一小组的 A1~ A4 、B1~B4有关，称它为第一小组的本地进位记GI;另一部分不仅
与这一小组的4位操作数有关，而且与低位小组的小组进位有关，如
1.行波进位
也称为串进位，它是指并行加法器进位从低位向高位逐位的产生与传送，高一位的依赖于低位的产生与传送。
2.先行进位
先行进位也称并行进位，指加法器各位的进位是各自独立且同时产生的，高一位的进位不依赖低位的进位产生与传送。
并行加法器任何一位的进位：
Ci = AiBi +(Ai⊕ Bi) Ci-1 = AiBi +(Ai +Bi) Ci-1 它可以分为两个部分：AiBi和(Ai⊕ Bi) Ci-1 ，前者仅与这
一位的两个操作数有关与低位的进位无关称它为本地进位或进位生成函数，记Gi；后者不仅与操作数有关还与低位
的进位有关称它为传递进位，称Ai⊕ Bi或Ai +Bi为传递函
数记Pi。因此可写成：
Ci = Gi + Pi Ci-1
以16为加法器为例，在行波进位器中有如下进位关系：
C1 = G1 + P1 C0 C2 = G2 + P2 C1
(1)组内并行、组间串行的分组进位方式
以16位并行加法器为例，将其按每组4位划分为4个组，组内4位按类似公式（3.6）设计如（图3.7）所示的先行进位电路。4个小组的进位电路按图(3.8)所示的关系将其串联起来。

第4组 3位串行加法器

第4组3位串行加法器_课程报告项目名称:可数字显示的3位串行进位加法器组员：邵捷(1111122217)罗洪强(1111122216)姜帅(1111122204)指导教师：张凡上课时间：2013/9/16 ~2013/9/27项目摘要：将三个一位全加器串联，实现0到7的十进制加法运算，加数以二进制的形式从两端口输入。

并分别对两个加数与和数进行译码，输出到三个数码管上，以十进制的形式分别显示出两个加数的输入值与和数的输出值。

关键字：全加器FPGA 数字显示一、实验目的实现0到7的十进制加法运算，加数以二进制的形式从两端口输入。

并给出三个数码管，以十进制的形式分别显示出两个加数的输入值与和数的输出值。

二、实验设备FPGA器件、USB JTAG调试工具、Quarts9.0软件、VHDL硬件设计语言。

三、硬件设计3.1 框图数据显示器1 数据显示器2 数据显示器3A0 A1 A2 B0 B1 B2 S0 S1 S2 CO求和输出值S0 CO S1 CO S2 CO1位全加器1位全加器1位全加器A0 B0 A1 B1 A2 B2A0 A1 A2 B0 B1 B2输入端口1 输入端口23.2 原理阐述取3只全加器，依次将低位全加器的进位输出端接到高位全加器的进位输入端，便可得到3位串行进位加法器，此时有六个输入端口A0、B0、A1、B1、A2、B2和四个输出端口S0、S1、S2、CO 。

分别将六个端口通过6只开关与5V 直流电源连接起来当相应输入端口所对应的开关闭合，该端口就被输入二进制数1；开关断开，该端口就被输入二进制数0。

再将A0、A1、A2端口从低位到高位依次接到DCD_HEX_ORANGE 上，B0、B1、B2端口从低位到高位依次接到另一只DCD_HEX_ORANGE 上。

这样当两个相加的数A2A1A0、B2B1B0被以二进制的形式输入时，其对应的DCD_HEX_ORANGE 上就会以十进制的形式显示出其数值。

计算机组成原理加法器和ALU

B16~B13
B12~B9
B8~B5
B4~B1
3.4 加法器和ALU
3.4.2 ALU电路
为了实现算术/逻辑多功能运算，则必须对全加器（FA）的功能进行扩展，具体方法是：先不将输入Ai、Bi和下一位的进位数Ci直接进行全加，而是将Ai和Bi先组合成由控制参数S0、S1、S2、S3控制的组合函数Xi、Yi，如图3-16所示，然后再将 Xi、Yi和下一位进位数通过全加器进行全加。这样，不同的控制参数可以得到不同的组合函数，因而能够实现多种算术运算和逻辑运算。
3.4 加法器和ALU
C4=G4+P4C3 C5=G5+P5C4= G5+ P5G4+ P5P4C3 C6=G6+P6C5= G6+ P6G5+ P6P5G4+ P6 P5P4C3 C7=G7+P7C6= G7+ P7G6+ P7P6G5+ P7P6 P5 G4+ P7P6 P5P4C3
C8=G8+P8C7 C9=G9+P9C8= G9+ P9G8+ P9P8C7 C10=G10+P10C9= G10+ P10G9+ P10P9G8+ P10 P9P8C7 C11=G11+P11C10= G11+ P11G10+ P11P10G9+ P11P10 P9 G8+ P11P10 P9P8C7
最高数值位与符号位相同，此时尾数连续左移，直到最高数值位与符号位的值不同为止。同时从E中减去移位的位数，这称之为“向左规格化”，简称“左规”。
4.舍入
右规或对阶时尾数低位上的数值会移掉，使数值精度受影响，常用“0”舍“1”入法。当移掉的最高位为1时，在尾数的末位加 1，如果加1后又使尾数溢出，则要进行右规。

八位串行加法器

八位串行加法器实验内容：设计一个8位串行加法器，并将计算结果转换为十进制数在数码管上进行显示。

实现电路图：前言8位二进制加法器，它的功能主要是实现两个8位二进制数的相加，其结果的范围应该在00000000到111111110之间，即000到510之间。

那么我们如何设计一个8位二进制加法器呢？在实际应用中，我们通常输入的是十进制数，一个八位二进制数所对应的最大的十进制数是255，于是输入两个范围在000到255之间的数，首先通过二-十进制编码器将输入的三位十进制数的个位、十位、百位分别转换为8421BCD码，得到两个十二位字码，再通过加法器将它们相加，逢10进1，得到一个新的十二位字码，再用7447数字显示译码器将这个十二位字码还原到原来的三位十进制数。

最后输出的就是一个三位十进制数，其范围在000到510之间。

通过上述方法我们实现了八位二进制数的相加，从而达到了题目的要求。

为实现上述目的，我们查阅相关资料。

通过查阅，理解以及加以运用，我们认识到了收集资料的不易性，但同时也得到了不少收获，可以说是有苦有甜。

同时，虽然我们基本设计出了这个八位二进制加法器，但是不必可避免地会产生一些问题，比如说在连线上可能有更简便的途径，在元件的选用上可能还有其它更简便的方法，在控制上可能还不够精简，等等。

我们希望在以后的实践中能找出更好的方法，也希望能吸取这次设计中的不足，逐渐改善。

另外，在电子设计的过程中，与同组同学之间的合作配和是十分重要的。

本次课程设计介绍了一种基于数字电子技术的八位二进制加法器,实现了如下功能:1、八位二进制加数与被加数输入2、三位数码管显示3、三位十进制加数与被加数的输入该电路系统主要分为八位二进制加法器和三位十进制加法器两个系统4个模块组成：八位二进制加法器系统由①二进制输入电路②二进制加法运算电路③二进制码到十进制8421BCD码的转换电路④三位数码管显示输出三位十进制加法器系统由3个模块组成②进制的输入电路②三位十进制8421BCD码加法运算电路③四位数码管显示输出。

Verilog实现的4位串行进位加法器

Verilog实现的4位串行进位加法器以下是一个使用Verilog语言实现的4位串行进位加法器的示例代码：```verilogmodule serial_carry_adder(input wire clk, reset, input wirea0, b0, a1, b1, a2, b2, a3, b3, input wire cin, output wire cout, output wire [3:0] sum);reg [3:0] s;reg c;if (reset)s<=4'b0;else begins<={s[2:0],a0^b0^c};c<=(a0&b0)，(a0&c)，(b0&c);endendassign sum = s;assign cout = c;endmodule```这个示例代码中，定义了一个名为`serial_carry_adder`的模块，包含了输入端口`clk`（时钟信号）、`reset`（复位信号）、`a0`、`b0`、`a1`、`b1`、`a2`、`b2`、`a3`、`b3`（4位加数和被加数的各位）、`cin`（进位输入）、以及输出端口`cout`（进位输出）和`sum`（和）。

在`always`块中，根据时钟信号和复位信号的边沿变化来更新和`s`和进位输出`c`的值。

当复位信号为高电平时，和`s`被清零；否则，和`s`的值是上一次和的低3位与当前的加法和（即`a0`、`b0`和进位`c`的异或结果）拼接而成，进位输出`c`的值则根据加法和的三个输入的与运算和或运算结果来决定。

最后，使用`assign`语句将和`s`和进位输出`c`分别赋值给输出端口`sum`和`cout`。

这个模块可以通过在顶层模块中实例化并连接适当的时钟、复位、输入和输出信号来使用。

四位串行进位加法器设计教学文稿

四位串行进位加法器设计集成电路CAD课程设计报告四位串行加法器设计1串行进位加法器简介1.1加法器实现多为二进制数相加的电路，称为加法器。

根据进位方式不同，有串行进位加法器和超前进位加法器之分。

采用串行进位方式，优点是电路简单，连接方便；缺点是运算速度不高。

原理：把四个全加器（例如两片74LS183）依次级联起来，便可构成四位串行进位加法器。

因此四位串行进位加法器的设计可以分以下两步进行：（1）全加器设计；（2）将全加器级联，构成四位串行进位加法器（a）（b）图（1）四位串行加法器74831.2 图2为四位串行加法器7483逻辑图图（2）四位串行加法器2 四位串行进位加法器的设计实现：2.1 输出级电路设计与TTL电路兼容驱动10个TTL①输出高电平时｜IoH｜<=20ｕＡ VoHmin=4.4V②输出低点平时｜IoH｜<=20mＡ VoHmax=0.4V③输出级充放电时间tr=tf计算电路如图3所示①以15个PF 的电容负载代替10个TTL 电路来计算tr 、tf ②输入V 为的前一级的输出被认为是理想的输出，即：ViL=Vss,ViH=Vdd③计算电流时，负载为电流负载，有拉电流的灌电流。

图3（1）CMOS N 管（W/L ）N 的计算：当输入为高电平时（Vi=Vdd ）,N 管导通后级TTL 电路有较大的灌电流输入，此时（表示成对称形式）使方括号中的值和栅电容Cox 及电子迁移率un 为最小值:o u t00f f[]200200)()(2V V V V V V C L W I tn i s tn ox N n dsn -----⎪⎭⎫ ⎝⎛=μm ax0m in 2ox SiO ox t C εε=(2) CMOS P 管（W/P ）p 的计算｜IoH ｜<=20ｕＡ时有 VoHmin=4.4Vtr=tf① 以Ioh<=20ｕＡ时VoHmin=4.4V 的条件计算最坏的情况下Vdd=4.5V,Vohmin=4.4v,Vtp=0.8V,230m ax 0m in -⎪⎪⎭⎫ ⎝⎛=T T n n μμ∆∆===⎪⎭⎫ ⎝⎛233034956.164m in n L W []202)()(2oh tp i dd tp i ox p p oh V V V V V V C L W I -----⎪⎭⎫ ⎝⎛=μm ax 0m in 2ox SiO ox t C εε=230m ax 0m in -⎪⎪⎭⎫ ⎝⎛=T T n p μμ经计算可得②tr=tp 的条件计算：CMOS 中αp=αn所以 ∆∆===⎪⎭⎫ ⎝⎛21532227.7pL W dd tp p V V =αddtn n V V =αdd p L p V k C =τ()⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡-⎪⎪⎭⎫ ⎝⎛--+--=p n n n n f arth t αααατ111.011)1.0(2p p n n p n n p f r L W L W k k t tμμττ⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛===⎪⎪⎭⎫ ⎝⎛∆∆===⎪⎭⎫ ⎝⎛233034956.164minn L W ∆∆==⎪⎭⎫ ⎝⎛275931138minn L W2.2 输入级设计输入电平Vih 可能为2.4V（1）拉管P2为了节省面积，同时又能使Vih 较快上升，取图4(2)CMOS 反向器的P1管此P1管应取内部基本反向器的尺寸∆===⎪⎭ ⎝236.164minn L ∆∆===⎪⎭⎫ ⎝⎛223312p L W∆∆==⎪⎭⎫ ⎝⎛231.546内p L W（3）CMOS 反相器的N 管TTL 的输出电平在0.4-2.4之间V1*=ViLmax+Vihmin=1.4V式中βk=kn/kp,Vdd=5V,Vtn=0.7V,Vi*=1.4V, βk=17.162.3 内部基本反相器中各MOS 管尺寸的计算内部反相器的负载电容：①本级漏极的PN 结电容Cpn1K k V V k V p n TP DD p *I+++=+++=R TP DD TN R TN N V V V V k ββ）（∆∆=⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛2230W n p R plnl L L W μμβ∆∆==⎪⎭⎫ ⎝⎛22303345nl L W ∆∆==⎪⎭⎫ ⎝⎛231.546plL W ∆∆===⎪⎭⎫ ⎝⎛223312p L W②下级的栅电容Cc1③连线杂散电容CsCpn+Cc1=10CsCs :铝线宽5um,长100um ，在场区上面，此铝线的电容为Cpn 和Cl ：N 管其衬底是P 型，所以 NB=2⨯1016 cm-3设结深Xi=0.5um R □=20Ω/□对于P 管Cpn= )(10726.1100.19.31085.8101005C 14482014F t A s oxF SiO Al ---⨯=⨯⨯⨯⨯⨯⨯==-εεϕεε2021021C C p jn n jp Si qN C jpn ===++2l n iB n N N q k T =ϕ318õ10862.7R 1N -⨯==cm x q j μ28/10195.2cm F C p jN -+⨯=28/101396.1cm F C N jP -+⨯=Cp n Cn p+++而CC1可以由：Cc1=10Cs-Cpn求出。

组合逻辑电路(加法器)

Ci m3 m5 Ai Bi ( Ai Bi )Ci 1 Ai Bi
全加器的逻辑图和逻辑符号
Si m1 m2 m4 m7 Ai BiCi 1 Ai BiCi 1 Ai BiCi 1 Ai BiCi 1 Ai ( BiCi 1 BiCi 1 ) Ai ( BiCi 1 BiCi 1 ) Ai ( Bi Ci 1 ) Ai ( Bi Ci 1 ) Ai Bi Ci 1
加法器
半加器和全加器
1、半加器
能对两个1位二进制数进行相加而求得和及进位的逻辑电路称为半加器.
半加器真值表 Ai Bi 0 1 0 1 Si 0 1 1 0 Ci 0 0 0 1
本位的和向高位的进位
Ai Bi
=1
Si Ci
加数
0 0 1 1
&
半加器电路图 Ai Bi ∑
CO
Si Ci
Si Ai Bi Ai Bi Ai Bi Ci Ai Bi
0
0
1
1
被加数/被减数
加数/减数
加减控制
BCD码+0011=余3码
C0-1＝0时，B0=B，电路执行A+B运算；当C0-1＝1 时，B1=B，电路执行A －B=A+B运算。
3、二-十进制加法器
修正条件 C C3 S3S2 S3S1
8421 BCD 输出 S3 ' S2 ' S1 ' S0' 4 位二进制加法器 C0-1 A1 A0 B3 B2 B1 B0
4位超前进位加法器递推公式
S 2 P2 C1 1G0 P 2P 1P 0C0 1 C2 G2 P2C1 G2 P2G1 P2 P S3 P3 C2 1G0 P 3P 2P 1P 0C0 1 C3 G3 P3C2 G3 P3G2 P3 P2G1 P3 P2 P

串行加法器和并行加法器工作原理

串行加法器和并行加法器工作原理
串行加法器和并行加法器是数字电路中常用的加法器。

它们的工作原理如下：
1. 串行加法器是采用逐位相加的方式来实现加法运算。

它从最低位（最右端）开始，逐位将两个加数和进位相加，得到当前位的和与进位。

然后将当前位的和输出，并将进位传递给下一位。

这样依次循环，直到最高位（最左端）计算完毕。

串行加法器的速度较慢，因为需要按位逐个计算。

2. 并行加法器是将所有位的运算同时进行，以提高计算速度。

它将加法器拆分成多个子加法器，每个子加法器负责计算一位的和。

每个子加法器同时接收两个加数的对应位和进位，并输出当前位的和与进位。

这样所有子加法器的输出可以同时得到，并且通过电路连接，将进位传递给下一位的子加法器。

并行加法器的速度较快，因为可以同时计算多个位。

总而言之，串行加法器是按位逐个计算的，速度较慢；而并行加法器是同时计算多个位的和，速度较快。

(完整版)计算机组成原理知识点总结

第2章数据的表示和运算主要内容：（一）数据信息的表示1.数据的表示2.真值和机器数（二）定点数的表示和运算1.定点数的表示：无符号数的表示；有符号数的表示。

2.定点数的运算：定点数的位移运算；原码定点数的加/减运算；补码定点数的加/减运算；定点数的乘/除运算；溢出概念和判别方法。

（三）浮点数的表示和运算1.浮点数的表示：浮点数的表示范围；IEEE754标准2.浮点数的加/减运算（四）算术逻辑单元ALU1.串行加法器和并行加法器2.算术逻辑单元ALU的功能和机构2.3 浮点数的表示和运算2.3.1 浮点数的表示（1）浮点数的表示范围•浮点数是指小数点位置可浮动的数据，通常以下式表示：N=M·RE其中，N为浮点数，M为尾数，E为阶码，R称为“阶的基数（底）”，而且R为一常数，一般为2、8或16。

在一台计算机中，所有数据的R都是相同的，于是不需要在每个数据中表示出来。

浮点数的机内表示浮点数真值：N=M ×2E浮点数的一般机器格式：数符阶符阶码值 . 尾数值1位1位n位m位•Ms是尾数的符号位，设置在最高位上。

•E为阶码，有n+1位，一般为整数，其中有一位符号位EJ，设置在E的最高位上，用来表示正阶或负阶。

•M为尾数，有m位，为一个定点小数。

Ms=0，表示正号，Ms=1，表示负。

•为了保证数据精度，尾数通常用规格化形式表示：当R＝2，且尾数值不为0时，其绝对值大于或等于0.5。

对非规格化浮点数，通过将尾数左移或右移，并修改阶码值使之满足规格化要求。

浮点数的机内表示阶码通常为定点整数，补码或移码表示。

其位数决定数值范围。

阶符表示数的大小。

尾数通常为定点小数，原码或补码表示。

其位数决定数的精度。

数符表示数的正负。

浮点数的规格化字长固定的情况下提高表示精度的措施：•增加尾数位数（但数值范围减小）•采用浮点规格化形式尾数规格化：1/2≤M <1 最高有效位绝对值为1浮点数规格化方法：调整阶码使尾数满足下列关系：•尾数为原码表示时，无论正负应满足1/2 ≤M <1即：小数点后的第一位数一定要为1。

串行进位加法器原理

串行进位加法器原理
串行进位加法器是一种通过串行方式逐位进行加法运算并传递进位的电路。

它用于实现大型数字加法器中的高速运算。

下面是串行进位加法器的一般原理：
1. 输入：串行进位加法器有两组输入，分别是被加数（A）和加数（B）。

每个输入位都通过时钟信号逐位输入。

2. 加法器：串行进位加法器使用逐位加法器，每个逐位加法器负责实现单独位的加法运算。

3. 进位传递：串行进位加法器中最重要的部分是进位传递逻辑。

每个逐位加法器会生成一个局部进位（Carry-out）信号，表示该位的进位情况。

4. 串行运算：串行进位加法器从最低有效位（LSB）开始，通过时钟信号按位进行加法运算。

每个逐位加法器都将被加数位、加数位和上一位的进位信号作为输入，并输出当前位的和输出位。

5. 进位传递：当一个位的运算结果中产生了进位时，这个进位会被
传递到下一个更高位，成为下一位的输入进位。

这个进位传递过程会一直持续到最高有效位（MSB）。

6. 输出：串行进位加法器的输出是所有位的和输出和最高位的进位
输出。

和输出表示两个数的和，进位输出表示需要进位到更高位的情况。

串行进位加法器通过逐位运算和进位传递实现多位数相加的功能。

它的优点是可以使用较少的硬件资源实现高位数的加法运算。

它广泛应用于数字信号处理、通信系统等需要高速和高精度加法运算的应用中。

8位串行进位加法器

8位串行进位加法器实验报告一、实验目的使对quartus II的使用进行初步的了解，对于一些芯片的组合应用更加掌握。

二、实验内容设计8位串行进位加法器用半加器设计一个全加器元件，然后根据图4-38，在顶层设计中用8个1位全加器构成8位串行进位加法器。

给出时序仿真波形并说明之、引脚锁定编译、编程下载于FPGA中进行硬件测试。

完成实践报告。

三、实验步骤及各步结果1、分析8位串行全加器的层次结构2、半加器3、一位全加器output S,CO;wire S1,D1,D2;halfadder HA1(S1,D1,A,B);halfadder HA2(S,D2,S1,CI);or g1(CO,D2,D1);endmodule//8-bit full addermodule _8bit_adder(S,C7,A,B,C_1);input[7:0]A,B;input C_1;output [7:0]S;output C7;wire C0,C1,C2,C3,C4,C5,C6,C7;fulladderFA0(S[0],C0,A[0],B[0],C_1),FA1(S[1],C1,A[1],B[1],C0),FA2(S[2],C2,A[2],B[2],C1),FA3(S[3],C3,A[3],B[3],C2),FA4(S[4],C4,A[4],B[4],C3),FA5(S[5],C5,A[5],B[5],C4),FA6(S[6],C6,A[6],B[6],C5),FA7(S[7],C7,A[7],B[7],C6);endmodule4、软件使用（1）、新建一个工程，工程名为_8bit_adder(2)、新建一个Verilog HDL File文件并写入程序代码（3）、对写完的代码进行编译，发现没有错误（4）、新建一个波形文件（5）、新建（6）、插入程序后双击输入数值进行数据的输入（7）、输入相应的值（8）、仿真出来的结果（9）、按时序给输入端输入不同的数据（10）、继续仿真，波形如图（11）、时序仿真（12）、放大后这里出现了冒险竞争。

[转]串、并行加法器

[转]串、并⾏加法器转⾃：的百度空间加法器逻辑结构的改进1.全加器(加法单元)加法单元是⼀个三端输⼊，两端输出的加法⽹络·串⾏加法器和并⾏加法器串⾏加法器：只设⼀个全加器称串⾏加法器典型的串⾏加法器只⽤⼀位全加器，由移位寄存器从低位到⾼位串⾏地提供操作数进⾏相加并⾏加法器：让各位数据同时相加，就产⽣了并⾏加法器并⾏加法器解决了同时对数的各位相加，减少了本⾝求和延迟。

但是。

低位向⾼位产⽣的进位却姗姗来迟。

·进位链通常我们将各位之间传递进位信号的逻辑连接构成的进位线路称进位链(1)串⾏进位⽅式：每⼀级进位直接依赖于前⼀级的进位(2)并⾏进位⽅式：从数学的⾓度去掉数据的相关项(3) 分组并⾏进位⽅式：并⾏进位⽅式逻辑表达式没有问题，但是会使得硬件电路结构变得⼗分复杂，⽽且受到元器件前⼊系数的限制，使得完全采⽤并⾏⽅式变得不现实。

所以进⾏分组并⾏进位⽅式，具体做法如下：设加法器字长16位，每4位为⼀组，则可将进位链分成两级，第⼀级在⼩组内采⽤并⾏进位链，第⼆级在⼩组间并⾏进位链串⾏加法器和并⾏加法器加法器是算术逻辑单元的重要组成部分，它是⼀种⽤于加法运算的器件，其本⾝主要由全加器再配以其他必要的逻辑电路组成，根据组成加法器的全加器个数，可以将加法器分为串⾏加法器和并⾏加法器。

1．串⾏加法器在串⾏加法器中，只有⼀个全加器，数据逐位串⾏送⼊加法器进⾏运算，如图2-15所⽰。

图中FA是全加器，A、B是两个具有右移功能的寄存器，C为进位触发器。

由移位寄存器从低位到⾼位逐位串⾏提供操作数相加。

如果操作数长n位，加法就要分n次进⾏，每次产⽣⼀位和，并串⾏地送回A寄存器。

进位触发器⽤来寄存进位信号，以便参与下⼀次的运算。

串⾏加法器具有器件少、成本低的优点，但运算速度太慢，所以除去某些低速的专⽤运算器外很少采⽤。

2．并⾏加法器并⾏加法器由多个全加器组成，其全加器个数的多少取决于机器的字长，由于并⾏加法器可同时对数据的各位相加，读者可能会认为数据的各位能同时运算，其实并不是这样的。

利用原理图输入法实现4位串行进位加法器

VHDL（一）模拟部分电子线路仿真实验报告实验名称：软件和实验箱介绍姓名：申红霞学号： 080404108班级： 08通信一班时间： 10.02南京理工大学紫金学院电光系一、实验目的1.讲解QuartusⅡ软件和实验箱的使用。

2.利用原理图输入法实现4位串行进位加法器。

3.重点掌握软件使用过程中工程建立、原理图输入方法、编译、仿真、管脚配置等。

二、实验原理1.加法器原理全加器真值表如图1所示：加法器真值表全加器表达式为：Si=Ai⊕Bi⊕Ci-1Ci=（Ai⊕Bi）Ci-1+AiBi全加器逻辑符号如图2所示：全加器逻辑符号2.利用全加器可以构成4位串行进位加法器，逻辑符号如图3所示：4位串行进位加法器逻辑符号图三、实验内容1.新建文件夹，在所新建的文件夹中利用QuartusⅡ软件建立新工程，设计原理图输入的一位全加器电路，如图4所示：图4、一位全加器电路2.对该图进行全编译，编译成功后，建立矢量波形文件，验证所设计的一位全加器电路的正确性，时序仿真结果和功能仿真结果如下图所示：图5、时序仿真结果图6、功能仿真结果由仿真波形分析可知，该全加器设计正确。

3.将设计好的全加器生成一个模块，如图7所示：图7、一位全加器器件4.将4个全加器串联,再添加相应的管脚和原件构成四位串行进位加法器，如图8所示:图8、四位串行进位加法器电路图5．将此文件设置为顶层文件，对该图进行全编译，编译成功后，建立矢量波形文件，添加相应的节点，为输入信号赋初值，功能仿真结果和时序仿真结果如下图：图9、功能仿真结果图10、时序仿真结果由仿真波形可知，电路设计正确。

6．利用模式实验箱来验证设计电路的正确性，设置管脚，管脚配置图如图11所示：图11、管脚配置图配置好使用管脚后，器件上未使用管脚也需进行设置，将它们设置为高阻状态。

7．管脚配置完，一定要重新编译一次。

编译后如图12所示：图12、配置管脚后电路图8．下载到实验箱中，对实验箱进行操作，验证电路是否正确。

数字系统设计实验---32位串行加法器实验综述

Port ( a : in STD_LOGIC; b : in STD_LOGIC; cin : in STD_LOGIC; s : out STD_LOGIC; cout : out STD_LOGIC); end component; component DFF is ---------------D 触发器 Port ( D : in STD_LOGIC; clk : in STD_LOGIC; rst,CE : in STD_LOGIC; Q: out STD_LOGIC); end component; signal Sh,load,Xi,Yi,Si,cin,sum,cout:std_logic; -----中间变量 begin A1: controller port map(clk,n,k,Sh,load); A2: registers_jiashu port map(inputB,Sh,load,clk,Yi); A3: registers_add port map(inputA,clk,load,Sh,sum,Xi,outputA); A4: full_adder port map(Xi,Yi,cin,sum,cout); A5: DFF port map (cout,clk,load,Sh,cin); end Behavioral;
------------------控制器------------------------------------------------------------library IEEE; use IEEE.STD_LOGIC_1164.ALL; use ieee.std_logic_unsigned.all; entity controller is Port ( clk : in STD_LOGIC; N : in STD_LOGIC; K,Sh,load : out STD_LOGIC); end controller; architecture Behavioral of controller is signal state,nextstate:integer range 0 to 2; ---设置状态 signal counter:std_logic_vector(4 downto 0); begin process(clk) begin if(clk'event and clk='1') then state<=nextstate; ---上升沿触发启动 end if; end process; process(clk,N) begin if(clk'event and clk='1') then case state is ---设置各状态 when 0 => sh<='0';K<='0';load<='0';counter<="00000"; if N='1' then load<='1'; nextstate<=1; else nextstate<=0; end if; when 1 => sh<='1';K<='0';load<='0'; if counter="11110" then counter<=counter+1; nextstate<=2; else counter<=counter+1; nextstate<=1; end if;