实验标准差和平均值实验标准差
平均值和标准差

平均值和标准差首先,让我们来了解一下平均值和标准差的定义。
平均值,也称为均值,是一组数据所有数值之和除以数据个数所得的结果。
它可以用来表示数据的集中趋势,是最常用的描述数据集中趋势的统计量之一。
而标准差则是一组数据离均值的平均距离的平方根。
它可以用来衡量数据的离散程度,标准差越大,数据的离散程度越大,反之则越小。
接下来,我们来介绍一下平均值和标准差的计算方法。
计算平均值的方法非常简单,只需要将一组数据所有数值之和除以数据个数即可。
而计算标准差的方法则稍显复杂,需要经过多个步骤。
首先,计算每个数据与平均值的差值,然后将这些差值求平方,再将平方后的差值求和,最后再除以数据个数并取平方根,即可得到标准差。
在实际应用中,平均值和标准差都具有重要的意义。
平均值可以帮助我们了解数据的集中趋势,比如一组考试成绩的平均值可以反映出整个班级的学习水平;而标准差则可以帮助我们了解数据的分布情况,比如一组商品的价格标准差可以反映出价格的波动程度。
因此,平均值和标准差在数据分析、科学研究、商业决策等领域都有着重要的应用价值。
最后,让我们来总结一下平均值和标准差在实际应用中的作用。
通过计算平均值和标准差,我们可以更好地理解和描述数据的特征,从而为我们的决策提供更加准确的依据。
比如在财务管理中,我们可以通过计算标准差来衡量投资组合的风险;在医学研究中,我们可以通过计算平均值来评估药物的疗效。
因此,平均值和标准差在实际应用中发挥着不可替代的作用。
综上所述,平均值和标准差是统计学中两个非常重要的概念,它们可以帮助我们更好地理解和描述数据的特征。
通过计算平均值和标准差,我们可以了解数据的集中趋势和离散程度,从而为我们的决策提供更加准确的依据。
希望本文能够帮助读者更好地理解和应用平均值和标准差这两个概念。
实验数据误差分析与数据处理

实验数据误差分析与数据处理在实验中,数据误差是不可避免的,它可能来自于多种各方面的因素,如仪器的不精确性、环境条件的影响、样本变化的随机性等等。
因此,在实验数据分析中需要对误差进行合理的处理和分析。
首先,我们需要了解误差的类型。
误差可以分为系统误差和随机误差两种类型。
系统误差是由不可避免的系统偏差引起的,它会导致实验结果的偏离真实值的方向始终相同。
而随机误差是由于随机因素引起的,它会导致实验结果的波动性,其方向和大小是不确定的。
对于系统误差,我们可以采取一些校正措施来减小或消除它们的影响。
例如,我们可以校正仪器的零点,减少仪器本身的偏差。
另外,我们还可以进行实验重复,然后取平均值来消除系统偏差的影响。
对于随机误差,我们可以采取统计方法来分析和处理。
最常见的方法是计算测量值的平均值和标准差。
平均值可以反映实验结果的中心位置,而标准差可以反映实验结果的散布程度。
如果实验数据符合正态分布,我们可以使用正态分布的性质来计算置信区间,从而确定实验结果的误差范围。
此外,还有其他一些常见的数据处理方法,如线性回归分析、方差分析等。
这些方法可以用于分析变量之间的关系、对比实验组和对照组之间的差异等。
通过这些方法,我们可以从实验数据中获取更多的信息和结论。
最后,我们需要注意数据的合理性和可靠性。
在进行数据处理之前,我们应该首先对实验数据进行筛选和清洗,排除异常值和明显错误的数据。
同时,应该确保实验过程的可重复性和可靠性,提高实验数据的准确性和可信度。
总之,实验数据误差分析与数据处理是实验研究中不可或缺的环节。
通过对数据误差的分析和处理,我们可以更好地理解实验结果的可靠性和准确性,并从中提取有效的信息和结论。
因此,在进行实验研究时,我们应该重视数据误差的分析和处理,以确保实验结果的科学性和可信度。
平均值和标准差

平均值和标准差在统计学中,平均值和标准差是两个常用的统计量,它们可以帮助我们更好地理解数据的分布和变异程度。
本文将对平均值和标准差进行详细介绍,包括它们的定义、计算方法以及在实际应用中的意义和作用。
首先,让我们来看一下平均值。
平均值,也称为均值,是一组数据的总和除以数据的个数。
它是对数据集中心位置的一种度量,可以帮助我们了解数据的集中趋势。
计算平均值的公式如下:\[ \bar{x} = \frac{1}{n} \sum_{i=1}^{n} x_i \]其中,\( \bar{x} \) 表示平均值,\( n \) 表示数据的个数,\( x_i \) 表示第 \( i \) 个数据点。
平均值的计算方法比较简单,只需要将所有数据相加,然后除以数据的个数即可。
它可以帮助我们快速了解数据的集中程度,但在某些情况下,平均值可能会受到极端值的影响,因此在分析数据时需要谨慎对待。
接下来,让我们来介绍标准差。
标准差是一组数据的离散程度的度量,它可以帮助我们了解数据的分散程度和稳定性。
标准差的计算方法如下:\[ s = \sqrt{\frac{1}{n} \sum_{i=1}^{n} (x_i \bar{x})^2} \]其中,\( s \) 表示标准差,\( n \) 表示数据的个数,\( x_i \) 表示第 \( i \) 个数据点,\( \bar{x} \) 表示平均值。
标准差的计算相对复杂一些,需要先计算每个数据点与平均值的差值的平方,然后将其相加并除以数据的个数,最后再取平方根。
标准差越大,表示数据的离散程度越高;标准差越小,表示数据的离散程度越低。
在实际应用中,平均值和标准差经常被用来描述和比较不同数据集的特征。
例如,在财务分析中,我们可以用平均值来表示公司的平均收入或利润水平,用标准差来表示收入或利润的波动程度;在医学研究中,我们可以用平均值来表示患者的平均年龄或体重,用标准差来表示年龄或体重的变异程度。
数学里面标准差是什么意思

数学里面标准差是什么意思数学里面标准差是什么意思?下面是店铺为你整理出来的关于标准差的解释,希望对你学习有所帮助!1计算公式编辑标准差( Standard Deviation),在概率统计中最常使用作为统计分布程度(statistical dispersion)上的测量。
标准差定义是总体各单位标准值与其平均数离差平方的算术平均数的平方根。
它反映组内个体间的离散程度。
测量到分布程度的结果,原则上具有两种性质:为非负数值,与测量资料具有相同单位。
一个总量的标准差或一个随机变量的标准差,及一个子集合样品数的标准差之间,有所差别。
标准计算公式:假设有一组数值X₁,X₂,X₃,......Xn(皆为实数),其平均值( 算术平均值)为μ,公式如图1。
标准差也被称为标准偏差,或者实验标准差,公式为。
简单来说,标准差是一组数据平均值分散程度的一种度量。
一个较大的标准差,代表大部分数值和其平均值之间差异较大;一个较小的标准差,代表这些数值较接近平均值。
例如,两组数的集合 {0,5,9,14} 和 {5,6,8,9} 其平均值都是 7 ,但第二个集合具有较小的标准差。
标准差可以当作不确定性的一种测量。
例如在物理科学中,做重复性测量时,测量数值集合的标准差代表这些测量的精确度。
当要决定测量值是否符合预测值,测量值的标准差占有决定性重要角色:如果测量平均值与预测值相差太远(同时与标准差数值做比较),则认为测量值与预测值互相矛盾。
这很容易理解,因为如果测量值都落在一定数值范围之外,可以合理推论预测值是否正确。
标准差应用于投资上,可作为量度回报稳定性的指标。
标准差数值越大,代表回报远离过去平均数值,回报较不稳定故风险越高。
相反,标准差数值越小,代表回报较为稳定,风险亦较小。
例如,A、B两组各有6位学生参加同一次语文测验,A组的分数为95、85、75、65、55、45,B组的分数为73、72、71、69、68、67。
这两组的平均数都是70,但A组的标准差约为17.08分,B组的标准差约为2.16分,说明A组学生之间的差距要比B组学生之间的差距大得多。
标准差

简介公式标准差也被称为标准偏差,或者实验标准差,公式如图。
简单来说,标准差是一组数据平均值分散程度的一种度量。
一个较大的标准差,代表大部分数值和其平均值之间差异较大;一个较小的标准差,代表这些数值较接近平均值。
例如,两组数的集合 {0, 5, 9, 14} 和 {5, 6, 8, 9} 其平均值都是7 ,但第二个集合具有较小的标准差。
标准差可以当作不确定性的一种测量。
例如在物理科学中,做重复性测量时,测量数值集合的标准差代表这些测量的精确度。
当要决定测量值是否符合预测值,测量值的标准差占有决定性重要角色:如果测量平均值与预测值相差太远(同时与标准差数值做比较),则认为测量值与预测值互相矛盾。
这很容易理解,因为如果测量值都落在一定数值范围之外,可以合理推论预测值是否正确。
标准差应用于投资上,可作为量度回报稳定性的指标。
标准差数值越大,代表回报远离过去平均数值,回报较不稳定故风险越高。
相反,标准差数值越细,代表回报较为稳定,风险亦较小。
例如,A、B两组各有6位学生参加同一次语文测验,A组的分数为95、85、75、65、55、45,B组的分数为73、72、71、69、68、67。
这两组的平均数都是70,但A组的标准差为17.07分,B组的标准差为2.37分(此数据时在R统计软件中运行获得),说明A组学生之间的差距要比B组学生之间的差距大得多。
如是总体,标准差公式根号内除以n如是样本,标准差公式根号内除以(n-1)因为我们大量接触的是样本,所以普遍使用根号内除以(n-1)公式意义所有数减去其平均值的平方和,所得结果除以该组数之个数(或个数减一),再把所得值开根号,所得之数就是这组数据的标准差。
标准差越高,表示实验数据越离散,也就是说越不精确反之,标准差越低,代表实验的数据越精确离散度标准差是反应一组数据离散程度最常用的一种量化形式,是表示精密度的最要指标。
说起标准差首先得搞清楚它出现的目的。
我们使用方法去检测它,但检测方法总是有误差的,所以检测值并不是其真实值。
平均值和标准差

平均值和标准差在统计学中,平均值和标准差是两个重要的概念,它们在描述和分析数据分布和变异性方面起着至关重要的作用。
本文将对平均值和标准差进行详细的介绍和解释,帮助读者更好地理解这两个概念及其在实际应用中的意义。
首先,我们来讨论平均值。
平均值,也称为均值,是一组数据的总和除以数据的个数所得到的值。
它是描述数据集中趋势的一种统计量,通常用来代表数据的集中趋势。
计算平均值的公式为,平均值 = 总和 / 数据个数。
例如,如果我们有一组数据,2, 4, 6, 8, 10,那么这组数据的平均值为(2+4+6+8+10)/5=6。
平均值的计算方法比较简单直观,但它对异常值比较敏感。
当数据中存在异常值时,平均值会受到异常值的影响,不再能够准确地代表数据的集中趋势。
因此,在一些情况下,为了更好地描述数据的集中趋势,我们会使用其他统计量,如中位数和众数。
接下来,我们来讨论标准差。
标准差是衡量数据分散程度的一种统计量,它能够反映数据的离散程度或变异程度。
标准差的计算方法是先求出每个数据与平均值的差值,然后将这些差值的平方求和,再除以数据的个数,最后取平方根。
标准差的计算公式为,标准差 = √[((x1-平均值)^2 + (x2-平均值)^2 + … + (xn-平均值)^2)/n]。
标准差的大小反映了数据的离散程度,标准差越大,数据的离散程度越大;标准差越小,数据的离散程度越小。
在正态分布的情况下,大约68%的数据落在平均值加减一个标准差的范围内,大约95%的数据落在平均值加减两个标准差的范围内,大约99.7%的数据落在平均值加减三个标准差的范围内。
因此,标准差也可以用来判断数据是否符合正态分布。
平均值和标准差在实际应用中有着广泛的用途。
在质量控制中,我们可以使用平均值和标准差来评估产品的质量稳定性;在金融领域,我们可以使用平均值和标准差来评估投资组合的风险和收益;在医学研究中,我们可以使用平均值和标准差来比较不同治疗方法的疗效等等。
大学物理实验数据的有效数字保留方法

⼤学物理实验数据的有效数字保留⽅法
⽂档
⼤学物理实验数据的有效数字保留⽅法
1、测量数据:根据所⽤仪器的最⼩分度,有效数字保留到分度值的下⼀位。
(即估读⼀位,
游标卡尺除外)
2、实验数据的平均值及标准差:保留数字⽐测量数据的数字多⼀位;标准差保留三位有效数字。
(数据保留均采⽤四舍六⼊、五凑偶原则)
3、A类和B类不确定度:均保留三位有效数字。
(数据保留均采⽤⾮零即进原则)
4、合成不确定度:当数据的⾸位数字⼤于或等于三时,取⼀位有效数字;当数据的⾸位数字⼩于三时,去两位有效数字。
(数据保留采取⾮零即进的原则)
5、由测量得出的所测物理量的测量结果:该数据为平均值和合成不确定度的加减关系,此时平均值的数字的保留要与合成不确定度保持末位对齐。
6、由测量数据间接得出的数据的平均值:数字保留应与所测数据的最少的有效数字保持⼀致。
7、相对不确定度:保留三位有效数字。
(数据保留⽤⾮零即进原则)
8、有所测数据间接得出的物理量的不确定度:当⾸位数字⼤于或等于三时,取⼀位有效数字;当数据的⾸位数字⼩于三时,去两位有效数字。
(数据保留采取⾮零即进的原则)
9、所求物理量的测量结果:应为⽤所测数据计算出的平均值与其对应的不确定度的加减关系。
此时平均值的数字的保留要与合成不确定度保持末位对齐。
10、相对误差:当数据的百分数的⾸位数字⼤于⼀时,保留整数位;当数据的百分数的⾸位数字⼩于⼀时,保留⼀位有效数字。
(数据保留采取⾮零即进的原则)。
算术平均值的实验标准差和单次测量值的实验标准差的区别

一、问题的提出在不等精度直接测量时,由各测量值x i及其σi计算加权算术平均值的时,有两个计算公式式中:p i——各测量值的权;σi——各测量值的标准差;σ——单位权标准差;——加权算术平均值的标准差。
但这两个公式的计算结果有时会相差很大。
那么,在这种情况下,采用哪个公式更为合理呢本文对此从公式的推导到公式的选用进行探讨,并给出了一般性的原则。
二、公式的数学推导在不等精度测量时,各测量值的权的定义式为:测量结果的最佳估计值为:则测量结果的不确定度评定为:对式(5)求方差有设各测量值x i的方差都存在,且已知分别为,即D(x i)=由(4)式有=σ2/p i从公式(1)的推导,我们可以看出,此时各测量值的方差(或标准差)必须是已知的。
而在实际测量中,常常各测量值的方差(或标准差)是未知的,无法直接应用公式(1)进行不确定度评定。
但是,从分析来看,如果能由各测量值的残差(其权等于测量值的权)求出单位权标准差的估计值,并将其代入公式(1)中,就可计算出加权算术平均值标准差的估计值。
为此,作如下推导:由残差νi=x i-i=1,2,……n对νi单位权化由于v i的权都相等,因而可设为1,故用v i代替贝塞尔公式中的ν可得单位权标准差的估计值i将此式代入公式(1),即得到加权算术平均值标准差的估计值从上面的推导我们可以看出,公式(1)是在各测量值的标准差已知时计算出的不等精度测量结果的不确定度的准确值;而公式(2)是在各测量值的标准差未知时计算出的不等精度测量结果的不确定度的估计值。
从概率论与数理统计知识可知,只有在n→∞时,其单位权标准差的估计值才能等于单位权的标准差,而由于测量次数的有限性和随机抽样取值的分散性,这两者是不相等的,所以由公式(1)和公式(2)确定的不确定度的值是也不相同的。
三、公式选用的一般原则笔者用了较大的篇幅来进行公式的数学推导,主要是为了说明这两个公式推导的前提是不一样的,其应用当然也就不同。
算术平均值的实验标准差和单次测量值的实验标准差的区别

一、问题的提出在不等精度直接测量时,由各测量值x i及其标准差σi计算加权算术平均值的标准差时,有两个计算公式式中:p i——各测量值的权;σi—-各测量值的标准差;σ-—单位权标准差;——加权算术平均值的标准差。
但这两个公式的计算结果有时会相差很大。
那么,在这种情况下,采用哪个公式更为合理呢?本文对此从公式的推导到公式的选用进行探讨,并给出了一般性的原则。
二、公式的数学推导在不等精度测量时,各测量值的权的定义式为:测量结果的最佳估计值为:则测量结果的不确定度评定为:对式(5)求方差有设各测量值x i的方差都存在,且已知分别为,即D(x i)=由(4)式有=σ2/p i从公式(1)的推导,我们可以看出,此时各测量值的方差(或标准差)必须是已知的.而在实际测量中,常常各测量值的方差(或标准差)是未知的,无法直接应用公式(1)进行不确定度评定。
但是,从分析来看,如果能由各测量值的残差(其权等于测量值的权)求出单位权标准差的估计值,并将其代入公式(1)中,就可计算出加权算术平均值标准差的估计值.为此,作如下推导:由残差νi=x i—i=1,2,……n对νi单位权化由于v i的权都相等,因而可设为1,故用v i代替贝塞尔公式中的ν可得单位权标准差的估计值i将此式代入公式(1),即得到加权算术平均值标准差的估计值从上面的推导我们可以看出,公式(1)是在各测量值的标准差已知时计算出的不等精度测量结果的不确定度的准确值;而公式(2)是在各测量值的标准差未知时计算出的不等精度测量结果的不确定度的估计值.从概率论与数理统计知识可知,只有在n→∞时,其单位权标准差的估计值才能等于单位权的标准差,而由于测量次数的有限性和随机抽样取值的分散性,这两者是不相等的,所以由公式(1)和公式(2)确定的不确定度的值是也不相同的.三、公式选用的一般原则笔者用了较大的篇幅来进行公式的数学推导,主要是为了说明这两个公式推导的前提是不一样的,其应用当然也就不同.我们分两种情况来进行讨论。
标准差和平均值的计算公式

标准差和平均值的计算公式标准差和平均值这两个概念,在咱们的数学学习中可是相当重要的!它们能帮我们更好地理解数据的分布和集中趋势。
平均值,简单来说就是一组数据的“平均水平”。
比如说,咱们班这次数学考试的成绩分别是 85 分、90 分、78 分、95 分和 88 分。
那这组数据的平均值怎么算呢?就是把这几个分数加起来,然后除以数据的个数。
也就是(85 + 90 + 78 + 95 + 88)÷ 5 = 86.6 分,这个 86.6 分就是这组数据的平均值啦。
再来说说标准差。
标准差反映的是数据的离散程度。
还是拿刚刚考试成绩的例子来说,假如这几个同学的成绩分别是 60 分、70 分、80 分、90 分和 100 分,那这组数据的离散程度就比较大。
计算标准差的公式稍微复杂一点,但也别害怕。
我记得有一次给学生们讲这个知识点的时候,有个特别调皮的小家伙一脸迷茫地问我:“老师,这标准差和平均值到底有啥用啊?我们生活中又用不到!”我笑着回答他:“你想想看呀,假如你去买苹果,一家水果店的苹果大小差不多,重量的平均值是 200 克,标准差很小;另一家的苹果大小参差不齐,平均值也是 200 克,但标准差很大。
那你会选哪家的苹果呢?”这小家伙眨巴眨巴眼睛,好像突然明白了。
咱们接着说标准差的计算公式。
首先要算出每个数据与平均值的差值,然后把这些差值平方,再求这些平方值的平均值,最后开平方就得到标准差啦。
举个具体的例子,有一组数据3,5,7,9,11。
它们的平均值是7。
那每个数与 7 的差值分别是 -4,-2,0,2,4。
平方之后就是 16,4,0,4,16。
这些平方值的平均值是(16 + 4 + 0 + 4 + 16)÷ 5 = 8 。
最后开平方,标准差就约等于 2.83 。
在实际应用中,标准差和平均值经常一起出现。
比如说在工厂生产零件的时候,通过测量零件的尺寸,计算平均值和标准差,可以判断生产过程是否稳定。
算术平均值的实验标准差和单次测量值的实验标准差的区别

一、问题的提出在不等精度直接测量时,由各测量值x i及其标准差σi计算加权算术平均值的标准差时,有两个计算公式式中:p i——各测量值的权;σi——各测量值的标准差;σ——单位权标准差;——加权算术平均值的标准差。
但这两个公式的计算结果有时会相差很大。
那么,在这种情况下,采用哪个公式更为合理呢?本文对此从公式的推导到公式的选用进行探讨,并给出了一般性的原则。
二、公式的数学推导在不等精度测量时,各测量值的权的定义式为:测量结果的最佳估计值为:则测量结果的不确定度评定为:对式(5)求方差有设各测量值x i的方差都存在,且已知分别为,即D(x i)=由(4)式有=σ2/p i从公式(1)的推导,我们可以看出,此时各测量值的方差(或标准差)必须是已知的。
而在实际测量中,常常各测量值的方差(或标准差)是未知的,无法直接应用公式(1)进行不确定度评定。
但是,从分析来看,如果能由各测量值的残差(其权等于测量值的权)求出单位权标准差的估计值,并将其代入公式(1)中,就可计算出加权算术平均值标准差的估计值。
为此,作如下推导:由残差νi=x i-i=1,2,……n对νi单位权化由于v i的权都相等,因而可设为1,故用v i代替贝塞尔公式中的ν可得单位权标准差的估计值i将此式代入公式(1),即得到加权算术平均值标准差的估计值从上面的推导我们可以看出,公式(1)是在各测量值的标准差已知时计算出的不等精度测量结果的不确定度的准确值;而公式(2)是在各测量值的标准差未知时计算出的不等精度测量结果的不确定度的估计值。
从概率论与数理统计知识可知,只有在n→∞时,其单位权标准差的估计值才能等于单位权的标准差,而由于测量次数的有限性和随机抽样取值的分散性,这两者是不相等的,所以由公式(1)和公式(2)确定的不确定度的值是也不相同的。
三、公式选用的一般原则笔者用了较大的篇幅来进行公式的数学推导,主要是为了说明这两个公式推导的前提是不一样的,其应用当然也就不同。
均值、方差、标准差

87 112 94 94 99 90 120 98 95 119
108 100 96 115 111 104 95 108 111 105
104 107 119 107 93 102 98 112 112 99
92 102 93
85 90 80 80 85 75 100 计算这组样本数据的极差、方差和标准差.
例2.甲、乙两种水稻试验品种连续5年的平均单位 面积产量如下(单位:t/hm2),试根据这组数据估 计哪一种水稻品种的产量比较稳定。
品种 第1年 第2年 第3年 第4年 第5年
甲
9.8 9.9 10.1 10 10.2
1500元,平均月工资怎么能是1695元呢?”经理拿出
如下表所示的工资表说:“你看,平均周工资就是
1695元。”
某公司内部结构以及工资分布:
人员 经理 管理人员 技工 工人 学徒 合计
月工资 11000 1250 1100 1000 500
人数 1
6
5 10 10 23
在这个问题中,总体月平均数能客观地反映工人的 月工资水平吗?为什么?
收入范围
所占百分 比
10000 至 15000 10%
15000 至 20000 15%
20000 至 25000 20%
25000 至 30000 25%
30000 至 35000 15%
35000 至 40000 10%
40000 至 50000
5%
平均数的计算方法:
(1)定义法:已知 x1,x2,x3,…,xn 为某样本的 n 个数据,则这 n 个数据的平均数为: x = x1+x2+xn3+…+xn.
偏差、标准偏差等概念

偏差、标准偏差、实验标准偏差一、 偏差(deviation )定义为一个值减去其参考值1。
二、标准偏差(standard deviation )又称总体标准偏差(population standard deviation ),以σ表示,计算公式为: ()n x n i i ∑=-=12μσ (1)式中,μ为总体均值(见式1-1);n 为重复测量次数,且n →∞。
σ也称为真标准偏差,表示在这一给定条件下,n 个xi 中任意一个结果的偏差,即共同的偏差,其含义为n 个xi 的分散性,表达分散构成的一个区间。
由于n →∞,因此它只能是统计学上的一个概念。
三、实验标准偏差(experimental standard deviation )指给定的测量条件下,对同一被测量Q 进行n 次测量,得到n 个测量结果xi (i=1,2,3,…,n ),按下式计算得出的表示测量结果分散性的一个参数,以s 表示:()112--=∑=n x x s n i i (2)1 定义中的“一个值”与“参考值”分别是什么?有各种不同的情况。
分述如下:①对实物量具来说,如砝码,可以其标称值为“参考值”,而制造出的质量是“一个值”。
这时的偏差即制造的偏差。
②在某给定条件下,对某量Q 进行了若干次重复检测,某一测定结果q k 减去其平均值q ,也就是一种偏差,即对平均值的偏差。
③以Q 的约定真值作为参考值,测量结果作“一个值”,则偏差为该测量结果误差的估计,甚至有“系统偏差”、“随机偏差”的概念。
日前习惯上多使用第二种偏差。
式中n-1统计学中称自由度2,一般以v 表示。
s 的含义为任一次测量结果xi 的实验标准偏差,它是总体标准偏差σ的一个估计值。
这个估计值随所测量次数n 的增加而变得更加可靠。
式(1-9)计算过程相对复杂,实际计算时可用下面的等效公式代替: ()1212--=∑∑n x x s i n i (3)四、其它常用的各种偏差1. 绝对偏差指一次测量结果与样本均值之差,以di 表示。
实验数据误差分析与数据处理

实验数据误差分析与数据处理实验数据误差分析主要包括两个方面:系统误差和随机误差。
系统误差是由于实验仪器、实验方法或实验条件等产生的固定的、有方向性的误差,它的大小和方向在一定范围内是恒定的。
而随机误差是由于实验过程中的偶然性因素导致的误差,其大小和方向是随机的。
对于系统误差,我们可以通过改进实验仪器或实验方法来减小其影响;对于随机误差,我们可以通过多次实验取平均值或者进行统计处理来减小其影响。
在数据处理中,我们常用的方法有拟合曲线、计算平均值和标准差等。
拟合曲线方法主要用于实验数据呈现出一定的规律性和趋势性时,通过曲线拟合来找到其中的关系式,并预测出实验数据在其他条件下的取值。
计算平均值和标准差方法主要用于对大量实验数据进行统计处理。
平均值可以反映实验结果的集中趋势,而标准差则可以反映实验结果的离散程度。
当我们得到一组实验数据时,可以计算其平均值和标准差,并通过比较不同组数据的平均值和标准差,来判断实验结果的可靠性和误差的大小。
另外,还有一些常用的统计学方法和误差分析方法可以用于数据处理,例如方差分析法、卡方检验法、t检验法等。
方差分析法适用于多组实验数据之间的比较,可以通过分析组间和组内的方差来判断实验结果是否显著。
卡方检验法适用于对分类数据的处理,可以通过比较实际观测频数和理论计算频数的差异来判断数据是否符合其中一种假设。
t检验法适用于小样本数据的处理,可以通过比较样本均值和总体均值之间的差异来判断数据是否显著。
在进行数据处理之前,我们还需要对实验数据进行合理的选择和处理。
首先,要注意选择适当的实验方法和仪器,以确保实验数据的准确性和可靠性。
其次,要注意采样的代表性,即所选样本应该具有一定的代表性,能够反映出总体的特征。
此外,还要注意避免数据中的异常值或者异常结果对数据处理的影响,可以通过排除异常值或者重新进行实验来解决。
平均值和标准差的关系

平均值和标准差的关系在统计学中,平均值和标准差是两个常用的统计量,它们可以帮助我们更好地理解数据的分布和变化情况。
本文将探讨平均值和标准差之间的关系,以及它们在统计分析中的作用。
首先,让我们来了解一下平均值和标准差分别代表什么意思。
平均值是一组数据的总和除以数据的个数,它代表了数据的集中趋势,可以帮助我们了解数据的中心位置。
而标准差则是一组数据与其平均值的偏差的平方的平均数的平方根,它代表了数据的离散程度,可以帮助我们了解数据的分散程度。
平均值和标准差之间的关系可以通过以下几点来说明:1. 平均值和标准差都是用来描述数据分布的统计量,它们之间存在密切的关联。
在一定程度上,平均值可以代表数据的集中趋势,而标准差可以代表数据的离散程度。
当数据的平均值较大时,标准差通常也会较大;反之,当数据的平均值较小时,标准差通常也会较小。
2. 在正态分布的情况下,平均值和标准差之间存在着特定的关系。
正态分布是一种对称的、钟形的概率分布,其均值和标准差可以完全描述这种分布的特征。
具体来说,大约68%的数据落在均值加减一个标准差的范围内,大约95%的数据落在均值加减两个标准差的范围内,大约99.7%的数据落在均值加减三个标准差的范围内。
这个规律被称为“三个标准差原则”,它说明了在正态分布下,标准差可以帮助我们更好地理解数据的分布情况。
3. 平均值和标准差还可以一起用来比较不同数据集之间的差异。
通过比较两个数据集的平均值和标准差,我们可以了解它们的集中趋势和离散程度,从而判断它们之间的相似性和差异性。
在实际的统计分析中,平均值和标准差经常被用来描述和分析数据的特征。
通过对数据的平均值和标准差进行计算和分析,我们可以更好地理解数据的分布情况,从而进行更深入的统计推断和决策分析。
总之,平均值和标准差之间存在着密切的关系,它们可以帮助我们更好地理解数据的分布和变化情况。
在统计分析中,我们可以通过对平均值和标准差的计算和分析,来揭示数据的特征和规律,从而为决策提供更可靠的依据。
平均值的实验标准差

平均值的实验标准差在统计学中,平均值和标准差是两个重要的概念,它们可以帮助我们更好地理解数据的分布和变化程度。
本文将重点讨论平均值的实验标准差,以及如何计算和解释这一指标。
平均值是一组数据的总和除以数据的个数,它代表了这组数据的中心位置。
在实际应用中,平均值经常被用来描述一组数据的集中趋势。
然而,仅仅知道平均值并不能完全揭示数据的特征,因为它无法反映数据的分散程度。
这时候,我们就需要用到标准差这一指标。
标准差是一组数据与其平均值的偏离程度的平方的平均数的平方根。
它代表了数据的离散程度,即数据的波动范围。
标准差越大,数据的波动范围越广;标准差越小,数据的波动范围越窄。
通过计算标准差,我们可以更好地了解数据的分散情况,从而更准确地描述数据的特征。
在实验中,我们通常会进行多次测量或观察,得到一系列的数据。
这些数据可能会存在一定的波动,因此我们需要计算实验数据的平均值和标准差,以便更好地理解实验结果。
下面,我们将介绍如何计算实验数据的平均值和标准差,并解释这些指标的意义。
首先,我们需要计算实验数据的平均值。
假设我们进行了n次实验,得到了n 组数据,分别为x1, x2, ..., xn。
那么这些数据的平均值可以用下式表示:平均值 = (x1 + x2 + ... + xn) / n。
接下来,我们计算实验数据的标准差。
标准差的计算公式如下:标准差 = sqrt(( (x1-平均值)^2 + (x2-平均值)^2 + ... + (xn-平均值)^2 ) / n )。
通过计算平均值和标准差,我们可以得到实验数据的中心位置和离散程度。
平均值告诉我们数据的集中趋势,而标准差告诉我们数据的波动范围。
这两个指标结合起来,能够更全面地描述实验数据的特征。
在实际应用中,平均值和标准差常常被用来比较不同实验结果之间的差异,或者评估同一实验在不同条件下的稳定性。
例如,如果我们对同一种药物在不同剂量下的疗效进行实验,我们可以计算不同剂量下病人的平均病情改善程度和标准差,从而比较不同剂量的药物在疗效上的差异和稳定性。
实验结果标准差的计算

实验结果标准差的计算
在实验数据分析中,标准差是一个重要的统计量,用于衡量数据点的离散程度。
标准差越大,说明数据点的离散程度越大;标准差越小,说明数据点的离散程度越小。
以下是计算实验结果标准差的步骤:
1.计算平均值
对实验数据进行分析前,首先需要计算数据的平均值。
平均值是将所有数据点相加后,再除以数据点的数量得出。
平均值计算公式:
μ = Σx/N
其中μ为平均值,Σx为所有数据点之和,N为数据点的数量。
2.计算每个数据点与平均值的差的平方
接下来,我们需要计算每个数据点与平均值之间的差的平方。
这个步骤是为了消除正负偏差的影响,以便在后续计算中得到正确的标准差。
偏差计算公式:
xi-μ=(xi-μ)²
其中xi为每个数据点,μ为平均值。
3.计算偏差的平均值
接下来,我们需要计算偏差的平均值。
偏差的平均值是将所有偏差相加后,再除以数据点的数量得出。
这个步骤是为了得到标准差的平方。
偏差平均值计算公式:
σ² = Σ(xi-μ)²/N
其中σ²为偏差的平均值,Σ(xi-μ)²为所有偏差平方之和,N为数据点的数量。
4.计算标准差
最后一步是计算标准差。
标准差是偏差的平均值的平方根。
通过这个步骤,我们可以得到实验结果的标准差。
标准差计算公式:
σ = √σ²
其中σ为标准差,σ²为偏差的平均值。
需要注意的是,在计算标准差时,我们需要取正值,因为标准差是一个非负数。
均值和标准差的关系

均值和标准差的关系在统计学中,均值和标准差是两个非常重要的概念,它们分别代表了数据的集中趋势和离散程度。
均值是一组数据的平均值,而标准差则是数据偏离均值的程度的一种度量。
本文将重点讨论均值和标准差之间的关系,以及它们在数据分析中的作用。
首先,我们来看一下均值和标准差的计算公式。
对于一组包含n个数据的样本,其均值可以通过将所有数据相加后除以n来得到。
而标准差的计算则稍显复杂,它需要先计算每个数据与均值的差值的平方,然后将这些差值的平方相加并除以n,最后再取平方根。
标准差的计算公式如下所示:\[ \sigma = \sqrt{\frac{1}{n}\sum_{i=1}^{n}(x_i\bar{x})^2} \]其中,σ代表标准差,n代表样本数量,xi代表第i个数据,而 \(\bar{x}\) 则代表均值。
接下来,我们来讨论均值和标准差之间的关系。
一般来说,当一组数据的均值较大时,数据的分布中心就偏向于整体的较大数值,而标准差则代表了数据的离散程度。
换句话说,均值和标准差之间存在着一种关系,即当数据的均值增大时,数据的离散程度也会相应增大。
这是因为数据的均值较大时,数据中可能存在着一些相对较大的数值,从而导致数据整体的离散程度增大。
反之,当数据的均值较小时,数据的离散程度则相对较小。
此外,我们还可以通过标准差来衡量数据的稳定性。
当一组数据的标准差较小时,说明数据的波动程度较小,数据相对稳定;而当标准差较大时,则说明数据的波动程度较大,数据相对不稳定。
因此,均值和标准差之间的关系也可以反映出数据的稳定性。
在实际数据分析中,均值和标准差经常被用来描述和分析数据的特征。
通过计算均值和标准差,我们可以更好地了解数据的分布情况,从而进行更准确的数据分析和预测。
例如,在财务分析中,我们可以通过计算公司收入的均值和标准差来评估公司的盈利稳定性;在科学实验中,我们可以通过计算实验数据的均值和标准差来评估实验结果的可靠性。
实验标准差和平均值实验标准差
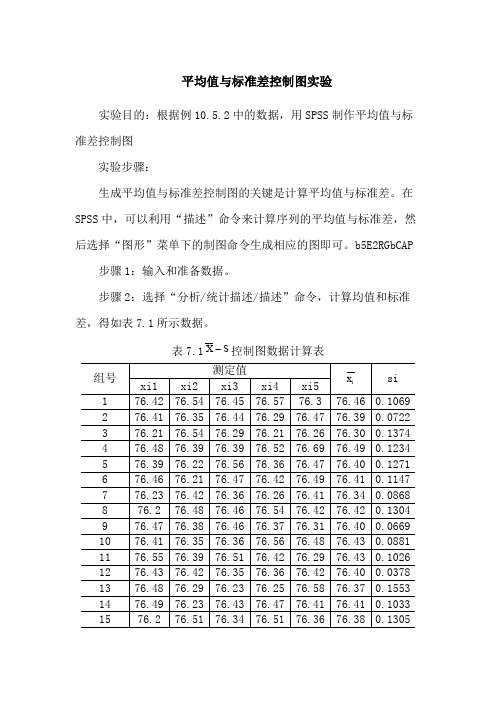
平均值与标准差控制图实验
实验目的:根据例10.5.2中的数据,用SPSS制作平均值与标准差控制图
实验步骤:
生成平均值与标准差控制图的关键是计算平均值与标准差。
在SPSS中,可以利用“描述”命令来计算序列的平均值与标准差,然后选择“图形”菜单下的制图命令生成相应的图即可。
b5E2RGbCAP 步骤1:输入和准备数据。
步骤2:选择“分析/统计描述/描述”命令,计算均值和标准差,得如表7.1所示数据。
X 控制图数据计算表
表7.1S
步骤3:查S X 控制图系数表,得控制界限。
步骤4:整理均值数据和方差数据,形成序列,选择“图形/线图”,生成如图7.1的均值控制图和7.2所示的标准差控制图。
p1EanqFDPw
图7.1 均值控制图
图7.2 方差控制图
申明:
所有资料为本人收集整理,仅限个人学习使用,勿做商业用途。
算术平均值的实验标准差和单次测量值的实验标准差的区别

一、问题的提出在不等精度直接测量时,由各测量值x i及其标准差σi计算加权算术平均值的标准差时,有两个计算公式式中:p i——各测量值的权;σi——各测量值的标准差;σ——单位权标准差;——加权算术平均值的标准差。
但这两个公式的计算结果有时会相差很大。
那么,在这种情况下,采用哪个公式更为合理呢?本文对此从公式的推导到公式的选用进行探讨,并给出了一般性的原则。
二、公式的数学推导在不等精度测量时,各测量值的权的定义式为:测量结果的最佳估计值为:则测量结果的不确定度评定为:对式(5)求方差有设各测量值x i的方差都存在,且已知分别为,即D(x i)=由(4)式有=σ2/p i从公式(1)的推导,我们可以看出,此时各测量值的方差(或标准差)必须是已知的。
而在实际测量中,常常各测量值的方差(或标准差)是未知的,无法直接应用公式(1)进行不确定度评定。
但是,从分析来看,如果能由各测量值的残差(其权等于测量值的权)求出单位权标准差的估计值,并将其代入公式(1)中,就可计算出加权算术平均值标准差的估计值。
为此,作如下推导:由残差νi=x i-i=1,2,……n对νi单位权化由于v i的权都相等,因而可设为1,故用v i代替贝塞尔公式中的ν可得单位权标准差的估计值i将此式代入公式(1),即得到加权算术平均值标准差的估计值从上面的推导我们可以看出,公式(1)是在各测量值的标准差已知时计算出的不等精度测量结果的不确定度的准确值;而公式(2)是在各测量值的标准差未知时计算出的不等精度测量结果的不确定度的估计值。
从概率论与数理统计知识可知,只有在n→∞时,其单位权标准差的估计值才能等于单位权的标准差,而由于测量次数的有限性和随机抽样取值的分散性,这两者是不相等的,所以由公式(1)和公式(2)确定的不确定度的值是也不相同的。
三、公式选用的一般原则笔者用了较大的篇幅来进行公式的数学推导,主要是为了说明这两个公式推导的前提是不一样的,其应用当然也就不同。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验标准差和平均值实验标准差
部门: xxx
时间: xxx
整理范文,仅供参考,可下载自行编辑
平均值与标准差控制图实验
实验目的:根据例10.5.2中的数据,用SPSS制作平均值与标准差控制图
实验步骤:
生成平均值与标准差控制图的关键是计算平均值与标准差。
在SPSS中,可以利用“描述”命令来计算序列的平均值与标准差,然后选择“图形”菜单下的制图命令生成相应的图即可。
b5E2RGbCAP 步骤1:输入和准备数据。
步骤2:选择“分析/统计描述/描述”命令,计算均值和标准差,得如表7.1所示数据。
X 控制图数据计算表
表7.1S
步骤3:查S X 控制图系数表,得控制界限。
步骤4:整理均值数据和方差数据,形成序列,选择“图形/线图”,生成如图7.1的均值控制图和7.2所示的标准差控制图。
p1EanqFDPw
图7.1 均值控制图
图7.2 方差控制图
申明:
所有资料为本人收集整理,仅限个人学习使用,勿做商业用途。
