2023年中考九年级数学高频考点拔高训练--圆的动点问题

合集下载

2024 河北数学中考备考重难专题：圆的综合题动点问题(课后练)

2024河北数学中考备考重难专题：圆的综合题动点问题考情分析年份题号题型分值考查内容设问形式202022解答题9(1)①圆上的点到圆心的距离都相等（即为半径），全等三角形的判定（SAS）②全等三角形的对应角相等，三角形内外角关系(2)切线性质，扇形面积计算(1)①求证三角形全等②写出三个角间的数量关系，并证明(2)指出线段与半圆的位置关系，求扇形面积20222510(1)弧长公式，锐角三角函数，平行线的性质(2)点圆最值，直线与圆的位置关系，勾股定理(3)分类讨论思想，勾股定理，锐角三角函数(1)求角度数及x的值(2)求x最小值，指出直线与圆的位置关系(3)求x的值例(2022河北预测卷)如图，点A是⊙O外一点，连接AO交⊙O于点B，点P从点B出发，在⊙O上按顺时针方向运动一周，过点P且垂直于AO的射线PM也随之运动，PM交AO于点C，交⊙O于点Q.连接AQ，OP，AP.例题图(1)求证：AP＝AQ；(2)若AO＝2PO＝6.最大时，求AQ的值；①当S△APO②当AP与⊙O相切时，求点P运动路径的长．练习(2022河北定心卷)如图，∠AOC＝90°，OA＝OC＝3，以点O为圆心，OA为半径作⊙O，分别过点A，C，作⊙O的切线AB，CB，两切线交于点B，点M是线段OA上一点(不与点A，O重合)，连接CM并延长交⊙O于点D，OE平分∠AOD交DC于点E.练习题图(1)求证：四边形OABC为正方形；(2)连接AC，若OD∥AC，求∠ODC的度数；(3)随着点M位置的改变，直接写出点E所经过的路径l的取值范围．练习(2022河北定制卷)如图，在Rt△ABC中，∠B＝90°，AB＝6cm，BC＝8cm，动点M 从点A出发，以2cm/s的速度沿AB向点B运动，同时动点N从点C出发，以3cm/s的速度沿CA向点A运动，当一点停止运动时，另一点也随即停止运动．以AM为直径作⊙O，连接MN，设运动时间为t(s)(t>0).练习题图(1)试用含t的代数式表示出AM及AN的长度，并直接写出t的取值范围；(2)当t为何值时，MN与⊙O相切？(3)若线段MN与⊙O有两个交点，求t的取值范围．答案典例精讲例(1)证明：∵PQ⊥AO于点C，OB为⊙O的半径，∴PC＝QC，∠ACP＝∠ACQ＝90°，在△ACP和△ACQ中，A＝A∠A＝∠AA＝A，∴△ACP≌△ACQ(SAS),∴AP＝AQ；(2)解：①如解图①，∵S△APO＝12×AO·PC，且AO＝6，＝3PC，∴当PC最大时，S△APO最大，∴S△APO最大，∴当点C与点O重合时，PC最大，即S△APO∵AO＝2PO＝6，∴PO＝3，在Rt△AOP中，AP＝B2＋B2＝62＋32＝35，由(1)得AP＝AQ，∴AQ＝35；解图①②当AP与⊙O相切时，则AP⊥PO，即∠APO＝90°，当点P在AO上方时，如解图②，∵AO＝2PO＝6，∠APO＝90°，∴PO＝3，∴cos∠AOP＝B B＝12，∴∠AOP＝60°，∴点P运动路径的长为60H3180＝π；解图②解图③例题图当点P在AO下方时，如解图③，根据圆的轴对称性可得点P运动路径的长为300H3180＝5π.综上所述，点P的运动路径长为π或5π.课堂练兵练习(1)证明：∵BA，BC是⊙O的切线，∴∠BAO＝∠BCO＝90°.又∵∠AOC＝90°，∴四边形OABC为矩形.∵OA＝OC，∴四边形OABC为正方形；(2)解：如解图，连接AC，∵在Rt△AOC中，∠AOC＝90°，OA＝OC，∴∠OAC＝∠OCA＝45°.又∵OD∥AC，∴∠DOC＝180°－∠OCA＝135°.∵OD＝OC，∴∠ODC＝180°－135°2＝22.5°；解图(3)在⊙O中，已知∠AOD=2∠DCA，∵OE平分∠AOD，∴∠EOA=∠DCA∴A、C、O、E四点共圆∵∠AOC＝90°，∴AC为直径如解图，连接AC ，取AC 的中点Q ，AQ 为半径∴点E 在以AC 的中点Q 为圆心，AQ 为半径的圆弧OA 上运动．连接QO ，∵OA ＝OC ＝3，Q 为AC 的中点，∴∠OQA ＝90°，AC ＝32，∴QA ＝322，∴OA ︵的长为90×π×322180＝32π4.∴点E 所经过的路径l 的取值范围为0＜l ＜32π4.例题解图课后小练练习解：(1)由题意得，AM ＝2t ，CN ＝3t ，在Rt △ABC 中，AC ＝B 2＋A 2＝62＋82＝10，∴AN ＝AC －CN ＝10－3t ，∵AB ＝6cm ，动点M 速度为2cm /s ，∴动点M 的最长运动时间为62＝3s ，∵AC ＝10cm ，动点N 的速度为3cm /s ，∴动点N 的最长运动时间为103s ，∴t 的取值范围为0＜t ≤3；(2)若MN 与⊙O 相切，则AB ⊥MN ，即∠AMN ＝90°，∵∠ABC ＝90°，∴∠AMN ＝∠ABC ，∵∠MAN ＝∠BAC ，∴△AMN ∽△ABC ，A B ＝A A ，即26＝10－310，解得t ＝3019，∴当t ＝3019时，MN 与⊙O 相切；(3)由(2)得，当t＞3019时，直线MN与⊙O有两个交点，如解图，当点N恰好在⊙O上时，线段MN与⊙O的两个交点恰好为M，N，∵AM为⊙O的直径，∴∠ANM＝90°＝∠B，∵∠MAN＝∠CAB，∴△AMN∽△ACB，A A＝A B，即210＝10－36，解得t＝5021，∴若线段MN与⊙O有两个交点，则t的取值范围为3019<t≤5021.解图。

2023年九年级中考数学高频考点专题训练圆的综合题(含解析)

2023年中考数学高频考点专题训练--圆的综合题1．已知：△ABC内接于△O，直径AM平分△BAC．（1）如图1，求证AB＝AC；（2）如图2，弦FG分别交AB、AC于点D、E，AE＝BD，当△ADE+△DEC＝90°时，连接CD，直径AM分别交DE、CD、BC于N、H、R，若CD△AB，求证：△NDC＝△ACB；（3）在（2）的条件下，若DE长为√2，求△ACH的面积．2．在平面直角坐标系xOy中，对于点P，Q和图形G，给出如下定义：若图形G上存在一点C，使△PQC＝90°，则称点Q为点P关于图形G的一个“直角联络点”，称Rt△PCQ为其对应的“联络三角形”．如图为点P关于图形G的一个“直角联络点”及其对应的“联络三角形”的示例．（1）已知点A（4，0），B（4，4）①在点Q1（2，2），Q2（4，﹣1）中，点O关于点A的“直角联络点”是；②点E的坐标为（2，m），若点E是点O关于线段AB的“直角联络点”，直接写出m的取值范围；（2）△T的圆心为（t，0），半径为√10，直线y＝﹣x+2与x，y轴分别交于H，K两点，若在△T上存在一点P，使得点P关于△T的一个“直角联络点”在线段HK 上，且其对应的“联络三角形”是底边长为2的等腰三角形，直接写出t的取值范围．3．对于平面直角坐标系xOy中的点P和△C，给出如下定义：若△C上存在一个点M，使得PM = MC，则称点P为△C的“等径点”．已知点D (12，13)，E(0，2√3)，F (−2，0)．（1）当△O的半径为1时，①在点D，E，F中，△O的“等径点”是；②作直线EF，若直线EF上的点T（m，n）是△O的“等径点”，求m的取值范围．（2）过点E作EG△EF交x轴于点G，若△EFG上的所有点都是某个圆的“等径点”，求这个圆的半径r的取值范围．4．问题背景：如图①，在四边形ADBC中，△ACB=△ADB=90°，AD=BD，探究线段AC，BC，CD之间的数量关系．小吴同学探究此问题的思路是：将△BCD绕点D，逆时针旋转90°到△AED处，点B，C分别落在点A，E处（如图②），易证点C，A，E在同一条直线上，并且△CDE 是等腰直角三角形，所以CE= √2CD，从而得出结论：AC+BC= √2CD．简单应用：（1）在图①中，若AC= √2，BC=2 √2，则CD=．（2）如图③，AB是△O的直径，点C、D在△上，AD̂= BD̂，若AB=13，BC=12，求CD的长．拓展规律：（3）如图④，△ACB=△ADB=90°，AD=BD，若AC=m，BC=n（m＜n），求CD 的长（用含m，n的代数式表示）（4）如图⑤，△ACB=90°，AC=BC，点P为AB的中点，若点E满足AE= 1 3AC，CE=CA，点Q为AE的中点，则线段PQ与AC的数量关系是．5．如图，等边三角形ABC中，AB= 2√3，AH△BC于点H，过点B作BD△AB交线段AH的延长线于点D，连结CD. 点E为线段AD上一点(不与点A，D重合)，过点E作EF△AB交BC于点F，以EF为直径作△O. 设AE的长为x.（1）求线段CD的长度.（2）当点E在线段AH上时，用含x的代数式表示EF的长度.（3）当△O与四边形ABDC的一边所在直线相切时，求所有满足条件的x的值. 6．如图1，⊙O是ΔABC的外接圆，AB是直径，D是⊙O外一点且满足∠DCA=∠B，连接AD.（1）求证：CD是⊙O的切线；（2）若AD⊥CD，AB=8，AD=6，求AC的长；（3）如图2，当∠DAB=45°时，AD与⊙O交于E点，试写出AC、EC、BC 之间的数量关系并证明.7．问题探究（1）如图1，在△ABC中，BC=8，D为BC上一点，AD=6，则△ABC面积的最大值是。

2023年中考九年级数学高频考点提升练习--圆的综合题(含答案)

2023年中考九年级数学高频考点提升练习--圆的综合题1．如图，在⊙ O中，弦AC，BD相交于点M，且∠OAC=∠OBD．（1）求证：AC=BD；（2）若OA=4，∠OAC=30°，当AC⊥BD时，求：①图中阴影部分面积．②弧CD的长．2．已知⊙O中，弦AB＝AC，⊙BAC＝120°（1）如图①，若AB＝3，求⊙O的半径．（2）如图②，点P是⊙BAC所对弧上一动点，连接PB、PA、PC，试请判断PA、PB、PC之间的数量关系并说明理由．3．如图（1），已知矩形ABCD中，AB=6cm，BC=2√3cm，点E为对角线AC 上的动点.连接BE，过E作EB的垂线交CD于点F.（1）探索BE与EF的数量关系，并说明理由.（2）如图（2），过F作AC垂线交AC于点G，交EB于点H，连接CH.若点E从A出发沿AC方向以2√3cm/s的速度向终点C运动，设E的运动时间为ts.①是否存在t，使得H与B重合？若存在，求出t的值；若不存在，说明理由；②t为何值时，△CFH是等腰三角形；③当CG=GH时，求△CGH的面积.4．如图，AB是⊙O的直径，BC为⊙O的切线，D为⊙O上的一点，CD＝CB，延长CD交BA的延长线于点E.（1）求证：CD是⊙O的切线；（2）求证：⊙C＝2⊙DBE.（3）若EA＝AO＝2，求图中阴影部分的面积.（结果保留π）5．定义：三角形一边上的点将该边分为两条线段，且这两条线段的积等于这个点到该边所对顶点连线的平方，则称这个点为三角形该边的“好点”.如图1，⊙ABC中，点D 是BC边上一点，连结AD，若AD2=BD⋅CD，则称点D是⊙ABC中BC边上的“好点”.（1）如图2，⊙ABC的顶点是4×3网格图的格点，请仅用直尺画出AB边上的一个“好点”.（2）⊙ABC中，BC=9，tanB=43，tanC=23，点D是BC边上的“好点”，求线段BD的长.（3）如图3，⊙ABC是⊙O的内接三角形，OH⊙AB于点H，连结CH并延长交⊙O于点D.①求证：点H是⊙BCD中CD边上的“好点”.②若⊙O的半径为9，⊙ABD=90°，OH=6，请直接写出CHDH的值.6．如图，⊙O为等边⊙ABC的外接圆，半径为2，点D在劣弧上运动（不与点A，B 重合），连接DA，DB，DC.（1）求证：DC是⊙ADB的平分线；（2）设四边形ADBC的面积为S，线段DC的长为x，试用含x的代数式表示S；（3）若点M，N分别在线段CA，CB上运动（不含端点），经过探究发现，点D 运动到每一个确定的位置，⊙DMN的周长有最小值t，随着点D的运动，t的值会发生变化，求所有t值中的最大值.7．在⊙ABC中，D，E分别是⊙ABC两边的中点，如果弧DE（可以是劣弧、优弧或半圆）上的所有点都在⊙ABC的内部或边上，则称弧DE为⊙ABC的中内弧．例如，图1中弧DE是⊙ABC其中的某一条中内弧．（1）如图2，在边长为4 √3的等边⊙ABC中，D，E分别是AB，AC的中点．画出⊙ABC的最长的中内弧DE，并直接写出此时弧DE的长；（2）在平面直角坐标系中，已知点A（2 √3，6），B（0，0），C（t，0），在⊙ABC中，D，E分别是AB，AC的中点．①若t＝2 √3，求⊙ABC的中内弧DE所在圆的圆心P的纵坐标的取值范围；②请写出一个t的值，使得⊙ABC的中内弧DE所在圆的圆心P的纵坐标可以取全体实数值．8．如图，⊙O是⊙ABC的外接圆，AC是直径，过点O作OD⊙AB于点D，延长DO 交⊙O于点P，过点P作PE⊙AC于点E，作射线DE交BC的延长线于F点，连接PF．（1）若⊙POC=60°，AC=12，求劣弧PC的长；（结果保留π）（2）求证：OD=OE；（3）求证：PF是⊙O的切线．9．如图，点A和动点P在直线l上，点P关于点A的对称点为Q，以AQ为边作Rt△ABQ，使∠BAQ=90°，AQ：AB=3：4，作△ABQ的外接圆O.点C在点P右侧，PC=4，过点C作直线m⊥l，过点O作OD⊥m于点D，交AB右侧的圆弧于点E.在射线CD上取点F，使DF=32CD，以DE，DF为邻边作矩形DEGF.设AQ=3x.（1）用关于x的代数式表示BQ=，DF=.（2）当点P在点A右侧时，若矩形DEGF的面积等于90，求AP的长.（3）当点P在点A右侧时，作直线BG交⊙O于点N，若BN的弦心距为1，求AP的长.10．如图，⊙ABC中，⊙ACB=90°，D是边AB上一点，且⊙A=2⊙DCB．E是BC边上的一点，以EC为直径的⊙O经过点D．（1）求证：AB是⊙O的切线；（2）若CD的弦心距为1，BE=EO，求BD的长．11．已知：A、B两点在直线l的同一侧，线段AO，BM均是直线l的垂线段，且BM 在AO的右边，AO=2BM，将BM沿直线l向右平移，在平移过程中，始终保持⊙ABP=90°不变，BP边与直线l相交于点P．（1）当P与O重合时（如图2所示），设点C是AO的中点，连接BC．求证：四边形OCBM是正方形；（2）请利用如图1所示的情形，求证：ABPB=OMBM；（3）若AO=2 √6，且当MO=2PO时，请直接写出AB和PB的长．12．（问题情境）如图①，小区A、B位于一条笔直的道路l的同侧，为了方便A，B两个小区居民投放垃圾，现在l上建一个垃圾分类站C，使得C与A，B的距离之比为2：1.（1）（初步研究）在线段AB上作出点C，使CACB=2.如图，做法如下：第一步：过点A作射线AM，以A为圆心，任意长为半径画弧，交AM于点P1；以P1为圆心，AP1长为半径画弧，交AM于点P2；以P2为圆心，AP1长为半径画弧，交AM于点P3.第二步：连接BP3，作∠AP2C=∠AP3B，交AB于点C.则点C即为所求.请证明所作的点C满足CACB=2.（2）（深入思考）如图，点C在线段AB上，点D在直线AB外，且DADB=CACB=2.求证：DC是∠ADB的平分线.（3）（问题解决）如图，已知点A，B和直线l，点C在线段AB上，且CACB=2.用直尺和圆规完成下列作图.（保留作图痕迹，不写作法）（⊙）在直线AB上作出点E（异于点C），使EAEB=2；（⊙）在直线l上作出点F，使FAFB=2.13．在矩形ABCD中，BC=2AB，点E是对角线AC上任意一点，过点E作AD的垂线分别交AD，BC于点F，G，作FH平行AC交CD于点H．（1）证明：EF=CH．（2）连结GH交AC于点K，若AE：CK=3，求AE：EK的值．（3）作⊙FGH的外接圆⊙O，且AB=1．①若⊙O与矩形的边相切时，求CH的长．②作点E关于GH的对称点E'，当E'落在⊙O上时，直接写出⊙FGH的面积。

2023年中考数学高频考点专题训练-- 圆的综合题

2023年中考数学高频考点专题训练-- 圆的综合题1．（1）[问题提出]如图1，已知线段AB＝4，点C是一个动点，且点C到点B的距离为2，则线段AC长度的最大值是；（2）[问题探究]如图2，以正方形ABCD的边CD为直径作半圆O，E为半圆O上一动点，若正方形的边长为2，求AE长度的最大值；（3）[问题解决]如图3，某植物园有一块三角形花地ABC，经测量，AC＝20√3米，BC＝120米，∠ACB＝30°，BC下方有一块空地（空地足够大），为了增加绿化面积，管理员计划在BC下方找一点P，将该花地扩建为四边形ABPC，扩建后沿AP修一条小路，以便游客观赏.考虑植物园的整体布局，扩建部分△BPC需满足∠BPC＝60°.为容纳更多游客，要求小路AP的长度尽可能长，问修建的观赏小路AP的长度是否存在最大值？若存在，求出AP的最大长度；若不存在，请说明理由.2．如图，在Rt△ABC中，∠ABC=90°，AC的垂直平分线分别与AC，BC及AB的延长线相交于点D，E，F，且BF=BC．⊙O是△BEF的外接圆，∠EBF的平分线交EF于点G，交⊙O于点H，连接BD、FH．（1）求证：△ABC≌△EBF；（2）试判断BD与⊙O的位置关系，并说明理由；（3）若AB=1，求HG⋅HB的值．3．如图，点C是以AB为直径的半圆O上一点，且AB=2，AD平分∠BAC交BC于点D，CP 平分∠BCA交AD于点P，PF⊥AC，PE⊥BC.（1）求证：四边形CEPF为正方形；（2）求AC⋅BC的最大值；（3）求1AC+1DC的最小值.4．如图，已知∠ABC内接于∠O，点C在劣弧AB上（不与点A，B重合），点D为弦BC的中点，DE∠BC，DE与AC的延长线交于点E，射线AO与射线EB交于点F，与∠O交于点G，设∠GAB=α，∠ACB=β，∠EAG+∠EBA=γ，（1）点点同学通过画图和测量得到以下近似数据：（2）猜想：β关于ɑ的函数表达式，γ关于ɑ的函数表达式，并给出证明；若γ=135°，CD=3，∠ABE的面积为∠ABC的面积的4倍，求∠O半径的长5．如图1，点P是平面内任意一点，点A，B是⊙C上不重合的两个点，连结PA,PB．当∠APB=60°时，我们称点P为⊙C的“关于AB的关联点”．（1）如图2，当点P在⊙C上时，点P是⊙C的“关于AB的关联点”时，画出一个满足条件的∠APB，并直接写出∠ACB的度数；（2）在平面直角坐标系中有点M(1,√3)，点M关于y轴的对称点为点N．①以点O为圆心，OM为半径画⊙O，在y轴上存在一点P，使点P为⊙O“关于MN的关联点”，直接写出点P的坐标；②点D(m,0)是x轴上一动点，当⊙D的半径为1时，线段MN上至少存在一点是⊙D的“关于某两个点的关联点”，求m的取值范围．6．如图，点A在∠0上，点P是∠0外一点.PA切∠0于点A.连接OP交∠0于点D，作AB∠OP于点C，交∠0于点B，连接PB.（1）求证：PB是∠0的切线；（2）若PC=9，AB=6 √3，求图中阴影部分的面积.7．如图，已知线段AB=2，MN∠AB于点M，且AM=BM，P是射线MN上一动点，E，D分别是PA，PB的中点，过点A，M，D的圆与BP的另一交点C（点C在线段BD上），连结AC，DE．̂的度数；（1）当∠APB=28°时，求∠B和CM（2）求证：AC=AB．（3）在点P的运动过程中①当MP=4时，取四边形ACDE一边的两端点和线段MP上一点Q，若以这三点为顶点的三角形是直角三角形，且Q为锐角顶点，求所有满足条件的MQ的值；②记AP与圆的另一个交点为F，将点F绕点D旋转90°得到点G，当点G恰好落在MN上时，连结AG，CG，DG，EG，直接写出∠ACG和∠DEG的面积之比．8．如图1，在矩形ABCD中．点E以1cm／s的速度从点A向点D运动，运动时间为t(s)．连结BE，过点E作EF∠BE，交CD于F，以EF为直径作∠O ．（1）求证：∠1=∠2；（2）如图2，连结BF，交∠O于点G，并连结EG．已知AB=4，AD=6．①用含t的代数式表示DF的长；②连结DG．若∠EGD是以EG为腰的等腰三角形。

2023年中考九年级数学高频考点拔高训练--圆的切线的证明综合题(含答案)

2023年中考九年级数学高频考点拔高训练--圆的切线的证明综合题1．如图，已知：射线PO与⊙O交于A、B两点，PC、PD分别切⊙O于点C、D．（1）请写出两个不同类型的正确结论；（2）若CD=12，tan⊙CPO= 12，求PO的长．2．如图，⊙ABC内接于⊙O，AB是⊙O的直径，过⊙O外一点D作DG//BC，DG交线段AC于点G，交AB于点E，交⊙O于点F，连接DB，CF，⊙A＝⊙D．（1）求证：BD与⊙O相切；（2）若AE＝OE，CF平分⊙ACB，BD＝12，求DE的长．3．如图，已知⊙O的直径为AB，AC⊙AB于点A，BC与⊙O相交于点D，在AC上取一点E，使得ED=EA．（1）求证：ED是⊙O的切线．（2）当OA=3，AE=4时，求BC的长度．4．如图，AB是⊙O的直径，点F，C是⊙O上两点，且点C是弧FB̀的中点，连接AC，AF，过点C作CD⊙AF，垂足为点D．（1）求证：CD是⊙O的切线；（2）若AB=10，AC=8，求DC的长．5．如图，⊙O是⊙ABC的外接圆，点O在BC边上，⊙BAC的平分线交⊙O于点D，连接BD、CD，过点D作BC的平行线与AC的延长线相交于点P.（1）求证：PD是⊙O的切线；（2）求证：AB·CP=BD·CD；（3）若tan∠ABC=2，AB=2√5，求线段DP的长.6．如图，AB是⊙O的直径，C是⊙O上一点，D在AB的延长线上，且⊙CAD＝⊙D，给出下列三个信息：①sin⊙CAB＝12；②BO＝BD；③DC是⊙O的切线.（1）请在信息①或②中选择一个作为条件，剩下的两个信息中选择一个作为结论，组成一个真命题．．．.你选择的条件是，结论是（只要填写序号）.（2）证明（1）中你写出的真命题.7．如图，AB是⊙O的直径，点C在⊙O上，点D在AB的延长线上，且⊙BCD =⊙A.（1）求证：CD是⊙O的切线；（2）若AC =2，AB =32CD，求⊙O半径.8．如图，四边形ABCD为菱形，以AD为直径作⊙O交AB于点F，连接DB 交⊙O于点H，E是BC上的一点，且BE=BF，连接DE.（1）求证：ΔDAF≌ΔDCE.（2）求证：DE是⊙O的切线.（3）若BF=2，DH=√5，求四边形ABCD的面积.9．如图，在矩形ABCD中，点E是BC边上一点，且AD=DE，以AB为半径作⊙A，交AD边于点F，连接EF．（1）求证：DE是⊙A的切线；（2）若AB＝2，BE＝1，求AD的长；（3）在（2）的条件下，求tan⊙FED．10．等腰三角形ABC，AB=AC，CD⊥AB于点D，AE⊥BC于点E，AE、CD交于点F，⊙O为⊙ADF的外接圆，连接DE．（1）求证：DE是⊙O的切线：（2）若CF＝5，DF＝3，求⊙O的直径．11．如图，在Rt△OAB中，∠AOB=90°,OA=OB=4，以点O为圆心、2为半径画圆，过点A作⊙O的切线，切点为P，连接OP．将OP绕点O按逆时针方向旋转到OH时，连接AH,BH．设旋转角为α(0°<α<360°)．（1）当α=90°时，求证：BH是⊙O的切线；（2）当BH与⊙O相切时，求旋转角α和点H运动路径的长；（3）当△AHB面积最大时，请直接写出此时点H到AB的距离．12．如图，AB是⊙O的直径，点C是AB的中点，连接AC并延长至点D，使CD＝AC，点E是OB上一点，且OEEB=23，CE的延长线交DB的延长线于点F，AF交⊙O于点H，连接BH．（1）求证：BD是⊙O的切线；（2）当OB＝2时，求BH的长．13．如图，AB是 ⊙O的直径，点C是 ⊙O上一点，AC平分⊙DAB，直线DC与AB的延长线相交于点P，AD与PC延长线垂直，垂足为点D，CE平分⊙ACB，交AB于点F，交 ⊙O于点E.（1）求证：PC与⊙O相切；（2）求证：PC＝PF；（3）若AC＝8，tan⊙ABC＝43，求线段BE的长.14．如图，已知二次函数图象的对称轴为直线x=2，顶点为点C，直线y=x+m与该二次函数的图象交于点A，B两点，其中点A的坐标为（5，8），点B在y轴上．（1）求m的值和该二次函数的表达式．P为线段AB上一个动点（点P不与A，B 两点重合），过点P作x轴的垂线，与这个二次函数的图象交于点E．①设线段PE的长为h，求h与x之间的函数关系式，并写出自变量x的取值范围．②若直线AB与这个二次函数图象的对称轴的交点为D，求当四边形DCEP是平行四边形时点P的坐标．（2）若点P（x，y）为直线AB上的一个动点，试探究：以PB为直径的圆能否与坐标轴相切？如果能请求出点P的坐标，如果不能，请说明理由．15．如图，PA为⊙O的切线，A为切点，点B在⊙O上，且PA=PB，连AO并延长交PB的延长线于点C，交⊙O于点D.（1）求证：PB为⊙O的切线；（2）连接OB、DP交于点E.若CD=2，CB=4，求PEDE的值.16．如图，AB是⊙O的直径，AC是⊙O的切线，切点为A，BC交⊙O于点D，点E 是AC的中点．（1）试判断直线DE与⊙O的位置关系，并说明理由；（2）若⊙O的半径为2，⊙B＝50°，AC＝4.8，求图中阴影部分的面积．答案解析部分1．【答案】（1）解：不同类型的正确结论有：①PC=PD ，②⊙CPO=⊙DP ，③CD⊙BA ，④⊙CEP=90°，⑤PC 2=PA•PB（2）解：连接OC ∵PC 、PD 分别切⊙O 于点C 、D ∴PC=PD ，⊙CPO=⊙DPA∴CD⊙AB∵CD=12∴DE=CE= 12CD=6． ∵tan⊙CPO= 12， ∴在Rt⊙EPC 中，PE=12∴由勾股定理得CP=6 √5∵PC 切⊙O 于点C∴⊙OCP=90°在Rt⊙OPC 中，∵tan⊙CPO= 12， ∴OC PC =12∴OC=3 √5 ，∴OP= √OC 2+PC 2 =152．【答案】（1）证明：如图1，延长 DB 至 H ，∵DG//BC ，∴∠CBH =∠D ，∵∠A=∠D，∴∠A=∠CBH，∵AB是⊙O的直径，∴∠ACB=90°，∴∠A+∠ABC=90°，∴∠CBH+∠ABC=90°，∴∠ABD=90°，∴AB⊙BD，∴BD与⊙O相切；（2）解：如图2，连接OF，∵CF平分∠ACB，∴∠ACF=∠BCF，∴AF=BF，∴⊙AOF＝⊙BOF＝90°，∴OF⊥AB，∵BD⊥AB，∴OF//BD，∴△EFO∽△EDB，∴OFBD=OE BE，∵AE=OE，∴OEEB=1 3，∴OF12=13，∴OF=4，∴OA=OB=OF=4，∴BE =OE +OB =2+4=6 ，∴DE =√BD 2+BE 2=√122+62=6√5 ．3．【答案】（1）证明：如图：首先连接OD ．∵AC⊙AB ，∴⊙BAC=90°，即⊙OAE=90°．在⊙AOE 与⊙DOE 中，OA=OD ，ED=EA ，OE=OE ，∴⊙AOE⊙⊙DOE （SSS ），∴⊙OAE=⊙ODE=90°，即OD⊙ED ．又∵OD 是⊙O 的半径，∴ED 是⊙O 的切线；（2）解：如图，在⊙OAE 中，⊙OAE=90°，OA=3，AE=4，∴由勾股定理求得OE=5．∵AB 是直径，∴⊙ADB=90°（直径所对的圆周角是直角），即AD⊙BC ．又∵OA=OD ，AE=DE ，∴OE 垂直平分AD （到线段两个端点距离相等的点在这条线段的垂直平分线上）， ∴OE⊙AD ，∴OE⊙BC ，∴OA AB =OE BC =12（平行线分线段成比例定理）． ∴BC=2OE=2×5=10，即BC 的长度是10．4．【答案】（1）解：如图1，连接OC ，∵C 是弧FB ̀的中点， ∴弧FC=弧BC ̀̀，∴⊙FAC=⊙BAC ，∵OA=OC ，∴⊙OCA=⊙BAC ，∴⊙FAC=⊙OCA ，∴AD⊙OC ，∵CD⊙AF ，∴CD⊙OC ，即CD 是⊙O 的切线；（2）解：如图2，连接BC ，∵AB 是⊙O 的直径，∴⊙ACB=90°，∴⊙D=⊙ACB ，又⊙DAC=⊙CAB ，∴⊙DAC⊙⊙CAB ，∴AD AC =AC AB，解得，AD= AC 2AB=6.4，在Rt⊙ADC 中，CD= √AC 2−AD 2 =4.8．5．【答案】（1）证明：如图，连接OD ，∵BC 是⊙O 的直径，∴⊙BAC=90°，∵AD 平分⊙BAC ，∴⊙BAC=2⊙BAD ，∵⊙BOD=2⊙BAD ，∴⊙BOD=⊙BAC=90°，∵DP⊙BC ，∴⊙ODP=⊙BOD=90°，∴PD⊙OD ，∵OD 是⊙O 半径，∴PD 是⊙O 的切线；（2）证明：∵PD⊙BC ，∴⊙ACB=⊙P ，∵⊙ACB=⊙ADB ，∴⊙ADB=⊙P ，∵⊙ABD+⊙ACD=180°，⊙ACD+⊙DCP=180°，∴⊙DCP=⊙ABD ，∴⊙ABD⊙⊙DCP ，∴AB CD =BD CP∴AB•CP=BD•CD.（3）解：在 RtΔABC 中，∵tan∠ABC =2 ， AB =2√5 ，∴AC =2AB =4√5 ，∴BC =√AB 2+AC 2=10 ，∴OD =5 ，过点 C 作 CG ⊥DP ，垂足为 G ，则四边形 ODGC 为正方形，∴DG =CG =OD =5 ，∵BC ∥PD ，∴∠CPG =∠ACB ，∴tan∠CPG =tan∠ACB ，∴CG GP =AB AC，即 5GP =2√54√5 ，解得， GP =10 ，∴DP =DG +GP =15 .6．【答案】（1）①；②（或①，③；或②，①；或②，③；答案不唯一）（2）解：条件:①，结论:②；连接BC ，∵AB是⊙O的直径，∴⊙ACB=90°，∵sin⊙CAB= 1 2，∴BC= 12AB=BO，⊙D=⊙CAB=30°，∴⊙ABC=60°，∴⊙BCD=⊙ABC-⊙D=30°=⊙D，∴BD=BC，∴BD=BO；条件:①，结论:③；连接CO，∵sin⊙CAB= 1 2，∴⊙D=⊙CAB=30°，∵OA=OC，∴⊙OCA=⊙CAB=30°，在⊙DCA中，⊙DCO =180°-⊙D-⊙CAB-⊙OCA =180°-30°-30°-30°=90°，∴OC⊙DC，∴DC是⊙O的切线；条件:②，结论:①；连接BO、CO，∵AB是⊙O的直径∴⊙ACB=90°∵BO=BD，BO=AO，∴DO=AB，在⊙DCO与⊙ACB中，{CD=CA∠D=∠CAD DO=AB，∴⊙DCO⊙⊙ACB，∴BC=CO= 12AB，∴sin⊙CAB= 1 2；条件:②，结论:③；连接BO、CO，∵AB是⊙O的直径，∴⊙ACB=90°，∵BO=BD，BO=AO，∴DO=AB，在⊙DCO与⊙ACB中，{CD=CA ∠D=∠CAD DO=AB∴⊙DCO⊙⊙ACB，∴⊙DCO=⊙ACB=90°，∴CO⊙DC，∴DC是⊙O的切线.7．【答案】（1）证明：如图，连接OC.∵AB 是⊙O 的直径，C 是⊙O 上一点，∴⊙ACB=90°，即⊙ACO+⊙OCB=90°.∵OA=OC ，⊙BCD=⊙A ，∴⊙ACO=⊙A=⊙BCD ，∴⊙BCD+⊙OCB=90°，即⊙OCD=90°，∴CD 是⊙O 的切线.（2）解：设CD 为x ，则AB= 32 x ，OC=OB= 34x ， ∵⊙OCD=90°，∴OD= √OC 2+CD 2=√(34x)2+x 2 = 54 x ， ∴BD=OD ﹣OB= 54x ﹣ 34 x= 12 x ， ∵⊙BCD ＝⊙A ，⊙BDC ＝⊙CDA ，∴⊙ADC⊙⊙CDB ，∴AC CB =CD BD，即 2CB =x 12，解得CB=1，∴AB= √AC 2+BC 2 =√5∴⊙O 半径是 √52. 8．【答案】（1）证明：如图1，连接 DF ，∵四边形 ABCD 为菱形，∴AB =BC =CD =DA ， AD//BC ， ∠DAB =∠C ，∵BF=BE，∴AB−BF=BC−BE，即AF=CE，∴ΔDAF≌ΔDCE（2）解：∵ΔDAF≌ΔDCE∴∠DFA=∠DEC.∵AD是⊙O的直径，∴∠DFA=90°，∴∠DEC=90°.∵AD//BC，∴∠ADE=∠DEC=90°，∴OD⊥DE.∵OD是⊙O的半径，∴DE是⊙O的切线（3）解：如图2，连接AH，∵AD是⊙O的直径，∴∠AHD=∠DFA=90°，∴∠DFB=90°，∵AD=AB，DH=√5，∴DB=2DH=2√5，在RtΔADF和RtΔBDF中，∵DF2=AD2−AF2，DF2=BD2−BF2，∴AD2−AF2=DB2−BF2，∴AD2−(AD−BF)2=DB2−BF2，∴AD2−(AD−2)2=(2√5)2−22，∴AD=5．∴AF=3∴DF=√AD2−AF2=4∴四边形ABCD的面积=AB⋅DF=5×4=20．9．【答案】（1）证明：过点A作AG⊙DE，∴⊙AGD=90°在矩形ABCD 中，AD⊙BC ，⊙C=90°，∴⊙AGD=⊙C ，⊙ADG=⊙DEC∵AD=DE ，∴⊙ADG⊙⊙DEC∴AG=DC ，DG=EC ，∵AB=DC ，∴AG=AB ，即AG 为⊙A 的半径∴DE 是⊙A 的切线（2）解：连接AE ，由（1）可知，AG=AB ，⊙ABE=⊙AGE=90°，AE=AE ，∴⊙ABE⊙⊙AGE （HL ），∴BE=EG ，设DG=EC=x ，∵AB=2，BE=1，∴DE=x+1，DC=AB=2，在Rt⊙DEC 中，由勾股定理可得，x 2+22=(x +1)2解得，x =32， ∴AD=DE=52（3）解：过点F 作FH⊙DE ，∵AD =52，AF =AB =2， ∴DF =AD −AF =52−2=12， ∵FH⊙DE ，AG ⊥DE ，∴FH ∥AG ，∴⊙DFH⊙⊙DAG ，∴DF AD =FH AG ，即1252=FH 2，解得FH =25， ∵DH =√(12)2−(25)2=310，DE =√(32)2−22=52， ∴EH =52−310=115∴tan⊙FED =FH EH =211， 10．【答案】（1）证明：如下图所示，连接OD ．∵AB ＝AC ，AE⊙BC ，∴CE ＝EB ，⊙DCE ＋⊙CFE ＝90°．∴CE =12BC ． ∵CD⊙AB ，∴DE =12BC ，⊙ADF=90°． ∴DE=CE ，⊙FAD ＋⊙AFD ＝90°，⊙ODA ＋⊙ODF ＝90°．∴∠DCE =∠CDE ．∵⊙AFD 和⊙CFE 是对顶角，∴⊙AFD ＝⊙CFE ．∴⊙FAD ＝⊙DCE ．∴⊙FAD=⊙CDE ．∵OA ＝OD ，∴⊙FAD ＝⊙ODA ．∴⊙ODA ＝⊙CDE ．∴⊙ODE=⊙ODF ＋⊙CDE ＝⊙ODF+⊙ODA=90°．∴OD⊙DE ．∵OD 为半径，∴DE 是⊙O 的切线．（2）解：如下图所示，连接BF ．∵CE ＝BE ，AE⊙BC ，CF=5，∴BF ＝CF ＝5．∵DF=3，∴DB =√BF 2−DF 2=4，CD =CF +DF =8．∵CD⊙AB ，∴⊙ADF=⊙CDB=90°．∴AF 是⊙O 直径．∵⊙FAD=⊙DCE ，即⊙FAD=⊙BCD ，∴⊙ADF⊙⊙CDB ．∴AD CD =DF DB． ∴AD 8=34． ∴AD ＝6．∴AF =√AD 2+DF 2=√62+32=3√5．11．【答案】（1）解： ∵α=90°=∠AOB ，∴∠AOP =∠BOH ，又 ∵OP =OH, OA =OB ，∴△AOP ≌△BOH ，∴∠OPA =∠OHB ，∵AP 是⊙O 的切线，∴∠OPA =90° ，∴∠OHB =90° ，即 OH ⊥BH 于点H ，∴BH是⊙O的切线；（2）解：如图，过点B作⊙O的切线BC、BD，切点分别为C、D，连接OC，OD，则有OC⊥BC,OD⊥BD，∵OC=2,OB=4，∴cos∠BOC=OCOB=24=12，∴∠BOC=60°，同理∠BOD=60°，当点H与点C重合时，由（1）知：α=90°，∴∠OHB=90°，∵OP=2，∴PH的长为90π×2180=π；当点H与点D重合时，α=∠POC+∠BOC+∠BOD=90°+2×60°=210°，∴PH的长为210π×2180=73π，∴当BH与⊙O相切时，旋转角α=90°或210°，点H运动路径的长为π或73π．（3）2+2√212．【答案】（1）解：连接OC，∵AB是⊙O的直径，点C是AB的中点，∴⊙AOC＝90°，∵OA＝OB，CD＝AC，∴OC是⊙ABD是中位线，∴OC⊙BD，∴⊙ABD ＝⊙AOC ＝90°，∴AB⊙BD ，∵点B 在⊙O 上，∴BD 是⊙O 的切线（2）解：由（1）知，OC⊙BD ，∴⊙OCE⊙⊙BFE ，∴OC BF =OE EB， ∵OB ＝2，∴OC ＝OB ＝2，AB ＝4， OE EB =23， ∴2BF =23， ∴BF ＝3，在Rt⊙ABF 中，⊙ABF ＝90°，根据勾股定理得，AF ＝5， ∵S ⊙ABF ＝ 12 AB•BF ＝ 12AF•BH ， ∴AB•BF ＝AF•BH ，∴4×3＝5BH ，∴BH ＝ 125． 13．【答案】（1）证明：连接OC ，∵AC 平分⊙DAB ，∴⊙DAC ＝⊙CAB ，∵OA ＝OC ，∴⊙OCA ＝⊙CAB ，∴⊙DAC ＝⊙OCA ，∴OC⊙AD ，又AD⊙PD ，∴OC⊙PD ，∴PC 与⊙O 相切（2）证明：∵CE 平分⊙ACB ，∴⊙ACE ＝⊙BCE ，∴AE =BE ，∴⊙ABE ＝⊙ECB ，∵OC ＝OB ，∴⊙OCB ＝⊙OBC ，∵AB 是⊙O 的直径，∴⊙ACB ＝90°，∴⊙CAB+⊙ABC ＝90°，∵⊙BCP+⊙OCB ＝90°，∴⊙BCP ＝⊙BAC ，∵⊙BAC ＝⊙BEC ，∴⊙BCP ＝⊙BEC ，∵⊙PFC ＝⊙BEC+⊙ABE ，⊙PCF ＝⊙ECB+⊙BCP ，∴⊙PFC ＝⊙PCF ，∴PC ＝PF（3）解：连接AE ，在Rt⊙ACB 中，tan⊙ABC ＝ 43，AC ＝8， ∴BC ＝6，由勾股定理得，AB ＝ √AC 2+BC 2=√82+62=10 ，∵AE =BE ，∴AE ＝BE ，则⊙AEB 为等腰直角三角形，∴BE ＝ √22AB ＝5 √2 . 14．【答案】（1）解： A 的坐标为（5，8）在直线y=x+m 上，∴8=5+m ，∴m=3，∴直线AB 解析式为y=x+3，∴B （0，3），设抛物线解析式为y=a （x ﹣2）2+k ，∵点A ，B 在抛物线上，∴{9a +k =8a +k =0， ∴{a =1k =−1， ∴抛物线解析式为y=（x ﹣2）2﹣1=x 2﹣4x+3，顶点C （2，﹣1）①∵点P在线段AB上，∴P（x，x+3）（0≤x≤5），∵PE⊙x轴，交抛物线与E，P （x，x+3），∴E（x，x2﹣4x+3），∴h=PE=x+3﹣（x2﹣4x+3）=﹣x2+5x，（0≤x≤5）②∵直线AB与这个二次函数图象的对称轴的交点为D，∴D（2，5），∴DC=6，∵四边形DCEP是平行四边形，∴PE=DC=6，∵PE=|﹣x2+5x|，⊙、当0≤x≤5时，﹣x2+5x=6，∴x1=2（舍），x2=3，∴P（3，6），⊙、当x＜0，或x＞5时，x2﹣5x=6，∴x3=﹣1，x4=6，∴P（﹣1，2）或P（6，9），（舍）即：点P的坐标为（3，6）（2）解：∵点P（x，y）为直线AB上的一个动点，∴P（x，x+3），∴点P到x轴的距离为|x+3|，到y轴的距离为|x|，∵点B（0，3），∴BP= √x2+(x+3−3)2=√2 |x|，∵以PB为直径的圆能与坐标轴相切，∴①以PB为直径的圆能与y轴相切，∴|x|= √22|x|，∴x=0（舍），②以PB为直径的圆能与x轴相切，∴|x+3|= √22|x|，∴x=﹣6﹣3 √2或x=﹣6+3 √2，∴P（﹣6﹣3 √2，﹣3+3 √2）或P（﹣6﹣3√2，﹣3﹣3 √2）．故存在点P，坐标为P（﹣6+3 √2，﹣3+3 √2）或P（﹣6﹣3 √2，﹣3﹣3 √2）时，以PB为直径的圆能与坐标轴相切15．【答案】（1）证明：连接OB，OP，∵PA为⊙O的切线，∴OA⊥PA，∠OAP=90°，∵OA=OB，PA=PB，OP=OP，∴∠OBP=∠OAP=90°∴OB⊥PB∴PB为⊙O切线；（2）解：设OB=OD=r，在Rt△OBC中，BC2+OB2=OC2∴r2+42=(2+r)2，∴r=3，∴OB=OD=3，AC=OA+OD+CD=3，设PB=PA=x，在Rt△PAC中，AC2+PA2=PC2∴x2+82=(x+4)2，解得x=6，∴PB=PA=6，在Rt△PAO中，OP=√OA2+AP2=3√5，连接AB与OP交于G，连接BD，∵OA=OB，PA=PB，∴AB⊙OP，AG=BG，∴S△AOP=12AG⋅OP=12OA⋅AP，即S△AOP=12AG⋅3√5=12×3×6，∴AG=65√5，在Rt△OAG中，OG=√OA2−AG2=35√5，∵OA=OD，AG=BG，∴BD=2OG=65√5，∵AD为直径，∴∠ABD=90°，∴OP//BD，∴∠BDP=∠OPD，∠DBO=∠POE，∴PEDE=OPDB=52.16．【答案】（1）解：直线DE与⊙O相切．理由如下：连接OE、OD，如图，∵AC是⊙O的切线，∴AB⊙AC，∴⊙OAC＝90°，∵点E是AC的中点，O点为AB的中点，∴OE⊙BC，∴⊙1＝⊙B，⊙2＝⊙3，∵OB＝OD，∴⊙B＝⊙3，∴⊙1＝⊙2，在⊙AOE和⊙DOE中{OA=OD∠1=∠2 OE=OE，∴⊙AOE⊙⊙DOE，∴⊙ODE＝⊙OAE＝90°，∴OA⊙AE，∴DE为⊙O的切线（2）解：∵点E是AC的中点，∴AE＝12AC＝2.4，∵⊙AOD＝2⊙B＝2×50°＝100°，∴图中阴影部分的面积＝2• 12×2×2.4﹣100⋅π⋅22360＝4.8﹣109π。

2023年中考复习二轮九年级数学高频考点拔高训练--圆的综合

2023年中考复习二轮九年级数学高频考点拔高训练--圆的综合一、单选题1．如图，在正方形ABCD中，点E、F分别是DC、AD边上的动点，且AE⊥BF，垂足为P，连接CP．若正方形的边长为1，则线段CP的最小值为（）A．√55B．√22C．√5−12D．√542．如图，正方形ABCD中，P为CD边上任意一点，DE⊥AP于点E，点F在AP延长线上，且EF ＝AE，连结DF、CF，⊥CDF的平分线DG交AF于G，连结BG.给出以下结论：①DF＝DC；②⊥DEG是等腰直角三角形；③⊥AGB＝45°；④DG+BG＝√2AG.所有正确的结论是（）A．①②B．①②③C．①③④D．①②③④3．如图，点P（3,4），⊥P半径为2，A（2.8，0），B（5.6,0）.点M是P上的动点，点C是MB的中点，则AC的最小值为（）A．14B．32C．52D．264．有一圆内接正八边形ABCDEFGH，若⊥ADE的面积为10，则正八边形ABCDEFGH的面积为()A．40B．50C．60D．805．如图，已知A、B两点的坐标分别为(8,0)，(0,8)，点C、F分别是直线x=−5和x轴上的动点，CF=10,点D是线段CF的中点，连接AD交y轴于点E；当⊥ ABE面积取得最小值时，tan∠BAD的值是（）A．817B．717C．49D．596．已知⊥O的半径为10，P为⊥O内一点，且OP＝6，则过P点，且长度为整数的弦有（）A．5条B．6条C．8条D．10条7．如图，⊥ABC是⊥O的内接三角形，把BC⌢沿BC折叠后，与弦AB交于点P，恰好OP⊥AB．若OP=1，AB=4，则BC：AC等于（）A．3√107B．3√55C．4√57D．2√1058．如图,点A,B,C在一条直线上,⊥ABD,⊥BCE均为等边三角形,连接AE和CD,AE分别交CD,BD于点M,P,CD交BE于点Q,连接PQ,BM,下面的结论:①⊥ABE⊥⊥DBC;②⊥DMA=60°;③⊥BPQ为等边三角形;④MB平分⊥AMC,其中结论正确的有()A．1个B．2个C．3个D．4个二、填空题9．自行车车轮的辐条编制方式是多种多样的，同样大小的车轮，辐条编法不同，辐条的长度是不一样的，图2和图3是某种“24吋（指轮圈直径）”车轮一侧的辐条编法示意图，两个同心圆分别代表轮圈和花鼓，连接两圆的线段代表辐条，轮圈和花鼓上的穿辐条的孔都等分圆周，图2是直拉式编法，每根辐条的延长线都过圆心，优点是编法简单，缺点是轮强度较低，且力传递的效果较差，所以一般都采用如图3（两图中孔的位置一样）这样的错位式编法，若弧DC的长度和弧AB相等，则BE的长度为吋.10．如图，△ABC中，∠ACB=90°，AC=BC，点D是边BC上任意一点，连结AD，过点C 作CE⊥AD于点E，过点C作CF⊥CE，且CF=CE，连结FE并延长交AB于点M，连结BF.若四边形AMEC的面积是8，CE=2，则四边形ABFC的面积是.11．如图，在⊥ABC中，⊥C=45°，⊥B=60°，BC为√3+1，点P为边AB上一动点，过点P作PD⊥BC于点D，PE⊥AC于点E，则DE的最小值为.12．如图，已知∠ΑΟΒ=30∘，在射线ΟΑ上取点Ο1，以Ο1为圆心的圆与ΟΒ相切；在射线Ο1Α上取点Ο2，以Ο2为圆心，Ο2Ο1为半径的圆与ΟΒ相切；在射线Ο2Α上取点Ο3，以Ο3为圆心，Ο3Ο2为半径的圆与ΟΒ相切；⋅⋅⋅；在射线Ο9Α上取点Ο10，以Ο10为圆心，Ο10Ο9为半径的圆与ΟΒ相切．若⊙Ο1的半径为1，则⊙Ο10的半径长是．13．如图，在矩形ABCD中，AB=√3，AD=1，延长AD至点F，使得DF=AD，以点A 为圆心，AD的长为半径画弧，交AB于点E，P为上一动点，连接FP并延长交AB于点G，当BG 的长度最短时，阴影部分的周长为.14．如图Rt⊥ABC中，⊥ACB＝90°，⊥O是⊥ABC的外接圆，E为⊥O上一点，连结CE，过C作CD⊥CE，交BE于点D，已知tanA＝12，AB＝2 √10，DE＝5，则tan⊥ACE＝．三、综合题15．如图，在平面直角坐标系中，已知A（-3，0），B（0，3√3），点D与点A关于y轴对称，C在第一象限内且四边形ABCD是平行四边形.（1）求点C、点D的坐标并用尺规作图确定两点位置（保留作图痕迹）（2）若半径为1的⊥P从点A出发，沿A—D—B—C以每秒4个单位长的速度匀速移动，同时⊥P的半径以每秒0.5个单位长的速度增加，运动到点C时运动停止，当运动时间为t秒时①t为何值时，⊥P与y轴相切？②在整个运动过程中⊥P与y轴有公共点的时间共有几秒？简述过程.（3）若线段AB绕点O顺时针旋转90°，线段AB扫过的面积是多少？16．如图1，AB为圆O直径，点D为AB下方圆上一点，点C为弧ABD中点，连结CD，CA．（1）若⊥ABD=70°，求⊥BDC的度数；（2）如图2，过点C作CE⊥AB于点H，交AD于点E，⊥CAD=α，求⊥ACE（用含α的代数式表示）；（3）在（2）的条件下，若OH=5，AD=24，求线段DE的长．17．定义：平面直角坐标系xOy中，过二次函数图象与坐标轴交点的圆，称为该二次函数的坐标圆.（1）已知点P(2，2)，以P为圆心，√5为半径作圆.请判断⊥ P是不是二次函数y=x2−4x+3的坐标圆，并说明理由；（2）已知二次函数y=x2−4x+4图象的顶点为A，坐标圆的圆心为P，如图1，求△POA周长的最小值；（3）已知二次函数y=ax2−4x+4(0<a<1)图象交x轴于点A，B，交y轴于点C，与坐标圆的第四个交点为D，连结PC，PD，如图2.若∠CPD=120°，求a的值. 18．定义：三角形内部有一小三角形与原三角形相似，其中小三角形的三个顶点在原三角形的三边上（顶点可重合），则称这两个三角形是星相似三角形例如：如图1，Rt△ABC中，∠BCA=∠CEA=90°，△ACE和△ABC是星相似三角形.如图2，D是AB的中点，以CD为直径画圆，交AB，BC于点E，F，AC=1.（1）①若BC=2，求DE的长..②设BC=x，GDGO=y，试写出y与x的函数关系式（2）若CG=CE，则△CEG与哪个三角形星相似，并证明.（3）在（2）的条件下，求BC的长.19．如图，⊥O是⊥ABC的外接圆，AB是⊥O的直径，FO⊥AB，垂足为点O，连接AF并延长交⊥O于点D，连接OD交BC于点E，⊥B=30°，FO=2√3（1）求AC的长度（2）求图中阴影部分的面积．（计算结果保留根号）20．如图，CD为⊥O的直径，弦AB垂直于CD，垂足为H，⊥EAD=⊥HAD．（1）求证：AE为⊥O的切线；（2）延长AE与CD的延长线交于点P，过D 作DE⊥AP，垂足为E，已知PA=2，PD=1，求⊥O 的半径和DE的长．答案解析部分1．【答案】B 2．【答案】D 3．【答案】B 4．【答案】A 5．【答案】B 6．【答案】C 7．【答案】B 8．【答案】D 9．【答案】√7 10．【答案】1811．【答案】√6+3√2412．【答案】512 13．【答案】π6+√3+1 14．【答案】1315．【答案】（1）解：由题可知：AD=AB=6，⊥DAB=60°．∵⊥AOB=90°，∴AO=3，OB=3 √3 ∴OD=AD-OA=3．∵四边形ABCD 是平行四边形， ∴BC=AD=6．∴点C 的坐标为（6，3 √3 ），点D 的坐标为（3，0）．作法：①以点A 为圆心，AB 为半径画弧，与x 轴交点即为点D ；②以点D 为圆心，AB 为半径画弧；以点B 为圆心，AD 为半径画弧，两弧的交点即为点C ．如图1所示．（2）解：①当点P在AO上时，如图所示：设时间为t，则r=1+0.5t,此时⊥P与y轴相切，则AP=4t∵AP+OP=AO∴4t+1+0.5t=3,∴t= 4 9;当点P在OD上时，如图所示：设时间为t，则r=1+0.5t,此时⊥P与y轴相切，OP＝4t－3,∴4t-3=1+0.5t,∴t= 8 7,当点P在BD上时，作PE ⊥OB，如图所示：设时间为t，则r=1+0.5t,此时⊥P与y轴相切，由PD＝4t-6,∵BD= √32+(3√3)2=6,BP=BD-DP,∴BP=6-(4t-6)=12-4t,∵cos⊥ODB= ODBD=36=12, ⊥ODB=⊥EPB∴cos⊥EPB= EPBP=1+0.5t12−4t=12∴t=2;当点P在BC上时，如图所示：设时间为t，则r=1+0.5t,此时⊥P与y轴相切，PB=4t-12∴4t-12=1+0.5t∴t= 26 7;∴当运动时间为49、87、2、267时，⊥P与y轴相切；②当圆P在AO上与y轴相切至圆P在OD上与y轴相切时，圆与y轴有交点，则时间为：87−4 9=4463，当圆P在BD上与y轴相切至圆P在BC上与y轴相切时，圆与y轴有交点，则时间为：267−2=127，所以总时间为4463+127=15263；（3）解：若线段AB绕点O顺时针旋转90°，线段AB扫过的图形如图8所示，过点O作OH⊥AB，垂足为H，过点O作OH′⊥A′B′，垂足为H′，如图所示，则有OH=OA•sin⊥HAO=3× √32=3√32，同理可得：OH′= 3√32，∵S 弓形AR =S 扇形OAR -S 正⊥OAR = 60π×32360−12×3×3√32=3π2−9√34，S 扇形OBB′= 90π×(3√3)2360=27π4，S 扇形OHH′= 90π×(3√32)2360=27π16S ⊥OHB =S ⊥OH′B′∴S 阴影=S 弓形AR +S ⊥OHB +S 扇形OBB′-S 扇形OHH′-S ⊥OH′B′ =S 弓形AR +S 扇形OBB′-S 扇形OHH′ ＝ 3π2−9√34+27π4−27π16＝ 105π−36√316∴线段AB 扫过的面积是 105π−36√316。

2023年中考九年级数学高频考点拔高训练--圆的综合题

2023年中考九年级数学高频考点拔高训练--圆的综合题一、单选题1．如图，已知正方形ABCD的边长是4，点E是AB边上一动点，连接CE，过点B 作BG⊥CE于点G，点P是AB边上另一动点，则PD+PG的最小值是（）A．2√10−2B．4√3−2C．2√13−2D．2√14−22．如图所示，已知直线l的解析式是y＝43x−4，并且与x轴、y轴分别交于A、B两点．一个半径为1.5的⊥C，圆心C从点（0，1.5）开始以每秒0.5个单位的速度沿着y 轴向下运动，当⊥C与直线l相切时，则该圆运动的时间为（)A．3秒或6秒B．6秒或10秒C．3秒或16秒D．6秒或16秒3．《九章算术》商功章有题：一圆柱形谷仓，高1丈3尺3 13寸，容纳米2000斛（1丈=10尺，1尺=10寸，斛为容积单位，1斛≈1.62立方尺，π=3），则圆柱底周长约为（注：圆柱体的体积=底面积×高）（）A．1丈3尺B．5丈4尺C．9丈2尺D．48丈6尺4．已知在平面直角坐标系xOy中，点A的坐标为(3，4)，M是抛物线y=ax2+bx+ 2(a≠0)对称轴上的一个动点，小明经探究发现：当b a的值确定时，抛物线的对称轴上能使⊥AOM为直角三角形的点M的个数也随之确定．当ba满足（）时，抛物线y= ax2+bx+2(a≠0)的对称轴上存在4个不同的点M，使⊥AOM为直角三角形.A．0<ba<2B．−8<ba<2C．−3≤ba<0D．−6≤ba<05．如图，点E为ΔABC的内心，过点E作MN∥BC交AB于点M，交AC于点N，若AB=7，AC=5，BC=6，则MN的长为（）A．3.5B．4C．5D．5.5 6．已知抛物线y＝a(x﹣3)2+254过点C(0，4)，顶点为M，与x轴交于A、B两点.如图所示以AB为直径作圆，记作⊥D，下列结论：①抛物线的对称轴是直线x＝3；②点C在⊥D外；③在抛物线上存在一点E，能使四边形ADEC为平行四边形；④直线CM与⊥D相切。

2023年中考数学几何模型之动点最值之阿氏圆模型(讲+练)(解析版)

专题15动点最值之阿氏圆模型背景故事：“阿氏圆”又称为“阿波罗尼斯圆”，如下图，已知A 、B 两点，点P 满足PA ：PB=k （k≠1），则满足条件的所有的点P 的轨迹构成的图形为圆．这个轨迹最早由古希腊数学家阿波罗尼斯发现，故称“阿氏圆”.模型建立：当点P 在一个以O 为圆心，r 为半径的圆上运动时，如图所示：易证：△BOP ∽△POA，，∴对于圆上任意一点P 都有.对于任意一个圆，任意一个k 的值，我们可以在任意一条直径所在直线上，在同侧适当的位置选取A 、B点，则需【技巧总结】计算PA k PB 的最小值时，利用两边成比例且夹角相等构造母子型相似三角形问题：在圆上找一点P 使得PA k PB 的值最小，解决步骤具体如下：①如图，将系数不为1的线段两端点与圆心相连即OP ，OB ②计算出这两条线段的长度比OPk OB③在OB 上取一点C ，使得OC k OP ，即构造△POM ∽△BOP ，则PCk PB，PC k PB ④则=PA k PB PA PC AC ，当A 、P 、C 三点共线时可得最小值例1.如图，在Rt △ABC 中，∠ACB ＝90°，CB ＝7，AC ＝9，以C 为圆心、3为半径作⊙C ，P 为⊙C 上一动点，连接AP 、BP ，则13AP ＋BP 的最小值为（）A ．7B ．C ．4D ．【答案】B【详解】如图，在CA 上截取CM ，使得CM ＝1，连接PM ，PC ，BM ．∵PC ＝3，CM ＝1，CA ＝9，∴PC 2＝CM •CA ，∴PC CMCA CP，∵∠PCM ＝∠ACP ，∴△PCM ∽△ACP ，∴13PM PC PA AC ，∴PM 13 PA ，∴13AP +BP ＝PM +PB ，∵PM +PB ≥BM ，在Rt △BCM 中，∵∠BCM ＝90°，CM ＝1，BC ＝7，∴BM ，∴13AP +BP ∴13AP +BP 的最小值为．故选：B ．例2.在ABC 中，AB =9，BC =8，∠ABC =60°，⊙A 的半径为6，P 是A 上一动点，连接PB ，PC ，则32PC PB 的最小值_____________73PB PC 的最小值_______【答案】21【详解】①连接AP ，在AB 上取点Q ，使AQ =4，连接CQ ，∵⊙A 的半径为6，即AP =6，∴23AB AP ，又6923AP AB ，且PAQ BAP ，∴APQ ABP ∽，∴23PQ AP P AB B ，∴23PQ BP ，∴ 232333PC PB PC BP PC PQ，当P C Q 、、三点共线时，PC PQ 的值最小，最小值为CQ 的长，过C 作CI ⊥AB 于I ，∴90CIB CIQ ，在Rt △CIB 中，∵60CBI ，BC =8，sin CI CBI BC，∴CI∴4BI ，9441QI AB AQ BI ，在Rt △CIQ 中，7CQ ，∴32PC PB 的最小值为 321PC PQ ；故答案为：21；②连接AP ，由①得：在Rt △CIA 中，AC在AC 上取点G ，使AG ，连接PG ，BG ，∴73673AG AP ，∵67373AP AC ，∴P P AC A AG A ，且GAP PAC ，∴AGP APC ∽，∴73GP AG A P P C，∴73GP PC，∴73PB PB GP ，当G P B 、、三点共线时，PB GP 的值最小，最小值为BG 的长，过G 作GH ⊥AB 于H ，∴90GHA GHB ，在Rt △CIA 中，sin C CI AI ACRt △GAH 中，sin GH GAH AG∴GH ，∴18073AH，180********BH AB AH ，在Rt △GHB中，73BG ，∴73PB PC的最小值为73．故答案为：73．例题3.如图，已知正方ABCD 的边长为6，圆B 的半径为3，点P 是圆B 上的一个动点，则12PD PC 的最大值为_______．AB CDP【解析】当P 点运动到BC 边上时，此时PC=3，根据题意要求构造12PC ，在BC 上取M 使得此时PM=32，则在点P 运动的任意时刻，均有PM=12PC ，从而将问题转化为求PD-PM的最大值．连接PD ，对于△PDM ，PD-PM ＜DM ，故当D 、M 、P 共线时，PD-PM=DM 为最大值152．【变式训练1】如图，已知菱形ABCD 的边长为4，60B ，B 的半径为2，P 为B 上一动点，则12PD PC 的最小值_______．PC PD 的最小值_______3【详解】①如图，在BC 上取一点G ，使得BG =1，连接PB 、PG 、GD ，作DF ⊥BC 交BC 延长线于F ．∵221PB BG ，422BC PB ，∴PB BC BG PB ，∵PBG PBC ，∴PBG CBP ，∴12PG BG PC PB ，∴12PG PC ，∴12PD PC DP PG，∵DP PG DG ，∴当D 、P 、G 共线时，PD +12PC 的值最小，最小值为DG ，在Rt △CDF 中，∠DCF =60°，CD =4，∴DF =CD •sin CF =2，在Rt △GDF 中，DG ；②如图，连接BD ，在BD 上取一点M ，使得BM 连接PB 、PM 、MC ，过M 作MN ⊥BC 于N ．∵四边形ABCD 是菱形，且60ABC ，∴AC ⊥BD ，∠AOB =90 ，∠ABO =∠CBO =12∠ABC =30 ，∴AO =12AB =2，BO ∴BD =2BO =∴326BM PB ，6PB BD，∴BM PB PB BD ∠MBP =∠PBD ，∴△MBP ~△PBD ，∴PM PB PD BD∴PM ，∴PC PC PM MC ，∴当M 、P 、C 共线时，PC 的值最小，最小值为CM ，在Rt △BMN 中，∠CBO =30 ，BM ∴MN =12BM BN 12 ，∴CN =4-1722，∴MC，∴PC 的最小值为1113．【变式训练2】如图，正方形ABCD 的边长为4，圆B 的半径为2，点P 是圆B 上一动点，则的最小值为，的最大值为.【答案】最小值为5，最大值为5【解析】在BC 上取一点G ，使得BG ＝1，连接PG 、DG ，如图所示：∵∠PBG＝∠PBC，∴△PBG∽△CBP，，∴，在△PDG中，DP＋PG≥DG，∴当D、G、P共线时，；当点P在DG的延长线时，DG，最大值为5.【变式训练3】如图，在平面直角坐标系中，点A（4，0），B（4，4），点P在半径为2的圆O上运动，则的最小值是.【答案】5【解析】取点K（1，0），连接OP、PK、BK，如图所示：∵OP ＝2，OA ＝4，OK ＝1，∵∠POK ＝∠AOP ，∴△POK ∽△AOP ，在△PBK 中，，的最小值为BK 的长，∵B （4，4），K （1，0），，∴的最小值为5.【变式训练4】如图，菱形ABCD 的边长为2，锐角大小为60 ，A 与BC 相切于点E ，在A上任取一点P ，则2PB PD的最小值为___________．【答案】2．【详解】解：在AD 上截取AH =1.5，连接PH 、AE ，过点B 作BF ⊥DA 延长线，垂足为F ，∵AB =2，∠ABC =60°，∴BE =AF =1，AE =BF ，∴3AP AD AH AP，∵∠PAD =∠PAH ，∴△ADP ∽△APH ，∴3DP AD PH AP，∴PH ，当B 、P 、H 共线时，PB 的最小，最小值为BH 长，BH课后训练1.如图，矩形ABCD 中，4,2AB AD ，以B 为圆心，以BC 为半径画圆交边AB 于点E ，点P 是弧CE 上的一个动点，连结,PD PA ，则12AP DP 的最小值为（）A BC D 【答案】C【详解】解：如图，连接BP ，取BE 的中点G ，连接PG ，∵2AD BC BP ，4AB ，∴2142BP BA ，∵G 是BE 的中点，∴12BG BP ，∴BP BGBA BP，∵PBG ABP ，∴BPG BAP ，∴12PG BP AP BA ，∴12PG AP ，则12AP DP PG DP ，当P 、D 、G 三点共线时，取最小值，即DG 长，DG C ．2.如图，在平面直角坐标系中，A （2，0）、B （0，2）、C （4，0）、D （3，2），P 是△AOB 外部的第一象限内一动点，且∠BPA ＝135º，则2PD ＋PC 的最小值是.【解析】依题意可得OA＝OB＝2，∠BPA＝135º，∴点P的轨迹是以原点为圆心，OA长为半径的圆O上的劣弧AB，构造圆O，连接OP，在OC上截取OE＝1，连接PE、ED，过点D作DF⊥OC于点F，如图所示：∠POC＝∠EOP，∴△POC∽△EOP，，，，当E、P、D三点共线时，PD＋PE的值最小，最小值为DE的值，∵DF⊥OC于点F，则DF＝2，EF＝2，的最小值为2DE.3.如图，在Rt ABC中，∠C=90°，CA=3，CB=4．C 的半径为2，点P是C 上一动点，则12AP BP的最小值______________23PB PA的最小值_______【详解】①在BC 上取点D ，使CD =14BC =1，连接AD ，PD ，PC ，由题意知：PC =2，∵12DC PC PC BC ，∠PCD =∠BCP ，∴PDC BPC ∽，∴12PD PB ，且12PA PB PA PD AD，∴AD∴2PA PB ；②在AC 上取点E ，使CE =43，连接PE ，BE ，PC ，∵42323CE PC ，23PC AC ，∴23CE PC PC AC ，且∠PCE =∠ACP ，∴PEC APC ∽，∴23PE PC PA AC ，∴23PE PA ，∴23PB PA PB PE BE ，∴BE ∴23 PB PA 的最小值为3，故答案为：3．4.如图，半圆的半径为1，AB 为直径，AC 、BD 为切线，AC ＝1，BD ＝2，点P 为弧AB上一动点，求的最小值.【答案】【解析】当A、P、D三点共线时，的值最小.连接PB、CO，AD与CO相交于点M，如图所示：∵AB＝BD＝2,BD是⊙O的切线,∴∠ABD＝90º,∠BAD＝∠D＝45º,∵AB是⊙O直径,∴∠APB＝90º,∴∠PAB＝∠PBA＝45º,∴PA＝PB,PO⊥AB,∵AC是⊙O的切线,∴AC⊥AB,∴AC∥PO,∠CAO＝90º∵AC＝PO＝1,∴四边形AOPC是平行四边形,而OA＝OP,∠CAO＝90º,∴四边形AOPC是正方形,PC＋PD＝PM＋PD＝DM,∵DM⊥OC,∴由"垂线段最短"可知此时＋PD的值最小，最小值为.5.（1）如图1，在△ABC中，AB＝AC，BD是AC边上的中线，请用尺规作图做出AB边上的中线CE，并证明BD＝CE：（2）如图2，已知点P是边长为6的正方形ABCD内部一动点，PA＝3，求PC+PD的最小值；（3）如图3，在矩形ABCD中，AB＝18，BC＝25，点M是矩形内部一动点，MA＝15，当MC+MD最小时，画出点M的位置，并求出MC+MD的最小值．【解答】解：（1）如图1中，作线段AB的垂直平分线MN交AB于点E，连接EC．线段EC即为所求；∵AB＝AC，AE＝EC，AD＝CD，∴AE＝AD，∵AB＝AC，∠A＝∠A，AD＝AE，∴△BAD≌△CAE（SAS），∴BD＝CE．（2）如图2中，在AD上截取AE，使得AE＝．∵PA2＝9，AE•AD＝×6＝9，∴PA2＝AE•AD，∴＝，∵∠PAE＝∠DAP，∴△PAE∽△DAP，∴＝＝，∴PE＝PD，∴PC+PD＝PC+PE，∵PC+PE≥EC，∴PC+PD的最小值为EC的长，在Rt△CDE中，∵∠CDE＝90°，CD＝6，DE＝，∴EC＝＝，∴PC+PD的最小值为．（3）如图3中，如图2中，在AD上截取AE，使得AE＝9．∵MA2＝225，AE•AD＝9×25＝225，∴MA2＝AE•AE，∴＝，∵∠MAE＝∠DAM，∴△MAE∽△DAM，∴＝＝＝，∴ME＝MD，∴MC+MD＝MC+ME，∵MC+ME≥EC，∴MC+MD的最小值为EC的长，在Rt△CDE中，∵∠CDE＝90°，CD＝18，DE＝16，∴EC＝＝2，∴MC+MD的最小值为2．6.如图1，抛物线y＝ax2＋（a＋3）x＋3（a≠0）与x轴交于点A（4，0），与y轴交于点B，在x轴上有一动点E（m，0）（0＜m＜4），过点E作x轴的垂线交直线AB于点N，交抛物线于点P，过点P作PM⊥AB于点M．（1）求a的值和直线AB的函数表达式；（2）设△PMN的周长为C1，△AEN的周长为C2，若＝，求m的值；（3）如图2，在（2）条件下，将线段OE绕点O逆时针旋转得到OE′，旋转角为α（0°＜α＜90°），连接E′A、E′B，求E’A＋E’B的最小值．【解答】（1）；（2）m＝2；（3）【解析】（1）令y＝0，则ax2＋（a＋3）x＋3＝0，∴（x＋1）（ax＋3）＝0，∴x＝﹣1或，∵抛物线y＝ax2＋（a＋3）x＋3（a≠0）与x轴交于点A（4，0），∴＝4，∴a．∵A（4，0），B（0，3），设直线AB解析式为y＝kx＋b，则，解得，∴直线AB解析式．（2）如图1中，∵PM⊥AB，PE⊥OA，∴∠PMN＝∠AEN，∵∠PNM＝∠ANE，∴△PNM∽△ANE，∵NE∥OB，∴AN（4﹣m），∵抛物线解析式为，∴PN＝﹣（）＝，，解得m＝2．（3）如图2中，在y轴上取一点M′使得OM′＝，连接AM′，在AM′上取一点E′使得OE′＝OE．∵OE′＝2，OM′•OB×3＝4，∴OE′2＝OM′•OB，，∵∠BOE′＝∠M′OE′，∴△M′OE′∽△E′OB，，∴M′E′＝BE′，∴AE BE′＝AE′＋E′M′＝AM′，此时AE′＋BE′最小（两点间线段最短，A、M′、E′共线时），最小值＝AM′＝．。

2023年九年级数学中考压轴复习专题几何综合——动点问题课件

6−5
∴
=

4

Rt△ADH中，AD=5，tanA= = 3
6−5
∴y与x的函数关系式为
=
∴DH=4，AH=3.在Rt△EDH中，DH=4，

25
EH=x-3，
( 6 ≤≤35)
∴DE²=DH²＋EH²=4²＋(x-3)²=x²-6x＋
4
例题在△ABC中,AC=25,AB =35,tanA=3,D为AC边上的一点，且AD=5 ,E,F都为AB边上的动
所以结合已知条件与所给图形进行认真分析是非常重要的，
当然这样的分析是建立在熟练运用常见图形的几何性质之上
的.
（2）类似于例题这样的几何计算型的压轴题，同学们
要切实体会解直角三角形与相似三角形在计算中所发挥的
重要作用.
（3）对于类似于例题这样的动态几何，应时刻谨记
“动静结合”、“数形结合”的处理原则，以及“分类
∴∠EDF＋∠ADF=90°，即
∠ADE=90°.在Rt△ADE中，AD=5，

4
tanA= = 3
4
20
5
25
∴DE=3AD= 3 ，AE=3AD= 3
∴△EDF∽△EAD，

∴ =
∴DE²=AE·EF=x·（x一y）=x²-xy.∴x²-6x＋25=x²xy
（2）如下图，作DH⊥AE于点H，在
目录
01
研究背景
03
典型例题探究
动态几何研究重要性
总结分析动态问题处理技巧
05
02
知识脉络梳理
初中阶段几何知识梳理
04 小试能手
技巧，
挑战自我
展

2023年九年级中考数学高频考点突破-圆的动点问题

2023年中考数学高频考点突破--圆的动点问题一、单选题1．如图，在ΔABC中，AB=10，AC=8，BC=6，以边AB的中点O为圆心，作半圆与AC相切，点P，Q分别是边BC和半圆上的动点，连接PQ，则PQ长的最大值与最小值的和是（）A．6B．2√13+1C．323D．92．如图，直角△ABC中，∠ACB=90°，BC=2√3，点P是△ABC内部一动点，总满足∠APC=150°，连接BP，则BP的最小值为（）A．2√7−4B．2√31−8C．4−√3D．23√183−83√3 3．点A，B的坐标分别为A (4，0)，B(0，4)，点C为坐标平面内一点，BC﹦2，点M为线段AC的中点，连接OM，则OM的最大值为（）A．2 √2＋1B．2 √2＋2C．4 √2＋1D．4 √2-24．如图，点A的坐标是（−2，0），点C是以OA为直径的∠B上的一动点，点A关于点C的对称点为点P. 当点C在∠ B上运动时，所有这样的点P组成的图形与直线y=kx－3（k＞0）有且只有一个公共点，则k的值是（）A．23B．√53C．6√55D．√525．如图，A是∠B上任意一点，点C在∠B外，已知AB＝2，BC＝4，∠ACD是等边三角形，则△BCD的面积的最大值为（）A．4 √3＋4B．4C．4 √3＋8D．66．如图，A（12，0），B（0，9）分别是平面直解坐标系xOy坐标轴上的点，经过点O且与AB相切的动圆与x轴、y轴分别相交于点P、Q，则线段PQ长度的最小值是（）A．6√2B．10C．7.2D．6√37．设O为坐标原点，点A、B为抛物线y=x2上的两个动点，且OA⊥OB．连接点A、B，过O 作OC⊥AB于点C，则点C到y轴距离的最大值（）A．12B．√22C．√32D．18．已知∠O的半径为3，A为圆内一定点，AO＝1，P为圆上一动点，以AP为边作等腰∠APQ，AP ＝PQ，∠APQ＝120°，则OQ的最大值为（）A．1+3√3B．1+2√3C．3+√3D．3√3−19．如图，在Rt△ABC中，∠C=90°，AC=6，BC=8，点F在边AC上，且CF= 2，点E为射线CB上一动点，连接EF．将△CEF沿直线EF折叠，使点C落在点P处，连接AP，BP，则△APB的面积最小值为（）A．3B．6C．245D．1210．如图，在ΔABC中，AB=10，AC=8，BC=6，以边AB的中点O为圆心作半圆，使BC与半圆相切，点P,Q分别是边AC和半圆上的动点，连接PQ，则PQ长的最大值与最小值的和是（）A．8B．9C．10D．1211．如图，A是⊙B上任意一点，点C在⊙B外，已知AB=2，BC=4，△ACD是等边三角形，则△BCD的面积的最大值为（）A．4√3+4B．4√3C．4√3+8D．6√312．如图，在等边∠ABC中，AB＝6，点D，E分别在边BC，AC上，且BD＝CE，连接AD，BE 交于点F，连接CF，则CF的最小值是（）A．3B．2 √3C．4D．3 √3二、填空题13．在平面直角坐标系中，已知点A (2√3，0)，点B (−6√3，0)，点C是y轴上的一个动点，当∠BCA＝30°时，点C的坐标为．14．如图，在平面直角坐标系xOy中，半径为4的∠O与x轴的正半轴交于点A，点B是∠O上一动点，点C为弦AB的中点，直线y=34x−6与x轴、y轴分别交于点D、E，则△CDE面积的最小值为.15．如图，AB为半圆的直径，AB=10，点O到弦AC的距离为4，点P从B出发沿BA 方向向点A以每秒1个单位长度的速度运动，连接CP，经过秒后，ΔAPC为等腰三角形．16．如图，AB是⊙O的直径，M、N是AB̂异于A，B的两点，C是MN̂一动点，∠ACB的角平分线交⊙O于点D，∠BAC的平分线交CD于点E．当点C从点M运动到点N时，则E，C两点的运动路径长的比是．三、综合题17．如图，在平面直角坐标系中，边长为6的正方形ABCD的四条边与坐标轴平行，顶点A、B 分别在第一象限、第二象限，对角线AC、BD的交点与坐标原点O重合，当正方形ABCD的边上存在点Q，满足PQ≤2时，称点P为正方形ABCD的伴随点．（1）点A的坐标为点，B的坐标为，点C的坐标为，点D的坐标为．（2）当正方形ABCD的伴随点P的坐标为(3，0)时，点Q的坐标可以为（写出一个即可）．（3）在点P1(0，0)、P2(5.5，5.5)、P3(−4，2)、P4(1，−2)中，正方形ABCD的伴随点是．（4）点P在直线y=x上．若点P为正方形ABCD的伴随点，直接写出点P横坐标m的取值范围．18．如图，已知∠MON=90°，OT是∠MON的平分线，A是射线OM上一点，OA=12cm．动点P从点A出发，以1cm/s的速度沿AO水平向左做匀速运动，与此同时，动点Q从点O出发，也以1cm/s 的速度沿ON竖直向上做匀速运动．连接PQ，交OT于点B．经过O，P，Q三点作圆，交OT于点C，连接PC，QC．设运动时间为t(s)，其中0<t<12．（1）若tan∠OCQ =13，求t 的值；（2）当△PBC 为等腰三角形时，求t 的值；（3）若△OPQ 的内心为点I ，求线段IC 长度的最小值．19．在平面直角坐标系xOy 中，已知点M(a ，b)，N.对于点P 给出如下定义：将点P 向右(a ≥0)或向左(a <0)平移|a|个单位长度，再向上(b ≥0)或向下(b <0)平移|b|个单位长度，得到点P′，点P′关于点N 的对称点为Q ，称点Q 为点P 的“对应点”．（1）如图，点M(1，1)，点N 在线段OM 的延长线上，若点P(−2，0)，点Q 为点P 的“对应点”．①在图中画出点Q ；②连接PQ ，交线段ON 于点T.求证：NT =12OM ；（2）⊙O 的半径为1，M 是⊙O 上一点，点N 在线段OM 上，且ON =t(12<t <1)，若P 为⊙O 外一点，点Q 为点P 的“对应点”，连接PQ.当点M 在⊙O 上运动时直接写出PQ 长的最大值与最小值的差（用含t 的式子表示）20．如图①，在矩形ABCD 中，BC ＝60cm.动点P 以6cm/s 的速度在矩形ABCD 的边上沿A→D 的方向匀速运动，动点Q 在矩形ABCD 的边上沿A→B→C 的方向匀速运动.P 、Q 两点同时出发，当点P 到达终点D 时，点Q 立即停止运动.设运动的时间为t （s ），∠PDQ 的面积为S （cm 2），S 与t 的函数图象如图②所示.（1）AB＝cm，点Q的运动速度为cm/s；（2）在点P、Q出发的同时，点O也从CD的中点出发，以4cm/s的速度沿CD的垂直平分线向左匀速运动，以点O为圆心的∠O始终与边AD、BC相切，当点P到达终点D时，运动同时停止.①当点O在QD上时，求t的值；②当PQ与∠O有公共点时，求t的取值范围.答案解析部分1．【答案】D 2．【答案】B 3．【答案】A 4．【答案】D 5．【答案】A 6．【答案】C 7．【答案】A 8．【答案】A 9．【答案】B 10．【答案】C 11．【答案】A 12．【答案】B13．【答案】(0，12+6√5) 或 (0，−12−6√5) 14．【答案】815．【答案】145 或4或516．【答案】√217．【答案】（1）(3，3)；(−3，3)；(−3，−3)；(3，−3)（2）(3，1) 答案不唯一（3）P 3 、 P 4（4）解：如图符合条件的临界点P 有4个，如图，过点 P 5 作 P 5E ⊥x 轴于E ，过点 P 6 作 P 6F ⊥x 轴于F ，∵点P5，点P6在y=x上，∴∠P5OE=45°，∵正方形ABCD边长为6，∴OG=AG=3，∴OA=3√2，P6F=OF=1，∴OP5=3√2+2，∴OE=P5E=√2+2√2=3+√2，∴P5(3+√2，3+√2)，P6(1，1)，∴1≤m≤3+√2，同理可得P7(−1，−1)，P8(−3−√2，−3−√2)，∴−3−√2≤m≤−1，综上，−3−√2≤m≤−1或1≤m≤3+√2．18．【答案】（1）解：由题意得：OQ=t，OP=12−t，∠MON=90°，∵OQ⌢=OQ⌢，∴∠OPQ=∠OCQ，∴tan∠OPQ=tan∠OCQ=1 3，在Rt△OPQ，tan∠OPQ=OQ OP，∴t12−t=13，解得：t=3；（2）解：∵∠BPC=∠QOC，∠PBC=∠POC+∠OPQ，∵∠MON=90°，OT是∠MON的平分线，∴∠QOC=∠POC=12∠MON=45°，∴∠BPC=45°，∠PBC>45°，∴当△PBC为等腰三角形时，则PB=PC或BC=BP，当PB=PC时，则∠PBC=∠PCB，如图，作BH⊥OQ，BG⊥OP，∵∠PCB=∠OQB，∠PBC=∠OBQ，∴∠OBQ=∠OQB，∴OB=OQ=t，∵∠QOC=∠POC=12∠MON=45°，∴BH=BG=√22t，∵S△OPQ=S△OBQ+S△OBP，∴12OQ⋅OP=12OQ⋅BH+12OP⋅BG，即：12t⋅(12−t)=12t×√22t+12(12−t)×√22t，解得：t=12−6√2；如图，当BC=BP时，则∠BPC=∠BCP=∠QOC=45°，∴∠OQP=∠BCP=45°，∴∠OPQ是等腰直角三角形，∴OP=OQ，即：12−t=t，解得：t=6；综上所述，当△PBC为等腰三角形时，求t的值为12−6√2或6.（3）解：设PQ的中点为D，∵△OPQ的内心为点I，OC平分∠MON，∴点I在OC上，∴ID+CD≥IC，∴当点I、D、C共线时，即点D与点B重合时，线段IC长度的值最小，如图，过点I作IE∠OQ于E，IF∠OP于F，∵点B为PQ中点，为圆心，∴OC为圆的直径，∴∠OPC=∠OQC=90°，∴∠OCP=∠POC=45°，∵∠OCP=∠OQP，∴∠OQP=∠OPQ=45°，∴OP=OQ，OB∠PQ，∴IE=IF=IB，即：12−t=t，解得：t=6；∴OC=√2OQ=6√2，OB=BC=3√2，∵∠QOC=45°，∴OI=√2EI，∵EI=FI=BI，OB=OI+BI，∴OB=√2BI+BI，即：3√2=√2BI+BI，解得：BI=6−3√2，IC=BC+BI=6−3√2+3√2=6，∴线段IC长度的最小为6．19．【答案】（1）解：①点Q如下图所示．∵点M(1，1)，∴点P(−2，0)向右平移1个单位长度，再向上平移1个单位长度，得到点P′，∴P′(−1，1)，∵点P′关于点N的对称点为Q，N(2，2)，∴点Q的横坐标为：2×2−(−1)=5，纵坐标为：2×2−1=3，∴点Q(5，3)，在坐标系内找出该点即可；②证明：如图延长ON至点A(3，3)，连接AQ，∵AQ//OP，∴∠AQT=∠OPT，在ΔAQT与Δ∠OPT中，{∠AQT =∠OPT∠ATQ =∠OTP AQ =OP，∴ΔAQT ≅ΔOPT(AAS)，∴TA =TO =12OA ， ∵A(3，3)，M(1，1)，N(2，2)，∴OA =√32+32=3√2，OM =√12+12=√2，ON =√22+22=2√2，∴TO =12OA =32√2， ∴NT =ON −OT =2√2−32√2=√22， ∴NT =12OM ；（2）解：PQ 长的最大值与最小值的差为4t −2．20．【答案】（1）30；6（2）解：①如图1，设AB ，CD 的中点分别为E ，F ，当点O 在QD 上时，QC ＝AB+BC ﹣6t ＝90﹣6t ，OF ＝4t ，∵OF∠QC 且点F 是DC 的中点，∴OF ＝12QC ，即4t ＝12（90﹣6t ），解得，t ＝457； ②设AB ，CD 的中点分别为E ，F ，∠O 与AD ，BC 的切点分别为N ，G ，过点Q 作QH∠AD 于H ，如图2﹣1，当∠O 第一次与PQ 相切于点M 时，∵AH+AP＝6t，AB+BQ＝6t，且BQ＝AH，∴HP＝QH＝AB＝30，∴∠QHP是等腰直角三角形，∵CG＝DN＝OF＝4t，∴QM＝QG＝90﹣4t﹣6t＝90﹣10t，PM＝PN＝60﹣4t﹣6t＝60﹣10t，∴QP＝QM+MP＝150﹣20t，∵QP＝√2QH，∴150﹣20t＝30√2，；∴t＝15−3√22如图2﹣2，当∠O第二次与PQ相切于点M时，∵AH+AP＝6t，AB+BQ＝6t，且BQ＝AH，∴HP＝QH＝AB＝30，∴∠QHP是等腰直角三角形，∵CG＝DN＝OF＝4t，∴QM＝QG＝4t﹣（90﹣6t）＝10t﹣90，PM＝PN＝4t﹣（60﹣6t）＝10t﹣60，∴QP＝QM+MP＝20t﹣150，∵QP＝√2QH，∴20t ﹣150＝30√2，∴t ＝15+3√22，综上所述，当PQ 与∠O 有公共点时，t 的取值范围为：15−3√22≤t≤15+3√22.。

2024年中考数学高频压轴题训练——圆-动点问题及参考答案

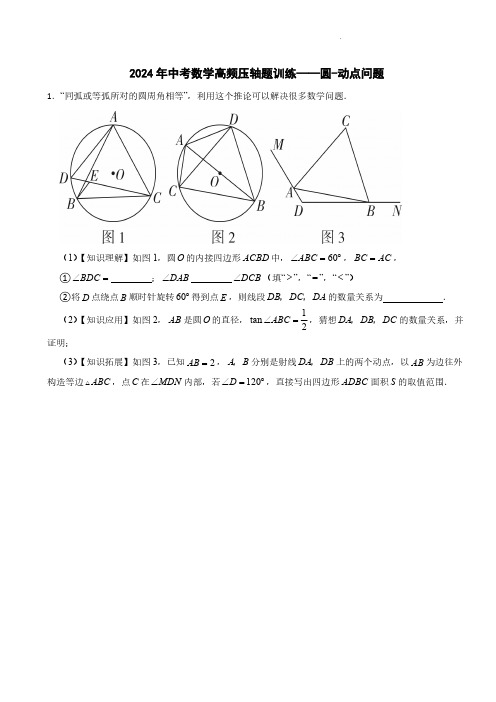
2024年中考数学高频压轴题训练——圆-动点问题1．“同弧或等弧所对的圆周角相等”，利用这个推论可以解决很多数学问题．（1）【知识理解】如图1，圆O 的内接四边形ACBD 中，60ABC ∠=︒，BC AC =，①BDC ∠=；DAB ∠DCB ∠（填“>”，“=”，“<”）②将D 点绕点B 顺时针旋转60︒得到点E ，则线段DB DC DA ，，的数量关系为．（2）【知识应用】如图2，AB 是圆O 的直径，1tan 2ABC ∠=，猜想DA DB DC ，，的数量关系，并证明；（3）【知识拓展】如图3，已知2AB =，A B ，分别是射线DA DB ，上的两个动点，以AB 为边往外构造等边ABC ，点C 在MDN ∠内部，若120D ∠=︒，直接写出四边形ADBC 面积S 的取值范围．2．如图1，对于PMN 的顶点P 及其对边MN 上的一点Q ，给出如下定义：以P 为圆心，PQ 为半径的圆与直线MN 的公共点都在线段MN 上，则称点Q 为PMN 关于点P 的内联点．在平面直角坐标系xOy 中：（1）如图2，已知点(70)A ，，点B 在直线1y x =+上．①若点(34)B ，，点(30)C ，，则在点O ，C ，A 中，点是AOB 关于点B 的内联点；②若AOB 关于点B 的内联点存在，求点B 纵坐标n 的取值范围；（2）已知点(20)D ，，点(42)E ，，将点D 绕原点O 旋转得到点F ．若EOF 关于点E 的内联点存在，直接写出点F 横坐标m 的取值范围．3．在平面直角坐标系xOy 中，O 的半径为1，对于点A 和线段BC ，给出如下定义：若将线段BC 绕点A 旋转可以得到O 的弦B C ''（B C ''，分别是B C ，的对应点），则称线段BC 是O 的以点A 为中心的“关联线段”．（1）如图，点112233A B C B C B C ，，，，，，的横､纵坐标都是整数．在线段112233B C B C B C ，，中，O 的以点A 为中心的“关联线段”是；（2）ABC 是边长为1的等边三角形，点()0A t ，，其中0t ≠．若BC 是O 的以点A 为中心的“关联线段”，求t 的值；（3）在ABC 中，12AB AC ==，．若BC 是O 的以点A 为中心的“关联线段”，直接写出OA 的最小值和最大值，以及相应的BC 长．4．已知：点C 为⊙O 的直径AB 上一动点，过点C 作CD ⊥AB ，交⊙O 于点D 和点E ，连接AD 、BD ，∠DBA 的角平分线交⊙O 于点F ．（1）若DF ＝BD ，求证：GD ＝GB ；（2）若AB ＝2cm ，在（1）的条件下，求DG 的值；（3）若∠ADB 的角平分线DM 交⊙O 于点M ，交AB 于点N ．当点C 与点O 重合时，AD BD DM+＝；据此猜想，当点C 在AB （不含端点）运动过程中，AD BD DM +的值是否发生改变？若不变，请求其值；若改变，请说明理由．5．在平面直角坐标系xOy 中，O 的半径为1，对于ABC 和直线l 给出如下定义：若ABC 的一条边关于直线l 的对称线段PQ 是O 的弦，则称ABC 是O 的关于直线l 的“关联三角形”，直线l 是“关联轴”．（1）如图1，若ABC 是O 的关于直线l 的“关联三角形”，请画出ABC 与O 的“关联轴”（至少画两条）；（2）若ABC 中，点A 坐标为(23)，，点B 坐标为(41)，，点C 在直线3y x =-+的图像上，存在“关联轴l ”使ABC 是O 的关联三角形，求点C 横坐标的取值范围；（3）已知A ，将点A 向上平移2个单位得到点M ，以M 为圆心MA 为半径画圆，B ，C 为M 上的两点，且2AB =（点B 在点A 右侧），若ABC 与O 的关联轴至少有两条，直接写出OC 的最小值和最大值，以及OC 最大时AC 的长．6．如图，在⊙O 中，AB 为弦，CD 为直径，且AB ⊥CD ，垂足为E ，P 为 AC 上的动点（不与端点重合），连接PD ．（1）求证：∠APD ＝∠BPD ；（2）利用尺规在PD 上找到点I ，使得I 到AB 、AP 的距离相等，连接AD （保留作图痕迹，不写作法）．求证：∠AIP+∠DAI ＝180°；（3）在（2）的条件下，连接IC 、IE ，若∠APB ＝60°，试问：在P 点的移动过程中，IC IE 是否为定值？若是，请求出这个值；若不是，请说明理由．7．在平面直角坐标系xOy 中，已知线段AB 和点P ，给出如下定义：若PA PB =且点P 不在线段AB 上，则称点P 是线段AB 的等腰顶点．特别地，当90APB ∠≥︒时，则称点P 是线段AB 的非锐角等腰顶点．（1）已知点(20)A ，，(42)B ，．①在点(40)C ，，(31)D ，，(15)E -，，(05)F ，中，是线段AB 的等腰顶点的是▲；②若点P 在直线3(0)y kx k =+≠上，且点P 是线段AB 的非锐角等腰顶点，求k 的取值范围；（2）直线33y x =-+与x 轴交于点M ，与y 轴交于点N ．⊙P 的圆心为(0)P t ，，半径为，若⊙P 上存在线段MN 的等腰顶点，请直接写出t 的取值范围．8．在平面直角坐标系xOy中，⊙O的半径为1，T（0，t）为y轴上一点，P为平面上一点．给出如下定义：若在⊙O上存在一点Q，使得△TQP是等腰直角三角形，且∠TQP＝90°，则称点P为⊙O的“等直点”，△TQP为⊙O的“等直三角形”．如图，点A，B，C，D的横、纵坐标都是整数．（1）当t＝2时，在点A，B，C，D中，⊙O的“等直点”是；（2）当t＝3时，若△TQP是⊙O“等直三角形”，且点P，Q都在第一象限，求CPOQ的值．9．综合与实践动手操作利用正方形纸片的折叠开展数学活动．探究体会在正方形折叠过程中，图形与线段的变化及其蕴含的数学思想方法．如图1，点E 为正方形ABCD 的AB 边上的一个动点，3AB =，将正方形ABCD 对折，使点A 与点B 重合，点C 与点D 重合，折痕为MN ．思考探索（1）将正方形ABCD 展平后沿过点C 的直线CE 折叠，使点B 的对应点B '落在MN 上，折痕为EC ，连接DB '，如图2．①点B '在以点E 为圆心，的长为半径的圆上；②B M '=；③DB C ' 为三角形，请证明你的结论．（2）拓展延伸当3AB AE =时，正方形ABCD 沿过点E 的直线l （不过点B ）折叠后，点B 的对应点B '落在正方形ABCD 内部或边上．①ABB ' 面积的最大值为；②连接AB '，点P 为AE 的中点，点Q 在AB '上，连接PQ AQP AB E ∠=∠'，，则2B C PQ '+的最小值为．10．在平面直角坐标系xOy 中，过⊙T （半径为r ）外一点P 引它的一条切线，切点为Q ，若0＜PQ≤2r ，则称点P 为⊙T 的伴随点．（1）当⊙O 的半径为1时，①在点A(4，0)，B(0，)，C(1，)中，⊙O 的伴随点是▲；②点D 在直线y ＝x+3上，且点D 是⊙O 的伴随点，求点D 的横坐标d 的取值范围；（2）⊙M 的圆心为M(m ，0)，半径为2，直线y ＝2x ﹣2与x 轴，y 轴分别交于点E ，F ．若线段EF 上的所有点都是⊙M 的伴随点，直接写出m 的取值范围．11．定义：在平面直角坐标系xOy 中，点P 为图形M 上一点，点Q 为图形N 上一点．若存在OP OQ =，则称图形M 与图形N 关于原点O “平衡”．（1）如图，已知⊙A 是以()1,0为圆心，2为半径的圆，点()1,0C -，()2,1D -，()3,2E ．①在点C ，D ，E 中，与⊙A 关于原点O “平衡”的点是；②点H 为直线y x =-上一点，若点H 与⊙A 关于原点O “平衡”，点H 的横坐标的取值范围为：；（2）如图，已知图形G 是以原点O 为中心，边长为2的正方形．⊙K 的圆心在x 轴上，半径为2．若⊙K 与图形G 关于原点O “平衡”，请直接写出圆心K 的横坐标的取值范围．12．阅读下列材料，并按要求解答相关问题：【思考发现】根据直径所对的圆周角是直角，我们可以推出“如果一条定边所对的角始终为直角，那么所有满足条件的直角顶点组成的图形是以定边为直径的圆或圆弧（直径的两个端点除外）”这一正确的结论．如图1，若AB 是一条定线段，且90APB ∠=︒，则所有满足条件的直角顶点P 组成的图形是定边AB 为直径的O （直径两端点A 、B 除外）（1）已知：如图2，四边形ABCD 是边长为8的正方形，点E 从点B 出发向点C 运动，同时点F 从点C 出发以相同的速度向点D 运动，连接AE ，BF 相交于点P ．①当点E 从点B 运动到点C 的过程中，APB ∠的大小是否发生变化？若发生变化，请说明理由；若不发生变化，请直接写出APB ∠的度数．②当点E 从点B 运动到点C 的过程中，点P 运动的路径是（）A ．线段；B ．弧；C ．半圆；D ．圆③点P 运动的路经长是▲．（2）已知：如图3，在图2的条件下，连接CP ，请直接写出E 、F 运动过程中，CP 的最小值．13．对于平面内的图形1G 和图形2G ，记平面内一点P 到图形1G 上各点的最短距离为1d ，点P 到图形2G 上各点的最短距离为2d ，若12d d =，就称点P 是图形1G 和图形2G 的一个“等距点”．在平面直角坐标系xOy 中，已知点()60A ，，(0B ．（1）在()30R ，，()20S ，，(1T 三点中，点A 和点B 的等距点是；（2）已知直线2y =-．①若点A 和直线2y =-的等距点在x 轴上，则该等距点的坐标为▲；②若直线y a =上存在点A 直线2y =-的等距点，求实数a 的取值范围；（3）记直线AB 为直线1l ，直线2l ：33y x =-，以原点O 为圆心作半径为r 的O ．若O 上有m 个直线1l 和直线2l 的等距点，以及n 个直线1l 和y 轴的等距点（0m ≠，0n ≠），求m n ≠时，求r 的取值范围．14．如图，平面上存在点P 、点M 与线段AB ．若线段AB 上存在一点Q ，使得点M 在以PQ 为直径的圆上，则称点M 为点P 与线段AB 的共圆点．已知点P （0，1），点A （﹣2，﹣1），点B （2，﹣1）．（1）在点O （0，0），C （﹣2，1），D （3，0）中，可以成为点P 与线段AB 的共圆点的是；（2）点K 为x 轴上一点，若点K 为点P 与线段AB 的共圆点，请求出点K 横坐标x K 的取值范围；（3）已知点M （m ，﹣1），若直线y ＝12x +3上存在点P 与线段AM 的共圆点，请直接写出m 的取值范围．15．如图，在ABC 中，AB BC =，30CAB ∠=︒，8AC =，半径为2的O 从点A 开始（如图1）沿直线AB 向右滚动，滚动时始终与直线AB 相切（切点为D ），当O 与ABC 只有一个公共点时滚动停止，作OG AC ⊥于点G ．（1）图1中，O 在AC 边上截得的弦长AE =；（2）当圆心落在AC 上时，如图2，判断BC 与O 的位置关系，并说明理由．（3）在O 滚动过程中，线段OG 的长度随之变化，设AD x =，OG y =，求出y 与x 的函数关系式，并直接写出x 的取值范围．16．在平面直角坐标系xOy 中，给出如下定义：若点P 在图形M 上，点Q 在图形N 上，称线段PQ 长度的最小值为图形M ，N 的“近距离”，记为d(M ，N)，特别地，若图形M ，N 有公共点，规定d(M ，N)＝0．已知：如图，点A(2-，0)，B(0，．（1）如果⊙O 的半径为2，那么d(A ，⊙O)＝，d(B ，⊙O)＝．（2）如果⊙O 的半径为r ，且d （⊙O ，线段AB ）=0，求r 的取值范围；（3）如果C(m ，0)是x 轴上的动点，⊙C 的半径为1，使d （⊙C ，线段AB ）<1，直接写出m 的取值范围．17．在平面直角坐标系xOy 中，对于点()P m n ，，我们称直线y mx n =+为点P 的关联直线.例如，点()24P ，的关联直线为24y x =+．（1）已知点()12A ，．①点A 的关联直线为；②若O 与点A 的关联直线相切，则O 的半径为；（2）已知点()02C ，，点()0.D d ，点M 为直线CD 上的动点．①当2d =时，求点O 到点M 的关联直线的距离的最大值；②以()11T -，为圆心，3为半径作.T 在点M 运动过程中，当点M 的关联直线与T 交于E ，F 两点时，EF 的最小值为4，请直接写出d 的值．18．在平面直角坐标系xOy 中，给定圆C 和点P ，若过点P 最多可以作出k 条不同的直线，且这些直线被圆C 所截得的线段长度为正整数，则称点P 关于圆C 的特征值为.k 已知圆O 的半径为2，（1）若点M 的坐标为()11，，则经过点M 的直线被圆O 截得的弦长的最小值为，点M 关于圆O 的特征值为；（2）直线y x b =+分别与x ，y 轴交于点A ，B ，若线段AB 上总存在关于圆O 的特征值为4的点，求b 的取值范围；（3）点T 是x 轴正半轴上一点，圆T 的半径为1，点R ，S 分别在圆O 与圆T 上，点R 关于圆T 的特征值记为r ，点S 关于圆O 的特征值记为.s 当点T 在x 轴正轴上运动时，若存在点R ，S ，使得3r s +=，直接写出点T 的横坐标t 的取值范围．答案解析部分1．【答案】（1）60︒；=；DC DB DA=+（2）解：在AB 上取一点E ，使ADE BDC ∠=∠，如图所示：∵AB 是圆O 的直径，1tan 2ABC ∠=，∴1tan 2AC ABC BC BC =∠⋅=，∴在Rt ACB 中，52AB BC ==，∵ BD BD =，∴DAB DCB ∠=∠，∵ADE BDC ∠=∠，∴ADE CDB ∽，∴ADAECD CB =，∴AD CB CD AE ⋅=⋅，∵ AD AD =，∴DBA DCA ∠=∠，∵ADE CDE CDB CDE ∠-∠=∠-∠，即ADC BDE ∠=∠，∴BDE CDA ∽，∴BDBECD AC =，∴BD AC CD BE ⋅=⋅，∴()AD CB AC BD CD AE CD BE CD AE BE CD AB⋅+⋅=⋅+⋅=⋅+=⋅，∴AB CD AC DB AD BC ⋅=⋅+⋅，∴122BC CD BC DB AD BC ⋅=⋅+⋅，∴5122CD DB AD ⋅=⋅+，∴5122CD DB AD =+，即2DB AD =+，故答案为：2DB AD =+．（3）解：∵A B ，分别是射线DA DB ，上的两个动点，120D ∠=︒，ABC 是等边三角形，∴四边形ADBC 的两个对角180ADB ACB ∠+∠=︒，∴构造四边形ADBC 的外接圆，∴根据四边形外接圆的性质可得：当点A 和点D 重合时，四边形ADBC 面积S 最小；当CD AB ⊥时，四边形ADBC 面积S 最大，①当点A 和点D 重合时，四边形ADBC 面积S 最小，∵CBD 时等边三角形，且2AB =，∴60CBD ∠=︒，2AB BD BC ===∴1sin 602CBD S BC BD =⋅⋅⋅= ，②当CD AB ⊥时，四边形ADBC 面积S 最大，∵CBD 时等边三角形，且2AB =，∴30ACD ∠=︒，2AC =，∴tan 233AD ACD AC =∠⋅==，∴11232322233ADC S AD DC =⋅⋅=⨯= ，∴23ADC ADBC S S == 四边形；433S <≤．2．【答案】（1）解：①O ，C ②当点B 的坐标为（0，1）时，如图，此时以BO 为半径的B 与线段OA 相切于点O ，∴点O 是OAB 关于点B 的内联点；当点B 移动到在y 轴左侧时，作图发现B 与x 轴有相交，且有一个交点不在线段OA 上，∴不再有OAB 关于点B 的内联点；当点B 的坐标为（7，8）时，以BA 为半径的B 与x 轴相切于点A ，∴点A 是OAB 关于点B 的内联点；当点B 直线x=7的右侧时，以BA 为半径的B 与x 轴相交，且有一个交点不在线段OA 上∴不再有OAB 关于点B 的内联点；综上所述，若AOB 关于点B 的内联点存在，求点B 纵坐标n 的取值范围为18n ≤≤；（2）80m 555m -≤≤≤≤或3．【答案】（1）22B C （2）解：由题意可得：当BC 是O 的以点A 为中心的“关联线段”时，则有AB C '' 是等边三角形，且边长也为1，当点A 在y 轴的正半轴上时，如图所示：设B C ''与y 轴的交点为D ，连接OB '，易得B C y ''⊥轴，∴12B D DC ''==，∴32OD ==，32==，∴OA =，∴t =；当点A 在y 轴的正半轴上时，如图所示：同理可得此时的OA =，∴t =；（3）当1min OA =时，此时BC =；当2max OA =时，此时2BC =．4．【答案】（1）证明：∵CD ⊥直径AB ，∴ BDBE =，∵DF ＝BD ，∴ DFBD =，∴ BEDF =，∴∠1＝∠2，∴DG ＝BG（2）解：∠DBA 的角平分线交⊙O 于点F ，∴∠2＝∠3，由（1）知，∠1＝∠2，∴∠1＝∠2＝∠3，∵∠BCD ＝90°，∴∠1+∠2+∠3＝90°，∴∠1＝∠2＝∠3＝30°，∵AB 是⊙O 的直径，∴∠ADB ＝90°，∴∠4＝90°﹣∠2﹣∠3＝30°，∵AB ＝2，∴BD ＝1，在Rt △BCD 中，∠1＝30°，∴BC ＝12BD ＝12，在Rt △BCG 中，∠3＝30°，∴CG ＝＝6，∴BG ＝2CG ＝33，由（1）知，DG ＝BG ＝33（3）5．【答案】（1）解：如图1，作BM ⊥x 轴，垂足为M ，根据题意AB=AE=EF=BF=，且∠EFO=∠BFM=45°，∴∠EFB=90°，∴四边形ABFE 是正方形，∴边AE ，BF 的中点所在直线就是ABC 与O 的一条“关联轴”；∵O 的半径为1，∴，且∠EFG=90°，∴四边形EFGH 是正方形，∵∠EFG+∠EFB=180°，∴B 、F 、G 三点共线，∴直线EF 是ABC 与O 的一条“关联轴”．（2）解：如图2，根据A （2，3），B （4，1），C （4，1），计算2=，故AB 不能落在圆的内部；过点A 作AN ⊥y 轴，垂足为N ，则AN=2，等于圆的直径，存在“关联轴l ”使ABC 是O 的关联三角形，此时0C x =；作点B 关于x 轴的对称点P ，此时BP=2，等于圆的直径，存在“关联轴l ”使ABC 是O 的关联三角形，此时4C x =，综上所述，点C 横坐标的范围是04C x ≤≤．（3）解：OC 的最小值为2-；OC 最大，根据勾股定理，AC=4.6．【答案】（1）证明：∵直径CD ⊥弦AB ，∴ AD BD=，∴∠APD=∠BPD ；（2）解：如图，作∠BAP 的平分线，交PD 于I ，证：∵AI 平分∠BAP ，∴∠PAI=∠BAI ，∴∠AID=∠APD+∠PAI=∠APD+BAI ，∵ AD BD=，∴∠DAB=∠APD ，∴∠DAI=∠DAB+∠BAI=∠APD+∠BAI ，∴∠AID=∠DAI ，∵∠AIP+∠DAI=180°，∴∠AIP+∠DAI=180°；（3）解：如图2，连接BI ，AC ，OA ，OB ，∵AI 平分∠BAP ，PD 平分∠APB ，∴BI 平分∠ABP ，∠BAI=12∠BAP ，∴∠ABI=12∠ABP ，∵∠APB=60°，∴∠PAB+∠PBA=120°，∴∠BAI+∠ABI=12（∠BAP+∠ABP ）=60°，∴∠AIB=120°，∴点I 的运动轨迹是 AB ，∴DI=DA ，∵∠AOB=2∠APB=120°，∵AD ⊥AB ，∴ AD BD=，∴∠AOB=∠BOD=60°，∵OA=OD ，∴△AOD 是等边三角形，∴AD=AO ，∵CD 是⊙O 的直径，∴∠DAC=90°，∵CD ⊥AB ，∴∠AED=90°，∴∠AED=∠CAD ，∵∠ADC=∠ADE ，∴△ADE ∽△CDA ，∴AD DE CD AD=，∴AD 2=DE•CD ，∵DI′=DI=AD ，∴DI 2=DE•CD ，∵∠I′DE 是公共角，∴△DIE ∽△DCI ，∴2IC CD IE DI==．7．【答案】（1）解：①C(4，0)，E(-1，5)；②（Ⅰ）当点(40)，在直线3y kx =+上时，430k +=，34k =-；（Ⅱ）当点(31)，在直线3y kx =+上时，331k +=，23k =-；（Ⅲ）当点(22)，在直线3y kx =+上时，232k +=，12k =-；结合图象可得3142k -≤≤-且23k ≠-；（2）解：直线333y x =-+与x 轴的交点M 坐标为()30，，与y 轴交点N 的坐标为(03，，∴tan 3NMO ∠=，∴30NMO ∠=︒，如图，作出线段MN 的垂直平分线，如图为两个临界情况：，利用待定系数法求得MN 垂直平分线解析式为y =，∴(0R -，，12230ORQ P RQ ∠=∠=︒，∴1112PR PQ ==，2222P R P Q ==，∴(10P ，(20P -，，∴t -≤<．8．【答案】（1）A 、B 、D（2）解：如图，依题意作⊙O 的“等直三角形”△TQP∴TQ=PQ ，∠TQP=90°过Q 点作MH //x 轴，交y 轴于M 点，过点P 作PH ⊥MH 于H 点∴∠TMQ=∠QHP=90°∴∠TQM+∠MTQ=∠TQM+∠HQP=90°∴∠MTQ=∠HQP∴△TMQ ≌△QHP （AAS ）∴TM=QH ，MQ=HP设Q （x ，y ）∴HM=MQ+QH=MQ+TM=x+3-y ，PH=MQ=x∴P （x-y+3，x+y ）∵C （3，0）∴∵∴CP OQ ．9．【答案】（1）BE ；3332-；等边；证明：B′D=BC CD ==，∴△DB'C 为等边三角形（2）310．【答案】（1）B ，C ；解：②如图2中，设点D 的坐标为(3)d d +，当过点D 的切线长为22r =时，OD ==由两点之间的距离公式得：OD =解得1221d d =-=-，结合图象可知，点D 的横坐标d 的取值范围是21d -≤≤-；（2）解：对于22y x =-当0y =时，220x -=，解得1x =，则点E 的坐标为(10)E ，当0x =时，2y =-，则点F 的坐标为(02)F -，⊙M 的半径为2，⊙M 的圆心为(0)M m ，24r ∴=，OM m=由题意，由以下两种情况：如图3-1中，点M 在点E 的右侧设FT 是⊙M 的切线则有两个临界位置：4FT =和点E 对应的切线长为0当4FT =时，则4OM m FT ===当点E 对应的切线长为0，即2EM =12EM m ∴=-=解得3m =结合图象得，当34m <≤时，线段EF 上的所有点都是⊙M 的伴随点②如图3-2和3-3中，点M 在点E 的左侧则有如下两个临界位置：如图3-2，设ET 是⊙M 的切线，连接MT ，则90MTE ∠=︒当4ET =时，2222245EM MT ET =+=+此时15m -=解得15m =-如图3-3，当⊙M 在直线EF 的左侧与EF 相切时，设切点为T ，连接MT∵(10)(02)E F -，，，∴12OE OF ==，∴22125EF =+=∵EF 是切线∴EF MT⊥∴90MTE FOE ∠=∠=︒∵MET FEO∠=∠∴MTE FOE~ ∴EM MTEF OF =，即22=解得EM =，即1m -=解得1m =-结合图象得，当11m -≤<-时，线段EF 上的所有点都是⊙M 的伴随点综上，m 的取值范围是11m -≤<-或34m <≤．11．【答案】（1）点C 、D ；22H x -≤≤-或22H x ≤≤（2）解：图形G 是以原点O 为中心，边长为2的正方形，∴原点O 到正方形的最短距离是1d =，最长距离是d =，⊙K 与图形G 关于原点O “平衡”，∴原点O 到⊙K 上一点的距离1d ≤≤，⊙K 的圆心在x 轴上，半径为2，∴当⊙K 在x 轴正半轴时，圆心K 的横坐标的取值范围为：22x -≤≤+，当⊙K 在x 轴负半轴时，圆心K 的横坐标的取值范围为：22x --≤≤，综上所述，圆心K 的横坐标的取值范围22x -≤≤+或22x --≤≤．12．【答案】（1）解：①90°；②B ；③2π（2）解：413．【答案】（1）S(2，0)（2）解：①（4，0）或（8，0）；②如图，设直线y a =上的点Q 为点A 和直线2y =-的等距点，连接QA ，过点Q 作直线2y =-的垂线，垂足为点C ．点Q 为点A 和直线2y =-的等距点，QA QC ∴=．22QA QC ∴=．点Q 在直线y a =上，∴可设点Q 的坐标为()Q x a ，．()()22262x a a ∴-+=--⎡⎤⎣⎦．整理得2123240x x a -+-=．由题意得关于x 的方程2123240x x a -+-=有实数根．()()()212413241610a a ∴∆=--⨯⨯-=+≥．解得1a ≥-．（3）解：如图．直线l 1和直线l 2的等距点在直线l 3：33y x =-+上，直线l 1和y 轴的等距点在直线4l y =+：或33y x =+上，点O 与l 4的距离为32，点O 与l 3的距离为，点O 与l 5的距离为3，当r ＜时，n=0不符合题意，当r=时，m=2，n=0，符合题意，当＜r ＜3时，m=n=2，不符合题意，当r≥3时，m=2，n=3或4，符合题意，综上所述，r=或r≥3.14．【答案】（1）C（2）解：∵P （0，1），点A （﹣2，﹣1），点B （2，﹣1）．∴AP ＝BP ＝＝2，如图2，分别以PA 、PB 为直径作圆，交x 轴于点K 1、K 2、K 3、K 4，∵OP＝OG＝1，OE∥AB，∴PE＝AE＝，∴OE＝12AG＝1，∴K1（﹣1﹣，0），k2（1﹣，0），k3（﹣1，0），k4（1+，0），∵点K为点P与线段AB的共圆点，∴﹣1﹣≤x k≤1﹣或﹣1≤x k≤1+（3）解：分两种情况：①如图3，当M在点A的左侧时，Q为线段AM上一动点，以PQ为直径的圆E与直线y＝12x+3相切于点F，连接EF，则EF⊥FH，当x＝0时，y＝3，当y＝0时，y＝12x+3＝0，x＝﹣6，∴ON＝3，OH＝6，∵tan∠EHF＝ON EFOH FH＝36＝12，设EF＝a，则FH＝2a，EH＝a，∴OE＝6﹣a，Rt △OEP 中，OP ＝1，EP ＝a ，由勾股定理得：EP 2＝OP 2+OE 2，∴2221(6)a =+-，解得：a ＝2+（舍去）或2，∴QG ＝2OE ＝2（6﹣a ）＝﹣3+2，∴m≤3﹣2；②如图4，当M 在点A 的右侧时，Q 为线段AM 上一动点，以PQ 为直径的圆E 与直线y ＝12x+3相切于点F ，连接EF ，则EF ⊥FH ，同理得QG ＝3+2，∴m≥3+2，综上，m 的取值范围是m≤3﹣2或m≥3+215．【答案】（1）2（2）解：BC 与O 相切；理由：如图2，过点O 作OH BC ⊥于H ，连接OD ，∵O 与AB 相切于D ，∴OD AB ⊥，在Rt AOD 中，30BAC ∠=︒，∴24OA OD ==，∵8AC =，∴4OC =，在ABC 中，AB BC =，∴30C BAC ∠=∠=︒，在Rt OHC 中，30C ∠=︒，∴122OH OC OD ===，∴BC 与O 相切，（3）解：①当点O 在AC 的左侧时，连接OD 交AC 于F ，如备用图1，∵O 与AB 相切于D ，∴OD AB ⊥，∵OG AC ⊥，∴30FOG BAC ∠=∠=︒，在Rt FDA 中，tan FD BAC AD ∠=，∴tan 3FD AD BAC x =⋅∠=，∴23OF x =-，在Rt FOG 中，331cos 2322y OG OF FOG ⎛⎫==⋅∠=-⨯-+ ⎪ ⎪⎝⎭，即12y x =-+，此时x 的取值范围为0x ≤≤；②当点O 在AC 的右侧时，连接DO 并延长交AC 于F ，如备用图2，同①的方法得，33FD x =，∴23OF x =-，∵FD AB ⊥，∴90BAC AFD ∠+∠=︒，∴30FOG BAC ∠=∠=︒，在Rt FOG 中，331cos 2322y OG OF FOG x x ⎛⎫==⋅∠=-⨯- ⎪⎪⎝⎭，即12y x =-，此时x 的取值范围为1433x ≤≤．16．【答案】（1）0；2-（2）解：过点O 作OD ⊥AB 于点D ，∵点A(2-，0)，B(0，．∴2OA OB ==，，∴4AB ==，∵1122OA OB AB OD ⋅=⋅，∴112422OD ⨯⨯=⨯⨯∴DO =，∵d （⊙O ，线段AB ）=0，∴当⊙O 的半径等于OD 时最小，当⊙O 的半径等于OB 时最大，∴r r ≤≤（3）43423m -<<-17．【答案】（1）2y x =+（2）解：①当2d =时，()20D ，，设直线CD 的解析式为：y kx b =+，()02C ，，202k b b +=⎧∴⎨=⎩，解得：12k b =-⎧⎨=⎩，∴直线CD 的解析式为：y x =-+，设点M 的坐标为()2m m -+，，∴点M 的关联直线为：()212y mx m m x =-+=-+，∴点M 的关联直线经过定点()12N ，，如图2，过点O 作直线2y mx m =--+的垂线，垂足为H ，连接ON ，ON OH ∴≥，∴当点H与点N重合时，OH最大，即点O到点M的关联直线的距离最大，∴点O到点M=；2 d=②或2 3-18．【答案】（1）；3（2）解：设点G是O的特征值为4的点，∴经过一点G且弦长为4(最长弦)的直线有1条，弦长为3的直线有2条，弦长为2的直线有且只有1条，经过点G的直线被O截得的弦长的最小值为2，=，∴关于O的特征值为4的所有点都在以O为半径的圆周上，直线y x b=+分别与x，y轴交于点A、B，()0A b∴-，，()B b，，OA OB b∴==，45OBH∴∠=︒，当0b>时，线段AB与以O为半径的圆相切时，点G特征值为4，设切点为为H，连接OH，则OH=，OB∴==，b∴=，设以O 为半径的圆与y 轴正半轴的交点记为1B ，则1OB =，当线段AB 与以O 1B 时，可得b =，b ≤≤同理可求当0b <时，b ≤≤，综上，b b b ≤≤-≤（3）当372122t -≤≤+时，存在点R ，S ，使得3r s +=。

九上圆动点、暗动点、最值问题拔高提优知识点+例题+练习（分类全面）

九上圆动点、暗动点、最值问题拔高提优知识点+例题+练习（分类全面）3、如图，在直角梯形ABCD中，AD∥BC，∠B＝90°, AD＝13cm，BC＝16cm，CD ＝5cm，AB为⊙O的直径，动点P沿AD方向从点A开始向点D以1 cm/s的速度运动，动点Q沿CB方向从点C开始向点B以2 cm/s的速度运动，点P、Q分别从A、C两点同时出发，当其中一点停止时，另一点也随之停止运动．（1）求⊙O的直径；4（2）求四边形PQCD的面积y关于P、Q运动时间t的函数关系式，并求四边形PQCD为等腰梯形时，四边形PQCD的面积．（3）是否存在某一时刻t，使直线PQ与⊙O相切，若存在，求出t的值；若不存在，请说明理由．（2）s=2t+26T=3分之19S=3分之116（3）PQ=16-tH=43t-16T=4-根号14或 T=4+根号14相切，说明理由。

O ADBCE F二、最值问题1、如图，在Rt △ABC 中，∠ACB=90°，AC=8，BC=6，点D 是平面内的一个动点，且AD=4，M 为BD 的中点，在D 点运动过程中，线段CM 长度的取值范围是． 2分之3,2分之72、如图，在△ABC 中，∠C=90°，AC=12，BC=5，经过点C 且与边AB 相切的动圆与CA 、CB 分别相交于点P 、Q ，则PQ 长的最小值为．13分之603、如图，在等腰Rt △ABC 中，∠A=90°，AB=AC=10，D 是BC 的中点，点E 在AB 边上运动（点E 不与点A 重合），过A 、D 、E 三点作⊙O ，⊙O 交AC 于另一点F ，在此运动变化的过程中，线段EF 长度的最小值为．2倍跟24、如图，AB是⊙O的一条弦，点C是⊙O上一动点，且∠ACB=30°，点E、F分别是AC、BC的中点，直线EF与⊙O交于G、H两点．若⊙O的半径为6，则GE+FH的最大值为．10.55、如图，在Rt△AOB中，OA=OB=5，⊙O的半径为2，点P是AB边上的动点，过点P作⊙O的一条切线PQ（点Q为切点），则切线PQ的最小值为．2倍根号26、在平面直角坐标系xOy中，以原点O为圆心的圆过点A（13，0），直线y=kx ﹣3k+4与⊙O交于B、C两点，则弦BC的长的最小值为．247、如图，90MON ∠=? , Rt ABC ?的顶点,A B 分别在,OM ON 上，90ACB ∠=?，点A 从点O 出发沿射线OM 运动，同时点B 从点O 出发沿射线ON 运动，连接OC .若AB = 10，则OC 长的最大值是 .58、如图，定长弦CD 在以AB 为直径的⊙O 上滑动（点C 、D 与点A 、B 不重合），M 是CD 的中点，过点C 作CP ⊥AB 于点P ，若CD=3，AB=10，则PM 的最大值是．49、如图，矩形ABCD 中，AB=4，AD=6，点E 、F 分别为AD 、DC 边上的点，且 EF=4，点G 为EF 的中点，点P 为BC 上一动点，则PA+PG 的最小值为___________ 410、在平面直角坐标系中，M（3，4），P是以M为圆心，2为半径的⊙M上一动点，A（-1，0）、B（1，0），连接PA、PB，则PA2+PB2最大值是 .100P（x,y）PA2=(X+1)2+y2PB2=(x-1)2+y2PA2+PB2 =2（x2+y2）+2x2+y2最大值为72=4911、在⊙O中，直径AB=6，BC是弦，∠ABC=30°，点P在BC上，点Q在⊙O上，且OP⊥PQ．（1）如图1，当PQ//AB时，求PQ的长度；根号6（2）如图2，当点P在BC上移动时，求PQ长的最大值．2分之3倍根号3PQ2=OQ2-OP2OP最小，PQ最大12、如图，圆O的半径为1，A，P，B，C是圆O上的四个点，∠APC=∠CPB=60°．（1）判断三角形ABC的形状：；等边（2）试探究线段PA，PB，PC之间的数量关系，并证明你的结论；PA+PB=PC （3）当点P位于的什么位置时，四边形APBC的面积最大？求出最大面积．中点，根号313、如图，已知圆O的直径AB=12cm，AC是圆O的弦，过点C作圆O的切线交BA 的延长线于点P，连接BC．（1）求证：∠PCA=∠B；（2）已知∠P=40°，点Q在优弧ABC上，从点A开始逆时针运动到点C停止（点Q与点C不重合），当三角形ABQ与三角形ABC 的面积相等时，求动点Q所经过的弧长．3分之5π3分之13π3分之23π三、暗动点、隐圆1、如图，OA ⊥OB ，垂足为O ，P 、Q 分别是射线OA 、OB 上的两个动点，点C 是线段PQ 的中点，且PQ=4.则动点C 运动形成的路径长是___.π2、已知边长为a 的正三角形ABC ，两顶点A B 、分别在平面直角坐标系的x 轴、y 轴的正半轴上滑动，点C 在第一象限，连结OC ，则OC 的长的最大值是． 2（分之根号3+1）a3．如图，∠MON=90°，矩形ABCD 的顶点A 、B 分别在边OM 、ON 上，当B 在边ON 上运动时，A 随之在OM 上运动，矩形ABCD 的形状保持不变，其中AB=2，BC=1，运动过程中，点D 到点O 的最大距离为（）AA 、21B 、5C 、1455D 、524、如图，在Rt ABC ?中，90ACB ∠=?，30CAB ∠=?，1BC =，点D 是斜边AB 上的一个动点(不与点A 重合)，AED ?为等边三角形.过D 点作DE 的垂线，F 为垂线上任意一点，G 为EF 的中点，则线段CG 长的最小值是 . 2分之35、如图，E 是正方形ABCD 的边AD 上的动点，过点A 作AH BE ⊥于点H . 若正方形的边长为4，则线段DH 的最小值是多少? 2分之根号5-26、如图，E 、F 是正方形ABCD 的边AD 上的两个动点，满足AE=DF ．连接CF 交BD 于G ，连接BE 交AG 于H ．已知正方形ABCD 的边长为4cm ，解决下列问题：（1）求证：BE ⊥AG ；（2）求线段DH 的长度的最小值．2分之根号5-27、如图，在正方形ABCD中，动点E、F分别从D、C两点同时出发，以相同的速度在边DC、CB上移动，连接AE和DF交于点P，由于点E、F的移动，使得点P也随之运动.若，线段CP的最小值是_____________根号5-18、如图，在Rt△ABC中，∠ACB=90°，将△ABC绕顶点C逆时针旋转得到△A′B′C，M是BC的中点，P是A′B′的中点，连接PM，若BC=2，∠BAC=30°，求线段PM 的最大值39、如图,以y轴上一点M为圆心作M,分别与坐标轴交于点A,B,C,其中A(0,3),B(1,0),动点P在劣弧BC上由点B运动到C,过点B作BQ⊥AP于点Q,求垂足Q在此过程中经过的路径。

2023年中考九年级数学高频考点提升练习--圆的综合(含答案)

2023年中考九年级数学高频考点提升练习--圆的综合1．如图，AB是⊙O的直径，点C为⊙O上一点，OE⊥BC于点H，交⊙O于点E，点D为OE的延长线上一点，DC的延长线与BA的延长线交于点F﹐且∠BOD=∠BCD，连结BD、AC、CE.（1）求证：DF为⊙O的切线；（2）过E作EG⊥FD于点G，求证：△CHE≌△CGE；（3）如果AF=1，sin∠FCA=√33，求EG的长.2．如图，在平面直角坐标系中，直线y=−12x+2与x轴交于点A，与y轴交于点B，抛物线y=−23x 2+bx+c过点B且与直线相交于另一点C(52,34).（1）求抛物线的解析式；（2）点P是抛物线上的一动点，当∠PAO=∠BAO时，求点P的坐标；（3）点N(n,0) (0<n<52)在x轴的正半轴上，点M(0,m)是y轴正半轴上的一动点，且满足∠MNC=90°.①求m与n之间的函数关系式；②当m在什么范围时，符合条件的N点的个数有2个？3．综合与探究如图，抛物线y=−x2+bx+c经过A(−1,0)，D(3,4)两点，直线AD与y 轴交于点Q．点P(m,n)是直线AD上方抛物线上的一个动点，过点P作PF⊥x轴，垂足为F，并且交直线AD于点E．（1）请直接写出抛物线与直线AD的函数关系表达式；（2）当CP//AD时，求出点P的坐标；（3）是否存在点P，∠CPE=∠QFE？若存在，求出m的值；若不存在，请说明理由．4．如图，在梯形ABCD中，AD⊙BC，⊙B=90°，BC=6，AD=3，⊙DCB=30°．点E、F同时从B点出发，沿射线BC向右匀速移动，已知F点移动速度是E点移动速度的2倍，以EF为一边在CB的上方作等边⊙EFG，设E点移动距离为x（x＞0）．（1）⊙EFG的边长是（用含有x的代数式表示），当x=2时，点G的位置在；（2）若⊙EFG与梯形ABCD重叠部分面积是y，求y与x之间的函数关系式；（3）探究（2）中得到的函数y在x取何值时，存在最大值？并求出最大值．5．如图，抛物线y=−34x2+bx+c与x轴交于点A(4，0)，与y轴交于点B(0，3)，点M(m，0)为线段OA上一动点，过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P，N．（1）求抛物线的解析式，并写出此抛物线的对称轴；（2）如果以点P、N、B、O为顶点的四边形为平行四边形，求m的值；（3）若△BPN与△OPM面积相等，直接写出点M的坐标．6．在平面直角坐标系xOy中，⊙C的半径为r(r＞1)，点P是圆内与圆心C不重合的点，⊙C的“完美点”的定义如下：过圆心C的任意直线CP与⊙C交于点A，B，若满足|PA﹣PB|＝2，则称点P为⊙C的“完美点”，如图点P为⊙C的一个“完美点”.（1）当⊙O的半径为2时，﹣12)⊙O的“完①点M( 32，0)⊙O的“完美点”，点(﹣√32美点”；(填“是”或者“不是”)②若⊙O的“完美点”P在直线y＝34x上，求PO的长及点P的坐标；（2）设圆心C的坐标为(s，t)，且在直线y＝﹣2x+1上，⊙C半径为r，若y轴上存在⊙C的“完美点”，求t的取值范围.7．平面直角坐标系xOy中有点P和某一函数图象M，过点P作x轴的垂线，交图象M 于点Q ，设点P ，Q 的纵坐标分别为 y P ， y Q ．如果 y P >y Q ，那么称点P 为图象M 的上位点；如果 y P =y Q ，那么称点P 为图象M 的图上点；如果 y P <y Q ，那么称点P 为图象M 的下位点．（1）已知抛物线 y =x 2−2 .① 在点A (-1，0)，B (0，-2)，C (2，3)中，是抛物线的上位点的是；② 如果点D 是直线 y =x 的图上点，且为抛物线的上位点，求点D 的横坐标 x D 的取值范围；（2）将直线 y =x +3 在直线 y =3 下方的部分沿直线 y =3 翻折，直线 y =x +3 的其余部分保持不变，得到一个新的图象，记作图象G ．⊙H 的圆心H 在x 轴上，半径为 1 ．如果在图象G 和⊙H 上分别存在点E 和点F ，使得线段EF 上同时存在图象G 的上位点，图上点和下位点，求圆心H 的横坐标 x H 的取值范围．8．在平面直角坐标系xOy 中，⊙O 的半径为1，点A 在⊙O 上，点P 在⊙O 内，给出如下定义：连接AP 并延长交⊙O 于点B ，若AP =kAB ，则称点P 是点A 关于⊙O 的k 倍特征点．（1）如图，点A 的坐标为(1，0)．①若点P 的坐标为(−12，0)，则点P 是点A 关于⊙O 的 ▲倍特征点；②在C 1(0，12)，C 2(12，0)，C 3(12，−12)这三个点中，点 ▲是点A 关于⊙O 的12倍特征点； ③直线l 经过点A ，与y 轴交于点D ，∠DAO =60°.点E 在直线l 上，且点E 是点A 关于⊙O 的12倍特征点，求点E 的坐标；（2）若当k取某个值时，对于函数y=−x+1(0<x<1)的图象上任意一点M，在⊙O上都存在点N，使得点M是点N关于⊙O的k倍特征点，直接写出k的最大值和最小值．9．如图，已知抛物线y=x2+bx-3c经过点A(1,0)和点B(0,-3)，与x 轴交于另一点C ．（1）求抛物线的解析式；（2）若点P 是抛物线上的动点，点Q 是抛物线对称轴上的动点，是否存在这样的点P ，使以点A、C、P、Q 为顶点的四边形是平行四边形？若存在，求出点P 的坐标；若不存在，请说明理由．10．如图，在⊙ABC中，⊙ACB =90°，AB=10，AC=8，CD是边AB的中线．动点P 从点C出发，以每秒5个单位长度的速度沿折线CD-DB向终点B运动．过点P作PQ⊙AC于点Q，以PQ为边作矩形PQMN，使点C、N始终在PQ的异侧，且PN= 2．设矩形PQMN与⊙ACD重叠部分图形的面积是S，点P的运动时间为t(s)3PQ（t>0）．（1）当点P在边CD上时，用含t的代数式表示PQ的长．（2）当点N落在边AD上时，求t的值．（3）当点P在CD上时，求S与t之间的函数关系式．（4）连结DQ，当直线DQ将矩形PQMN分成面积比为1：2的两部分时，直接写出t的值．11．如图1，在平面直角坐标系中，抛物线y= √36x2﹣114x+3 √3与x轴交于点A、B两点（点A在点B的左侧），与y轴交于点C，过点C作CD⊙x轴，且交抛物线于点D，连接AD，交y轴于点E，连接AC．（1）求S⊙ABD的值；（2）如图2，若点P是直线AD下方抛物线上一动点，过点P作PF⊙y轴交直线AD于点F，作PG⊙AC交直线AD于点G，当⊙PGF的周长最大时，在线段DE上取一点Q，当PQ+ 35QE的值最小时，求此时PQ+35QE的值；（3）如图3，M是BC的中点，以CM为斜边作直角⊙CMN，使CN⊙x轴，MN⊙y 轴，将⊙CMN沿射线CB平移，记平移后的三角形为⊙C′M′N′，当点N′落在x轴上即停止运动，将此时的⊙C′M′N′绕点C′逆时针旋转（旋转度数不超过180°），旋转过程中直线M′N′与直线CA交于点S，与y轴交于点T，与x轴交于点W，请问⊙CST是否能为等腰三角形？若能，请求出所有符合条件的WN′的长度；若不能，请说明理由．12．在平面直角坐标系xOy中，把与x轴交点相同的二次函数图象称为“共根抛物线”．如图，抛物线L1：y=12x2−32x−2的顶点为D，交x轴于点A、B（点A在点B左侧），交y轴于点C．抛物线L2与L1是“共根抛物线”，其顶点为P．（1）若抛物线L2经过点（2，﹣12），求L2对应的函数表达式；（2）当BP﹣CP的值最大时，求点P的坐标；（3）设点Q是抛物线L1上的一个动点，且位于其对称轴的右侧．若⊙DPQ与⊙ABC相似，求其“共根抛物线”L2的顶点P的坐标．13．如图，已知抛物线与x轴交于A(−1，0)、B(3，0)两点，与y轴交于点C(0，3)．（1）求抛物线的解析式；（2）点D是第一象限内抛物线上的一个动点（与点C、B不重合），过点D作DF⊥x 轴于点F，交BC于点E，过点D作DM⊥BC，垂足为M．求线段DM的最大值；（3）已知P为抛物线对称轴上一动点，若△PBC是直角三角形，求出点P的坐标．14．如图，D是⊙ABC的BC边上一点，连接AD，作⊙ABD的外接圆，将⊙ADC沿直线AD折叠，点C的对应点E落在⊙O上.（1）求证：AE＝AB.（2）填空：①当⊙CAB＝90°，cos⊙ADB＝13，BE＝2时，边BC的长为.②当⊙BAE＝时，四边形AOED是菱形.15．如图，在平面直角坐标系xOy中，已知点A（0，4），点B是x轴正半轴上一点，连结AB，过点A作AC⊙AB，交x轴于点C，点D是点C关于点A的对称点，连结BD，以AD为直径作⊙Q交BD于点E，连结AE并延长交x轴于点F，连结DF.（1）求线段AE的长；（2）若AB﹣BO＝2，求tan⊙AFC的值；（3）若⊙DEF与⊙AEB相似，求BEDE的值.16．如图，已知AB为⊙O的直径，C为⊙O上一点，BG与⊙O相切于点B，交AC的延长线于点D（点D在线段BG上），AC = 8，tan⊙BDC = 4 3（1）求⊙O的直径；（2）当DG= 52时，过G作GE//AD，交BA的延长线于点E，说明EG与⊙O相切.答案解析部分1．【答案】（1）证明：如图，连结OC ，∵OE⊙BC ， ∴⊙OHB=90°， ∴⊙OBH+⊙BOD=90°， ∵OB=OC ， ∴⊙OBH=⊙OCB ， ∵⊙BOD=⊙BCD ， ∴⊙BCD+⊙OCB=90°， ∴OC⊙CD ，∵点C 为⊙O 上一点， ∴DF 为⊙O 的切线（2）证明：∵⊙OCD=90°， ∴⊙ECG+⊙OCE=90°， ∵OC=OE ， ∴⊙OCE=⊙OEC ， ∴⊙ECG+⊙OEC=90°， ∵⊙OEC+⊙HCE=90°， ∴⊙ECG=⊙HCE ，在⊙CHE 和⊙CGE 中， {∠CHE ＝∠CGE ＝90°∠ECG ＝∠HCE CE ＝CE，∴⊙CHE⊙⊙CGE （AAS ）（3）解：∵AB 是⊙O 的直径，∴⊙ACB=90°， ∴⊙ABC+⊙BAC=90°， ∵DF 为⊙O 的切线， ∴⊙OCA+⊙FCA=90°， ∵OA=OC ， ∴⊙OAC=⊙OCA ， ∴⊙FCA=⊙ABC ，∴sin∠ABC =sin∠FCA =√33，设AC= √3a ，则AB=3a ，∴BC =√AB 2−AC 2=√(3a)2−(√3a)2=√6a ， ∵⊙FCA=⊙ABC ，⊙AFC=⊙CFB ， ∴⊙ACF⊙⊙CFB ，∴AF CF =CF BF =AC BC =1√2，∵AF=1， ∴CF= √2 ， ∴BF =(√2)21=2 ，∴BF-AF=AB=1，∴OC =12,BC =√63，∵OE⊙BC ，∴CH =12BC =√66，∴OH =√OC 2−CH 2=(12)2−(√66)2=√36，∴HE=OE-OH= 12−√36，∵⊙CHE⊙⊙CGE ，∴EG=HE= 12−√36.2．【答案】（1）解：∵直线 y =−12x +2 与x 轴交于点A ，与y 轴交于点B ，令x=0，则y=2，令y=0，则x=4， ∴A （4，0），B （0，2），∵抛物线 y =−23x 2+bx +c 经过B （0，2）， C(52,34) ，∴{2=c 34=−23×254+52b +c ，解得： {b =76c =2 ， ∴抛物线的表达式为： y =−23x 2+76x +2 ；（2）解：当点P 在x 轴上方时，点P 与点C 重合，满足 ∠PAO =∠BAO ， ∵C(52,34) ，∴P(52,34) ，当点P 在x 轴下方时，如图，AP 与y 轴交于点Q ，∵∠PAO =∠BAO ，∴B ，Q 关于x 轴对称，∴Q （0，-2），又A （4，0），设直线AQ 的表达式为y=px+q ，代入，{−2=q0=4p +q ，解得： {p =12q =−2 ，∴直线AQ 的表达式为： y =12x −2 ，联立得：{y =12x −2y =−23x 2+76x +2，解得：x=3或-2，∴点P 的坐标为（3， −12 ）或（-2，-3），综上，当 ∠PAO =∠BAO 时，点P 的坐标为： (52,34) 或（3，−12 ）或（-2，-3）；（3）解：①如图，⊙MNC=90°，过点C 作CD⊙x 轴于点D ，∴⊙MNO+⊙CND=90°，∵⊙OMN+⊙MNO=90°，∴⊙CND=⊙OMN,又⊙MON=⊙CDN=90°，∴⊙MNO⊙⊙NCD ，∴MO ND =NO CD ，即 m 52−n =n 34 ，整理得： m =−43n 2+103n ； ②如图，∵⊙MNC=90°，以MC 为直径画圆E ，∵N(n,0) (0<n <52) ， ∴点N 在线段OD 上（不含O 和D ），即圆E 与线段OD 有两个交点（不含O 和D ）， ∵点M 在y 轴正半轴，当圆E 与线段OD 相切时，有NE= 12 MC ，即NE 2= 14MC 2， ∵M （0，m ）， C(52,34) ， ∴E （ 54， 38+m 2 ）， ∴(38+m 2)2 = 14[(52)2+(m −34)2] ，解得：m= 2512，当点M 与点O 重合时，如图，此时圆E 与线段OD （不含O 和D ）有一个交点，∴当0＜m ＜ 2512时，圆E 与线段OD 有两个交点，故m 的取值范围是：0＜m ＜ 2512. 3．【答案】（1）解：∵抛物线 y =−x 2+bx +c 经过 A(−1,0) ， D(3,4) 两点，∴{−(−1)2+b ×(−1)+c =0−32+b ×3+c =4，解之得： {b =3c =4 ∴抛物线的函数关系表达式为 y =−x 2+3x +4 ，设直线 AD 的函数关系表达式为 y =kx +b ，∵直线 AD 经过 A(−1,0) ， D(3,4) 两点，∴{k ×(−1)+b =0k ×3+b =4，解之得： {k =1b =1 ∴直线 AD 的函数关系表达式为 y =x +1 ．（2）解：把 x =0 代入 y =−x 2+3x +4 ，得 y =4 ．∴点 C 坐标是（0，4），∵CP//AD∴k CP =k AD =1 ，设直线 CP 的函数关系表达式为 y =x +b ，∵将点 C （0，4），代入 y =x +b 得： b =4 ，∴直线 CP 的函数关系表达式为 y =x +4 ，∵直线 CP 与抛物线 y =−x 2+3x +4 相交于 P ，则有： x +4=−x 2+3x +4 ，解之得： x 1=0 ， x 2=2 ，把 x =2 代入 y =x +4 ，得 y =6 ，∴点P 的坐标是（2，6）．（3）解：存在点 P ，使得 ∠CPE =∠QFE ．过点 C 作 CG ⊥PF ，垂足为 G ．过点 Q 作 QH ⊥PF ，垂足为 H ．则四边形CGHQ为矩形．∴CG=QH，∠CGP=∠QHF=90°．∴当PG=HF时，△CGP≌△QHF，这时∠CPG=∠QFH，即∠CPE=∠QFE．设P(m,−m2+3m+4)，则PG=−m2+3m+4−4=−m2+3m．∵HF=QO=1．∴−m2+3m=1，解得m=3+√52或m=3−√52．4．【答案】（1）x；D（2）解：①当0＜x≤2时，⊙EFG在梯形ABCD内部，所以y= √34x2；②分两种情况：⊙．当2＜x＜3时，如图1，点E、点F在线段BC上，⊙EFG与梯形ABCD重叠部分为四边形EFNM，∵⊙FNC=⊙FCN=30°，∴FN=FC=6﹣2x．∴GN=3x﹣6．∵在Rt⊙NMG中，⊙G=60°，GN=3x﹣6，∴GM= 12（3x﹣6），由勾股定理得：MN= √32（3x﹣6），∴S⊙GMN= 12×GM×MN= 12× 12（3x﹣6）× √32（3x﹣6）= √38（3x﹣6）2，所以，此时y= √34x2﹣√38（3x﹣6）2=﹣7√38x2+9√32x−9√32；⊙．当3≤x≤6时，如图2，点E在线段BC上，点F在射线CH上，⊙EFG与梯形ABCD重叠部分为⊙ECP，∵EC=6﹣x，∴y= √38（6﹣x）2= √38x2﹣3√32x+ 9√32，⊙．当x＞6时，点E，F都在线段BC的延长线上，没公共部分，∴y=0（3）解：当0＜x≤2时，∵y= √34x2，在x＞0时，y随x增大而增大，∴x=2时，y最大= √3；当2＜x＜3时，∵y=﹣9√37x 2+9√32x−9√32在x= 187时，y最大= 9√37；当3≤x≤6时，∵y= √38x−3√32x+9√32，在x＜6时，y随x增大而减小，∴x=3时，y最大= 9√38．综上所述：当x= 187时，y最大=9√37．5．【答案】（1）解：∵抛物线y=−34x2+bx+c与x轴交于点A(4，0)，与y轴交于点B(0，3)，∴{−34×16+4 b+c=0c=3，解得{b=94c=3，∴抛物线y=−34x 2+94x+3=−34(x−32)2+7516；∴抛物线的对称轴为直线x=32（2）解：设直线A(4，0)，B(0，3)的解析式为y=ax+d，∴{4a+d=0d=3，解得{a=−34 d=3，∴直线AB的表达式为：y=−34x+3；∵点M(m，0)为线段OA上一动点，过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P，N，∴PN//y轴，即PN//OB，且点N在点P上方，若以点P、N、B、O为顶点的四边形为平行四边形，则只需要PN=OB，∴−34m2+94m+3−(−34m+3)=3，解得m=2；即当m=2时，以点P、N、B、O为顶点的四边形为平行四边形．（3）解：M（1，0）6．【答案】（1）不是；是；解：如图1，根据题意，|PA−PB|＝2，∴|OP+2−(2−OP)|＝2，∴OP＝1. 若点P在第一象限内，作PQ⊙x轴于点Q，∵点P在直线y＝34x上，OP＝1，∴OQ=45,PQ=3 5 .∴P( 45,35). 若点P在第三象限内，根据对称性可知其坐标为(﹣45，﹣35). 综上所述，PO的长为1，点P的坐标为( 45,35)或（−45,−35）).（2）解：对于⊙C的任意一个“完美点”P都有|PA﹣PB|＝2，∴|CP+r﹣(r﹣CP)|＝2.∴CP＝1.∴对于任意的点P，满足CP＝1，都有|CP+r﹣(r﹣CP)|＝2，∴|PA﹣PB|＝2，故此时点P为⊙C的“完美点”.因此，⊙C的“完美点”是以点C为圆心，1为半径的圆.设直线y＝﹣2x+1与y轴交于点D，如图2，当⊙C 移动到与y 轴相切且切点在点D 的上方时，t 的值最大.设切点为E ，连接CE ，∵⊙C 的圆心在直线y ＝﹣2x+1上，∴此直线和y 轴，x 轴的交点D(0，1)，F( 12，0)， ∴OF ＝ 12，OD ＝1， ∵CE⊙OF ，∴⊙DOF⊙⊙DEC ，∴OD DE =OF CE， ∴1DE =12， ∴DE ＝2，∴OE ＝3，t 的最大值为3，当⊙C 移动到与y 轴相切且切点在点D 的下方时，t 的值最小.同理可得t 的最小值为﹣1.综上所述，t 的取值范围为﹣1≤t≤3.7．【答案】（1）解：① A ，C ②∵点D 是直线 y =x 的图上点，∴点D 在 y =x 上. 又∵点D 是 y =x 2−2 的上位点， ∴点D 在 y =x 与y =x 2−2 的交点R ，S 之间运动. ∵{y =x 2−2,y =x.∴{x 1=−1,y 1=−1. {x 2=2,y 2=2.∴点R( −1 ， −1 )，S( 2 ， 2 ). ∴−1<x D <2 .（2）解：如图，当圆与两条直线的反向延长线相切时，为临界点，临界点的两边都满足要求.将y=x+3沿直线y=3翻折后的直线的解析式为y=−x+3当y=x+3=0时，x=−3，∴A(-3,0),OA=3当x=0时，y=x+3=3∴C(0,3),OC=3∴OA=OC∵∠AOC=90°∴∠CAO=45°∴AH1=rsin45°=1√22=√2∵A(-3,0)∴x H1=−3+√2同理可得x H2=3−√2∴线段EF上同时存在图象G的上位点，图上点和下位点，圆心H的横坐标x H的取值范围为x H>3−√2或x H<−3+√2.8．【答案】（1）解：①34②C3③如图所示，设直线AD交圆O于B，连接OE，过点E作EF⊙x轴于F，∵点E 是点A 关于⊙O 的12倍的特征点， ∴AE AB =12， ∴E 是AB 的中点，∴OE⊙AB ，∵⊙EAO=60°，∴⊙EOA=30°，∴AE =12OA =12，EF =12OE ， ∴OE =√OA 2−AE 2=√32， ∴EF =√34， ∴OF =√OE 2−EF 2=34， ∴点E 的坐标为（34，√34）；（2）k 的最小值为2−√24，k 有最大值为2+√249．【答案】（1）解：把A （1，0），B （0，-3）代入 y=x 2+bx-3c ，得 {1+b −3c =0−3c =−3解得 {b =2c =1∴抛物线的解析式为y=x 2+2x-3；（2）解：对于y=x 2+2x-3，∵x =−b 2a=−1 ，A(1，0)∴C 点坐标为（-3,0），AC=4，Q点的横坐标为-1.如图所示：若以点A、C、P、Q 为顶点的平行四边形以AC为边，则PQ=AC=4.①当P点的横坐标为x1=-1-4=-5时，y1=x2+2x−3=25−10−3=12，即P1(-5,12）②当P点的横坐标为x2=-1+4=3时，y2=x2+2x−3=9+6−3=12，即P2(3,12）；若以点A、C、P、Q为顶点的平行四边形以AC为对角线，则设P3的横坐标为x3，则有x3−12=−3+12，解得x3=-1，y3=x2+2x−3=1−2−3=−4，即P3(-1，-4)。

2023年初三数学九上圆所有知识点总结和常考题型练习题

圆知识点一、圆旳概念集合形式旳概念： 1、圆可以看作是到定点旳距离等于定长旳点旳集合；2、圆旳外部：可以看作是到定点旳距离不小于定长旳点旳集合；3、圆旳内部：可以看作是到定点旳距离不不小于定长旳点旳集合轨迹形式旳概念：1、圆：到定点旳距离等于定长旳点旳轨迹就是以定点为圆心，定长为半径旳圆；（补充）2、垂直平分线：到线段两端距离相等旳点旳轨迹是这条线段旳垂直平分线（也叫中垂线）；3、角旳平分线：到角两边距离相等旳点旳轨迹是这个角旳平分线；4、到直线旳距离相等旳点旳轨迹是：平行于这条直线且到这条直线旳距离等于定长旳两条直线；5、到两条平行线距离相等旳点旳轨迹是：平行于这两条平行线且到两条直线距离都相等旳一条直线。

二、点与圆旳位置关系1、点在圆内⇒d r<⇒点C在圆内；2、点在圆上⇒d r=⇒点B在圆上；3、点在圆外⇒d r>⇒点A在圆外；三、直线与圆旳位置关系1、直线与圆相离⇒d r>⇒无交点；2、直线与圆相切⇒d r=⇒有一种交点；3、直线与圆相交⇒d r<⇒有两个交点；四、垂径定理垂径定理：垂直于弦旳直径平分弦且平分弦所对旳弧。

推论1：（1）平分弦（不是直径）旳直径垂直于弦，并且平分弦所对旳两条弧；（2）弦旳垂直平分线通过圆心，并且平分弦所对旳两条弧；（3）平分弦所对旳一条弧旳直径，垂直平分弦，并且平分弦所对旳另一条弧A以上共4个定理，简称2推3定理：此定理中共5个结论中，只要懂得其中2个即可推出其他3个结论，即：①AB 是直径 ②AB CD ⊥ ③CE DE = ④ 弧BC =弧BD ⑤ 弧AC =弧AD 中任意2个条件推出其他3个结论。

推论2：圆旳两条平行弦所夹旳弧相等。

即：在⊙O 中，∵AB ∥CD ∴弧AC =弧BD五、圆心角定理圆心角定理：同圆或等圆中，相等旳圆心角所对旳弦相等，所对旳弧相等，弦心距相等。

此定理也称1推3定理，即上述四个结论中，只要懂得其中旳1个相等，则可以推出其他旳3个结论，即：①AOB DOE ∠=∠；②AB DE =；③OC OF =；④ 弧BA =弧BD 六、圆周角定理1、圆周角定理：同弧所对旳圆周角等于它所对旳圆心旳角旳二分之一。

2023年中考九年级数学高频考点拔高训练-圆的综合

2023年中考九年级数学高频考点拔高训练-圆的综合1．如图，在⊙O中，AB为⊙O的直径，过O点作OC⊙AB且交⊙O于C点，延长AB到D，过点D 作⊙O的切线DE，切点为E，连接CE交AB于F点.（1）求证：DE＝DF；（2）若⊙O的半径为2，求CF·CE的值；（3）若⊙O的半径为2，⊙D＝30°，则阴影部分的面积.2．如图，⊙O为等腰⊙ABC的外接圆，直径AB＝12，P为弧BC⌢上任意一点（不与B，C重合），直线CP交AB延长线于点Q，⊙O在点P处切线PD交BQ于点D，（1）若PD⊙BC，求证：AP平分⊙CAB；（2）若PB＝BD，求PD的长度；⌢上的位置如何变化，CP•CQ为定值．（3）证明：无论点P在弧BC3．（1）知识储备①如图1，已知点P 为等边⊙ABC 外接圆的弧BC 上任意一点．求证：PB+PC= PA.②定义：在⊙ABC 所在平面上存在一点P，使它到三角形三顶点的距离之和最小，则称点P 为⊙ABC的费马点，此时PA+PB+PC 的值为⊙ABC 的费马距离．（2）知识迁移①我们有如下探寻⊙ABC (其中⊙A，⊙B，⊙C 均小于120°)的费马点和费马距离的方法：如图2，在⊙ABC 的外部以BC 为边长作等边⊙BCD 及其外接圆，根据(1)的结论，易知线段的长度即为⊙ABC 的费马距离.②在图3 中，用不同于图2 的方法作出⊙ABC 的费马点P(要求尺规作图).（3）知识应用①判断题：⊙.任意三角形的费马点有且只有一个（）；⊙.任意三角形的费马点一定在三角形的内部（）.②已知正方形ABCD，P 是正方形内部一点，且PA+PB+PC 的最小值为√6+√2，求正方形ABCD 的边长．4．已知：如图，B,C,D三点在⊙A上，∠BCD=45°，PA是钝角⊙ABC的高线，PA的延长线与线段CD交于点E.（1）请在图中找出一个与⊙CAP相等的角，这个角是；（2）用等式表示线段AC，EC，ED之间的数量关系，并证明.5．如图，已知⊙O上依次有A、B、C、D四个点，AD̂= BĈ，连接AB、AD、BD，弦AB不经过圆心O，延长AB到E，使BE=AB，连接EC，F是EC的中点，连接BF．（1）若⊙O的半径为3，⊙DAB=120°，求劣弧BD̂的长；（2）求证：BF= 12BD；（3）设G是BD的中点，探索：在⊙O上是否存在点P（不同于点B），使得PG=PF？并说明PB 与AE的位置关系．6．图1、图2为同一长方体房间的示意图，图3为该长方体的表面展开图．（1）蜘蛛在顶点A′处．①苍蝇在顶点B处时，试在图1中画出蜘蛛为捉住苍蝇，沿墙面爬行的最近路线．②苍蝇在顶点C处时，图2中画出了蜘蛛捉住苍蝇的两条路线，往天花板ABCD爬行的最近路线A′GC和往墙面BB′C′C爬行的最近路线A′HC，试通过计算判断哪条路线更近．（2）在图3中，半径为10dm的⊙M与D′C′相切，圆心M到边CC′的距离为15dm，蜘蛛P在线段AB上，苍蝇Q在⊙M的圆周上，线段PQ为蜘蛛爬行路线，若PQ与⊙M相切，试求PQ长度的范围．7．如图，AB是⊙O的直径，点E在AB的延长线上，点D为⊙O上一点，且∠EDB=∠EAD.（1）求证：ED是⊙O的切线、8．如图，AB是⊙O的直径，C，G是⊙O上两点，且AC⌢=CG⌢，过点C的直线CD⊙BG于点D，交BA的延长线于点E，连接BC，交OD于点F．（1）求证：CD是⊙O的切线；（2）若OFFD=23，求证：AE=AO；（3）连接AD，在（2）的条件下，若CD = √2，求AD的长．9．如图1，有一块直角三角板，其中AB=16，∠ACB=90∘，∠CAB=30∘，A、B在x轴上，点A的坐标为(20,0)，圆M的半径为3√3，圆心M的坐标为(−5,3√3)，圆M以每秒1个单位长度的速度沿x轴向右做平移运动，运动时间为t秒；（1）求点C的坐标；（2）当点M在∠ABC的内部且⊙M与直线BC相切时，求t的值；（3）如图2，点E、F分别是BC、AC的中点，连接EM、FM，在运动过程中，是否存在某一时刻，使∠EMF=90∘？若存在，直接写出t的值，若不存在，请说明理由.10．如图1，四边形ABCD内接于圆O，AC是圆O的直径，过点A的切线与CD的延长线相交于点P.且∠APC=∠BCP（1）求证：∠BAC=2∠ACD；（2）过图1中的点D作DE⊥AC，垂足为E（如图2），当BC=6，AE=2时，求圆O 的半径.11．（1）问题提出如图①，已知直线a//b，点A，B在直线a上，点C，D在直线b上，则S△ACDS△BCD（填“＞”“＜”或“＝”）；（2）问题探究如图②，⊙O的直径为20，点A，B，C都在⊙O上，AB=12，求△ABC面积的最大值；（3）问题解决如图③，在△ABC中，∠ACB=90°，AB=20，BC=10，根据设计要求，点D为∠ABC内部一点，且∠ADB=60°，过点C作CE//AD交BD于点E，连接AE，CD，试求满足设计要求的四边形ADCE的最大面积.12．如图，AB是⊙O的直径，E，C是⊙O上两点，且EC⌢=BC⌢，连接AE，AC，过点C 作CD⊥AE交AE的延长线于点D.（1）判定直线CD与⊙O的位置关系，并说明理由；（2）若AB=4，CD=√3，求图中阴影部分的面积.13．问题提出：（1）如图①，半圆O的直径AB=10，点P是半圆O上的一个动点，则⊙PAB的面积最大值是.（2）如图②，在边长为10的正方形ABCD中，点G是BC边的中点，E、F分别是AD和CD 边上的点，请探究并求出四边形BEFG的周长的最小值.（3）如图③，四边形ABCD中，AB=AD=6，⊙BAD=60°，⊙BCD=120°，四边形ABCD的周长是否存在最大值，若存在，请求出最大值；若不存在，请说明理由.14．如图，四边形ABCD内接于圆O，⊙BAD=90°，AC为直径，过点A作圆O的切线交CB的延长线于点E，过AC的三等分点F（靠近点C）作CE的平行线交AB于点G，连结CG．（1）求证：AB=CD；（2）求证：CD2=BE•BC；（3）当CG= √3，BE= 92时，求CD的长．15．如图，四边形ABCD为平行四边形，以AD为直径的⊙O交AB于点E，连接DE，DA＝2√2，DE=√7，DC＝5．过点E作直线l．过点C作CH⊙l，垂足为H．（1）若l⊙AD，且l与⊙O交于另一点F，连接DF，求DF的长；（2）连接BH，当直线l绕点E旋转时，求BH的最大值；（3）过点A作AM⊙l，垂足为M，当直线l绕点E旋转时，求CH﹣4AM的最大值．16．如图，点E是正方形ABCD边BC上一点（点E不与B、C重合），连接AE交对角线BD于点F，△ADF的外接圆O交边CD于点G，连接GA、GE，设BECE=α.（1）求∠EAG的度数.（2）当α=12时，求tan∠AEG.（3）用α的代数式表示DGCG，并说明理由.答案解析部分1．【答案】（1）证明：连接OE.∵DE是⊙O的切线，∴DE⊙OE，∴⊙OED＝90°，∴⊙DEF+⊙OEC＝90°，∵OC⊙AB，∴⊙COB＝90°，∴⊙C+⊙OFC＝90°，∵OE＝OC，∴⊙OEC＝⊙C，∵⊙OFC＝⊙DFE，∴⊙DEF＝⊙EFD，∴DE＝DF.（2）解：延长CO交⊙O于H，连接EH.∵CH为直径，∴⊙CEH＝90°，∵OC⊙AB，∴⊙COF＝90°，∴⊙COF＝⊙CEH，∵⊙C＝⊙C，∴⊙COF⊙⊙CEH，∴COCE＝CFCH，∴CE•CF＝CO•CH＝2×4＝8.（3）2 √3﹣23π2．【答案】（1）证明：如图，连接OP，∵PD是⊙O的切线，∴OP⊙PD，∵PD⊙BC，∴OP⊙BC，∴CP＝BP，∴⊙PAC＝⊙PAB，∴AP平分⊙CAB；（2）解：∵PB＝BD，∴⊙BPD＝⊙BDP，∵OP⊙PD，∴⊙BPD+⊙BPO＝⊙BDP+⊙BOP，∴⊙BOP＝⊙BPO，∴BP＝BO＝PO＝6，即⊙BOP是等边三角形，∴在Rt⊙OPD中，PD＝√OD2−OP2＝6 √3；（3）证明：∵AC＝BC，∴⊙BAC＝⊙ABC，∵⊙ABC＝⊙APC，∴⊙APC＝⊙BAC，又∵⊙ACP＝⊙QCA，∴⊙ACP⊙⊙QCA，∴CPCA＝CACQ，即CP•CQ＝CA2＝72，即CP•CQ为定值．3．【答案】（1）①证明：在PA上取一点E，使PE=PC，连接CE，∵正三角形ABC∴⊙APC=⊙ABC=60°又∵PE=PC，∴⊙PEC是正三角形∴CE=CP ⊙ACB=⊙ECP=60°∴⊙1=⊙2又∵⊙3=⊙4 BC=AC∴⊙ACE⊙⊙BCP (ASA)∴AE=BP即：BP+CP=AP（2）AD；解：过AB和AC分别向外作等边三角形，连接CD，BE，交点即为P0．（3）正确；错误；解：将⊙ABP沿点B逆时针旋转60°到⊙A1BP1，过A1作A1H⊙BC，交CB的延长线于H，连接P1P，易得：A1B=AB，PB=P1B，PA=P1 A1，⊙P1BP=⊙A1BA=60°∵PB=P1B⊙P1BP=60°∴⊙P1PB是正三角形∴PP1=PB∵PA+PB+PC的最小值为√6+√2∴P1A1+PP1+PC的最小值为√6+√2∴A1，P1，P，C在同一直线上，即A1C= √6+√2设正方形的边长为2x∵⊙A1BA=60° ⊙CBA=90°∴⊙1=30°在Rt⊙A1HB中，A1B=AB=2x，⊙1=30°得：A1H=x，BH= √3x在Rt⊙A1HC中，由勾股定理得：x2+(√2+3)2x2=(√6+√2)2解得：x1=1x2=−1（舍去）∴正方形ABCD的边长为2．4．【答案】（1）⊙BAP（2）解：AC，EC，ED满足的数量关系：EC2+ED2=2AC2. 证明：连接EB，与AD交于点F∵点B，C两点在⊙A上,∴AC=AB，∴⊙ACP=⊙ABP.∵PA是钝角⊙ABC的高线,∴PA是⊙CAB的垂直平分线.∵PA的延长线与线段CD交于点E，∴EC=EB.∴⊙ECP=⊙EBP.∴⊙ECP-⊙ACP =⊙EBP -⊙ABP.即⊙ECA=⊙EBA.∵AC=AD，∴⊙ECA=⊙EDA∴⊙EBA=⊙EDA∵⊙AFB=⊙EFD, ⊙BCD=45°,∴⊙AFB+⊙EBA =⊙EFD+⊙EDA=90°即⊙BAD=⊙BED=90°∴EB2+ED2=BD2.∵BD2=AB2+AD2，∴ BD2=2AB2,∴EB2+ED2=2AB2，∴EC2+ED2=2AC25．【答案】（1）解：连接OB，OD，∵⊙DAB=120°，∴BCD̂ 所对圆心角的度数为240°， ∴⊙BOD=360°﹣240°=120°， ∵⊙O 的半径为3，∴劣弧 BD̂ 的长为： 120180×π×3=2π；（2）证明：连接AC ，∵AB=BE ，∴点B 为AE 的中点，∵F 是EC 的中点，∴BF 为⊙EAC 的中位线， ∴BF= 12AC ，∵AD̂ = BC ̂ ， ∴AD̂ + AB ̂ = BC ̂ + AB ̂ ， ∴DAB̂ = CBA ̂ ， ∴BD=AC ， ∴BF= 12BD ；（3）解：过点B 作AE 的垂线，与⊙O 的交点即为所求的点P ， ∵BF 为⊙EAC 的中位线， ∴BF⊙AC ， ∴⊙FBE=⊙CAE ，∵AD̂ = BC ̂ ， ∴⊙CAB=⊙DBA ， ∵由作法可知BP⊙AE ， ∴⊙GBP=⊙FBP ， ∵G 为BD 的中点， ∴BG= 12 BD ，∴BG=BF ，在⊙PBG 和⊙PBF 中， {BG =BF∠PBG =∠PBF BP =BP ，∴⊙PBG⊙⊙PBF （SAS ）， ∴PG=PF ．6．【答案】（1）【解答】解：①根据“两点之间，线段最短”可知：线段A′B为最近路线，如图1所示．②⊙．将长方体展开，使得长方形ABB′A′和长方形ABCD在同一平面内，如图2①．在Rt⊙A′B′C中，⊙B′=90°，A′B′=40，B′C=60，∴AC=√402+602=√5200=20√13．⊙．将长方体展开，使得长方形ABB′A′和长方形BCC′B′在同一平面内，如图2②．在Rt⊙A′C′C中，⊙C′=90°，A′C′=70，C′C=30，∴A′C=√702+302=√5800=10√58．∵√5200＜√5800，∴往天花板ABCD爬行的最近路线A′GC更近；（2）【解答】过点M作MH⊙AB于H，连接MQ、MP、MA、MB，如图3．∵半径为10dm的⊙M与D′C′相切，圆心M到边CC′的距离为15dm，BC′=60dm，∴MH=60﹣10=50，HB=15，AH=40﹣15=25，根据勾股定理可得AM=√AH2+MH2=√252+502=√3125，MB=√BH2+MH2=√152+502=√2725，∴50≤MP≤√3125．∵⊙M与D′C′相切于点Q，∴MQ⊙PQ，⊙MQP=90°，∴PQ=√MP2−MQ2=√MP2−100．当MP=50时，PQ=√2400=20√6；当MP=√3125时，PQ=√3025=55．∴PQ长度的范围是20√6dm≤PQ≤55dm．7．【答案】（1）证明：如图，连接OD.∵AB是⊙O的直径，∴∠ADB=90°，∴∠EAD+∠DBA=90°.∵OB=OD，∴∠ODB=∠DBA.∵∠EDB=∠EAD，∴∠ODE=∠ODB+∠EDB=∠DBA+∠EAD=90°，∴ED⊥OD，∴ED是⊙O的切线（2）过点A作⊙O的切线AC，交ED的延长线于点C，若AE=15,BE= 5，求EC的长.解：∵AE=15,BE=5，∴AB=AE−BE=15−5=10，∴OD=OB=12AB=5,∴OE=OB+EB=5+5=10.∴∠ODE=90°.∵OD=5,OE=10，∴DE=5√3.∵CA是⊙O的切线，∴∠CAE=90°，∴∠ODE=∠CAE.∵∠E=∠E，∴△ODE∽△CAE，∴ODCA=DEAE∵5 AC=5√3 15.∴AC=5√3，∴CE=√(5√3)2+152=10√3. 8．【答案】（1）证明：连接OC，∵OC=OB，AC⌢=CG⌢，∴∠OCB=∠OBC，∠OBC=∠DBC，∴∠DBC=∠OCB，∴OC∥BD，∴∠BDC＝∠ECO，∵CD⊥BD，∴∠BDC＝90°，∴∠ECO＝90°，∵OC是⊙O的半径，（2）解：由（1）知，OC∥BD，∴∠OCF＝∠DBF，∠COF＝∠BDF，∴△OCF∼△DBF，∴OF DF=OC DB，∵OF FD=2 3，∴OC DB=2 3，∵OC∥BD，∴△EOC∼△EBD，∴OC BD=EO EB，∴EO EB=2 3，设OE=2a，则EB=3a，∴OB=a，∴AO=a，∴AE=a，∴AE=AO；（3）解：在（2）的条件下，∵OC=OA=a，∴OC=12OE，∵∠OCE=90°，∴∠E=30°，∵∠BDE=90°，∠OBC=∠DBC，∴∠EBD=60°，∠OBC=∠DBC=30°，∵CD=√2，∴BC=2√2，BD=√6，∵OC DB=2 3，∴OC=23√6，作DM⊥AB于点M，∴∠DMB=90°，∵BD=√6，∠DBM=60°，∴BM=√62，DM=3√22，∵OC=23√6，∴AB=43√6，∴AM=5√66，∵∠DMA=90°，DM=3√22，∴AD=√DM2+AM2=√783．9．【答案】（1）解：如图1中，作CH⊙AB于H.∵A（20，0），AB=16，∴OA=20，OB=4.在Rt⊙ABC中，∵⊙ACB=90°，AB=16，⊙CAB=30°，∴BC =12AB=8，CH=BC•sin60°=4 √3，BH=BC•cos60°=4，∴OH=8，∴C（8，4 √3）.（2）解：如图1﹣1中，设⊙M与直线BC相切于点N，作MH⊙AB于H.∵MN=MH=3 √3，MN⊙BC，MH⊙BA，∴⊙MBH=⊙MBN=30°，∴BH =√3MH=9，∴点M的运动路径的长为5+4+9=18，∴当点M在⊙ABC的内部且⊙M与直线BC相切时，t的值为18s.（3）解：∵C（8，4 √3），B（4，0），A（20，0）.∵CE=EB，CF=FA，∴E（6，2 √3），F（14，2 √3），设M（﹣5+t，3 √3），EF =12AB=8.∵⊙EMF=90°，∴EM2+MF2=EF2，∴（6+5﹣t）2+（√3）2+（14+5﹣t）2+（√3）2=82，整理得：t2﹣30t+212=0，解得：t=15± √13.10．【答案】（1）证明：作DF⊥BC于F，连接DB，∵AP是圆O的切线，∴∠PAC=90∘，即∠P+∠ACP=90∘，∵AC是圆O的直径，∴∠ADC=90∘，即∠PCA+∠DAC=90∘，∴∠P=∠DAC=∠DBC，∵∠APC=∠BCP，∴∠DBC=∠DCB，∴DB=DC，∵DF⊥BC，∴DF是BC的垂直平分线，∴DF经过点O，∵OD=OC，∴∠ODC=∠OCD，∵∠BDC=2∠ODC，∴∠BAC=∠BDC=2∠ODC=2∠OCD（2）解：∵DF经过点O，DF⊥BC，∴FC =12BC =3 ，在 ΔDEC 和 ΔCFD 中， {∠DCE =∠FDC ∠DEC =∠CFD DC =CD ，∴ΔDEC ⊙ ΔCFD (AAS) ∴DE =FC =3 ，∵∠ADC =90∘ ， DE ⊥AC ， ∴DE 2=AE •EC ，则 EC =DE 2AE =92，∴AC =2+92=132，∴圆 O 的半径为 13411．【答案】（1）=（2）解：取优弧 AB⌢ 的中点记为 C 1 ，过 C 1 作AB 的垂线，垂足为D ，由垂径定理知 C 1D 过O 且AD=BD ，如下图②所示.过C 作AB 的平行线a ，∵当直线a 向上平移时，a 距AB 的距离增大，即 △ABC 的AB 边上的高增大，得当a 运动到最高点C1时，△ABC的AB边上的高最大，又AB为常数，∴当C运动到C1时△ABC的面积最大，下面计算△ABC1的面积.连接OB在Rt⊙OBD中：∵AB=12、圆O的直径为20∴BD=6、BO=10、OC1=10由勾股定理得OD=√BO2−BD2=√102−62=8∴C1D=OD+OC1=8+10=18∴△ABC1的面积为12AB⋅C1D=12×12×18=108，∴△ABC面积的最大值为108；（3）解：过C作CF⊙BD交AD的延长线于F，如下图③-1所示∴⊙F=⊙ADB=60°∵AD⊙CE∴四边形DECF是平行四边形∴DF=CE，FC=DE又DC=CD∴⊙DFC⊙⊙CED∴S△DFC=S△CED又由（1）的结论知S△DAC=S△DAE∴S四边形ADCE=S△DAE+S△CED=S△DAC+S△DFC=S△ACF所以只需求得SΔACF最大值即得S四边形ADCE的最大值.以AC为边向△ABC外作等边三角形△AGC，再作等边△AGC的外接圆，过G作GJ⊙AC于J，如下图③-2所示.∵⊙F=60°∴点F在△AGC的外接圆上，由第（2）问的解决知，当F运动到点G时，SΔACF最大= SΔACG.在Rt⊙ABC中：由勾股定理得AC=√AB2−BC2=√202−102=10√3∴AJ=12AC=5√3∴GJ=√32×10√3=15∴SΔACG=12AC×GJ=12×10√3×15=75√3∴四边形ADCE的最大面积是75√3. 12．【答案】（1）证明：直线DC与⊙O相切. 理由如下：连接OC，如图，∵EC⌢=BC⌢∴⊙EAC＝⊙OAC∵OA＝OC，∴⊙ACO＝⊙OAC，∴⊙ACO＝⊙DAC，∴OC⊙AD，∵CD⊙AE，∴OC⊙CD，∴DC是⊙O的切线；（2）解：连接OC、OE、CB，过C作CH⊙AB于H，∵CH⊙AB，CD⊙AE∴⊙ADC=⊙AHC，∵⊙EAC＝⊙OAC，AC=AC∴⊙ADC⊙⊙AHC∴CH= CD=√3，AH=AD，∵⊙CAH+⊙ACH=⊙BCH+⊙ACH=90°∴⊙CAH=⊙BCH，又∵⊙CHA=⊙BHC，∴⊙CAH⊙⊙BCH∴CHBH=AHCH∴√34−AH=AH √3∴AH=3或1（舍去1）∴BH= 1∴S⊙ACH= 12×3×√3=3√3 2在Rt⊙CHB中，BH=1，HC= √3∴⊙BCH=30°=⊙CAB∴⊙COB=⊙EOC=60°∴S阴影=S梯形OCDE-S扇形OCE=S⊙ACD-S扇形OCE= S⊙ACH-S扇形OCE=3√32- 60×22π360= 3√32- 23π13．【答案】（1）25 问题探究：（2）解：如图2，作点G关于CD的对称点G'，作点B关于AD的对称点B'，连接B'G'，B'E，FG'，∵EB=EB'，FG=FG'，∴BE+EF+FG+BG=B'E+EF+FG'+BG，∵EB'+EF+FG'≥B'G'，∴四边形BEFG的周长的最小值=BG+B'G'，∵BG =12BC=5，BB'=20，BG'=15，∴B'G' =√BG′2+BB′2=√152+202=25，∴四边形BEFG的周长的最小值为30；问题解决：（3）解：如图3，连接AC、BD，在AC上取一点，使得DM=DC，∵⊙DAB=60°，⊙DCB=120°，∴⊙DAB+⊙DCB=180°，∴A、B、C、D四点共圆，∵AD=AB，⊙DAB=60°，∴⊙ADB是等边三角形，∴⊙ABD=⊙ADB=60°，∴⊙ACD=⊙ADB=60°，∵DM=DC，∴⊙DMC是等边三角形，∴⊙ADB=⊙MDC=60°，CM=DC，∴⊙ADM=⊙BDC，∵AD=BD，∴⊙ADM⊙⊙BDC(SAS)，∴AM=BC，∴AC=AM+MC=BC+CD，∵四边形ABCD的周长=AD+AB+CD+BC=AD+AB+AC，∵AD=AB=6，∴当AC最大时，四边形ABCD的周长最大，∴当AC为⊙ABC的外接圆的直径时，四边形ABCD的周长最大，∵6AC=sin60°，∴AC的最大值=4 √3，∴四边形ABCD的周长最大值为12+4 √3. 14．【答案】（1）证明：∵AC为⊙O的直径，∴⊙ABC=⊙ADC=90°，∵⊙BAD=90°，∴四边形ABCD是矩形，∴AB=CD；（2）∵AE为⊙O的切线，∴AE⊙AC，∴⊙EAB+⊙BAC=90°，∵⊙BAC+⊙ACB=90°，∴⊙EAB=⊙ACB，∵⊙ABC=90°，∴⊙ABE⊙⊙CBA，∴ABBC=BEAB，∴AB2=BE•BC，由（1）知：AB=CD，∴CD2=BE•BC；（3）∵F是AC的三等分点，∴AF=2FC，∵FG⊙BE，∴⊙AFG⊙⊙ACB，∴AFFC=AGBG=2，设BG=x，则AG=2x，∴AB=3x，在Rt⊙BCG中，CG= √3，∴BC2=（√3）2﹣x2，BC= √3−x2，由（2）得：AB2=BE•BC，（3x）2= 92√3−x2，4x4+x2﹣3=0，（x2+1）（4x2﹣3）=0，x=± √32，∵x＞0，∴x= √32，∴CD=AB=3x= 3√32．15．【答案】（1）解：如图所示，连接DF，∵AD⊙l，∴⊙ADE=⊙DEF，∴AE=DF，∵AD是圆O的直径，∴⊙AED=90°，∴DF=AE=√AD2−DE2=1；（2）解：如图所示，连接CE，取CE中点K，过点K作KM⊙BE于M，∵CH⊙EH，∴⊙CHE=90°，∴H在以K为圆心，以CE为直径的圆上，∵BH≤HK+BK，∴如图所示，当H运动到H的位置时，即此时H，B，K三点共线，BH有最大值BH，∵四边形ABCD是平行四边形，∴AB=CD=5，AB⊙CD，∴BE=AB-AE=4，⊙CDE=⊙AED=90°，⊙DCE=⊙MEK，∴CE=KE=√DE2+CD2=4√2，∴KH=12CE=2√2，∵⊙CDE=⊙EMK=90°，∴⊙CDE⊙⊙EMK，∴KMDE=EKCE=EMCD=12，∴KM=12DE=√72，EM=12CD=52，∴BM=AB−AE−EM=3 2，∴BK=√KM2+BM2=2，∴BH=2+2√2，∴BH的最大值为2+2√2；（3）解：如图3-1所示，过点B作BN⊙l于N，过点B作BT⊙l交CH于T，∵BN⊙l，CH⊙l，∴BN⊙CH，∴四边形BCHN是平行四边形，∴HT=BN，同理可证AM⊙BN，∴⊙AME⊙⊙BNE，∴BNAM=BEAE=4，∴BN=4AM，∴HT=4AM，∴CH-4AM=CH-HT=CT，又∵CT≤BC∴当直线l与直线BC垂直时，CT=BC，如图3-2所示，即此时CH-4AM的最大值即为BC，∵四边形ABCD是平行四边形，∴BC=AD=2√2，∴CH-4AM的最大值为2√2．16．【答案】（1）解：∵BD是正方形ABCD的对角线，∴∠BDC=45°，∵FG⌢=FG⌢，∴∠GAF=∠FDG，∴∠EAG=45°，（2）解：连接GF，∵在正方形ABCD中，∠ADG=90°，又∵在圆O的内接四边形ADGF中，∠AFG+∠ADG=180°，∴∠AFG=90°由（1）得∠GAE=45°，∴∠AGF=45°，∴∠FAG=∠AGF，∴AF=GF，∵∠GFE=180°−∠AFG=90°，∴tan∠AEG=GF FE，∴tan∠AEG=AF FE，∵α=BECE=12，BE+CE=BC，∴BCBE=3，∵正方形ABCD中，AD∕∕BC，AD=BC ∴△BEF∼△DAF，∴AFFE=ADBE=BCBE，∴tan∠AEG=3，（3）解：过F作FH⊥CD，垂足为H，连接CF，利用正方形轴对称可得CF=AF，由（2）知AF=GF∴CF=GF，∵FH⊥CD，∴CH=HG，∵BECE=α，AD=BC=BE+CE，∴ADBE=BCBE=α+1α，∵△BEF∼△DAF，∴DFBF=ADBE=α+1α，∵FH⊥CD,∠ACB=90°，∴HF⊙BC，∴DHCH=DFBF，∴DHCH=α+1α，∵DG=DH−GH,GH=CH，∴DGGC=DH−GHCH+GH=DH−CH2CH=α+1−α2α=12α.。