平抛运动知识点总结及解题方法归类总结.doc
(完整版)平抛运动的知识点总结

(完整版)平抛运动的知识点总结平抛运动是一种常见的物理现象,它涉及到物体在重力作用下沿水平方向以恒定速度运动的情况。
以下是平抛运动的关键知识点总结:1. 基本概念:- 平抛运动是指物体在水平方向上以初速度抛出,同时受到竖直方向重力加速度(g)作用的运动。
- 这种运动可以看作是水平方向的匀速直线运动和竖直方向的自由落体运动的叠加。
2. 运动方程:- 水平方向:$x = v_{0x}t$,其中$v_{0x}$是水平方向的初速度,$t$是时间。
- 竖直方向:$y = v_{0y}t - \frac{1}{2}gt^2$,其中$v_{0y}$是竖直方向的初速度(在纯平抛运动中通常为0),$g$是重力加速度。
3. 速度和位移:- 水平方向的速度保持不变,为$v_{0x}$。
- 竖直方向的速度随时间变化,为$v_{y} = gt$。
- 总速度$v$可以通过速度分量合成得到,使用勾股定理:$v =\sqrt{v_{0x}^2 + v_{y}^2}$。
- 位移分量同样可以通过水平和竖直方向的位移合成得到。
4. 运动时间:- 平抛运动的最大高度由公式$h = \frac{1}{2}gt^2$给出,解出时间$t = \sqrt{\frac{2h}{g}}$。
- 物体落地时间是指从抛出到落地的时间,可以通过竖直位移来计算。
5. 能量分析:- 动能:物体在水平和竖直方向上的动能分别为$K_x =\frac{1}{2}m v_{0x}^2$和$K_y = \frac{1}{2}m v_{y}^2$,总动能为两者之和。
- 势能:由于竖直方向的初速度通常为0,物体在初始时刻的势能为$E_p = mgh$,其中$h$是初始高度。
6. 实验验证:- 平抛运动可以通过实验来验证,例如使用高速摄像机捕捉物体的运动轨迹,或者通过测量不同时间点的位置来计算速度和加速度。
7. 应用场景:- 平抛运动的原理广泛应用于各种领域,如体育运动中的投掷项目、军事中的炮弹发射等。
高一物理必修2《平抛运动》知识点总结

由 h 1 gt 2 得: t 2h
2
g
②水平飞行射程由高度和水平初速度共同决定:
x
v0t
v0
2h g
③平抛物体任意时刻瞬时速度 夹角 θ正切值的两倍。
v 与平抛初速度 v0夹角 θa 的正切值为位移 s 与水平位移 x
④平抛物体任意时刻瞬时速度方向的反向延长线与初速度延长线的交点到抛出点的距离 都等于水平位移的一半。
证明: tan
gt
1 gt2 2
v0
s
sx 2
⑤平抛运动中, 任意一段时间内速度的变化量 Δv=gΔt,方向恒为竖直向下 (与 g 同向)。 任意相同时间内的 Δv 都相同(包括大小、方向) ,如右图。
V0 V1 △V V2 △V
V3 △V
⑥以不同的初速度,从倾角为 θ的斜面上沿水平方向抛出的物体,再次落到斜面上时速 度与斜面的夹角 a 相同,与初速度无关。 (飞行的时间与速度有关,速度越大时间越长。 )
⑧从动力学的角度看:由于做平抛运动的物体只受到重力,因此物体在整个运动过程中
机械能守恒。
7、平抛运动的实验探究
①如图所示,用小锤打击弹性金属片,金属片把
A球沿水平方向抛出,同时 B球松开,自
由下落, A、 B两球同时开始运动。观察到两球同时落地,多次改变小球距地面的高度和打
击力度, 重复实验, 观察到两球落地, 这说明了小球 A在竖直方向上的运动为自由落体运动。
在初速度 v0 方向做匀速直线运动,在合外力方向做初速度为零的匀加速直线运动,加速
度 a F合 。处理时和平抛运动类似,但要分析清楚其加速度的大小和方向如何,分别运用 m
两个分运动的直线规律来处理。
合位移(实际位移)的大小: s x 2 y 2
总结平抛知识点

总结平抛知识点一、平抛的基本概念1. 平抛的定义平抛是指物体在一定速度的情况下,在重力的作用下做抛体运动。
在平抛运动中,物体在水平方向做匀速直线运动,在竖直方向上受重力作用而做加速直线运动。
2. 平抛的特点平抛运动具有以下特点:(1)水平速度恒定:物体在水平方向上的速度是恒定的,即物体做匀速直线运动。
(2)竖直加速度恒定:物体在竖直方向上受到重力的影响,因此有竖直方向上的加速度,且加速度大小是恒定的,即重力加速度。
(3)运动轨迹为抛物线:考虑到水平速度恒定、竖直加速度恒定的特点,平抛物体的运动轨迹为抛物线。
二、平抛的运动规律1. 平抛的运动方程在平抛运动中,物体的水平运动与竖直运动是相互独立的,因此可以分别考虑。
设物体水平方向上的速度为v0,竖直方向上的初速度为v0y,竖直方向上的加速度为-g(g为重力加速度),水平方向上的位移为x,竖直方向上的位移为y,则有以下运动方程:(1)水平方向运动方程:x = v0*t(2)竖直方向运动方程:y = v0y*t - 0.5*g*t^22. 平抛的运动参数在平抛运动中,有一些重要的运动参数需要了解:(1)飞行时间:物体在竖直方向上的运动时间,记为T。
当物体抛出后再次回到初始高度时,飞行时间为T。
(2)最大高度:物体在竖直方向上所达到的最大高度,记为H。
最大高度可以通过竖直方向的运动方程求得。
(3)飞行距离:物体在水平方向上的飞行距离,记为D。
飞行距离可以通过水平方向的运动方程求得。
三、平抛的受力分析1. 平抛物体的受力在平抛运动中,物体受到的受力主要包括重力和空气阻力。
(1)重力:重力是所有物体都会受到的作用力,它的大小与物体的质量成正比,与重力加速度g成正比。
(2)空气阻力:当物体在空气中运动时,会受到空气的阻力作用。
空气阻力的大小与物体的速度成正比,与物体的表面积和空气密度成正比。
2. 平抛物体的受力分析考虑到物体的水平运动与竖直运动是相互独立的,在受力分析中可以单独考虑水平方向和竖直方向的受力情况。
平抛运动 知识点总结与典例(最新)

平抛运动知识点总结与典例【知识点梳理】知识点一 平抛运动的基本规律1.定义将物体以一定的初速度沿水平方向抛出,物体只在重力作用下所做的运动。
2.性质加速度为重力加速度的匀变速曲线运动,轨迹是抛物线。
3.条件:v 0≠0,沿水平方向;只受重力作用。
4.研究方法平抛运动可以分解为水平方向的匀速直线运动和竖直方向的自由落体运动。
5.基本规律(1)位移关系(2)速度关系6. 平抛运动的两个主要推论(1)做平抛运动的物体在任意时刻的瞬时速度的反向延长线一定通过此时水平位移的中点,如图所示,即x B =x A2。
推导:⎭⎬⎫tan θ=y A x A -x Btan θ=v yv 0=2yAxA→x B=x A2 (2)做平抛运动的物体在任意时刻任意位置处,有tan θ=2tan α。
推导:⎭⎬⎫tan θ=v y v 0=gt v 0tan α=y x =gt 2v→tan θ=2tan α知识点二、斜拋运动1.定义:将物体以初速度v 0沿斜向上方或斜向下方拋出,物体只在重力作用下的运动。
2.性质:加速度为重力加速度g 的匀变速运动,轨迹是拋物线。
3.研究方法:斜拋运动可以看作水平方向的匀速直线运动和竖直方向的竖直上拋运动的合运动。
4.与斜面有关的平拋运动常见的两种模型 斜面规律 方法 总结水平:v x =v 0 竖直:v y =gt合速度:v =v 2x +v 2y分解 速度分解速度,构建速度三角形.利用斜面倾角为θ这个约束条件可得tan θ=v 0v y水平:x =v 0t 竖直:y =12gt 2合位移:s =x 2+y 2分解 位移分解位移,构建位移三角形.利用斜面倾角为θ这个约束条件可得tan θ=yx ,可求得t 、x 、y【考点分类 深度解析】考点一 平抛运动的基本规律【典例1】 在一斜面顶端,将甲、乙两个小球分别以v 和v2的速度沿同一方向水平抛出,两球都落在该斜面上。
甲球落至斜面时的速率是乙球落至斜面时速率的( )A .2倍B .4倍C .6倍D .8倍 【答案】A【解析】甲、乙两球都落在同一斜面上,则隐含做平抛运动的甲、乙的最终位移方向相同,根据位移方向与末速度方向的关系,即末速度方向与水平方向夹角的正切值是位移方向与水平方向夹角的正切值的2倍,可得它们的末速度方向也相同,在速度矢量三角形中,末速度比值等于初速度比值,故A 正确。
平抛运动专题

平抛运动专题知识点一、平抛运动的规律:1、速度公式:0x v v = y v gt =合速度:()22220t x y v v v v gt =+=+ 0tan y xv gtv v θ==2、位移公式:20,2gt x v t y ==合位移:222222012s x y v t gt ⎛⎫=+=+ ⎪⎝⎭ 0tan 2y gt x v α==3、轨迹方程:2202gx y v =,顶点在原点(0、0),开口向下的抛物线方程。
4、任何相等的时间t ∆内,速度改变量v ∆=g t ∆相等,且v g t ∆=∆,方向竖直向下。
知识点二、平抛运动的推论1、平抛运动是一个同时经历水平方向的匀速直线运动和竖直方向的自由落体运动的合运动。
即tx=ty (分运动的等时性)运行时间:2ht g=,由h,g 决定,与无关。
2、在同一时刻,平抛运动的速度(与水平方向之间的夹角为)方向和位移方向(与水平方向之间的夹角是)是不相同的,其关系式3、任意一点的速度延长线必交于此时物体位移的水平分量的中点。
4、描绘平抛运动的物理量有、、、、、θ、、,已知这八个物理量中的任意两个,可以求出其它六个。
知识点三、平抛运动和斜面结合问题1、落回斜面: 隐含条件:位移和斜面平行运用2、撞击斜面:隐含条件:速度方法与水平方向的夹角与斜面的倾角互余。
3、离斜面距离最远:合速度的矢量合成,沿斜面方向和垂直斜面方向。
知识点四、平抛运动的综合应用问题1、平抛运动与其它运动形式的综合。
2、多体平抛问题。
当堂练习:1、如图所示,一物体自倾角为θ的固定斜面顶端沿水平方向抛出后落在斜面上,物体与斜面接触时速度与水平方向的夹角φ满足( )A . tan φ=sin θ B. tan φ=cos θ C. tan φ=tan θ D. tanφ=2tan θ2、物体以v的速度水平抛出,当其竖直分位移与水平分位移大小相等时,以下说法正确的是()A。
竖直分速度等于水平分速度 B.瞬时速度的大小为5vC.运动时间为2v0/g D.运动的位移大小为g222v/3、在“研究平抛物体运动”的实验中,某同学只记录了小球运动途中的A、B、C三点位置,取A点为坐标原点(0、0),则各点位置坐标如图所示,g取10m/s2,那么(注意:A点不一定是抛出点)①平抛运动的初速度是多少?②小球抛出点的位置坐标是多少?4、平抛运动的物体,在落地前的最后1s内,其速度方向由跟竖直方向成60°角变为跟竖直方向成45°角,求:物体抛出时的速度和高度分别是多少?5、如图1所示,某人骑摩托车在水平道路上行驶,要在A处越过的壕沟,沟面对面比A处低,摩托车的速度至少要有多大?g取106、以10m/s的初速度水平抛出的物体,飞行一段时间后,垂直地撞在倾角为的斜面上。
平抛运动·知识要点

v2y2-v1y2=2gy12
同理,在任何连续相等的时间内,竖直方向的位移之差一定满足关系:
Δy=y23-y12=g(Δt)2.
2.合速度方向时刻变化
随着运动时间的推移,平抛物体的竖直速度分量越来越大,因此,合速度也不断增大,它与竖直方向间的夹角θ越来越小,即速度方向越来越陡直.但在运动过程中每经过相等时间速度变化Δv的大小和方向恒定,如图4-2所示.
平抛运动·知识要点
平抛运动的性质
平抛物体仅受恒定的重力作用,因此是一种匀变速曲线运动,其加速度a=g,方向竖直向下.平抛物体的轨迹是一条抛物线.
平抛运动的规律
几个要点
1.抓住竖直方向的Байду номын сангаас动规律
平抛物体在竖直方向是加速度a=g的匀加速运动,因此在运动过程中任何两位置上(图4-1),速度的竖直分量与运动时间、竖直高度之间一定满足关系:
高一物理必修平抛运动知识点总结

高一物理必修2《平抛运动》知识点总结平抛运动1、定义:平抛运动是指物体只在重力作用下,从水平初速度开始的运动。
2、条件:a 、只受重力;b 、初速度与重力垂直.3、运动性质:尽管其速度大小和方向时刻在改变,但其运动的加速度却恒为重力加速度g ,因而平抛运动是一个匀变速曲线运动。
g a =4、研究平抛运动的方法:通常,可以把平抛运动看作为两个分运动的合动动:一个是水平方向(垂直于恒力方向)的匀速直线运动,一个是竖直方向(沿着恒力方向)的匀加速直线运动。
水平方向和竖直方向的两个分运动既具有独立性,又具有等时性.5、平抛运动的规律①水平速度:v x =v 0,竖直速度:v y =gt 合速度(实际速度)的大小:22y x v v v += 物体的合速度v 与x 轴之间的夹角为:②水平位移:t v x 0=,竖直位移221gt y =合位移(实际位移)的大小:22y x s +=物体的总位移s 与x 轴之间的夹角为:可见,平抛运动的速度方向与位移方向不相同。
而且θαtan 2tan =而θα2≠轨迹方程:由t v x 0=和221gt y =消去t 得到:2202x v g y =。
可见平抛运动的轨迹为抛物线。
6、平抛运动的几个结论①落地时间由竖直方向分运动决定: 由221gt h =得:gh t 2= ②水平飞行射程由高度和水平初速度共同决定:③平抛物体任意时刻瞬时速度v 与平抛初速度v 0夹角θa 的正切值为位移s 与水平位移x 夹角θ正切值的两倍。
④平抛物体任意时刻瞬时速度方向的反向延长线与初速度延长线的交点到抛出点的距离都等于水平位移的一半。
证明:221tan 20x s s gt v gt =⇒==α ⑤平抛运动中,任意一段时间内速度的变化量Δv =gΔt,方向恒为竖直向下(与g 同向)。
任意相同时间内的Δv 都相同(包括大小、方向),如右图。
⑥以不同的初速度,从倾角为θ的斜面上沿水平方向抛出的物体,再次落到斜面上时速度与斜面的夹角a 相同,与初速度无关。
平抛实验知识点总结

平抛实验知识点总结一、引言平抛实验是物理学中的一种基础实验,通过对物体在水平方向上做抛掷运动的实验研究,可以深入了解运动学和动力学的知识,同时也可以帮助学生掌握实验方法和数据处理的技巧。
在平抛实验中,我们通常会研究物体的抛射运动规律和抛射运动的相关参数。
二、平抛运动的基本规律1. 抛射运动的基本特点平抛运动是指物体在水平面上进行抛掷运动的运动形式。
在平抛运动中,物体在竖直方向上受到重力的作用,而在水平方向上则不受力的作用,因此物体在水平方向上做匀速直线运动。
平抛运动的基本特点有以下几点:(1)水平速度恒定。
在平抛运动中,物体在水平方向上的速度保持恒定。
(2)竖直速度变化。
在平抛运动中,物体在竖直方向上受到重力的作用,竖直速度逐渐增大。
(3)运动轨迹呈抛物线。
由于物体在水平方向上做匀速直线运动,而在竖直方向上做匀变速直线运动,所以物体的运动轨迹呈抛物线。
2. 平抛运动的基本参数在研究平抛运动时,我们通常会关注以下几个基本参数:(1)初速度。
即物体抛出时的速度,通常用v₀表示。
(2)水平方向的位移。
即物体在水平方向上移动的距离,通常用S表示。
(3)竖直方向的位移。
即物体在竖直方向上移动的距离,通常用H表示。
(4)飞行时间。
即物体从抛出到落地所经历的时间,通常用t表示。
(5)最大高度。
即物体抛出后达到的最高点,通常用Hmax表示。
(6)落地速度。
即物体落地时的速度,通常用v表示。
3. 平抛运动的运动方程在平抛运动中,我们可以根据运动学和动力学的知识推导出物体在水平方向和竖直方向上的运动方程。
假设物体在水平方向上的速度为vx,竖直方向上的速度为vy,竖直上抛,重力加速度为g,初始速度为v₀,抛射角为θ,我们有以下几个基本的物理关系式:(1)水平方向的运动方程:S = vx * t(2)竖直方向的运动方程:H = v₀ * t + (1/2) * g * t²(3)时间关系式:t = S / vx(4)最大高度:Hmax = (v₀² * sin²θ) / (2 * g)(5)落地速度:v = √(v₀² + 2 * g * H)通过上述关系式,我们可以分析物体在平抛运动中的运动规律,计算出物体的运动参数,并与实验测量值进行比较,从而检验运动方程的有效性。
(完整版)平抛运动知识点总结及解题方法归类总结

三、平抛运动及其推论平抛运动是一个同时经历水平方向的匀速直线运动和竖直方向的自由落体运动的合平抛运动在竖直方向上是自由落体运动,加速度。
=g 恒定,所以竖直方向上在相 珂:为:旳=1:$:5… 竖直方向上在相等的时间内相邻 审'(T 表示相等的时间间隔)。
(4)在同一时刻, 水平方向之间的夹角是日)是不相同的,其关系式他(即任意一点的速度延长线 必交于此时物体位移的水平分量的中点)。
一、知识点巩固:1. 定义:①物体以一定的初速度沿 水平方向抛出,②物体仅在重力作用下、加速度为重力加 速度g,这样的运动叫做平抛运动。
2. 特点:①受力特点:只受到重力作用。
② 运动特点:初速度沿水平方向,加速度方向竖直向下,大小为 g,轨迹为抛物线。
③ 运动性质:是加速度为 3. 平抛运动的规律:①速度公式:g 的匀变速曲线运动。
V x V o V y gt合速度: V ttan aV ygV x V ov/a^ a vv②位移公式:x V o t, ygt 22合位移:s^t 2如2tanegt 2V o③轨迹方程:顶点在原点(0、0),开口向下的抛物线方程。
注: (1) 运动。
(2) 平抛运动的轨迹是一条抛物线,其一般表达式为丿= (3) 等的时间内相邻的位移的高度之比为的位移之差是一个恒量平抛运动的速度(与水平方向之间的夹角为 a )方向和位移方向(与l描绘平抛运动的物理量有卩0、"*、¥、疋、尸、占、a 0、兰,已知这八个物理量中的任意两个,可以求出其它六个。
运动分类加速度速度位移轨迹分运动龙方向o 直线丿方向g 1 a直线合运动大小g 抛物线与K方向的夹角90 口ton —tan 日=2^04.平抛运动的结论:①运行时间:t (至,由h,g决定,与V o无关。
③任何相等的时间t内,速度改变量 v=g t相等,且④以不同的初速度,从倾角为0的斜面上沿水平方向抛出的物体,再次落到斜面上时速度与斜面的夹角a相同,与初速度无关。
平抛的知识点

平抛的知识点一、知识概述《平抛运动》①基本定义:平抛就是水平方向扔出去一个东西,这东西只受重力的影响,就这么直直地往前面飞呀飞,在空中划出一道弧线,这就是平抛运动啦。
比如说你水平扔出一个小石子(当然要确保安全,别砸到人和东西哦),这个小石子的运动就是平抛运动。
②重要程度:在物理学里这可是很重要的呢,它是运动学里的一个很典型的例子。
很多复杂的运动都可以通过对平抛运动的研究来找到思路,就好比它是一座桥梁,能帮我们连接到更多关于运动、力等知识概念。
③前置知识:你得先知道什么是运动,比如匀速直线运动啦,还有重力是怎么回事。
要是这些不懂的话,平抛运动可就不好理解了。
就像盖房子,你地基没打好,楼肯定盖不稳。
④应用价值:在现实生活中平抛可以用来测量一些距离。
比如说测量一条河的宽度,我们如果知道一块石头平抛出去的初速度和在空中运动的时间,就可以算出石头飞出去的水平距离,可能就等于河的宽度呢。
二、知识体系①知识图谱:在运动学这个大板块里,平抛运动算是比较关键和基础的一个。
它和自由落体运动、斜抛运动都有联系,可以说是运动学家族里的一个重要成员。
②关联知识:和力的知识尤其是重力联系紧密,毕竟是在重力作用下产生这种运动的。
还有和速度、位移这些运动学概念也分不开,它们就像小伙伴一样,手拉手构成了平抛运动。
③重难点分析:重点就是理解平抛运动水平和竖直方向的运动特点。
难点的话,说实话我觉得对于初学者来讲,把水平方向的匀速直线运动和竖直方向的自由落体运动结合起来理解挺难的。
这就像是要同时协调两只手做不同的动作,有点费脑筋。
④考点分析:在考试里经常出现哦。
一般会直接考查平抛运动的概念、速度或者位移的计算。
考查方式可能是给你一些已知条件,像初速度、下落高度之类的,然后让你算出水平位移或者落地时间。
也可能会和其他知识联合起来出题,像让你在电场或者磁场里分析一个类似平抛运动的带电粒子的运动。
三、详细讲解【理论概念类】①概念辨析:平抛运动就是有一个初始速度沿着水平方向,然后忽略空气阻力的情况下,只在重力的作用下所做的曲线运动。
平抛运动知识点总结总结

平抛运动知识点总结总结一、定义平抛运动是指一个物体在水平方向上以一定初速度抛出后,在竖直方向上只受重力的作用,不受空气阻力的运动。
在这种运动中,物体的水平速度保持不变,而竖直方向的速度受到重力加速度的影响而不断变化。
二、特点1. 水平速度恒定:在平抛运动中,物体的水平速度是恒定的,不会因为重力的作用而改变。
2. 竖直速度变化:物体在竖直方向上受到重力的影响,其竖直速度会随着时间的推移而改变。
3. 运动轨迹是抛物线:由于水平速度恒定,竖直速度发生变化,物体的轨迹呈现出一个抛物线的形状。
三、运动规律1. 距离和时间关系:在平抛运动中,物体的水平速度恒定,所以它在同样时间内所运动的距离是相等的。
在一定时间内,水平速度乘以时间即为水平方向上的位移。
2. 竖直方向运动:由于物体在竖直方向上受重力的作用,其竖直速度会随着时间的推移而改变。
根据运动学知识,我们可以得到物体在竖直方向上的运动规律为:s = ut + 1/2gt^2,其中s为竖直方向上的位移,u为初速度,g为重力加速度,t为时间。
3. 飞行时间:在平抛运动中,物体的水平速度是恒定的,所以物体飞行的时间只与竖直方向上的运动有关。
根据竖直方向上的运动规律,我们可以得到物体飞行的时间为t = 2u/g。
其中u为初速度,g为重力加速度。
4. 飞行距离:由于物体的水平速度是恒定的,则物体的飞行距离与其水平速度和飞行时间有关。
物体的水平速度乘以飞行时间即为飞行距离。
四、实例分析假设一个物体以初速度 u 被抛出,求其飞行时间、飞行距离和最大高度。
解:根据平抛运动的运动规律,我们可以得到物体的飞行时间为 t = 2u/g,飞行距离为 d = ut,最大高度为 h = 1/2 u^2/g。
五、应用1. 运动装置设计:在工程领域中,平抛运动的知识被广泛应用于设计各种物体的投放装置,比如我们需要将物体投放到某一指定位置,就可以利用平抛运动的知识来设计相应的装置。
2. 运动轨迹研究:在科学研究中,平抛运动的知识可以帮助我们研究物体在空中的运动轨迹,从而帮助我们理解相关现象和定律。
《平抛运动》 知识清单

《平抛运动》知识清单一、平抛运动的定义平抛运动是指将物体以一定的初速度沿水平方向抛出,物体仅在重力作用下所做的运动。
在平抛运动中,物体的初速度水平,且在运动过程中只受到重力的作用,重力方向竖直向下。
二、平抛运动的特点1、水平方向物体在水平方向上不受力,具有水平方向的初速度,做匀速直线运动。
水平方向的速度保持不变,即:$v_x = v_0$ (其中$v_0$为平抛运动的初速度)水平方向的位移:$x = v_0 t$ ($t$为运动时间)2、竖直方向物体在竖直方向上只受重力作用,加速度为重力加速度$g$,做自由落体运动。
竖直方向的速度:$v_y = gt$竖直方向的位移:$y =\frac{1}{2}gt^2$3、合速度与合位移合速度大小:$v =\sqrt{v_x^2 + v_y^2} =\sqrt{v_0^2 +(gt)^2}$合速度方向:与水平方向夹角的正切值为$\tan\theta =\frac{v_y}{v_x} =\frac{gt}{v_0}$合位移大小:$s =\sqrt{x^2 + y^2} =\sqrt{(v_0 t)^2 +(\frac{1}{2}gt^2)^2}$合位移方向:与水平方向夹角的正切值为$\tan\alpha =\frac{y}{x} =\frac{\frac{1}{2}gt^2}{v_0 t} =\frac{gt}{2v_0}$三、平抛运动的规律1、速度规律水平方向速度不变,竖直方向速度均匀增加。
2、位移规律水平方向位移与时间成正比,竖直方向位移与时间的平方成正比。
3、轨迹方程平抛运动的轨迹是一条抛物线,其方程为:$y =\frac{g}{2v_0^2}x^2$四、平抛运动的时间和水平射程1、运动时间由竖直方向的自由落体运动可得:$y =\frac{1}{2}gt^2$,所以运动时间$t =\sqrt{\frac{2y}{g}}$。
可见,平抛运动的时间只取决于下落的高度,与初速度无关。
(完整)必修2平抛运动知识点总结及经典练习题,推荐文档.docx
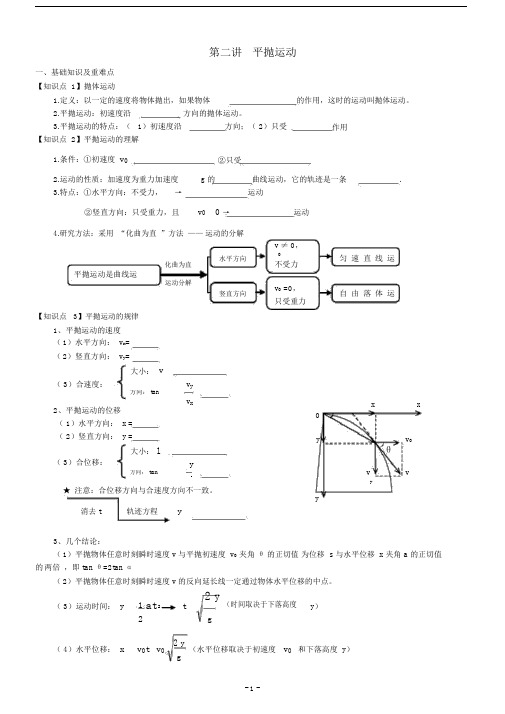
第二讲平抛运动一、基础知识及重难点【知识点 1】抛体运动1.定义:以一定的速度将物体抛出,如果物体的作用,这时的运动叫抛体运动。
2.平抛运动:初速度沿方向的抛体运动。
3.平抛运动的特点:( 1)初速度沿方向;( 2)只受作用【知识点 2】平抛运动的理解1.条件:①初速度v0②只受2.运动的性质:加速度为重力加速度g 的曲线运动,它的轨迹是一条.3.特点:①水平方向:不受力,→运动②竖直方向:只受重力,且v0 0 →运动4.研究方法:采用“化曲为直”方法——运动的分解v ≠ 0,水平方向0匀速直线运化曲为直不受力平抛运动是曲线运运动分解v0 =0,竖直方向自由落体运只受重力【知识点3】平抛运动的规律1、平抛运动的速度(1)水平方向: v x=(2)竖直方向: v y=大小:v( 3)合速度:v y方向: tan2、平抛运动的位移v x x x( 1)水平方向: x =( 2)竖直方向: y =y v大小: l ( 3)合位移:θy方向: tan v vxy ★ 注意:合位移方向与合速度方向不一致。
y消去 t轨迹方程y3、几个结论:(1)平抛物体任意时刻瞬时速度v 与平抛初速度 v0夹角θ的正切值为位移 s 与水平位移 x 夹角 a 的正切值的两倍,即 tan θ=2tan α(2)平抛物体任意时刻瞬时速度v 的反向延长线一定通过物体水平位移的中点。
( 3)运动时间:y 1 at2t 2 y(时间取决于下落高度y)2g2 y( 5)落地速度:v v02v y2v022gy (取决于初速度v0和下落高度y)【知点 4】平抛运的特点1、理想化特点 :物理上提出的平抛运是一种理想化模型,即把物体看出点,抛出后只考重力作用,忽略空气阻力。
2、匀速特点:平抛运的加速度恒定,始重力加速度 g 所以平抛运是一种运。
3、速度化特点:平抛运中,任意一段内速度的化量v=g t,方向恒直向下(与 g 同向),即任意两个相等的隔内速度的化相同,如右所示。
平抛运动总结

高一物理必修 2《平抛运动》知识点总结平抛运动1、 定义:平抛运动是指物体只在重力作用下,从水平初速度开始的运动。
2、 条件:a 、只受重力:b 、初速度与重力垂直.3、 运动性质:尽管其速度大小和方向时刻在改变, 但其运动的加速度却恒为重力加速度 g ,因而平抛运动是一个匀变速曲线运动。
a = g4、 研究平抛运动的方法: 通常,可以把平抛运动看作为两个分运动的合动动:一个是水平方向(垂直于恒力方向)的匀速直线运动,一个是竖直方向(沿着恒力方向)的匀加速直 线运动。
水平方向和竖直方向的两个分运动既具有独立性,又具有等时性.5、平抛运动的规律①水平速度:V x =V o ,竖直速度:V y =gt合速度(实际速度)的大小:v = v x 2 v y 2物体的合速度v 与x 轴之间的夹角为:v x v o1②水平位移:x =v°t ,竖直位移y gt 22合位移(实际位移)的大小: s = : x 2• y 2物体的总位移s 与x 轴之间的夹角为:可见,平抛运动的速度方向与位移方向不相同。
而且tan 〉=2tan^而二=公轨迹方程:12g 2由x -v °t 和ygt 消去t 得到:y2x 。
可见平抛运动的轨迹为抛22v物线。
6、平抛运动的几个结论① 落地时间由竖直方向分运动决定:vygttan 二x 2v o由 h jgt 2得:t 二2h2g② 水平飞行射程由高度和水平初速度共同决定:|2hx = Vot = Vo ,—V g③平抛物体任意时刻瞬时速度 v 与平抛初速度V 0夹角B 的正切值为位移s 与水平位移xv s 夹角B 正切值的两倍,即:tan-= 2tanr - 2 。
V x x④平抛物体任意时刻瞬时速度方向的反向延长线与初速度延长线的交点到抛出点的距离 都等于水平位移的一半。
1X 2t _ gt证明:tan 〉= 2 = 2 ——V o S⑤平抛运动中,任意一段时间内速度的变化量A V = g A t 方向恒为竖直向下(与g 同向)。
平抛运动知识点总结

平抛运动知识点总结
抛体平抛运动是物理学中的基本运动形式,它是指一个体在重力场中以恒定的初始速度以的运动,体的质心水平运动,在不考虑空气阻力的前提下可描述为一次函数。
1.初始速度:抛出物体的初始速度是抛体运动的基本参数,也是运动的控制因素。
其大小直接影响抛出物体的位置移动轨迹和半径,而它的方向则决定是否存在水平分量或者垂直分量,从而影响该运动的行程和时间。
2.重力加速度:地球表面重力加速度g,在运动过程中,重力加速度给抛体施加的垂直向下的重力作用使其向下运动。
3.速度的变化:抛体运动的特点是速度的变化规律是匀减速的。
考虑重力加速度的作用下,抛出物体在水平方向上的速度是不变的,而在垂直方向上则一直在减小,最终趋于0。
4.位置的变化:由于抛出物体在水平方向上的速度不变,抛出物体在水平方向上的变化是匀速运动;在垂直方向上则受重力加速度的作用,由于速度一直在减小,抛出物体在垂直方向上的变化也是匀减速运动。
5.平抛运动的静止时间:抛出物体在重力场中位置的变化,它的实际位置受初速度、重力加速度及空气阻力等因素的影响。
在抛物体的运动过程中会出现一个极点,即物体最高点的位置,此时物体的速度为0,物体会出现一个静止的瞬间。
完整word版高考复习平抛运动解题方法归类解析

平抛运动解题方法归类例析一、平抛运动的研究方法运动的合成与分解是研究曲线运动的基本方法. 根据运动的合成与分解,可以把平抛运动分解为水平方向的匀速运动和竖直方向的自由落体运动,然后研究两分运动的规律,必要时可以再用合成方法进行合成。
二、平抛运动规律以抛出点为坐标原点,水平初速度v方向为x轴正方向,竖直向下的方向为y轴正方向,建立如图所0示的坐标系,则平抛运动规律如下表:的飞镖以速处,将质量m h、离靶面距离L【典例精析1】:(双选)(2010 年广州一模)人在距地面高四个量中的一个,可使飞镖投中靶心v、L、m、水平投出,落在靶心正下方,如图所示.只改变hv度00) 的是(B.适当提高hv A.适当减小 0LD.适当减小C.适当减小m从题意中判断,要使飞镖投中靶心,可以在保持水平距离的条[解析]只会使下落时间更长,故v件下相应提升出手高度,或者,如出手高度不变,则需减少其下落时间,减小0BD。
应适当减小水平距离L。
质量对其运动无影响,综上,选【问题探究】:平抛物体落在水平面上时,物体在空中运动时间和水平射程分别由什么决定。
无关,而物体v][解析当平抛物体落在水平面上时,物体在空中运动的时间由高度h决定,与初速度0两者共同决定。
的水平射程由高度h及初速度v0三、对平抛运动规律的进一步理解1.速度的变化规律Δ时间,t,从抛出点起,每隔不变;竖直方向加速度恒为=vg,速度v=gtv水平方向分速度保持yx0速度的矢量关系如右图所示,这一矢量关系有三个特点;。
v(1)任意时刻的速度水平分量均等于初速度0ΔΔ的方向均竖直向内的速度改变量t(2)任意相等时间间隔vΔΔΔ=v=tg。
下,大小均为v y平抛运动的速率并不随时间均匀变化,但速度随时间是注意:均匀变化的。
随着时间的推移,末速度与竖直方向的夹角越来越大,但永(3) 远不会等于°。
90 1.位移的变化规律2ΔΔt。
(1)任意相等时间间隔内,水平位移不变,且=xv02ΔΔΔt内,竖直方向上的位移差不变,即。
《平抛运动》 知识清单

《平抛运动》知识清单一、平抛运动的定义平抛运动是指将物体以一定的初速度沿水平方向抛出,物体只在重力作用下所做的运动。
想象一下,你站在高处,水平抛出一个小球,这个小球在空中的运动轨迹就是平抛运动。
在平抛运动中,物体的初速度方向是水平的,而加速度方向是竖直向下的,始终为重力加速度 g。
二、平抛运动的特点1、水平方向平抛运动在水平方向上不受力,所以水平方向的分运动是匀速直线运动。
这意味着物体在水平方向上的速度始终保持不变。
例如,一个水平初速度为 v₀的物体,经过时间 t 后,水平方向移动的距离 x = v₀t 。
2、竖直方向在竖直方向上,物体只受到重力的作用,所以竖直方向的分运动是自由落体运动。
竖直方向的初速度为 0 ,加速度为 g 。
经过时间 t ,竖直方向下落的高度 h = 1/2gt²,竖直方向的速度 vᵧ= gt 。
3、合运动平抛运动的轨迹是一条抛物线,它是水平方向的匀速直线运动和竖直方向的自由落体运动的合运动。
合速度的大小 v =√(v₀²+ vᵧ²) ,合速度的方向与水平方向的夹角θ ,满足 tanθ = vᵧ/ v₀。
三、平抛运动的规律1、速度规律水平速度vₓ = v₀,竖直速度 vᵧ= gt ,合速度 v =√(v₀²+(gt)²) 。
2、位移规律水平位移 x = v₀t ,竖直位移 y = 1/2gt²,合位移 s =√(x²+ y²) 。
四、平抛运动的重要推论1、平抛运动任意时刻速度的反向延长线交于此时水平位移的中点。
假设某一时刻平抛物体的速度与水平方向夹角为θ ,位移与水平方向夹角为α ,则有tanθ =2tanα 。
2、平抛运动的时间由下落高度决定,与初速度无关。
因为 h = 1/2gt²,所以 t =√(2h/g) 。
五、平抛运动的应用1、体育项目在许多体育项目中,如铅球、标枪的投掷,运动员的动作都近似于平抛运动。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三、平抛运动及其推论一、 知识点巩固:1. 定义:①物体以一定的初速度沿 水平方向 抛出,②物体 仅在重力 作用下、加速度为重力加速度 g ,这样的运动叫做平抛运动。
2. 特点:①受力特点:只受到重力作用。
②运动特点:初速度沿水平方向,加速度方向竖直向下,大小为 g ,轨迹为抛物线。
③运动性质:是加速度为 g 的匀变速曲线运动。
3. 平抛运动的规律:①速度公式:v x v 0v y gt0x2xV合速度: v t222gt 2/xv x v y v 0O θαv ygtx =V 0tanɑv xv 0S( ,y )V②位移公式:xgt 2v 0t, yPx2yV y V合位移: sx 2y 2v 02t 21 gt 222y gttanθ x 2v 0gx 2 ③轨迹方程: y,顶点在原点 (0 、 0) ,开口向下的抛物线方程。
22v 0注:(1)平抛运动是一个同时经历水平方向的匀速直线运动和竖直方向的自由落体运动的合运动。
(2)平抛运动的轨迹是一条抛物线,其一般表达式为 。
(3)平抛运动在竖直方向上是自由落体运动,加速度恒定,所以竖直方向上在相等的时间内相邻的位移的高度之比为竖直方向上在相等的时间内相邻的位移之差是一个恒量(T 表示相等的时间间隔)。
(4)在同一时刻,平抛运动的速度(与水平方向之间的夹角为ɑ)方向和位移方向(与水平方向之间的夹角是)是不相同的,其关系式ɑ(即任意一点的速度延长线必交于此时物体位移的水平分量的中点)。
描绘平抛运动的物理量有、、、、、、ɑ、θ、,已知这八个物理量中的任意两个,可以求出其它六个。
运动分类加速度速度位移轨迹方向0直线分运动方向直线合运动大小抛物线与方向ɑ的夹角4. 平抛运动的结论:2h,由 h,g 决定,与v0无关。
V0△ V①运行时间: t V1gV2 △ V②水平射程: x v0 2h ,由 h,g,v0 共同决定。
V3 △V g③任何相等的时间t 内,速度改变量v =g t 相等,且v g t ,方向竖直向下。
④以不同的初速度,从倾角为θ的斜面上沿水平方向抛出的物体,再次落到斜面上时速度与斜面的夹角 a 相同,与初速度无关。
(飞行的时间与速度有关,速度越大时间越长。
)Av0yθx v xαv y 如上图:所以t2v0tangvθv y gt tan(a)v x v0所以 tan( a) 2 tan,θ为定值故a也是定值,与速度无关。
⑤速度 v 的方向始终与重力方向成一夹角,故其始终为曲线运动,随着时间的增加,tan变大,,速度 v 与重力的方向越来越靠近,但永远不能到达。
⑥从动力学的角度看:由于做平抛运动的物体只受到重力,因此物体在整个运动过程中机械能守恒。
5、斜抛运动:定义:将物体以一定的初速度沿与水平方向成一定角度抛出,且物体只在重力作用下(不计空气阻力)所做的运动,叫做斜抛运动。
它的受力情况与平抛完全相同,即在水平方向上不受力,加速度为 0;在竖直方向上只受重力,加速度为 g。
设初速度 v0与水平方向夹角为θ。
速度: v x v0 cos 位移: x v0 cos tv y v0 sin gty v0 sin t 1 gt 222 v sin回落原水平面时间: t xV 0v0 cos g2sin 2水平射程: x V v0 当45时, x 最大。
g y6、类平抛运动问题:平抛运动是典型的匀变速曲线运动,应掌握这类问题的处理思路、方法并迁移到讨论类平抛运动 ( 如带电粒子在匀强电场中的偏转等 ) 的问题上来.(1) 类平抛运动的特点是物体所受的合力为恒力,且与初速度方向垂直( 初速度v0的方向不一定是水平方向,即合力的方向也不一定是竖直方向,且加速度大小不一定等于重力加速度 g) .(2)类平抛运动可看成是某一方向的匀速直线运动和垂直此方向的匀加速直线运动的合运动.处理类平抛运动的方法与处理平抛运动类似,但要分析清楚其加速度的大小和方向如何.7、平抛运动中的临界问题:分析平抛运动中的临界问题时一般运用极端分析的方法,即把要求的物理量设定为极大或极小,让临界问题突现出来,找出产生临界的条件.例:如图所示,排球场总长为l8m,球网高度为 2m,运动员站在离网3m的线上 ( 图中虚线所示) 正对网向上跳起将球水平击出 ( 球在飞行过程中所受空气阻力不计, g 取 10m/s2) .(1)设击球点在 3m线的正上方高度为 2.5m 处,试问击球的速度在什么范围内才能使球既不触网也不越界 ?(2)若击球点在 3m线正上方的高度小于某个值,那么无论水平击球的速度多大,球不是触网就是越界,试求这个高度.二、平抛运动的常见问题及求解思路:关于平抛运动的问题,有直接运用平抛运动的特点、规律的问题,有平抛运动与圆周运动组合的问题、有平抛运动与天体运动组合的问题等。
本文主要讨论直接运用平抛运动的特点和规律来求解的问题,即有关平抛运动的常见问题。
1.从同时经历两个运动的角度求平抛运动的水平速度:求解一个平抛运动的水平速度的时候,我们首先想到的方法,就应该是从竖直方向上的自由落体运动中求出时间,然后,根据水平方向做匀速直线运动,求出速度。
[ 例 1]如图所示,某人骑摩托车在水平道路上行驶,要在 A 处越过的壕沟,沟面对面比 A 处低,摩托车的速度至少要有多大?g 取 10m/s2。
解析:在竖直方向上,摩托车越过壕沟经历的时间在水平方向上,摩托车能越过壕沟的速度至少为对于一个做平抛运动的物体来说,如果知道了某一时刻的速度方向,则我们常常是“从分解速度”的角度来研究问题。
[ 例 2]如图甲所示,以9.8m/s的初速度水平抛出的物体,飞行一段时间后,垂直地撞在倾角为的斜面上。
可知物体完成这段飞行的时间是()A. B. C.D.解析:先将物体的末速度分解为水平分速度和竖直分速度(如图乙所示)。
根据平抛运动的分解可知物体水平方向的初速度是始终不变的,所以;又因为与斜面垂直、与水平面垂直,所以与间的夹角等于斜面的倾角。
再根据平抛运动的分解可知物体在竖直方向做自由落体运动,那么我们根据就可以求出时间了。
则所以根据平抛运动竖直方向是自由落体运动可以写出:所以所以答案为 C。
3.从分解位移的角度进行解题:对于一个做平抛运动的物体来说,如果知道了某一时刻的位移方向(如物体从已知倾角的斜面上水平抛出,这个倾角也等于位移与水平方向之间的夹角),则我们可以把位移分解成水平方向和竖直方向,然后运用平抛运动的运动规律来进行研究问题(这种方法,暂且叫做“分解位移法”)[ 例 3] 如图所示,在坡度一定的斜面顶点以大小相同的速度同时水平向左与水平向右抛出两个小球 A 和 B,两侧斜坡的倾角分别为和,小球均落在坡面上,若不计空气阻力,则 A 和 B 两小球的运动时间之比为多少?解析:和都是物体落在斜面上后,位移与水平方向的夹角,则运用分解位移的方法可以得到所以有同理则4.从竖直方向是自由落体运动的角度出发求解:在研究平抛运动的实验中,由于实验的不规范,有许多同学作出的平抛运动的轨迹,常常不能直接找到运动的起点(这种轨迹,我们暂且叫做“残缺轨迹”),这给求平抛运动的初速度带来了很大的困难。
为此,我们可以运用竖直方向是自由落体的规律来进行分析。
[ 例 4]某一平抛的部分轨迹如图 4 所示,已知,,,求。
解析: A 与 B、 B 与 C 的水平距离相等,且平抛运动的水平方向是匀速直线运动,可设 A 到 B、B到 C的时间为 T,则又竖直方向是自由落体运动,则代入已知量,联立可得5.从平抛运动的轨迹入手求解问题:[ 例 5]从高为H的A点平抛一物体,其水平射程为,在A点正上方高为 2H的 B 点,向同一方向平抛另一物体,其水平射程为。
两物体轨迹在同一竖直平面内且都恰好从同一屏的顶端擦过,求屏的高度。
解析:本题如果用常规的“分解运动法”比较麻烦,如果我们换一个角度,即从运动轨迹入手进行思考和分析,问题的求解会很容易,如图 5 所示,物体从 A、B 两点抛出后的运动的轨迹都是顶点在轴上的抛物线,即可设 A、B 两方程分别为,则把顶点坐标 A(0,H)、 B(0,2H)、 E( 2 , 0)、F(,0)分别代入可得方程组这个方程组的解的纵坐标,即为屏的高。
6.灵活分解求解平抛运动的最值问题[ 例 6] 如图所示,在倾角为的斜面上以速度水平抛出一小球,该斜面足够长,则从抛出开始计时,经过多长时间小球离开斜面的距离的达到最大,最大距离为多少?解析:将平抛运动分解为沿斜面向下和垂直斜面向上的分运动,虽然分运动比较复杂一些,但易将物体离斜面距离达到最大的物理本质凸显出来。
取沿斜面向下为轴的正方向,垂直斜面向上为轴的正方向,如图 6 所示,在轴上,小球做初速度为、加速度为的匀变速直线运动,所以有①②当时,小球在轴上运动到最高点,即小球离开斜面的距离达到最大。
由①式可得小球离开斜面的最大距离当时,小球在轴上运动到最高点,它所用的时间就是小球从抛出运动到离开斜面最大距离的时间。
由②式可得小球运动的时间为7.利用平抛运动的推论求解:推论 1:任意时刻的两个分速度与合速度构成一个矢量直角三角形。
[ 例 1] 从空中同一点沿水平方向同时抛出两个小球,它们的初速度大小分别为和,初速度方向相反,求经过多长时间两小球速度之间的夹角为?解析:设两小球抛出后经过时间,它们速度之间的夹角为,与竖直方向的夹角分别为和,对两小球分别构建速度矢量直角三角形如图所示,由图可得和又因为所以由以上各式可得,解得推论 2:任意时刻的两个分位移与合位移构成一个矢量直角三角形[ 例 2]宇航员站在一星球表面上的某高度处,沿水平方向抛出一个小球,经过时间,小球落到星球表面,测得抛出点与落地点之间的距离为,若抛出时初速度增大到两倍,则抛出点与落地点之间的距离为。
已知两落地点在同一水平面上,该星球的半径为 R,万有引力常数为G,求该星球的质量M。
解析:设第一次抛出小球,小球的水平位移为,竖直位移为,如图 8 所示,构建位移矢量直角三角形有:若抛出时初速度增大到 2 倍,重新构建位移矢量直角三角形,如图所示有由以上两式得令星球上重力加速度为,由平抛运动的规律得由万有引力定律与牛顿第二定律得由以上各式解得推论 3:平抛运动的末速度的反向延长线交平抛运动水平位移的中点。
[ 例 3]如图所示,与水平面的夹角为的直角三角形木块固定在地面上,有一质点以初速度从三角形木块的顶点上水平抛出,求在运动过程中该质点距斜面的最远距离。
解析:当质点做平抛运动的末速度方向平行于斜面时,质点距斜面的距离最远,此时末速度的方向与初速度方向成角。
如图所示,图中 A 为末速度的反向延长线与水平位移的交点, AB即为所求的最远距离。
根据平抛运动规律有:,和由上述推论 3 知据图 9 中几何关系得由以上各式解得即质点距斜面的最远距离为推论 4:平抛运动的物体经时间后,其速度与水平方向的夹角为,位移与水平方向的夹角为,则有[ 例 4] 如图所示,从倾角为斜面足够长的顶点 A,先后将同一小球以不同的初速度水平向右抛出,第一次初速度为,球落到斜面上前一瞬间的速度方向与斜面的夹角为,第二次初速度,球落在斜面上前一瞬间的速度方向与斜面间的夹角为,若,试比较和的大小。
