1 球杆系统建模分析
一种精简化的球杆系统控制器建模方法

一种精简化的球杆系统控制器建模方法钟秉翔;高国芳【摘要】To simulate human behaviors or actions and solve the problem of dimension disaster of behavior functional simulation model in complicated control, with the cue system as the researching object, the simplified control model for cue system is designed. For this model, the methods of kernel principal component analysis (KPCA) and false nearest neighbor point are applied. In addition, variable selection is implemented through phase-space reconstruction; the least square method is used to realize linear regression to fit the regression mathematical model from simplified input space to output space. The test shows that the control algorithm of this controller is effective, and the controller possesses higher control accuracy and stability.%为了模拟人的控制行为,解决复杂控制中行为功能模拟模型的维度灾难问题,以球杆系统为研究对象,设计了精简化的球杆系统控制器模型.该模型采用核主元分析法和虚假最近邻点法,通过重构相空间实现变量选择;同时,利用最小二乘法进行线性回归,拟合从精简的输入空间到输出空间的回归数学模型.试验证明,该控制器的控制算法有效,具有较高的控制精度和稳定性.【期刊名称】《自动化仪表》【年(卷),期】2012(033)003【总页数】4页(P53-56)【关键词】球杆系统;嵌入维数;虚假最近邻点法;相空间重构;系统建模【作者】钟秉翔;高国芳【作者单位】重庆科技学院电气与信息工程学院, 重庆401331;重庆科技学院电气与信息工程学院, 重庆401331【正文语种】中文【中图分类】TP273+.10 引言在实际生活或工程实践中,一个熟练的操作人员凭借丰富的生活经验或实践经验,可以非常娴熟、巧妙地控制一个复杂过程,并得到满意的控制效果。
1 球杆系统建模分析

《线性系统理论》课程设计报告书课题名称球杆系统姓名孟禹漆铖刘泽文孟凡强杨佐龙日期2013年2 月25日老师陈玮1 球杆系统建模分析本章将对球杆系统进行简单的介绍,然后采用拉格朗日方程建立其数学模型,并在此基础上分析其特性。
1.1球杆系统介绍球杆系统(Ball & Beam )是由球杆执行系统、控制器和直流电源等部分组成。
该系统对控制系统设计来说是一种理想的实验模型。
正是由于系统的结构相对简单,因此比较容易理解该模型的控制过程。
球杆执行系统(如图1 所示)由一根V 型轨道和一个不锈钢球组成。
V 型槽轨道一侧为不锈钢杆,另一侧为直线位移电阻器。
当球在轨道上滚动时,通过测量不锈钢杆上输出电压可测得球在轨道上的位置。
V 型槽轨道的一端固定,而另一端则由直流电机(DC motor )的经过两级齿轮减速,再通过固定在大齿轮上的连杆带动进行上下往复运动。
V 型槽轨道与水平线的夹角可通过测量大齿轮转动角度和简单的几何计算获得。
这样,通过设计一个反馈控制系统调节直流电机的转动,就可以控制小球在轨道上的位置。
图1 球杆系统执行机构原理图1.2拉格朗日方程介绍建立一个力学体系的动力学方程所需要的独立坐标称为广义坐标,广义坐标一旦确定,体系在空间的位置状态也就可以唯一确定。
广义坐标可以是坐标变量,也可能是是角动量或其他独立变量,凡能用来表述体系的位形、运动和动力学状态的独立参量都可作为广义坐标。
广义坐标的条件是:互相独立、满足约束方程、唯一确定体系的位形式动力学状态。
拉格朗日方程方法建模可以表述为:设一个机械系统的自由度为n ,对于系统可以采用广义坐标12(,,...,)n q q q q =,12(,,...)n q q q q =来描述,记该系统的总体动能为(,)T q q ,总体势能为()V q ,系统的运动特性可以用以下的拉格朗日方程描述:d 1,2,...,d i i iL Li n t q q τ⎛⎫∂∂-== ⎪∂∂⎝⎭ (1.1)其中,方程组中方程式的数目等于质点系的自由度数,i τ为作用在第i 个广义坐标i q 方向的外部力或力矩之和。
1球杆系统
球杆系统GBB1004实验报告一、球杆系统的数学模型一、实验目的1) 分析并推导系统的数学模型;2) 求解系统的状态空间方程和传递函数方程;3) 在Matlab 下建立系统的模型并进行阶跃响应仿真。
4) 完成实验报告二、实验步骤1. 球杆系统在Simulink 下的模型建立在Simulink 下建立系统的模型:仿真结果如下:二、球杆系统的数字控制器实验报告一、实验目的学习使用根轨迹法设计一个稳定的系统,进一步理解根轨迹的基本概念和根轨迹图所代表的含义,通过实验来验证增加零、极点以及开环增益对系统性能有何影响。
二、实验步骤1、开环根轨迹实验程序:m=0.028;R=0.0145;g=-9.8;L=0.40;d=0.045;J=0.4*m*R^2;K=(m*g*d)/(L*(J/R^2+m));num=[-K]; den=[1 0 0];plant=tf(num,den);rlocus(plant)运行结果:2、可以看到系统在原点有两个极点沿虚轴伸向无穷远处使用sgrid 命令可以将设计目标也显示在根轨迹上m=0.028;R=0.0145;g=-9.8;L=0.40;d=0.045;J=0.4*m*R^2;K=(m*g*d)/(L*(J/R^2+m));num=[-K];den=[1 0 0];plant=tf(num,den);rlocus(plant)sgrid(0.7,1.9)axis([-5 5 -2 2])运行结果:3、超前补偿器;在上面那个程序前添加以下程序:zo=0.01;po=5;contr=tf([1 zo],[1 po])rlocus(contr*plant)sgrid(0.7,1.9)运行结果:4、现在,根轨迹的分支已经在设计目标范围内。
使用rlocfind 命令来确定系统的增益。
在m文件中加入以下几行[k,poles]=rlocfind(contr*plant)到图形显示窗口选择用十字形光标一点。
综合课程设计A任务书0111(1)球杆控制系统

综合课程设计任务书(球杆控制系统)二O一一年十二月1 自学部分1.1 MATLAB 软件应用。
1.2 小组自学教材第六章线性系统的校正方法。
1.3 完成教材习题:P.296 6-3;P.297 6-5;P.298 6-9;P.299 6-14;P.301-304 6-19到6-26任选两题。
要求:理论分析和MATLAB 软件仿真设计。
理论分析要有推导过程; MATLAB 软件设计要有程序框图、清单和运行结果、仿真曲线。
2 综合部分——球杆控制系统2.1系统建模。
球杆控制系统装置该装置由球杆装置、IPM 智能驱动器、计算机、电机、齿轮减速器、直线位移传感器所组成。
通过计算机可以输入小球的控制位置,由计算机把数据传输给IPM 智能驱动器,产生相应的控制量,使电机转动,带动杠杆臂运动,使小球的位置得到控制。
球杆系统建模对小球在导轨上滚动的动态过程的完整描述是非常复杂的,设计者的目的是对于该控制系统给出一个相对简单的模型。
实际上使小球在导轨上加速滚动的力是小球的重力在同导轨平行方向上的分力同小球受到的摩擦力的合力。
考虑小球滚动的动力学方程,小球在V 型杆图2.1 球杆控制系统直线位移传感器上滚动的加速度: ααμsin cos g g a -=(1)其中μ为小球与轨道之间的摩擦系数,而α为轨道杆与水平面之间的夹角。
但在进行数学建模的过程中,我们忽略了摩擦力,因此,其基本的数学模型转换成如下方式:xm mg =αsin (2)当α<<1时,将上式线性化,得到传递函数如下2)()(sgs s x =α (3)其中X(s)为小球在轨道上的位置。
但是,在实际控制的过程中,杆的仰角α是由电动机的转角输出来实现的。
影响电动机转角θ和杆仰角α之间关系的主要因素就是齿轮的减速比和连杆机构。
因此,我们把该模型进一步简化:)()(s b s αθ∙= (4)把(4)式代入(3)式,我们可以得到另一个模型:2)()(s cs s x =θ (5)其中c 是一个包含了b 和g 的影响的参数。
建模仿真_球杆实验_实验报告

《建模仿真与相似原理》課程实验报告第一章简化模型的建立和稳定性分析一、实验目的1.了解机理法建模的基本步骤;2.会用机理法建立球杆系统的简化数学模型;3.掌握控制系统稳定性分析的基本方法;二、实验要求1.采用机理法建立球杆系统的数学模型;2.分析的稳定性,并在 matlab 中仿真验证;三、实验设备1.球杆系统;2.计算机 matlab 平台;四、实验分析及思考题Simulink模型:Matlab仿真结果:思考题:1.根据建模的过程,总结机理法建模的基本步骤:1)根据系统运动的物理规律建立方程;2)化简为微分方程;3)根据小偏差线性化的理论化简为线性系统的传递函数;2.实验结果分析、讨论和建议。
答:影响系统稳定的因素是闭环系统的极点位置,闭环极点为[i,-i],在虚轴上,所以其阻尼为0,则系统震荡。
测量系统稳定性的方法之一是加入大小合适的阶跃信号,根据其输出的阶跃响应分析系统的稳定性和其他性能。
第二章仿真及实物模拟仿真实验2.1 PID仿真及实物模拟仿真实验一、实验目的1.会用 PID 法设计球杆系统控制器;2.设计并验证校正环节;二、实验要求1.根据给定的性能指标,采用凑试法设计 PID 校正环节,校正球杆系统,并验证之。
2.设球杆系统的开环传递函数为:设计 PID 校正环节,使系统的性能指标达到: St ≤10s,δ≤30%。
三、实验设备1.球杆系统;2.计算机 matlab 平台;四、实验过程1.未校正系统仿真Simulink模型及仿真结果如第一章所示;2.PID校正法仿真Simulink模型:Matlab仿真结果:参数设定:Kp=10 Ki=0 Kd=103.PID实时控制Simulink模型:实时控制结果:Step参数设定:Step time=1 Final value=0.25PID参数设定:P=3 I=1 D=1.54.实验记录五、实验分析1.怎样确定PID 控制器的参数?答:由于ID 控制器各校正环节的作用如下:比例环节:成比例地反映控制系统的偏差信号e(t),偏差一旦产生,控制器立即产生作用,以减少偏差;积分环节:主要用于消除稳态误差,提高系统的型别。
球杆系统建模与控制

球杆系统建模与控制
球杆系统可以被建模为一个旋转质点系统。
球杆的旋转可以由
两种力矩进行控制:外力矩和内部的惯性力矩。
外力矩可能来自于
球的运动,例如摩擦和空气阻力。
惯性力矩则来源于球杆的旋转惯性。
为了控制球杆系统,可以使用反馈控制算法。
这需要收集传感
器数据,例如加速度计和陀螺仪数据,来对球杆的位置和运动进行
实时监测。
然后使用控制器来计算所需的控制操作,例如力矩大小
和方向,以实现所需的旋转控制。
PID控制算法是常用的控制器类型之一。
它包括一个反馈回路,其中误差信号被用作输入。
PID控制器可调整三个参数:比例、积
分和微分增益。
这三个参数的好坏决定PID对期望跟踪的效果。
需要注意的是,球杆系统建模和控制算法的复杂度取决于所需
的控制精度和稳定性。
需要细致地考虑各种曲率半径、力矩大小、
空气动力学、杆膜弹性、重心偏移等物理因素对该系统的影响。
球杆系统的建模、仿真与控制器设计

球杆系统的建模、仿真与控制器设计
胖永新;金迪;孟宪东
【期刊名称】《武汉大学学报:工学版》
【年(卷),期】2005(38)6
【摘要】球杆系统是一个非线性不稳定系统,其中小球在导轨上滚动过程的动态描述十分复杂.通过建立球杆系统机械部分模型、角度模型和电机模型,简化后得到了整个球杆系统的传递函数.同时通过设计最优鲁棒控制器、最优瞬态控制器和二自由度控制器对其进行控制,证明了系统是可控的和稳定的.在Matlab的Simulink环境下的仿真试验也印证了上述结论.充分说明了球杆系统对学习控制理论来说是一个很好的实验装置.
【总页数】5页(P142-146)
【关键词】球杆系统;系统建模仿真;控制器设计;角度模型;电机模型
【作者】胖永新;金迪;孟宪东
【作者单位】广东蓄能发电有限公司;姚孟发电有限公司;三江集团江河化工厂【正文语种】中文
【中图分类】TP13
【相关文献】
1.基于Modelica的球杆平衡系统建模仿真 [J], 于红
2.一种精简化的球杆系统控制器建模方法 [J], 钟秉翔;高国芳
3.浅谈球杆系统的建模与仿真 [J], 刘阳;万隆君;徐轶群
4.球杆系统建模及其闭环控制器的设计 [J], 刘诗宇
5.基于模糊免疫PID控制器在球杆网络控制系统中的仿真研究 [J], 黄丽华
因版权原因,仅展示原文概要,查看原文内容请购买。
球杆系统

实验一球杆系统简化模型的建立和稳定性分析一、实验目的1、理解球杆系统模型建立的基本步骤;2、建立球杆系统的简化数学模型;3、掌握控制系统稳定性分析的基本方法;二、实验要求1、建立球杆系统的数学模型;2、分析的稳定性,并在matlab 中仿真验证;三、实验设备1、球杆系统;2、计算机、matlab 平台;四、实验原理系统建模可以分为两种:机理建模和实验建模。
机理建模是在了解研究对象的运动规律基础上,通过物理、化学的知识和数学手段建立起系统内部的输入——输出状态关系。
实验建模是通过在研究对象上加上一系列的研究者事先确定的输入信号,激励研究对象并通过传感器检测其可观测的输出,应用数学手段建立起系统的输入——输出关系。
这里面包括输入信号的设计选取,输出信号的精确检测,数学算法的研究等等内容。
在导轨上移动的系统,是一个典型的运动的刚体系统,可以在惯性坐标系内应用经典力学理论建立系统的动力学方程。
下面采用其中的牛顿——欧拉方法建立球杆的数学模型。
球杆系统的机械部分包括底座、小球、横杆、减速皮带轮、支撑部分、马达等。
如图1.1所示。
图1.1 球杆本体图小球可以在横杆上自由的滚动,横杆的一端通过转轴固定,另一端可以上下转动,通过控制直流伺服电机的位置,带动皮带轮转动,通过传动机构就可以控制横杆的倾斜角。
直流伺服电机带有增量式编码器(1000P/R),可以检测电机的实际位置,在横杆上的凹槽内,有一线性的电阻传感器用于检测小球的实际位置。
当带轮转动角度,横杆的转动角度为,当横杆偏离水平的平衡位置后,在重力作用下,小球开始沿横杆滚动。
如下图1.2所示。
图1.2 球杆运动示意图连线(连杆和同步带轮的连接点与齿轮中心的连线)和水平线的夹角为的角度存在一定的限制,在最小和最大的范围之间),连杆和齿轮的连接点与齿轮中心的距离为d ,横杆与支撑杆连接点的长度为L ,于是,横杆的倾斜角α和θ之间的有如下的数学关系:d Lαθ=角度θ和电机轴之间存在一个减速比4n =的同步带,控制器设计的任务是通过调整齿轮的角度θ,使得小球在某一位置平衡。
自动控制实验报告——球杆系统倒立摆bupt概要

球杆系统实验实验一小球位置的数据采集处理一、实验目的:学会用Simulink仿真与硬件连接并获得小球位置。
二、实验任务:1、在MatLab Simulink中通过添加功能模块完成球杆系统模型的建立;2、正确获得小球位置数据;三、实验原理:小球的位置通过电位计的输出电压来检测,它和IPM100的AD转换通道AD5相连,AD5(16位)的范围为0-65535,对应的电压为0-5V,相应的小球位置为0-400mm。
MatLab Simulink环境下的数据采集处理工具箱提供了强大的功能。
可以编写扩展名为mdl的图形文件,采集小球的位置信号,并进行数字滤波。
四、实验设备及仪器:1、球杆系统;2、计算机MATLAB平台;五、实验步骤:将MatLab主窗口的Current Directory文本框设置为球杆控制程序的系统文件夹;在MatLab主窗口点击进入Simulink Library Brower窗口,打开工具箱Googol Education Products\4. Ball & Beam\A. Data Collection and Filter Design,运行Data Collection and Filter Design程序,确认串行口COM Port为1后,双击Start Real Control模块,打开数据采集处理程序界面;已有的模块不需再编辑设置,其中Noise Filter1模块是专门设计的滤波器,用来抑制扰动。
请参考以下步骤完成剩余部分:1、添加、设置模块:添加User-Defined Functions组中的S-Function模块,双击图标,设置name为AD5;parameters为20.添加Math Operations组中的Gain模块,双击图标,设置Gain为0.4/65535.0.添加Sinks组中的Scope模块,双击图标,打开窗口,点击(Parameters),设置General 页中的Number of axes为2,Time Range为20000,点击OK退出,示波器屏成双;分别右击双屏,选Axes properties,设置Y-min为0,Y-max为0.4.2、连接模块:顺序连接AD5、Gain、Noise Filter1、Scope模块,完成后的程序界面如图所示:图1.1.1 完成后的数据采集处理程序界面点击运行程序,双击Scope模块,显示滤波前后的小球位置-时间图,拨动小球在横杆上往返滚动,可得如下实验结果:图1.1.2 小球位置的数据采集处理六、实验总结通过这个实验、我学会了球杆系统模型的建立以及小球位置的获取。
固高球杆控制模型的建模与分析

固高球杆控制模型的建模与分析作者:任宏宇来源:《西部论丛》2019年第17期摘要:当代社会,自动控制的思想已经渗透到生活的方方面面,在军事、航空、工业、农业和手工业等各个方面都广泛应用。
而自动控制系统中最常见的是二阶系统,二阶系统的种类有很多,本文主要以最典型的二阶系统之一固高球杆模型为列具体介绍其建模过程。
关键词:自动控制二阶固高球杆模型建模1 系统数学模型的建立典型的球杆系统主要由两个部分组成,分别是控制部分和执行部分。
在执行部分中,横杆由一根带刻度的钢杆和一个直线位移传感器构成,并保证横杆的一端保持不动,而另一端通过杠杆臂与减速齿轮边缘相连,可以保证其上下转动。
如果横杆的倾斜角与水平面夹角成时,小球将会由于重力沿横杆滚动。
只要通过控制部分控制横杆与水平面的夹角,就可以进一步控制小球在横杆上的位置,横杆倾斜角度的控制是通过调节电机的转速来完成的。
控制部分包括IPM100智能控制器、计算机、传感器、光电码盘等组成,是基于由DSP控制技术的36 V、3 A智能伺服驱动单元。
球杆运动的具体过程为:小球的位置通过线性传感器采集信号反馈给控制单元,控制单元由位置误差公式计算控制量,从而控制电机使减速齿轮转动角度,从而进一步控制横杆的倾斜角,让小球稳定到指定位置。
传统的球杆系统是一个开环不稳定的系统,其精确的数学模型很难准确建立,为此我们需要做一些简化。
为了便于分析,将球杆系统的模型分为三部分:机械模型,角度模型和电机模型。
机械模型用来反映小球的位置和横杆倾斜角之间的关系,角度模型用来反映横杆倾斜角和减速齿轮转角的关系,电机模型用来反映电机的电压和减速齿轮转角的关系。
1.1 机械模型。
通过受力分析小球在横杆上应受到三个力的作用:第一个为重力作用产生的沿着轴向下的力,第二个为使小球产生旋转的力以及第三个让小球在横杆上滚动时受到的摩擦力。
其三个力的表达式分别如下:(1)(2)(3)式中,为横杆的倾斜角,为小球的质量,为重力加速度,为小球的加速度,为横杆和小球的静摩擦系数。
球杆系统
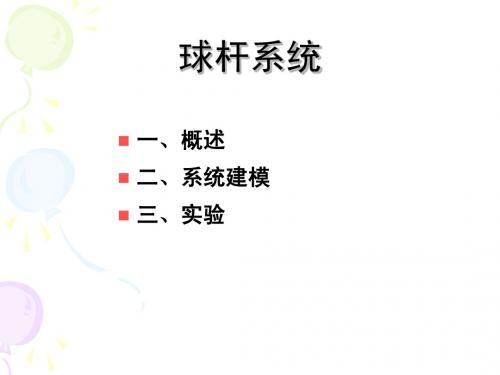
(2)
2 在Simulink中建立球杆系统的模型
3 电气模型
电机轴的位置通过电机附带的编码器进行检测, θ和电机轴存在一个减速比n=4 编码器输出脉冲信号,并反馈给IPM100,驱 动器接收增量式编码器的信号,信号由两路信号 (A,B信号)以及一路index信号组成,两路信 号为方波信号,两者之间相位差为90度,A信号超 前B信号说明电机正转,否则说明电机反转。 控制器对编码器信号进行4分频,电机的位置 精度提高到四倍。电机转动一圈,index信号产生 一个负脉冲,用于同步控制或精确的控制。
三、实验
1.球杆系统的开环模型
X (s)和 (s)分别为系统输出(小球的位置)和输 入(齿轮的角度)的拉普拉斯变换。
2.球杆系统的PID控制
PID控制器的传递函数为:
KP, KI 和KD为PID控制器的比例,积分和微分参数。
3.完成报告内容
(1)在Simulink中建立球杆系统的模型 (2)假设控制的性能指标要求如下: ♦ 调整时间小于1秒(2%误差) ♦ 超调量小于10% 分别对球杆系统实现P控制、PD控制、PID控制, 对其稳定性进行理论分析,并在实际系统上验 证,给出控制实验结果曲线。 可假设: m = 0.11 R = 0.015 g = -9.8; L = 0.4 d = 0.04 J =2*m*R^2/5
传递函数包含一个积分项1/s,具有积分的特 性,通常Ra、Tm和J0都很小,伺服电机可以看作 为一个积分器。
♦ 球杆系统采用电位计检测小球的位置,电位 计安装在横杆上,小球位置对应的电压信号输 送给IPM100智能驱动的AD转换器。
4 控制结构
球杆系统的闭环控制系统结构图如下:
自动控制原理实验报告——球杆系统

自动控制原理实验报告——球杆系统一、实验目的1、了解自动控制中的反馈控制原理。
2、通过对球杆系统的建模,实现对球杆运动的自动控制。
3、了解PID控制器的基本原理及其参数调节方法。
二、实验器材1、单轴直线滚动导轨2、步进电机3、直流电机5、万用表6、电脑三、实验原理反馈控制是控制系统中的一种常见方法。
其工作过程是测量输出量,与设定值进行比较,然后用输出的误差信号来调整控制器,从而控制输入量,使输出量达到设定值。
这种工作方式的主要特点是能够在一定程度上处理外部干扰和系统变化。
2、控制对象球杆系统具有非线性和时变特点,建模时常用的方法是状态空间法,即用矩阵方程来描述系统的状态和动态特性,从而实现系统的控制。
其中,球杆系统的状态向量可以表示为:式中,α和θ分别表示球杆的角度和倾斜角度,u则是系统的输入。
3、PID控制器PID控制器是一种基本的反馈控制器,其主要特点是能够在一定程度上克服系统的非线性和时变性。
其控制策略是将误差信号经Proportional、Integral、Derivative三个环节处理后再输出控制信号。
具体来说,PID控制器的输出可以表示为:式中,e表示当前误差,T为采样时间,Kp、Ki和Kd分别为比例系数、积分系数和微分系数。
这些系数是PID控制器的重要参数,在控制实际物理系统时需要进行合理调节。
四、实验过程1、球杆系统建模根据上述原理,我们采用模型参数估计法,对球杆系统的状态方程进行求解和建模。
下图为球杆系统的实物模型:其中,Θ为球杆的倾斜角度,α为球杆相对于竖直方向的偏角。
此外,球杆的长度为L,质量为m,转动惯量为I。
考虑到系统的非线性和时变性,我们采用状态空间法进行建模,得到以下的状态方程:根据系统的动态特性,我们选择PID控制器进行调节,以使球杆系统达到平衡状态。
首先我们需要调节PID控制器的三个系数,通过试验寻找较为合适的值。
其中,Kp控制系统的快速性,Ki控制系统的稳定性,Kd则是控制系统的抗干扰性。
合肥工业大学自动控制理论综合实验球杆实验报告

实验一 球杆系统的数学模型实验目的l 掌握对实际物理模型的建模方法l 掌握在Matlab 中利用Simulink 等工具对系统进行模型分析的方法。
实验内容:1) 分析并推导系统的数学模型;2) 求解系统的状态空间方程和传递函数方程;在matlab 中建立一下m 文件并运行:m=0.028;R=0.0145;g=-9.8;J=0.4*m*R^2;a=-m*g/(J/R^2+m);A=[0 1 0 0;0 0 a 0;0 0 0 1;0 0 0 0] B=[0;0;0;1] C=[1 0 0 0] D=0[n,d]=ss2tf(A,B,C,D);G=tf(n,d); 返回:A = 0 1.0000 0 0 0 0 7.0000 0 0 0 0 1.0000 0 0 0 0B = 0 0 0 1C = 1 0 0 0D = 0Transfer function:-4.441e-016 s^3 + 1.998e-015 s^2 + 3.997e-015 s + 7 --------------------------------------------------- s^4上式即为传递函数方程。
3) 在Matlab 下建立系统的模型并进行阶跃响应仿真。
为得到阶跃响应,输入命令: step(G) 得到阶跃响应曲线如下:Step ResponseTime (sec)A m p l i t u d e实验二 球杆系统的数字P 控制器设计实验目的了解P 控制器原理及其对球杆系统的控制作用 实验原理:实验内容:1. 在matlab 下仿真比例控制时系统的响应情况。
在matlab 中建立m 文件并运行: m = 0.028; R = 0.0145; g = -9.8; L = 0.40; d = 0.045; J = 0.4*m*R^2;K = (m*g*d)/(L*(J/R^2+m)); %simplifies input num = [-K]; den = [1 0 0]; ball=tf(num,den) kp = 1;sys_cl=feedback(kp*ball,1) %建立闭环系统 step(0.25*sys_cl) %阶跃响应2. 进入BallBeamControl 应用控制程序进行实时控制;实验步骤如下:1) 让小球稳定在一个位置,设为200;2) 设置Kp=const(常数),Kd=0,Ki=0(拖动相应滑块到最低位置即为0); 3) 拖动小球目标位置滑块往右移动到需要位置,设置此处为300; 4) 松开鼠标即刷新参数,系统开始运动 5) 改变Kp 的值,观察响应变化Step ResponseTime (sec)A m p l i t u d e从结构可以看出,系统实际输出和matlab 仿真结果很相似,但是由于参数不一样,系统忽略了很多次要因素,而在实际系统中,这些因素又在起作用,所以有时候振幅会收敛(阻力),有时候发散9比例系数过大,并有迟延环节作用)(此处可能需要另外加图,以表示不同的kp 对系统的影响)实验三 球杆系统的数字PD 控制器设计实验目的掌握PD 控制器的控制原理和对球杆系统的控制效果 实验原理:实验内容:1、 在matlab 中仿真PD 控制器下球杆系统的响应情况。
球杆系统完整版

实验一 简化模型的建立和稳定性分析一、 实验目的1、了解机理法建模的基本步骤;2、会用机理法建立球杆系统的简化数学模型;3、掌握控制系统稳定性分析的基本方法;二、 实验要求1、采用机理法建立球杆系统的数学模型;2、分析系统的稳定性,并在Matlab 中仿真验证;三、 实验设备1、球杆系统;2、计算机,Matlab 平台;四、实验内容1、根据微分方程求取传递函数当以θ为系统输入量时,位置r 和θ的传递函数为:()()21.853r s s sθ= 2、 球杆闭环系统稳定性分析构建如图 2.1.4 所示单位负反馈闭环系统,则系统的闭环极点为【+1.36i 】,【-1.36i 】:3、仿真Matlab 仿真结果如下:五、实验记录内容数据开环系统传递函数()()21.853c s u s s = 闭环系统输入 0.25m 闭环系统输出信号振荡六、实验分析及思考题影响系统稳定的因素是闭环系统的极点位置,闭环极点为【i ,-i 】,则系统震荡。
测量系统稳定性的方法之一是加入大小合适的阶跃信号,根据其输出的阶跃响应分析系统的稳定性和其他性能。
思考题:1、根据建模的过程,总结机理法建模的基本步骤; 答: 1)根据系统运动的物理规律建立方程;2)化简为微分方程;3)根据小偏差线性化的方法化简为线性系统的传递函数;2、实验结果分析、讨论和建议。
答:由Matlab 仿真结果来看,系统闭环极点在虚轴上,进行等幅振荡,应设计控制控制器进行调节。
实验二 PID 校正一、实验目的1、会用PID 法设计球杆系统控制器;2、设计并验证校正环节;二、 实验要求1、根据给定的性能指标,采用凑试法设计PID 校正环节,校正球杆系统,并验证之。
2、设球杆系统的开环传递函数为:()021.853G s s =,设计PID 校正环节,使系统的性能指标达到:10s t s ≤,30%p σ≤。
三、实验设备1、球杆系统;2、计算机,Matlab 平台;四、实验内容1、PID 校正法仿真其中PID 参数为: 1.5p K = 0.3i K = 1.5d K = 仿真运行结果如下:2、PID 实时控制系统框图如下:其中PID 参数为: 1.5p K = 0.3i K = 1.5d K =运行结果如下:五、实验记录控制器参数性能指标 未校正系统系统振荡校正系统仿真 1.5p K = 0.3i K = 1.5d K = t s= 3.15秒,σp=20% 校正改进系统实测 1.5p K = 0.3i K = 1.5d K =t s= 11.32秒,σp=52%六、 实验分析1、 怎样确定PID 控制器的参数?答:通过试凑法来不断地调节PID 信号参数,观察系统响应信号,直至系统达到稳定,性能比较好时,确定此时的PID 参数。
球杆平衡系统分析
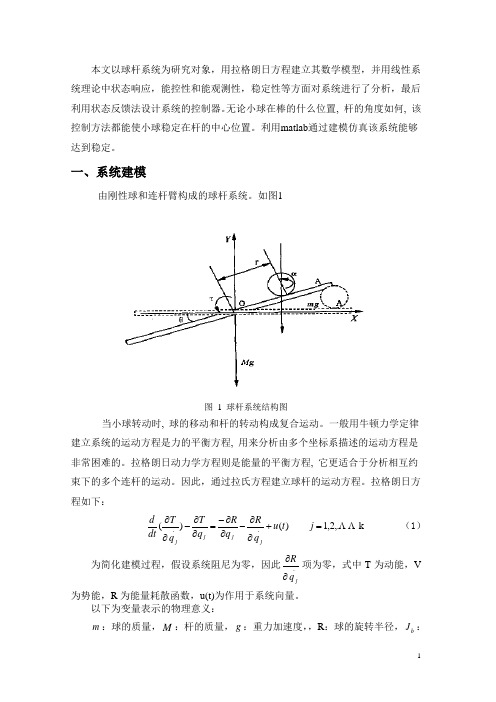
本文以球杆系统为研究对象,用拉格朗日方程建立其数学模型,并用线性系统理论中状态响应,能控性和能观测性,稳定性等方面对系统进行了分析,最后利用状态反馈法设计系统的控制器。
无论小球在棒的什么位置, 杆的角度如何, 该控制方法都能使小球稳定在杆的中心位置。
利用matlab 通过建模仿真该系统能够达到稳定。
一、系统建模由刚性球和连杆臂构成的球杆系统。
如图1图 1 球杆系统结构图当小球转动时, 球的移动和杆的转动构成复合运动。
一般用牛顿力学定律建立系统的运动方程是力的平衡方程, 用来分析由多个坐标系描述的运动方程是非常困难的。
拉格朗日动力学方程则是能量的平衡方程, 它更适合于分析相互约束下的多个连杆的运动。
因此,通过拉氏方程建立球杆的运动方程。
拉格朗日方程如下:k .,2,1)()(.. =+∂∂-∂∂-=∂∂-∂∂j t u q Rq R q T q T dt d jj j j(1)为简化建模过程,假设系统阻尼为零,因此.jq R ∂∂项为零,式中T 为动能,V为势能,R 为能量耗散函数,u(t)为作用于系统向量。
以下为变量表示的物理意义:m :球的质量,M :杆的质量,g :重力加速度,,R :球的旋转半径,b J :小球的转动惯量,l J :横杆的转动惯量,l :横杆的长度,α:小球绕轴线旋转的角度。
该系统可看作是二维空间运动的相互约束的两个质点,选取θ和r 作为广义坐标,设刚球在直角坐标系下的位置坐标为(x,y ),则与广义坐标之间的关系为:⎩⎨⎧==θθsin cos r y r x (2)所以,其速度关系为⎪⎩⎪⎨⎧+=-=θθθθθθcos sin sin cos ......r r y r r x (3) 系统的动能主要包括小球沿横杆运动的动能,小球绕自身轴线转动的动能和横杆绕固定点转动的动能三部分,分别设为321,,T T T 。
小球在r 方向运动的动能1T 为)(21)(21.22.2.2.21θr r m y x m T +=+= (4)小球绕轴线旋转的角度Rr=α (5) 对时间求导的角速度Rr..=α (6) 小球绕自身轴线转动的动能.22.22221r RJ J T b b ==α (7) 其中252mR J b =。
基于LabVIEW的球杆系统建模、仿真及实验研究的开题报告

基于LabVIEW的球杆系统建模、仿真及实验研究的开题报告1. 研究背景和意义高尔夫运动是一项需要高度技术的运动,提高球杆运动质量对于提高球手比赛排名和经济收益都有重要意义。
将工程控制技术应用于高尔夫球杆系统建模与仿真这一问题上,可以有效地提高球杆运动质量,提高球员的竞争力。
基于LabVIEW平台的球杆系统建模、仿真及实验研究,可以为高尔夫球员的训练提供更高质量的数据支持。
2. 研究内容和目标本研究的目标是基于LabVIEW平台,建立高尔夫球杆系统的数学模型和控制模型,并进行仿真和实验研究。
具体研究内容包括:- 研究高尔夫球杆系统的力学特性,建立球杆系统的数学模型;- 设计球杆系统的控制模型,以提高球杆运动的质量;- 基于LabVIEW平台,开发球杆系统的仿真模型;- 进行实验研究,验证仿真模型的正确性和可靠性;- 对实验结果进行分析,总结球杆系统的运动规律和特性。
3. 研究方法和技术路线本研究使用的研究方法包括理论分析、数值求解、建模与仿真、实验研究等。
技术路线如下:- 研究高尔夫球杆系统的力学特性,建立数学模型,利用数值求解方法求解模型;- 设计球杆系统的控制模型,包括开环控制和闭环控制;- 基于LabVIEW平台,开发球杆系统的仿真模型,进行仿真研究;- 进行实验研究,设计实验方案,对球杆运动进行记录和数据分析;- 分析模拟与实验结果,优化球杆系统的控制方式。
4. 预期成果和意义本研究的预期成果包括:- 建立球杆系统的力学模型和控制模型,分析球杆运动规律和特性;- 基于LabVIEW平台,开发球杆系统仿真模型,验证模拟结果;- 进行实验研究,验证仿真模型的正确性和可靠性;- 分析实验结果,总结球杆系统的运动规律和特性,为球员训练提供科学依据。
本研究的意义在于,提高球杆系统的运动质量,为球员提供更加科学的训练方案。
另外,本研究也为基于LabVIEW平台的控制系统研究提供实践经验。
球杆系统仿真
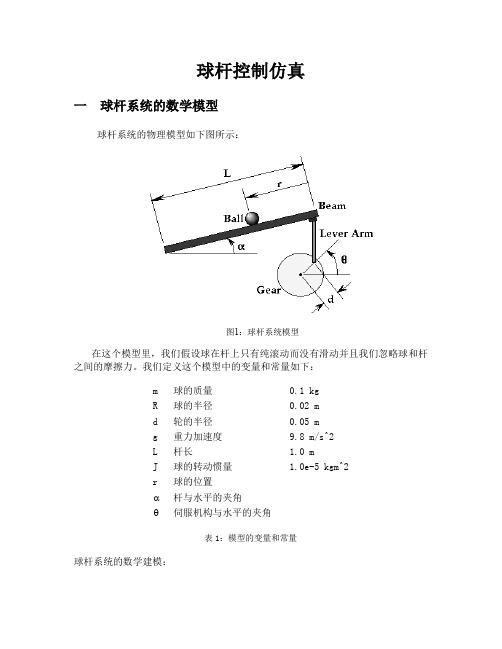
球杆控制仿真一球杆系统的数学模型球杆系统的物理模型如下图所示:图1:球杆系统模型在这个模型里,我们假设球在杆上只有纯滚动而没有滑动并且我们忽略球和杆之间的摩擦力。
我们定义这个模型中的变量和常量如下:m 球的质量0.1 kgR 球的半径0.02 md 轮的半径0.05 mg 重力加速度9.8 m/s^2L 杆长 1.0 mJ 球的转动惯量 1.0e-5 kgm^2r 球的位置α杆与水平的夹角θ伺服机构与水平的夹角表1:模型的变量和常量球杆系统的数学建模:系统的动能:222])r L [(m 21rm 21)R r(J 21T α-++= 系统的势能:α-=sin mgr U该系统的拉格朗日方程为:0rUr T )r T (dt d =∂∂+∂∂-∂∂ 通过拉格朗日法得到球的运动方程:0))(r L (m sin mg r)m RJ(22=α-+α-+ 若我们假设杆与水平的夹角是小角度且0≈α ,对上面的方程进行线性化,我们得到:α=+mg r)m RJ(2 杆的角度与伺服机构的角度的关系可以近似的线性化为:θ=αLd综合上面几个方程我们得到:θ=+Ldmg r)m R J (2对方程两边做拉普拉斯变换:)s (Ld mg s )s (R )m R J (22Θ=+ 整理后我们得到系统线性化后的开环传递函数:22s1)m R J (L mgd )s ()s (R +=Θ二 控制器的设计在这里,我们采用普遍使用的PID 控制器。
整个系统的闭环框图可以表达为:图2:线性化后的控制框图令 )S ()S (R )S (H Θ=,得: )S (R )s (H SK S K S K ))S (R )S (r (IP 2D =⋅++-我们取p K =21,I K =0,D K =14,将球稳定在杆的中点,仿真结果如下图所示:图3:仿真结果通过仿真结果表明将系统线性化后,该系统的超调量小于1%,上升时间3秒。
如果我们进一步考虑该模型的非线性性,可以得到⎪⎪⎩⎪⎪⎨⎧θ=α+α--α=L d )m R J ())(r L (m sin mg r 22在Matlab Simulink 中我们可以用如下方框图表示θ和r 的关系:图4:θ到r 的方框图其中f(u)是 (m*g*sin(u[3])- m*(L-u[1])*(u[4])^2) /(J/(R^2)+m),u[1]是r , u[2]是r,u[3]是α, u[4]是α 。
1 球杆系统建模剖析

2020年军人自荐书范文下面是整理的关于年军人自荐书优秀范文,欢迎借鉴!2020年军人自荐书优秀范文一尊敬的领导:您好!对您百忙之中抽出宝贵的时间阅览我的求职自荐书,对此表示由衷地感激,希望它与您手中若干份求职材料不相雷同,同时也希望它能够有助您在求职浪潮之中寻求到令您满意的人才。
我叫**,今年25岁,在空军部队服役8年。
因为考虑个人问题选择退伍。
因为出自空军部队,感谢部队这么多年的培养,我热爱空军,就像歌曲的歌词一样,我爱祖国的蓝天。
在军队,我们空军的职责就是守卫祖国的蓝天,因为家庭原因不得不脱下心爱的军装。
经过深思熟虑,决定申请加入贵公司发展,因为了解贵公司所从事的事业与本人以前所从事的工作大庭相径,也能继续更好我报效祖国的使命。
儿时的梦想就是有天能够当上飞行员,傲游在蓝天,长大后,才发现这只是梦想。
所以,我毅然加入空军部队,希望能够有所建树。
望领导审查,给予机会。
在部队期间,虽不说有惊天地泣鬼神的伟大壮举,但平时兢兢业业工作。
05年,服役在警卫连,平时的工作就是站岗执勤和军事训练,当时自己还是一名新兵,在各方面都特别能吃苦,思想和身体素质有很大提升,作为军人的自豪感和荣誉感从这里开始得到升华。
每日站岗执勤,保卫重点部位和首长安全,高度警觉性和责任心,也是从中磨练学习来的,最后得到单位领导肯定,授予嘉奖一次。
年底,得单位领导信任,负于我在新兵连以义务兵身份,代理新训班长职务,不负重托,圆满完成上级交予的任务,并得到表扬。
09年,这是在部队的第5年,走过懵懵懂懂的年少时光,日趋成熟。
06年初,因为工作需要调入试训岗位,从事光电经纬仪工作。
期间通过领导培养,自己认真学习,再加入伍前,有过钳工方面的技术学习,所以在技术学习进展较快很快就在岗位上有了一点成绩。
由于技术比较成熟在08年被评技师。
每次参加各项军演、试训都有一部分贡献,期间单位领导要给予我嘉奖,自己觉得这都是自己的本职工作,所以婉言谢绝,不是自己不重视荣誉,而是觉得比我更年轻的同志更需要鼓励成长。
西安工业大学实验三 球杆系统建模分析与控制

实验三:球杆系统建模、分析与控制实验(综合实验)一.实验目的:1、建立球杆系统的数学模型,掌握系统建模的一般方法及在Matlab中对系统进行建模的方法;2、对球杆系统进行性能分析,在Matalab Simulink中对系统进行仿真;3、理解PID控制的原理和方法,进行系统控制;4、掌握如何设计和调整PID参数,使系统达到设计的要求。
二.实验内容:1、对球杆系统进行受力分析,建立球杆系统的数学模型2、在Matlab下建立球杆系统的数学模型,3、对球杆系统进行性能分析与仿真4、P控制器的设计5、PD控制器的设计6、PID控制器的设计三.实验设备:1 固高科技球杆机械传动系统2 球杆系统运动控制箱3 计算机四.实验原理:1. PID 简介任何闭环控制系统的首要任务是要稳(稳定)、快(快速)、准(准确)的响应命令。
PID调整的主要工作就是如何实现这一任务。
增大比例系数P将加快系统的响应,它的作用于输出值较快,但不能很好稳定在一个理想的数值,不良的结果是虽较能有效的克服扰动的影响,但有余差出现,过大的比例系数会使系统有比较大的超调,并产生振荡,使稳定性变坏。
积分能在比例的基础上消除余差,它能对稳定后有累积误差的系统进行误差修整,减小稳态误差。
微分具有超前作用,对于具有容量滞后的控制通道,引入微分参与控制,在微分项设置得当的情况下,对于提高系统的动态性能指标,有着显著效果,它可以使系统超调量减小,稳定性增加,动态误差减小。
综上所述,P---比例控制系统的响应快速性好,快速作用于输出;I---积分控制系统的准确性好,消除过去的累积误差;D---微分控制系统的稳定性好,具有超前控制作用。
在调整的时候,你所要做的任务就是在系统结构允许的情况下,在这三个参数之间权衡调整,达到最佳控制效果,实现稳、快、准的控制特点。
根据要求添加PID控制器后,闭环系统的结构图如下:PID 控制器闭环结构图PID 控制器的传递函数为:)1()(sK s K K s G I D P PID ++=, K D 和 K I 对应于积分和微分控制,K P 为比例增益。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《线性系统理论》课程设计报告书课题名称球杆系统姓名孟禹漆铖刘泽文孟凡强杨佐龙日期2013年2 月25日老师陈玮1 球杆系统建模分析本章将对球杆系统进行简单的介绍,然后采用拉格朗日方程建立其数学模型,并在此基础上分析其特性。
1.1球杆系统介绍球杆系统(Ball & Beam )是由球杆执行系统、控制器和直流电源等部分组成。
该系统对控制系统设计来说是一种理想的实验模型。
正是由于系统的结构相对简单,因此比较容易理解该模型的控制过程。
球杆执行系统(如图1 所示)由一根V 型轨道和一个不锈钢球组成。
V 型槽轨道一侧为不锈钢杆,另一侧为直线位移电阻器。
当球在轨道上滚动时,通过测量不锈钢杆上输出电压可测得球在轨道上的位置。
V 型槽轨道的一端固定,而另一端则由直流电机(DC motor )的经过两级齿轮减速,再通过固定在大齿轮上的连杆带动进行上下往复运动。
V 型槽轨道与水平线的夹角可通过测量大齿轮转动角度和简单的几何计算获得。
这样,通过设计一个反馈控制系统调节直流电机的转动,就可以控制小球在轨道上的位置。
图1 球杆系统执行机构原理图1.2拉格朗日方程介绍建立一个力学体系的动力学方程所需要的独立坐标称为广义坐标,广义坐标一旦确定,体系在空间的位置状态也就可以唯一确定。
广义坐标可以是坐标变量,也可能是是角动量或其他独立变量,凡能用来表述体系的位形、运动和动力学状态的独立参量都可作为广义坐标。
广义坐标的条件是:互相独立、满足约束方程、唯一确定体系的位形式动力学状态。
拉格朗日方程方法建模可以表述为:设一个机械系统的自由度为n ,对于系统可以采用广义坐标12(,,...,)n q q q q =,12(,,...)n q q q q =来描述,记该系统的总体动能为(,)T q q ,总体势能为()V q ,系统的运动特性可以用以下的拉格朗日方程描述:d 1,2,...,d i i iL Li n t q q τ⎛⎫∂∂-== ⎪∂∂⎝⎭ (1.1)其中,方程组中方程式的数目等于质点系的自由度数,i τ为作用在第i 个广义坐标i q 方向的外部力或力矩之和。
若函数L 表示系统动能T 与势能V 的差值即L=T —V ,L 称为拉格朗日函数。
即:(,)(,)()L q q T q q V q =-。
因势能不是广义速度i q 的函数,所以0iVq ∂=∂这样,系统的拉格朗日方程用L 表示为:d 1,2,...,d i i i iT T Vi n t q q q τ⎛⎫∂∂∂-=-+= ⎪∂∂∂⎝⎭ (1.2)显然,拉格朗日函数具有能量的量纲。
这不但在机械系统中成立,在电动力学中,有些问题也可求出拉格朗日函数,从而通过拉格朗日方程,来建立电动力学的运动微分方程,因此拉格朗日函数及拉格朗日方程,具有更为普遍的意义。
1.3球杆系统建模过程为了简化和清晰建模过程,可将球杆系统分解为三个部分——球杆机械部分模型,球杆角度转换部分模型和直流电机部分模型。
1.3.1球杆系统机械部分建模对于球杆系统中球和横杆的运动方程可以采用拉格朗日方法建模。
定义广义坐标(x ,α),x 、α分别表示小球相对固定轴端的位移和导轨相对水平位置绕固定轴逆时针方向的转角,x 、α分别表示相应的位移速度和角速度。
当然,建立拉氏方程一般分以下四个步骤:1)用广义坐标表示笛卡尔坐标:12(,,...,)k k n x x q q q = 2)用广义速度表示笛卡尔坐标下的速度:d d k kk x q x x q q t q∂∂=⋅=∂∂3)(,)()L T V T q q V q =-=- 4)求出i L q ∂∂及iLq ∂∂,按自由度数建立拉格朗日方程组。
①求系统动能选取球杆系统的广义坐标为(,)q x α,系统的自由度为2,用广义坐标表示笛卡尔坐标为:1cos x x α=⋅,1sin y x α=⋅,广义速度之间的关系为:1cos sin x x x ααα=⋅-⋅⋅, (1.3)1sin cos y x x ααα=⋅+⋅⋅ (1.4) 小球沿广义坐标1x 方向运动的动能:221111()2T m x y =+2221()2m x x α=+⋅ (1.5) 小球绕径向转动的动能为:2212m T J ω=(1.6) 式中ω表示小球转动的角速度,由小球在横杆上的滚动速度和横杆的转动速度两部分组成,即:xRωα=+ (1.7) 22222x x x R R R ωααα⎛⎫⎛⎫=+=++ ⎪ ⎪⎝⎭⎝⎭(1.8)因α数值很小,故可做一下近似22x R ω⎛⎫= ⎪⎝⎭,故有:2212m x T J R ⎛⎫= ⎪⎝⎭(1.9)其中m J 为小球的转动惯量,225m J mR = 横杆绕固定端转动时的动能为:2312M T J α=(1.10) 其中M J 为横杆的转动惯量,213M J ML =故系统总动能:22222123111()222m M x T T T T m x x J J R αα⎛⎫=++=+⋅++ ⎪⎝⎭ (1.11)②求系统势能 小球的势能:1sin V mgx α= (1.12)横杆本身引起的势能为:21sin 2V MgL α=(1.13) 故系统总势能:12V V V =+1sin sin 2mgx MgL αα=+(1.14) 对式1.11做以下处理,得到:222222111()222m M T x m x x J J mx x x R ααα⎡⎤∂∂⎛⎫=+⋅++=⎢⎥ ⎪∂∂⎝⎭⎢⎥⎣⎦ (1.15) 222222111()222m m M T x J m x x J J m x x x R R αα⎡⎤∂∂⎛⎫⎛⎫=+⋅++=+⎢⎥ ⎪ ⎪∂∂⎝⎭⎝⎭⎢⎥⎣⎦ (1.16) 1sin sin sin 2V mgx MgL mg x x ααα∂∂⎛⎫=+= ⎪∂∂⎝⎭(1.17) 对式1.15做以下处理,得到:22d d d d m m T J J m x m x t x t R R ∂⎡⎤⎛⎫⎛⎫⎛⎫=+=+ ⎪ ⎪ ⎪⎢⎥∂⎝⎭⎝⎭⎝⎭⎣⎦ (1.18) 根据式1.2,得到广义坐标下x 的拉格朗日方程,即有:d d T TV t xxx ∂∂∂⎛⎫-=- ⎪∂∂∂⎝⎭ (1.19) 综合以上式1.14、1.15、1.16、1.17,得出关于广义坐标下x 的方程为:22sin m J m x mx mg R αα⎛⎫+-=- ⎪⎝⎭(1.20) 当系统处于平衡状态时,α等于零,在零点附近对系统进行线性化处理,可取sin αα≈,cos 1α≈,2x α表示离心加速度,实际中其数值很小,可忽略,于是可得到近似方程:2m J m x mg R α⎛⎫+=- ⎪⎝⎭ (1.21) 对上式进行拉氏变换即可得球杆系统机械部分模型为:图2球杆系统的近似模型22()1()m X s mg J s s m R α=-*+ (1.22)1.3.2球杆系统角度转换部分模型在球杆的执行机构中,横杆一端固定,大齿轮、连杆与横杆一起组成了一个四连杆结构,齿轮的转动就通过连杆作用到横杆上,从而使横杆绕固定轴转动。
齿轮转角θ和横杆的转角α之间的关系可以用下式表示:()()2221cos 1cos (sin sin )L r L l r l αθαθ---++-=⎡⎤⎣⎦ (1.23)在横杆水平位置附近,齿轮转角在50±之间,故可以将其近似为一个比例关系:r Lαθ= (1.24)1.3.3球杆系统直流电机部分模型球杆系统中的电机由智能驱动器控制,其响应速度相当快且电机转角()t θ对电压()u t 的响应时间常数也很小。
因此可将直流伺服电机数学模型近似为一个纯增益K 。
1.4球杆系统状态空间描述根据以上模型的推导过程,整个球杆系统的模型可以近似为如图2所示。
故整个系统的传递函数近似为:22()1()m X s mgrK J U s s m L R =-*⎛⎫+ ⎪⎝⎭线性化的系统方程还可以用状态空间方程来表示。
我们将小球的位置(r)和 速度(r 的一阶导数 )作为变量, 将齿轮角度θ作为输入,状态方程如下所示:θm)R J L(mgd 0r r 0010r r 2⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡++⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡ 不过,在本实验中, 我们不用角度θ,而是用α的二阶导数来控制小球位置,这本质上就是控制横梁的转矩。
状态方程变为:u 1000ααr r 0010000m R J mg00010ααr r2⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡[]⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=ααr r 0001y注意: 对于本系统是采用电机在横杆上施加转矩来控制小球的位置的。
2.球杆系统性能分析根据第一部分球杆系统的状态空间描述在这章中对球杆系统的能控性,能观性进行等方面进行分析。
2.1球杆系统的能控能观性利用matlab工具箱对球杆系统进行的能控能观性分析如下:A = [0 1 0 0;0 0 1 0;0 0 0 1;0 0 0 0];B = [0 ;0; 0; 1];C = [1 0 0 0];D = [0];N = size(A);n = N(1);CAM=ctrb(A,B);rcam=rank(CAM);if rcam == ndisp('System is controlled');elseif rcam < ndisp('System is not controlled');endob = obsv(A,C);roam=rank(ob);if roam == ndisp('System is observable');elseif rcam<ndisp('System is not observable');end结果为:所以系统是能控能观的。
2.2球杆系统的稳定性分析根据系统的状态空间方程容易得知系统有四个特征根且四个特征跟均为零,对于高阶非线性系统的平衡状态X e的稳定性要由高阶导数项G(y)来决定的;通过查取资料分析该球杆系统是非稳定的。
(查取资料前用分别用李亚普诺夫第一方法和第二法进行了分析,在采取第二法分析中由于求取的矩阵P不唯一,得不到相关的结果,最后查取资料进行了分析,并将资料付在论文最后)。
2.3球杆系统极点配置与控制器设计极点配置的方法就是通过一个适当的状态反馈增益矩阵的状态反馈方法 ,将闭环系统的极点配置到任意期望的位置。
()()()X t Ax t Bu t ,其中x 是状态变量(n 维),u 是控制信号,这里选取控制信号为u Kx ,)()()(t x BK A t x *-= ,该方程的解为()()(0)ABK tx t e x ,系统的稳态响应和瞬态响应特性由矩阵 A - B K 的特征决定。
