一次函数和几何综合题含答案
中考数学专题《一次函数与几何综合》高分必刷原卷

(培优特训)专项19.3 一一次函数与几何综合高分必刷1.(2023春•普兰店区期中)已知△ABC中,∠C=90°,AC=3,CD=4,BD =AD.点F从点A出发,沿AC﹣CD运动,速度为1cm/s,同时点E从点B 出发,沿BD﹣DA运动,运动速度为1cm/s,一个点到达终点,另一点也停止运动.(1)求BD的长;(2)设△AEF的面积为S,点P、Q运动时间为t,求S与的函数关系式,并写出的取值范围.2.(2023春•鼓楼区期中)如图1,已知直线l1:y=ax﹣6a交x轴于点A,交轴y于点B,直线l2:y=bx﹣18a交x轴于点C,交y轴于点D,交直线l1于点E.(1)求点A的坐标;(2)若点B为线段AE的中点,求证:EC=EA;(3)如图2,已知P(0,m),将线段P A绕点P逆时针方向旋转90°至PF,连接OF,求证:点F在某条直线上运动,并求OF的最小值.3.(2023春•苍南县期中)如图,在平面直角坐标系中,▱OABC的顶点A落在x轴上,点B的坐标为(7,4),AB=2,点D是OC的中点,点E是线段AD上一动点,EF⊥BC于点F,连结DF.(1)求点A、C的坐标.(2)求直线AD的函数表达式.(3)若△DEF是等腰三角形,求CF的长.4.(2023•佳木斯一模)如图,将矩形纸片OABC放在平面直角坐标系中,O为坐标原点.点A在y轴上,点C在x轴上,OA,OB的长是x2﹣16x+60=0的两个根,P是边AB上的一点,将△OAP沿OP折叠,使点A落在OB上的点Q处.(1)求点B的坐标;(2)求直线PQ的解析式;(3)点M在直线OP上,点N在直线PQ上,是否存在点M,N,使以A,C.M,N为顶点的四边形是平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由.5.(2023春•顺德区校级月考)如图,请根据图象所提供的信息解答下列问题:(1)当x时,kx+b≥mx﹣n;(2)不等式kx+b<0的解集是;(3)求两个一次函数表达式;(4)若直线l1分别交x轴、y轴于点M、A,直线l2分别交x轴、y轴于点B、N,求点M的坐标和四边形OMPN的面积.6.(2023春•北碚区校级期中)如图,在平面直角坐标系中,直线y=2x﹣2与x 轴、y轴分别交于点A、点B,与直线CD:y=kx+b(k≠0)交于点P,OC =OD=4OA.(1)求直线CD的解析式;(2)连接OP、BC,若直线AB上存在一点Q,使得S△PQC =S四边形OBCP,求点Q的坐标;(3)将直线CD向下平移1个单位长度得到直线,直线l与x轴交于点E,点N为直线l上的一点,在平面直角坐标系中,是否存在点M,使以点O,E,N,M为顶点的四边形是矩形?若存在,请直接写出点M的坐标;若不存在,请说明理由.7.(2023春•宜兴市期中)如图,在平面直角坐标系中,已知A(0,4),点B、C都在x轴上,BC=12,AD∥BC,CD所在直线的函数表达式为y=﹣x+9,E是BC的中点,点P是BC边上一个动点.(1)当PB=时,以点P、A、D、E为顶点的四边形为平行四边形;(2)点P在BC边上运动过程中,以点P、A、D、E为顶点的四边形能否构成菱形?试说明理由.8.(2023春•工业园区校级期中)如图,在平面直角坐标系中,点A、点B分别在x轴与y轴上,直线AB的解析式为,以线段AB、BC为边作平行四边形ABCD.(1)如图1,若点C的坐标为(3,7),判断四边形ABCD的形状,并说明理由;(2)如图2,在(1)的条件下,P为CD边上的动点,点C关于直线BP的对称点是Q,连接PQ,BQ.①当∠CBP=°时,点Q位于线段AD的垂直平分线上;②连接AQ,DQ,设CP=x,设PQ的延长线交AD边于点E,当∠AQD=90°时,求证:QE=DE,并求出此时x的值.9.(2023•沈阳一模)如图,在平面直角坐标系中,直线y=kx+b与x轴交于点B(﹣5,0),与y轴交于点A,直线过点A,与x轴交于点C,点P 是x轴上方一个动点.(1)求直线AB的函数表达式;(2)若点P在线段AB上,且S△APC =S△AOB,求点P的坐标;(3)当S△PBC =S△AOB时,动点M从点B出发,先运动到点P,再从点P运动到点C后停止运动.点M的运动速度始终为每秒1个单位长度,运动的总时间为t(秒),请直接写出t的最小值.10.(2023春•鼓楼区期中)如图1,已知函数与x轴交于点A,与y轴交于点B,点C与点A关于y轴对称.(1)求直线BC的函数解析式;(2)设点M是x轴上的一个动点,过点M作y轴的平行线,交直线AB于点P,交直线BC于点Q.①若△PQB的面积为,求点M的坐标;②连接BM,如图2,若∠BMP=∠BAC,求点P的坐标.11.(2023春•顺德区校级期中)一次函数y=kx+b的图象经过点A(﹣2,0)、B(﹣1,1),且和一次函数y=﹣2x+a的图象交于点C,如图所示.(1)填空:不等式kx+b<0的解集是;(2)若不等式kx+b>﹣2x+a的解集是x>1,求点C的坐标;(3)在(2)的条件下,点P是直线y=﹣2x+a上一动点.且在点C上方,当∠P AC=15°时,求点P的坐标.12.(2023春•重庆期中)如图,已知函数y=x+1的图象与y轴交于点A,一次函数y=kx+b的图象经过点B(0,﹣1),与x轴以及y=x+1的图象分别交于点C,D,且点D的坐标为(1,n).(1)则k=,b=,n=;(2)求四边形AOCD的面积;(3)在x轴上是否存在点P,使得以点P,C,D为顶点的三角形是直角三角形,请求出点P的坐标.13.(2023春•崇川区校级月考)模型建立:如图1,等腰直角三角形ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过A作AD⊥ED于D,过B作BE⊥ED于E.(1)求证:△BEC≌△CDA;(2)模型应用:已知直线l1:y=﹣x﹣4与y轴交于A点.将直线l1绕着A 点逆时针旋转45°至l2,如图2,求l2的函数解析式.14.(2023春•崇川区校级月考)如图,在平面直角坐标系中,直线l1:y=﹣x+4分别与x轴,y轴交于点B,C.直线l2:y=x.(1)直接写出点B,C的坐标:B,C.(2)若D是直线l2上的点,且△COD的面积为6,求直线CD的函数表达式;(3)在(2)的条件下,且当点D在第一象限时,设P是射线CD上的点,在平面内存在点Q.使以O,C,P,Q为顶点的四边形是菱形,请直接求点Q的坐标.15.(2023•城固县模拟)如图,A、B两个长方体水箱放置在同一水平桌面上,开始时水箱A中没有水,水箱B盛满水,现以6dm3/min的流量从水箱B中抽水注入水箱A中,直至水箱A注满水为止.设注水时间为t(min),水箱A 的水位高度为y A(dm),水箱B中的水位高度为y B(dm).(抽水水管的体积忽略不计)(1)分别求出y A,y B与t之间的函数表达式;(2)当水箱A与水箱B中的水的体积相等时,求出此时两水箱中水位的高度差.16.(2022秋•常州期末)在平面直角坐标系中,一次函数的图象l1与x轴交于点A,一次函数y=x+6的图象l2与x轴交于点B,与l1交于点P.直线l3过点A且与x轴垂直,C是l3上的一个动点.(1)分别求出点A、P的坐标;(2)设直线PC对应的函数表达式为y=kx+b,且满足函数值y随x的增大而增大.若△PCA的面积为15,分别求出k、b的值;(3)是否存在点C,使得2∠PCA+∠P AB=90°?若存在,直接写出点C的坐标;若不存在,请说明理由.17.(2023春•靖江市期中)如图,平面直角坐标系中,已知点A(0,a)在y 轴正半轴上,点B(0,b)(a>b),点C(c,0)在x轴正半轴上,且a2﹣2ab+b2(1)如图1,求证:AB=OC;(2)如图2,当a=3,b=1时,过点B的直线与AC成45°夹角,试求该直线与AC交点的横坐标;(3)如图3,当b<0时,点D在OC的延长线上,且CD=OB,连接AD,射线BC交AD于点E.当点B在y轴负半轴上运动时,∠AEB的度数是否为定值?如果是,请求出∠AEB的度数;如果不是,请说明理由.18.(2023春•沙坪坝区校级期中)如图,在平面直角坐标系xOy中,直线AB:与直线CD:y=kx﹣2相交于点M(4,a),分别交坐标轴于点A,(1)求直线CD的解析表达式;(2)如图,点P是直线CD上的一个动点,当△PBM的面积为20时,求点P的坐标;(3)直线AB上有一点F,在平面直角坐标系内找一点N,使得以BF为一边,以点B,D,F,N为顶点的四边形是菱形,请直接写出符合条件的点N的坐标.19.(2023春•揭西县校级月考)在平面直角坐标系中,直线y1=kx+b经过点P (2,2)和点Q(0,﹣2),与x轴交于点A,与直线y2=mx+n交于点P.(1)求出直线y1=kx+b的解析式;(2)当m<0时,直接写出y1<y2时自变量x的取值范围;(3)直线y2=mx+n绕着点P任意旋转,与x轴交于点B,当△P AB是等腰三角形时,请直接写出符合条件的所有点B的坐标.20.(2023春•溧阳市校级月考)如图,四边形OABC是矩形,点A、C在坐标轴上,△ODE是由△OCB绕点O顺时针旋转90°得到的,点D在x轴上,直线BD交y轴于点F,交OE于点H,线段BC、OC的长是2和4;(1)求直线BD的表达式;(2)求△OFH的面积;(3)点M在坐标轴上,平面内是否存在点N,使以点D、F、M、N为顶点的四边形是矩形?若存在,请直接写出点N的坐标;若不存在,请说明理由.21.(2023春•江都区月考)如图,在平面直角坐标系中,直线y=﹣x+3与x 轴、y轴相交于A、B两点,动点C在线段OA上,将线段CB绕着点C顺时针旋转90°得到CD,此时点D恰好落在直线AB上时,过点D作DE⊥x轴于点E.(1)求证:△BOC≌△CED;(2)求点D的坐标;(3)若点P在y轴上,点Q在直线AB上,是否存在以C、D、P、Q为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的Q点坐标;若不存在,请说明理由.22.(2023春•新城区校级月考)如图,在平面直角坐标系中,直线l1的解析式为y=x,直线l2的解析式为,与x轴、y轴分别交于点A、点B,直线l1与l2交于点C.(1)若直线l2上存在点P(不与B重合),满足S△COP=S△COB,求出点P的坐标;(2)在y轴右侧有一动直线平行于y轴,分别与l1,l2交于点M、N,且点M 在点N的下方,y轴上是否存在点Q,使△MNQ为等腰直角三角形?若存在,请直接写出满足条件的点Q的坐标;若不存在,请说明理由.23.(2022秋•宿豫区期末)如图,直线l分别与x轴、y轴交于点A(4,0)、B (0,5),把直线l沿y轴向下平移3个单位长度,得到直线m,且直线m分别与x轴、y轴交于点C、D.(1)求直线l对应的函数表达式;(2)求四边形ABDC的面积.24.(2022秋•临淄区期末)如图,在直角坐标系中,四边形ABCD的顶点坐标分别为A(﹣1,0),B(0,2),C(2,3),D(4,0).(1)求直线BC的表达式;(2)线段AB与BC相等吗?请说明理由;(3)求四边形ABCD的面积;(4)已知点M在x轴上,且△MBC是等腰三角形,求点M的坐标.25.(2022秋•金牛区期末)如图1,在平面直角坐标系xOy中,直线AB:y=2x+b 与x轴交于点A(﹣2,0),与y轴交于点B.(1)求直线AB的解析式;(2)若直线CD:y=﹣x+与x轴、y轴、直线AB分别交于点C、D、E,求△BDE面积;(3)如图2,在(2)的条件下,点F为线段AC上一动点,将△EFC沿直线EF翻折得到△EFN,EN交x轴于点M.当△MNF为直角三角形时,求点N 的坐标.26.(2022秋•婺城区期末)如图,直线y=x+4与x轴、y轴分别交于点A、点B,点P是射线BO上的动点,过点B作直线AP的垂线交x轴于点Q,垂足为点C,连结OC.(1)当点P在线段BO上时,①求证:△AOP≌△BOQ;②若点P为BO的中点,求△OCQ的面积.(2)在点P的运动过程中,是否存在某一位置,使得△OCQ成为等腰三角形?若存在,求点P的坐标;若不存在,请说明理由.27.(2022秋•郫都区期末)在直角坐标系xOy中,直线l1:y=﹣x+4与x轴、y 轴分别交于点A,点B.直线l2:y=mx+m(m>0)与x轴,y轴分别交于点C,点D,直线l1与l2交于点E.(1)若点E坐标为(,n).ⅰ)求m的值;ⅱ)点P在直线l2上,若S△AEP=3S△BDE,求点P的坐标;(2)点F是线段CE的中点,点G为y轴上一动点,是否存在点F使△CFG 为以FC为直角边的等腰直角三角形.若存在,求出m的值,若不存在,请说明理由.28.(2022秋•市中区期末)如图,直线y=kx+b经过点,点B(0,25),与直线交于点C,点D为直线AB上一动点,过D点作x轴的垂线交直线OC于点E.(1)求直线AB的表达式和点C的坐标;(2)当时,求△CDE的面积;(3)连接OD,当△OAD沿着OD折叠,使得点A的对应点A'落在直线OC 上,直接写出此时点D的坐标.29.(2022秋•新都区期末)如图1,在平面直角坐标系中,点A的坐标为(4,4),点B的坐标为(﹣4,0).(1)求直线AB的表达式;(2)点M是坐标轴上的一点,若以AB为直角边构造Rt△ABM,请求出满足条件的所有点M的坐标;(3)如图2,以A为直角顶点作∠CAD=90°,射线AC交x轴的正半轴于点C,射线AD交y轴的负半轴于点D,当∠CAD绕点A旋转时,求OC﹣OD 的值.30.(2022秋•皇姑区期末)如图,在平面直角坐标系中,直线AD:y=﹣x+4交y轴于点A,交x轴于点D.直线AB交x轴于点B(﹣3,0),点P为直线AB上的动点.(1)求直线AB的关系式;(2)连接PD,当线段PD⊥AB时,直线AD上有一点动M,x轴上有一动点N,直接写出△PMN周长的最小值;(3)若∠POA=∠BAO,直接写出点P的纵坐标.31.(2022秋•新都区期末)如图所示,直线l1:y=x﹣1与y轴交于点A,直线l2:y=﹣2x﹣4与x轴交于点B,直线l1与l2交于点C.(1)求点A,C的坐标;(2)点P在直线l1上运动,求出满足条件S△PBC=S△ABC且异于点A的点P的坐标;(3)点D(2,0)为x轴上一定点,当点Q在直线l1上运动时,请直接写出|DQ﹣BQ|的最大值.32.(2022秋•鸡西期末)如图,直角三角形ABC在平面直角坐标系中,直角边BC在y轴上,AB,BC的长分别是一元二次方程x2﹣14x+48=0的两个根,AB<BC,且BC=2OB,P为BC上一点,且∠BAP=∠C.(1)求点A的坐标;(2)求直线AP的解析式;(3)M为x轴上一点,在平面内是否存在点N,使以A,C,M,N为顶点的四边形为矩形?若存在,请直接写出点N的坐标;若不存在,请说明理由.33.(2022秋•锦江区校级期末)如图,直线y=kx+b与x轴、y轴分别交于点A 和点B,点C在线段AO上,将△ABC沿BC所在直线折叠后,点A恰好落在y轴上点D处,若OA=4,OD=2.(1)求直线AB的解析式.(2)求S△ABC :S△OCD的值.(3)直线CD上是否存在点P使得∠PBC=45°,若存在,请直接写出P的坐标.34.(2022秋•福田区校级期末)已知:如图,一次函数的图象分别与x 轴、y轴相交于点A、B,且与经过点C(2,0)的一次函数y=kx+b的图象相交于点D.点D的横坐标为4,直线CD与y轴相交于点E.(1)直线CD的函数表达式为:;(2)点Q为线段DE上的一个动点,连接BQ.①若直线BQ将△BDE的面积分为1:2两部分,求点Q的坐标;②点Q是否存在某个位置,将△BQD沿着直线BQ翻折,使得点D恰好落在直线AB下方的坐标轴上?若存在,请直接写出点Q的坐标;若不存在,请说明理由.35.(2022秋•抚州期末)如图,在平面直角坐标系xOy中,直线AP交x轴于点P(p,0),与y轴交于点A(0,a),且a,p满足=0.(1)求直线AP的解析式;(2)如图1,直线x=﹣2与x轴交于点N,点M在x轴上方且在直线x=﹣2上,若△MAP的面积等于6,请求出点M的坐标;(3)如图2,已知点C(﹣2,4),若点B为射线AP上一动点,连接BC,在坐标轴上是否存在点Q,使△BCQ是以BC为底边,点Q为直角顶点的等腰直角三角形,若存在,请直接写出点Q坐标;若不存在,请说明理由.36.(2022秋•天桥区期末)如图1,在平面直角坐标系xOy中,点O是坐标原点,直线AB:y=kx+与直线AC:y=﹣2x+b交于点A,两直线与x轴分别交于点B(﹣3,0)和C(2,0).(1)求直线AB和AC的表达式.(2)点P是y轴上一点,当P A+PC最小时,求点P的坐标.(3)如图2,点D为线段BC上一动点,将△ABD沿直线AD翻折得到△ADE,线段AE交x轴于点F,若△DEF为直角三角形,求点D坐标.37.(2023•桐乡市校级开学)如图,一次函数y=x+6的图象与x轴交于点A,与y轴交于点B,OC⊥AB于点C,点P在直线AB上运动,点Q在y轴的正半轴上运动.(1)求点A,B的坐标;(2)求OC的长;(3)若以O,P,Q为顶点的三角形与△OCP全等,求点Q的坐标.38.(2022秋•秦都区期末)如图,平面直角坐标系中,直线AB与x轴交于点A (﹣3,0)与y轴交于点B(0,6),点C是直线AB上的一点,它的坐标为(m,4),经过点C作直线CD∥x轴交y轴于点D.(1)求点C的坐标;(2)已知点P是直线CD上的动点,①若△POC的面积为4,求点P的坐标;②若△POC为直角三角形,请求出所有满足条件的点P的坐标.39.(2022秋•南海区期末)如图,在平面直角坐标系中,直线y=x+1分别交x 轴,y轴于点A、B.另一条直线CD与直线AB交于点C(a,6),与x轴交于点D(3,0),点P是直线CD上一点(不与点C重合).(1)求a的值.(2)当△APC的面积为18时,求点P的坐标.(3)若直线MN在平面直角坐标系内运动,且MN始终与AB平行,直线MN 交直线CD于点M,交y轴于点N,当∠BMN=90°时,求△BMN的面积.40.(2023•丰顺县校级开学)问题提出:如图,等腰Rt△ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过点A作AD⊥ED于点D,过点B作BE⊥ED于点E,求证:△BEC≌△CDA;问题探究:如图2,在平面直角坐标系中,一次函数与x轴交于点A,与y轴交于点B,以AB为腰在第二象限作等腰直角△ABC,∠BAC=90°,求点C的坐标;问题解决:古城西安已经全面迎来地铁时代!继西安地铁2号线于2011年9月16日通车试运行以来,共有八条线路开通运营,极大促进了西安市的交通运输,目前还有多条线路正在修建中.如图,地铁某线路原计划按OA﹣AB的方向施工,由于在AB方向发现一处地下古建筑,地铁修建须绕开此区域.经实地勘测,若将AB段绕点A顺时针或逆时针方向旋转45°至AC或AD方向,则可以绕开此区域.已知OA长为1千米,以点O为原点,OA所在直线为x轴,1千米为单位长度,建立平面直角坐标系,且射线AB与直线y=﹣2x平行,请帮助施工队计算出AC和AD所在直线的解析式.41.(2022秋•碑林区校级期末)(1)模型建立:如图1,在等腰直角三角形ABC中,∠ACB=90°,CA=CB,直线ED经过点C,过点A作AD⊥ED于点D,过点B作BE⊥ED于点E,请直接写出图中相等的线段(除CA=CB);模型应用:(2)如图2,在平面直角坐标系xOy中,直线与x,y轴分别交于A、B两点,C为第一象限内的点,若△ABC是以AB为直角边的等腰直角三角形,请求出点C的坐标和直线BC的表达式;探究提升:(3)如图3,在平面直角坐标系xOy中,A(3,0),点B在y轴上运动,将AB绕点A顺时针旋转90°至AC,连接OC,求CA+OC的最小值,及此时点B坐标.42.(2023•南岸区校级开学)如图,已知直线l1:y=﹣x+b与直线l2:y=kx+3相交于y轴的B点,且分别交x轴于点A、C,已知OC=OA.(1)如图,求点C的坐标及k的值;(2)如图,若E为直线l1上一点,且E点的横坐标为,点P为y轴上一个动点,求当|PC﹣PE|最大时,点P的坐标;(3)若M为x轴上一点,当△ABM是等腰三角形时,直接写出点M的坐标.43.(2022秋•驿城区校级期末)(1)操作思考:如图1,在平面直角坐标系中,等腰直角△ACB的直角顶点C在原点,将其绕着点O旋转,若顶点A恰好落在点(1,2)处.则:①OA的长为;②点B的坐标为.(直接写结果)(2)感悟应用:如图2,在平面直角坐标系中,将等腰直角△ACB如图放置,直角顶点C(﹣1,0),点A(0,4),试求直线AB的函数表达式.(3)拓展研究:如图3,在直角坐标系中,点B(4,3),过点B作BA⊥y 轴,垂足为点A,作BC⊥x轴,垂足为点C,P是线段BC上的一个动点,点Q是直线y=2x﹣8上一动点,存在以点P为直角顶点的等腰直角△APQ,请直接写出点P的坐标.。
一次函数代数几何综合问题

一次函数代几综合问题一.填空题(共6小题)1.如图,直线和x轴、y轴分别交于点A、B.若以线段AB为边作等边三角形ABC,则点C的坐标是.2.一次函数y=x+4分别交x轴、y轴于A、B两点,在x轴上取一点,使△ABC为等腰三角形,则这样的点C的坐标为.3.如图,平面直角坐标系中,已知直线y=x上一点P(1,1),C为y轴上一点,连接PC,线段PC绕点P顺时针旋转90°至线段PD,过点D作直线AB⊥x轴,垂足为B,直线AB与直线y=x交于点A,且BD=2AD,连接CD,直线CD与直线y=x交于点Q,则点Q的坐标为.4.如图,已知直线l:y=x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;…;按此作法继续下去,则点A4的坐标为.5.在直角坐标系中,正方形A1B1C1O1、A2B2C2C1、…、A n B n C n C n﹣1按如图所示的方式放置,其中点A1、A2、A3、…、A n均在一次函数y=kx+b的图象上,点C1、C2、C3、…、C n均在x轴上.若点B1的坐标为(1,1),点B2的坐标为(3,2),则点A n的坐标为.6.如图,直线1:与x轴、y轴分别相交于点A、B,△AOB与△ACB关于直线l对称,则点C的坐标为.二.解答题(共24小题)7.已知一次函数y=2x﹣4的图象与x轴、y轴分别相交于点A、B,点P在该函数的图象上,P到x轴、y 轴的距离分别为d1、d2.(1)当P为线段AB的中点时,求d1+d2的值;(2)直接写出d1+d2的范围,并求当d1+d2=3时点P的坐标;(3)若在线段AB上存在无数个P点,使d1+ad2=4(a为常数),求a的值.8.在平面直角坐标系xOy中,边长为6的正方形OABC的顶点A,C分别在x轴和y轴的正半轴上,直线y=mx+2与OC,BC两边分别相交于点D,G,以DG为边作菱形DEFG,顶点E在OA边上.(1)如图1,当CG=OD时,直接写出点D和点G的坐标,并求直线DG的函数表达式;(2)如图2,连接BF,设CG=a,△FBG的面积为S.①求S与a的函数关系式;②判断S的值能否等于等于1?若能,求此时m的值,若不能,请说明理由;(3)如图3,连接GE,当GD平分∠CGE时,m的值为.9.认真阅读材料,然后回答问题:我们知道,在数轴上,x=1表示一个点.而在平面直角坐标系中,x=1表示一条直线;我们还知道,以二元一次方方程2x﹣y+1=0的所有解为坐标的点组成的图形就是一次函数y=2x+1的图象,它也是一条直线,如图1可以得出:直线x=1与直线y=2x+1的交点P的坐标(1,3)就是方程组在直角坐标系中,x≤1表示一个平面区域,即直线x=1以及它左侧的部分,如图2;y≧2x+1也表示一个平面区域,即直线y=2x+1以及它上方的部分,如图3.回答下列问题:请你自己作一个直角坐标系,并在直角坐标系中(1)用作图象的方法求出方程组的解.(2)用阴影表示,所围成的区域.10.如图,直线l1的解析表达式为:y=3x﹣3,且l1与x轴交于点D,直线l2经过点A,B,直线l1,l2交于点C.(1)求△ADC的面积;(2)在直线l2上存在异于点C的另一点P,使得△ADP与△ADC的面积相等,则点P的坐标为;(3)若点H为坐标平面内任意一点,在坐标平面内是否存在这样的点H,使以A、D、C、H为顶点的四边形是平行四边形?若存在,请直接写出点H的坐标;若不存在,请说明理由.11.如图,在平面直角坐标系中,已知直线l1和l2相交于点A,它们的解析式分别为l1:y=x,l2:y=﹣x+.直线l2与两坐标轴分别相交于点B和点C,点P在线段OB上从点O出发.以每秒1个单位的速度向点B运动,同时点Q从点B出发以每秒4个单位的速度沿B→O→C→B的方向向点B运动,过点P作直线PM⊥OB分别交l1,l2于点M,N.连接MQ.设点P,Q运动的时间是t秒(t>0)(1)求点A的坐标;(2)点Q在OC上运动时,试求t为何值时,四边形MNCQ为平行四边形;(3)试探究是否存在某一时刻t,使MQ∥OB?若存在,求出t的值;若不存在,请说明理由.12.已知,将边长为5的正方形ABCO放置在如图所示的直角坐标系中,使点A在x轴上,点C在y轴上.点M(t,0)在x轴上运动,过A作直线MC的垂线交y轴于点N.(1)当t=1时,求直线MC的解析式;(2)设△AMN的面积为S,求S关于t的函数解析式并写出相应t的取值范围;(3)在该平面直角坐标系中,第一象限内取点P(2,y),是否存在以M、N、C、P为顶点的四边形是直角梯形?若存在,直接写出点P的坐标;若不存在,请说明理由.13.如图①,以四边形AOCD的顶点O为原点建立直角坐标系,点A、C、D的坐标分别为(0,2)、(2,0)、(2,2),点P(m,0)是x轴上一动点,m是大于0的常数,以AP为一边作正方形APQR(QR落在第一象限),连接CQ.(1)请判断四边形AOCD的形状,并说明理由:(2)连接RD,请判断△ARD的形状,并说明理由:(3)如图②,随着点P(m,0)的运动,正方形APQR的大小会发生改变,若设CQ所在直线的表达式为y=kx+b(k≠0),求k的值.14.如图,将边长为4的正方形纸片,置于平面直角坐标系内,顶点A在坐标原点,AB在x轴正方向上,E、F分别是AD、BC的中点,M在DC上,将△ADM沿折痕AM折叠,使点D折叠后恰好落在EF上的P点处.(1)求点M、P的坐标;(2)求折痕AM所在直线的解析式;(3)设点H为直线AM上的点,是否存在这样的点H,使得以H、A、P为顶点的三角形为等腰三角形?若存在,请直接写出点H的坐标;若不存在,请说明理由.15.如图①,在平面直角坐标系中,A点坐标为(3,0),B点坐标为(0,4).动点M从点O出发,沿OA方向以每秒1个单位长度的速度向终点A运动;同时,动点N从点A出发沿AB方向以每秒个单位长度的速度向终点B运动.设运动了x秒.(1)点N的坐标为(,);(用含x的代数式表示)(2)当x为何值时,△AMN为等腰三角形;(3)如图②,连接ON得△OMN,△OMN可能为正三角形吗?若不能,点M的运动速度不变,试改变点N的运动速度,使△OMN为正三角形,并求出点N的运动速度.16.已知直线y=﹣x+4与x轴和y轴分别交与B、A两点,另一直线经过点B和点D(11,6).(1)求AB、BD的长度,并证明△ABD是直角三角形;(2)在x轴上找点C,使△ACD是以AD为底边的等腰三角形,求出C点坐标;(3)一动点P速度为1个单位/秒,沿A﹣﹣B﹣﹣D运动到D点停止,另有一动点Q从D点出发,以相同的速度沿D﹣﹣B﹣﹣A运动到A点停止,两点同时出发,PQ的长度为y(单位长),运动时间为t(秒),求y关于t的函数关系式.17.如图:直线y=kx+3与x轴、y轴分别交于A、B两点,,点C(x,y)是直线y=kx+3上与A、B不重合的动点.(1)求直线y=kx+3的解析式;(2)当点C运动到什么位置时△AOC的面积是6;(3)过点C的另一直线CD与y轴相交于D点,是否存在点C使△BCD与△AOB全等?若存在,请求出点C的坐标;若不存在,请说明理由.18.如图,在平面直角坐标系中,已知O为原点,四边形ABCD为平行四边形,A、B、C的坐标分别是A(﹣5,1),B(﹣2,4),C(5,4),点D在第一象限.(1)写出D点的坐标;(2)求经过B、D两点的直线的解析式,并求线段BD的长;(3)将平行四边形ABCD先向右平移1个单位长度,再向下平移1个单位长度所得的四边形A1B1C1D1四个顶点的坐标是多少?并求出平行四边形ABCD与四边形A1B1C1D1重叠部分的面积.19.如图1,在平面直角坐标系中,已知△AOB是等边三角形,点A的坐标是(0,4),点B在第一象限,点P是x轴上的一个动点,连接AP,并把△AOP绕着点A按逆时针方向旋转,使边AO与AB重合,得到△ABD.(1)求直线AB的解析式;(2)当点P运动到点(,0)时,求此时DP的长及点D的坐标;(3)是否存在点P,使△OPD的面积等于?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.20.已知,直线y=﹣x+1与x轴,y轴分别交于点A、B,以线段AB为直角边在第一象限内作等腰Rt△ABC,∠BAC=90度.且点P(1,a)为坐标系中的一个动点.(1)求三角形ABC的面积S△ABC;(2)证明不论a取任何实数,三角形BOP的面积是一个常数;(3)要使得△ABC和△ABP的面积相等,求实数a的值.21.如图,在直角坐标系xoy中,一次函数的图象与x轴交于点A,与y轴交于点B.(1)已知OC⊥AB于C,求C点坐标;(2)在x轴上是否存在点P,使△PAB为等腰三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.22.如图1,在正方形ABOC中,BD平分∠OBC,交OA于点D.(1)若正方形ABOC的边长为2,对角线BC与OA相交于点E.则:①BC的长为;②DE的长为;③根据已知及求得的线段OB、BC、DE的长,请找出它们的数量关系?(2)如图2,当直角∠BAC绕着其顶点A顺时针旋转时,角的两边分别与x轴正半轴、y轴正半轴交于点C1和B1,连接B1C1交OA于P.B1D平分∠OB1C1,交OA于点D,过点D作DE⊥B1C1,垂足为E,请猜想线段OB、B1C1、DE三者之间的数量关系,并证明你的猜想;(3)在(2)的条件下,当B1E=6,C1E=4时,求直线B1D的解析式.23.如图,一次函数的函数图象与x轴、y轴分别交于点A、B,以线段AB为直角边在第一象限内作Rt△ABC,且使∠ABC=30°;(1)如果点P(m,)在第二象限内,试用含m的代数式表示四边形AOPB的面积,并求当△APB与△ABC面积相等时m的值;(2)如果△QAB是等腰三角形并且点Q在坐标轴上,请求出点Q所有可能的坐标;(3)是否存在实数a,b使一次函数和y=ax+b的图象关于直线y=x对称?若存在,求出的值;若不存在,请说明理由.24.一次函数的图象与x轴、y轴分别交于点A(8,0)和点B(0,6).(1)确定此一次函数的解析式.(2)求坐标原点O到直线AB的距离.(3)点P是线段AB上的一个动点,过点P作PM垂直于x轴于M,作PN垂直于y轴于N,记L=PM+PN,问L是否存在最大值和最小值?若存在,求出此时P点到原点O的距离,若不存在请说明理由.25.已知直线y=2x+4与x轴交于点A,与y轴交于点B,点P在坐标轴上,且PO=2AO.求△ABP的面积.26.已知A(1,5),B(3,﹣1)两点,在x轴上取一点M,使AM﹣BM取得最大值时,则M的坐标为.27.如图,在平面直角坐标系中,直线分别交于x轴,y轴于B、A两点,D、E分别是OA、OB的中点,点P从点D出沿DE方向运动,过点P作PQ⊥AB于Q,过点Q作QR∥OA交OB于R,当点Q与B点重合时,点P停止运动.(1)求A、B两点的坐标;(2)求PQ的长度;(3)是否存在点P,使△PQR为等腰三角形?若存在,请求出所有满足要求的点R的坐标;若不存在,请说明理由.28.如图,直线y=﹣2x+2与x轴、y轴分别交于A、B两点,将△OAB绕点O逆时针方向旋转90°后得到△OCD.(1)填空:点C的坐标是(,),点D的坐标是(,);(2)设直线CD与AB交于点M,求线段BM的长;(3)在y轴上是否存在点P,使得△BMP是等腰三角形?若存在,请求出所有满足条件的点P的坐标;若不存在,请说明理由.29.已知△ABC,∠BAC=90°,AB=AC=4,BD是AC边上的中线,分别以AC,AB所在直线为x轴,y 轴建立直角坐标系(如图).(1)在BD所在直线上找出一点P,使四边形ABCP为平行四边形,画出这个平行四边形,并简要叙述其过程;(2)求直线BD的函数关系式;(3)直线BD上是否存在点M,使△AMC为等腰三角形?若存在,求点M的坐标;若不存在,说明理由.30.如图,一次函数的图象与x轴、y轴交于点A、B,以线段AB为边在第一象限内作等边△ABC,(1)求△ABC的面积;(2)如果在第二象限内有一点P(a,);试用含有a的代数式表示四边形ABPO的面积,并求出当△ABP的面积与△ABC的面积相等时a的值;(3)在x轴上,是否存在点M,使△MAB为等腰三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由.。
一次函数和几何综合题含答案

一次函数和几何综合题含答案1.(2013•天水)如图1,在平面直角坐标系中,已知△AOB是等边三角形,点A的坐标是(0,4),点B在第一象限,点P是x轴上的一个动点,连接AP,并把△AOP绕着点A按逆时针方向旋转,使边AO与AB重合,得到△ABD.(1)求直线AB的解析式;(2)当点P运动到点(,0)时,求此时DP的长及点D的坐标;(3)是否存在点P,使△OPD的面积等于?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.2.(2013•济宁)如图,直线y=﹣x+4与坐标轴分别交于点A、B,与直线y=x交于点C.在线段OA上,动点Q以每秒1个单位长度的速度从点O出发向点A做匀速运动,同时动点P从点A出发向点O做匀速运动,当点P、Q其中一点停止运动时,另一点也停止运动.分别过点P、Q作x轴的垂线,交直线AB、OC于点E、F,连接EF.若运动时间为t秒,在运动过程中四边形PEFQ总为矩形(点P、Q重合除外).(1)求点P运动的速度是多少?(2)当t为多少秒时,矩形PEFQ为正方形?(3)当t为多少秒时,矩形PEFQ的面积S最大?并求出最大值.3.(2013•绥化)如图,直线MN与x轴,y轴分别相交于A,C两点,分别过A,C两点作x轴,y轴的垂线相交于B 点,且OA,OC(OA>OC)的长分别是一元二次方程x2﹣14x+48=0的两个实数根.(1)求C点坐标;(2)求直线MN的解析式;(3)在直线MN上存在点P,使以点P,B,C三点为顶点的三角形是等腰三角形,请直接写出P点的坐标.4.(2013•齐齐哈尔)如图,平面直角坐标系中,直线l分别交x轴、y轴于A、B两点(OA<OB)且OA、OB的长分别是一元二次方程x2﹣(+1)x+=0的两个根,点C在x轴负半轴上,且AB:AC=1:2(1)求A、C两点的坐标;(2)若点M从C点出发,以每秒1个单位的速度沿射线CB运动,连接AM,设△ABM的面积为S,点M的运动时间为t,写出S关于t的函数关系式,并写出自变量的取值范围;(3)点P是y轴上的点,在坐标平面内是否存在点Q,使以A、B、P、Q为顶点的四边形是菱形?若存在,请直接写出Q点的坐标;若不存在,请说明理由.5.(2013春•屯留县期末)如图,四边形OABC是菱形,点C在x轴上,AB交y轴于点H,AC交y轴于点M.已知点A(﹣3,4).(1)求AO的长;(2)求直线AC的解析式和点M的坐标;(3)点P从点A出发,以每秒2个单位的速度沿折线A﹣B﹣C运动,到达点C终止.设点P的运动时间为t秒,△PMB 的面积为S.①求S与t的函数关系式;②求S的最大值.6.(2012•鞍山)如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标(3,3),将正方形ABCO绕点A顺时针旋转角度α(0°<α<90°),得到正方形ADEF,ED交线段OC于点G,ED的延长线交线段BC于点P,连AP、AG.(1)求证:△AOG≌△ADG;(2)求∠PAG的度数;并判断线段OG、PG、BP之间的数量关系,说明理由;(3)当∠1=∠2时,求直线PE的解析式.7.(2012•桃源县校级自主招生)如图,点A在y轴上,点B在x轴上,且OA=OB=1,经过原点O的直线l交线段AB于点C,过C作OC的垂线,与直线x=1相交于点P,现将直线L绕O点旋转,使交点C从A向B运动,但C点必须在第一象限内,并记AC的长为t,分析此图后,对下列问题作出探究:(1)当△AOC和△BCP全等时,求出t的值;(2)通过动手测量线段OC和CP的长来判断它们之间的大小关系并证明你得到的结论;(3)①设点P的坐标为(1,b),试写出b关于t的函数关系式和变量t的取值范围.②求出当△PBC为等腰三角形时点P的坐标.8.(2012秋•海陵区期末)如图1,在平面直角坐标系中,直线AB与x轴交于点A,与y轴交于点B,与直线OC交于点C.(1)若直线AB解析式为y=﹣2x+12,直线OC解析式为y=x,①求点C的坐标;②求△OAC的面积.(2)如图2,作∠AOC的平分线ON,若AB⊥ON,垂足为E,△OAC的面积为6,且OA=4,P、Q分别为线段OA、OE上的动点,连接AQ与PQ,试探索AQ+PQ是否存在最小值?若存在,求出这个最小值;若不存在,说明理由.9.(2012秋•成都校级期末)如图,在平面直角坐标系xOy中,已知直线PA是一次函数y=x+m(m>0)的图象,直线PB是一次函数y=﹣3x+n(n>m)的图象,点P是两直线的交点,点A、B、C、Q分别是两条直线与坐标轴的交点.(1)用m、n分别表示点A、B、P的坐标及∠PAB的度数;(2)若四边形PQOB的面积是,且CQ:AO=1:2,试求点P的坐标,并求出直线PA与PB的函数表达式;(3)在(2)的条件下,是否存在一点D,使以A、B、P、D为顶点的四边形是平行四边形?若存在,求出点D的坐标;若不存在,请说明理由.10.(2012秋•綦江县校级期末)如图,一次函数的函数图象与x轴、y轴分别交于点A、B,以线段AB 为直角边在第一象限内作Rt△ABC,且使∠ABC=30°.(1)求△ABC的面积;(2)如果在第二象限内有一点P(m,),试用含m的代数式表示△APB的面积,并求当△APB与△ABC面积相等时m的值;(3)是否存在使△QAB是等腰三角形并且在坐标轴上的点Q?若存在,请写出点Q所有可能的坐标;若不存在,请说明理由.参考答案与试题解析一.解答题(共10小题)1.(2013•天水)如图1,在平面直角坐标系中,已知△AOB是等边三角形,点A的坐标是(0,4),点B在第一象限,点P是x轴上的一个动点,连接AP,并把△AOP绕着点A按逆时针方向旋转,使边AO与AB重合,得到△ABD.(1)求直线AB的解析式;(2)当点P运动到点(,0)时,求此时DP的长及点D的坐标;(3)是否存在点P,使△OPD的面积等于?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.考点:一次函数综合题.专题:压轴题.分析:(1)过点B作BE⊥y轴于点E,作BF⊥x轴于点F.依题意得BF=OE=2,利用勾股定理求出OF,然后可得点B的坐标.设直线AB的解析式是y=kx+b,把已知坐标代入可求解.(2)由△ABD由△AOP旋转得到,证明△ABD≌△AOP.AP=AD,∠DAB=∠PAO,∠DAP=∠BAO=60°,△ADP是等边三角形.利用勾股定理求出DP.在Rt△BDG中,∠BGD=90°,∠DBG=60°.利用三角函数求出BG=BD•cos60°,DG=BD•sin60°.然后求出OH,DH,然后求出点D的坐标.(3)本题分三种情况进行讨论,设点P的坐标为(t,0):①当P在x轴正半轴上时,即t>0时,关键是求出D点的纵坐标,方法同(2),在直角三角形DBG中,可根据BD即OP的长和∠DBG的正弦函数求出DG的表达式,即可求出DH的长,根据已知的△OPD的面积可列出一个关于t的方程,即可求出t的值.②当P在x轴负半轴,但D在x轴上方时.即<t≤0时,方法同①类似,也是在直角三角形DBG用BD的长表示出DG,进而求出GF的长,然后同①.③当P在x轴负半轴,D在x轴下方时,即t≤时,方法同②.综合上面三种情况即可求出符合条件的t的值.解答:解:(1)如图1,过点B作BE⊥y轴于点E,作BF⊥x轴于点F.由已知得:BF=OE=2,OF==,∴点B的坐标是(,2)设直线AB的解析式是y=kx+b(k≠0),则有.解得.∴直线AB的解析式是y=x+4;(2)如图2,∵△ABD由△AOP旋转得到,∴△ABD≌△AOP,∴AP=AD,∠DAB=∠PAO,∴∠DAP=∠BAO=60°,∴△ADP是等边三角形,∴DP=AP=.如图2,过点D作DH⊥x轴于点H,延长EB交DH于点G,则BG⊥DH.方法(一)在Rt△BDG中,∠BGD=90°,∠DBG=60°.∴BG=BD•cos60°=×=.DG=BD•sin60°=×=.∴OH=EG=,DH=∴点D的坐标为(,)方法(二)易得∠AEB=∠BGD=90°,∠ABE=∠BDG,∴△ABE∽△BDG,∴;而AE=2,BD=OP=,BE=2,AB=4,则有,解得BG=,DG=;∴OH=,DH=;∴点D的坐标为(,).(3)假设存在点P,在它的运动过程中,使△OPD的面积等于.设点P为(t,0),下面分三种情况讨论:①当t>0时,如图,BD=OP=t,DG=t,∴DH=2+t.∵△OPD的面积等于,∴,解得,(舍去)∴点P1的坐标为(,0).②∵当D在y轴上时,根据勾股定理求出BD==OP,∴当<t≤0时,如图,BD=OP=﹣t,DG=﹣t,∴GH=BF=2﹣(﹣t)=2+t.∵△OPD的面积等于,∴,解得,,∴点P2的坐标为(,0),点P3的坐标为(,0).③当t≤时,如图3,BD=OP=﹣t,DG=﹣t,∴DH=﹣t﹣2.∵△OPD的面积等于,∴(﹣t)[﹣(2+t)]=,解得(舍去),∴点P4的坐标为(,0),综上所述,点P的坐标分别为P1(,0)、P2(,0)、P3(,0)、P4(,0).点评:本题综合考查的是一次函数的应用,包括待定系数法求解析式、旋转的性质、相似三角形的判定和性质、三角形面积公式的应用等,难度较大.2.(2013•济宁)如图,直线y=﹣x+4与坐标轴分别交于点A、B,与直线y=x交于点C.在线段OA上,动点Q以每秒1个单位长度的速度从点O出发向点A做匀速运动,同时动点P从点A出发向点O做匀速运动,当点P、Q其中一点停止运动时,另一点也停止运动.分别过点P、Q作x轴的垂线,交直线AB、OC于点E、F,连接EF.若运动时间为t秒,在运动过程中四边形PEFQ总为矩形(点P、Q重合除外).(1)求点P运动的速度是多少?(2)当t为多少秒时,矩形PEFQ为正方形?(3)当t为多少秒时,矩形PEFQ的面积S最大?并求出最大值.考点:一次函数综合题.专题:压轴题.分析:(1)根据直线y=﹣x+4与坐标轴分别交于点A、B,得出A,B点的坐标,再利用EP∥BO,得出==,据此可以求得点P的运动速度;(2)当PQ=PE时,以及当PQ=PE时,矩形PEFQ为正方形,分别求出即可;(3)根据(2)中所求得出s与t的函数关系式,进而利用二次函数性质求出即可.解答:解:(1)∵直线y=﹣x+4与坐标轴分别交于点A、B,∴x=0时,y=4,y=0时,x=8,∴==,当t秒时,QO=FQ=t,则EP=t,∵EP∥BO,∴==,∴AP=2t,∵动点Q以每秒1个单位长度的速度从点O出发向点A做匀速运动,∴点P运动的速度是每秒2个单位长度;(2)如图1,当PQ=PE时,矩形PEFQ为正方形,则∵OQ=FQ=t,PA=2t,∴QP=8﹣t﹣2t=8﹣3t,∴8﹣3t=t,解得:t=2;如图2,当PQ=PE时,矩形PEFQ为正方形,∵OQ=t,PA=2t,∴OP=8﹣2t,∴QP=t﹣(8﹣2t)=3t﹣8,∴t=3t﹣8,解得:t=4;(3)如图1,当Q在P点的左边时,∵OQ=t,PA=2t,∴QP=8﹣t﹣2t=8﹣3t,∴S矩形PEFQ=QP•QF=(8﹣3t)•t=8t﹣3t2,当t=﹣=时,S矩形PEFQ的最大值为:=,如图2,当Q在P点的右边时,∵OQ=t,PA=2t,∴2t>8﹣t,∴t,∴QP=t﹣(8﹣2t)=3t﹣8,∴S矩形PEFQ=QP•QF=(3t﹣8)•t=3t2﹣8t,∵当点P、Q其中一点停止运动时,另一点也停止运动,∴<t≤4,当t=﹣=时,S矩形PEFQ的最大,∴t=4时,S矩形PEFQ的最大值为:3×42﹣8×4=16,点评:此题主要考查了二次函数与一次函数的综合应用,得出P,Q不同的位置进行分类讨论得出是解题关键.3.(2013•绥化)如图,直线MN与x轴,y轴分别相交于A,C两点,分别过A,C两点作x轴,y轴的垂线相交于B 点,且OA,OC(OA>OC)的长分别是一元二次方程x2﹣14x+48=0的两个实数根.(1)求C点坐标;(2)求直线MN的解析式;(3)在直线MN上存在点P,使以点P,B,C三点为顶点的三角形是等腰三角形,请直接写出P点的坐标.考点:一次函数综合题.专题:压轴题.分析:(1)通过解方程x2﹣14x+48=0可以求得OC=6,OA=8.则C(0,6);(2)设直线MN的解析式是y=kx+b(k≠0).把点A、C的坐标分别代入解析式,列出关于系数k、b的方程组,通过解方程组即可求得它们的值;(3)需要分类讨论:PB为腰,PB为底两种情况下的点P的坐标.根据等腰三角形的性质、两点间的距离公式以及一次函数图象上点的坐标特征进行解答.解答:解:(1)解方程x2﹣14x+48=0得x1=6,x2=8.∵OA,OC(OA>OC)的长分别是一元二次方程x2﹣14x+48=0的两个实数根,∴OC=6,OA=8.∴C(0,6);(2)设直线MN的解析式是y=kx+b(k≠0).由(1)知,OA=8,则A(8,0).∵点A、C都在直线MN上,∴,解得,,∴直线MN的解析式为y=﹣x+6;(3)∵A(8,0),C(0,6),∴根据题意知B(8,6).∵点P在直线MNy=﹣x+6上,∴设P(a,﹣a+6)当以点P,B,C三点为顶点的三角形是等腰三角形时,需要分类讨论:①当PC=PB时,点P是线段BC的中垂线与直线MN的交点,则P1(4,3);②当PC=BC时,a2+(﹣a+6﹣6)2=64,解得,a=,则P2(﹣,),P3(,);③当PB=BC时,(a﹣8)2+(a﹣6+6)2=64,解得,a=,则﹣a+6=﹣,∴P4(,﹣).综上所述,符合条件的点P有:P1(4,3),P2(﹣,)P3(,),P4(,﹣).点评:本题考查了一次函数综合题.其中涉及到的知识点有:待定系数法求一次函数解析式,一次函数图象上点的坐标特征,等腰三角形的性质.解答(3)题时,要分类讨论,防止漏解.另外,解答(3)题时,还利用了“数形结合”的数学思想.4.(2013•齐齐哈尔)如图,平面直角坐标系中,直线l分别交x轴、y轴于A、B两点(OA<OB)且OA、OB的长分别是一元二次方程x2﹣(+1)x+=0的两个根,点C在x轴负半轴上,且AB:AC=1:2(1)求A、C两点的坐标;(2)若点M从C点出发,以每秒1个单位的速度沿射线CB运动,连接AM,设△ABM的面积为S,点M的运动时间为t,写出S关于t的函数关系式,并写出自变量的取值范围;(3)点P是y轴上的点,在坐标平面内是否存在点Q,使以A、B、P、Q为顶点的四边形是菱形?若存在,请直接写出Q点的坐标;若不存在,请说明理由.考点:一次函数综合题.专题:压轴题.分析:(1)通过解一元二次方程x2﹣(+1)x+=0,求得方程的两个根,从而得到A、B两点的坐标,再根据两点之间的距离公式可求AB的长,根据AB:AC=1:2,可求AC的长,从而得到C点的坐标;(2)分①当点M在CB边上时;②当点M在CB边的延长线上时;两种情况讨论可求S关于t的函数关系式;(3)分AQ=AB,BQ=BA,BQ=QA三种情况讨论可求Q点的坐标.解答:解:(1)x2﹣(+1)x+=0,(x﹣)(x﹣1)=0,解得x1=,x2=1,∵OA<OB,∴OA=1,OB=,∴A(1,0),B(0,),∴AB=2,又∵AB:AC=1:2,∴AC=4,∴C(﹣3,0);(2)∵AB=2,AC=4,BC=2,∴AB2+BC2=AC2,即∠ABC=90°,由题意得:CM=t,CB=2.①当点M在CB边上时,S=2﹣t(0≤t);②当点M在CB边的延长线上时,S=t﹣2(t>2);(3)存在.①当AB是菱形的边时,如图所示,在菱形AP1Q1B中,Q1O=AO=1,所以Q1点的坐标为(﹣1,0),在菱形ABP2Q2中,AQ2=AB=2,所以Q2点的坐标为(1,2),在菱形ABP3Q3中,AQ3=AB=2,所以Q3点的坐标为(1,﹣2),②当AB为菱形的对角线时,如图所示的菱形AP4BQ4,设菱形的边长为x,则在Rt△AP4O中,AP42=AO2+P4O2,即x2=12+(﹣x)2,解得x=,所以Q4(1,).综上可得,平面内满足条件的Q点的坐标为:Q1(﹣1,0),Q2(1,﹣2),Q3(1,2),Q4(1,).点评:考查了一次函数综合题,涉及的知识点有:解一元二次方程,两点之间的距离公式,三角形面积的计算,函数思想,分类思想的运用,菱形的性质,综合性较强,有一定的难度.5.(2013春•屯留县期末)如图,四边形OABC是菱形,点C在x轴上,AB交y轴于点H,AC交y轴于点M.已知点A(﹣3,4).(1)求AO的长;(2)求直线AC的解析式和点M的坐标;(3)点P从点A出发,以每秒2个单位的速度沿折线A﹣B﹣C运动,到达点C终止.设点P的运动时间为t秒,△PMB 的面积为S.①求S与t的函数关系式;②求S的最大值.考点:一次函数综合题;解二元一次方程组;待定系数法求一次函数解析式;三角形的面积;角平分线的性质;勾股定理;菱形的性质.专题:计算题.分析:(1)根据A的坐标求出AH、OH,根据勾股定理求出即可;(2)根据菱形性质求出B、C的坐标,设直线AC的解析式是y=kx+b,把A(﹣3,4),C(5,0)代入得到方程组,求出即可;(3)①过M作MN⊥BC于N,根据角平分线性质求出MN,P在AB上,根据三角形面积公式求出即可;P 在BC上,根据三角形面积公式求出即可;②求出P在AB的最大值和P在BC上的最大值比较即可得到答案.解答:(1)解:∵A(﹣3,4),∴AH=3,OH=4,由勾股定理得:AO==5,答:OA的长是5.(2)解:∵菱形OABC,∴OA=OC=BC=AB=5,5﹣3=2,∴B(2,4),C(5,0),设直线AC的解析式是y=kx+b,把A(﹣3,4),C(5,0)代入得:,解得:,∴直线AC的解析式为,当x=0时,y=2.5∴M(0,2.5),答:直线AC的解析式是,点M的坐标是(0,2.5).(3)①解:过M作MN⊥BC于N,∵菱形OABC,∴∠BAC=∠OCA,∵MO⊥CO,MN⊥BC,∴OM=MN,当0≤t<2.5时,P在AB上,MH=4﹣2.5=,S=×BP×MH=×(5﹣2t)×=﹣t+,∴,当t=2.5时,P与B重合,△PMB不存在;当2.5<t≤5时,P在BC上,S=×PB×MN=×(2t﹣5)×=t﹣,∴,答:S与t的函数关系式是(0≤t<2.5)或(2.5<t≤5).②解:当P在AB上时,高MH一定,只有BP取最大值即可,即P与A重合,S最大是×5×=,同理在BC上时,P与C重合时,S最大是×5×=,∴S的最大值是,答:S的最大值是.点评:本题主要考查对勾股定理,三角形的面积,菱形的性质,角平分线性质,解二元一次方程组,用待定系数法求一次函数的解析式等知识点的理解和掌握,综合运用这些性质进行计算是解此题的关键.6.(2012•鞍山)如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标(3,3),将正方形ABCO绕点A顺时针旋转角度α(0°<α<90°),得到正方形ADEF,ED交线段OC于点G,ED的延长线交线段BC于点P,连AP、AG.(1)求证:△AOG≌△ADG;(2)求∠PAG的度数;并判断线段OG、PG、BP之间的数量关系,说明理由;(3)当∠1=∠2时,求直线PE的解析式.考点:一次函数综合题.专题:压轴题.分析:(1)由AO=AD,AG=AG,利用“HL”可证△AOG≌△ADG;(2)利用(1)的方法,同理可证△ADP≌△ABP,得出∠1=∠DAG,∠DAP=∠BAP,而∠1+∠DAG+∠DAP+∠BAP=90°,由此可求∠PAG的度数;根据两对全等三角形的性质,可得出线段OG、PG、BP之间的数量关系;(3)由△AOG≌△ADG可知,∠AGO=∠AGD,而∠1+∠AGO=90°,∠2+∠PGC=90°,当∠1=∠2时,可证∠AGO=∠AGD=∠PGC,而∠AGO+∠AGD+∠PGC=180°,得出∠AGO=∠AGD=∠PGC=60°,即∠1=∠2=30°,解直角三角形求OG,PC,确定P、G两点坐标,得出直线PE的解析式.解答:(1)证明:∵∠AOG=∠ADG=90°,∴在Rt△AOG和Rt△ADG中,∵,∴△AOG≌△ADG(HL);(2)解:PG=OG+BP.由(1)同理可证△ADP≌△ABP,则∠DAP=∠BAP,由(1)可知,∠1=∠DAG,又∠1+∠DAG+∠DAP+∠BAP=90°,所以,2∠DAG+2∠DAP=90°,即∠DAG+∠DAP=45°,故∠PAG=∠DAG+∠DAP=45°,∵△AOG≌△ADG,△ADP≌△ABP,∴DG=OG,DP=BP,∴PG=DG+DP=OG+BP;(3)解:∵△AOG≌△ADG,∴∠AGO=∠AGD,又∵∠1+∠AGO=90°,∠2+∠PGC=90°,∠1=∠2,∴∠AGO=∠AGD=∠PGC,又∵∠AGO+∠AGD+∠PGC=180°,∴∠AGO=∠AGD=∠PGC=60°,∴∠1=∠2=30°,在Rt△AOG中,AO=3,AG=2OG,AG2=AO2+OG2,∴OG=,则G点坐标为:(,0),CG=3﹣,在Rt△PCG中,PG=2CG=2(3﹣),PC==3﹣3,则P点坐标为:(3,3﹣3),设直线PE的解析式为y=kx+b,则,解得,所以,直线PE的解析式为y=x﹣3.点评:本题考查了一次函数的综合运用.关键是根据正方形的性质证明三角形全等,根据三角形全等的性质求角、边的关系,利用特殊角解直角三角形,求P、G两点坐标,确定直线解析式.7.(2012•桃源县校级自主招生)如图,点A在y轴上,点B在x轴上,且OA=OB=1,经过原点O的直线l交线段AB于点C,过C作OC的垂线,与直线x=1相交于点P,现将直线L绕O点旋转,使交点C从A向B运动,但C点必须在第一象限内,并记AC的长为t,分析此图后,对下列问题作出探究:(1)当△AOC和△BCP全等时,求出t的值;(2)通过动手测量线段OC和CP的长来判断它们之间的大小关系并证明你得到的结论;(3)①设点P的坐标为(1,b),试写出b关于t的函数关系式和变量t的取值范围.②求出当△PBC为等腰三角形时点P的坐标.考点:一次函数综合题.专题:压轴题;探究型.分析:(1)△AOC和△BCP全等,则AO=BC=1,又∵AB=,t=AB﹣BC=﹣1;(2)过点C作x轴的平行线,交OA与直线BP于点T、H,证△OTC≌△CHP即可;(3)根据题意可直接得出b=1﹣t;当t=0或1时,△PBC为等腰三角形,即P(1,1),P(1,1﹣),但t=0时,点C不在第一象限,所以不符合题意.解答:解:(1)△AOC和△BCP全等,则AO=BC=1,又AB=,所以t=AB﹣BC=﹣1;(2)OC=CP.证明:过点C作x轴的平行线,交OA与直线BP于点T、H.∵PC⊥OC,∴∠OCP=90°,∵OA=OB=1,∴∠OBA=45°,∵TH∥OB,∴∠BCH=45°,又∠CHB=90°,∴△CHB为等腰直角三角形,∴CH=BH,∵∠AOB=∠OBH=∠BHT=90°,∴四边形OBHT为矩形,∴OT=BH,∴OT=CH,∵∠TCO+∠PCH=90°,∠CPH+∠PCH=90°,∴∠TCO=∠CPH,∵HB⊥x轴,TH∥OB,∴∠CTO=∠THB=90°,TO=HC,∠TCO=∠CPH,∴△OTC≌△CHP,∴OC=CP;(3)①∵△OTC≌△CHP,∴CT=PH,∴PH=CT=AT=AC•cos45°=t,∴BH=OT=OA﹣AT=1﹣t,∴BP=BH﹣PH=1﹣t,∴;(0<t<)②t=0时,△PBC是等腰直角三角形,但点C与点A重合,不在第一象限,所以不符合,PB=BC,则﹣t=|1﹣t|,解得t=1或t=﹣1(舍去),∴当t=1时,△PBC为等腰三角形,即P点坐标为:P(1,1﹣).点评:主要考查了函数和几何图形的综合运用.解题的关键是会灵活的运用函数的性质和点的意义表示出相应的线段的长度,再结合三角形全等和等腰三角形的性质求解.试题中贯穿了方程思想和数形结合的思想,请注意体会.8.(2012秋•海陵区期末)如图1,在平面直角坐标系中,直线AB与x轴交于点A,与y轴交于点B,与直线OC交于点C.(1)若直线AB解析式为y=﹣2x+12,直线OC解析式为y=x,①求点C的坐标;②求△OAC的面积.(2)如图2,作∠AOC的平分线ON,若AB⊥ON,垂足为E,△OAC的面积为6,且OA=4,P、Q分别为线段OA、OE上的动点,连接AQ与PQ,试探索AQ+PQ是否存在最小值?若存在,求出这个最小值;若不存在,说明理由.考点:一次函数综合题.专题:综合题;数形结合.分析:(1)①联立两个函数式,求解即可得出交点坐标,即为点C的坐标.②欲求△OAC的面积,结合图形,可知,只要得出点A和点C的坐标即可,点C的坐标已知,利用函数关系式即可求得点A的坐标,代入面积公式即可.(2)在OC上取点M,使OM=OP,连接MQ,易证△POQ≌△MOQ,可推出AQ+PQ=AQ+MQ;若想使得AQ+PQ存在最小值,即使得A、Q、M三点共线,又AB⊥OP,可得∠AEO=∠CEO,即证△AEO≌△CEO(ASA),又OC=OA=4,利用△OAC的面积为6,即可得出AM=3,AQ+PQ存在最小值,最小值为3.解答:解:(1)①由题意,(2分)解得所以C(4,4)(3分)②把y=0代入y=﹣2x+12得,x=6,所以A点坐标为(6,0),(4分)所以.(6分)(2)存在;由题意,在OC上截取OM=OP,连接MQ,∵OQ平分∠AOC,∴∠AOQ=∠COQ,又OQ=OQ,∴△POQ≌△MOQ(SAS),(7分)∴PQ=MQ,∴AQ+PQ=AQ+MQ,当A、Q、M在同一直线上,且AM⊥OC时,AQ+MQ最小.即AQ+PQ存在最小值.∵AB⊥ON,所以∠AEO=∠CEO,∴△AEO≌△CEO(ASA),∴OC=OA=4,∵△OAC的面积为6,所以AM=12÷4=3,∴AQ+PQ存在最小值,最小值为3.(9分)点评:本题主要考查一次函数的综合应用,具有一定的综合性,要求学生具备一定的数学解题能力,有一定难度.9.(2012秋•成都校级期末)如图,在平面直角坐标系xOy中,已知直线PA是一次函数y=x+m(m>0)的图象,直线PB是一次函数y=﹣3x+n(n>m)的图象,点P是两直线的交点,点A、B、C、Q分别是两条直线与坐标轴的交点.(1)用m、n分别表示点A、B、P的坐标及∠PAB的度数;(2)若四边形PQOB的面积是,且CQ:AO=1:2,试求点P的坐标,并求出直线PA与PB的函数表达式;(3)在(2)的条件下,是否存在一点D,使以A、B、P、D为顶点的四边形是平行四边形?若存在,求出点D的坐标;若不存在,请说明理由.考点:一次函数综合题.专题:开放型.分析:(1)已知直线解析式,令y=0,求出x的值,可求出点A,B的坐标.联立方程组求出点P的坐标.推出AO=QO,可得出∠PAB=45°.(2)先根据CQ:AO=1:2得到m、n的关系,然后求出S△AOQ,S△PAB并都用字母m表示,根据S四边形PQOB=S△PAB ﹣S△AOQ积列式求解即可求出m的值,从而也可求出n的值,继而可推出点P的坐标以及直线PA与PB的函数表达式.(3)本题要依靠辅助线的帮助.求证相关图形为平行四边形,继而求出D1,D2,D3的坐标.解答:解:(1)在直线y=x+m中,令y=0,得x=﹣m.∴点A(﹣m,0).在直线y=﹣3x+n中,令y=0,得.∴点B(,0).由,得,∴点P(,).在直线y=x+m中,令x=0,得y=m,∴|﹣m|=|m|,即有AO=QO.又∵∠AOQ=90°,∴△AOQ是等腰直角三角形,∴∠PAB=45°.(2)∵CQ:AO=1:2,∴(n﹣m):m=1:2,整理得3m=2n,∴n=m,∴==m,而S四边形PQOB=S△PAB﹣S△AOQ=(+m)×(m)﹣×m×m=m2=,解得m=±4,∵m>0,∴m=4,∴n=m=6,∴P().∴PA的函数表达式为y=x+4,PB的函数表达式为y=﹣3x+6.(3)存在.过点P作直线PM平行于x轴,过点B作AP的平行线交PM于点D1,过点A作BP的平行线交PM于点D2,过点A、B分别作BP、AP的平行线交于点D3.①∵PD1∥AB且BD1∥AP,∴PABD1是平行四边形.此时PD1=AB,易得;②∵PD2∥AB且AD2∥BP,∴PBAD2是平行四边形.此时PD2=AB,易得;③∵BD3∥AP且AD3∥BP,此时BPAD3是平行四边形.∵BD3∥AP且B(2,O),∴y BD3=x﹣2.同理可得y AD3=﹣3x﹣12,得,∴.点评:本题的综合性强,主要考查的知识点为一次函数的应用,平行四边形的判定以及面积的灵活计算.难度较大.10.(2012秋•綦江县校级期末)如图,一次函数的函数图象与x轴、y轴分别交于点A、B,以线段AB 为直角边在第一象限内作Rt△ABC,且使∠ABC=30°.(1)求△ABC的面积;(2)如果在第二象限内有一点P(m,),试用含m的代数式表示△APB的面积,并求当△APB与△ABC面积相等时m的值;(3)是否存在使△QAB是等腰三角形并且在坐标轴上的点Q?若存在,请写出点Q所有可能的坐标;若不存在,请说明理由.考点:一次函数综合题.专题:综合题.分析:(1)先求出A、B两点的坐标,再由一个角等于30°,求出AC的长,从而计算出面积;(2)过P作PD⊥x轴,垂足为D,先求出梯形ODPB的面积和△AOB的面积之和,再减去△APD的面积,即是△APB的面积;根据△APB与△ABC面积相等,求得m的值;(3)假设存在点Q,使△QAB是等腰三角形,求出Q点的坐标即可.解答:解:(1)∵一次函数的解析式为函数图象与x轴、y轴分别交于点A、B,∴A(1,0),B(0,),∴AB=2,设AC=x,则BC=2x,由勾股定理得,4x2﹣x2=4,解得x=,S△ABC==;(2)过P作PD⊥x轴,垂足为D,S△APB=S梯形ODPB+S△AOB﹣S△APD==,﹣=,解得m=;(3)∵AB==2,∴当AQ=AB时,点Q1(3,0),Q2(﹣1,0),Q3(0,﹣);当AB=BQ时,点Q4(0,+2),Q2(0,﹣2),Q2(﹣1,0);当AQ=BQ时,点Q6(0,),Q2(﹣1,0),综上可得:(0,),(0,),(﹣1,0)(3,0),(0,),(0,)点评:此题主要考查平面直角坐标系中图形的面积的求法.解答此题的关键是根据一次函数的特点,分别求出各点的坐标再计算.。
2024年中考数学复习重难点题型训练—一次函数与几何图形综合题一(含答案解析)

2024年中考数学复习重难点题型训练—一次函数与几何图形综合题二(含答案解析)类型一与三角形有关1.(2022·天津)如图,△OAB的顶点O(0,0),顶点A,B分别在第一、四象限,且AB⊥x 轴,若AB=6,OA=OB=5,则点A的坐标是()A.(5,4)B.(3,4)C.(5,3)D.(4,3)【答案】D【分析】利用HL证明△ACO≌△BCO,利用勾股定理得到OC=4,即可求解.【详解】解:∵AB⊥x轴,∴∠ACO=∠BCO=90°,∵OA=OB,OC=OC,∴△ACO≌△BCO(HL),∴AC=BC=12AB=3,∵OA=5,∴=4,∴点A的坐标是(4,3),故选:D.【点睛】本题考查了坐标与图形,全等三角形的判定和性质,勾股定理,解题的关键是灵活运用所学知识解决问题.2.(2020·宁夏中考真题)如图,直线542y x =+与x 轴、y 轴分别交于A 、B 两点,把AOB 绕点B 逆时针旋转90°后得到11AO B ,则点1A的坐标是_____.【答案】(4,125)【解析】【分析】首先根据直线AB 来求出点A 和点B 的坐标,A 1的横坐标等于OB ,而纵坐标等于OB-OA ,即可得出答案.【详解】解:在542y x =+中,令x=0得,y=4,令y=0,得5042x =+,解得x=8-5,∴A (8-5,0),B (0,4),由旋转可得△AOB ≌△A 1O 1B ,∠ABA 1=90°,∴∠ABO=∠A 1BO 1,∠BO 1A 1=∠AOB=90°,OA=O 1A 1=85,OB=O 1B=4,∴∠OBO 1=90°,∴O 1B ∥x 轴,∴点A 1的纵坐标为OB-OA 的长,即为48-5=125;横坐标为O 1B=OB=4,故点A 1的坐标是(4,125),故答案为:(4,125).【点睛】本题主要考查了旋转的性质以及一次函数与坐标轴的交点问题,利用基本性质结合图形进行推理是解题的关键.3.(2021·广西贺州市·中考真题)如图,一次函数4y x =+与坐标轴分别交于A ,B 两点,点P ,C 分别是线段AB ,OB 上的点,且45OPC ∠=︒,PC PO =,则点P 的标为________.【答案】(--【分析】过P 作PD ⊥OC 于D ,先求出A ,B 的坐标,得∠ABO=∠OAB=45°,再证明△PCB ≌△OPA ,从而求出BD =,OD =,进而即可求解.【详解】如图所示,过P 作PD ⊥OC 于D ,∵一次函数4y x =+与坐标轴分别交于A ,B 两点,∴A(-4,0),B(0,4),即:OA=OB ,∴∠ABO=∠OAB=45°,∴△BDP 是等腰直角三角形,∵∠PBC=∠CPO=∠OAP=45°,∴∠PCB+∠BPC=135°=∠OPA+∠BPC,∴∠PCB=∠OPA,又∵PC=OP,∴△PCB≌△OPA(AAS),∴AO=BP=4,∴Rt△BDP中,BD=PD=2=2,∴OD=OB−BD=2,∴P(2,2).故答案是:P(2,2).【点睛】本题主要考查了一次函数图象上点的坐标特征以及等腰三角形的性质,结合等腰三角形的性质,判定全等三角形是解决问题的关键.4.(2022·湖北黄冈)如图1,在△ABC中,∠B=36°,动点P从点A出发,沿折线A→B→C 匀速运动至点C停止.若点P的运动速度为1cm/s,设点P的运动时间为t(s),AP的长度为y(cm),y与t的函数图象如图2所示.当AP恰好平分∠BAC时,t的值为________.【答案】252+##2+25【分析】根据函数图像可得AB=4=BC ,作∠BAC 的平分线AD ,∠B =36°可得∠B =∠DAC =36°,进而得到ADC BAC △△,由相似求出BD 的长即可.【详解】根据函数图像可得AB=4,AB+BC=8,∴BC=AB=4,∵∠B =36°,∴72BCA BAC ∠∠︒==,作∠BAC 的平分线AD ,∴∠BAD =∠DAC =36°=∠B ,∴AD=BD ,72BCA DAC ∠∠︒==,∴AD=BD=CD ,设AD BD CD x ===,∵∠DAC =∠B =36°,∴ADC BAC △△,∴AC DC BC AC =,∴x 4x 4x-=,解得:1225x =-+,225x =--,∴252AD BD CD ===,此时521AB BD t +==(s),故答案为:52.【点睛】此题考查了图形与函数图象间关系、相似三角形的判定与性质、解一元二次方程,关键是证明ADC BAC △△.5.(2020·四川内江?中考真题)如图,在平面直角坐标系中,点A (-2,0),直线33:33l y x =+与x 轴交于点B ,以AB 为边作等边1ABA ∆,过点1A 作11//A B x 轴,交直线l 于点1B ,以11A B 为边作等边112A B A ∆,过点2A 作22//A B x 轴,交直线l 于点2B ,以22A B 为边作等边223A B A ∆,以此类推……,则点2020A 的纵坐标是______________【答案】20203(21)2-【解析】【分析】如图,过A 1作A 1C ⊥AB 与C ,过A 2作A 2C 1⊥A 1B 1于C 1,过A 3作A 3C 2⊥A 2B 2于C 2,先根据直线方程与x 轴交于点B (-1,0),且与x 轴夹角为30º,则有AB=1,然后根据平行线的性质、等边三角形的性质、含30º的直角三角形的性质,分别求的A 1、A 2、A 3、的纵坐标,进而得到A n 的纵坐标,据此可得A 2020的纵坐标,即可解答.【详解】如图,过A 1作A 1C ⊥AB 与C ,过A 2作A 2C 1⊥A 1B 1于C 1,过A 3作A 3C 2⊥A 2B 2于C 2,先根据直线方程与x 轴交于点B (-1,0),与y 轴交于点D (0,33),∴OB=1,OD=33,∴∠DBO=30º由题意可得:∠A 1B 1B=∠A 2B 2B 1=30º,∠B 1A 1B=∠B 2A 2B 1=60º∴∠A 1BB 1=∠A 2B 1B 2=90º,∴AB=1,A 1B 1=2A 1B=21,A 2B 2=2A 2B 1=22,A 3B 3=2A 3B 2=23,…A n B n =2n∴A 1C=2AB=2×1,A 1纵坐标为32×1=13(21)2-;A 2C 1=32A 1B 1=1322⨯,A2的纵坐标为32×1+1322⨯=013(22)2+=332⨯=23(21)2-;A 3C 2=32A 2B 2=2322⨯,A 3的纵坐标为32×1+1322⨯+2322⨯=0123(222)2++=372⨯=33(21)2-;…由此规律可得:A n C n-1=1322n -⨯,A n 的纵坐标为01213(2222)2n -++++ =3(21)2n -,∴A 2020=20203(21)2-,故答案为:20203(21)2-【点睛】本题是一道点的坐标变化规律探究,涉及一次函数的图象、等边三角形的性质、含30º角的直角三角形的性质,数字型规律等知识,解答的关键是认真审题,观察图象,结合基本图形的有关性质,找到坐标变化规律.6.(2022·陕西)如图,ABC 的顶点坐标分别为(23)(30)(11)A B C ----,,,,,.将ABC 平移后得到A B C '''V ,且点A 的对应点是(23)A ',,点B 、C 的对应点分别是B C '',.(1)点A 、A '之间的距离是__________;(2)请在图中画出A B C '''V .【答案】(1)4(2)见解析【分析】(1)由(23)A -,,(23)A ',得,A 、A '之间的距离是2-(-2)=4;(2)根据题意找出平移规律,求出103-1B C ''(,),(,),进而画图即可.(1)解:由(23)A -,,(23)A ',得,A 、A '之间的距离是2-(-2)=4.故答案为:4.(2)解:由题意,得103-1B C ''(,),(,),如图,A B C '''V 即为所求.【点睛】本题考查了坐标系中两点之间的距离求解以及平移求点坐标画图,题目相对较简单,掌握平移规律是解决问题的关键.7.(2021·贵州毕节市·中考真题)如图,在平面直角坐标系中,点()11,1N 在直线:l y x =上,过点1N 作11N M l ⊥,交x 轴于点1M ;过点1M 作12M N x ⊥轴,交直线l 于点2N ;过点2N 作22N M l ⊥,交x 轴于点2M ;过点2M 作23M N x ⊥轴,交直线l 于点3N ;…;按此作法进行下去,则点2021M 的坐标为_____________.【答案】(20212,0).【分析】根据题目所给的解析式,求出对应的1M 坐标,然后根据规律求出n M 的坐标,最后根据题目要求求出最后答案即可.【详解】解:如图,过点N 作NM ⊥x 轴于M将1x =代入直线解析式y x =中得1y =∴1OM MN ==,MON ∠=45°∵1ONM =∠90°∴1ON NM =∵1ON NM ⊥∴11OM MM ==∴1M 的坐标为(2,0)同理可以求出2M 的坐标为(4,0)同理可以求出3M 的坐标为(8,0)同理可以求出n M 的坐标为(2n ,0)∴2021M 的坐标为(20212,0)故答案为:(20212,0).【点睛】本题主要考查了直线与坐标轴之间的关系,解题的关键在于能够发现规律.8.(2020·湖南湘西?中考真题)在平面直角坐标系中,O 为原点,点(6,0)A ,点B 在y 轴的正半轴上,30ABO ∠=︒.矩形CODE 的顶点D ,E ,C 分别在,,OA AB OB 上,2OD =.将矩形CODE 沿x 轴向右平移,当矩形CODE 与ABO 重叠部分的面积为时,则矩形CODE 向右平移的距离为___________.【答案】2【解析】【分析】先求出点B 的坐标(0,3),得到直线AB 的解析式为:33y =+,根据点D 的坐标求出OC 的长度,利用矩形CODE 与ABO 重叠部分的面积为63列出关系式求出3D G '=,再利用一次函数关系式求出OD '=4,即可得到平移的距离.【详解】∵(6,0)A ,∴OA=6,在Rt △AOB 中,30ABO ∠=︒,∴63tan 30OA OB ==∴B (0,63),∴直线AB 的解析式为:33y =+,当x=2时,y=43∴E (2,3,即DE=3∵四边形CODE 是矩形,∴OC=DE=43设矩形CODE 沿x 轴向右平移后得到矩形C O D E '''',D E ''交AB 于点G ,∴D E ''∥OB ,∴△AD G '∽△AOB ,∴∠AGD '=∠AOB=30°,∴∠EGE '=∠AGD '=30°,∴GE ''=,∵平移后的矩形CODE 与ABO 重叠部分的面积为,∴五边形C O D GE '''的面积为∴12O D O C EE GE ''''''⋅-⋅=,∴122EE ''⨯-⨯=,∴2EE '=,∴矩形CODE 向右平移的距离DD '=2EE '=,故答案为:2.【点睛】此题考查了锐角三角函数,求一次函数的解析式,矩形的性质,图形平移的性质,是一道综合多个知识点的综合题型,且较为基础的题型.9.(2021·浙江金华市·中考真题)在平面直角坐标系中,点A 的坐标为(,点B 在直线8:3l y x =上,过点B 作AB 的垂线,过原点O 作直线l 的垂线,两垂线相交于点C .(1)如图,点B ,C 分别在第三、二象限内,BC 与AO 相交于点D .①若BA BO =,求证:CD CO =.②若45CBO ∠=︒,求四边形ABOC 的面积.(2)是否存在点B ,使得以,,A B C 为顶点的三角形与BCO 相似?若存在,求OB 的长;若不存在,请说明理由.【答案】(1)①见解析;②552;(2)存在,44+-4,9,1【分析】(1)①等腰三角形等角对等边,则BAD AOB ∠=∠,根据等角的余角相等和对顶角相等,得到CDO COD ∠=∠,根据等角对等边,即可证明CD CO =;②添加辅助线,过点A 作AH OB ⊥于点H ,根据直线l 的解析式和角的关系,分别求出线段AB 、BC 、OB 、OC 的长,则11+22ABC CBO ABOC S S S AB BC OB OC =+=⨯⨯ 四边形;(2)分多钟情况进行讨论:①当点C 在第二象限内,ACB CBO ∠=∠时;②当点C 在第二象限内,ACB BCO ∠=∠时;③当点C 在第四象限内,ACB CBO ∠=∠时.【详解】解:(1)①证明:如图1,∵BA BO =,∴12∠=∠.∴BA BC ⊥,∴2590∠+∠=︒.而45∠=∠,∴2490∠+∠=︒.∵OB OC ⊥,∴1390∠+∠=︒.∴34∠=∠,∴CD CO =.②如图1,过点A 作AH OB ⊥于点H .由题意可知3tan 18∠=,在Rt AHO 中,3tan 18AH OH ∠==.设3m AH =,8m OH =.∵222AH OH OA +=,∴()()22238m m +=,解得1m =.∴38AH OH ==,.∵4590CBO ABC ∠=︒∠=︒,,∴45ABH ∠=︒,∴3,tan 45sin 45AH AH BH AB ====︒︒∴5OB OH BH =-=.∵45OB OC CBO ⊥∠=︒,,∴tan 455,cos 45OB OC OB BC =⨯︒===︒,∴111522ABC S AB BC =⨯=⨯= ,112555222CBO S OB OC =⨯=⨯⨯= :∴552ABC CBO ABOC S S S =+= 四边形.(2)过点A 作AH OB ⊥于点H ,则有38AH OH ==,.①如图2,当点C 在第二象限内,ACB CBO ∠=∠时,设OB t=∵ACB CBO ∠=∠,∴//AC OB .又∵AH OB OC OB ⊥⊥,,∴3AH OC ==.∵AH OB AB BC ⊥⊥,,∴12902390∠+∠=︒∠+∠=︒,,∴13∠=∠,∴AHB BOC ∽,∴AH HB BO OC=,∴383t t -=,整理得2890t t -+=,解得4t =±∴4OB =±②如图3,当点C 在第二象限内,ACB BCO ∠=∠时,延长AB CO ,交于点G ,则ACB GCB ≌,∴AB GB =.又∵AH OB OC OB ⊥⊥,,∴90AHB GOB ∠=∠=︒,而ABH GBO ∠=∠,∴ABH GBO ≌,∴142OB HB OH ===③当点C 在第四象限内,ACB CBO ∠=∠时,AC 与OB 相交于点E ,则有BE CE =.(a)如图4,点B 在第三象限内.在Rt ABC 中,1290,90ACB CAB ∠+∠=︒∠+∠=︒,∴2CAB∠=∠∴AE BE CE ==,又∵,AH OB OC OB ⊥⊥,∴90AHE COE ∠=∠=︒,而AEH CEO∠=∠∴AHE COE ≌,∴142HE OE OH ===∴225AE AH HE =+=,∴5BE =,∴9OB BE OE =+=(b)如图5,点B 在第一象限内.在Rt ABC 中90,90ACB CAB CBO ABE ∠+∠=︒∠+∠=︒∴CAB ABE ∠=∠,∴AE BE CE ==.又∵,AH OB OC OB ⊥⊥,∴90AHE COE ∠=∠=︒而AEH CEO ∠=∠,∴AHE COE≌∴142HE OE OH ===∴5AE ==,∴5BE =,∴1OB BE OE =-=综上所述,OB 的长为44+4,9,1.【点睛】本题涉及到等腰三角形、等角的余角相等、利用切割法求四边形的面积和相似三角形等知识,综合性较强.在题中已知两个三角形相似时,要分情况考虑.10.(2020·河南中考真题)小亮在学习中遇到这样一个问题:如图,点D 是弧BC 上一动点,线段8,BC cm =点A 是线段BC 的中点,过点C 作//CF BD ,交DA 的延长线于点F .当DCF ∆为等腰三角形时,求线段BD 的长度.小亮分析发现,此问题很难通过常规的推理计算彻底解决,于是尝试结合学习函数的经验研究此问题,请将下面的探究过程补充完整:()1根据点D 在弧BC 上的不同位置,画出相应的图形,测量线段,,BD CD FD 的长度,得到下表的几组对应值.操作中发现:①"当点D 为弧BC 的中点时, 5.0BD cm =".则上中a 的值是②"线段CF 的长度无需测量即可得到".请简要说明理由;()2将线段BD 的长度作为自变量x CD ,和FD 的长度都是x 的函数,分别记为CD y 和FD y ,并在平面直角坐标系xOy 中画出了函数FD y 的图象,如图所示.请在同一坐标系中画出函数CD y 的图象;()3继续在同一坐标系中画出所需的函数图象,并结合图象直接写出:当DCF ∆为等腰三角形时,线段BD 长度的近似值.(结果保留一位小数).【答案】(1)①5.0;②见解析;(2)图象见解析;(3)图象见解析;3.5cm 或5.0cm 或6.3cm ;【解析】【分析】(1)①点D 为弧BC 的中点时,△ABD ≌△ACD ,即可得到CD=BD ;②由题意得△ACF ≌△ABD ,即可得到CF=BD ;(2)根据表格数据运用描点法即可画出函数图象;(3)画出CF y 的图象,当DCF ∆为等腰三角形时,分情况讨论,任意两边分别相等时,即任意两个函数图象相交时的交点横坐标即为BD 的近似值.【详解】解:(1)①点D 为弧BC 的中点时,由圆的性质可得:AB AC BAD CAD AD AD =⎧⎪∠=∠⎨⎪=⎩,∴△ABD ≌△ACD ,∴CD=BD=5.0,∴ 5.0a =;②∵//CF BD ,∴BDA CFA ∠=∠,∵BDA CFA BAD CAF AD AF ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ACF ≌△ABD ,∴CF=BD ,∴线段CF 的长度无需测量即可得到;(2)函数CD y的图象如图所示:(3)由(1)知=CF BD x =,画出CF y 的图象,如上图所示,当DCF ∆为等腰三角形时,①CF CD =,BD 为CF y 与CD y 函数图象的交点横坐标,即BD=5.0cm ;②CF DF =,BD 为CF y 与DF y 函数图象的交点横坐标,即BD=6.3cm ;③CD DF =,BD 为CD y 与DF y 函数图象的交点横坐标,即BD=3.5cm ;综上:当DCF ∆为等腰三角形时,线段BD 长度的近似值为3.5cm 或5.0cm 或6.3cm .【点睛】本题考查一次函数结合几何的应用,学会用描点法画出函数图象,熟练掌握一次函数的性质以及三角形全等的判定及性质是解题的关键.11.(2020·河北中考真题)如图1和图2,在ABC ∆中,AB AC =,8BC =,3tan 4C =.点K 在AC 边上,点M ,N 分别在AB ,BC 上,且2AM CN ==.点P 从点M 出发沿折线MB BN-匀速移动,到达点N时停止;而点Q在AC边上随P移动,且始终保持APQ B∠=∠.(1)当点P在BC上时,求点P与点A的最短距离;(2)若点P在MB上,且PQ将ABC∆的面积分成上下4:5两部分时,求MP的长;(3)设点P移动的路程为x,当03x≤≤及39x≤≤时,分别求点P到直线AC的距离(用含x的式子表示);(4)在点P处设计并安装一扫描器,按定角APQ∠扫描APQ∆区域(含边界),扫描器随点P从M到B再到N共用时36秒.若94AK=,请直接..写出点K被扫描到的总时长.【答案】(1)3;(2)43MP=;(3)当03x≤≤时,24482525d x=+;当39x≤≤时,33355d x=-+;(4)23t s=【解析】【分析】(1)根据当点P在BC上时,PA⊥BC时PA最小,即可求出答案;(2)过A点向BC边作垂线,交BC于点E,证明△APQ∽△ABC,可得2APQABCS APS AB∆∆⎛⎫= ⎪⎝⎭,根据SS上下=45可得24=9APQABCS APS AB∆∆⎛⎫= ⎪⎝⎭,可得23APAB=,求出AB=5,即可解出MP;(3)先讨论当0≤x≤3时,P在BM上运动,P到AC的距离:d=PQ·sinC,求解即可,再讨论当3≤x≤9时,P在BN上运动,BP=x-3,CP=8-(x-3)=11-x,根据d=CP·sinC即可得出答案;(4)先求出移动的速度=936=14,然后先求出从Q 平移到K 耗时,再求出不能被扫描的时间段即可求出时间.【详解】(1)当点P 在BC 上时,PA ⊥BC 时PA 最小,∵AB=AC ,△ABC 为等腰三角形,∴PA min =tanC·2BC =34×4=3;(2)过A 点向BC 边作垂线,交BC 于点E,S 上=S △APQ ,S 下=S 四边形BPQC ,∵APQ B ∠=∠,∴PQ ∥BC ,∴△APQ ∽△ABC ,∴AP AD PQ AB AC BC==,∴2APQABC S AP S AB ∆∆⎛⎫= ⎪⎝⎭,当S S 上下=45时,24=9APQ ABC S AP S AB ∆∆⎛⎫= ⎪⎝⎭,∴23AP AB =,AE=2BC ·tan 3C =,根据勾股定理可得AB=5,∴2253AP MP AB +==,解得MP=43;(3)当0≤x≤3时,P 在BM 上运动,P 到AC 的距离:d=PQ·sinC ,由(2)可知sinC=35,∴d=35PQ ,∵AP=x+2,∴25AP x PQ AB BC+==,∴PQ=285x +⨯,∴d=23855x +⨯⨯=24482525x +,当3≤x≤9时,P 在BN 上运动,BP=x-3,CP=8-(x-3)=11-x ,d=CP·sinC=35(11-x )=-35x+335,综上()()24480325253333955x x d x x ⎧+≤≤⎪⎪=⎨⎪-+≤≤⎪⎩;(4)AM=2<AQ=94,移动的速度=936=14,①从Q 平移到K ,耗时:92414-=1秒,②P 在BC 上时,K 与Q 重合时CQ=CK=5-94=114,∵∠APQ+∠QPC=∠B+∠BAP ,APQ B∠=∠∴∠QPC=∠BAP ,又∵∠B=∠C ,∴△ABP ∽△PCQ ,设BP=y ,CP=8-y ,AB BP PC CQ =,即51184y y =-,整理得y 2-8y=554-,(y-4)2=94,解得y 1=52,y 2=112,52÷14=10秒,112÷14=22秒,∴点K 被扫描到的总时长36-(22-10)-1=23秒.【点睛】本题考查了相似三角形的判定和性质,锐角三角函数,一次函数的应用,结合知识点灵活运用是解题关键.12.(2020·湖南衡阳?中考真题)如图1,平面直角坐标系xOy 中,等腰ABC ∆的底边BC 在x 轴上,8BC =,顶点A 在y 的正半轴上,2OA =,一动点E 从(3,0)出发,以每秒1个单位的速度沿CB 向左运动,到达OB 的中点停止.另一动点F 从点C 出发,以相同的速度沿CB 向左运动,到达点O 停止.已知点E 、F 同时出发,以EF 为边作正方形EFGH ,使正方形EFGH 和ABC ∆在BC 的同侧.设运动的时间为t 秒(0t ≥).(1)当点H 落在AC 边上时,求t 的值;(2)设正方形EFGH 与ABC ∆重叠面积为S ,请问是存在t 值,使得9136S =若存在,求出t 值;若不存在,请说明理由;(3)如图2,取AC 的中点D ,连结OD ,当点E 、F 开始运动时,点M 从点O 出发,以每秒OD DC CD DO ---运动,到达点O 停止运动.请问在点E 的整个运动过程中,点M 可能在正方形EFGH 内(含边界)吗?如果可能,求出点M 在正方形EFGH 内(含边界)的时长;若不可能,请说明理由.【答案】(1)t=1;(2)存在,143t =,理由见解析;(3)可能,3455t ≤≤或4533t ≤≤或35t ≤≤理由见解析【解析】【分析】(1)用待定系数法求出直线AC 的解析式,根据题意用t 表示出点H 的坐标,代入求解即可;(2)根据已知,当点F 运动到点O 停止运动前,重叠最大面积是边长为1的正方形的面积,即不存在t ,使重叠面积为9136S =,故t ﹥4,用待定系数法求出直线AB 的解析式,求出点H 落在BC 边上时的t 值,求出此时重叠面积为169﹤9136,进一步求出重叠面积关于t 的表达式,代入解t 的方程即可解得t 值;(3)由已知求得点D (2,1),AC=,结合图形分情况讨论即可得出符合条件的时长.【详解】(1)由题意,A(0,2),B(-4,0),C(4,0),设直线AC 的函数解析式为y=kx+b ,将点A 、C 坐标代入,得:402k b b +=⎧⎨=⎩,解得:122k b ⎧=-⎪⎨⎪=⎩,∴直线AC 的函数解析式为122y x =-+,当点H 落在AC 边上时,点E(3-t ,0),点H (3-t ,1),将点H 代入122y x =-+,得:11(3)22t =--+,解得:t=1;(2)存在,143t =,使得9136S =.根据已知,当点F 运动到点O 停止运动前,重叠最大面积是边长为1的正方形的面积,即不存在t ,使重叠面积为9136S =,故t ﹥4,设直线AB 的函数解析式为y=mx+n ,将点A 、B 坐标代入,得:402m n n -+=⎧⎨=⎩,解得:122m n ⎧=⎪⎨⎪=⎩,∴直线AC 的函数解析式为122y x =+,当t ﹥4时,点E (3-t ,0)点H (3-t ,t-3),G(0,t-3),当点H 落在AB 边上时,将点H 代入122y x =+,得:13(3)22t t -=-+,解得:133t =;此时重叠的面积为221316(3)(3)39t -=-=,∵169﹤9136,∴133﹤t ﹤5,如图1,设GH 交AB 于S ,EH 交AB 于T,将y=t-3代入122y x =+得:1322t x -=+,解得:x=2t-10,∴点S(2t-10,t-3),将x=3-t 代入122y x =+得:11(3)2(7)22y t t =-+=-,∴点T 1(3,(7))2t t --,∴AG=5-t ,SG=10-2t ,BE=7-t ,ET=1(7)2t -,211(7)24BET S BE ET t ∆==- ,21(5)2ASG S AG SG t ∆==- 所以重叠面积S=AOB BET ASG S S S ∆∆∆--=4-21(7)4t --2(5)t -=2527133424t t -+-,由2527133424t t -+-=9136得:1143t =,29215t =﹥5(舍去),∴143t =;(3)可能,35≤t≤1或t=4.∵点D 为AC 的中点,且OA=2,OC=4,∴点D (2,1),AC=,易知M 点在水平方向以每秒是4个单位的速度运动;当0﹤t ﹤12时,M 在线段OD 上,H 未到达D 点,所以M 与正方形不相遇;当12﹤t ﹤1时,12+12÷(1+4)=35秒,∴t =35时M 与正方形相遇,经过1÷(1+4)=15秒后,M 点不在正方行内部,则3455t ≤≤;当t=1时,由(1)知,点F 运动到原E 点处,M 点到达C 处;当1≤t≤2时,当t=1+1÷(4-1)=43秒时,点M 追上G 点,经过1÷(4-1)=13秒,点M 都在正方形EFGH 内(含边界),4533t ≤≤当t=2时,点M 运动返回到点O 处停止运动,当t=3时,点E 运动返回到点O 处,当t=4时,点F 运动返回到点O 处,当35t ≤≤时,点M 都在正方形EFGH 内(含边界),综上,当3455t ≤≤或4533t ≤≤或35t ≤≤时,点M 可能在正方形EFGH 内(含边界).【点睛】本题考查了一次函数与几何图形的综合,涉及求一次函数的解析式、正方形的性质、直角三角形的性质、不规则图形的面积、解一元二次方程等知识,解答的关键是认真审题,提取相关信息,利用待定系数法、数形结合法等解题方法确定解题思路,进而推理、探究、发现和计算.13.(2020·黑龙江哈尔滨?中考真题)已知,在平面直角坐标系中,点O 为坐标原点,直线AB 与x 轴的正半轴交于点A ,与y 轴的负半轴交于点B ,OA OB =,过点A 作x 轴的垂线与过点O 的直线相交于点C ,直线OC 的解析式为34y x =,过点C 作CM y ⊥轴,垂足为,9M OM =.(1)如图1,求直线AB 的解析式;(2)如图2,点N 在线段MC 上,连接ON ,点P 在线段ON 上,过P 点作PD x ⊥轴,垂足为D ,交OC 于点E ,若NC OM =,求PE OD的值;(3)如图3,在(2)的条件下,点F 为线段AB 上一点,连接OF ,过点F 作OF 的垂线交线段AC 于点Q ,连接BQ ,过点F 作x 轴的平行线交BQ 于点G ,连接PF 交x 轴于点H ,连接EH ,若,DHE DPH GQ FG ∠=∠-=,求点P 的坐标.【答案】(1)12y x =-;(2)94;(3)1236(,)55P .【解析】【分析】(1)根据题意求出A ,B 的坐标即可求出直线AB 的解析式;(2)求出N (3,9),以及ON 的解析式为y=3x ,设P (a ,3a ),表达出PE 及OD 即可解答;(3)如图,设直线GF 交CA 延长线于点R ,交y 轴于点S ,过点F 作FT ⊥x 轴于点T ,先证明四边形OSRA 为矩形,再通过边角关系证明△OFS ≌△FQR ,得到SF=QR ,进而证明△BSG ≌△QRG ,得到SG=RG=6,设FR=m ,根据GQ FG -=,以及在Rt △GQR 中利用勾股定理求出m 的值,得到FS=8,AR=4,证明四边形OSFT 为矩形,得到OT=FS=8,根据∠DHE=∠DPH ,利用正切函数的定义得到DE DH DH PD=,从而得到DH=32a ,根据∠PHD=∠FHT ,得到HT=2,再根据OT=OD+DH+HT ,列出关于a 的方程即可求出a 的值,从而得到点P 的坐标.【详解】解:(1)∵CM ⊥y 轴,OM=9,∴当y=9时,394x =,解得:x=12,∴C (12,9),∵CA ⊥x 轴,则A (12,0),∴OB=OA=12,则B (0,-12),设直线AB 的解析式为y=kx+b ,∴12012k b b +=⎧⎨=-⎩,解得:112k b =⎧⎨=-⎩,∴12y x =-;(2)由题意可得,∠CMO=∠OAC=∠MOA=90°,∴四边形MOAC 为矩形,∴MC=OA=12,∵NC=OM ,∴NC=9,则MN=MC-NC=3,∴N (3,9)设直线ON 的解析式为1y k x =,将N (3,9)代入得:193k =,解得:13k =,∴y=3x ,设P (a ,3a )∵PD ⊥x 轴交OC 于点E ,交x 轴于点D ,∴3(,)4E a a ,(a,0)D ,∴PE=39344a a a -=,OD=a ,∴9944a PE OD a ==;(3)如图,设直线GF 交CA 延长线于点R ,交y 轴于点S ,过点F 作FT ⊥x 轴于点T ,∵GF ∥x 轴,∴∠OSR=∠MOA=90°,∠CAO=∠R=90°,∠BOA=∠BSG=90°,∠OAB=∠AFR ,∴∠OSR=∠R=∠AOS=∠BSG=90°,则四边形OSRA为矩形,∴OS=AR,SR=OA=12,∵OA=OB,∴∠OBA=∠OAB=45°,∴∠FAR=90°-∠AFR=45°,∴∠FAR=∠AFR,∴FR=AR=OS,∵QF⊥OF,∴∠OFQ=90°,∴∠OFS+∠QFR=90°,∵∠SOF+∠OFS=90°,∴∠SOF=∠QFR,∴△OFS≌△FQR,∴SF=QR,∵∠SFB=∠AFR=45°,∴∠SBF=∠SFB,∴BS=SF=QR,∵∠SGB=∠RGQ,∴△BSG≌△QRG,∴SG=RG=6,设FR=m,则AR=m,∴QR=SF=12-m,∴=,-=,∵GQ FG∴66m m +-=+,∵QG 2=GR 2+QR 2,即222(6)6(12)m m +=+-,解得:m=4,∴FS=8,AR=4,∵∠OAB=∠FAR ,FT ⊥OA ,FR ⊥AR ,∴FT=FR=AR=4,∠OTF=90°,∴四边形OSFT 为矩形,∴OT=FS=8,∵∠DHE=∠DPH ,∴tan ∠DHE=tan ∠DPH ,∴DE DH DH PD=,由(2)可知,DE=34a ,PD=3a ,∴343a DH DH a=,解得:DH=32a ,∴tan ∠PHD=3232PD a DH a ==,∵∠PHD=∠FHT ,∴tan ∠FHT=2TF HT =,∴HT=2,∵OT=OD+DH+HT ,∴3282a a ++=,∴a=125,∴1236(,)55P 【点睛】本题考查了一次函数与几何综合问题,涉及了一次函数解析式的求法,矩形的判定与性质,全等三角形的判定与性质以及锐角三角函数的定义等知识点,第(3)问难度较大,解题的关键是正确做出辅助线,熟悉几何的基本知识,综合运用全等三角形以及锐角三角函数的概念进行解答.类型二与平行四边形有关14.(2022·山东泰安)如图,四边形ABCD 为平行四边形,则点B 的坐标为________.【答案】()2,1--【分析】根据平行四边形的性质以及点的平移即可得出结论.【详解】解: 四边形ABCD 为平行四边形,∴DA CB ∥,即将D 点平移到A 的过程与将C 点平移到B 的过程保持一致,将D 点平移到A 的过程是::134x --=-(向左平移4各单位长度);:220y -=(上下无平移);∴将C 点平移到B 的过程按照上述一致过程进行得到()24,1B --,即()2,1B --,故答案为:()2,1--.【点睛】本题考查平行四边形的性质及点的平移,掌握点的平移的代数表示是解决问题的关键.15.(2022·甘肃武威)如图1,在菱形ABCD 中,60A ∠=︒,动点P 从点A 出发,沿折线AD DC CB →→方向匀速运动,运动到点B 停止.设点P 的运动路程为x ,APB △的面积为y ,y 与x 的函数图象如图2所示,则AB 的长为()AB .C .D .【答案】B【分析】根据图1和图2判定三角形ABD 为等边三角形,它的面积为【详解】解:在菱形ABCD 中,∠A=60°,∴△ABD 为等边三角形,设AB=a ,由图2可知,△ABD 的面积为∴△ABD 的面积24a ==解得:a=故选B【点睛】本题考查了动点问题的函数图象,根据菱形的性质和函数图象,能根据图形得出正确信息是解此题的关键.16.(2020·黑龙江牡丹江?中考真题)如图,已知直线AB 与x 轴交于点A ,与y 轴交于点B ,线段OA 的长是方程27180x x --=的一个根,12OB OA =.请解答下列问题:(1)求点A ,B 的坐标;(2)直线EF 交x 轴负半轴于点E ,交y 轴正半轴于点F ,交直线AB 于点C .若C 是EF 的中点,6OE =,反比例函数k y x=图象的一支经过点C ,求k 的值;(3)在(2)的条件下,过点C 作CD OE ⊥,垂足为D ,点M 在直线AB 上,点N 在直线CD 上.坐标平面内是否存在点P ,使以D ,M ,N ,P 为顶点的四边形是正方形?若存在,请写出点P 的个数,并直接写出其中两个点P 的坐标;若不存在,请说明理由.【答案】(1)A (9,0),B (0,92);(2)-18;(3)存在5个,(9,12)或(9,-12)或(1,0)或(-7,4)或(-15,0).【解析】【分析】(1)解一元二次方程,得到点A 的坐标,再根据12OB OA =可得点B 坐标;(2)利用待定系数法求出直线AB 的表达式,根据点C 是EF 的中点,得到点C 横坐标,代入可得点C 坐标,根据点C 在反比例函数图像上求出k 值;(3)画出图形,可得点P 共有5个位置,分别求解即可.【详解】解:(1)∵线段OA 的长是方程27180x x --=的一个根,解得:x=9或-2(舍),而点A 在x 轴正半轴,∴A (9,0),∵12OB OA =,∴B (0,92);(2)∵6OE =,∴E (-6,0),设直线AB 的表达式为y=kx+b ,将A 和B 代入,得:0992k b b =+⎧⎪⎨=⎪⎩,解得:1292k b ⎧=-⎪⎪⎨⎪=⎪⎩,∴AB 的表达式为:1922y x =-+,∵点C 是EF 的中点,∴点C 的横坐标为-3,代入AB 中,y=6,则C (-3,6),∵反比例函数k y x=经过点C ,则k=-3×6=-18;(3)存在点P ,使以D ,M ,N ,P 为顶点的四边形是正方形,如图,共有5种情况,在四边形DM 1P 1N 1中,M 1和点A 重合,∴M 1(9,0),此时P 1(9,12);在四边形DP 3BN 3中,点B 和M 重合,可知M 在直线y=x+3上,联立:31922y x y x =+⎧⎪⎨=-+⎪⎩,解得:14x y =⎧⎨=⎩,∴M (1,4),∴P 3(1,0),同理可得:P 2(9,-12),P 4(-7,4),P 5(-15,0).故存在点P 使以D ,M ,N ,P 为顶点的四边形是正方形,点P 的坐标为P 1(9,12),P 2(9,-12),P 3(1,0),P 4(-7,4),P 5(-15,0).【点睛】本题考查了解一元二次方程,一次函数表达式,正方形的性质,反比例函数表达式,难度较大,解题的关键是根据图像画出符合条件的正方形.类型三最值问题17.(2020·江苏宿迁?中考真题)如图,在平面直角坐标系中,Q是直线y=﹣12x+2上的一个动点,将Q绕点P(1,0)顺时针旋转90°,得到点Q',连接OQ',则OQ'的最小值为()A.455B C.523D.655【答案】B【解析】【分析】利用等腰直角三角形构造全等三角形,求出旋转后Q′的坐标,然后根据勾股定理并利用二次函数的性质即可解决问题.【详解】解:作QM⊥x轴于点M,Q′N⊥x轴于N,设Q(m,122m-+),则PM=1m﹣,QM=122m-+,∵∠PMQ=∠PNQ′=∠QPQ′=90°,∴∠QPM+∠NPQ′=∠PQ′N+∠NPQ′,∴∠QPM=∠PQ′N ,在△PQM 和△Q′PN 中,'90''PMQ PNQ QPM PQ N PQ Q P ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩,∴△PQM ≌△Q′PN(AAS),∴PN=QM=122m -+,Q′N=PM=1m ﹣,∴ON=1+PN=132m -,∴Q′(132m -,1m ﹣),∴OQ′2=(132m -)2+(1m ﹣)2=54m 2﹣5m+10=54(m ﹣2)2+5,当m=2时,OQ′2有最小值为5,∴OQ′故选:B .【点睛】本题考查了一次函数图象上点的坐标特征,一次函数的性质,三角形全等的判定和性质,坐标与图形的变换-旋转,二次函数的性质,勾股定理,表示出点的坐标是解题的关键18.(2020·湖南永州?中考真题)已知点()00,P x y 和直线y kx b =+,求点P 到直线y kx b =+的距离d可用公式d =C 的圆心C 的坐标为()1,1,半径为1,直线l 的表达式为26y x =-+,P 是直线l 上的动点,Q 是C 上的动点,则PQ 的最小值是()A .355B .3515-C .6515-D .2【答案】B 【解析】【分析】过点C 作直线l 的垂线,交C 于点Q ,交直线l 于点P ,此时PQ 的值最小,利用公式计算即可.【详解】过点C 作直线l 的垂线,交C 于点Q ,交直线l 于点P ,此时PQ 的值最小,如图,∵点C 到直线l 的距离()00222116355112kx y b d k -+-⨯-+==++-,C 半径为1,∴PQ 的最小值是3515-,故选:B.【点睛】此题考查公式的运用,垂线段最短的性质,正确理解公式中的各字母的含义,确定点P与点Q最小时的位置是解题的关键.A B-,在x19.(2020·辽宁鞍山?中考真题)如图,在平面直角坐标系中,已知(3,6),(2,2)CD=,线段CD在x轴上平移,当轴上取两点C,D(点C在点D左侧),且始终保持1+的值最小时,点C的坐标为________.AD BC【答案】(-1,0)【解析】【分析】作点B关于x轴的对称点B′,将B′向右平移1个单位得到B″,连接AB″,与x轴交于点D,过点B′作AB″的平行线,与x轴交于点C,得到此时AD+BC的值最小,求出直线AB″,得到点D坐标,从而可得点C坐标.【详解】解:如图,作点B关于x轴的对称点B′,将B′向右平移1个单位得到B″,连接AB″,与x轴交于点D,过点B′作AB″的平行线,与x轴交于点C,可知四边形B′B″DC为平行四边形,则B′C=B″D,由对称性质可得:BC=B′C,∴AD+BC=AD+B′C=AD+B″D=AB″,则此时AB″最小,即AD+BC最小,∵A(3,6),B(-2,2),∴B′(-2,-2),∴B″(-1,-2),设直线AB″的表达式为:y=kx+b,则632k bk b=+⎧⎨-=-+⎩,解得:2kb=⎧⎨=⎩,∴直线AB″的表达式为:y=2x,令y=0,解得:x=0,即点D坐标为(0,0),∴点C坐标为(-1,0),故答案为:(-1,0).【点睛】本题考查了轴对称的性质,最短路径问题,一次函数表达式,解题的关键是找到AD+BC最小时的情形20.(2020•连云港)如图,在平面直角坐标系xOy中,半径为2的⊙O与x轴的正半轴交于点A,点B是⊙O上一动点,点C为弦AB的中点,直线y=34x﹣3与x轴、y轴分别交于点D、E,则△CDE面积的最小值为.【分析】如图,连接OB,取OA的中点M,连接CM,过点M作MN⊥DE于N.首先证明点C的运动轨迹是以M为圆心,1为半径的⊙M,设⊙M交MN于C′.求出MN,当点C与C′重合时,△C′DE的面积最小.【解析】如图,连接OB,取OA的中点M,连接CM,过点M作MN⊥DE于N.∵AC=CB,AM=OM,∴MC=12OB=1,∴点C的运动轨迹是以M为圆心,1为半径的⊙M,设⊙M交MN于C′.∵直线y=34x﹣3与x轴、y轴分别交于点D、E,∴D(4,0),E(0,﹣3),∴OD =4,OE =3,∴DE =32+42=5,∵∠MDN =∠ODE ,∠MND =∠DOE ,∴△DNM ∽△DOE ,∴MN OE=DM DE,∴MN 3=35,∴MN =95,当点C 与C′重合时,△C′DE 的面积最小,最小值=12×5×(95−1)=2,故答案为2.21.(2020·江苏连云港?中考真题)如图,在平面直角坐标系xOy 中,半径为2的O 与x 轴的正半轴交于点A ,点B 是O 上一动点,点C 为弦AB 的中点,直线334y x =-与x 轴、y 轴分别交于点D 、E ,则CDE △面积的最小值为________.【答案】2【解析】【分析】如图,连接OB ,取OA 的中点M ,连接CM ,过点M 作MN ⊥DE 于N .首先证明点C 的运动轨迹是以M 为圆心,1为半径的⊙M ,设⊙M 交MN 于C′.求出MN ,当点C 与C′重合时,△C′DE的面积最小.【详解】解:如图,连接OB,取OA的中点M,连接CM,过点M作MN⊥DE于N.∵AC=CB,AM=OM,∴MC=12OB=1,∴点C的运动轨迹是以M为圆心,1为半径的⊙M,设⊙M交MN于C′.∵直线y=34x-3与x轴、y轴分别交于点D、E,∴D(4,0),E(0,-3),∴OD=4,OE=3,∴5 DE===,∵∠MDN=∠ODE,∠MND=∠DOE,∴△DNM∽△DOE,∴MN DM OE DE=,∴3 35 MN=,∴95 MN=,当点C 与C′重合时,△C′DE 的面积最小,△C′DE 的面积最小值1951225⎛⎫=⨯⨯-= ⎪⎝⎭,故答案为2.【点睛】本题考查三角形的中位线定理,三角形的面积,一次函数的性质等知识,解题的关键是学会添加常用辅助线,构造三角形的中位线解决问题,属于中考常考题型.22.(2020·北京中考真题)在平面直角坐标系xOy 中,⊙O 的半径为1,A ,B 为⊙O 外两点,AB=1.给出如下定义:平移线段AB ,得到⊙O 的弦A B ''(,A B ''分别为点A ,B 的对应点),线段AA '长度的最小值称为线段AB 到⊙O 的“平移距离”.(1)如图,平移线段AB 到⊙O 的长度为1的弦12PP 和34P P ,则这两条弦的位置关系是;在点1234,,,P P P P 中,连接点A 与点的线段的长度等于线段AB 到⊙O 的“平移距离”;(2)若点A ,B 都在直线y =+上,记线段AB 到⊙O 的“平移距离”为1d ,求1d 的最小值;(3)若点A 的坐标为32,2⎛⎫ ⎪⎝⎭,记线段AB 到⊙O 的“平移距离”为2d ,直接写出2d 的取值范围.【答案】(1)平行,P 3;(2)32;(3)233922d ≤≤。
部编数学八年级下册专题09一次函数与几何图形综合的七种考法(解析版)含答案
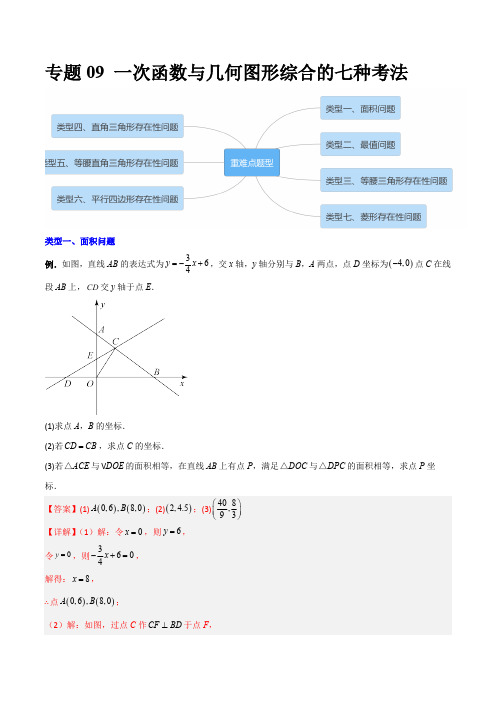
专题09 一次函数与几何图形综合的七种考法类型一、面积问题例.如图,直线AB 的表达式为364y x =-+,交x 轴,y 轴分别与B ,A 两点,点D 坐标为()4,0-点C 在线段AB 上,CD 交y 轴于点E .(1)求点A ,B 的坐标.(2)若CD CB =,求点C 的坐标.(3)若ACE △与DOE V 的面积相等,在直线AB 上有点P ,满足DOC △与DPC △的面积相等,求点P 坐标.∵CD CB =,∴DF BF =,∵点D 坐标为()4,0-,点B 的坐标为(∴12BD =,8OB =,∴6BF =,∴2OF =,∵DOC △与DPC △的面积相等,∴点O 和点P 到距离相等,此时OP ∥∴直线OP 的解析式为35y x =,联立得:36435y x y xì=-+ïïíï=ïî,解得:x y ì=ïïíï=ïî【变式训练1】如图,直线1:1l y kx =+与x 轴交于点D ,直线2:l y x b =-+与x 轴交于点A ,且经过定点(1,5)B -,直线1l 与2l 交于点(2,)C m .(1)填空:k =________;b =________;m =________;(2)在x 轴上是否存在一点E ,使BCE V 的周长最短?若存在,请求出点E 的坐标;若不存在,请说明理由;(3)若动点P 在射线DC 上从点D 开始以每秒1个单位的速度运动,连接AP ,设点P 的运动时间为t 秒.是否存在t 的值,使ACP △和ADP △的面积比为1:2?若存在,直接写出t 的值;若不存在,请说明理由.(3)∵点P 在射线DC 上从点∴(2,0)D -,∵(2,2)C ,∴22(22)225CD =++=,∵点P 的运动时间为t 秒.②点P 在线段DC 的延长线上,∵ACP △和ADP △的面积比为1:∴12CP DP =,∴22545DP =´=,综上:存在t 的值,使ACP △和【变式训练2】在平面直角坐标系中,O 为原点,点()4,0A ,()2,0B -,()3,2C -,点D 是y 轴正半轴上的动点,连接CD 交x 轴于点E .(1)如图①,若点D 的坐标为()0,2,求ACD V 的面积;(2)如图②,若12ABD ABC S S =V V ,求点D 的坐标.(3)如图③,若BDE ACE S S =△△,请直接写出点D 的坐标.【变式训练3】如图,平面直角坐标系中,直线AB :13y x b =-+交y 轴于点()0,1A ,交x 轴于点B .过点()1,0E 且垂直于x 轴的直线DE 交AB 于点D ,P 是直线DE 上一动点,且在点D 的上方,设()1,P n .(1)求直线AB 的解析式和点B 的坐标;(2)求ABP V 的面积(用含n 的代数式表示);(3)当ABP V 的面积为2时,以PB 为边在第一象限作等腰直角三角形BPC ,求出点C 的坐标.,则90PEB BP CGB Ð=Ð=Ð=°,PB BC =,∴90PBE BPE Ð+Ð=°,90BPE CPG Ð+Ð=°,∴BPE CPG Ð=Ð,∴()AAS BEP PGC ≌V V ,∴2BE PG ==,2PE CG ==,∴点()3,4C ;②以PB 为底时,如图,过点C 作CG PE ^于点G ,作CH x ^轴于点H ,则90PGC CGE CHB PEB PCB Ð=Ð=Ð=°=Ð=Ð,CP CB =,∴90GCH PCB Ð=°=Ð,∴PCG BCH Ð=Ð,∴∴()AAS BCH PCG ≌V V ,∴BH PG =,CH CG =,∴BE BH PE PG +=-,即22BH BH +=-,∴0BH PG ==,∴点()3,2C ;综上,符合题意的点C 坐标为()5,2或()3,4或()3,2.类型二、最值问题例.如图,在平面直角坐标系xOy 中,一次函数()0y kx b k =+¹的图像经过()4,0A 、()0,4B 两点.(1)k =______,b =______.(2)已知()1,0M -、()3,0N ,①在直线AB 上找一点P ,使PM PN =.用无刻度直尺和圆规作出点P (不写画法,保留作图痕迹);②点P 的坐标为______;③点Q 在y 轴上,那么PQ NQ +的最小值为______.【答案】(1)1-,4;(2)①见解析;②()1,3;③5【详解】(1)解:将()4,0A 、()0,4B 代入()0y kx b k =+¹中,得:044k b b =+ìí=î,解得;14k b =-ìí=î,故答案为:1-,4;(2)①如图,点P 即为所求;【变式训练1】在平面直角坐标系中,已知直线l经过1,32Aæöç÷èø和()3,2B-两点,且与x轴,y轴分别相交于C,D两点.(1)求直线l的表达式;V的面积等于2时,求点E的坐标;(2)若点E在直线AB上,当ODE-的值最小,则点P的坐标为______;(3)①在x轴上找一点P,使得PA PB-的值最大,则点Q的坐标为______.②在x轴上找一点Q,使得QA QB【变式训练2】如图,一次函数2y x =+的图象分别与x 轴和y 轴交于C ,A 两点,且与正比例函数y kx=的图象交于点()1,B m -.(1)求正比例函数的表达式;(2)点D 是一次函数图象上的一点,且OCD V 的面积是4,求点D 的坐标;(3)点P 是y 轴上一点,当BP CP +的值最小时,若存在,点P 的坐标是______.取点C 关于y 轴的对称点C ¢,则PC PC =CP BP C P BP C B ¢¢\+=+³,即点P 位于C B ¢与x 轴的交点时,BP +∵点(2,0)C - ,【变式训练3】如图,在平面直角坐标系内,()3,4A -,()3,2B ,点C 在x 轴上,AD x ^轴,垂足为D ,BE x ⊥轴,垂足为E ,线段AB 交y 轴于点F .若AC BC =,ACD CBE Ð=Ð.(1)求点C 的坐标;(2)如果经过点C 的直线y kx b =+与线段BF 相交,求k 的取值范围;(3)若点P 是y 轴上的一个动点,当PA PC -取得最大值时,求BP 的长.类型三、等腰三角形存在性问题例.如图,在平面直角坐标系中,一次函数21y x =--的图像分别交x 轴、y 轴于点A 和B .已知点C 的标为()3,0-,若点P 是x 轴上的一个动点.(1)A 的坐标是______,B 的坐标是______;(2)过点P 作y 轴的平行线交AB 于点M ,交BC 于点N ,当点P 恰好是MN 的中点时,求出P 点坐标.(3)若以点B 、P 、C 为顶点的BPC △为等腰三角形时、请求出所有符合条件的P 点坐标.【变式训练1】直线8y kx =-与x 轴、y 轴分别交于B C 、两点,且43OC OB =.(1)求OB 的长和k 的值:(2)若点A 是第一象限内直线8y kx =-上的一个动点,当它运动到什么位置时,AOB V 的面积是12?(3)在(2)成立的情况下,y 轴上是否存在点P ,使POA V 是等腰三角形?若存在,求出点P 的坐标;若不存在,请说明理由.(写过程)由题意得,12OB AD ´´=6OB =Q ,\解得,AD当21294OA OP =+==当397OA OP ==时,3P 当22AP OP =时,作2P H ^22AP OP =Q Q 2P 为线段OA 垂直平分线与【变式训练2】在平面直角坐标系中,直线MN 交x 轴正半轴于点M ,交y 轴负半轴于点()0,3N -,30Ð=°ONM ,作线段MN 的垂直平分线交x 轴于点A ,交y 轴于点B .(1)如图1,求直线MN 的解析式和A 点坐标;(2)如图2,过点M 作y 轴的平行线l ,P 是l 上一点,若ANP S =△P 坐标;(3)如图3,点Q 是y 轴的一个动点,连接QM 、AQ ,将MAQ V 沿AQ 翻折得到1M AQ △,当1M MN △是等腰三角形时,求点Q 的坐标.过T 作TS AM ^于S ,则AT ∴22333322AS æö=-=ç÷èø,同理2315Q P y x =--:,综上:()3,6P ,(3,P -(3)①如图,当MN MM =由轴对称的性质可得:AM ∵()223323AN =+=,∴()0,1Q .②当1NM NM =时,如图,由23AN NM AM ===,∴ANM V 为等边三角形,此时Q ,N 重合,∴()0,3Q -;③当11M M M N =时,1M 在直线∵30OAB Ð=°,【变式训练3】如图,一次函数()0y kx b k =+¹的图象与x 轴交于点C ,与y 轴交于点()0,5A ,与正比例函数12y x =的图象交于点B ,且点B 的横坐标为2,点P 为y 轴上的一个动点.(1)求B 点的坐标和k 、b 的值;(2)连接CP ,当ACP △与AOB V 的面积相等时,求点P 的坐标;(3)连接BP ,是否存在点P 使得PAB V 为等腰三角形?若存在,请求出点P 的坐标;若不存在,请说明理由.③当PA PB =时,如图2,设(0,P m 22(5)PA m =-,1PH m =-,所以PB 所以222(5)(1)2m m -=-+,解得m类型四、直角三角形存在性问题例.如图1,在平面直角坐标系xOy 中,点O 为坐标原点,直线AB :3y 4x b =+与直线AC :9y kx =+交于点(2,)A n ,与x 轴分别交于点0()6,B -和点C .点D 为线段BC 上一动点,将ABD △沿直线AD 翻折得到ADE V ,线段AE 交x 轴于点F .(1)直线AC 的函数表达式.(2)当点D 在线段BO 上,点E 落在y 轴上时,求点E 的坐标.(3)若DEF V 为直角三角形,求点D 的坐标.【变式训练1】综合与探究:如图,在平面直角坐标系中,直线2y x =+与x 轴,y 轴分别交于点A ,B ,与直线11433y x =-+交于点C .直线11433y x =-+与x 轴交于点D ,若点P 是线段AD 上的一个动点,点P 从点D 出发沿DA 方向,以每秒2个单位长度匀速运动到点A (到 A 停止运动).设点P 的运动时间为s t .(1)求点A 和点B 的坐标;△的面积为12时,求t的值;(2)当ACP△为直角三角形?若存在,请直接写出t的值;(3)试探究,在点P运动过程中,是否存在t的值,使ACP若不存在,请说明理由.【变式训练2】如图,平面直角坐标系中,直线AB 与x 轴交于点()30A -,与y 轴交于点()06B ,,点C 是直线AB 上的一点,它的坐标为()4m ,,经过点C 作直线CD x ∥轴交y 轴于点D .(1)求点C 的坐标;(2)已知点P 是直线CD 上的动点,①若POC △的面积为4,求点P 的坐标;②若POC △为直角三角形,请求出所有满足条件的点P 的坐标.②Q OCP Ð一定不是直角,当90OPC Ð=°时,点P 恰好在点D ,\()04P ,,当90POC Ð=°时,,由题可得221417OC =+=,2222416OP DP DP =+=+,()221CP DP =+,Q 222CP OC OP =+,\()2211716DP DP +=++,\16DP =,\()164P ,,综上所述,所有满足条件的点P 的坐标为()04,或()164P ,.【变式训练3】如图,已知函数1y x =+的图象与y 轴交于点A ,一次函数y kx b =+的图象经过点()0,1B -,与x 轴以及1y x =+的图象分别交于点C ,D ,且点D 的坐标为()1,n .(1)则k =______,b =______,n =______;(2)关于x ,y 的二元一次方程组y =x +1,y =kx +b的解为______;(3)求四边形AOCD 的面积;(4)在x 轴上是否存在点P ,使得以点P ,C ,D 为顶点的三角形是直角三角形,请求出点P 的坐标.①当P D DC ¢^时,22P C P D ¢¢=类型五、等腰直角三角形存在性问题例.模型建立:如图1,等腰直角三角形ABC 中,90ACB Ð=°,CB CA =,直线ED 经过点C ,过A 作AD ED ^于D ,过B 作BE ED ^于E .(1)求证:BEC CDA V V ≌.(2)模型应用:已知直线14:43l y x =+与y 轴交与A 点,将直线1l 绕着A 点顺时针旋转45°至2l ,如图2,求2l 的函数解析式.(3)如图3,矩形ABCO ,O 为坐标原点,B 的坐标为()8,6,A 、C 分别在坐标轴上,P 是线段BC 上动点,设PC m =,已知点D 在第一象限,且是直线26y x =-上的一点,若APD △是不以A 为直角顶点的等腰直角三角形,请直接写出点D 的坐标.∵45BAC Ð=°,∴ABC V 为等腰直角三角形,由(1)得:CBD BAO V V ≌∴BD AO =,CD OB =,∵直线4:4l y x =+,∴()626122AE x =--=-由(1)得:ADE DPF △△≌∴DF AE =,即1228x x -=-,解得:4x =;∴()4,2D ;∴266212BF x x =--=-;同(1)得,APB PDF △≌△∴8AB PF ==,PB DF ==∴()88BF PF PB x =-=--=∴21216x x -=-,解得:283x =;∴2838,33D æöç÷èø;【变式训练1】综合与探究:如图1,平面直角坐标系中,一次函数334y x =-+的图像分别与x 轴、y 轴交于点A ,B ,点C 是线段OA 的中点,点D 与点C 关于y 轴对称,作直线BD .(1)求A ,B 两点的坐标;(2)求直线BD 的函数表达式;(3)若点P 是直线BD 上的一个动点.请从A ,B 两题中任选一题作答.我选择______题.A .如图2,连接AP ,CP .直接写出ACP △为直角三角形时点P 的坐标.B .如图3,连接CP ,过点P 作PQ x ^轴于点Q .直接写出CPQ V 为等腰直角三角形时点P 的坐标.【变式训练2】如图,平面直角坐标系中,直线1:3AB y x b =-+交y 轴于点()0,1A ,交x 轴于点B .直线1x =交AB 于点D ,交x 轴于点E ,P 是直线1x =上一动点,且在点D 的上方,设()1,P n .(1)求直线AB 的解析式;(2)当2ABP S =△时,在第一象限内找一点C ,使BCP V 为等腰直角三角形,求点C 的坐标.∵1x =时,12133y x =-+=,P 在点∴23PD n =-,∴12PAB APD BPD S S S PD AM =+=×+V V V ∵2ABP S =△,3∵90,45CPB EPB Ð=°Ð=°,∴45NPC EPB Ð=Ð=°.又∵90,CNP PEB BP PC Ð=Ð=°=,∴CNP BEP ≌V V ,∴2PN =NC =EB =PE =,∴224NE NP+PE ==+=,∴()3,4C ;若90,PBC BP BC Ð=°=,如图,过点C 作CF x ^轴于点F .∵90,45PBC EBP Ð=°Ð=°,∴45CBF PBE Ð=Ð=°.又∵90,CFB PEB BC BP Ð=Ð=°=,∴CBF PBE ≌V V .∴2BF CF PE EB ====,∴325OF OB BF =+=+=,∴()5,2C ;若90,PCB CP EB Ð=°=,如图,∴45CPB EBP Ð=Ð=°,∵,,CP EB CPB EBP BP BP =Ð=Ð=,∴PCB PEB ≌V V ,∴2PC CB PE EB ====,∴()3,2C ;∴点C 的坐标是()3,4或()5,2或()3,2.【变式训练3】如图,在平面直角坐标系xOy 中,直线AP 交x 轴于点(),0P p ,与y 轴交于点()0,A a ,且a ,p ()230a +=.(1)求直线AP 的解析式;(2)如图1,直线2x =-与x 轴交于点N ,点M 在x 轴上方且在直线2x =-上,若MAP △的面积等于6,请求出点M 的坐标;(3)如图2,已知点()2,4C -,若点B 为射线AP 上一动点,连接BC ,在坐标轴上是否存在点Q ,使BCQ △是以BC 为底边,点Q 为直角顶点的等腰直角三角形,若存在,请直接写出点Q 坐标;若不存在,请说明理由.∵MD AP P ,MAP △的面积等于∴DAP V 的面积等于6,∴162A DP y ××=,即12DP ×∴4DP =,∴()3,0D -,y∴,33OE t BE t ==-,∵BCQ △是以BC 为底边的等腰直角三角形,∴BQ CQ =,90BQC Ð=∴90BQE NQC Ð=°-Ð=又∵BEQ QNC Ð=Ð,∴()AAS BEQ QNC V V ≌,∴BG t =,33OG t =-,∴BT t =,33OT t =-,同②可证CFQ QTB V V ≌∴QF BT t ==,QT CF =∴OQ OT QT OF =+=+∴52t =,∴513422OQ =+=,类型六、平行四边形存在性问题例.在平面直角坐标系xOy 中,直线36y x =+分别与x 、y 轴相交于A 、B 两点,将线段AB 绕点A 顺时针旋转90°得到线段AC .连接BC 交x 轴于点D .(1)求点C 的坐标;(2)P 为x 轴上的动点,连接PB ,PC ,当PB PC -的值最大时,求此时点P 的坐标.(3)点E 在直线AC 上,点F 在x 轴上,若以B 、D 、E 、F 为顶点的四边形是平行四边形,请直接写出点F 的坐标;【答案】(1)点C 的坐标为()4,2-(2)()6,0P (3)点F 的坐标为()17,0-或()13,0或()23,0【详解】(1)解:令0y =,则2x =-,()2,0A \-,令0x =,则6y =,()0,6B \,26OA BO \==,,过点C 作CH x ^轴于H ,9090CAD BAO BAO ABO ÐÐÐÐ+=°+=°Q ,,CAD ABO ÐÐ\=,90AHC BOA ÐÐ\==°,由旋转得AB AC =,()AAS ABO CAH \V V ≌,26CH OA AH BO \====,,4OH AH OA \=-=,\点C 的坐标为()4,2-;(2)作点C 关于x 轴的对称点C ¢,连接BC ¢延长交x 轴于点P ,则点P 就是所求的最大值点,\()4,2C ¢设直线BC ¢的解析式为y kx b =+,\642b k b =ìí+=î,解得16k b =-ìí=î,6y x \=-+,()6,0P \;(3)()()()2,04,20,6A C B --Q ,,,设直线AC 的解析式为y mx n =+,则2042m n m n -+=ìí+=-î【变式训练1】如图1,在平面直角坐标系中,直线AB 与x 轴交于点(),0A m ,与y 轴交于点()0,B n ,且m n ,满足:()260m n n ++-=.(1)求:AOB S V 的值;(2)D 为OA 延长线上一动点,以BD 为直角边作等腰直角BDE V ,连接EA ,求直线EA 与y 轴交点F 的坐标;(3)在(2)的条件下,当2AD =时,在坐标平面内是否存在一点P ,使以B E F Р、、、为顶点的四边形是平行四边形,如果存在,直接写出点Р的坐标,若不存在,说明理由.∵EDB △为等腰直角三角形,∴,90DE DB EDB =Ð=°,∴18090EDG ODB Ð+Ð=°-。
一次函数综合题(解析版)--2024年中考数学压轴题专项训练

一次函数综合题通用的解题思路:(1)一次函数与几何图形的面积问题首先要根据题意画出草图,结合图形分析其中的几何图形,再求出面积.(2)一次函数的优化问题通常一次函数的最值问题首先由不等式找到x 的取值范围,进而利用一次函数的增减性在前面范围内的前提下求出最值.(3)用函数图象解决实际问题从已知函数图象中获取信息,求出函数值、函数表达式,并解答相应的问题.1(2024•鼓楼区一模)如图,直线y =-3x +6与⊙O 相切,切点为P ,与x 轴y 轴分别交于A 、B 两点.⊙O 与x 轴负半轴交于点C .(1)求⊙O 的半径;(2)求图中阴影部分的面积.【分析】(1)由OP =OA ⋅sin60°,即可求解;(2)由图中阴影部分的面积=S 扇形COP -S ΔPOC ,即可求解.【解答】解:(1)对于直线y =-3x +6,令y =-3x +6=0,则x =23,即OA =23,由一次函数的表达式知,OB =6,则tan ∠BAC =OB AO =623=3,则∠BAC =60°连接OP ,则OP ⊥AB ,则OP =OA ⋅sin60°=23×32=3;(2)过点P 作PH ⊥AC 于点H ,∵∠POH =30°,则∠POC =150°,PH =12OP =32,则图中阴影部分的面积=S 扇形COP -S ΔPOC =150°360°×π×32-12×3×32=15π-94.【点评】本题考查了一次函数和圆的综合运用,涉及到圆切线的和一次函数的性质,解直角三角形,面积的计算等,综合性强,难度适中.2(2023•宿豫区三模)如图①,在平面直角坐标系中,直线l 1:y =x +1与直线l 2:x =-2相交于点D ,点A 是直线l 2上的动点,过点A 作AB ⊥l 1于点B ,点C 的坐标为(0,3),连接AC ,BC .设点A 的纵坐标为t ,ΔABC 的面积为s .(1)当t =2时,求点B 的坐标;(2)s 关于t 的函数解析式为s =14t 2+bt -54t -1或t 5 a t +1 t -5 (-1<t <5),其图象如图②所示,结合图①、②的信息,求出a 与b 的值;(3)在直线l 2上是否存在点A ,使得∠ACB =90°,若存在,请求出此时点A 的坐标;若不存在,请说明理由.【分析】(1)解法一:先根据t =2可得点A (-2,2),因为B 在直线l 1上,所以设B (x ,x +1),利用y =0代入y =x +1可得G 点的坐标,在Rt ΔABG 中,利用勾股定理列方程可得点B 的坐标;解法二:根据可以使用y =x +1与x 轴正半轴夹角为45度来解答;(2)先把(7,4)代入s =14t 2+bt -54中计算得b 的值,计算在-1<t <5范围内图象上一个点的坐标值:当t =2时,根据(1)中的数据可计算此时s =94,可得坐标2,94,代入s =a (t +1)(t -5)中可得a 的值;(3)存在,设B (x ,x +1),如图5和图6,分别根据两点的距离公式和勾股定理列方程可解答.【解答】解:(1)解法一:如图1,连接AG ,当t =2时,A (-2,2),设B (x ,x +1),在y =x +1中,当x =0时,y =1,∴G (0,1),∵AB ⊥l 1,∴∠ABG =90°,∴AB 2+BG 2=AG 2,即(x +2)2+(x +1-2)2+x 2+(x +1-1)2=(-2)2+(2-1)2,解得:x 1=0(舍),x 2=-12,∴B -12,12;解法二:如图1-1,过点B 作BE ⊥x 轴于E ,过点A 作AH ⊥BE 于H ,当x =0时,y =1,当y =0时,x +1=0,则x =-1,∴OF =OG =1,∵∠GOF =90°,∴∠OGF =∠OFG =45°,∴BE =EF ,∵∠ABD =90°,∴∠ABH =∠BAH =45°,∴ΔABH 是等腰直角三角形,∴AH =BH ,当t =2时,A (-2,2),设B (x ,x +1),∴x +2=2-(x +1),∴x =-12,∴B -12,12 ;(2)如图2可知:当t =7时,s =4,把(7,4)代入s =14t 2+bt -54中得:494+7b -54=4,解得:b =-1,如图3,过B 作BH ⎳y 轴,交AC 于H ,由(1)知:当t =2时,A (-2,2),B -12,12 ,∵C (0,3),设AC 的解析式为:y =kx +n ,则-2k +n =2n =3 ,解得k =12n =3 ,∴AC 的解析式为:y =12x +3,∴H -12,114,∴BH =114-12=94,∴s=12BH⋅|x C-x A|=12×94×2=94,把2,9 4代入s=a(t+1)(t-5)得:a(2+1)(2-5)=94,解得:a=-1 4;(3)存在,设B(x,x+1),当∠ACB=90°时,如图5,∵∠ABD=90°,∠ADB=45°,∴ΔABD是等腰直角三角形,∴AB=BD,∵A(-2,t),D(-2,-1),∴(x+2)2+(x+1-t)2=(x+2)2+(x+1+1)2,(x+1-t)2=(x+2)2,x+1-t=x+2或x+1-t=-x-2,解得:t=-1(舍)或t=2x+3,RtΔACB中,AC2+BC2=AB2,即(-2)2+(t-3)2+x2+(x+1-3)2=(x+2)2+(x+1-t)2,把t=2x+3代入得:x2-3x=0,解得:x=0或3,当x=3时,如图5,则t=2×3+3=9,∴A(-2,9);当x=0时,如图6,此时,A(-2,3),综上,点A的坐标为:(-2,9)或(-2,3).【点评】本题考查二次函数综合题、一次函数的性质、等腰直角三角形的判定和性质、三角形的面积、两点间距离公式等知识,解题的关键是灵活运用所学知识解决问题.3(2023•溧阳市一模)如图1,将矩形AOBC放在平面直角坐标系中,点O是原点,点A坐标为(0,4),点B坐标为(5,0),点P是x轴正半轴上的动点,连接AP,ΔAQP是由ΔAOP沿AP翻折所得到的图形.(1)当点Q落在对角线OC上时,OP= 165 ;(2)当直线PQ经过点C时,求PQ所在的直线函数表达式;(3)如图2,点M是BC的中点,连接MP、MQ.①MQ的最小值为;②当ΔPMQ是以PM为腰的等腰三角形时,请直接写出点P的坐标.【分析】(1)通过Q 点在OC 上,可以通过∠BOC 的三角函数和∠OAP 的三角函数来导出对应的边的关系,求得结果;(2)通过直角ΔAQC 中,得到QC 的长度,然后通过OP =PQ =x ,可以在Rt ΔBCP 中,得到对应的x 值然后求出结果;(3)通过QA =OA =4,可得出Q 点的运动轨迹,是以A 点为圆心,4为半径长度的圆弧,从而可知,MA 的连线上的Q 点为最短的MQ 长度,通过分类讨论,PM =PQ ,PM =QM ,PQ =QM 来求得对应的P 的坐标.【解答】解:(1)如图1,∵∠OAP +∠AOE =90°,∠BOC +∠AOE =90°,∴∠OAP =∠BOC ,又∵∠AOP =∠OBC =90°,∴ΔOAP ∽ΔBOC ,∴OP BC =OA OB ,即OP 4=45,∴OP =165,故答案为:165;(2)如图,∵AQ ⊥PQ ,∴∠AQC =90°,∴QC =AC 2-AQ 2=52-42=3,∵AQ =AO =4,设OP =PQ =x ,则CP =3+x ,PB =5-x ,∴CP 2=BP 2+BC 2,(3+x )2=(5-x )2+42,x =2,∴P 点的坐标为(2,0),将P (2,0)和C (5,4)代入y =kx +b 中,0=2k +b 4=5k +b ,解得:k =43b =-83,∴PQ 所在直线的表达式为:y =43x -83;(3)如图,①∵AQ =AO =4,∴Q 点的运动轨迹,是以A 为圆心,4为半径的圆弧,∴MQ 的最小值在AM 的连线上,如图,MQ ′即为所求,∵M 是BC 中点,CM =12BC =2,∴AM =52+22=29,MQ ′=MA -AQ ′=29-4,故答案为:29-4;②如图,设OP =PQ =x ,BP =5-x ,∴PM 2=(5-x )2+22=x 2-10x +29,当PM =PQ 时,PM 2=PQ 2,∴x 2-10x +29=x 2,x =2910,∴P 2910,0,当MP =MQ 时,如图,若点Q 在AC 上,则AQ =OA =4,∵MP =MQ ,MB =MC ,∠PBM =∠QCM ,∴ΔPMB ≅ΔQMC (HL ),∴PB =QC ,QC =AC -AQ =5-4=1,∴PB =1,∴OP =BO -PB =5-1=4,∴P (4,0);若点Q 在AC 上方时,由对称性可知OM =MQ ,∵MQ =MQ ,∴MO =MP ,∴P (10,0);当MQ =PQ 时,不符合题意,不成立,故P 点坐标为P 2910,0或P (4,0)或(10,0).【点评】本题考查一次函数的图象及应用,通过一次函数坐标图象的性质,三角函数的性质,全等三角形的性质和勾股定理,来求得对应的解.4(2022•启东市模拟)我们知道一次函数y =mx +n 与y =-mx +n (m ≠0)的图象关于y 轴对称,所以我们定义:函数y =mx +n 与y =-mx +n (m ≠0)互为“M ”函数.(1)请直接写出函数y =2x +5的“M ”函数;(2)如果一对“M ”函数y =mx +n 与y =-mx +n (m ≠0)的图象交于点A ,且与x 轴交于B ,C 两点,如图所示,若∠BAC =90°,且ΔABC 的面积是8,求这对“M ”函数的解析式;(3)在(2)的条件下,若点D 是y 轴上的一个动点,当ΔABD 为等腰三角形时,请求出点D 的坐标.【分析】(1)根据互为“M ”函数的定义,直接写出函数y =2x +5的“M ”函数;(2)现根据已知条件判断ΔABC 为等腰直角三角形,再根据互为“M ”函数的图象关于y 轴对称,得出OA =OB =OC ,再根据函数解析式求出点A 、B 、C 的坐标,再根据ΔABC 的面积是8求出m 、n 的值,从而求出函数解析式;(3)ΔABD 为等腰三角形,分以A 为顶点,以B 为顶点,以D 为顶点三种情况讨论即可.【解答】(1)解:根据互为“M ”函数的定义,∴函数y =2x +5的“M ”函数为y =-2x +5;(2)解:根据题意,y =mx +n 和y =-mx +n 为一对“M 函数”.∴AB =AC ,又∵∠BAC =90°,∴ΔABC 为等腰直角三角形,∴∠ABC =∠ACB =45°,∵OB =OC ,∴∠BAO =∠CAO =45°,∴OA =OB =OC ,又∵S ΔABC =12×BC ×AO =8且BC =2AO ,∴AO =22,∵A 、B 、C 是一次函数y =mx +n 与y =-mx +n (m ≠0)的图象于坐标轴的交点,∴A (0,n ),B -n m ,0 ,C n m ,0,∵OA =OB =n ,∴n m=22,∴m =1,∴y =x +22和y =-x +22;(3)解:根据等腰三角形的性质,分情况,∵AO =BO =22,∴AB =4,由(2)知,A (0,22),B (-22,0),C (22,0),∴①以A 为顶点,则AB =AD ,当点D 在点A 上方时,AD =22+4,当点D 在点A 下方时,AD =22-4,∴D 1(0,22+4),D 2(0,22-4),②以B 为顶点,则BA =BD ,此时点D 在y 轴负半轴,∴D 3(0,-22),③以D 为顶点,则DA =DB ,此时D 为坐标原点,∴D 4(0,0).∴D 点坐标为D 1(0,22+4),D 2(0,22-4),D 3(0,-22),∴D 4(0,0).【点评】本题考查一次函数的综合应用,以及新定义、等腰三角形的性质等知识,关键是理解新定义,用新定义解题.5(2024•新北区校级模拟)如图①,动点P 从矩形ABCD 的顶点A 出发,以v 1的速度沿折线A -B -C 向终点C 运动;同时,一动点Q 从点D 出发,以v 2的速度沿DC 向终点C 运动,当一个点到达终点时,另一个点也停止运动.点E 为CD 的中点,连接PE ,PQ ,记ΔEPQ 的面积为S ,点P 运动的时间为t ,其函数图象为折线MN -NF 和曲线FG (图②),已知,ON =4,NH =1,点G 的坐标为(8,0).(1)点P 与点Q 的速度之比v 1v 2的值为 85 ;AB AD的值为;(2)如果OM =15.①求线段NF 所在直线的函数表达式;②求FG 所在曲线的函数表达式;③是否存在某个时刻t ,使得S ≥154?若存在,求出t 的取值范围:若不存在,请说明理由.【分析】(1)由函数图象可知t =3时,Q 与E 重合,t =4时,P 与B 重合,t =6时,P 与C 重合,则Q 的速度v 2=DE 4,P 的速度v 1=AB 4,从而得出答案;(2)①当t =0时,P 与A 重合,Q 与D 重合,此时S ΔADE =2,可得AD =BC =DE =15,AB =CD =53AD =10,从而得出点P 与Q 的速度,即可得出点F 的坐标,利用待定系数法可得答案;②设FG 所在的曲线的数解析式为S =a (t -6)2+k (a ≠0),把F 5,154,G (8,0)代入解析式求得a ,k 值即可求解答;③利用待定系数法求出直线MN 的函数解析式,当S =154时,可得t 的值,根据图象可得答案.【解答】解:(1)∵ON =4,NH =1,G (8,0),∴N (4,0),H (5,0),由图象可知:t =4时,Q 与E 重合,t =5时,P 与B 重合,t =8时,P 与C 重合,∴Q 的速度v 2=DE 4,P 的速度v 1=AB 5,∵四边形ABCD 是矩形,∴AB =CD ,AD =BC ,∵E 为CD 的中点,∴DE =12CD =12AB ,∴v 1v 2=AB5DE 4=AB 5⋅4DE =85,∵P 从A 到B 用了5秒,从B 到C 用了3秒,∴AB =5v 1,BC =3v 1,∴AB =53BC ,∴AB :AD 的值为53,故答案为:85,53;(2)①∵OM =15,∴M (0,15),由题知,t =0时,P 与A 重合,Q 与D 重合,∴S ΔEPQ =12AD ⋅DE =15,∵AB :AD =53,DE =12AB ,∴DE =56AD ,∴12AD ⋅56AD =15,∴AD =BC =6(舍去负值),∴AB =CD =53AD =10,∴v 2=DE 4=54,当t =5时,DQ =v 2t =54×5=254,∴QE =DQ -DE =254-5=54,此时P 与B重合,∴S ΔEPQ =12EQ ⋅BC =12×54×6=154,∴F 5,154 ,设直线NF 的解析式为S =kt +b (k ≠0),将N (4,0)与F 5,154 代入得:4k +b =05k +b =154,∴k =154b =-15 ,∴线段NF 所在直线的函数表达式为S =154t -15(4<t ≤5);②设FG所在的曲线的数解析式为S=1254t-5(16-2t)=-54t2+15t-40,∴FG所在的曲线的函数解析式为S=-54t2+15t-40(5≤t≤8);③存在,分情况讨论如下:当Q在DE上,P在AB上时,∵直线MN经过点M(0,15),N(4,0),可求得直线MN的解析式为S=-54t+15(0≤t≤4),当s=154时,-154t+15=154,∴x=3,∵s随x的增大而减小,∴当0≤x≤3时,S≥154,当Q在CE上,P在BC上时,直线NF的解析式为S=154t-15(4<t≤5);由F5,15 4知:当t=5时,S=154,当S=154时,-54t2+15t-40=154,∴t=7或5,由图象知:当5≤x≤7,x的取值范围为0≤t≤3或5≤t≤7.【点评】本题是一次函数综合题,主要考查了待定系数法求函数解析式,三角形的面积,矩形的性质等知识,理解函数图象中每一个拐点的意义是解题的关键.6(2024•梁溪区校级模拟)在平面直角坐标系xOy 中,二次函数y =-ax 2+3ax +4a 的图象与x 轴交于A 、B 两点(点A 在点B 的左侧),与y 轴正半轴交于点C ,直线y =12x 交于第一象限内的D 点,且ΔABC 的面积为10.(1)求二次函数的表达式;(2)点E 为x 轴上一点,过点E 作y 轴的平行线交线段OD 于点F ,交抛物线于点G ,当GF =5OF 时,求点G 的坐标;(3)已知点P (n ,0)是x 轴上的点,若点P 关于直线OD 的对称点Q 恰好落在二次函数的图象上,求n 的值.【分析】(1)在y =-ax 2+3ax +4a 中,令y =0得A (-1,0),B (4,0),根据ΔABC 的面积为10,即得OC =4,C (0,4),用待定系数法即得二次函数的表达式为y =-x 2+3x +4;(2)设E (m ,0),则F m ,12m ,G (m ,-m 2+3m +4),由GF =5OF ,可得-m 2+52m +4=5×52m ,即可解得G (2,6);(3)连接PQ 交直线OD 于K ,过Q 作QT ⊥x 轴于T ,设Q (r ,s ),可得K n +r 2,s 2 ,即得s 2=12×n +r 2,n +r =2s ①,又r 2+s 2=n 2,(n +r )(n -r )=s 2②,可解得r =35n ,s =45n ,故Q 35n ,45n ,代入y =-x 2+3x +4得45n =-35n 2+3×35n +4,解得n =5或n =-209.【解答】解:(1)如图:在y =-ax 2+3ax +4a 中,令y =0得-ax 2+3ax +4a =0,解得x =4或x =-1,∴A (-1,0),B (4,0),∴AB =5,∵ΔABC 的面积为10,∴12AB ⋅OC =10,即12×5⋅OC =10,∴OC =4,∴C (0,4),把C (0,4)代入y =-ax 2+3ax +4a 得:4a =4,∴a =1,∴二次函数的表达式为y =-x 2+3x +4;(2)如图:设E (m ,0),则F m ,12m ,G (m ,-m 2+3m +4),∴OF =m 2+12m 2=52m ,GF =-m 2+3m +4-12m =-m 2+52m +4,∵GF =5OF ,∴-m 2+52m +4=5×52m ,解得m =2或m =-2(舍去),∴G (2,6);(3)连接PQ 交直线OD 于K ,过Q 作QT ⊥x 轴于T ,如图:∵P (n ,0)关于直线对称点为Q ,∴OQ =OP =|n |,K 是PQ 中点,设Q (r ,s ),∴K n +r 2,s 2,∵K 在直线y =12x 上,∴s 2=12×n +r 2,整理得:n +r =2s ①,∵OT 2+QT 2=OQ 2,∴r 2+s 2=n 2,变形得:(n +r )(n -r )=s 2②,把①代入②得:2s (n -r )=s 2,∵s ≠0,∴n -r =s2③,由①③可得r =35n ,s =45n ,∴Q 35n ,45n ,∵Q 在抛物线y =-x 2+3x +4上,∴45n =-35n 2+3×35n +4,解得n =5或n =-209,答:n 的值为5或-209.【点评】本题考查一次函数、二次函数综合应用,涉及待定系数法,三角形面积,对称变换等知识,解题的关键是用含n 的代数式表示Q 的坐标.7(2023•邗江区校级一模)如图1,在平面直角坐标系中,直线l :y =-33x +43分别与x 轴、y 轴交于点A 点和B 点,过O 点作OD ⊥AB 于D 点,以OD 为边构造等边ΔEDF (F 点在x 轴的正半轴上).(1)求A 、B 点的坐标,以及OD 的长;(2)将等边ΔEDF ,从图1的位置沿x 轴的正方向以每秒1个单位的长度平移,移动的时间为t (s ),同时点P 从E 出发,以每秒2个单位的速度沿着折线ED -DF 运动(如图2所示),当P 点到F 点停止,ΔDEF 也随之停止.①t =3或6(s )时,直线l 恰好经过等边ΔEDF 其中一条边的中点;②当点P 在线段DE 上运动,若DM =2PM ,求t 的值;③当点P 在线段DF 上运动时,若ΔPMN 的面积为3,求出t 的值.【分析】(1)把x =0,y =0分别代入y =-33x +43,即可求出点A 、B 的坐标,求出∠BAO =30°,根据直角三角形的性质,即可得出OD =12OA =6;(2)①当直线l 分别过DE 、DF 、EF 的中点,分三种情况进行讨论,得出t 的值,并注意点P 运动的最长时间;②分点P 在直线l 的下方和直线l 上方两种情况进行讨论,求出t 的值即可;③分点P 在DN 之间和点P 在NF 之间两种情况进行讨论,求出t 的值即可.【解答】解:(1)令x =0,则y =43,∴点B 的坐标为(0,43),令y =0,则-33x +43=0,解得x =12,∴点A 的坐标为(12,0),∵tan ∠BAO =OB OA=4312=33,∴∠BAO =30°,∵OD ⊥AB ,∴∠ODA =90°,∴ΔODA 为直角三角形,∴OD =12OA =6;(2)①当直线l 过DF 的中点G 时,∵ΔDEF 为等边三角形,∴∠DFE =60°,∵∠BAO =30°,∴∠FGA =60°-30°=30°,∴∠FGA =∠BAO ,∴FA =FG =12DF =3,∴OF =OA -FA =9,∴OE =OF -EF =9-6=3,∴t =3;当l 过DE 的中点时,∵DE ⊥l ,DG =EG ,∴直线l 为DE 的垂直平分线,∵ΔDEF 为等边三角形,∴此时点F 与点A 重合,∴t =12-61=6;当直线l 过EF 的中点时,运动时间为t =12-31=9;∵点P 从运动到停止用的时间为:6+62=6,∴此时不符合题意;综上所述,当t =3s 或6s 时,直线l 恰好经过等边ΔEDF 其中一条边的中点,故答案为:3或6;②∵OE =t ,AE =12-t ,∠BAO =30°,∴ME =6-t2,∴DM =DE -EM =t2,∵EP =2t ,∴PD =6-2t ,当P 在直线l 的下方时,∵DM =23DP ,∴t 2=23(6-2t ),解得:t =2411;当P 在直线l 的上方时,∵DM =2DP ,∴t2=2(6-2t ),解得t =83;综上所述:t 的值为2411或83;③当3<t ≤6时,∵∠D =60°,∠DMN =90°,DM =t2,∴∠DNM =90°-60°=30°,∴MN =DM ×tan60°=32t ,DN =2DM =2×t2=t ,∵DP =2t -6,∴PN =DN -DP =t -(2t -6)=6-t ,∵∠DNM =30°,∴边MN 的高h =12PN =3-12t ,∵ΔPMN 的面积为3,∴12×32t 3-12t =3,整理得:t 2-6t +8=0,解得t =2(舍)或t =4当点P 在NF 之间时,∵∠D =60°,∠DMN =90°,DM =t2,∴∠DNM =90°-60°=30°,∴MN =DM ×tan60°=32t ,DN =2DM =2×t2=t ,∵DP =2t -6,∴PN =DP -DN =2t -6-t =t -6,∵∠DNM =30°,∴∠FNA =∠DNM =30°,∴边MN 的高h =12PN =12t -3,∵ΔPMN 的面积为3,∴12×32t 12t -3 =3,解得t =3+17(舍)或t =3-17(舍),综上所述,t 的值为4s .【点评】本题主要考查了一次函数的性质、等边三角形的性质、直角三角形的性质、利用三角函数解直角三角形,熟练掌握含30°的直角三角形的性质并注意进行分类讨论是解题的关键.8(2023•武进区校级模拟)在平面直角坐标系xOy 中,对于任意两点P 1(x 1,y 1)与P 2(x 2,y 2)的“非常距离”,给出如下定义:若|x 1-x 2|≥|y 1-y 2|,则点P 1与点P 2的“非常距离”为|x 1-x 2|;若|x 1-x 2|<|y 1-y 2|,则点P 1与点P 2的“非常距离”为|y 1-y 2|.例如:点P 1(1,2),点P 2(3,5),因为|1-3|<|2-5|,所以点P 1与点P 2的“非常距离”为|2-5|=3,也就是图1中线段P 1Q 与线段P 2Q 长度的较大值(点Q 为垂直于y 轴的直线P 1Q 与垂直于x 轴的直线P 2Q 交点).(1)已知点A -12,0,B 为y 轴上的一个动点,①若点A 与点B 的“非常距离”为2,写出一个满足条件的点B 的坐标;②直接写出点A 与点B 的“非常距离”的最小值;(2)已知C 是直线y =34x +3上的一个动点,①如图2,点D 的坐标是(0,1),求点C 与点D 的“非常距离”的最小值及相应的点C 的坐标;②如图3,E 是以原点O 为圆心,1为半径的圆上的一个动点,求点C 与点E 的“非常距离”的最小值及相应的点E 与点C 的坐标.【分析】(1)①根据点B 位于y 轴上,可以设点B 的坐标为(0,y ).由“非常距离”的定义可以确定|0-y |=2,据此可以求得y 的值;②设点B 的坐标为(0,y ).因为-12-0 ≥|0-y |,所以点A 与点B 的“非常距离”最小值为-12-0 =12;(2)①设点C 的坐标为x 0,34x 0+3 .根据材料“若|x 1-x 2|≥|y 1-y 2|,则点P 1与点P 2的“非常距离”为|x 1-x 2|”知,C 、D 两点的“非常距离”的最小值为-x 0=34x 0+2,据此可以求得点C 的坐标;②根据“非常距离”的定义,点E 在过原点且与直线y =34x +3垂直的直线上,且C 与E 的横纵坐标差相等时,点C 与点E 的“非常距离”取最小值,据此求出C 与E 的坐标及“非常距离”的最小值.【解答】解:(1)①∵B 为y 轴上的一个动点,∴设点B 的坐标为(0,y ).∵-12-0 =12≠2,∴|0-y |=2,解得,y =2或y =-2;∴点B 的坐标是(0,2)或(0,-2);②点A 与点B 的“非常距离”的最小值为12.(2)①如图2,当点C 与点D 的“非常距离”取最小值时,需要根据运算定义“若|x 1-x 2|≥|y 1-y 2|,则点P 1与点P 2的“非常距离”为|x 1-x 2|”解答,此时|x 1-x 2|=|y 1-y 2|.即AC =AD ,∵C 是直线y =34x +3上的一个动点,点D 的坐标是(0,1),∴设点C 的坐标为x 0,34x 0+3 ,∴-x 0=34x 0+2,此时,x 0=-87,∴点C 与点D 的“非常距离”的最小值为:|x 0|=87,此时C -87,157;②如图3,当点E 在过原点且与直线y =34x +3垂直的直线上,且CF =EF 时,点C 与点E 的“非常距离”最小,设E (x ,y )(点E 位于第二象限).则y x=-43x 2+y 2=1 ,解得x =-35y =45,故E -35,45.设点C 的坐标为x 0,34x 0+3 ,-35-x 0=34x 0+3-45,解得x0=-8 5,则点C的坐标为-8 5,95,点C与点E的“非常距离”的最小值为1.【点评】本题考查了一次函数综合题.对于信息给予题,一定要弄清楚题干中的已知条件.本题中的“非常距离”的定义是正确解题的关键.9(2023•海安市一模)对于平面直角坐标系xOy中的图形W和点P,给出如下定义:F为图形W上任意一点,将P,F两点间距离的最小值记为m,最大值记为M,称M与m的差为点P到图形W的“差距离”,记作d(P,W),即d(P,W)=M-m,已知点A(2,1),B(-2,1)(1)求d(O,AB);(2)点C为直线y=-1上的一个动点,当d(C,AB)=1时,点C的横坐标是 (2-5)或(5-2,) ;(3)点D为函数y=x+b(-2≤x≤2)图象上的任意一点,当d(D,AB)≤2时,直接写出b的取值范围.【分析】(1)画出图形,根据点P到图形W的“差距离”的定义即可解决问题.(2)如图2中,设C(m,-1).由此构建方程即可解决问题.(3)如图3中,取特殊位置当b=6时,当b=-4时,分别求解即可解决问题.【解答】解:(1)如图1中,∵A(2,1),B(-2,1),∴AB⎳x轴,∴点O到线段AB的最小距离为1,最大距离为5,∴d(O,AB)=5-1.(2)如图2中,设C(m,-1).当点C在y轴的左侧时,由题意AC-2=1,∴AC=3,∴(2-m)2+22=9,∴m=2-5或2+5(舍弃),∴C(2-5,-1),当点C在y轴的右侧时,同法可得C(5-2,-1),综上所述,满足条件的点C的坐标为(2-5,-1)或(5-2,-1).故答案为:(2-5,-1)或(5-2,-1).(3)如图3中,当b=6时,线段EF:y=x+6(-2≤x≤2)上任意一点D,满足d(D,AB)≤2,当b=-4时,线段E′F′:y=x-4(-2≤x≤2)上任意一点D′,满足d(D′,AB)≤2,观察图象可知:当b≥6或b≤-4时,函数y=x+b(-2≤x≤2)图象上的任意一点,满足d(D,AB)≤2.【点评】本题属于一次函数综合题,考查了一次函数的性质,点P到图形W的“差距离”的定义等知识,解题的关键是理解题意,学会利用参数解决问题,学会寻找特殊位置解决问题,属于中考创新题型.10(2022•姑苏区校级模拟)平面直角坐标系xOy中,对于任意的三个点A、B、C,给出如下定义:若矩形的任何一条边均与某条坐标轴平行,且A,B,C三点都在矩形的内部或边界上,则称该矩形为点A,B,C的“三点矩形”.在点A,B,C的所有“三点矩形”中,若存在面积最小的矩形,则称该矩形为点A,B,C的“最佳三点矩形”.如图1,矩形DEFG,矩形IJCH都是点A,B,C的“三点矩形”,矩形IJCH是点A,B,C的“最佳三点矩形”.如图2,已知M(4,1),N(-2,3),点P(m,n).(1)①若m=2,n=4,则点M,N,P的“最佳三点矩形”的周长为18,面积为;②若m=2,点M,N,P的“最佳三点矩形”的面积为24,求n的值;(2)若点P在直线y=-2x+5上.①求点M,N,P的“最佳三点矩形”面积的最小值及此时m的取值范围;②当点M,N,P的“最佳三点矩形”为正方形时,求点P的坐标;(3)若点P(m,n)在抛物线y=ax2+bx+c上,当且仅当点M,N,P的“最佳三点矩形”面积为12时,-2≤m≤-1或1≤m≤3,直接写出抛物线的解析式.【分析】(1)①利用“最佳三点矩形”的定义求解即可,②利用“最佳三点矩形”的定义求解即可;(2)①利用“最佳三点矩形”的定义求得面积的最小值为12,②由“最佳三点矩形”的定义求得正方形的边长为6,分别将y=7,y=-3代入y=-2x+5,可得x分别为-1,5,点P的坐标为(-1,7)或(4,-3);(3)利用“最佳三点矩形”的定义画出图形,可分别求得解析式.【解答】解:(1)①如图,画出点M,N,P的“最佳三点矩形”,可知矩形的周长为6+6+3+3=18,面积为3×6=18;故答案为:18,18.②∵M(4,1),N(-2,3),∴|x M-x N|=6,|y M-y N|=2.又∵m=2,点M,N,P的“最佳三点矩形”的面积为24.∴此矩形的邻边长分别为6,4.∴n=-1或5.(2)如图,①由图象可得,点M,N,P的“最佳三点矩形”面积的最小值为12;分别将y=3,y=1代入y=-2x+5,可得x分别为1,2;结合图象可知:1≤m≤2;②当点M,N,P的“最佳三点矩形”为正方形时,边长为6,分别将y=7,y=-3代入y=-2x+5,可得x分别为-1,4;∴点P的坐标为(-1,7)或(4,-3);(3)设抛物线的解析式为y=ax2+bx+c,经过点(-1,1),(1,1),(3,3),∴a -b +c =1a +b +c =19a +3b +c =3,a =14b =0c =34,∴y =14x 2+34,同理抛物线经过点(-1,3),(1,3),(3,1),可求得抛物线的解析式为y =-14x 2+134,∴抛物线的解析式y =14x 2+34或y =-14x 2+134.【点评】本题主要考查了一次函数的综合题,涉及点的坐标,正方形及矩形的面积及待定系数法求函数解析式等知识,解题的关键是理解运用好“最佳三点矩形”的定义.11(2022•太仓市模拟)如图①,动点P 从矩形ABCD 的顶点A 出发,以v 1的速度沿折线A -B -C 向终点C 运动;同时,一动点Q 从点D 出发,以v 2的速度沿DC 向终点C 运动,当一个点到达终点时,另一个点也停止运动.点E 为CD 的中点,连接PE ,PQ ,记ΔEPQ 的面积为S ,点P 运动的时间为t ,其函数图象为折线MN -NF 和曲线FG (图②),已知,ON =3,NH =1,点G 的坐标为(6,0).(1)点P 与点Q 的速度之比v 1v 2的值为 32 ;AB :AD 的值为;(2)如果OM =2.①求线段NF 所在直线的函数表达式;②是否存在某个时刻t ,使得S ≥23?若存在,求出t 的取值范围;若不存在,请说明理由.【分析】(1)由函数图象可知t =3时,Q 与E 重合,t =4时,P 与B 重合,t =6时,P 与C 重合,则Q 的速度v 2=DE 3,P 的速度v 1=AB4,从而得出答案;(2)①当t =0时,P 与A 重合,Q 与D 重合,此时S ΔADE =2,可得AD =BC =DE =2,AB =CD =2AD =4,从而得出点P 与Q 的速度,即可得出点F 的坐标,利用待定系数法可得答案;②利用待定系数法求出直线MN 的函数解析式,当S =23时,可得t 的值,根据图象可得答案.【解答】解:(1)∵ON =3,NH =1,G (6,0),∴N (3,0),H (4,0),由图象可知:t =3时,Q 与E 重合,t =4时,P 与B 重合,t =6时,P 与C 重合,∴Q 的速度v 2=DE 3,P 的速度v 1=AB4,∵四边形ABCD 是矩形,∴AB =CD ,AD =BC ,∵E 为CD 的中点,∴DE =12CD =12AB ,∴v 1v 2=AB4DE 3=AB 4⋅3DE =AB 4⋅312AB =32,∵P 从A 到B 用了4秒,从B 到C 用了2秒,∴AB =4v 1,BC =2v 1,∴AB =2BC ,∴AB :AD 的值为2,故答案为:32,2;(2)①∵OM =2,∴M (0,2),由题知,t =0时,P 与A 重合,Q 与D 重合,∴S ΔEPQ =12AD ⋅DE =2,∵AB :AD =2,∴AD =DE =12AB ,∴12AD 2=2,∴AD =BC =DE =2,AB =CD =2AD =4,∴v 2=DE 3=23,当t =4时,DQ =v 2t =23×4=83,∴QE =DQ -DE =83-2=23,此时P 与B 重合,∴S ΔEPQ =12EQ ⋅BC =12×23×2=33,∴F 4,23,设直线NF 的解析式为S =kx +b (k ≠0),将N (3,0)与F 4,23 代入得:3k +b =04k +b =23 ,∴k =23b =-2,∴线段NF 所在直线的函数表达式为S =23x -2(3<x ≤4);②存在,分情况讨论如下:当Q 在DE 上,P 在AB 上时,∵直线MN 经过点M (0,2),N (3,0),同理求得直线MN 的解析式为S =-23x +2(0≤x ≤3),当s =23时,-23x +2=2,∴x =2,∵s随x的增大而减小,∴当0≤x≤2时,S≥23,当Q在CE上,P在AB上时,直线NF的解析式为S=23x-2(3<x≤4),由F4,2 3知:当x=4时,S=23,当Q在CE上,P在BC上时,SΔEPQ=12EQ⋅CP,∵DQ=v2t=23t,∴EQ=DQ-DE=23t-2,∵v1=AB4=44=1,∴AB+BP=v1t=t,∵AB+BC=4+2=6,∴CP=6-t,∴S=1223t-2(6-t)=-13t2+3t-6(4<x≤6),当S=23时,-13t2+3t-6=23,∴t=4或5,由图象知:当4<x≤5时,S≥2 3,综上,S≥23时,x的取值范围为0≤x≤2或4≤x≤5.【点评】本题是一次函数综合题,主要考查了待定系数法求函数解析式,三角形的面积,矩形的性质等知识,理解函数图象中每一个拐点的意义是解题的关键.12(2022•邗江区校级一模)在平面直角坐标系xOy中,对于点P和线段ST,我们定义点P关于线段ST的线段比k=PSST(PS<PT)PTST(PS≥PT) .(1)已知点A(0,1),B(1,0).①点Q(2,0)关于线段AB的线段比k= 22 ;②点C(0,c)关于线段AB的线段比k=2,求c的值.(2)已知点M(m,0),点N(m+2,0),直线y=x+2与坐标轴分别交于E,F两点,若线段EF上存在点使得这一点关于线段MN的线段比k≤14,直接写出m的取值范围.【分析】(1)①求出QA、QB、AB,根据线段比定义即可得到答案;②方法同①,分c>0和c≤0讨论;(2)分两种情况,画出图象,根据线段比定义,分别在M(N)为“临界点”时列出不等式,即可得到答案.【解答】解:(1)①∵A(0,1),B(1,0),Q(2,0),∴AB=2,QA=5,QB=1,根据线段比定义点Q(2,0)关于线段AB的线段比k=QBAB=22;故答案为:22;②∵A (0,1),B (1,0),C (0,c ),∴AB =2,AC =|1-c |,BC =1+c 2,AC 2=1+c 2-2c ,BC 2=1+c 2,当c >0时,AC 2<BC 2,即AC <BC ,由C (0,c )关于线段AB 的线段比k =2可得:|1-c |2=2,解得c =3或c =-1(舍去),∴c =3,当c ≤0时,AC 2≥BC 2,即AC ≥BC ,由C (0,c )关于线段AB 的线段比k =2可得:1+c 22=2,解得c =3(舍去)或c =-3,∴c =-3,综上所述,点C (0,c )关于线段AB 的线段比k =2,c =3或c =-3;(2)∵直线y =x +2与坐标轴分别交于E ,F 两点,∴E (-2,0),F (0,2),∵点M (m ,0),点N (m +2,0),∴MN =2,N 在M 右边2个单位,当线段EF 上的点到N 距离较小时,分两种情况:①当M 、N 在点E 左侧时,如图:线段EF 上存在点使得这一点关于线段MN 的线段比k ≤14,∴NE MN≤14,即-2-(m +2)2≤14,解得:m ≥-92,②当N 在E 右侧,M 在E 左侧时,过M 作MG ⊥EF 于G ,如图:线段EF 上存在点使得这一点关于线段MN 的线段比k ≤14,∴GM MN ≤14,即GM 2≤14,∴GM ≤12,而E (-2,0),F (0,2),∴∠FEO =45°,∴ΔHEM 时等腰直角三角形,∴GM =22EM ,∴22EM ≤12,即22[(m +2)-(-2)]≤12,解得m ≤-4+22,∴线段EF 上存在点使得这一点关于线段MN 的线段比k ≤14,线段EF 上的点到N 距离较小时,-92≤m ≤-4+22,当线段EF 上的点到M 距离较小时,也分两种情况:①当N 在E 右侧,M 在E 左侧时,如图:线段EF 上存在点使得这一点关于线段MN 的线段比k ≤14,∴ME MN≤14,即-2-m 2≤14,解得m ≥-52,②当M 、N 在点E 右侧时,过M 作MH ⊥EF 于H ,如图:线段EF 上存在点使得这一点关于线段MN 的线段比k ≤14,∴HM MN ≤14,即HM 2≤14,∴HM ≤12,而E (-2,0),F (0,2),∴∠FEO =45°,∴ΔHEM 时等腰直角三角形,∴HM =22EM ,∴22EM ≤12,即22[m -(-2)]≤12,解得:m ≤-2+22,∴线段EF 上存在点使得这一点关于线段MN 的线段比k ≤14,线段EF 上的点到M 距离较小时,-52≤m ≤-2+22,综上所述,线段EF 上存在点使得这一点关于线段MN 的线段比k ≤14,则-92≤m ≤-4+22或-52≤m ≤-2+22.【点评】本题考查一次函数应用,解题的关键是读懂线段比的定义,找出“临界点”列不等式.13(2022•泰州)定义:对于一次函数y 1=ax +b 、y 2=cx +d ,我们称函数y =m (ax +b )+n (cx +d )(ma +nc ≠0)为函数y 1、y 2的“组合函数”.(1)若m =3,n =1,试判断函数y =5x +2是否为函数y 1=x +1、y 2=2x -1的“组合函数”,并说明理由;(2)设函数y 1=x -p -2与y 2=-x +3p 的图像相交于点P .①若m +n >1,点P 在函数y 1、y 2的“组合函数”图像的上方,求p 的取值范围;②若p ≠1,函数y 1、y 2的“组合函数”图像经过点P .是否存在大小确定的m 值,对于不等于1的任意实数p ,都有“组合函数”图像与x 轴交点Q 的位置不变?若存在,请求出m 的值及此时点Q 的坐标;若不存在,请说明理由.【分析】(1)由y =5x +2=3(x +1)+(2x -1),可知函数y =5x +2是函数y 1=x +1、y 2=2x -1的“组合函数”;(2)①由y =x -p -2y =-x +3p得P (2p +1,p -1),当x =2p +1时,y =m (2p +1-p -2)+n (-2p -1+3p )=(p-1)(m +n ),根据点P 在函数y 1、y 2的“组合函数”图象的上方,有p -1>(p -1)(m +n ),而m +n >1,可得p <1;②由函数y 1、y 2的“组合函数” y =m (x -p -2)+n (-x +3p )图象经过点P ,知p -1=m (2p +1-p -2)+n (-2p -1+3p ),即(p -1)(1-m -n )=0,而p ≠1,即得n =1-m ,可得y =(2m -1)x +3p -(4p +2)m ,令y =0得(2m -1)x +3p -(4p +2)m =0,即(3-4m )p +(2m -1)x -2m =0,即可得m =34时,“组合函数”图象与x 轴交点Q 的位置不变,Q (3,0).【解答】解:(1)函数y =5x +2是函数y 1=x +1、y 2=2x -1的“组合函数”,理由如下:∵3(x +1)+(2x -1)=3x +3+2x -1=5x +2,∴y =5x +2=3(x +1)+(2x -1),∴函数y =5x +2是函数y 1=x +1、y 2=2x -1的“组合函数”;(2)①由y =x -p -2y =-x +3p得x =2p +1y =p -1 ,∴P (2p +1,p -1),∵y 1、y 2的“组合函数”为y =m (x -p -2)+n (-x +3p ),∴x =2p +1时,y =m (2p +1-p -2)+n (-2p -1+3p )=(p -1)(m +n ),∵点P 在函数y 1、y 2的“组合函数”图象的上方,∴p -1>(p -1)(m +n ),∴(p -1)(1-m -n )>0,∵m +n >1,∴1-m -n <0,∴p -1<0,∴p <1;②存在m =34时,对于不等于1的任意实数p ,都有“组合函数”图象与x 轴交点Q 的位置不变,Q (3,0),理由如下:由①知,P (2p +1,p -1),∵函数y 1、y 2的“组合函数”y =m (x -p -2)+n (-x +3p )图象经过点P ,∴p -1=m (2p +1-p -2)+n (-2p -1+3p ),∴(p -1)(1-m -n )=0,∵p ≠1,∴1-m -n =0,有n =1-m ,∴y =m (x -p -2)+n (-x +3p )=m (x -p -2)+(1-m )(-x +3p )=(2m -1)x +3p -(4p +2)m ,令y =0得(2m -1)x +3p -(4p +2)m =0,变形整理得:(3-4m )p +(2m -1)x -2m =0,∴当3-4m =0,即m =34时,12x -32=0,∴x =3,∴m =34时,“组合函数”图象与x 轴交点Q 的位置不变,Q (3,0).【点评】本题考查一次函数综合应用,涉及新定义,函数图象上点坐标的特征,一次函数与一次方程的关系等,解题的关键是读懂“组合函数“的定义.14(2024•钟楼区校级模拟)在同一平面内,具有一条公共边且不完全重合的两个全等三角形,我们称这两个三角形叫做“共边全等”.(1)下列图形中两个三角形不是“共边全等”是③;AB,点E、F分别在AC、BC边(2)如图1,在边长为6的等边三角形ABC中,点D在AB边上,且AD=13上,满足ΔBDF和ΔEDF为“共边全等”,求CF的长;(3)如图2,在平面直角坐标系中,直线y=-3x+12分别与直线y=x、x轴相交于A、B两点,点C是OB 的中点,P、Q在ΔAOB的边上,当以P、B、Q为顶点的三角形与ΔPCB“共边全等”时,请直接写出点Q 的坐标.【分析】(1)由于第③个图不符合共边要求,所以图③即为答案;(2)DF为两个全等三角形的公共边,由于F点在BC边上,E在AC边上,两个三角形的位置可以如图②,在公共边异侧,构成一个轴对称图形,也可以构成一个平行四边形(将图③的两条最长边重合形成),分两类讨论,画出图形,按照图②构图,会得到一个一线三等角模型,利用相似,列出方程来解决,按照平行四边形构图,直接得到ΔADE为等边三角形,计算边长即可求得;(3)由题目要求,可以知道两个全等三角形的公共边为PB边,由于要构成ΔPCB,所以P点只能在OA和OB边上,当P在OA边上,两个三角形可以在PB同侧,也可以在PB异侧,当在PB异侧构图时,可以得到图3和图4,在图3中,当在PB同侧构图时,可以得到图6,当P在OB边上时,Q只能落在OA上,得到图7,利用已知条件,解三角形,即可求出Q点坐标.【解答】解:(1)①②均符合共边全等的特点,只有③,没有公共边,所以③不符合条件,∴答案是③;(2)①如图1,当ΔBDF≅ΔEFD,且是共边全等时,∠BFD=∠EDF,∴DE⎳BC,∵ΔABC是等边三角形,∴ΔADE是等边三角形,AB=2,∵AD=13∴DE=AE=BF=2,∴CF=BC-BF=4,②如图2,当ΔBDF≅ΔEDF,且是共边全等时,BD=DE=6-AD=4,∠DEF=∠B=60°,EF=BF,∴∠AED+∠FEC=120°,又∠AED+∠EDA=120°,。
2023年九年级数学下册中考数学综合培优测试卷:一次函数图像与几何变换【含答案】

2023年九年级数学下册中考数学综合培优测试卷:一次函数图像与几何变换一、单选题1.在平面直角坐标系中,把直线y=3x 向左平移2个单位长度,平移后的直线解析式是( )A .y=3x+2B .y=3x-2C .y=3x+6D .y=3x-62.若一次函数y=2x-3的图象平移后经过点(3,1),则下列叙述正确的是( )A .沿x 轴向右平移3个单位长度B .沿x 轴向右平移1个单位长度C .沿x 轴向左平移3个单位长度D .沿x 轴向左平移1个单位长度3.在平面直角坐标系中,将直线沿y 轴向下平移6个单位后,得到一条新的直线,该直y =−32x +3线与x 轴的交点坐标是( )A .B .C .D .(0,3)(−2,0)(4,0)(6,0)4.已知直线向下平移2个单位长度后得到直线,且直线与直线关于l 1:y =kx +3l 2l 2l 3:y =−x +1y 轴对称,则k 的值为( ).A .B .1C .2D .3−15.在平面直角坐标系中,将函数 的图象向上平移6个单位长度,则平移后的图象与x 轴的y =3x 交点坐标为( ) A .(2,0)B .(-2,0)C .(6,0)D .(-6,0)6.把直线y=-x+1向上平移3个单位长度后得到的直线的解析式为( )A .y=-x+4B .C .y=x+4D .y=x-27.将直线沿x 轴向左平移3个单位得到直线L ,则直线L 的解析式是( )y =2x +5A .y =2x +2B .y =2x +8C .y =2x -1D .y =2x +118.对于一次函数y =﹣2x+4,下列结论错误的是( )A .函数的图象不经过第三象限B .函数的图象与x 轴的交点坐标是(2,0)C .函数的图象向下平移4个单位长度得y =﹣2x 的图象D .若两点A(x 1,y 1),B(x 2,y 2)在该函数图象上,且x 1<x 2,则y 1<y 29.将一次函数y =﹣3x 的图象沿y 轴向下平移4个单位长度后,所得图象的函数表达式为( )A .y =﹣3(x ﹣4)B .y =﹣3x +4C .y =﹣3(x +4)D .y =﹣3x ﹣410.在平面直角坐标系中,将直线 先关于 轴作轴对称变换,再将所得直线关于y =−3x +4x y 轴作轴对称变换,则经两次变换后所得直线的表达式是( )A .B .C .D .y =4x−3y =−4x +3y =3x +4y =−3x−411.将直线向上平移2个单位长度,则平移后的直线所对应的函数解析式为( )y =−2x +3A .B .C .D .y =−2x +1y =−4x +5y =−2x +5y =−4x +112.将直线向上平移5个单位长度后得到直线,则下列关于直线的说y =x +1y =kx +b y =kx +b 法错误的是( )A .函数图象经过第一、二、三象限B .函数图象与轴的交点在轴的正半轴x xC .点在函数图象上(−2,4)D .随的增大而增大y x 二、填空题13.直线 +3的图像是由正比例函数 图像向 (填上或下)平移 y =3x 个单位得到或由正比例函数 图像向 (填左或右)平移 个单位得到可以得到的一条直线14.直线 沿 轴平移3个单位,则平移后直线与 轴的交点坐标为 .y =2x−1y y 15.在平面直角坐标系中,把直线y=2x 向左平移1个单位长度,平移后的直线解析式是 .16.将正比例函数y=﹣2x 的图象沿y 轴向上平移5个单位,则平移后所得图象的解析式是 .17.如图,在平面直角坐标系中,A (1,0),B (3,0),点C 在第一象限,∠ABC=90°,AC=25,直线l 的关系式为: .将△ABC 沿x 轴向左平移,当点C 落在直线l 上时,线段AC 扫y =−x−3过的面积为 平方单位.18.已知直线与直线关于y 轴对称,当时,,当y 1=ax +b(a ≠0)y 2=kx +5(k ≠0)x >−52y 1>0时,,则直线 .x >52y 2<0y 1=三、综合题19.如图,直线 与 轴、 轴交于点 、 ,直线 与 轴l 1:y =2x +1x y D A l 2:y =mx +4x y 轴分别交于点 、 ,两直线相交于点 .C B P(1,b)(1)求 , 的值; b m (2)求 的值;S △PDC −S △PAB (3)垂直于 轴的直线 与直线 , 分别交于点 , ,若线段 的长为x x =a l 1l 2M N MN 2,求 的值.a 20.如图,直线y =kx +4的图象与y 轴交于点A ,与x 轴交于点B (2,0),直线AF 交x 轴负半轴于点F ,且OF =2OA .(1)求出k 的值为 ,直线AF 的解析式为 ;(2)若将直线AB 沿y 轴向下平移,平移后的直线恰好经过C (﹣3,0),与y 轴相交于点D ,且直线CD 与直线AF 交于点E ,求点E 的坐标.21.如图,一次函数 的图象与反比例函数( 为常数且 )的图象相交于y =x +5y =kx k k ≠0 , 两点.A(−1,m)B(1)求反比例函数的表达式;(2)将一次函数 的图象沿 轴向下平移 个单位 ,使平移后的图象与反y =x +5y b (b >0)比例函数的图象有且只有一个交点,求 的值.y =kx b 22.已知反比例函数与正比例函数 相交于 .y 1=kx y 2=x A(2,2)(1)求 值.k (2)画出反比例函数的图象.(3)当 时,直接写出 的范围?y 1>y 2x (4)根据图象,解不等式 .kx <x−323.背景知识:已知两直线 , ,若 ,则m :y 1=k 1x +b 1n :y 2=k 2x +b 2(k 1k 2≠0)m ⊥n ;若 ,则 .k 1k 2=−1m//n k 1=k 2应用:在平面直线坐标系 中,直线 交x 轴于点C ,交y 轴于点D ,若 xoy l 1:y =x−1l 2⊥l 1于点 ,交y 轴于点A ,交x 轴于点B.P(2,1)(1)求直线 的表达式; l 2(2)求 的面积;△ABC (3)若将直线 向下平移 个单位,得到新的直线 ,交y 轴于点E ,交直线 于点F ,l 1q l 3l 2使得 ,求 的值.S △AEF =16q 24.已知:如图1,在平面直角坐标系中,一次函数y = x+3交x 轴于点A ,交y 轴于点B ,点C34是点A 关于y 轴对称的点,过点C 作y 轴平行的射线CD ,交直线AB 与点D ,点P 是射线CD 上的一个动点.(1)求点A ,B 的坐标.(2)如图2,将△ACP 沿着AP 翻折,当点C 的对应点C′落在直线AB 上时,求点P 的坐标. (3)若直线OP 与直线AD 有交点,不妨设交点为Q(不与点D 重合),连接CQ ,是否存在点P ,使得S △CPQ =2S △DPQ ,若存在,请求出对应的点Q 坐标;若不存在,请说明理由.答案解析部分1.【答案】C 2.【答案】B 3.【答案】B 4.【答案】B 5.【答案】B 6.【答案】A 7.【答案】D 8.【答案】D 9.【答案】D 10.【答案】D 11.【答案】C 12.【答案】B13.【答案】y=3x ;上;3;y=3x ;左;114.【答案】(0,2)或(0, )−415.【答案】y=2x+216.【答案】y =-2x+517.【答案】4018.【答案】或2x +55+2x19.【答案】(1)解:∵点 在直线 上,∴ ,P(1,b)l 1:y =2x +1b =2×1+1=3∵ 在直线 上,∴ ,∴P(1,3)l 2:y =mx +43=m +4m =−1(2)解:∵直线 与 轴、 轴交于点 、 ,l 2:y =−x +4x y D A ∴ ,,A(0,1)D(−12,0)∵直线 与 轴、 轴分别交于点 、 ,l 2:y =−x +4x y C B ∴ , ,B(0,4)C(4,0)∴S △PDC −S △PAB =12DC ⋅y P −12AB ⋅x P =12×(12+4)×3−12×(4−1)×1=214(3)解:设直线 与直线 , 分别交于点 , , x =a l 1l 2M N 当 时, ;当 时, ,x =a y M =2a +1x =a y N =4−a ∵ ,∴ ,解得或 ,MN =2|2a +1−(4−a)|=2a =13a =53所以 的值为 或 a 135320.【答案】(1)-2;y =+412x (2)解:∵直线AB 沿y 轴向下平移,平移后的直线恰好经过C (﹣3,0), ∴设直线DC 的解析式为y =﹣2x+d ,把C (﹣3,0)代入得d =﹣6,∴直线DC 的解析式为y =﹣2x﹣6.解得,{y =−2x−6y =12x +4{x =−4y =2∴E (﹣4,2).21.【答案】(1)解:由题意,将点 代入一次函数 得: A(−1,m)y =x +5m =−1+5=4∴A(−1,4)将点 代入得: ,解得 A(−1,4)y =k x k−1=4k =−4则反比例函数的表达式为;y =−4x (2)解:将一次函数 的图象沿 轴向下平移 个单位得到的一次函数的解析式为 y =x +5y b y =x +5−b 联立{y =x +5−by =−4x 整理得: x 2+(5−b)x +4=0一次函数 的图象与反比例函数 的图象有且只有一个交点∵y =x +5−b y =−4x 关于x 的一元二次方程 只有一个实数根∴x 2+(5−b)x +4=0 此方程的根的判别式 ∴Δ=(5−b)2−4×4=0解得 b 1=1,b 2=9则b 的值为1或9.22.【答案】(1)解:∵反比例函数y 1= 与正比例函数y 2=x 相交于A (2,2).kx ∴k=2×2=4(2)解:描出点(1,4),(2,2),(4,1), 用平滑的曲线连接,画出反比例函数的图象如图,(3)解:由图象可知,当0<x<2和x<-2时,y1>y2.(4)解:观察图象,直线y=x向下平移3个单位,与反比例函数的交点为(4,1)和(-1,-4),∴不等式 <x-3的解集为:-1<x <0和x >4.kx 23.【答案】(1)解:由 ,得 ,l 1:y =x−1k 1=1 , ,∵l 2⊥l 1∴k 2⋅k 1=−1,∴k 2=−1设 ,把 代入解析式得:b=3,l 2:y =−x +b P(2,1) ;∴l 2:y =−x +3(2)解:由图象可得:, 与x 轴交于点B 、C , 令y=0,则有 ∵l 2:y =−x +3l 1:y =x−1∴B(3,0),C(1,0),又 与y 轴交于点A , 令x=0,则有 ,∵l 2:y =−x +3∴A(0,3) OA=3,BC=2, ;∴∴S △ABC =12BC ⋅OA =3(3)解: 将直线 向下平移 个单位,得到新的直线 ,∵l 1q l 3 ,令x=0则 , ,∴l 3:y =x−1−q y =−1−q ∴E(0,−1−q) ,∴AE =3−(−1−q)=4+q 交直线 于点F , 解得,∵l 3l 2∴{y =−x +3y =x−1−q {x =4+q 2y =2−q 2 , ,∵S △AEF =12AE ⋅F x =16∴12×(4+q)⋅4+q 2=16解得 (不符题意,舍去).q 1=4,q 2=−12 .∴q =424.【答案】(1)解:令x=0,则y=3,∴B (0,3),令y=0,则 x+3=0,34∴x=﹣4,∴A (﹣4,0);(2)解:∵点C 是点A 关于y 轴对称的点, ∴C (4,0),∵CD ⊥x 轴,∴x=4时,y=6,∴D (4,6),∴AC=8,CD=6,AD=10,由折叠知,AC'=AC=8,∴C'D=AD﹣AC'=2,设PC=a ,∴PC'=a ,DP=6﹣a ,在Rt △DC'P 中,a2+4=(6﹣a )2,∴a= ,83∴P (4, );83(3)解:设P (4,m ), ∴CP=m ,DP=|m﹣6|,∵S △CPQ =2S △DPQ ,∴CP=2PD ,∴2|m﹣6|=m ,∴m=4或m=12,∴P (4,4)或P (4,12),∵直线AB 的解析式为y= x+3①,34当P (4,4)时,直线OP 的解析式为y=x ②,联立①②解得,x=12,y=12,∴Q (12,12),当P (4,12)时,直线OP 解析式为y=3x ③,联立①③解得,x= ,y=4,43∴Q ( ,4),43。
一次函数与几何综合(通用版)(含答案)

一次函数与几何综合(通用版)试卷简介:一次函数与几何综合一、单选题(共10道,每道10分)1.如图,已知一条直线经过A(0,2),B(1,0)两点,将这条直线向左平移与x轴,y轴分别交于点C,点D.若DB=DC,则直线CD的函数解析式为( )A. B.C. D.答案:C解题思路:由题意可求得直线AB的解析式为y=-2x+2,AB∥CD.由DB=DC,DO⊥BC可得,OC=OB=1,∴C(-1,0).由AB∥CD可设直线CD的解析式为y=-2x+b,把C点坐标代入可得,b=-2,∴直线CD的函数解析式为y=-2x-2.试题难度:三颗星知识点:一次函数图象与几何变换2.如图,一束光线从点A(3,3)出发,经过y轴上的点C反射后经过点B(1,0),则光线从点A到点B 经过的路径长为( )A. B.C. D.5答案:D解题思路:如图,延长AC交x轴于点B′.则点B,B′关于y轴对称,CB=CB′.作AD⊥x轴于点D,则AD=3,DB′=3+1=4,AB′=5.∴AC+CB=AC+CB′=AB′=5.即光线从点A到点B经过的路径长为5.试题难度:三颗星知识点:坐标与图形性质3.如图,△ABC的内心在y轴上,点C的坐标为(2,0),点B的坐标为(0,2),直线AC的解析式为,则tanA的值是( )A. B.C. D.答案:B解题思路:根据三角形内心的定义可知∠ABO=∠CBO,∵C(2,0),B(0,2),∴OB=OC,∠CBO=∠ABO=45°,,∴∠ABC=90°即AB⊥BC,可求得直线AB的表达式为:,由得,,即A(-6,-4),∴,在Rt△ABC中,.试题难度:三颗星知识点:一次函数综合题4.如图,直线⊥x轴于点(1,0),直线⊥x轴于点(2,0),直线⊥x轴于点(3,0)…,直线⊥x轴于点(n,0).函数y=x的图象与直线,,,…,分别交于点,…,;函数y=2x的图象与直线,,,…,分别交于点,…,.如果△的面积为,四边形的面积为,四边形的面积为,…,四边形的面积为,那么=( )A.4025B.4023C. D.答案:C解题思路:∵函数y=x的图象与直线,,,…,分别交于点,∴∵函数y=2x的图象与直线,,,…,分别交于点∴,,…….当n=2013时,.试题难度:三颗星知识点:一次函数综合题5.如图,在平面直角坐标系中,直线经过原点O,且与x轴正半轴的夹角为30°.点M在x轴上,⊙M的半径为2,⊙M与直线相交于A,B两点.若△ABM为等腰直角三角形,则点M的坐标为( )A. B.C. D.答案:B解题思路:如图,当点M在原点右边时,过点M作MN⊥AB,垂足为N,则,∵△ABM为等腰直角三角形,∴AN=MN,∴,∵AM=2,∴,∴,∵直线与x轴正半轴的夹角为30°,∴,∴点M的坐标为,由对称性可知,点M′的坐标为.试题难度:三颗星知识点:一次函数之存在性6.已知在直角坐标系中有两条直线,直线所对应的函数解析式为y=x-2,如果将坐标纸折叠,使与重合,则点(-1,0)与点(0,-1)也重合,那么直线所对应的函数解析式为( )A.y=x-2B.y=x+2C.y=-x-2D.y=-x+2答案:B解题思路:∵折叠坐标纸可以使点(-1,0)与点(0,-1)重合,∴是沿直线y=x折叠的(也就是对称轴为直线y=x).∵y=x-2过点(0,-2),(2,0),折叠后的对应点为(-2,0),(0,2),即直线过两点(-2,0),(0,2).可以求得:y=x+2.试题难度:三颗星知识点:一次函数图象与几何变换7.如图,有一种动画程序,屏幕上正方形ABCD是黑色区域(含正方形边界),其中A(1,1),B(2,1),C(2,2),D(1,2),用信号枪沿直线发射信号,当信号遇到黑色区域时,区域便由黑变白,则能够使黑色区域变白的b的取值范围是( )A.3<b<6B.2<b<6C.3≦b≦6D.2<b<5答案:C解题思路:题干意思是指直线与小正方形有交点时,求b的取值范围.我们知道直线是由直线向上平移b个单位得到的,若直线与小正方形有交点,可知当直线经过A(1,1)时b的值最小,此时b=3;当直线经过C(2,2)时,b最大,此时b=6.∴能够使黑色区域变白的b的取值范围为3≦b≦6.试题难度:三颗星知识点:一次函数综合题8.已知矩形ABCD中,AB=9,AD=3,将此矩形置于平面直角坐标系中,使AB在x轴正半轴上,若经过点C的直线与x轴交于点E,则四边形AECD的面积为( )A.9B.18C.6D.21答案:B解题思路:在矩形ABCD中,要求四边形AECD的面积,只需求出△EBC的面积即可,即求BE的长.∵点C的纵坐标是3,代入直线解析式可得点C(10,3),∴OB=10,∵直线与x轴交于点E,∴点E(4,0),∴OE=4,BE=6,则△EBC的面积为9,∴四边形AECD的面积为18.试题难度:三颗星知识点:一次函数综合题9.如图,在平面直角坐标系xOy中,A(0,2),B(0,6),动点C在直线y=x上.若以A,B,C三点为顶点的三角形是等腰三角形,则满足条件的点C的个数为( )A.2B.3C.4D.5答案:B解题思路:由于点A,B是固定点,要使△ABC是等腰三角形,只需根据一线两圆,判断与直线的交点即可.①作线段AB的垂直平分线,交直线于点,则是以AB为底的等腰三角形;②以点A为圆心,AB长为半径作圆,交直线于两点,,则,分别是以为底的等腰三角形;③以点B为圆心,AB长为半径作圆,我们发现该圆与直线无交点,原因在于:过点B作直线的垂线BM,垂足为M,.试题难度:三颗星知识点:一次函数之存在性10.如图,在以点O为原点的平面直角坐标系中,一次函数的图象与x轴交于点A,与y轴交于点B,点C在直线AB上,且,反比例函数的图象经过点C,则所有可能的k值为( )A. B.C. D.答案:C解题思路:由题意得,A(2,0),B(0,1),.显然当点为线段AB的中点时,有,此时点的坐标为,.如图,以点O为圆心,的长为半径作圆,交直线AB于另一点,则点也符合条件.过点O作OE⊥AB于点E,过点作⊥x轴于点F,则,.在中,,,则;在中,,且,则,∴点,综上:,试题难度:三颗星知识点:一次函数综合题。
专题5.5 一次函数的几何综合压轴题专项讲练浙教版解析版

专题5.5 一次函数的几何综合【典例1】如图1 , 在平面直角坐标系中, 一次函数y =−23x +4与x 轴交于点B , 与y 轴交于点A , 点C 为线段AB 的中点, 过点C 作DC ⊥x 轴, 垂足为D .(1)求A 、B 两点的坐标;(2)若点E 为y 轴负半轴上一点, 连接CE 交x 轴于点F , 且CF =FE , 在直线CD 上有一点P , 使得AP +EP 最小, 求P 点坐标;(3)如图2, 直线CD 上是否存在点Q 使得∠ABQ =45°,若存在, 请求出点Q 的坐标, 若不存在, 请说明理由.(1)已知一次函数y =−23x +4与x 轴交于点B , 与y 轴交于点A ,利用点在坐标轴上的特点,代数求值即可;(2)已知点C 为线段AB 的中点,DC ⊥x 轴,可求出C(2,3),且CF =FE ,得到△OFE≅△DFC ,进而F(32,0),E(0,−2),要求AP +EP 最小,则根据最短路径原理,作对称点连线求值即可;(3)直线CD 上存在点Q 使得∠ABQ =45°,分两种情况,点Q 分别在x 轴的上方和下方,画图找点证明即可.(1)解:一次函数y =−23x +4与x 轴交于点B ,即y =0时,x =6,点B(6,0),与y 轴交于点A ,即x =0时,y =4,点A(0,4)(2)解:点C 为线段AB 的中点, 由(1)得A(0,4)、B(6,0),所以根据中点坐标C 为(062,402),即C(3,2),∵ CF =FE ,DC ⊥x 轴,∴ △OFE≅△DFC ,∴ OF =FD,OE =CD ,∴ F(32,0),E(0,−2),作点A 关于直线CD 的对称点A ′,坐标为(6,4),连接A ′E ,与直线CD 交于点P ,根据最短路径原理,此时AP +EP 最小,设直线A ′E 为一次函数y =kx +b ,将A ′ (6,4)、E(0,−2)代入得:4=6k +b −2=b ,解得k =1b =−2 ,∴ y =x−2,∴当x =3时,y =1,即点P 坐标为(3,1);(3)解:如图1当点Q 在x 轴上方时,∠ABQ =45°,过点A 作AM ⊥AB ,交BQ 于点M ,过点M 作MH ⊥y 轴于点H ,则△ABM 为等腰直角三角形,∴ AM =AB∵ ∠HAM +∠OAB =∠OAB +∠ABO =90°,∴ ∠HAM =∠ABO ,∵ ∠AHM =∠AOB =90°,∴ △AMH≅△ABO(AAS),∴ MH =AO =4,AH =BO =6,∴ OH =AH +AO =10,∴ M(4,10)设直线BM 为一次函数y =k 1x +b 1,将M(4,10)、B(6,0)代入得:10=4k 1+b 10=6k 1+b 1 ,解得k 1=−5b 1=30 ,∴ y =−5x +30∴当x =3时,y =15,即点Q 坐标为(3,15);如图2,当点Q 在x 轴下方时,∠ABQ =45°,过点A 作AN ⊥AB ,交BQ 于点N ,过点N 作NG ⊥y 轴于点G ,则△ABN 为等腰直角三角形,同理可得△ANG≅△ABO ,∴ NG =AO =4,AG =BO =6,∴ N(−4,−2)设直线BN 为一次函数y =k 2x +b 2,将N(−4,−2)、B(6,0)代入得:−2=−4k 2+b 20=6k 2+b 2 ,解得k 2=15b 2=−65,∴ y =15x−65∴当x=3时,y=−35,即点Q坐标为(3,−35);所以Q坐标(3,15)或(3,−35)1.(2022春·广东深圳·八年级校考期中)如图,在平面直角坐标系xOy中,直线y=−34x+6交x轴于点A,交y轴于点B.(1)求点A、点B的坐标及△OAB的面积;(2)线段OA上存在一动点P从点O出发沿OA以每秒2个单位的速度向A运动,设P点运动时间为t秒,连接BP,当t为何值时BP平分∠ABO;(3)在(2)的前提下,过点P作PC⊥AB于点C,试问x轴上是否存在一动点M,使得△CPM为等腰三角形,若存在请直接写出M坐标,若不存在,请说明理由.【思路点拨】(1)在y=−34x+6中,求出当x=0时,y的值,求出y=0时,x的值即可得到答案;(2)先利用勾股定理求出AB=10,再根据角平分线的性质得到OP=PC,利用面积法求出OP的长即可得到答案;(3)分当PC=PM=3时,当PC=MC时,当MP=MC时,三种情况根据等腰三角形的定义和性质进行分类讨论求解即可.【解题过程】(1)解:在y=−34x+6中,令x=0,则y=6;令y=0,则x=8,∴A(8,0),B(0,6);即,OA=8,OB=6,∴S△OAB=12⋅OA⋅OB=12×8×6=24(2)如图所示,连接BP ,作PC ⊥AB ,∵A(8,0),B(0,6),∴OA =8,OB =6,∴ AB 10;∵BP 平分∠ABO ,PC ⊥AB ,∠BOP =90°,∴OP =PC ,∵S △AOB =S △POB +S △ABP ,∴ 12OB ⋅OA =12OB ⋅OP +12AB ⋅PC ,∴ 12×6×8=12×6⋅OP +12×10⋅OP ,∴ OP =3,即2t =3∴t =32;当t =32时,BP 平分∠ABO ;(3)由(2)得PC =3,P(3,0),则AP =8−3=5,在Rt △APC 中,AC =4,如图,当PC =PM =3时,则M(0,0)或(6,0);如图所示,当PC =MC 时,过点C 作CN ⊥PM 于N ,则MP =2PN ,∵ S △APC =12AC ⋅PC =12AP ⋅CN ,∴CN =PC⋅AC AP =125,在Rt △CPN 中,由勾股定理得PN =95,∴ MP =185,∴ OM =OP +MP =335,∴ M(335,0);当MP =MC 时,设M(m,0),由上一问可知ON =OP +PN =3+95=245,即C(245,125),∴CM 2=m−+0−∵P(3,0),∴PM 2=(m−3)2,∴ (m−3)2=(m−245)2+(0−125)2,∴ m =112,∴ M(112,0);综上所述,点M 的坐标为(0,0)或(6,0)或(335,0)或(112,0).2.(2023秋·上海普陀·八年级校考期中)如图,已知直线l 1:y =kx(k >0)上有一点A ,直线l 1绕着原点O 旋转45°得直线l 2,过点A 作AB ⊥l 1,交直线l 2于点B .,且点A的横坐标是4,点B在第一象限内时,求点B的坐标和直线l2的解析式.2(2)当点A的横坐标是m(m>0)时,求旋转后直线的解析式.(用含字母k的式子表示).【思路点拨】(1)如图:过A作x轴的垂线与过B作y轴的垂线交于点M,即BM⊥AM,然后证△ABM≌△AOC可得BM=AC、AM=OC,再根据坐标与图形求得AM=OC=4,BM=AC=2,进而确定点B的坐标,最后运用待定系数法即可解答;(2)直线l1逆时针旋转和顺时针旋转两种情况,分别按照(1)的方法解答即可.【解题过程】(1)解:如图:过A作x轴的垂线与过B作y轴的垂线交于点M,即BM⊥AM,∴∠OCA=∠BMA=90°,∠BAM+∠ABM=90°,∵AB⊥l1,∴∠BAM+∠CAO=90°,∴∠ABM=∠CAO∵AB⊥l1,∠BOA=45°,∴∠OBA=∠BOA=45°,∴AB=OA,∴△ABM≌△AOC,∴BM=AC,AM=OC,∵k=1,2x,∴直线l1的解析式为y=12∵点A的横坐标是4,∴点A的纵坐标坐标是2,∴AM=OC=4,BM=AC=2∴点B的横坐标为4−2=2,纵坐标为4+2=6,即点B的坐标为(2,6),设直线l2的解析式为y=k1x,则有6=2k1,解得:k1=3,∴直线l2的解析式为y=3x.(2)解:①如图:当直线l1逆时针旋转时,∵点A的横坐标是m,y=kx,∴点A纵坐标为km,即OC=m,AC=km,由(1)可证:∴△ABM≌△AOC,∴BM=AC,AM=OC,∴点B的横坐标为m−km=m(1−k),纵坐标为m+km=m(k+1),即点B的坐标为(m(1−k),m(1+k)),;设直线l2的解析式为y=k2x,则有m(1+k)=m(1−k)k2,解得:k2=1k1−k∴直线l 2的解析式为y =1k 1−k x ;②当直线l 1顺时针旋转时,同理可得:直线l 2的解析式为y =1−k 1k x .综上,当点A 的横坐标是m (m >0)时,旋转后直线的解析式为y =1k 1−k x 或y =1−k 1k x .3.(2023秋·广东深圳·八年级深圳市大鹏新区华侨中学校联考期中)如图,一次函数y =kx +b 的图象与x 轴交于点A ,与y 轴交于点B(0,3),且OA =OB .(1)点A 的坐标为___________;点AB 的表达式为___________;(2)在y 轴上有一点C(0,4),在x 轴上是否存在点P ,使△ACP 是等腰三角形?若存在,求出所有符合条件的点P 的坐标;若不存在,请说明理由:(3)若x 轴上的动点Q 在点A 的右侧,以Q 为直角顶点,BQ 为腰在第一象限内作等腰直角△BQD ,连接DA 并延长,交y 轴于点E ,当Q 运动时,点E 的位置是否发生变化?若不变,请求出点E 的坐标;若变化,请说明理由.【思路点拨】(1)由OA =OB,B(0,3),得OA =3,从而得到A(3,0),再用待定系数法求出直线AB 的解析式即可;(2)设点P(x,0),可得AC =5,分情况三种:CP =CA ;PC =PA ;AP =AC ,分别求出x 的值即可得解;(3)过点D 作DF ⊥x 轴,由AAS 证得△BOQ≌△QFD ,从而得到OQ =DF,BO =QF ,进而推导出△AFD 为等腰直角三角形,OE =OA =3,故E (0,−3).【解题过程】(1)解:∵B(0,3),OA =OB∴OA =3,∴A(3,0),设直线AB 的解析式为y =kx +b ,把A(3,0),B (0,3)分别代入得:3k +b =0b =3,故直线AB 的解析式为y =−x +3;故答案为:(3,0);y=−x+3;(2)在x轴上存在点P,使△ACP是等腰三角形,设P(x,0).依题意得,AC5,当CP=CA时,点P位置如图中的点P1,如图,∵CO⊥AP1,∴OP1=OA,∴P1(−3,0);当PC=PA,时点P位置如图1中的点P2,此时,P2A=3−x,在Rt△COP2中,(3−x)2=x2+16,.解得:x=−76∴P2−7,0;6当AP=AC=5时,点P位置如图1中的点P3、P4,∴|x−3|=5,解得:x=8或−2.∴P3(8,0),P4(−2,0),综上所述,点P的坐标为(−3,0)或−7,0或(8,0)或(−2,0);6(3)当Q运动时,点E的位置不发生变化,点E的坐标为(0,−3),理由如下:过点D作DF⊥x轴,则∠2=90°,则∠1=∠2,如图,∵△BQD 为等腰直角三角形,∠BQD =90°,∴∠BQO +∠DQF =90°,BQ =DQ ,在Rt △BOA 中,∠OBQ +∠BQO =90°,∴∠OBQ =∠DQF ,在△BOQ 和△QFD 中,∠OBQ =∠DQF ∠1=∠2BQ =QD∴△BOQ≌△QFD(AAS),∴OQ =DF ,BO =QF ,设AQ =a ,则AF =a +3,DF =a +3,∴△AFD 为等腰直角三角形,∴∠OAE =∠DAF =45°,∴OE =OA =3,∴E(0,−3).4.(2023秋·重庆渝中·八年级重庆巴蜀中学校考阶段练习)如图所示,在直角坐标系中,C (6,0),D (6,6),线段AB 在y 轴上平移,且满足AB =2,连接AD 、BC 、CD .(1)当∠OBC =30°时,BC =__________;(2)当四边形ABCD 的周长取得最小值时,求出此时点B 的坐标及四边形的最小周长;(3)在(2)的条件下,连接BD ,当BD 向下平移的过程中,x 轴上是否存在一点P ,使△BDP为等腰直角三角形?若存在,请求出点P的坐标,若不存在,请说明理由.【思路点拨】(1)根据直角三角形的性质,即可求解;(2)作点C关于y轴的对称点E,连接BE,将AD沿y轴平移至点B交CD于点F,连接EF,则点E(−6,0),BE=BC,CE=12,根据平移的性质可得当点E,B,F三点共线时,四边形ABCD的周长取得最小值,再求出直线EF的解析式,即可求解;(3)分三种情况讨论,结合全等三角形的判定和性质,即可求解.【解题过程】(1)解:∵C(6,0),∴OC=6,∵∠OBC=30°,∠BOC=90°,∴BC=2OC=12;故答案为:12(2)解:如图,作点C关于y轴的对称点E,连接BE,将AD沿y轴平移至点B交CD于点F,连接EF,则点E(−6,0),BE=BC,CE=12,∵C(6,0),D(6,6),∴CD∥y轴,CD=6,∴BF=AD,AB=DF=2,∴BC+AD=BE+BF≥EF,∴AB+BC+CD+AD≥AB+CD+EF,即当点E,B,F三点共线时,四边形ABCD的周长取得最小值,∵CD=6,DF=2,∴CF=4,∴点F的坐标为(6,4),∴EF==∴四边形ABCD 的周长的最小值为2+6+=8+设直线EF 的解析式为y =kx +b (k ≠0),把点E (−6,0),F (6,4)代入得:−6k +b =06k +b =4 ,解得:k =13b =2,∴直线EF 的解析式为y =13x +2,当x =0时,y =2,∴点B 的坐标为(0,2);(3)解:存在,由(2)得:BD=当∠BDP =90°,BD =PD 时,如图,过点B 作BM ⊥CD 于点M ,则∠BDM +∠PDC =90°,∠BMD =∠DCP =90°,∴∠BDM +∠DBM =90°,∴∠DBM =∠PDC ,∴△BDM≌△DPC ,∴CP =DM,BM =DC =6,∴CP =DM =4,∴OP =10,∴此时点P 的坐标为(10,0);当∠DBP =90°,BD =PB 时,如图,过点B 作DM ⊥y 轴于点M ,则∠DBM +∠PBO =90°,∠BMD =∠BOP =90°,∴∠PBO+∠OPB=90°,∴∠DBM=∠OPB,∴△BDM≌△PBO,∴OP=BM,DM=OB=6,∴OP=BM=4,∴此时点P的坐标为(−4,0);当∠BPD=90°,BP=PD时,如图,过点D作DM⊥x轴于点M,则∠OPD+∠DPM=90°,∠PMD=∠BOP=90°,∴△BOP≌△PMD,∴OP=DM,BP=PM,设此时点B的坐标为(0,a),则BD向下平移(2−a)个单位,PM=OB=−a,∴OP=DM=2−a−6=−a−4,∵OP+PM=6,∴−a−4−a=6,解得:a=−5,∴OP=1,∴此时点P的坐标为(1,0);综上所述,点P的坐标为(10,0)或(−4,0)或(1,0).5.(2023春·重庆涪陵·八年级西南大学附中校考开学考试)如图,直线l AB:y=+3的图像与x轴和y轴分别交于点A和点B,将△AOB沿直线l对折使点A和点B重合,直线l与x轴交于点C,与AB交于点D,连接BC.(1)求线段OC的长;(2)若点E是点C关于y轴的对称点,求△BED的面积;(3)已知y轴上有一点P,若以点B,C,P为顶点的三角形是等腰三角形,请求出所有满足条件的点P的坐标.【思路点拨】(1)根据坐标轴上点的特征,求出点A、B的坐标,设OC=a,由折叠的性质可得BC=AC=,利用勾股定理求解即可;(2)先求出点E的坐标,然后由S△BED=S△ABE−S△ADE,即可获得答案;(3)设点P(0,m),分三种情况利用等腰三角形两腰相等的性质,建立方程并求解即可获得答案.【解题过程】(1)解:对于直线l AB:y=+3,令x=0,则y=3,∴点B(0,3),令y=0,则有0=+3,解得x=∴点,设OC=a,∵将△AOB沿直线l对折使点A和点B重合,直线l与x轴交于点C,与AB交于点D,∴BC=AC=,在Rt△OBC中,可有OB2+OC2=BC2,即32+a2=2,解得a=∴线段OC(2)如下图,连接DE,∵点E是点C关于y轴的对称点,线段OC∴,∴AE=AC=∵,B(0,3),∴,∴S△BED=S△ABE−S△ADE=12AE⋅OB−12AE×|y D|=12×3−12××32=(3)∵线段OC∴,设点P(0,m),∵点B(0,3),∴BC2=32+2=12,CP2=2+m2=3+m2,BP2=(m−3)2,∵△PCB为等腰三角形,∴①当CP=BP时,可有3+m2=(m−3)2,解得m=1,∴点P的坐标为(0,1);②当CP=BC时,可有3+m2=12,解得m=3(舍去)或m=−3,∴点P的坐标为(0,−3);③当BP=BC时,可有(m−3)2=12,解得m=3+m=∴点P的坐标为(0,3+或.综上所述,点P的坐标为(0,1)或(0,−3)或(0,3+或.6.(2022春·湖南岳阳·八年级校考阶段练习)如图,直线y=kx+k分别交x轴、y轴于点A,C,直线BCOC,∠CBA=45°,点P是直线BC上的一点.过点C交x轴于点B,且OA=13(1)求直线BC的解析式;(2)若动点P从点B出发沿射线BC/秒,连接AP,设△PAC的面积为S,点P的运动时间为t秒,求S与t之间的函数关系式,并写出t的取值范围;(3)若点Q是直线AC上且位于第三象限图象上的一个动点,点M是y轴上的一个动点,当以点B、M、Q 为顶点的三角形为等腰直角三角形时,求点Q和点M的坐标.【思路点拨】(1)先求得点A坐标,进而求得点C、B坐标,然后利用待定系数法求解即可;(2)分点P在线段BC上和点P在射线BC上两种情况,可画出图形,利用S=S△ABC−S△ABP或S=S△ABP−S△ABC求解即可;(3)分∠BMQ=90°、∠BQM=90°、∠QBM=90°三种情况,利用等腰直角三角形的性质和全等三角形的判定与性质,结合坐标与图形性质求解即可.【解题过程】(1)解:令y=0,由kx+k=0得x=−1,则A(−1,0),OA=1,OC,∴OC=3,则C(0,3),∵OA=13∵∠CBA=45°,∠BOC=90°,∴OB=OC=3,则B(3,0),设直线BC的表达式为y=mx+n,将C (0,3)、B (3,0)代入,得3m +n =0n =3,解得m =−1n =3 ,∴直线BC 的表达式为y =−x +3;(2)解:当点P 在线段BC 上时,过P 作PH ⊥x 轴于H ,如图,∵∠CBA =45°,∠PHB =90°,PB =,∴PH =BH ==t ,又AB =OB +OA =4,OC =3,∴S =S △ABC −S △ABP =12AB ⋅OC−12AB ⋅PH =12×4×3−12×4⋅t =6−2t ,∵BC =∴0≤t ≤3;当点P 在射线BC 上时,如图,同理可得S =S △ABP −S △ABC =2t−6,t >3,综上,S 与t 之间的函数关系式为S =6−2t,(0≤t ≤3)2t−6,(t >3) ;(3)解:将C (0,3)代入y =kx +k 中得k =3,∴直线AC 的表达式为y =3x +3设M (0.m ),Q (n,3n +3),n <−1,①当∠BMQ =90°时,当点M 在x 轴上方,如图,分别过Q 、B 作y 轴的平行线,分别交过点M 与x 轴平行的直线于点G 、H ,则∠QGM =∠BHM =∠BMQ =90°,∴∠GMQ +∠MQG =∠GMQ +∠HMB =90°,∴∠MQG =∠HMB ,又MQ =MB ,∴△QGM≌△MHB (AAS),∴GQ =MH ,GM =BH ,则m−3n−3=3,−n =m ,解得m =32,n =−32,又3n +3=−32,∴M 0,Q −32同理,当点M 在x 轴下方时,3n +3−m =3,−n =−m ,解得m =n =0,不符合题意,舍去;②当∠BQM =90°时,如图,过Q 作y 轴的平行线,交过点M 与x 轴平行的直线H ,交x 轴于点G ,则∠QGB =∠QHM =∠BQM =90°,∴∠GBQ +∠BQG =∠MQH +∠BQG =90°,∴∠GBQ =∠MQH ,又BQ =QM ,∴△QGB≌△MHQ (AAS),∴GQ =MH ,GB =QH ,则−3n−3=−n ,3−n =3n +3−m ,解得m =−6,n =−32,又3n +3=−32,∴M (0,−6),Q −32③当∠QBM =90°时,如图,同理证明△QGB≌△BHM (AAS),∴GQ =BH ,GB =MH ,则−3n−3=3,3−n =m ,解得m =5,n =−2,又3n +3=−3,∴M (0,5),Q (−2,−3),综上,满足题意的点M 、Q 坐标为;M 0,Q −32M (0,−6)、Q −32M (0,5)、Q (−2,−3).7.(2023秋·黑龙江哈尔滨·八年级哈尔滨市第四十九中学校校考阶段练习)如图,在平面直角坐标系中,点O 为坐标原点,点C 的坐标为(0,6),在x 轴的负半轴取点A ,在x 轴的正半轴取点B ,△ABC 面积等于36,AC =BC .(1)求点A 的坐标.(2)如图2,动点P 以每秒2个单位长度的速度从点A 出发沿AO 方向向终点O 运动,运动时间为t ,过点P作DP⊥OA交AC于点D,在CB的延长线上取点E,使得AD=BE,连接DE交x轴于点G,若△DPG的面积为S,求S与t的关系式.(3)如图3,在(2)的条件下,以DE为底边,在x轴的上方作等腰直角三角形,使得DF=FE,∠F=90°,CE交DF于点K,DF交y轴于点Q,连接GQ,若GQ⊥DF,求点K坐标.【思路点拨】(1)根据AC=BC,可得AB=2OB,再由△ABC面积等于36,可得AB=12,即可求解;(2)过点E作EH⊥x轴于点H,根据题意得:AP=2t,AC=BC=△ADF,△BEH都是等腰直角三角形,可得DP=AP=2t,再由△ADP≌△BEH,可得AP=BH=2t,可证明△DGP≌△EGH,从而得到PG=HG,即可求解;(3)过点E作EH⊥x轴于点H,过点D作DM⊥OC点M,则DM=OP=6−2t,根据题意可得点D(2t−6,2t) ,E(6+2t,−2t),可求出直线BC的解析式,再根据△DEF是等腰直角三角形,可得△DGQ是等腰直角三角形,再证明△DQM≌△QGO,可得DM=OQ=6−2t,QM=OG=2t,从而得到t=1,进而得到点Q(0,4),D (−4,2),可求出直线DF的解析式,然后联立两直线解析式,即可求解.【解题过程】(1)解:∵AC=BC,OC⊥AB,∴AB=2OB,∵点C的坐标为(0,6),∴OC=6,∵△ABC面积等于36,AB×OC=36,∴12∴AB=12,∴OB=6,∴点B的坐标为(6,0);(2)解:如图,过点E作EH⊥x轴于点H,根据题意得:AP =2t ,AC =BC =由(1)得:OA =OB =OC =6,∴∠BAC =∠ABC =∠ACO =∠BCO =45°,∴∠EBH =∠ABC =∠BAC =45°,∵DP ⊥OA ,∴△ADF,△BEH 都是等腰直角三角形,∴DP =AP =2t ,∵AD =BE ,∴△ADP≌△BEH ,∴AP =BH =2t ,∴PH =PB +BH =PB +AP =AB =12,∵∠DPO =∠EHG =90°,∠DGP =∠EGH ,∴△DGP≌△EGH ,∴PG =HG ,∴PG =GH =6,∴S 与t 的关系式为S =12DP ×PG =12×2t ×6=6t ;(3)解:如图,过点E 作EH ⊥x 轴于点H ,过点D 作DM ⊥OC 点M ,则DM =OP =6−2t ,由(2)得:DG =EG ,EH =DP =2t,OH =6+2t,OP =6−2t ,∴点D (2t−6,2t ),E (6+2t,−2t ),设直线BC 的解析式为y =k 1x +b 1,把点C (0,6),B (6,0)代入得:6k 1+b 1=0b 1=6 ,解得:k 1=−1b 1=6 ,∴直线BC 的解析式为y =−x +6,∵△DEF 是等腰直角三角形,∴∠EDF =45°,∵GQ ⊥DF ,∴△DGQ 是等腰直角三角形,∴DQ =GQ ,∵∠DMQ =∠GOQ =90°,∴∠DQO +∠OQG =∠OGQ +∠OQG =90°,∴∠DQO =∠OGQ ,∴△DQM≌△QGO ,∴DM =OQ =6−2t ,QM =OG =2t ,∴OQ =OM +QM =4t ,∴4t =6−2t ,即t =1,∴点Q (0,4),D (−4,2)设直线DF 的解析式为y =k 2x +b 2,把点Q (0,4),D (−4,2)代入得:−4k2+b2=2b2=4,解得:k2=12b2=4,∴直线DF的解析式为y=12x+4,联立得:y=−x+6y=12x+4,解得:x=43y=143,∴点K8.(2023春·黑龙江哈尔滨·八年级哈尔滨市第十七中学校校考期中)如图1,平面直角坐标系中,O为原点,直线AB的解析式为y=x+4,分别交x轴、y轴于B、A两点,过点A作AC⊥AB交x轴于C.(1)直接写出点A,点B的坐标;(2)如图1,点D在点A上方的y轴上,连接BD,延长CA交BD于E,DE<BE,作DF⊥BD交BA延长线于F,若线段AD的长度为t,四边形AEDF的面积为S,用含t的式子表示S;(3)如图2,在(2)问条件下,在线段BE上取一点G,使BG=DF,K为第一象限∠CAF内部一点,连接KG,KF,∠GKF=45°,过点K作KH⊥DF于H,KH=DF,连接CK,当S=8时,求线段CK的长度.【思路点拨】(1)令x=0,y=0,即可求解;(2)作DI⊥AD交BA的延长线于点I,证明△DEA≌△DFI(AAS),S=S△DAI=12t2;(3)过点F作FQ⊥FK交BD于点Q,证明△QFD≌△FKH(ASA),推出△QFK是等腰直角三角形,证得点Q与点G重合,再证明△BDO≌△DHA(SAS),得到H8,4,根据两直线的交点求得E−43EM⊥AD于点M,过点K作KN⊥AH交AH于点N,交x轴于点T,同理可证△DEM≌△KHN,求得K【解题过程】(1)解:∵直线AB的解析式为y=x+4,令x=0,则y=x+4=0+4=4;令y=0,则0=x+4,解得x=−4;∴点A的坐标为0,4;点B的坐标为−4,0;(2)解:∵DF⊥BD,AC⊥AB,∴∠BDF=∠EDF=90°,∴∠DEA+∠DFA=180°,∵A0,4,B−4,0,∴OA=OB,∴∠OAB=∠OBA=45°=∠DAF,∠DAE=∠OAC=90°−∠BAO=45°,作DI⊥AD交BA的延长线于点I,∴∠DAI=∠I=45°,∠DFI+∠DFA=180°,∴DI=AD=t,∠DEA=∠DFI,∠DAE=∠I=45°,∴△DEA≌△DFI(AAS),t2;∴S=S四边形DEAF=S△DAE+S△DAF=S△DAI=12(3)解:∵S=8,t2=8,解得t=4,∴12∴AD=4,D0,8,过点F作FQ⊥FK交BD于点Q,连接AH,∴∠QFD+∠KFH=90°=∠FKH+∠KFH,∴∠QFD=∠FKH,∵KH=DF,∴△QFD≌△FKH(ASA),∴FQ=FK,∴△QFK是等腰直角三角形,∴∠FQK=∠FKQ=45°,∵∠GKF=45°,∴点Q与点G重合,∴DG=FH,∵BG=DF,∴DB=DH;∵∠BDO=90°−∠ADH=∠DHA,BO=DA=4,∴△BDO≌△DHA(SAS),∴AH=OD=8,∠DAH=∠BOD=90°,∴AH∥x轴,∴H8,4,∵B−4,0,D0,8,设直线BD的解析式为y=kx+8,代入B−4,0,∴0=−4k+8,解得k=2,∴直线BD的解析式为y=2x+8,同理得直线AC的解析式为y=−x+4,联立2x +8=−x +4,解得x =−43,y =−−+4=163,∴E −43作EM ⊥AD 于点M ,过点K 作KN ⊥AH 交AH 于点N ,交x 轴于点T ,同理可证△DEM≌△KHN ,∴KN =DM =8−163=83,HN =EM =43,∴AN =8−43=203,KT =4−83=43,∴∴CT =203−4=83,∴CK ==9.(2023春·湖北武汉·八年级校考阶段练习)如图,平面直角坐标系中,直线y =−x +4分别交x 、y 轴于A 、B 两点,点P 为线段AB 的中点.(1)直接写出点P 的坐标 ;(2)如图1,点C 是x 轴负半轴上的一动点,过点P 作PD ⊥PC 交y 轴正半轴于点D ,连接CD ,点M 、N 分别是CD 、OB 的中点,连接MN ,求∠MNO 的度数;(3)如图2,点Q 是x 轴上的一个动点,连接PQ .把线段PQ 绕点Q 顺时针旋转90°至线段QT ,连接PT 、OT .当PT +OT 的值最小时,求此时点T 的坐标.【思路点拨】(1)求出A 、B 点的坐标,再由中点坐标公式求出P 点坐标即可;(2)过点P 作EF ⊥x 轴交于F 点,过D 点作DE ⊥EF 交于E 点,过M 点作MG ⊥y 轴交于G ,可证明△PED≌△CFP(AAS),设C(−x ,0),则D(0,4+x),M( x 2,x 2+2 ),求出GN =GM ,可得∠GNM =45°,即可求∠MNO =135°;(3)过点Q 作RS ⊥x 轴,过点P 作PR ⊥RS 交于点R ,延长PQ ,使PQ =QK ,过点T 作TS ⊥RS 交于S ,作O 点关于过点T 垂直于x 轴的直线的对称点O ′,连接O ′T ,当O ′、T 、K 三点共线时,PT +OT 的值最小,最小值为KO ′,可证明△PQR≌△QTS (AAS),设Q(t ,0),则T(t +2,t−2),O ′ (2t +4,0),K(2t−2,−2),求出直线Q 'K 的解析式为.y =13x−23t−43,再将T 点坐标代入即可求t 的值,从而求出T 点坐标.【解题过程】(1)解:在y =−x +4中,令x =0,则y =4,∴B(0,4),令y =0,则x =4,∴A(4,0),∵点P 为线段AB 的中点,,∴P(2,2),故答案为:(2,2);(2)解:过点P 作EF ⊥x 轴交于F 点,过D 点作DE ⊥EF 交于E 点,过M 点作MG ⊥y 轴交于G ,∵CP ⊥PD ,∴∠CPD =90°,∴∠EPD +∠FPC =90°,∵∠EPD +∠EDP =90°,∴∠FPC =∠EDP ,∵PF =ED =2,∴△PED≌△CFP(ASA),∴PE =FC ,设C(−x ,0),∴FC =x +2,∴EF =4+x ,∴D(0,4+x),∵M 是CD 的中点,∴M(− x 2,2+x 2 ),∴ GM =x 2,OG =2+x 2,∵N 是OB 的中点,∴N(0,2),∴GN = x 2,∴GN =GM ,∴∠GNM =45°,∴∠MNO =135°;(3)解:过点Q 作RS ⊥x 轴,过点P 作PR ⊥RS 交于点R ,延长PQ ,使PQ =QK ,过点T 作TS ⊥RS 交于S ,∵PQ =TQ ,∠PQT =90°,∴∠PTQ =45°,∵Q 点是PK 的中点,TQ ⊥QK ,∴TQ=PQ=KQ,∴∠PTK=90°,PT=KT,作O点关于过点T垂直于x轴的直线的对称点O′,连接O′T,∴OT+PT=O′T+TK,∴当O′、T、K三点共线时,PT+OT的值最小,最小值为KO′,如图所示,∴∠PQR+∠TQS=90°,∵∠PQR+∠QPR=90°,∴∠TQS=∠QPR,∴△PQR≌△QTS(AAS),∴PR=QS,RQ=TS,设Q(t,0),∴PR=2−t,RQ=2,∴T(t+2,t−2),∴O′(2t+4,0),∵Q是PK的中点,∴K(2t−2,−2),设直线O′K的解析式为y=kx+b,∴(2t+4)k+b=0 (2t−2)k+b=−2,解得k=13b=−2t−43∴ .y =13x−23t−43,∵T(t +2,t−2)在O ′K 上,∴ t−2=13(t +2)−23t−43,解得t =1,∴T(3,−1).10.(2023春·湖北武汉·八年级校考阶段练习)已知:直线y =x +b 分别与x 轴负半轴、y 轴正半轴交于点A 、B .(1)如图1,若直线AB 过P (1,3),求S △AOB .(2)如图2,点B 关于x 轴的对称点为B ′,将线段AB ′沿x 轴正半轴移动到MN ,直线MN 交直线AB 于点E ,直线BN 交x 轴于点F ,求NEAF 的值.(3)如图3,在(1)的条件下,在x 轴上是否存在一点Q ,使得∠PQO =∠APO ,若存在请求出Q 点坐标;若不存在,请说明理由.【思路点拨】(1)分别令x,y =0求得点A,B 的坐标,进而即可求解;(2)分别令x,y =0求得点A,B 的坐标,得出B ′(0,−b ),设线段AB ′沿x 轴正半轴移动到MN ,移动了t 个单位,得出直线MN 的解析式为y =−x +t−b ,联立y =−x +t−b y =x +b,得出NE ,进而得出直线BN 的解析式为y =−2b t x +b ,求得AF =t2+b ,即可求解;(3)以OP 为直角边在OP 的右侧作等腰Rt △POH ,连接PQ 交OH 于点G ,过点P 作EF ⊥y 轴于点E ,过点H 作HF ⊥EF 于点F ,根据已知得出∠GOQ =∠GQO ,则GQ =GO ,即点G 在OG 的垂直平分线上,证明△OPE≌△PHF ,可得H (4,2),进而得出OH 的解析式为y =12x ,设G a,12a ,则Q (2a,0),求得直线PQ 的解析式为y =31−2a x−61−2a ,将点G a,12a 代入求得a 的值,进而即可求解.【解题过程】(1)解:将点P (1,3)代入y =x +b ,得1+b =3∴b =2,即y =x +2当x =0时,y =2,则B (0,2),当y =0时,x =−2,则A (−2,0)∴S △AOB =12OA ×OB =12×2×2=2,(2)∵y =x +b ,当x =0时,y =b ,则B (0,b ),当y =0时,x =−b ,则A (−b,0),∴B ′(0,−b ),设线段AB ′沿x 轴正半轴移动到MN ,移动了t 个单位,则M (−b +t,0),N (t,−b ),t >0,设直线MN 的解析式为y =−x +c ,∴−b =−t +c 解得:c =t−b ,∴直线MN 的解析式为y =−x +t−b ,联立y =−x +t−b y =x +b∴x =t−2b 2y =t 2∴∴NE =b设直线BN 的解析式为y =mx +n ,将点B (0,b ),N (t,−b )代入,n =b mt +n =−b∴m =−2bt n =b ,∴直线BN 的解析式为y =−2bt x +b ,当y =0时,x =t2,+b,∴AF=t2∴NEAF t2(3)解:如图所示,以OP为直角边在OP的右侧作等腰Rt△POH,连接PQ交OH于点G,过点P作EF⊥y轴于点E,过点H作HF⊥EF于点F,∴∠POG=45°,∵P(3,1),∴EP=1,OE=3∵OA=OB,∠AOB=45°∴△AOB是等腰直角三角形,∵∠APO+∠EOP=45°,∠PQO=∠APO∴∠PQO+∠EOP=45°又∵∠EOP+∠GOQ=90°−∠POG=45°∴∠GOQ=∠GQO∴GQ=GO,即点G在OG的垂直平分线上,∵∠OEP=∠PFH=∠OPH=90°,∴∠OPE=90°−∠FPH=∠PHF,又PQ=PH,∴△OPE≌△PHF,∴EP=FH=1,PF=OE=3,∴H(4,2),设直线OH的解析式为y=k1x,则2=4k1,12∴OH 的解析式为y =12x 设G a,12a∵点G 在OG 的垂直平分线上,∴Q (2a,0)设PQ 的直线解析式为y =ex +f ,将点P (1,3),Q (2a,0)代入得,3=e +f 0=2ae +f解得:e =31−2af =−6a1−2a∴直线PQ 的解析式为y =31−2a x−61−2a将点G a,12a 代入得,12a =3a1−2a −6a1−2a∵a ≠0,∴12=31−2a −61−2a解得:a =72(经检验,是原方程的解)∴Q (7,0).11.(2023春·湖北武汉·八年级统考期末)在平面直角坐标系中,已知A (−4,0),B (0,2)两点.(1)请直接写出直线AB的解析式;(2)如图(1),点C 坐标为(0,−1),动点D 在线段OA 上,直线CD 交直线AB 于点E ,若S △ADE =S △CDO ,求点D 的坐标;(3)如图(2),F 为y 轴负半轴上任意一点,有一宽度为1的直尺平行于y 轴,在点A ,O 之间平行移动,直尺两长边被线段AB 和线段AF 截得两线段PQ,MN .设点P 的横坐标为t ,且−4<t <−1,试比较线段MN 与2PQ 的大小.【思路点拨】(1)根据待定系数法求出直线解析式即可得到答案;(2)如图所示,由S △ADE =S △CDO ,得到S △ADE +S 四边形DOBE =S △CDO +S 四边形DOBE ,从而有S △BCE =S △AOB =4,则3(−x E )2=4,解得x E =−83,代入直线AB 的解析式中即可得到E −83再求出y CE =−58x−1,当y D =0时,解得x D =−85,即得到点D 坐标为−85,0;(3)如图,设F (0,m )(m <0),根据直线AF 过A (−4,0)得−4p +m =0,即p =14m, 从而y AF =14mx +m ,则y P =12t +2,y Q =mt 4+m ,即可得到PQ =t 2−mt 4+2−m ,再由直尺的宽度为1,且MN ∥PQ ,求出MN =t 2−mt4+52−5m4,进而表示出MN−2PQ【解题过程】(1)解:∵ A (−4,0),B (0,2),设直线AB 的解析式是y =kx +b ,则0=−4k +b2=b,解得k =12b =2,∴ 直线AB 的解析式是y =12x +2;(2)解:如图所示:∵S △ADE =S △CDO ,∴S △ADE +S 四边形DOBE=S △CDO +S 四边形DOBE ,∴S △BCE =S △AOB =4×22=4,∵C (0,−1),B (0,2),∴BC =3,∴3(−x E )2=4,解得x E =−83,∴y E =12×−+2=23,即E −83设y CE =k ′x +b ′(k ′≠0),分别将C (0,−1)和E −83代入,可得b ′=−1−83k ′+b ′=23,解得k =−58b =−1 ,∴y CE =−58x−1,当y D =0时,x D =−85,即点D 坐标为−85,0;(3)解:如图,设F (0,m )(m <0),设直线AF 的解析式为y AF =px +m,(p ≠0),将A (−4,0)代入,得−4p +m =0,即p =14m, ∴y AF =14mx +m ,∵PQ ∥y 轴,且点P 的横坐标为t ,则x Q =x P =t ,∴y P =12t +2,y Q =mt 4+m ,∴PQ =+2m =t2−mt4+2−m ,∵直尺的宽度为1,且MN ∥PQ ,∴x M =x N =t +1,∴y M =12(t +1)+2=t2+52,y Q =m (t 1)4+m =mt 4+5m 4,∴MN ==t 2−mt4+52−5m 4,∴MN−2PQ =mt 4+52−mt4+2−m =mt 4−t 2−32+3m4=(t 3)(m−2)4,∵m <0,∴m−2<0,令MN−2PQ =0,可得(t 3)(m−2)4=0,∵m−2≠0,∴t +3=0,解得t =−3,①当−4<t <−3>0,∴MN−2PQ >0,∴MN >2PQ ;②当t =−3时,(t 3)(m−2)4=0,∴MN−2PQ =0,∴MN =2PQ ;③当−3<t <−1时,(t 3)(m−2)4<0,∴MN−2PQ <0,∴MN <2PQ .综上所得:当−4<t <−3时,MN >2PQ ;当t =−3时,MN =2PQ ;当−3<t <−1时,MN <2PQ .12.(2023春·湖北随州·八年级统考期末)已知矩形OABC 的边OA ,OC 在坐标轴上,点B (4,3),直线y =2x−3分别交线段AB 及x 轴、y 轴于点D,E,F .(1)直接写出点D,E,F的坐标;(2)如图1,P为线段DF(不包括端点)上一动点,连接AP,设点P的横坐标为t,△ADP的面积为S,求S关于t的函数关系式,并写出自变量t的取值范围;(3)如图2,M是线段BC上一动点,点N在第一象限,且在直线y=2x−3上,若△AMN是以MN为直角边的等腰直角三角形,请直接写出点N的坐标.【思路点拨】(1)根据线段AB及x轴、y轴上点的坐标特征解答;(2)过点P作PH⊥AB于点H,由题意用t表示出PH的值,然后根据三角形的面积公式可以得解;(3)分点M为直角顶点、点N为直角顶点三种情况讨论.【解题过程】(1)解:在y=2x−3中分别令y=3、y=0及x=0可得:x=3,x=3,y=−3,2∴D(3,3),,0,F(0,−3);(2)解:如图,过点P作PH⊥AB于点H,∵点P在直线y=2x−3上,∴点P(t,2t−3),∴PH=3−(2t−3)=6−2t,∵AD=3,×3×(6−2t)=−3t+9.∴S=12∵点P在线段DF上,∴0<t<3.(3)解:①若点M为直角顶点时,点N在第一象限,如图,过点N作NH⊥CB,交CB的延长线于点H,∵△AMN是等腰直角三角形,∴AM=MN,∠AMN=90°,∵∠AMH+∠MAB=90°,∠AMH+∠HMN=90°,∴∠MAB=∠HMN,∴Rt△ABM≌Rt△MHN(AAS),∴AB=MH=4,HN=BM,设N x,2x−3,则HN=x−4,∴2x−3=4+3−(x−4),∴x=14,3∴②若点N为直角顶点,点N在第一象限,当点N在点D下方时,如图,设N′x,2x−3,过点N′作N′G′⊥OA于点G′,交BC于点H′,∴∠G′N′A+∠H′N′M=90°,∠G′N′A+∠G′AN′=90°,∴∠H′N′M=∠G′AN′,∵∠AG′N′=∠N′H′M=90°,AN′=N′M,∴△AG′N′≌△N′H′M(AAS),∴AG′=N′H′=3−(2x−3),∴x+3−(2x−3)=4,∴x=2,∴N′2,1,如图,当点N在点D上方时,过点N″作N″G″⊥OA于点G″,交BC于点H″,设N″(x,2x−3),同理可得x+2x−3−3=4,∴x=10,3∴N综上所述,点N的坐标可以为:N(2,1)或.13.(2023春·四川成都·八年级统考期末)如图1,在平面直角坐标系xOy中,直线y=kx+b分别与x轴,y轴交于点A(−1,0),B(0,2),过点C(2,0)作x轴的垂线,与直线AB交于点D.(1)求点D的坐标;(2)点E是线段CD上一动点,直线BE与x轴交于点F.i)若△BDF的面积为8,求点F的坐标;ii)如图2,当点F在x轴正半轴上时,将直线BF绕点B逆时针旋转45°后的直线与线段CD交于点M,连接FM,若OF=MF+1,求线段MF的长.【思路点拨】(1)根据题意,易求AD 的函数解析法y =2x +2,点D 在直线AB 上,可求出点D 坐标;(2)i )解:E 在线段CD 上,且C(2,0),D(2,6),设点F(m,0),分两种情况:①F 在C 点右侧时,根据题图表示△ADF 和△ABF 、△BDF 的关系列出方程,即:3(m +1)=m +1+8,解之得m =3;②F 点在A 点左侧时根据△ADF 、△ABF 、△BDF 三者之间的关系列出方程:(−3−3m)−(−1−m)=8,解得m =−5.综上所述F(−5,0)或(3,0);ii )出现45°想到构造等腰直角三角形,证明三角形全等,再利用勾股定理和方程思想求MF .【解题过程】(1)解:∵y =kx +b 分别与x 轴,y 轴交于点A(−1,0),B(0,2),∴ −k +b =0b =2 ,解得k =2b =2 ,∴y =2x +2,∴x =2时,y D =2×2+2=6,∴D(2,6);(2)解:i )E 在线段CD 上,且C(2,0),D(2,6),设点F(m,0),分两种情况:①当F 在x 轴正半轴上时,如图所示:∵D(2,6),A(−1,0),B(0,2),DC ⊥x 轴,∴S △ADF =12AF ⋅DC =12(m +1)×6=3(m +1),S △ABF =12AF ⋅OB =12(m +1)×2=m +1,∵S △DBF =8,∴S △ADF =S △ABF +S △DBF ,即3(m +1)=m +1+8,解得m =3,∴F(3,0);②当F 在x 轴负半轴上时,如图所示:∵点A(−1,0),B(0,2),C(2,0),D(2,6),∴S △ADF =12×AF ×CD =12×(−1−m)×6=−3−3m ,S △ABF =12×AF ×OB =12×(−1−m)×2=−1−m ,∵S △BDF =S △ADF −S △ABF =8,∴(−3−3m)−(−1−m)=8,解得m =−5,∴F(−5,0);综上所述:F(−5,0)或(3,0);ii )过M 作MN 垂直于y 轴,垂足为N ,过B 作MB 的垂线交x 轴于G 点,如图所示:∵∠NMB +∠NBM =90°,∠OBG +∠NBM =90°,∴∠NMB =∠OBG ,在△MNB 与△BOG 中,∠NMB =∠OBG MN =BO =2∠MNB =∠BOG =90°,∴△MNB≌△BOG(ASA),∴NB =OG ,BM =BG ,在△MBF 与△GBF 中,BM =BG ∠MBF =∠GBF BF =BF,∴△MBF≌△GBF(SAS),∴MF=GF,又∵OF=MF+1,OF=GF+OG,∴OG=1,∴NB=1,∴ON=MC=3,设MF=t,则CF=OF−2=t+1−2=t−1,在Rt△MCF中,由勾股定理可得MC2+CF2=MF2,∴32+(t−1)2=t2,解得t=5,∴MF=5.14.(2023秋·北京朝阳·八年级校考开学考试)在平面直角坐标系xOy中,若P(a,b),Q(c,d),式子|a−c|+ |b−d|的值就叫做线段PQ的“勾股距”,记作d PQ=|a−c|+|b−d|.同时,我们把两边的“勾股距”之和等于第三边的“勾股距”的三角形叫做“等距三角形”.在平面直角坐标系xOy中,A(2,3),B(4,2),C(m,n).(1)线段OA的“勾股距”d OA=______________;(2)已知点P(m,−2),Q(m+4,−2),E(m+4,6),F(m,6),若以点P、Q、E、F为顶点的四边形边上存在一点K,使得d KO=6,则m的最小值为________,最大值为_________;(3)若点C在第三象限,且d OC=2d AB,求d AC并判断△ABC是否为“等距三角形”;(4)若点C在x轴上,△OBC是“等距三角形”,请直接写出m的取值范围________.【思路点拨】(1)根据线段“勾股距”,由O,A两点的坐标求出线段OA的“勾股距”;(2)根据线段“勾股距”定义,由d KO=6在平面直角坐标系中作出图形,分情况讨论,列式求解即可得到答案;(3)现根据“勾股距”的定义求出d AB,d AC,d BC,再根据等距三角形的定义判断即可;(4)根据“等距三角形”分三种情况讨论m的取值.【解题过程】(1)解:由“勾股距”的定义知d OA=|2−0|+|3−0|=2+3=5,故答案为:5;(2)解:若设K(x,y),则由“勾股距”的定义知d KO=|x|+|y|=6,当x>0,y>0时,x+y=6,即y=−x+6;当x>0,y<0时,x−y=6,即y=x−6;当x<0,y>0时,−x+y=6,即y=x+6;当x<0,y<0时,−x−y=6,即y=−x−6;已知点P(m,−2),Q(m+4,−2),E(m+4,6),F(m,6),则PQ=4在直线y=−2上移动,EF=4在直线y=6上移动,若以点P、Q、E、F为顶点的四边形边上存在一点K(x,y),则四边形PQEF的两边在直线y=−2和直线y=6上移动,在平面直角坐标系中作出直线y=−x+6、y=x−6、y=x+6、y=−x−6及四边形PQEF,如图所示:∴K(x,y)是四边形PQEF与四边形MNHL的交点,若EQ边过点M(−6,0),则K(m+4,y)与M(−6,0)重合,此时m有最小值,如图所示:若FP边过点H(6,0),则K(m,y)与H(6,0)重合,此时m有最大值,如图所示:则m=6,即m最大值为m=6;故答案为:−10;6;(3)解:∵d AB=|4−2|+|2−3|=2+1=3,∴2d AB=6,∵点C在第三象限,∴m<0,n<0,d OC=|m−0|+|n−0|=|m|+|n|=−m−n=−(m+n),∵d OC=2d AB,∴−(m+n)=6,即m+n=−6,∴d AC=|2−m|+|3−n|=2−m+3−n=5−(m+n)=5+6=11,d BC=|4−m|+|2−m|=4−m+2−n=6−(m+n)=6+6=12,∵3+11≠12,11+12≠3,12+3≠11,∴△ABC不是为“等距三角形”;(4)解:∵点C在x轴上时,点C(m,0),则d AC=|2−m|+3,d BC=|4−m|+2,①当m<2时,d AC=2−m+3=5−m,d BC=4−m+2=6−m,若△ABC是“等距三角形”,∴5−m+6−m=11−2m=3,解得:m=4(不合题意),又∵5−m+3=8−m≠6−m,6−m+3=9−m≠5−m,∴△ABC不是“等距三角形”,∴当m<2时,△ABC不是“等距三角形”;②当2≤m<4时,d AC=m−2+3=m+1,d BC=4−m+2=6−m,若△ABC是“等距三角形”,则m+1+6−m=7≠3;若6−m+3=m+1,解得m=4(不合题意);若m+1+3=6−m,解得:m=1(不合题意);∴当2≤m<4时,△ABC不是“等距三角形”;③当m≥4时,d AC=m+1,d BC=m−2,若△ABC是“等距三角形”,则m+1+m−2=3,解得m=2(不合题意);且m−2+3=m+1恒成立;∵当m=8时,A,B,C三点共线,∴m≥4且m≠8时,△ABC是“等距三角形”,综上所述:△ABC是“等距三角形”时,m的取值范围为m≥4且m≠8.x−3交x轴于点A,交y轴15.(2022秋·全国·八年级专题练习)如图,在平面直角坐标系中,直线y=−34于点B,交直线x=a于点C,点D与点B关于x轴对称,连接AD交直线x=a于点E.(1)求直线AD的解析式;(2)在x轴上存在一点P,使得PE+PD的和最小,并求出其最小值;(3)当−4<a<0时,点Q为y轴上的一个动点,使得△QEC为等腰直角三角形,求点Q的坐标.【思路点拨】(1)分别计算A、D的坐标,再利用待定系数法可得直线AD的解析式;(2)根据轴对称的最短路径先确认P的位置:连接BE交x轴于P,此时,PD+PE最小,即是BE的长,面积法即可计算BE的长;(3)存在三种情况:分别以Q、E、C三个顶点为直角顶点,画图可得Q的坐标.【解题过程】(1)∵直线y=−34x−3交x轴于点A,交y轴于点B,令x=0,得y=−3,∴B(0,−3),令y=0,0=−34x−3,∴x=−4,∴A(−4,0),∵点D与点B关于x轴对称,∴D(0,3),设直线AD的解析式为y=kx+b,将A(−4,0),D(0,3)代入得,∴−4k+b=0b=3,。
一次函数与几何图形综合题10及答案

一次函数与几何图形综合题10及答案1、1) AC的解析式为y=-x-2;2) 设BP与PQ的交点为R,由相似三角形可得BP/PQ=OB/OQ,即BP/PQ=1/2,故BP=2PQ。
证明如下:设BP=x,PQ=y,则由OC=OB可得AC=-x-2,又由直线AC和BP的垂线PQ相似可得y/x=(x+2)/(y+2),解得y=2x,代入AC 的解析式可得BP=2PQ,结论得证。
3) 正确结论为①(MQ+AC)/PM的值不变。
证明如下:由(2)可得BP=2PQ,又由相似三角形可得MQ/PM=OB/OQ,即MQ/PM=1/3,代入AC的解析式可得(MQ+AC)/PM=-2/3,为定值。
而(MQ-AC)/PM=(MQ+AC)/PM-2AC/PM=-2/3-2x/(x+2),不是定值。
故正确结论为①。
2、1) 直线L的解析式为y=-x+5;2) 由相似三角形可得MN/BN=AM/AB=4/(4+3),即MN=12/7;3) 猜想PB的长为定值,其值为2.证明如下:设点B在y轴上的坐标为h,则BP=h,由△OBF和△ABE相似可得BE=BF=h/2,EF=AB-BE=5-h/2,由相似三角形可得FP/EF=BP/BE=h/(5-h/2),所以FP=5h/(5-h/2),由于P在y轴上,故FP=2h,解得h=2,即PB=2,结论得证。
3、1) 直线l2的解析式为y=-x+1;2) 画图如下,由相似三角形可得BE/BC=AB/AC,即BE/(BE+CF)=(AB+BC+AC)/AC,代入AB=1,BC=3,AC=4可得BE/(BE+CF)=5/4,即BE=5CF/3,代入△BEC的勾股定理可得CF=3/2,BE=5/2,故BE+CF=8/2=4=EF,结论得证。
3) 正确结论为①OM为定值,其值为1/2.证明如下:设△ABC沿y轴向下平移的距离为h,则BP=CQ=h,由相似三角形可得OM/AB=OC/AC,即OM/1=(h+2)/(h+4),解得OM=(2h+4)/(h+4),为定值。
一次函数与几何综合(k的几何意义、垂直关系)(人教版)(含答案)

一次函数与几何综合(k的几何意义、垂直关系)(人教版)一、单选题(共6道,每道16分)1.如图,直线:y=x+2与y轴交于点A,将直线绕点A旋转90°后,所得直线的解析式为( )A.y=x-2B.y=-x+2C.y=-x-2D.y=-2x-1答案:B解题思路:试题难度:三颗星知识点:一次函数与几何转化2.在平面直角坐标系中,把直线y=2x+4绕着原点O顺时针旋转90°后,所得的直线一定经过下列各点中的( )A.(2,0)B.(2,3)C.(4,2)D.(6,-1)答案:D解题思路:试题难度:三颗星知识点:一次函数与几何转化3.如图,点A的坐标为(-1,0),点B在直线y=x-3上运动,则AB的最小值为( )A. B.4C. D.答案:C解题思路:试题难度:三颗星知识点:k的几何意义4.如图,点A的坐标为(-2,0),点B在直线上运动,当线段AB最短时,点B的坐标是( )A. B.C. D.答案:D解题思路:试题难度:三颗星知识点:一次函数与几何综合5.如图,一次函数y=kx+b的图象经过点B(0,1)和点C(1,3),交x轴于点A,过点A 的另一直线l与直线AB垂直,且交y轴负半轴于点P,则点P的坐标为( )A.(0,)B.(0,)C.(,0)D. (0,)答案:A解题思路:试题难度:三颗星知识点:k的几何意义、两条直线的垂直关系6.如图,直线AB与x轴交于点B,与y轴交于点A,已知C(0,),D(,0),且C,D两点关于直线AB对称,则直线AB的表达式为( )A. B.C. D.答案:D解题思路:试题难度:三颗星知识点:k的几何意义、两条直线垂直关系。
2023学年北师大版八年级数学上学期压轴题专题09 一次函数与几何图形综合问题的五种类型含解析

专题09 一次函数与几何图形综合问题的五种类型类型一、面积问题例1.在平面直角坐标系xOy 中,已知直线AB 与x 轴交于A 点 (2,0)与y 轴交于点B (0,1). (1)求直线AB 的解析式;(2)点M (-1,y 1),N (3,y 2)在直线AB 上,比较y 1与y 2的大小. (3)若x 轴上有一点C ,且S △ABC =2,求点C 的坐标【变式训练1】已知一次函数12y kx =+的图象与x 轴交于点(2,0)B -,与正比例函数2y mx =的图象交于点(1,)A a .(1)分别求k ,m 的值;(2)点C 为x 轴上一动点,如果ABC 的面积是6,请求出点C 的坐标.【变式训练2】如图,在正方形ABCD 中,4AB =,点P 为线段DC 上的一个动点.设DP x =,由点,,,A B C P 首尾顺次相接形成图形的面积为y .(1)求y 关于x 的函数表达式及x 的取值范围;(2)设(1)中函数图象的两个端点分别为M N 、,且P 为第一象限内位于直线MN 右侧的一个动点,若MNP △正好构成一个等腰直角三角形,请求出满足条件的P 点坐标;(3)在(2)的条件下,若l 为经过(1,0)-且垂直于x 轴的直线,Q 为l 上的一个动点,使得MNQNMPS S=,请直接写出符合条件的点Q 的坐标.【变式训练3】如图,已知直线1:3l y x =+与过点A (3,0)的直线2l 交于点C (1,m ),且与x 轴交于点B ,与y 轴交于点D . (1)求直线2l 的解析式;(2)若点D 关于x 轴的对称点为P ,求△PBC 的面积.类型二、一次函数与平行四边形例1.如图,在平面直角坐标系中,直线AB 与x ,y 轴分别交于点(4,0)A ,(0,3)B ,点C 是直线554y x =-+上的一个动点,连接BC .(1)求直线AB 的函数解析式;(2)如图1,若//BC x 轴,求点C 到直线AB 的距离;(3)如图2,点(1,0)E ,点D 是直线AB 上的动点,试探索点C ,D 在运动过程中,是否存在以B ,C ,D ,E 为顶点的四边形是平行四边形,若存在,请直接写出点C ,D 的坐标;若不存在,请说明理由.【变式训练1】一次函数y = kx+1(k ≠ 0)的图象过点P (-3,2),与x 轴交于点A ,与y 轴交于点B .(1)求k 的值及点A 、B 的坐标;(2)已知点C (-1,0),若以A ,B ,C ,D 为顶点的四边形是平行四边形,请直接写出所有符合条件的点D 的坐标.【变式训练2】平面直角坐标系xOy 中,直线1l :2y x b =+与直线2l :12y x =交于点()2,P m . (1)求m ,b 的值;(2)直线()0x n n =≠与直线1l ,2l 分别交于M ,N 两点,当MN =3时,若以M ,N ,P ,Q 为顶点的四边形是平行四边形,请直接写出点Q 的坐标.类型三、一次函数与等腰三角形例1.一次函数的图像与x 轴、y 轴分别交于点A 0),B (0,1),以AB 为边在第一象限内做等边△ABC . (1)线段AB 的长是 ,△BAO = °,点C 的坐标是 ;(2)如果在第二象限内有一点P (a ,1),试用含a 的代数式表示四边形ABPO 的面积. (3)在y 轴上存在点M ,使△MAB 为等腰三角形,请直接写出点M 的坐标.【变式训练1】如图一,已知直线l :6y x =-+与x 轴交于点A ,与y 轴交于点B ,直线m 与v 轴交于点(0,2)C -,与直线l 交于点(,1)D t .(1)求直线m 的解析式;(2)如图二,点P 在直线l 上且在y 轴左侧,过点P 作//PQ y 轴交直线m 于点Q ,交x 轴于点G ,当2PCG QCG S S ∆∆=,求出P ,Q 两点的坐标;(3)将直线l :6y x =-+向左平移12个单位得到直线n 交x 轴于E 点,点F 是点C 关于原点对称点.过点F 作直线//k x 轴.点M 在直线k 上,写出以点C ,E ,M ,为顶点且CE 为腰的等腰三角形,并把求其中一个点M 的坐标的过程写出来.【变式训练2】在如图的平面直角坐标系中,直线n 过点A (0,﹣2),且与直线l 交于点B (3,2),直线l 与y 轴交于点C .(1)求直线n 的函数表达式;(2)若△ABC 的面积为9,求点C 的坐标;(3)若△ABC 是等腰三角形,求直线l 的函数表达式.【变式训练3】如图,直线1:l y ax a =-,1l 与x 轴交于点B ,直线2l 经过点(4,0)A ,直线1l ,2l 交于点(2,3)C -.(1)a =______;点B 的坐标为______. (2)求直线2l 的解析表达式; (3)求ABC 的面积;(4)在直线2l 上存在异于点C 的另一点P ,使得ABP △为等腰三角形,请直接写出P 点的横坐标?类型四、一次函数与直角三角形例1.如图,在平面直角坐标系中,函数y =-x +2的图象与x 轴,y 轴分别交于点A ,B ,与函数y =13x +b 的图象交于点C (-2,m ). (1)求m 和b 的值;(2)函数y =-x +b 的图象与x 轴交于点D ,点E 从点D 出发沿DA 向,以每秒2个单位长度匀速运动到点M (到A 停止运动),设点E 的运动时间为t 秒. ①当ΔACE 的面积为12时,求t 的值;②在点E 运动过程中,是否存在t 的值,使ΔACE 为直角三角形?若存在,请求出t 的值;若不存在,请说明理由.【变式训练1】如图1,在菱形ABCD 中,60ABC ∠=︒,对角线AC BD 、交于点,O P 从B 点出发,沿B DC →→方向匀速运动,P 点运动速度为1cm/s .图2是点P 运动时,APC △的面积2()cm y 随P 点运动时间()s x变化的函数图像.(1)AB =_______cm,a =_____;(2)P 点在BD 上运动时,x 为何值时,四边形ADCP ; (3)在P 点运动过程中,是否存在某一时刻使得APB △为直角三角形,若存在,求x 的值;若不存在,请说明理由.【变式训练2】在平面直角坐标系xOy 中,将直线2y x =向下平移2个单位后,与一次函数132y x =-+的图象相交于点A .(1)将直线2y x =向下平移2个单位后对应的解析式为 ; (2)求点A 的坐标;(3)若P 是x 轴上一点,且满足△OAP 是等腰直角三角形,直接写出点P 的坐标.类型五、最值问题例1.如图,将直线34y x=-向上平移后经过点()4,3A,分别交x轴y轴于点B、C.(1)求直线BC的函数表达式;(2)点P为直线BC上一动点,连接OP.问:线段OP的长是否存在最小值?若存在,求出线段OP的最小值,若不存在,请说明理由.【变式训练1】如图,四边形OABC是张放在平面直角坐标系中的正方形纸片,点O与坐标原点重合,点A在x轴正半轴上,点C在y轴正半轴上,5OC=,点E在边BC上.(1)若点N的坐标为(3,0),过点N且平行于y轴的直线MN与EB交于点M,将纸片沿直线OE折叠,顶点C恰好落在MN上,并与MN上的点G重合.①求点G、点E的坐标;②若直线:l y mx n=+平行于直线OE,且与长方形ABMN有公共点,请直接写出n的取值范围.(2)若点E为BC上的一动点,点C关于直线OE的对称点为G,连接BG,请求出线段BG的最小值.专题09 一次函数与几何图形综合问题的五种类型类型一、面积问题例1.在平面直角坐标系xOy 中,已知直线AB 与x 轴交于A 点 (2,0)与y 轴交于点B (0,1). (1)求直线AB 的解析式;(2)点M (-1,y 1),N (3,y 2)在直线AB 上,比较y 1与y 2的大小. (3)若x 轴上有一点C ,且S △ABC =2,求点C 的坐标 【答案】(1)112y x =-+;(2)y 1>y 2;(3)()6,0C 或()2,0-. 【解析】(1)解:设直线AB 的解析式为y kx b =+△A (2,0)B (0,1),△201k b b +=⎧⎨=⎩,解得:k =12-,b =12△直线AB 的解析式为112y x =-+ (2)△y =﹣12x +1中k =﹣12<0,△y 值随x 值的增大而减小, △﹣1<3,△y 1>y 2;(3)△x 轴上有一点C ,设点C (x ,0),△AC =|2﹣x |, △S △ABC =2,△12×|2﹣x |×1=2,△x =﹣2或x =6, △C (﹣2,0)或C (6,0). 故答案为:(1)112y x =-+;(2)y 1>y 2;(3)()6,0C 或()2,0-. 【变式训练1】已知一次函数12y kx =+的图象与x 轴交于点(2,0)B -,与正比例函数2y mx =的图象交于点(1,)A a .(1)分别求k ,m 的值;(2)点C 为x 轴上一动点,如果ABC 的面积是6,请求出点C 的坐标. 【答案】(1)1k =,3m =;(2)点C 的坐标为(2,0)或(6,0)- 【解析】(1)一次函数1=2y kx +的图象与x 轴交于点2,0B -(),220k ∴-+=1k ∴=12y x ∴=+一次函数12y x =+的图象与正比例函数2y mx =的图象交于点(1,)A a ,12a ∴=+,a m =,3m ∴=; (2)设点C 的坐标为(,0)n ,过点A 作AD x ⊥轴,垂足为点D .ABC 的面积是6,162BC AD ∴⋅=,1|(2)|362n ∴--⨯=,2n ∴=或6n =-∴点C 的坐标为(2,0)或(6,0)-,或过点A 作AD x ⊥轴,垂足为点D .ABC 的面积是6,162BC AD ∴⋅=,1362BC ∴⨯=,4BC ∴=,点B 的坐标为(2,0)-,∴点C 的坐标为(2)0,或(60)-,. 【变式训练2】如图,在正方形ABCD 中,4AB =,点P 为线段DC 上的一个动点.设DP x =,由点,,,A B C P 首尾顺次相接形成图形的面积为y .(1)求y 关于x 的函数表达式及x 的取值范围;(2)设(1)中函数图象的两个端点分别为M N 、,且P 为第一象限内位于直线MN 右侧的一个动点,若MNP △正好构成一个等腰直角三角形,请求出满足条件的P 点坐标;(3)在(2)的条件下,若l 为经过(1,0)-且垂直于x 轴的直线,Q 为l 上的一个动点,使得MNQNMPS S=,请直接写出符合条件的点Q 的坐标.【答案】(1)y =-2x +16,0<x <4;(2)(12,12)或(8,20)或(6,14);(3)(-1,-2)或(-1,8)或(-1,38)或(-1,28)【解析】(1)由线段的和差,得PC =(4-x ),由梯形的面积公式,得y =-2x +16, △四边形ABCD 是正方形,△AB =CD =4,△x 的取值范围是0<x <4; (2)设P 点坐标是(a ,b ),M (0,16),N (4,8),以MN 为边,在MN 右侧做正方形,MNAB ,正方形中心为H ,则易知A ,B ,H 即为所求P 的坐标;示意图如下求得A (12,12),B (8,20),O (6,14),故P 点可能的坐标为(12,12)或(8,20)或(6,14); (3)由S △MNQ =S △NMP ,设Q (-1,m ),QN 所在直线方程为y =kx +b , 把Q 和N 代入方程,求得b =845m +,则可求S △NMP =12|16-b |×[4-(-1)]=|36-2m |当P 为(12,12)时,S △MNQ =40,△|36-2m |=40;解得m =-2或38,当P (8,20),同理解得m =-2或38,当P (8,20),有S △MNQ =20,解得m =8或28, 综上,符合条件的Q 的坐标为(-1,-2)或(-1,8)或(-1,38)或(-1,28).【变式训练3】如图,已知直线1:3l y x =+与过点A (3,0)的直线2l 交于点C (1,m ),且与x 轴交于点B ,与y 轴交于点D . (1)求直线2l 的解析式;(2)若点D 关于x 轴的对称点为P ,求△PBC 的面积.【答案】(1)-26y x =+;(2)12.【解析】(1)把(1,)C m 代入y =x +3,得1+3=m ,△m =4,△(1,4)C设2l 的解析式为:y =kx +b (k ≠0),将点A ,C 的坐标代入,则430k b k b +=⎧⎨+=⎩ 解得26k b =-⎧⎨=⎩,△2l 的解析式为:-26y x =+(2)当y =0时,30x += ,△3x =-,△(3,0)B -, 当x =0时,y =3,△(0,3)D ,△点P 、D 关于x 轴对称,△(0,3)P - ,如图,连接BP ,PC ,设PC 与x 轴的交点为Q ,设直线PC 的解析式为(0)y kx b k =+≠,将点(1,4),(0,3)C P -代入:43k b b +=⎧⎨=-⎩,解得73k b =⎧⎨=-⎩,△直线PC 的解析式为:73y x =-,令y =0,解得37x =, △BPCBQP BQCSSS=+1122c BQ OP BQ y =+1124()712227c BQ OP y =+=⨯⨯=.类型二、一次函数与平行四边形例1.如图,在平面直角坐标系中,直线AB 与x ,y 轴分别交于点(4,0)A ,(0,3)B ,点C 是直线554y x =-+上的一个动点,连接BC .(1)求直线AB 的函数解析式;(2)如图1,若//BC x 轴,求点C 到直线AB 的距离;(3)如图2,点(1,0)E ,点D 是直线AB 上的动点,试探索点C ,D 在运动过程中,是否存在以B ,C ,D ,E 为顶点的四边形是平行四边形,若存在,请直接写出点C ,D 的坐标;若不存在,请说明理由.【答案】(1)334y x =-+;(2)2425;(3)17(2,45)8-、15(2-,69)8或1(2-,45)8、1(2,21)8或17(2,45)8-、15(2,21)8- 【解析】(1)设直线AB 的表达式为y kx b =+,则304b k b =⎧⎨=+⎩,解得343k b ⎧=-⎪⎨⎪=⎩,故AB 的表达式为334y x =-+;(2)//BC x 轴,故点C 的纵坐标为3,当3y =时,即5534y x =-+=,解得85x =,即点C 的坐标为8(5,3),则85BC =;由点A 、B的坐标得,5AB ==,过点C 作CH AB ⊥于点H ,在△ABC 中,S △ABC =1122BC OB AB CH ⨯⨯=⨯⨯,即18135252CH ⨯⨯=⨯⨯,解得:2425CH =,即点C 到直线AB 的距离为2425;(3)设点C 、D 的坐标分别为5(,5)4m m -+、3(,3)4n n -+,当EB 是对角线时,由中点坐标公式得:01m n +=+且53305344m n +=-+-+,解得172152m n ⎧=⎪⎪⎨⎪=-⎪⎩,故点C 、D 的坐标分别为17(2,45)8-、15(2-,69)8;当EC 是对角线时,同理可得:1m n +=且5353344m n -+=-++,解得,1212m n ⎧=-⎪⎪⎨⎪=⎪⎩故点C 、D 的坐标分别为1(2-,45)8、1(2,21)8;当ED 是对角线时,同理可得:1n m +=且35035344n m -+=-++,解得152172m n ⎧=⎪⎪⎨⎪=⎪⎩,故点C 、D 的坐标分别为17(2,45)8-、15(2,21)8-.综上,点C 、D 的坐标分别为17(2,45)8-、15(2-,69)8或1(2-,45)8、1(2,21)8或17(2,45)8-、15(2,21)8-.【变式训练1】一次函数y = kx+1(k ≠ 0)的图象过点P (-3,2),与x 轴交于点A ,与y 轴交于点B .(1)求k 的值及点A 、B 的坐标;(2)已知点C (-1,0),若以A ,B ,C ,D 为顶点的四边形是平行四边形,请直接写出所有符合条件的点D 的坐标.【答案】(1)13k =-,与x 轴交于点A (3,0),与y 轴交于点B (0,1);(2)D (4,1)或D (2,-1)或D (-4,1).【解析】(1)将P (-3,2)代入()10y kx k =+≠,得:13k =-函数表达式:113y x =-+,令y =0,x =3,令x =0,y =1,△与x 轴交于点A (3,0),与y 轴交于点B (0,1);(2)分三种情况:①BC 为对角线时,点D 的坐标为(-4,1);②AB 为对角线时,点D 的坐标为(4,1),③AC 为对角线时,点D 的坐标为(2,-1).综上所述,点D 的坐标是(4,1)或(-4,1)或(2,-1).【变式训练2】平面直角坐标系xOy 中,直线1l :2y x b =+与直线2l :12y x =交于点()2,P m . (1)求m ,b 的值;(2)直线()0x n n =≠与直线1l ,2l 分别交于M ,N 两点,当MN =3时,若以M ,N ,P ,Q 为顶点的四边形是平行四边形,请直接写出点Q 的坐标.【答案】(1)13m b ==-,;(2)点Q 的坐标为()2,4,()2,2-或()6,6 【解析】(1)△直线1l :2y x b =+与直线2l :12y x =交于点()2,P m ,△4122m b m =+⎧⎪⎨=⨯⎪⎩,△1 3.m b ==-, (2)依题意可得直线1l :23y x =-,△直线1l 与y 轴的交点为(0,-3) △直线()0x n n =≠与直线1l ,2l 分别交于M ,N 两点, MN =3, △M ,N 不是y 轴上的点,设M (x ,2x -3),则N (x ,12x ) 由MN =3,得(2x -3)-12x =3,解得x =4,△M (4,5),则N (4,2) △以M ,N ,P ,Q 为顶点的四边形是平行四边形,①当MN 为四边形MPNQ 的对角线时,MN 的中点坐标为(4,3.5) 故()2,1P 、Q 关于(4,3.5)对称,△点Q 的坐标为()6,6,②当MN 为四边形MNQP 的一边时,MN =PQ =3,且PQ 与y 轴平行,故点Q 的坐标为()2,4或()2,2- 综上,点Q 的坐标为()2,4,()2,2-或()6,6. 类型三、一次函数与等腰三角形例1.一次函数的图像与x 轴、y 轴分别交于点A0),B (0,1),以AB 为边在第一象限内做等边△ABC . (1)线段AB 的长是 ,△BAO = °,点C 的坐标是 ;(2)如果在第二象限内有一点P (a ,1),试用含a 的代数式表示四边形ABPO 的面积. (3)在y 轴上存在点M ,使△MAB 为等腰三角形,请直接写出点M 的坐标.【答案】(1)2,30,C2);(22a-;(3)(0,-1)或(0,3)【解析】(1)(3A ,0),(0,1)B ,在Rt AOB ∆中,2AB =,2OB =AB ,可30BAO ∴∠=︒,以AB 为边在第一象限内做等边ABC ∆,60ACB ∠=︒∴,AB AC =,90OAC ∴∠=︒,C ∴2),故答案为2,30,C 2);(2)四边形ABPO 的面积BAO =∆的面积OBP +∆的面积1111()222a a =+⨯⨯-=;(3)2AB =,30BAO ∠=︒,60OBA ∴∠=︒,①当AB BM =时,2BM =,(0,1)M -或(0,3)M ;②当AB AM =时,ABM ∆是等边三角形,M ∴与B 关于x 轴对称,(0,1)M ∴-; ③当BM AM =时,ABM ∆是等边三角形,M ∴与B 关于x 轴对称,(0,1)M ∴-; 综上所述:MAB ∆为等腰三角形时,M 点坐标为(0,1)-或(0,3).【变式训练1】如图一,已知直线l :6y x =-+与x 轴交于点A ,与y 轴交于点B ,直线m 与v 轴交于点(0,2)C -,与直线l 交于点(,1)D t .(1)求直线m 的解析式;(2)如图二,点P 在直线l 上且在y 轴左侧,过点P 作//PQ y 轴交直线m 于点Q ,交x 轴于点G ,当2PCG QCG S S ∆∆=,求出P ,Q 两点的坐标;(3)将直线l :6y x =-+向左平移12个单位得到直线n 交x 轴于E 点,点F 是点C 关于原点对称点.过点F 作直线//k x 轴.点M 在直线k 上,写出以点C ,E ,M ,为顶点且CE 为腰的等腰三角形,并把求其中一个点M 的坐标的过程写出来. 【答案】(1)直线m 的解析式为325y x =-;(2)P 点的坐标为(-10,16),Q 点坐标为(-10,-8);(3)当CE 为腰时,点M 的坐标为:M (2)或M (-2)或M (0,2).过程见解析. 【解析】(1)△D (t ,1)在直线l :y =-x +6上,△1=-t +6,△t =5,△D (5,1),设直线m 的解析式为y =kx +b ,将点C ,D 代入得,512k b b +=⎧⎨=-⎩,解得,352k b ⎧=⎪⎨⎪=-⎩,所以,直线m 的解析式为325y x =-; (2)设P (a ,6-a ),△点P 在x 轴的左侧,△0a < △PQ △轴,G (a ,0),Q (a ,325a -),如图,点P 、Q 在x 轴两侧,△S △PCG =12PG •(-a ),S △QCG =12GQ •(-a )且S △PCG =2S △QCG , △PG =2QG ,△6-a =2(2-35a ),解得:a =-10, △66(10)16a -=--=,332(10)2855a -=⨯--=-△P 点的坐标为(-10,16),Q 点坐标为(-10,-8);(3)对于直线l :y =-x +6,当x =0时,y =6;当y =0时,x =6.△A (6,0),B (0,6),△将直线l :y =-x +6向左平移12个单位得直线n 交x 轴于点E ,点F 是点C 关于原点的对称点.点C (0,-2), △E (-6,0),F (0,2), 如图,△将直线l :y =-x +6向左平移12个单位得直线n ,△直线n :y =-x -6, 又△F (0,2)△k 的解析式为:y =2,设M (a ,2),则MCME,CE ,当△MCE 为等腰三角形,且CE 为腰,有:①CE =MCa =a =-M (2).M (-2), ②ME =CE解得,a =0或a =-12(此时三点共线,不构成三角形,舍去),即M (0,2),综上,当CE 为腰时,点M 的坐标为:M (2)或M (-2)或M (0,2).【变式训练2】在如图的平面直角坐标系中,直线n 过点A (0,﹣2),且与直线l 交于点B (3,2),直线l 与y 轴交于点C .(1)求直线n 的函数表达式;(2)若△ABC 的面积为9,求点C 的坐标;(3)若△ABC 是等腰三角形,求直线l 的函数表达式.【答案】(1)y =43x ﹣2;(2)C (0,4)或(0,﹣8);(3)直线l 的解析式为:y =﹣13x +3或y =3x ﹣7或y =﹣43x +6或y =724x +98 【解析】(1)设直线n 的解析式为:y =kx +b ,△直线n :y =kx +b 过点A (0,﹣2)、点B (3,2),△232b k b =-⎧⎨+=⎩ ,解得:432k b ⎧=⎪⎨⎪=-⎩ ,△直线n 的函数表达式为:y =43x ﹣2; (2)△△ABC 的面积为9,△9=12•AC •3,△AC =6, △OA =2,△OC =6﹣2=4或OC =6+2=8,△C (0,4)或(0,﹣8); (3)分四种情况:①如图1,当AB =AC 时,△A (0,﹣2),B (3,2),△AB 22(22)=5,△AC =5,△OA =2,△OC =3,△C (0,3),设直线l 的解析式为:y =mx +n ,把B (3,2)和C (0,3)代入得:323m n n +=⎧⎨=⎩ ,解得:133m n ⎧=-⎪⎨⎪=⎩ ,△直线l 的函数表达式为:y =13-x +3; ②如图2,AB =AC =5,△C (0,﹣7),同理可得直线l 的解析式为:y =3x ﹣7; ③如图3,AB =BC ,过点B 作BD △y 轴于点D ,△CD =AD =4,△C (0,6),同理可得直线l 的解析式为:y =43-x +6; ④如图4,AC =BC ,过点B 作BD △y轴于D ,设AC =a ,则BC =a ,CD =4﹣a ,根据勾股定理得:BD 2+CD 2=BC 2,△32+(4﹣a )2=a 2,解得:a =258, △OC =258﹣2=98 ,△C (0,98),同理可得直线l 的解析式为:y =724x +98; 综上,直线l 的解析式为:y =13-x +3或y =3x ﹣7或y =43-x +6或y =724x +98. 【变式训练3】如图,直线1:l y ax a =-,1l 与x 轴交于点B ,直线2l 经过点(4,0)A ,直线1l ,2l 交于点(2,3)C -.(1)a =______;点B 的坐标为______. (2)求直线2l 的解析表达式; (3)求ABC 的面积;(4)在直线2l 上存在异于点C 的另一点P ,使得ABP △为等腰三角形,请直接写出P 点的横坐标?【答案】(1)3a =-,()10B ,;(2)362y x =-;(3)92;(4)52,2813【解析】(1)△直线1:l y ax a =-经过点(2,3)C -,32a a ∴-=-,解得:3a =-;即直线1:l y ax a =-的解析式为33y x =-+;当y =0时,-3x +3=0,解得1x =,则()10B ,;故答案为:-3,(1,0);(2)设直线2l 的解析式为:y kx b =+, △经过点()4,0A 和点(2,3)C -,△0432k b k b=+⎧⎨-=+⎩,解得:32k ,6b =-.△直线2l 的解析式为:362y x =-; (3)设ABC 的面积的面积为ABC S ;则413AB =-=,ABC 的高为3,则193322ABCS=⨯⨯=; (4)存在,设点P 的坐标为(x ,362x ),分三种情况: ①当AP=BP 时,点P 在线段AB 的垂直平分线上,△A (4,0),B (1,0),△点P 的横坐标为:41522+=; ②当AP=AB =3时,过点P 作PH △x 轴于点H ,△222PH AH AP +=,△2223(6)(4)32x x -+-=,解得x③当AB=BP =3时,作PM △x 轴于点M , △222PM BM BP +=,△2223(6)(1)32x x -+-=,解得x =2813或x =4(舍去);综上,符合条件的P 点的横坐标是52,2813,5213± 类型四、一次函数与直角三角形例1.如图,在平面直角坐标系中,函数y =-x +2的图象与x 轴,y 轴分别交于点A ,B ,与函数y =13x +b 的图象交于点C (-2,m ). (1)求m 和b 的值;(2)函数y =-x +b 的图象与x 轴交于点D ,点E 从点D 出发沿DA 向,以每秒2个单位长度匀速运动到点M (到A 停止运动),设点E 的运动时间为t 秒. ①当ΔACE 的面积为12时,求t 的值;②在点E 运动过程中,是否存在t 的值,使ΔACE 为直角三角形?若存在,请求出t 的值;若不存在,请说明理由.【答案】(1)m =4,b =143;(2)①t =5;②t =4或t =6 【解析】(1)△点C (−2,m )在直线y =−x +2上, △m =−(−2)+2=2+2=4,△点C (−2,4), △函数y =13x +b 的图象过点C (−2,4),△4=13×(−2)+b ,得b =143,即m 的值是4,b 的值是143; (2)①△函数y =−x +2的图象与x 轴,y 轴分别交于点A ,B ,△点A (2,0),点B (0,2), △函数y =13x +143的图象与x 轴交于点D ,△点D 的坐标为(−14,0),△AD =16, △△ACE 的面积为12,△(16−2t )×4÷2=12,解得,t =5.即当△ACE 的面积为12时,t 的值是5; ②当t =4或t =6时,△ACE 是直角三角形,理由:当△ACE =90°时,AC △CE , △点A (2,0),点B (0,2),点C (−2,4),点D (−14,0),△OA =OB ,AC =,△△BAO =45°,△△CAE =45°,△△CEA =45°,△CA =CE =,△AE =8, △AE =16−2t ,△8=16−2t ,解得,t =4;当△CEA =90°时,△AC =,△CAE =45°,△AE =4, △AE =16−2t ,△4=16−2t ,解得,t =6;由上可得,当t =4或t =6时,△ACE 是直角三角形.【变式训练1】如图1,在菱形ABCD 中,60ABC ∠=︒,对角线AC BD 、交于点,O P 从B 点出发,沿B DC →→方向匀速运动,P 点运动速度为1cm/s .图2是点P 运动时,APC △的面积2()cm y 随P 点运动时间()s x变化的函数图像.(1)AB =_______cm,a =_____;(2)P 点在BD 上运动时,x 为何值时,四边形ADCP; (3)在P 点运动过程中,是否存在某一时刻使得APB △为直角三角形,若存在,求x 的值;若不存在,请说明理由.【答案】(1)2;(2;(3或1【解析】(1)在菱形ABCD 中,60ABC ∠=︒,则ABC ∆、ACD ∆为全等的两个等边三角形,设ABC ∆的边长为a,则其面积为24a , 由图2知,当点P 在点A 时,y ABC =∆的面积2=,解得2a =(负值已舍去), 即菱形的边长为2,则2()AB cm =,由题意知,点P 与点O 重合时,对于图2的a 所在的位置,则1AO =,故a BO ====2(2)由(1)知点P 在BO 段运动时,对于图2第一段直线,而该直线过点、0),设其对应的函数表达式为y kx t =+,则0t t ⎧=⎪+=,解得1k t =-⎧⎪⎨=⎪⎩,故该段函数的表达式为=-+y x ,当点P 在BD 上运动时,四边形ADCP,则点P 只能在BO 上,则四边形ADCP 的面积ACD S y ∆=+=x x =;(3)存在,理由:由(1)知,菱形的边长为2,则BP =1AO =,过点A 作AP DC ''⊥于点P ''交BD 于点P ',ABC ∆、ACD ∆均为等边三角形,则30PAP DAP ∠'=∠''=︒,①当点P 和点O 重合时,APB ∠为直角,则x BP ==②当BAP ∠'为直角时,则同理可得:PP '=x BP PP =+'=;③当BAP ∠''为直角时,则112x BD DP AD =+''=+=,综上,x 或1. 【变式训练2】在平面直角坐标系xOy 中,将直线2y x =向下平移2个单位后,与一次函数132y x =-+的图象相交于点A .(1)将直线2y x =向下平移2个单位后对应的解析式为 ; (2)求点A 的坐标;(3)若P 是x 轴上一点,且满足△OAP 是等腰直角三角形,直接写出点P 的坐标.【答案】(1)22y x =-;(2)(2,2);(3)(2,0)或(4,0).【解析】(1)根据题意,得22y x =-;故答案为:22y x =-.(2)由题意得:22132y x y x =-⎧⎪⎨=-+⎪⎩,解得:22x y =⎧⎨=⎩,△点A 的坐标为(2,2); (3)如图所示,△P 是x 轴上一点,且满足△OAP 是等腰直角三角形,当OA =OP 时,P 点坐标为(4,0),当OP =AP 时,P 点坐标为(2,0), 综上,P 点的坐标为:(2,0)或(4,0). 类型五、最值问题 例1.如图,将直线34y x =-向上平移后经过点()4,3A ,分别交x 轴y 轴于点B 、C .(1)求直线BC 的函数表达式;(2)点P 为直线BC 上一动点,连接OP .问:线段OP 的长是否存在最小值?若存在,求出线段OP 的最小值,若不存在,请说明理由. 【答案】(1)364y x =-+;(2)存在,线段OP 的最小值为4.8.【解析】(1)设平移后的直线BC 的解析式为34y x b =-+,代入()4,3A 得3344b =-⨯+,解得6b = △直线BC 的解析式为364y x =-+; (2)存在,理由如下:令x =0,得y =6,△C (0,6),故OC =6令y =0,得x =8,△B (8,0)故OB =8△BC 10= △OP △BC 时,线段OP 最小, △S △ABC =12BO CO ⨯=12BC OP ⨯,△OP = 4.8BO COBC⨯=,即线段OP 的最小值为4.8. 【变式训练1】如图,四边形OABC 是张放在平面直角坐标系中的正方形纸片,点O 与坐标原点重合,点A 在x 轴正半轴上,点C 在y 轴正半轴上,5OC =,点E 在边BC 上.(1)若点N 的坐标为(3,0),过点N 且平行于y 轴的直线MN 与EB 交于点M ,将纸片沿直线OE 折叠,顶点C 恰好落在MN 上,并与MN 上的点G 重合. ①求点G 、点E 的坐标;②若直线:l y mx n =+平行于直线OE ,且与长方形ABMN 有公共点,请直接写出n 的取值范围. (2)若点E 为BC 上的一动点,点C 关于直线OE 的对称点为G ,连接BG ,请求出线段BG 的最小值.【答案】(1)①G (3,4),E (53,5);②-15≤n ≤-4;(2)5【解析】(1)由折叠的性质可知,OG =OC =5,由勾股定理得,GN 4=, △点G 的坐标为(3,4);设CE =x ,则EM =3-x ,由折叠的性质可知:EG =CE =x , △GN =4,△GM =5-4=1,在Rt △EMG 中,222EG EM MG =+,即()22231x x =-+,解得:x =53, △点E 的坐标为(53,5);设OE所在直线的解析式为:y=kx,则53k=5,解得,k=3,△OE所在直线的解析式为:y=3x,△直线l:y=mx+n平行于直线OE,△m=3,即直线l的解析式为y=3x+n,当直线l经过点M(3,5)时,5=3×3+n,解得,n=-4,当直线l经过点A(5,0)时,0=3×5+n,解得,n=-15,△直线l与长方形ABMN有公共点时,-15≤n≤-4;(3)连接OB,OG,△OC=BC=5,△OCB=90°,△BC OC=△点C关于直线OE的对称点为点G,△OC=OG=5,△BG≥OB-OG,△当O、B、G三点共线时,BG取得最小值,△BG的最小值为5.。
中考数学总复习《一次函数-动态几何问题》练习题附带答案

中考数学总复习《一次函数-动态几何问题》练习题附带答案一、单选题(共12题;共24分)1.如图,在矩形ABCD中,AB=2,BC=3,点P在矩形的边上沿B→C→D→A运动.设点P运动的路程为x,△ABP的面积为y,则y关于x的函数图象大致是()A.B.C.D.2.如图,点P是▱ABCD边上一动点,沿A→D→C→B的路径移动,设P点经过的路径长为x,△BAP的面积是y,则下列能大致反映y与x的函数关系的图象是()A.B.C.D.3.如图,在正方形ABCD中,点P从点A出发,沿着正方形的边顺时针方向运动一周,则△APC的面积y与点P运动的路程x之间形成的函数关系图象大致是()A.B.C.D.4.在数轴上,点A表示-2,点B表示4.P,Q为数轴上两点,点Р从点A出发以每秒1个单位长度的速度向左运动,同时点Q从点B出发以每秒2个单位长度的速度向左运动,点Q到达原点О后,立即以原来的速度返回,当点Q回到点B时点Р与点Q同时停止运动.设点Р运动的时间为x秒,点Р与点Q之间的距离为y个单位长度,则下列图像中表示y与x的函数关系的是()A.B.C.D.5.如图,在矩形ABCD中AB=8cm,BC=6cm动点P从点B出发,沿B→C→D→A方向匀速运动至点A 停止,已知点P的运动速度为2cm/s,设点P的运动时间为x(s),△PAB的面积为y(cm2),则下列图象中,能正确表示y与x的关系的是()A.B.C.D.6.如图1,在四边形ABCD中DC//AB,∠DAB=90°点E沿着B→C→D的路径以2cm/s 速度匀速运动,到达点D停止运动,EF始终与直线BC保持垂直,与AB或AD交于点F,设线段EF的长度为d(cm),运动时间为t(s),若d与t之间的关系如图2所示,则图中a的值为()A.3.8B.3.9C.4.5D.4.87.如图1,在矩形MNPQ中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止.设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图2所示,则当x=9时点R应运动到()A .M 处B .N 处C .P 处D .Q 处8.如图,一次函数y= 34x+6的图像与x 轴、y 轴分别交于点A ,B ,过点B 的直线l 平分△ABO 的面积,则直线l 相应的函数表达式为( )A .y= 35 x+6B .y= 53 x+6C .y= 23 x+6D .y= 32x+69.如图1,在矩形 ABCD 中,动点 E 从点 B 出发,沿 BADC 方向运动至点 C 处停止,设点 E运动的路程为 x ,△BCE 的面积为 y ,如果 y 关于 x 的函数图象如图2所示,则当 x =7 时点 E 应运动到( )A .点 处B .点 处C .点 处D .点 处10.如图,AD,BC 是⊙O 的两条互相垂直的直径,点P 从点O 出发,沿O →C →D →O 的路线匀速运动,设∠APB=y (单位:度),点P 运动的时间为x (单位:秒),那么表示y 与x 关系的图象是( )A .B .C .D .11.如图,正方形ABCD 的边长为4,P 为正方形边上一动点,沿A →D →C →B →A 的路径匀速移动,设P点经过的路径长为x,△APD的面积是y,则下列图象能大致反映y与x的函数关系的是()A.B.C.D.12.如图,过点A0(2,0)作直线l:y= √33 x的垂线,垂足为点A1,过点A1作A1A2⊥x轴,垂足为点A2,过点A2作A2A3⊥l,垂足为点A3,…,这样依次下去,得到一组线段:A0A1,A1A2,A2A3,…则线段A2016A2107的长为()A.(√32)2015B.(√32)2016C.(√32)2017D.(√32)2018二、填空题(共6题;共10分)13.如图,把△ABC放在平面直角坐标系内,其中∠CAB=90°,BC=10点A,B的坐标分别为(2,0),(8,0)当直线y=2x+b(b为常数)与△ABC有交点时则b的取值范围是.14.已知两点M(3,5),N(1,1),点P是x轴上一动点,若使PM+PN最短,则点P的坐标应为.15.如图1,AB//CD,E是直线CD上的一点,且∠BAE=30°,P是直线CD上的一动点,M是AP的中点,直线MN⊥AP且与CD交于点N,设∠BAP=x°和∠MNE=y°.(1)在图2中,当x=12时∠MNE=;在图3中,当x=50时∠MNE=;(2)研究及明:y与x之间关系的图象如图4所示(y不存在时用空心点表示,请你根据图象直接估计当y=100时x=.(3)探究:当x=时点N与点E重合,并在答题卡上画出此时图形.(4)探究:当x>105时求y与x之间的关系式.16.如图1,在矩形ABCD中,动点P从点A出发,沿A−B−C的方向在AB和BC上运动,记PA=x,点D到直线PA的距离为y,且y关于x的函数图象如图2所示.当△PCD的面积与△PAB的面积相等时y的值为.17.如图,直线y=−12x+2与坐标轴分别交于点A,B,与直线y=12x交于点C,Q是线段OA上的动点,连接CQ,若OQ=CQ,则点Q的坐标为.18.如图,在平面直角坐标系中,点P的坐标为(0,4),直线y=34 x-3与x轴、y轴分别交于点A、B,点M是直线AB上的一个动点,则PM的最小值为.三、综合题(共6题;共69分)19.如图,在平面直角坐标系中,A,B,C三点的坐标分别为(2,0),(1,2),(4,3),直线l的解析式为y=kx+4﹣3k(k≠0).(1)当k=1时直线l与x轴交于点D,点D的坐标是,S△ABD=.(2)小明认为点C在直线l上,他的判断是否正确,请说明理由;(3)若线段AB与直线l有交点,则k的取值范围为.20.如图所示,在平面直角坐标系中,过点A(√3,0)的两条直线分别交y轴于B、C两点,且B、C两点的纵坐标分别是一元二次方程x2﹣2x﹣3=0的两个根(1)试问:直线AC与直线AB是否垂直?请说明理由;(2)若点D在直线AC上,且DB=DC,求点D的坐标;(3)在(2)的条件下,在直线BD上寻找点P,使以A、B、P三点为顶点的三角形是等腰三角形,请直接写出P点的坐标.21.如图,在平面直角坐标系中,直线y=x+2与x轴、y轴分别交A、B两点,与直线y=−12x+b相交于点C(2,m)(1)求点A、B的坐标;(2)求m和b的值;(3)若直线y=−12x+b与x轴相交于点D.动点P从点D开始,以每秒1个单位的速度向x轴负方向运动,设点P的运动时间为t秒①若点P在线段DA上,且ΔACP的面积为10,求t的值;②是否存在t的值,使ΔACP为等腰三角形?若存在,求出t的值;若不存在,请说明理由.22.如图,直线l与x轴交于点A,与y轴交于点B(0,2) .已知点C(−1,3)在直线l上,连接OC.(1)求直线l的解析式;(2)P为x轴上一动点,若ΔACP的面积是ΔBOC的面积的2倍,求点P的坐标. 23.如图,一次函数y=2x+b的图像经过点M(1,3),且与x轴,y轴分别交于A,B两点.(1)填空:b=;(2)将该直线绕点A顺时针旋转45∘至直线l,过点B作BC⊥AB交直线l于点C,求点C的坐标及直线l的函数表达式.24.当m,n为实数,且满足m+nm=n时就称点P(m,mn)为“状元点”.已知点A(0,7)和点M都在直线y=x+b上,点B,C是“状元点”,且B在直线AM上.(1)求b的值及判断点F(2,6)是否为“状元点”;(2)请求出点B的坐标;(3)若AC≤5√2,求点C的横坐标的取值范围.参考答案1.【答案】B 2.【答案】A 3.【答案】C 4.【答案】B 5.【答案】A 6.【答案】B 7.【答案】D 8.【答案】D 9.【答案】B 10.【答案】B 11.【答案】B 12.【答案】B13.【答案】-16≤b ≤4 14.【答案】(43,0)15.【答案】(1)102°;40°(2)10或170 (3)15或105 (4)y =270−x16.【答案】√2 17.【答案】(54,0)18.【答案】28519.【答案】(1)(−1,0);3(2)解:小明的判断不符合题意,理由如下: ∵y =kx +4−3k ∴ 当 x =4 时 ∵k +4 不一定为3∴ 点 C(4,3) 不一定在直线 l 上,小明的判断不符合题意; (3)1⩽k ⩽420.【答案】(1)解:结论:AC ⊥AB .理由如下:∵由x 2﹣2x ﹣3=0得:∴x 1=3,x 2=﹣1∴B (0,3),C (0,﹣1)∵A ( √3 ,0),B (0,3),C (0,﹣1)∴OA= √3 ,OB=3,OC=1∴tan ∠ABO= OA BO = √33,tan ∠ACO= OA OC = √3 ∴∠ABO=30°,∠ACO=60°∴∠BAC=90°∴AC ⊥AB(2)解:如图1中,过D 作DE ⊥x 轴于E .∴∠DEA=∠AOC=90°∵tan ∠ACO= OA OC= √3 ∵∠DCB=60°∵DB=DC∴△DBC 是等边三角形∵BA ⊥DC∴DA=AC∵∠DAE=∠OAC在△ADE 和△ACO 中∴△ADE ≌△ACO∴DE=OC=1,AE=OA= √3∴OE=2 √3∴D 的坐标为(﹣2 √3 ,1)(3)解:设直线BD 的解析式为:y=mx+n ,直线BD 与x 轴交于点E把B (0,3)和D (﹣2 √3 ,1)代入y=mx+n∴{n =31=−2√3m +n解得 {m =√33n =3∴直线BD 的解析式为:y= √33 x+3令y=0代入y= √33 x+3∴x=﹣3 √3∴E (﹣3 √3 ,0)∴OE=3 √3∴tan ∠BEC= OB OE = 33√3 = √33∴∠BEO=30°同理可求得:∠ABO=30°∴∠ABE=30°当PA=AB 时如图2此时∠BEA=∠ABE=30°∴EA=AB∴P 与E 重合 ∴P 的坐标为(﹣3 √3 ,0)当PA=PB 时如图3此时∠PAB=∠PBA=30°∵∠ABE=∠ABO=30°∴∠PAB=∠ABO∴PA ∥BC∴∠PAO=90° ∴点P 的横坐标为﹣ √3 令x=﹣ √3 代入y= √33 x+3∴y=2 ∴P (﹣ √3 ,2)当PB=AB 时如图4∴由勾股定理可求得:AB=2 √3 ,EB=6若点P 在y 轴左侧时记此时点P 为P 1过点P 1作P 1F ⊥x 轴于点F ∴P 1B=AB=2 √3∴EP 1=6﹣2 √3∴sin ∠BEO= FP 1EP 1∴FP 1=3﹣ √3令y=3﹣ √3 代入y= √33x+3 ∴x=﹣3∴P 1(﹣3,3﹣ √3 )若点P 在y 轴的右侧时记此时点P 为P 2过点P 2作P 2G ⊥x 轴于点G∴P 2B=AB=2 √3∴EP 2=6+2 √3∴sin ∠BEO= GP 2EP 2∴GP 2=3+ √3令y=3+ √3 代入y= √33x+3 ∴x=3∴P 2(3,3+ √3 )综上所述,当A 、B 、P 三点为顶点的三角形是等腰三角形时点P 的坐标为(﹣3 √3 ,0),(﹣√3 ,2),(﹣3,3﹣ √3 ),(3,3+ √3 )21.【答案】(1)解:在y=x+2中当x=0时当y=0时∴A(−2,0)(2)解:∵点C(2,m)在直线y=x+2上∴m=2+2=4又∵点C(2,4)也在直线y=−12x+b上∴即4=12x+5解得b=5(3)解:在y=−12x+5中当x=0时∴D(10,0)∵A(−2,0)∴AD=12①设PD=t,则AP=12−t过C作CE⊥AP于E,则CE=4由ΔACP的面积为10得12(12−t)×4=10解得t=7②过C作CE⊥AP于E则CE=4∴AC=4√2 a.当AC=CP时如图①所示则AP=2AE=8∴PD=AD−AP=4∴t=4b.当AP1=AP2=AC=4√2时如图②所示DP1=t=12−4√2c.当CP=AP时如图③所示设EP=a则CP=√a2+42∴√a2+42=a+4解得a=0∴AP=4∴PD=8∴t=8综上所述,当t=4或t=12−4√2或t=12+4√2或t=8时ΔACP为等腰三角形22.【答案】(1)解:设直线l的解析式为y=kx+b∵点B(0,2)、C(−1,3)在直线l上∴{b=2−k+b=3解得{b=2 k=−1∴直线l的解析式为y=−x+2(2)解:把y=0代入方程y=−x+2得x=2∴点A(2,0)SΔBOC=12|x c|⋅OB=12×1×2=1设P(a,0),则AP=|a−2|∴ΔACP△ACP 的面积是: 12×3×|a−2|令SΔACP=2SΔBOC即12×3×|a−2|=2解得a=103或a=23∴A点的坐标数是(103,0)或(23,0)23.【答案】(1)1(2)由(1)可知,直线AB的解析式为:y=2x+1令x=0,则y=1令y=0,则 x =−12∴点A 为( −12 ,0),点B 为(0,1) ∴OA= 12 ,OB=1;由旋转的性质,得 AB =BC∵BC ⊥AB∴∠ABC=90°过点C 作CD ⊥y 轴,垂足为D ,如图:∵∠BDC=90°∴∠CBD+∠BCD=∠CBD+∠ABD=90° ∴∠BCD=∠ABD同理,∠CBD=∠BAO∵AB=BC∴△ABO ≌△BCD∴BD=AO= 12 ,CD=BO=1∴OD= OB −BD =1−12=12∴点C 的坐标为(1, 12 );设直线l 的表达式为 y =mx +n ∵直线经过点A 、C ,则{m +n =12−12m +n =0 ,解得: {m =13n =16∴直线l 的表达式为 y =13x +16 .24.【答案】(1)解:∵m+mn=n 且m ,n 是正实数 ∴m n +m=1,即m n =1-m∴P (m ,1-m )∴点P 在直线y=1-x 上当x=2时1-x=-1∴点F (2,6)不是“状元点”;∵点A (0,7)在直线y=x+b 上∴7=0+b∴b=7;(2)解:由(1)求得直线AM :y=x+7∵“状元点”B 在直线AM 上,且满足y=1-x∴{y =1−x y =x +7解得:{x =−3y =4∴点B 的坐标为(-3,4);(3)解:∵点C 是“状元点”∴设C (n ,1-n )∴AC=√n 2+(7−1+n)2=√2n 2+12n +36≤5√2 整理得n 2+6n −7≤0解得:-7≤n ≤1.。
一次函数与几何图形综合题及答案

专题训练:一次函数与几何图形综合1、直线y=-x+2与x 轴、y 轴交于A 、B 两点,C 在y 轴的负半轴上,且OC=OB(1) 求AC 的解析式;(2) 在OA 的延长线上任取一点P,作PQ ⊥BP,交直线AC 于Q,试探究BP 与PQ 的数量关系,并证明你的结论。
(3) 在(2)的前提下,作PM ⊥AC 于M,BP 交AC 于N,下面两个结论:①(MQ+AC)/PM 的值不变;②(MQ-AC)/PM 的值不变,期中只有一个正确结论,请选择并加以证明。
2.(本题满分12分)如图①所示,直线L :5y mx m =+与x 轴负半轴、y 轴正半轴分别交于A 、B 两点。
(1)当OA=OB 时,试确定直线L 的解析式;xyo BA CPQxyo BA CPQM第2题图①(2)在(1)的条件下,如图②所示,设Q 为AB 延长线上一点,作直线OQ ,过A 、B 两点分别作AM ⊥OQ 于M ,BN ⊥OQ 于N ,若AM=4,BN=3,求MN 的长。
(3)当m 取不同的值时,点B 在y 轴正半轴上运动,分别以OB 、AB 为边,点B 为直角顶点在第一、二象限内作等腰直角△OBF 和等腰直角△ABE ,连EF 交y 轴于P 点,如图③。
问:当点B 在 y 轴正半轴上运动时,试猜想PB 的长是否为定值,若是,请求出其值,若不是,说明理由。
3、如图,直线1l 与x 轴、y 轴分别交于A 、B 两点,直线2l 与直线1l 关于x 轴对称,已知直线1l 的解析式为3y x =+,(1)求直线2l 的解析式;(3分)第2题图②第2题图③CB Al 2l 1xy(2)过A 点在△ABC 的外部作一条直线3l ,过点B 作作CF ⊥3l 于F 分别,请画出图形并求证:BE +CF =(3)△ABC 沿y 轴向下平移,AB 边交x 轴于点P ,过P 点的直线与AC 边的延长线相交于点Q ,与y 轴相交与点M ,且BP =CQ ,在△ABC 平移的过程中,①OM 为定值;②MC 为定值。
部编数学八年级下册专题38一次函数的应用之几何问题(解析版)含答案

专题38一次函数的应用之几何问题1.如图,在平面坐标系中,直线:l y kx b =+分别与x 轴,y 轴交于点3,02A æö-ç÷èø,点()0,3B .(1)求直线l 的解析式;(2)若点C 是y 轴上一点,且ABC V 的面积是154,求点C 的坐标;(3)在(2)的条件下,当点C 在y 轴负半轴时,在平面内是否存在点D ,使以A ,B ,C ,D 为顶点的四边形是平行四边形?若存在,直接写出点D 的坐标;若不存在,请说明理由.2.如图①,在矩形OACB 中,点A 、B 分别在x 轴、y 轴正半轴上,点C 在第一象限,8OA =,6OB =.(1)请直接写出点C 的坐标;(2)如图②,点F 在BC 上,连接AF ,把ACF V 沿着AF 折叠,点C 刚好与线段AB 上一点C ¢重合,求线段CF 的长度;(3)如图③,点(,)P x y 为直线26y x =-在第一象限内的图象上的个动点,点D 在线段AC 上(不与点A 、C 重合),是否存在直角顶点为P 的等腰直角BDP △,若存在,请求出点P 的坐标:若不存在,请说明理由.Q BPD D 是等腰三角形,\ BP PD =,90BPD Ð=°,\EF BC ∥,\BEP Ð=90PFD Ð=°,\BPE DPF DPF PDF Ð+Ð=Ð+Ð,\BPE PDF Ð=Ð,\()BPE PDF AAS D D ≌,\6(26)122PF BE a a ==--=-,EP DF =,Q 1228EF EP PF a a =+=+-=,\4a =,\点(4,2)P ,点D 为(8,6)在端点上,点(4,2)P 不符合题意,舍去;②当点P 在BC 的上方时,如图④,过点P 作EF BC ∥,交y 轴于E ,交AC 的延长线于F ,同理可证BPE PDF D D ≌,\266212BE PF a a ==--=-,3.如图,在平面直角坐标系中,正方形OABC的边OA,OC分别在x轴,y轴的正半轴上,直线y =2x-6经过线段OA的中点D,与y轴交于点G,E是线段CG上一点,作点E关于直线DG的对称点F,连接BE,BF,FG.设点E的坐标为(0,m).(1)写出点B的坐标是( , );(2)当43OABCBEGFS S=正方形四边形时,求点E的坐标;(3)在点E的整个运动过程中,①当四边形BEGF为菱形时,求点E的坐标;②若N为平面内一点,当以B,E,F,N为顶点的四边形为矩形时,m的值为 .(请直接写出答案)4.如图,在平面直角坐标系中,过点B(4,0)的直线AB与直线OA相交于点A(3,1),动点M 在线段OA和射线AC上运动.(1)求直线AB的解析式;(2)直线AB交y轴于点C,求△OAC的面积;(3)当△OAC的面积是△OMC面积的3倍时,求出这时点M的坐标.5.如图1,在平面直角坐标系中,直线AB 分别交x 轴、y 轴于A(a ,0)、B(0,b)两点,且a ,b 满足(a ﹣b )2+|a ﹣4t|=0,且t >0,t 是常数.直线BD 平分∠OBA ,交x 轴于D 点.(1)若AB 的中点为M ,连接OM 交BD 于N ,求证:ON =OD ;(2)如图2,过点A 作AE ⊥BD ,垂足为E ,猜想AE 与BD 间的数量关系,并证明你的猜想;(3)如图3,在x 轴上有一个动点P (在A 点的右侧),连接PB ,并作等腰Rt △BPF ,其中∠BPF =90°,连接FA 并延长交y 轴于G 点,当P 点在运动时,OG 的长是否发生改变?若改变,请求出它的变化范围;若不变,求出它的长度.【答案】(1)见解析;(2)BD =2AE ,证明见解析;(3)OG 的长不变,OG =4t【分析】(1)根据直线解析式求出点A 、B 的坐标,然后得出AOB D 是等腰直角三角形,再根据角平分线的定义求出22.5ABD Ð=°,根据等腰三角形三线合一的性质OM AB ^,然后根据直角三角形两锐角互余的性质与三角形的一个外角等于与它不相邻的两个内角的和求出67.5OND Ð=°,67.5ODB Ð=°,利用等角对等边得到ON OD =;(2)延长AE 交BO 于C ,得ABE CBE D @D ,得到2AC AE =,再证OAC OBD D @D 得到BD AE =,从而得到2BD AE =;()ABE CBE ASA \D @D ,AE CE \=,2AC AE \=,AE BD ^Q ,90OAC ADE \Ð+Ð=°,又90OBD BDO Ð+Ð=°,ADE BDO Ð=Ð(对顶角相等),OAC OBD \Ð=Ð,在OAC D 与OBD D 中,OAC OBD OA OB BOD AOCìÐ=Ðïïïï=íïïïÐ=Ðïî,()OAC OBD ASA \D @D ,BD AC \=,2BD AE \=;(3)OG 的长不变,且4OG t =.过F 作FH OP ^,垂足为H ,90FPH PFH \Ð+Ð=°,90BPF Ð=°Q ,90BPO FPH \Ð+Ð=°,FPH BPO \Ð=Ð,BPF D Q 是等腰直角三角形,BP FP \=,在OBP D 与HPF D 中,90FPH BPO BOP FHP BP FPìÐ=ÐïïïïÐ=Ð=°íïïï=ïî,()OBP HPF AAS \D @D ,FH OP \=,4PH OB t ==,=,Q,OA OB=+=+AH PH AP OB AP\=+=,AH OA OP OP\=,FH AH\Ð=Ð=°,45GAO FAH\D是等腰直角三角形,AOG\==.OG OA t4【点睛】本题综合考查了一次函数,全等三角形的判定与全等三角形的性质,以及等腰直角三角形的性质,角平分线的定义,等腰三角形三线合一的性质等等知识点,熟悉相关性质是解题的关键.6.如图,在平面直角坐标系中,边长为3的正方形ABCD在第一象限内,AB∥x轴,点A的坐标为(5,4)经过点O、点C作直线l,将直线l沿y轴上下平移.(1)当直线l与正方形ABCD只有一个公共点时,求直线l的解析式;(2)当直线l在平移过程中恰好平分正方形ABCD的面积时,直线l分别与x轴、y轴相交于点E、点F,连接BE、BF,求△BEF的面积.【点睛】本题主要考查一次函数的图象的平移和正方形的性质的综合,掌握待定系数法和求直线和坐标轴的交点坐标是解题的关键.7.已知,一次函数364y x =-+的图像与x 轴、y 轴分别交于点A 、点B ,与直线54y x = 相交于点C ,过点B 作x 轴的平行线l .点P 是直线l 上的一个动点.(1)求点A ,点B 的坐标.(2)若AOC BCP S S =△△,求点P 的坐标.(3)若点E 是直线54y x =上的一个动点,当△APE 是以AP 为直角边的等腰直角三角形时,求点E 的坐标.8.如图,将一矩形纸片OABC 放在平面直角坐标系中,()0,0O ,()6,0A ,()0,3C .动点F 从点O 出发以每秒1个单位长度的速度沿OC 向终点C 运动,运动23秒时,动点E 从点A 出发以相同的速度沿AO 向终点O 运动,当点E 、F 其中一点到达终点时,另一点也停止运动.设点E 的运动时间为t (秒).(Ⅰ)OE =_____________,OF =_____________;(用含t 的代数式表示)(Ⅱ)当1t =时,将OEF V 沿EF 翻折,点O 恰好落在CB 边上的点D 处.①求点D 的坐标及直线DE 的解析式;②点M 是射线DB 上的任意一点,过点M 作直线DE 的平行线,与x 轴交于N 点,设直线MN 的解析式为y kx b =+,当点M 与点B 不重合时,S 为MBN △的面积,当点M 与点B 重合时,0S =.求S 与b 之间的函数关系式,并求出自变量b 的取值范围.∵OEF V 沿EF 翻折得到DEF V ,∴53FD OF ==.∴1410BM b=-+.9.已知,直线y=2x-2与x轴交于点A,与y轴交于点B.(1)如图①,点A的坐标为_______,点B的坐标为_______;(2)如图②,点C是直线AB上不同于点B的点,且CA=AB.①求点C的坐标;②过动点P(m,0)且垂直与x轴的直线与直线AB交于点E,若点E不在线段BC上,则m的取值范围是_______;(3)若∠ABN=45º,求直线BN的解析式.令y=0,则2x-2=0,即x=1过点C 作CD⊥x 轴,垂足是D,∵∠BOA=∠ADC=90°,∠BAO=∠CAD,CA=AB,∴△BOA≌△CAD(AAS),∴CD=OB=2,AD=OA=1,∴C(2,2);②由①可知D(2,0),观察图②,可知m的取值范围是:m<0或m>2.故答案是:m<0或m>2;(3)如图③,作AN⊥AB,使得AN=AB,作NH⊥x轴于H,则△ABN是等腰直角三角形,∠ABN=45°.∵∠AOB=∠BAN=∠AHN=90°,∴∠OAB+∠ABO=90°,∠OAB+∠HAN=90°,∴∠ABO=∠HAN,∵AB=AN,∴△ABO≌△NAH(AAS),∴AH=OB=2,NH=OA=1,∴N(3,-1),设直线BN的解析式为y=kx+b,则有:312k bb+=-ìí=-î,解得132kbì=ïíï=-î,∴直线BN的解析式为y=13x-2,当直线BN′⊥直线BN时,直线BN′也满足条件,直线BN′的解析式为:y3x2=--.∴满足条件的直线BN的解析式为y=13x-2或y=-3x-2.【点睛】本题考查一次函数的性质、全等三角形的判定和性质、等腰直角三角形的性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.10.如图,将一矩形纸片OABC放在平面直角坐标系中,O(0,0),A(6,0),C(0,3),动点F从点O出发以每秒1个单位长度的速度沿OC向终点C运动,运动23秒时,动点E从点A出发以相同的速度沿AO向终点O运动,当点E、F其中一点到达终点时,另一点也停止运动设点E的运动时间为t:(秒)(1)OE= ,OF= (用含t的代数式表示)(2)当t=1时,将△OEF沿EF翻折,点O恰好落在CB边上的点D处①求点D的坐标及直线DE的解析式;②点M是射线DB上的任意一点,过点M作直线DE的平行线,与x轴交于N点,设直线MN的解析式为y=kx+b,当点M与点B不重合时,S为△MBN的面积,当点M与点B重合时,S=0.求S 与b之间的函数关系式,并求出自变量b的取值范围.11.如图,一次函数y=kx+b的图象为直线l1,经过A(0,4)和D(4,0)两点;一次函数y=x+1的图象为直线l2,与x轴交于点C;两直线l1,l2相交于点B.(1)求k、b的值;(2)求点B的坐标;(3)求△ABC的面积.12.已知11y kx =+过点(2,-1),与x 轴交于点A,F 点为(1,2).(Ⅰ)求k 的值及A 点的坐标;(Ⅱ)将函数1y 的图象沿y 轴方向向上平移得到函数2y ,其图象与y 轴交于点Q,且OQ=QF,求平移后的函数2y 的解析式;(Ⅲ)若点A 关于2y 的对称点为K,请求出直线FK 与x 轴的交点坐标.13.在平面直角坐标系中,直线1l:142y x=-+分别与x轴、y轴交于点A、点B,且与直线2l:y x=于点C.(Ⅰ)如图①,求出B、C两点的坐标;(Ⅱ)若D是线段OC上的点,且BODV的面积为4,求直线BD的函数解析式.(Ⅲ)如图②,在(Ⅱ)的条件下,设P是射线BD上的点,在平面内是否存在点Q,使以O、B、P、Q为顶点的四边形是菱形?若存在,直接写出点Q的坐标;若不存在,请说明理由.14.如图1,直线AB交x轴于点A(4 ,0),交y轴于点B(0 ,-4),(1)如图,若C的坐标为(-1, ,0),且AH⊥BC于点H,AH交OB于点P,试求点P的坐标;(2)在(1)的条件下,如图2,连接OH ,求证:∠OHP=45°;(3)如图3,若点D 为AB 的中点,点M 为y 轴正半轴上一动点,连结MD ,过点D 作DN ⊥DM 交x 轴于N 点,当M 点在y 轴正半轴上运动的过程中,式子BDM ADN S S -V V 的值是否发生改变?如发生改变,求出该式子的值的变化范围;若不改变,求该式子的值.【答案】(1)P (0 ,-1);(2)证明见解析;(3)不变;4.【分析】(1)利用坐标的特点,得出△OAP ≌△OB ,得出OP=OC=1,得出结论;(2)过O 分别做OM ⊥CB 于M 点,ON ⊥HA 于N 点,证出△COM ≌△PON ,得出OM=ON ,HO 平分∠CHA ,求得结论;(3)连接OD ,则OD ⊥AB ,证得△ODM ≌△ADN ,利用三角形的面积进一步解决问题.试题解析:(1)由题得,OA=OB=4.【详解】解:∵AH ⊥BC 于H ,∴∠OAP +∠OPA=∠BPH +∠OBC=90°,∴∠OAP=∠OBC在△OAP 和△OBC 中,90COB POA OA OB OAP OBC Ð=Ð=°ìï=íïÐ=Ðî∴△OAP ≌△OBC (ASA ),∴OP=OC=1,则点P (0 ,-1)(2)过点O 分别作OM ⊥CB 于M 点,ON ⊥HA 于N 点,15.如图,直线12y x b=-+与x轴,y轴分别交于点A,点B,与函数y=kx的图象交于点M(1,2).(1)直接写出k,b的值和不等式012x b kx£-+£的解集;(2)在x轴上有一点P,过点P作x轴的垂线,分别交函数y=﹣12x+b和y=kx的图象于点C,点D.若2CD=OB,求点P的坐标.16.无刻度直尺作图:图1 图2(1)直接写出四边形ABCD的形状.(2)在图1中,先过E点画一条直线平分四边形ABCD的面积,再在AB上画点F,使得AF=AE.(3)在图2中,先在AD上画一点G,使得∠DCG=45°;连接AC,再在AC上画点H,使得GH=GA.【答案】(1)四边形ABCD是菱形,理由见解析(2)见解析(3)见解析【分析】(1)只需要证明AB=CD=AD=BC即可得到结论;(2)如图连接AC,BD交于点T,作直线ET交BC于G,连接AG交BD于H,连接CH并延长交AB于F,则直线EG,点F即为所求;(3)如图所示,取格点T,连接CT交AD于G,取格点M、N,连接MN交BC于P,连接GP交AC于H,则点G、H即为所求;(1)求直线AB 的解折式;(2)如图2,已知P 为直线l :152y x =-+上一点,且512ABI ABCO S S =四边形△,求点P 的坐标;(3)若点D 为第一象限内一动点,且45ODC Ð=°,求BD 的最小值.∴∠BDA =90°,∵BC ∥OA ,BC =2,OA =6,∴AD =6−2=4,在Rt △ABD 中,BD =(22213AB AD -=∴PQ=|yQ−yP|=31922m m -++∵xA−xB=6−2=4,∴S△ABP=12PQ•(xA−xB)=12×4×|4−S四边形ABCO=12×(2+6)×6=24,∵∠ODC=45°,∠MOD=90°,18.如图,直线y =x +9与直线y =-2x -3交于点C ,它们与y 轴分别交于A 、B 两点.(1)求A 、B 、C 三点的坐标;(2)点F 在x 轴上,使10BFC S =△,求点F 的坐标;(3)点P 在x 轴上,使∠PBO +∠PAO =90°,直接写出点P 的坐标.。
一次函数与几何综合(k,b的几何意义一)(人教版)(含答案)

一次函数与几何综合(k,b的几何意义一)(人教版)一、单选题(共7道,每道14分)1.如图,点B,C分别在直线y=3x和直线y=kx上,A,D是x轴上两点,若四边形ABCD是长方形,且,则k的值是( )A. B.C. D.答案:C解题思路:试题难度:三颗星知识点:k的几何意义2.如图,点B,C分别在两条直线和上,点A,D是x轴上的两点,已知四边形ABCD是正方形,则k的值为( )A.2B.C. D.1答案:A解题思路:试题难度:三颗星知识点:一次函数k的几何意义3.如图,已知点A的坐标为(5,0),直线y=x+b(b>0)与x轴、y轴分别交于点B,C,连接AC,,则点B的坐标为( )A. B.C. D.答案:B解题思路:试题难度:三颗星知识点:k的几何意义4.如图,直线AP的解析式为,且点P的坐标为(4,2),PA=PB,则点B的坐标是( )A.(5,0)B.(6,0)C.(7,0)D.(8,0)答案:C解题思路:试题难度:三颗星知识点:k的几何意义5.如图,已知一条直线经过A(0,2),B(1,0)两点,将这条直线向左平移,与x轴、y 轴分别交于点C,点D.若DB=DC,则直线CD的函数解析式为( )A. B.C. D.答案:C解题思路:试题难度:三颗星知识点:一次函数、坐标、几何三角通道互转6.已知点,B(0,0),,AE平分∠BAC,交BC于点E,则直线AE的函数表达式是( )A. B.y=x-2C. D.答案:D解题思路:试题难度:三颗星知识点:一次函数、坐标、几何三角通道互转7.如图,在平面直角坐标系中,直线交x轴于点A,交y轴于点B,点C 是线段AB的中点,连接OC,然后将直线OC绕点C逆时针旋转30°交x轴于点D,则直线CD的表达式为( )A. B.C. D.答案:D解题思路:试题难度:三颗星知识点:一次函数、坐标、几何三角通道互转。
一次函数练习题及答案(较难------实用)

初二一次函数与几何题(附答案)1、 平面直角坐标系中,点A 的坐标为(4,0),点P 在直线y=-x-m 上,且AP=OP=4,则m 的值是多少?2、如图,已知点A 的坐标为(1,0),点B 在直线y=-x 上运动,当线段AB 最短时,试求点B 的坐标。
3、如图,在直角坐标系中,矩形OABC 的顶点B 的坐标为(15,6),直线y=1/3x+b 恰好将矩形OABC 分为面积相等的两部分,试求b 的值。
4、如图,在平面直角坐标系中,直线y= 2x —6与x 轴、y在x 轴上,若△ABC是等腰三角形,试求点C 的坐标。
5、在平面直角坐标系中,已知A (1,4)、B (3,1),P AP+BP 取最小值,最小值为多少? 当P 的坐标为多少时,AP-BP6、如图,已知一次函数图像交正比例函数图像于第二象限的A AOB 的面积为15,且AB=AO ,求正比例函数和一次函数的解析式。
7、已知一次函数的图象经过点(2,20)式。
8、已经正比例函数Y=k1x 的图像与一次函数y=k2x-9的图像相交于点P(3,-6)求k1,k2的值如果一次函数y=k2x-9的图象与x 轴交于点A 求点A 坐标9、正方形ABCD 的边长是4,将此正方形置于平面直角坐标系中,使AB 在x 轴负半轴上,A 点的坐标是(-1,0),(1)经过点C 的直线y=-4x-16与x 轴交于点E ,求四边形AECD 的面积;(2)若直线L 经过点E 且将正方形ABCD 分成面积相等的两部分,求直线L 的解析式。
10、在平面直角坐标系中,一次函数y=Kx+b(b 小于0)的图像分别与x 轴、y 轴和直线x=4交于A 、B 、C ,直线x=4与x 轴交于点D ,四边形OBCD 的面积为10,若A 的横坐标为-1/2,求此一次函数的关系式11、在平面直角坐标系中,一个一次函数的图像过点B(-3,4),与y 轴交于点A ,且OA=OB :求这个一次函数解析式12、如图,A 、B 分别是x 轴上位于原点左右两侧的点,点P (2,m )在第一象限,直线PA 交y 轴于点C (0,2),直线PB 交y 轴于点D ,S AOP =6.求:(1)△COP 的面积(2)求点A 的坐标及m 的值;(3)若S BOP =S DOP ,求直线BD 的解析式13、一次函数y=-33x+1的图像与x 轴、y 轴分别交于点A 、B ,以AB 为边在第一象限内做等边△ABC (1)求△ABC 的面积和点C 的坐标;(2)如果在第二象限内有一点P (a ,21),试用含a 的代数式表示四边形ABPO 的面积。
一次函数与几何综合(学生版)

x轴
试求这个一次函数的表达式 若△POB≌△EPA 求这个一次函数的表达式
有一定点 E ( 2,0 )
9 /15
电话 024-22823262
一次函数与动态问题
36. 如图 直线 y = kx + b
y 轴 x 轴分别相交于点 A ( 0,4 ) B ( 6,0 )
点 C 的坐标为 ( 2,0 )
B ( 4 2)
C
在x轴
取一点 P
使点 P 到点 A 和点 B 的距离
D
(2
0)
(0
0)
2 /15
电话 024-22823262
8.
在平面直角坐标系中
BP + AP 最小时
x轴
一动点 P 到定点 A (1 1)
B ( 5 7 ) 的距离分别为 AP 和 BP
那 当
P 点坐标为_______________
OP ⋅ OQ = ________
11. 已知点 P 坐标是 ( 4,0 )
点 Q 坐标是 ( 6,2 )
在直线 y = x
找一点 M
使得 △QMP 的周长最小
则点 M 的坐标为_________
12. 如 图 牧童在 A 处放牛 其家在 B 处 CD = 8m
A
B 到河岸的距离分别为 AC
BD 且 AC = BD = 3m
25. 已知一次函数 y = kx + b 的图象 过点 ( 0, −3)
a 的值 k b 的值 这两个函数图象
且
比例函数 y =
1 x 的图象相交于点 ( 2, a ) 2
求
x 轴所围
的
角形面
一次函数与几何综合(k,b的几何意义二)(人教版)(含答案)

一次函数与几何综合(k,b的几何意义二)(人教版)一、单选题(共7道,每道14分)1.如图,将正方形ABCD置于平面直角坐标系的第一象限内,使AB落在x轴正半轴上,直线经过点C,与x轴交于点E,若点A的坐标是(1,0),则四边形AECD的面积是( )A.4B.6C.10D.16答案:C解题思路:试题难度:三颗星知识点:一次函数与几何综合2.如图,已知直线与直线相交于点F,分别交x轴于点E,G,矩形ABCD顶点C,D分别在直线上,顶点A,B都在x轴上,且点B与点G 重合,则长方形ABCD的面积为( )A.12B.18C.24D.32答案:B解题思路:试题难度:三颗星知识点:一次函数、坐标、几何三角通道互转3.正方形……按照如图所示的方式放置,点……和点……分别在直线l和x轴上,已知点(1,1),(3,2),则的坐标是( )A. B.C. D.答案:C解题思路:试题难度:三颗星知识点:一次函数k的几何意义4.已知函数的图象为直线,点P的坐标为(2,1),则点P到直线的距离为( )A. B.C. D.答案:C解题思路:试题难度:三颗星知识点:一次函数k的几何意义5.如图,点A的坐标为(-1,0),点B在直线y=x-3上运动,则线段AB最短为( )A. B.4C. D.答案:C解题思路:试题难度:三颗星知识点:k的几何意义6.已知直线PQ的斜率为,将直线PQ绕点P(,0)顺时针旋转60°所得直线的表达式为( )A. B.C. D.答案:B解题思路:试题难度:三颗星知识点:一次函数与几何综合7.如图,直线与x轴相交于点A,与y轴相交于点B,将△ABO沿着AB翻折,得到△ABC,则直线BC的表达式为( )A. B.C. D.答案:A解题思路:试题难度:三颗星知识点:一次函数与几何综合。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.(2013•天水)如图1,在平面直角坐标系中,已知△AOB是等边三角形,点A的坐标是(0,4),点B在第一象限,点P是x轴上的一个动点,连接AP,并把△AOP绕着点A按逆时针方向旋转,使边AO与AB重合,得到△ABD.(1)求直线AB的解析式;(2)当点P运动到点(,0)时,求此时DP的长及点D的坐标;(3)是否存在点P,使△OPD的面积等于?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.2.(2013•济宁)如图,直线y=﹣x+4与坐标轴分别交于点A、B,与直线y=x交于点C.在线段OA上,动点Q以每秒1个单位长度的速度从点O出发向点A做匀速运动,同时动点P从点A出发向点O做匀速运动,当点P、Q其中一点停止运动时,另一点也停止运动.分别过点P、Q作x轴的垂线,交直线AB、OC于点E、F,连接EF.若运动时间为t秒,在运动过程中四边形PEFQ总为矩形(点P、Q重合除外).(1)求点P运动的速度是多少?(2)当t为多少秒时,矩形PEFQ为正方形?(3)当t为多少秒时,矩形PEFQ的面积S最大?并求出最大值.3.(2013•绥化)如图,直线MN与x轴,y轴分别相交于A,C两点,分别过A,C两点作x轴,y轴的垂线相交于B 点,且OA,OC(OA>OC)的长分别是一元二次方程x2﹣14x+48=0的两个实数根.(1)求C点坐标;(2)求直线MN的解析式;(3)在直线MN上存在点P,使以点P,B,C三点为顶点的三角形是等腰三角形,请直接写出P点的坐标.4.(2013•齐齐哈尔)如图,平面直角坐标系中,直线l分别交x轴、y轴于A、B两点(OA<OB)且OA、OB的长分别是一元二次方程x2﹣(+1)x+=0的两个根,点C在x轴负半轴上,且AB:AC=1:2(1)求A、C两点的坐标;(2)若点M从C点出发,以每秒1个单位的速度沿射线CB运动,连接AM,设△ABM的面积为S,点M的运动时间为t,写出S关于t的函数关系式,并写出自变量的取值范围;(3)点P是y轴上的点,在坐标平面内是否存在点Q,使以A、B、P、Q为顶点的四边形是菱形?若存在,请直接写出Q点的坐标;若不存在,请说明理由.5.(2013春•屯留县期末)如图,四边形OABC是菱形,点C在x轴上,AB交y轴于点H,AC交y轴于点M.已知点A(﹣3,4).(1)求AO的长;(2)求直线AC的解析式和点M的坐标;(3)点P从点A出发,以每秒2个单位的速度沿折线A﹣B﹣C运动,到达点C终止.设点P的运动时间为t秒,△PMB 的面积为S.①求S与t的函数关系式;②求S的最大值.6.(2012•鞍山)如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标(3,3),将正方形ABCO绕点A顺时针旋转角度α(0°<α<90°),得到正方形ADEF,ED交线段OC于点G,ED的延长线交线段BC于点P,连AP、AG.(1)求证:△AOG≌△ADG;(2)求∠PAG的度数;并判断线段OG、PG、BP之间的数量关系,说明理由;(3)当∠1=∠2时,求直线PE的解析式.7.(2012•桃源县校级自主招生)如图,点A在y轴上,点B在x轴上,且OA=OB=1,经过原点O的直线l交线段AB于点C,过C作OC的垂线,与直线x=1相交于点P,现将直线L绕O点旋转,使交点C从A向B运动,但C点必须在第一象限内,并记AC的长为t,分析此图后,对下列问题作出探究:(1)当△AOC和△BCP全等时,求出t的值;(2)通过动手测量线段OC和CP的长来判断它们之间的大小关系并证明你得到的结论;(3)①设点P的坐标为(1,b),试写出b关于t的函数关系式和变量t的取值范围.②求出当△PBC为等腰三角形时点P的坐标.8.(2012秋•海陵区期末)如图1,在平面直角坐标系中,直线AB与x轴交于点A,与y轴交于点B,与直线OC交于点C.(1)若直线AB解析式为y=﹣2x+12,直线OC解析式为y=x,①求点C的坐标;②求△OAC的面积.(2)如图2,作∠AOC的平分线ON,若AB⊥ON,垂足为E,△OAC的面积为6,且OA=4,P、Q分别为线段OA、OE上的动点,连接AQ与PQ,试探索AQ+PQ是否存在最小值?若存在,求出这个最小值;若不存在,说明理由.9.(2012秋•成都校级期末)如图,在平面直角坐标系xOy中,已知直线PA是一次函数y=x+m(m>0)的图象,直线PB是一次函数y=﹣3x+n(n>m)的图象,点P是两直线的交点,点A、B、C、Q分别是两条直线与坐标轴的交点.(1)用m、n分别表示点A、B、P的坐标及∠PAB的度数;(2)若四边形PQOB的面积是,且CQ:AO=1:2,试求点P的坐标,并求出直线PA与PB的函数表达式;(3)在(2)的条件下,是否存在一点D,使以A、B、P、D为顶点的四边形是平行四边形?若存在,求出点D的坐标;若不存在,请说明理由.10.(2012秋•綦江县校级期末)如图,一次函数的函数图象与x轴、y轴分别交于点A、B,以线段AB 为直角边在第一象限内作Rt△ABC,且使∠ABC=30°.(1)求△ABC的面积;(2)如果在第二象限内有一点P(m,),试用含m的代数式表示△APB的面积,并求当△APB与△ABC面积相等时m的值;(3)是否存在使△QAB是等腰三角形并且在坐标轴上的点Q?若存在,请写出点Q所有可能的坐标;若不存在,请说明理由.参考答案与试题解析一.解答题(共10小题)1.(2013•天水)如图1,在平面直角坐标系中,已知△AOB是等边三角形,点A的坐标是(0,4),点B在第一象限,点P是x轴上的一个动点,连接AP,并把△AOP绕着点A按逆时针方向旋转,使边AO与AB重合,得到△ABD.(1)求直线AB的解析式;(2)当点P运动到点(,0)时,求此时DP的长及点D的坐标;(3)是否存在点P,使△OPD的面积等于?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.考点:一次函数综合题.专题:压轴题.分析:(1)过点B作BE⊥y轴于点E,作BF⊥x轴于点F.依题意得BF=OE=2,利用勾股定理求出OF,然后可得点B的坐标.设直线AB的解析式是y=kx+b,把已知坐标代入可求解.(2)由△ABD由△AOP旋转得到,证明△ABD≌△AOP.AP=AD,∠DAB=∠PAO,∠DAP=∠BAO=60°,△ADP是等边三角形.利用勾股定理求出DP.在Rt△BDG中,∠BGD=90°,∠DBG=60°.利用三角函数求出BG=BD•cos60°,DG=BD•sin60°.然后求出OH,DH,然后求出点D的坐标.(3)本题分三种情况进行讨论,设点P的坐标为(t,0):①当P在x轴正半轴上时,即t>0时,关键是求出D点的纵坐标,方法同(2),在直角三角形DBG中,可根据BD即OP的长和∠DBG的正弦函数求出DG的表达式,即可求出DH的长,根据已知的△OPD的面积可列出一个关于t的方程,即可求出t的值.②当P在x轴负半轴,但D在x轴上方时.即<t≤0时,方法同①类似,也是在直角三角形DBG用BD的长表示出DG,进而求出GF的长,然后同①.③当P在x轴负半轴,D在x轴下方时,即t≤时,方法同②.综合上面三种情况即可求出符合条件的t的值.解答:解:(1)如图1,过点B作BE⊥y轴于点E,作BF⊥x轴于点F.由已知得:BF=OE=2,OF==,∴点B的坐标是(,2)设直线AB的解析式是y=kx+b(k≠0),则有.解得.∴直线AB的解析式是y=x+4;(2)如图2,∵△ABD由△AOP旋转得到,∴△ABD≌△AOP,∴AP=AD,∠DAB=∠PAO,∴∠DAP=∠BAO=60°,∴△ADP是等边三角形,∴DP=AP=.如图2,过点D作DH⊥x轴于点H,延长EB交DH于点G,则BG⊥DH.方法(一)在Rt△BDG中,∠BGD=90°,∠DBG=60°.∴BG=BD•cos60°=×=.DG=BD•sin60°=×=.∴OH=EG=,DH=∴点D的坐标为(,)方法(二)易得∠AEB=∠BGD=90°,∠ABE=∠BDG,∴△ABE∽△BDG,∴;而AE=2,BD=OP=,BE=2,AB=4,则有,解得BG=,DG=;∴OH=,DH=;∴点D的坐标为(,).(3)假设存在点P,在它的运动过程中,使△OPD的面积等于.设点P为(t,0),下面分三种情况讨论:①当t>0时,如图,BD=OP=t,DG=t,∴DH=2+t.∵△OPD的面积等于,∴,解得,(舍去)∴点P1的坐标为(,0).②∵当D在y轴上时,根据勾股定理求出BD==OP,∴当<t≤0时,如图,BD=OP=﹣t,DG=﹣t,∴GH=BF=2﹣(﹣t)=2+t.∵△OPD的面积等于,∴,解得,,∴点P2的坐标为(,0),点P3的坐标为(,0).③当t≤时,如图3,BD=OP=﹣t,DG=﹣t,∴DH=﹣t﹣2.∵△OPD的面积等于,∴(﹣t)[﹣(2+t)]=,解得(舍去),∴点P4的坐标为(,0),综上所述,点P的坐标分别为P1(,0)、P2(,0)、P3(,0)、P4(,0).点评:本题综合考查的是一次函数的应用,包括待定系数法求解析式、旋转的性质、相似三角形的判定和性质、三角形面积公式的应用等,难度较大.2.(2013•济宁)如图,直线y=﹣x+4与坐标轴分别交于点A、B,与直线y=x交于点C.在线段OA上,动点Q以每秒1个单位长度的速度从点O出发向点A做匀速运动,同时动点P从点A出发向点O做匀速运动,当点P、Q其中一点停止运动时,另一点也停止运动.分别过点P、Q作x轴的垂线,交直线AB、OC于点E、F,连接EF.若运动时间为t秒,在运动过程中四边形PEFQ总为矩形(点P、Q重合除外).(1)求点P运动的速度是多少?(2)当t为多少秒时,矩形PEFQ为正方形?(3)当t为多少秒时,矩形PEFQ的面积S最大?并求出最大值.考点:一次函数综合题.专题:压轴题.分析:(1)根据直线y=﹣x+4与坐标轴分别交于点A、B,得出A,B点的坐标,再利用EP∥BO,得出==,据此可以求得点P的运动速度;(2)当PQ=PE时,以及当PQ=PE时,矩形PEFQ为正方形,分别求出即可;(3)根据(2)中所求得出s与t的函数关系式,进而利用二次函数性质求出即可.解答:解:(1)∵直线y=﹣x+4与坐标轴分别交于点A、B,∴x=0时,y=4,y=0时,x=8,∴==,当t秒时,QO=FQ=t,则EP=t,∵EP∥BO,∴==,∴AP=2t,∵动点Q以每秒1个单位长度的速度从点O出发向点A做匀速运动,∴点P运动的速度是每秒2个单位长度;(2)如图1,当PQ=PE时,矩形PEFQ为正方形,则∵OQ=FQ=t,PA=2t,∴QP=8﹣t﹣2t=8﹣3t,∴8﹣3t=t,解得:t=2;如图2,当PQ=PE时,矩形PEFQ为正方形,∵OQ=t,PA=2t,∴OP=8﹣2t,∴QP=t﹣(8﹣2t)=3t﹣8,∴t=3t﹣8,解得:t=4;(3)如图1,当Q在P点的左边时,∵OQ=t,PA=2t,∴QP=8﹣t﹣2t=8﹣3t,∴S矩形PEFQ=QP•QF=(8﹣3t)•t=8t﹣3t2,当t=﹣=时,S矩形PEFQ的最大值为:=,如图2,当Q在P点的右边时,∵OQ=t,PA=2t,∴2t>8﹣t,∴t,∴QP=t﹣(8﹣2t)=3t﹣8,∴S矩形PEFQ=QP•QF=(3t﹣8)•t=3t2﹣8t,∵当点P、Q其中一点停止运动时,另一点也停止运动,∴<t≤4,当t=﹣=时,S矩形PEFQ的最大,∴t=4时,S矩形PEFQ的最大值为:3×42﹣8×4=16,综上所述,当t=4时,S矩形PEFQ的最大值为:16.点评:此题主要考查了二次函数与一次函数的综合应用,得出P,Q不同的位置进行分类讨论得出是解题关键.3.(2013•绥化)如图,直线MN与x轴,y轴分别相交于A,C两点,分别过A,C两点作x轴,y轴的垂线相交于B 点,且OA,OC(OA>OC)的长分别是一元二次方程x2﹣14x+48=0的两个实数根.(1)求C点坐标;(2)求直线MN的解析式;(3)在直线MN上存在点P,使以点P,B,C三点为顶点的三角形是等腰三角形,请直接写出P点的坐标.考点:一次函数综合题.专题:压轴题.分析:(1)通过解方程x2﹣14x+48=0可以求得OC=6,OA=8.则C(0,6);(2)设直线MN的解析式是y=kx+b(k≠0).把点A、C的坐标分别代入解析式,列出关于系数k、b的方程组,通过解方程组即可求得它们的值;(3)需要分类讨论:PB为腰,PB为底两种情况下的点P的坐标.根据等腰三角形的性质、两点间的距离公式以及一次函数图象上点的坐标特征进行解答.解答:解:(1)解方程x2﹣14x+48=0得x1=6,x2=8.∵OA,OC(OA>OC)的长分别是一元二次方程x2﹣14x+48=0的两个实数根,∴OC=6,OA=8.∴C(0,6);(2)设直线MN的解析式是y=kx+b(k≠0).由(1)知,OA=8,则A(8,0).∵点A、C都在直线MN上,∴,解得,,∴直线MN的解析式为y=﹣x+6;(3)∵A(8,0),C(0,6),∴根据题意知B(8,6).∵点P在直线MNy=﹣x+6上,∴设P(a,﹣a+6)当以点P,B,C三点为顶点的三角形是等腰三角形时,需要分类讨论:①当PC=PB时,点P是线段BC的中垂线与直线MN的交点,则P1(4,3);②当PC=BC时,a2+(﹣a+6﹣6)2=64,解得,a=,则P2(﹣,),P3(,);③当PB=BC时,(a﹣8)2+(a﹣6+6)2=64,解得,a=,则﹣a+6=﹣,∴P4(,﹣).综上所述,符合条件的点P有:P1(4,3),P2(﹣,)P3(,),P4(,﹣).点评:本题考查了一次函数综合题.其中涉及到的知识点有:待定系数法求一次函数解析式,一次函数图象上点的坐标特征,等腰三角形的性质.解答(3)题时,要分类讨论,防止漏解.另外,解答(3)题时,还利用了“数形结合”的数学思想.4.(2013•齐齐哈尔)如图,平面直角坐标系中,直线l分别交x轴、y轴于A、B两点(OA<OB)且OA、OB的长分别是一元二次方程x2﹣(+1)x+=0的两个根,点C在x轴负半轴上,且AB:AC=1:2(1)求A、C两点的坐标;(2)若点M从C点出发,以每秒1个单位的速度沿射线CB运动,连接AM,设△ABM的面积为S,点M的运动时间为t,写出S关于t的函数关系式,并写出自变量的取值范围;(3)点P是y轴上的点,在坐标平面内是否存在点Q,使以A、B、P、Q为顶点的四边形是菱形?若存在,请直接写出Q点的坐标;若不存在,请说明理由.考点:一次函数综合题.专题:压轴题.分析:(1)通过解一元二次方程x2﹣(+1)x+=0,求得方程的两个根,从而得到A、B两点的坐标,再根据两点之间的距离公式可求AB的长,根据AB:AC=1:2,可求AC的长,从而得到C点的坐标;(2)分①当点M在CB边上时;②当点M在CB边的延长线上时;两种情况讨论可求S关于t的函数关系式;(3)分AQ=AB,BQ=BA,BQ=QA三种情况讨论可求Q点的坐标.解答:解:(1)x2﹣(+1)x+=0,(x﹣)(x﹣1)=0,解得x1=,x2=1,∵OA<OB,∴OA=1,OB=,∴A(1,0),B(0,),∴AB=2,又∵AB:AC=1:2,∴AC=4,∴C(﹣3,0);(2)∵AB=2,AC=4,BC=2,∴AB2+BC2=AC2,即∠ABC=90°,由题意得:CM=t,CB=2.①当点M在CB边上时,S=2﹣t(0≤t);②当点M在CB边的延长线上时,S=t﹣2(t>2);(3)存在.①当AB是菱形的边时,如图所示,在菱形AP1Q1B中,Q1O=AO=1,所以Q1点的坐标为(﹣1,0),在菱形ABP2Q2中,AQ2=AB=2,所以Q2点的坐标为(1,2),在菱形ABP3Q3中,AQ3=AB=2,所以Q3点的坐标为(1,﹣2),②当AB为菱形的对角线时,如图所示的菱形AP4BQ4,设菱形的边长为x,则在Rt△AP4O中,AP42=AO2+P4O2,即x2=12+(﹣x)2,解得x=,所以Q4(1,).综上可得,平面内满足条件的Q点的坐标为:Q1(﹣1,0),Q2(1,﹣2),Q3(1,2),Q4(1,).点评:考查了一次函数综合题,涉及的知识点有:解一元二次方程,两点之间的距离公式,三角形面积的计算,函数思想,分类思想的运用,菱形的性质,综合性较强,有一定的难度.5.(2013春•屯留县期末)如图,四边形OABC是菱形,点C在x轴上,AB交y轴于点H,AC交y轴于点M.已知点A(﹣3,4).(1)求AO的长;(2)求直线AC的解析式和点M的坐标;(3)点P从点A出发,以每秒2个单位的速度沿折线A﹣B﹣C运动,到达点C终止.设点P的运动时间为t秒,△PMB 的面积为S.①求S与t的函数关系式;②求S的最大值.考点:一次函数综合题;解二元一次方程组;待定系数法求一次函数解析式;三角形的面积;角平分线的性质;勾股定理;菱形的性质.专题:计算题.分析:(1)根据A的坐标求出AH、OH,根据勾股定理求出即可;(2)根据菱形性质求出B、C的坐标,设直线AC的解析式是y=kx+b,把A(﹣3,4),C(5,0)代入得到方程组,求出即可;(3)①过M作MN⊥BC于N,根据角平分线性质求出MN,P在AB上,根据三角形面积公式求出即可;P 在BC上,根据三角形面积公式求出即可;②求出P在AB的最大值和P在BC上的最大值比较即可得到答案.解答:(1)解:∵A(﹣3,4),∴AH=3,OH=4,由勾股定理得:AO==5,答:OA的长是5.(2)解:∵菱形OABC,∴OA=OC=BC=AB=5,5﹣3=2,∴B(2,4),C(5,0),设直线AC的解析式是y=kx+b,把A(﹣3,4),C(5,0)代入得:,解得:,∴直线AC的解析式为,当x=0时,y=2.5∴M(0,2.5),答:直线AC的解析式是,点M的坐标是(0,2.5).(3)①解:过M作MN⊥BC于N,∵菱形OABC,∴∠BAC=∠OCA,∵MO⊥CO,MN⊥BC,∴OM=MN,当0≤t<2.5时,P在AB上,MH=4﹣2.5=,S=×BP×MH=×(5﹣2t)×=﹣t+,∴,当t=2.5时,P与B重合,△PMB不存在;当2.5<t≤5时,P在BC上,S=×PB×MN=×(2t﹣5)×=t﹣,∴,答:S与t的函数关系式是(0≤t<2.5)或(2.5<t≤5).②解:当P在AB上时,高MH一定,只有BP取最大值即可,即P与A重合,S最大是×5×=,同理在BC上时,P与C重合时,S最大是×5×=,∴S的最大值是,答:S的最大值是.点评:本题主要考查对勾股定理,三角形的面积,菱形的性质,角平分线性质,解二元一次方程组,用待定系数法求一次函数的解析式等知识点的理解和掌握,综合运用这些性质进行计算是解此题的关键.6.(2012•鞍山)如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标(3,3),将正方形ABCO绕点A顺时针旋转角度α(0°<α<90°),得到正方形ADEF,ED交线段OC于点G,ED的延长线交线段BC于点P,连AP、AG.(1)求证:△AOG≌△ADG;(2)求∠PAG的度数;并判断线段OG、PG、BP之间的数量关系,说明理由;(3)当∠1=∠2时,求直线PE的解析式.考点:一次函数综合题.专题:压轴题.分析:(1)由AO=AD,AG=AG,利用“HL”可证△AOG≌△ADG;(2)利用(1)的方法,同理可证△ADP≌△ABP,得出∠1=∠DAG,∠DAP=∠BAP,而∠1+∠DAG+∠DAP+∠BAP=90°,由此可求∠PAG的度数;根据两对全等三角形的性质,可得出线段OG、PG、BP之间的数量关系;(3)由△AOG≌△ADG可知,∠AGO=∠AGD,而∠1+∠AGO=90°,∠2+∠PGC=90°,当∠1=∠2时,可证∠AGO=∠AGD=∠PGC,而∠AGO+∠AGD+∠PGC=180°,得出∠AGO=∠AGD=∠PGC=60°,即∠1=∠2=30°,解直角三角形求OG,PC,确定P、G两点坐标,得出直线PE的解析式.解答:(1)证明:∵∠AOG=∠ADG=90°,∴在Rt△AOG和Rt△ADG中,∵,∴△AOG≌△ADG(HL);(2)解:PG=OG+BP.由(1)同理可证△ADP≌△ABP,则∠DAP=∠BAP,由(1)可知,∠1=∠DAG,又∠1+∠DAG+∠DAP+∠BAP=90°,所以,2∠DAG+2∠DAP=90°,即∠DAG+∠DAP=45°,故∠PAG=∠DAG+∠DAP=45°,∵△AOG≌△ADG,△ADP≌△ABP,∴DG=OG,DP=BP,∴PG=DG+DP=OG+BP;(3)解:∵△AOG≌△ADG,∴∠AGO=∠AGD,又∵∠1+∠AGO=90°,∠2+∠PGC=90°,∠1=∠2,∴∠AGO=∠AGD=∠PGC,又∵∠AGO+∠AGD+∠PGC=180°,∴∠AGO=∠AGD=∠PGC=60°,∴∠1=∠2=30°,在Rt△AOG中,AO=3,AG=2OG,AG2=AO2+OG2,∴OG=,则G点坐标为:(,0),CG=3﹣,在Rt△PCG中,PG=2CG=2(3﹣),PC==3﹣3,则P点坐标为:(3,3﹣3),设直线PE的解析式为y=kx+b,则,解得,所以,直线PE的解析式为y=x﹣3.点评:本题考查了一次函数的综合运用.关键是根据正方形的性质证明三角形全等,根据三角形全等的性质求角、边的关系,利用特殊角解直角三角形,求P、G两点坐标,确定直线解析式.7.(2012•桃源县校级自主招生)如图,点A在y轴上,点B在x轴上,且OA=OB=1,经过原点O的直线l交线段AB于点C,过C作OC的垂线,与直线x=1相交于点P,现将直线L绕O点旋转,使交点C从A向B运动,但C点必须在第一象限内,并记AC的长为t,分析此图后,对下列问题作出探究:(1)当△AOC和△BCP全等时,求出t的值;(2)通过动手测量线段OC和CP的长来判断它们之间的大小关系并证明你得到的结论;(3)①设点P的坐标为(1,b),试写出b关于t的函数关系式和变量t的取值范围.②求出当△PBC为等腰三角形时点P的坐标.考点:一次函数综合题.专题:压轴题;探究型.分析:(1)△AOC和△BCP全等,则AO=BC=1,又∵AB=,t=AB﹣BC=﹣1;(2)过点C作x轴的平行线,交OA与直线BP于点T、H,证△OTC≌△CHP即可;(3)根据题意可直接得出b=1﹣t;当t=0或1时,△PBC为等腰三角形,即P(1,1),P(1,1﹣),但t=0时,点C不在第一象限,所以不符合题意.解答:解:(1)△AOC和△BCP全等,则AO=BC=1,又AB=,所以t=AB﹣BC=﹣1;(2)OC=CP.证明:过点C作x轴的平行线,交OA与直线BP于点T、H.∵PC⊥OC,∴∠OCP=90°,∵OA=OB=1,∴∠OBA=45°,∵TH∥OB,∴∠BCH=45°,又∠CHB=90°,∴△CHB为等腰直角三角形,∴CH=BH,∵∠AOB=∠OBH=∠BHT=90°,∴四边形OBHT为矩形,∴OT=BH,∴OT=CH,∵∠TCO+∠PCH=90°,∠CPH+∠PCH=90°,∴∠TCO=∠CPH,∵HB⊥x轴,TH∥OB,∴∠CTO=∠THB=90°,TO=HC,∠TCO=∠CPH,∴△OTC≌△CHP,∴OC=CP;(3)①∵△OTC≌△CHP,∴CT=PH,∴PH=CT=AT=AC•cos45°=t,∴BH=OT=OA﹣AT=1﹣t,∴BP=BH﹣PH=1﹣t,∴;(0<t<)②t=0时,△PBC是等腰直角三角形,但点C与点A重合,不在第一象限,所以不符合,PB=BC,则﹣t=|1﹣t|,解得t=1或t=﹣1(舍去),∴当t=1时,△PBC为等腰三角形,即P点坐标为:P(1,1﹣).点评:主要考查了函数和几何图形的综合运用.解题的关键是会灵活的运用函数的性质和点的意义表示出相应的线段的长度,再结合三角形全等和等腰三角形的性质求解.试题中贯穿了方程思想和数形结合的思想,请注意体会.8.(2012秋•海陵区期末)如图1,在平面直角坐标系中,直线AB与x轴交于点A,与y轴交于点B,与直线OC交于点C.(1)若直线AB解析式为y=﹣2x+12,直线OC解析式为y=x,①求点C的坐标;②求△OAC的面积.(2)如图2,作∠AOC的平分线ON,若AB⊥ON,垂足为E,△OAC的面积为6,且OA=4,P、Q分别为线段OA、OE上的动点,连接AQ与PQ,试探索AQ+PQ是否存在最小值?若存在,求出这个最小值;若不存在,说明理由.考点:一次函数综合题.专题:综合题;数形结合.分析:(1)①联立两个函数式,求解即可得出交点坐标,即为点C的坐标.②欲求△OAC的面积,结合图形,可知,只要得出点A和点C的坐标即可,点C的坐标已知,利用函数关系式即可求得点A的坐标,代入面积公式即可.(2)在OC上取点M,使OM=OP,连接MQ,易证△POQ≌△MOQ,可推出AQ+PQ=AQ+MQ;若想使得AQ+PQ存在最小值,即使得A、Q、M三点共线,又AB⊥OP,可得∠AEO=∠CEO,即证△AEO≌△CEO(ASA),又OC=OA=4,利用△OAC的面积为6,即可得出AM=3,AQ+PQ存在最小值,最小值为3.解答:解:(1)①由题意,(2分)解得所以C(4,4)(3分)②把y=0代入y=﹣2x+12得,x=6,所以A点坐标为(6,0),(4分)所以.(6分)(2)存在;由题意,在OC上截取OM=OP,连接MQ,∵OQ平分∠AOC,∴∠AOQ=∠COQ,又OQ=OQ,∴△POQ≌△MOQ(SAS),(7分)∴PQ=MQ,∴AQ+PQ=AQ+MQ,当A、Q、M在同一直线上,且AM⊥OC时,AQ+MQ最小.即AQ+PQ存在最小值.∵AB⊥ON,所以∠AEO=∠CEO,∴△AEO≌△CEO(ASA),∴OC=OA=4,∵△OAC的面积为6,所以AM=12÷4=3,∴AQ+PQ存在最小值,最小值为3.(9分)点评:本题主要考查一次函数的综合应用,具有一定的综合性,要求学生具备一定的数学解题能力,有一定难度.9.(2012秋•成都校级期末)如图,在平面直角坐标系xOy中,已知直线PA是一次函数y=x+m(m>0)的图象,直线PB是一次函数y=﹣3x+n(n>m)的图象,点P是两直线的交点,点A、B、C、Q分别是两条直线与坐标轴的交点.(1)用m、n分别表示点A、B、P的坐标及∠PAB的度数;(2)若四边形PQOB的面积是,且CQ:AO=1:2,试求点P的坐标,并求出直线PA与PB的函数表达式;(3)在(2)的条件下,是否存在一点D,使以A、B、P、D为顶点的四边形是平行四边形?若存在,求出点D的坐标;若不存在,请说明理由.考点:一次函数综合题.专题:开放型.分析:(1)已知直线解析式,令y=0,求出x的值,可求出点A,B的坐标.联立方程组求出点P的坐标.推出AO=QO,可得出∠PAB=45°.(2)先根据CQ:AO=1:2得到m、n的关系,然后求出S△AOQ,S△PAB并都用字母m表示,根据S四边形PQOB=S△PAB ﹣S△AOQ积列式求解即可求出m的值,从而也可求出n的值,继而可推出点P的坐标以及直线PA与PB的函数表达式.(3)本题要依靠辅助线的帮助.求证相关图形为平行四边形,继而求出D1,D2,D3的坐标.解答:解:(1)在直线y=x+m中,令y=0,得x=﹣m.∴点A(﹣m,0).在直线y=﹣3x+n中,令y=0,得.∴点B(,0).由,得,∴点P(,).在直线y=x+m中,令x=0,得y=m,∴|﹣m|=|m|,即有AO=QO.又∵∠AOQ=90°,∴△AOQ是等腰直角三角形,∴∠PAB=45°.(2)∵CQ:AO=1:2,∴(n﹣m):m=1:2,整理得3m=2n,∴n=m,∴==m,而S四边形PQOB=S△PAB﹣S△AOQ=(+m)×(m)﹣×m×m=m2=,解得m=±4,∵m>0,∴m=4,∴n=m=6,∴P().∴PA的函数表达式为y=x+4,PB的函数表达式为y=﹣3x+6.(3)存在.过点P作直线PM平行于x轴,过点B作AP的平行线交PM于点D1,过点A作BP的平行线交PM于点D2,过点A、B分别作BP、AP的平行线交于点D3.①∵PD1∥AB且BD1∥AP,∴PABD1是平行四边形.此时PD1=AB,易得;②∵PD2∥AB且AD2∥BP,∴PBAD2是平行四边形.此时PD2=AB,易得;③∵BD3∥AP且AD3∥BP,此时BPAD3是平行四边形.∵BD3∥AP且B(2,O),∴y BD3=x﹣2.同理可得y AD3=﹣3x﹣12,得,∴.点评:本题的综合性强,主要考查的知识点为一次函数的应用,平行四边形的判定以及面积的灵活计算.难度较大.10.(2012秋•綦江县校级期末)如图,一次函数的函数图象与x轴、y轴分别交于点A、B,以线段AB 为直角边在第一象限内作Rt△ABC,且使∠ABC=30°.(1)求△ABC的面积;(2)如果在第二象限内有一点P(m,),试用含m的代数式表示△APB的面积,并求当△APB与△ABC面积相等时m的值;(3)是否存在使△QAB是等腰三角形并且在坐标轴上的点Q?若存在,请写出点Q所有可能的坐标;若不存在,请说明理由.考点:一次函数综合题.专题:综合题.分析:(1)先求出A、B两点的坐标,再由一个角等于30°,求出AC的长,从而计算出面积;(2)过P作PD⊥x轴,垂足为D,先求出梯形ODPB的面积和△AOB的面积之和,再减去△APD的面积,即是△APB的面积;根据△APB与△ABC面积相等,求得m的值;(3)假设存在点Q,使△QAB是等腰三角形,求出Q点的坐标即可.解答:解:(1)∵一次函数的解析式为函数图象与x轴、y轴分别交于点A、B,∴A(1,0),B(0,),∴AB=2,设AC=x,则BC=2x,由勾股定理得,4x2﹣x2=4,解得x=,S△ABC==;(2)过P作PD⊥x轴,垂足为D,S△APB=S梯形ODPB+S△AOB﹣S△APD==,﹣=,解得m=;(3)∵AB==2,∴当AQ=AB时,点Q1(3,0),Q2(﹣1,0),Q3(0,﹣);当AB=BQ时,点Q4(0,+2),Q2(0,﹣2),Q2(﹣1,0);当AQ=BQ时,点Q6(0,),Q2(﹣1,0),综上可得:(0,),(0,),(﹣1,0)(3,0),(0,),(0,)点评:此题主要考查平面直角坐标系中图形的面积的求法.解答此题的关键是根据一次函数的特点,分别求出各点的坐标再计算.。
